A Fully Coupled Electro-Vibro-Acoustic Benchmark-Model for Evaluation of Self-Adaptive Control Strategies

1. Introduction

The design of noise control strategies is impossible without basic knowledge on the theory of sound and vibration. The latter is described in many textbooks, for example in [1,2,3]. To design active noise control treatments, it is in addition also necessary to understand electro-mechanical coupling effects in order to describe actuators, filter-structures and sensors. These aspects of the theory of vibrations are for example described in [4,5]. If finally self-adaptive control strategies are taken into account, adaptive signal processing as described in [6,7,8,9] has to be studied in great detail. Especially the so-called Filtered-x Least Mean Square (FxLMS) algorithm [6,7,8] that is used to minimize the squared error signal detected at a well-chosen sensor position considering both a proper reference signal and the transfer behavior between actuator and sensor plays an important role in many applications as described in [5,7,8,9]. This algorithms is well understood and implemented in many applications. It is used for decades also considering variations of the original implementation [10].

For many applications it has been sufficient to concentrate on Linear Time-Invariant (LTI) systems. An actual survey on the application of Active Noise Control (ANC) considering linear system behaviour has been presented in [11]. However, in many situations it is also necessary to cover non-linear effects. An actual survey on the application of ANC to non-linear system is to be found in [12]. Recently, a novel approach using a so-called Brain Storm Optimization (BSO) algorithm for active control of non-linear systems has been proposed in [13].

Considering the above named referenced that represent only a non-complete selection of all publications in this filed one can conclude that the concept of self-adaptive ANC as well as its application to LTI systems is well understood. Thus, its application should be in the spot light of ongoing research. One can also conclude that nowadays research is also focussed on non-linear effects. For this reason it is obvious to ask: Is it necessary to write another paper focussing on linear systems? From the point of view of the author the answer is yes. This is especially true, if the aspect of benchmarking is taken into account.

It is of course possible to study a wide range of publications reporting on the design as well as on the performance evaluation of ANC. This is especially true for active control of plane waves in one-dimensional wave guides [14,15,16]. However, a drawback of many publications is that the electro-mechanical parameters describing the electro-mechanical parts are not documented in such a way that a reproduction of the relevant findings is supported without limitations. In contrast to the above named references also sophisticated mathematical models have been presented to describe the multi-physical problem of ANC based on detailed description of the model parameter, compare [17]. Unfortunately self-adaptive control has not been taken into account in this particular reference.

Summarizing these findings a simple Electro-Vibro-Acoustic (EVA) model that can be used to benchmark self-adaptive ANC approaches is (from the viewpoint of the author) still missing in the scientific community. For this reason the present paper proposes such a simple EVA model that is based on a limited number of Degrees Of Freedom (DOF). The latter are introduced to describe the propagation of sound in a one-dimensional wave guide without non-linear effects. This model is presented in combination with a detailed description of the physical parameter of the electro-mechanical components as well as of the acoustic wave guide. It consists of discrete electrical and mechanical networks that are applied to model the electro-acoustic behavior of noise and anti-noise sources. The acoustic field inside a duct, terminated by the electro-acoustic sources, is modelled using the Finite Element Method (FEM). The resulting EVA model is capable to describe all relevant coupling effects and enables an efficient evaluation of self-adaptive control strategies such as local control of sound pressure or active control of acoustic absorption. It is designed as a benchmark model for the benefit of the scientific community.

The paper is structured as follows. Multi-physical modelling and self-adaptive control strategies based on the FxLMS algorithm are described in section 2. This section also includes comments on numerical integration. The behaviour of the passive system (without active control) is analysed in section 3, whereas the noise control potential of two control strategies is discussed in section 4. The paper closes with section 5 presenting a short summary of the main findings.

2. Multi-Physical Modelling and Self-Adaptive Control Strategies

In order to study self-adaptive control of sound, a multi-physical approach to an EVA system is proposed in the upcoming section. LTI system behavior is assumed for all subsystems. The latter are given by electro-dynamical loudspeaker and an acoustic duct. This subsystem represents the one-dimensional acoustic wave guide. At first the fully-coupled EVA model is introduced. Afterwards some comments will be given on the numerical solution of this model. In a second step two self-adaptive control strategies based on the FxLMS algorithm will be outlined.

2.1. A fully Coupled Electro-Vibro-Acoustical Model

As described in section 1 the proposed benchmark model is given by an acoustic duct of length $L$ and cross section $S=\pi \cdot r^2$ terminated by the primary noise source at position x = 0 and the secondary source (anti-noise source). The latter terminates the duct at the position x = L. For further investigations five “sensor-positions” $i=I,II,III,IV,V$ have been considered. The position of the primary source is identical to the position $I$, and the position of the secondary source is identical to the position $V$.

The equations of motion of these electro-mechanical networks are based on the electric charge $q_i\left(t\right)$, the displacement of the loudspeaker membrane $x_i\left(t\right)$, and the sound pressure $p_i\left(t\right)$ defined at the positions $i=I,V$. The associated ordinary differential equations (ODE’s) are given by

$$\begin{array}{l}{L}_i{\ddot{q}}_i\left(t\right)+R_i{\dot{q}}_i\left(t\right)+{\displaystyle \frac{1}{C_i}}{q}_i\left(t\right)+T_i{\dot{x}}_i\left(t\right)=u_i\left(t\right)\hspace{0.17em}\\ M_i{\ddot{x}}_i\left(t\right)+B_i{\dot{x}}_i\left(t\right)+K_i{x}_i\left(t\right)+S{p}_i\left(t\right)-T_i{\dot{q}}_i\left(t\right)=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{with}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=I,V\end{array}$$

(1)

where $L_i$ is the inductance of the electrical network at position $\hspace{0.17em}i$, $R_i$ is the electric resistance, $C_i$ is the capacity and $T_i$ is the electromagnetic force factor. $M_i$ is mass of the loudspeaker membrane at position $\hspace{0.17em}i$, $B_i$ is its viscosity, and $K_i$ is the mechanical stiffness of the membrane. The external excitation is given by the voltage $u_i\left(t\right)\hspace{0.17em}$ with $i=I,V$ applied at the primary and secondary loudspeaker.

As proposed in [5] the acoustic field inside the duct is modelled by finite elements, considering the speed of sound $c$ and the density $\rho$ as the relevant material properties. In the present approach four finite elements of length $L/4$ with linear shape functions have been used to establish a simple discrete model. The latter is given by

$$\begin{array}{l}{\displaystyle \frac{S\left(L/4\right)}{6c^2}}\left[\begin{array}{ccccc}2& 1& & & \\ 1& 4& 1& & \\ & 1& 4& 1& \\ & & 1& 4& 1\\ & & & 1& 2\end{array}\right]\left[\begin{array}{c}{\ddot{p}}_I\left(t\right)\\ {\ddot{p}}_{II}\left(t\right)\\ {\ddot{p}}_{III}\left(t\right)\\ {\ddot{p}}_{IV}\left(t\right)\\ {\ddot{p}}_V\left(t\right)\end{array}\right]+\mathrm{...}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\displaystyle \frac{S}{\left(L/4\right)}}\left[\begin{array}{ccccc}1& -1& & & \\ -1& 2& -1& & \\ & -1& 2& -1& \\ & & -1& 2& -1\\ & & & -1& 1\end{array}\right]\left[\begin{array}{c}{p}_I\left(t\right)\\ p_{II}\left(t\right)\\ p_{III}\left(t\right)\\ p_{IV}\left(t\right)\\ p_V\left(t\right)\end{array}\right]-\rho S\left[\begin{array}{c}{\ddot{x}}_I\left(t\right)\\ 0\\ 0\\ 0\\ {\ddot{x}}_V\left(t\right)\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\end{array}\right],\end{array}$$

(2)

where $p_i\left(t\right)$ are the sound pressure data determined at the positions $i=I,II,\mathrm{...},V$. Acoustic sources inside the duct have not been taken into account. For this reason the right hand side of (2) is zero in every row.

The EVA model proposed in this paper contains nine DOF’s summarized in the (9x1) column matrix $u\left(t\right)$ such as

$$u\left(t\right)={\left[\begin{array}{ccccccccc}{q}_I& x_I& p_I& p_{II}& p_{III}& p_{IV}& p_V& x_V& q_V\end{array}\right]}^T$$

(3)

The right hand side is also represented by a (9x1) column matrix that contains the external excitation prescribed at the loudspeaker such as

$$r\left(t\right)={\left[\begin{array}{ccccccccc}{u}_I& 0& 0& 0& 0& 0& 0& 0& u_V\end{array}\right]}^T$$

(4)

The fully coupled EVA model can be established in matrix notation such as

$$M\ddot{u}\left(t\right)+C\dot{u}\left(t\right)+Ku\left(t\right)=r\left(t\right)$$

(5)

where $M$ is the (9x9) generalized mass matrix, $C$ is the (9x9) generalized damping matrix, and $K$ is the (9x9) generalized stiffness matrix. It should be noticed that all these matrices are non-symmetric. Thus the proposed model can also be used as a benchmark in a bi-modal decoupling approach as described in [18]. Using the abbreviations

$$\alpha :={\displaystyle \frac{S\left(L/4\right)}{6c^2}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{and}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\beta :={\displaystyle \frac{S}{\left(L/4\right)}}$$

(6)

the elements of these matrices can be presented such as

$$M=\alpha \left[\begin{array}{ccccccccc}L/\alpha & & & & & & & & \\ & M/\alpha & & & & & & & \\ & -\rho S/\alpha & 2& 1& & & & & \\ & & 1& 4& 2& & & & \\ & & & 1& 4& 1& & & \\ & & & & 1& 4& 1& & \\ & & & & & 1& 2& -\rho S/\alpha & \\ & & & & & & & M/\alpha & \\ & & & & & & & & L/\alpha \end{array}\right]\hspace{0.17em}$$

(7)

$$C=\left[\begin{array}{ccccccccc}R& T& & & & & & & \\ -T& B& & & & & & & \\ & & & & & & & & \\ & & & & & & & & \\ & & & & & & & & \\ & & & & & & & & \\ & & & & & & & & \\ & & & & & & & B& -T\\ & & & & & & & T& R\end{array}\right]\hspace{0.17em}$$

(8)

$$K=\beta \left[\begin{array}{ccccccccc}{C}^{-1}/\beta & & & & & & & & \\ & K/\beta & S/\beta & & & & & & \\ & & 1& -1& & & & & \\ & & -1& 2& -1& & & & \\ & & & -1& 2& -1& & & \\ & & & & -1& 2& -1& & \\ & & & & & -1& 1& & \\ & & & & & & S/\beta & K/\beta & \\ & & & & & & & & C^{-1}/\beta \end{array}\right]\hspace{0.17em}$$

(9)

2.2. Comments on Numerical Integration, Frequency Domain Analysis and Generalized Eigenvalues

Considering only time-harmonic excitation signals, the EVA model defined by (5) – (9) can be solved analytically in time-domain. However, if also more sophisticated excitation signals have to be taken into account, a numerical solution is more convenient. Following the implementation of the original Newmark algorithm [19] that is proposed in [20] it is possible to analyze a broad range of excitation signals using a simple and robust algorithm for the numerical solution of second-order ODE’s. This integration schema can be summarized as follows. The new values of the dependent variables $u_{n+1}$ at the discrete time step $t_{n+1}$ are obtained from the dependent variables $u_n$ at the previous time $t_n$ as well as from their first $v_n$ and second $a_n$ time derivative such as

$$u_{n+1}=u_n+T_s\cdot v_n+{\displaystyle \frac{1}{2}}\cdot T_s^2\cdot a_n,$$

(9)

where $T_s$ is the sample time. The new value for the second time derivative is calculated such as

$$a_{n+1}={\left\{M+{\displaystyle \frac{1}{2}}\cdot T_s\cdot C\right\}}^{-1}\cdot \left\{\begin{array}{l}{r}_{n+1}-C\cdot \left(v_n+{\displaystyle \frac{1}{2}}\cdot T_s\cdot a_n\right)-\mathrm{...}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}K\cdot \left(u_n+T_s\cdot v_n+{\displaystyle \frac{1}{2}}\cdot T_s^2\cdot a_n\right)\end{array}\right\},$$

(10)

where $r_{n+1}$ represents the right hand side of (9) at the discrete time step $t_{n+1}$. The new value of the first time derivative $v_{n+1}$ can subsequently be determined such as

$$v_{n+1}=v_n+{\displaystyle \frac{1}{2}}\cdot T_s\cdot a_n+{\displaystyle \frac{1}{2}}\cdot T_s\cdot a_{n+1}.$$

(11)

Initial values must be defined for all these quantities such as

$$\begin{array}{l}u\left(t=0\right)=u_0\\ v\left(t=0\right)=v_0\\ a\left(t=0\right)=M^{-1}\cdot \left\{r\left(t=0\right)-C\cdot v_0-K\cdot u_0\right\}.\end{array}$$

(12)

For time-harmonic excitation the solution of the EVA model described by (5) – (9) can be written in matrix notation such as

$$H\left(j\Omega \right)={\left(-{\Omega }^2\cdot M+j\Omega \cdot C+K\right)}^{-1},$$

(13)

where $j=\sqrt{-1}$ is the imaginary unit and $\Omega =2\pi f$ is the angular frequency that is associated to the excitation frequency $f$. The (9x9) complex compliance matrix $H\left(j\Omega \right)$ contains all Frequency Response Functions (FRF’s) of the system.

To study operational mode shapes at a given frequency $f$ it is possible to use the so called Transmissibility Functions (TMF’s). In order to define these quantities it is necessary to define one FRF as reference. If the response at position 1 due to excitation at position 1 is used as reference, it is possible to define eight non-trivial TMF’s out of the first column of $H\left(j\Omega \right)$ such as.

$$T_{i+1,1}\left(j\Omega \right)={\displaystyle \frac{H_{i+1,1}\left(j\Omega \right)}{H_{1,1}\left(j\Omega \right)}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{with}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=0,1,\mathrm{...},8,$$

(14)

where $T_{k,1}\left(j\Omega \right)$ contains the deviation in both magnitude and phase between the response at position $k$ compared to the chosen reference position at the specific angular frequency $\Omega .$ Please notice that in contrast to a FRF a TMF can only be interpreted frequency by frequency because it describes an operational mode shape and not the response characteristic of a dynamic system.

In order to verify the results of numerical simulations it can be useful to determine the eigenvalues of the EVA model. Based on the state variables

$$y\left(t\right)={\left[\begin{array}{cc}u\left(t\right)& \dot{u}\left(t\right)\end{array}\right]}^T,$$

(15)

It is possible to define a first order system of ODE’s on the state variables such as

$$A\dot{y}\left(t\right)=By\left(t\right),$$

(16)

where the (18x18) matrices $A$ and $B$ are given by

$$A=\left[\begin{array}{cc}C& M\\ M& 0\end{array}\right],\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{and}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}B=\left[\begin{array}{cc}-K& 0\\ 0& M\end{array}\right].$$

(17)

If the (18x1) column matrix $y\left(t\right)$ is described by $y\left(t\right)=\widehat{y}\cdot e^{\lambda t}$ the associated complex eigenvalues $\lambda ={\lambda }_{\mathrm{Re}}+j\cdot {\lambda }_{\mathrm{Im}}$ can be derived from the generalized Eigenvalue Problem (EVP),

$$\left(\lambda \cdot A-B\right)\widehat{y}=0.$$

(18)

The imaginary part of these eigenvalues can be used to verify the resonance frequencies hat can be determined in time-harmonic analysis and numerical simulations.

2.3. Comments on Adaptive Algorithms

The self-adaptive control strategies applied in this investigation are based on the LMS algorithm. The latter has been originally proposed in [21]. However, in order to include the effect of the so called secondary path, the power normalized FxLMS algorithm, compare [6,7,8,9,10] considering one reference signal has been used.

In an approach to active control of sound this algorithm can be applied to adapt $M$ FIR filter (each of length $I$ ) in order to drive $M$ control sources. The signals generated by these anti-noise sources are passed though $\left(L\times M\right)$ secondary paths in order to minimize the instantaneous squared error determined at $L$ sensor positions.

$$\begin{array}{l}\mathrm{for}\hspace{0.17em}m=1\hspace{0.17em}:M\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{Compute}\hspace{0.17em}\mathrm{output} \mathrm{of} \mathrm{the} m-\mathrm{th} \mathrm{controller}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{q}_m\left(n\right)={\displaystyle \sum _{i=0}^{I-1}{w}_{m,i}\left(n\right)}\cdot x\left(n-i\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{for}\hspace{0.17em}l=1\hspace{0.17em}:L\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{Calculate} \mathrm{the} m,l-\mathrm{th} \mathrm{sample} \mathrm{of} \mathrm{filtered} \mathrm{reference} \mathrm{at} \mathrm{discrete} \mathrm{time} n\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{x^{\prime }}_{l,m}\left(n\right)={\displaystyle \sum _{j=0}^{J-1}{h}_{l,m,j}\left(n\right)\cdot x\left(n-j\right)}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{end}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{for}\hspace{0.17em}i=0\hspace{0.17em}:I-1\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{Update} \mathrm{the} i-\mathrm{th} \mathrm{control}-\mathrm{filter} \mathrm{coefficient} \mathrm{of} \mathrm{the} m-\mathrm{th} \mathrm{controller}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{w}_{m,i}\left(n+1\right)=w_{m,i}\left(n\right)-{\displaystyle \sum _{l=1}^L{\mu }_l\left(n\right)\cdot {x^{\prime }}_{l,m}\left(n-i\right)\cdot e_l\left(n\right)}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{end}\\ \mathrm{end}\\ \mathrm{for}\hspace{0.17em}l=1\hspace{0.17em}:L\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{Update}\hspace{0.17em}\mathrm{the} l-\mathrm{th} \mathrm{normalized} \mathrm{step} \mathrm{size}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mu }_l\left(n\right)={\displaystyle \frac{\tilde{\mu }}{{\displaystyle \sum _{m=1}^M{‖{x^{\prime }}_{l,m}\left(n\right)‖}^2+\epsilon }}}\\ \mathrm{end}\end{array}$$

(19)

An algorithmic summary of the $\left(1\times L\times M\right)$ FxLMS algorithm is given in (19), where ${\mu }_l$ is the l-th power normalized step size and $\tilde{\mu }$ is its non-normalized counterpart. In order to prevent a division by zero it is also necessary to introduce a minimum value of the signal energy. The latter is represented by $\epsilon$.

If self-adaptive control can be limited to one reference signal as well as to one controller driving only one secondary source in order to reduce one error signal at one sensor position (19) reduced to the $\left(1\times 1\times 1\right)$ version or single-channel version of the FxLMS algorithm that is easy to implement. In such a situation it is only necessary to identify one secondary path $h$.

A compact summary on single-channel self-adaptive filtering based on the power normalized LMS algorithm applied to system identification has recently been presented by the author [22]. Secondary path modelling is for this reason not again commented in the present publication.

2.4. Two Examples for Self-Adaptive Noise Control Strategies

In the present paper two self-adaptive strategies to active control of sound will be discussed. Both approaches can be interpreted as illustrative examples. The first one is known as local control of the acoustic potential energy or active control of local sound pressure in front of the secondary source, compare [8]. Thus, considering the EVA model presented in this publication, the instantaneous error is in this case defined by the sound pressure determined at position $V$ such as

$$e_{A1}\left(n\right)=p_V\left(n\right).$$

(20)

The second approach was originally proposed in [23] and is based on active control of acoustic absorption. Its self-adaptive implementation has been proposed in [24] in order to motivate the design of a sound intensity probe with an actively generated free-field. The latter is generated, if only the reflected part of a one-dimensional plane standing wave is suppressed by active control. To apply this approach in combination with the EVA model presented in this publication, it is necessary to include the sound pressure data determined at position $IV$ and $V$ having the spacing $\Delta x=L/4$. The time delay associated with this distance is given by $\tau =\Delta x/c=N_{\tau }\cdot T_s$, where $N_{\tau }$ is the number of time steps in this time delay. The total sound pressure at discrete time step $n$ measured at both sensor positions reads

$$\begin{array}{l}{p}_V\left(n\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=p_{V,i}\left(L,n\right)+p_{V,r}\left(L,n\right)\\ p_{IV}\left(n\right)=p_{IV,i}\left(L-\Delta x,n\right)+p_{IV,r}\left(L-\Delta x,n\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=p_{IV,i}\left(L,n+N_{\tau }\right)+p_{IV,r}\left(L,n-N_{\tau }\right),\end{array}$$

(21)

where the index i represents the incident component of the wave and the index r represents the reflected component of the wave. If $p_{IV}\left(n\right)$ is delayed by $\tau$, the delayed sound pressure is defined as

$$p_{IV,\tau }\left(n\right)=p_{IV}\left(n-N_{\tau }\right)=p_{IV,i}\left(L,n\right)+p_{IV,r}\left(L,n-2\cdot N_{\tau }\right).$$

(21)

The instantaneous error that has to be minimized by self-adaptive control is for this control strategy given by

$$e_{A2}\left(n\right)=p_{IV,\tau }\left(n\right)-p_V\left(n\right)=p_r\left(L,n-2\cdot N_{\tau }\right)-p_r\left(L,n\right).$$

(22)

In order to fulfill Shannon’s law, the number time delay steps are limited by $1<N_{\tau }\le T_{\min }/\left(2\cdot T_s\right)$, where $T_{\min }=1/f_{\max }$ is associated with the highest frequency of interest $f_{\max }$.

It is of course possible to include other and more sophisticated control approaches such as the active control of the total power input or the active control of the total acoustic potential energy, compare [8,9] into such a study. However, the main goal of the present publication is the motivation of the EVA benchmark model as well as its illustration by the above named control approaches.

The use of this model to compare or evaluate other and new control strategies is up to the interest of the scientific community, likewise on the basis of the proposed simple but fully coupled EVA approach. For this reason the present study is limited to the discussion of two “easy to understand” control strategies.

3. Numerical Evaluation of System Dynamics Without Self-Adaptive Control

The EVA model introduced in the previous section is analyzed numerically. In a first step the passive system (without active control) is analyzed. The dynamic behavior can be characterized by it’s eigenvalues as well as by the resonance frequencies and the associated mode shapes. The upcoming section will therefore report on these types of investigations. Furthermore, the results of time-discrete simulations based on random excitation signals will be discussed.

3.1. Comments on Parameter Used for Numerical Evaluation

To simulate the dynamical behavior it is necessary to define both physical parameter as well as parameter for the numerical algorithm. These data are summarized in Table 1. It should be noticed that the electromagnetic force factor $T=a\cdot b$ is given by the product of the length of the coil $a$ and the magnetic flux constant $b$.

Beside these physical parameter also the parameter used in time-discrete simulations are listed in Table 1. The sampling frequency determines the sample time $T_s=1/f_s$. Furthermore, it should be noticed that a number of 1e5 discrete time steps have been used in all time-discrete simulations.

In order to distinguish between the responses determined at the different sensor position Table 2 contains the associated color labels. This is especially relevant for the discussion of the mode shapes at the resonance frequencies based on the TMF’s introduced in (14).

3.2. Evaluation of Eigenvalues and Time-Harmonic Response

At first the generalized EVP defined in (18) has been solved numerically. Table 3 contains all non-zero Eigenvalues (EV) of the system. Please notice that the imaginary part of each EV represents one natural frequency ${\lambda }_{\mathrm{Im}i}=f_{0i}$ of the system. These data are to be find in the third column of Table 3. Six eigenvalues have been taken into account. In order to ease the use of these data in benchmarks five digits have been considered in the documentation of these results.

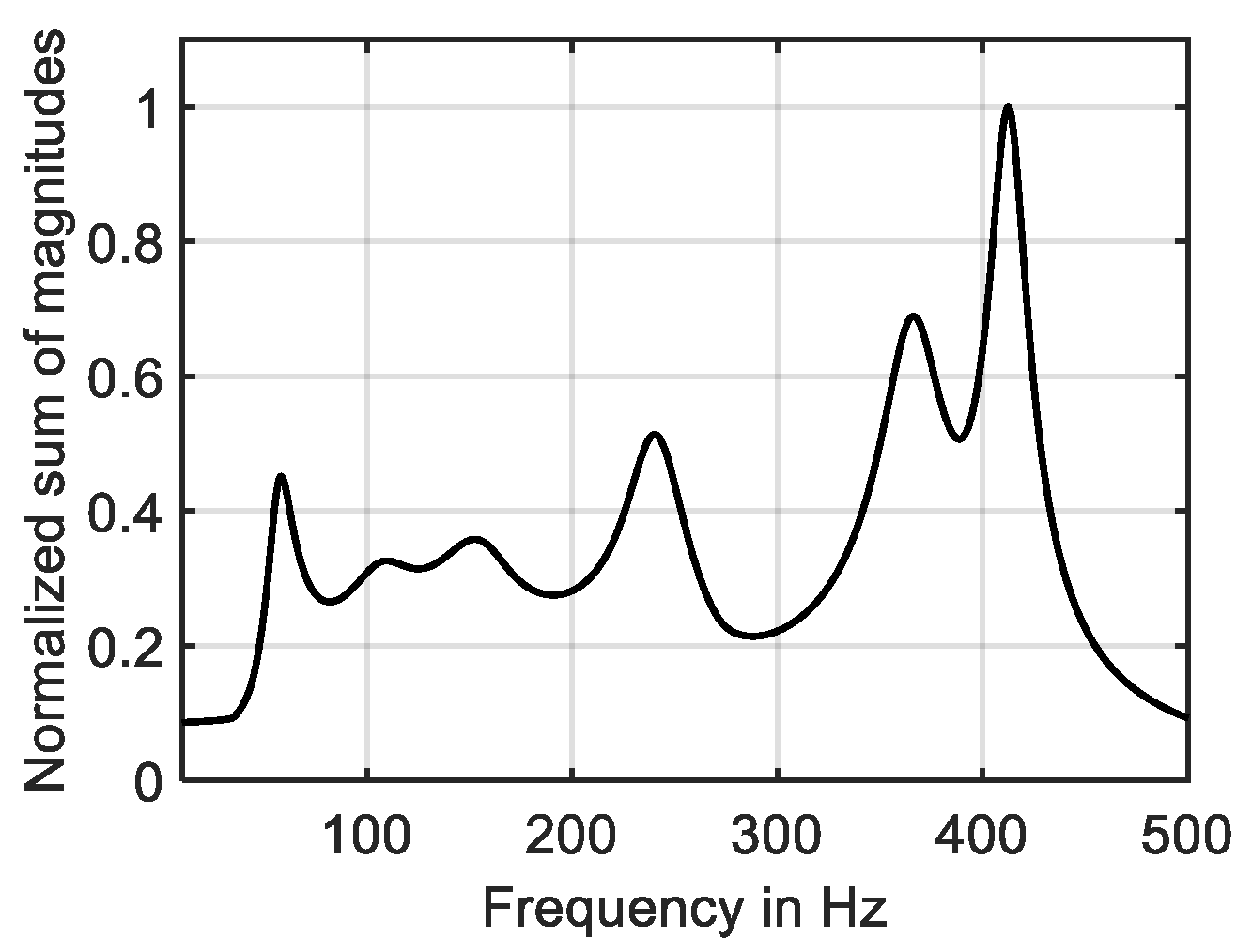
To determine the associated resonance frequencies $f_{Ri}$, time-harmonic analysis based on (13) has been performed. The results are shown in Figure 1 as well as in the fourth column of Table 3. Figure 1 presents the sum of all magnitude response curves determined for all five acoustic DOF’s ( $p_i\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{with}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=I,II,\mathrm{...},V$ ) caused by excitation at position I. Normalization has been performed by the maximum value. In other words the curve shown in this figure represents the overall acoustic magnitude response of the system due to the voltage applied at position I.

The relative deviation between the natural frequencies and the resonance frequencies is presented in the fifth column of Table 3. Due to the fact that a relevant amount of damping is included in the model of the electro-mechanical networks the natural frequencies (connected with free vibrations of the system) are not fully identical with the resonance frequencies (connected with forced vibrations of the system). However, the deviation is small. For this reason, the numerical implementation of the model is verified by comparison of these proper numbers.

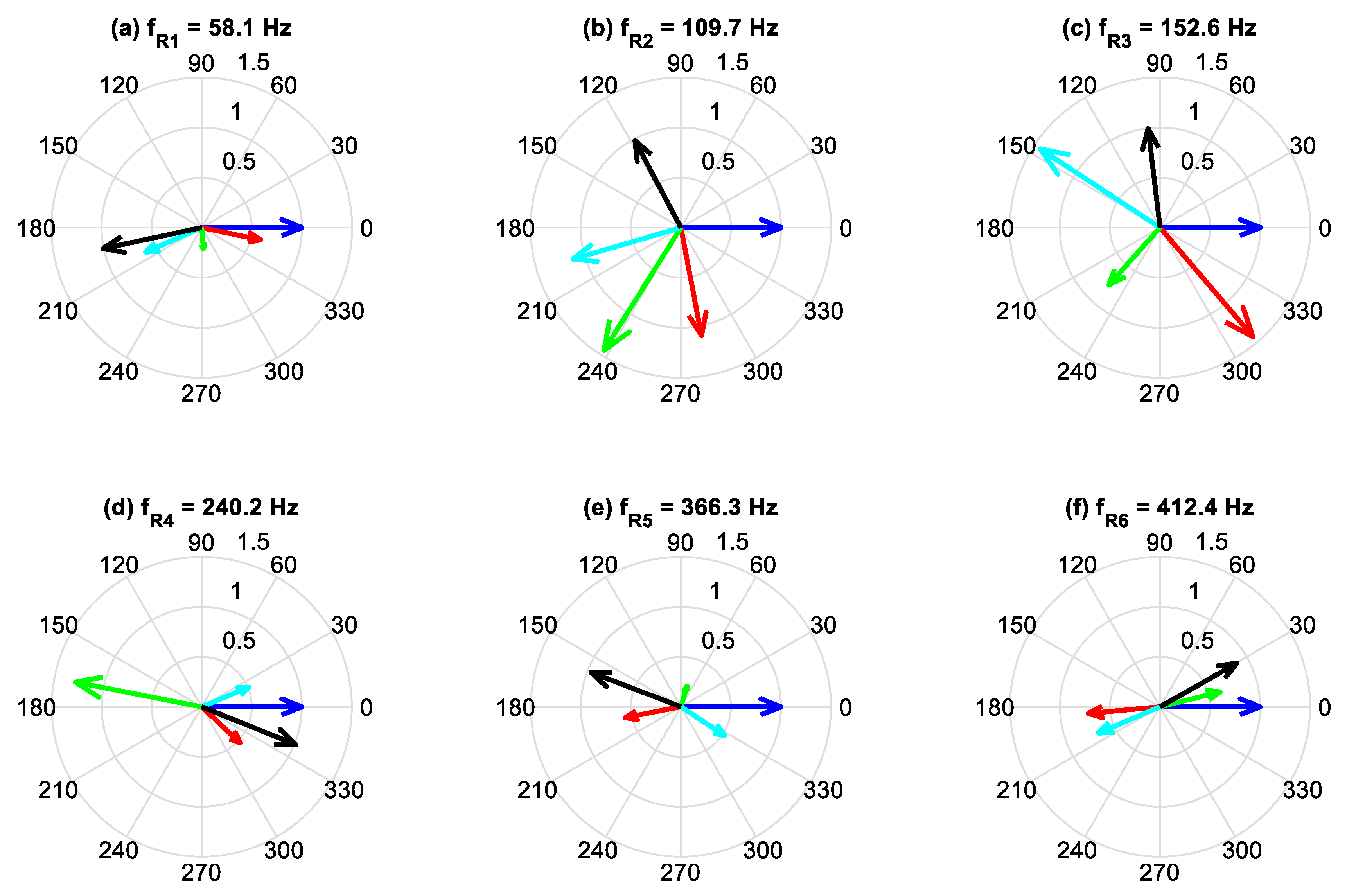
In order to understand the relative mode shapes associated with the resonance frequencies the TMF’s have been analyzed for the response of sound pressure determined at the positions I, II, III, IV, and IV caused by the electric voltage applied at position I. The FRF describing the acoustic response at position I due to electric excitation at position I has been chosen as reference by calculating the TMF’s. The associated data are shown in Figure 2 as well as in Table 4 and 5.

Combining these results and considering the information given in Table 2 it is possible to interpret the relative mode shapes in resonance as standing waves. An example is given for Figure 2 (a). The arrows shown in this subplot prove that the wave length associated with the first resonance frequency is twice the length of the acoustic duct. This is true because the relative response at the positions I and II is in phase, but opposite in phase to the relative response determined at position IV and V. Furthermore, the relative response at position I has nearly the same magnitude as the relative response at position V. The same holds for the relative response at position II compared to the relative response determined at position IV. Thus, one half of a full wave represents the mode shape.

3.3. Discrete time-domain analysis using random excitation signals

The behavior of the passive system has also been analyzed for broadband excitation considering band limited noise (25 Hz < f < 500 Hz). To solve the model the Newmark algorithm, compare (9) – (12) has been applied. To prepare the evaluation of the two noise control strategies introduced in the previous section, system identification based on adaptive filtering has been applied using the parameter listed in Table 6. The result is given by the impulse response in terms of the sound pressure at position V caused by the voltage applied to the secondary source at the same position.

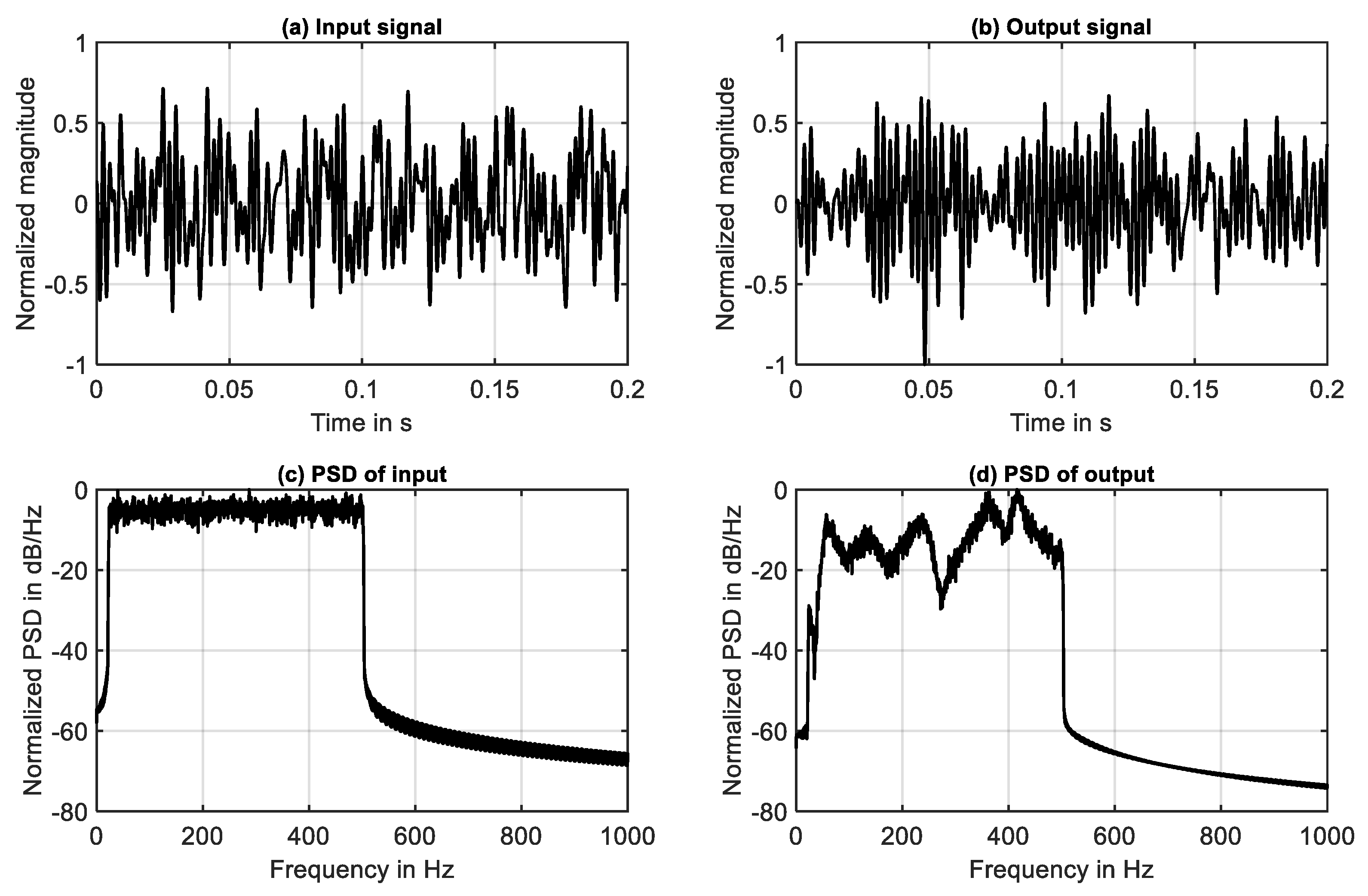
Both input signal (voltage applied at the secondary source) and output signal (sound pressure in front of the secondary source) are shown in Figure 3. The time-domain behavior is shown in Figure 3a,b considering 0.2 s out of 10.0 s simulation time. Both signals are normalized to their maximum values. The random nature of both signals is obvious. However, it should be noticed that the output signal shown in Figure 3b is colored by the response characteristic of the investigated system.

This can clearly be observed, if the power spectral density (PSD) of the input signal (shown in Figure 3c) is compared to the PSD of the output signal (shown in Figure 3d). The input signal is nearly white in the frequency range of excitation (25 Hz < f < 500 Hz), while the PSD of the output signal contains maxima and minima that clearly correspond to the resonances and anti-resonances presented in Figure 1 and Table 4.

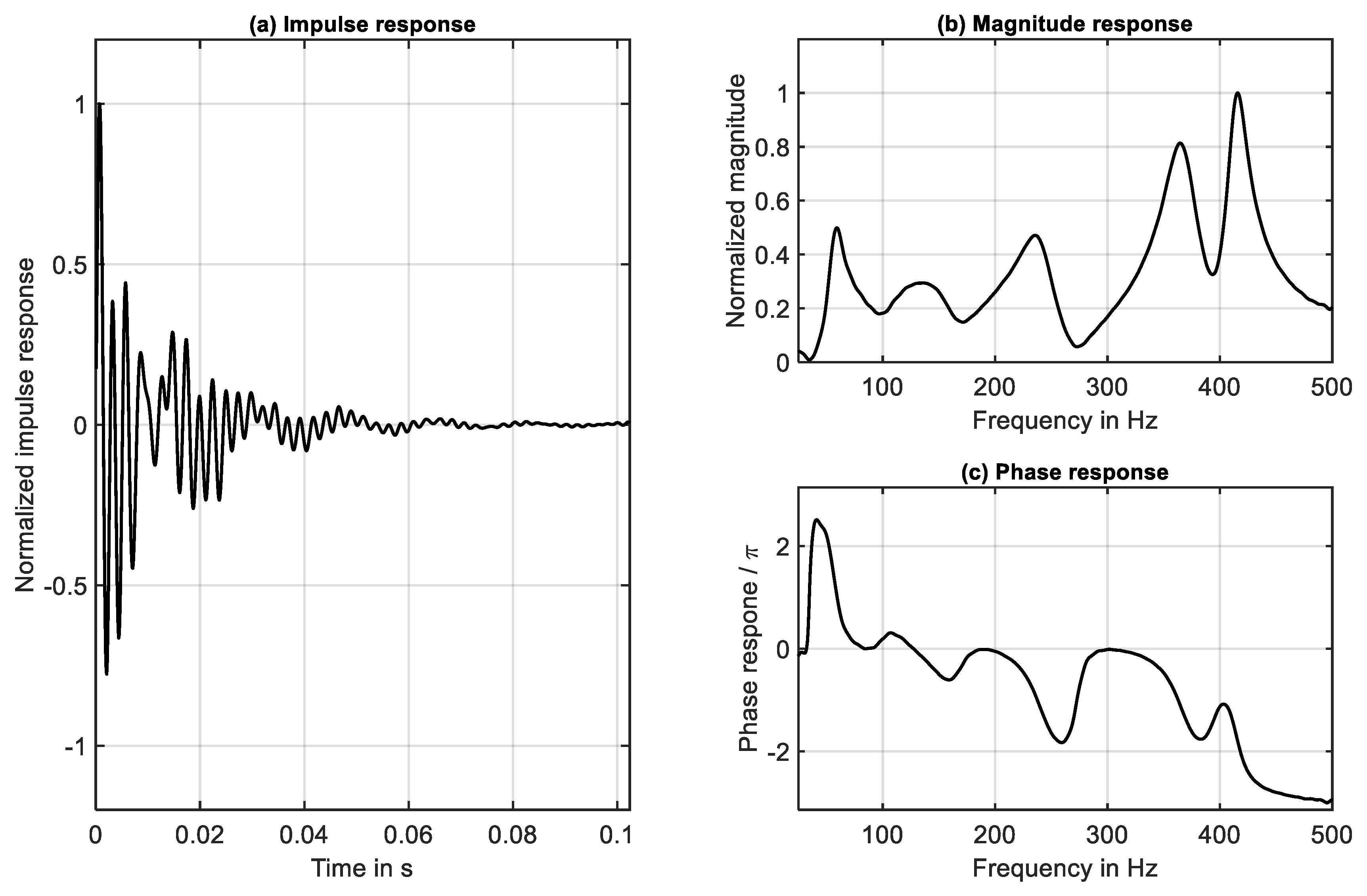
The identified impulse response $h_{p_V,u_V}$ that represents the sound pressure determined at position V due to the voltage applied at position V is shown in Figure 4a. Because of the damping modeled in the electro-mechanical networks the decay time has a small value of only 0.1 s. Thus, the system reaches the steady sate in a time period that is about 1% of the total simulation time. The associated FRF $H_{p_V,u_V}$ is show in Figure 4b,c. The normalized magnitude response is shown in Figure 4b. The shape of this curve is in fair agreement with the results shown in in Figure 1 and Table 4. The same holds for the phase response. The latter is shown in Figure 4c.

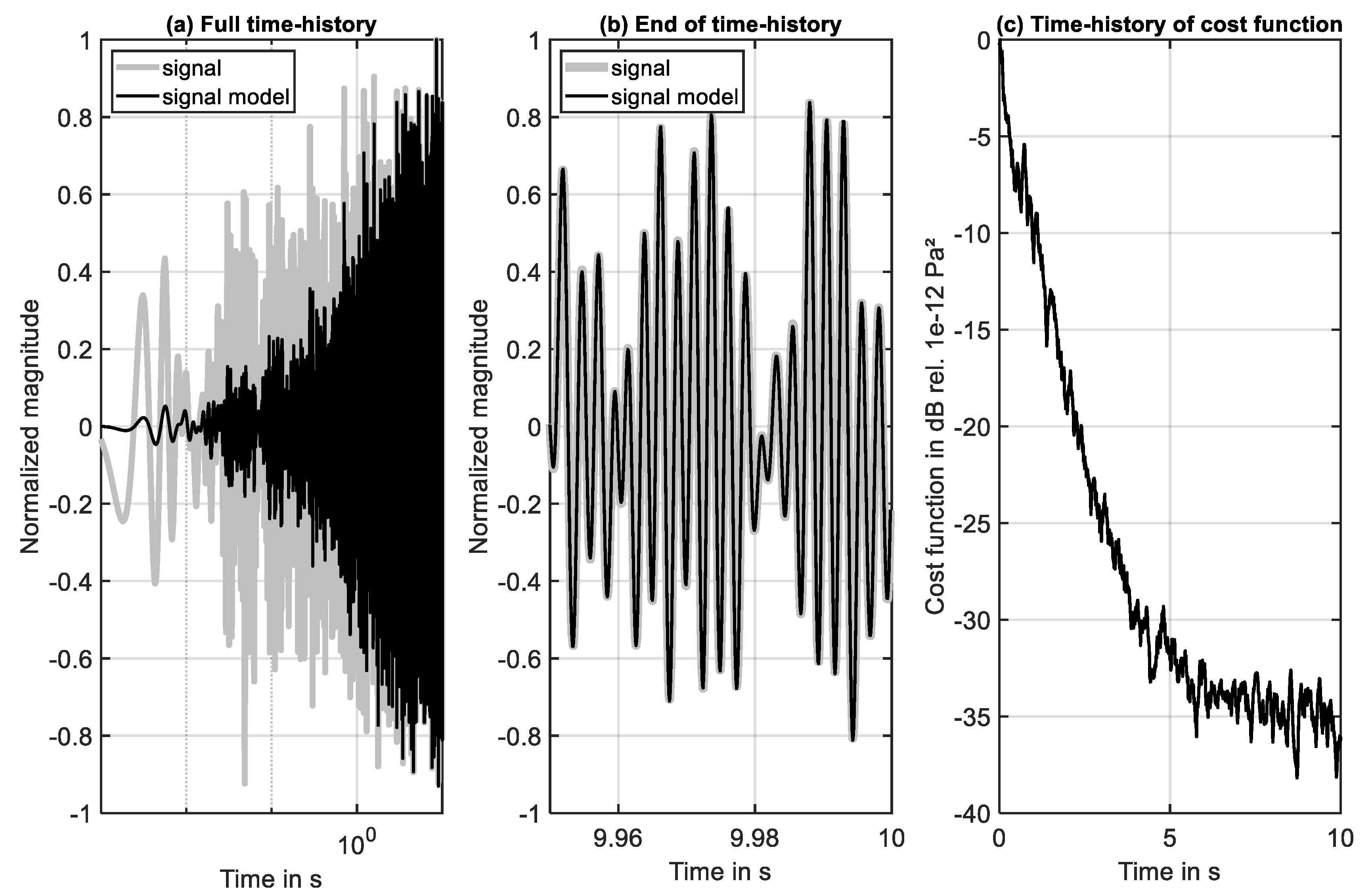
To discuss the quality of the system identification based on adaptive filtering, the time-history of the system output, the time history of the model system output, and the time-history of the cost function are shown in Figure 5. Figure 5a contains the whole time-history considering a logarithmic scale for the abscissa. For this reason it is possible to see that the response of the system model (black curve) develops with time. The last 0.05 s of the time-history is shown in Figure 5b. Here, the identification reached a steady state. The perfectly overlapping curves indicate that the identification has been successful.

This finding is also supported by the time-history of the cost function

$$J={\left[p_V-{\widehat{p}}_V\right]}^2,$$

(23)

where ${\widehat{p}}_V$ is the model of the original system output $p_V$. The development of the cost function defined in (23) is shown using a logarithmic scale for the ordinate such as

$$NR=\hspace{0.17em}10\cdot {\log }_{10}\left({\displaystyle \frac{J}{{10}^{-12}\cdot \mathrm{Pa}{}_2}}\right).$$

(24)

With a noise reduction (NR) of more than -35 dB at the end of the simulation the transfer behavior can be seen as fully identified.

4. Numerical Evaluation of Noise Control Potential

In the previous section the dynamic behavior of the passive system without active control has been discussed. Besides the evaluation of proper frequencies and associated mode shapes a time-discrete model for the secondary path has been identified. Based on these findings the upcoming section presents results that have been obtained from numerical simulations of two self-adaptive control strategies. In a first step the concept of active control of the local sound pressure is discussed. Further on the results of simulating active control of acoustic absorption will be presented.

4.1. Self-Adaptive Control of Local Sound Pressure

The first control approach is based on the minimization of the instantaneous squared error defined of the sound pressure in front of the secondary source. The associated cost function is in this case defined by

$$J\left(n\right)={\left[p_V\left(n\right)\right]}^2,$$

(25)

where $p_V\left(n\right)$ is given by the superposition of the sound pressure caused by the primary source at position I and the secondary source located at position V. The parameter used for the FxLMS algorithm are summarized in Table 7.

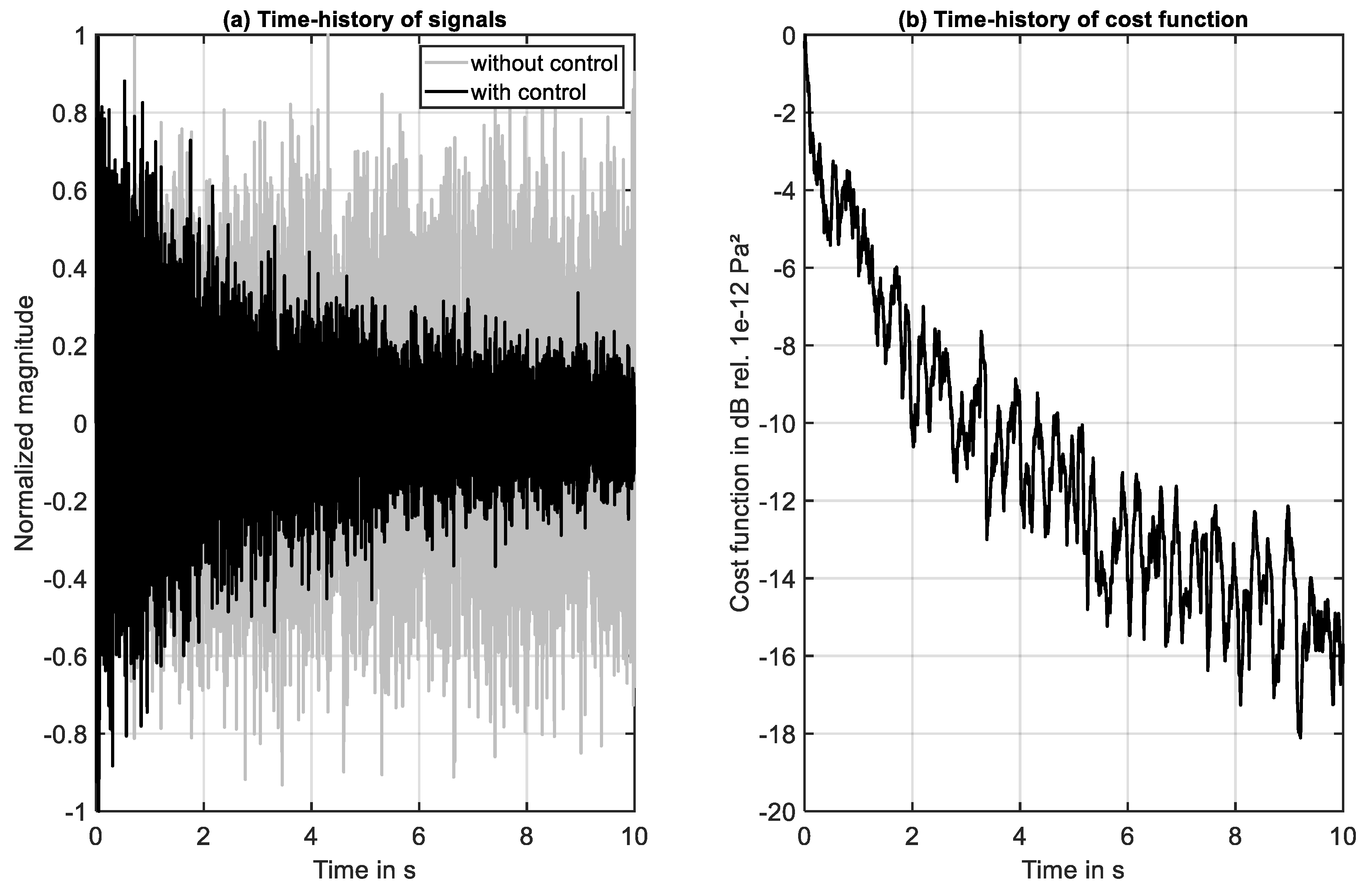
The results of this simulation are shown in Figure 6 and Figure 7. Figure 6 presents the time-history, whereas frequency-domain results are presented in Figure 7. The results (normalized to the maximum values) presented in Figure 6a indicate that active control of local sound pressure is very effective. At the end of the simulation a NR of about -15 dB has been realized, compare Figure 6b.

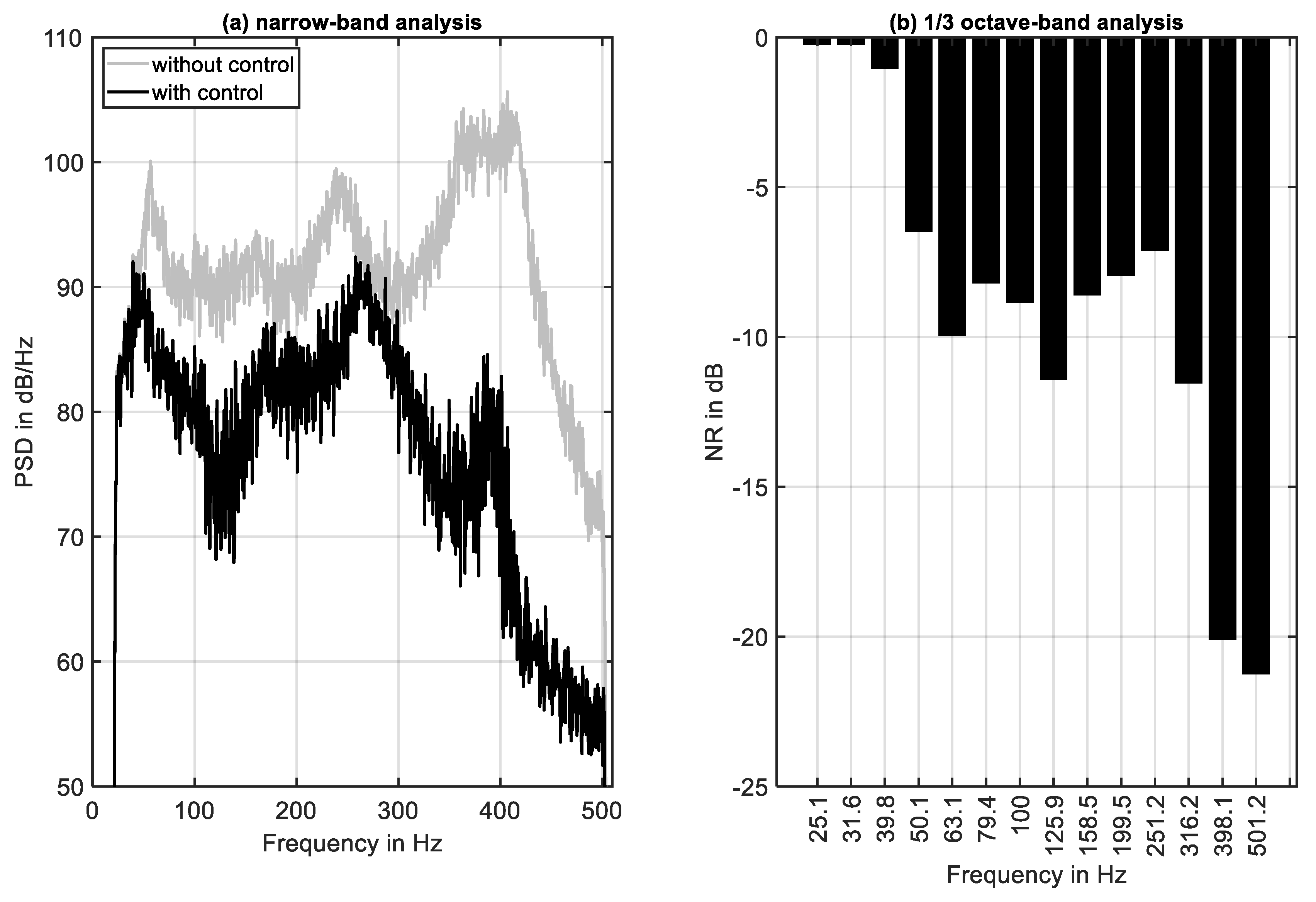
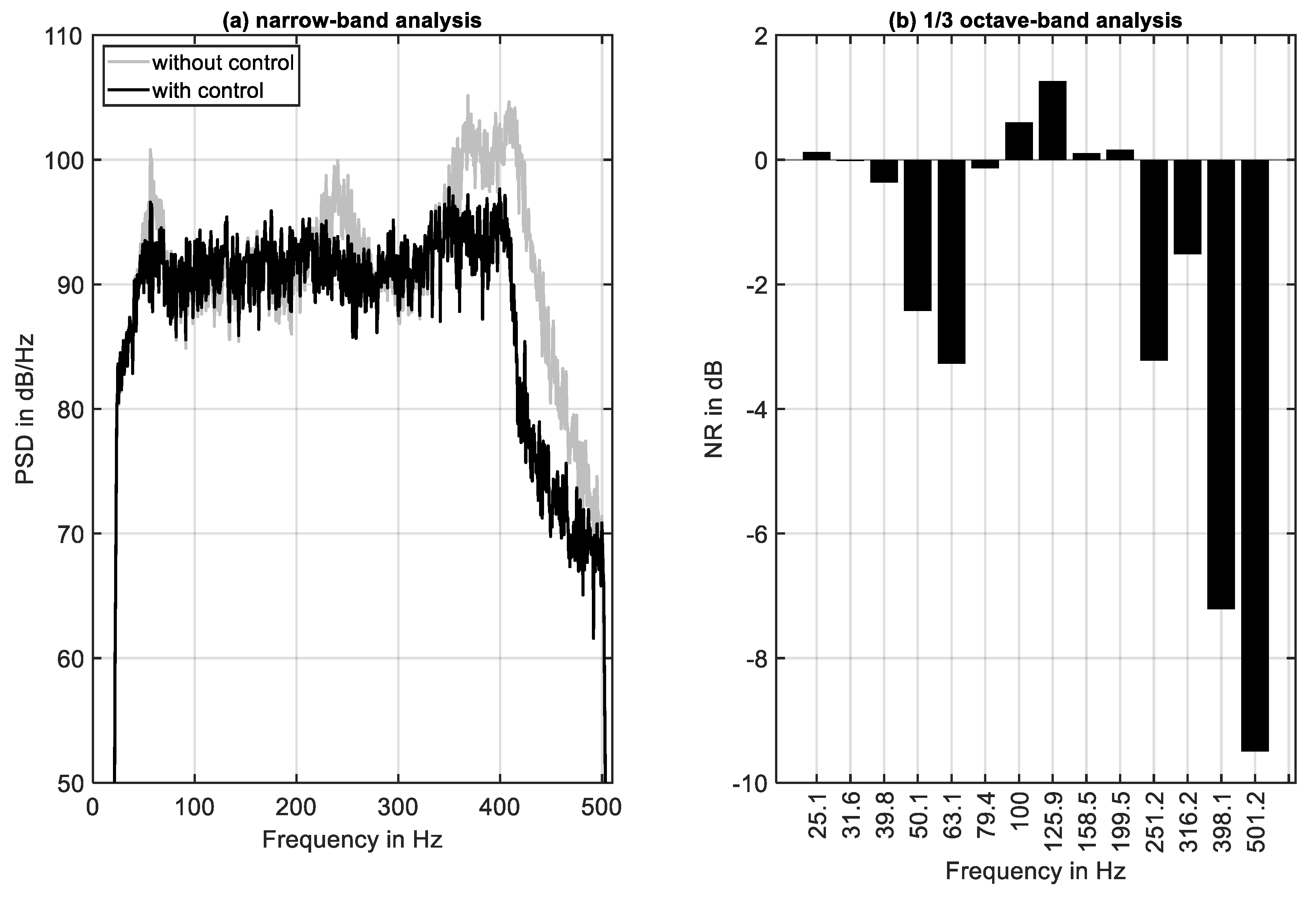
The frequency domain illustration of the control approach is based on a narrow-band analysis as well as on a 1/3-octave band analysis. The first one is shown in Figure 7a. The second one is presented in Figure 7b. It is obvious that this control approach is especially effective at the acoustic resonances. However, as it can be concluded from the results shown in Figure 7b, the NR is not constant over frequency. This is a well-known finding in ANC and caused by the transfer behavior of the secondary path that has not been equalized in the present investigation.

4.2. Self-Adaptive Control of Acoustic Absorption

In order to analyze the second control approach that is based on the minimization of the instantaneous squared error defined of the reflected sound pressure in front of the secondary source the cost function has to be modified such as

$$J\left(n\right)={\left[p_{IV,\tau }\left(n\right)-p_V\left(n\right)\right]}^2,$$

(26)

where $p_V\left(n\right)$ is given by the superposition of the sound pressure caused by the primary source at position I and the secondary source located at position V. $p_{IV,\tau }\left(n\right)$ is the delayed sound pressure at the position IV. The parameter used for the FxLMS algorithm are summarized in Table 8.

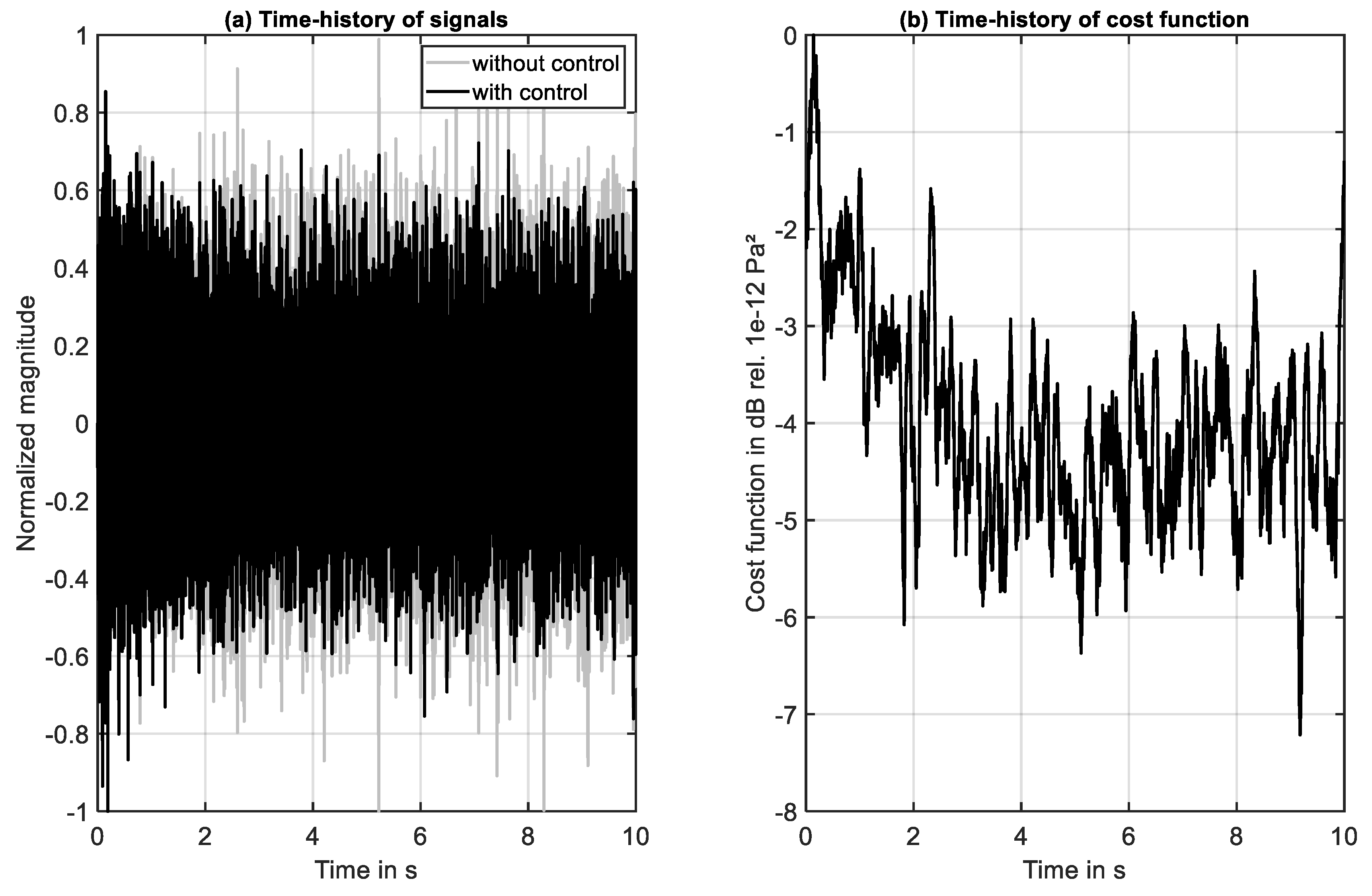
The results of this simulation are shown in Figure 8 and Figure 9. Figure 8 presents the time-history, whereas frequency-domain results are presented in Figure 9. Please notice that the total sound pressure at position V is shown (not the reflected wave component). The results (normalized to the maximum values) presented in Figure 8(a) indicate that active control of acoustic absorption has an effect on the local sound pressure. The latter is determined for position V. At the end of the simulation a NR of about -4 dB has been realized, compare Figure 8(b). Thus, nearly one half of the signal energy is suppressed. The missing part is naturally the energy of the reflected wave component.

The frequency domain illustration of the control approach is again based on a narrow-band analysis as well as on a 1/3-octave band analysis. The first one is shown in Figure 9(a). The second one is presented in Figure 9b. It is interesting to notice that this control approach is only effective at the acoustic resonances. The PSD of the controlled signal is equalized, because the reflected wave component is suppressed. For this reason the magnitude response is reduced at the resonances but at the same time increased outside the resonances. This can clearly be observed by the results presented in Figure 9b. However, the application of this control strategy can be adventurous, if the goal of active control is to transform a standing wave into a traveling wave. For this reason active control of acoustic absorption has a global effect on the controlled system in such a way that the magnitude response will be equalized. Thus, significant amplification at sensor positions that are not included in the error signal that is known from the application of local control of potential acoustic energy, compare, [8,9], will not be occur, if active control of acoustic absorption is applied.

5. Conclusions

A fully coupled EVA model has been presented that can be used as benchmark system in the evaluation of active noise control strategies. This model represents a LTI system with significant damping. On the one hand it is simple, because only nine DOF’s have been taken into account. On the other hand it is non-trivial, because the associated system matrices are non-symmetric. For this reason, the proposed EVA model can also be used to benchmark bi-modal decoupling strategies.

The model has been used to illustrate two well-known approaches to active noise control - local control of acoustic potential energy and active control of acoustic absorption. In both scenarios self-adaptive control based on the FxLMS algorithm has been simulated. Because of its simplicity, the proposed EVA model is not only suited for research but also for teaching – especially in the field of mechatronics. It can be used as representative multi-physical system with active components.