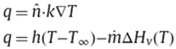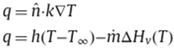A Multiphysics Modelling Approach of Stripping Ethanol from Ethanol-Water Mixture Using Hot Microbubbles

1.1. Background

1.1.1. Bioethanol

Bioethanol is the bio-based derivative of the component ‘ethanol’. Ethanol is a five-carbon chain organic alcohol. Synthetically, ethanol is produced using ethene. The market share of ethanol production process even though is quite low for synthetically produced ethanol, the side-effects of the toxic gases which are released as a result of synthetic production could cause a damage to the ecosystem and make it unfit for human consumption and use.

Ethanol as discussed above is a five-chain organic molecule with a hydroxy group attached at the end of the chain.

Figure 1. Ethanol Structure.

Figure 1. Ethanol Structure.

Ethanol has a molecular weight of 46.07 g/mol. The substance is colourless and flammable in nature. In general, ethanol is volatile in nature and has a boiling point of 78.37℃ which is relatively close to that of water.

Ethanol also forms an azeotrope with water when the ethanol content in the binary mixture is at 95% leaving 5% of water in the mixture. An azeotrope is a point where the contents of the binary mixture remain equal which makes it hard to separate than a non-azeotropic mixture.

Table 1. Ethanol Properties.

S. No	Property	Value/Description
1	Boiling point	78.37℃
2	Flammability	Highly flammable
3	Molecular weight	46.068 g/mol
4	Formula	C2H5OH
5	IUPAC Name	Ethyl Alcohol
6	Azeotrope Point	78℃ and 95.5% ethanol and rest water

Table 1. Ethanol Properties.

S. No	Property	Value/Description
1	Boiling point	78.37℃
2	Flammability	Highly flammable
3	Molecular weight	46.068 g/mol
4	Formula	C2H5OH
5	IUPAC Name	Ethyl Alcohol
6	Azeotrope Point	78℃ and 95.5% ethanol and rest water

The costs associated with the production of ethanol biologically can be rather high than the cost of producing ethanol synthetically [ref (costs)]. To reduce the costs associated to production of bioethanol, process intensification techniques are utilised. Process intensification can be achieved when multiple unit operations are performed in the same equipment.

Bioethanol is produced using the Embden-Meyerhof-Parnas (EMP) pathway where glucose is converted into ethanol by conversion of ATP to ADP.

Figure 2. EMP pathway to produce ethanol.

Figure 2. EMP pathway to produce ethanol.

Bioethanol is produced using bio-stock with aid of microorganisms which can facilitate the production of bioethanol. Microorganisms like P. Pastoris, S. Cerevisiae facilitate the production of Bioethanol from bio feedstock. The addition of microbes in the fermentation medium triggers the beginning of the EMP pathway by removal of phosphate group and converting Adenosine Triphosphate to Adenosine Diphosphate and releasing energy in the process. The process continues until energy is gained when converting acetaldehyde into ethanol by removal of hydroxide to form ethanol.

The production of bioethanol is divided into various generations based on the raw materials used in the process. In the first generation of bioethanol production, the raw materials primarily used are mostly direct sugars and molasses. Sugars and molasses are generally in form of direct glucose and sucrose which can be easily broken down into ethanol and other useful products.

The second generation of bioethanol production’s raw materials involve the indirect sugars like cellulosic materials. The cellulosic materials have to be broken down into useful sugars like glucose before being processed into ethanol. Cellulosic sources usually contain holocellulose, hemicellulose and lignocellulose. The purification process of cellulose usually involves hydrolysing the raw materials and treating the hydrolysed materials to form bioethanol. Third generation of bioethanol involves in the usage of algal sources to produce bioethanol.

1.1.2. Microbubbles

Microbubbles going by its arbitrary definition is defined as the bubbles of a fluid with a radius of size measured in micrometres or in simple terms microns. Spheres also tend to have the highest surface area which makes a bubble have an effectively higher mass/heat transfer area than using conventional jacketed type heaters where the heat transfer takes place when the liquid of interest is coming in contact with the jacket located on the walls of the vessel. In the case of microbubbles, the heat transfer takes place withing the fluid level and the bubbles are dissolved in the liquid of interest once the heat transfer takes place.

Although there are various other ways to facilitate heat transfer in fluids, the better and more economical way is to disperse the heating medium into the system without disturbing the dynamics of the system in a drastic way.

Hot microbubbles tend to do the same by facilitating better mass and heat transfer by cutting down the costs associated with heating/cooling the fluid. A microbubble is formed by passing a stream of fluid of interest through a fluidic oscillator to streamline the fluid and the fluid is then passed through a microporous diffuser.

Although each microbubble has a quite low surface area, the net surface area of multiple (more than thousand) of similar microbubbles which are fluidically non-interacting could result in hectares of net surface area.

There could be an option to skip passing the fluid of interest through a fluidic oscillator and send it directly through the microporous diffuser. Even though this could be a possible solution to increase the heat and mass transfer characteristics, the bubbles are often not distributed equally in its shapes and sizes and can increase in the size after passing through the diffuser.

Figure 3. Microbubbles Produced as a result of fluidic oscillations.

Figure 3. Microbubbles Produced as a result of fluidic oscillations.

Figure 4. Microbubbles produced as a result without fluidic oscillations.

Figure 4. Microbubbles produced as a result without fluidic oscillations.

As we can observe in the above figure, the difference between microbubbles generated when the fluid is passed through a microporous diffuser with and without passing through a fluidic oscillator, the distribution of the bubbles is more even in the earlier than the latter where the bubbles after passing though the diffuser collude with each other forming a bigger bubble which defeats the purpose to facilitate better heat and mass transfer by concentrating mostly in certain places rather than the entire estimated area it supposes to focus.

1.1.3. Multiphysics Modelling and COMSOL

Multiphysics modelling is defined as modelling various physical and chemical parameters which tend to change with respect to time. For a parameter to change with respect to time, the best type of equation to use to describe the model with multiple parameters mathematically is to use a partial differential equation. A modelled equation gives the best representation of the system with respect to time for various parameters.

There have been many software packages to perform Multiphysics modelling which are heavily reliant on high power computing.

A Multiphysics modelling software package simulates the model over a said geometry which can be specified by its user and an appropriate mesh can be applied over the geometry and the model can be simulated over the formed mesh across the surface or throughout the geometry.

COMSOL is a software package which simulates various Multiphysics models pertaining to fluid dynamics, heat and mass transfer, electrical and magnetic simulations. COMSOL can combine any of the models present within the package into one single geometry which is defined by the user.

COMSOL also has a model builder with various primitives which eases up the process of developing the geometry for the model. COMSOL can simulate its models in various geometries ranging from a single dimension to a 3-D simulation including a 2-D axisymmetric simulation which sweeps a 2-D model into a 3-D model around a specified axis.

There are other software packages which does Multiphysics modelling which are open source or under a licensing fee. Next popular modelling software is ansys which predominantly deals with fluid dynamics and is more accessible.

Open-sourced software packages like OpenFOAM performs the same simulations but the user must download and install the package as a compiler rather than a finished GUI (graphical user interface). Graphical interfaces like Opensim is compatible for OpenFOAM.

COMSOL is built using Java in the backend and the models developed in the package is recorded as a java code. In addition to the java code recorded with edits in the model, the user can make edits to the model by editing the code recorded and can be compiled in their local java environment provided the system has the libraries related to COMSOL installed.

Figure 5. Java code generated as a result of building model.

Figure 5. Java code generated as a result of building model.

Apart from Java, the models can be edited according to the user’s specifications in few other ways. One method is using the inbuilt application developer where the user codes the modifications to the model using a java method which can be added to the model.

This method is the most preferred method of making modifications to the model as it is done without having any issues with compatibility related issues.

Figure 6. Application builder in COMSOL.

Figure 6. Application builder in COMSOL.

A user can also modify their models using COMSOL’s built-in live-link feature to MATLAB where one can use MATLAB instead of Java. Users often prefer MATLAB over Java to make edits to the model as MATLAB code is easier to build and execute than compared to build and execute a java method.

Python also developed its own MPh library where a user could create, modify and run their COMSOL models using Python provided the user has COMSOL installed in their systems and has the module JPype which connects Java runtime environment (JRE) to Python. The project utilises the first method to modify the built model in COMSOL and the Java method is run in the model developer to modify the model.

1.2. Overview

In common literature, bioethanol is produced as a result of fermentation of glucose or complex sugars with action of S.Cerevisiae in the fermentation broth, the glucose breaks down as we have seen in the previous section, the glucose breaks down into ethanol through the EMP pathway. There are few other products which is also produced during the breakdown as discussed by [5] which can inhibit the growth of S.Cerevisiae which can in return inhibit the growth of ethanol. To maximise the growth of microorganism and ethanol, constant removal of ethanol is required while production is taking place.

A typical system with a fermenter along with a sidearm distiller is recommended to remove ethanol constantly and re-circulate the cells back to the fermenter to produce more ethanol from the feedstock which is also supplied into the fermenter.

As a general knowledge, it is known that alcohols are volatile in nature, and it is quite easy to remove by adding heat to the system. In certain cases, the alcohols tend to form azeotropes with the solvents used which makes it a challenge to separate the alcohol from the mixture as the contents has the same boiling point. To properly remove the alcohols from the mixture, a third component is added to the mixture which helps the alcohol bind with the third solvent but not form an azeotrope and can be separated easily.

Using a third solvent to extract can be quite tedious of a task to execute, to avoid the addition of third component, various other methods such as pervaporation, vacuum distillation can be carried out. These methods are usually not cost effective; to develop a solution more cost effective, addition of microbubbles is an effective way where hot microbubbles can evaporate ethanol around the bubble’s surface and carry along with the bubble until it evaporates the surrounding molecules of ethanol.

This project explores developing a Multiphysics model of a hotter single microbubble in a 2-D axisymmetric model than the one produced by earlier studies. The earlier studies had an empirical solution to the temperature of air bubble entering the reservoir containing the binary mixture of ethanol and water is quite lower than the practical nature of the system where the bubbles entering the system is hotter than the prior study’s model described due to the physical aspects of the system. The project tends to do a parametric sweep of the bubble to incorporate hotter microbubbles. The study is later scaled up to a 2-microbubble system to find out the optimal separation between the bubbles where the bubbles do not interact with each other fluidically to form a bigger bubble.

The project aims to further develop a geometry which abides the results from the model and uses the optimal separation between the bubbles and using an automated java code written in COMSOL’s application developer to generate bubbles in a geometry in a random fashion in a vessel.

2.1. General Survey

The current world’s economy as described by Sarkar et.al [1] is heavily dependant on conventional sources of energy derived using fossil fuels and its derivatives like coal, petroleum and natural gases to produce power, energy and other goods essential for the world. The high increase in usage of conventional sources of fuels leads to increase in the emissions of greenhouse gases and a steady decline of the conventional fuels as the sources present are limited which could lead to a shortage of the resources.

With heavier legislation being introduced to move towards a cleaner type of fuels as discussed in the news article [2], the move towards production of bioethanol is starting to gain traction even in countries like India where the speed to make a 20% ethanol blended fuel available in all fuel stations, a sustainable method to produce ethanol is necessary.

Often with sustainable production and production of bio-based products as a general, the costs associated with production often is significantly higher than conventional production as described in Li et.al [3], the cost to product ethanol synthetically is significantly lesser than the biological method of producing ethanol which involves fermentation and separation in later stages.

2.2. Production of Bioethanol

Raw materials used in the production of bioethanol describes its generation. As discussed in the previous sections, using molasses or direct glucose is the easiest and most convenient way as glucose directly breaks down through the EMP pathway to form bioethanol and other bioproducts like biobutanol. Production of bioethanol is highly dependent in countries like India using produced sugars rather than cellulosic materials. There might be various reasons to that, probably some of them are:

1)

Reduced complexity of the process:

Using direct sugars which are sucrose and glucose mix, the complexity of the process decreases drastically. When using cellulosic materials as a source of raw material, they need to be pre-processed in order to be converted to glucose and remove undesirable materials like hemi and holo celluloses [20].

The pre-treatment of the raw materials can be a time taking process where the raw materials are hydrolysed to remove the undesirable substances and to convert lignocellulose into glucose. The process can be heavy on manpower and energy as well.

Using direct sugars to produce ethanol can be a lesser complex process which needs lesser equipment which often leads to lower capital investment by the manufacturers.

2)

Decreased costs associated with production:

Cost can contribute to a huge factor in determining things as one cannot simply go behind “green” and “sustainable” production. This is a main reason why producers usually go with synthetic ethanol rather than bioethanol as the costs associated with production is far cheaper than compared to bioethanol as discussed in Li et.al [3]. Higher costs to the production are usually not favoured by the manufacturers as they tend to be recurring and not a one-time investment. Added process line involving pre-treatment of raw materials can increase the costs associated as the operators need to maintain the process at a certain temperature to properly pre-treat.

For the fermentation alone, O₂ supply as described by Raghavendran et.al [5] accounts to up to 15% of the total cost of production. In order to reduce the costs associated to production, process intensification techniques are utilised. In certain cases in pharmaceutical production units, the reaction takes place in a pressurised vessel or a jacketed vessel where post reaction process, the undesirable or the desirable is extracted in the same vessel by heating the unit or decreasing or increasing the pressure for volatile products and also could perform liquid-liquid extractions to remove undesirable or desirable products depending on the process.

3)

Surplus of sugar stocks:

India is currently the largest producer of sugar and the third largest exporter of sugar. This means that the country is producing the most sugar and is exporting a small fraction of sugar which leaves a huge surplus in the sugar stock in the Indian godowns. An estimate of around 35 lakh tonnes or 3.5 million tonnes of sugar is produced in excess [23]. With the excess in mind, the resources are more than sufficient to keep its citizens supplied with sugar and also focus on the blended fuel which is termed as ethanol blending program (EBP).

Although there is a hitch where the sugarcane is a seasonal harvest which is planted in the months of December through March and is harvested in the months of January through March. This leaves with a limited supply of sugarcane throughout the year and the plants being operational only in few months of the year i.e., during the harvest period, the main challenge is to store the produced sugars suitable for ethanol production throughout the year.

This might be a temporary feather in the cap for India as the farmers are distressed/ dissatisfied on the prices offered for their crops by the private authorities and the government authorities, the farmers are bailing out from planting a sugarcane crop. [26]

Keeping the above points into mind, a producer would prefer an easier production of bioethanol rather than a complex second or third generation method to produce bioethanol even though they can be produced using more cleaner sources of energy.

2.3. Microbubbles

As defined in the previous section, microbubbles are the bubbles where the radii are in the range between 100-200 micrometres. Microbubbles produced using a Tesar-Zimmerman fluidic oscillator (T-Z Oscillator) [7] regulates the flow of fluid are steady and evenly distributed when passed through a microporous diffuser as discussed in Abdulrazzaq et.al [11] and Zimmerman et.al [12].

As discussed in Zimmerman et.al [12], the set of model equations describing the evaporation dynamics of a hot microbubble rising in a reservoir of fluid. The same paper discusses certain assumptions for the microbubbles.

○

Surface tensions on the bubbles prevent any deformities to occur on the bubble’s surface due to the size of the bubbles.

○

A fully laminar flow is achieved instantaneously.

Table 2. Model equations for the system described by Zimmerman et.al [12], abdulrazzaq et.al [11].

Model	Equation
Internal Velocity	${\mathit{V}}_{\mathit{z}}={\mathit{U}}_{\mathit{t}}\left(1-{\left({\displaystyle \frac{\mathit{z}}{\mathit{R}}}\right)}^2-2{\left({\displaystyle \frac{\mathit{r}}{\mathit{R}}}\right)}^2\right)$ ${\mathit{v}}_{\mathit{r}}={\mathit{U}}_{\mathit{t}}{\displaystyle \frac{\mathit{r}}{\mathit{R}}}{\displaystyle \frac{\mathit{z}}{\mathit{R}}}$ ${\mathit{U}}_{\mathit{t}}={\displaystyle \frac{1}{3}}{\displaystyle \frac{\mathit{g}{\mathit{R}}^2}{\mathit{\mu }}}\mathsf{\Delta }\mathit{\rho }$
Mass Transport	${\displaystyle \frac{\partial \mathit{c}}{\partial \mathit{t}}}+\mathit{v}.\nabla \mathbf{c}=\mathbf{D}{\nabla }^2\mathit{c}$
Heat Transfer	${\displaystyle \frac{\partial \mathit{T}}{\partial \mathit{t}}}+\mathit{v}.\nabla \mathbf{T}=\mathsf{\alpha }{\nabla }^2\mathit{T}$
Partial Pressure	${\mathit{p}}_{\mathit{w}|{\mathit{r}}^2+{\mathit{z}}^2={\mathit{R}}^2}=\mathit{p}\mathit{*}\left(\mathit{T}\right)$ $\mathit{C}{|}_{{\mathit{r}}^2+{\mathit{z}}^2={\mathit{R}}^2}=\mathit{C}\mathit{*}\left(\mathit{T}\right)$
Boundary Condition

Table 2. Model equations for the system described by Zimmerman et.al [12], abdulrazzaq et.al [11].

Model	Equation
Internal Velocity	${\mathit{V}}_{\mathit{z}}={\mathit{U}}_{\mathit{t}}\left(1-{\left({\displaystyle \frac{\mathit{z}}{\mathit{R}}}\right)}^2-2{\left({\displaystyle \frac{\mathit{r}}{\mathit{R}}}\right)}^2\right)$ ${\mathit{v}}_{\mathit{r}}={\mathit{U}}_{\mathit{t}}{\displaystyle \frac{\mathit{r}}{\mathit{R}}}{\displaystyle \frac{\mathit{z}}{\mathit{R}}}$ ${\mathit{U}}_{\mathit{t}}={\displaystyle \frac{1}{3}}{\displaystyle \frac{\mathit{g}{\mathit{R}}^2}{\mathit{\mu }}}\mathsf{\Delta }\mathit{\rho }$
Mass Transport	${\displaystyle \frac{\partial \mathit{c}}{\partial \mathit{t}}}+\mathit{v}.\nabla \mathbf{c}=\mathbf{D}{\nabla }^2\mathit{c}$
Heat Transfer	${\displaystyle \frac{\partial \mathit{T}}{\partial \mathit{t}}}+\mathit{v}.\nabla \mathbf{T}=\mathsf{\alpha }{\nabla }^2\mathit{T}$
Partial Pressure	${\mathit{p}}_{\mathit{w}|{\mathit{r}}^2+{\mathit{z}}^2={\mathit{R}}^2}=\mathit{p}\mathit{*}\left(\mathit{T}\right)$ $\mathit{C}{|}_{{\mathit{r}}^2+{\mathit{z}}^2={\mathit{R}}^2}=\mathit{C}\mathit{*}\left(\mathit{T}\right)$
Boundary Condition

The above equations described in the papers by Abdulrazzaq et.al [11] and Zimmerman et.al [12] represent the system containing a hot microbubble rising in a reservoir of liquid and converts the fluid around it into a vapor state.

Abdulrazzaq et.al [10] conducted practical studies to test their effectiveness in a binary system of ethanol and water but with varying heights of liquid levels. The study resulted in a clear consensus where the liquid levels does in fact plays a huge role in separation of ethanol from the binary system.

Figure 7. Depth of liquid vs separation as evaporation %.

Figure 7. Depth of liquid vs separation as evaporation %.

As in the graph we can see above that the liquid level height plays a significant role in evaporation percentage where the maximum evaporation occurs when the liquid level is kept minimum from 2mm to 4mm.

2.4. Microbubble Generation

Traditionally a bubble is formed when a stream of fluid passes through an opening of a surface and the size is determined by the opening of the surface. In the case of microbubbles, the stream is passed through a microporous diffuser but in this case, when the stream of gas is passed through a microporous diffuser, the bubbles are distributed in an uneven fashion through the area as shown in previous section.

In order to counter the effects of uneven distribution of bubble through the vessel, the fluid of interest has to be streamlined to alter the pressure to create evenly sized small bubbles. In order to do so, Brittle et.al [21] conducted various studies on how to do the same by starting out with acoustic speakers to induce pressure on the fluid by oscillating the airstream.

Based on the observation, the T-Z oscillator was built with having no moving parts. A question might arise on how the fluid of interest is oscillated if there are no moving parts. A simple answer to that is by creating a pressure difference between the flow path of the stream. The pressure difference in between the flow path of the stream, the pressure difference drives a change in pressure of the stream.

The T-Z oscillator consists of a supply terminal as the name suggests, it supplies the gas of interest to be sent as microbubbles. A fluid is sent through control terminals from high pressure to low pressure to create a pressure difference between the control terminals.

Figure 8. T-Z Oscillator.

Figure 8. T-Z Oscillator.

Figure 9. Working of T-Z oscillator.

Figure 9. Working of T-Z oscillator.

The Coanda effect as defined by Constantin (2010) [22] says that any fluid has a tendency to adhere itself to a curved surface due to the reduced pressure caused by an acceleration of flow around the surface. Zimmerman et.al [7] described in detail that the pressure difference between the two control terminals causes a resonance in the fluid flow inducing the Coanda effect.

2.5. Multiphysics Modelling and COMSOL

FEATool Multiphysics [15] defines Multiphysics modelling as “process if computer simulation of coupled and interacting physical phenomena such as heat, mass transfers and fluid flows”. In simple words, a multiphysics simulation consists of set of model equations which are simulated over a defined geometry to get a visual representation of the behaviour of the geometry to the model equations.

In studies conducted by Abdulrazzaq [11] which focussed on developing the model for a single hot microbubble injected into the reservoir containing a binary mixture of ethanol and water. The model equations used in the development of model were similar to the models produced in Zimmerman et.al [12]. The model was developed in a 2-D axisymmetric environment with a semicircle on the ‘r’ axis. An axisymmetric domain sweeps the 2-D model around a 360-degree axis making a 2-D model into a 3-D model.

COMSOL is a specialised software package which performs Multiphysics modelling where a user can create a geometry of interest and add equations of interest to study at and simulate the specified equations over the said geometry. COMSOL offers various geometry domains ranging from a zero-dimensional point to a 3-D geometry.

Figure 10. Dimensions available in COMSOL.

Figure 10. Dimensions available in COMSOL.

Figure 11. Various physics and models available in COMSOL.

Figure 11. Various physics and models available in COMSOL.

3.1. A Brief to COMSOL

COMSOL is a software package built to simulate Multiphysics models over a defined geometry. COMSOL was built using Java in the backend and the front end was built using C# which evolved from Visual basic. COMSOL was founded in the year of 1986 and released a Multiphysics modelling software named FEMLAB in 1998 which evolved to be known today as COMSOL.

Traditionally COMSOL is used to simulate computational fluid dynamics (CFD) models involving single phase or multiphase models. Single phase models are the models where the fluid dynamics studied in the problem are because of a single phase of fluid interacting with the defined geometry. This often results in lesser the complication and the computational power required by COMSOL to execute the simulation.

Although other packages like Ansys and OpenFOAM exists, the variety of packages available ranging from classic computational fluid dynamics to electrodynamics and magnetic simulations. In COMSOL, one can combine different models altogether to one geometry and visualise its behaviour to the equations and materials.

COMSOL has a huge material library where one can choose from biological materials to common chemicals like ethanol, butanol and other materials. The user also has the freedom to create ‘blank’ materials to which they can add their own properties like the material type, state, properties like density, viscosity, kinematic and dynamic viscosities etc. The benefit of adding own materials makes COMSOL a suited software package to simulate Multiphysics models.

COMSOL also connects with other software packages used by researchers and people in the industry. COMSOL has inbuilt and third-party connections to software packages like MATLAB using MATLAB Livelink and Python’s mph library.

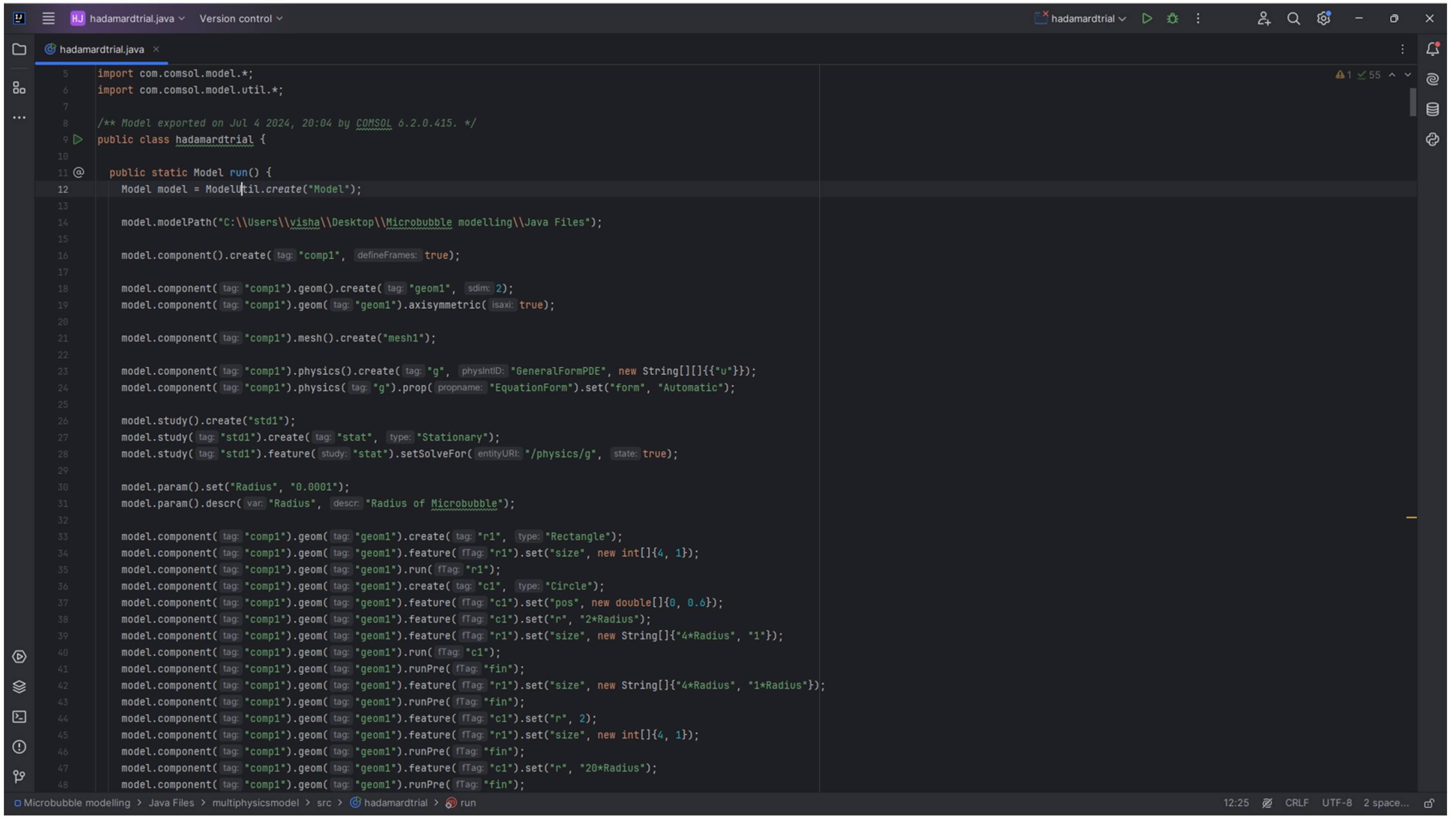
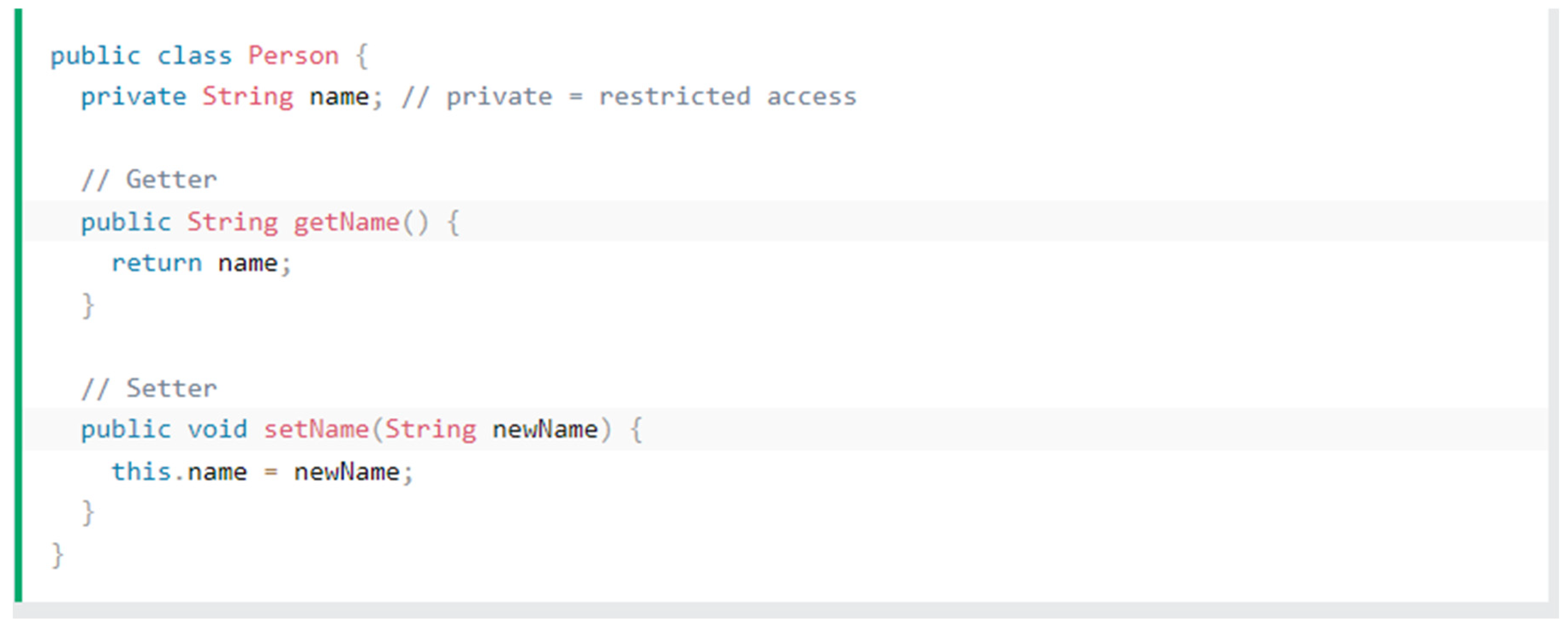
Though COMSOL has various models it can run the models and algorithms can be computationally challenging to work with as the backend of the models which records every click and edit as a Java code. Certain parts of the models like the geometry have to be initialised in Java as a getter and a setter for the model to be initialised properly.

Java being an object-oriented programming language, depends on the principles of object-oriented programming. COMSOL’s models rely heavily on encapsulation where its main function is to hide certain variables by taking the variable to a certain name by the get method and the set method call the method separately.

Figure 12. Get and set methods in Java.

Figure 12. Get and set methods in Java.

As we can see in the above image [24] we can see that the get method gets the name and returns the property name as a string which is a collection of characters. The setter method or the set method receives the string initialised from the get method and calls the method using a new parameter newName and it assigns to the variable initialised in the get method.

A question might arise, why not make the variables public? Using encapsulation makes sure that the model is protected by making only the essentials to be visible in the set method and in turn making it a read only item. In case of the user being a programmer, they can edit one part of the code and not worry about changing the name of the variable in each instance which would lessen the complications to make changes in the code.

COMSOL also has the ability to link with MATLAB where a user proficient with MATLAB can make edits to the model by using COMSOL’s inbuilt Livelink feature available to a subscribed user which links COMSOL’s model with MATLAB.

Python also built a library which can connect to COMSOL’s interface and control, build and edit models in Python’s environment. Using a programming language helps the users to make edits to models, visualise the results by adding certain specific plots which brings and extra customization options to the way we build and visualise the models.

The model built in COMSOL comprises of built in equations from COMSOL for heat transfer in fluids for heat exchange system of bubbles, transport of diluted species for mass transfer properties of the bubbles and level set model for the fluid dynamics and the movement of bubbles.

After lots of trials and errors, level set was chosen to be a fitting algorithm to execute the movement of microbubbles for the vessel. Often with using other algorithms like multiphase flow and bubbly flow, the results for a time dependant study resulted in a singular value which made no sense. Upon investigating the log file for the model, the Linear error or the LinError was constantly found to be zero. This occurred for various other model equations and proper simulation occurred in model set in level set with phase initialisation in a time dependant study. The details to the error will be discussed in the following subsections.

3.2. Model Equations

The model equations used to build the model were taken from Zimmerman et.al [12] where the model equations were built for a single bubble responsible for facilitating heat and mass transfer and is treated phenomenologically which means no external factors affect its dynamics. This assumption cannot be true when adding a second bubble as the two bubbles can interact with each other in all the three ways, i.e., fluidically by merging into a larger bubble and settle down in the reservoir rather than travelling up or creating a super-hot zone between bubbles.

To reduce the complications, Zimmerman et.al [12] came up with model equations with some additional hypothesis which makes further ease in complications, which are:

• The bubbles are small enough that the surface tensions exerted by the bubbles oppose any deformations to the spherical shape.
• The time to achieve a fully developed laminar flow is instantaneous so that laminar flow can be considered throughout the model and the travel of the bubble.

Additional assumptions were also considered to ease out the process of scaling up to multiple bubbles which were:

• The bubbles act individually and does not merge into each other to form larger bubbles.
• The bubbles are shaped evenly and are sized and spaced equally to reduce complications and travels parallel to the z-axis.

Model equations are given as following:

1)

Fluid dynamics:

As we know from the assumptions that the time to assume a fully developed laminar flow is instantaneous which leads to an assumption that the microbubble’s fluid dynamics equation can be solved using a solution to the Navier-Stokes equation adapted by the Hadamard-Rybcynski method which solves for the rising bubble under buoyancy.

The equation is solved using the internal velocity component which is given by:

$${\mathit{V}}_{\mathit{z}}={\mathit{U}}_{\mathit{t}}\left(1-{\left({\displaystyle \frac{\mathit{z}}{\mathit{R}}}\right)}^2-2{\left({\displaystyle \frac{\mathit{r}}{\mathit{R}}}\right)}^2\right)$$

Where,

$${\mathit{V}}_{\mathit{z}}={\mathit{U}}_{\mathit{t}}\left(1-{\left({\displaystyle \frac{\mathit{z}}{\mathit{R}}}\right)}^2-2{\left({\displaystyle \frac{\mathit{r}}{\mathit{R}}}\right)}^2\right)$$

And

$${\mathit{U}}_{\mathit{t}}={\displaystyle \frac{1}{3}}{\displaystyle \frac{\mathit{g}{\mathit{R}}^2}{\mathit{\mu }}}\mathsf{\Delta }\mathit{\rho }$$

The components v_z and v_r are the axial and the radial components respectively, R denotes the radius of the bubble, and the terminal velocity is given by U_t. The equation also considers gravitational forces to count. $\mathsf{\Delta }\rho$ denotes the difference in the densities of the fluids.

2)

Heat and mass transfers:

In case of mass and heat transfer for the system the set of equations is given by the following equations:

$${\displaystyle \frac{\partial \mathit{c}}{\partial \mathit{t}}}+\mathit{v}.\nabla \mathbf{c}=\mathbf{D}{\nabla }^2\mathit{c}$$

$${\displaystyle \frac{\partial \mathit{T}}{\partial \mathit{t}}}+\mathit{v}.\nabla \mathbf{T}=\mathsf{\alpha }{\nabla }^2\mathit{T}$$

The equations look similar but with a change in the variables used in the equations. T denotes the temperature and concentration is denoted by c. in the concentration equation, D denotes the molecular diffusivity of the system and $\mathsf{\alpha }$ denotes the thermal diffusivity in the air. The boundary condition for the heat transfer systems is given by the following equations:

3.3. Model Set-Up

The model considered to be studied was from a previous study where the model was constructed to study the behaviour of single microbubble made of air towards a reservoir of a binary mixture of ethanol and water. The model was part of a PhD thesis submitted at The University of Sheffield [25] and the corresponding paper submitted by Abdulrazzaq et.al [11].

Initial studies were conducted in this project to find out the optimal separation between identical air microbubbles which are hot wherein there wouldn’t be any interaction between the bubbles fluidically, but they share or interact with each other to cause an effect of heat and mass transfer amongst each other.

The initial studies were conducted in a 2-D geometry domain rather than the model built in the earlier studies to understand the working of COMSOL and to understand how the bubbles would also move freely in an x-y plane which can’t be studied in an r-z plane.

The model as discussed earlier is built in an x-y plane. In order to define the model, also keeping a decreased level of complexity in mind, a level set with phase initialization study was chosen to simulate the bubbles flowing in the binary mixture of ethanol and water. A time dependant study was chosen where the model will be simulated across a set time which would lead to a study analysed through a timeframe giving more realistic and readable results which would possibly replicate the real experiment.

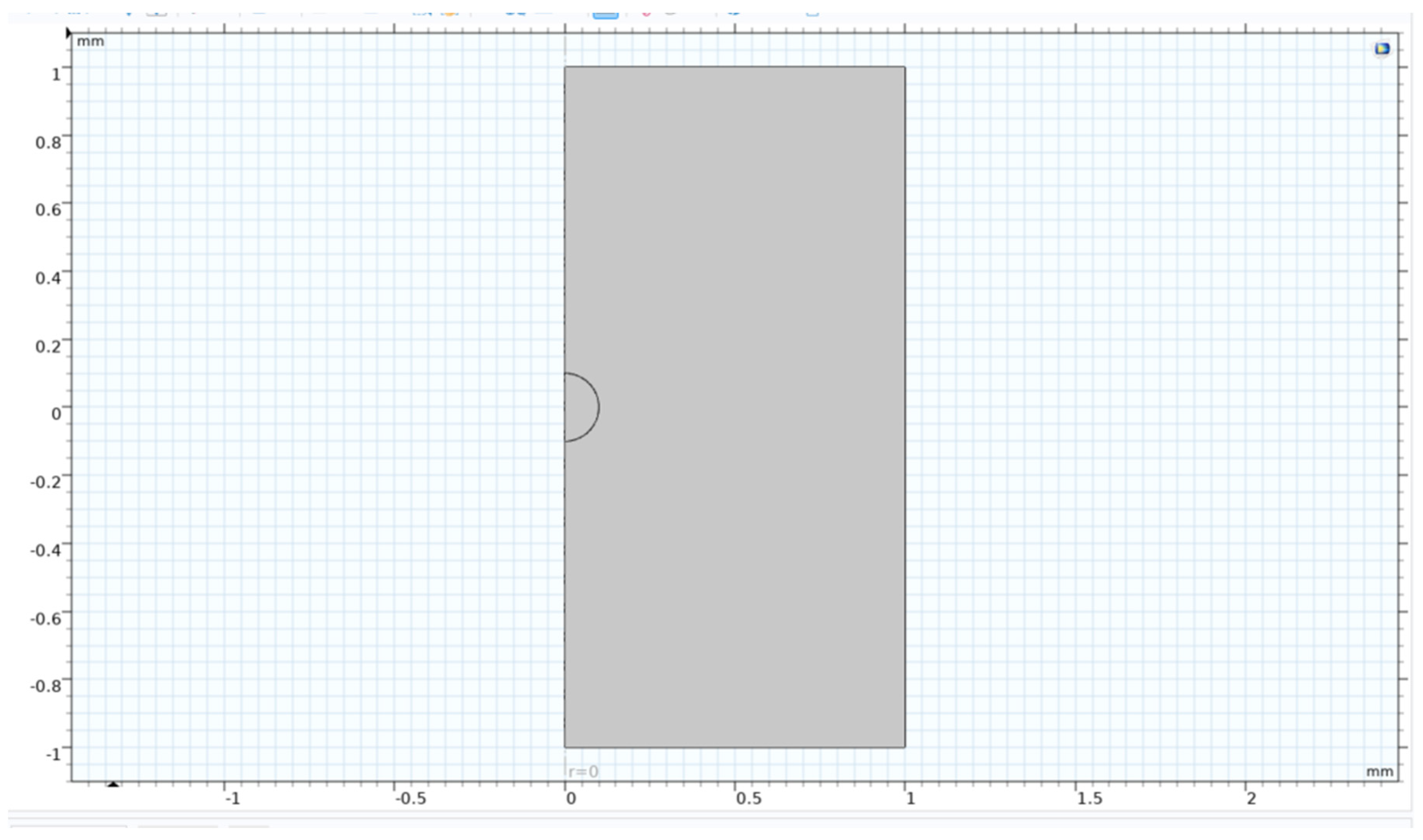
In the beginning, a single microbubble of radius 100µm was set in the reservoir under the same conditions and simulated using level set algorithm to study the rise of bubble on the x-y plane. A finer mesh was taken into consideration to get a more accurate simulation. A varied size of mesh was even studied to find out if there indeed was a variation in values upon changing mesh size or a simple coarse or a normal mesh would do the job.

With the computational power available in hand which amounted to around 16GB of DDR-4 RAM with a virtual RAM up to extra of 30GB, with a 8GB of Graphical Processing Unit (GPU), all the trials for this project were initially made on a coarser mesh and later scaled up to a finer mesh and occasionally extremely fine mesh.

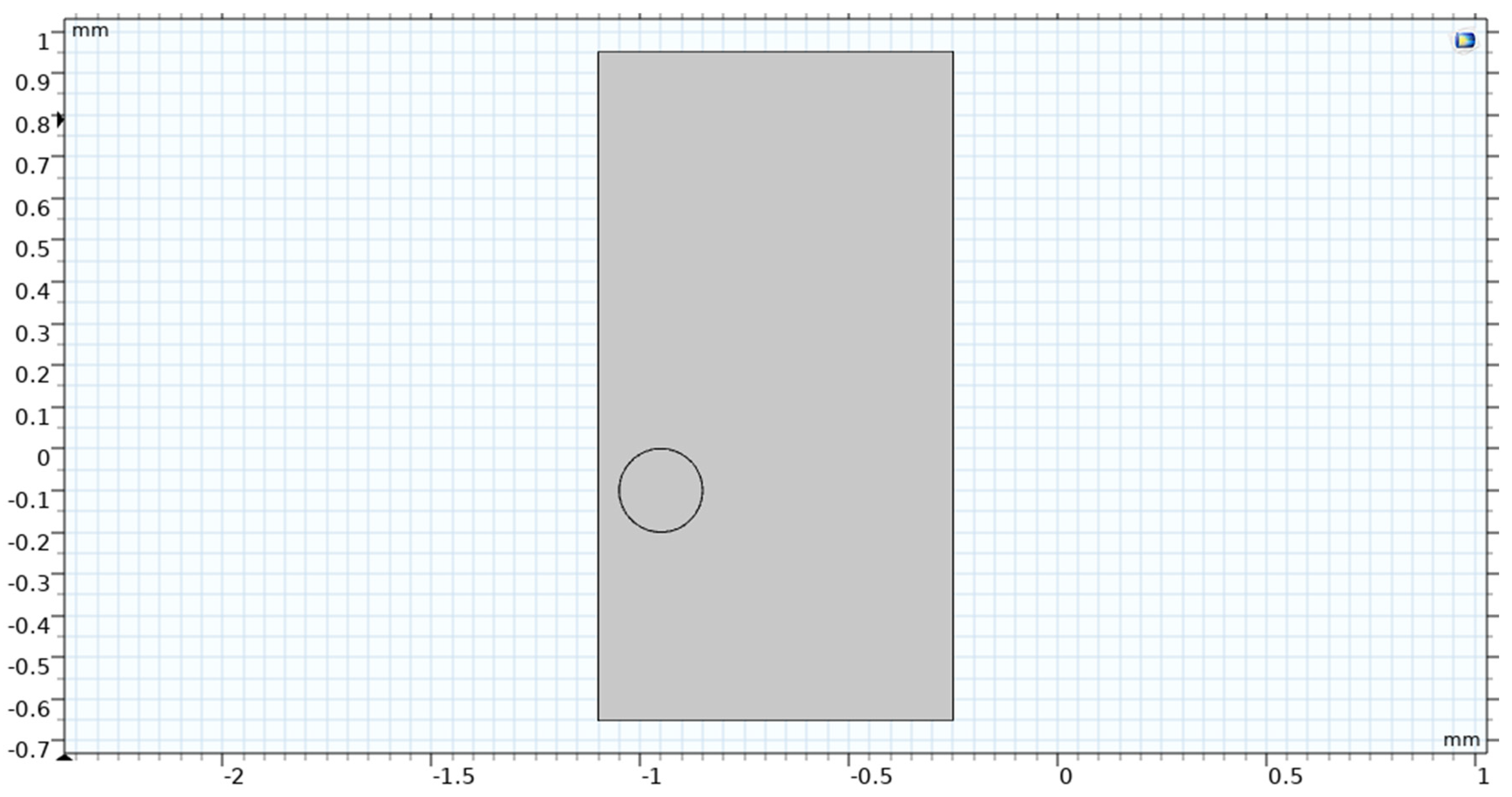
Figure 13. Geometry of single bubble study.

Figure 13. Geometry of single bubble study.

The simulation showed a variety of results for the single microbubble on its residence time in the vessel and its travel path and behaviour towards the vessel geometry and boundaries. To scale up this study to find out the optimal separation between the bubbles so that they wouldn’t interact with each other fluidically but could possibly interact with each other to promote better heat transfer between the bubbles.

The model for the single bubble built in a 2-D environment was scaled up by changing the bubble’s position and another bubble was added and tested in various configurations like placing the bubbles side by side and above each other to find the optimal separation.

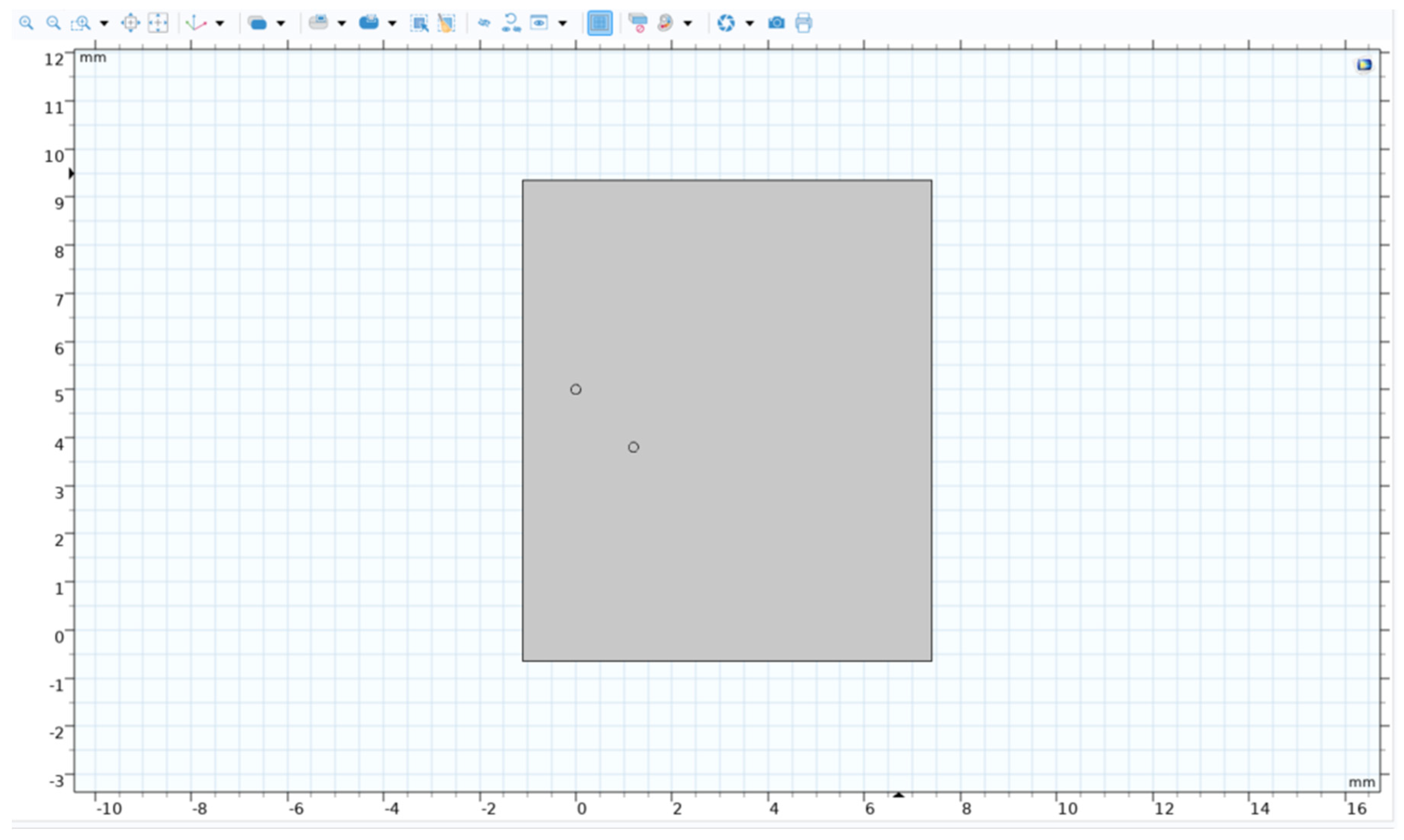
Figure 14. Double bubble system with 2 bubbles of 100 microns separated with a certain distance.

Figure 14. Double bubble system with 2 bubbles of 100 microns separated with a certain distance.

Figure 15. Geometry of single bubble axisymmetric model (previous study).

Figure 15. Geometry of single bubble axisymmetric model (previous study).

Figure 16. Double bubble system of previous study model.

Figure 16. Double bubble system of previous study model.

The optimal distance was sought out and a second bubble was added to the model developed in previous studies and was studied the effect of adding a second bubble to the model. There also was a problem where the previous study was more empirical in nature which led to the hot air microbubble being not as hot as it seemed to be. In order to study the effect of even hotter microbubble, a parametric based study was conducted where the temperature of the hot air bubble (T0_air) was varied across different values of temperature in Kelvin from 350K to 450 with increments of 50K.

The parametric sweep was studied, and the second bubble was added to the study and the effects were studied by making sure the fluid properties were added for the second bubble and the model incorporated the second bubble. The radius and the properties of the bubble were made identical to each other, and the bubble was placed on the r-axis in order to sweep the geometry along the r-axis to form a 3D geometry. If the bubble was placed anywhere except along the r-axis, the bubble would not be sphere but rather be a torus or a doughnut.

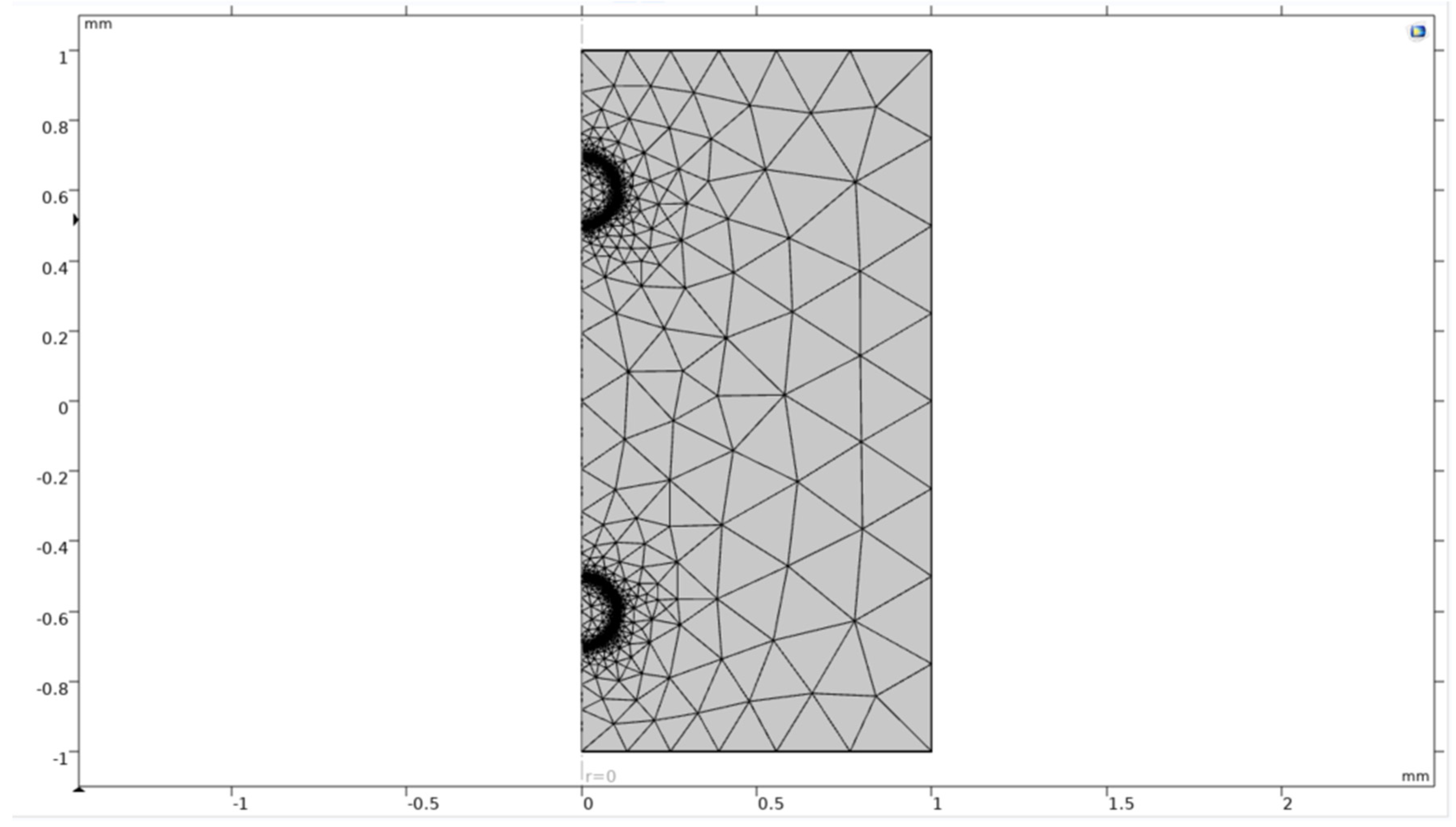
3.4. Mesh Selection and Meshing

What is meshing and why is it important?

The process of meshing of the model enables us to discretize the model into smaller units which are simple shapes which are referred to as mesh elements. The combination of mesh elements altogether is known as a mesh. Meshing allows the users to control the finetuning of the model by allowing the number elements to be defined over the geometry to get either a low number of elements where the equations could be applied over by choosing a coarse mesh or by using a fine mesh or extremely fine mesh to incorporate more number of nodes onto the geometry to increase the number of computations. According to COMSOL’s discussion boards and articles published on their websites, it clearly states that meshing is one of the most computationally demanding part of the simulation throughout the process of simulating Multiphysics models.

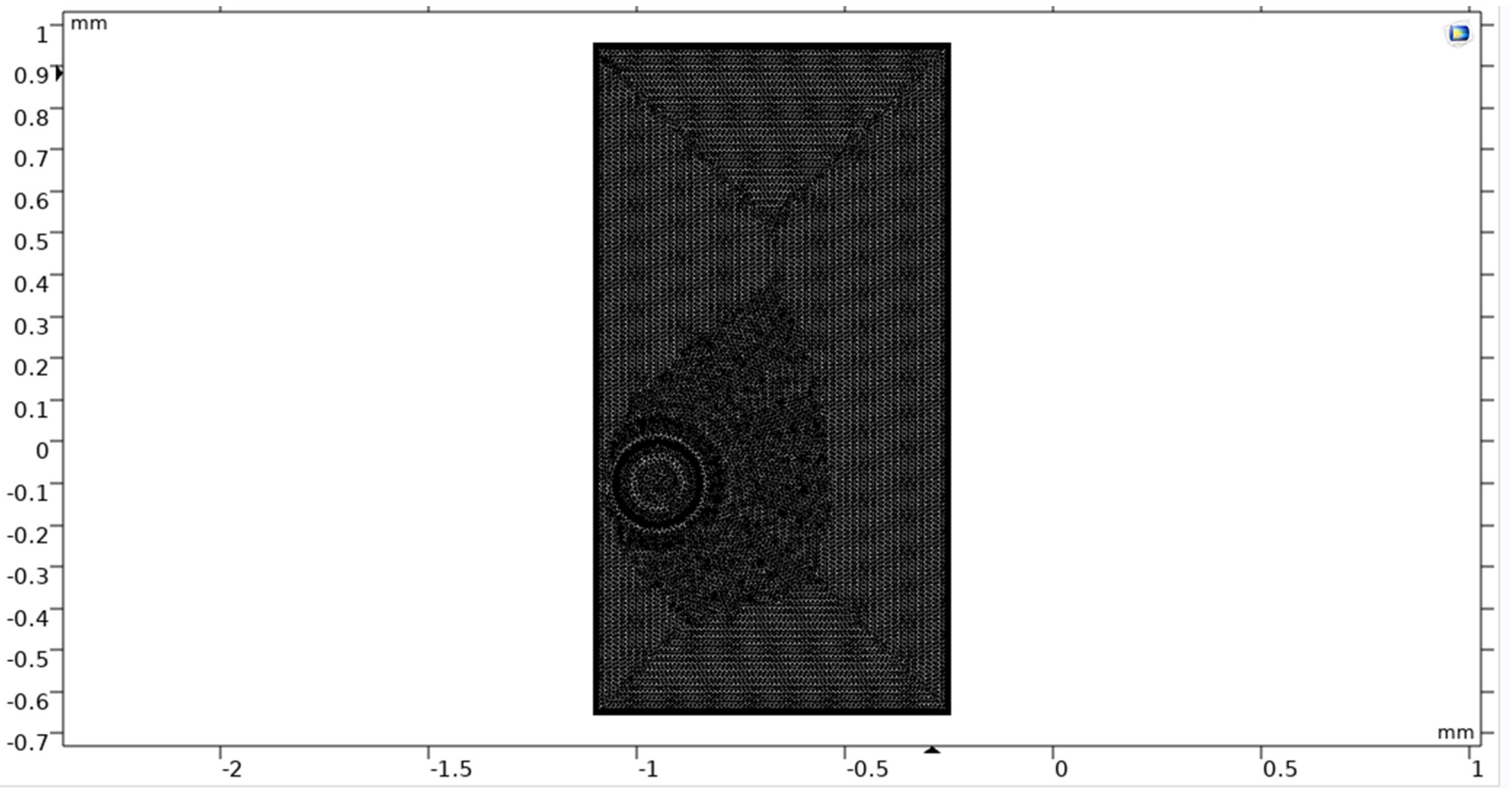
For initial studies considering a single and double microbubble study, a fine mesh was chosen where the mesh’s shape was a free tetrahedral. A triangular mesh of small element size was chosen and applied over the boundaries of bubbles which move under buoyancy making the mesh around the bubble to act like a moving mesh where it moves along with the geometry while simulating the equations. Since the models are not complex or computationally demanding, the mesh took less than 2-3 seconds to build on the geometry.

Figure 17. Meshing of single bubble system.

Figure 17. Meshing of single bubble system.

Figure 18. Meshing of double bubble system.

Figure 18. Meshing of double bubble system.

Figure 19. Meshing over double bubble axisymmetric system.

Figure 19. Meshing over double bubble axisymmetric system.

For the model from previous studies, a finer mesh was initially studied on. A tetrahedral mesh of fine size was constructed over the geometry containing a single microbubble along the z-axis at r=0. Around the bubble’s surface, a fine triangular mesh was constructed to get a finer simulation around the bubble’s surface. Since the mesh is more detailed, the computational burden was a bit more than the single or the double microbubble systems. The mesh to build around the geometry took approximately 5-6 seconds to build over it.

3.5. Application Builder

Application builder is a feature unique to COMSOL where a user can make edits to models either to build a model from scratch or to make edits to any part of the model ranging from geometry to the visualisation part of the model after simulation using results obtained from simulation. The application builder can be used through writing custom Java methods and importing those methods onto the model builder.

The java code generated in model builder as a result of actions like click and edits are recorded as a long and tedious code of nearly 1000+ lines of code for a simple model involving a simple mathematical equation over a rectangle. In software engineering terminologies, this type of programming is termed as brute force coding. A brute force code though it is easy to understand, the computation burden is heavy in this case and the code when is reviewed in the case of making complex software packages gets hard to review and make edits to it.

In order to reduce complexity of the code behind the model, often people in certain cases would prefer to build the model completely on the application builder although it is a tedious task. In ideal conditions, the application builder is generally used to write smaller methods to make certain edits in the model which are sometimes very tedious to execute manually in the model builder. As discussed earlier, the application builder can be used to benefit for recurring tasks which can be coded to ease out the model solving process or the building process.

Processes like generating geometries over a certain range could be possible automated and edits to the model such as adding certain ranges of parameters and custom input data and creating custom visualisation graphs and plots could be added. Since a user can use Java in the application builder, a user can also make use of various other java elements like making use of the object-oriented programming concepts and various other Java features to disposal.

COMSOL models are heavily dependent on object-oriented programming elements where the code generated in the model builder and encapsulated with getters and setters. As discussed in previous sections, encapsulation is an object-oriented programming concept where certain features which are paramount the code or the model are hidden and only the attributes related to that model are revealed to the user which would protect the integrity of the code.

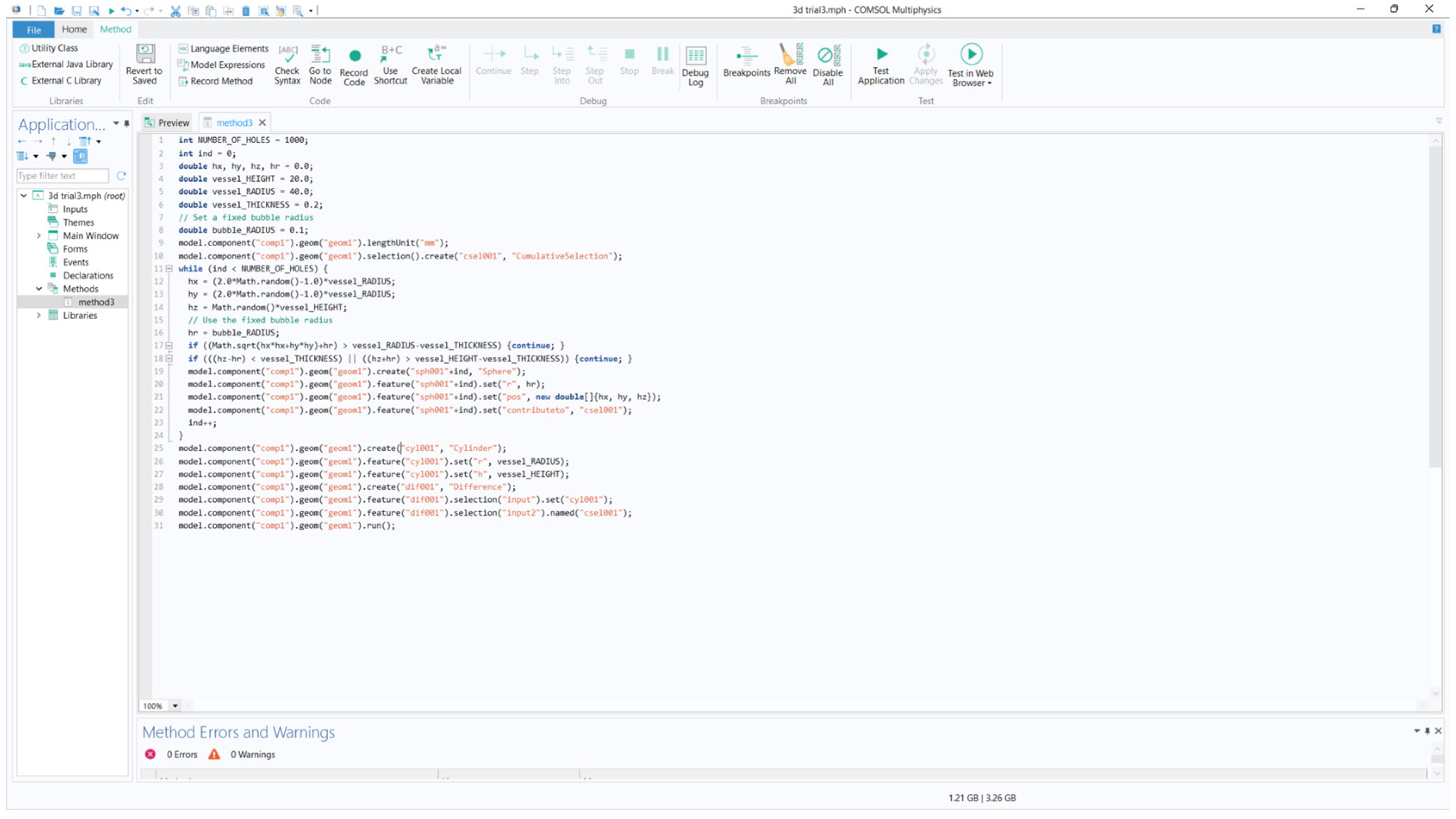
This project utilised the Application builder in a way where a complex 3D geometry was generated with respect to the results obtained from the initial studies of the model to find out the optimal separation between the microbubbles. The separation between the bubbles where the bubbles are non-interacting with each other fluidically are set as the separating distance and a Java method is written to execute the same. For reference to the Java method, refer appendix-1.

Figure 20. Geometry generated as a result of Java method in COMSOL.

Figure 20. Geometry generated as a result of Java method in COMSOL.

3.6. Model Studies

The models are studied using COMSOL’s study tab where usually a study is added and the parameters of the study are added and modified according to the requirements of the study. In the case of this project, a time dependant study was considered where the model’s behaviour could be studied with respect to a time change to study the behaviour of the equation over time. Usually, a time dependant study takes a while as the model equations depending on the mesh must compute the behaviour of the geometry over the range of time.

In this project, time dependant study was considered where the model equations were studied over a range of time to study the behaviour of bubbles. A parametric sweep study was added ad discussed in prior sections to study the effect of bubbles with higher temperature than 390K which was the base study of the previous model.

3.7. Overall Methodology

In a summary of the methodology followed in the project, the model used to evaluate the behaviour of hot microbubbles in a reservoir containing a binary mixture of ethanol and water was obtained from previous studies. Although there was an issue with the previous model where the model was more empirical than the practical experiment where the air microbubbles tend to be hotter than the model described it to be.

Also, the model dealt with studying the behaviour of a single microbubble rising rather than a cloud of microbubbles which posed an opportunity to scale up the model to a cloud of microbubbles. In order to scale up to a cloud, the model initially had to be tested to a double-bubble system where the interaction between the bubbles are to be studied. There posed a threat to the system where bubbles if placed close to each other, they often tend to merge and form a bigger microbubble as to be seen in the results section. The importance of finding the optimal separation of bubbles plays a major part in the third part of the project wherein by using the application builder module of COMSOL, using the distance of separation of microbubbles, a java method is written to generate random bubbles inside a cylinder of radius 100µm with bubbles separated evenly throughout the geometry.

In order to counter the problem where the model was more empirical than it meant to be, a parametric study was added to the model with varying inlet bubble temperatures ranging from 350K to 550K with increments of 50K. The varying inlet air bubble temperatures gave a good understanding of how a cloud of microbubbles could if simulated could work together in unison.

4.1. Initial Test

The motive behind the initial test’s purpose was of the following:

1)

Test the features available in COMSOL available with respect to microbubbles.

2)

Check the residence time of microbubbles in the reservoir.

3)

Study the fluid dynamic effects of the single microbubble system in a 2-D plane.

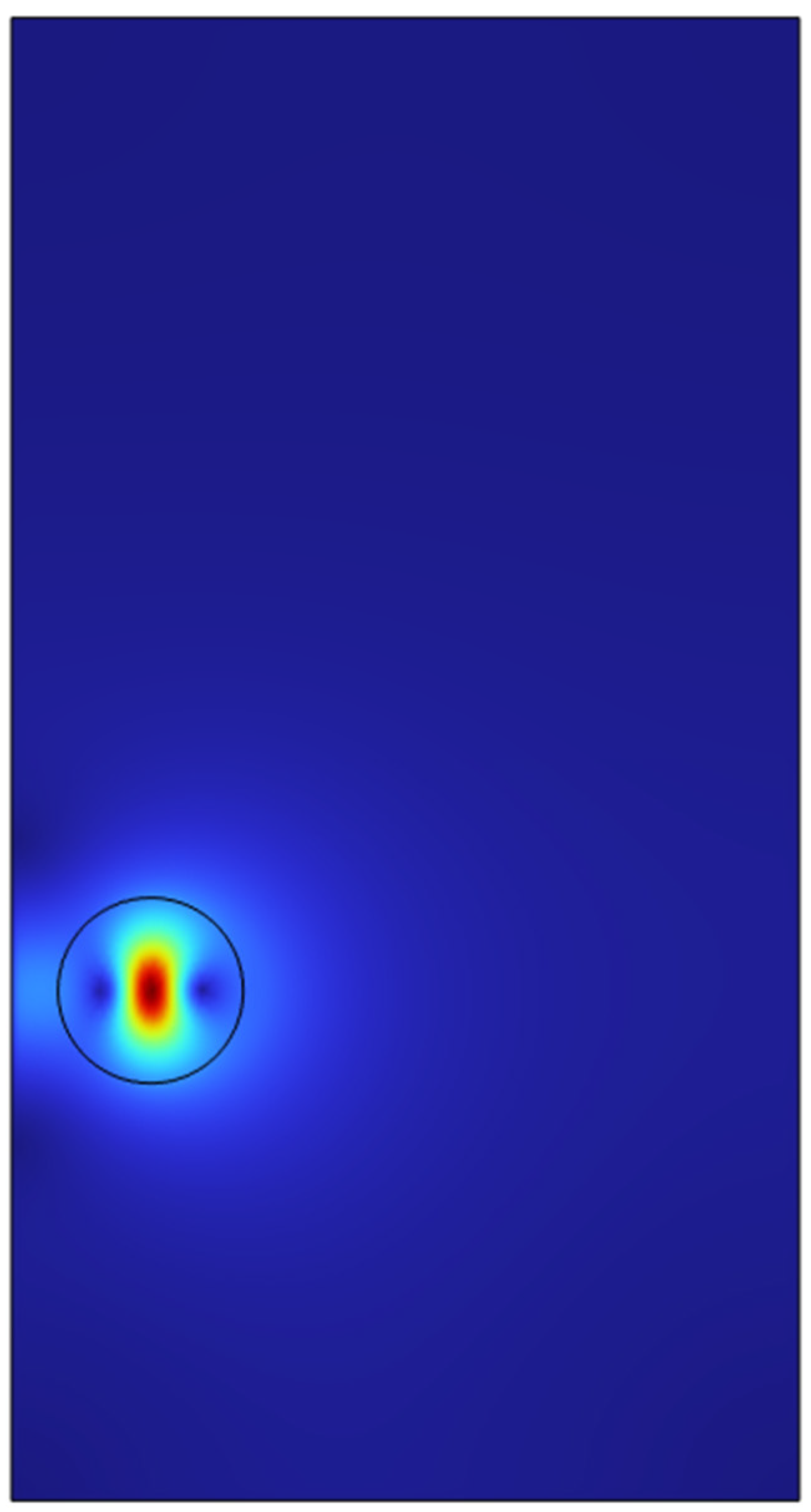
The model was studied in a level set with phase initialization study. A single air microbubble of 100 microns was added to the reservoir containing ethanol (100%) taken from COMSOL’s inbuilt material bank. A time dependant study was chosen with time from 0 seconds to 1 second with an increment of 0.1 seconds.

The results for the initial study conducted in a 2-D domain showed a residence time of 0.1 seconds in the vessel and the bubble travels through the vessel and escapes through the centre of the vessel. The solution time took around 10 minutes with a physics controlled finer mesh.

Figure 21. Velocity surface plot of single microbubble at 0 seconds.

Figure 21. Velocity surface plot of single microbubble at 0 seconds.

Figure 22. Velocity surface plot at time 0.1 seconds.

Figure 22. Velocity surface plot at time 0.1 seconds.

Figure 23. Velocity surface plot at 0.3 seconds.

Figure 23. Velocity surface plot at 0.3 seconds.

Figure 24. Velocity surface plot at 0.4 seconds.

Figure 24. Velocity surface plot at 0.4 seconds.

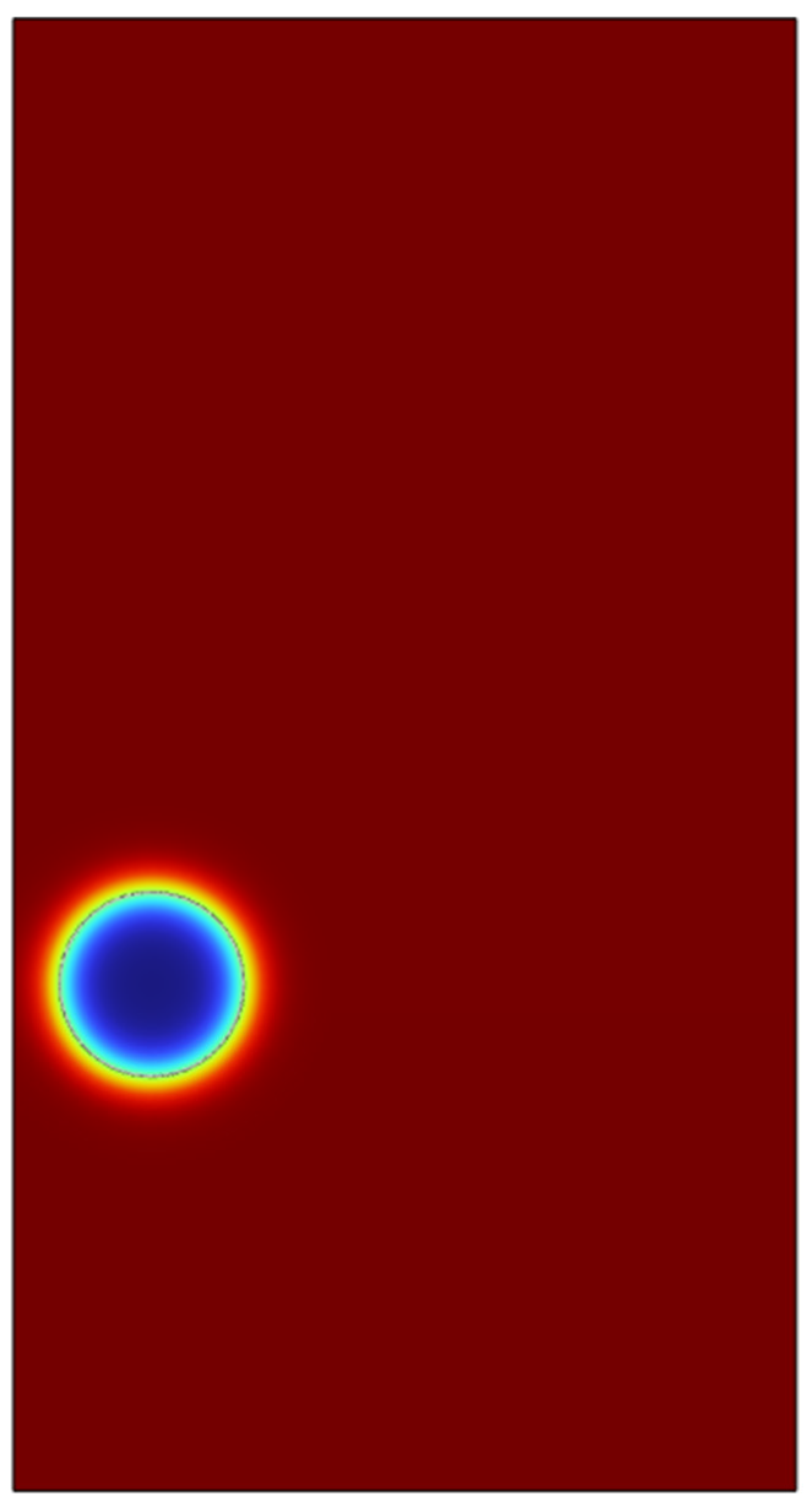
Figure 25. Liquid fraction at time t=0.

Figure 25. Liquid fraction at time t=0.

Figure 26. Volume fraction at time t= 0.1 seconds.

Figure 26. Volume fraction at time t= 0.1 seconds.

Figure 27. Volume fraction at time t= 0.3 seconds.

Figure 27. Volume fraction at time t= 0.3 seconds.

4.2. Double Microbubble System in 2-D Domain

In order to test the viability of the system for a possibility to scale up to a clous of identical microbubbles, the viability of double microbubble systems have to be explored where the double microbubbles do not interact with each other fluidically. Various bubble separation distances were tested from bubble’s diameter (200 microns) to a couple of centimetres.

It was found out that bubbles placed too close to each other coalesced with each other to form a bigger microbubble and defeats the purpose of effective heat and mass transfer if the bubbles are coalescing and increasing its size. After various testing and studies of the double bubble system, it was found that with a separation of 1.2 mm between the bubbles, the bubbles do not coalesce and moves up separately.

Figure 28. Velocity plot of double bubble system at t=0s.

Figure 28. Velocity plot of double bubble system at t=0s.

Figure 29. Velocity plot at t=0.1s.

Figure 29. Velocity plot at t=0.1s.

Figure 30. Volume fraction at time t=0s.

Figure 30. Volume fraction at time t=0s.

Figure 31. VOl frac at time t=0.1s.

Figure 31. VOl frac at time t=0.1s.

Figure 32. Vol frac at time t=0.3s.

Figure 32. Vol frac at time t=0.3s.

As we can see in the above surface plots generated by COMSOL for the system containing two microbubbles. The surface plots generated are for velocity profiles and volume fractions respectively. We can see that there is no interaction between the air bubbles when placed 1.2mm apart from each other. Although there seems to be an interaction at the velocity profile but considering the surface tension assumption from the previous sections, the volume fraction of the liquids which shows the different fluids interacting with each other, we can see the that the microbubbles sized 100 microns do not interact until they reach the surface of the liquid. A point of note, the system built here was just to consider the fluid dynamics of the system and neglecting the interaction between the phases in perspective of heat and mass transfer.

4.3. Axisymmetric Results of Original Model with Parametric Sweep

The initial model as discussed in previous sections was more on the theoretical side where the temperature of the air bubble (T0_air in the model) was lower than the practical side. In order to study the effects of hotter microbubbles, a parametric based study was added where a sweep of various values of the air bubble temperature was studied. Values ranging from 350K to 550K with increments of 50K was chosen to be the parameter values to be tried and tested.

Figure 33. Average temperature of fluids in reservoir over time.

Figure 33. Average temperature of fluids in reservoir over time.

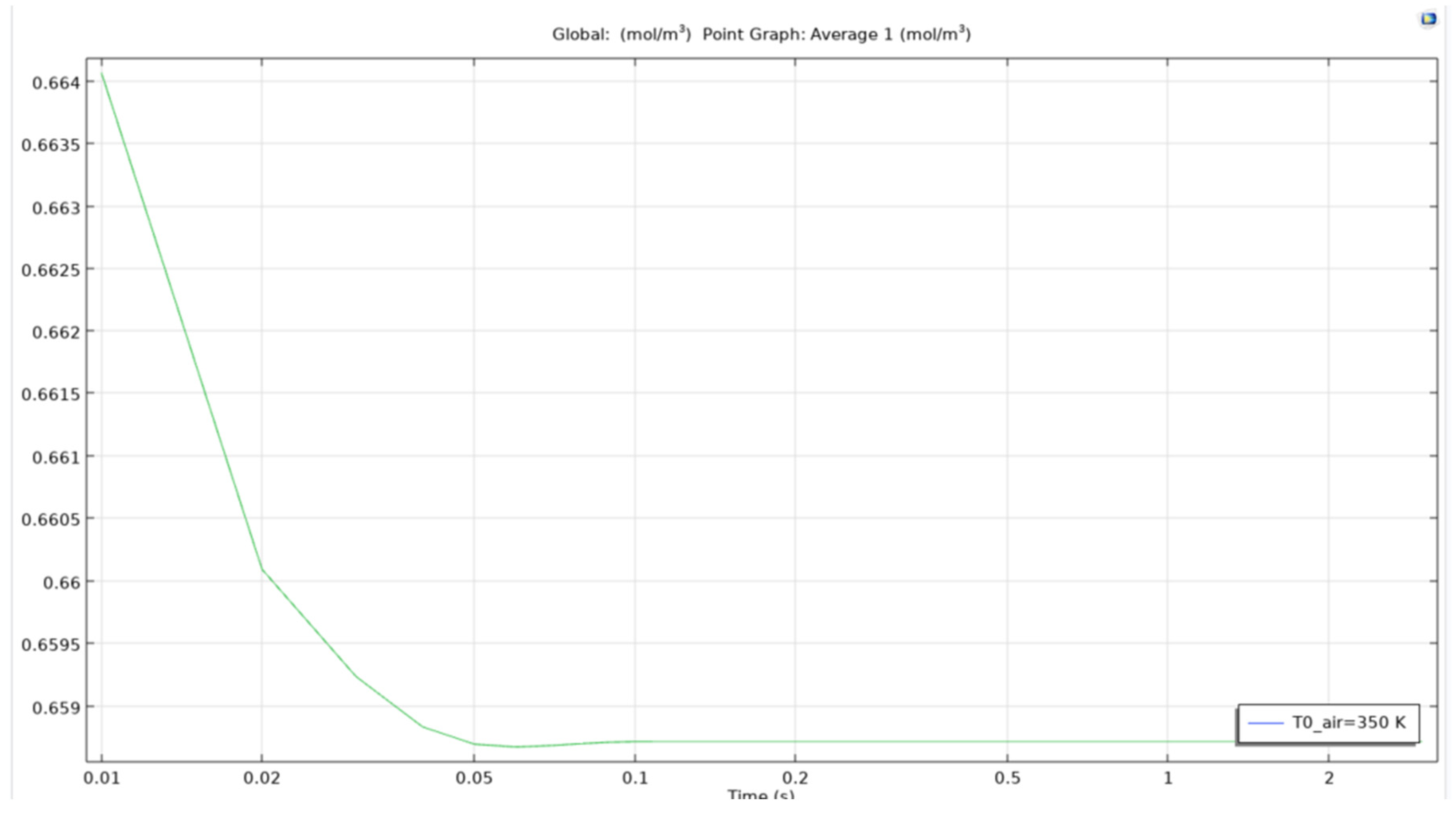
Figure 34. Average ethanol conc when air microbubble at 350K.

Figure 34. Average ethanol conc when air microbubble at 350K.

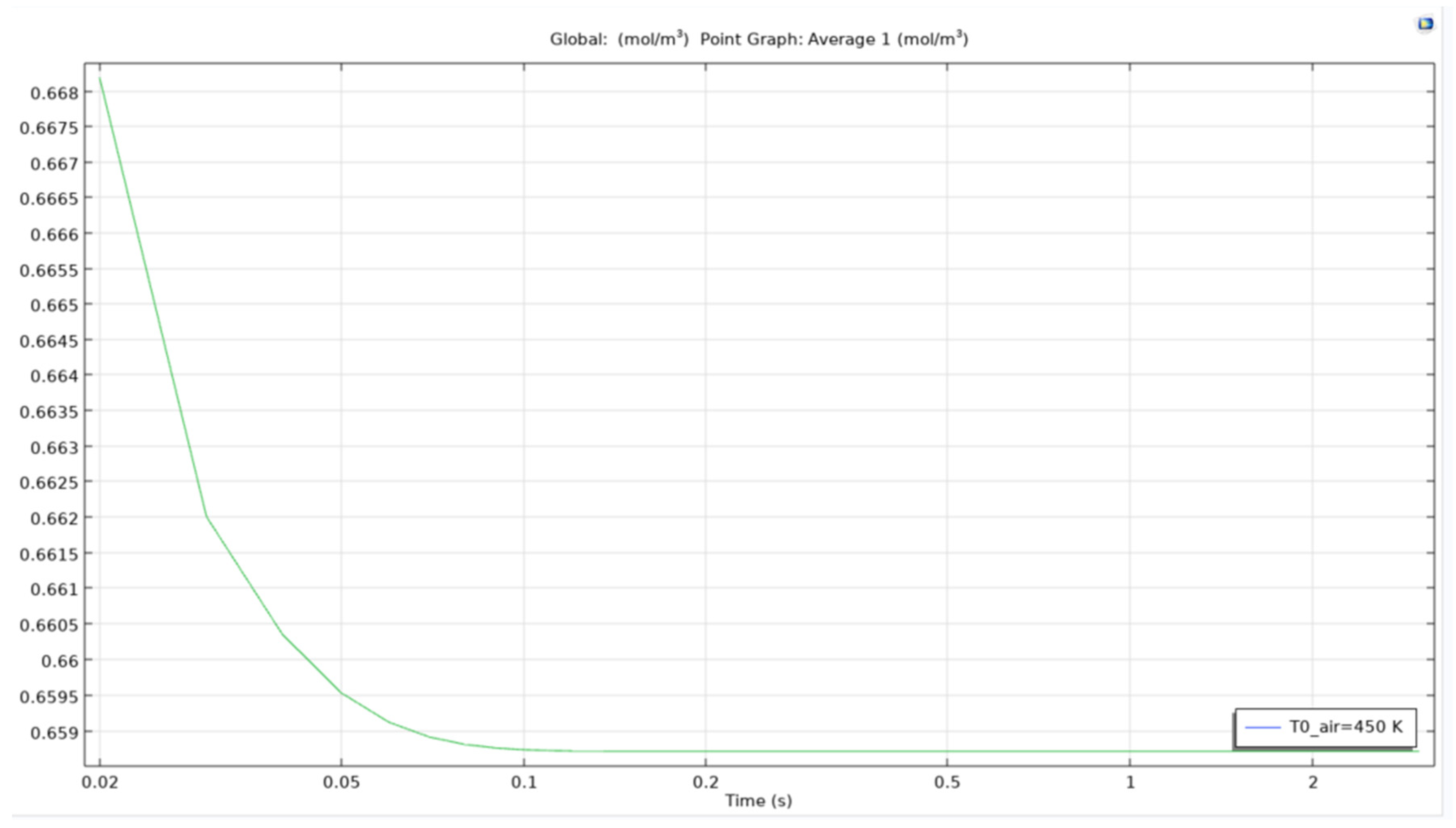
Figure 35. Average ethanol conc for air microbubble at 450K.

Figure 35. Average ethanol conc for air microbubble at 450K.

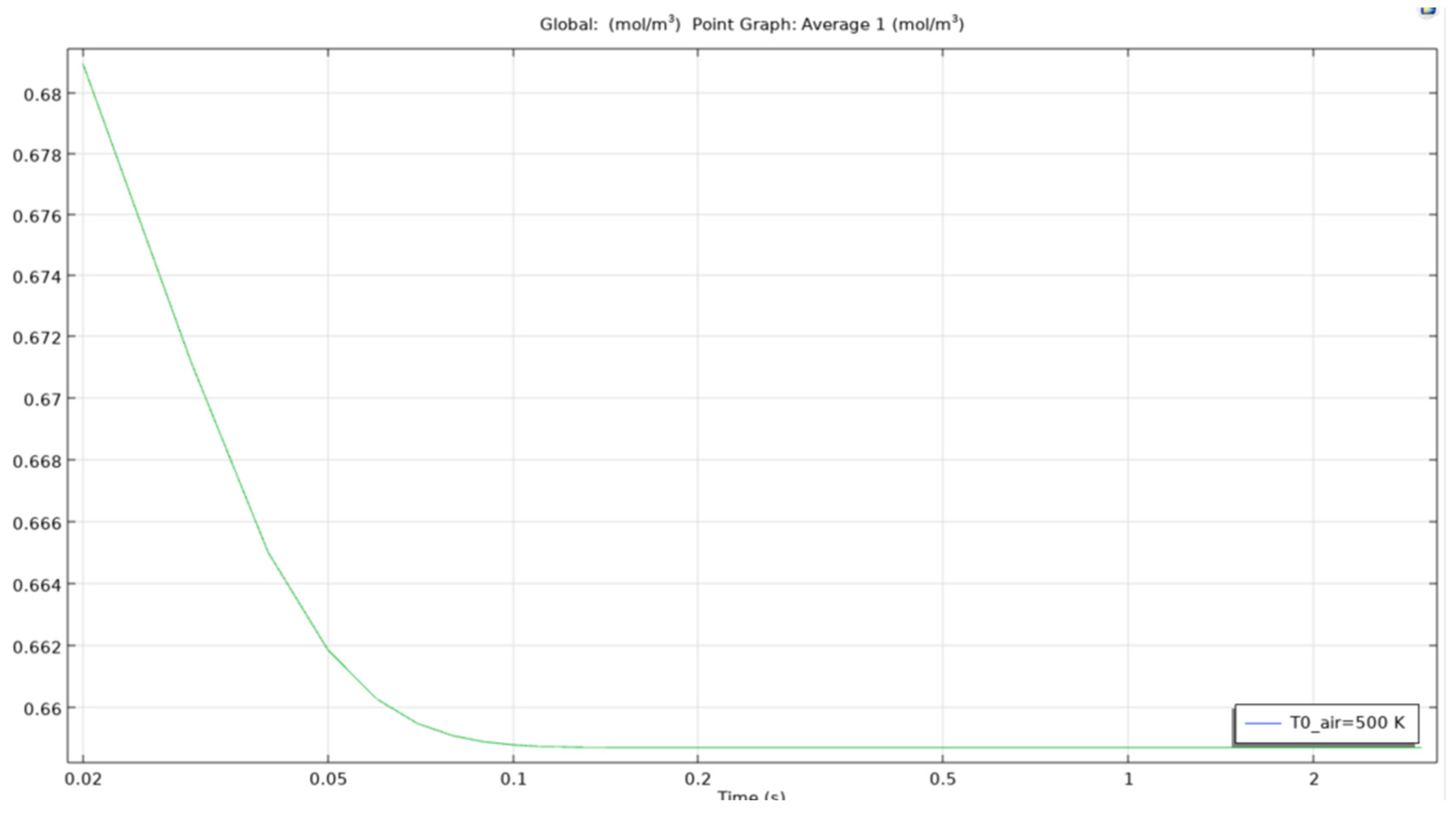
Figure 36. Average ethanol conc for microbubble at 500K.

Figure 36. Average ethanol conc for microbubble at 500K.

As we can see in figure that the average concentration of computed ethanol in the vessel when the air bubble entering the reservoir is at 350K, the total average concentration drops from an approximate 0.664 mol/m³ to below 0.659 mol/m³ in less than 0.05 seconds. This clearly shows that the microbubbles are effective to recover ethanol from constituent mixtures in a short period of time. Even though the change is low from 0.664 to 0.659, the time taken to achieve this reduction is quite low. This could be scaled to 10 minutes for an almost complete removal of ethanol from the mixture.

The reason for leaving behind other temperatures is that of the similarity between the curves obtained. The study found out that there Is not much difference between the values and curves obtained in certain temperatures of the parametric sweep.

For an air bubble with temperature of 450K, the time to reach the same results as when bubble with temperature 350K passes through the reservoir is lesser and the curve obtained as seen in the image is smoother and straighter. This matters as when scaling up the time for simulating the model, easier it is to estimate the time for removal of certain quantity.

4.4. Double Bubble Axisymmetric Results

From the results of the parametric sweep of the single bubble model, it shows us clearly that a hotter bubble has an effect over the reservoir containing ethanol and water where it does indeed evaporate ethanol and reduce it concentration in the mixture in a quick manner. The study from the double bubble system also shows the viability of scaling up without interaction between the bubbles where the bubbles coalesce with each other and defeats the purpose of being a microbubble and converting into a milli bubble.

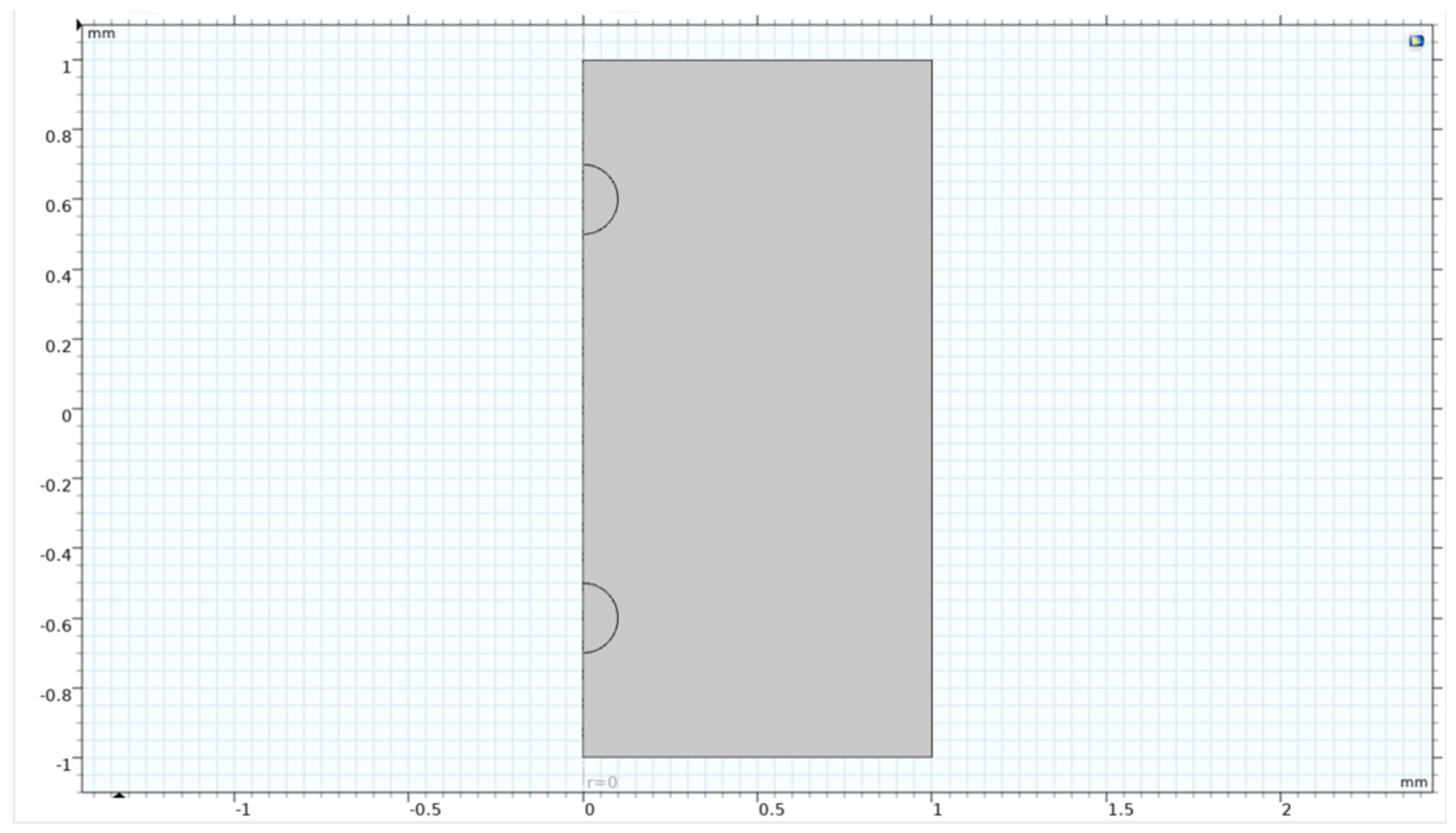
The model with parametric sweep was scaled up to a two-bubble system where the bubbles are 1.2mm apart on the z axis in the r-z plane. The model as described is in the COMSOL’s 2D axisymmetric domain. A second bubble is added to the model by adding a circle with an angle of 180 degrees and a rotation of 270 degrees or -90 degrees which yield the same result which is a microbubble in the middle of the vessel when the r-axis is swept around itself as the semicircle becomes a sphere when swept around.

Figure 37. Double microbubble axisymmetric geometry.

Figure 37. Double microbubble axisymmetric geometry.

The addition of the second bubble in the model along with the parametric sweep showed similar results to the double bubble system simulated earlier to find the optimal distance between the bubbles. The bubbles showed a similar residence period in the vessel which prompted the accuracy of the earlier model constructed to simulate the fluidical behaviour of the microbubbles in the reservoir.

The parametric sweep also showed a wide range of results of the reservoir’s behaviour towards the pair of hot microbubbles of various temperatures rather than the pre-defined 390K.

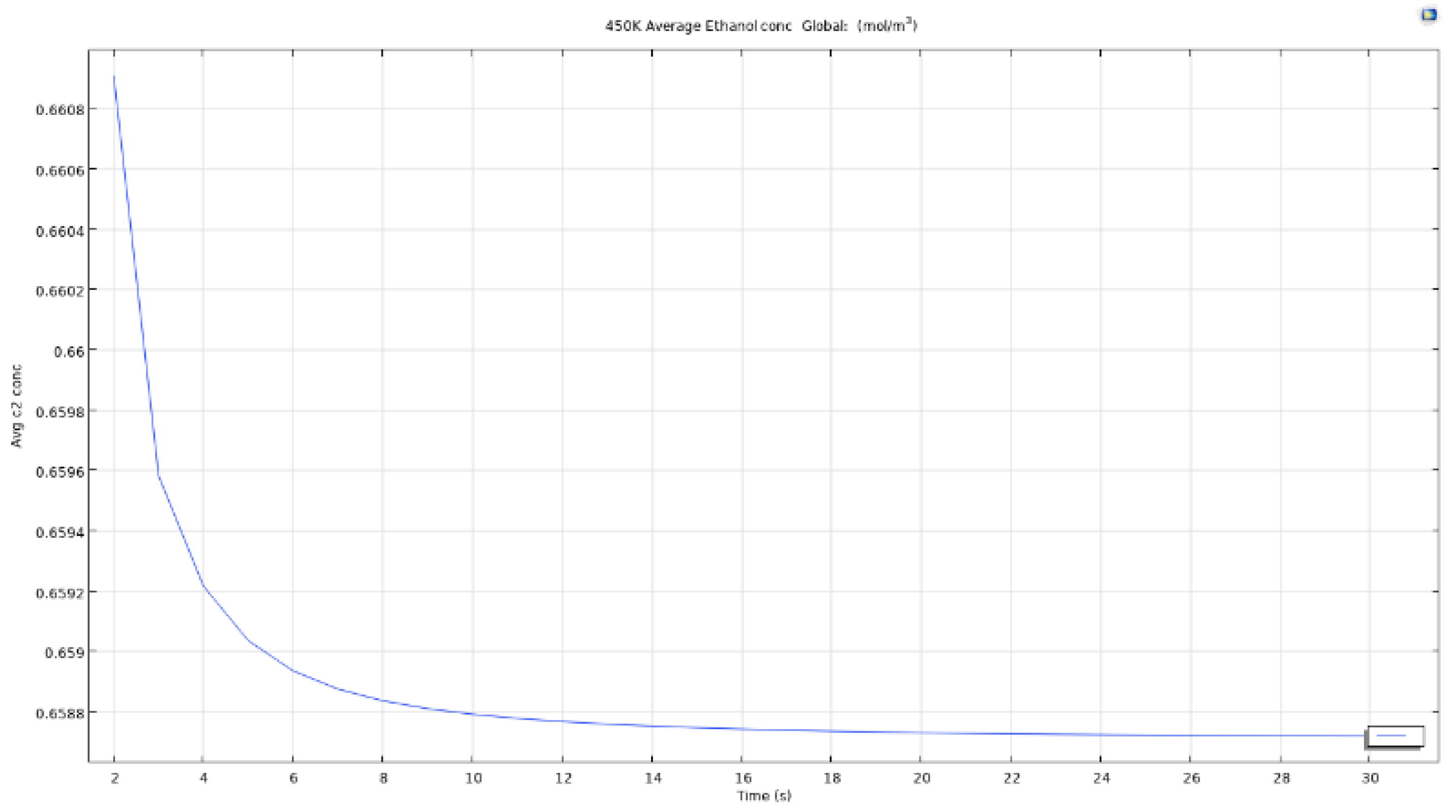
Figure 38. 450K average ethanol concentration.

Figure 38. 450K average ethanol concentration.

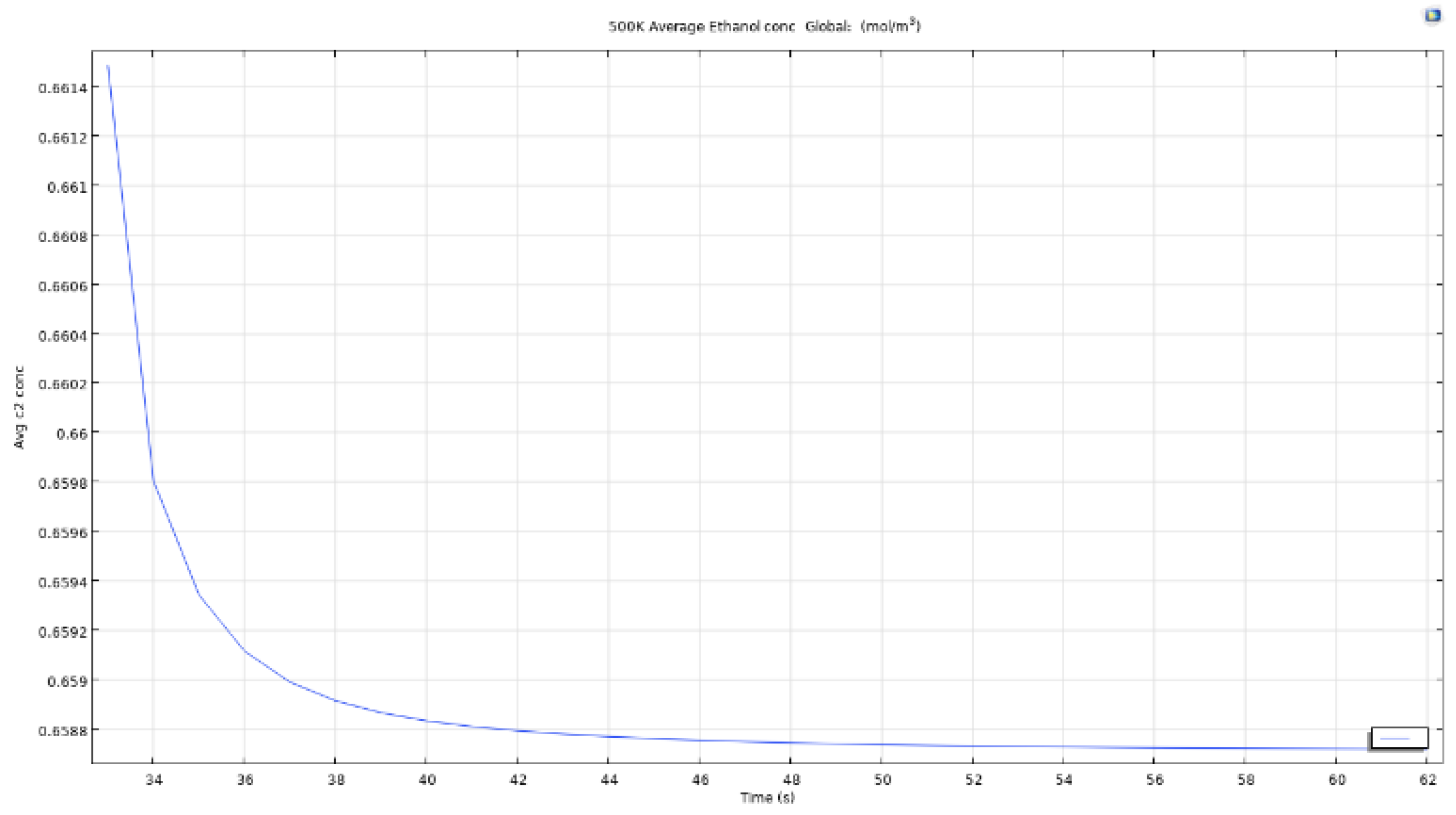
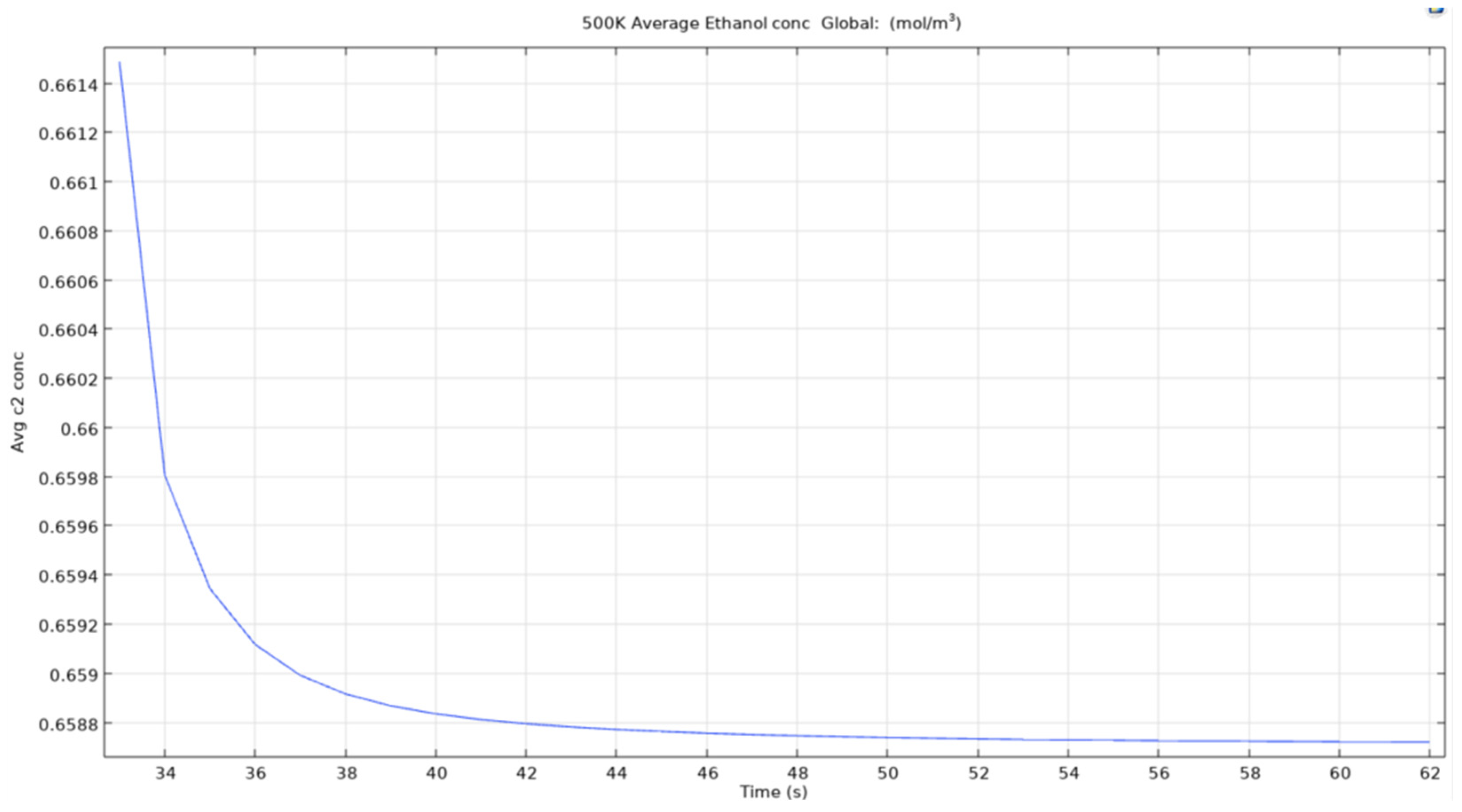
Figure 39. 500K average ethanol concentration.

Figure 39. 500K average ethanol concentration.

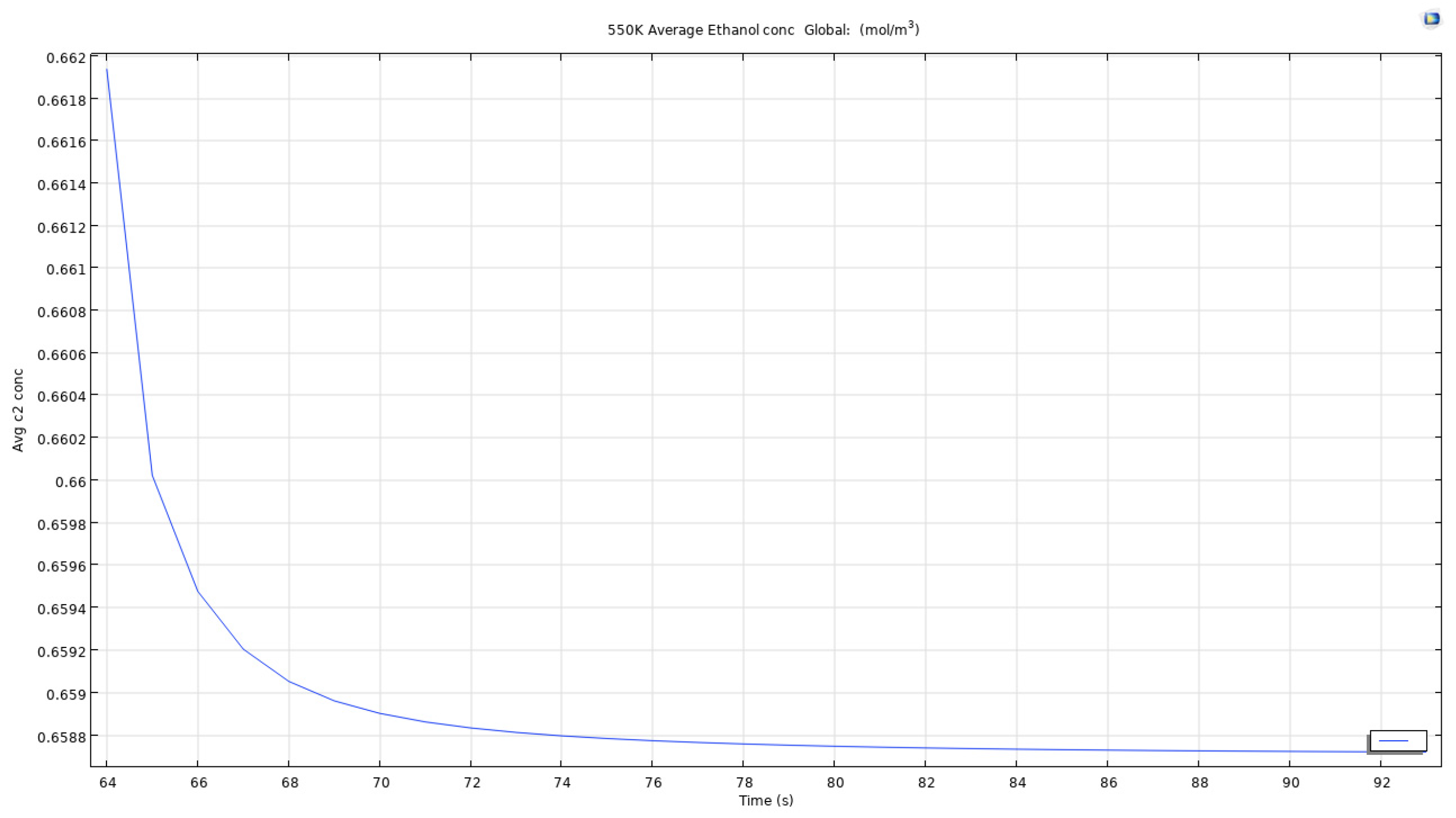
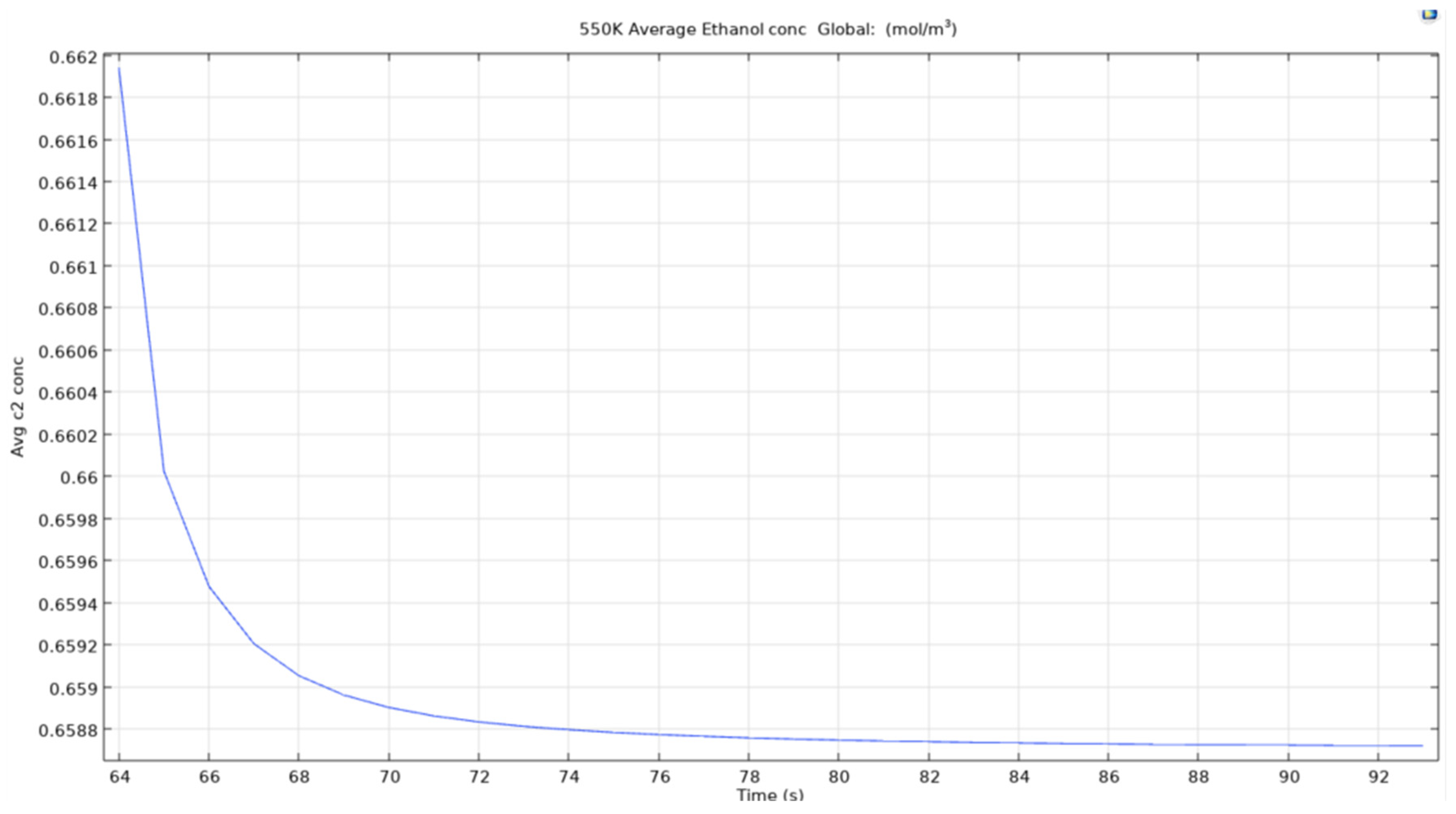
Figure 40. 550K average ethanol concentration.

Figure 40. 550K average ethanol concentration.

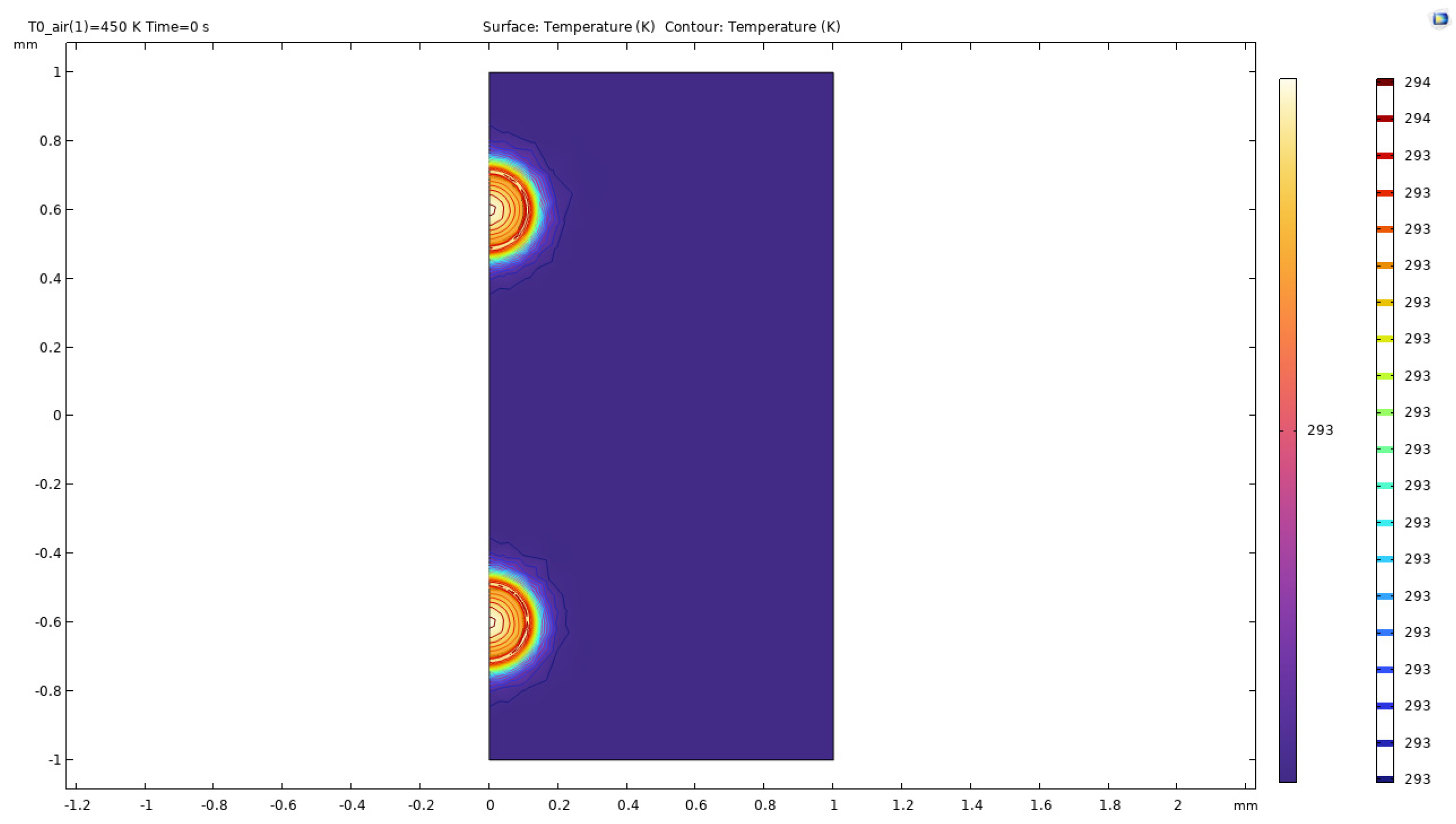
Figure 41. Temperature distribution of double bubble system.

Figure 41. Temperature distribution of double bubble system.

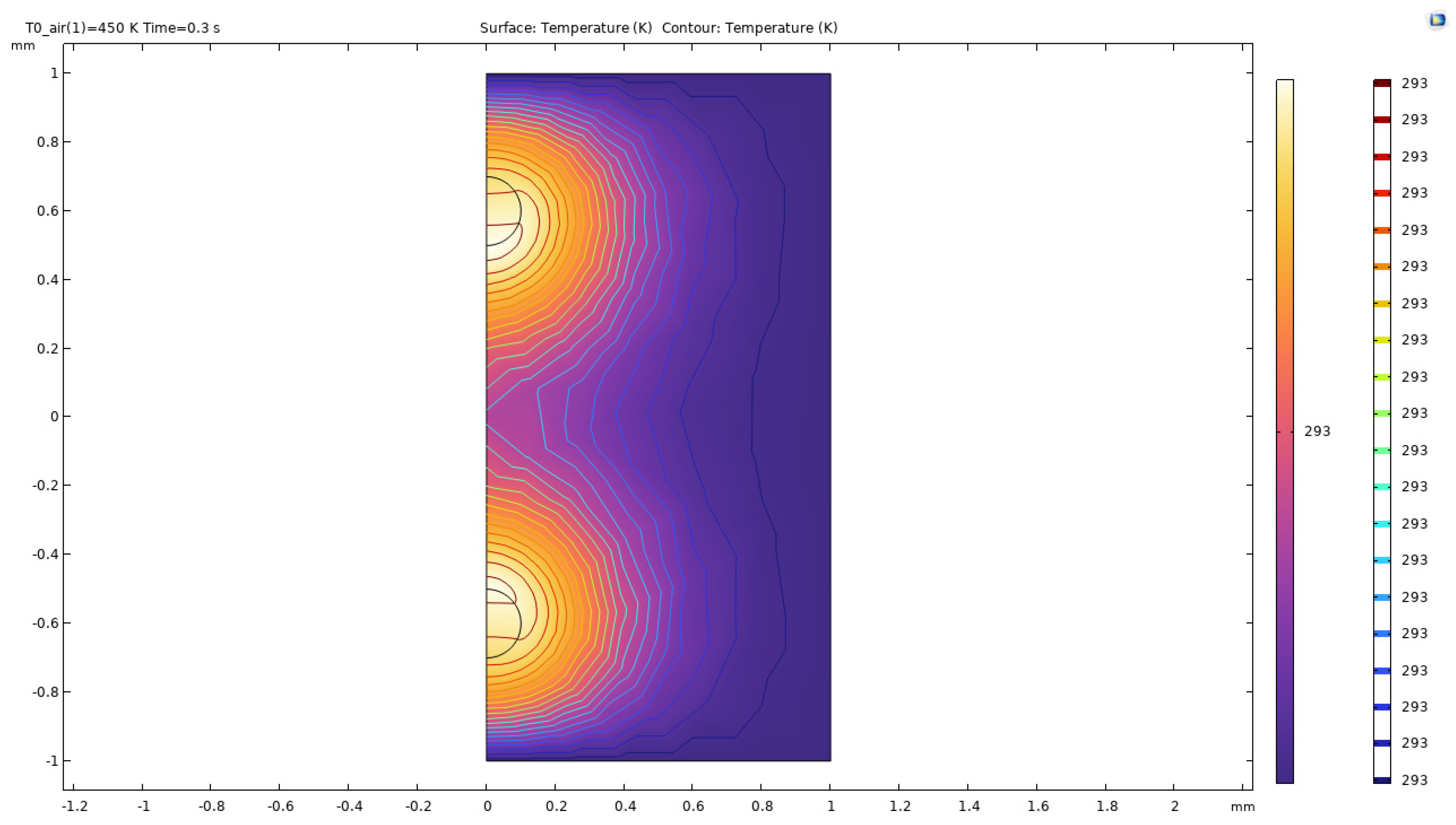
Figure 42. Temperature distribution of double bubble system at time t=0.1s.

Figure 42. Temperature distribution of double bubble system at time t=0.1s.

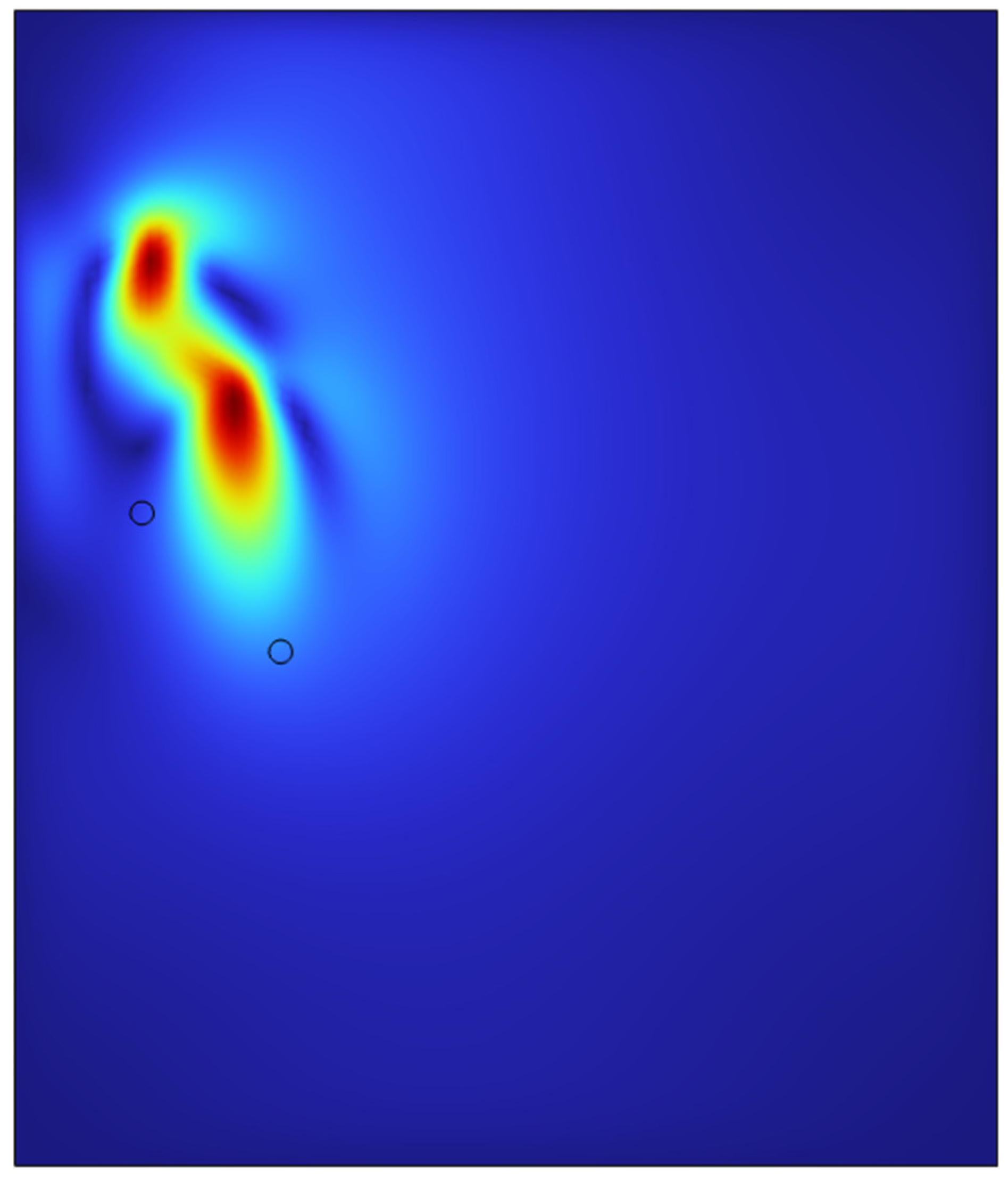
The above surface plots describe the action of hot microbubbles on the binary mixture of ethanol and water. As we can see that the microbubbles dissipate heat onto the mixture equally and quickly. From the surface plots, one can assume that the temperature of the two-bubble system comes together and forms a “pocket” of heat between the bubbles forming an extra area of heating in the middle of the bubbles. The results for the surface plots of the temperature distribution is similar to the other parameters considered as the heat distribution plots remain similar to each other.

Figure 43. Average ethanol concentration at 450K.

Figure 43. Average ethanol concentration at 450K.

Figure 44. Average ethanol concentration at 500K.

Figure 44. Average ethanol concentration at 500K.

Figure 45. Average ethanol concentration at 550K.

Figure 45. Average ethanol concentration at 550K.

The plots above show the average concentration of ethanol in the mixture of the double bubble axisymmetric simulation. One can assume that the temperatures of the bubbles have similar behaviour to that of single bubble system to that of the double bubbles system. This could be due to various reasons where the most predominant or the logical one could be where COMSOL treats the microbubbles in the model as similar ones and applies the equations over the entire model and in particular the bubbles similarly.

On comparing the plots on the effects of hot microbubbles, it is clearly visible that the effects of the hot microbubbles are similar to that of the model for single microbubbles study due to the model applying same set of equations for the bubbles. Although this could be a problem as the heat overlaps between the bubbles as seen in previous explanations of the double bubble model system, a superhot zone forms between the bubbles assuming the bubbles maintain the same head and travels in a uniform path and maintains an equal distance from each other. Although one knows that this situation is impossible to recreate, the best is to find the interactions between the bubbles when the bubbles flow freely and interactions between the bubbles are taken into consideration.

From the above discussion, the model showed a positive viability towards the double bubble system in the axisymmetric domain and an initiative can be taken to simulate a cloud of similar and identical microbubbles in either a 2D or a 3D domain. Although a more accurate representation of the system could be described in a 3D domain, the model could also be represented in a 2D domain to ease up the computational power required for COMSOL to solve the model as a normal 3D model running on a normal system containing 32GB RAM and a normal CPU chip with a decent Graphic Processing Unit (GPU) could take hours to run the model and for an even normal day to day system, a 3D model would take up a day or even two to solve the model or could possibly crash the system. In these cases, the user would prefer to go ahead with a less complicated study with ease in computation power.

4.5. 3D Model Development—An Initiative

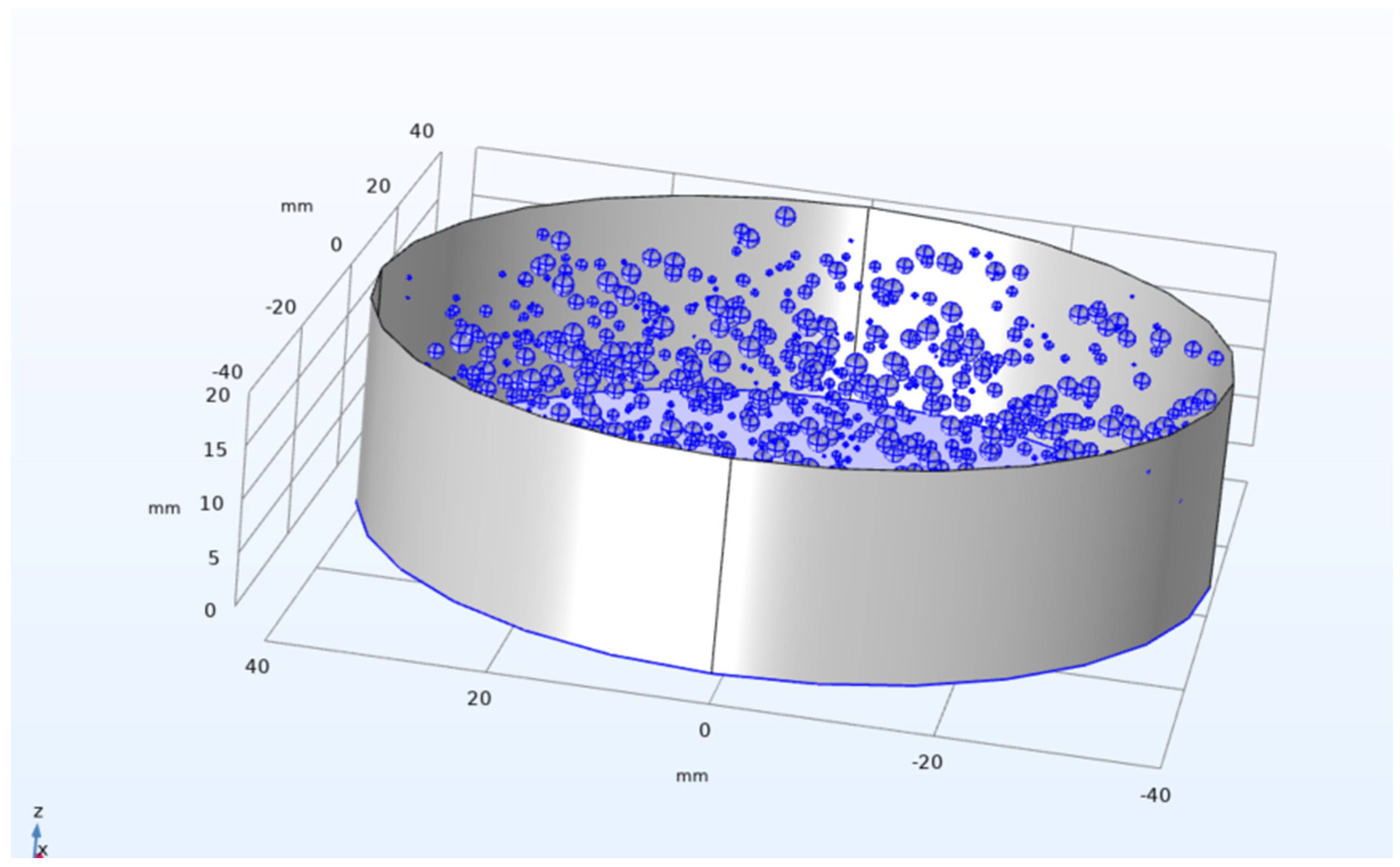
From the results of the previous studies in this project, an attempt to the creation of a possible 3-D simulation was attempted using the application builder in COMSOL from scratch. The model was pre-defined in a 3D domain initially for the codes to be written to generate and work with 3D entities ad the codes written to work with 3D geometries wouldn’t generally work with any other domain other than 3D.

This might be due to many reasons as when a person chooses a certain domain to work with, the best guess on what COMSOL does automatically is that it grabs that particular JAR files’ references into that model. Since COMSOL is built on Java, the best guess is that the Jar files are encapsulated and only its attributes are brought into the source code of the model which saves a lot of time when the model is executed or compiled.

With using the programming guide issued by COMSOL which recaps the essential programming required to make edits in the Application builder to make changes in the model. The application builder guide or as COMSOL names it, “The Programming Guide” [ add reference to the programming guide] states the various ways one can make use of java to affect changes to the model as desired. The guide also offers a refresher to Java with various syntaxes and “easy to write” templates for creating Java methods to interact with the model.

Figure 46. 3D geometry generated using Java method.

Figure 46. 3D geometry generated using Java method.

The above geometry was generated using the application builder in COMSOL using Java method (refer to Appendix-A). The method considers a microbubble if radius of 100 microns distributed randomly with a minimum spacing of 1.2mm from each other. The method uses a loop function to ease up the code writing process and making the code easier to read. The code was borrowed and edited from a random 3D generator code to generate cheese. The code was refactored to accommodate microbubbles [27].

5.1. Insight

The insight from the project clearly shows the possibility of separation of ethanol from a binary mixture of ethanol and water. The project initially focussed on simulating the behaviour of microbubbles with the liquid reservoir and the study was scaled up to a double bubble system. The single bubble study showed a residence time of 0.1 seconds for the single bubble to escape the liquid reservoir containing ethanol. A short residence time for the microbubble shows the quick action of microbubbles and the time taken for the microbubble to effect changes in the system.

Although a short residence time in conventional chemical engineering could refer to an inefficient process and leaves residue of the materials to be extracted behind, in the case of microbubbles, the net surface area per second of processing time is in the scale of acres and hectares in a small area as the surface area to volume ratio of a perfect sphere is the maximum compared to other shapes. Assumptions related to the formation of microbubbles assume that the microbubbles are perfect spheres and due to the surface tensions on the surface, deformations are unlikely to occur.

The double bubble system proved the assumptions that when bubbles are spaced at a certain distance from each other (approx. 1.2mm), the bubbles does not interact with each other fluidically, but they can interact with each other in factors affecting the bubbles but the volume fractions of the fluids in the double bubble systems form the previous sections suggest differently where the bubbles does not interact with each other. Parameters like velocity and other fluid parameters could interact with each other like the velocity profiles as seen in previous section.

When the model built in previous studies was incorporated to accommodate higher temperatures as the model was built more empirical or theoretical, the higher bubble temperature showed a similar trend to that of the initial temperature of the air bubble, but the plots generated a smoother and slightly quick approach to achieve the separation quickly. This showed a viability of the model to accommodate hotter bubbles. And regardless of the temperature, the microbubbles tend to cause an effect rather quickly than expected for a normal process or intensification process.

When the same model and the parametric sweep was studied not under one bubble and was scaled up to a two-bubble system where the bubbles are placed 1.2mm away from each other from the study conducted before, the bubbles tend to follow the same trend where the bubbles do not interact with each other when placed 1.2 mm away from each other thereby proving the safe distance between the bubbles. The study showed a viability of the double bubble system of the model. Also the study pointed out that there is not much of a difference between in the results of the single bubble and the double bubble study. This could be due to many reasons where the simple explanation to this may be due to the model considering the bubbles similar and doesn’t take its interactions into account. For example, the interaction of heat between the bubbles where in between the bubbles as suggested by the surface plots in the previous section, where the heat from the bubbles form a heated pocket zone in between the bubbles suggests a possibility of expansion of study where the concentration profile and the heat distribution could be studied in the pocket zone.

The double bubble system showed a promise of the possibility to scale up the system of microbubbles affecting change on the reservoir containing binary mixture of ethanol and water. To start the scale up process for the model, a 3D domain was selected and in cases of manual geometry addition and positioning, it could result in a longer time to generate objects and position them in the vessel. In order to quicken up the process, a Java method was written named method3 in COMSOL’s Application builder (code in appendix) where it generated random microbubbles in the vessel. The number of microbubbles can be randomised or be generated up to an x number of bubbles in the vessel. Using a 3D domain could help in visualising the practical applications of said microbubbles in stripping ethanol from binary mixture. Since the local system conducting the simulations was of low spec day to day usage, proper simulations were unable to be studied for the 3D model. Though this does provide a scope for the future where 3D simulations could be used to study the process.

5.2. Room for Improvements- What Could’ve Been Better

Though this project helped in understanding the behaviour of microbubbles (mainly two bubble systems), it was not the most ideal project or model to simulate the system. A model is said to be perfect or ideal when it completely simulates the exact behaviour of the system taking in all errors and parameters into account, but such model could be really hard to replicate the errors and various parameters but the system could may or may not have that errors in the system or could have even other factors which are not taken into account while building the model. In the case of this project, a better model can be constructed in the future consisting of interactions of the heat and concentration profiles caused by the double bubble systems and how the fluid behaves to the heat pockets between the bubbles could be studied in the future.