Submitted:
22 May 2024
Posted:
23 May 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
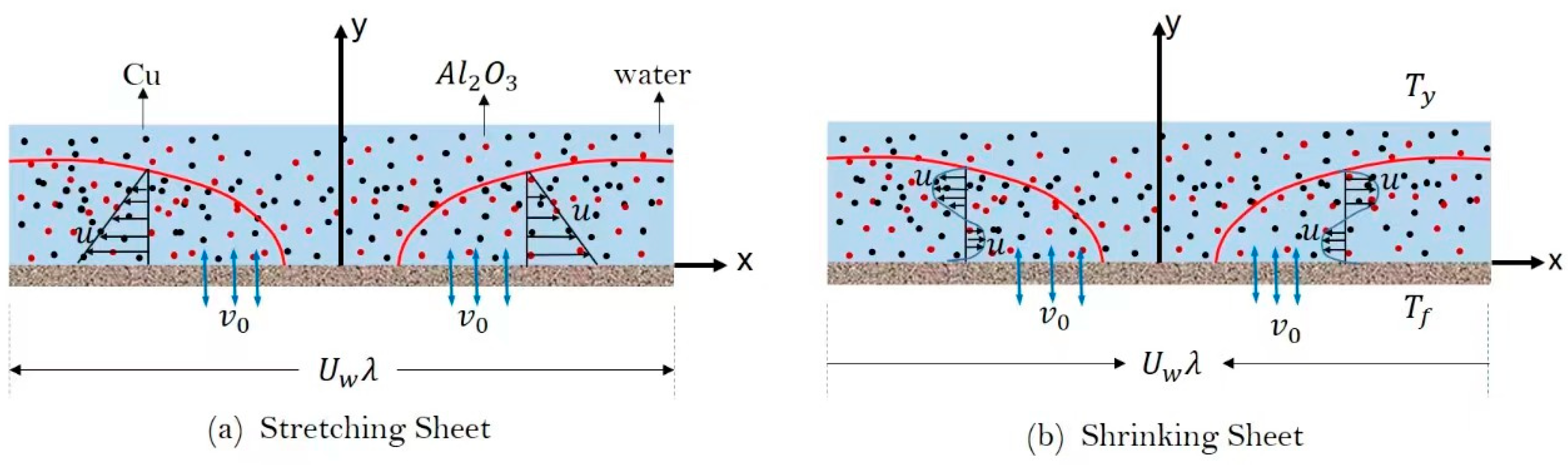
- The mathematical 2-D flow model of HNF over porous stretch/shrink sheet using water as the base fluid and as nanoparticles.
- This analysis investigates an appropriate interpretation of Darcy-Forchhiemer and Buongiorno models of HNF flow on stretch/shrink sheet.
- The use of significant mechanisms such as heat generation/absorption, viscous dissipation, and Joule heating effect, homogeneous and heterogeneous reaction enhances the originality of this work.
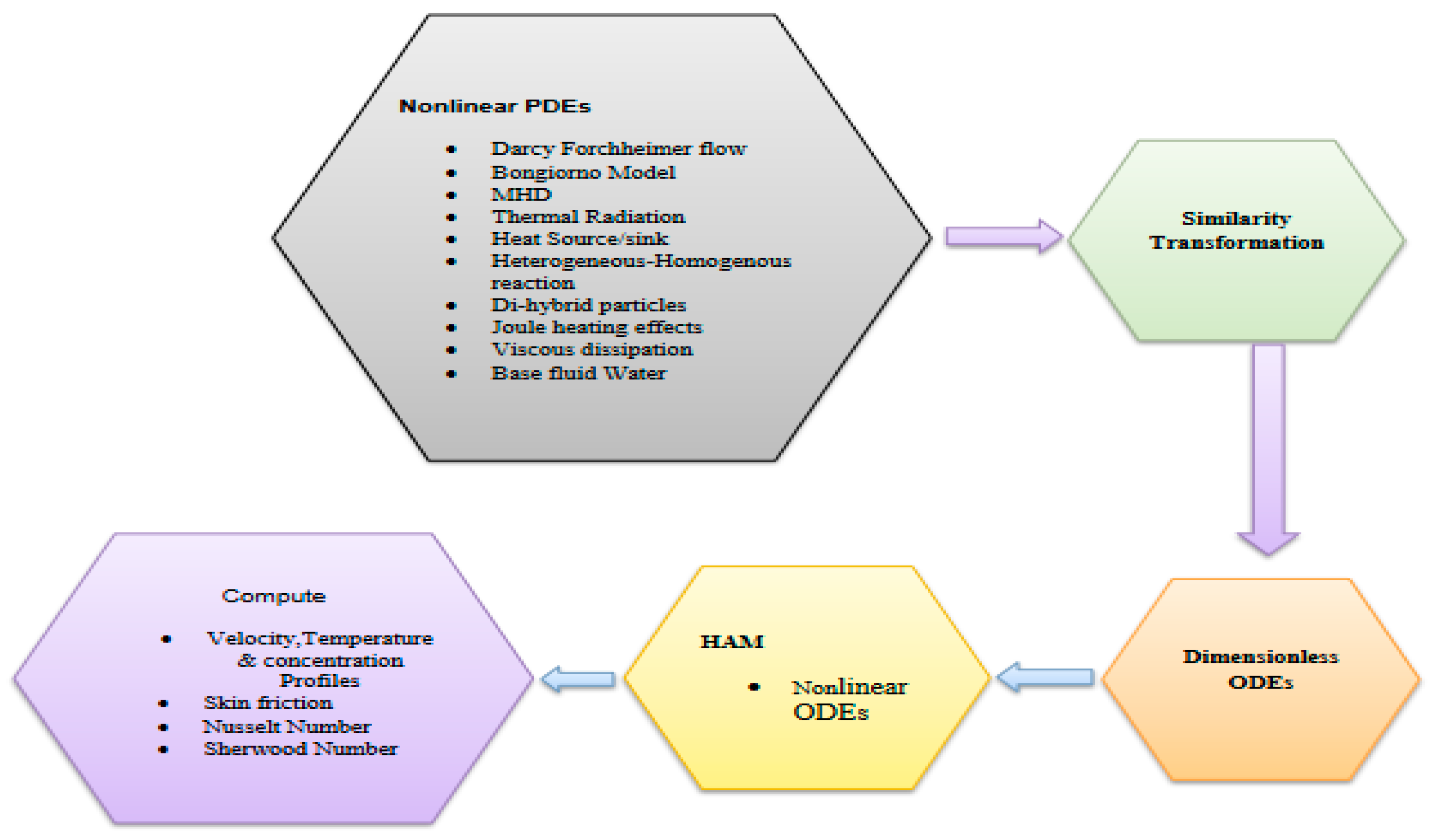
- A system of PDEs is converted into a set of ODEs using similarity variables, and then HAM is applied for the solution of the obtained ODEs.
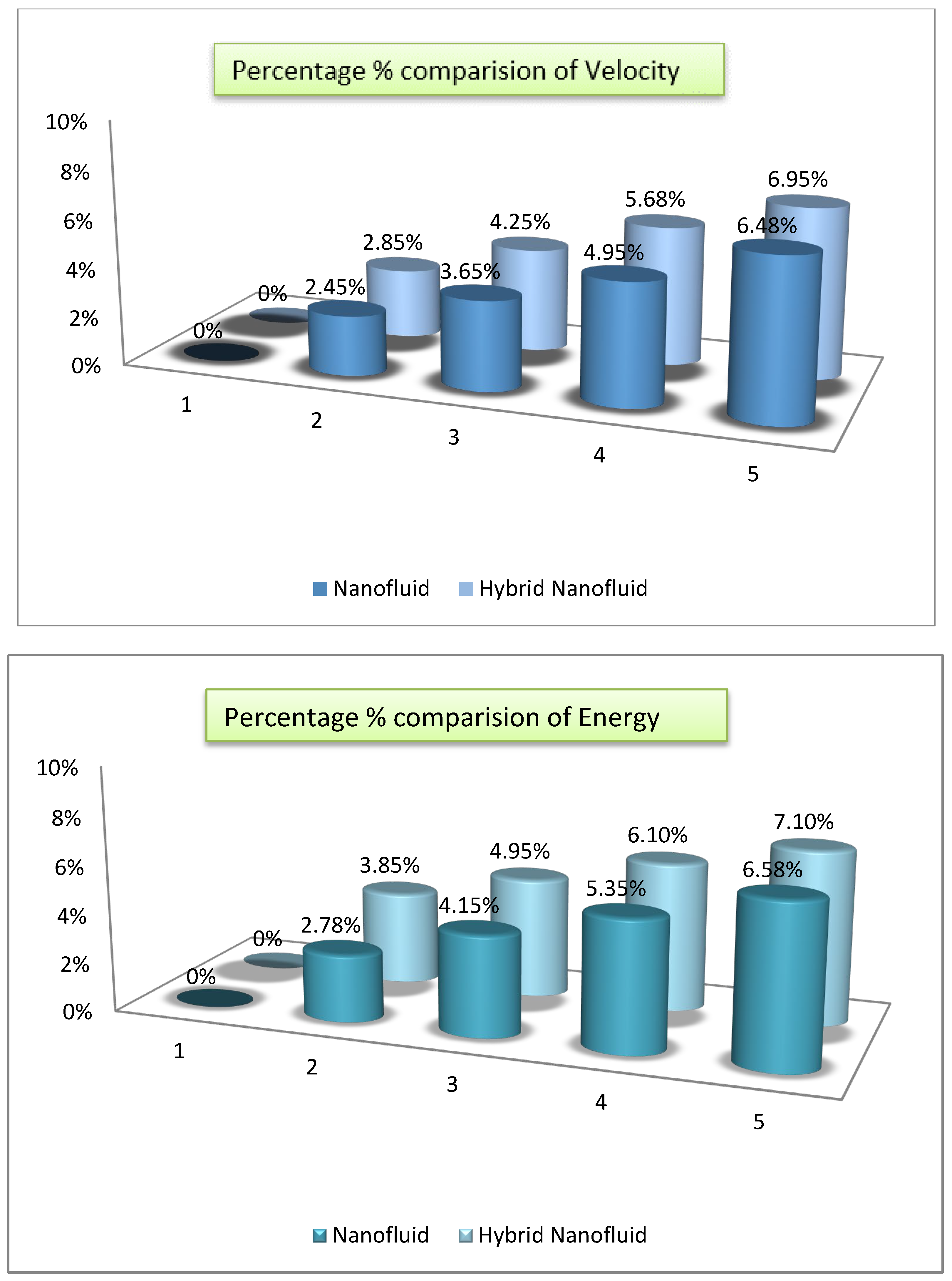
- Tables and graphs are used to explain the results of the numerical analysis. The percentage % comparison of NF and HNF of velocity and energy are shown through graph.
2. Problem Formulation
3. HAM Solution
4. Result and Discussion
5. Table Discussion
6. Conclusions
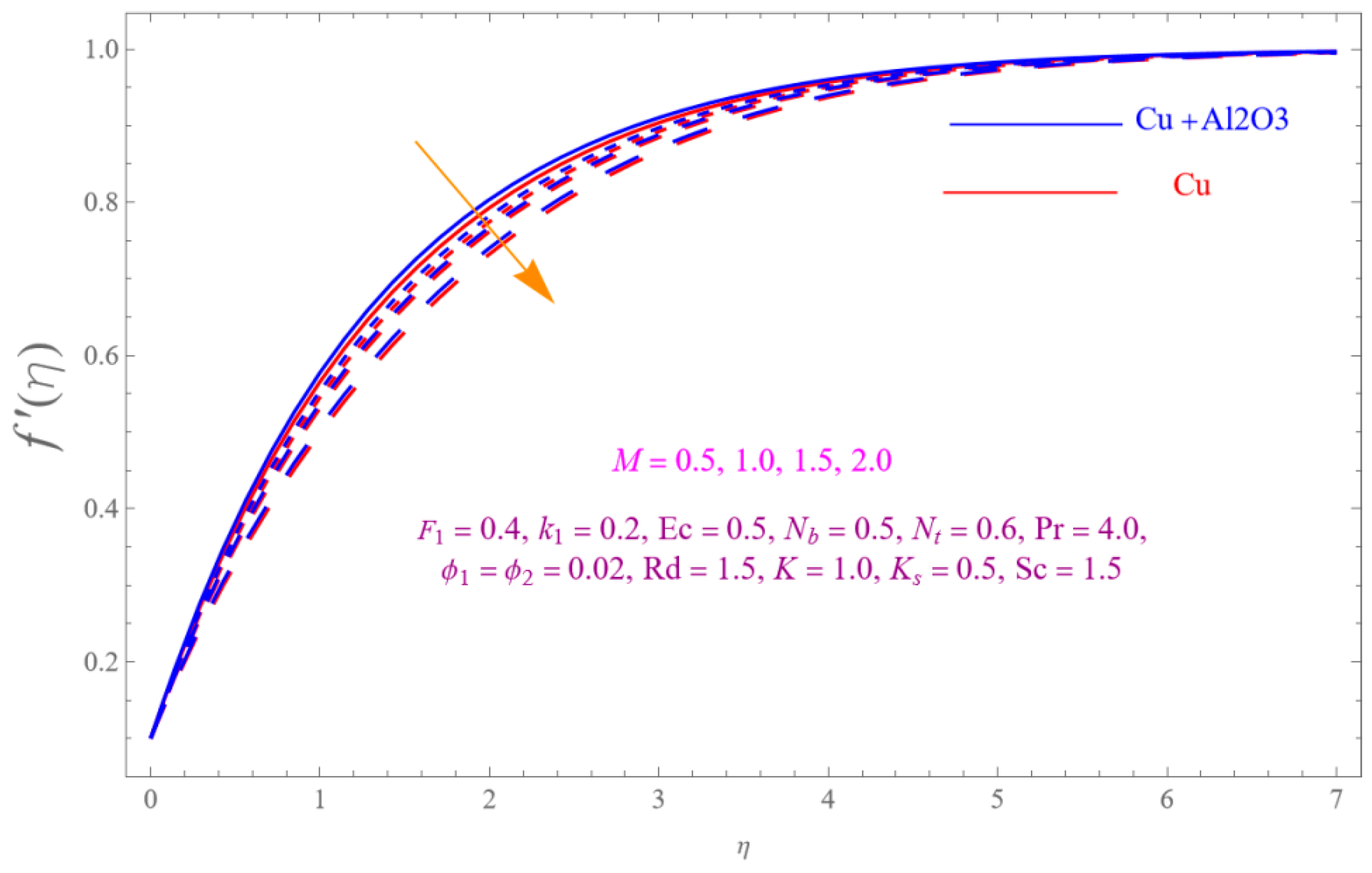
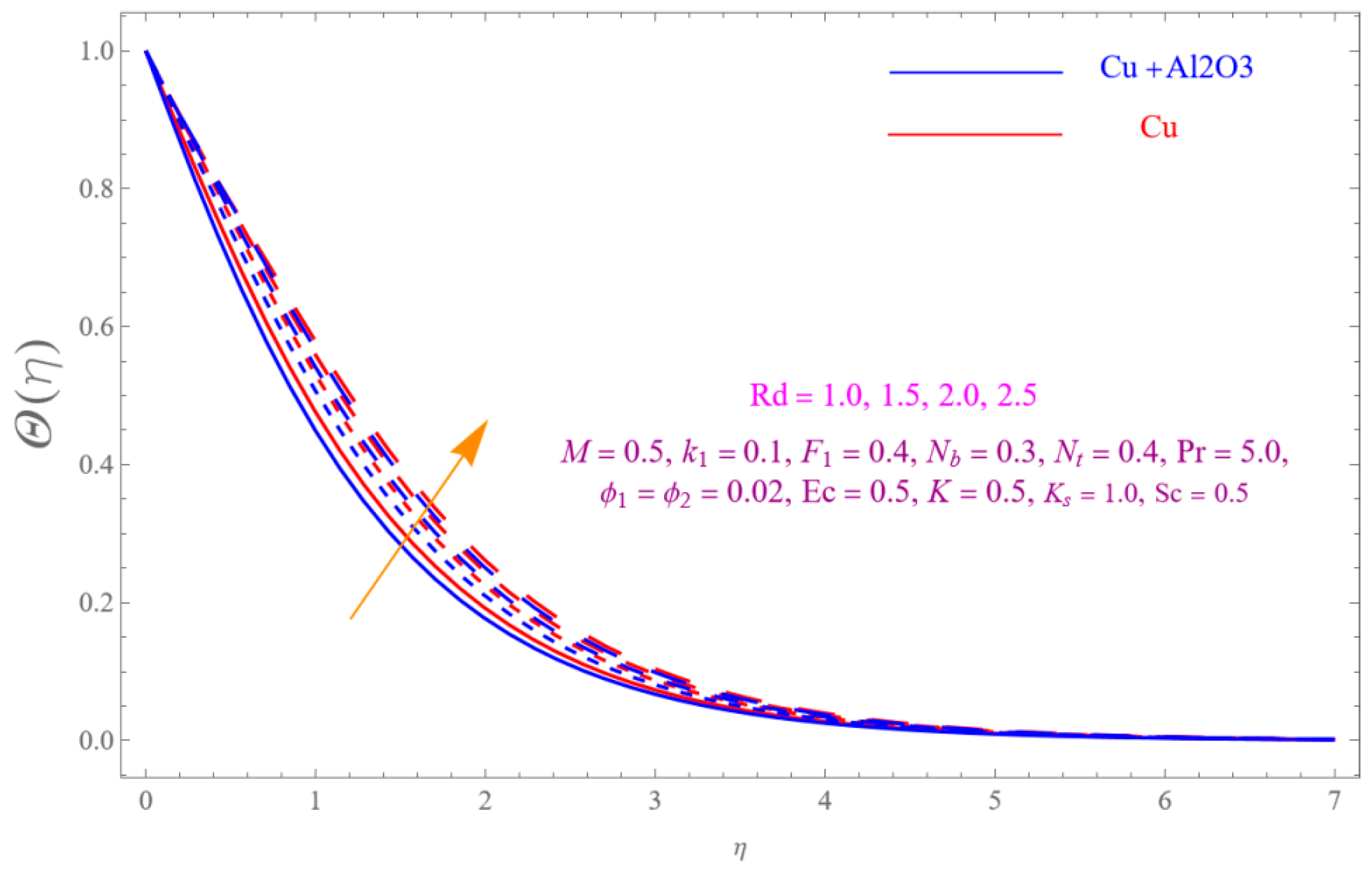
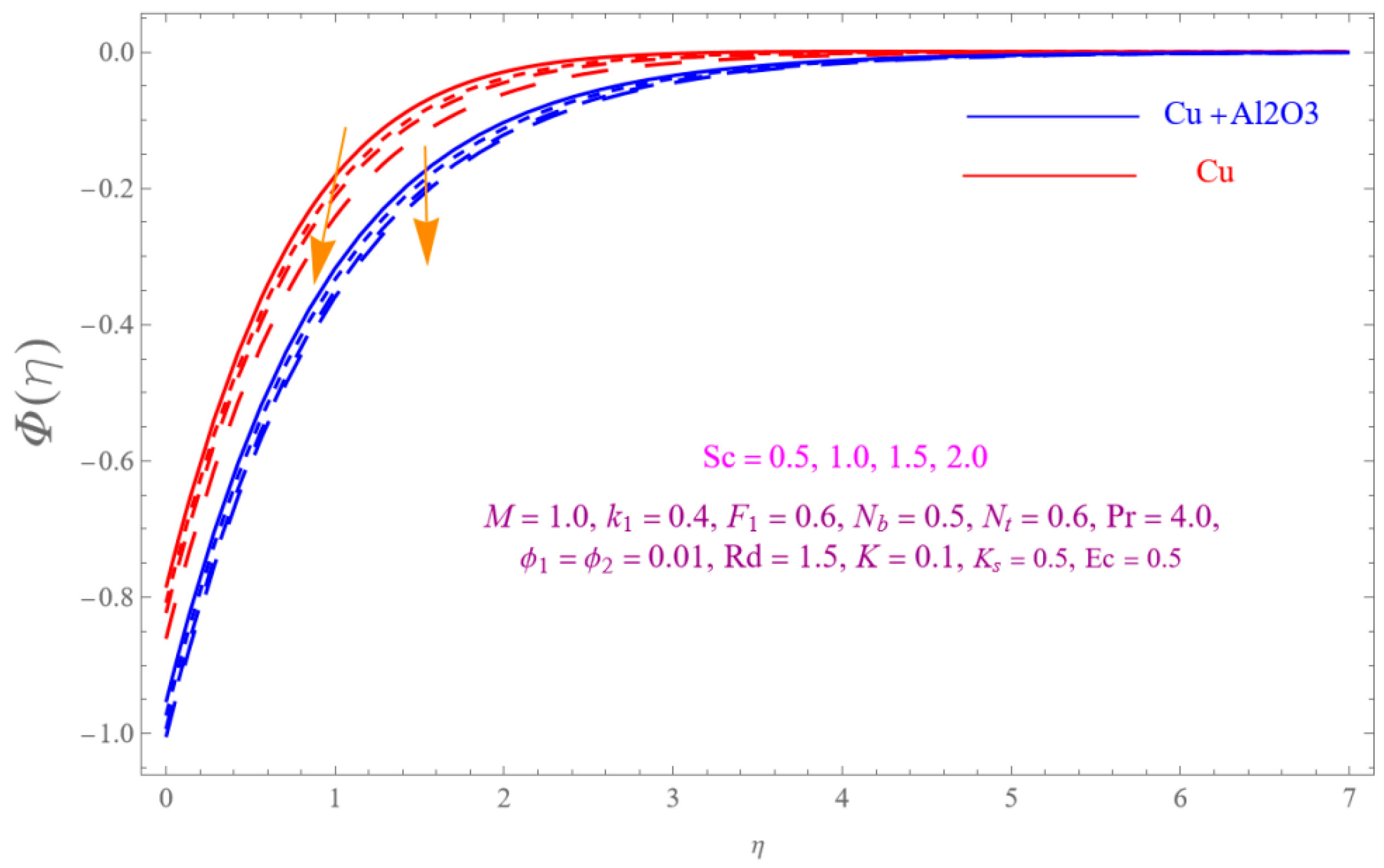
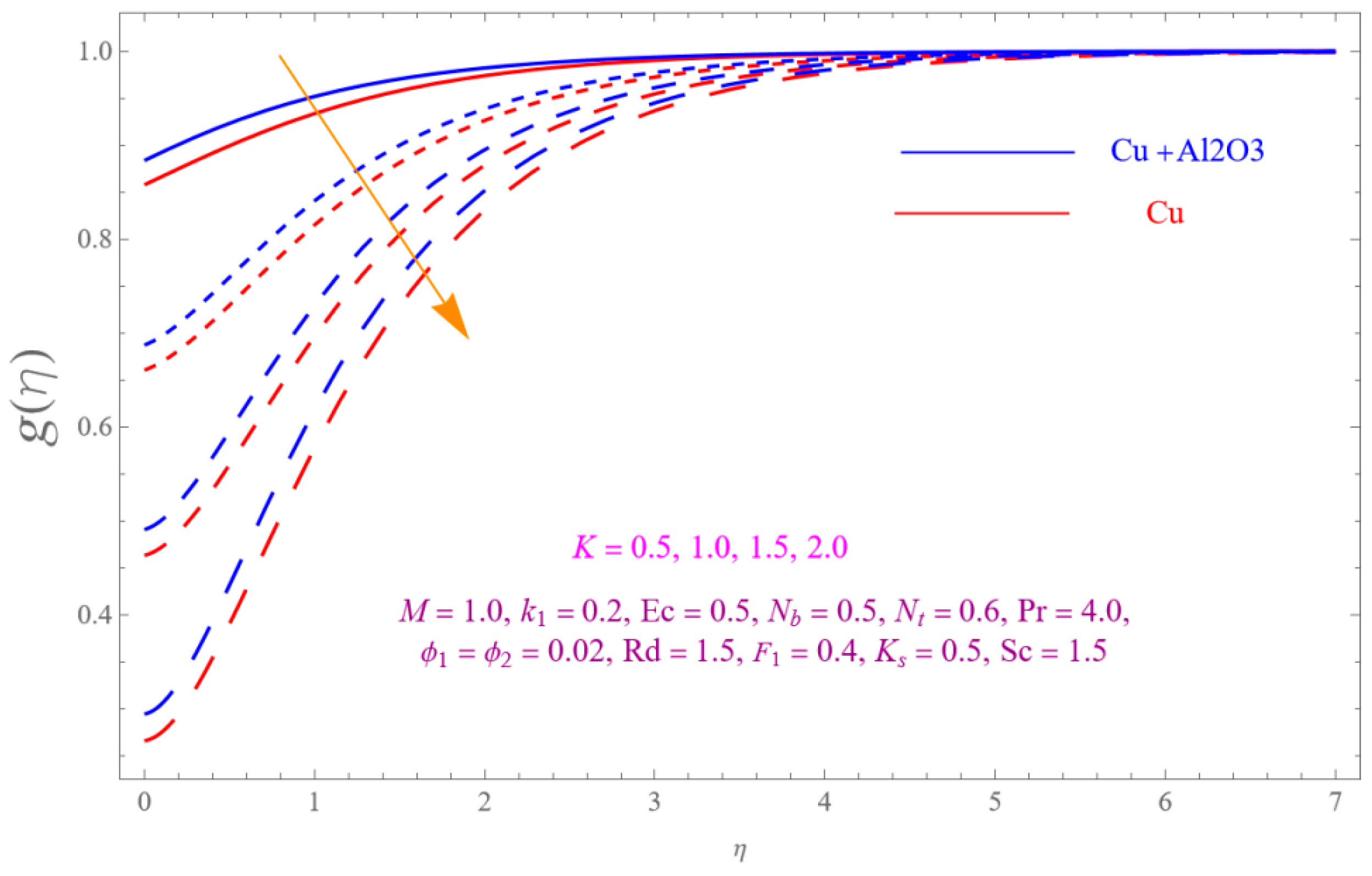
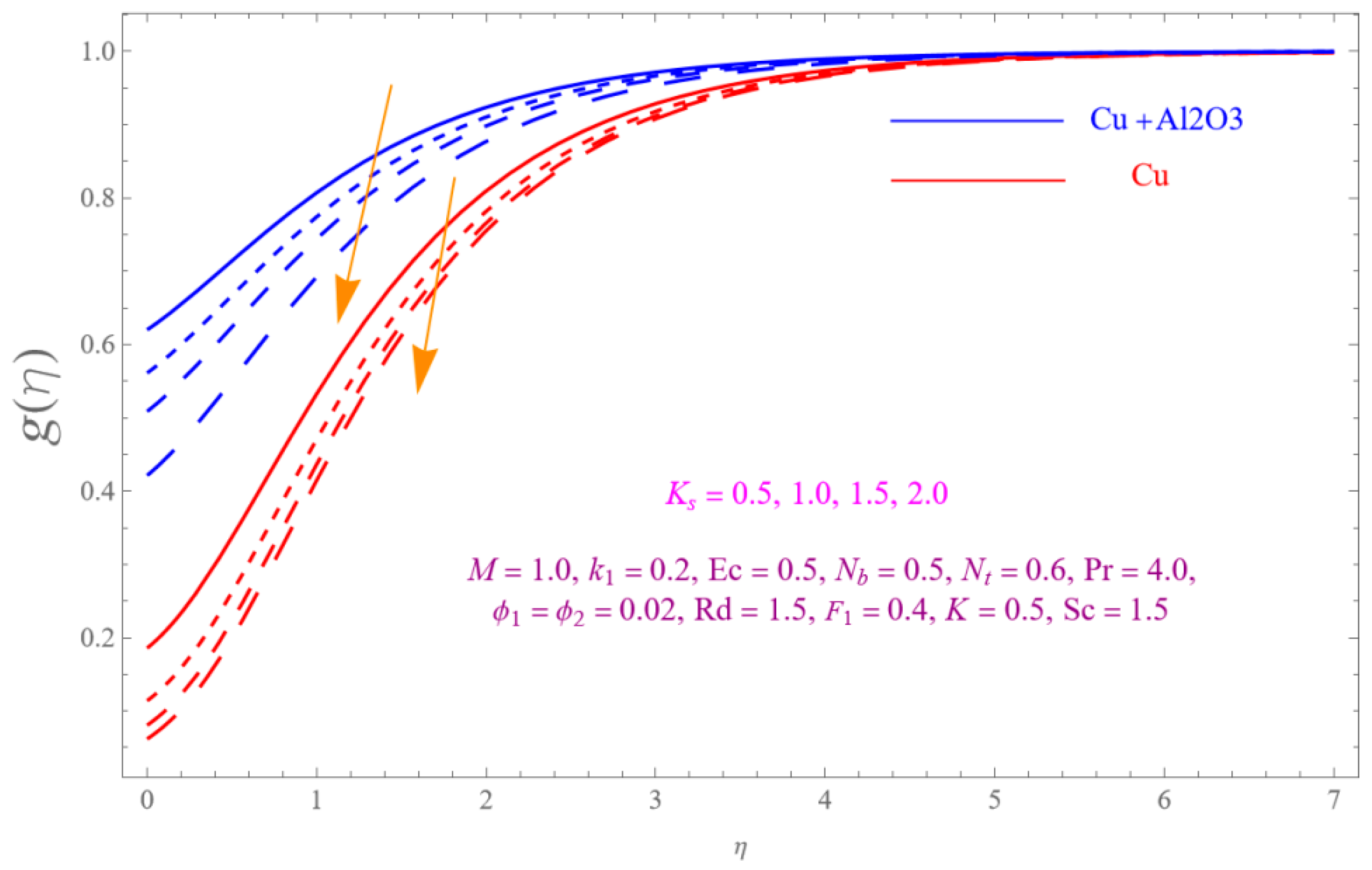
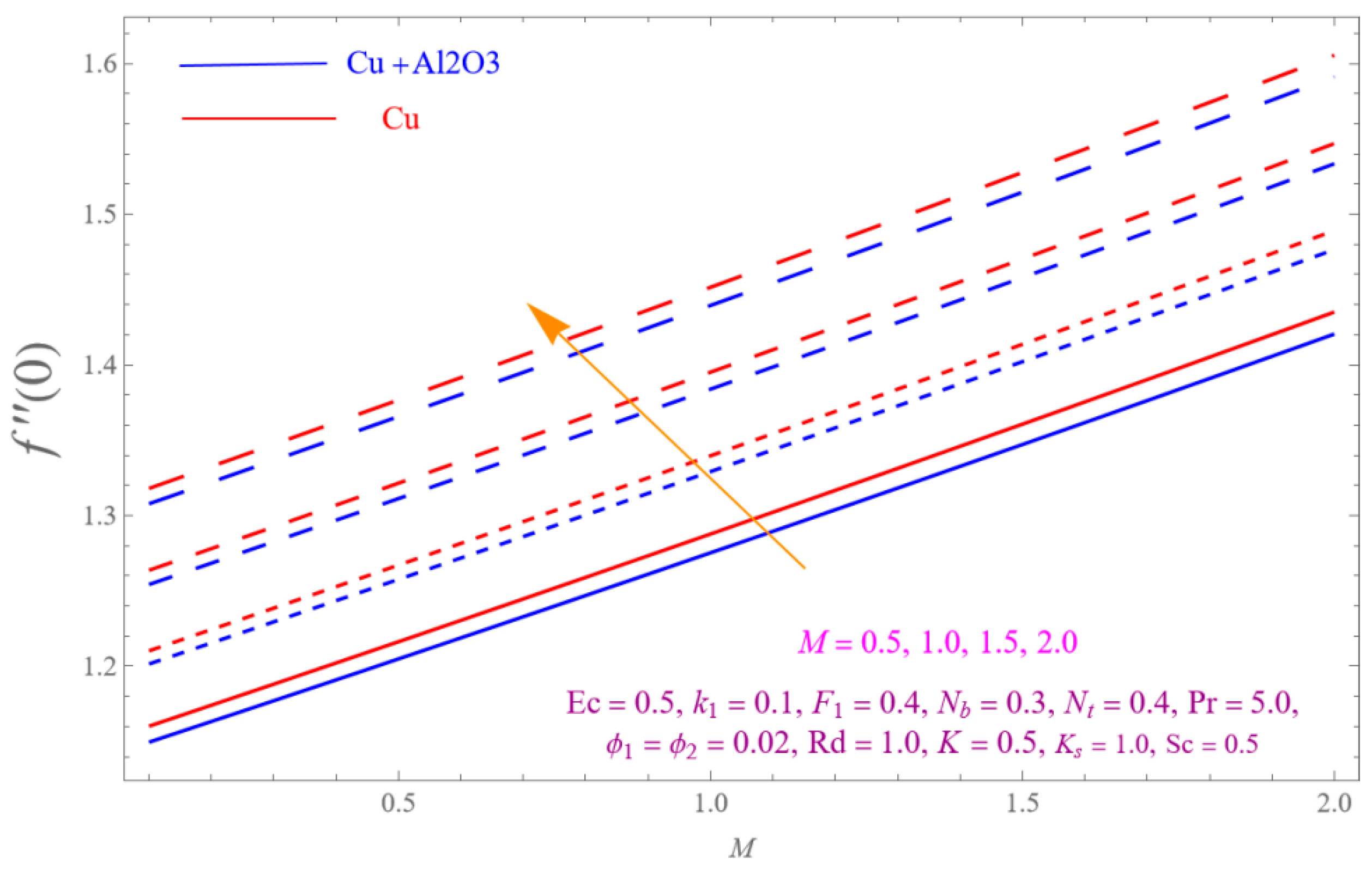
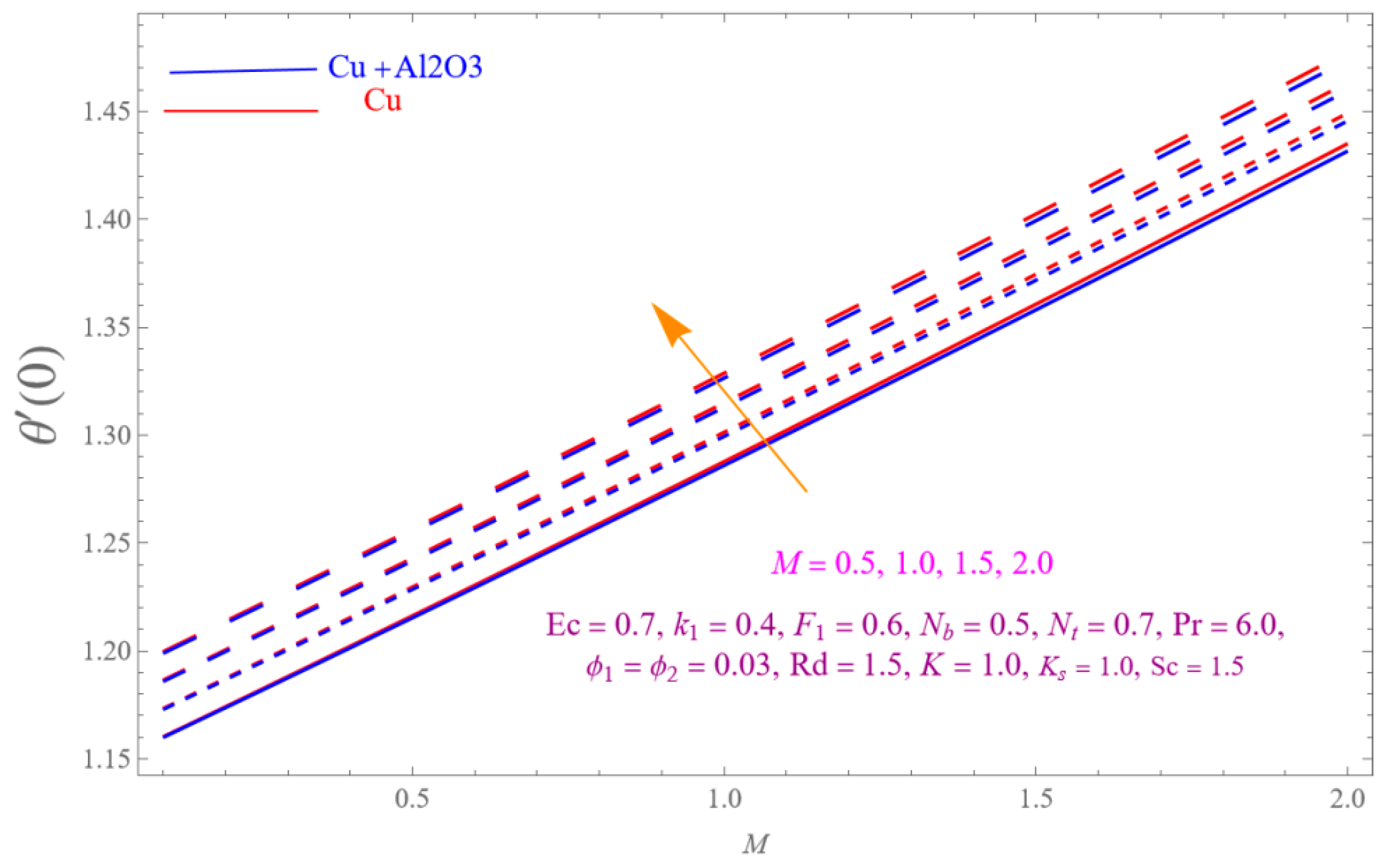
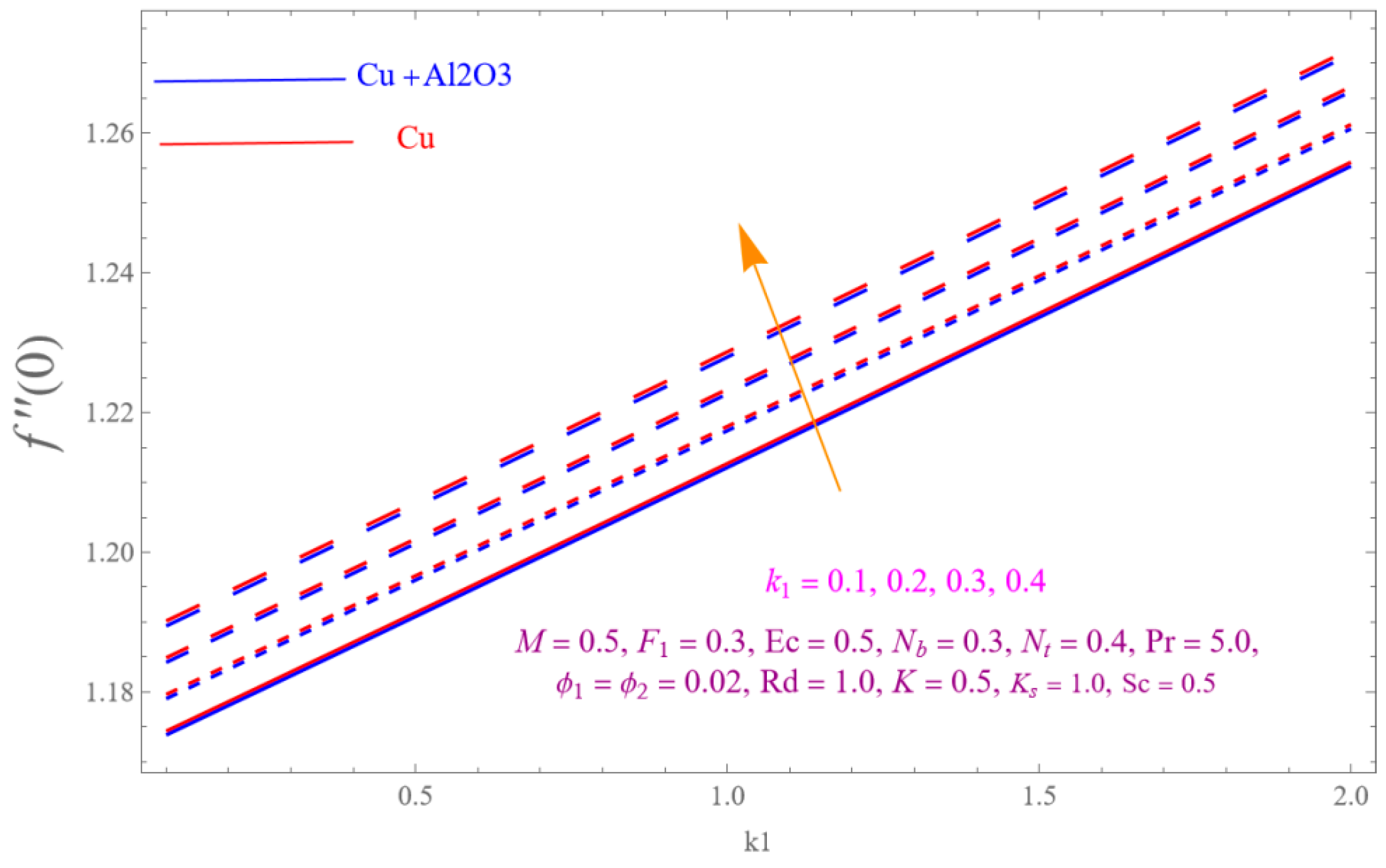
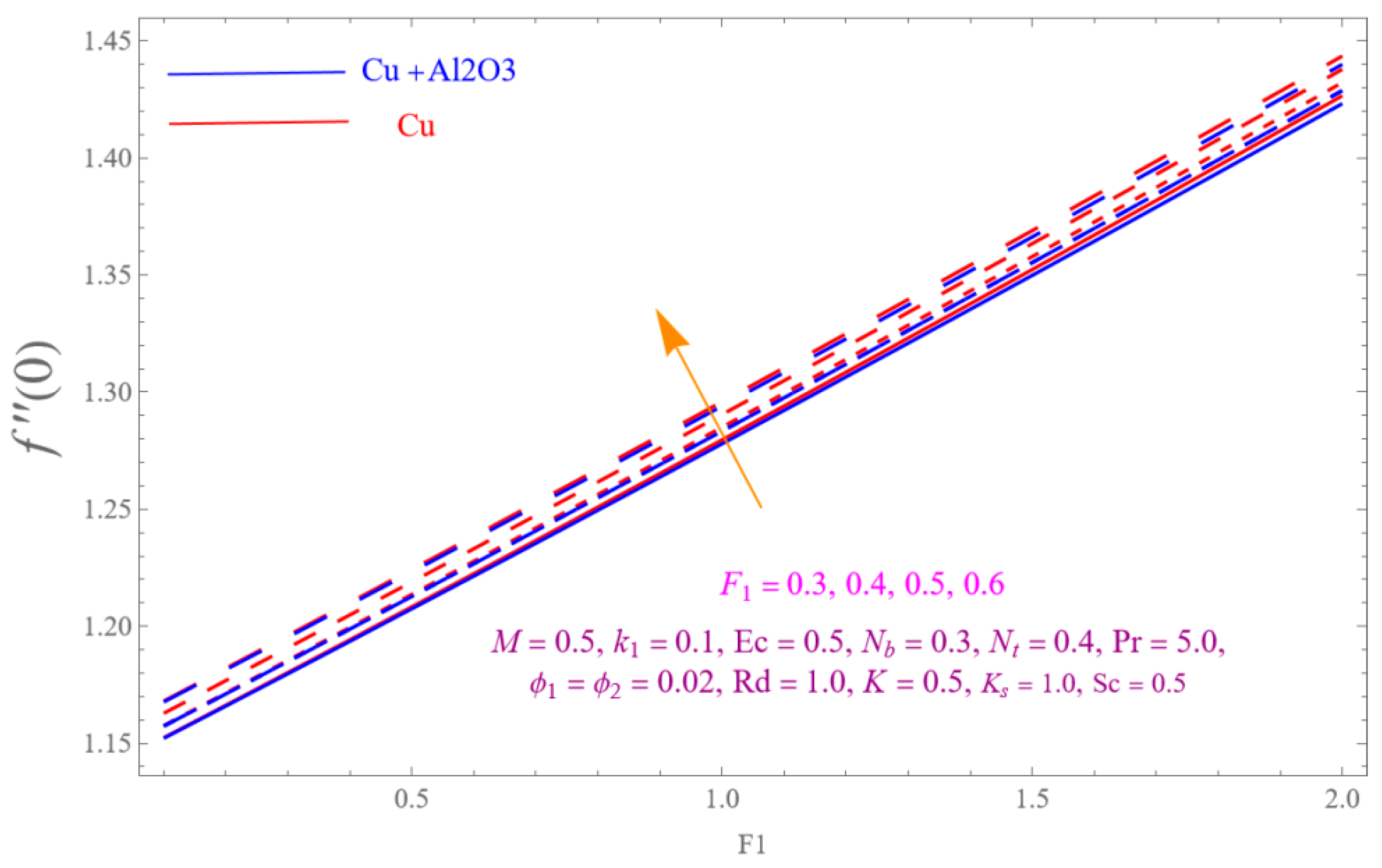
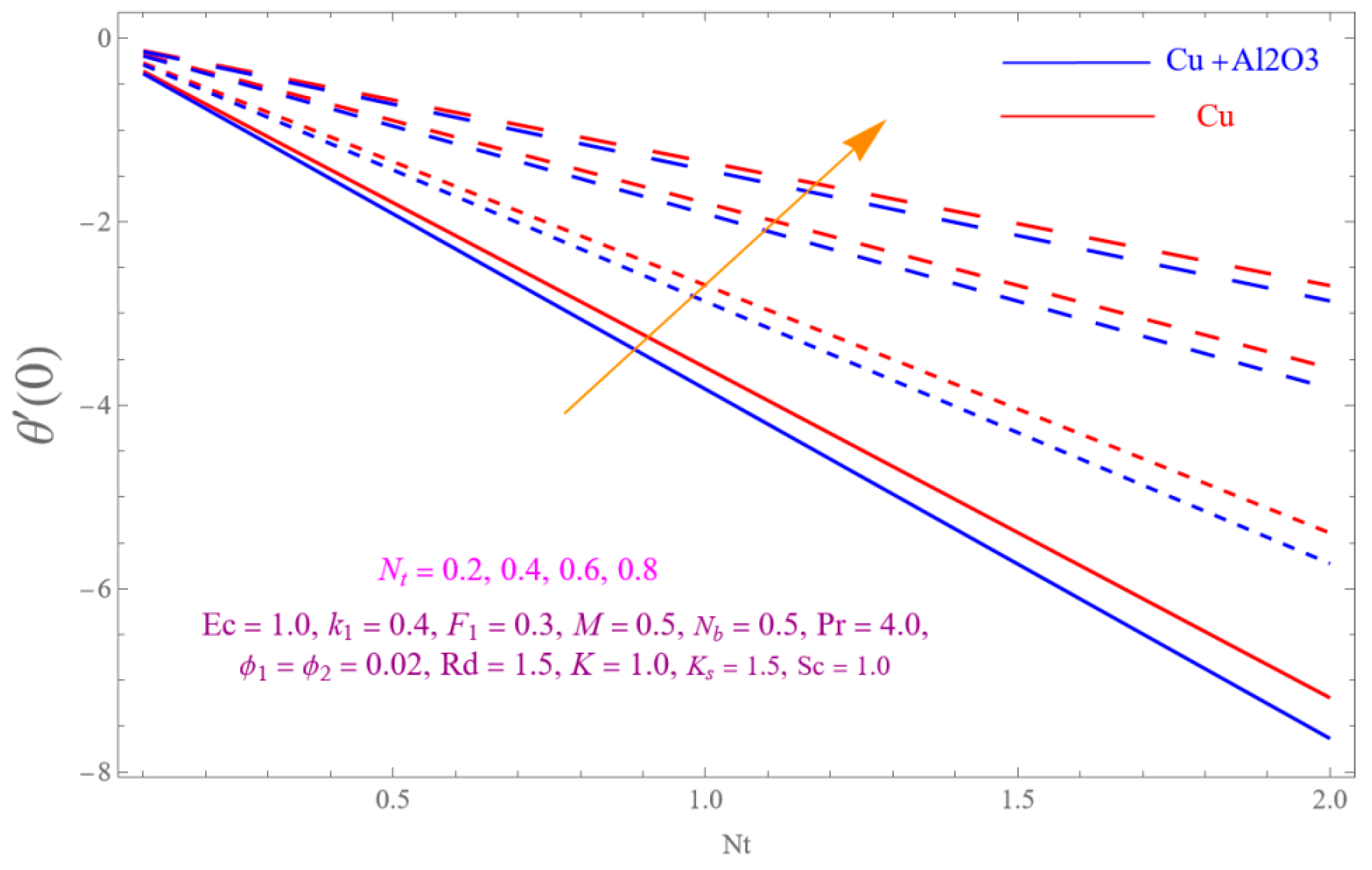
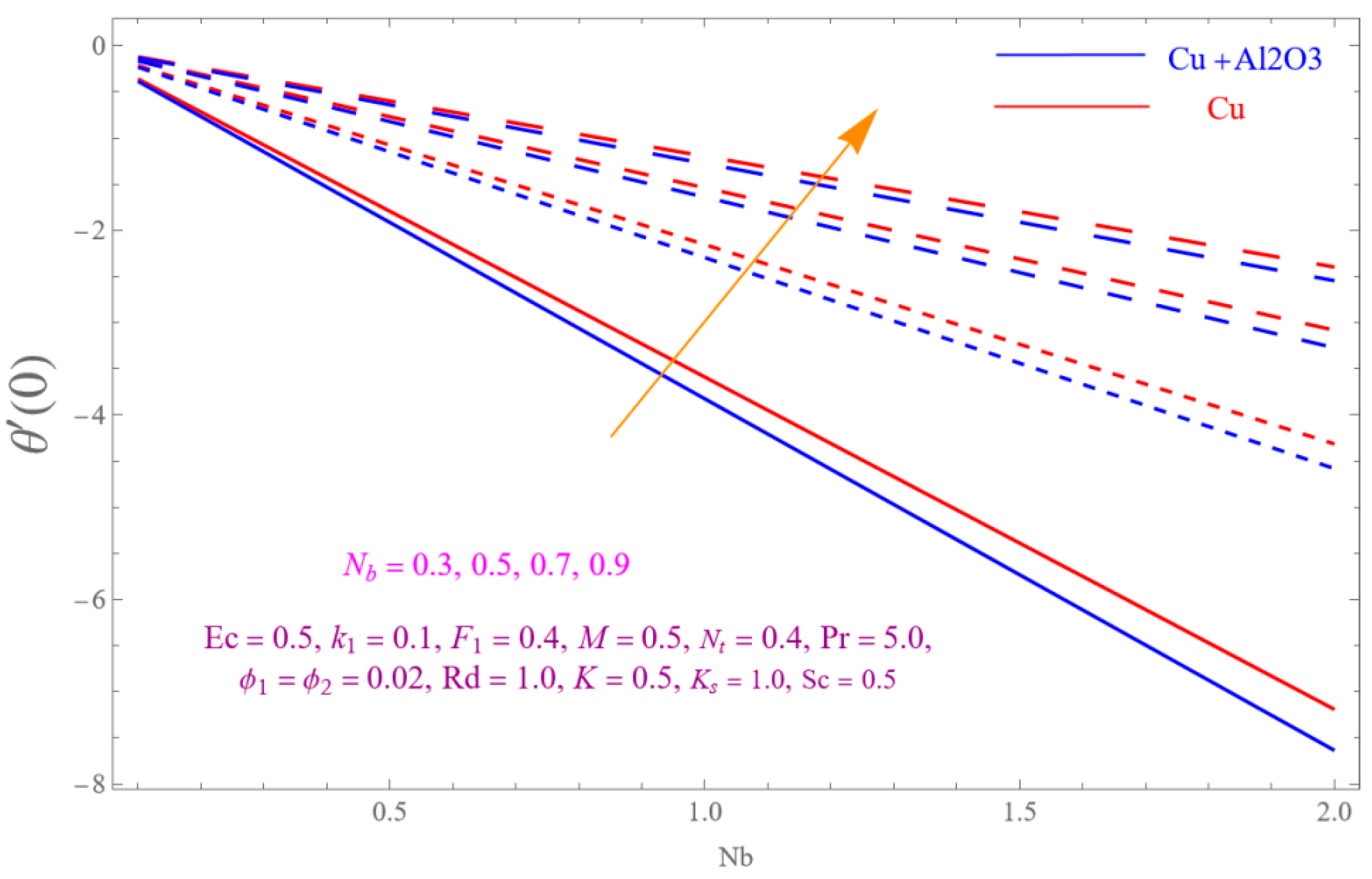
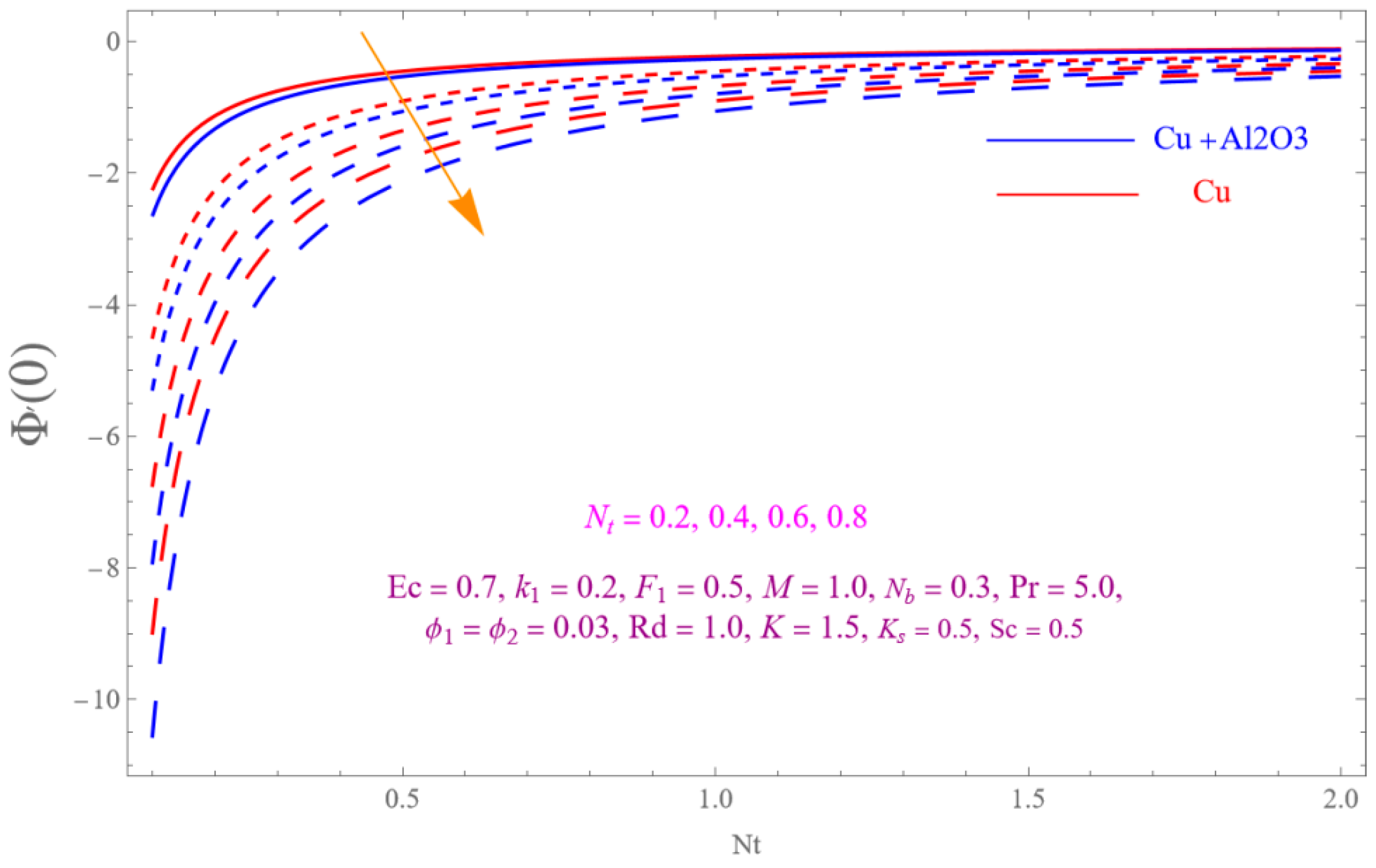
- The is a declining function of .
- Increasing in is decreased.
- Augmenting in decline the .
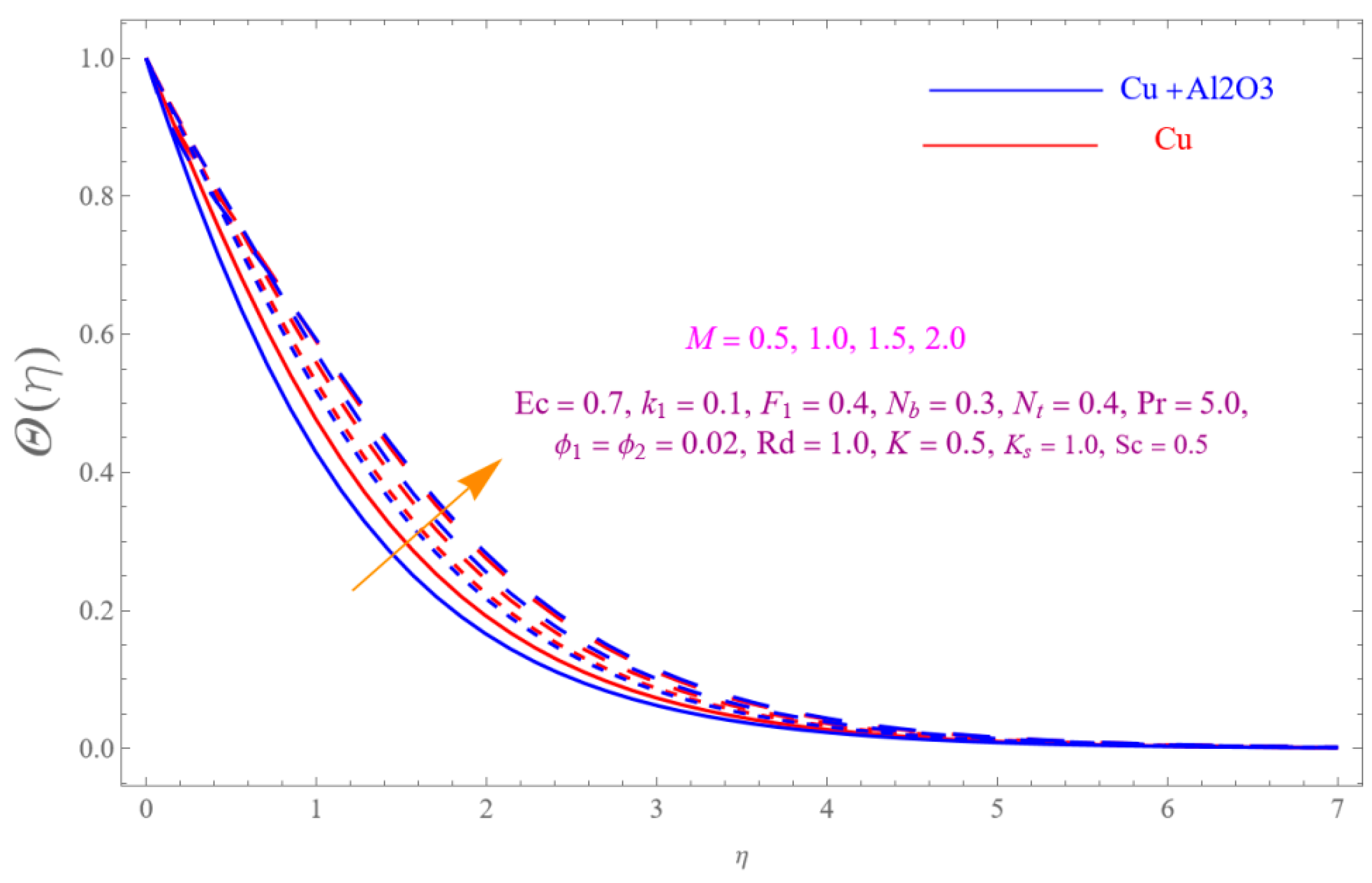
- The decreasing pattern of is observed for increasing in .
- is the growing function of Nu and is the growing function of.
- The reverse impact is observed for and , while increasing in .
Declaration of Interest
Competing interests
Nomenclature
| Surface velocity | For injection | ||
| Ambient temperature | Velocity components in and directions. | ||
| For suction | Mass flux velocity | ||
| Density of base fluid | Ambient concentration | ||
| Dynamic viscosity of HNF | Rate constant | ||
| Chemical concentration | Temperature | ||
| Diffusion coefficients of species | Thermophoretic diffusion | ||
| Inertia coefficient | Surface concentration | ||
| Specific heat capacity of HNF | Electrical conductivity of HNF | ||
| Surface temperature | Kinematic viscosity of base fluid | ||
| Thermal conductivity of base fluid | Thermal conductivity of HNF | ||
| Density of HNF | Electrical conductivity of base fluid | ||
| Nanoparticles volume friction | Schmidth number | ||
| Porosity Parameter | Magnetic parameter | ||
| Inertial parameter | Prandtl number | ||
| Ratio of Diffusion Cosfficient | Strength of homogeneous | ||
| Thermophoresis parameter | Nusselt number | ||
| Brownian motion parameter | Sherwood number | ||
| Strength of hetrogeneous | Skin friction | ||
| Eckert number | Dimensionless concentration | ||
| Dimensionless velocity | Dimensionless temperature | ||
| ODEs | Ordinary differential equations | HNPs | Hybrid nanoparticles |
| PDEs | Partial differential equations | HAM | Homotopy Analysis Method |
| HNF | Hybrid nanofluid | NF | Nanofluid |
| BL | Boundary layer |
References
- Choi, S.U. Enhancing thermal conductivity of fluids with nanoparticles, developments and applications of non-Newtonian flows. ASME, FED, MD 1995, 231, 99–105. [Google Scholar]
- Xuan, Y.; Roetzel, W. Conceptions for heat transfer correlation of nanofluids. Int. J. Heat Mass Transf. 2000, 43, 3701–3707. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective Transport in Nanofluids. J. Heat Transfer. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Dharmalingam, R.; Sivagnanaprabhu, K.; Kumar, B.S.; Thirumalai, R. Nano Materials and Nanofluids: An Innovative Technology Study for New Paradigms for Technology Enhancement. Procedia Eng. 2014, 97, 1434–1441. [Google Scholar] [CrossRef]
- Tielke, J., Maas, M., Castillo, M., Rezwan, K. and Avila, M., 2021. Statistical analysis of thermal conductivity experimentally measured in water-based nanofluids. Proceedings of the Royal Society A, 477(2250), p.20210222.
- Coccia, G.; Tomassetti, S.; Di Nicola, G. Thermal conductivity of nanofluids: A review of the existing correlations and a scaled semi-empirical equation. Renew. Sustain. Energy Rev. 2021, 151, 111573. [Google Scholar] [CrossRef]
- Alami, A.H.; Ramadan, M.; Tawalbeh, M.; Haridy, S.; Al Abdulla, S.; Allahu, H.; Ayoub, M.; Alashkar, A.; Abdelkareem, M.A.; Olabi, A.G. A critical insight on nanofluids for heat transfer enhancement. Sci. Rep. 2023, 13, 1–14. [Google Scholar] [CrossRef]
- Rao, M.E.; Sankari, M.S.; Nagalakshmi, C.; Rajkumar, S. On the Role of Bioconvection and Activation Energy for MHD-Stretched Flow of Williamson and Casson Nanofluid Transportation across a Porous Medium Past a Permeable Sheet. J. Nanomater. 2023, 2023, 1–11. [Google Scholar] [CrossRef]
- Alahmadi, R.A.; Raza, J.; Mushtaq, T.; Abdelmohsen, S.A.M.; Gorji, M.R.; Hassan, A.M. Optimization of MHD Flow of Radiative Micropolar Nanofluid in a Channel by RSM: Sensitivity Analysis. Mathematics 2023, 11, 939. [Google Scholar] [CrossRef]
- Ali, A.; Khan, H.S.; Saleem, S.; Hussan, M. EMHD Nanofluid Flow with Radiation and Variable Heat Flux Effects along a Slandering Stretching Sheet. Nanomaterials 2022, 12, 3872. [Google Scholar] [CrossRef] [PubMed]
- Jawad, M.; Shah, Z.; Islam, S.; Bonyah, E.; Khan, A.Z. Darcy-Forchheimer flow of MHD nanofluid thin film flow with Joule dissipation and Navier’s partial slip. J. Phys. Commun. 2018, 2, 115014. [Google Scholar] [CrossRef]
- Jawad, M.; Saeed, A.; Khan, A.; Islam, S. MHD bioconvection Darcy-Forchheimer flow of Casson nanofluid over a rotating disk with entropy optimization. Heat Transf. 2020, 50, 2168–2196. [Google Scholar] [CrossRef]
- Jawad, M.; Saeed, A.; Kumam, P.; Shah, Z.; Khan, A. Analysis of boundary layer MHD Darcy-Forchheimer radiative nanofluid flow with soret and dufour effects by means of marangoni convection. Case Stud. Therm. Eng. 2020, 23, 100792. [Google Scholar] [CrossRef]
- Roşca, N.C.; Roşca, A.V.; Aly, E.H.; Pop, I. Flow and Heat Transfer Past a Stretching/Shrinking Sheet Using Modified Buongiorno Nanoliquid Model. Mathematics 2021, 9, 3047. [Google Scholar] [CrossRef]
- Hayat, T.; Nadeem, S. Heat transfer enhancement with Ag–CuO/water hybrid nanofluid. Results Phys. 2017, 7, 2317–2324. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow and heat transfer past a permeable stretching/shrinking surface with a convective boundary condition. J. Physics: Conf. Ser. 2019, 1366, 012022. [Google Scholar] [CrossRef]
- El-Zahar, E.R., Rashad, A.M., Saad, W. and Seddek, L.F., 2020. Magneto-hybrid nanofluids flow via mixed convection past a radiative circular cylinder. Scientific Reports, 10(1), p.10494.
- Rasheed, T.; Hussain, T.; Anwar, M.T.; Ali, J.; Rizwan, K.; Bilal, M.; Alshammari, F.H.; Alwadai, N.; Almuslem, A.S. Hybrid Nanofluids as Renewable and Sustainable Colloidal Suspensions for Potential Photovoltaic/Thermal and Solar Energy Applications. Front. Chem. 2021, 9. [Google Scholar] [CrossRef] [PubMed]
- Jaafar, A.; Waini, I.; Jamaludin, A.; Nazar, R.; Pop, I. MHD flow and heat transfer of a hybrid nanofluid past a nonlinear surface stretching/shrinking with effects of thermal radiation and suction. Chin. J. Phys. 2022, 79, 13–27. [Google Scholar] [CrossRef]
- Nadeem, M.; Siddique, I.; Awrejcewicz, J.; Bilal, M. Numerical analysis of a second-grade fuzzy hybrid nanofluid flow and heat transfer over a permeable stretching/shrinking sheet. Sci. Rep. 2022, 12, 1–17. [Google Scholar] [CrossRef]
- Sarfraz, M.; Yasir, M.; Khan, M. Multiple solutions for non-linear radiative mixed convective hybrid nanofluid flow over an exponentially shrinking surface. Sci. Rep. 2023, 13, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Jawad, M.; Khan, Z.; Bonyah, E.; Jan, R. Analysis of Hybrid Nanofluid Stagnation Point Flow over a Stretching Surface with Melting Heat Transfer. Math. Probl. Eng. 2022, 2022, 1–12. [Google Scholar] [CrossRef]
- Jawad, M., Khan, A. and Shah, S.A.A., 2021. Examination of couple stress hybrid nanoparticles (CuO-Cu/blood) as a targeted drug carrier with magnetic effects through porous sheet. Brazilian Journal of Physics, 51(4), pp.1096-1107.
- Jawad, M.; Saeed, A.; Tassaddiq, A.; Khan, A.; Gul, T.; Kumam, P.; Shah, Z. Insight into the dynamics of second grade hybrid radiative nanofluid flow within the boundary layer subject to Lorentz force. Sci. Rep. 2021, 11, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Waini, I.; Ishak, A.; Pop, I. Hybrid Nanofluid Flow with Homogeneous-Heterogeneous Reactions. Comput. Mater. Contin. 2021, 68, 3255–3269. [Google Scholar] [CrossRef]
- Xu, N.-L.; Xu, H.; Raees, A. Homogeneous-heterogeneous reactions in flow of nanofluids near the stagnation region of a plane surface: The Buongiorno’s model. Int. J. Heat Mass Transf. 2018, 125, 604–609. [Google Scholar] [CrossRef]
- Alarabi, T.H.; Rashad, A.M.; Mahdy, A. Homogeneous–Heterogeneous Chemical Reactions of Radiation Hybrid Nanofluid Flow on a Cylinder with Joule Heating: Nanoparticles Shape Impact. Coatings 2021, 11, 1490. [Google Scholar] [CrossRef]
- Ramzan, M.; Chaudhry, H.; Ghazwani, H.A.S.; Kadry, S.; Shahmir, N.; Abbas, M.; Saleel, C.A. Impact of homogeneous–heterogeneous reactions on nanofluid flow through a porous channel – A Tiwari and Das model application. Numer. Heat Transfer, Part A: Appl. 2023; 14. [Google Scholar] [CrossRef]
- Anuar NS, Bachok N, Pop I. Cu-Al2O3/water hybrid nanofluid stagnation point flow past MHD stretching/shrinking sheet in presence of homogeneous-heterogeneous and convective boundary conditions. Mathematics. 2020 Jul 28;8(8):1237.
- Reddy, P.B.A.; Suneetha, S.; Subbarayudu, K.; Al-Arabi, T.; Rashad, A. Exploration of physical features of homogeneous–heterogeneous chemical action in a nanofluid film dispensed with MOS2 in diathermic oils. J. Taibah Univ. Sci. 2021, 15, 826–839. [Google Scholar] [CrossRef]
- Khashi’Ie, N.S.; Arifin, N.M.; Pop, I. Magnetohydrodynamics (MHD) boundary layer flow of hybrid nanofluid over a moving plate with Joule heating. Alex. Eng. J. 2021, 61, 1938–1945. [Google Scholar] [CrossRef]
- Reddy, Y.D.; Goud, B.S.; Nisar, K.S.; Alshahrani, B.; Mahmoud, M.; Park, C. Heat absorption/generation effect on MHD heat transfer fluid flow along a stretching cylinder with a porous medium. Alex. Eng. J. 2023, 64, 659–666. [Google Scholar] [CrossRef]
- Abbas, N.; Shatanawi, W.; Shatnawi, T.A.M.; Hasan, F. Theoretical analysis of induced MHD Sutterby fluid flow with variable thermal conductivity and thermal slip over a stretching cylinder. AIMS Math. 2023, 8, 10146–10159. [Google Scholar] [CrossRef]
- Rashad, A.M.; Nafe, M.A.; Eisa, D.A. Heat variation on MHD Williamson hybrid nanofluid flow with convective boundary condition and Ohmic heating in a porous material. Sci. Rep. 2023, 13, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Kumar, Y.S.; Hussain, S.; Raghunath, K.; Ali, F.; Guedri, K.; Eldin, S.M.; Khan, M.I. Numerical analysis of magnetohydrodynamics Casson nanofluid flow with activation energy, Hall current and thermal radiation. Sci. Rep. 2023, 13, 1–19. [Google Scholar] [CrossRef] [PubMed]
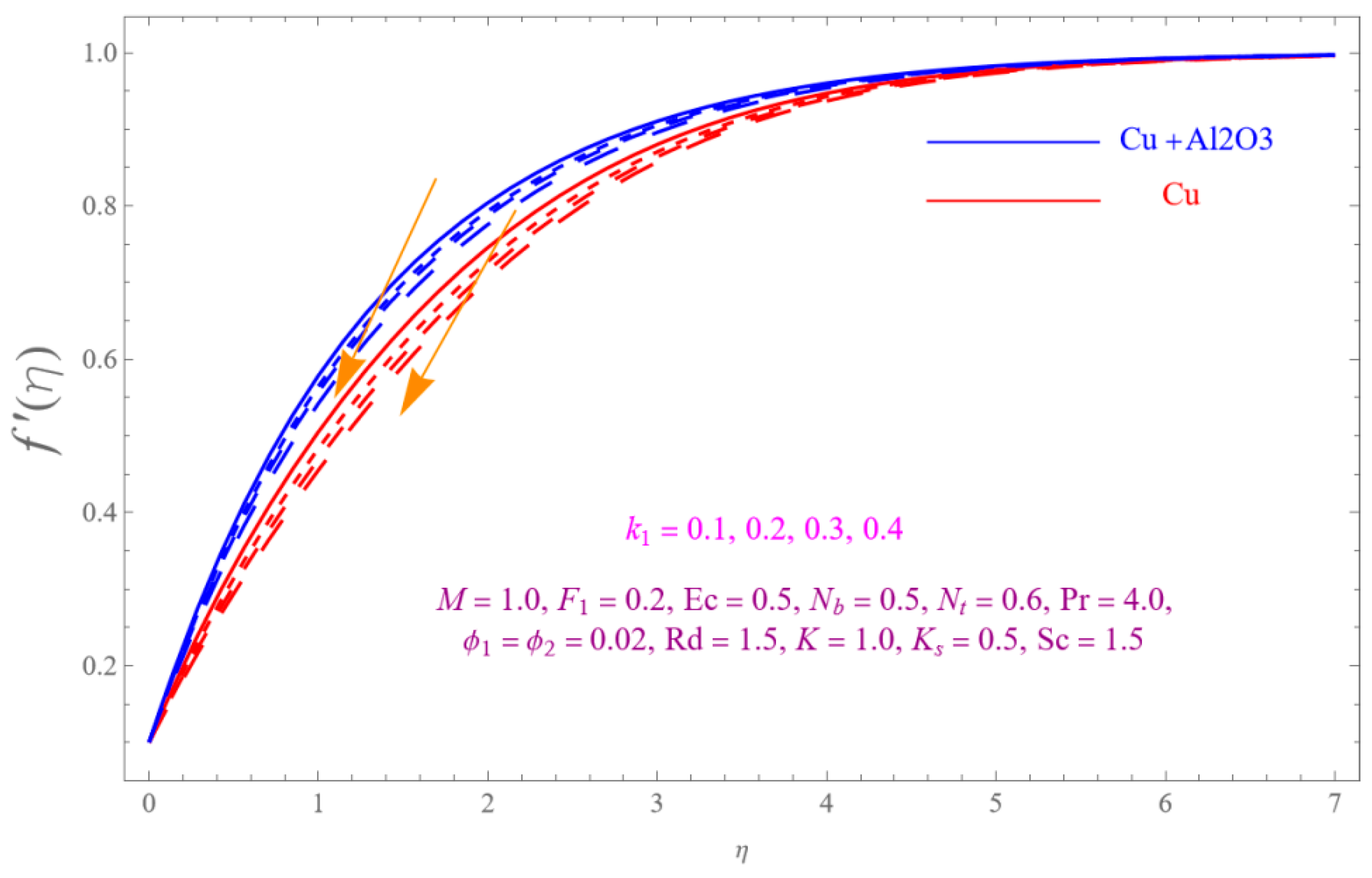
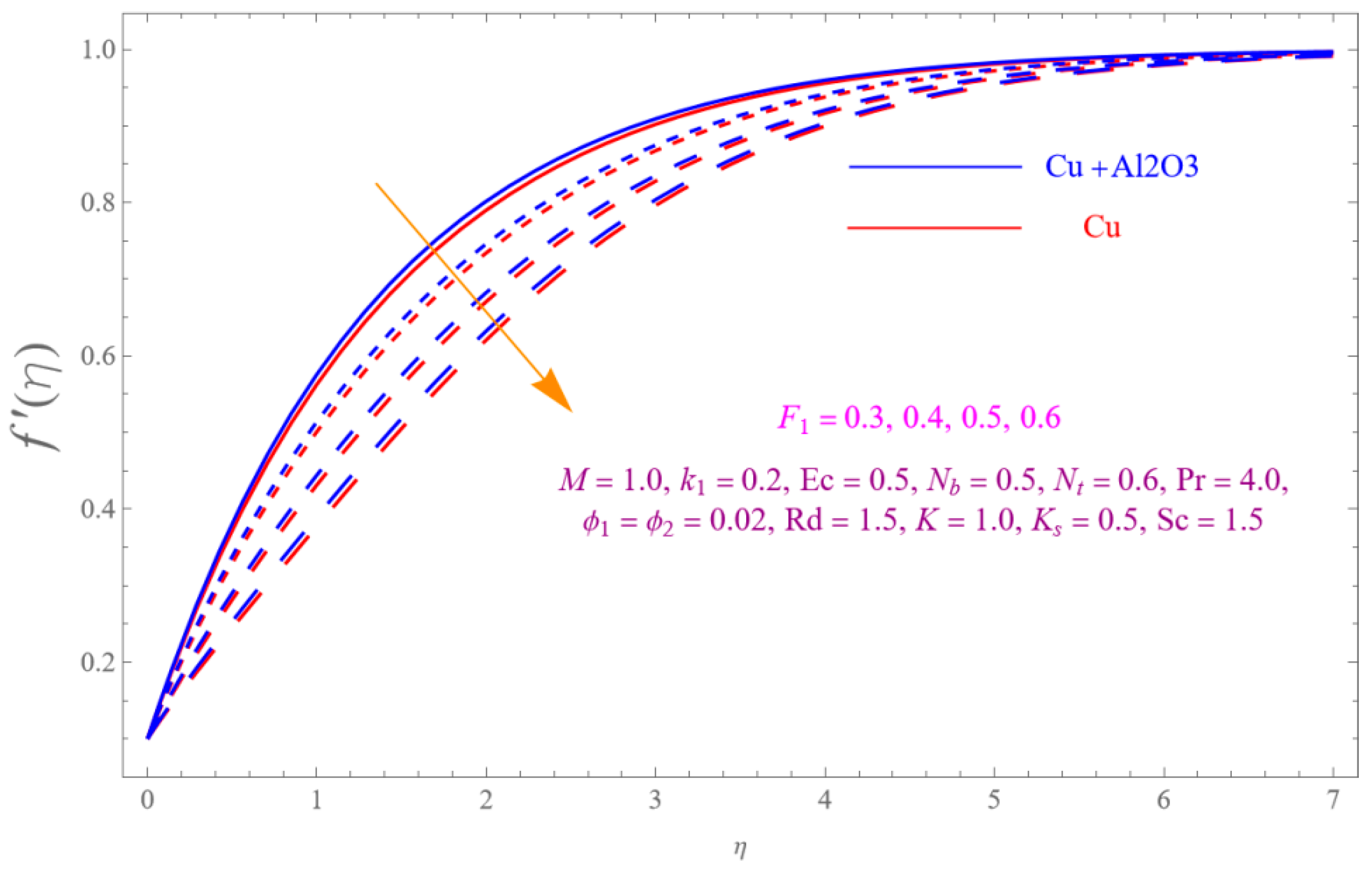
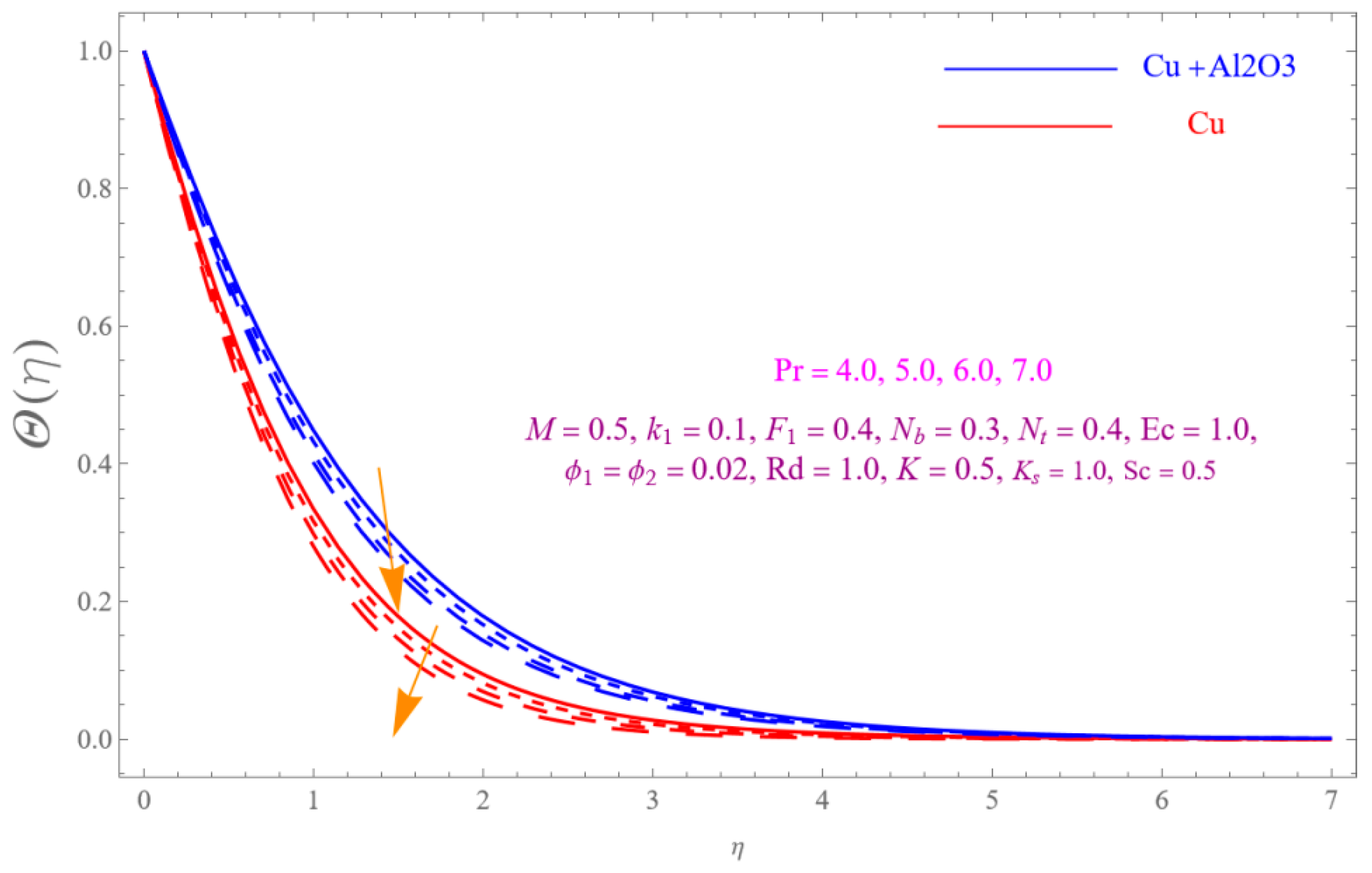
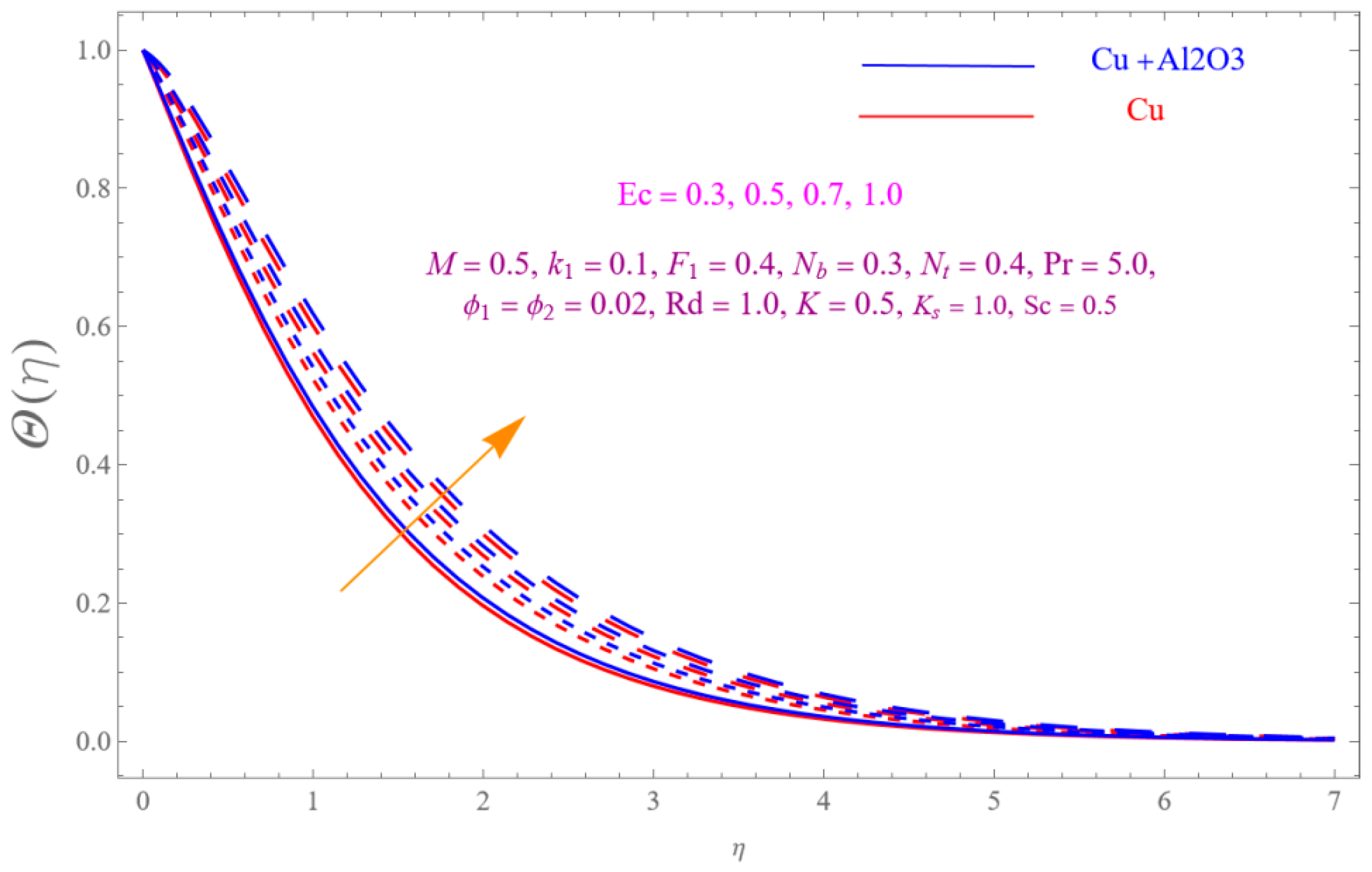


| 0.3 | 0.1 | 0.5 | 4.0 | 0.3 | 0.2 | 1.0 | 0.3 | 00.01 | 00.01 | ............ | |
| 0.4 | ............ | ||||||||||
| 0.5 | ............ | ||||||||||
| 0.1 | ............ | ||||||||||
| 0.2 | ............ | ||||||||||
| 0.3 | ............ | ||||||||||
| 0.5 | |||||||||||
| 1.0 | |||||||||||
| 1.5 | |||||||||||
| 4.0 | ............ | ||||||||||
| 5.0 | ............ | ||||||||||
| 6.0 | ............ | ||||||||||
| 0.3 | ............ | ||||||||||
| 0.5 | ............ | ||||||||||
| 0.7 | ............ | ||||||||||
| 0.2 | ............ | ||||||||||
| 0.4 | ............ | ||||||||||
| 0.6 | ............ | ||||||||||
| 1.0 | ............ | ||||||||||
| 1.5 | ............ | ||||||||||
| 2.0 | ............ | ||||||||||
| 0.3 | ............ | ||||||||||
| 0.5 | ............ | ||||||||||
| 0.7 | ............ | ||||||||||
| 0.01 | ............ | ||||||||||
| 0.02 | ............ | ||||||||||
| 0.03 | ............ | ||||||||||
| 0.01 | ............ | ||||||||||
| 0.02 | ............ | ||||||||||
| 0.03 | ............ |
| 0.5 | 0.3 | 0.2 | 0.01 | 0.01 | |
| 1.0 | |||||
| 1.5 | |||||
| 0.3 | |||||
| 0.5 | |||||
| 0.7 | |||||
| 0.2 | |||||
| 0.4 | |||||
| 0.6 | |||||
| 0.01 | |||||
| 0.02 | |||||
| 0.03 | |||||
| 0.01 | |||||
| 0.02 | |||||
| 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





