The Solution to the Crisis in Cosmology: Current Cosmology is a Distorted Internal View of a Uniformly Expanding Spherical Universe

1. Introduction

Kuhn [1] changed the classical understanding of the gradual evolution of science into a sequence of leapfrog scientific revolutions, where a new paradigm based on new principles is established. As an example, he gives the Copernican revolution and the jump from the Geocentric to the Heliocentric description of the Solar System. New paradigms solve generally recognized problems while preserving the ability to solve problems through previous paradigms.

In particle physics, due to the statistical nature of the measurements, the minimum limit for accepting new discoveries is a signal for which the probability to be only a statistical fluctuation is at the level of 5 σ. The value of the cosmological important Hubble constant H₀ measured directly by type Ia supernovae (SNe) or determined from the Cosmic Microwave Background radiation spectrum (CMB) by the Lambda Cold Dark Mater (ΛCDM) cosmological model gives different values. This deviation is now at the level of 5 σ so this should also be accepted as a fact.

One way to solve this problem is to introduce another new parameter into the ΛCDM model, for example, by changing the amount ω_DM = -1 from the dark energy state equation, so that ΛCDM would become the ωΛCDM model. This is like inserting new circles within circles into a Geocentric model. There are other problems besides this so-called Hubble tension: S₈ tension, the problem of primordial lithium (Li⁷/H ratio), unexpected new measurement results by the James Webb Space Telescope (JWST). It is time for a new paradigm in cosmology.

Kuhn's paradigm shift requires the “sacrifice” of some “obvious” and “common-sense” but wrong unconscious understanding that is implicitly implied until it is realized that it is wrong and is replaced with another principle, sometimes difficult to accept. For example, the “obvious fact” of the Earth's quiescence is replaced by its rotation on its axis and around the Sun while “sacrificing” the idea that the Earth is at the center of the universe. There is an almost perfect mathematical “isomorphism” between “mappings”:

New Perspective: Geocentric Model → Heliocentric Model and:

A new perspective: ΛCDM cosmology → a 3D-spherical universe that spreads uniformly.

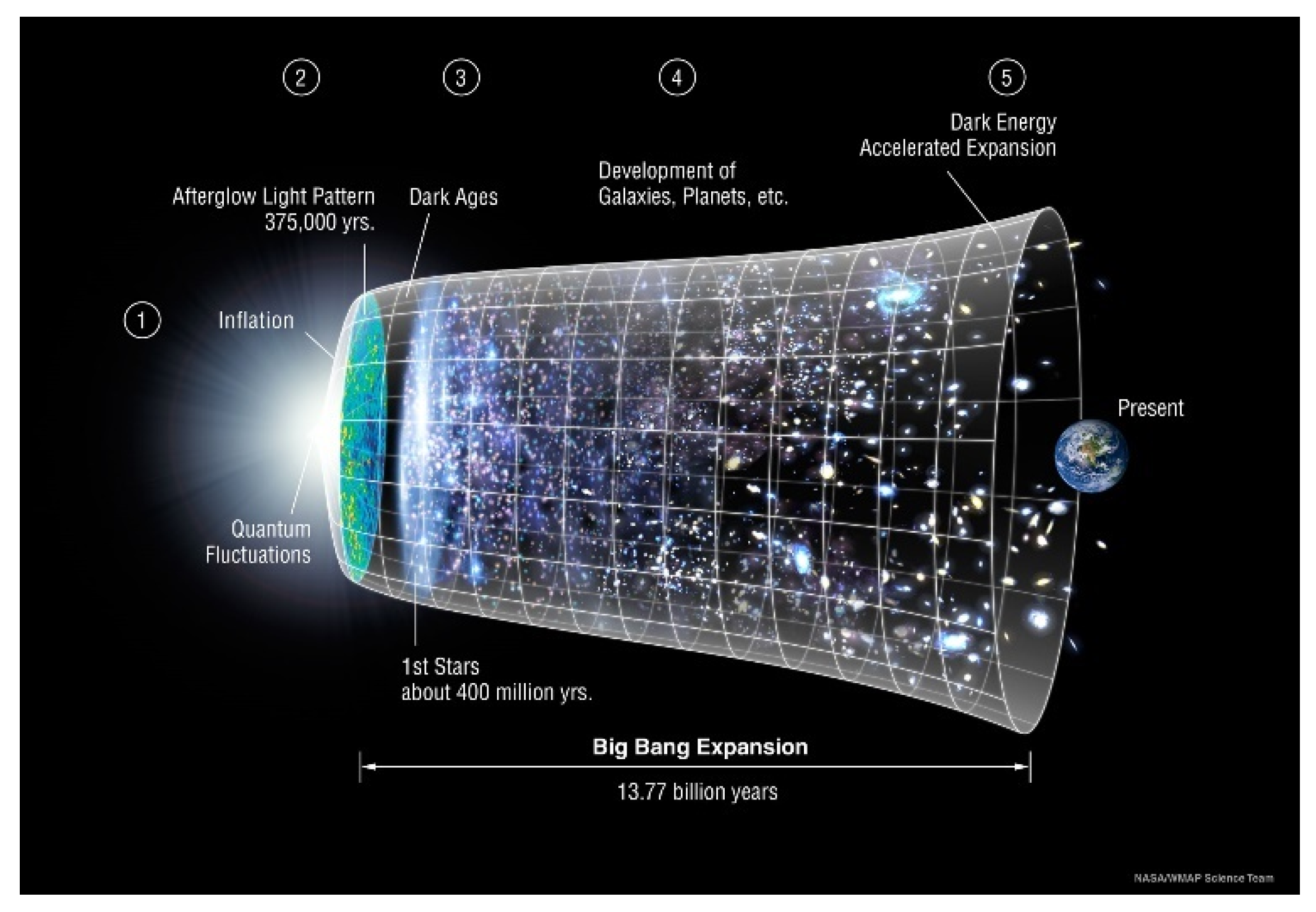
All the great truths later become almost banal, and that is why they are difficult to reach, as the conclusion of the fish that it is in the water. Figure 1 is a popular representation of the universe from the Big Bang (BB) to the present day, according to ΛCDM cosmology. There is something unusual about that picture. Without going into the question of the existence of the Creator, Figure 1 is a representation of the universe from God's perspective because, by definition, God is OUTSIDE (OUT) of space and time, and we are INSIDE (IN) space and time, and all our measurements are INSIDE the universe. Do (IN)-measurements give an accurate (OUT)-cosmology? The mentioned “isomorphism” indicates that it does not.

Just as the constant light speed principle is sufficient for the development of the Special Theory of Relativity (STR), so the distinction between (IN) and (OUT) cosmological quantities is sufficient to reproduce the (ω)ΛCDM model from a simple (OUT) model of a uniformly expanding 3D-spherical universe. For the cosmological expansion of the universe beyond the Hubble radius, the following argument is used:

In Einstein's STR, velocities greater than c = 299,792,458 m/s are not possible, but they are possible in GTR because it is not the motion of the body but the expansion of the space itself. For simplicity, I use dimensionless quantities in this work (time t = 0 for BB, t = 1 now, scale a(t) = t, Hubble constant H₀ = 1, Hubble radius D_H = 1, speed of light c = 1). Next to the cosmological parameters, if necessary, I add (IN) or (OUT). All dependencies of all quantities (INside and OUTside) as time functions, arise from the identity equation a(t) = t and can be easily reproduced using some Graphing Calculator (for example Desmos).

2. Model Development

2.1. (IN) and (OUT) recessionary velocity

Here are two thought experiments (Earth, A, and B are on the same line):

• Let at R = 0.5 galaxy A move away from us at a speed of 0.5 c, and at a distance R = 1, galaxy B moves away from galaxy A at a speed of 0.5 c. Then in GTR galaxy B is moving away from us at a speed of 0.5 c + 0.5 c = c .
• Let rocket A move away from us at a speed of 0.5 c, and rocket B moves away from rocket A at a speed of 0.5 c. Then rocket B moves away from us at a speed of 0.8 c, because in STR the relativistic addition of velocities applies (for c = 1):

$$u\oplus v={\displaystyle \frac{u+v}{1+uv}} .$$

(1)

The differences in the summing of velocities in 1 and 2 are because (implicitly) GTR and cosmology are defined from the (OUT) perspective and STR from the (IN) perspective. The collateral victim of this distinction is the so-called Warp drive, the idea of traveling faster than light in a space-time “bubble” in which the rocket is stationary. Equidistant galaxies on the line with R(Milky-Way) = R(0) = 0 are (now) moving away according to Hubble's law at an (OUT) velocity v(R) = H₀∙R = R , and their (IN) velocity is v(R) = tanh(R), which is always less than c=1 and less than (OUT) R = v(R). For this (OUT) a(t) = t model radial (OUT) comoving distance is

$$R\left(t\right)=\underset{t}{\overset{1}{\int }}{\displaystyle \frac{dt}{a\left(t\right)}}=-\mathit{ln}\left(t\right) ,$$

(2)

so, (IN) velocity is v(R(t)) = tanh(-ln(t)) = (1-t²)/(1+t²) and (OUT) v(t) = -ln(t). There are as many as three different definitions of redshift z: Doppler, cosmological and gravitational. For (IN) v(t) from the expression for Doppler redshift, we get:

$$1+z=\sqrt{{\displaystyle \frac{1+v}{1-v}}}=\sqrt{{\displaystyle \frac{1+\frac{1-t^2}{1+t^2}}{1-\frac{1-t^2}{1+t^2}}}}=\sqrt{{\displaystyle \frac{1+t^2+1-t^2}{1+t^2-1+t^2}}}=\sqrt{{\displaystyle \frac{2}{2t^2}}}={\displaystyle \frac{1}{a\left(t\right)}}$$

(3)

Thus, the relativistic Doppler redshift for the (IN) recessionary velocity of the galaxy due to the expansion of the universe is equal to the cosmological redshift due to the change in the scale a(t). This is the same cosmological redshift seen from (IN) and (OUT) perspective (Doppler and cosmological).

2.2. (IN) and (OUT) radial comoving distance

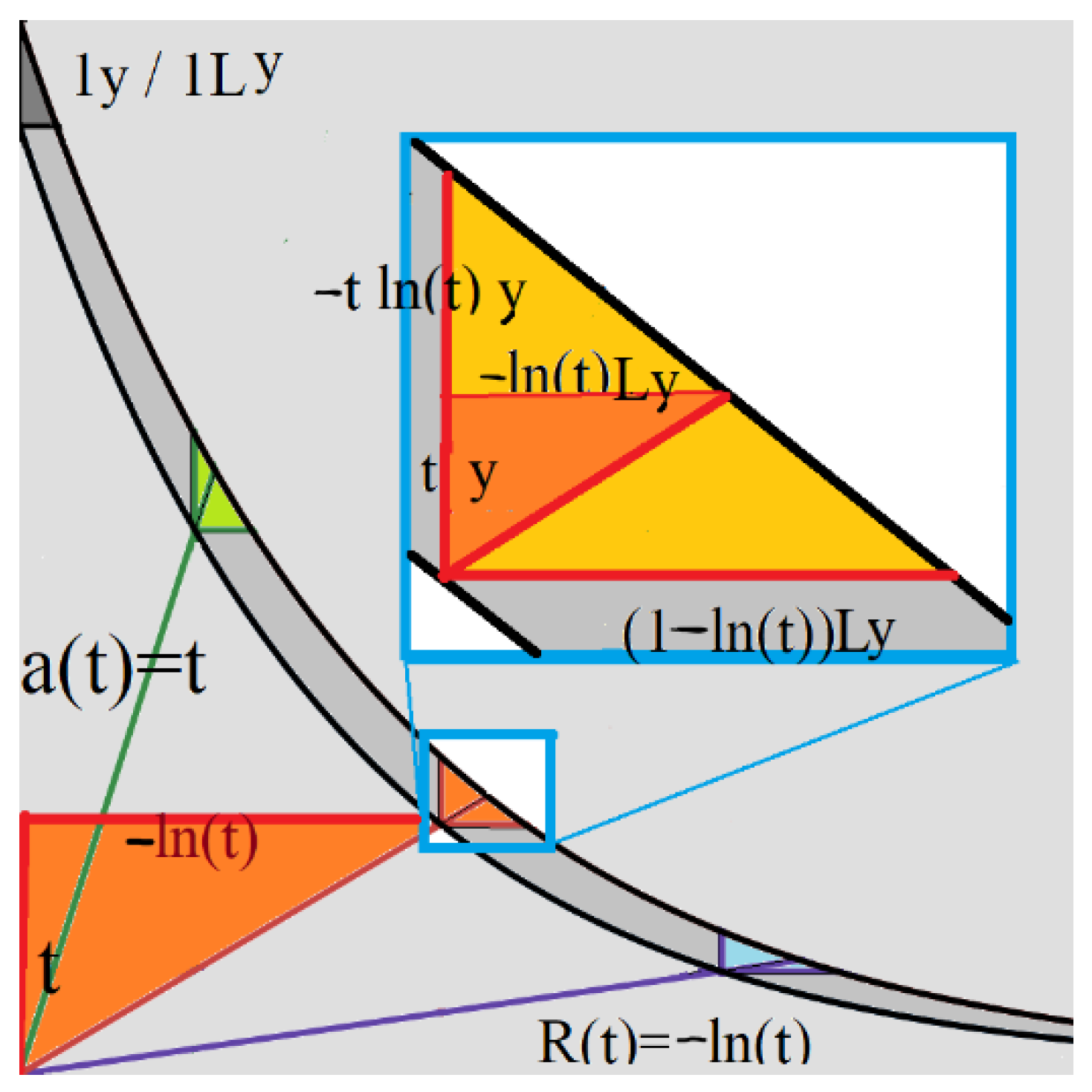
Figure 2 shows a schematized representation of the dependence of the (OUT) radial comoving distance of (OUT) R(t) for symbolical one-year cosmological (IN) measurement. The space-time “stairs” for the 3 different distances is shown, for the central one enlarged, corresponding to HERE and NOW “stair” of 1 light year / 1 year. From similar triangles and using the relativistic contraction of the “stairs” by 1/γ factor, it is easy to obtain that the infinitesimal (IN) length of the “stairs” is:

$$dR\left(t\right)={\displaystyle \frac{2\left(1-\mathit{ln}\left(t\right)\right)}{1+t^2}}dt ,$$

(4)

with

$${\displaystyle \frac{1}{\gamma }}=\sqrt{1-{\left({\displaystyle \frac{1-t^2}{1+t^2}}\right)}^2}={\displaystyle \frac{2t}{1+t^2}} .$$

(5)

It is also

$$1+v=1+{\displaystyle \frac{1-t^2}{1+t^2}}={\displaystyle \frac{2}{1+t^2}} ,$$

(6)

so:

$${\displaystyle \frac{\left(1+\left(out\right)v\right)}{t\cdot \left(in\right)\gamma }}dt=\left(1+\left(in\right)v\right)d{t}^{\text{'}}.$$

(7)

Thus, (IN) dR(t) can be understood in two complementary ways: either as the product of the (now) time interval dt and the scaled sum of the speed of light and the recessional (OUT) velocity (1+v)/t, contracted via the gamma factor for the (IN) velocity γ, or as the product of the (past) time interval dt’ and the sum of the light and (IN) velocity (1+v). The (IN) radial comoving distance is

$$(in)R\left(t\right)=\underset{t}{\overset{1}{\int }}{\displaystyle \frac{\left(1+\left(out\right)R\left(x\right)\right)}{\gamma x}}dx=2\underset{t}{\overset{1}{\int }}{\displaystyle \frac{\left(1-\mathit{ln}\left(x\right)\right)}{1+x^2}}dx .$$

(8)

With the substitution r = -ln(t), the (IN) radial distance R(t) expressed over the (OUT) radial distance r(t) is obtained:

$$R\left(r\right)=\underset{0}{\overset{r}{\int }}{\displaystyle \frac{1+x}{\mathit{cosh}\left(x\right)}}dx .$$

(9)

3. Results

3.1. The (OUT) SCC cosmology reproduces (IN) ΛCMD cosmology

Analogous to the problem of deformation in cartographic projections from a curved to a flat surface (or vice versa), there is a similar problem of "projection" of the universe from the OUT perspective to the IN perspective. Thus, it is possible to "deform" the OUT into the IN perspective in several different ways. For example, in a "projection" used here time is equal in the IN and OUT perspectives. This leads to a slightly nonlinear function a(t) = t + ε(t) where the function ε(t) takes on small values. A "projection" is possible in which the OUT scale is equal to the IN scale "a" where t(a) = a + δ(a). Again, the function δ(t) takes small values. It is also possible to express the IN scale and time parametrically, of the form a(x) and t(x), a slightly nonlinear functions of the parameter x.

The (IN) radial distance R(r) (Eq. 9) is finite even for the infinite (OUT) distance (r) and is equal to 3.4027. According to the ΛCDM model, the observable universe has an age of 13.77 Gy and a radius of 46.6 Gly, giving a ratio of 3.3842. This is only 0.54% less than the 3.4027 obtained from (OUT) a(t) = t, within the limits of measurement precision, which is the first, extremely accurate confirmation of this new paradigm.

From Hubble's law (for any epoch) H(t) = v(R(t))/R(t), and a(t) = t it follows that v(R) = const = (OUT)R, where the radial comoving distance (OUT) R is constant for a given galaxy, but due to the expansion is v(R(t)) = R(t)/t = -ln(t)/t and (OUT) R(t) = -ln(t) so, (OUT) H(t) = v(R(t))/(OUT)R(t) = 1/t. On the other hand, (IN) H(t) = (-ln(t)/t)/((IN)R(t)). (IN) R(t) is defined by Eq. (8). The reciprocal of 1/(OUT)H(t) is equal to the Hubble radius D_H(t) = t = (OUT)T(t). The reciprocal of (IN) H(t) is a slightly nonlinear function (IN) T(t). The deceleration parameter q(t) is defined as

$$q=-{\displaystyle \frac{\ddot{a}a}{{\dot{a}}^2}}={\displaystyle \frac{{\dot{a}}^2-\ddot{a}a}{{\dot{a}}^2}}-1={\displaystyle \frac{d}{dt}}\left({\displaystyle \frac{a}{\dot{a}}}\right)-1=\dot{T}-1 ,$$

(10)

where obviously (OUT) q(t) = const = 0. However, due to the (apparent) nonlinearity of (IN) T(t), it is obtained that for t > 0.5523 the (IN) q(t) becomes negative, i.e. the universe expansion apparently accelerates and for t = 1 (IN) q₀(t=1) is exactly -1/2. This is another confirmation of this paradigm since, according to the ΛCMD model, q₀= -0.55. The (IN) q(t) becomes negative for t = 0.5523 for any epoch of the universe and has a value of -1/2 at the end of each epoch, since this is the apparent effect (such as a rainbow or a mirage) because of (IN)-measurements. From the apparent (IN) H(t) scale (IN) a(t) is determined as follows:

$$\left(in\right)a\left(t\right)=\mathit{exp}\left(-\underset{t}{\overset{1}{\int }}\left(in\right)H\left(x\right)dx\right) .$$

(11)

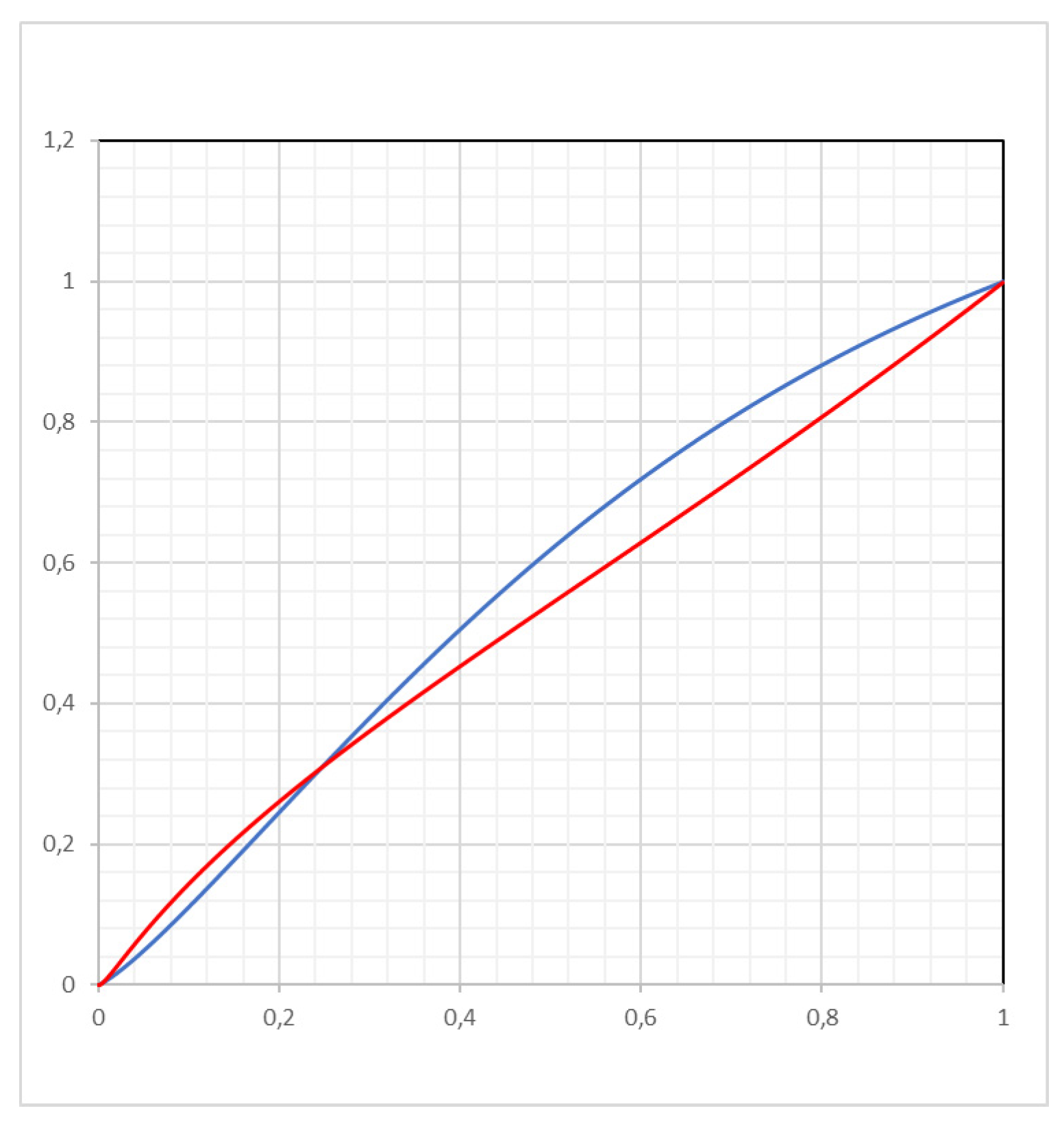
The scale (IN) a(t) is slightly nonlinear too. Figure 3 shows the (apparent) (IN) a(t) and (IN) T(t) which are (OUT)-identity functions (a(t) = t and T(t) = t). For t = 0.5523, when (IN) q(t) becomes negative, is (IN) a(t) = 0.5886 (according to Planck data [2] this occurs when a is about 0.6).

According to the ΛCMD model, when the expansion of the universe changes from deceleration to acceleration scale a is equal to (Ω_M/2Ω_DE)^1/3, q₀ = (Ω_M+(1+3ω_DE)Ω_DE)/2. So, with the condition Ω_M + Ω_DE = 1 by including a = 0.5886 and q₀ = -1/2 the solutions of these three equations are:

Ω_M = 0.2897, Ω_DE = 0.7103 and ω_DE = -0.9386, for ωΛCMD model

With fixed ω = -1, q₀ = -1/2, and the conditions Ω_M + Ω_DE = 1, the solutions are

Ω_M = 1/3 = 0.3333, Ω_DE = 2/3 = 0.6667, and a = 4^-1/3 = 0.6300 for ΛCMD model

The data from the analysis of CMB radiation [2] are

Ω_M = 0.315 ± 0.007, Ω_DE = 0.6847 ± 0.0073 (with the assumed ω_DE= -1),

which are roughly somewhere between the two (IN) solutions. This match, paradoxically, confirms that ΛCMD or here extended ωΛCMD is a distorted (IN)-image of a 3D-spherical universe with scale a(t) = t. So, Ω_M, Ω_DE (and added ω_DE) should be understood only as the parameters by which this distorted image fits.

According to the ΛCDM model, it is

$$T\left(t\right)\approx {\left({\displaystyle \frac{{\Omega }_M}{a{\left(t\right)}^3}}+1-{\Omega }_M\right)}^{-0.5}=T\text{'}\left(x\right) .$$

(12)

It is possible to find Ω_M via (IN) T(t) and (IN) a(t) so that δ(t) is minimal:

$$\delta \left(t\right)=\sqrt{{\displaystyle \frac{1}{1-t}}\underset{t}{\overset{1}{\int }}{\left(T\left(x\right)-T^{\text{'}}\left(x\right)\right)}^{2}dx} .$$

(13)

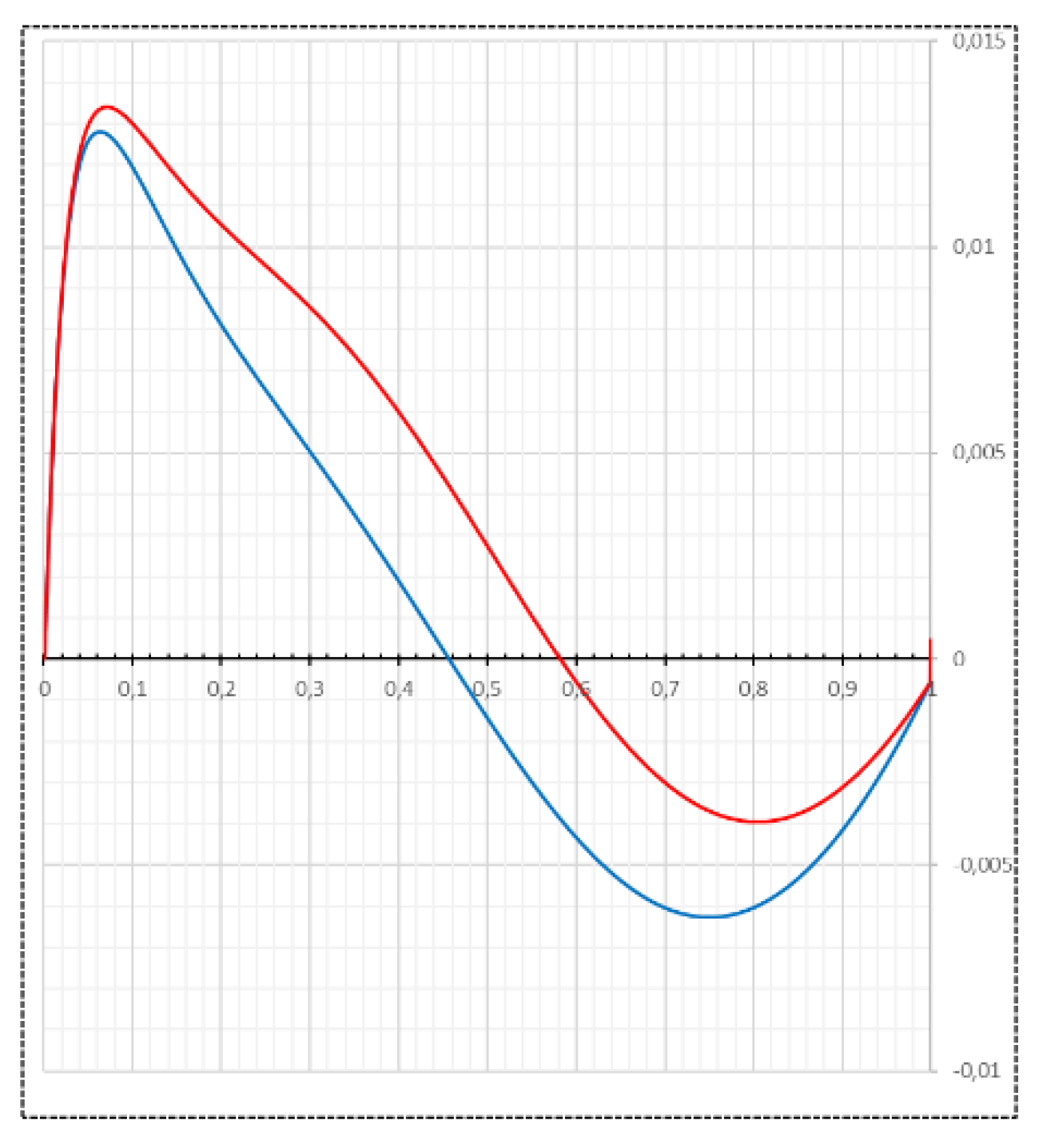
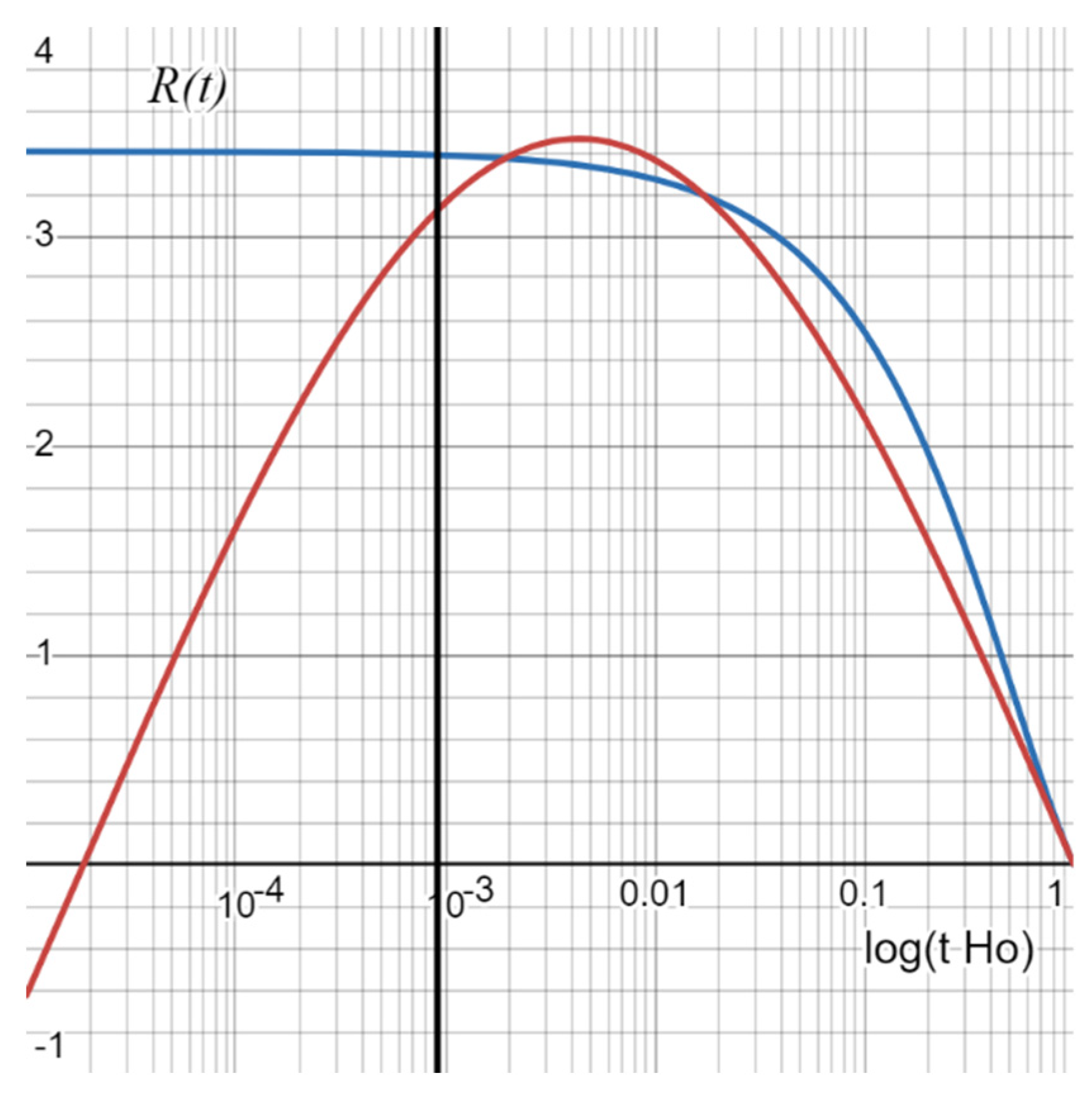
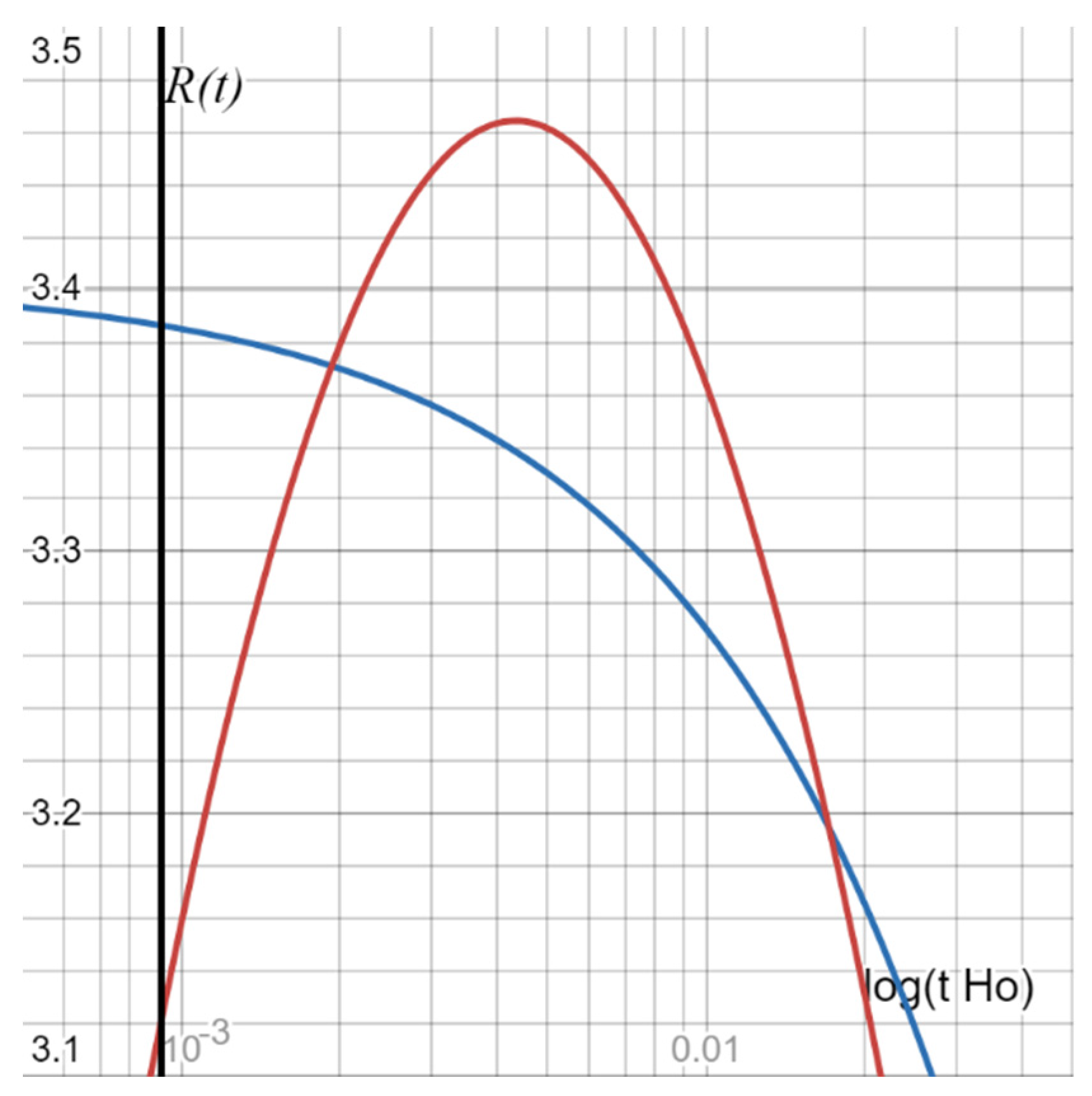
Figure 4 shows the difference (T(t) - T’(t)) for the minimum values δ(0) (blue) and δ(0.4) (red). For t = 0, the minimum δ(0) = 0.00584, which is extremely small, considering that the calculation of apparent (IN) a(t) and (IN) T(t) has nothing to do with the ΛCDM model. This minimum δ(0) is achieved for

Ω_M = 0.3041 and Ω_DE = 0.6959.

For t = 0.4 (corresponding to the measurement limit of Type Ia supernovae (SNe) to z < 1.4 [3]) the minimum is δ(0.4) = 0.00282, for

Ω_M = 0.3104 and Ω_DE = 0.6896.

For the distance of the angular diameter, which is determined by measuring the angle at which an object of known size can be seen, the following applies:

$${\displaystyle \frac{dD}{dt}}=-\left(\mathit{ln}\left(t\right)+1\right)$$

(14)

so, the maximum angular diameter distance for a(t) = 1/e where e = 2.71828 is Euler's constant, which corresponds to the redshift z_max = 1.71828. This is another example of the perfect cosmological principle that the universe is always and everywhere homogeneous, isotropic and stationary in time, has the same (OUT) (due to linearity) and apparent (IN) characteristics in every epoch.

There are many authors ([4], and the literature attached there), starting with Milne [5], who use some variant of the linear model a(t) = t. Thus, Melia and Yennapureddy [6], who using a sample of 140 quasar nuclei obtained z_max = 1.70 ± 0.20 and conclude that the linear model of the expansion of the universe has the highest (92.8 %) probability of being correct, greater than the ΛCDM model.

3.2. The "weakest link" of this model

The CMB spectrum confirms that we live in a flat universe, which is problematic for all models of a linearly growing universe, because for z = 1089.8, the (OUT) radial comoving distance is R = 6.9947, and it should be R_ΛCDM = 3.3140. Although (IN) R= 3.3862 is only 2.2 % larger than R_ΛCDM, this does not detract from the problem, since for a flat universe the transverse distance remains D = 6.9947. The only solution, which is also the weakest “link in the chain” of this new paradigm, is that we live in a 3-sphere universe with these three unlikely coincidences:

• The universe is (OUT) spherically curved that at a certain z the radial (IN) R and the transverse (IN) D comoving distance are equal.
• This z must correspond to the time of CMB formation (recombination).
• The GTR should be modified to contain the (OUT) cosmological solution a(t) = t with Ω_k which satisfies conditions 1 and 2.

Such coincidences are not unknown to the history of science (for example, Hoyle's resonance state C¹², the opacity of water, the apparent size of the Moon and the Sun from Earth). For z = 1089.8 (OUT) comoving distance is R = 6.9947, (IN) comoving distance is R = 3.3862, so (IN) transverse comoving distance must be D = 3.3862 to make the (IN) universe look flat for CMB spectrum. This gives the condition

$$3.3862={\displaystyle \frac{1}{\sqrt{\left|{\Omega }_k\right|}}}\mathit{sin}\left(6.9947\cdot \sqrt{\left|{\Omega }_k\right|}\right).$$

(15)

The numerical solution of this nonlinear equation gives Ω_k = (-1/13.1048) ≈ (-1/13). There are many alternatives to GTR offered, but I have narrowed my search down to those theories that contain GTR as a special case, that is, Brans-Dicke (BD) theories of gravity. Kofinas [7] identifies only three possible types of “natural” generalizations of BD theories in which the stress-energy tensor is not conserved. One of these theories of the second type is Barber's model of cosmology [8, 9, 10] which Barber calls Self Creation Cosmology (SCC), for which the cosmological solution is a(t) = t and Ω_k = (-1/12).

3.3. becomes the crowning proof of (OUT) SCC cosmology

Like the story of the Dirac equation, the biggest problem with this (OUT) a(t) = t model, thanks to Barber's SCC model, becomes its greatest triumph. Because 13.1048 is NOT equal to 12, the three unlikely matches disappear. After 42 years, since the publication of Barber's first paper on the SCC model of cosmology, it follows that the ΛCDM is just a distorted (IN) view of a simple (OUT)-SCC universe of radius R₀ = 12^1/2. It should be R₀ = 13.1048^1/2, because with that (OUT) curvature of the universe it would look perfectly flat for the CMB from the (IN) perspective.

This is a kind of cosmic “mimicry”, in which the spherical universe “pretends” to be flat, just as the Moon “pretends” to be equal to the Sun. Every mimicry is imperfect, including this cosmic one, which resolves Hubble's tension. The (IN) radial comoving distance R(t) (see Eq. 8) for a flat universe should be equal to the (IN) transverse comoving distance D(t) which according to the SCC model is equal to:

$$D\left(t\right)=\sqrt{12}\mathit{sin}\left({\displaystyle \frac{-\mathit{ln}\left(t\right)}{\sqrt{12}}}\right)$$

(16)

Figure 5 shows time dependence of (IN) radial R(t) and (IN) transversal D(t) distances (on a logarithmic scale for time t), and Figure 6 shows a detail of Figure 5. The vertical black line is the recombination time t_CMB = 1/1090.8 for which R(t_CMB) = 3.3862 and D (t_CMB) = 3.1217 which gives the ratio:

$$\left({\displaystyle \frac{R}{D}}\right)={\displaystyle \frac{3.3862}{3.1217}}=1.0847$$

(17)

3.4. Solution of Hubble tension

The Hubble tension is a 5 σ level discrepancy for the Hubble constant determined over the CMB spectrum (Planck) [2] H₀ = (67.27 ± 0.60) km/s/Mpc at 68% CL and the most recent (SH0ES) values [11] H₀ = (73.04 ± 1.04) km/s/Mpc at 68% CL, based on SNe Ia calibrated by Cepheids. From these data, the experimental ratio is:

$${\left({\displaystyle \frac{R}{D}}\right)}_{Experiment}={\displaystyle \frac{H_0\left(SHOES\right)}{H_0\left(Planck\right)}}={\displaystyle \frac{73.04\pm 1.04}{67.27\pm 0.60}}=1.0858\pm 0.0127$$

(18)

A factor of 1.0847, the ratio of radial and transverse comoving distances on the CMB sphere, represents a deviation from the perfect “mimicry” of the (IN) flat universe (R/D = 1) from an IN-perspective. The experimental ratio of radial and transverse distance of the CMB sphere deviates from the theoretical (OUT) SCC value (R/D) = 1.0847 by Δ(R/D) = 0.0011, which is a confirmation of the extremely high accuracy of H₀ measurements for both methods.

Of course, the direct measurement of H₀ from SNe is correct, and the deviation of the H₀ value obtained from the CMB measurement is due to the wrong assumption that the universe is (IN) flat.

With a correction for this theoretical factor of 1.0847, the exact value determined by the CMB measurement is H₀ = (72.97 ± 0.65) km/s/Mpc. Mean value is H₀(corr CMB + SNe) = (73.00 ± 0.87) km/s/Mpc. This value corresponds to the slightly lower age of the universe then from the ΛCDM model, t₀ = (13.394 ± 0.160) Gy.

4. Discussion

The assumed measurement errors amount to about 1 % of the H₀ values, but they are probably much smaller, because the deviation from the mean value (corr CMB + SNe) is only ΔH₀ = (± 0.04) km/s/Mpc, at the relative error of 5.48∙10^-4. This confirms that both series of measurements were extremely precise, accurate, which gives an answer to one, somewhat awkward question, related to the discovery of dark energy and the accelerated expansion of the universe, for which Nobel Prizes were awarded, and this paper convincingly suggests that this is “just like a mirage” of the (IN) view of a simple (OUT)-SCC universe.

Are these awards then “undeserved”? Far from it, because without the dedicated work of thousands of scientists who have been measuring this “mirage” of radial and transverse (IN) distances so precisely for years, there would be neither Kuhn's crisis in cosmology, nor this new paradigm, which is so convincing precisely because there are such precise measurements of the Hubble constant H₀ determined in two different ways.

That's how science works. Old models are replaced with new ones using new paradigms based on new principes. The so-called Hubble tension, which no longer exists, confirms very precisely that we live in a 3-sphere universe with today's radius of curvature:

$$R_0=\sqrt{12}\cdot T\left(BB-NOW\right)=(46.398\pm 0.554)\mathrm{G}\mathrm{l}\mathrm{y}$$

The so-called S₈ tension is also resolved. Data from Planck TT, TE, EE + low E in combination with secondary CMB anisotropies yield

S₈ = (0.834 ± 0.013), which is a factor of 1.0847 greater than the actual value. So, the CMB corrected value is

S₈ = (0.769 ± 0.012) compared to a combination of local large-scale structure probes [12]

S₈ = 0.766 (+0.020/-0.014). Here too, the limits of 68% CL are probably excessively large, because the deviation from their mean value

S₈(corr CMB + local) = 0.7675 is (± 0.0015), at the level of the relative error of 19.5∙10^-4.

The relative error of the deviation of S₈ from the (corr CMB + local measurements) mean value is about 4 times higher than the relative error of the deviation of H₀ from the (corr CMB + Sne measurements) mean value.

Many astronomers and astrophysicists who deal with the formation and evolution of structures of different scales in the universe do not have to doubt their theories and models, confused by the data sent by the JWST, because all these problems come down to the unexpected (incorrectly determined) early time of occurrence of these structures, earlier than previously thought.

Everything is probably fine with theories and models, especially for JWST measurements for large redshift z, because t(z) should be calculated using this simple expression t(z) = 13.394/(1+z) Gy.

For example, the galaxy JADES-GS-z14-0 has a redshift z = 14.32 (+0.08/-0.20), which is currently the most distant known galaxy. We see this galaxy when, according to ΛCDM t(z) is only 290 My after BB. The correct value is 935 My after BB.

5. Conclusion

Because all results presented in this work convincingly suggests that standard ΛCDM comology is distorted IN-side view of a much simpler SCC cosmology, I hope that this work will be an incentive and inspiration to many cosmologists for the development of this new paradigm of cosmology, new cosmological research, measurement, theorizing, questioning, and reinterpreting old and new data and models from this literally new perspective of looking at cosmology:

(IN)-ΛCDM model → (OUT)-SCC model,

analogous to jumping from Geocentric to Heliocentric system. This time, I hope, much faster and more painlessly.