Submitted:
19 November 2024
Posted:
20 November 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
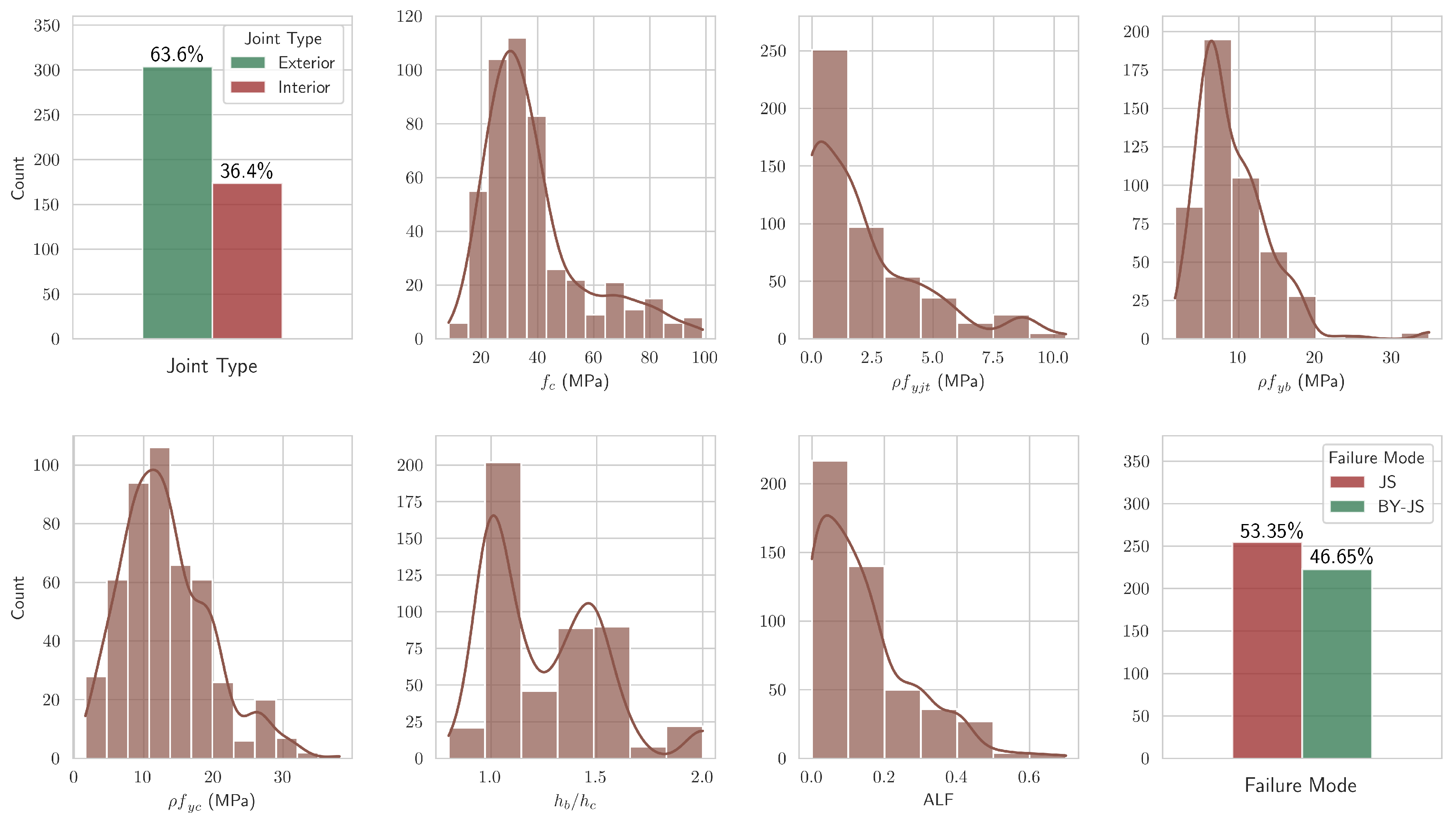
2.1. Dataset Overview and Feature Engineering
- The joint type: This categorical variable, describes whether the joint is “interior”, i.e., beams are attached on two opposing sides, or “exterior”.
- : The compressive strength of the concrete, measured in MPa.
- : The amount of transverse reinforcement, i.e., stirrups, in the joint, expressed as a percentage of its area.
- : The yield strength of the stirrups in the joint, measured in MPa.
- : The amount of longitudinal reinforcement in the beam and column, respectively, expressed as a percentage of the respective cross-sectional areas.
- : The yield strength of the longitudinal reinforcement in the beam and column, respectively, measured in MPa.
- : The height (h) and width (b) of the beam and column, respectively, measured in mm.
- ALF: The Axial Load Factor,i.e., the axial load applied to the column normalized to the respective compressive strength .
- The failure mode: This is the dependent variable in the present study and takes two distinct values. Specifically, the value “Joint Shear” (“JS”) corresponds to cases where the joint failed suddenly in a brittle, shear manner and the beam had not yet reached its yield capacity. Accordingly, the value “Beam Yield-Joint Shear” (“BY-JS”) pertains to specimens wherein the ductile flexural yielding of the beam reinforcement preceded the brittle shear failure of the joint [3].
2.2. Machine Learning Modeling
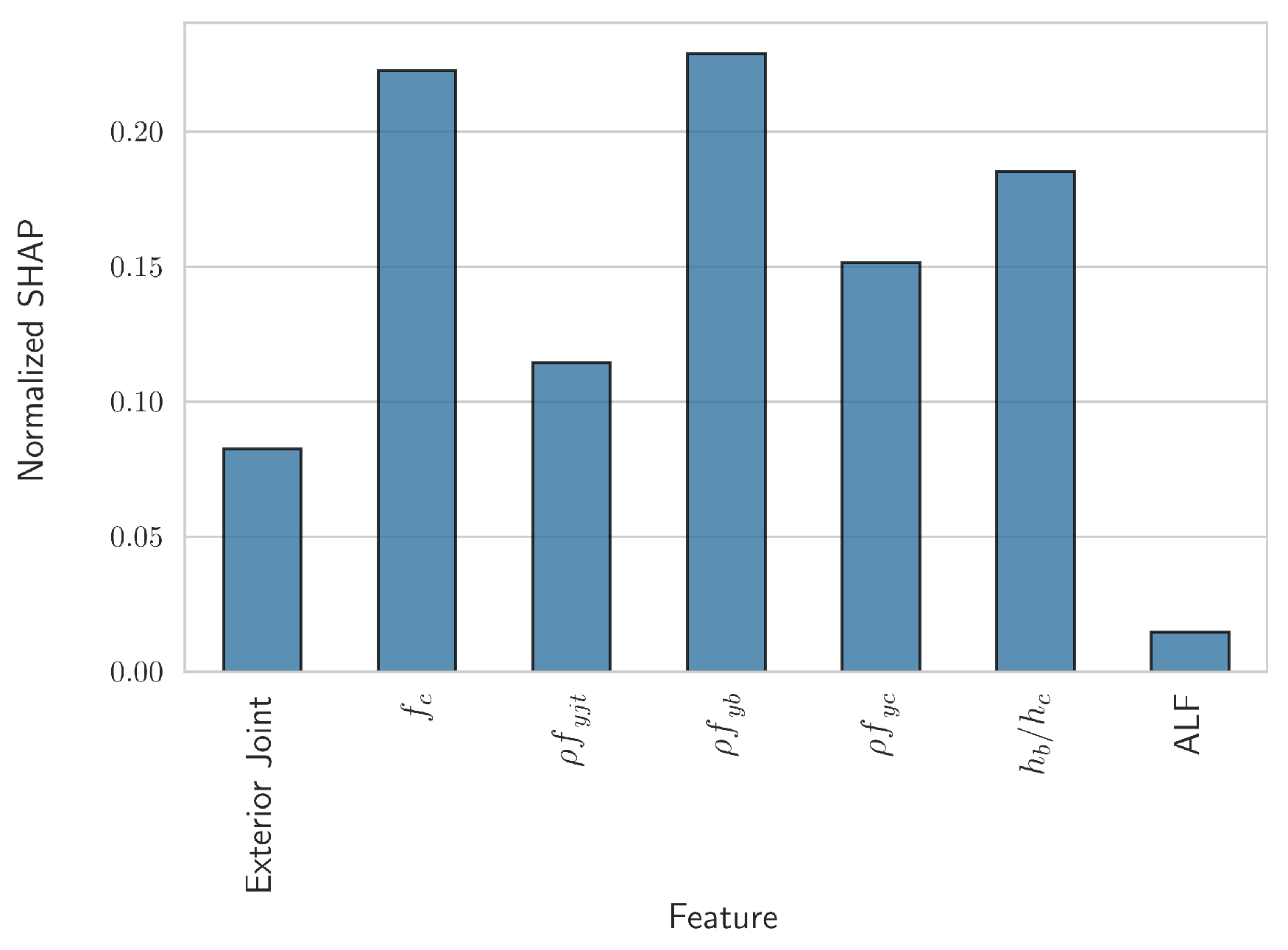
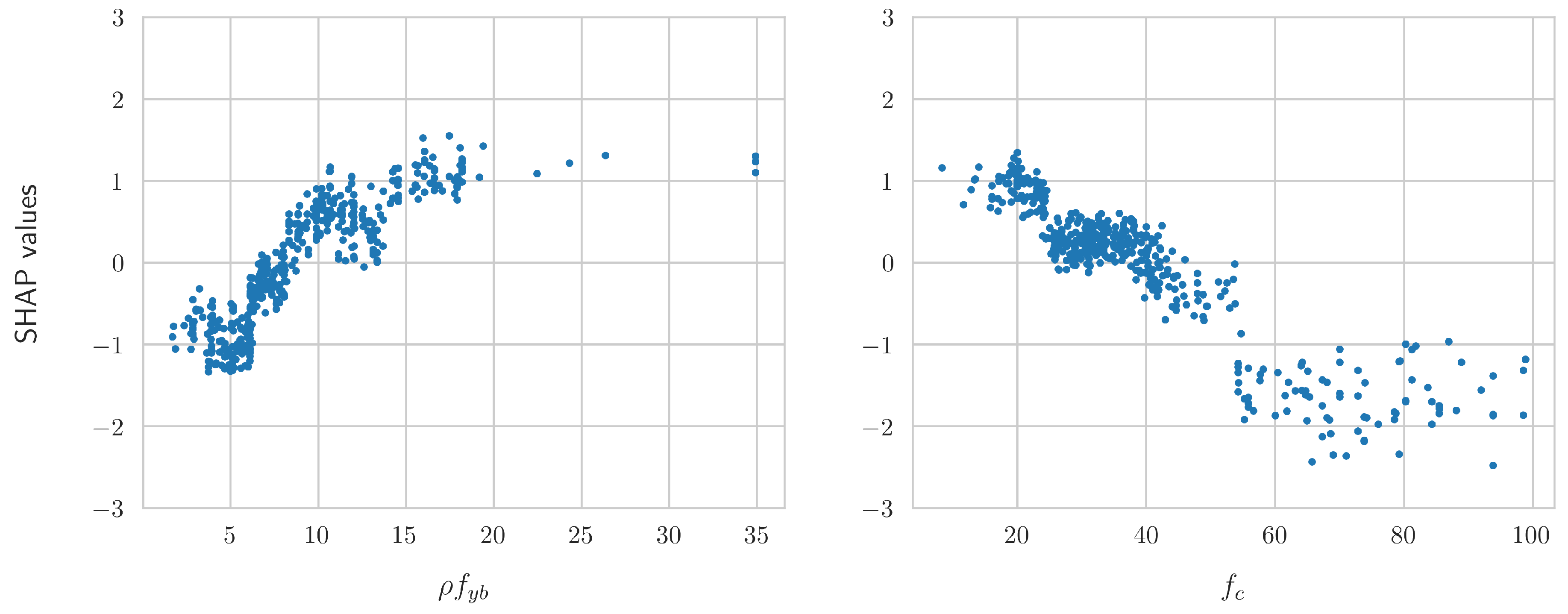
2.3. Shapley Additive Explanations (SHAP values)
3. Results
3.1. Xgboost Classification Results
3.2. Derivation of the Analytical Equations
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| RC | Reinforce Concrete |
| ML | Machine Learning |
| ANN | Artifical Neural Network |
| SHAP | SHapley Additive exPlanations |
| k-NN | k-Nearest Neighbors |
| SVM | Support Vector Machine |
| OLS | Ordinary Least Squares |
| XGBoost | eXtreme Gradient Boosting |
| P-R | Precision-Recall |
References
- Najafgholipour, M.; Dehghan, S.; Dooshabi, A.; Niroomandi, A. Finite element analysis of reinforced concrete beam-column connections with governing joint shear failure mode. Latin American Journal of Solids and Structures 2017, 14, 1200–1225. [Google Scholar] [CrossRef]
- Karabini, M.; Karampinis, I.; Rousakis, T.; Iliadis, L.; Karabinis, A. Machine Learning Ensemble Methodologies for the Prediction of the Failure Mode of Reinforced Concrete Beam–Column Joints. Information 2024, 15, 647. [Google Scholar] [CrossRef]
- Kuang, J.; Wong, H. Behaviour of Non-seismically Detailed Beam-column Joints under Simulated Seismic Loading: A Critical Review. fib Symposium on Concrete Structures: the Challenge of Creativity, Avignon, France, 2004.
- Braga, F.; Caprili, S.; Gigliotti, R.; Salvatore, W.; others. Hardening slip model for reinforcing steel bars. Earthquakes and Structures 2015, 9, 503–539. [Google Scholar] [CrossRef]
- Recommendations for Design of Beam-Column Connections in Monolithic Reinforced Concrete Structures (ACI 352R-02). Technical report, American Concrete Institute, Indianapolis, IN, USA, 2002.
- Retrofitting of Concrete Structures by Externally Bonded FRPs with Emphasis on Seismic Applications (FIB-35). Technical report, TheInternational Federation for Structural Concrete, Lausanne, Switzerland, 2002.
- EN 1992 Eurocode 2 Part 1-1: General rules and rules for buildings. Technical report, European Committee for Standardization, Brussels, Belgium, 2004.
- Karayannis, C.G.; Sirkelis, G.M. Strengthening and rehabilitation of RC beam–column joints using carbon-FRP jacketing and epoxy resin injection. Earthquake Engineering & Structural Dynamics 2008, 37, 769–790. [Google Scholar]
- Tsonos, A.; Stylianidis, K. Pre-seismic and post-seismic strengthening of reinforced concrete structural subassemblages using composite materials (FRP). Proc., 13th Hellenic Concrete Conference, 1999, Vol. 1, pp. 455–466.
- Park, R.; Paulay, T. Reinforced concrete structures; John Wiley & Sons: Hoboken, NJ, USA, 1991. [Google Scholar]
- Tsonos, A.G. Cyclic load behaviour of reinforced concrete beam-column subassemblages of modern structures. WIT Transactions on The Built Environment 2005, 81. [Google Scholar]
- Antonopoulos, C.P.; Triantafillou, T.C. Experimental investigation of FRP-strengthened RC beam-column joints. Journal of Composites for Construction 2003, 7, 39–49. [Google Scholar] [CrossRef]
- Nikolić, Ž.; Živaljić, N.; Smoljanović, H.; Balić, I. Numerical modelling of reinforced-concrete structures under seismic loading based on the finite element method with discrete inter-element cracks. Earthquake Engineering & Structural dynamics 2017, 46, 159–178. [Google Scholar]
- Thai, H.T. Machine learning for structural engineering: A state-of-the-art review. Structures. Elsevier, 2022, Vol. 38, pp. 448–491. [CrossRef]
- Kaveh, A. Applications of Artificial Neural Networks and Machine Learning in Civil Engineering. Studies in Computational Intelligence 2024, 1168, 472. [Google Scholar]
- Kotsovou, G.M.; Cotsovos, D.M.; Lagaros, N.D. Assessment of RC exterior beam-column Joints based on artificial neural networks and other methods. Engineering Structures 2017, 144, 1–18. [Google Scholar] [CrossRef]
- Suwal, N.; Guner, S. Plastic hinge modeling of reinforced concrete Beam-Column joints using artificial neural networks. Engineering Structures 2024, 298, 117012. [Google Scholar] [CrossRef]
- Mangalathu, S.; Jeon, J.S. Classification of failure mode and prediction of shear strength for reinforced concrete beam-column joints using machine learning techniques. Engineering Structures 2018, 160, 85–94. [Google Scholar] [CrossRef]
- Oviedo, F.; Ferres, J.L.; Buonassisi, T.; Butler, K.T. Interpretable and explainable machine learning for materials science and chemistry. Accounts of Materials Research 2022, 3, 597–607. [Google Scholar] [CrossRef]
- Marie, H.S.; Abu El-hassan, K.; Almetwally, E.M.; El-Mandouh, M.A. Joint shear strength prediction of beam-column connections using machine learning via experimental results. Case Studies in Construction Materials 2022, 17, e01463. [Google Scholar] [CrossRef]
- Gao, X.; Lin, C. Prediction model of the failure mode of beam-column joints using machine learning methods. Engineering Failure Analysis 2021, 120, 105072. [Google Scholar] [CrossRef]
- Karampinis, I.; Morfidis, K.; Iliadis, L. Derivation of Analytical Equations for the Fundamental Period of Framed Structures Using Machine Learning and SHAP Values. Applied Sciences 2024, 14, 9072. [Google Scholar] [CrossRef]
- Verdonck, T.; Baesens, B.; Óskarsdóttir, M.; vanden Broucke, S. Special issue on feature engineering editorial. Machine learning 2024, 113, 3917–3928. [Google Scholar] [CrossRef]
- Ahsan, M.M.; Mahmud, M.P.; Saha, P.K.; Gupta, K.D.; Siddique, Z. Effect of data scaling methods on machine learning algorithms and model performance. Technologies 2021, 9, 52. [Google Scholar] [CrossRef]
- Lee, H.; Yun, S. Strategies for Imputing Missing Values and Removing Outliers in the Dataset for Machine Learning-Based Construction Cost Prediction. Buildings 2024, 14, 933. [Google Scholar] [CrossRef]
- Ghosh, K.; Bellinger, C.; Corizzo, R.; Branco, P.; Krawczyk, B.; Japkowicz, N. The class imbalance problem in deep learning. Machine Learning 2024, 113, 4845–4901. [Google Scholar] [CrossRef]
- Kumar, P.; Bhatnagar, R.; Gaur, K.; Bhatnagar, A. Classification of imbalanced data: review of methods and applications. IOP conference series: materials science and engineering. IOP Publishing, 2021, Vol. 1099, p. 012077. [CrossRef]
- Wongvorachan, T.; He, S.; Bulut, O. A comparison of undersampling, oversampling, and SMOTE methods for dealing with imbalanced classification in educational data mining. Information 2023, 14, 54. [Google Scholar] [CrossRef]
- Jeong, D.H.; Kim, S.E.; Choi, W.H.; Ahn, S.H. A comparative study on the influence of undersampling and oversampling techniques for the classification of physical activities using an imbalanced accelerometer dataset. Healthcare 2022, 10, 1255. [Google Scholar] [CrossRef]
- Sen, P.C.; Hajra, M.; Ghosh, M. Supervised classification algorithms in machine learning: A survey and review. Emerging Technology in Modelling and Graphics: Proceedings of IEM Graph 2018. Springer, 2020, pp. 99–111. [CrossRef]
- Kotsiantis, S.B.; Zaharakis, I.D.; Pintelas, P.E. Machine learning: a review of classification and combining techniques. Artificial Intelligence Review 2006, 26, 159–190. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August, 2016, pp. 785–794.
- Friedman, J.H. Greedy function approximation: a gradient boosting machine. Annals of Statistics, 1189. [Google Scholar]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I. From local explanations to global understanding with explainable AI for trees. Nature Machine Intelligence 2020, 2, 56–67. [Google Scholar] [CrossRef]
- Lundberg, S.; Su-In, L. A unified approach to interpreting model predictions. arXiv preprint arXiv:1705.07874, arXiv:1705.07874 2017.
- Linardatos, P.; Papastefanopoulos, V.; Kotsiantis, S. Explainable AI: A review of machine learning interpretability methods. Entropy 2020, 23, 18. [Google Scholar] [CrossRef]
- Shapley, L. Notes on the n-Person Game-II: The Value of an n-Person Game. RAND Corporation, Santa Monica, CA, USA,.
- Aas, K.; Jullum, M.; Løland, A. Explaining individual predictions when features are dependent: More accurate approximations to Shapley values. Artificial Intelligence 2021, 298, 103502. [Google Scholar] [CrossRef]
- Norton, E.C.; Dowd, B.E. Log odds and the interpretation of logit models. Health Services Research 2018, 53, 859–878. [Google Scholar] [CrossRef]
- Raschka, S. An overview of general performance metrics of binary classifier systems. arXiv preprint arXiv:1410.5330, arXiv:1410.5330 2014.
- Allgaier, J.; Pryss, R. Cross-Validation Visualized: A Narrative Guide to Advanced Methods. Machine Learning and Knowledge Extraction 2024, 6, 1378–1388. [Google Scholar] [CrossRef]
- Karampinis, I.; Iliadis, L.; Karabinis, A. Rapid Visual Screening Feature Importance for Seismic Vulnerability Ranking via Machine Learning and SHAP Values. Applied Sciences 2024, 14, 2609. [Google Scholar] [CrossRef]
- Buckland, M.; Gey, F. The relationship between recall and precision. Journal of the American society for Information Science 1994, 45, 12–19. [Google Scholar] [CrossRef]
- Gordon, M.; Kochen, M. Recall-precision trade-off: A derivation. Journal of the American Society for Information Science 1989, 40, 145–151. [Google Scholar] [CrossRef]
- Sofaer, H.R.; Hoeting, J.A.; Jarnevich, C.S. The area under the precision-recall curve as a performance metric for rare binary events. Methods in Ecology and Evolution 2019, 10, 565–577. [Google Scholar] [CrossRef]
- Miao, J.; Zhu, W. Precision-recall curve (PRC) classification trees. Evolutionary intelligence 2022, 15, 1545–1569. [Google Scholar] [CrossRef]
- Fan, J.; Upadhye, S.; Worster, A. Understanding receiver operating characteristic (ROC) curves. Canadian Journal of Emergency Medicine 2006, 8, 19–20. [Google Scholar] [CrossRef]
- Yang, S.; Berdine, G. The receiver operating characteristic (ROC) curve. The Southwest Respiratory and Critical Care Chronicles 2017, 5, 34–36. [Google Scholar] [CrossRef]
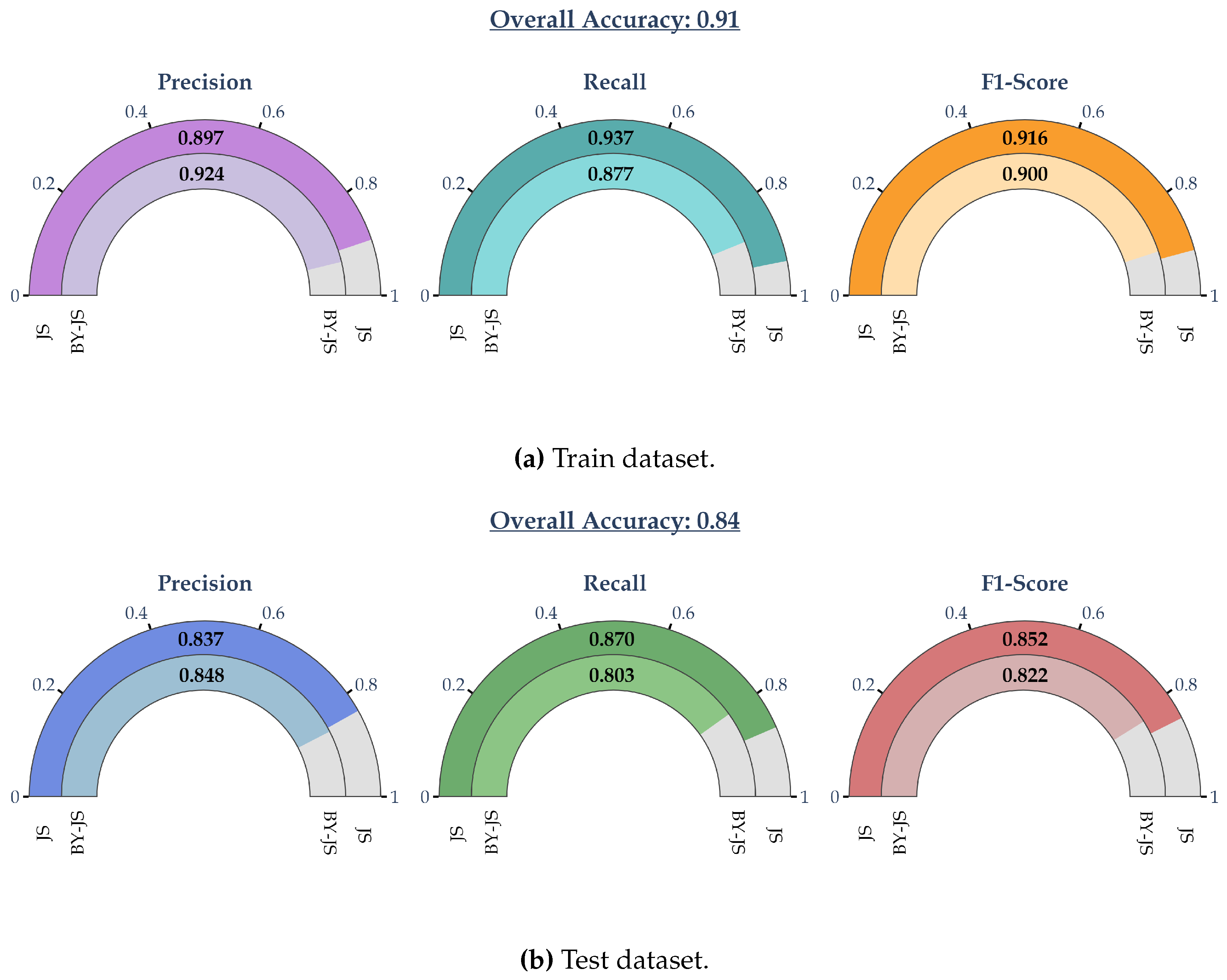
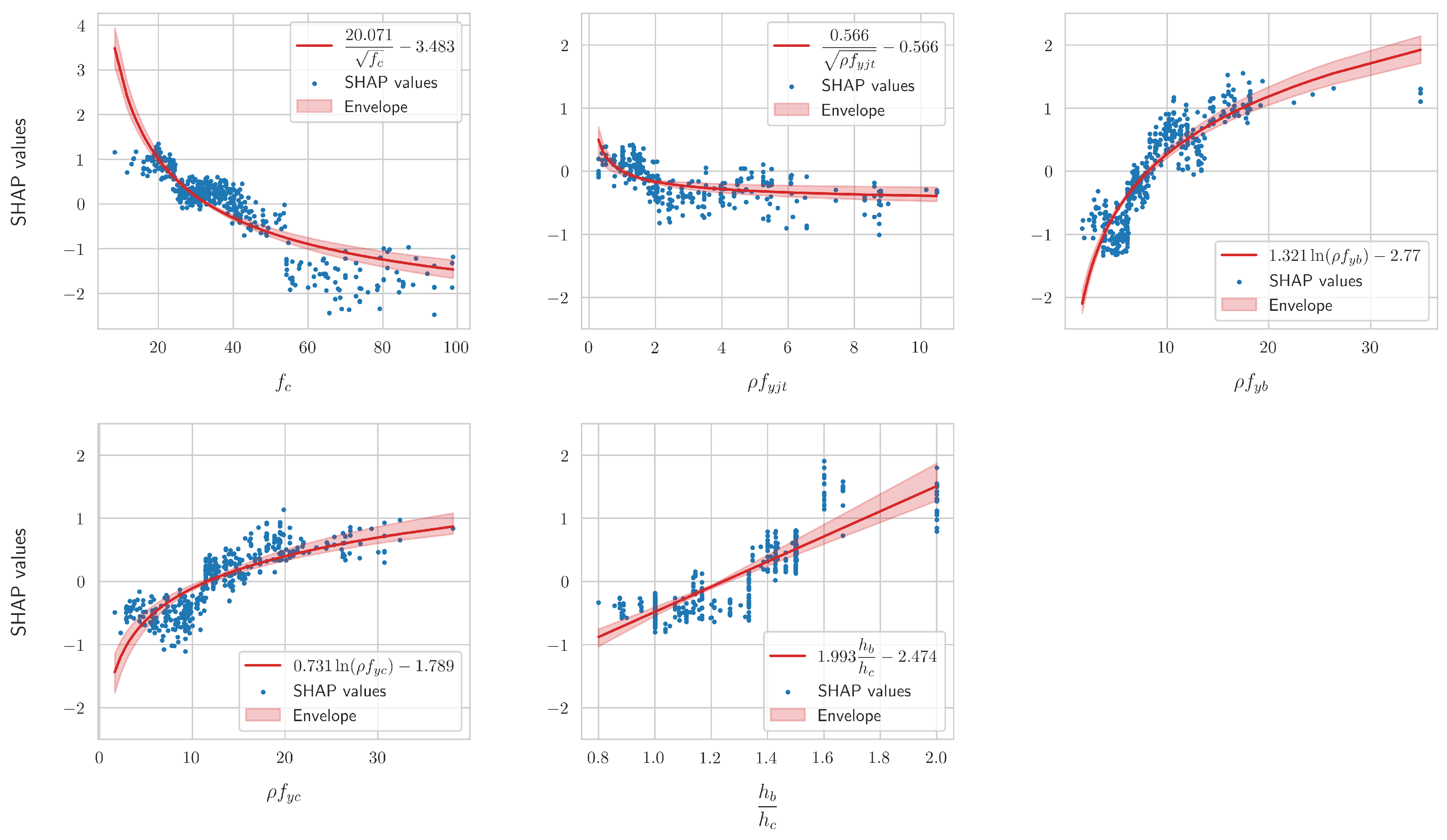
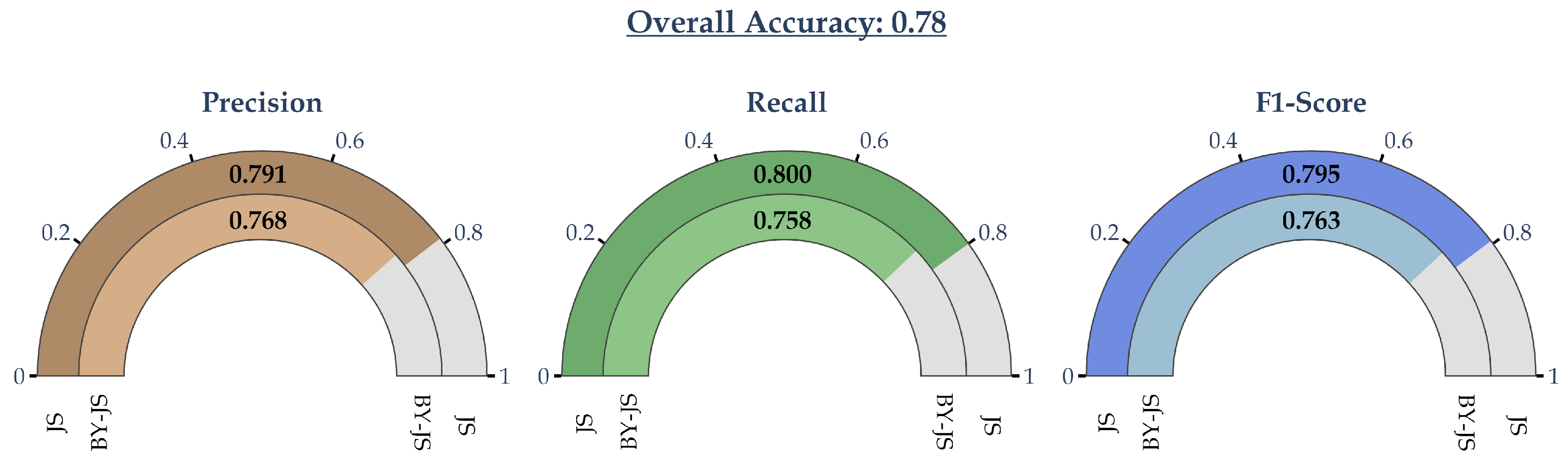
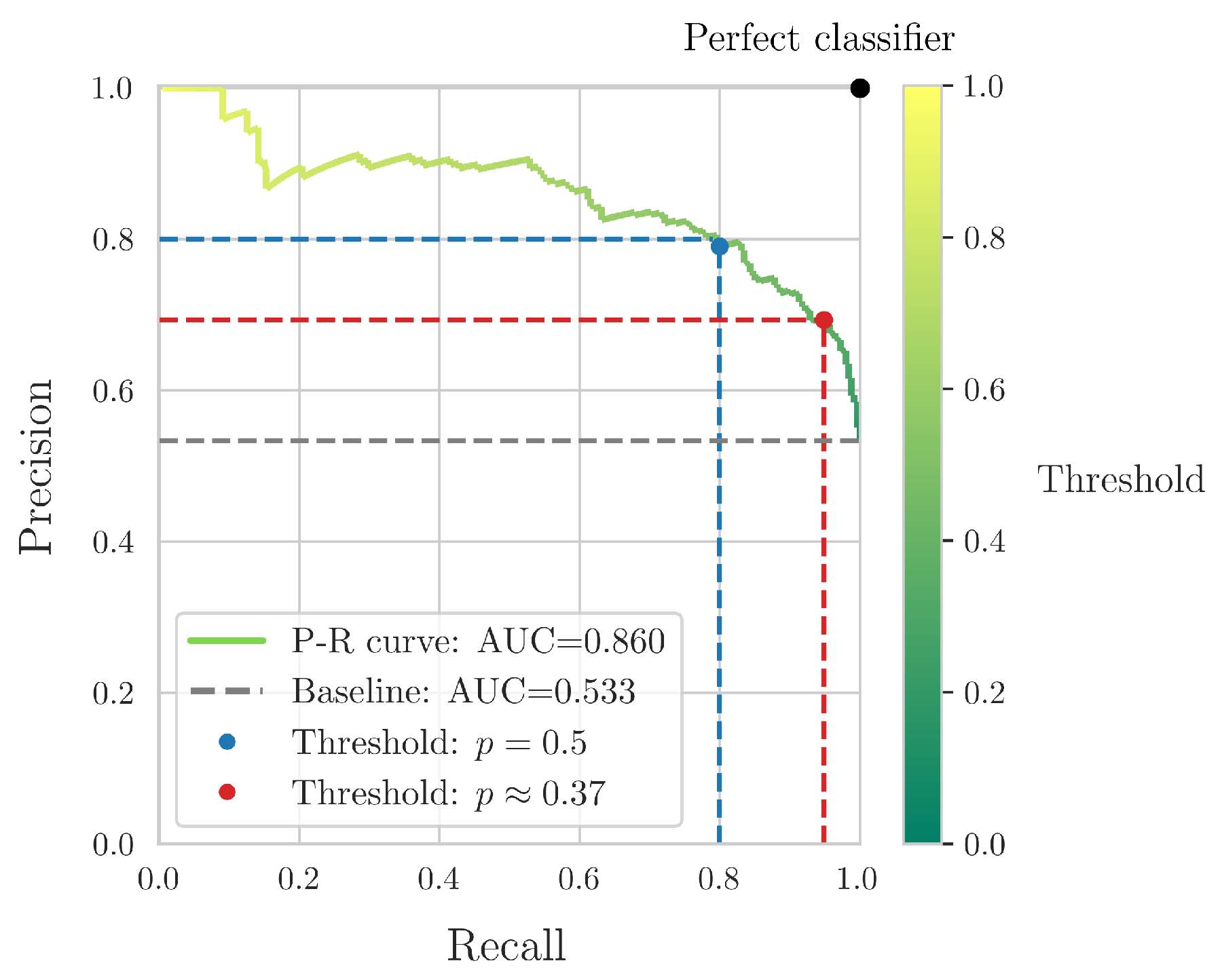
| Training set | Testing set | |||
|---|---|---|---|---|
| BY-JS | JS | BY-JS | JS | |
| Precision | ||||
| Recall | ||||
| F1-Score | ||||
| Accuracy | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





