Gravitational Sensors and the Structure of the Gravitational Field in Six Dimensions of Space and Time

1. Introduction

Gravitational waves have long been a cornerstone prediction of general relativity, and their existence has subsequently been confirmed through experimental observation [1]. In parallel, gravitational wave detectors have achieved extraordinarily high accuracies, enabling the precise measurement of these elusive signals [2,3]. Moreover, recent theoretical advancements based on six-dimensional space–time frameworks suggest that time may possess two mutually orthogonal dimensions, both of which can be influenced by gravitational waves [4]. Although electromagnetic waves are known to induce distortions in both space and time, no direct interaction between electromagnetic phenomena and the gravitational field has yet been observed.

In this article, we employ the distinctive properties of Möbius space to establish a direct link between electromagnetism and gravity. In doing so, we demonstrate that distortions of the gravitational field can be detected and quantitatively measured using specially engineered Möbius coils. Despite the relatively high noise levels and error margins associated with our initial test samples, our experimental setup is capable of capturing and recording minute changes in the gravitational field.

An important aspect of our findings is the dimensional distinction between gravitational waves and gravitational field distortions: while gravitational waves appear to oscillate in five dimensions, the measured distortions of the gravitational field are confined to four dimensions. This observation lays the groundwork for the theoretical development of antigravity mechanisms, as explored further in this work [5,6,7].

2. Field Stricture

The gravitational field is modeled as a hypercone in five-dimensional space (Figure 1). This hypercone rotates within a closed Möbius space. The field is composed of discrete layers characterized by variations in space-time density, with the intervals between layers analogous to the intervals between musical notes. Furthermore, the spacing of prime numbers in six distinct groups conforms to the theorem stated in .(2.1) Table 1

$$\begin{array}{l}{Log}_2\left({\displaystyle \frac{f_2}{f_1}}\right)=c\\ e^{\pi }+\phi =24.758\\ {Log}_{24}\left({\displaystyle \frac{72}{3}}\right)=1\sec ({sin}^{-1}({Log}_n\left({\displaystyle \frac{s}{k}}\right)={\displaystyle \frac{1}{\sqrt{1-\frac{{\left(\ln \left(\frac{s}{k}\right)\right)}^2}{{\left(\ln \left(n\right)\right)}^2}}}}\equiv {\displaystyle \frac{1}{\sqrt{1-\frac{{\left(v\right)}^2}{{\left(c\right)}^2}}}}\\ \Rightarrow sec({sin}^{-1}({Log}_n\left({\displaystyle \frac{s}{k}}\right)y={\displaystyle \frac{1}{\sqrt{1+\frac{{-y^2\left(ln\right(\frac{s}{k}\left)\right)}^2}{{\left(ln\right(n\left)\right)}^2}}}} \end{array}$$

2.1

In a six-dimensional spacetime framework, time is decomposed into two mutually orthogonal dimensions. The gravitational field affects both dimensions. Figure 2

Mass arises from variations in the density of space over time. Fluctuations in density can drive the emergence or dissolution of mass. (2.2) The eccentricity of the ellipse along one axis induces a reciprocal centralization (or reverse centrality) in the other axis. Mass is attributed to the absence of three-dimensional matter within higher-dimensional spaces. Consequently, the eccentricity of a three-dimensional ellipse within a gravitational field results in hyperbolic equations that describe free-fall motion. Time is defined as a geometric potential difference, and mass originates from variations in geometric density over time. The three-dimensional structure of matter interacts with tensions arising from two real temporal dimensions, which are analogous to spatial dimensions. These tensions, governed by fundamental forces such as Planck's constant and the gravitational constant, result in a twofold stress in temporal dimensions compared to the single-fold stress in spatial dimensions. This dynamic forms reverse elliptical eccentricity, directly governed by the golden ratio $\phi$. Consequently, the fractal growth observed in nature is fundamentally influenced by variations in density and the golden constant, establishing a profound connection between geometry, density, and symmetry in both space and time. There are two types of mass: the mass arising from motion in space, known as relativistic mass, and the mass originating from motion in temporal dimensions, referred to as intrinsic mass. Intrinsic mass emerges from the quantized oscillation of a three-dimensional rigid body within a rotating, expanding Möbius-like space. This space, involving higher dimensions, experiences internal tension, which is termed intrinsic mass. By substituting hν into the mass-energy equivalence equation, the essence of intrinsic mass can be defined. Furthermore, Newton's equation relating mass to acceleration illustrates the emergence of mass from geometric transformations or density variations.(2.2)

$$\begin{array}{l}{m}_t={\displaystyle \frac{h\nu }{c^2}}{m}_x={\displaystyle \frac{F}{a}}\\ \sec ({sin}^{-1}({Log}_n\left({\displaystyle \frac{{\rho }_2}{{\rho }_1}}\right)\left(-\sqrt{{\displaystyle \frac{2GM}{r}}}\right)={\displaystyle \frac{1}{\sqrt{1+\frac{-2GM}{r{c}^2}}}}\Rightarrow \ln \left(n\right)=c\\ \left({\displaystyle \frac{{\left(\frac{1}{2\pi }\right)}^3+{\left(\frac{1}{2}\right)}^6{\pi }^3\left(\frac{1}{6}\right){\pi }^3\left(\frac{\left(\frac{3\pi -6}{2\pi }\right)}{360}\right){\phi }^3}{c}}\right)\cong G\end{array}$$

2.2

The different layers of the gravitational field follow groups of prime numbers. Also, these layers have a direct relationship with the wave function. (2.3) Table 1

$$\begin{array}{c}{\int }_{-\rho }^{+\rho }{\int }_{-t}^{+t}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{\left|\psi (\rho ,t,x)\right|}^{2}d\rho dtdx=1,\left|\mathsf{\Psi }⟩=b_1\left|{\tilde{\psi }}_1⟩+b_2\left|{\tilde{\psi }}_2⟩+\dots +b_n\left|{\tilde{\psi }}_n⟩\right.\right.\right.\right.\\ \left|\tilde{\psi }⟩={\alpha }_1\left|A_1⟩+{\alpha }_2\left|A_2⟩+{\alpha }_3\left|A_3⟩+{\alpha }_4\left|A_4⟩+\right.\right.\right.\right.\right.{\alpha }_5\left|A_5⟩+{\alpha }_6\left|A_6⟩\right.\right.\end{array}$$

2.3

3. Result

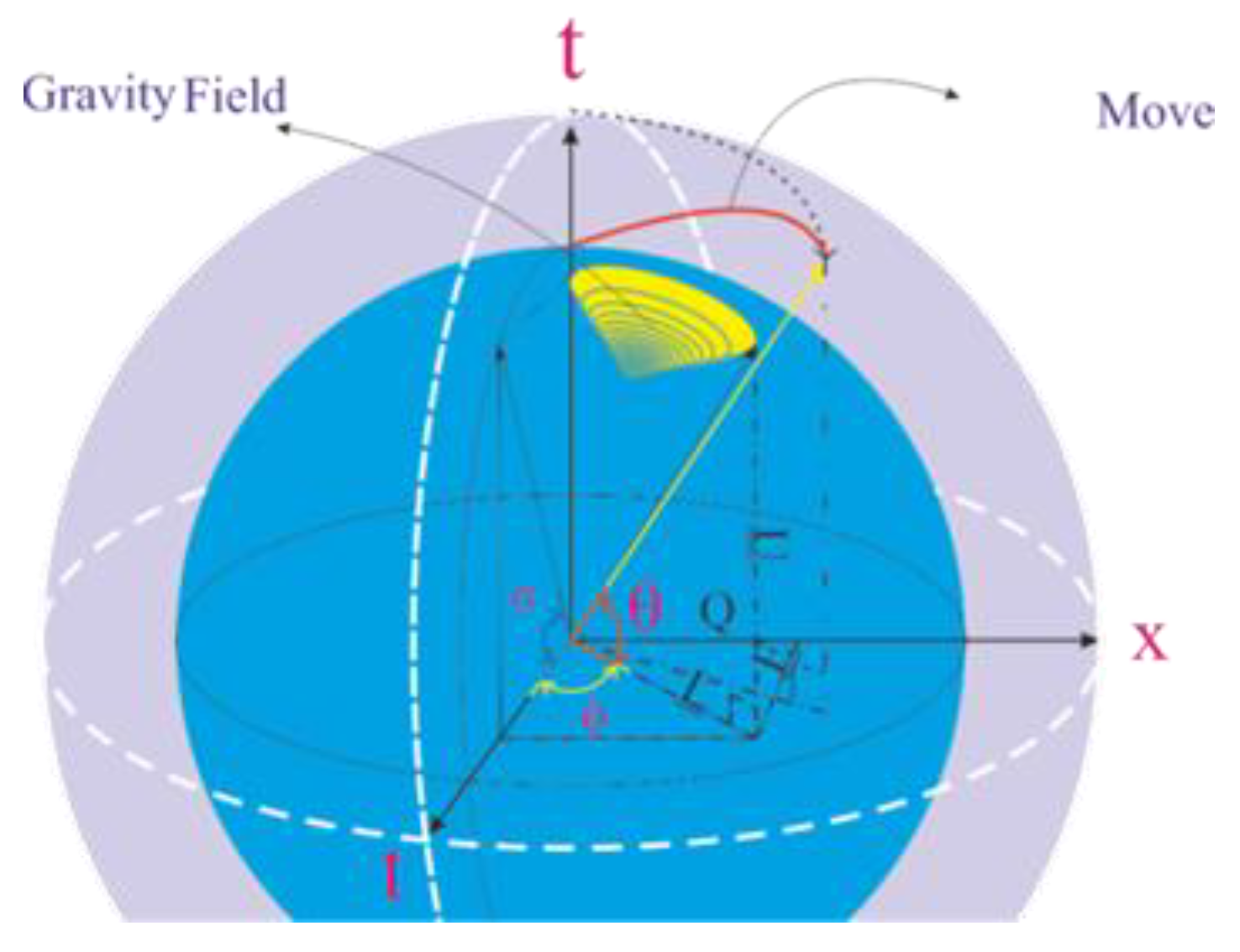
A. Time Evolution in Möbius Space

Time emerges as a result of geometric potential differences. Within the six-dimensional space-time framework, three-dimensional matter moves under tension in the closed, five-dimensional Möbius space while progressing through the real dimensions of time. Density variations (Δρ) directly influence the evolution of time, signifying that without the passage of time, neither mass nor magnetic fields could exist. Mass arises from inhomogeneities in space and time, leading to negative density and movement of mass across temporal dimensions.

This principle explains why, without the passage of time, objects in a gravitational field do not fall but instead follow the geodesics of space-time (e.g., the motion of a ball and feather). Consequently, movement through space slows time or reduces motion through the temporal dimensions, manifesting as relativistic mass.

In the Möbius-Klein bottle geometry, density and pressure changes in gravitational fields follow a generalized Bernoulli principle. This principle governs the meta-geometric distribution of mass into six-dimensional wave function packets, modeled by a six-dimensional Fourier series. These packets depict the relationship between density variations and field dynamics, aligning gravitational behavior with the Riemann zeta function via prime number distributions.

Based on this framework, the relationship between density variations and the passage of time takes on a deeper meaning. Density (ρ) can be equivalently expressed as a spatial length (Δx) within space-time, emphasizing that these two are fundamentally interchangeable in this context. This equivalence allows us to reinterpret density variations in terms of spatial changes, leading to the replacement of velocity (v) with density changes (Δρ) in relevant formulations.

In this extended understanding, time (t) becomes equivalent to a geometric potential difference (Δɸ), further solidifying the link between temporal flow and variations in space and geometry.

Thus, the relationship can be refined as

Based on the framework, the relationship between density variations and the passage of time can be expressed as follows: (3.1)

$${\displaystyle \frac{1}{sin\left({cos}^{-1}\left(\frac{\mathrm{v}}{\mathrm{c}}\right)\right)}}={\displaystyle \frac{m_0}{m}}={\displaystyle \frac{t_0}{t}}\equiv ∆\rho \propto ∆t$$

3.1

Density and Geometric Potential:

$$sec\left({sin}^{-1}\left(\theta \right)\right)={\displaystyle \frac{1}{∆\rho }}$$

3.2

and equivalently:

$$∆x^2=\rho c∆t^2={\displaystyle \frac{1}{\rho c}}∆t^2+∆x^2=c^2∆t=∆\varphi$$

3.3

The logarithmic base k in Möbius space follows the regular spacing between prime numbers in sextuple groups. Moreover, this equation can also have a foundation based on photon density and the speed of light. Accordingly, the general equation is expressed as follows :(3.4)

$$\mathrm{s}\mathrm{e}\mathrm{c}({sin}^{-1}({\log }_k\left({\displaystyle \frac{\rho }{{\rho }_0}}\right))={\displaystyle \frac{1}{\sqrt{1-\frac{{\left(\ln \left(\frac{\rho }{{\rho }_0}\right)\right)}^2}{{\left(\mathit{ln}\left(k\right)\right)}^2}}}}$$

3.4

The analysis of prime gaps within sextuple groups demonstrates a structured distribution influenced by periodic density variations in space-time. The observed gaps, predominantly values such as 18, 36, 54, and 72, align with a logarithmic model where differences between consecutive primes follow periodic patterns. These patterns reflect the evolving dynamics of time and density in higher-dimensional geometries, such as a five-dimensional Möbius framework expanding into a sixth dimension. The relationships incorporate correlations with photon density and the speed of light, emphasizing the interconnectedness of prime distribution and geometric structures. (3.5) Table 1:

$${∆}_n=P_n-P_{n-1}\Rightarrow {∆}_n=a.P_n+b.\ln \left(P_{n-1}\right)+c.f\left(n\right)$$

3.5

f(n) represents a periodic function capturing the alternation of gaps, aligned with observed values like 18,36,54, and 72.

Constants a, b, and c adjust based on the prime density in the analyzed group.

In Möbius geometry, such distributions could mirror the regular spacing of structural "geodesics," with density variations reflecting curvature within the space-time manifold.

This formulation underlines how spatial density variations inherently drive both the temporal evolution of a system and its geometric potential, offering a cohesive interpretation of density, space, and time within a unified framework. Thus, density behaves like a length over time, rotating around the mass field and creating the dual-state spin of an object in two temporal dimensions. The radius of the field is directly proportional to the variations in density. Additionally, the generalized principle of Bernoulli’s equation, derived from the motion of objects in the temporal dimension and the preservation of the constancy of time passage, determines the wave function states in the closed Möbius space based on prime numbers and the meta-geometric distribution of mass. Accordingly, the connection between the cosmological constant, the golden ratio, the gravitational constant, and Planck's constant is determined within a five-dimensional space expanding into the sixth dimension:(3.6)

$$\begin{array}{l}\mathrm{P}=\mathrm{P}\left(\mathrm{static}\right)+\mathrm{P}\left(\mathrm{dynamic}\right)+\mathrm{P}\left(\mathrm{gravitational}\right)+\mathrm{P}\left(\mathrm{topological}\right)\\ \Rightarrow h^2{G}^2{e}^{{\pi }^3{\phi }^2}=\mathsf{\Lambda }\\ {\int }_{-\rho }^{+\rho }{\int }_{-t}^{+t}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{\left|\psi (\rho ,t,x)\right|}^{2}d\rho dtdx=1,\left|\mathsf{\Psi }⟩=b_1\left|{\tilde{\psi }}_1⟩+b_2\left|{\tilde{\psi }}_2⟩+\dots +b_n\left|{\tilde{\psi }}_n⟩\right.\right.\right.\right.\\ \left|\tilde{\psi }⟩={\alpha }_1\left|A_1⟩+{\alpha }_2\left|A_2⟩+{\alpha }_3\left|A_3⟩+{\alpha }_4\left|A_4⟩+\right.\right.\right.\right.\right.{\alpha }_5\left|A_5⟩+{\alpha }_6\left|A_6⟩\right.\right.\\ \mathsf{\Psi }\left(\rho ,x,t\right)={\displaystyle \sum _{n=1}^4}{\displaystyle \sum _{m=1}^4}{\displaystyle \sum _{k=1}^4}{C}_{nmk}cos\left({\displaystyle \frac{2\pi n}{L_{\rho }}}\right)+sin\left({\displaystyle \frac{2\pi m}{L_x}}\right)+isec\left({\displaystyle \frac{2\pi k}{T}}\right)\end{array}$$

3.6

$$\begin{array}{l}{\mathsf{\Psi }}^{\mathrm{*}}\left(\rho ,x,t\right)={\displaystyle \sum _{n=1}^4}{\displaystyle \sum _{m=1}^4}{\displaystyle \sum _{k=1}^4}{C}_{nmk}cos\left({\displaystyle \frac{2\pi n}{L_{\rho }}}\right)+sin\left({\displaystyle \frac{2\pi m}{L_x}}\right)-isec\left({\displaystyle \frac{2\pi k}{T}}\right)\\ \mathit{\xi }\left(\mathbf{0.5}\mathbf{\pm }\mathit{i}\mathit{t}\right)\mathbf{=}{\displaystyle \frac{\mathbf{1}}{{\mathit{P}}^{\mathit{S}}}}\mathbf{\Rightarrow }\mathit{\xi }{\mathit{\xi }}^{\mathrm{*}}\mathbf{=}{\mathit{s}\mathit{i}\mathit{n}}^{\mathbf{2}}\left(\mathit{\theta }\right)\mathit{\xi }{\mathit{\xi }}^{\mathrm{*}}\mathbf{=}{\mathit{c}\mathit{o}\mathit{s}}^{\mathbf{2}}\left(\mathit{\theta }\right)\mathit{\xi }{\mathit{\xi }}^{\mathrm{*}}\mathbf{=}{\mathit{s}\mathit{i}\mathit{n}}^{\mathbf{2}}\left(\mathit{\varphi }\right)\mathit{\xi }{\mathit{\xi }}^{\mathrm{*}}\mathbf{=}{\mathit{c}\mathit{o}\mathit{s}}^{\mathbf{2}}\left(\mathit{\varphi }\right)\\ \mathit{\xi }\left(\mathit{x}\pm \mathit{i}\mathit{t}\right)\mathbf{=}{\displaystyle \frac{\mathbf{1}}{{\mathit{n}}^{\mathit{s}}}}\mathbf{\Rightarrow }\mathit{\xi }{\mathit{\xi }}^{\mathrm{*}}\mathbf{=}{\mathit{s}\mathit{e}\mathit{c}}^{\mathbf{2}}\left(\mathit{\varphi }\right)\mathit{\xi }{\mathit{\xi }}^{\mathrm{*}}\mathbf{=}{\mathit{c}\mathit{e}\mathit{c}}^{\mathbf{2}}\left(\mathit{\varphi }\right)\\ \mathbf{1}\mathbf{+}{\displaystyle \sum _{\mathit{x}\mathbf{=}\mathbf{1}}^{\mathit{n}}}\left(\left({\displaystyle \frac{\mathit{x}\mathbf{!}\mathbf{+}\mathbf{2}\mathit{x}\mathbf{!}}{\mathbf{2}}}\right)\right)\mathbf{=}\mathbf{1}\mathbf{+}{\displaystyle \frac{\mathbf{3}}{\mathbf{2}}}\mathit{H}\mathit{G}\left(\left[\mathbf{1}\mathbf{,}\mathbf{2}\right]\mathbf{,}\left[\right]\mathbf{,}\mathbf{1}\right)\mathbf{-}{\displaystyle \frac{\mathbf{3}}{\mathbf{2}}}\mathit{\Gamma }\left(\mathit{n}\mathbf{+}\mathbf{2}\right)\mathit{H}\mathit{G}\mathbf{(}\left[\mathbf{1}\mathbf{,}\mathit{n}\mathbf{+}\mathbf{2}\right]\mathbf{,}\left[\right]\mathbf{,}\mathbf{1}\mathbf{)}\end{array}$$

Two-dimensional waves oscillate in three dimensions, while three-dimensional waves oscillate in the fourth dimension. Due to the presence of two orthogonal temporal dimensions, the electric field oscillates in one dimension and the magnetic field oscillates in the other. Over time, they periodically interchange within the temporal dimensions, and this interchange within the closed Möbius space introduces a novel definition of superposition.(3.7)

$$\mathsf{\Psi }\left(t_1,t_2\right)=E_0\cos \left(\omega t_1\right)+B_0\cos \left(\omega t_2\right)$$

3.7

Parallel transport in the closed Möbius space remains stable when the governing laws are homogeneous and isotropic. Accordingly, the necessity of displacement based on prime numbers in the wave function introduces the presence of a wave tensor and a force tensor, which are linked to the fundamental constants of nature, into the final equation.(3.8)

$${\mathit{G}}_{\mathit{\mu }\mathit{\nu }}\mathbf{=}\left[\begin{array}{cccccc}{\displaystyle \frac{\mathbf{10}}{{\mathit{r}}^{\mathbf{2}}}}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\displaystyle \frac{\mathbf{4}}{{\mathit{r}\mathit{c}\mathit{o}\mathit{s}}^{\mathbf{2}}\mathit{\varphi }}}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& {\displaystyle \frac{\mathbf{4}}{\mathit{r}{{\mathit{c}\mathit{o}\mathit{s}}^{\mathbf{2}}\mathit{\theta }\mathit{c}\mathit{o}\mathit{s}}^{\mathbf{2}}\mathit{\varphi }}}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& {\displaystyle \frac{\mathbf{4}}{\mathit{r}{{\mathit{c}\mathit{o}\mathit{s}}^{\mathbf{2}}\mathit{\theta }\mathit{c}\mathit{o}\mathit{s}}^{\mathbf{2}}\mathit{\varphi }}}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& {\displaystyle \frac{\mathbf{4}{\mathit{sin}}^{\mathbf{2}}\mathbf{}\mathit{\theta }}{{{\mathit{r}\mathit{c}\mathit{o}\mathit{s}}^{\mathbf{2}}\mathit{\theta }\mathit{c}\mathit{o}\mathit{s}}^{\mathbf{2}}\mathit{\varphi }}}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& {\displaystyle \frac{\mathbf{4}{\mathit{sin}}^{\mathbf{2}}\mathbf{}\mathit{\theta }{\mathit{sin}}^{\mathbf{2}}\mathit{\varphi }}{{{\mathit{r}\mathit{a}\mathit{c}\mathit{o}\mathit{s}}^{\mathbf{2}}\mathit{\theta }\mathit{c}\mathit{o}\mathit{s}}^{\mathbf{2}}\mathit{\varphi }}}\end{array}\right]$$

$$K_{\mu \nu }=\left[\begin{array}{cccccc}{\displaystyle \frac{r_t}{\pi c}}& A_{\iota }& A_{\iota }& A_{\iota }& A_{\iota }& A_{\iota }\\ A_{\iota }& {\displaystyle \frac{{r_{t}he}^{{\pi }^3}}{c}}& A_{\iota }& A_{\iota }& A_{\iota }& A_{\iota }\\ A_{\iota }& A_{\iota }& {\displaystyle \frac{r_t\sqrt{G}h{e}^{{\phi }^2}}{c}}& A_{\iota }& A_{\iota }& A_{\iota }\\ A_{\iota }& A_{\iota }& A_{\iota }& {\displaystyle \frac{\sqrt{G}}{r_x}}& A_{\iota }& A_{\iota }\\ A_{\iota }& A_{\iota }& A_{\iota }& A_{\iota }& {\displaystyle \frac{\sqrt{G}}{r_x}}& A_{\iota }\\ A_{\iota }& A_{\iota }& A_{\iota }& A_{\iota }& A_{\iota }& {\displaystyle \frac{\sqrt{G}}{r_x}}\end{array}\right]$$

3.8

$${\mathsf{\Psi }}_{\mu \nu }=\left[\begin{array}{cccccc}{cos}^2\theta {cos}^2\varphi & A_{\iota }& A_{\iota }& A_{\iota }& A_{\iota }& A_{\iota }\\ A_{\iota }& {cos}^2\varphi & A_{\iota }& A_{\iota }& A_{\iota }& A_{\iota }\\ A_{\iota }& A_{\iota }& e^{-i\pi \phi }& A_{\iota }& A_{\iota }& A_{\iota }\\ A_{\iota }& A_{\iota }& A_{\iota }& e^{i\pi \phi }& A_{\iota }& A_{\iota }\\ A_{\iota }& A_{\iota }& A_{\iota }& A_{\iota }& {sin}^2\theta & A_{\iota }\\ A_{\iota }& A_{\iota }& A_{\iota }& A_{\iota }& A_{\iota }& {sin}^2\theta {sin}^2\varphi \end{array}\right]$$

$$\begin{array}{l}{A}_{\sigma }=\pm \left({\displaystyle \frac{\pi }{3}}\right)+iz,A_2=\pm \left({\displaystyle \frac{2\pi }{3}}\right)+iz,A_3=\pm \left(\pi \right)+iz,A_4=\pm \left({\displaystyle \frac{4\pi }{3}}\right)+iz,A_5=\pm \left({\displaystyle \frac{5\pi }{3}}\right)+iz,A_6=\pm \left(2\pi \right)+iz\\ \mathsf{\mu },\nu =1,2,3,4,5,6\\ {\mathsf{\Psi }}_{\mathit{\mu }\mathit{\nu }}\mathbf{+}{\mathit{R}}_{\mathit{\mu }\mathit{\nu }}-{\displaystyle \frac{\mathbf{1}}{\mathbf{2}}}\mathit{R}{\mathit{g}}_{\mathit{\mu }\mathit{\nu }}\mathbf{+}\mathsf{\Lambda }{\mathit{g}}_{\mathit{\mu }\mathit{\nu }}\mathbf{=}{\left({\displaystyle \frac{\mathit{\pi }\mathbf{-}\mathbf{2}}{\mathbf{2}}}\right)}^{\mathbf{6}}\left({\displaystyle \frac{\mathit{h}\mathit{e}}{\mathit{c}}}\right){\mathit{T}}_{\mathit{\mu }\mathit{\nu }}\mathbf{+}{\mathit{K}}_{\mathit{\mu }\mathit{\nu }}\end{array}$$

The topology of electron orbitals represents the structure of Möbius space. The structure of the orbitals of an atom is shaped by density changes in six-dimensional space-time. These changes in energy states and the connections between orbitals are regular and have an underlying periodicity of the topology of the gravitational field. A Klein bottle serves as an example of Möbius space, capable of adopting more complex states based on density variations. For instance, the reflection of light from the curved surface of a small stream of water indicates changes in the geometric structure of a surface manifold. Naturally, the distribution of prime numbers over time is influenced by these density variations. Phase shifts between the distances of prime numbers in the defined groups of six reflect the presence of the Bernoulli principle within the geometry of Möbius space. Periodic jumps correspond to instantaneous changes in geodesics at the "neck" and "belly" of the function, resembling wormholes. As a result, when two masses exert gravitational influence on one another, they form distinct geometric orbitals that represent orthogonal density domains within the field of each mass. When electrons move between energy levels, or orbitals, the gaps between these energy levels follow patterns similar to those observed in prime numbers. For example, in the six-digit prime groups, common gaps such as 18, 36, 54, and 72 appear periodically. These gaps are influenced by density and energy fluctuations, both of which can be modeled in the Möbius framework. The gaps between energy levels are a periodic function of density fluctuations with changes in the state of the wave function, which overlaps perfectly with the orbital phenomena of the electron.

Δn = Pn - Pn-1, where Δn denotes the energy gap, and Pn and Pn-1 represent consecutive orbital energy levels modeled by prime spacing. The preservation of symmetry, based on homogeneity and isotropy in Möbius space, causes the reflection of density changes in its geometric structure. Based on the number of electrons, the orbitals not only adopt different geometric structures but also express the effects of electrons in regions of negative density within the orbital's geometric structure. This includes the relationship between the absence of density and quantum phenomena such as tunneling. In the universe, dark energy reflects the effects originating from density changes over time. The intensified reflection of negative density, similar to fluid flow in Bernoulli's principle, influences the expansion and expansion rate of the universe. The rotation of Möbius space, governed by prime numbers, encodes the wavefunction of each particle based on the hypergeometric distribution of mass.

B. Gravity Sensors

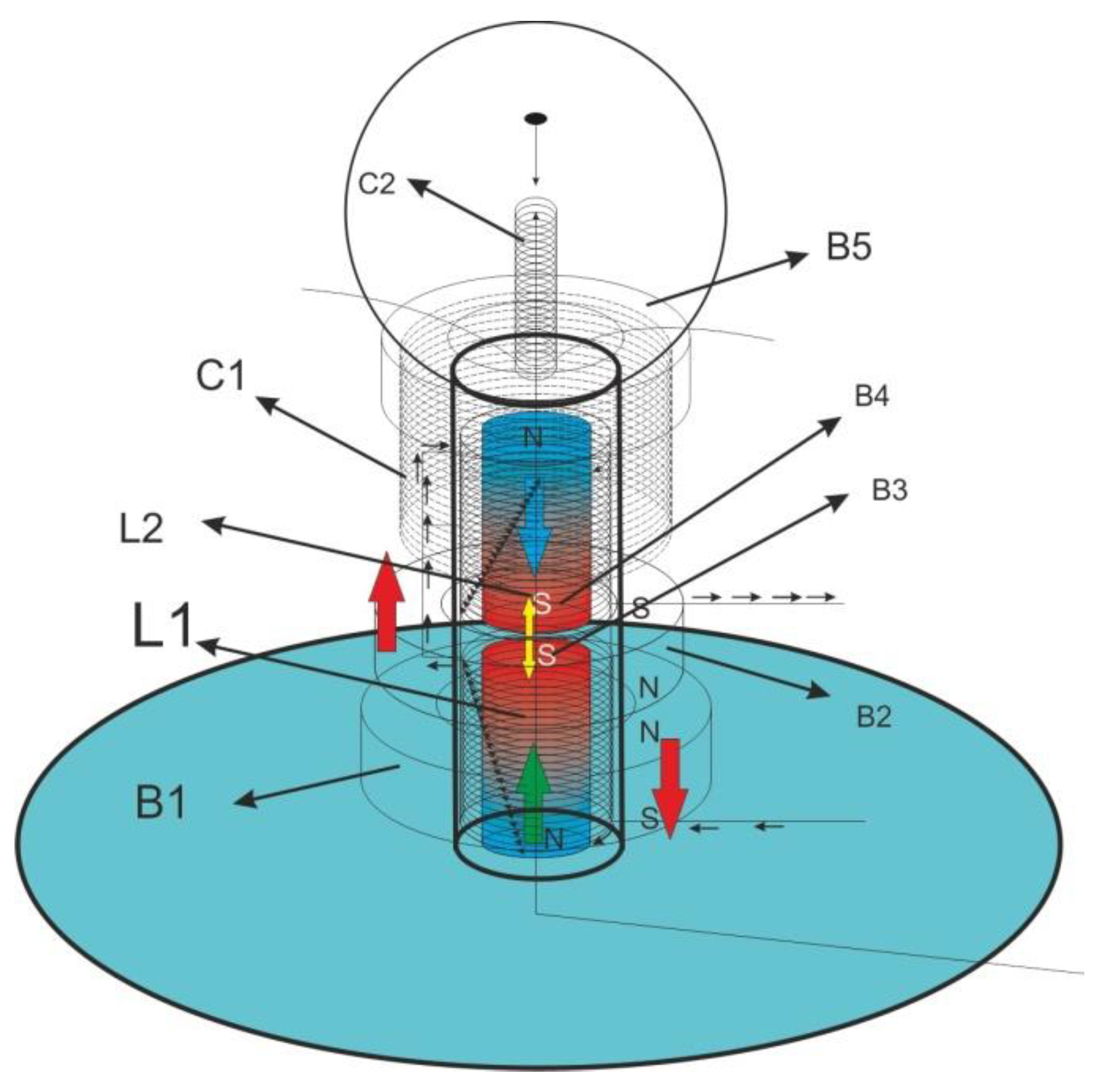
To mitigate the effects of inductance, Möbius inductors were designed. Additionally, Möbius capacitors were simulated in series with these inductors. This device demonstrates the ability to generate both positive and negative gravitational fields and can also produce a weak current derived from the gravitational field.

Its application as a distortion detection sensor within a gravitational field utilizes variations in the generated current. The sensor operates by monitoring fluctuations in this current, which directly correspond to changes in the gravitational field. By analyzing these fluctuations, the device can identify subtle distortions indicative of momentum-induced perturbations or wave-like distortions. Figure 3

Möbius coil, composed of two opposing windings connected in series and sharing a common magnetic core. The windings remain magnetically isolated, ensuring no mutual interaction. Initially, high-voltage, low-current pulses are prevented from passing through due to inductance. As the magnetic properties of the core diminish—modulated by weight variations of external magnets in a gravitational field—a specific current is discharged through the second winding as an instantaneous flux. The reverse current flow in the second winding, combined with its lower inductance, filters most of the wire resistance, allowing the amplified current to detect minute oscillations in the core. Figure 4

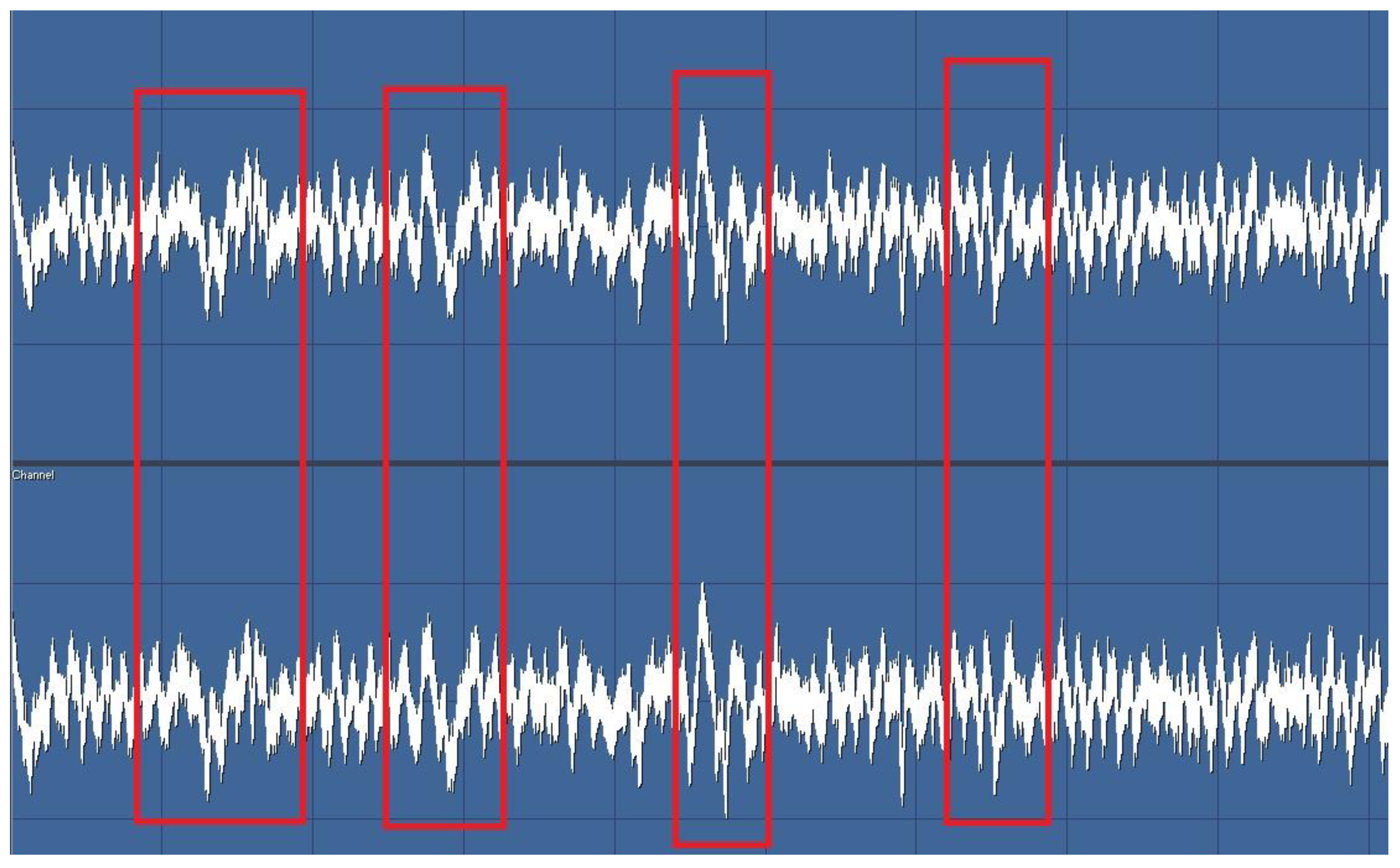
The external magnetic field, induced by natural magnets suspended in isolated conditions and interacting with the gravitational field, transmits distortions caused by the combined effects of gravitational potential energy and magnetic field density changes. Möbius inductors relay these distortions to Möbius capacitors, which are designed with a Möbius geometry and variable dielectric properties. The dielectric variations in the capacitors depend on the current discharged from the Möbius coil. The resulting current undergoes amplification within a loop, generating oscillations whose intervals resemble the structured gaps of prime numbers, akin to the systematic intervals of musical scales. These oscillations, governed by the six-group prime distribution, enable precise identification of the smallest momentum associated with each layer. Such momentum variations can be mapped in spatial coordinates using fast Fourier transformation techniques.

The Möbius coil system operates through interactions of inductance, current, and magnetic flux. The instantaneous current is influenced by the time-dependent magnetic flux and is governed by the inductance of the Möbius coil. Variations in magnetic flux, modulated by the gravitational field, determine the flow of current.(3.9)

$$I\left(t\right)={\displaystyle \frac{d\Phi }{L}}$$

3.9

The Möbius capacitor exhibits unique dielectric properties that vary based on the discharged current from the Möbius coil. The capacitance adjusts according to changes in the dielectric constant, which are directly tied to flux discharge variations.(3.10)

$$C\left(ϵ\right)={\displaystyle \frac{1}{L}}{\displaystyle \frac{\partial \varphi }{\partial t}}$$

3.10

The system generates oscillations that reflect structured intervals, comparable to the patterns of musical scales. These oscillations resonate in harmony with the prime number gaps distributed across six groups, forming a connection between mathematical intervals and physical oscillations:(3.11) Figure 4

$$J\left(t\right)=A \mathrm{s}\mathrm{i}\mathrm{n}\left(2\pi ft\right)$$

3.11

This framework integrates the dynamic interactions within the Möbius system, establishing parallels between physical behaviors and the mathematical distribution of prime numbers.

4. Conclusions

This section discusses the analysis of the Möbius coil and capacitor system and its dynamics, examining the correlations between geometric design, physical principles, and their resulting interactions. The focus of this study was to assess the distribution of current and the oscillatory patterns linked to gravitational and magnetic distortions, with an emphasis on prime number intervals. By systematically connecting the behavior of the Möbius inductors and capacitors to theoretical frameworks, this research explores the broader implications of harmonic oscillations and their alignment with six distinct prime number groups.

The analysis indicates that variations in the gravitational and magnetic field distortions directly influence the inductance and capacitance properties of the Möbius components. This was reflected in the dynamic interactions between magnetic flux and current within the Möbius coil, resulting in the amplification and transfer of oscillations to the Möbius capacitors. The dielectric variations, modulated by the discharged currents, produce oscillations resonating in structured intervals analogous to musical scales, correlating with prime number gaps.