Submitted:
17 November 2024
Posted:
18 November 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
2.1. Materials and Solvents
2.2. Experimental
2.3. Retention Volume
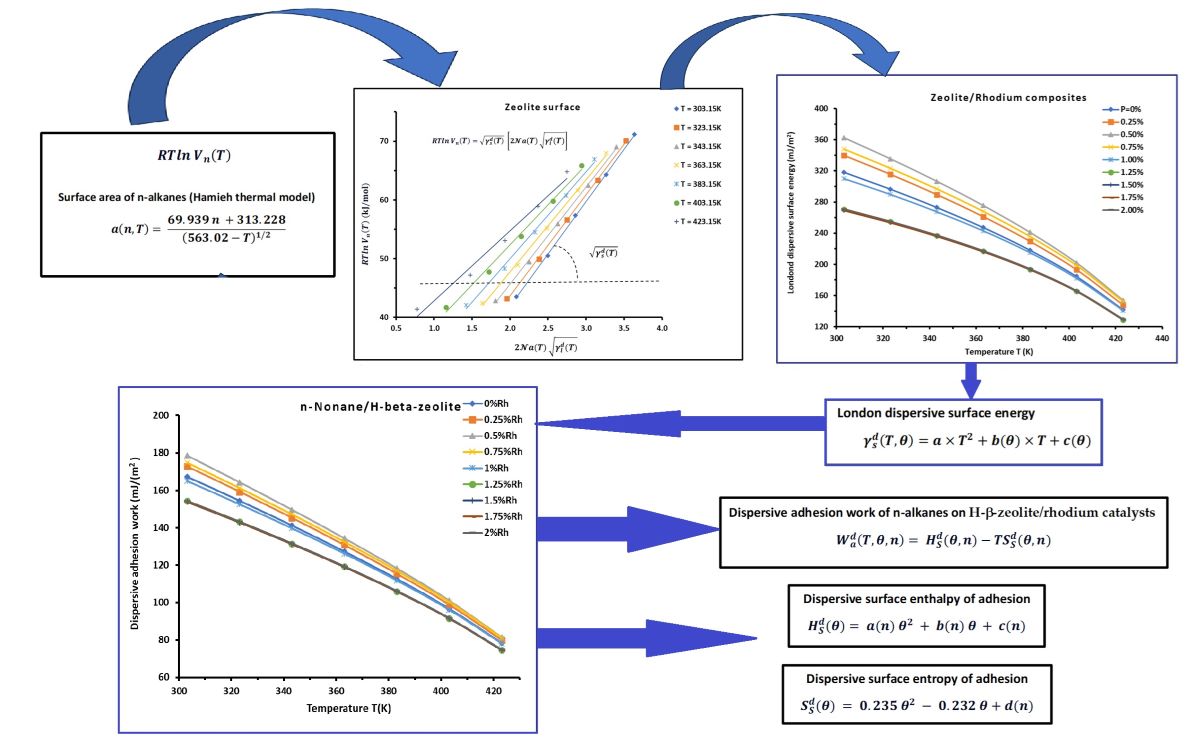
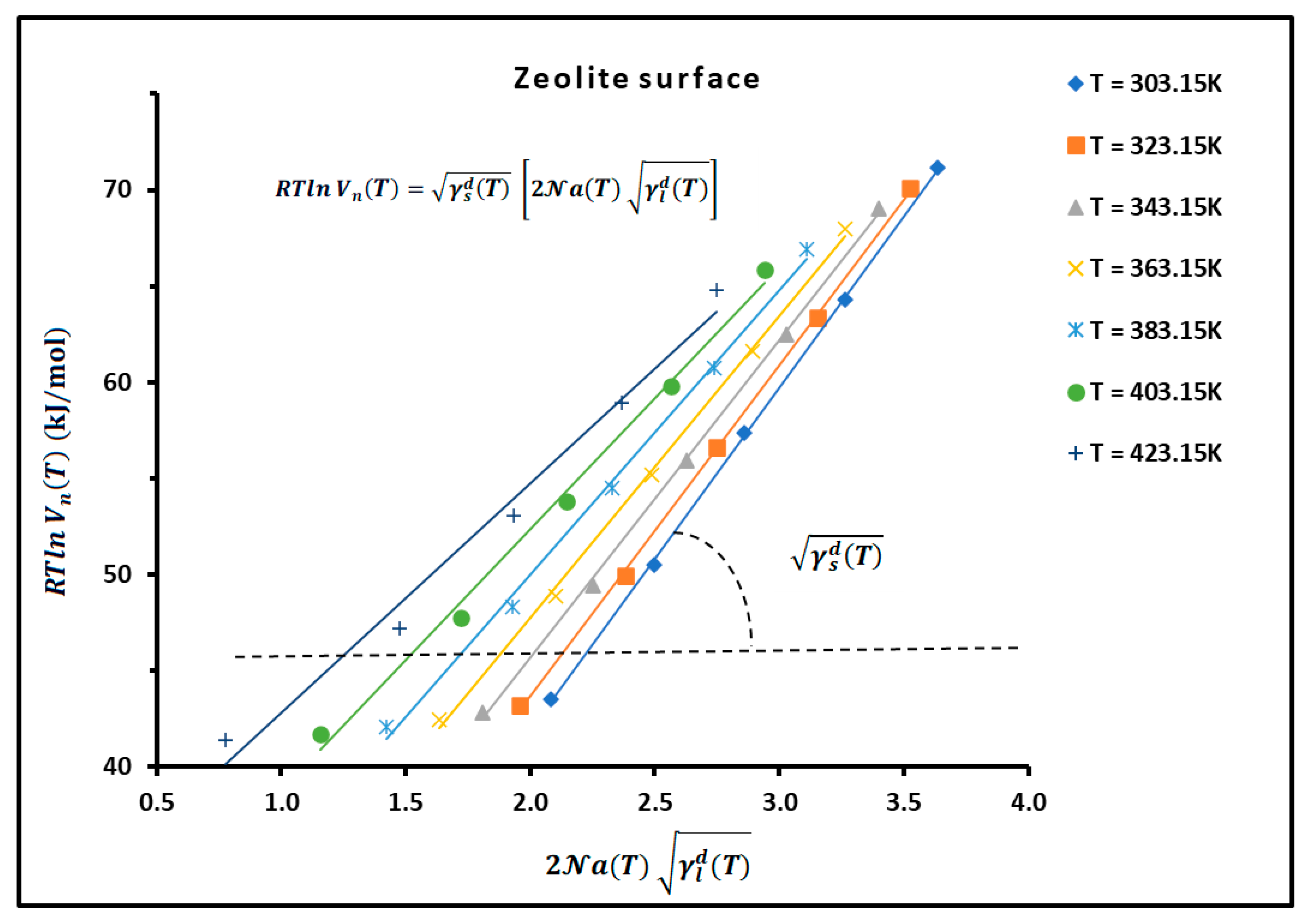
2.4. London Dispersive Surface Energy of Catalysts Using the Hamieh Thermal Model
3. Results
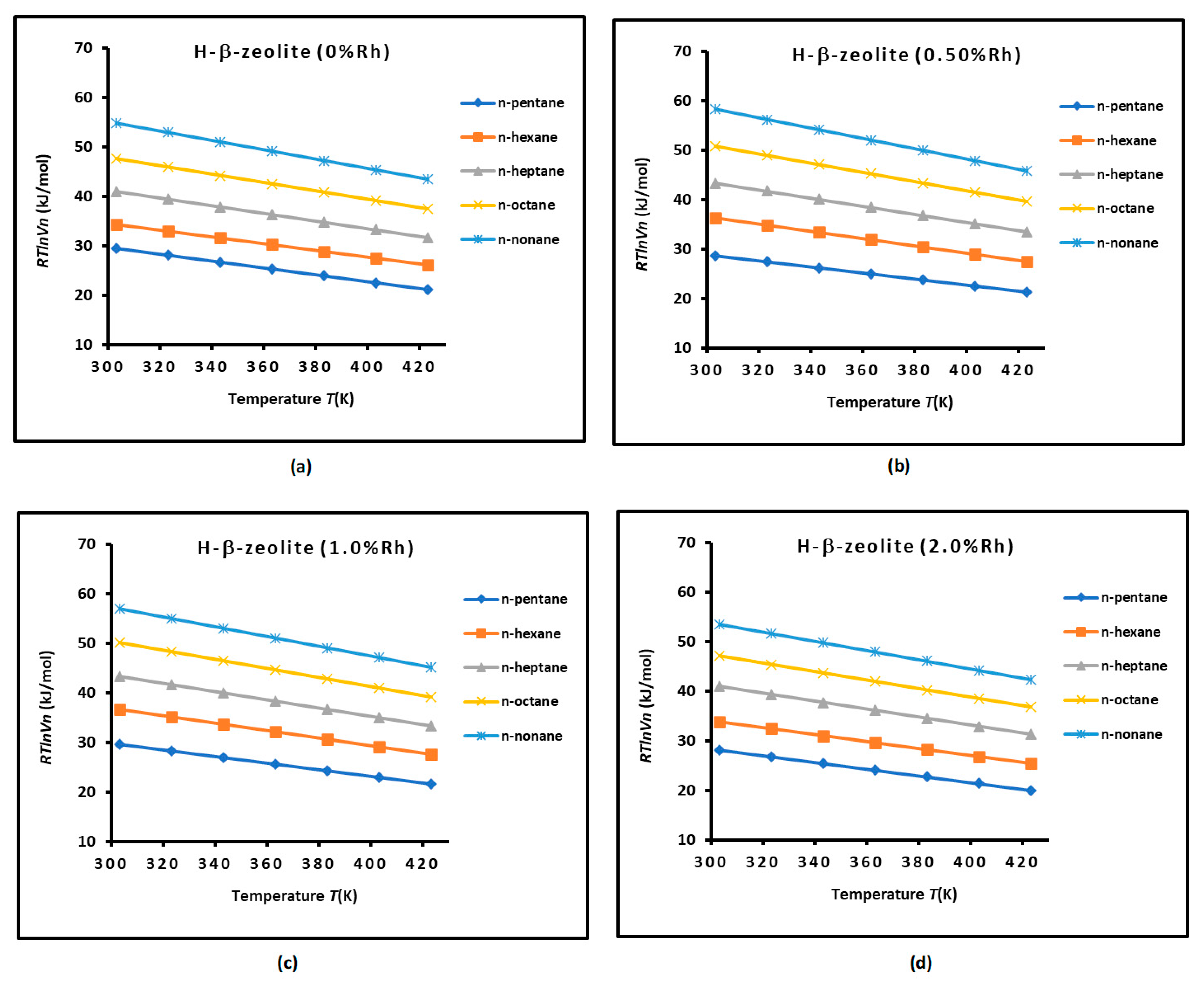
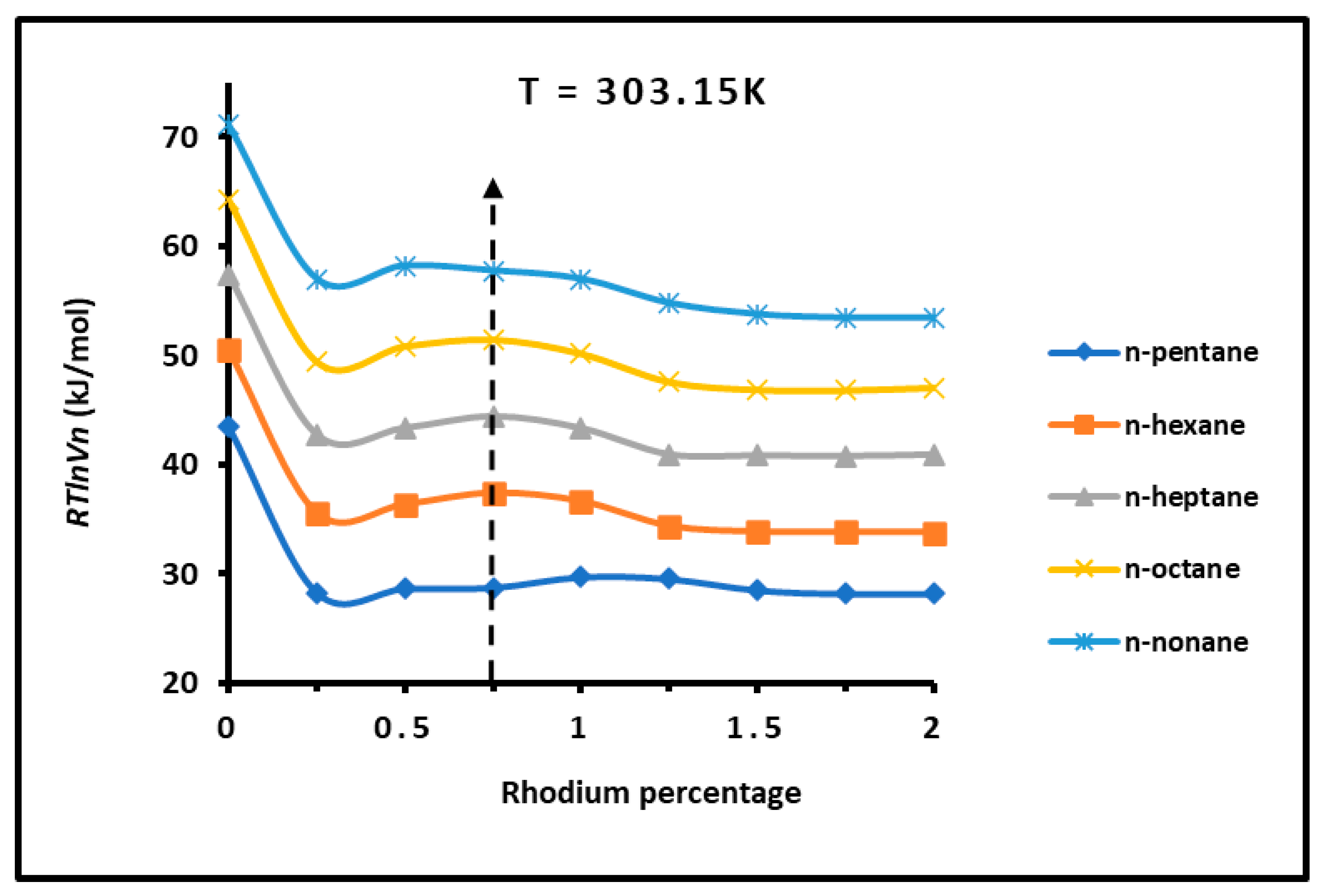
3.1. Determination of of n-Alkanes Adsorbed on H−β−Zeolite/Rhodium Catalysts
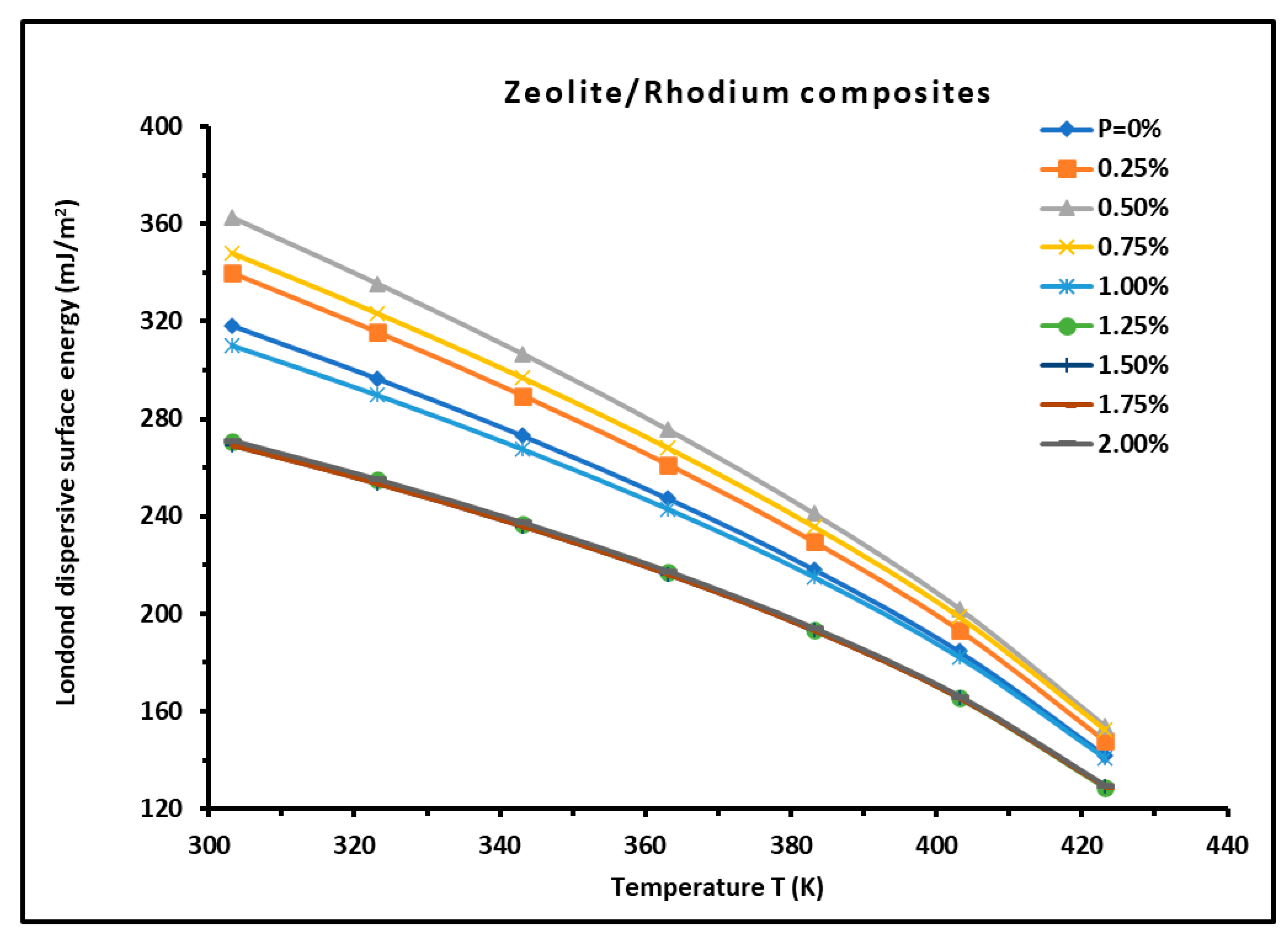
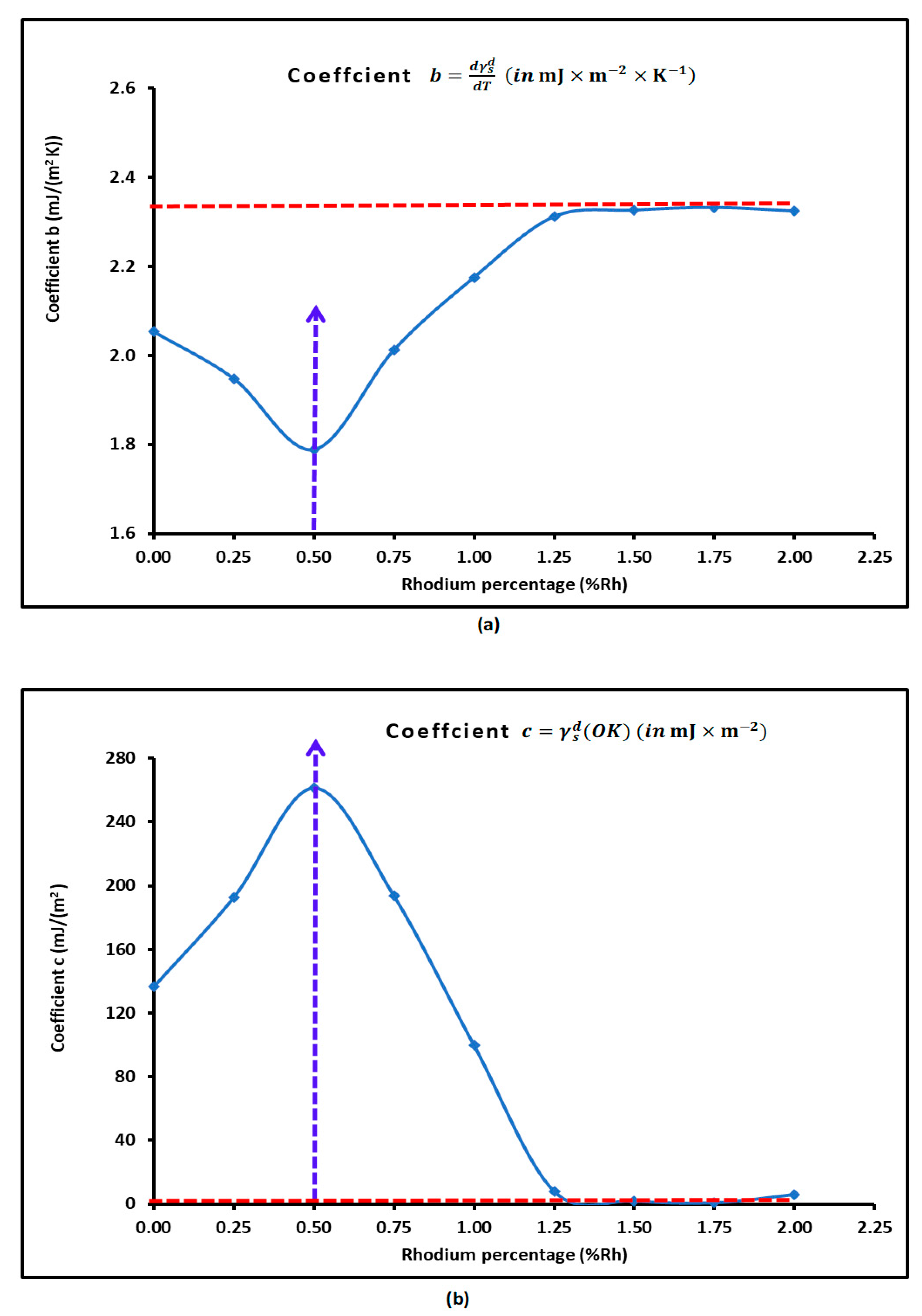
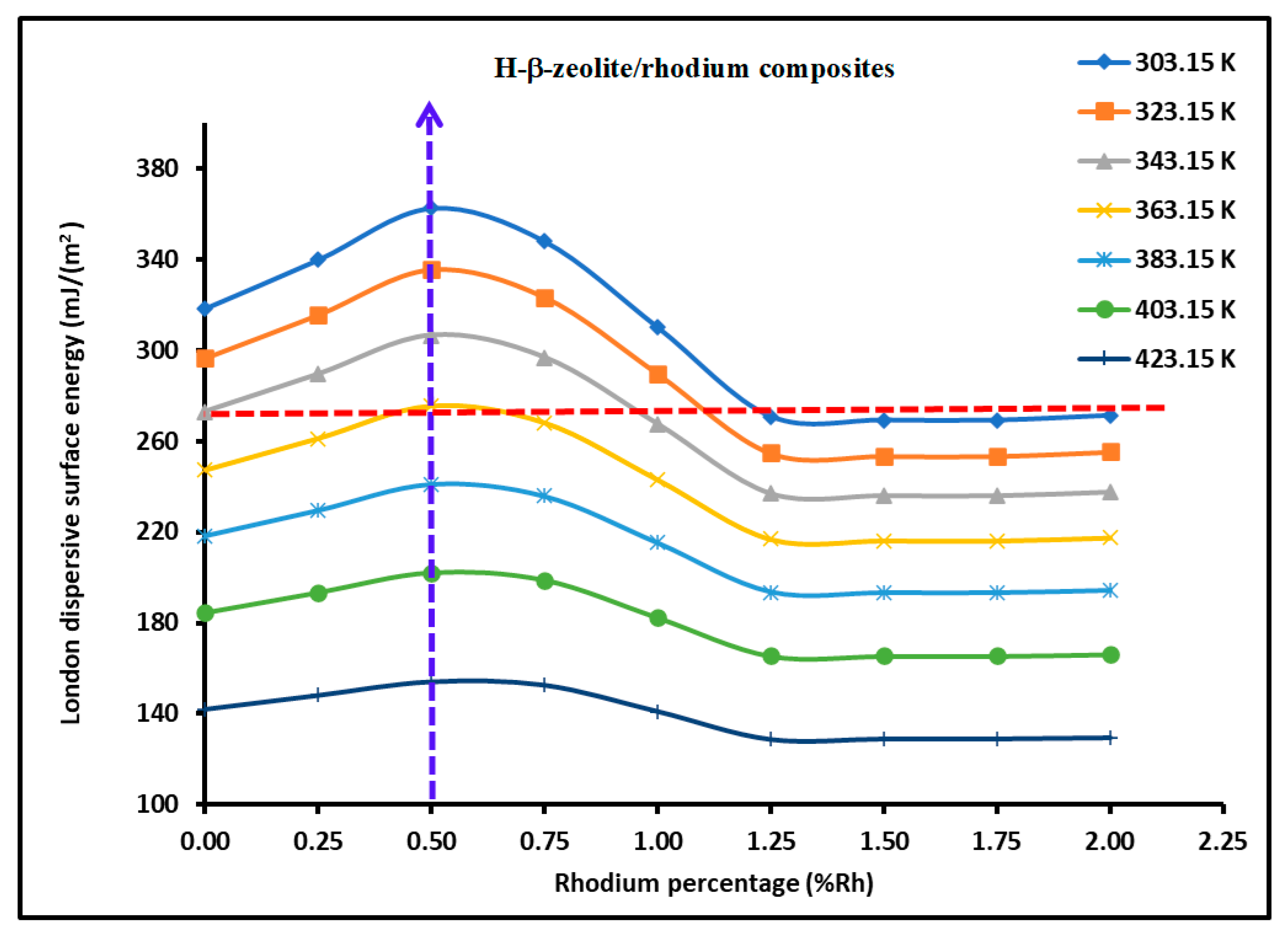
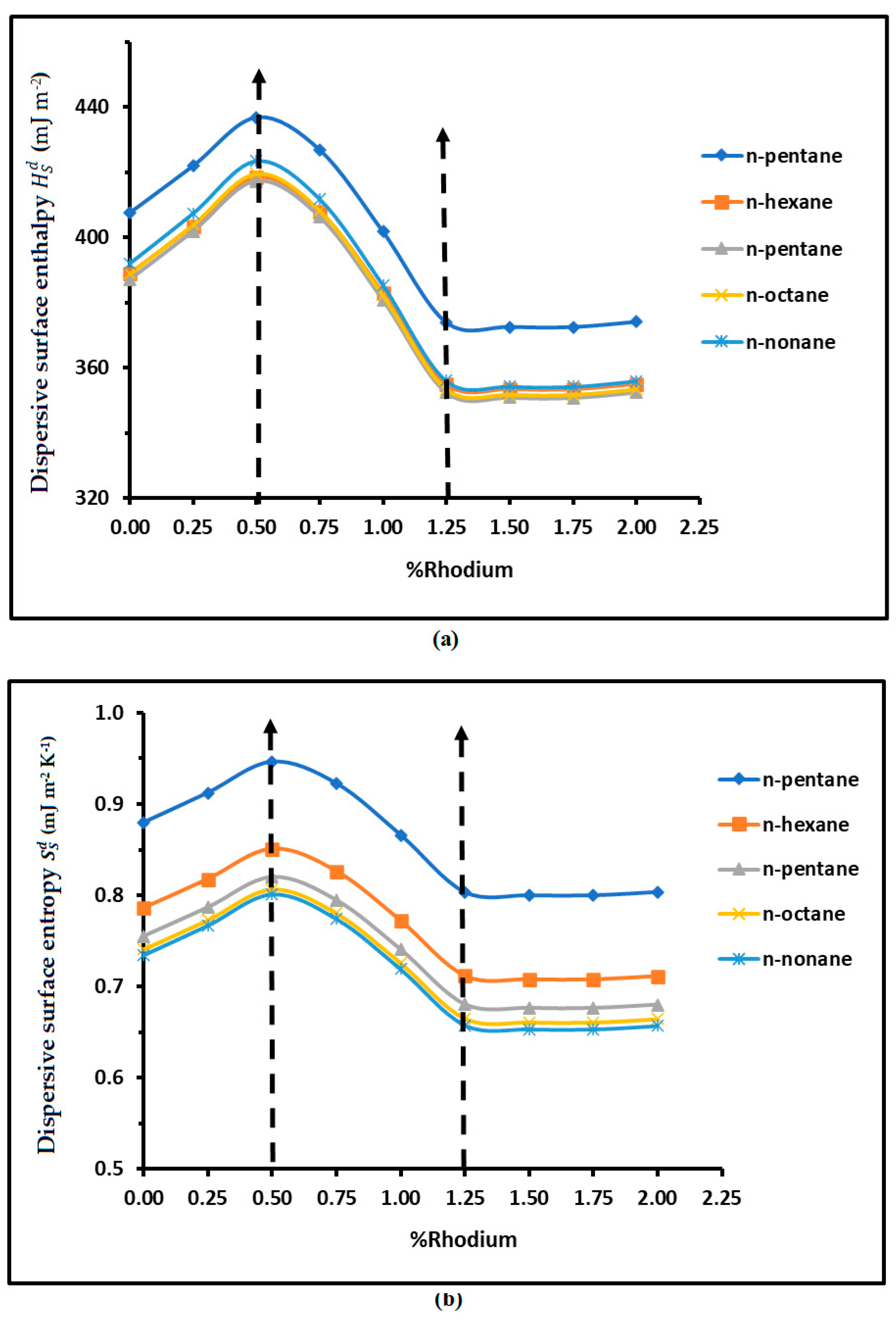
3.2. London Dispersive Surface Energy of H−β-Zeolite/Rhodium Catalysts
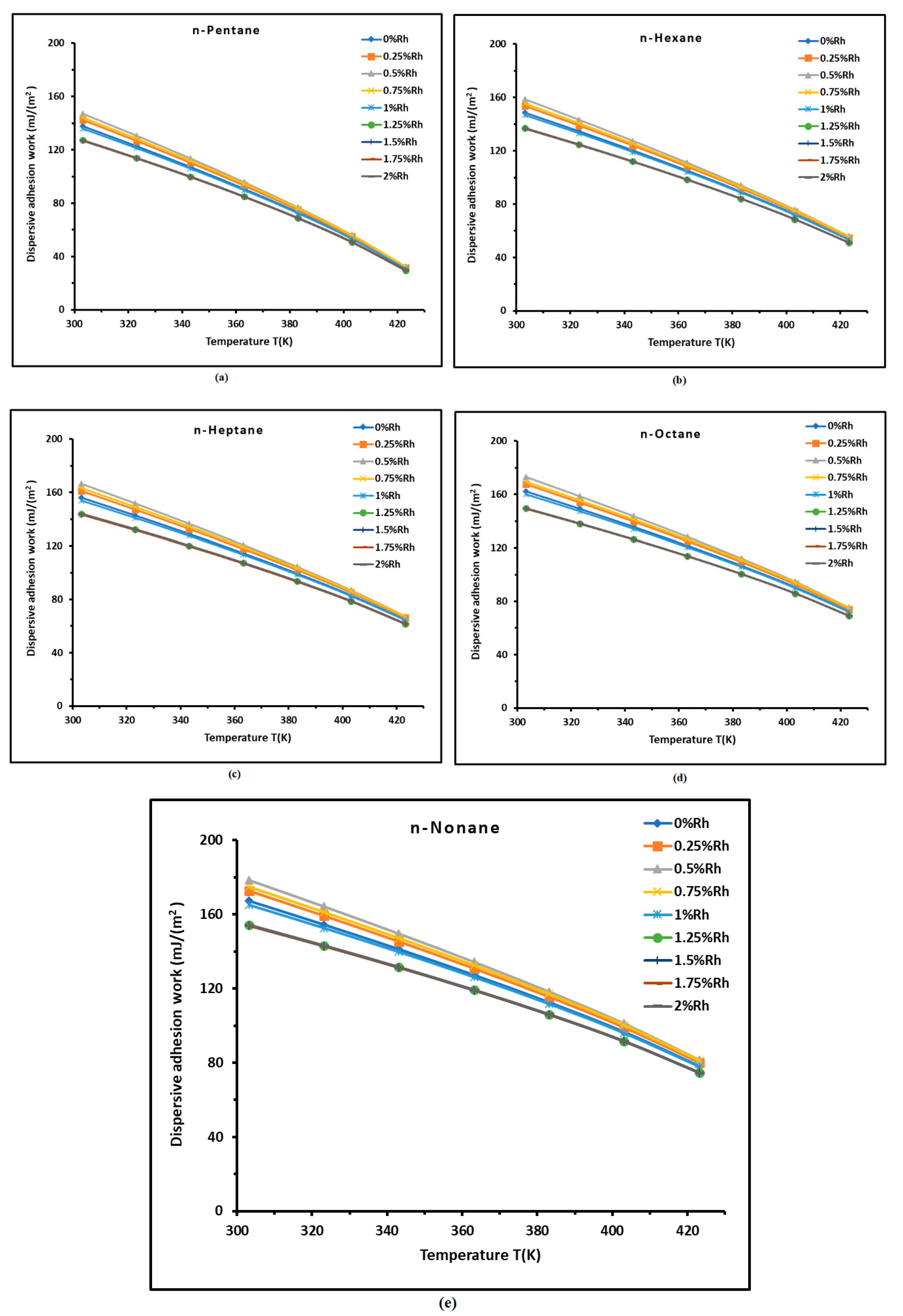
3.2. Dispersive Adhesion Work of n-Alkanes on H−β-Zeolite/Rhodium Catalysts
5. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Conflicts of Interest
References
- Voelkel, A.; Strzemiecka, B.; Adamska, K.; Milczewska, K. Inverse gas chromatography as a source of physiochemical data. J. Chromatogr. A 2009, 1216, 1551. [Google Scholar] [CrossRef]
- Papadopoulou, S.K.; Panayiotou, C. Thermodynamic characterization of poly(1,1,1,3,3,3-hexafluoroisopropyl methacrylate) by inverse gas chromatography. J. Chromatogr. A 2012, 1229, 230. [Google Scholar] [CrossRef]
- Coimbra, P.; Coelho, M. S.N.; Gamelas, J. A.F. Surface characterization of polysaccharide scaffolds by inverse gas chromatography regarding application in tissue engineering. Surface and Interface Analysis 2019, 51 (11), 1070–1077. [Google Scholar] [CrossRef]
- Kołodziejek, J.; Voelkel, A.; Heberger, K. Characterization of hybrid materials by means of inverse gas chromatography and chemometrics. J. Pharm. Sci. 2013, 102, 1524. [Google Scholar] [CrossRef]
- Belgacem, M.N.; Czeremuszkin, G.; Sapieha, S.; Gandini, A. Surface by XPS characterization and inverse gas of cellulose fibres chromatography. Cellulose 1995, 2, 145–157. [Google Scholar] [CrossRef]
- Donnet, J.B.; Custodéro, E.; Wang, T.K.; Hennebert, G. Energy site distribution of carbon black surfaces by inverse gas chromatography at finite concentration conditions. Carbon 2002, 40, 163–167. [Google Scholar] [CrossRef]
- Balard, H.; Maafa, D.; Santini, A.; Donnet, J.B. Study by inverse gas chromatography of the surface properties of milled graphites. J. Chromatogr. A 2008, 1198–1199, 173–180. [Google Scholar] [CrossRef]
- Bogillo, V.I.; Shkilev, V.P.; Voelkel, A. Determination of surface free energy components for heterogeneous solids by means of inverse gas chromatography at finite concentrations. J. Mater. Chem. 1998, 8, 1953–1961. [Google Scholar] [CrossRef]
- Das, S.C.; Zhou, Q.; Morton, D.A.V.; Larson, I.; Stewart, P.J. Use of surface energy distributions by inverse gas chromatography to understand mechanofusion processing and functionality of lactose coated with magnesium stearate. Eur. J. Pharm. Sci. 2011, 43, 325–333. [Google Scholar] [CrossRef]
- Das, S.C.; Stewart, P.J. Characterising surface energy of pharmaceutical powders by inverse gas chromatography at finite dilution. J. Pharm. Pharmacol. 2012, 64, 1337–1348. [Google Scholar] [CrossRef]
- Bai, W.; Pakdel, E.; Li, Q.; Wang, J.; Tang, W.; Tang, B.; Wang, X. Inverse gas chromatography (IGC) for studying the cellulosic materials surface characteristics: a mini review. Cellulose 2023, 30, 3379–3396. [Google Scholar] [CrossRef]
- Dong, S.; Brendlé, M.; Donnet, J.B. Study of solid surface polarity by inverse gas chromatography at infinite dilution. Chromatographia 1989, 28, 469–472. [Google Scholar] [CrossRef]
- Gamble, J.F.; Leane, M.; Olusanmi, D.; Tobyn, M.; Supuk, E.; Khoo, J.; Naderi, M. Surface energy analysis as a tool to probe the surface energy characteristics of micronized materials—A comparison with inverse gas chromatography. Int. J. Pharm. 2012, 422, 238–244. [Google Scholar] [CrossRef]
- Newell, H.E.; Buckton, G.; Butler, D.A.; Thielmann, F.; Williams, D.R. The use of inverse gas chromatography to measure the surface energy of crystalline, amorphous, and recently milled lactose. Pharm. Res. 2001, 18, 662–666. [Google Scholar] [CrossRef]
- Newell, H.E.; Buckton, G. Inverse gas chromatography: Investigating whether the technique preferentially probes high energy sites for mixtures of crystalline and amorphous lactose. Pharm. Res. 2004, 21, 1440–1444. [Google Scholar] [CrossRef]
- Kołodziejek, J.; Głowka, E.; Hyla, K.; Voelkel, A.; Lulek, J.; Milczewska, K. Relationship between surface properties determined by inverse gas chromatography and ibuprofen release from hybrid materials based on fumed silica. Int. J. Pharm. 2013, 441, 441–448. [Google Scholar] [CrossRef]
- Calvet, R.; Del Confetto, S.; Balard, H.; Brendlé, E.; Donnet, J.B. Study of the interaction polybutadiene/fillers using inverse gas chromatography. J. Chromatogr. A 2012, 1253, 164–170. [Google Scholar] [CrossRef]
- Hamieh, T. Temperature Dependence of the Polar and Lewis Acid–Base Properties of Poly Methyl Methacrylate Adsorbed on Silica via Inverse Gas Chromatography. Molecules 2024, 29, 1688. [Google Scholar] [CrossRef]
- Basivi, P.K.; Hamieh, T.; Kakani, V.; Pasupuleti, V.R.; Sasikala, G.; Heo, S.M.; Pasupuleti, K.S.; Kim, M.-D.; Munagapati, V.S.; Kumar, N.S.; Wen, J.-H.; Kim, C.W. Exploring advanced materials: Harnessing the synergy of inverse gas chromatography and artificial vision intelligence, TrAC Trends in Analytical Chemistry, 2024, 173, 117655, . [CrossRef]
- Sawyer, D.T.; Brookman, D.J. Thermodynamically based gas chromatographic retention index for organic molecules using salt-modified aluminas and porous silica beads. Anal. Chem. 1968, 40, 1847–1850. [Google Scholar] [CrossRef]
- Saint-Flour, C.; Papirer, E. Gas-solid chromatography. A method of measuring surface free energy characteristics of short carbon fibers. 1. Through adsorption isotherms. Ind. Eng. Chem. Prod. Res. Dev. 1982, 21, 337–341. [Google Scholar] [CrossRef]
- Saint-Flour, C.; Papirer, E. Gas-solid chromatography: Method of measuring surface free energy characteristics of short fibers. 2. Through retention volumes measured near zero surface coverage. Ind. Eng. Chem. Prod. Res. Dev. 1982, 21, 666–669. [Google Scholar] [CrossRef]
- Donnet, J.B.; Park, S.J.; Balard, H. Evaluation of specific interactions of solid surfaces by inverse gas chromatography. Chromatographia 1991, 31, 434–440. [Google Scholar] [CrossRef]
- Brendlé, E.; Papirer, E. A new topological index for molecular probes used in inverse gas chromatography for the surface nanorugosity evaluation, 2. Application for the Evaluation of the Solid Surface Specific Interaction Potential. J. Colloid Interface Sci. 1997, 194, 217–224. [Google Scholar] [CrossRef]
- Brendlé, E.; Papirer, E. A new topological index for molecular probes used in inverse gas chromatography for the surface nanorugosity evaluation, 1. Method of Evaluation. J. Colloid Interface Sci. 1997, 194, 207–216. [Google Scholar] [CrossRef]
- Hamieh, T.; Schultz, J. New approach to characterise physicochemical properties of solid substrates by inverse gas chromatography at infinite dilution. I. II. And III. J. Chromatogr. A 2002, 969, 17–47. [Google Scholar] [CrossRef]
- Hamieh, T. The Effect of Temperature on the Surface Energetic Properties of Carbon Fibers Using Inverse Gas Chromatography. Crystals 2024, 14, 28. [Google Scholar] [CrossRef]
- Hamieh, T. New Progress on London Dispersive Energy, Polar Surface Interactions, and Lewis’s Acid–Base Properties of Solid Surfaces. Molecules 2024, 29, 949. [Google Scholar] [CrossRef]
- Hamieh, T. London Dispersive and Lewis Acid-Base Surface Energy of 2D Single-Crystalline and Polycrystalline Covalent Organic Frameworks. Crystals 2024, 14, 148. [Google Scholar] [CrossRef]
- Hamieh, T. Inverse Gas Chromatography to Characterize the Surface Properties of Solid Materials. Chem. Mater. 2024, 36, 5–2231. [Google Scholar] [CrossRef]
- Hamieh, T. Some Irregularities in the Evaluation of Surface Parameters of Solid Materials by Inverse Gas Chromatography. Langmuir 2023, 39, 17059–17070. [Google Scholar] [CrossRef]
- Hamieh, T.; Ahmad, A.A.; Roques-Carmes, T.; Toufaily, J. New approach to determine the surface and interface thermodynamic properties of H-β-zeolite/rhodium catalysts by inverse gas chromatography at infinite dilution. Sci. Rep. 2020, 10, 20894. [Google Scholar] [CrossRef] [PubMed]
- G.M. Dorris, D.G. Gray, Adsorption of n-alkanes at zero surface coverage on cellulose paper and wood fibers, J. Colloid Interface Sci., 77 (1980) 353–362. [CrossRef]
- F.M. Fowkes, in: Surface and interfacial aspects of biomedical polymers, Vol. I, pp. 337-372, Ed: J. D. Andrade, Plenum Press, New York (1985).
- Hamieh, T. Study of the temperature effect on the surface area of model organic molecules, the dispersive surface energy and the surface properties of solids by inverse gas chromatography. J. Chromatogr. A 2020, 1627, 461372. [Google Scholar] [CrossRef]
- Hamieh, T. New methodology to study the dispersive component of the surface energy and acid–base properties of silica particles by inverse gas chromatography at infinite dilution. J. Chromatogr. Sci. 2022, 60, 126–142. [Google Scholar] [CrossRef]
- Schultz, J.; Lavielle, L.; Martin, C. The role of the interface in carbon fibre-epoxy composites. J. Adhes. 1987, 23, 45–60. [Google Scholar] [CrossRef]
- Navio, J.A.; Colon, G.; Litter, M.I.; Bianco, G.N. J. Mol. Catal. A: Chem. 1996, 106 (3), 267–276.
- Zhang, X.; Qian, L.; Xu, P.; He, H.; Du, Q. Study of H-βzeolite supported Rh catalyst by inverse gas chromatography, Chemical Engineering Journal, 2008, 137, 579–586. [CrossRef]
- Gutmann, V. The Donor-Acceptor Approach to Molecular Interactions; Plenum: New York, NY, USA, 1978. [Google Scholar]
- Hamieh, T.; Rageul-Lescouet, M.; Nardin, M.; Haidara, H.; Schultz, J. Study of acid-base interactions between some metallic oxides and model organic molecules. Colloids and Surfaces A: Phys. and Eng. Aspects 1997, 125, 155–161. [Google Scholar] [CrossRef]
- Conder, J.R.; Young, C.L. Physical measurements by gas chromatography. Eds: Wiley J and Sons, New York, 1979.
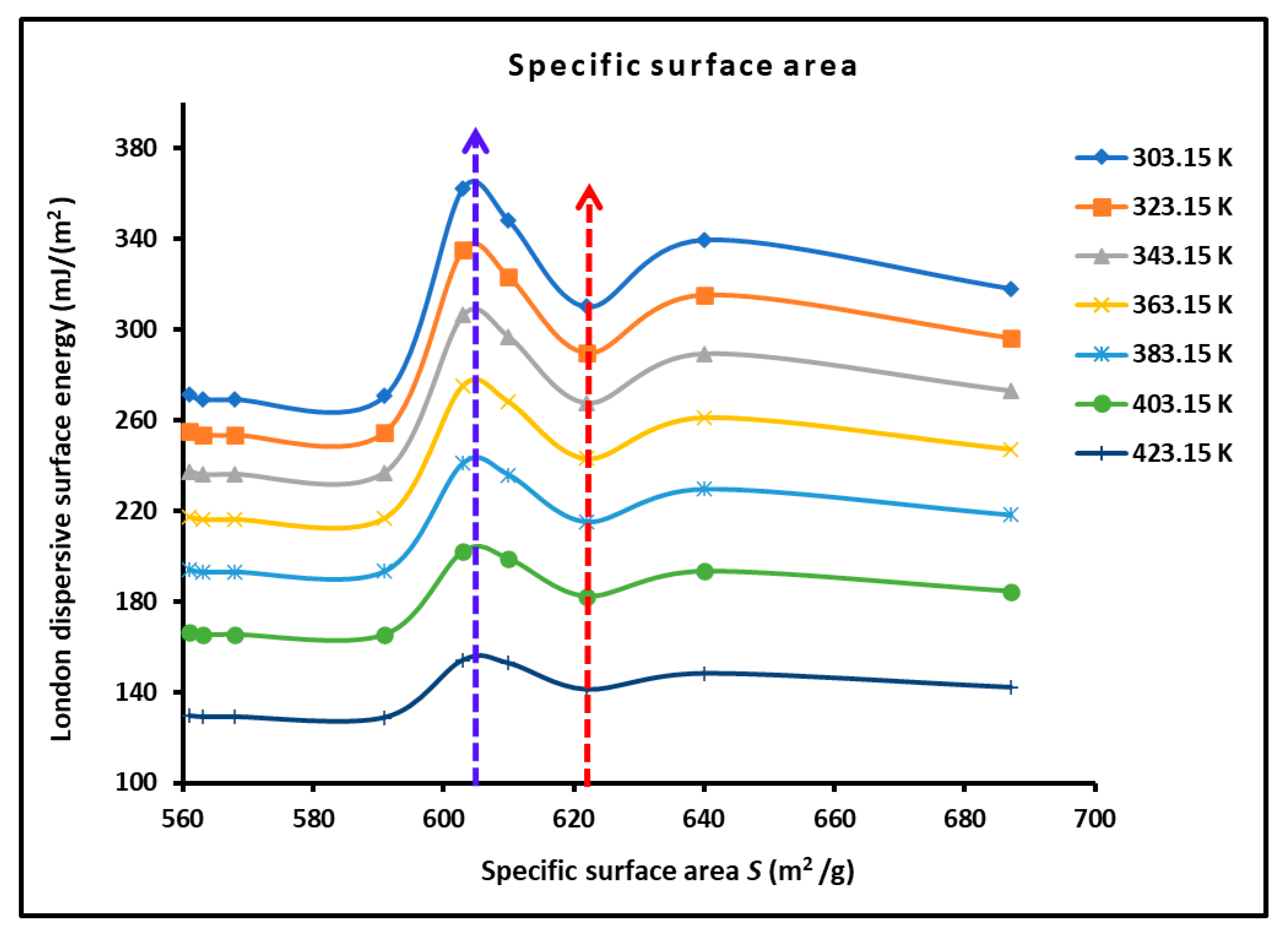
| %Rh | SBET (m2/g) | Vm (cm3/g) |
| 0 | 687 | 0.198 |
| 0.25 | 640 | 0.185 |
| 0.5 | 603 | 0.175 |
| 0.75 | 610 | 0.177 |
| 1 | 622 | 0.182 |
| 1.25 | 591 | 0.172 |
| 1.5 | 568 | 0.165 |
| 1.75 | 563 | 0.164 |
| 2 | 561 | 0.163 |
| %Rh | of catalysts | R² |
|---|---|---|
| 0.00% | 0.9993 | |
| 0.25% | 0.9994 | |
| 0.50% | 0.9995 | |
| 0.75% | 0.9994 | |
| 1.00% | 0.9993 | |
| 1.25% | 0.999 | |
| 1.50% | 0.999 | |
| 1.75% | 0.999 | |
| 2.00% | 0.999 |
| n-pentane | ||||
|---|---|---|---|---|
| %Rhodium | (mJ m-2) | (mJ m-2 K-1) | (mJ m-2) | R² |
| 0 | = -0.8797T + 407.51 | 0.8797 | 407.51 | 0.995 |
| 0.25 | = -0.9123T + 421.94 | 0.9123 | 421.94 | 0.9955 |
| 0.5 | = -0.9463T + 436.84 | 0.9463 | 436.84 | 0.996 |
| 0.75 | = -0.9226T + 426.85 | 0.9226 | 426.85 | 0.9955 |
| 1 | = -0.866T + 401.7 | 0.866 | 401.7 | 0.9946 |
| 1.25 | = -0.8032T + 373.84 | 0.8032 | 373.84 | 0.9935 |
| 1.5 | = -0.7998T + 372.46 | 0.7998 | 372.46 | 0.9933 |
| 1.75 | = -0.7997T + 372.42 | 0.7997 | 372.42 | 0.9933 |
| 2 | = -0.8034T + 374.02 | 0.8034 | 374.02 | 0.9934 |
| n-hexane | ||||
| %Rhodium | (mJ m-2) | (mJ m-2 K-1) | (mJ m-2) | R² |
| 0 | = -0.786T + 388.86 | 0.786 | 388.86 | 0.9973 |
| 0.25 | = -0.8177T + 403.34 | 0.8177 | 403.34 | 0.9976 |
| 0.5 | = -0.8509T + 418.39 | 0.8509 | 418.39 | 0.998 |
| 0.75 | = -0.8264T + 407.87 | 0.8264 | 407.87 | 0.9976 |
| 1 | = -0.772T + 382.78 | 0.772 | 382.78 | 0.997 |
| 1.25 | = -0.7115T + 354.95 | 0.7115 | 354.95 | 0.9961 |
| 1.5 | = -0.7077T + 353.42 | 0.7077 | 353.42 | 0.996 |
| 1.75 | = -0.7076T + 353.38 | 0.7076 | 353.38 | 0.9961 |
| 2 | = -0.7112T + 355.01 | 0.7112 | 355.01 | 0.9961 |
| n-heptane | ||||
| %Rhodium | (mJ m-2) | (mJ m-2 K-1) | (mJ m-2) | R² |
| 0 | = -0.7554T + 387.11 | 0.7554 | 387.11 | 0.9971 |
| 0.25 | = -0.7872T + 401.88 | 0.7872 | 401.88 | 0.9975 |
| 0.5 | = -0.8206T + 417.27 | 0.8206 | 417.27 | 0.9978 |
| 0.75 | = -0.7952T + 406.3 | 0.7952 | 406.3 | 0.9974 |
| 1 | = -0.7408T + 380.79 | 0.7408 | 380.79 | 0.9968 |
| 1.25 | = -0.6804T + 352.47 | 0.6804 | 352.47 | 0.9959 |
| 1.5 | = -0.6764T + 350.84 | 0.6764 | 350.84 | 0.9958 |
| 1.75 | = -0.6763T + 350.8 | 0.6763 | 350.8 | 0.9958 |
| 2 | = -0.68T + 352.47 | 0.68 | 352.47 | 0.9959 |
| n-octane | ||||
| %Rhodium | (mJ m-2) | (mJ m-2 K-1) | (mJ m-2) | R² |
| 0 | = -0.7408T + 388.78 | 0.7408 | 388.78 | 0.9967 |
| 0.25 | = -0.7729T + 403.85 | 0.7729 | 403.85 | 0.9971 |
| 0.5 | = -0.8067T + 419.57 | 0.8067 | 419.57 | 0.9975 |
| 0.75 | = -0.7805T + 408.24 | 0.7805 | 408.24 | 0.997 |
| 1 | = -0.7258T + 382.27 | 0.7258 | 382.27 | 0.9964 |
| 1.25 | = -0.665T + 353.43 | 0.665 | 353.43 | 0.9954 |
| 1.5 | = -0.6608T + 351.72 | 0.6608 | 351.72 | 0.9952 |
| 1.75 | = -0.6607T + 351.68 | 0.6607 | 351.68 | 0.9953 |
| 2 | = -0.6644T + 353.39 | 0.6644 | 353.39 | 0.9953 |
| n-nonane | ||||
| %Rhodium | (mJ m-2) | (mJ m-2 K-1) | (mJ m-2) | R² |
| 0 | = -0.7343T + 392.02 | 0.7343 | 392.02 | 0.9962 |
| 0.25 | = -0.7667T + 407.38 | 0.7667 | 407.38 | 0.9966 |
| 0.5 | = -0.801T + 423.42 | 0.801 | 423.42 | 0.9971 |
| 0.75 | = -0.7742T + 411.77 | 0.7742 | 411.77 | 0.9966 |
| 1 | = -0.719T + 385.33 | 0.719 | 385.33 | 0.9959 |
| 1.25 | = -0.6576T + 355.97 | 0.6576 | 355.97 | 0.9948 |
| 1.5 | = -0.6532T + 354.2 | 0.6532 | 354.2 | 0.9947 |
| 1.75 | = -0.6531T + 354.15 | 0.6531 | 354.15 | 0.9947 |
| 2 | = -0.6569T + 355.9 | 0.6569 | 355.9 | 0.9948 |
| n-alkanes | R² | R² | ||
|---|---|---|---|---|
| n-pentane | = -106.2 2 + 105.4 + 406.4 | 0.9777 | = 0.24 2 - 0.24 - 0.877 | 0.977 |
| n-hexane | = -106.3 2 + 105.3 + 387.82 | 0.9771 | = 0.23 2 - 0.23 - 0.784 | 0.9762 |
| n-pentane | = -108.3 2 + 107.1 + 386.08 | 0.9768 | = 0.23 2 - 0.23 - 0.754 | 0.9756 |
| n-octane | = -110.4 2 + 109.1 + 387.75 | 0.9766 | = 0.23 2 - 0.23 - 0.739 | 0.9752 |
| n-nonane | = -112.4 2 + 111.1 + 390.99 | 0.9765 | = 0.24 2 - 0.23 - 0.732 | 0.9749 |
| = -0.282 2 + 2.297 - 110.41 | R² = 0.9866 |
| = 0.313 2 - 2.872 + 111.73 | R² = 0.9827 |
| = 3.361 2 - 50.139 + 571.38 | R² = 0.9095 |
| = -0.014 2 + 0.223 - 1.648 | R² = 0.9770 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





