A New Varying-Factor Finite-Time Recurrent Neural Network to Online Solving Time-Varying Sylvester Equation

1. Introduction

As we all know, the Sylvester equation $UP-PV+W=0$, as a kind of linear matrix equation, plays an crucial role in many fields,especially linear algebra and matrix theory. For some mathematics, dynamic control system, and computer vision problems, Sylvester equation can be used to solve them, like designing the feedback control system by pole assignment optimization, linear least-squares regression, image fusion [1], clustering [2,3], and so on. In recent years, there exist many methods proposed by other scholars to solve real-time linear algebra problems [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19].Among these methods, several methods are efficient and representative, like GNN methods and ZNN methods. It is notable that GNN and ZNN methods both use the thought to force the time derivative of the error function declining and further to force the error function gain on zero. The proposal of GNNs, as a emblematic recurrent neural network, is very representational for solving real-time linear algebra problems[20,21,22].Generally speaking, different GNNs are designed to solve different linear algebra problems. By itself, for solving the Sylvester equation, GNN methods are able to roughly stated as follows:

1)

The first step, the error function is defined as $E=||UP-PV+{W||}^2/2$. In order to acquire the solution of Sylvester equation, the error function should converge to zero.

2)

In the next step, for purpose of acquiring the minimum point of the error function, GNN methods use a negative gradient descent direction. In addition to this, GNN methods employ a constant scalar-type parameter, which parameter is accelerating the convergence rate of the error function so that solving Sylvester equation efficiently.

However, GNN cannot track the ideal solution for the time-varying Sylvester equation well, because the GNN method is a kind of gradient-based method, which may makes the error definition $E={\displaystyle \frac{||UP-PV+{W||}^2}{2}}$ of GNN unable to converge to 0 [23].Therefore, GNN cannot solve the Sylvester function with time-varying effectively. But in practice, time-varying problems are everywhere, so we need a neural network to better track solutions locus to time-varying issues in real-time. Under this background, many kinds of neural networks have been proposed to solve this kind of time-varying algebraic problems. Among these neural networks, the ZNN proposed by Zhang $et$$al.$ proved to be efficient[17].ZNN is a kind of implicit dynamic neural network, that skillfully replaces the gradient dynamic with implicit dynamic, so that the computation error can achieve better convergence, that is, with the increase of time, the solution of the network can approach the theoretical solution in real time[24,25,26,27,28,29,30,31,32].However, ZNN also has some shortcomings, such as its convergence speed is not fast enough, convergence parameters are difficult to set, and other issues. Aiming at the above shortcomings, Li $et$$al.$ proposed a finite time ZNN [24]. The sign-bi-power activation function has been used in this network, as effectively activates this network, makes the convergence speed much faster and can achieve finite-time convergence. In addition, Zhang $et$$al.$ proposed a variable parameter convergence differential neural network (VP-CDNN)[33]. Different from the initial ZNN, the convergence parameter of VP-CDNN change with time, which makes the network hardware implementation much more reasonable than ZNN, and the convergence speed has reached the super-exponential convergence speed. But despite this, VP-CDNN cannot achieve finite-time convergence. Based on the above discussion, this paper proposes a recurrent neural network (VFFTNN) for solving the time-varying Sylvester equation. The network not only has the speed of super-exponential convergence but also can achieve finite-time convergence.

The rest of this paper is divided into four parts. The second section introduces some tools needed to solve the Sylvester equation, and briefly describes the solution steps of ZNN. In the third section, the implicit dynamic equation of the proposed VFFTNN and the general steps of solving time-varying problems with the network are given, and the convergence and robustness of VFFTNN under different conditions are analyzed theoretically. In the fourth section, the simulation results of MATLAB are given and compared with the simulation results of ZNN. In the last section, the thesis is summarized.

Before concluding this section, some highlights of the paper are listed below:

1)

Propose a VFFTNN algorithm for solving the Sylvester equation;

2)

Compared with VP-CDNN, this network can achieve finite-time convergence;

3)

Theoretically proved the convergence time of the network in the case of three activation functions;

4)

In the situation considering the existence of disturbances, the robustness of VFFTNN is discussed;

5)

Data simulation results show that the proposed VFFTNN has better convergence and robustness than the traditional ZNN model under the same initial conditions.

2. Problem Formulation And Prepare Knowledge

Let us observe the following Sylvester equation with smooth time-varying expressed as:

$$\begin{array}{c}\hfill U\left(t\right)P\left(t\right)-P\left(t\right)V\left(t\right)+W\left(t\right)=0,\forall t\in [0,+\infty )\end{array}$$

(1)

where time is expressed as the variable t. The time-varying smooth coefficient matrices $W\left(t\right)\in {\Re }^{m\times n}$, $V\left(t\right)\in {\Re }^{n\times n}$ as well as $U\left(t\right)\in {\Re }^{m\times m}$. Besides, $\dot{W}\left(t\right)=$ d$W\left(t\right)$/dt, $\dot{V}\left(t\right)=$ d$V\left(t\right)$/dt, and $\dot{U}\left(t\right)=$ d$U\left(t\right)$/dt are their time derivative respectively and assuming these time derivatives are known or can be found exactly. Furthermore, $P\left(t\right)\in {\Re }^{m\times n}$ is uncharted but real, and our purpose is to find it so that to approach or even equal the unique ideal solution $P^{*}\left(t\right)$ in finite time for the above Sylvester equation.

In order to facilitate the subsequent discussion and to solve equation (1) more simply, (1) is best to be transformed into a vector form. So the next Theorem (1) is introduced.

Theorem 1.

The Sylvester’s equation in matrix form (i.e., equation (1)) can be transform into the vector form as following:

$$\begin{array}{c}\hfill \left(I_n\otimes U\left(t\right)-V^T\left(t\right)\otimes I_m\right)vec\left(P\left(t\right)\right)+vec\left(W\left(t\right)\right)=0\end{array}$$

(2)

where $I_n$, as well as $I_m$, represent n-dimensional as well as m-dimensional identity matrices, respectively. Besides, the symbol T represents the transpose of the matrix. The symbol ⊗ represents the Kronecker product. In other words, $U\otimes V\in {\Re }^{mn\times mn}$ represents one large matrix, which is equivalent to turning the $ith$ row and $j-$column position element $u_{ij}$ in the matrix U into a matrix $u_{ij}V$. Operate $vec\left(P\left(t\right)\right)\in {\Re }^{mn}$ represents a column vector that puts totally of the columns of the matrix $P\left(t\right)\in {\Re }^{m\times n}$ in sequence.

Proof. 

See Section II as well as [17, Appendix]. □

Furthermore, if we want to obtain the only solution of equation (1), then it must meet the regularity condition [17,34], which is described in the following Theorem (2).

Theorem 2.

If the Sylvester equation (1) satisfies the following regularity condition, then it has one and only one solution.

$$\begin{array}{c}\hfill I_n\otimes \left(U^T\left(t\right)U\left(t\right)\right)-V^T\left(t\right)\otimes U^T\left(t\right)-V\left(t\right)\otimes U\left(t\right)\\ \hfill +\left(V\left(t\right)V^T\left(t\right)\right)\otimes I_m\ge \alpha I_{mn},\exists \alpha >0,\forall t\in [0,+\infty )\end{array}$$

(3)

where $I_{mn}$ represents mn-dimensional identity matrix.

Proof. 

See Section II and [17, Appendix]. □

With the continuous development of neural dynamics and the proposal of ZNNs, the idea of ZNNs is employed in many engineering and scientific fields to solve time-varying problems. For showing the details of this paper more clearly, next, we will briefly introduce how to solve the Sylvester equation (1) using a typical ZNN method.

In the first step,an error function about equation (1) is defined as follows:

$$\begin{array}{c}\hfill E\left(t\right):=U\left(t\right)P\left(t\right)-P\left(t\right)V\left(t\right)+W\left(t\right)\end{array}$$

(4)

Next, since our goal is to get a unique solution to equation(1), then when we set the error function approach 0, the unique solution of equation(1) will be acquired naturally. In the light of the design idea of neurodynamics, the following differential equations about the error function $E\left(t\right)$ could be designed :

$$\begin{array}{c}\hfill {\displaystyle \frac{dE\left(t\right)}{dt}}=\dot{E}\left(t\right)=-\mu \mathsf{\Phi }\left(E\left(t\right)\right)\end{array}$$

(5)

where the scale-valued factor $\mu$ is a positive design constant (i.e., $\mu >0$), which can adjust the convergence velocity of this network(5) through vary its value. $\mathsf{\Phi }(·):{\Re }^{m\times n}\to {\Re }^{m\times n}$ is an array including the same activation functions. $\mathsf{\Phi }(·)$ can be different kinds of activation functions, like linear-type, bipolar-sigmoid-type, power-type, sign-bi-power-type and so on. When we use the activation function with linear-type, (5) is a typical ZNN.

Based on (5), we can acquire the following implicit dynamic equation:

$$\begin{array}{c}\hfill U\left(t\right)\dot{P}\left(t\right)-\dot{P}\left(t\right)V\left(t\right)+\dot{U}\left(t\right)P\left(t\right)-P\left(t\right)\dot{V}\left(t\right)\\ \hfill +\dot{W}\left(t\right)=-\mu \mathsf{\Phi }\left(U\left(t\right)P\left(t\right)-P\left(t\right)V\left(t\right)+W\left(t\right)\right)\end{array}$$

(6)

where the starting value of $P\left(t\right)$ is $P\left(0\right)=P_0\in R^{m\times n}$. Besides, the state matrix $P\left(t\right)$ is an approximate solution that will gradually approach the theoretical solution, and it will approach to only one solution of $\left(1\right)$. In the light of the following lemma [17], the ZNNs performance to solve Sylvester equation can be guaranteed to exponential convergence.

Lemma 1.

Considering Sylvester-equation (1), its time-varying coefficient matrices $U\left(t\right)\in {\Re }^{m\times m},V\left(t\right)\in {\Re }^{n\times n}$, and $W\left(t\right)\in {\Re }^{m\times n}$, assuming that they satisfy inequality (3), and the activation function of the implicit dynamic equation (6) is chosen to be linear, then its state matrix $P\left(t\right)$ will be exponential convergence from any original state $P_0$ to the time-varying ideal solution $P^{*}\left(t\right)$ of (1).

3. Varying-Factor Finite-Time Recurrent Neural Networks

ZNN can achieve better convergence performance by means of using different activation functions or setting a larger constant factor [35], but its convergence performance still has room for further improvement. Inspired by classic ZNN design ideas, a novel recurrent neural network is put forward in this paper. It can realize a neural network with super-exponential convergence in a limited time, and because the factor before its activation function changes with time, it is called VFFTNN. It could be expressed as

$$\begin{array}{cc}\hfill \dot{E}\left(t\right)& =-\mathsf{\Gamma }\left(t\right)\left(\mathsf{\Phi }\left(E\left(t\right)\right)+\mathsf{\Phi }\left(E^{\lambda }\left(t\right)\right)\right)\hfill \\ \hfill & =-(t^{\alpha }+\alpha )\left(\mathsf{\Phi }\left(E\left(t\right)\right)+\mathsf{\Phi }\left(E^{\lambda }\left(t\right)\right)\right)\hfill \end{array}$$

(7)

where $\mathsf{\Gamma }\left(t\right)$ is a function about t, and it can be set to different functions. Here, for simplicity, we use exponential time-varying parameters $(t^{\alpha }+\alpha )$, and $\alpha$ is a positive scalar-valued factor, i.e., $\alpha >0$, and the positive scalar-valued factor $\lambda ={\displaystyle \frac{s}{q}}\in (0,1)$, where s and q both are odd numbers. In the light of (7), we can reformulate its implicit dynamic equation form:

$$\begin{array}{cc}\hfill \dot{U}\left(t\right)& P\left(t\right)+U\left(t\right)\dot{P}\left(t\right)-\dot{P}\left(t\right)V\left(t\right)-P\left(t\right)\dot{V}\left(t\right)+\dot{W}\left(t\right)\hfill \\ \hfill =& -(t^{\alpha }+\alpha )(\mathsf{\Phi }\left(U\left(t\right)P\left(t\right)-P\left(t\right)V\left(t\right)+W\left(t\right)\right)\hfill \\ \hfill & +\mathsf{\Phi }{\left(U\left(t\right)P\left(t\right)-P\left(t\right)V\left(t\right)+W\left(t\right)\right)}^{\lambda })\hfill \end{array}$$

(8)

In addition, in the light of Theorem 1 and equation (2) in Section I, we are able to obtain the vector form of the above implicit dynamic equation (8):

$$\begin{array}{cc}\hfill N\left(t\right)\dot{p}\left(t\right)=& -\dot{N}\left(t\right)p\left(t\right)-vec\left(\dot{W}\left(t\right)\right)\hfill \\ \hfill & -(t^{\alpha }+\alpha )(\mathsf{\Phi }\left(N\left(t\right)p\left(t\right)+vec\left(W\left(t\right)\right)\right)\hfill \\ \hfill & +\mathsf{\Phi }{\left(N\left(t\right)p\left(t\right)+vec\left(W\left(t\right)\right)\right)}^{\lambda })\hfill \end{array}$$

(9)

where $N\left(t\right):=I_n\otimes U\left(t\right)-V^T\left(t\right)\otimes I_m\in {\Re }^{mn\times mn}$ is a matrix, $p\left(t\right):=vec\left(P\left(t\right)\right)\in {\Re }^{mn}$ is a vector,and $\mathsf{\Phi }(·):{\Re }^{mn\times 1}\to {\Re }^{mn\times 1}$ is a activation function array. It is notable that the transformation dimensions of $\mathsf{\Phi }(·)$ in (9) are different with (5). 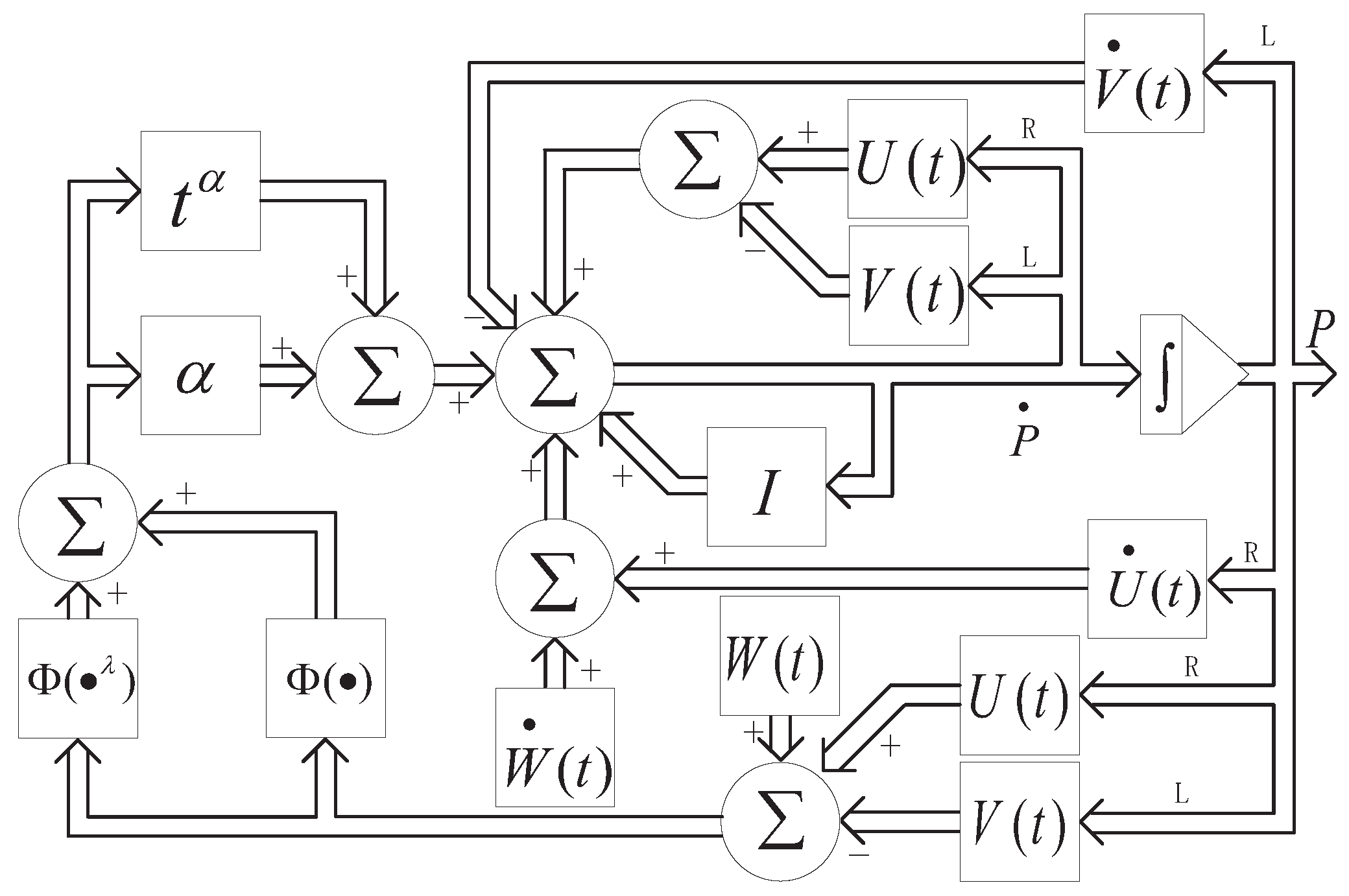The block diagram of VFFTNN can be drawn in the light of the implicit dynamic equation (8). As shown in Figure 1, ∫ and ∑ represent the integrator and accumulator respectively. The symbols L and R represent left and right multiplication of matrices, severally.

3.1. Convergence Analysis

The following theorem will lay the foundation which will come into play later when discussing VFFTNN global convergence.

Theorem 3.

For the time-varying Sylvester equation (1), its coefficient matrices $U\left(t\right)\in {\Re }^{m\times m}$, $V\left(t\right)\in {\Re }^{n\times n}$, and $W\left(t\right)\in {\Re }^{m\times n}$ have been given. If equation (1) satisfies inequality (3), and the activation function sequence is opted to be monotonous and oddly increasing, then the state matrix $P\left(t\right)$ of the VFFTNN model (8) can be global convergence from any original state $P_0$ to the time-varying ideal solution $P^{*}\left(t\right)$ of Sylvester equation (1).

Proof. 

First, we can convert VFFTNN system (7) into scalar form as

$$\begin{array}{c}\hfill {\dot{e}}_{ij}\left(t\right)=-(t^{\alpha }+\alpha )\left(\varphi \left(e_{ij}\left(t\right)\right)+\varphi \left(e_{ij}^{\lambda }\left(t\right)\right)\right)\\ \hfill \forall i\in \{1,2,...m\},j\in \{1,2,...n\}\end{array}$$

(10)

where $e_{ij}\left(t\right)$ represents the the $ith$ row and $j-$column position element on $E\left(t\right)$. In addition the $\varphi (·)$ represents the activation subfunction of matrix elements.

Next, we will proof its global convergence. Let us define a Lyapunov function as shown below:

$$v_{ij}\left(t\right)={\displaystyle \frac{1}{2}}{e}_{ij}^2\left(t\right),\forall i\in \{1,2,...m\},j\in \{1,2,...n\}$$

(11)

according to the above, we can calculate its derivative in time:

$$\begin{array}{cc}\hfill {\dot{v}}_{ij}\left(t\right)& =e_{ij}\left(t\right){\dot{e}}_{ij}\left(t\right)\hfill \\ \hfill & =-(t^{\alpha }+\alpha )e_{ij}\left(\varphi \left(e_{ij}\left(t\right)\right)+\varphi \left(e_{ij}^{\lambda }\left(t\right)\right)\right)\hfill \end{array}$$

It can be seen from the previous definition that $\alpha >0$ and $\varphi (·)$ is monotonous and oddly increasing. So for arbitrary $t\ge 0$ and $e_{ij}\left(t\right)$, we have

$$\begin{array}{c}\hfill {\dot{v}}_{ij}\left(t\right)\left\{\begin{array}{c}=0e_{ij}\left(t\right)=0\hfill \\ \le 0e_{ij}\left(t\right)\ne 0.\hfill \end{array}\right.\end{array}$$

In the light of Lyapunov stability theory, error function (10) is global asymptotical convergent. Therefore for any, i and j in the domain, the error function $e_{ij}\left(t\right)$ in scalar form will asymptotically converge to zero. In other words, the online solution $P\left(t\right)$ by using VFFTNN will approach its theoretical solution $P^{*}\left(t\right)$ when $t\to +\infty$.

In a word, the proof about Theorem 3 has been completed. That is, VFFTNN has global asymptotic convergence. □

In the next step, we will demonstrate finite-time convergence of VFFTNN under various activation functions (i.e., linear, bipolar-sigmoid, and power functions). See the following theorem for the specific convergence time.

Theorem 4.

For the time-varying Sylvester equation (1), its coefficient matrices $U\left(t\right)\in {\Re }^{m\times m}$, $V\left(t\right)\in {\Re }^{n\times n}$ and $W\left(t\right)\in {\Re }^{m\times n}$ have been given. If equation (1) satisfies the regularity condition (3) and the activation function sequence is monotonous and oddly increasing, then the VFFTNN system (8) can converge to the theoretical solution $P^{*}\left(t\right)$ of equation ( 1) in finite time from an arbitrary original state. In addition, the specific convergence time of neural system $\left(7\right)$ in the cases of different activation functions is:

1)

When we choose the linear activation function (i.e., $\varphi \left(x\right)=x$), the convergence time of VFFTNN $t_c<t_L$.

2)

When we choose the bipolar-sigmoid activation function (i.e., $\varphi \left(x\right)=(1-exp(-\xi x\left)\right)/(1+exp(-\xi x\left)\right)$, $\xi >0$), the convergence time of VFFTNN $t_c<t_B$.

3)

When we choose the power activation function (i.e., $\varphi \left(x\right)=x^s$, $\lambda s<1$ and s is an odd number), the convergence time of VFFTNN $t_c<t_P$.

The above $t_L$, $t_B$ and $t_P$ is respectively

$$\begin{array}{cc}\hfill & t_L=\sqrt[\alpha +1]{{\displaystyle \frac{\alpha +1}{1-\lambda }}ln({\chi }_1^{1-\lambda }+1)}\hfill \\ \hfill & t_B=\left\{\begin{array}{cc}\sqrt[\alpha +1]{{\displaystyle \frac{\alpha +1}{\omega (1-\lambda )}}ln({\chi }_1^{1-\lambda }+1)}\hfill & if{\chi }_1\le 1\hfill \\ \sqrt[\alpha +1]{{\displaystyle \frac{\alpha +1}{\omega (1-\lambda )}}ln2+{\displaystyle \frac{(\alpha +1)({\chi }_1-1)}{\omega }}}\hfill & ifotherwise.\hfill \end{array}\right.\hfill \\ & t_P=\left\{\begin{array}{cc}\sqrt[\alpha +1]{{\displaystyle \frac{\alpha +1}{2(1-\lambda s)}}{\chi }_1^{1-\lambda s}}\hfill & if{\chi }_1\le 1\hfill \\ \sqrt[\alpha +1]{{\displaystyle \frac{\alpha +1}{2(1-\lambda s)}}+{\displaystyle \frac{(\alpha +1)({\chi }_1^{1-s}-1)}{2(1-s)}}}\hfill & ifotherwise.\hfill \end{array}\right.\hfill \end{array}$$

(12)

where ${\chi }_1$ represents $max(|e_{ij}\left(0\right)|)$.

Proof. 

In the following, we will prove the convergence time of the VFFTNN system under three different activation functions one by one.

1)

Linear-type: For linear-type case, the following equation can be obtained from (10).

$${\dot{e}}_{ij}\left(t\right)=-(t^{\alpha }+\alpha )\left(e_{ij}\left(t\right)+e_{ij}^{\lambda }\left(t\right)\right)$$

(13)

In the light of the differential function theory [35], we can acquire the solution of (13).

$$e_{ij}\left(t\right)={\left((e_0^{1-\lambda }+1)exp\left((\lambda -1)(\alpha t+{\displaystyle \frac{t^{\alpha +1}}{\alpha +1}})\right)-1\right)}^{{\displaystyle \frac{1}{1-\lambda }}}$$

(14)

where $e_0=e_{ij}\left(0\right)$. Let $e_{ij}\left(t\right)$ in (13) be equal to zero, we can acquire the following:

$$\begin{array}{c}\hfill \alpha t+{\displaystyle \frac{t^{\alpha +1}}{\alpha +1}}={\displaystyle \frac{ln(e_0^{1-\lambda }+1)}{1-\lambda }}\ge {\displaystyle \frac{t^{\alpha +1}}{\alpha +1}}\end{array}$$

then we can easily find $t\le \sqrt[\alpha +1]{{\displaystyle \frac{\alpha +1}{1-\lambda }}ln(e_0^{1-\lambda }+1)}$. In other words, for any i and j on the definitional domain, we have when $t\to \sqrt[\alpha +1]{{\displaystyle \frac{\alpha +1}{1-\lambda }}ln(e_0^{1-\lambda }+1)}$, the scalar value $e_{ij}\left(t\right)\to 0$. Note the definition of $e_{ij}\left(t\right)$ above, at this time, the error function $E\left(t\right)$ in the form of a matrix will also approach zero, which means that the convergence of state matrix $P\left(t\right)\to P^{*}\left(t\right)$ is guaranteed.

To sum up, we can acquire the convergence time when VFFTNN system has used the linear-type activation function as follow:

$$t_L=\sqrt[\alpha +1]{{\displaystyle \frac{\alpha +1}{1-\lambda }}ln({\chi }_1^{1-\lambda }+1)}$$

(15)

where ${\chi }_1=max(|e_{ij}\left(0\right)|)$. It shows that in the case where the activation function is linear, VFFTNN method can achieve finite time convergence in the problem solving Sylvester equation.

2)

Bipolar-Sigmoid-Type: In this situation, we can easily know that the activation function form is $\varphi \left(x\right)=(1-exp(-\xi x\left)\right)/(1+exp(-\xi x\left)\right)$ where $\varphi \ge 1$ and $x\in R$ are scalar factors. So the following equation can be obtained from (10).

$$\begin{array}{cc}\hfill & {\dot{e}}_{ij}\left(t\right)=-(t^{\alpha }+\alpha )\left(R\left(t\right)+Q\left(t\right)\right)=\hfill \\ \hfill & -(t^{\alpha }+\alpha )\left({\displaystyle \frac{1-exp(-\xi e_{ij}\left(t\right))}{1+exp(-\xi e_{ij}\left(t\right))}}+{\displaystyle \frac{1-exp(-\xi e_{ij}^{\lambda }\left(t\right))}{1+exp(-\xi e_{ij}^{\lambda }\left(t\right))}}\right)\hfill \end{array}$$

where $R\left(e_{ij}\left(t\right)\right)={\displaystyle \frac{1-exp(-\xi e_{ij}\left(t\right))}{1+exp(-\xi e_{ij}\left(t\right))}}$, $Q\left(e_{ij}\left(t\right)\right)={\displaystyle \frac{1-exp(-\xi e_{ij}^{\lambda }\left(t\right))}{1+exp(-\xi e_{ij}^{\lambda }\left(t\right))}}$. In the light of relevant knowledge of the differential theory, we can rewritten (15) as

$$\begin{array}{c}\hfill {\displaystyle \frac{dy}{dt}}=-(t^{\alpha }+\alpha )\left(R\left(y\right)+Q\left(y\right)\right)\end{array}$$

where $y=e_{ij}\left(t\right)$. According to the Lyapunov function of this system, we can know that $e_{ij}\left(t\right)$ increases or decreases monotonically with the increase of t. So for simplicity, next we will only discuss the case of $e_{ij}\left(0\right)=y_0\ge 0$. Then we can acquire the following

$${\int }_0^t(t^{\alpha }+\alpha )dt=-{\int }_{y_0}^0{\displaystyle \frac{1}{R\left(y\right)+Q\left(y\right)}}dy$$

(16)

At this time we consider the following two situations.

a.

When $y_0\le 1$, noticing that $R\left(y\right)$ and $Q\left(y\right)$ are convex, solving for (16) can acquire

$$\begin{array}{cc}\hfill \alpha t+{\displaystyle \frac{t^{\alpha +1}}{\alpha +1}}& ={\int }_0^{y_0}{\displaystyle \frac{1}{R\left(y\right)+Q\left(y\right)}}dy\hfill \\ \hfill & \le {\displaystyle \frac{1}{\omega }}{\int }_0^{y_0}{\displaystyle \frac{1}{y+y^{\lambda }}}dy\hfill \\ \hfill & ={\displaystyle \frac{1}{\omega (1-\lambda )}}ln(y_0^{1-\lambda }+1)\hfill \end{array}$$

(17)

where $\omega =R\left(1\right)=Q\left(1\right)=(1-exp(-\xi \left)\right)/(1+exp(-\xi \left)\right)$ is a constant, determined by the scalar factor $\xi$. Similar to linear-type, solve for (17), we can acquire

$$t\le \sqrt[\alpha +1]{{\displaystyle \frac{\alpha +1}{\omega (1-\lambda )}}ln(y_0^{1-\lambda }+1)}$$

(18)

b.

When $y_0>1$, in the light of (16) and (17), (19) can be acquired

$$\begin{array}{cc}\hfill & \alpha t+{\displaystyle \frac{t^{\alpha +1}}{\alpha +1}}\hfill \\ \hfill & ={\int }_0^1{\displaystyle \frac{1}{R\left(y\right)+Q\left(y\right)}}dy+{\int }_1^{y_0}{\displaystyle \frac{1}{R\left(y\right)+Q\left(y\right)}}dy\hfill \\ \hfill & \le {\displaystyle \frac{1}{\omega (1-\lambda )}}ln2+{\int }_1^{y_0}{\displaystyle \frac{1}{R\left(y\right)+Q\left(y\right)}}dy\hfill \end{array}$$

(19)

Notice that $R\left(y\right)$ and $Q\left(y\right)$ are monotonically increasing over the interval $y>0$, so when $y>1$, $R\left(y\right)>R\left(1\right)>\omega$ and $Q\left(y\right)>Q\left(1\right)>\omega$. Therefor, we have

$$\begin{array}{c}\hfill {\int }_1^{y_0}{\displaystyle \frac{1}{R\left(y\right)+Q\left(y\right)}}dy\le {\int }_1^{y_0}{\displaystyle \frac{1}{\omega }}dy={\displaystyle \frac{y_0-1}{\omega }}\end{array}$$

(20)

Substitute (20) into (19) and solve for it, we can acquire

$$t\le \sqrt[\alpha +1]{{\displaystyle \frac{\alpha +1}{\omega (1-\lambda )}}ln2+{\displaystyle \frac{(\alpha +1)(y_0-1)}{\omega }}}$$

(21)

In the light of the results (18) and (21) of above two situations, it is can be known that when $t\to \sqrt[\alpha +1]{{\displaystyle \frac{\alpha +1}{\omega (1-\lambda )}}ln(y_0^{1-\lambda }+1)}$ or $t\to \sqrt[\alpha +1]{{\displaystyle \frac{\alpha +1}{\omega (1-\lambda )}}ln2+{\displaystyle \frac{(\alpha +1)(y_0-1)}{\omega }}}$, the scalar value $e_{ij}\left(t\right)\to 0$ for any i and j on the definitional domain. Which means that the convergence of state matrix $P\left(t\right)\to P^{*}\left(t\right)$ is guaranteed. The convergence time of the bipolar-sigmoid-type can be represented as

$$\begin{array}{cc}\hfill t& <\left\{\begin{array}{cc}\sqrt[\alpha +1]{{\displaystyle \frac{\alpha +1}{\omega (1-\lambda )}}ln({\chi }_1^{1-\lambda }+1)}\hfill & \mathrm{if}{\chi }_1\le 1\hfill \\ \sqrt[\alpha +1]{{\displaystyle \frac{\alpha +1}{\omega (1-\lambda )}}ln2+{\displaystyle \frac{(\alpha +1)({\chi }_1-1)}{\omega }}}\hfill & \mathrm{if} \mathrm{otherwise}.\hfill \end{array}\right.\hfill \\ \hfill & =t_B\hfill \end{array}$$

(22)

3)

Power-Type: For power-type case, we can easily know that the activation function form is $\varphi \left(x\right)=x^s$, where s is an odd number and $\lambda s<1$. So the following equation can be obtained from (10).

$${\dot{e}}_{ij}\left(t\right)=-(t^{\alpha }+\alpha )\left(e_{ij}^s\left(t\right)+e_{ij}^{\lambda s}\left(t\right)\right)$$

(23)

Similar to (16), we have

$${\displaystyle \frac{t^{\alpha +1}}{\alpha +1}}+\alpha t={\int }_0^{y_0}{\displaystyle \frac{1}{y^s+y^{\lambda s}}}dy$$

(24)

The discussion is divided into the following two situations:

a.

When $y_0\le 1$, it can be found easily that $1>\lambda s>s$, so $y^s>y^{\lambda s}$. In the light of (24), we can acquire

$$\begin{array}{c}\hfill {\displaystyle \frac{t^{\alpha +1}}{\alpha +1}}+\alpha t\le {\int }_0^{y_0}{\displaystyle \frac{1}{2y^{\lambda s}}}dy={\displaystyle \frac{1}{2(1-\lambda s)}}{y}_0^{1-\lambda s}\end{array}$$

Then the result (25) can be acquired

$$t<\sqrt[\alpha +1]{{\displaystyle \frac{\alpha +1}{2(1-\lambda s)}}{y}_0^{1-\lambda s}}$$

(25)

b.

When $y_0>1$, we know that for all $y>1$, we have $y^p<y^{\lambda s}$. So similarly:

$$\begin{array}{cc}\hfill {\displaystyle \frac{t^{\alpha +1}}{\alpha +1}}+\alpha t& \le {\int }_0^1{\displaystyle \frac{1}{2y^{\lambda s}}}dy+{\int }_1^{y_0}{\displaystyle \frac{1}{2y^s}}dy\hfill \\ \hfill & ={\displaystyle \frac{1}{2(1-\lambda s)}}+{\displaystyle \frac{y_0^{1-s}-1}{2(1-s)}}\hfill \end{array}$$

Then the follwing result (26) can be acquired

$$t<\sqrt[\alpha +1]{{\displaystyle \frac{\alpha +1}{2(1-\lambda s)}}+{\displaystyle \frac{(\alpha +1)(y_0^{1-s}-1)}{2(1-s)}}}$$

(26)

In conclusion, when $t\to \sqrt[\alpha +1]{{\displaystyle \frac{\alpha +1}{2(1-\lambda s)}}{y}_0^{1-\lambda s}}$ or $t\to \sqrt[\alpha +1]{{\displaystyle \frac{\alpha +1}{2(1-\lambda s)}}+{\displaystyle \frac{(\alpha +1)(y_0^{1-s}-1)}{2(1-s)}}}$, the scalar value $e_{(ij}\left(t\right)\to 0$ for any i and j on the definitional domain.It means that the convergence of state matrix $P\left(t\right)\to P^{*}\left(t\right)$ is guaranteed. The convergence time of the power-type can be represented as

$$\begin{array}{cc}\hfill t& <\left\{\begin{array}{cc}\sqrt[\alpha +1]{{\displaystyle \frac{\alpha +1}{2(1-\lambda s)}}{\chi }_1^{1-\lambda s}}\hfill & if{\chi }_1\le 1\hfill \\ \sqrt[\alpha +1]{{\displaystyle \frac{\alpha +1}{2(1-\lambda s)}}+{\displaystyle \frac{(\alpha +1)({\chi }_1^{1-s}-1)}{2(1-s)}}}\hfill & ifotherwise.\hfill \end{array}\right.\hfill \\ \hfill & =t_P\hfill \end{array}$$

(27)

In the light of the above analysis, it can be find that VFFTNN can achieve finite time convergence on the problem to solve Sylvester equation (1), no matter which of the three activation functions is used. So the proof of the finite time convergence Theorem 4 is completed. □

Remark 1: Regardless of choosing any one above activation functions, the convergence time for VFFTNN is determined by original error $E\left(0\right)$ (i.e., $E\left(0\right)=U\left(0\right)P\left(0\right)+P\left(0\right)V\left(0\right)-W\left(0\right)$) and the design factor $\alpha$ and $\lambda$.

Next, we will analyze the influence of the factor $\alpha$ and $\lambda$ for the convergence time under different activation functions one by one.

1)

Linear-Type:

a.

For $\alpha$, in the light of (14), $t_L$ can be rewritten as

$$t_L={\left({\chi }_2{\alpha }_1\right)}^{{\displaystyle \frac{1}{{\alpha }_1}}}$$

(28)

where ${\chi }_2={\displaystyle \frac{ln({\chi }_1^{1-\lambda }+1)}{1-\lambda }}>0$ and ${\alpha }_1=\alpha +1>1$. Then let us take the partial derivative with respect to ${\alpha }_1$.

$${\displaystyle \frac{\partial t_L}{\partial {\alpha }_1}}={\left({\chi }_2{\alpha }_1\right)}^{{\displaystyle \frac{1}{{\alpha }_1}}}{\displaystyle \frac{1-ln\left({\chi }_2{\alpha }_1\right)}{{\alpha }_1^2}}$$

(29)

We know that if ${\alpha }_1$ is enough large, the $1-ln\left({\chi }_2{\alpha }_1\right)$ is going to be less than zero. Therefore for ${\displaystyle \frac{\partial t_L}{\partial {\alpha }_1}}$, there exist two situation:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \frac{\partial t_L}{\partial {\alpha }_1}}<0\forall {\alpha }_1>1\hfill \\ {\displaystyle \frac{\partial t_L}{\partial {\alpha }_1}}>0\exists {\alpha }_1>1\hfill \end{array}\right.\end{array}$$

For the first situation, $t_L$ decreases as ${\alpha }_1$ increases. In other words, when $\alpha$ increases, $t_L$ decreases at the same time. Similarly, for the second situation, $t_L$ will increase first and then decrease as $\alpha$ increases, which means when $\alpha$ is a certain specific number associated with initial error $E\left(0\right)$, $t_L$ is going to be a maximum.

b.

For $\lambda$, in the light of (15), it can be known easily that we just need to analyze ${\displaystyle \frac{ln({\chi }_1^{1-\lambda }+1)}{1-\lambda }}$. Take the partial derivative of it:

$${\displaystyle \frac{\partial \eta }{\partial {\lambda }_1}}={\displaystyle \frac{{\lambda }_1{\chi }_1^{{\lambda }_1}ln{\chi }_1-({\chi }_1^{{\lambda }_1}+1)ln({\chi }_1^{{\lambda }_1}+1)}{{\lambda }_1^2}}$$

(30)

where $\eta ={\displaystyle \frac{ln({\chi }_1^{1-\lambda }+1)}{1-\lambda }}$ and ${\lambda }_1=1-\lambda \in (0,1)$. Due to the denominator of (30) is always greater than zero, we just need to analyze its numerator

$${\lambda }_1{\chi }_1^{{\lambda }_1}ln{\chi }_1-({\chi }_1^{{\lambda }_1}+1)ln({\chi }_1^{{\lambda }_1}+1)$$

(31)

If ${\chi }_1\le 1$, then ${\lambda }_1{\chi }_1^{{\lambda }_1}ln{\chi }_1\le 0$, ${\lambda }_1{\chi }_1^{{\lambda }_1}ln{\chi }_1-({\chi }_1^{{\lambda }_1}+1)ln({\chi }_1^{{\lambda }_1}+1)<0$, the value of (30) is always less than zero; If ${\chi }_1>1$, let ${\chi }_1^{{\lambda }_1}={\lambda }_2>1$, then ${\lambda }_1={\displaystyle \frac{ln{\lambda }_2}{ln{\chi }_1}}$. Its numerator can be rewritten as

$$\begin{array}{cc}\hfill & {\lambda }_1{\chi }_1^{{\lambda }_1}ln{\chi }_1-({\chi }_1^{{\lambda }_1}+1)ln({\chi }_1^{{\lambda }_1}+1)\hfill \\ \hfill & ={\lambda }_{2}ln{\lambda }_2-({\lambda }_2+1)ln({\lambda }_2+1)\hfill \end{array}$$

(32)

Note that for the function $f\left(x\right)=xlnx$ is monotonically increasing when $x>1$. Therefore the value of (32) is always less than zero. In other words, the value of (30) is always less than zero.

In the light of the above discussion, we can know that for any ${\lambda }_1$, it is always true that ${\displaystyle \frac{\partial \eta }{\partial {\lambda }_1}}<0$. And noticing the relationship between ${\lambda }_1$ and $\lambda$, we can acquire the conclusion that when $\lambda$ is larger, $t_L$ is smaller.

2)

Bipolar-Sigmoid-Type:

a.

For $\alpha$, in the light of (22), $t_B$ can be rewritten as

$$\begin{array}{c}\hfill t_B={\left({\chi }_3{\alpha }_1\right)}^{{\displaystyle \frac{1}{{\alpha }_1}}}\end{array}$$

(33)

where ${\chi }_3=\left\{\begin{array}{c}{\displaystyle \frac{ln({\chi }_1^{1-\lambda }+1)}{\omega (1-\lambda )}}>0,{\chi }_1\le 1\hfill \\ {\displaystyle \frac{ln2}{\omega (1-\lambda )}}+{\displaystyle \frac{{\chi }_1-1}{\omega }}>0,{\chi }_1>1\hfill \end{array}\right.$. Similar to the analysis of linear-type above, there exists two situations:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \frac{\partial t_B}{\partial {\alpha }_1}}<0\forall {\alpha }_1>1\hfill \\ {\displaystyle \frac{\partial t_B}{\partial {\alpha }_1}}>0\exists {\alpha }_1>1\hfill \end{array}\right.\end{array}$$

For the first situation, when $\alpha$ increases, $t_B$ decreases. For the second situation, there exists a certain value where $t_B$ is maximized.

b.

For $\lambda$, analyzing the structure of (22), we can know that we just care about ${\displaystyle \frac{ln({\chi }_1^{1-\lambda }+1)}{1-\lambda }}$ when ${\chi }_1\le 1$ and ${\displaystyle \frac{ln2}{1-\lambda }}$ when ${\chi }_1>1$. Due to the bigger $\lambda$ is, the bigger ${\displaystyle \frac{ln2}{1-\lambda }}$ and the derivation of $1)$ above, it is not hard to acquire that for any $\lambda \in (0,1)$, the bigger $\lambda$ is, the bigger $t_B$ is.

In addition, consider the influence of the factor $\xi$ to convergence time $t_B$. We know $\omega ={\displaystyle \frac{1-e^{-\xi }}{1+e^{-\xi }}}$, and the bigger $\xi$ is, the bigger $\omega$ is. Further according to (22), the bigger $\omega$ is, the smaller $t_B$ is.

3)

Power-Type:

a.

For $\alpha$, let ${\chi }_4=\left\{\begin{array}{c}{\displaystyle \frac{{\chi }_1^{1-\lambda s}}{2(1-\lambda s)}}>0,{\chi }_1\le 1\hfill \\ {\displaystyle \frac{1}{2(1-\lambda s)}}+{\displaystyle \frac{1-{\chi }_1^{s-1}}{2(s-1)}}>0,{\chi }_1>1\hfill \end{array}\right.$, then we have

$$t_P={\left({\chi }_4{\alpha }_1\right)}^{{\displaystyle \frac{1}{{\alpha }_1}}}$$

(34)

Similar to the analysis of linear-type above, there exists two situations:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \frac{\partial t_P}{\partial {\alpha }_1}}<0\forall {\alpha }_1>1\hfill \\ {\displaystyle \frac{\partial t_P}{\partial {\alpha }_1}}>0\exists {\alpha }_1>1\hfill \end{array}\right.\end{array}$$

For the first situation, when $\alpha$ increases, $t_P$ decreases. For the second situation, there exists a certain value where $t_P$ is maximized.

b.

For $\lambda$, according to (27), we can know that the bigger $\lambda$ is, the bigger $t_P$ is also when ${\chi }_1>0$. In addition, when ${\chi }_1\le 1$, we just consider ${\displaystyle \frac{{\chi }^{1-\lambda s}}{1-\lambda s}}$. Let ${\lambda }_3=1-\lambda s\in (0,1)$, then

$${\displaystyle \frac{\partial }{\partial {\lambda }_3}}\left({\displaystyle \frac{{\chi }_1^{{\lambda }_3}}{{\lambda }_3}}\right)={\displaystyle \frac{{\chi }_1^{{\lambda }_3}({\lambda }_{3}ln{\chi }_1-1)}{{\lambda }_3^2}}<0$$

(35)

So in conclusion, it is not hard to see that for $\forall \lambda \in (0,1)$, when $\lambda$ is larger, $t_P$ is larger.

In the light of above derivation, the following conclusions can be acquired:

1)

For $\alpha$, its relation to the convergence time is always divided into two cases. In the first case, the larger $\alpha$ is, the smaller the convergence time is. In the second case, the convergence time increases first and then decreases. It is worth noting that even if $\alpha =0$, the VFFTNN system will still converge in finite time.

2)

For $\lambda$, the convergence time always increases with the increase of $\lambda$, no matter what kind of activation function is chosen. Obviously, the factor $\lambda$ speeds up the convergence process of the proposed VFFTNN. If $\lambda =1$, then the proposed VFFTNN will become VP-CDNN and further, if the factor $\alpha =0$, then the proposed VFFTNN will become ZNN.

3.2. Robustness Analysis

As we all know, in actual application, the circumstance is always not prefect. Because of various reasons, such as such as errors in digital implementations or higher-order residues of circuit elements (such as diodes) in hardware implementations, there exist plenty of factors that interfere with the VFFTNN model all the time. And they are three common negative factors that coefficient matrices disturbances, differentiation error and model-implementation error. Next, we disscuss the robustness of the VFFNTT model when these negative factors are present.

1)

Coefficient Matrix Perturbation:

Theorem 5.

If uncharted smooth coefficient matrices perturbations $\mathsf{\Delta }U\left(t\right)\in {\Re }^{m\times m}$, $\mathsf{\Delta }V\left(t\right)\in {\Re }^{n\times n}$ and $\mathsf{\Delta }W\left(t\right)\in {\Re }^{m\times n}$ have existed in VFFTNN model, which satisfy the following conditions:

$$\begin{array}{cc}\hfill & ||N^{-1}\left(t\right)|{|}_F\le {\upsilon }_1,||{\widehat{N}}^{-1}\left(t\right)|{|}_F\le {\upsilon }_2\hfill \\ \hfill & ||W\left(t\right)|{|}_F\le {\iota }_1,||\mathsf{\Delta }W\left(t\right)|{|}_F\le {\iota }_2,\forall t\in [0,+\infty )\hfill \end{array}$$

where the mass matrices $N^{-1}\left(t\right):={\left(I_n\otimes U\left(t\right)-V{\left(t\right)}^T\otimes I_m\right)}^{-1}$, ${\widehat{N}}^{-1}\left(t\right):={\left(I_n\otimes (U\left(t\right)+\mathsf{\Delta }U\left(t\right))-{(V\left(t\right)+\mathsf{\Delta }V\left(t\right))}^T\otimes I_m\right)}^{-1}$, then its calculation error $||\widehat{\tilde{P}}{\left(t\right)||}_F=||\widehat{P}\left(t\right)-P^{*}\left(t\right){||}_F$ is bounded.

Proof. 

The following proof takes the linear activation function as an example. First, we define a variable $\tilde{P}\left(t\right)=P\left(t\right)-P^{*}\left(t\right)$ which can scale the error of state matrix $P\left(t\right)\to P^{*}\left(t\right)$. Then its Frobenius norm can be written as

$$||\tilde{P}\left(t\right)|{|}_F=\sqrt{\sum _{i=1}^m\sum _{j=1}^n{{\tilde{p}}^2}_{ij}\left(t\right)}=||\tilde{p}\left(t\right)|{|}_2$$

where $\tilde{p}\left(t\right):=vec\left(\tilde{P}\left(t\right)\right)\in {\Re }^{mn\times 1}$. Besides, in the light of (1), We can get an expression of W

$$W\left(t\right)=-U\left(t\right)P^{*}\left(t\right)+P^{*}\left(t\right)V\left(t\right)$$

(36)

Substitute (36) into (4)

$$E\left(t\right)=U\left(t\right)\tilde{P}\left(t\right)-\tilde{P}\left(t\right)V\left(t\right)$$

In the light of Theorem 1, we can acquire its vector form

$$e\left(t\right)=N\left(t\right)\tilde{p}\left(t\right)=N\left(t\right)\left(p\left(t\right)-p^{*}\left(t\right)\right)$$

(37)

where $e\left(t\right):=vec\left(E\left(t\right)\right)$ as well as $p^{*}\left(t\right):=vec\left(P^{*}\left(t\right)\right)$. From Theorem 2 as well as inequality (3), it is not difficult to know that matrix $N\left(t\right)$ is a invertible matrix. Therefore we know

$$\begin{array}{cc}\hfill ||\tilde{P}\left(t\right)|{|}_F=||\tilde{p}\left(t\right)|{|}_2& \le ||N^{-1}\left(t\right)|{|}_F||e\left(t\right)|{|}_2\hfill \\ \hfill & \le {\upsilon }_1\sqrt{\sum _{i=1}^m\sum _{j=1}^n{e}_{ij}^2\left(t\right)}\hfill \end{array}$$

(38)

Substitute (13) into (38), we can acquire

$$\begin{array}{cc}\hfill & ||\tilde{P}\left(t\right)|{|}_F\hfill \\ \hfill & \le {\upsilon }_1\sqrt{\sum _{i=1}^m\sum _{j=1}^n{((e_{ij}^{1-\lambda }\left(0\right)+1)e^{(\lambda -1)(\alpha t+{\displaystyle \frac{t^{\alpha +1}}{\alpha +1}})}-1)}^{{\displaystyle \frac{2}{1-\lambda }}}}\hfill \\ \hfill & \le {\upsilon }_1\sqrt{mn}{(({\chi }_1^{1-\lambda }+1)e^{(\lambda -1)(\alpha t+{\displaystyle \frac{t^{\alpha +1}}{\alpha +1}})}-1)}^{{\displaystyle \frac{1}{1-\lambda }}}\hfill \\ \hfill & \le {\upsilon }_1{\tau }_1{e}^{-(\alpha t+{\displaystyle \frac{t^{\alpha +1}}{\alpha +1}})}\hfill \end{array}$$

(39)

where ${\tau }_1=\sqrt{mn}{({\chi }_1^{1-\lambda }+1)}^{{\displaystyle \frac{1}{1-\lambda }}}>0$. The results show that the VFFTNN model to solve the Sylvester equation has super-exponential convergence in the case of linear-type activation function.

Next, we consider the situation existing coefficient matrix perturbation. In the light of (8), it is not difficult for us to write the implicit dynamic equation of the VFFTNN system when exists perturbation.

$$\begin{array}{cc}\hfill \dot{\widehat{U}}(& t)\widehat{P}\left(t\right)+\widehat{U}\left(t\right)\dot{\widehat{P}}\left(t\right)-\dot{\widehat{P}}\left(t\right)\widehat{V}\left(t\right)-\widehat{P}\left(t\right)\dot{\widehat{V}}\left(t\right)+\dot{\widehat{W}}\left(t\right)\hfill \\ \hfill =& -(t^{\alpha }+\alpha )(\mathsf{\Phi }(\widehat{U}\left(t\right)\widehat{P}\left(t\right)-\widehat{P}\left(t\right)\widehat{V}\left(t\right)+\widehat{W}\left(t\right))\hfill \\ \hfill & +\mathsf{\Phi }{(\widehat{U}\left(t\right)\widehat{P}\left(t\right)-\widehat{P}\left(t\right)\widehat{V}\left(t\right)+\widehat{W}\left(t\right))}^{\lambda })\hfill \end{array}$$

(40)

where $\widehat{U}\left(t\right)=U\left(t\right)+\mathsf{\Delta }U\left(t\right)$, $\widehat{V}\left(t\right)=V\left(t\right)+\mathsf{\Delta }V\left(t\right)$ and $\widehat{W}\left(t\right)=W\left(t\right)+\mathsf{\Delta }W\left(t\right)$. $\widehat{P}\left(t\right)$ denotes the solution to the VFFTNN system existing perturbation.

Besides, in the light of (36), its vector form can be written as

$$w\left(t\right)=-N\left(t\right)p^{*}\left(t\right)$$

where $w\left(t\right):=vec\left(W\right(t\left)\right)$, then we can acquire

$$p^{*}\left(t\right)=-N^{-1}\left(t\right)w\left(t\right)$$

Therefore we can acquire the inequality about the theoretical solution $P^{*}\left(t\right)$.

$$\begin{array}{cc}\hfill ||P^{*}\left(t\right)|{|}_F& =||p^{*}\left(t\right)|{|}_2=||N^{-1}\left(t\right)w\left(t\right)|{|}_2\hfill \\ \hfill & \le ||N^{-1}\left(t\right)|{|}_F||w\left(t\right)|{|}_F\le {\upsilon }_1{\iota }_1\hfill \end{array}$$

(41)

Let us assume that the theoretical solution for VFFTNN system with the perturbation is ${\widehat{P}}^{*}\left(t\right)$. Similar to (40), we can easily know

$$\begin{array}{cc}\hfill ||{\widehat{P}}^{*}\left(t\right)|{|}_F& \le ||{\widehat{N}}^{-1}\left(t\right)|{|}_F||\widehat{W}\left(t\right)|{|}_F\hfill \\ \hfill & \le {\upsilon }_2(||W\left(t\right)|{|}_F+||\mathsf{\Delta }W\left(t\right)|{|}_F)\le {\upsilon }_2({\iota }_1+{\iota }_2)\hfill \end{array}$$

(42)

In addition, similar to (39), it can be acquired

$$||\widehat{P}\left(t\right)-{\widehat{P}}^{*}\left(t\right)|{|}_F\le {\upsilon }_2{\tau }_2{e}^{-(\alpha t+{\displaystyle \frac{t^{\alpha +1}}{\alpha +1}})}$$

(43)

where ${\tau }_2=\sqrt{mn}{({\chi }_5^{1-\lambda }+1)}^{{\displaystyle \frac{1}{1-\lambda }}}$ and ${\chi }_5=max|{(\widehat{U}\left(0\right)\widehat{P}\left(0\right)-\widehat{P}\left(0\right)\widehat{V}\left(0\right)+\widehat{W}\left(0\right))}_{ij}|$.

Then, according to (41), (42) and (43), we can acquire an upper bound on the computation error $||\widehat{\tilde{P}}\left(t\right){||}_F$.

$$\begin{array}{cc}\hfill ||\widehat{\tilde{P}}\left(t\right){||}_F& =||\widehat{P}\left(t\right)-P^{*}\left(t\right)|{|}_F\hfill \\ \hfill & \le ||\widehat{P}\left(t\right)-{\widehat{P}}^{*}\left(t\right)|{|}_F+||{\widehat{P}}^{*}\left(t\right)-P^{*}\left(t\right)|{|}_F\hfill \\ \hfill & \le {\upsilon }_2{\tau }_2{e}^{-(\alpha t+{\displaystyle \frac{t^{\alpha +1}}{\alpha +1}})}+||{\widehat{P}}^{*}\left(t\right)|{|}_F+||P^{*}\left(t\right)|{|}_F\hfill \\ \hfill & \le {\upsilon }_2{\tau }_2{e}^{-(\alpha t+{\displaystyle \frac{t^{\alpha +1}}{\alpha +1}})}+{\upsilon }_1{\iota }_1+{\upsilon }_2({\iota }_1+{\iota }_2)\hfill \end{array}$$

(44)

In the light of above analysis, we have a conclusion when using linear-type activation function, the computation error $||\widehat{\tilde{P}}\left(t\right){||}_F$ of the VFFTNN system with the perturbation is bounded. In addition, it is worth mentioning that the solution process has a super-exponential convergence rate.

Similarly, for sigmoid or power activation functions, we are not hard to prove that the computation error of the VFFTNN system with the perturbation is bounded. Thinks to the limited space of this paper, the situation of these two activation functions will not be presented here. So the proof of the robustness Theorem 5 of matrix perturbation is completed. □

2)

Differentiation and Model-Implementation Errors:

In the process of hardware implementation, it is inevitable to appear the dynamics implementation error and differential error about $U\left(t\right)$, $V\left(t\right)$ and $W\left(t\right)$. Besides, these errors are collectively referred to as model-implementation error [36]. So here, we will analyze the robustness of the VFFTNN system in the presence of these errors. Let us suppose that these differential errors for time derivatives matrices $\dot{U}\left(t\right)$, as well as $\dot{V}\left(t\right)$, are severally $\mathsf{\Lambda }\left(t\right)\in {\Re }^{m\times m}$ and $\mathsf{\Omega }\left(t\right)\in {\Re }^{n\times n}$, the model-implementation error is $\mathsf{\Delta }\left(t\right)\in R^{m\times n}$. Then in the light of (8),the implicit dynamic equation for VFFTNN system with these errors is written as

$$\begin{array}{cc}\hfill & U\left(t\right)\dot{P}\left(t\right)+(\dot{U}\left(t\right)+\mathsf{\Lambda }\left(t\right))P\left(t\right)-\dot{P}\left(t\right)V\left(t\right)\hfill \\ \hfill & -P\left(t\right)(\dot{V}\left(t\right)+\mathsf{\Omega }\left(t\right))+\dot{W}\left(t\right)-\mathsf{\Delta }\left(t\right)\hfill \\ \hfill & =-(t^{\alpha }+\alpha )(\mathsf{\Phi }(U\left(t\right)P\left(t\right)-P\left(t\right)V\left(t\right)+W\left(t\right))\hfill \\ \hfill & +\mathsf{\Phi }\left({(U\left(t\right)P\left(t\right)-P\left(t\right)V\left(t\right)+W\left(t\right))}^{\lambda }\right))\hfill \end{array}$$

(45)

Theorem 6.

If there exist unknown smooth differentiation errors $\mathsf{\Lambda }\left(t\right)$, $\mathsf{\Omega }\left(t\right)$ and model-implementation error $\mathsf{\Delta }\left(t\right)$ in VFFTNN model, which satisfy the following conditions:

$$\begin{array}{c}\hfill ||\mathsf{\Lambda }\left(t\right)|{|}_F\le {\epsilon }_1||\mathsf{\Omega }\left(t\right)|{|}_F\le {\epsilon }_2||\mathsf{\Delta }\left(t\right)|{|}_F\le {\epsilon }_3\\ \hfill ||N^{-1}\left(t\right)|{|}_F\le {\upsilon }_1||W\left(t\right)|{|}_F\le {\iota }_1,\forall t\in [0,+\infty )\end{array}$$

then its computation error $||P\left(t\right)-P^{*}\left(t\right){||}_F$ is bounded.

Proof. 

Let us convert (45) from matrix form to vector form in order to analyze more easily.

$$\begin{array}{cc}\hfill N\left(t\right)\dot{p}\left(t\right)=& -(\dot{N}\left(t\right)+\mathsf{\Psi }\left(t\right))p\left(t\right)-\dot{w}\left(t\right)+\delta \left(t\right)\hfill \\ \hfill & -(t^{\alpha }+\alpha )(\mathsf{\Phi }(N\left(t\right)p\left(t\right)+w\left(t\right))\hfill \\ \hfill & +\mathsf{\Phi }\left({(N\left(t\right)p\left(t\right)+w\left(t\right))}^{\lambda }\right))\hfill \end{array}$$

(46)

where $\mathsf{\Psi }\left(t\right):=I_n\otimes \mathsf{\Lambda }\left(t\right)-{\mathsf{\Omega }}^T\left(t\right)\otimes I_m$ and $\delta \left(t\right):=vec\left(\mathsf{\Delta }\right(t\left)\right)$. In addition, we can simply tell that $e\left(t\right)=N\left(t\right)p\left(t\right)+w\left(t\right)$, than the derivative about times is $\dot{e}\left(t\right)=\dot{N}\left(t\right)p\left(t\right)+N\left(t\right)\dot{p}\left(t\right)+\dot{w}\left(t\right)$. Therefore equation (48) can reformulate as

$$\dot{e}\left(t\right)=-(t^{\alpha }+\alpha )\left(\mathsf{\Phi }\left(e\left(t\right)\right)+\mathsf{\Phi }\left(e^{\lambda }\left(t\right)\right)\right)+\delta \left(t\right)-\mathsf{\Psi }\left(t\right)p\left(t\right)$$

(47)

In the light of (37), we can acquire

$$x\left(t\right)=N^{-1}\left(t\right)e\left(t\right)+p^{*}\left(t\right)$$

(48)

Substitute (47) into (48), we have

$$\begin{array}{cc}\hfill \dot{e}\left(t\right)=& -(t^{\alpha }+\alpha )\left(\mathsf{\Phi }\left(e\left(t\right)\right)+\mathsf{\Phi }\left(e^{\lambda }\left(t\right)\right)\right)\hfill \\ \hfill & +\mathrm{H}\left(t\right)e\left(t\right)+\mathrm{K}\left(t\right)\hfill \end{array}$$

(49)

where $\mathrm{H}\left(t\right)=-\mathsf{\Psi }\left(t\right)N^{-1}\left(t\right)\in {\Re }^{mn\times mn}$, as well as $\mathrm{K}\left(t\right)=\delta \left(t\right)-\mathsf{\Psi }\left(t\right)p^{*}\left(t\right)\in {\Re }^{mn\times 1}$.

After that, we construct a Lyapunov function candidate in this form that $v:={\displaystyle \frac{1}{2}}{e}^T\left(t\right)e\left(t\right)$ and we can acquire its time derivative:

$$\begin{array}{cc}\hfill \dot{v}=e^T\left(t\right)\dot{e}\left(t\right)=& -(t^{\alpha }+\alpha )e^T\left(t\right)\left(\mathsf{\Phi }\left(e\left(t\right)\right)+\mathsf{\Phi }\left(e^{\lambda }\left(t\right)\right)\right)\hfill \\ \hfill & +e^T\left(t\right)\mathrm{H}\left(t\right)e\left(t\right)+e^T\left(t\right)\mathrm{K}\left(t\right)\hfill \end{array}$$

(50)

Observing the composition of (50) and (41), we can get

$$\begin{array}{cc}\hfill & e^T\left(t\right)\mathrm{H}\left(t\right)e\left(t\right)\hfill \\ \hfill & \le ||e^T\left(t\right)|{|}_2||\mathrm{H}\left(t\right)|{|}_F||e\left(t\right)|{|}_2\le e^T\left(t\right)e\left(t\right)||\mathrm{H}\left(t\right)|{|}_F\hfill \\ \hfill & \le ||\mathsf{\Psi }\left(t\right)|{|}_F||M^{-1}\left(t\right)|{|}_F{e}^T\left(t\right)e\left(t\right)\hfill \\ \hfill & \le {\upsilon }_1(||I_n\otimes \mathsf{\Lambda }\left(t\right)|{|}_F+||{\mathsf{\Omega }}^T\left(t\right)\otimes I_m|{|}_F)e^T\left(t\right)e\left(t\right)\hfill \\ \hfill & \le {\upsilon }_1({\epsilon }_1\sqrt{n}+{\epsilon }_2\sqrt{m})\sum _{i=1}^m\sum _{j=1}^n{e}_{ij}^2\left(t\right)\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & e^T\left(t\right)\mathrm{K}\left(t\right)\le ||e^T\left(t\right)|{|}_2||\mathrm{K}\left(t\right)|{|}_F\hfill \\ \hfill & \le ||e^T\left(t\right)|{|}_2(||\mathsf{\Delta }\left(t\right)|{|}_F+||\mathsf{\Psi }\left(t\right)|{|}_F||P^{*}\left(t\right)|{|}_F)\hfill \\ \hfill & \le \left({\epsilon }_3+({\epsilon }_1\sqrt{n}+{\epsilon }_2\sqrt{m}){\upsilon }_1{\iota }_1\right)\sqrt{\sum _{i=1}^m\sum _{j=1}^n{e}_{ij}^2\left(t\right)}\hfill \\ \hfill & \le \left({\epsilon }_3+({\epsilon }_1\sqrt{n}+{\epsilon }_2\sqrt{m}){\upsilon }_1{\iota }_1\right)\sum _{i=1}^m\sum _{j=1}^n|e_{ij}\left(t\right)|\hfill \end{array}$$

Substitute the above two equations into (51), and we can get

$$\begin{array}{cc}\hfill \dot{v}\le -\sum _{i=1}^m\sum _{j=1}^n|e_{ij}\left(t\right)|(& (t^{\alpha }+\alpha )\left(\varphi (|e_{ij}\left(t\right)|)+\varphi (|e_{ij}^{\lambda }\left(t\right)|)\right)\hfill \\ \hfill & -{\zeta }_1{\upsilon }_1|e_{ij}\left(t\right)|-{\zeta }_2)=\mathsf{{\rm Y}}\left(t\right)\hfill \end{array}$$

(51)

where ${\zeta }_1={\epsilon }_1\sqrt{n}+{\epsilon }_2\sqrt{m}$ and ${\zeta }_2={\epsilon }_3+{\zeta }_1{\upsilon }_1{\iota }_1$.

We know that $\varphi (|e_{ij}\left(t\right)|)\ge |e_{ij}\left(t\right)|$ for any t, and $t^{\alpha }+\alpha$ is increased with t increasing. So there always exists a value $t_0$, when for all $t>t_0$, $(t^{\alpha }+\alpha )\left(\varphi (|e_{ij}\left(t\right)|)+\varphi (|e_{ij}^{\lambda }\left(t\right)|)\right)-{\zeta }_1{\upsilon }_1|e_{ij}\left(t\right)|-{\zeta }_2)>0$. Therefore for (51), we should consider the following two cases:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\alpha \left(\varphi \right(|e_{ij}\left(0\right)|)+\varphi (|e_{ij}^{\lambda }\left(0\right)|))-{\zeta }_1{\upsilon }_1|e_{ij}\left(0\right)|-{\zeta }_2\ge 0\hfill \\ \forall i\in \{1,...,m\},j\in \{1,...,n\}\hfill \\ \alpha \left(\varphi \right(|e_{ij}\left(0\right)|)+\varphi (|e_{ij}^{\lambda }\left(0\right)|))-{\zeta }_1{\upsilon }_1|e_{ij}\left(0\right)|-{\zeta }_2<0\hfill \\ \exists i\in \{1,...,m\},j\in \{1,...,n\}\hfill \end{array}\right.\end{array}$$

(52)

1)

For first situation, it is easy to know $\mathsf{{\rm Y}}\left(t\right)<0$, i.e., $\dot{v}\le 0$. Therefore the error $e\left(t\right)$ will be going to be monotonically decreasing as time t increases, which shows that $P\left(t\right)$ eventually converges on $P^{*}\left(t\right)$ with time increases, i.e., $||P\left(t\right)-P^{*}\left(t\right){||}_F$ will approach to 0.

2)

For second situation, due to the symbol of $\mathsf{{\rm Y}}\left(0\right)$ is uncertain, we should subdivide it into two cases. If $\mathsf{{\rm Y}}\left(0\right)\le 0$, then the analysis is the same as 1). Besides, if $\mathsf{{\rm Y}}\left(0\right)>0$, then there exists a number $t_0$ that makes $\mathsf{{\rm Y}}\left(t\right)\le 0$ for any $t>t_0$. It shows that the error $e\left(t\right)$ will increase first and then decrease. In the light of paper [37], we can acquire the upper bound of $||\tilde{P}{\left(t\right)||}_F=||P\left(t\right)-P^{*}\left(t\right){||}_F$ when using linear activation function:

$$\begin{array}{c}\hfill ||\tilde{P}\left(t\right){||}_F\le {\displaystyle \frac{{\upsilon }_1{\zeta }_2(mn+\sqrt{mn})}{2(\rho (t^{\alpha }+\alpha )-{\upsilon }_1{\zeta }_1)}}\end{array}$$

(53)

Because of ${\zeta }_2>0$ and $(mn+\sqrt{mn})>0$, it is pledged that (52) hold true. The design factor $\rho$ should be set to greater than ${\displaystyle \frac{{\upsilon }_1{\zeta }_2}{\alpha }}$ in order to the denominator of the fraction is greater than zero. Therefore when $t\to +\infty$, the computation error $||\tilde{P}\left(t\right){||}_F$ will approach to 0.

Summing up the above, as time increases, the computation error $||\tilde{P}\left(t\right){||}_F$ tends to zero in both cases. The difference is that in first situation, the computation error $||\tilde{P}\left(t\right){||}_F$ is going to go down, whereas in second situation, the computation error $||\tilde{P}\left(t\right){||}_F$ is going to go up and down, and there is an upper bound ${\displaystyle \frac{{\upsilon }_1{\zeta }_2(mn+\sqrt{mn})}{2(\rho (t^{\alpha }+\alpha )-{\upsilon }_1{\zeta }_1)}}$. □

Table 1. Comparisons of Convergence Time of ZNN and VFFTNN when solving Sylvester equation.

$\mathit{P}\mathit{a}\mathit{r}\mathit{a}\mathit{m}\mathit{e}\mathit{t}\mathit{e}\mathit{r}(\mathit{\alpha }=\mathit{\mu })$	${\mathit{T}}_{\mathit{Z}\mathit{N}\mathit{N}\left(\mathit{s}\right)}$	${\mathit{T}}_{\mathit{V}\mathit{F}\mathit{F}\mathit{T}\mathit{N}\mathit{N}\left(\mathit{s}\right)}$
0.01	Cannot converge	2.39
0.1	67.55	2.25
0.2	34.20	1.99
0.5	13.88	1.69
1	6.98	1.41
2	3.48	1.02
5	1.37	0.49

Table 1. Comparisons of Convergence Time of ZNN and VFFTNN when solving Sylvester equation.

$\mathit{P}\mathit{a}\mathit{r}\mathit{a}\mathit{m}\mathit{e}\mathit{t}\mathit{e}\mathit{r}(\mathit{\alpha }=\mathit{\mu })$	${\mathit{T}}_{\mathit{Z}\mathit{N}\mathit{N}\left(\mathit{s}\right)}$	${\mathit{T}}_{\mathit{V}\mathit{F}\mathit{F}\mathit{T}\mathit{N}\mathit{N}\left(\mathit{s}\right)}$
0.01	Cannot converge	2.39
0.1	67.55	2.25
0.2	34.20	1.99
0.5	13.88	1.69
1	6.98	1.41
2	3.48	1.02
5	1.37	0.49

4. Illustrative Example

We will verify the capability for proposed VFFTNN and compare with ZNN by giving specific example in this part. Let us set the coefficients on the time-varying Sylvester equation (1) as follows:

$$\begin{array}{cc}\hfill & U\left(t\right)=\left[\begin{array}{cc}{\displaystyle \frac{\sin t}{10}}& {\displaystyle \frac{\cos t}{10}}\\ {\displaystyle \frac{-\cos t}{10}}& {\displaystyle \frac{\sin t}{10}}\end{array}\right],V\left(t\right)=\left[\begin{array}{cc}{\displaystyle \frac{\sin t}{100}}& 0\\ 0& {\displaystyle \frac{\cos t}{50}}\end{array}\right]\hfill \\ \hfill & W\left(t\right)=\left[\begin{array}{cc}{\displaystyle \frac{{\sin }^{2}t}{10}}-1& -{\displaystyle \frac{{\cos }^{2}t}{5}}\\ {\displaystyle \frac{\sin t\cos t}{10}}& {\displaystyle \frac{\sin t\cos t}{5}}-1\end{array}\right].\hfill \end{array}$$

Then its theoretical solution $P^{*}\left(t\right)$ can be easily obtained:

$$\begin{array}{c}\hfill P^{*}\left(t\right)=\left[\begin{array}{cc}10\sin t& -10\cos t\\ 10\cos t& 10\sin t\end{array}\right].\end{array}$$

In addition, we write $P\left(t\right)$ solved by VFFTNN in following form:

$$\begin{array}{c}\hfill P\left(t\right)=\left[\begin{array}{cc}{p}_{11}& p_{12}\\ p_{21}& p_{22}\end{array}\right]\end{array}$$

where $p_{ij}$ denotes the $ith$ row and $j-$column position element of $P\left(t\right)$. For the sake of discussion, let us set the initial state $P_0$ as follows :

$$\begin{array}{c}\hfill P_0=\left[\begin{array}{cc}{p}_a& p_b\\ p_c& p_d\end{array}\right]\end{array}$$

where $p_a$, $p_b$, $p_c$ and $p_d$ are all numbers created by MATLAB and all in the range $[-25,25]$.

Generally, the system is considered to have converged completely to solve Sylvester equation (1) when the computation error $||P\left(t\right)-P^{*}\left(t\right){||}_F$ is less than $0.1\%$ of the range(i.e., $||P\left(t\right)-P^{*}\left(t\right)||\le 50\times 0.1\%=0.05$). In other words, we only need to measure the time point when the calculation error $||P\left(t\right)-P^{*}\left(t\right){||}_F$ is less than 0.05, then we can get the convergence time.

4.1. Convergence Discussion

In this section, we will talk about their convergence performance by comparing with VFFTNN and ZNN to solve Sylvester equation in different situations.

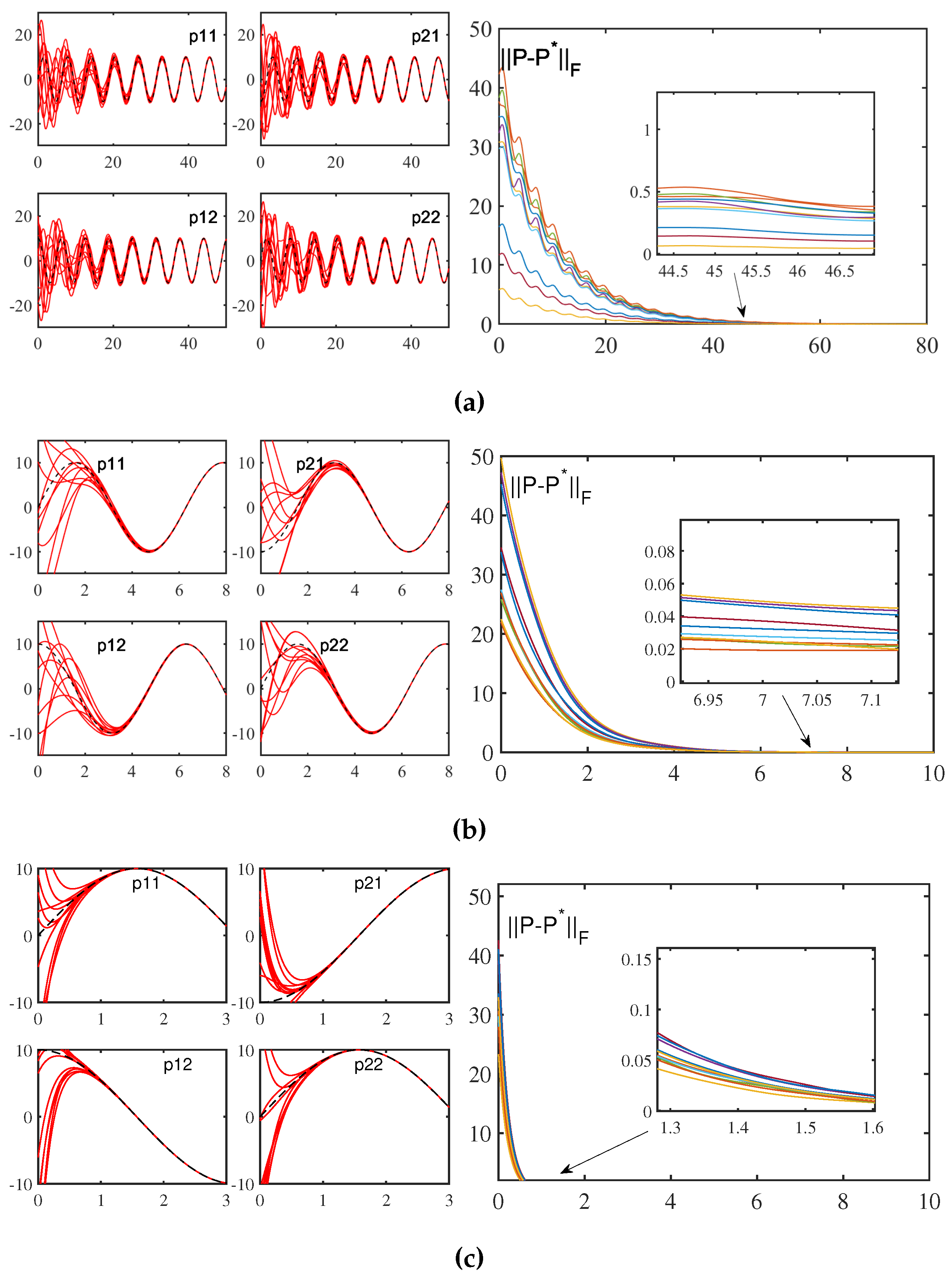
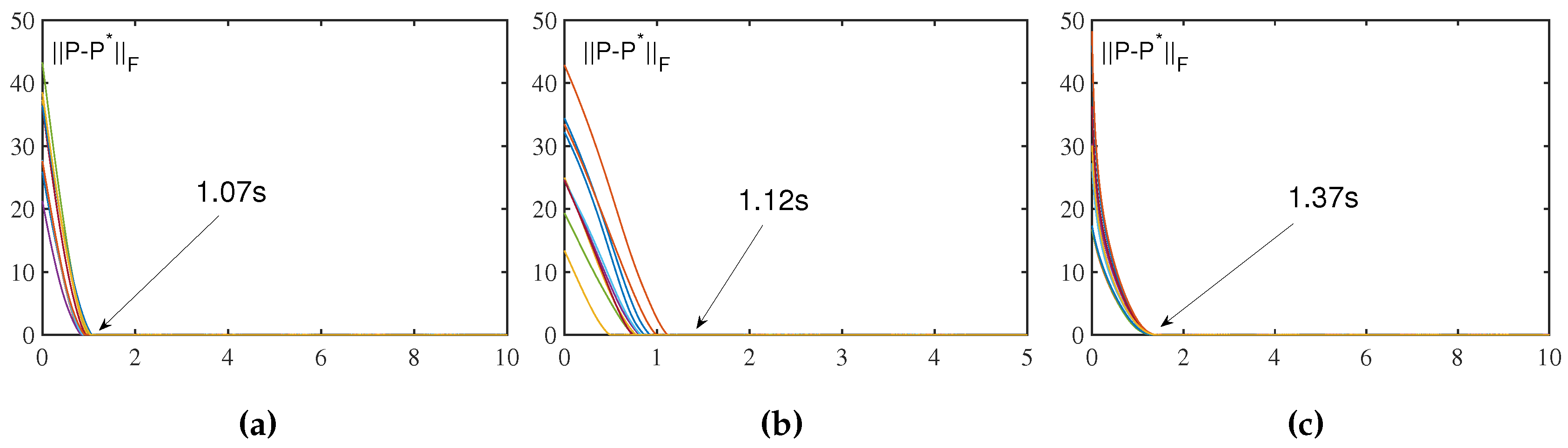
First, the effects of different factors on the convergence performance of ZNN and VFFNTNN were observed when the same activation function was used. In TABLE I, we enumerate the comparison of the convergence time of ZNN and VFFTNN under several different design factors. And in Figure 2 as well as Figure 3, we give detailed simulation results of ZNN and VFFTNN under different factors when $\alpha =\mu =0.1$, $\alpha =\mu =1$ and $\alpha =\mu =5$. It can be seen that when $\mu$ is small enough, such as $\mu =0.01$, ZNN cannot complete the convergence. When $\mu =0.1$, the convergence time of ZNN is $67.55$ seconds. With the increase of design factor $\mu$, the convergence performance of ZNN gradually get better. As you can see from Figure2, when $\mu =1$, it takes $6.98$ seconds for the computation error $||P\left(t\right)-P^{*}\left(t\right){||}_F$ to converge to 0, which is nearly ten times faster than with $\mu =0.1$. And when $\mu =5$, it only takes $1.37$ seconds to get $||P\left(t\right)-P^{*}\left(t\right){||}_F$ converge to 0. Next, let us look at the time when the computation error converges to zero by using VFFTNN. When design factor is set to $\alpha =0.01$ or $\alpha =0.1$, tt only takes $2.39$ or $2.35$ seconds for the computation error $||P\left(t\right)-P^{*}\left(t\right){||}_F$ to converge to 0, that is much faster than ZNN. In addition, no matter what the factors are set, it can be seen from the results comparison of Table I as well as Figure 2 and Figure 3 that the convergence performance of VFFTNN is much better than that of ZNN. Deserve to be mentioned, linear-type activation function is used in the above simulation results.

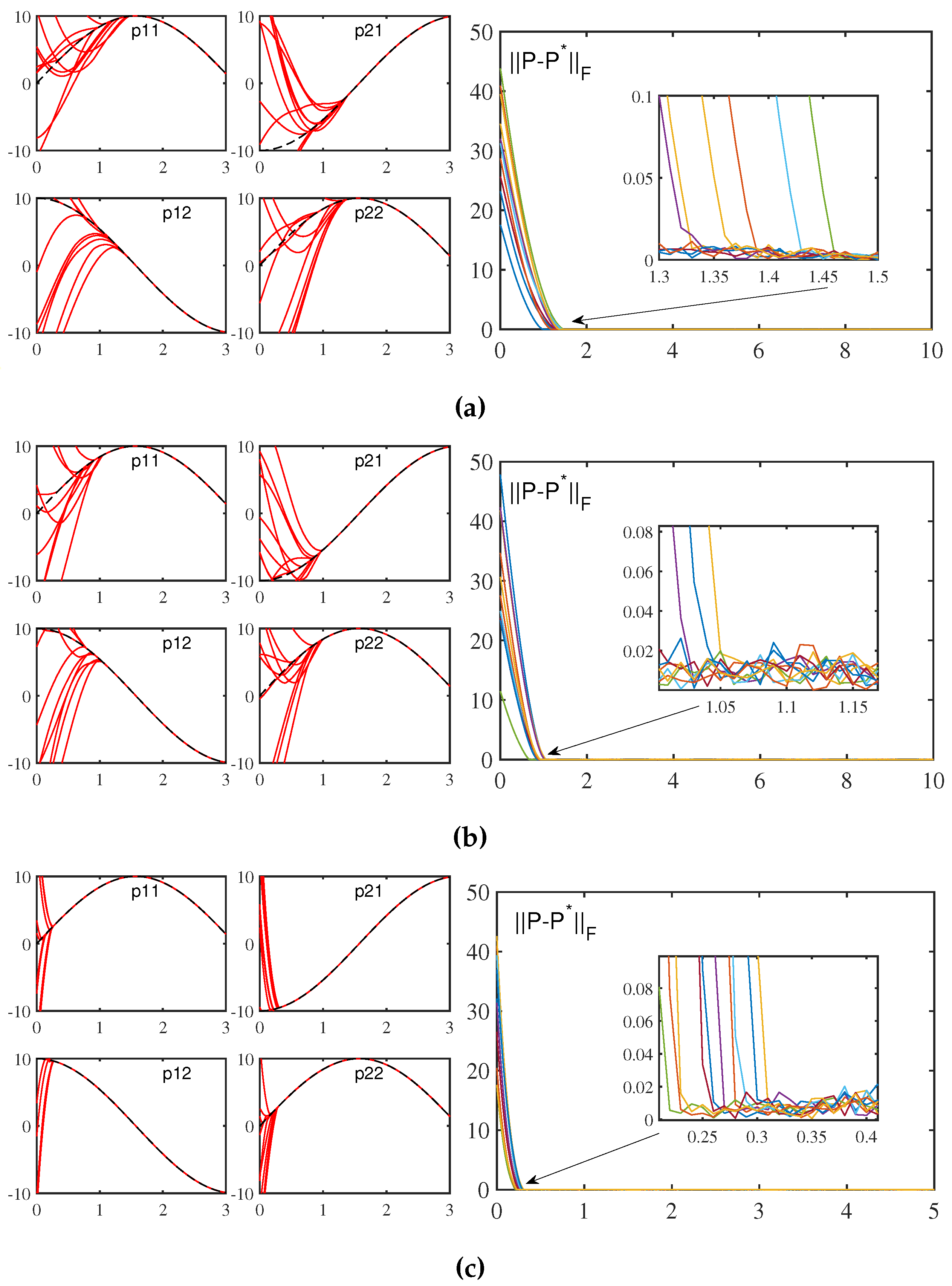
Second, the effects of different activation functions on the convergence performance of ZNN and VFFNTNN were observed when the same factors were set. In Figure 4 and Figure 5, we have plotted computation error $||P\left(t\right)-P^{*}\left(t\right){||}_F$ curves of ZNN and VFFTNN under these three activation functions(i.e., linear, bipolar-sigmoid and power-type) respectively. In the case to use linear activation function, it can be observed that ZNN needs to take 6.98 seconds to converge to zero, but VFFTNN only takes $1.05$ seconds. Likewise, when bipolar-sigmoid activation function, as well as power activation function, are used, the convergence time of VFFTNN is also much smaller than that of ZNN. This fully demonstrates the excellent performance of VFFTNN system compared with ZNN, and also verifies the finite-time convergence performance of VFFTNN under different activation functions for solving Sylvester equation. It is worth mentioning that the factors are respectively set to $\mu =\alpha =1$ and $\lambda ={\displaystyle \frac{1}{5}}$ in the above simulation results.

4.2. Robustness Discussion

In this section, we will verify the robustness of VFFTNN and compare it with ZNN. In order not to lose generality and simplicity, the differentiation and model-implementation errors are considered. For simulation purposes, let us set the differentiation and model-implementation errors as follows

$$\begin{array}{cc}\hfill & \mathsf{\Lambda }\left(t\right)={\beta }_1\left[\begin{array}{cc}\cos 2t& 0\\ 0& \sin 2t\end{array}\right],\mathsf{\Omega }\left(t\right)={\beta }_2\left[\begin{array}{cc}0& \cos 2t\\ \sin 2t& 0\end{array}\right]\hfill \\ \hfill & \mathsf{\Delta }\left(t\right)={\beta }_3\left[\begin{array}{cc}\sin 2t& 0\\ 0& \cos 2t\end{array}\right].\hfill \end{array}$$

where ${\beta }_1$, ${\beta }_2$ and ${\beta }_3$ are the settable factors, which can adjust the size of these disturbances.

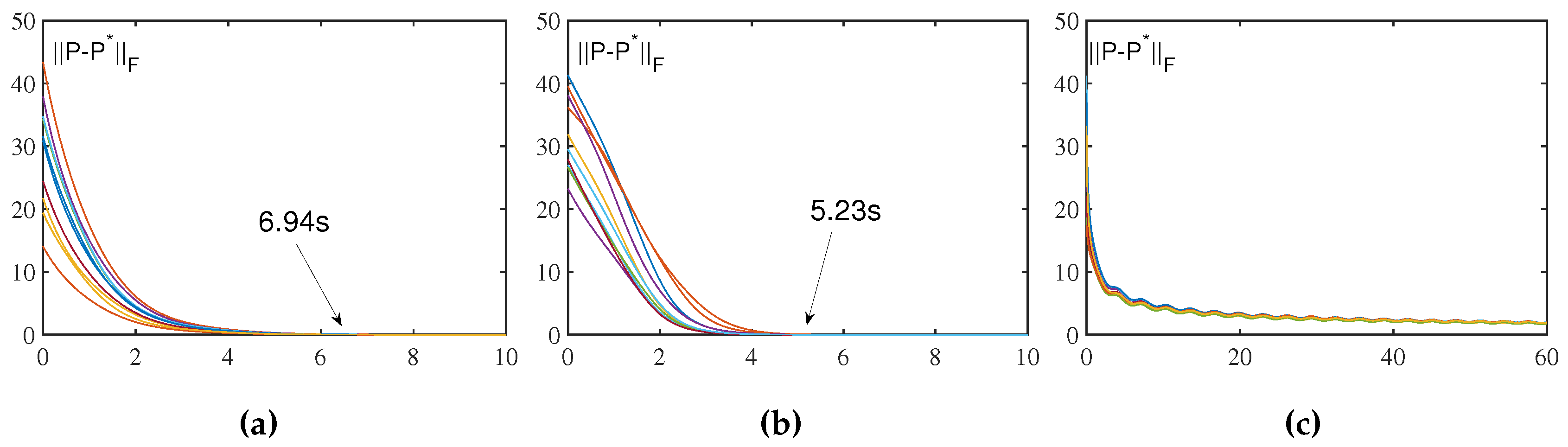
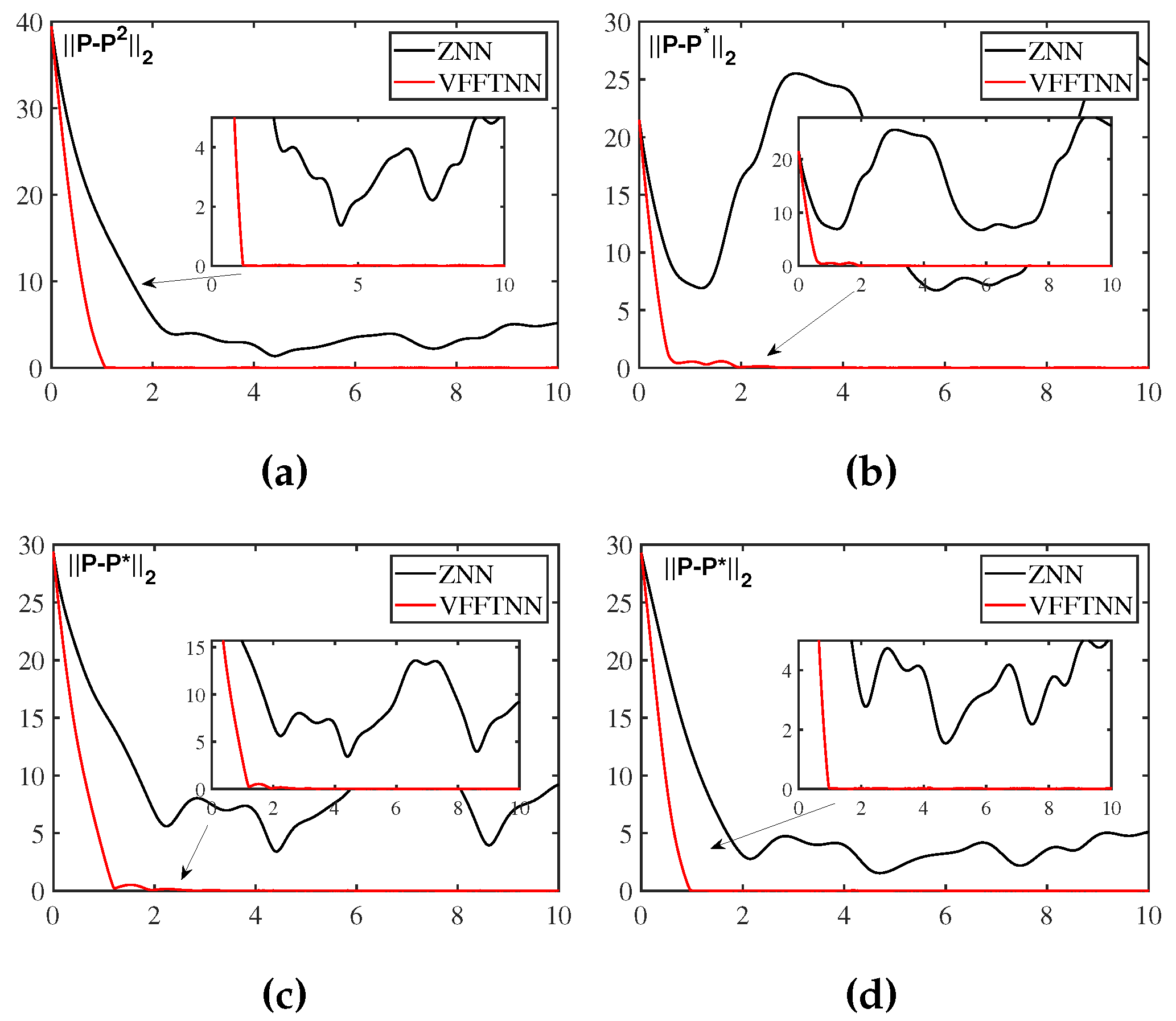
Here, we will take the four cases in Figure 6 as examples to compare the robustness of VFFTNN and ZNN. Form Figure 6, it can be seen that when ${\beta }_1={\beta }_2={\beta }_3$, even though the disturbances are small, but the computation error $||P\left(t\right)-P^{*}\left(t\right){||}_F$ of ZNN cannot converge to 0. On the contrary, when we look at the curve of VFFTNN, we can see that the computation error has converged around 4 seconds. Then look at the other three cases, the computation error of VFFTNN converges to zero, although the disturbances are much larger. Deserving to be mentioned, the convergence time of VFFTNN will be smaller with the design factors $\alpha$ increases or $\lambda$ decreases.

In conclusion, although the convergence performance of VFFTNN will get worse in the presence of disturbance, it can still complete the convergence and no matter how big the disturbance is, it can converge to 0 in a finite time, which well confirms the robustness of VFFTNN.

5. Conclusions

In this paper, we propose a new neural network called VFFTNN, and discuss the finite-time convergence and robustness of the network for solving Sylvester equation under three different activation functions. Compared with the typical ZNN, the proposed VFFTNN increases the time-varying coefficient and the fractional power term, which accelerates the convergence speed of VFFTNN and enhances the anti-jamming ability. More importantly, VFFTNN can guarantee not only finite time convergence, but also super-exponential convergence rate. Simulation results show the superior performance of the neural network for solving Sylvester equation problem. Therefore, in the real hardware implementation, the new neural network has more advantages.