Greek Classical Literature: A Multi–Dimensional Mathematical Analysis of Texts and Their Connections

1. Introduction

A multi–dimensional mathematical theory of alphabetical texts can reveal interesting connections between authors, between texts belonging to the same author or even between texts belonging to different languages, including translations, regardless of the epoch of writing. In recent years I have developed, in a series of papers [1,2,3,4,5,6,7,8,9,10], what I believe is a mathematical/statistical theory that fits the purpose of studying texts in a multi–dimensional mathematical framework by using parameters authors are not aware of. For example, this kind of analysis has recently [11] revealed strong connections between The Lord of the Rings (J.R.R. Tolkien) and The Chronicles of Narnia and The Space Trilogy (C.S. Lewis), therefore confirming both the conclusions reached by scholars of English Literature and the power of the mathematical theory, based on simple and easily calculable parameters. The theory can also reveal connections with the extended short–term memory (E–STM) of readers and writers as well, since writers are also readers of their own texts.

The theory considers number of words, sentences and interpunctions. It defines deep–language parameters and linguistic communication channels within texts which are due to writer’s unconscious design and, therefore, can reveal connections between texts far beyond writers’ awareness.

Since meaning is not considered by the theory, any text of any alphabetical language can be studied exactly with the same mathematical/statistical tools. Today, many scholars are working hard to arrive at a “semantic communication” theory, or “semantic information” theory which, according to their statements, should include at least some rudiments on meaning, but the results are still, in my opinion, in their infancy and very far from useful applications [12,13,14,15,16,17,18,19,20]. These theories, as those concerning the short–term memory [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48], have not considered most of the main “ingredients” of my theory, which can be very easily retrieved and studied in alphabetical texts of any epoch.

In the present paper my aim is to apply the theory to some important texts of the classical Greek Literature and New Testament (NT). The analysis will indicate that these ancient writers, and their readers, were not significantly different from the modern writers/readers. This finding is quite interesting because in a society in which most people were illitterate and used to memorize oral information more than modern people do, the ancient writers wrote almost exactly, mathematically speaking, as the modern writers do and for readers with similar characteristics, therefore underlining the long–term persistence of hunam mind processing tools. Of course, differences are found, as in modern texts, only because of the subject of the text.

After this introductory section, Section 2 presents the database of the classical Greek Literature texts studied. Section 3 defines the deep–language parameters and establishes some inequalities in calculating their mena values; Section 4 applies a useful graphical tool, namely a vector representation of the texts; Section 5 recalls the theory of linguistic channels; Section 6 reports and discusses the perfomance of important linguistic channels; Section 7 recalls and calculates a universal readability index for each text and compares them; Section 8 and Section 9 study the E–STM memory of ancient Greek writers/readers, and show that it is just like that of modern writers/readers. Finally, Section 10 draws a conclusion. Several Appendices report numerical data useful for applying the theory in each section.

2. Database of Ancient Greek Literary Texts

In this section I introduce the database of classical Greek Literature texts mathematically studied in the present paper. Table 1 lists authors and books concerning history, geography and philosophy (referred to as Greek–1 texts), poetry and theatre (Greek–2 texts). This is a large sample of classical Greek Literature. Notice that Iliad and Odissey, although traditionally attributed to the mythical Homer, are studied separately because they were likely written by different persons. Table 2 lists the texts of the New Testament.

I have used the digital texts (WinWord digitral files) and counted the number of characters, words, sentences and interpunctions (punctuation marks). Before doing so, I have deleted the titles, footnotes and other extraneous material present in the digital texts, a burdensome work. The count is very simple, although time–consuming. Winword directly provides the number of total words and their characters. The number of total sentences is calculated by using WinWord to replace every full stop with a full stop: of course, this action does not change the text, but it gives the number of these substitutions and therefore the number of full stops. The same procedure was repeated for question marks and exclamation marks. The sum of the three totals gives the total number of sentences in the text analyzed. The same procedure gives the total number of commas, colons and semicolons. The sum of these latter values with the total number of sentences gives the total number of interpunctions. The same procedure was applied to the New Testament books listed in Table 2. These data were also used for previous studies [4,6,7,49].

The original Greek texts of Table 1 were downloadef from https://www.perseus.tufts.edu/ (last accessed on 19 October 2024). The New Testament books were downloaded as indicated in [4,6,7,49].

Interpunctions were introduced in the scriptio continua by ancient readers acting as “editors” [50,51,52,53,54,55,56,57,58]. They were well–educated readers respectful of the original text and its meaning, therefore, very likely they maintained a correct subdivision in sentences and word intervals within sentences, for not distorting the correct meaning and emphasis. In other wirds, we can reasonably assume as if interpunctions were effectively introduced by the author. The mathematical theory, however, is very robust against slightly different versions of the Greek texts because it never considers meaning. If a word is not written, or it is substituted with another one, or if a small text is not present in a version, it does not significantly affect the statistical analysis. This applies also to the quality of the Greek used. This a point of force of the theory.

In the next section I recall the theory of deep–language parameters.

3. Deep–Language Parameters of Texts, Statistical Means and Minimum Values

Let us start to define and explore four linguistic variables termed deep–language parameters [1,2]. Very likely these parameters are not consciously managed by writers who, of course, act also as readers of their own text. To avoid possible misunderstandings, these parameters refer to the “surface” structure of texts, not to the “deep” structure mentioned in cognitive theory. I first recall their definition then prove useful inequalities.

3.1. Deep–Language Parameters

Let $n_C$, $n_W$ and $n_I$ be respectively the number of characters, words and interpunctions (punctuation marks) calculated in disjoint blocks of texts, such as chapters or any other subdivisions, then four deep–language parameters are defined (Appendix A lists the mathematical symbols used in the present paper).

The number of characters per word, $C_P$:

$${\mathit{C}}_{\mathit{P}}={\displaystyle \frac{{\mathit{n}}_{\mathit{C}}}{{\mathit{n}}_{\mathit{W}}}}$$

(1)

The number of words per sentence, $P_F$:

$${\mathit{P}}_{\mathit{F}}={\displaystyle \frac{{\mathit{n}}_{\mathit{W}}}{{\mathit{n}}_{\mathit{S}}}}$$

(2)

The number of interpunctions per word, referred to as the word interval, $I_P$:

$${\mathit{I}}_{\mathit{P}}={\displaystyle \frac{{\mathit{n}}_{\mathit{I}}}{{\mathit{n}}_{\mathit{W}}}}$$

(3)

The number of word intervals, ${\mathit{n}}_{{\mathit{I}}_{\mathit{P}}}$, per sentence, $M_F$:

$${\mathit{M}}_{\mathit{F}}={\displaystyle \frac{{\mathit{n}}_{{\mathit{I}}_{\mathit{P}}}}{{\mathit{n}}_{\mathit{S}}}}$$

(4)

Equation (4) can be written also as $M_F=P_F/I_P$. Table 3 and Table 4 report the mean values of these parameters, the other parameters in Table 3 and Table 4 will be discussed in following sections.

Notice that all mean values have been calculated by weighing each text with its number of words to avoid that shorter texts weigh statistically as much as long ones. In other words, any text considered weighs as the number of its words, compared to the total number of words. I have used this method also to calculate the mean values of the data bank of Greek–1 plus Greek–2 (last line in Table 3). In this case, for example, the statistical weight of Aeneas Tactitian is $13035/3225839\approx 0.004$ (see Table 1) while the weight of Aristotle is $509646/3225839\approx 0.1580$.

The mean values of these parameters can be calculated from the sample totals listed in Table 1 and Table 2. However, for not being misled, these values are not equal to the arithmetic or to the statistical means, as I prove now.

3.2. Inequalities

Let $M$ be the number of samples (i.e., number of disjoint blocks of text, such as chapters or books), then, for example, the statistical mean value $<P_F>$, is given by

$$<{\mathit{P}}_{\mathit{F}}>={\sum }_{\mathit{k}=1}^{\mathit{M}}{\mathit{P}}_{\mathit{F},\mathit{k}}\times \left({\mathit{n}}_{\mathit{W},\mathit{k}}/\mathit{W}\right)$$

(5)

where $W={\sum }_{k=1}^M{n}_{W,k}$ is the total number of words. Notice that $<P_F>\ne {\displaystyle \frac{1}{M}}{\sum }_{k=1}^M{P}_{F,k}\ne {\sum }_{k=1}^M{n}_{W,k}/{\sum }_{k=1}^M{n}_{S,k}$=$W/S$, where $S$ is the total number of sentences.

For example, for Aristotle $W=509646$ and $S=17790$, Table 1. These values would give the average $P_F=W/S=509646/17790=28.65$, while the statistical mean (calculated on the nine books listed in Table 1) $<P_F>=29.29>28.65$.

In general, the average values calculated from sample totals are always smaller than their statistical means, therefore they give lower bounds, as I prove in the following.

Let us consider, for example, the parameter $P_F$. Because of Chebyshev’s inequality ([59], inequality 3.2.7), we can write Eq.(5) as:

$${<P}_F>=\sum _{k=1}^M{\displaystyle \frac{n_{W_k}}{n_{S_k}}}{\displaystyle \frac{n_{W_k}}{W}}\ge {\displaystyle \frac{1}{M}}\sum _{k=1}^M{\displaystyle \frac{n_{W_k}}{n_{S_k}}}\sum _{k=1}^M{\displaystyle \frac{n_{W_k}}{W}}={\displaystyle \frac{1}{M}}\sum _{k=1}^M{\displaystyle \frac{n_{W_k}}{n_{S_k}}}$$

(6)

Eq.(6) states that the mean calculated with samples weighted $1/M$ (arithmetic mean) is smaller than (or equal to) the mean calculated with samples weighted $n_{W_k}/W$.

Now, again for Chebyshev’s inequality, we get:

$$\sum _{k=1}^M{\displaystyle \frac{n_{W_k}}{n_{S_k}}}\ge {\displaystyle \frac{1}{M}}\sum _{k=1}^M{n}_{W_k}\sum _{k=1}^M{\displaystyle \frac{1}{n_{S_k}}}={\displaystyle \frac{W}{M}}\sum _{k=1}^M{\displaystyle \frac{1}{n_{S_k}}}$$

(7)

Further, for Cauchy–Schawarz’s inequality (or by the fact that the harmonic mean is less than, or equal to, the arithmetic mean), we get:

$${\sum }_{k=1}^M{\displaystyle \frac{1}{n_{S_k}}}\ge {\displaystyle \frac{M^2}{{\sum }_{k=1}^M{n}_{S_k}}}$$

Finally, by inserting these inequalities in (6), we get:

$${<P}_F>\ge {\displaystyle \frac{W}{M^2}}{\displaystyle \frac{M^2}{{\sum }_{k=1}^M{n}_{S_k}}}={\displaystyle \frac{W}{S}}$$

(9)

Eq.(9) establishes that the statistical mean calculated with samples weighted $n_{W_k}/W$ is greater than (or equal to) the average calculated with sample totals. The values given by these three methods of calculation coincide only if all texts are perfectly identical, i.e. with the same number of characters, words, sentences and interpunctions, a case improbable.

The mean values of Table 3 and Table 4 (or their minimum values directly calculated from the totals, as discussed above) can be used for a first assessment of how “close”, or mathematically similar, texts are in a Cartesian plane by defining linear combinations of deep–language parameters [1]. Texts are then modeled as vectors, the representation of which is briefly recalled in the next section.

4. Vector Representation of Texts

Let us consider the six vectors of the indicated components of deep–language parameters, $\overrightarrow{R_1}=({<C}_P>,{<P}_F>$), $\overrightarrow{R_2}=({<M}_F>,{<P}_F>$), $\overrightarrow{R_3}=(<I_P>,<P_F>$), $\overrightarrow{R_4}=({<C}_P>,{<M}_F>$), $\overrightarrow{R_5}=({<I}_P>,{<M}_F>$), and $\overrightarrow{R_6}=({<I}_P>,<C_P>$), and their resulting vector sum:

$$\overrightarrow{R}={\sum }_{k=1}^6\overrightarrow{R_k}$$

(10)

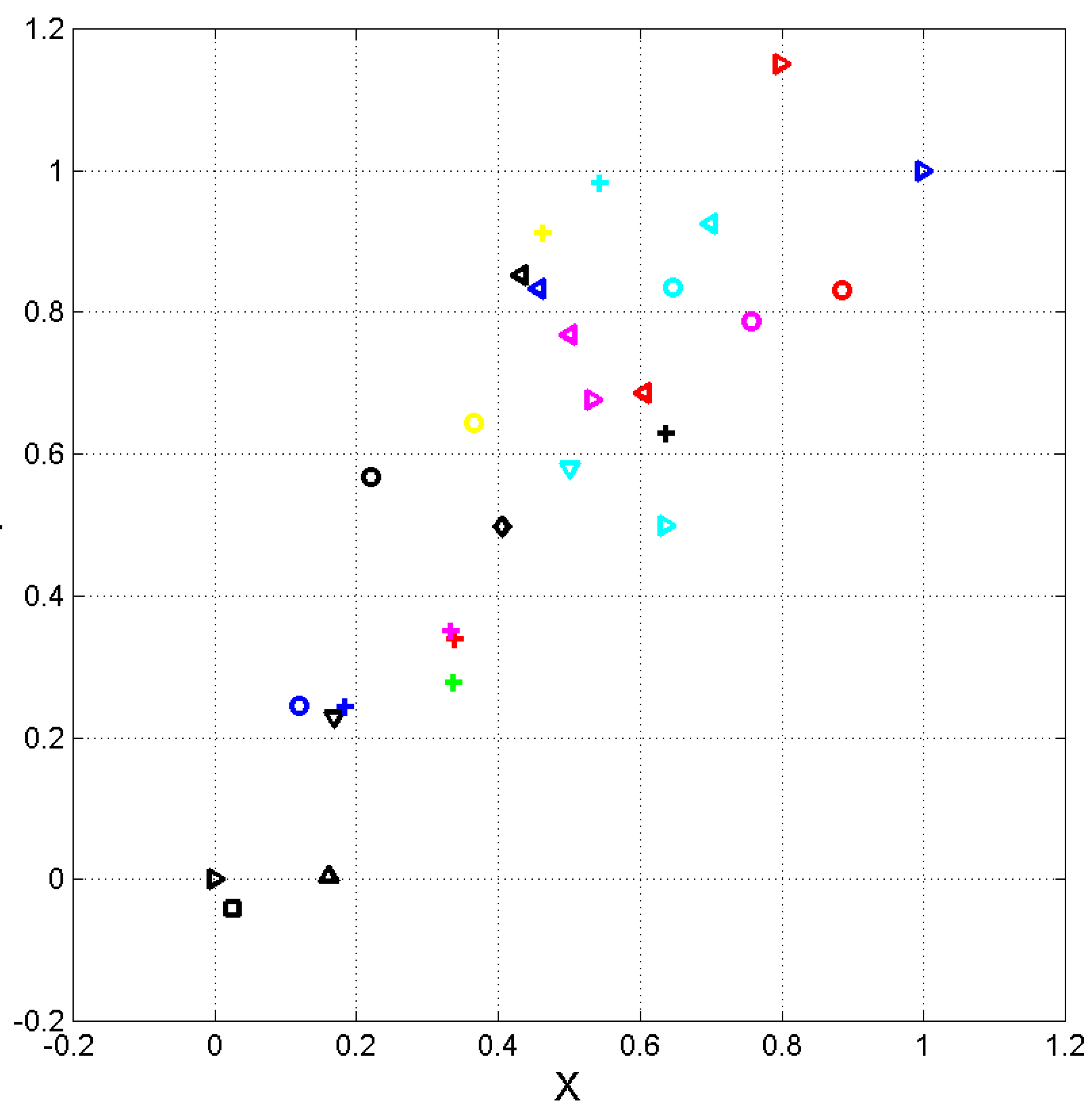
By considering the coordinates $x$ and $y$ of Equation (10), the scatterplot of their ending points is shown in Figure 1, where $X$ and $Y$ are normalized coordinates so that Sofocles (black triangle) is at the origin $(X=0,Y=0)$ and Flavius Josephus (blue triangle) is is at $(X=1,Y=1)$, through the linear transformations:

$$X={\displaystyle \frac{x–x_{Sofocles}}{x_{Flavius}–x_{Sofocles}}}$$

(11)

$$Y={\displaystyle \frac{y–y_{Sofocles}}{y_{Flavius}–y_{Sofocles}}}$$

Notice that the scatterplot using minimum values of the deep–language parameters – not shown for brevity, slightly displaced towards the origin in both coordinates – almost coincide with that shown in Figure 1, therefore the relative distances between texts are not significantly changed.

From Figure 1 we can observe the following characteristics.

1)

Texts on poetry and theatre (Greek–2) are significantly distant and separated from those on history and other disciplines (Greek–1). We will find that the authors/texts located towards the origin (such as Euripides, Sofocles and Aeschylus) have greater readability index (Section 7) and greater multiplicity factor (Section 9). An exception is Homer’s Iliad very near Aristotle, and Plato near Aesop.

2)

Iliad and Odissey are significantly distant, although they are traditionally attributed to Homer.

3)

The three synoptic gospels (Matthew, Mark and Luke) are each other very close. John almost coincides with Aesop. The gospels are nearer to Greek–2 than to Greek–1. Acts is nearer to historians (e.g. Herodotus) than to the synoptics. Hebrews and Apocalypse are each other near and are clearly distict from the other NT books, likely indicating they were written either by the same writer or by writers belonging to the same Christian group [6]. More studies, connections and details on these NT books can be found in [4,6,7].

5. Linguistic Channels and Signal–to–Noise Ratio

The representation of texts as vectors gives a necessary but not sufficient condition of possible connections and influence of authors on each other, e.g., see in [6] the discussione about the couple Aesop–John. The linguistic channels, always present in texts [3], can further assess similarity and likely dependence because they provide a “fine–tuning” analysis of authors/texts’ connections.

First, I briefly recall the definition of these channels and secondly the basic theory, for readers’s benefit. The “performance” of a channel is measured by a suitable signal–to–noise ratio.

5.1. Linguisic Channels

In texts we can always define at least four linguistic linear channels [3,11], namely:

(a).

Sentence channel (S–channel)

(b).

Interpunctions channel (I–channel)

(c).

Word interval channel (WI–channel)

(d).

Characters channel (C–channel).

In S‒channels, the number of sentences of two texts is compared for the same number of words. Notice that, as far as I know, only the theory of lingusitic channels allows this comparison. These channels describe how many sentences the author of text $j$ writes, compared to the writer of text $k$ (reference text), by using the same number of words. Therefore, these channels are more linked to $P_F$ than to the other parameters. Very likely they reflect the style of the writer.

In I‒channels, the number of word intervals $I_P\text{'}\mathrm{s}$of two texts is compared for the same number of sentences. These channels describe how many short texts between two contiguous punctuation marks (of length $I_P$ words) two authors use; therefore, these channels are more linked to $M_F$ than to the other parameters. Since $M_F$ is connected to the E–STM, I‒channels are more related to the second buffer of readers’ E–STM than to the style of the writer.

In WI‒channels, the number of words (i.e., $I_P$) contained in a word interval is compared for the same number of interpunctions. These channels are more linked to $I_P$ than to other parameters, therefore WI‒channels are more related to the first buffer of readers’ E–STM than to the style of the writer.

In C‒channels, the number of characters of two texts is compared for the same number of words. These channels are more related to the language used, e.g. Greek in this case, than to the other parameters.

5.1. Theory of Linguisic Channels

In a text, an independent (reference) variable $x$ (e.g., $n_W$in S–channels) and a dependent variable $y$ (e.g., $n_S)$ can be related by a regression line (slope $m$) passing through the origin:

$$y=mx$$

(12)

Let two diverse texts $Y_k$ and $Y_j$. For both we can write Equation (12) for the same couple of parameter; however, in both cases, Equation (12) does not give their full relationship because it links only mean conditional values. More general linear relationships consider also the scattering of the data—measured by the correlation coefficients $r_k$ and $r_j$, not considered in Equation (12)—around the regression lines (slopes $m_k$ and $m_j$):

$$y_k=m_{k}x+n_k$$

(13)

$$y_j=m_{j}x+n_j$$

while Equation (12) connects the dependent variable $y$ to the independent variable $x$only on the average, Equation (13) introduces additive “noise” $n_k$ and $n_j$, with zero mean value. The noise is due to the correlation coefficient $\left|r\right|\ne 1$, not considered by Equation (12).

We can compare two texts by eliminating $x$. In the example just mentioned, we can compare the number of sentences in two texts—for an equal number of words—by considering not only the mean relationship, Equation (13), but also the scattering of the data. Equation (13).

As recalled before, we refer to this communication channel as the “sentences channel” and to this processing as “fine tuning” because it deepens the analysis of the data and provides more insight into the relationship between two texts. The mathematical theory follows.

By eliminating $x$, from Equation (13) we obtain the linear relationship between—now—the sentences in text $Y_k$ (reference, input text) and the sentences in text $Y_j$ (output text):

$$y_j={\displaystyle \frac{m_j}{m_k}}{y}_k-{\displaystyle \frac{m_j}{m_k}}{n}_k+n_j$$

(14)

Compared with the independent (input) text $Y_k$, the slope $m_{jk}$ is given by

$$m_{jk}={\displaystyle \frac{m_j}{m_k}}$$

(15)

The noise source that produces the correlation coefficient between $Y_k$ and $Y_j$ is given by

$$n_{jk}=-{\displaystyle \frac{m_j}{m_k}}{n}_k+n_j=-m_{jk}{n}_k+n_j$$

(16)

The “regression noise–to–signal ratio”, $R_m$, due to $\left|m_{jk}\right|\ne 1$, of the channel is given by:

$$R_m={(m_{jk}-1)}^2$$

(17)

The unknown correlation coefficient $r_{jk}$ between $y_j$ and $y_k$ is given by:

$$r_{jk}=\mathrm{c}\mathrm{o}\mathrm{s}\left|\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\left(r_j\right)-\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\left(r_k\right)\right|$$

(18)

The “correlation noise–to–signal ratio”, $R_r$, due to $\left|r_{jk}\right|<1$, of the channel that connects the input text $Y_k$ to the output text $Y_j$ is given by:

$$R_r={\displaystyle \frac{1-r_{jk}^2}{r_{jk}^2}}{m}_{jk}^2$$

(19)

Because the two noise sources are disjoint, the total noise–to–signal ratio of the channel connecting text $Y_k$ to text $Y_j$ is given by:

$$R={(m_{jk}-1)}^2+{\displaystyle \frac{1-r_{jk}^2}{r_{jk}^2}}{m}_{jk}^2$$

(20)

Finally, the total signal–to–noise ratio is given by

$$\gamma =1/R$$

(21)

$$\mathsf{\Gamma }=10\times {\mathrm{l}\mathrm{o}\mathrm{g}}_{10}\gamma$$

$\mathsf{\Gamma }$ is in dB.

Notice that no channel can yield $\left|r_{jk}\right|=1$and $\left|m_{jk}\right|=1$ (i.e., $\mathsf{\Gamma }=\infty$), a case referred to as the ideal channel, unless a text is compared with itself (self–comparison, self–channel). In practice, we always find $\left|r_{jk}\right|<1$and $\left|m_{jk}\right|\ne 1$. The slope $m_{jk}$ measures the multiplicative “bias” of the dependent variable compared to the independent variable; the correlation coefficient $r_{jk}$measures how “precise” the linear best fit is. The slope $m_{jk}$ is the source of the regression noise of the channel, the correlation coefficient $r_{jk}$is the source of the correlation noise.

In the next section I study the four channels mentioned above.

6. Perfomance of Linguistic Channels

By using the regression lines reported in Appenix B, the signal–to–noise ratio $\mathsf{\Gamma }$ in the four channels is calculated as recalled in Section 5. Let us study the texts of Greek–1 and Greek–2.

6.1. Greek–1

Table 5 reports, for example, $\mathsf{\Gamma }$ in the S–channels. Appendices B and C report $\mathsf{\Gamma }$ for the other three channels.

Table 5 is interpreted as follows. The author/text in the first row is the reference author/text, i.e. the channel input author/text $Y_k$ of the theory; the author/text in the first column is the channel dependent output author/text $Y_j$.

For example, if Aristides is the input and Demosthenes is the output, then $\mathsf{\Gamma }=22.59$ dB $(\gamma =181.55)$; viceversa, if Demosthenes is the input and Aristides is the output, then $\mathsf{\Gamma }=23.16$ $(\gamma =207.01)$, a small asymmetry always found in linguistic channels [3]. In other words, for the same number of words, the number of sentences in Aristides is transformed into the number of sentences, for the same number of words in Demosthenes with a high $\mathsf{\Gamma },$ and viceversa. This finding means the two texts share very much a common style, as far sentences are concerned. The channel is little noisy, the regression line that relates $n_S$ of Demosthenes (dependent variable) to $n_S$ of Aristides (independent variable) has $m_{jk}=1.0392$ and $r_{jk}=0.9982$.

Now, in this example since Aristides lived before Demosthenes the large $\mathsf{\Gamma }$ may indicate that Aristides influenced Demosthenes’ style. In any case, the two texts are much correlated in the S–Channel.

The red and blue colours in Table 5 highlight the channels with $\mathsf{\Gamma }\ge 15$ dB ($\gamma \ge 31.62)$, with the following meaning: blue indicates not only that the number of sentences of the input and output texts are much correlated but also that the input author might have influenced the output author because he lived before. Red indicates a large correlation, as in the blue cases, but no likely influence can be supposed because the input author lived after the output author. Similar observations can be done for the other authors/texts and linguistic channels (see Appendix B).

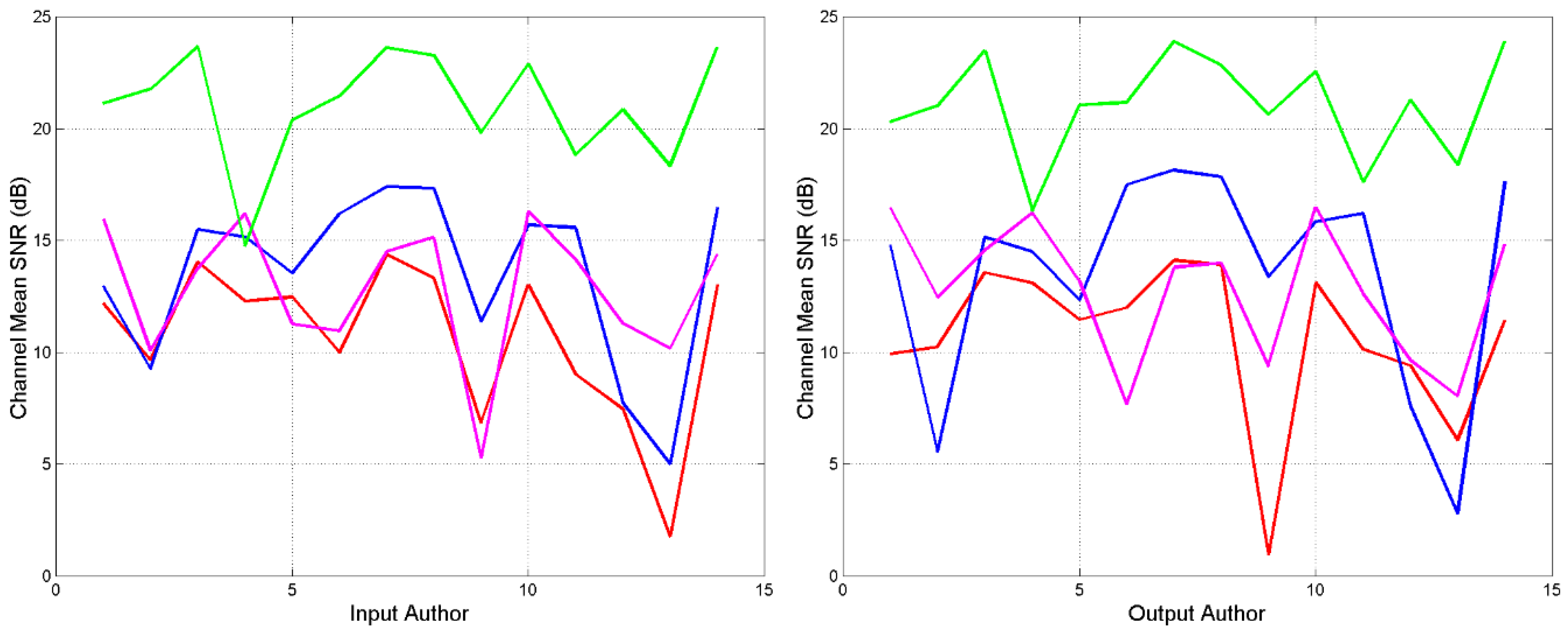
Figure 2 syntesizes the results of the four channels by showing the average $\mathsf{\Gamma }$ calculated by considering the input author (left panel, arithmetic average of the values reported in the corresponding column of Table 5) or the output author (right panel, arithmetic average of the values reported in the corresponding row). The asymmetry typical of linguisic channels is clearly evident.

For example, Aristides (no. 3) has large $\mathsf{\Gamma }$ both when he is the input author (left panel) and when he is the output author (right panel). The authors who are very uncorrerated with all others are Plato (no. 9) and Thucydides (no. 13).

From Figure 2, we can conclude that:

• C–Channels (green line) give large Γ for all authors, in any case. These large values are just saying that all authors use the same language because C_p changes little from author to author. The minumum is found with Aristotle (no. 4) which is not a historian or georgrapher like the other authors. These channels are not very apt to distinguish or assess large differences between texts or authors [11].
• S–Channels (red line) and WI–Channels (magenta line) are the most similar. This may be due to the fact that both are linked to the E–STM capacity (see Section 8).
• I–Channels (blue line) give Γ just smaller than that of C–Channels. I–Channels deal with I_p, therefore the word interval used by all authors is not very different (see Table 3 and Section 8).

6.2. Greek–2

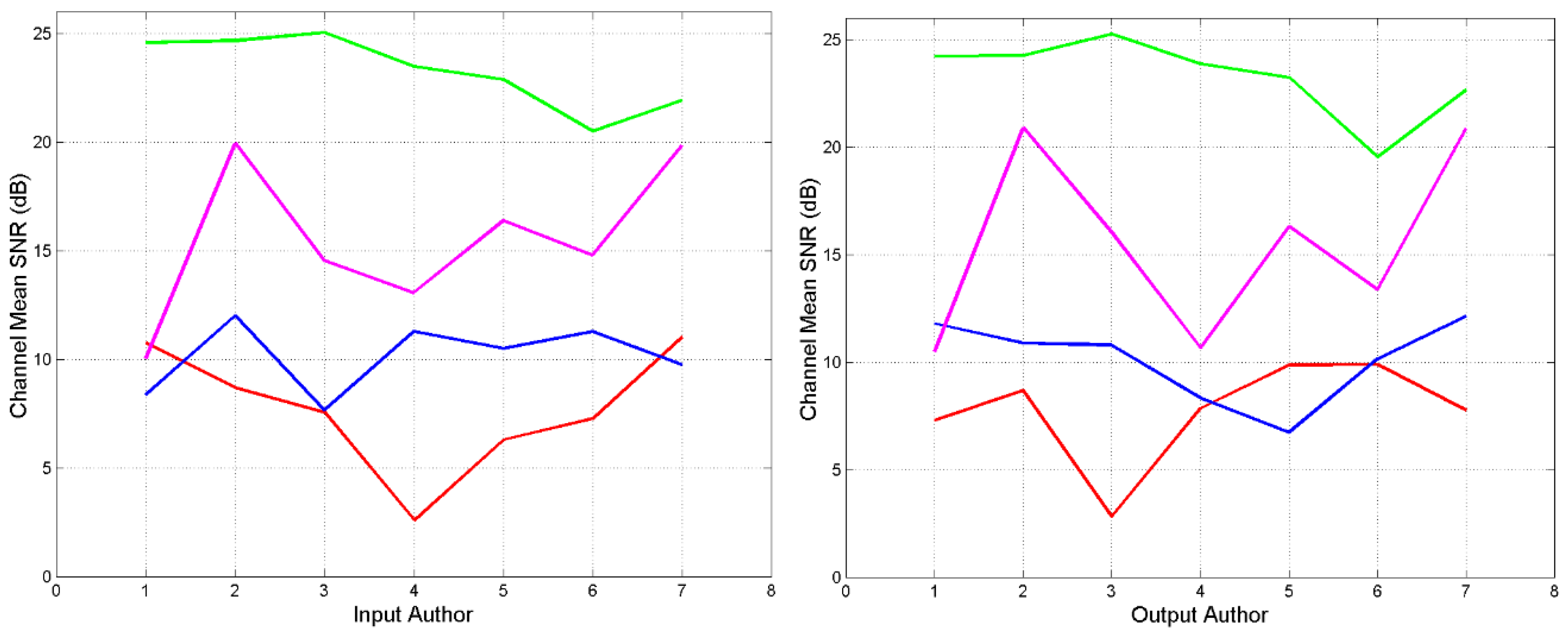
Table 6 shows the results in the S–channel for Greek–2, Appendix C reports $\mathsf{\Gamma }$ for the other three channels. We can notice that the cases of similarity or likely dependence are very few. Sofocles may be influenced by Aeschylus, and Pindarus by the writer of Odissey therefore confirming their closeness in Figure 1.

Notice that Iliad and Odissey have significant different $\mathsf{\Gamma }$ in the three channels able to distinguish better authors/texts. They are also distant in Figure 1. Now, modern scholars generally agree that Homer composed the Iliad most likely relying on oral traditions, and at least inspired the composition of the Odyssey but did not write it [60].

Figure 3 syntesizes the results of the four channels of Greek–2. We notice that the channels are less correlated that those of Greek–1, therefore texts are significantly different (details are reported in Appendix C). C–Channels (green line) give the largest $\mathsf{\Gamma }$, in the same range of Greek–1 because the authors use the same language.

In the next section, I will estimate the readability of these authors by considering a universal readabilty index.

7. Universal Readability Index

In Reference [8], I proposed a universal readability index given by:

$$G_U=89–10k{C}_P+300/P_F–6\left(I_P–6\right)$$

(22)

$$k=<C_{P,ITA}>/<C_{P,Lan}>$$

(23)

In Equation (23), ${<C}_{p,ITA}>=4.48$, ${<C}_{p,Lan}>$ is the mean statistical value in the language considered. By using Equations (22) and (23), the mean value ${<kC}_P>$ of any language is forced to be equal to that found in Italian, namely $4.48$. The rationale for this choice is that $C_P$ is a parameter typical of a language which, if not scaled, would bias $G_U$ without really quantifying the reading difficulty of readers, who in their own language are used, on average, to read shorter or longer words than in Italian. This scaling, therefore, avoids changing $G_U$ only because a language has, on the average, words shorter (as English) or longer (as classical Greek) than Italian. In any case, $C_p$ affects Equation (22) much less than $P_F$ or $I_P$ [1]. In this paper, from Table 3, ${<C}_{p,Lan}>=5.29$.

Table 3 and Table 4 report the mean value $<G_U>$ of each author/text. Notice that $<G_U>$ is always larger (more optimistic) than the value calculated by inserting in Equations (22)(23) the mean values $<P_F>$, $<I_P>$ (proof in Appendix A of [11]).

It is interesting to “decode” these mean values into the minimum number of school years, $Y$, necessary to assess that a text/author passes from being “very difficult” to being only “difficult” to read, according to the modern Italian school system, assumed as a common reference, see Figure 1 of [8]. The results are listed in Table 3 and Table 4. Of course, this assumption does not mean that ancient Greek readers attended school for the same number of years of the modern students, but it is only a way to do relative comparisons, otherwise difficult to assess from the mere values of $<G_U>$. In other words, we should consider $Y$ as an “equivalent” number of school years.

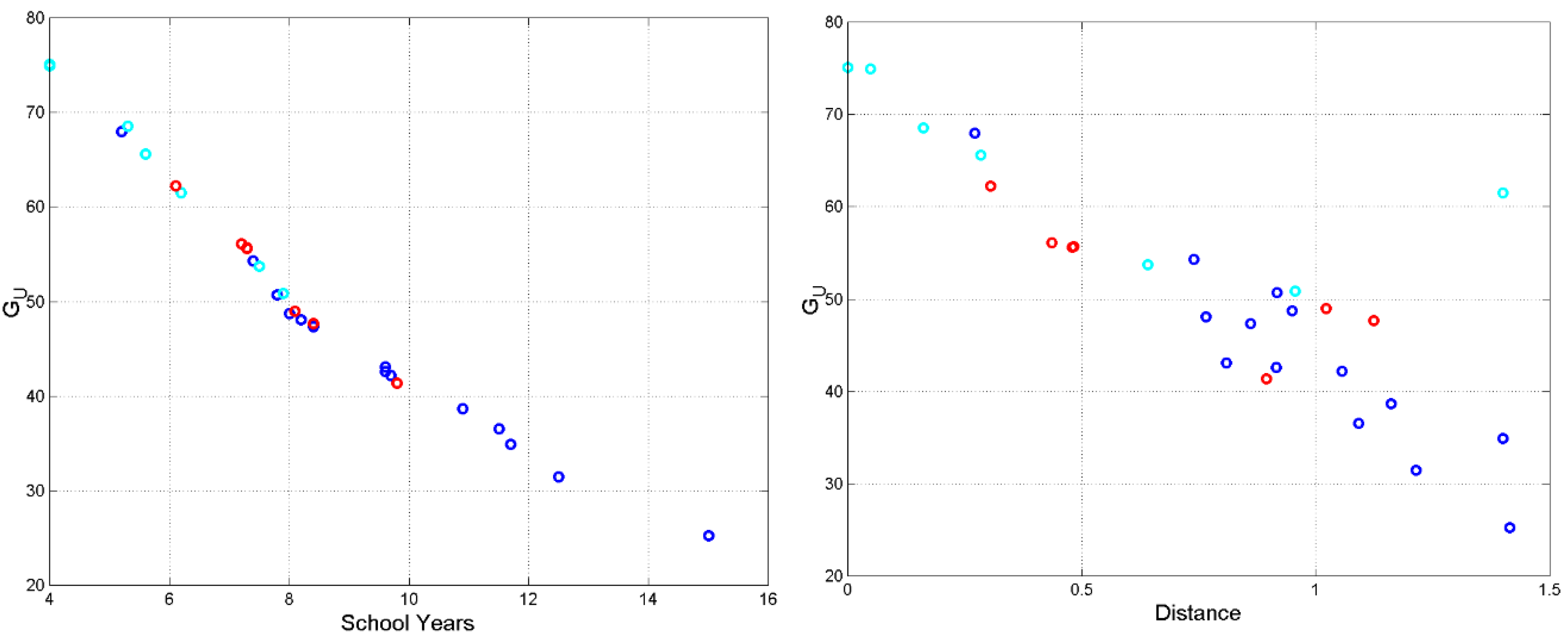
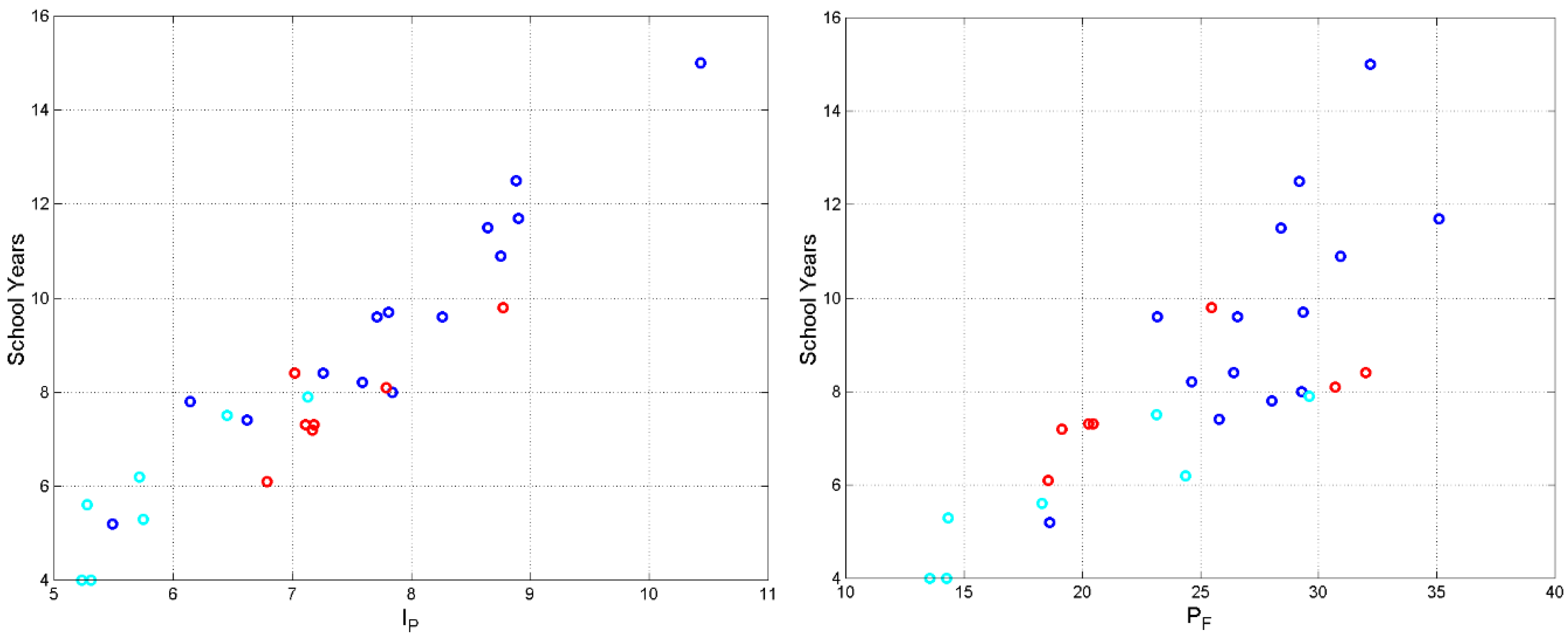
Figure 4 (left panel) shows $<G_U>$ versus $Y$. An inverse proportionality is clearly evident: The more the readability index decreases, the more school years are required for reading the text “with difficulty”. The author with the greatest readability index (74..9) is Euripides, whose readers require only 4 years of school, therefore, “elementary” school; the author with the smallest readability index ($<G_U>=25.2$, due to the large values of both $I_P$ and $P_F$) is Flavius Josephus, whose readers require about 15 years of school, therefore, “university”.

The synoptic gospels have very similar readability indices: Matthew and Luke practically coincide (55.61 and 55.68); Mark is very near (56.14). These gospels are more similar to the texts of Greek–2 than to those of Greek–1. John is the most readable book ($<G_U>=62.21$), Acts is the least readable ($<G_U>=41.35$) and requires more school years (about 10 years) than John (6.1 years, about like Aesop, 5.6 years, see their vicinity in Figure 1. Notice that Acts is more similar to the texts of Greek–1 (e.g., Herodotus) than to those of Greek–2 (see also [4]).

The readability indices of Hebrews and Apocalypse are very similar ($<G_U>=47.1$ and $<G_U>=48.95$) and both require about 8 years of school. See [6] for the possibility that both texts were written either by the same author or by two authors of the same early Christian group.

Figure 4 (right panel) shows $<G_U>$ versus the distance $d=\sqrt{X^2+Y^2}$ from the origin (0,0) in the vector plane (Figure 1); the “outlier” point is due to Odyssey. An inverse proportionality is also clearly evident: The more $<G_U>$ decreases the more $d$ increases, therefore, as anticipated in Section 4, the distance from a reference text/author is a relative measure of readability.

The remarks in SEction 4 on the NT books can be reiterated, because Matthew and Luke are each other superposed ($d=0.48$), Mark is very near ($d=0.44$). John is the nearest gospel to the origin ($d=0.31$). Acts, Hebrews and Apocalypse are the most distant texts. Hebrews and Apocalypse are each other close.

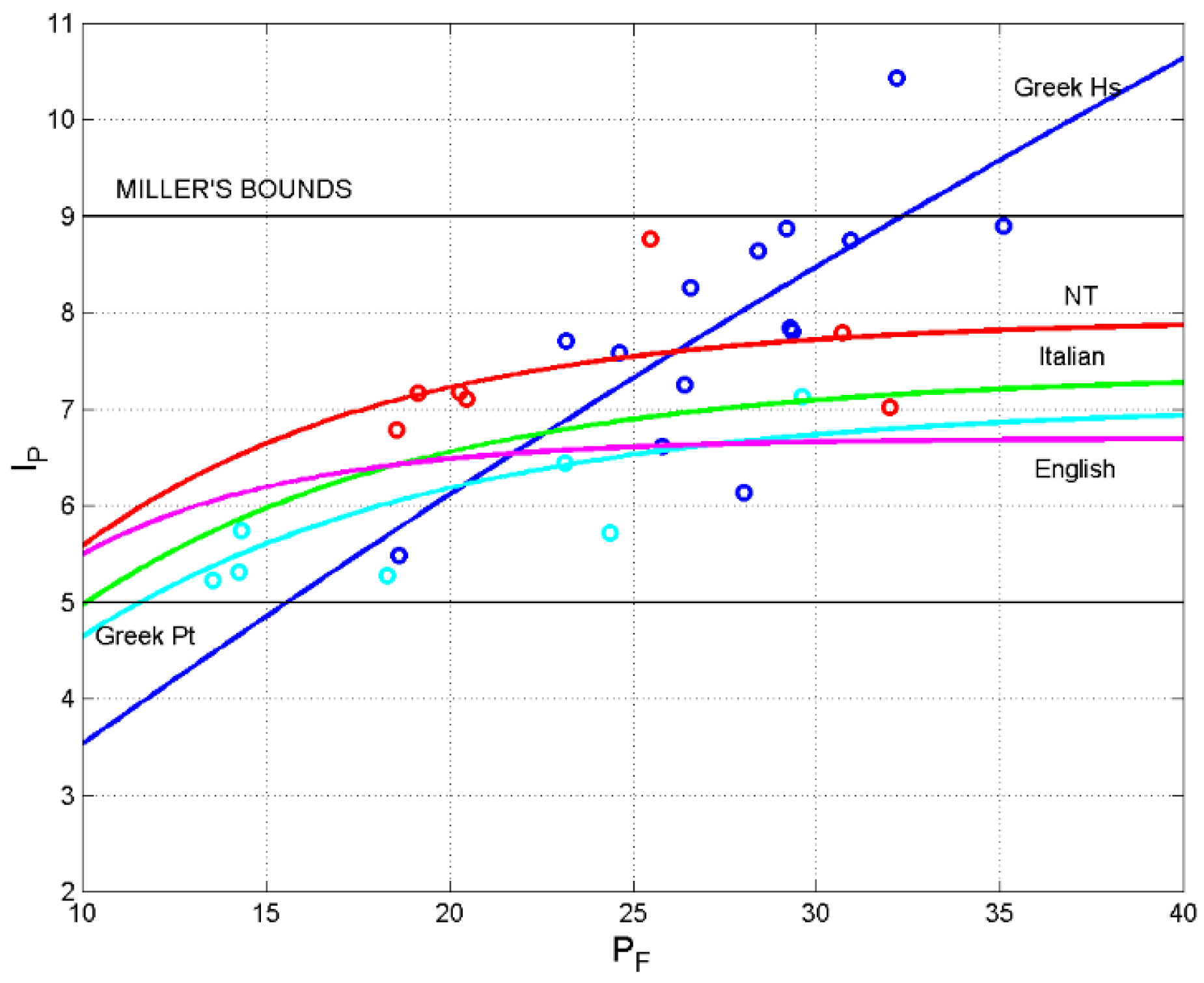
Figure 5 shows $Y$ versus $<I_P>$ (left panel) and versus $<P_F>$ (right panel). In both cases $Y$ increases as $<I_P>$ and $<P_F>$ increase. The authors/texts that use long word intervals and sentences engage more readers’ E–STM and, for this reason, are better matched to readers with longer schooling.

In the next section, I use $<P_F>$, ${<I}_P>$ and $<M_F>$ to calculate interesting indices connected to the E–STM of readers and writers, as well.

8. Short–Term Memory of Writers/Readers

Recently, I have proposed and applied a well–grounded conjecture that a sentence – read or pronounced, the two activities are similarly processed by the brain [9,10,11,12,13,14,15,16] – is elaborated by the E–STM with two independent processing units in series, with similar buffers size. The clues for conjecturing this model have emerged by considering a large number of novels belonging to the Italian and English Literatures. I have shown that there are no significant mathematical/statistical differences between the two literary corpora, according to deep–language parameters. In other words, the mathematical surface structure of alphabetical languages – a creation of human mind – seems to be deeply rooted in humans, independently of the particular language used. In this section, I show that this is true also for the ancient readers of Greek Literature.

A two–unit E–STM processing is justified according to how a human mind seems to memorize “chunks” of information written in a sentence. Although simple and related to the surface of language, the model seems to describe mathematically the input–output characteristics of a complex mental process largely unknown.

The first processing unit is linked to the number of words between two contiguous interpunctions, variable indicated by$I_p$ – the word interval – approximately ranging in Miller’s $7\pm 2$ law range [1,22]. The second unit is linked to the number $M_F$of word intervals contained in a sentence ranging approximately from 1 to 6. I have shown that the capacity (expressed in words) required to process a sentence ranges from $8.3$ to $61.2$ words, values that can be converted into time by assuming a reading speed. This conversion gives the range $2.6~19.5$ seconds for a fast–reading reader [32], and $5.3~30.1$ seconds for a common reader of novels, values well supported by experiments [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48].

The E–STM must not be confused with the intermediate memory [61,62]. It is not modelled by studying neuronal activity, but by studying only surface aspects of human communication, such as words, sentences and interpunctions, whose effects writers and readers have experienced since the invention of writing. In this section I show that these two independent units are also present in ancient Greek texts.

8.1. EW–STM First Buffer (Linked to $I_P$)

Figure 6 shows ${<I}_P>$ versus $<P_F>$ and the non–linear best–fit regression curves for Greek–1, Greek–2 and NT. As I have already established in modern languages and Latin [1,2,4], if $<P_F>$ increases $<I_p>$ tends to approach a horizontal asymptote. In other words, even if a sentence gets longer, $<I_p>$ cannot become larger than about the upper limit of $7\pm 2$Millers’ law (namely about 9), because of the constraints imposed by the E–STM capacity of readers and writers.

The coincidence of ${<I}_P>$ with the bounds of Miller’s law is clearly evident in Figure 6, just like in modern languages as the best–fit curves found in Italian and English novels [9], in modern languages [4] – also drawn in Figure 6 – clearly show.

From Figure 6, we can draw the following conclusions:

1)

There is a marked distinction between the regression curves concerning Greek–1, Greek–2 and NT.

2)

The regression curves of Italian and English, which refer only to novels, agree very well with the regression curves of Greek–2 and NT.

3)

Greek–1 is clearly mathematically different of Greek–2. The difference between novels and other types of writings, such as essays, was clearly found also in Italian writers as well [1].

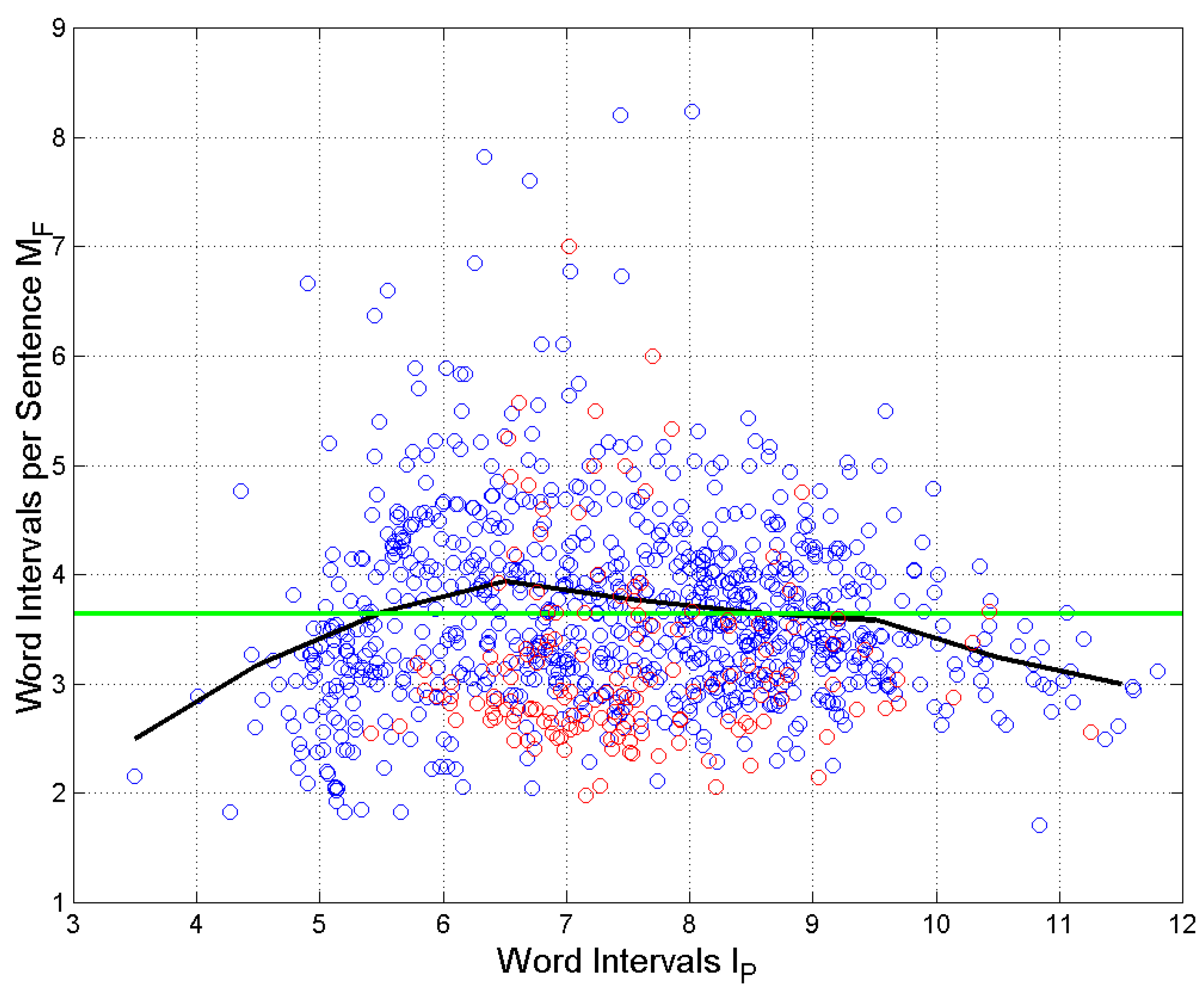
8.2. E–STM Second Buffer (Linked to $M_F$)

Figure 7 shows the scatterplot between $M_F$ and $I_P$ for the samples of the entire data bank used to calculate the statistical means of Figure 6. The horizontal green line reports the unconditional statistical mean ${<M}_F>,$ the black line reports the conditional mean versus $I_P$.

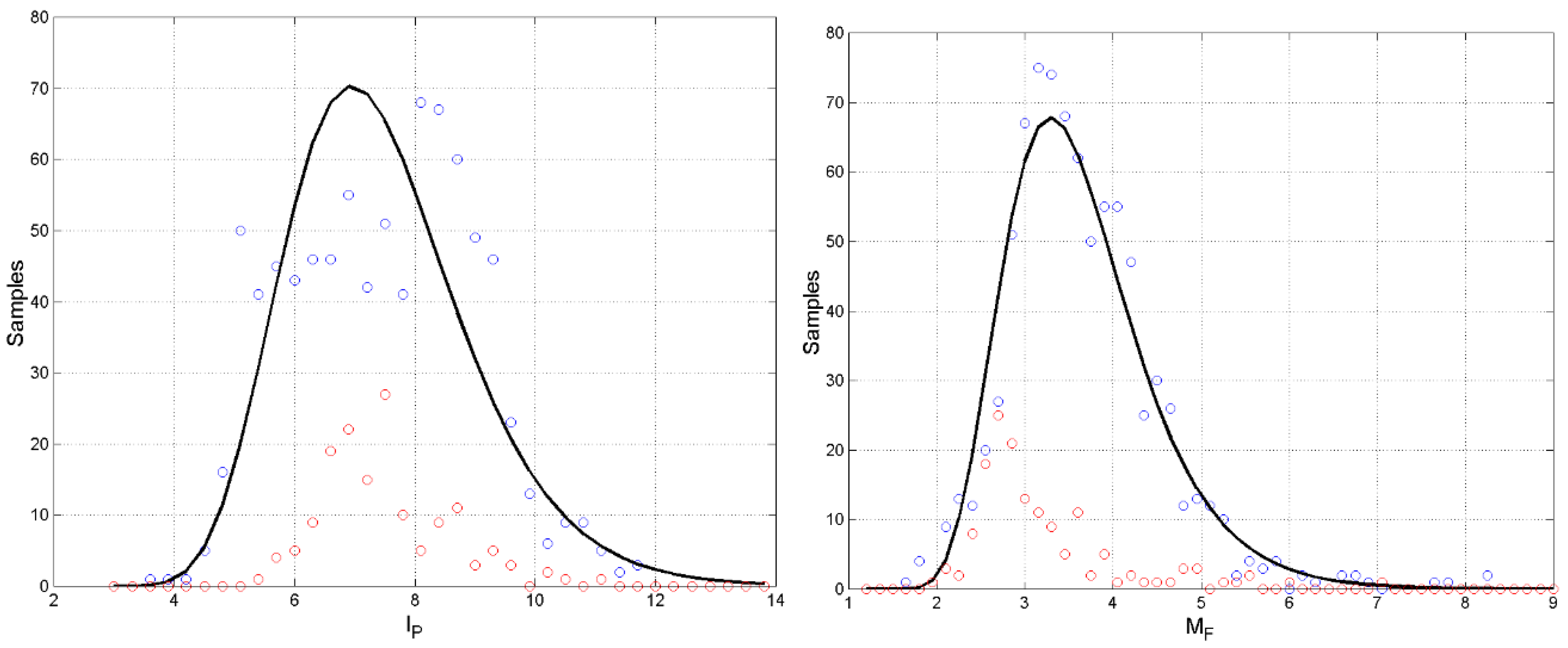
Now, the correlation coefficient between $I_P$ and $M_F$ in Figure 7 is practically zero (namely 0.03). The probability density of $I_P$ samples (Figure 8, left panel) and $M_F$ samples (Figure 8, right panel) can be modelled with a three–parameter log–normal density function – because $I_P\ge 1$, $M_F\ge 1$ – as in Italian and English [9]. Since a bivariate log–normal density function can be a sufficiently good model for the joint density of ${\mathrm{l}\mathrm{o}\mathrm{g}(I}_P)$ and ${\mathrm{l}\mathrm{o}\mathrm{g}(M}_F)$, at least in the central part of the marginal distributions, it follows that, if the correlation coefficient is zero, ${\mathrm{l}\mathrm{o}\mathrm{g}(I}_P)$ and ${\mathrm{l}\mathrm{o}\mathrm{g}(M}_F)$ are not only uncorrelated but also independent in the Gaussian case. Therefore, $I_P$ and $M_F$ are also independent and the two processing units of the E–STM work sufficiently independently, as with modern readers.

The size of the second E–STM buffer is in the same range found in modern languages, as the bulk of the data in Figure 7 is the range from $M_F\approx 2$ to $M_F\approx 6$ word intervals per sentence.

In conclusion, these texts were processed by a two–unit E–STM very similar to the E–STM of modern readers, even if these ancient readers were more accustomed to memorize oral information than modern ones. The specific size of the two buffers required in reading a text depended only on the kind of text, as for modern readers.

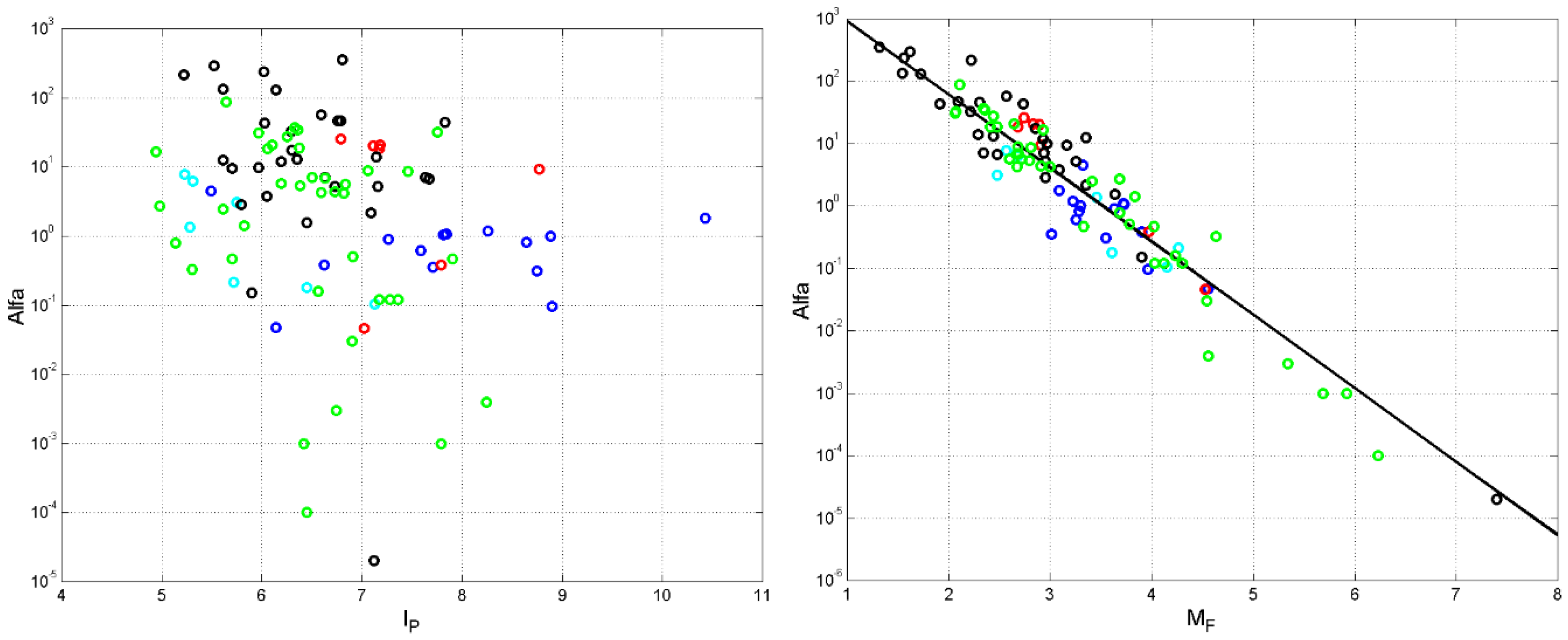
9. Multiplicity Factor and Mismatch Index

In [10], I studied the number of sentences that theoretically can be theoretically recorded in the E–STM. These numbers were compared with those of novels of Italian and English Literatures. I found that most authors write for readers with E–STM buffers and, consequently, are forced to reuse sentence patterns to convey multiple meanings. This behavior is quantified by the multiplicity factor $\alpha$, defined as the ratio between the number of sentences in a text and the number of sentences theoretically allowed.

I found that $\alpha >1$ is more likely than $\alpha <1$ and often $\alpha \gg 1$. In the latter case, writers reuse many times the same pattern of number of words. Few novels show $\alpha <1$; in this case, writers do not use some or most of them.

Another useful index is the mismatch index, $I_M,$in the range $\pm 1$, which measures to what extent a writer uses the number of sentences theoretically available, defined by:

$$I_M={\displaystyle \frac{\alpha -1}{\alpha +1}}$$

(24)

If $\alpha =1$ then $I_M=0$, therefore the number of sentences in a text equals the number of sentences theoretically allowed by the STM, a perfect match. If $\alpha >1$then $I_M>0$ therefore the number of sentences in a text is greater than and the number of sentences theoretically allowed (overmatching, the authors repeats patterns); if $\alpha <1$ then $I_M<0$, the number of sentences in a text is smaller than and the number of sentences theoretically allowed (undermatching, the authors use fewer patterns than those available).

Table 3 and Table 4 report $\alpha$ and $I_M$ for each author. From these results, we find that the authors who show practically perfect match are Aristides, Aristote, Plutarch and Polybius. No book of the NT shows a perfect match.

Figure 9 shows $\alpha$ versus $<I_P>$ (left panel) and versus ${<M}_F>$ (right panel). We can see that $\mathrm{l}\mathrm{o}\mathrm{g}\left(\alpha \right)$ and $<I_P>$ (first STM buffer) are substantially uncorrelated, while $\mathrm{l}\mathrm{o}\mathrm{g}\left(\alpha \right)$ and ${<M}_F>$ (second E–STM buffer) are significantly correlated. This latter findings mean that the number of sentence patterns is due only to the second E–STM buffer. 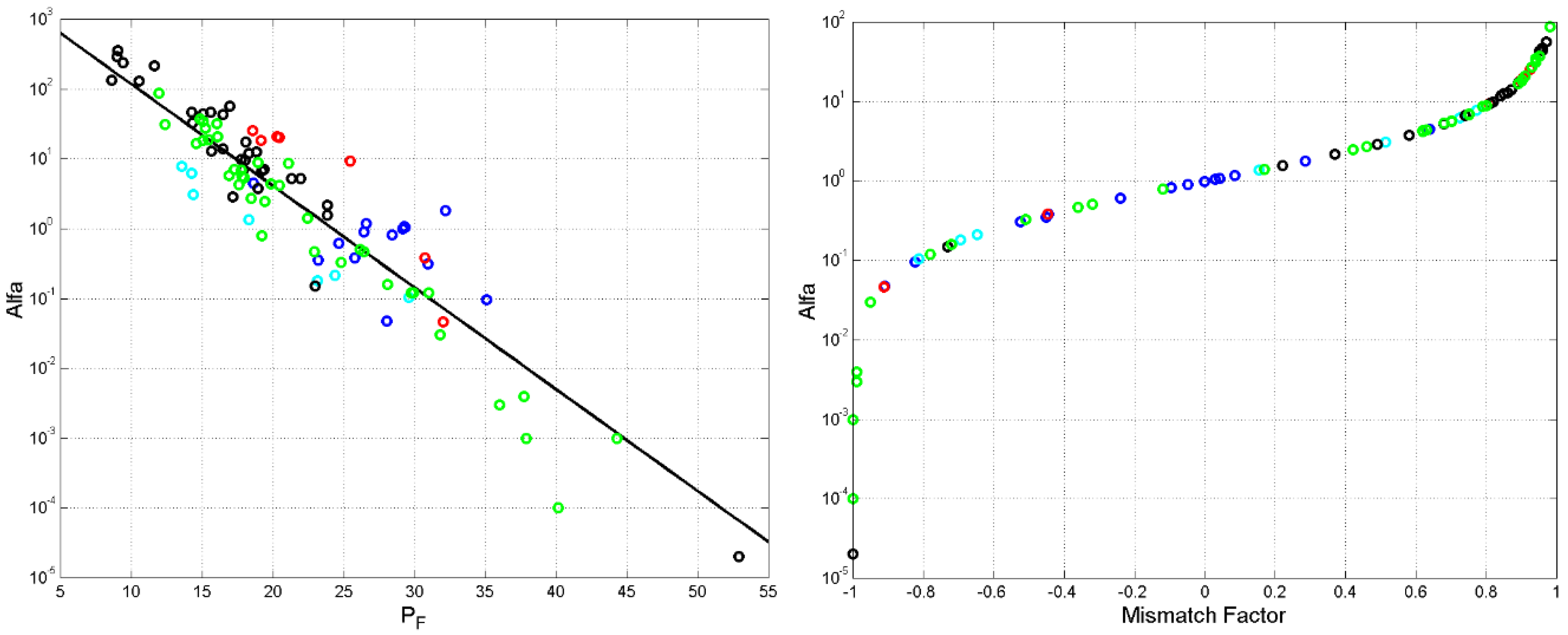The findngs concerning Italian and English Literatures [10] are scattered just like te Greek, therefore underlining no significant changes in more than 2000 years.

Figure 10 shows $\alpha$ versus $<P_F>$ (left panel) and the mistmath index ${<I}_M>$ (right panel). We can see that $\mathrm{l}\mathrm{o}\mathrm{g}\left(\alpha \right)$ and $<P_F>$ are correlated because large values of $<P_F>$ can contain many word intervals $I_P$, therefore large values of ${<M}_F>$. The mismatch index follows, of course, Eq.(24) and clearly indicates where texts/authors are located, including Italian and English ones.

10. Conclusions

After the punctual discussion on the findings reported in each section, I can conclude that the multi–dimensional mathematical theory and analysis of texts belonging to the classical Greek Literature – spanning eight centuries – have revealed interesting connections between authors/texts, just like it has done in modern literatures. It has also revealed connections with the extended short–term memory of ancient readers.

The theory considers the number of characters, words, sentences and interpunctions, and it defines surface deep–language parameters and linguistic communication channels within texts. All these mathematical entities are due to writer’s unconscious design and can, therefore, reveal connections between texts or authros far beyond writers’ awareness.

The analysis, based on 3,225,839 words contained in 118,952 sentences, has shown that ancient Greek writers, and their readers, were not significantly different from modern writers/readers.

Their sentences were processed by the extended short–term memory, modelled with two independent processing units in series, just like in modern readers. This finding is very interesting because in a society in which people were used to memorize information more than modern people do, authors write almost exactly, mathematically speaking, as modern writers do and for readers of similar characteristics. Since meaning is not considered, any text of any alphabetical language can be studied exactly with the same mathematical/statistical tools and, therefore, comparisons can be done, regardless of different languages and epoch of writing.