1. Introduction
The Kaiser-Hamming sharpening [
1] of comb decimation filters was first introduced in [
2] to improve the passband and stopband characteristics of the filters. Later, various improvements to the Kaiser sharpening method were presented [
3,
4,
5,
6,
7]. The Chebyshev sharpening of comb decimation filters first introduced Coleman in [
8]. This filter provides a high predetermined attenuation in all folding bands. However, the passband has a high passband droop. The author also proposed a pre-sharpening version in which the passband droop is decreased but still needs to be improved. The authors in [
9] proposed a novel structure for Chebyshev sharpening, while in [
10,
11], are proposed different Chebyshev sharpening polynomials and the optimal filters to compensate for the passband droop. In [
12], the method to design an optimal compensator for Chebyshev sharpening combs provides better compensation than the compensators in [
11]. The method is based on particle swarm optimization (PSO) and sinusoidal magnitude response.
This paper extends the previous paper [
12]. Three compensators for Chebyshev sharpened comb filters from the literature are introduced to enhance passband compensation and increase the flexibility of the design. The novelty of this work includes the following:
The paper is organized as described in continuation. Next Section introduces three compensators of different complexity and describes the design procedure.
Section 3 presents the passband compensation of the Chebyshev sharpened combs introduced in [
8] and [
11].
Section 4 presents the comparisons with the methods from the literature.
2. Design of Compensators
Compensators are a key area of research in the field of comb filters. They are designed to improve the passband characteristics of comb filters [
13,
14,
15,
16,
17] or modified comb filters [
18] at a low sample rate, i.e., after the decimation. Typically, compensators are designed as finite impulse responses (FIR) filters using various optimization methods to ensure that the cascade of the filter and the compensator provides as low as possible deviation in the passband of interest. We will adopt the denotations, as shown in the continuation.
The comb filter of order
K and the decimation factor
M is denoted as:
The Chebyshev sharpened comb is denoted as G(z) and the compensator as C(z).
Since the compensator works at a low rate, using the multirate identity [
19] the cascade of the Chebyshev sharpened comb and compensator is given as:
As the comb compensator introduced in [
13,
14,
15,
16] has sinusoidal magnitude characteristics while exhibiting high-quality compensation, we also propose to use the sinusoidal magnitude responses for the proposed compensators. We consider narrowband and wideband designs, as described in the following.
2.1. Narrowband Design
In this design, the passband frequency
ωp <1/4
M. The magnitude characteristic is chosen as in [
13],
where
C11 is the parameter of the design.
The system function of this filter is given as [
13],
The compensator requires three adders and one multiplier. In a multiplierless design, the number of required adders equals:
where
N11 is the number of adders in the signed-power-of-two (SPT) form of
C11.
2.2. Wideband Design
In the wideband design the passband frequency ωp equals 1/4M≤ ≤1/2M.
We consider two sinusoidal compensators.
2.2.1. Extension of Narrowband Design
The magnitude response is given as [
14]
where
C21 and
C22 are the parameters of the design.
The system function of this compensator is given as:
The compensator requires nine adders and two multipliers
C21 and
C22. The number of the required adders in a multiplierless design is given as
where
N21 and
N22 are the number of adders in SPT forms of
C21 and
C22, respectively.
To increase the flexibility of the design, we also consider the less complex compensator from [
16] introduced in the next subsection.
2.2.2. Simplified Version of Compensator in (6)
The magnitude response is given as [
16]:
where
C31 and
C32 are parameters of the design.
The system function is given as [
16],
The compensator requires six adders and two multipliers
C31 and
C32. The number of the required adders in a multiplierless design is,
where
N31 and
N32 are the number of adders in SPT forms of
C31 and
C32, respectively.
2.3. How to Obtain the Compensator Design Parameters?
We first consider optimum design to get the parameters in compensators (3), (6), and (9) in a way that a minimum of the maximum passband deviation
δo in the passband of interest, defined by the passband edge
ωp equals
where
is given in (2), and the compensators are given in (3), (6), and (9).
The optimal design is obtained using particle swarm optimization (PSO) in MATLAB [
20].
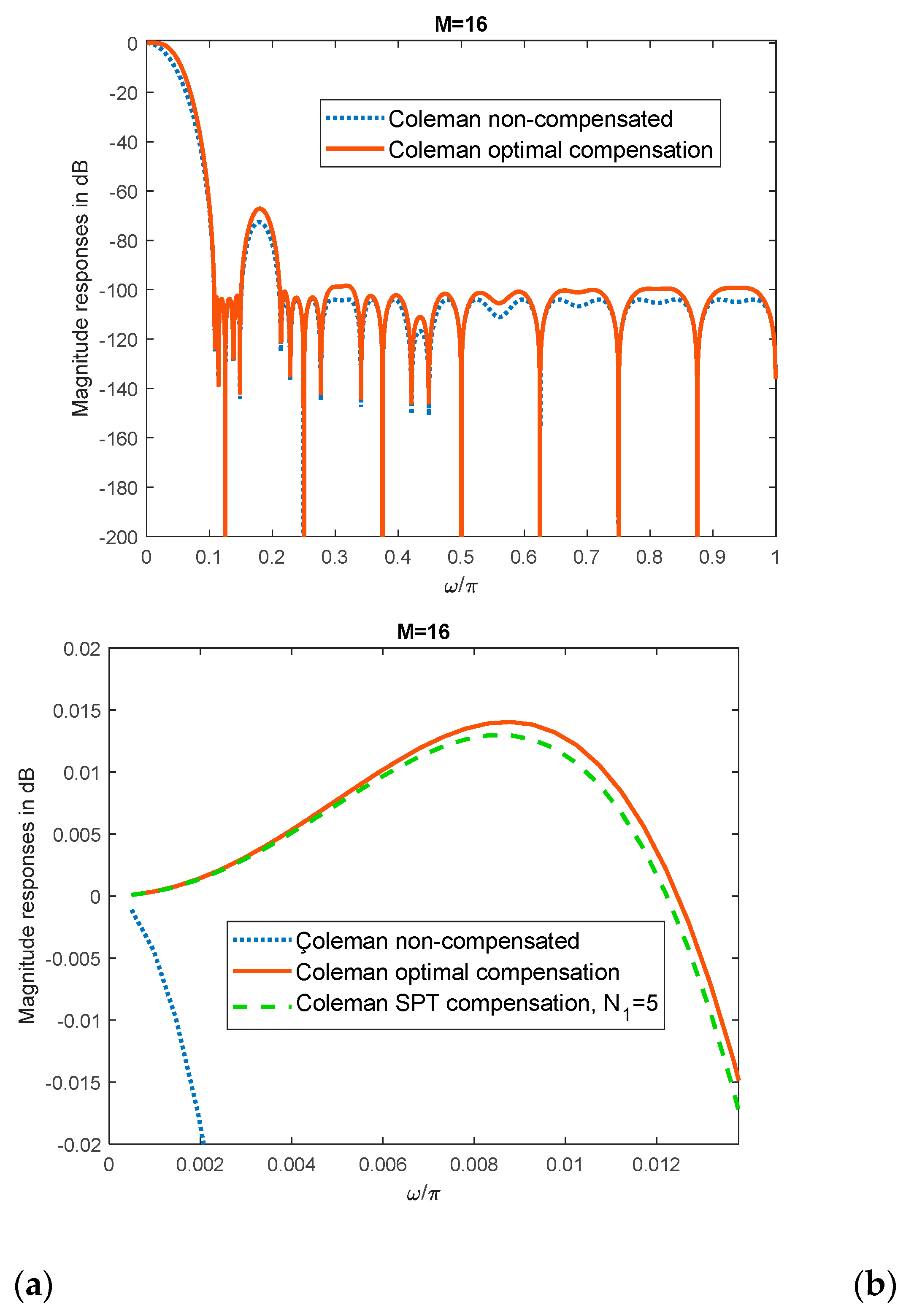
Figure 1.
Compensation with the narrowband filter C1. Overall magnitude responses and passband zooms: (a) Overall magnitude responses of Coleman non-compensated and optimal compensated filters; (b) Passband zoom od Coleman non-compensated, optimal compensated, and SPT compensated filters with N1=5.
Figure 1.
Compensation with the narrowband filter C1. Overall magnitude responses and passband zooms: (a) Overall magnitude responses of Coleman non-compensated and optimal compensated filters; (b) Passband zoom od Coleman non-compensated, optimal compensated, and SPT compensated filters with N1=5.
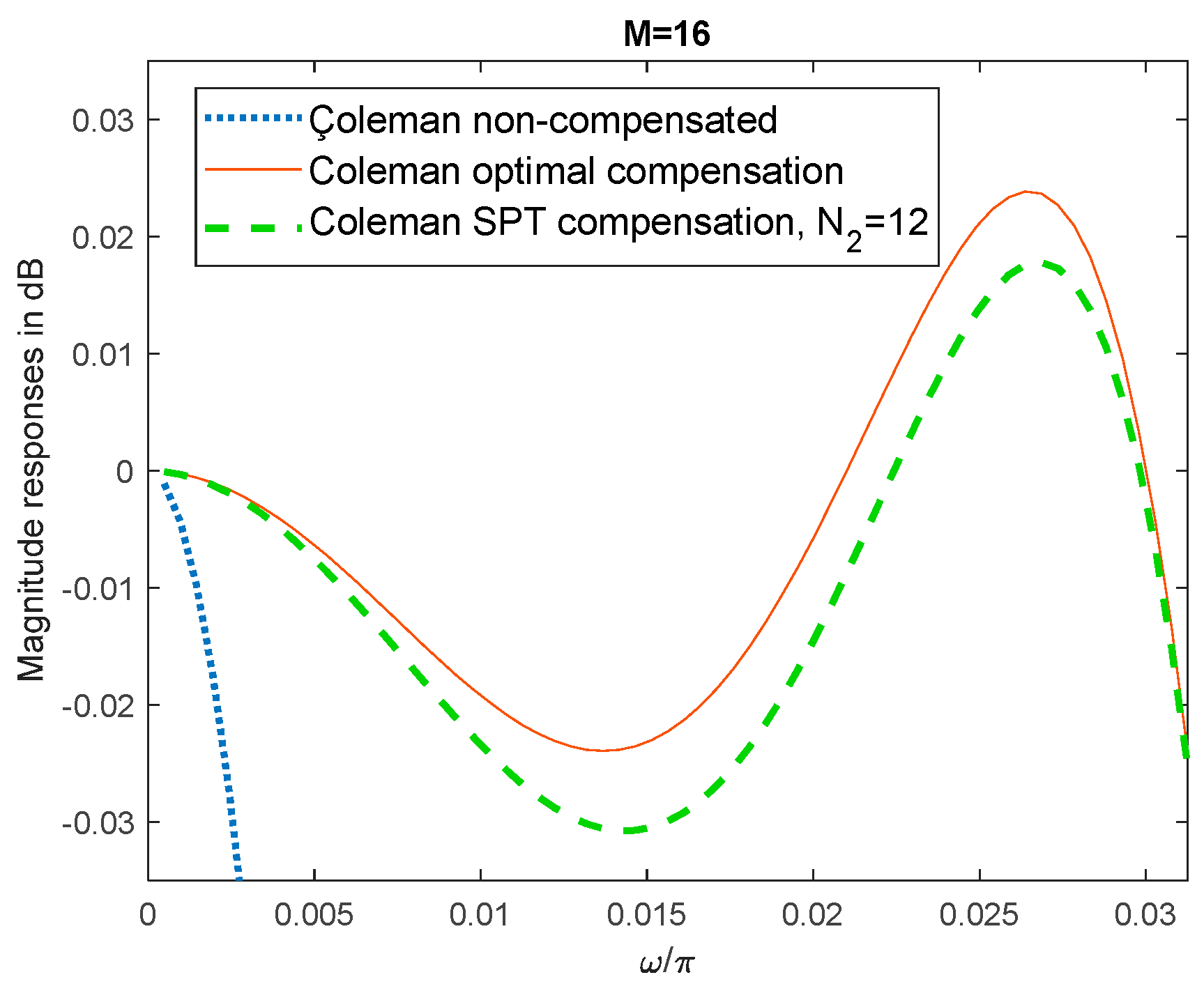
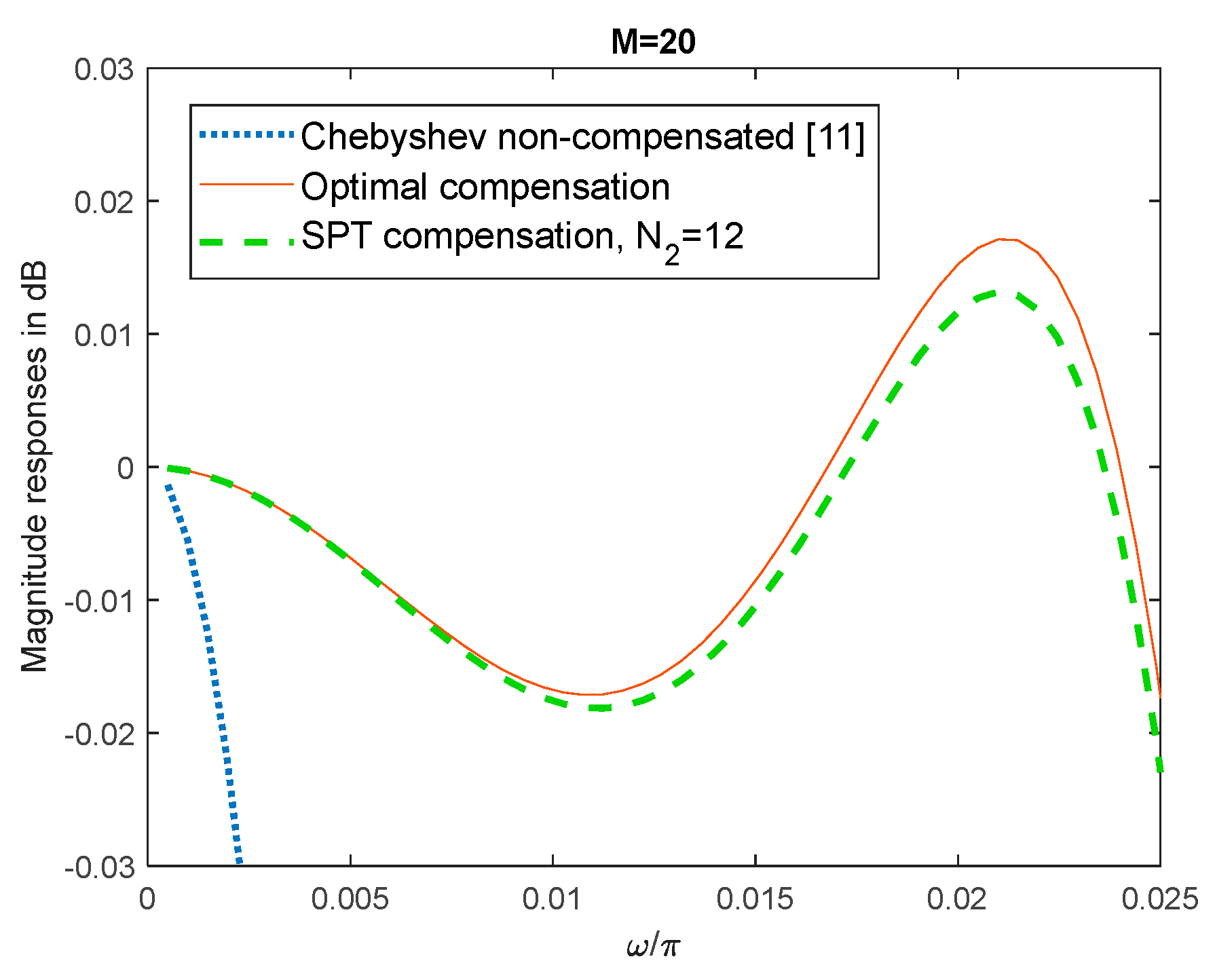
Figure 2.
Compensation with the wideband filter C2. Passband magnitude responses of non-compensated, optimal compensated, and SPT compensated Coleman sharpening comb filters with N2=12.
Figure 2.
Compensation with the wideband filter C2. Passband magnitude responses of non-compensated, optimal compensated, and SPT compensated Coleman sharpening comb filters with N2=12.
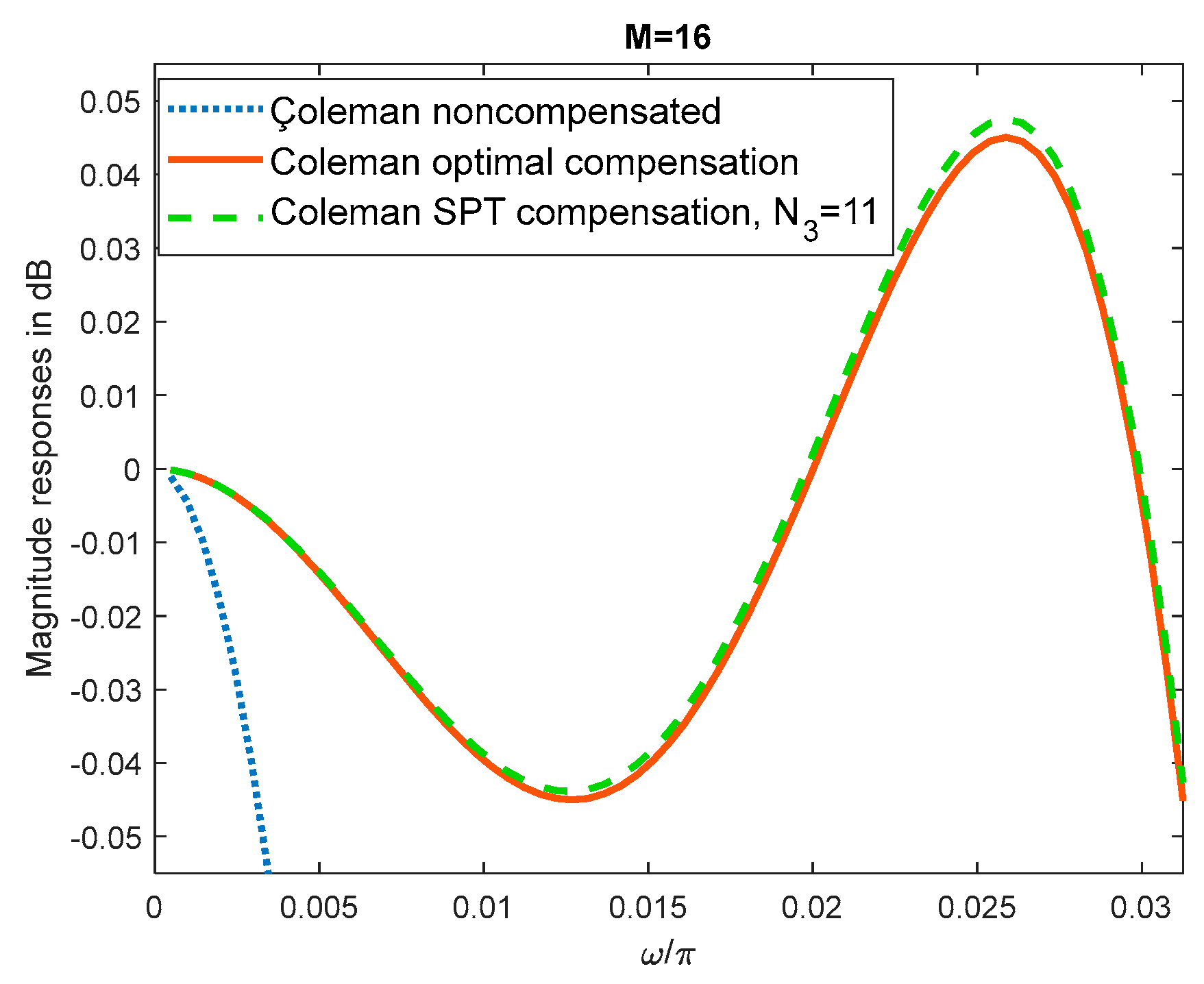
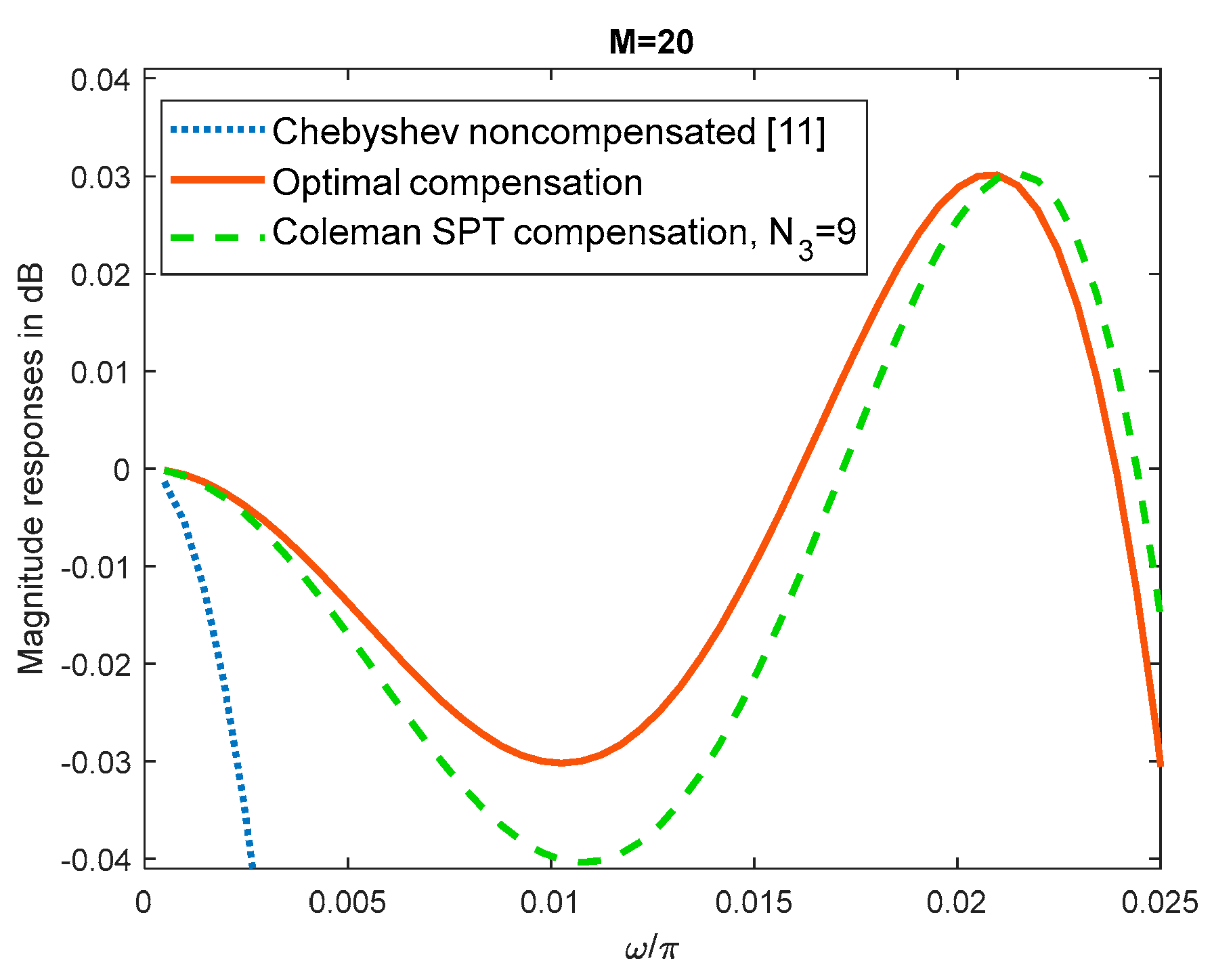
Figure 3.
Compensation with the wideband filter C3. Passband magnitude responses of non-compensated, optimal compensated, and SPT compensated Coleman sharpening comb filters, with N3=11.
Figure 3.
Compensation with the wideband filter C3. Passband magnitude responses of non-compensated, optimal compensated, and SPT compensated Coleman sharpening comb filters, with N3=11.
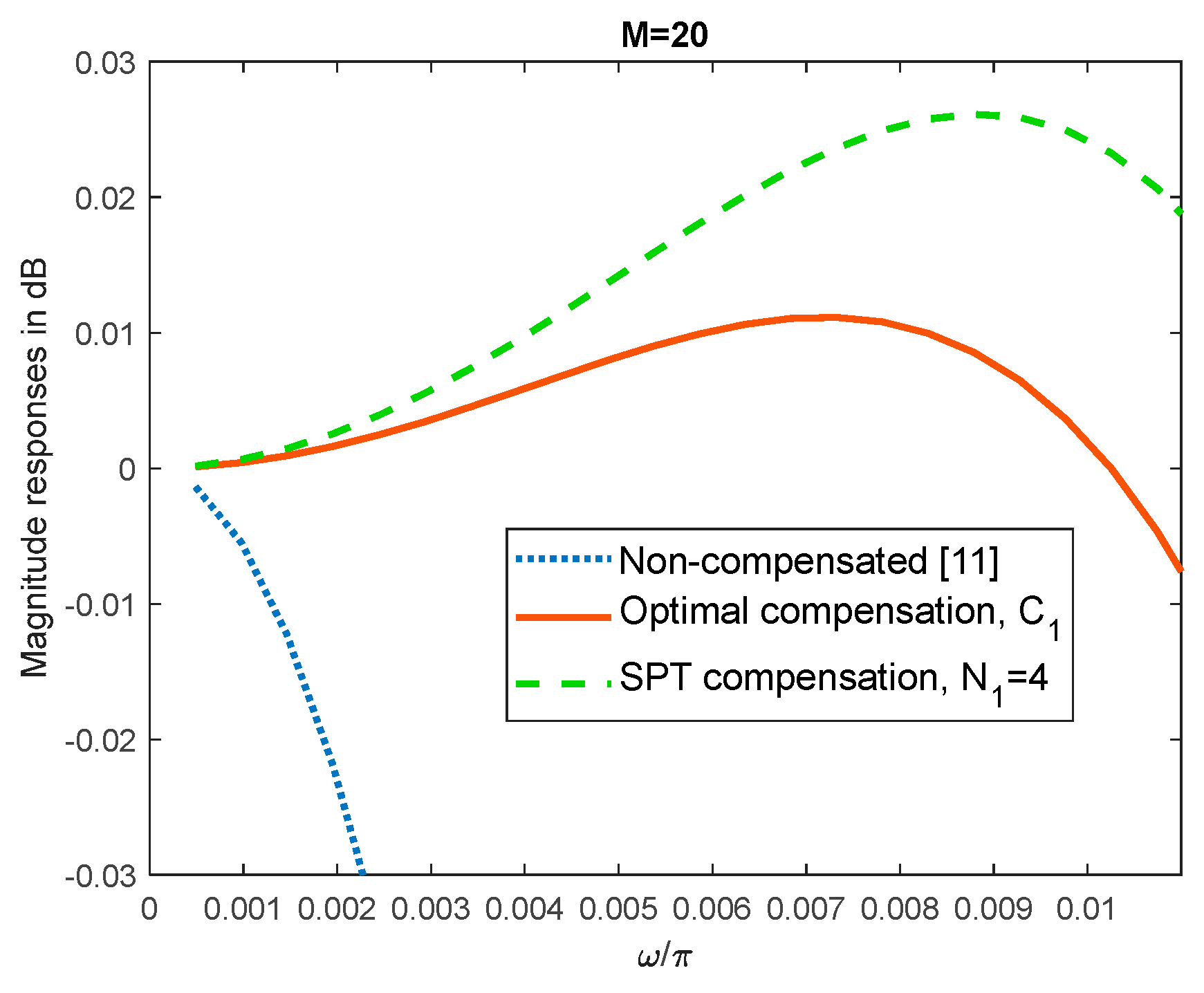
Figure 4.
Compensation with the narrowband filter C1. Passband magnitude responses of non-compensated, optimal compensated, and SPT compensated, N1=4, Chebyshev sharpening comb filters.
Figure 4.
Compensation with the narrowband filter C1. Passband magnitude responses of non-compensated, optimal compensated, and SPT compensated, N1=4, Chebyshev sharpening comb filters.
Figure 5.
Compensation with the wideband filter C2. Passband magnitude responses of non-compensated, optimal compensated, and SPT compensated, N1=4, Chebyshev sharpening comb filters.
Figure 5.
Compensation with the wideband filter C2. Passband magnitude responses of non-compensated, optimal compensated, and SPT compensated, N1=4, Chebyshev sharpening comb filters.
Figure 6.
Compensation with the wideband filter C3. Passband magnitude responses of non-compensated, optimal compensated, and SPT compensated, N1=4, Chebyshev sharpening comb filters.
Figure 6.
Compensation with the wideband filter C3. Passband magnitude responses of non-compensated, optimal compensated, and SPT compensated, N1=4, Chebyshev sharpening comb filters.
Table 1.
SPT compensator C1 coefficients, passband deviation, and the number of adders.
Table 1.
SPT compensator C1 coefficients, passband deviation, and the number of adders.
| C11 |
δ1 [dB] |
N1 |
| 20-2-4
|
0.0274 |
4 |
| 20-2-3+2-5
|
0.0165 |
5 |
| 20-2-3+2-5+2-8
|
0.0145 |
6 |
| 20-2-3+2-5+2-8-2-10
|
0.0142 |
7 |
Table 2.
SPT compensator C2 coefficients, passband deviations, and the number of adders.
Table 2.
SPT compensator C2 coefficients, passband deviations, and the number of adders.
| C21 |
C22 |
δ2 [dB] |
N2 |
|
|
| 20-2-2
|
20-2-3
|
0.1232 |
11 |
|
|
| 20-2-2+2-5
|
20-2-3
|
0.0307 |
12 |
|
|
| 20-2-2+2-5
|
20-2-3+2-7
|
0.0297 |
13 |
|
|
| 20-2-2+2-5+2-8
|
20-2-3-2-10
|
0.0271 |
14 |
|
|
| 20-2-2+2-5+2-7
|
20-2-3-2-6+2-8
|
0.0247 |
15 |
|
|
Table 3.
SPT compensator C3 coefficients, passband deviations, and the number of adders.
Table 3.
SPT compensator C3 coefficients, passband deviations, and the number of adders.
| C31 |
C32 |
δ3 [dB] |
N3 |
|
|
| 20-2-2
|
20-2-2+2-6
|
0.0616 |
9 |
|
|
| 20-2-2-2-8
|
20-2-2+2-6
|
0.0532 |
10 |
|
|
| 20-2-2-2-5+2-7
|
20+2-2+2-4
|
0.0474 |
11 |
|
|
| 20-2-2-2-5+2-7
|
20+2-2+2-4-2-9
|
0.04591 |
12 |
|
|
| 20-2-2-2-5+2-7-2-10
|
20-2-2+2-4-2-14
|
0.0452 |
13 |
|
|
Table 4.
SPT compensator C1 coefficients, passband deviation and the number of adders.
Table 4.
SPT compensator C1 coefficients, passband deviation and the number of adders.
| C11 |
δ1 [dB] |
N1 |
| 20-2-2
|
0.0299 |
4 |
| 20-2-2-2-5
|
0.0125 |
6 |
| 20-2-2-2-5-2-8
|
0.0115 |
7 |
| 20-2-2-2-5-2-8+2-11
|
0.0110 |
8 |
Table 5.
SPT compensator C2 coefficients, passband deviations, and the number of adders.
Table 5.
SPT compensator C2 coefficients, passband deviations, and the number of adders.
| C21 |
C22 |
δ2 [dB] |
N2 |
|
|
| 2-1+2--3
|
2-1+2-3
|
0.0485 |
11 |
|
|
| 2-1+2-3+2-7
|
2-1+2-3
|
0.0227 |
12 |
|
|
| 2-1+2-3+2-7
|
2-1+2-3+2-8
|
0.00177 |
13 |
|
|
| 2-1+2-3+2-7+2-11
|
2-1+2-3+2-9
|
0.0174 |
14 |
|
|
| 2-1+2-3+2-7+2-10
|
2-1+2-3+2-10+2-12
|
0.0172 |
15 |
|
|
Table 6.
SPT compensator C3 coefficients, passband deviations, and the number of adders.
Table 6.
SPT compensator C3 coefficients, passband deviations, and the number of adders.
| C31 |
C32 |
δ3 [dB] |
N |
|
|
| 2-1-2-4
|
20-2-4
|
0.0597 |
8 |
|
|
| 2-1+2-4-2-6
|
20-2-4
|
0.0404 |
9 |
|
|
| 2-1+2-3+2-6
|
20-2-3-2-6
|
0.0373 |
10 |
|
|
| 2-1+2-3-2-5+2-9
|
20-2-3+2-6
|
0.0317 |
11 |
|
|
| 2-1+2-3-2-5+2-11
|
20-2-3+2-6+2-8
|
0.0304 |
12 |
|
|
Table 7.
SPT compensator C1 coefficients, passband deviation, and the number of adders.
Table 7.
SPT compensator C1 coefficients, passband deviation, and the number of adders.
| C11 |
δ1 [dB] |
N1 |
| 2-1-2-3
|
0.0169 |
4 |
| 2-1-2-3-2-6
|
0.0064 |
5 |
| 2-1-2-3-2-6-2-8
|
0.0045 |
6 |
| 2-1-2-3-2-6-2-8-2-11
|
0.0043 |
7 |
Table 8.
SPT compensator C1 coefficients, passband deviation, and the number of adders.
Table 8.
SPT compensator C1 coefficients, passband deviation, and the number of adders.
| C11 |
δ1 [dB] |
N1 |
| 2-1-2-3
|
0.0157 |
4 |
| 2-1-2-3-2-5
|
0.0015 |
5 |
| 2-1-2-3-2-5-2-11
|
0.0012 |
6 |
| |
|
|
Table 9.
SPT compensator C1 coefficients, passband deviation, and the number of adders.
Table 9.
SPT compensator C1 coefficients, passband deviation, and the number of adders.
| C11 |
δ1 [dB] |
N1 |
| 2-1+2-5
|
0.0056 |
4 |
| 2-1+2-5-2-8
|
0.0042 |
5 |
| 2-1+2-5-2-7+2-9
|
0.0036 |
6 |
| 2-1+2-5-2-7+2-9-2-11
|
0.0035 |
7 |
Table 10.
SPT compensator C3 coefficients, passband deviations, and the number of adders.
Table 10.
SPT compensator C3 coefficients, passband deviations, and the number of adders.
| C31 |
C32 |
δ3 [dB] |
N3 |
|
|
| 2-1-2-13
|
2-1-2-4
|
0.0101 |
8 |
|
|
| 2-1-2-13-2-16
|
2-1-2-4
|
0.0100 |
9 |
|
|
| 2-1-2-11-2-13
|
2-1-2-4+2-10
|
0.0098 |
10 |
|
|
Table 11.
SPT compensator C1 coefficient, passband deviations and the number of adders.
Table 11.
SPT compensator C1 coefficient, passband deviations and the number of adders.
| C11 |
δ1 [dB] |
N1 |
| 2-1-2-3
|
0.0169 |
4 |
| 2-1-2-3-2-6
|
0.0064 |
5 |
| 2-1-2-3-2-6-2-8
|
0.0045 |
6 |
| 2-1-2-3-2-6-2-8-2-11
|
0.0043 |
7 |
Table 12.
SPT compensator C3 coefficients, passband deviations, and the number of adders.
Table 12.
SPT compensator C3 coefficients, passband deviations, and the number of adders.
| C31 |
C32 |
δ3 [dB] |
N3 |
|
|
| 20-2-3
|
21-2-3
|
0.0776 |
8 |
|
|
| 20-2-3+2-7
|
21-2-3
|
0.0601 |
9 |
|
|
| 20-2-3+2-6-2-9
|
21-2-3-2-7
|
0.0587 |
10 |
|
|
| 20-2-3+2-6+2-9
|
21-2-2+2-4+2-7
|
0.0555 |
11 |
|
|
Table 13.
SPT compensator C2 coefficients, passband deviations, and the number of adders.
Table 13.
SPT compensator C2 coefficients, passband deviations, and the number of adders.
| C21 |
C22 |
δ2 [dB] |
N2 |
|
|
| 2-1+2--5
|
2-2+2-6
|
0.0307 |
11 |
|
|
| 2-1-2--5+2-8
|
2-1+2-7
|
0.0276 |
12 |
|
|
| 2-1-2--5+2-8
|
2-1+2-7+2-9
|
0.0273 |
13 |
|
|
| 2-1-2--5+2-8+2-10
|
2-1+2-7-2-11
|
0.0266 |
14 |
|
|
| 2-1+2-5+2-7-2-9-2-11
|
2-1+2-7-2-9+2-11
|
0.0262 |
16 |
|
|