Submitted:
04 April 2025
Posted:
07 April 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Preliminaries
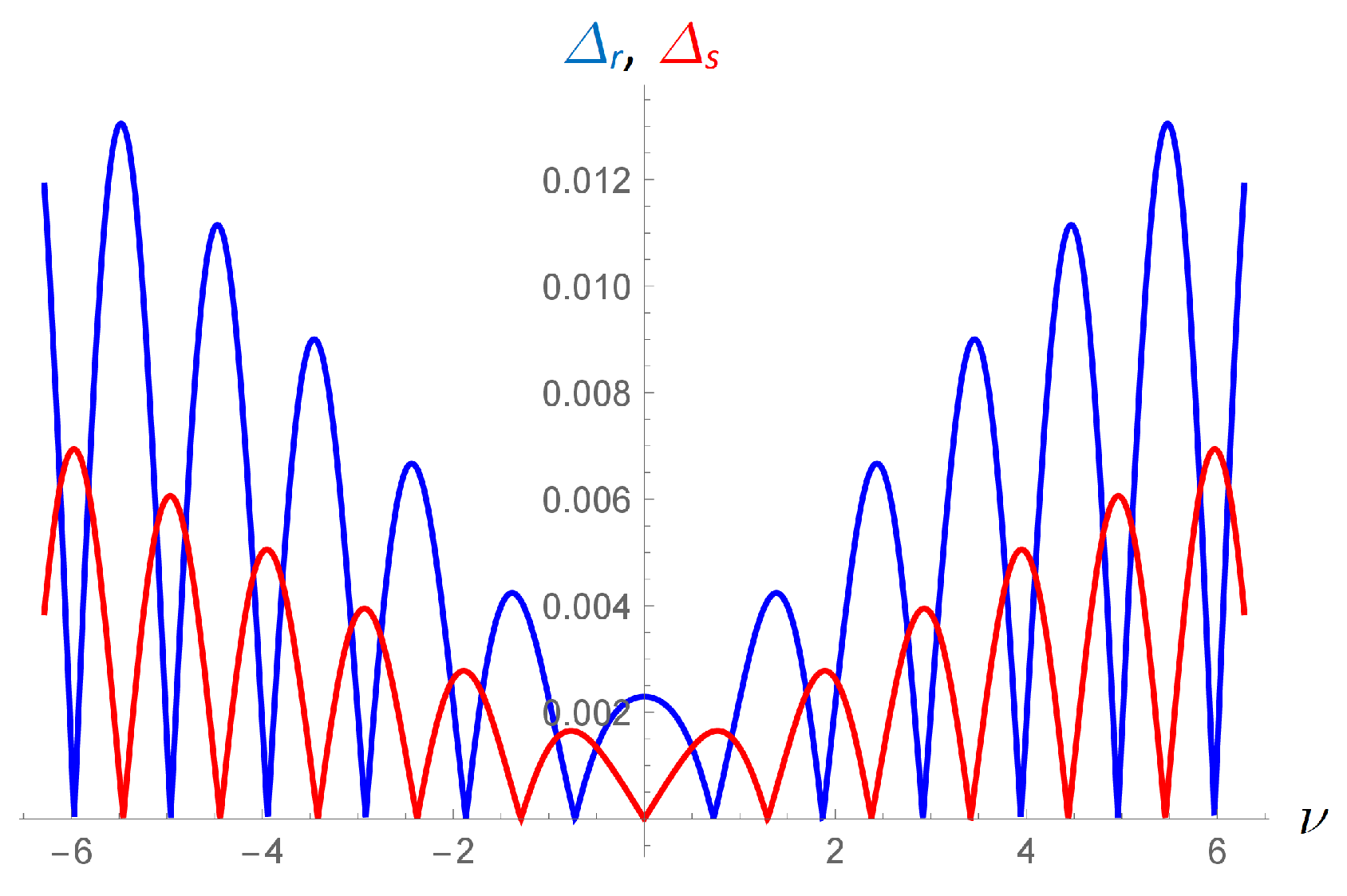
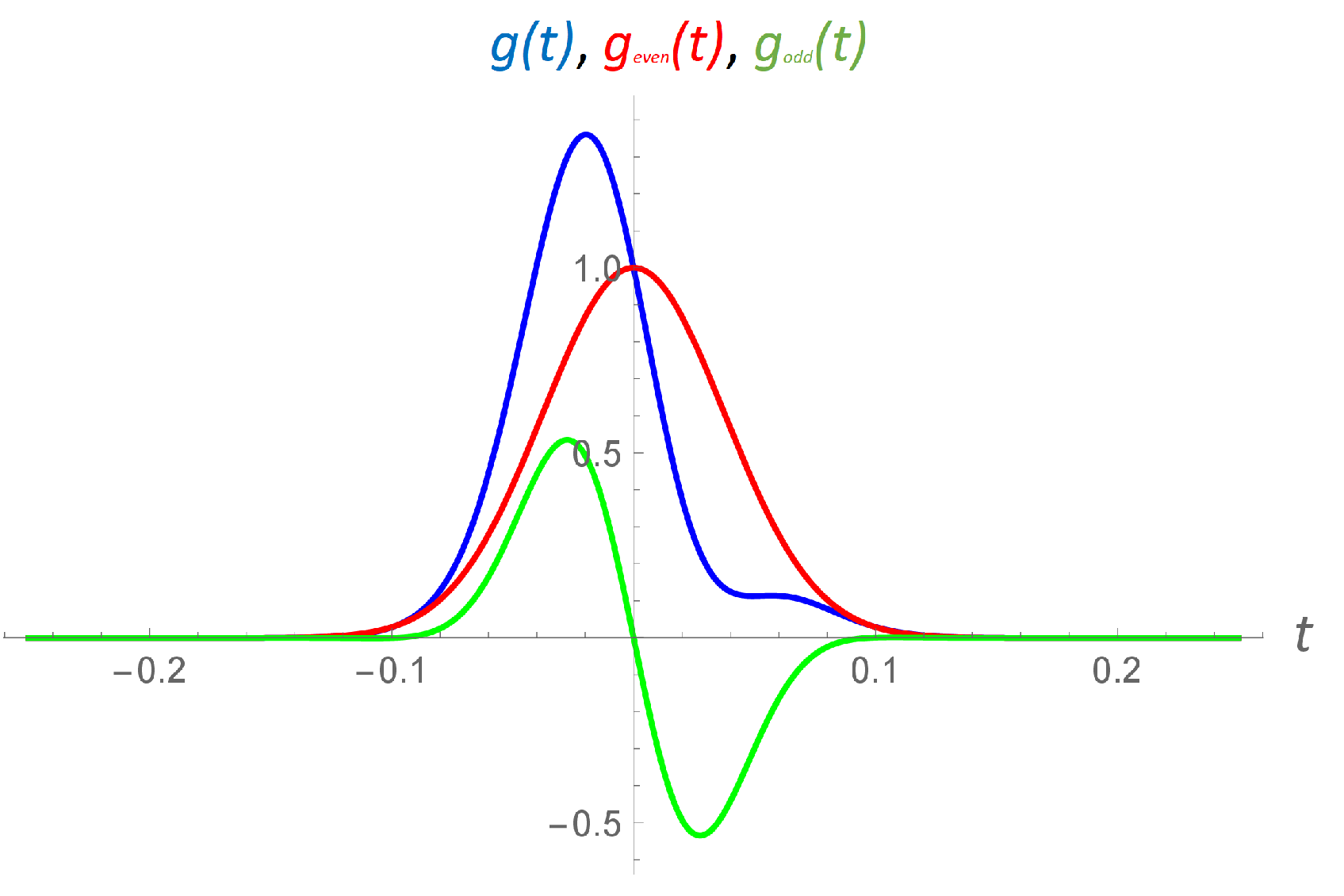
3. Results and Discussion
3.1. Methodology
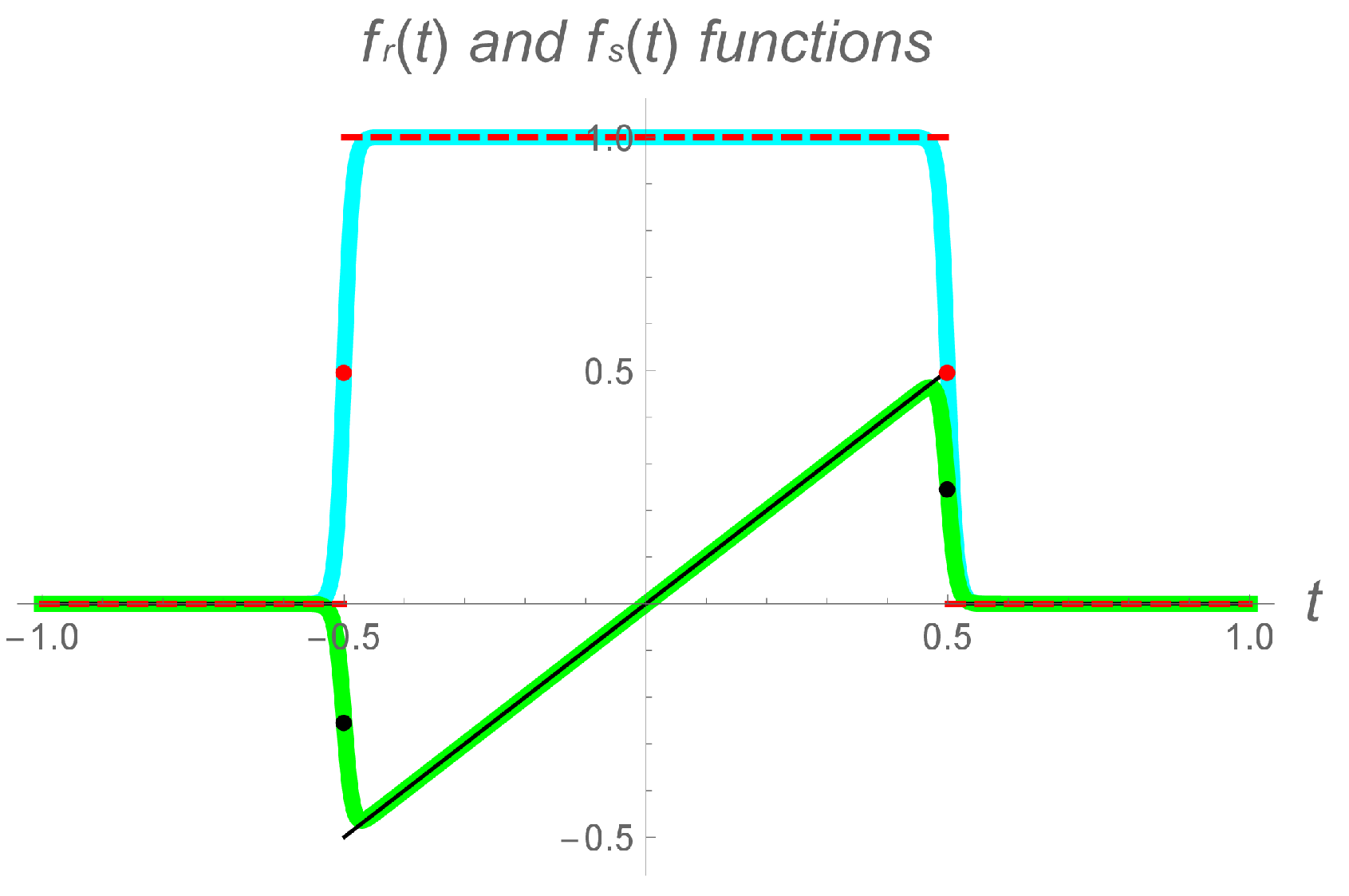
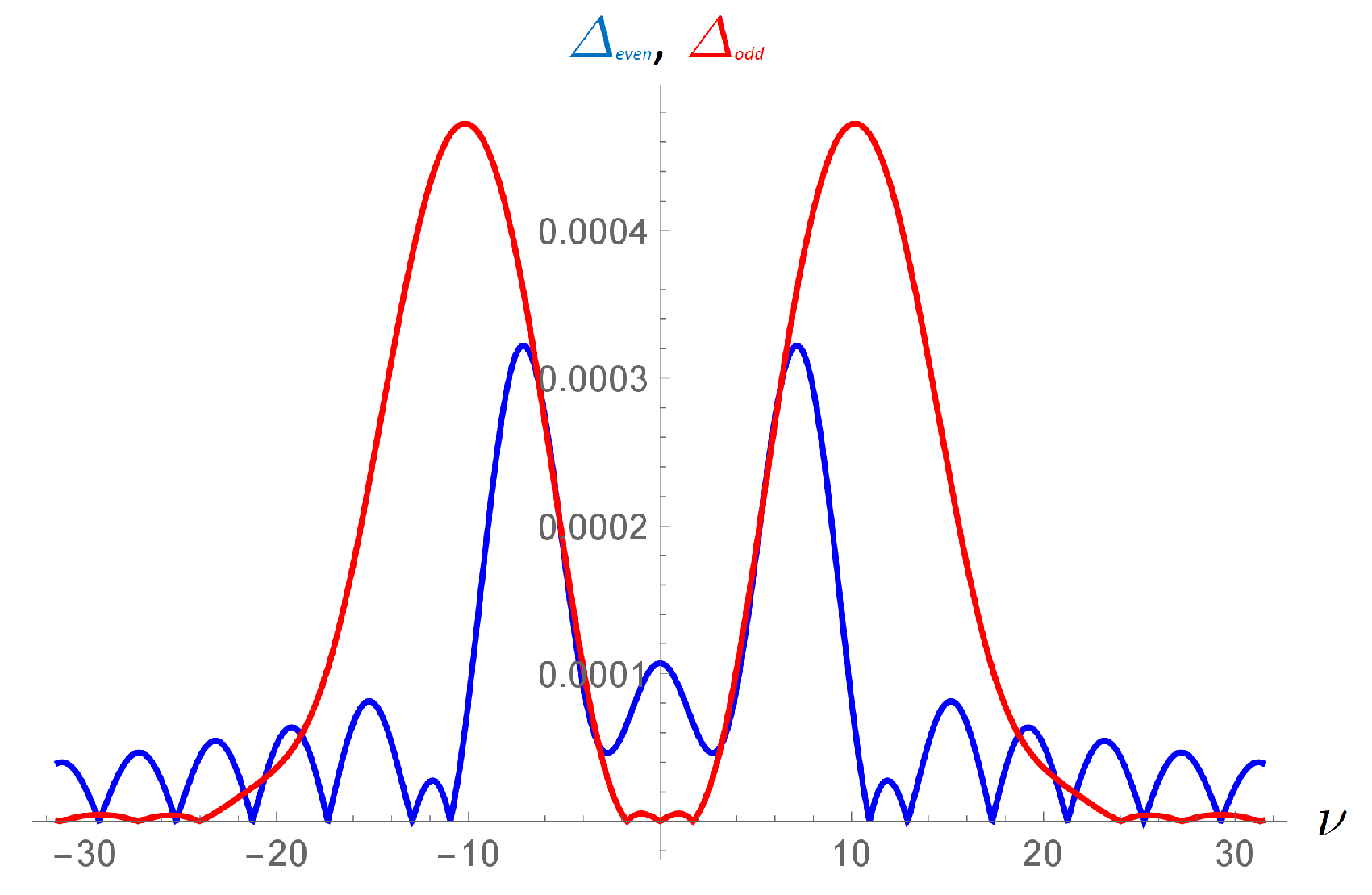
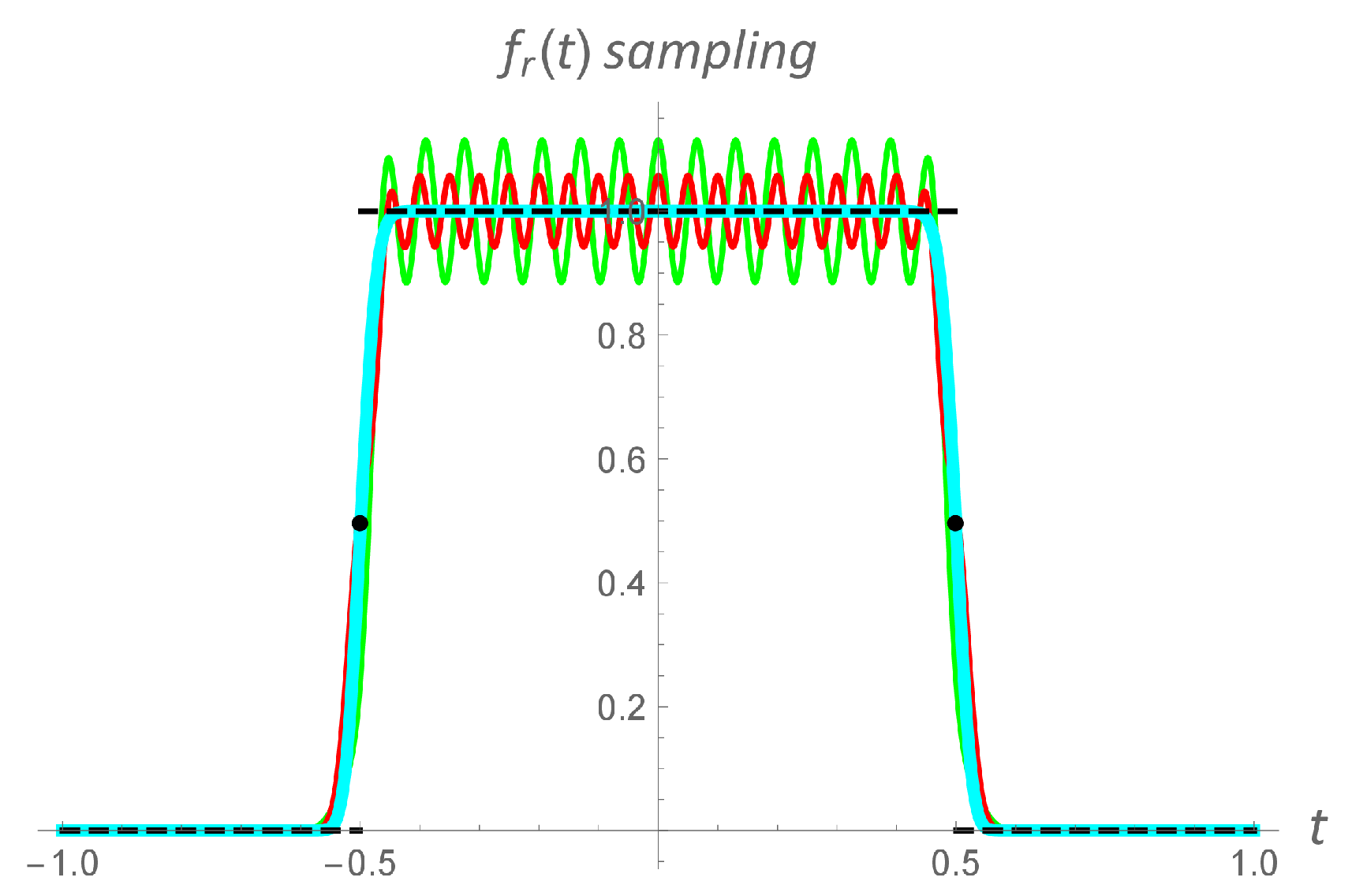
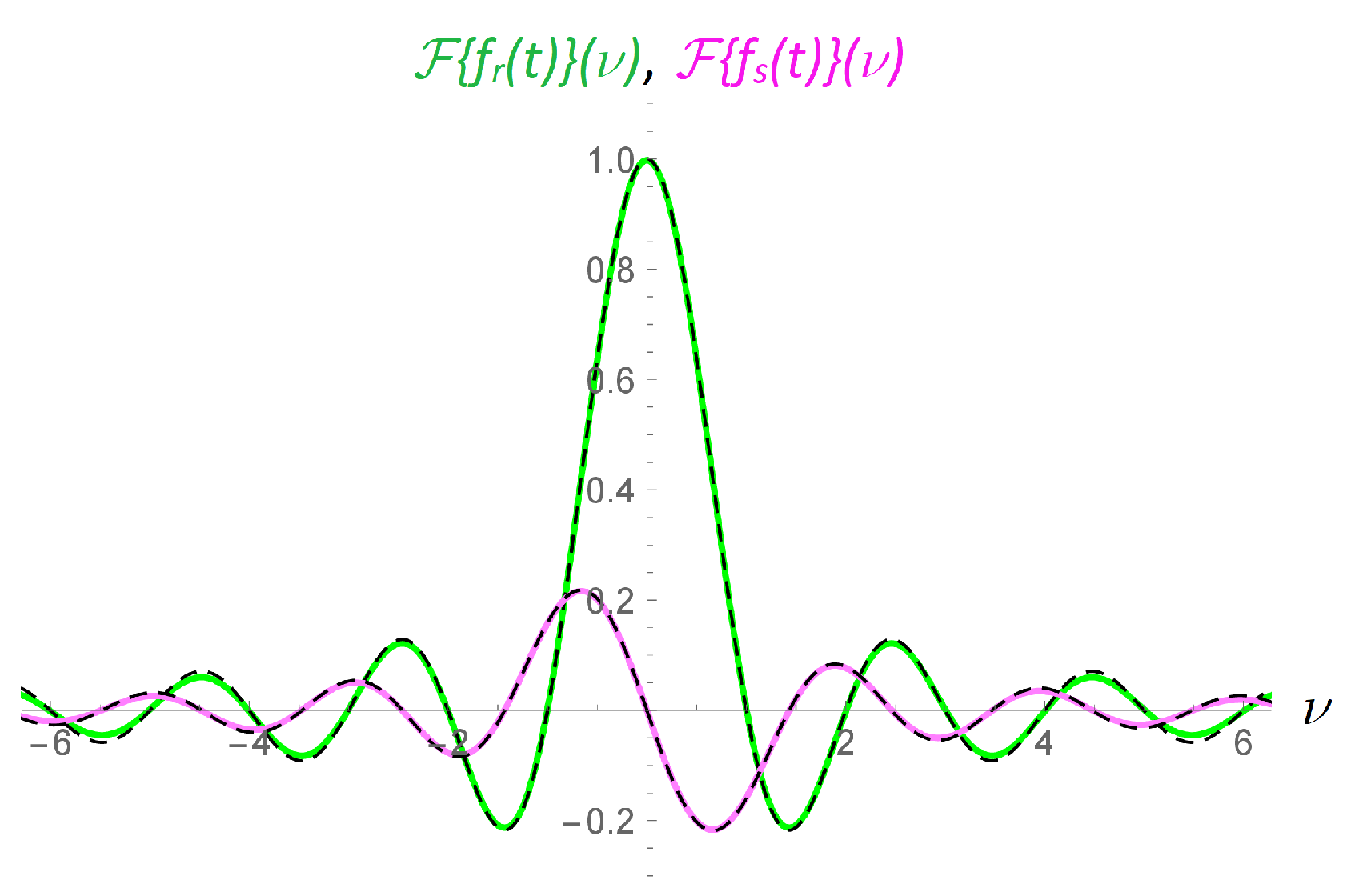
3.2. Numerical Results
3.3. Trigonometric Forms
4. Mathematica Codes
4.1. Complex Error Function
4.2. Fourier Transform
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| FT | Fourier transform |
| DFT | Discrete Fourier transform |
References
- Hansen, E.W. ; Fourier Transforms: Principles and Applications; John Wiley & Sons, Hoboken, 2014.
- Bracewell, R.N. ; The Fourier Transform and Its Applications; 3rd Edition, McGraw-Hill, New York, 2000.
- Abrarov, S.M.; Siddiqui, R.; Jagpal, R.K.; Quine, B.M. A rational approximation of the Fourier Transform by integration with exponential decay multiplier. Appl. Math. 2021, 12, 947–962. [Google Scholar] [CrossRef]
- Baker Jr., G. A.; Gammel, J.L; Wills, J.G. An investigation of the applicability of the Padé approximant method. J. Math. Anal. Appl. 1961, 2, 405–418. [Google Scholar] [CrossRef]
- Brezenski, C. Extrapolation algorithms and Padé approximations. Appl. Numer. Math. 1996, 20, 299–318. [Google Scholar] [CrossRef]
- Filip, S.-I.; Nakatsukasa, Y.; Trefethen, L.N.; Beckermann, B. Rational minimax approximation via adaptive barycentric representations. SIAM J. Sci. Comput. 2018, 40, A2427–A2455. [Google Scholar] [CrossRef]
- Nakatsukasa, Y.; Trefethen, L.N. An algorithm for real and complex rational minimax approximation. SIAM J. Sci. Comput. 3157. [Google Scholar] [CrossRef]
- Pachón, R.; Trefethen, L.N. Barycentric-Remez algorithms for best polynomialap proximation in the chebfun system. BIT Numer. Math. 2009, 49, 721–741. [Google Scholar] [CrossRef]
- Hofreither, C. An algorithm for best rational approximation based on barycentric rational interpolation. Numer. Algor. 2021, 88, 365–388. [Google Scholar] [CrossRef]
- Abrarov, S.M.; Quine, B.M. Sampling by incomplete cosine expansion of the sinc function: application to the Voigt/complex error function. Appl. Math. Comput. 2015, 258, 425–435. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I. ; Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical tables; 9th Ed. Dover, New York, 1972.
- Armstrong, B.H.; Nicholls, B.W. Emission, Absorption and Transfer of Radiation in Heated Atmospheres. Pergamon Press, New York, 1972.
- Schreier, F. The Voigt and complex error function: a comparison of computational methods. J. Quant. Spectrosc. Radiat. Transfer. 1992, 48, 743–762. [Google Scholar] [CrossRef]
- Armstrong, B.H. Spectrum line profiles: the Voigt function. J. Quant. Spectrosc. Radiat. Transfer. 1967, 61–88. [Google Scholar] [CrossRef]
- Zaghloul, M.R.; Ali, A.N. Algorithm 916: Computing the Faddeyeva and Voigt functions. ACM Trans. Math. Soft. 2012, 38, 1–22. [Google Scholar] [CrossRef]
- Berk, A.; Hawes, F. Validation of MODTRAN®6 and its line-by-line algorithm. J. Quant. Spectrosc. Radiat. Transfer. 2017, 203, 542–556. [Google Scholar] [CrossRef]
- Pliutau, D.; Roslyakov, K. Bytran -|- spectral calculations for portable devices using the HITRAN database. Earth Sci. Inf. 2017, 10, 395404. [Google Scholar] [CrossRef]
- Pliutau, D. Combined “Abrarov/Quine-Schreier-Kuntz (AQSK)” algorithm for the calculation of the Voigt function. J. Quant. Spectrosc. Radiat. Transfer. 2021, 272. [Google Scholar] [CrossRef]
- Balazs, N.L.; Tobias, I. Semiclassical dispersion theory of lasers. Phil. Trans. Royal Soc. A. 1969, 264, 1–29. [Google Scholar] [CrossRef]
- Chan, L.K.P. Equation of atomic resonance for solid-state optics. Appl. Opt. 1986, 25, 1728–1730. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Miller, E.A. A unified presentation of the Voigt function. Astrophys. Space Sci. 1987, 135, 111–118. [Google Scholar] [CrossRef]
- Abrarov, S.M.; Quine, B.M. A new application of the Fourier transform for rational approximation of the complex error function. J. Math. Research, 2016, 8, 14–23. [Google Scholar] [CrossRef]
- Humlíček, J. An efficient method for evaluation of the complex probability function: The Voigt function and its derivatives. J. Quant. Spectrosc. Radiat. Transfer. 1979, 2, 309–313. [Google Scholar] [CrossRef]
- Weideman, J.A.C. Computation of the complex error function. SIAM J. Numer. Anal. 1994, 31, 1497–1518. [Google Scholar] [CrossRef]
- Wells, R.J. Rapid approximation to the Voigt/Faddeeva function and its derivatives. J. Quant. Spectrosc. Radiat. Transfer. 1999, 62, 29–48. [Google Scholar] [CrossRef]
- Letchworth, K.L.; Benner, D.C. Rapid and accurate calculation of the Voigt function. J. Quant. Spectrosc. Radiat. Transfer. 2007, 107, 173–192. [Google Scholar] [CrossRef]
- Schreier, F. Optimized implementations of rational approximations for the Voigt and complex error function. J. Quant. Spectrosc. Radiat. Transfer. 2011, 112, 1010–1025. [Google Scholar] [CrossRef]
- Schreier, F. The Voigt and complex error function: Humlíček’s rational approximation generalized. Month. Not. Roy. Astron. Soc. 2018, 479, 3068–3075. [Google Scholar] [CrossRef]
- Abrarov, S.M.; Quine, B.M.; Jagpal, R.K. A sampling-based approximation of the complex error function and its implementation without poles. Appl. Numer. Math. 2018, 129, 181–191. [Google Scholar] [CrossRef]
- Abrarov, S.M.; Quine, B.M. A rational approximation of the Dawson’s integral for efficient computation of the complex error function. Appl. Math. Comput. 2018, 321, 526–543. [Google Scholar] [CrossRef]
- Al Azah, M.; Chandler-Wilde, S.N. Computation of the complex error function using modified trapezoidal rules. SIAM J. Numer. Anal. 2021, 59, 2346–2367. [Google Scholar] [CrossRef]
- Thompson, I. Algorithm 1046: an improved recurrence method for the scaled complex error function. ACM Trans. Math. Soft. 2024, 50, 1–18. [Google Scholar] [CrossRef]
- J. Mangaldan, Evaluate the Faddeeva function. Available online: https://tinyurl.com/2bmf9m4f (accessed on March 21, 2025).
- Kac, M. ; Statistical independence in probability, analysis and number theory; Washington, DC: Mathecal Association of America, 1959. [Google Scholar]
- Gearhart, W.B.; Shultz, H.S. The function sin(x)/x. College Math. J. 1990, 21, 90–99. [Google Scholar] [CrossRef]
| 1 | Matlab code can be copy-pasted from this link: arXiv:2001.07533
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).