1. Introduction
Mutual neutralization (MN) is the process where oppositely charged ions collide, and as a result of electron transfer, neutral fragments are formed. It is, in general, driven by non-adiabatic couplings arising from avoided crossings between electronic states of ionic and covalent characters, occurring at large internuclear distances. Usually, highly excited electronic states are involved. For an
ab initio description of the reaction, the potential energy curves of the relevant states of the reaction complex must be computed, as well as the corresponding non-adiabatic coupling elements. In the present study, MN in collisions of Li
− and O
+ is investigated using an
ab intio fully quantum mechanical approach. The reaction is
where one of the neutral atoms formed in the process can be excited.
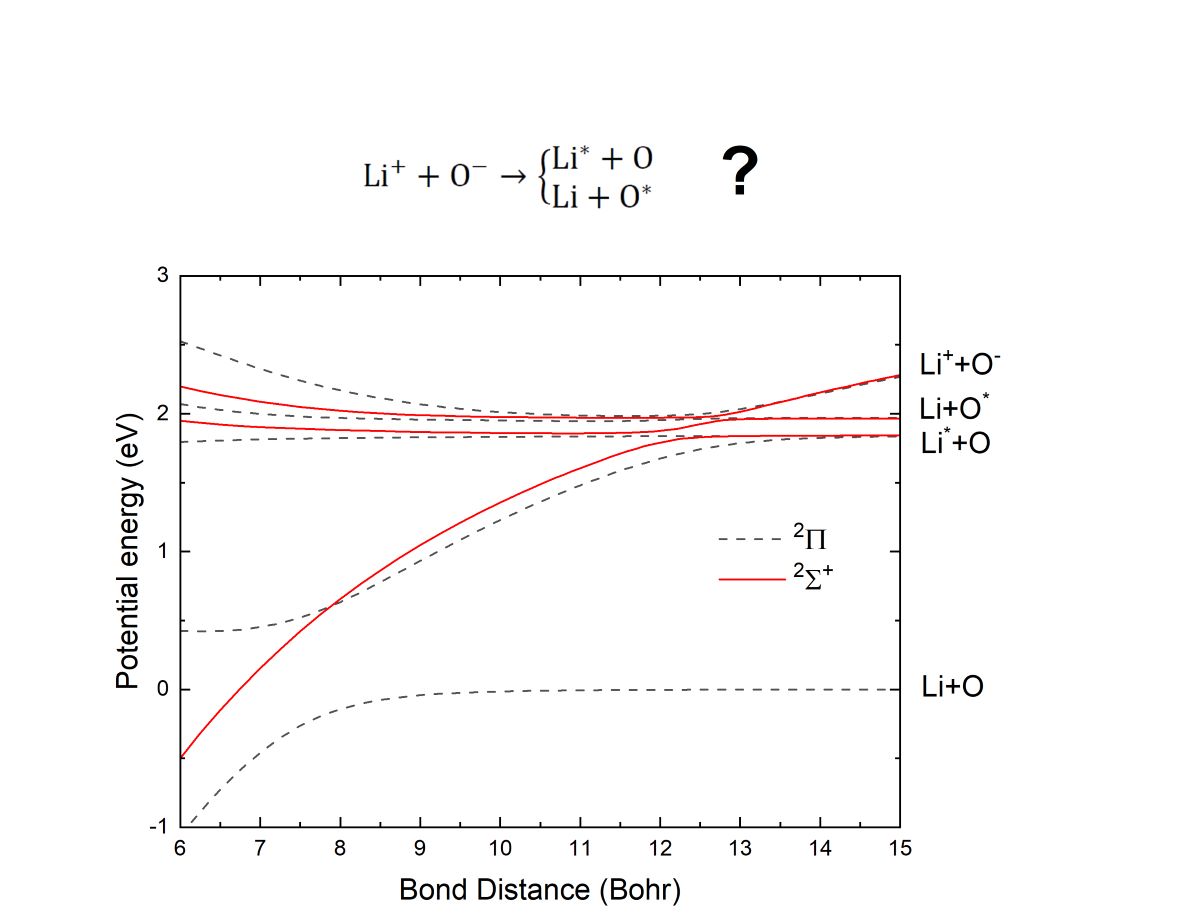
The system LiO is particularly interesting due to the energetics. In both cases, channels leading to excited oxygen and ground state lithium, or ground state oxygen and excited lithium are open at low energy collisions. The crossings between the potentials of these excited neutral states and the ion-pair channel are at very similar internuclear distances ( and for the Li*(2)+O(3) and Li(2)+O*(1) channels, respectively).
In low energy MN reactions of atomic ions, it is generally assumed that the electron is transferred to a virtual orbital of the cation, forming an excited state of the neutral atom. This corresponds to a one-electron process. This is what has been observed experimentally and theoretically for the majority of other systems. Some measurements (
e.g. on O
− with N
+) show contributions from core-excited states of the electron-accepting atom [
1]. Two-electron processes are required to form these channels. Also, the process by which the neutralized anion becomes excited requires two-electron rearrangement. There are some MN measurements indicating the formation of excited states of electron-donating atom (in collisions of C
++S
− as well as N
++D
−) [
2].
For a system such as LiO where the avoided crossings between the excited states of Li*+O and Li+O* occur at very similar internuclear distances, the MN reaction cannot be described using the multi-state Landau-Zener modeling [
1,
3]. Several states will simultaneously interact and the electron transfer cannot be modeled using successive two-state Landau-Zener Hamiltonians. An
ab initio description is required. We have investigated the importance of two-electron rearrangement by the formation of the Li+O* channel.
We have performed multi-reference configuration interaction calculations of the adiabatic potential energy curves and non-adiabatic couplings. Lower lying LiO molecular states of 2Σ+ and 2Π symmetries are involved in the reaction since the ion-pair forms molecular states of these symmetries. The MN reaction is studied by solving the nuclear radial Schrödinger equation numerically in a strict diabatic representation.
The article is organized as follows. In
Section 2, it is described how the relevant potential energy curves and couplings of LiO are computed.
Section 3 briefly describes the diabatization of the electronic states and how the coupled Schrödinger equation for the nuclear motion is solved. Finally, in
Section 4, the calculated total mutual neutralization cross section, differential cross section, and final state distributions are displayed. Throughout the article, atomic units are used.
2. Potential Energy Curves and Couplings
In this section we will discuss the calculations used to generate potential energy curves and non-adiabatic couplings for electronic states of
2Σ
+ and
2Π symmetries of LiO. The quantum chemistry calculations were carried out using the MOLPRO program [
4]. A series of calculations using the aug-cc-pVXZ basis sets with X = D, T, Q, 5 were carried out to check the convergence with respect to the size of the basis.
For LiO, molecular orbitals were generated using a state-averaged CASSCF (Complete Active Space Self Consistent Field) calculation where the lowest two orbitals were frozen and the active space was composed of the following six and three orbitals. A state averaged calculation was performed including the lowest 20 electronic states (five 2, five 2, five 2 and in symmetry, corresponding to three 2Σ+, three 2Σ−, five 2Π and two 2Δ states in ). These are all states associated with the asymptotic limits Li(2)+O(3), Li*(2)+O(3), Li(2)+O*(1), as well as the ion-pair, Li++O−. The ion-pair potential crosses some higher excited covalent states at larger internuclear distances ( a0). For these states, the ionic-covalent diabatic transition probabilities can be neglected, and hence, these states are not included in the model.
The adiabatic potential energy curves of the relevant electronic states were calculated using the MRCI (Multi Reference Configuration Interaction) method with the orbitals generated from the CASSCF calculations. The same active space was used in the MRCI and single and double excitations out of the reference configurations were included. The
2Σ
+ and
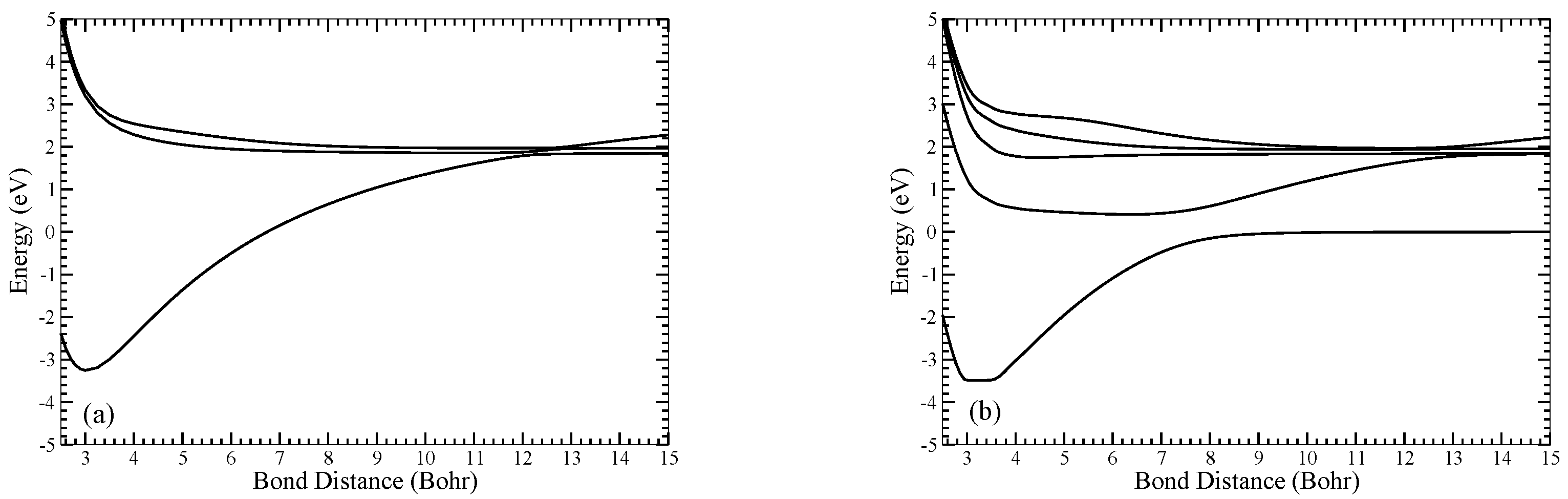
2Π adiabatic potential energy curves calculated in using MRCI with the aug-cc-pV5Z basis set are displayed in
Figure 1.
The MN cross section is sensitive to the bond distances where the avoided crossing between the states of ionic and covalent characters occurs. To check for convergence of the calculation, the potential energy curves are calculated using the aug-cc-pVXZ basis sets with X = D, T, Q, 5. In
Table 1, the calculated asymptotic limits are compared with experimental values. We also provide the experimental curve crossing distances between the ionic and covalent states. The curve crossing distances were estimated by assuming constant asymptotic potentials of the covalent states and an ion-pair state with the potential
. Here
a.u. is the sum of polarizabilities of the atomic ions [
5,
6].
Figure 2 displays adiabatic potential energy curves of
2Σ
+ symmetry calculated using the different basis sets. Larger basis sets provide a better description of the ion-pair state and the covalent state associated with Li+O*. With larger basis set, the avoided crossings are shifted towards larger internuclear distances.
Using the MRCI wavefunctions, the non-adiabatic couplings were calculated via finite difference with a step length of
a
0. The non-adiabatic coupling elements,
, among the lowest three states of
2Σ
+ symmetry and the five states of
2Π symmetry were computed.
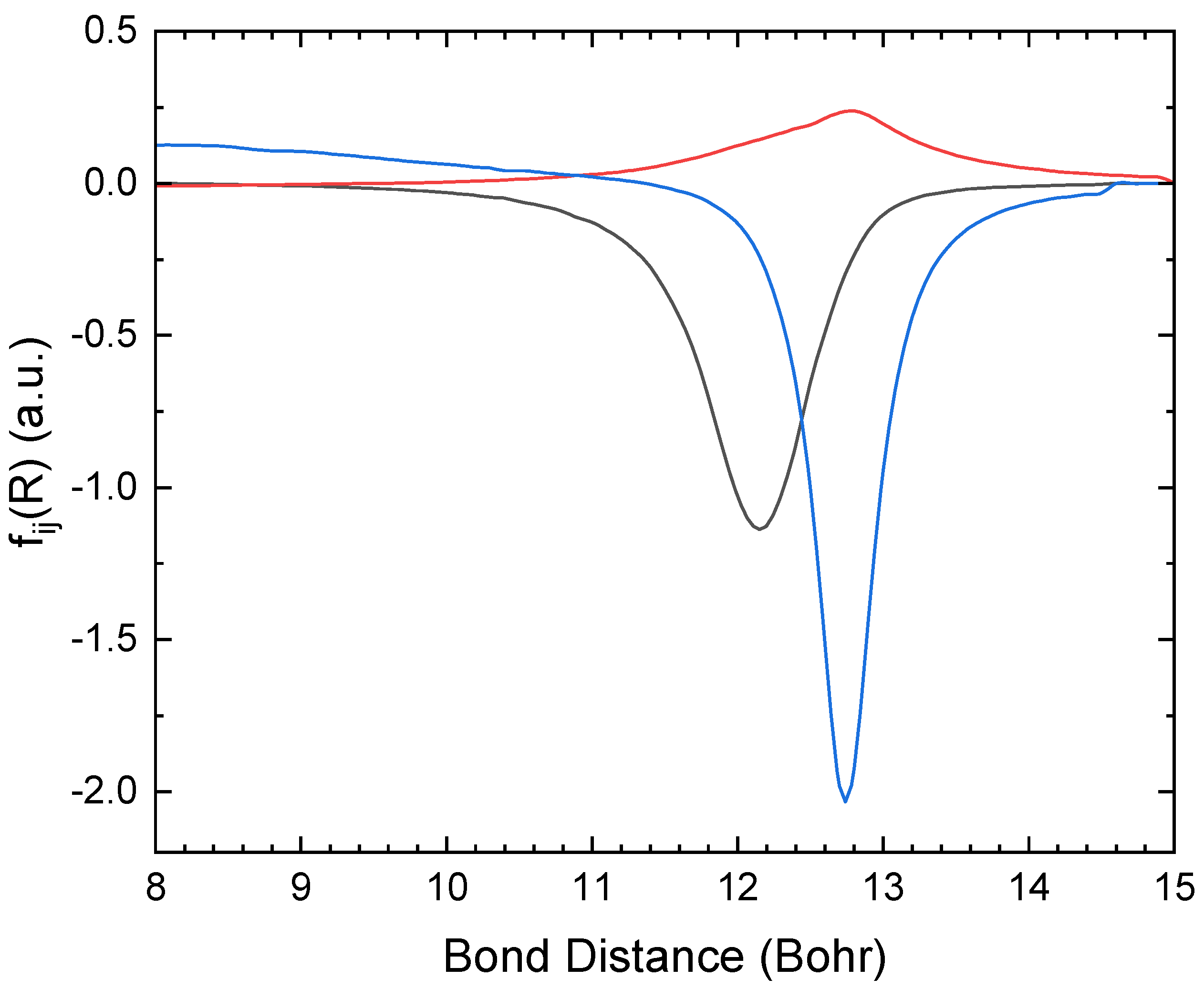
Figure 3 shows the non-adiabatic coupling elements between the three
2Σ
+ states, calculated using the aug-cc-pV5Z basis set. These are the states most important for the mutual neutralization reaction, and as demonstrated in the figure, the non-adiabatic coupling elements are similar in magnitude. The non-adiabatic coupling peaks at the avoided crossings. The adiabatic wave functions will change character in these regions, and as a result, there will be significant non-adiabatic coupling elements. All three states will interact simultaneously, so successive
state interactions cannot describe the charge transfer process.
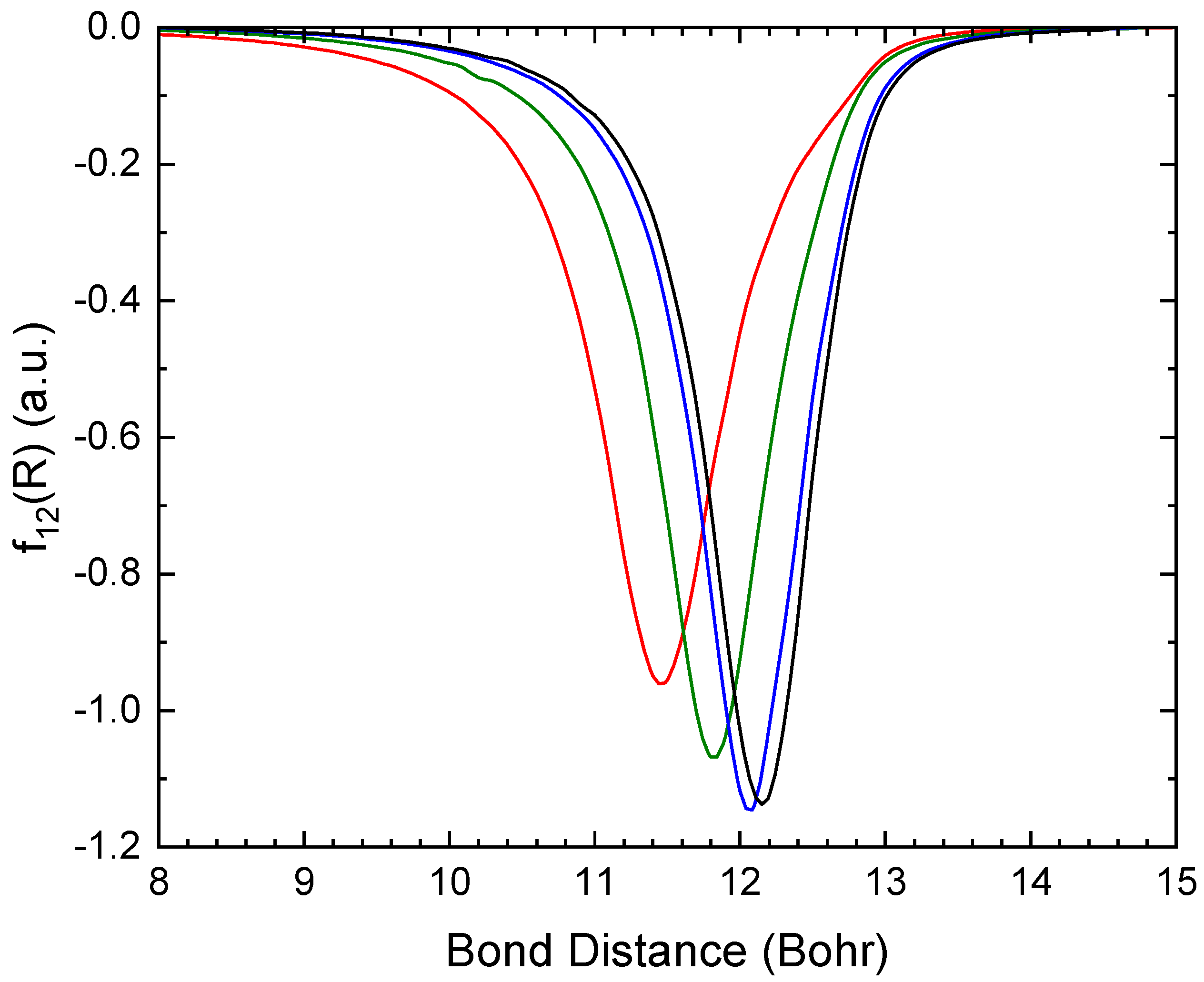
Figure 4 displays the non-adiabatic coupling element between the lowest two
2Σ
+ states, calculated using the different basis sets. As the basis set is improved and the avoided crossing is shifted towards a larger bond length, the coupling elements become more narrow.
We conclude that the calculation using the aug-cc-pV5Z basis set is converged and this is the calculation we use to compute the cross section for mutual neutralization.
3. Dynamics
The adiabatic potential energy curves were transformed to a strict diabatic representation. We included three
2Σ
+ states and five states of
2Π symmetry. Non-adiabatic couplings to higher lying electronic states were neglected. The orthogonal transformation matrix (
) that transforms between the adiabatic and diabatic basis was obtained by numerically integrating the equation [
7]
where
is the anti-symmetric matrix containing the non-adiabatic first derivative coupling elements. At large internuclear distances, all non-adiabatic coupling elements are assumed to be zero, and the asymptotic transformation matrix is an identity matrix. Non-zero asymptotic non-adiabatic couplings do not significantly affect the Li
++O
− mutual neutralization reaction. This is tested by varying the value for the integration stop.
The diabatic potential matrix is obtained by the similarity transformation
of the adiabatic potential matrix. The radial coupled Schrödinger equation in the diabatic representation is obtained using a partial wave expansion. This equation is solved by numerically integrating the matrix Riccati equation for the logarithmic derivative of the radial wave function using Johnson’s log-derivative method [
8]. Details on the numerical procedure can be found in [
9]. The scattering matrix,
, is obtained by combining the value of the log-derivative at the asymptotic boundary with the correct asymptotic solutions of the open or closed covalent or ionic channels, respectively. From the open partitioning of the scattering matrix, the cross section for scattering from channel
j to channel
i is given by
Here,
is the asymptotic wave number of the incoming channel.
The mutual neutralization cross section is calculated for energies ranging from 0.001 to 50 eV. The matrix Riccati equation is solved numerically from a0 to 15 a0 with an integration step size of 0.005 a0. The total mutual neutralization cross section is then obtained by summing all contributions from the partial waves and all channels. The program was set up so that the sum is truncated when the ratios of the partial cross sections and the accumulated integral cross sections remained less than for 50 terms in succession. The cross section to a specific final channel was obtained by adding the contributions from states of 2Σ+ and 2Π symmetry associated with that channel. The final state distribution was obtained by dividing the cross section of a specific channel with the total mutual neutralization cross section.
From the calculation of the scattering matrix, the differential cross section can be computed using [
10]
Here,
is the the Coulomb phase present due to scattering from the ion-pair state (channel
j). The Coulomb phase is given by [
10]
, where
is Euler’s gamma function and
is the Sommerfeld parameter. The Coulomb phase will influence the differential cross section, but not the total cross section for mutual neutralization.
are the Legendré polynomials and
is the scattering angle.
4. Results and Discussion
Our final converged calculation corresponds to the results obtained using potentials and non-adiabatic couplings calculated with the aug-cc-pV5Z basis set. To analyze the convergence of the MN cross section and branching ratios, results using the other basis sets are also displayed.
4.1. Total Cross Section
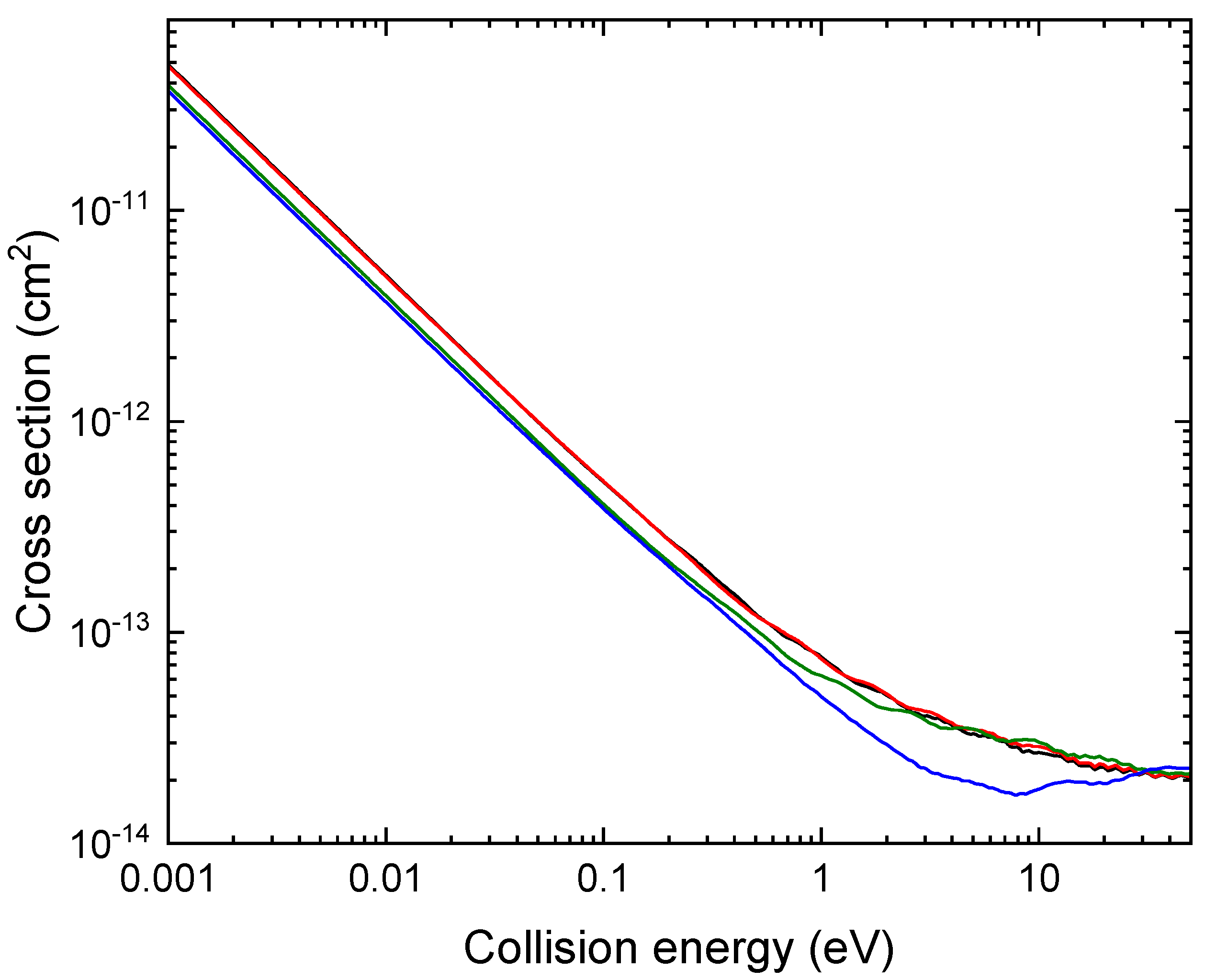
A comparison of the total MN cross section for Li
+ + O
− as a function of basis set is shown in
Figure 5 for energies in the range of 1 meV to 50 eV .
At low collision energies, the mutual neutralization cross section has the
behavior as expected from attractive Coulomb interactions [
11]. We notice a convergence of the total cross section with respect to the basis set from the aug-cc-pVQZ level.
4.2. Final State Distributions
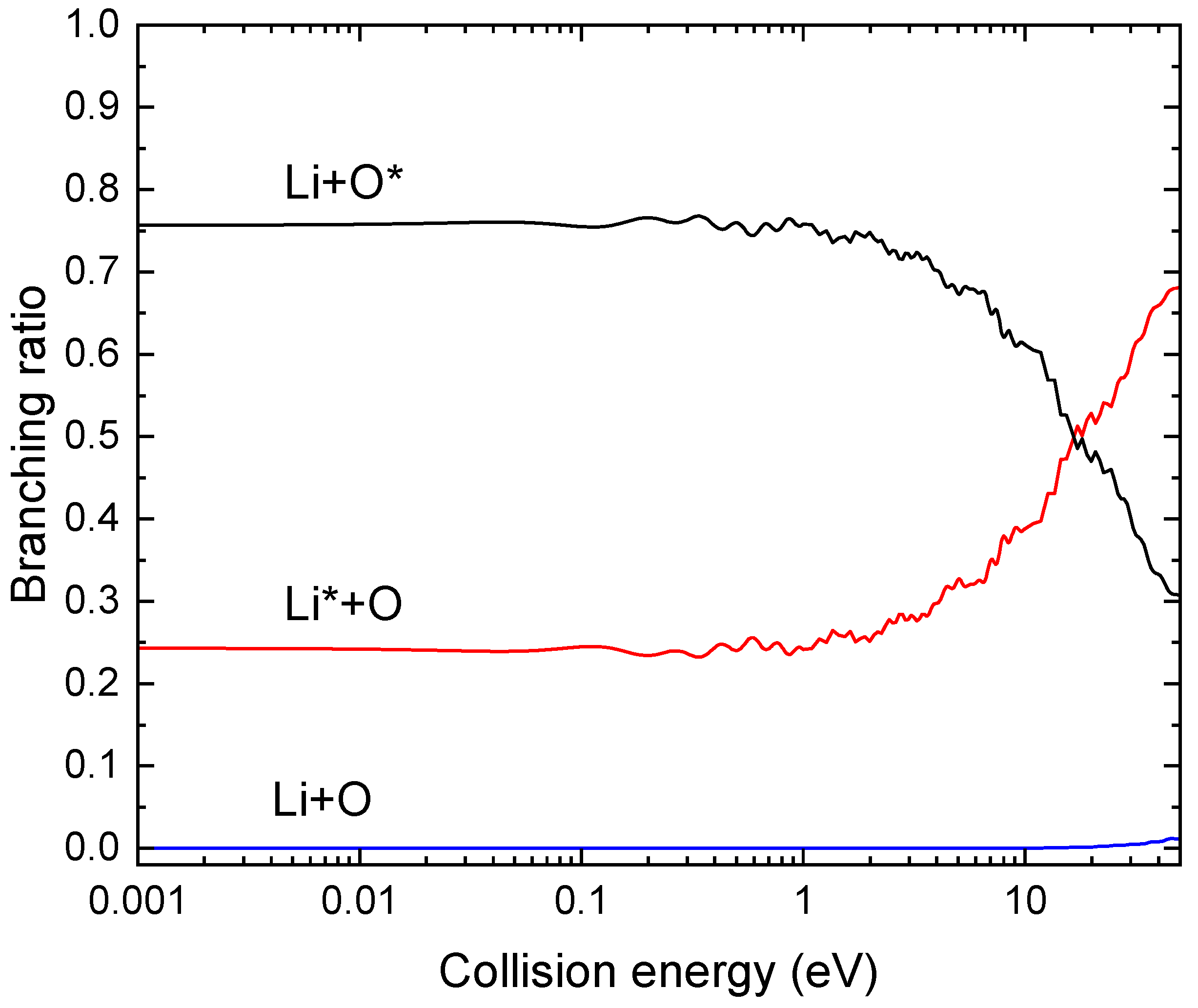
The MN final state distributions calculated using the aug-cc-pV5Z basis set are displayed in
Figure 6.
At a collision energy of 1 meV, the branching ratio for the Li+O* channel is
. The ratio for forming Li*+O is
, and the formation is ground state atoms is negligible (
). Thus, MN in Li
++O
− will primarily result in fragments where the neutralized anion is excited. This is different from other MN processes studied so far. The non-adiabatic coupling operator (in the limit of a complete basis set) can be expressed in terms of one-electron operators, and hence it is shown to be equivalent to a one-electron operator [
12]. The production of O* states requires a two-electron rearrangement - first the electron must move from O
− to Li
+, and then the O atom must be excited. Therefore, the production of O* states indicates a strong electron correlation in the wave functions of the interacting states.
At higher collision energies (
eV), the Li*+O channel will start to dominate, as seen in
Figure 6.
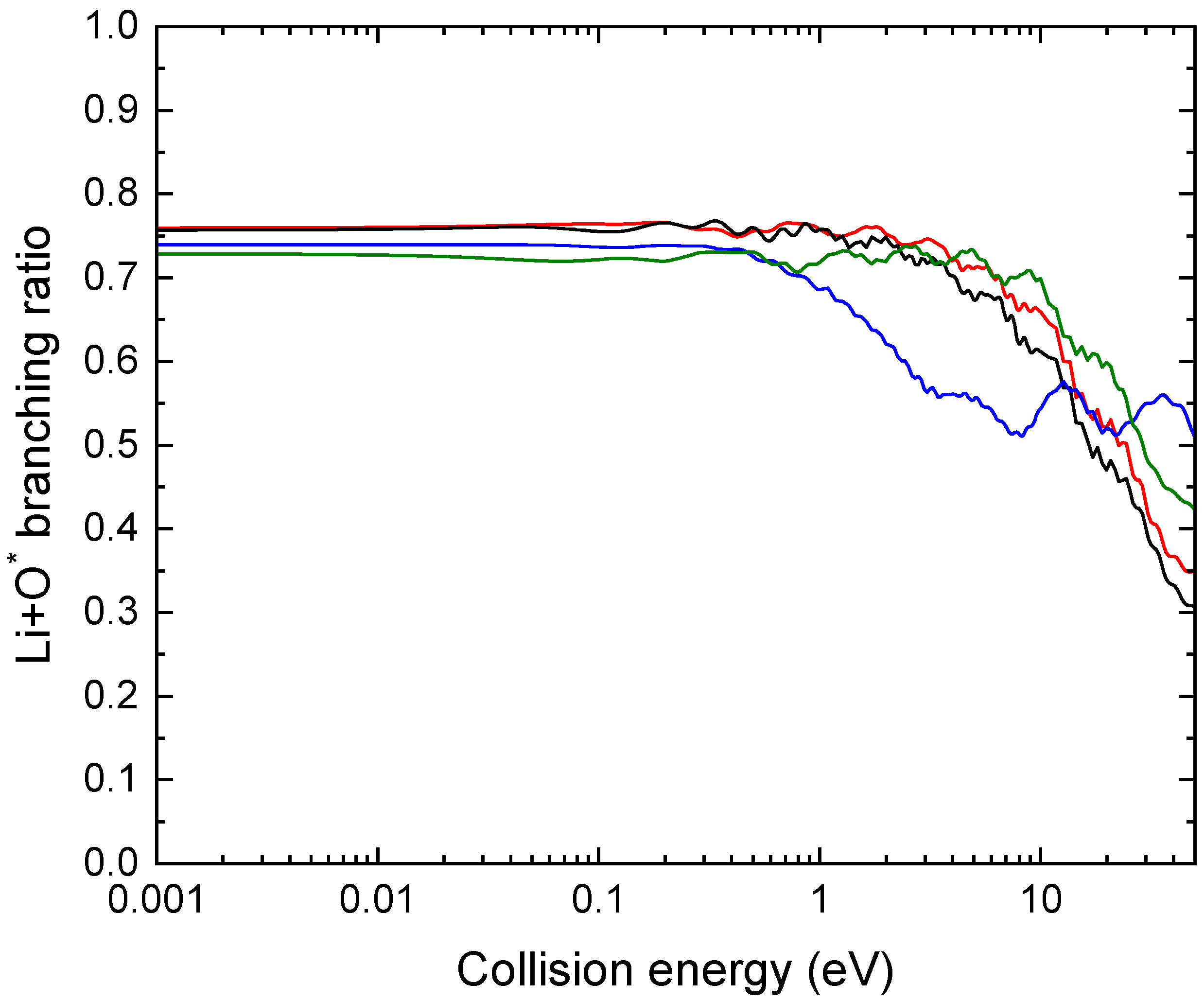
Previous theoretical studies have demonstrated that a convergence of the final state distributions is generally more difficult to achieve than a convergence of the total cross section.
Figure 7 shows the branching ratio to the channel Li+O*, as a function of the collision energy, computed using the different basis sets.
As opposed to the total cross section, the branching ratios are much more sensitive to basis set size. To ensure convergence, the aug-cc-pV5Z basis was necessary.
4.3. Differential Cross Section
The differential cross section, calculated using equation (
4), provides information about the angular distribution of the fragments. Using merged-beam experiments, information about the differential cross section can be obtained. As discussed in [
10,
13], the shape of the differential cross section is very sensitive to the magnitudes of the electronic couplings and to the detailed shapes of the interacting potentials.
The differential cross section for scattering into different final states can be computed by adding the contributions from all molecular states associated with the same channels. In
Figure 8, the differential cross sections for the channels Li+O* (black) and Li*+O (red), at a scattering energy of 1 meV, are displayed. The calculation is carried out using potentials and non-adiabatic couplings obtained with the aug-cc-pV5Z basis set. The grey dashed curve shows the sum of the differential cross section for all channels.
The differential cross sections are displayed as function of
. Notice that the shapes of the differential cross sections for the two channels are different. The differential cross section for Li+O* is more peaked in the forward direction and display longer oscillations. The shape of the minima of the two differential cross section (around
for Li+O* and
for Li*+O) depend on the shape of the potentials and non-adiabatic couplings in the vicinity if the avoided crossings. The drop in the differential cross section for
is due to the classical rainbow scattering arising from the attractive ion-pair potential [
13].
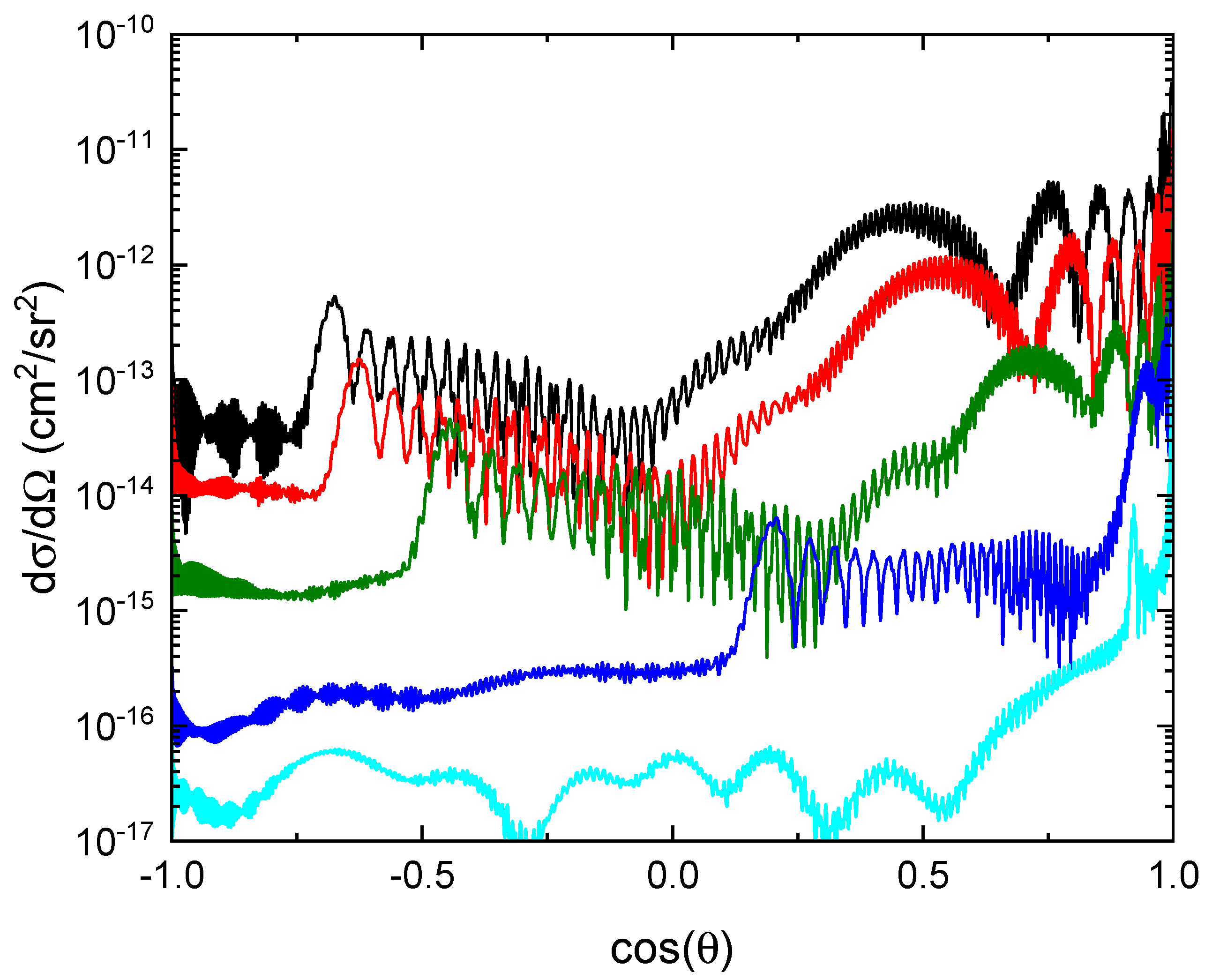
In
Figure 9, the differential MN cross sections (summed over all channels) are displayed for the electron collision energies 1 meV, 10 meV, 100 meV, 1 eV and 10 eV.
As the energy is increased the differential cross sections become more peaked in the forward direction. With increased collision energy, the rainbow scattering angle becomes smaller, as seen for other similar reactions [
10,
14].
5. Conclusion
The Li++O− MN reaction is interesting since the avoided crossing between the ionic and covalent states associated with Li*+O and Li+O* are very close. An ab initio approach based on computations of non-adiabatic couplings is needed to describe the process theoretically. Our study reveals that the Li+O* channel will primarily be produced in low energy MN. Two-electron rearrangement is thus needed. Calculated differential cross sections for the two channels are different. The Li+O* differential cross section has more pronounced oscillations and are more peaked in the forward direction.
We are not aware of any experimental studies on Li
++O
− MN. It would be interesting to compare our calculated final state branching ratios with measurements using e.g. the double ion storage ring DESIREE [
15,
16] or a single pass merged-beam setup such as the one at Université catholique de Louvain [
1,
2,
17].
Supplementary Materials
The following supporting information can be downloaded at the website of this paper posted on
Preprints.org
Author Contributions
Project administration, formal analysis, investigation, data curation and visualization: Å.L. and A.E.O., writing - original draft preparation : A.E.O., writing – review and editing: Å.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the project “Probing charge- and mass-transfer reactions on the atomic level” supported by the Knut and Alice Wallenberg Foundation (Grant No. 2018.0028).
Data Availability Statement
Adiabatic potential energy curves and non-adiabatic coupling elements, as well as total mutual neutralization cross section and final state distributions, calculated using the aug-cc-pV5Z basis set, are available as supplemental material. Other data presented in this study are available on request from the corresponding author.
Acknowledgments
Valuable discussion with A. Dochain are acknowledged.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CASSCF |
Complete Active Space Self Consistent Field |
| MN |
Mutual Neutralization |
| MRCI |
Multi Reference Configuration Interaction |
References
- de Ruette, N.; Dochain, A.; Launoy, T.; Nascimento, R.F.; Kaminska, M.; Stockett, M.H.; Vaeck, N.; Schmidt, H.T.; Cederquist, H.; Urbain, X. Mutual Neutralization of O− with O+ and N+ at Subthermal Collision Energies. Phys. Rev. Lett. 2018, 121, 083401. [Google Scholar] [CrossRef] [PubMed]
- Dochain, A. Systematic study of mutual neutralization reactions between atomic species using the merged beam method and an asymptotic model. "Ph.D. thesis", UCLouvain, 2022. see http://hdl.handle.net/2078.1/263451.
- Hedberg, H.M.; M., N.S.; Å., L. Landau–Zener studies of mutual neutralization in collisions of H+ + H− and Be++ H−. J. Phys. B: At. Mol. Opt. Phys. 2014, 47, 225206. [Google Scholar] [CrossRef]
- Werner, H.J.; Knowles, P.J.; others. MOLPRO, version , a package of ab initio programs. see https://www.molpro.net.
- Chung, K.T. Dynamic Polarizabilities and Refractive Indexes of H− and Li+ Ions. Phys. Rev. A 1971, 4, 7–11. [Google Scholar] [CrossRef]
- Dalgarno, A. Atomic polarizabilities and shielding factors. Advances in Physics 1962, 11, 281–315. [Google Scholar] [CrossRef]
- Mead, C.A.; Truhlar, D.G. Conditions for the definition of a strictly diabatic electronic basis for molecular systems. The Journal of Chemical Physics 1982, 77, 6090–6098. [Google Scholar] [CrossRef]
- Johnson, B. The multichannel log-derivative method for scattering calculations. Journal of Computational Physics 1973, 13, 445–449. [Google Scholar] [CrossRef]
- Stenrup, M.; Larson, A.; Elander, N. Mutual neutralization in low-energy H++H− collisions: A quantum ab initio study. Phys. Rev. A 2009, 79, 012713. [Google Scholar] [CrossRef]
- Hedvall, P.; Odelius, M.; Larson, Å. Charge transfer in sodium iodide collisions. J. Chem. Phys. 2023, 158, 014305. [Google Scholar] [CrossRef] [PubMed]
- Wigner, E.P. On the Behavior of Cross Sections Near Thresholds. Phys. Rev. 1948, 73, 1002–1009. [Google Scholar] [CrossRef]
- Sidis, V. SSimple Expression for the Off-Diagonal Matrix Elements of the d/dR Operator between Exact Electronic States of a Diatomic Molecule. The Journal of Chemical Physics 1971, 55, 5838–5839. [Google Scholar] [CrossRef]
- Delvigne, G.; Los, J. Rainbow, Stueckelberg oscillations and rotational coupling on the differential cross section of Na + I → Na+ + I−. Physica 1973, 67, 166–196. [Google Scholar] [CrossRef]
- Hörnquist, J.; Hedvall, P.; Larson, A.; Orel, A.E. Mutual neutralization in H+ + H− collisions: An improved theoretical model. Phys. Rev. A 2022, 106, 062821. [Google Scholar] [CrossRef]
- Thomas, R.D.; Schmidt, H.T.; Andler, G.; Björkhage, M.; Blom, M.; Brännholm, L.; Bäckström, E.; Danared, H.; Das, S.; Haag, N.; Halldén, P.; Hellberg, F.; Holm, A.I.S.; Johansson, H.A.B.; Källberg, A.; Källersjö, G.; Larsson, M.; Leontein, S.; Liljeby, L.; Löfgren, P.; Malm, B.; Mannervik, S.; Masuda, M.; Misra, D.; Orbán, A.; Paál, A.; Reinhed, P.; Rensfelt, K.G.; Rosén, S.; Schmidt, K.; Seitz, F.; Simonsson, A.; Weimer, J.; Zettergren, H.; Cederquist, H. The double electrostatic ion ring experiment: A unique cryogenic electrostatic storage ring for merged ion-beams studies. Rev. Sci. Instrum. 2011, 82, 065112. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, H.T.; Thomas, R.D.; Gatchell, M.; Rosén, S.; Reinhed, P.; Löfgren, P.; Brännholm, L.; Blom, M.; Björkhage, M.; Bäckström, E.; Alexander, J.D.; Leontein, S.; Hanstorp, D.; Zettergren, H.; Liljeby, L.; Källberg, A.; Simonsson, A.; Hellberg, F.; Mannervik, S.; Larsson, M.; Geppert, W.D.; Rensfelt, K.G.; Danared, H.; Paál, A.; Masuda, M.; Halldén, P.; Andler, G.; Stockett, M.H.; Chen, T.; Källersjö, G.; Weimer, J.; Hansen, K.; Hartman, H.; Cederquist, H. First storage of ion beams in the Double Electrostatic Ion-Ring Experiment: DESIREE. Rev. Sci. Instrum. 2013, 84, 055115. [Google Scholar] [CrossRef] [PubMed]
- Launoy, T.; Loreau, J.; Dochain, A.; Liévin, J.; Vaeck, N.; Urbain, X. Mutual Neutralization in Li+–D−Collisions: A Combined Experimental and Theoretical Study. The Astrophysical Journal 2019, 883, 85. [Google Scholar] [CrossRef]
Figure 1.
(a) Adiabatic 2Σ+ and (b) 2Π potential energy curves of LiO calculated using MRCI with the aug-cc-pV5Z basis set.
Figure 1.
(a) Adiabatic 2Σ+ and (b) 2Π potential energy curves of LiO calculated using MRCI with the aug-cc-pV5Z basis set.
Figure 2.
Adiabatic potential energy curves of LiO of 2Σ+ symmetry, calculated using the basis sets aug-cc-pVXZ, where X=D (blue), T (green), Q (red), 5 (black).
Figure 2.
Adiabatic potential energy curves of LiO of 2Σ+ symmetry, calculated using the basis sets aug-cc-pVXZ, where X=D (blue), T (green), Q (red), 5 (black).
Figure 3.
Non-adiabatic coupling elements between the 2Σ+ states of LiO, calculated using aug-cc-pV5Z (: black, : red and : blue).
Figure 3.
Non-adiabatic coupling elements between the 2Σ+ states of LiO, calculated using aug-cc-pV5Z (: black, : red and : blue).
Figure 4.
Non-adiabatic coupling element () between the lowest two 2Σ+ states of LiO, calculated using aug-cc-pVXZ with X=D (red), T (green), Q (blue) and 5 (black).
Figure 4.
Non-adiabatic coupling element () between the lowest two 2Σ+ states of LiO, calculated using aug-cc-pVXZ with X=D (red), T (green), Q (blue) and 5 (black).
Figure 5.
Li++O− MN cross sections as a function collision energy. The cross section is computed using potentials and couplings obtained with the basis sets aug-cc-pVXZ with X=D (blue), T (green), Q (red) and 5 (black).
Figure 5.
Li++O− MN cross sections as a function collision energy. The cross section is computed using potentials and couplings obtained with the basis sets aug-cc-pVXZ with X=D (blue), T (green), Q (red) and 5 (black).
Figure 6.
Final state distributions in Li++O− MN calculated using the aug-cc-PV5Z basis set.
Figure 6.
Final state distributions in Li++O− MN calculated using the aug-cc-PV5Z basis set.
Figure 7.
Branching ratio for the Li+O* channel calculated using different basis sets, aug-cc-pVXZ with X=D (blue), T (green), Q (red) and 5 (black).
Figure 7.
Branching ratio for the Li+O* channel calculated using different basis sets, aug-cc-pVXZ with X=D (blue), T (green), Q (red) and 5 (black).
Figure 8.
Differential MN cross sections at 1 meV for the Li+O* (black) and Li*+O (red) channels, as well as the sum of all channels (grey dashed curve).
Figure 8.
Differential MN cross sections at 1 meV for the Li+O* (black) and Li*+O (red) channels, as well as the sum of all channels (grey dashed curve).
Figure 9.
Differential MN cross sections (summed over all final states) at 1 meV (black), 10 meV (red), 100 meV (green), 1 eV (blue) and 10 eV (cyan).
Figure 9.
Differential MN cross sections (summed over all final states) at 1 meV (black), 10 meV (red), 100 meV (green), 1 eV (blue) and 10 eV (cyan).
Table 1.
Calculated and experimental asymptotic limits (in eV) . Also, experimental curve crossing distances, (a0), are given.
Table 1.
Calculated and experimental asymptotic limits (in eV) . Also, experimental curve crossing distances, (a0), are given.
| State |
DZ |
TZ |
QZ |
5Z |
Expt |
|
| Li + O |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
6.7 |
| Li* + O |
1.85 |
1.84 |
1.84 |
1.84 |
1.85 |
13.0 |
| Li + O* |
2.12 |
2.01 |
1.98 |
1.96 |
1.97 |
13.8 |
| Li− + O+
|
4.24 |
4.16 |
4.11 |
4.10 |
3.93 |
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).