Introduction
The description of the pressure and temperature dependence of viscosity has been an unresolved dilemma for classical elastohydrodynamic lubrication (EHL) since the founding. Because of the widespread use of the Roelands hoax [
1], classical EHL may be seen to be the study of the lubrication of concentrated contacts by a hypothetical liquid which may never be discovered. Quantitative EHL employs viscosity measured in viscometers and fitted to correlations which are, at least, capable of describing the universal previtreous response [
2] of glass-forming liquids, a group of liquids that includes lubricating oils. The classical approach has treated the effect of pressure on viscosity as a parameter to be adjusted to validate the present hypothesis. For example, note the method of extracting pressure-viscosity coefficients from film thickness measurements [
3]. These coefficients are unrelated to the piezoviscous strength [
4] of the liquid.
The universal piezoviscous response is faster than exponential [
5] as the glass pressure is approached from lower pressure. Usually, the super-Arrhenius behavior occupies the greatest range of pressure from ambient to the glass pressure and cannot be ignored. Correlations that are accurate for this regime are written in terms of a pressure for which the viscosity would be unbounded, the divergence pressure or idealized glass transition pressure,
. One of the first such expressions was by Johari and Whalley [
6] in 1972. The existence of the glass transition pressure is rarely acknowledged in classical EHL. Therefore, the previtreous response is unanticipated and the divergence pressure is not considered. Furthermore, ignoring the previtreous piezoviscous response made the traction calculated with the Eyring assumption appear to be reasonable [
7]. The difficulty in measuring very large viscosities means that there have been few measurements of viscosity at pressures up to the glass pressure. Therefore, a need exists for a piezoviscous model that extrapolates accurately and the Hybrid model fills that need [
8]. Here, an improved relation for the temperature dependence of the divergence pressure is offered.
The Hybrid Model
Correlations that are appropriate for modeling the pressure and temperature dependence of viscosity of glass formers are based upon free-volume theory or thermodynamic scaling. However, these are inaccurate for pressure extrapolation and the former is not as precise as the viscometer. A phenomenological model for the same purpose is the Hybrid [
9], which is the only model known to extrapolate well to pressures greater than those for which there are data [
8], possibly because it is a precise description of the phenomenon.
The isothermal form of the Hybrid model [
9] is
The Hybrid model is useful for pressure extrapolation [
8] and can be made temperature dependent in the following manner.
This
is not a pressure-viscosity coefficient because the Johari and Whalley term influences the pressure dependence at low pressures. The divergence pressure (ideal glass transition pressure) has been given [
8] until now as
Equation (3) combined with (1) and (2) has been shown to provide reasonable results over an interval of temperature of about 60 degrees when applied to EHL reference liquids [
10]. The pressure fragility parameter,
, has been assumed to be equal to the temperature fragility parameter,
, because evaluating them separately does not improve the accuracy. The curve fitting was accomplished by minimizing the relative standard deviation with the Solver add-in for Microsoft Excel.
Temperature Dependence of the Divergence Pressure
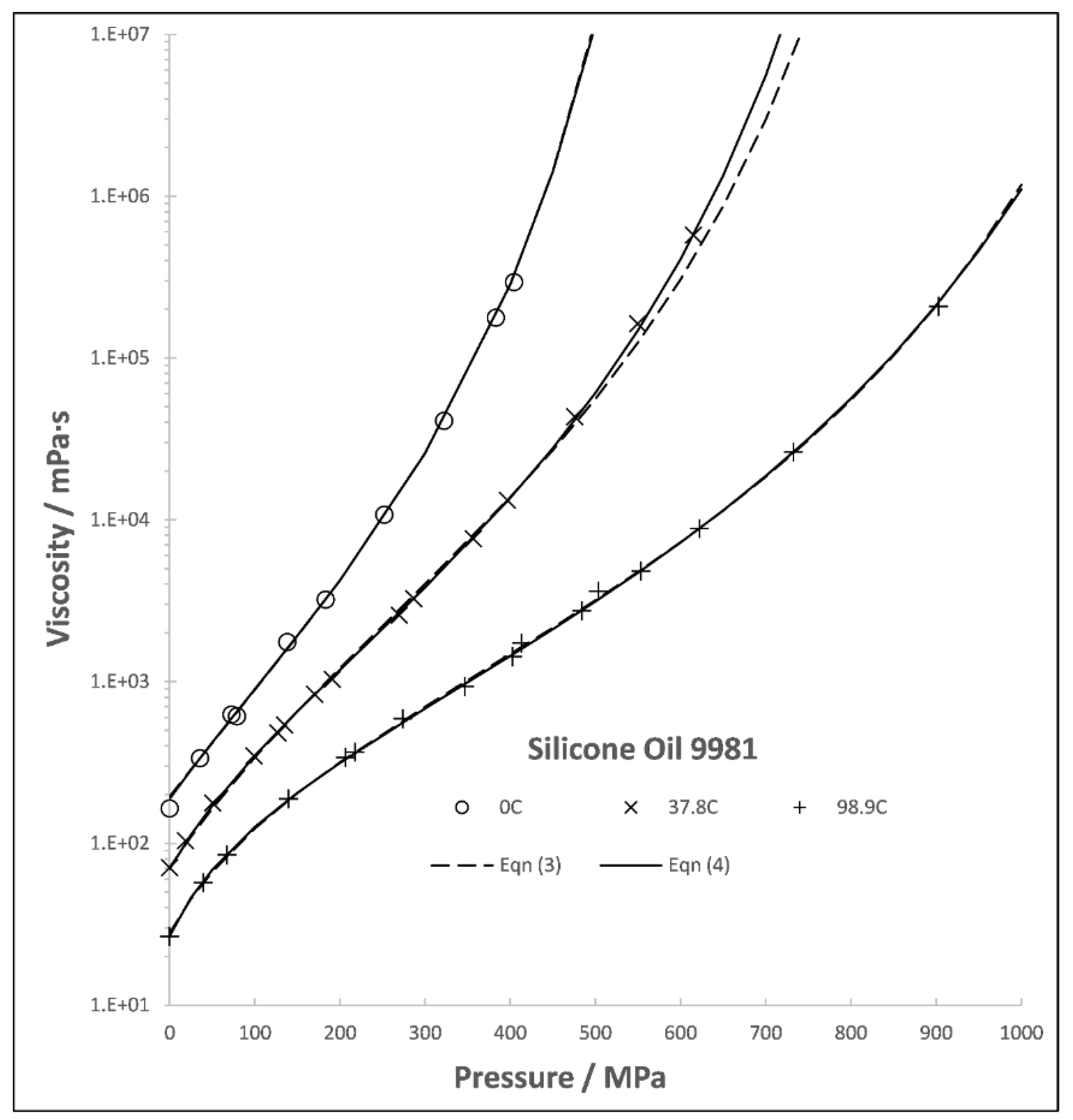
The framework above is deficient when applied to the viscosity of a silicone oil reported in the 1953 pressure-viscosity report of the ASME Research Committee on Lubrication [
11]. This problem is shown in
Figure 1 where the Hybrid model with equation (3) successfully describes the viscosity at 0°C and 99°C; however, at the intermediate temperature of 38°C, it is shown that the divergence pressure specified (by equation (3)) is overstated and must be reduced to match the data. The predicted viscosity at 615 MPa and 38°C is only 78% of the measured value. The parameters regressed from the ASME data are given in
Table 1. Dimethyl silicones are extremely compressible and, therefore, the sigmoidal shape of a log viscosity versus pressure curve can be observed at relatively small ranges of pressure as in
Figure 1. The free volume fraction is significantly reduced with unusually small increases in pressure.
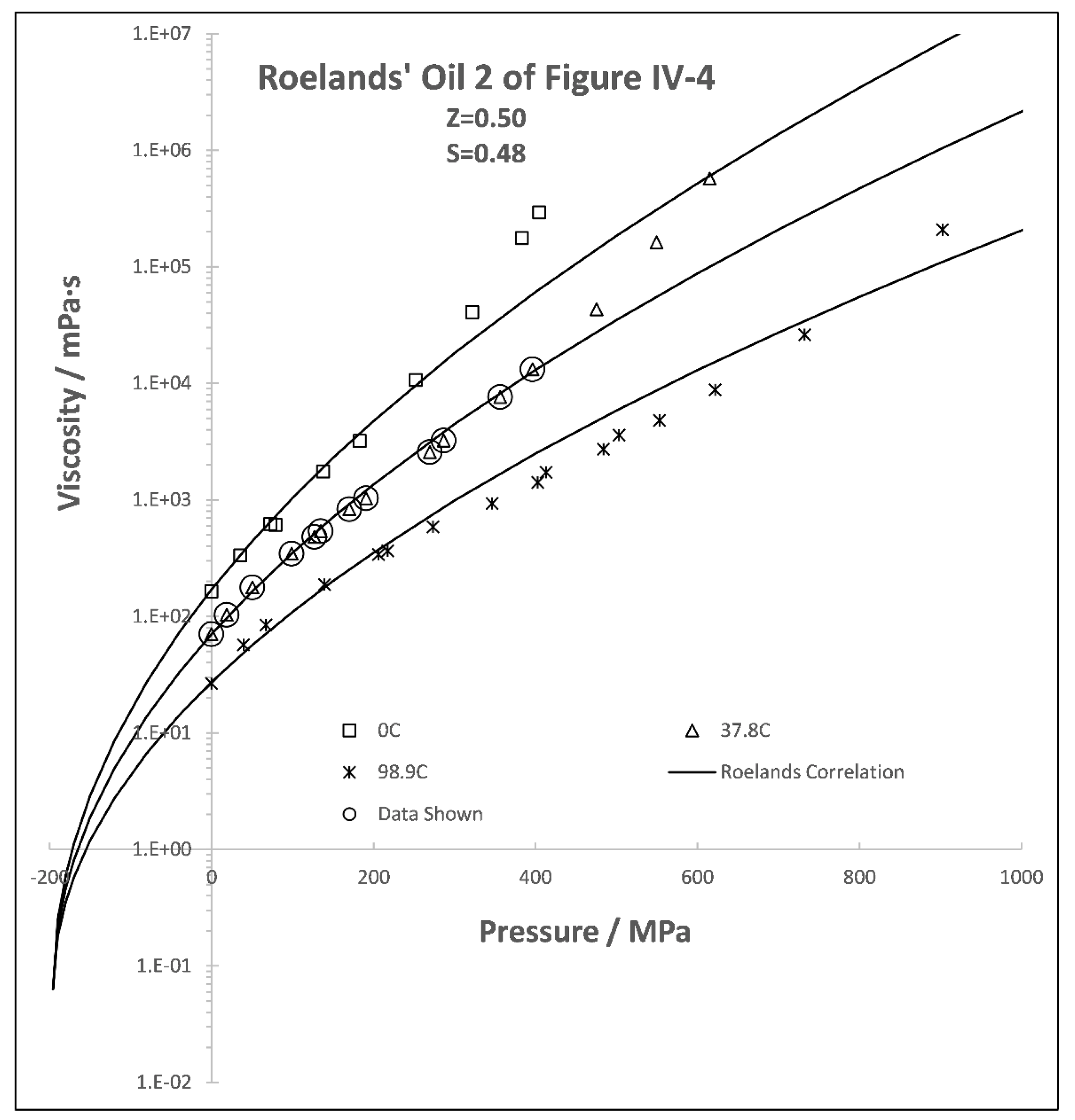
This silicone oil was oil 2 in Roelands’ Figure IV-4 [
12] with pressure viscosity index,
, and slope index,
. See
Figure 2. However, Roelands showed only 12 of the data points, those which could be successfully fitted to his correlation. For three temperatures, the data not discarded by Roelands and his correlation are given in
Figure 2 where it is shown that the correlation cannot describe the pressure dependence at some low pressures and at high pressures [
1].
The physics literature regarding previtreous response [
13] suggests a linear relation between the divergence pressure and temperature.
To investigate the use of a linear form for
, the regression was repeated substituting equation (4) for (3). This model is shown in
Figure 1 and the parameters are listed in
Table 1. The average absolute relative deviation (AARD) has improved from 6% to 3% and the agreement at the intermediate temperature is now excellent.
It will be useful to apply the Hybrid model with linear
to the EHL reference liquids of Reference [
10]. The resulting parameters are listed in
Table 2. These liquids are:
Squalane
diisodecyl phthalate (DIDP)
dipentaerythritol hexaisononanoate (DiPEiC9)
tri(2-ethylhexyl) trimellitate (TOTM)
Gear Research Center, FZG, reference gear oil (FVA3)
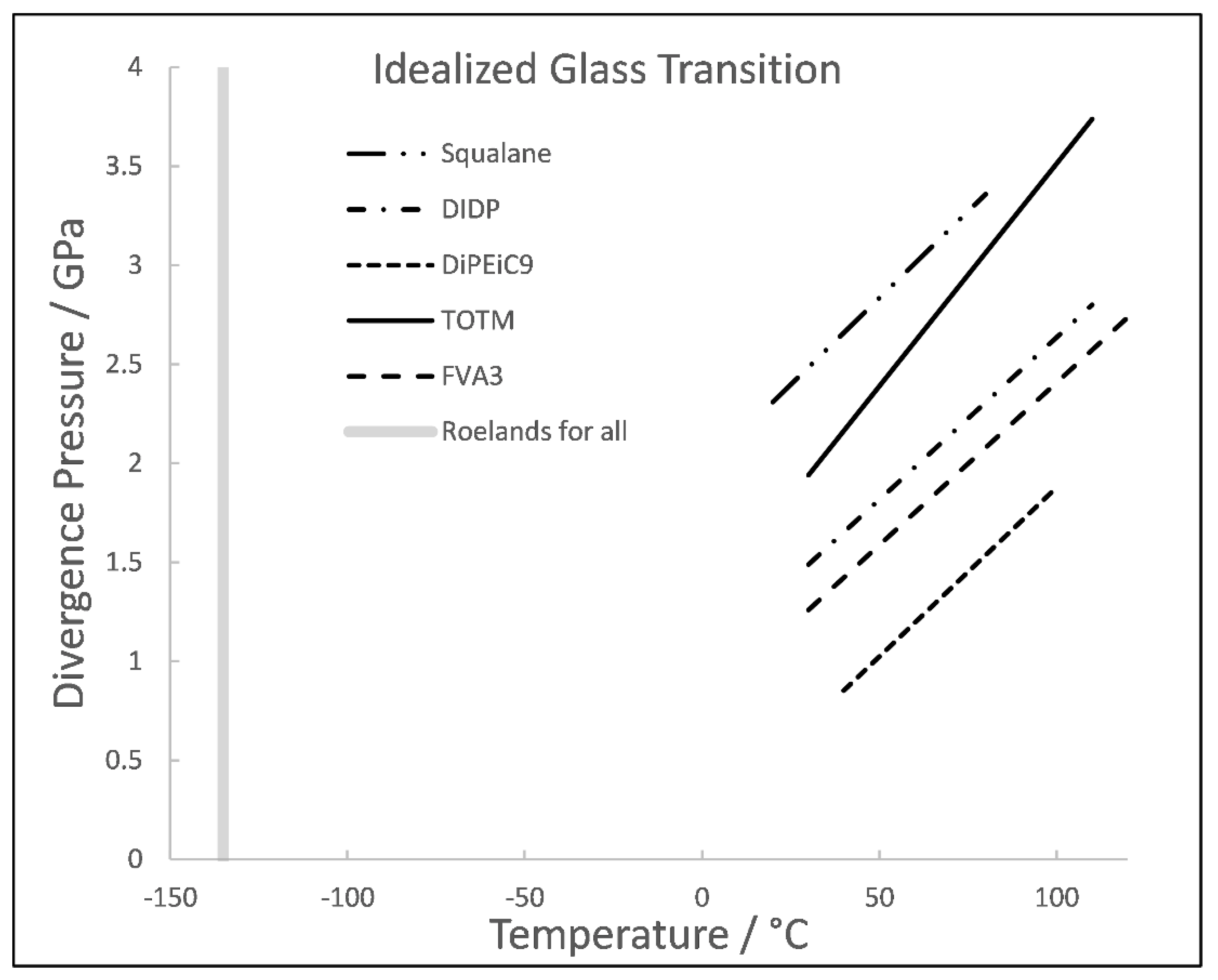
There is only a small improvement in AARD. The idealized glass pressure calculated from the Hybrid model with a linear
is plotted in
Figure 3. For the standard form of the Roelands correlation, the viscosity is unbounded only at -135°C [
12] for all finite pressures as shown in
Figure 3.
For an ambient pressure isobar, if the linear relation (4) for holds for low temperatures, then should be equal to . This is not correct and in every case. Therefore, the response of to temperature may not be linear for sub-ambient temperature or the pressure fragility parameter, in equation (1), may not be assumed to be equal to the temperature fragility parameter, in equation (2). A regression was made for DiPEiC9 assuming and varying and independently. There was no change in the AARD averaged over the entire data set. However, the accuracy of the prediction at the highest viscosities was poorer. Because the usefulness of the Hybrid correlation lies in pressure extrapolation, any degradation of the accuracy at high pressure is not welcome.
. The universal idealized glass pressure of Roelands is shown.
Examples of Special Importance
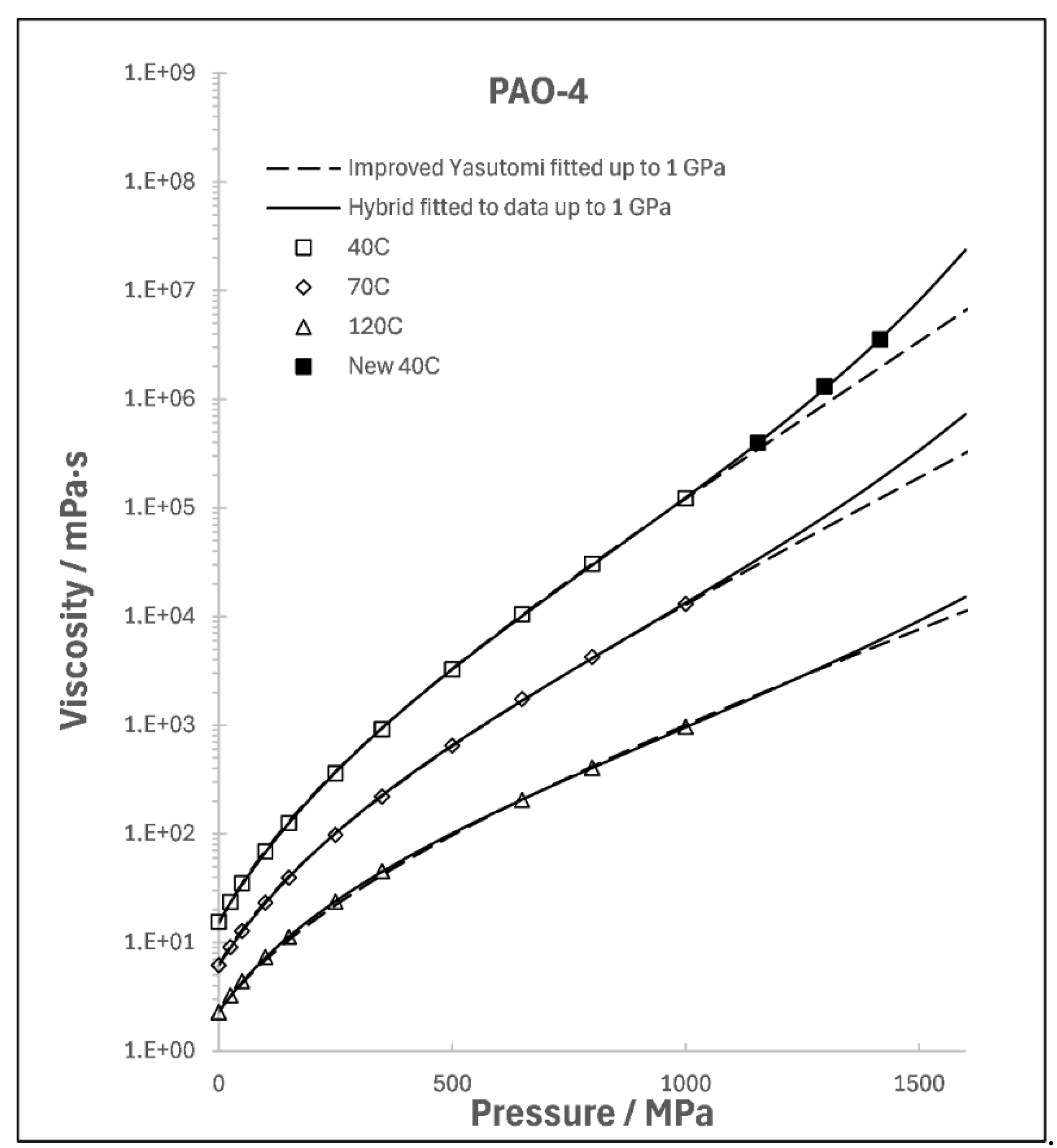
A polyalphaolefin of 4 centistokes grade at 100°C, PAO-4, is a common base oil for blending oils used in EHL. The viscosity of a PAO-4 has been measured to 1 GPa at 40 to 120°C and these data have been fitted to the improved Yasutomi correlation in reference [
14] as shown in
Figure 4. The Yasutomi parameters are given in [
14]. The improved Yasutomi correlation is a free volume model which fits the data very well with fewer parameters than the Hybrid. The ten parameters of the Hybrid model with linear
were fitted to these data and listed in
Table 2. Additional results are available from a 1.4 GPa falling cylinder viscometer [
15] at 40°C and these have been added to
Figure 4. The improved Yasutomi model extrapolated to 10.42 GPa predicted the low shear viscosity to be 44% of the measured value. Whereas the Hybrid model was within 2%. Clearly, the Hybrid model extrapolates well, although the 2% was clearly fortuitous, and the Yasutomi model should not be used for this purpose.
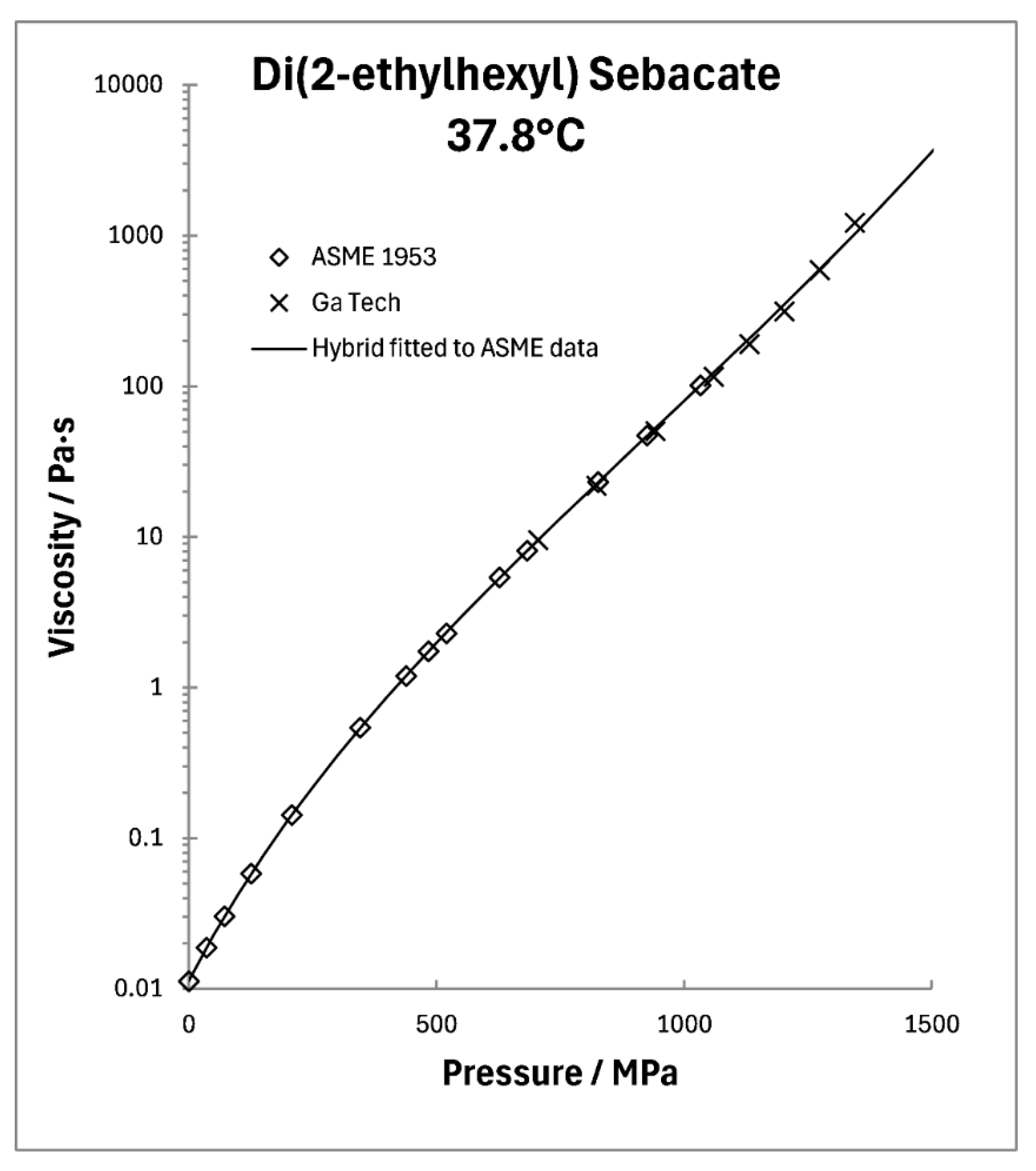
A diester, di(2-ethylhexyl) sebacate, DEHS or DOS, was the original MIL-L-7808 jet engine oil [
16]. It is also the most widely used pressure transmitting medium for high pressures because of the relatively weak piezoviscous response. It is one of the oils investigated in the 1953 ASME viscosity report [
11]. The isothermal form of the Hybrid model, equation (1) was fitted to the ASME data for 37.8°C and the parameters are
0.0113 Pa·s,
12.88 GPa
-1,
4.79,
6.36, and
3.44 GPa. See
Figure 5. There are published viscosities to 1.4 GPa for this oil at this temperature [
15] and these have been added to
Figure 5. The extrapolation from the ASME data is reasonable, even more so considering that there is no inflection in the ASME data to guide the characterization of
. If the glass transition viscosity is 10
7 Pa·s, then the glass transition pressure at 38°C is 2.2 GPa. This large pressure range of the liquid state explains the usefulness of DOS as a pressure medium.
Conclusion
Currently, most high-pressure viscometers used in EHL are limited in pressure capability to about 1 GPa. The limitation is often to lower pressure because of the difficulty in measuring very large viscosities. The Hybrid model provides useful extrapolation to pressures of the glass transition [
10,
17] which will be helpful in predicting minimum film thickness [
18] and traction. A linear relation for the temperature dependence of the divergence pressure improves the fit of the Hybrid model to viscometer measurements.
Nomenclature
pressure fragility parameter
temperature fragility parameter
p pressure, Pa
divergence pressure, Pa
McEwen exponent
T temperature, K
divergence temperature, K
parameter in the McEwen equation, Pa-1
➢ limiting low-shear viscosity, Pa·s
low-shear viscosity at , low-shear viscosity for unbounded temperature,
References
- Bair, S. Roelands' missing data. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology 2004, 218, 57–60. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A. , Rzoska, S. J., Roland, C. M., & Imre, A. R. On the pressure evolution of dynamic properties of supercooled liquids. Journal of Physics: Condensed Matter 2008, 20, 244103. [Google Scholar]
- Spikes, H. Basics of EHL for practical application. Lubrication science 2015, 27, 45–67. [Google Scholar] [CrossRef]
- Bair, S. A critical evaluation of film thickness-derived pressure–viscosity coefficients. Lubrication Science 2015, 27, 337–346. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A. Pressure-related universal previtreous behavior of the structural relaxation time and apparent fragility. Frontiers in Materials 2019, 6, 103. [Google Scholar] [CrossRef]
- Johari, G. P. , & Whalley, E. (1972). Dielectric properties of glycerol in the range 0.1–10 5 Hz, 218–357 K, 0–53 kb. In Faraday Symposia of the Chemical Society (Vol. 6, pp. 23–41). Royal Society of Chemistry.
- Houpert, L. , 1985, “New results of traction force calculations in elastohydrodynamic contacts,” Journal of Lubrication Technology, 107, pp. 241–248.
- Bair, S. A discussion of Arana, A., Larrañaga, J., & Ulacia, I.(2019). Partial EHL friction coefficient model to predict power losses in cylindrical gears. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, Vol. 233 (2) 303–316. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology 2020, 234, 1168–1170. [Google Scholar]
- Bair, S. Choosing pressure-viscosity relations. High Temperatures-High Pressures 2015, 44. [Google Scholar]
- Bair, S. Application of the Hybrid Model to EHL Reference Liquids for Pressure Extrapolation. Tribology Transactions 2024, 1–10. [Google Scholar] [CrossRef]
- American Society of Mechanical Engineers. Research Committee on Lubrication, 1953, “Viscosity and Density of Over 40 Lubricating Fluids of Known Composition at Pressures to 150,000 Psi and Temperatures to 425 F,” American Society of Mechanical Engineers, N.Y., New York.
- Roelands C. J., A. , 1966, “Correlational Aspects of the Viscosity-Temperature-Pressure Relationship of Lubricating Oils,” PhD Thesis, Technische Hogeschool Delft, The Netherlands.
- Paluch, M. , Dendzik, Z., & Rzoska, S. J. Scaling of high-pressure viscosity data in low-molecular-weight glass-forming liquids. Physical Review B 1999, 60, 2979. [Google Scholar]
- Bair, S. , & Flores-Torres, S. The viscosity of polyalphaolefins mixtures at high pressure and stress. Journal of Tribology 2019, 141, 021802. [Google Scholar]
- Bair, S. Pressure-viscosity behavior of lubricants to 1.4 GPa and its relation to EHD traction. Tribology Transactions 2000, 43, 91–99. [Google Scholar] [CrossRef]
- James, F. , Murphy, C. M., & O'Rear, J. G. Diester-Base Jet Engine Oils. Industrial & Engineering Chemistry 1959, 51, 673–674. [Google Scholar]
- Bair, S. , & Habchi, W. Quantitative Elastohydrodynamic Lubrication—Seventeen Years In. Journal of Tribology 2024, 146. [Google Scholar]
- Habchi, W. , Sperka, P., & Bair, S. The role of the glass transition for EHL minimum film thickness. Tribology International 2023, 190, 109061. [Google Scholar]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).