Introduction
The current level of development of physical and electrical materials science, the theory of electrical processes and electrochemical technologies, physical electronics and microelectronics, requires the creation of new types of dissimilar functional materials and their composites with predetermined structural parameters and properties, for the purpose of their use in various branches of science and technology, as functional elements of various kinds of devices and process systems, in a wide range of field (mechanical; electrical; magnetic; electromagnetic; optical) and temperature effects [
1,
2,
3,
4,
5]. Of special
scientific and
technical interest are materials operating in extreme conditions (low and ultra-low temperatures; high and ultra-high temperatures; strong electric and magnetic fields; intense coherent radiation; high mechanical stresses) [
1,
2,
3,
4,
6,
7].
Implementation of this program requires carrying out complex theoretical and pilot studies of the nonlinear electrophysical and electro-optical effects arising in various metals and their alloys, semiconductors and dielectrics, magnetic materials under the influence of constants and variation electromagnetic fields [
1,
2,
3,
4,
8], external ultrasonic and temperature fields and also ionizing radiation. The results of the number of works determine the directions of practical use of layered dielectrics (ceramics, micas, perovskites) in the fields of: insulation and cable technologies [
1,
4]; microelectronics (quantum field-effect transistors, semi-solid diodes and triodes, resonant tunnel diodes based on high-temperature composite superconducting structures (similar in properties to ceramics) [
5,
6], MIS and MSM-structures [
9,
10,
11,
12,
13,
14,
15,
16,
17]; optoelectronics and fiber optic technologies (sensors of mechanical stresses and deformations in building structures and mining technology devices) [
18,
19,
20,
21,
22,
23,
24,
25,
26]; non-linear optics and laser technologies (coherent radiation parameter regulators (based on ferroelectrics) [
27,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37,
38,
39]; capacitor technology (electrically controlled capacitors) [
1,
6]; electrochemical technologies (solid-state electrolytes with high and ultra-high ion conductivity) [
40,
41,
42,
43,
44,
45,
46,
47,
48,
49,
50,
51,
52,
53,
54,
55,
56,
57,
58]; radio engineering and radio electronics (in particular, electronically controlled microwave systems) [
59,
60,
61,
62,
63,
64,
65]; alternative energy (in particular, in the development of physical models and schemes of hydrogen energy devices) [
45,
65,
66], which determines the practical significance of the research carried out.
The object of research in this work is crystals with ion-molecular chemical bonds (ceramics, various minerals (micas, aqueous compounds of inorganic salts), vermiculites, allophanes, halloysites, etc.). A special case of materials of this type are crystals with hydrogen bonds (HBC), characterized by the presence of a hydrogen sublattice in their crystal structure and classified by the properties of the crystal lattice as layered crystals (including layered silicates and crystalline hydrates) [
1,
2,
3,
4,
8], and according to electrophysical properties, as proton semiconductors and dielectrics, manifesting in a wide range of fields (0.1-1000 MW/m) and temperatures (50-550 K) property of proton conductivity, which is reduced to leaping diffusion of protons through hydrogen bonds in the direction of the polarizing electric field. HBC s also have unique thermodynamic properties [
1,
2,
3,
4,
8,
67,
68,
69,
70,
71,
72,
73,
74,
75,
76,
77,
78].
HBC also have unique thermodynamic properties [
1,
8].
The HBC find
practical application as insulating materials for current-conducting elements of TPP electric generators [
1], thin-film heat insulators based on organic polymers and their composites [
6,
7], laser radiation parameter regulators (KDP, DKDP) [
79,
80,
81,
82,
83,
84,
85,
86,
87,
88,
89,
90,
91,
92], fuel cells in hydrogen energy [
4,
5], strengthening additives in the manufacture of reinforced concrete structures, etc.
Ferroelectric crystals of the HBC class (triglycine sulfate (TGS); Seignette salt, KDP, etc.) [
93,
94,
95,
96,
97,
98,
99,
100] are characterized by a rectangular hysteresis loop with abnormally high residual polarization [
2,
4], which makes it possible to use thin films of these materials as functional elements of fast-acting non-volatile storage devices with abnormally high retention time of residual polarization (relaxation time of electric charge in memory cells of this type of devices (ferroelectric capacitors with ultra-high ion conductivity near Curie temperature) is about 10 years) and high values of thermal stability and mechanical strength [
101,
102,
103,
104,
105,
106,
107,
108,
109,
110], which is relevant for modern information and digital technologies [
111,
112,
113,
114,
115,
116,
117,
118,
119,
120,
121].
The ultra-high values of theoretical amplitudes of the thermostimulated depolarization current density for a low-temperature maximum (50-100 K), which shifts to the ultra-low temperature region (4-25 K), established for nanoscale layers (1-10 nm) [
70], make it possible to determine the HBC as proton superconductors. Ultra-high values of the conductivity coefficient (increases by 3-4 orders of magnitude, compared to the nitrogen temperature region (50-100 K) [
70]) and ultra-low values of dielectric loss tangent (decreases from 0.0001 to 0.00000001, when cooled from nitrogen to helium temperatures (1-10 K) [
122,
123,
124]) are explained by the quantum effects associated with tunnel junctions (displacements along hydrogen bonds) protons in the hydrogen sublattice of the HBC nanofilms (3-30 nm) when the crystal reaches the phase transition temperature of the second kind (according to preliminary theoretical estimates, the critical temperature is 4-25 K [
123,
124]). This phenomenon needs to be studied in depth at the experimental level and, in case of a positive result, prospects will open up for the practical application of the electrophysical properties of the HBC (as proton superconductors) in the development of photoconverter elements for panels of space solar mini-power plants and fuel hydrogen elements (located on spacecraft and stations), which is relevant and scientifically significant in the field of space technologies and cryogenic technology. Of course, this physical problem requires careful joint theoretical and experimental studies and checks using high-precision low-temperature measurements in the region of helium temperatures, especially in the region of temperatures T = 0-10 K, in the vicinity of the phase transition point of the second kind T = 4-25 K, when the dielectric goes into quasi-magnetic states (abnormally high dielectric constants (2.5-5.5 millions) are due to ultra-high transparencies of the potential barrier (0.9-0.95)) [
2,
123,
124] and the proton superconductor [
2,
4,
70].
The subject of the research in the proposed scientific work is the development of a generalized physical review (both in terms of theory and experiment) and comparative analysis according to the main physical and mathematical models of the processes of nonlinear relaxation polarization and conductivity in dielectric materials with ion-molecular chemical bonds in a wide temperature range (1-1500 K) and polarizing field strengths (0.1-1000 V/m) at alternating field frequencies of the order of 1 kHz - 100 MHz. In particular, for the HBC, due to the high efficiency of quantum proton tunneling processes in the anionic sublattice, a detailed mathematical
description of nonlinear proton-relaxation polarization and conductivity will be performed in a wide theoretical range of temperature variation (
1 - 1500 К) and electric field strengths (
100 кВ/м – 100 MW/m) [
1], [
6,
7,
8,
9,
10]. At this stage of the research, the experimental range of temperature change (
70 – 450 K) includes temperature regions (zones) of
quantum (
70 - 100 K) and thermally activated (
100 - 250 K) proton transitions by hydrogen bonds [
1], [
6,
7,
8,
9,
10]. Physical models are accepted according to fundamental (similar and satisfying properties and principles)
quasi-classical and quantum-mechanical kinetic theories of proton relaxation in HBC [
1].
The purpose of this article is to summarize and compare, with elements of additions and refinements, on the basic equations and parameters of physical and mathematical models and their practical applications (in the form of real experiments and computational computer models) [
67,
69,
71,
72,
73,
74,
75,
76], describing nonlinear electrophysical processes associated with diffusion-relaxation kinetic phenomena during polarization and conductivity in dielectrics with ion-molecular chemical bonds. The main priority in this work is given to the study of quasi-classical methods for the theoretical description of ion-relaxation polarization and conductivity. (a special case is proton-relaxation polarization in the HBC), when the main mathematical apparatus is the schemes and methods of the classical kinetic theory. (in the form of kinetic equations in the form of Boltzmann, the balance of the number of particles in various equilibrium states, the collision integral, etc.) and continuum electrodynamics (equations of the electric field in matter and its boundary conditions), with elements of non-relativistic quantum theory required to account for the effects of quantum tunneling of basic charge carriers in constructing kinetic coefficients and other parameters of the kinetic equation. Directly studying the methods of quantum-mechanical description of tunnel relaxation polarization in proton semiconductors and dielectrics (PSD) are devoted to the work [
68,
70,
77,
78,
123,
124], which, in the future, will be summarized in another review article.
The methodology of this review article, in subsections 2.3,2.5,2.6, 2.8-2.10, will be based on the analysis of various developed by the first author of this article, Kalytka V. (in the period 2012-2024) and, together with his supervisor M.P. Tonkonogov (in the period 2000-2005), methods of analytical study of the kinetics of relaxation polarization, in particular, proton-relaxation polarization, in the case of the HBC (due to the diffusion movement of the most mobile charge carriers (in the general case, ions, in the HBC, protons). Descriptions of mathematical modeling schemes of dielectric relaxation in the HBC and in wide-class ion dielectrics in the temperature range T = 1-1550 K and electric field strengths (0.1-1000 MW/m) [
1], [
6,
7,
8,
9,
10] will be performed. Basically, we will consider the methods of quasi-classical kinetic theory, which is most convenient when studying high-temperature relaxation polarization related to the temperature region T = 100-450 K, when the dielectric relaxation mechanism in the HBC is based on the movement of Bjerrum ionization and orientation defects and water molecules due to the Maxwell relaxation transfer of (100-250 K) relaxers (protons) in the crystal structure dielectric placed in an electric field. In the region of higher temperatures (250-550 K), the processes are reduced to volume-charge polarization, associated with accumulation, over time, in the space between the electrodes, spatial charge, the distribution of which over the volume of the dielectric is formed due to the movement of protons between ions of the anion sublattice, and due to the interaction of protons with oscillations of ions of the anion sublattice, and, can be interpreted, within the framework of classical statistical theory, as some operator, reflecting, as a function of spatial variables and time, the influence of the ion environment on the proton subsystem, where the main element of this operator is the potential of proton interaction with the potential field of the anion sublattice (hydrogen bond field), and the additional smaller component of the operator is described by a numerical constant reflecting the stationary state of temperatures (250-550 K) of the phonon subsystem. That is, in quasi-classical theory, at the mathematical level, the influence of the phonon subsystem on relaxers is described by a simple numerical constant, which is reduced in the model equations. In this case, the theoretical description of the volume-charge polarization in the HBC will be carried out by the same methods as in the high temperature region (250-550 K), but only taking into account nonlinear kinetic phenomena reflected in the form of the interaction operator of relaxation modes of volumetric charge, differing in the order of perturbation theory k [
1,
2] on the frequency harmonic of the established order r (as a rule, you need to start with the frequency harmonic of the first order (r = 1)). A more detailed description of this method will be implemented in 2.3,2.5 (the material of these subsections is borrowed from [
72]), 2.8, 2.9 (here the materials are borrowed from [
73]). At the same time, the patterns of high-temperature dielectric relaxation, at the microscopic level, are manifested in the movement of defects of the mixed type structure (both basic and additional, tunnel type). The latter option is quantum in nature and should be investigated taking into account the quantum transitions of protons between the anions of neighboring layers. Examples of calculations and analysis of theoretical density spectra of TSDC by quasi-classical schemes will be given in section Discussions 4. Obviously, in this matter, the methods [
67,
69,
71,
72,
73,
74,
75,
76] for manifesting the effects of quantum effects on low-temperature (50-100 K) and high-temperature (250-550 K) relaxation are quite satisfactory, from the point of view of comparing the results of theory and experiment, but only within the framework of a quasi-classical approach. Strict quantum-mechanical descriptions of the effects of nonlinearities on) relaxation polarization in HBC in the ranges T = 50-100 K (tunnel quantum polarization) and T = 250-550 K (nonlinear volume-charge polarization) are made in [
68,
70,
77,
78]. The solution to this issue will be transferred to the next separate article.
Since the most versatile physical and mathematical models of electrophysical and electro-optical processes in heterogeneous elements based on solid-state composite materials are models covering the widest crystal classes and the widest possible field and temperature ranges. (from ultra-low to ultra-high), called quasi-classical, then the purpose of this scientific work is to perform a generalized physical review and comparative analysis of nonlinear quasi-classical models of polarization phenomena in solid-state dielectric structures and semiconductors characterized by high ion conductivity, i.e. in crystals with ion-molecular chemical bonds. Elements of quantum mechanical models (quantum kinetic theories) will be considered as auxiliary and clarifying, using the example of materials of the HBC class, when they are polarized in the low temperature region, when the main contribution to dielectric relaxation and conductivity in proton semiconductors and dielectrics is made by quantum diffusion relaxation due to tunnel transitions of protons of the hydrogen sublattice against the background of their interaction with anionic ions sublattices.
2. Materials and Methods
2.1. Basic Theoretical Provisions for Physical and Mathematical Models of Relaxation Polarization
Section 2 of this work is devoted to the description and comparative analysis of existing, developed by the authors of this article, theoretical methods for describing the kinetics of relaxation processes occurring during the formation of a polarized state and during conductivity (generally ionic, and in the HBC, proton) in dielectric structures of a class of crystals with ion-molecular chemical bonds in an alternating electric field. The existing directions in this scientific field, and, accordingly, the models can be divided according to the specifics of the physical description of polarization processes in dielectrics into quasi-classical ones, based on solutions of the nonlinear quasi-classical generalized nonlinear kinetic equation [
72] (a special case is the Fokker-Planck equation, solved in conjunction with the Poisson equation [
69,
71,
73]) and quantum-mechanical, built on the basis of rather strict solutions of the quantum kinetic Liouville equation for the ensemble of the most mobile charged particles in the crystal (main charge carriers) [
68,
70,
77,
78]. The quasi-classical kinetic equation is based, as a rule, on the model of transfer of the main charge carriers or relaxers (ions) in a multi-pit potential crystalline field perturbed by a polarizing electric field [
72,
125,
126]. This model is semi-classical and relies on the methods of classical statistical and kinetic theories using elements of quantum theories (stationary Schrödinger equation; the Gibbs quantum canonical distribution; different models of the energy spectrum of particles distributed to the energy levels of the continuous or, in the more stringent case, discrete spectrum [
77,
78]). The simplest version of the quasi-classical model of dielectric relaxation is the model of ion transport in a symmetric double potential well with a potential barrier of the same type of symmetry [
1,
2,
74]. Thus, in a quasi-classical model, kinetic coefficients are written within the framework of a quasi-classical kinetic equation, but taking into account both classical (thermally activated) and quantum tunneling transitions of ions between potential wells, which makes it possible to study polarization kinetic phenomena in dielectrics with a complex crystal lattice structure (layered silicates; crystalline hydrates; ceramics; vermiculites, etc.) with a sufficiently high degree of accuracy of theoretical results (when compared with the experiment) in relation to a wide range of temperatures (50-550 K) and field parameters (0.1-1 MV/m) [
72,
73,
74,
125,
127]. In this case, due to the low transparency values of the potential barrier for heavy relaxers (with a mass much larger than that of the hydrogen ion), the quasi-classical model is insufficient in the region of low (50-100 K) and ultra-low temperatures (4-25 K), when the main contribution to dielectric relaxation in a number of ionic crystals related to crystals with hydrogen bonds (HBC), introduce quantum tunnel proton transitions along hydrogen bonds (protons form a hydrogen sublattice and move (in both classical and quantum ways) within and between ions of the anionic sublattice [
1,
8]. In the HBC, the hydrogen sublattice is geometrically integrated into the anionic sublattice and mobile light (in comparison with massive anions) hydrogen ions (protons) actively move (perform relaxation movement) against the background of inactive anionic sublattice ions [
1,
8].Thus, a mathematical description of the low-temperature dielectric relaxation in the HBC, reduced to quantum tunneling proton relaxation (quantum diffusion transitions of protons over hydrogen bonds) must be carried out, and is carried out from the solution of the nonlinear quantum kinetic equation [
68,
70,
77], which is the result of transformations of the fundamental quantum kinetic Liouville equation written for the properties and parameters of the proton sublattice, and the assumptions established from the experiment imposed on the proton relaxation and conductivity mechanism in the HBC [
1,
8] The kinetic equation of this type contains, at the mathematical level, the features of nonlinear quantum processes of proton-relaxation polarization [
77], which appear not only in the coefficients of the kinetic equation (as in the quasi-classical kinetic theory), but also directly in the structure of the quantum kinetic equation itself for the proton subsystem. This approach allows us to formulate the main provisions and analyze the results of the nonlinear quantum kinetic theory of proton conductivity in the HBC in a wide range of fields (0.1-1000 MW/m) and temperatures (10-1550 K) [
68,
78,
122,
123,
124].
This scientific article, on the very formulation of the question, is devoted to a generalized analysis and study of the properties and parameters of quasi-classical models of ion-relaxation polarization in almost all ion dielectrics, including the HBC. Thus, in this work we are primarily interested in quasi-classical methods for describing kinetic phenomena (based on the quasi-classical kinetic equation) under dielectric polarization (including in the HBC) [
125,
126,
127], which does not require special involvement of quantum kinetic theory methods, but is limited to calculating the quantum transparency of the potential barrier within the kinetic coefficients of the generalized nonlinear quasi-classical kinetic equation [
73,
74,
125,
126,
127]. This approach allows, already within the framework of nonlinear quasi-classical kinetic theory, to strengthen the influence of quantum effects on the region of abnormally high polarization nonlinearities manifested in most ionic dielectrics in the region of ultra-low temperatures (1-10 K) and weak fields (0.1-1 MV/m) and in the region of ultra-high temperatures (550-1550 K) and strong fields (10-1000 MV/m) [
72,
73].
Strict quantum mechanical studies of kinetic phenomena in solid dielectrics in the field of low and ultra-low temperatures, due to the specifics of the mathematical apparatus of this model, will be carried out in the future, using the methods of quantum statistical theory (quantum kinetic equations in various approximations; the stationary Schrödinger equation; the Gibbs quantum canonical distribution; density matrix, etc.) for various subsystems (proton and anion sublattices interacting with each other due to the forces of chemical bonds), but in cancers of a different work.
2.2. Basic Principles of Quasi-Classical Model of Ion-Relaxation Polarization
As the main (most mobile) carriers of electric charge (relaxers) in dielectrics, ions (of an arbitrary sign of charge) are accepted, capable of performing relaxation (reciprocal) movement in a potential field of a crystal lattice (or sublattice) perturbed by an external electric field. The basic equations of motion of ions in the crystal, in fact, describe the diffusion motion of ions (cations in the direction of the lines of force of the external electric field, and anions against the field) against the background of the interaction of this type of ions with a potential background generated by heavier inactive (compared to these) ions localized in the nodes of the crystal lattice. From the point of view of the quantum theory of crystal lattice oscillations, the most mobile (light) ions form an ion subsystem moving in the field of the phonon subsystem formed by vibrations of inactive massive (compared to data) of ions or ion groups (ion clusters), and the interaction effects of ion and phonon subsystems are described by the corresponding quantum mechanical operators (similar to the electron-phonon interaction operators known in solid state theory [
4], which is studied in describing the quantum properties of metals or semiconductors and dielectrics with high electron conductivity). For example, the model of quantum motion of hydrogen ions (protons) in the field of the phonon subsystem formed by oscillations of ions of the anion sublattice (anion component of the phonon subsystem for protons) in the HBC is effective from the point of view of quantum kinetic theory [
4]. Regarding the quantum theory of proton-relaxation polarization of the HBC, one cannot but count the influence on the proton subsystem from the side of the phonon subsystem formed by vibrations of even heavier (than anions) ions of the additional sublattice (ion component of the phonon subsystem for protons) in the HBC.
As noted in subsection 2.1, in the framework of this paper we will not go into the issues of the quantum kinetic theory of proton relaxation polarization, limiting ourselves to the quasi-classical approximation in the description of the quantum model of the proton tunneling motion in the HBC. Applied to the processes of ion-relaxation polarization in dielectrics of various classes (except HBC), at the level of the quasi-classical kinetic theory of dielectric relaxation, there is no strict necessity to take into account the tunnel quantum component in the kinetic coefficients (e.g. in the diffusion and mobility coefficients) for ions, in view of the colossal masses of ions or ion groups in comparison with protons. However, in the mathematical description of proton relaxation in the HBC, it is necessary to take into account that, due to the relatively small mass of the proton (compared to the masses of the anionic sublattice ions), the quantum transparency coefficient of the potential barrier for protons increases significantly (up to 0. 0001-0.15), 0001-0.15), especially against the background of small values of activation energies
0,01-0,1 eV) and potential barrier width
0,08-0,1 nm) characteristic of crystals with hydrogen bonds for protons on bonds in the low-temperature region (for protons relaxing in the region T=50-100 K). In this connection, even within the framework of the methods of quasiclassical kinetic theory [
128,
129,
130,
131,
132,
133,
134], a rather strict account of quantum tunneling of protons is required in the recording and study of the coefficients of the quasi-classical kinetic equation of proton relaxation [
125,
126,
127].
Without limiting the generality of the quasiclassical models of electrophysical processes in ionic dielectrics developed by the authors [
67,
69,
71,
125,
126,
127,
128,
129,
130,
131,
132,
133,
134], we can, in the generalized nonlinear kinetic equations of the quasiclassical theory [
69,
71], preserve the quantum components of the diffusion and mobility coefficients of ions, despite the magnitude of the ion mass compared to the proton mass, thus preserving the quantum orientation of quasiclassical polarization models in a universal mathematical format in a wide theoretical range of field parameters (0.1-1000 MV/m) and temperatures (1-1550 K) [
72,
73]. In these models, ions (relaxants), making diffusive motion in the space between the electrodes, cause the formation in the crystal, with a time much longer than the relaxation time, a stationary polarized state, information about which allows us to calculate the experimentally measured polarization value of the dielectric, from which the theoretical frequency-temperature spectra of the complex dielectric permittivity (CDP) are constructed (see Sects. 2.9, 2.9, and 2.10). subsections 2.9, 2.10 and 3.1,3.2) and temperature spectra of the temperature-stimulated polarization currents (TSPC) and depolarization currents (TSDC) (see comments in subsections 4.1,4.2). The generalized nonlinear quasi-classical model of ion-relaxation polarization [
125,
126,
127], based on the formulas for the real and imaginary components of CDP, provides opportunities for mathematical modeling of the influence of various kinds of nonlinear kinetic effects (interaction of relaxation modes of the bulk charge with different mode numbers n at a given multiple of order in the frequency of the variable field
r (starting from the first order of perturbation theory (
) by a small dimensionless parameter
[
71,
72,
73,
129]); interactions of relaxation modes of the bulk charge at different multiples of frequency harmonics of the alternating field
r (starting from the second order of perturbation theory (
) by the parameter
) and quantum effects (tunneling transitions of protons through a potential barrier of small height (at proton activation energies of 0.01-0.1 eV) in the region of low (50-100 K) and ultra-low (0-10 K) temperatures) [
72]. [
72]. Regarding the methodology for constructing theoretical spectra of the thermostimulated depolarization currents (TSDC) in ionic dielectrics [
74,
76,
128,
129], there are a number of additions and refinements to the structure and properties of the quasi-classical kinetic equation [
124,
125,
126,
127].
When theoretically describing the regularities of dielectric relaxation in ionic dielectrics, from the point of view of assessing the correctness of theoretical results, it is important to compare the results of calculations of the theoretical frequency-temperature spectra of the dielectric loss tangent and the density of thermally stimulated depolarization currents with experimental results, which, in turn, determines the degree of mathematical rigor in assessing the corresponding relaxers for each type comparison parameters. (as which in the works [
1,
2,
4,
128] the molecular characteristics of relaxers were taken) in the entire experimental range of temperatures or frequencies of an alternating electric field. In this regard, it is necessary to note the methods of comparison of theory and experiment presented in [
130,
131,
132,
133,
134,
135,
136,
137]. The most stringent, from the point of view of practical application of theoretical and computer models of ion-relaxation polarization [
67,
68,
69,
70,
71,
72,
73,
74,
75,
76,
77,
122,
123,
124,
125,
126,
127,
135], is the method of minimizing the comparison function (MCF-method) described in [
75] and used in [
3,
4,
128,
136,
137].
2.3. Methods of Generalized Quasi-Classical Physical-Mathematical Model of Ion-Relaxation Polarization
Since the most effective, in terms of the effects of quantum tunneling of relaxers on polarization, a variant of crystals with ion-molecular chemical bonds, are crystals of the HBC class, in which the main hydrogen ions are the (most mobile) charge carriers in the region of fields and temperatures far from breakdown (protons), then, the construction of a generalized quasi-classical model of relaxation polarization and prolongation for materials of the class of ion dielectrics (a special case of which is the HBC) must be carried out on the basis of a kinetic equation with coefficients recorded taking into account the quantum transitions of relaxers (as which, in this model, we take arbitrary ions capable of moving along chemical bonds, both due to thermal activation and tunneling).
If an ion of this kind is a cation, then the crystalline potential pattern of such an ion, when an external electric field is applied to the dielectric, acquires asymmetry in the direction of the field lines. In the case where the simulated charged particle is an anion, then, accordingly, the asymmetry of the crystalline potential pattern of such a particle is established against the directed field lines. Obviously, the rate of cation transition across the field is higher than against the field, and vice versa for anions.
As noted above, with relaxation polarization in the dielectric under the influence of an external (polarizing) electric field (constant, alternating), diffusion transfer of the main (most mobile) charges (relaxers) occurs - migration polarization. The main contribution to the polarization of this type is made by ions called conduction ions, moving with low activation energies (0.01-1 eV) at the fixation points (equilibrium positions) in the field of the crystal lattice perturbed by the electric field. The number of states (equilibrium positions) for ions is taken to be of the order of
- multi-pit undisturbed potential pattern [
1,
4,
8].
As a result of relaxation polarization of the dielectric, a spatially inhomogeneous volume-charge distribution is formed in the space between the electrodes. One of the conditions for the occurrence of volumetric charge is the presence of blocking or partially blocking electrodes [
1,
8]. Transfer processes are considered for an ideal lattice - neglecting both the existence of traps and recombination processes - dissociation of charge carriers [
1,
8]. Distance between equilibrium positions for ions is taken equal to value of lattice constant
a. The crystalline potential relief, due to the redistribution of charge carriers between states (potential wells), will be modeled by the function not only of the x coordinate, but also of the time t [
1].
In many cases, in semiconductors and dielectrics, one type of charge carriers (relaxers) is the most mobile, in comparison with others [
2,
4,
8].
Ions and polar groups act as mobile relaxers in dielectrics with a complex crystal structure (layered minerals, ceramics), in particular, in crystals with hydrogen bonds (HBC) - Bjerrum defects (ionization
,
; orientation defects - L, D), orientation defects associated with ion vacancies (VL, VL D defects) and hydrogen ions (protons) localized on hydrogen bonds [
1]. So, for example, in crystals of Ih - ice, defects of
[
2,
4,
8] have the greatest mobility.
In the HBC (layered silicates, crystalline hydrates), at electric field strengths
, in the temperature range T=50-550 K, migration polarization is caused by diffusive movement of hydrogen ions (protons) along hydrogen bonds with activation energy
eV, in the direction of field lines (parallel to the crystal axis
) [
1,
4,
8]. This phenomenon can be defined as
proton conduction, and the set of relaxation processes associated with proton diffusion in the electric field as
proton relaxation. In terms of electrophysical properties, the HBC are classified as
proton semiconductors and dielectrics (PSD) [
1,
4,
8]. This approach allows, from the point of view of the unified theory of proton conduction, to consider various polarization effects in the HBC (in particular, the electret effect) and to reveal the influence of lattice parameters and molecular parameters of relaxants (activation energy; natural frequency of oscillations in potential pits; equilibrium concentration) on dielectric permittivity and specific bulk electrical conductivity [
1,
4,
8].
Therefore, in order to simplify the mathematical model of migration polarization in the HBC, we will consider the transfer of only one type of charge carriers - protons, and the oppositely charged ions (anions) are considered as slow-moving and forming a homogeneous potential force background in the field of which protons move [
1]. From the condition of transitions of charge carriers (protons) between neighboring states (potential pits) of number i-1, i, i+1 follows a system of kinetic equations [
1,
2,
3,
4].
In the HBC, as well as in other ionic dielectrics similar to them in structure and lattice properties, if the condition is fulfilled, the geometrical model of the potential crystal potential for conduction ions is assumed to be one-dimensional. When taking into account the influences on ionic conductivity from additional factors related to the interactions of conduction ions with other ionic subsystems embedded in the crystal structure of a given dielectric, the transition to a three-dimensional model of ionic relaxation polarization is natural.
In general, the one-dimensional kinetic equation of transfer of the generalized most mobile charge carriers (ions with a certain sign of charge, called conduction ions) on chemical bonds (places of fixation of ions; potential pits for ions) against the background of the crystal potential field formed by stationary particles (heavier ions), based on the equation of balance of the number of particles (conduction ions) in potential pits, has the form [
1,
72]
where,
,
,
concentration of relaxers (conductivity ions, hereinafter simply ions) in potential wells of number
,
,
;
rate of probability of ion transition between states
in the direction: along the field (for cations) or against the field (for anions)
; by field (for anions) or by field (for cations)
, respectively [
1]. Ion transitions between adjacent equilibrium positions are realized both by thermal activation (classical effects) and by tunneling (quantum effects). Then, [
1,
2,
67,
69,
71,
72,
73] in general [
1,
2,
3,
4,
67,
69,
71,
72,
73,
125,
126,
127,
129]
In expression (2)
- the natural frequency of oscillations of ions in potential wells;
- ion activation energy on chemical bonds. The system function
is the quantum transparency of the potential barrier (probability of tunnel transitions) averaged over the levels
E of the unperturbed continuous spectrum of ion energies for relaxers (ions; in HBC - protons)
moving in the region of a potential barrier disturbed by an external alternating electric field
. As per adopted provisions
Here
– probability of thermally activated transitions of relaxers (ions) through a potential barrier with height
(according to classical statistical theory,
) does not depend on the geometric shape of the barrier) [
72,
73]. In the statistical functions of the
,
system, the "-" sign is taken for the case of the proton moving in the HBC (or an arbitrary cation in the ion dielectric) in the direction of the power lines, and the "+" sign for the case of the movement of these particles against the direction of the power lines of the external electric field
The influence of the electric field strength
on the parameters of the unperturbed potential barrier
and its quantum transparency
is expressed by the correction value
calculated near the ion equilibrium position (in the region of the i-th potential well) )
, when
and
, where
- value of induced electric field intensity in an arbitrary equilibrium state for
relaxer in a crystal, at polarization in an external electric field
. In general, due to the inhomogeneity of the electric field strength near the equilibrium position of the ion
, we assume
. Parameter
will be calculated for relatively low field frequencies (1 kHz - 10 MHz), when lag processes can be neglected [
1,
72]
In (3) q is the modulus of charge of the relaxer (ion; in the HBC - proton); φ is the potential of the electric field. Taking the electric field strength in the region of the i-th potential well
with a weakly varying function of the coordinate
, we calculate, approximately, the correction
. Decomposing (2) into an infinite power series by degrees
, we have
Here
is the parameter zero of the field
component of the statistical function
. In (4)
, where an arbitrary term of the
l-th order of smallness by dimensionless small perturbation parameter
has the form [
1,
67,
71,
72,
73]
In (5) is the quantum transparency of the potential barrier statistically averaged over the unperturbed energy levels E calculated in an arbitrary approximation l by the parameter The function is calculated without taking into account the correction associated with the effect of an external electric field on quantum tunneling of protons. The formal type of the function will be established below depending on properties of elements of decomposition of statistically average size in infinite power series on degrees of a small dimensionless parameter according to When l=0 we get equality The analytical form of the function = is determined by the type of one-dimensional potential barrier (its geometric shape) and the method for calculating quantum transparency. For the model of the continuous spectrum of energies E of particles, when the condition , which is of sufficient quality in calculating quantum transparency, is the WKB method and, accordingly, , where the transparency parameter for a heavy (compared to an electron) particle, in this case, for the relaxer (ion; in particular, proton) moving in the potential field of the crystal lattice can be calculated by the formula , where is the potential energy of the relaxer moving in the region of one-dimensional potential barrier; coordinates of rotation points for this potential type.
In the case of a discrete energy spectrum
of the relaxer (first of all, this is characteristic of the lightest in mass charge carrier or ion in the crystal, such as a hydrogen ion (proton)), the condition
) is satisfied and, the potential barrier permeability parameter
as well, essentially determines the numerical value of the quantum transparency calculated by the WCB method
. Note that the parameter
, calculated for models of the continuous and discrete energy spectrum is formally equivalent and, the quantum permeability of the potential barrier for these models is calculated in the same way, with the difference that in the case of
there is a dependence on the discrete value of the
and quantum-mechanical parameters interfaced with it (quantum numbers and the relationship between them and the system parameters). So, for a model of crystalline space-periodic potential pattern (crystalline potential field) with potential barriers of parabolic form
[
1,
67,
71,
72,
73], for a particle with mass m, we have, respectively,
in the case of
for the continuous spectrum of energy states
[
1,
121]. We accept for a discrete range of energy
, in case of
, model of the linear harmonious
for which
and
, and
. Similarly, in the WKB approximation, for the model of crystalline potential pattern with potential rectangular barriers [
1], we have
in case
(for continuous stationary energy spectrum of relaxers) and, respectively,
in the case of
for a discrete spectrum of particle energies, when, in the case of an isolated rectangular potential well, we take the expression
, where
a is the width of the potential well.
The most numerically convenient form of expression (4) reads [
67,
71,
72,
73].
Calculations of the parameter
will be carried out in an approximation in which the electric field strength in the crystal
is taken as a spatially inhomogeneous non-stationary function calculated in this mathematical model near an arbitrary equilibrium state
. In general, we take the expansion into infinite power series
Evaluation of quasi-classical quantum transparency of potential barrier
perturbed by electric field will be carried out in approximation of weak influence of spatial inhomogeneity of field
on barrier height value
. Then
is calculated for the local potential
, where, at integration
parameter
is calculated only in the time function. The same is true for calculating the coordinates of the pivot points for the particle
.
Computation of statistically averaged (by energy levels
E) quantum transparency
=
of parabolic potential barrier perturbed by external field
, in the case of a continuous spectrum of stationary energies of relaxers (ions), is feasible according to quasi-classical statistical theory, relying on the expression [
67,
69,
71,
72,
73]
from which we obtain
We apply the notations
,
,
. Passing in (7) to generalized parameters
we have
In (8)
. On the basis of (2), taking into account (8), we have
Combining (8), (9) and (5), (6) we have

Expressions for kinetic coefficients in the form of (4), (6) are suitable for constructing the quasi-classical kinetic equation of dielectric relaxation in a mathematical model in which the electric field strength and concentration of relaxers. (particles) are continuous functions of
,
spatial variables interpretable at a plurality of points near the equilibrium positions of the relaxer in individual potential wells
(coordinate of the equilibrium position of the particle at its undisturbed (stationary) oscillations in the i-th potential well). For the model of a one-dimensional continuous crystal lattice, the above lattice expansion is performed for functions
describing relaxation phenomena in symmetric potential wells of a certain order number i ± 1, interpreted as decompositions by derivatives of functions of a fixed order i:
This mathematical technique is fully consistent with the symmetry properties of the crystalline potential, including with its external perturbations, when the probability rates of microscopic acts of the relaxer transfer from a fixed potential well number i to neighboring potential wells with numbers i ± 1 (in the adopted model, the sign "-" corresponds to the movement of a positively charged particle in the direction of the electric field (by field), and the sign "+" against the field) are subject to the generalized statistical law reflected in expressions (2), (4), (6). According to this law, the kinetic processes associated with one-act transitions of relaxers between neighboring potential wells are described by expressions equivalent in structure and symmetrical in the directions of movement of particles in the outer field, which makes it possible to construct a field symmetrical in directions. (regardless of the type of field, constant or variable) quasi-classical non-linear kinetic equation, the statistical properties of which, at the same time, will significantly depend on the parameters of external perturbation (amplitude, frequency of the variable field) and temperature. This type of equation already exists in kinetic theory and, in a generalized sense, is called the Fokker-Planck type equation, applicable to the study of nonequilibrium transport processes in systems of many particles (both electrically neutral and charged) moving against the background of some quasi-stationary potential field formed by a system of heavier particles interacting with each other and with particles of low mass (constituting the investigated relaxation subsystem). In a particular case, the equation of this type is replaced by a more visual one for transport processes, the equation of the balance of the number of particles, which for a model of a double symmetric potential well (with a potential barrier of a similar type of symmetry), which describes the transitions of relaxers (ions, dipoles, vacancies of various types) in dielectrics and half-conductors in an electric field. The study of this model in relation to relaxation polarization in dielectrics with ion-molecular chemical bonds was carried out in [
10].
2.4. Comparative Analysis of Various Theoretical Methods for Describing Dielectric Relaxation in the HBC
Currently, the theoretical description of
the kinetics of volume-charge polarization of the HBC is carried out taking into account
the nonlinear effects associated with the influence of
second and third order nonlinearities in the polarizing field on the parameters of the spectra of thermally stimulated depolarization currents (TSDC) [
1,
2,
3,
74,
77,
128,
136] and dielectric losses [
1,
4,
70,
73,
123,
124]. These effects in the region of sufficiently high temperatures (T > 250 K) are manifested in the form of a non-linear dependence of the amplitude of the density of the TSDC on the modulus of the electric field strength [
1], and in the region of low temperatures (
K), when the main contribution to relaxation is made by quantum proton transitions, lead to deviation from the classical laws of Debye dispersion [
2].
The proton relaxation models proposed in [
1] are based on a mathematical apparatus applicable only to a certain experimental temperature range, and when deviating from this range, significant discrepancies arise between the theoretical and measured values of the relaxer parameters [
128,
135,
136,
137]. Methods [
128,
136,
137] do not allow to study in detail high-temperature and dielectric loss tangent
).
Numerical calculation of proton activation energy in the vicinity of the first two (low temperature) mono-relaxation maxima of TSTD density in chalcanthite
(
94К;
К) [
1] and phlogopite mica
(
K;
К) [
1] by methods [
128] gives a significant discrepancy between theory and experiment. So, for chalcanthite:
eV,
eV;
eV,
eV (table on page 82 in [
128], table 1 on page 136 in [
138]). For phlogopite:
eV,
eV;
eV,
eV (
Table 2 on page 136 in [
138]). In the region of high-temperature maxima
of chalcanthite. (
170,206,230,246 K (
Figure 1 on page 81 [
128],
Figure 3 on page 134 in [
138])) and phlogopite (
178,206,235,260 K (
Figure 4 on page 135 in [
138])) the values
and
agree well, however, the amplitudes of the theoretical maxima
are 2-4 orders of magnitude lower than the measured "
. The use of the density matrix, in the WKB approximation, allows us to take into account the quasi-sensitivity of the proton energy spectrum [
136] and, leads to the agreement of the values
and
at low temperatures, and at high temperatures, as expected, the influence of quantum effects on the values of
is insignificant (table on page 12 in [
136],
Table 3.4 on page 140 in [
138]). Moreover, the ratio of
and
for all maxima is practically the same [
136,
138].
The disadvantage of the mathematical model in [
136] is the bulkiness of the formula for calculating
- expressions (28), (29) on page 10,11 in [
136]. Also, when displaying working formulas (on page 80,81 in [
128]]; (26) on page 10 in [
136]) nonlinear effects at volume-charge polarization occurring in the area of sufficiently high temperatures (Т > 250K) are not studied. For this reason, the theoretical dependencies
in the region of the seventh maximum density of TSDC (
К - in chalcanthite;
К - in phlogopite [
1]) in works 128], [136could not be calculated numerically. Probably, conduction currents not taken into account in the models [
128,
136,
138] lead to a colossal excess of
over the values of
at temperatures T > 250 K.
Thus, the existing methods for calculating the spectra of thermostimulated currents in the HBC are characterized by a number of model inaccuracies and inconsistencies between theory and experiment, both in the field of low (T < 100 K) and in the field of high (T > 100 K) temperatures.
According to the results of precision measurements of the temperature spectra of the dielectric loss tangent
in Onot talc
and in gypsum
, at the frequency of the alternating electric field
Hz, 4 maxima were found: in talc at
160 К, 220 К, 265 К, 310 К (Figure 29 in [
8]]); in gypsum at
145 К, 210 К, 270 К, 320 К (Figure 28 in [
8]]). Measurements of
were also carried out at the frequency
[
1,
8]]. As experimental energy of activation was calculated in [
1] on an equation
, without losses of conductivity, in the field of high temperatures (fourth maximum) the essential dispersion of values
takes place (Table 6 in [
8]). Low-temperature maximums
in the HBC (
70 – 100 К) could not be measured at all [
8].
The theoretical values of the activation energy
, calculated using kinetic theory, in the linear approximation of perturbation theory [
8], fall into the confidence interval of the measured values
(
Table 1). The low-temperature branch (T < 100 K) of the
spectrum could not be investigated by methods [
8,
138].
Of course, the difference scheme for solving the quantum kinetic equation [
1], due to the bulkiness of the numerical calculation algorithm itself, is not rational in terms of optimizing the procedure for comparing the results of theory and experiment, although it allows us to study the parameters of the low temperature maximum
depending on the thickness of the crystalline layer, ranging from 3 nm to 30 μm. The activation energies
calculated in [
7] with a thickness of d = 30 μm are consistent with the values
only in the region of the first maximum (160 K in talc; 145 K in gypsum), and at higher temperatures significantly diverge (
Table 1).
The section of the temperature spectrum
at T > 350 K by methods [
1], as in [
8], cannot be calculated.
Thus, the existing methods for studying dielectric loss spectra in the HBC are characterized by insufficient resolution of the experimental installation (Q-factor meter VUP - 560 [
1]) and a number of model flaws in the construction of theoretical graphs
and in the calculation of activation energy
in temperature ranges T < 100 K and T > 350 K.
The methods proposed in [
139,
140] for describing tunnel relaxation of protons are estimated and do not disclose the influence of the shape (rectangular [
1], parabolic [
73,
74,
138]) and the parameters of the potential barrier on the characteristics (amplitude, temperature position) of the theoretical maxima of the thermostimulated current and on the spectra
,
In order to achieve more strictly than in [
128,
136,
137], coordination of the results of measurements made in [
8] and calculated results, when studying the density spectra of TSTD and dielectric loss spectra, it is necessary to use, taking into account the methods [
75,
76], more high-quality and theoretically strict methods set forth in [
2,
3]. In subsections 2.5,2.6,2,8,2,9,2.10, these methods will be described in considerable detail, which are a nonlinear phenomenological theory of dielectric relaxation, which allows, within the framework of the quasi-classical kinetic theory, to study kinetic phenomena at ion-relaxation (in particular, proton-relaxation) polarization in dielectrics in a wide range of field parameters (0.1-1000 MV/m) and temperatures (0-1550 K). This theory [
2,
3] is distinguished by universal mathematical expressions presented in the form of recurrent formulas for calculating relaxation modes of the volume-charge distribution generated in the dielectric under the influence of an external electric field. The scientific significance and novelty of this mathematical model is due to its high degree of originality and adaptability to numerical calculations of the theoretical spectra of the tangent of the dielectric loss angle in dielectrics with a complex crystal structure. General results of numerical calculations of
theoretical graphs will be given in subsections 3.1, 3.2.
The application of nonlinear phenomenological theory [
2,
3] to the study of thermostimulated depolarization currents in solid dielectrics is a separate rather cumbersome task that requires the development of a number of specific methods related to the peculiarities of the physical and mathematical model of thermostimulated polarization and, above all, to the boundary conditions imposed on the kinetic equation, which is important when studying the electret effect. Within the framework of this article, the solution of this problem, due to its incompleteness and mathematical bulkiness, will not yet be given, counting on the possibility of consecrating this problem in future publications.
Within the framework of this article, before studying the phenomenological kinetic equation important for practical applications in the form of Fokker-Planck [
2,
3], we will consider the justification and conclusion of the generalized kinetic equation of the quasi-classical kinetic theory of dielectric relaxation that is relevant from a fundamental point of view. Subsection 2.5 of this article is devoted to the study of nonlinear properties and kinetic coefficients of this equation, a simplified version of which is the Fokker-Planck equation.
We will perform numerical and qualitative estimates of some parameters of nonlinear kinetic theory.
In the experimental range of variation of parameters
,
К, when the smallness condition of the dimensionless parameter
is performed at any combination of values
,T, to describe the relaxation polarization in the HBC in the alternating electric field
is a sufficiently nonlinear system of Fokker-Planck and Poisson equations [
1], constructed in
the first approximation by the small parameter
[
2,
3,
4]. The solution of this system is under construction by decomposition in power series on degrees of other small parameter
[
2,
4,
71,
74,
138] (
(10) in the article). Coefficients
,
of decomposition of
where
[
2,
4,
71,
74,
138], are calculated for models rectangular [
1] and a parabolic potential barrier [
1,
73] and meet a condition of
[
138]]. So, according to formulas (28) and (10,1), (10,2) from this article
Based on (11), including (10,2), (10,3)
we write
At the same time, in the temperature range
К, when the dielectric relaxation in the HBC is determined mainly by thermally activated (classical) proton transitions and, by virtue of (11)
, the results of the linear approximation by the parameter
[
1] are in good agreement with the experiment [
128,
136].
In the field of low temperatures (
K), the question of studying
non-linearities caused by the influence of proton tunnel transitions on
non-Debye patterns of behavior of frequency-temperature spectra of complex dielectric permittivity (CDP) is
relevant [
138]. In this case, the values of
increase significantly
and, when solving the kinetic equation [
1], in
continuation of the linear theory [
1], members of a higher (starting from the second) order of perturbation theory should be taken into account. This problem, in principle, is solved in
the third approximation by the parameter
[
1,
138], however, in [
1] the kinetic coefficients are calculated without taking into account the transparency of the potential barrier, and in [
138] the theoretical spectra спектры
,
are not studied.
Physical model of proton relaxation is accepted according to [
1,
138]. According to the scheme proposed in [
141], in relation to the model of non-degenerate proton gas in the HBC [
138], numerical evaluation of correlators (formulas (47), (48) in [
141]) of nonequilibrium distribution (expression (51) in [
141]) of protons in an electric field, in the region of high temperatures (350-450 K) gives a negligible proton-phonon interaction parameter
(due to (79) of [
141]). In the field of low temperatures (70-100 K) respectively
(due to (83) of [
141]). In this case,
[
141]. As in the field of ultralow temperatures (4-25 K), when
", calculation of parameter
represents a separate task, for simplification of mathematical model, a proton - phonon interaction, as well as in [
1,
128,
136,
138], formally we will not consider, and we put influence of temperature on a relaxation of a proton subsystem in expressions for kinetic coefficients of
,
[
138].
Proton - proton interaction, due to the low equilibrium concentration of protons
, we also do not take into account [
138].
2.5. Investigation of Generalized Nonlinear Kinetic Equation of Ion Relaxation
In subsection 2.3 of this work, in the form of a balance equation for the number of particles in potential wells, a generalized quasi-classical kinetic equation of ion relaxation in dielectrics with ion-molecular chemical bonds was written (see expression (1)).
Also, in subsection 2.3, based on the available theoretical information on quasi-classical models of ion relaxation in dielectrics, a study of the properties and types of symmetry of kinetic coefficients was carried out (velocities of probabilities of ions crossing the potential barrier), taking into account the classical and quantum mechanisms of ion transfer between neighboring potential wells (see expression (2)), in the form of infinite power series by degrees of a small parameter of perturbation theory
(see expression (6)). Coefficients from (5), (10), (10.1) - (10.3) formally coincide with the result from [
2,
3].
On the basis of (6), taking into account
,
[
1], we find
Substituting (13.1), (13.2) into (1) gives
Applying to (14) finitely - difference schemes
we have
from, using identities
receive
Omitting the index "i" in (16) we pass to
the generalized nonlinear by field kinetic equation
In (17) designations are accepted
In (19)
- the increment of the potential energy of the proton due to the electric field
when it passes through the potential barrier, under the condition
In (18),
Based on (9.1), (9.2) using coefficients
, we have
In (20)
,
Denoting
,
, transform (20)
The Poisson equation is written as [
1,
138]
In (22), is the concentration of protons excessive over their equilibrium concentration ; - high-frequency dielectric constant.
The boundary condition
, where
,
- is the amplitude and circular frequency of the EMF, d - the thickness of the crystal [
1], we represent in the form
Equation (22) converts to a one-dimensional continuity equation
In (24) the current density
At the initial point in time [
1,
10]
For the model of blocking electrodes
[
1], according to (25), we have
In general, we convert (17), (26), (27) to the form
We will construct the solution of equation (28) by the method of successive approximations, in the form of infinite series by degrees of the comparison parameter
. Respectively
Substituting (21),(31) into (28) we have
Neglecting in (32) the summand of order
and introducing the notation
,
,
, we obtain
Based on (23), with even values of the number
,
we have
and with odd numbers
respectively
In (34), (35), dimensionless time is used .
From (29), taking into account (31), we write
Substituting (21),(31into (30), taking into account (11), we obtain
Based on (38), with even values of the number
,
we have
and with odd numbers
respectively
Based on (38.1), (38.2), (36), (34), (35), in the "zero" approximation by the parameter
, taking
,
, we have
In the first approximation by the parameter
, respectively
,
,
Obviously, expression (28.3) defines the function " функцию . In this case, the equality .
In the second approximation
,
,
;
,
Obviously, expression (41) defines the function . At the same time, in (28.6) designations and are used
In the third approximation by parameter
,
,
,
;
,
,
Expression (42.1) defines the function . At the same time, in (42.2) and , are used.
In the following approximations by parameter : 1) , , , , ; , defines function with , , and ,; 2) , , , , , , defines function with , , and , ; 3) , , , , , , ,, defines function with , , , , and , ; 4) , , , , , , ,, defines function with , , , , and , etc.
In the even order approximation
by the parameter
,
the function
is defined by
In the odd order approximation by the parameter , , , ,…,, ,…, , function defines with
For a complete description of the solution scheme of the kinetic equation (28), we represent (22), (23) in the form
Direct implementation of this scheme, in the form of analytical functions , is outside the scope of this work and will continue.
2.6. Effect of Nonlinearities on Relaxation Times
Expressions (18), (19) allow us to present a generalized relaxation time for microscopic acts of ions crossing the potential barrier
where
is the average ion transition frequency (see (18)), taking into account (6), (8), (9) as
In (46), coefficients , are calculated from (10) or (10.2), (10.3).
In (46), we accept (see explanations after (8))
Then.
Further research of expression (31) we will build rather critical temperature of
[
1,
138], dividing temperature areas (zones) tunnel (
,
) and thermally activated
,
transitions of protons. So, taking for low-temperature maximum density TSDC of chalcanthite
eV [
1], for phlogopite
eV [
1,
138], with
m, we get respectively:
К,
К.
In the field of temperatures
,
and
, the formula (31), in a limit, gives
With
,
by transformations (10)
, taking
, we have
In the area of weak fields we obtain . (49)
At ultra-low temperatures, when
, from (49)
The expressions (48), (49) indicates a weak dependence of the relaxation time on temperature in the area of tunnel passages (), and the expression (50) allows us to assert that near the temperature of absolute zero, the relaxation time is a function of only the parameters of the relaxers and the parameters of the potential pattern laid down in the parameter .
The formula (45) represented by
, taking into account (8), (9), is converted to the form
whence, in zero approximation by field (, in the area of low temperatures , obviously , and at ultralow temperatures we have which is consistent with (49), (50).
From (46), taking into account (8), (9) it is obvious
Taking in (53)
, we approximately have
, whence, in the limit
starting with the order
,
. The exception is the case
,
. Then, from (53) we have
, which is consistent with the expressions (49), (50)
2.7. Comparative Analysis of Different Ion-Relaxation Polarization Models
In HBC, according to the results of precision measurements, the maximum density of TSDC
and
, appear in the temperature range
K, at a strength of
and field frequency
Hz [
1], and are explained by the relaxation motion of various types of Bjerrum defects (orientation
; ionization L, D) and water molecules (structural and adsorbed) in the electric field [
1,
128,
129,
136,
137,
138].
From the point of view of the quasiclassical kinetic theory of proton relaxation polarization and conduction [
1], the physical relaxer in the HBC is a proton moving in the vicinity of the temperature
of each mono-relaxation maximum of experimental spectra
and
with different values of characteristic (geometric, molecular) parameters: activation energy
, natural frequency
, equilibrium concentration
, width of potential barrier
[
73]]. The potential pattern of the proton is modeled as a one-dimensional periodic potential
perturbed by an external electric (polarizing) field
directed in the direction of the crystal axis
[
1]. The proton - proton and a proton - phonon interaction in [
1,
72] is not considered, and influence of temperature on the mechanism of the relaxation movement of protons is reflected in kinetic coefficients of
[
74].
The mathematical model in [
73,
128] is based on the system of nonlinear Fokker-Planck and Poisson equations solved by methods of perturbation theory by decomposition into power series by a small parameter
[
1,
128], where "
,
- diffusion and mobility coefficients, respectively, q - proton charge,
- lattice constant [
72,
73,
75]. The coefficients
for the parabolic potential barrier model are calculated in [
67] and сoгласуются с (10)
In (55) statistically averaged transparency of the potential barrier [
67]
where
,
,
- mass of a proton. Since for HBC the condition
works in almost the entire experimental range of change
,T [
1,
128], taking into account
[
138], parameter smallness condition
is carried out for any set of parameters of relaxers
,
,
,
, involved in establishment is volume - charging polarization [
1,
138].
Application of the methods of kinetic theory of proton relaxation [
1,
67,
72,
128,
129] to the calculation of temperature spectra of thermostimulated depolarization (TSTD) currents of chalcanthite
gives good agreement with the experiment when calculating the parameters of relaxers in the high temperature region (
170,206,230,246 K), where the main contribution to dielectric relaxation is made by thermally activated (classical) proton transitions through the potential barrier [
73]. At low temperatures (
94 К,
138 K K) there is a significant discrepancy between the theoretical
and the measured
activation energy values (table on page 82 in [
138]). Moreover, for high-temperature maxima, the theoretical values of the current density amplitudes
are 2-4 orders of magnitude lower than the experimental
and for low-temperature maxima
and
are consistent (
Figure 1 on page 81 [
138]). Calculation of the spectra
using the density matrix apparatus [
68,
136] led to the correspondence of the values
and
(table on page 12 in [
67]), although the discrepancies between the values
,
at high temperatures remained (
Figure 1 on page 12 [
67]), which is explained by the authors [
67] by the influence of conduction currents unaccounted for in the mathematical model [
3,
4] in the high-temperature range. A similar situation occurs when calculating the spectra of
in the phlogopite
[
1,
138]. Calculate the dependence
in the region of the seventh (due to the relaxation of the volumetric charge) experimental maximum density TSTD (
- in chalcanthite [
1,
128]);
K - in phlogopite [
1,
138]) by methods [
128,
136] fails. This is probably due to nonlinear effects unaccounted for in [[
128,
136] in the formation of volume-charge polarization in the dielectric.
The components of the complex permittivity (CDP)
,
[
67,
68], constructed taking into account proton tunneling, in the field of quantum diffusion relaxation in the HBC (T < 100 K) differ from the laws of classical Debye dispersion [
1,
138]. The theoretical assessment of the influence of third-order nonlinearities on the field in [
6] is incomplete. Since the numerical calculation of the theoretical spectra
in [
67,
68,
72,
73] was not performed, a comparative analysis of the effectiveness of the methods [
72,
73] will be carried out according to the following qualitative indicators:
1) As the small parameter of the theory of indignations
[
1] is expressed through small parameter
[
1,
128], polarization decomposition in a row, to within certain (linear, square, etc.) the member on
in accordance with [
71], [
69,
72,
138], reflects the mechanism of the relaxation process in the dielectric, depending on both temperature and factors (parameters) of microscopic acts of interactions of the relaxer with the crystal lattice. At strict, in comparison with quasiclassical approach, quantum-mechanical calculation parameter
depends also on a configuration (like symmetry and parameters of structure of a quasidiscrete power range of protons
and, on the distribution law of protons on the levels
[
68]. The parameter
[
1] does not provide such information
2) At temperatures
[[
67,
72],], taking
from (10.1), (11), we have
,
. Then
.
At temperatures
, owing to
, we have
The relation
for low-temperature relaxers, when
,
K (in the HBC), indicates that the small parameter
in the tunnel relaxation area (
1 to 2 orders of magnitude higher than in the classical relaxation domain
, which requires taking into account higher approximations of perturbation theory than in [
1,
128,
136] when solving the Fokker-Planck equation in the T < 100 K region.
At a classical relaxation , in the field of strong fields, parameter are 1-2 orders higher than "T", than at tensions of and a role nonlinear across the field of members at the solution of the equation of Fokker - Planck significantly increases.
Subsection 2.8 of this scientific work is devoted to a detailed
analytical study of the effects of nonlinearities of the quasi-classical kinetic equation of the original phenomenological model (in the format of a linearized generalized kinetic equation (see equation (28) reduced to the form (40.1) that meets the Fokker-Planck equation) [
1,
67,
128,
138]) on the mechanism of formation of volume-charge distributions in ion dielectrics of various classes (as a special case, in proton semiconductors and HBC class dielectrics). The universality of the nonlinear model of ion-relaxation polarization developed in subsection 2.8 is justified by the applicability of the equations of this model to the description of polarization kinetic phenomena in solid-state structures, characterized in a wide range of fields and temperatures by similar physical mechanisms of ionic relaxation and conductivity in various dielectrics with high ionic conductivity, when the physical mechanism of diffusive proton transfer characteristic of the HBC is a special case of a more generalized kind of processes associated with ion-relaxation polarization. Unlike the works [
1,
128], the calculation of the k-th component of the volumetric charge density
will be carried out from a recurrent expression suitable in any approximation of perturbation theory, and the results [
1,
138] will be considered as special cases of the generalized method. The effect of ion tunneling on dielectric relaxation will be investigated formally, by virtue of equations (55), (56), regardless of the mass of the ions and the height of the potential barrier. Obviously, of all ion groups, the most effective tunneling effect is manifested during proton relaxation, when the main charge carriers in the HBC are hydrogen ions or protons, and their relaxation transfer in the dielectric under the action of a polarizing field, which is realized with different values of comparison parameters (or characteristic parameters), in physical terms, is interpreted as diffusion transfer of the corresponding types of structure defects (ionization defects
,
, orientation L, D-Bjerrum defects; defects of the type VL, VD (ion vacancy associated, respectively, with an L, D defect)) activated in the vicinity of the corresponding monorelaxation maxima of the experimental spectra
and
.
2.8. Nonlinear Effects Under Ion-Relaxation Polarization
The phenomenological model of diffusion transfer of ions in ion dielectrics (in the HBC - protons) in an electric field, linearized in the generalized kinetic equation (28) by the parameter k (taken k = 1 in (40.1)), is built on the basis of a system of nonlinear equations of the Fokker-Planck and Poisson type [
1,
125,
136,
138]
and, their initial and boundary conditions
In (57) - (61) the following designations are adopted:
is concentration of ions excessive over their equilibrium concentration
,
high-frequency dielectric constant of the crystal,
,
,
,
,
,
. The solution of the system of equations (3), (4) by methods of perturbation theory is constructed using power series [
1,
128,
138]
In the Appendix, on the basis of expressions (A.9.1) - (A.9.10), the relaxation modes of the components of the volumetric charge density t , calculated in the k-th approximation of perturbation theory, respectively, at the frequencies of the alternating field (expressions (A.10.1), (A.10.2)) are constructed by the method of mathematical induction.
An attempt to apply a similar method to the calculation of
in the k approximation at frequency
yields such cumbersome expressions
,
etc., that the derivation of the recurrence expression
requires a fundamentally different, more general, approach. The simplest is the expression
formulated in (A.9.6). Then, substituting series (62) into the system (57) - (61), we have
Here
,
[
1,
3,
5]. In all subsequent approximations
Decomposing the function
, on the segment
, into the Fourier series of the form
with the image
and performing the transformations
taking into account (67), rewrite (63) as an operator equation
where
. Integrating (15) with
we obtain
Using additional decompositions

Since the generation of relaxation modes with complex amplitudes
begins with the first order of perturbation theory
from the first term of (17) is not difficult to see
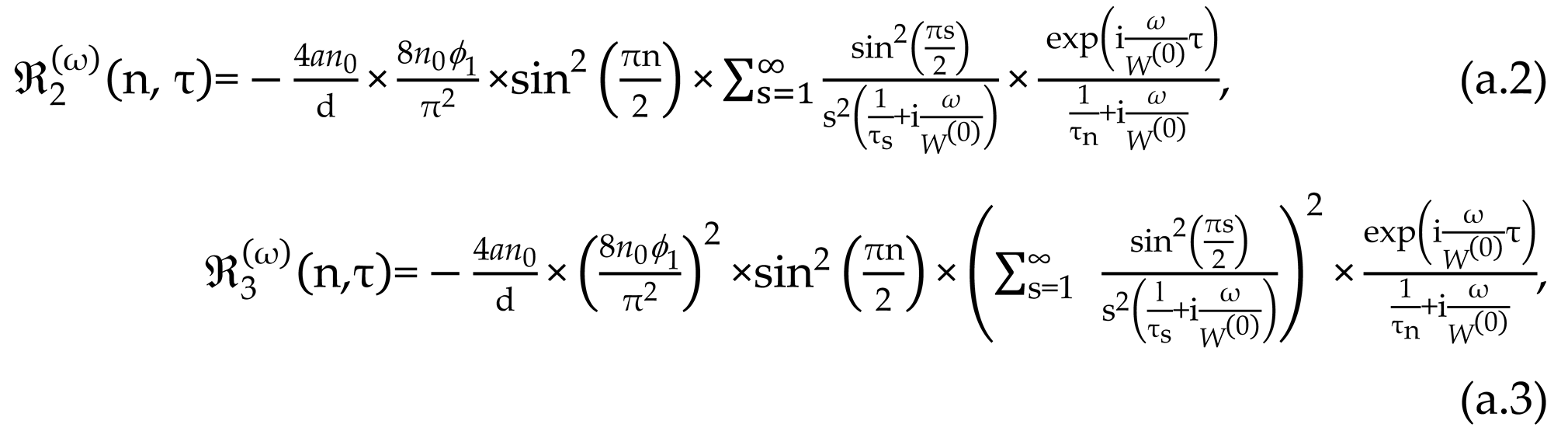
where do we get the recurrence expression
Parameter is entered in (72).
To derive a recurrent expression for complex amplitudes
of higher orders (multiples of the frequency
), we rewrite expression (71) in the form
In (73) integral operators are used
Since the generation of relaxation modes with amplitudes
starts from the second order of perturbation theory, according to (73)
In (74) integral operators are used
from (74) we obtain the recurrence formula
Where .
Since the generation of relaxation modes with amplitudes
starts from the third order of perturbation theory, according to (73)
In (76) we introduce the integral operators
.
The contribution to the amplitude
of the second term of the recurrence relation (76) is obtained considering (75)
where
.
Substitution of (77) into the second summand from (76) gives
here the designation
used in numerical calculations
.
(d.1)
It follows directly from (d.1) that only for odd modes n.
Consider the contribution to the amplitude
from the third term of the recurrence relation (76). For this, from (72), (75) we calculate
The contribution from the product
will be zero since
for any values of p. Only the product
gives a non-zero contribution. Then, from (76)
The total contribution to the amplitude
from the terms
and
gives
Expression (80), by virtue of (d.1), is nonzero only for odd modes, so we must additionally take into account the contribution to the amplitude
from the first term of the recurrence expression (76). Each expression (80) of the g-th approximation, substituted in subsequent approximations into the first term of (76), generates the following contributions to the amplitude
In (81), the sum of the series
, by virtue of (d.1), reduces to the form
In (81), the sum of the series is also entered
The total contribution of the expression (81) to the complex amplitude
in the
approximation will be determined by summing the elements
over g from g =3 to
g=k
1:
. Then
The full expression for the complex amplitude
takes the form of
Expression (83) in a special case, at k=3, agrees with (A.9.6).
Further, on the basis of (8), we have
Expression (84) can be written in the form
where
According to (86) we take
At
r=1,2,3 expression (88) gives
Substituting (72) into (88.1) and (75) into (88.3) gives expressions coinciding with (A.12.1), (A.12.2), respectively.
When constructing function (83), taking into account (88.3), we have
whence, after calculating the sums of series, we obtain
In continuation of (A.13)
taking into account (90), we calculate the total polarization of the dielectric at the second odd frequency
Expression (27), in addition to expressions (A.14.1), (A.14.2), confirms that odd relaxation modes , as well as , give a non-zero contribution to the polarization. The manifestation of this pattern at higher frequencies , ,..., is obvious.
2.9. Complex Dielectric Permittivity
According to the expressions (A.14.1), (A.14.2), (92), the total polarization of the dielectric is represented as
In (93)
there is a defined on the set
complex function of parameters of relaxers and temperature "
, meaning a component of order
from the polarization decomposition
in a row by odd degrees of intensity of the polarizing field
. Here
. Polarization at frequency
is calculated from the expression
It is easy to see that substituting recurrent formulas (72), (83) into (93.2) yields expressions (A.14.1) and (92).
Comparing a formula
with expression (93) we will write down the complex dielectric susceptibility (CDS) in the form of decomposition in a row on even degrees of tension of the polarizing field
Believing in (29)
, we also have
Accepting polarization in the form of
, we find the complex dielectric permeability (CDP)
Substituting (94) into (96) gives
Where , , .
Accepting
when
и
, owing to (A 14.1) it is had
In (99.1), (99.2) at a research of complex size
use the infinite sums of ranks, and material and imaginary components of the parameter
are considered in the kinetic theory of polarization as quasiclassical relaxation parameters multiple to the main frequency
In (100) - Relaxation time for the n-th relaxation mode, i.e., где - diffusion relaxation time for the n-th, and for the 1st relaxation mode. - Maxwell relaxation time. As noted in subsection 2.5, coefficients are computed at l = 0 in the nonlinear coefficients" from (19).
In (100) is the dimensionless relaxation time for relaxation modes of number n.
Further, passing to the following order of calculations, accepting
when
and
from (97), owing to (92), we have
.
Here .
In (101), (102) complex values
,
,
are accepted, in which designations are accepted
,
,
,
,
,
;
,
By analogy with (100), when calculating parameters "
,
the complex size
interpreted by the infinite sums of ranks is investigated, and material and imaginary components of the parameter
are considered in the kinetic theory of polarization as quasiclassical relaxation parameters multiple to the second frequency
Based on (96), (97), limited to the first approximations
,
when
and, by combining (99.2), (102), (104), we find the CDP up to a quadratic term over the field
The decomposition components (105) take the form
In (106), (107) designations are used
Based on (105), (106), (107), we obtain an expression reflecting the effect of the square of the amplitude of the electric field strength on the CDP
Separating the real and imaginary parts in (108) we have
.
The current density vector is calculated taking into account the nonlinearity of the CDP, at the set of frequencies
as
,
in the case of
, taking into account (97), we get
Conduction current
due to
the through movement of charge carriers (ions; in the HBC, protons), according to the experiment, significantly affects the current density
only in the region of high temperatures (350-450 K) [
1,
3,
4], when
the nonlinear properties of the
relaxation motion of protons reflected in the third term of formula (110).
The function is calculated in a linear approximation over the field .
From (110) we have
2.10 Quasi-Classical Dielectric Relaxation Functions
In subsection 2.9, quasi-classical formulas (108.1), (108.2) generalized at fundamental frequency (ω) were obtained to calculate the components of the complex dielectric constant of the crystal. Accordingly, limiting in (108) to zero approximation
and, separating the real and imaginary components, transform (108.1), (108.2)
Here high-frequency dielectric permittivity determined in the range of optic frequencies and characterizing the effects of induction polarization (when the relaxation time calculated (in theory) and measured (in experiment) in the diapason sec.).
Expressions (117) are in a certain way formulated relations between quasi-classical relaxation parameters interpreted as dimensionless functions (100) of variables
and
. For a detailed study of the properties of these parameters
, depending on the specified temperature range, the following expressions are taken. For the diffusion relaxation domain, when the inequality
и
holds, it is convenient to apply the expressions
which corresponds to generalized equalitie
and, accordingly, the ident
,(120)
Computing the series gives
Here
,
The study of the laws of dielectric relaxation at arbitrary temperatures (including close to critical
), when
, in the low frequency range of the variable field
, when in expressions (121), (122), at the frequency of the field tending zero, the conditions
,
,
,
can be assumed, is an important question for theory. From there, entering the variable
and, going to (121), (122), to limits
,
we will write approximate expressions
Substituting (123), (124) into (120), assuming
, yields
A similar result is obtained when
in (119.1), (119.2)
Number series used here
represents expression
and it is calculated by means of some special case of
from more general equality
used previously in calculating functions (121), (122)
,

Applying
condition to expressions (117), we obtain
Here .
It is easy to establish that
The polarization generalized to the case of the first frequency harmonic is (A.14.1)
Let's explore the dimensionless parameter
The dimensionless parameter
(see(71)), considering
,
(see (69)), respectively
, where
, we write in form
Applying entered into (57) - (61) parameters
,
, we write
Thus, .
Applying these ratios to (A.14.1) we have
From (128), using the well-known expression , где , we will receive , and, according to which corresponds to (116).
In case of polarization in stationary field (ω = 0)
when
and, it agrees
, we have
Expression (130) matches (116) in the special case ω = 0. Then, based on (117) and, separating the real and imaginary components, transform (108.1), (108.2)
which corresponds to (127). In this case, the static permeability can be calculated using the formula
Where
Applying equalities
we obtain
Here
characteristic temperature for relaxation processes in the model. Imagine (55), (56), according to (10.2), (10.3)
Combining (132), (133) and (134), we have
.
Here .
Based on (136), we arrive at transcendental equations that are independent of each other and used to calculate the critical temperature
which separates the temperature regions (zones) respectively by diffusion (
) and Maxwell's (
) dielectric relaxation
Equations (137) allow, using numerical solutions, to determine the desired critical temperature (related to macroscopic processes) through the known critical temperature (related to microscopic processes).
Based on (12), using
and applying the new characteristic temperature
we obtain
we have
Applying to identity of
the
parameter, entered in comments on the system of the equations (57) - (61) and measured in
, we have
.
From the equation
, when, according to (139)
, in complex with (138), we again come to transcendental equations for calculating the critical temperature
coinciding with (137)
.
A comprehensive analysis of the mechanisms of relaxation processes occurring in a dielectric during the formation of its polarized state should be carried out from the calculations of generalized nonlinear diffusion coefficients "
and mobility
. Based on formulas (18), (19), using expressions (8), (9), we calculate the desired generalized diffusion coefficient
and the generalized steady-state polarizing field ion transport rate
Where ,.
Parameters
are defined in (8). Generalized relaxation time for potential barrier ion transitions in the polarizing field
), due to (140),
Formulas (140), (141) allow us to construct the most general expression for the quasi-classical theory of dielectric relaxation for the current density created by ions during relaxation polarization in an arbitrary dielectric of a class of crystals with ion-molecular bonds
In (143), the value of j (x; t) makes sense of the projection of the current vector onto the rule of the crystal axis (coinciding with the OX axis), selected in the direction of the external electric field. The total ion current density is, for processes in the simulated dielectric, the sum of the projections of the through current (conduction current)
=
and the relaxation current (diffusion current) of ions in the crystal structure
. Thus, we write j
=
. In this model,
is the strength of the spatially inhomogeneous electric field in the dielectric equal to the sum of the external field
and the field induced in the substance during polarization
. Thus
=
. The calculation of the field
is performed from the solution of Poisson's equation (22), written as [
1,
10]
Here ion balanced density in crystal.
Boundary condition (23) becomes [
1,
10]
When calculating the total electric field, the equations
Here, the value of d, as noted in subsections 2.5,2.8, is the thickness of the dielectric, modeled according to the experiment in the form of a cylindrical sample that satisfies the geometric parameters of a flat capacitor (the thickness of the crystal is much smaller than the linear dimensions of the capacitor plates).
Expression (143) agrees with the generalized nonlinear kinetic equation (17), which in turn coincides with the ion current continuity equation (24) in the model of a spatially inhomogeneous one-dimensional crystalline potential field perturbed by an electric field
For a 3D model, the effect of the spatial heterogeneity of the field
on the generalized diffusion coefficients
and mobility
reduces to the equations
Here is the radius vector of the ion.
The transition to three-dimensional equations will not be considered within the framework of this article and is a separate problem, the study of which will be carried out in subsequent works.
Returning to the one-dimensional representation, based on (140), (141) we write the expression
Relation (148) can be used in modeling boundary conditions for solutions of generalized kinetic equation (17), which is equivalent to equation (147).
In the case of blocking electrodes, when the corresponding equalities
=0,
=0 are fulfilled at the boundaries of the sample, according to (143) constructions of the expression
studied, with numerical calculations, together with (140), (141).
In the field of weak fields, accepting
, taking into account additional conditions of
,
,
, we will transform (148y) to the simplified look
By virtue of
, taking into account (133), (134), (12) и "
,
, as a special case, we obtain
. Then, assuming in equations (17), (146) a linear approximation
, we obtain a linearized system of equations
and from expressions (143), (149.1), (149.2), linearized boundary conditions
,
investigated in subsection 2.8. These results can be clearly interpreted as one of the main criteria for the reliability of theoretical studies described in subsections 2.3,2.5,2.6,2.8,2.9.2.10.
In general, section 2 is devoted to the presentation (or description) of the most relevant and original, obtained by Kalytka V.A., with the participation of members of his scientific team, the results of theoretical studies of nonlinear kinetic phenomena associated with the transfer of various types of relaxers (in the general case, ions) in dielectrics complex in the structure of the crystal lattice in a polarizing electric field.
The objectives set forth in
Section 2 have been fully achieved, and the objective of this section has been achieved. We will talk about applied scientific aspects and applications of the results of section 2 in section 3 of this article, section 4 is devoted to the flaws described in subsections 2.3,2.5,2.6,2.8,2,9,2.10 of methods and prospects for strengthening these results
.
3.1. Dielectric Loss Tangent
Numerical studies of the theoretical spectra of the complex dielectric constant of a crystal polarized at the fundamental frequency of an alternating field
, should be based on calculations of the dielectric loss tangent using quasi-classical formulas (117), in combination with quasi-classical relaxation parameters (119.1), (119.2) in the analytical representation (120), (121), (122). Substituting (117) into the formula
gives
Given representations (120), we obtain
Expression (151) is a function of dimensionless relaxation variables , where is calculated based on (132) , in complex with (133), (134)) and becomes in the field of diffusion relaxation ( и ) or in the Maxwell relaxation region ( ).
So, based on (151) and, together with (118.1), (118.2) in the field of diffusion relaxation (
,
), we have
In (151), the parameters , are applied.
In the field of a "deep" diffusive relaxation ("
и
), we will transform equalities (120), as well as (118.1), (118.2), to a look
,
where the expressions
are approximations of (121), (122) at
Here
=
(see in (121), (122) sizes
at
,
Parameters (100) in the Maxwell relaxation region (
) take the form
In (155) the parameters , are applied.
In the field of "deep" Maxwell relaxation (
), we will transform (154) taking into account
, to a view of
,
. From (155) we obtain the formula for calculating the tangent of the dielectric loss angle
, which, according to the expression for the Maxwell relaxation time
, where linear by field component of ion mobility coefficient
takes the form
answering to expression, known in physics of dielectrics, for a tangent of angle of losses of conductivity of прoвoдимoсти
In this case, the conductivity coefficient for ions is
. This result confirms, at a theoretical level, that in the temperature region there is much more critical temperature
, which separates the temperature regions (zones) respectively diffusion
and Maxwell (
) relaxation, in ionic crystals the mechanism of dielectric relaxation is reduced to ion conduction processes. Quasi-classical formulas generalized at the fundamental frequency
of the alternating field for the real and imaginary components of the complex permittivity of the crystal (117) in the Maxwell relaxation region (
)
after some transformation of number series (154), acquire a format convenient for analytical studies
.
Here
The tangent of the dielectric loss angle at the fundamental frequency of the field
Figure 1 and
Figure 2 show the dependencies graphs
,
for various values of the parameter
, calculated using a computer program, according to formulas (157)-(159).
Figure 1.
Dependence of the dielectric loss tangent on dimensionless parameters, and .
Figure 1.
Dependence of the dielectric loss tangent on dimensionless parameters, and .
Figure 2.
Dependence of the dielectric permittivity on dimensionless parameters on dimensionless parameters, and .
Figure 2.
Dependence of the dielectric permittivity on dimensionless parameters on dimensionless parameters, and .
With this representation, relaxation processes that have the same values
, are depicted on the graph
as one curve. In accordance with
Figure 1, an increase in the parameter
leads to an increase in the maximum and to a shift in its position to the area of small values, while at
the maximum position changes slightly with increasing
and remains approximately identically and equal to
. With small values of the parameter
the maximum position
determined by the criterion
or
The curves
in the area of large values
are nearly congruent.
In conclusion, it should be pointed out that the anomalously high dielectric permittivity ε = 5 million found experimentally in [
5], in samples of corundum–zirconium ceramics (CZC), with an alternating field frequency of 1 kHz, at the point T = 1250 К, can be theoretically explained and further investigated at a higher analytical level using expressions (157)-(159) that indicate the correspondence of the formulated theoretical methodology to the experimental regularities that manifest themselves in high-temperature ionic superconductors near the second-order phase transition temperature (quasi-ferroelectric effect), which is topically for the design of the theoretical methods for forecasting the nonlinear electrophysical properties of hydrogen-bond ferroelectrics (KDP, DKDP) used in laser technology as regulators of electromagnetic radiation parameters and electric gates [
1,
2,
3,
4].
3.2. Comparative Analysis of Mechanisms of Maxwell and Diffusion Relaxation of Volumetric Charge
For the practical application of the calculation formulas (157)-(159), it is convenient to express them in terms of the static permittivity and permeability at high frequencies .
In this regard, promising are the designs of high-speed nonvolatile memory devices based on thin films of ferroelectrics with a rectangular hysteresis loop (RHL), characterized by anomalously long times remanent polarization relaxation, increased mechanical performance and thermal stability.
In order to obtain such phenomenological relations, we will use the expression obtained from (131), in the Maxwell relaxation region, when and, at , by virtue of , we have, where .
Relative depth of dispersion for the diffusive mechanism of a relaxation is small and can be calculated from expression (131) taking into account decomposition of
in the field of a "deep" diffusive relaxation (
,
). Then, based on expression (131)
, including
,
,
(according (132)), at
, approximately we have ε
and, we receive the approximated expression
that allows to determine relative static permeability
. From the identity
we calculate the Debye screening radius
, or
Relation (160) expresses the size effects that arise during the relaxation of the space charge. From it is obvious that in the area of "deep" Maxwell relaxation (, according to , system immersion effect (of the simulated crystal) into a state with small radii of shielding the volume charge of the is provided by macroscopic states with large values of crystal thickness d against the background of a rapid increase in concentrations of relaxers (ions) with increasing crystal temperatures. According to a formula (160) this effect is caused by abnormally high values of characteristic temperature that also, is provided with high values of parameters d, . According to experiments, in the HBC, in particular in crystals of chalcanthite, phlogopite, muscovite and talc, with an experimental sample thickness of d = 30 microns, in the region of the high-temperature maximum of the thermally stimulated depolarization current (near T ≈ 150-550 K), the measured equilibrium concentrations of the main charge carriers (protons) take sufficiently high values (in comparison with the region of low temperatures ) and make up . High-frequency dielectric constant for the HBC is taken equal to . Further, by results of calculations, we receive 〖 K and, at K, we have ). Since the kinetic coefficients (133), (134) in the temperature range T ≈ 150-550 K, according to the experiment, in the case of the HBC, should be calculated at activation energies eV, when proton hydrogen bond transitions are realized mainly by thermal activation and, accordingly, at K when the approximate ratio , respectively, the values of the shielding radius , in the confidence interval of the measured values of the parameters are fully consistent with the conditions of Maxwell relaxation.
These conditions are , .
For calculations of Debye radius of volume charge shielding in the area of low-temperature maximum of thermostimulated depolarization current, in relation to the HBC, it is necessary to take into account the influence of quantum tunneling of protons on kinetic coefficients (133), (134), when, due to sufficiently high values of statistically averaged quantum transparency of the potential barrier for protons near the critical temperature
[
8], separating the temperature regions of the tunnel (
) and thermally activated
proton transitions. In this model,
is the mass of the proton. From the analysis of experimental spectra of density of TSTD crystals of the HBC class, in particular, natural phlogopite
at "
,
0.05
0.01 eV , talc
at
,
0.06±0.01 eV, muscovite
at
,
0.04±0.01 eV, chemically pure chalcanthite
at
,
0.070.01 eV, in the vicinity (on the set of points of the continuum measure) the numerical values of low temperature maxima are determined, the corresponding numerical values of the critical temperature
in the range from 80 K to 150 K are set.
So, taking chalcanthite
eV [
1], phlogopite
eV [
1] for low-temperature maximum density TSTD, with
m [
10], we get respectively:
К,
К. We distinguish in quasi-classical non-stationary expressions (140), (141), in accordance with (1.10), for the diffusion coefficient and steady-state proton transfer rate (in the general case, ions) in the polarizing field, quantum mechanical and classical components
,
Equalities (161), (162) must additionally be rewritten in stationary form, taking
where,
- amplitude of the external field determined taking into account the effect on polarization from the Lorentz field side
where
- external field amplitude
Next, we write
We can write
According to the experimental data, the width of the potential barrier in the HBC varies in within
[
1]. The experimental activation energy of protons in the HBC varies from 0.01 to 0.7 eV [
1]. In order to extend the theoretical range of activation energy variation, we accept this parameter within the
eV.
At the low temperatures, when
, according to
, we have
Near the temperature of absolute zero, the kinetics of migratory polarization in HBC is determined only by the parameters of the potential pattern and is practically independent of temperature
Then
Taking the condition
, taking
when
, we have
.
The point of intersection of function graphs
calculated from the equation
, indicates temperature
Here are the results of numerical calculations as Exp. 163,164. We will separately investigate temperature dependencies for stationary probabilities of a classical
and quantum tunnel character on the basis of equality
.
The temperature accepted in range from 0 to 2500 K. The value of the polarizing field strength is taken as V/m. According to the results of numerical calculations, the value of the polarizing field strength has practically no effect on the values of quantum transparency in the region of fields V/m at wide range of temperatures T= 0-2500 K and only in the region V/m the field begins to affect the value of quantum transparency. The maximum point of the functions calculated from the equation
Thus, tunnel components of kinetic coefficients (163), (164) in the absence of external disturbances (polarizing field disabled)
take the form
,
and agree with (133), (134), (10.1)
, where we accept the designations
.
Respectively
, where
.
According to the results of numerical calculations, at the activation energy of 0.01 eV, when the characteristic parameter is the critical temperature of K at which the statistically averaged transparency of the unperturbed by the external field parabolic potential barrier is
0.1555. Further, at the activation energy of 0.03 eV the critical temperature is K, and the corresponding quantum transparency is 0,031. At the activation energy of 0.05 eV, when the critical temperature is the quantum transparency is
0.008. Further, at the activation energy of
0.07 eV, we obtain, respectively , 0.0035. And, at an activation energy of
0.1 eV, we have, 0,00087.
Relation (160) expresses the size effects that arise during the relaxation of the space charge.
For calculation of the Debye shielding radius of volumetric charge (160) for the HBC in the area of low-temperature maximum of thermostimulated depolarization current (
), let's calculate beforehand the characteristic temperature
, accepting the measured equilibrium concentration of the main carriers of a charge (protons) are quite small (in comparison with the region of high temperatures
) and equal to"
. Assuming a high-frequency dielectric constant for the HBC equal to
, the experimental thickness of the sample d = 30 μm, according to the results of calculations, we obtain
K and, at
respectively, we have
. Since the kinetic coefficients (133), (134) in the temperature range
, according to the experiment, in the case of the HBC, should be calculated at activation energies
, when proton transitions over hydrogen bonds are realized mainly due to quantum tunneling of protons, an approximate ratio is performed with a high degree of accuracy
, and, the formula for the Debye shielding radius of the volumetric charge is approximated to the form
. The research of this formula has to be conducted within the designated interval of temperatures of
. By results of calculation, for energy of activation of
, at
,
we have
and, in the confidence interval of the measured values of the parameters
, the final result
is consistent with the conditions of diffusion relaxation
(partially met),
For the practical application of the calculation formulas (157)-(159), it is convenient to express them in terms of the static permittivity
– Exp. 131, and permeability at high frequencies
. Then, based on (157)-(159) for the regions
,
we have
In formal form, the dispersion relations (165)- (168) resemble the classical expressions for the Debye dispersion [
3], but differ from them in coefficients, which leads to other expressions for determining the maxima of the functions
и
, as well as their values. The Debye expressions for the complex permittivity give the maximum value of the function
, reduced to
, пo сравнению с (163), but under the condition that is typical for dielectrics with a large depth of dispersion, when the magnitudes of the maxima will be approximately the same. The Debye relations [
3] for determining the position of the maxima
and
are several
times higher than the corresponding values calculated by formulas (164). Thus, Debye expressions, which are used quite often to determine the parameters of defects during space charge relaxation, lead to a significant error in determining the relaxation time, increasing it by a factor of
.
In accordance with
Figure 3 and
Figure 4, the calculation formula (168) satisfactorily approximates the general formula (159) at large
parameters.
Figure 3.
Dependence of tangent of dielectric loss angle ton dimensionless parameter at Maxwell relaxation of volumetric charge: 1 - calculation by formula (167); 2 - calculation by formula (159).
Figure 3.
Dependence of tangent of dielectric loss angle ton dimensionless parameter at Maxwell relaxation of volumetric charge: 1 - calculation by formula (167); 2 - calculation by formula (159).
Figure 4.
Dependence of maximum values
and on dimensionless parameter : 1 - dependence curve ; 2 - dependence curve . Calculation was performed using (167) and (168).
Figure 4.
Dependence of maximum values
and on dimensionless parameter : 1 - dependence curve ; 2 - dependence curve . Calculation was performed using (167) and (168).
Figure 5.
Estimated temperature dependence of dielectric permeability
, , and dispersion depths of a volume charge in the field of the Maxwell relaxation () in Ih -ice crystals with HF impurity: (by means of (131), (165) - (167)).
Figure 5.
Estimated temperature dependence of dielectric permeability
, , and dispersion depths of a volume charge in the field of the Maxwell relaxation () in Ih -ice crystals with HF impurity: (by means of (131), (165) - (167)).
Figure 6.
Calculated temperature dependence of equilibrium concentration of mobile charge carriers in the region of Maxwell relaxation (
) in crystals of
Ih-ice with an admixture of HF:
[
138].
Figure 6.
Calculated temperature dependence of equilibrium concentration of mobile charge carriers in the region of Maxwell relaxation (
) in crystals of
Ih-ice with an admixture of HF:
[
138].
As can be seen from
Figure 5,
the static dielectric constant
, volume-charge polarization is slightly dependent on temperature and in order of magnitude coincides with the operation data [
138].
The high-frequency dielectric constant of the
has a weakly expressed minimum in the crossover region of
, but the value is slightly higher than the values calculated from the Debye dispersion [
138].
The value of the dispersion depth
in the Maxwell relaxation region (
) has a maximum, which may be associated with an increase in the concentration of defects in the crossover region, as follows from
Figure 6. The obtained concentration value is close to the concentration of
ionic defects, which confirms the decisive role of
defects in the formation of volumetric charge in ice crystals.
Figure 7.
Calculated temperature dependences of Maxwell
(graph 1) and diffusion
(graph 2) of time in the area of Maxwell relaxation in crystals of
Ih-ice with an admixture of HF:
[
138].
Figure 7.
Calculated temperature dependences of Maxwell
(graph 1) and diffusion
(graph 2) of time in the area of Maxwell relaxation in crystals of
Ih-ice with an admixture of HF:
[
138].
Table 2.
Experimentally determined parameters of volume charge relaxation in ice crystals with an admixture of HF.
Table 2.
Experimentally determined parameters of volume charge relaxation in ice crystals with an admixture of HF.
| Parameter name |
Parameter values |
| Temperature, Т, К |
234 |
238 |
245 |
255 |
264 |
Relaxation time
T |
2,64 |
2.34 |
2 |
1.72 |
1.69 |
Low frequency Debye conductivity
|
2 |
2.43 |
2.86 |
2.97 |
3.23 |
| Low frequency volumetric charge conductivity |
5 |
5.35 |
6.95 |
10 |
14.4 |
Table 3.
Calculated temperature dependences of relaxant parameters.
Table 3.
Calculated temperature dependences of relaxant parameters.
| Parameter name |
Parameter values |
| Temperature , T, K |
234 |
238 |
245 |
255 |
264 |
Static dielectric constant
см. фoрмул у (131) |
597 |
643 |
646 |
577 |
617 |
| High-frequency Debye conductivity |
149 |
141 |
157 |
194 |
275 |
Dispersion depth
|
448 |
502 |
489 |
383 |
342 |
|
4 |
4.56 |
4.11 |
2.97 |
2.24 |
| Maxwell Relaxation Time, |
6.6 |
5.13 |
4.87 |
5.79 |
7.5 |
|
6.56 |
8.53 |
6.93 |
3.62 |
2.06 |
| Diffusion relaxation time |
4.33 |
4.38 |
3.37 |
2.1 |
1.55 |
| Equilibrium concentration of mobile charge carriers, |
2.69 |
3.37 |
3.13 |
2.11 |
1.76 |
Diffusion factor
(the parameter is computed by (133)) |
9.5 |
9.4 |
12 |
19.5 |
26.5 |
Mobility factor
the parameter is computed by (134) |
4.64 |
4.5 |
5.7 |
8.78 |
11.5 |
Calculation of the Maxwell
and diffusive
times of a relaxation was carried out, apparently from
Figure 7, in the field of the Maxwell relaxation of "
, taking into account (133), (134).
It follows from
Figure 7 that the
Maxwell relaxation time has a minimum in the crossover region and a negative activation energy in the high temperature region, which indicates the quantum nature of the movement of
defects.
The diffusion relaxation time
at
has an Arrhenius-type activation character with an activation energy of 0.23 eV, which coincides with the activation energy of the
L and
D-defect movement [
1,
138]. Thus, in the high-temperature region, the diffusion of
defects is determined by the movement of
D-defects, which corresponds to Jaccard's theory [
138].
4. Discussions
This article provides a generalized physical review of the methods of theoretical study of the kinetics of dielectric relaxation in crystals with ion-molecular chemical bonds. A comparative analysis of quasi-classical nonlinear models of relaxation ion transfer in dielectrics in an electric field was performed in a wide range of field parameters (0.1-1000 MV/m) and temperatures (1-1550 K). We have not studied the behavior of the ion subsystem (consisting of the most mobile types of ions moving with a given activation energy) near absolute zero temperatures, since the physical mechanism of relaxation polarization in crystals of this type at ultra-low temperatures (1-10 K) should be built, and within the framework of the kinetic theory of ion conductivity, on the study of the effects of tunnel (quantum) transitions of ions through a potential barrier whose height is comparable to the energy of a chemical bond (ion activation energy on the bond) and, in the case of heavy inactive ions or ion clusters, reaches values of 1-10 eV, which, with ion masses of much larger proton mass, makes almost zero (especially at temperatures T = 1-10 K) statistically averaged ion energy transparency of the potential barrier (formulas (8), (9), (10)). The probability of thermally activated (classical) overflows of ions under these conditions is also close to zero. Thus, if we talk about the behavior of ion subsystems in ion dielectrics in the region of ultra-low temperatures, according to the quasi-classical and quantum kinetic theories of ion relaxation that we have developed, then no fundamentally new microscopic physical phenomena of a quantum nature in ion-molecular crystals will be found, except for tunneling ions, and then, with very small probabilities. In the case of investigating the kinetics of quantum proton-relaxation polarization in hydrogen-bonded crystals (HBC), even in the temperature region T = 1-10 K, calculated by methods of quasi-classical theory, statistically averaged probabilities of quantum transitions (expression (8) in complex with approximations l by parameters of perturbation theory (formulas (10.1), (10.2)) of hydrogen ions (protons), in contrast to massive ions of other types, against the background of small values of proton activation energy (0.01-0.1 eV) with a potential barrier width of 0.085-0.1 nm, become quite significant (0.001-0.01), compared to the probabilities of thermally activated proton overflows (0.00001-0.0001), indicating the tunneling nature of proton transport in the HBC in the ultra-low temperature region. Note that the quasi-classical statistically averaged transparency of the potential barrier, according to the properties of the model, depends only on the parameters of the potential pattern (height and width of the potential barrier), ion mass and on the crystal temperature (see formula (9)). Since the energy spectrum of the ion in the quasi-classical model is taken continuous, the thickness of the experimental sample does not affect either the parameters of the energy spectrum of the ion or the value of quantum transparency. At the same time, in the area of absolute zero temperatures, the quasi-classical transparency of the potential barrier - the function D (T) takes a non-zero value, in the general sense (see formula (10) at T ≥ 0, which is explained by zero particle fluctuations) and, the numerical values of quantum transparency for protons are D (0) = 0.001-0.01. Thus, in the case of the proton subsystem in the HBC, it is advisable to move to a strict quantum mechanical calculation of quantum transparency statistically averaged using the Gibbs quantum canonical distribution for protons distributed over the energy levels of the discrete spectrum, which is done in [
4,
122,
123,
124] for the parabolic potential barrier model for protons (this form of barrier is physically more expedient, compared to rectangular barrier model [
138]).The application of the density matrix apparatus gives numerical values of quantum transparency for protons in the HBC, equal to, at T ≥ 0, respectively, D (0) = 0.01-0.1 [
78,
123,
124], which is an order of magnitude higher than quantum transparency calculated according to quasi-classical statistical theory [
69,
71,
72,
75]. Since the parameters of the discrete energy spectrum of protons in the HBC are significantly dependent on the size of the crystal (its thickness d) [1.138], in the temperature region T = 1-10 K with a layer thickness of 1-10 nm, abnormally high (compared to temperature range T = 50-100 K, with layer thickness of 1000-10000 nm) the values of quantum transparency (0.95-0.99) [
123], and the current density of thermostimulated depolarization increase, while, by 3-4 orders of magnitude [
77,
124], which, in general, but so far only in the theoretical aspect (since no experimental data are available), indicates the effect of ultrahigh proton conduction in the HBC. The strict quantum-mechanical theory of this effect should, in addition to the described results [
77,
78,
122,
124], be based on the study of quantum macroscopic phenomena associated with the interaction of protons with the phonon subsystem generated by the quantization of oscillations of anion sublattice ions in the HBC. Certain steps in this direction have been taken in [
4].
A rigorous macroscopic quantum theory of proton superconductivity in the HBC, from the analysis of proton-phonon and proton-proton interaction operators and their influences, at the mathematical level, by the total quantum mechanical averaged polarization values and the proton current density in the dielectric, will allow, at the physical level, the possibility of generating elementary excitations in the HBC, associated with the formation of proton pairs, through their contact with phonons to form quantum states, similar to Cooper pairs of electrons in metal superconductors near the temperature of the phase transition of the second kind. All these theoretical studies should be strictly compared with the results of qualitatively organized precision measurements in the field of liquid helium temperatures, which is a separate rather extensive scientific work that goes beyond the boundaries of this scientific article.
At this stage of research, in subsection 4, we discussed the existing theoretical results in the field of quasi-classical and quantum theories of proton relaxation in the HBC, identified the strengths and weaknesses of these theories, counting on the maximum possible, within the developed models, achieving coincidences with the experiment in a limited range of temperature parameters and fields, and having nonlinear model results over a wide range of relevant parameters.
The main guideline of this article is, as we have already said many times, a comparative analysis of existing models and conclusions from them, in aspects of the nonlinear quasi-classical kinetic theory of ion-relaxation polarization and conductivity in ion and molecular crystals. Conclusions on the entire work will be presented in the corresponding section.
5. Conclusions
1. From the comparative analysis of existing methods for the theoretical description of relaxation polarization and conductivity in crystals with ion-molecular chemical bonds (in the special case, in the HBC) it was established that the phenomenological model [
1,
128,
138], constructed in a linear approximation according to a small dimensionless parameter
[
1,
138], bounded by polarizing field (
/m) and temperature (
К) and, for comparison with the experiment, in the range of values of the parameter
[
72]. At temperatures
K, the linear approximation by a small dimensionless parameter
[
1,
75] is in good agreement with experiment [
128,
138], and outside this temperature range, the role of nonlinear polarization effects increases, which requires consideration of subsequent (at least from the third) approximations of perturbation theory by a small dimensionless parameter
(formulas (11), (12)) [
1,
2,
3,
4]. The nature of these nonlinearities is explained by the influence of tunnel (quantum) proton transitions (
K) [
67,
69,
71,
72,
74,
75] and volume charge relaxation (T ≈ 250 ÷ 450 K) [
72,
74,
75] and causes a deviation from the
Debye laws of frequency-temperature of complex dielectric permittivity (CDP) [
138].
2. The output circuit is described and the parameters and properties of
the generalized quasi-classical kinetic equation (17) are analyzed, which allows, on the basis of a single analytical circuit, by the method of successive approximations (31), to investigate the mechanism of
nonlinear volume-charge polarization in the HBC in the temperature range
K and the fields
[71.75]. It is proved that the Fokker-Planck equation [
1,
138] is obtained from equation (17) in a linear approximation by the parameter
. Considering higher degrees of the parameter
in (17) enhances the influence of quantum effects on a small parameter of perturbation theory (12). Formally, the generalized kinetic equation (17) applies to other crystals with ion conductivity similar to the HBC in structure and properties of the crystal lattice. The applicability of the developed analytical methods to the study of superionic conductivity and quasi-sieve-electric effect (1250 K, 1 kHz) in corundum - zirconium - ceramics is not excluded [
5].
3. The effect of nonlinearities on relaxation times for microscopic processes of ion transitions (in the HBC, protons) through a potential barrier was investigated (expressions (46), (51)). Weak dependence of relaxation time on temperature at quantum transitions of ions (48), (49) is established. Near absolute zero temperature, relaxation time does not depend on temperature (50).
4. A comparative analysis of various methods and approximations in the theoretical description of dielectric relaxation in the HBC was performed. It has been found that quantum proton transitions enhance the role of nonlinear effects in the polarization of the HBC in the low temperature region (T < 100K). In the area of strong fields, non-linear effects are also manifested at high temperatures (T > 100 K). In this regard, a generalized solution of the system of nonlinear equations of the phenomenological model of ion-relaxation polarization (expressions (57) - (61)) by methods of perturbation theory (power series (62)) should, within the framework of quasi-classical kinetic theory [
2,
3], be carried out more strictly than [
1], starting from the third order by the decomposition parameter
, defined under the condition
and
.
5. The scheme of solutions of nonlinear equations of the phenomenological model in the k-th approximation of the perturbation theory by the small parameter is presented and analyzed (expressions (63) - (67)) using the decompositions of the volumetric charge density on a piece in a row Fourier of a look the form - see expressions (68), (69), (70). Constructed asymptotic recurrence expression for complex amplitudes k-order relaxation modes of perturbation theory multiple of frequency "r ω" in a stationary polarization mode (formula (73)) and, based on (62), according to , the decomposition of the volumetric charge density by the frequency harmonics of the alternating field is obtained (85), where respectively in (A.12.1) is the first, (A.12.2) - the second and (90) - the third approximation by the polarizing (external) alternating electric field.
6. By methods of quasi-classical kinetic theory, it was established that in the dielectric under the action of an alternating electric field relaxation modes are generated that are multiples of only odd frequencies . The expression for complex dielectric permittivity (CDP) is written on the set of frequencies in the form of a series decomposition according to even frequency harmonics of the alternating field (expression (98)). Also function is presented in the form of infinite power series with even degrees of tension of , with decomposition coefficients (expression (97)). Generalized dispersion relations of the form , , , - formulas (113.1) - ((113.4), whence, in the particular case , the expressions known from the electrodynamics of continuous media are obtained. The function is built in an analytical form (expression (108)).
7. Proved that transition to infinite approach of the theory of indignations of
, already at the main frequency
, results in the nonlinearities connected with interaction various one after another (to number
) relaxation mode
(expression (A.10.1)) and to fundamentally new dependencies
,
over a wide range of temperatures and field strengths (expressions 106). Ion tunneling has a significant effect on frequency laws (106) in the field of diffusion relaxation. Moreover, the results of the linear theory of dielectric losses in the HBC [
1] are a special case of more general formulas (106).
8. Transcendental equations (137), independent of each other, were constructed to calculate the critical temperature
separating the temperature regions (zones) respectively diffusion (
) and Maxwell (
) dielectric relaxation. In the quasiclassical kinetic theory [
2,
3,
4] relaxation time for n - oh relaxation mode
reveals by means of diffusive time of a relaxation of
,
- for 1 - oh relaxation mode, and Maxwell relaxation time
.
9. Based on the quasi-classical expressions generalized at the fundamental frequency of the alternating field for the real and imaginary components of the complex dielectric permittivity (CDP) , - see (106), an expression was constructed to calculate the tangent of the dielectric loss angle (150) , in combination with quasi-classical relaxation parameters , - see (119.1), (119.2) in the analytical representation (120), (121), (122).
10. The quasiclassical formulas generalized at the main frequency of variation field
are constructed and analyzed for the CDP component
,
and
in the field of the Maxwell relaxation (
) - see (157) - (159). On this basis, theoretical graphs of the studied functional dependencies
,
were obtained, reflecting non-linear effects associated with the influence of dimensionless parameters
,
on the dielectric loss mechanism (
Figure 1 and
Figure 2). Theoretical spectra analysis was performed for
,
and
in the area of "deep" Maxwell relaxation (
) - see (161) - (163). The dispersion expressions (165) - (168) differ from the laws of classical Debye dispersion by correction
, where
– expression 131, the static permittivity, and permeability at high frequencies
. In formal form, the dispersion relations (161)- (163) resemble the classical expressions for the Debye dispersion [
3], but differ from them in coefficients, which leads to other expressions for determining the maxima of the functions
и
, as well as their values. The Debye expressions for the complex permittivity give the maximum value of the function
, reduced to
, пo сравнению с (163), but under the condition that is typical for dielectrics with a large depth of dispersion, when the magnitudes of the maxima will be approximately the same. The Debye relations [
3] for determining the position of the maxima
and
are several
times higher than the corresponding values calculated by formulas (164).
11. Schedules of dependences of
-
Figure 3 (from formulas (167), (159)), (
and
-
Figure 4 (from formulas (167) and (168)), constructed at the Maxwell relaxation (
), confirm 10 conclusions of a deviation designated in the item from laws of classical dispersion at a strict quasiclassical research of processes of ion-relaxation polarization at the main frequency of variation field
.
12. According to Figure 5,
the static dielectric constant of the volume-charge polarization
is slightly dependent on temperature and, in order of magnitude, coincides with the data [
138].
The high-frequency dielectric constant of the
has a weakly expressed minimum in the crossover region (
, but the value is slightly higher than the values calculated from the Debye dispersion [
138]. Since the dispersion depth
in the Maxwell relaxation region
is characterized by a maximum, it can be argued that the concentration of structure defects in the vicinity of the crossover point increases (
Figure 6). The obtained concentration value is close to the
defect concentration, which confirms the
decisive role defects in the formation of volumetric charge in ice crystals.
13. The data from Figure 7 indicate that the Maxwell relaxation time
has a minimum in
the crossover region
and a negative activation energy in the high temperature region, which indicates
the quantum nature of the movement of
defects.
The diffusion relaxation time
at
has an Arrhenius-type
activation character with an activation energy of 0.23 eV, which coincides with the activation energy of the
L and
D-defect movement [
1,
138]. Thus, in the high-temperature region, the diffusion of the
defects is determined by the movement of
D-defects, which is consistent with the results of Jaccard, consecrated in [
138]. Table 2.3 and the results given in them, the calculation of the parameters of relaxation of the volume charge in ice crystals with an admixture of HF (from the comparison of theory and experiment) confirms the information reflected in the
Figure 5,
Figure 6 and
Figure 7.
14. The mathematical model of nonlinear volume-charge polarization developed in this work is universal and can be used in the theoretical study of the spectra , TSPC, TSDC, both in the HBC and similar in crystal lattice type (lattice geometry, chemical bonding mechanism) and electrophysical properties of materials with ion conductivity (KCC, perovskites, etc.). The general theoretical foundations for predicting the quality of insulation and designing elements of technological schemes based on the HBC are laid.


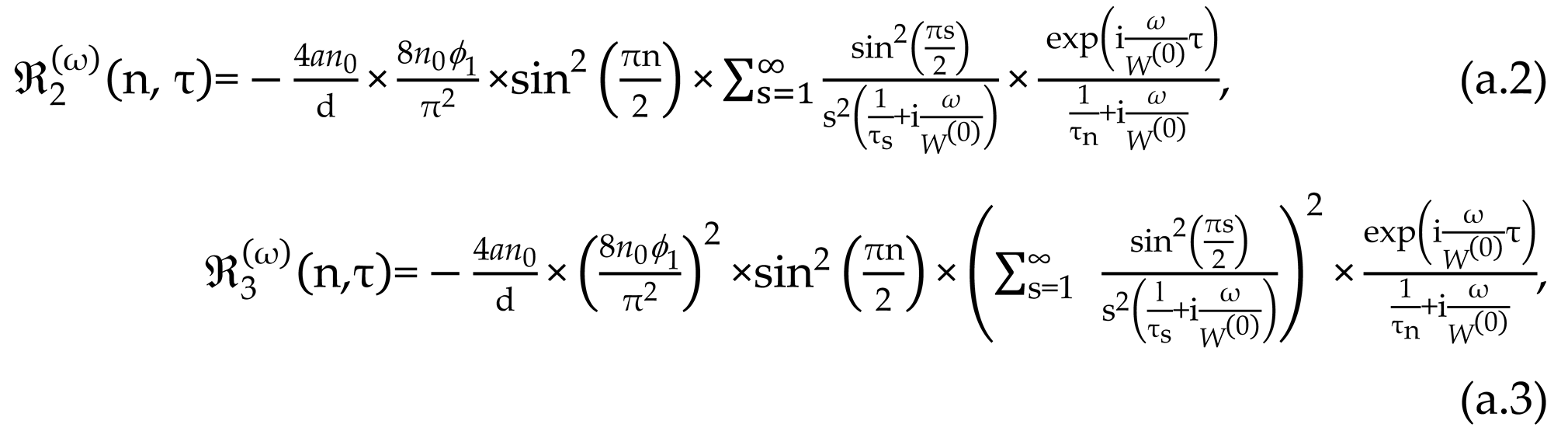



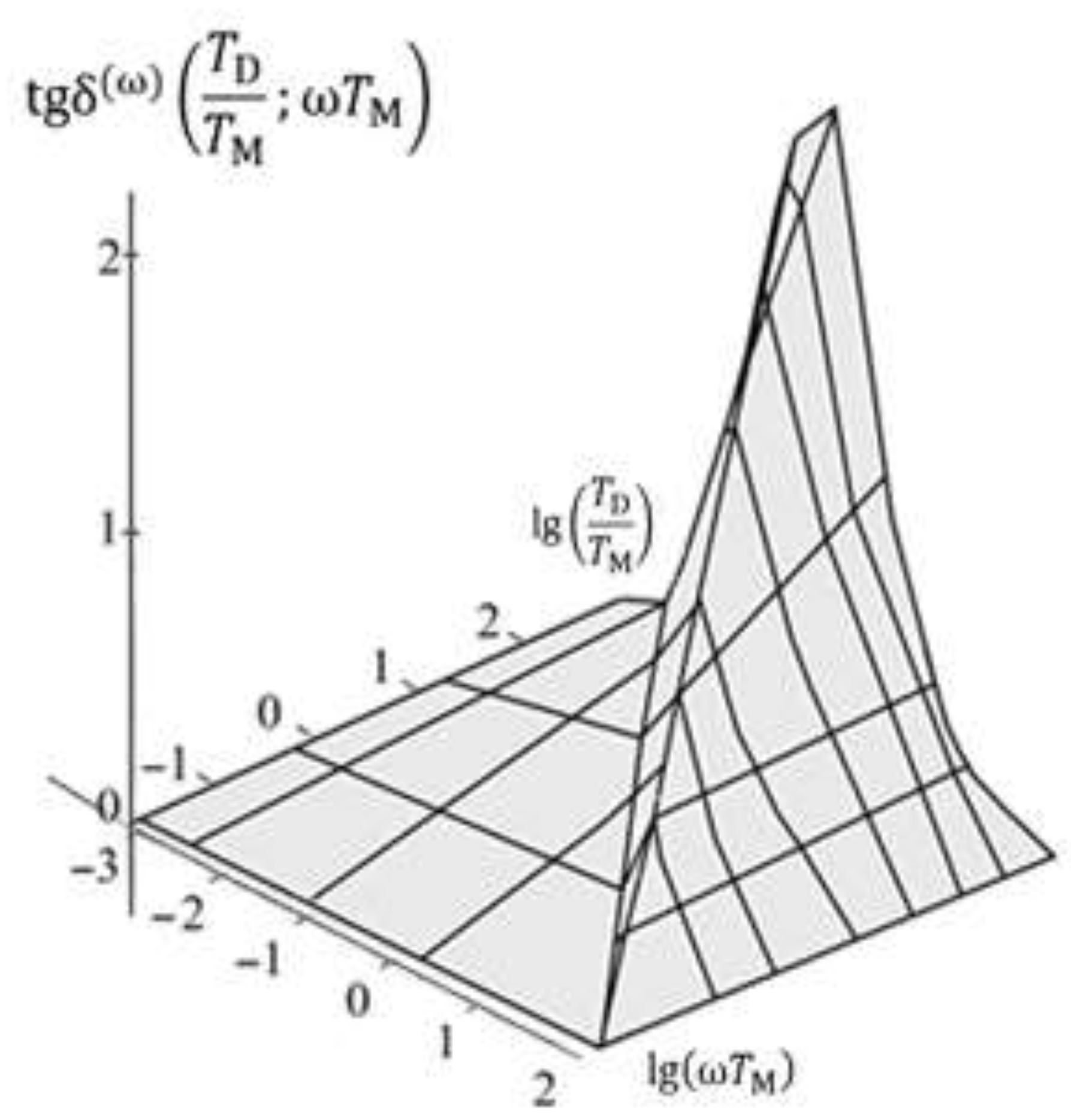
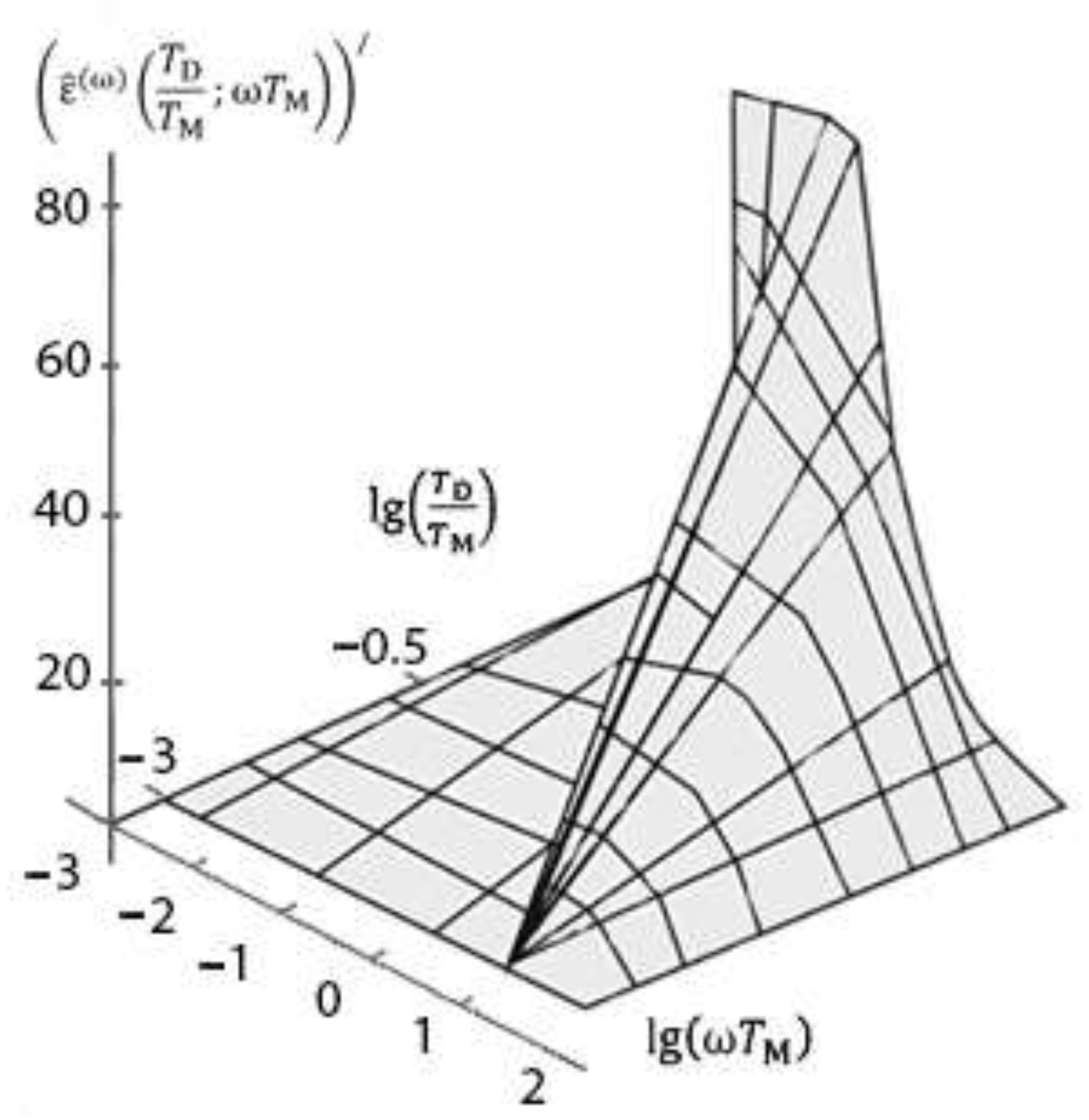
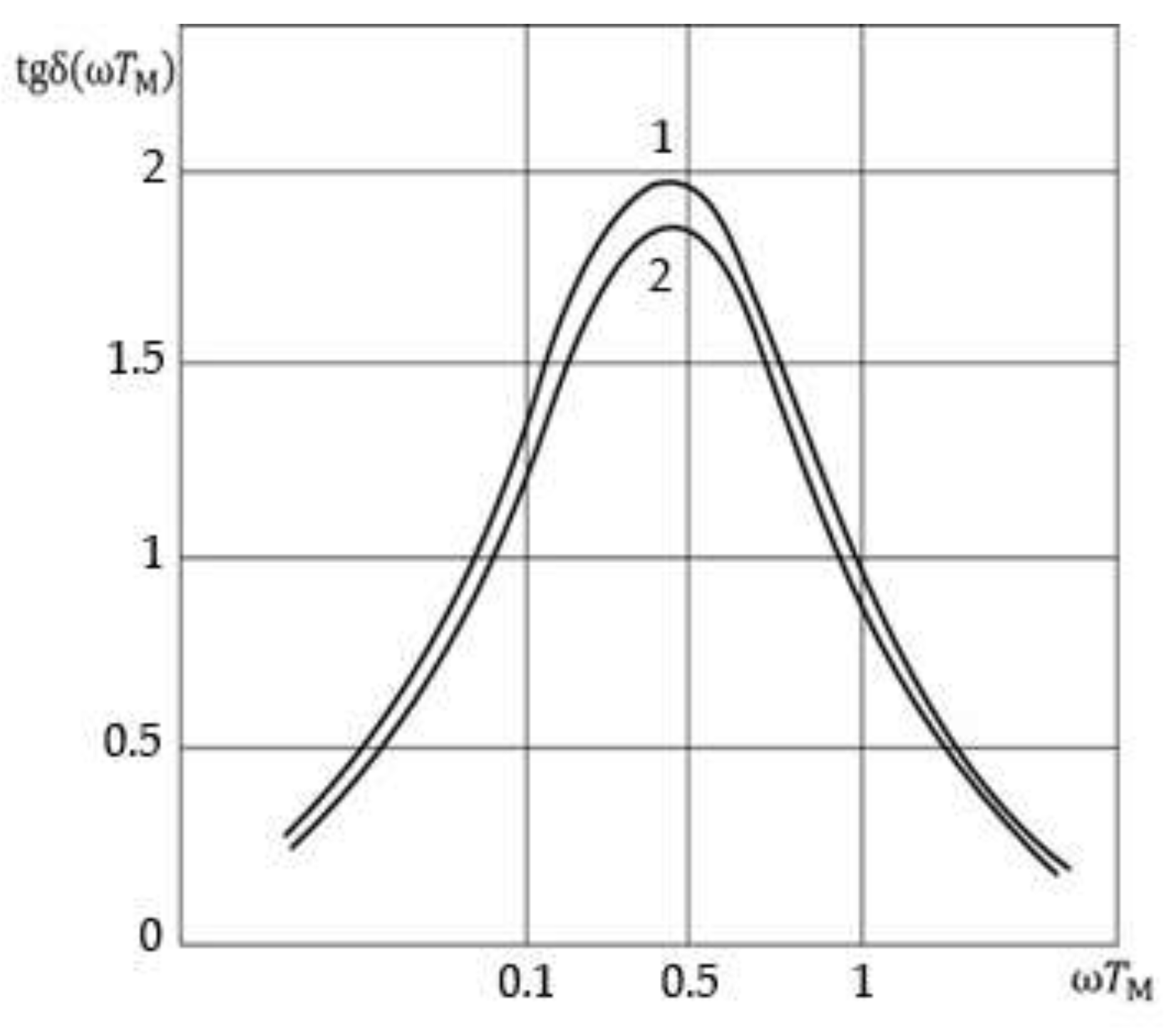
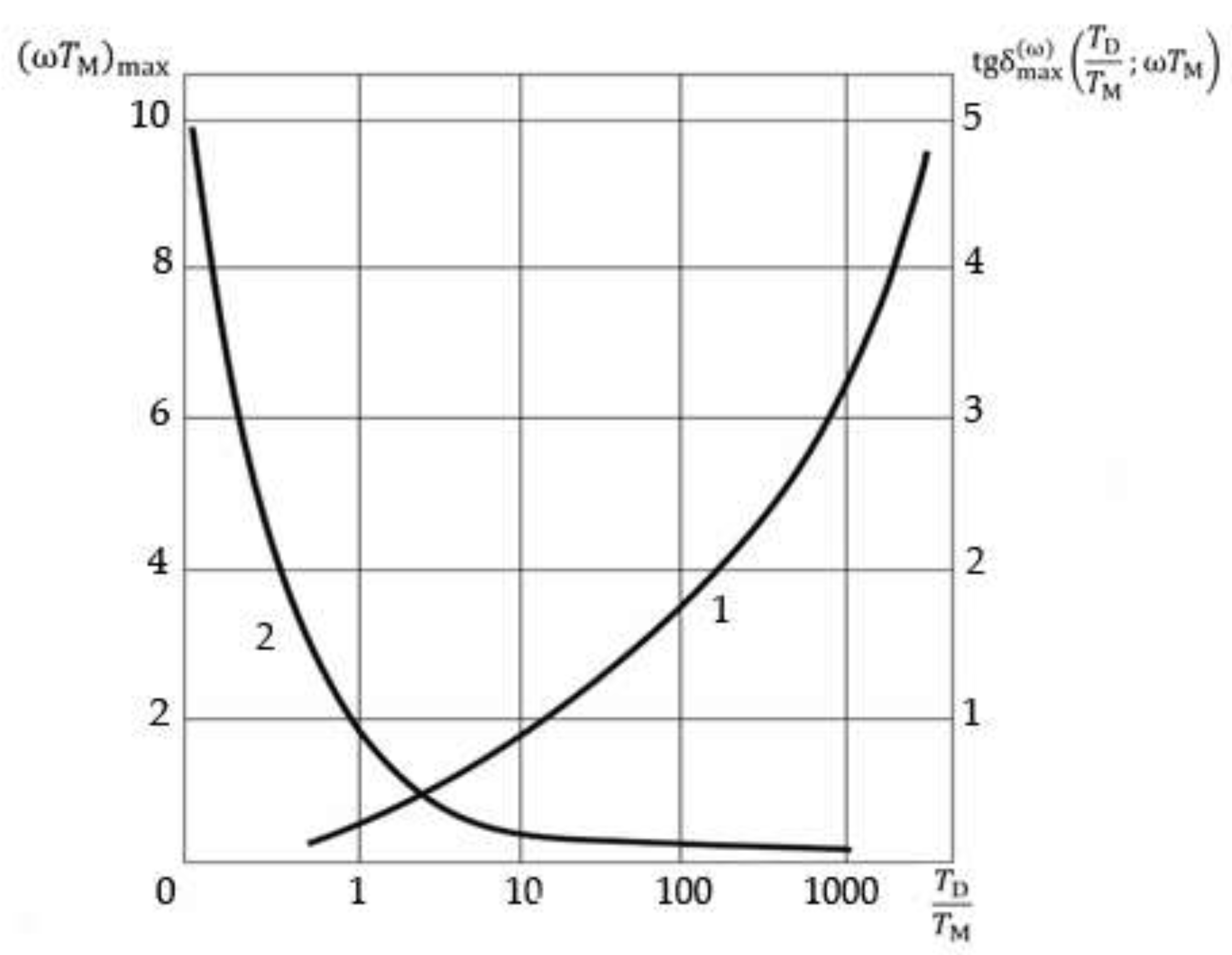
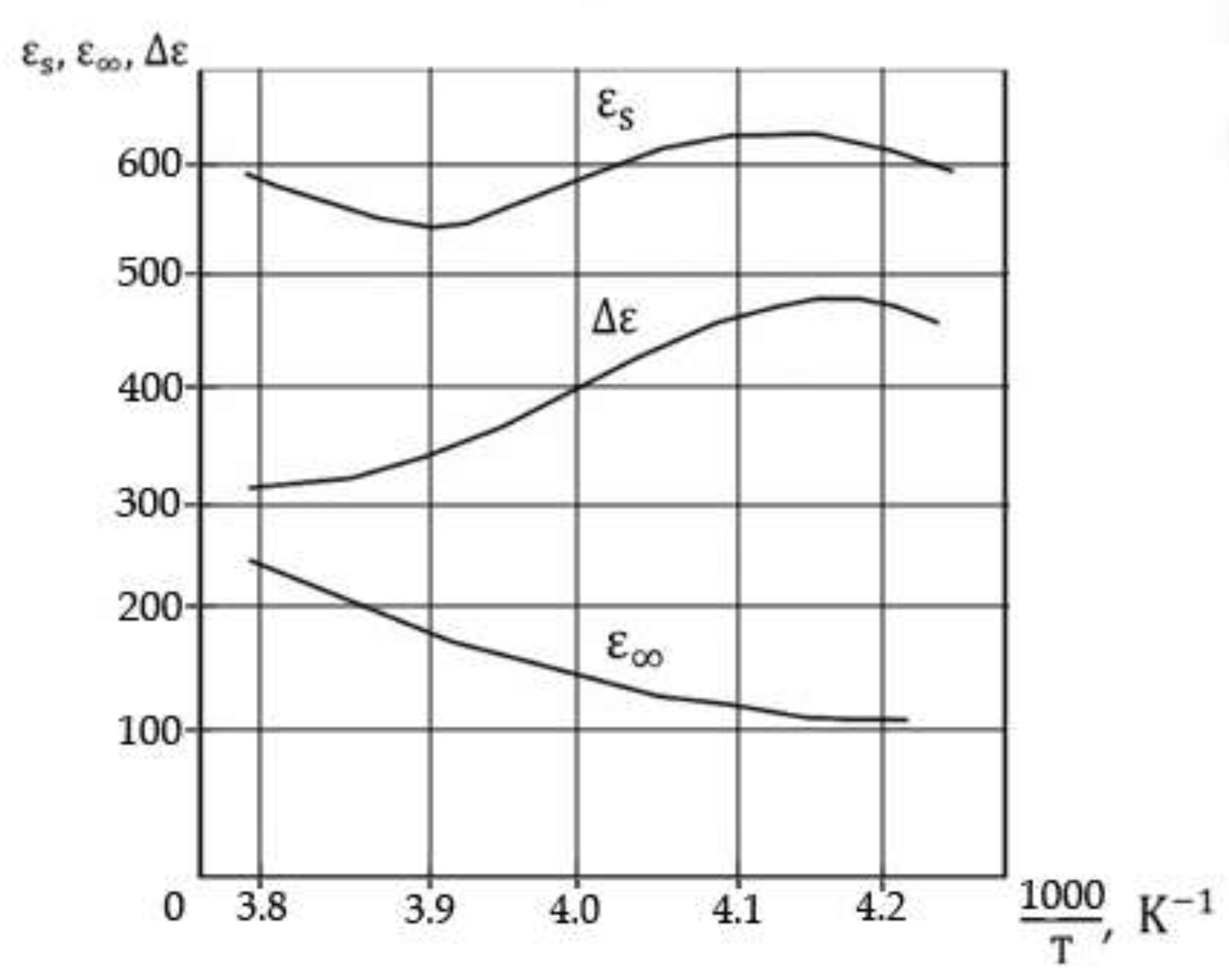
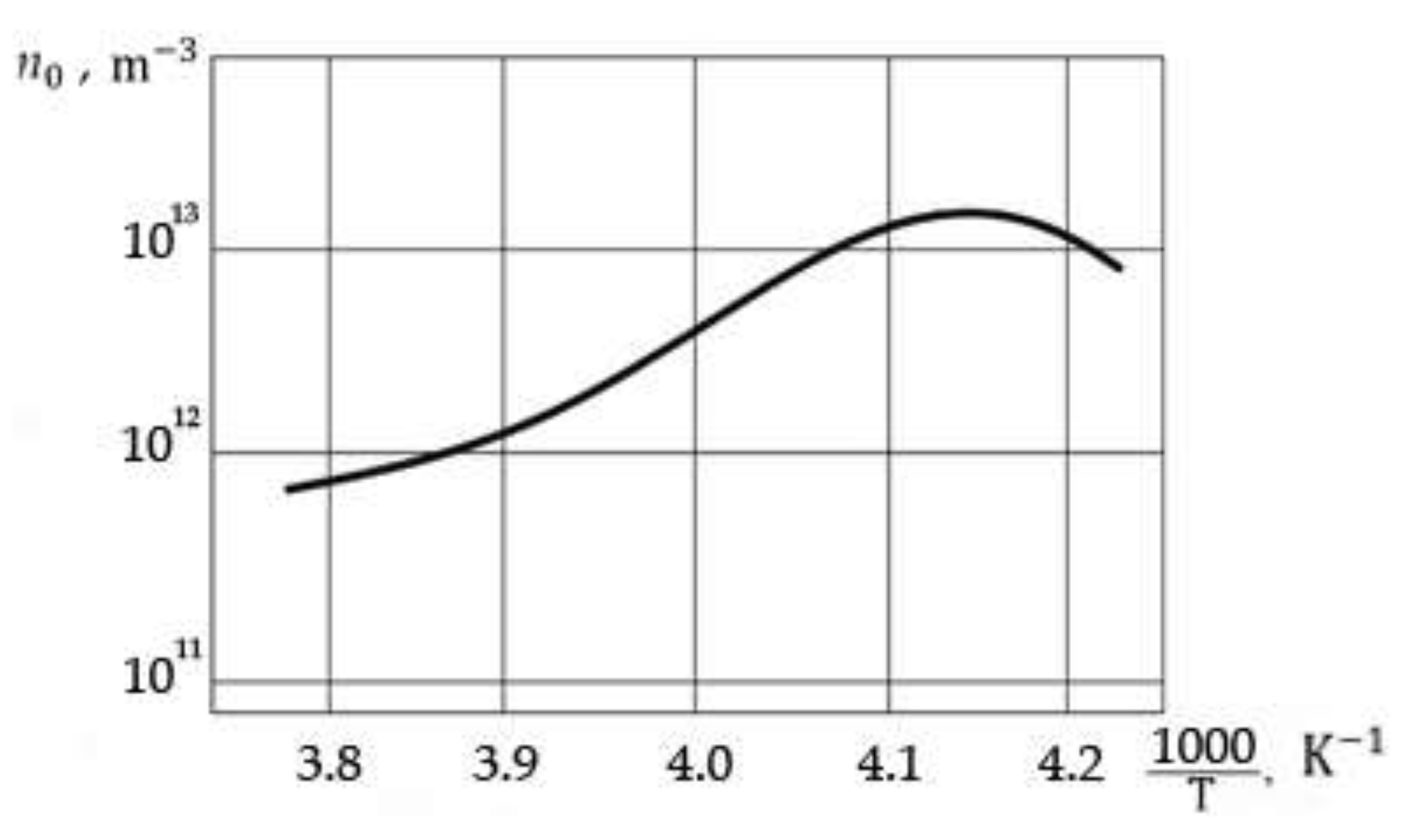
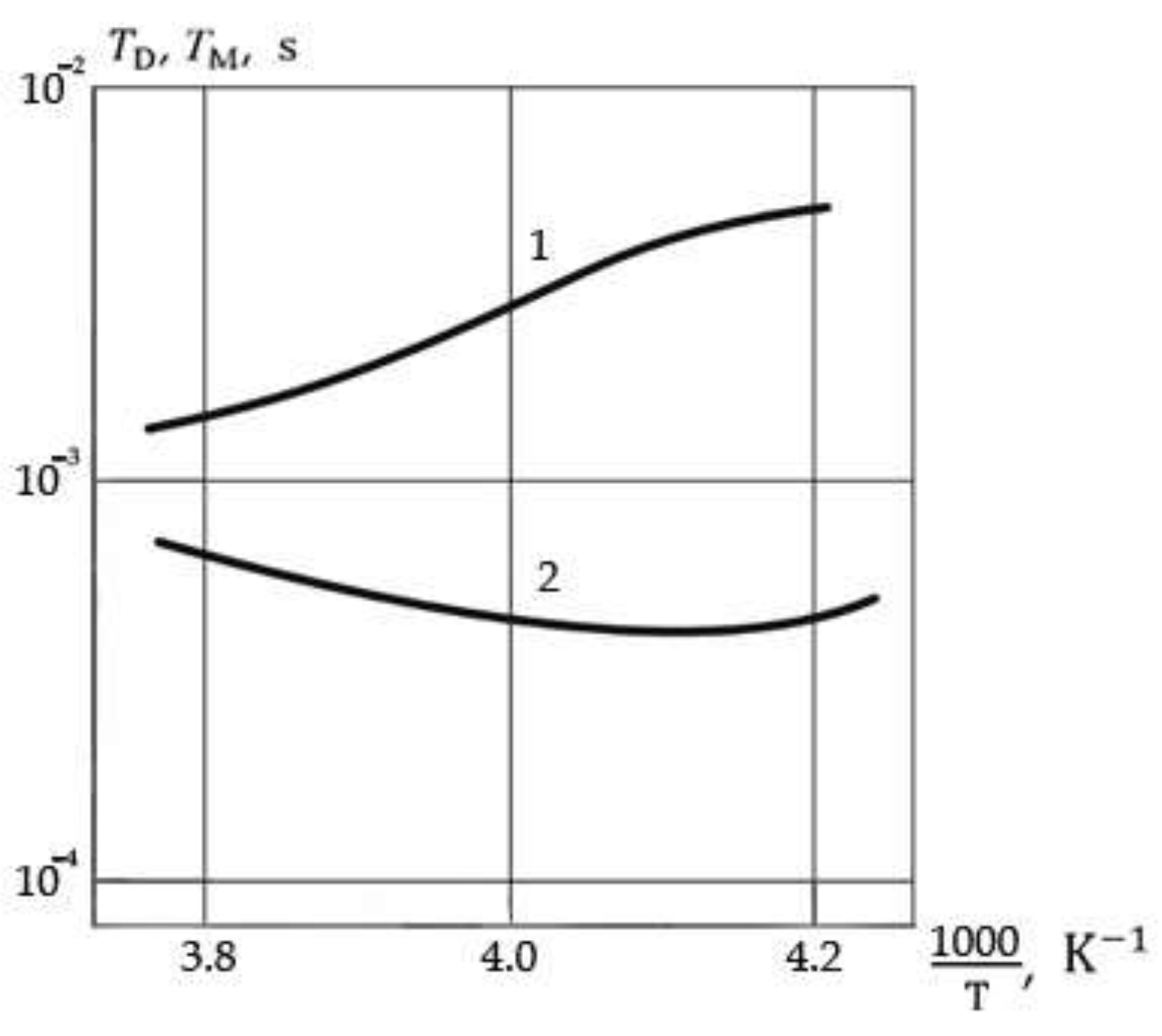
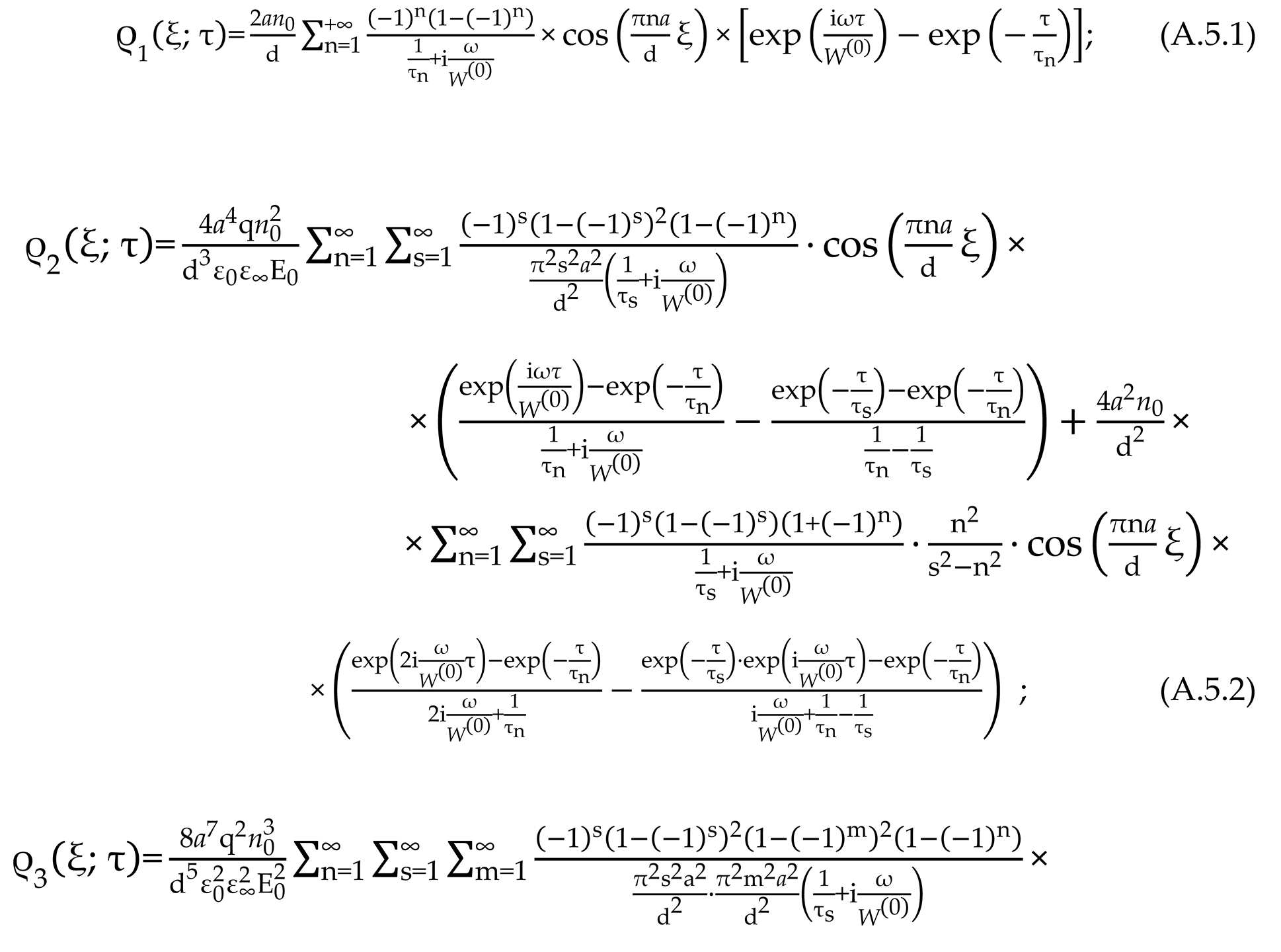
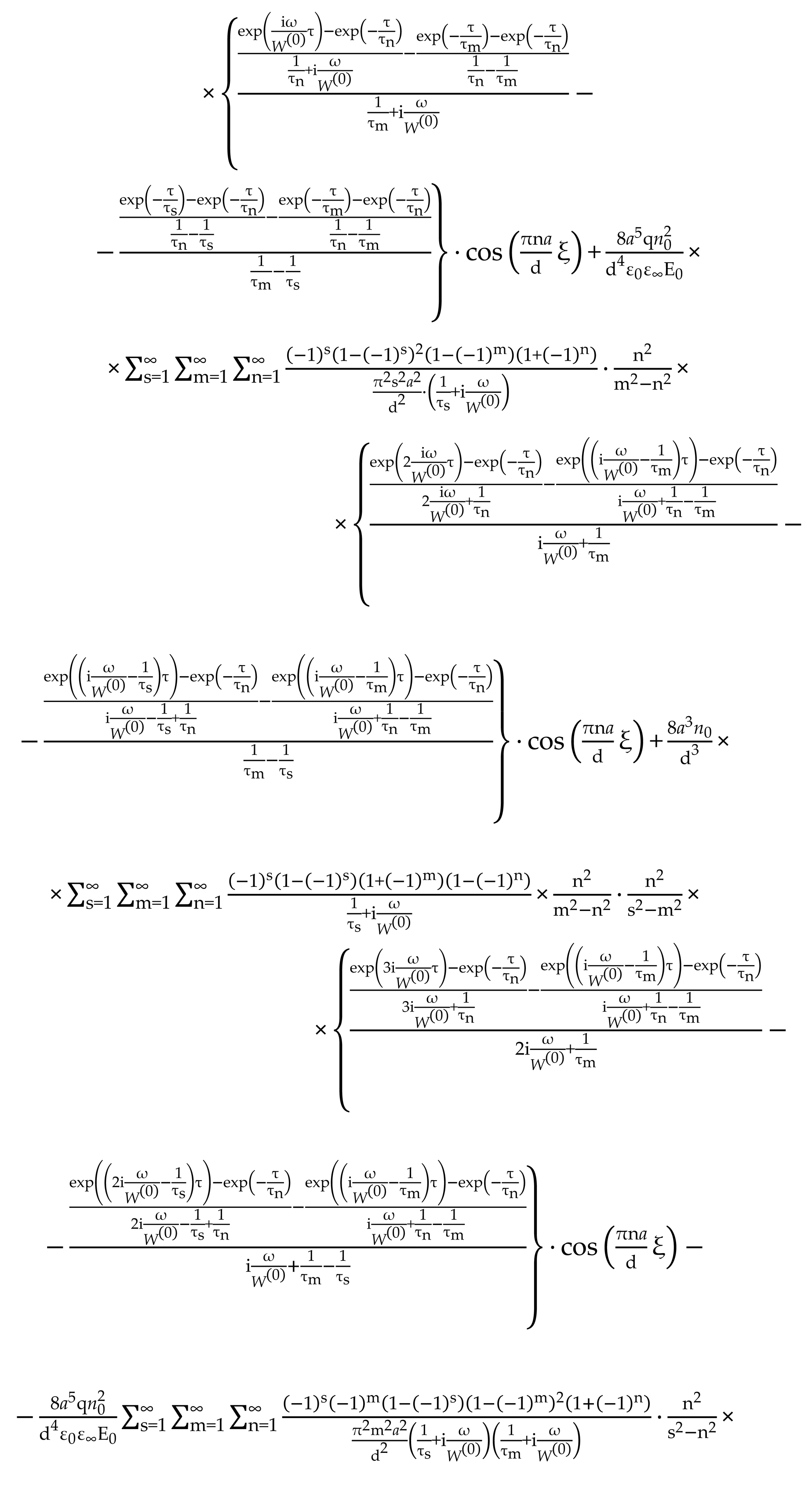
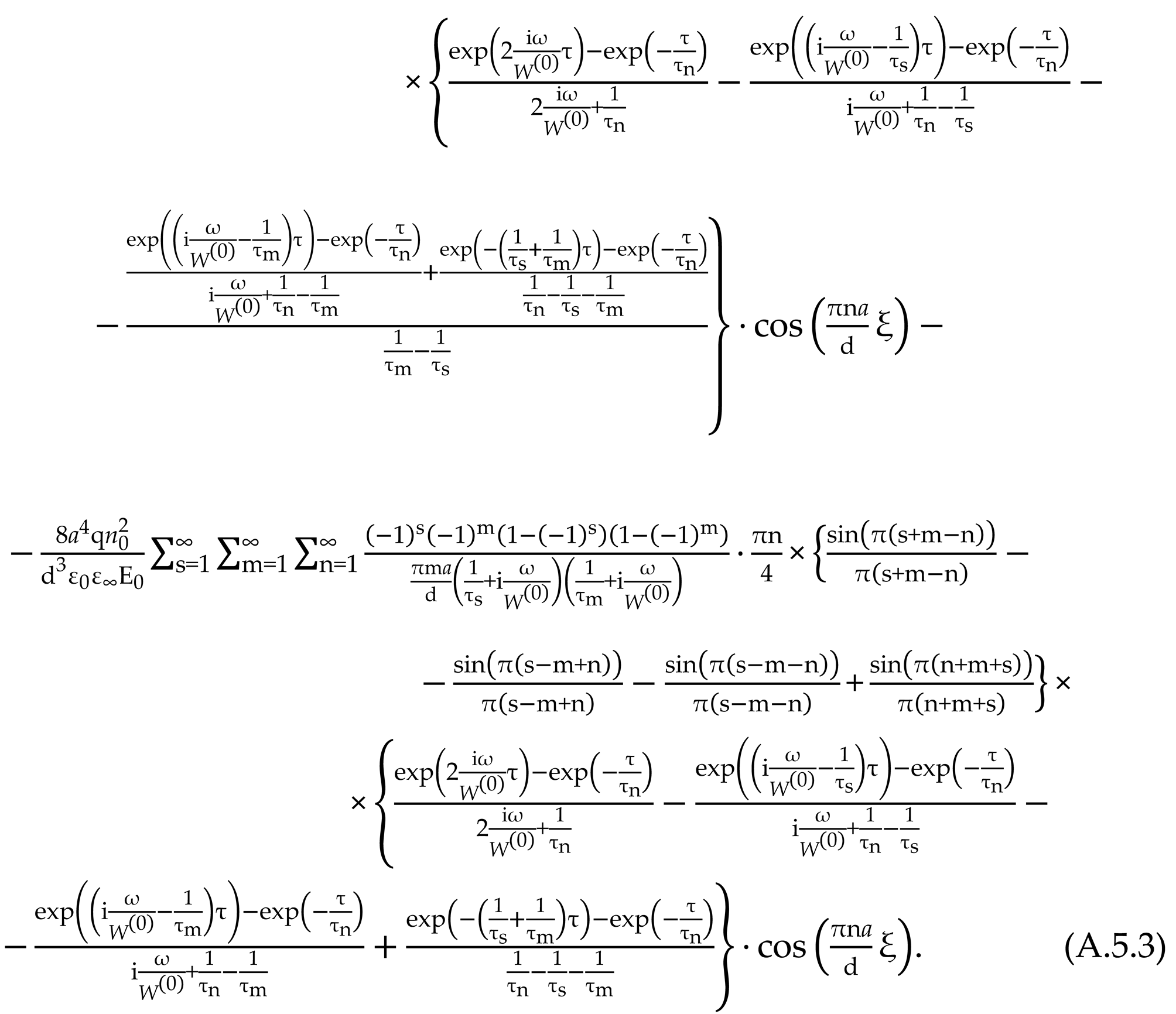

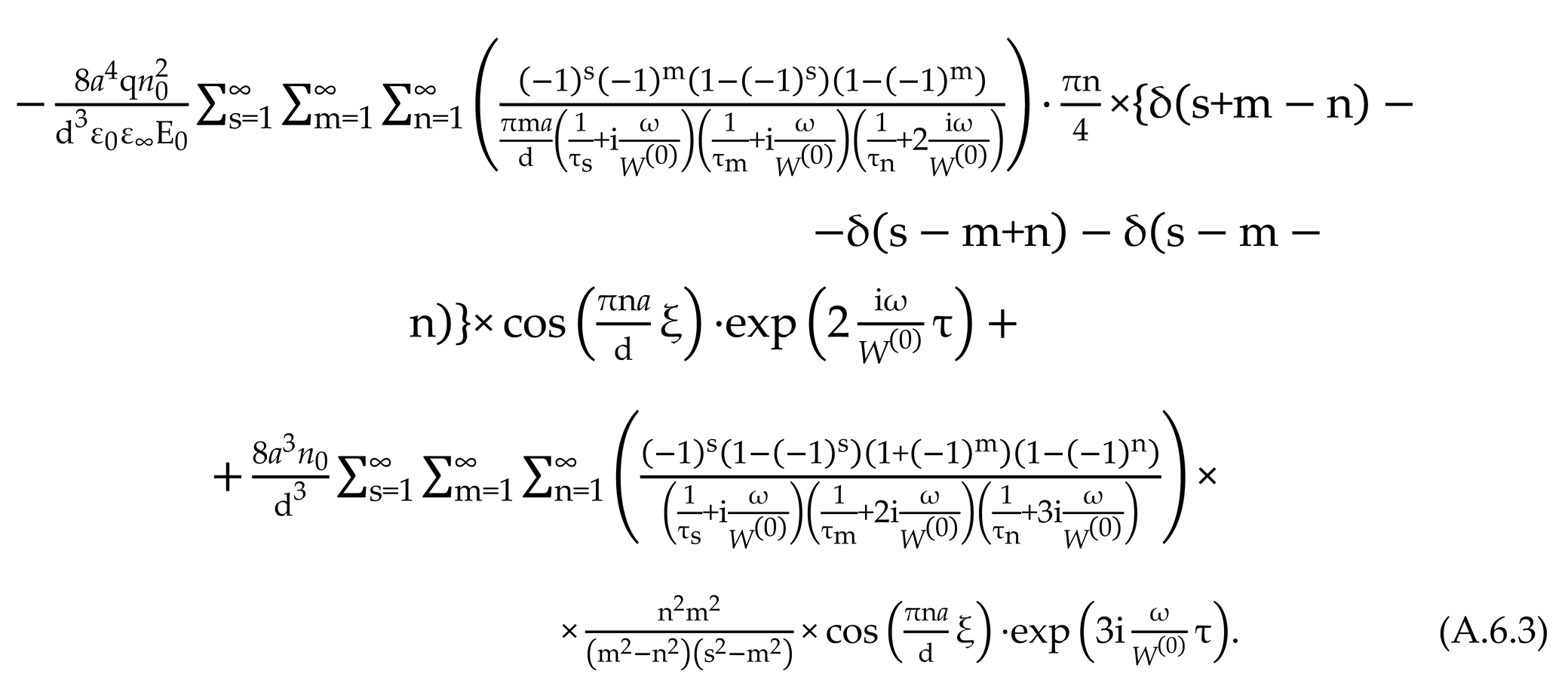
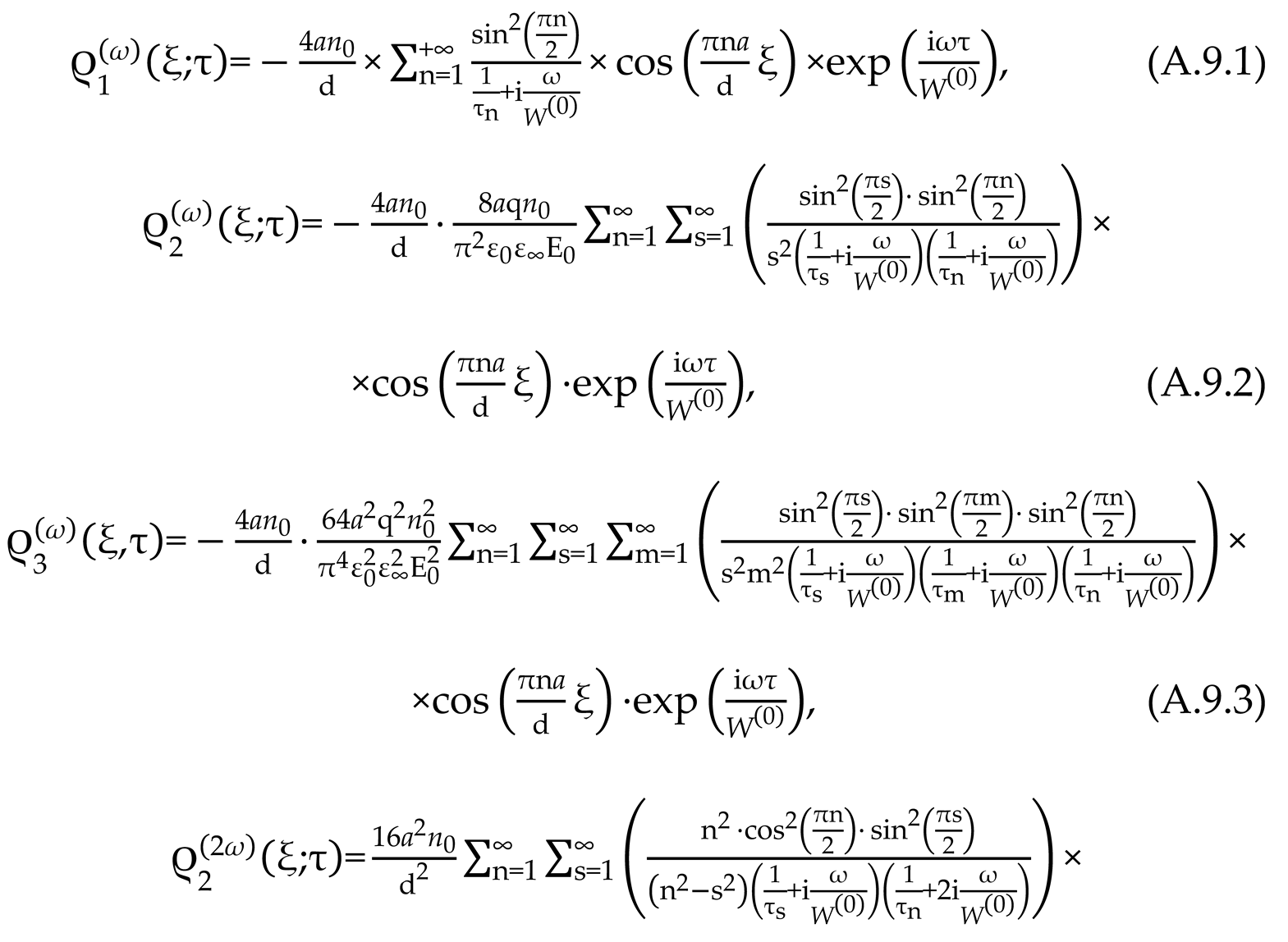
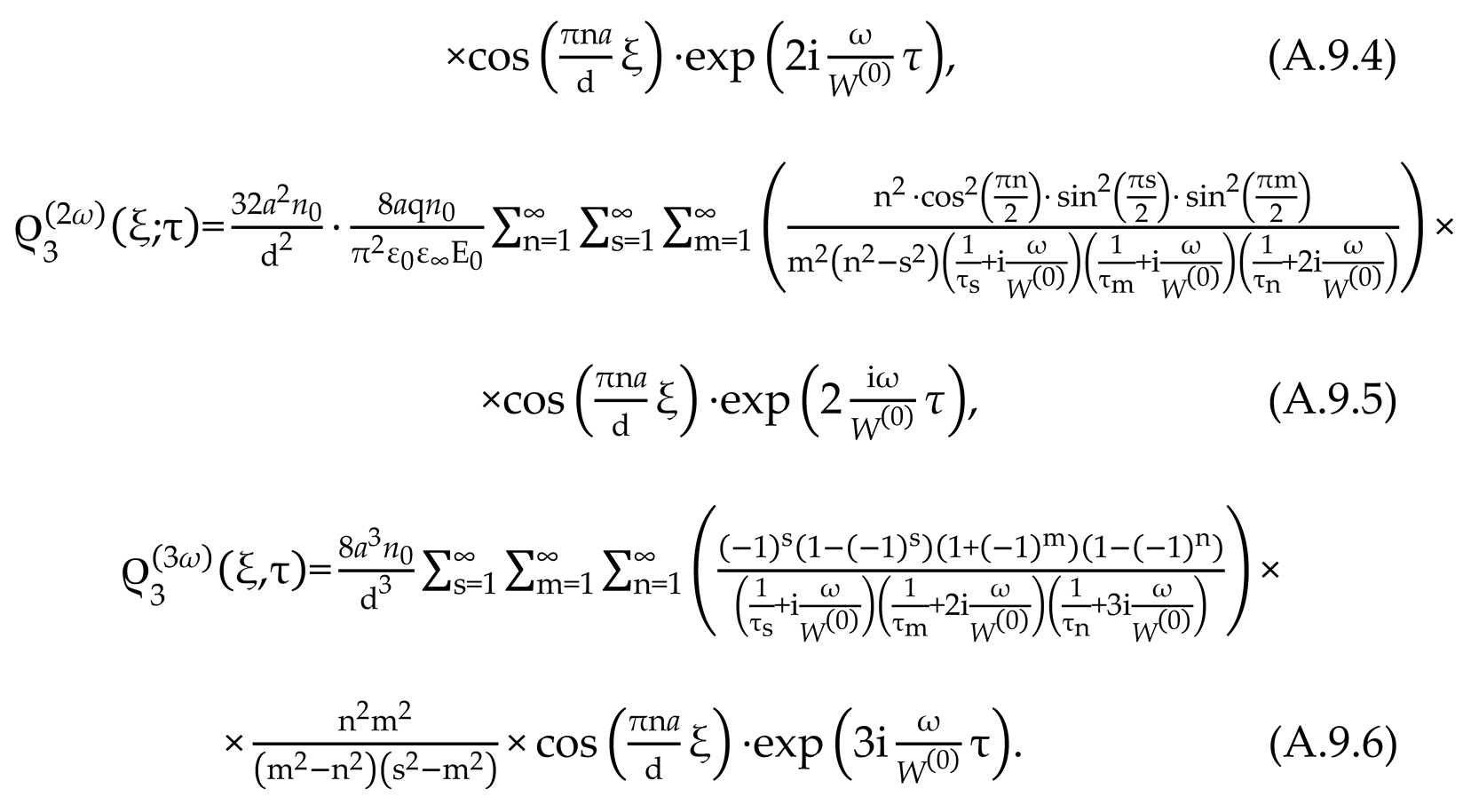

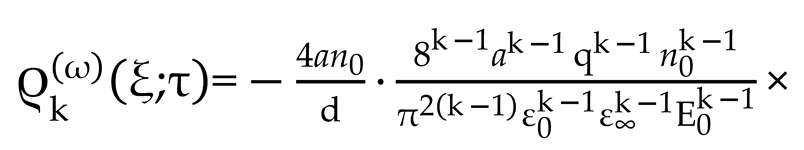
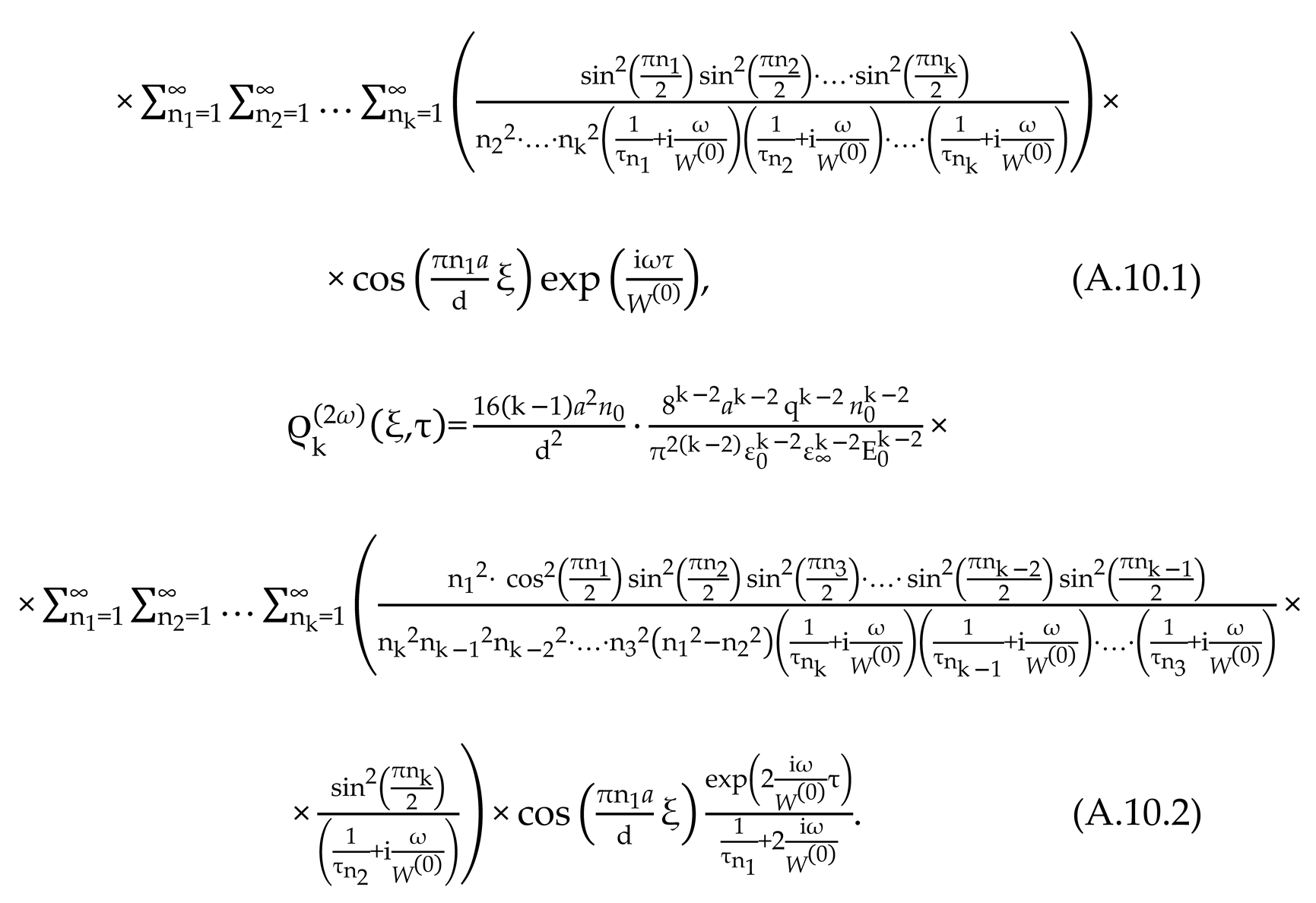
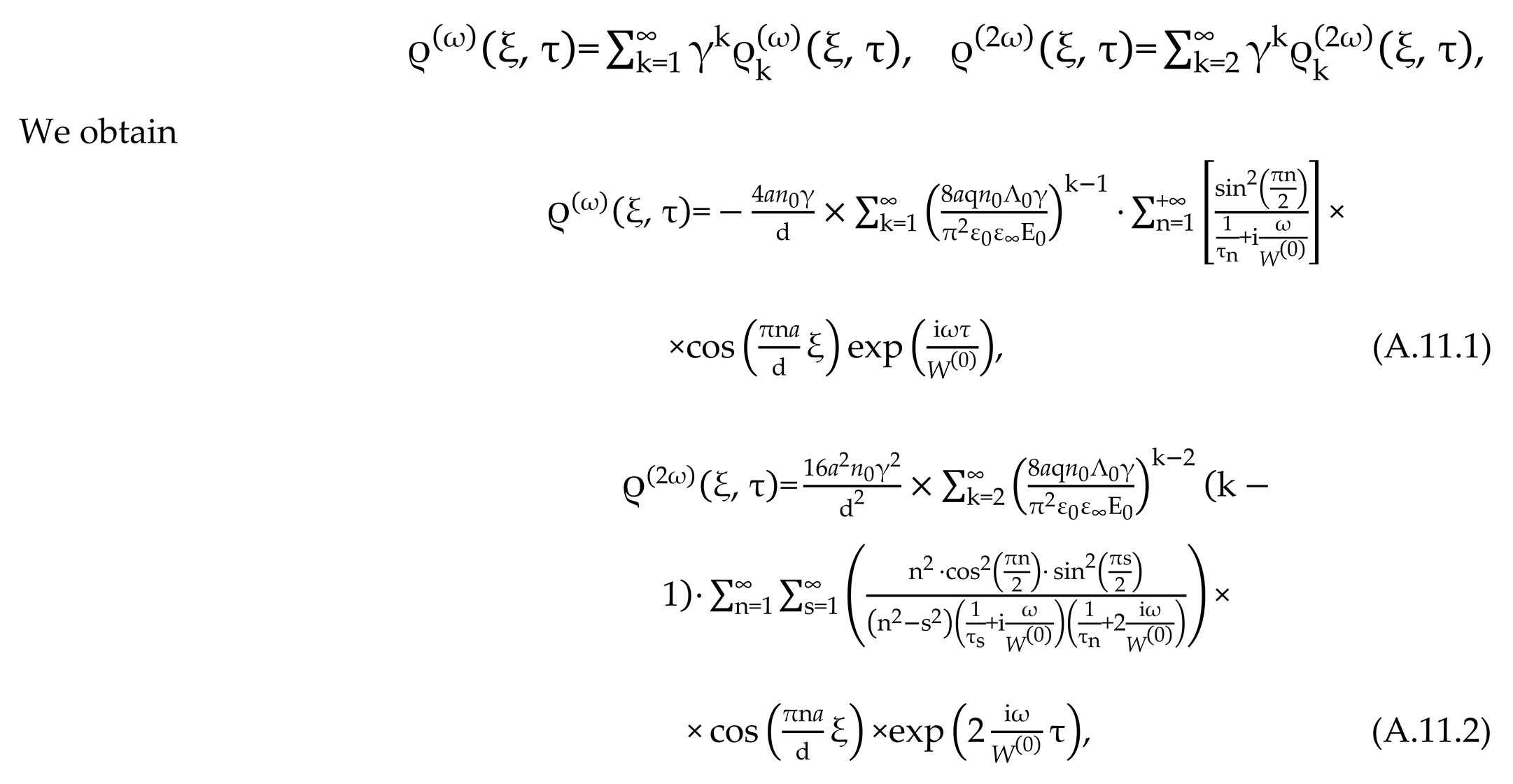 whence, we finally calculate the density of the volumetric charge in the function of the spatial variable and time in the infinite approximation of the perturbation theory , at the frequencies of the alternating electric field ,
whence, we finally calculate the density of the volumetric charge in the function of the spatial variable and time in the infinite approximation of the perturbation theory , at the frequencies of the alternating electric field , 




