Universe Expanding vs Non-Expanding Interpretation of Friedmann Lemaître Robertson Walker (FLRW) Metric

1. Foundations of the Expanding Universe

The expanding universe rest on the Einstein’s field equation given by

$$\begin{array}{c}\hfill R_{\mu \nu }-{\displaystyle \frac{1}{2}}{g}_{\mu \nu }R+\Lambda g_{\mu \nu }={\displaystyle \frac{8\pi G}{c^4}}{T}_{\mu \nu }\end{array}$$

(1)

where $R_{\mu \nu }$ is the Ricci curvature tensor, ${\displaystyle R}$ is the scalar curvature, $T_{\mu \nu }$ is the energy momentum tensor and $g_{\mu \nu }$ metric tensor. The form of $g_{\mu \nu }$ for a homogeneous and isotropic universe is know as the FLRW metric and is given by

$$\begin{array}{c}\hfill -c^{2}d{\tau }^2=-c^{2}d{t}^2+a{\left(t\right)}^2\left[{\displaystyle \frac{d{r}^2}{1-k{r}^2}}+r^{2}d{\Omega }^2\right]\end{array}$$

(2)

being

$$\begin{array}{c}\hfill d{\Omega }^2=d{\theta }^2+si{n}^2\theta d{\varphi }^2\end{array}$$

(3)

where k describes the curvature, while a(t) is a time-dependent factor commonly interpreted as the scale factor of an expanding universe. There are different distance ladders relating theory and observations. Let us to provide a brief summary of some distance definitions and their relations with normalized densities (${\Omega }_M$, ${\Omega }_r$, ${\Omega }_{\Lambda }$, ${\Omega }_k$), corresponding to matter, radiation, cosmological constant and curvature ([18]) respectively. The first Friedmann equation can be expressed from the Hubble parameter H at any time, and the Hubble constant $H_0$ today as

$$\begin{array}{c}\hfill {\displaystyle \frac{\dot{a}{\left(t\right)}^2}{a{\left(t\right)}^2}}=H^2=H_0^{2}E{\left(z\right)}^2\end{array}$$

(4)

where

$$\begin{array}{c}\hfill E\left(z\right)=\sqrt{{\Omega }_K{(1+z)}^2+{\Omega }_{\Lambda }+{\Omega }_M{(1+z)}^3+{\Omega }_r{(1+z)}^4}\end{array}$$

(5)

By integrating Equation 2 along with Equation 4 one can obtain the line of sight comoving distance $d_C$ as

$$\begin{array}{c}\hfill d_C=d_H{\int }_0^z{\displaystyle \frac{d{z}^{\prime }}{E\left(z^{\prime }\right)}}\end{array}$$

(6)

where $d_H=c/H_0=3000h^{-1}Mpc$ is the Hubble distance. From the same equations one can get the transverse comoving distance$d_M$ as

$$\begin{array}{c}\hfill d_M=\left\{\begin{array}{ccc}{d}_H{\displaystyle \frac{1}{{\&\#x003A9;}_k}}sinh[{\&\#x003A9;}_k{d}_C/d_H]& for& {\Omega }_k>0\\ d_c& for& {\Omega }_k=0\\ d_H{\displaystyle \frac{1}{\sqrt{|{\Omega }_k|}}}sin[\sqrt{|{\Omega }_k|}{d}_C/d_H]& for& {\Omega }_k<0\end{array}\right\}\end{array}$$

(7)

With respect to observable quantities, the angular diameter distance $d_A$ is defined as the ratio between the object physical size S and its angular size $\theta$

$$\begin{array}{c}\hfill d_A={\displaystyle \frac{S}{\theta }}\end{array}$$

(8)

The angular diameter distance is related to the transverse comoving distance by

$$\begin{array}{c}\hfill d_M=d_A(1+z)\end{array}$$

(9)

where z is the redshift. On the other hand, the luminosity distance defines the relation between the bolometric flux energy f received at earth from an object, to its bolometric luminosity L by means of

$$\begin{array}{c}\hfill f={\displaystyle \frac{L}{4\pi d_L^2}}\end{array}$$

(10)

or finding $d_L$

$$\begin{array}{c}\hfill d_L=\sqrt{{\displaystyle \frac{L}{4\pi f}}}\end{array}$$

(11)

The relation between $d_L$ and $d_M$ is given by

$$\begin{array}{c}\hfill d_L=d_M(1+z)\end{array}$$

(12)

and taking into account Equation 9

$$\begin{array}{c}\hfill d_L^2=d_A^2{(1+z)}^4\end{array}$$

(13)

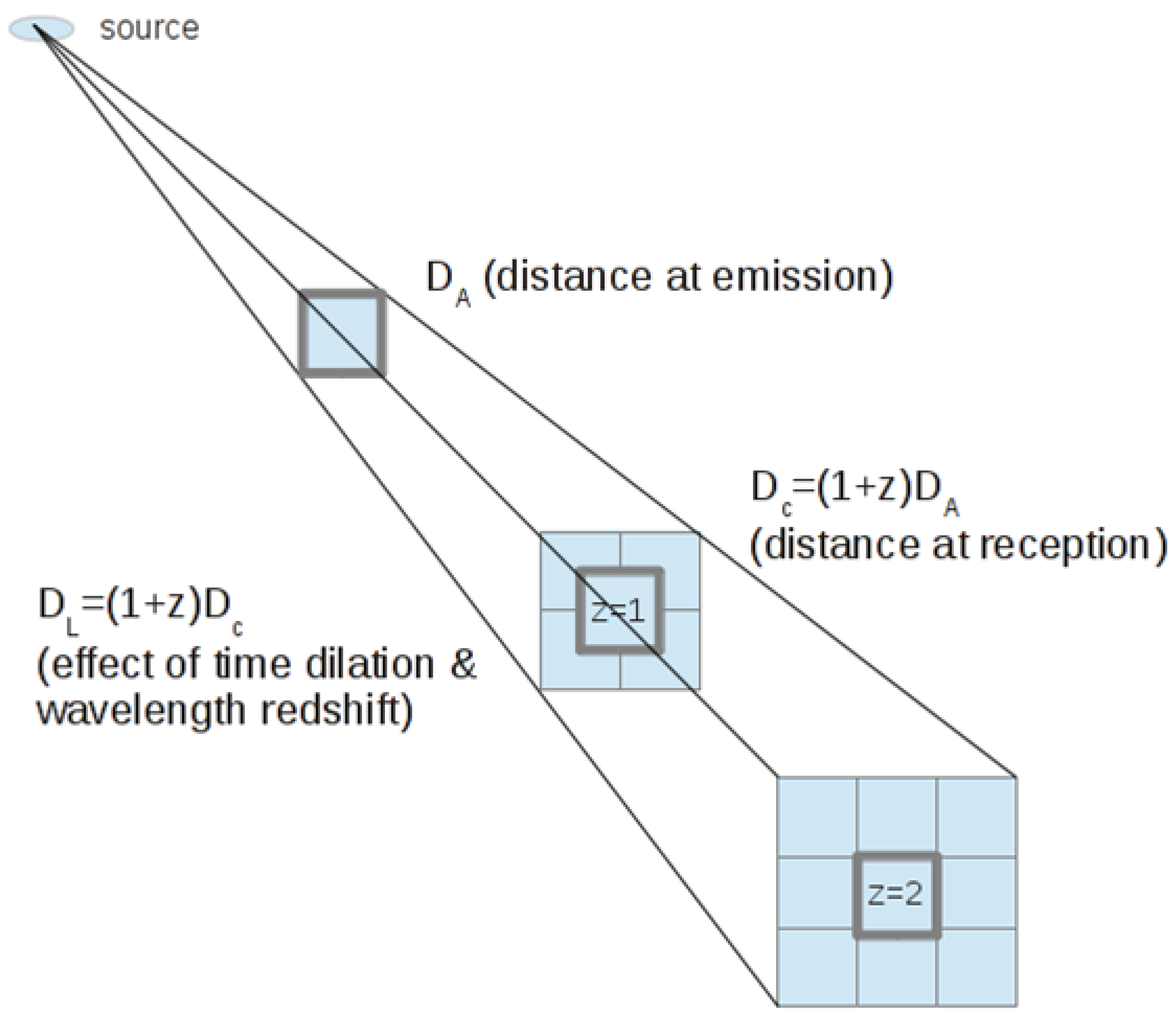
There are four (1+z) factors affecting to flux energy diminution (Figure 1). Two come from the elongation of the initial distance $d_A$ by a factor of $(1+z)$ due to universe expansion according to the inverse square law. Another factor comes from the time dilation due to universe expansion that reduces the photon emission/reception rate by ${(1+z)}^{-1}$. The last factor comes from the cosmological wavelength redshift that decrease the energy of photons by ${(1+z)}^{-1}$. Therefore, a relevant relation is established between the angular diameter distance and the luminosity distance in the expanding universe as

$$\begin{array}{c}\hfill d_L=d_A{(1+z)}^2\left(expandinguniverse\right)\end{array}$$

(14)

Equation 14 is commonly known as Etherington distance-duality relation.

2. Weakness of the Expanding Interpretation of FLRW Metric

Let us to focus on the expanding interpretation of the FLRW metric. The radial coordinate r in Equation 2 is commonly interpreted as a comoving radial coordinate and hence the base for comoving distance ($d_M$) computation, rather than luminosity distance $d_L$. Thus, note the observable luminosity distance $d_L$ given by Equation 11, which depends on the flux of energy, is not related with the energy momentum tensor $T_{\mu \nu }$ in spite of both treat with energy. It is required to define an additional equation

$$\begin{array}{c}\hfill d_L=d_M(1+z)\end{array}$$

(15)

to relate the luminosity distance $d_L$ with the comoving distance $d_M$, and hence with Einstein’s field equation. Note that it is not $a\left(t\right)$, but the consideration of r in FLRW metric as a radial comoving coordinate, that push the FLRW model to be interpreted as an expanding one.

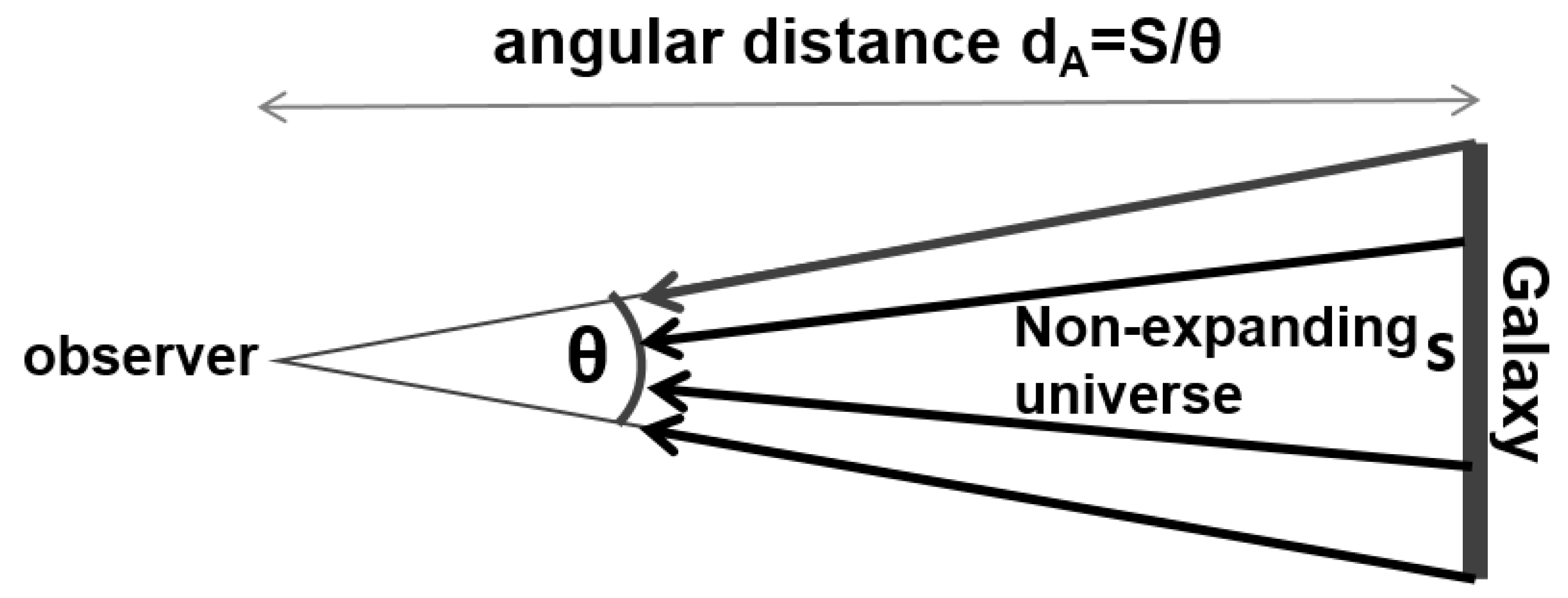
A similar question arise with respect to Etherington relation. Figure 2 shows the relation between the luminosity distance $\Delta$ and the angular diameter distance ${\Delta }^{\prime }$ derived by Etherington from general relativity. Thus, the Etherington equation is the reciprocity theorem for a local (i.e. non-expanding) universe:

$$\begin{array}{c}\hfill d_L=d_A(1+z)(non-expandinguniverse)\end{array}$$

(16)

Note that this equation can be adapted for an expanding universe by the introduction of an additional intermediate variable $d_M$ (comoving distance), that through equations Equation 9 and Equation 15, gives the Equation 14, known as Etherington distance-duality relation. Therefore, it is by the definition of these two intermediate external equations (Equation 9 and Equation 15), that the expanding paradigm is supported.

3. Non-Expanding Interpretation of FLRW Metric

Let us reflect on the same FLRW metric considered in the previous section given by

$$\begin{array}{c}\hfill -c^{2}d{\tau }^2=-c^{2}d{t}^2+a{\left(t\right)}^2\left[{\displaystyle \frac{d{r}^2}{1-k{r}^2}}+r^{2}d{\Omega }^2\right]\end{array}$$

(17)

and let us to analyze the behavior of light rays considering a non-expanding universe (Figure 3). Let the origin of coordinates be at the observer O, and considers an extended cosmological object (galaxy) initially located at a distance $d_A$ from O at time of emission $t_e$. According to general relativity, light rays follow null geodesics where $d{\tau }^2=0$. Substituting this value in Equation 17, light rays follow the equation

$$\begin{array}{c}\hfill c^{2}d{t}^2=a{\left(t\right)}^2\left[{\displaystyle \frac{d{r}^2}{1-k{r}^2}}+r^{2}d{\Omega }^2\right]\end{array}$$

(18)

Note from Figure 3 that the light rays propagate on the radial direction (leaving apart non pure cosmological effects as gravitational lensing or astrophysical events). Therefore $\theta =cte$, $d\theta =0$, $\varphi =cte$, $d\varphi =0$ in Equation 3, and hence $d\Omega =0$ . Substituting $d\Omega =0$ in Equation 18, the light rays that will arrive to the observer meet

$$\begin{array}{c}\hfill c^{2}d{t}^2=a{\left(t\right)}^2{\displaystyle \frac{d{r}^2}{1-k{r}^2}}\end{array}$$

(19)

Now, integrating Equation 19 from time of emission $t_e$ to time of observation $t_o$, and considering r simply as the radial coordinate rather than the radial comoving coordinate, the integration limit becomes directly the luminosity distance, dropping out the intermediate comoving distance concept. Thus, in this case we obtain

$$\begin{array}{c}\hfill {\int }_{t_e}^{t_o}{\displaystyle \frac{cdt}{a\left(t\right)}}={\int }_0^{d_L}{\displaystyle \frac{dr}{\sqrt{1-k{r}^2}}}(non-expandinguniverse)\end{array}$$

(20)

rather than

$$\begin{array}{c}\hfill {\int }_{t_e}^{t_o}{\displaystyle \frac{cdt}{a\left(t\right)}}={\int }_0^{d_M}{\displaystyle \frac{dr}{\sqrt{1-k{r}^2}}}\left(expandinguniverse\right)\end{array}$$

(21)

Note that in a non-expanding universe, the comoving distance $d_M$ loose its meaning and it should be substituted by the luminosity distance $d_L$ in all equations.

$$\begin{array}{c}\hfill d_M=d_L(non-expandinguniverse)\end{array}$$

(22)

As a consequence, the radial comoving coordinate r of the expanding FLRW model, should be interpreted as the radial coordinate on the non-expanding FLRW model. In the simplest case of a flat non-expanding universe ($k=0$), we would have

$$\begin{array}{c}\hfill d_L={\int }_0^t{\displaystyle \frac{cdt}{a\left(t\right)}}(non-expandinguniverse)\end{array}$$

(23)

where $a\left(t\right)$ still would be the factor responsible of time dilation and cosmological redshift in a non-expanding universe, but with another meaning.

On the other hand, since the comoving concept disappear, we can substitute Equation 22 on Equation 7, obtaining

$$\begin{array}{c}\hfill d_L=\left\{\begin{array}{ccc}{d}_H{\displaystyle \frac{1}{{\Omega }_k}}sinh[{\Omega }_k{d}_C/d_H]& for& {\Omega }_k>0\\ d_c& for& {\Omega }_k=0\\ d_H{\displaystyle \frac{1}{\sqrt{|{\Omega }_k|}}}sin[\sqrt{|{\Omega }_k|}{d}_C/d_H]& for& {\Omega }_k<0\end{array}\right\}\end{array}$$

(24)

that directly relates the first Friedmann equation with the observable luminosity distance $d_L$, without the need to define additional intermediate equations.

In an expanding universe, the Friedmann equations constraints the form of the scale factor $a\left(t\right)$ with the different species of the universe as radiation, matter, curvature and cosmological constant. In the non-expanding interpretation of the FLRW model, $a\left(t\right)$ also depends exactly in the same way on the relative content of these species along cosmic time. Even more, the stability of the FLRW non-expanding universe resides on the same argumentation given for the expanding universe, but with a different interpretation, since $a\left(t\right)$ is not related to the size of the universe. The standard model demonstrates that the geodesics for a free particle (galaxy) corresponds to fixed FLRW comoving coordinates. The same demonstration applies to non-expanding-FLRW by interpreting the radial comoving coordinate simply as the radial coordinate. Thus, geodesics for a free particle in a non-expanding universe corresponds to fixed FLRW coordinates. Therefore, it is the own FLRW metric that ensure the stability of the non-expanding universe.

Let us to consider an alternative view of the FLRW metric dividing both sides of Equation 17 by $a{\left(t\right)}^2$. In this case we have

$$\begin{array}{c}\hfill -{\left({\displaystyle \frac{cd\tau }{a\left(t\right)}}\right)}^2=-{\left({\displaystyle \frac{cdt}{a\left(t\right)}}\right)}^2+\left[{\displaystyle \frac{d{r}^2}{1-k{r}^2}}+r^{2}d{\Omega }^2\right]\end{array}$$

(25)

In this view, we see that a(t) may affect not only to the spatial coordinates of the FLRW metric, but alternatively to temporal behaviour or to the speed of light. In the case of constant speed of light, $c=cte$, a(t) affects to the temporal behaviour as a time down-scaling rather than a space scaling. From Equation 23, we can define

$$\begin{array}{c}\hfill \Delta t^{\prime }={\int }_0^t{\displaystyle \frac{dt}{a\left(t\right)}}(non-expandinguniverse)\end{array}$$

(26)

in such a way that $d_A=c\Delta t$ and $d_L=c\Delta t^{\prime }$, and therefore

$$\begin{array}{c}\hfill {\displaystyle \frac{d_L}{d_A}}={\displaystyle \frac{\Delta t^{\prime }}{\Delta t}}=(1+z)(non-expandinguniverse)\end{array}$$

(27)

which would explain the redshift as a time dilation.

In the next section, we explore the case of a feasible variable speed of light with cosmic time.

4. Exploring Variable Magnetic Permeability with Cosmic Time as a Possible Cause of Cosmological Redshift

In this section, we explore the possibility of variable speed of light (VSL) with cosmic time as a feasible cause of the redshift. The cosmological principle assumes a universe spatially homogeneous and spatially isotropic. It does not state that the universe is the same over time. Thus, according to the cosmological principle, we can allow a space property to change overtime. That is the case of the scale factor in the expanding universe or the speed of light in the non-expanding one. There are different VSL theories as those addressing the horizon problem ([19,20]) or the ones allowing the variation of speed of light between free-falling observers ([21]). Other depart from FLRW metric as the one that assumes both expansion and VLS ([22])(which would requires a value of $\gamma \ge 3$) or those assuming photons emitted at higher speed of light at earlier times, but maintaining such high velocities up to earth ([23]), events not observed experimentally.

Though less known, there is a plausible alternative explanation to redshift based on variable speed of light with cosmic time ([24]). Such approach would still require a spatially constant speed of light among all free falling observes as the general relativity demands. In this case, from Equation 23 we can write

$$\begin{array}{c}\hfill d_L={\int }_0^{t}c\left(t\right)dt(non-expandinguniverse)\end{array}$$

(28)

where

$$\begin{array}{c}\hfill c\left(t\right)={\displaystyle \frac{c}{a\left(t\right)}}(non-expandinguniverse)\end{array}$$

(29)

The process of photon redshift based on a speed of light decreasing with cosmic time can be described as follow: a galaxy emits a photon at speed $c_z$ due to an electron transition between atomic levels at its corresponding energy $h{\nu }_0$, being lambda stretched out at emission due to the equation ${\lambda }_z=c_z/{\nu }_0$. In the travel of the photon to earth, ${\lambda }_z$ remains constant, while the frequency decrease up to ${\nu }_z$ due to speed of light drop ${\nu }_z=c_0/{\lambda }_z$.

Such behaviour would agree with the observed redshift.

Given that the speed of light is

$$\begin{array}{c}\hfill c={\displaystyle \frac{1}{\sqrt{{ϵ}_0{\mu }_0}}}\end{array}$$

(30)

some of the vacuum properties, either dielectric permittivity ${ϵ}_0$ or magnetic permeability ${\mu }_0$, have to change with cosmic time. Since the gross atomic structure of redshifted galaxies and its corresponding energy levels depend on ${ϵ}_0$, it should remain constant. Thus, we assume

$$\begin{array}{c}\hfill c\left(t\right)={\displaystyle \frac{1}{\sqrt{{ϵ}_0{\mu }_0^{\prime }\left(t\right)}}}\end{array}$$

(31)

being

$$\begin{array}{c}\hfill {\mu }_0^{\prime }\left(t\right)={\mu }_0{a}^2\left(t\right)\end{array}$$

(32)

in such a way that only magnetic fields and the fine structure constant would be affected along cosmic time. Therefore, in this case the time dependent function $a\left(t\right)$ defined in $FLRW$ metric would not correspond to an expansion, but to the square root of an increasing magnetic permeability. Consequently, the speed of light would decreases with cosmic time àccording to Equation 31, while the electric permittivity ${ϵ}_0$ remains constant allowing the observed atomic structures. The model can be denominated ${\mu }_0^{\prime }-FLRW$ to differentiate it from other possible alternatives.

Note that ${\mu }_0^{\prime }-FLRW$ universe does not change the FLRW equation, but reinterpreted it. Thus, ${\mu }_0^{\prime }-FLRW$ may assumes the main ideas of the standard model as that the early universe was hotter and dominated by radiation. But in this case, the cause of the drop in the temperature of the universe would not be expansion, but the drop of the speed of light with cosmic time. Thus, the cosmic microwave background would have been emitted at the same energy as in the standard model with values ${\nu }_z={\nu }_{cmb}(1+zcmb)$, $c_z=c(1+zcmb)$ and ${\lambda }_{cmb}=c_z/{\nu }_z$, and is received as c, ${\nu }_{cmb}$ and ${\lambda }_{cmb}$.

In the same sense, ${\mu }_0^{\prime }-FLRW$ would meet the Friedmann equations, being the value of ${\mu }_0^{\prime }$ modulated by the same cosmological species as radiation, matter, curvature or dark energy.

5. Conclusions

The FLRW metric is a solution of the Einstein’s field equations for a homogeneous and isotropic universe. The FLRW metric is characterized by a time varying factor $a\left(t\right)$, which is considered as the scale factor of an expanding universe. Even more, $a\left(t\right)$ is related through Friedman equations with the different constituents of the universe as radiation, matter, curvature or dark energy.

In this work, we show that $a\left(t\right)$ may affect not only to the spatial part of the metric, but alternatively to the temporal behaviour or to the speed of light, whenever the FLRW radial comoving coordinate is considered simply as a radial coordinate. Consequently, the cosmological redshift can be explained by a time downscaling or a variable magnetic permeability with cosmic time respectively, rather that by a space scaling, while maintaining the main principles of the standard model.

Finally remark that the relation between the luminosity distance and the angular diameter distance is the key to elucidate between the different alternatives. Much experimental work should be focused on this topic.