Submitted:
14 October 2024
Posted:
16 October 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
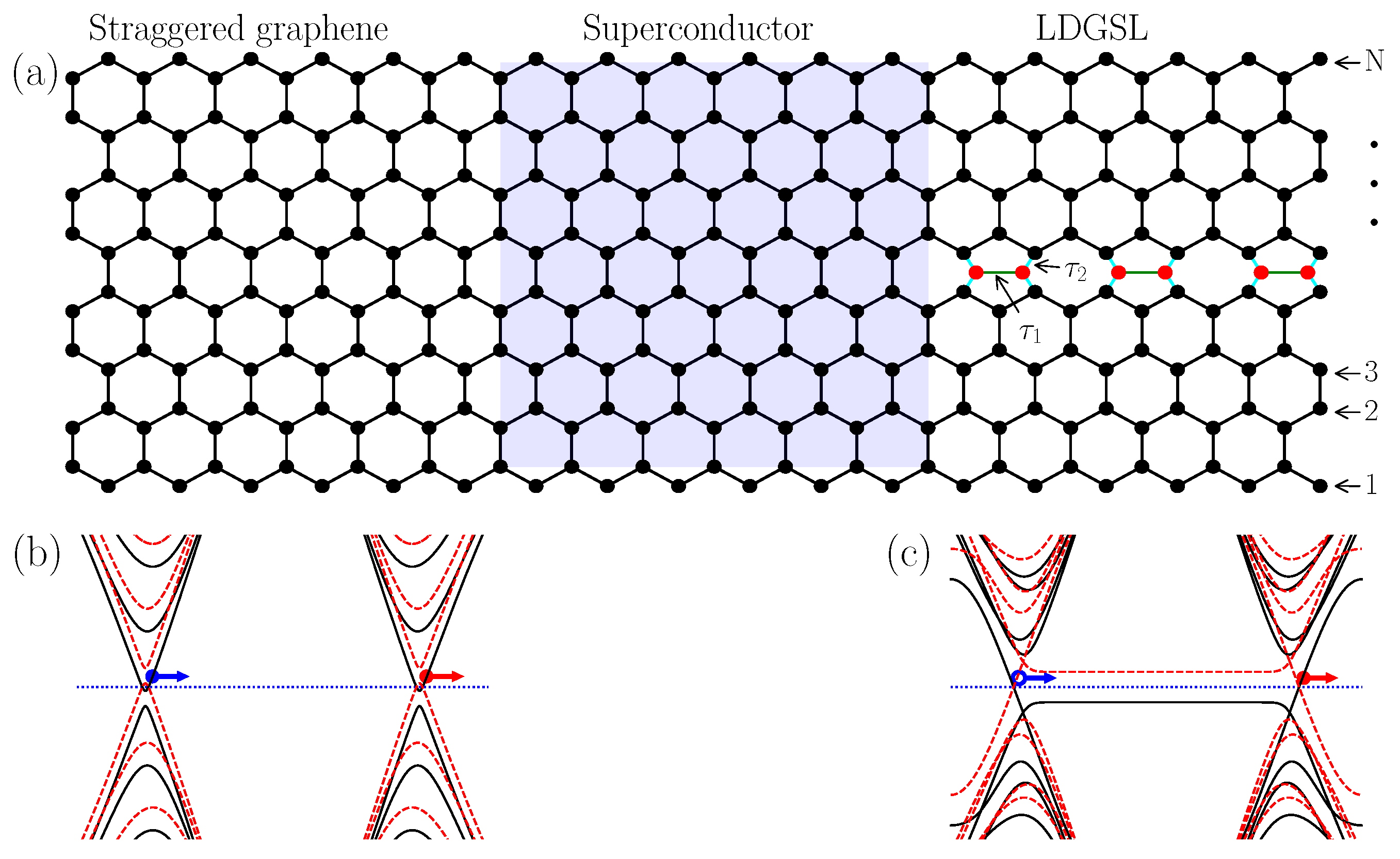
2. Theoretical Modeling
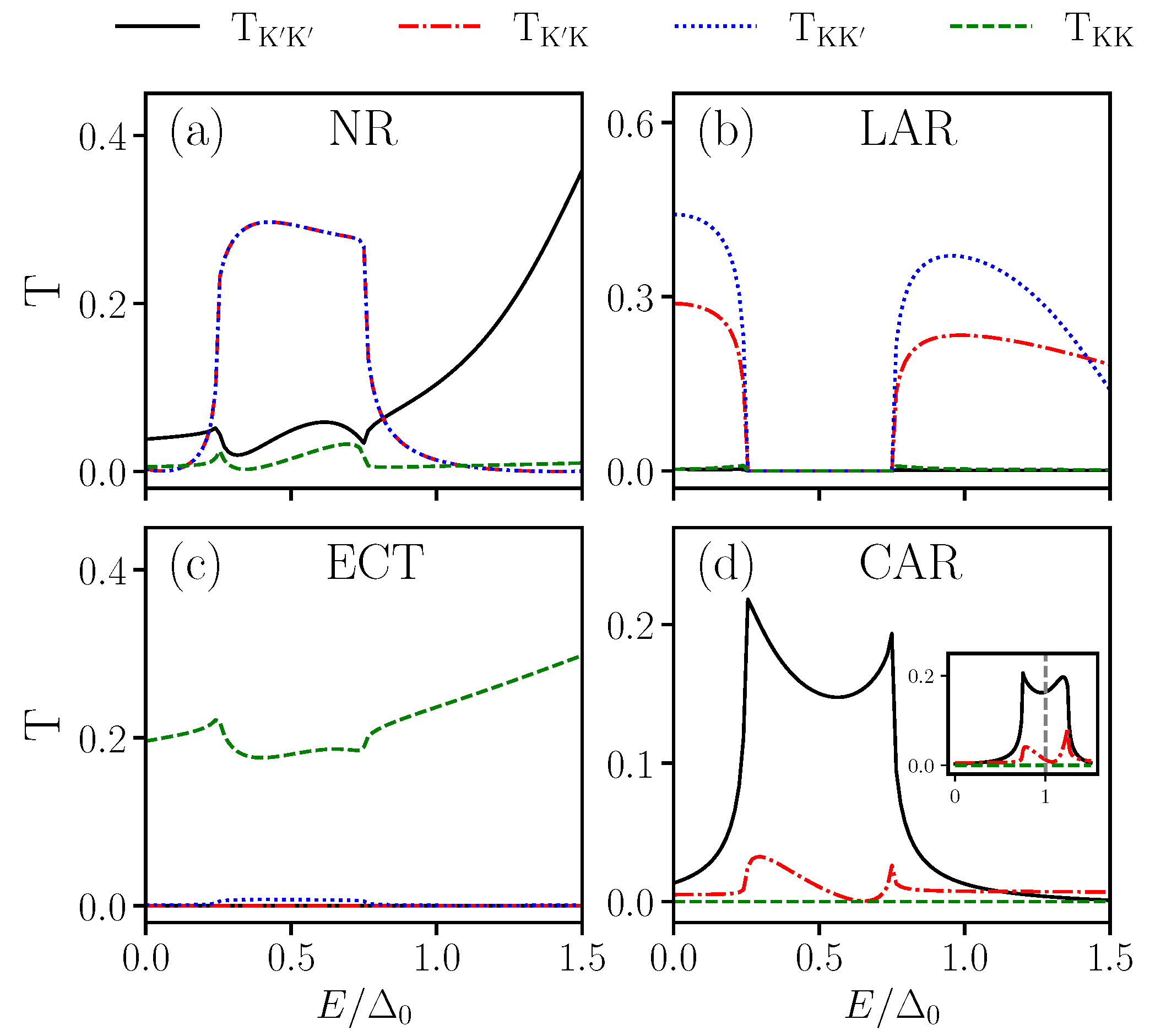
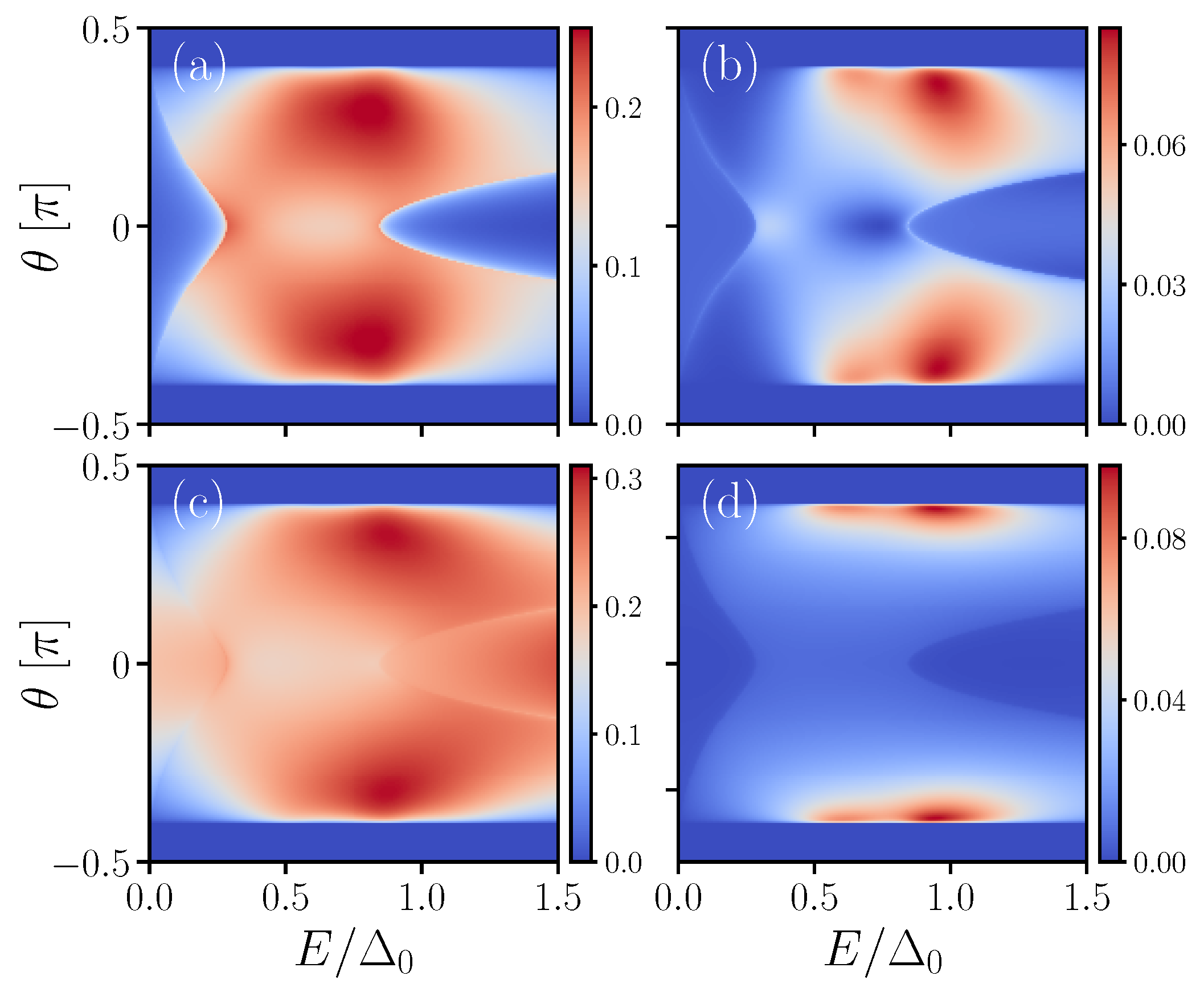
3. Numerical Results
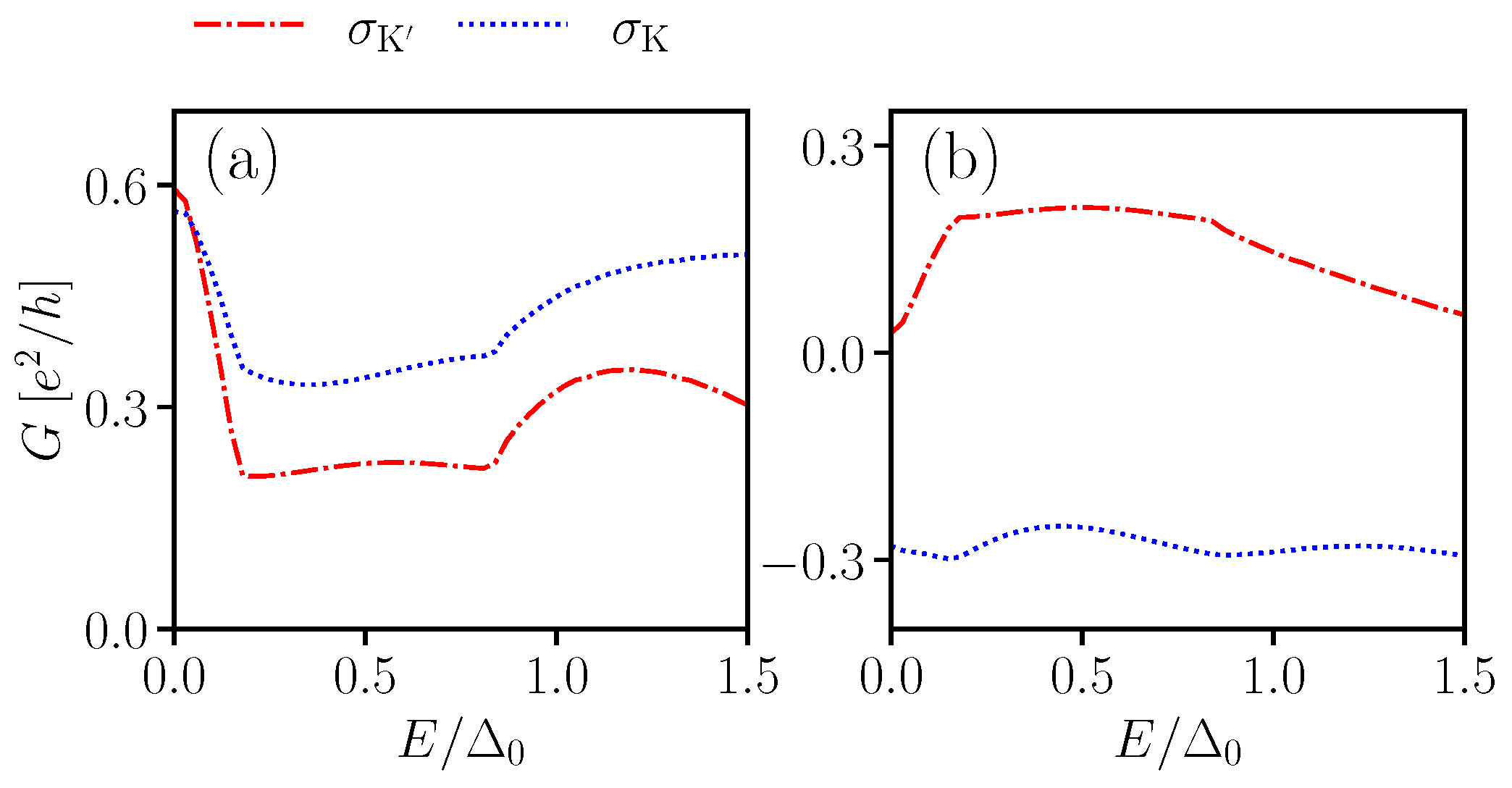
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vidal, G. Efficient classical simulation of slightly entangled quantum computations. Physical review letters 2003, 91, 147902. [Google Scholar] [CrossRef] [PubMed]
- Chtchelkatchev, N.M.; Blatter, G.; Lesovik, G.B.; Martin, T. Bell inequalities and entanglement in solid-state devices. Physical Review B 2002, 66, 161320. [Google Scholar] [CrossRef]
- Sauret, O.; Martin, T.; Feinberg, D. Spin-current noise and Bell inequalities in a realistic superconductor-quantum dot entangler. Physical Review B 2005, 72, 024544. [Google Scholar] [CrossRef]
- Nilsson, J.; Akhmerov, A.R.; Beenakker, C.W.J. Splitting of a Cooper pair by a pair of Majorana bound states. Physical review letters 2008, 101, 120403. [Google Scholar] [CrossRef] [PubMed]
- Hofstetter, L.; Csonka, S.; Nygård, J.; Schönenberger, C. Cooper pair splitter realized in a two-quantum-dot Y-junction. Nature 2009, 461, 960–963. [Google Scholar] [CrossRef]
- Veldhorst, M.; Brinkman, A. Nonlocal Cooper Pair Splitting in a pSn Junction. Physical Review Letters 2010, 105, 107002. [Google Scholar] [CrossRef]
- Hofstetter, L.; Csonka, S.; Baumgartner, A.; Fülöp, G.; d’Hollosy, S.; Nygård, J.; Schönenberger, C. Finite-bias Cooper pair splitting. Physical review letters 2011, 107, 136801. [Google Scholar] [CrossRef]
- Tan, Z.B.; Cox, D.; Nieminen, T.; Lähteenmäki, P.; Golubev, D.; Lesovik, G.B.; Hakonen, P.J. Cooper pair splitting by means of graphene quantum dots. Physical review letters 2015, 114, 096602. [Google Scholar] [CrossRef]
- Pandey, P.; Danneau, R.; Beckmann, D. Ballistic Graphene Cooper Pair Splitter. Physical review letters 2021, 126, 147701. [Google Scholar] [CrossRef]
- Recher, P.; Sukhorukov, E.V.; Loss, D. Andreev tunneling, Coulomb blockade, and resonant transport of nonlocal spin-entangled electrons. Physical Review B 2001, 63, 165314. [Google Scholar] [CrossRef]
- Zhu, Y.; Sun, Q.f.; Lin, T.h. Andreev reflection through a quantum dot coupled with two ferromagnets and a superconductor. Physical Review B 2001, 65, 024516. [Google Scholar] [CrossRef]
- Yamashita, T.; Takahashi, S.; Maekawa, S. Crossed Andreev reflection in structures consisting of a superconductor with ferromagnetic leads. Physical Review B 2003, 68, 174504. [Google Scholar] [CrossRef]
- Mélin, R.; Peysson, S. Crossed Andreev reflection at ferromagnetic domain walls. Physical Review B 2003, 68, 174515. [Google Scholar] [CrossRef]
- Mélin, R.; Feinberg, D. Sign of the crossed conductances at a ferromagnet/superconductor/ferromagnet double interface. Physical Review B 2004, 70, 174509. [Google Scholar] [CrossRef]
- Beckmann, D.; Weber, H.B.; Löhneysen, H.V. Evidence for crossed Andreev reflection in superconductor-ferromagnet hybrid structures. Physical review letters 2004, 93, 197003. [Google Scholar] [CrossRef]
- Benjamin, C. Crossed Andreev reflection as a probe for the pairing symmetry of ferromagnetic superconductors. Physical Review B 2006, 74, 180503. [Google Scholar] [CrossRef]
- Cadden-Zimansky, P.; Chandrasekhar, V. Nonlocal correlations in normal-metal superconducting systems. Physical review letters 2006, 97, 237003. [Google Scholar] [CrossRef]
- Chen, W.; Shen, R.; Sheng, L.; Wang, B.G.; Xing, D.Y. Resonant nonlocal Andreev reflection in a narrow quantum spin Hall system. Physical Review B 2011, 84, 115420. [Google Scholar] [CrossRef]
- Liu, J.; Song, J.; Sun, Q.f.; Xie, X.C. Even-odd interference effect in a topological superconducting wire. Physical Review B 2017, 96, 195307. [Google Scholar] [CrossRef]
- Reeg, C.; Klinovaja, J.; Loss, D. Destructive interference of direct and crossed Andreev pairing in a system of two nanowires coupled via an s -wave superconductor. Physical Review B 2017, 96, 081301. [Google Scholar] [CrossRef]
- Zhang, K.; Zeng, J.; Dong, X.; Cheng, Q. Spin dependence of crossed Andreev reflection and electron tunneling induced by Majorana fermions. Journal of Physics: Condensed Matter 2018, 30, 505302. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Yu, Z.M.; Liu, J.; Jiang, H.; Yang, S.A. Transverse shift in crossed Andreev reflection. Physical Review B 2018, 98, 195141. [Google Scholar] [CrossRef]
- Wang, Y.X.; Wang, X.; Li, Y.X. Double local and double nonlocal Andreev reflections in nodal-line semimetal-superconducting heterostructures. Physical Review B 2022, 105, 195402. [Google Scholar] [CrossRef]
- Galambos, T.H.; Ronetti, F.; Hetényi, B.; Loss, D.; Klinovaja, J. Crossed Andreev reflection in spin-polarized chiral edge states due to the Meissner effect. Physical Review B 2022, 106, 075410. [Google Scholar] [CrossRef]
- Gül, Ö.; Ronen, Y.; Lee, S.Y.; Shapourian, H.; Zauberman, J.; Lee, Y.H.; Watanabe, K.; Taniguchi, T.; Vishwanath, A.; Yacoby, A.; Kim, P. Andreev Reflection in the Fractional Quantum Hall State. Physical Review X 2022, 12, 021057. [Google Scholar] [CrossRef]
- Reinthaler, R.W.; Recher, P.; Hankiewicz, E.M. Proposal for an all-electrical detection of crossed Andreev reflection in topological insulators. Physical review letters 2013, 110, 226802. [Google Scholar] [CrossRef]
- Wang, J.; Hao, L.; Chan, K.S. Quantized crossed-Andreev reflection in spin-valley topological insulators. Physical Review B 2015, 91, 085415. [Google Scholar] [CrossRef]
- Zhang, Y.T.; Hou, Z.; Xie, X.C.; Sun, Q.f. Quantum perfect crossed Andreev reflection in top-gated quantum anomalous Hall insulator–superconductor junctions. Physical Review B 2017, 95, 245433. [Google Scholar] [CrossRef]
- Zhou, Y.F.; Hou, Z.; Zhang, Y.T.; Sun, Q.f. Chiral Majorana fermion modes regulated by a scanning tunneling microscope tip. Physical Review B 2018, 97, 115452. [Google Scholar] [CrossRef]
- Zhang, S.B.; Trauzettel, B. Perfect Crossed Andreev Reflection in Dirac Hybrid Junctions in the Quantum Hall Regime. Physical review letters 2019, 122, 257701. [Google Scholar] [CrossRef]
- Li, Q.; Han, Y.; Zhang, K.; Zhang, Y.T.; Liu, J.J.; Qiao, Z. Multiple Majorana edge modes in magnetic topological insulator–superconductor heterostructures. Physical Review B 2020, 102, 205402. [Google Scholar] [CrossRef]
- Jakobsen, M.F.; Brataas, A.; Qaiumzadeh, A. Electrically Controlled Crossed Andreev Reflection in Two-Dimensional Antiferromagnets. Physical Review Letters 2021, 127, 017701. [Google Scholar] [CrossRef] [PubMed]
- Lu, W.T.; Sun, Q.f. Electrical control of crossed Andreev reflection and spin-valley switch in antiferromagnet/superconductor junctions. Physical Review B 2021, 104, 045418. [Google Scholar] [CrossRef]
- Fuchs, J.; Barth, M.; Gorini, C.; Adagideli, İ.; Richter, K. Crossed Andreev reflection in topological insulator nanowire T junctions. Physical Review B 2021, 104, 085415. [Google Scholar] [CrossRef]
- Cayssol, J. Crossed Andreev Reflection in a Graphene Bipolar Transistor. Physical Review Letters 2008, 100, 147001. [Google Scholar] [CrossRef] [PubMed]
- Benjamin, C.; Pachos, J.K. Detecting entangled states in graphene via crossed Andreev reflection. Physical Review B 2008, 78, 235403. [Google Scholar] [CrossRef]
- Wang, J.; Liu, S. Crossed Andreev reflection in a zigzag graphene nanoribbon-superconductor junction. Physical Review B 2012, 85, 035402. [Google Scholar] [CrossRef]
- Crépin, F.; Hettmansperger, H.; Recher, P.; Trauzettel, B. Even-odd effects in NSN scattering problems: Application to graphene nanoribbons. Physical Review B 2013, 87, 195440. [Google Scholar] [CrossRef]
- Beconcini, M.; Polini, M.; Taddei, F. Nonlocal superconducting correlations in graphene in the quantum Hall regime. Physical Review B 2018, 97, 201403. [Google Scholar] [CrossRef]
- Zhao, S.C.; Gao, L.; Cheng, Q.; Sun, Q.f. Perfect crossed Andreev reflection in the proximitized graphene/superconductor/proximitized graphene junctions. Physical Review B 2023, 108, 134511. [Google Scholar] [CrossRef]
- Xiao-Ling, L.; Zhe, L.; Hai-Bo, Y.; Li-Wei, J.; Wen-Zhu, G.; Yi-Song, Z. Valley polarized electronic transmission through a line defect superlattice of graphene. Physical Review B 2012, 86, 045410. [Google Scholar] [CrossRef]
- Zihlmann, S.; Cummings, A.W.; Garcia, J.H.; Kedves, M.; Watanabe, K.; Taniguchi, T.; Schönenberger, C.; Makk, P. Large spin relaxation anisotropy and valley-Zeeman spin-orbit coupling in WSe2 /graphene/ h -BN heterostructures. Physical Review B 2018, 97, 075434. [Google Scholar] [CrossRef]
- Zollner, K.; Fabian, J. Proximity effects in graphene on monolayers of transition-metal phosphorus trichalcogenides MPX3(M:Mn, Fe, Ni, Co, and X: S, Se). Physical Review B 2022, 106, 035137. [Google Scholar] [CrossRef]
- Khatibi, Z.; Power, S.R. Proximity spin-orbit coupling in graphene on alloyed transition metal dichalcogenides. Physical Review B 2022, 106, 125417. [Google Scholar] [CrossRef]
- Zollner, K.; Cummings, A.W.; Roche, S.; Fabian, J. Graphene on two-dimensional hexagonal BN, AlN, and GaN: Electronic, spin-orbit, and spin relaxation properties. Physical Review B 2021, 103, 075129. [Google Scholar] [CrossRef]
- Wakamura, T.; Reale, F.; Palczynski, P.; Zhao, M.Q.; Johnson, A.T.C.; Guéron, S.; Mattevi, C.; Ouerghi, A.; Bouchiat, H. Spin-orbit interaction induced in graphene by transition metal dichalcogenides. Physical Review B 2019, 99, 245402. [Google Scholar] [CrossRef]
- Frank, T.; Gmitra, M.; Fabian, J. Theory of electronic and spin-orbit proximity effects in graphene on Cu(111). Physical Review B 2016, 93, 155142. [Google Scholar] [CrossRef]
- Waintal, X.; Wimmer, M.; Akhmerov, A.; Groth, C.; Nikolic, B.K.; Istas, M.; Rosdahl, T.Ö.; Varjas, D. Computational quantum transport. [CrossRef]
- Groth, C.W.; Wimmer, M.; Akhmerov, A.R.; Waintal, X. Kwant: a software package for quantum transport. New Journal of Physics 2014, 16, 063065. [Google Scholar] [CrossRef]
- Jana, K.; Muralidharan, B. Robust all-electrical topological valley filtering using monolayer 2D-Xenes. npj 2D Materials and Applications 2022, 6, 19. [Google Scholar] [CrossRef]
- Blonder, G.E.; Tinkham, M.; Klapwijk, T.M. Transition from metallic to tunneling regimes in superconducting microconstrictions: Excess current, charge imbalance, and supercurrent conversion. Physical Review B 1982, 25, 4515–4532. [Google Scholar] [CrossRef]
- Liu, Y.; Song, J.; Li, Y.; Liu, Y.; Sun, Q.f. Controllable valley polarization using graphene multiple topological line defects. Physical Review B 2013, 87, 195445. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




