Quantum-Relativistic Diffusion in Nano-Transport

1. Introduction

Nanomaterials are largely utilized in various applications considering their special properties, which are dependent on size, composition, and structure; the deep understanding of the diffusion process is of high importance for its stability and controlled synthesis. Nanomaterials have peculiar optical, electronic, magnetic, and chemical properties, which significantly differ from that of their bulk counterparts; these particular properties (higher reactivity, higher saturation magnetization, modified electronic band structures, etc.) arise from the fact that they have a large surface-to-volume ratio. Therefore, the investigation of the local structure of nanomaterials is theoretically and technologically highly important. Both a need of new techniques probing the diffusion process for nanoparticles and nano-structures in general, and theoretical efforts in the profound comprehension of transport processes are useful and fruitful for the improve of innovation in science and technology.

X-rays have been widely utilized in imaging and structure determination of materials, in the range from biomolecules to electronics materials, for its penetrating power and short wavelength. With the synchrotron radiation sources and free electron lasers, progress in X-ray science is fast increasing and new imaging techniques are being realized.

The proper understanding of diffusion processes for nanomaterials is important in the synthesis and determination of the material suitability for specific applications, for obtaining desired properties. There are several conventional methods used to study the diffusion in solids (Table I) [1].

At the same time, the theoretical study at level of mathematical modeling is essential, considering always new models which incorporate the characteristics of the previous ones and offer new peculiarities too.

In this paper a generalization of the Drude-Lorentz model for transport processes in nanostructures, performed at classical [2], quantum [3], and relativistic level [4], is generalized to the case of quantum-relativistic effect inside a nanostructure.

Table 1. Conventional experimental methods for direct and indirect diffusion studies in solids [1].

Direct Methods		Indirect Methods
Tracer diffusion Chemical diffusion Spreading resistance profiling (SRP) Rutherford backscattering (RBS) Nuclear reaction analysis (NRA) Field gradient NMR (FG-NMR) Pulsed field-gradient NMR (PFG-NMR)		Mechanical spectroscopy Magnetic relaxation Nuclear magnetic relaxation (NMR) Impedance spectroscopy (IS) Mössbauer spectroscopy (MBS) Quasi-elastic neutron scattering (QENS)

Table 1. Conventional experimental methods for direct and indirect diffusion studies in solids [1].

Direct Methods		Indirect Methods
Tracer diffusion Chemical diffusion Spreading resistance profiling (SRP) Rutherford backscattering (RBS) Nuclear reaction analysis (NRA) Field gradient NMR (FG-NMR) Pulsed field-gradient NMR (PFG-NMR)		Mechanical spectroscopy Magnetic relaxation Nuclear magnetic relaxation (NMR) Impedance spectroscopy (IS) Mössbauer spectroscopy (MBS) Quasi-elastic neutron scattering (QENS)

The analysis of the function $D(t)$ is considered, and this step completes the quantum-relativistic study together to that performed for the velocities correlation function ${〈\overrightarrow{v} (t) \cdot \overrightarrow{v} (0)〉}_T$ [5] and the mean square deviation of position $R^2(t)$ [6].

The paper considers the key elements of this recent generalization of the Drude-Lorentz model (§2), the general expressions of the quantum-relativistic diffusion function D(t) (§3), some examples of application (§4) and ends with the conclusion (§5).

2. A Recent Analytical Generalization of the Drude-Lorentz Model

A recent analytical generalization of the Drude-Lorentz model for transport processes is showing to fit very well with experimental data and presents interesting new predictions of various peculiarities in nanostructures. The model studies the dynamics of processes from sub-pico-level to macro-level; it is based on the complete Fourier transform of the frequency-dependent complex conductivity $\sigma (\omega )$, as deduced by linear response theory [7,8], through a Cauchy integration and the use of the residue theorem in the complex plane [9].

The new introduced key idea is to perform the integration on the entire time axis (-∞, +∞) and not on the half time axis (0, +∞), as usually considered in literature [10].

The new model has its core in the inversion of the Fourier transform in the complex plane considering the whole time axis:

$$< {\overrightarrow{v}}^{\alpha } (0) {\overrightarrow{v}}^{\beta } (t){>}_T = {\displaystyle \frac{k_B T V}{\pi e^2}} {\displaystyle \underset{- \infty }{\overset{+ \infty }{\int }}d\omega \mathrm{Re} {\sigma }_{\beta \alpha }}(\omega ) e^{i \omega t}.$$

(1)

The carrier dynamics is studied considering, in addition to the velocities correlation function ${〈\overrightarrow{v} (t) \cdot \overrightarrow{v} (0)〉}_T$, also the mean square deviation of position of particles $R^2(t)$ and the diffusion function D(t). $R^2(t)$ is defined as:

$$R^2(t)=〈{[\overrightarrow{R} (t) - \overrightarrow{R} (0)]}^2〉.$$

(2)

Eq. (2) is connected to Eq. (1) by the relation:

$$R^2(t)= 2 {\displaystyle \underset{0}{\overset{t}{\int }}dt\text{'} \left(t-t\text{'}\right)} 〈\overrightarrow{v} (t\text{'}) \cdot \overrightarrow{v} (0)〉.$$

(3)

With the residue theorem is therefore possible to obtain the analytical expressions of ${〈\overrightarrow{v} (t) \cdot \overrightarrow{v} (0)〉}_T$, $R^2(t)$ and of the diffusion function $D (t)$, defined as [2,3]:

$$D(t)= {\displaystyle \frac{1}{2}}{\displaystyle \frac{d{R}^2(t)}{dt}} .$$

(4)

3. General Analytical Expressions of the Quantum-Relativistic Diffusion Function D(t)

About the quantum aspects, we considered a frequency-dependent electric field of the form $\overrightarrow{E} = {\overrightarrow{E}}_0 e^{- i \omega t}$in the contest of the time-dependent perturbation theory, with the factor $e \overrightarrow{E} \cdot \overrightarrow{r}$ as perturbing potential.

Written the matrix elements of the dipole moment of the charge in the direction of the electric field as:

$$x_{j 0} = {\displaystyle \int {\mathsf{\Phi }}_j^{*}} e x {\mathsf{\Phi }}_0 dr,$$

(5)

defining the oscillator strength of the j-th transition as:

$$f_j = {\displaystyle \frac{2 m}{{\hslash }^2}} {\displaystyle \sum _j\hslash {\omega }_j} {\left|x_{0 j}\right|}^2,$$

(6)

and keeping into account the relation between permittivity and conductivity of a system, we obtained the relation:

$${\displaystyle \frac{i \sigma (\omega )}{\omega }} = {\displaystyle \frac{1}{4 \pi }} {\displaystyle \sum _i\frac{{\omega }_{p_i}^2}{({\omega }_i^2 - {\omega }^2) - i \omega {\mathsf{\Gamma }}_i}} ,$$

(7)

with:

$${{\omega }_{p_i}}^2 = {\displaystyle \frac{4 \pi N e^2}{m}} f_i$$

(8)

and:

- ${\omega }_i = (E_i - E_0)/\hslash$;

- $E_i$, $E_0$ energies of the excited and the ground states respectively;

- ${\mathsf{\Gamma }}_i = 1/{\tau }_i$ inverse of the decay time of every mode;

- N density of carriers.

Unlike the classical case, the real part of conductivity is calculated at quantum level through the weights $f_i$. The relaxation times can be obtained by ${\tau }_i = 1/{\mathsf{\Gamma }}_i$ and weights $f_i$. The calculation of N can be exactly obtained by Eq. (8), considering that it holds: ${\displaystyle {\sum }_i{f}_i} = 1$.

About the relativistic behavior, we considered the possibility of relativistic velocities of carriers inside a nanostructure through the study of the condition of relativistic variation of the mass along the x-axis on which a nanostructure is placed, in the fixed ground reference frame. About the forces acting on the carrier (electrons, but this is not restrictive), we considered the following outer forces:

- a passive elastic-type force of the form $F_{el} = K x$;

- a passive friction-type force of the form $F_{fr} = \lambda \dot{x}$, with $\lambda = m_{part}/\tau$;

- the force deriving by an oscillating electric field $E = e E_0 e^{- i \omega t}$.

Performing the calculation as for the velocities correlation function ${〈\overrightarrow{v} (t) \cdot \overrightarrow{v} (0)〉}_T$ [5] and the mean square deviation of position $R^2(t)$ [6], the quantum-relativistic analytical expressions of D(t) are as follows:

Q-R₁) Case ${\Delta }_{i R_{Q - R}} > 0$

$$D (t) = 2 \left({\displaystyle \frac{k_B T}{m_0}}\right) \left({\displaystyle \frac{1}{\gamma }}\right) {\displaystyle \sum _i\left\{\left(\frac{f_i {\tau }_i}{{\alpha }_{i R_{Q - R}}}\right) \left[\exp \left(- \frac{1}{2 \rho } \frac{t}{{\tau }_i}\right) \sin \left(\frac{{\alpha }_{i R_{Q - R}}}{2 \rho } \frac{t}{{\tau }_i}\right)\right]\right\}}$$

(9)

with:

$${\alpha }_{i R_{Q - R}} = \sqrt{4 \gamma {\omega }_i^2 {{\tau }_i}^2 - 1 }\in {\Re }^{+}(positiverealnumbers);$$

Q-R₂) Case ${\Delta }_{i I_{Q - R}} < 0$

$$D (t) = \left({\displaystyle \frac{k_B T}{m_0}} \right) \left({\displaystyle \frac{1}{\gamma }}\right) {\displaystyle \sum _i\left\{\left(\frac{f_i {\tau }_i}{{\alpha }_{i I_{Q - R}}}\right) \left[\exp \left(- \frac{(1 - {\alpha }_{i I_{Q - R}})}{2 \rho } \frac{t}{{\tau }_i}\right) - \exp \left(- \frac{(1 + {\alpha }_{i I_{Q - R}})}{2 \rho } \frac{t}{{\tau }_i}\right)\right]\right\}}$$

(10)

with:

$${\alpha }_{i I_{Q - R}} = \sqrt{1 - 4 \gamma {\omega }_i^2 {{\tau }_i}^2}\in ( 0, 1 ) \subset \Re$$

It holds: ${\alpha }_{i I_{Q - R}} = \sqrt{{\Delta }_{i I_{Q - R}} }$, ${\alpha }_{i R_{Q - R}} = \sqrt{{\Delta }_{i R_{Q - R}} }$, $\gamma = 1 /\sqrt{1 - {\beta }^2}$, $\beta = v/c$, $\rho = 1 + {\beta }^2 {\gamma }^2 = {\gamma }^2$ [5,6].

4. Examples of Application

As first example of application we considered relativistic velocities of electrons in ZnO nanowires [11,12]. Changing the nanomaterial, we must consider the right effective mass and relaxation time; for non-relativistic velocities, the electron rest mass m₀ and the effective mass m_eff are practically the same. The used data in Eqs (9,10) are resumed in Table 2.

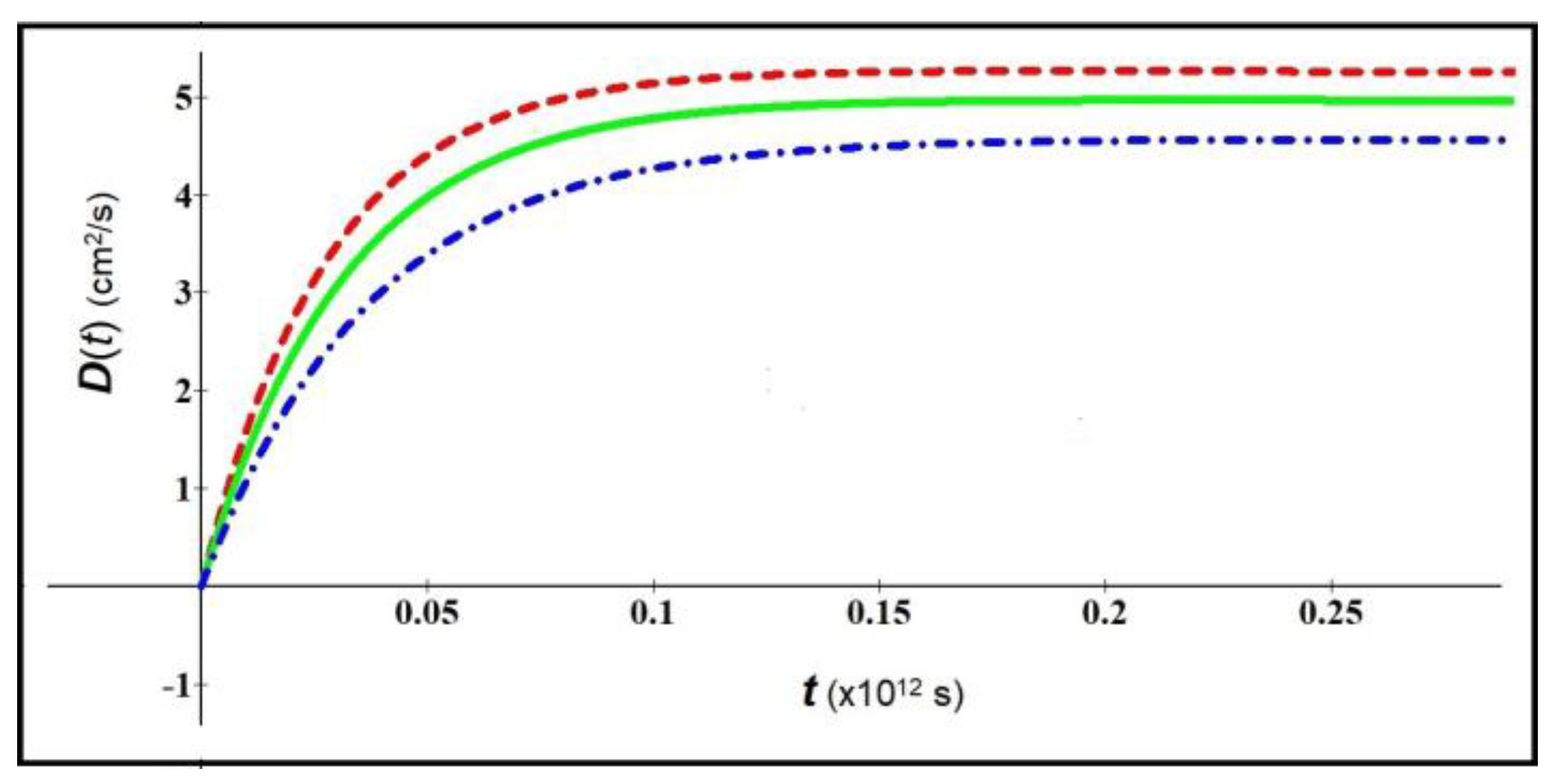
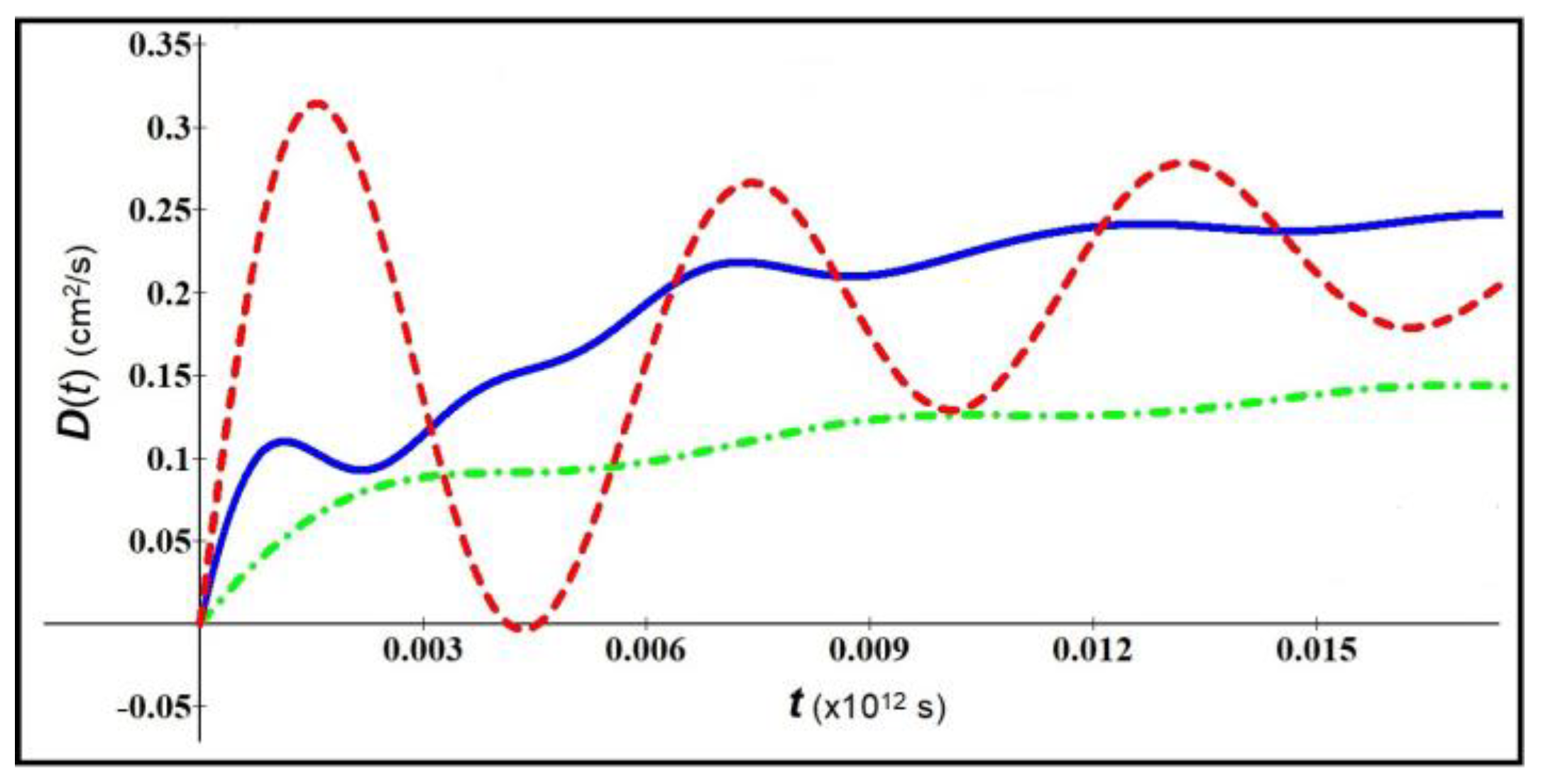
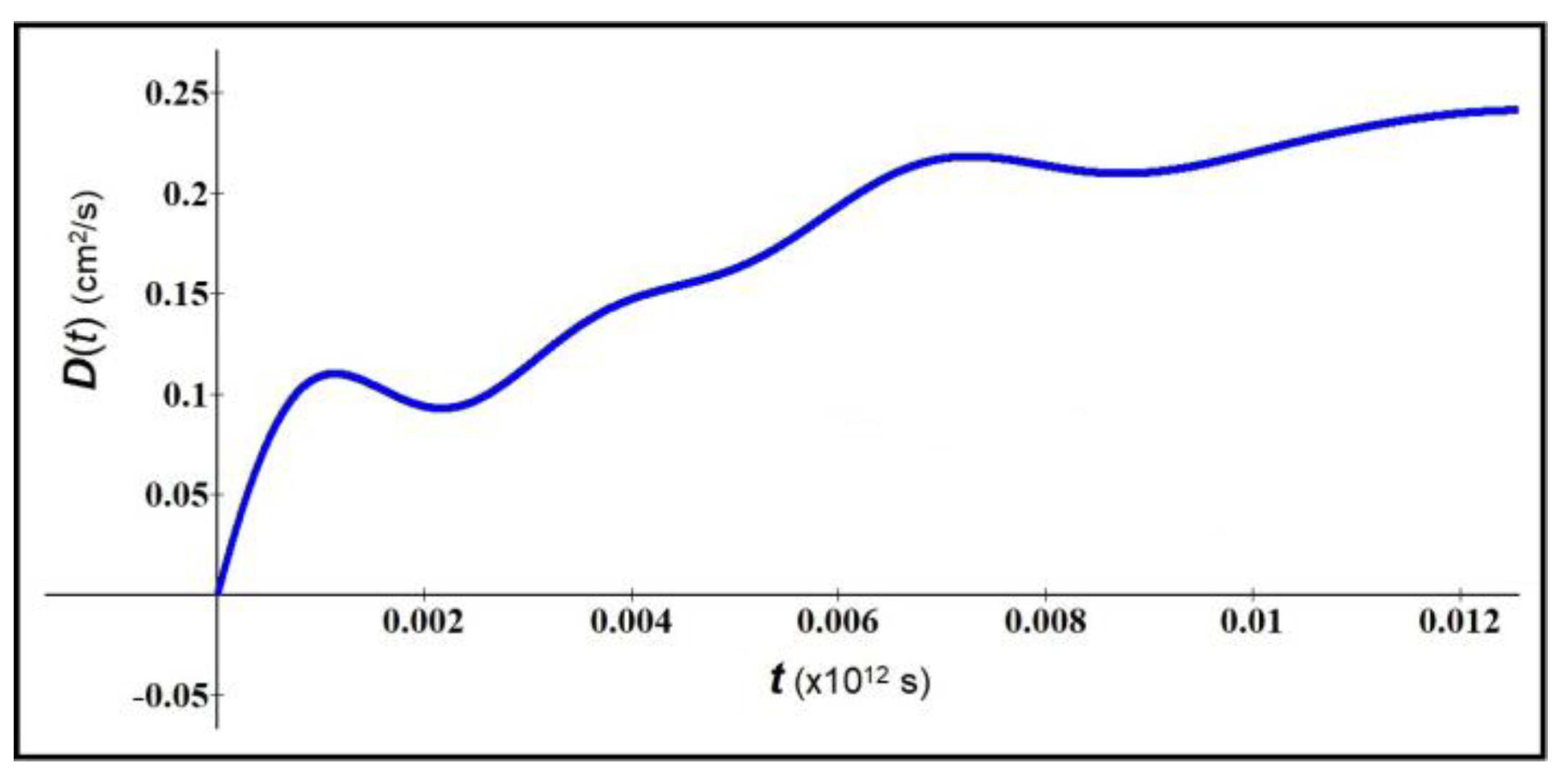
Figure 1 represents the behavior of $D (t)$ vs time for electrons inside a ZnO nanowire [11,12], considering the parameters: $T = 300 K$, ${\tau }_1 = 0.28 \cdot {10}^{- 13} s$, $v_1$, ${\omega }_1$ (red dashed line), $v_2$, ${\omega }_1$ (green solid line), and $v_3$, ${\omega }_1$ (blue dot-dashed line).

With the increase of velocity, we note a decrease in diffusion, as expected considering that the mass increases with $v$ (see Eqs (9,10)).

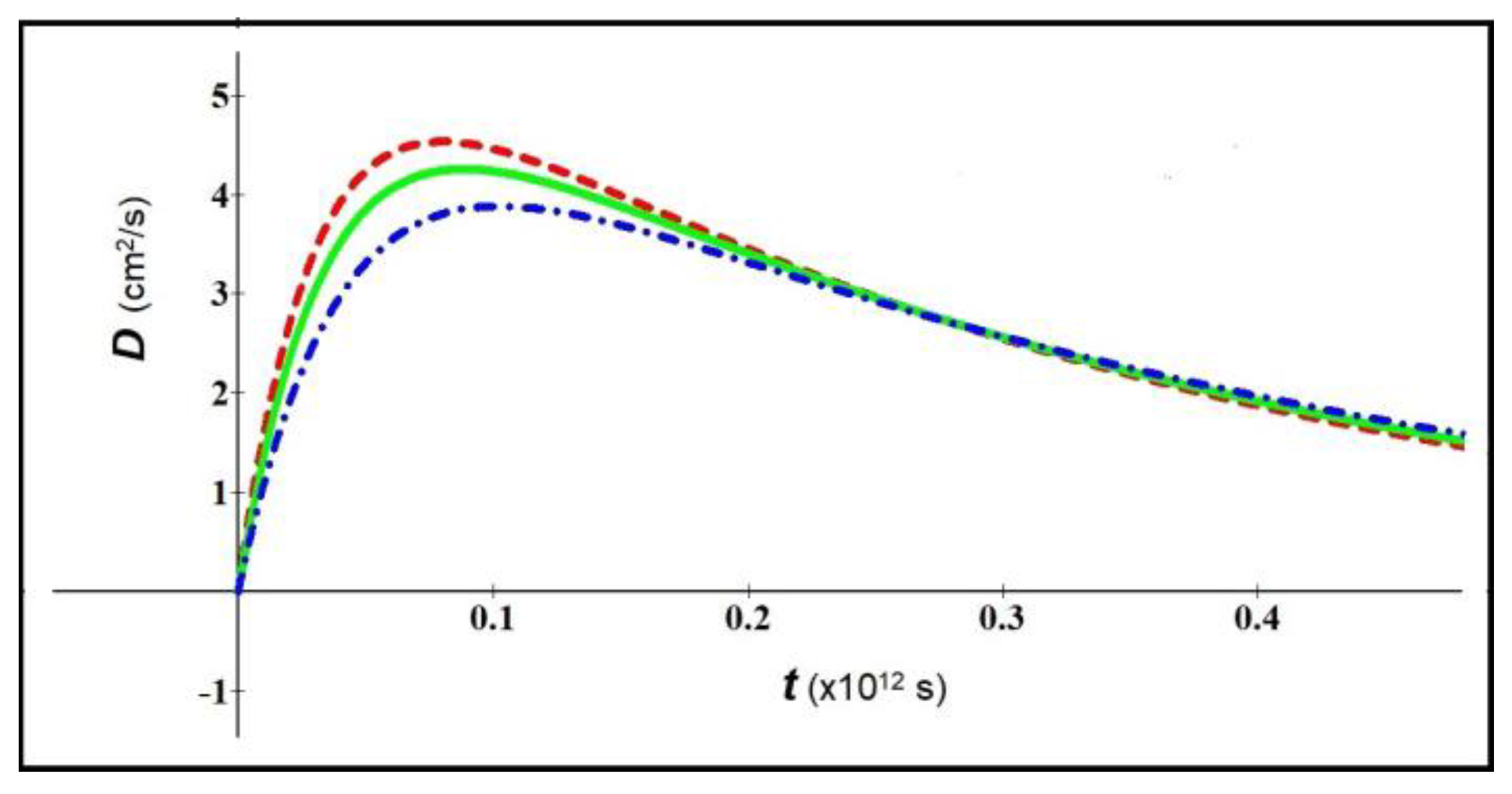
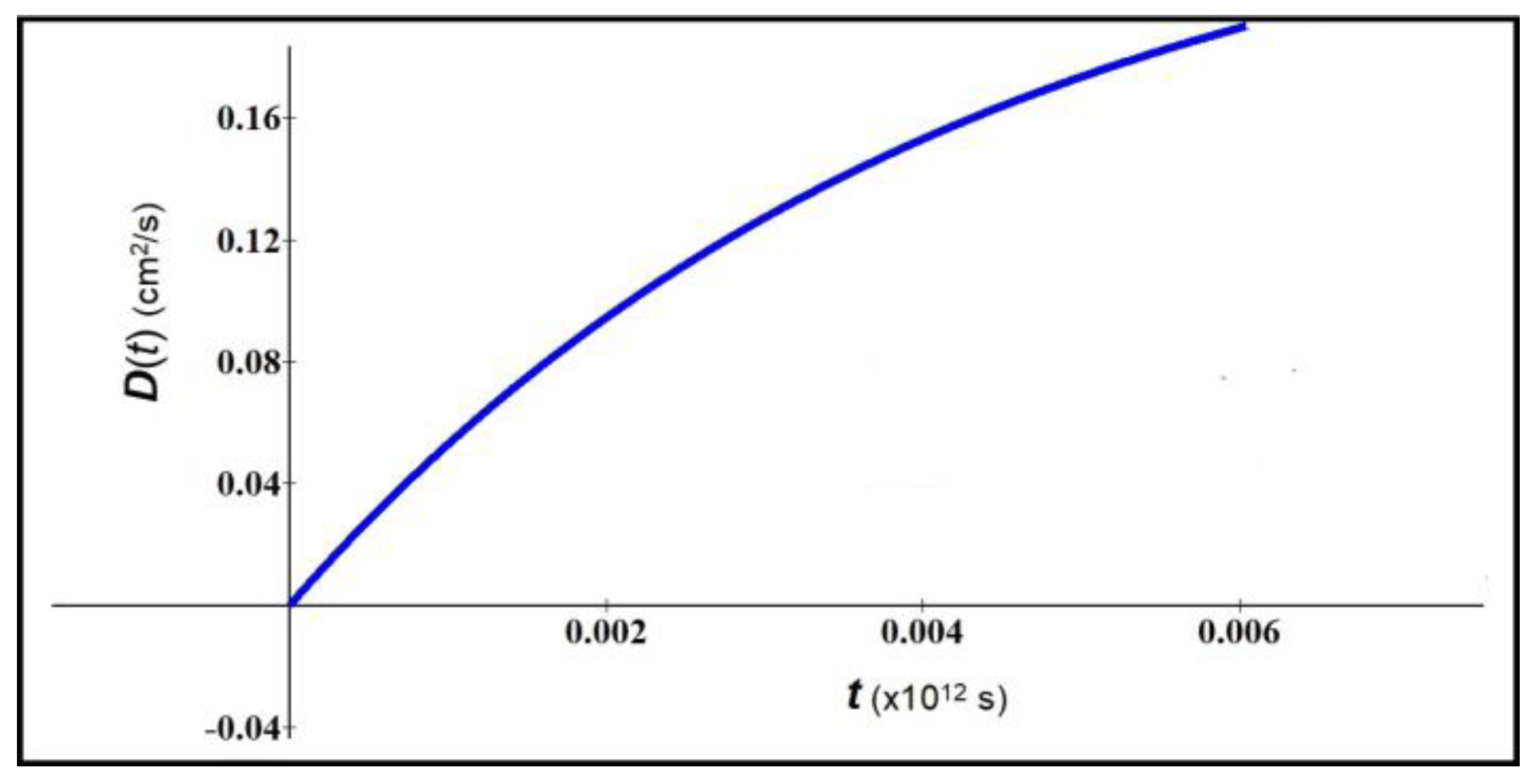
In Figure 2 we consider ZnO nanowires using the same parameters of Figure 1, with exception of the value of $\omega = {\omega }_2$. We note that, in these conditions, the D function decreases more rapidly.

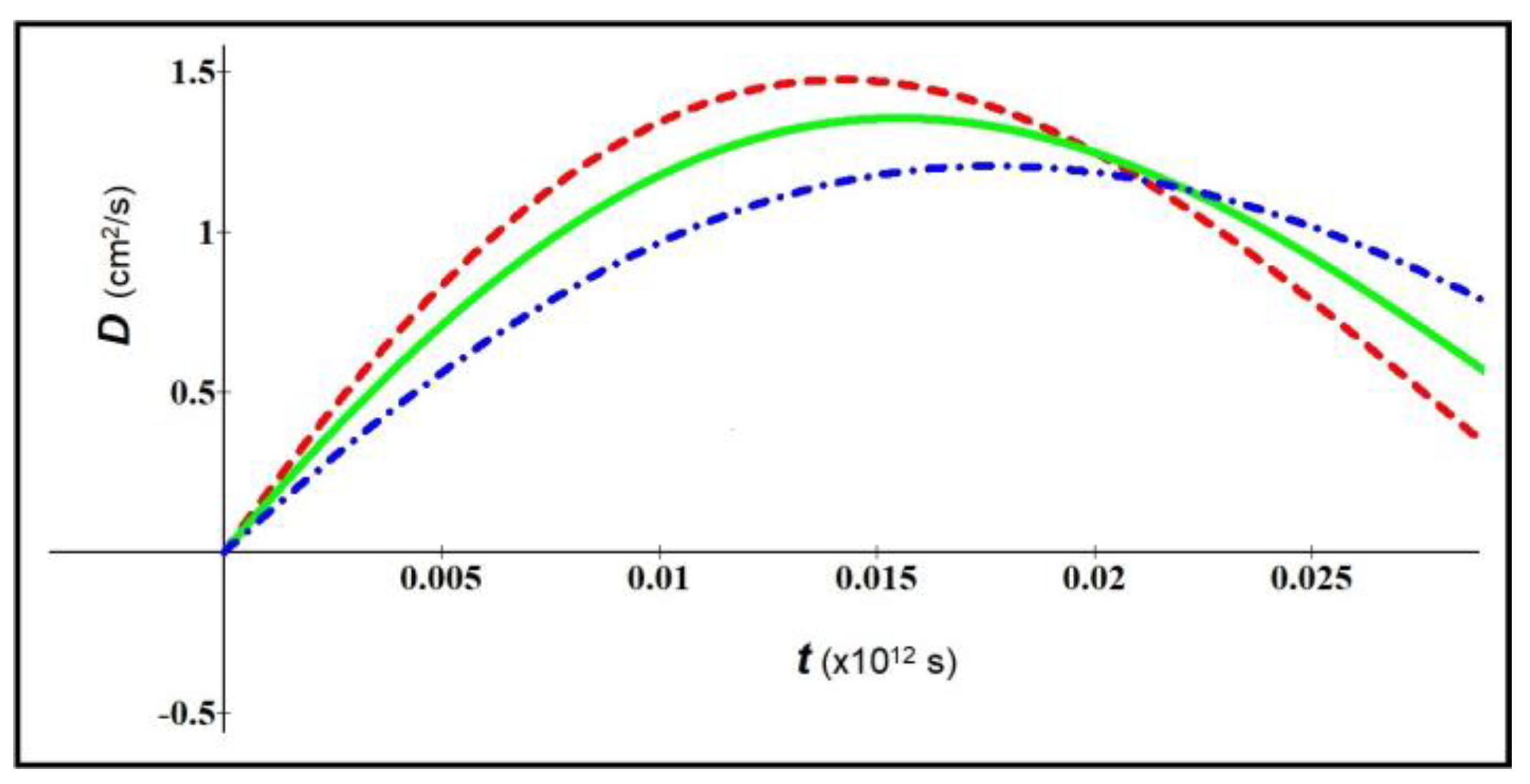
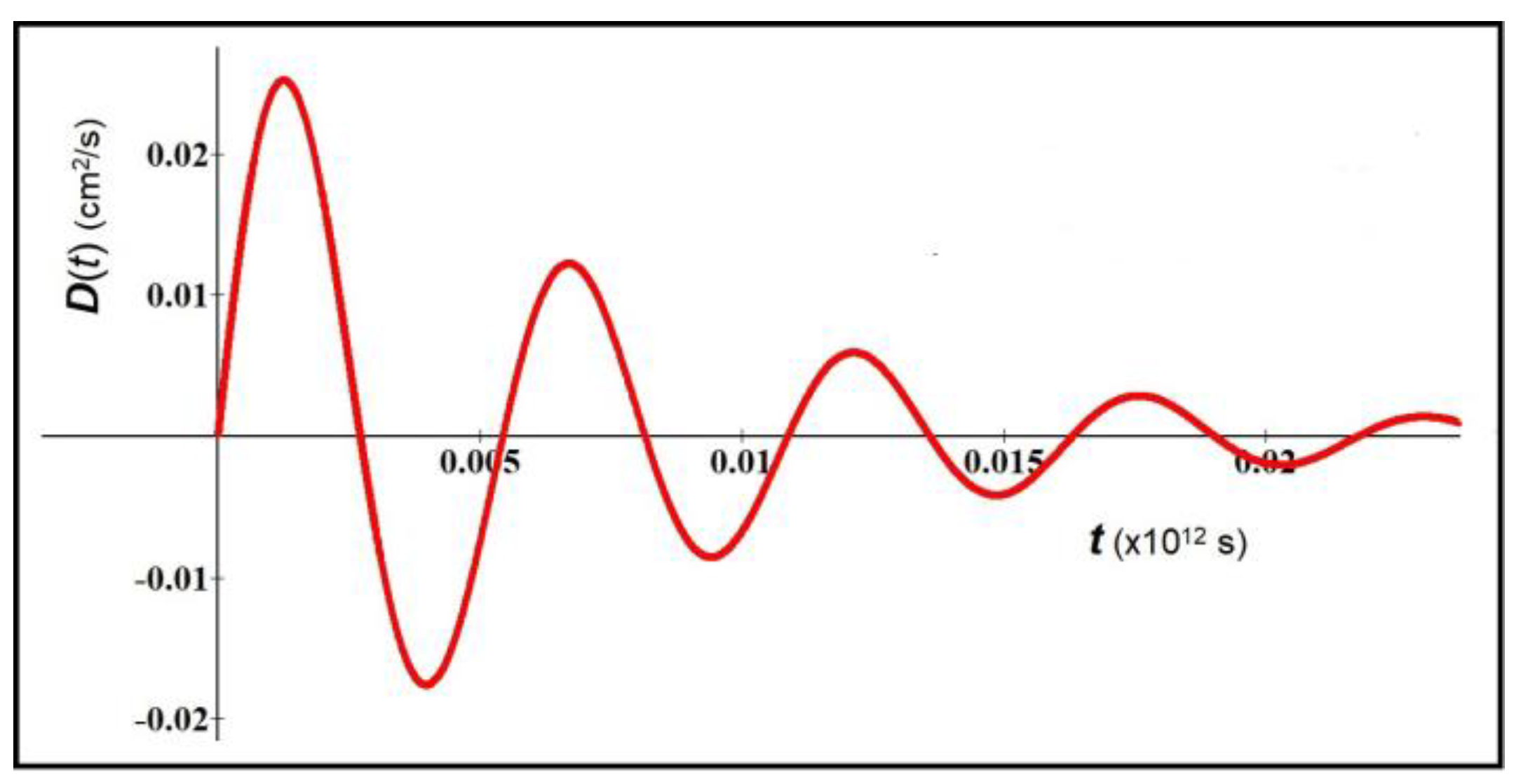
In Figure 3 we consider the parameters of Figure 1, with exception of the value of $\omega = {\omega }_3$.

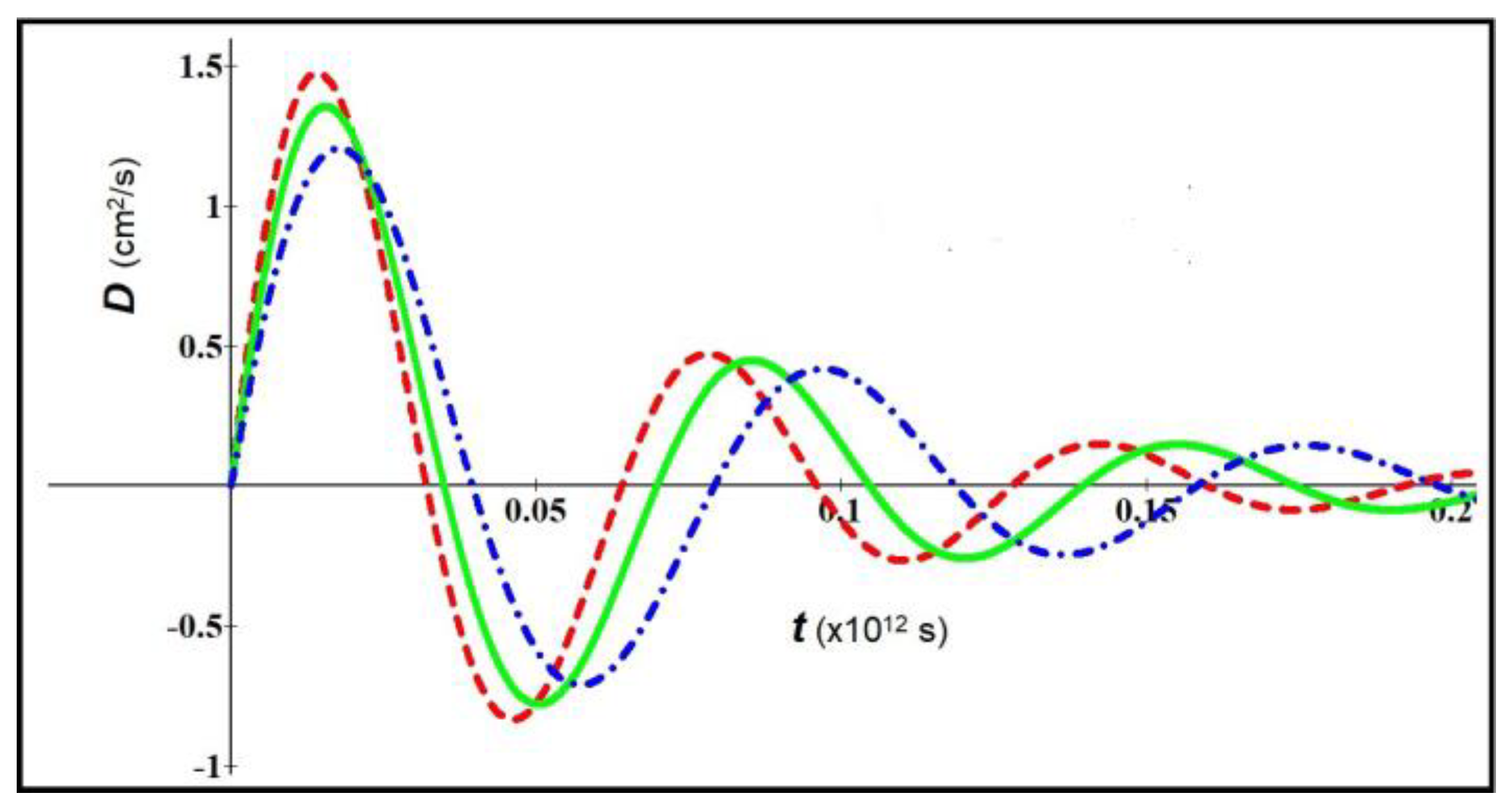
In this last case, the chosen parameters bring to the condition $\Delta > 0$, therefore to Eq. 9; the oscillatory damped behavior is well visible for long times (Figure 4).

The obtained results can explain the ultra-short times and high mobilities, with which charges diffuse in mesoporous systems, of high interest in photocatalitic and photovoltaic systems. The short times of few $\tau$ show easy charge diffusion inside the nanoparticles. The undescribed experimental ultrashort injection of charge carriers, particularly in Grätzel’s cells, can be linked to this phenomenon [13]. Deviations by the Drude model become powerful in nanostructured materials, such as photoexcited TiO₂ nanoparticles, ZnO films, InP nanoparticles, semiconducting polymer molecules and CNTs [14,15,16,17,18,19].

About the quantum-relativistic case, as examples of application, we considered experimental data by literature, from which three states were extracted through a personal elaboration (Table 3). Data are related to single-walled carbon nanotube films at the temperature of 300 K [20,21].

The corresponding values of ${\alpha }_{I - R}$, calculated for each considered velocity, are resumed in Table 4.

Figure 5, Figure 6 and Figure 7 show the behavior of each single weight f_i (i = 1,2,3) considering v = v₁, in Figure 8 the graph represents their sum. In this last one, the presence of both ${\alpha }_I$ and ${\alpha }_R$ implies that the D function is a mix of Eq. (9) and Eq. (10), with consequent damped oscillating increased behavior.

Figure 9 shows the general quantum-relativistic case, i.e. considering the quantum-relativistic behavior related to the presence of all considered states, with variation of velocity.

From the examples we understand that it is possible to perform a general fine-tuned quantum-relativistic study of the charge transport in nanostructures.

The assumption of quantum-relativistic aspects inside a nanostructure is a desirable feature; quantum processes with ultra-high velocities of carriers are concerning both the current science and technology and the future of theoretical and phenomenological (nano)physics.

What discussed here can be considered as the starting point of an investigation pathway linked to physical assumptions, i.e. how scattering, ballistic transport, influence of temperature [22], size effect, etc., can impact on the studied phenomenon. This research presents a challenge for phenomenologists, whose insights and inspirations could usefully support this theoretical effort, through, but not only, TRTS [23,24,25,26], Photon-Induced Near-Field Electron Microscopy [27,28] and Graphene based Plasmonics [29,30,31].

5. Conclusion

In this work it has been presented a new theoretical result: the complete analytical form of the function $D (t)$ considering the possibility of quantum-relativistic effects inside a nanostructure. We have generalized a new analytical model, appeared in classical, quantum and relativistic form [2,3,4], and tested during last years with fine accordance with experimental existing data. Eqs (9,10) become those of the classical case, when the carriers velocity is classic and we do not consider quantum effects. The introduced formulae for the diffusion function $D (t)$ complete the quantum-relativistic form of this model, said DS model [5,6].

The considered extension is mathematically accurate and fine, because of the analytical approach, which overcome time-consuming numerical approaches. It is able to give also new interesting information, potentially useful in the design phase of new nano-bio-devices with dedicated and specific features. These new information may be appropriately tested through current experimental techniques, like TRTS, PINEM, Graphene based Plasmonics.

Considering all parameters influencing the system at chemical, physical, structural and model-intrinsic level, as the system’s temperature T, the parameters ${\alpha }_{i I_{Q - R}}$ and ${\alpha }_{i R_{Q - R}}$, the values of ${\tau }_i$ and ${\omega }_i$, possible variations of the effective mass $m*$ [32], variations of the chiral vector, the quantum weights $f_i$ of modes, the carrier density N, the velocity of carriers, it is possible to perform a precise tuning of the three fundamental functions related to the dynamics of charge transport, i.e. ${〈\overrightarrow{v} (t) \cdot \overrightarrow{v} (0)〉}_T$, $R^2(t)$, and $D (t)$. The model works adequately on the theoretical analysis of phenomena of ultrafast carrier dynamics [33,34,35].