Submitted:
10 October 2024
Posted:
12 October 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Numerical Method and Simulations
2.1. Numerical Method
2.2. Numerical Simulations and Results
3. Conclusion
Data Availability Statement
References
- Martin, G.D.; Hoath, S.D.; Hutchings, I.M. Inkjet printing-the physics of manipulating liquid jets and drops. Journal of Physics: Conference Series. IOP Publishing, 2008, Vol. 105, p. 012001. [CrossRef]
- Kim, B.H.; Kim, T.G.; Lee, T.K.; Kim, S.; Shin, S.J.; Kim, S.J.; Lee, S.J. Effects of trapped air bubbles on frequency responses of the piezo-driven inkjet printheads and visualization of the bubbles using synchrotron X-ray. Sensors and Actuators A: Physical 2009, 154, 132–139. [Google Scholar] [CrossRef]
- van der Bos, A. AIR ENTRAPMENT DROP FORMATION INKJET PRINTING. Ph.D. thesis,University of Twente 2011.
- Åmand, L.; Olsson, G.; Carlsson, B. Aeration control–a review. Water Science and Technology 2013, 67, 2374–2398. [Google Scholar] [CrossRef] [PubMed]
- Harja, G.; Nascu, I.; Muresan, C.; Nascu, I. Improvements in dissolved oxygen control of an activated sludge wastewater treatment process. Circuits, Systems, and Signal Processing 2016, 35, 2259–2281. [Google Scholar] [CrossRef]
- Skouteris, G.; Rodriguez-Garcia, G.; Reinecke, S.; Hampel, U. The use of pure oxygen for aeration in aerobic wastewater treatment: a review of its potential and limitations. Bioresource Technology 2020, 312, 123595. [Google Scholar] [CrossRef]
- Kim, T.; Hite, M.; Rogacki, L.; Sealock, A.W.; Sprouse, G.; Novak, P.J.; LaPara, T.M. Dissolved oxygen concentrations affect the function but not the relative abundance of nitrifying bacterial populations in full-scale municipal wastewater treatment bioreactors during cold weather. Science of the Total Environment 2021, 781, 146719. [Google Scholar] [CrossRef]
- Melville, W.K. The role of surface-wave breaking in air-sea interaction. Annual review of fluid mechanics 1996, 28, 279–321. [Google Scholar] [CrossRef]
- Deane, G.B.; Stokes, M.D. Scale dependence of bubble creation mechanisms in breaking waves. Nature 2002, 418, 839–844. [Google Scholar] [CrossRef]
- Wanninkhof, R.; Asher, W.E.; Ho, D.T.; Sweeney, C.; McGillis, W.R. Advances in quantifying air-sea gas exchange and environmental forcing. Annual review of marine science 2009, 1, 213–244. [Google Scholar] [CrossRef]
- Kiger, K.T.; Duncan, J.H. Air-entrainment mechanisms in plunging jets and breaking waves. Annual Review of Fluid Mechanics 2012, 44, 563–596. [Google Scholar] [CrossRef]
- Wilson, T.W.; Ladino, L.A.; Alpert, P.A.; Breckels, M.N.; Brooks, I.M.; Browse, J.; Burrows, S.M.; Carslaw, K.S.; Huffman, J.A.; Judd, C.; others. A marine biogenic source of atmospheric ice-nucleating particles. Nature 2015, 525, 234–238. [Google Scholar] [CrossRef]
- Veron, F. Ocean spray. Annual Review of Fluid Mechanics 2015, 47, 507–538. [Google Scholar] [CrossRef]
- Lubin, P.; Glockner, S. Numerical simulations of three-dimensional plunging breaking waves: generation and evolution of aerated vortex filaments. Journal of Fluid Mechanics 2015, 767, 364–393. [Google Scholar] [CrossRef]
- Deike, L.; Melville, W.K.; Popinet, S. Air entrainment and bubble statistics in breaking waves. Journal of Fluid Mechanics 2016, 801, 91–129. [Google Scholar] [CrossRef]
- Chan, W.H.R.; Mirjalili, S.; Jain, S.S.; Urzay, J.; Mani, A.; Moin, P. Birth of microbubbles in turbulent breaking waves. Physical Review Fluids 2019, 4, 100508. [Google Scholar] [CrossRef]
- Ruan, S.p.; Wu, J.h.; Wu, W.w.; Xi, R.z. Hydraulic research of aerators on tunnel spillways. Journal of Hydrodynamics, Ser. B 2007, 19, 330–334. [Google Scholar] [CrossRef]
- Park, C.P.; Kim, D.P. Dual-channel microreactor for gas- liquid syntheses. Journal of the American Chemical Society 2010, 132, 10102–10106. [Google Scholar] [CrossRef]
- Ren, X.; Bachman, M.; Sims, C.; Li, G.; Allbritton, N. Electroosmotic properties of microfluidic channels composed of poly (dimethylsiloxane). Journal of Chromatography B: Biomedical Sciences and Applications 2001, 762, 117–125. [Google Scholar] [CrossRef] [PubMed]
- Cheng, M.; Lou, J.; Lim, T. Motion of a bubble ring in a viscous fluid. Physics of Fluids 2013, 25, 067104. [Google Scholar] [CrossRef]
- Martínez-Bazán, C. About bubbles and vortex rings. Journal of Fluid Mechanics 2015, 780, 1–4. [Google Scholar] [CrossRef]
- Abadie, T.; Matar, O. Numerical modelling of bubble dynamics and growth in supersaturated water using a Front-Tracking method. Bulletin of the American Physical Society 2021, 66. [Google Scholar]
- Taylor, G.I. The dynamics of thin sheets of fluid II. Waves on fluid sheets. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences 1959, 253, 296–312. [Google Scholar] [CrossRef]
- Culick, F.E. Comments on a ruptured soap film. Journal of applied physics 1960, 31, 1128–1129. [Google Scholar] [CrossRef]
- De Gennes, P.G.; Brochard-Wyart, F.; Quéré, D.; Phenomena, W. Drops, bubbles, pearls, waves, 2004. [CrossRef]
- Ma, Y.; Cheng, Y.; Zhang, D.; Zhang, K.; Wang, F. Numerical prediction of breakup mode of contracting gas filament in liquid. Int J Numer Meth Fluids. 2021, 1–12. [Google Scholar] [CrossRef]
- Osama, M.; Deng, P.; Thoraval, M.J.; Agbaglah, G.G. Dynamics of finite-size air filaments in a static liquid. Physics of Fluids 2022, 34, 062106. [Google Scholar] [CrossRef]
- Popinet, S. Basilisk, a free-software program for the solution of partial differential equations on adaptive cartesian meshes. URL http://basilisk. fr () 2018.
- Osama, M. Computational Analysis of Finite Size Air Filaments in Static Liquid. Master’s thesis, Wayne State University, 2024.
- Osama, M.; Agbaglah, G.G. Breakup regimes of the long-time dynamics of a finite-size air filament in a dense fluid. Physics of Fluids 2023, 35. [Google Scholar] [CrossRef]
- Van Hooft, J.A.; Popinet, S.; Van Heerwaarden, C.C.; Van der Linden, S.J.; de Roode, S.R.; Van de Wiel, B.J. Towards adaptive grids for atmospheric boundary-layer simulations. Boundary-layer meteorology 2018, 167, 421–443. [Google Scholar] [CrossRef]
- Popinet, S. An accurate adaptive solver for surface-tension-driven interfacial flows. J. Comput. Phys. 2009, 228, 5838–5866. [Google Scholar] [CrossRef]
- Pierson, J.L.; Soares, E.J.; Popinet, S. Revisiting the Taylor-Culick approximation: Retraction of an axisymmetric filament. Phys. Rev. Fluids 2020, 5, 073602. [Google Scholar] [CrossRef]
- Hoepffner, J.; Paré, G. Recoil of a liquid filament: Escape from pinch-off through creation of a vortex ring. J. Fluid Mech. 2013, 734, 183–197. [Google Scholar] [CrossRef]
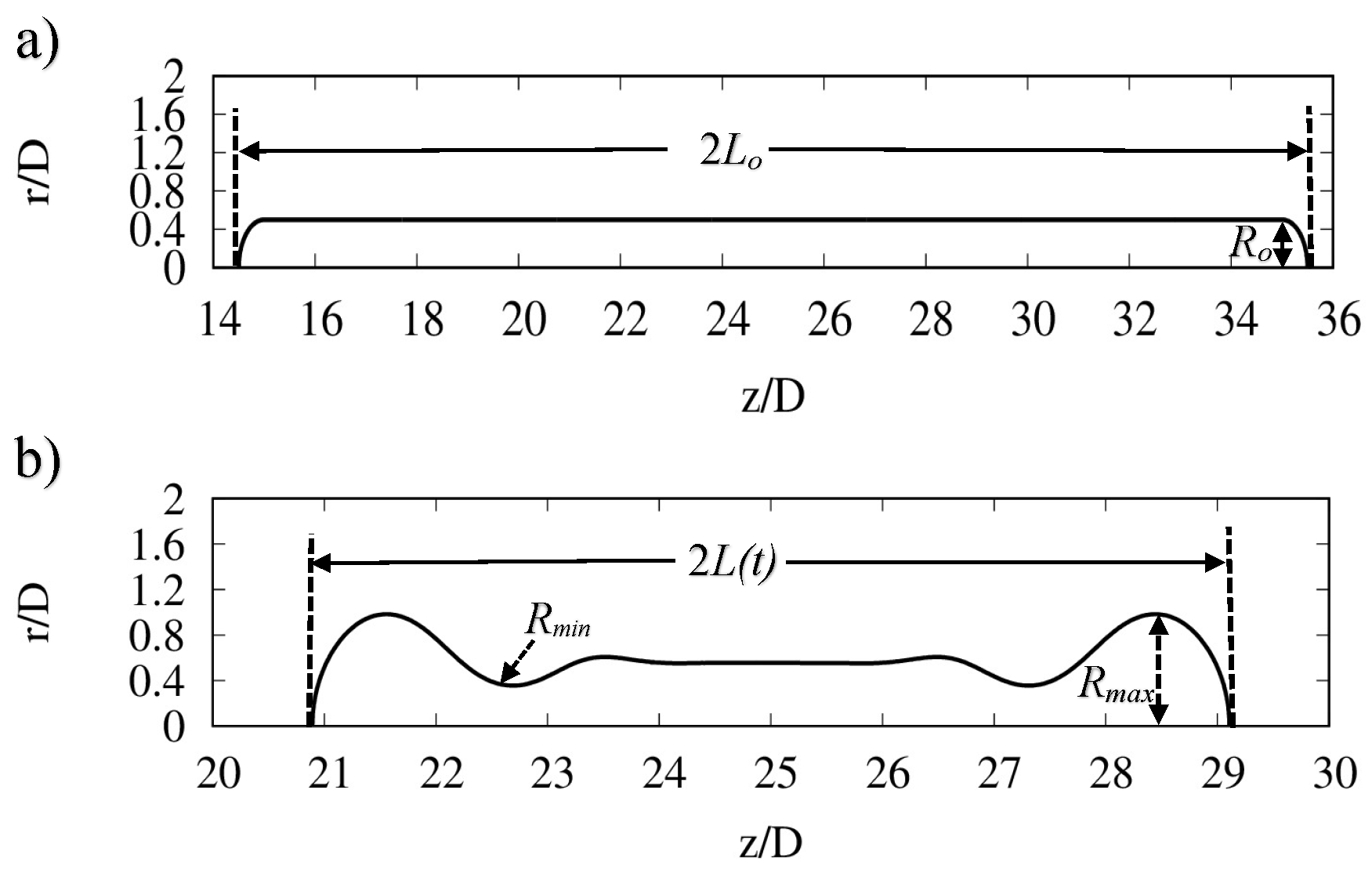


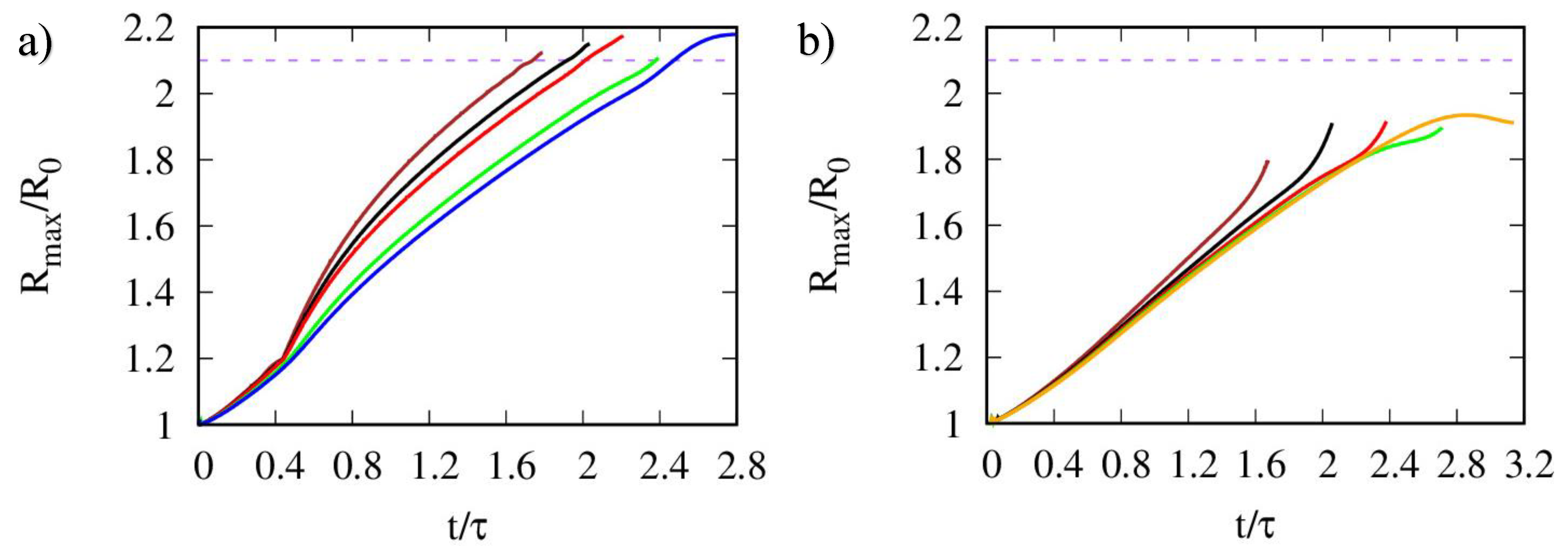


| Phase | (kg ) | (Pa s) | (N ) | |
|---|---|---|---|---|
| Liquid | 1000 | 0.069 | – | |
| Gas | 1.2 | – | 6 – 15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





