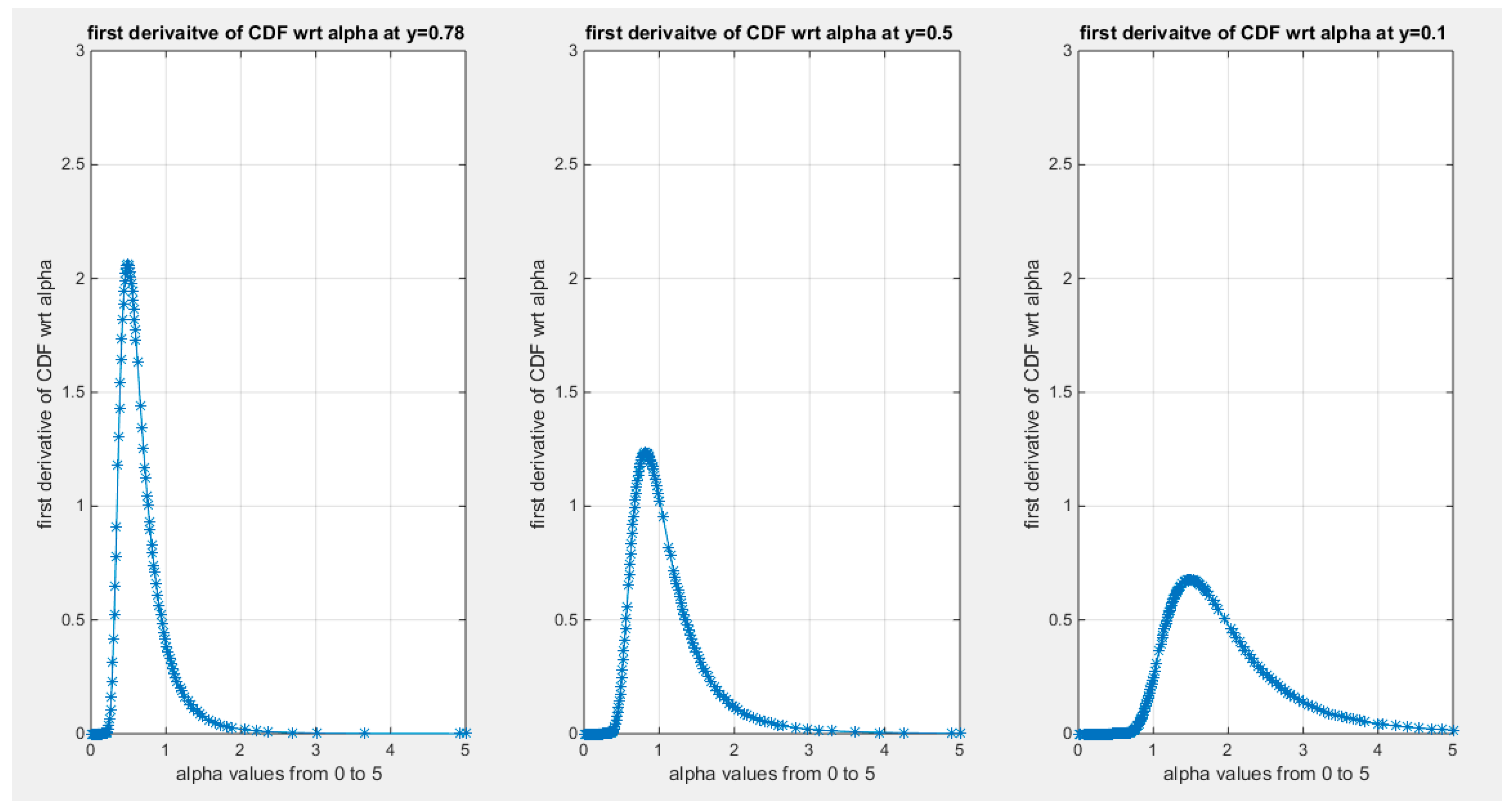
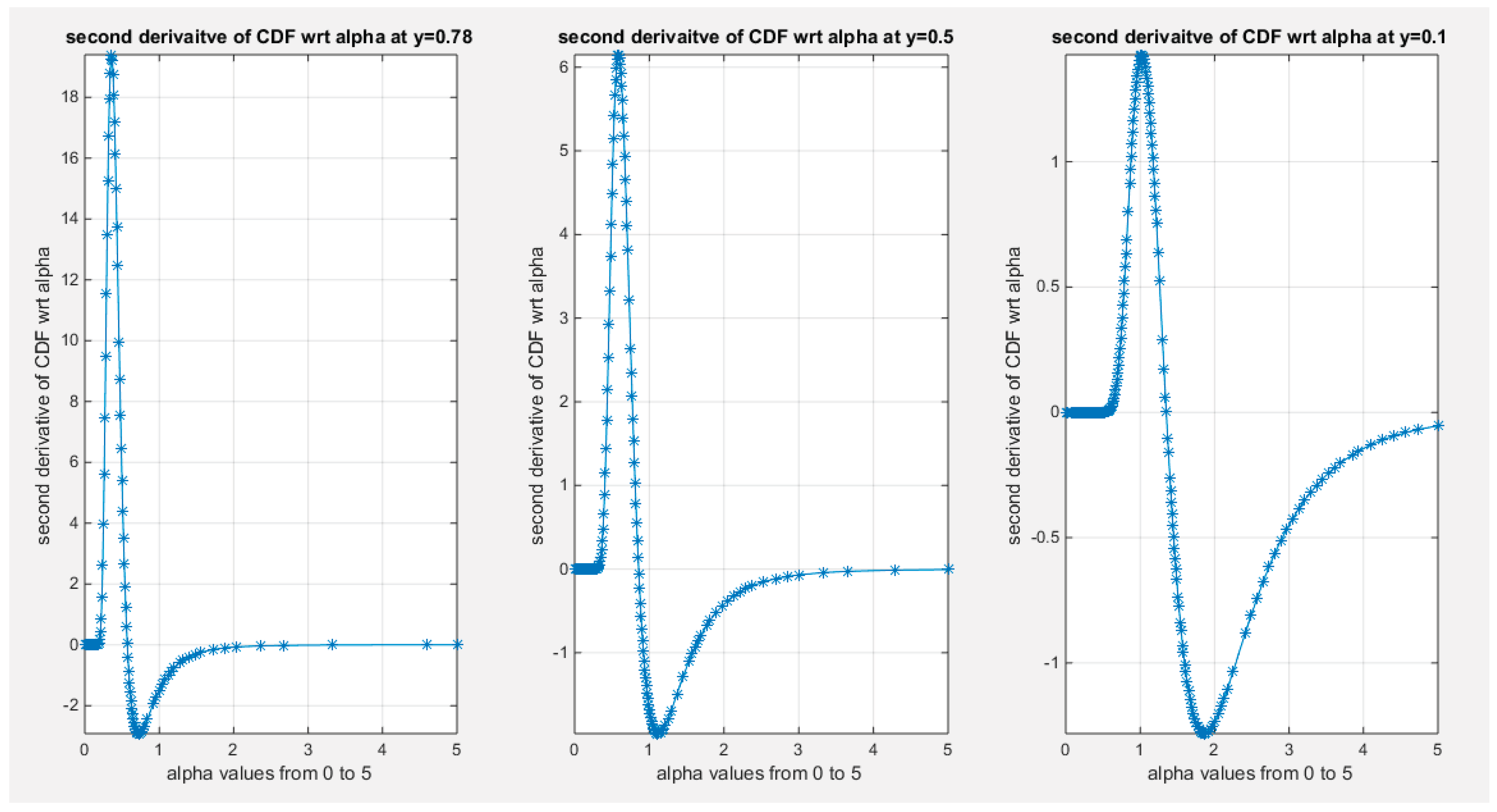
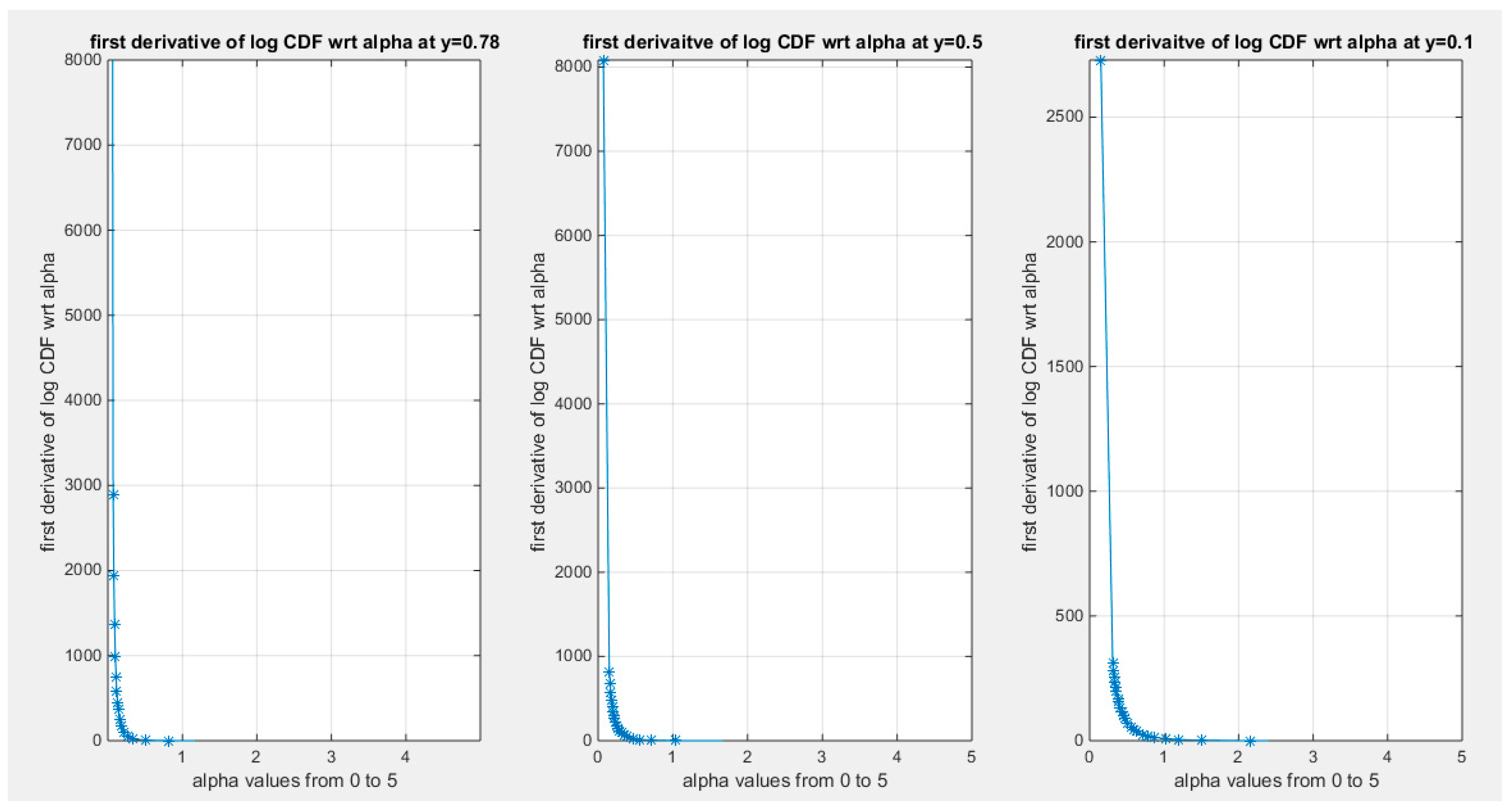
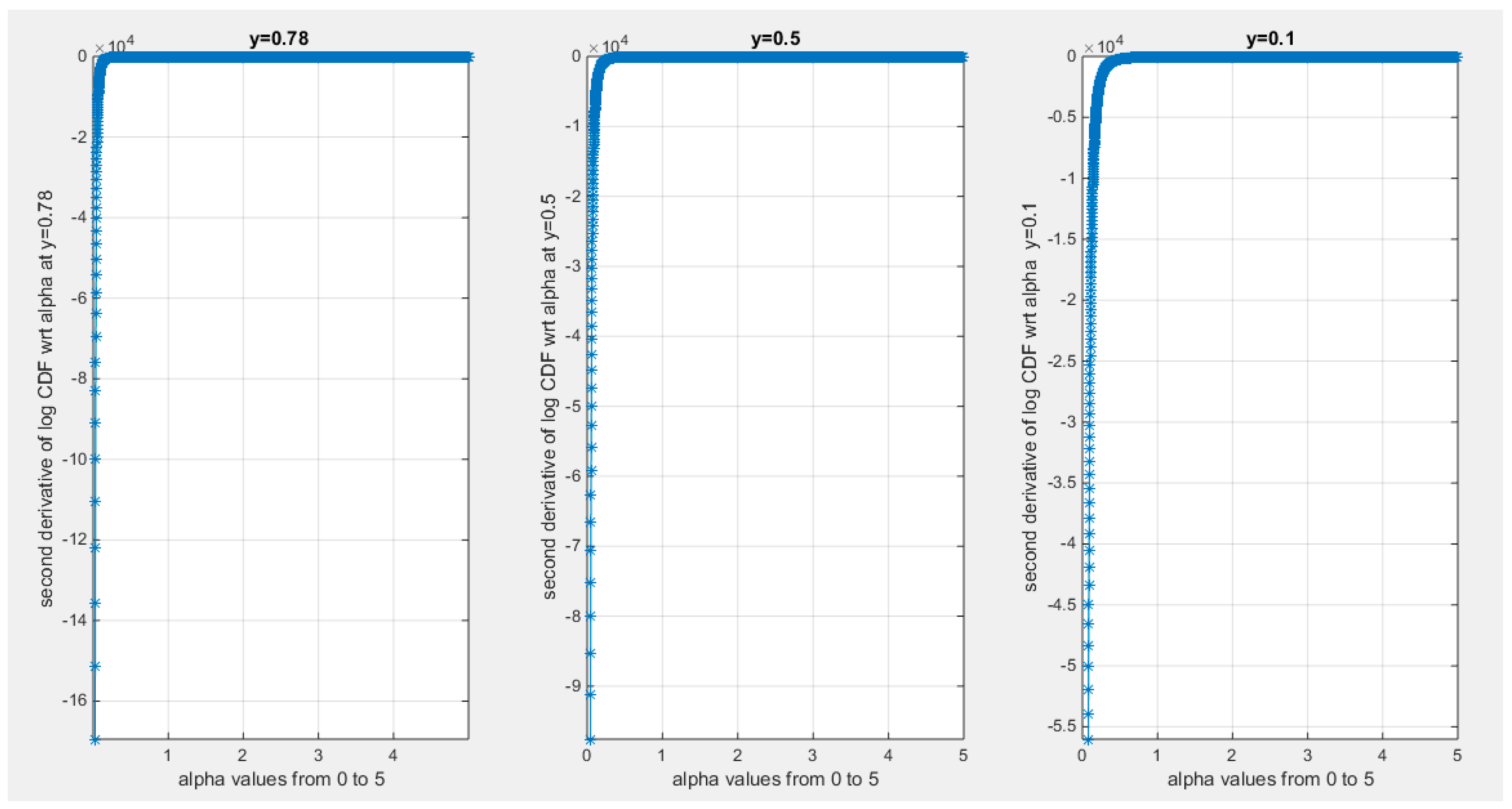
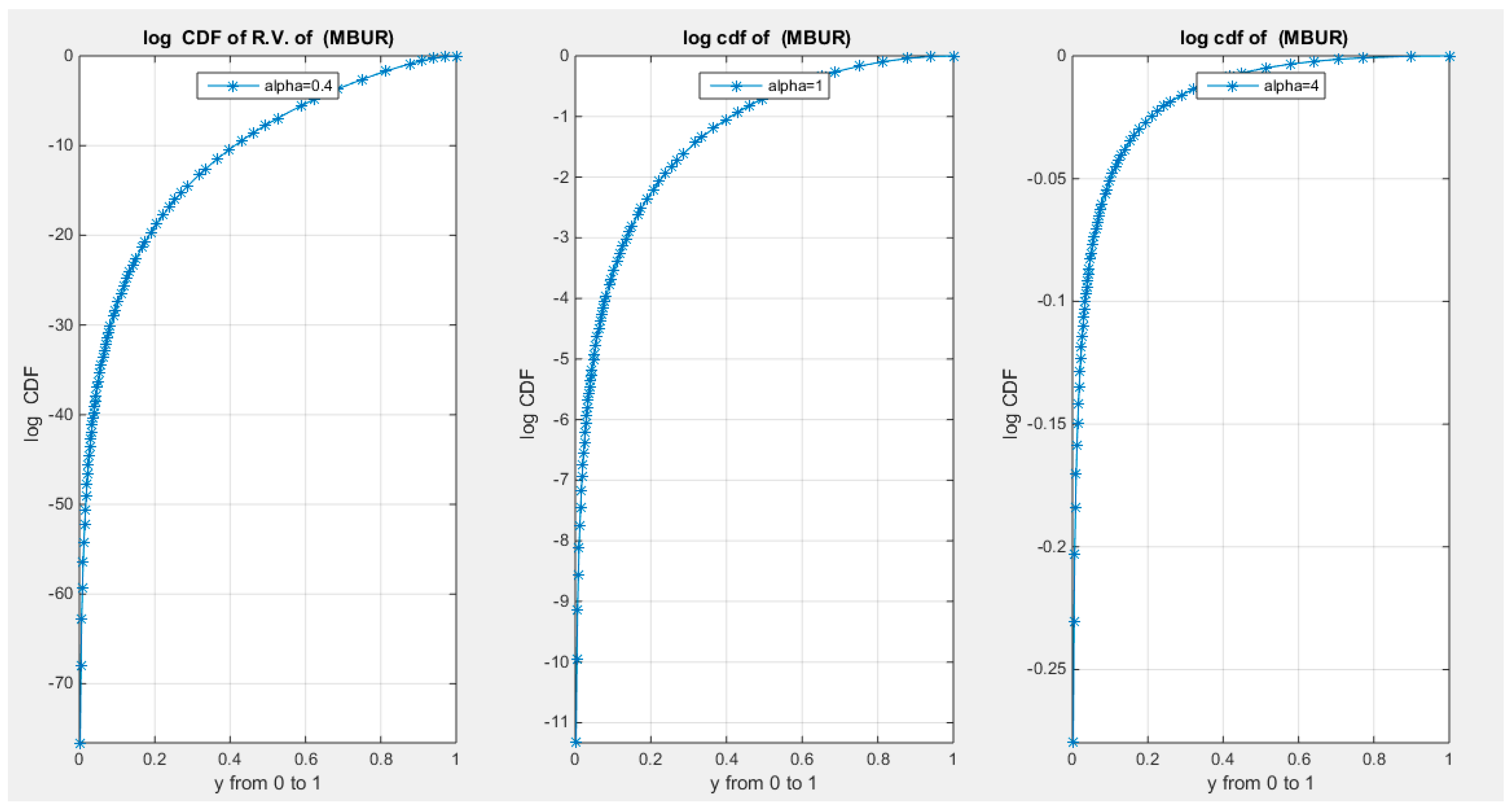
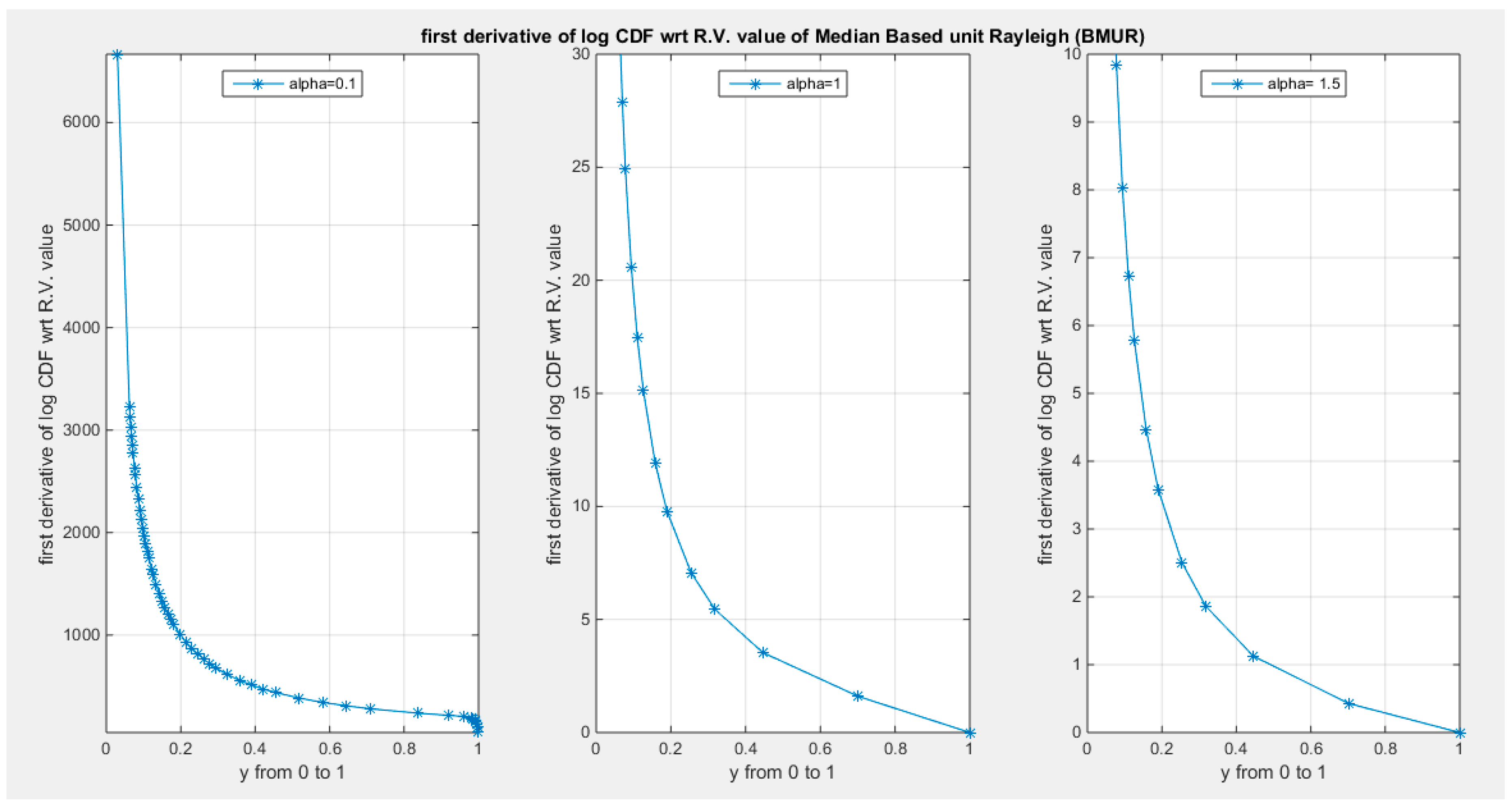
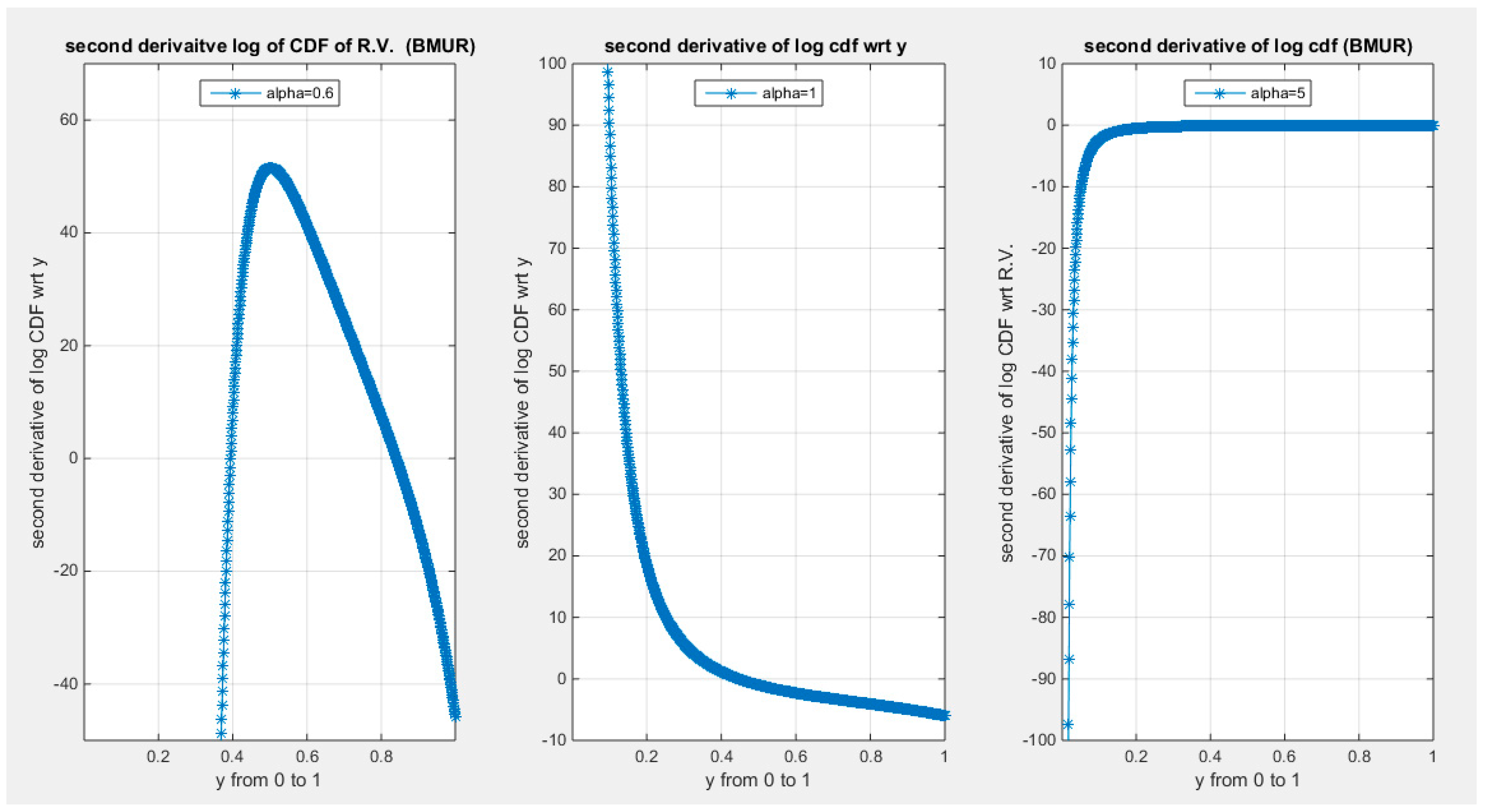
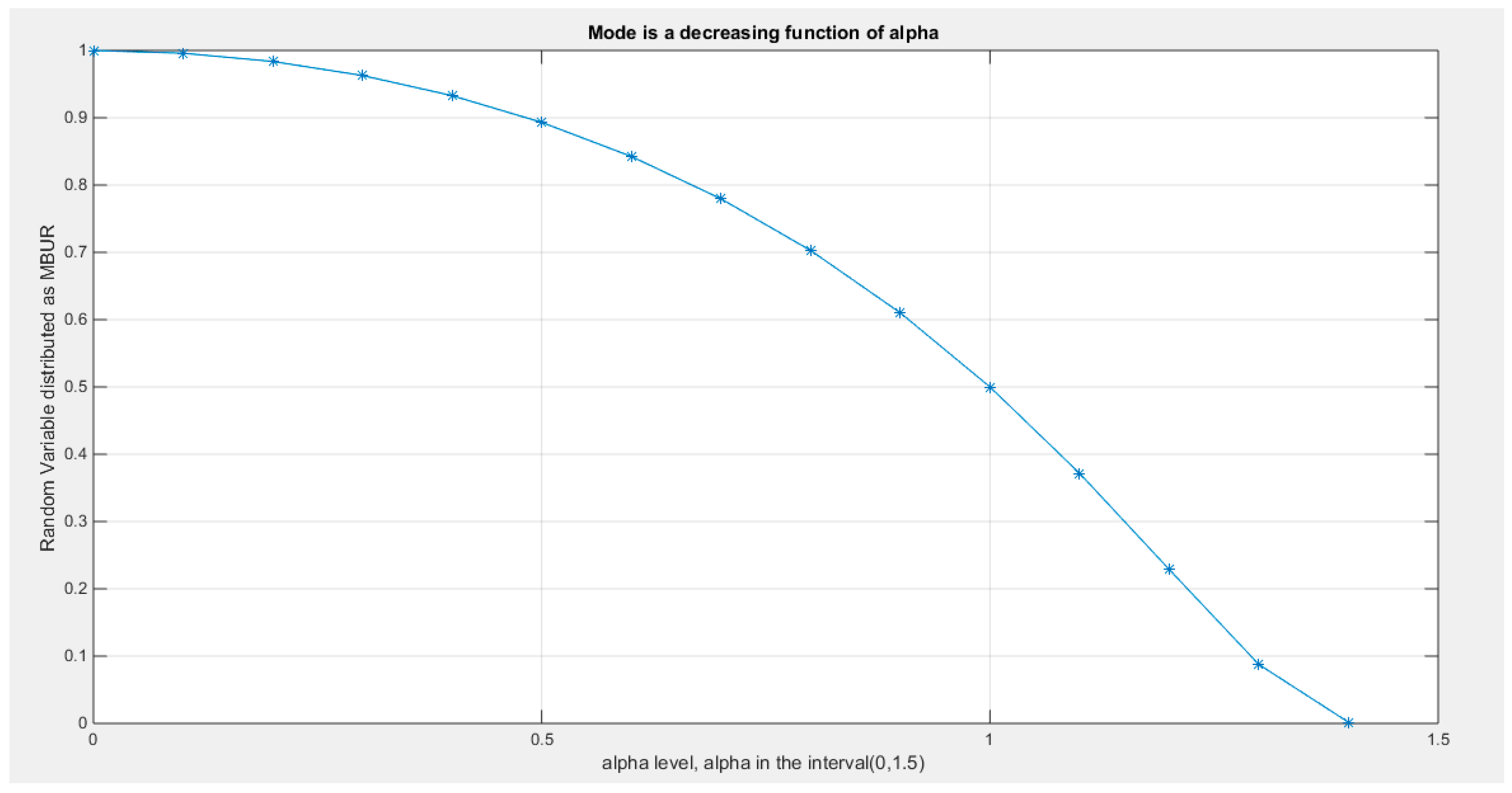
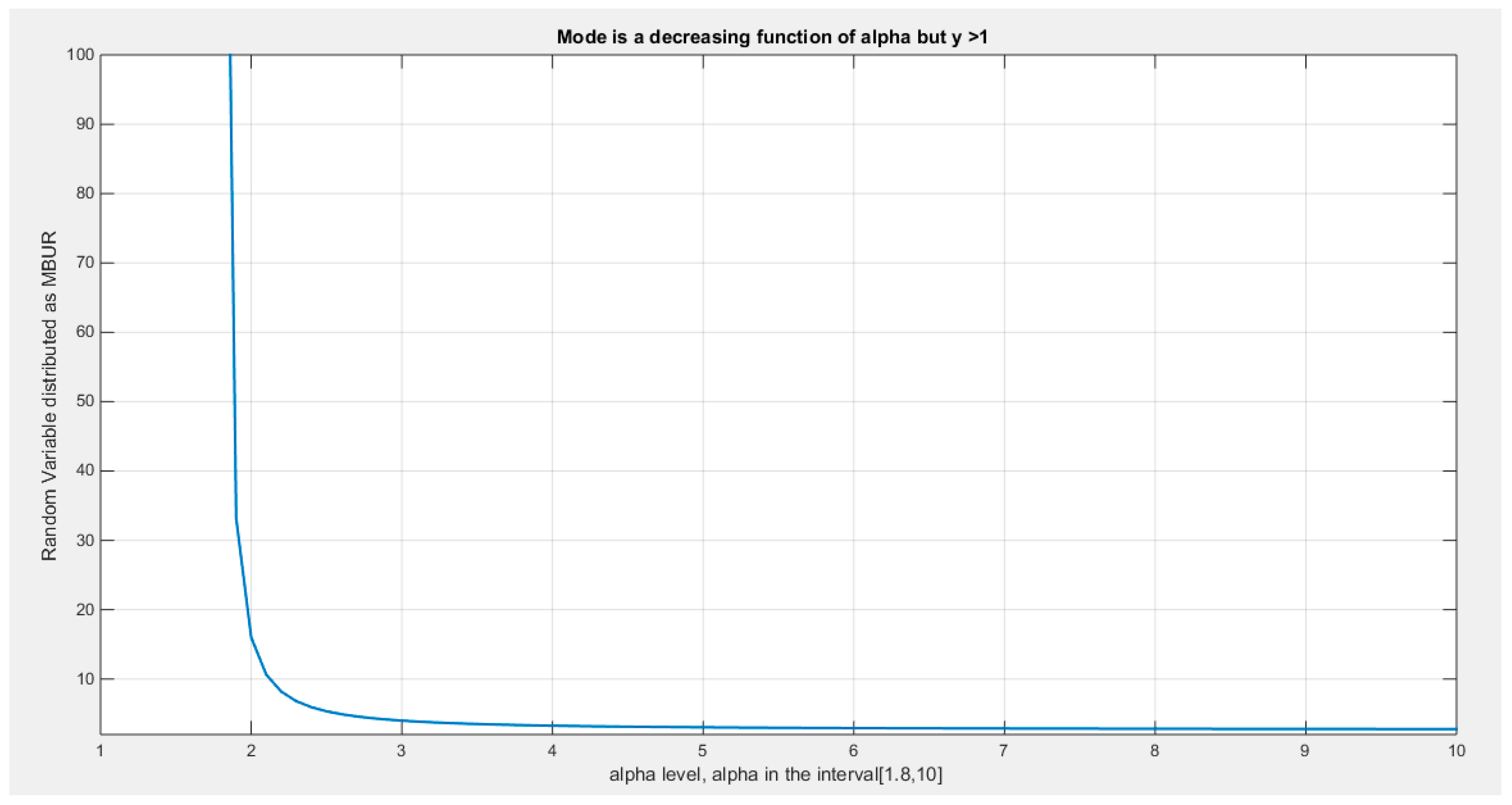
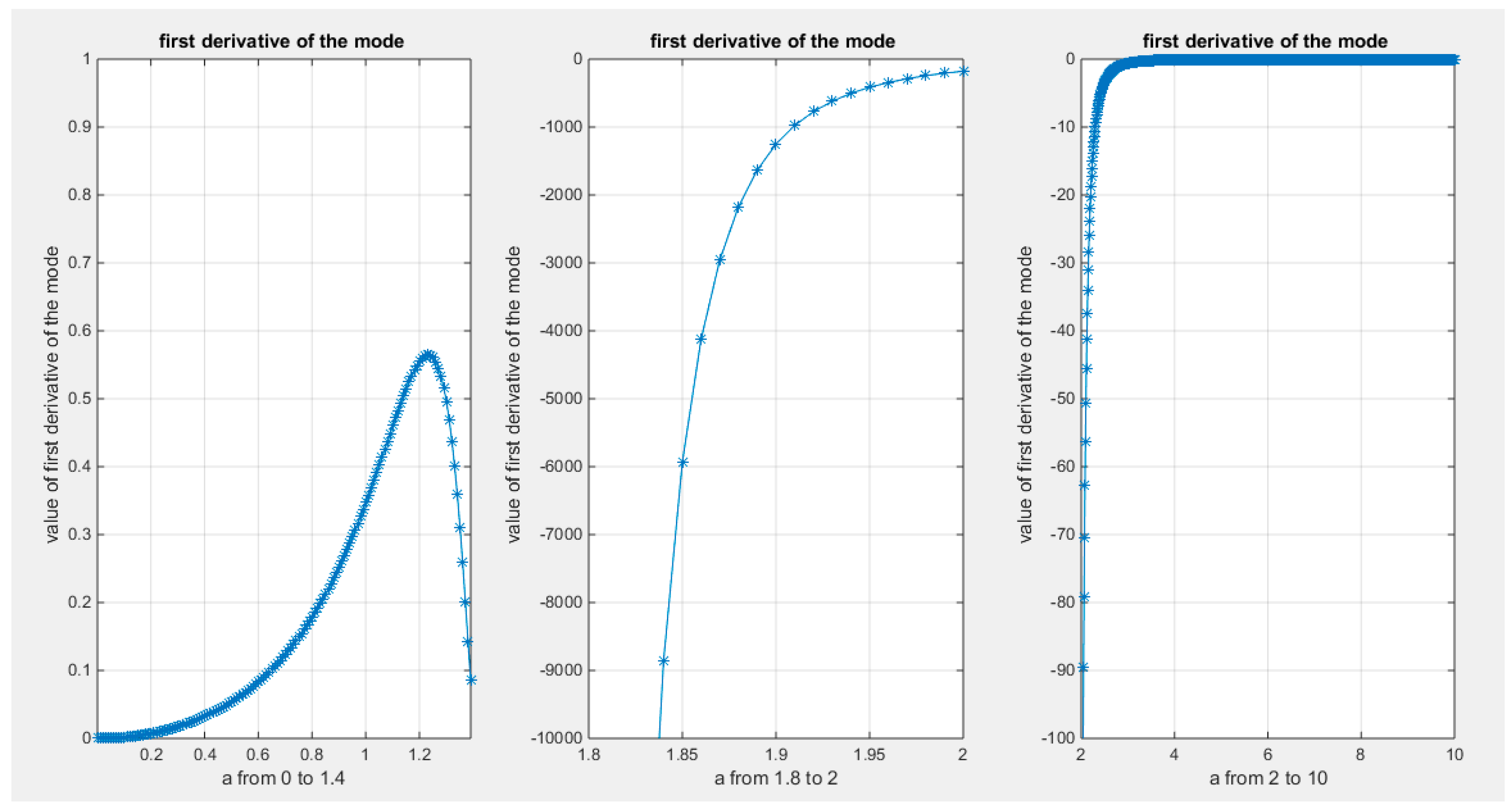
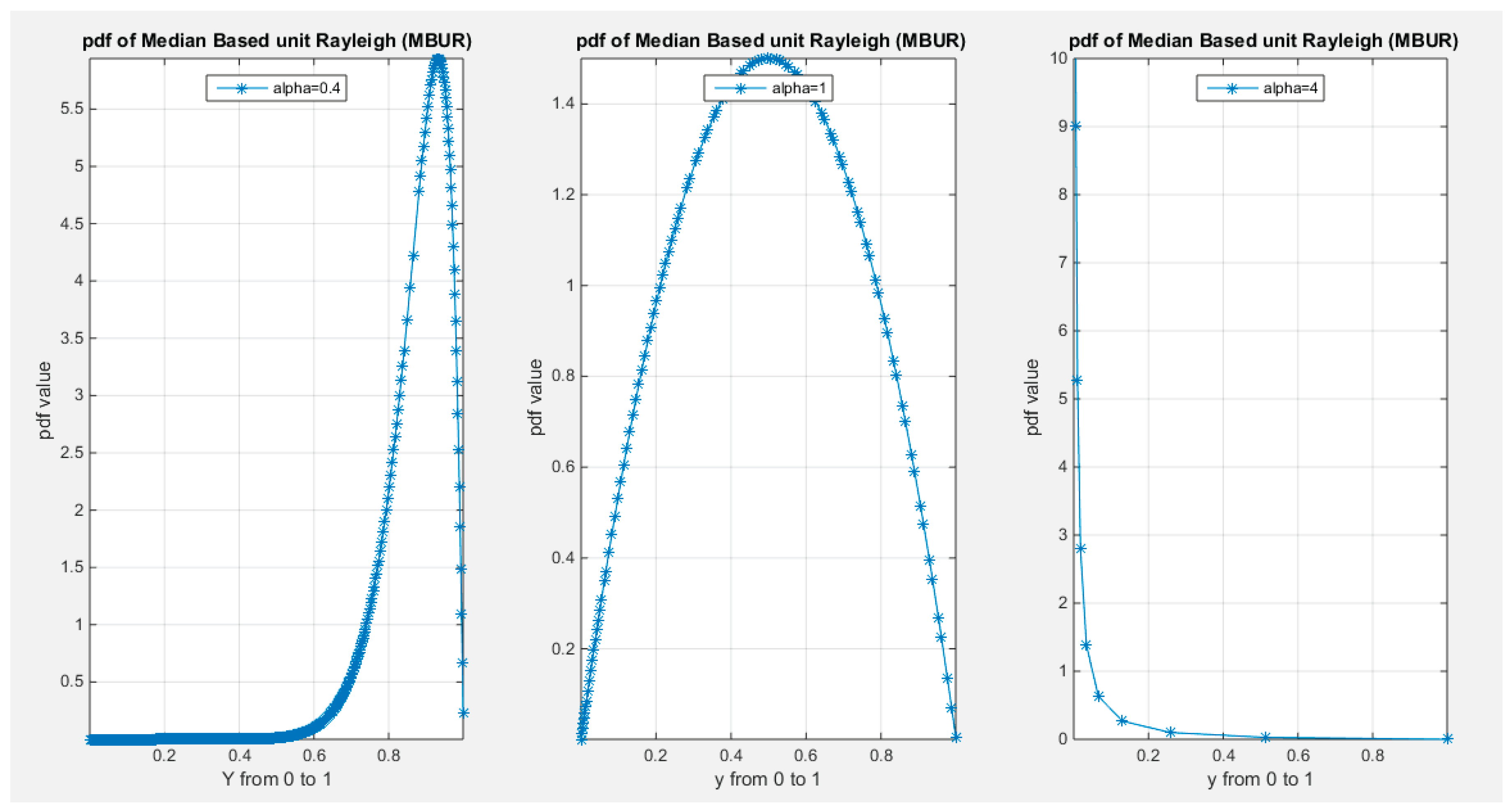
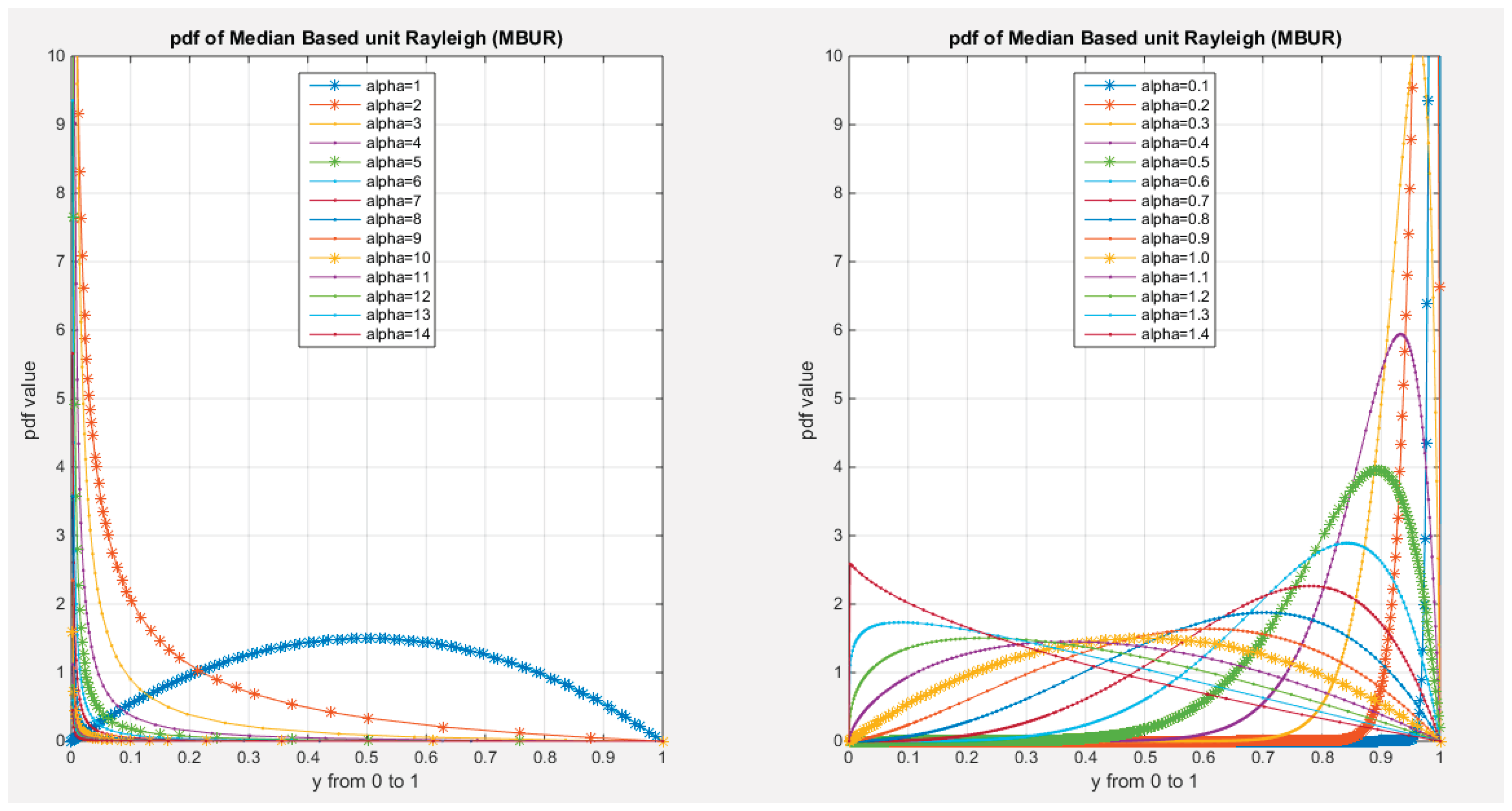
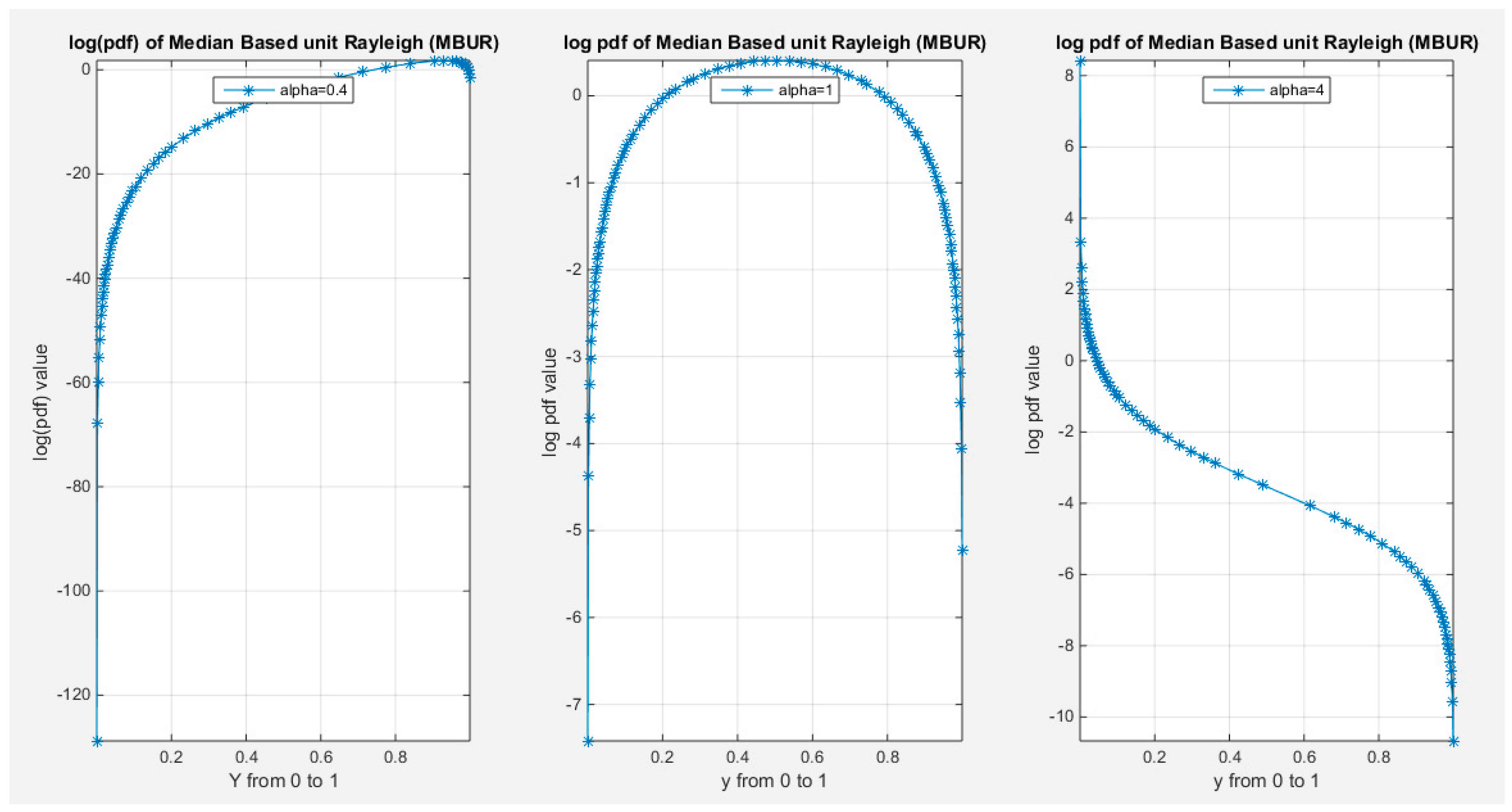
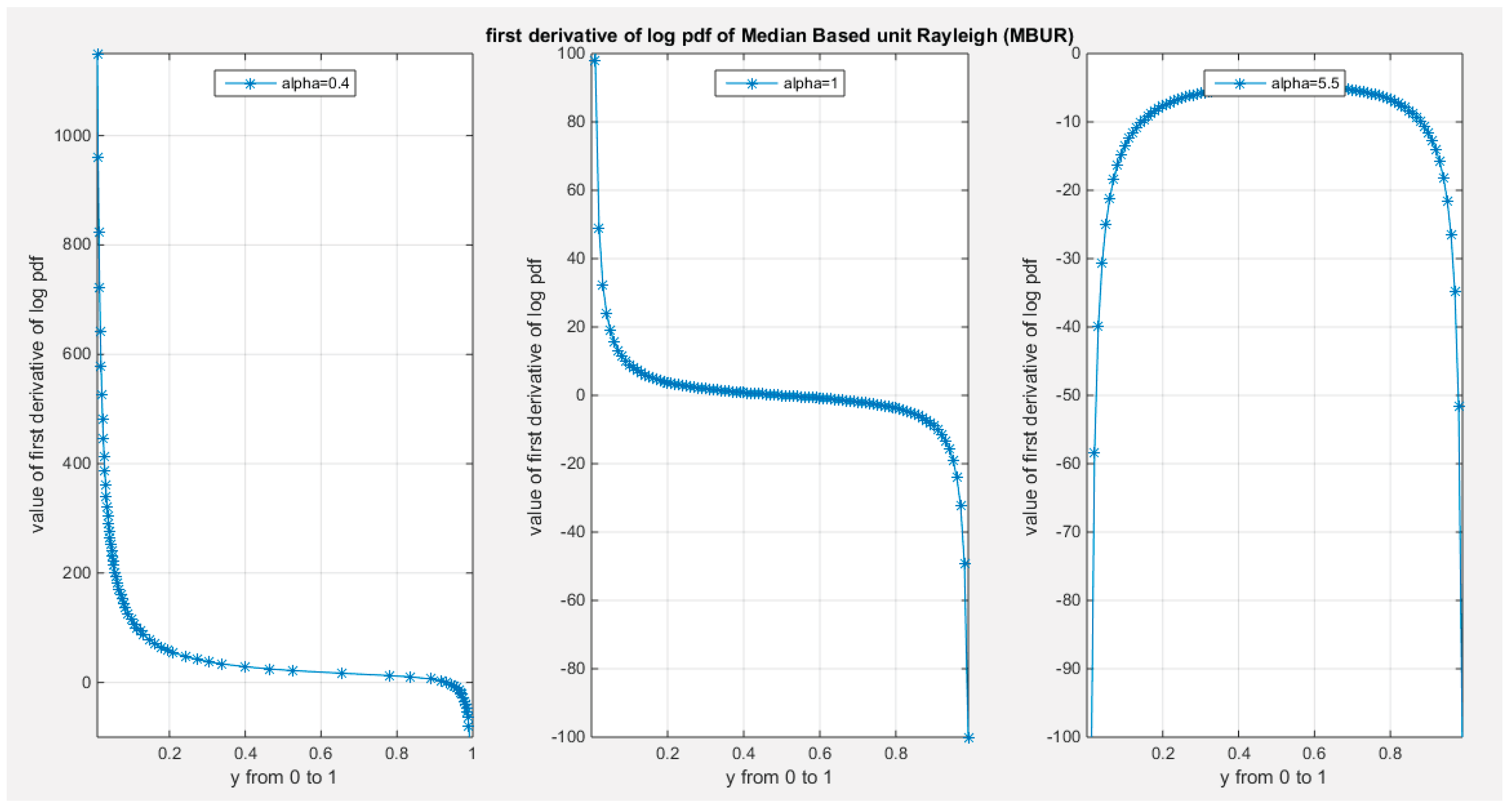
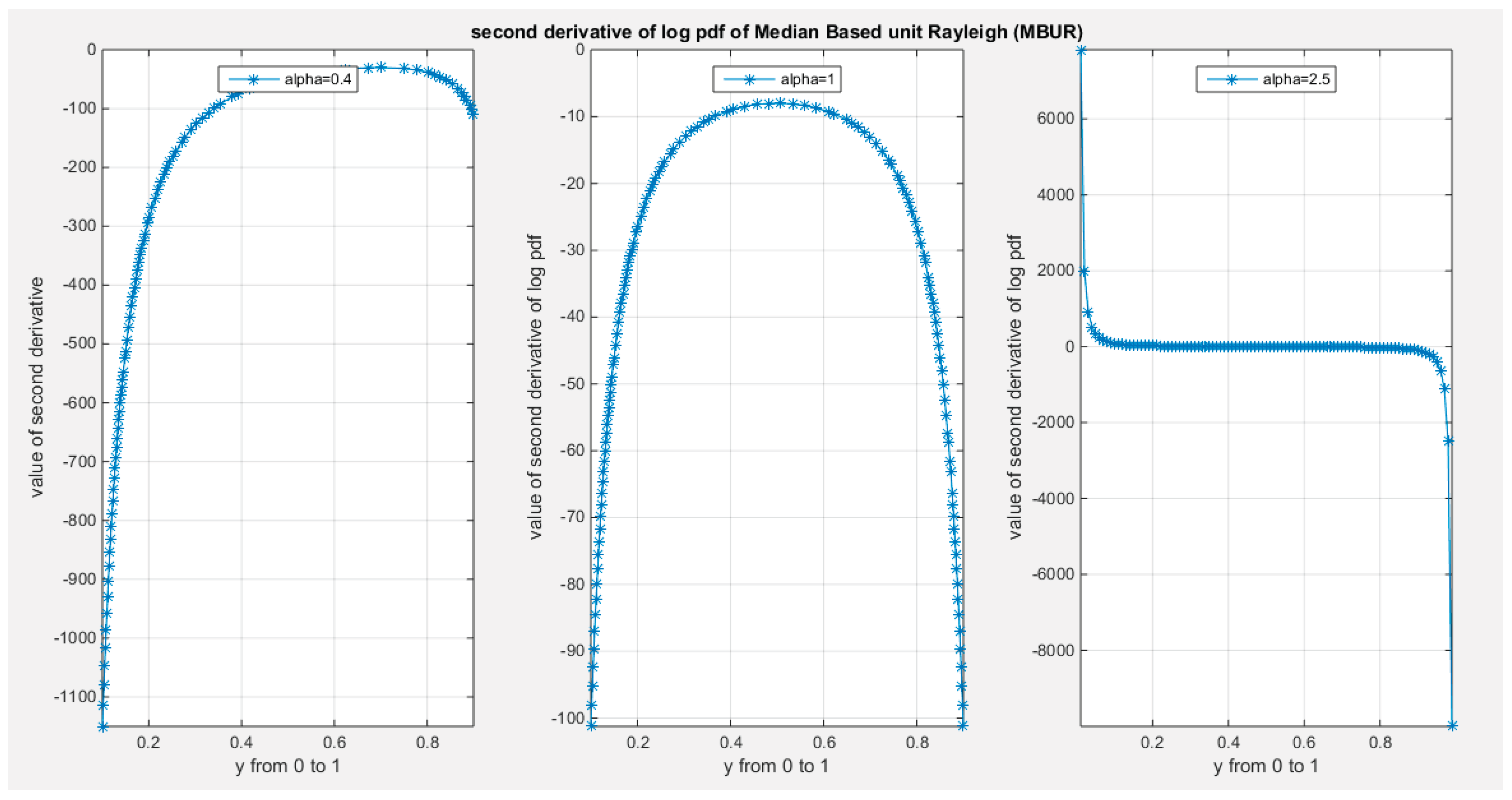
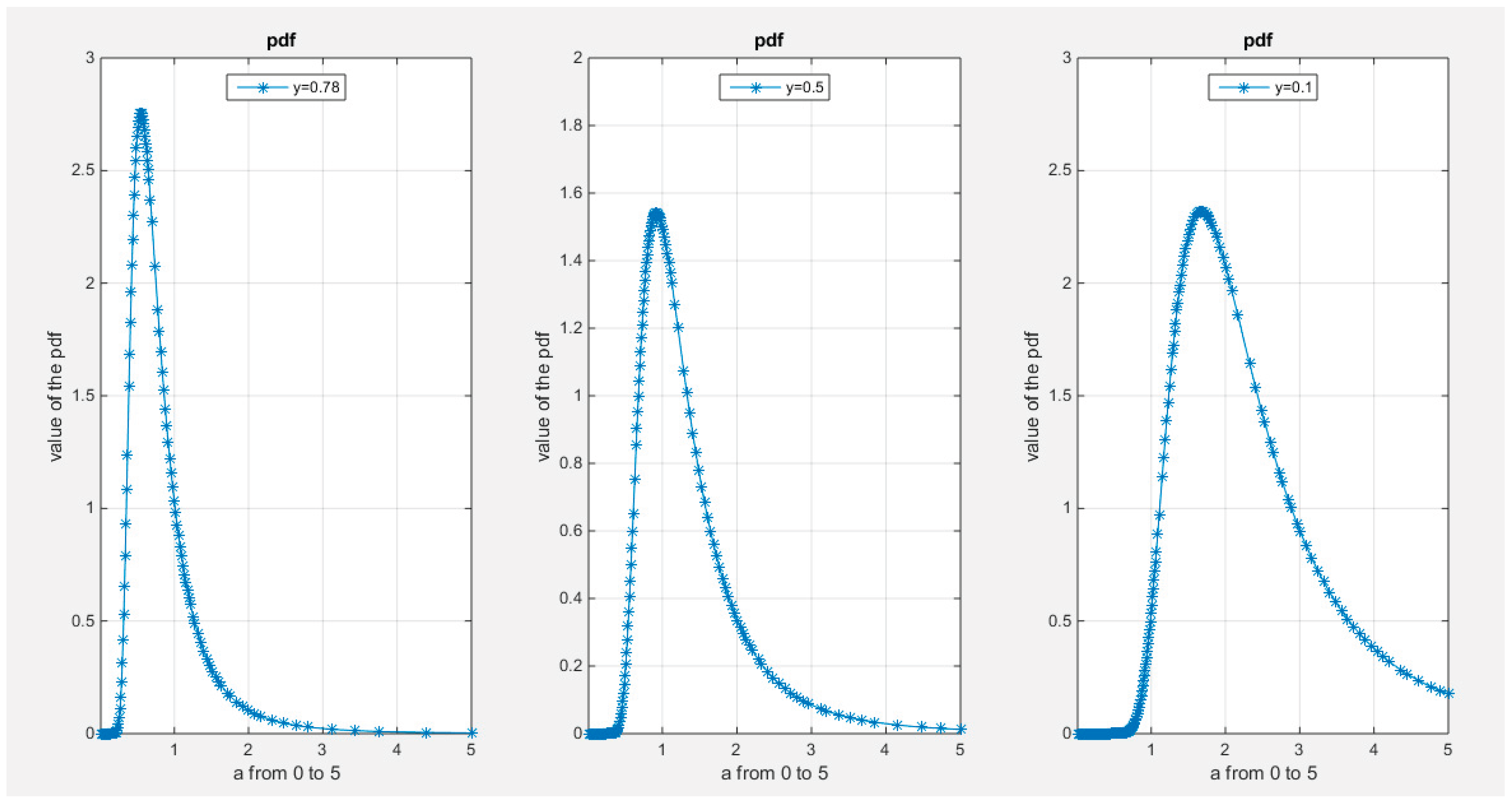
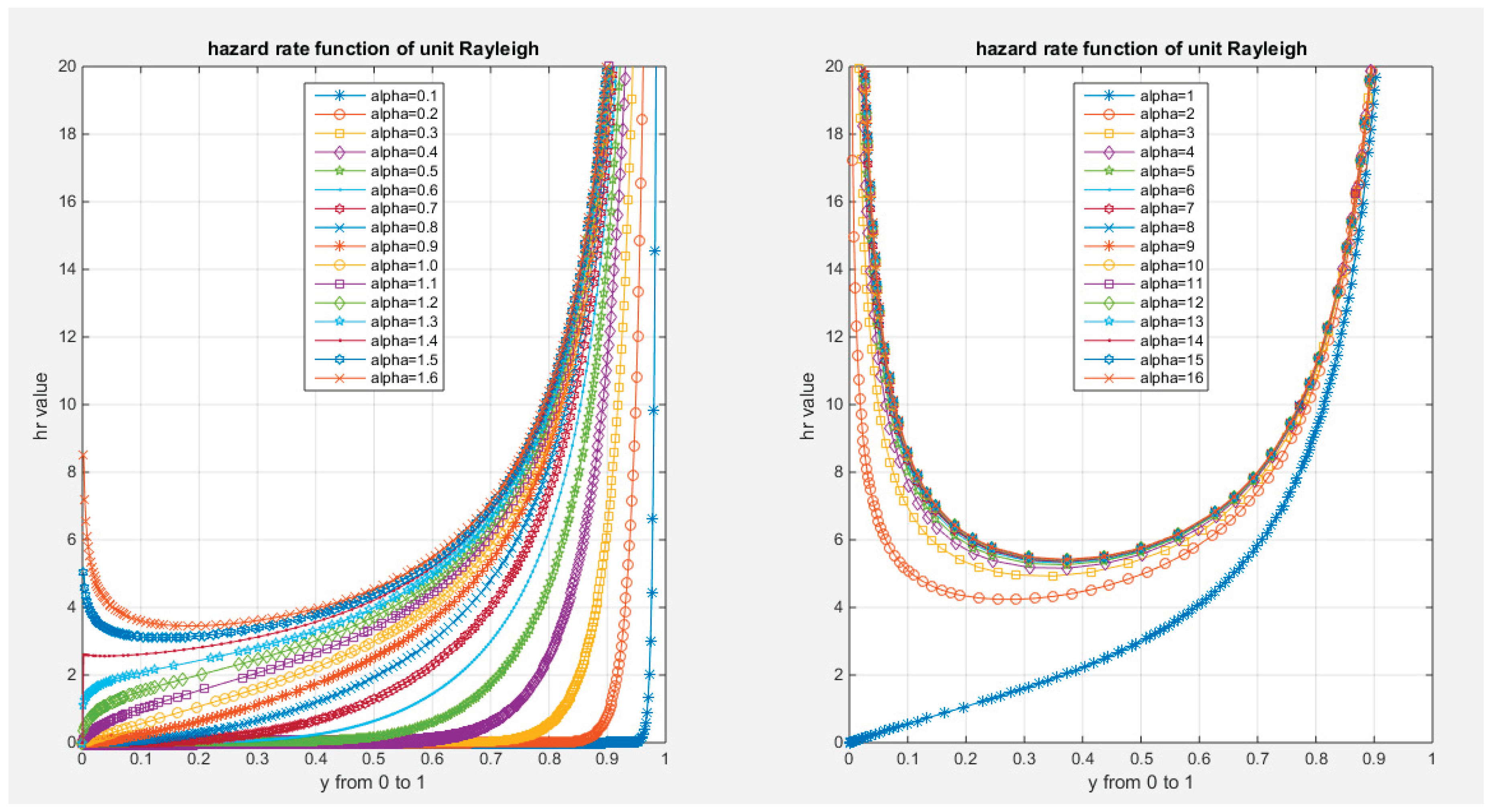
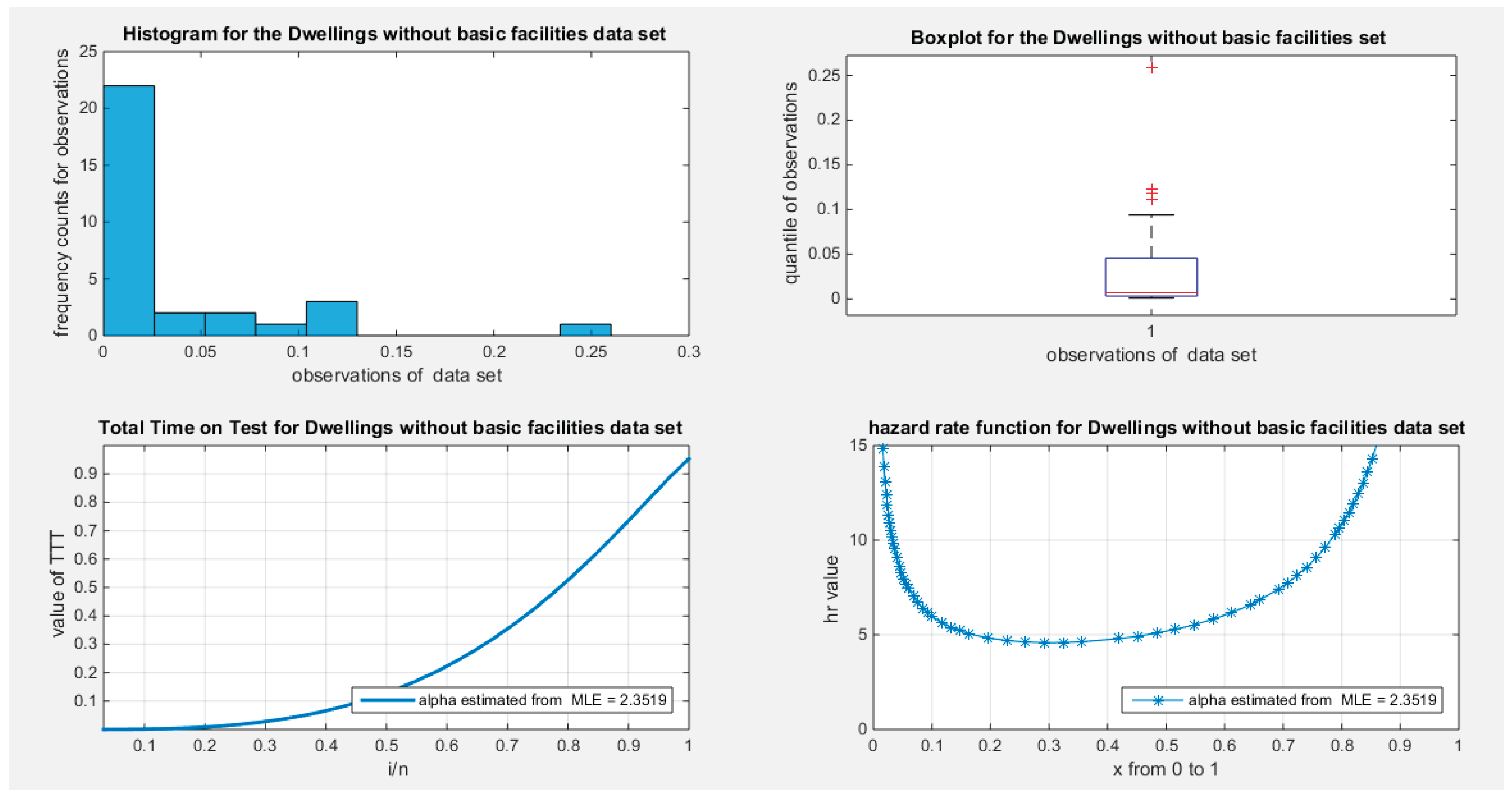
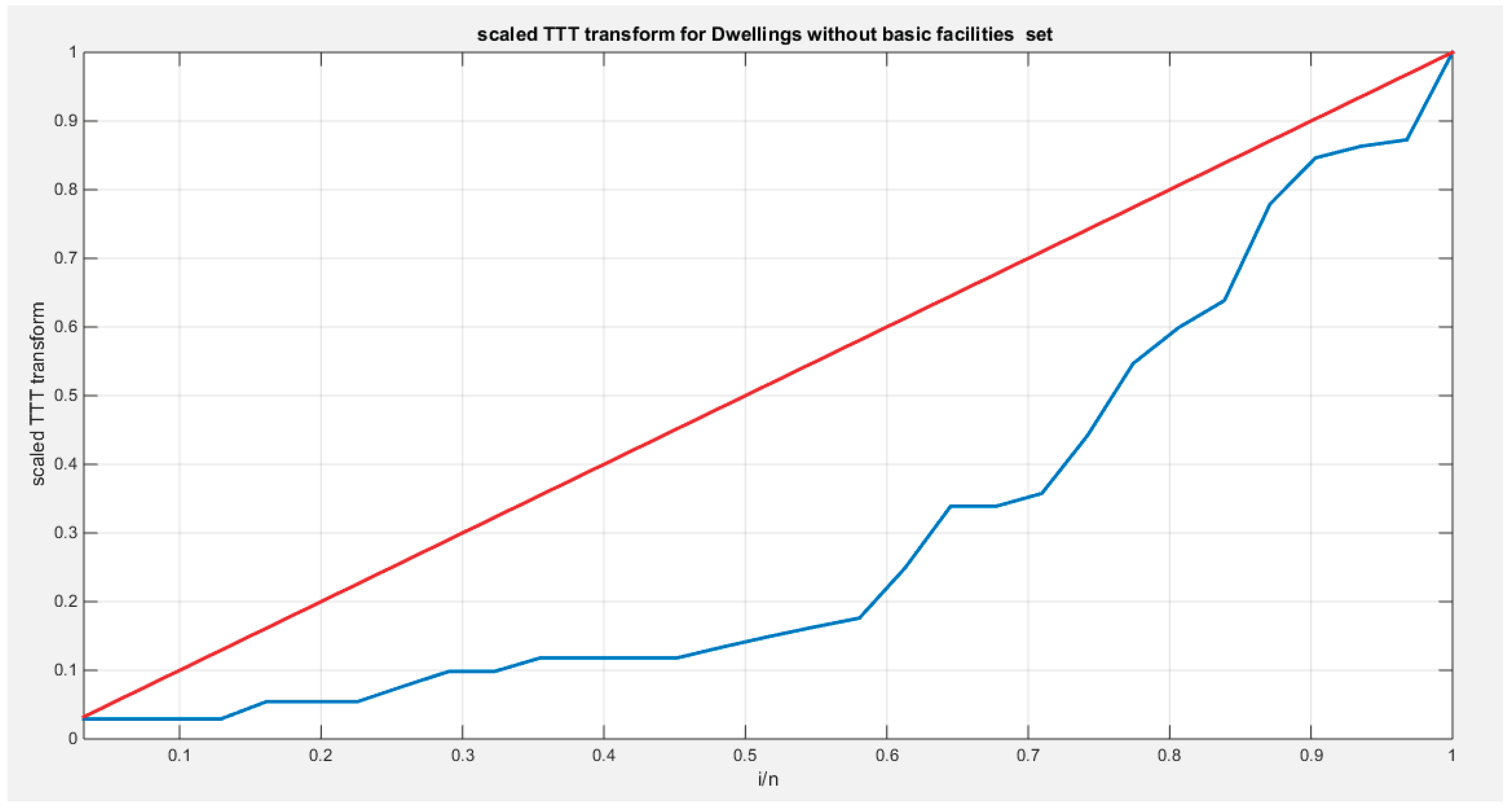
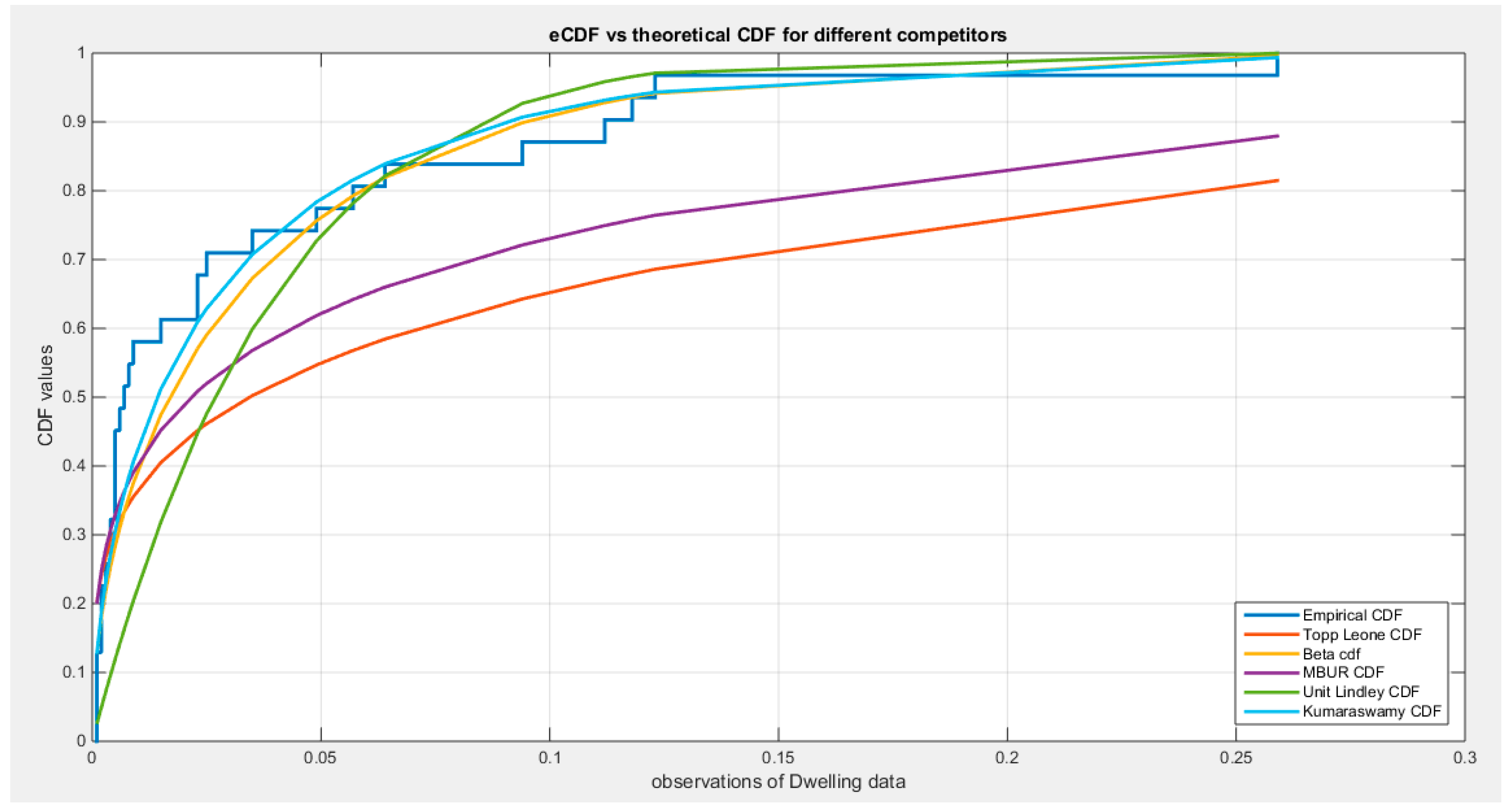
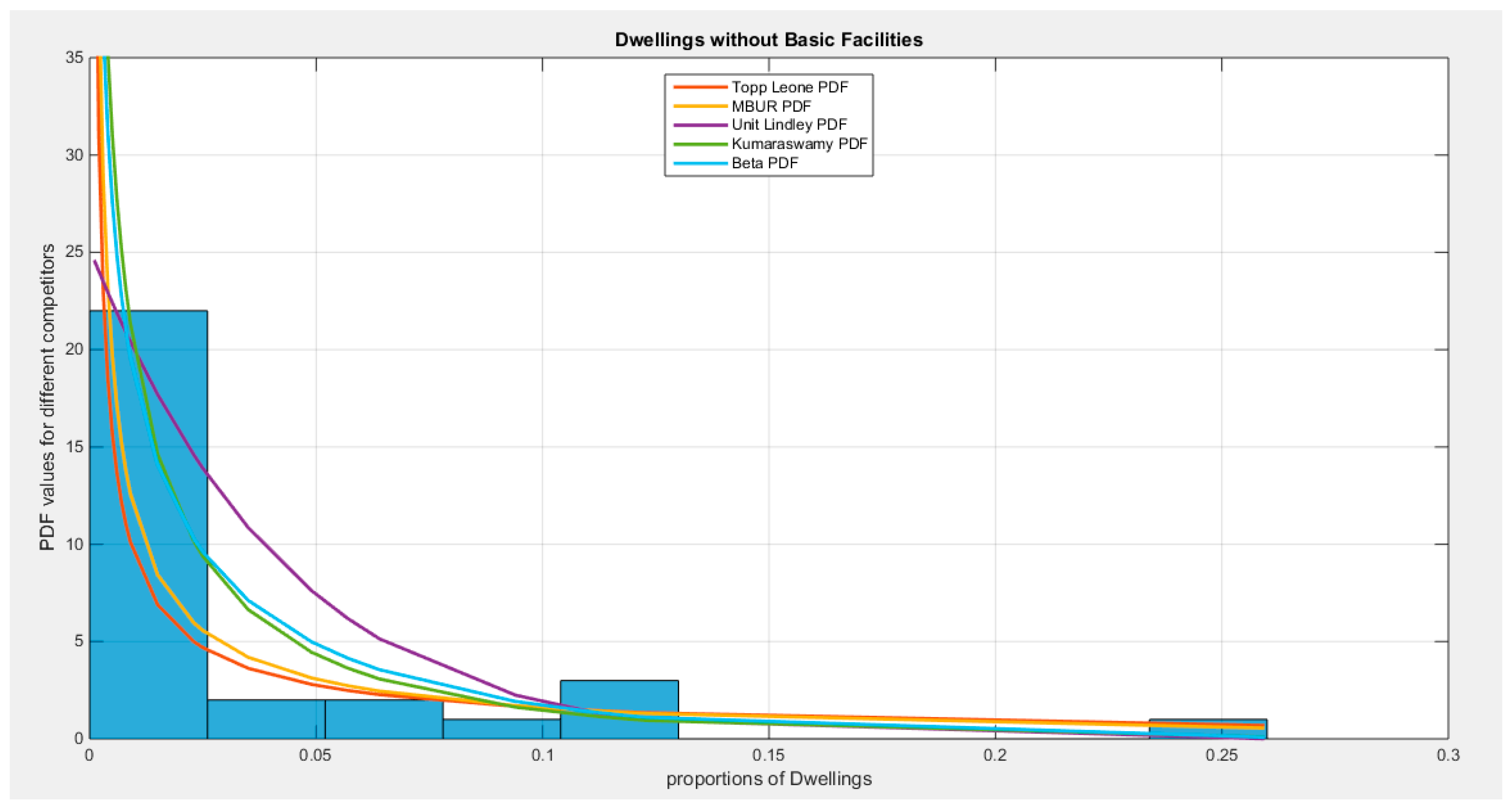
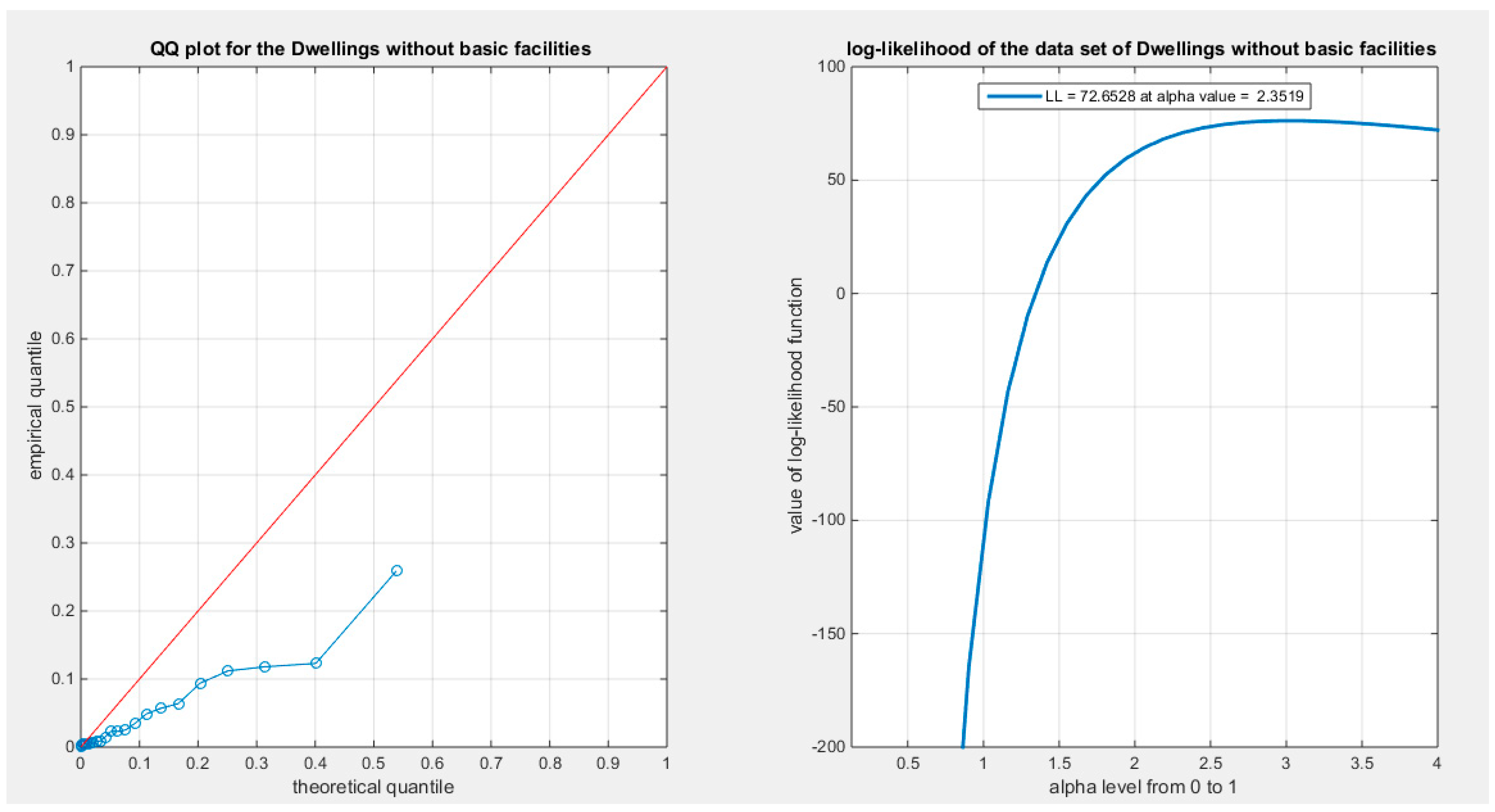
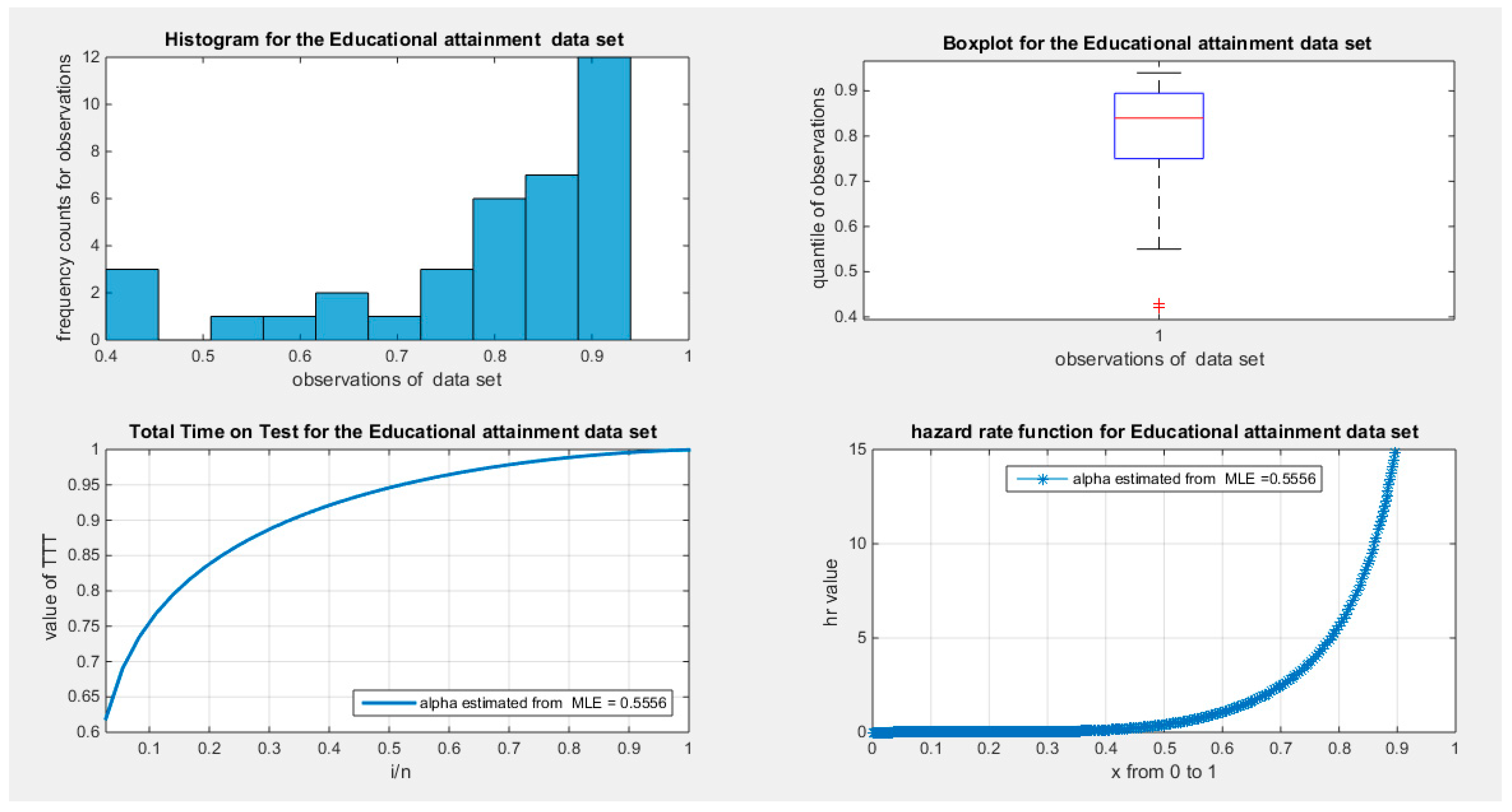
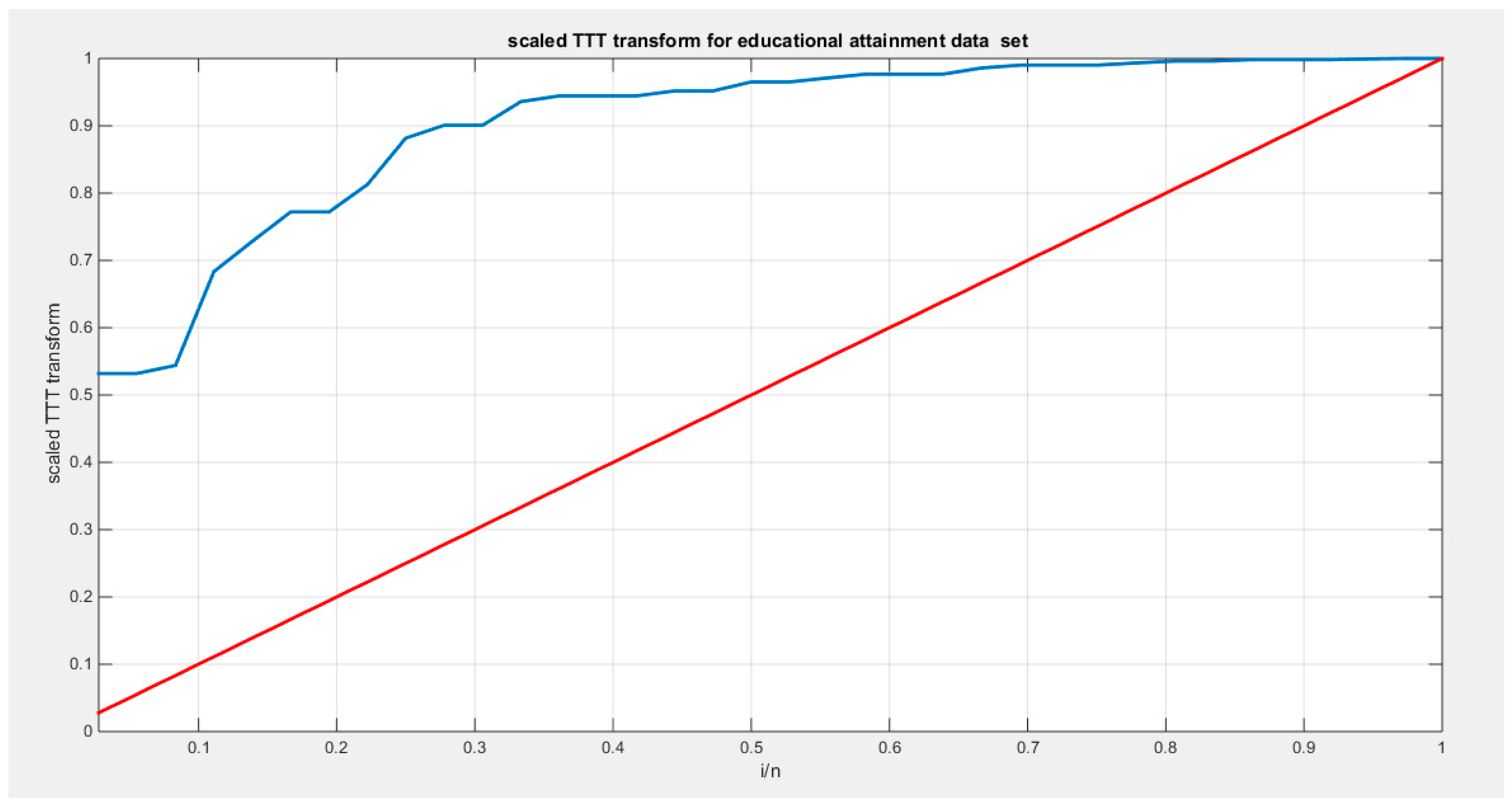
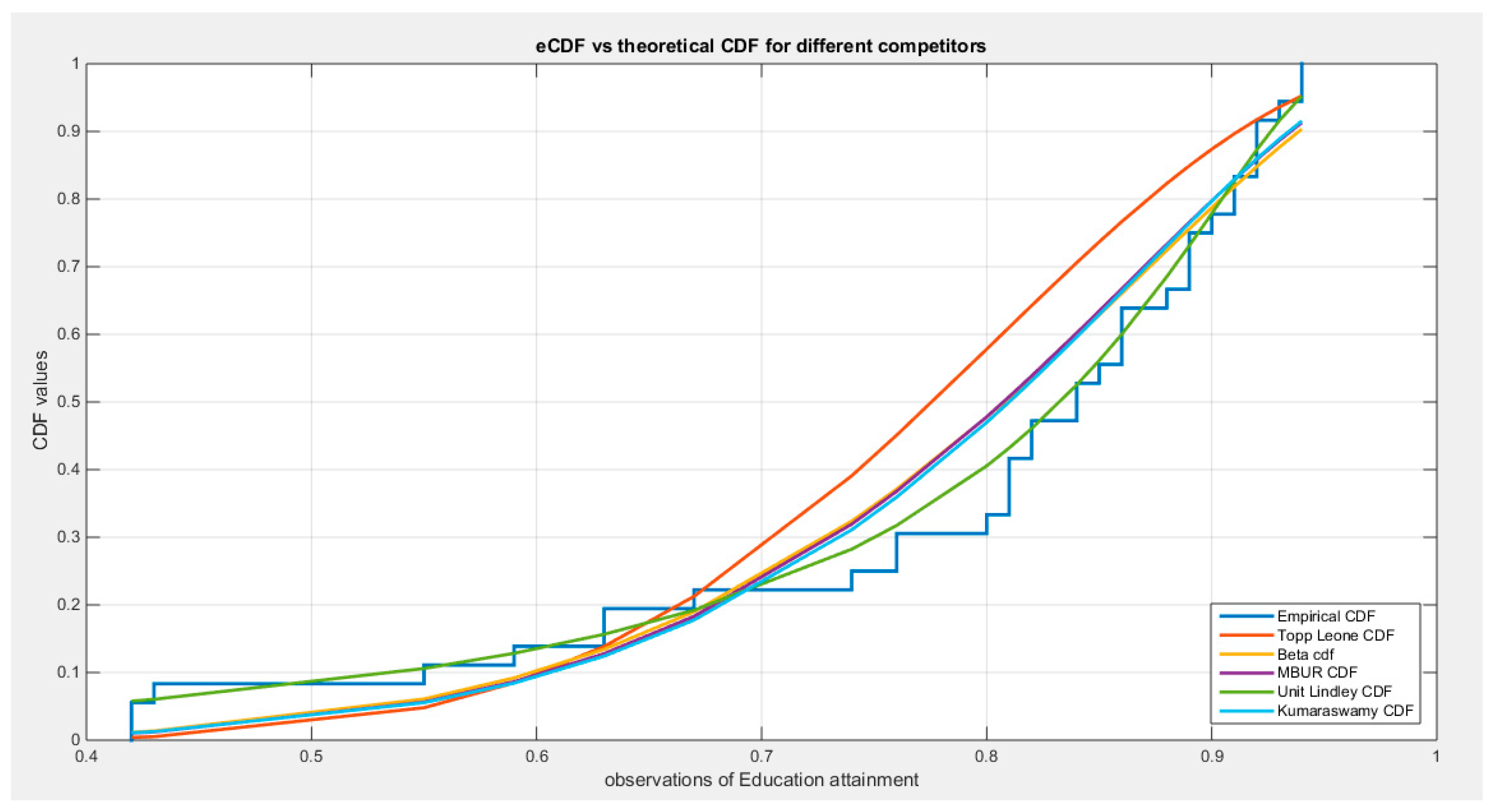
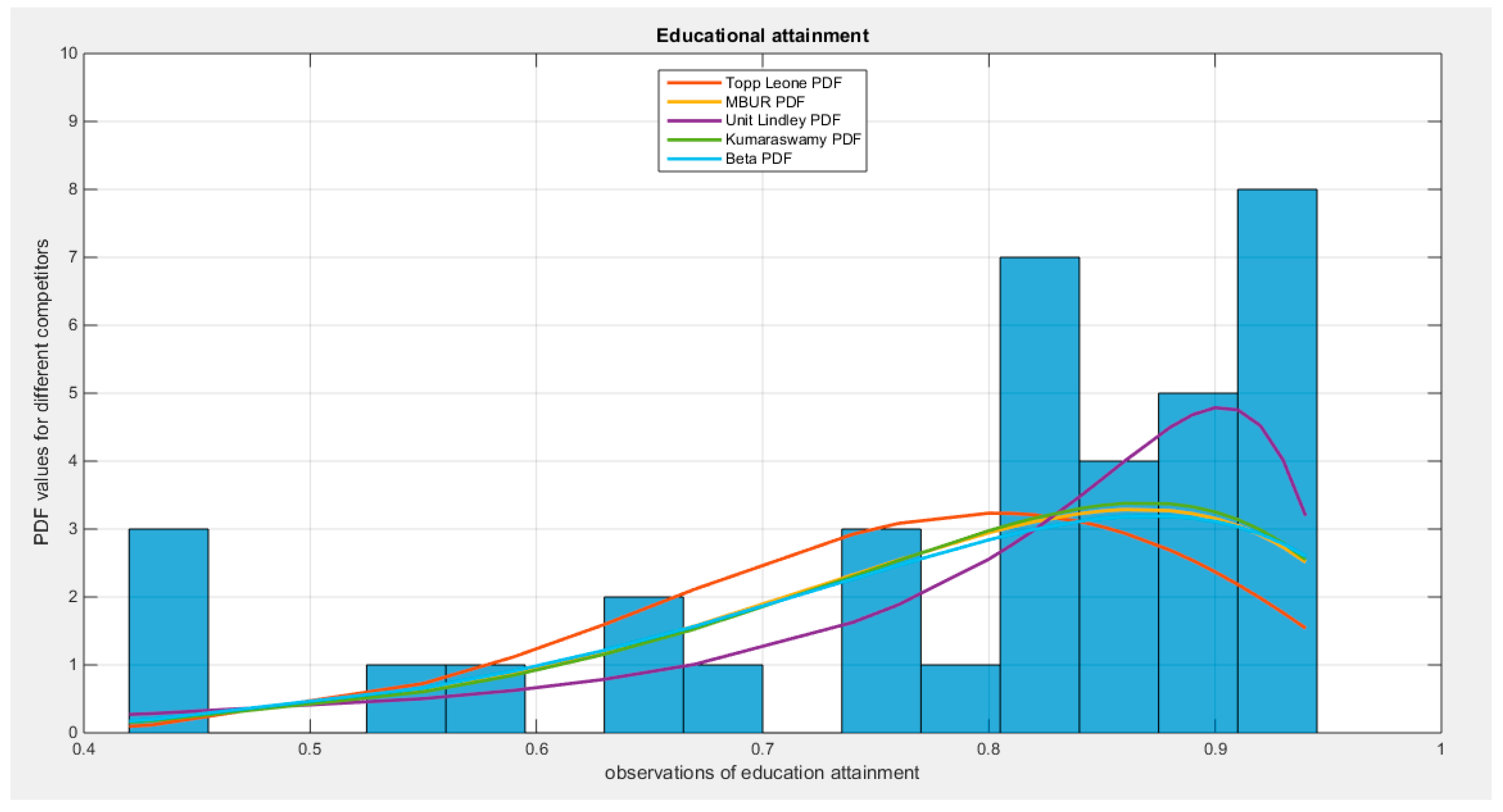
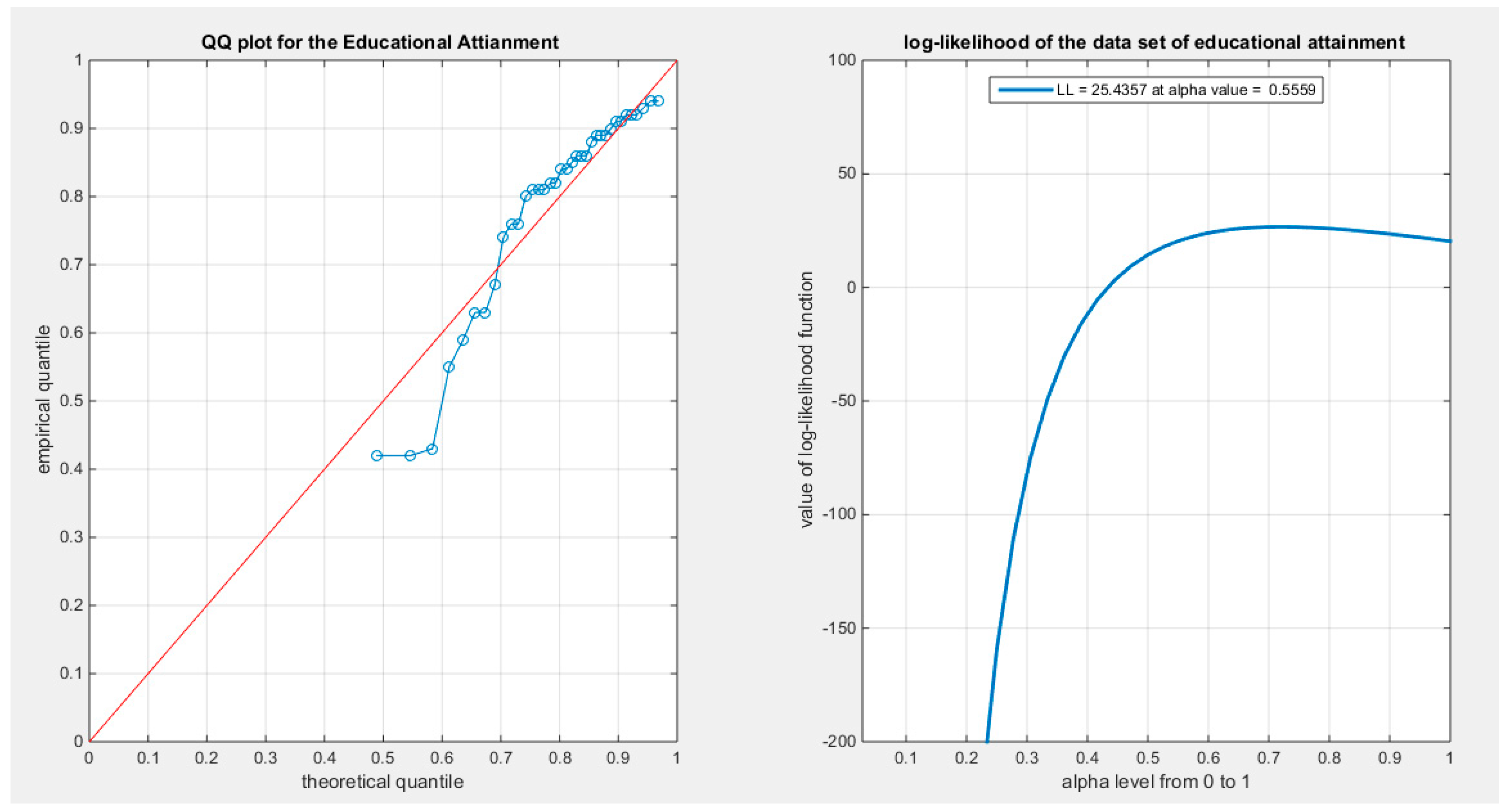
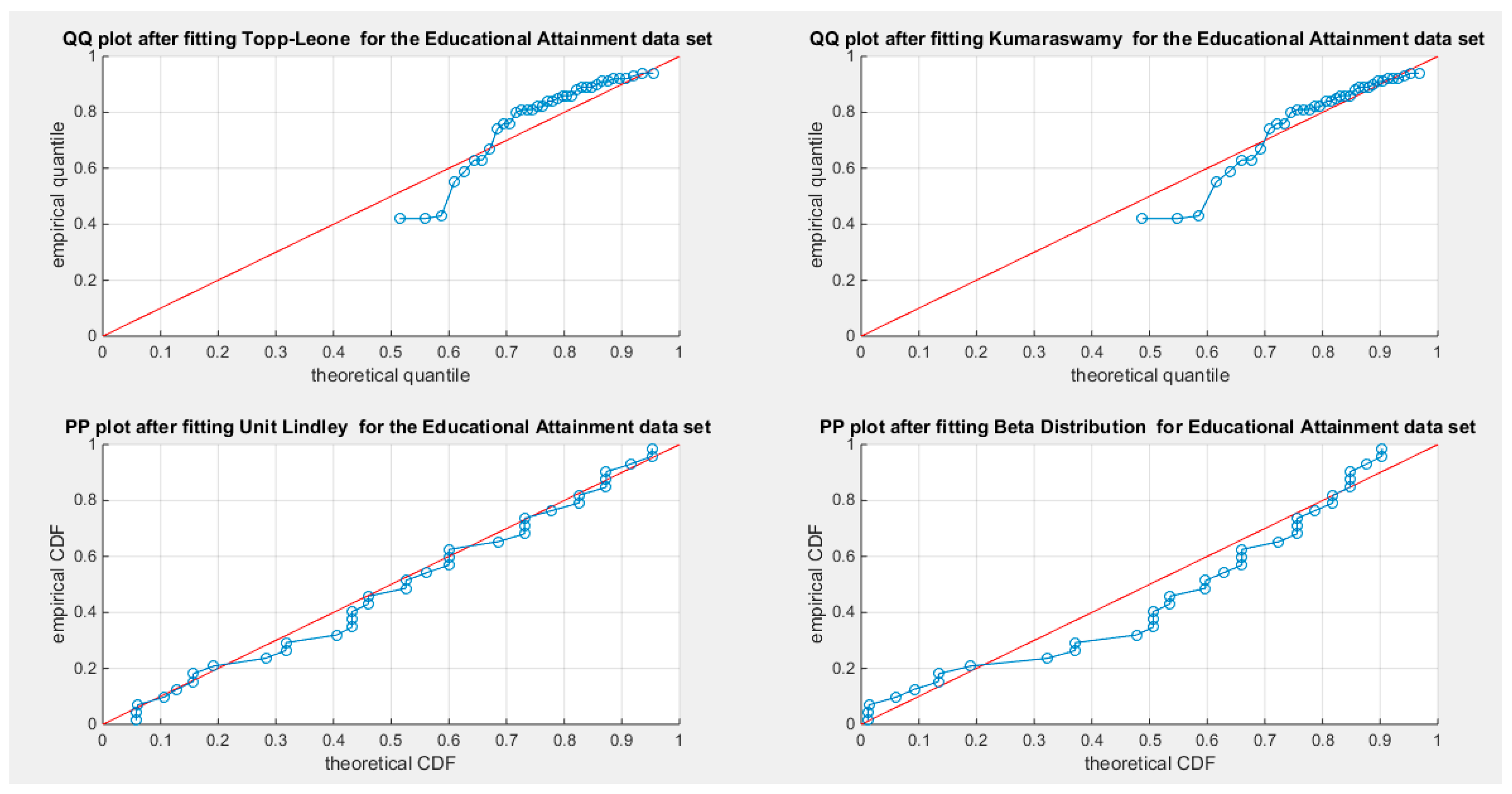
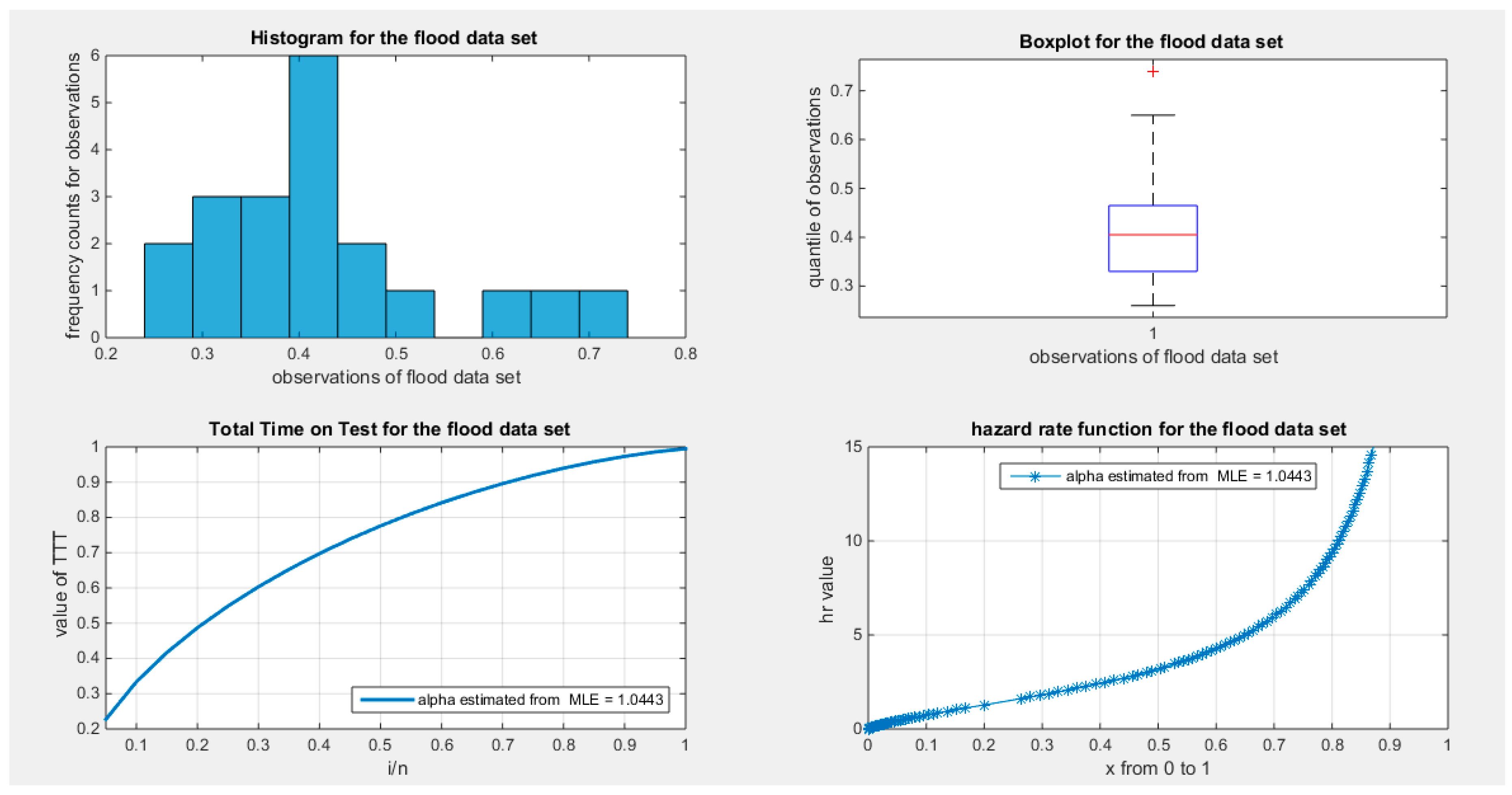
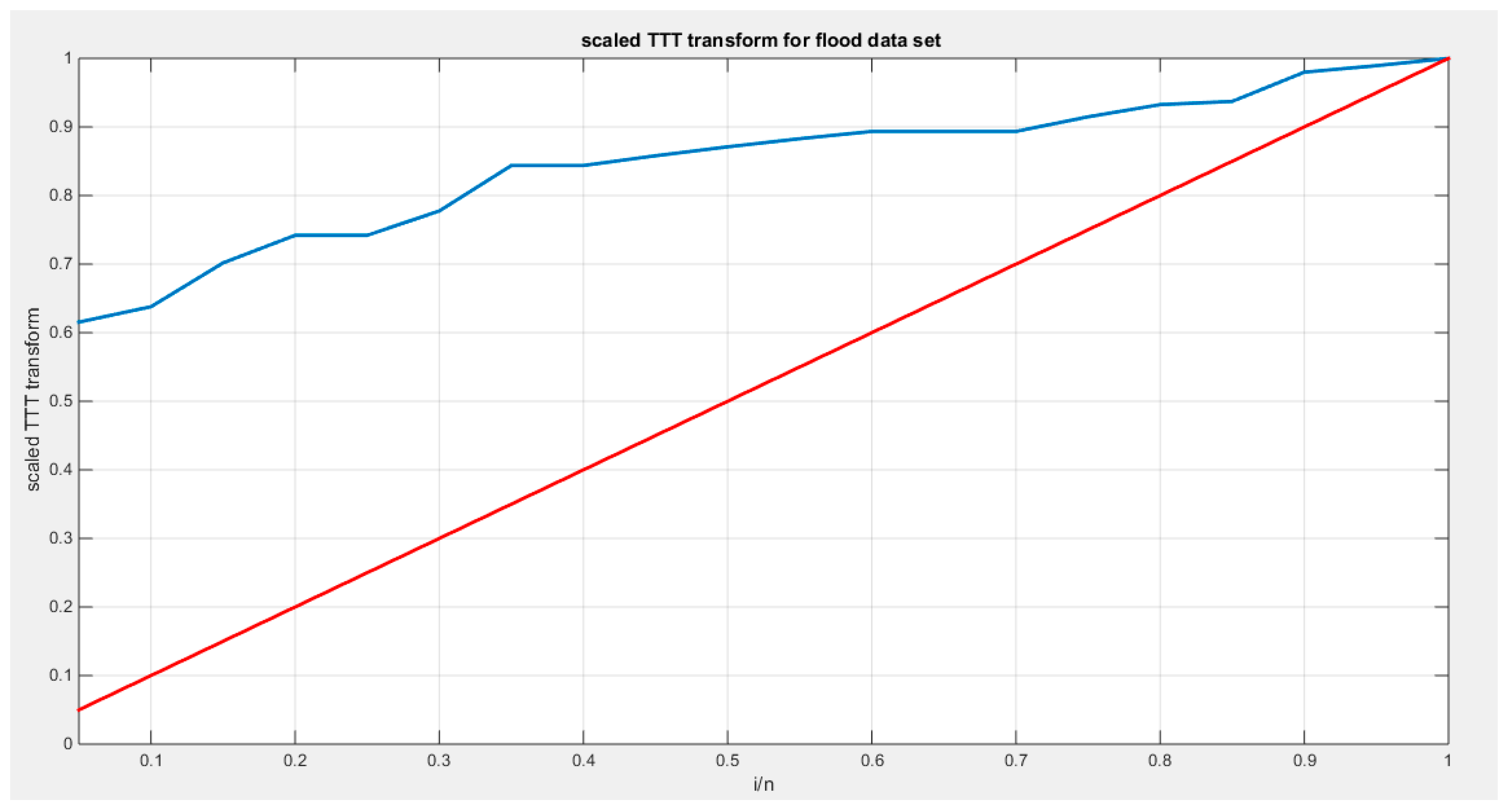
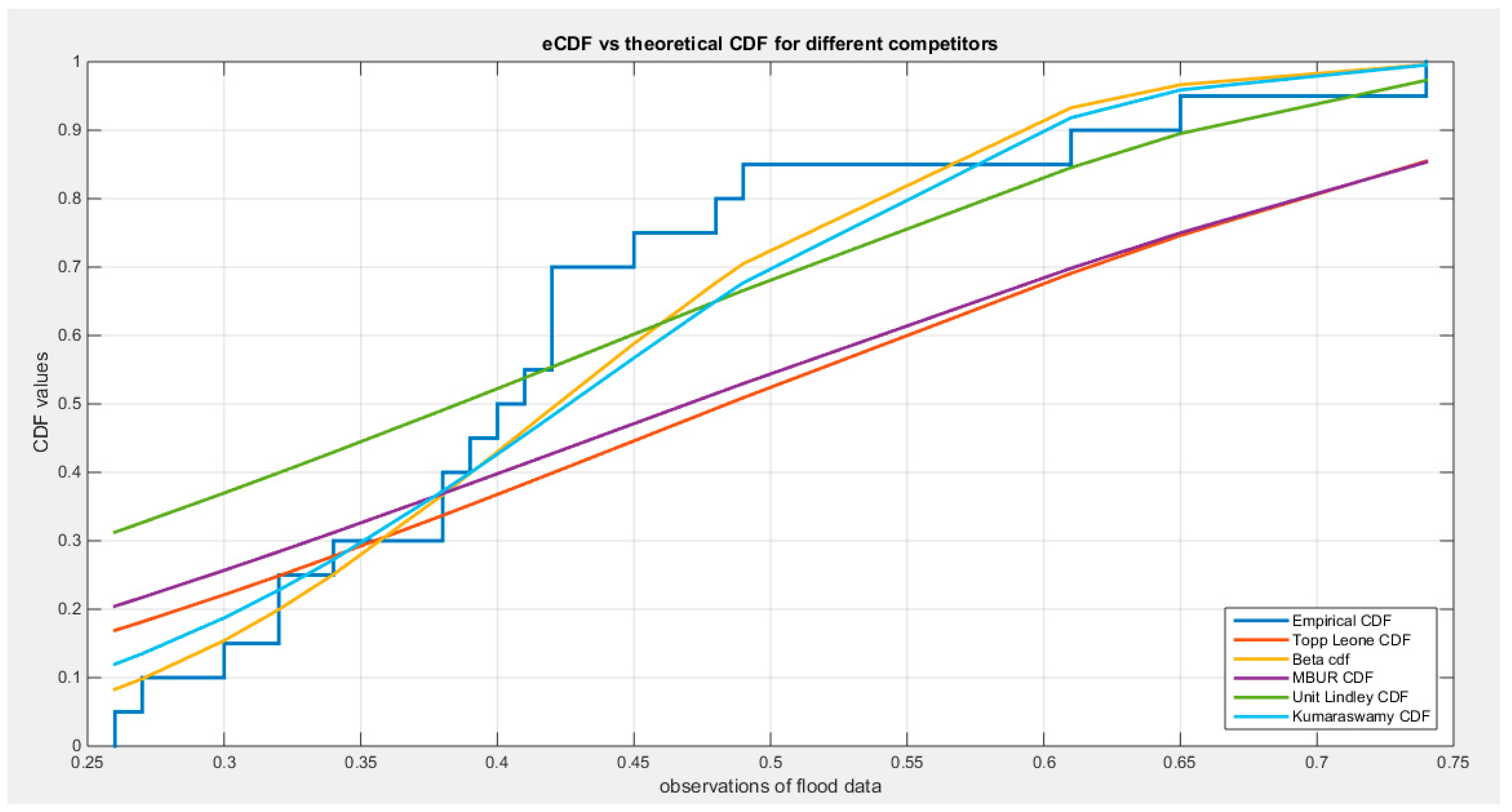
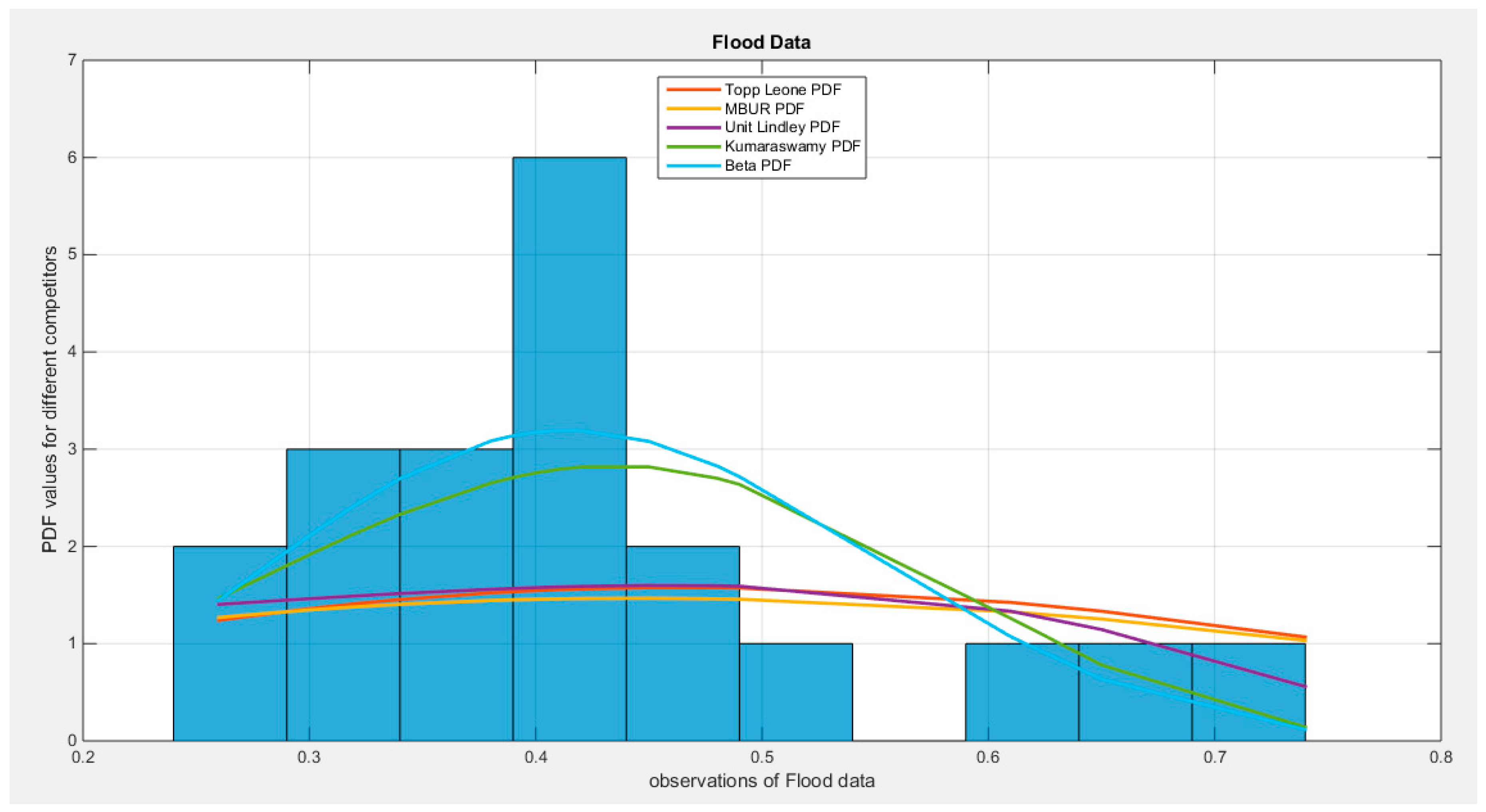
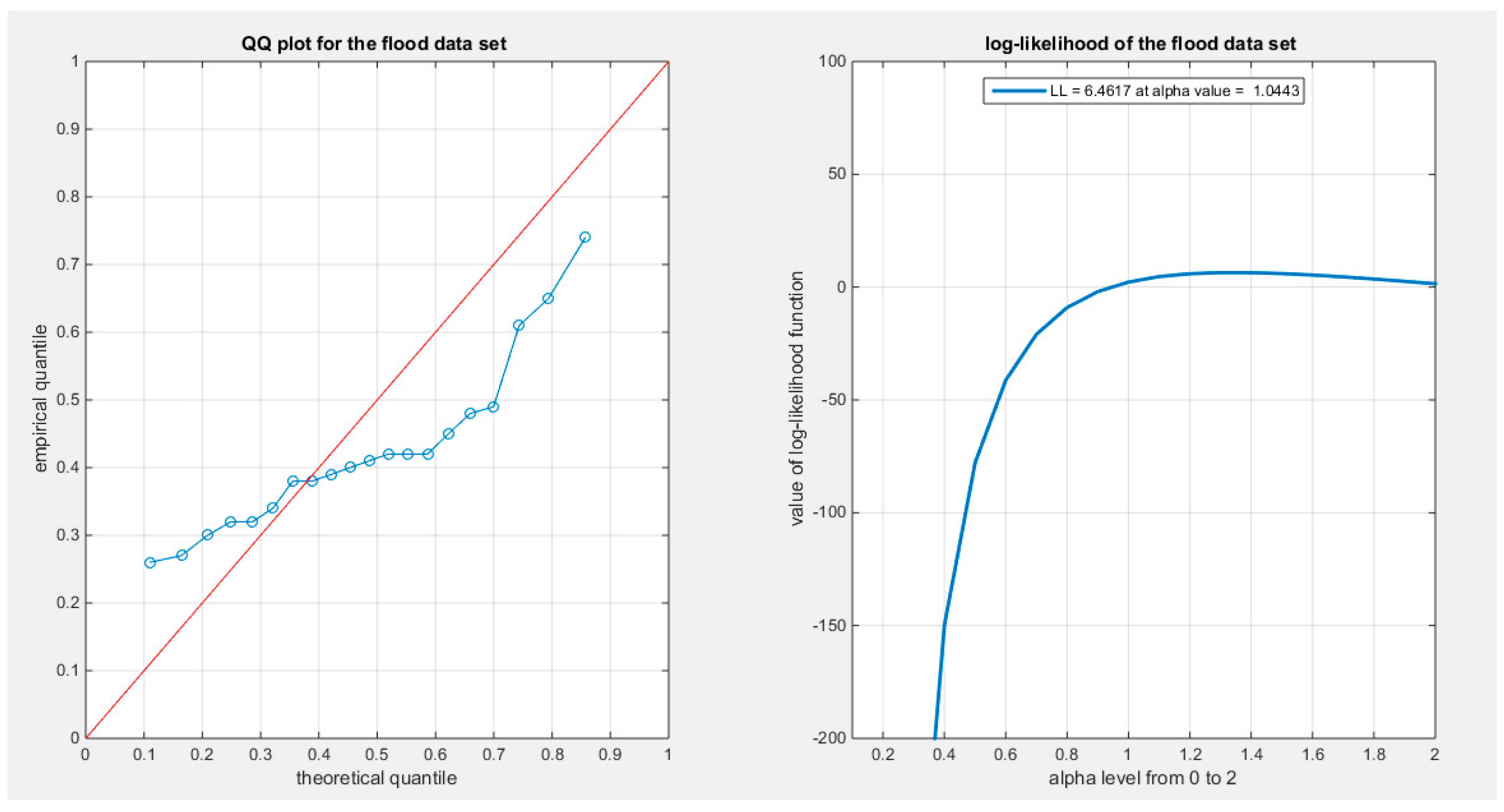
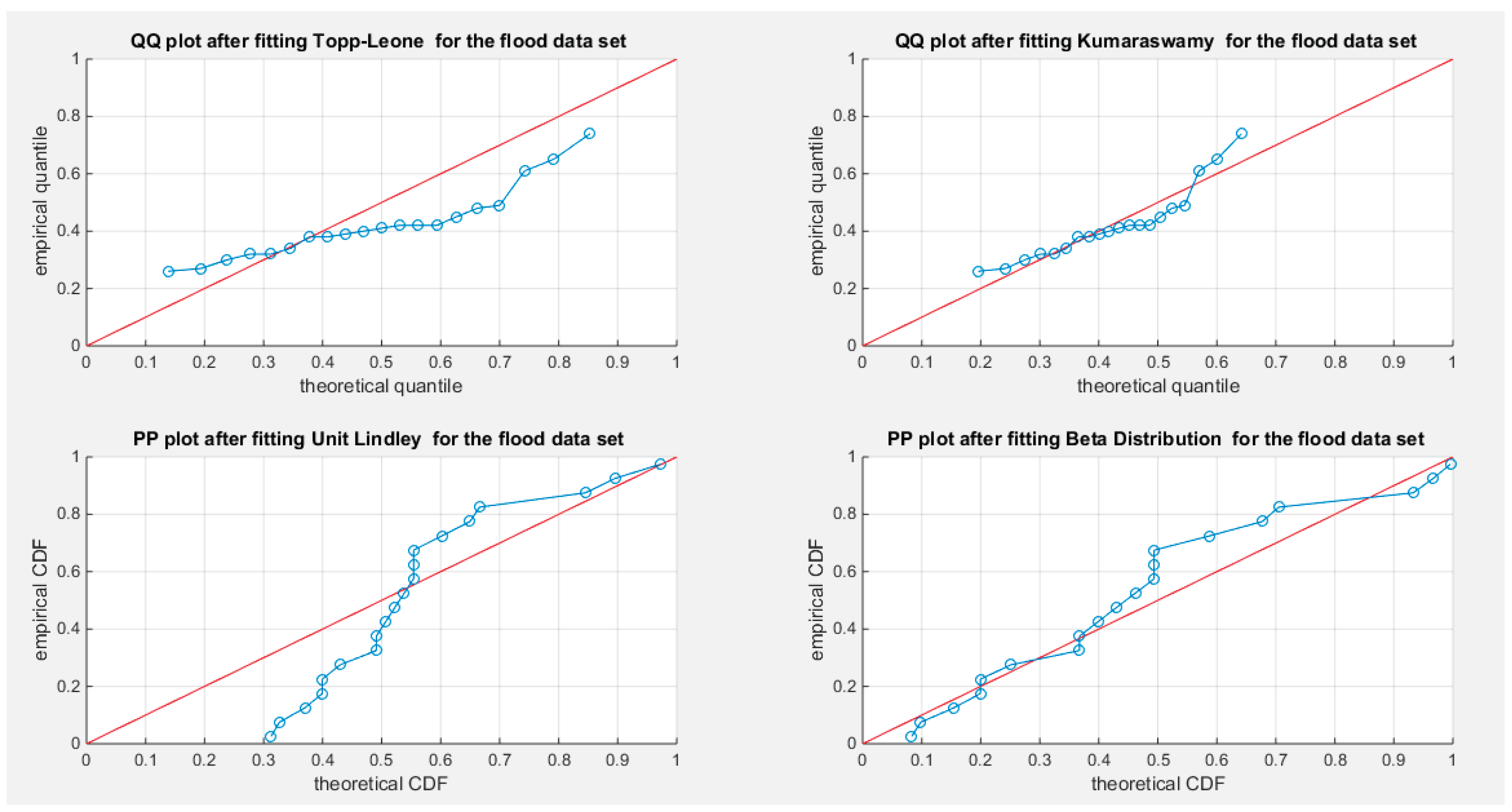
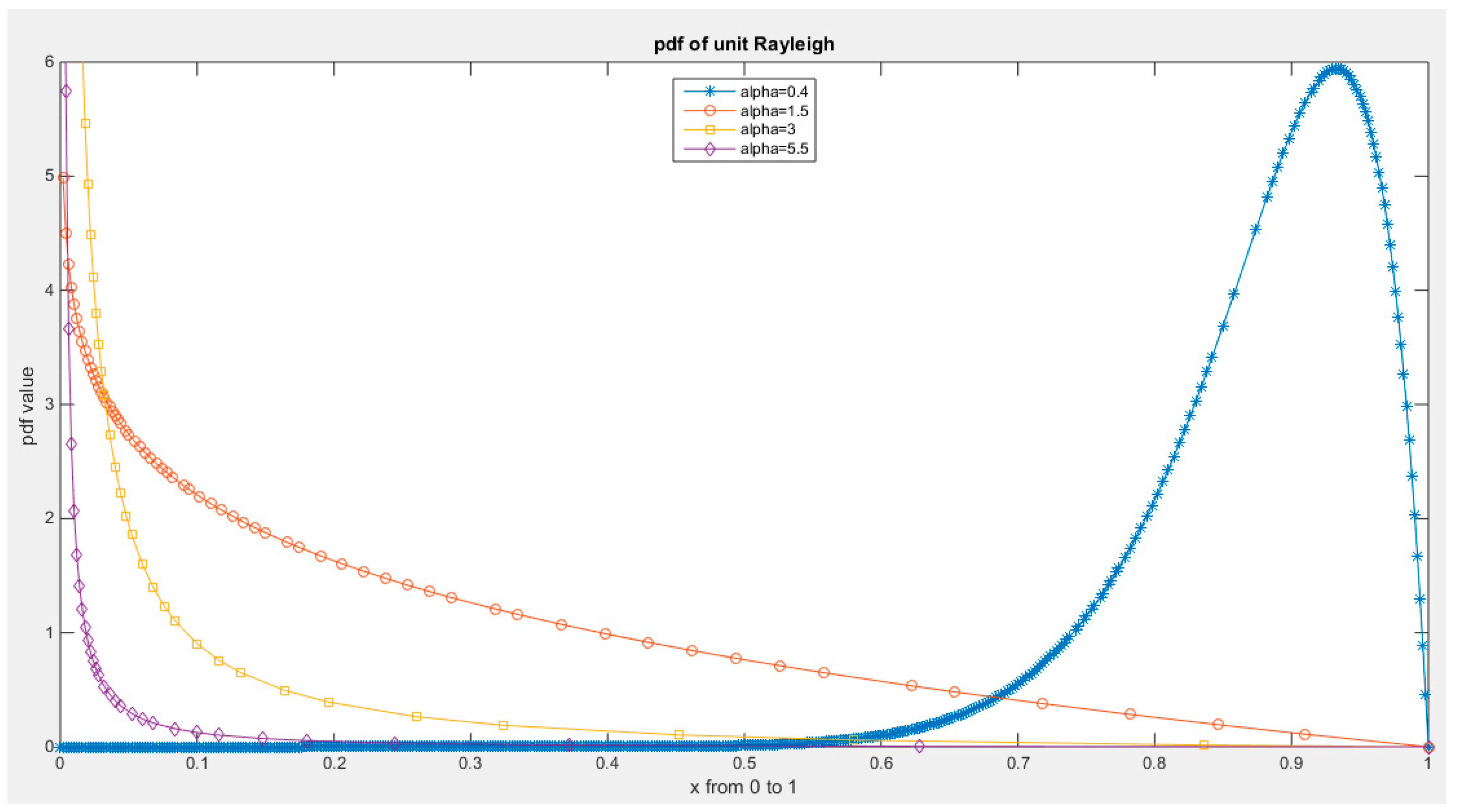
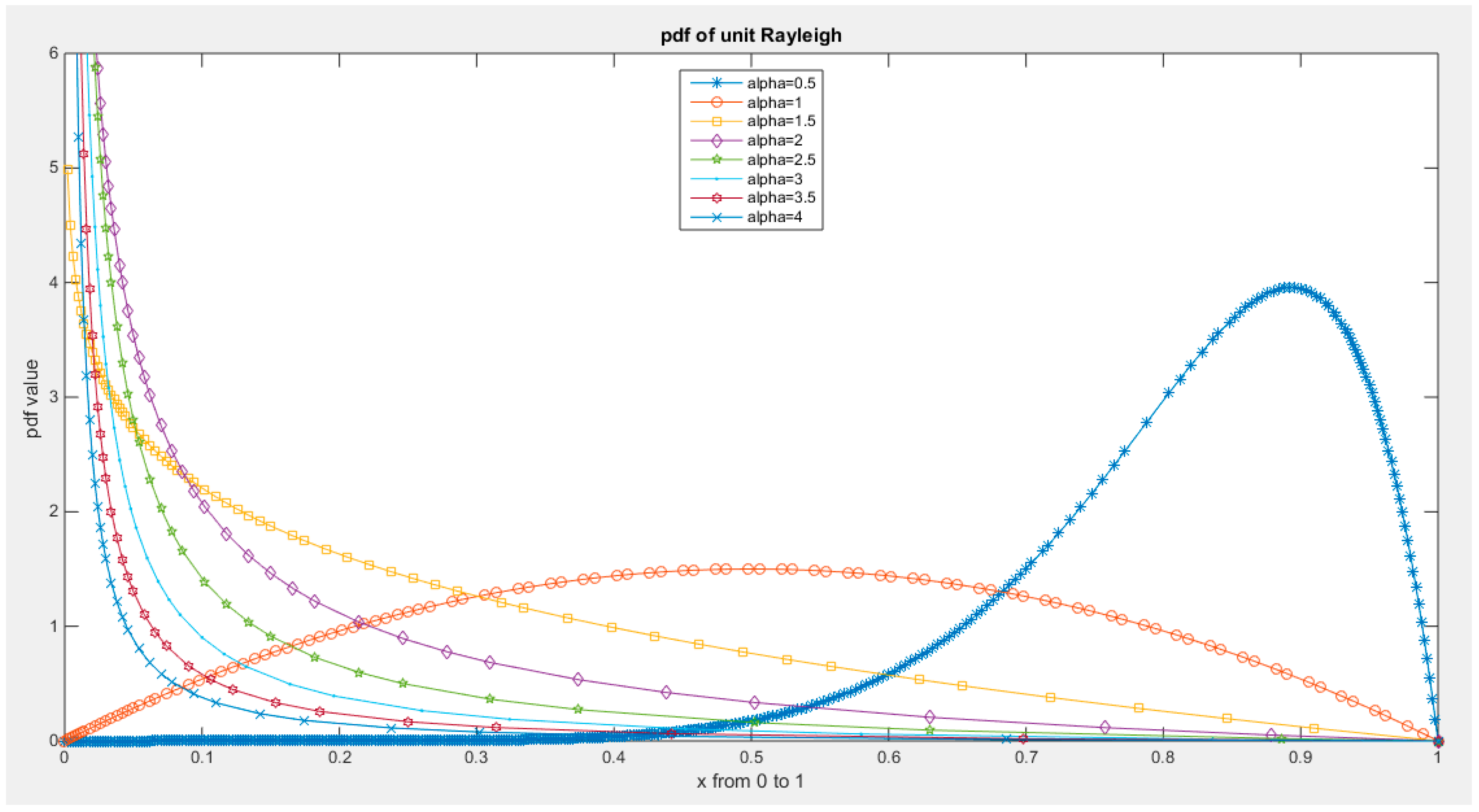
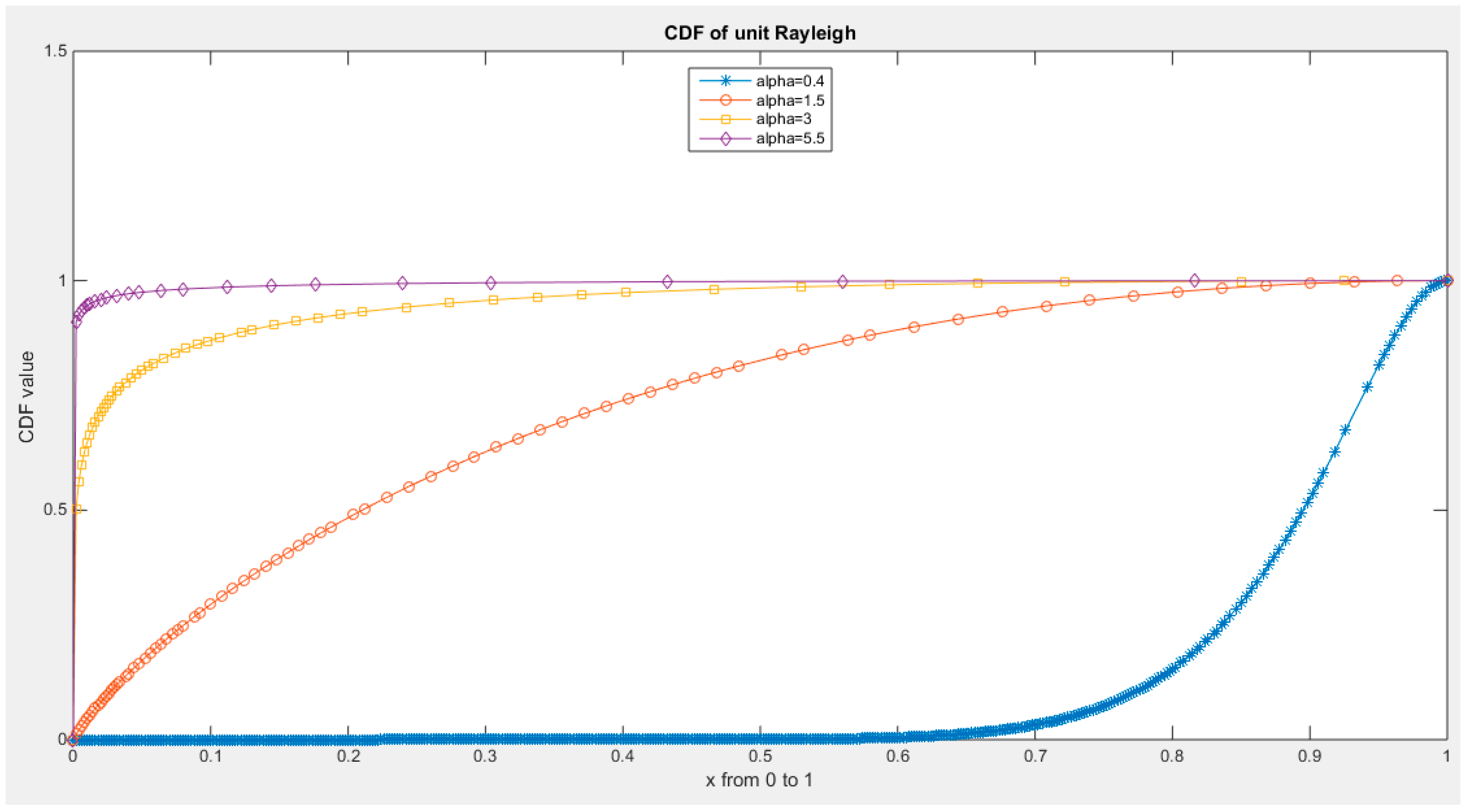
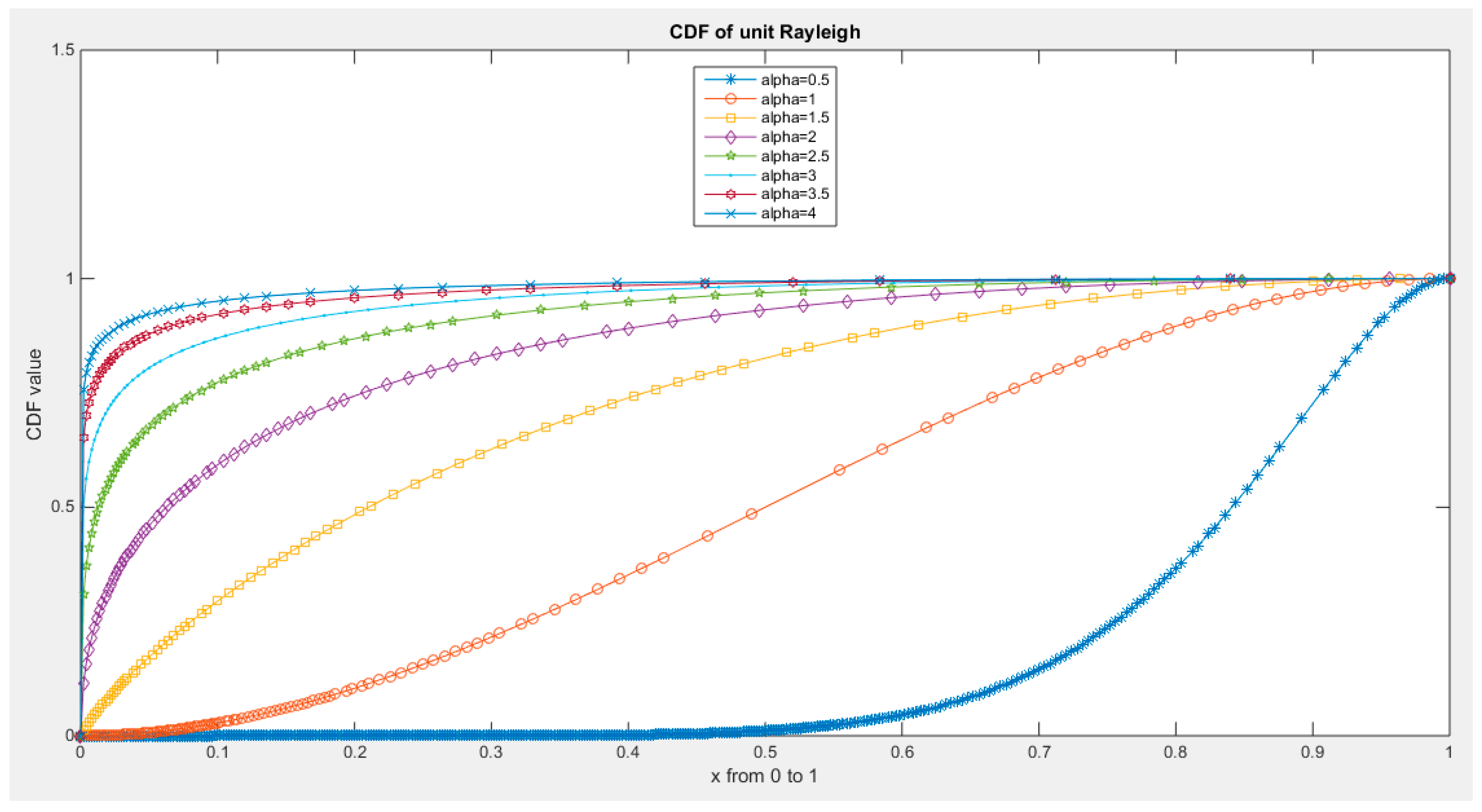
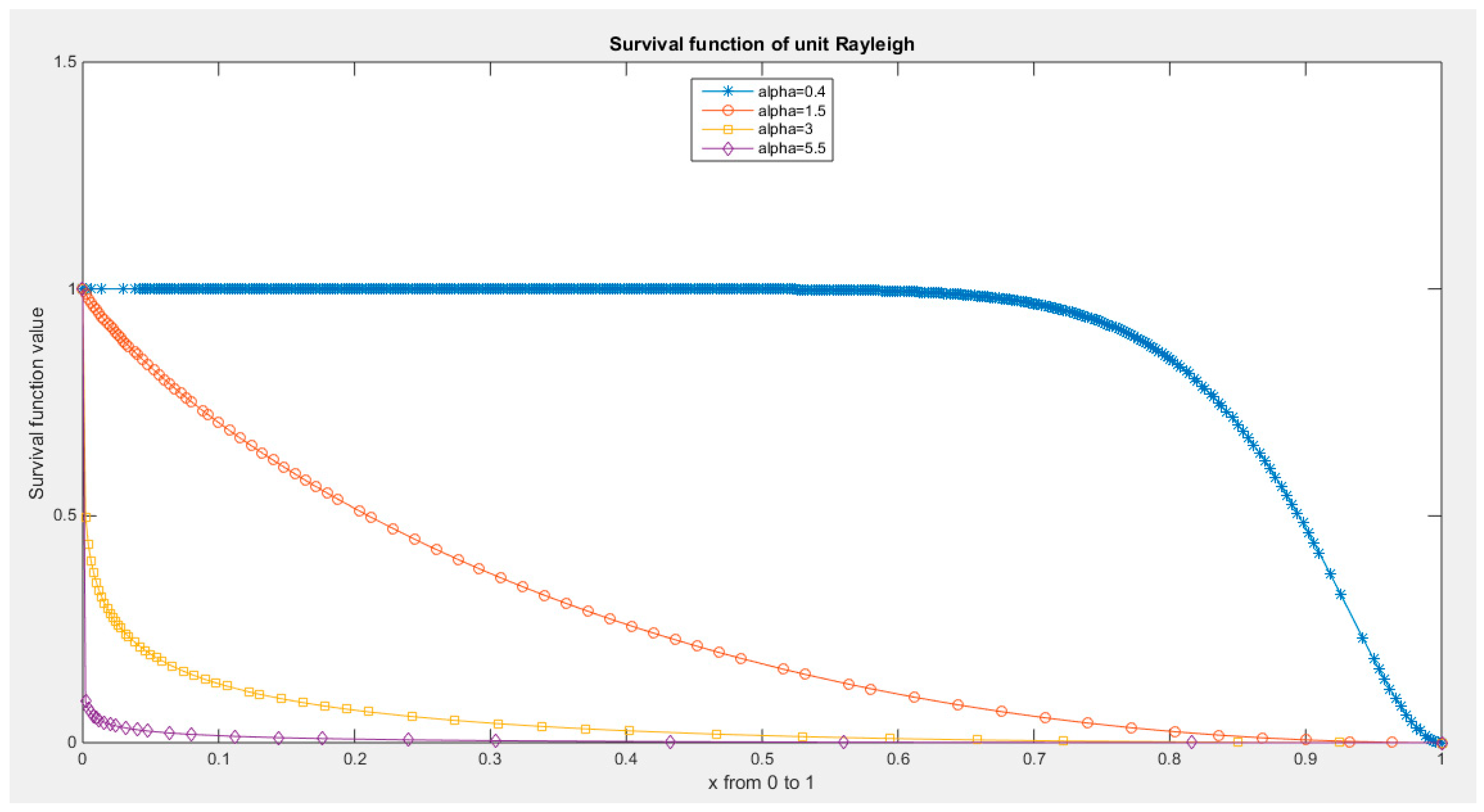
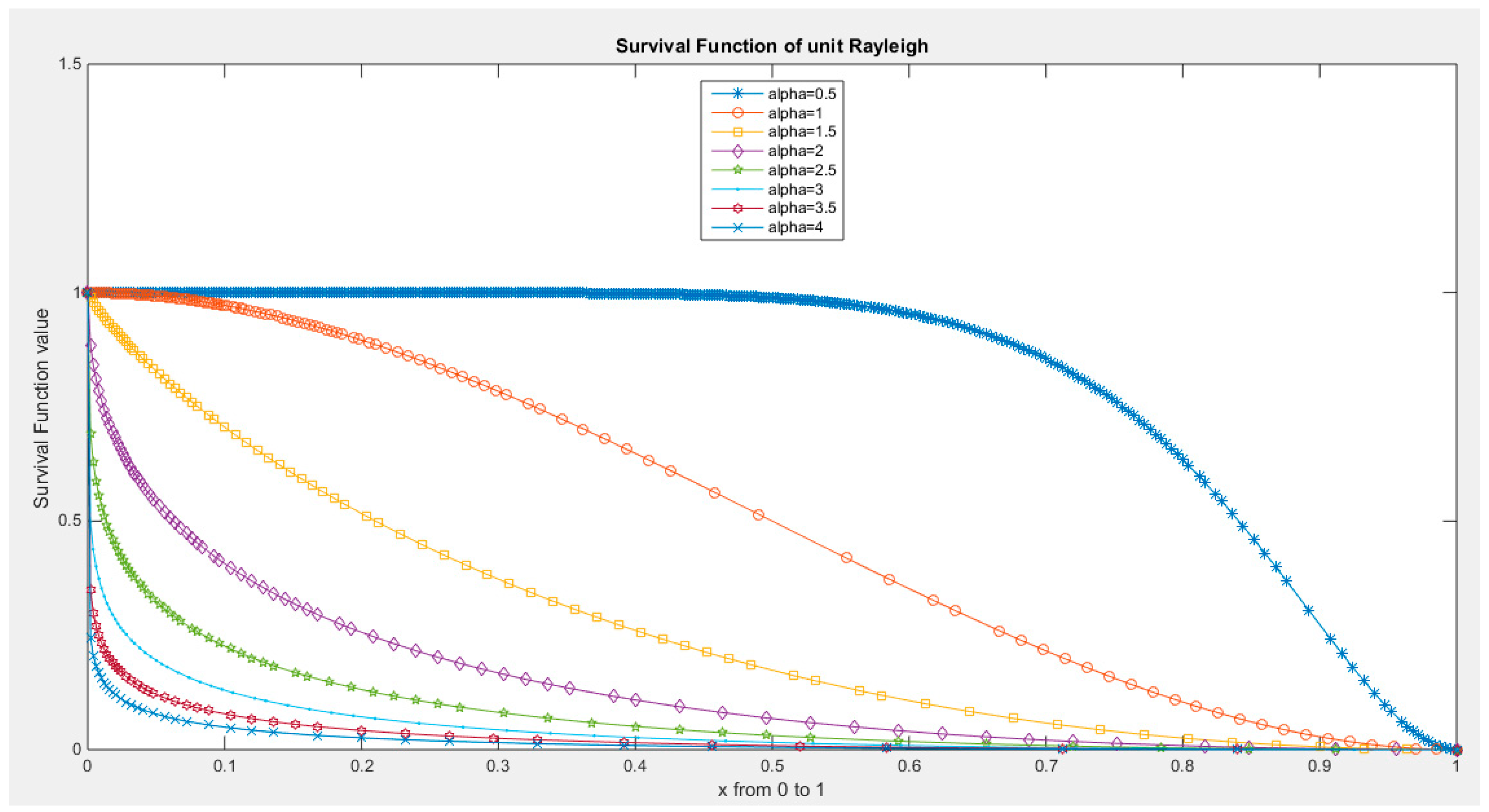
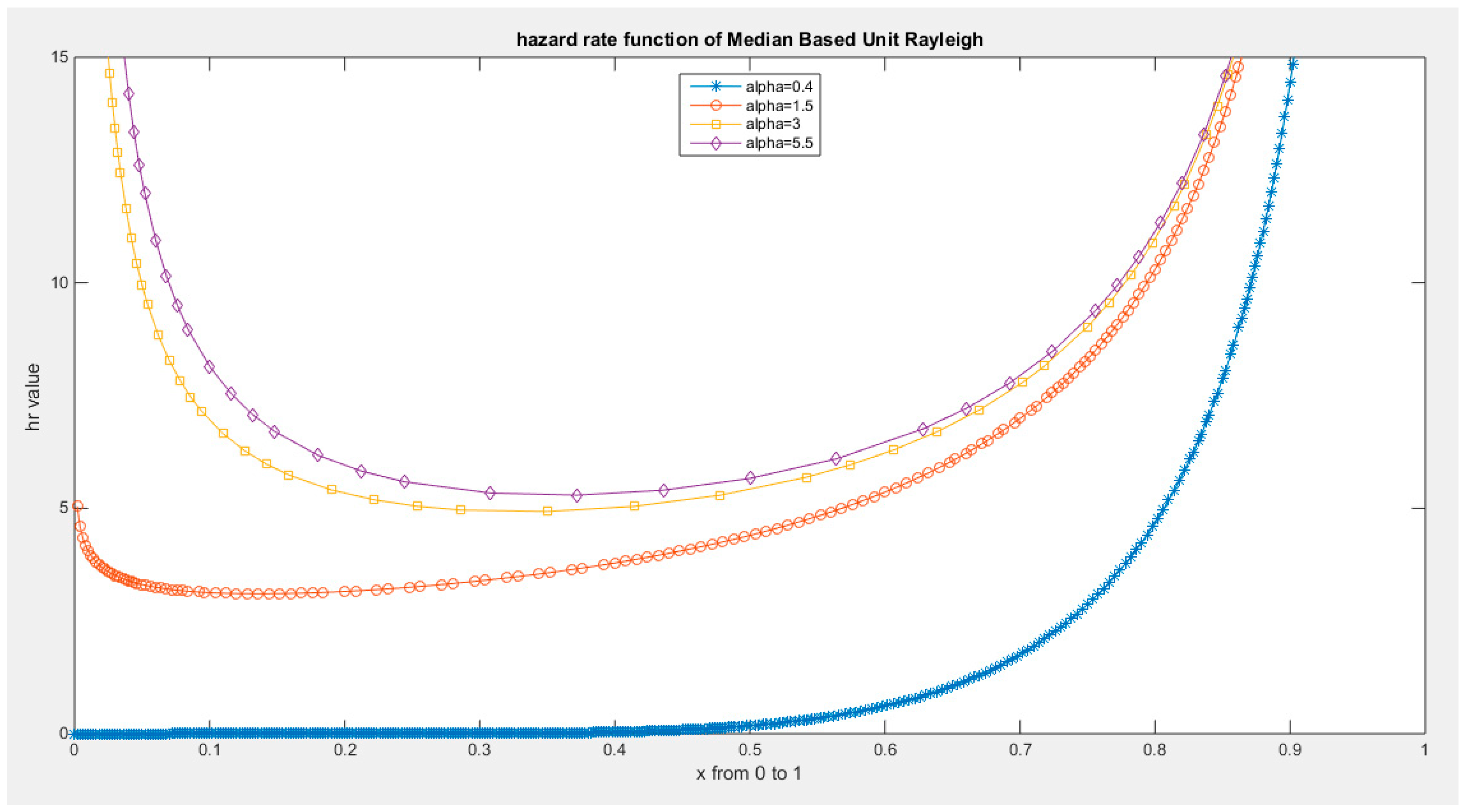
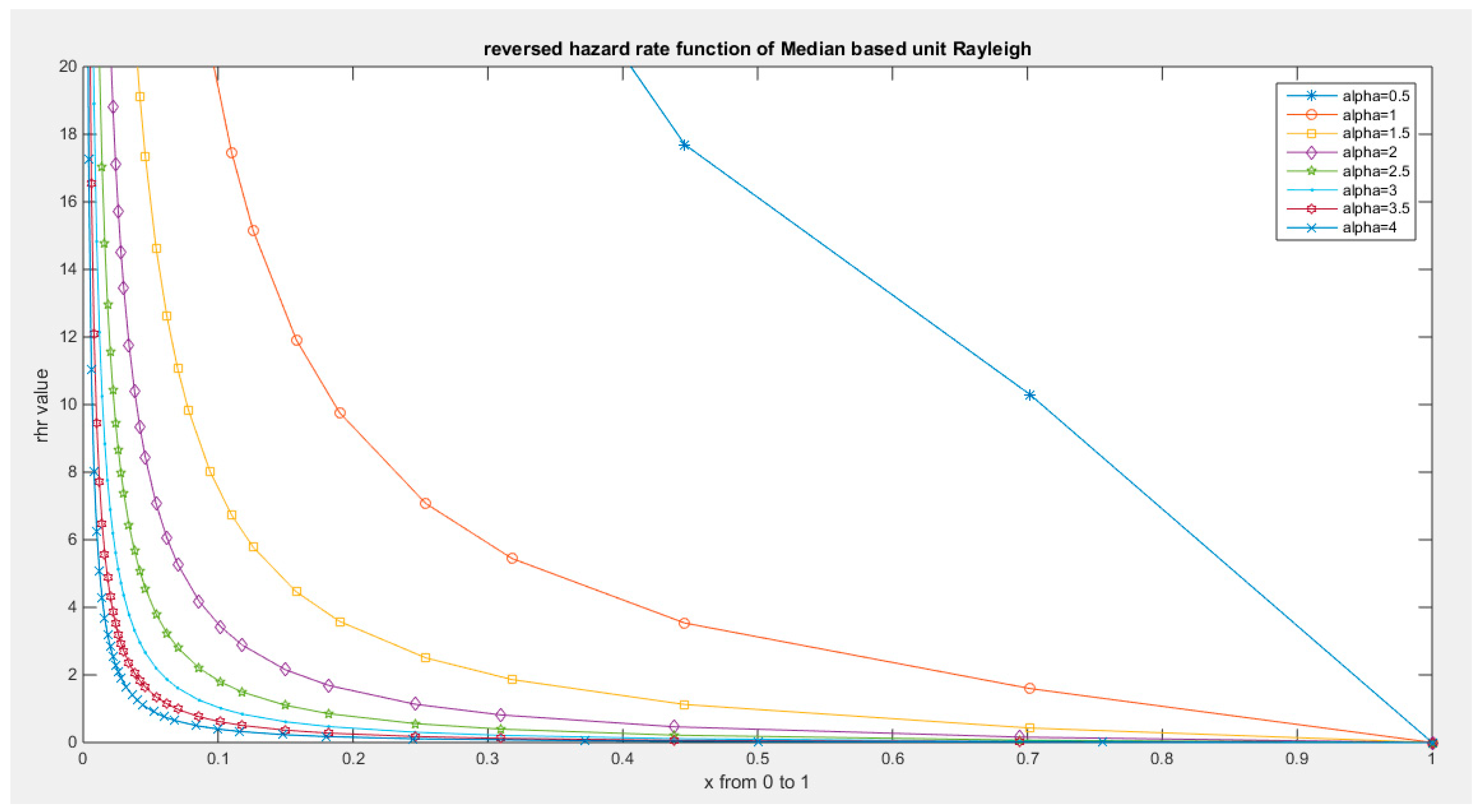
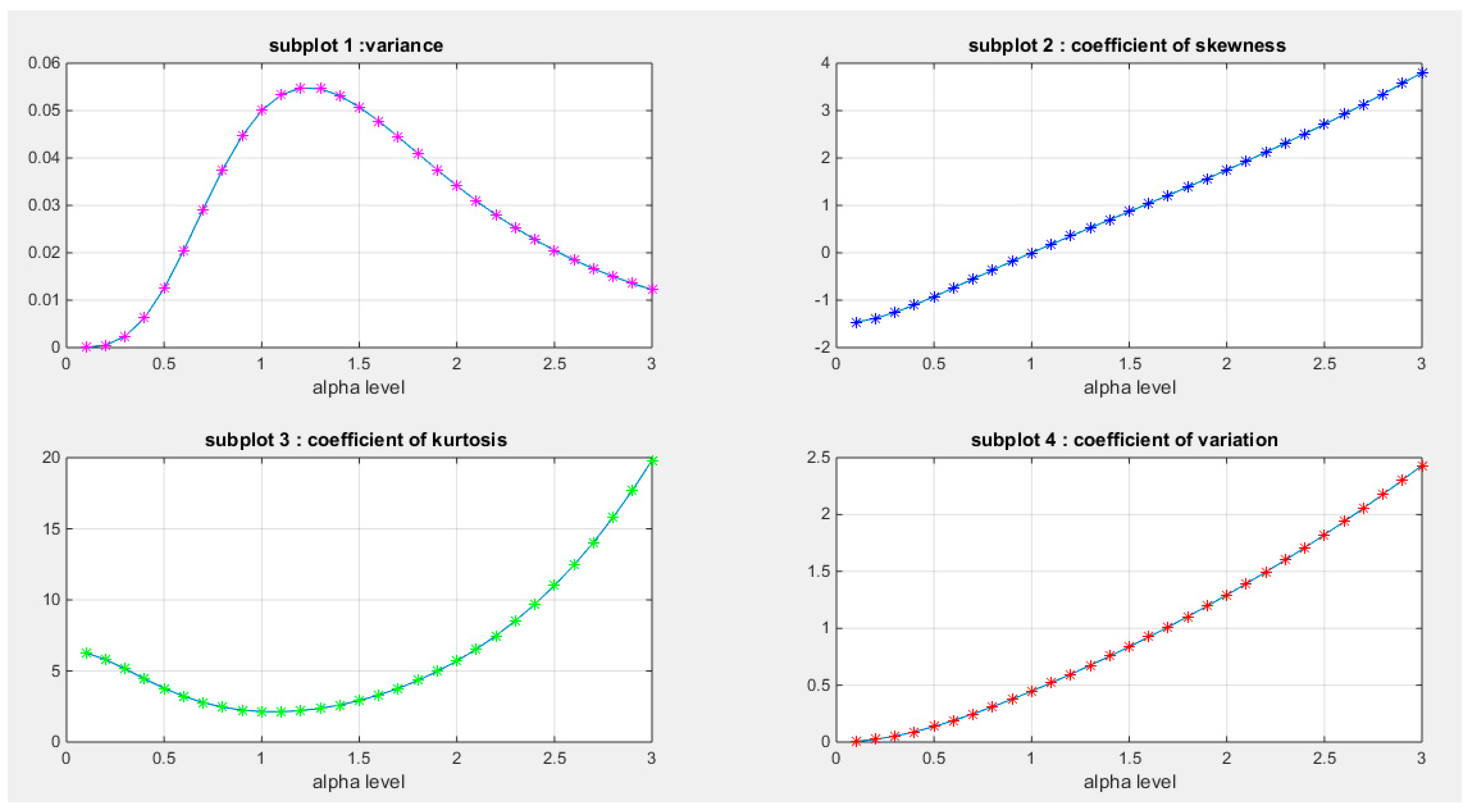
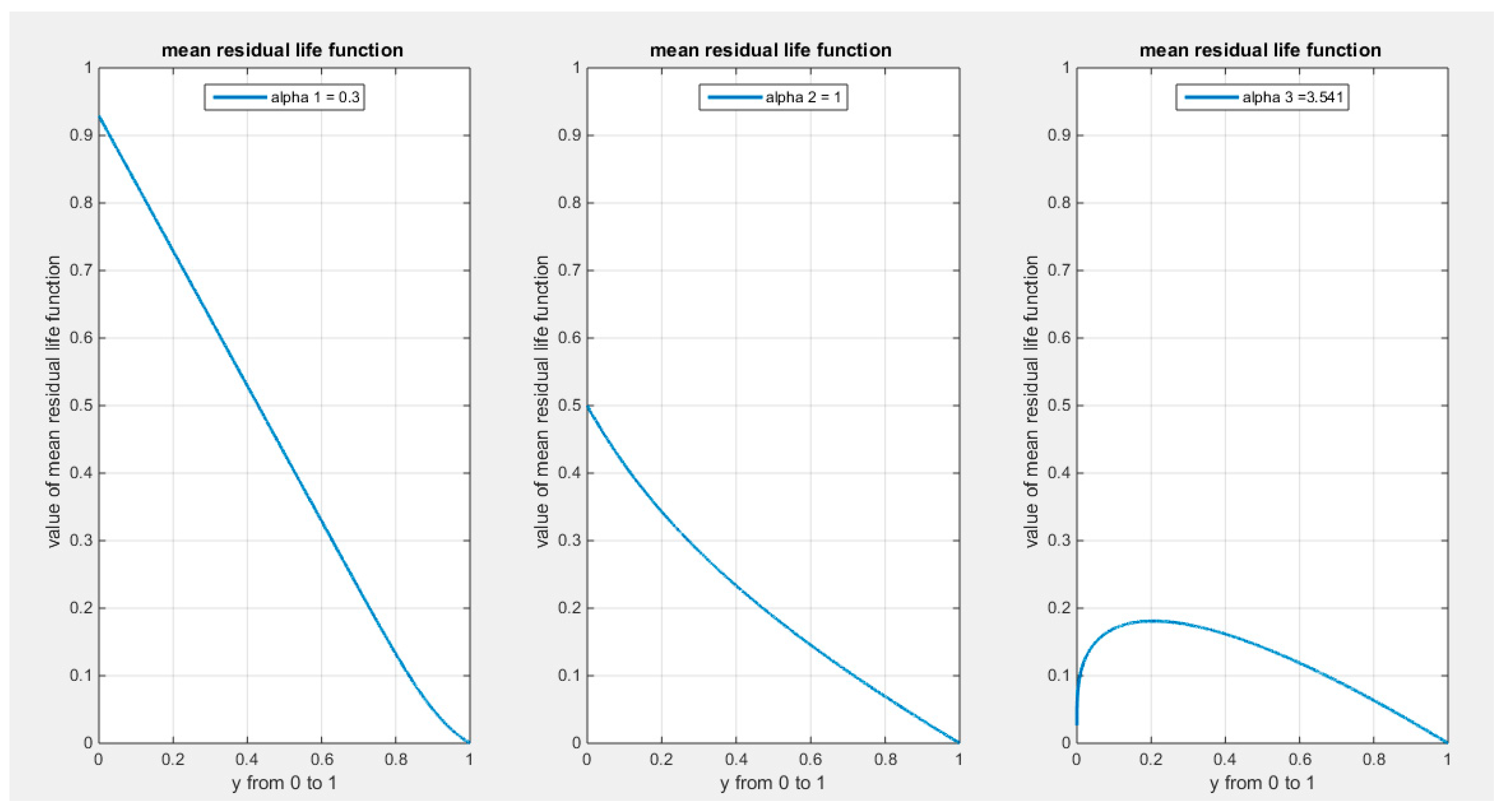
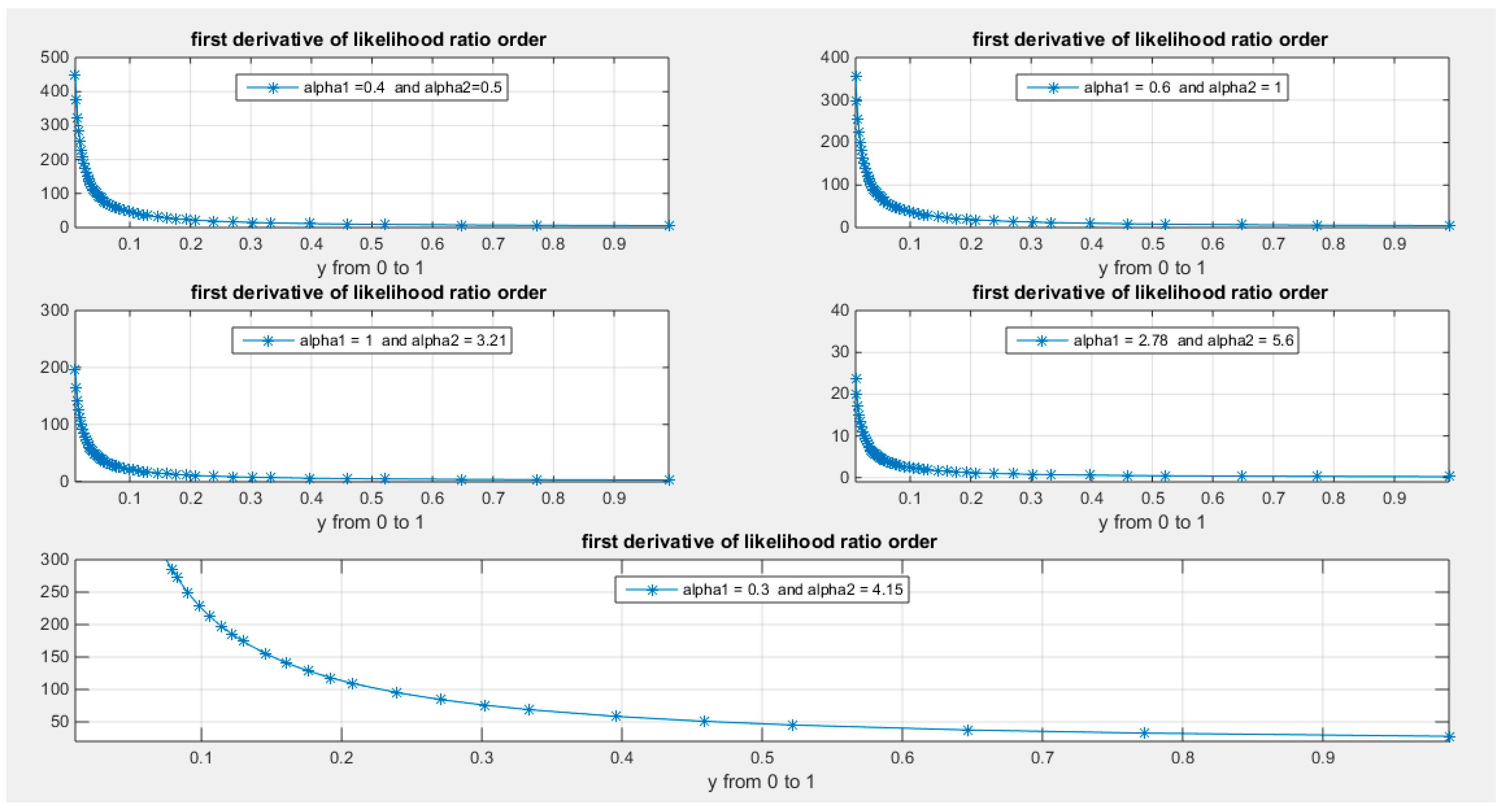
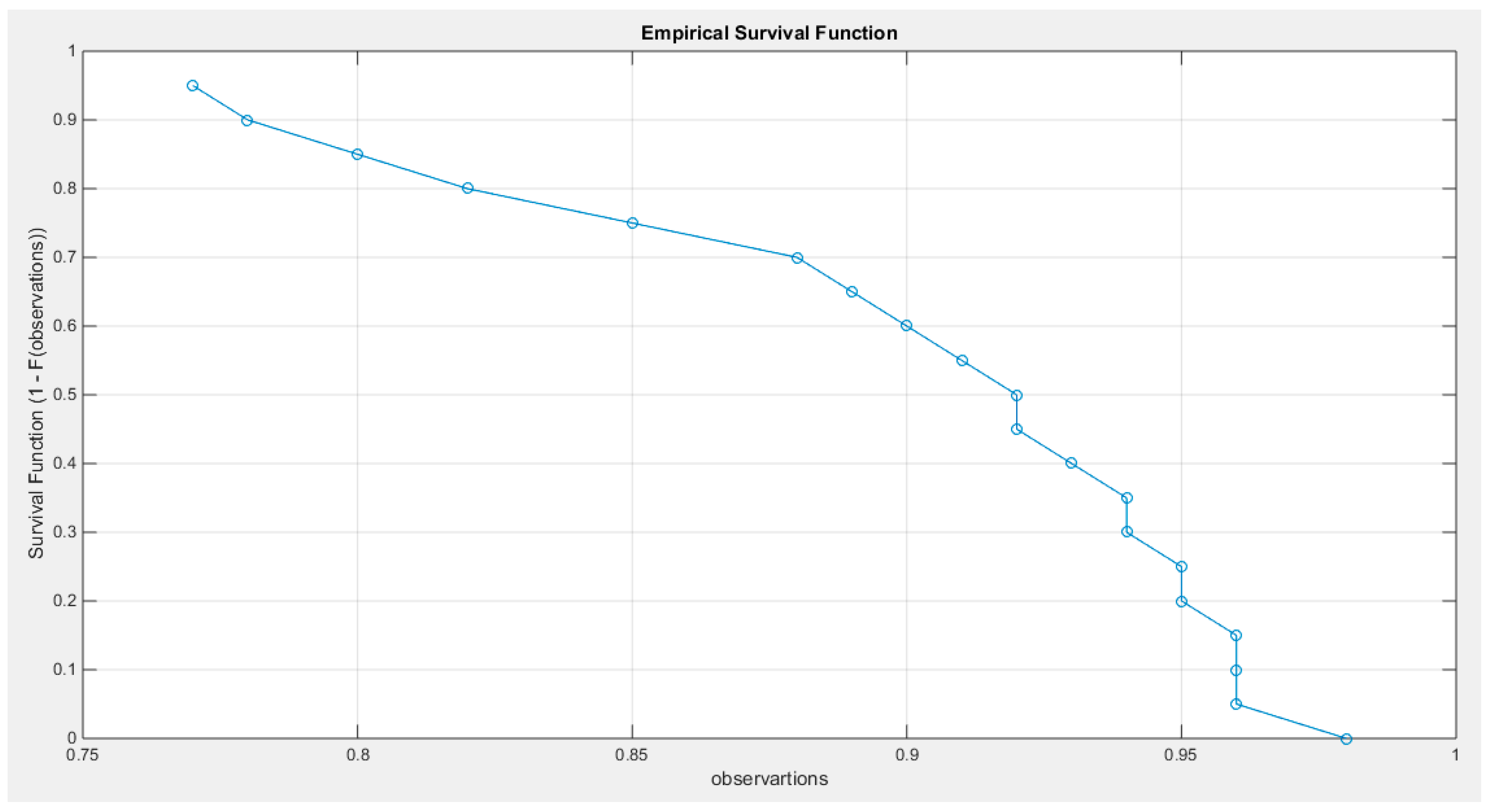
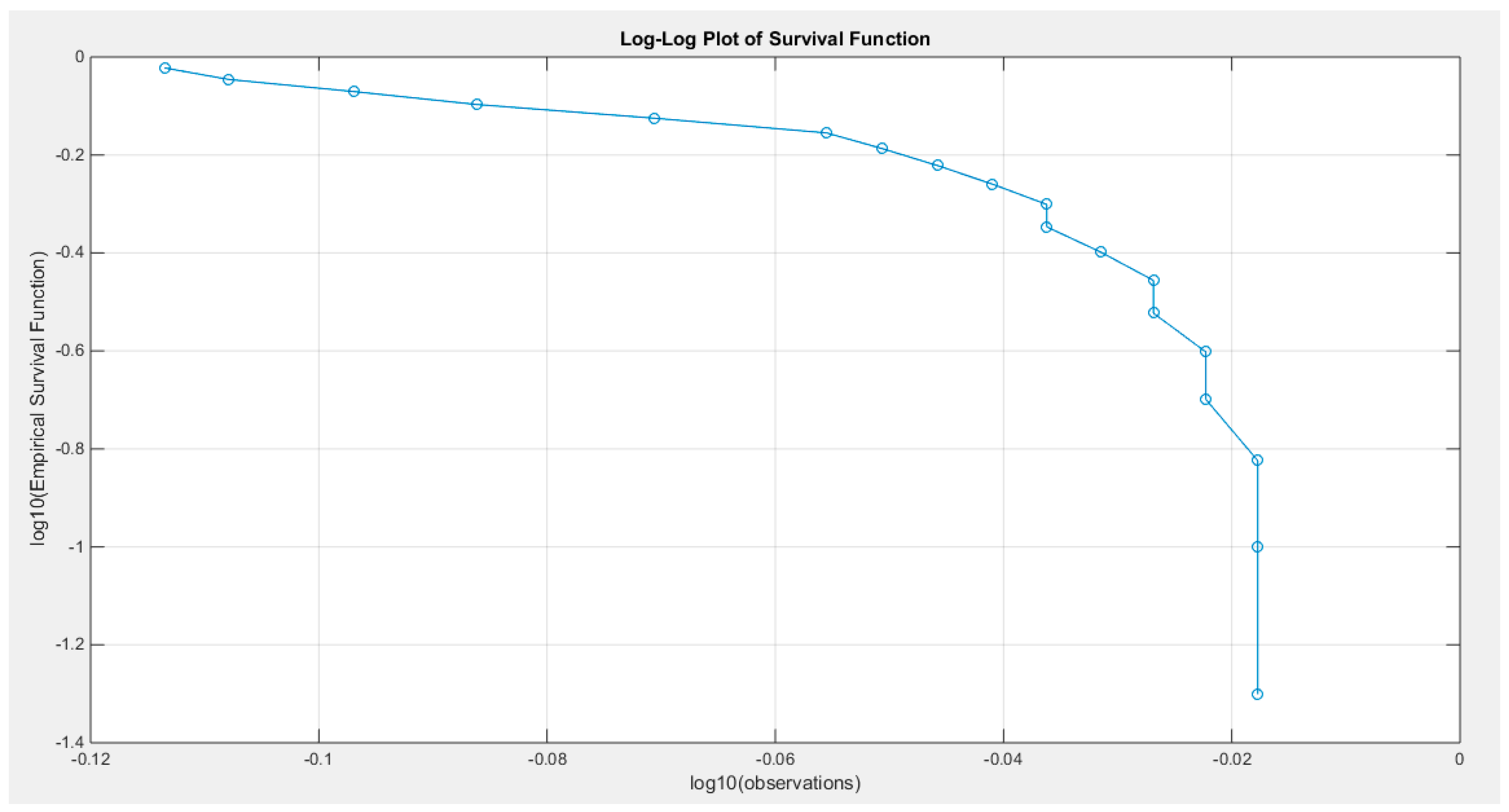
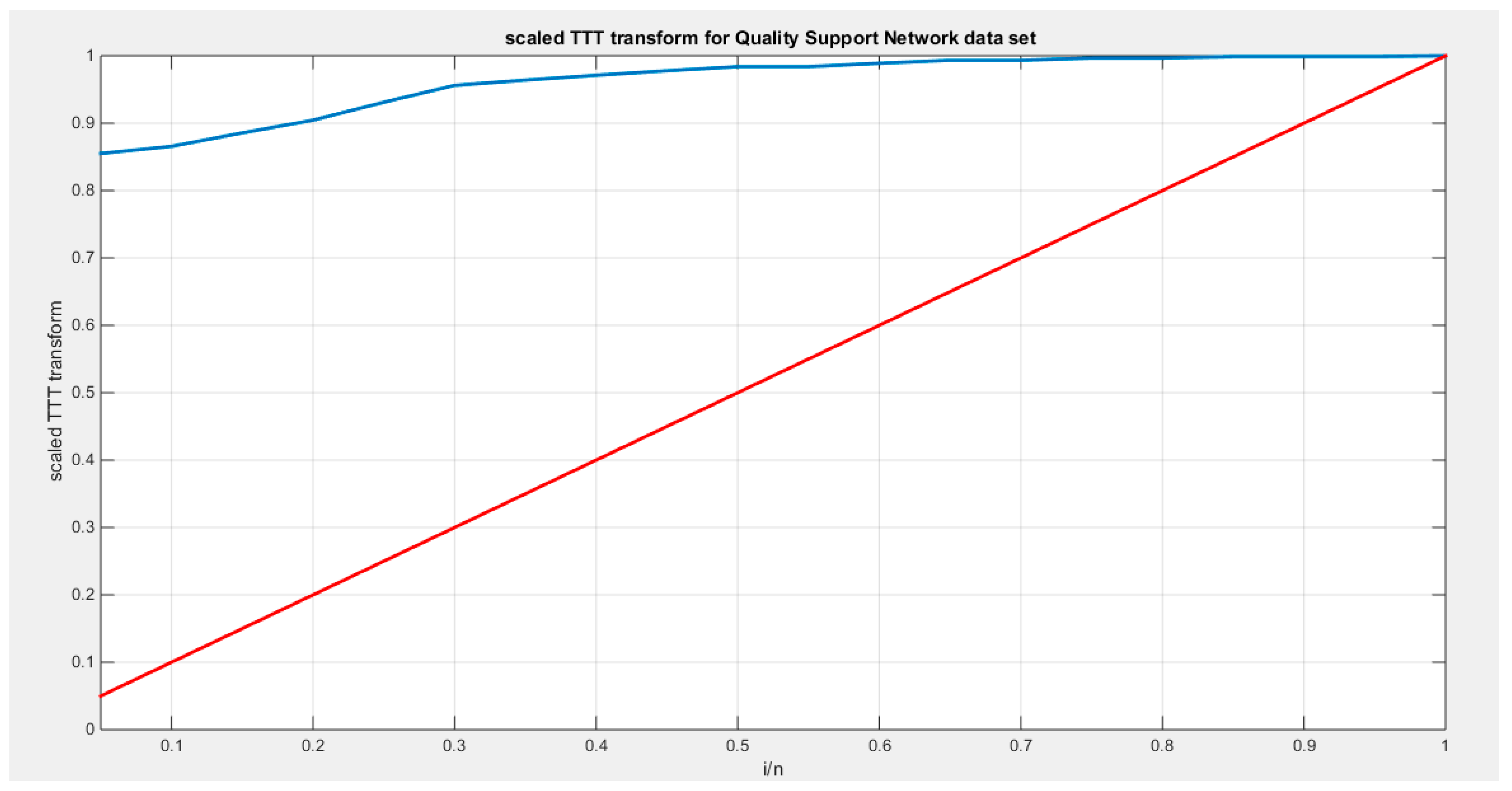
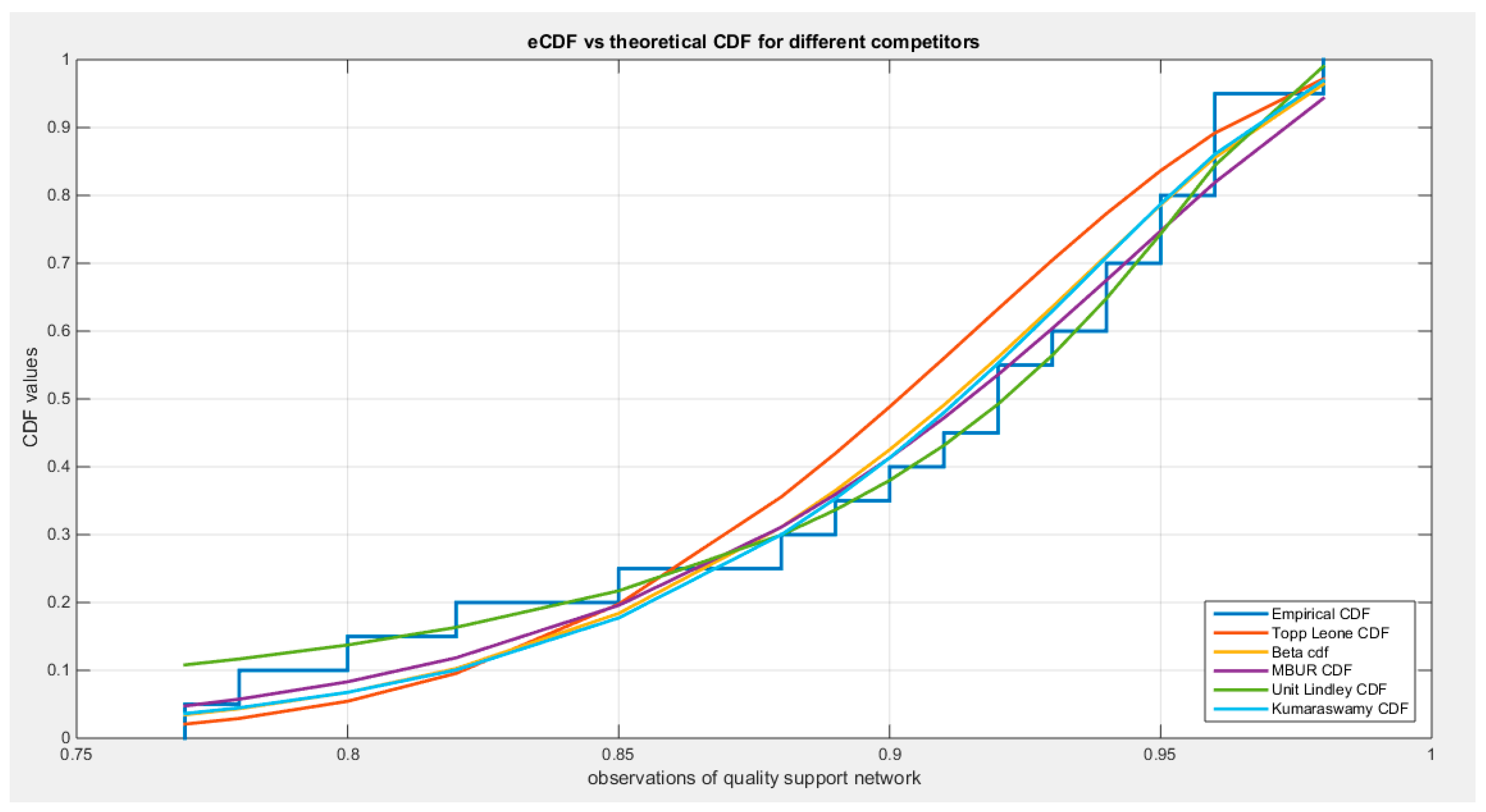
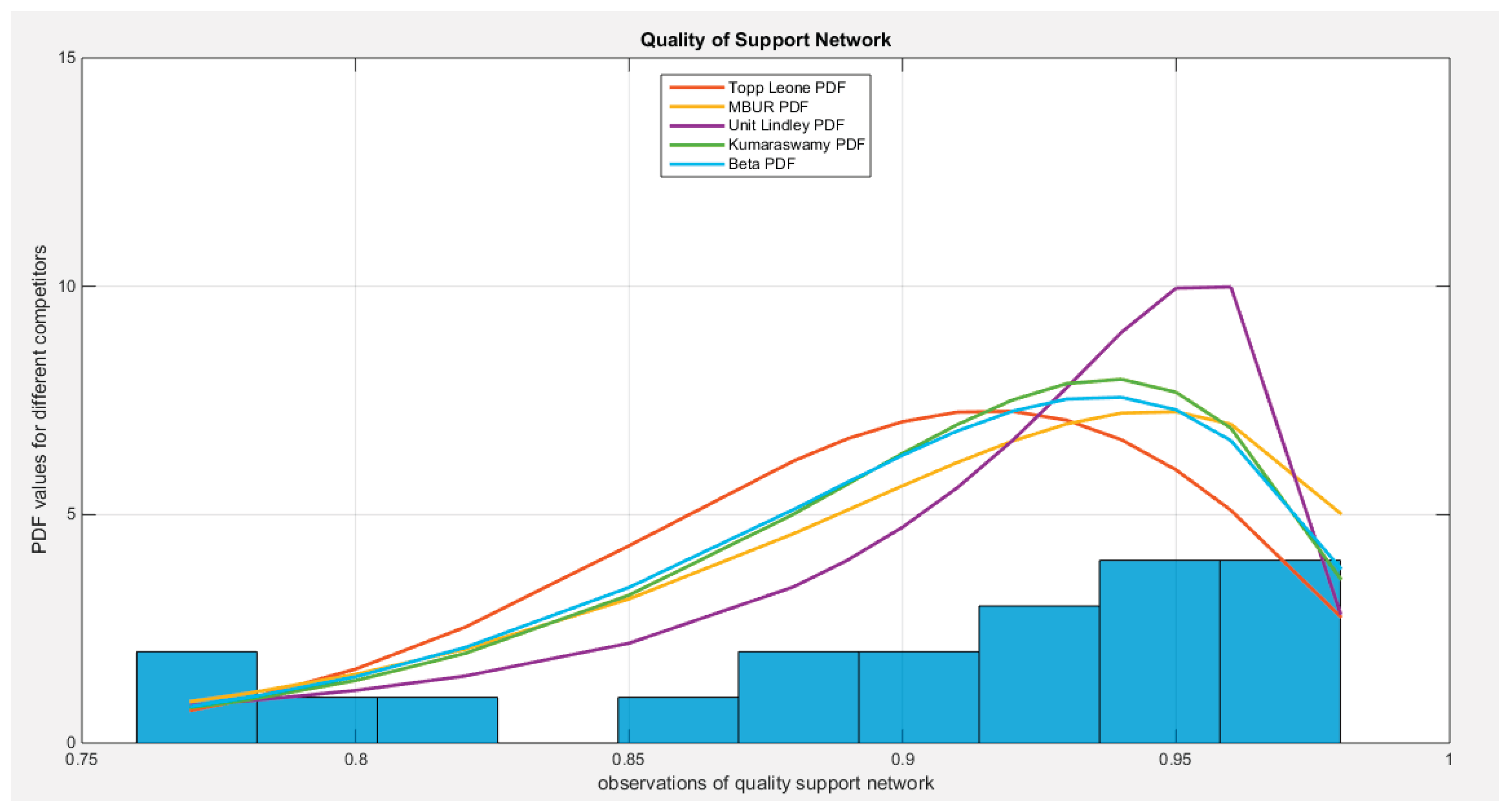
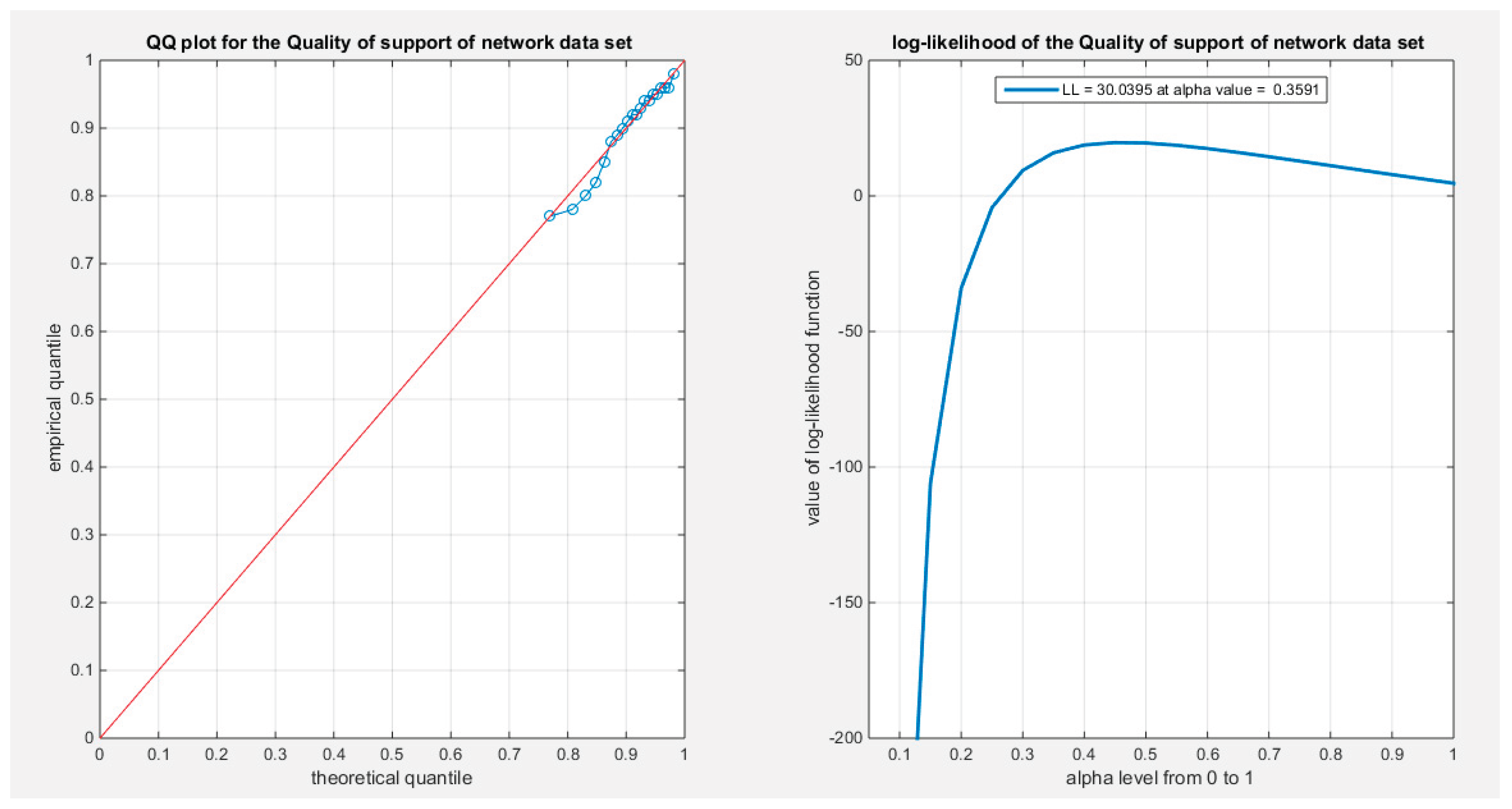
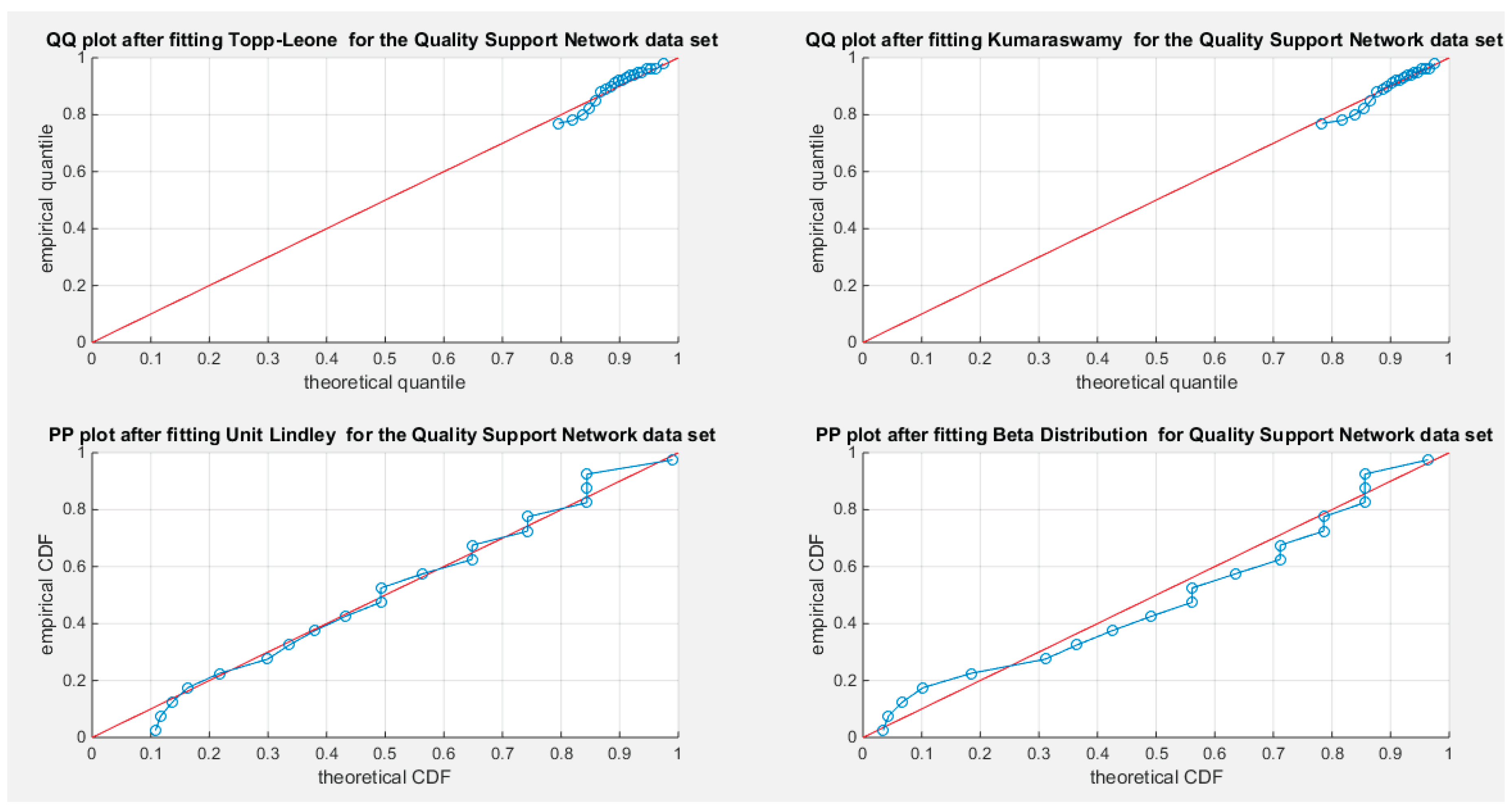
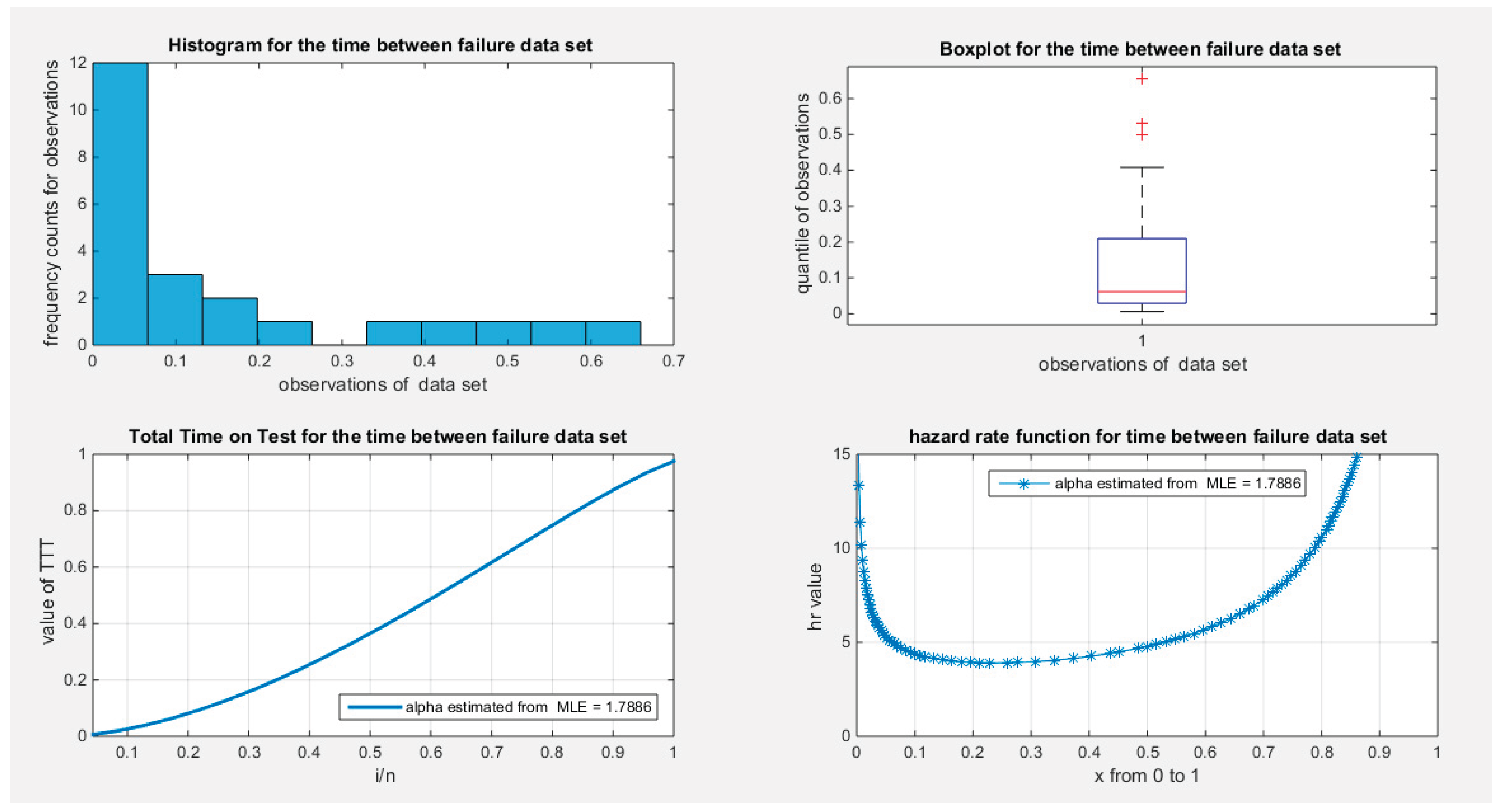
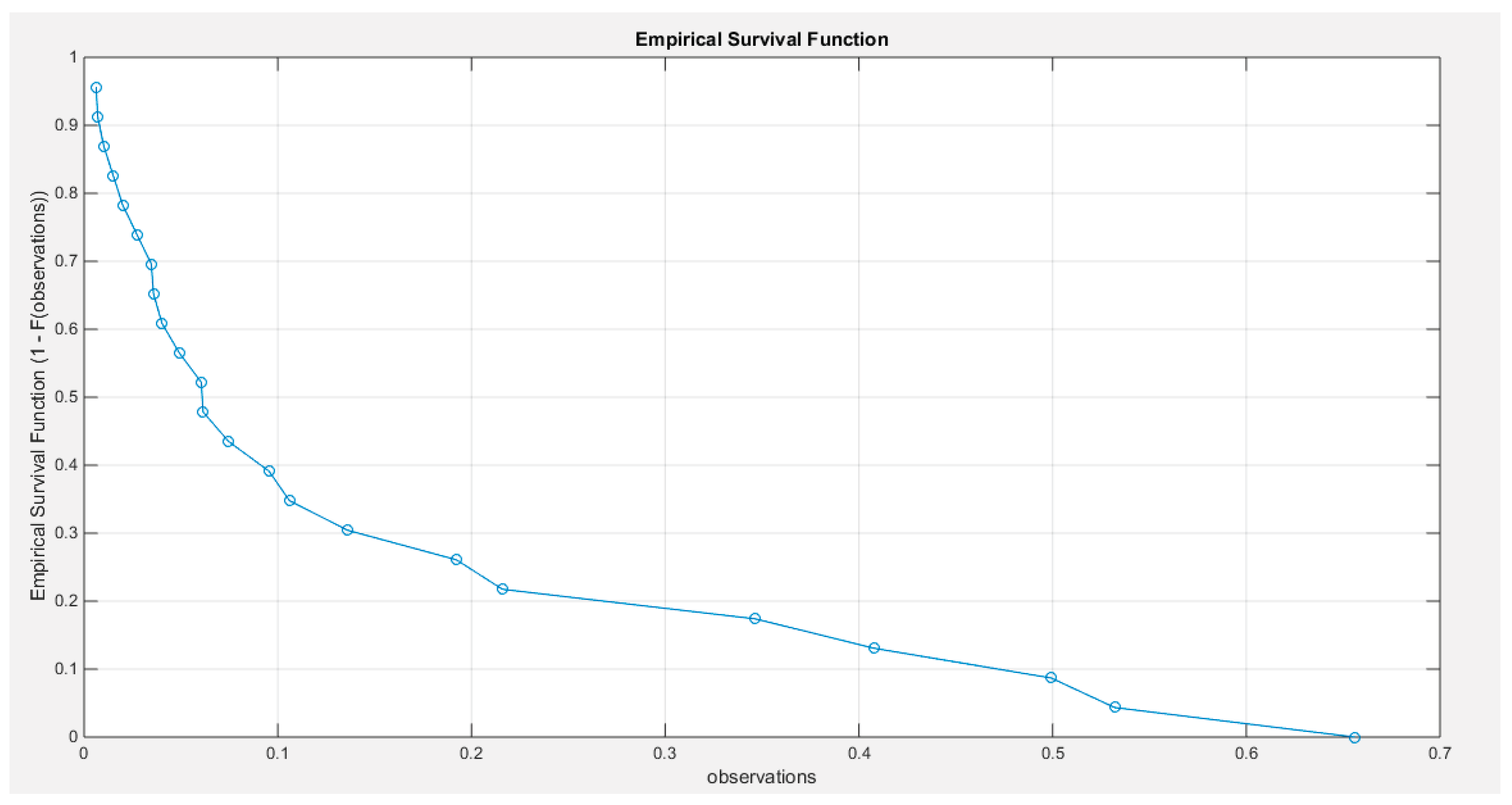
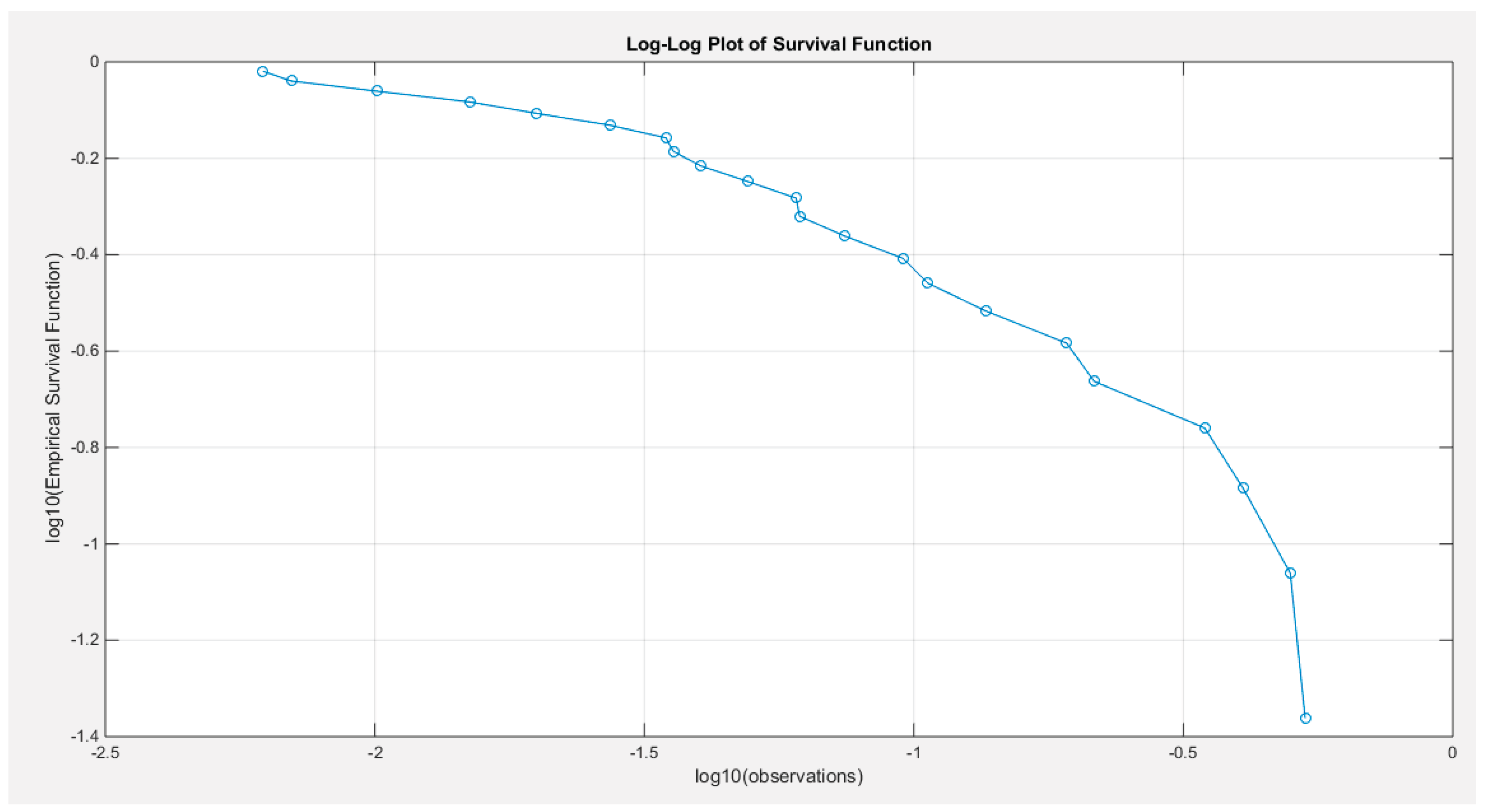
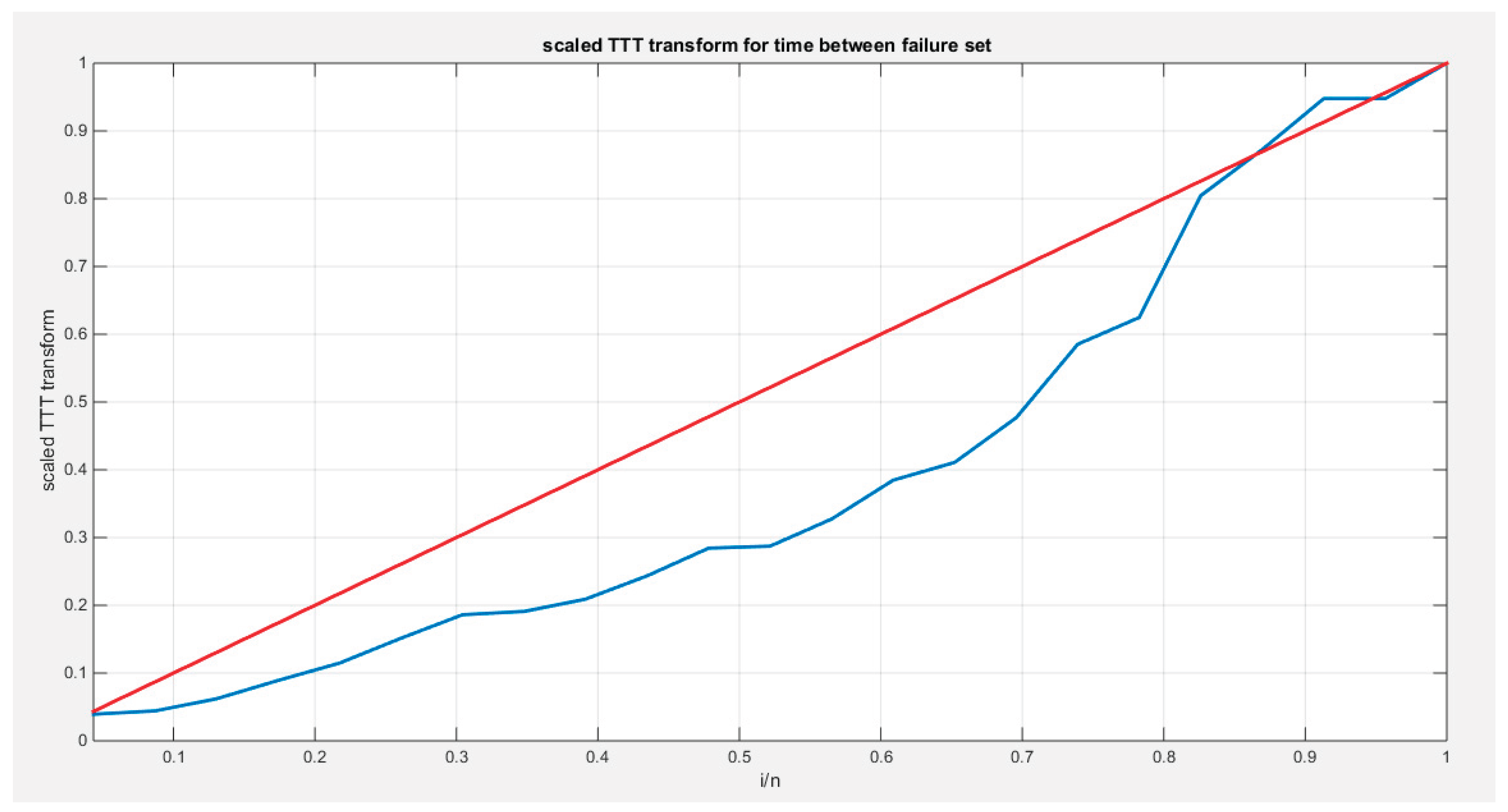
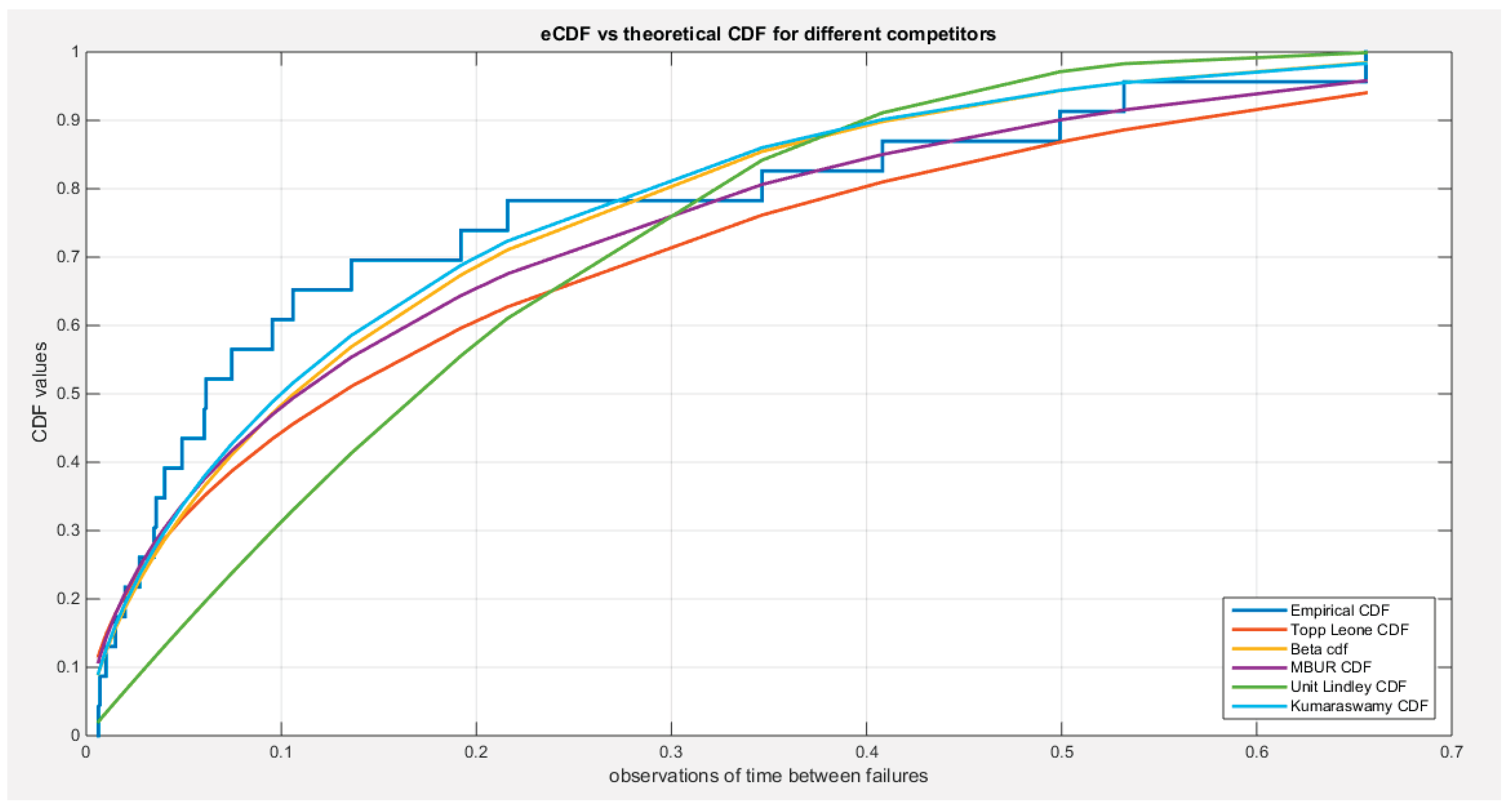
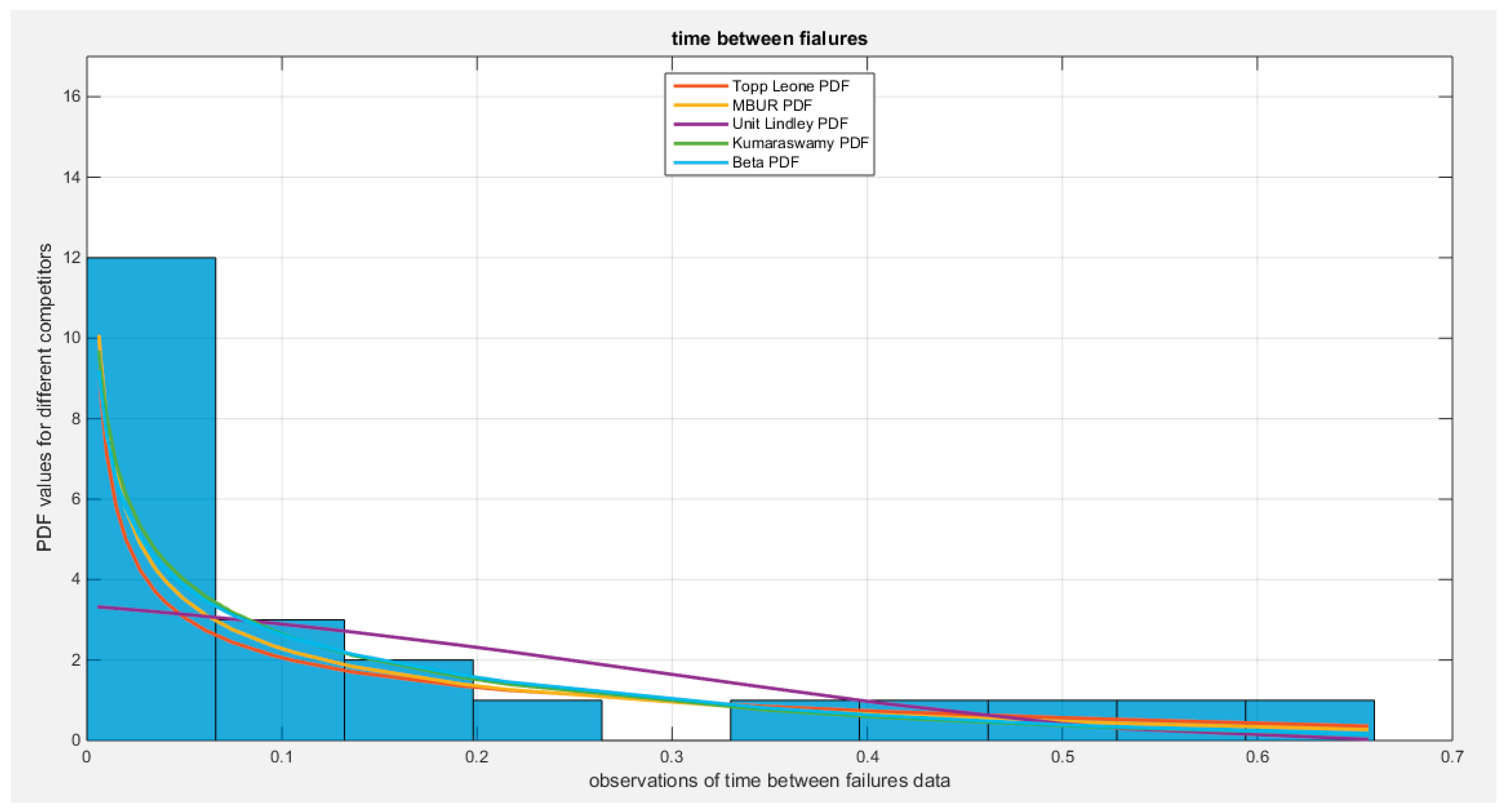
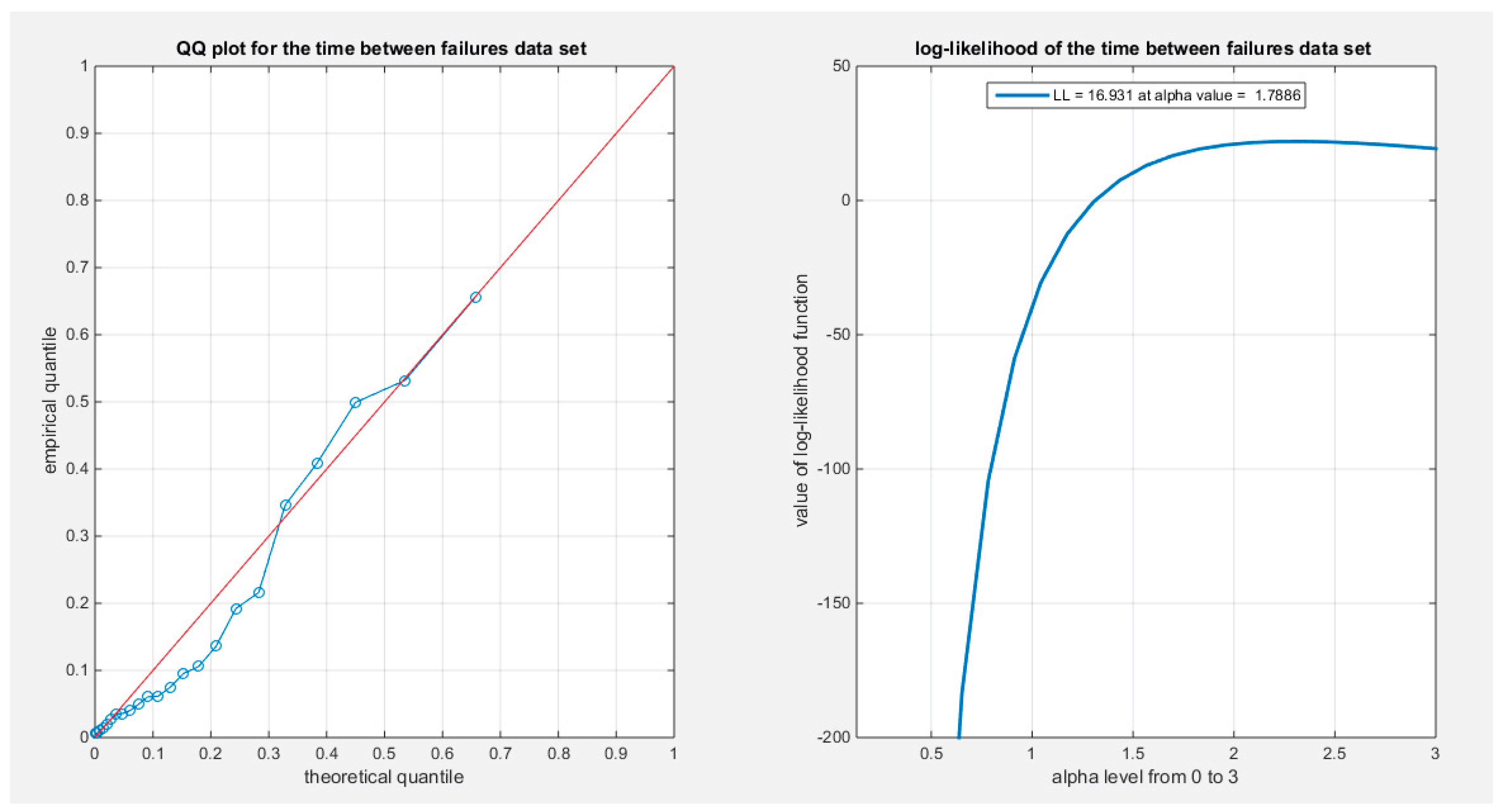
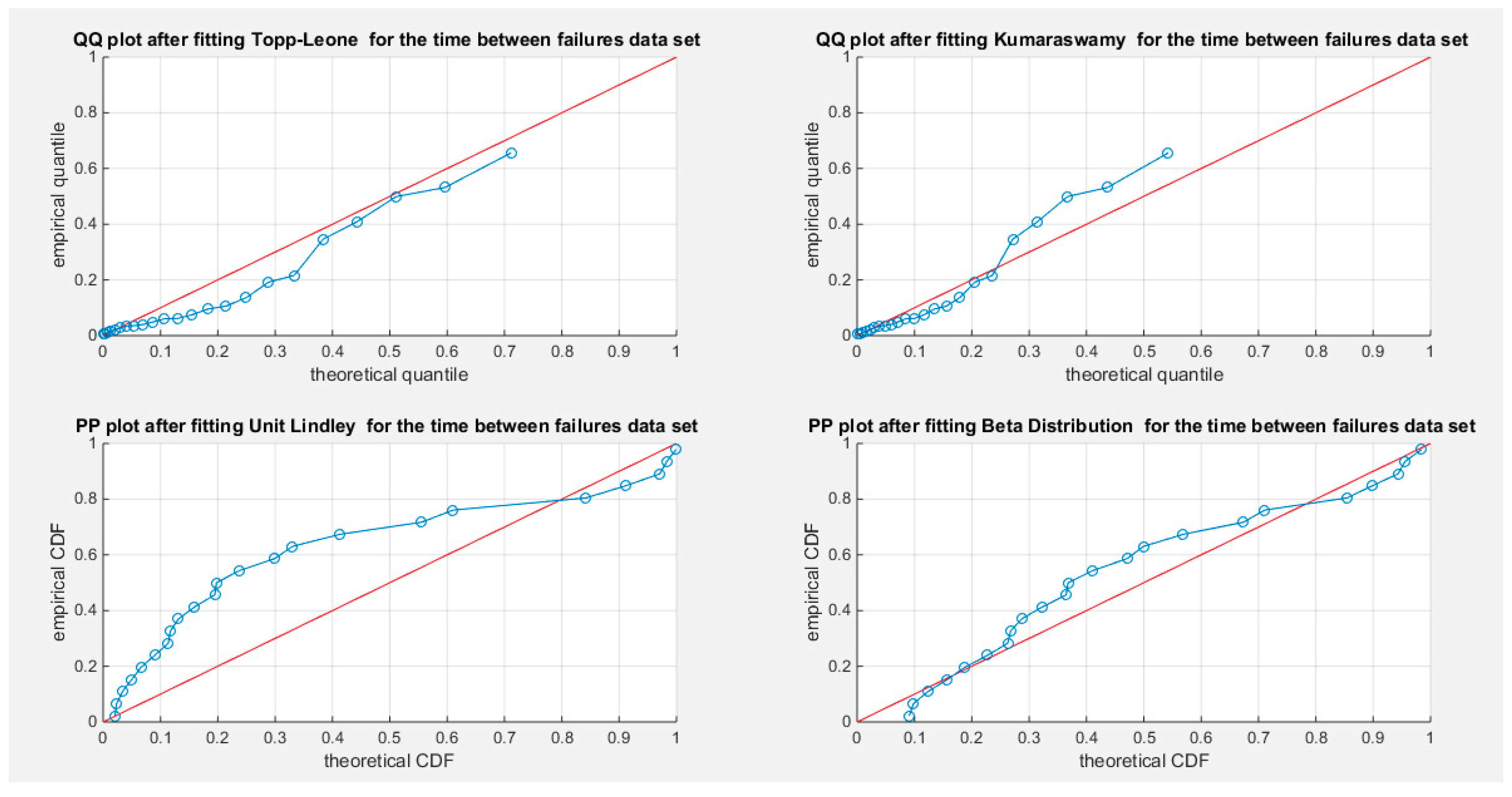
Supplementary Materials (Section 2)
ALPHA LEVEL =2.5
Table 1.
characteristics of empirical distribution of estimated alpha using MOM.
Table 1.
characteristics of empirical distribution of estimated alpha using MOM.
| MOM |
n=20 |
n=80 |
n=160 |
n=260 |
n=500 |
| 2.5 Q |
1.9635 |
2.2062 |
2.2705 |
2.3197 |
2.3647 |
| 97.5 Q |
3.5095 |
2.9080 |
2.7614 |
2.7171 |
2.6581 |
| Skewness |
0.8381 |
0.4247 |
0.1649 |
0.2798 |
0.2249 |
| Kurtosis |
4.3346 |
3.2498 |
2.9082 |
3.0278 |
3.1826 |
| Fit N (5%) |
H0=1
(0.001) |
H0=1
(0.0053) |
H0=0
(0.4899) |
H0=0
(0.1637) |
H0=0
(0.2444) |
| Fit N (1%) |
H0=1
(0.001) |
H0=1
(0.0053 |
H0=0
(0.4899) |
H0=0
(0.1637) |
H0=0
(0.2444) |
The empirical distribution of the estimated parameter alpha using MOM is shown in table 1. Each column represents a specific sample size with 1000 replicates in each size. The 2.5 th quantile and the 97.5 th quantile of the 1000 values of the estimated parameter in each sample shows that as the sample size increases the 2.5 quantile rises while the 97.5 quantile decreases. In other words, the distance between the two quantiles decreases as the sample size increases and this is reflected on the confidence interval (CI). As the sample size increases the CI becomes narrower. The distribution exhibits a mild right skewness and a high positive excess kurtosis (leptokurtic shape) at small sample size. As sample size increases the skewness decreases trying to approach the zero level (skewness of standard normal) and kurtosis decreases trying to approach the kurtosis of standard normal. The empirical distribution fits standard normal starting at size 160 and larger than this at significance level 5% and 1% with associated P-value as shown in the table. H0=1 means reject the null hypothesis that states the parameter distribution follows the standard normal distribution. While H0=0 means fail to reject the null hypothesis. See the following Figures (1-4)
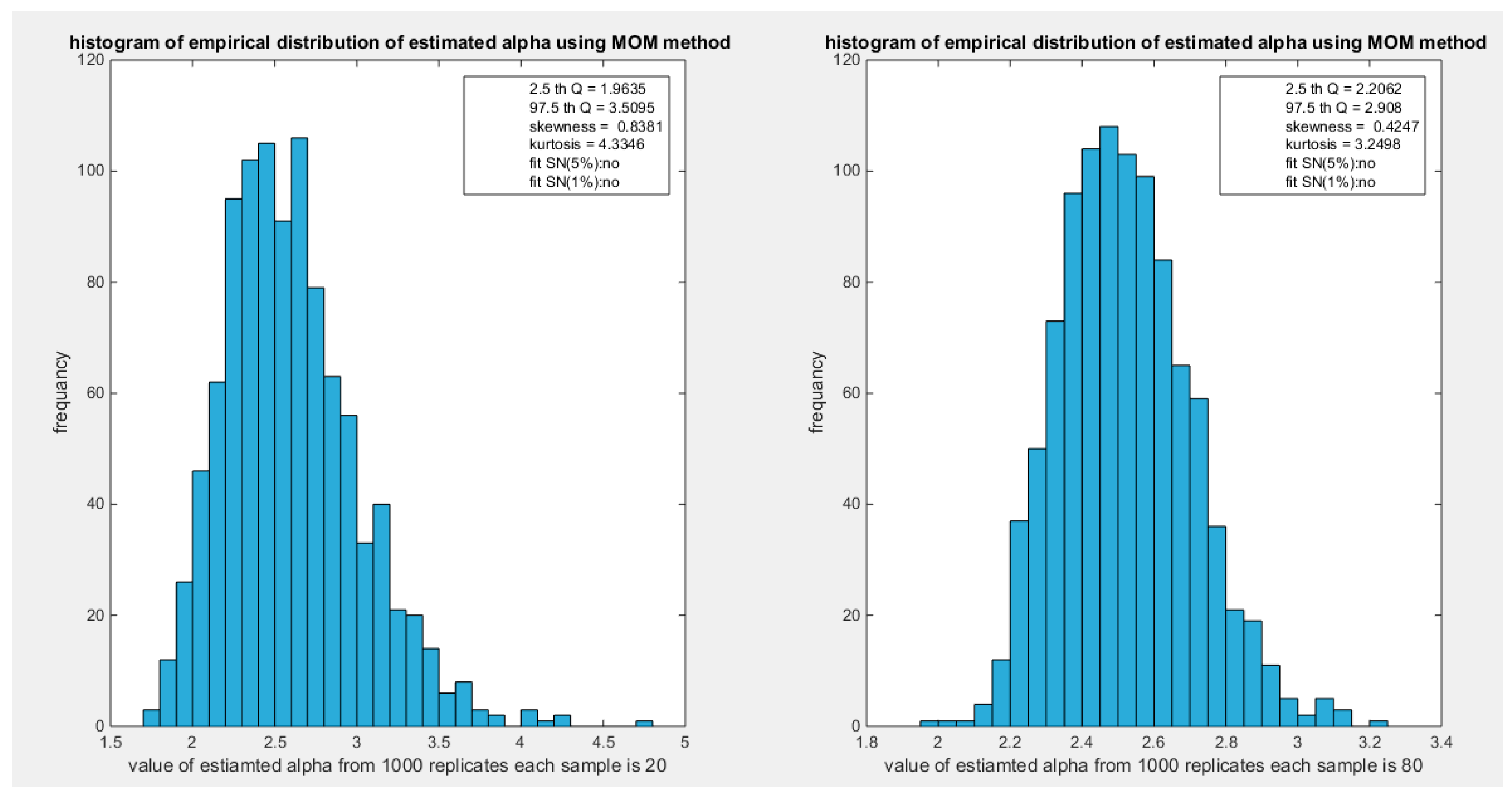
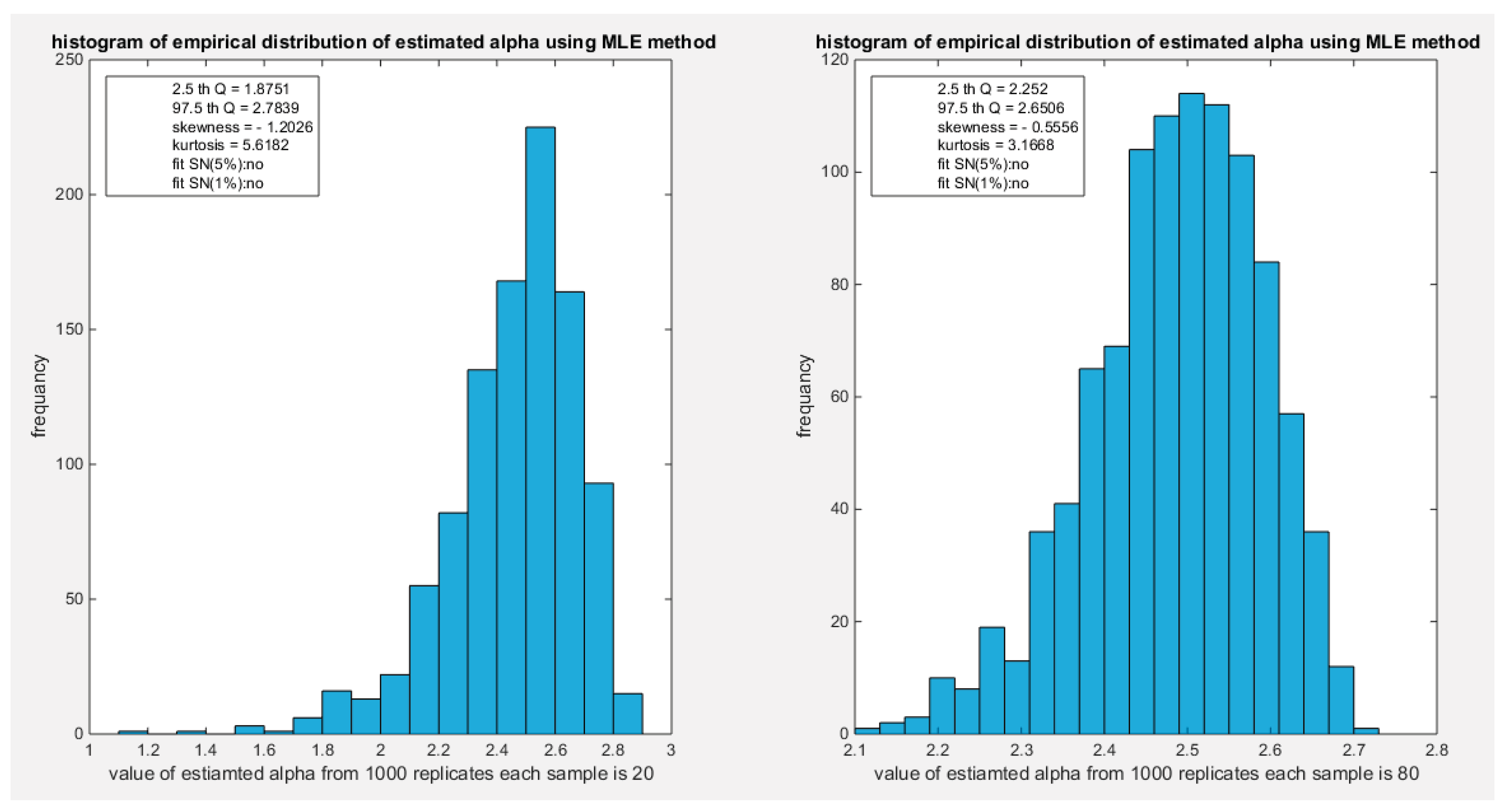
Figure 1.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using MOM method.
Figure 1.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using MOM method.
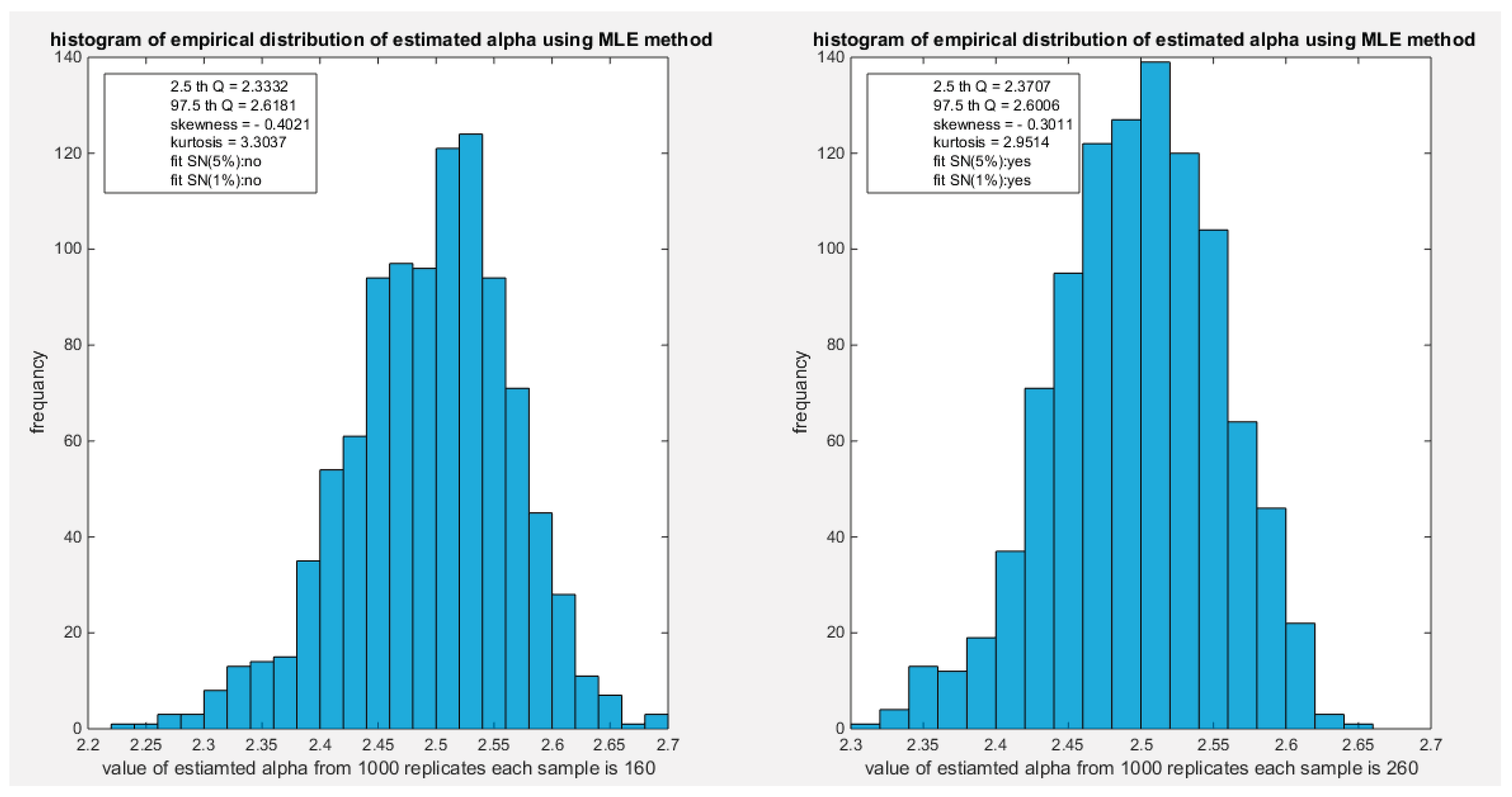
Figure 2.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using MOM method.
Figure 2.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using MOM method.
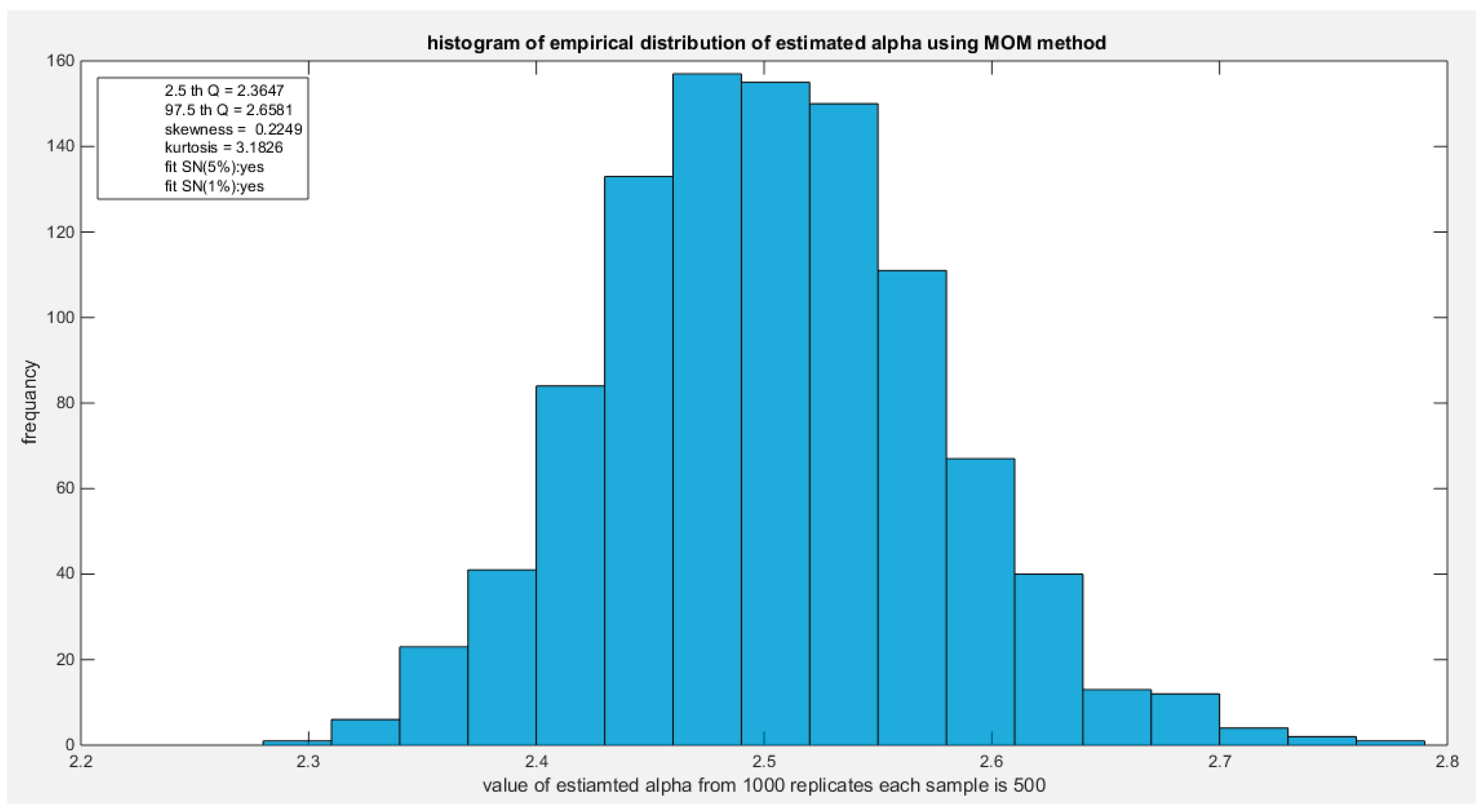
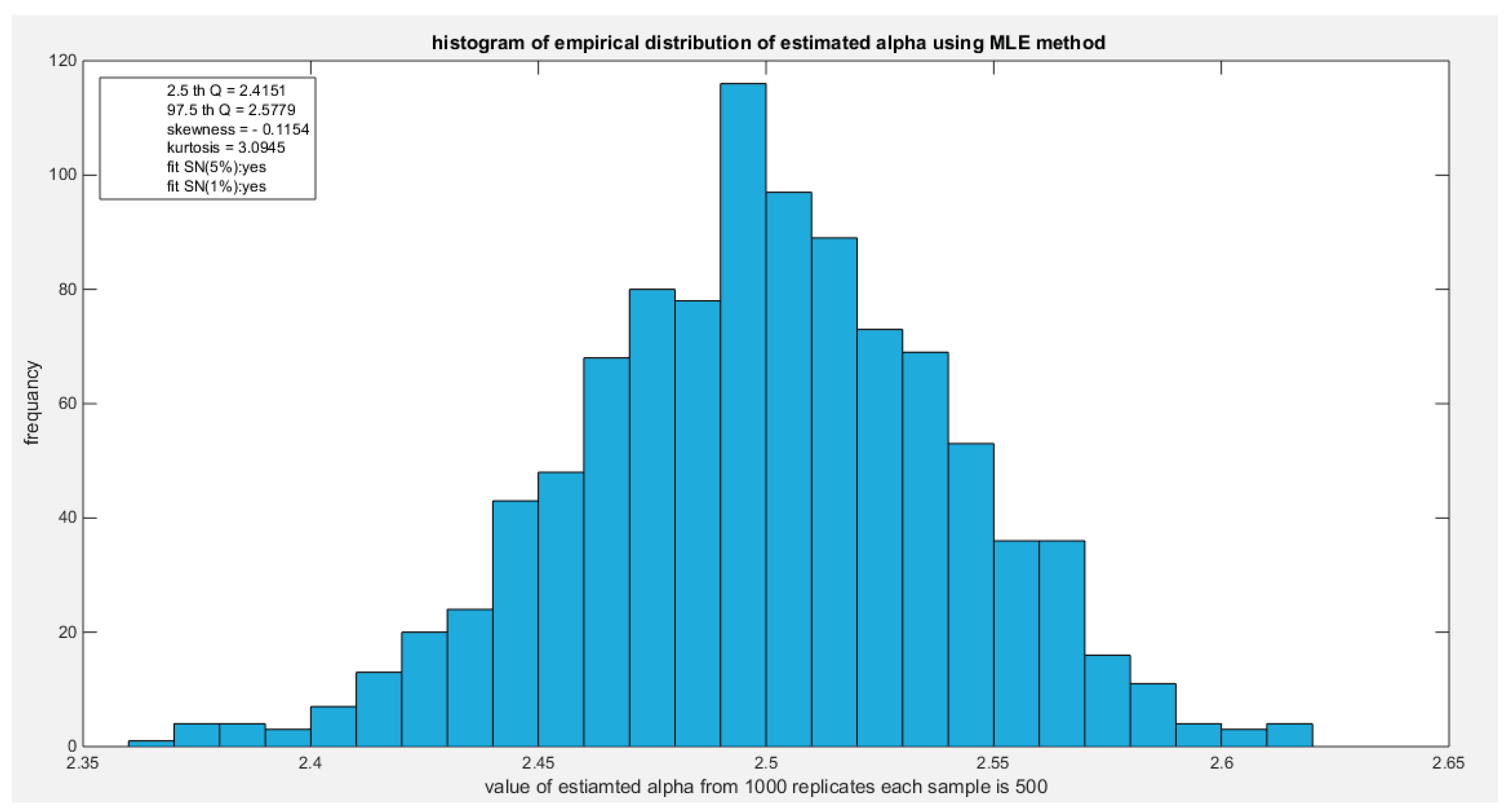
Figure 3.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=500) using MOM method.
Figure 3.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=500) using MOM method.
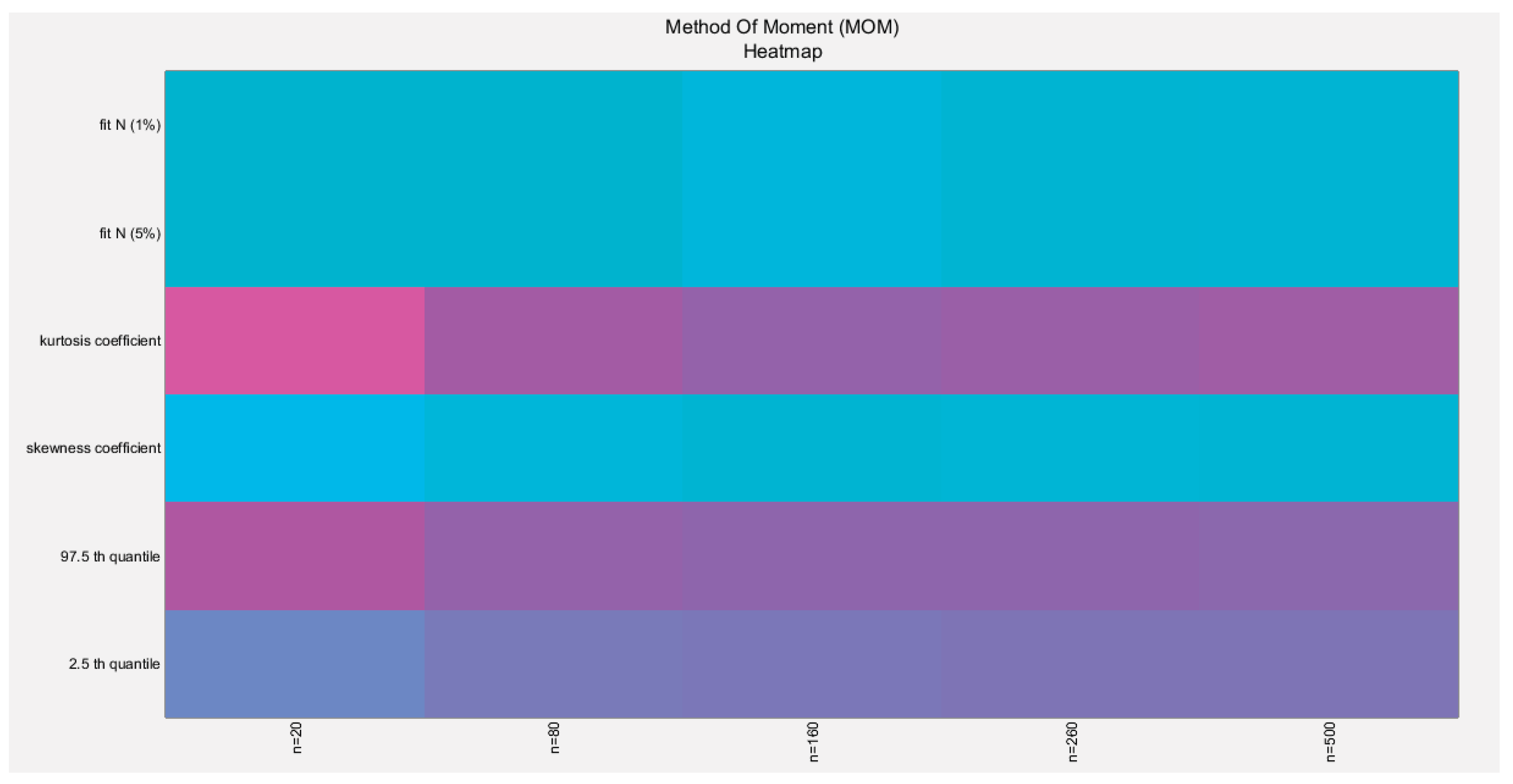
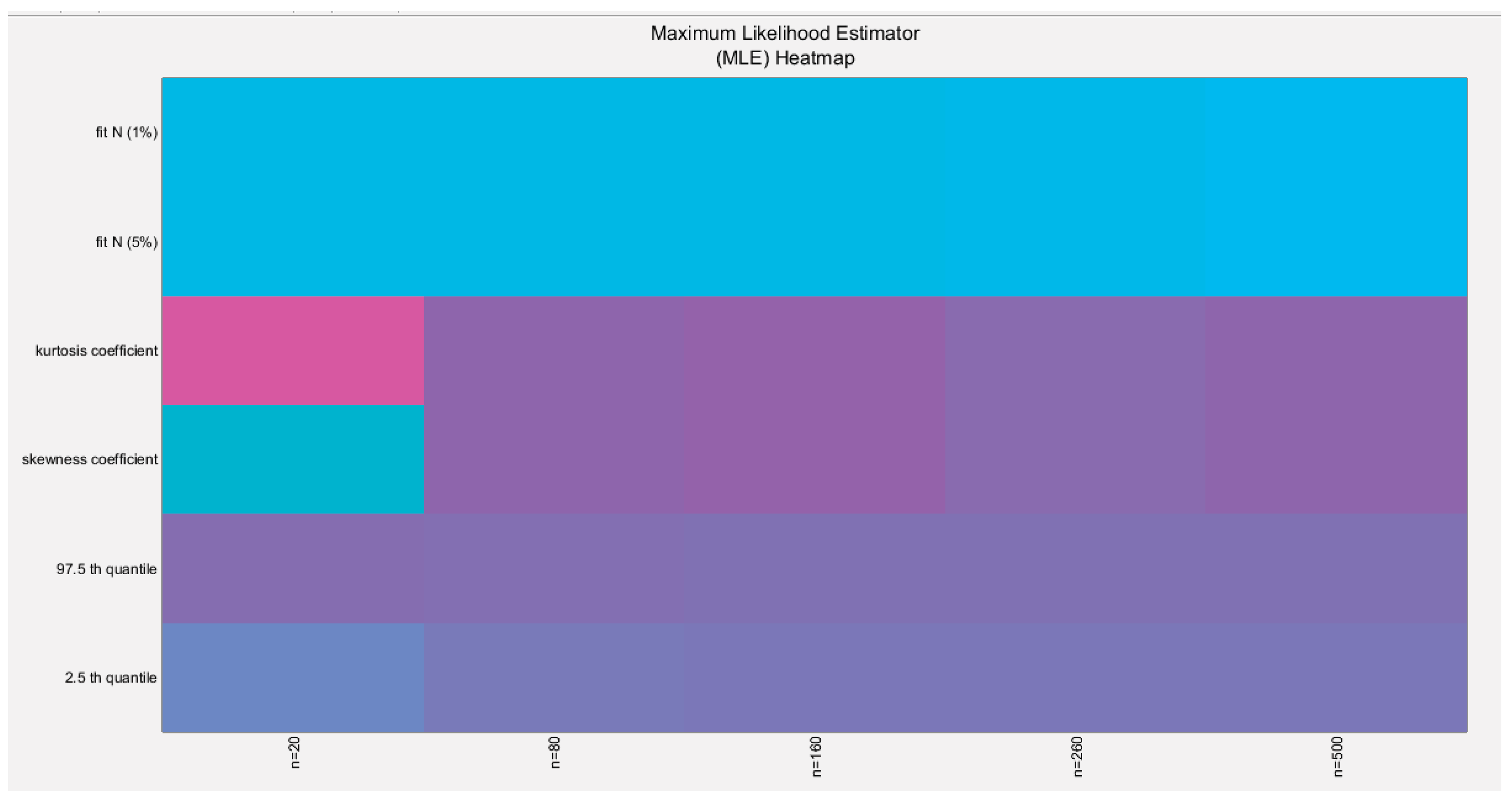
Figure 4.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (MOM) method and how these indices change with changing the sample size from 20 to 500. (p values are shown).
Figure 4.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (MOM) method and how these indices change with changing the sample size from 20 to 500. (p values are shown).
Table 2.
characteristics of empirical distribution of estimated alpha using MLE.
Table 2.
characteristics of empirical distribution of estimated alpha using MLE.
| MLE |
n=20 |
n=80 |
n=160 |
n=260 |
n=500 |
| 2.5 Q |
1.8751 |
2.252 |
2.3332 |
2.3707 |
2.4151 |
| 97.5 Q |
2.7839 |
2.6506 |
2.6181 |
2.6006 |
2.5779 |
| Skewness |
-1.2026 |
-0.5556 |
-0.4021 |
-0.3011 |
-0.1154 |
| Kurtosis |
5.6182 |
3.1668 |
3.3037 |
2.9514 |
3.0945 |
| Fit N (5%) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=0
(0.1318) |
H0=0
(0.3172) |
| Fit N (1%) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=0
(0.1318) |
H0=0
(0.3172) |
The empirical distribution of the estimated parameter alpha using MLE is shown in Table 2. Each column represents a specific sample size with 1000 replicates in each size. The 2.5 th quantile and the 97.5 th quantile of the 1000 values of the estimated parameter in each sample shows that as the sample size increases the 2.5 quantile rises while the 97.5 quantile decreases. In other words, the distance between the two quantiles decreases as the sample size increases and this is reflected on the confidence interval (CI). As the sample size increases the CI becomes narrower. The distribution exhibits a moderate left skewness and a high positive excess kurtosis (leptokurtic shape) at small sample size. As sample size increases the skewness decreases trying to approach the zero level (skewness of standard normal) and kurtosis decreases trying to approach the kurtosis of standard normal. The empirical distribution fits standard normal starting at size 260 and larger than this at significance level 5% and 1% with associated P-value as shown in the table. H0=1 means reject the null hypothesis that states the parameter distribution follows the standard normal distribution. While H0=0 means fail to reject the null hypothesis. The test used is the Lillietest in all the following tables. See following Figures (5-8)
Figure 5.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using MLE method.
Figure 5.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using MLE method.
Figure 6.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using MLE method.
Figure 6.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using MLE method.
Figure 7.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=500) using MLE method.
Figure 7.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=500) using MLE method.
Figure 8.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (MLE) method and how these indices change with changing the sample size from 20 to 500. (p values are shown).
Figure 8.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (MLE) method and how these indices change with changing the sample size from 20 to 500. (p values are shown).
Table 3.
characteristics of empirical distribution of estimated alpha using MPS.
Table 3.
characteristics of empirical distribution of estimated alpha using MPS.
| MPS |
n=20 |
n=80 |
n=160 |
n=260 |
n=500 |
| 2.5 Q |
2.1020 |
2.278 |
2.3455 |
2.3797 |
2.4192 |
| 97.5 Q |
2.9075 |
2.6649 |
2.6247 |
2.6056 |
2.5818 |
| Skewness |
-0.4654 |
-0.5367 |
-0.3972 |
-0.2999 |
-0.1177 |
| Kurtosis |
3.8161 |
3.1241 |
3.2465 |
2.9476 |
3.1013 |
| Fit N (5%) |
H0=1
(0.0066) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=0
(0.0663) |
H0=0
(0.3267) |
| Fit N (1%) |
H0=1
(0.0066) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=0
(0.0663) |
H0=0
(0.3267) |
The empirical distribution of the estimated parameter alpha using MPS is shown in Table 3. Each column represents a specific sample size with 1000 replicates in each size. The 2.5 th quantile and the 97.5 th quantile of the 1000 values of the estimated parameter in each sample shows that as the sample size increases the 2.5 quantile rises while the 97.5 quantile decreases. In other words, the distance between the two quantiles decreases as the sample size increases and this is reflected on the confidence interval (CI). As the sample size increases the CI becomes narrower. The distribution exhibits a mild left skewness and a mild positive excess kurtosis (leptokurtic shape) at small sample size. As sample size increases the skewness decreases trying to approach the zero level (skewness of standard normal) and kurtosis decreases trying to approach the kurtosis of standard normal. The empirical distribution fits standard normal starting at size 260 and larger than this at significance level 5% and 1% with associated P-value as shown in the table. H0=1 means reject the null hypothesis that states the parameter distribution follows the standard normal distribution. While H0=0 means fail to reject the null hypothesis. See following Figures (9-12).
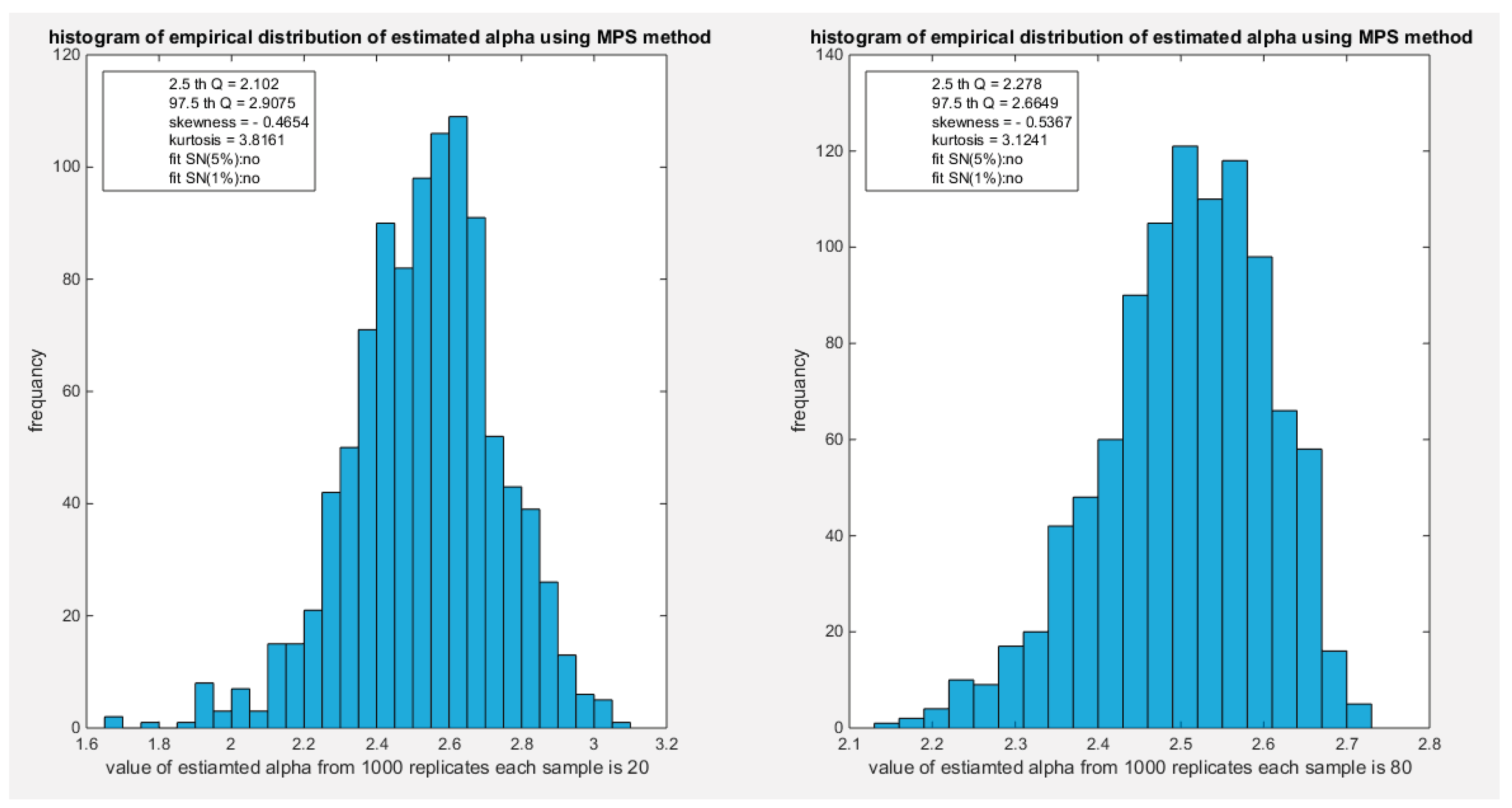
Figure 9.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using MPS method.
Figure 9.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using MPS method.
Figure 10.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using MPS method.
Figure 10.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using MPS method.
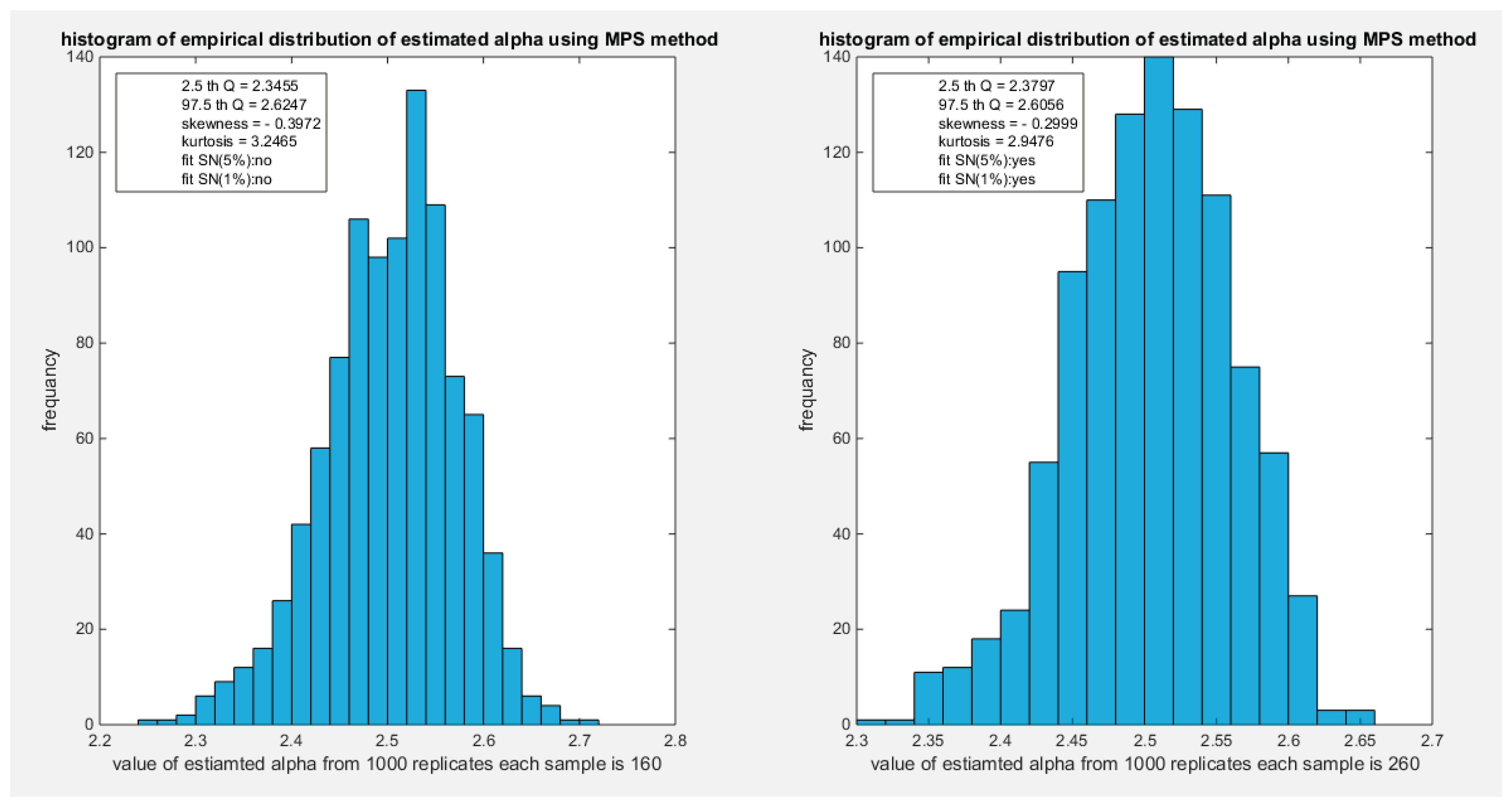
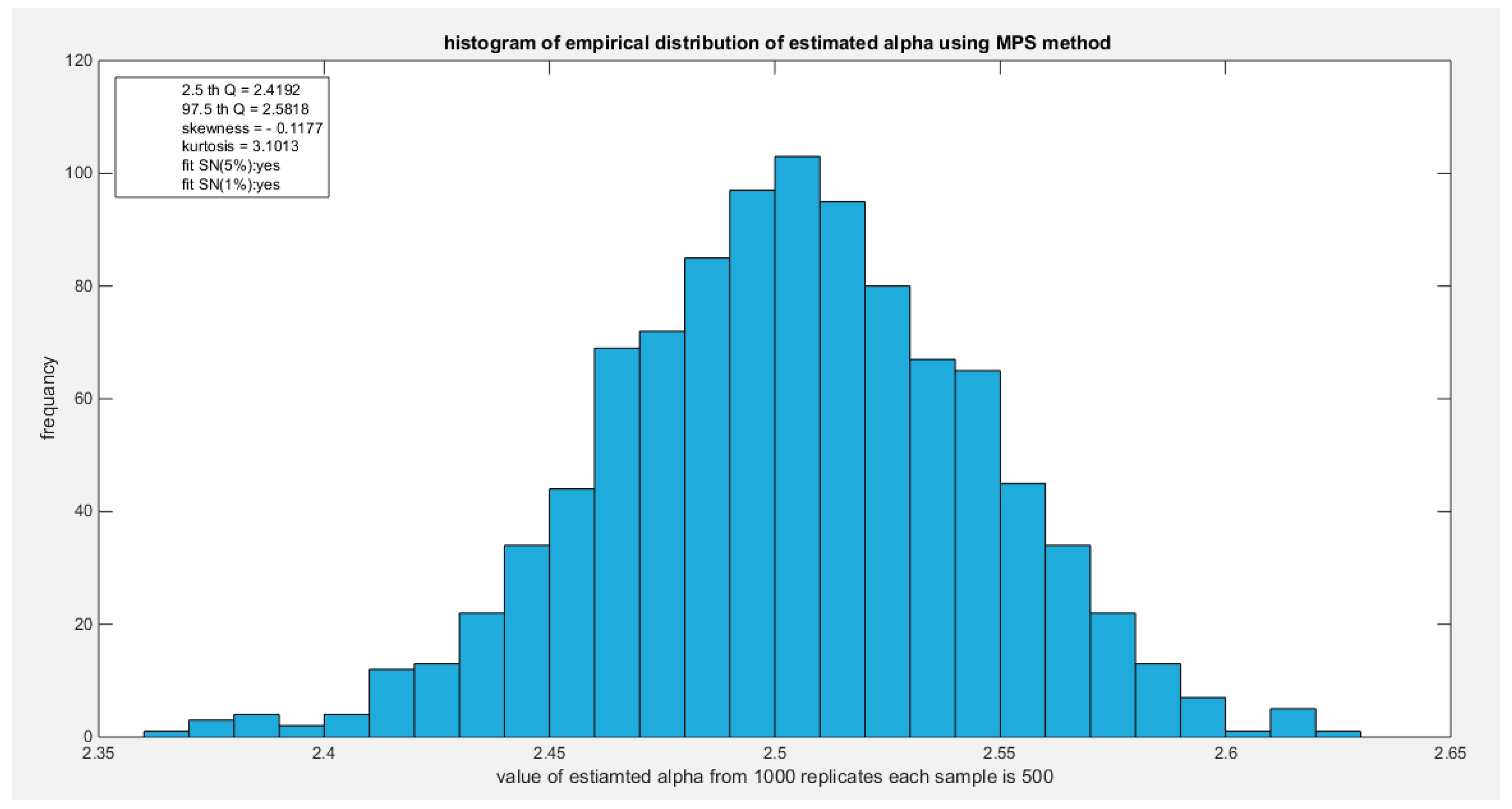
Figure 11.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=500) using MPS method.
Figure 11.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=500) using MPS method.
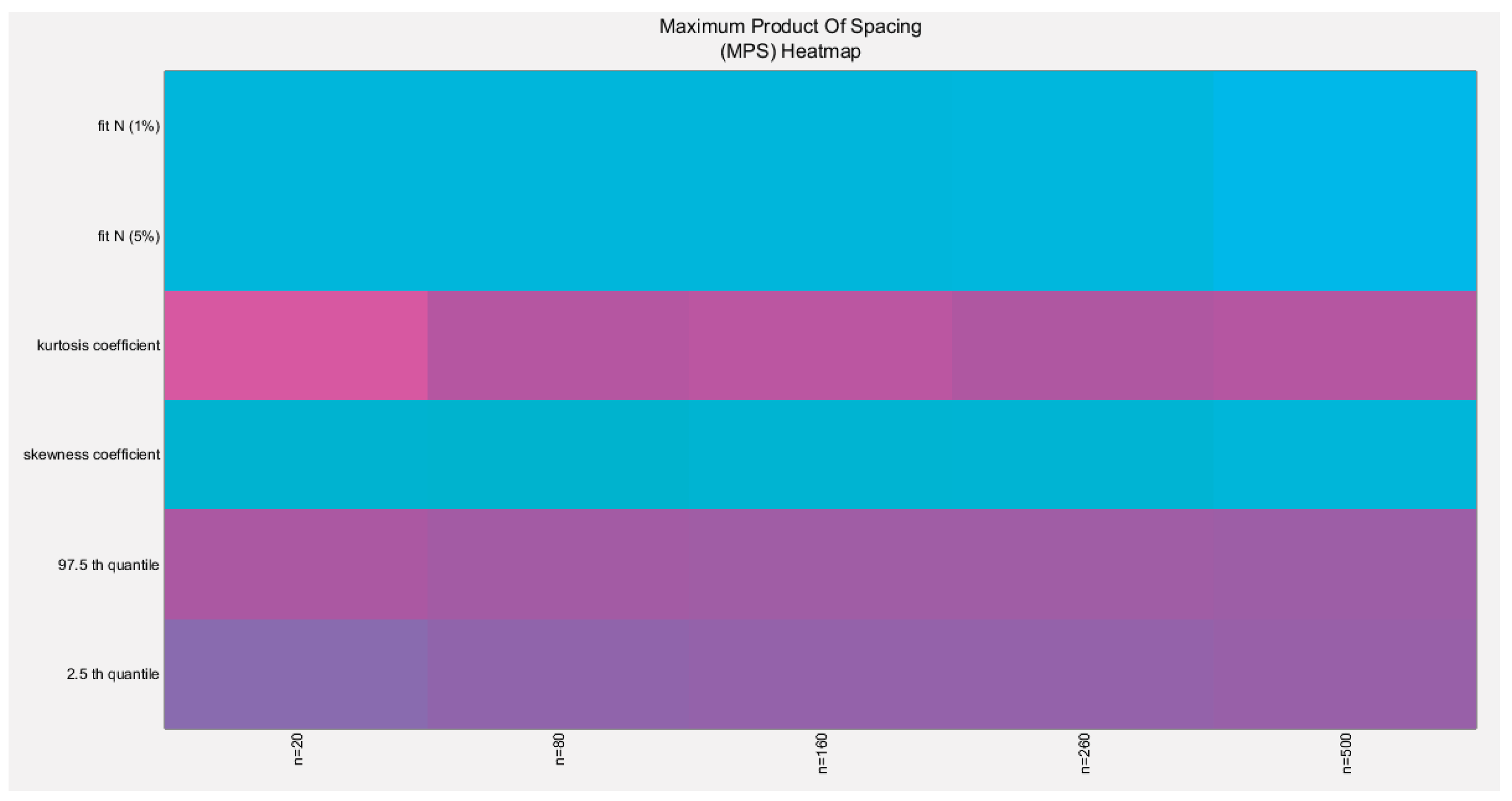
Figure 12.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (MPS) method and how these indices change with changing the sample size from 20 to 500.(p values are shown).
Figure 12.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (MPS) method and how these indices change with changing the sample size from 20 to 500.(p values are shown).
Table 4.
characteristics of empirical distribution of estimated alpha using AD.
Table 4.
characteristics of empirical distribution of estimated alpha using AD.
| AD |
n=20 |
n=80 |
n=160 |
n=260 |
n=500 |
| 2.5 Q |
1.9191 |
2.245 |
2.3306 |
2.3754 |
2.4105 |
| 97.5 Q |
2.8090 |
2.6669 |
2.6243 |
2.6072 |
2.5793 |
| Skewness |
-1.0612 |
-0.6927 |
-0.3771 |
-0.2281 |
-0.0795 |
| Kurtosis |
4.8814 |
3.7495 |
3.3002 |
2.9371 |
2.9561 |
| Fit N (5%) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=1
(0.0107) |
H0=0
(0.2142) |
H0=0
(0.5) |
| Fit N (1%) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=1
(0.0107) |
H0=0
(0.2142) |
H0=0
(0.5) |
The empirical distribution of the estimated parameter alpha using AD is shown in Table 4. Each column represents a specific sample size with 1000 replicates in each size. The 2.5 th quantile and the 97.5 th quantile of the 1000 values of the estimated parameter in each sample shows that as the sample size increases the 2.5 quantile rises while the 97.5 quantile decreases. In other words, the distance between the two quantiles decreases as the sample size increases and this is reflected on the confidence interval (CI). As the sample size increases the CI becomes narrower. The distribution exhibits a moderate left skewness and a moderate positive excess kurtosis (leptokurtic shape) at small sample size. As sample size increases the skewness decreases trying to approach the zero level (skewness of standard normal) and kurtosis decreases trying to approach the kurtosis of standard normal. The empirical distribution fits standard normal starting at size 260 and larger than this at significance level 5% and 1% with associated P-value as shown in the table. H0=1 means reject the null hypothesis that states the parameter distribution follows the standard normal distribution. While H0=0 means fail to reject the null hypothesis. See the following Figures (13-16).
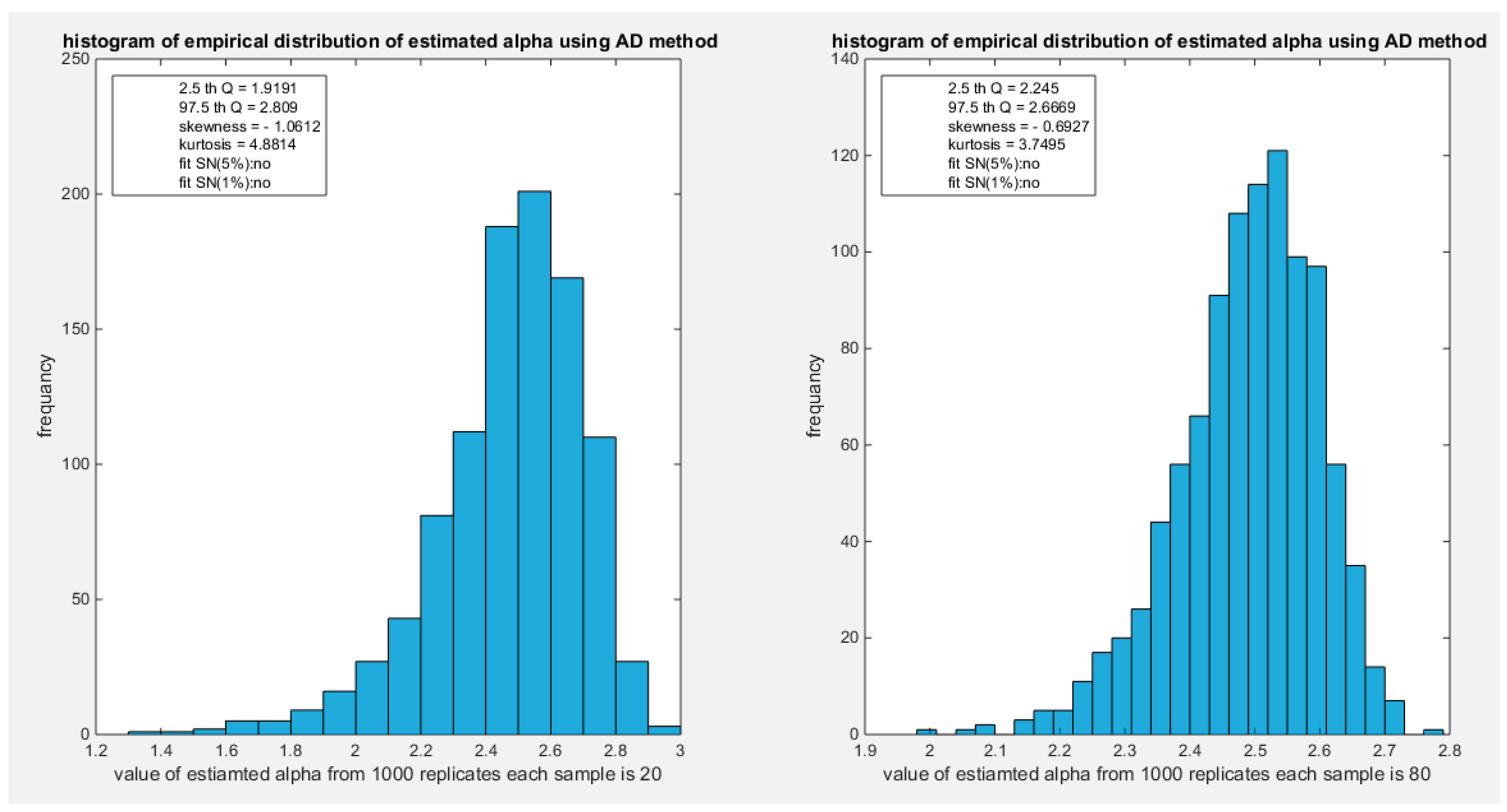
Figure 13.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using AD method.
Figure 13.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using AD method.
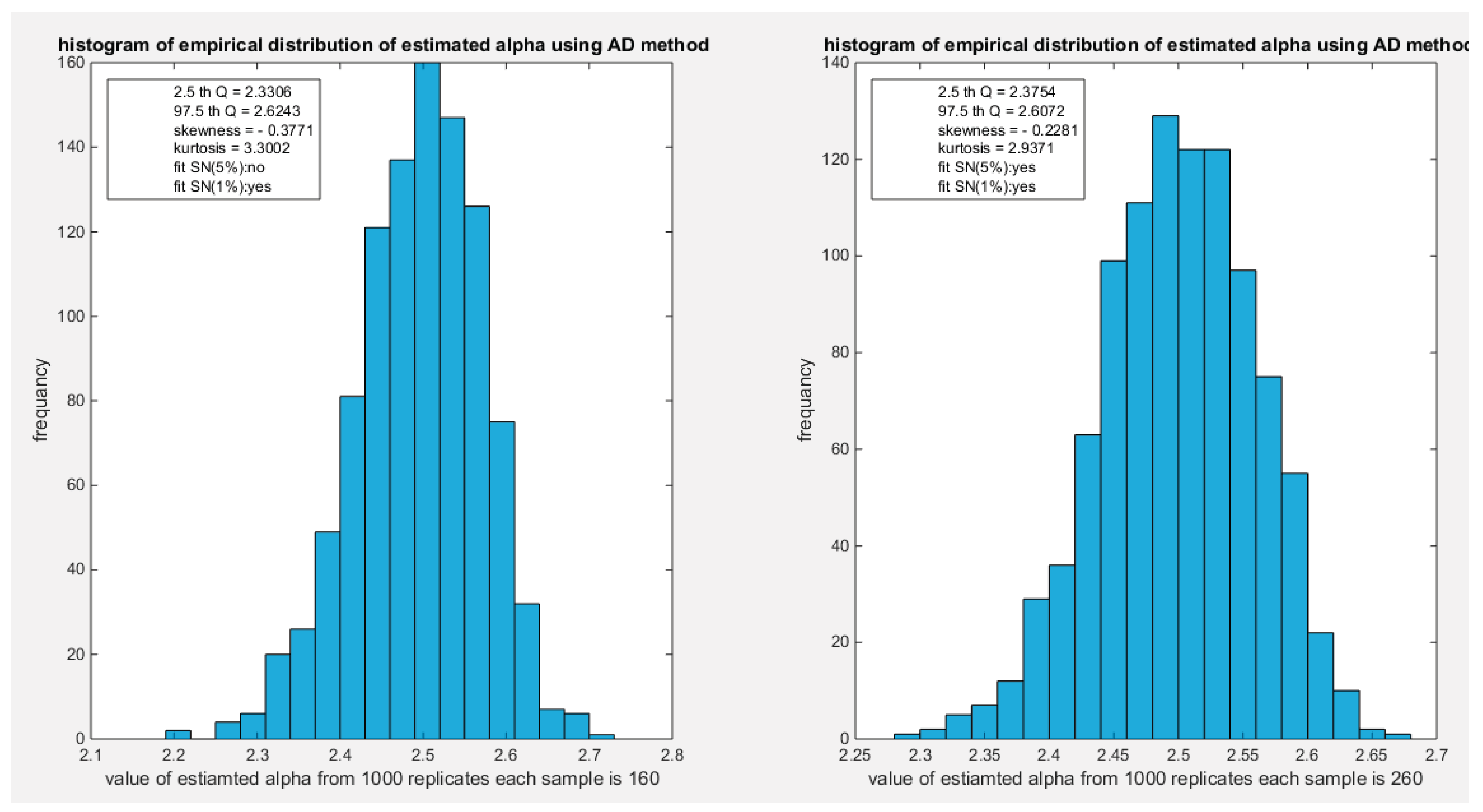
Figure 14.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using AD method.
Figure 14.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using AD method.
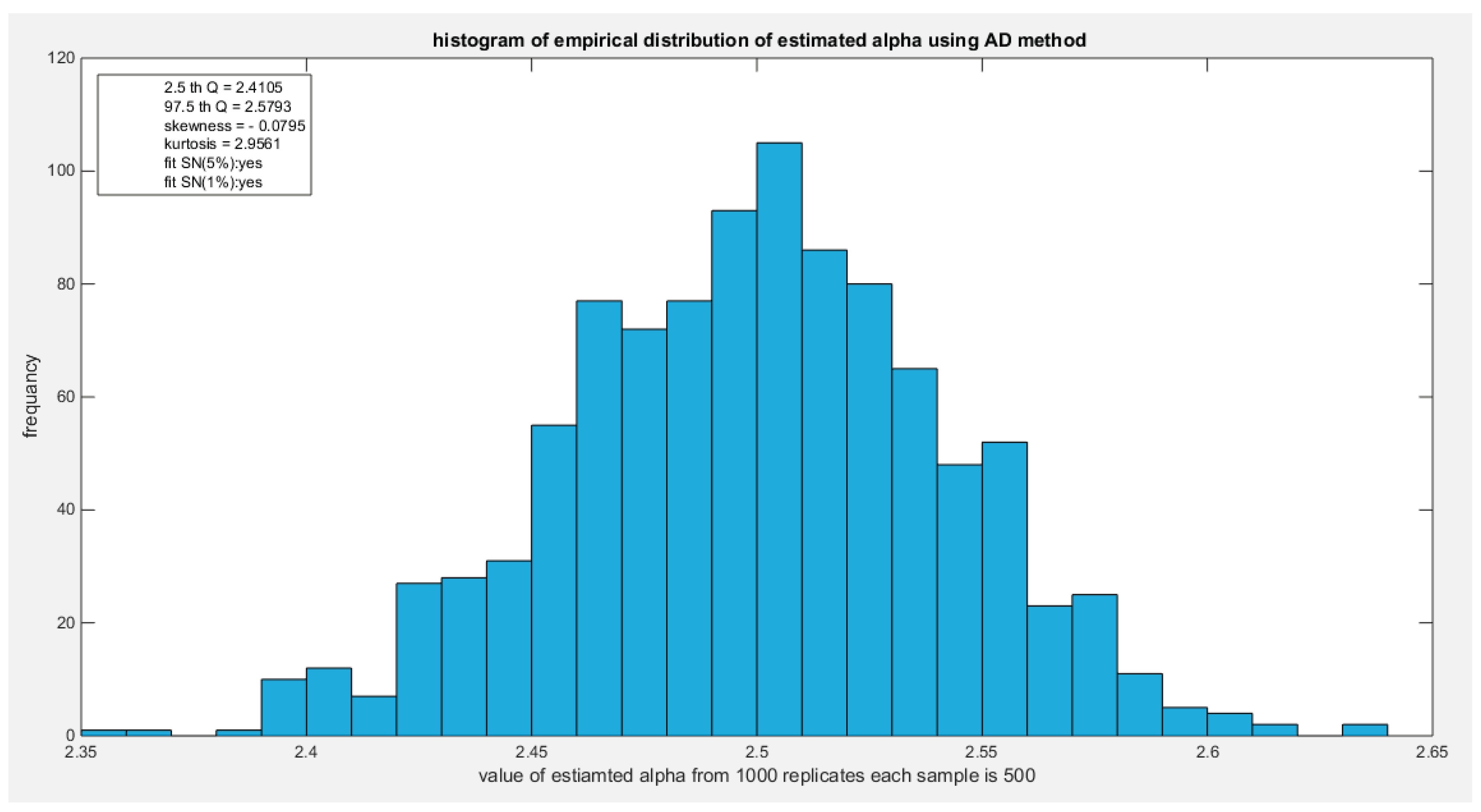
Figure 15.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=500) using AD method.
Figure 15.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=500) using AD method.
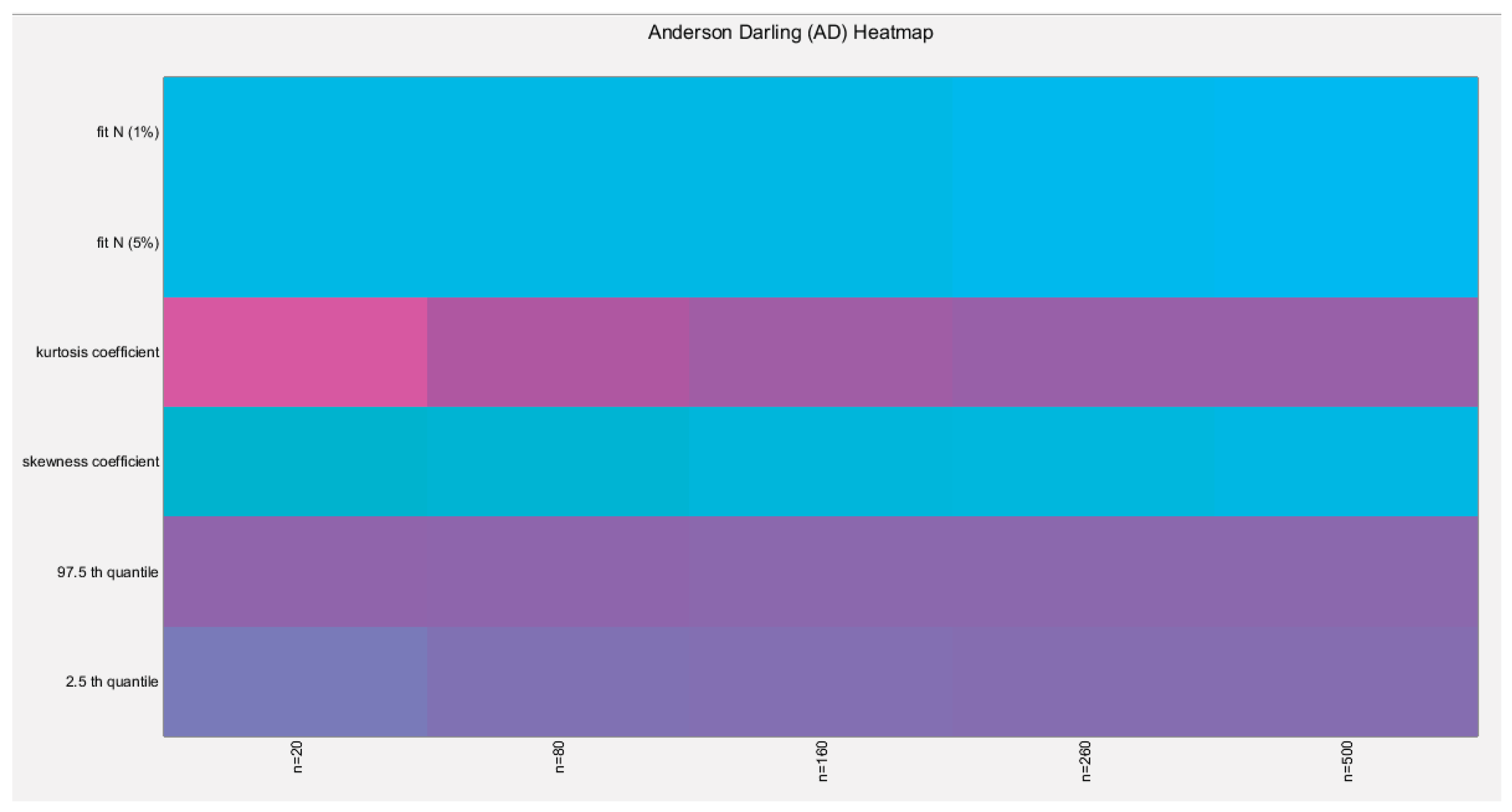
Figure 16.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (AD) method and how these indices change with changing the sample size from 20 to 500. (p=values are shown).
Figure 16.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (AD) method and how these indices change with changing the sample size from 20 to 500. (p=values are shown).
Table 5.
characteristics of empirical distribution of estimated alpha using CVM.
Table 5.
characteristics of empirical distribution of estimated alpha using CVM.
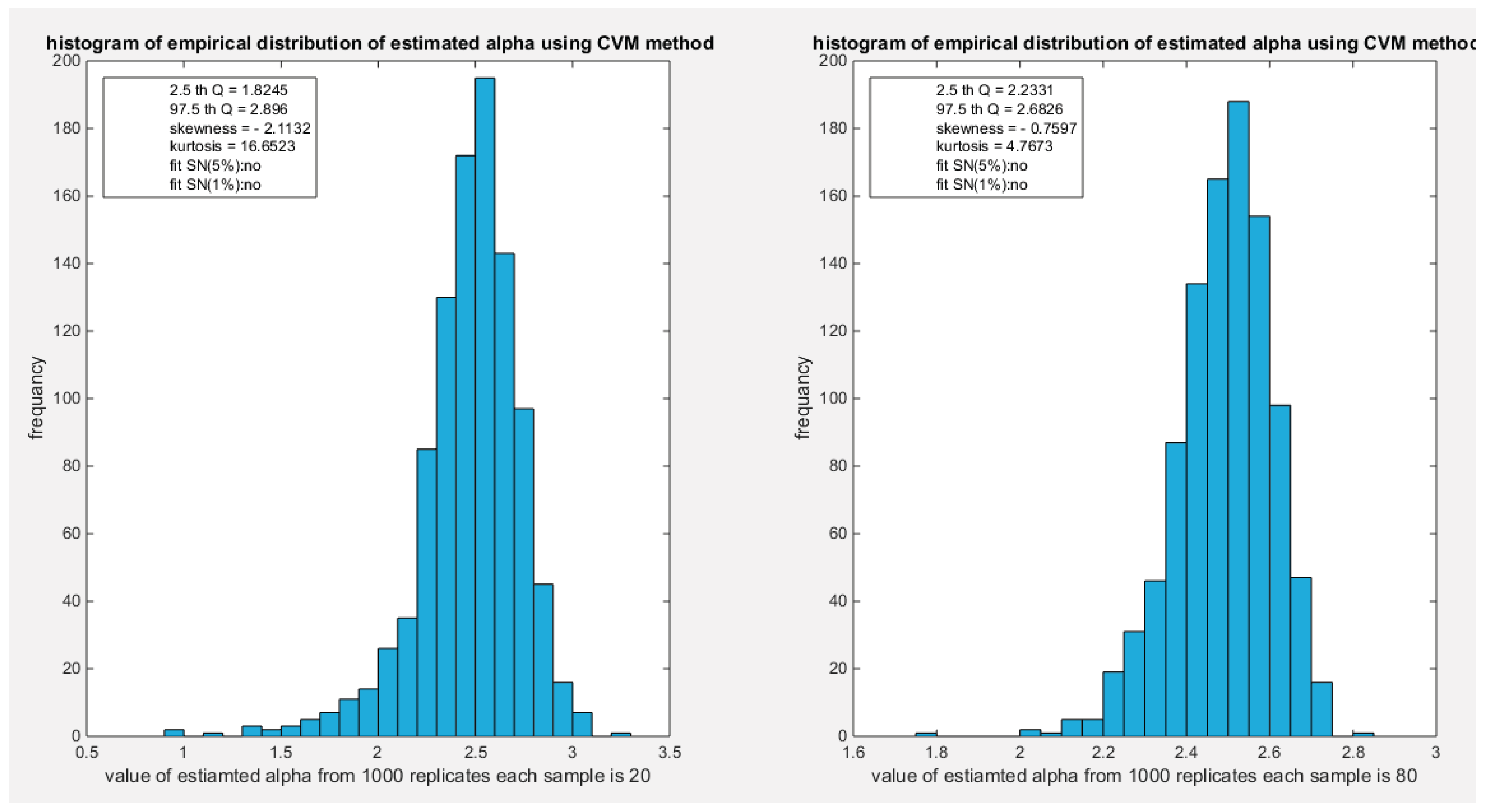
| CVM |
n=20 |
n=80 |
n=160 |
n=260 |
n=500 |
| 2.5 Q |
1.8245 |
2.2331 |
2.3265 |
2.3754 |
2.4088 |
| 97.5 Q |
2.896 |
2.6826 |
2.6384 |
2.6137 |
2.5853 |
| Skewness |
-2.1132 |
-0.7597 |
-0.2994 |
-0.1571 |
-0.0392 |
| Kurtosis |
16.6523 |
4.7673 |
3.3267 |
2.9688 |
2.9101 |
| Fit N (5%) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=0
(0.1544) |
H0=0
(0.326) |
H0=0
(0.5) |
| Fit N (1%) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=0
(0.1544) |
H0=0
(0.326) |
H0=0
(0.5) |
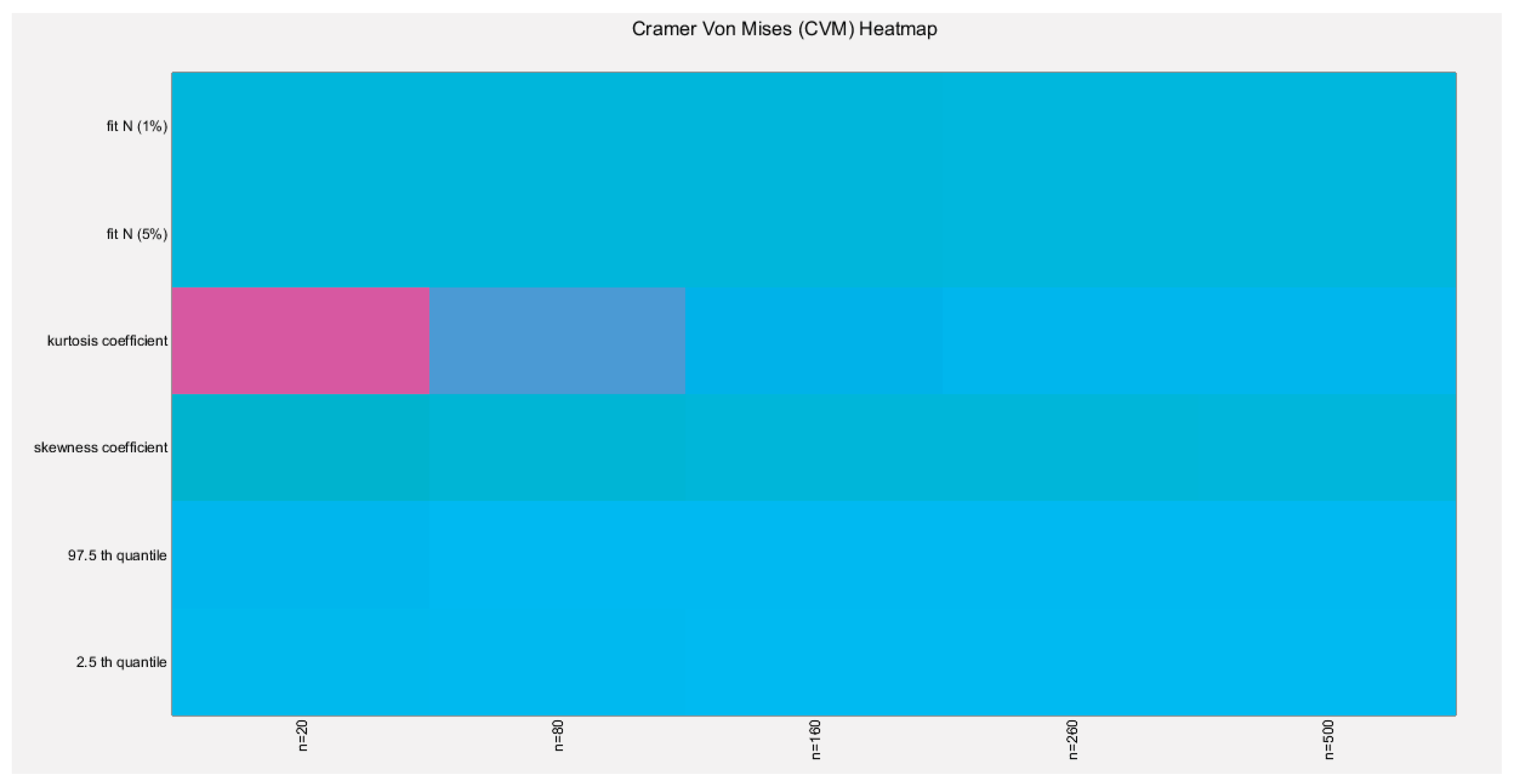
The empirical distribution of the estimated parameter alpha using CVM is shown in Table 5. Each column represents a specific sample size with 1000 replicates in each size. Each column depicts the characteristics of the empirical distribution of the estimated alpha. The 2.5 th quantile and the 97.5 th quantile of the 1000 values of the estimated parameter in each sample shows that as the sample size increases the 2.5 th quantile rises while the 97.5 th quantile decreases. In other words, the distance between the two quantiles decreases as the sample size increases and this is reflected on the confidence interval (CI). As the sample size increases the CI becomes narrower. The distribution exhibits a moderate left skewness and a high positive excess kurtosis (leptokurtic shape) at small sample size. As sample size increases the skewness decreases trying to approach the zero level (skewness of standard normal) and kurtosis decreases trying to approach the kurtosis of standard normal. The empirical distribution fits standard normal starting at size 160 and larger than this at significance level 5% and 1% with associated P-value as shown in the table. H0=1 means reject the null hypothesis that states the parameter distribution follows the standard normal distribution. While H0=0 means fail to reject the null hypothesis. See the following Figures (17-20).
Figure 17.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using CVM method.
Figure 17.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using CVM method.
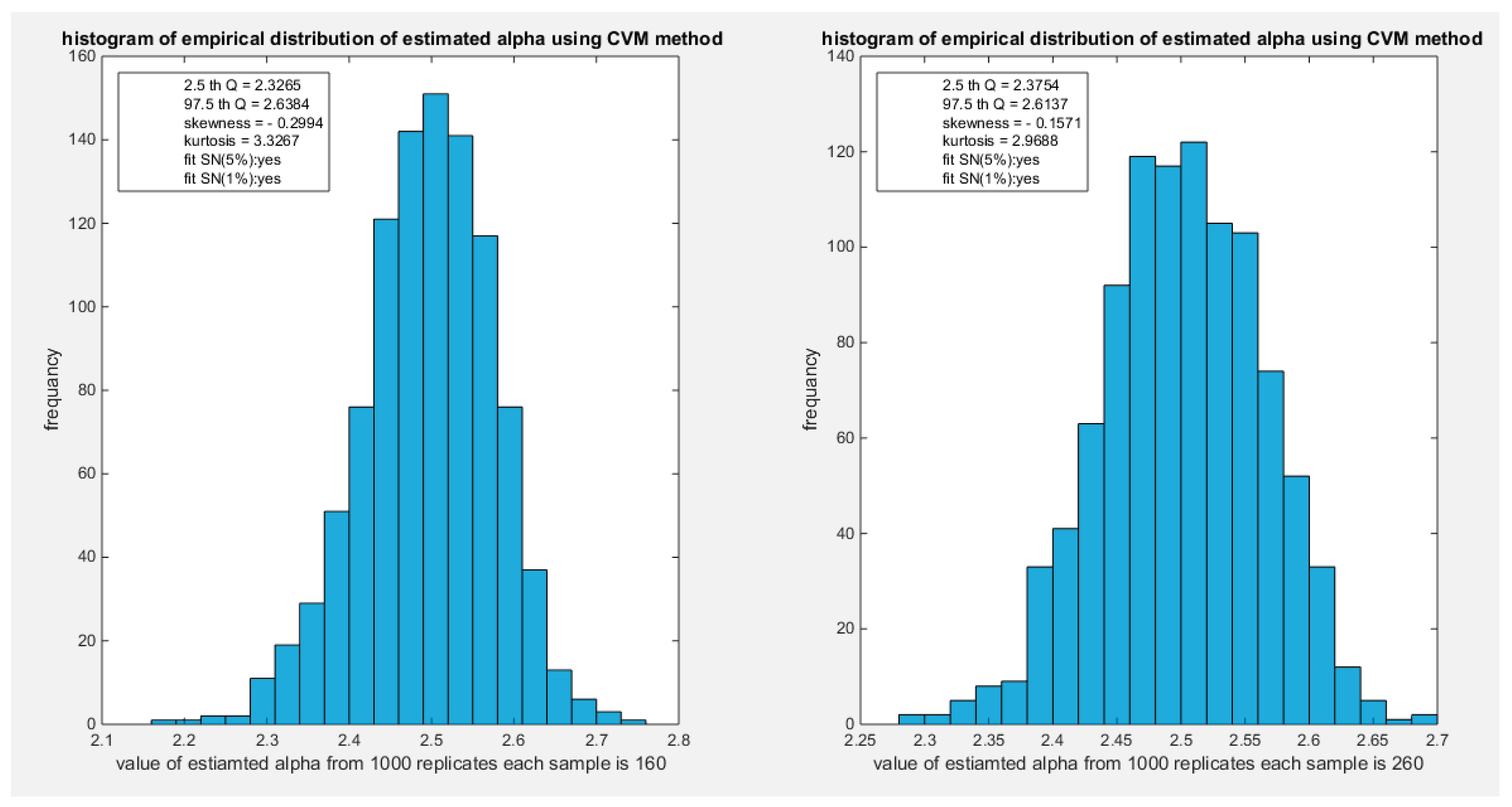
Figure 18.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using CVM method.
Figure 18.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using CVM method.
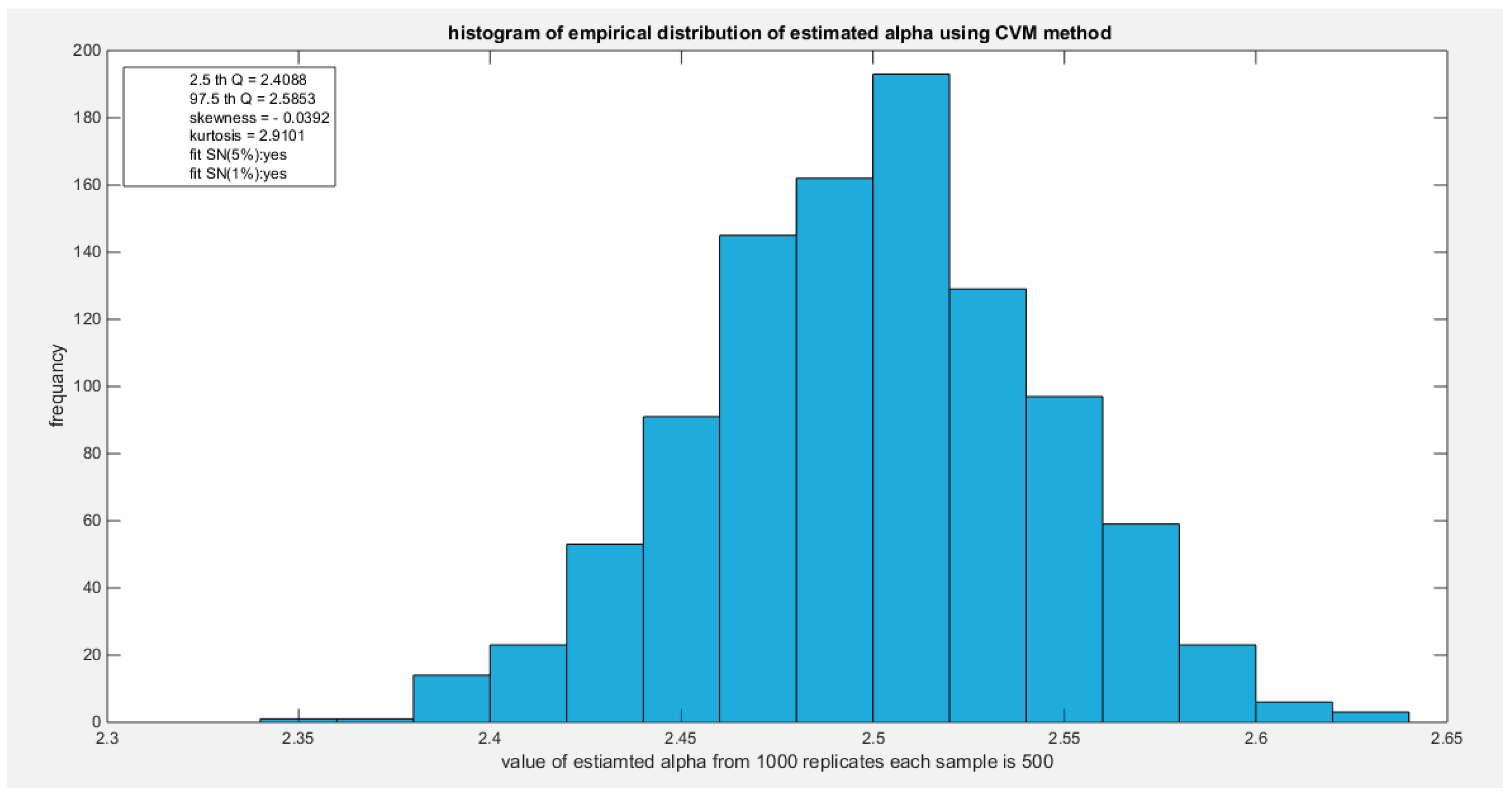
Figure 19.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n =500) using CVM method.
Figure 19.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n =500) using CVM method.
Figure 20.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (CVM) method and how these indices change with changing the sample size from 20 to 500. (p value shown).
Figure 20.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (CVM) method and how these indices change with changing the sample size from 20 to 500. (p value shown).
Table 6.
characteristics of empirical distribution of estimated alpha using LS.
Table 6.
characteristics of empirical distribution of estimated alpha using LS.
| LS |
n=20 |
n=80 |
n=160 |
n=260 |
n=500 |
| 2.5 Q |
1.8885 |
2.2345 |
2.3275 |
2.3758 |
2.4112 |
| 97.5 Q |
2.9203 |
2.6842 |
2.6390 |
2.6142 |
2.5855 |
| Skewness |
-1.1974 |
-0.7647 |
-0.2988 |
-0.1567 |
-0.0182 |
| Kurtosis |
7.1553 |
4.7783 |
3.3263 |
2.9686 |
2.8689 |
| Fit N (5%) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=0
(0.1454) |
H0=0
(0.3256) |
H0=0
(0.5) |
| Fit N (1%) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=0
(0.1454) |
H0=0
(0.3256) |
H0=0
(0.5) |
The empirical distribution of the estimated parameter alpha using CVM is shown in Table 6. Each column represents a specific sample size with 1000 replicates in each size. Each column depicts the characteristics of the empirical distribution of the estimated alpha. The 2.5 th quantile and the 97.5 th quantile of the 1000 values of the estimated parameter in each sample shows that as the sample size increases the 2.5 th quantile rises while the 97.5 th quantile decreases. In other words, the distance between the two quantiles decreases as the sample size increases and this is reflected on the confidence interval (CI). As the sample size increases the CI becomes narrower. The distribution exhibits a moderate left skewness and a high positive excess kurtosis (leptokurtic shape) at small sample size. As sample size increases the skewness decreases trying to approach the zero level (skewness of standard normal) and kurtosis decreases trying to approach the kurtosis of standard normal. The empirical distribution fits standard normal starting at size 160 and larger than this at significance level 5% and 1% with associated P-value as shown in the table. H0=1 means reject the null hypothesis that states the parameter distribution follows the standard normal distribution. While H0=0 means fail to reject the null hypothesis. See following Figures (21-24)
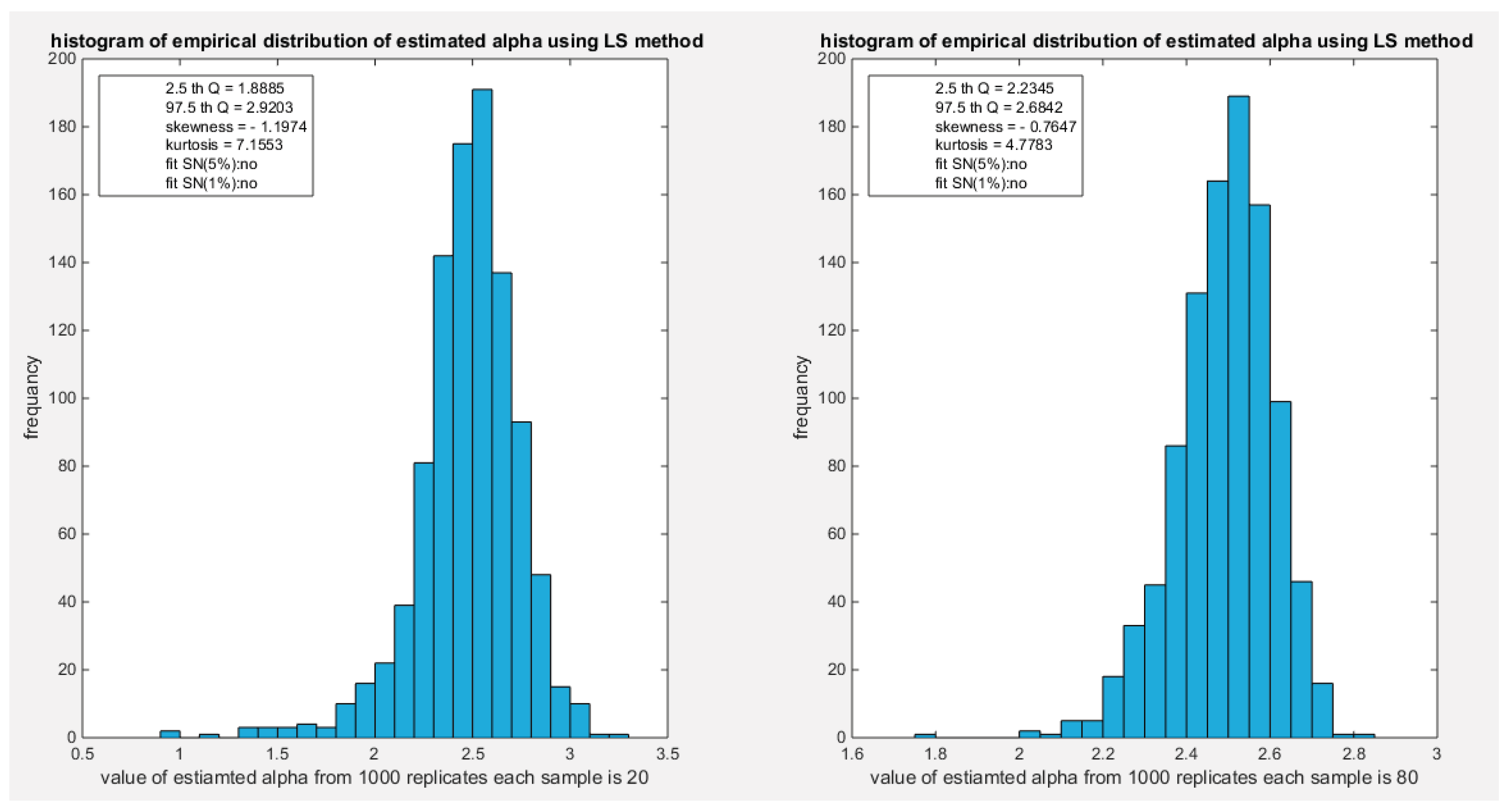
Figure 21.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using LS method.
Figure 21.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using LS method.
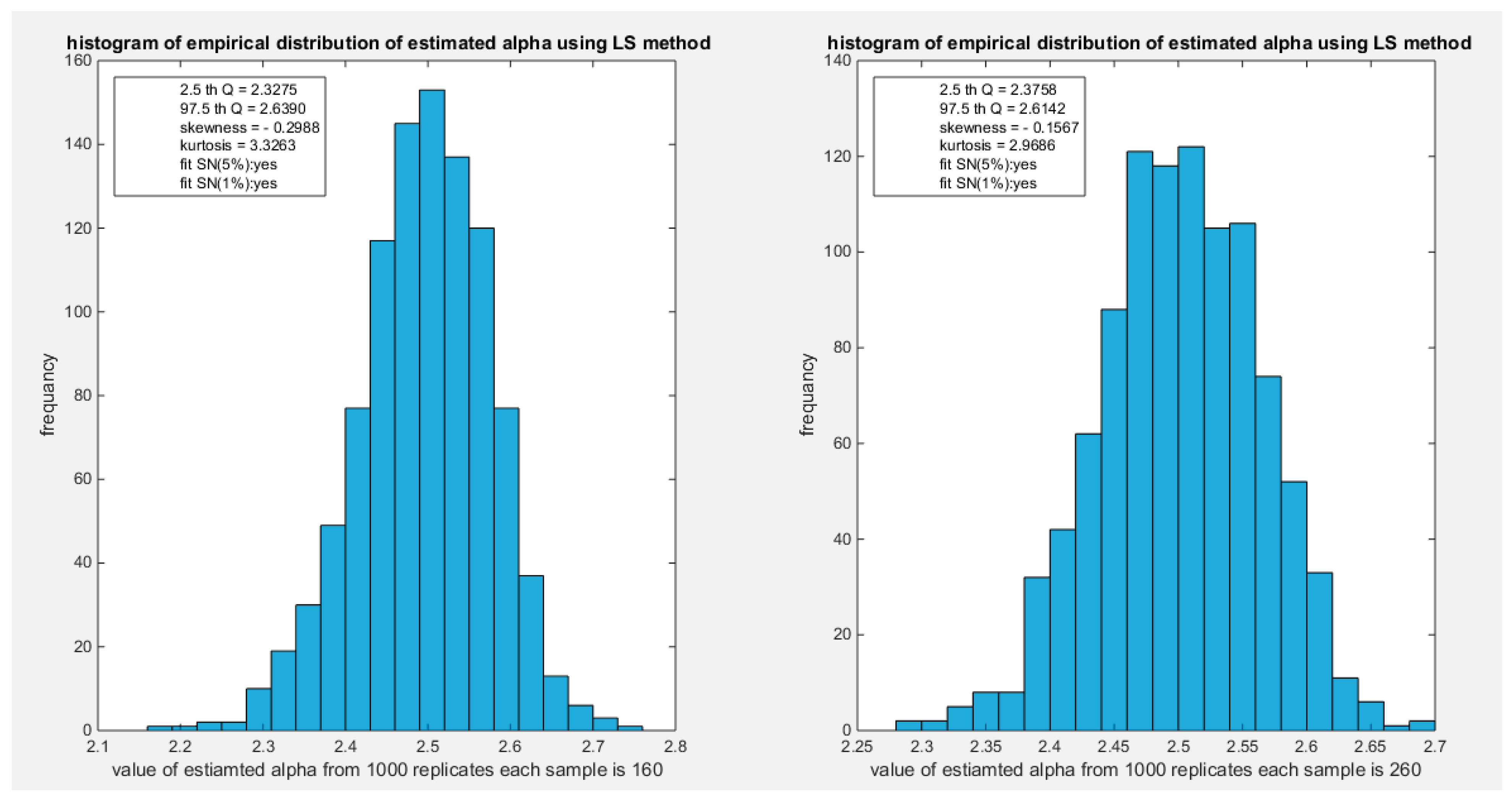
Figure 22.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using LS method.
Figure 22.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using LS method.
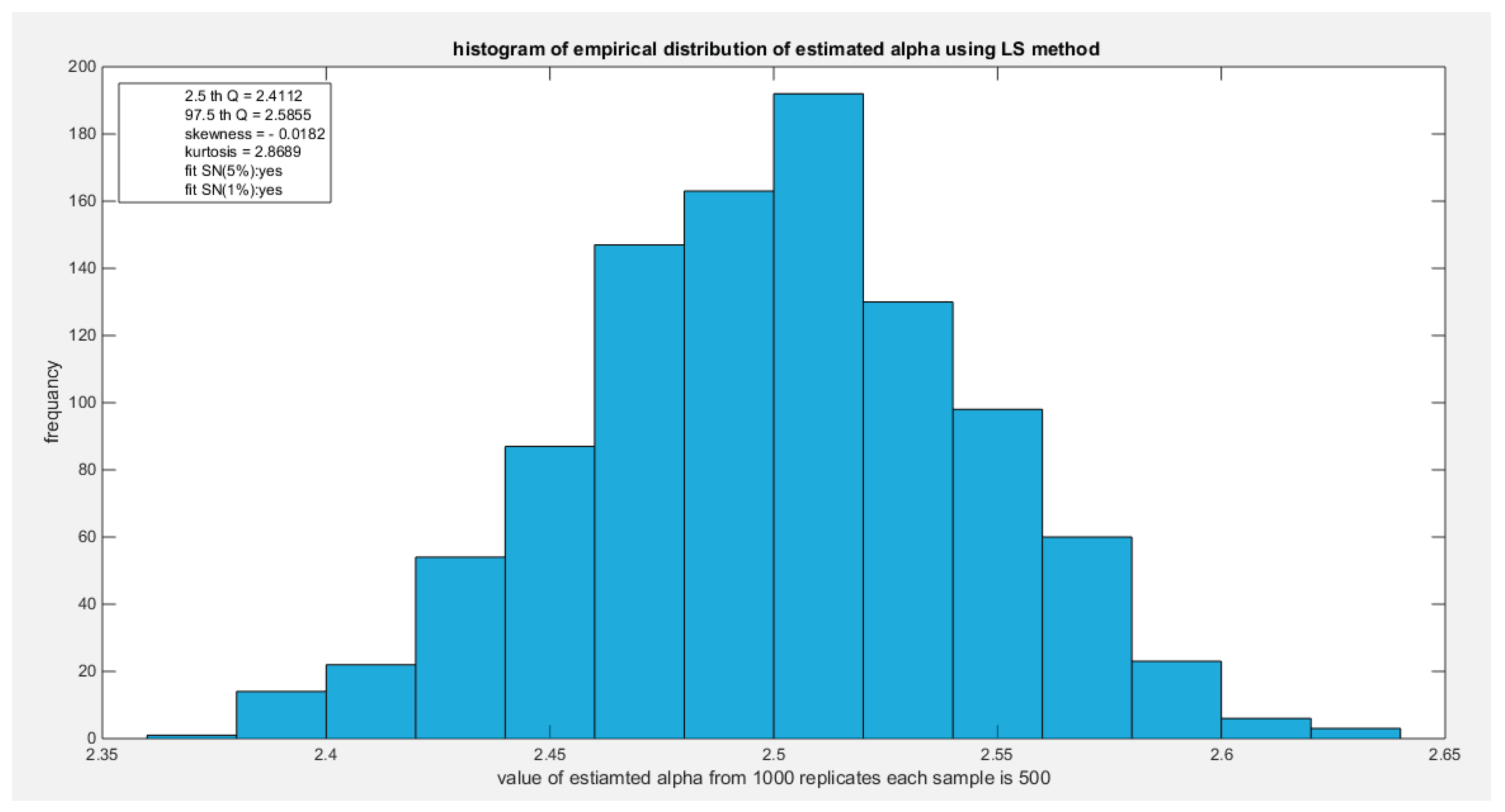
Figure 23.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n =500) using LS method.
Figure 23.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n =500) using LS method.
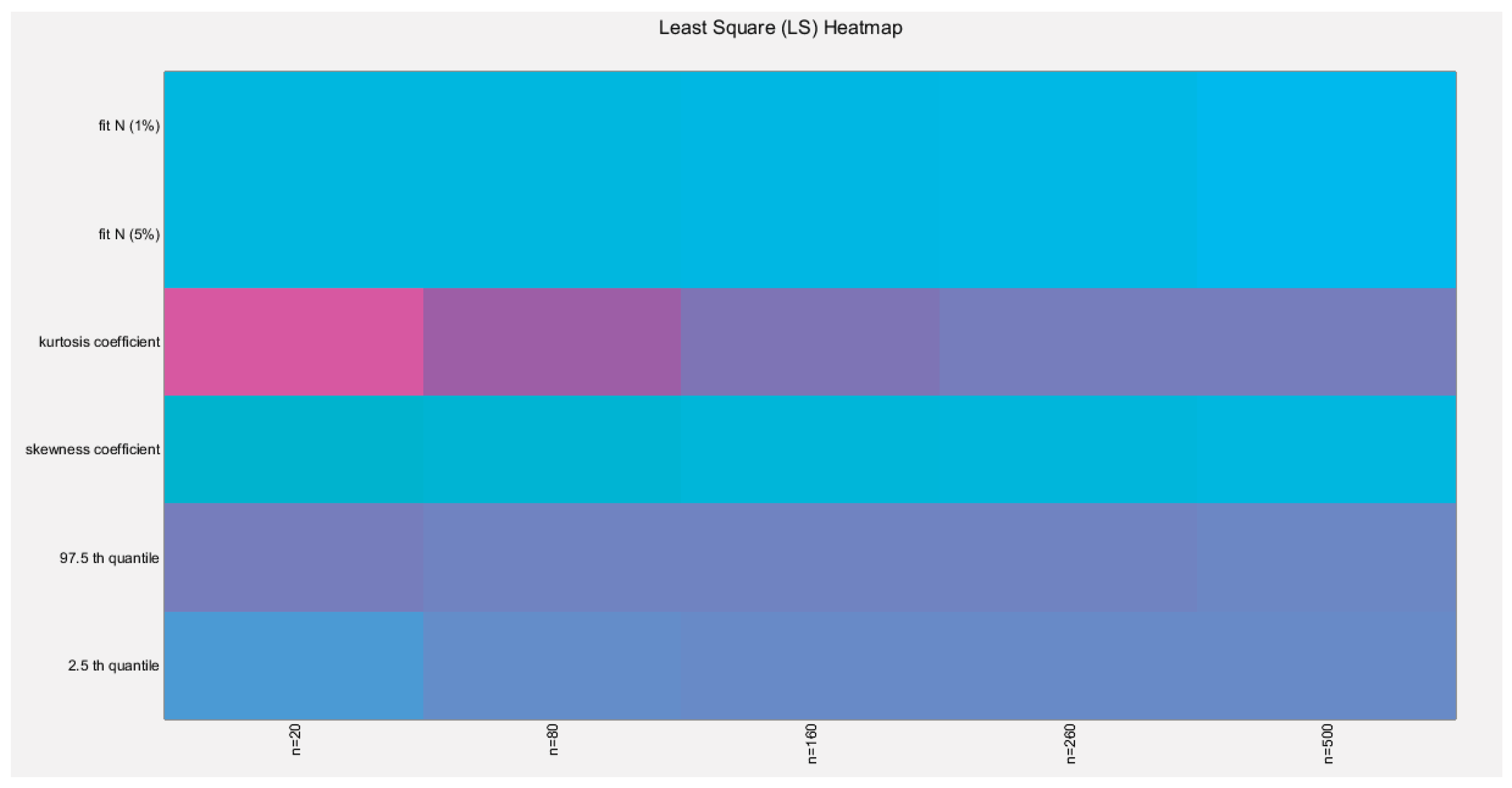
Figure 24.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (LS) method and how these indices change with changing the sample size from 20 to 500. (p values are shown).
Figure 24.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (LS) method and how these indices change with changing the sample size from 20 to 500. (p values are shown).
Table 7.
characteristics of empirical distribution of estimated alpha using percentile.
Table 7.
characteristics of empirical distribution of estimated alpha using percentile.
| PERCENTILE |
n=20 |
n=80 |
n=160 |
n=260 |
n=500 |
| 2.5 Q |
1.5756 |
2.0858 |
2.1745 |
2.2574 |
2.3239 |
| 97.5 Q |
3.0543 |
2.8417 |
2.7483 |
2.7020 |
2.6533 |
| Skewness |
-0.2107 |
0.0299 |
-0.1196 |
0.0412 |
0.0296 |
| Kurtosis |
2.6405 |
2.8171 |
2.8136 |
2.8258 |
3.0752 |
| Fit N (5%) |
H0=1
(0.0035) |
H0=0
(0.5) |
H0=0
(0.4261) |
H0=0
(0.5) |
H0=0
(0.3554) |
| Fit N (1%) |
H0=1
(0.0035) |
H0=0
(0.5) |
H0=0
(0.4261) |
H0=0
(0.5) |
H0=0
(0.3554) |
The empirical distribution of the estimated parameter alpha using percentile method is shown in Table 7. Each column represents a specific sample size with 1000 replicates in each size. Each column depicts the characteristics of the empirical distribution of the estimated alpha. The 2.5 th quantile and the 97.5 th quantile of the 1000 values of the estimated parameter in each sample shows that as the sample sizes increase the 2.5 th quantile rises while the 97.5 th quantile decreases. In other words, the distance between the two quantiles decreases as the sample size increases and this is reflected on the confidence interval (CI). As the sample size increases the CI becomes narrower. As sample size increases the distribution exhibits oscillation between a mild left skewness and a mild right skewness. In contrast, it exhibits gradual mild increase in negative excess kurtosis (platykurtic shape) as sample size rises and it approaches mesokurtic shape (kertosis coefficient=3) of the standard normal at sample size 500. The empirical distribution fits standard normal starting at size 80 and larger than this size at significance level 5% and 1% with associated P-value as shown in the table. H0=1 means reject the null hypothesis that states the parameter distribution follows the standard normal distribution. While H0=0 means fail to reject the null hypothesis. See following Figures (25-28)
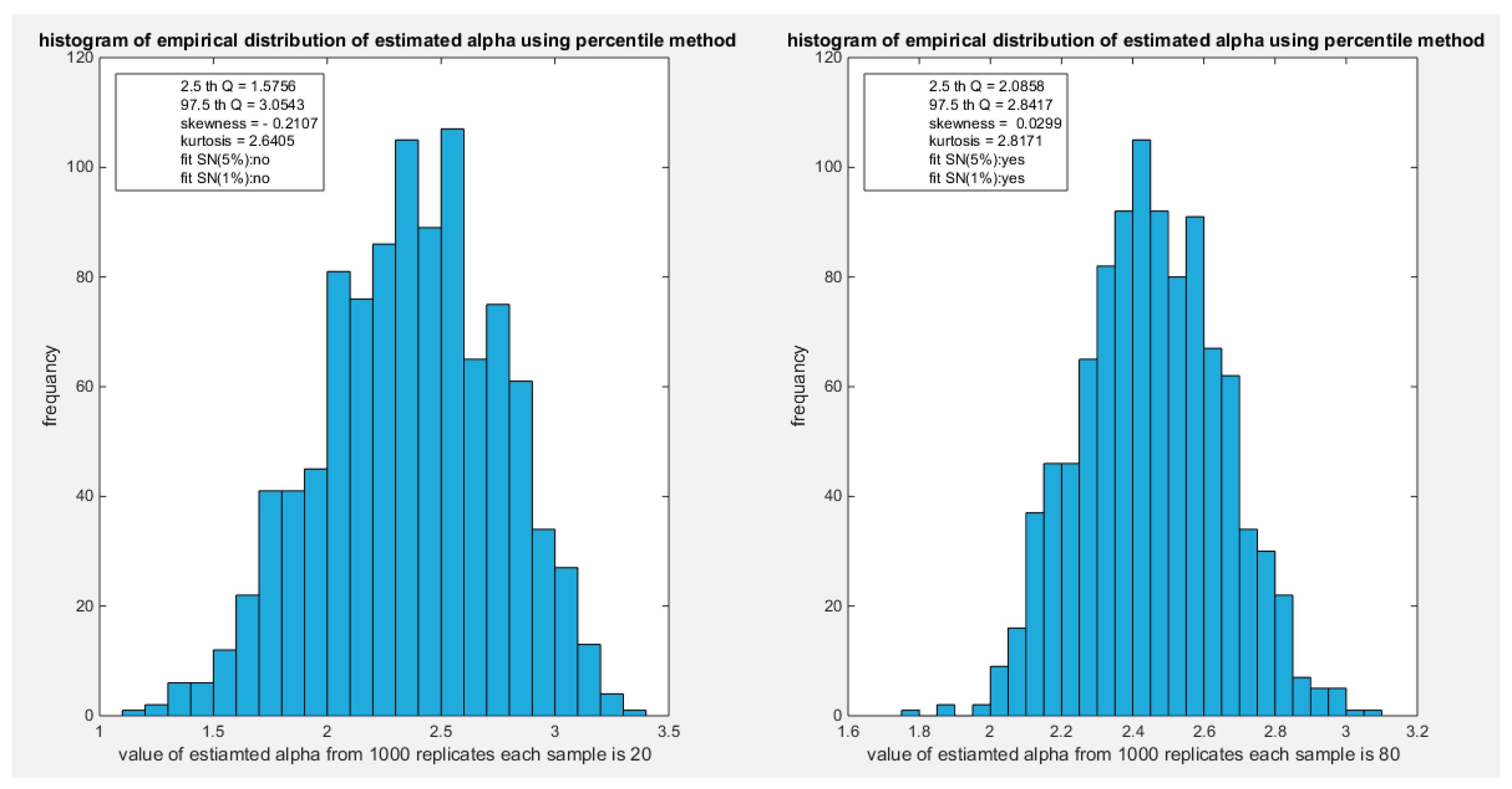
Figure 25.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using percentile method.
Figure 25.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using percentile method.
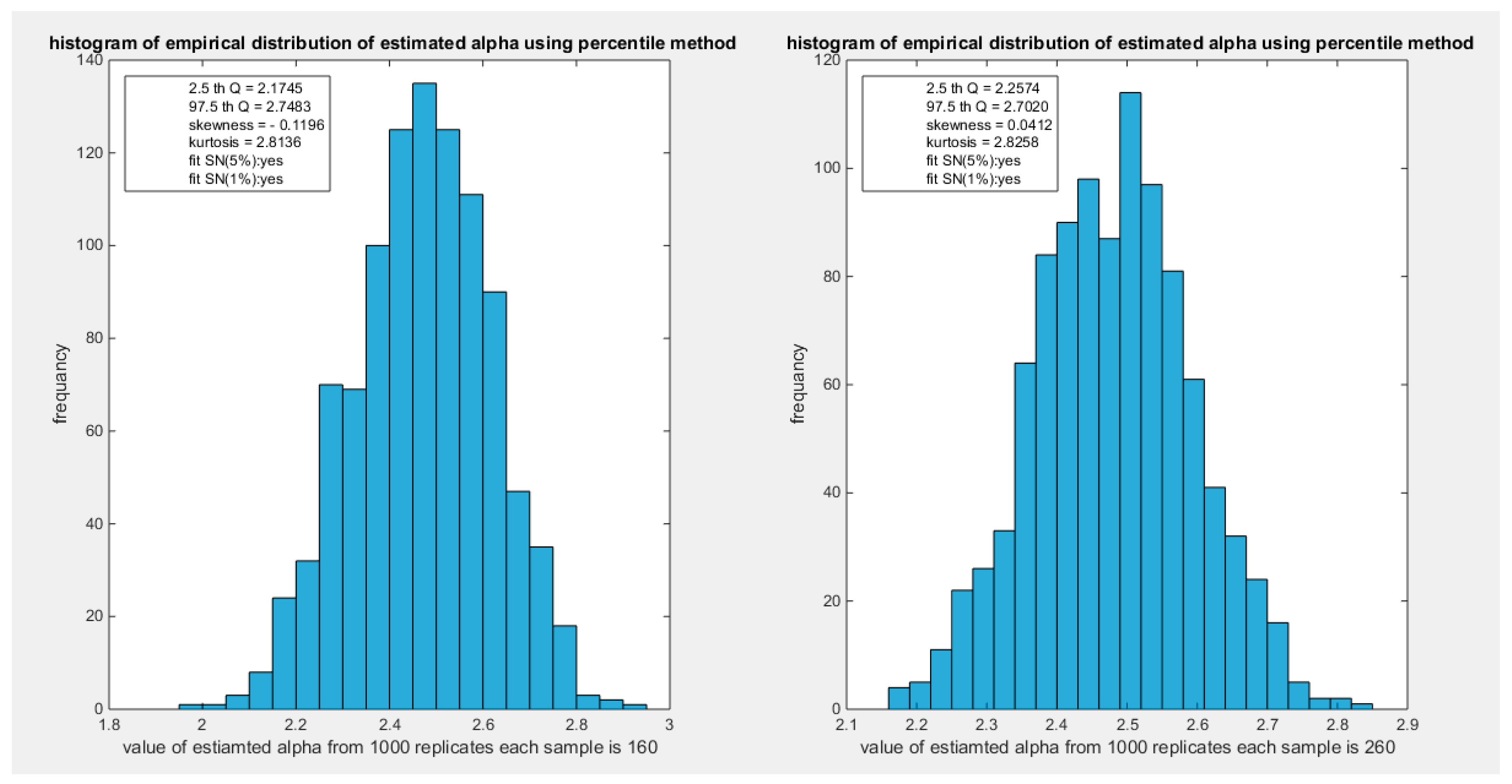
Figure 26.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using percentile method.
Figure 26.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using percentile method.
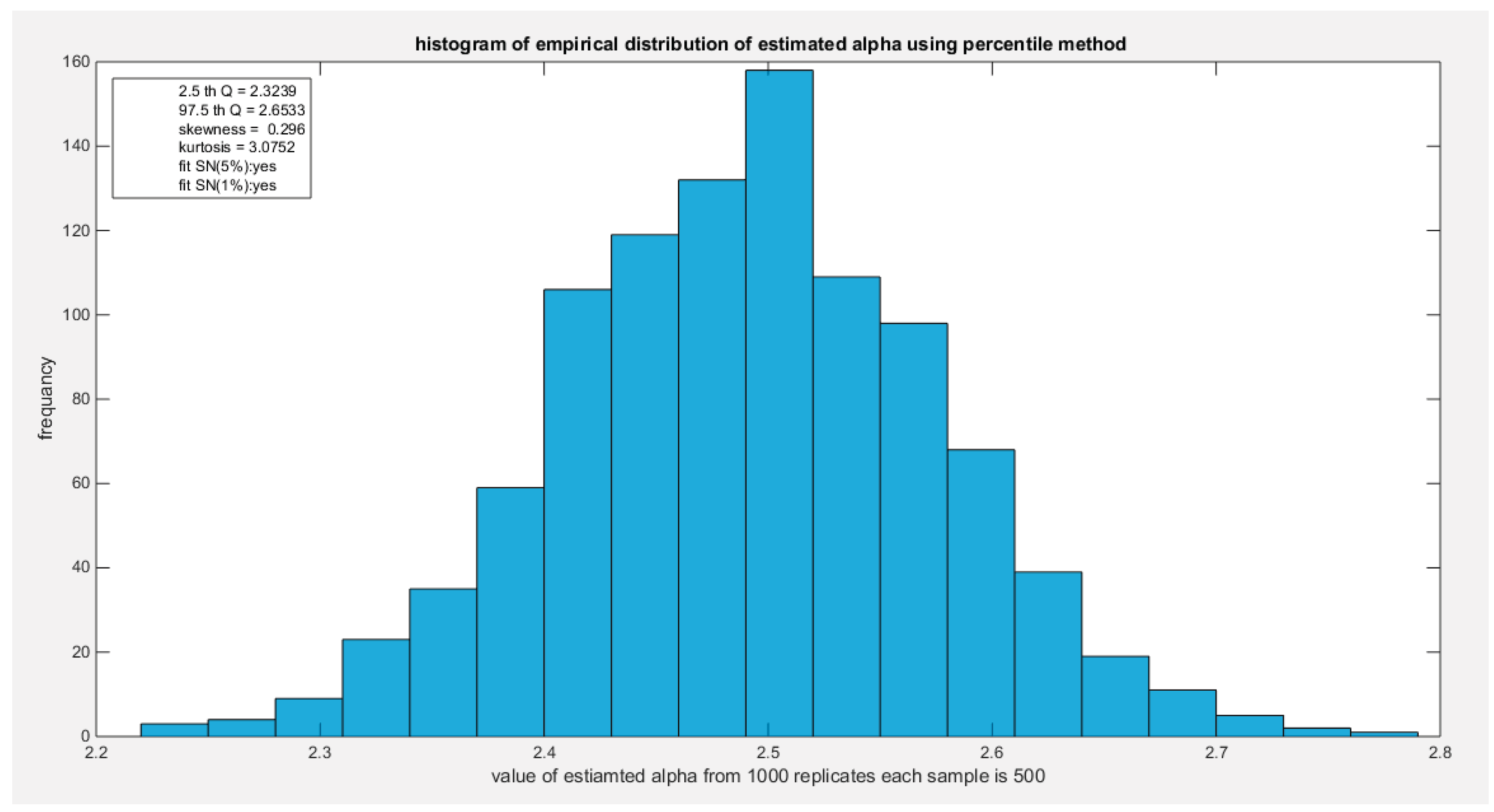
Figure 27.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n =500) using percentile method.
Figure 27.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n =500) using percentile method.
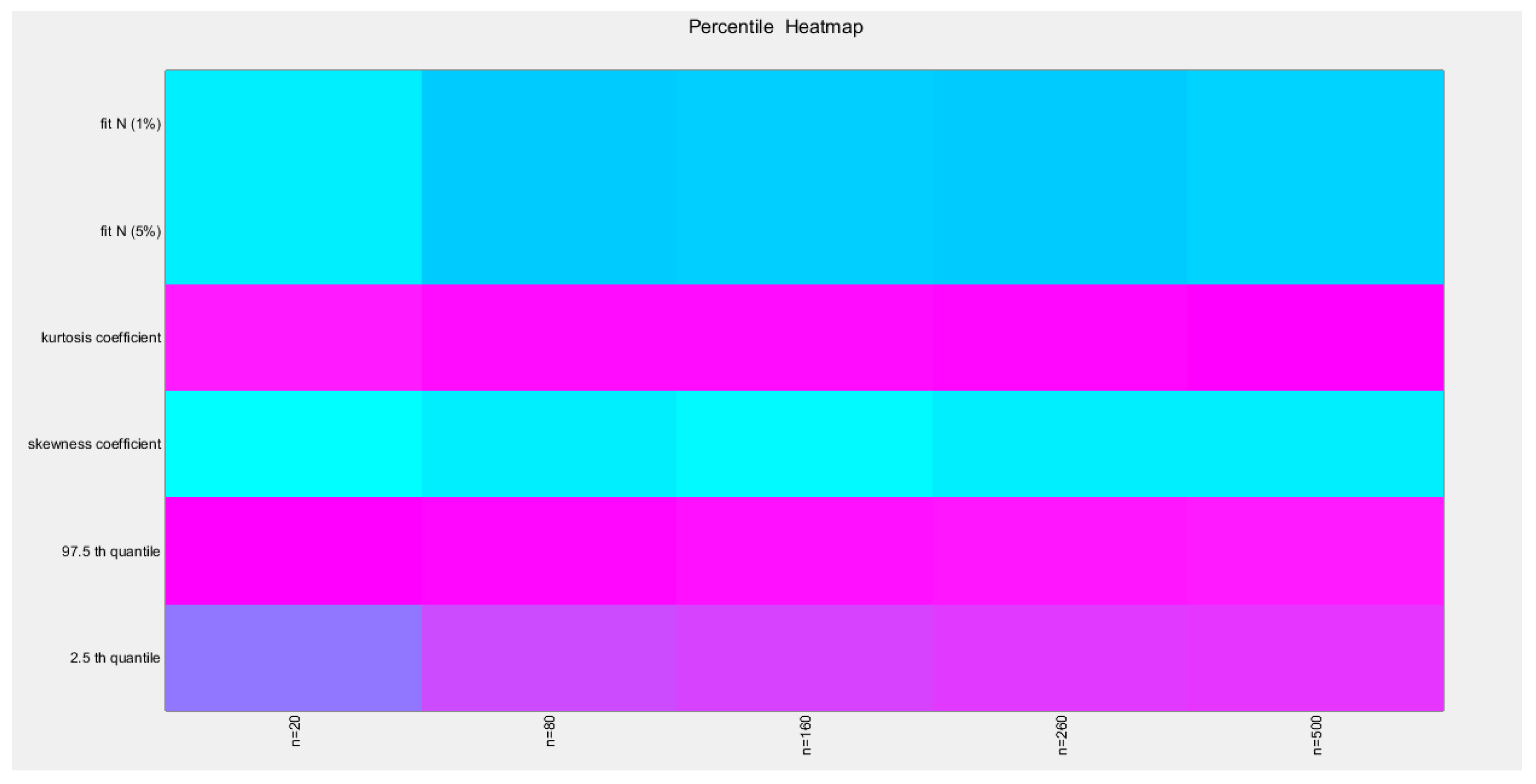
Figure 28.
shows the heat map of the indices of the empirical distribution of the estimated alpha using percentile method and how these indices change with changing the sample size from 20 to 500. (p values are shown).
Figure 28.
shows the heat map of the indices of the empirical distribution of the estimated alpha using percentile method and how these indices change with changing the sample size from 20 to 500. (p values are shown).
Table 8.
characteristics of empirical distribution of estimated alpha using WLS.
Table 8.
characteristics of empirical distribution of estimated alpha using WLS.
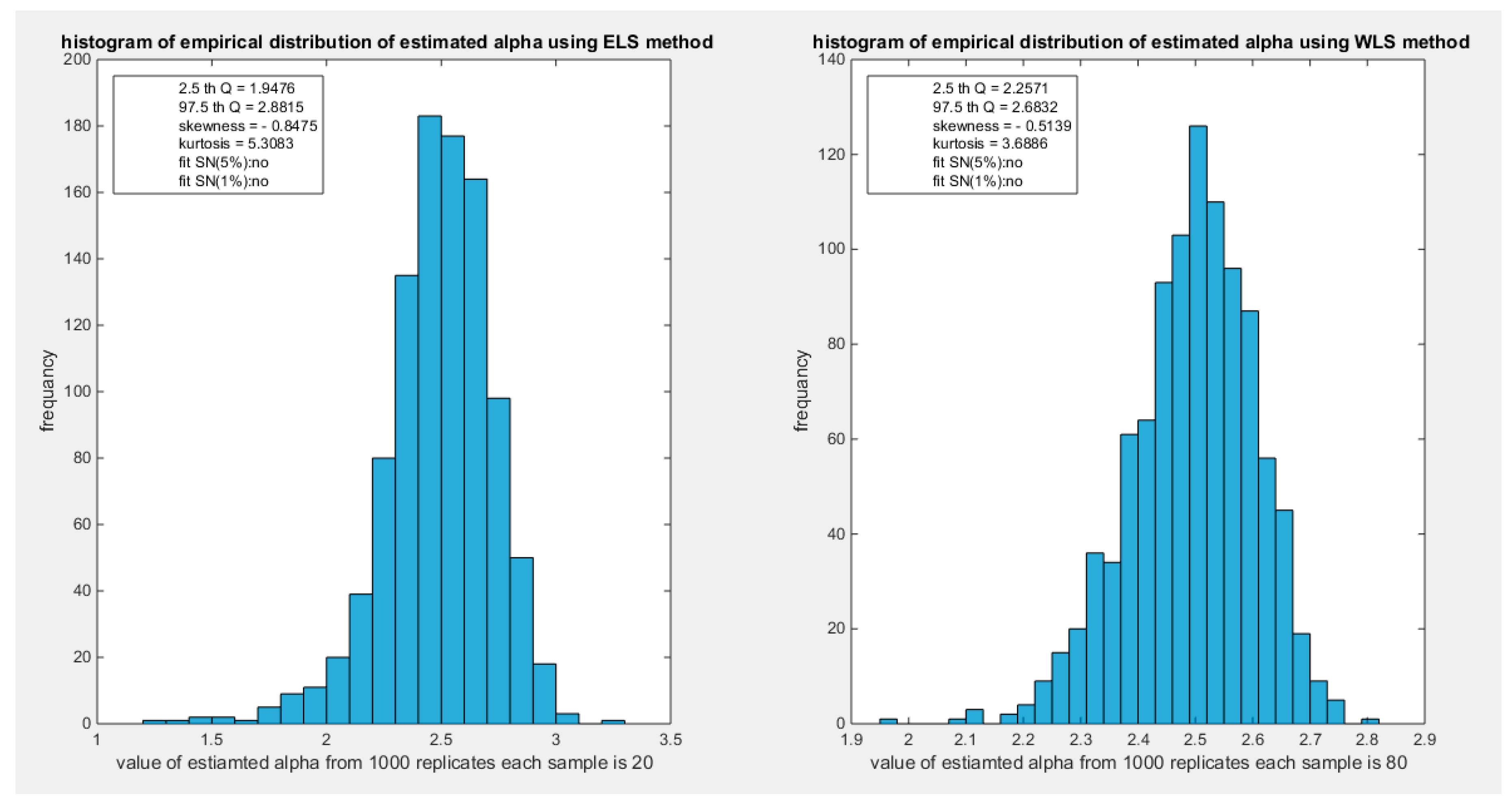
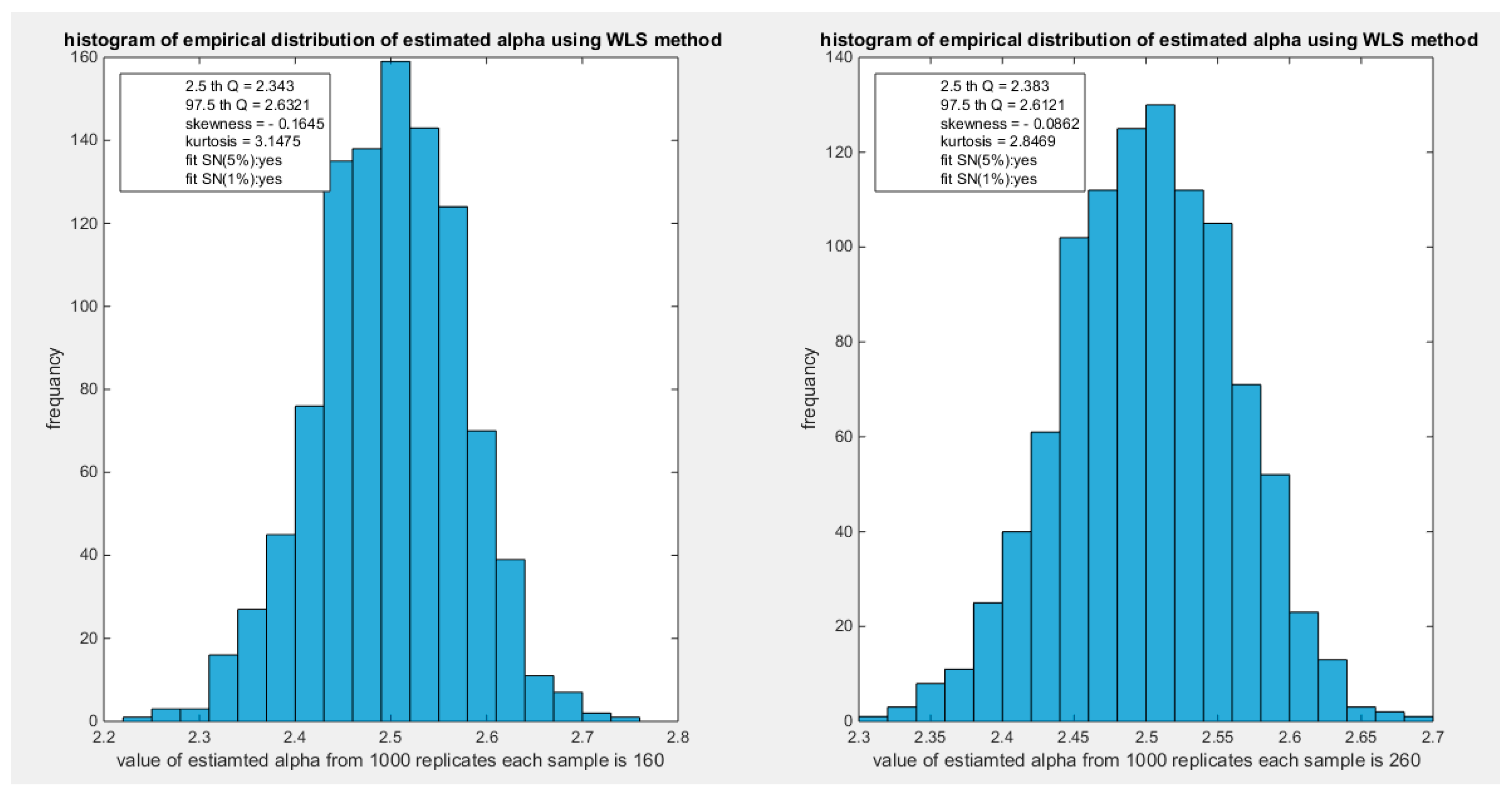
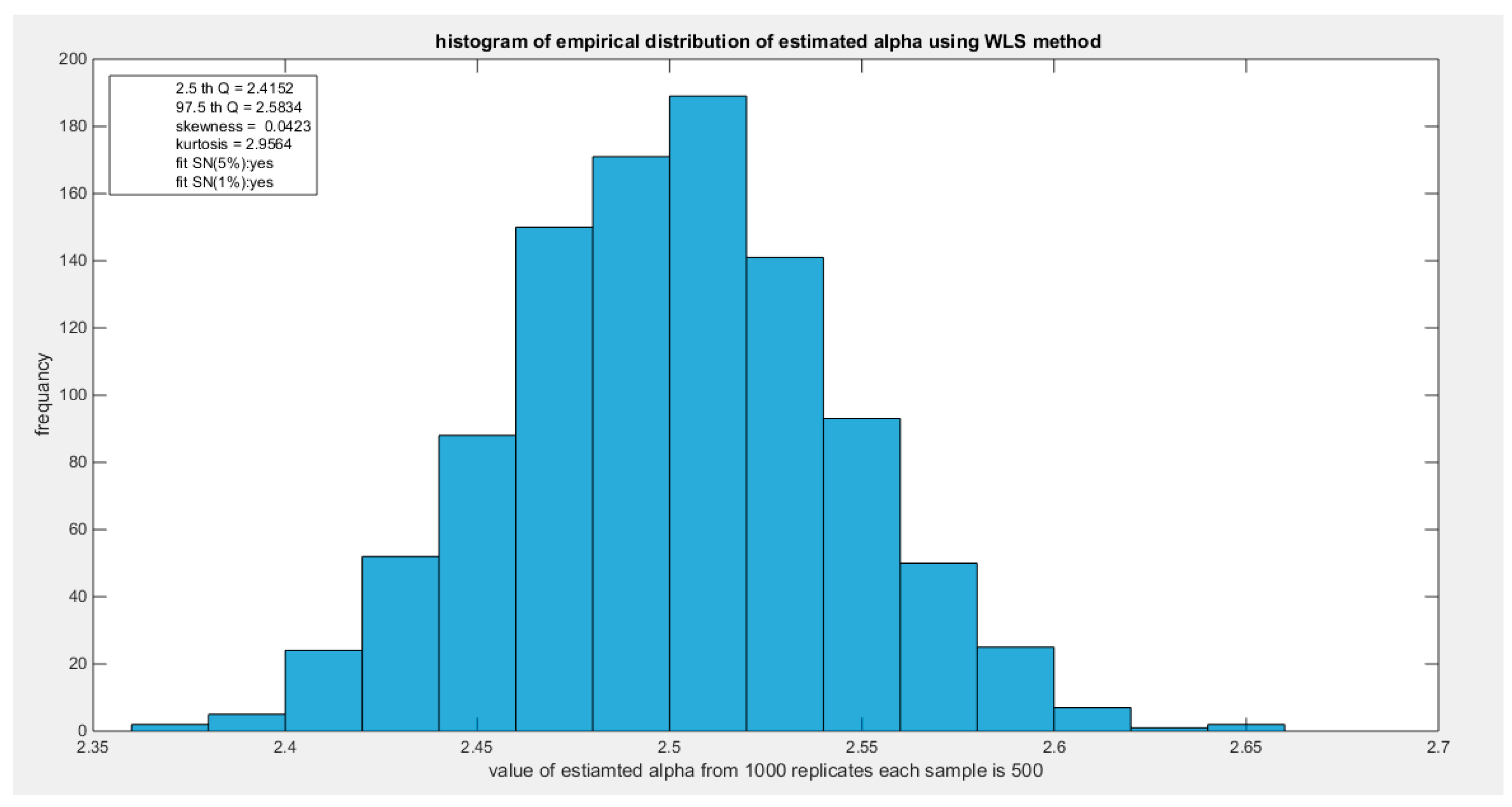
| WLS |
n=20 |
n=80 |
n=160 |
n=260 |
n=500 |
| 2.5 Q |
1.9476 |
2.2571 |
2.343 |
2.383 |
2.4152 |
| 97.5 Q |
2.8815 |
2.6832 |
2.6321 |
2.6121 |
2.5834 |
| Skewness |
-0.8475 |
-0.5139 |
-0.1645 |
-0.0862 |
0.0423 |
| Kurtosis |
5.3083 |
3.6886 |
3.1475 |
2.8469 |
2.9564 |
| Fit N (5%) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=0
(0.5) |
H0=0
(0.5) |
H0=0
(0.5) |
| Fit N (1%) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=0
(0.5) |
H0=0
(0.5) |
H0=0
(0.5) |
The empirical distribution of the estimated parameter alpha using WLS method is shown in Table 8. Each column represents a specific sample size with 1000 replicates in each size. Each column depicts the characteristics of the empirical distribution of the estimated alpha. The 2.5 th quantile and the 97.5 th quantile of the 1000 values of the estimated parameter in each sample shows that as the sample size increases the 2.5 th quantile rises while the 97.5 th quantile decreases. In other words, the distance between the two quantiles decreases as the sample size increases and this is reflected on the confidence interval (CI). As the sample size increases the CI becomes narrower. The distribution exhibits a mild left skewness and a high positive excess kurtosis (leptokurtic shape) at small sample size. As sample size increases the skewness decreases trying to approach the zero level (skewness of standard normal) and kurtosis decreases trying to approach the kurtosis of standard normal. The empirical distribution fits standard normal starting at size 160 and larger than this size at significance level 5% and 1% with associated P-value as shown in the table. H0=1 means reject the null hypothesis that states the parameter distribution follows the standard normal distribution. While H0=0 means fail to reject the null hypothesis. See the following Figures (29-32)
Figure 29.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using WLS method.
Figure 29.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using WLS method.
Figure 30.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using WLS method.
Figure 30.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using WLS method.
Figure 31.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n =500) using WLS method.
Figure 31.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n =500) using WLS method.
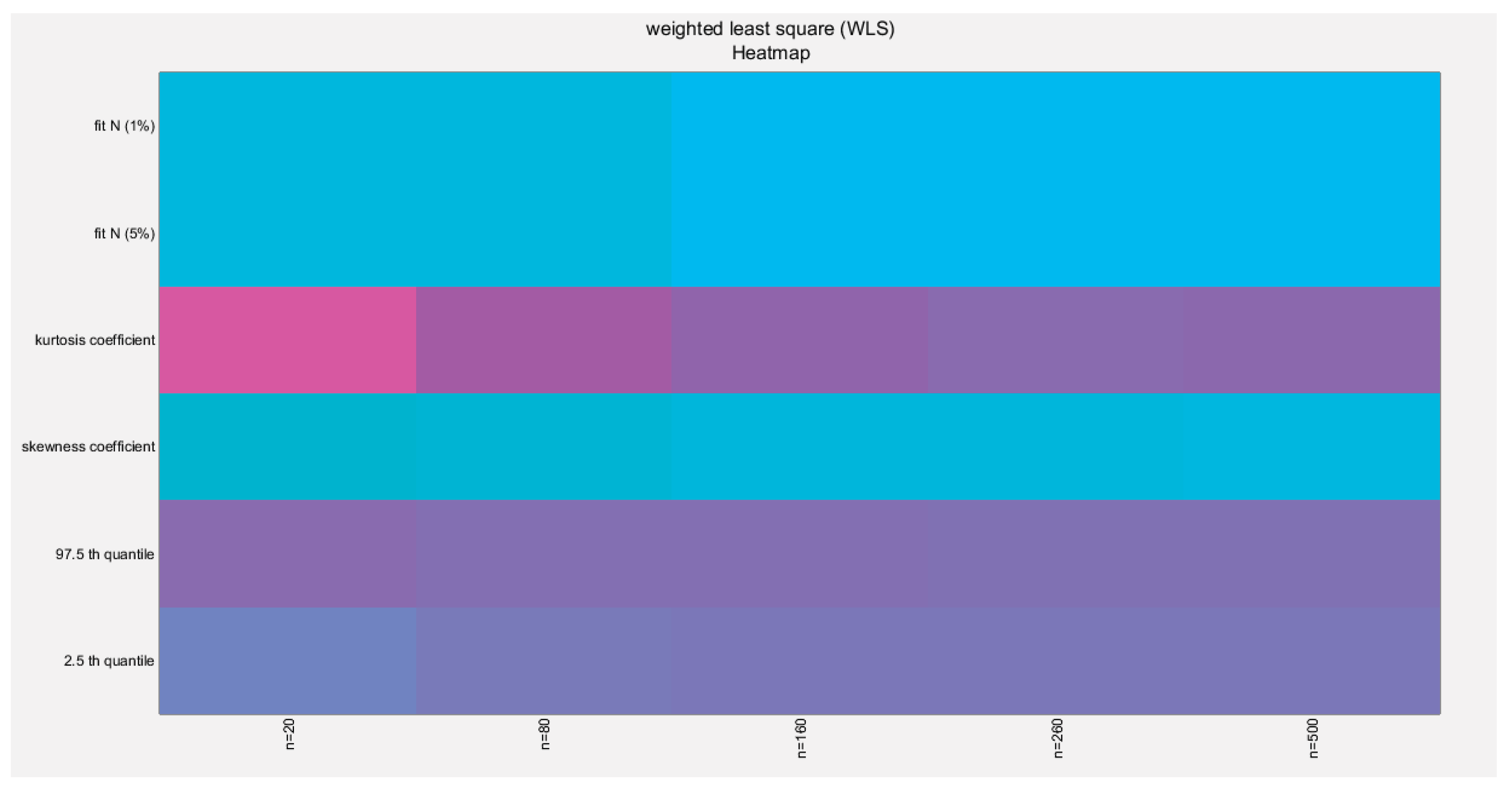
Figure 32.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (WLS) method and how these indices change with changing the sample size from 20 to 500. (p values are shown).
Figure 32.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (WLS) method and how these indices change with changing the sample size from 20 to 500. (p values are shown).
ALPHA LEVEL =0.5
A simulation study is conducted utilizing the following sample sizes
, and replicate N=1000 times. Various methods of estimation are utilized and compared with one another. The parameter alpha value chosen is .
Table 9 shows that as sample size increases, the estimated parameter approaches the true value. The different methods are approximately equally efficient to approach the true value regardless the sample size. Figure 33 visually illustrates these results.
Table 9.
shows the SE from the 1000 replicates for each method.
Table 9.
shows the SE from the 1000 replicates for each method.
| MEAN |
MOM |
MLE |
MPS |
AD |
PERC |
CVM |
LS |
WLS |
| n=20 |
0.4988 |
0.4888 |
0.4994 |
0.4925 |
0.5108 |
0.4921 |
0.4932 |
0.4961 |
| n=80 |
0.4989 |
0.4965 |
0.5002 |
0.4974 |
0.5033 |
0.4975 |
0.4978 |
0.4983 |
| n=160 |
0.4992 |
0.498 |
0.5001 |
0.4985 |
0.5016 |
0.4987 |
0.4989 |
0.4991 |
| n=260 |
0.4997 |
0.4991 |
0.5006 |
0.4995 |
0.5013 |
0.4996 |
0.4996 |
0.4997 |
| n=500 |
0.4999 |
0.4995 |
0.5004 |
0.4997 |
0.5008 |
0.4998 |
0.4999 |
0.4999 |
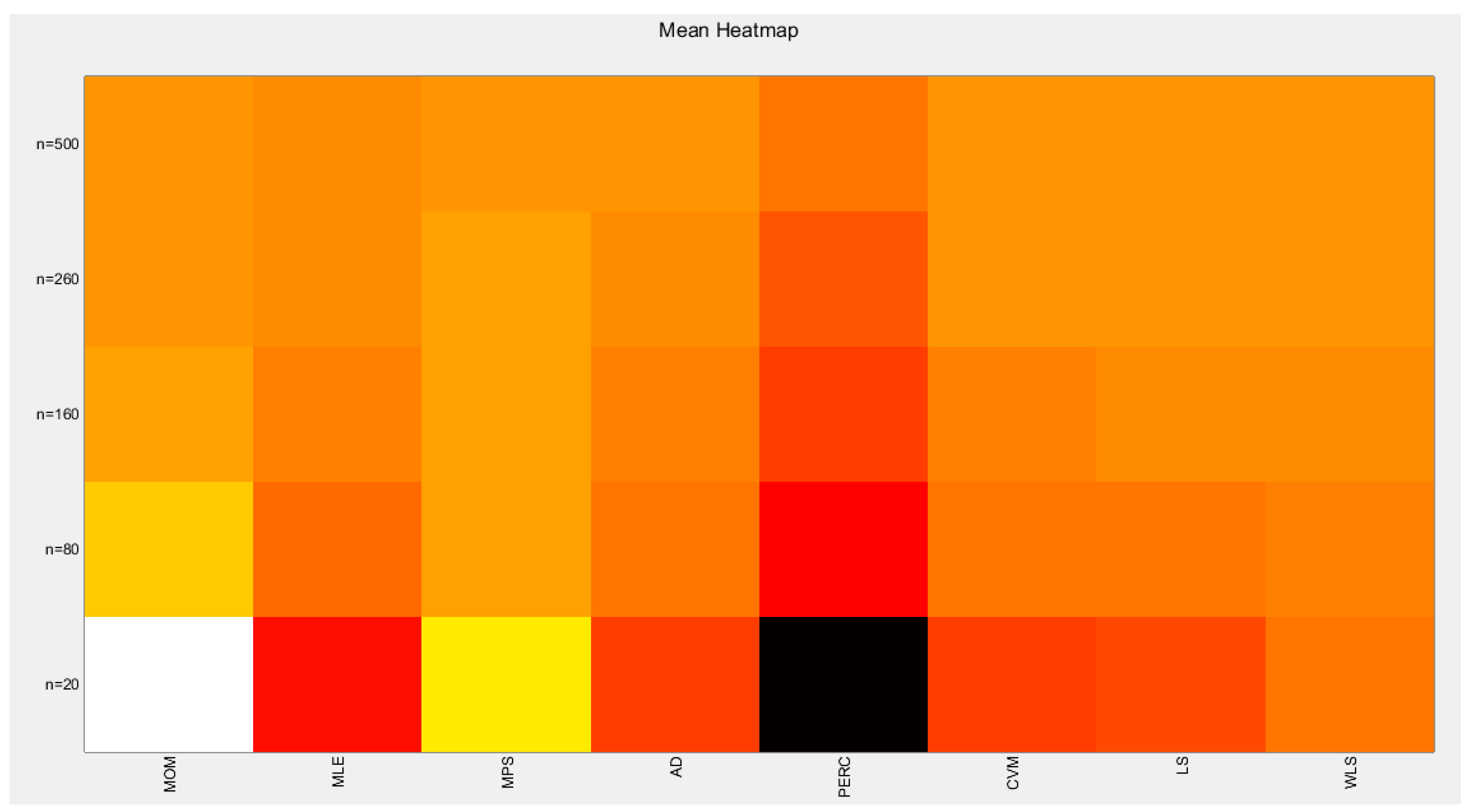
Figure 33.
shows the Heat-map for the mean of the estimated alpha parameter from running the simulation using different estimation methods with alpha value 0.5.
Figure 33.
shows the Heat-map for the mean of the estimated alpha parameter from running the simulation using different estimation methods with alpha value 0.5.
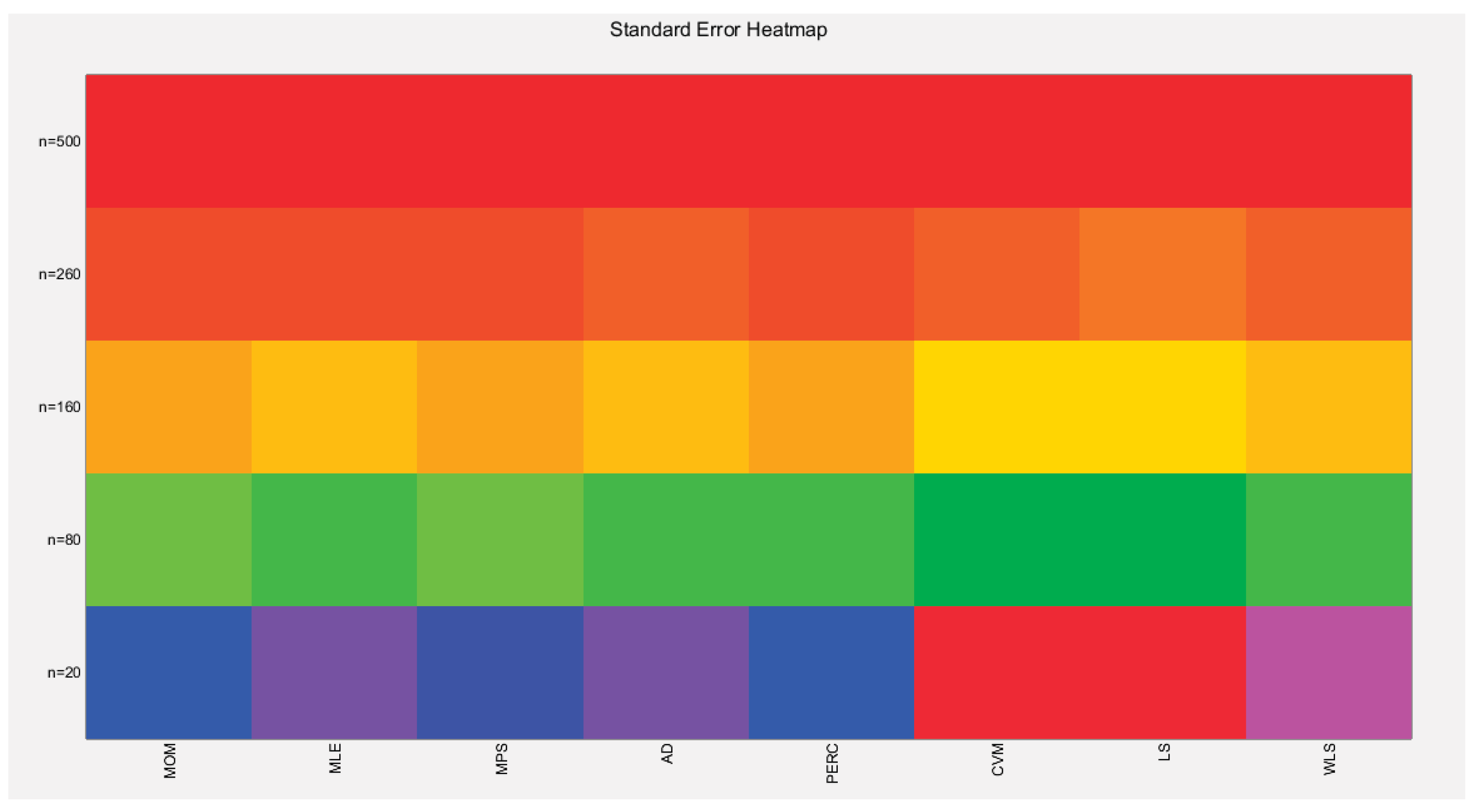
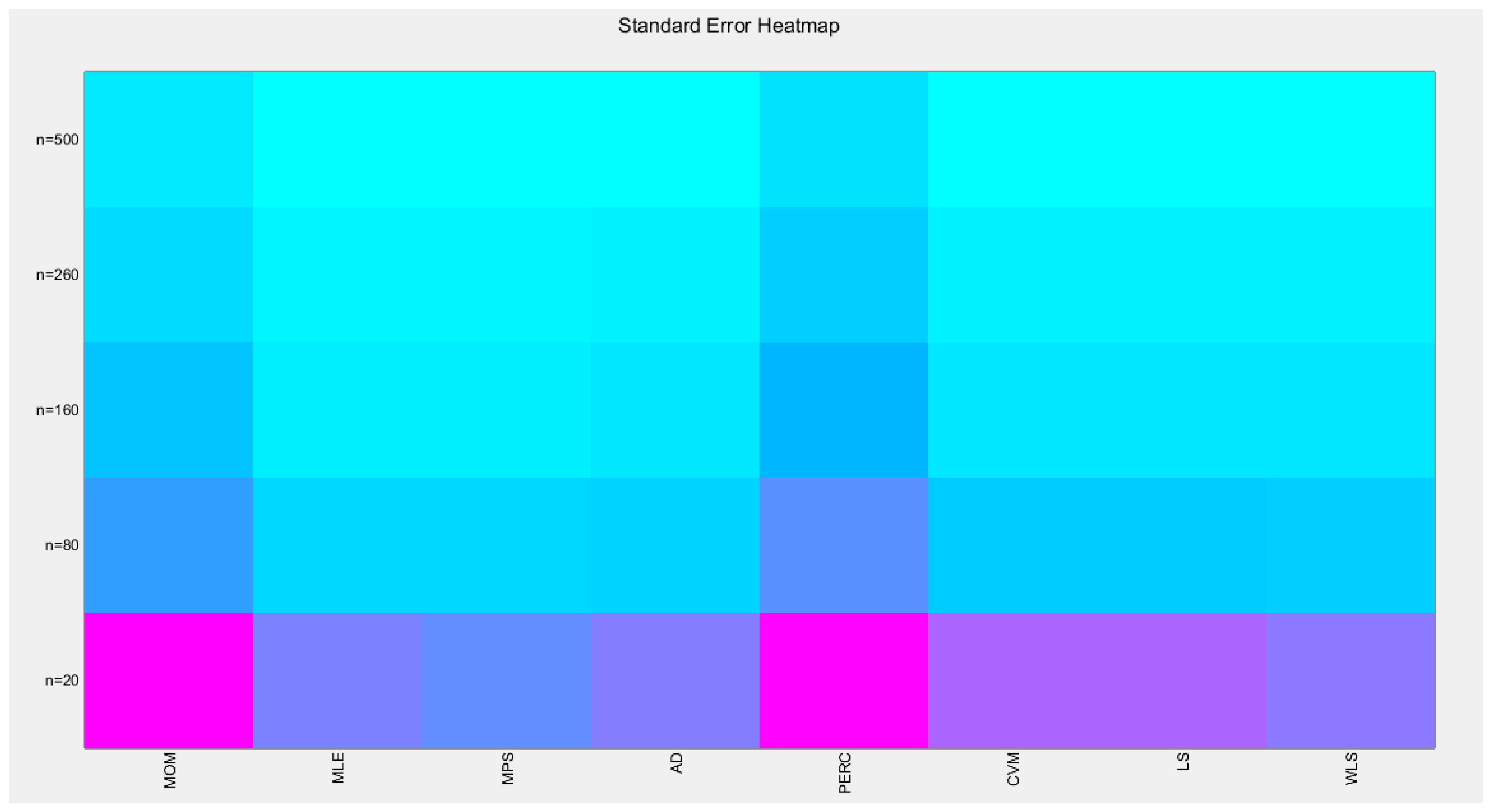
Table 10 shows that as sample size increases the standard error (SE) decreases. CVM and LS methods have the highest SE at all different sample sizes. The MOM & MPS have the lowest SE at n=500. MOM and MPS have nearly equal results at different sample sizes. This is also true as regards the pair of AD and WLS methods and the pair of CVM and LS methods. Figure 34 visually demonstrates these results.
Table 10.
shows the SE from the 1000 replicates for each method.
Table 10.
shows the SE from the 1000 replicates for each method.
| SE |
MOM |
MLE |
MPS |
AD |
PERC |
CVM |
LS |
WLS |
| n=20 |
0.0013 |
0.0015 |
0.0014 |
0.0015 |
0.0013 |
0.0019 |
0.0019 |
0.0016 |
| n=80 |
0.00065 |
0.00068 |
0.00066 |
0.00069 |
0.00067 |
0.00074 |
0.00074 |
0.00069 |
| n=160 |
0.00046 |
0.00047 |
0.00046 |
0.00049 |
0.00046 |
0.00051 |
0.00051 |
0.00049 |
| n=260 |
0.00035 |
0.00035 |
0.00035 |
0.00037 |
0.00035 |
0.00038 |
0.00039 |
0.00037 |
| n=500 |
0.00026 |
0.00027 |
0.00026 |
0.00027 |
0.00027 |
0.00028 |
0.00028 |
0.00027 |
Figure 34.
shows the Heat-map for the SE of the estimated alpha parameter from running the simulation using different estimation methods with alpha value 0.5.
Figure 34.
shows the Heat-map for the SE of the estimated alpha parameter from running the simulation using different estimation methods with alpha value 0.5.
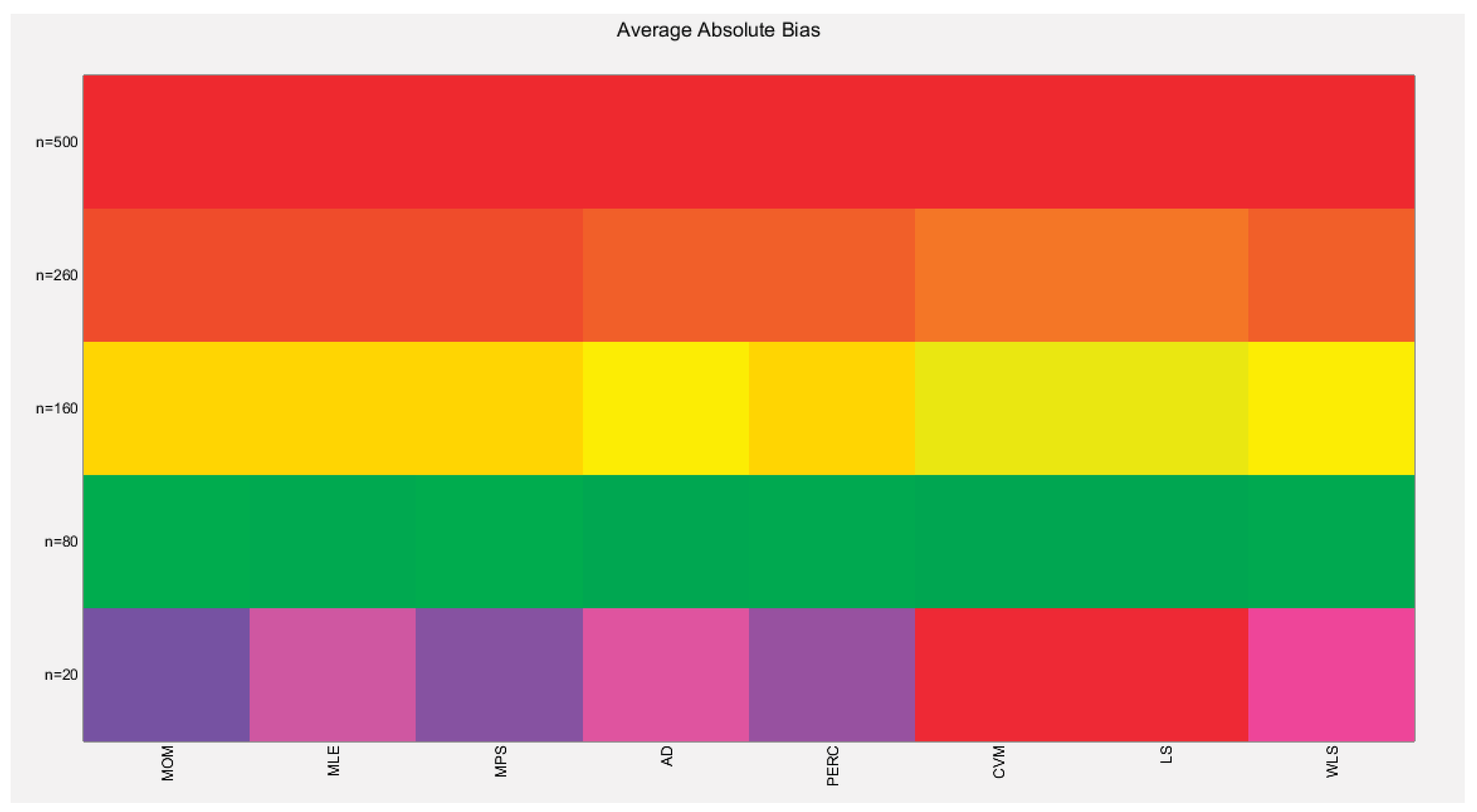
Table 11 shows that as sample size increases the average absolute bias (AAB) decreases. CVM and LS methods have the highest AAB at all different sample sizes. The MOM, MLE, & MPS have the lowest AAB at n=500. The MOM, MLE, & MPS have nearly equal results at different sample sizes. This is also true as regards the pair of AD and WLS methods and the pair of CVM and LS methods. Figure 35 visually demonstrates these results.
Table 11.
shows the SE from the 1000 replicates for each method.
Table 11.
shows the SE from the 1000 replicates for each method.
| AAB |
MOM |
MLE |
MPS |
AD |
PERC |
CVM |
LS |
WLS |
| n=20 |
0.0332 |
0.0361 |
0.0337 |
0.0367 |
0.0344 |
0.0418 |
0.0418 |
0.0378 |
| n=80 |
0.0166 |
0.0171 |
0.0167 |
0.0176 |
0.0172 |
0.0184 |
0.0184 |
0.0175 |
| n=160 |
0.0117 |
0.0119 |
0.0118 |
0.0122 |
0.0118 |
0.0127 |
0.0127 |
0.0122 |
| n=260 |
0.0085 |
0.0086 |
0.0085 |
0.0092 |
0.0088 |
0.0096 |
0.0097 |
0.0091 |
| n=500 |
0.0066 |
0.0066 |
0.0066 |
0.0068 |
0.0068 |
0.0070 |
0.0071 |
0.0068 |
Figure 35.
shows the Heat-map for the AAB of the estimated alpha parameter from running the simulation using different estimation methods with alpha value 0.5.
Figure 35.
shows the Heat-map for the AAB of the estimated alpha parameter from running the simulation using different estimation methods with alpha value 0.5.
Table 12.
shows the MSE from the 1000 replicates for each method.
Table 12.
shows the MSE from the 1000 replicates for each method.
| MSE |
MOM |
MLE |
MPS |
AD |
PERC |
CVM |
LS |
WLS |
| n=20 |
0.0017 |
0.0025 |
0.002 |
0.0024 |
0.0019 |
0.0037 |
0.0037 |
0.0026 |
| n=80 |
0.00043 |
0.00047 |
0.00044 |
0.00049 |
0.000455 |
0.00055 |
0.00056 |
0.00049 |
| n=160 |
0.0002 |
0.00022 |
0.00022 |
0.00024 |
0.00021 |
0.00026 |
0.00026 |
0.00024 |
| n=260 |
0.00012 |
0.00012 |
0.00012 |
0.00014 |
0.00013 |
0.00015 |
0.00015 |
0.00013 |
| n=500 |
0.000068 |
0.000071 |
0.000070 |
0.000075 |
0.000071 |
0.00008 |
0.00008 |
0.000074 |
Table 13.
shows the MRE from the 1000 replicates for each method.
Table 13.
shows the MRE from the 1000 replicates for each method.
| MRE |
MOM |
MLE |
MPS |
AD |
PERC |
CVM |
LS |
WLS |
| n=20 |
0.0664 |
0.0722 |
0.0674 |
0.0735 |
0.0689 |
0.0836 |
0.0836 |
0.0756 |
| n=80 |
0.0333 |
0.0342 |
0.0333 |
0.0351 |
0.0344 |
0.0368 |
0.0367 |
0.0351 |
| n=160 |
0.0233 |
0.0238 |
0.0235 |
0.0244 |
0.0237 |
0.0254 |
0.0254 |
0.0243 |
| n=260 |
0.017 |
0.0171 |
0.0170 |
0.0183 |
0.0176 |
0.0192 |
0.0194 |
0.0183 |
| n=500 |
0.0131 |
0.0133 |
0.0132 |
0.013 |
0.0135 |
0.014 |
0.0141 |
0.0136 |
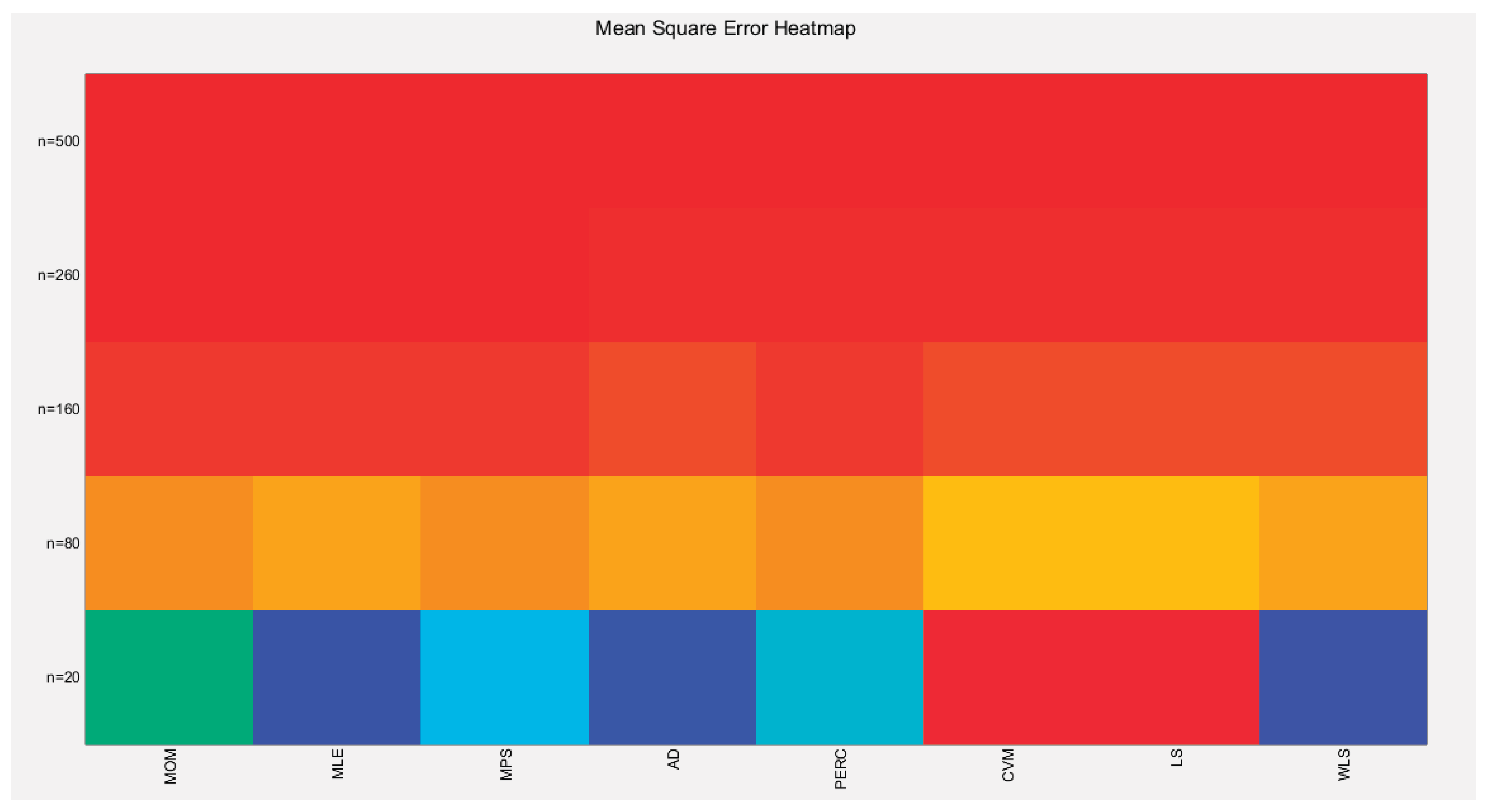
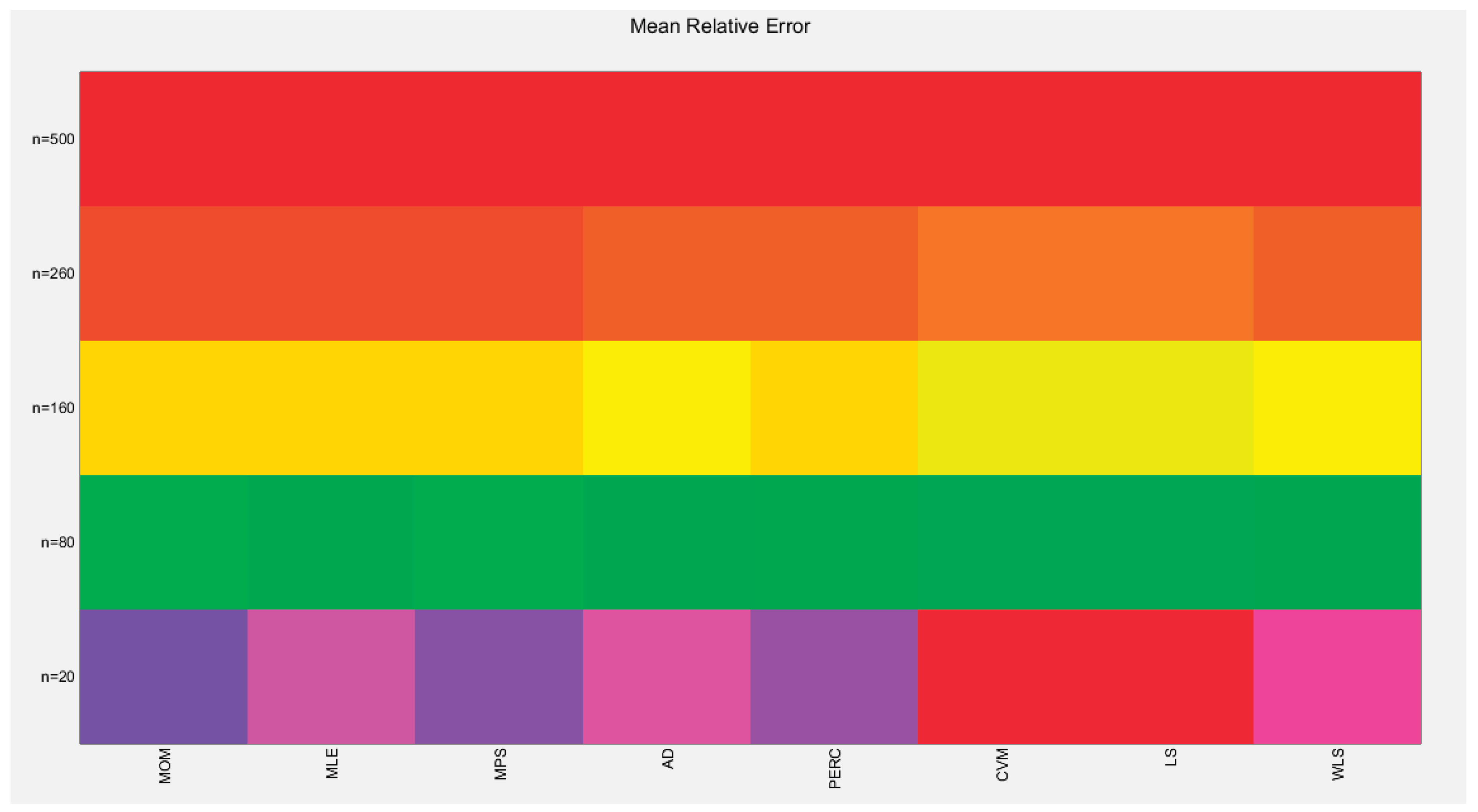
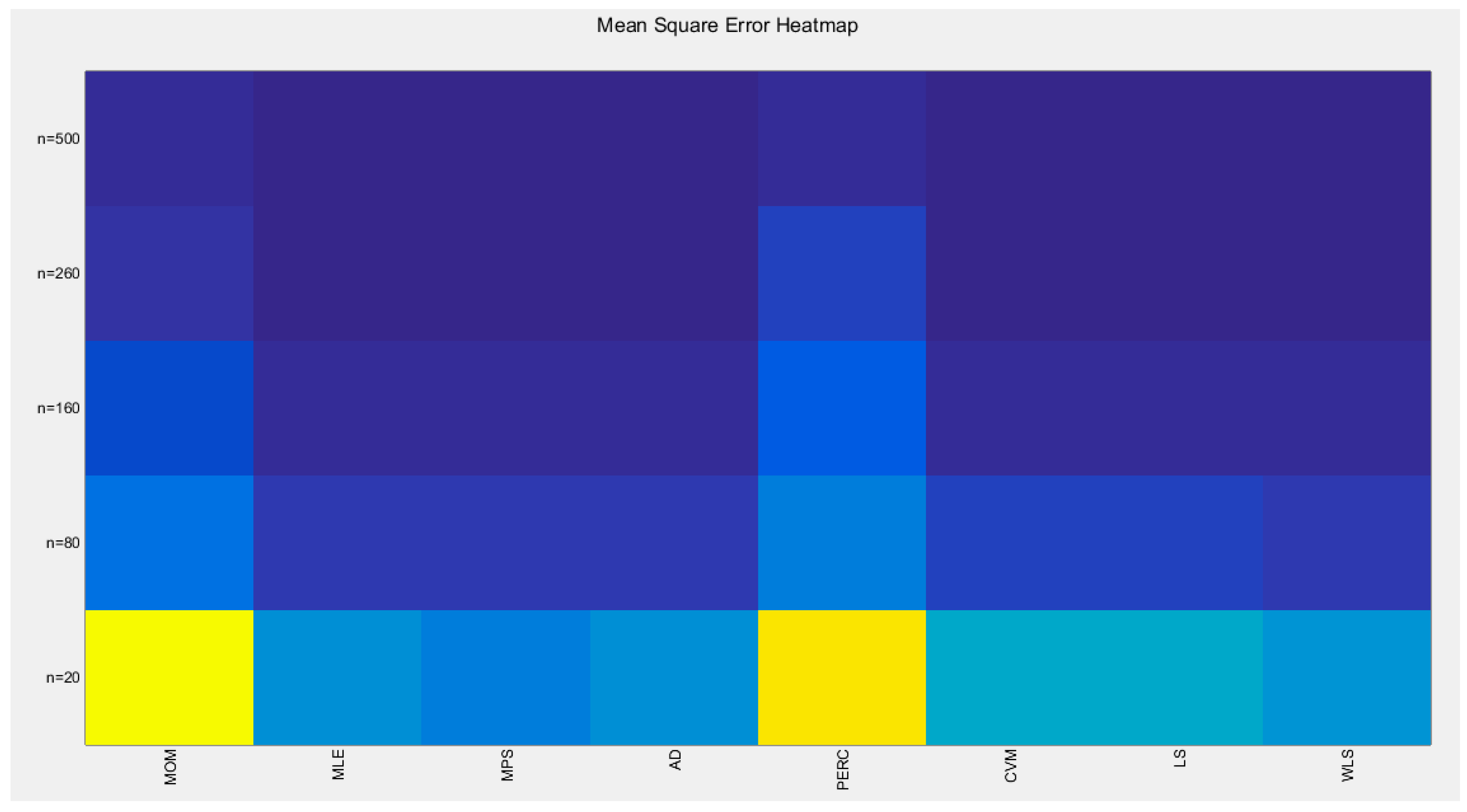
The tables indicate that increasing the sample size leads to a decrease in the SE, AAB, MSE and MRE indices. For each method used, the indices decrease as the sample size increases. The values obtained from the MLE and MPS methods are nearly equal, especially with larger sample sizes (n=260 and n=500). Similarly, the AD and WLS methods yield comparable results. Additionally, the CVM and LS methods show approximately equal indices as the sample size increases. Overall, the methods demonstrate consistent results regarding the estimation values. Figure 36-37 display these findings
Figure 36.
shows the Heat-map for the MSE of the estimated alpha parameter from running the simulation using different estimation methods with alpha value 0.5.
Figure 36.
shows the Heat-map for the MSE of the estimated alpha parameter from running the simulation using different estimation methods with alpha value 0.5.
Figure 37.
shows the Heat-map for the MRE of the estimated alpha parameter from running the simulation using different estimation methods with alpha value 0.5.
Figure 37.
shows the Heat-map for the MRE of the estimated alpha parameter from running the simulation using different estimation methods with alpha value 0.5.
Table 14.
characteristics of empirical distribution of estimated alpha using MOM.
Table 14.
characteristics of empirical distribution of estimated alpha using MOM.
| MOM |
n=20 |
n=80 |
n=160 |
n=260 |
n=500 |
| 2.5 Q |
0.424 |
0.4607 |
0.4704 |
0.4776 |
0.4830 |
| 97.5 Q |
0.5801 |
0.5424 |
0.5277 |
0.5221 |
0.5156 |
| Skewness |
0.1049 |
0.0987 |
0.0338 |
-0.0750 |
-0.1145 |
| Kurtosis |
2.892 |
2.9217 |
2.9082 |
3.2618 |
3.0662 |
| Fit N (5%) |
H0=0
(0.1041) |
H0=0
(0.5) |
H0=0
(0.2235) |
H0=1
(0.0222) |
H0=0
(0.3337) |
| Fit N (1%) |
H0=0
(0. 1041) |
H0=0
(0.5) |
H0=0
(0. 2235) |
H0=0
(0.0222) |
H0=0
(0. 3337) |
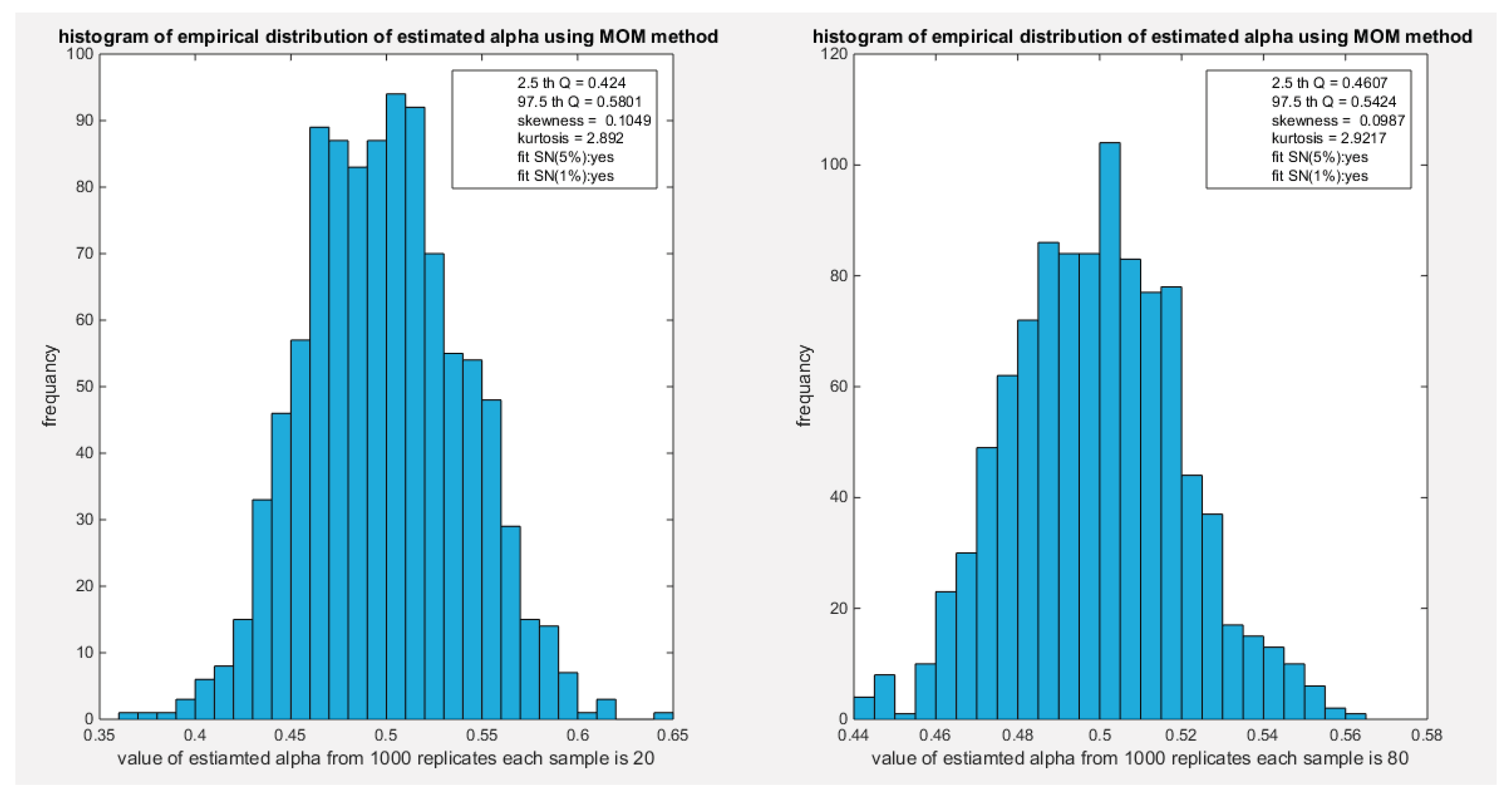
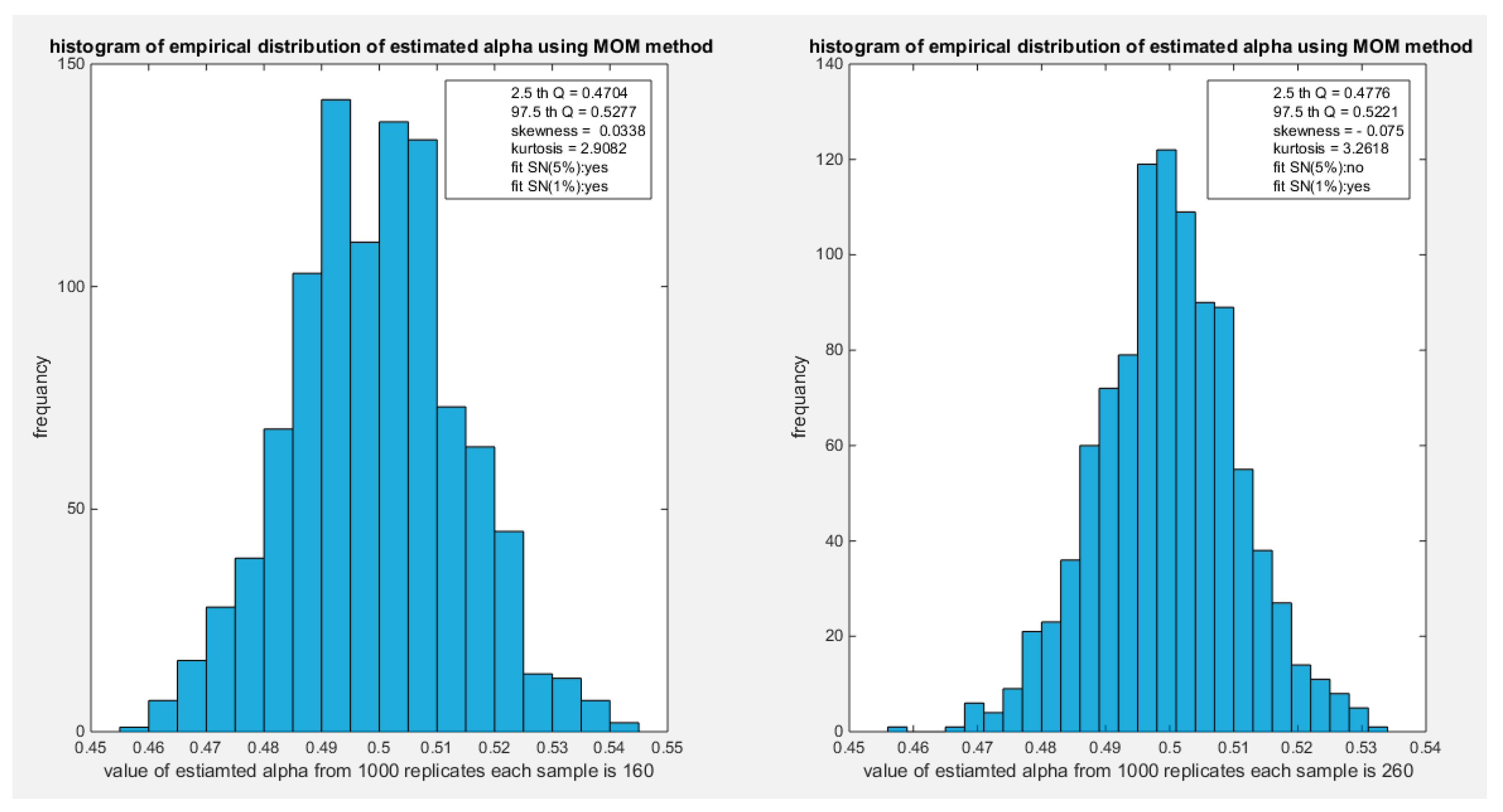
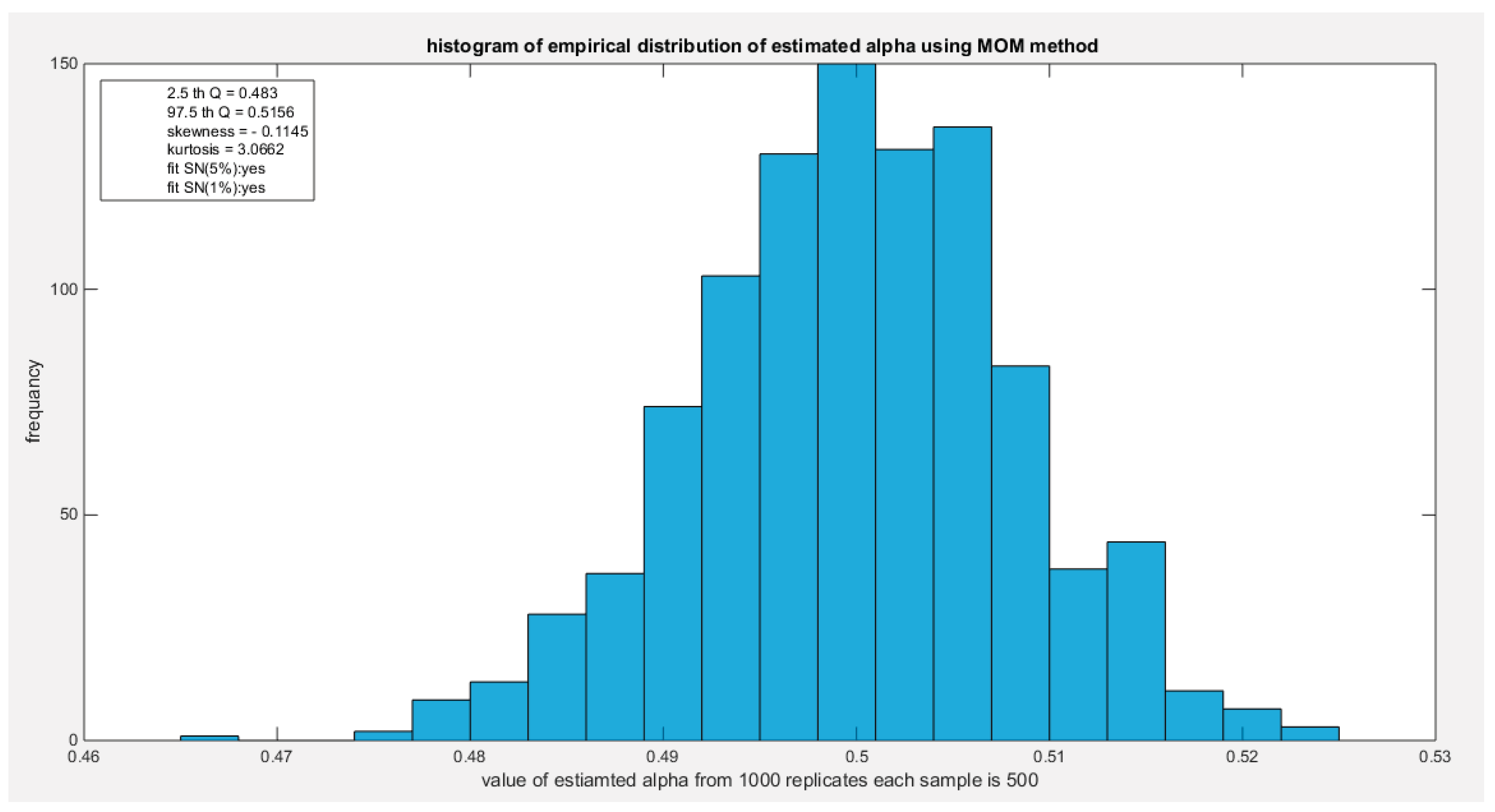
The empirical distribution of the estimated parameter alpha using MOM is shown in Table 14. Each column represents a specific sample size with 1000 replicates in each size. The 2.5 th quantile and the 97.5 th quantile of the 1000 values of the estimated parameter in each sample shows that as the sample size increases the 2.5 quantile rises while the 97.5 quantile decreases. In other words, the distance between the two quantiles decreases as the sample size increases and this is reflected on the confidence interval (CI). As the sample size increases the CI becomes narrower. The distribution exhibits a mild right skewness and a mild negative excess kurtosis (platykurtic shape) at small sample size. As sample size increases the skewness decreases trying to approach the zero level (skewness of standard normal) and kurtosis increases trying to approach the kurtosis of standard normal. The empirical distribution does not fit standard normal at size n=260 and at 5% significance level, otherwise, it fits standard normal distribution at different sample sizes and at significance level 5% and 1% with associated P-value as shown in the table. H0=1 means reject the null hypothesis that states the parameter distribution follows the standard normal distribution. While H0=0 means fail to reject the null hypothesis. See the following Figures (38-41)
Figure 38.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using MOM method.
Figure 38.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using MOM method.
Figure 39.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using MOM method.
Figure 39.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using MOM method.
Figure 40.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n =500) using MOM method.
Figure 40.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n =500) using MOM method.
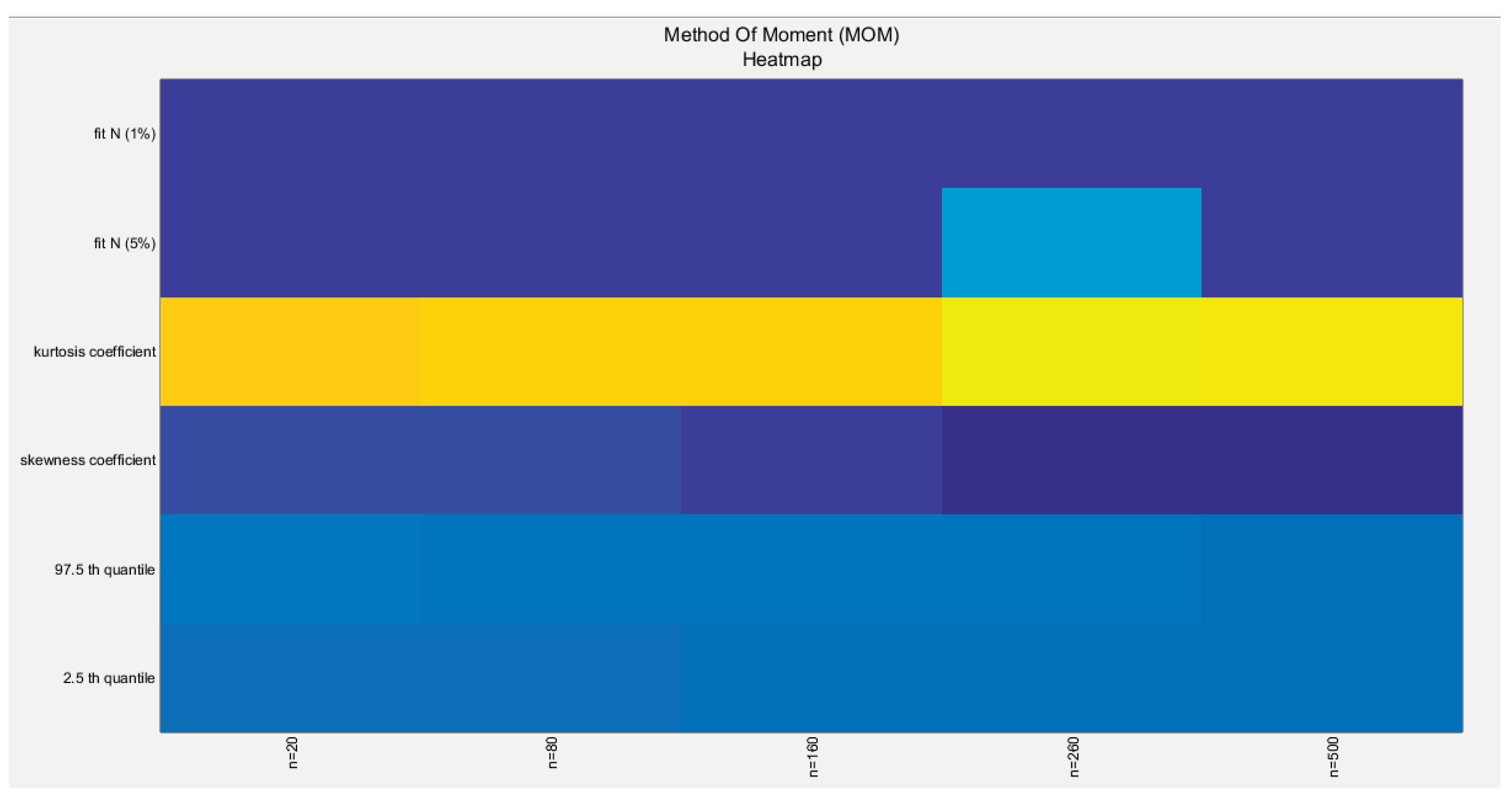
Figure 41.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (MOM) method and how these indices change with changing the sample size from 20 to 500.( h0 values reported).
Figure 41.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (MOM) method and how these indices change with changing the sample size from 20 to 500.( h0 values reported).
Table 15.
characteristics of empirical distribution of estimated alpha using MLE.
Table 15.
characteristics of empirical distribution of estimated alpha using MLE.
| MLE |
n=20 |
n=80 |
n=160 |
n=260 |
n=500 |
| 2.5 Q |
0.381 |
0.4508 |
0.465 |
0.474 |
0.4814 |
| 97.5 Q |
0.5569 |
0.5344 |
0.524 |
0.5192 |
0.5144 |
| Skewness |
-1.6493 |
-0.5355 |
-0.3951 |
-0.4555 |
-0.3762 |
| Kurtosis |
9.6769 |
3.4636 |
3.1770 |
3.6191 |
3.3215 |
| Fit N (5%) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=1
(0.0098) |
| Fit N (1%) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=1
(0.0098) |
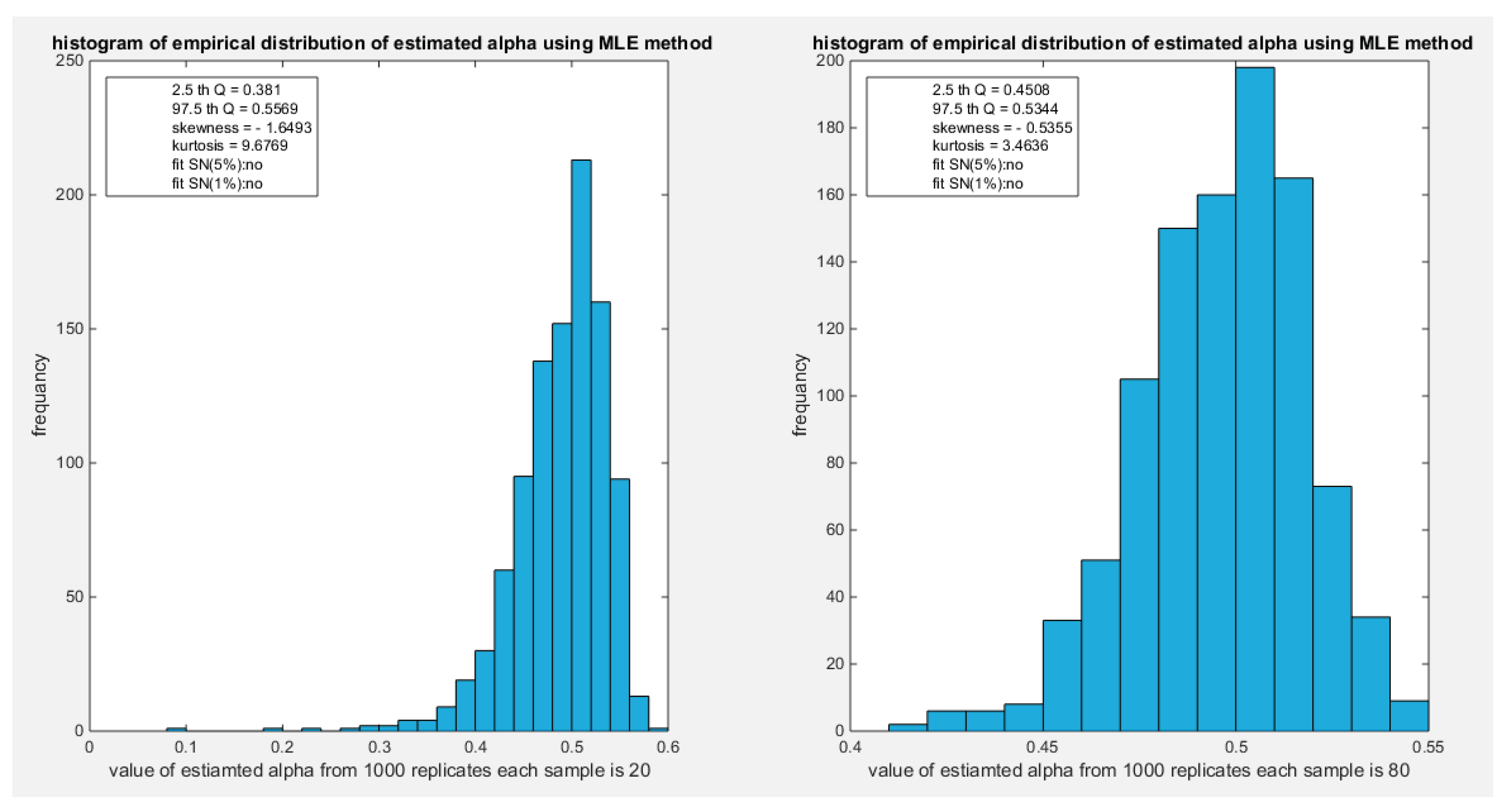
The empirical distribution of the estimated parameter alpha using MLE is shown in Table 15. Each column represents a specific sample size with 1000 replicates in each size. The 2.5 th quantile and the 97.5 th quantile of the 1000 values of the estimated parameter in each sample shows that as the sample size increases the 2.5 quantile rises while the 97.5 quantile decreases. In other words, the distance between the two quantiles decreases as the sample size increases and this is reflected on the confidence interval (CI). As the sample size increases the CI becomes narrower. The distribution exhibits a moderate left skewness and a high positive excess kurtosis (leptokurtic shape) at small sample size. As sample size increases the skewness decreases trying to approach the zero level (skewness of standard normal) and kurtosis decreases trying to approach the kurtosis of standard normal. The empirical distribution does not fit standard normal at any size and at either significance level 5% or 1% with associated P-value as shown in the table. The distribution may fit the standard normal at sample sizes more than 500. H0=1 means reject the null hypothesis that states the parameter distribution follows the standard normal distribution. While H0=0 means fail to reject the null hypothesis. See the following Figures (42-45).
Figure 42.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using MLE method.
Figure 42.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using MLE method.
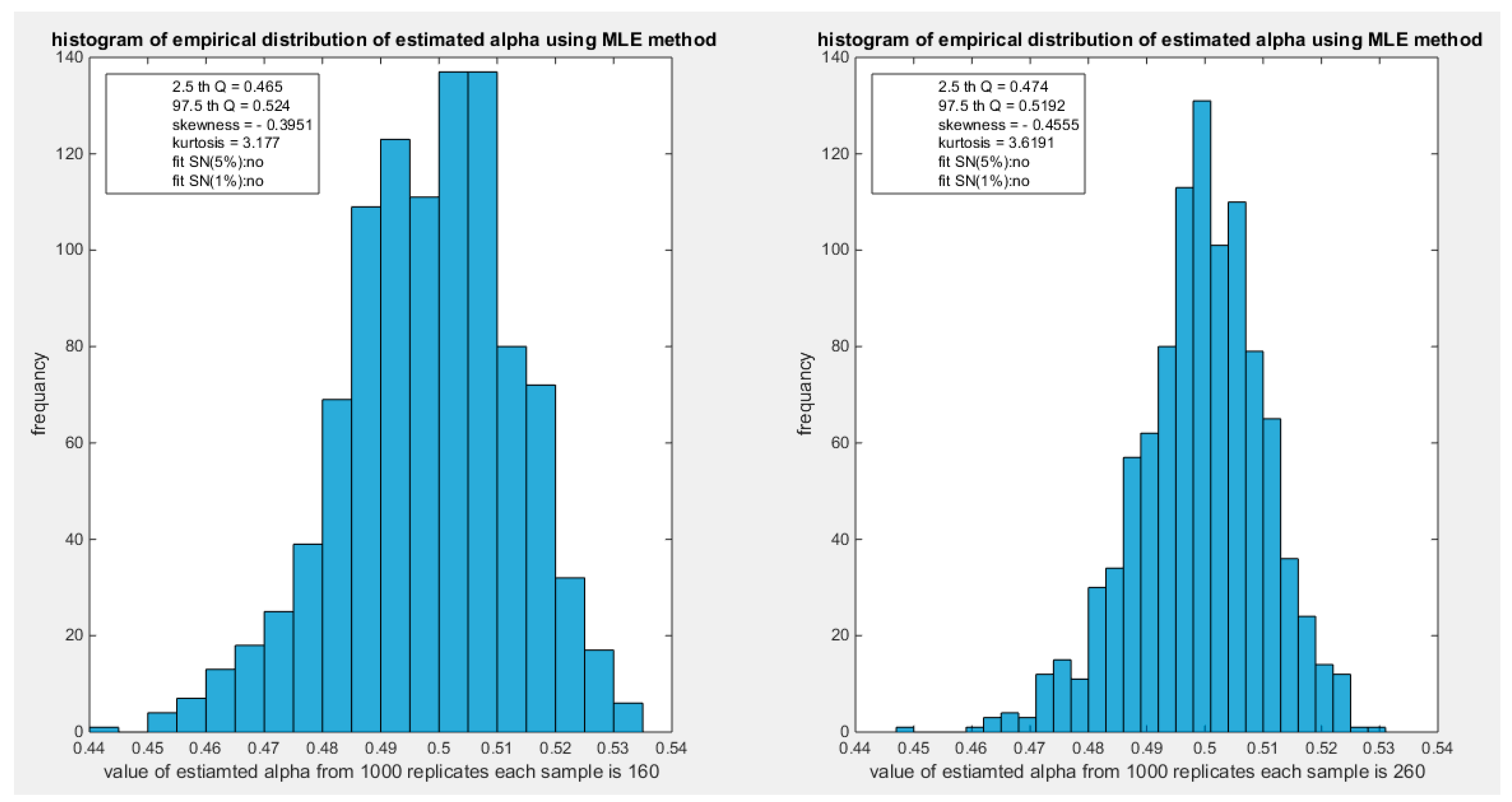
Figure 43.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using MLE method.
Figure 43.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using MLE method.
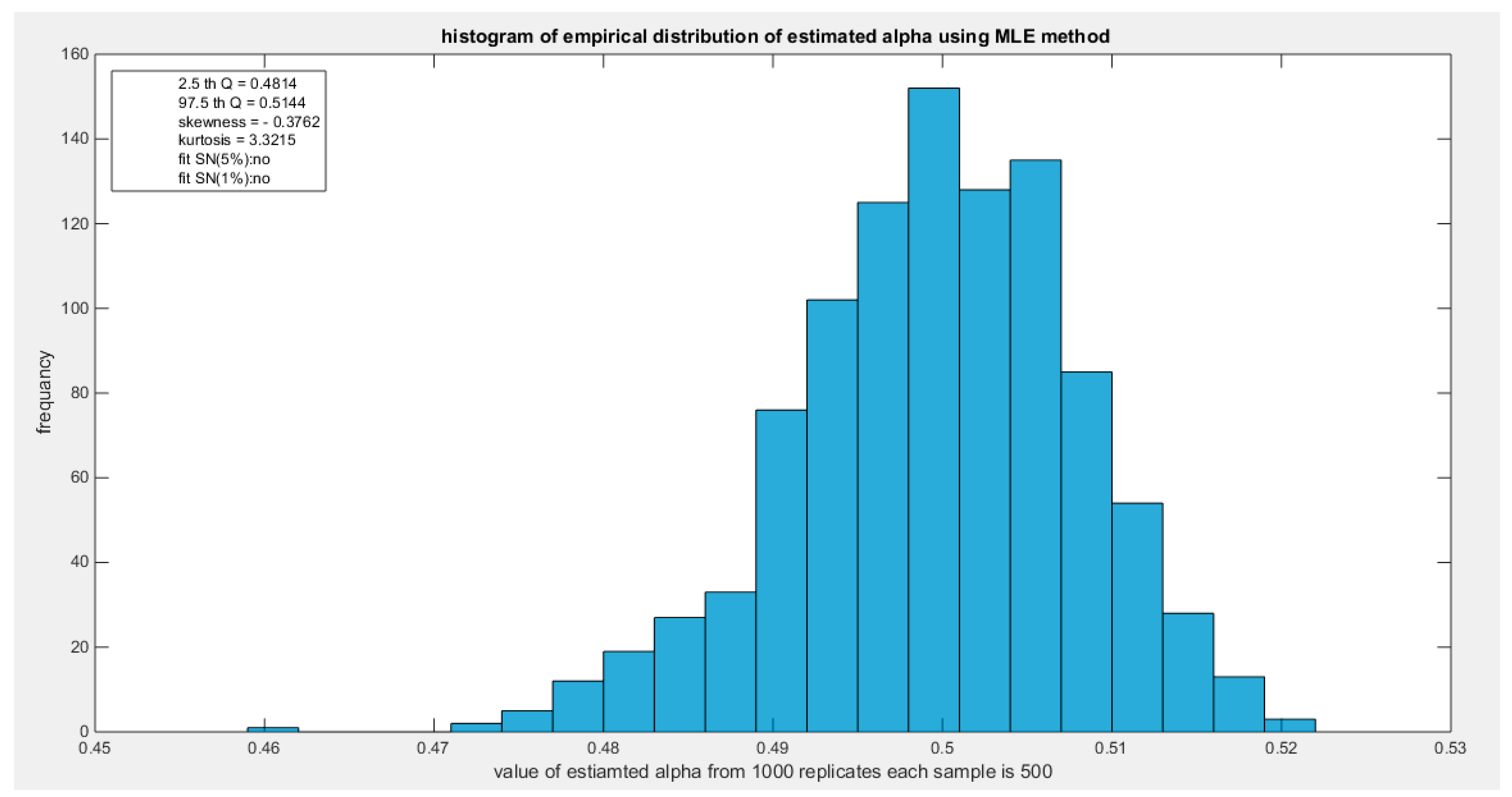
Figure 44.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n =500) using MLE method.
Figure 44.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n =500) using MLE method.
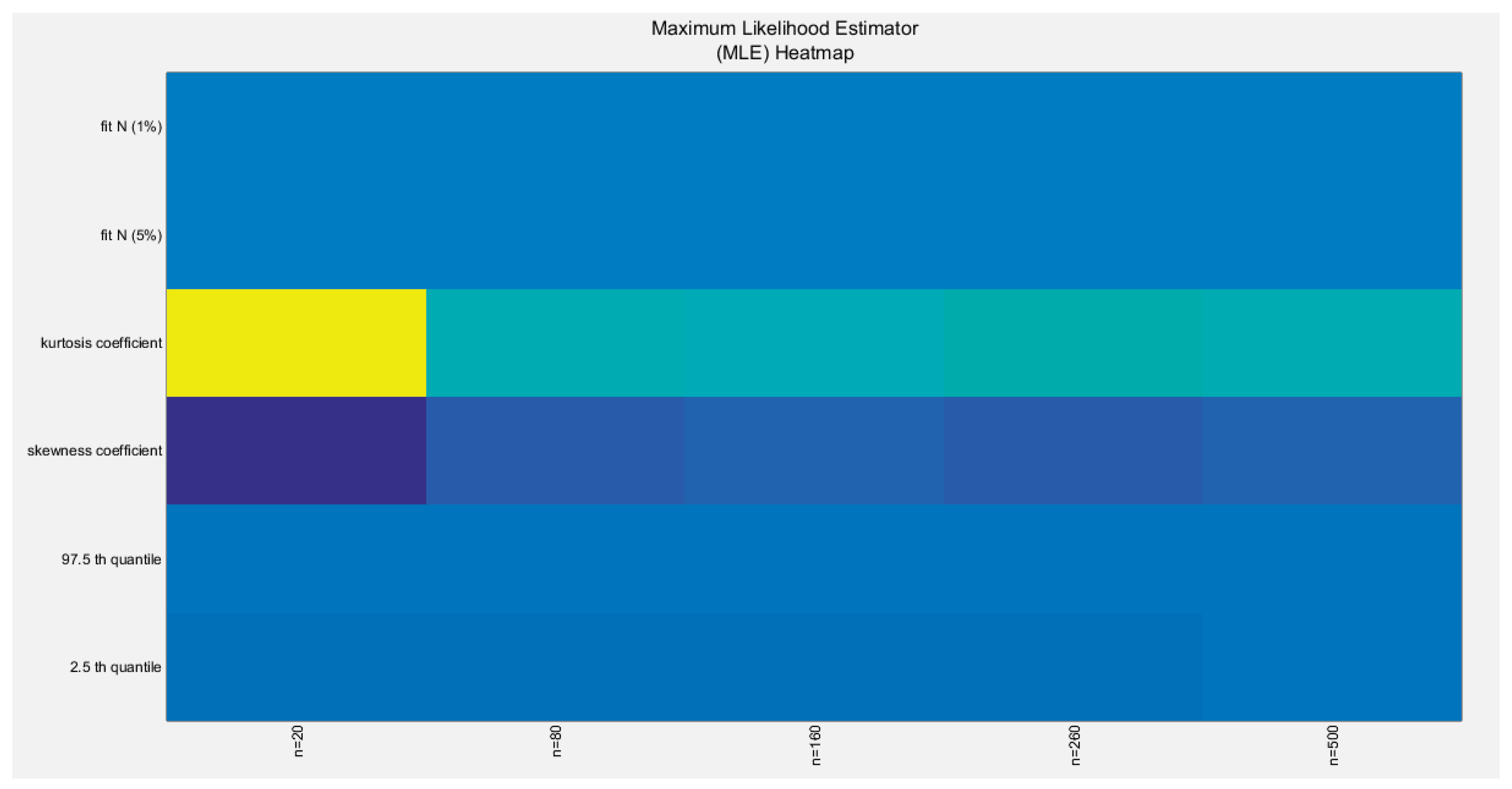
Figure 45.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (MLE) method and how these indices change with changing the sample size from 20 to 500. (h value is shown).
Figure 45.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (MLE) method and how these indices change with changing the sample size from 20 to 500. (h value is shown).
Table 16.
characteristics of empirical distribution of estimated alpha using MPS.
Table 16.
characteristics of empirical distribution of estimated alpha using MPS.
| MPS |
n=20 |
n=80 |
n=160 |
n=260 |
n=500 |
| 2.5 Q |
0.399 |
0.4557 |
0.4671 |
0.4757 |
0.4823 |
| 97.5 Q |
0.5631 |
0.537 |
0.5262 |
0.5203 |
0.5152 |
| Skewness |
-1.5438 |
-0.5296 |
-0.3834 |
-0.4521 |
-0.3794 |
| Kurtosis |
8.894 |
3.4477 |
3.1806 |
3.6063 |
3.3356 |
| Fit N (5%) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=1
(0.0147) |
| Fit N (1%) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=0
(0.0147) |
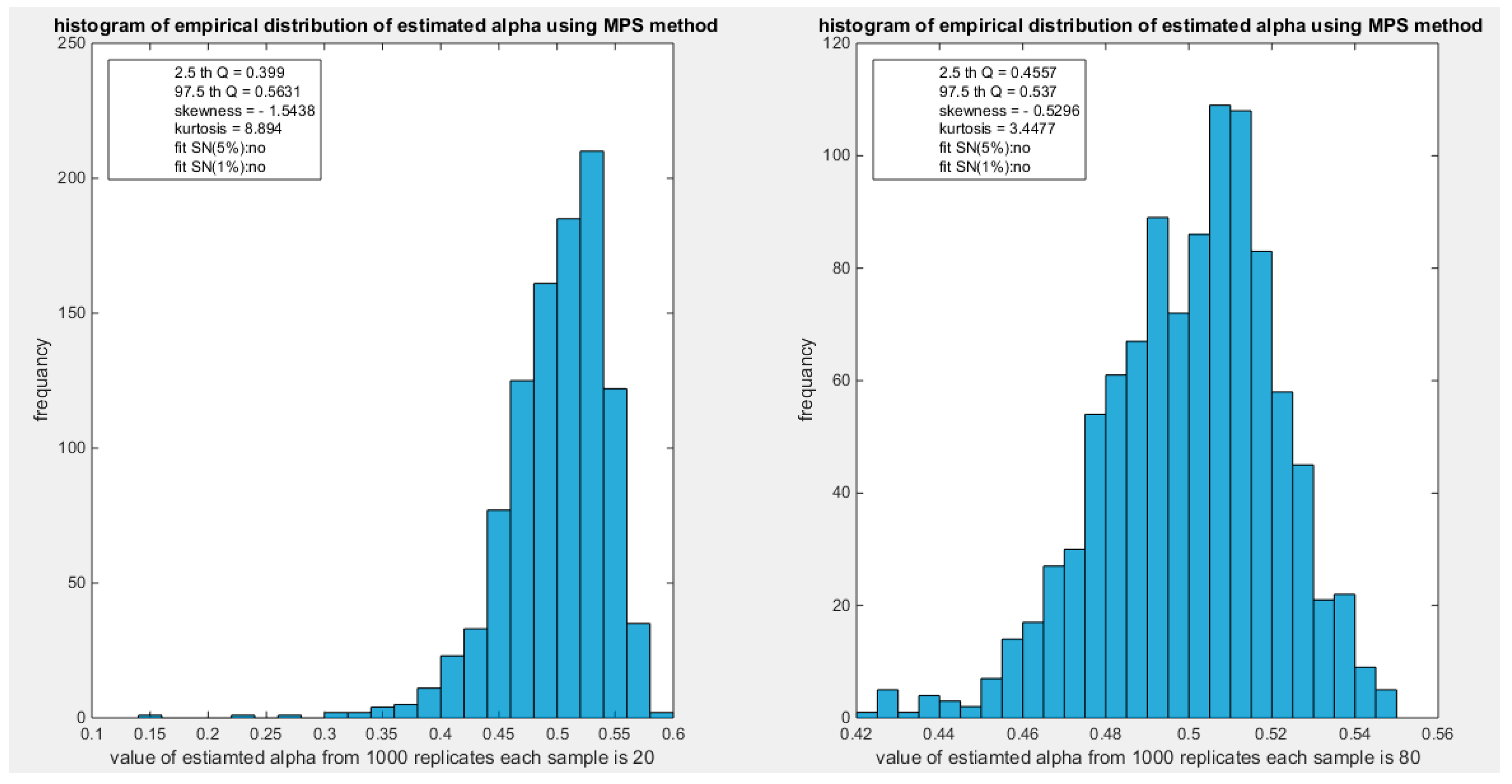
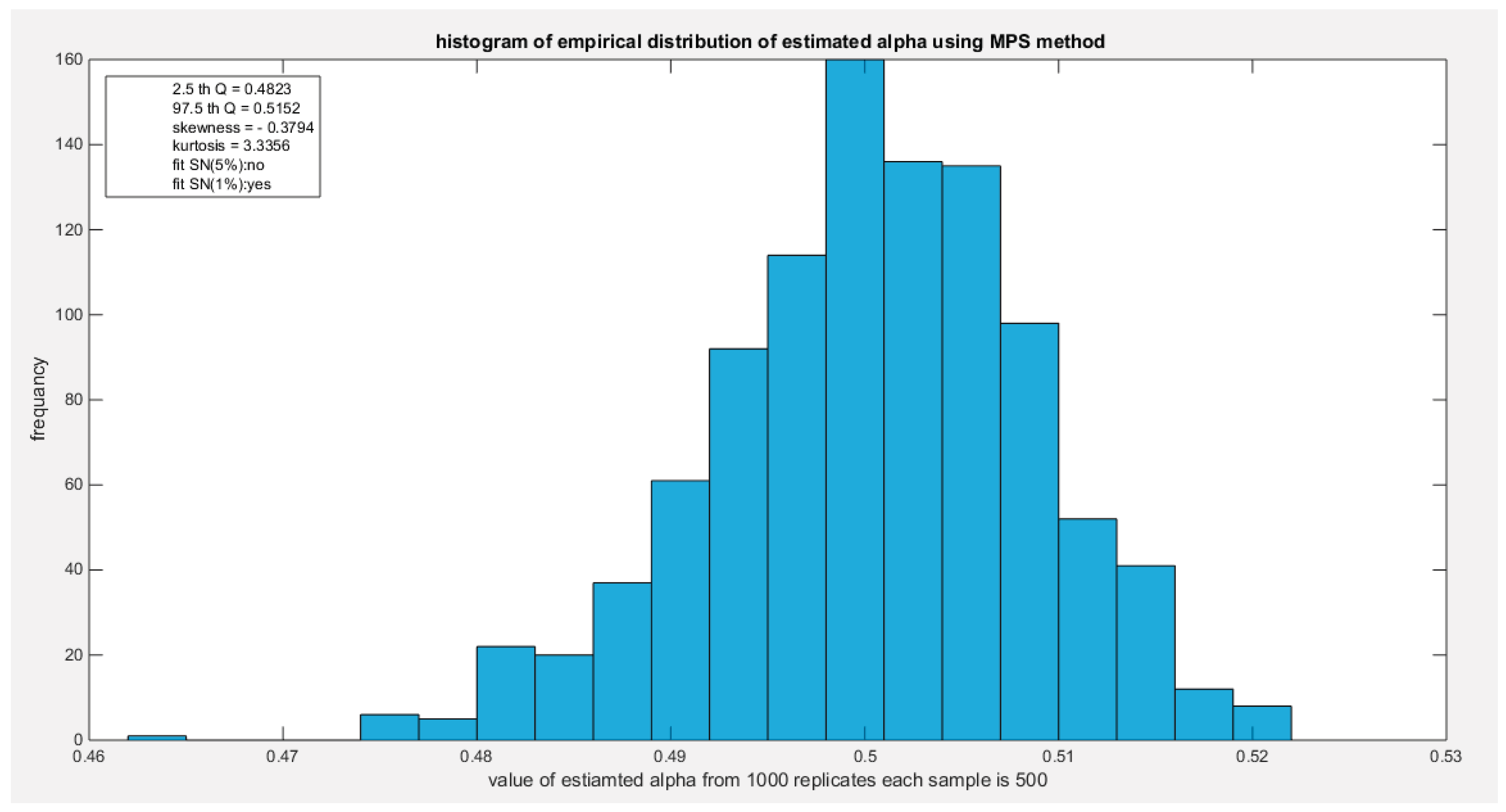
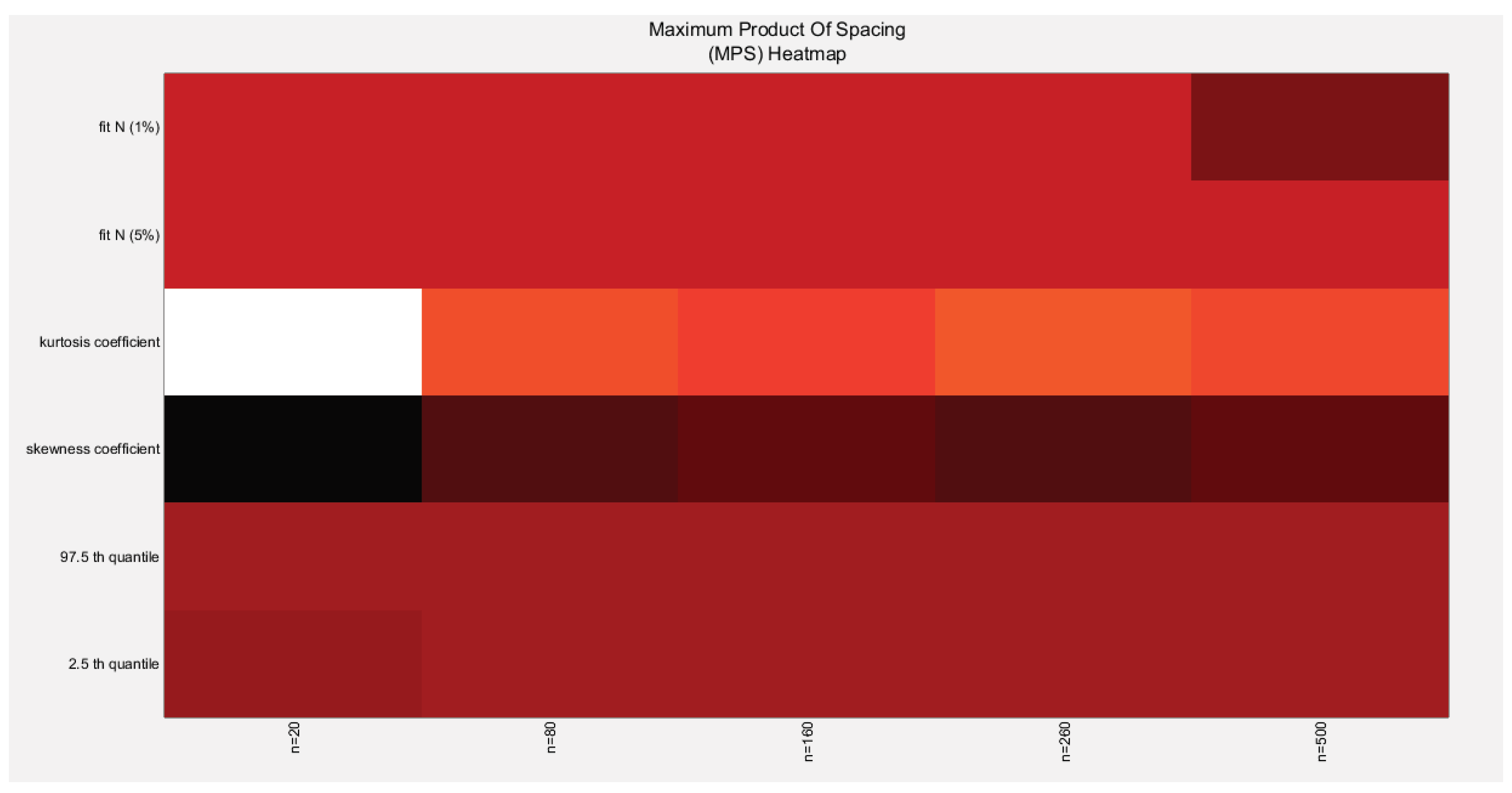
The empirical distribution of the estimated parameter alpha using MPS is shown in Table 16. Each column represents a specific sample size with 1000 replicates in each size. The 2.5 th quantile and the 97.5 th quantile of the 1000 values of the estimated parameter in each sample shows that as the sample sizes increases the 2.5 quantile rises while the 97.5 quantile decreases. In other words, the distance between the quantiles decreases as the sample size increases and this is reflected on the confidence interval (CI). As the sample size increases the CI becomes narrower. The distribution exhibits a moderate left skewness and high positive excess kurtosis (leptokurtic shape) at small sample size. As sample size increases the skewness decreases trying to approach the zero level (skewness of standard normal) and kurtosis decreases trying to approach the kurtosis of standard normal. The empirical distribution does not fit the standard normal at different sample sizes except at sample size 500 and at significance level 1% with associated P-value as shown in the table. H0=1 means reject the null hypothesis that states the parameter distribution follows the standard normal distribution. While H0=0 means fail to reject the null hypothesis. See following Figures (46-49).
Figure 46.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using MPS method.
Figure 46.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using MPS method.
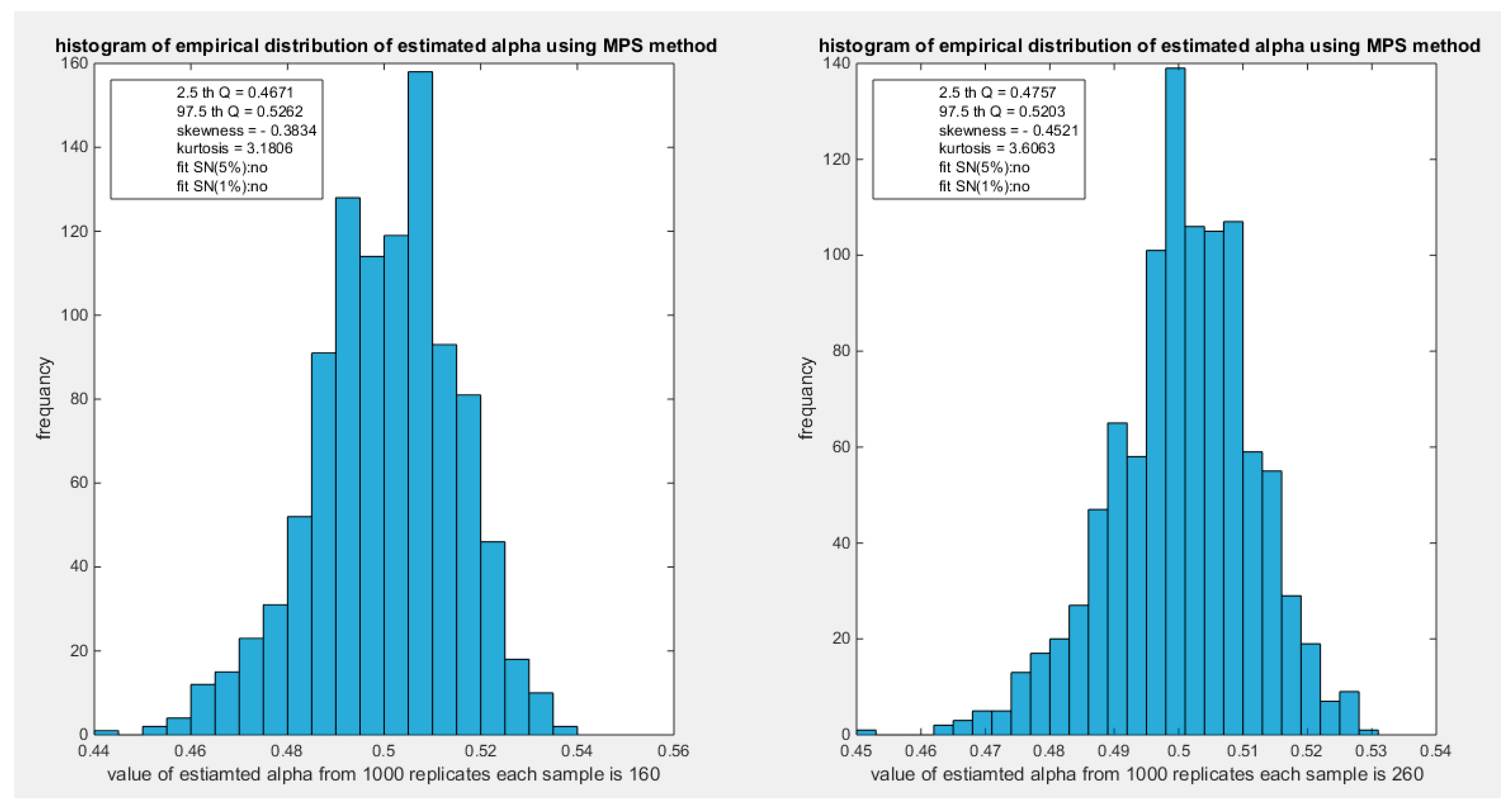
Figure 47.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using MPS method.
Figure 47.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using MPS method.
Figure 48.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n =500) using MPS method.
Figure 48.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n =500) using MPS method.
Figure 49.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (MPS) method and how these indices change with changing the sample size from 20 to 500.(h value shown).
Figure 49.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (MPS) method and how these indices change with changing the sample size from 20 to 500.(h value shown).
Table 17.
characteristics of empirical distribution of estimated alpha using AD.
Table 17.
characteristics of empirical distribution of estimated alpha using AD.
| AD |
n=20 |
n=80 |
n=160 |
n=260 |
n=500 |
| 2.5 Q |
0.3812 |
0.4523 |
0.4651 |
0.4748 |
0.4813 |
| 97.5 Q |
0.5622 |
0.537 |
0.5278 |
0.5220 |
0.5154 |
| Skewness |
-1.3644 |
-0.3869 |
-0.312 |
-0.4046 |
-0.3145 |
| Kurtosis |
7.2624 |
3.0839 |
3.0796 |
3.5645 |
3.3159 |
| Fit N (5%) |
H0=1
(0.001) |
H0=1
(0.0011) |
H0=1
(0.0025) |
H0=1
(0.0115) |
H0=1
(0.0418) |
| Fit N (1%) |
H0=1
(0.001) |
H0=1
(0.0011) |
H0=1
(0.0025) |
H0=0
(0.0115) |
H0=0
(0.0418) |
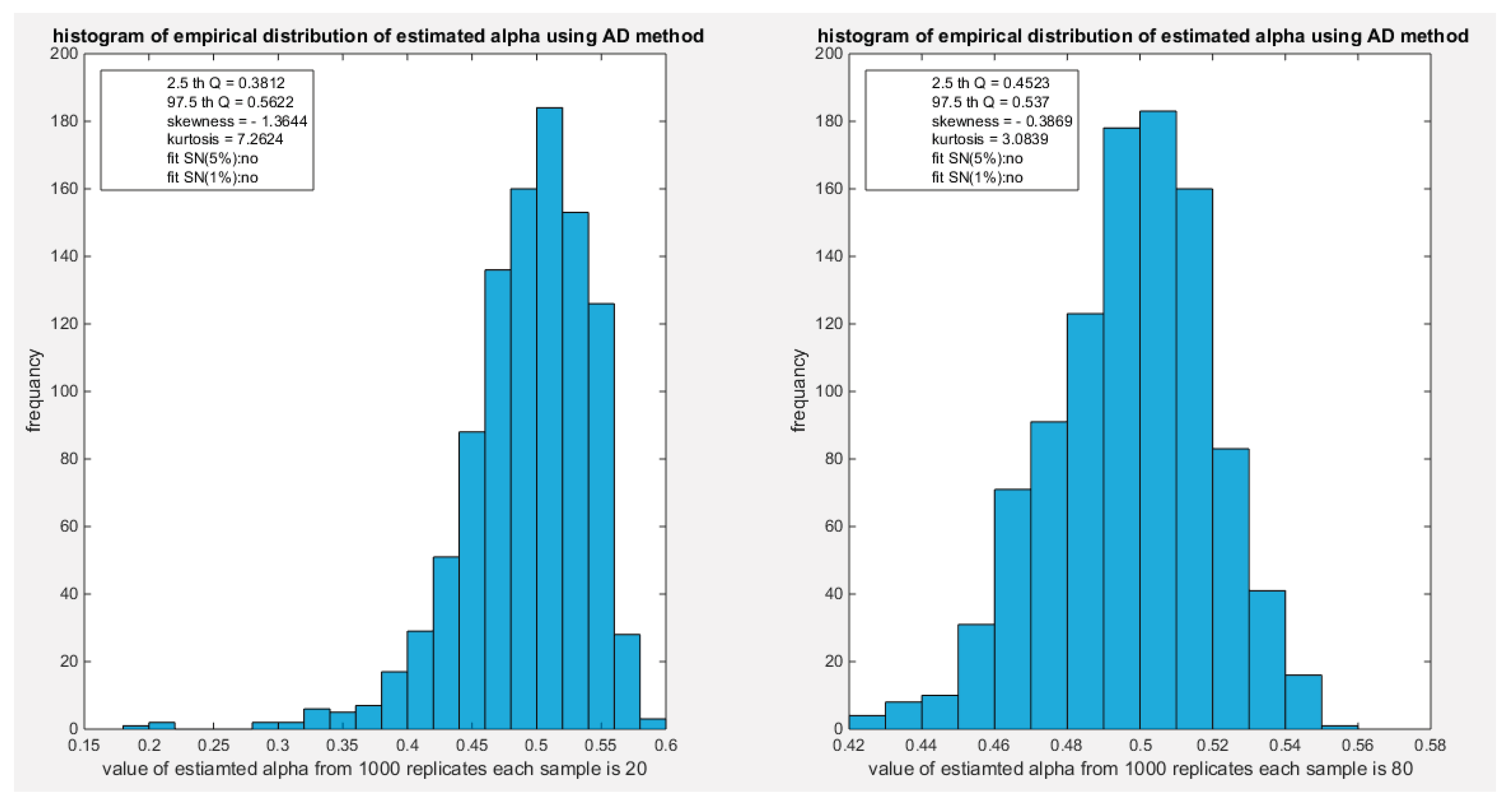
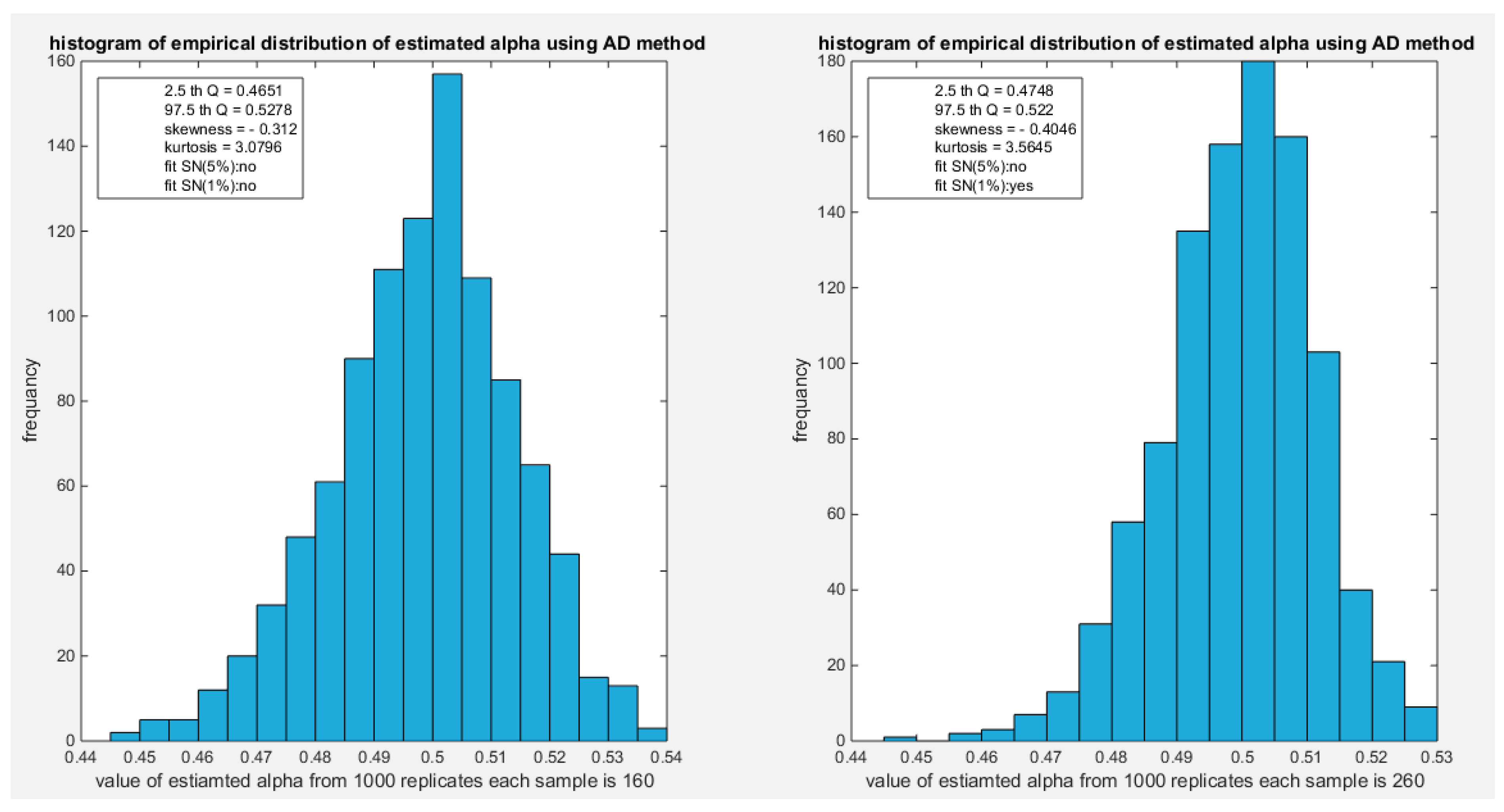
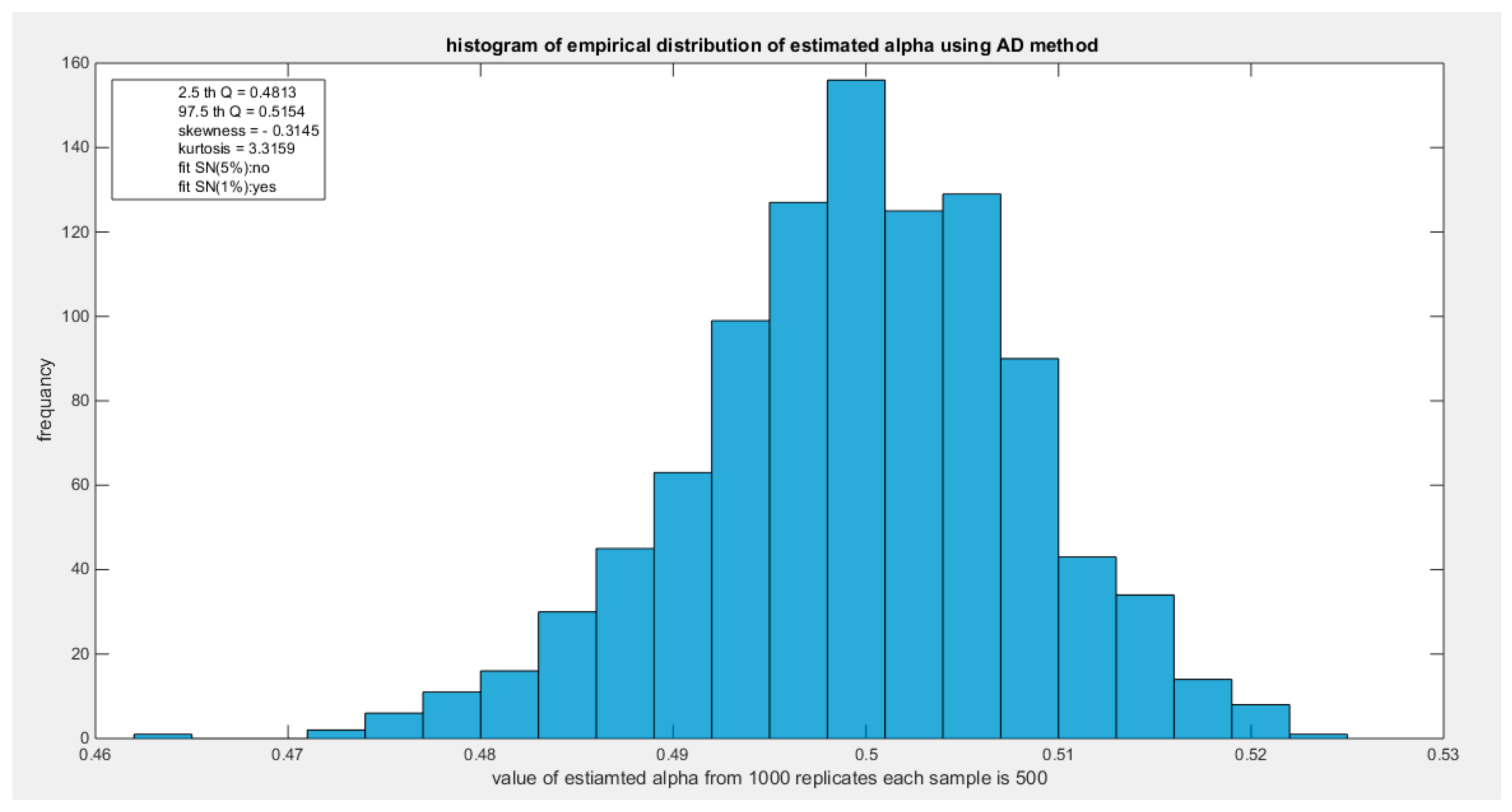
The empirical distribution of the estimated parameter alpha using AD is shown in Table 17. Each column represents a specific sample size with 1000 replicates in each size. The 2.5 th quantile and the 97.5 th quantile of the 1000 values of the estimated parameter in each sample shows that as the sample sizes increases the 2.5 quantile rises while the 97.5 quantile decreases. In other words, the distance between the two quantiles decreases as the sample size increases and this is reflected on the confidence interval (CI). As the sample size increases the CI becomes narrower. The distribution exhibits a moderate left skewness and a moderate positive excess kurtosis (leptokurtic shape) at small sample size. As sample size increases the skewness decreases trying to approach the zero level (skewness of standard normal) and kurtosis decreases trying to approach the kurtosis of standard normal. The empirical distribution fits standard normal starting at size 260 and larger than this at significance level 1% with associated P-value as shown in the table. H0=1 means reject the null hypothesis that states the parameter distribution follows the standard normal distribution. While H0=0 means fail to reject the null hypothesis. See the following Figures (50-53)
Figure 50.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using AD method.
Figure 50.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using AD method.
Figure 51.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using AD method.
Figure 51.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using AD method.
Figure 52.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n =500) using AD method.
Figure 52.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n =500) using AD method.
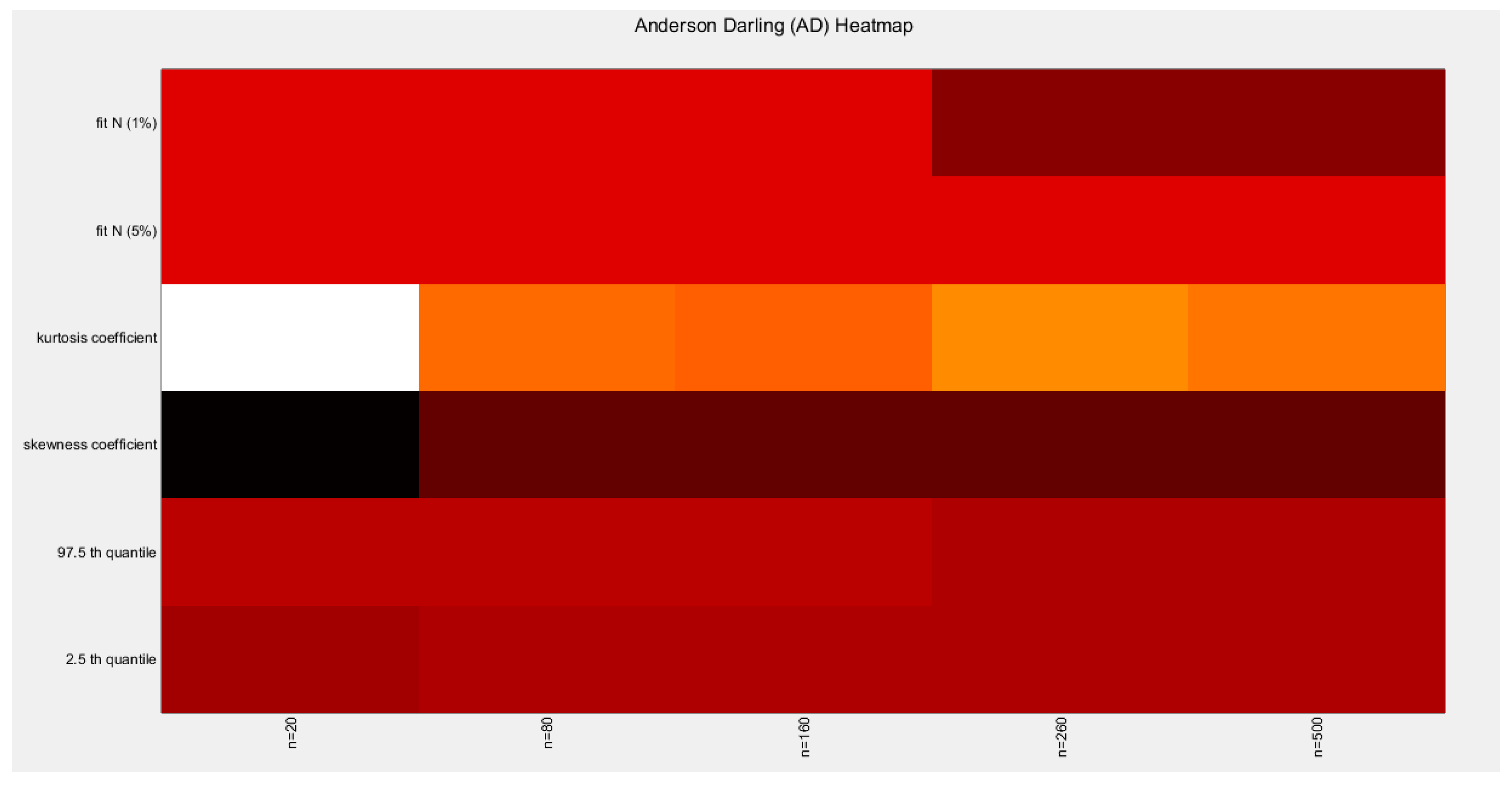
Figure 53.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (AD) method and how these indices change with changing the sample size from 20 to 500. (h value shown).
Figure 53.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (AD) method and how these indices change with changing the sample size from 20 to 500. (h value shown).
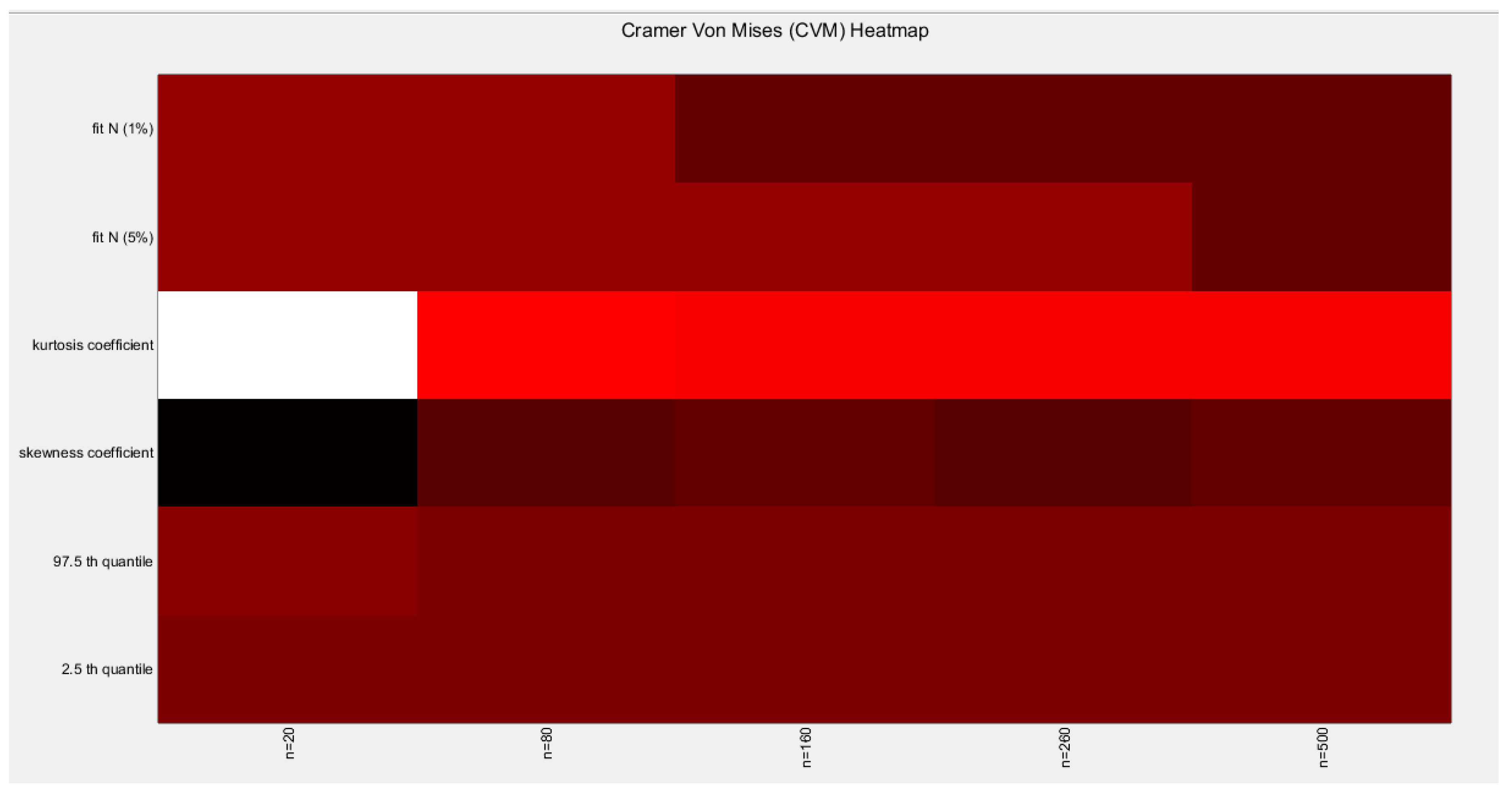
Table 18.
characteristics of empirical distribution of estimated alpha using CVM.
Table 18.
characteristics of empirical distribution of estimated alpha using CVM.
| CVM |
n=20 |
n=80 |
n=160 |
n=260 |
n=500 |
| 2.5 Q |
0.3675 |
0.45 |
0.465 |
0.4745 |
0.481 |
| 97.5 Q |
0.5804 |
0.5408 |
0.5292 |
0.5219 |
0.5166 |
| Skewness |
-2.2301 |
-0.349 |
-0.2116 |
-0.2663 |
-0.2296 |
| Kurtosis |
15.7352 |
3.4125 |
3.1182 |
3.2822 |
3.3211 |
| Fit N (5%) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=1
(0.0447) |
H0=1
(0.0369) |
H0=0
(0.1806) |
| Fit N (1%) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=0
(0.0447) |
H0=0
(0.0369) |
H0=0
(0.1806) |
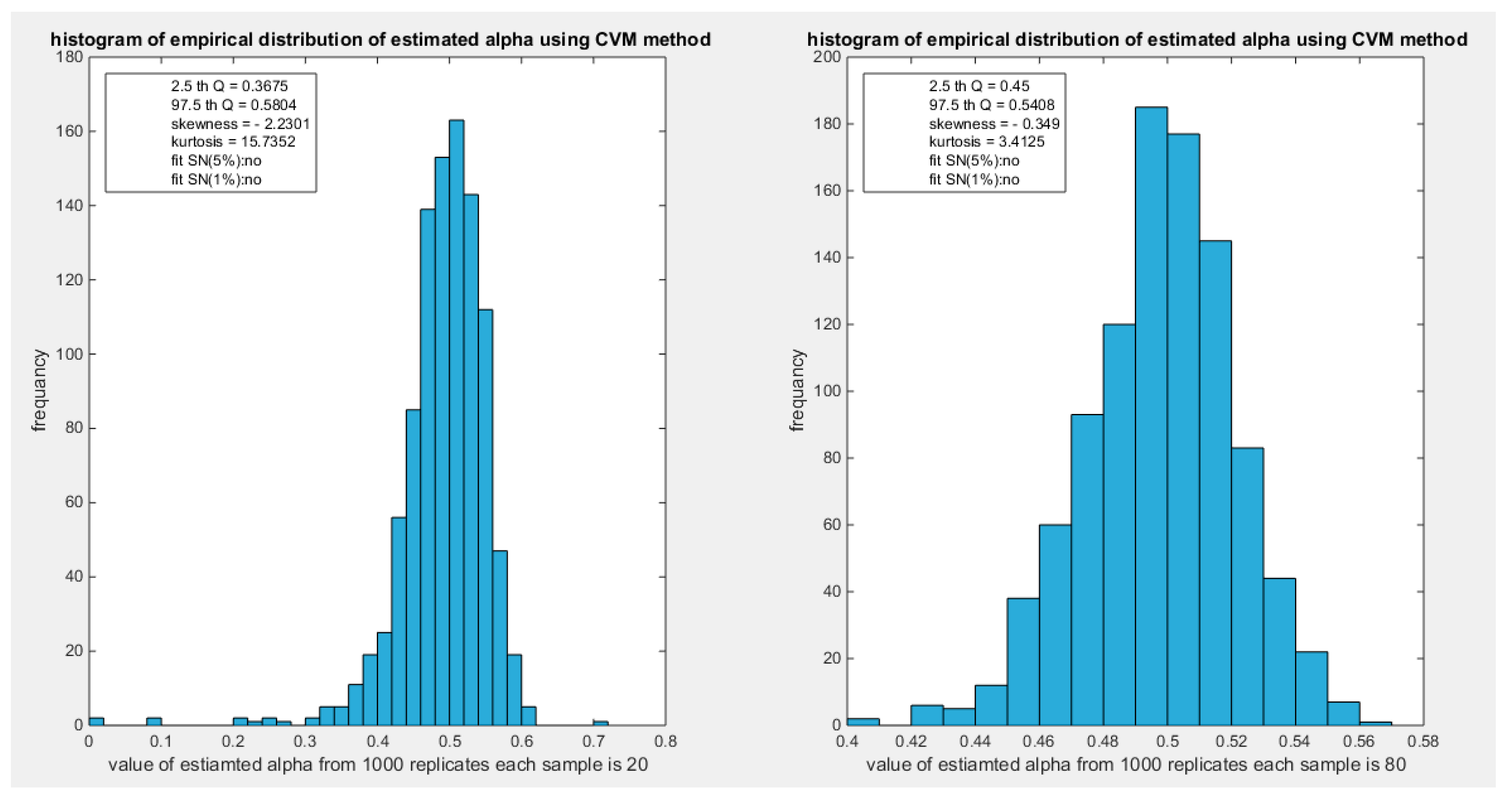
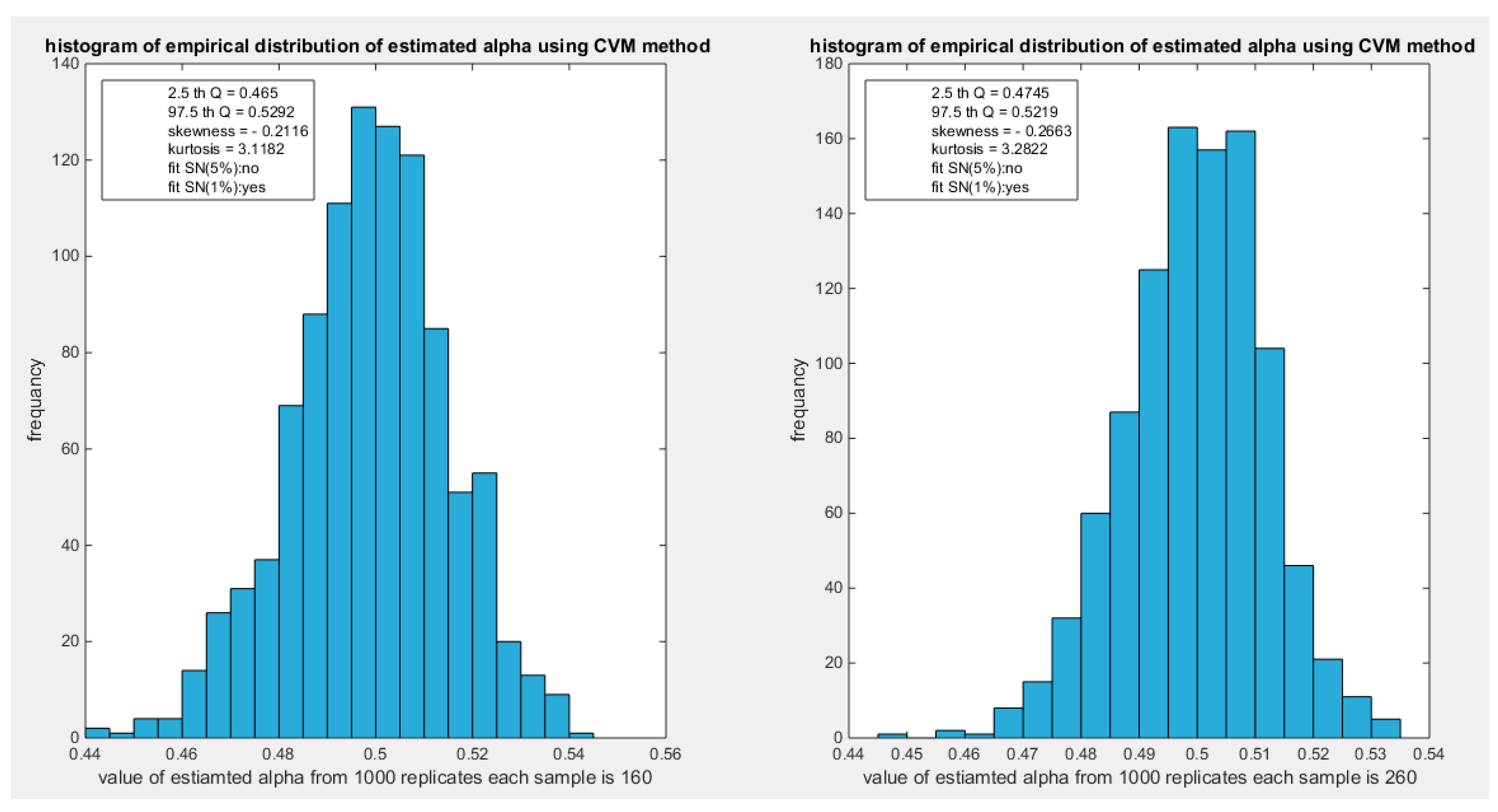
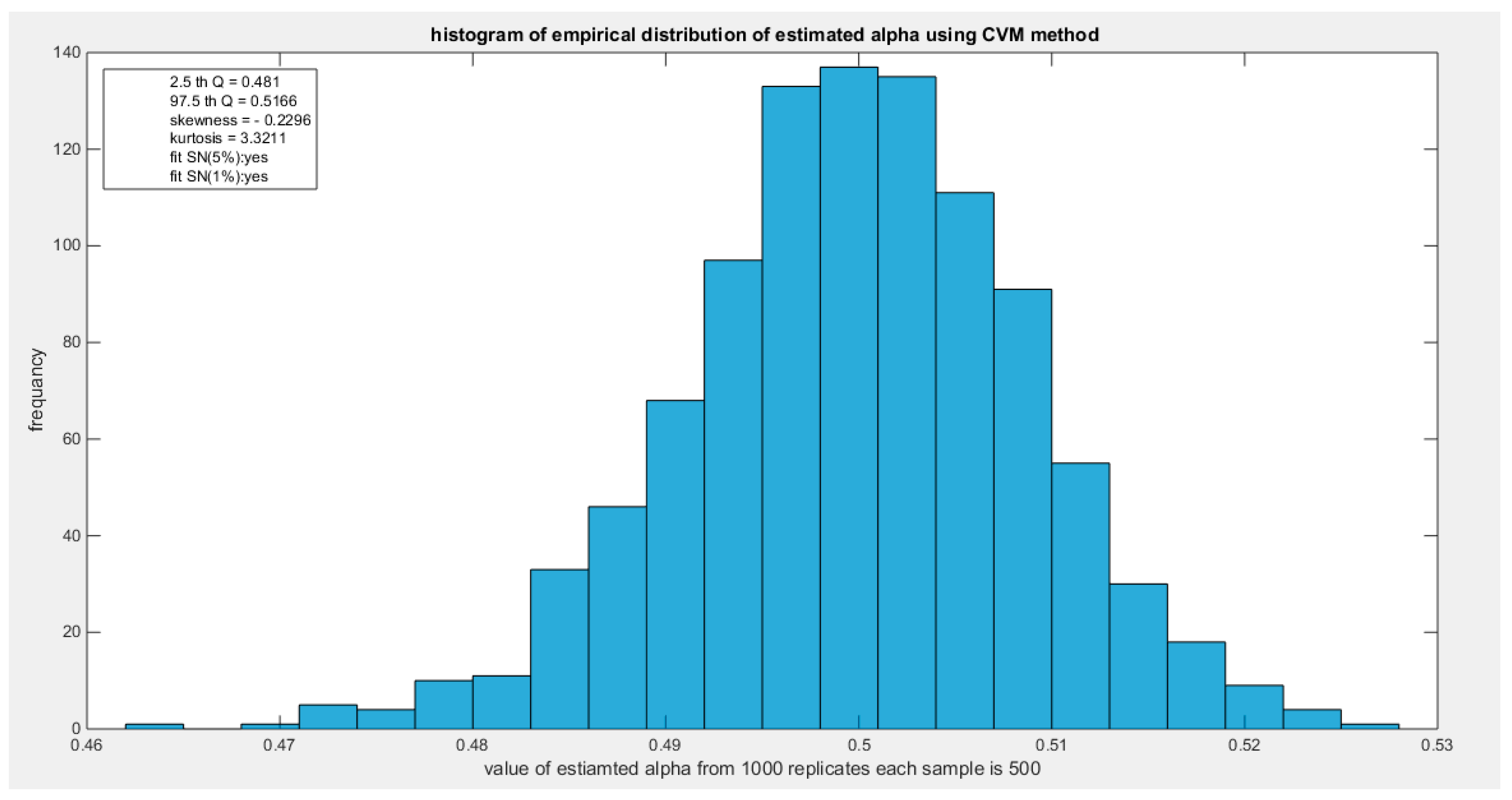
The empirical distribution of the estimated parameter alpha using CVM is shown in Table 18. Each column represents a specific sample size with 1000 replicates in each size. Each column depicts the characteristics of the empirical distribution of the estimated alpha. The 2.5 th quantile and the 97.5 th quantile of the 1000 values of the estimated parameter in each sample shows that as the sample size increases the 2.5 th quantile rises while the 97.5 th quantile decreases. In other words, the distance between the quantiles decreases as the sample size increases and this is reflected on the confidence interval (CI). As the sample size increases the CI becomes narrower. The distribution exhibits a moderate left skewness and a high positive excess kurtosis (leptokurtic shape) at small sample size. As sample size increases the skewness decreases trying to approach the zero level (skewness of standard normal) and kurtosis decreases trying to approach the kurtosis of standard normal. The empirical distribution fits standard normal starting at size 160 and larger than this at significance level 5% and 1% with associated P-value as shown in the table. H0=1 means reject the null hypothesis that states the parameter distribution follows the standard normal distribution. While H0=0 means fail to reject the null hypothesis. See the following Figures (54-57)
Figure 54.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using CVM method.
Figure 54.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using CVM method.
Figure 55.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using CVM method.
Figure 55.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using CVM method.
Figure 56.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n =500) using CVM method.
Figure 56.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n =500) using CVM method.
Figure 57.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (cvm) method and how these indices change with changing the sample size from 20 to 500. (h value show).
Figure 57.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (cvm) method and how these indices change with changing the sample size from 20 to 500. (h value show).
Table 19.
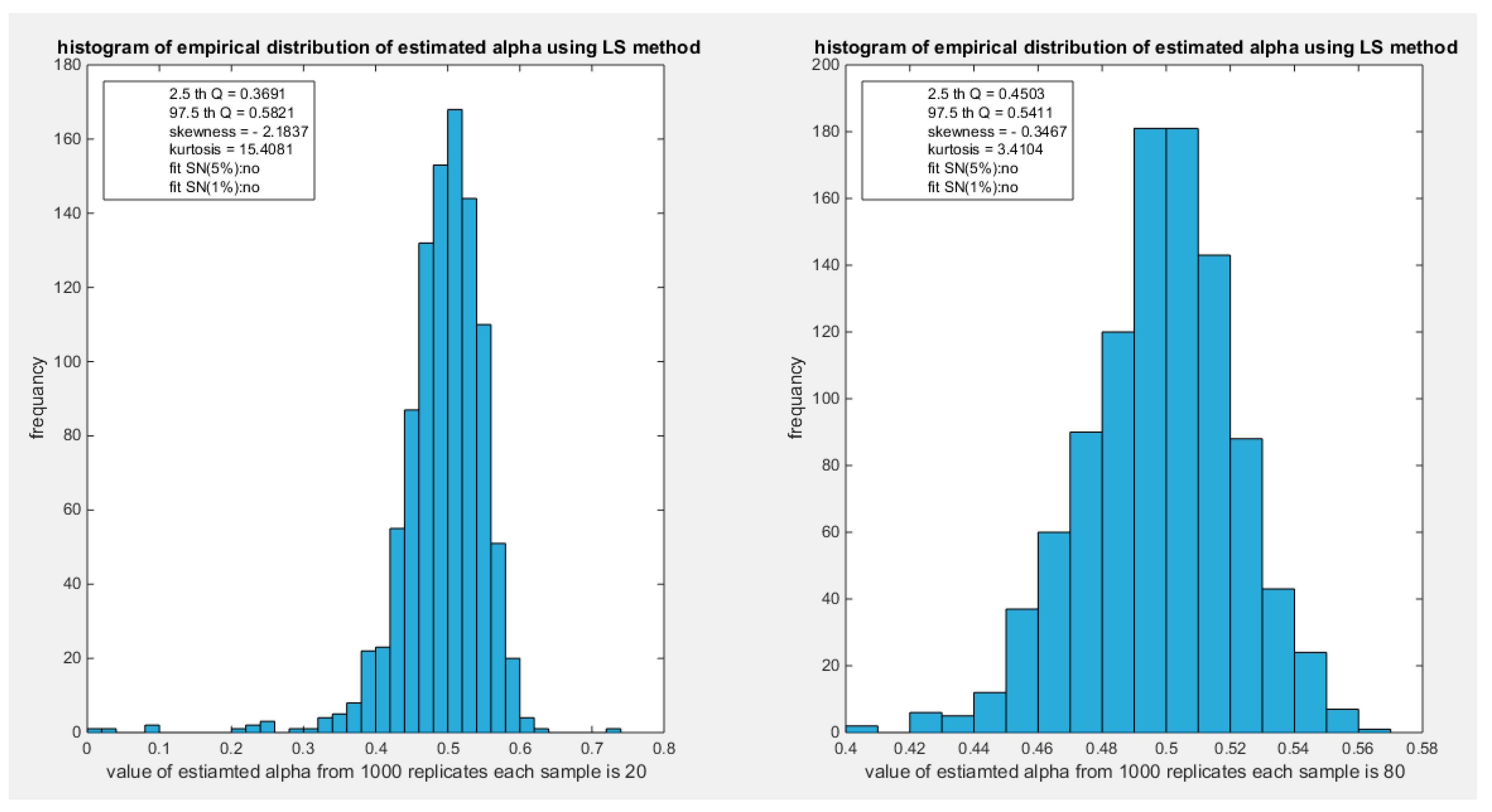
characteristics of empirical distribution of estimated alpha using LS.
Table 19.
characteristics of empirical distribution of estimated alpha using LS.
| LS |
n=20 |
n=80 |
n=160 |
n=260 |
n=500 |
| 2.5 Q |
0.3691 |
0.4503 |
0.4651 |
0.4741 |
0.4809 |
| 97.5 Q |
0.5821 |
0.5411 |
0.5297 |
0.5218 |
0.5167 |
| Skewness |
-2.1837 |
-0.3467 |
-0.2108 |
-0.3274 |
-0.2461 |
| Kurtosis |
15.4081 |
3.4104 |
3.1182 |
3.4525 |
3.3134 |
| Fit N (5%) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=1
(0.0405) |
H0=1
(0.0213) |
H0=0
(0.1329) |
| Fit N (1%) |
H0=1
(0.001) |
H0=1
(0.001) |
H0=0
(0.0405) |
H0=0
(0.0213) |
H0=0
(0.1329) |
The empirical distribution of the estimated parameter alpha using LS is shown in Table 19. Each column represents a specific sample size with 1000 replicates in each size. Each column depicts the characteristics of the empirical distribution of the estimated alpha. The 2.5 th quantile and the 97.5 th quantile of the 1000 values of the estimated parameter in each sample shows that as the sample size increases the 2.5 th quantile rises while the 97.5 th quantile decreases. In other words, the distance between the quantiles decreases as the sample size increases and this is reflected on the confidence interval (CI). As the sample size increases the CI becomes narrower. The distribution exhibits a moderate left skewness and a high positive excess kurtosis (leptokurtic shape) at small sample size. As sample size increases the skewness decreases trying to approach the zero level (skewness of standard normal) and kurtosis decreases trying to approach the kurtosis of standard normal. The empirical distribution fits standard normal starting at size 160 and larger than this at significance level 5% and 1% with associated P-value as shown in the table. H0=1 means reject the null hypothesis that states the parameter distribution follows the standard normal distribution. While H0=0 means fail to reject the null hypothesis. See the following Figures (58-61)
Figure 58.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using LS method.
Figure 58.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using LS method.
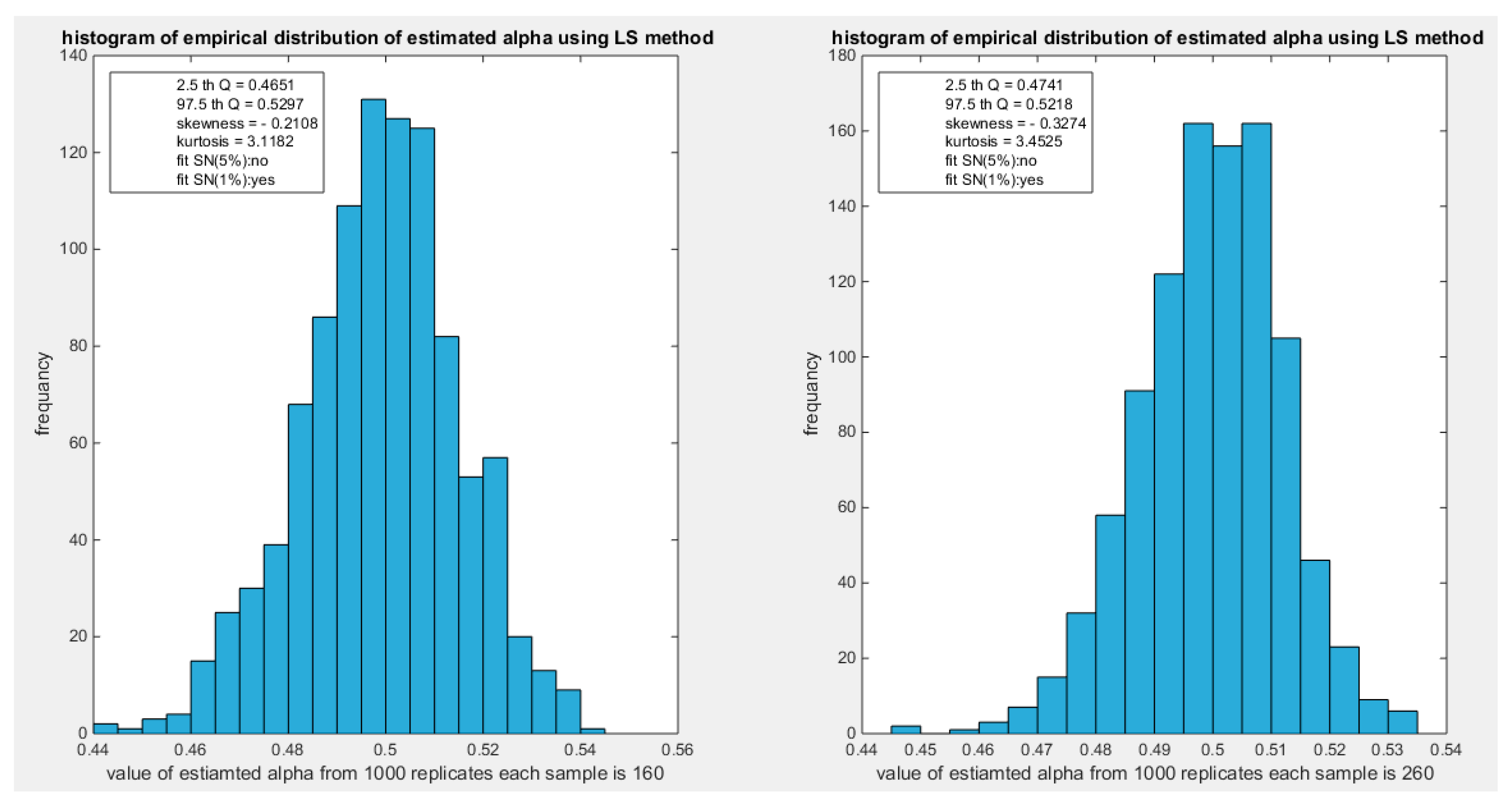
Figure 59.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using LS method.
Figure 59.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using LS method.
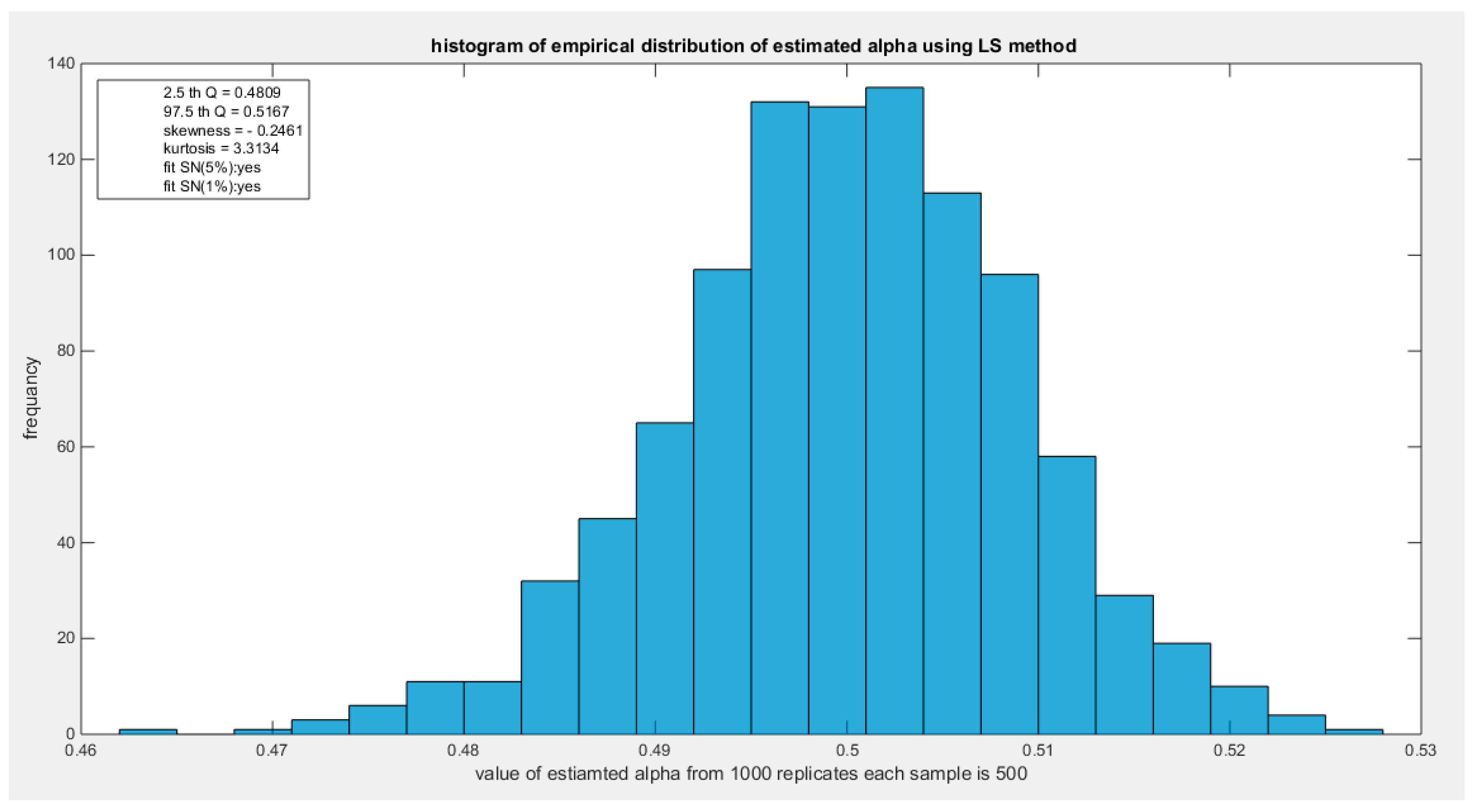
Figure 60.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n =500) using LS method.
Figure 60.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n =500) using LS method.
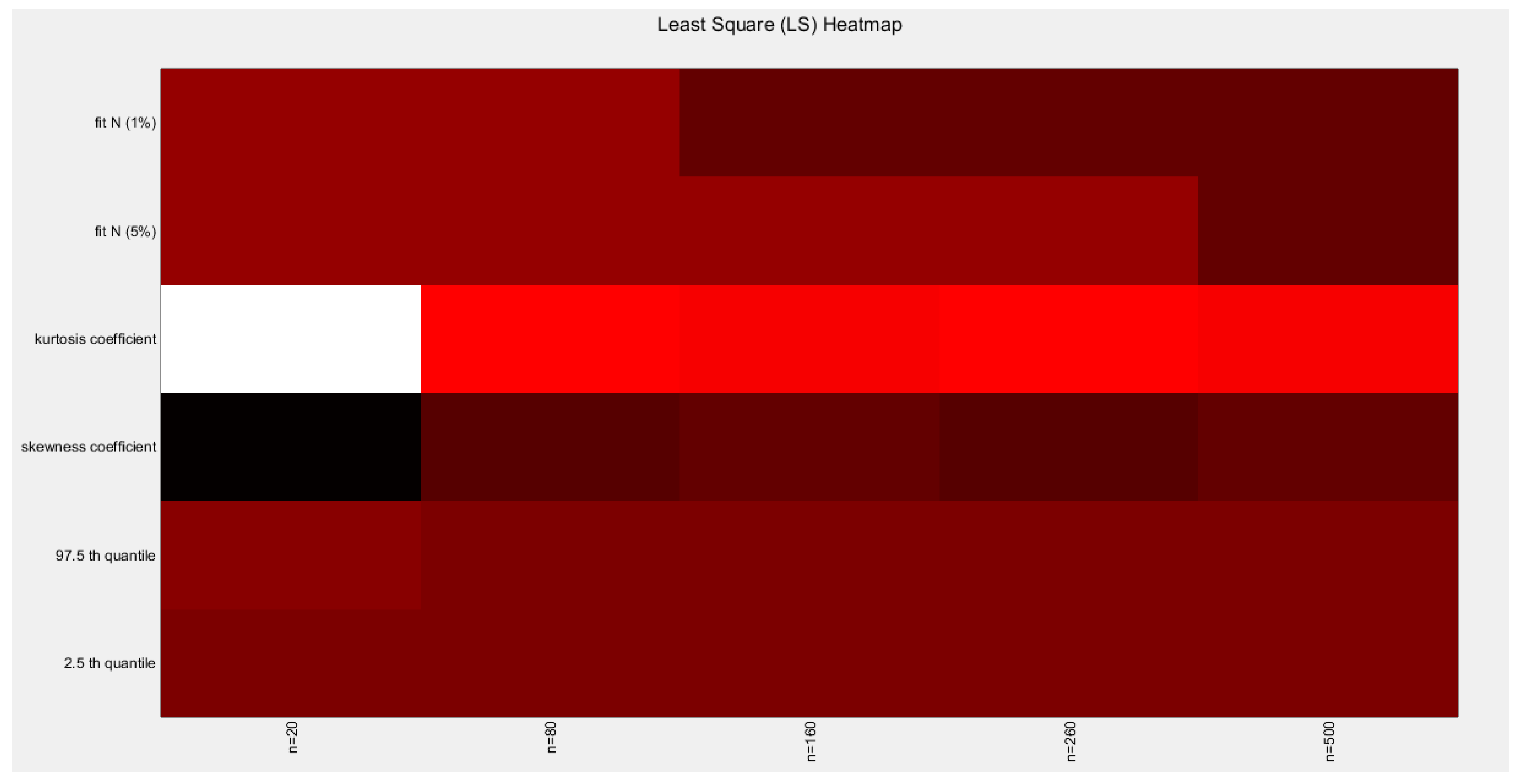
Figure 61.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (LS) method and how these indices change with changing the sample size from 20 to 500. (h value is shown).
Figure 61.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (LS) method and how these indices change with changing the sample size from 20 to 500. (h value is shown).
Table 20.
characteristics of empirical distribution of estimated alpha using percentile.
Table 20.
characteristics of empirical distribution of estimated alpha using percentile.
| PERCENTILE |
n=20 |
n=80 |
n=160 |
n=260 |
n=500 |
| 2.5 Q |
0.4386 |
0.463 |
0.4736 |
0.4782 |
0.4836 |
| 97.5 Q |
0.6012 |
0.5473 |
0.5304 |
0.5246 |
0.5172 |
| Skewness |
0.3592 |
0.1697 |
0.0348 |
-0.0114 |
-0.1044 |
| Kurtosis |
3.1173 |
2.9065 |
2.8661 |
3.1032 |
2.9806 |
| Fit N (5%) |
H0=1
(0.0078) |
H0=1
(0.0299) |
H0=1
(0.046) |
H0=0
(0.1917) |
H0=0
(0.5) |
| Fit N (1%) |
H0=1
(0.0078) |
H0=0
(0.0299) |
H0=0
(0.046) |
H0=0
(0.1917) |
H0=0
(0.5) |
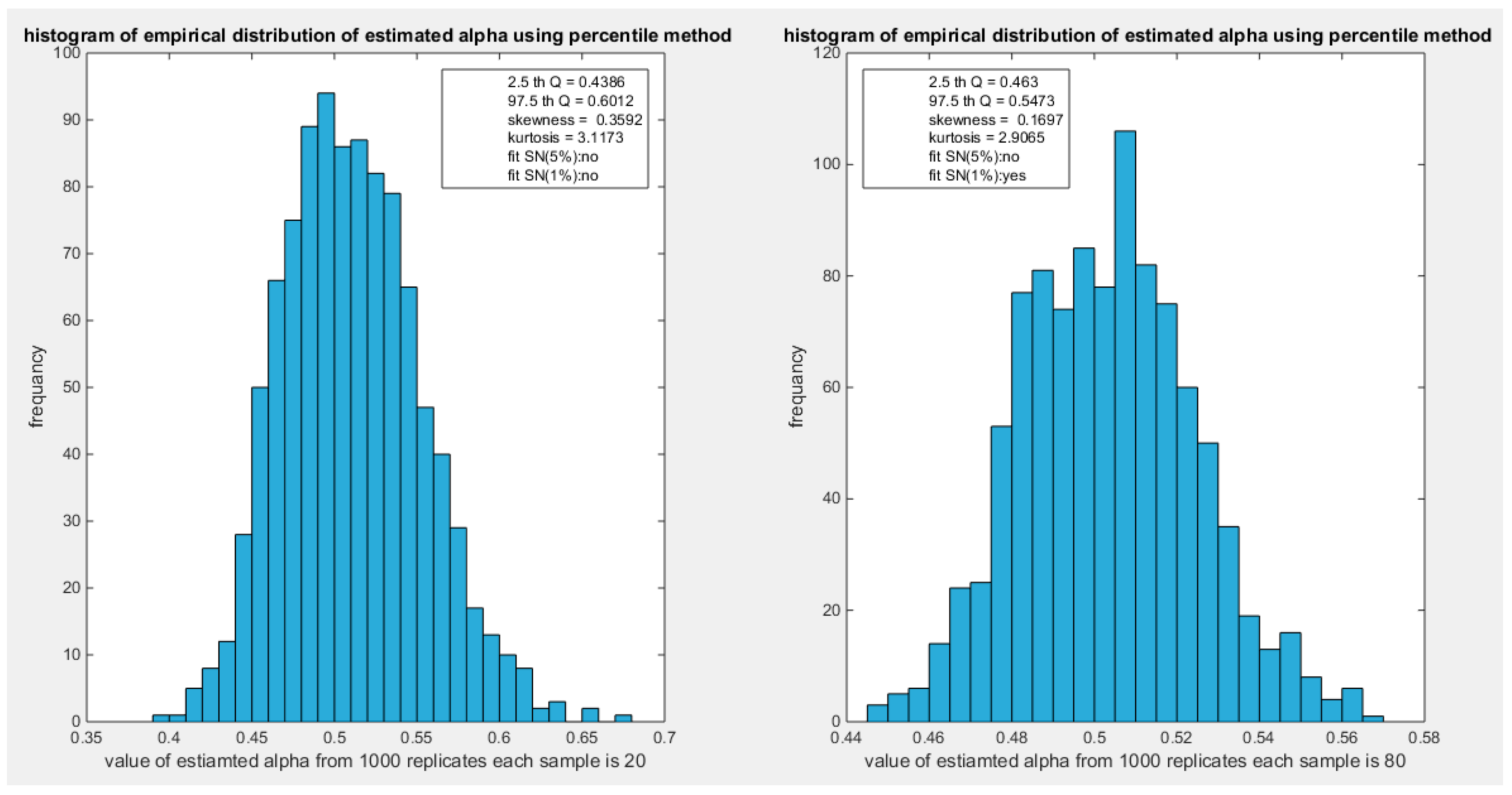
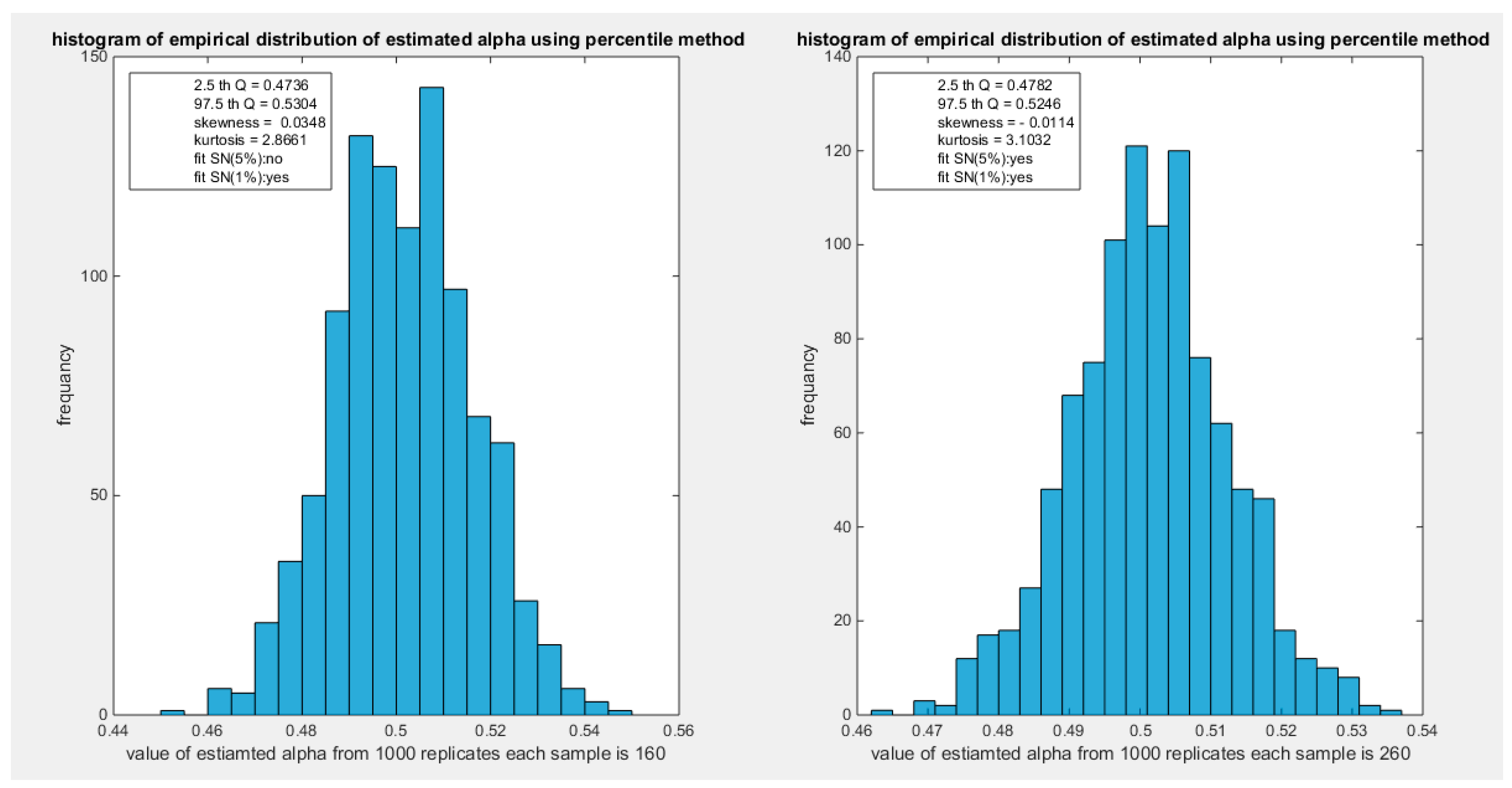
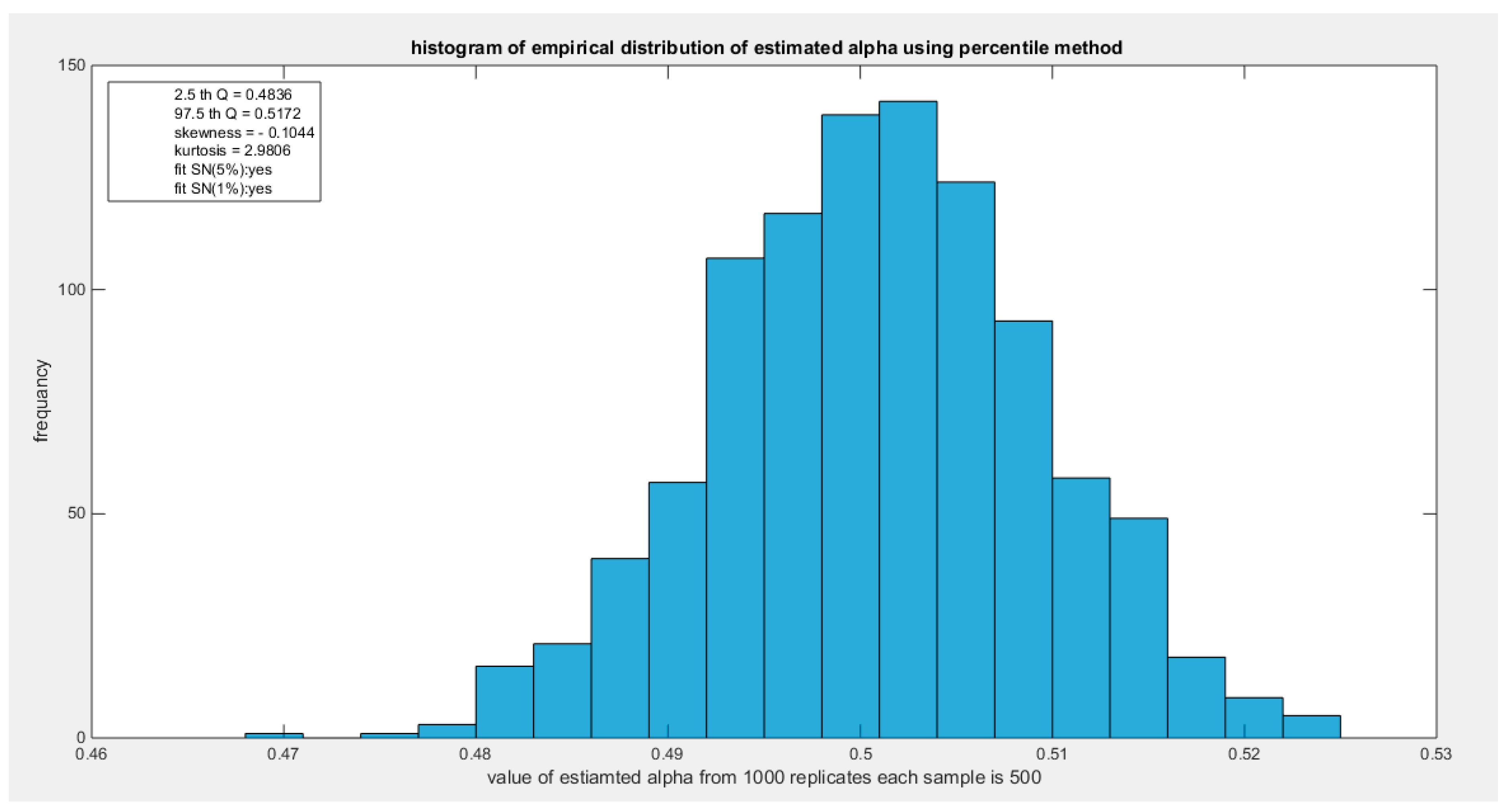
The empirical distribution of the estimated parameter alpha using percentile method is shown in Table 20. Each column represents a specific sample size with 1000 replicates in each size. Each column depicts the characteristics of the empirical distribution of the estimated alpha. The 2.5 th quantile and the 97.5 th quantile of the 1000 values of the estimated parameter in each sample shows that as the sample sizes increases the 2.5 th quantile rises while the 97.5 th quantile decreases. In other words, the distance between the quantiles decreases as the sample size increases and this is reflected on the confidence interval (CI). As the sample size increases the CI becomes narrower. As sample size increases the distribution exhibits oscillation between a mild left skewness and a mild right skewness. In contrast, it exhibits gradual mild decrease in kurtosis (platykurtic shape) as sample size rises and it approaches mesokurtic shape (kertosis coefficient=3) of the standard normal at sample size 500. The empirical distribution fits standard normal starting at size 80 and larger than this size at significance level 5% and 1% with associated P-value as shown in the table. H0=1 means reject the null hypothesis that states the parameter distribution follows the standard normal distribution. While H0=0 means fail to reject the null hypothesis. See figures (62-65)
Figure 62.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using percentile method.
Figure 62.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using percentile method.
Figure 63.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using percentile method.
Figure 63.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using percentile method.
Figure 64.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n =500) using percentile method.
Figure 64.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n =500) using percentile method.
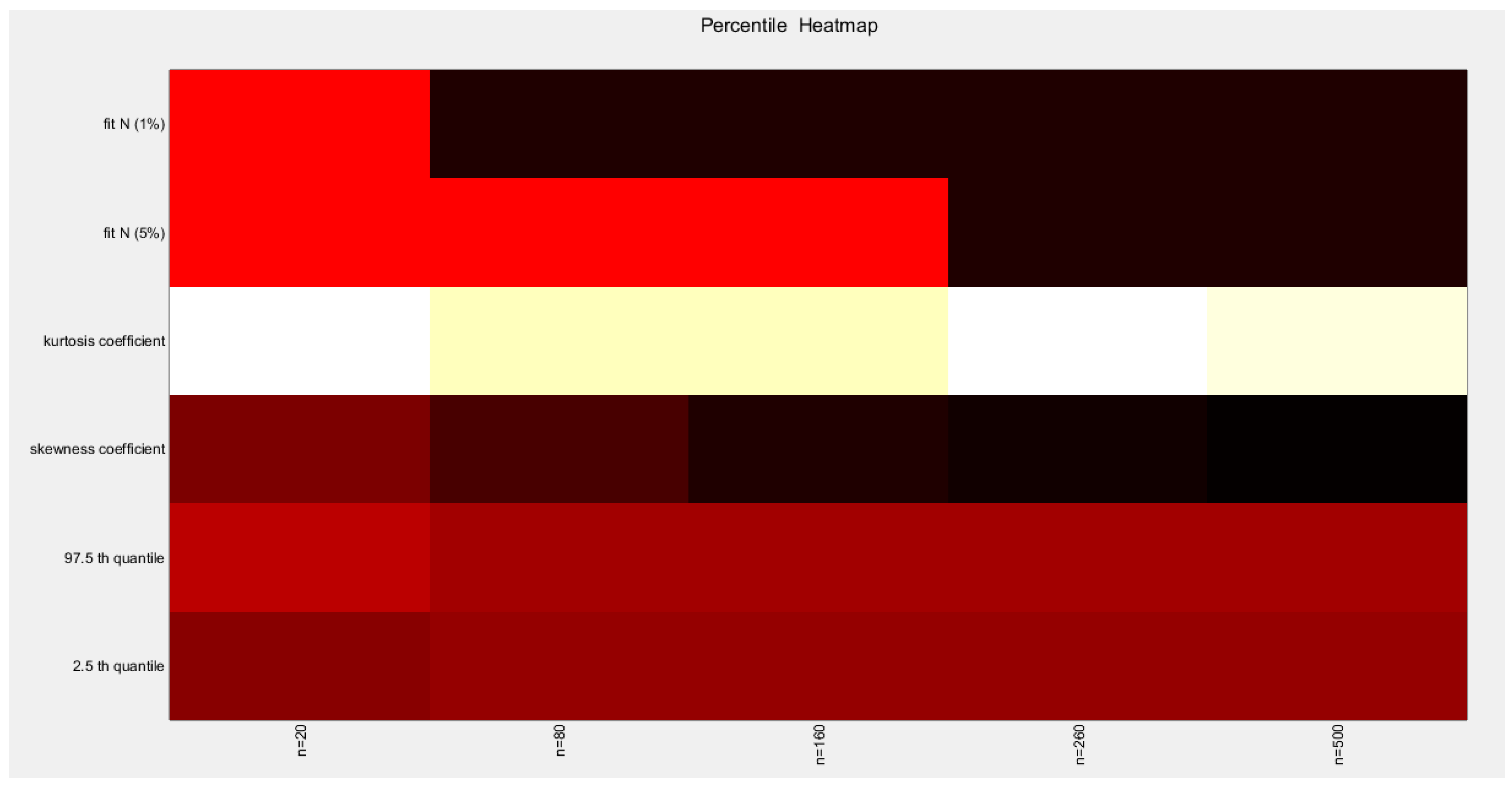
Figure 65.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (percentile) method and how these indices change with changing the sample size from 20 to 500. (h value is shown).
Figure 65.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (percentile) method and how these indices change with changing the sample size from 20 to 500. (h value is shown).
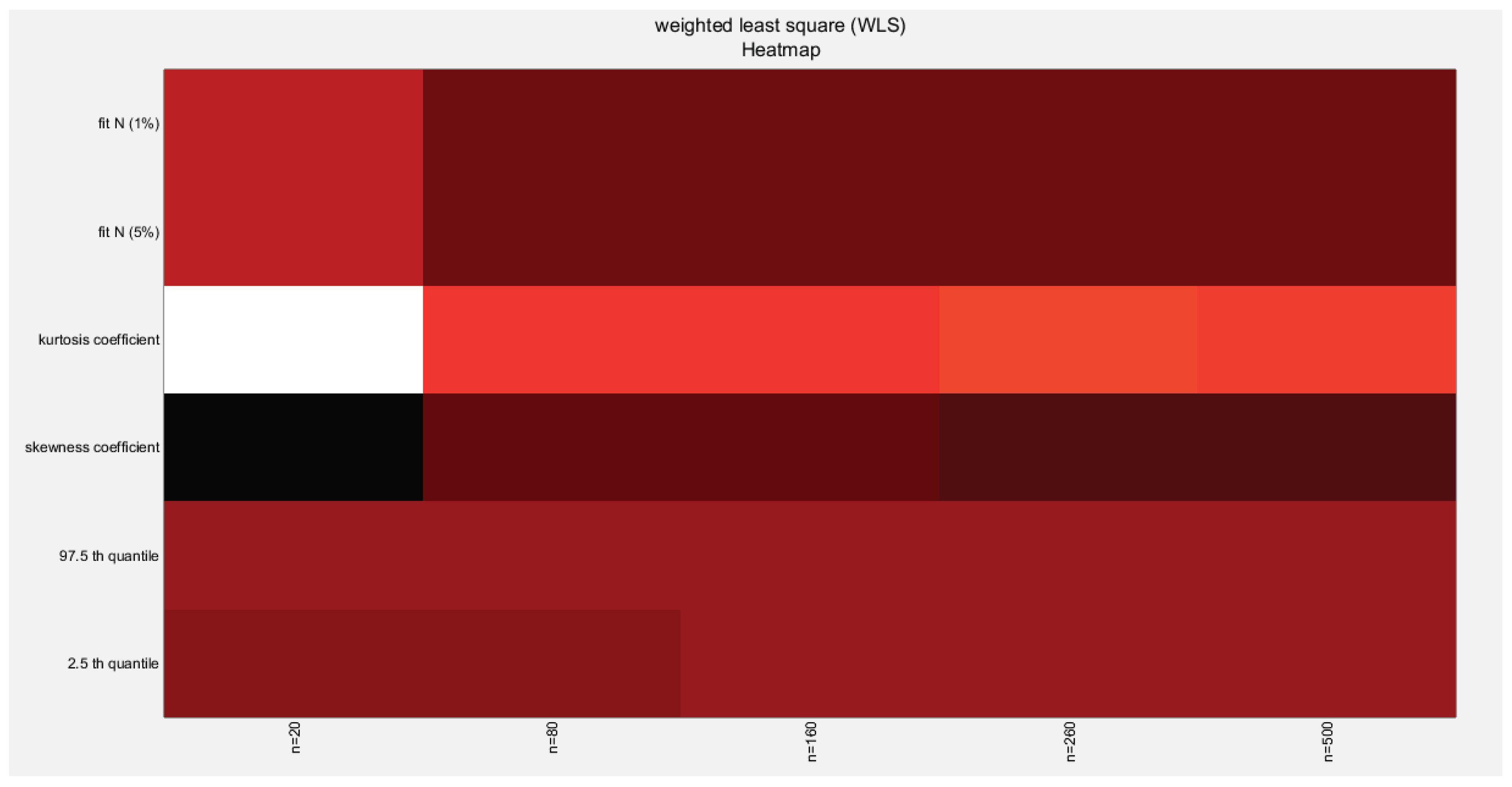
Table 21.
characteristics of empirical distribution of estimated alpha using WLS.
Table 21.
characteristics of empirical distribution of estimated alpha using WLS.
| WLS |
n=20 |
n=80 |
n=160 |
n=260 |
n=500 |
| 2.5 Q |
0.3885 |
0.4547 |
0.4676 |
0.4756 |
0.4816 |
| 97.5 Q |
0.5784 |
0.5406 |
0.5299 |
0.5222 |
0.5162 |
| Skewness |
-1.2701 |
-0.1687 |
-0.113 |
-0.2175 |
-0.1815 |
| Kurtosis |
8.7862 |
3.1044 |
3.0195 |
3.338 |
3.1696 |
| Fit N (5%) |
H0=1
(0.001) |
H0=0
(0.2563) |
H0=0
(0.296) |
H0=0
(0.182) |
H0=0
(0.1715) |
| Fit N (1%) |
H0=1
(0.001) |
H0=0
(0.2563) |
H0=0
(0.296) |
H0=0
(0.182) |
H0=0
(0.1715) |
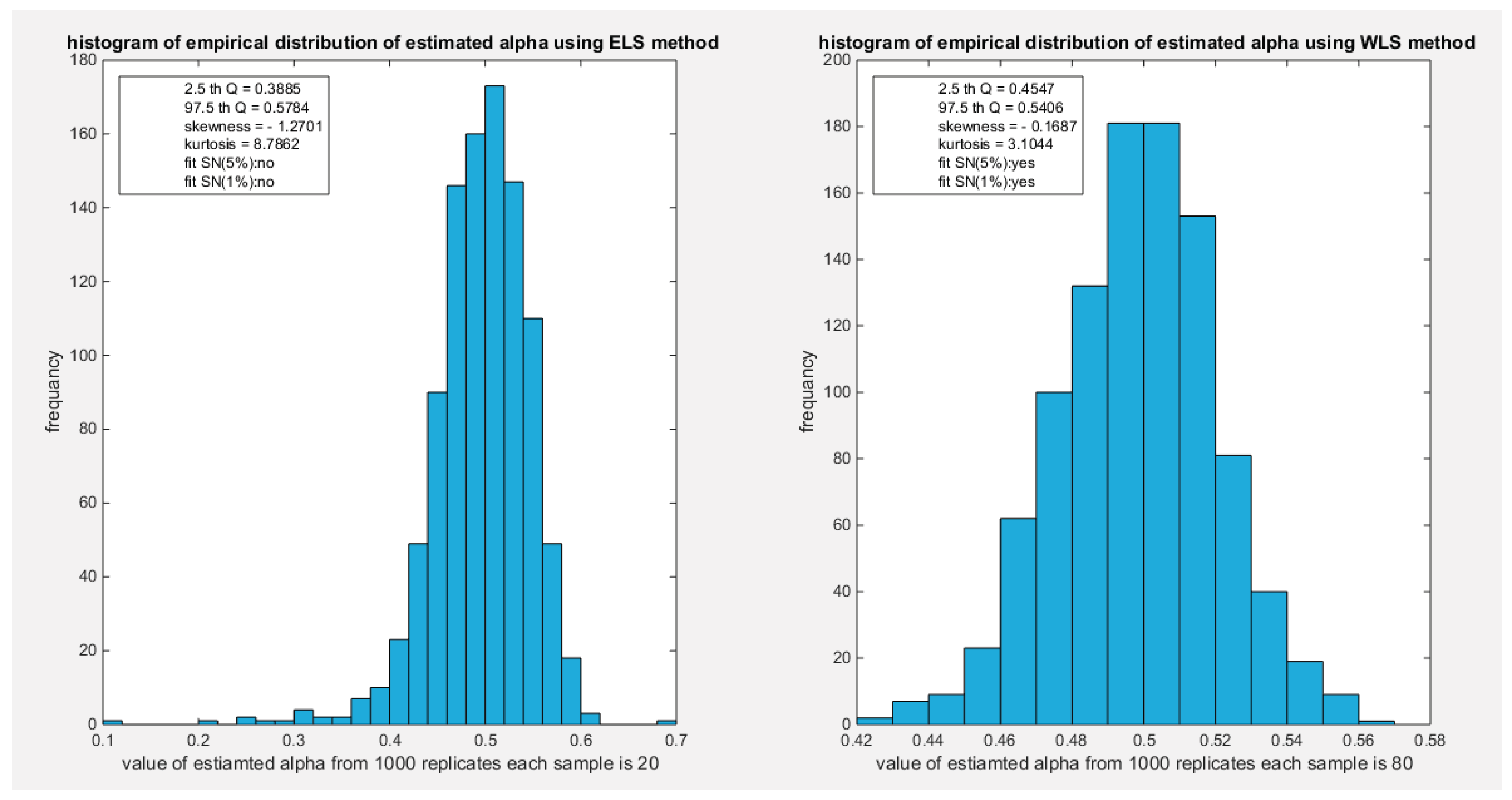
The empirical distribution of the estimated parameter alpha using WLS method is shown in Table 21. Each column represents a specific sample size with 1000 replicates in each size. Each column depicts the characteristics of the empirical distribution of the estimated alpha. The 2.5 th quantile and the 97.5 th quantile of the 1000 values of the estimated parameter in each sample shows that as the sample sizes increases the 2.5 th quantile rises while the 97.5 th quantile decreases. In other words, the distance between the quantiles decreases as the sample size increases and this is reflected on the confidence interval (CI). As the sample size increases the CI becomes narrower. The distribution exhibits mild left skewness and high positive excess kurtosis (leptokurtic shape) at small sample size. As sample size increases the skewness decreases trying to approach the zero level (skewness of standard normal) and kurtosis decreases trying to approach the kurtosis of standard normal. The empirical distribution fits standard normal starting at size 80 and larger than this size at significance level 5% and 1% with associated P-value as shown in the table. H0=1 means reject the null hypothesis that states the parameter distribution follows the standard normal distribution. While H0=0 means fail to reject the null hypothesis. See the following figures (66-69)
Figure 66.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using percentile method.
Figure 66.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=20) on the left and (n=80) on the right using percentile method.
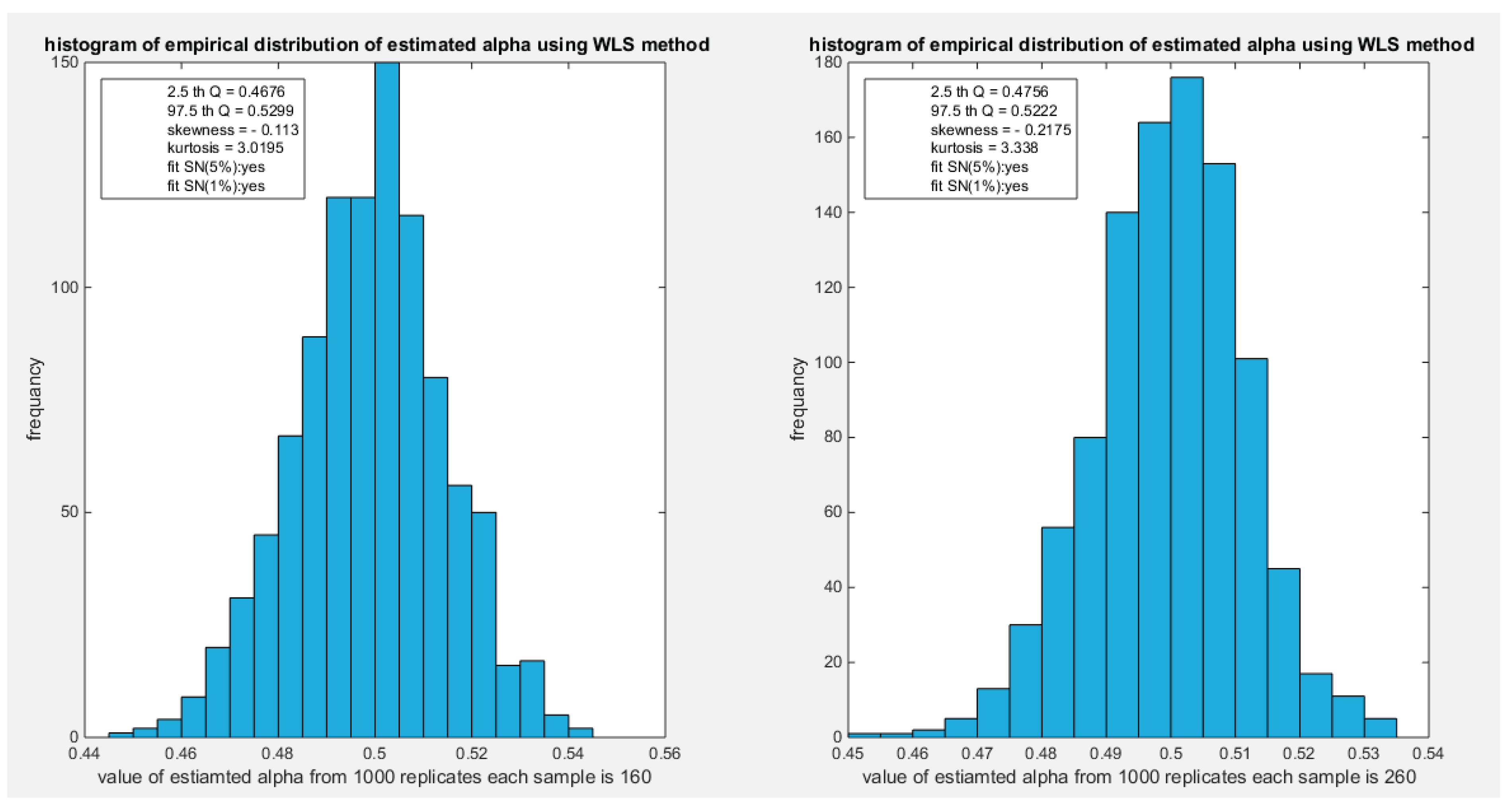
Figure 67.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using percentile method.
Figure 67.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n=160) on the left and (n=260) on the right using percentile method.
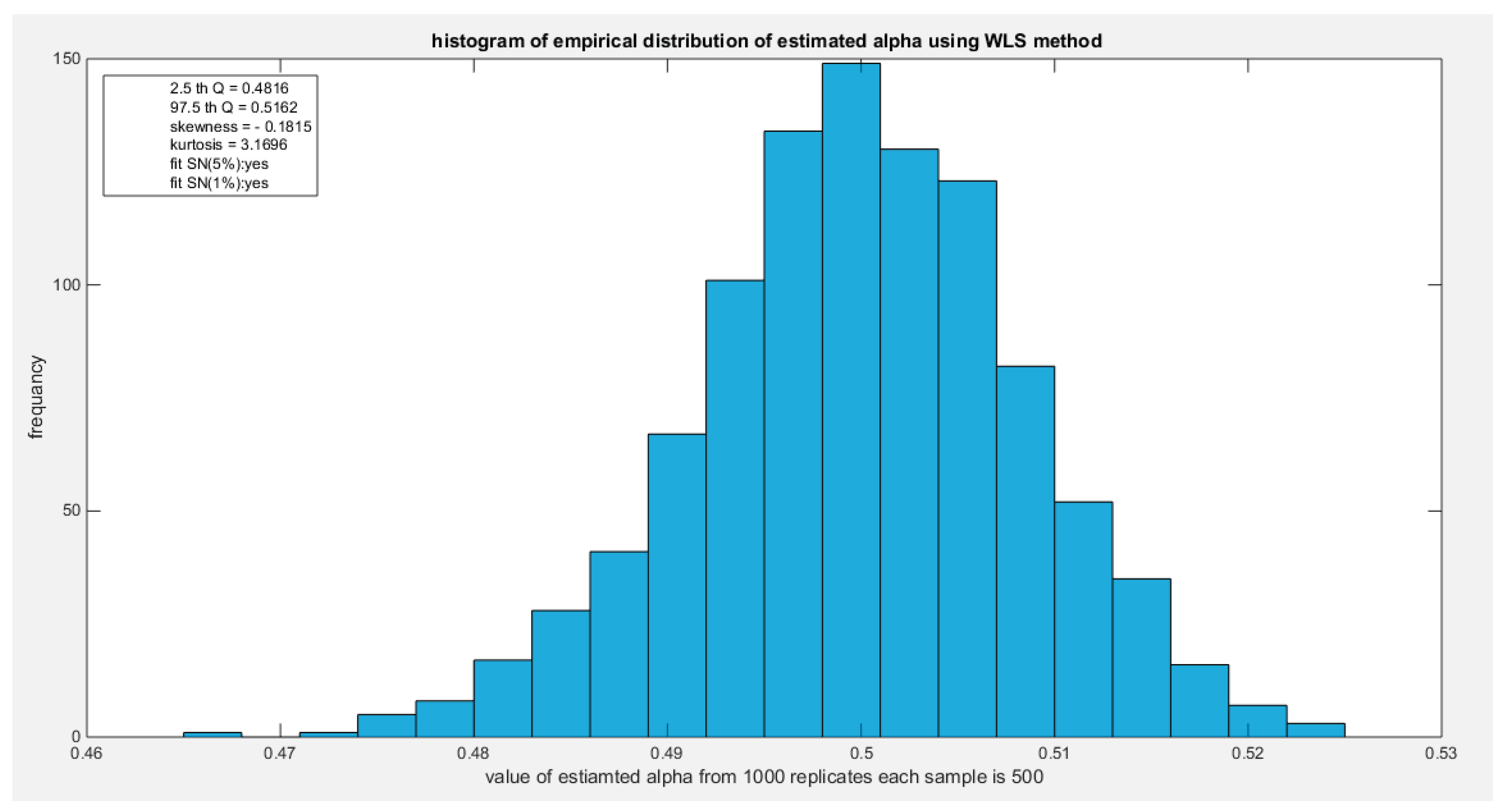
Figure 68.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n =500) using percentile method.
Figure 68.
shows the histogram of the empirical distribution of the estimated alpha from the 1000 replicates with sample size (n =500) using percentile method.
Figure 69.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (percentile) method and how these indices change with changing the sample size from 20 to 500.
Figure 69.
shows the heat map of the indices of the empirical distribution of the estimated alpha using (percentile) method and how these indices change with changing the sample size from 20 to 500.