Submitted:
25 September 2024
Posted:
26 September 2024
You are already at the latest version
Abstract
Keywords:
MSC: 65M06; 26A33; 65M12
1. Introduction
2. 4WSGD Operators for Riemann-Liouville VO Fractional Derivatives
3. IE-4WSGD Scheme for 1D SRVONFDE
3.1. IE-4WSGD Scheme
3.2. Stability and Convergence Analysis
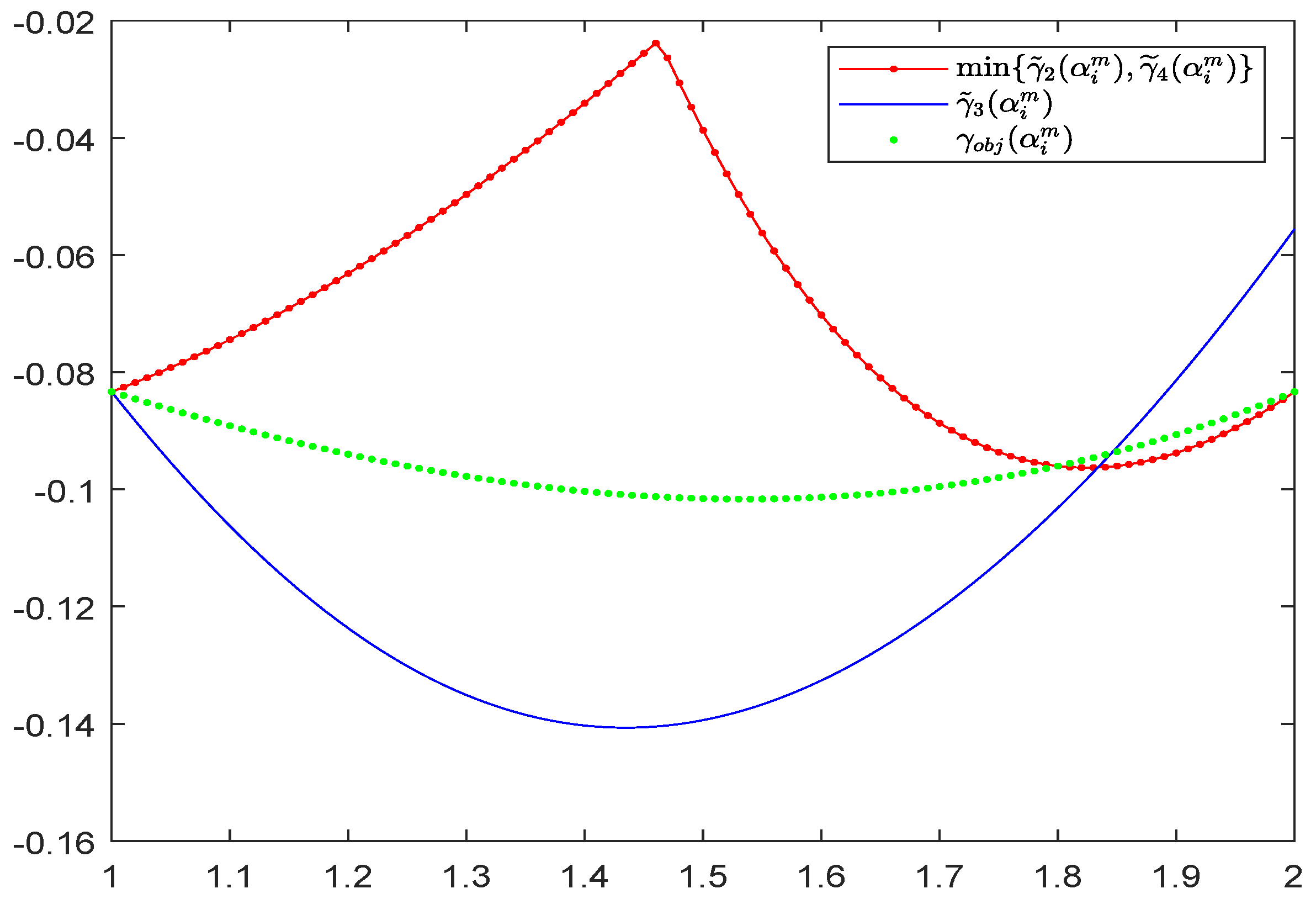
- Objective:
- Lower bound:
- Upper bound:
4. Preconditioning Techniques
- (i)
- The spectrum radius of is bounded as follows:
- (ii)
- The condition number of the preconditioned matrix is bounded as follows:
- (i)
- The spectrum radius of is bounded as follows:
- (ii)
- The condition number of the preconditioned matrix is bounded as follows:
5. IE-4WSGD Scheme for 2D SRVONFDE
6. Numerical Results
7. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Axelsson, O.; Kolotilina, L. Montonicity and discretization error eatimates. SIAM J. Numer. Anal. 1990, 27, 1591–1611. [Google Scholar] [CrossRef]
- Bai, J.; Feng, X.C. Fractional-order anisotropic diffusion for image denoising. IEEE Trans. Image Proc. 2007, 16, 2492–2502. [Google Scholar] [CrossRef] [PubMed]
- Benson, D.A.; Wheatcraft, S.W.; Meerschaert, M.M. Application of a fractional advection-dispersion equation. Water Resour. Res. 2000, 36, 1403–1412. [Google Scholar] [CrossRef]
- Benson, D.A.; Wheatcraft, S.W.; Meerschaert, M.M. The fractional-order governing equation of Lévy motion. Water Resour. Res. 2000, 36, 1413–1423. [Google Scholar] [CrossRef]
- Çelik, C.; Duman, M. Crank-Nicolson method for the fractional diffusion equation with the Riesz fractional derivative. J. Comput. Phys. 2012, 231, 1743–1750. [Google Scholar] [CrossRef]
- Chechkin, A.V.; Gorenflo, R.; Sokolov, I.M. Fractional diffusion in inhomogeneous media. J. Phys. A 2005, 38, L679–L684. [Google Scholar] [CrossRef]
- Coimbra, C. F. Mechanics with variable-order differential operators. Ann. Phys. 2003, 515, 692–703. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations; Spring-Verlag, Berlin and Heidelberg, 2010.
- Ding, H.F.; Li, C.P.; Chen, Y.Q. High-order algorithms for Riesz derivative and their applications (I). Abstr. Appl. Anal. 2014, 2014, 653797. [Google Scholar] [CrossRef]
- Du, R.; Alikhanov, A.A.; Sun, Z.Z. Temporal second order difference schemes for the multi-dimensional variable-order time fractional sub-diffusion equations. Comput. Math. Appl. 2020, 79, 2952–2972. [Google Scholar] [CrossRef]
- Henry, B.I.; Wearne, S.L. Fractional reaction-diffusion. Physica A 2000, 276, 448–455. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Toptics in Matrix Analysis; Academic Press, Cambridge, 1994.
- Ingman, D.; Suzdalnitsky, J. Control of damping oscillations by fractional differential operator with time-dependent order. Comput. Methods Appl. Mech. Engrg. 2004, 193, 5585–5595. [Google Scholar] [CrossRef]
- Jin, B.T.; Lazarov, R.; Pasciak, J.; Zhou, Z. Error analysis of a finite element method for the space-fractional parabolic equation. SIAM J. Numer. Anal. 2014, 52, 2272–2294. [Google Scholar] [CrossRef]
- Kameni, S.N.; Djida, J.D.; Atangana, A. Modelling the movement of groundwater pollution with variable order derivative. J. Nonlinear Sci. Appl. 2017, 10, 5422–5432. [Google Scholar] [CrossRef]
- Kheirkhah, F.; Hajipour, M.; Baleanu, D. The performance of a numerical scheme on the variable-order time-fractional advection-reaction-subdiffusion equations. Appl. Numer. Math. 2022, 178, 25–40. [Google Scholar] [CrossRef]
- Lin, F.R.; Wang, Q.Y.; Jin, X.Q. Crank-Nicolson-weighted-shifted-Grünwald difference schemes for space Riesz variable-order fractional diffusion equations. Numer. Algor. 2021, 87, 601–631. [Google Scholar] [CrossRef]
- Lin, F.R.; Yang, S.W.; Jin, X.Q. Preconditioned iterative methods for fractional diffusion equation. J. Comput. Phys. 2014, 256, 109–117. [Google Scholar] [CrossRef]
- Lin, R.; Liu, F.; Anh, V.; Turner, I. Stability and convergence of a new explicit finite-difference approximation for the variable-order nonlinear fractional diffusion equation. Appl. Math. Comput. 2009, 212, 435–445. [Google Scholar] [CrossRef]
- Liu, F.; Zhuang, P.; Turner, I.; Burrage, K.; Anh, V. A new fractional finite volume method for solving the fractional diffusion equation. Appl. Math. Model. 2014, 38, 3871–3878. [Google Scholar] [CrossRef]
- Lorenzo, C.F.; Hartley, T.T. Variable-order and distributed order fractional operators. Nonlinear Dyn. 2002, 29, 57–98. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Tadjeran, C. Finite difference approximtionns for fractional advection-dispersion flow equations. J. Comput. Appl. Math. 2004, 172, 65–77. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Tadjeran, C. Finite difference approximations for two-sided space-fractional partial differential equations. Appl. Numer. Math. 2006, 56, 80–90. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley, New York, 1993.
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press, New York, 1974.
- Ortigueira, M.D. Riesz potential operators and inverses via fractional centred derivatives. Int. J. Math. Math. Sci. 2006, 2006, 048391. [Google Scholar] [CrossRef]
- Pang, H.K.; Sun, H.W. A fast algorithm for the variable-order spatia fractional advection-diffusion equation. J. Sci. Comput. 2021, 87, 15. [Google Scholar] [CrossRef]
- Patnaik, S.; Hollkamp, J.P.; Semperlotti, F. Applications of variable-order fractional operators: a review. Proc. R. Soc. A 2020, 87476, 20190498. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Cambridge University Press, New York, 1999.
- Ruiz-Medina, M.D.; Anh, V.; Angulo, J.M. Fractional generalized random fields of variable order. Stochastic Anal. Appl. 2004, 22, 775–799. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integerals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers, 1993.
- Samko, S.G.; Ross, B. Integration and differentiation to a variable fractional order. Integr. Transf. Special Funct. 1993, 1, 277–300. [Google Scholar] [CrossRef]
- Seki, K.; Wojcik, M.; Tachiya, M. Fractional reaction-diffusion equation. J. Chem. Phys. 2003, 119, 2165–2174. [Google Scholar] [CrossRef]
- She, Z.H. A class of unconditioned stable 4-point WSGD schemes and fast iteration methods for space fractional diffusion equations. J. Sci. Comput. 2022, 92, 18. [Google Scholar] [CrossRef]
- She, Z.H.; Lao, C.X.; Yang, H.; Lin, F.R. Banded preconditioners for Riesz space fractional diffusion equations. J. Sci. Comput. 2021, 86, 31. [Google Scholar] [CrossRef]
- Sokolov, I.M.; Klafter, J.; Blumen, A. Fractional kinetics. Phys. Today 2002, 55, 48–54. [Google Scholar] [CrossRef]
- Sun, H.; Chang, A.; Zhang, Y.; Chen, W. A review on variable-order fractional differential equations: mathematical foundations, physical models, numerical methods and applications. Fract. Calc. Appl. Anal. 2019, 22(1), 27–59. [Google Scholar] [CrossRef]
- Sun, Z.Z.; Gao, G.H. Finite Difference Method for Fractional Differential Equations (Chinese version). Science Press, Beijing, 2015.
- Tian, W.; Zhou, H.; Deng, W. A class of second order difference approximations for solving space fractional diffusion equations. Math. Comput. 2015, 84, 1703–1727. [Google Scholar] [CrossRef]
- Wang, D.L.; Xiao, A.G.; Yang, W. Maximum-norm error analysis of a difference scheme for the space fractional CNLS. Appl. Math. Comput. 2015, 257, 241–251. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Lin, F.R. Banded preconditioners for two-sided space variable-order fractional diffusion equations with a nonlinear source term. Accepted by Commun. Appl. Math. Comput.
- Wang, Q.Y.; She, Z.H.; Lao, C.X.; Lin, F.R. Fractional centered difference schemes and banded preconditioners for nonlinear Riesz space variable-order fractional diffusion equations. Numer. Algor. 2023, 95, 859–895. [Google Scholar] [CrossRef]
- Zeng, F.H.; Zhang, Z.Q.; Karniadakis, G.E. A generalized spectral collocation method with tunable accuracy for variable-order fractional differential equations. SIAM J. Sci. Comput. 2015, 37, A2710–A2732. [Google Scholar] [CrossRef]
- Zhao, X.; Sun, Z.Z.; Karniadakis, G.E. Second-order approximations for variable order fractional derivatives: Algorithms and applications. J. Comput. Phys. 2015, 293, 184–200. [Google Scholar] [CrossRef]
- Zhuang, P.; Liu, F.; Anh, V.; Turner, I. Numerical methods for the variable-order fractional advection-diffusion equation with a nonlinear source term SIAM J. Numer. Anal. 2009, 47, 1760–1781. [Google Scholar] [CrossRef]
| N | M | Error | GE | |||
| 1.6776e-01 | – | (–, 0.0216) | (6.00, 0.0369) | (26.00, 0.0394) | ||
| 8.6713e-03 | 4.26 | (–, 0.0895) | (3.92, 0.1379) | (13.81, 0.1398) | ||
| 5.3568e-04 | 4.02 | (–, 2.3517) | (1.01, 2.3228) | (1.01, 2.2034) | ||
| 3.3459e-05 | 4.00 | (–, 175.5498) | (1.00, 156.8173) | (1.00, 149.2442) |
| N | M | Error | GE | |||
| 1.0610e-01 | – | (–, 0.0212) | (4.00, 0.0365) | (28.50, 0.0391) | ||
| 5.7878e-03 | 4.20 | (–, 0.0918) | (2.94, 0.1334) | (22.73, 0.1488) | ||
| 3.5884e-04 | 4.01 | (–, 2.4540) | (1.01, 2.4022) | (1.22, 2.3063) | ||
| 2.2415e-05 | 4.00 | (–, 177.6686) | (1.00, 161.0472) | (1.00, 152.0569) |
| N | M | Error | GE | |||
| 1.4136e-01 | – | (–, 0.1455) | (7.33, 0.1474) | (6.67, 0.1569) | ||
| 7.8665e-03 | 4.17 | (–, 0.2134) | (2.60, 0.2876) | (3.03, 0.3827) | ||
| 4.8806e-04 | 4.01 | (–, 126.3812) | (1.05, 11.7302) | (1.10, 13.8425) | ||
| 3.0296e-05 | 4.01 | (–, 29107.2033) | (1.00, 748.1152) | (1.02, 753.8003) |
| N | M | Error | GE | |||
| 1.3983e-01 | – | (–, 0.1073) | (16.00, 0.1375) | (16.00, 0.1886) | ||
| 7.6815e-03 | 4.19 | (–, 0.2687) | (4.68, 0.4383) | (5.59, 0.4450) | ||
| 4.7459e-04 | 4.02 | (–, 139.7812) | (1.09, 13.7007) | (1.17, 12.0109) | ||
| 2.9450e-05 | 4.01 | (–, 13772.3810) | (1.02, 1010.3408) | (1.07, 1216.1459) |
| N | M | Error | |
| 5.6644e-02 | – | ||
| 6.1470e-03 | 3.20 | ||
| 4.0610e-04 | 3.92 | ||
| 2.5891e-05 | 3.97 |
| N | M | Error | |
| 6.7791e-02 | – | ||
| 3.9463e-03 | 4.10 | ||
| 2.5590e-04 | 3.95 | ||
| 1.6331e-05 | 3.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





