Submitted:
24 September 2024
Posted:
26 September 2024
Read the latest preprint version here
Abstract
Keywords:
1. Introduction
3. Results
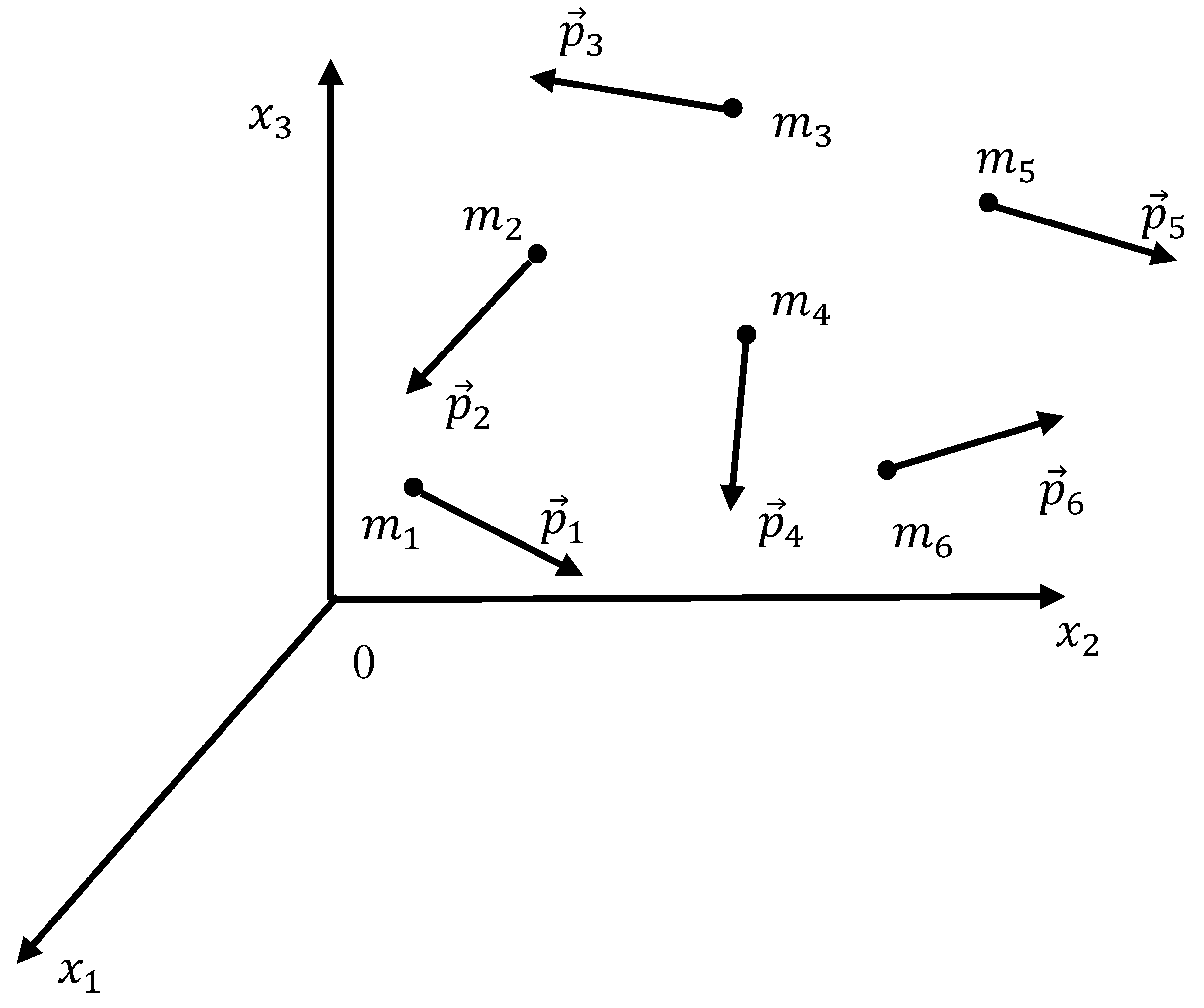
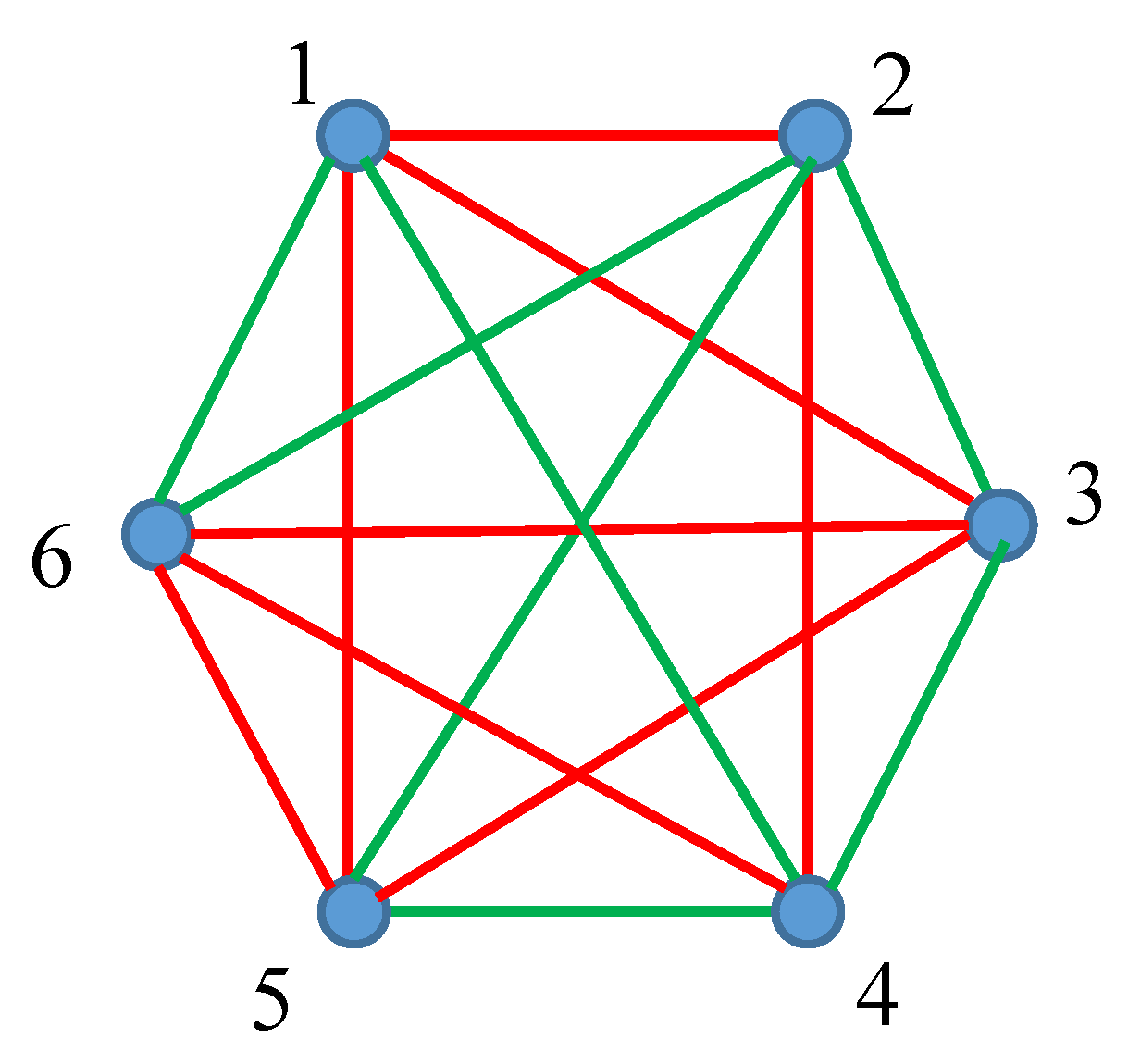
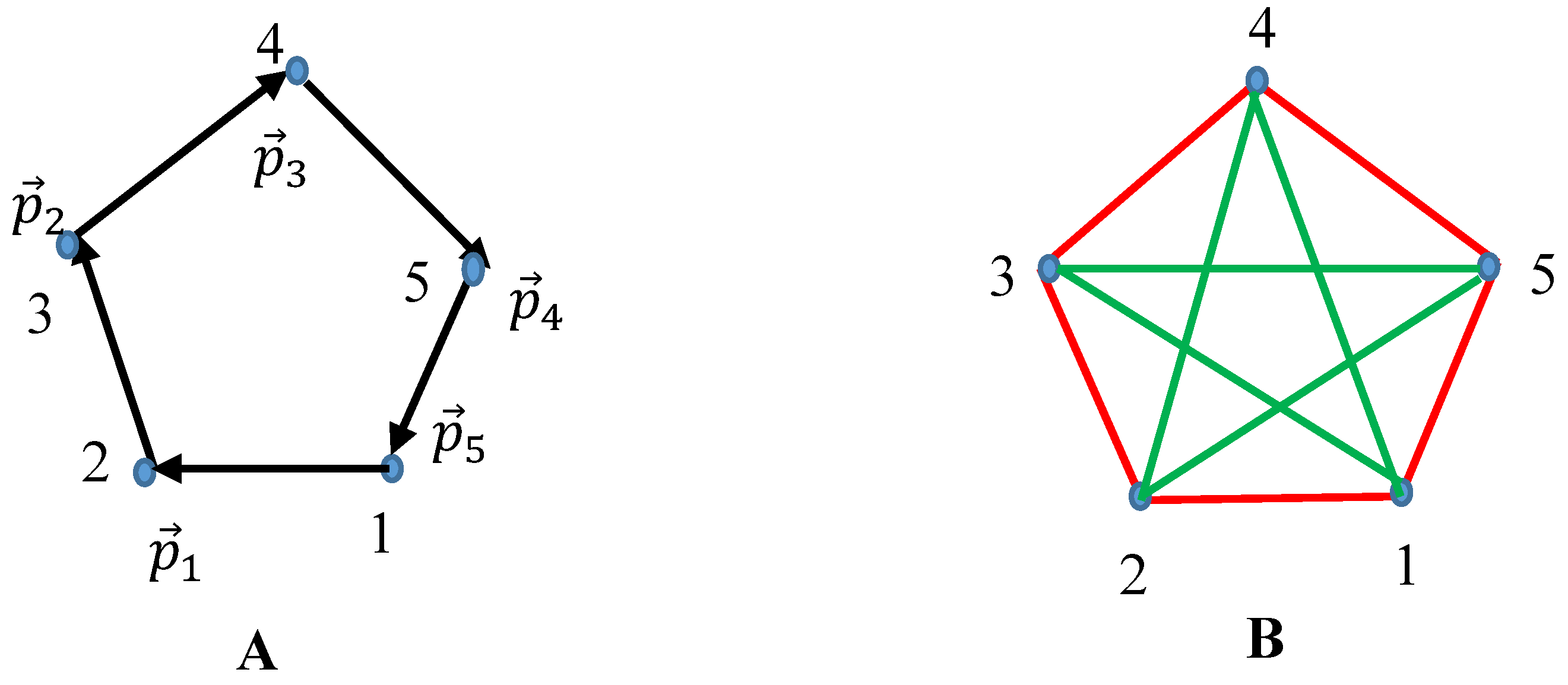
3.1. Isolated System of Point Masses and Its Analysis with the Ramsey Theory
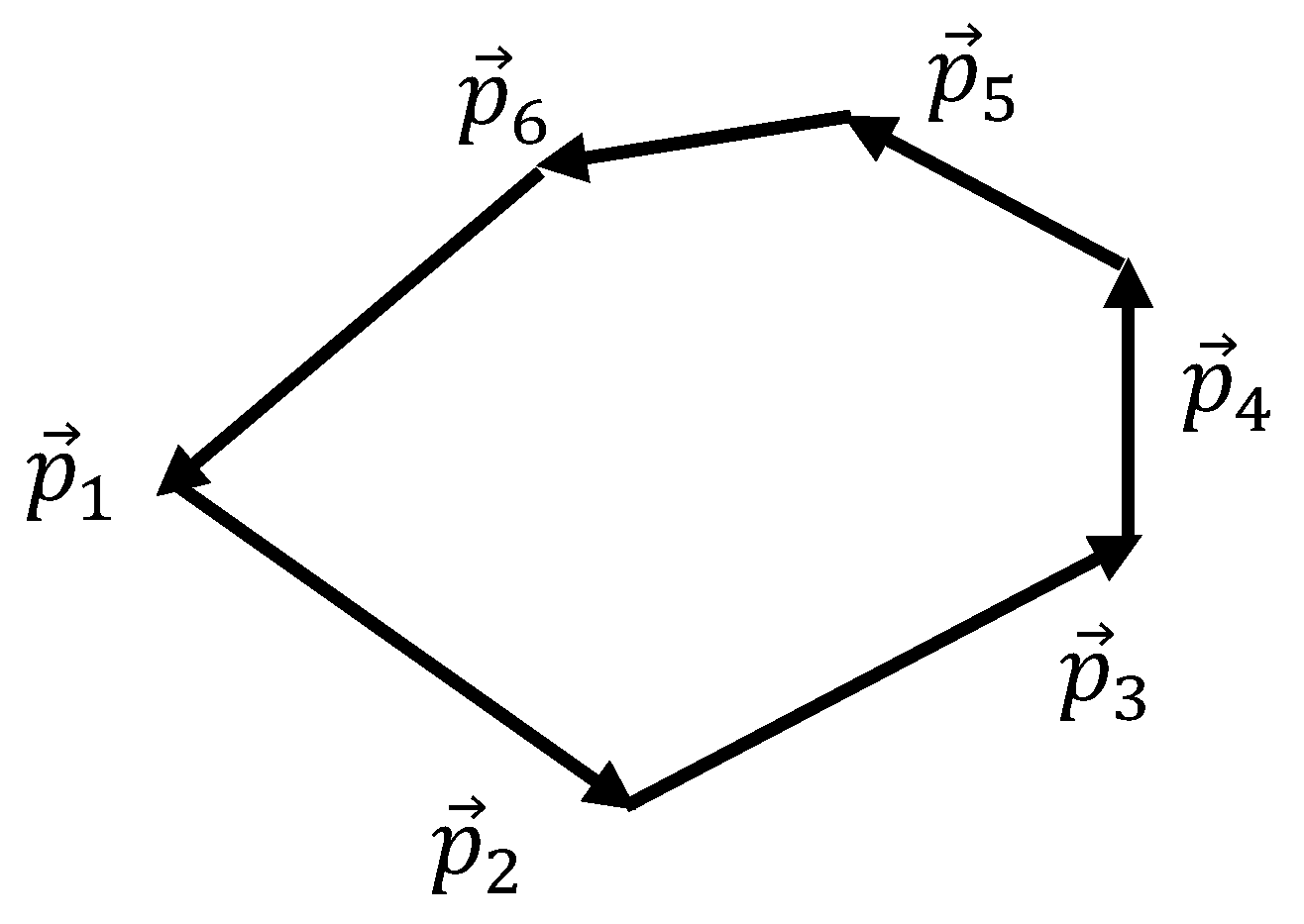
3.2. The Ring-like System of Momenta and Its Properties
3.3. Extension of the Suggested Analysis for the Angular Momenta of the Particles
4. Discussion
- i)
- to investigate Hamiltonian interpretation of the introduced graphs, emerging from the Hamiltonian of a given mechanical system.
- ii)
- to study the relativistic generalization of the introduced graphs.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ramsey, F. P. On a Problem of Formal Logic. In: Gessel, I., Rota, GC. (eds) Classic Papers in Combinatorics. Modern Birkhäuser Classics. Birkhäuser Boston, 2009, pp. 264-286.
- Chartrand, G.; Zhang, P. New directions in Ramsey theory. Discrete Math. Lett. 2021, 6, 84–96. [Google Scholar]
- Graham, R. L.; Rothschild, B.L.; Spencer, J, H. Ramsey theory, 2nd ed., Wiley-Interscience Series in Discrete Mathematics and Optimization, John Wiley & Sons, Inc., New York, A Wiley-Interscience Publication, 1990, pp. 10-110.
- Graham, R.; Butler, S. Rudiments of Ramsey Theory (2nd ed.). American Mathematical Society: Providence, Rhode Island, USA, 2015; pp. 7–46.
- Di Nasso, M.; Goldbring, I.; Lupini, M. , Nonstandard Methods in Combinatorial Number Theory, Lecture Notes in Mathematics, vol. 2239, Springer-Verlag, Berlin, 2019.
- Katz, M.; Reimann, J. Introduction to Ramsey Theory: Fast Functions, Infinity, and Metamathematics, Student Mathemati-cal Library Volume: 87; 2018; pp. 1-34.
- Erdős, P. , Gyárfás, A. A variant of the classical Ramsey problem. Combinatorica 1997, 17, 459–467. [Google Scholar] [CrossRef]
- Erdős, P. Solved and unsolved problems in combinatorics and combinatorial number theory, Congressus Numerantium, 1981, 32, 49–62.
- Conlon, J. Fox, B. Sudakov, Recent developments in graph Ramsey theory, Surveys in Combinatorics, 2015, 424, 49–118. [Google Scholar]
- Dubo, F. D.; Stein, M. On the Ramsey number of the double star, Discrete Mathematics, 2025, 348 (1), 114227.
- Hu, X.; Li, Q. Ramsey numbers and a general Erdős-Rogers function, Discrete Mathematics, 2024, 347 (12), 114203.
- Wouters, J.; Giotis, A.; Kang, R.; Schuricht, D.; Fritz, L. Lower bounds for Ramsey numbers as a statistical physics problem. J. Stat. Mech. 2022, 2022, 0332. [Google Scholar] [CrossRef]
- Shvalb, N.; Frenkel, M.; Shoval, Sh.; Bormashenko, Ed. Dynamic Ramsey Theory of Mechanical Systems Forming a Complete Graph and Vibrations of Cyclic Compounds, Dynamics 2023, 3(2), 272-281.
- Frenkel, M.; Shoval, Sh.; Bormashenko, Ed. Fermat Principle, Ramsey Theory and Metamaterials. Materials 2023, 16(24), 7571.
- Landau, L. D.; Lifshitz, E. M. Mechanics, Vol. 1 (3rd ed.), Butterworth-Heinemann, Oxford, UK, 1976.
- Choudum, S. A.; Ponnusamy, B. Ramsey numbers for transitive tournaments, Discrete Mathematics 1999, 206, 119–129.
- Shvalb, N.; Frenkel, M. Shoval, S.; Bormashenko Ed. A Note on the Geometry of Closed Loops, Mathematics 2023, 11(8), 1960.
- Li, Y.; Lin, Q. Elementary methods of the graph theory, Applied Mathematical Sciences. Springer, pp. 3-44, Cham, Switzerland, 2020.
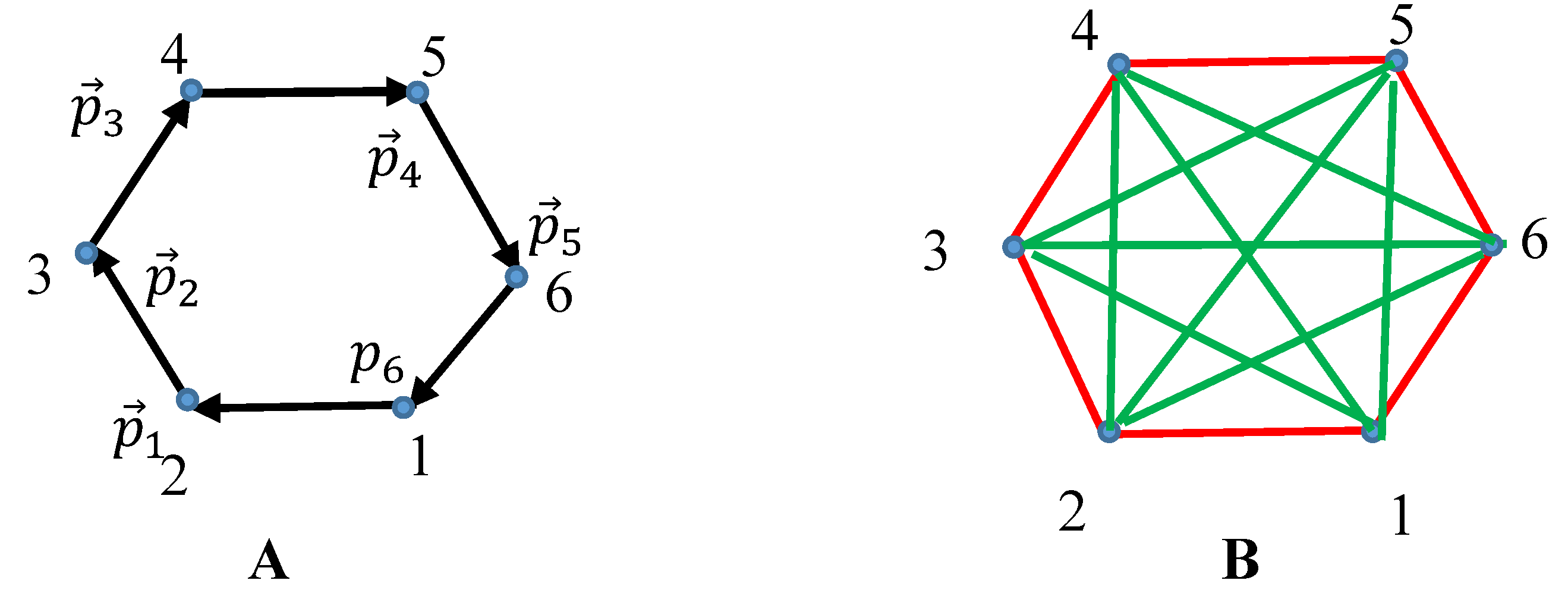
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




