1. Introduction
Automation in agriculture has experienced significant advancements in recent decades, with robotics playing an increasingly vital role. These developments have been driven by the need to enhance efficiency, reduce labor costs, and increase productivity in the agricultural sector [
2]. Robotic arms specifically designed for fruit harvesting must exhibit precision, speed, and adaptability to various working conditions, as these characteristics are essential for handling the diversity and delicacy of agricultural products [
15].
A 4-degree-of-freedom (DOF) robotic arm presents a suitable solution due to its balance of simplicity and functionality, providing the capability to achieve varied positions and orientations. These robotic arms operate with four independent movements: base rotation, arm lift, arm extension, and wrist rotation. This configuration enables the arm to access a wide range of positions, crucial for the precise handling required in fruit harvesting. Additionally, the simpler design of 4-DOF robotic arms, compared to those with more degrees of freedom, reduces control complexity and programming effort, leading to faster implementation and lower maintenance costs [
11].
As a versatile tool in agricultural automation, the 4-DOF robotic arm is particularly effective in fruit harvesting applications. Its ability to move in multiple independent directions allows for a high degree of flexibility and precision in handling fruits. This flexibility is essential for ensuring efficient, accurate harvesting while minimizing the risk of damaging delicate produce [
10].
Fruit harvesting poses unique challenges due to the variability in the size, shape, and location of fruits, as well as the need to prevent product damage. Robotic arms must be capable of adapting to these variations, accurately identifying and selecting fruits, and applying the appropriate amount of force to avoid bruising or other damage. The flexibility of a 4-DOF robotic arm makes it well-suited to these tasks. Moreover, advanced programming and control algorithms can be employed to optimize the arm’s movements according to specific environmental conditions, such as different tree types or varying weather conditions [
9].
Incorporating robotic arms into fruit harvesting represents a promising solution for automating this labor-intensive process. By integrating advanced sensors and computer vision algorithms, these robotic systems can identify and select ripe fruits, differentiating them from unripe or damaged ones. This capability not only enhances the efficiency of the harvest but also improves the quality of the final product by ensuring that only fruits in optimal condition are picked [
1]. Furthermore, automating fruit harvesting reduces dependence on seasonal labor, which is often scarce and costly, while enabling continuous operation without fatigue, thereby significantly increasing productivity [
18].
2. Methodology
The methodology for the analysis and development of a 4-degree-of-freedom (DOF) robotic arm for fruit harvesting, using MATLAB, can be organized into several key stages. Each stage plays a crucial role in ensuring the thorough analysis, precise design, and optimized performance of the robotic system.
Kinematic Modeling: This stage involves the formulation of the kinematic equations governing the robotic arm’s movement. MATLAB provides a powerful platform for this, enabling the development of precise models that define the position, velocity, and acceleration of each joint and link in the robotic arm. By using MATLAB’s symbolic math tools and the Robotics System Toolbox, researchers can model both forward and inverse kinematics, ensuring that the robotic arm can reach the necessary positions with the required accuracy and speed [
6]. This model is essential for understanding the robot’s range of motion and operational limits.
Simulation in MATLAB: The simulation phase is where the kinematic model is tested under different conditions to verify its functionality and efficiency. MATLAB’s Robotics System Toolbox provides pre-built functions and toolsets that simplify the simulation of robotic arms, including the ability to simulate joint movements, control algorithms, and sensor integration. Through these simulations, researchers can visualize the robot’s behavior in real-time, identify potential issues, and make necessary adjustments before physical implementation [
12].
Trajectory Planning: MATLAB offers advanced trajectory planning tools that allow researchers to program the robotic arm to follow specific paths while avoiding obstacles and minimizing energy consumption. These tools enable the arm to efficiently navigate complex environments, such as fruit orchards, by generating smooth and optimized trajectories. MATLAB’s visualization capabilities allow researchers to observe the robotic arm’s performance and ensure that the trajectories are feasible for real-world applications. This step is crucial for reducing the risk of fruit damage and optimizing the harvesting speed [
12].
Control and Optimization: Once the robotic arm has been successfully modeled and simulated, control algorithms must be developed to govern its real-time behavior. MATLAB can be integrated with physical hardware, allowing the transfer of simulated models to actual robotic systems. Additionally, MATLAB’s optimization tools can be used to refine the control algorithms, ensuring that the arm operates with maximum efficiency in terms of speed, precision, and power consumption. The ability to fine-tune the robot’s performance through MATLAB ensures that the system can handle the challenges of agricultural environments, such as uneven terrain and varying fruit positions [
12].
Several studies have demonstrated the effectiveness of this methodology. For example, [
5] developed a robotic system for cucumber harvesting, utilizing MATLAB for both simulation and control. Their research showed that by accurately modeling the system and using MATLAB for simulation, the efficiency of the harvesting process was significantly improved, reducing manual labor and increasing overall productivity. Similarly, [
2] investigated the use of robotic arms for pepper harvesting, leveraging MATLAB to simulate the robot’s kinematic behavior and optimize its trajectories. Their work demonstrated that optimized trajectory planning not only increased harvesting efficiency but also minimized fruit damage by ensuring precise and gentle handling.
This methodology highlights the importance of integrating kinematic modeling, simulation, trajectory planning, and control optimization into the development of a 4-DOF robotic arm for fruit harvesting. By utilizing MATLAB’s comprehensive toolboxes and capabilities, researchers can refine both the design and performance of agricultural robots, ultimately contributing to more efficient and cost-effective automation in the agricultural industry.
3. Background
Robotics in agriculture has gained prominence in recent decades due to the need to improve efficiency and reduce labor costs. The agricultural industry faces significant challenges, such as labor shortages and the need to increase production to meet global food demand. In this context, the adoption of advanced technologies such as robotics has become a viable and effective solution to address these problems. Robotic arms have been used for various agricultural tasks, from planting to harvesting, contributing to greater automation and optimization of agricultural processes [
13].
The use of robotic arms in agriculture has allowed a significant improvement in the accuracy and efficiency of critical tasks. For example, in planting, robots can plant seeds evenly and at precise depths, which improves germination rates and crop yields. At harvest, robotic arms can operate continuously and consistently, without the constraints of human fatigue, resulting in higher productivity and lower operating costs [
3].
A 4-degree-of-freedom (4 DOF) robotic arm is particularly suitable for fruit picking because of its ability to move in three-dimensional space with sufficient precision. The 4 DOFs allow the arm to perform complex movements that are essential for reaching and picking fruits located in varying positions on trees. The ability to rotate, extend, and raise the arm, as well as rotate the wrist, provides the flexibility needed to maneuver around branches and other natural obstacles, minimizing the risk of damage to both the fruit and the tree [
17].
In addition, a 4-DOF robotic arm can be equipped with advanced sensors, such as cameras and machine vision systems, which allow real-time detection and analysis of the fruits to be picked. These sensors can identify the degree of ripeness of the fruit, its size and its exact position, allowing the robotic arm to adjust its movement for optimal picking. This precision in picking not only improves the quality of the final product by preventing the harvesting of unripe or damaged fruits, but also reduces waste and increases process efficiency [
1].
The flexibility and precision of the 4 DOF robotic arms also make them ideal for picking different types of fruits, from apples and pears to more delicate fruits such as strawberries and grapes. The ability to adapt to the specific characteristics of each type of fruit, such as its size, shape and fragility, is essential to ensure effective and damage-free harvesting. This is particularly important in the context of modern agriculture, where crop diversity and variations in growing conditions require highly adaptable and efficient robotic solutions [
15].
The adoption of 4-DOF robotic arms in agriculture represents a significant breakthrough in the automation and optimization of fruit picking. Its ability to move precisely in a three-dimensional space, combined with the integration of advanced sensors, allows for efficient, accurate harvesting that is adaptable to various working conditions. This not only improves productivity and reduces labor costs, but also contributes to the sustainability and competitiveness of the agricultural industry in the long term [
17].
4. Importance of Kinematics Analysis in 4 Degrees of Freedom Robots
4.1. Precision and Motion Control
Direct (or direct) kinematics are used to determine the position and orientation of the robot’s end effector (or tool) based on the angles of the joints. This is essential for tasks that require high precision, such as assembly, welding, and robotic surgery.
Inverse kinematics, on the other hand, are used to calculate the joint angles required to achieve a desired position and orientation of the end effector. This capability is critical for robot control and programming in industrial and automation applications.
4.2. Mechanical Design Optimization
Kinematic analysis allows engineers to evaluate different design configurations to maximize the robot’s range, flexibility, and efficiency. This includes determining the optimal link length and joint arrangement. It helps to identify and avoid singularities, which are positions in which the robot loses degrees of freedom and becomes unable to move in certain directions.
4.3. Development of Control Algorithms
Motion and trajectory control algorithms are based on kinematic models to ensure smooth and precise movements. This includes the use of mathematical models for trajectory interpolation and real-time motion planning. Kinematics is also critical for the development of force controllers and haptic feedback in collaborative robots and teleoperation systems.
4.4. Simulation and Validation
Kinematic models are used in simulations to predict and visualize robot behavior prior to physical deployment. This reduces the costs and risks associated with developing and testing new robotic systems. Simulations allow for case studies and sensitivity analysis to understand how variations in system parameters affect robot performance.
4.5. Multidisciplinary Applications
In medicine, 4-DOF surgical robots are used to perform precise and minimally invasive procedures, improving patient outcomes and reducing recovery time. In manufacturing, robots with 4 DOFs are common in assembly and handling tasks, where a combination of linear and rotational movements is required. In research and development, kinematic analysis is crucial for the creation of autonomous robots and artificial intelligence systems that interact with dynamic, unstructured environments.
5. Benefits of Using Matlab for Analysis
Matlab software is a tool that allows you to perform motion analysis for a robotic component, its use is due to certain advantages explained below.
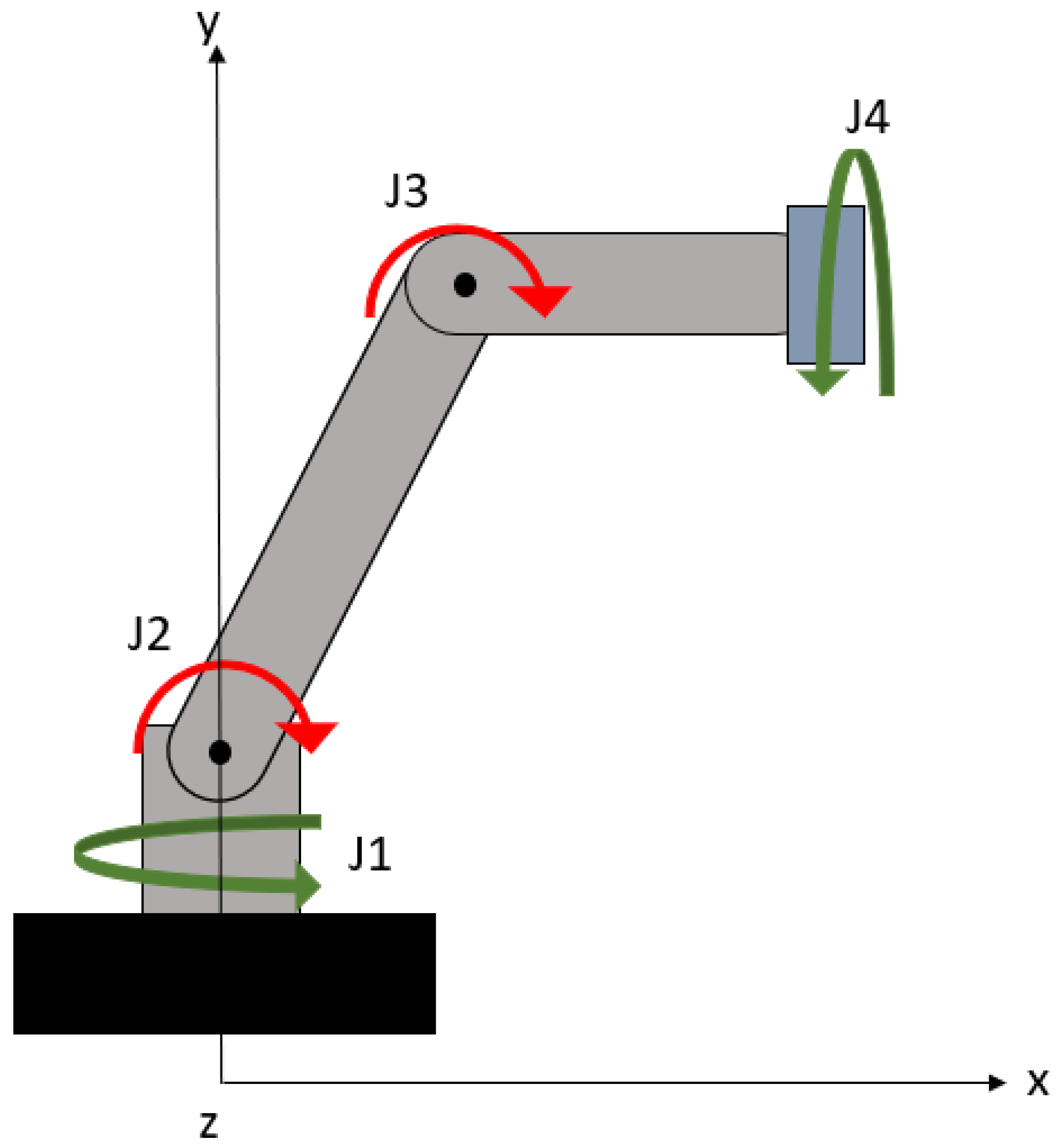
6. System Description
Degrees of Freedom and Structure of the Robotic Arm A 4-DOF robotic arm typically consists of the following joints:
Base rotation (J1).
Arm Raise (J2).
Arm extension (J3).
Wrist rotation (J4).
Each joint is controlled by an electric motor that provides the necessary movement. The combination of these movements allows the arm to reach and manipulate fruit in different positions within its operational range.
7. Direct Kinematics
Direct kinematics is a fundamental component in the analysis of manipulator robots, allowing the position and orientation of the end effector to be determined based on the configurations of the joints. The 4 DOF robotic arm consists of four joints connected in series, each controlled by a motor that determines its angle of rotation. Joints typically are:
Rotational base (J1): Allows rotational movement around a vertical axis, usually the z-axis.
Shoulder (J2): Allows the arm to be raised from the base, rotation around the x-axis.
Elbow (J3): Controls the extension of the arm forward or backward, rotation around the x-axis.
Wrist (J4): Controls the final orientation of the effector, rotation around the x-axis.
These joints are connected by rigid segments of variable length, defined by geometric parameters and the angles of the joints. For each joint of the robot, we define the D-H parameters that describe the geometry and relative orientation between two consecutive joints. These parameters are:
: Angle of rotation around the anterior .
d: Distance along the anterior to the point of intersection of the axes.
a: Length of the link along the current .
: Rotation angle around the current to carry a .
For each joint, the homogeneous transformation matrix
is calculated using the following general formula:
Where:
: Matrix rotation around the x axis by an angle .
: Translation matrix along the z axis for a distance .
: Translation matrix along the x axis for a distance .
: Matrix rotation around the z axis by an angle .
For the mathematical description of the movement of the robotic arm, homogeneous coordinates and Denavit-Hartenberg (DH) parameters are used. The DH parameters for the 4 DOF arm are:
Table 1.
Homogeneous coordinates and DH parameters
Table 1.
Homogeneous coordinates and DH parameters
| Joint |
|
|
|
|
| P1 |
|
|
0 |
|
| P2 |
|
0 |
|
0 |
| P3 |
|
0 |
|
0 |
| P4 |
|
0 |
0 |
0 |
Where:
: angle of rotation around the z-axis.
: distance along the z-axis.
: distance along the x-axis.
: angle of rotation around the x-axis.
8. Kinematics for the 4-Degree-of-Freedom Robot
To write the homogeneous matrix of a 4-degree-of-freedom robotic arm according to
Figure 1, we must first define the Denavit-Hartenberg (DH) parameters for each of the joints.
The homogeneous transformation matrix for each joint i is calculated as:
The total homogeneous matrix is obtained by multiplying the matrices of each joint:
For a 4-degree-of-freedom articulated robot, the final homogeneous transformation matrix provides a complete description of the position and orientation of the end effector (or the last link) in three-dimensional space in relation to the robot’s base.
In robot calibration, transform matrices are used to adjust and correct deviations in the position and orientation of the end effector, ensuring precision in tasks. This information is critical for a variety of applications, from trajectory planning and control to robot simulation and calibration, enabling accurate and efficient operation of the robotic system.
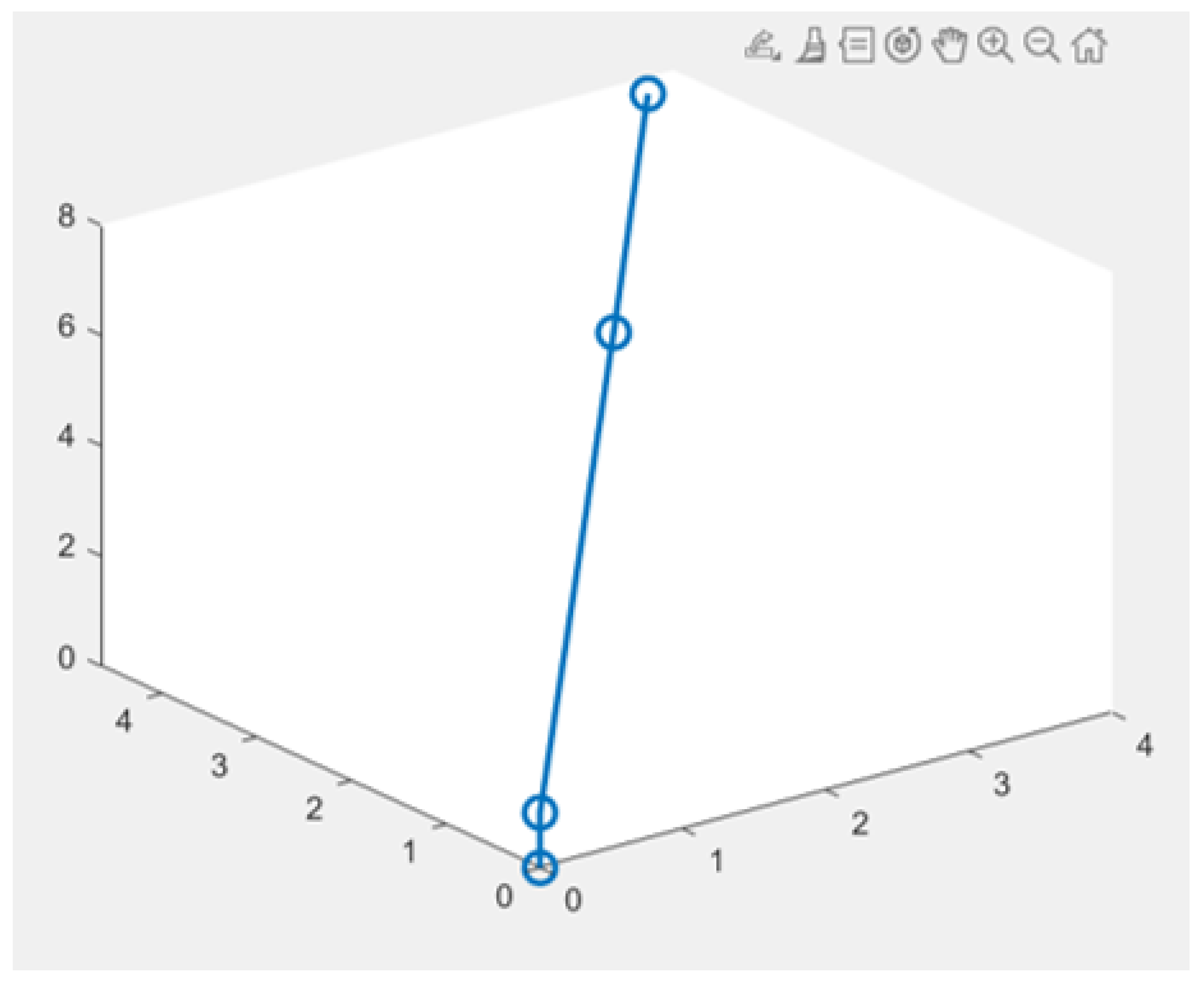
Figure 2.
Result obtained using Matlab software for graphical representation of the robotic arm.
Figure 2.
Result obtained using Matlab software for graphical representation of the robotic arm.
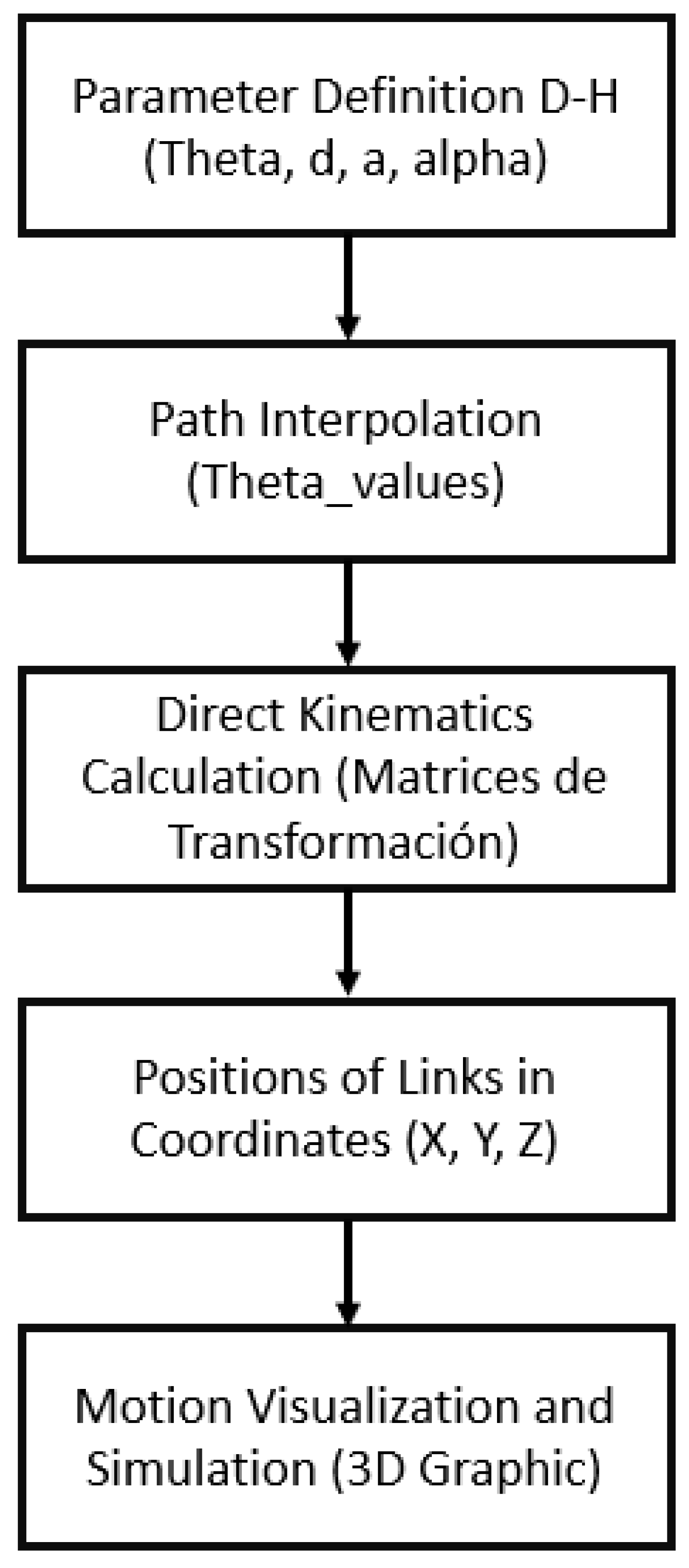
9. Trajectory Analysis
An optimal trajectory allows the robotic arm to move efficiently between fruits, reducing the overall time needed for harvesting. By reducing downtime and unnecessary movements, the robot can harvest more fruit in a given period, increasing overall productivity. Well-planned trajectories ensure that the arm moves smoothly and accurately, minimizing the risk of damaging the fruits during harvesting. Careful handling is crucial to maintaining the quality of fruits, which is essential for their commercial value. A detailed trajectory analysis allows arm movements to be adjusted to suit different sizes, shapes, and locations of the fruits. Trajectories can be adjusted to suit different terrain conditions and tree configurations, improving the robot’s adaptability. More direct and efficient movements reduce the system’s energy consumption, extending battery life and reducing operating costs. Lower energy consumption contributes to more sustainable and environmentally friendly agricultural practices. A trajectory analysis makes it possible to predict and avoid collisions with branches, leaves or other obstacles, protecting both the robot and the work environment. It ensures that the robotic arm operates safely, avoiding sudden movements that could endanger nearby human workers. In previous studies, such as the one conducted by [
18], it has been shown that optimizing the trajectories of a harvesting robotic arm can significantly improve harvesting efficiency and the quality of the fruits picked. In this study, a kinematic model was used to plan smooth and precise trajectories, reducing harvest time and damage to fruits. For the analysis of the trajectory in Matlab, the following steps were carried out:
Defining D-H Parameters
The Denavit-Hartenberg parameters are established for each of the links of the robotic arm. These parameters include joint angles (theta), displacements (d), link lengths (a), and torsional angles (alpha).
Path Interpolation
The start and end points of each joint’s path are defined and interpolated to obtain a series of intermediate configurations. This is done by using the linspace function in MATLAB to generate a sequence of joint angles that the robot will follow.
Direct Kinematics Calculation
Using the joint configurations (interpolated angles), homogeneous transformation matrices are calculated for each joint. These arrays describe the spatial relationship between the different links of the robotic arm.
Link Positions in Coordinates (X, Y, Z)
From the transformation matrices, the positions of each link in three-dimensional space are calculated. The coordinates (X, Y, Z) of the key points of each link are extracted.
Motion Visualization and Simulation
A 3D graph is generated that shows the trajectory of the robotic arm. The robot’s movement along the interpolated path is simulated, visualizing the positions of the links in each joint configuration.
Figure 3.
Block diagram representing the simulation of arm movement with 4 degrees of freedom.
Figure 3.
Block diagram representing the simulation of arm movement with 4 degrees of freedom.
Figure 4.
Start of the simulation process with the help of Matlab software .
Figure 4.
Start of the simulation process with the help of Matlab software .
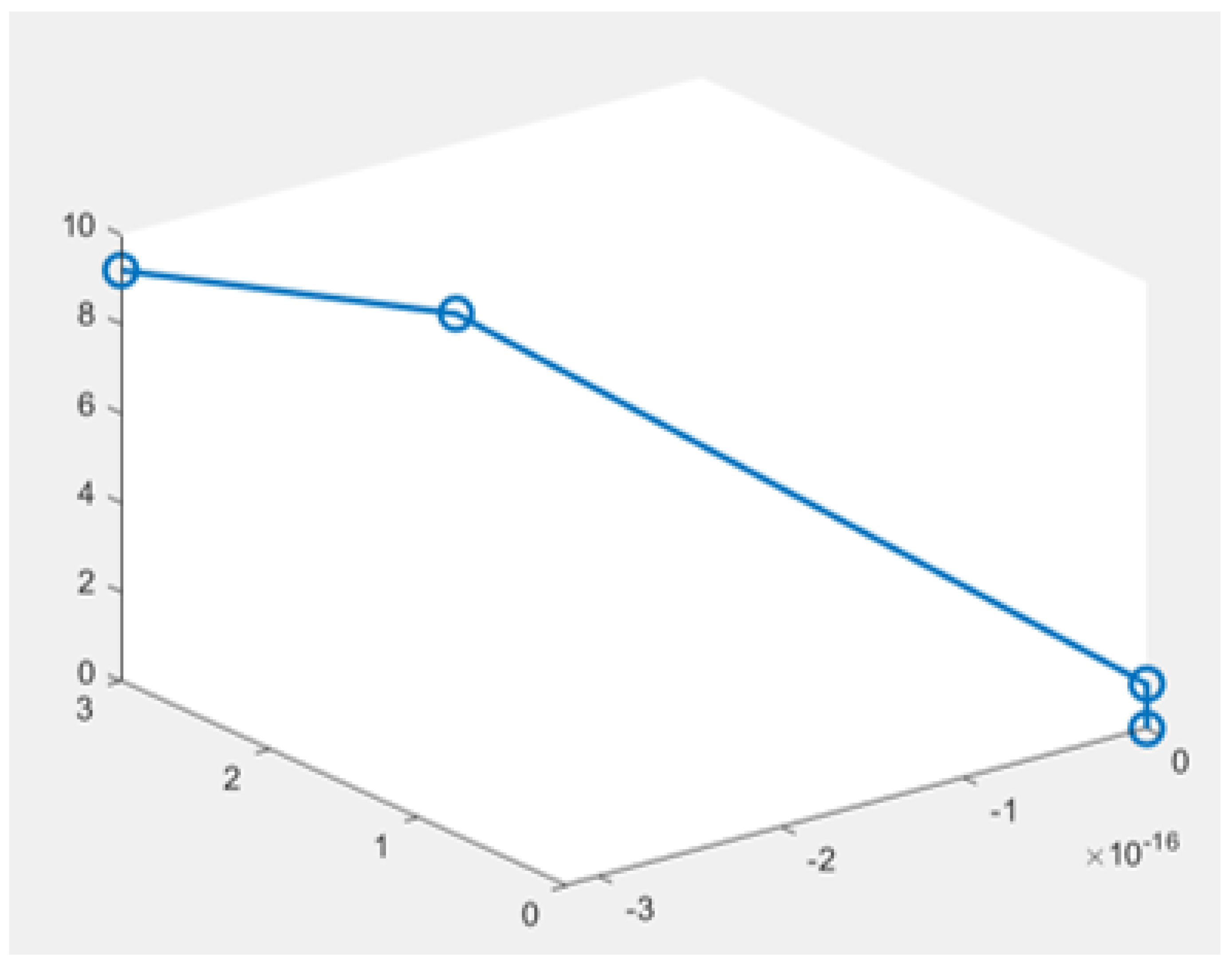
Figure 5.
Final stage of simulating the movement of the robotic arm with Matlab software
Figure 5.
Final stage of simulating the movement of the robotic arm with Matlab software
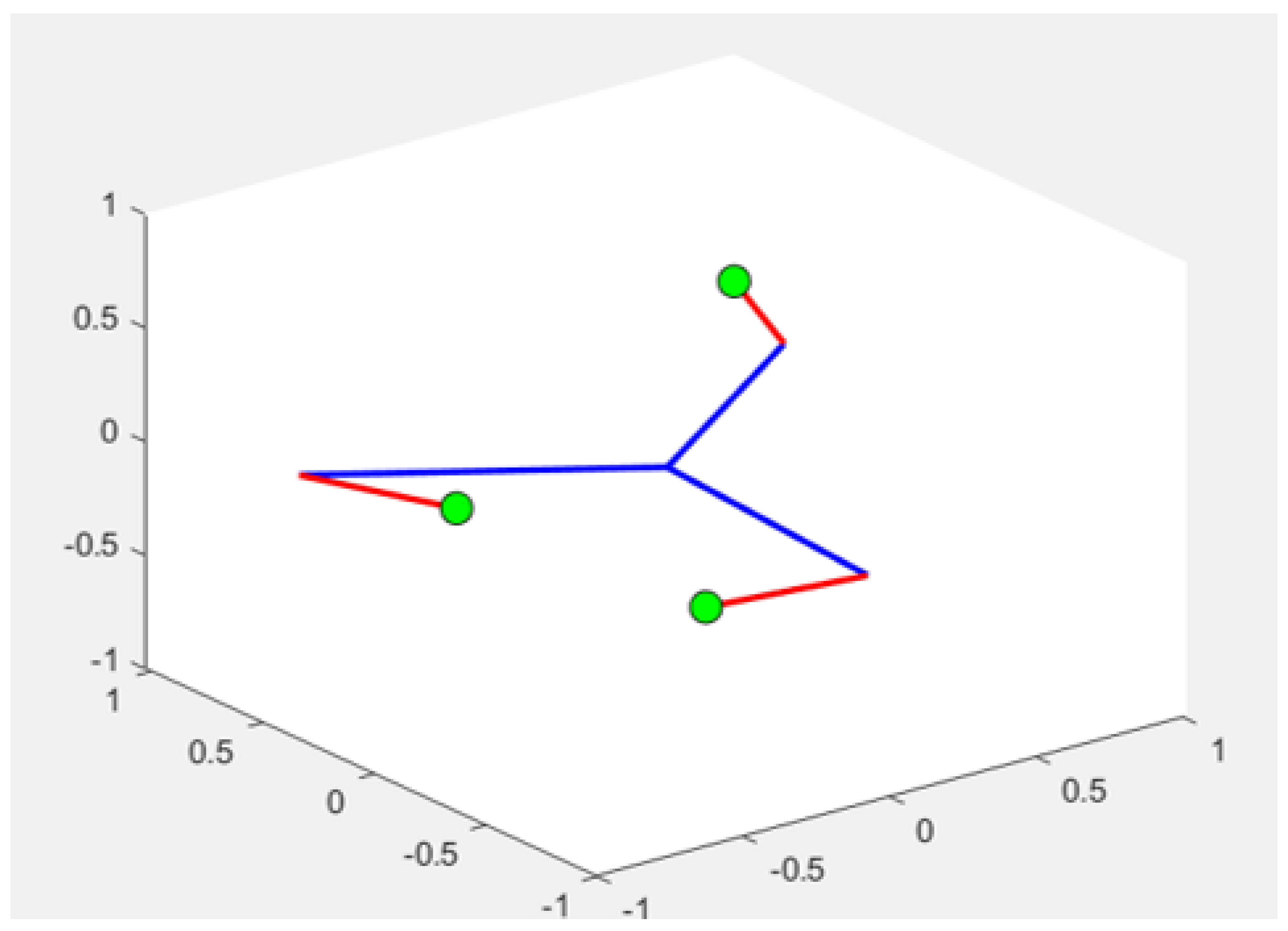
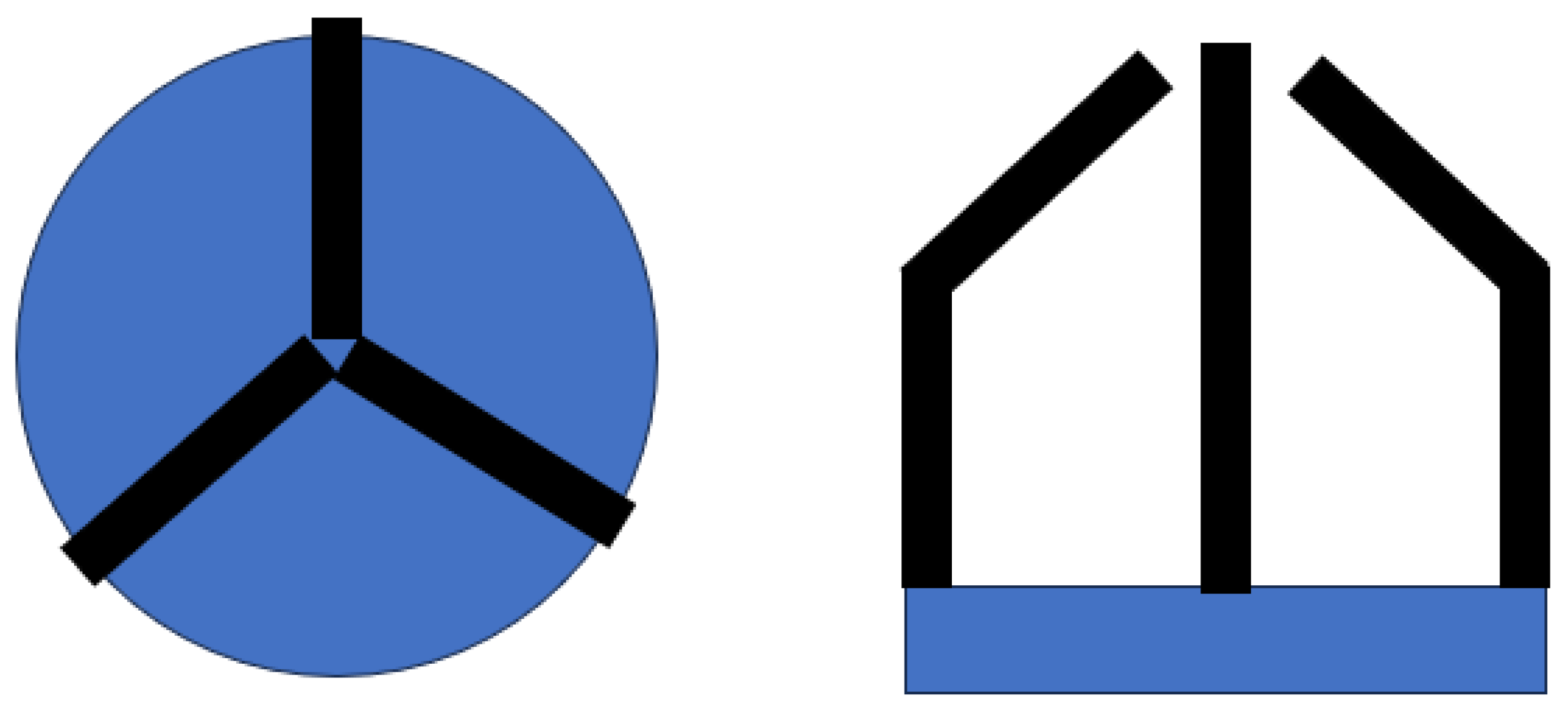
10. 3-Point Gripper Analysis
The proposed harvested robot has a gripper at the end of the arm which takes care of harvesting when opened and closed. The Matlab is used to analyze its movement, with the help of equations that will facilitate its subsequent analysis, when the exact position is determined, along with the trajectory of the articulated arm.
10.1. Conceptual Design
The gripper is the most important element of the harvesting arm as it interacts directly with the fruits, therefore the analysis must be very detailed to achieve the most optimal grip. It consists of 3 tips for a better grip which work independently but with synchrony, that is, the same movement.
Figure 6 shows the schematic representation of the gripper that will be added to the robotic arm to complete the autonomous harvesting process. The design of the clamp is 3-point to improve the grip of the fruits without compromising their size or weight. Each gripper works individually with its own motor.
10.2. Simulation in Matlab
To simulate the process of opening and closing a robotic 3-point gripper in MATLAB, we’re going to define the kinematics of each tip of the gripper and then interpolate the movement from an open position to a closed position.
Using MATLAB for the analysis of a 3-prong gripper in your opening and closing process offers multiple benefits ranging from ease of implementation to robustness in data analysis and visualization.
MATLAB provides an intuitive and easy-to-use programming environment, making it easy to quickly implement complex algorithms without the need for a steep learning curve. It also allows you to observe the dynamic behavior of the gripper in real time. This is crucial to understand how the gripper tips behave during the opening and closing process, and to identify potential improvements in the design.
MATLAB facilitates kinematic and dynamic analysis of robotic systems. It allows you to calculate trajectories, positions, speeds and accelerations of the different parts of the gripper, providing a detailed understanding of the gripper’s movement and performance. It can be easily integrated with other software and hardware systems, enabling real-time simulation and control of robotic grippers. This is especially useful for practical applications where gripper behavior needs to be tested and validated in a controlled environment before deploying it in the real world.
MATLAB includes optimization tools that can be used to improve gripper design and efficiency. In addition, it allows you to implement and test various control algorithms, such as PID controllers, adaptive controllers, and artificial intelligence algorithms, to improve gripper performance under different operating conditions.
For example, when analyzing the trajectory of a 3-point gripper in MATLAB, you can:
Model each link of the clamp and their respective joints.
Simulate the opening and closing movement in real time.
Visualize the positions of the points and joints in a 3D graph.
Optimize the trajectory to minimize operating time or maximize grip accuracy.
Implement and test different control strategies to improve the stability and performance of the gripper.
Figure 7.
Figure shows the process of simulating the gripper when it is opened
Figure 7.
Figure shows the process of simulating the gripper when it is opened
11. Discussion
The kinematic analysis of the 4-degree-of-freedom (4-DOF) robotic arm with a 3-finger gripper designed for fruit harvesting presents several key insights into the effectiveness and potential of agricultural automation. The integration of a homogeneous transformation matrix and inverse kinematics solutions within MATLAB facilitated precise motion control and simulation, demonstrating the feasibility of this robotic system in practical applications.
The kinematic modeling provided a comprehensive framework for understanding the motion capabilities of the robotic arm. By deriving the motion equations and implementing them in MATLAB, we were able to simulate various trajectories and optimize the design for maximum efficiency. The results showed that the arm could effectively navigate complex environments, reaching and grasping fruits with high precision. The accuracy of the homogeneous transformation matrices in representing the arm’s position and orientation in 3D space was particularly noteworthy.
One of the primary challenges in robotic fruit harvesting is the precise control of the gripper to avoid damaging the fruit. Our analysis revealed that the 4-DOF configuration, coupled with advanced trajectory planning algorithms, allowed for smooth and controlled movements. The MATLAB simulations demonstrated that the arm could follow predefined paths with minimal deviation, ensuring gentle handling of the fruits. This level of control is crucial for maintaining the quality of the harvested produce.
The successful kinematic analysis and simulation underscore the potential of robotics in agricultural applications. This robotic arm design can significantly reduce the labor-intensive nature of fruit harvesting, increase efficiency, and potentially lower costs. However, further research is needed to address environmental factors such as varying fruit positions and external disturbances. Future work will focus on integrating advanced sensors and machine learning algorithms to enhance the arm’s adaptability and autonomous decision-making capabilities.
Additionally, field tests in real-world agricultural settings are essential to validate the laboratory findings and identify practical challenges. Collaborations with agricultural experts will be crucial in refining the design to meet the specific needs of different crops and harvesting conditions.
12. Conclusions
The methodology described provides a structured and detailed approach to the analysis and development of a 4-degree-of-freedom robotic arm for fruit harvesting using MATLAB. From spec definition to hardware implementation, every stage is crucial to ensure an efficient and effective design that can significantly improve efficiency and accuracy in fruit picking.
In summary, the use of 4-DOF robotic arms in fruit harvesting offers numerous advantages including flexibility, precision, and the ability to adapt to different working conditions. These arms are capable of handling variability in size, shape, and location of fruits, while minimizing damage to the product. Implementing advanced robotics in agriculture not only improves efficiency and reduces labor costs, but can also ensure greater consistency and quality in fruit harvesting. For these reasons, 4-DOF’s robotic arms represent a valuable and promising tool for agricultural automation, contributing to the advancement and modernization of the industry.
The analysis of the trajectory of a robotic arm involves the precise definition of the robot’s kinematic parameters, the planning of appropriate trajectories, and the simulation of its movement. Path analysis is critical to maximizing system efficiency, accuracy, and adaptability. By optimizing these aspects, productivity can be improved, operating costs can be reduced, and the quality of the final product can be assured, contributing to more sustainable and profitable agricultural practices.
MATLAB provides a complete and versatile environment for the analysis, simulation, and optimization of 3-prong robotic grippers. Its powerful visualization tools, advanced simulation capabilities, and ease of integration with other systems make MATLAB an ideal choice for engineers and researchers in the field of robotics.
Author Contributions
Conceptualization, M.S.; Methodology, M.S.; Formal Analysis, M.S. and P.P.; Investigation, M.S. and P.P.; Data Curation, P.P.; Writing—Original Draft Preparation, M.S.; Writing—Review and Editing, P.P.; Supervision, P.P.; Validation, M.S. All authors have read and agreed to the published version of the manuscript.
Funding
The author(s) declared having received the following financial support for the research, authorship, and/or publication of this article: This work was supported by the Universitario Rumiñahui as part of the research department.
Acknowledgments
The activities that gave rise to the results presented were carried out in the context of the project to develop a fruit harvesting robot. This project is in its initial stage and the research gave rise to the results presented, with the support of the Rumiñahui University Institute. We deeply appreciate the collaboration of all the researchers, students and professionals involved in this project, whose dedication and effort have been fundamental to achieving our objectives.
Conflicts of Interest
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
References
- Arad, B., Balendonck, J., Sadeh, Y., Alchanatis, V., & van Tuijl, B. A. (2020). A review of the advances in robotic harvesting and handling of tree fruits. Computers and Electronics in Agriculture, 172, 105375.
- Bac, C. W., Hemming, J., van Tuijl, B. A. J., Barth, R., Wais, E., & Henten, E. J. (2014). Performance evaluation of a harvesting robot for sweet-pepper. Journal of Field Robotics, 31(6), 834-851.
- Bac, C. W., van Henten, E. J., Hemming, J., & Edan, Y. (2014). Harvesting robots for high-value crops: State-of-the-art review and challenges ahead. Journal of Field Robotics, 31(6), 888-911.
- Behera, S. K. (2019). Advantages and Disadvantages of MATLAB. Retrieved from https://www.researchgate.net/publication/334567234_ Advantages_and_Disadvantages_of_MATLAB.
- Bontsema, J., Van Henten, E. J., & Hemming, J. (1996). Robot for cucumber harvesting: A case study of biannual automation conferences. IFAC Proceedings Volumes, 29(1), 1653-1658.
- Corke, P. (2017). Robotics, Vision and Control: Fundamental Algorithms in MATLAB (Vol. 118). Springer.
- Craig, J. J. (2005). Introduction to Robotics: Mechanics and Control (3rd ed.). Pearson Prentice Hall.
- Denavit, J., & Hartenberg, R. S. (1955). A kinematic notation for lower-pair mechanisms based on matrices. Journal of Applied Mechanics, 22, 215-221.
- Hemming, J., Bac, C. W., van Tuijl, B. A., Barth, R., & van Henten, E. J. (2014). A robot for harvesting sweet-pepper in greenhouses. IEEE Robotics and Automation Magazine, 21(3), 105-114.
- Kragh, M. F., Christiansen, P., Laursen, M. S., Jørgensen, R. N., & Andersen, H. J. (2017). Agricultural robot for plant-specific weed control and harvesting. Journal of Field Robotics, 34(6), 1099-1111.
- Lehnert, C., English, A., McCool, C., Tow, A., & Perez, T. (2017). Autonomous sweet pepper harvesting for protected cropping systems. IEEE Robotics and Automation Letters, 2(2), 872-879.
- MathWorks. (2023). Robotics System Toolbox. Retrieved from https://www.mathworks.com/products/robotics.html.
- Siciliano, B., & Khatib, O. (2008). Springer Handbook of Robotics. Springer.
- Siciliano, B., Sciavicco, L., Villani, L., & Oriolo, G. (2010). Robotics: Modelling, Planning and Control. Springer.
- Silwal, A., Davidson, J. R., Karkee, M., Mo, C., Zhang, Q., & Lewis, K. (2017). Design, integration, and field evaluation of a robotic apple harvester. Journal of Field Robotics, 34(6), 1140-1159.
- Spong, M. W., Hutchinson, S., & Vidyasagar, M. (2005). Robot Modeling and Control. John Wiley & Sons.
- Zhao, J., Gong, L., Huang, Y., & Liu, C. (2016). A review of key techniques of vision-based control for harvesting robot. Computers and Electronics in Agriculture, 127, 311-323.
- Zhao, X., et al. (2016). "Trajectory Planning for a Robotic Apple Harvesting System." Journal of Field Robotics, 33(1), 99-120.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).