Assembly Theory - Formalizing Assembly Spaces, Discovering Patterns and Bounds

1. Introduction

Assembly theory quantifies the minimum number of constructive steps required to generate an object, providing a principled measure of its structural complexity. It is built around two fundamental concepts: an assembly pool (a predefined set of basic items and a set of hitherto assembled subitems) and an assembly step (joining a pair of items taken from the assembly pool in a predefined order and cloning [1] such an assembled subitem to the assembly pool if it is not there), which together define the assembly index (ASI) as the minimal number of steps necessary to construct the object. Since its original formulation in 2017 [2], AT has been generalized to a broad range of theoretical and practical settings. A considerable body of work on AT [3,4,5,6,7,8,9,10,11,12,13,14,13,14] showcased the scale invariance of AT: its implementations, whether based on graphs, building blocks, DNA nucleobases, bounded structures, or more abstract units assembled in various spaces, share the same fundamental characteristics.

Intrinsic purpose-driven mechanics implementing global combinatorics (heuristics) of AT provides a genuinely different perspective from classical notions of algorithmic or statistical complexity, despite the fact that AT appears to share many methodological features with classical dictionary-based [15,16,17] and more particularly grammar-based [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33] data compression schemes. This resemblance stems from the fact that both AT and compression algorithms seek to capture redundancy, identify reusable substructures, and derive concise generative descriptions of data. However, instead of quantifying randomness or compressibility, AT focuses on causal construction pathways and structural regularities encoded in minimal assembly pathways (i.e., in the ASI). This perspective naturally raises the question of how such regularities can be efficiently detected, represented, and exploited by formal computational methods.

In this study, we focus on the general string version of AT. The paper is organized as follows. Section 2 introduces definitions and basic theorems used in the paper. Section 3 concerns the minimum complexity strings of AT, showing certain relations between the minimum ASI, assembly depth, depth index, and the Shannon entropy. Section 4 concerns the maximum complexity strings of AT, provides certain bounds of the maximum ASI as a function of a string length and the number of basic symbols, as well as certain methods of constructing high ASI strings. Section 5 concerns results common to the minimum and maximum complexity strings of AT, including a correlation between the expected waiting time for a string of outcomes obtainable from a uniform categorical distribution and the ASI of this string. Section 6 discusses the supremacy of ASI compression over all polynomial-time compression algorithms. Finally, Section 7 summarizes the findings of this study. In general, the proofs of theorems and lemmas, methods, and tables are given in Appendices.

2. General Framework

Consider a string $C_k^{(N,b)}$ (we often write it simply as $C_k$) of length N made of b distinct basic symbols (unit-length strings) c. We shall label the symbols c using decimal digits $\{0,1,\dots ,b_{-1}\}$ and letters if $b>10$, where $b_{-k}b-k$. We can assume that all strings $C_k$ belong to a set C and are vertices of a graph, where certain strings are connected via edges e from a set E. The Definition 2.1 and Lemma 2.1 were already stated in our previous studies [10,12]. We restate them here for clarity.

Definition 2.1  

(Assembly Space). An assembly space $\Omega =(C,E)$ is an acyclic digraph of strings $C=\left\{C_k\right\},k\in \mathbb{N}$, where all $b\in \mathbb{N}$ unit length strings (basic symbol(s)) are source vertices and the remaining strings are 2-in-regular assembly steps vertices, and E is a set of edges.

Definition 2.2  

(Assembly Step). An assembly step s is the formation of a new string $C_z$ in an assembly space Ω from two, not necessarily different, strings $C_x$, $C_y$ by concatenating $C_z=C_x\circ C_y=\mathrm{strcat}(C_x,C_y)$ which establishes the edges $e=(C_x,C_z)$ and $e^{\prime }=(C_y,C_z)$.

Thus, any edge $e=(C_x,C_z)$ unambiguously resolves to either $e=(C_x,C_x\circ C_y)$ or $e=(C_x,C_y\circ C_x)$. For example, the edge $e=\left(\right[010],[0101\left]\right)$ unambiguously resolves to $e=\left(\right[010],[010]\circ [1\left]\right)$. Even though all the $\Omega$ vertices are strings, it is convenient to separate this set into a set $BC\setminus \{C_k^{(N,b)}\in C:N\ne 1\}$ of source vertices, and a set $SC\setminus \{C_k^{(N,b)}\in C:N=1\}$ of 2-in-regular assembly steps vertices.

Definitions 2.1 and 2.2 are consistent: all vertices are unique (in any standard graph, all vertices should be unique) and all are strings. Since an assembly step always consists of joining two parts only [2], this can be thought of as the left and right fragments of the newly formed string, and those strings that can be the result of the concatenation of two shorter strings are assembly step 2-in-regular vertices. The uniqueness of each vertex is a sufficient criterion to establish the admissibility of an assembly step and to introduce the notion of an assembly pool: vertices (strings) present in the assembly space can not be assembled again as new vertices of $\Omega$, as they would not be unique.

Definition 2.3  

(String Assembly Space). An assembly space ${\Omega }_{C_s}$ of a string $C_s$ is the assembly space 2.1 containing the vertex $C_s$ and all the vertices leading to the string $C_s$.

There can be more than one assembly space for a target string, reflecting different assembly pathways leading to it. However, the ASI $a^{(N,b)}\left(C_s\right)$ of a string $C_s^{(N,b)}$ is the minimum cardinality $\left|S\right({\Omega }_{C_s}\left)\right|$ of the set of the assembly step vertices $S\left({\Omega }_{C_s}\right)$ of all assembly spaces ${\Omega }_{C_s}$ of the string $C_s$.

Strings in an assembly space 2.1 can form 2-grams, 3-grams, 4-grams,..., n-grams, in general, wherein the following holds.

Lemma 2.1.  

For all b a 4-gram is the shortest string that allows for more than one ASI.

$N=2$ provides $b^2$ available 2-grams with unit ASI. $N=3$ provides $b^3$ available 3-grams with ASI equal to two. Only $N=4$ provides $b^4$ 4-grams that include $b^2$ 4-grams with ASI equal to two, that is b 4-grams $C_{k,\min }^{(4,b)}=[****]$ and $b(b-1)$ 4-grams $C_{l,\min }^{(4,b)}=[*★*★]$, while the ASI of the remaining $b^4-b^2$ 4-grams is three. For example, to assemble the 4-gram $C_{k,\min }^{(4,4)}=\left[0202\right]$, we need to assemble the 2-gram $\left[02\right]$ and reuse it, while there is nothing available to reuse, in the case of the 4-gram $C_l^{(4,4)}=\left[0123\right]$.

Definition 2.4  

(Clear/Mixed String). We call a string (an n-gram) containing only one symbol a clear string (a clear n-gram). We call a string (an n-gram) which is not clear a mixed string (a mixed n-gram).

Theorem 2.1.  

Each $k_r$ copies of an $n_r$-gram $C_r^{(n_r,b)}$ contained in a string $C_m^{(N,b)}$ decrease its ASI at least by $k_r(n_r-1)-a^{(n_r,b)}\left(C_r\right)$. That is

$$a^{(N,b)}\left(C_m\right)\le N-1-\sum _{r=1}^R\left[k_r(n_r-1)-a^{(n_r,b)}\left(C_r\right)\right],$$

(1)

where R is the total number of repeated $n_r$-grams.

For example, due to the presence of three copies of a 5-gram $\left[01001\right]$, each with $a^{(5,6)}\left(\left[01001\right]\right)=3$, in a string

$$C_k^{(24,6)}=\left[12\right|01001\left|21\right|01001\left|235\right|01001\left|52\right],$$

(2)

its ASI amounts to $a^{(24,6)}\left(C_k\right)=24-1-(3·(5-1)-3)=14$. The relation (1) provides the upper bound on ASI as it does not describe a situation in which n-gram for $n>2$ is assembled based on a $(n-1)$-gram also present in the string $C_m^{(N,b)}$, outside of this n-gram. For example, the ASI $a^{(14,9)}\left(\right[56\left|101\right|78\left|101\right|43\left|01\right])=10$, while $14-1-\left(2\right(3-1)-2)=11$.

Consider the strings $C_k$ and $C_l$, where $C_l$ is $C_k$ in reverse order. The string $C_k$ can have a distribution of $n_r$-grams leading to its ASI decrease (1). But the string $C_l$ will have the same distribution of $n_r$-grams in reverse order. Consequently, the strings $C_k$ and $C_l$ have the same ASI.

Definition 2.5  

(AT String Equivalence). We consider two strings $C_k$ and $C_l$ to be AT-equivalent if they have the same ASI because $C_l$ is $C_k$ in reverse order and/or if $C_l$ and $C_k$ differ at most in symbol permutations.

If it is not otherwise clear from the context, in this study, we consider equivalent strings (e.g., $\left\{\right[001222],[111200],\dots \}$) as one string.

Another measure of a string’s complexity is the assembly depth [34].

Definition 2.6  

(Assembly Depth). The assembly depth (ASD)

$$d_s^{(N_k,b)}\left(C_k\right)\max \left(d^{(N_l,b)}\left(C_l\right),d^{(N_m,b)}\left(C_m\right)\right)+1,$$

(3)

where $d_0^{(1,b)}\left(c\right)0$, and $d^{(N_l,b)}\left(C_l\right)$ and $d^{(N_m,b)}\left(C_m\right)$ are the ASDs of two substrings $C_l$, $C_m$ of the string $C_k$ that were joined in step s. For $N>3$, and if there are more assembly pathways with different depths $w_j$ leading to a string, which happens if at least two independent assembly steps are possible, the minimum pathway depth is the ASD of this string. Hence, the ASD captures the notion of an independent assembly step.

The ASD naturally divides the lengths of strings into sections $2^{d-1}<N\le 2^d$ (cf. Figure 4 and Figure 5).

Theorem 2.2.  

If an assembly space Ω contains strings having the same (non-zero) ASD they were assembled in independent assembly steps.

In other words, if two strings $C_l$, $C_m$ in $\Omega$ have the same ASD, their assembly pathways are unrelated to each other; by the defining equation (3), neither of them could have been used in the assembly pathway of the other.

Corollary 2.1.  

If ASI and ASD of a string are equal to each other, an assembly space of this string cannot contain independent assembly steps.

Lemma 2.2.  

For all b the maximum length N of any string that can be assembled with the ASD $d_s^{\left(N\right)}$ (3) satisfies

$$N\le 2^{d_s^{\left(N\right)}}.$$

(4)

Theorem 2.3.  

For all b the minimum ASD (minASD) as a function of a string length N, is given by

$$d_{\min }^{\left(N\right)}=⌈{log}_2\left(N\right)⌉,$$

(5)

where $⌈x⌉$ denotes the ceiling function.

The ASD need not be a monotonically nondecreasing function of the assembly step. For example

$$\begin{array}{cc}\hfill & \left[11\right]d_1=1;\left[110\right]d_2=2;\left[01\right]d_3=1;\left[00\right]d_4=1;\left[0001\right]d_5=2;\left[0001110\right]d_6=3.\hfill \end{array}$$

(6)

Figure 1. Assembly spaces of bitstrings $C_{\max }^{(N,2)}$ (a, c) and $C_{\min }^{(N,2)}$ (b, d) for $N=2^s=16$ (a, b) and $N=15\ne 2^s$ (c, d), where the assembly index is a number in a string (final string for (a, c)) and the assembly depth corresponds to the level. For $N=2^s$, $d_{a_{\max }}^{(2^s,b)}=d_{a_{\min }}^{(2^s,b)}=s$. In general, for $N\ne 2^s$, the assembly depth $d_{a_{\max }}^{(N,b)}<d_{a_{\min }}^{(N,b)}$.

Figure 1. Assembly spaces of bitstrings $C_{\max }^{(N,2)}$ (a, c) and $C_{\min }^{(N,2)}$ (b, d) for $N=2^s=16$ (a, b) and $N=15\ne 2^s$ (c, d), where the assembly index is a number in a string (final string for (a, c)) and the assembly depth corresponds to the level. For $N=2^s$, $d_{a_{\max }}^{(2^s,b)}=d_{a_{\min }}^{(2^s,b)}=s$. In general, for $N\ne 2^s$, the assembly depth $d_{a_{\max }}^{(N,b)}<d_{a_{\min }}^{(N,b)}$.

Figure 2. Assembly space $\Omega$, assembly index, and assembly depth. The assembly space of all eight binary 3-grams with all pathways (a). Blue edge provides the 1^st string, red edge provides the 2^nd string in the assembly step, and the order is irrelevant for two green edges or green edge provides the 1^st or 2^nd string in dependence of the color of the complementary edge. Dotted edges and question marks indicate alternative pathways. The assembly space of the bitstring $C_6^{(7,2)}=\left[0001110\right]$ showing that its assembly index $a^{(7,2)}\left(C_6\right)=6$ (b). The evolution of assembly spaces of strings $\left[0101\right]$ and $\left[0110\right]$ (c-e). Strings $\left[0101\right]$ and $\left[0110\right]$ are initially assembled from 3-grams and basic symbols, increasing the assembly depth (c). New pathways increasing the number of independent assembly steps are found (d), and the edges of $\Omega$ are reconfigured, decreasing the number of assembly steps of the string $\left[0101\right]$ from three to two steps and the assembly depth of both 4-grams from three to two. Five assembly spaces of the bitstrings $\left[0101\right]$, $\left[010\right]$ (two alternatives, one encircled), $\left[011\right]$, and $\left[0110\right]$ (e)

Figure 2. Assembly space $\Omega$, assembly index, and assembly depth. The assembly space of all eight binary 3-grams with all pathways (a). Blue edge provides the 1^st string, red edge provides the 2^nd string in the assembly step, and the order is irrelevant for two green edges or green edge provides the 1^st or 2^nd string in dependence of the color of the complementary edge. Dotted edges and question marks indicate alternative pathways. The assembly space of the bitstring $C_6^{(7,2)}=\left[0001110\right]$ showing that its assembly index $a^{(7,2)}\left(C_6\right)=6$ (b). The evolution of assembly spaces of strings $\left[0101\right]$ and $\left[0110\right]$ (c-e). Strings $\left[0101\right]$ and $\left[0110\right]$ are initially assembled from 3-grams and basic symbols, increasing the assembly depth (c). New pathways increasing the number of independent assembly steps are found (d), and the edges of $\Omega$ are reconfigured, decreasing the number of assembly steps of the string $\left[0101\right]$ from three to two steps and the assembly depth of both 4-grams from three to two. Five assembly spaces of the bitstrings $\left[0101\right]$, $\left[010\right]$ (two alternatives, one encircled), $\left[011\right]$, and $\left[0110\right]$ (e)

We cannot consider the ASD apart from the ASI. For example, the ASD of a string $C_{\max }^{(7,2)}=\left[0001110\right]$ is $d_{a_{\max }}^{(7,2)}=⌈{log}_2\left(7\right)⌉=3$ even though this string can be assembled in six steps with three larger pathway depths $w_6\in \{4,5,6\}$ as

$$\begin{array}{cccc}\left[00\right]d_1=1,\hfill & \left[00\right]w_1=1,\hfill & \left[00\right]w_1=1,\hfill & \left[00\right]w_1=1,\hfill \\ \left[01\right]d_2=1,\hfill & \left[01\right]w_2=1,\hfill & \left[01\right]w_2=1,\hfill & \left[000\right]w_2=2,\hfill \\ \left[11\right]d_3=1,\hfill & \left[11\right]w_3=1,\hfill & \left[0001\right]w_3=2,\hfill & \left[0001\right]w_3=3,\hfill \\ \left[110\right]d_4=2,\hfill & \left[0001\right]w_4=2,\hfill & \left[00011\right]w_4=3,\hfill & \left[00011\right]w_4=4,\hfill \\ \left[0001\right]d_5=2,\hfill & \left[000111\right]w_5=3,\hfill & \left[000111\right]w_5=4,\hfill & \left[000111\right]w_5=5,\hfill \\ \left[0001110\right]d_6=3,\hfill & \left[0001110\right]w_6=4,\hfill & \left[0001110\right]w_6=5,\hfill & \left[0001110\right]w_6=6.\hfill \end{array}$$

(7)

Similarly, the ASD of a string $C_{\max }^{(8,2)}=\left[00011101\right]$ is $d_{a_{\max }}^{(8,2)}=⌈{log}_2\left(8\right)⌉=3$ as

$$\begin{array}{cccc}\left[00\right]d_1=1,\hfill & \left[00\right]w_1=1,\hfill & \left[00\right]w_1=1,\hfill & \left[01\right]w_1=1,\hfill \\ \left[01\right]d_2=1,\hfill & \left[01\right]w_2=1,\hfill & \left[01\right]w_2=1,\hfill & \left[001\right]w_2=2,\hfill \\ \left[11\right]d_3=1,\hfill & \left[11\right]w_3=1,\hfill & \left[0001\right]w_3=2,\hfill & \left[0001\right]w_3=3,\hfill \\ \left[0001\right]d_4=2,\hfill & \left[0001\right]w_4=2,\hfill & \left[00011\right]w_4=3,\hfill & \left[00011\right]w_4=4,\hfill \\ \left[1101\right]d_5=2,\hfill & \left[000111\right]w_5=3,\hfill & \left[000111\right]w_5=4,\hfill & \left[000111\right]w_5=5,\hfill \\ \left[00011101\right]d_6=3,\hfill & \left[00011101\right]w_6=4,\hfill & \left[00011101\right]w_6=5,\hfill & \left[00011101\right]w_6=6.\hfill \end{array}$$

(8)

However, the non-maximum and non-minimum ASI string $C_k^{(8,2)}=\left[01001011\right]$ has only two 2-grams that can be assembled in independent steps. Hence, its ASD cannot be decreased to $⌈{log}_2\left(8\right)⌉=3$

$$\begin{array}{cc}\left[01\right]d_1=1,\hfill & \left[01\right]w_1=1,\hfill \\ \left[11\right]d_2=1,\hfill & \left[010\right]w_2=2,\hfill \\ \left[010\right]d_3=2,\hfill & \left[010010\right]w_3=3,\hfill \\ \left[010010\right]d_4=3,\hfill & \left[0100101\right]w_4=4,\hfill \\ \left[01001011\right]d_5=4,\hfill & \left[01001011\right]w_5=5.\hfill \end{array}$$

(9)

In general, the $\Omega$ that contains a $2^d$-gram having the ASD d can also contain $\{2^{d-1}+1,2^{d-1}+2,\dots ,2^d-1\}$-grams having the ASD d and based on the shorter n-grams of length $n<2^{d-1}+1$.

Theorem 2.4.  

For all b the ASD of any maximum ASI string $C_{\max }^{(N,b)}$, corresponds to the minASD (5) of Theorem 2.3, that is

$$d_{a_{\max }}^{(N,b)}=⌈{log}_2\left(N\right)⌉,$$

(10)

For example, as shown in Figure 1c,d, the string $C_{\max }^{(15,2)}=\left[010101000011100\right]$ has the ASI $a_{\max }^{(15,2)}=10$ and the ASD $d_{a_{\max }}^{(15,2)}=4$, while the string $C_{\min }^{(15,2)}=\left[010010100101001\right]$ has smaller ASI $a_{\min }^{\left(15\right)}=5$ but larger ASD $d_{a_{\min }}^{(15,2)}=5$. On the other hand, the ASD of the maxASI string $C_{(N-5)}^{(16,2)}=\left[0101010000001110\right]$ and the minASI string $C_{\min }^{(16,2)}=\left[0101010101010101\right]$, shown in Figure 1a,b, is the same.

Here, we introduce the following definition, which — as we shall see — is also related to the independent assembly step.

Definition 2.7  

(Depth Index). We call the number of steps ${\widehat{a}}_{\min }^{\left(N\right)}$ to reach 1 starting from $N{N}_0$ and assigning

$$N_{s+1}=\left\{\begin{array}{cc}{N}_s-1\hfill & \mathrm{if}{N}_s\mathrm{is}\mathrm{odd},\hfill \\ N_s-2\hfill & \mathrm{if}{N}_s=2^s+2,s\in \mathbb{N},\hfill \\ N_s/2\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(11)

the depth index (DPI).

The relation (11) yields the same number of steps as the Chandah-sutra method (OEIS A014701) and, unlike the minimum ASI, is an analytical function of N. For example, ${\widehat{a}}_{\min }^{\left(2^s\right)}=s$ and ${\widehat{a}}_{\min }^{(2^s-1)}=2(s-1)$.

Applying AT to evolutionary biology, we can assume that initially, a new string of length N is formed in an assembly space based on a basic symbol and a string of length $N-1$. Subsequently, this string assembly space evolves to reduce the cardinality $\left|S\right({\Omega }_{C_s}\left)\right|$ of the set of the assembly step vertices until it equals the ASI of this string, that is until $|S\left({\Omega }_{C_s}\right)|=a^{(N,b)}\left(C_s\right)$. Hence, the assembly spaces evolve by reconfiguring the network of edges to decrease the ASD of newly assembled strings, possibly finding shorter pathways for these strings, and if only such a decrease would not result in ASI increase (Length $N=15$ shown in Figure 1d is the shortest length, where $5=d_{a_{\min }}^{\left(15\right)}>⌈{log}_2\left(15\right)⌉=4$).

The concepts of assembly space, string assembly space, ASI, and ASD, as well as the evolution of assembly spaces, are illustrated in Figure 2. Although the alternative pathways shown in Figure 2a demonstrate that the mixed 2-gram $\left[01\right]$ is not required to construct all 3-grams in two steps, this 2-gram is necessary to achieve the ASI of longer strings (Cf. a constrained AT* version shown in list (38) discusses in Section 6.).

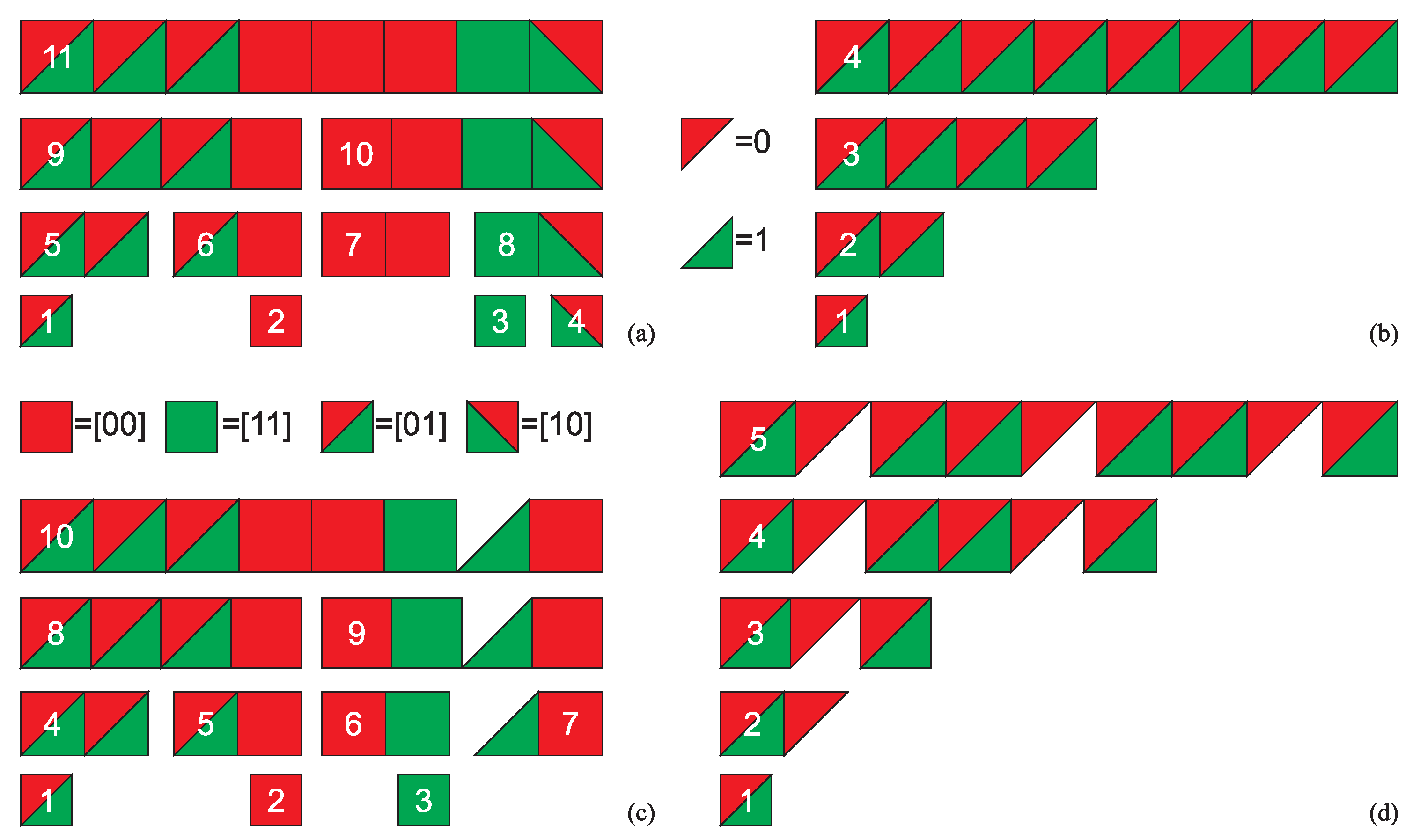
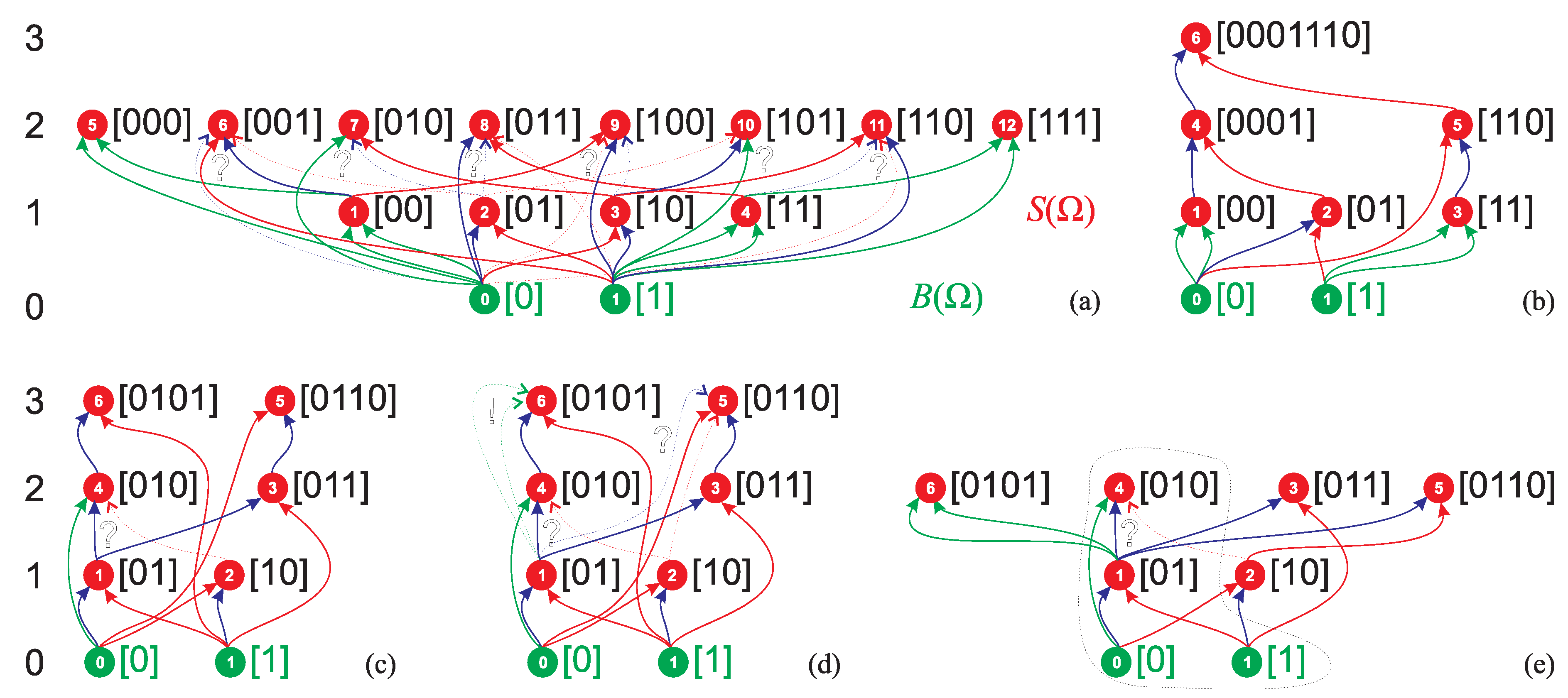
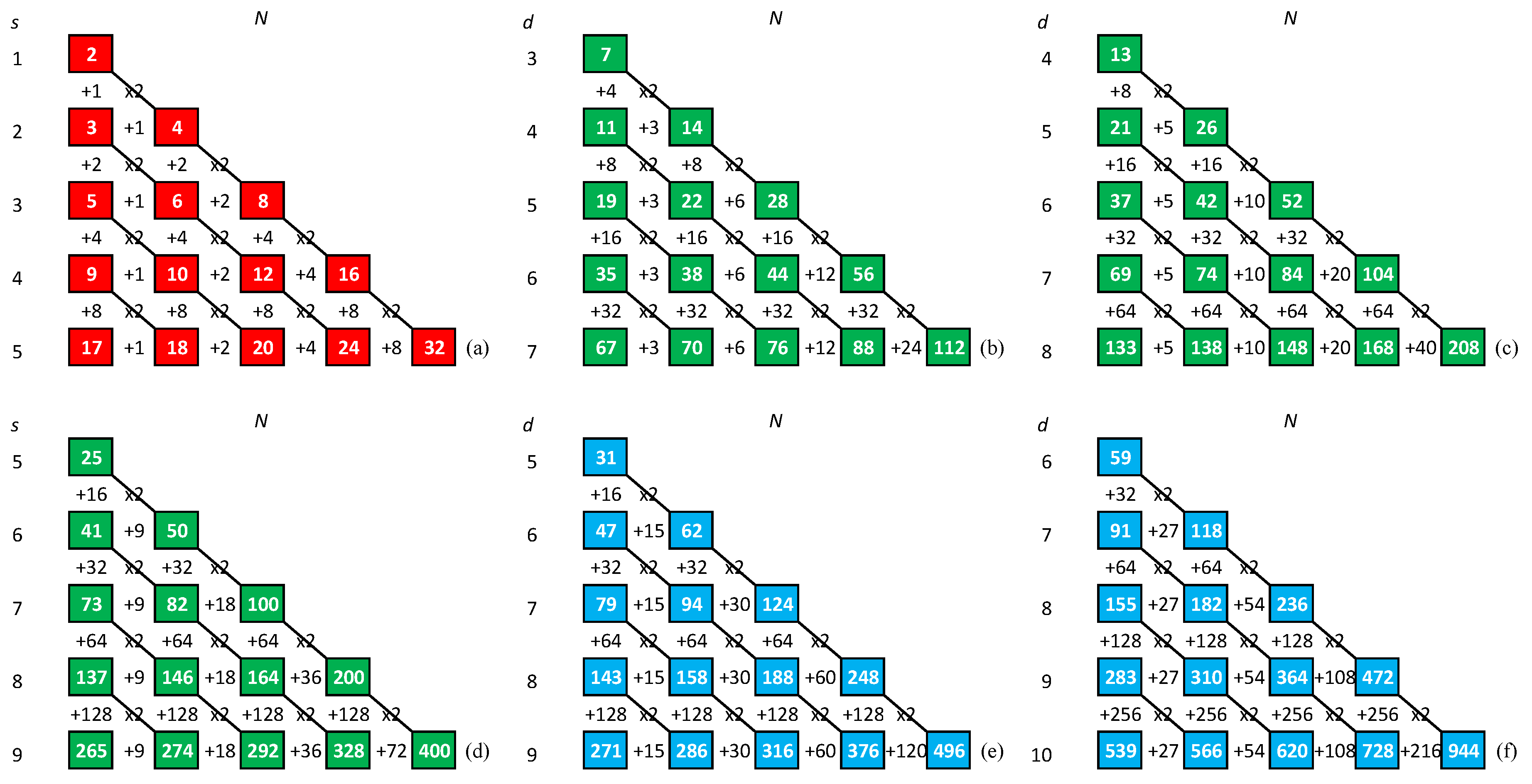
3. Minimum Complexity Strings of AT

In this section, we consider factors relevant to the minimum string complexity in the context of AT. The Theorem 3.1 was already stated in our previous study [10]; we restate it here for clarity.

Theorem 3.1.  

For all b the minimum ASI (minASI) $a^{\left(N\right)}\left(C_{\min }\right)$ as a function of N corresponds to the shortest addition chain for N (OEIS A003313).

Any shortest addition chain for n starts with one, not zero, as zero is the neutral element of addition. For the same reason, two is considered the smallest prime, as one is the neutral element of multiplication. Hence, the fundamental theorem of arithmetic can be thought of as the shortest multiplication chain for N. It is conjectured that the largest prime factor must appear in some shortest addition chain for N [35].

Theorem 3.2.  

The strings $C_{\min }^{(2^s,b)}$ can contain at most two distinct symbols if $b>1$. Other minASI strings of length $N\ne 2^s$ can contain at most three distinct symbols if $b>2$.

Proof. 

Minimum ASI strings of length $N=2^s$ are formed by joining the newly assembled string to itself, where a clear or mixed 2-gram is assembled in the first step. Minimum ASI strings of other lengths admit a 2-gram and a 3-gram containing this 2-gram and an additional basic symbol.

To formally prove the first part, we can also use mathematical induction on the assembly step s. If $s=1$, then the minASI strings $C_{\min }^{(2,b)}$ are 2-grams of the form $\left[c_1{c}_2\right]$, where $c_1,c_2\in B\left(\Omega \right)$. If $c_1=c_2$, the string contains one distinct symbol, and if $c_1\ne c_2$, the string contains two distinct symbols. In both cases, the string has a form (A13) and the number of distinct symbols does not exceed two. Now assume that for some $k\in \mathbb{N}$, all minASI strings $C_{\min }^{(2^k,b)}$ contain at most two distinct symbols. We must show that $C_{\min }^{(2^{k+1},b)}$ also contains at most two distinct symbols. We construct $C_{\min }^{(2^{k+1},b)}$ by joining two identical minASI strings $C_{\min }^{(2^k,b)}$

$$C_{\min }^{(2^k,b)}\circ C_{\min }^{(2^k,b)}=C_{\min }^{(2^{k+1},b)},$$

(12)

with each other. By the inductive hypothesis, each $C_{\min }^{(2^k,b)}$ contains at most two distinct symbols. Therefore, their concatenation also contains at most two distinct symbols. By induction, for all $s\in \mathbb{N}$, the minASI string $C_{\min }^{(2^s,b)}$ contains at most two distinct symbols.

We will now show that other minASI strings of length $N\ne 2^s$ can contain at most three distinct symbols if $b>2$. We provide the construction of minASI strings with three symbols. In the first step $s=1$, we assemble a 2-gram $\left[c_1{c}_2\right]$ where $c_1,c_2\in B\left(\Omega \right)$ and $c_1\ne c_2$. Next, we join the existing 2-gram $\left[c_1{c}_2\right]$ with a new symbol $c_3\in B\left(\Omega \right)$ where $c_3\notin \{c_1,c_2\}$. This forms a 3-gram $\left[c_1{c}_2{c}_3\right]$, introducing a third distinct symbol and further increasing the ASI by 1. We continue assembling by joining the longest string formed so far with itself or with previously formed strings, maintaining the minimal ASI increase.

Assume a contrario that there exists a minASI string $C_{\min }^{(N,b)}$ of length $N\ne 2^s$ that contains four or more distinct symbols. But, incorporating such a fourth symbol is equivalent to assembling a maxASI 4-gram, which contradicts the minimality of $C_{\min }^{(N,b)}$ (only a 2-gram must be assembled from basic symbols and a 3-gram must be assembled from a basic symbol and a 2-gram). Thus, Theorem 3.2 is proven. □

By Theorem 2.1 the maximum ASI decrease is provided by minASI $2^s$-grams and amounts to $k(2^s-1)-s$. On the other hand, 1-symbol n-grams are guaranteed to have the minimum ASI for all n. Therefore, the maxASI string will tend to contain only one such long n-gram for each b. We have found, for example, that the sum of the lengths of an $n_0$-gram of zeros and an $n_1$-gram of ones should preferably be greater than or equal to $N/2$ of a maxASI string.

The assembly spaces of strings $a_{\min }^{\left(N\right)}$ of length $N\ne 2^s$ are not unique [36]. For example, a string $C_{\min }^{(5,b)}=\left[01010\right]$ can be assembled in three steps from four assembly spaces with $S\left(\Omega \right)=\left\{\right[01],[010\left]\right\}$, $S\left(\Omega \right)=\left\{\right[01],[0101\left]\right\}$, $S\left(\Omega \right)=\left\{\right[10],[010\left]\right\}$, or $S\left(\Omega \right)=\left\{\right[10],[1010\left]\right\}$.

Strings with non-minASI can contain all symbols. For example, the string [37]

$$C_k=\left[01234012340123401234\right],$$

(13)

has ASI $a^{(20,5)}\left(C_k\right)=6=a_{\min }^{\left(20\right)}+1$ and contains all five basic symbols $B\left(\Omega \right)\{0,1,2,3,4\}$.

The minASD as a function of the length of a string $d_{\min }^{\left(N\right)}$ (5), the ASD of a minASI string $d_{a_{\min }}^{\left(N\right)}$ (which we call here the minASI ASD), the minASI as a function of the length of a string $a_{\min }^{\left(N\right)}$ (OEIS A003313), and DPI ${\widehat{a}}_{\min }^{\left(N\right)}$ (OEIS A014701) define four distinct sets illustrated in Figure 4, wherein $d_{\min }^{\left(N\right)}\le d_{a_{\min }}^{\left(N\right)}\le a_{\min }^{\left(N\right)}\le {\widehat{a}}_{\min }^{\left(N\right)}$. We observed certain salient regularities among them.

Theorem 3.3.  

If a minASI string has length $N{2}^s$, $s\in {\mathbb{N}}_0$, then the minimum ASD, minASI ASD, minASI, and DPI are equal to s.

Theorem 3.3 can be generalized as follows.

Theorem 3.4.  

The minASD, minASI ASD, minASI, and DPI of a minASI string are equal to $s\in \mathbb{N}$ iff ${\widehat{N}}_1{2}^{s-1}+2^l,l=0,1,\dots ,s-1,s\ge 1$ or, in other words

$${\widehat{N}}_1{2}^{s-1}+2^l,l=0,1,\dots ,s-1,s\ge 1\iff d_{\min }^{\left({\widehat{N}}_1\right)}=d_{a_{\min }}^{\left({\widehat{N}}_1\right)}=a_{\min }^{\left({\widehat{N}}_1\right)}={\widehat{a}}_{\min }^{\left({\widehat{N}}_1\right)}=s.$$

(14)

Figure 3. Lengths of all strings having the property of $d_{\min }^{\left({\widehat{N}}_1\right)}=a_{\min }^{\left({\widehat{N}}_1\right)}=d_{a_{\min }}^{\left({\widehat{N}}_1\right)}={\widehat{a}}_{\min }^{\left({\widehat{N}}_1\right)}=s$ (a). Lengths ${\tilde{N}}_3$, ${\tilde{N}}_5$, ${\tilde{N}}_9$ of certain strings having the property of $a_{\min }^{\left({\tilde{N}}_{*}\right)}=d_{\min }^{\left({\tilde{N}}_{*}\right)}+1$ (b-d). Lengths ${\tilde{N}}_{15}$, ${\tilde{N}}_{27}$ of certain strings having the property of $a_{\min }^{\left({\tilde{N}}_{*}\right)}=d_{\min }^{\left({\tilde{N}}_{*}\right)}+2$ (e,f)

Figure 3. Lengths of all strings having the property of $d_{\min }^{\left({\widehat{N}}_1\right)}=a_{\min }^{\left({\widehat{N}}_1\right)}=d_{a_{\min }}^{\left({\widehat{N}}_1\right)}={\widehat{a}}_{\min }^{\left({\widehat{N}}_1\right)}=s$ (a). Lengths ${\tilde{N}}_3$, ${\tilde{N}}_5$, ${\tilde{N}}_9$ of certain strings having the property of $a_{\min }^{\left({\tilde{N}}_{*}\right)}=d_{\min }^{\left({\tilde{N}}_{*}\right)}+1$ (b-d). Lengths ${\tilde{N}}_{15}$, ${\tilde{N}}_{27}$ of certain strings having the property of $a_{\min }^{\left({\tilde{N}}_{*}\right)}=d_{\min }^{\left({\tilde{N}}_{*}\right)}+2$ (e,f)

The assembly spaces of other minASI strings can contain independent assembly steps. The first such case occurs for $N=7$, where, for example, the $S\left(\Omega \right)$

$$\begin{array}{cc}\hfill [01]& d_1=1\hfill \\ \hfill [001],[0101]& d_2=d_3=2\hfill \\ \hfill [0010101]& d_4=3\hfill \end{array}$$

(15)

results in a string having ma $a_{\min }^{\left(7\right)}=4$ and $d_{a_{\min }}^{\left(7\right)}=⌈{log}_2\left(7\right)⌉=3$, since both $\left[001\right]$ and $\left[0101\right]$ were assembled from the 2-gram $\left[01\right]$ in two independent assembly steps at the same depth $d_2=d_3=2$, which is congruent with Theorem 2.2.

Lemma 3.1.  

The minASI strings [10] (strings (15)) of lengths

$${\tilde{N}}_3{2}^{d-1}+3·2^l,l=0,1,\dots ,d-3,d\ge 3\iff a_{\min }^{\left({\tilde{N}}_3\right)}=d+1=⌈{log}_2\left({\tilde{N}}_3\right)⌉+1,$$

(16)

have only one independent assembly step in their assembly spaces, and excluding this step, they are assembled by joining the longest string assembled so far with itself. Therefore, their ASI is one greater than the minASD (5).

Lemma 3.2.  

The minASI strings of lengths

$${\tilde{N}}_5{2}^{d-1}+5·2^l,l=0,1,\dots ,d-4,d\ge 4\iff a_{\min }^{\left({\tilde{N}}_5\right)}=d+1=⌈{log}_2\left({\tilde{N}}_5\right)⌉+1,$$

(17)

have only one independent assembly step in their assembly spaces, and excluding this step, they are assembled by joining the longest string assembled so far with itself. Therefore, their ASI is one greater than the minASD (5).

Lemma 3.3.  

The minASI strings of lengths

$${\tilde{N}}_9{2}^{d-1}+9·2^l,l=0,1,\dots ,d-5,d\ge 5\iff a_{\min }^{\left({\tilde{N}}_9\right)}=d+1=⌈{log}_2\left({\tilde{N}}_9\right)⌉+1,$$

(18)

have only one independent assembly step in their assembly spaces, and excluding this step, they are assembled by joining the longest string assembled so far with itself. Therefore, their ASI is one greater than the minASD (5).

Lemmas 3.1–3.3 allow for the following generalization.

Theorem 3.5.  

The minASI strings of lengths

$${\tilde{N}}_{2^n+1}{2}^{d-1}+\left(2^{k-4}+1\right)2^l,k\ge 5,d\ge k-2,l=0,1,\dots ,d-(k-2),\iff a_{\min }^{\left({\tilde{N}}_{2^n+1}\right)}=d+1=⌈{log}_2\left({\tilde{N}}_{2^n+1}\right)⌉+1,$$

(19)

have only one independent assembly step in their assembly spaces, and excluding this step, they are assembled by joining the longest string assembled so far with itself. Therefore, their ASI is one greater than the minASD (5).

Proof. 

The lengths of the strings (19) are listed in rows in Table A1 starting after the length of the substring assembled in an independent assembly step marked green. Hence, the first row contains the lengths of strings of Theorem 3.1 shown on the diagonal of Figure 3b, and so on. □

Theorem 3.6.  

The minASI strings [10] of lengths

$${\tilde{N}}_7{2}^{d-1}+7·2^{d-4}\in \{15,30,60,\dots \},d\ge 4\iff a_{\min }^{\left({\tilde{N}}_7\right)}=d_{a_{\min }}^{\left({\tilde{N}}_7\right)}=d_{\min }^{\left({\tilde{N}}_7\right)}+1={\widehat{a}}_{\min }^{\left({\widehat{N}}_1\right)}-1=⌈{log}_2\left({\tilde{N}}_7\right)⌉+1,$$

(20)

are assembled by joining the longest string assembled so far with itself. Their ASI and ASD are the same, one greater than the minASD (5) and one smaller than the DPI.

Theorem 3.6 seems to allow for the following generalization, which we have validated numerically based on the sequence OEIS A003313 for $N\le {10}^5$. For d, l, and ${\tilde{N}}_{2^n+1}$ defined by the relation (19), the following holds

$${\tilde{N}}_{2^n+1,a}{\tilde{N}}_{2^n+1}+2^d=3·2^{d-1}+\left(2^{k-4}+1\right)2^l\wedge k=5\iff a_{\min }^{\left({\tilde{N}}_{2^n+1,a}\right)}=d+2=⌈{log}_2\left({\tilde{N}}_{2^n+1,a}\right)⌉+1,$$

(21a)

$${\tilde{N}}_{2^n+1,b}{\tilde{N}}_{2^n+1}+2^{d+1}=5·2^{d-1}+\left(2^{k-4}+1\right)2^l\wedge k\in \{5,6\}\iff a_{\min }^{\left({\tilde{N}}_{2^n+1,b}\right)}=d+3=⌈{log}_2\left({\tilde{N}}_{2^n+1,b}\right)⌉+1.$$

(21b)

The lengths of the strings (21a) and (21b) are listed in rows in Table A1. Furthermore, we have numerically validated the following conjecture. The minASI strings of lengths

$${\tilde{N}}_{15}{2}^{d-1}+15·2^l,l=0,1,\dots ,d-5,d\ge 5,$$

(22a)

$${\tilde{N}}_{27}{2}^{d-1}+27·2^l,l=0,1,\dots ,d-6,d\ge 6,$$

(22b)

$${\tilde{N}}_{50.9}50·2^{d-6}+9·2^l,l=0,1,\dots ,d-6,d\ge 6,$$

(22c)

have the property of

$$a_{\min }^{\left({\tilde{N}}_{*}\right)}=d+2=⌈{log}_2\left({\tilde{N}}_{*}\right)⌉+2.$$

(22d)

Figure 4. The minimum assembly depth ($⌈{log}_2\left(N\right)⌉$, blue), the assembly depth of the minimum assembly index string (magenta), the minimum assembly index (OEIS A003313, red; ${log}_2\left(N\right)$, red, dash-dot), depth index (OEIS A014701, green), and $\lfloor {log}_2\left(N\right)\rfloor +N_1-2$, where $N_1$ is the Hamming weight of the binary representation of N (black) for $1<N\le 65$.

Figure 4. The minimum assembly depth ($⌈{log}_2\left(N\right)⌉$, blue), the assembly depth of the minimum assembly index string (magenta), the minimum assembly index (OEIS A003313, red; ${log}_2\left(N\right)$, red, dash-dot), depth index (OEIS A014701, green), and $\lfloor {log}_2\left(N\right)\rfloor +N_1-2$, where $N_1$ is the Hamming weight of the binary representation of N (black) for $1<N\le 65$.

Figure 5. The Shannon entropy of the most balanced bitstrings having the minimum assembly index for $1<N\le 65$

Figure 5. The Shannon entropy of the most balanced bitstrings having the minimum assembly index for $1<N\le 65$

Strings of lengths (14), (16), and (20), revealed in [10] based on the degree of causation, showed that there are certain regularities among the minASI strings. Here, we extended these results to strings of lengths (19), (21), and (22). In general, Theorems 3.4–3.6 (in particular Theorem 3.6) and Conjectures Section 3 and Section 3 show a peculiar interdependence among the minASD (5), minASI ASD, minASI, and DPI, as shown in Figure 4. In particular, they show that

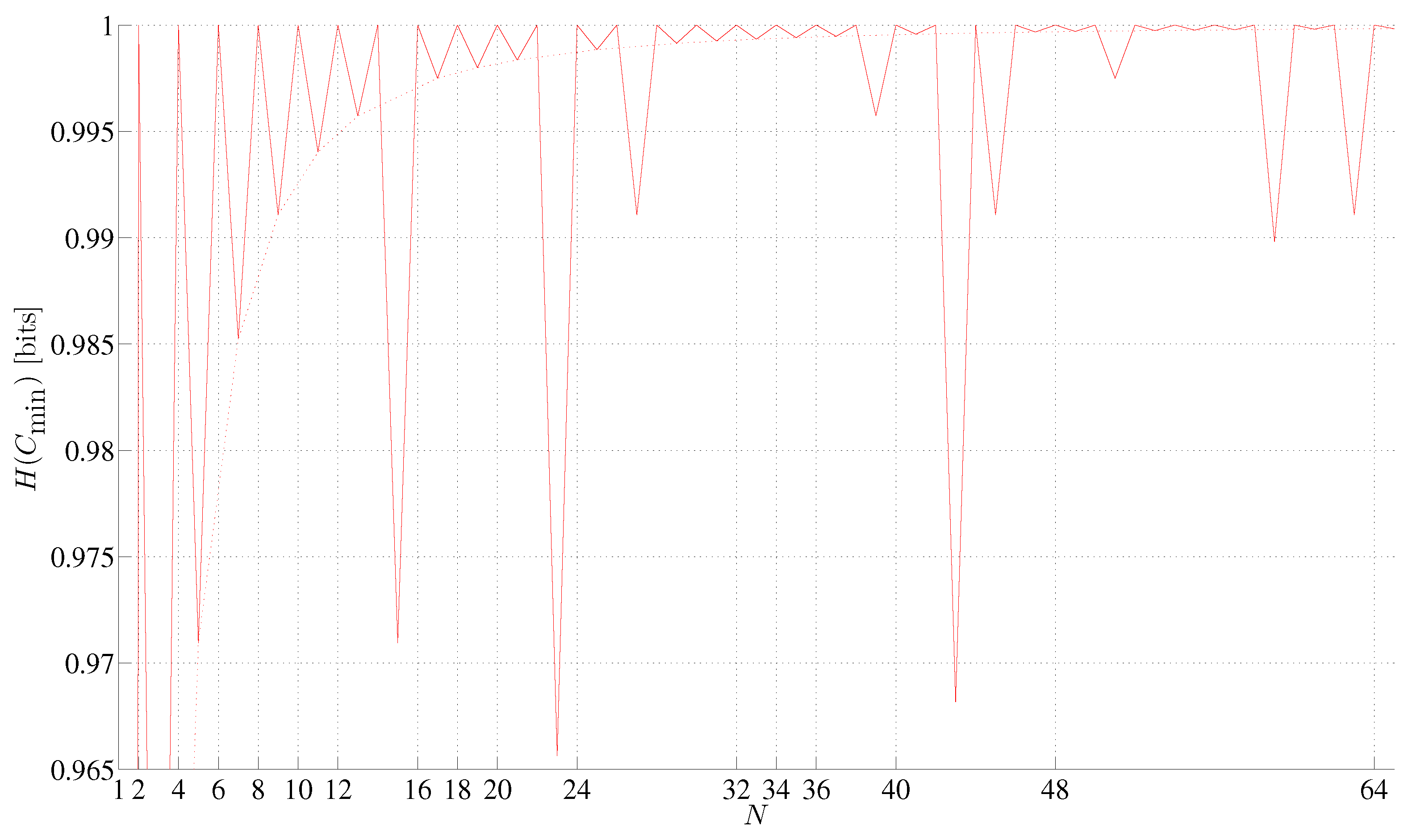
• the $\Omega$ of minASI strings having ASI equal to DPI cannot contain strings assembled in independent assembly steps,
• the $\Omega$s of other minASI strings can contain at least two such strings, and therefore
• the assembly space of a maxASI string will tend to maximize the number of strings assembled in independent assembly steps in the $\Omega$, taking into account the saturation of the $\Omega$ as it cannot contain more than $b^n$ distinct n-grams, and hence to minimize the possible ASD.

We note that, in general, the difference between the DPI and minASI is larger than 1.

Lemma 3.4.  

The minASI bitstrings assembled along the pathway given by the DPI 2.7 and beginning with $C_{\min }^{\left(2\right)}=[*★]$ are balanced bitstrings if N is even or nearly balanced bitstrings ($N_0=N_1+1$) if N is odd.

In other words, the Definition 2.7 removes the imbalance propagation. For example, an imbalanced pathway $\{2,4,5,10,20\}$ ($N_1=8$) becomes a balanced pathway $\{2,4,8,10,20\}$ ($N_1=10=N/2$) and $2^s+2\to 2^{s-1}+1\to 2^{s-1}\iff 2^s+2\to 2^s\to 2^{s-1}$. We have also examined the Shannon entropy

$$H\left(C_{\min }^{\left(N\right)}\right)=-p_0{log}_2\left(p_0\right)-p_1{log}_2\left(p_1\right),$$

(23)

of the most balanced minASI bitstrings, where $p_0=N_0/N$ and $p_1=N_1/N$ are fractions of the respective symbols $\{0,1\}$ within the string ($N_1$ is the Hamming weight). Although by Theorem 3.1, the minASI as a function of the length of a string does not depend on b, we have chosen the most balanced bitstrings, as they maximize the Shannon entropy (23). This choice is also supported by physics [38,39,40]. For the same reason, we preferred the pathway $\{2,3,5,10,15\}$ (cf. Figure 1d) over $\{2,3,6,12,15\}$, for example, as the string assembled using the former pathway is more balanced ($N_1=6$) than the one assembled using the latter one ($N_1=5$). Similarly, we preferred the pathway that provided a more balanced string over the one that provided independent assembly steps. $N=14$ is the first exception. $C_{\min }^{\left(14\right)}$ assembled in five steps along the pathway $\{2,(3,4),7,14\}$ with the independent assembly steps 3 and 4 has the hamming weight $N_1=6$ as compared to $C_{\min }^{\left(14\right)}$ assembled in five steps along the pathway $\{2,4,8,12,14\}$ with no independent assembly steps and the hamming weight $N_1=N/2=7$. The resulting pathways of the minASI strings maximizing the number of independent assembly steps or the binary Shannon entropy (23) are listed in Table A2 for $N\le 65$. As shown in Figure 5, the Shannon entropy (23) of the most balanced minASI bitstrings rapidly converges to one with exceptions for lengths $N\in \{15,23,27,39,43,45,51,59,63,\dots \}$ substantially corresponding to lengths at which DPI is larger than the minASI (cf. Figure 4), which highlights the interdependence among the minASI and DPI.

We demonstrated in this section that minimum complexity AT strings cannot be fully derived by any rule-based system. The same is true for the maxASI strings, as we shall show in a subsequent section.

4. Maximum Assembly Index Strings of AT

A seven-bit string is the longest string that can have the maxASI $a_{\max }^{(7,2)}=N-1=6$. It contains two clear 3-grams

$$C_{(N-1)}^{(7,2)}=\left[0001110\right],$$

(24)

and its length cannot be increased without a repetition of a 2-gram, which keeps the ASI at the same level $a_{\max }^{(8,2)}=8-2=6$. This led us to seek a general method to construct the longest possible string having the maxASI $a_{\max }^{(N,b)}\left(C_{(N-1)}\right)=N-1$, as a function of the radix b. We denote the length of this string by $N_{(N-1)}$ and we call this string a $C_{(N-1)}$ string. We developed two methods of constructing a string $C_{(N-1)}$ of the form

$$C_{(N-1)}=[0001112\dots b_{-2}{b}_{-1}{b}_{-1}{b}_{-1}\dots 0].$$

(25)

In both methods, we start with an initial balanced string of length $3b$ containing b clear 3-grams ordered as

$$[0001112\dots b_{-2}{b}_{-1}{b}_{-1}{b}_{-1}].$$

(26)

The 2-grams that can be inserted into the initial string (26) can be arranged in a $b\times b$ matrix

$$\left[\begin{array}{ccccc}00& 01& 02& \dots & 0b_{-1}\\ 10& 11& 12& \dots & 1b_{-1}\\ 20& 21& 22& \dots & 2b_{-1}\\ \dots & \dots & \dots & \dots & \dots \\ b_{-2}0& b_{-2}1& b_{-2}2& \dots & b_{-2}{b}_{-1}\\ b_{-1}0& b_{-1}1& b_{-1}2& \dots & b_{-1}{b}_{-1}\end{array}\right],$$

(27)

where the crossed out entries on a diagonal cannot be reused, as they would form repetitions in this string. Due to the order of 3-grams in the string (26) we can also cross out the entries in the first superdiagonal of the matrix (27). By construction, the starting string (26) has length $3b$ and contains only $b+(b-1)=2b-1$ 2-grams $\left[ll\right]$ and $\left[m\right(m+1\left)\right]$, where $0\le l\le b_{-1}$ and $0\le m\le b_{-2}$.

In the 1st step of the 1st method, we begin by forming a string containing 2-grams on the first subdiagonal of the matrix (27), starting with 10

$$[102132\dots b_{-2}{b}_{-3}{b}_{-1}{b}_{-2}],$$

(28)

and we append it to the string (26). With this step, we also eliminate the 2-grams on the second superdiagonal starting with the 2-gram 02, as well as the 2-gram $b_{-1}1$. In the 2nd step, we form a string containing 2-grams on the third superdiagonal beginning with the 2-gram 03

$$[0314\dots b_{-5}{b}_{-2}{b}_{-4}{b}_{-1}],$$

(29)

and append it to the string formed so far. With this step, we also remove the 2-gram $b_{-2}0$ and the middle part of the second subdiagonal containing $\{31,42,\dots ,b_{-2}{b}_{-4}\}$. And so on. Finally, we append 0 if b is even. This process is illustrated in Figure 6 and generates the following $C_{(N-1)}^{(N,b)}$ strings

$$\begin{array}{cc}\hfill C_{(N-1)}^{(3,1)}& =\left[000\right],\hfill \\ \hfill C_{(N-1)}^{(7,2)}& =\left[000111\right|0],\hfill \\ \hfill C_{(N-1)}^{(13,3)}& =\left[000111222\right|10\left|20\right],\hfill \\ \hfill C_{(N-1)}^{(21,4)}& =\left[000111222333\right|102132\left|03\right|0],\hfill \\ \hfill C_{(N-1)}^{(31,5)}& =\left[000111222333444\right|10213243\left|0314\right|20\left|40\right],\hfill \\ \hfill C_{(N-1)}^{(43,6)}& =\left[000111222333444555\right|1021324354\left|031425\right|0415\left|2053\right|0],\hfill \\ \hfill C_{(N-1)}^{(57,7)}& =\left[000111222333444555666\right|102132435465\left|03142536\right|041526\left|2064\right|0516\left|30\right],\hfill \\ \hfill C_{(N-1)}^{(73,8)}& =\left[000111222333444555666777\right|10213243546576\left|0314253647\right|04152637\left|2075\right|051627\left|306174\right|0],\hfill \\ \hfill C_{(N-1)}^{(91,9)}& =[\dots |1021324354657687\left|031425364758\right|0415263748\left|2086\right|05162738\left|30617285\right|0718\left|40\right],\hfill \\ \hfill & \dots \hfill \end{array}$$

(30)

We discuss the 2nd method in Appendix A.15.

Figure 6. 2-gram matrices for $1\le b\le 16$ that illustrate the generation of $C_{(N-1)}$ strings according to a method presented in this section. Coloured 2-grams are appended to the initial string of clear 3-grams in the order indicated by arrows starting from the 1st column or row. Finally, 0 is appended at the end if b is even.

Figure 6. 2-gram matrices for $1\le b\le 16$ that illustrate the generation of $C_{(N-1)}$ strings according to a method presented in this section. Coloured 2-grams are appended to the initial string of clear 3-grams in the order indicated by arrows starting from the 1st column or row. Finally, 0 is appended at the end if b is even.

The longest length of a string that has the ASI of $N-1$ (a $C_{(N-1)}$ string) is given by

$$N_{(N-1)}=3b+{(b-1)}^2=b{N}_c+1=b^2+b+1$$

(31)

(OEIS A353887), where $N_c=b+1$ is the number of occurrences of all but one symbol within the string, so this string has odd length and is nearly balanced. To be the longest, a $C_{(N-1)}$ string must contain all 2-grams from the matrix (27) and all clear 3-grams. A string that contains all k-grams is a linear, minimal de Bruijn string (e.g., $\left\{\right[00110],[01100],\dots \}$ for $b=k=2$), which must start and end with the same symbol. Its length is given by $N_{\mathrm{de}\mathrm{Bruijn}}=b^k+k-1$, and there are ${(b!)}^{b^{k-1}}$ such strings. We consider $k=2$ and have to add b symbols to turn b clear 2-grams of a de Bruijn string into b clear 3-grams, which clearly does not introduce any disjoint occurrences [41]. This leads to the formula (31). For $b=1$ the upper and the lower bound on the ASI are the same, $a_{\max }^{(N,1)}=a_{\min }^{\left(N\right)}$, and this is the only case where the maxASI is not a monotonically non-decreasing function of N. Otherwise, the maxASI must rise. If it were to become constant for $N>{\widehat{N}}_{max}$, then at some even larger N it would inevitably become lower than the minASI bound of Theorem 3.1, which also rises, and this would be a contradiction.

Subsequently, we considered other strings with the maxASI. A $C_{(N-1)}$ string contains all 2-grams. Hence, inserting any basic symbol into any position inevitably leads to a repetition of a 2-gram. Without loss of generality (w.l.o.g.) we append it at the start of the $C_{(N-1)}$ string, obtaining a string $[*000111\dots ]$. Another symbol can be introduced to this string without an additional 2-gram repetition, for example, as another prefix $[★*000111\dots ]$ leading to the repetition of the 2-gram $★*$ or $*0$ but not both of them (here we allow $★=*$). Hence, both the length and the ASI of this string increase by one. Finally, 0 can be appended at the start of this string without an additional 2-gram repetition, provided that $★=1$ and $*=0$. For $b=2$ there are only four1 bitstrings containing only two copies of a 2-gram having the ASI $a_{\max }^{(10,2)}=8$

$$\begin{array}{c}\hfill \left[01\right|0000\left|1110\right],\left[1\right|0000\left|11101\right],\left[101\right|0000\left|111\right],\left[1\right|0000\left|10111\right],\end{array}$$

(32)

where the leftmost one is the only unbalanced string within this set ($N_0\ne N_1$). Each 10-bit string (32) has one clear 4-gram surrounded by the same symbol ($[\dots 1|0000|1\dots ]$) and one clear 3-gram ($[\dots 111\dots ]$), which can be concatenated ($[\dots 1|0000|111\dots ]$) in eight bits or separated ($[\dots 1|0000|1\dots 111\dots ]$) in nine bits. The first three strings (32) correspond to the former case, while the last one to the latter. Each of the strings (32) contains three pairs of mutually exclusive 2-grams, so that only one pair can be reused to decrease the maximum $N-1$ ASI by one.

We developed two methods of constructing generalized $C_{(N-b)}$ strings (32) for $b>2$. They have $b-1$ clear 4-grams ($c_l{c}_l{c}_l{c}_l$), one clear 3-gram and $(b-1)\times 3$ of mutually exclusive 2-grams $\{c_k{c}_l,c_l{c}_l,c_l{c}_m\}$ overlapped in patterns $[\dots c_k|c_l{c}_l{c}_l{c}_l|c_k\dots ]$ surrounding clear 4-gram, so that only one pair from each pattern can be reused in $3^{b-1}$ ways to reduce the maxASI to $N-b$. The 1st method is based on the balanced $C_{(N-2)}$ string (32) $\left[101\right|0000\left|111\right]$ and generates the most balanced $C_{(N-b)}$ strings. It starts with a string of length $6b-2$ containing all $b-1$ clear 4-grams in the form

$$\left[b_{-1}01\right|0000\left|12\right|1111|2\dots b_{-1}|b_{-2}{b}_{-2}{b}_{-2}{b}_{-2}\left|b_{-1}{b}_{-1}{b}_{-1}\right],$$

(33)

to which the missing $b^2-2b$ symbols are appended using the patterns shown in Figure 7 yielding the $C_{(N-b)}$ strings of the form

$$\begin{array}{cc}\hfill C_{(N-1)}^{(3,1)}=[& 000],\hfill \\ \hfill C_{(N-2)}^{(10,2)}=[& 101\left|0000\right|111],\hfill \\ \hfill C_{(N-3)}^{(19,3)}=[& 201\left|0000\right|12\left|1111\right|222\left|102\right],\hfill \\ \hfill C_{(N-4)}^{(30,4)}=[& 301\left|0000\right|12\left|1111\right|23\left|2222\right|333\left|103\right|202\left|13\right],\hfill \\ \hfill C_{(N-5)}^{(43,5)}=[& 401\left|0000\right|12\left|1111\right|23\left|2222\right|34\left|3333\right|444\left|104\right|30313202\left|1424\right],\hfill \\ \hfill C_{(N-6)}^{(58,6)}=[& 501\left|0000\right|12\left|1111\right|23\left|2222\right|34\left|3333\right|45\left|4444\right|555\left|105\right|404142430313202\left|152535\right],\hfill \\ \hfill C_{(N-7)}^{(75,7)}=[& 601\left|0000\right|12\left|1111\right|23\left|2222\right|34\left|3333\right|45\left|4444\right|56\left|5555\right|666\left|106\right|505152535404142430313202\left|16263646\right],\hfill \\ \hfill C_{(N-8)}^{(94,8)}=[& 701\left|0000\right|12\left|1111\right|23\left|2222\right|34\left|3333\right|45\left|4444\right|56\left|5555\right|67\left|6666\right|777|\hfill \\ \hfill & 107\left|60616263646505152535404142430313202\right|1727374757],\hfill \\ \hfill & \dots \hfill \\ \hfill C_{(N-b)}^{(b^2+4b-2,b)}=[& b_{-1}01\left|0000\right|12\left|1111\right|2\dots b_{-1}|b_{-2}{b}_{-2}{b}_{-2}{b}_{-2}|b_{-1}{b}_{-1}{b}_{-1}|10b_{-1}|b_{-2}0b_{-2}\dots 21\dots b_{-1}].\hfill \end{array}$$

(34)

Figure 7. 2-gram matrices for $1\le b\le 9$ that illustrate the generation of the most balanced $C_{(N-b)}$ strings (33). Coloured 2-grams are appended to the initial string of clear 4-grams in the order indicated by colours.

Figure 7. 2-gram matrices for $1\le b\le 9$ that illustrate the generation of the most balanced $C_{(N-b)}$ strings (33). Coloured 2-grams are appended to the initial string of clear 4-grams in the order indicated by colours.

We discuss the 2nd method, generating non-balanced $C_{(N-b)}$ strings, in Appendix A.16.

The mutually exclusive 2-grams of any $C_{(N-b)}$ string comprise $b-1$ adjoining clear 2-grams on the diagonal of the 2-grams matrix (27) and $2(b-1)$ 2-grams on its sub- and super-diagonals, as shown in Figure 7, so that each clear 4-gram is surrounded by the same symbol only one pair from each pattern can be reused. In particular, $C_{(N-b)}$ strings can have forms (A25) or (34) with all clear 4-grams separated by 2-grams and forming 7-gram patterns in the form $[\dots c_l{c}_k{c}_l{c}_l{c}_l{c}_l{c}_k\dots ]$. However, this is not necessary. For example, the string $C_{(N-3)}=\left[1\right|0000\left|102\right|1111\left|21\right|222\left|01\right]$ does not follow this rule. $C_{(N-b)}$ strings are not the maximum length maxASI strings having the property of maxASI incremented by one with every three symbols. For example, the string (34) for $b=3$ can be suffixed with 202, yielding a string with $a^{(22,3)}=18$ which still is not the maxASI string with this property for $b=3$ (cf. Table A5).

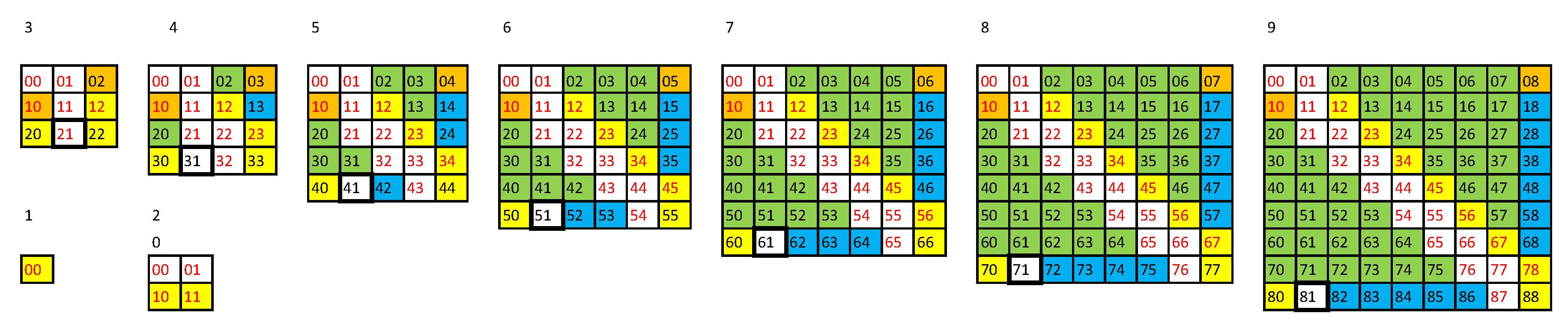
5. Results Common to the Minimum and Maximum Complexity Strings

The minASI and maxASI bounds are illustrated in Figure 8 for $b=\{2,3,4\}$. For each b, maxASI initially equals $N-1$ up to the 1st threshold (31). Then it flattens and decreases by one every 3 symbols: once for $b=2$ and $2b$ times for $b>2$, as we conjecture based on the results for $b=3$.

Figure 8. The minimum assembly index (red; ${log}_2\left(N\right)$, red, dash-dot) and the maximum assembly index (green) for $b\in \{2,3,4,5\}$ and $N\le 81$.

Figure 8. The minimum assembly index (red; ${log}_2\left(N\right)$, red, dash-dot) and the maximum assembly index (green) for $b\in \{2,3,4,5\}$ and $N\le 81$.

Figure 9. The ASI of all bitstrings of lengths $N=8$ (a), $N=10$ (b), $N=12$ (c), $N=14$ (d), and $N=16$ (e), as a function of their decimal representations, in squares with sides equal to $\sqrt{2^N}$. Red dots indicate maxASI strings.

Figure 9. The ASI of all bitstrings of lengths $N=8$ (a), $N=10$ (b), $N=12$ (c), $N=14$ (d), and $N=16$ (e), as a function of their decimal representations, in squares with sides equal to $\sqrt{2^N}$. Red dots indicate maxASI strings.

The ASI of a string is also related to the expected waiting time (EWT) of this string. The EWT is the expected number of trials until a specific string appears in a sequence of independent and identically distributed (i.i.d.) random variables taking values in a finite set of $b>1$ equiprobable outcomes, called a uniform categorical distribution. The general formula for the EWT of a string, which can be determined using Markov chains, is [42]

$$\mathrm{E}\left[C_l^{(N,b)}\right]=\sum _{k=1}^N{b}^k·{\mathrm{I}}_k,$$

(35)

where ${\mathrm{I}}_k$ is an indicator function that is 1 if the prefix of length k is also the suffix of the string $C_l^{(N,b)}$ and 0 otherwise. Thus, the EWT is bounded from below and from above as

$$b^N\le \mathrm{E}\left[C_l^{(N,b)}\right]\le {\displaystyle \frac{b}{b-1}}\left(b^N-1\right).$$

(36)

The upper EWT bound (36) is attained by clear strings, that is, also by the minASI strings, in which case ${\mathrm{I}}_k=1,\forall k$ and the formula (35) simplifies to a geometric series $\mathrm{E}\left[C_l^{(N,b)}\right]={\sum }_{k=1}^N{b}^k$ which resolves to the upper EWT bound (36). The minASI strings containing two or three symbols do not satisfy this relation and hence have shorter EWT. For example, the minASI alternating strings have the EWT given by $\mathrm{E}\left[C_l^{(N,b)}\right]={\sum }_{m=1}^{N/2}{b}^{2m}$ if N is even and $\mathrm{E}\left[C_l^{(N,b)}\right]={\sum }_{m=1}^{\lceil N/2\rceil }{b}^{2m-1}$ if N is odd, that is $\mathrm{E}\left[C_k^{(N,b)}\right]\in \{2,4,10,20,42,84,\dots \}$ given by $\{\times 2,\times 2+2,\times 2,\dots \}$ (OEIS A026644). The non-alternating minASI bitstrings can have the EWT even closer to the lower bound (36). For example, $\mathrm{E}\left[010010100101001\right]=33828$ (cf. Figure 1d) lies firmly at the lower end of the spectrum, being positioned just $3.24\%$ of the way through the total range. The lower EWT bound (36) is attained by the strings having no prefixes matching suffixes, in which case, for $k=N$ the whole string matches itself. The maxASI strings feature the EWT values equal to or close to this bound.

Applying AT to evolutionary biology, the inverse proportionality between the EWT of a string and its ASI is anticipated but also feels counterintuitive, as common sense would suggest that strings of low complexity should be provided earlier than more complex ones.

We found a correlation between the maxASI and the decimal representation of a string providing an intuitive geometric interpretation of the complexity landscape. For example, Figure 9 shows the ASI of all bitstrings of even lengths $N\in \{8,10,12,14,16\}$ distributed in squares of sides equal to $2^{N/2}$, starting from the top-left corner (${\mathrm{val}}_2[00\dots ]=0$) and ending at the bottom-right corner (${\mathrm{val}}_2[11\dots ]=2^N-1$). The decimal value of each pixel is given by $r{2}^{N/2}+c$, where $0\le r,c\le 2^{N/2}-1$ are the row and column indices. The low ASI strings naturally occur on diagonals and oblique lines because of the internal symmetries they exhibit. For example, minASI strings naturally occur on the main diagonal, as $r(2^{N/2}+1)$ for $r=c$ corresponds to a bitstring containing a prefix of length $N/2$ equal to its suffix. Thus, the EWT (35) of a main diagonal bitstring $C_d$ is bounded from below by $\mathrm{E}\left[C_d^{(N,2)}\right]\ge 2^N+2^{N/2}$, and its ASI, taking ito account the relation (1), is bounded by

$$a_{\min }^{(N,2)}\le a^{(N,2)}\left(C_d\right)\le N-1-2(N/2-1)+a_{\max }^{(N/2,2)}=a_{\max }^{(N/2,2)}+1.$$

(37)

For example, for $N=8$, the ASI of all main diagonal strings $C_d$ satisfy $3\le a^{(8,2)}\left(C_d\right)\le 4$, and they include the four minASI strings $\left\{\right[00\dots ],[01\dots \left]\right\}\times 2$ corresponding to equidistributed decimals 0, 85, 170, and 255. For $N=10$, the depleted sixteen maxASI strings correspond to $\{94,122,270,286,376,450,482,488,535,541,573,647,737,753,901,929\}$ decimal values. For $N=12$, the ten minASI strings $\left\{\right[00\dots ],[001\dots ],[010\dots ],[01\dots ],[011\dots \left]\right\}\times 2$ are equidistributed on the main square diagonal every 585 and every 1365. Finally, for $N=16$, the small ASI strings are aligned on diagonals and skewed lines with the four minASI strings again equidistributed on the main square diagonal, while the 506 maxASI strings tend to attain row-like and column-like arrangements.

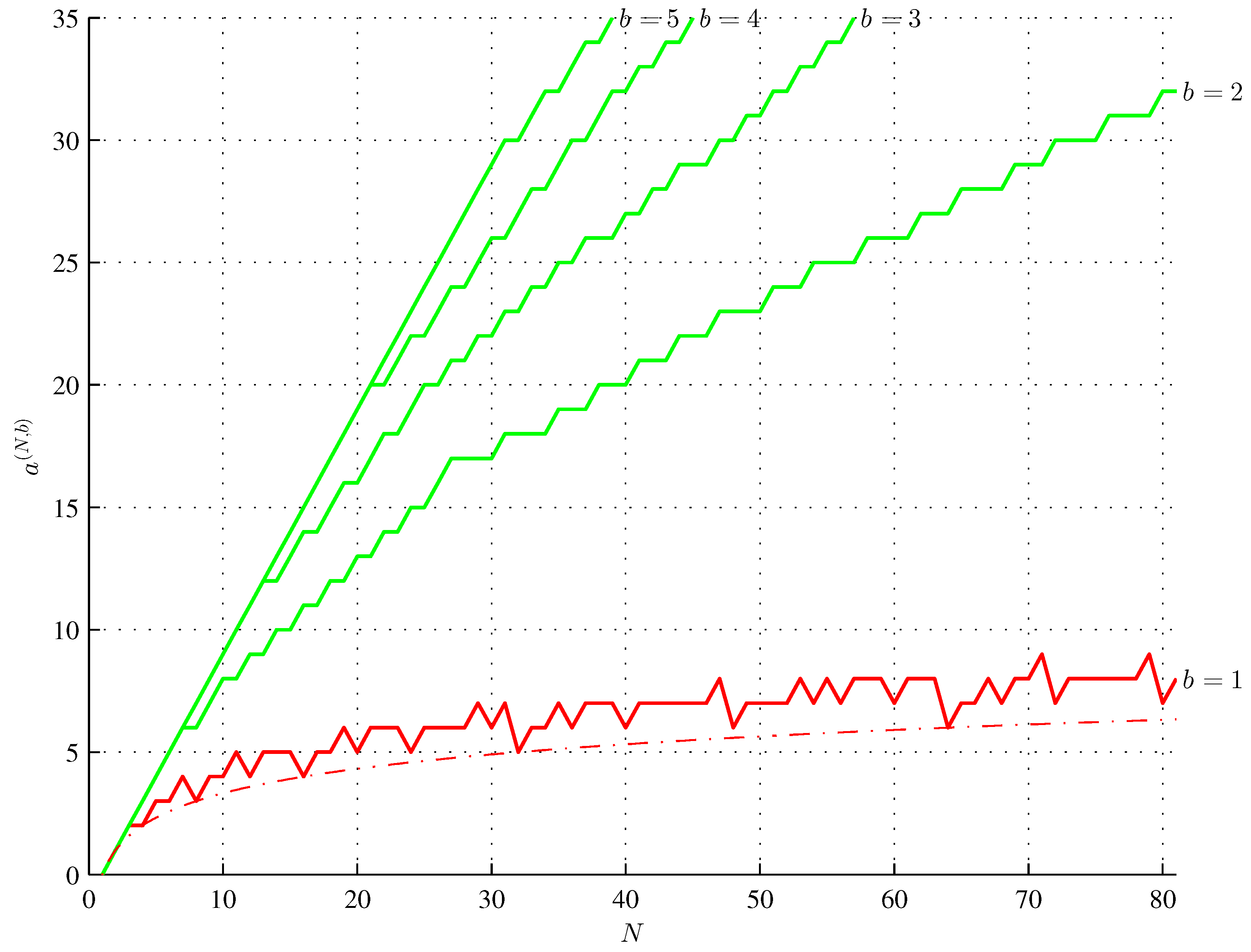
6. Supremacy of the ASI Compression over Polynomial-Time Compression Algorithms

Calculating the ASI of a string can be contrasted with compression algorithms that run in polynomial time, such as basic dictionary (LZ-type) schemes [43,44,45] or grammar-based algorithms, such as Re-Pair. Indeed, Turing’s universality and algorithmic complexity show that any computable transformation, including the ASI, can be simulated symbolically with no loss of information [43]. This naturally raised doubts regarding the trivial computability of the ASI and its potential equivalence to popular lossless compression algorithms [43].

Yet these doubts proved moot. As the length of a string increases, computing the ASI becomes a hyper-exponentially hard, exhaustive process over all possible combinations and repeated substrings due to the enormous combinatorial space of possible construction pathways and the need to globally evaluate which fragments are most efficient to create early versus later; such a pathway minimization cannot be resolved entirely through local heuristics; there is no local strategy of finding optimal substrings in AT. This ASI problem is widely known in AT literature (cf. [13,46,47,48]). It was conjectured [10] that the ASI problem is NP-complete. A certificate-dependent (assembly-step) proof of this conjecture within predefined assembly spaces [12,47] was found [48] by providing a Karp reduction from the vertex cover problem. A complete, self-contained proofs of NP-completeness of the ASI problem for both decision and optimization variants and for all assembly spaces were found [14] by establishing a correspondence between string assembly spaces and straight-line grammars. Since, for each ASI, there exists a naïve algorithm (exhaustive search of the entire assembly tree), the ASI is computable for all finite objects [7]. Thus, one can say that determining ASI is computable and algorithmically trivial, but it is also computationally non-trivial because the assembly tree grows exponentially with N. One can see this non-triviality by noting that integrating machine-learning–driven methods does not improve ASI computation, even for moderately sized molecules [49]. Interestingly, human intuition can often identify structural patterns or regularities enabling rapid non-algorithmic qualitative estimation of the ASI that remains inaccessible to sequential algorithms.

The computational non-triviality of the ASI raised a second question: whether a worse and slower algorithm [43], such as NP-complete ASI exhaustive search, merits consideration if it provides the same explanatory power and predictive accuracy as known algorithms. Indeed, if additional constraints are imposed on AT, such as restricting assembly steps to substrings of predefined length, allowing/excluding certain assembly steps [12,48], etc., then certain variants of calculating the ASI may yield the same, or even worse results as compared to known compression algorithms, given the large number of the latter.

Figure 10. The ASI (a) and Re-Pair steps (b) of all bitstrings of length $N=10$, as a function of their decimal representations ($\{0,1,\dots ,1023\}$), in squares with sides equal to 32 pixels. Visible lack of perfect correlation between the ASI and Re-Pair: the number of Re-Pair steps is higher than ASI for 100 strings (e.g., 7=Re-Pair(34) > ASI(34)=5 for $\left[0000100010\right]$, 8=Re-Pair(95) > ASI(95)=7 for $\left[0001011111\right]$).

Figure 10. The ASI (a) and Re-Pair steps (b) of all bitstrings of length $N=10$, as a function of their decimal representations ($\{0,1,\dots ,1023\}$), in squares with sides equal to 32 pixels. Visible lack of perfect correlation between the ASI and Re-Pair: the number of Re-Pair steps is higher than ASI for 100 strings (e.g., 7=Re-Pair(34) > ASI(34)=5 for $\left[0000100010\right]$, 8=Re-Pair(95) > ASI(95)=7 for $\left[0001011111\right]$).

As an example, let us compare AT, a constrained AT* version that prohibits mixed 2-gram $\left[10\right]$ in the assembly pool (cf. Figure 2b), and the grammar-based Re-Pair method. The Re-Pair method involves counting all 2-grams in a string, selecting the most frequent 2-gram that occurs at least twice, replacing all its occurrences with a new symbol, and repeating these steps until no 2-gram occurs more than once. This is illustrated in the list (38) for an exemplary maxASI bitstring $\left[1111110000001001101010110\right]$ of length $N=25$. As shown, the ASI of this string is fifteen, while the ASI* obtained by such a constrained AT* version is sixteen, which corresponds to the number of steps required to compress this string into a Re-Pair compressed version $\left[DAEB1BACC0A0\right]$.

$$\begin{array}{cccc}\mathrm{step}\hfill & \mathrm{ASI}\hfill & \mathrm{ASI}*(\mathrm{no}2-\mathrm{gram}\left[10\right])\hfill & \mathrm{Re}-\mathrm{Pair}\hfill \\ 1.\hfill & \left[00\right]\hfill & \left[00\right]\hfill & \left[11\right]\times 7\to A,\left[AAA000000100A01010A0\right]\hfill \\ 2.\hfill & \left[01\right]\hfill & \left[11\right]\hfill & \left[00\right]\times 6\to B,\left[AAABBB1BA01010A0\right]\hfill \\ 3.\hfill & \left[10\right]\hfill & \left[01\right]\hfill & \left[01\right]\times 2\to C,\left[AAABBB1BACC0A0\right]\hfill \\ 4.\hfill & \left[11\right]\hfill & \left[000\right]\hfill & \left[AA\right]\times 2\to D,\left[DABBB1BACC0A0\right]\hfill \\ 5.\hfill & \left[0110\right]\hfill & \left[111\right]\hfill & \left[BB\right]\times 2\to E.\left[DAEB1BACC0A0\right]\hfill \\ 6.\hfill & \left[1111\right]\hfill & \left[111111\right]\hfill & \left[DA\right]\hfill \\ 7.\hfill & \left[111111\right]\hfill & \left[111111000\right]\hfill & \left[DAE\right]\hfill \\ 8.\hfill & \left[11111100\right]\hfill & \left[111111000000\right]\hfill & \left[DAEB\right]\hfill \\ 9.\hfill & \left[1111110000\right]\hfill & \left[1111110000001\right]\hfill & \left[DAEB1\right]\hfill \\ 10.\hfill & \left[111111000000\right]\hfill & \left[111111000000100\right]\hfill & \left[DAEB1B\right]\hfill \\ 11.\hfill & \left[11111100000010\right]\hfill & \left[11111100000010011\right]\hfill & \left[DAEB1BA\right]\hfill \\ 12.\hfill & \left[111111000000100110\right]\hfill & \left[1111110000001001101\right]\hfill & \left[DAEB1BAC\right]\hfill \\ 13.\hfill & \left[11111100000010011010\right]\hfill & \left[111111000000100110101\right]\hfill & \left[DAEB1BACC\right]\hfill \\ 14.\hfill & \left[111111000000100110101\right]\hfill & \left[11111100000010011010101\right]\hfill & \left[DAEB1BACC0\right]\hfill \\ 15.\hfill & \left[1111110000001001101010110\right]\hfill & \left[111111000000100110101011\right]\hfill & \left[DAEB1BACC0A\right]\hfill \\ 16.\hfill & \hfill & \left[1111110000001001101010110\right]\hfill & \left[DAEB1BACC0A0\right]\hfill \end{array}$$

(38)

However, an unconstrained AT provides different results. The distributions of ASI and Re-Pair steps for all the bitstrings of length $N=10$ illustrated in Figure 10, show that ASI compression is superior to the one provided by the Re-Pair algorithm. We encourage the reader to conduct an independent comparison of the ASI (e.g., for the maxASI strings provided in Table A3–Table A6) with the results produced by well-known compression algorithms.

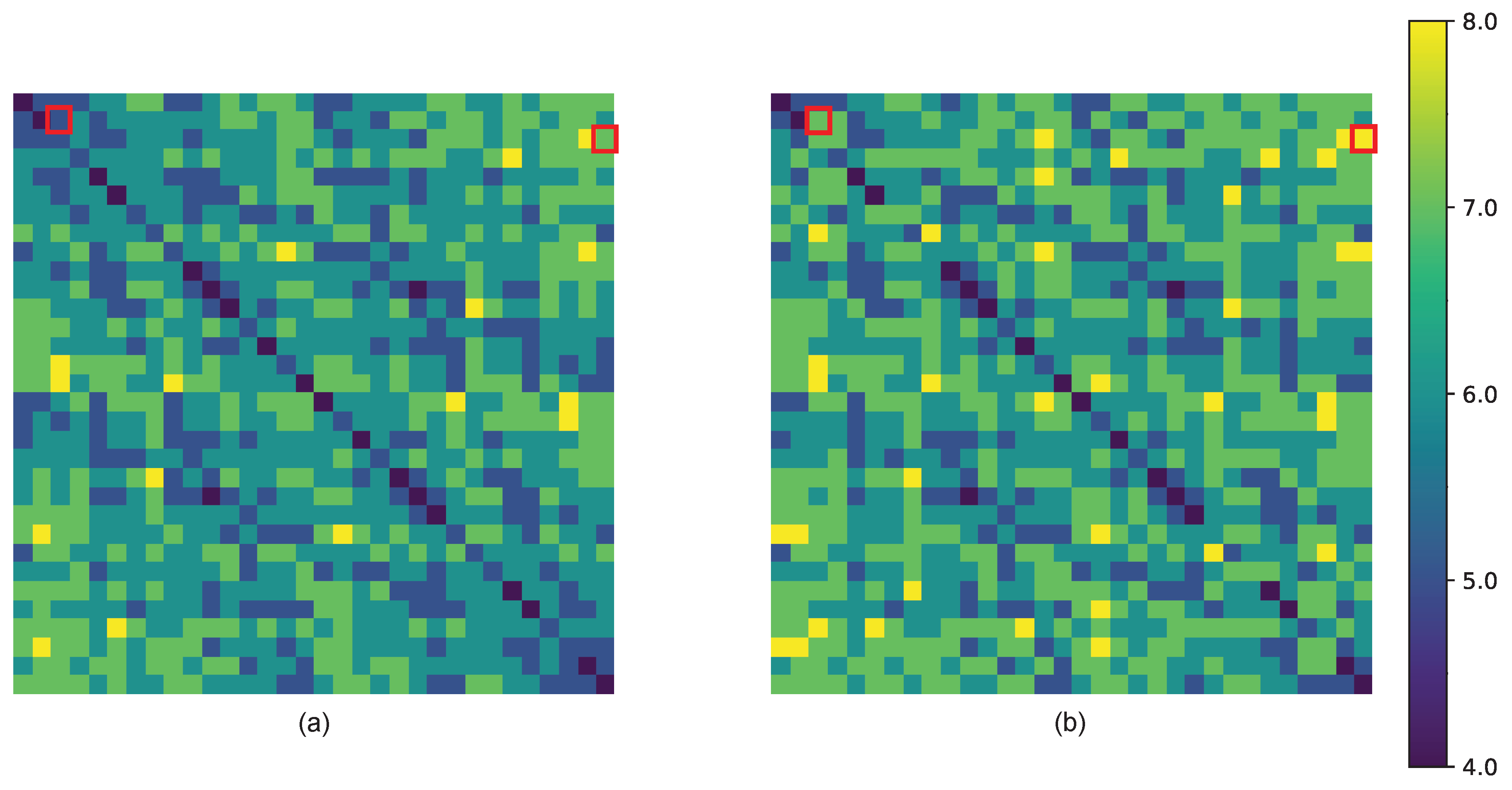
7. Discussion

The present study provides a general mathematical framework for the general AT string version and demonstrates how this formalization enables efficient computation of assembly indices across various diverse structural sequences. Clarifying the theory’s conceptual structure provides suggestions for its computational implementation. This allowed us to formalize bounding and pruning processes (an approach also proposed in [13,46]) and to develop software capable of effectively computing the ASI of a string, significantly reducing the number of potential configurations to explore. This, in turn, resulted in substantial efficiency gains, allowing us to find the exemplary long maxASI strings (cf. Table A3–Table A6) and determine the maxASI bounds shown in Figure 8, overcoming important limitations exhibited by all the other known implementations of the algorithms to compute the ASI of big objects [50].

Fortunately, the non-triviality of computing the ASI does not close the field but rather delineates a structured landscape for algorithmic exploration. The framework developed here is equally applicable to symbolic representations of various real world patterns within the context of AT, such as detecting biosignatures [6], describing the evolution of music [51], and, as we conjecture, natural language processing (AI-generated text detection, authorship style analysis, plagiarism detection, time series analysis, etc.), financial data changes (distinction between random and predictable behaviour), sensor data anomaly analysis, medical signal analysis, etc.

The implications of our findings extend beyond the formal structure of AT itself. Traditional physics, while offering predictive power from past initial conditions to future states, lacks a functional perspective necessary to differentiate meaningful novelty from random fluctuations. AT may offer a unifying language for describing how information becomes structure. It can do so by showing how biological sequences are governed by foundational mathematical principles, for instance, for understanding the rules underlying the assembly of macromolecules such as proteins and DNA. Evolutionary biology explains the survival and prevalence of certain traits, but it does not address the mechanisms for generating novel phenotypic variants. We have shown, for example, that a DNA strand of length N containing four nucleobases cannot represent a minASI string without violating Chargaff’s rules and Theorem 3.2. Theorem 3.2 establishes that a minASI string can contain at most three distinct symbols (if $N\ne 2^s$, as otherwise it can contain at most two), while the first Chargaff’s rule (for double-stranded DNA) states that four nucleobases A, T, and G, C should be pairwise balanced. On the other hand, biological systems tend to deviate from the equilibrium of maximum entropy [10,52] corresponding to balanced strings,

For $b=1$, the information entropy (23) vanishes, as the bit ($b=2$) is the smallest amount and the quantum of information. Yet AT explains the assembly of such minASI strings, extending beyond the minimal two-valued system necessary to convey any information. Our results clarify that AT is a formal system for describing the generative and causal structure of objects, positioning it as a theoretical extension of information theory, emphasizing not the description of information but the effort required to construct it.

Appendix A.1. Proof of Theorem 2.1

Consider the following two strings of the same length $N+8$ with $*★\ne 01$ and the same distributions of other repetitions (if any)

$$C_k=[\dots 01\dots 01\dots 01\dots *★\dots ],C_l=[\dots 01\dots 01\dots 22\dots 22\dots ].$$

(A1)

Assembling a 2-gram takes one assembly step. Each appending of a 2-gram to an assembled string counts as another assembly step. Hence, in a general case (i.e., for strings $C_k$, $C_l$ containing also other symbols), the string $C_k$ requires six additional assembly steps, the same as the string $C_l$. Thus, a string containing the same three 2-grams has the same ASI as a string containing two pairs of the same 2-grams, provided that both strings have the same distributions of other repetitions and have the same lengths.

Consider the following two strings of the same length $N+6$ with the same distributions of other repetitions

$$C_k=[\dots 01\dots 01\dots 01\dots ],C_l=[\dots 010\dots 010\dots ].$$

(A2)

The assembly of a 3-gram takes two steps. Hence, in the general case, the string $C_k$ requires four additional assembly steps, the same as the string $C_l$. Thus, a string containing the same three 2-grams has the same ASI as a string containing the same two 3-grams, provided that both strings have the same distributions of other repetitions.

Similarly, a string containing the same two 3-grams has the same ASI as a string containing two pairs of the same 2-grams, provided that both strings have the same distributions of other repetitions and have the same lengths.

Consider the following two strings of the same length $N+9$ with the same distributions of other repetitions

$$C_k=[\dots 0101\dots 0101\dots ★\dots ],C_l=[\dots 010\dots 010\dots 010\dots ].$$

(A3)

The assembly of such a 4-gram takes two steps. Hence, in a general case, the string $C_k$ requires five additional assembly steps, the same as the string $C_l$. Thus, a string containing the same two 4-grams of the minASI has the same ASI as a string containing the same three 3-grams, provided that both strings have the same distributions of other repetitions and have the same lengths.

Consider the following two strings of the same length $N+8$ with the same distributions of other repetitions

$$C_k=[\dots 0001\dots 0001\dots ],C_l=[\dots 110\dots 10\dots 110\dots ].$$

(A4)

The assembly of such a 4-gram takes three steps. Hence, in a general case, the string $C_k$ requires five additional assembly steps, the same as the string $C_l$. Thus, a string containing the same two 4-grams of the maxASI has the same ASI as a string containing a 2-gram and the same two 3-grams based on this 2-gram, provided that both strings have the same distributions of other repetitions.

Consider the following two strings of the same length $N+10$ with the same distributions of other repetitions

$$C_k=[\dots 110\dots 00\dots 110\dots 00\dots ],C_l=[\dots 110\dots 10\dots 110\dots *★\dots ],$$

(A5)

where $*★\notin \{11,10\}$. In a general case, the string $C_k$ requires seven additional assembly steps, the same as the string $C_l$. Thus, a string containing the same two 2-grams and the same two 3-grams not based on this 2-gram has the same ASI as a string containing a 2-gram and the same two 3-grams based on this 2-gram, provided that both strings have the same distributions of other repetitions and have the same lengths.

In general, the above considerations show that

• k copies of a 2-gram in a string decrease the ASI of this string at least by $k-1$;
• k copies of a 3-gram in a string decrease the ASI of this string at least by $2k-2$;
• k copies of a minASI 4-gram in a string decrease the ASI of this string at least by $3k-2$;
• k copies of a maxASI 4-gram in a string decrease the ASI of this string at least by $3k-3$;

where, the phrase "at least" is meant to indicate that other repetitions, such as e.g. 2-grams forming multiple 4-grams, etc. can further decrease the ASI of the string. W.l.o.g., consider the following string

$$C_m^{(N,b)}=[\dots [c_1{c}_2\dots c_n]\dots [c_1{c}_2\dots c_n]\dots ],$$

(A6)

containing two copies of an n-gram $C_l^{(n,b)}=[c_1{c}_2\dots c_n]$. The n-gram $C_l^{(n,b)}$ can be assembled in at least $a^{(n,b)}\left(C_l\right)$ steps and appended to the assembled string $C_m$ in one step. Consider that the ASI of the n-gram $C_l^{(n,b)}$ is $a^{(n,b)}\left(C_l\right)=n-1$, i.e. the n-gram does not have any repetitions that can be reused and $n<8$. Then one copy of this n-gram - as expected - does not decrease the ASI of the string $C_m^{(N,b)}$, as $1(n-1)-(n-1)=0$, while more copies k decrease it by $(n-1)(k-1)$. On the other hand, if $a^{(n,b)}\left(C_l\right)<n-1$ then even a single copy of this n-gram will decrease the ASI of $C_m$.

Appendix A.2. Proof of Theorem 2.2

Without loss of generality (w.l.o.g.) assume a contrario that $\Omega$ contains two strings $C_l$, $C_m$ having the same ASD, i.e., $d^{(N_l,b)}\left(C_l\right)=d^{(N_m,b)}\left(C_m\right)\ne 0$, that were not assembled in independent assembly steps, i.e., that $C_m$ was used in the assembly of $C_l$ along with a basic symbol c in some previous step s. Then

$$d_s^{(N_l,b)}\left(C_l\right)=\max \left(d^{(N_m,b)}\left(C_m\right),d^{(1,b)}\left(c\right)\right)+1=d^{(N_m,b)}\left(C_m\right)+1\ne d^{(N_m,b)}\left(C_m\right),$$

(A7)

which contradicts our assumption and completes the proof.

Appendix A.3. Proof of Lemma 2.2

Assume a contrario that $N>2^{d_s^{\left(N\right)}}$. Then for the ASD $d_s^{\left(N\right)}=0$, we have $N>2^0=1$ which is a contradiction as all basic symbols c are unit-length strings and $N=1$. Similarly, for $d_s^{\left(N\right)}=1$, $N>2$ is also contradiction in the case of 2-grams, and so on. This is a consequence of the ASD Definition (3).

Appendix A.4. Proof of Theorem 2.3

$d_s^{\left(N\right)}\ge {log}_2\left(N\right)$ follows from the relation (4). $d_{\min }^{\left(2\right)}=⌈{log}_2\left(2\right)⌉=1$ satisfies both the definition (3) and our hypothesis (5). Similarly $N=3$. Using induction on length N, assume that for some $N>3$, we can assemble a minASD string with ASD (5). We need to show that for $N+1$, we can assemble a string with the ASD satisfying

$$d_{\min }^{(N+1)}=⌈{log}_2(N+1)⌉.$$

(A8)

Since, by definition (3), the ASD as a function of N is monotonously nondecreasing and can increase at most by one between N and $N+1$, we have

$$d_{\min }^{(N+1)}=d_{\min }^{\left(N\right)}=⌈{log}_2\left(N\right)⌉\mathrm{or}{d}_{\min }^{(N+1)}=d_{\min }^{\left(N\right)}+1=⌈{log}_2\left(N\right)⌉+1,$$

(A9)

where we used relations (5) and (A8). Solving the relation (A9) for N yields

$$d_{\min }^{(N+1)}=\left\{\begin{array}{cc}{d}_{\min }^{\left(N\right)}=s\hfill & \mathrm{if}{2}^{s-1}<N<2^s,\hfill \\ d_{\min }^{\left(N\right)}+1=s+1\hfill & \mathrm{if}N=2^s,\hfill \end{array}\right.$$

(A10)

and completes the proof.

Appendix A.5. Proof of Theorem 2.4

Using the property of the ceiling function $n=\lceil x\rceil \iff n-1<x\le n$ valid for $n\in \mathbb{N},x\in \mathbb{R}$, we have

$$d_{a_{\max }}^{(N,b)}=⌈{log}_2\left(N\right)⌉\iff d_{a_{\max }}^{(N,b)}-1<{log}_2\left(N\right)\le d_{a_{\max }}^{(N,b)},$$

(A11)

The non-strict inequality (A11) corresponds to the non-strict inequality (4) valid for any N and any ASD. Therefore, we need to prove that the strict inequality $d_{a_{\max }}^{(N,b)}<{log}_2\left(N\right)+1$ holds for all $C_{\max }$ strings. Assume, for contradiction, that there exists a maxASI string $C_{\max }^{(N,b)}$ such that

$$d_{a_{\max }}^{(N,b)}\ge {log}_2\left(N\right)+1={log}_2\left(2N\right)\Rightarrow 2^{d_{a_{\max }}^{(N,b)}}\ge 2N\Rightarrow N\le 2^{d_{a_{\max }}^{(N,b)}-1}.$$

(A12)

But this relation does not hold for the maxASI string $C_{\max }^{(N,b)}$.

Appendix A.6. Proof of Theorem 3.1

Strings $C_{\min }$ for which $a^{\left(N\right)}\left(C_{\min }\right)=\underset{k}{min}\left(\left\{a^{(N,b)}\left(C_k\right)\right\}\right)$, $\forall k\in \{1,2,\dots ,b^N\}$ can be formed in subsequent steps s by joining the longest string assembled so far with itself until $N=2^s$ is reached. Therefore, if $N=2^s$, then $\underset{k}{min}\left(\left\{a^{\left(2^s\right)}\left(C_k\right)\right\}\right)=s={log}_2\left(N\right)$. Only $b^2$ strings have such ASI if $N=2^s$, including respectively b and $b(b-1)$ strings

$$C_k^{(2^s,b)}=[**\dots ],C_l^{(2^s,b)}=[*★*★\dots ],$$

(A13)

and the assembly space of each of the strings (A13) is unique. At each assembly step, its length doubles.

An addition chain for $N\in \mathbb{N}$ having the shortest length $s\in \mathbb{N}$ (commonly denoted as $l\left(N\right)$) is defined as a sequence $1=a_0<a_1<\dots <a_s=N$ of integers such that $\forall j\ge 1$, $a_j=a_k+a_l$ for $k\le l<j$. Hence, $j=1\Rightarrow k=l=0$ and the first step in forming an addition chain for N is always $a_1=a_0+a_0=1+1=2$, which is equivalent to saying that the ASI of any 2-gram is one. The second step in forming an addition chain can be $a_2=a_0+a_1=1+2=3$ or $a_2=a_1+a_1=2+2=4$, which corresponds to assembling a 3-gram based on the previously assembled 2-gram or to assembling a minASI 4-gram (A13) from this 2-gram. The maxASI 4-gram can be assembled in a third step, $a_3=a_2+a_0=3+1=4$, which corresponds to joining a basic symbol to a 3-gram. Therefore, four is the smallest number achievable in two ways according to Theorem 2.1.

Thus, finding the shortest addition chain for N corresponds to finding the ASI of a string containing basic symbols and/or 2-grams and/or 3-grams containing these 2-grams if $N\ne 2^s$ since due to Theorem 2.1 only they provide the same assembly indices $\{0,1,2\}$ with no internal repetitions.

Appendix A.7. Proof of Theorem 3.3

To prove that the minASI ASD equals the minASI, we use mathematical induction on the length N of the string. For the base case ($N=2^0=1$), the string consists of a single basic symbol $c\in P_0^{\left(b\right)}$, where $P_s^{\left(b\right)}$ denotes the assembly pool. Hence, its ASI is $a_{\min }^{\left(1\right)}0$ and its ASD $d_{a_{\min }}^{\left(1\right)}0$. Therefore, $d_{a_{\min }}^{\left(1\right)}=a_{\min }^{\left(1\right)}=0$. Assume now that for all strings of length $2^s$ less than N, the ASD equals the minASI, that is

$$d_{a_{\min }}^{\left(2^s\right)}=a_{\min }^{\left(2^s\right)}\forall 2^s<N.$$

(A14)

For some integer s, we construct the minASI string as follows. First, we assemble a 2-gram from two basic symbols:

$$c_1\circ c_2=C^{(2,b)},c_1,c_2\in P_0^{\left(b\right)}.$$

(A15)

Its ASI is $a_{\min }^{\left(2\right)}=1$ and its ASD is $d_{a_{\min }}^{\left(2\right)}=1$. Then for each $s\ge 2$ we have $C^{(2^{s-1},b)}$ with the ASI $a_{\min }^{\left(2^{s-1}\right)}=s-1$ and the ASD $d_{a_{\min }}^{\left(2^{s-1}\right)}=s-1$ and we construct $C^{(2^s,b)}$ by joining two copies of $C^{(2^{s-1},b)}$

$$C^{(2^{s-1},b)}\circ C^{(2^{s-1},b)}=C^{(2^s,b)}.$$

(A16)

The ASI of the string $C^{(2^s,b)}$ is equal to

$$a_{\min }^{\left(2^s\right)}=a_{\min }^{\left(2^{s-1}\right)}+1=(s-1)+1=s,$$

(A17)

and, similarly, its ASD is equal to

$$d_{a_{\min }}^{\left(2^s\right)}max\left(d_{a_{\min }}^{\left(2^{s-1}\right)},d_{a_{\min }}^{\left(2^{s-1}\right)}\right)+1=(s-1)+1=s.$$

(A18)

Therefore, $a_{\min }^{\left(2^s\right)}=d_{a_{\min }}^{\left(2^s\right)}=s$. At any step, we assemble strings (A13), and no two assembly steps can be independent, which follows from Theorem 3.1. The equation (A10) establishes that $N=2^s$ is the largest N for which $d_{\min }^{\left(N\right)}=s$. This proves $d_{\min }^{\left(2^s\right)}=d_{a_{\min }}^{\left(2^s\right)}=a_{\min }^{\left(2^s\right)}=s$. Finally, the even part of the definition of the DPI 2.7 is the only defining part of this definition iff $N=2^s$. Hence, $d_{\min }^{\left(2^s\right)}=d_{a_{\min }}^{\left(N\right)}=a_{\min }^{\left(2^s\right)}={\widehat{a}}_{\min }^{\left(2^s\right)}=s$.

Appendix A.8. Proof of Theorem 3.4

The lengths (14) (OEIS A173786 or OEIS A048645) are the generalization of the strings of length $N=2^{s-1}+2^{s-1}=2^s$ of the Theorem 3.3. For other lengths of the strings (14), the base case for $s=2,l=0$ describes the assembly of a 3-gram, by joining a symbol to a 2-gram made in the first step, so that both the ASI and the ASD of this 3-gram increase by one. And so on. For any s we can join a symbol to a string of length $N=2^{s-1}$ assembled in $s-1$ steps or join two such strings, as shown in Figure 3a.

To see that ${\widehat{a}}_{\min }^{\left({\widehat{N}}_1\right)}=s$ (14) holds for ${\widehat{N}}_1\ne 2^s$ note that there is only one odd part of the definition of the DPI 2.7 that restores$N=2^s$. For example, we reach one starting from ${\widehat{N}}_1=20$ in five consecutive steps $20\to 10\to \mathit{5}\to 4\to 2\to 1$.

Appendix A.9. Proof of Lemma 3.1

We begin at $d=3$ by assembling a $C_{\min }^{\left(7\right)}$ using a 4-gram and a 3-gram assembled independently (e.g., using an assembly space (15)) with $a_{\min }^{\left(7\right)}=4$ and $d_{a_{\min }}^{\left(7\right)}=⌈{log}_2\left(7\right)⌉=3$. For $d=4$, the string (16) $C_{\min }^{\left(11\right)}$ can be assembled by joining the string $C_{\min }^{\left(8\right)}$ assembled in three steps and the 3-gram, while the string $C_{\min }^{\left(14\right)}$ by joining two strings $C_{\min }^{\left(7\right)}$ made in the previous step. For any d, the shortest string (16) $C_{\min }^{\left({\tilde{N}}_3\right)}$ can be assembled by joining the string $C_{\min }^{\left(2^{d-1}\right)}$ (A13) assembled in $d-1$ steps and the 3-gram, while the remaining strings $C_{\min }^{\left({\tilde{N}}_3\right)}$ - by joining two strings made in a previous step $d-1$, as shown in Figure 3b.

Appendix A.10. Proof of Lemma 3.2

We begin at $d=4$ by assembling a $C_{\min }^{\left(13\right)}$ through $\{2,4,(5,8),13\}$ with $a_{\min }^{\left(13\right)}=d_{\min }^{\left(13\right)}+1=5$. For any d, the shortest string (17) $C_{\min }^{\left({\tilde{N}}_5\right)}$ can be assembled by joining the string $C_{\min }^{\left(2^{d-1}\right)}$ (A13) assembled in $d-1$ steps with the 5-gram assembled in the independent assembly step, while the remaining strings $C_{\min }^{\left({\tilde{N}}_5\right)}$ - by joining two strings made in a previous step $d-1$, as shown in Figure 3c.

Appendix A.11. Proof of Lemma 3.3

We begin at $d=5$ by assembling a $C_{\min }^{\left(25\right)}$ with $a_{\min }^{\left(25\right)}=d_{\min }^{\left(25\right)}+1=6$. For any d, we assemble the shortest strings (18) as

$$\begin{array}{c}\hfill \begin{array}{ccccccccc}\{2,\hfill & 4,\hfill & 8,\hfill & (9,\hfill & 16),\hfill & 25\},\hfill & \hfill & & \\ \{\dots \hfill & \hfill & & \hfill & & 32,\hfill & 41\},\hfill & \hfill & \\ \{\dots \hfill & \hfill & & \hfill & & \hfill & 64,\hfill & 73\},\hfill & \\ \{\dots \hfill & \hfill & & \hfill & & \hfill & & 128,\hfill & 137\},\hfill \\ \dots \hfill & \hfill & & \hfill & & \hfill & & \hfill & \end{array}\end{array}$$

(A19)

with one independent assembly step $(9,16)$ to assemble the string of length $N=2^{d-1}$ and joining 9-gram at the last step, while the remaining strings $C_{\min }^{\left({\tilde{N}}_9\right)}$ - by joining two strings made in a previous step $d-1$, as shown in Figure 3d.

Appendix A.12. Proof of Theorem 3.6

The equality of ASI and ASD of the strings (20) follows from the proof of Theorem 3.4. Furthermore $\forall d$,

$$\begin{array}{cc}\hfill & 2^{d-1}<2^{d-1}+7·2^{d-4}<2^d/-2^{d-1}\hfill \\ \hfill & 0<7·2^{d-4}<2^d-2^{d-1}=2^{d-1}/·2^{4-d}\hfill \\ \hfill & 0<7<2^{d-1}{2}^{4-d}=8,\hfill \end{array}$$

(A20)

shows that $d_{a_{\min }}^{\left({\tilde{N}}_7\right)}=⌈{log}_2\left({\tilde{N}}_7\right)⌉+1$. Finally, ${\widehat{a}}_{\min }^{\left({\widehat{N}}_1\right)}=⌈{log}_2\left({\tilde{N}}_7\right)⌉+2$ follows from the DPI Definition 2.7: six steps are required to reach one starting from fifteen and additional steps for thirty, sixty, etc., which completes the proof.

Appendix A.13. Support for Conjecture Section 3

The shortest strings of length ${\tilde{N}}_{15}$ (22a) can be assembled with the pathways

$$\begin{array}{c}\hfill \begin{array}{ccccccccccc}\{2,\hfill & 4,\hfill & (5,\hfill & 8),\hfill & 13,\hfill & 26,\hfill & 31\}\hfill & \hfill & & \hfill & \\ \{\dots \hfill & \hfill & & \hfill & & \hfill & 39,\hfill & 47\},\hfill & \hfill & & \\ \{\dots \hfill & \hfill & & \hfill & & \hfill & & 78,\hfill & 79\},\hfill & \hfill & \\ \dots \hfill & \hfill & & \hfill & & \hfill & & \hfill & & \hfill & \end{array}\end{array}$$

(A21)

shown in Figure 3e; the shortest strings of length ${\tilde{N}}_{27}$ (22b) can be assembled with the pathways

$$\begin{array}{c}\hfill \begin{array}{ccccccccccc}\{2,\hfill & (3,\hfill & 4),\hfill & 7,\hfill & 14,\hfill & 28,\hfill & 31,\hfill & 59\}\hfill & \hfill & & \\ \{\dots \hfill & \hfill & & \hfill & 14\hfill & 28,\hfill & 56,\hfill & 84,\hfill & 91\}\hfill & \hfill & \\ \{\dots \hfill & \hfill & & \hfill & 11\hfill & 18,\hfill & 36,\hfill & 72,\hfill & 144,\hfill & 155\}\hfill & \\ \dots \hfill & \hfill & & \hfill & & \hfill & & \hfill & & \hfill & \end{array}\end{array}$$

(A22)

shown in Figure 3f; and for any d, the shortest strings of length ${\tilde{N}}_{50.9}$ (22c) can be assembled as

$$\begin{array}{c}\hfill \begin{array}{cccccccccc}\{2,\hfill & 4,\hfill & 8,\hfill & (9,\hfill & 16),\hfill & 25,\hfill & 50,\hfill & 59\},\hfill & \hfill & \\ \{\dots \hfill & \hfill & & \hfill & & \hfill & & 100,\hfill & 109\},\hfill & \\ \{\dots \hfill & \hfill & & \hfill & & \hfill & & \hfill & 200,\hfill & 209\}\hfill \\ \dots \hfill & \hfill & & \hfill & & \hfill & & \hfill & & \end{array}\end{array}$$

(A23)

The remaining strings of length ${\tilde{N}}_{15}$, ${\tilde{N}}_{27}$, and ${\tilde{N}}_{50.9}$ (Section 3) can be assembled by joining two strings made in a previous step $d-1$.

Appendix A.14. Proof of Lemma 3.4

By Theorems 3.1 and 3.2, a minASI string of length $N=2^s$ assembled beginning with $C_{\min }^{\left(2\right)}=[*★]$ is a balanced bitstring. To assemble a longer string of other lengths, we assign $N_{s+1}=N_s+1$ or $N_{s+1}=N_s+2$. However, the Definition 2.7 removes the longest string of an odd length $N=2^s+1$ from the sequence if it is not the first one in the sequence. Strings longer than this string of length $N=2^s+1$ are assembled by joining the longest string assembled so far with itself ($N_{s+1}=2N_s$) or by joining a basic symbol chosen to preserve the balance of the string ($N_{s+1}=N_s+1$).

Appendix A.15. The 2nd Method for Generating C (N-1) Strings

This method is similar to the 1^st method discussed in Section 4. We also start with a string of clear 3-grams (26) and the matrix of 2-grams (27) with a crossed diagonal and the first superdiagonal. In the first step, we append the 2-gram $0b_{-1}$ (top right 2-gram of the matrix of 2-grams (27)) at the end of the string (26). Next, we generally perform the following pairs of iterations:

(1)

we check subsequent subdiagonals until we find one that does not contain a 2-gram present in the string formed so far, we append it at the end of this string and proceed to step 2;

(2)

we check subsequent superdiagonals until we find one that does not contain a 2-gram present in the string formed so far, we append it at the end of this string and proceed to step 1.

Finally, we append 0 if b is even. The method is illustrated in Figure A1 and generates the $C_{(N-1)}$ strings in the form

$$\begin{array}{cc}\hfill C_{(N-1)}^{(3,1)}=[& 000],\hfill \\ \hfill C_{(N-1)}^{(7,2)}=[& 000111\left|0\right],\hfill \\ \hfill C_{(N-1)}^{(13,3)}=[& 000111222\left|02\right|10],\hfill \\ \hfill C_{(N-1)}^{(21,4)}=[& 000111222333\left|03\right|102132\left|0\right],\hfill \\ \hfill C_{(N-1)}^{(31,5)}=[& 000111222333444\left|04\right|10213243\left|0314\right|20],\hfill \\ \hfill C_{(N-1)}^{(43,6)}=[& 000111222333444555\left|05\right|1021324354\left|031425\right|304152\left|0\right],\hfill \\ \hfill C_{(N-1)}^{(57,7)}=[& 000111222333444555666\left|06\right|102132435465\left|03142536\right|405162\left|041526\right|30],\hfill \\ \hfill C_{(N-1)}^{(73,8)}=[& 000111222333444555666777\left|07\right|10213243546576\left|0314253647\right|3041526374\left|051627\right|506172\left|0\right],\hfill \\ \hfill C_{(N-1)}^{(91,9)}=[& \dots \left|08\right|1021324354657687\left|031425364758\right|304152637485\left|05162738\right|607182\left|061728\right|40],\hfill \\ \hfill C_{(N-1)}^{(111,10)}=[& \dots \left|09\right|102132435465768798\left|03142536475869\right|30415263748596\left|0516273849\right|5061728394|\hfill \\ \hfill & 071829\left|708192\right|0],\hfill \\ \hfill C_{(N-1)}^{(133,11)}=[& \dots \left|0a\right|102132435465768798a9\left|031425364758697a\right|30415263748596a7\left|05162738495a\right|\hfill \\ \hfill & 60718293a4\left|061728394a\right|8091a2\left|08192a\right|50],\hfill \\ \hfill C_{(N-1)}^{(157,12)}=[& \dots \left|0b\right|102132435465768798a9ba\left|031425364758697a8b\right|30415263748596a7b8\left|05162738495a6b\right|\hfill \\ \hfill & 5061728394a5b6\left|0718293a4b\right|708192a3b4\left|091a2b\right|90a1b2\left|0\right],\hfill \\ \hfill C_{(N-1)}^{(183,13)}=[& \dots \left|0c\right|102132435465768798a9bacb\left|031425364758697a8b9c\right|30415263748596a7b8c9\left|05162738495a6b7c\right|\hfill \\ \hfill & 5061728394a5b6c7\left|0718293a4b5c\right|8091a2b3c4\left|08192a3b4c\right|a0b1c2\left|0a1b2c\right|60],\hfill \\ \hfill & \dots \hfill \end{array}$$

(A24)

Figure A1. 2-gram matrices for $1\le b\le 13$ that illustrate the generation of $N_{(N-1)}$ strings according to the 2^nd method. Coloured 2-grams are appended to the initial string of clear 3-grams in the order indicated by arrows starting from the 1st column or row. Finally, 0 is appended at the end if b is even.

Figure A1. 2-gram matrices for $1\le b\le 13$ that illustrate the generation of $N_{(N-1)}$ strings according to the 2^nd method. Coloured 2-grams are appended to the initial string of clear 3-grams in the order indicated by arrows starting from the 1st column or row. Finally, 0 is appended at the end if b is even.

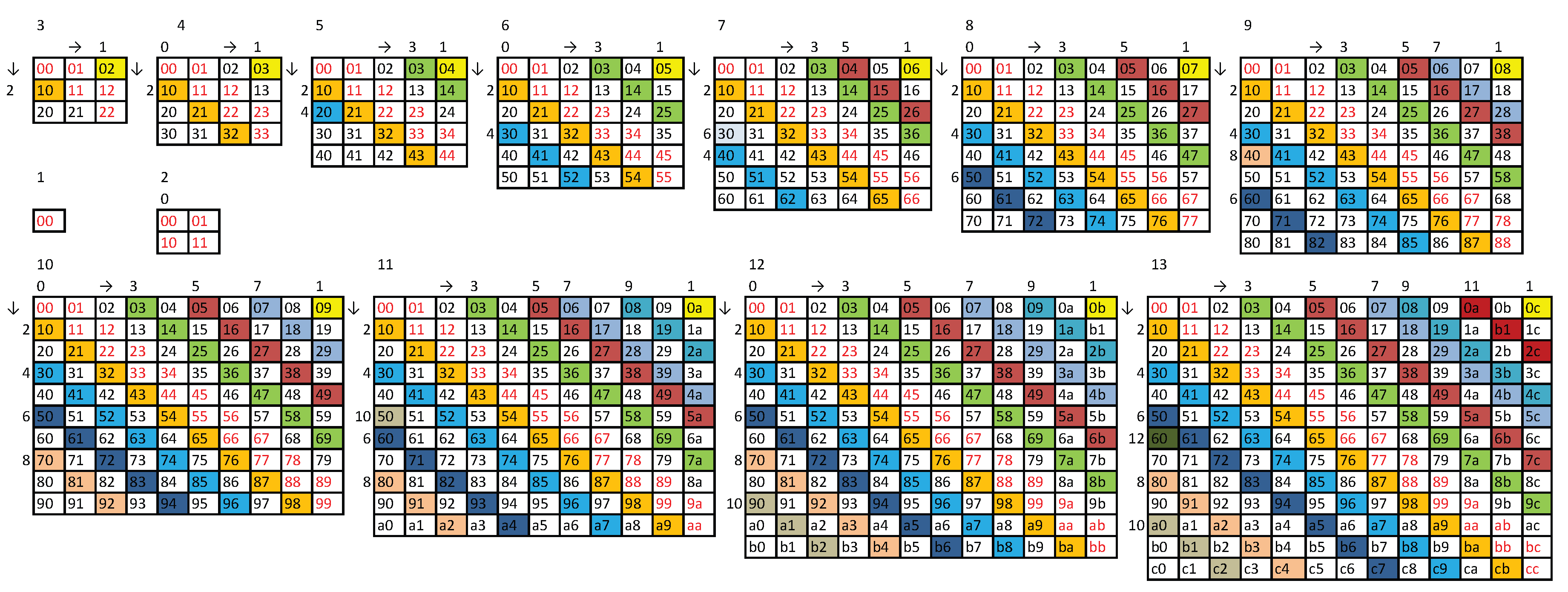
Appendix A.16. Method for Generating Non-Balanced C (N-b) Strings

The $C_{(N-b)}$ strings can also have the following non-balanced (e.g. $N_0=6,N_1=4$ for $C_{(N-2)}$) form

$$\begin{array}{cc}\hfill C_{(N-1)}^{(3,1)}=[& 000],\hfill \\ \hfill C_{(N-2)}^{(10,2)}=[& 01\left|0000\right|1110],\hfill \\ \hfill C_{(N-3)}^{(19,3)}=[& 01\left|0000\right|12\left|1111\right|2221020],\hfill \\ \hfill C_{(N-4)}^{(30,4)}=[& 01\left|0000\right|12\left|1111\right|23\left|2222\right|333102132030],\hfill \\ \hfill C_{(N-5)}^{(43,5)}=[& 01\left|0000\right|12\left|1111\right|23\left|2222\right|34\left|3333\right|444\left|1021324303142040\right],\hfill \\ \hfill C_{(N-6)}^{(58,6)}=[& 01\left|0000\right|12\left|1111\right|23\left|2222\right|34\left|3333\right|45\left|4444\right|555\left|1021324354031425041520530\right],\hfill \\ \hfill C_{(N-7)}^{(75,7)}=[& 01\left|0000\right|12\left|1111\right|23\left|2222\right|34\left|3333\right|45\left|4444\right|56\left|5555\right|666102132435465031425360415262064051630],\hfill \\ \hfill C_{(N-8)}^{(94,8)}=[& 01\left|0000\right|12\left|1111\right|23\left|2222\right|34\left|3333\right|45\left|4444\right|56\left|5555\right|67\left|6666\right|\hfill \\ \hfill & 7771021324354657603142536470415263720750516273061740],\hfill \\ \hfill & \dots \hfill \\ \hfill C_{(N-b)}^{(b^2+4b-2,b)}=[& 01\left|0000\right|12\left|1111\right|2\dots b_{-1}|b_{-2}{b}_{-2}{b}_{-2}{b}_{-2}|b_{-1}{b}_{-1}{b}_{-1}1021\dots b_{-1}{b}_{-2}\dots 0].\hfill \end{array}$$

(A25)