Experimental State Observer of the Population Inversion of a Multistable Erbium-Doped Fiber Laser

1. Introduction

The dynamics of even the simplest lasers are intimately connected to the fundamental models of nonlinear systems, linking them to a wide range of phenomena observed in various fields such as physics, engineering, and other scientific disciplines. From weather patterns to economic, chemical, and biological systems, chaotic dynamics appear to dominate [1]. Unlike these more complex systems, lasers are relatively simple, and uniquely, controlling their degrees of freedom is possible. Historically, the first experimental evidence of chaotic behavior was observed in laser physics [2], particularly in single-mode CO₂ lasers [3,4]. Studies of laser dynamics not only offer practical insights but also contribute to a broader understanding of complex yet unresolved phenomena. From the perspective of nonlinear dynamics, laser research presents clear advantages over the investigation of various physical phenomena, such as neuron dynamics [5,6,7], electronics, optoelectronics, potentially population dynamics [8,9,10], as well as epidemiological models [11]. Another advantage of studying lasers is that the number of degrees of freedom, such as the number of modes, can be easily controlled. In laser research, the key parameters are typically well-known and controllable, and the experimental conditions are well-defined.

From a theoretical perspective, studying a specific laser system involves solving differential equations analytically or, more commonly, numerically for a wide range of initial and experimental conditions. This process often generates an overwhelming amount of data, making it challenging to understand the system’s behavior fully. As a result, techniques or methods to reduce the information or the number of degrees of freedom are essential, ensuring that the core properties of dynamic evolution are retained. Experimentally, measuring or analyzing the complete temporal evolution of all the dynamic variables in a laser is typically impossible. Only partial information is recorded, which must still capture the essential dynamic characteristics of the system. In recent years, dynamic exploration of lasers has primarily focused on reduced state variables, especially optical intensity [1]. However, there has been limited attention to studying laser dynamics using the experimental state observer of the laser’s population inversion, which accounts for all state variables. Investigating the population inversion in laser models provides a way to explore chaos experimentally and draw comparisons with other well-known nonlinear systems, as discussed by Sprott [12], Rössler [13], Chen [14,15,16], Chua [17,18], and Lorenz [19]. In 1975, Haken [20] demonstrated that the Lorenz model is analogous to a laser, thereby linking their dynamics.

On the other hand, state observers are commonly employed in control systems to estimate unmeasured states based on available measurements. Various methodologies have been developed for both linear and nonlinear systems. In linear systems, least squares methods can be utilized to design observers. More recent studies have concentrated on observers for uncertain nonlinear systems, employing Lyapunov stability criteria and linear matrix inequalities [21]. Critical factors in observer design include stability, convergence, and robustness against measurement noise and model uncertainties. Observers can enhance the performance of control systems by providing more precise state estimates for feedback control.

Observers have been applied across a wide range of applications, such as in walking robots [22], machine vision [23,24], power systems [25], and electric motors [26,27]. Nonlinear observer designs include Luenberger-type observers [28] and methods inspired by sliding mode control [23,24].

On the other hand, the Luenberger observer, originally designed for linear systems, has been extended to nonlinear systems in various ways. Researchers have proposed distributed Luenberger observers for networked systems [29] and developed observers for specific applications like robot manipulators [30]. Some approaches combine state and parameter estimation [31], while others focus on existence conditions and dimensionality of Kazantzis-Kravaris/Luenberger observers [32,33]. Nonlinear extensions include the Luenberger-like observer for continuous-time systems [28] and the extended Luenberger observer for multivariable systems [34]. Numerical investigations have been conducted for infinite-dimensional vibrating systems [35]. These extensions have broadened the applicability of Luenberger-type observers to a wide range of nonlinear systems, offering improved state estimation capabilities and addressing challenges such as observability and convergence in various contexts.

This work presents the design of a Luenberger state observer for the unmeasurable variable of a Multistable Erbium-Doped Fiber Laser (Population inversion). The aim is to design neural identifiers and controllers that can be applied in real-time in future works.

The sections of this paper are organized as follows: in Section 2, the theoretical model of the Multistable Erbium-Doped Fiber Laser and normalized equations are presented; Section 3 presents the State Observer Design; Section 4 shows the simulation results; the experimental setup and the experimental results are given in Section 5; discussion, conclusion and some remarks about the application of state observer are drawn in Section 6.

2. Laser Model

The operation of a laser in a single emission mode is governed by three coupled equations. The key state variables are the optical field, population inversion, and polarization, each of which decays at different time scales. When one of these variables dominates, it relaxes quickly and adiabatically adjusts to the other variables, reducing the number of equations required to describe the laser.

Lasers where both population inversion and polarization decay rapidly compared to the optical field are categorized as class A lasers. In contrast, lasers where only the polarization relaxes quickly are known as class B lasers, while those where all three variables have similar relaxation rates are referred to as class C lasers. Class A lasers typically have a single constant output solution. Class B lasers exhibit energy oscillations between the optical field and population inversion, leading to relaxation oscillations. Class C lasers can display undamped periodic or non-periodic (chaotic) pulsations in their laser emissions. Furthermore, class B lasers can also exhibit periodic or chaotic dynamics if influenced externally, such as through parameter modulation. Solid-state and semiconductor lasers are examples of class B lasers. The semiconductor laser is modeled by the Lang and Kobayashi (LK) model [36]. The LK equation describes the complex dynamics of these lasers through the electric field E and population inversion (electron-hole pairs) N within the laser. Due to their rapid chaotic dynamics, these lasers have been considered for cryptographic applications in secure communication systems [37,38,39,40,41].

From a nonlinear dynamics perspective, rare-earth-doped fiber lasers with external modulation, such as solid-state, semiconductor, and gas lasers with electric discharge (e.g., CO2 and CO lasers), fall under the category of class B lasers [42]. In these systems, polarization is adiabatically eliminated, and the dynamics are described by two rate equations for the optical field and population inversion. Despite extensive research on complex laser dynamics, the nonlinear behavior of erbium-doped fiber lasers (EDFLs) has only recently been explored. The dynamic characteristics of these lasers closely resemble those of other class B lasers, with various chaotic motion scenarios being identified in EDFLs [43].

2.1. Complete EDFL Model

The dynamics of the EDFL studied here are modeled using two differential equations, known as power-balance equations, which incorporate excited state absorption (ESA). For erbium ions, this occurs at a wavelength of 1.5 $\mu$m. The model averages the population inversion of the EDFL and includes key factors characteristic of fiber lasers, such as ESA at the laser emission wavelength and the depletion of the pump wave as it propagates through the doped fiber. These factors lead to undamped natural oscillations in the laser, which have been experimentally observed in setups without external modulation [44,45].

The power-balance equations describe the intracavity laser emission P (defined as the sum of the intensities of the counter-propagating waves inside the cavity, measured in $s^{-1}$) and the averaged population N of the upper laser level 2 (a dimensionless variable, but considering $0\le N\le 1$ ), as follows:

$$\begin{array}{cc}\hfill \dot{P}& ={\displaystyle \frac{2L}{T_r}}P\{r_w{\alpha }_0(N[\xi -\eta ]-1)-{\alpha }_{th}\}+P_{sp},\hfill \\ \hfill \dot{N}& =-{\displaystyle \frac{{\sigma }_{12}{r}_{w}P}{\pi r_0^2}}(\xi N-1)-{\displaystyle \frac{N}{\tau }}+P_{pump}.\hfill \end{array}$$

(1)

The system of equations (1) has been widely applied in previous studies [44,46,47]. In these equations, L denotes the length of the erbium-doped fiber (EDF), and $T_r={\displaystyle \frac{2n_0(L+l_0)}{c}}$ represents the photon lifetime within the cavity, where $l_0$ is the length of the intra-cavity tails of the fiber Bragg grating (FBG) couplers. The variable P corresponds to the intracavity laser emission, with its value initially set as an initial condition.

The other parameters in equation (1) include $r_w=1+exp\left[2{\left({\displaystyle \frac{r_0}{w_0}}\right)}^2\right]$, a factor that accounts for the match between the laser’s fundamental mode and the erbium-doped core volumes within the active fiber. Here, $r_0$ is the fiber core radius, and $w_0$ is the radius of the fundamental fiber mode. The parameter ${\alpha }_0=N_0{\sigma }_{12}$ represents the small-signal absorption of the erbium fiber at the laser emission wavelength. $N_0=N_1+N_2=2.4^{19}c{m}^{-3}$ denotes the total number of erbium ions in the active fiber, while N is defined as:

$$N={\displaystyle \frac{1}{n_{0}L}}{\int }_0^L{N}_2\left(z\right)dz,$$

where $N_2$ is the population of the upper laser level 2, and $n_0$ is the refractive index of a "cold" erbium-doped fiber core. The coefficient for the ratio between the excited-state absorption (ESA) ${\sigma }_{23}$ and the ground-state absorption cross-sections at the laser wavelength, expressed as $\xi ={\displaystyle \frac{{\sigma }_{12}+{\sigma }_{21}}{{\sigma }_{12}}}=2$ and $\eta ={\displaystyle \frac{{\sigma }_{23}}{{\sigma }_{12}}}$, considering that the cross-section of the return stimulated transition ${\sigma }_{12}$ has nearly the same intensity. The parameter ${\alpha }_{th}={\gamma }_0+{\displaystyle \frac{1}{2L}}ln\left({\displaystyle \frac{1}{R}}\right)$ represents the intra-cavity losses at the threshold, where ${\gamma }_0$ corresponds to the non-resonant fiber loss, and R defines the reflection coefficient of the FBG couplers. Additionally,

$$P_{sp}={\displaystyle \frac{{10}^{-3}N}{\tau T_r}}{\left({\displaystyle \frac{{\lambda }_g}{w_0}}\right)}^2{\displaystyle \frac{r_0^2{\alpha }_{0}L}{4{\pi }^2{\sigma }_{12}}},$$

represents the spontaneous emission into the fundamental laser mode, where $\tau$ is the lifetime of erbium ions in the excited state 2, and ${\lambda }_g$ is the laser wavelength. Finally, the pump power $P_{\mathrm{pump}}$ is defined as

$$P_{\mathrm{pump}}=P_p{\displaystyle \frac{1-exp[-\beta {\alpha }_{0}L(1-N)]}{n_0\pi r_0^{2}L}},$$

where $P_p$ denotes the pump power at the fiber input, and $\beta ={\alpha }_p/{\alpha }_0$ is the ratio of the absorption coefficients of the erbium fiber at the pump wavelength ${\lambda }_p$ and the laser wavelength ${\lambda }_g$. This study set the laser spectrum width to ${10}^{-3}$ of the erbium luminescence spectral bandwidth.

Additionally, it is important to mention that the system of equations (1) describes the dynamics of the EDFL without considering modulation. However, a harmonic modulation of $P_p$ is introduced as

$$\begin{array}{c}\hfill P_p=P_p^0(1+m_{0}sin\left(2\pi F_{0}t\right)),\end{array}$$

(2)

where $m_0$ and $F_0$ are the modulation depth and frequency, respectively, and $P_p^0$ is the pump power without modulation at $m_0=0$.

The following parameter values were used for the numerical implementation of the results presented in this study, consistent with those in previous works [44].

Table 1. Parameters used in numerical simulations.

Parameter	Value		Parameter	Value		Parameter	Value
L	70 cm		$n_0$	1.45		$r_0$	$1.5\times {10}^{-4}$ cm
$T_r$	8.7 nm		$l_0$	20 cm		${\omega }_0$	$3.5\times {10}^{-4}$ cm

Table 1. Parameters used in numerical simulations.

Parameter	Value		Parameter	Value		Parameter	Value
L	70 cm		$n_0$	1.45		$r_0$	$1.5\times {10}^{-4}$ cm
$T_r$	8.7 nm		$l_0$	20 cm		${\omega }_0$	$3.5\times {10}^{-4}$ cm

The experimentally measured value of ${\omega }_0$ was slightly higher than $2.5\times {10}^{-4}$ cm, as predicted by the formula for a step-index single-mode fiber: $w_0=r_0(0.65+1.619/V^{1.5}+2.879/V^6)$. In this expression, the parameter V is linked to the numerical aperture $NA$ and $r_0$ by $V=2\pi r_{0}NA/{\lambda }_g$, while the values of $r_0$ and $w_0$ yield $r_w=0.308$.

The coefficients that describe the resonant absorption characteristics of the erbium-doped fiber at the emission and laser wavelengths, directly measured from a heavily doped fiber with an erbium concentration of 2300 ppm, are listed in Table 2.

By applying the specified values to the system of equations (1), the generated wavelength ${\lambda }_g=1.56\times {10}^{-4}$ cm ($h\nu =1.274\times {10}^{-19}$ J) is experimentally observed, with the peak reflection coefficients of both FBGs aligned at this wavelength. The pump parameters are expressed in terms of the excess above the laser threshold $\epsilon$, where $P_p=\epsilon P_{th}$, and the threshold pump power is defined as follows

$$P_{th}={\displaystyle \frac{N_{th}}{\tau }}{\displaystyle \frac{n_{0}L\pi w_p^2}{1-exp\left[-{\alpha }_{0}L\beta (1-N_{th})\right]}},$$

the threshold population of level 2 is defined as

$$N_{th}={\displaystyle \frac{1}{\xi }}\left(1+{\displaystyle \frac{{\alpha }_{th}}{r_w{\alpha }_0}}\right),$$

with the pump beam radius, for simplicity, assumed to be the same as that of the generated beam (${\omega }_p={\omega }_0$).

2.2. Normalized Equations of EDFL

To synthesize and generalize the laser model, we modified the complete system (1) into the next compact expression

$$\begin{array}{c}\hfill {\displaystyle \frac{d{x}_1}{d\theta }}=x_1{x}_2-c_1{x}_1+c_2{x}_2+c_3,\end{array}$$

(3)

$$\begin{array}{c}\hfill {\displaystyle \frac{d{x}_2}{d\theta }}=-x_1{x}_2-d_1{x}_2-d_2+P_0\left(1-d_3{e}^{x_2}\right),\end{array}$$

(4)

the changes have been made in the variables:

$$\begin{array}{ccc}\hfill x_1& =& {\displaystyle \frac{{\sigma }_{12}{\Gamma }_s{T}_r{\alpha }_p}{2\pi r_0^2{\alpha }_0}}{\displaystyle \frac{{\xi }_1}{{\xi }_1-{\xi }_2}}P,\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill x_2& =& {\alpha }_{p}L\left(N-{\displaystyle \frac{1}{{\xi }_1}}\right),\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill \theta & =& {\displaystyle \frac{2r_w{\alpha }_0}{T_r{\alpha }_p}}\left({\xi }_1-{\xi }_2\right)t\hfill \end{array}$$

(7)

and in the parameters:

$$\begin{array}{ccc}\hfill c_1& =& {\displaystyle \frac{{\alpha }_{p}L}{{\xi }_1-{\xi }_2}}\left({\displaystyle \frac{{\alpha }_{th}}{{\alpha }_0{r}_w}}+{\displaystyle \frac{{\xi }_2}{{\xi }_1}}\right),\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill c_2& =& {\displaystyle \frac{{\xi }_1{\alpha }_p}{\pi r_w{\alpha }_0}}{\displaystyle \frac{T_r}{\tau }}{\left[{\displaystyle \frac{{\lambda }_g}{4\pi w_0\left({\xi }_1-{\xi }_2\right)}}\right]}^2\times {10}^{-3},\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill c_3& =& {\displaystyle \frac{L}{\pi r_w{\alpha }_0}}{\displaystyle \frac{T_r}{\tau }}{\left[{\displaystyle \frac{{\lambda }_g{\alpha }_p}{4\pi w_0\left({\xi }_1-{\xi }_2\right)}}\right]}^2\times {10}^{-3},\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill d_1& =& {\displaystyle \frac{{\alpha }_p}{2r_w{\alpha }_0\left({\xi }_1-{\xi }_2\right)}}{\displaystyle \frac{T_r}{\tau }},\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill d_2& =& {\displaystyle \frac{{\alpha }_p^{2}L}{2r_w{\alpha }_0{\xi }_1\left({\xi }_1-{\xi }_2\right)}}{\displaystyle \frac{T_r}{\tau }},\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill d_3& =& exp\left[-{\alpha }_{p}L\left(1-{\displaystyle \frac{1}{{\xi }_1}}\right)\right],\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill P_0& =& {\displaystyle \frac{{\alpha }_p^2{T}_r}{2\pi r_0^2{N}_0{r}_w{\alpha }_0\left({\xi }_1-{\xi }_2\right)}}{P}_p.\hfill \end{array}$$

(14)

The variable $x_1$ represents the normalized laser intensity, while $x_2$ corresponds to the population inversion. The parameter $P_0$ denotes the pump power, and the pump modulation, $P_p$, is given by Equation (2).

The values of the parameters used in the simulations are listed in Table 3 [48].

3. State Observer Design

Normalized equations of EDFL are given by

$$\begin{array}{cc}\hfill {\dot{x}}_1& =x_1{x}_2-c_1{x}_1+c_2{x}_2+c_3,\hfill \\ \hfill {\dot{x}}_2& =-x_1{x}_2-d_1{x}_2-d_2+u_{pump},\hfill \\ \hfill y& =x_1,\hfill \end{array}$$

(15)

where ${\dot{x}}_1$ = $d{x}_1/d\theta$, ${\dot{x}}_2$ = $d{x}_2/d\theta$ and $u_{pump}=P_0\left(1-d_3{e}^{x_2}\right)$. These equations are represented in the general form

$$\begin{array}{cc}\hfill \dot{x}& =f\left(x\right)+g\left(x\right)u_{pump},\hfill \\ \hfill y& =h\left(x\right).\hfill \end{array}$$

(16)

For system (16), the following state observer is proposed

$$\begin{array}{c}\hfill \dot{\tilde{x}}=f\left(\tilde{x}\right)+g\left(\tilde{x}\right)u_{pump}+L(y-\tilde{y}),\end{array}$$

(17)

where $\tilde{x}$ is the estimated state of $x\left(t\right)$ and $\tilde{y}\left(t\right)$ is the output from state observer, L is a constant parameter. Defining $e\left(t\right)=x\left(t\right)-\tilde{x}\left(t\right)$, the following dynamic error system results

$$\begin{array}{c}\hfill \dot{\tilde{e}}=f\left(x\right)+g\left(x\right)u_{pump}-f\left(\tilde{x}\right)-g\left(\tilde{x}\right)u_{pump}+L(y-\tilde{y}).\end{array}$$

(18)

For system (15), Eq. (17) becomes

$$\begin{array}{cc}\hfill {\dot{\tilde{x}}}_1& ={\tilde{x}}_1{\tilde{x}}_2-c_1{\tilde{x}}_1+c_2{\tilde{x}}_2+c_3+L_1(x_1-{\tilde{x}}_1),\hfill \\ \hfill {\dot{x}}_2& =-{\tilde{x}}_1{\tilde{x}}_2-d_1{\tilde{x}}_2-d_2+u_{pump}+L_2(x_1-{\tilde{x}}_1),\hfill \\ \hfill \tilde{y}& ={\tilde{x}}_1.\hfill \end{array}$$

(19)

For the purpose of this work, the state observer is designed for the state variable population investment ($x_2$), given that in real time the variable cannot be measured because the electronic equipment does not exist to carry out this measurement.

4. Simulation Results

This section shows the simulation results of the estimation of the variable of the EDFL, equations (15) through the state observer, equations (19), the simulation in Matlab/Simulink has been implemented.

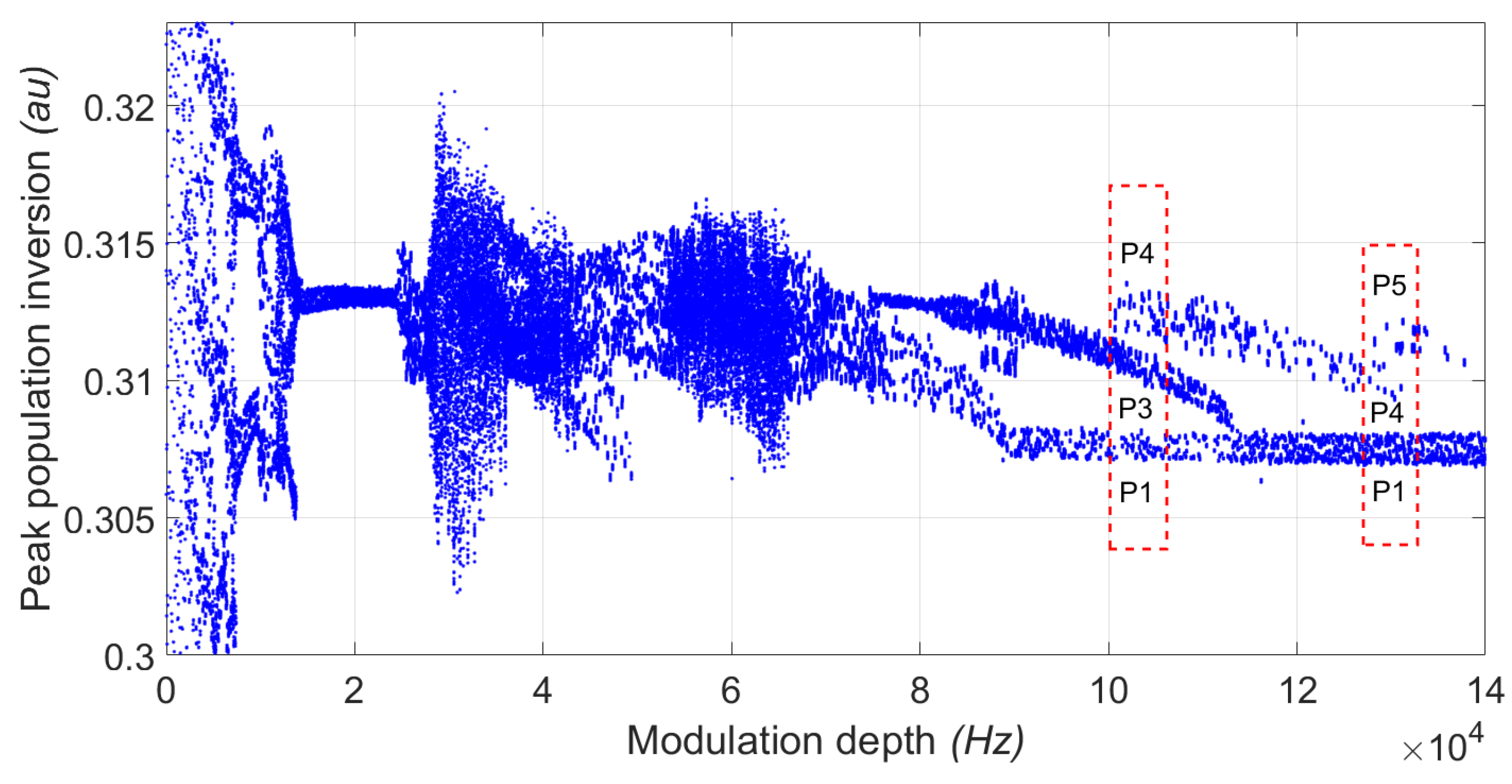
Figure 1 shows an extract of the numerical laser intensity bifurcation diagram, which was obtained through the time series of the multistable region corresponding to the coexistence of attractors, shown by ($P1$, $P3$, $P4$, $P5$), for a modulation frequency of 80 Hz. The complete bifurcation diagram can be consulted in the work [49].

The parameters used in the mathematical model of the EDFL and numerical state observer are shown in Table 2, in addition, the gains used for the state observer are $L1=0.2$ and $L2=18$.

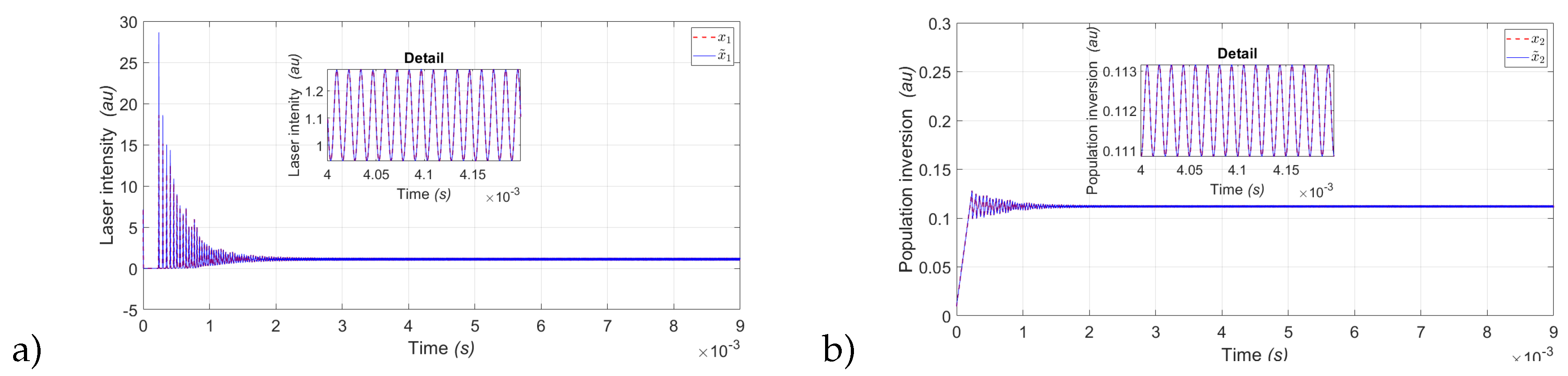
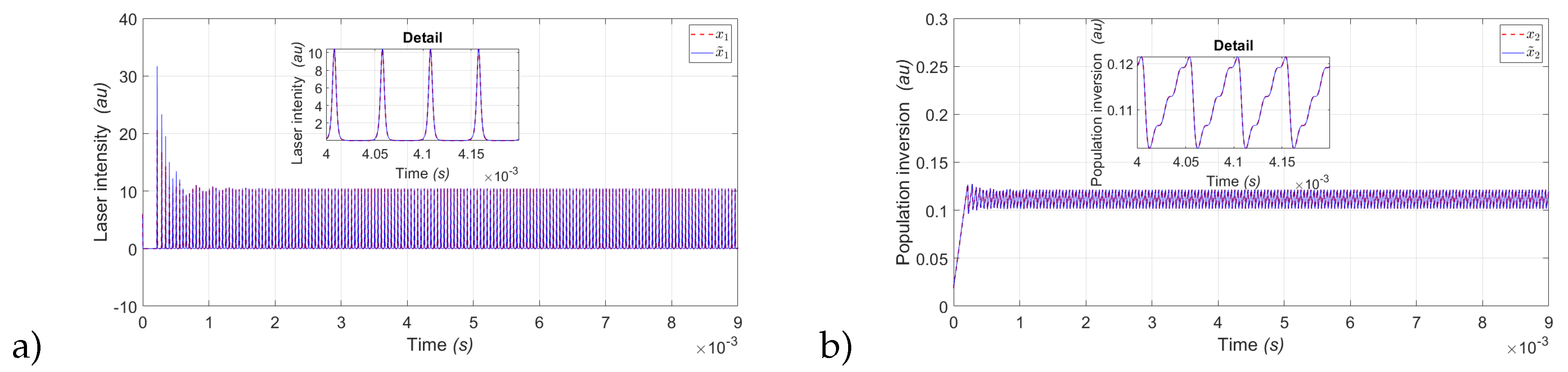
Figure 2 shows the simulation results of the state observer for the EDFL state variables. Since the laser states in simulation can be measured, the observation of both variables for different periods is presented ($P1$, $P3$, $P4$, and $P5$). Figure 2a) shows the estimation of the Laser intensity ($x_1$) represented by the variable (${\tilde{x}}_1$), where can see the convergence of the observer and Figure 2b) shows the estimation of the Population inversion ($x_2$) represented by the variable (${\tilde{x}}_2$), both variables are for period $P1$.

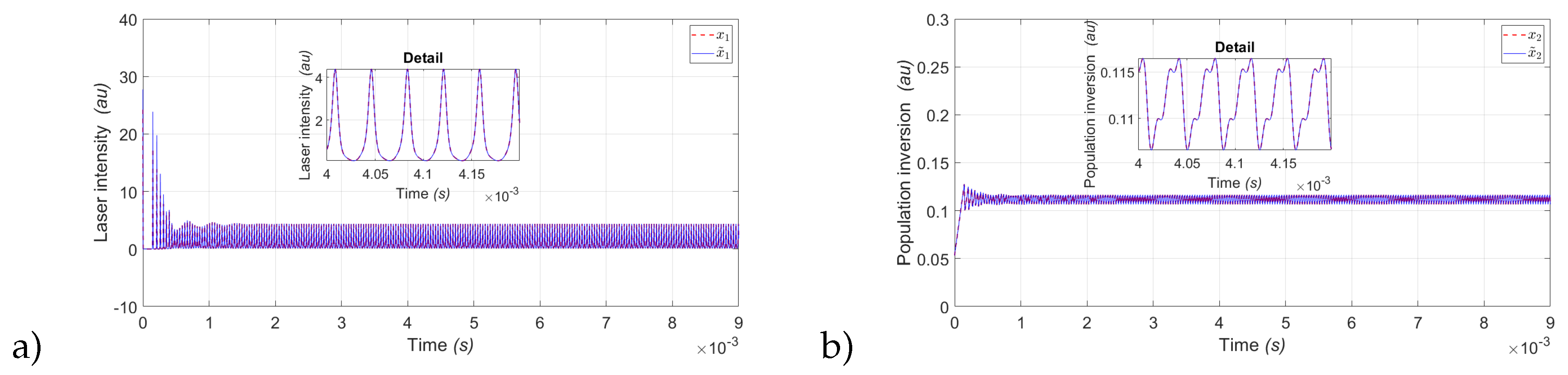
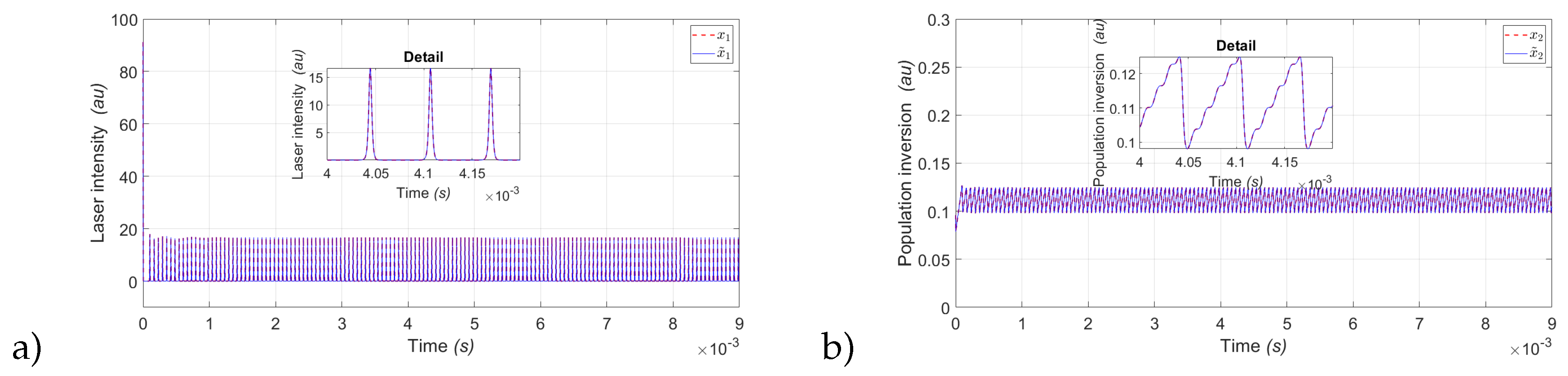
In the same way as Figure 2, Figure 3, Figure 4 and Figure 5 show the estimation of the laser intensity ($x_1$) represented by the variable (${\tilde{x}}_1$) and the estimate of the Population inversion ($x_2$) represented by the variable (${\tilde{x}}_2$) of the periods $P3$, $P4$ and $P5$.

The effectiveness of the state observer depended on the correct selection of parameters and the design of the observer to ensure that the observer could provide accurate and reliable estimates. In addition, the experimental implementation of the state observer must consider aspects such as accuracy and effectiveness, as shown in the next section.

5. Experimental Setup

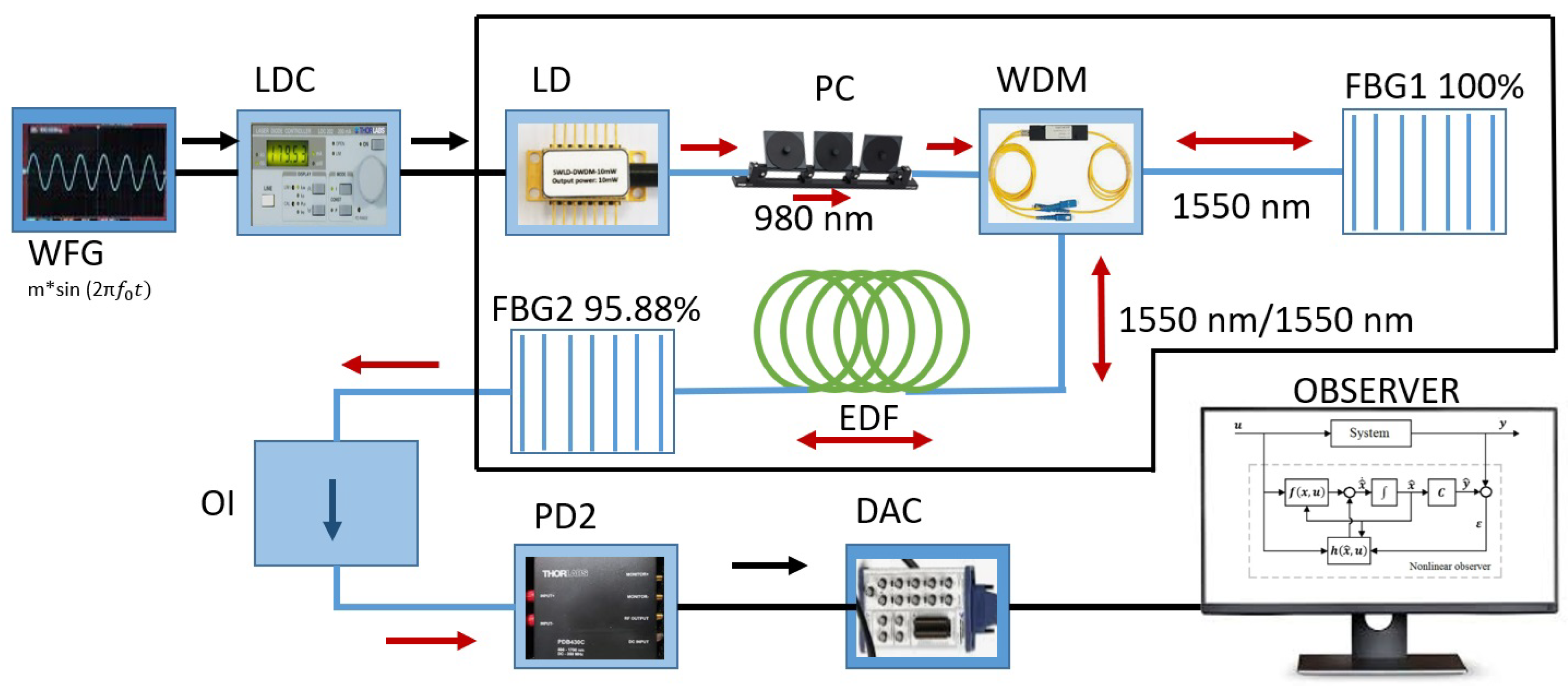
The implementation of the EDFL in the laboratory is shown in Figure 6. This laser has a 6.5 m resonator with a 70-centimeter erbium fiber active region, made of fiber with a core diameter of 2.7 micrometers, including a wavelength division multiplexing coupler (WDM-WD9850FD) and two fiber Bragg gratings (FBG1 and FBG2). The FBGs have reflectivities of 100% and 95% for use at a ${\lambda }_g=1550$nm. The optical components are made with single-mode fiber (SMF-28) with a cladding diameter of 200 micrometers. The EDFL is pumped using a 977-nm laser diode (LD-BL976PAG500) through a polarization controller (PC), by using a laser diode controller (LDC-ITC510). During the experiments, the diode current was set to 145.5 mA, having an EDFL threshold at 110 mA. The system was modulated with a sinusoidal signal $msin\left(2\pi f_{d}t\right)$ from a periodic function generator (WFG-AFG3102) applied to the pump current. An optical isolator (OI) prevents back-reflections into the laser cavities. The optical output signal $P\left(t\right)$ from the FBG2 fiber Bragg grating is directed to the PD2 photodiode, which is connected to a data acquisition card (DAC) NI-BNC-2110 for subsequent analysis. Data is collected using the DAC.

5.1. Experimental Bifurcation Diagrams and Time Series

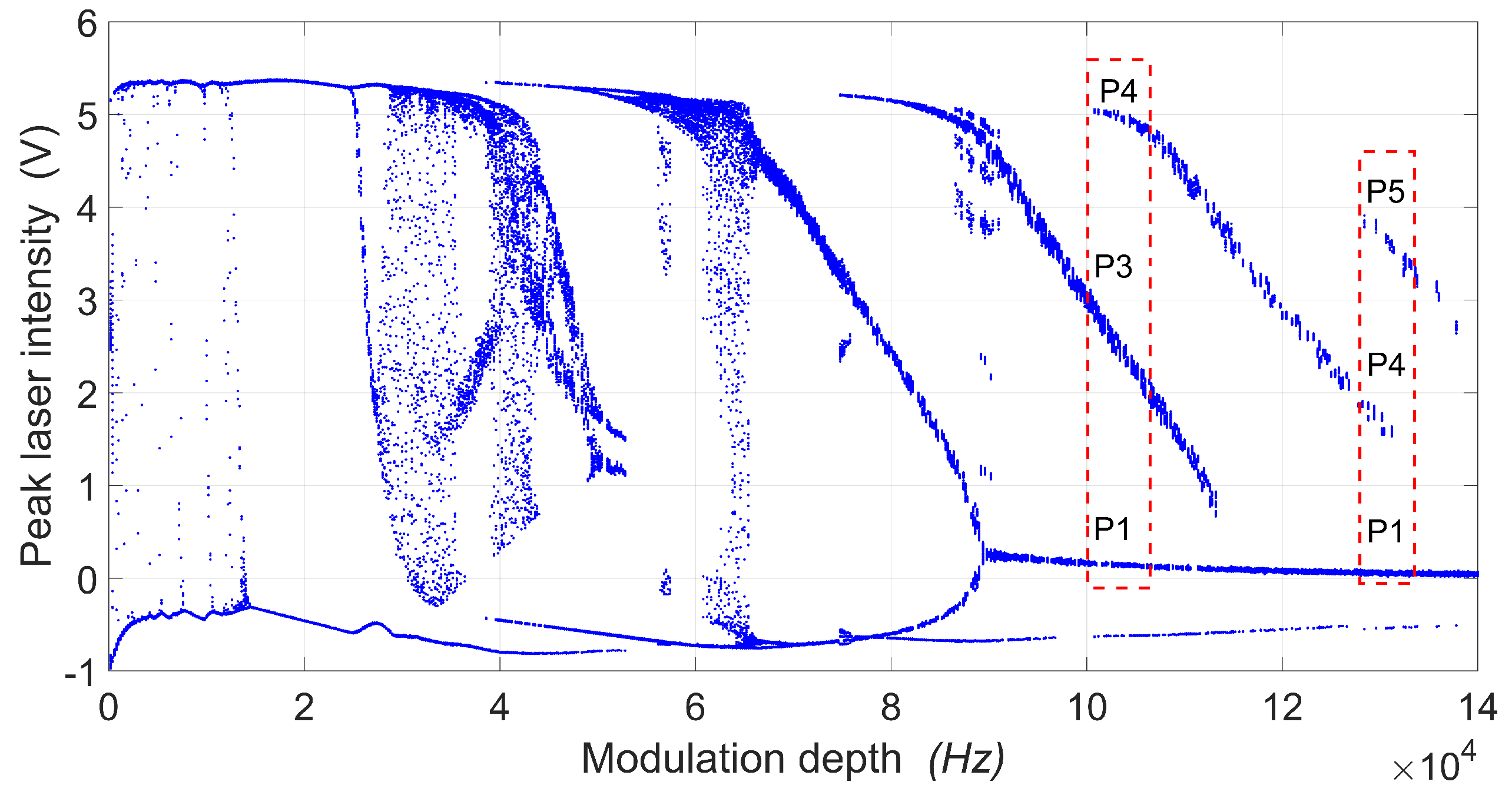
Using periodic modulation $msin\left(2\pi f_{d}t\right)$, where m is the modulation amplitude and $f_d$ represents the frequency applied to the diode pump current via a periodic function generator (WFG). This EDFL has multistable behavior, having up to four periodic states, defined as Period 1 (P1), Period 3 (P3), Period 4 (P4), and Period 5 (P5) [44]. The output signal of the laser was detected by a photodiode (PD2) and recorded through a data acquisition card (DAC) (Figure 6). 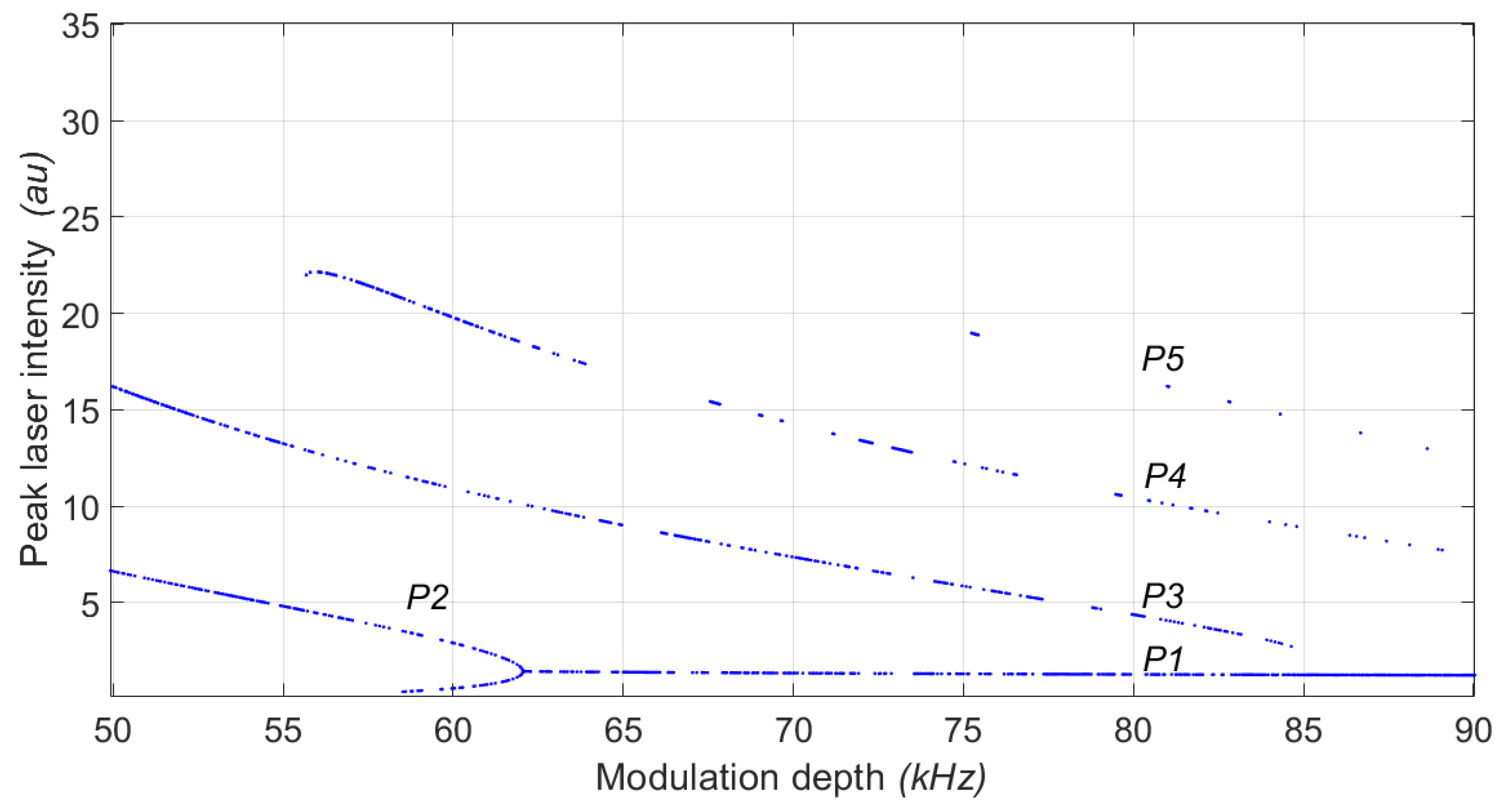Figure 7 shows a bifurcation diagram (BD) constructed by randomly changing the system’s initial conditions by turning off and on the WFG ten times for $m=1$. The bifurcation diagram can show the system evolution corresponding to different dynamic regimes through saddle-node bifurcations when increasing the control parameter $f_d$. The attractor’s coexistence is present in different BD regions. We can see that in the range 100 kHz $<f_d<115$ kHz, P1, P3 and P4 coexist, and in the range 125 kHz $<f_d<135$ kHz, P1, P4 and P5 also coexist. The local maximum intensity in the different regimes with longer periods is significantly higher than in P1.

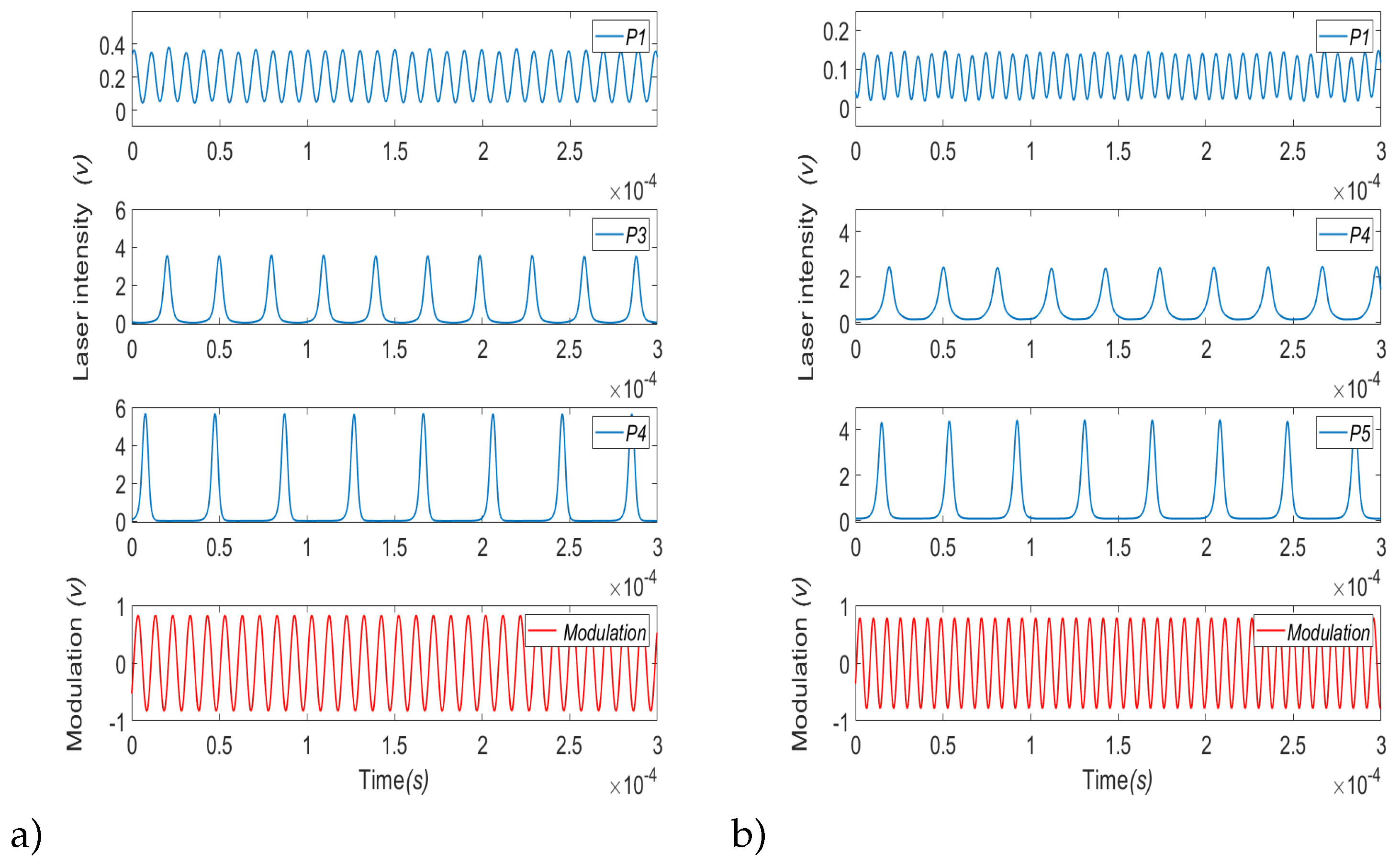
This section presents the experimental results for estimating the unmeasurable variables of the EDFL using the state observer equations (19). The parameters used in the state observer equations (19) are listed in Table 2. In addition, the gains of the experimental state observer are $L1=95550.4\times 6$ and $L2=200$. The time series of the laser intensity corresponding to different coexisting periodic regimes are shown for a modulation frequency of $f_0=100800$ Hz and amplitude $m_0=1$ in Figure 8 a) and for a modulation frequency of $f_0=129600$ Hz and amplitude $m_o=1$ in Figure 8 b) is shown. A modulation signal $m_{0}sin\left(2\pi f_{0}t\right)$ is shown in the bottom panel of both Figures.

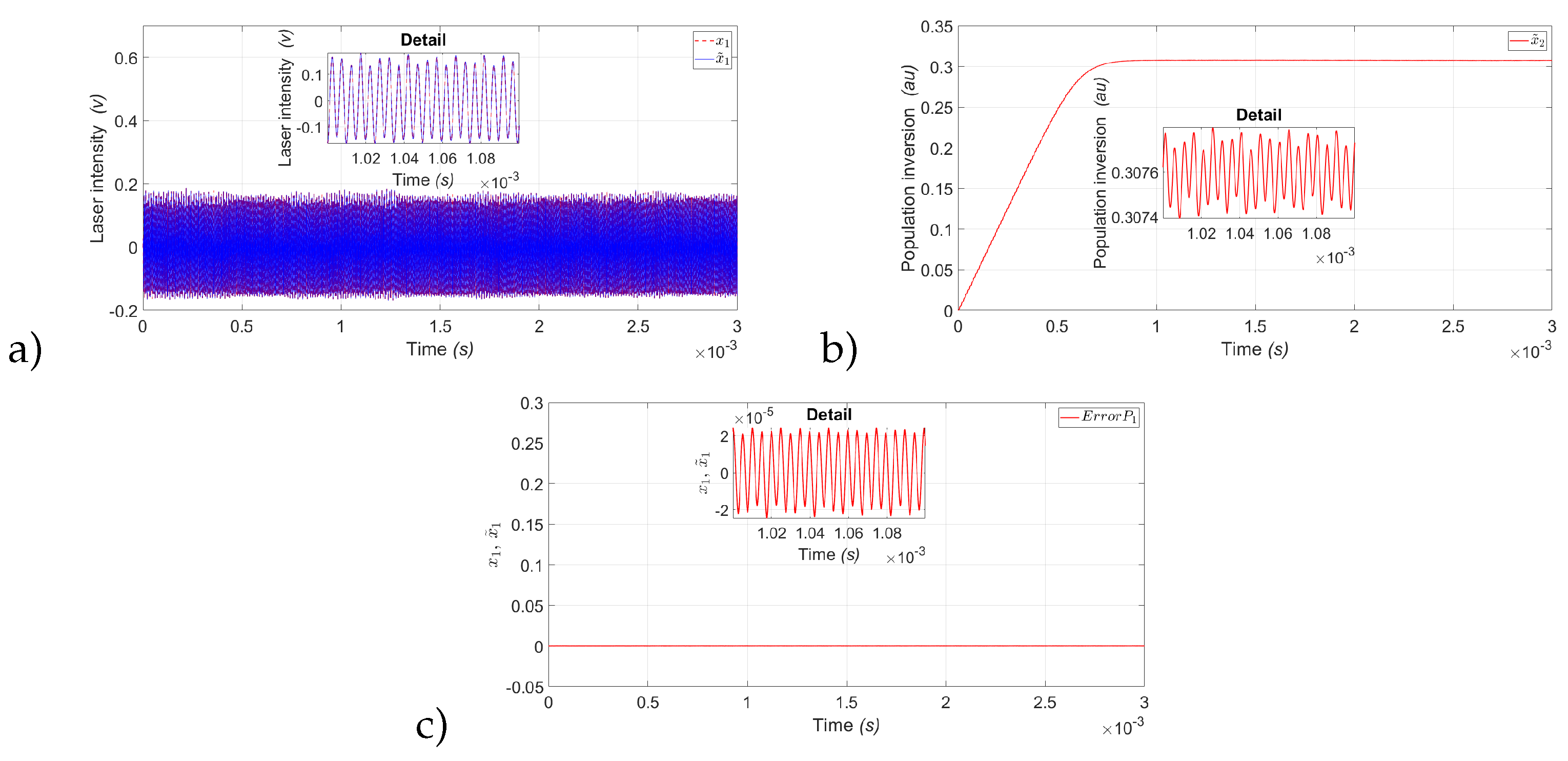
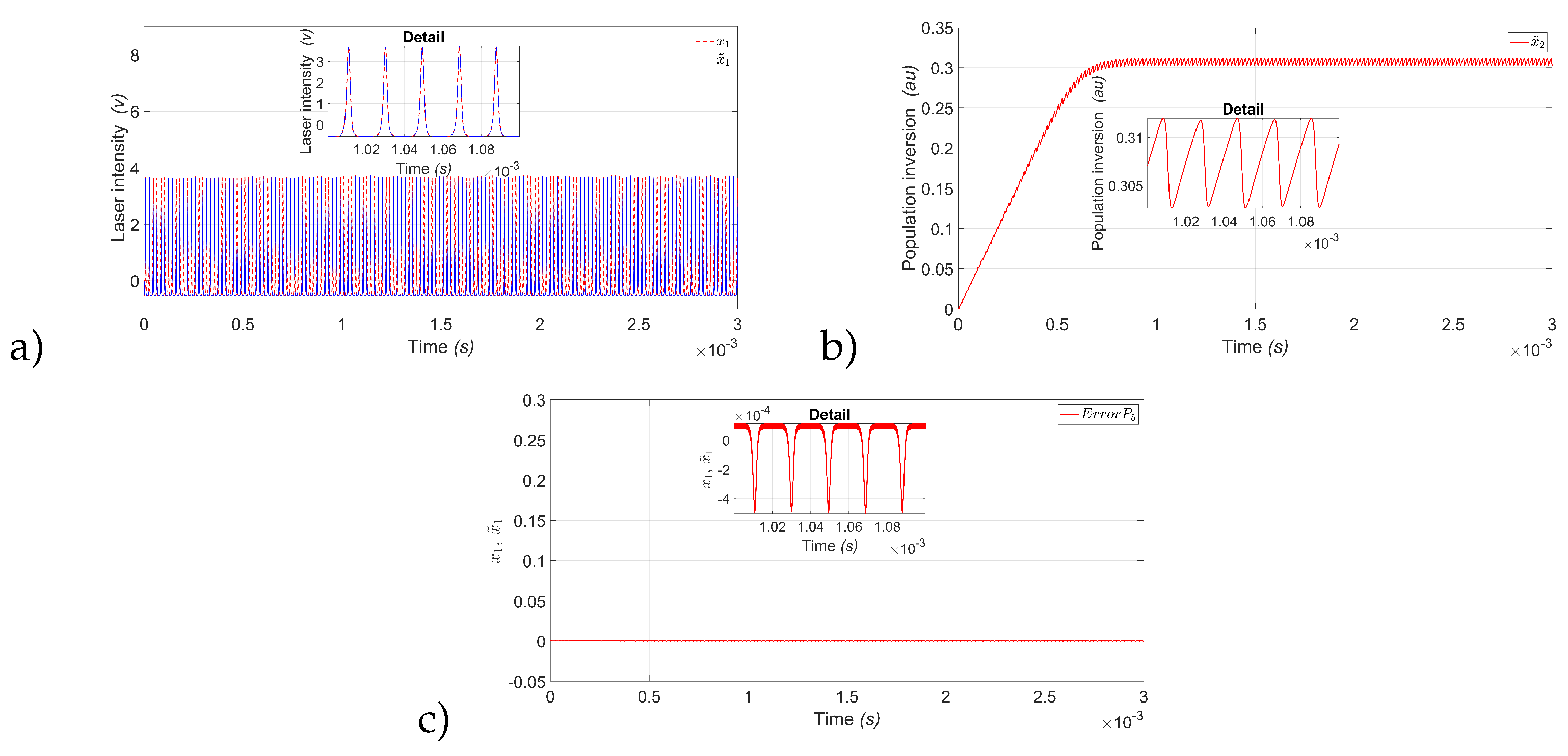
Figure 10 shows the experimental results of the state observer for the EDFL state variables for $P1$. Figure 10a) shows the estimation of the Laser intensity ($x_1$) represented by the variable (${\tilde{x}}_1$), although the variable can be measured physically, the procedure is carried out to guarantee good estimation of the second non-measurable variable of EDFL. Figure. Figure 10b) shows the estimation of the Population inversion (${\tilde{x}}_2$), and Figure 10c) shows the estimation error between $x_1$ and ${\tilde{x}}_1$ where can see that the error is very close to zero, which guarantees the good estimate of the population inversion variable.

Figure 9. Experimental bifurcation diagram for Population inversion ($x_2$).

Figure 9. Experimental bifurcation diagram for Population inversion ($x_2$).

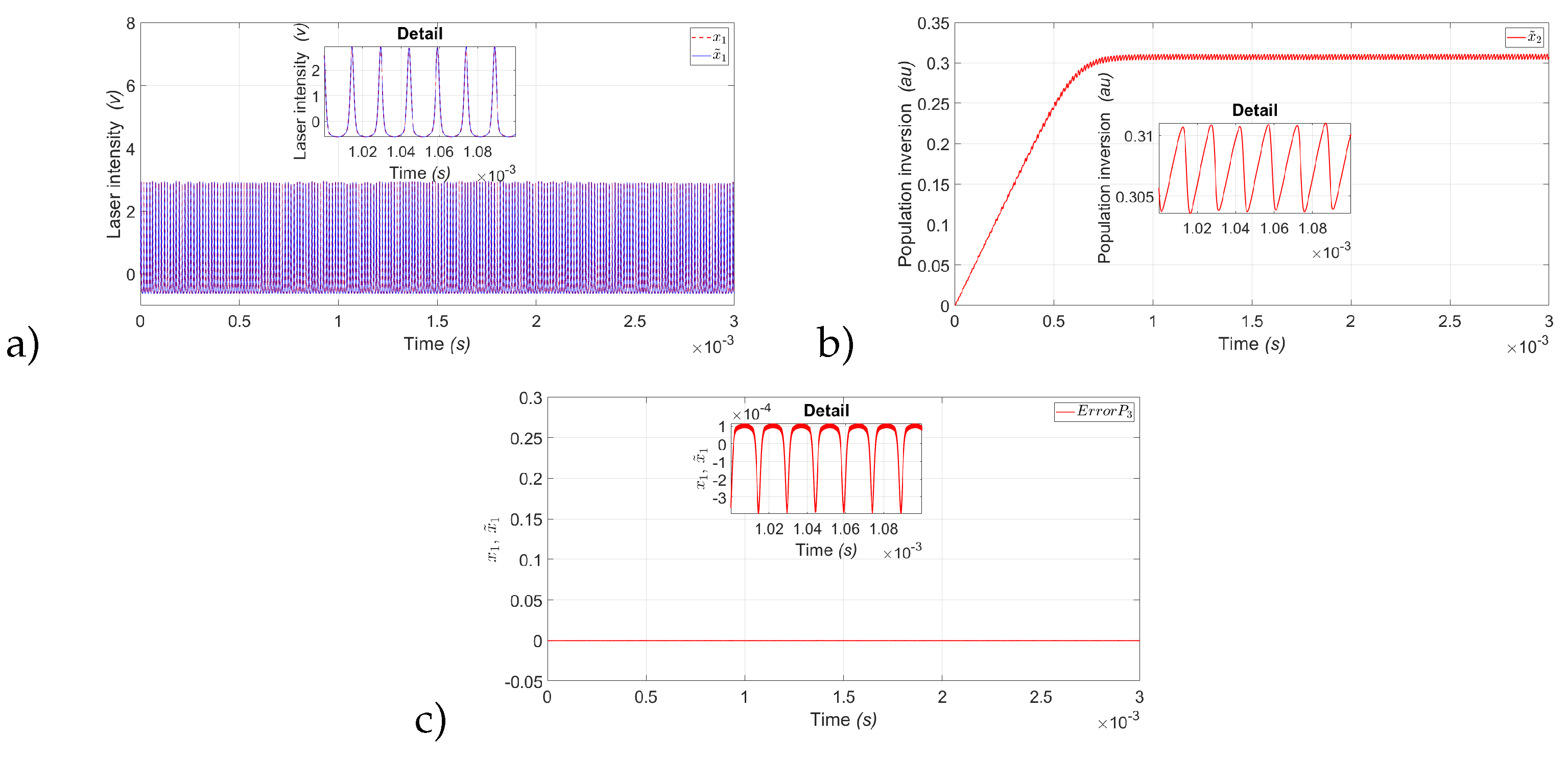
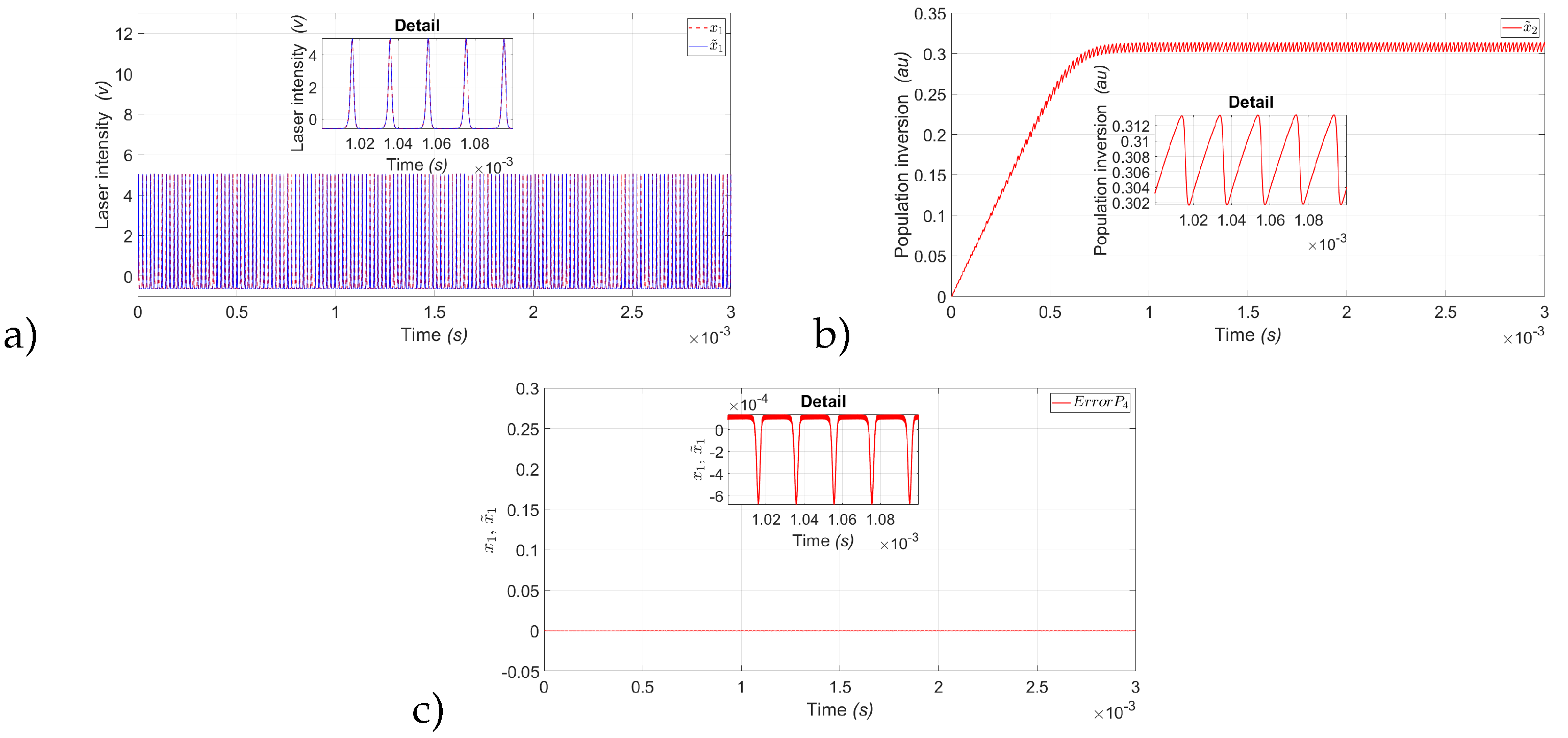
In the same way as Figure 10, Figure 11 and Figure 12 show the estimation of the laser intensity ($x_1$) represented by the variable (${\tilde{x}}_1$) and the estimate of the Population inversion, represented by the variable (${\tilde{x}}_2$) of the periods $P3$, $P4$ and $P5$.

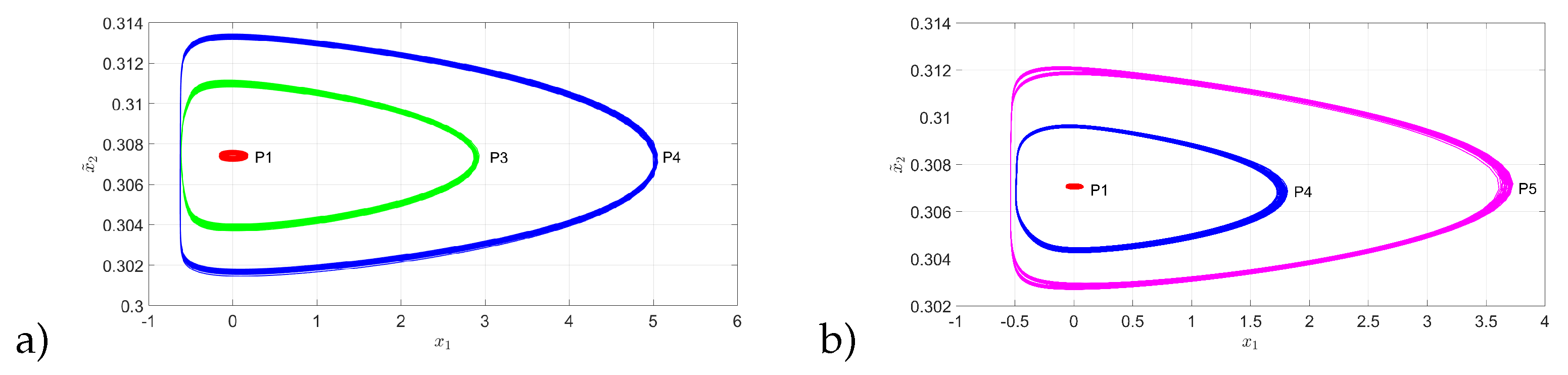
5.2. Experimental Phase space

Figure 14a) shows the phase space for periods P1, P3, and P4 of a multistable region, shown in Figure 7a) with a red box at a modulation frequency of $f_0=100.8$ kHz. Similarly, for Figure 14, the phase space of the periods P1, P4, and P5 of a multistable region is observed in Figure 7 with a red box at a modulation frequency of $f_0=129.6$ kHz. It is worth mentioning that although the periods are at different frequencies, the state observer was able to estimate each period of the multistable regions.

5.3. Mean Square Error

The results of Table 4 show that the MSE is very small for any of the periods (P1, P3, P4 and P5), which guarantees a good estimate of the measurable laser intensity variable ($x_1$), which leads to a good estimate of the (EDFL) population inversion (${\tilde{x}}_2$).

6. Conclusions

This paper presents the design and implementation of a nonlinear state observer to identify the non-measurable variables of an erbium-doped fiber laser (EDFL). The experimental identification of the population inversion enabled the reconstruction of the laser dynamics and the construction of a state-space model using the measurable variable (laser intensity) and the observed variable (population inversion). The mean square error (MSE) analysis confirms the accurate observation of the non-measurable variable. Furthermore, the population inversion bifurcation diagram was constructed, revealing that the multistable regions of the population inversion align with those of the laser intensity bifurcation diagram. To our knowledge, this is the first report of experimental results using a state observer for the population inversion variable in an erbium-doped fiber laser or any other type of laser. The proposed state observer technique advances the understanding of multistable dynamics in EDFLs and offers potential applications in power enhancement and intra-cavity loss control. This approach contributes significantly to the field of optics and lasers. Finally, the estimation of EDFL state variables by state observer is crucial for effectively implementing advanced controls and improving the overall performance of dynamic systems.