Beyond Network Switching: FPGA-based Switch Architecture for Fast and Accurate Ensemble Learning

1. Introduction

The explosive increase in data has led to a surge in moving machine learning tasks to the cloud. This is driven by the need of fast training and inference for large models, which is done by distributing the computational workload across multiple servers. Additionally, the geographically dispersed sources of training data also contribute to this shift. Consequently, cloud providers are continually updating their infrastructure to get adapted to this computational pattern.

Network acceleration can take place at various levels [1], from directly connected acceleration devices to network components. Specifically, FPGA, as a flexible hardware platform, has shown success in cloud networks in recent years, ranging from PCIe-connected accelerator cards [2] to smart Network Interface Controllers (NICs) [3].

In the context of acceleration using switches, ASIC-based switches are typically fixed in functionality and lack computing resources, providing limited programmablility and computational power to handle computationally intensive tasks. Another type of ASIC-based switch utilises the protocol-independent switch architecture to gain programmability through reconfigurable match tables (RMT) [4]. This type of switch is typically used for packet classification and network anomaly detection [5,6]. By modifying the lookup tables, it can also be adapted for in-network computing for machine learning tasks [7,8,9,10]. However, the functionality and performance of these tasks are constrained by the design’s reliance on lookup tables and the limited number of tables available.

FPGA-based network switches, due to their customizability, offer multiple benefits to data center networks. They support custom transport protocols, in-network acceleration, aggregation, and network function customization [11,12]. FPGAs can be tuned to match the performance of ASIC-based switches. Previous work [13,14,15,16] demonstrates the capability of FPGAs for implementing network switches while saturating the ASIC-transceiver bandwidth. However, such designs typically leave computational resources, such as Digital Signal Processing (DSP) blocks unused. For example, 6840 DSPs on the Xilinx vu9p FPGA, as presented in [13]. Further details can be found in Section 5.

We therefore propose an FPGA-based network switch architecture that utilises these computational resources. As an example, we demonstrate the benefits of this architecture with a fast and accurate ensemble classification system utilising random projection (RP) across multiple servers. Due to the stream processing nature of the design, the data processing block does not affect the throughput of the switch with little latency overhead. Further analysis can be found in Section 5 and Section 7.

Given that the architecture is designed to be applicable to all models, we demonstrate the benefits of the FPGA-based system through two types of models. We choose MLP-based classifiers to represent machine learning models that require training and kNN-based classifiers to represent those without the training phase. In the MLP-based classifier, since the training happens on servers, the switch is responsible for distributing training data and applying random projection using DSPs. Our system accelerates the training process for Multilayer Perceptron (MLP) models with a speedup of 2.1-6.7 times across four high-dimensional datasets.

For the kNN-based classifier, the proposed system is modified to show the feasibility of replacing the computationally expensive cosine distance metric with Hamming distance without losing accuracy and gaining speed-up at the same time. This achieves a worst-case speedup of 2.3-8.7 times and a memory reduction of 3.9-27.7 times compared to CPU-based kNN classifiers using cosine distance

Moreover, the proposed architecture is not limited to classification tasks. It extends to data processing and aggregation, making it compatible with applications beyond classification.

The challenges of designing the proposed systems are: (C1) Processing large dimensional data requires a large amount of FPGA resources, thereby limiting the scalability of the system. (C2) Performing fast computation requires storing the RP matrices on-chip, and this becomes challenging as the dimensionality of input data increases due to limited on-chip storage. (C3) How to support kNN on an FPGA-based network switch with high performance and minimised resources. (C4) How to completely offload the kNN tasks from downstream servers. Through model analysis, we tackle the aforementioned challenges, and provide a generalisable solution for various scenarios. In summary, C1 is addressed by the hierarchical switch topology, C2 is managed through the efficient representation of the RP matrix, C3 and C4 are handled by incorporating the Hamming code within the FPGA. These solutions are discussed in more detail in Section 3.

The contributions of this paper are as follows:

• A novel system architecture for random projection ensemble method that utilises the spare resources of an FPGA-based switch.
• A novel system architecture that enables kNN classification within FPGA-based network switches through an ensemble of classifiers with Hamming distance as the metric. The system can be easily adapted to FPGA-based NICs due to their similar architecture.
• Potential speedups in training whilst maintaining or even surpassing the single model accuracy for MLP-based classifiers.
• Achieving high memory reduction on high-dimensional dataset whilst retaining accuracy for kNN-based classifiers.
• A parameterised system model for hardware-software co-analysis that allows prediction and analysis of the system performance, for datasets of different sizes or FPGAs with different resources.

To the best of our knowledge, this is the first work that uses an FPGA-based network switch to accelerate ensemble learning using random projection.

2. Background

2.1. FPGAs in the Network

An FPGA, due to its flexibility and reconfigurability, is a perfect candidate for balancing the growing cost of hardware updates and the fast-evolving algorithms. The Azure SmartNIC [3], which utilises FPGA as a bump-in-the-wire accelerator next to the ASIC NIC (Network Interface Card), shows a reduction in latency and an increase in throughput for Azure services. Studies such as [17,18,19] utilise the SmartNIC to offload CPU/GPU workload to gain better overall performance.

FPGA-based network switches take a step further in bringing FPGA to the data center. Because the network switch is located at a higher level than the NIC, it is supposed to bring similar benefits to the network applications with the NIC whilst reducing the response latency. There are two major types of studies on FPGA-based network switches: 1) The infrastructure design targeting FPGAs such as [15,20] focusing on designing high throughput and low latency switching fabric on the FPGA. 2) Applications utilising FPGA-based switches such as [12] focus on reducing the latency of distributed training by moving the aggregation step into the switch. [11] also conducts a series of experiments analysing the impact of FPGA accelerators based on their relative distance in an IoT network.

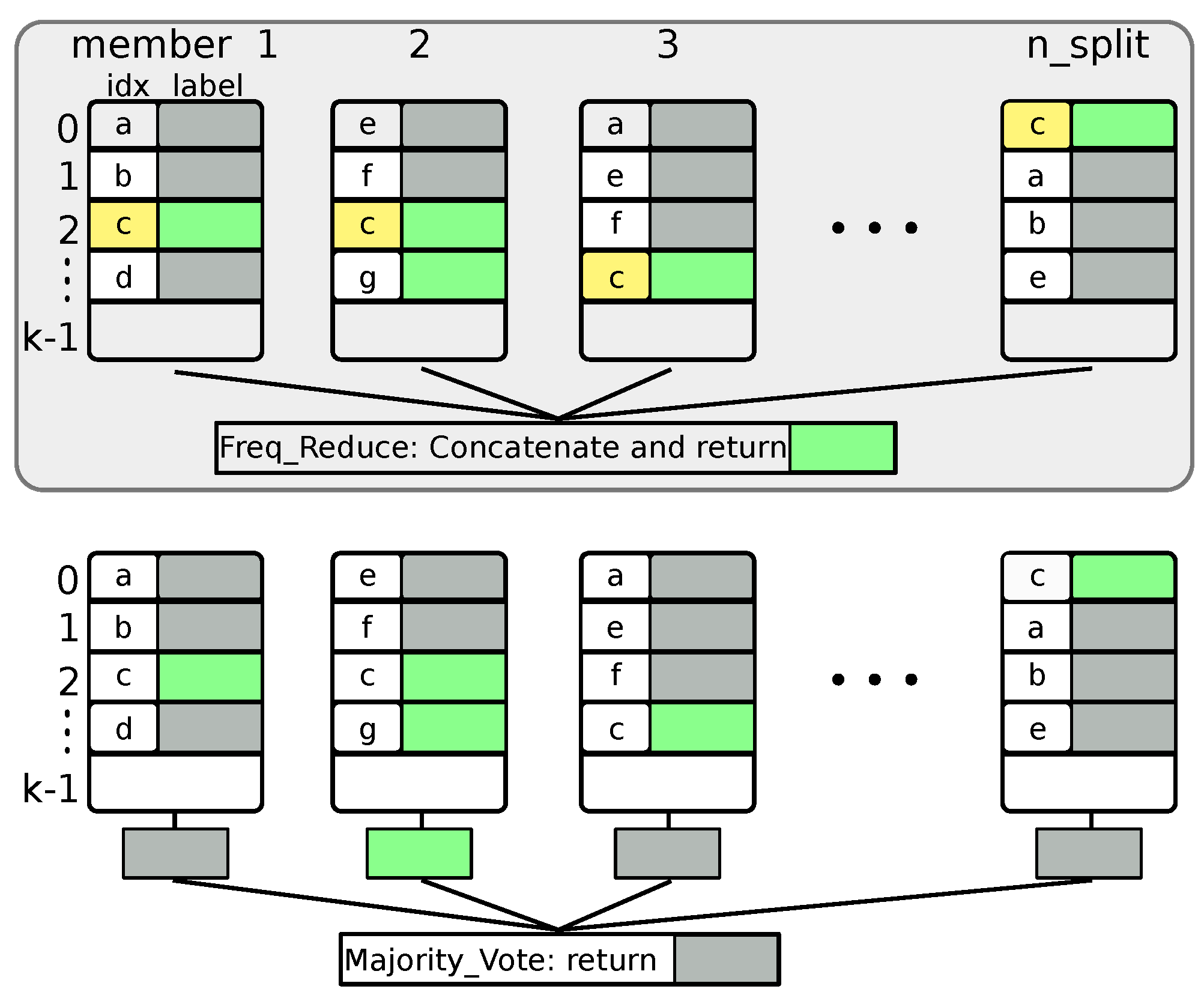
2.2. Random Projection and Ensemble Classification

Random projection as a technique to reduce the feature size and inject randomness into the dataset has been well studied. The most popular random projection methods are Gaussian random projection and Sparse random projection [21,22]. Fox et al. [23] propose the first FPGA-based RP method to make training scalable on FPGAs. However, the limited resources left for RP in their design force them to use high-sparsity RP matrices for hardware simplicity, which results in large errors for the projected subspace. It also limits their design to low-dimensional datasets, whereas the benefits of RP are more significant for high-dimensional datasets. In contrast, our work devotes all the idle computational resources on an FPGA-based switch to performing RP, allowing us to explore RP using Li’s method [22] without introducing additional error.

An ensemble classification system comprises multiple classifiers, which can vary in model type and predictive accuracy. The diversity of classifiers allows them to correct and compensate for each other’s shortcomings, thereby achieving collective accuracy higher than that of individual classifiers. Combining RP with ensemble systems allows classifiers to gain diversity from data in different sub-spaces, and the ensemble system recovers the accuracy loss.

2.3. Previous Work on FPGA-Based kNN Design

Most previous research on FPGA-based k-nearest neighbour focus on designing specialised hardware to efficiently run kNN. Lu [24] implemented an HLS-based kNN accelerator that optimises memory access with multiple DDR and HBM memory banks, the design was tested on data with dimensions up to 128, using single-precision floating-point type for data representation. The high memory bandwidth comes at the cost of routing resources, especially in LUTs. This high resource usage does not suit the current FPGA switch based application design scenario. In addition, the high-precision data representation used in this work limits the data size that can be stored onboard. Pu [25] proposed an OpenCL-based high-speed kNN accelerator utilising a modified parallel bubble sort, their design was tested on data with dimensions equal to 64, also using a floating-point representation. Song [26] implemented an HLS-based memory-efficient kNN leveraging PCA filtering and low-precision data representation. Their design uses at least 4 bits to represent each feature, however, it was only tested on a single dataset.

2.4. Distance Metrics

Distance metrics, also known as similarity measures or dissimilarity measures, are mathematical methods used to quantify the similarity or dissimilarity between two objects or data points in a space. They play a crucial role in various fields and applications.

• In classification, k-nearest neighbours (kNN) classifiers make predictions based on the distances between the input data point and its neighbours in the feature space.
• In kernel methods, certain kernel functions are related to specific distance metrics. For instance, the linear kernel is related to the dot product between vectors. The RBF Kernel (Gaussian Kernel) uses the Gaussian function, and its value is related to the Euclidean distance between data points.
• In recommendation systems, collaborative filtering often relies on distance metrics to measure the similarity between users or items. Similar users or items are recommended based on their historical preferences.
• In text mining and information retrieval, distance metrics, especially cosine similarity, are commonly used to compare and measure the similarity between documents or text snippets.
• In pattern recognition, distance metrics are utilised to quantify the similarity or dissimilarity between different patterns, whether they are in the form of images, sounds, or other types of data.

Different distance metrics are suitable for different types of data and applications. Let $\mathbf{p}$ and $\mathbf{q}$ be two vectors with the same length n whose elements are indexed by an integer between 1 to n. Below are some commonly used distance metrics:

• Euclidean Distance: $d(\mathbf{p},\mathbf{q})=\sqrt{{\sum }_{i=1}^n{(p_i-q_i)}^2}$, which is often used in geometric contexts and when the dimensions are comparable.
• Manhattan Distance (L1 Norm): $d(\mathbf{p},\mathbf{q})={\sum }_{i=1}^n|p_i-q_i|$, which represents the distance between two points as the sum of the absolute differences along each dimension.
• Minkowski Distance: $d(\mathbf{p},\mathbf{q})={\left({\sum }_{i=1}^n{|p_i-q_i|}^p\right)}^{{\displaystyle \frac{1}{p}}}$, which is a generalisation of both Euclidean and Manhattan distances. When $p=2$, it reduces to the Euclidean distance; when $p=1$, it becomes the Manhattan distance.
• Cosine Similarity: cosine_similarity$(\mathbf{p},\mathbf{q})={\displaystyle \frac{\mathbf{p}·\mathbf{q}}{\parallel \mathbf{p}\parallel \parallel \mathbf{q}\parallel }}$, which measures the cosine of the angle between two vectors and is commonly used for text similarity and document clustering.
• Hamming Distance: $d(\mathbf{p},\mathbf{q})={\sum }_{i=1}^n\delta (p_i\ne q_i)$, which is often used to compare strings of equal length, counting the number of positions at which the corresponding symbols differ.

2.5. Previous kNN Designs That Use Hamming Distance as the Metric

An [27] implemented an associative-memory-based online learning method that uses fully-parallel associative memory to reduce query time for nearest neighbour finding. However, the data is pre-processed heavily before entering the FPGA. Besides, the tested dataset is a binary dataset which is sufficient to use Hamming distance without losing accuracy. Lee [28] proposed a similarity search design on an Automata Processor (AP) that uses Hamming encoding to solve the sorting phase of kNN in linear time. This ASIC design on the AP platform achieves great speedup. However, this design assumes dataset vectors are processed offline, meaning it only needs to work on datasets with small dimensions. Compared with previous designs, our system supports a much higher input dimensionality. The comparison is summarised in Table 8. In particular, [29] proposed a parameterised kNN IP core that supports either a large number of training instances or a large feature dimension. However, achieving high in one aspect inevitably brings down the other. For example, the IP core theoretically supports dimensions up to 16384, but for only 15 data entries.

2.6. LSH Hashing

The hyperplane technique described in [30] gives: $Pr[h_{\overrightarrow{r}}\left(\overrightarrow{u}\right)=h_{\overrightarrow{r}}\left(\overrightarrow{v}\right)]=1-{\displaystyle \frac{\theta (\overrightarrow{u},\overrightarrow{v})}{\pi }}$, where $\theta (\overrightarrow{u},\overrightarrow{v})$ measures the angle between vectors $\overrightarrow{u}$ and $\overrightarrow{v}$. Since $cos\left(\theta \right)$ can be estimated by $\theta$, this similarity on the right-hand side can be treated as cosine distance. Furthermore, Indyk and Motwani [31] show that the similarity between two vectors $\overrightarrow{u}$ and $\overrightarrow{v}$ can be adapted to measure the Hamming distance between them.

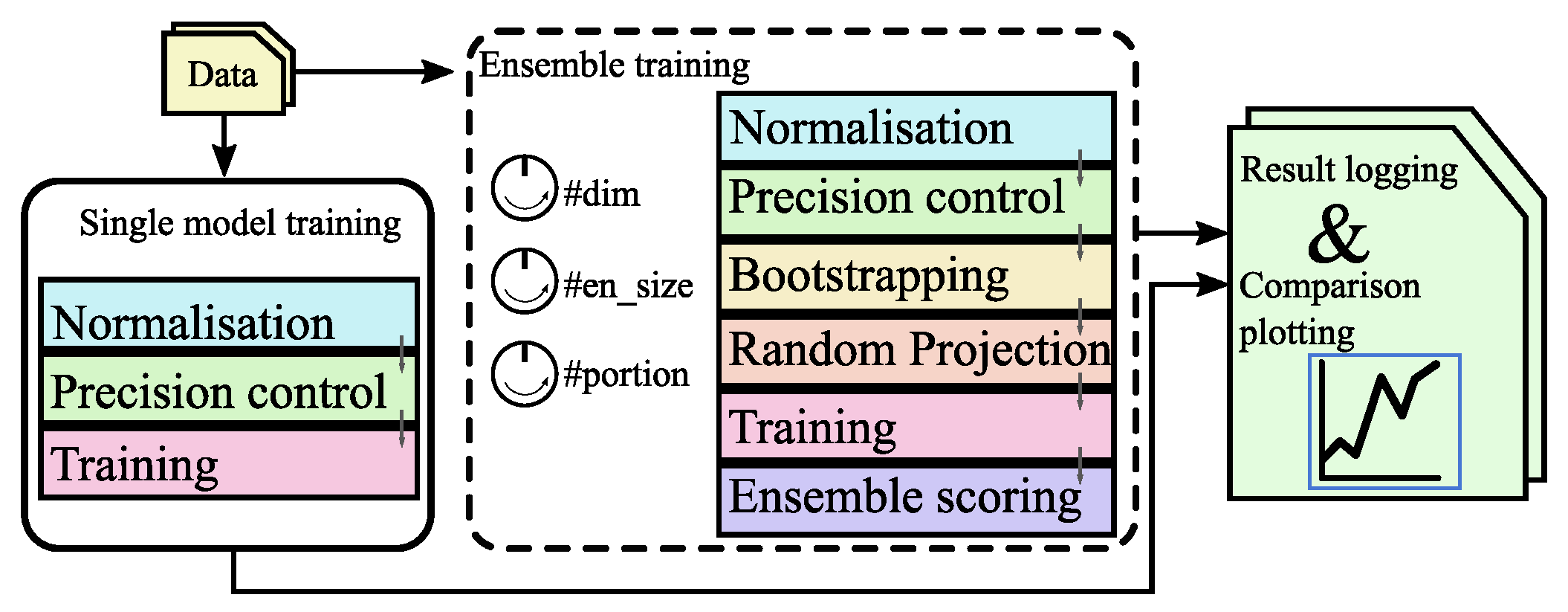
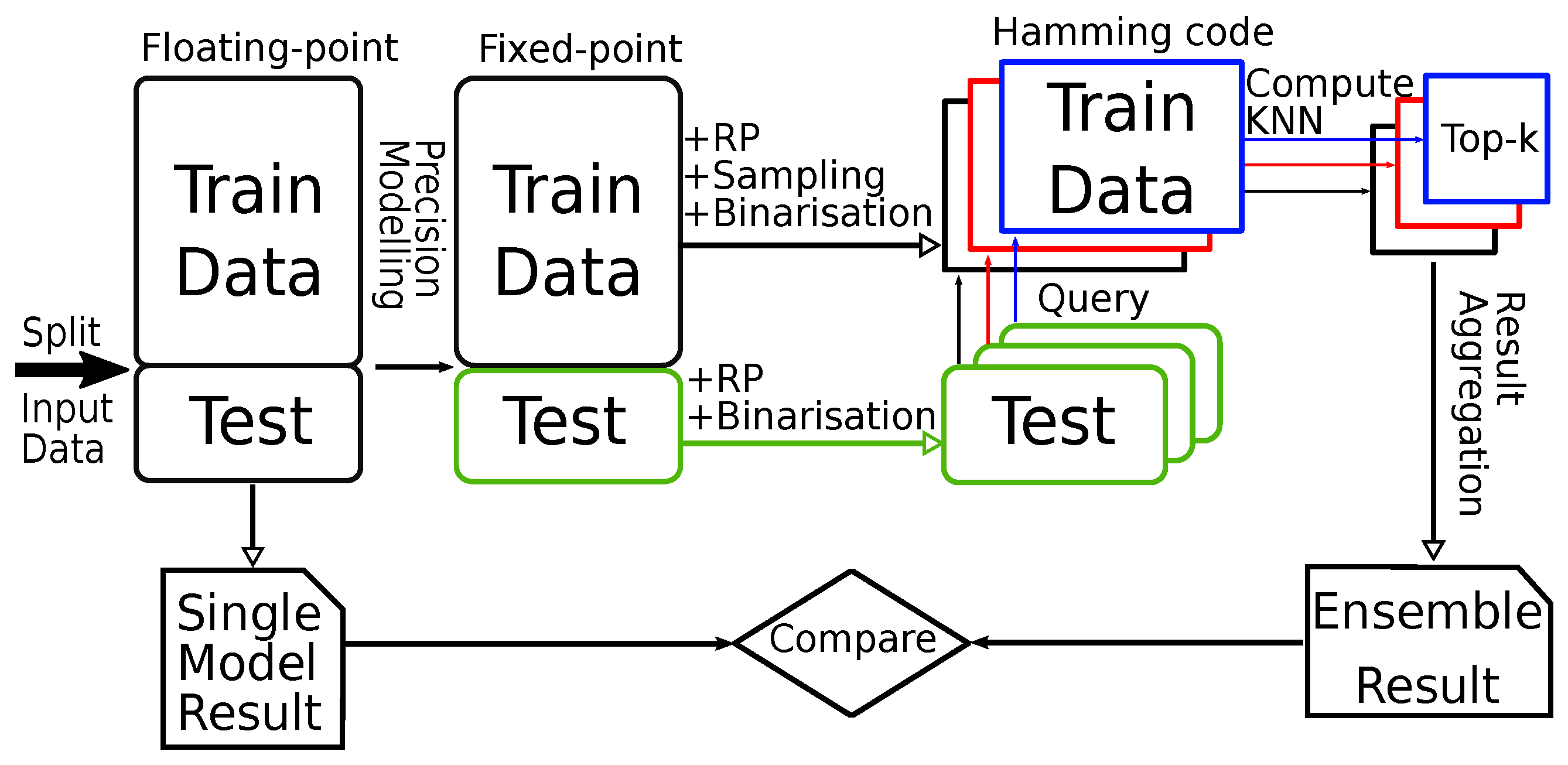
3. Proposed System Architecture

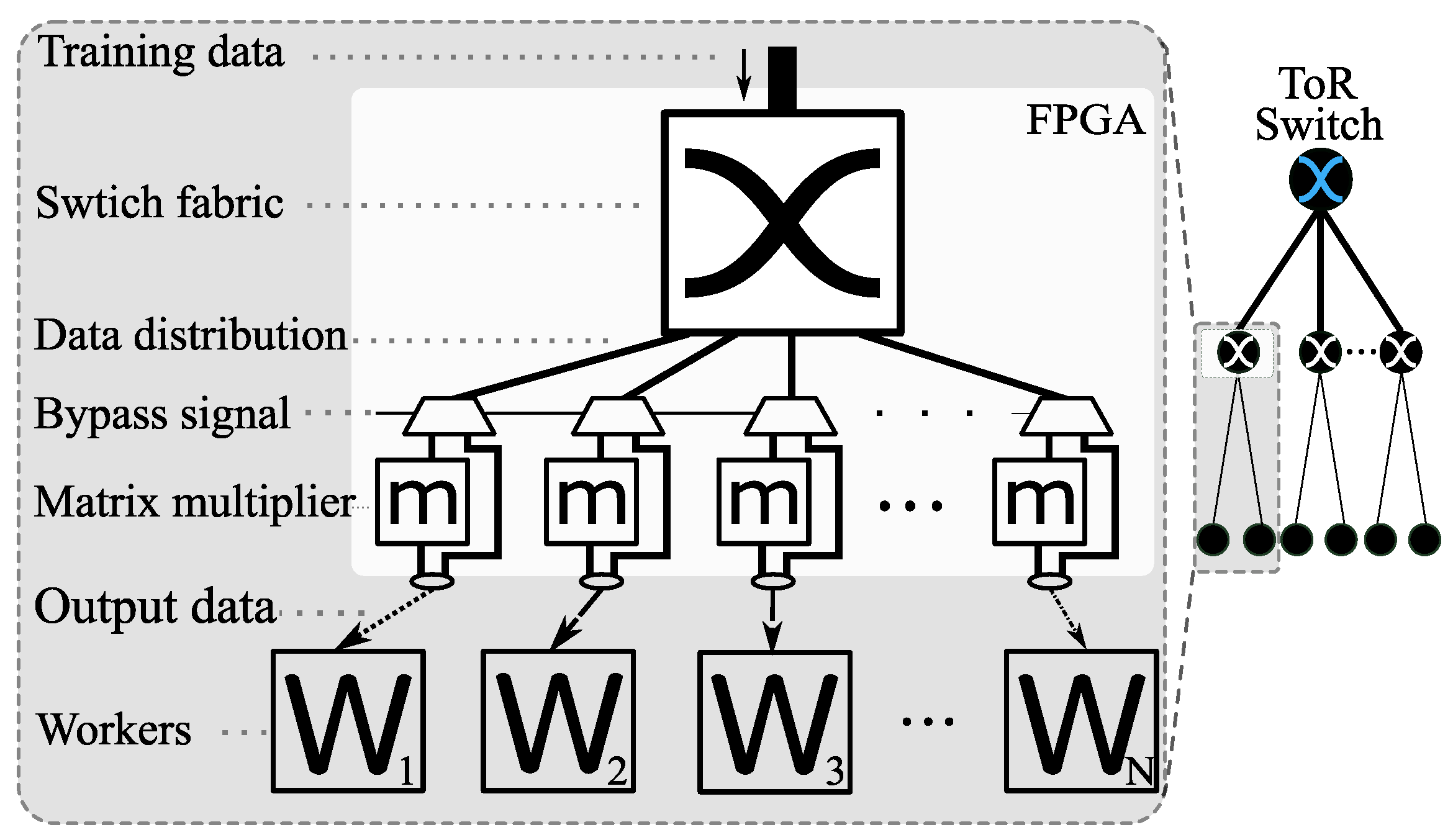
3.1. Overall System Design - for MLP-Based Models

The system comprises two major parts, as shown in Figure 1, the FPGA-based switch for data pre-processing and the worker nodes for training MLP-based models. We make no assumptions about the type of worker nodes, and they could range from edge devices to server clusters.

Our design can be deployed as an extra layer of switching between the ToR switch and server nodes, illustrated by the right half of Figure 1. This approach allows a reduction of the number of workers connected to each FPGA and keeps the functionality of the traditional rack. As a result, more resources on the FPGA can be utilised to compute random projection. Replacing the ToR switch with FPGA-based switches, in contrast, would require the FPGA to scale with the number of servers connected to the ToR switch and this would limit the resources available for computation. Such a hierarchical approach allows us to address C1 as the number of worker nodes increases.

On-chip storage avoids extra data transfer latency of the RP matrix from the off-chip memory and is necessary to perform fast data projection within the FPGA-based switch. However, the size of the projection matrix can become considerably larger than the capacity of the FPGA when the data dimension increases. Observing that the sparse matrix consists of only three types of values (positive, negative and zero) as shown in [22], we represent the matrix value with 2 bits, and restore values only when used. This enables storing the RP matrix on-chip with little logic resource overhead, thereby addressing challenge C2.

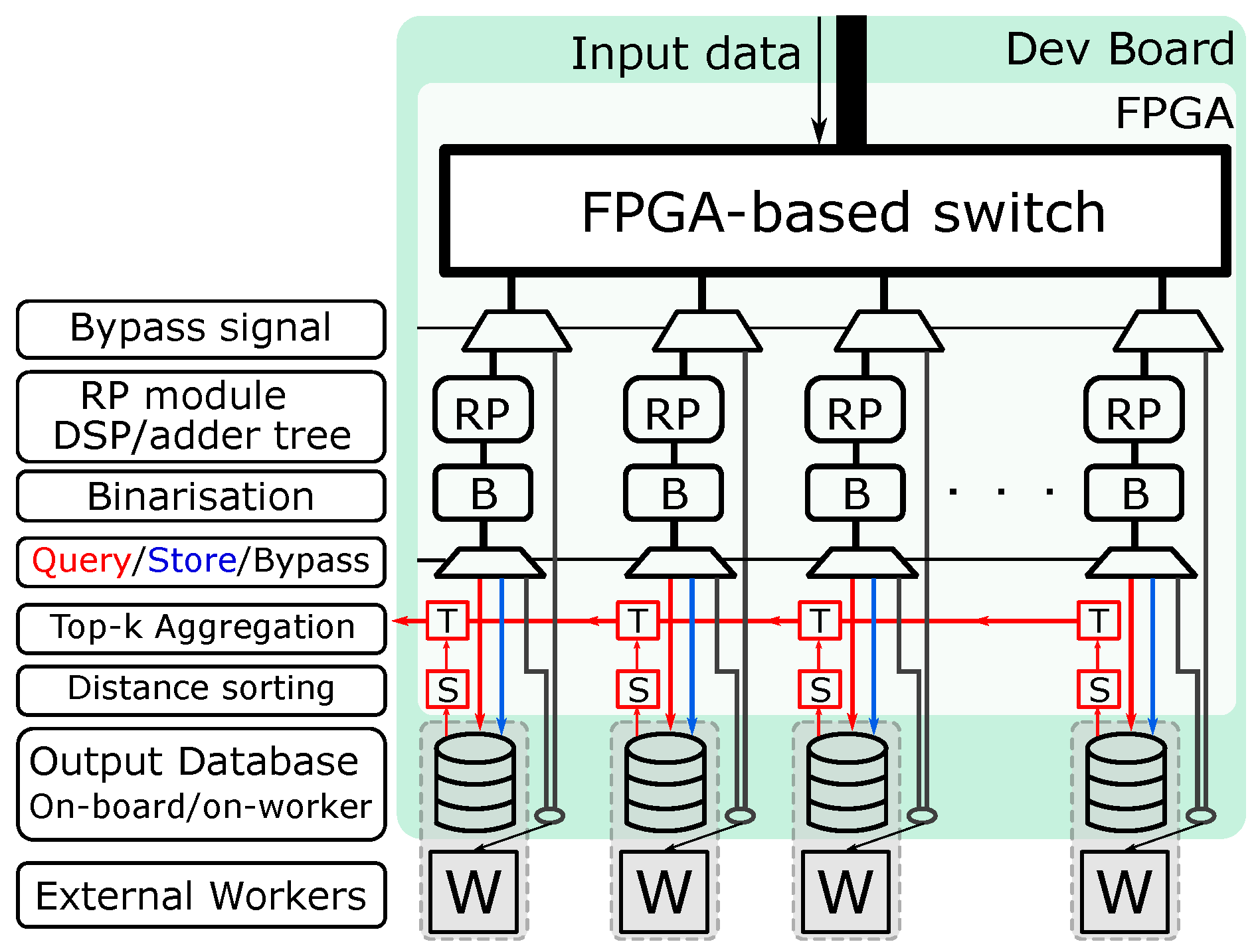
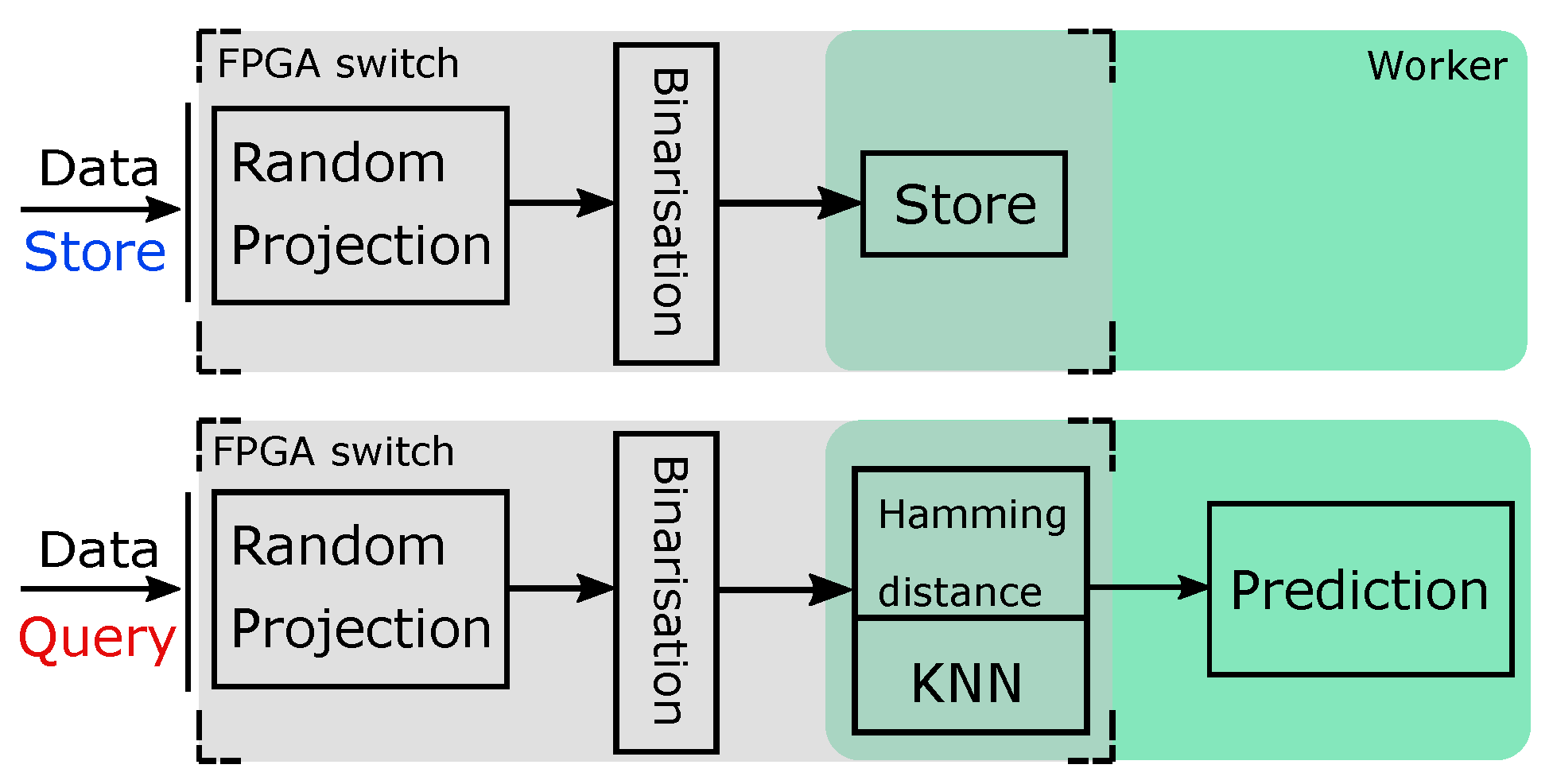
3.2. System Architecture for kNN Classifier with Hamming Distance as Metric

With the memory-efficient Hamming encoding method for dataset compression and computation-efficient Hamming distance metric for computing the distance of nearest neighbours, our design enables the possibility of removing the worker from the system, having the output database completely stored within the FPGA board. Distinguished from the overall system architecture, the novel features of this architecture include:

• An additional binarisation step to convert data to Hamming code and an additional level of multiplexing that supports the forward, store and query operations.
• In-FPGA top-k computation and aggregation on the Hamming code, which greatly reduces the computation overhead and, as a result, increases the performance. Converting to Hamming code also gives the FPGA the ability to store all data on-board. Therefore, the need to access data from the worker is eliminated (address challenge C3, C4).
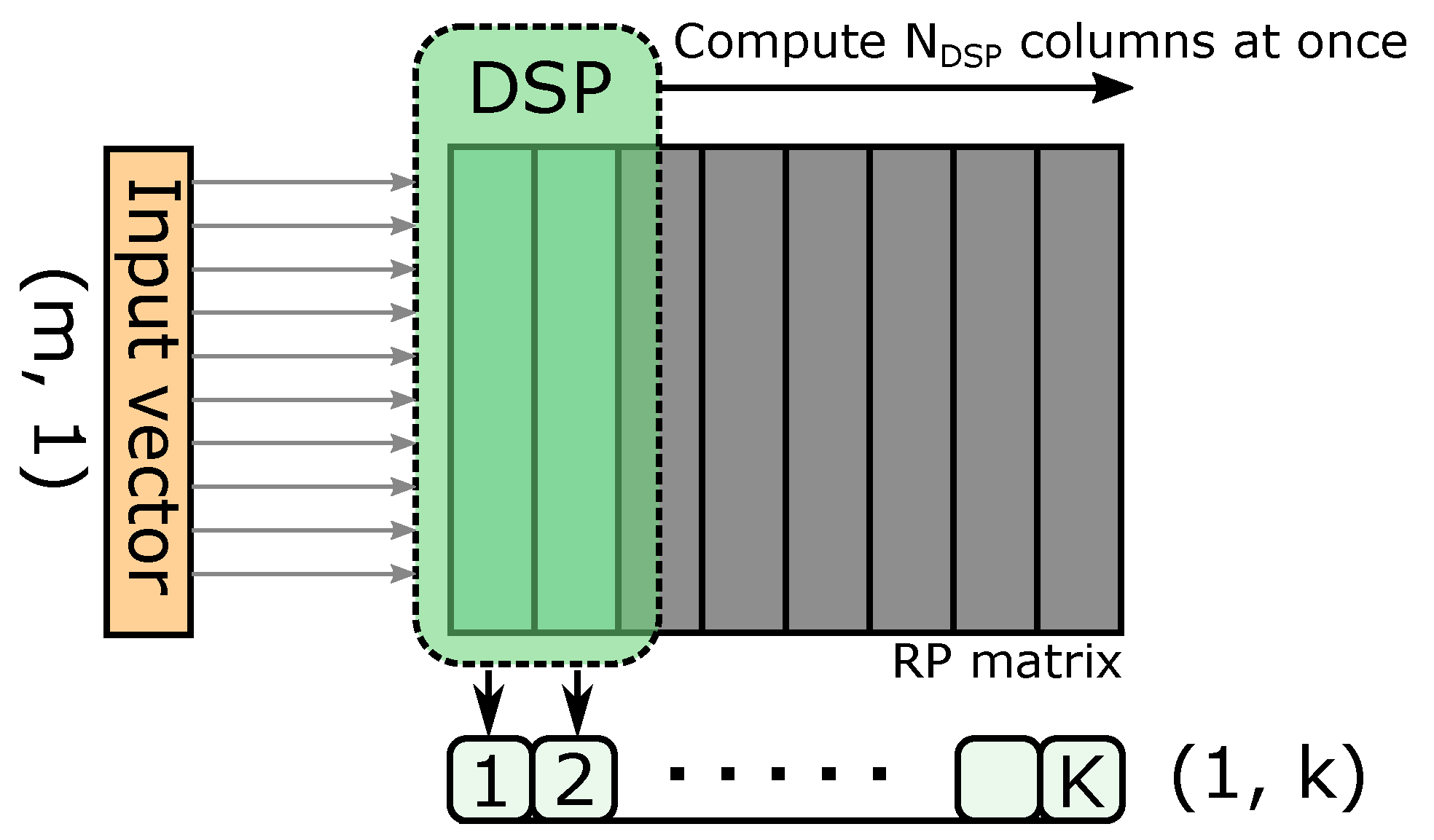
• The multiplier module is not restricted to a DSP-based design, which enables support for different types of RP matrix.

The proposed system architecture is shown in Figure 2, the descriptions of the blocks are presented on the left. In particular, the external workers are downstream platforms that carry out further data processing tasks. In the data center scope, they are normally referred to as the servers in the rack. Looking from top to bottom, first, data will be fed to the FPGA-based switch from an upper-stream storage source. Then based on the type of data, identified by the header field of the packet, the packet will be either directly forwarded to the corresponding output port or distributed to the computing pipeline through broadcasting. Each copy of the data will enter the RP module to be projected (through matrix multiplication) to a different latent space. Note in our design, based on the type of RP matrix used, the RP module can be implemented with either Digital Signal Processing (DSP) units or simple adder trees, which brings more flexibility to the resource usage. After the RP process, the binarisation module converts the data to the Hamming space by taking the sign bit of the projected data. This compresses the data from high bit-width representation to binary representation. Since datasets vary in all sizes and shapes, the hardware solution should also be flexible to support such variation. Therefore another stage of bypassing is introduced in our design. This solves the challenge when on-chip/on-board memory is limited in the development board, and allows us to analyse the impact of our method under different circumstances.

If bypass is enabled, the compressed dataset will be forwarded to the downstream worker for storage and computation of the nearest neighbours. Turning off the bypass is equivalent to removing the workers from the system, leaving storage and computation all on the development board. For the initialisation phase, i.e., building the database with the store operation, data will be stored in the onboard DDR RAM. For the prediction phase, i.e., query operation, the incoming binarised data will be compared with the database (using block T and S in Figure 2), and the top-k result will be aggregated to form the final result. The detail of the aggregation methods is presented in Figure 3.

Let us consider the scalability of the proposed approach. Limited by the manufacturing technology, current FPGA chips remain tight in resources after implementing a high throughput/high port count network switch. This challenges the types of applications that can be implemented on the FPGA-based switch, which potentially cuts out the benefit of in-network computing. To scale the system, a hierarchical design that contains two layer of switching should be used. The extra layer of switching will inevitably introduce additional latency overhead. We argue that this fixed latency is trivial when compared with the computation cost, therefore it is reasonable to adopt this architecture. In fact, when the dataset is large, the problem will be bounded by the computation with current FPGAs. In Section 7.3, we quantify this gap with an example dataset. As a summary, all dataset used in this work is presented in Table 1.

4. Theoretical Model for MLP-Based Classifiers

Our theoretical model analyses the system time using boundary conditions. Aiming to optimise the system time, it provides conditions when maximum computation power can be utilised by the system. However, the theoretical model is constructed under the condition that FPGA has enough resources to compute the RP in a fully pipelined way, its result could deviate with different implementations.

Random projection can be performed by the switch and/or by the server nodes. Let $\alpha$ be the fraction random projection computed by the switch, the rest $(1-\alpha )$ computed by the servers. The overall system time consists of three components (a) the random projection time $T_{project}\left(\alpha \right)$ (b) the release time of output ports $t_{release}\left(\alpha \right)$ and (c) the training time of the server $T_{train}$. It is possible to implement the random projection with systolic matrix multiplication. In this case, the output ports can send data to the servers while the random projection is in progress. In other words, the random projection time and data release time overlap. Therefore, we take the greater time of $T_{project}\left(\alpha \right)$ and $T_{release}\left(\alpha \right)$. Ignoring the latency caused by the network and the pipeline, the total system time is as follows:

$$\begin{array}{c}\hfill T\left(\alpha \right)=max(T_{project}\left(\alpha \right),T_{release}\left(\alpha \right))+T_{train}\end{array}$$

(1)

$$\begin{array}{c}\hfill T_{project}\left(\alpha \right)={\displaystyle \frac{\alpha X}{{\theta }_{project}^{switch}}}+{\displaystyle \frac{(1-\alpha )X}{{\theta }_{project}^{server}}}\end{array}$$

(2)

where X is the number of data points for training a sub-model in the ensemble; ${\theta }_{project}^D$ is the throughput of random projection for device D measured by the number of data instances projected per second.

The release rate of data should stay below the bandwidth of outgoing links due to congestion control. The release time to a server is the total data traffic $F\left(\alpha \right)$ divided by the bandwidth b from the switch to the server. The data traffic for each server includes the original data and projected data sent to the server, i.e.,

$$\begin{array}{c}\hfill F\left(\alpha \right)=\alpha Xk+(1-\alpha )Xm\end{array}$$

(3)

where m and k are respectively the number of dimensions of the original data and the projected data. Assume that all servers have the same bandwidth b measured by the number of data entries transferred per second, the release time is

$$\begin{array}{c}\hfill T_{release}\left(\alpha \right)={\displaystyle \frac{F}{b}}={\displaystyle \frac{\alpha Xk+(1-\alpha )Xm}{b}}\end{array}$$

(4)

We propose to handle all calculations for random projection in the FPGA-based switch with spared resources, which corresponds to $\alpha =1$. In contrast, in a conventional system with an ordinary switch, the random projection works solely on the servers, which corresponds to $\alpha =0$. The difference in performance is as follows:

$$\begin{array}{cc}\hfill T\left(1\right)-T\left(0\right)& =X\left[max({\displaystyle \frac{1}{{\theta }_{project}^{switch}}},{\displaystyle \frac{k}{b}})-max({\displaystyle \frac{1}{{\theta }_{project}^{server}}},{\displaystyle \frac{m}{b}})\right]\hfill \end{array}$$

(5)

The proposed system outperforms the conventional one if and only if

$$\begin{array}{c}\hfill T\left(1\right)-T\left(0\right)<0\end{array}$$

(6)

This inequality holds if and only if

$$\begin{array}{c}\hfill max({\displaystyle \frac{1}{{\theta }_{project}^{switch}}},{\displaystyle \frac{k}{b}})-max({\displaystyle \frac{1}{{\theta }_{project}^{server}}},{\displaystyle \frac{m}{b}})<0\end{array}$$

(7)

Note that inequality 7 is independent of the number of data points X or the time spent on sub-model training $T_{train}$.

Inequality 7 is very likely to hold under practical settings. In particular, there can only be four cases for the maximum operations.

• $max({\displaystyle \frac{1}{{\theta }_{project}^{switch}}},{\displaystyle \frac{k}{b}})={\displaystyle \frac{k}{b}}$ and $max({\displaystyle \frac{1}{{\theta }_{project}^{server}}},{\displaystyle \frac{m}{b}})={\displaystyle \frac{m}{b}}$. Since $k<m$ is the fundamental setting of random projection and $b>0$, we have ${\displaystyle \frac{k}{b}}<{\displaystyle \frac{m}{b}}$. Therefore inequality 7 obviously holds.
• $max({\displaystyle \frac{1}{{\theta }_{project}^{switch}}},{\displaystyle \frac{k}{b}})={\displaystyle \frac{k}{b}}$ and $max({\displaystyle \frac{1}{{\theta }_{project}^{server}}},{\displaystyle \frac{m}{b}})={\displaystyle \frac{1}{{\theta }_{project}^{server}}}$. In this case, ${\displaystyle \frac{k}{b}}<{\displaystyle \frac{m}{b}}\le {\theta }_{project}^{server}$. Therefore, similar to the previous case, inequality 7 still holds.
• $max({\displaystyle \frac{1}{{\theta }_{project}^{switch}}},{\displaystyle \frac{k}{b}})={\displaystyle \frac{1}{{\theta }_{project}^{switch}}}$ and $max({\displaystyle \frac{1}{{\theta }_{project}^{server}}},{\displaystyle \frac{m}{b}})={\displaystyle \frac{1}{{\theta }_{project}^{server}}}$. In other words, the random projection time is the bottleneck of both systems. In this case, the inequity holds if ${\theta }_{project}^{switch}>{\theta }_{project}^{server}$, which holds as long as DSPs on the FPGA have a speed advantage over the server in terms of matrix multiplication.
• $max({\displaystyle \frac{1}{{\theta }_{project}^{switch}}},{\displaystyle \frac{k}{b}})={\displaystyle \frac{1}{{\theta }_{project}^{switch}}}$ and $max({\displaystyle \frac{1}{{\theta }_{project}^{server}}},{\displaystyle \frac{m}{b}})={\displaystyle \frac{m}{b}}$. In this case, whether inequality 7 holds is more data-dependent and hardware-dependent. However, we found that the case is very unlikely to appear practically.

5. Experiment Setup and Performance Analysis for MLP-Based Classifier

The experiments are primarily carried out in simulation with binary classification datasets from the UCI repository [38]. A two-layer MLP classifier model from Keras [39] is used in our experiment. The simulation is open-sourced1. Based on Equation 8, training time is obtained from simulation and switch time is calculated based on our model. The simulation flow is illustrated in Figure 4. To study the impact of dimension reduction on the training time and accuracy, different numbers of workers ($\#en\_size$), size of dimensionalities ($\#dim$) and the portion size of bootstrapping ($\#portion$) are passed as input parameters to the simulator.

Figure 5 illustrates the system time flow more practically, with the top half showing the time for training without RP and the bottom half with RP. $t_0$ represents the time for the first element in the dataset to leave the switch. $t_{Ia}$ is the time interval for each packet to arrive at the worker. $T_t$ is the total training time taken by the worker. Without RP, training data are simply forwarded to the worker without processing, resulting in shorter $t_0$ and $t_{Ia}$ in the top graph than the ones in the bottom. Packet forwarding during random projection is also shown in the bottom graph, indicated by the grey arrows in between the packets with RP. From the time graph, it is not hard to observe that a speedup from our design requires $t_{diff}$ to be greater than zero.

To prove our point, four high-dimensionality datasets are tested with their performance improvements shown in Table 2. As a proof of concept, we assume a 4x4 10Gbps (256bit data width) switch is implemented on a Xilinx vu9p FPGA with 6840 DSPs, as presented in [13,20]. A previous 4x4 network switch designed by the NetFPGA-SUME project [40] shows less than 15% of on-chip memory usage and less than 10% logic usage on a Virtex-7 chip. The same implementation on an Ultrascale+ chip will leave us with more flexibility for the RP function. We further assume a 16-bit fixed-point number for data representation as it only requires a single DSP block. Floating-point multiplication is avoided for minimal resource utilisation. The impact of fixed-point versus floating-point is modelled by a conversion precision loss in the simulation.

Figure 6. Experimental results showing the impact of the proposed system on training time and accuracy.

Figure 6. Experimental results showing the impact of the proposed system on training time and accuracy.

Overall system time is represented by the sum of time spent on the switch ($T_{switch}$) and the training time of workers ($T_t$) as shown in Equation 8.

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill T_{single}& =T_{switch}^F+T_t^F,\hfill \\ \hfill T_{ensemble}& =T_{switch}^P+T_t^P\hfill \end{array}\end{array}$$

(8)

where superscripts F and P stand for the forwarding mode and processing mode of the switch respectively. On the switch side, time is measured by the difference between the first entry and the last departure of packets. $T_{switch}^P$ in terms of clock cycles is given by:

$$\begin{array}{c}\hfill T_{switch}^P=\underset{t_0}{\underbrace{t_{in}+t_{mult}}}+(X_{sub}-1)\ast t_{Ia}+t_{out}\end{array}$$

(9)

where $X_{sub}$ is the number of elements in the dataset for each sub-model; $t_{in}$ is the time for the first element to enter the switch; $t_{out}$ is the time for the last element to leave the switch, which is shorter than $t_{in}$ due to the dimension reduction; $t_{mult}$ is the time for multiplying a single element of the dataset with the RP matrix. $t_{Ia}$ equals to $t_{mult}$, as shown in Figure 7.

Packet forwarding time for single model training is shorter as no multiplication time is required. The switching latency is typically a few hundred nanoseconds and is a one-time expense for continuous packet transfer, which becomes negligible compared with the total forwarding time. It can be modelled as: $T_{switch}^F=X_s\ast t_{out}=X_s\ast t_{in}$, where $X_s$ denotes the number of elements in the single model training dataset.

The speedup S of our proposed system compared with a single model can then be calculated by:

$$\begin{array}{c}\hfill S={\displaystyle \frac{T_{single}}{T_{ensemble}}}={\displaystyle \frac{T_{switch}^F+T_t^F}{T_{switch}^P+T_t^P}}\end{array}$$

(10)

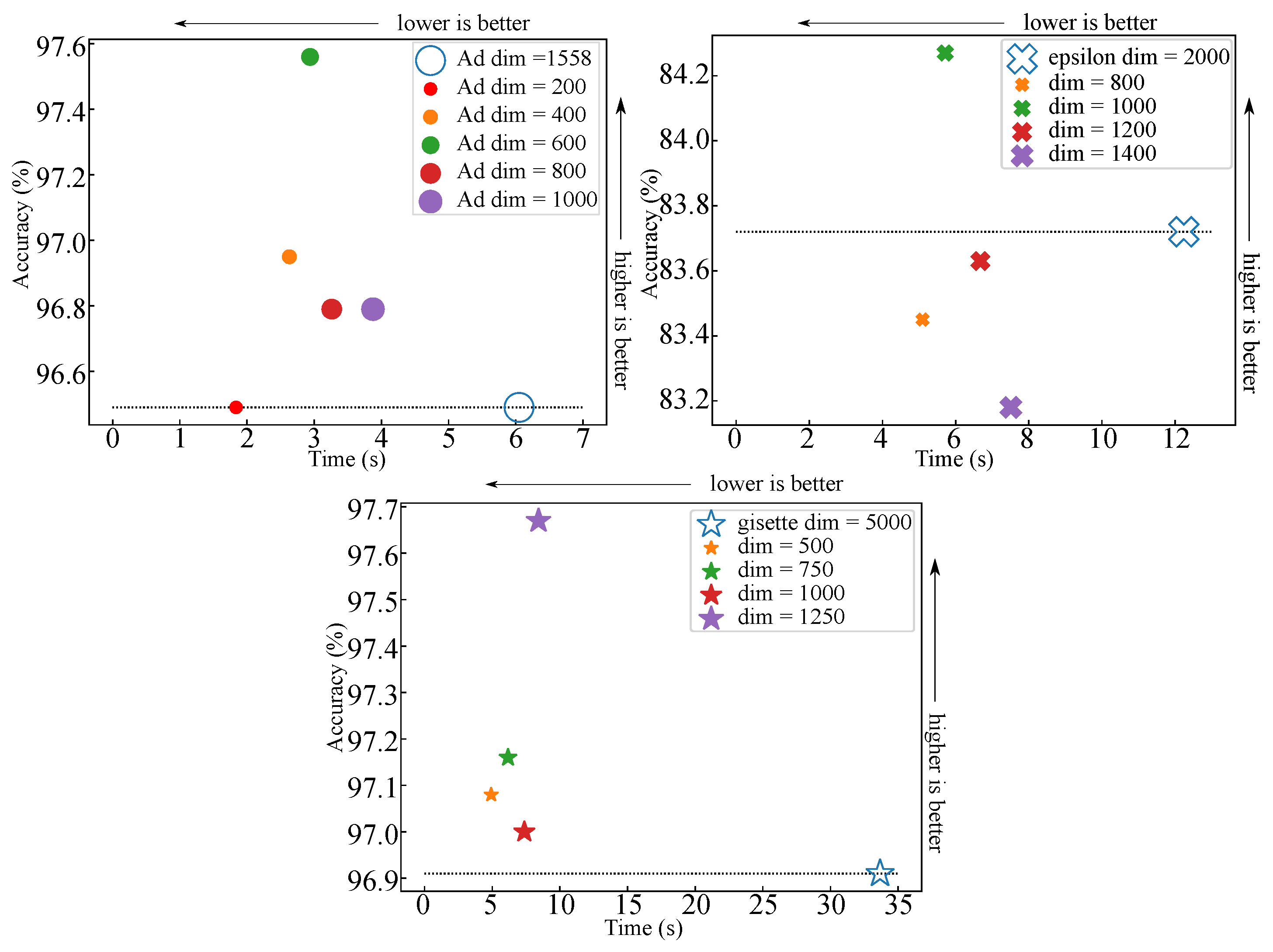
6. Dataset-Specific Case Study for MLP-Based Classifier

Take the Ad dataset as an example, the dataset has a total element of 3279, in which 80% ($X_s=2623$) is used for single model training and the rest 20% is used for testing. The training time and model accuracy of this single model are then severed as the baseline of the ensemble method. After bootstrapping, sub-training data is sampled for each server. The sub-training data can be less in quantity compared with the training data, and achieves the same model accuracy with less training time. A portion of 80% is chosen for this case study, which makes the sub-training data $X_{sub}=2098$.

Each element in the Ad dataset has 1558 dimensions. Transferring an element in a 16-bit fixed point over a 10Gbps switch with 256-bit data width requires $t_{in}=1558\ast 16/256=97.375\approx 98$ cycles. Assume the switch is running with a 200MHz clock, and let C denote its period which is 5ns. We then have $t_{in}=98C=0.49us$. This latency only needs to be considered once as matrix multiplication takes longer than receiving a packet. As mentioned in Figure 7, $t_{in}$ can be hidden under $t_{mult}$.

With limited DSP resources on the FPGA, matrix multiplication is broken down into vector multiplication. Each element in the dataset will be multiplied by the RP matrix column-wise. For a system with each FPGA switch connected to two servers, assume only DSPs-based multipliers are used for computation for worst-case analysis. To simplify the calculation, we allocate 1558*2 DSPs to each matrix multiplier module, which results in a total DSP usage of 6232 out of 6840.

As shown in Figure 8, the time for the multiplication process depends on the number of DSPs allocated for multiplication, which can be calculated as $m\ast k/N_{DSPs}$. Therefore, multiplication time $t_{mult}=1558/(1558\ast 2\ast k\ast C)=1/2kC$. Multiplication time $t_{mult}$ equals to $t_{Ia}$ in this case as multiplication takes longer than transmission. The remaining elements take $t_{mult}\times (X_{sub}-1)=209700C$. On the output side of the switch, the reduced dimension data requires fewer cycles to transfer. After dimension reduction, a vector of 200 dimensions takes $T_{out}=200\times 16/256\approx 13C$ cycles to transfer. In total, $T_{switch}^P=(98+209700+13)C=1.049e-3s$. Finally, the training time for the thin data set is 1.838s measured by the server, in this case, an Intel 7700k CPU. Therefore, $T_{ensemble}=0.001049+1.838=1.8390s$.

With our FPGA-based switch serving as a simple forwarding switch, the time spent on the switch is given by the total number of cycles that the dataset requires to be transferred. Therefore, $T_{switch}^F=X_s\ast t_{in}=2623\ast 98C=0.00128s$. Together with a training time of 6.049s obtained from the worker, $T_{single}=0.00128+6.049=6.0502s$. Using Equation 10, we obtain the speedup as $S\approx 3.288$. In addition, we determine the optimal value of $\alpha$ for the various models considered and summarise the results in Table 3.

6.1. Time Estimation for Very Large Dimension Size

For datasets with high dimensions, for example, the $realsim$ dataset, the m×k RP matrix becomes substantial in size, causing insufficient on-chip memory in small FPGAs. To solve this problem, off-chip DDR memory needs to be added to the system as a method of offloading the on-chip memory usage. However, extra latencies introduced by the DDR memory can cost 100-200 cycles. The data width of the memory controller can be chosen from 32-64bit for DDR4 and 32-512bit for DDR3 [42]. To estimate the worst case, we assume a transfer latency of 200 cycles and a memory interface of 512-bit wide. Moreover, RP matrices are assumed to be stored completely off-chip, despite the spare on-chip memory remaining idle. Note that our precomputed RP matrix is stored in the DDR memory in a compressed manner. Transfer for each column of the RP matrix from DDR to FPGA costs 20958*2/512 = 81.86 ≈ 82 cycles. Assume multiplication finishes as soon as one column of the RP matrix is transferred. In contrast with the case where no DDR is involved, it takes 82 instead of 20958/1000 ≈ 21 cycles to compute the one column of the RP matrix. Taking this into consideration, the new speedup becomes $S_{DDR}=1.89$.

7. Experiment Setup and Performance Analysis for kNN-Based Classifier

7.1. Software Modelling

Our baseline design computes kNN using cosine distance for the original dataset, operating on a multi-core CPU server. Because the official Scikit library implements different distance metrics with different levels of optimisation. For a fair comparison, we design our experiments in accordance with different optimisations in the library. When compared with the baseline, the CPU time is measured on the official KNeighborsClassifier library, which is implemented as a Cython extension that compiles down to C, leveraging OpenMP-based parallelism and allowing multi-core processing on the CPU. When measuring the time taken for the Hamming distance metric on the CPU, we implement our own kNN function for two reasons: 1) The official library implements the Hamming distance with normalisation and returns a double data type, whereas our experiment only requires an un-normalised distance with an integer distance. 2) When the Hamming distance metric is used, little optimisation is applied in the official library, causing an unfair comparison with the cosine distance metric. Our implementation first generates a distance list by comparing the query with all the data in the database, then returns the top-k element with the smallest distance (largest similarity) after a simple sorting on the distance list.

The proposed method uses an ensemble of models to recover the accuracy loss introduced by the Hamming space similarity. All data are first preprocessed, including standardisation and loss modelling for converting floating-point to fixed-point numbers. Then the processed data is projected to multiple latent spaces before converting to their Hamming encoding. These new sets of data are then stored in separate models waiting for queries to take place. The queries will go through the same process before turning into a Hamming vector in their corresponding latent space. Each model in the ensemble will return the top-k most similar elements in the dataset. Based on the aggregation type, each model can return either the label of the majority class, or the index of the top k element in their subspace. We will discuss the impact on the result of these two aggregation methods later. The software flow is summarised in Figure 9.

All datasets used are large datasets with high dimensionality, with a mixture of sparse and dense datasets. Due to the lack of dense high-dimensional datasets online, two dense datasets are created. The first one is created from a stock price dataset, the dataset is created with a window size of 1000 and each window corresponds to the trend of the market for the day after. The second dataset contains the image embedding of cats and dogs created using the openAI CLIP model [43], with an embedding length of 512.

As for the experiment setup, we run the experiment for all datasets with 4 types of random projection matrices. Gaussian, GaussianInt, Sparse and SparseInt, which correspond to dense and sparse matrices and their compressed version (using -1, 0, 1 to replace positive, zero, and negative values, identified by the Int suffix). Note that the dense RP matrix is used to compare with the DSP-based multiplier and the compressed version is used to compare with the adder tree-based multiplier. This is summarised in Table 4. For the number of data used, we split the dataset with a fixed train test split ratio = 0.8. For the ensemble, we provide a further sample portion of the training dataset to reduce the number of data to be stored.

7.2. Performance Modelling

The estimation is done using a combination of hardware estimation and software simulation. At a higher level, the time for our system can be summarised as the computation time plus the transmission time. We denote the time taken for the baseline as $T_{single}$, which represents kNN using the cosine distance metric operating on a single CPU without processing the dataset. The time taken with our proposed design is denoted as $T_{ensemble}$.

For the baseline model, the breakdown of the time can be expressed as:

$$T_{single}=T_{trans}+T_{cos}+T_{sort}$$

(11)

where $T_{trans}$ is the time taken to forward the data from the data server to the worker, $T_{cos}$ is the time taken for the CPU to compute the cosine distance, $T_{sort}$ for sorting the obtained distance table. Note that we assume no overlap between these operations, theoretically, sorting can start immediately after receiving a single data point if we maintain a priority queue, similar to a streaming top-k algorithm.

For the proposed model, the system time bifurcates into two expressions depending on the size of the dataset. They are:

$$T_{ensemble}=T_{rp}^{fpga}+T_{bin}^{fpga}+T_{trans}^{fpga}+T_{DDR}^{fpga}+T_{ham}^{fpga}+T_{sort}^{fpga}$$

(12)

if the data size is smaller than the onboard memory, otherwise,

$$T_{ensemble}=T_{rp}^{fpga}+T_{bin}^{fpga}+T_{trans}^{fpga}+T_{ham}+T_{sort}$$

(13)

where $T_{rp}$ is the time taken for random projection, $T_{bin}$ is the time taken for binarising the projected data, $T_{DDR}$ is the time for reading and writing data from the on-board DDR memory and $T_{ham}$ represents the time taken to compute the Hamming distance between the query and the dataset. Note that parameters with superscript represent operations that happen on the FPGA, whereas those without represent operations on the CPU. If the size of the database after compression can fit in onboard memory, then the top-k is performed on the FPGA, otherwise, performing top-k on the CPU worker. For simplicity, we skip the case that would store the data partially on the FPGA and partially on the workers, as this would require non-trivial algorithmic adaptation.

For worse case analysis, we assume only two columns of multipliers are implemented on the FPGA, i.e., generating two output dimensions at the same cycle. This reduces the execution time of the multiplier by half. Now $T_{rp}=M\ast m/N\ast C$, with M being the original dimensionality and m being the projected dimensionality. Note that N represents the number of multiplication units, which is the same for the adder tree and the DSP multiplier.

$T_{ensemble}$ contains two phases, namely the Store and Query phases. They can be calculated with:

$$T_{store}=sr\times sp\times n_{data}\times t_{rp}$$

(14)

$$T_{query}=n_{data}\times (1-sr)\times (T_{rp}^{fpga}+T_{ham}^{\ast }+T_{sort}^{\ast })+T_{init}$$

(15)

where $n_{data}$ is the total data size, $T_{init}$ is the initial latency of the sorter pipeline, $sr$ is the train test split ratio and $sp$ is the sample portion. Note that the sample portion only applies to the training data. The superscript * indicates the time taken in either a CPU or an FPGA. We will elaborate on Equation 14 and 15 with an example dataset in the next section.

The platforms used for our experiment are: 1) Xilinx U280 board [42] with a total DDR capacity of 32GB and 9027 DSP slices. 2) AMD EPYC 7543 32-Core Processor running at an average 2.8GHz, with 504GB total memory. For the performance estimation, we assume the FPGA is running at 200 MHz, which is equivalent to a clock period of 5ns.

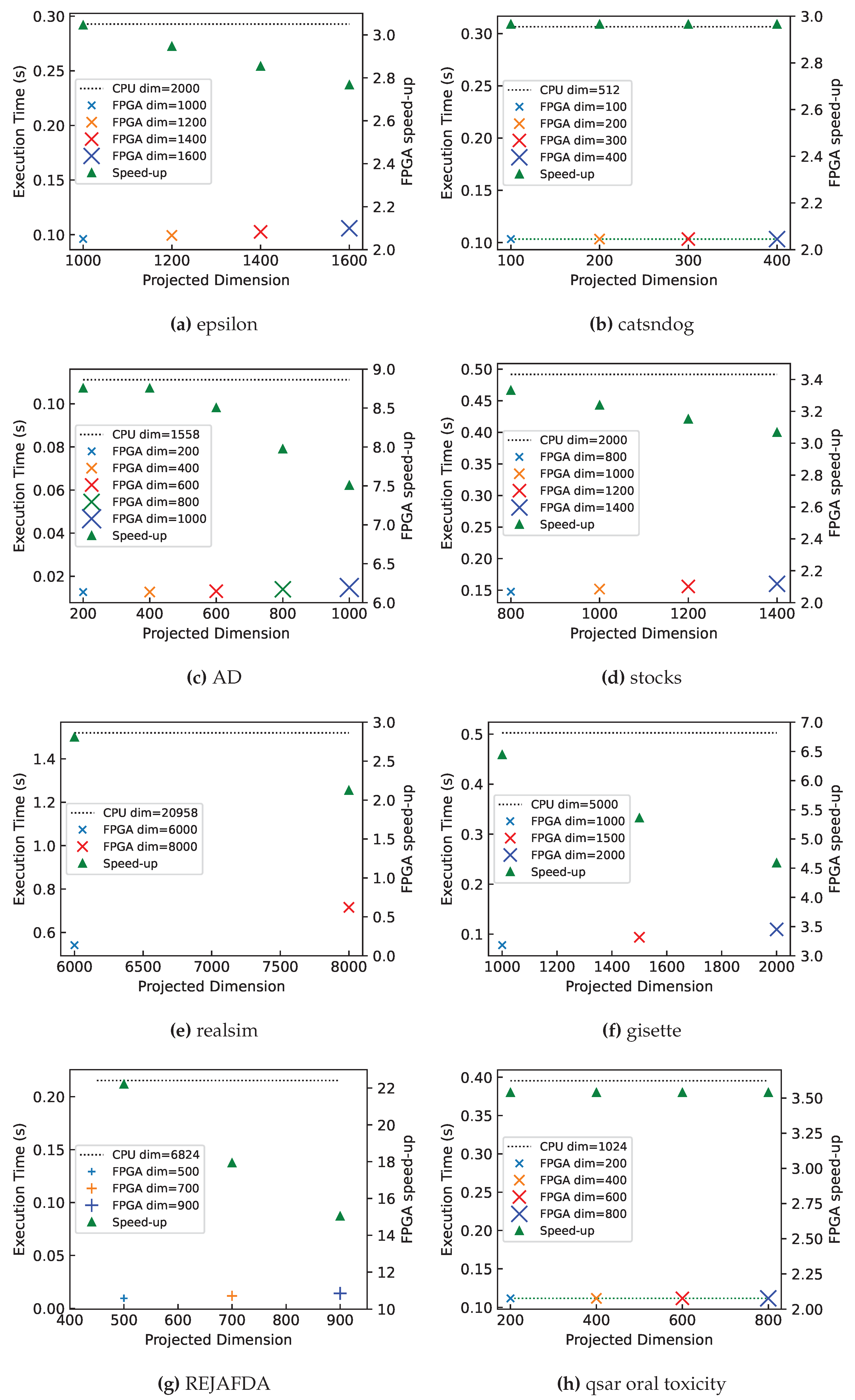
7.3. Dataset-Specific Case Study

The epsilon dataset is a dense dataset with high dimensionality, the original dataset contains 400000 entries with 2000 dimensions. To reduce the simulation time, a portion of the dataset is taken for simulation. In this case study, 7000 data entries are randomly sampled from the dataset for training and testing, and a train-test split portion of 0.8 is used.

To calculate $T_{single}$: According to Equation 11, the transmission time is simply the time spent forwarding the packet by the switch. This time is determined by the design of the network switch and the length of the packet. For simplicity, we assume that the packet is of fixed size, and the network switch operates the same as the NetFPGA-SUME [40] base design, but to match the state-of-the-art FPGA, we assume it is implemented on an AMD Alveo U280 FPGA. Based on [44], $T_{trans}$ contributes little to the total time due to the domination of the RP process. Another reason to ignore this parameter is that both the base case and our proposed design contain packet forwarding, reducing their impact on the speed up which is calculated by the ratio of the two cases. Therefore, $T_{single}$ is reduced to $T_{cos}+T_{sort}$. This gives us $T_{single}$ = 0.29270s. Note that $T_{single}$ includes the time taken for the fitting process, this is to ensure a fair comparison with the $T_{ensemble}$.

To calculate $T_{ensemble}$: As stated in Equation 12 and 13, there are two situations for $T_{ensemble}$, which can be further divided into two phases, $T_{store}$ and $T_{query}$, both sharing the $T_{rp}$ and $T_{bin}$ processes as illustrated in Figure 10.

Table 5. Experiment results

Name	# entry	M	m	sp	Lib Time CPU Cosine/s	Estimated time/s FPGA	FPGA speedup	Total memory reduction	Trigger size Terabytes
epsilon [32]	7000	2000	1000	0.9	0.2927	0.095917	3.05	3.95	1.138
catsndogs	10000	512	100	0.6	0.3065	0.103337	2.97	21.01	4.369
AD [33]	3279	1558	200	0.6	0.1111	0.012718	8.74	27.70	6.647
stock	10074	2000	1000	0.8	0.4916	0.151872	3.24	26.67	1.280
realsim [34]	3614	20958	8000	0.8	1.5200	0.652816	2.33	6.99	1.677
gisette [35]	6000	5000	1000	0.8	0.5027	0.078037	6.44	22.22	3.200
REJAFDA [36]	1996	6824	700	0.6	0.2153	0.012023	17.91	519.92	8.318
qsar_oral [37]	8992	1024	800	0.8	0.3953	0.111949	3.53	12.8	0.819

Table 5. Experiment results

Name	# entry	M	m	sp	Lib Time CPU Cosine/s	Estimated time/s FPGA	FPGA speedup	Total memory reduction	Trigger size Terabytes
epsilon [32]	7000	2000	1000	0.9	0.2927	0.095917	3.05	3.95	1.138
catsndogs	10000	512	100	0.6	0.3065	0.103337	2.97	21.01	4.369
AD [33]	3279	1558	200	0.6	0.1111	0.012718	8.74	27.70	6.647
stock	10074	2000	1000	0.8	0.4916	0.151872	3.24	26.67	1.280
realsim [34]	3614	20958	8000	0.8	1.5200	0.652816	2.33	6.99	1.677
gisette [35]	6000	5000	1000	0.8	0.5027	0.078037	6.44	22.22	3.200
REJAFDA [36]	1996	6824	700	0.6	0.2153	0.012023	17.91	519.92	8.318
qsar_oral [37]	8992	1024	800	0.8	0.3953	0.111949	3.53	12.8	0.819

Situation 1 — when the on-board memory can hold the dataset. In this case, there is no packet transmissions between the FPGA and the workers, removing one level of data transmission. The Store and Query in Figure 10 will both run on the FPGA-based switch. However, we do need to consider the DDR RAM latency for storing and reading. For worst-case analysis, we assume the read and write latency takes 200 cycles = 1 us. Since it is smaller than $T_{rp}$, it can be hidden within the 2.5us window. Therefore $T_{DDR}^{fpga}$ can be replaced by the initial latency of 1us, assuming read and write have the same latency.

For the Store phase, with the random projection being a time-consuming part of the design and to support different RP matrices, we design our system to choose between two types of matrix multiplication modules. A DSP-based multiplier for the RP matrices with large fixed-point values, or an adder tree-based multiplier for RP matrices contains only 0, -1 and 1. To avoid over utilising the resources, we assume that each switch will implement only two copies of the RP module.

With the DSP-based multiplier already discussed in [44], we implemented an adder tree with 2000 input of type 16-bit fixed-point using Vivado HLS. It only uses 5% LUT on the U280 board. Since the epsilon dataset has an input dimension equal to 2000, we allocate 4000 DSPs or two 2000 input adder trees for random projection. Using FPGA to binarise a vector can be simply done by extracting the sign bit of each element in the vector, this is included in our adder tree design. The overhead of this operation is trivial, thus adding this functionality to the DSP-based multiplier will not affect the estimation outcome. Therefore, $T_{rp}$ = 0.5*1000*5ns = 2.5us, meaning the projected data will be generated every 2.5us. The total time to generate the entire projected dataset in the store phase is $T_{store}$ = 0.9 * 0.8 * 7000 * 2.5us = 12.60 ms.

In the Query Phase, the query data is first projected to the same latent space using the database, which takes 2.5us. Then this projected query will be compared with the entire database, computing the Hamming distance along the way; Burst reading from the DRAM can be initiated within this 2.5us window, and by the time the projection is ready, the entire database will be ready to use. To compute the Hamming distance, another adder tree is implemented. This adder tree only takes as input a single bit, therefore significantly reducing resource usage. This circuit is much simpler than the adder tree for random projection, and our implementation result shows less than one per cent of LUT is used on the target platform.

If pipelined, the initial latency can be calculated as $lo{g}_{2}N$, where N is the length of the input bit vector. For an input of 1000 bits, the initial latency is around 11 cycles. The initial latency can be amortised with a large input dataset. For the sake of simplicity, we will ignore this latency in our estimation as the datasets used in our experiments are relatively large. When reading the data from DRAM, with a reading port data width of 1024, it is possible to read one data from the DRAM every cycle. Therefore, computing the Hamming distance of a single vector can be achieved every cycle, and the total time is taken $n_{data}$ cycles. For the epsilon dataset, this is $T_{ham}^{fpga}$ = 0.9 * 0.8 * 7000 * 5ns = 25.2us.

Finally, for the sorting time, we need to sort an integer vector of length $n_{data}$. We implemented an iterative merge sorter using Vivado HLS with 6300 inputs using a short data type (signed 16-bit), the latency result is shown in Table 6. Since the size of each input is bounded by the number of elements in the input vector, this allows further optimisation of the input data width of the design. We use this simple design as a proof of concept, since designing a high-performance sorter is not the main object of this paper. We are aware that better designs for retrieving top-k exist, this design serves as the upper bound of taking the top-k element. The implementation result shows little resource usage and is able to run under 200MHz. In fact, it is designed to return the result in log2(N) stages, so the output latency is deterministic given the running frequency.

In practice, our pipelined implementation with minimum optimisation (array partition) using Vivado HLS has an initial latency of 0.410ms and an interval latency of 6304 cycles = 31.52 us, as shown in Table 6. In theory, the interval latency (N) is the latency of a single stage and the initial latency ($Nlog2\left(N\right)$) is the total length of the pipeline and the latency. The implementation summary shows the actual latency corresponds to the theoretical value. The resource usage is shown in Table 7. Putting everything together, the total time taken by test data is $T_{query}$ = 7000 * (1 - 0.8) * (2.5us + 25.2us + 31.52us) + 0.410ms = 83.318ms Adding the time for the two phases gives the $T_{ensemble}$ = 12.6 ms + 83.318 = 95.917 ms

Situation 2 — when all data are stored in the worker. Under this condition, the speed-up will be dominated by the CPU computation time. KNeighborClassifier uses SciPy’s hamming distance which returns a normalised distance with type double. This does not fit our design purpose which requires only a small non-normalised integer distance as the output type. As a result, we implemented our own version of kNN that can take our own hamming distance function as input. Re-running the experiments on our implementation and the speed up under this condition is 7.5. Although this speedup appears to be higher than it is in Situation 1, it does not reflect the real behaviour of our design. This is because our own implementation does not leverage parallel computing on the CPU. The problem then becomes memory bound, meaning the time difference is dominated by the memory retrieval time of a full-precision dataset and a hamming-encoded one, which outweighs the benefit of computing RP on the FPGA. Getting the same comparison of Situation 1 requires the exact same software implementation of the Scikit learning library, which is beyond the scope of this study. Fortunately, it requires the dataset to be massive to trigger Situation 2; this is presented in the last column of Table 5. The computation detail is shown in Section 8.2.2.

In respect of classification accuracy, our simulation results show that by configuring the experiment with [projection dimension=1000, sample portion=0.9, number of split=18], we could recover the accuracy loss caused by the RP and binarisation process. In terms of memory usage, depending on the data type of the original dataset, there is a fixed compression ratio W using the hamming space i.e., the bit width of the data type to 1. For example, W=32 for the epsilon dataset that uses floating-point numbers. The total memory reduction (the ratio of the original memory size to the compressed memory size) can be calculated as:

$$R={\displaystyle \frac{M}{m}}\times {\displaystyle \frac{W}{n\_split\times sp}}$$

(16)

where ${\displaystyle \frac{M}{m}}$ is the ratio between the original dimension and the projected dimension, $sp$ is the sample portion, and $n_{split}$ is the size of the ensemble to recover the accuracy.

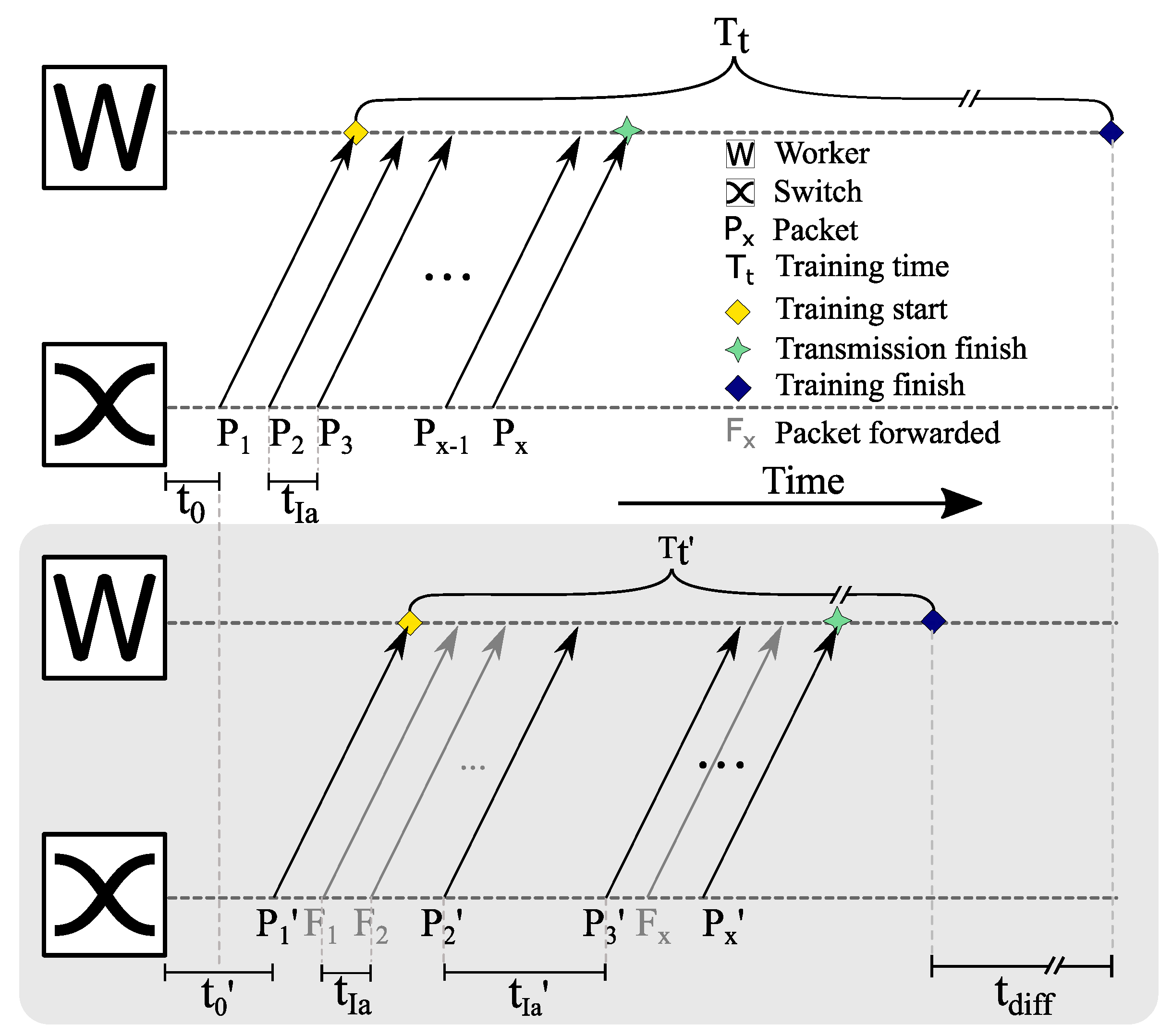
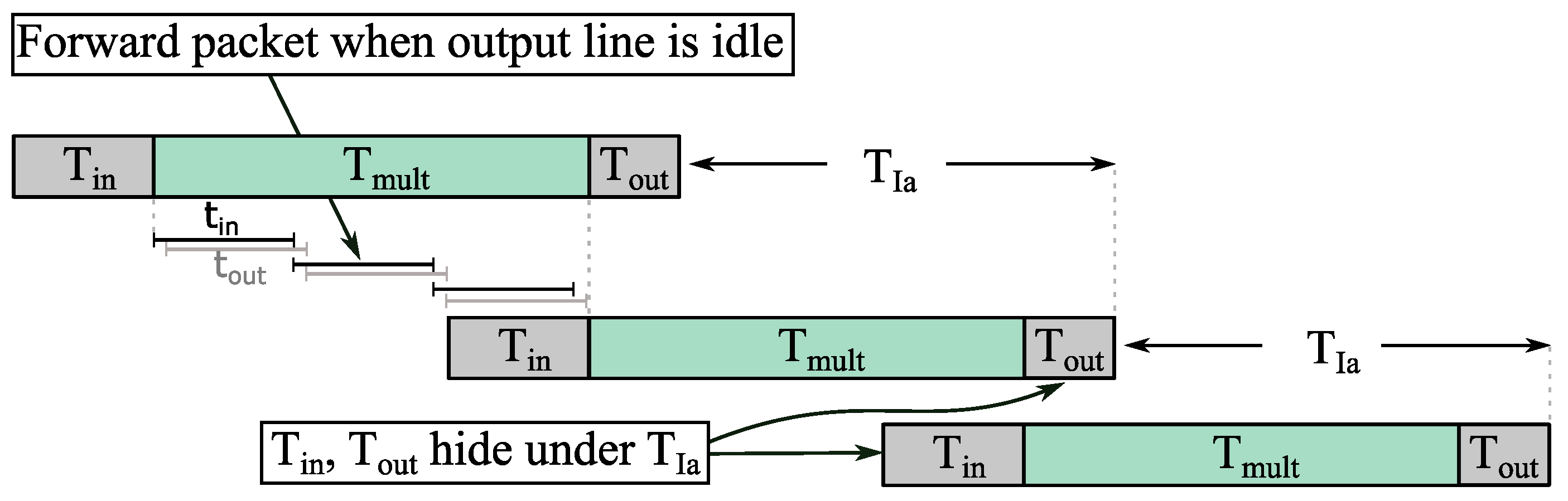
7.3.1. Quantifying the Gap between Forwarding Latency and Computation Latency

Based on the official NetFPGA-SUME wiki [14], the average port-to-port latency of the reference switch is 823ns. This corresponds to $T_{trans}^{fpga}$ in Equation 12 and Equation 13. For the epsilon dataset, $T_{rp}^{fpga}$ takes more than 3 times longer than $T_{trans}^{fpga}$. As long as the total transmission latency is shorter than $T_{rp}^{fpga}$, it can be hidden under the random projection latency, therefore, we could keep increasing the levels of the hierarchy until $T_{trans}^{fpga}$ saturates $T_{rp}^{fpga}$. In addition, if a certain level of buffering is enabled in the hierarchy, then it is able to control the packet arriving interval by sending packets back-to-back, with a controlled burst interval. As long as the burst interval is smaller than $T_{rp}^{fpga}$, then it can also be hidden under $T_{rp}^{fpga}$. Therefore we only need to add the initial latency to the whole model, which is 823ns times the number of levels in the hierarchy. Compared to $T_{ensemble}$ which is in millisecond scale, this is still small.

8. Discussion

8.1. MLP-Based Classifier

In general, our software simulation result shows an increase in training accuracy and a decrease in training time with the ensemble method; the reduced dimension is typically less than half of the original. A member size of 15 is chosen for the ensemble method, as they achieve stable performance for most tested datasets. Figure 6 shows the training time against accuracy for different binary classification datasets. The original data are represented with hollow markers, whereas experimental data are represented with solid filled markers. Take the Ad dataset for example; our method uses only 12.83% of the original dimension and 30.38% of the original training time to achieve the same accuracy of single model training. Increasing the dimensionality to 50% extends the training time but results in even higher accuracy than single model training. For the epsilon data set, the proposed method experiences small variance in terms of accuracy, but with only less than 0.5% lower in accuracy for some dimensions. This can be explained as the result of an insufficient ensemble member size. The gisette dataset gives the highest time reduction among all the tests. Note that the training time of lower dimension data is given by the slowest member.

8.2. kNN-Based Classifier

Table 5 summarises the experiment results for all the datasets; it also contains all the information required to compute the speed up and the memory reduction. The # entry column represents the total number of data instances used to compute kNN. Column $sp$ is the minimum sample portion to successfully recover the accuracy given the ensemble size. The data shows that our FPGA-based design offers speedup for datasets of different sizes and dimensionality. Notice that for the REJAFDA dataset, the speedup is around 17 times, this is due to the high sparsity of the dataset, which results in a very high $M/m$ ratio. To generalise our performance model, we have created a function that takes as input the first four columns of the table and returns the estimated FPGA execution time.

8.2.1. Relationship between Speed-up and Projected Dimension

Figure 11 presents the speed-up under different projected dimensions. The dotted line at the top of each figure represents the based line execution time for the original dataset. The markers at the bottom of each figure represent the execution time of our system with different projected dimensionalities (the lower the better). The triangle markers in the middle of each figure show the speed-up for each projected dimension.

In general, the speed-up for FPGA decreases linearly with the projected dimension. With a few exceptions such as Figure 11b and Figure 11c, where a constant speed-up for the FPGA can be observed. This is because the projected dimension is smaller than the input size of the matrix multiplier. With the current design, all dimensions smaller than the input threshold will experience a constant speed-up. In terms of prediction accuracy, all the presented dimensions are able to achieve the same accuracy as the baseline. If speed-up is vital, it is possible to further reduce the project dimension to gain higher speed-up, with the sacrifice of the prediction accuracy.

8.2.2. The Effect of Memory Reduction on System Scalability

Equation 16 presents the memory reduction ratio after summing all copies of data stored in all members of the ensemble. Multiply Equation 16 by $n\_split$ gives the memory reduction ratio ($R_s$) for a single copy of the dataset. Taking the epsilon dataset which utilises 18 splits as an example. $R_s$ = 18 * 3.95 = 71.11, which means for a single FPGA board, we will be able to store 71.11 times more data. If we only consider off-chip memory for storage, for an FPGA board with 32GB available DDR RAM, based on the assumption that each FPGA board holds two copies of the dataset, which means 16GB for each copy. With the memory reduction, we are able to store data with sizes up to 1.138TB on a single FPGA node, which is enough for most available datasets online.

Table 8. Comparison with previous designs

Designs	Platform	Metrics	Input Data dimension
[45]	AP	Euclidean	unspecified
[28]	AP	Hamming	64 - 256
CHIP-kNN [24]	Cloud FPGA	Euclidean	2 - 128
PRINS [46]	In-storage	Euclidean	1 - 384
kNN-MSDF [47]	FPGA SoC	Euclidean	4 - 17
[48]	FPGA SoC	Hamming	64
[29]	FPGA	Manhattan	16384
Rosetta [49]	FPGA	Hamming	unspecified
[50]	FPGA	Hamming	<24
kNN-STUFF [51]	FPGA	Euclidean	<50
[25]	FPGA	Euclidean	64
[52]	FPGA	Euclidean	1 - 16
[26]	FPGA	Euclidean	16
[53]	FPGA	Hamming	<50
This work	FPGA network switch	Hamming	<20958

Table 8. Comparison with previous designs

Designs	Platform	Metrics	Input Data dimension
[45]	AP	Euclidean	unspecified
[28]	AP	Hamming	64 - 256
CHIP-kNN [24]	Cloud FPGA	Euclidean	2 - 128
PRINS [46]	In-storage	Euclidean	1 - 384
kNN-MSDF [47]	FPGA SoC	Euclidean	4 - 17
[48]	FPGA SoC	Hamming	64
[29]	FPGA	Manhattan	16384
Rosetta [49]	FPGA	Hamming	unspecified
[50]	FPGA	Hamming	<24
kNN-STUFF [51]	FPGA	Euclidean	<50
[25]	FPGA	Euclidean	64
[52]	FPGA	Euclidean	1 - 16
[26]	FPGA	Euclidean	16
[53]	FPGA	Hamming	<50
This work	FPGA network switch	Hamming	<20958

9. Conclusion and Future Works

Our approach achieves a higher training accuracy for ensemble learning with reduced training time compared with single-model training. Small datasets are manageable on current FPGAs, whereas for datasets with very large dimensionality, current FPGAs may not have sufficient resources to exploit our method. Our proposed architecture is not limited to a single FPGA-based switch; it can be deployed with multiple FPGA-based switches to form larger ensemble clusters.

By combining random projection and ensemble techniques for a binarised Hamming embedding database. Our system is able to host the kNN classification entirely within an FPGA-based platform equipped with customised network switches while gain promising speedup through software hardware co-analysis. This indicates our system is able to completely offload kNN applications from downstream servers, which preserves the server resource for other applications. Because the system is designed with simple (least optimised) modules for worse-case analysis, there is plenty of space for optimisation in the future.

Ensemble machine learning is not the only application that can benefit from our proposed FPGA-switch-based method; further work will explore how our design can benefit other demanding computations, and how such computations can be implemented automatically and efficiently on the switch.