Adaptive Dataflow and Precision Optimization for Deep Learning on Configurable Hardware Architectures

1. Introduction

The rapid proliferation of artificial intelligence (AI) and machine learning (ML) applications across diverse domains—ranging from computer vision, speech recognition, and autonomous systems to financial forecasting and medical diagnostics—has fueled a concomitant demand for high-performance, energy-efficient computing platforms capable of accelerating deep neural networks (DNNs). These models, particularly convolutional neural networks (CNNs), recurrent neural networks (RNNs), and transformers, are characterized by immense computational and memory requirements that challenge the capabilities of traditional general-purpose processors. As Moore’s Law and Dennard scaling reach their practical limits, novel hardware solutions are imperative to sustain the momentum of AI innovation. Field-Programmable Gate Arrays (FPGAs) have emerged as a compelling platform for accelerating neural networks due to their unique blend of programmability, parallelism, energy efficiency, and low-latency processing. Unlike application-specific integrated circuits (ASICs), which offer high performance at the cost of flexibility, FPGAs provide a reconfigurable fabric that enables tailored architectural designs without incurring the non-recurring engineering (NRE) costs and time-to-market delays associated with ASIC development. Furthermore, in contrast to graphics processing units (GPUs), which excel at data-parallel workloads but suffer from high power consumption and memory bandwidth bottlenecks, FPGAs offer fine-grained control over hardware resources and the potential for deterministic performance, making them suitable for real-time and embedded inference applications. The suitability of FPGAs for DNN acceleration stems from several architectural features. First, the abundance of logic elements, digital signal processing (DSP) blocks, and block RAMs (BRAMs) facilitates the implementation of highly parallel and pipelined computation paths [1]. Second, the programmable interconnect fabric allows for customized dataflows, enabling optimizations such as weight reuse, data locality, and reduced off-chip memory access [2]. Third, modern high-level synthesis (HLS) tools and machine learning compilers (e.g., Xilinx Vitis AI, Intel OpenVINO, hls4ml, and TVM) have significantly lowered the barrier to entry for FPGA development, allowing researchers and practitioners to explore a wide design space with relative ease. Despite these advantages, the design of efficient FPGA-based neural network accelerators remains a challenging task that demands careful consideration of multiple, often conflicting, objectives [3]. These include maximizing throughput and energy efficiency while minimizing latency, resource utilization, and design complexity [4]. Design choices must account for model characteristics (e.g., layer types, precision requirements, sparsity), hardware constraints (e.g., logic and memory resources, I/O bandwidth, operating frequency), and deployment scenarios (e.g., edge vs [5]. cloud, static vs [6]. dynamic workloads). Consequently, a rich body of literature has emerged that explores architectural innovations, optimization techniques, and design methodologies to harness the full potential of FPGAs for DNN acceleration [7]. This review aims to provide a comprehensive and structured survey of FPGA-based neural network accelerators, highlighting key trends, architectural paradigms, and trade-offs in the design space [8]. We systematically categorize existing accelerator architectures based on their target network types, dataflow models, and level of customization. Additionally, we examine the impact of quantization, pruning, and model compression on FPGA implementation efficiency, and discuss emerging directions such as dynamic reconfiguration, hardware/software co-design, and support for evolving network architectures like transformers and spiking neural networks. Through this survey, we seek to inform researchers, engineers, and system designers of the state-of-the-art in FPGA-based DNN acceleration and provide insights into future research opportunities in this dynamic and interdisciplinary field.

2. Background and Mathematical Foundations of Neural Network Computations

In order to design efficient FPGA-based accelerators for neural networks, it is essential to first understand the mathematical operations that underpin modern deep learning models. Neural networks are, at their core, compositions of affine transformations and non-linear activation functions. These operations are computationally intensive and highly parallelizable, making them ideal candidates for hardware acceleration [9].

2.1. Fundamentals of Neural Network Layers

A neural network can be mathematically represented as a parameterized function $f_{\theta }:{\mathbb{R}}^n\to {\mathbb{R}}^m$, where $\theta$ denotes the set of learnable parameters (weights and biases), n is the dimension of the input feature vector, and m is the dimension of the output [10]. The function $f_{\theta }$ is typically composed of L sequential layers:

$$f_{\theta }\left(\mathbf{x}\right)=f^{\left(L\right)}\circ f^{(L-1)}\circ \dots \circ f^{\left(1\right)}\left(\mathbf{x}\right)$$

Each layer $f^{\left(l\right)}$ is generally defined by an affine transformation followed by a non-linear activation:

$${\mathbf{z}}^{\left(l\right)}={\mathbf{W}}^{\left(l\right)}{\mathbf{a}}^{(l-1)}+{\mathbf{b}}^{\left(l\right)},{\mathbf{a}}^{\left(l\right)}={\varphi }^{\left(l\right)}\left({\mathbf{z}}^{\left(l\right)}\right)$$

where:

• ${\mathbf{W}}^{\left(l\right)}\in {\mathbb{R}}^{n_l\times n_{l-1}}$ is the weight matrix for layer l,
• ${\mathbf{b}}^{\left(l\right)}\in {\mathbb{R}}^{n_l}$ is the bias vector,
• ${\varphi }^{\left(l\right)}:{\mathbb{R}}^{n_l}\to {\mathbb{R}}^{n_l}$ is the activation function (e.g., ReLU, sigmoid, tanh),
• ${\mathbf{a}}^{\left(l\right)}\in {\mathbb{R}}^{n_l}$ is the output (activation) of layer l,
• ${\mathbf{a}}^{\left(0\right)}=\mathbf{x}\in {\mathbb{R}}^{n_0}$ is the input vector.

2.2. Convolutional Layers

A convolutional layer is a special case where the affine transformation is implemented via a discrete convolution operation. Given an input feature map $\mathbf{X}\in {\mathbb{R}}^{C_{\mathrm{in}}\times H\times W}$, a convolutional kernel $\mathbf{K}\in {\mathbb{R}}^{C_{\mathrm{out}}\times C_{\mathrm{in}}\times K_H\times K_W}$, and stride s, the output feature map $\mathbf{Y}\in {\mathbb{R}}^{C_{\mathrm{out}}\times H^{\prime }\times W^{\prime }}$ is computed as:

$${\mathbf{Y}}_{c_{\mathrm{out}},h,w}=\sum _{c_{\mathrm{in}}=1}^{C_{\mathrm{in}}}\sum _{i=1}^{K_H}\sum _{j=1}^{K_W}{\mathbf{K}}_{c_{\mathrm{out}},c_{\mathrm{in}},i,j}·{\mathbf{X}}_{c_{\mathrm{in}},s·h+i,s·w+j}$$

This operation can be reformulated as a generalized matrix multiplication (GEMM) through techniques such as im2col, which enables a more straightforward mapping to hardware primitives like multiply-accumulate (MAC) units.

2.3. Activation Functions

Non-linear activation functions are essential to introduce non-linearity into the model. Some common activation functions include:

• Rectified Linear Unit (ReLU): $\varphi \left(z\right)=max(0,z)$
• Sigmoid: $\varphi \left(z\right)={\displaystyle \frac{1}{1+e^{-z}}}$
• Hyperbolic Tangent: $\varphi \left(z\right)=tanh\left(z\right)={\displaystyle \frac{e^z-e^{-z}}{e^z+e^{-z}}}$
• Softmax (for classification):

  $$\varphi {\left(\mathbf{z}\right)}_i={\displaystyle \frac{e^{z_i}}{{\sum }_{j=1}^n{e}^{z_j}}},\mathrm{for}i=1,\dots ,n$$

From a hardware perspective, the ReLU is particularly attractive due to its simplicity, requiring only a comparison and a multiplexer [11].

2.4. Fully Connected Layers

Fully connected (dense) layers can be expressed as:

$${\mathbf{a}}^{\left(l\right)}=\varphi ({\mathbf{W}}^{\left(l\right)}{\mathbf{a}}^{(l-1)}+{\mathbf{b}}^{\left(l\right)})$$

This operation is a straightforward matrix-vector multiplication, which can be parallelized at various granularities depending on the available hardware resources. FPGAs can implement this using systolic arrays, parallel MAC units, or pipelined architectures.

2.5. Loss Functions and Backpropagation

The loss function $\mathcal{L}(\mathbf{y},\widehat{\mathbf{y}})$ quantifies the discrepancy between the predicted output $\widehat{\mathbf{y}}$ and the ground truth $\mathbf{y}$. Common loss functions include mean squared error (MSE) and categorical cross-entropy. For training, the backpropagation algorithm computes gradients of the loss with respect to each parameter ${\theta }_i$ using the chain rule:

$${\displaystyle \frac{\partial \mathcal{L}}{\partial {\theta }_i}}={\displaystyle \frac{\partial \mathcal{L}}{\partial {\mathbf{a}}^{\left(L\right)}}}·{\displaystyle \frac{\partial {\mathbf{a}}^{\left(L\right)}}{\partial {\mathbf{z}}^{\left(L\right)}}}·{\displaystyle \frac{\partial {\mathbf{z}}^{\left(L\right)}}{\partial {\theta }_i}}$$

While training is generally performed offline on GPUs or cloud-based infrastructures, FPGAs are increasingly being explored for on-device training and inference fine-tuning.

2.6. Quantization and Fixed-Point Arithmetic

To reduce memory footprint and power consumption, neural networks are often quantized from floating-point to fixed-point representations. Let $x\in \mathbb{R}$ be a real number and $\widehat{x}\in \mathbb{Q}$ its quantized approximation. The quantization function $Q\left(x\right)$ can be defined as:

$$\widehat{x}=Q\left(x\right)=\mathrm{clip}\left(\mathrm{round}\left({\displaystyle \frac{x}{s}}\right),q_{min},q_{max}\right)·s$$

where $s\in \mathbb{R}$ is the scaling factor, and $q_{min},q_{max}$ define the range of quantized values (e.g., for 8-bit integers, $q_{min}=-128$, $q_{max}=127$) [12]. Fixed-point arithmetic is particularly well-suited for FPGAs due to its low hardware cost and predictable latency.

2.7. Sparsity and Pruning

Sparsity, the property of having a large number of zero-valued weights or activations, can be exploited to reduce the computational load:

$$\mathbf{y}=\mathbf{W}\mathbf{x},\mathrm{with}{W}_{ij}=0\Rightarrow \mathrm{skip}\mathrm{MAC}$$

Let ${\delta }_{ij}\in \{0,1\}$ be a binary mask denoting whether a weight is active:

$${\mathbf{y}}_i=\sum _{j=1}^n{\delta }_{ij}·W_{ij}·x_j$$

Sparse representations can be efficiently mapped to custom FPGA architectures using zero-skipping techniques and compressed storage formats (e.g., CSR, CSC).

2.8. Parallelism and Dataflow Models

FPGAs allow the exploitation of various forms of parallelism in neural network computations:

• Data-level parallelism (DLP): Simultaneous computation across input batches.
• Model-level parallelism: Distribution of model layers or channels across parallel units.
• Instruction-level parallelism: Pipelined operations at the arithmetic unit level [13].
• Bit-level parallelism: Use of bit-serial or mixed-precision computation.

Dataflow models such as weight stationary (WS), output stationary (OS), and row stationary (RS) determine how data is reused and moved within the accelerator. Each has implications for on-chip buffer design, memory bandwidth usage, and throughput [14].

2.9. Summary

The mathematical operations discussed above form the computational backbone of modern deep learning models [15]. Understanding these operations in their algebraic and numerical context is a prerequisite for designing efficient FPGA-based accelerators [16]. The next sections will delve into architectural strategies, dataflow optimization, memory management, and real-world implementations that leverage these mathematical principles to achieve high-performance inference and training on reconfigurable hardware platforms [17].

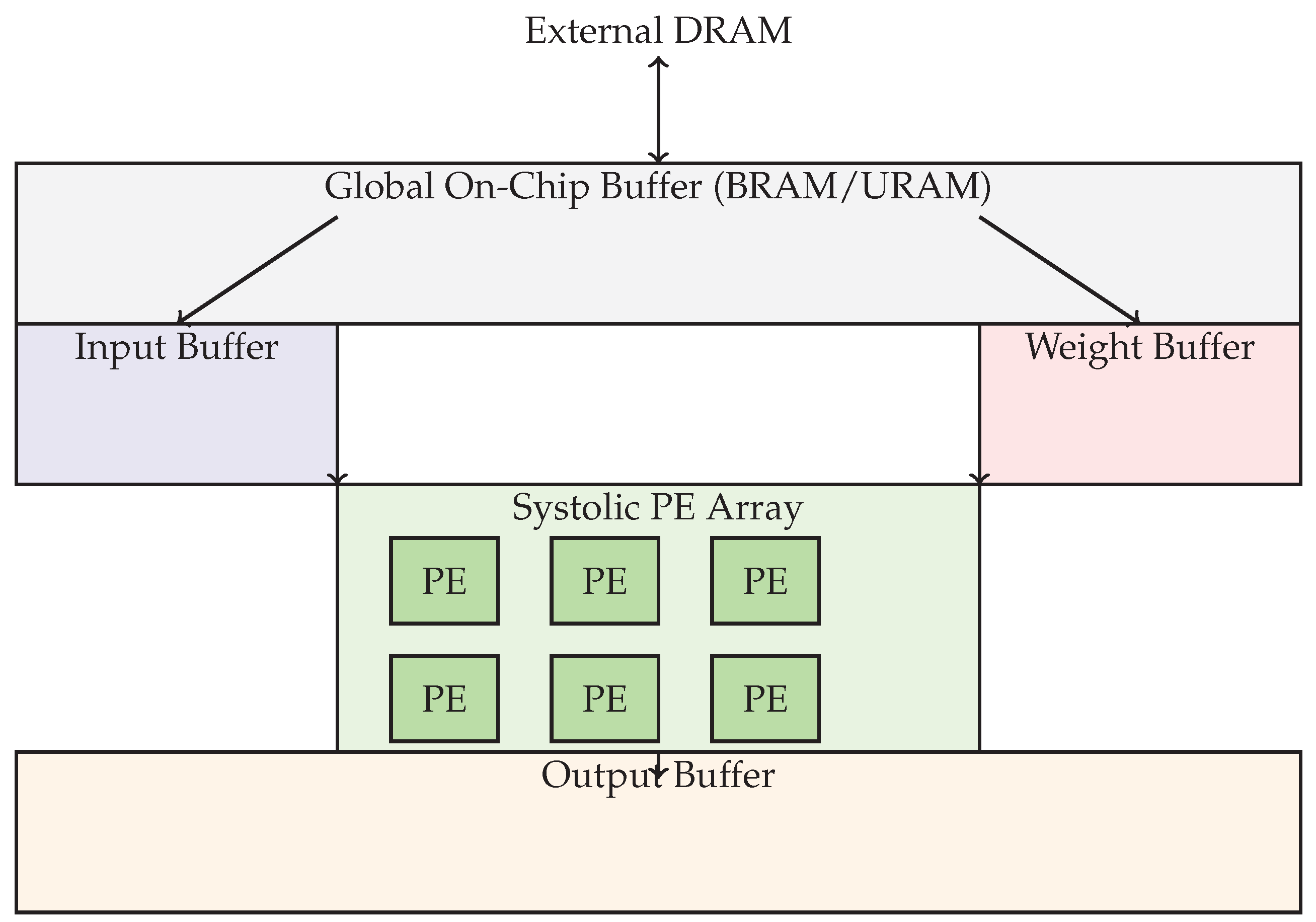
3. Architectural Design of FPGA-Based Neural Network Accelerators

Designing high-performance neural network accelerators on FPGAs necessitates a meticulous exploration of the hardware architecture that supports massively parallel, low-latency computation. Unlike general-purpose processors, FPGAs offer a reconfigurable substrate composed of logic elements, block RAMs (BRAMs), digital signal processors (DSPs), and programmable interconnects, allowing for highly customized datapaths [18]. This section presents a comprehensive analysis of architectural strategies employed in FPGA-based neural network accelerators, organized around fundamental hardware design principles and components.

3.1. Computation Units: Multiply-Accumulate (MAC) Engines

At the core of virtually every neural network accelerator lies the multiply-accumulate (MAC) unit, responsible for performing operations of the form:

$$y=\sum _{i=1}^n{w}_i·x_i$$

MAC units are implemented using FPGA DSP slices, which are optimized for fixed-point and floating-point multiplication and accumulation. A single MAC operation typically maps to:

$$\mathrm{MAC}(x_i,w_i)=\mathrm{DSP}\leftarrow (x_i·w_i)+\mathrm{acc}$$

Designers often instantiate arrays of MAC units to process multiple inputs and outputs concurrently [19]. For a layer with $N_{\mathrm{in}}$ inputs and $N_{\mathrm{out}}$ outputs, a fully parallel implementation would require $N_{\mathrm{in}}\times N_{\mathrm{out}}$ MAC units—often impractical due to resource constraints. Therefore, partial parallelism combined with time-multiplexing is commonly adopted [20].

3.2. Systolic Arrays

Systolic arrays provide a scalable architecture for implementing matrix multiplication, which underpins both fully connected and convolutional layers. A 2D systolic array comprises a grid of processing elements (PEs) that communicate in a pipelined fashion [21]. Each PE performs a MAC operation:

$${\mathrm{PE}}_{i,j}:y_{i,j}\leftarrow y_{i,j}+x_i·w_j$$

The systolic architecture is advantageous due to its regular structure, local communication, and high throughput. The matrix multiplication $\mathbf{Y}=\mathbf{W}·\mathbf{X}$, where $\mathbf{W}\in {\mathbb{R}}^{m\times n}$ and $\mathbf{X}\in {\mathbb{R}}^{n\times p}$, can be computed over a $m\times p$ PE array with input and weight matrices streamed from the edges.

3.3. On-Chip Memory Hierarchy

Efficient memory management is critical for minimizing off-chip data movement and maximizing computational efficiency [22]. FPGA designs typically employ a multi-level memory hierarchy:

• Registers: Hold temporary data within PEs (lowest latency) [23].
• Block RAMs (BRAMs): Serve as scratchpads for activations, weights, and intermediate results.
• UltraRAM (URAM): In large FPGAs, URAM provides higher capacity than BRAM [24].
• Off-chip DRAM: Stores full network parameters and batch inputs when on-chip resources are insufficient [25].

Let $A_{\mathrm{on}}$ and $W_{\mathrm{on}}$ be the sets of activations and weights stored on-chip. The goal is to maximize:

$${\displaystyle \frac{|A_{\mathrm{on}}|+|W_{\mathrm{on}}|}{|A_{\mathrm{total}}|+|W_{\mathrm{total}}|}}$$

while adhering to capacity constraints:

$$|A_{\mathrm{on}}|·b_a+\left|W_{\mathrm{on}}\right|·b_w\le M_{\mathrm{BRAM}}+M_{\mathrm{URAM}}$$

where $b_a,b_w$ denote the bit widths of activations and weights, respectively [26].

3.4. Dataflow Models

The choice of dataflow model significantly impacts buffer reuse, interconnect traffic, and latency [27]. Common models include:

• Weight Stationary (WS): Keep weights static in PEs while inputs and outputs move [28].

  $$\mathrm{Reuse}\text{:}{w}_{ij}\mathrm{used}{N}_{\mathrm{in}}\mathrm{times}$$
• Output Stationary (OS): Keep partial sums in registers, accumulating contributions from streamed weights and inputs.

  $$y_j^{\left(k\right)}=y_j^{\left(k\right)}+w_{ij}·x_i$$
• Row Stationary (RS): Optimizes reuse of weights, inputs, and partial sums by tiling the computation.
• No Local Reuse (NLR): Stream-based architectures that do not exploit data reuse but allow pipelining and high throughput for small models.

Let $R_w,R_x,R_y$ be the number of times a weight, input, or output is reused in a given schedule. The goal is to maximize reuse:

$$max\left({\alpha }_w{R}_w+{\alpha }_x{R}_x+{\alpha }_y{R}_y\right)$$

subject to memory and PE bandwidth constraints [29].

3.5. Control Logic and Scheduling

Control logic orchestrates the flow of data and execution of operations across PEs. A static schedule assumes a fixed topology and order of operations, whereas a dynamic schedule supports control flow for models with conditional branches, loops, or varying layer configurations. For example, a control FSM (finite state machine) might be used to sequence the following phases:

• Load weights from DRAM to BRAM.
• Stream activations into the systolic array [30].
• Accumulate results and apply activation.
• Store output to BRAM or DRAM.

Designers aim to minimize idle cycles and maximize PE utilization:

$$\mathrm{Utilization}={\displaystyle \frac{T_{\mathrm{active}}}{T_{\mathrm{total}}}}$$

where $T_{\mathrm{active}}$ denotes the time PEs are performing valid MAC operations [31].

3.6. Pipeline and Parallelism Strategies

Pipeline parallelism is exploited at multiple granularities:

• Inter-layer pipelining: Consecutive layers process different data samples in parallel [32].
• Intra-layer pipelining: Separate pipeline stages for fetch, compute, accumulate, and write-back.
• Loop unrolling: Explicit replication of hardware for inner loops of MAC operations.

Given a loop nest:

$$\mathtt{for}i=1\mathtt{to}N\mathtt{do}y+=w_i·x_i$$

an unrolling factor U yields a speedup of approximately:

$$\mathrm{Speedup}\approx min\left(U,{\displaystyle \frac{N}{L}}\right)$$

where L is the latency per MAC.

3.7. Parameterization and Design Space Exploration

Modern accelerators are often fully parameterized in terms of:

$$\left\{T_x,T_y,P_w,P_a,b_w,b_a\right\}$$

where:

• $T_x,T_y$: Tiling factors for input and output.
• $P_w,P_a$: Parallelism factors for weights and activations.
• $b_w,b_a$: Bit widths of weights and activations.

Exploring this design space involves a multi-objective optimization problem:

$$\underset{\theta \in \Theta }{max}\left[\mathrm{Throughput}\left(\theta \right),\mathrm{Energy}\mathrm{Efficiency}\left(\theta \right)\right]\mathrm{s}.\mathrm{t}\left[33\right].\mathrm{Resource}\mathrm{Usage}\left(\theta \right)\le R_{\max }$$

Techniques such as analytical modeling, design space pruning, and evolutionary algorithms are employed to identify Pareto-optimal configurations.

3.8. Summary

The architectural design of FPGA-based neural network accelerators involves a rich interplay between algorithmic properties, hardware constraints, and system-level objectives. By leveraging fine-grained parallelism, reconfigurable datapaths, and customized memory hierarchies, FPGAs offer a unique platform for efficient deep learning inference. The next section will delve into optimization techniques, including quantization, pruning, and mixed-precision computation, that further enhance performance and resource efficiency in these architectures[34].

4. Optimization Techniques for FPGA-Based Neural Network Accelerators

The inherent flexibility of FPGAs makes them well-suited for implementing a wide array of architectural and algorithmic optimizations that are crucial for accelerating deep neural networks [35]. These optimizations are necessary not only to meet stringent constraints on power, area, and latency but also to fully exploit the potential of reconfigurable hardware in domains such as edge computing, embedded vision, and autonomous systems. In this section, we explore a range of key optimization strategies in extreme detail, beginning with numerical precision reduction techniques and proceeding through structural network simplification, dataflow enhancement, and hardware-aware neural architecture search [36]. One of the most impactful optimizations for FPGA-based neural network accelerators is numerical precision reduction through quantization. Unlike GPUs and CPUs, which are often optimized for IEEE 754 floating-point arithmetic, FPGAs allow designers to choose arbitrary bit widths and numeric representations, enabling a fine-grained trade-off between accuracy, resource utilization, and throughput [37]. Quantization involves converting the high-precision weights and activations of a neural network (typically 32-bit floating-point) into lower-precision fixed-point or integer representations. Let $w\in \mathbb{R}$ be a real-valued weight, and let $\widehat{w}=Q\left(w\right)\in \mathbb{Z}$ be its quantized form. The quantization function Q can be linear (uniform quantization) or non-linear (logarithmic, k-means-based, etc.). Uniform affine quantization maps a continuous value to an integer as $\widehat{w}=\mathrm{round}(w/s)$, where s is the scaling factor. During inference, this is reversed via dequantization: $w\approx \widehat{w}·s$[38]. On FPGAs, quantized operators reduce both computation time and memory bandwidth, allowing, for instance, an 8-bit MAC unit to consume one-fourth the resources of a 32-bit floating-point equivalent. More aggressive schemes, such as binary neural networks (BNNs) and ternary weight networks, push this concept further by restricting weights and activations to {−1, +1} or {−1, 0, +1}, enabling the replacement of multipliers with XNOR or multiplexing logic. However, aggressive quantization introduces accuracy degradation, which must be compensated by retraining or fine-tuning [39]. FPGA accelerators often support mixed-precision designs, where critical layers (e.g., first and last layers) operate at higher bit widths (e.g., 16-bit) while intermediate layers use lower precision (e.g., 4- or 8-bit), thus balancing accuracy and efficiency. Bit-serial arithmetic and approximate computing techniques may also be employed to further reduce logic usage, although this increases control complexity and may introduce non-negligible latency overheads. Another major optimization technique is network pruning, which aims to eliminate redundant parameters and computations from neural networks [40]. By leveraging the observation that many weights in a trained network contribute negligibly to its final output, pruning algorithms generate sparse networks by zeroing out small-magnitude weights or removing entire neurons, channels, or filters. Mathematically, pruning can be viewed as applying a sparsity-inducing regularizer (e.g., ${\ell }_1$ norm) during training, leading to a weight tensor $\mathbf{W}$ such that ${\parallel \mathbf{W}\parallel }_0\ll \mathrm{dense}\left(\mathbf{W}\right)$. For example, structured pruning eliminates entire rows or columns of the weight matrix, preserving compatibility with parallel computation, whereas unstructured pruning leads to arbitrary sparsity patterns that require index bookkeeping and zero-skipping logic during execution. On FPGAs, sparsity is particularly advantageous, as unnecessary MAC operations can be completely omitted, reducing dynamic power and enabling higher clock frequencies due to lower switching activity. To efficiently map sparse networks onto FPGAs, accelerators may use compressed sparse row (CSR), compressed sparse column (CSC), or coordinate list (COO) representations, alongside custom decoders and address generators to fetch non-zero values and their indices [41]. However, the irregular access patterns introduced by unstructured sparsity can negate the performance benefits unless carefully managed [42]. Structured pruning, by contrast, allows entire computation blocks to be bypassed or removed at compile-time, resulting in more predictable and scalable performance. Pruning is often combined with quantization, a synergy known as quantization-aware pruning, which maximizes the reduction in memory footprint while minimizing accuracy loss [43]. Data reuse and locality-aware scheduling are additional critical optimizations for FPGAs, where the high cost of off-chip memory accesses necessitates minimizing redundant data transfers [44]. Convolutional neural networks, in particular, exhibit substantial input, weight, and output reuse, which can be exploited through loop tiling, loop interchange, and caching strategies [45]. For example, in a convolutional layer with kernel size $K\times K$, stride S, and input feature map of size $H\times W$, each weight element is reused $\left({\displaystyle \frac{H-K}{S}}+1\right)·\left({\displaystyle \frac{W-K}{S}}+1\right)$ times, assuming no padding. Likewise, input pixels participate in multiple overlapping convolution windows [46]. An efficient accelerator must schedule operations such that these reused values remain on-chip as long as possible, residing in local registers or BRAMs. Tiling breaks down the input/output tensors into smaller blocks that fit within the available memory, allowing temporal reuse of weights and activations while avoiding off-chip memory thrashing. Loop interchange further helps by adjusting the order of nested loops to maximize reuse factors [47]. Designers often employ analytical models or performance simulators to derive optimal tiling factors and buffer sizes that balance latency, memory usage, and parallelism. Data reuse is especially effective when combined with output-stationary or row-stationary dataflows, which preserve partial sums in registers or local BRAMs throughout the computation, thereby minimizing intermediate data movement [48]. At a higher level, DMA engines and burst-mode memory access patterns are used to optimize DRAM transactions, and double buffering is adopted to overlap data transfer with computation [49]. Finally, a rapidly emerging field of optimization is hardware-aware neural architecture search (NAS), which aims to automatically discover network topologies that are co-optimized for accuracy and hardware efficiency [50]. Unlike traditional NAS that searches purely for accuracy under generic constraints (e.g., FLOPs), hardware-aware NAS explicitly incorporates metrics such as latency, LUT/DSP/BRAM usage, and energy into its search objective. Let $\mathcal{A}=\{a_1,a_2,\dots ,a_n\}$ be the space of architectural candidates, and let $\mathcal{O}:\mathcal{A}\to {\mathbb{R}}^k$ be a vector-valued objective function capturing k design goals (e.g., accuracy, power, inference time). Then NAS solves:

$$\underset{a\in \mathcal{A}}{min}\mathcal{L}\left(a\right)={\lambda }_1·\mathrm{Loss}\left(a\right)+{\lambda }_2·\mathrm{Latency}\left(a\right)+{\lambda }_3·\mathrm{Resources}\left(a\right)$$

where ${\lambda }_i$ are weights reflecting design trade-offs. In practice, latency and resource usage must be estimated or measured on a target FPGA using cost models or hardware emulation. Search strategies such as reinforcement learning, evolutionary algorithms, or differentiable architecture search (DARTS) guide the exploration of this vast design space [51]. Importantly, the discovered architectures often feature non-standard operations (e.g., separable convolutions, group convolutions, channel shuffle) that can be challenging to implement efficiently on FPGAs unless the accelerator is highly modular and reconfigurable [52]. Therefore, a co-design methodology, where both the neural network and hardware architecture evolve in tandem, is critical to achieving optimal performance. In summary, optimization techniques for FPGA-based neural network accelerators span a diverse array of numerical, structural, and architectural domains. Quantization reduces arithmetic complexity, pruning eliminates redundancy, data reuse enhances memory efficiency, and NAS introduces automation and intelligence into the design loop [53]. Each of these techniques can be implemented at various granularities and may be interdependent, requiring careful integration into the accelerator design process. As neural networks grow in complexity and deployment moves toward resource-constrained environments, such optimizations are not merely desirable but essential for achieving real-time, energy-efficient inference on reconfigurable hardware.

5. Case Studies and Benchmarking of FPGA-Based Neural Network Accelerators

To concretely demonstrate the practical relevance and performance trade-offs of FPGA-based neural network accelerators, it is instructive to examine a variety of case studies drawn from the literature and industrial implementations. These case studies highlight diverse application domains—such as image classification, object detection, natural language processing, and anomaly detection—and reveal the impact of architectural decisions, optimization techniques, and hardware resource allocation on critical metrics including throughput, latency, energy efficiency, and logic utilization. Despite the diversity of platforms and neural network workloads, certain architectural themes and performance trends consistently emerge, providing valuable insights for future accelerator design [54]. Consider, for example, the Xilinx Deep Learning Processing Unit (DPU), a commercial FPGA IP core designed for high-throughput CNN inference [55]. The DPU adopts a deeply pipelined, VLIW-style architecture that features parallel MAC engines, configurable weight/activation bit widths, and multiple compute units operating in parallel. In representative configurations targeting the Zynq UltraScale+ MPSoC platform, the DPU achieves performance levels of over 200 GOPS (giga-operations per second) while sustaining a power envelope below 5W. Performance is achieved by integrating multiple optimization techniques described in previous sections: quantization-aware training (INT8 inference), aggressive loop tiling, a unified on-chip memory for fast data reuse, and a compiler-assisted instruction scheduling engine that statically analyzes data dependencies. Importantly, the DPU is tailored for specific workload classes such as MobileNet and ResNet, and it incorporates prefetching and caching strategies to mitigate DRAM access latency. Academic designs such as the MIT Eyeriss architecture also illustrate key trade-offs. Eyeriss introduced the concept of row-stationary dataflow, which prioritizes on-chip reuse of partial sums and weights over raw throughput. This design choice leads to a more balanced use of resources, favoring energy efficiency and flexibility. Eyeriss maps each processing element in a 2D array to a spatially-aware data reuse pattern, which, combined with on-chip global buffers and a hierarchical NoC (network-on-chip), allows it to dynamically adjust to different layers of a CNN [56]. While its peak performance may be lower than purely throughput-optimized designs, its energy per inference is significantly reduced, making it ideal for embedded and mobile environments. To provide a generalized abstraction of these types of FPGA accelerators, we can visualize a parameterized hardware architecture that illustrates the interaction between computation units, memory hierarchies, and control infrastructure. Figure 1 presents a simplified but representative model.

This architecture comprises several major subsystems [58]. At the top lies the global on-chip buffer, typically composed of BRAM or URAM blocks, responsible for staging data transferred from external DRAM [59]. Input activations and weights are partitioned and routed to dedicated local buffers, which in turn feed a 2D systolic array of processing elements. Each PE performs a multiply-accumulate operation on incoming streams of activations and weights, either broadcasting or shifting data through the array depending on the dataflow strategy. Outputs are accumulated either within the array or in a dedicated accumulator buffer and then passed to the output buffer, which stores the final results or intermediate feature maps before offloading to DRAM [60]. Throughout the system, control logic orchestrates data transfers, synchronization, and instruction sequencing, while DMA engines ensure burst transfers and memory coalescing. Benchmarking results across various platforms and networks underscore the performance variability introduced by hardware configuration, optimization depth, and workload characteristics. For instance, on an Intel Stratix 10 FPGA, a hand-optimized design implementing ResNet-50 with INT8 quantization and pipelined convolution blocks achieved over 500 GOPS at 250 MHz, with resource utilization peaking at 80% of available DSPs and 60% of BRAM [61]. In contrast, a design targeting a smaller Artix-7 FPGA implementing a binarized neural network (BNN) reported inference latencies under 1 ms with power consumption under 1 W, albeit with lower classification accuracy [62]. Such comparisons emphasize the importance of matching design objectives to application constraints, and they highlight the tunability of FPGAs as a unique advantage over fixed-architecture ASICs or GPUs [63]. To enable fair benchmarking, standardized datasets (e.g., ImageNet, CIFAR-10), reference networks (e.g., AlexNet, VGG, MobileNet), and open-source design flows (e.g., FINN, hls4ml, VTA) are increasingly employed by the FPGA research community [64]. Metrics such as GOPS/W (operations per watt), inference per second (IPS), resource utilization breakdown (LUTs, FFs, DSPs, BRAMs), and end-to-end latency are typically reported. However, care must be taken in comparing results due to differences in precision, batch size, clock frequency, and toolchain efficiency [65]. Despite these challenges, case studies remain an essential part of evaluating and advancing the state of FPGA-based neural network acceleration, serving as both proof of concept and validation of architectural innovation.

6. Comparison with GPU and ASIC Accelerators

While FPGAs have emerged as a powerful and flexible platform for accelerating deep neural networks, they coexist in a broader ecosystem of specialized hardware that includes graphics processing units (GPUs) and application-specific integrated circuits (ASICs). Each of these platforms exhibits distinct strengths and limitations in terms of performance, energy efficiency, programmability, scalability, and cost, and the decision to adopt a particular solution depends heavily on the target application domain, deployment context, and workload characteristics. This section provides an in-depth comparative analysis of FPGAs versus GPUs and ASICs, examining architectural differences, design trade-offs, toolchain maturity, and real-world deployment considerations [66]. At a high level, the most prominent advantage of GPUs lies in their extremely high throughput, enabled by hundreds to thousands of parallel cores and a SIMT (single instruction, multiple threads) execution model. GPUs excel in batch processing of large datasets, especially in training scenarios, due to their optimized floating-point arithmetic units and fast global memory bandwidth. In contrast, ASICs represent the pinnacle of specialization; they are designed for a single application or a narrow range of tasks and can achieve unmatched energy efficiency and throughput-per-watt by eliminating all unnecessary logic, tailoring every aspect of the microarchitecture to the target workload. FPGAs occupy the space between these two extremes: more flexible and reprogrammable than ASICs, yet more energy-efficient and application-customizable than GPUs. Their unique value proposition lies in their ability to implement application-specific parallelism, custom data paths, and non-standard precision formats, while still allowing post-fabrication reconfiguration. Table 1 summarizes the comparative characteristics of FPGAs, GPUs, and ASICs across multiple dimensions relevant to neural network acceleration [67].

As shown in Table 1, the trade-off between performance and flexibility is central to the choice among FPGA, GPU, and ASIC accelerators. FPGAs offer a compelling balance for edge deployment scenarios where inference must be performed under tight power and latency budgets, and where workloads may evolve post-deployment. Unlike ASICs, which cannot be reconfigured once manufactured, FPGAs allow for iterative updates, making them suitable for prototyping, low-volume deployment, and field-reprogrammable systems such as autonomous drones, smart cameras, or portable medical devices [68]. They are also advantageous in situations where custom dataflows or exotic network topologies (e.g., transformer variants or sparse CNNs) must be mapped efficiently, something that GPUs often struggle with due to rigid memory hierarchies and SIMT constraints. However, FPGAs also come with notable challenges. Their programming model is more complex and less accessible than that of GPUs, often requiring domain-specific hardware knowledge or the use of high-level synthesis (HLS) tools that may not generate optimal hardware by default [69]. Despite significant advances in design automation (e.g., vendor platforms such as Xilinx Vitis AI and Intel OpenVINO), the development cycle remains longer than for GPU-based inference. Moreover, FPGAs tend to have lower clock frequencies than GPUs or ASICs and may suffer from underutilization if the accelerator is not properly tailored to the specific workload [70]. On the other hand, ASICs, while representing the gold standard in terms of energy and throughput, require enormous up-front investment in design, verification, and silicon fabrication, which limits their use to high-volume deployments such as smartphone SoCs, data center TPUs, or automotive-grade ADAS chips. In conclusion, while GPUs remain dominant in large-scale deep learning training and ASICs deliver unmatched efficiency in mass-produced products, FPGAs offer a unique middle ground that blends flexibility, efficiency, and customizability. Their ability to support custom numeric formats, layer-specific acceleration strategies, and dataflow-aware architectures make them an essential tool in the hardware acceleration toolbox, particularly as the field shifts toward edge intelligence, heterogeneous computing, and rapid deployment of new model variants. Understanding the detailed trade-offs among these platforms is therefore critical for system architects aiming to deploy robust, efficient, and scalable AI systems.

7. Challenges and Future Directions in FPGA-Based Neural Network Acceleration

Despite the growing maturity and demonstrated success of FPGA-based neural network accelerators, the domain continues to grapple with numerous technical, practical, and systemic challenges [71]. These challenges span from low-level hardware limitations to high-level software abstraction barriers and deployment ecosystem gaps. Overcoming these issues is essential not only for scaling current FPGA-based solutions to meet the increasingly complex demands of modern AI workloads, but also for expanding their accessibility to a broader community of developers, researchers, and system integrators. At the same time, the field presents an abundance of future opportunities—from tighter hardware-software co-design methodologies to the integration of emerging memory technologies and adaptive runtime systems—which collectively point toward a vibrant and innovative trajectory for the next generation of FPGA-accelerated machine learning systems [72]. One of the most persistent challenges in this space is the difficulty of achieving both high performance and ease of programmability. Traditional hardware design using register-transfer level (RTL) languages such as Verilog or VHDL is both time-consuming and error-prone, requiring deep expertise in digital logic design, timing analysis, and FPGA-specific constraints such as clock domain crossing, floorplanning, and resource budgeting [73]. High-Level Synthesis (HLS) has emerged as a promising alternative, allowing designers to describe functionality in C/C++ or OpenCL, but current HLS tools often suffer from suboptimal code generation, opaque optimization decisions, and steep learning curves when tuning performance-critical constructs such as loop unrolling, memory partitioning, and pipelining. Furthermore, machine learning models themselves are increasingly authored in high-level frameworks like PyTorch or TensorFlow, creating a semantic gap between network designers and hardware architects [74]. Bridging this divide requires a new generation of compiler and synthesis tools that can automatically map high-level neural network descriptions into efficient hardware implementations, with minimal manual intervention. Projects such as hls4ml, FINN, and VTA (Versatile Tensor Accelerator) are steps in this direction, but the general problem of automated, high-performance hardware generation from abstract model specifications remains unsolved. Resource limitations and hardware constraints also pose substantial hurdles. Unlike ASICs, which can be engineered to include precisely the resources needed for a given neural network workload, FPGAs must work within fixed budgets of logic elements, DSP blocks, on-chip memory (BRAM/URAM), and I/O bandwidth. For large-scale models such as BERT, GPT, or even deep convolutional networks with extensive parameter counts, naïve mappings onto FPGAs can easily exceed available resources, resulting in the need for aggressive quantization, pruning, or off-chip data transfers that reduce computational efficiency [75]. Moreover, managing memory hierarchy on FPGAs remains a complex task; the lack of hardware-managed caches necessitates explicit control over buffer sizing, data reuse, and access scheduling. Inefficient memory use not only limits performance but can also cause severe timing closure issues, as routing congestion and excessive fanout delay signal propagation across the FPGA fabric. The development of new memory-centric accelerator architectures, possibly leveraging high-bandwidth memory (HBM), 3D stacked memory, or near-memory compute primitives, represents a promising direction to address this bottleneck. Another pressing issue lies in the lack of robust support for dynamic workloads [76]. Most FPGA accelerators for neural networks are statically scheduled and optimized for fixed model architectures and dimensions [77]. This inflexibility can become a serious limitation in real-world deployment scenarios where models evolve, inputs vary in shape or size, or multiple applications share the same compute platform. Dynamically reconfigurable FPGAs and partial reconfiguration offer a path toward addressing this issue, but current toolchains for partial reconfiguration are immature, slow, and incompatible with rapid model iteration cycles [78]. Runtime-adaptive architectures that support multiplexed execution, elastic data paths, and configurable compute fabrics may alleviate these limitations, but they introduce additional complexity in control logic, verification, and resource sharing [79]. A future trend may involve hybrid solutions in which FPGAs act as dynamic co-processors working alongside general-purpose processors or ASICs, orchestrated by intelligent scheduling software that performs real-time workload profiling and accelerator tuning. Security and reliability are additional challenges that are increasingly important as FPGAs are deployed in edge environments with limited physical and cyber protections. Unlike ASICs or secure enclaves within CPUs/GPUs, FPGAs are often susceptible to side-channel attacks, bitstream manipulation, and denial-of-service conditions caused by hostile reconfiguration or logic overuse. Ensuring secure deployment involves encryption of bitstreams, attestation mechanisms, and possibly runtime monitoring of logic behavior, all of which add overhead and require standardized support from FPGA vendors and tool providers [80]. In mission-critical applications such as autonomous driving, healthcare diagnostics, and aerospace, the lack of fault tolerance and error recovery mechanisms in FPGA-based accelerators presents a potential liability [81]. Introducing redundancy, error-correcting codes, and self-healing fabrics may provide avenues to address these concerns, albeit at a cost in area and power [82]. Looking forward, the co-evolution of machine learning models and FPGA architectures is likely to define the next era of research. New model paradigms such as spiking neural networks, neuromorphic computing, and transformer-inspired lightweight attention mechanisms will push the boundaries of what FPGA-based accelerators must support [83]. These models may offer novel sparsity patterns, temporal computation styles, or graph-based connectivity that diverge significantly from the grid-based convolutional and MLP patterns commonly optimized today [84]. Adapting FPGA architectures to efficiently support such models will likely require novel interconnect topologies, more granular control over compute sequencing, and the exploration of non-Von Neumann paradigms such as in-memory computing. At the same time, advances in chiplet-based design and heterogeneous integration may allow FPGAs to be embedded more closely with other accelerators and memory devices on a shared interposer, enabling high-bandwidth, low-latency communication across system components [85]. In summary, while FPGA-based neural network accelerators have made significant strides in recent years, particularly in embedded and low-latency inference scenarios, they face a constellation of challenges that span hardware design, software tooling, resource constraints, and security. Addressing these challenges will require coordinated efforts from the broader computing research community, FPGA vendors, compiler developers, and machine learning practitioners [86]. By pushing forward on these fronts, the field can unlock the full potential of FPGAs as reconfigurable, efficient, and versatile platforms for next-generation AI [87].

8. Conclusions

The landscape of deep learning acceleration is increasingly shaped by the dual imperatives of performance and adaptability, and within this evolving context, FPGA-based neural network accelerators have emerged as a compelling and versatile solution. Their inherent reconfigurability, energy efficiency, and suitability for custom precision and dataflow optimizations position FPGAs as a uniquely powerful platform at the intersection of software-defined flexibility and hardware-level specialization. This review has examined the architectural foundations, design strategies, comparative performance metrics, and development ecosystems surrounding FPGA-based accelerators, offering a panoramic view of their capabilities, limitations, and trajectory.

Central to the appeal of FPGAs is their capacity for fine-grained control over computation. Unlike GPUs, which enforce a rigid SIMT model, or ASICs, which are locked into pre-defined execution pipelines, FPGAs enable architects to create deeply pipelined, parallel, and task-specialized hardware units that are precisely tailored to the structure and requirements of individual neural networks. This ability to co-optimize data movement, arithmetic precision, memory hierarchy, and control logic leads to highly efficient accelerators that outperform general-purpose hardware on specific workloads, particularly in low-batch, latency-sensitive, and edge-deployed inference applications. The support for customized low-precision formats—ranging from INT8 down to binary representations—not only reduces the hardware footprint and memory bandwidth requirements but also enables higher degrees of parallelism, directly improving throughput without sacrificing accuracy in many cases.

Moreover, the reprogrammable nature of FPGAs introduces an unparalleled level of post-deployment adaptability. As machine learning models evolve rapidly, and as new architectural innovations such as transformer variants, attention-based mechanisms, and sparsity-aware layers become more prevalent, FPGA accelerators can be updated via bitstream reconfiguration to accommodate these changes without the need for new silicon. This characteristic makes FPGAs highly suitable for prototyping, iterative model deployment, and field upgrades in long-lifecycle systems such as autonomous robots, IoT devices, and embedded medical platforms. In contrast, ASIC-based accelerators, while extremely efficient, are fundamentally limited by their static design and long development cycles, rendering them inflexible to evolving standards or emerging model innovations.

That said, the review has also identified significant challenges that continue to hinder the widespread adoption of FPGA-based accelerators in commercial and research applications. Chief among these are the steep learning curve associated with hardware development, the complexity of current toolchains, and the lack of seamless integration with mainstream deep learning frameworks. Although recent progress in high-level synthesis (HLS), domain-specific compilers, and open-source initiatives such as FINN, hls4ml, and VTA has narrowed this gap, the overall hardware design process remains more fragmented and less accessible compared to the well-established GPU programming ecosystem. Furthermore, issues related to timing closure, resource fragmentation, and memory management demand considerable hardware design expertise, limiting the speed and scalability with which new accelerators can be brought to deployment.

From a systems perspective, limitations in bandwidth, on-chip memory capacity, and dynamic reconfigurability continue to constrain the types of workloads that FPGAs can efficiently support. Large-scale transformer models, multi-tenant inference services, and training workloads with highly variable memory access patterns remain better served by GPU or ASIC platforms—at least for now. However, as the FPGA ecosystem begins to incorporate technologies such as high-bandwidth memory (HBM), chiplet integration, and runtime reconfigurable fabrics, it is plausible that many of these barriers will be gradually mitigated. The rise of heterogeneous computing platforms that combine CPUs, GPUs, FPGAs, and domain-specific accelerators under a unified programming interface also points toward a future in which FPGAs function not in isolation but as dynamically deployable components in an intelligent orchestration framework.

In light of the detailed analysis presented in this review, it is evident that the future of FPGA-based neural network acceleration is both promising and complex. The key to unlocking their full potential lies not only in advancing FPGA hardware itself but also in rethinking the broader compiler toolchains, abstraction layers, and co-design methodologies that underpin their integration into the machine learning development lifecycle. There is a pressing need for more expressive programming models, automated optimization flows, and flexible deployment frameworks that allow software engineers to harness the benefits of FPGA acceleration without requiring deep hardware expertise. Additionally, stronger standardization, open tooling, and ecosystem collaboration will be essential to reduce fragmentation and foster innovation.

Ultimately, as AI systems continue to permeate domains as diverse as healthcare, finance, robotics, and scientific discovery, the demand for efficient, scalable, and adaptable inference hardware will only intensify. FPGA-based neural network accelerators—by virtue of their unique combination of performance, efficiency, and programmability—are well-positioned to play a critical role in meeting this demand. Whether as standalone inference engines, co-processors in heterogeneous computing stacks, or adaptable edge platforms in the Internet of Things, FPGAs offer a path toward deploying advanced neural networks in environments that demand more than what general-purpose processors can deliver. Realizing this vision, however, will require sustained research, cross-disciplinary collaboration, and continued evolution in both hardware and software—a challenge that, if met, could significantly reshape the future of intelligent computation.