Submitted:
30 August 2024
Posted:
30 August 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Theoretical Formulation
2.1. Basic Equations
2.2. Modeling of the Fluid-Shell Interaction
2.3. Dispersion of State-Space Equations
2.4. Vibration Analysis
3. Numerical Results and Discussion
3.1. Convergence and Validation Studies
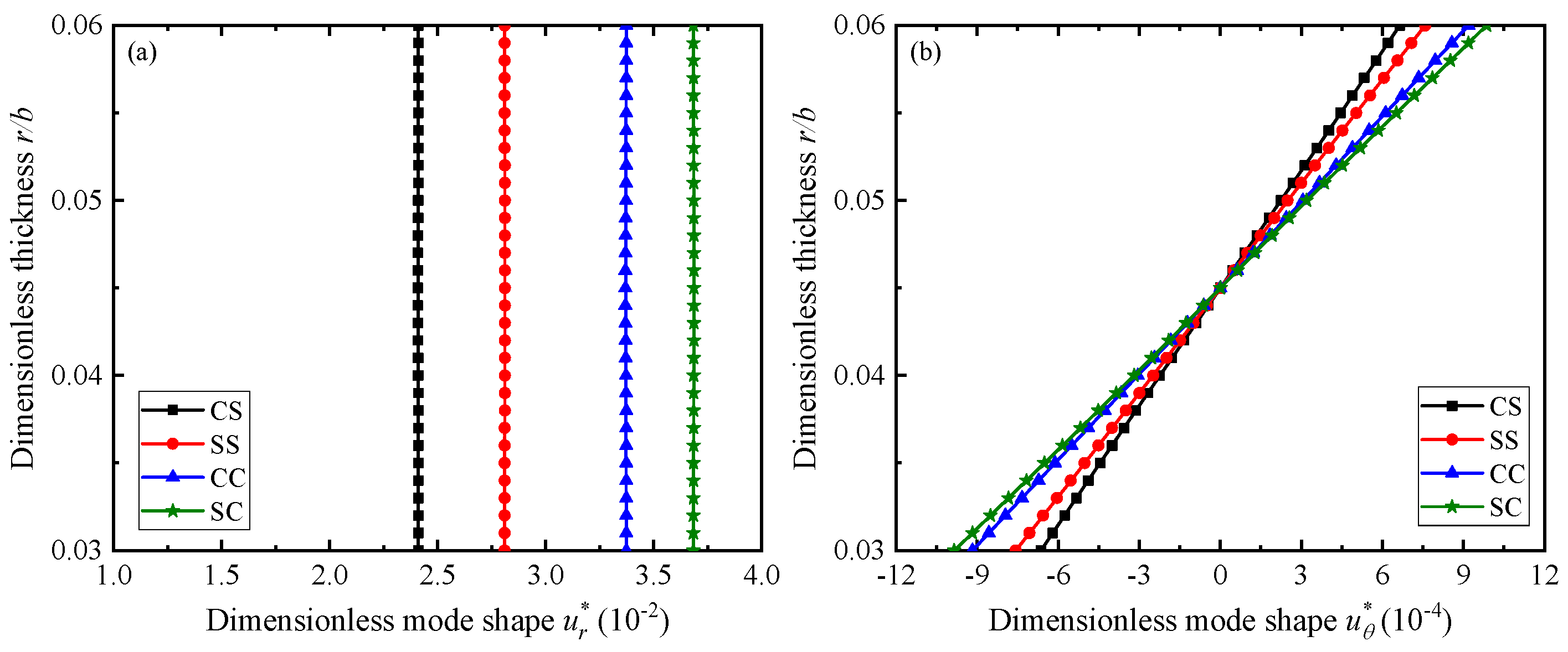
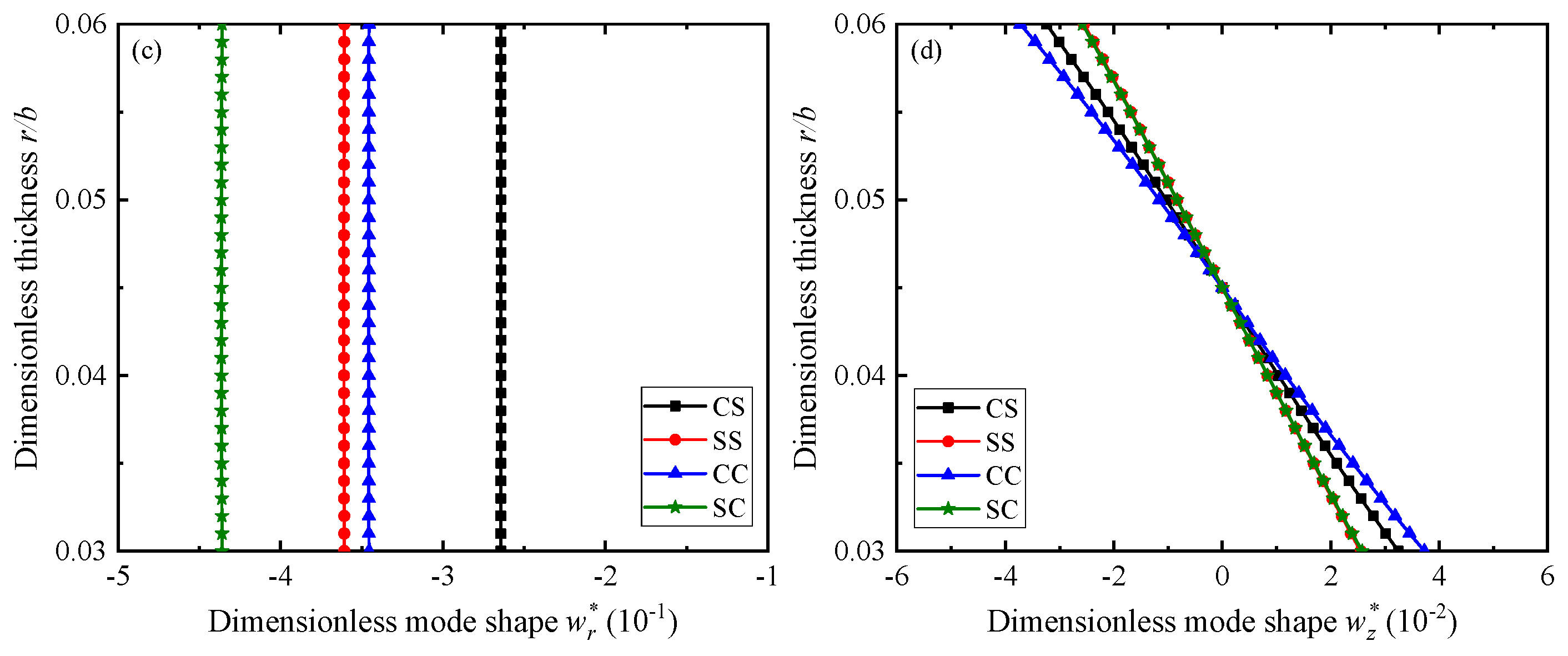
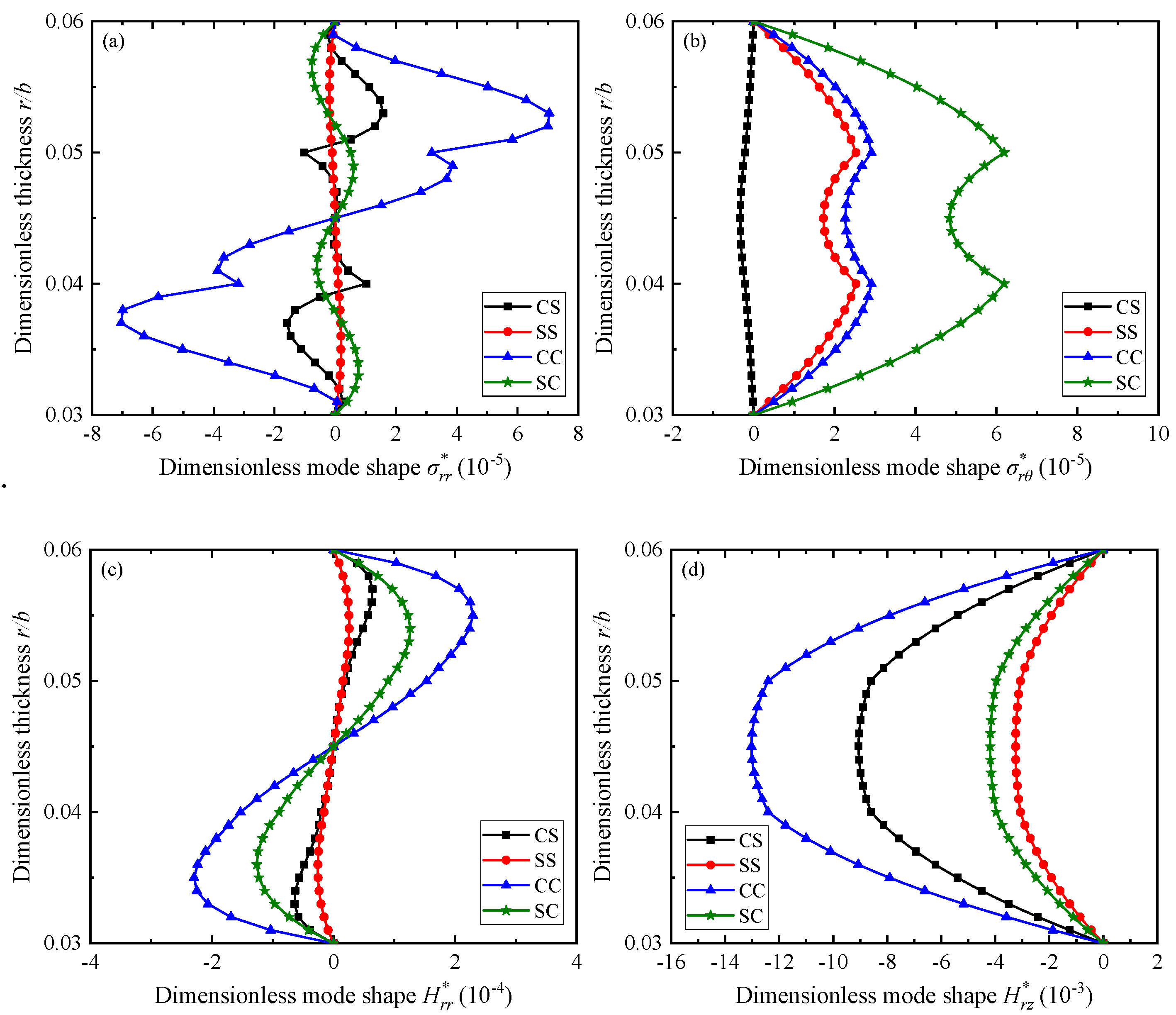
3.2. QC Annular Plates with Different Boundary Conditions
3.3. Dynamic Behavior of the Empty and Fluid-Filled Shell
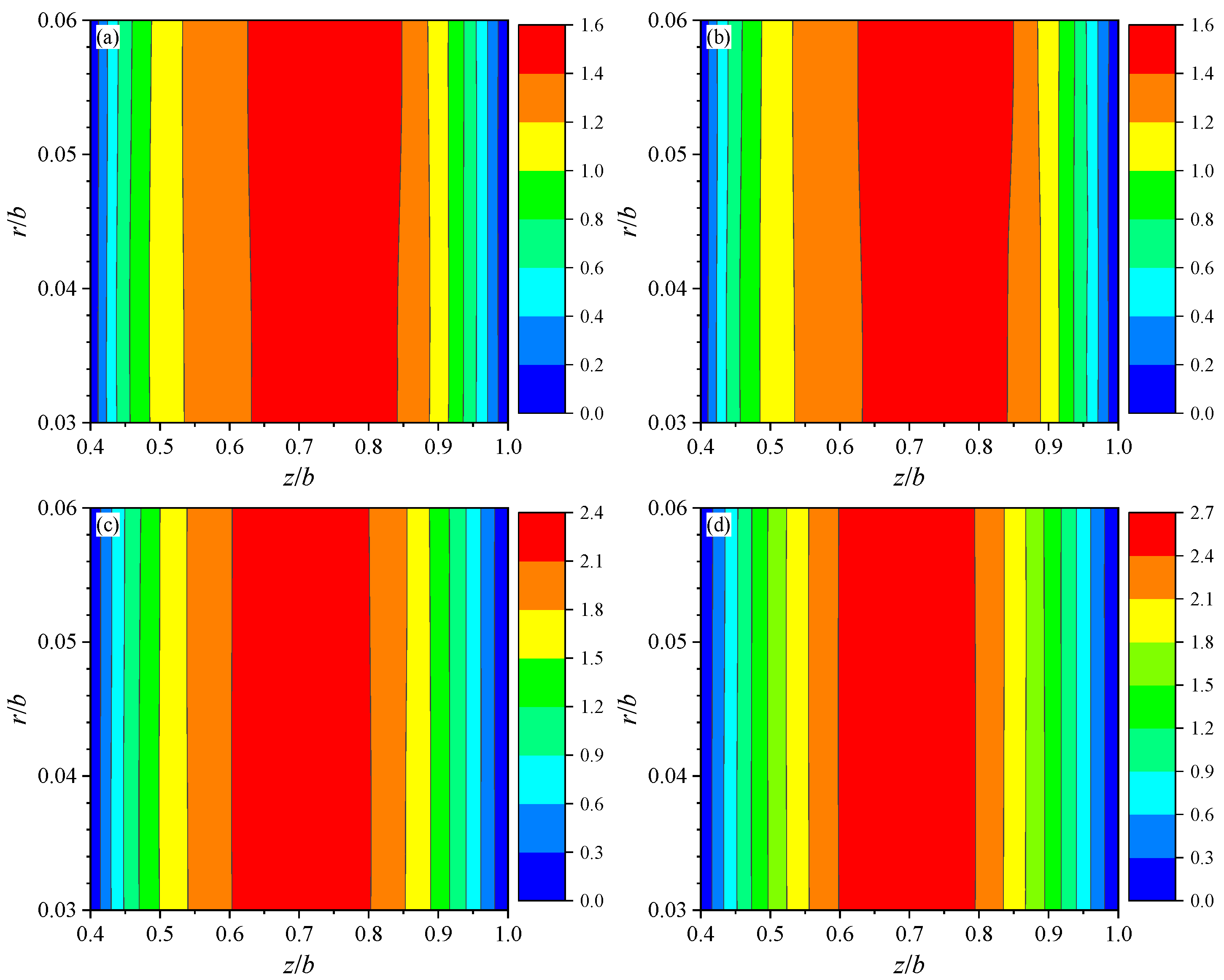

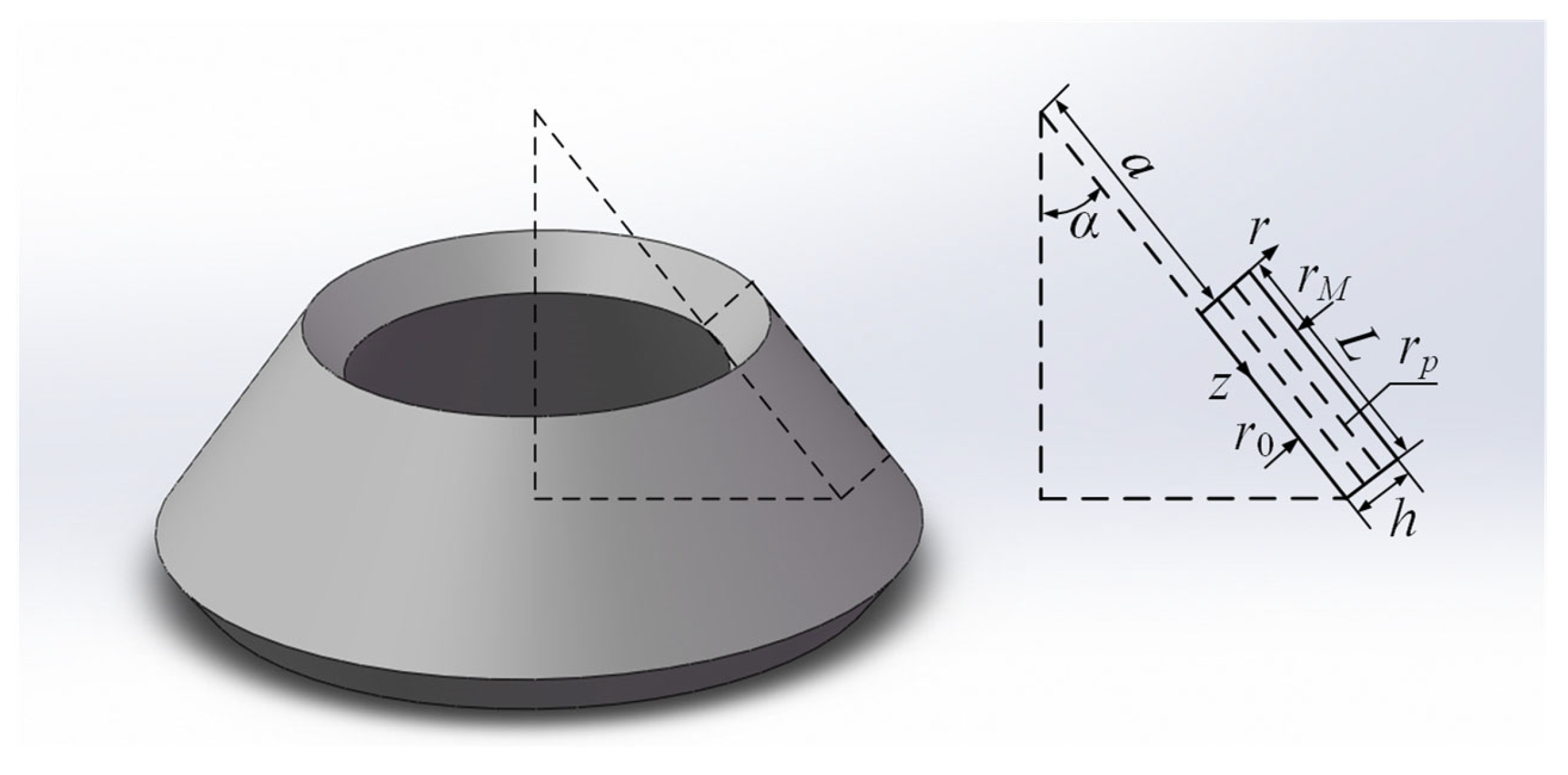
3.4. QC Truncated Conical Shells Containing Flowing Fluid
4. Conclusions
- The global propagator relation is reestablished to resolve numerical instabilities in the case of large discrete point numbers and high frequencies for three QC structures. Some cases such as one-dimensional and two-dimensional QC plates/shells could all be investigated according to the present methods.
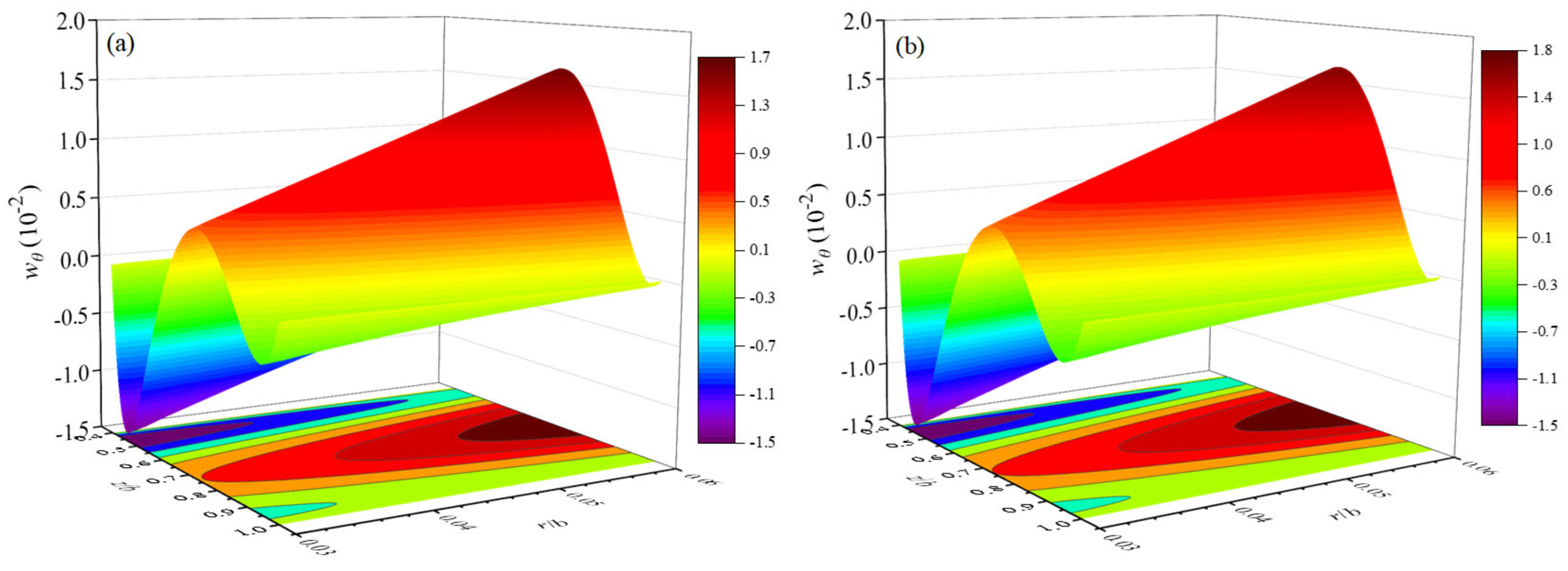
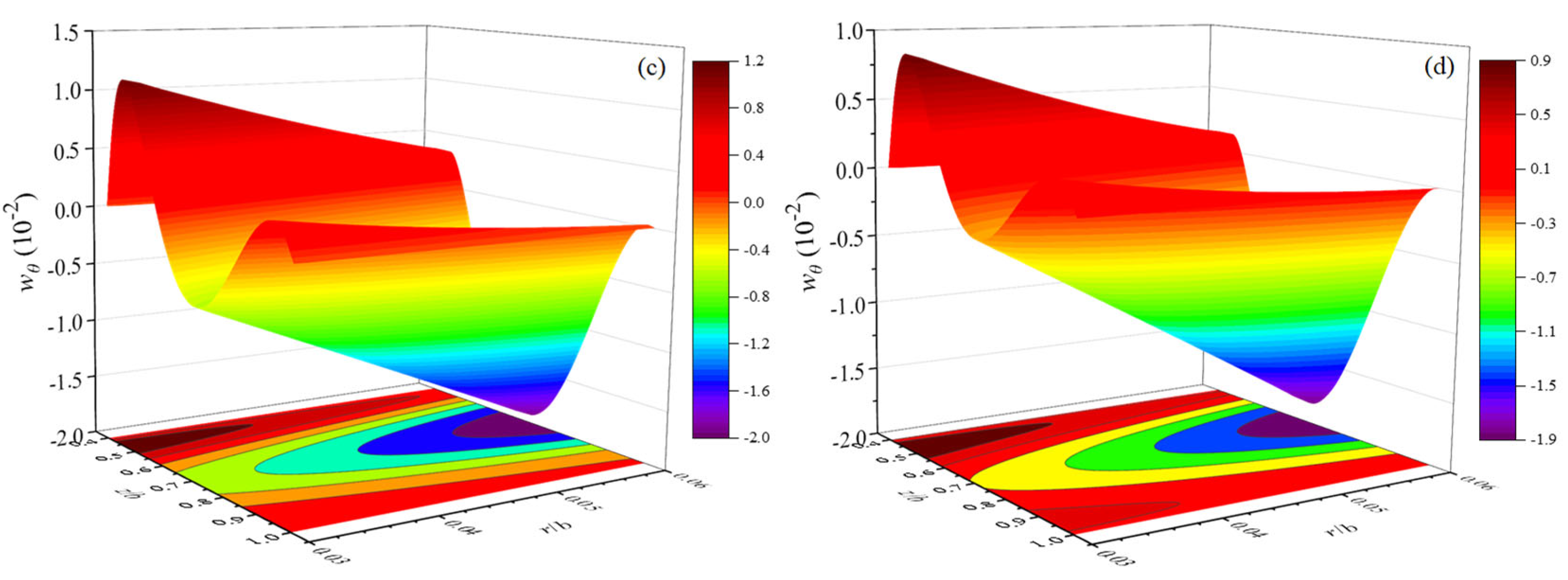
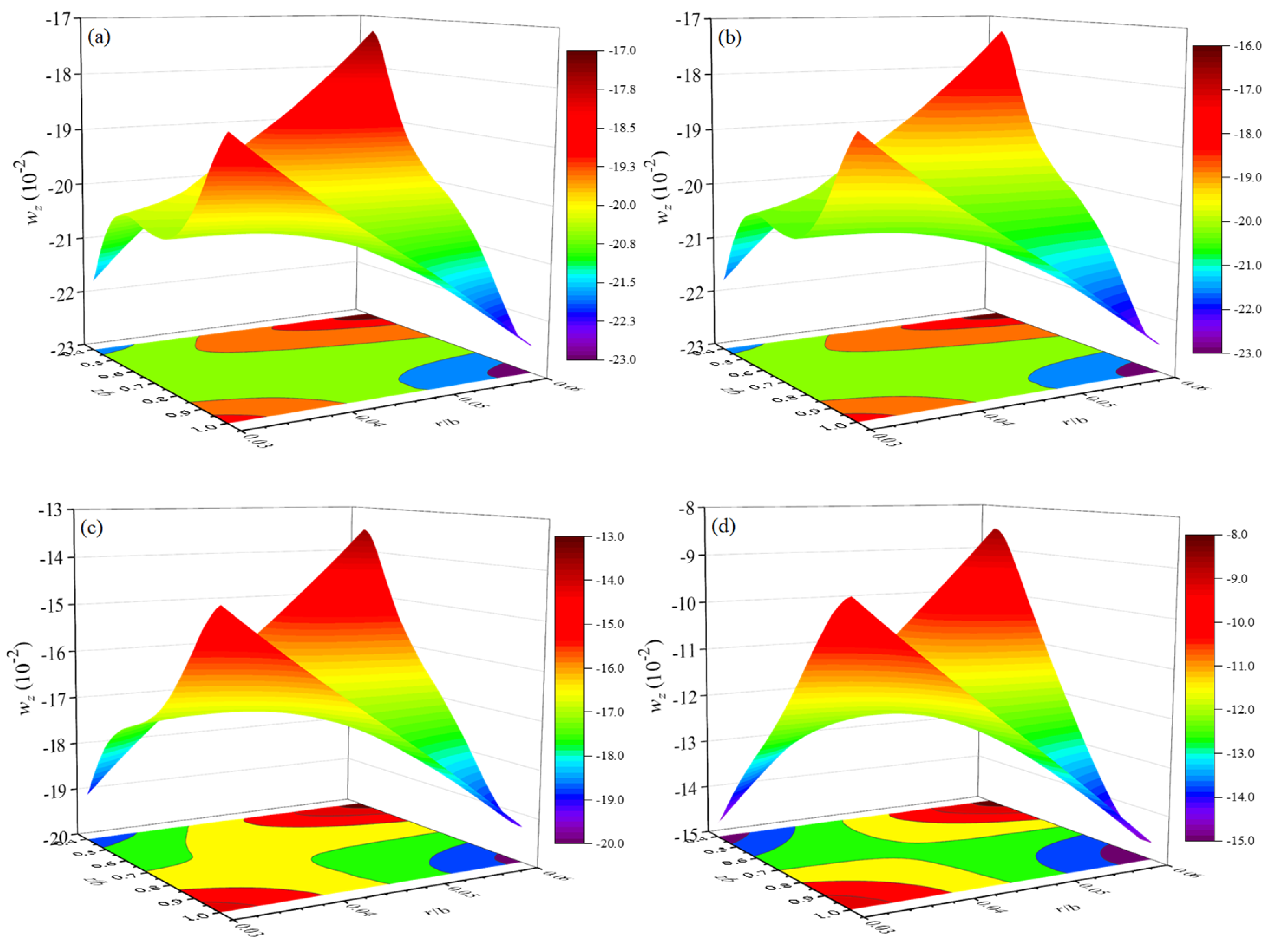
- Quiescent fluid improves the overall stiffness of the truncated conical shell. This shell with the higher semi-vertical angle α leads to smaller natural frequencies and phonon displacements mode shapes and larger phason displacements mode shapes. Meanwhile, QC truncated conical shells are more susceptible to external excitation with semi-vertical angle α increasing
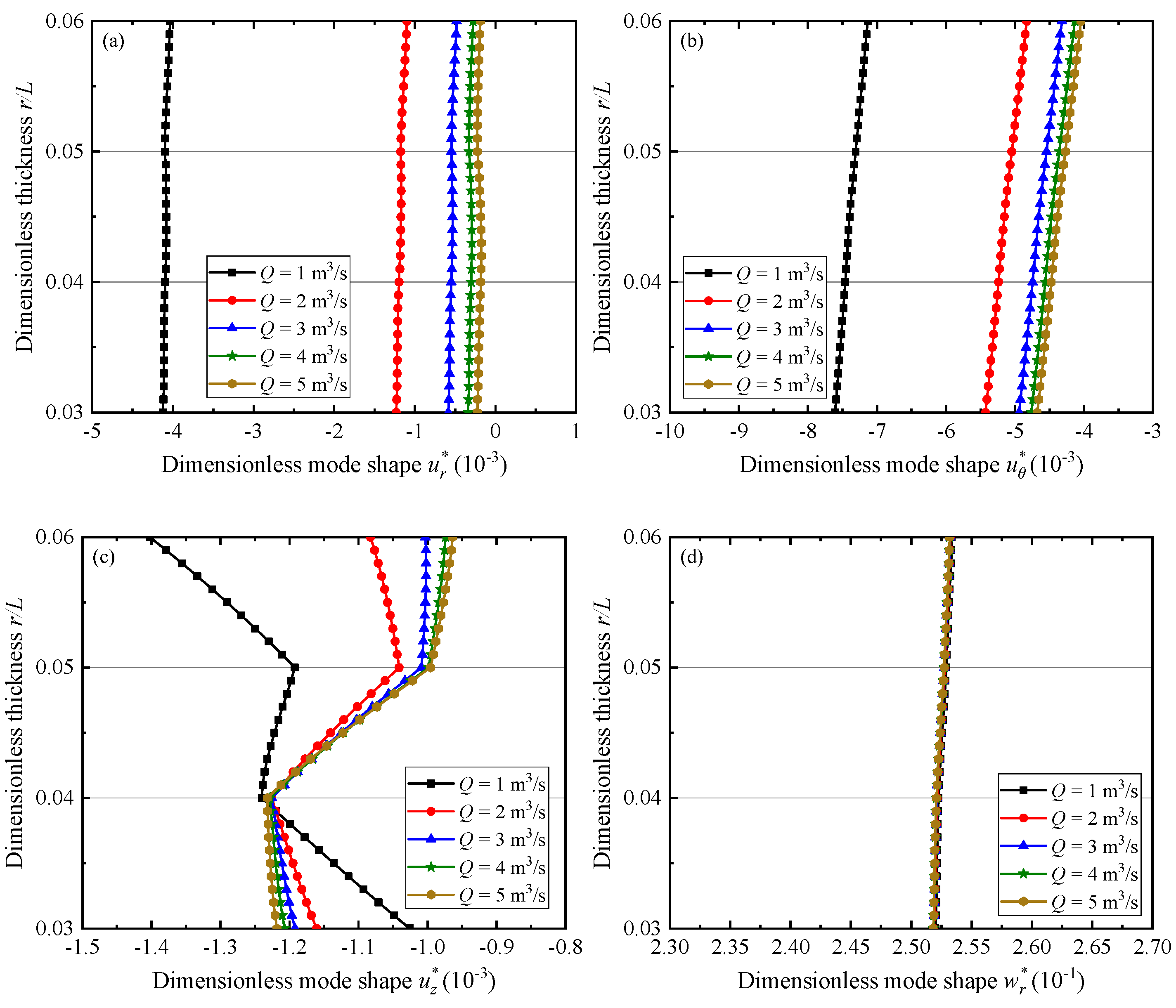
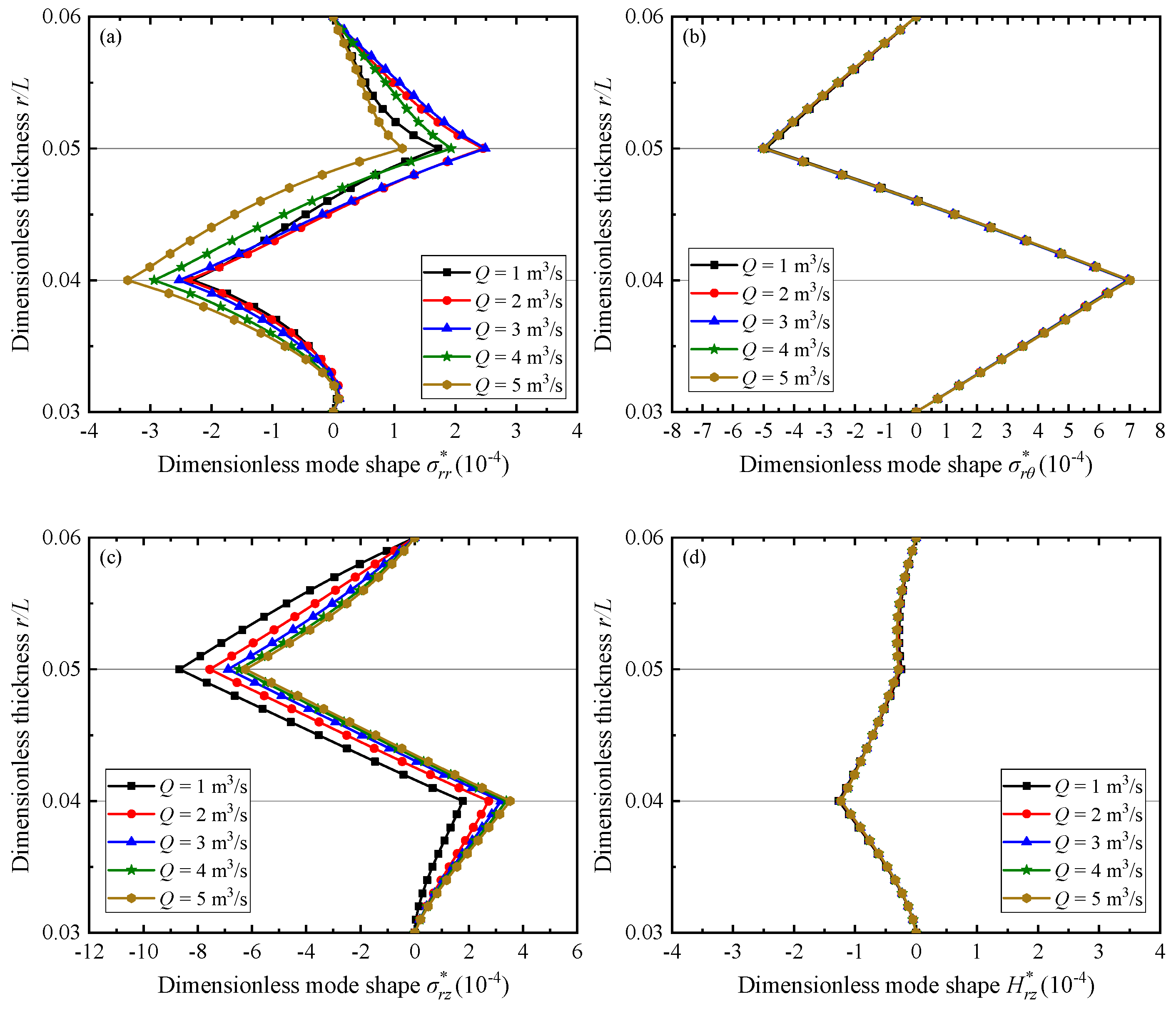
- Every order of natural frequencies increases in the order of SS, CS, SC, and CC for a fixed value of h/L. Higher fluid debits Q causes shells to experience larger frequencies in the case of all boundary conditions. All phason variables are insensitive to fluid debits Q.
Acknowledgments
Appendix A
References
- Fan T Y. Mathematical theory of elasticity of quasicrystals and its applications[M]. Heidelberg: Springer, 2011.
- Li X F. Elastohydrodynamic problems in quasicrystal elasticity theory and wave propagation[J]. Philosophical Magazine, 2013, 93(13): 1500-1519. [CrossRef]
- Wolf W, Schulz R, Savoie S, et al. Structural, mechanical and thermal characterization of an Al-Co-Fe-Cr alloy for wear and thermal barrier coating applications[J]. Surface Coatings Technology, 2017, 319: 241-248. [CrossRef]
- Ferreira T, Koga G Y, De Oliveira I L, et al. Functionally graded aluminum reinforced with quasicrystal approximant phases - Improving the wear resistance at high temperatures[J]. Wear, 2020, 462: 203507. [CrossRef]
- Zhang X J, Wang H W, Yan B, et al. The nanoscale strain assignment behavior of icosahedral quasicrystalline phase T2-Al6CuLi3 in cast Al-Li alloys[J]. Journal of Alloys and Compounds, 2021, 867(6): 159096. [CrossRef]
- Guo J H, Liu G T. Analytic solutions to problem of elliptic hole with two straight cracks in one-dimensional hexagonal quasicrystals[J]. Applied Mathematics and Mechanics-English Edition, 2008, 29(4): 485-493. [CrossRef]
- Sun T Y, Guo J H, Pan E. Nonlocal vibration and buckling of two-dimensional layered quasicrystal nanoplates embedded in an elastic medium[J]. Applied Mathematics and Mechanics, 2021, 42(8): 1077-1094. [CrossRef]
- Ye J Q. Laminated composite plates and shells: 3D modelling[M]. Springer Science and Business Media, 2002.
- Vattré A, Pan E. Thermoelasticity of multilayered plates with imperfect interfaces[J]. International Journal of Engineering Science, 2021, 158: 103409. [CrossRef]
- Farshidianfar A, Oliazadeh P. Free vibration analysis of circular cylindrical shells: comparison of different shell theories[J]. International Journal of Mechanics Applications, 2012, 2(5): 74-80.
- Żur K K. Free vibration analysis of discrete-continuous functionally graded circular plate via the Neumann series method[J]. Applied Mathematical Modelling, 2019, 73: 166-189. [CrossRef]
- Ersoy H, Mercan K, Civalek Ö. Frequencies of FGM shells and annular plates by the methods of discrete singular convolution and differential quadrature methods[J]. Composite Structures, 2018, 183: 7-20. [CrossRef]
- Eshaghi M, Sedaghati R, Rakheja S. Analytical and experimental free vibration analysis of multi-layer MR-fluid circular plates under varying magnetic flux[J]. Composite Structures, 2016, 157: 78-86. [CrossRef]
- Yas M H, Jodaei A, Irandoust S, et al. Three-dimensional free vibration analysis of functionally graded piezoelectric annular plates on elastic foundations[J]. Meccanica, 2011, 47(6): 1401-1423. [CrossRef]
- Yas M H, Moloudi N. Three-dimensional free vibration analysis of multi-directional functionally graded piezoelectric annular plates on elastic foundations via state space based differential quadrature method[J]. Applied Mathematics and Mechanics, 2015, 36(4): 439-464. [CrossRef]
- Safarpour M, Rahimi A, Alibeigloo A, et al. Parametric study of three-dimensional bending and frequency of FG-GPLRC porous circular and annular plates on different boundary conditions[J]. Mechanics Based Design of Structures and Machines, 2021, 49(5): 707-737. [CrossRef]
- Rahimi A, Alibeigloo A, Safarpour M. Three-dimensional static and free vibration analysis of graphene platelet–reinforced porous composite cylindrical shell[J]. Journal of Vibration and Control, 2020, 26(19-20): 1627-1645. [CrossRef]
- Safarpour M, Rahimi A R, Alibeigloo A. Static and free vibration analysis of graphene platelets reinforced composite truncated conical shell, cylindrical shell, and annular plate using theory of elasticity and DQM[J]. Mechanics Based Design of Structures and Machines, 2020, 48(4): 496-524. [CrossRef]
- Rahimi G H, Gazor M S, Hemmatnezhad M, et al. Free vibration analysis of fiber metal laminate annular plate by state-space based differential quadrature method[J]. Advances in Materials Science Engineering, 2014, 2014(3): 653-659. [CrossRef]
- Kerboua Y, Lakis A A. Numerical model to analyze the aerodynamic behavior of a combined conical–cylindrical shell[J]. Aerospace Science and Technology, 2016, 58: 601-617. [CrossRef]
- Naj R, Sabzikar Boroujerdy M, Eslami M R. Thermal and mechanical instability of functionally graded truncated conical shells[J]. Thin-Walled Structures, 2008, 46(1): 65-78. [CrossRef]
- Jooybar N, Malekzadeh P, Fiouz A, et al. Thermal effect on free vibration of functionally graded truncated conical shell panels[J]. Thin-Walled Structures, 2016, 103: 45-61. [CrossRef]
- Izyan M D N, Viswanathan K K, Aziz Z A, et al. Free vibration of layered truncated conical shells filled with quiescent fluid using spline method[J]. Composite Structures, 2017, 163: 385-398. [CrossRef]
- Hien V Q, Thinh T I, Cuong N M, et al. Free vibration analysis of joined composite conical-conical-conical shells containing fluid[J]. Vietnam Journal of Science echnology, 2016, 54(5): 650. [CrossRef]
- Hien V Q, Thinh T I, Cuong N M. Free vibration analysis of joined composite conical-cylindrical-conical shells containing fluid[J]. Vietnam Journal of Mechanics, 2016, 38(4): 249-265. [CrossRef]
- Rahmanian M, Firouz-Abadi R D, Cigeroglu E. Free vibrations of moderately thick truncated conical shells filled with quiescent fluid[J]. Journal of fluids structures, 2016, 63: 280-301. [CrossRef]
- Kerboua Y, Lakis A A, Hmila M. Vibration analysis of truncated conical shells subjected to flowing fluid[J]. Applied Mathematical Modelling, 2010, 34(3): 791-809. [CrossRef]
- Mohammadi N, Asadi H, Aghdam M M. An efficient solver for fully coupled solution of interaction between incompressible fluid flow and nanocomposite truncated conical shells[J]. Computer Methods in Applied Mechanics and Engineering, 2019, 351: 478-500. [CrossRef]
- Feng X, Fan X Y, Li Y, et al. Static response and free vibration analysis for cubic quasicrystal laminates with imperfect interfaces[J]. European Journal of Mechanics - A/Solids, 2021, 90(14): 104365. [CrossRef]
- Li X Y. Fundamental solutions of penny-shaped and half-infinite plane cracks embedded in an infinite space of one-dimensional hexagonal quasi-crystal under thermal loading[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2013, 469(2154): 20130023. [CrossRef]
- Huang Y Z, Li Y, Zhang L L, et al. Dynamic analysis of a multilayered piezoelectric two-dimensional quasicrystal cylindrical shell filled with compressible fluid using the state-space approach[J]. Acta Mechanica, 2020, 231(6): 2351-2368. [CrossRef]
- Li X Y, Wang T, Zheng R F, et al. Fundamental thermo-electro-elastic solutions for 1D hexagonal QC[J]. ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik, 2015, 95(5): 457-468. [CrossRef]
- Huang Y Z, Li Y, Yang L Z, et al. Static response of functionally graded multilayered one-dimensional hexagonal piezoelectric quasicrystal plates using the state vector approach[J]. Journal of Zhejiang University-Science A, 2019, 20(2): 133-147.
- Li Y, Li Y, Qin Q H, et al. Axisymmetric bending analysis of functionally graded one-dimensional hexagonal piezoelectric quasi-crystal circular plate[J]. Proceedings of the Royal Society A, 2020, 476(2241): 20200301. [CrossRef]
- Chen J Y, Guo J H, Pan E. Wave propagation in magneto-electro-elastic multilayered plates with nonlocal effect[J]. Journal of Sound and Vibration, 2017, 400: 550-563. [CrossRef]
- Vattré A, Pan E, Chiaruttini V. Free vibration of fully coupled thermoelastic multilayered composites with imperfect interfaces[J]. Composite Structures, 2021, 259: 113203. [CrossRef]
- Bellman R, Kashef B G, Casti J. Differential quadrature: A technique for the rapid solution of nonlinear partial differential equations[J]. Journal of Computational Physics, 1972, 10(1): 40-52. [CrossRef]
- Lü C F, Chen W Q, Shao J W. Semi-analytical three-dimensional elasticity solutions for generally laminated composite plates[J]. European Journal of Mechanics - A/Solids, 2008, 27(5): 899-917. [CrossRef]
- Korn G A, Korn T M. Mathematical handbook for scientists and engineers: definitions, theorems, and formulas for reference and review[M]. Courier Corporation, 2000.
- Yan W W, Xu M Z. Dependence of eigenvalues of second-order differential operator with eigen parameters contained in both boundary conditions[J]. Journal of Inner Mongolia University of Technology(Natural Science Edition), 2022, 41(14): 294-300.
- Chen W Q, Cai J B, Ye G R. Exact solutions of cross-ply laminates with bonding imperfections[J]. Aiaa Journal, 2003, 41(11): 2244-2250. [CrossRef]
- Hwu C. Anisotropic Elastic Plates[M]. Spring Science and Business Media, 2010.
- Hu C Z, Wang R H, Ding D H. Symmetry groups, physical property tensors, elasticity and dislocations in quasicrystals[J]. Reports on Progress in Physics, 2000, 63(1): 1-39. [CrossRef]
- Wu D, Zhang L L, Xu W S, et al. Electroelastic Green's function of one-dimensional piezoelectric quasicrystals subjected to multi-physics loads[J]. Journal of Intelligent Material Systems and Structures, 2017, 28(12): 1651-1661. [CrossRef]
| C11 | C12 | C44 | K11 | K12 | K44 | R1 | R2 | R3 | ρ | |
|---|---|---|---|---|---|---|---|---|---|---|
| QC1 | 234.33 | 57.41 | 70.19 | 122 | 24 | 12 | 8.846 | 4.578 | 3.125 | 4505 |
| QC2 | 112.1 | 60.3 | 32.8 | 60 | 20 | 10 | 5 | -2 | 7 | 5300 |
| Mode 1 | Mode 2 | Mode 3 | Mode 4 | Mode 5 | Mode 6 | Mode 7 | |
|---|---|---|---|---|---|---|---|
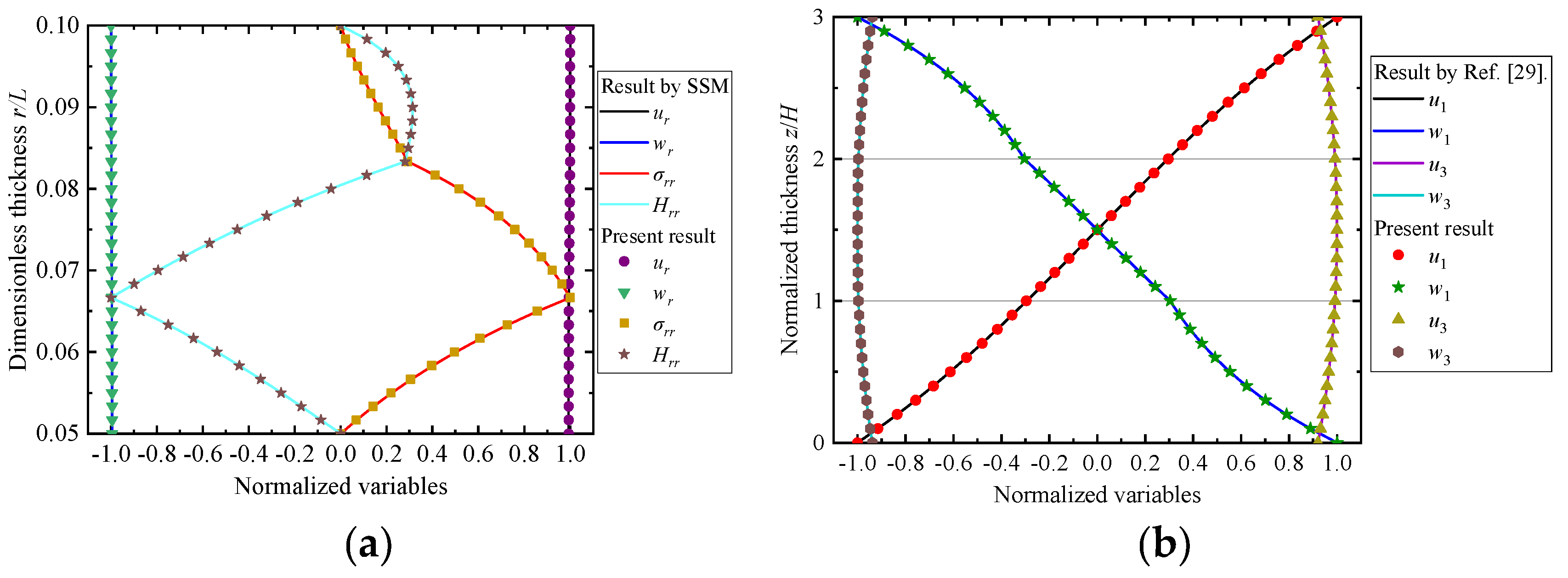
| Result by SSM | 0.50665 | 0.75775 | 6.26025 | 12.88351 | 18.83285 | 23.90636 | 26.45587 |
| Present result | 0.50665 | 0.75775 | 6.26026 | 12.88351 | 18.83285 | 23.90637 | 26.45588 |
| Mode 1 | Mode 2 | Mode 3 | Mode 4 | Mode 5 | |
|---|---|---|---|---|---|
| Result by Ref. [29] | 1.47999 | 2.38416 | 4.27451 | 8.32909 | 9.52440 |
| Present result | 1.47999 | 2.38417 | 4.27453 | 8.32911 | 9.52443 |
| Mode 1 | Mode 2 | Mode 3 | Mode 4 | Mode 5 | Mode 6 | Mode 7 | Mode 8 | Mode 9 | |
|---|---|---|---|---|---|---|---|---|---|
| SS | 0.18006 | 0.25376 | 0.66903 | 0.71981 | 0.95204 | 1.16316 | 1.40024 | 1.69379 | 2.05038 |
| CS | 0.25230 | 0.35814 | 0.79363 | 1.15242 | 1.30192 | 1.54856 | 1.96985 | 2.17479 | 2.32465 |
| SC | 0.28126 | 0.39808 | 0.82056 | 1.19096 | 1.52124 | 1.57224 | 2.23517 | 2.36010 | 2.53888 |
| CC | 0.36982 | 0.53056 | 0.94874 | 1.40814 | 1.54224 | 1.71593 | 2.57940 | 2.63754 | 2.78044 |
| Mode 1 | Mode 2 | Mode 3 | Mode 4 | Mode 5 | |
|---|---|---|---|---|---|
| α0 = π/6 | 0.55916 | 0.79145 | 1.13472 | 1.28815 | 1.60288 |
| α = π/6 | 0.55959 | 0.79158 | 1.15277 | 1.28852 | 1.63267 |
| α = π/4 | 0.38664 | 0.71957 | 1.01077 | 1.41469 | 1.60849 |
| α = π/3 | 0.28030 | 0.47297 | 0.82724 | 1.21100 | 1.36207 |
| Mode 1 | Mode 2 | Mode 3 | Mode 4 | Mode 5 | Mode 6 | Mode 7 | Mode 8 | Mode 9 | |
|---|---|---|---|---|---|---|---|---|---|
| Q = 1 m3/s | 0.83832 | 1.56236 | 1.75879 | 2.35217 | 2.42893 | 3.26236 | 3.84708 | 4.03837 | 4.17203 |
| Q = 2 m3/s | 0.83946 | 1.56357 | 1.75968 | 2.41162 | 2.43311 | 3.26878 | 3.85937 | 4.18399 | 4.58554 |
| Q = 3 m3/s | 0.83971 | 1.56387 | 1.75992 | 2.42240 | 2.43481 | 3.27066 | 3.85993 | 4.18815 | 4.59383 |
| Q = 4 m3/s | 0.83980 | 1.56399 | 1.76003 | 2.42608 | 2.43588 | 3.27141 | 3.86014 | 4.18988 | 4.59572 |
| Q = 5 m3/s | 0.83985 | 1.56405 | 1.76010 | 2.42784 | 2.43669 | 3.27177 | 3.86026 | 4.19075 | 4.59665 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





