Critical Points in the Noiseberg Achievable Region of the Gaussian Z-Interference Channel

The Gaussian signaling strategy with power control for the Gaussian Z-interference channel with weak interference is reviewed in this paper. In particular, we study the various communication strategies that may arise at various points of the capacity region and identify the locations of the phase transitions between the various strategies. The Gaussian Z-interference channel with weak interference is known to have two critical points in its capacity region, where the slope of the region shows a sudden change. They occur at the points of the unconditional maximum rate for one of the users and the maximum rate that can be accommodated by the other user. In this paper, we discuss two additional critical points (locations of phase transitions) in the achievable region of this channel. At these points, we do not observe a discontinuous slope in the achievable rate region, but there is a discontinuity in the second derivative of the rate contour of the achievable region. This review paper is mainly based on some of our ITA (Information Theory and Applications Workshop, UCSD, San Diego, CA, USA) papers since 2011.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

Many authors have studied scalar Gaussian interference channels since 1974 [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,18,19,20,21,22,23,24,25,26,27,28]. One of the key questions in this area, for which we do not have a definitive answer as yet, is whether Han–Kobayashi inner bound with Gaussian signaling achieves the capacity region. The model under investigation in this paper is the one-sided interference channel given by

Y_{1}^{'} = X_{1}^{'} + Z_{1}^{'}

and

Y_{2}^{'} = X_{2}^{'} + a X_{1}^{'} + Z_{2}^{'}

, where

X_{1}^{'}

and

X_{2}^{'}

are transmitter signals constrained to have average powers

Q_{1}

and

Q_{2}

, respectively, a is an interference gain in the interval

(0, 1)

Z_{1}^{'}

and

Z_{2}^{'}

are Gaussian noises of unit variance, and

Y_{1}^{'}

and

Y_{2}^{'}

are the two received signals. This model is depicted in Figure 1.

The receivers are interested in messages sent by their respective, same-indexed, transmitters. Thus

X_{1}^{'}

encodes a message addressed to receiver 1 and

X_{2}^{'}

conveys a message to receiver 2. This model is a particular case of the Gaussian interference channel, which exhibits interference in both directions. Like in the more general model, the problem of finding the associated capacity region has been open for almost 50 years. In the case of strong interference, when

a \geq 1

, the capacity region is known [18,27]. In this case, the unintended receiver can fully decode the interfering message. Therefore, the rate region coincides with the intersection of the two underlying multiple access channel regions. Also, when

a = 0

, the problem has a trivial solution. This paper uses the fact that the Gaussian Z-interference channel with interference parameter a in the range

(0, 1)

can be regarded as a degraded Gaussian interference channel [5], a model shown in Figure 2.

Like the Gaussian Z-interference channel, the degraded Gaussian interference channel is characterized by three parameters, namely the two powers

P_{1}

and

P_{2}

, and the additional independent noise in the second receiver, of power

N_{2}

. These parameters are related to the parameters of the original Z-interference channel by

P_{1} = Q_{1}

P_{2} = Q_{2} / a^{2}

and

N_{2} = (1 - a^{2}) / a^{2}

. Moreover, since

0 < a < 1

, the additional noise power

N_{2}

is always positive. For simplicity, we choose to use the more common notation, without the primes, in this channel, which will constitute our working model.

In this review paper, we investigate the behavior of the noiseberg encoding scheme [6], which has recently been shown [8] to coincide with the Han–Kobayashi region with Gaussian signaling. From a communication engineer’s perspective, knowing the optimal Gaussian signaling strategy for a given set of parameters is essential when one wishes to maximize

β R_{2} + R_{1}

. In particular, we investigate two additional critical points in the achievable region of the noiseberg scheme for the Gaussian Z-interference channel with weak interference. These critical points are associated with transitions between different modes of operation. A third critical point happens between the so-called multiplex and the overflow regions that are produced in the noiseberg encoding scheme [6]. A fourth critical point happens after the overflow mode is in effect, as the evolution of modes leads to a transition to pure superposition or, otherwise, reaches an extreme boundary in the

λ

x h parameter space.

From a mathematical perspective, a proof of the optimality of the Gaussian signaling - using the current techniques - necessitates the identification of parameters and the weight

β

corresponding to a weighted sum-rate

β R_{2} + R_{1}

, for which a pure superposition coding strategy is optimal.

2. Preliminaries

We focus on the degraded interference channel model depicted in Figure 2. Two extreme points in the channel capacity region have been identified for this channel. One extreme point occurs when

X_{1}

sends information at its maximum possible rate and

X_{2}

uses what is left of the channel, with

X_{1}

’s interference treated as noise. In this extreme point the achieved rate pair

(R_{1}, R_{2})

is given by

R_{1} = \frac{1}{2} log (1 + P_{1})

and

R_{2} = \frac{1}{2} log (1 + \frac{P_{2}}{1 + N_{2} + P_{1}})

(cf. Figure 3). There is a slope discontinuity for the capacity region at this extreme point, which follows from the capacity region of an associated degraded broadcast channel [5,26], establishing that this extreme point is a critical point. From this, it immediately follows that this point also maximizes

R_{1} + R_{2}

, the sum-rate, and therefore, this corner point will be referred to as the sum-rate corner point. Another extreme point in the achievable region occurs when all the privilege of operating at maximum rate is given to the second transmitter [5,23]. In this case, the first transmitter must lower its rate to the point where the second receiver is sure to decode and eliminate all the interference that its signaling might impose. The first transmitter then uses the noisy channel that sees noise power

1 + N_{2} + P_{2}

. Therefore, we have

R_{1} = \frac{1}{2} log (1 + \frac{P_{1}}{1 + N_{2} + P_{2}})

and

R_{2} = \frac{1}{2} log (1 + \frac{P_{2}}{1 + N_{2}})

. There is also a slope discontinuity for the capacity region at this extreme point, which follows from a recent outer bound developed in [15]. This corner point is referred to as the backoff corner point.

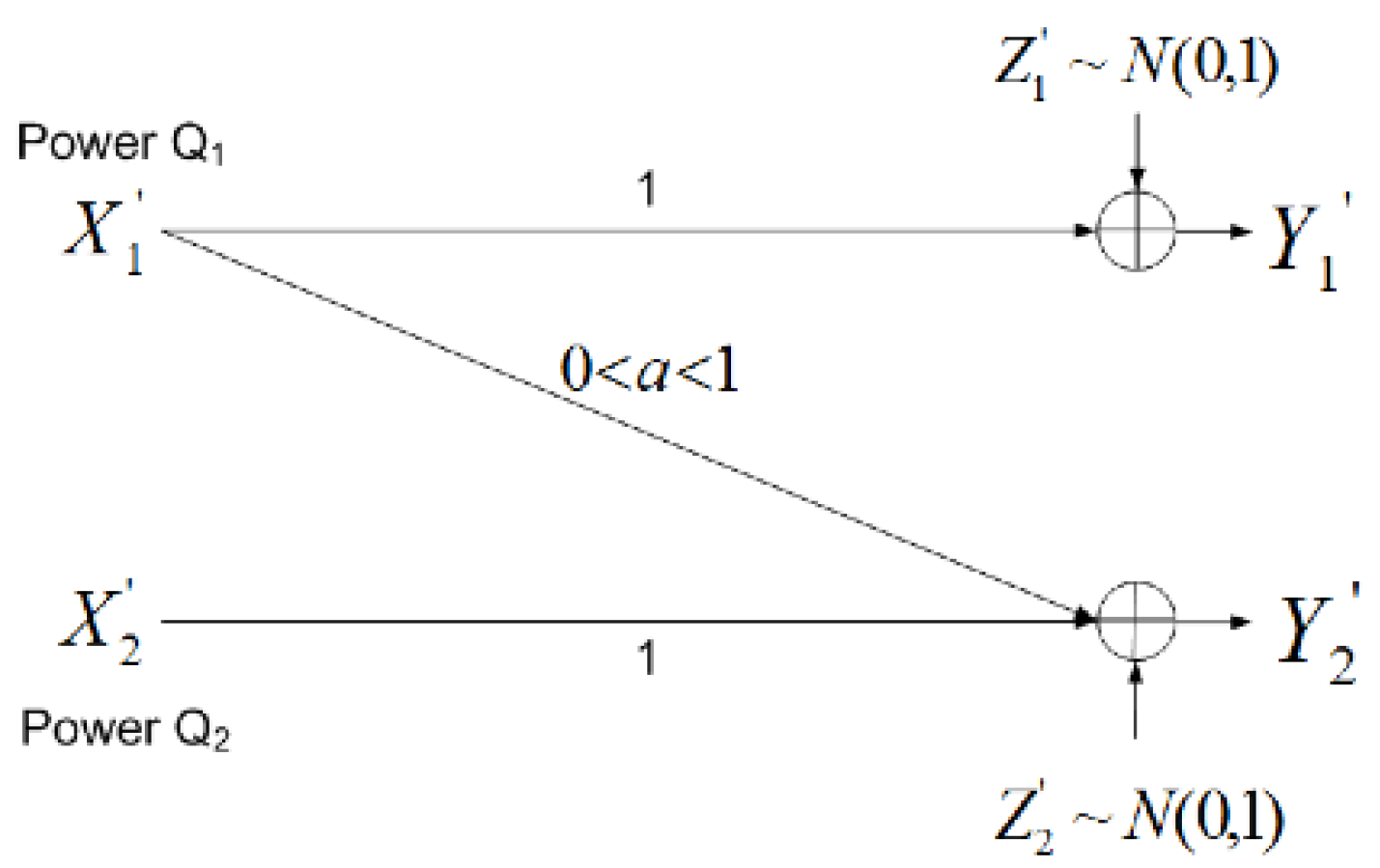
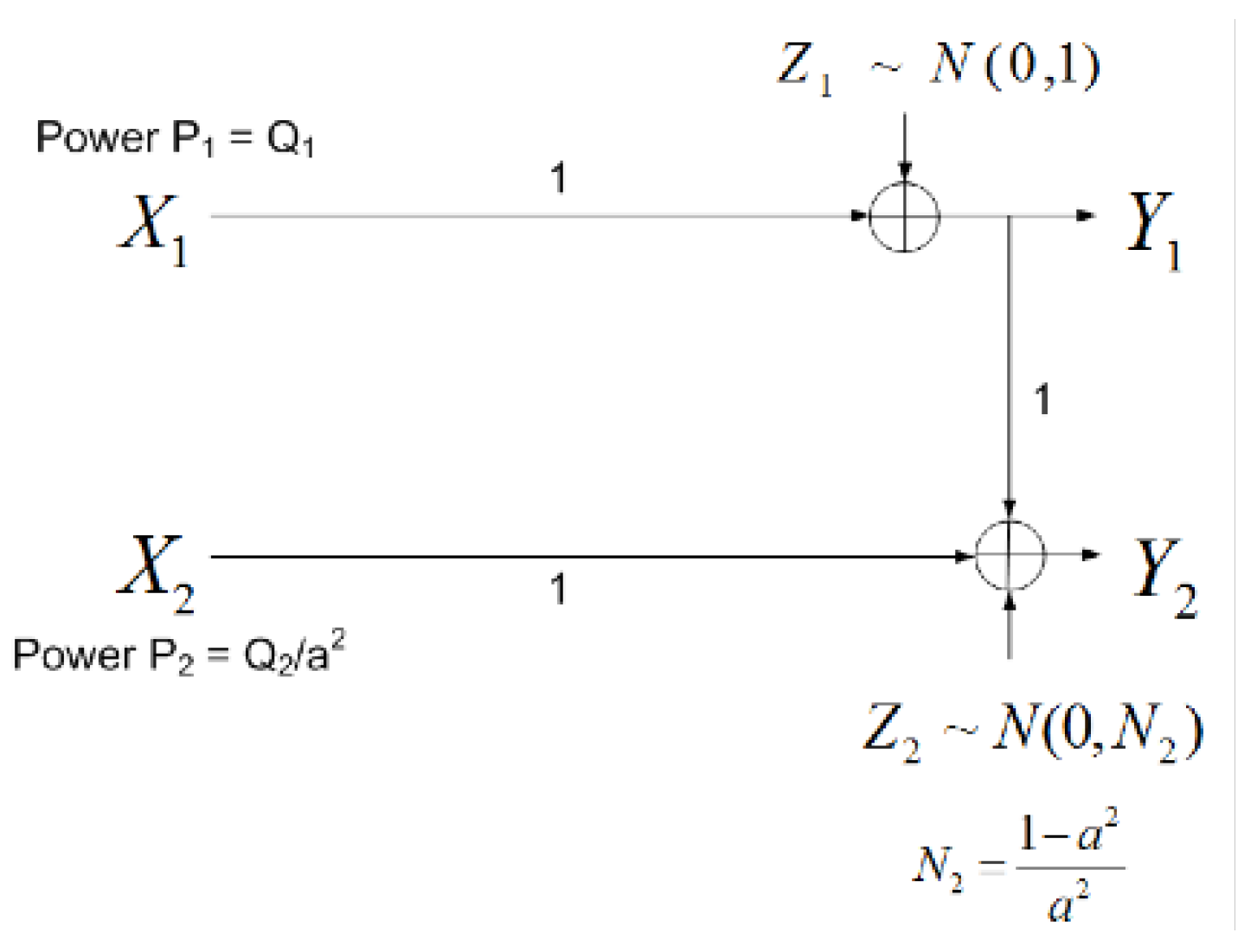
2.1. Noisebergs – A Brief Review

A noiseberg transmission scheme is a particular Gaussian signaling strategy with power control, with (only) six potential phases, depicted in Figure 4, Figure 6, Figure 5, Figure 7, Figure 8 , and Figure 9. In a nutshell, it is a scheme that combines superposition coding, non-naïve (i.e., power controlled) time sharing and water filling between the two spectral regions that get multiplexed. More specifically, it is a time-sharing/bandwidth-sharing between two signaling strategies, with the first strategy (depicted on the left) occupying

(1 - λ)

fraction of the time (band) and the second strategy occupying the remaining

λ

fraction of the time (band). In particular, the strategies in Figure 4, Figure 6, and Figure 5 can be considered as special instances of those in Figure 7, Figure 9, and Figure 8 respectively by setting

λ = 0

. In the leftmost strategy, one allocates part of the power budget to combine transmissions to both decoders in a pure superposition manner. In the second strategy the communication is solely accomplished between the first transmitter and the first receiver.

Consider the following six communication strategies, using Gaussian signaling, for the Gaussian interference channel:

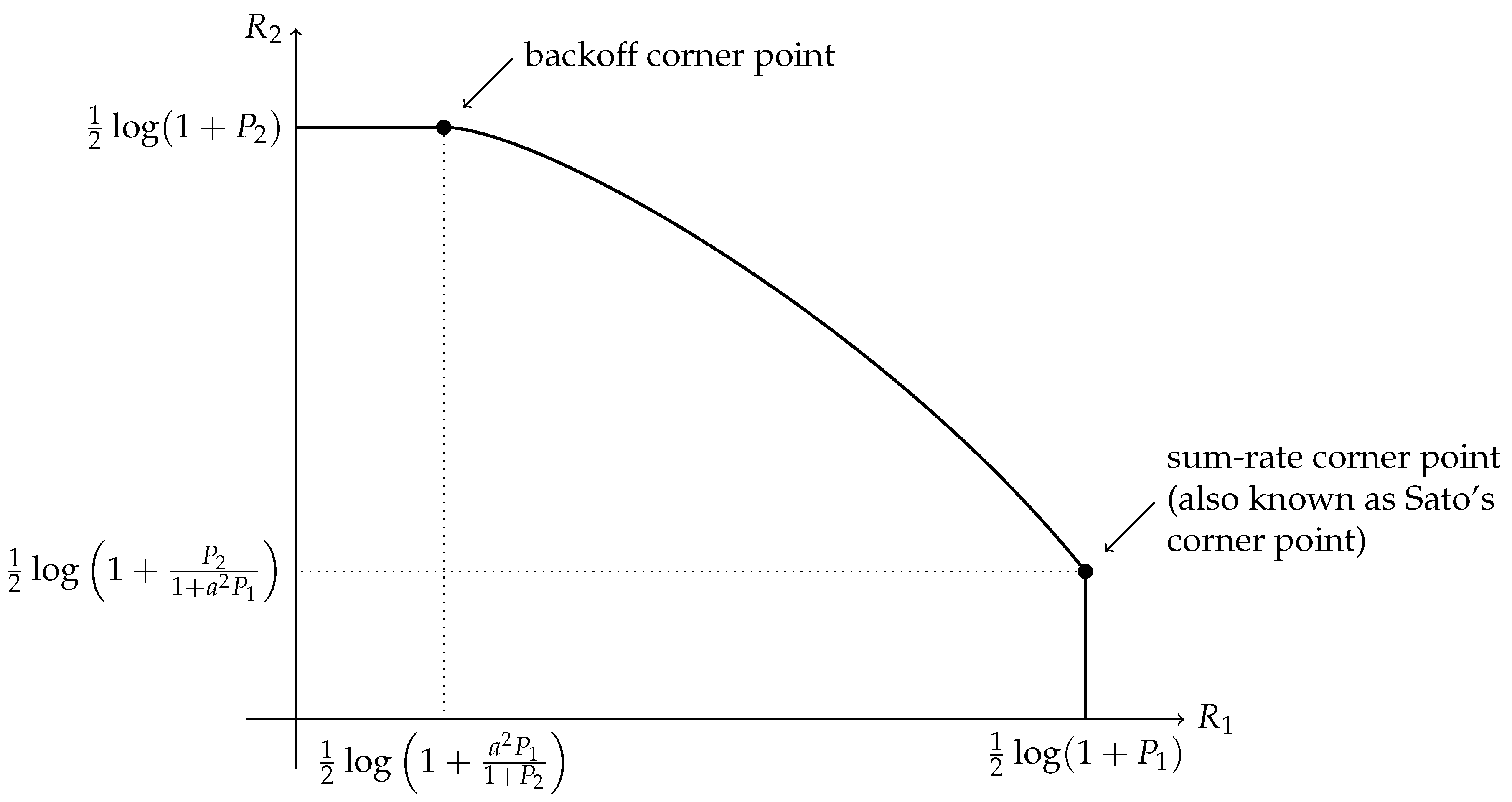
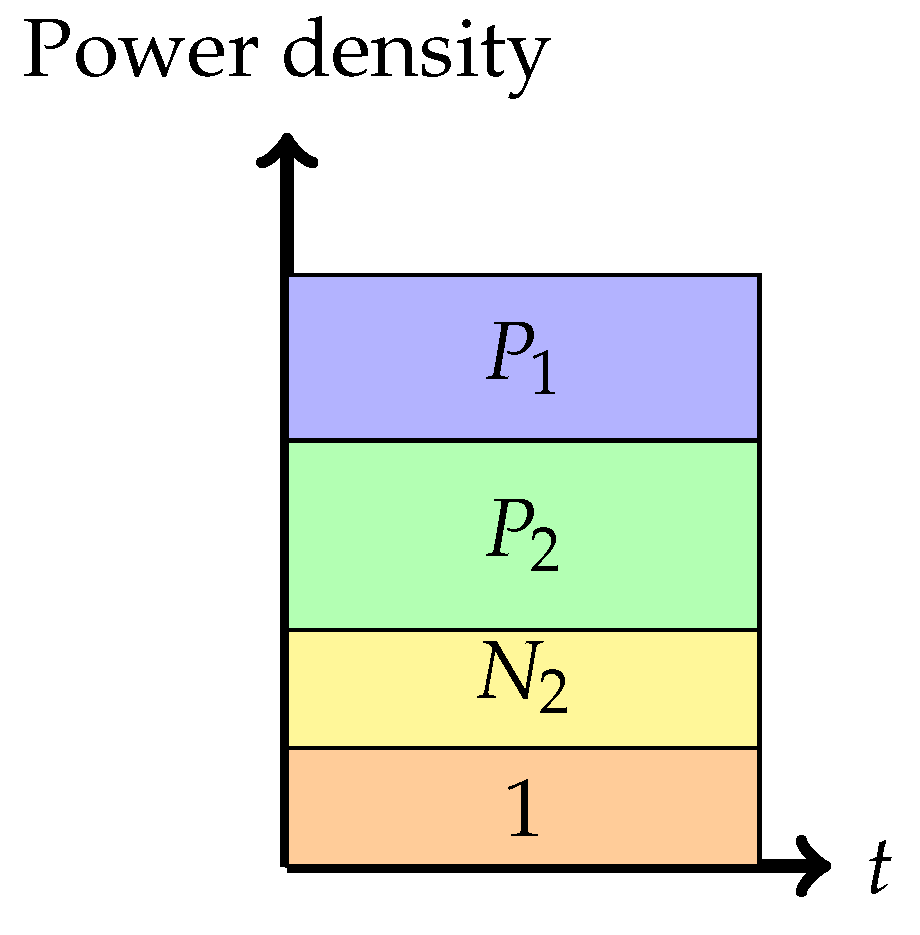
Phase 1: Treating interference to be noise at the weaker receiver (Sato’s corner point)

In this phase, the weaker receiver, $Y_{2}$ , decodes its message by treating $X_{1}$ as noise. This is depicted pictorially in Figure 4. The decoding order in the picture is assumed to go from top to bottom. Any receiver will decode all the messages on top of its message (including its message) in any band by treating those below it as noise. The rate pair achieved in this phase is

$\begin{matrix} R_{1} = \frac{1}{2} log (1 + P_{1}), R_{2} = \frac{1}{2} log (1 + \frac{P_{2}}{1 + P_{1} + N_{2}}) . \end{matrix}$
Phase 2: Partial interference cancellation at the weaker receiver (or pure superposition coding)

In this phase, the weaker receiver, $Y_{2}$ , decodes a part of $X_{1}$ first, subtracts this from the received signal, and then decodes its own signal $X_{2}$ . This is a mix of Phase 1 and Phase 3.

The rate pair achieved in this phase is

$\begin{matrix} R_{1} & = \frac{1}{2} log (1 + \frac{P_{1 C}}{1 + N_{2} + P_{2} + P_{1 A}}) + \frac{1}{2} log (1 + P_{1 A}), \\ R_{2} & = \frac{1}{2} log (1 + \frac{P_{2}}{1 + N_{2} + P_{1 A}}) . \end{matrix}$

Note that $P_{1 A} + P_{1 C} = P_{1}$ .
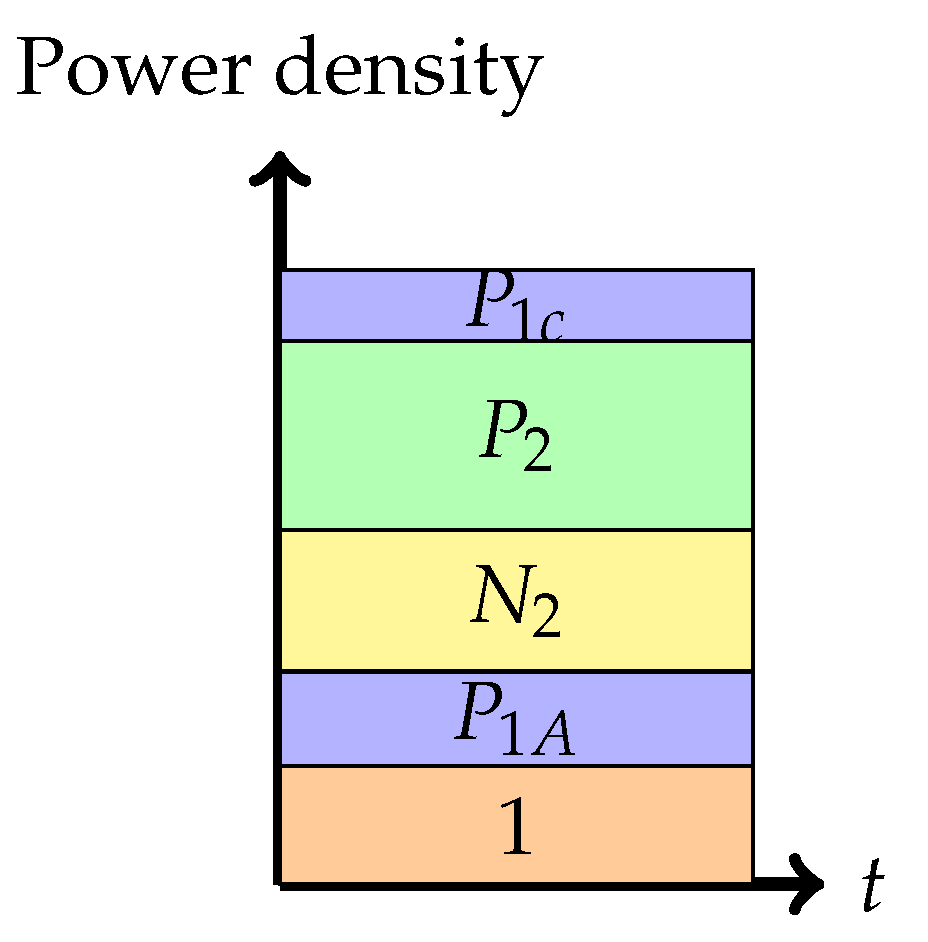
Phase 3: Interference cancellation at the weaker receiver (the backoff corner point)

In this phase, the weaker receiver, $Y_{2}$ , decodes $X_{1}$ first and then subtracts this from the received signal, and then decodes its own signal $X_{2}$ . The rate pair achieved in this phase is

$\begin{matrix} R_{1} = \frac{1}{2} log (1 + \frac{P_{1}}{1 + N_{2} + P_{2}}), R_{2} = \frac{1}{2} log (1 + \frac{P_{2}}{1 + N_{2}}) . \end{matrix}$

Note that the rate for message 1 is solely determined by the ability of the weaker decoder to decode it.
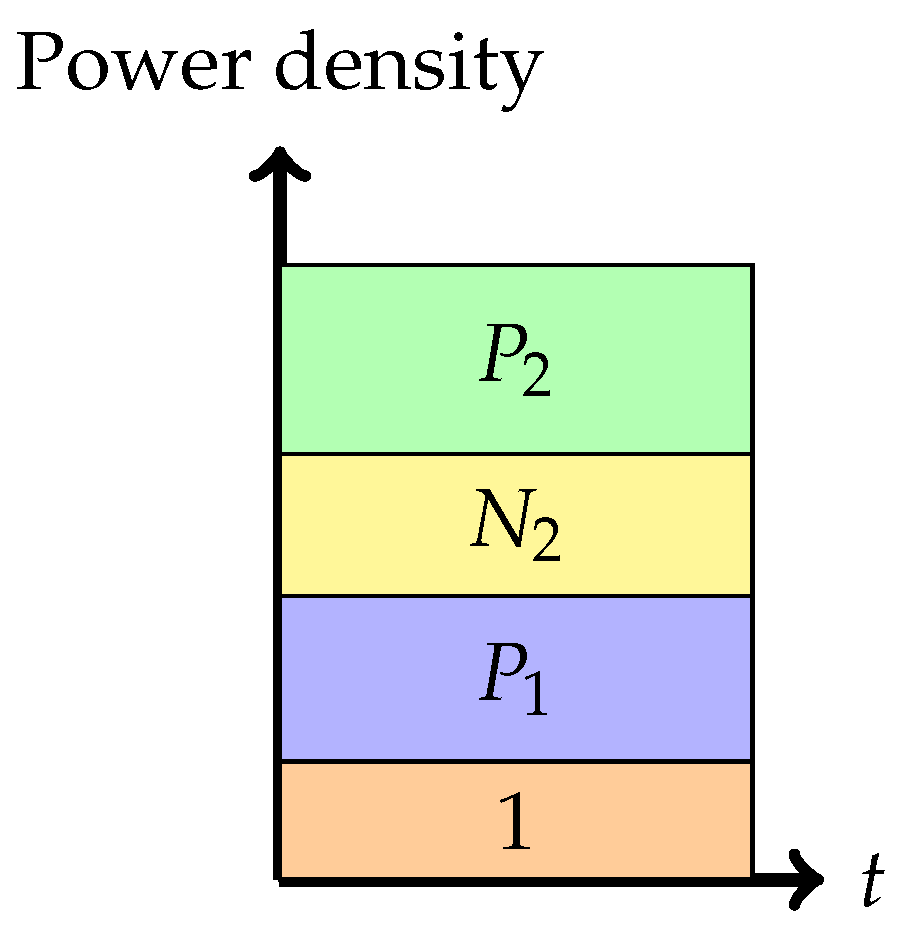
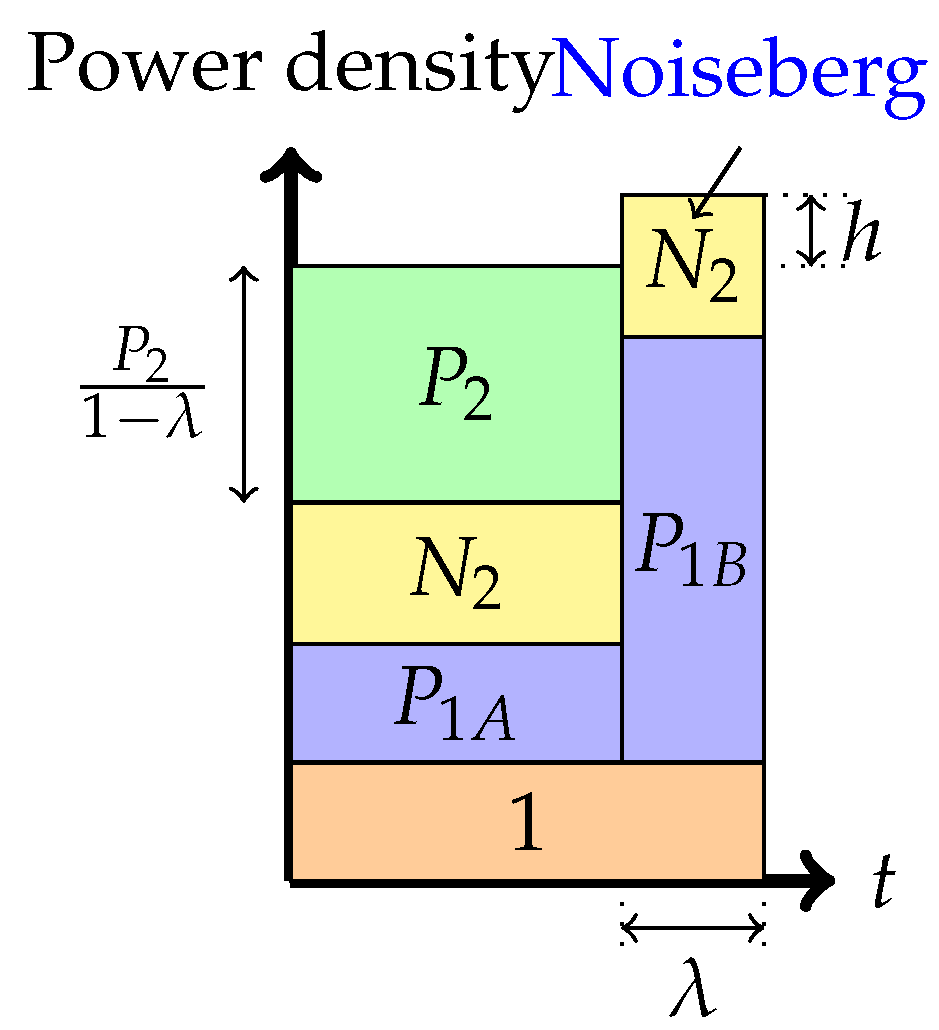
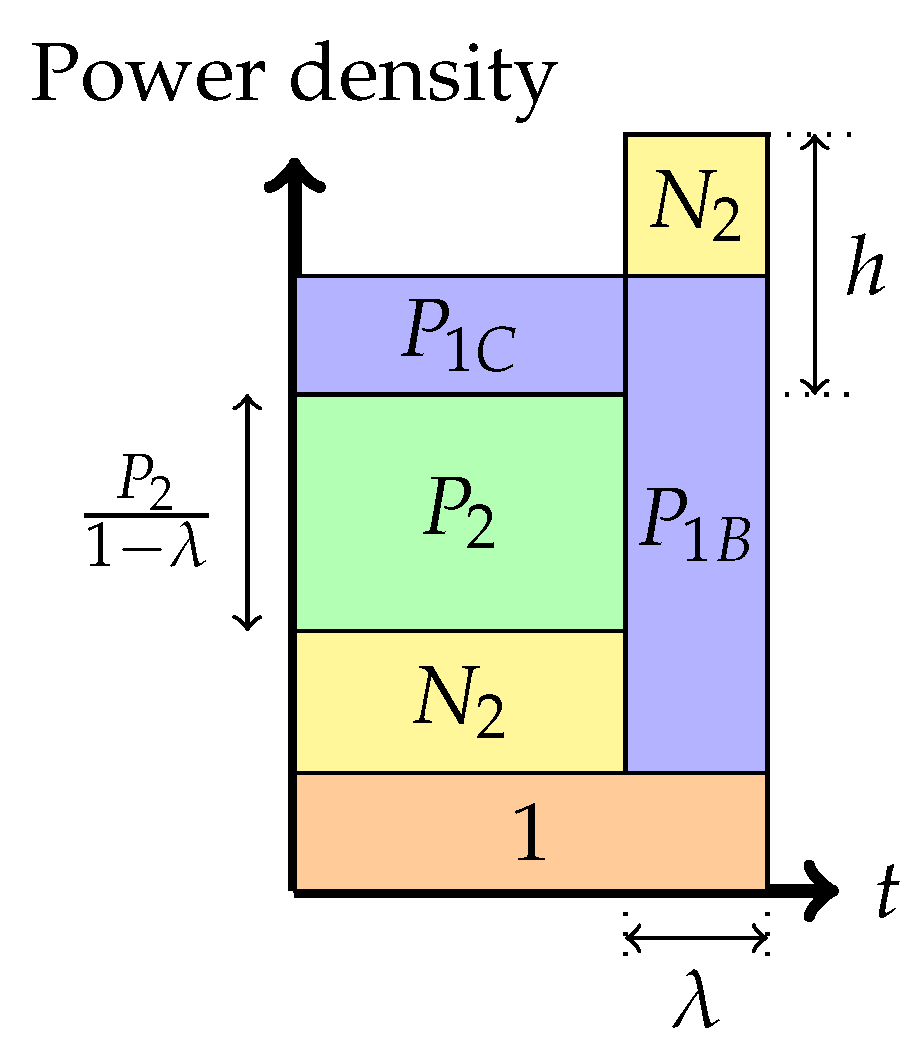
Phase 4: Time-sharing between the following two strategies: Treating interference to be noise at the weaker receiver and transmitting solely to the stronger receiver (or multiplex strategy)

In this phase, there is a time-sharing between two communication schemes. The first scheme, employed for $1 - λ$ fraction of the time, employs the Phase 1 strategy, and the second scheme consists of transmission only to the stronger receiver. The total average power in each band is indicated in the figure. Therefore, one needs to divide the power by the band duration to get the height. It is this phase that led to the noiseberg nomenclature. We denote by h, the height difference between the $N_{2}$ slab in the second band and the power level of $P_{2}$ in the first band. This height difference comes from part of the noise spectrum of $Z_{2}$ that floats above the signal level in the first band and characterizes what we call a noise-iceberg, or noiseberg. The flotation of the noise slab releases prime-rate space in the power × bandwidth plane, in a fashion that Archimedes would be sure to appreciate. In this phase, we get the following:

$\begin{matrix} P_{1} & = P_{1 A} + P_{1 B} \\ \frac{P_{1 A} + P_{2}}{1 - λ} & = \frac{P_{1 B}}{λ} - h . \end{matrix}$

(1)

The rate pairs achieved in this scheme are

$\begin{matrix} R_{1} & = \frac{\bar{λ}}{2} log (1 + \frac{\bar{λ} P_{1} - λ \bar{λ} h - λ P_{2}}{\bar{λ}}) + \frac{λ}{2} log (1 + P_{1} + P_{2} + \bar{λ} h), \\ R_{2} & = \frac{\bar{λ}}{2} log (1 + \frac{P_{2}}{\bar{λ} (1 + N_{2}) + \bar{λ} P_{1} - λ \bar{λ} h - λ P_{2}}) . \end{matrix}$

(2)
Phase 5: Time-sharing between the following two strategies: Partial interference cancellation at the weaker receiver and transmitting solely to the stronger receiver (or overflow strategy)

In this phase, as before, there is a time-sharing between two communication schemes. The first scheme, employed for $1 - λ$ fraction of the time, employs the Phase 2 strategy, and the second scheme consists of transmission only to the stronger receiver. The total average power in each band is indicated in the figure. We denote by h, the height difference between the top of the $N_{2}$ slab in the second band and the power level of $P_{2}$ in the first band. Again, as argued in [6,8], the total heights of the two bands must agree via a water-filling argument. In this phase, we get the following:

$\begin{matrix} P_{1} & = P_{1 A} + P_{1 B} + P_{1 C} \\ \frac{P_{1 B}}{λ} & = N_{2} + \frac{P_{2} + P_{1 A} + P_{1 C}}{\bar{λ}} \\ \frac{P_{1 C}}{1 - λ} & = h - N_{2} \end{matrix}$

(3)

$\begin{matrix} R_{1} & = \frac{\bar{λ}}{2} log (1 + \frac{\bar{λ} P_{1} - λ P_{2} - \bar{λ} h + {\bar{λ}}^{2} N_{2}}{\bar{λ}}) \\ + \frac{\bar{λ}}{2} log (1 + \frac{\bar{λ} (h - N_{2})}{\bar{λ} (1 + N_{2}) + \bar{λ} P_{1} - λ P_{2} - \bar{λ} h + {\bar{λ}}^{2} N_{2} + P_{2}}) \\ + \frac{λ}{2} log (1 + P_{1} + P_{2} + \bar{λ} h), \\ R_{2} & = \frac{\bar{λ}}{2} log (1 + \frac{P_{2}}{\bar{λ} (1 + N_{2}) + \bar{λ} P_{1} - λ P_{2} - \bar{λ} h + {\bar{λ}}^{2} N_{2}}) . \end{matrix}$

(4)
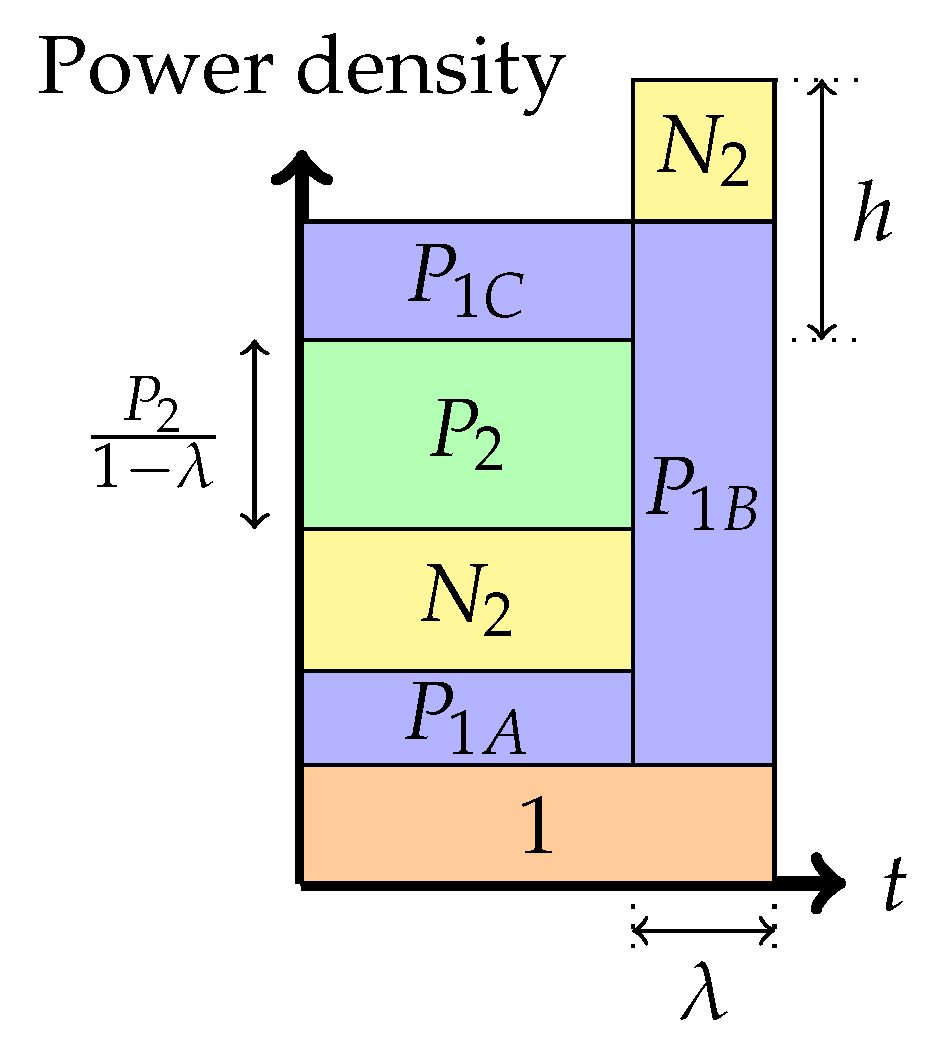
Phase 6: Time-sharing between the following two strategies: Interference cancellation at the weaker receiver and transmitting solely to the stronger receiver (boundary of the admissible region)

In this phase, there is also a time-sharing between two communication schemes. The first scheme, employed for $1 - λ$ fraction of the time, employs the Phase 3 strategy, and the second scheme consists of transmission only to the stronger receiver. The total average power in each band is indicated in the figure. We denote by h, the height difference between the top of the $N_{2}$ slab in the second band and the power level of $P_{2}$ in the first band. As argued in [6,8], the total heights of the two bands must agree via a water-filling argument. In this phase, we get the following:

$\begin{matrix} P_{1} & = P_{1 C} + P_{1 B} \\ \frac{P_{1 B}}{λ} & = N_{2} + \frac{P_{2} + P_{1 C}}{\bar{λ}} \\ \frac{P_{1 C}}{1 - λ} & = h - N_{2} \end{matrix}$

(5)

$\begin{matrix} R_{1} & = \frac{\bar{λ}}{2} log (1 + \frac{\bar{λ} P_{1} - λ \bar{λ} N_{2} - λ P_{2}}{\bar{λ} (1 + N_{2}) + P_{2}}) + \frac{λ}{2} log (1 + P_{1} + P_{2} + \bar{λ} N_{2}), \\ R_{2} & = \frac{\bar{λ}}{2} log (1 + \frac{P_{2}}{\bar{λ} (1 + N_{2})}) . \end{matrix}$

Remark 1.

A general Gaussian signaling strategy incorporating superposition coding and non-naïve (i.e., power-controlled) time-sharing will have many more phases than those described above. However, it was proposed in [6] and established in [8] that the boundary of the Gaussian signaling region is obtained by restricting to these six strategies.

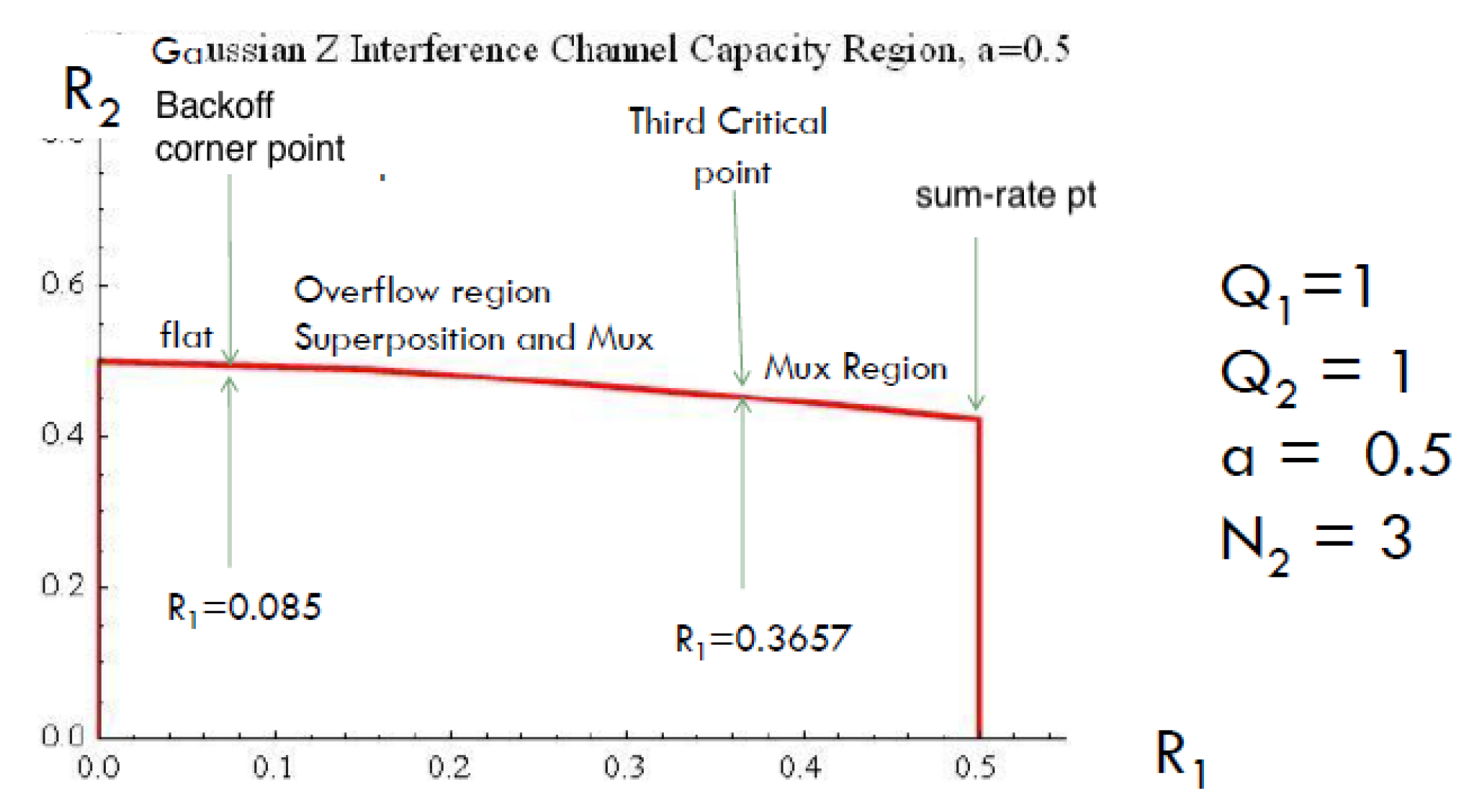
2.2. The Gaussian signaling region

One needs to optimize

R_{1} + β R_{2}

for

1 \leq β \leq \infty

, among the various signaling strategies or phases to compute the Gaussian signaling region.

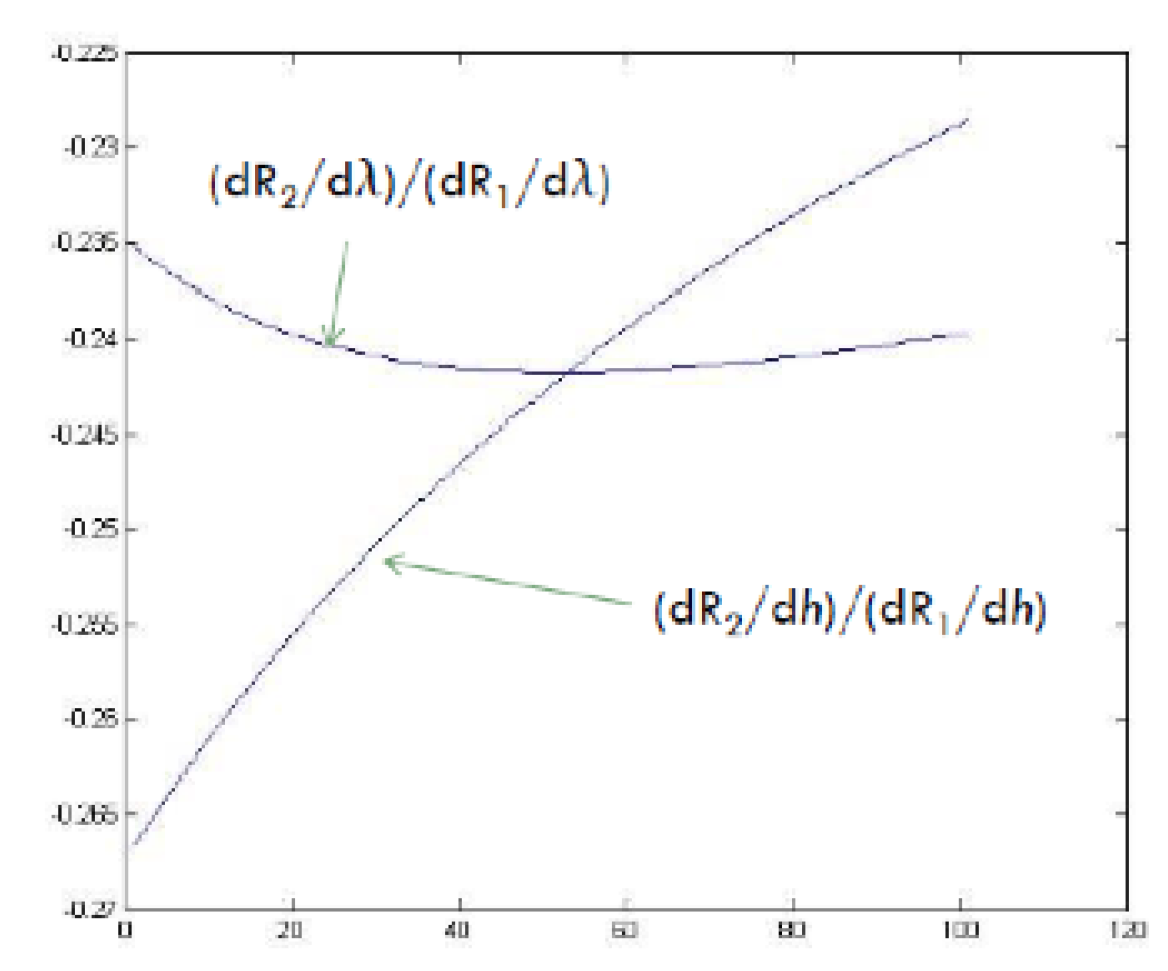
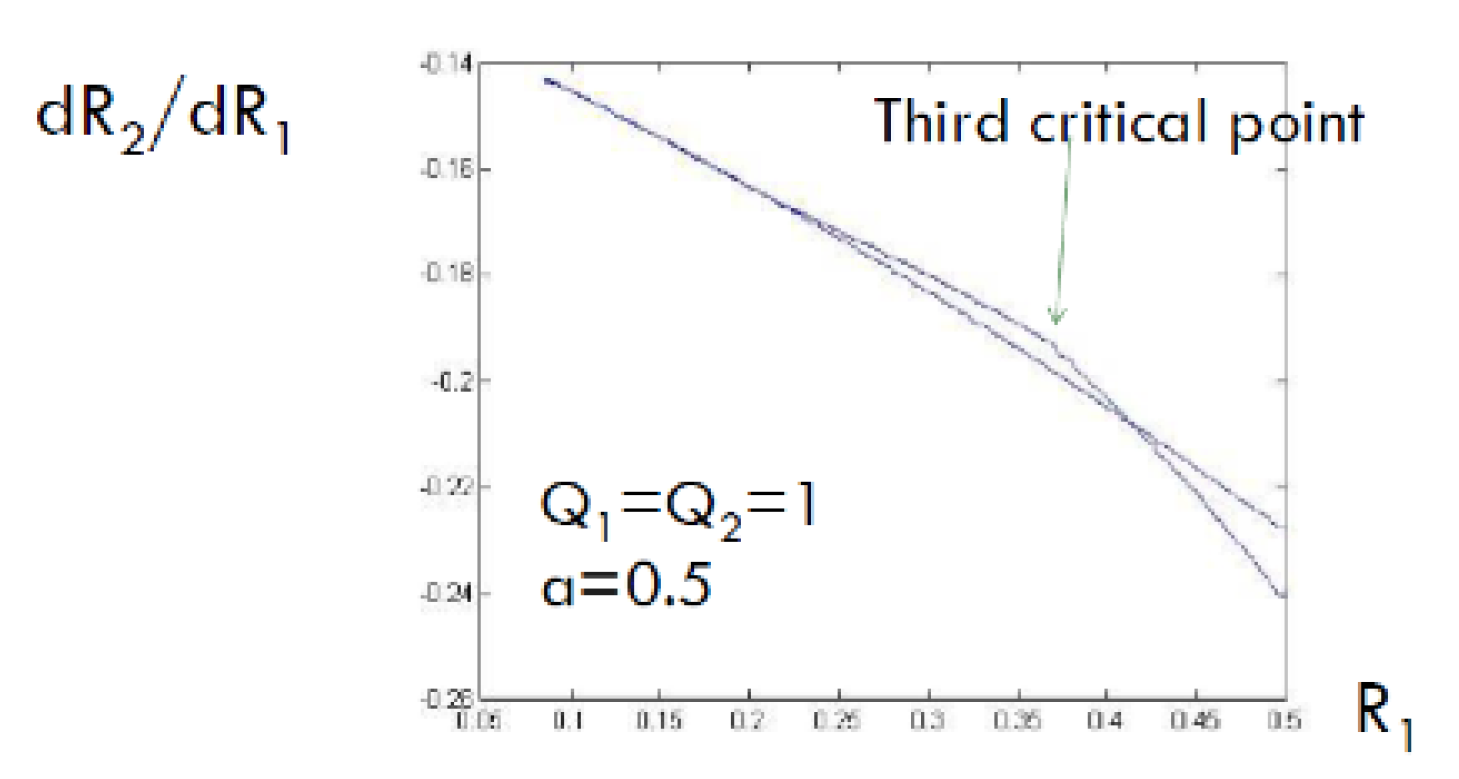
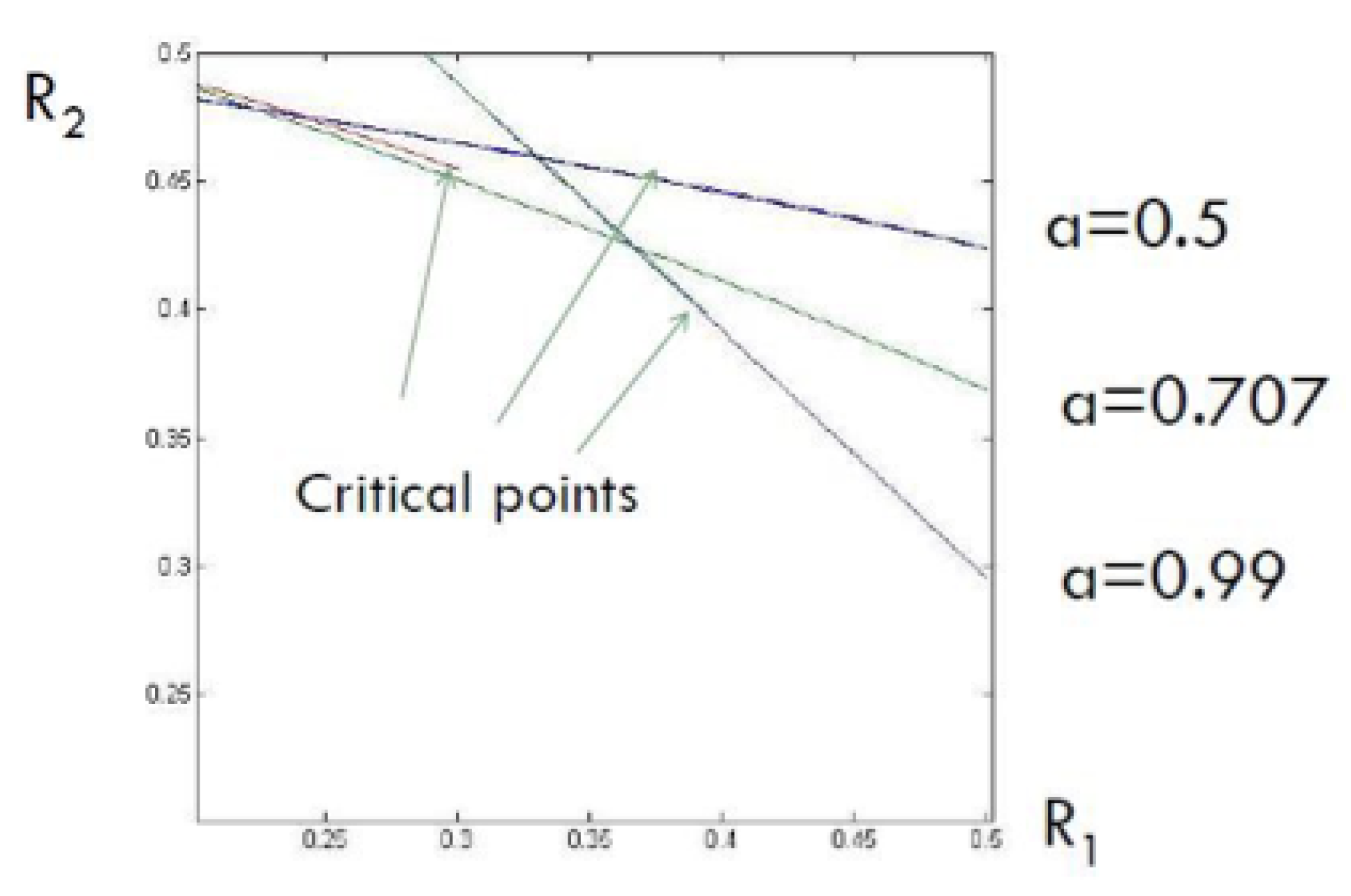
2.2.1. Slopes at the corner points

It is known [5,27] that

R_{1} + R_{2}

(i.e.

β = 1

) is maximized (for the capacity region) at the corner point 1

R_{1} = \frac{1}{2} log (1 + P_{1})

and

R_{2} = \frac{1}{2} log (1 + \frac{P_{2}}{1 + N_{2} + P_{1}})

. This corresponds to a Phase 1 communication strategy. In particular, it has been shown [12] that the supporting hyperplane,

R_{1} + β R_{2}

, will touch the Gaussian signaling region (or equivalently the noiseberg region) at the same corner point if and only if

β \leq β_{S a t o}

(defined below). Thus,

β_{S a t o}

marks the first critical (or phase-transition) point of the noiseberg region.

Theorem 1

([12]). For a GZIC, let

β_{S a t o}

be the largest value of

β \geq 1

such that

\begin{matrix} sup_{(R_{1}, R_{2}) \in R^{HK - GS}} (R_{1} + β R_{2}) = \frac{1}{2} log (1 + P_{1}) + \frac{λ}{2} log (1 + \frac{P_{2}}{1 + N_{2} + P_{1}}) . \end{matrix}

(6)

Then

\begin{matrix} β_{Sato} = min \{\frac{(N_{2} + P_{2}) (1 + N_{2} + P_{1})}{P_{2} (1 + P_{1})}, β^{*}\}, \end{matrix}

where

β^{*}

is the unique positive solution

ψ (β) = 0

, where

\begin{matrix} ψ (β) & : = β (log (1 + \frac{P_{2}}{1 + N_{2} + P_{1}}) - \frac{N_{2} P_{2}}{(1 + N_{2} + P_{1}) (1 + N_{2} + P_{1} + P_{2})}) \\ + log (1 - \frac{P_{2} (1 + P_{1})}{(1 + N_{2} + P_{1}) (1 + N_{2} + P_{1} + P_{2})} β) . \end{matrix}

Remark 2.

We do not yet have a matching converse (i.e. one that follows from an outer bound to the capacity region) that establishes the slope at this corner point. An interested reader may refer to [15] and [17] for some of the recent developments along these lines.

On the other hand, it is known that for large enough

β

the supporting hyperplanes to the Gaussian signaling region, [11], as well as the one to the capacity region [15] pass through the backoff corner point established in [23], namely

R_{1} = \frac{1}{2} log (1 + \frac{P_{1}}{1 + N_{2} + P_{2}})

and

R_{2} = \frac{1}{2} log (1 + P_{2})

. This corresponds to a Phase 3 communication strategy. 2

Theorem 2

([11]). Consider a Gaussian Z-interference channel. The smallest β such that the supporting hyperplane of the form

R_{1} + β R_{2}

of Han-Kobayashi signaling scheme with Gaussian inputs passes through the backoff corner point is given by

β_{b a c k o f f} = 1 + max \{\frac{N_{2} (1 + N_{2} + P_{2})}{P_{2}}, \frac{log (1 + N_{2}) - \frac{N_{2}}{(1 + N_{2} + P_{1} + P_{2})}}{log (\frac{1 + P_{2} + N_{2}}{1 + N_{2}}) - \frac{P_{2}}{1 + P_{2} + N_{2}}}\} .

Thus for all

β \geq β_{b a c k o f f}

the supporting hyperplane to the Gaussian signaling region (or the noiseberg region) passes through the above corner point.

Remark 3.

As with the sum-rate point, we do not yet have a matching converse (i.e. one that follows from an outer bound to the capacity region) that establishes the slope at this corner point. An interested reader may refer to [8,15], where upper bounds on the slope have been established.

2.2.2. The intermediate regime, $β : β_{S a t o} \leq β \leq β_{b a c k o f f}$

The main objective of this paper would be to review the known results for

β

in the regime

β : β_{S a t o} \leq β \leq β_{b a c k o f f}

. Initially, consider the leftmost (pure superposition coding) strategy, i.e we only consider Phases 1,2, and 3. In Phase 2, we need to compute

max_{0 \leq P_{1 A} \leq P_{1}} \frac{1}{2} log (1 + \frac{P_{1} - P_{1 A}}{1 + N_{2} + P_{2} + P_{1 A}}) + \frac{1}{2} log (1 + P_{1 A}) + \frac{β}{2} log (1 + \frac{P_{2}}{1 + N_{2} + P_{1 A}}) .

A little bit of calculus shows that the optimizing

\begin{matrix} P_{1 A} & = \{\begin{matrix} \begin{matrix} P_{1} & if β \leq \frac{P_{2} + N_{2}}{P_{2}} \frac{1 + P_{1} + N_{2}}{1 + P_{1}}, & (Phase 1) \\ 0 & if β \geq \frac{P_{2} + N_{2}}{P_{2}} (1 + N_{2}), & (Phase 3) \\ \frac{(1 + N_{2}) (P_{2} + N_{2}) - β P_{2}}{β P_{2} - (P_{2} + N_{2})} & otherwise . & (Phase 2) \end{matrix} \end{matrix} . \end{matrix}

In the above optimization problem, we observe that there are two transition values for

β

, defined by

β_{1} = \frac{P_{2} + N_{2}}{P_{2}} \frac{1 + P_{1} + N_{2}}{1 + P_{1}}

(marking the transition from Phase 1 to Phase 2) and

β_{2} = \frac{P_{2} + N_{2}}{P_{2}} (1 + N_{2})

(marking the transition from Phase 2 to Phase 3). Note that

β_{1}

corresponds to the first of the two terms in the minimization that defines

β_{S a t o}

, and

β_{2}

corresponds to the first of the two terms in the maximization that defines

β_{b a c k o f f}

. It turns out that the second of the two terms in the minimization that defines

β_{S a t o}

corresponds to a phase transition from Phase 1 to Phase 4. Similarly, the second of the two terms in the maximization that defines

β_{b a c k o f f}

corresponds to a phase transition from Phase 6 to Phase 3. Phases 1, 2, and 3 can be considered special instances of Phases 4, 5, and 6, respectively, by setting

λ = 0

. More specifically, Phase 1 (Sato’s corner point) is associated with the segment

λ = 0

and

0 \leq h \leq N_{2}

. Phase 2 (the pure superposition phase) is related to the middle segment formed by

λ = 0

and

N_{2} \leq h \leq N_{2} + P_{1} .

Finally, Phase 3 (the backoff corner point) is mapped to the single point,

λ = 0

and

h = N_{2} + P_{1}

. Further, the rate pairs

(R_{1}, R_{2})

in Phases 4, 5, and 6 can also be expressed in terms of the parameters

λ

and h as stated before. These parameters

λ, h

vary over a region, called the region of admissible points, defined by the conditions that

P_{1 A}

P_{1 B}

, and

P_{1 C}

are non-negative and sum to

P_{1}

. The region

h \leq N_{2}

and

λ > 0

corresponds to Phase 4. If

h \geq N_{2}

, then

P_{1 C} > 0

and is called the overflow region. This encompasses Phases 5 and 6. The admissible region in Phase 4, using (1), can be shown to be restricted by the expressions

0 \leq h \leq N_{2}

and

0 < λ \leq \frac{P_{1} + P_{2} + h - \sqrt{{(P_{1} + P_{2} + h)}^{2} - 4 P_{1} h}}{2 h},

The admissible region in Phase 5, using (5), can be shown to be restricted by the expressions

N_{2} < h \leq N_{2} + P_{1}

and

0 < λ < \frac{P_{1} + P_{2} + 2 N_{2} - h - \sqrt{{(P_{1} + P_{2} + 2 N_{2} - h)}^{2} - 4 N_{2} (P_{1} + N_{2} - h)}}{2 N_{2}} .

Finally, the admissible region in Phase 6, using (3), can be shown to be restricted by the expressions

N_{2} < h \leq N_{2} + P_{1}

and

λ = \frac{P_{1} + P_{2} + 2 N_{2} - h - \sqrt{{(P_{1} + P_{2} + 2 N_{2} - h)}^{2} - 4 N_{2} (P_{1} + N_{2} - h)}}{2 N_{2}} .

Figure 10 shows the admissible region of

λ

and h for the parameters

P_{1} = 1, P_{2} = 4, N_{2} = 3

. Phases 1,2, and 3 correspond to

λ = 0

and collapse to Y-axis. Phase 6 correspond to the upper boundary. The dotted line at

h = 3

marks the phase boundary between Phases 4 and 5.

To determine the phase, we need to maximize

R_{1} (h, λ) + β R_{2} (h, λ)

(using (2) or (4) depending on

h \leq N_{2}

h \geq N_{2}

, repectively) and this leads to a path of optimal extreme points in the admissible region. Numerical experiments suggest that the possible phase transitions are as follows:

Path 1: For some set of parameters (for example $P_{1} = 1, P_{2} = \frac{1}{a^{2}}, N_{2} = \frac{1}{a^{2}} - 1$ , with $a^{2} \leq 3 - 2 \sqrt{2}$ ) it appears that the optimal path is Phase 1 → Phase 2 → Phase 3. (This is the path of pure superposition evolution) and the locations of the phase transitions are $β_{1}$ and $β_{2}$ respectively. This implies that the trajectory in the admissible region is only along the h-axis, i.e., with $λ = 0$ .
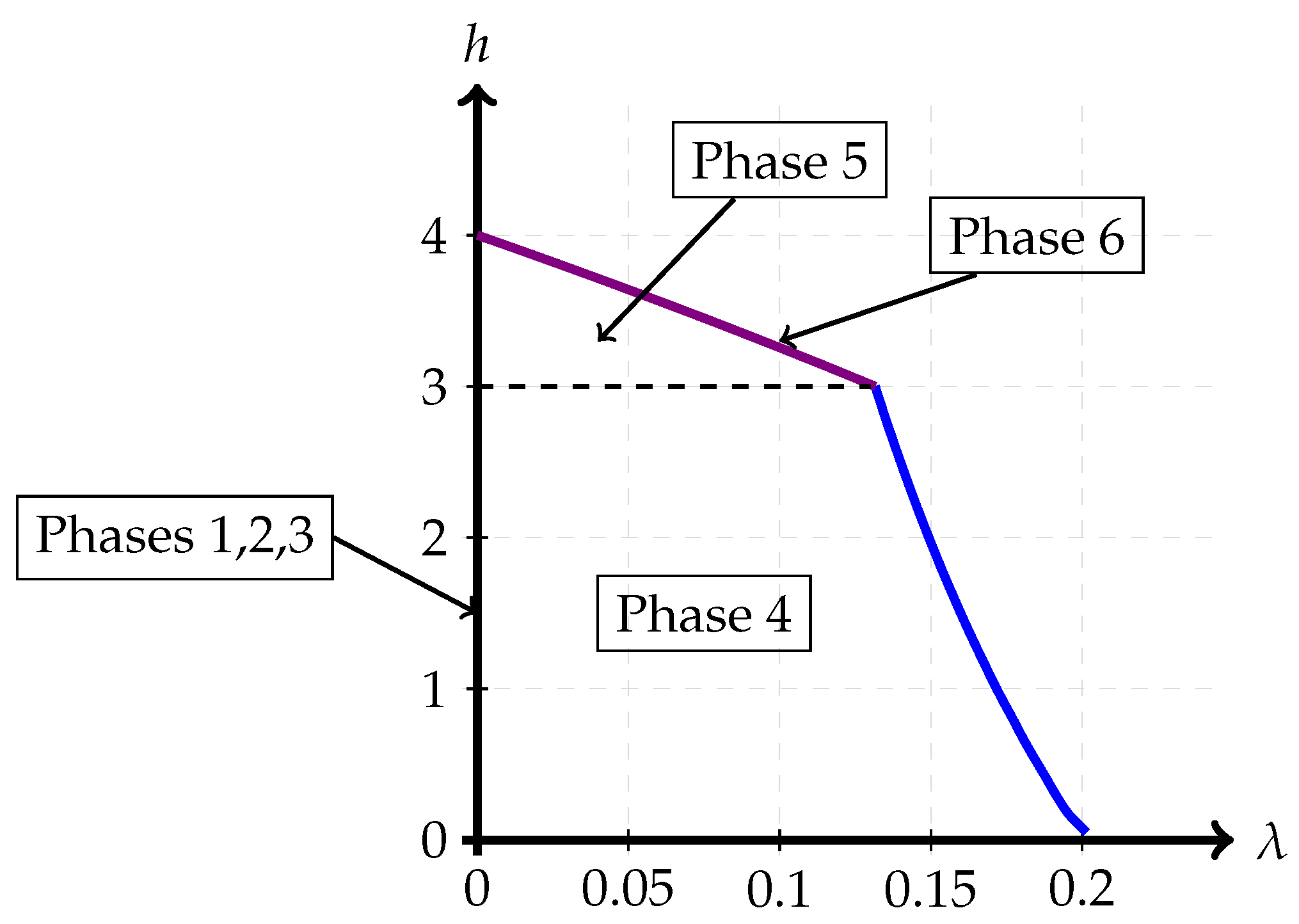
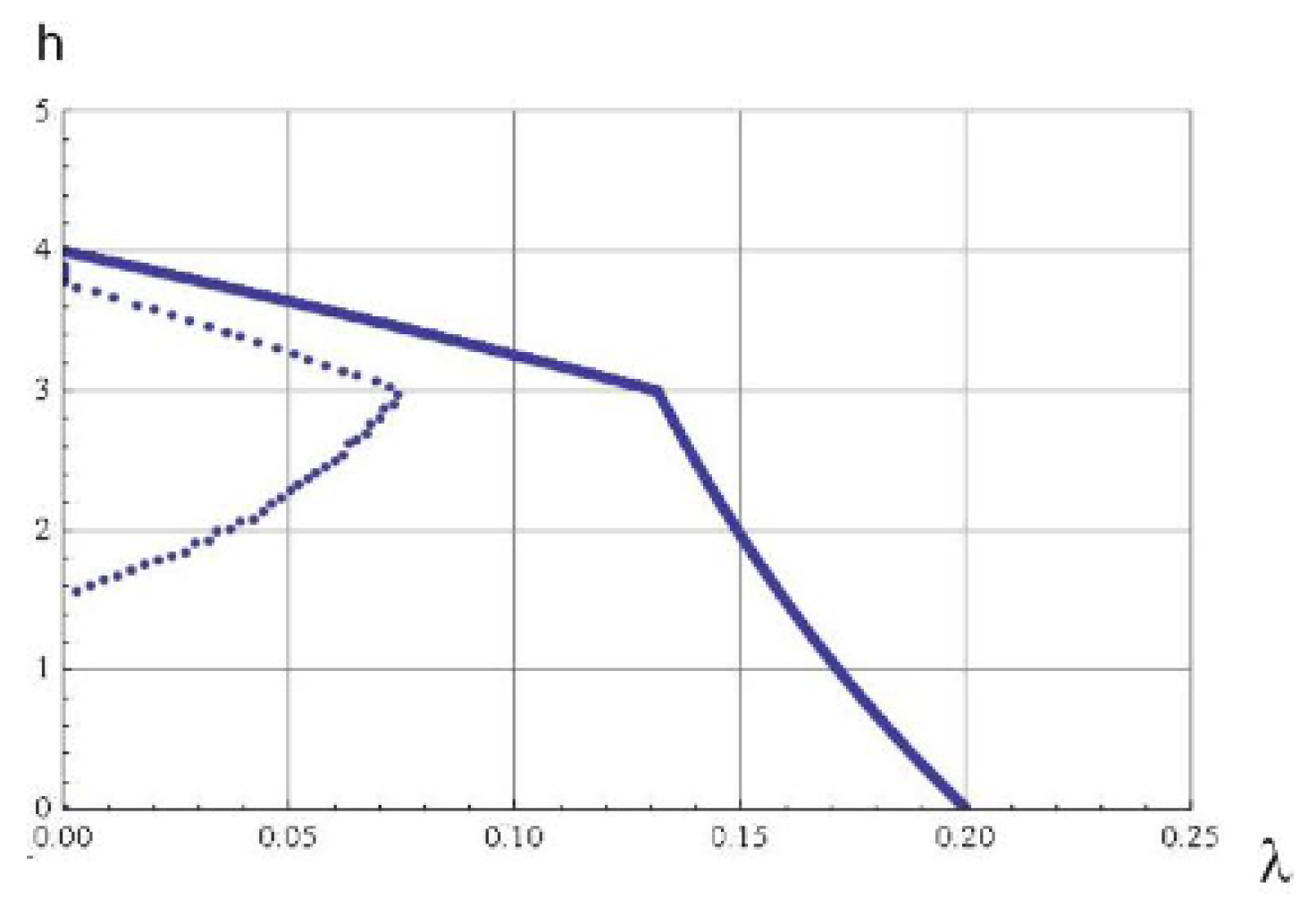
Path 2: For some set of parameters (for example $P_{1} = 1, P_{2} = \frac{1}{a^{2}}, N_{2} = \frac{1}{a^{2}} - 1$ , with $a^{2} = \frac{1}{4}$ ) the optimal path seems to be Phase 1 → Phase 4 → Phase 5 → Phase 2 → Phase 3. This path is depicted in Figure 11.

As the figure illustrates, it leaves Phase 1 (Sato point) and moves into Phase 4. Then at $h = 3$ , it moves from Phase 4 to Phase 5. Then, at $h \approx 3.8$ , it moves from Phase 5 to Phase 2. Finally at $h = 4$ , the trajectory reaches the other corner point.
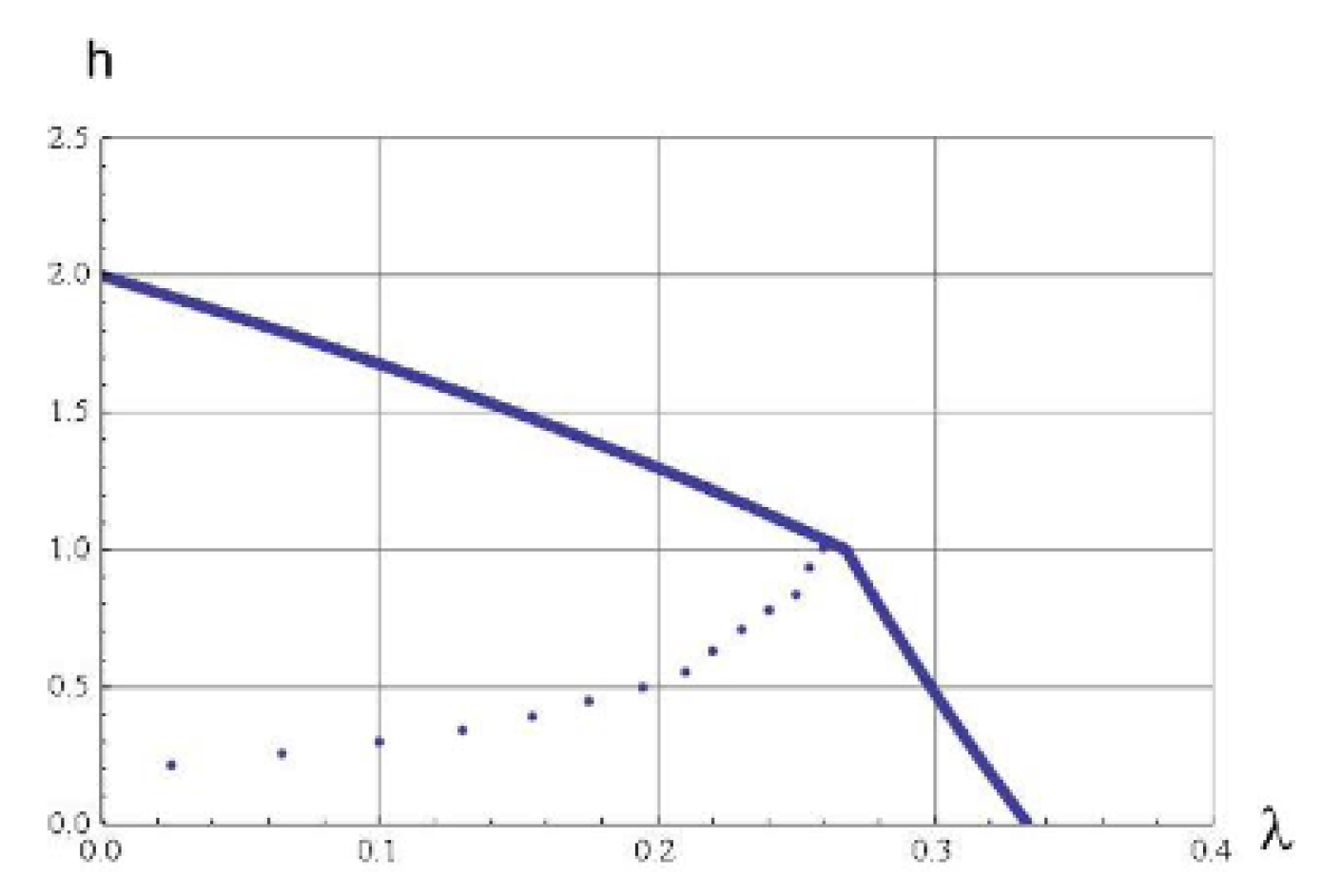
Path 3: For some set of parameters (for example $P_{1} = 1, P_{2} = \frac{1}{a^{2}}, N_{2} = \frac{1}{a^{2}} - 1$ , with $a^{2} = \frac{1}{2}$ ) the optimal path seems to be Phase 1 → Phase 4 → Phase 5 → Phase 6 → Phase 3. This path is depicted in Figure 12.

As the figure illustrates, it leaves Phase 1 (Sato point) and moves into Phase 4. Then at $h = N_{2} = 1$ , it moves from Phase 4 to Phase 5. Almost immediately, it enters into Phase 6 and remains there till it reaches the new corner point at Phase 3.

An extreme example of Path 3 is obtained for

a = 0.99

. In this case, the best trajectory follows very closely the right contour of the

(λ, h)

admissible region, with a noiseberg growing fast for small variations in

β

above 1, rapidly overflowing power over

P_{2}

, and following the top parabolic boundary of the admissible

(λ, h)

region. The resulting rate region is very close to the pentagon that is known to be the capacity region for

a = 1

. Apart from the phase transitions characterized in Theorems 1 and 2, namely, Phase 1 → Phase 2, Phase 1 → Phase 4, Phase 2 → Phase 3, and Phase 6 → Phase 3, the numerical experiments show that there are three more types of phase transitions in the Gaussian signaling scheme. These other ones represent the transitions from Phase 4 → Phase 5, Phase 5 → Phase 2, and Phase 5 → Phase 6, and let us define the corresponding

β

’s to be

β_{4 \to 5}

β_{5 \to 2}

, and

β_{5 \to 6}

respectively. These phase transitions can be implicitly characterizes as follows:

$β_{4 \to 5}$ : This corresponds to the $β$ at which $R_{1} (h, λ) + β R_{2} (h, λ)$ is maximized when $h = N_{2}$ and $λ > 0$ . This corresponds to the transition between the multiplex and overflow regions (please see Section 2.4).
$β_{5 \to 2}$ : This corresponds to the $β$ at which $R_{1} (h, λ) + β R_{2} (h, λ)$ is maximized when $h > N_{2}$ and $λ = 0$ . This corresponds to the transition from the overflow region to a pure superposition coding region.
$β_{5 \to 6}$ : This corresponds to the $β$ at which $R_{1} (h, λ) + β R_{2} (h, λ)$ is maximized when $h > N_{2}$ and $λ = \frac{P_{1} + P_{2} + 2 N_{2} - h - \sqrt{{(P_{1} + P_{2} + 2 N_{2} - h)}^{2} - 4 N_{2} (P_{1} + N_{2} - h)}}{2 N_{2}} .$ This corresponds to the transition from the interior of the admissible $(h, λ)$ admissible region to the boundary of this region.

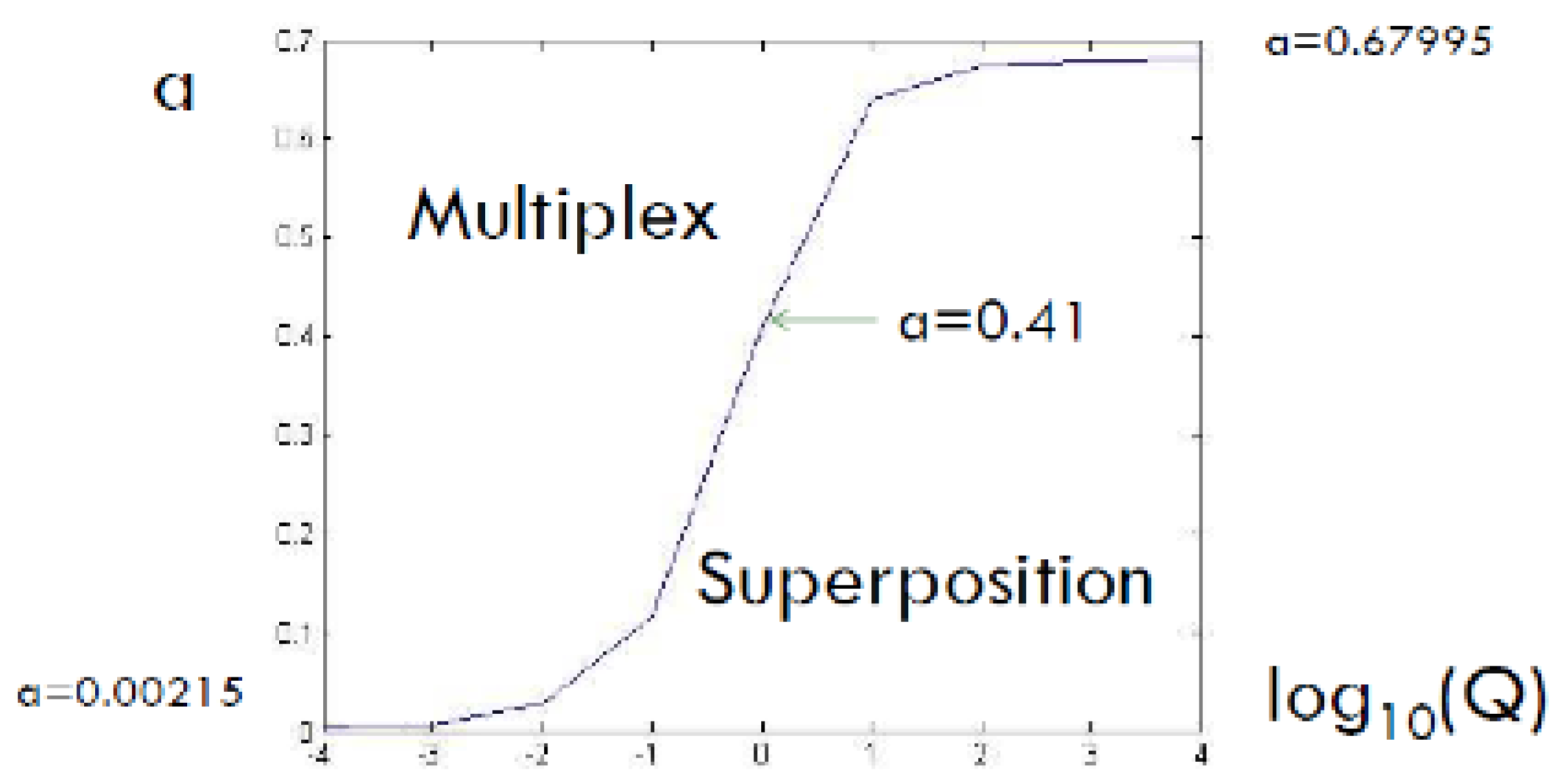
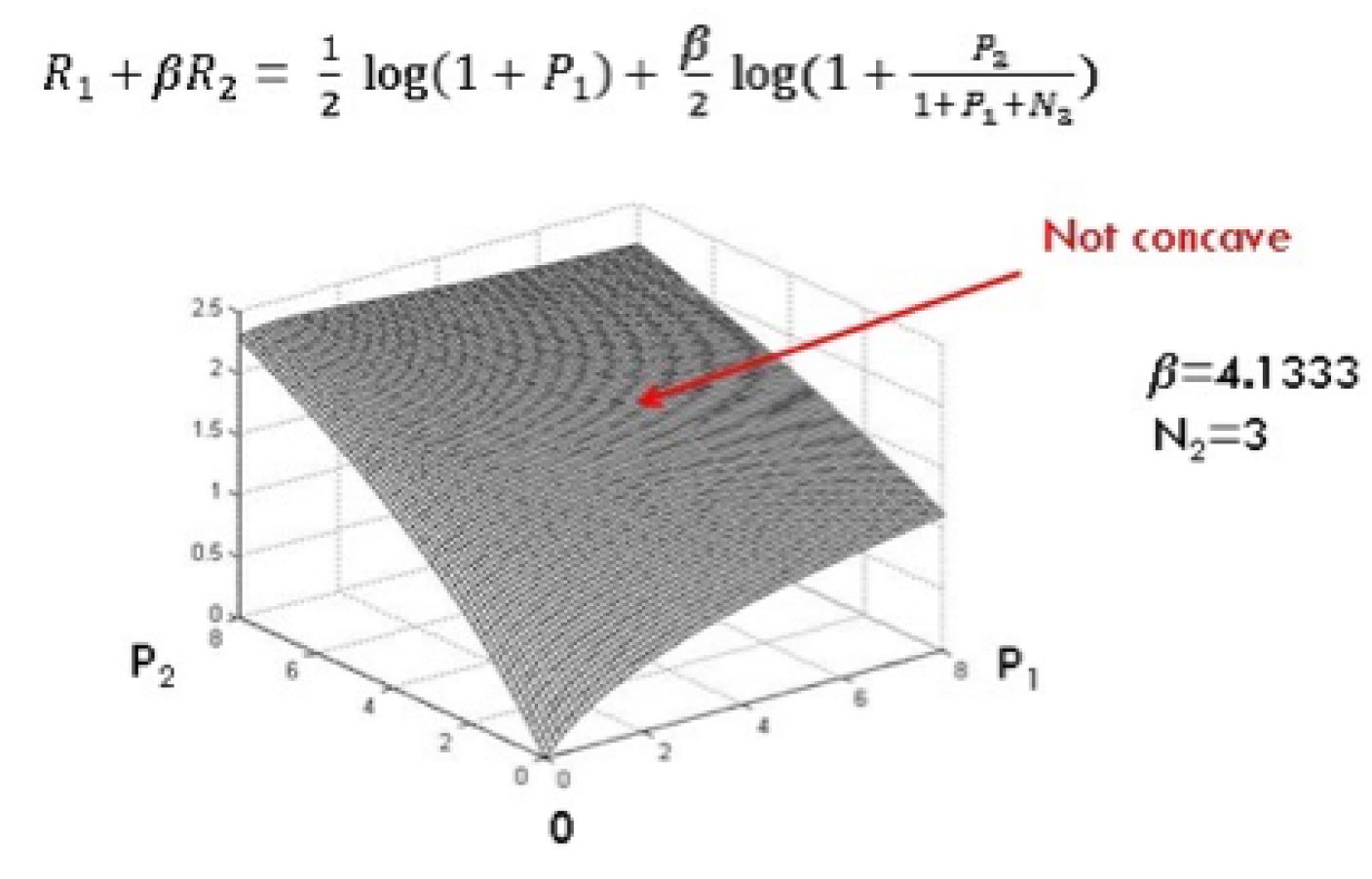
2.3. To Mux or Not to Mux

In this section we review in detail the transitions from Phases 1 to 2 (pure superposition option) and Phases 1 to 4 (multiplex option), and show the calculations needed to establish the results of Theorem 1, and settle the "mux or not to mux" competition. To understand the difference of pure superposition (i.e. no need for noisebergs) and the multiplex scheme (with noisebergs), we evaluate the gradient of

R_{1} (h, λ) + β R_{2} (h, λ)

that leads to a path of optimal extreme points in the rate region. Equating this gradient to 0 for the outmost rate contour (the boundary of the achievable rate region), we get that

\begin{matrix} \frac{d R_{2}}{d λ} / \frac{d R_{1}}{d λ} = \frac{d R_{2}}{d h} / \frac{d R_{1}}{d h} = - \frac{1}{β} . \end{matrix}

(7)

The first of these derivatives can be calculated to equal

\begin{matrix} \frac{d R_{2}}{d λ} / \frac{d R_{1}}{d λ} = \frac{- (F (\frac{P_{2}}{1 + N_{2} + P_{1}}) + \frac{h P_{2}}{(1 + N_{2} + P_{1} + P_{2}) (1 + N_{2} + P_{1})})}{F (\frac{P_{2} + h}{1 + P_{1}})} \end{matrix}

(8)

where the function

F (x)

is defined as

F (x) = x - log (1 + x)

. The second derivative in (7), with respect to h, can be computed to be

\begin{matrix} \frac{d R_{2}}{d h} / \frac{d R_{1}}{d h} = \frac{- P_{2} (1 + P_{1}) (1 + P_{1} + P_{2} + h)}{(P_{2} + h) (1 + N_{2} + P_{1}) (1 + N_{2} + P_{1} + P_{2})} \end{matrix}

(9)

Equating these two derivatives we can find the conditions for the maximum to occur in the

(h, λ)

segment of

0 \leq h \leq N_{2}

, and small

λ

values (more specifically, in the limit as

λ \to 0

). When there is a matching point in the two derivative curves, we conclude that the corresponding h value is the optimal height for the initial noiseberg, for very small

λ

. Alternatively, if the two derivatives do not meet as h varies from 0 to

N_{2}

, then this indicates that pure superposition is the best strategy to connect the two extreme points of the achievable rate region. An example of these solutions is shown in Figure 13, where we find the intersecting point of the two derivatives. The plot has the horizontal axis showing h scaled as a percentage of

N_{2}

. We see that the intersecting point occurs at approximately the midpoint of

0 \leq h \leq N_{2} = 3

, more precisely at

h = 1.54

. These techniques allow us to identify the regions of parameters

Q_{1}

Q_{2}

and a where we have optimal rate evolution between the extreme points with pure superposition alone, i.e., without the use of noisebergs. The results are shown in Figure 14.

2.3.1. Multiplexing × Pure superposition

Another way to present the boundary between the multiplexing and pure superposition regions is illustrated in Figure 15. For example, the boundary happens at

a = 0.41

for

Q_{1} = Q_{2} = Q = 1

. In addition, no superposition happens for a greater than about

0.68

, in the

Q_{1} = Q_{2} = Q

case. To find the point of intersection we can equate these two expressions and do some algebraic manipulations. Equivalently, we can take the derivative of (8) with respect to h and equate it to 0. We then get

\begin{matrix} (1 + P_{1} + P_{2} + N_{2}) G (\frac{P_{2}}{1 + P_{1} + N_{2}}) - N_{2} = (1 + P_{1} + P_{2} + h) G (\frac{P_{2} + h}{1 + P_{1}}) \end{matrix}

(10)

where the function

G (x)

is defined as

\frac{log (1 + x)}{x}

. Solving this equation numerically or graphically for h we obtain the optimal initial height of the noiseberg at Sato’s point, if

h < N_{2}

. Let this optimal value be denoted by

h^{*}

. Then we can use (8) or (9) with

h = h^{*}

, and then (7) to get the normal slope to the achievable region at Sato’s point. For example, if we take the case

P_{1} = 1

P_{2} = 4

and

N_{2} = 3

(equivalently,

Q_{1} = Q_{2} = 1

and

a = 0.5

), we get

h^{*} = 1.5415

, and

β = 4.1333

. If the

h^{*}

solution to (10) turns out to be equal or greater than

N_{2}

, then there is no need for multiplexing with a noiseberg band, and the optimal strategy to leave Sato’s point is pure superposition, that is moving along the path with

λ = 0

and h varying from

N_{2}

N_{2} + P_{1}

, in the admissible

(λ, h)

parameter region. In this case, the normal slope at Sato’s point is easily found to be

β = \frac{(1 + P_{1} + N_{2}) (P_{2} + N_{2})}{(1 + P_{1}) P_{2}} .

Remark 4.

Two points are worth noting here. Firstly, from the point of view of a converse to the capacity region, it may be helpful to realize that one does not need multiplexing for some parameters. Hence, there is a potential for the existing techniques for proving the optimality of Gaussian distributions to work. Secondly, Theorem 1 only establishes the behavior of the noiseberg region around the sum-rate corner point. A formal proof of the numerically observed phenomenon that if the first term is the minimizer, then only never encounters multiplexing phenomenon is absent at this point.

2.4. The Multiplex-Overflow Region Interface

In Figure 16 we show an example of achievable rate region and identify the two extreme point as well the new critical point,

β_{4 \to 5}

, that happens at the mux/overflow interface. Even though no change of derivative is shown in this new critical point, a discontinuous second derivative is observed, as depicted in Figure 17.

Figure 18 shows a portion of the achievable rate regions for three values of a (

0.5

0.707

, and

0.99

) including the transitional critical point. In all cases the optimized path preserved the continuity of the derivative of the curves. It can be shown that the second derivatives of the curves are discontinuous at these points.

Remark 5.

To illustrate the need for multiplexing for certain values of the channel parameters, we observe that the linear combination of rates

R_{1}

and

R_{2}

given by

R_{1} + β R_{2} = \frac{1}{2} log (1 + P_{1}) + \frac{β}{2} log (1 + \frac{P_{2}}{1 + P_{1} + N_{2}})

is not concave in certain regions of the

(P_{1}, P_{2})

plane and certain values of β. In these cases the best rate combination happens above the surface of the function, on the concave envelope, and requires the multiplexing of two superposition schemes. As an example, in Figure 19 we show a surface plot of this function in the plane

(P_{1}, P_{2})

with

β = 4.1333

and

N_{2} = 3

, for

0 \leq P_{1}, P_{2} \leq 8

. The shading of the surface indicates the non-concavity.

2.5. The Overflow-Superposition Interface

As mentioned earlier, for some range of parameters, as we increase

β

from one, we first encounter the multiplexing situation (Phase 4) and then the overflow scenario (Phase 5). As we continue to increase

β

, the optimizers of the

R_{1} (λ, h) + β R_{2} (λ, h)

will undergo another phase transition before reaching the back-off corner point. If

λ = 0

becomes the optimizer before (i.e. for a smaller value of

β

)

P_{1 A} = 0

, then the trajectory in the phase space

(h, λ)

reverts to the superposition region (Figure 11). On the other hand, if

P_{1 A} = 0

happens earlier, then the trajectory in the phase space follows the boundary of the phase space to the backoff point (Figure 12).

3. Conclusions

In this paper we show new critical points in the noiseberg achievable rate region of the Gaussian Z-interference channel. This region is known to have two critical points at its two corner points. A third critical point marks the transition of the noiseberg multiplex region into the overflow region. Somewhat surprisingly, the derivative of

R_{2}

with respect to

R_{1}

is continuous at this point, but the second derivative is discontinuous. A fourth critical point occurs in one of two possible phase transitions. One such phase transition occurs between the overflow region and the pure superposition region. The other phase transition that yields a critical point happens in the overflow region as it reaches the boundary of admissible points. At these fourth critical points, we also can verify that the derivative of

R_{2}

with respect to

R_{1}

is continuous, but the second derivative is discontinuous. This happens because there is a crossing of the curves of

β

that correspond to the two schemes that are involved in the transition. These critical points relate to a sudden change in the path of

β

, which correspond to a sudden change in the slope of

β

. But

β

is the slope of the normal to the tangent of the achievable rate pair curve. Therefore, the first derivatives of the achievable rate pair curve will not show a discontinuity at these extra critical points, but their second derivatives (the slope of the slope) will. We also evaluate the ratio of derivatives of the rates

R_{2}

and

R_{1}

with respect to

λ

and h, and identify the situations where pure superposition is the optimal strategy (i.e. with no use of noisebergs) to traverse the achievable rate region from the Sato extreme point to the newer extreme corner point.

4. Acknowledgement

The authors would like to thank Gustavo Fraidenraich, José Cândido Santos Filho, Dustin Wang, and Amin Gohari for their inspiring discussions.

References

R. Ahlswede. The capacity region of a channel with two senders and two receivers. The Annals of Probability, 2(5):805 – 814, 1974. [CrossRef]
V. Sreekanth Annapureddy and Venugopal V. Veeravalli. Gaussian interference networks: sum capacity in the low-interference regime and new outer bounds on the capacity region. IEEE Transactions on Information Theory, 55(7):3032–3050, 2009. [CrossRef]
A. Carleial. A case where interference does not reduce capacity (corresp.). IEEE Transactions on Information Theory, 21(5):569–570, 1975. [CrossRef]
A. Carleial. Interference channels. IEEE Transactions on Information Theory, 24(1):60–70, 1978. [CrossRef]
Max H. m. Costa. On the Gaussian interference channel. IEEE Transactions on Information Theory, 31(5):607–615, 1985. [CrossRef]
Max H. M. Costa. Noisebergs in Z Gaussian interference channels. In Proc. Information Theory and Applications Workshop (ITA), pages 1–6, 2011.
Max H. M. Costa. A third critical point in the achievable region of the z-Gaussian interference channel. In Information Theory and Applications Workshop (ITA), 2014.
Max H. M. Costa, Amin Gohari, Chandra Nair, and David Ng. A proof of the noiseberg conjecture for the Gaussian z-interference channel. In 2023 IEEE International Symposium on Information Theory (ISIT), pages 1824–1829, 2023.
Max H. M. Costa and Chandra Nair. On the achievable rate sum for symmetric Gaussian interference channels. In Proc. Information Theory and Applications Workshop (ITA), 2012.
Max H. M. Costa and Chandra Nair. Phase transitions in the achievable sum-rate of symmetric Gaussian interference channels. In Proc. Inf. Theory Appl. Workshop, pages 10–15, 2013.
Max H. M. Costa and Chandra Nair. Gaussian Z-interference channel: around the corner. In Proc. Information Theory and Applications Workshop (ITA), pages 1–6, 2016.
Max H. M. Costa, Chandra Nair, and David Ng. On the Gaussian Z-interference channel. In Proc. Information Theory and Applications Workshop (ITA), pages 1–15, 2017.
Max H. M. Costa, Chandra Nair, David Ng, and Yan Nan Wang. On the structure of certain non-convex functionals and the Gaussian Z-interference channel. In Proc. IEEE International Symposium on Information Theory (ISIT), pages 1522–1527, 2020.
Raul H. Etkin, David N. C. Tse, and Hua Wang. Gaussian interference channel capacity to within one bit. IEEE Transactions on Information Theory, 54(12):5534–5562, 2008. [CrossRef]
Amin Gohari and Chandra Nair. Outer bounds for multiuser settings: the auxiliary receiver approach. IEEE Transactions on Information Theory, 68(2):701–736, 2022. [CrossRef]
Amin Gohari, Chandra Nair, and David Ng. An information inequality motivated by the Gaussian Z-interference channel. In Proc. IEEE International Symposium on Information Theory (ISIT), 2021.
Amin Gohari, Chandra Nair, and Jinpei Zhao. On the capacity region of some classes of interference channels. In 2024 IEEE International Symposium on Information Theory (ISIT), pages 3136–3141, 2024.
Te Sun Han and Kingo Kobayashi. A new achievable rate region for the interference channel. IEEE Transactions on Information Theory, 27(1):49–60, 1981. [CrossRef]
G. Kramer. Outer bounds on the capacity of gaussian interference channels. IEEE Transactions on Information Theory, 50(3):581–586, 2004. [CrossRef]
G. Kramer. Review of rate regions for interference channels. In 2006 International Zurich Seminar on Communications, pages 162–165, 2006.
Omar Mehanna, John Marcos, and Nihar Jindal. On achievable rates of the two-user symmetric gaussian interference channel. In 2010 48th Annual Allerton Conference on Communication, Control, and Computing (Allerton), pages 1273–1279, 2010.
Abolfazl Seyed Motahari and Amir Keyvan Khandani. Capacity bounds for the Gaussian interference channel. IEEE Transactions on Information Theory, 55(2):620–643, 2009. [CrossRef]
Yury Polyanskiy and Yihong Wu. Wasserstein continuity of entropy and outer bounds for interference channels. CoRR, abs/1504.04419, 2015. [CrossRef]
I. Sason. On achievable rate regions for the Gaussian interference channel. IEEE Transactions on Information Theory, 50(6):1345–1356, 2004. [CrossRef]
H. Sato. Two-user communication channels. IEEE Transactions on Information Theory, 23(3):295–304, 1977. [CrossRef]
H. Sato. On degraded gaussian two-user channels (corresp.). IEEE Transactions on Information Theory, 24(5):637–640, 1978. [CrossRef]
H. Sato. The capacity of the Gaussian interference channel under strong interference (corresp.). IEEE Transactions on Information Theory, 27(6):786–788, 1981. [CrossRef]
Xiaohu Shang, Gerhard Kramer, and Biao Chen. A new outer bound and the noisy-interference sum-rate capacity for Gaussian interference channels. IEEE Transactions on Information Theory, 55(2):689–699, 2009. [CrossRef]

1	Note that $R_{1} + β R_{2}$ for $0 \leq β \leq 1$ will also pass through the same corner point, as this corresponds to the maximum value of $R_{1}$ .
2	At this corner point $R_{2}$ takes it maximum value.

Figure 1. Gaussian Z-interference channel.

Figure 2. Degraded Gaussian interference channel.

Figure 3. Critical points of the capacity region.

Figure 4. Phase 1.

Figure 5. Phase 2.

Figure 6. Phase 3.

Figure 7. Phase 4.

Figure 8. Phase 5.

Figure 9. Phase 6.

Figure 10. Contour of admissible region for a Z-interference channel with

Q_{1} = 1

Q_{2} = 1

a = 0.5

, i.e. a degraded channel with

P_{1} = 1

P_{2} = 4

N_{2} = 3

Figure 10. Contour of admissible region for a Z-interference channel with

Q_{1} = 1

Q_{2} = 1

a = 0.5

, i.e. a degraded channel with

P_{1} = 1

P_{2} = 4

N_{2} = 3

Figure 11. Contour of admissible region and optimized points (obtained numerically) for a Z-interference channel with

Q_{1} = 1

Q_{2} = 1

a = 0.5

, i.e. a degraded channel with

P_{1} = 1

P_{2} = 4

N_{2} = 3

Figure 11. Contour of admissible region and optimized points (obtained numerically) for a Z-interference channel with

Q_{1} = 1

Q_{2} = 1

a = 0.5

, i.e. a degraded channel with

P_{1} = 1

P_{2} = 4

N_{2} = 3

Figure 12. Admissible region and optimized points (obtained numerically) for a Z-interference channel with

Q_{1} = 1

Q_{2} = 1

a = \frac{1}{\sqrt{2}}

, i.e. a degraded channel with

P_{1} = 1

P_{2} = 2

N_{2} = 1

Figure 12. Admissible region and optimized points (obtained numerically) for a Z-interference channel with

Q_{1} = 1

Q_{2} = 1

a = \frac{1}{\sqrt{2}}

, i.e. a degraded channel with

P_{1} = 1

P_{2} = 2

N_{2} = 1

Figure 13. Intersecting derivatives with respect to h and

λ

plotted as a function of h given as a percentage of

N_{2}

(Curves for

P_{1} = 1

P_{2} = 4

N_{2} = 3

Figure 13. Intersecting derivatives with respect to h and

λ

plotted as a function of h given as a percentage of

N_{2}

(Curves for

P_{1} = 1

P_{2} = 4

N_{2} = 3

Figure 14. Boundaries between pure superposition and multiplex regions for different values of

Q_{1}

and

Q_{2}

Figure 14. Boundaries between pure superposition and multiplex regions for different values of

Q_{1}

and

Q_{2}

Figure 15. Boundary between mux region and pure superposition region for different values of a and Q, for the

Q_{1} = Q_{2} = Q

case.

Figure 15. Boundary between mux region and pure superposition region for different values of a and Q, for the

Q_{1} = Q_{2} = Q

case.

Figure 16. Achievable rate region showing the two extreme points and the transitional critical point in the mux/overflow boundary.

Figure 17. A discontinuous transition in the second derivative of

R_{2}

with respect to

R_{1}

at the critical point of the mux/overflow interface.

Figure 17. A discontinuous transition in the second derivative of

R_{2}

with respect to

R_{1}

at the critical point of the mux/overflow interface.

Figure 18. Zoom in on achievable rate regions showing critical transitional points,

β_{4 \to 5}

, for three values of a (

Q_{1} = Q_{2} = 1

Figure 18. Zoom in on achievable rate regions showing critical transitional points,

β_{4 \to 5}

, for three values of a (

Q_{1} = Q_{2} = 1

Figure 19. Surface plot of

R_{1} + β R_{2}

as a function of

P_{1}

and

P_{2}

with

β = 4.1333

and

N_{2} = 3

Figure 19. Surface plot of

R_{1} + β R_{2}

as a function of

P_{1}

and

P_{2}

with

β = 4.1333

and

N_{2} = 3

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Critical Points in the Noiseberg Achievable Region of the Gaussian Z-Interference Channel

Abstract

1. Introduction

2. Preliminaries

2.1. Noisebergs – A Brief Review

2.2. The Gaussian signaling region

2.2.1. Slopes at the corner points

2.2.2. The intermediate regime, β : β S a t o ≤ β ≤ β b a c k o f f

2.3. To Mux or Not to Mux

2.3.1. Multiplexing × Pure superposition

2.4. The Multiplex-Overflow Region Interface

2.5. The Overflow-Superposition Interface

3. Conclusions

4. Acknowledgement

References

MDPI Initiatives

Important Links

Subscribe

2.2.2. The intermediate regime, $β : β_{S a t o} \leq β \leq β_{b a c k o f f}$