Submitted:
02 August 2024
Posted:
02 August 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Quark Model and Wave Functions
2.1. The Chiral Quark Model
2.2. The Olor Screening Model
2.3. Wave Functions
3. Calculation Method
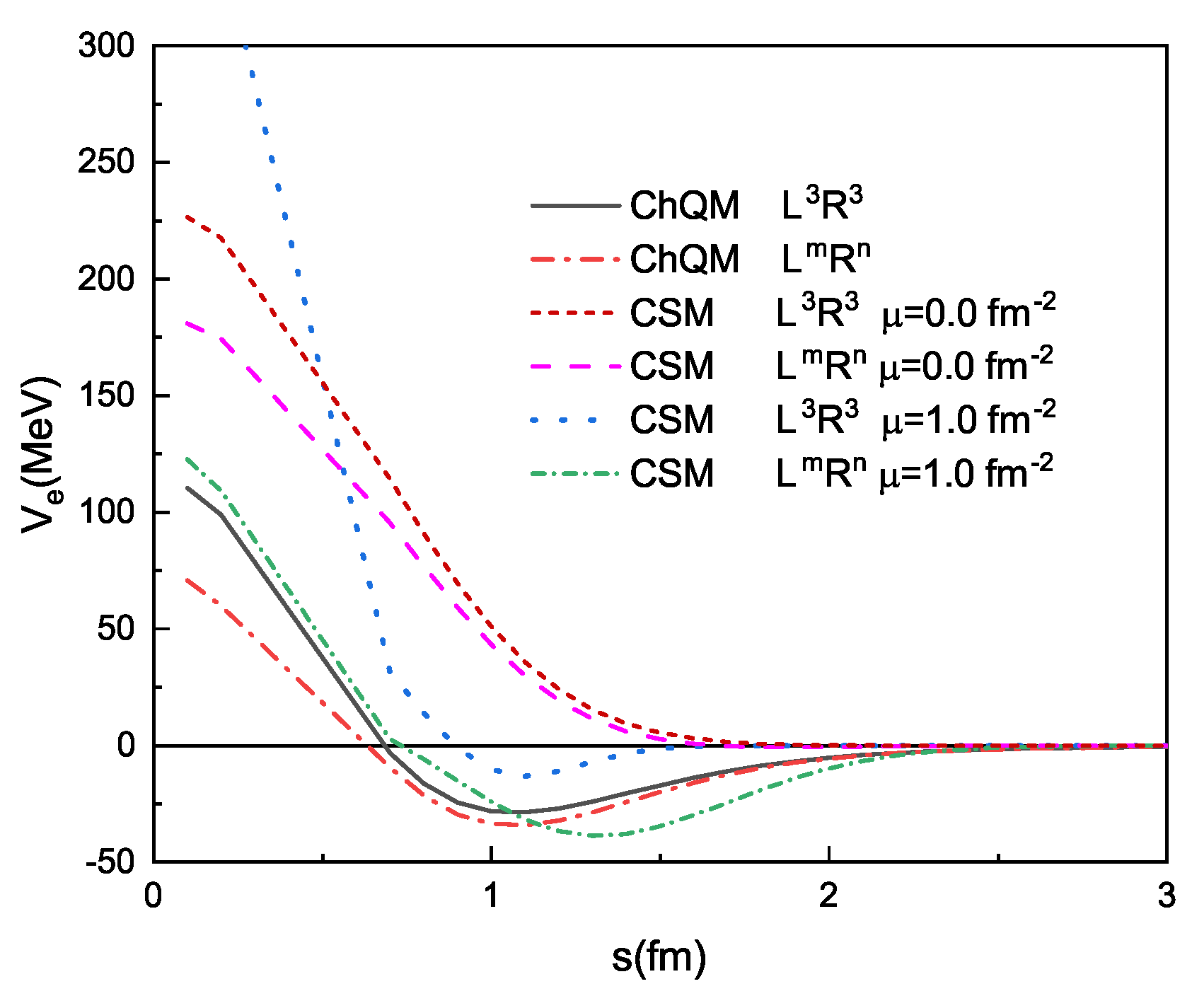
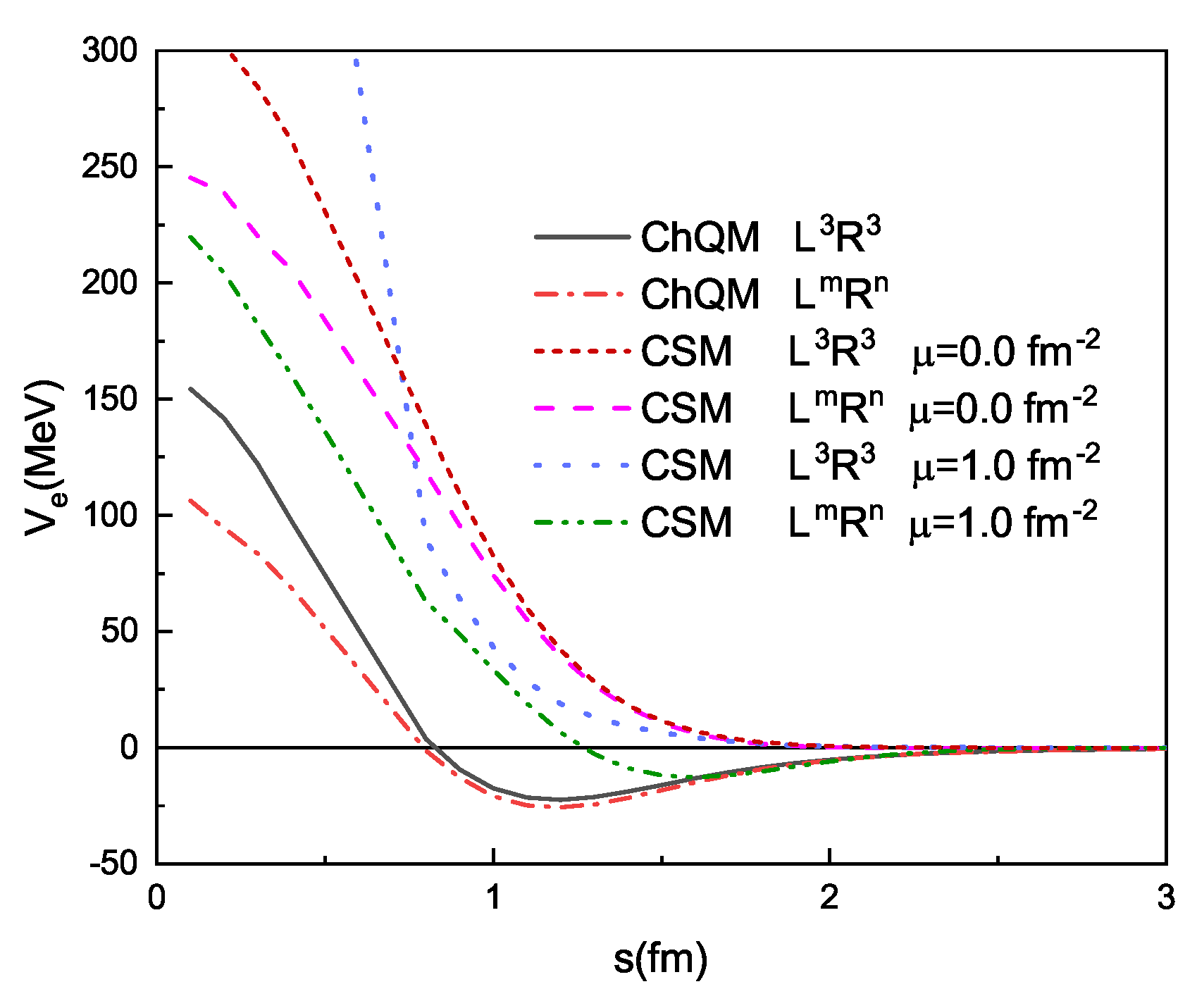
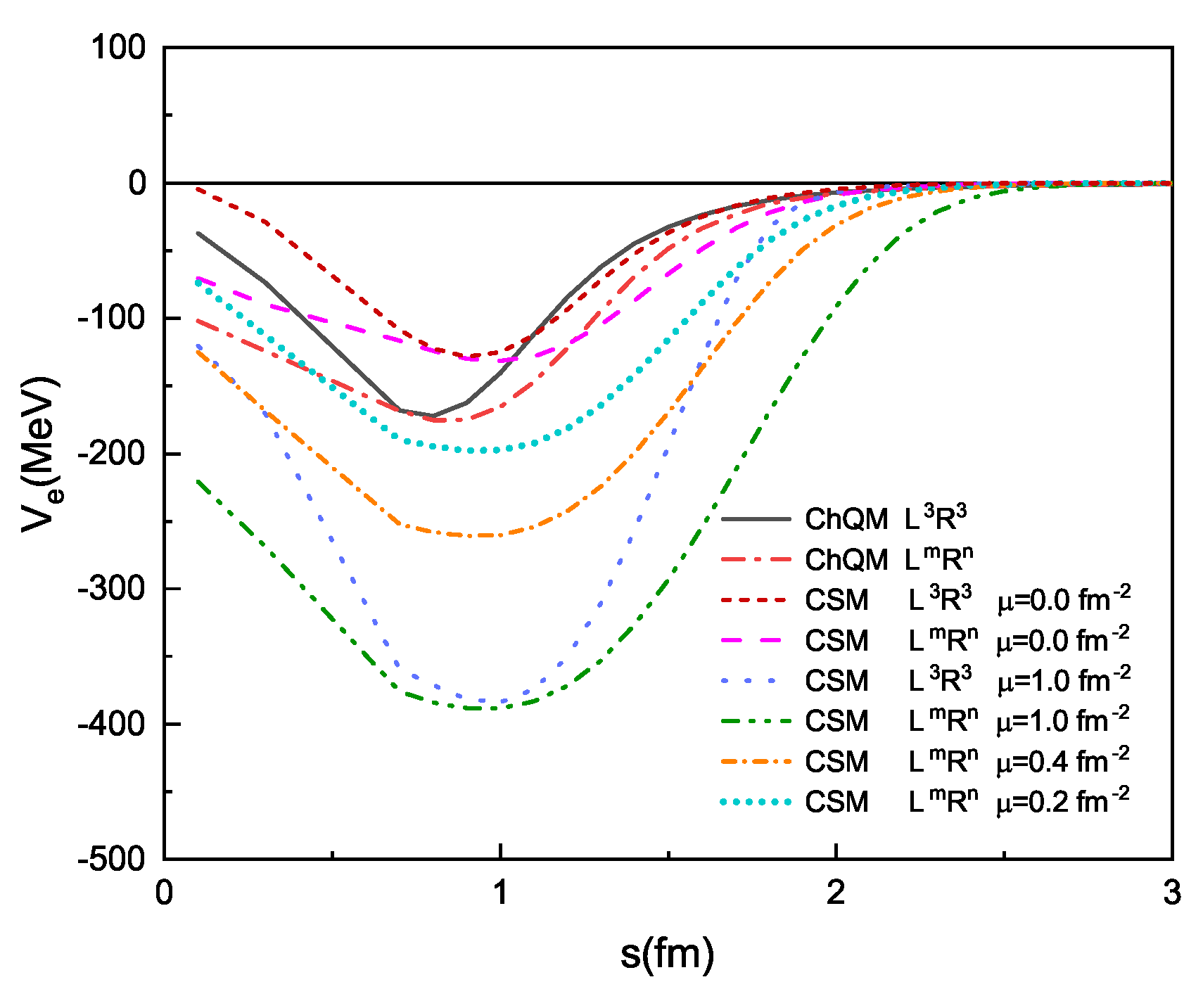
4. The Results and Discussions
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. The 27 Symmetry Bases, for the State with α = (IJ) = (01)
Appendix B. The Matrix Element in the Configuration of L3 R3
References
- Jaffe, R. L. Phys. Rev. Lett. 1977, 38, 195. [Google Scholar] [CrossRef]
- Bashkanov, M. [CELSIUS-WASA Collab.] Phys. Rev. Lett. 2009, 102, 052301.
- Adam, J. et al. [STAR Collab.] Phys. Lett. B 2019, 790, 490. [Google Scholar] [CrossRef]
- Machleidt, R.; Holinde, K.; Elster, Ch. Phys. Rep. 1987, 149, 1. [Google Scholar] [CrossRef]
- Nagels, M. M.; Rijken, T. A.; de Swart, J. J. Ann. Phys. 1973, 79, 338. [Google Scholar]
- Nagels, M. M.; Rijken, T. A.; de Swart, J. J. Phys. Rev. D 1975, 12, 744; 1977, 15, 2547.
- Cottingham W., N. et al. Phys. Rev. D 1973, 8, 800. [Google Scholar]
- Maessen, P. M. M.; Rijken, T. A.; de Swart, J. J. Phys. Rev. C 1989, 40, 2226. [Google Scholar]
- Holzenkamp, B.; Holinde, K.; Speth, J. Nucl. Phys. A 1989, 500, 485. [Google Scholar]
- Oka, M.; Shimizu, K.; Yazaki, K. Nucl. Phys. A 1987, 464, 700. [Google Scholar]
- Koike, Y.; Shimizu, K. Yazaki, K. Nucl. Phys. A 1990, 513, 653. [Google Scholar] [CrossRef]
- Shimizu, K. Rep. Prog. Phys. 1989, 52, 1. [Google Scholar] [CrossRef]
- Yazaki, K. Properties and interactions of hyperons, ed. B. F. Gibson et al, World Scientific, Singapore, 1994, p.189.
- Straub, U.; Zhang, Z. Y.; Bräuer, K.; Faessler, A.; Khadkikar, S. H.; Lübeck, G. Nucl. Phys. A 1988, 483, 686. [Google Scholar]
- Straub, U. et al Phys. Lett. B 1988, 200, 241. [Google Scholar] [CrossRef]
- Fujiwara, Y.; Nakamoto, C.; Suzuki, Y. Phys. Rev. Lett. 1996, 76, 2242. [Google Scholar] [CrossRef] [PubMed]
- Fujiwara, Y.; Nakamoto, C.; Suzuki, Y. Prog. Theor. Phys. 1995, 94, 215; 94, 353.
- Nakamoto, C.; Suzuki, Y.; Fujiwara, Y. Prog. Theor. Phys. 1995, 94, 65. [Google Scholar] [CrossRef]
- Wang, F.; Wu, G. H.; Teng, L. J. Goldman, T. Phys. Rev. Lett. 1992, 69, 2901. [Google Scholar] [CrossRef] [PubMed]
- Ping, J. L.; Wang, F.; Goldman, T. Nucl. Phys. A 1999, 657, 95. [Google Scholar]
- Wang, F.; Ping, J. L.; Goldman, T. Phys. Rev. A 1995, 51, 1648. [Google Scholar]
- Valcarce, A.; Garcilazo, H. et al. Rep. prog. Phys. 2005, 2005 68, 965. [Google Scholar] [CrossRef]
- Ping, J. L.; Huang, H. X.; Pang, H. R.; Wang, F.; Wong, C. W. Phys. Rev. C 2009, 79, 024001. [Google Scholar]
- Valcarce, A.; Gonzalez, P.; Garcilazo, H.; Fernandez, F.; Vento, V. Phys. Lett. B 1996, 367, 35. [Google Scholar] [CrossRef]
- Entem, D. R.; Fernández, F.; Valcarce, A. Phys. Rev. C 2000, 62, 034002. [Google Scholar]
- Chen, J. Q. Tables of the Clebsh-Gordan, Racah and Subduction Coefficients of SU(n) Groups, World Scientific, Singapore, 1987.
- Chen, J. Q. Tables of the SU(mn)⊃SU(m)×SU(n) Coefficients of Fractional Parentage, World Scientific, Singapore. 1991. n.
- Bashkanova, M.; Brodsky, S. Phys. lett. B 2013, 727, 438. [Google Scholar]
- Ping, J. L.; Wang, F.; Goldman, T. Nucl. Phys. A 2001, 688, 871. [Google Scholar]
- Valcarce, A.; Garcilazo, H.; Fernandez, F.; Gonzalez, P. Rep. Prog. Phys. 2005, 68, 965 and references there in.
- Chen, L. Z.; Pang, H. R.; Huang, H. X.; Ping, J. L.; Wang, F. Phys. Rev. C 2007, 76, 014001. [Google Scholar]
| Model | ChQM | CSM | |
|---|---|---|---|
| Quarks | b (fm) | 0.518 | 0.603 |
| (MeV) | 313 | 313 | |
| (MeV) | 313 | 313 | |
| Confinements | (MeV·fm) | 46.938 | 25.13 |
| (fm) | − | ||
| (fm) | − | ||
| OGE | 0.485 | 1.54 | |
| Goldstone bosons | (MeV) | 675 | − |
| (MeV) | 138 | − | |
| (fm) | − |
| K | |||||||
|---|---|---|---|---|---|---|---|
| 01 | [6][44] | [51][321] | [42][51] | [42][33] | [42][2211] | [42][321] | [42][411] |
| 10 | [6][33] | [51][321] | [42][51] | [42][33] | [42][2211] | [42][321] | [42][411] |
| 03 | [6][33] | [42][33] | |||||
| [6] | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| [51] | 0 | 1 | 1 | 1 | 1 | 1 | 0 | |
| [42] | 0 | 0 | 1 | 1 | 1 | 0 | 0 | |
| [33] | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| fm | fm | fm | ||||
|---|---|---|---|---|---|---|
| ChQM | CSM | ChQM | CSM | ChQM | CSM | |
| 0.15 | 0.15 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.00 | 0.01 | 0.00 | 0.08 | 0.00 | 0.01 | |
| 0.13 | 0.19 | 0.17 | 0.03 | 0.01 | 0.12 | |
| 0.44 | 0.30 | 0.66 | 0.78 | 0.78 | 0.74 | |
| 0.13 | 0.19 | 0.17 | 0.03 | 0.01 | 0.12 | |
| 0.00 | 0.01 | 0.00 | 0.08 | 0.00 | 0.01 | |
| 0.15 | 0.15 | 0.00 | 0.00 | 0.00 | 0.00 | |
| fm | fm | fm | ||||
| ChQM | CSM | ChQM | CSM | ChQM | CSM | |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.00 | 0.09 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 1.00 | 0.82 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 0.00 | 0.09 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| fm | fm | fm | ||||
|---|---|---|---|---|---|---|
| ChQM | CSM | ChQM | CSM | ChQM | CSM | |
| 0.13 | 0.07 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.00 | 0.00 | 0.01 | 0.01 | 0.00 | 0.00 | |
| 0.14 | 0.15 | 0.18 | 0.22 | 0.00 | 0.04 | |
| 0.46 | 0.56 | 0.63 | 0.54 | 1.00 | 0.92 | |
| 0.14 | 0.15 | 0.18 | 0.22 | 0.00 | 0.04 | |
| 0.00 | 0.00 | 0.01 | 0.01 | 0.00 | 0.00 | |
| 0.13 | 0.07 | 0.00 | 0.00 | 0.00 | 0.00 | |
| fm | fm | fm | ||||
| ChQM | CSM | ChQM | CSM | ChQM | CSM | |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.00 | 0.04 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 0.00 | 0.04 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| fm | fm | fm | ||||
|---|---|---|---|---|---|---|
| ChQM | CSM | ChQM | CSM | ChQM | CSM | |
| 0.29 | 0.15 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.00 | 0.01 | 0.02 | 0.03 | 0.00 | 0.01 | |
| 0.11 | 0.19 | 0.05 | 0.08 | 0.05 | 0.11 | |
| 0.20 | 0.30 | 0.86 | 0.78 | 0.90 | 0.76 | |
| 0.11 | 0.19 | 0.05 | 0.08 | 0.05 | 0.11 | |
| 0.00 | 0.01 | 0.02 | 0.03 | 0.00 | 0.01 | |
| 0.29 | 0.15 | 0.00 | 0.00 | 0.00 | 0.00 | |
| fm | fm | fm | ||||
| ChQM | CSM | ChQM | CSM | ChQM | CSM | |
| 0.00 | 0.07 | 0.00 | 0.03 | 0.00 | 0.00 | |
| 0.00 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.00 | 0.04 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 1.00 | 0.76 | 1.00 | 0.94 | 1.00 | 1.00 | |
| 0.00 | 0.04 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.00 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.00 | 0.07 | 0.00 | 0.03 | 0.00 | 0.00 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).





