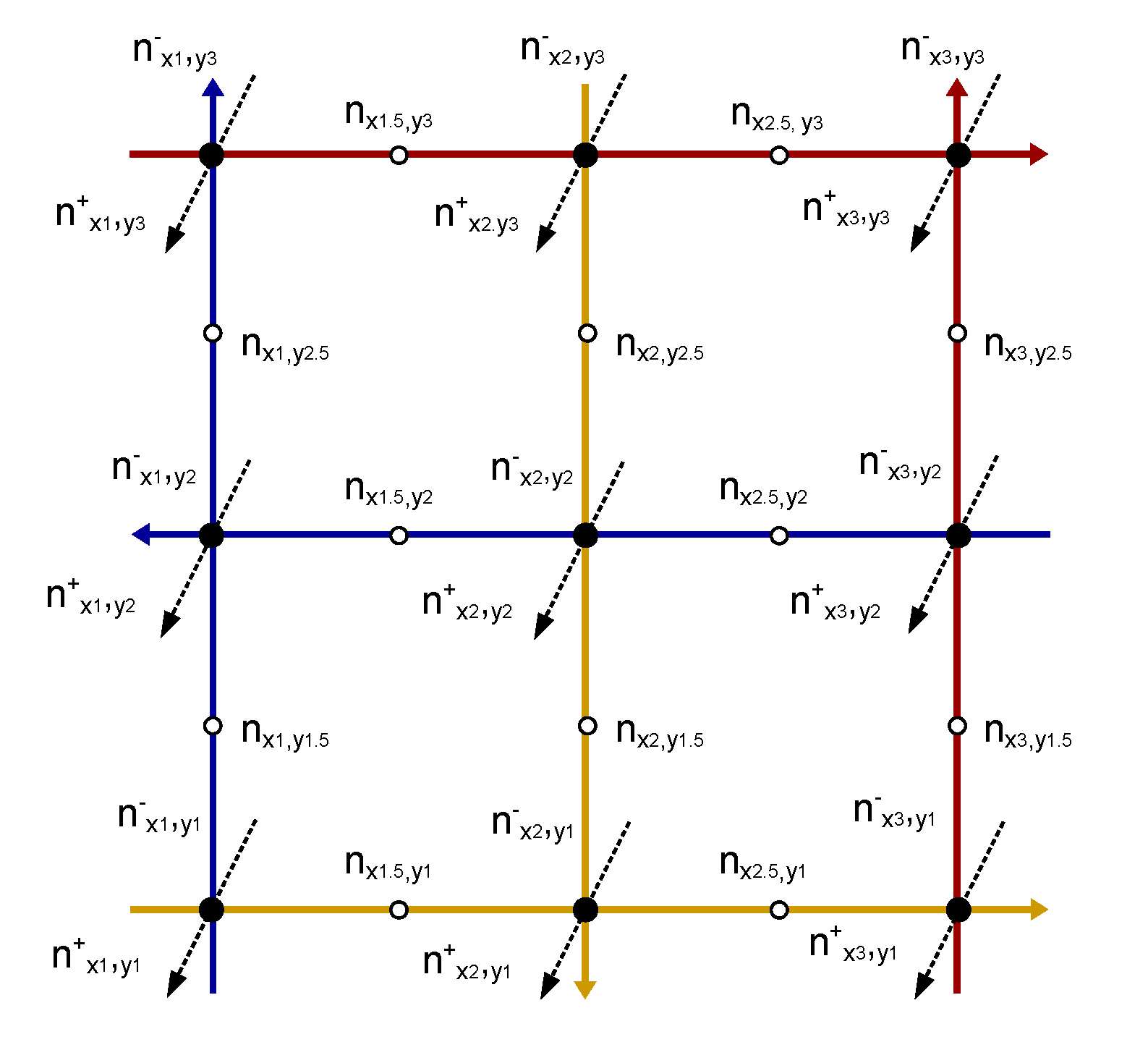
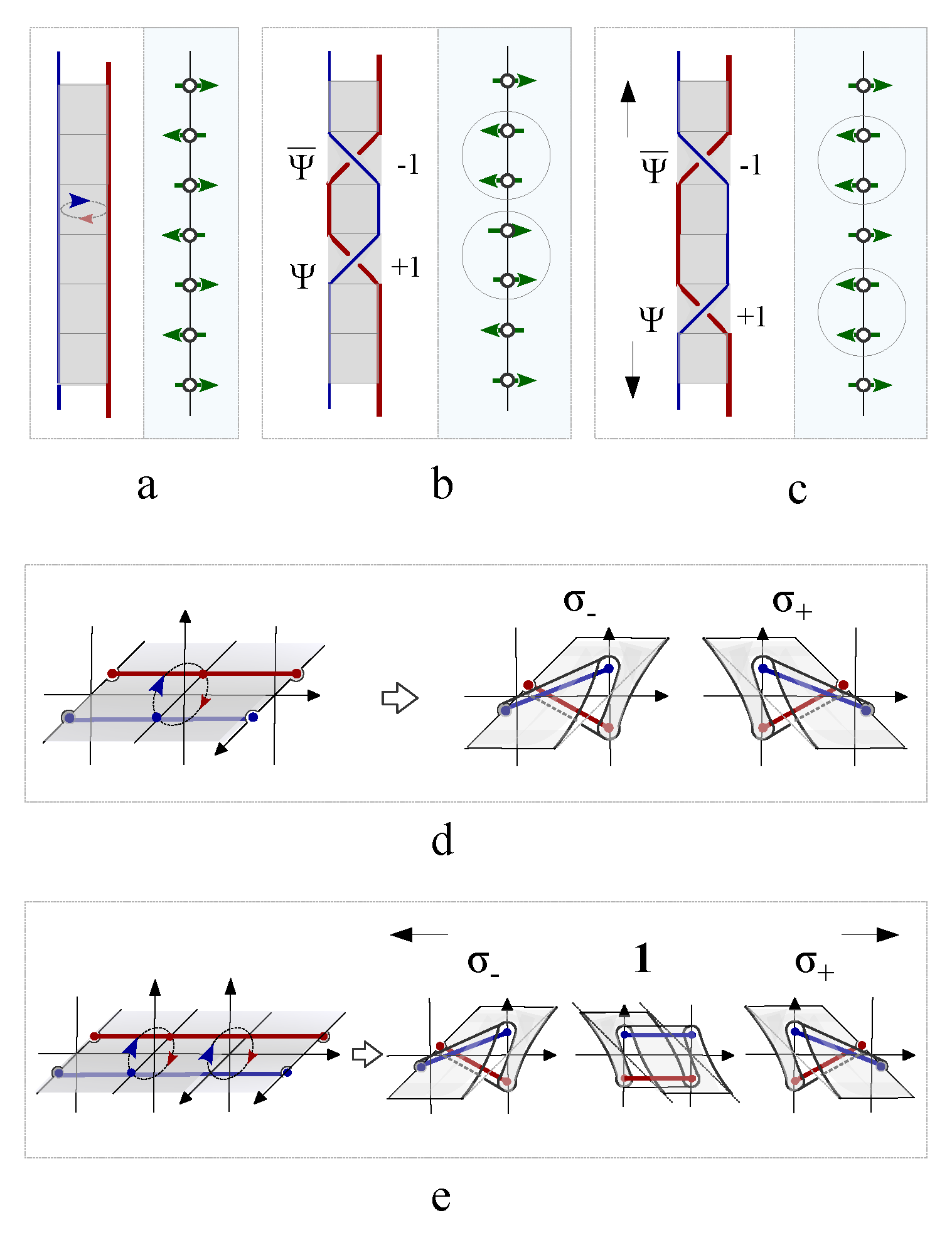
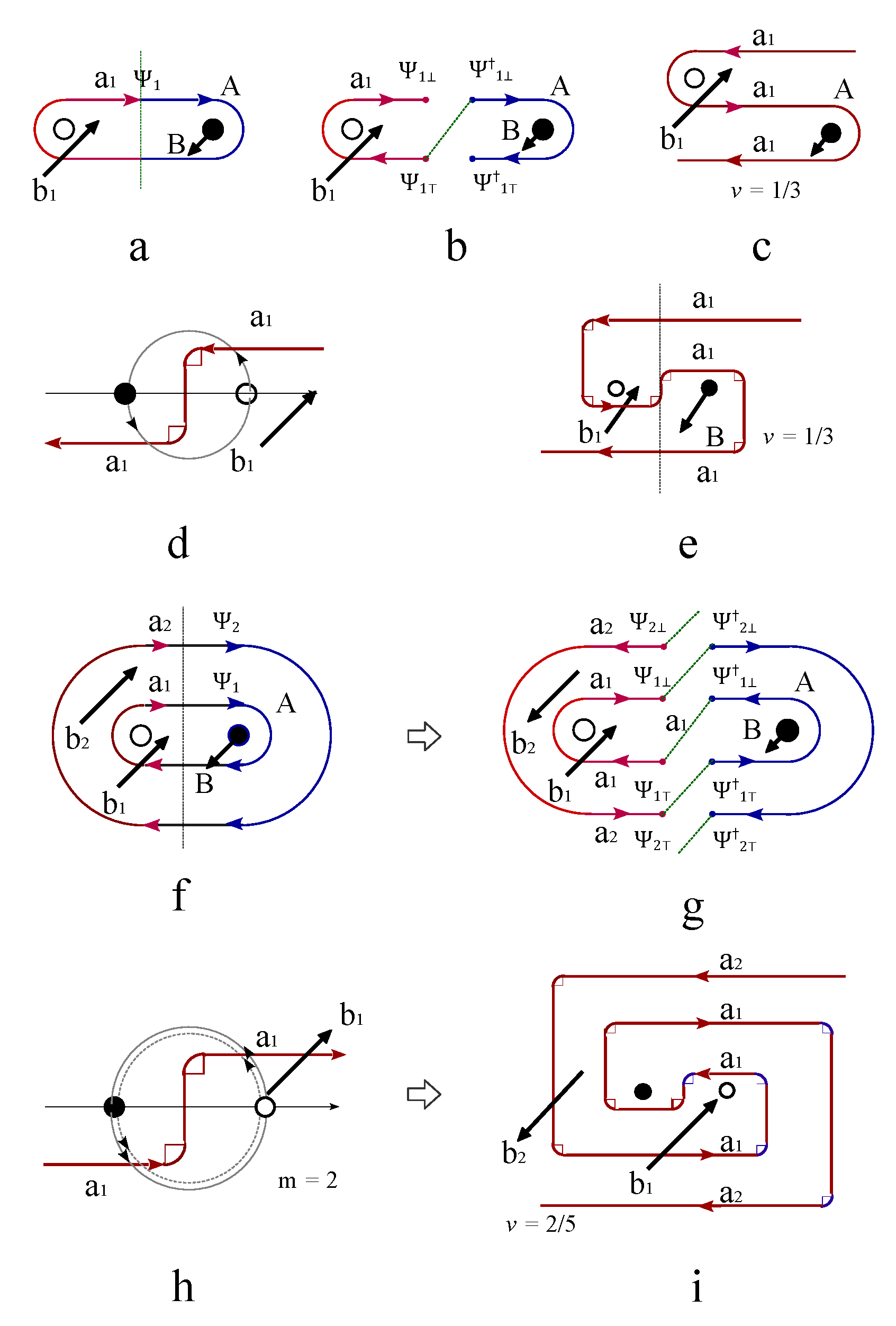
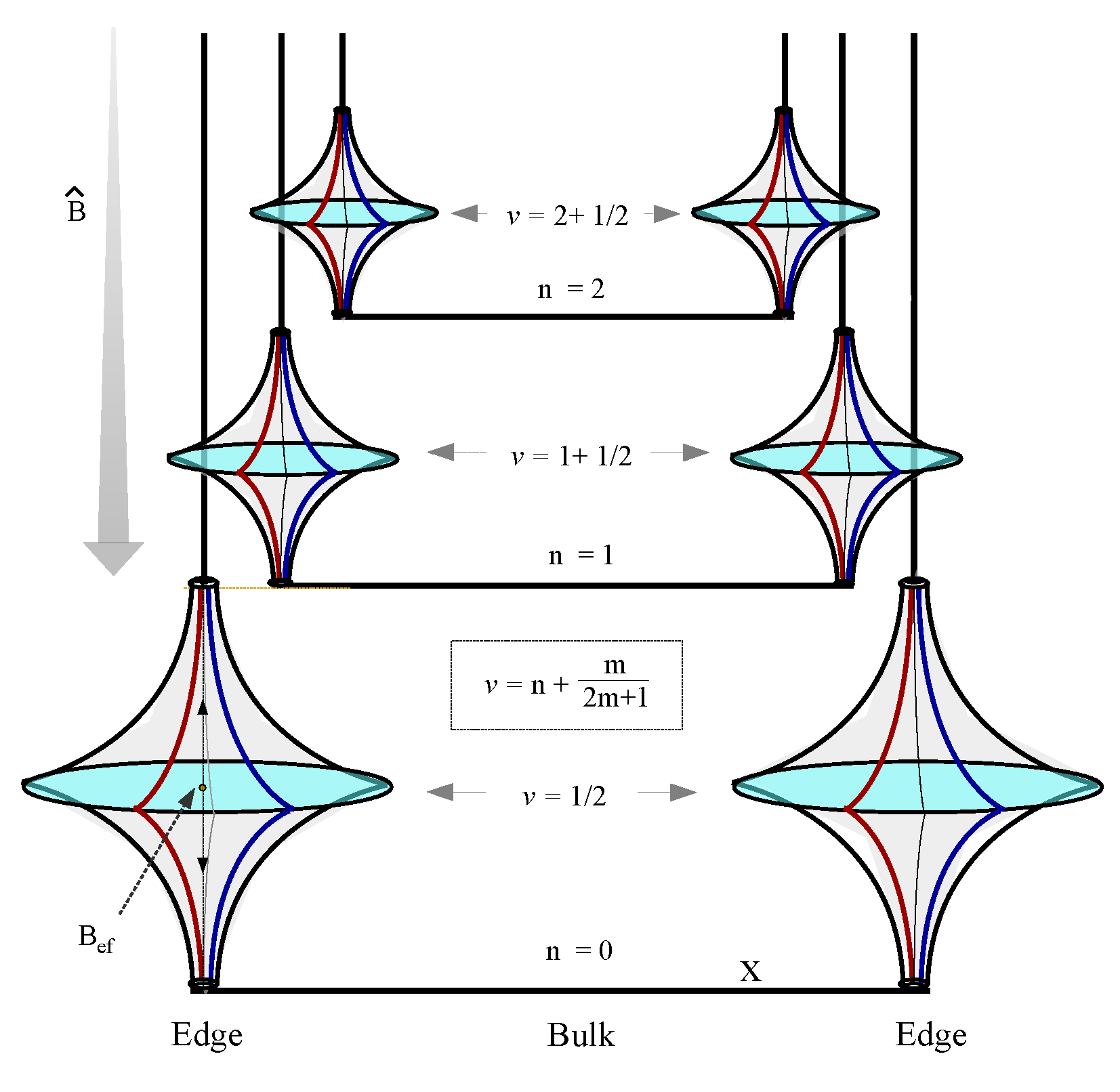
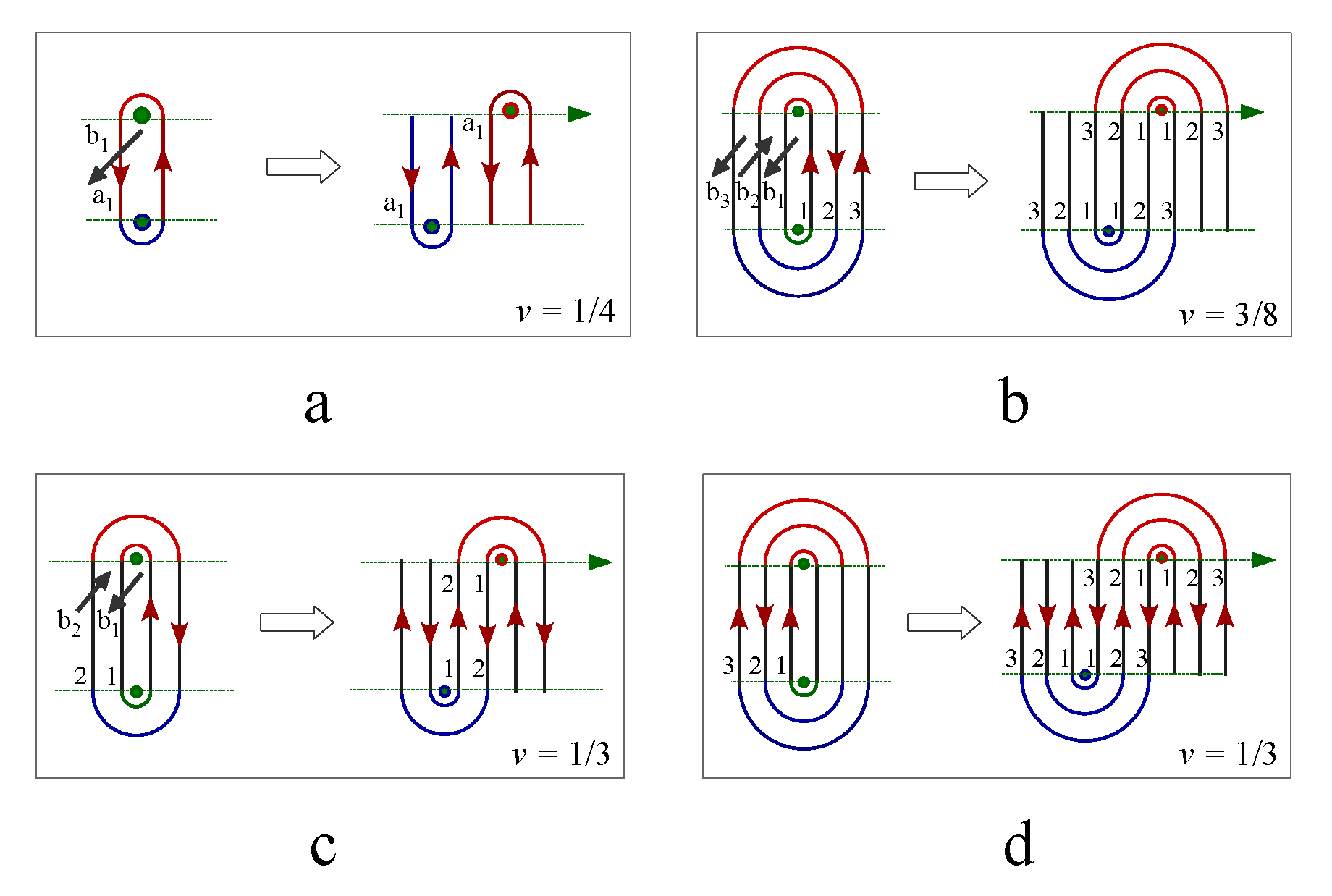
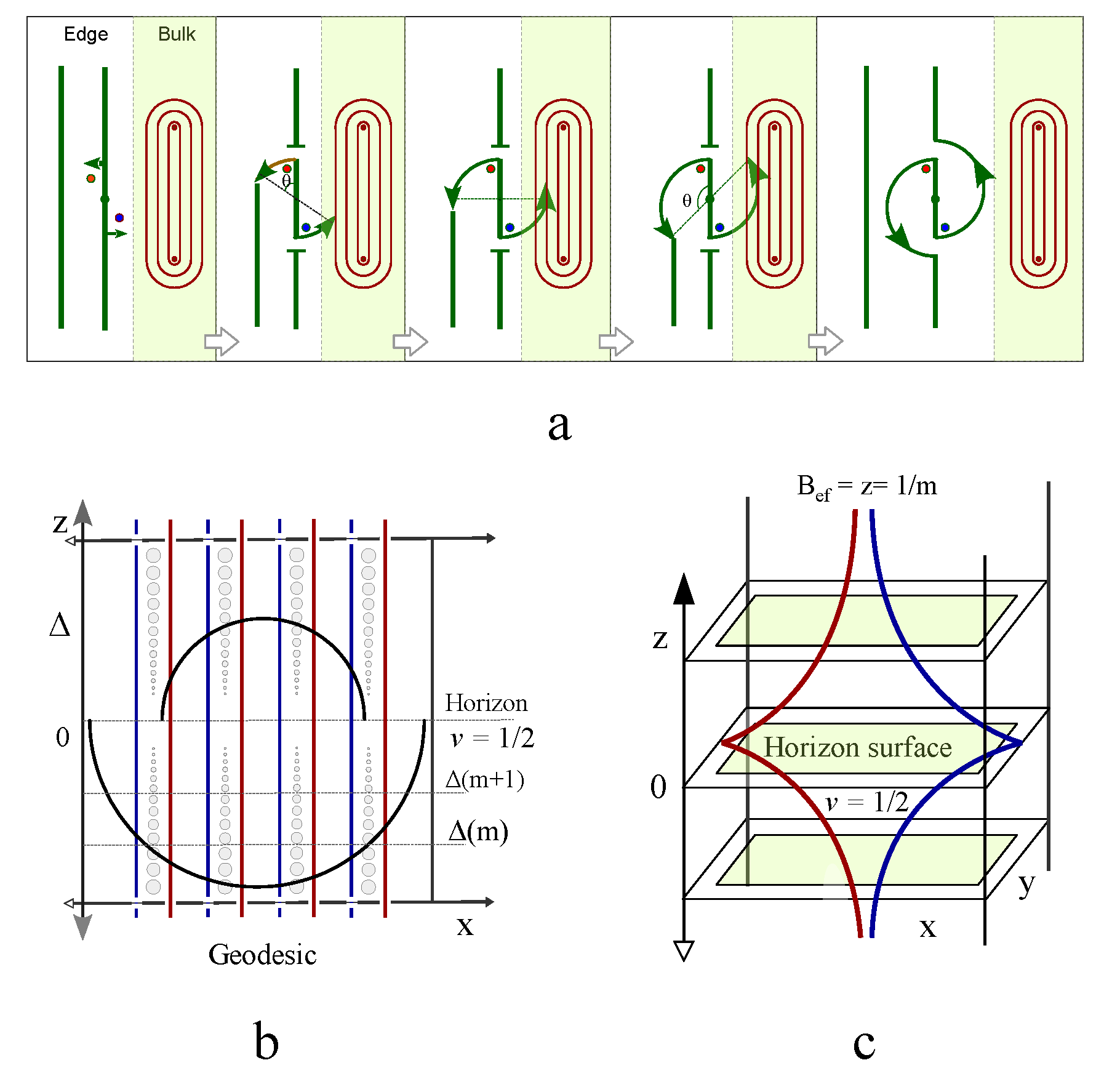
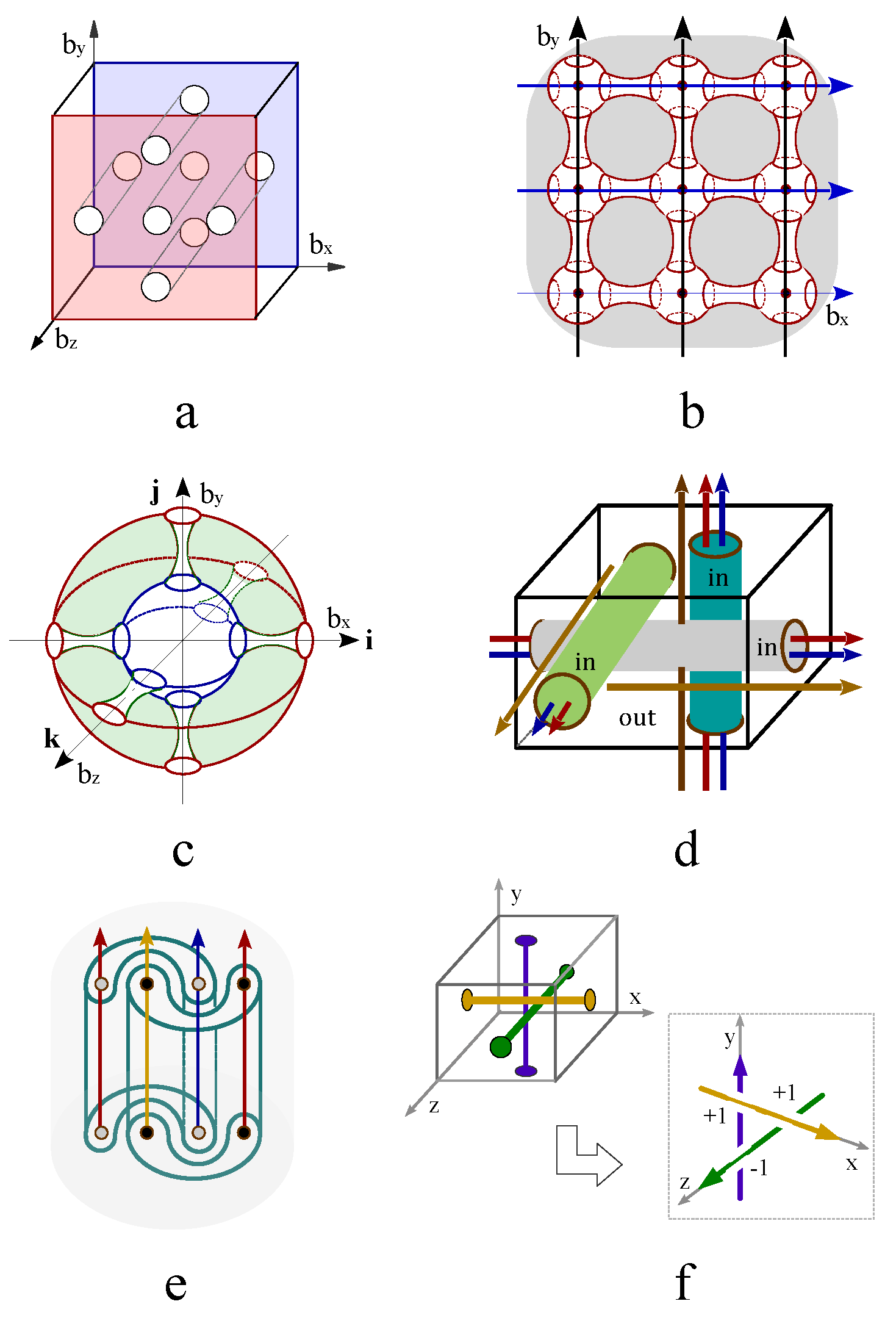
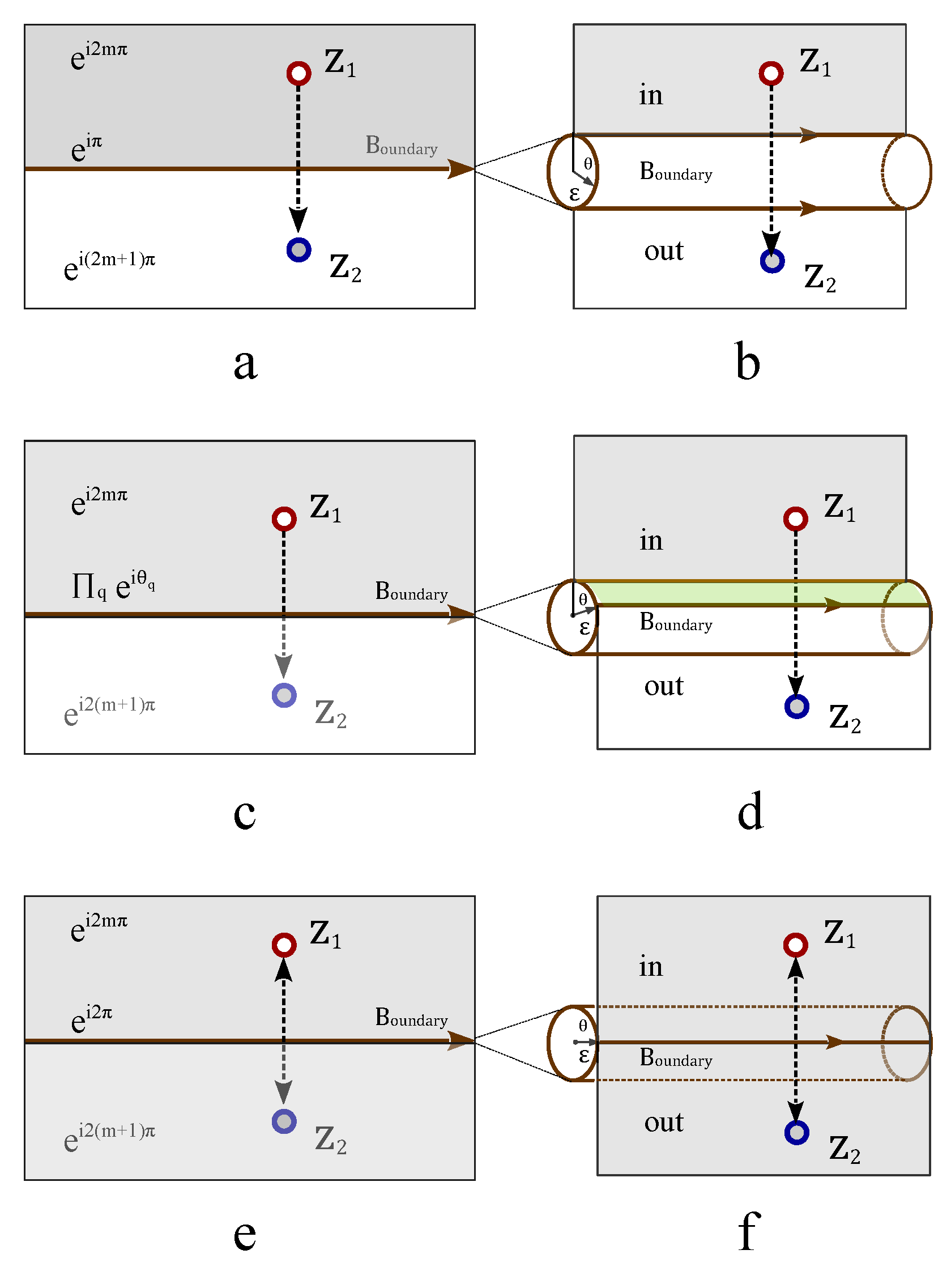
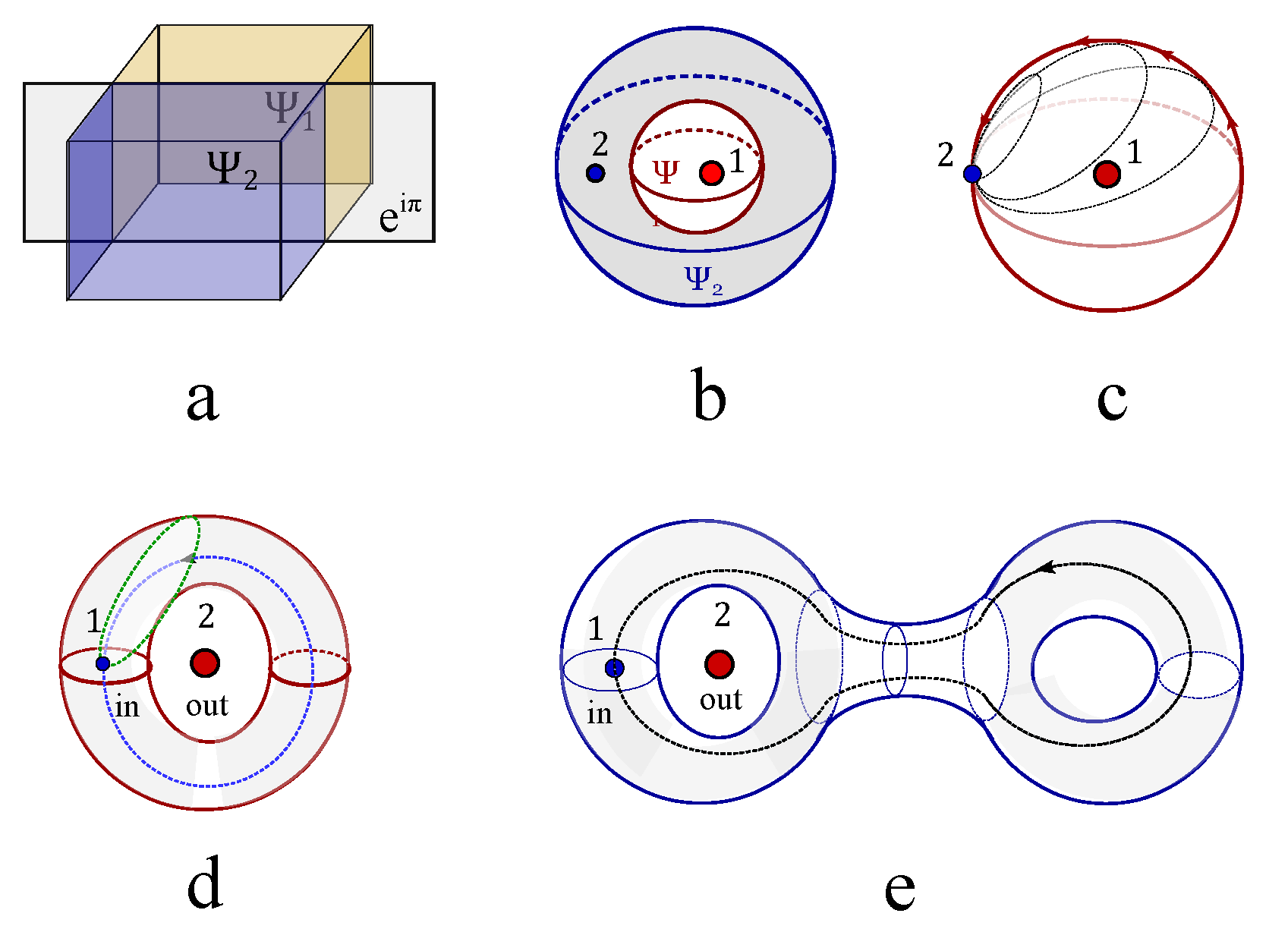
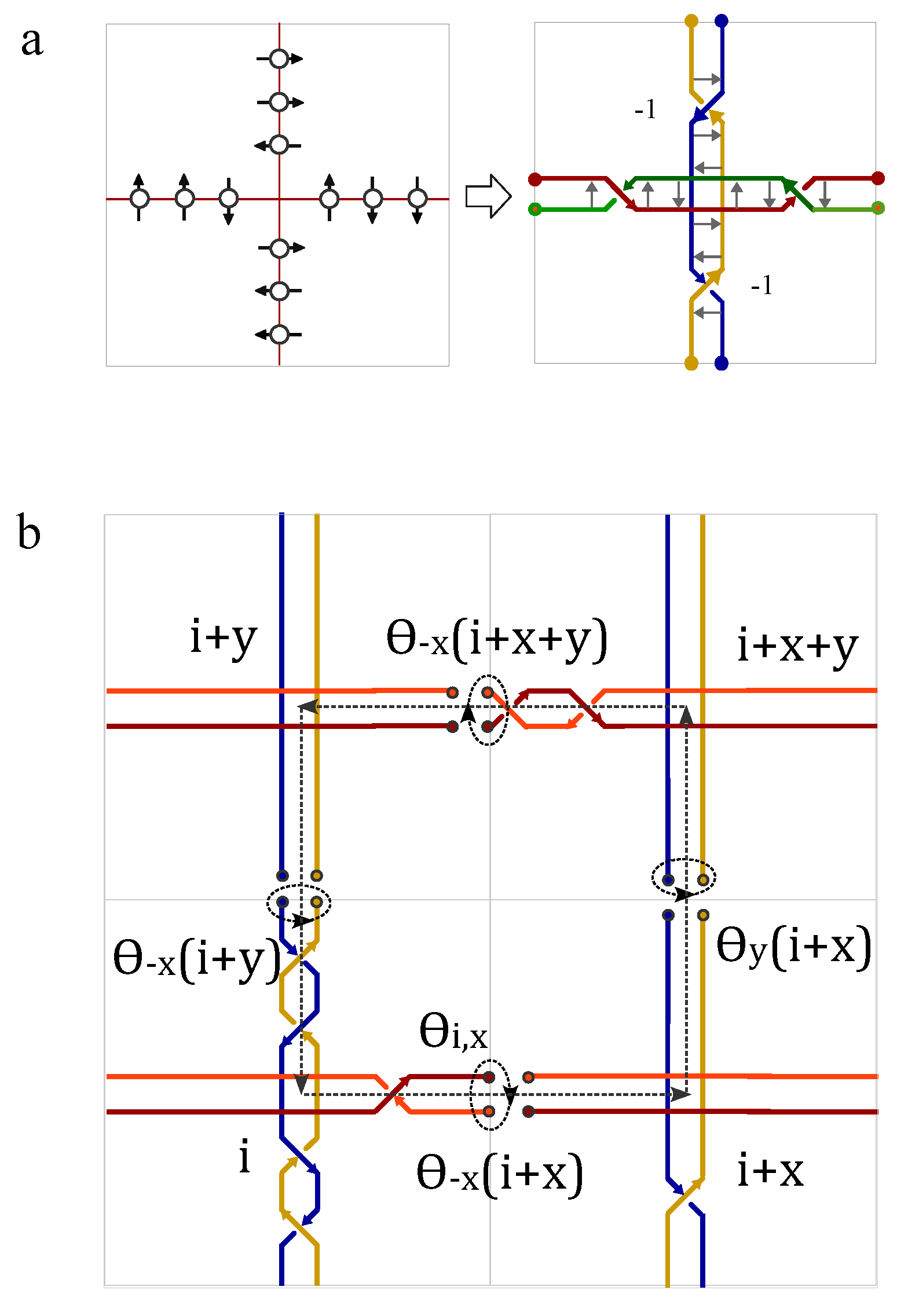
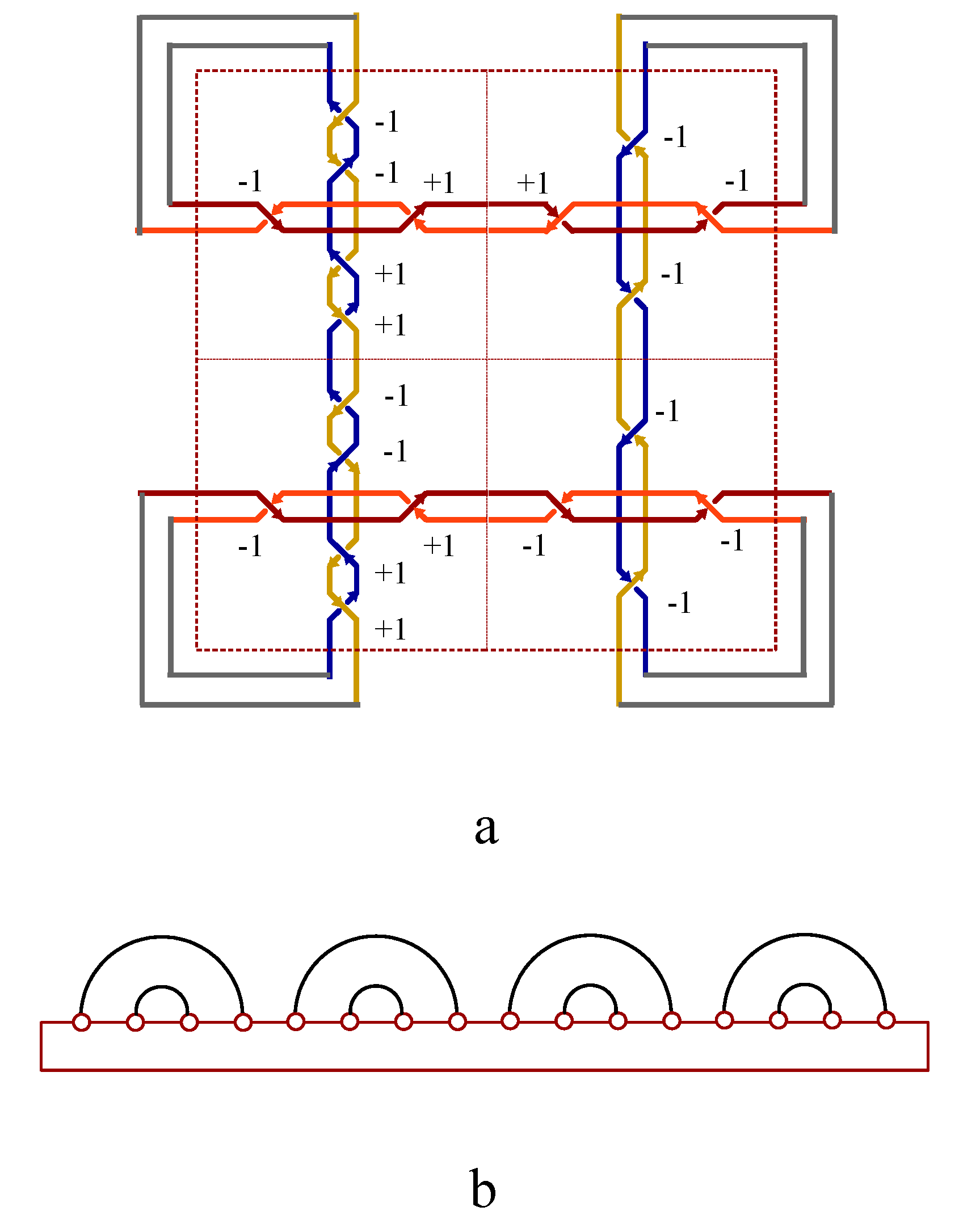
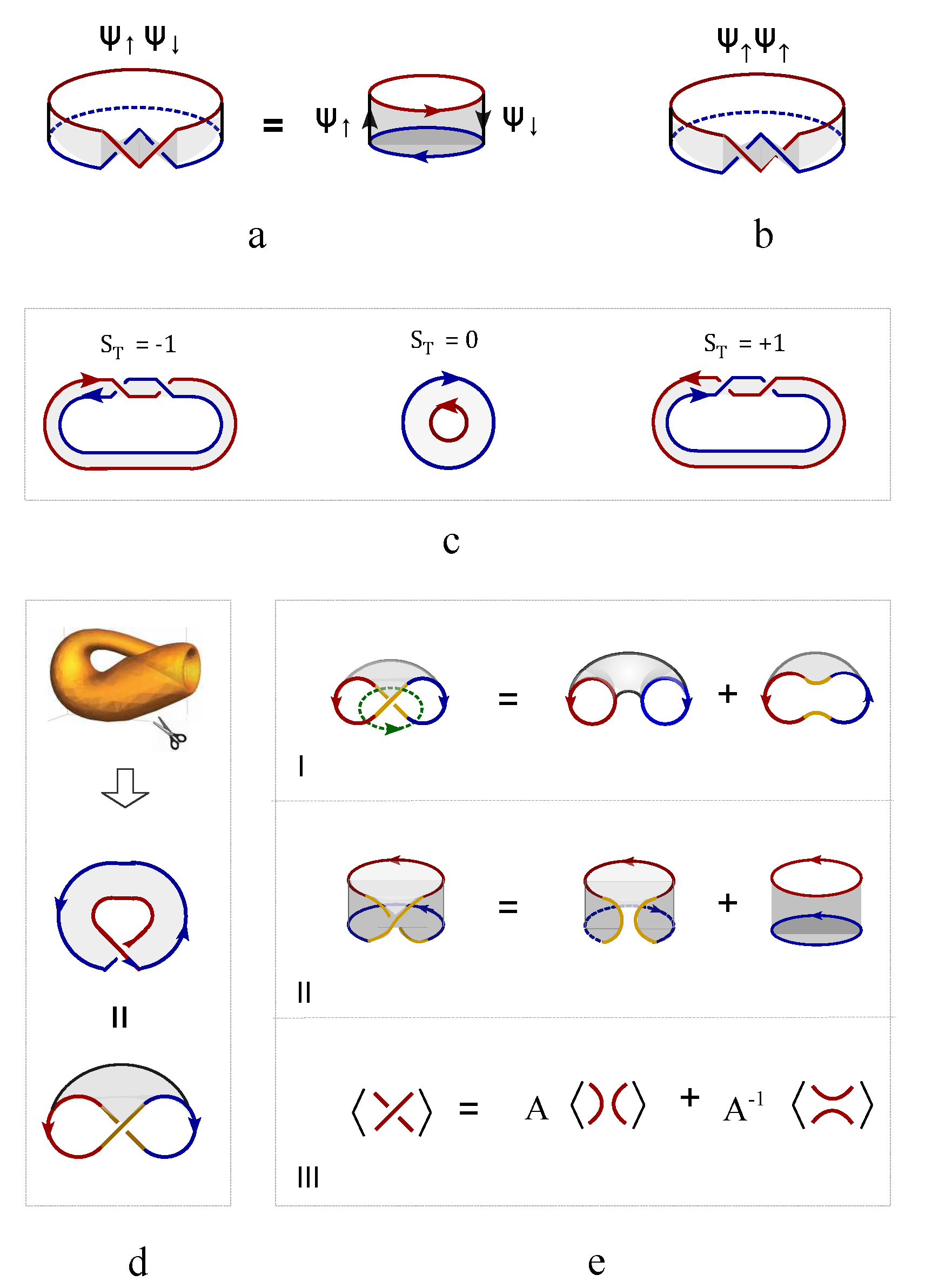
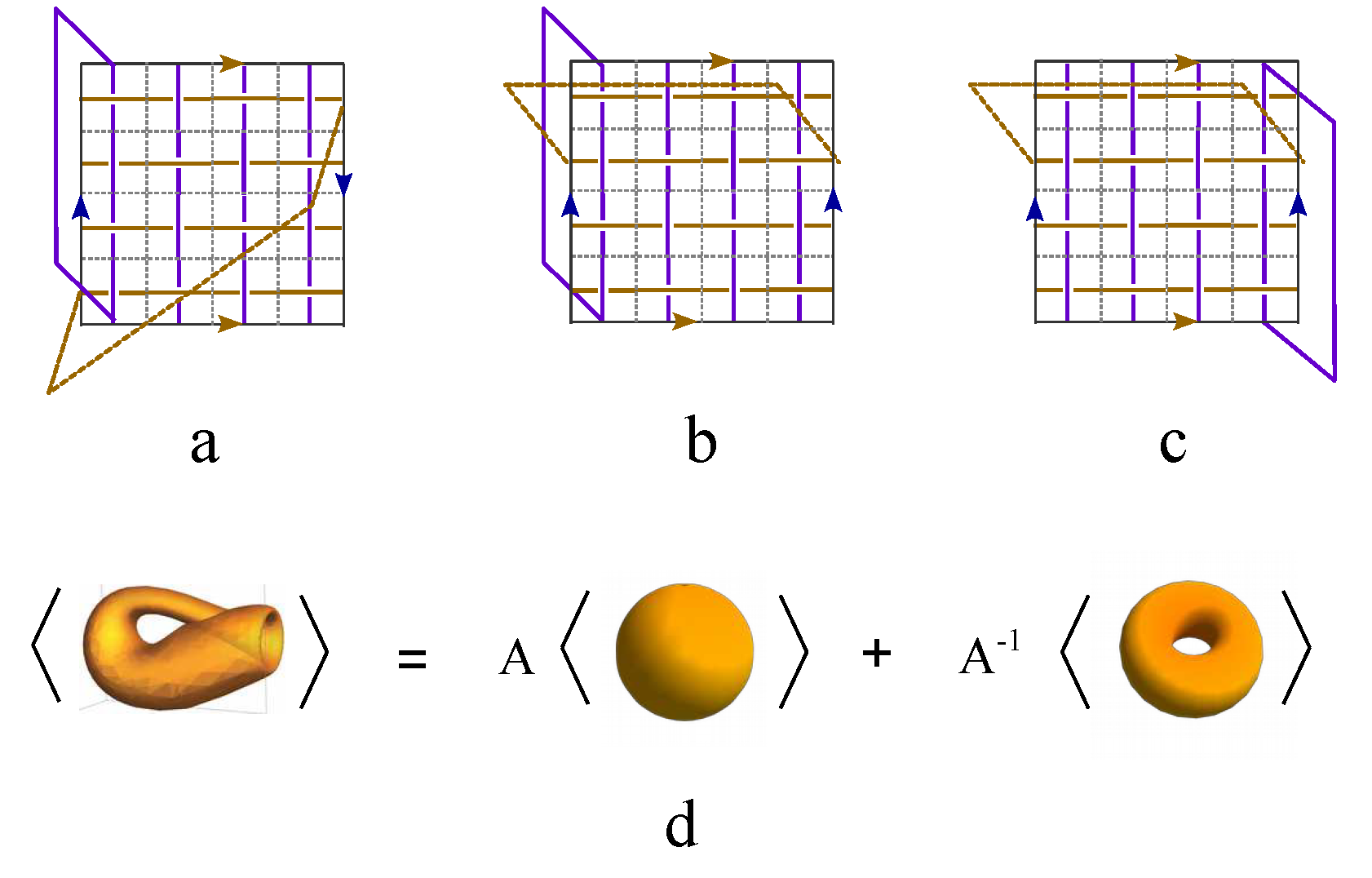
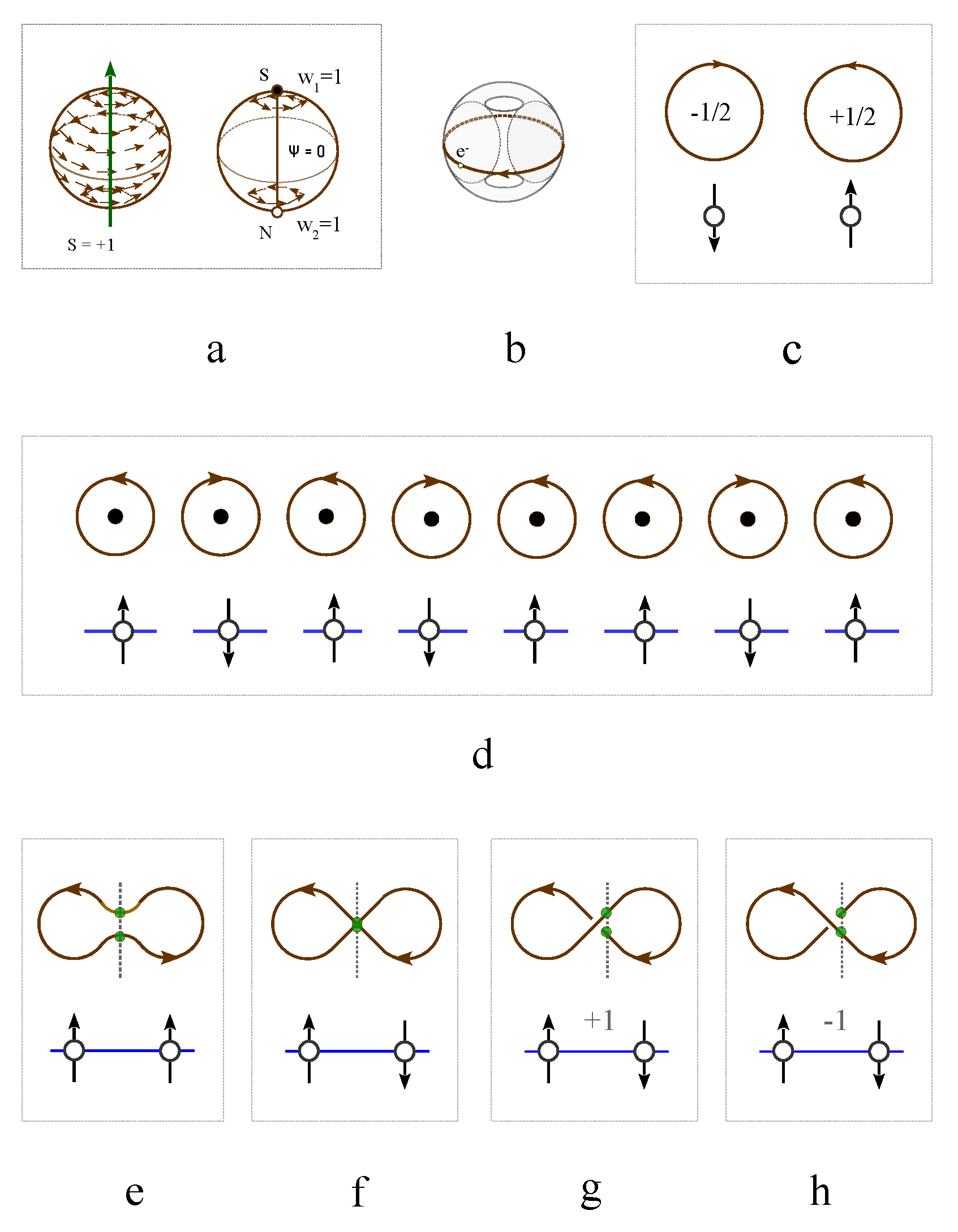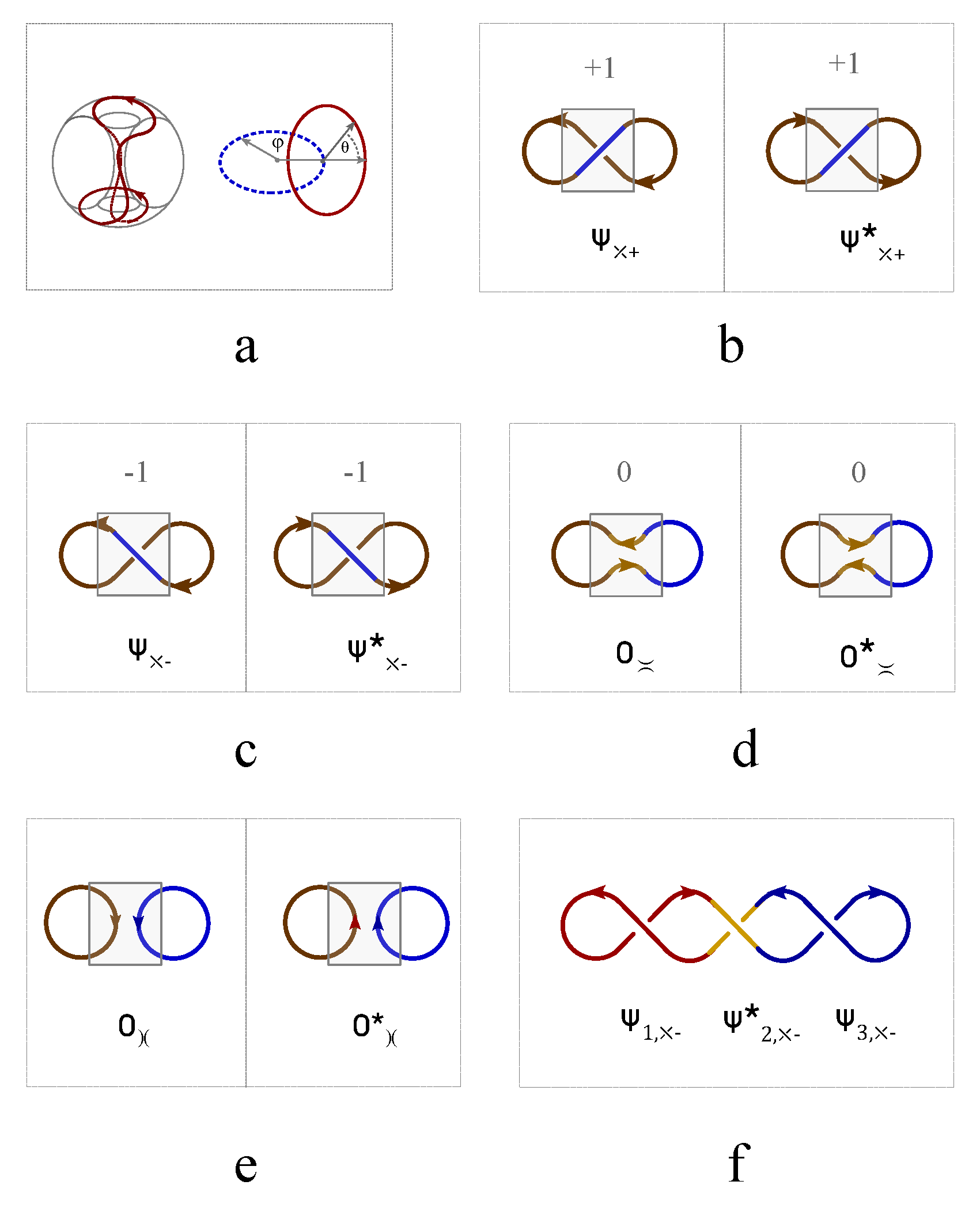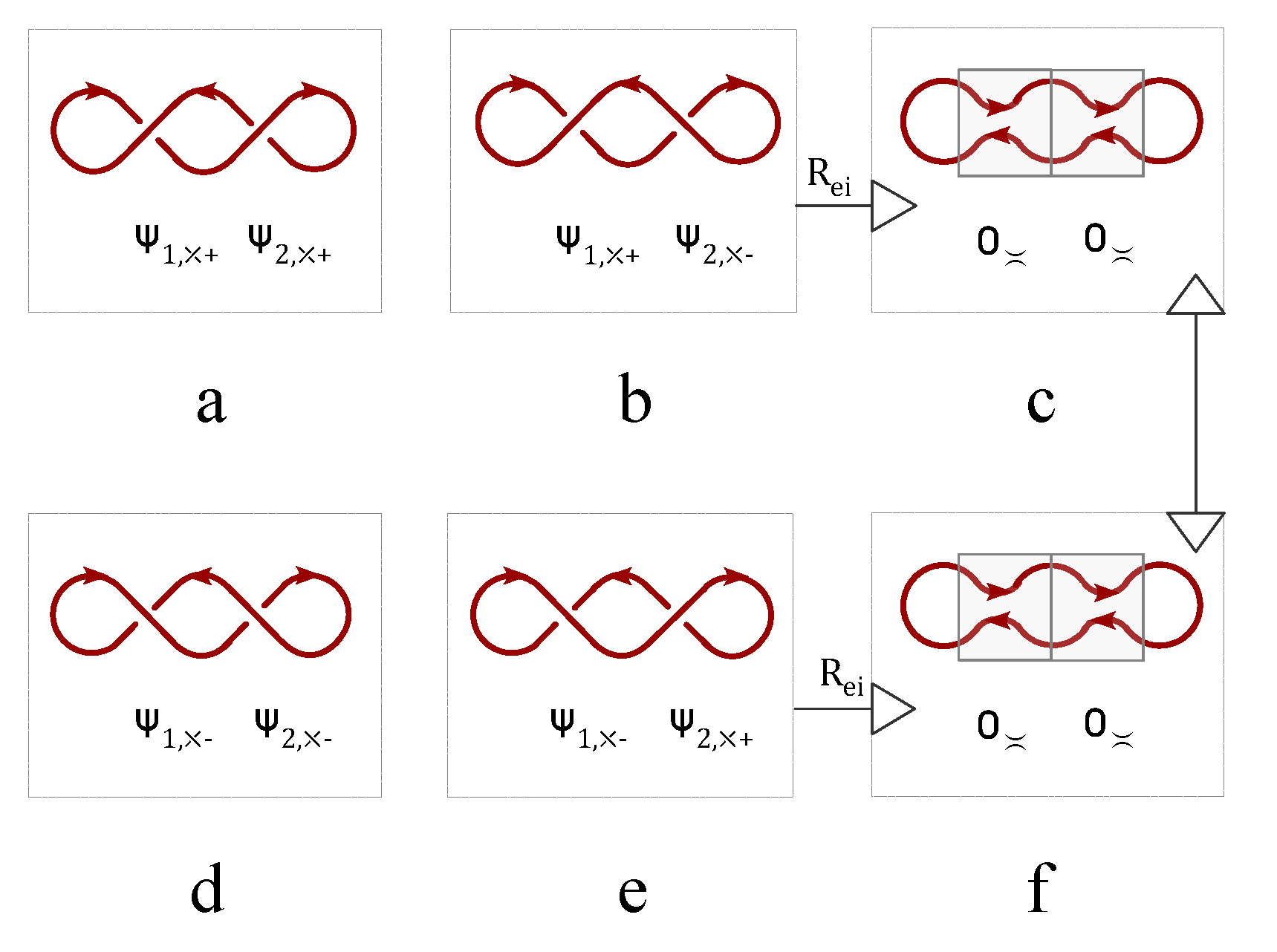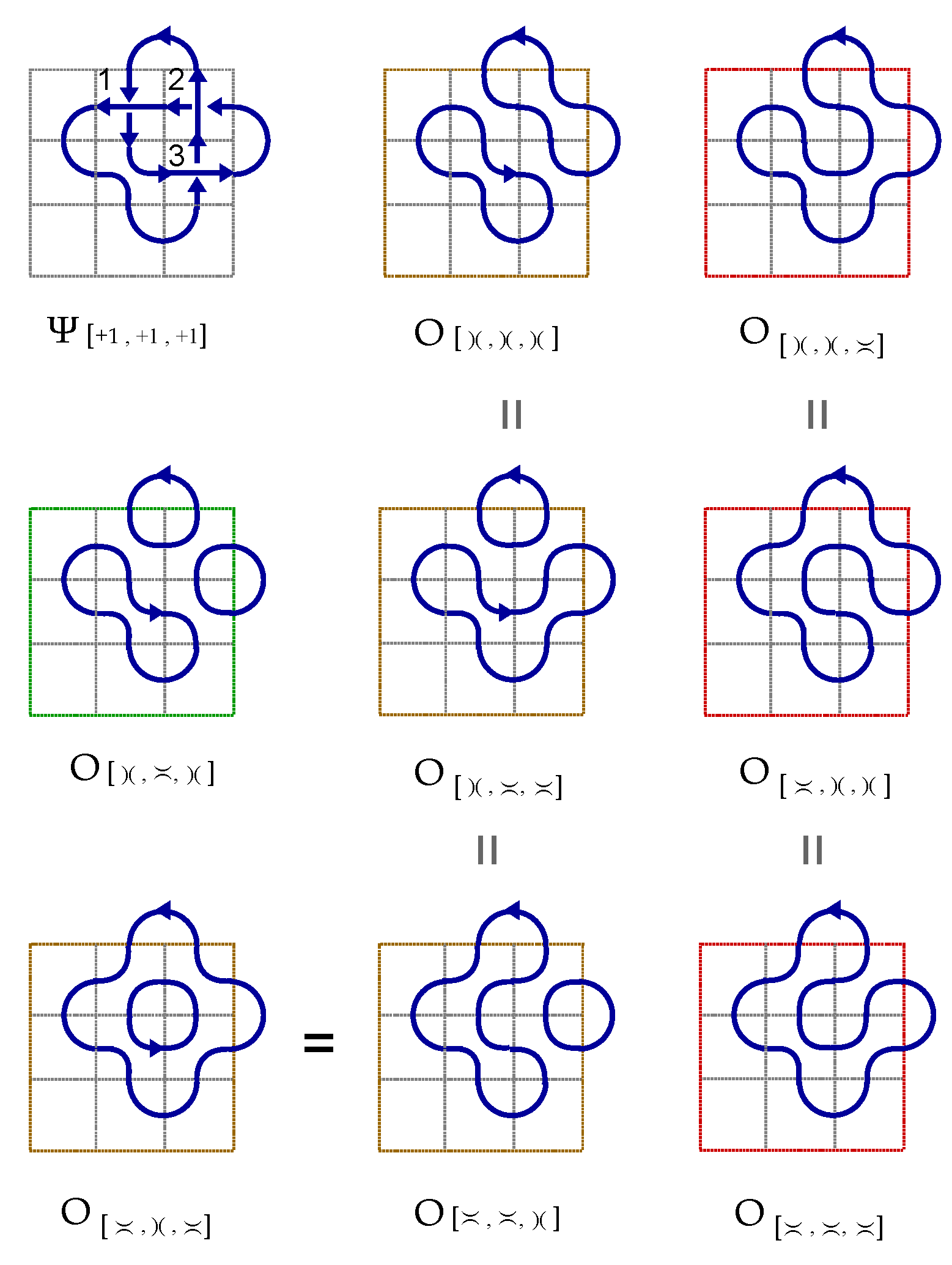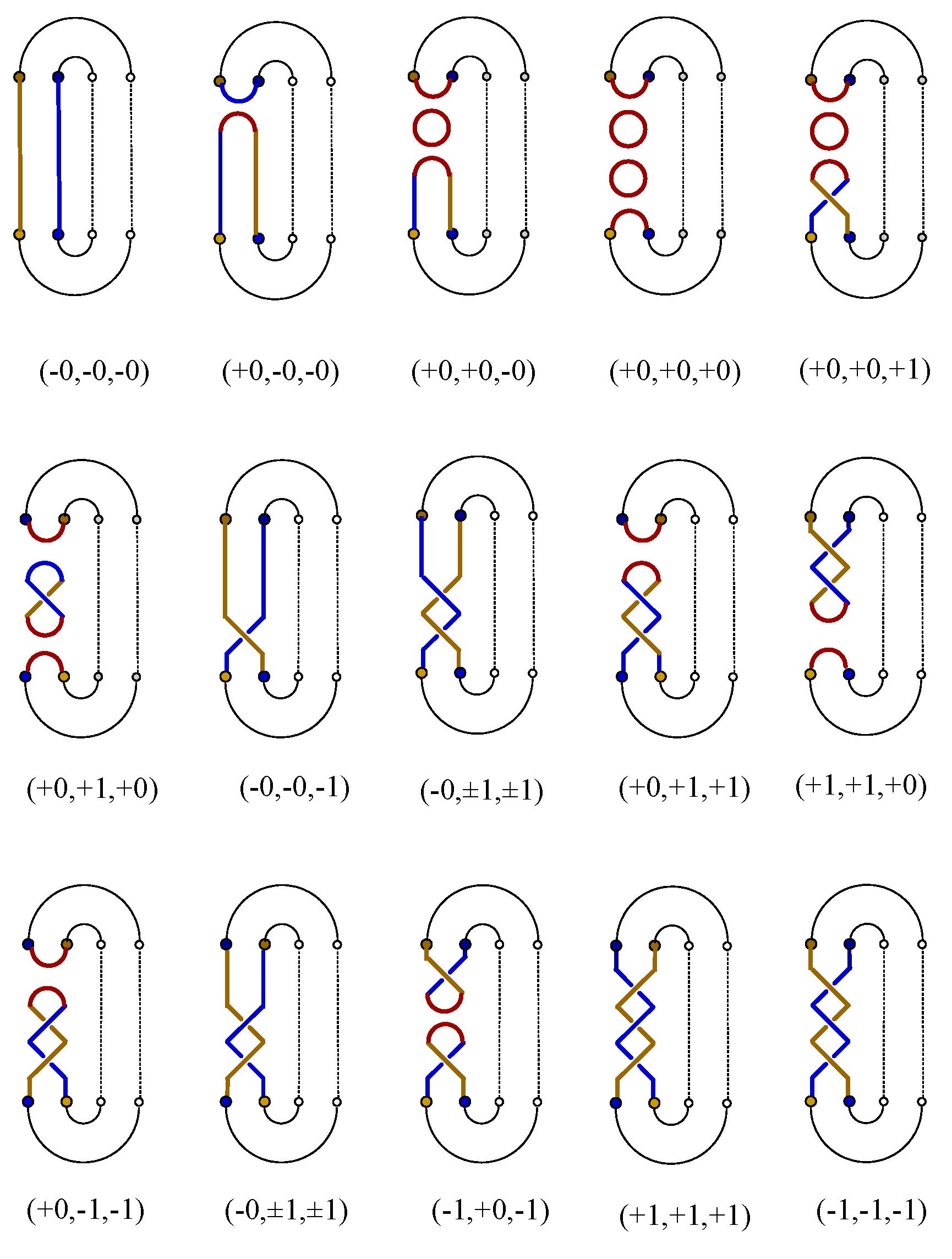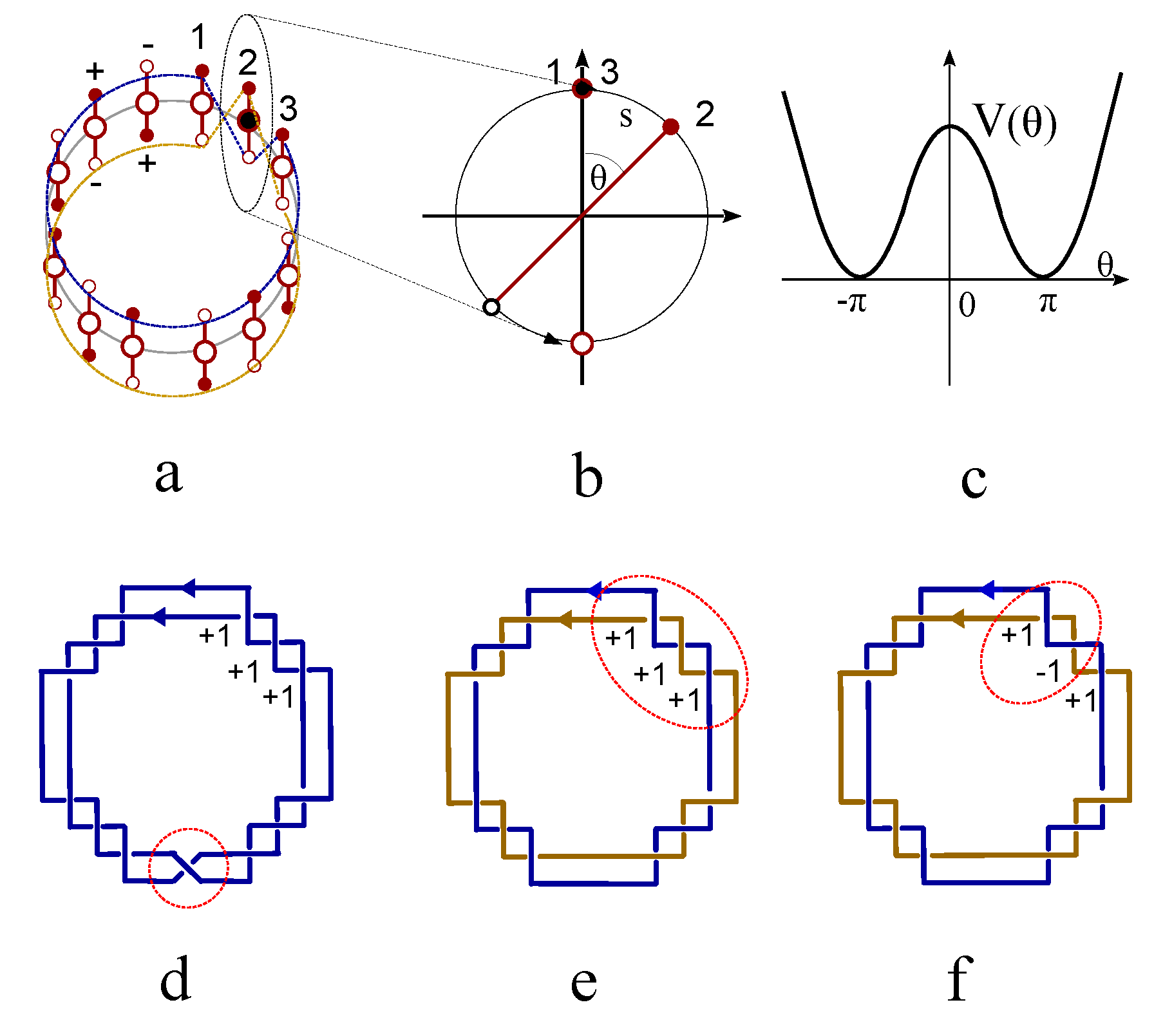2.1. The topological representation of spin by knot
The classical Ising spin
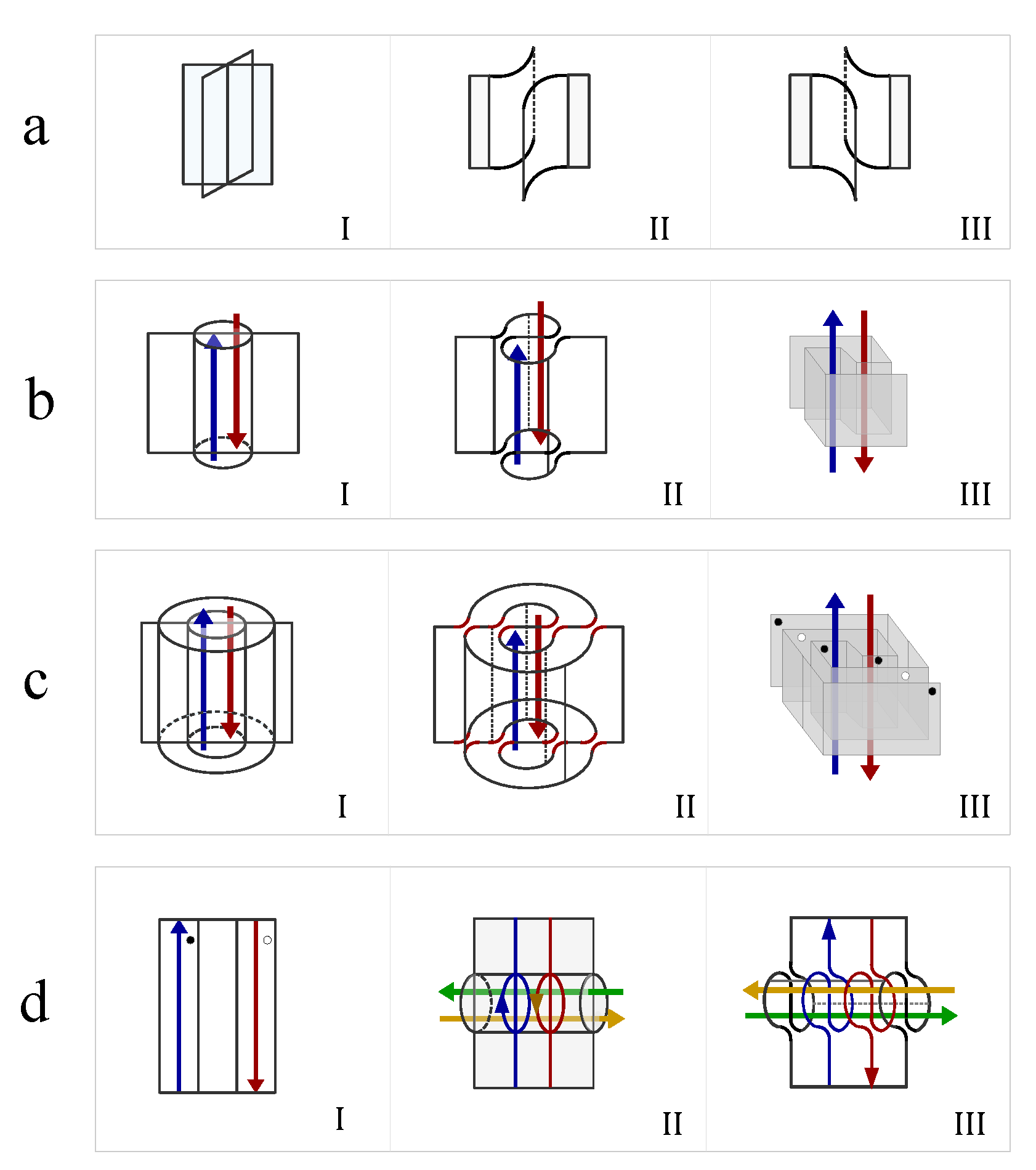
is modeled as a rotating quantum fluid droplet, featuring two topological defects at the north and south poles, each carrying an identical winding number
(
Figure 1a). This Ising spin characterize the angular momentum of a rotating charged fluid, which is ideally simplified into an electric current loop (
Figure 1b). The Ising spin represents the two opposite states of magnetic dipole moment (
Figure 1b). This topological representation of Ising spin satisfies the topological constraint that the sum of the winding numbers equals the Euler number (or Chern number) of the underlying manifold,
. The spherical surface of quantum droplet results in
. Duan’s topological current theory [
21] suggests there exist a topological line defect along which the density of wave function vanishes (
Figure 1a),
where
the vectorial velocity field that is tangential to the surface of the droplet. The line defect connects the north pole and south pole. Even though the two topological defects carry the same topological charge, but are assigned with opposite magnetic charges (
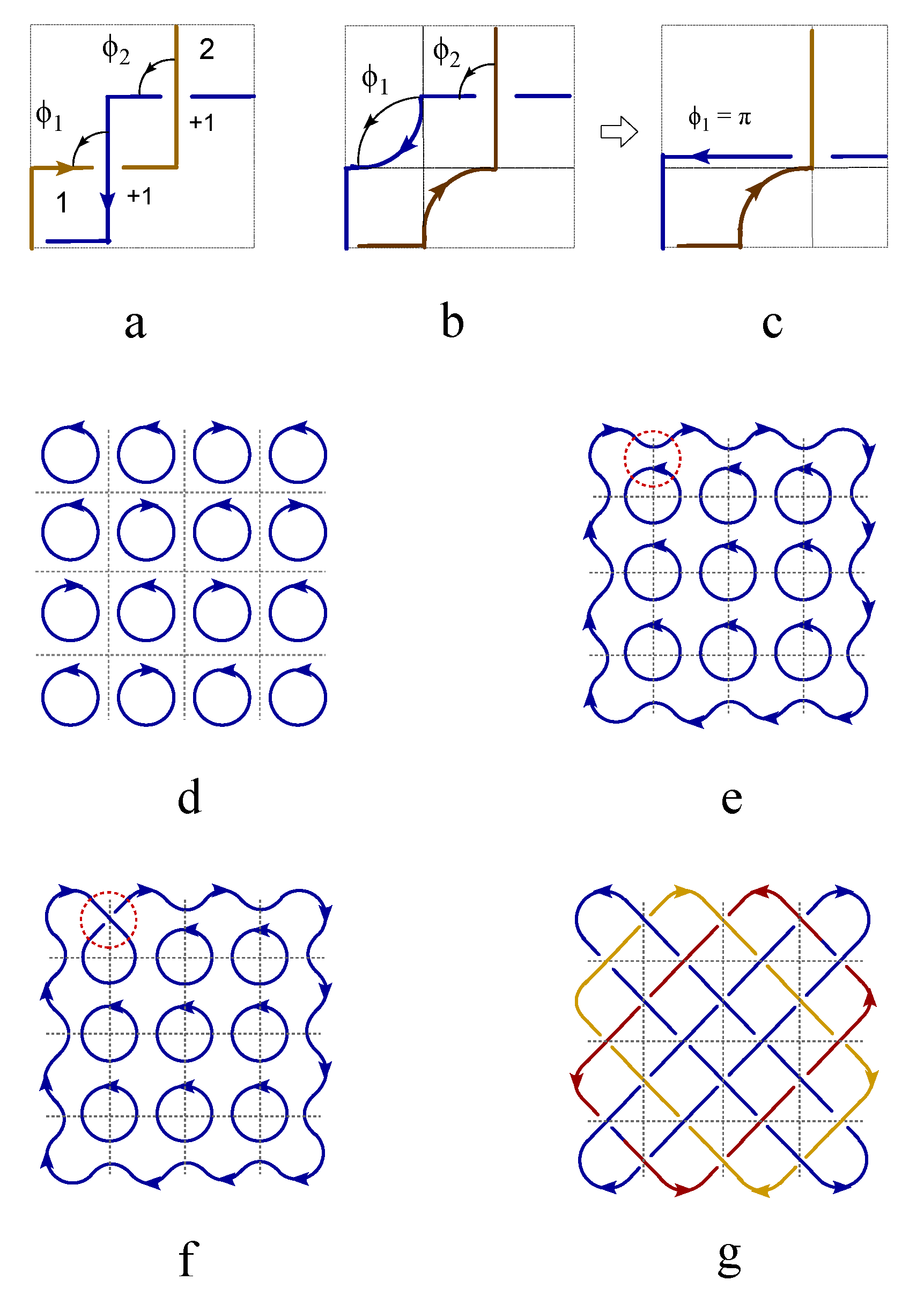
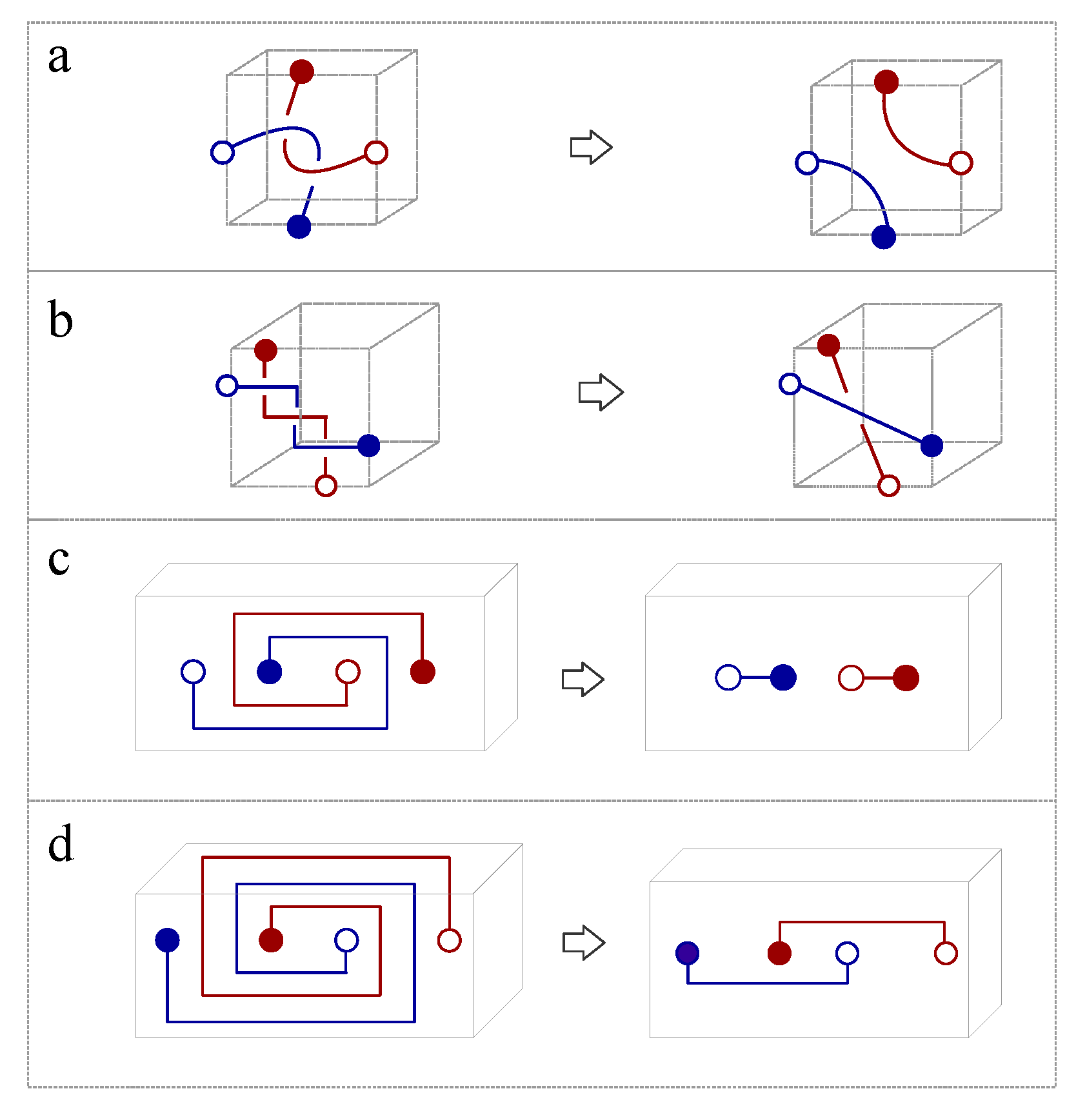
Figure 1c). Free spins without interaction are represented by directed loops without intersections (
Figure 1d). Interacted spins are represented by intersecting loops(
Figure 1e-h), i.e., cutting each loop current to generate two ending points and glue them with the open endings of another loop (
Figure 1e-h). The ferromagnetic coupling is represented by one giant loop made of the fusion of two small loops without self-crossings (
Figure 1e). For the antiferromagnetic coupling, the self-crossing of the giant loop made of two nearest neighboring loops is inevitable (
Figure 1f). Different crossing states are characterized by chiral index,
, where
indicated a positive chirality that the four fingers of the right hand first point into the direction of the current above the crossing point and then bend to the direction of the current underneath the crossing point (
Figure 1g), while the opposite case is labeled by a negative crossing index (
Figure 1h).
A classical rotating droplet is a good representation of Ising spin, but is inadequate to take into account of the phase factor of a quantum particle. A quantum fluid droplet is described by a wavefunction
that obeys Schr
dinger equation
. The Schr
dinger equation is equivalently transformed into a pair of fluid dynamic equations by Bohm [
20],
The quantum character of a particle is governed by the potential combination of a classical potential
V and the well known Bohm potential
,
Here we substitute the identity equations,
into the Bohm potential Eq. (
3) to decomposes
into the sum of two terms,
The Bohm potential approaches to negative infinity at the zero points of wave function
. For a nonzero wave function
, the first term on the right hand side of Bohm potential Eq. (
5) vanishes. The second term of Bohm potential Eq. (
5) is determined by the gradient of wavefunction. The Bohm potential turns into zero at the extremal points of wavefunction, i.e.,
. According to Duan’s topological current theory [
21], the sum of topological charges of zero points of wavefunction is determined by the topology of spacetime manifold. Therefore a quantum particle is born to carry the topological information of the space time manifold at
, which usually is eliminated in local dynamics. The Bohm potential reaches the minimal (maximal) point when the gradient of wavefunction
is positive (negative). The particle moves along the minimal points of Bohm potential under the mathematical constraints
. The quantum fluid droplet deforms into different oscillating modes following Bohm potential. The velocity field on the surface of quantum droplet is defined as
The velocity field
as showed in
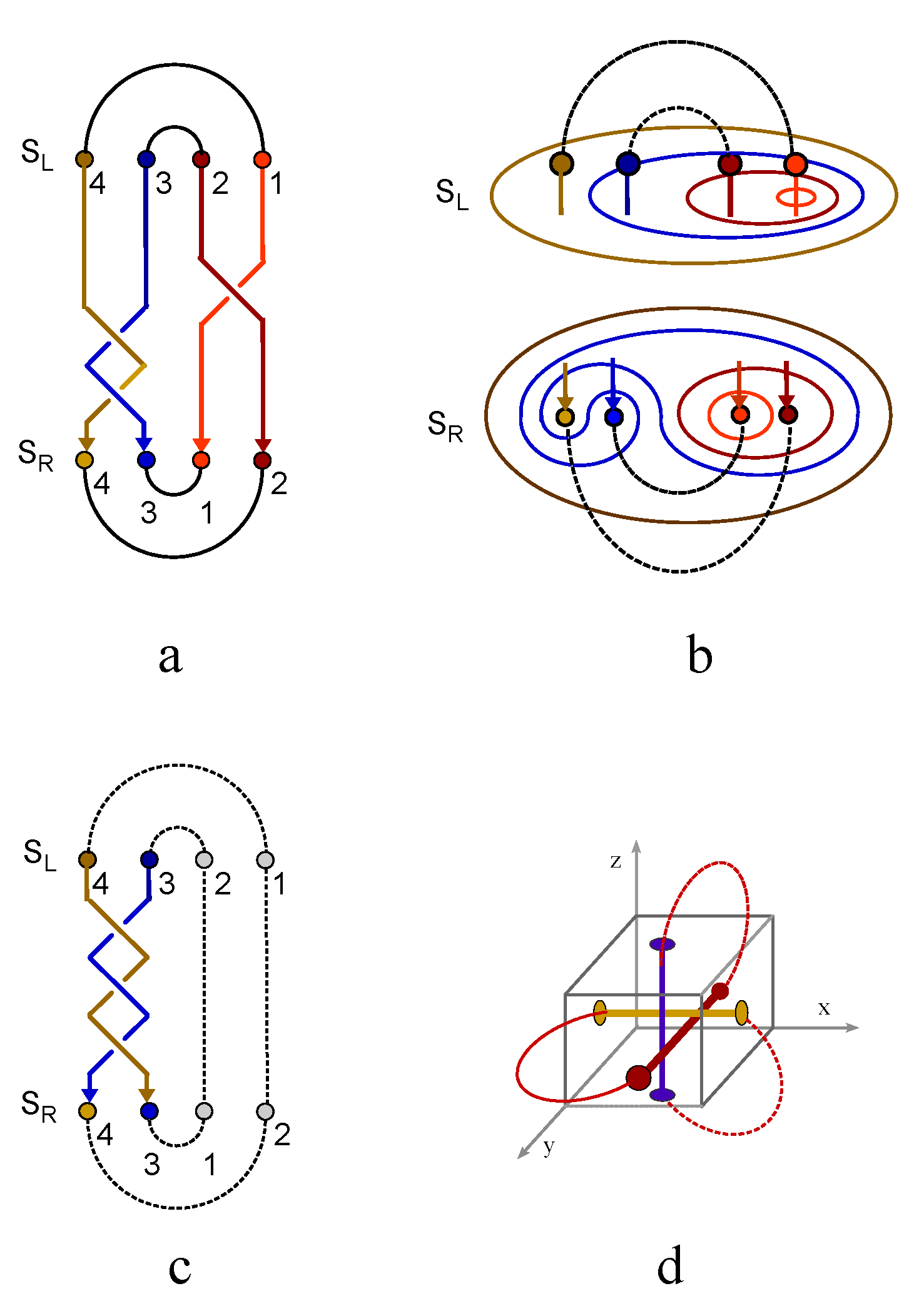
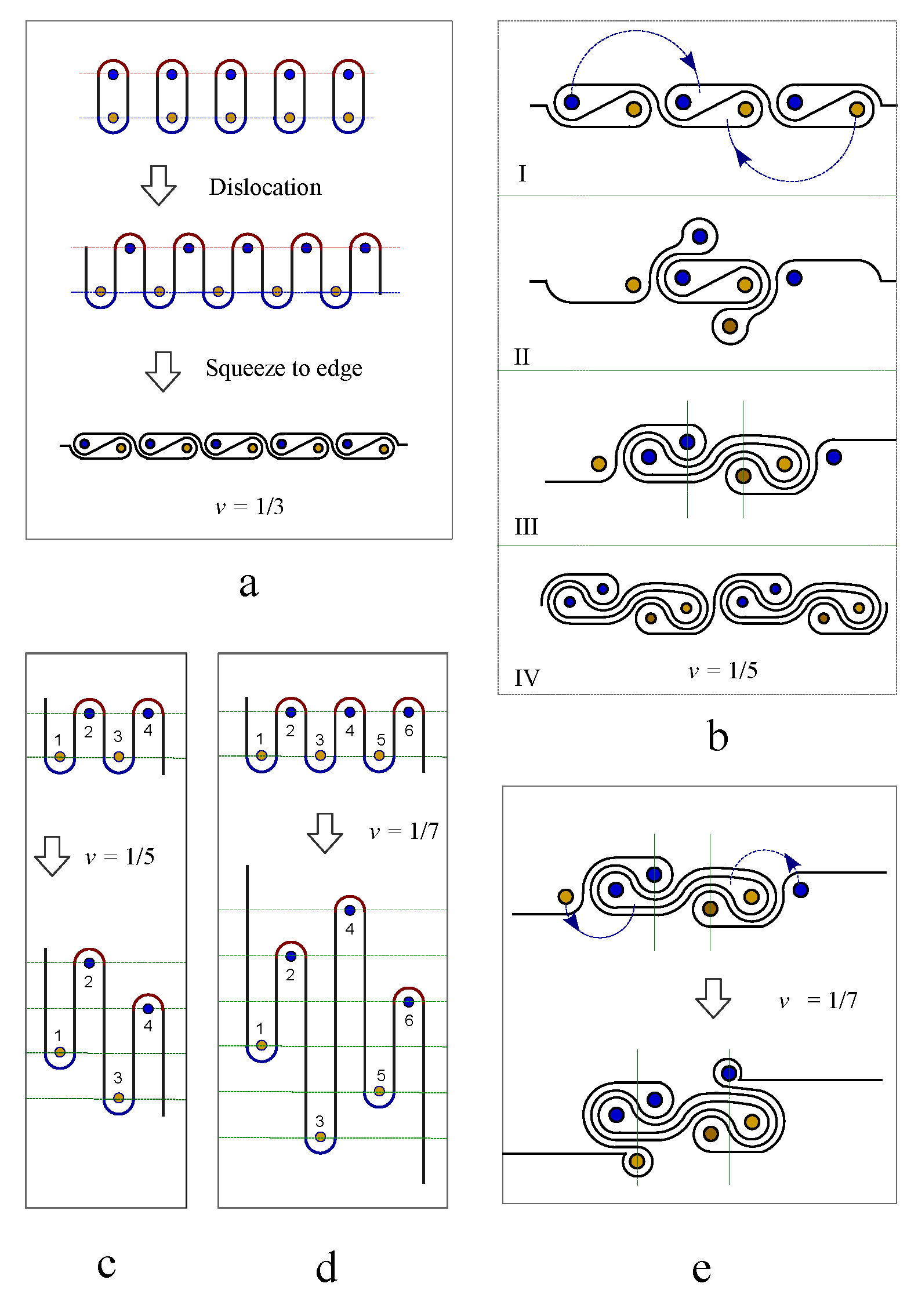
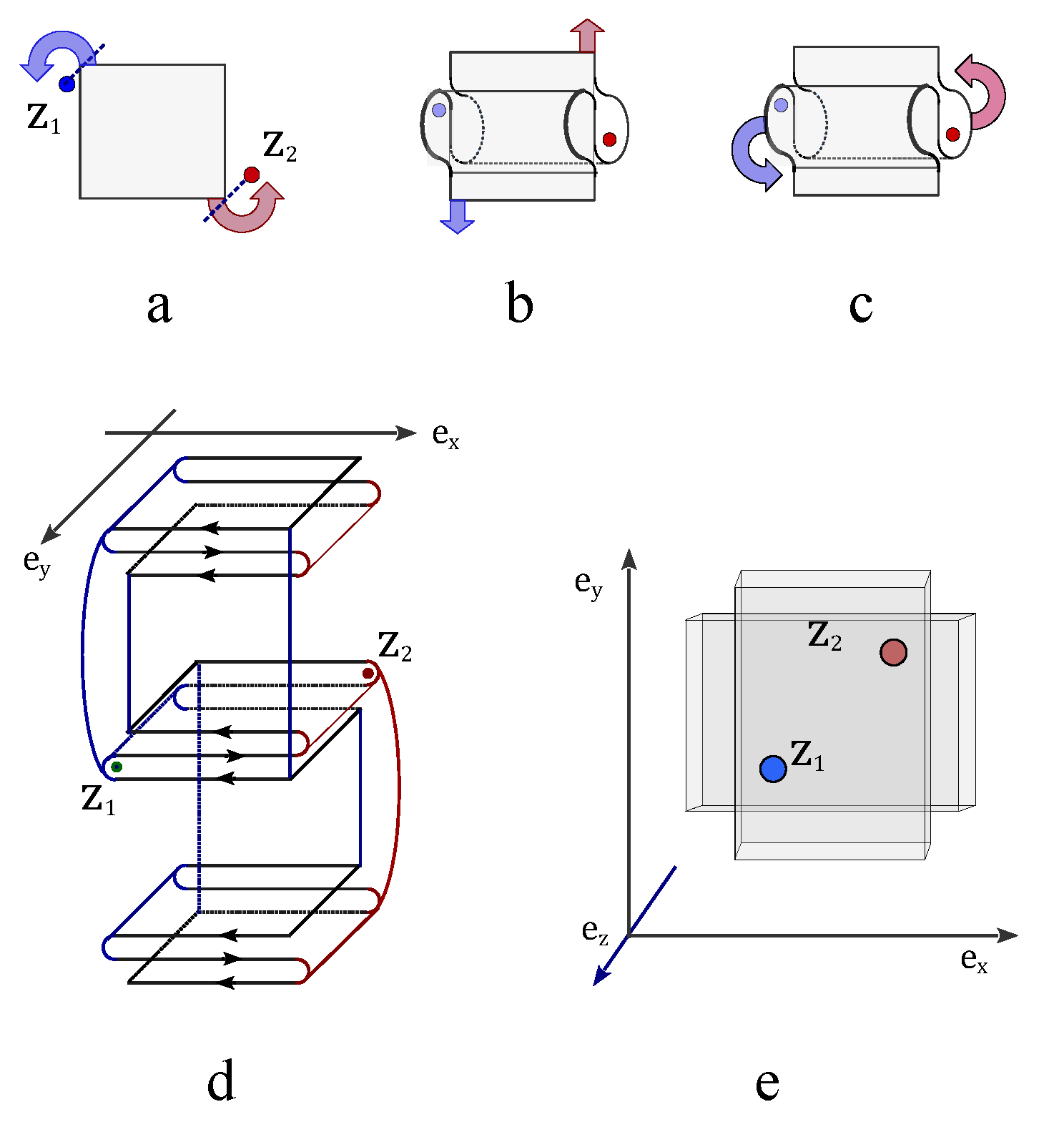
Figure 1a shows two topological defect on the north pole and south pole of the spherical droplet. The spherical droplet deforms into a solid torus when the line defect penetrate through the north pole, south pole and the mass center. A moving particle going around the topological line defect twice provides an effective representation of spinor wavefunction for
(
Figure 2a),
An equivalent topological deformation of solid torus is M
bius strip. The edge of the M
bius strip locates along the extremal points of Bohm potential. An electron winds around the topological line defect
to form a closed path in
Figure 2a. The periodicity of the other phase factor
is still
. The eigenvalues of the spin operator are
, which represents the chirality of flowing current in M
bius strip.
Unfolding the edge of M
bius strip into an
∞-shaped knot preserves the topology of quantum fluid torus and the
periodicity of spinor wavefunction. The
Figure 2a represents the wavefunction of topological spin state
, which defines a topological representation of electron spin
. The spin states of
∞-shaped knot crossing,
and
, are represented by complex wavefunctions with four components,
It must be pointed out that magnitude of wave function for knot crossing is not normalized to unity, instead it is normalized by Jones polynomial,
.
Figure 2b (
Figure 2c) represents the two components of wavefunction for topological spin state with
(
). The tangential velocity of circling fluid in the knots of
Figure 2b-c is determined by the gradient of phase field of wavefunction. Opposite gradient fields generate opposite tangential flow fields. A crossing state in
Figure 2a-b transforms into uncrossing state in two different ways, as showed in
Figure 2d-e. The uncrossing states are topological vacuum states, denoted by
and
,
Both the topological crossing basis and vacuum basis are not normalized and orthogonal, but a set of orthogonal basis always exists to expand the two sets of topological basis into the same Hilbert space,
The conventional Jones polynomial are projected into the orthogonal basis
. The eigenvalue of topological spin with respect to vacuum states is zero,
or
. Once the two currents are oriented to form the horizontal vacuum state
, the vertical vacuum state
is forbidden under continuity constraint of topological invariant. The magnitude polynomial of the topological spin states transform into one another following Kauffman decomposition rule in knot theory[
18],
which are further reformulated into matrix equation,
Substituting the orthogonal Eq. (
9) of topological vacuum states into the decomposition Eq. (
12) yields the transformation equation between the crossing basis
and uncrossing basis
,
The basis transformation equation an unitary matrix, which is expanded by the generators of SU(2) group,
where the crossing state vector
and uncrossing state vector
are denoted as
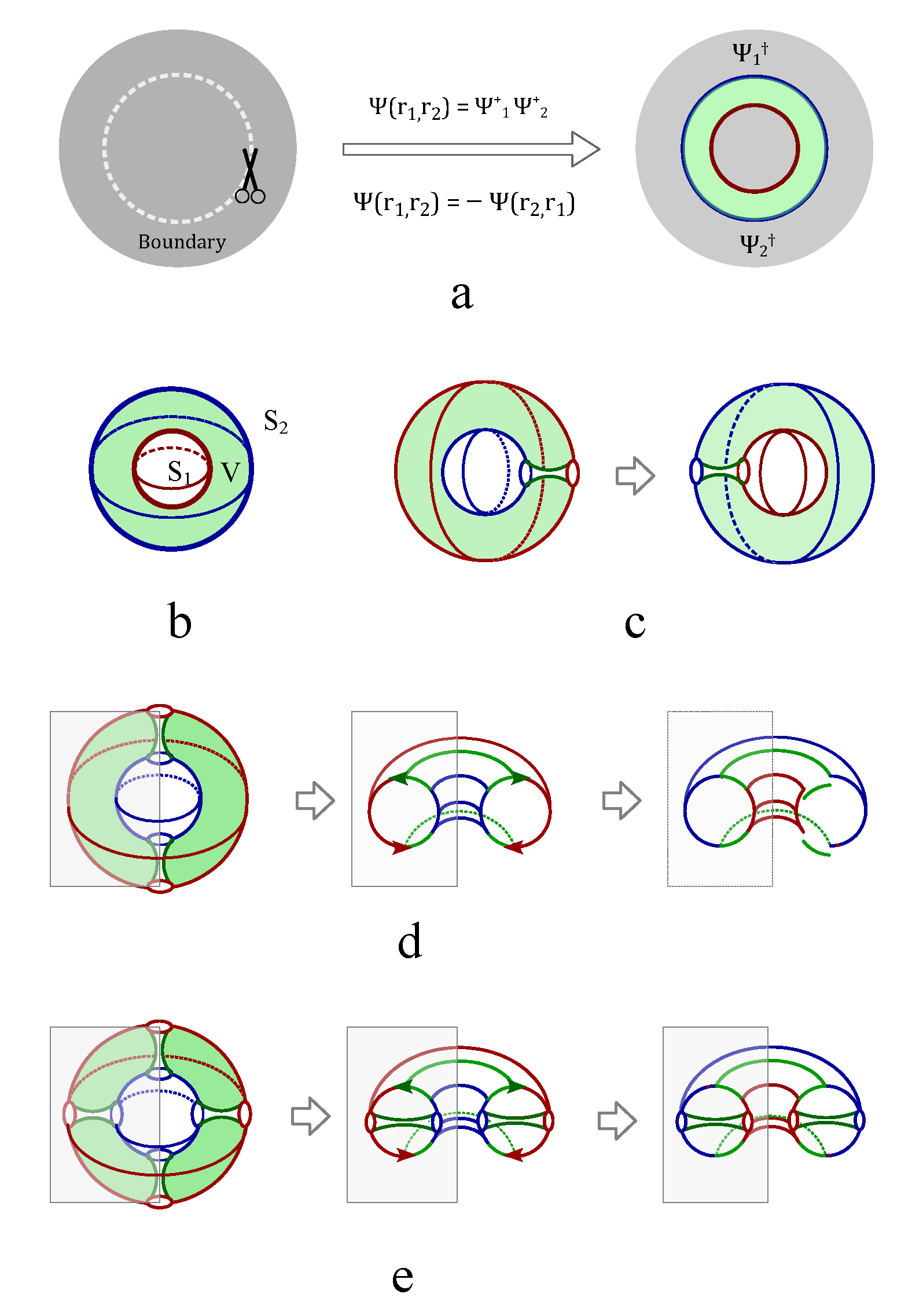
Both the crossing state and uncrossing state have four open endings. In order to form closed path that is topologically equivalent to circles, edge states with two open endings are introduced as following.
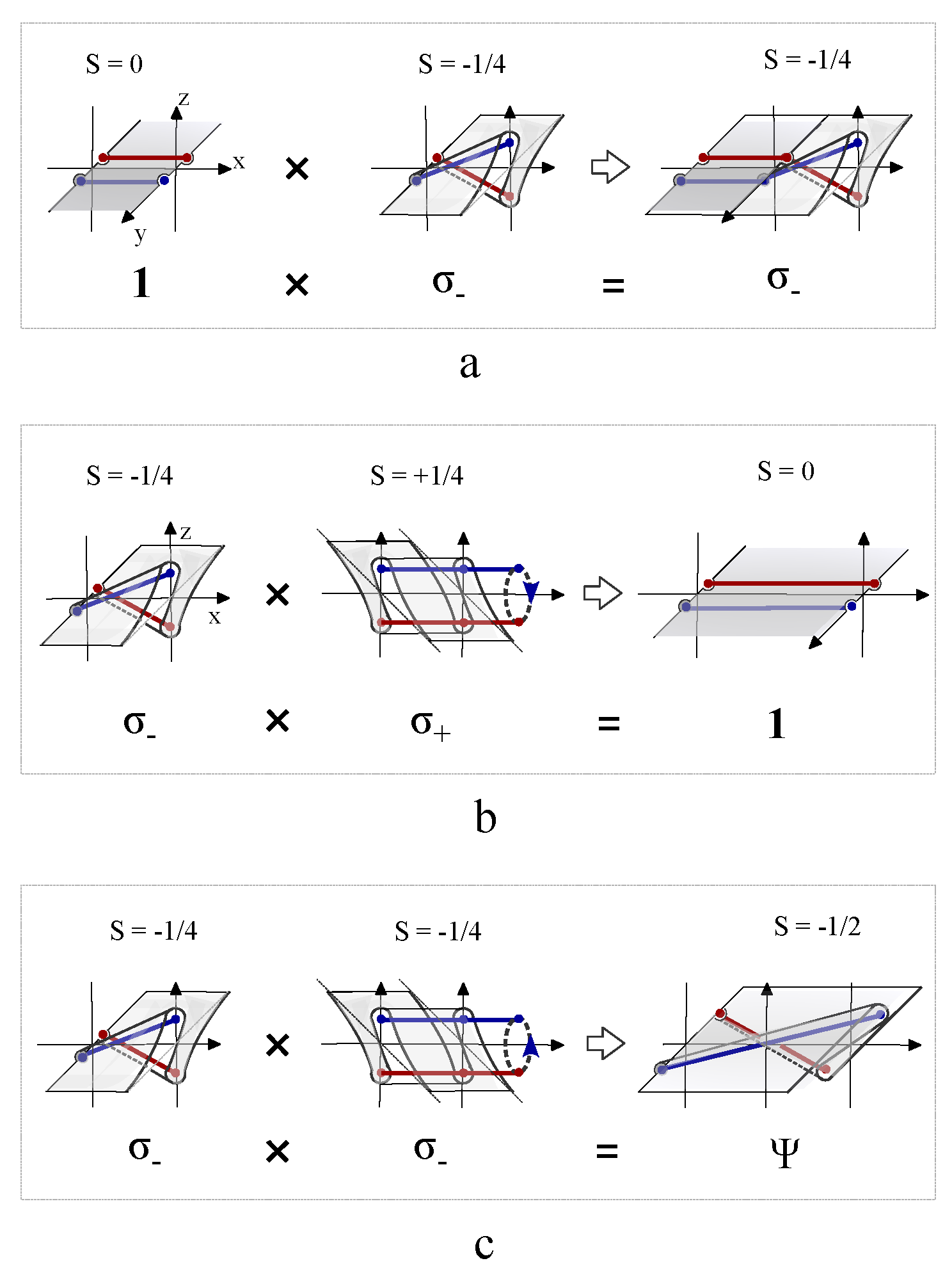
where
,
represents the left, the right, the top and the bottom edges respectively. The topological edge state of single current branch locates along the edge of knot lattice. Once the edge current configuration is fixed, its collective configuration remains invariant when the bulk knot lattice transform from the crossing basis to the uncrossing basis. The product of two edge states of opposite semicircles,
or
, are defined as closed vacuum state
. The closed vacuum state can be represented by unit matrix. The simplest representation of
is U(1) group element,
In knot theory [
18], the polynomial with respect to the combination of a closed loop and general link is defined as
This decomposition rule is derived from two coupled crossings, that decomposes according to Eq. (
11).
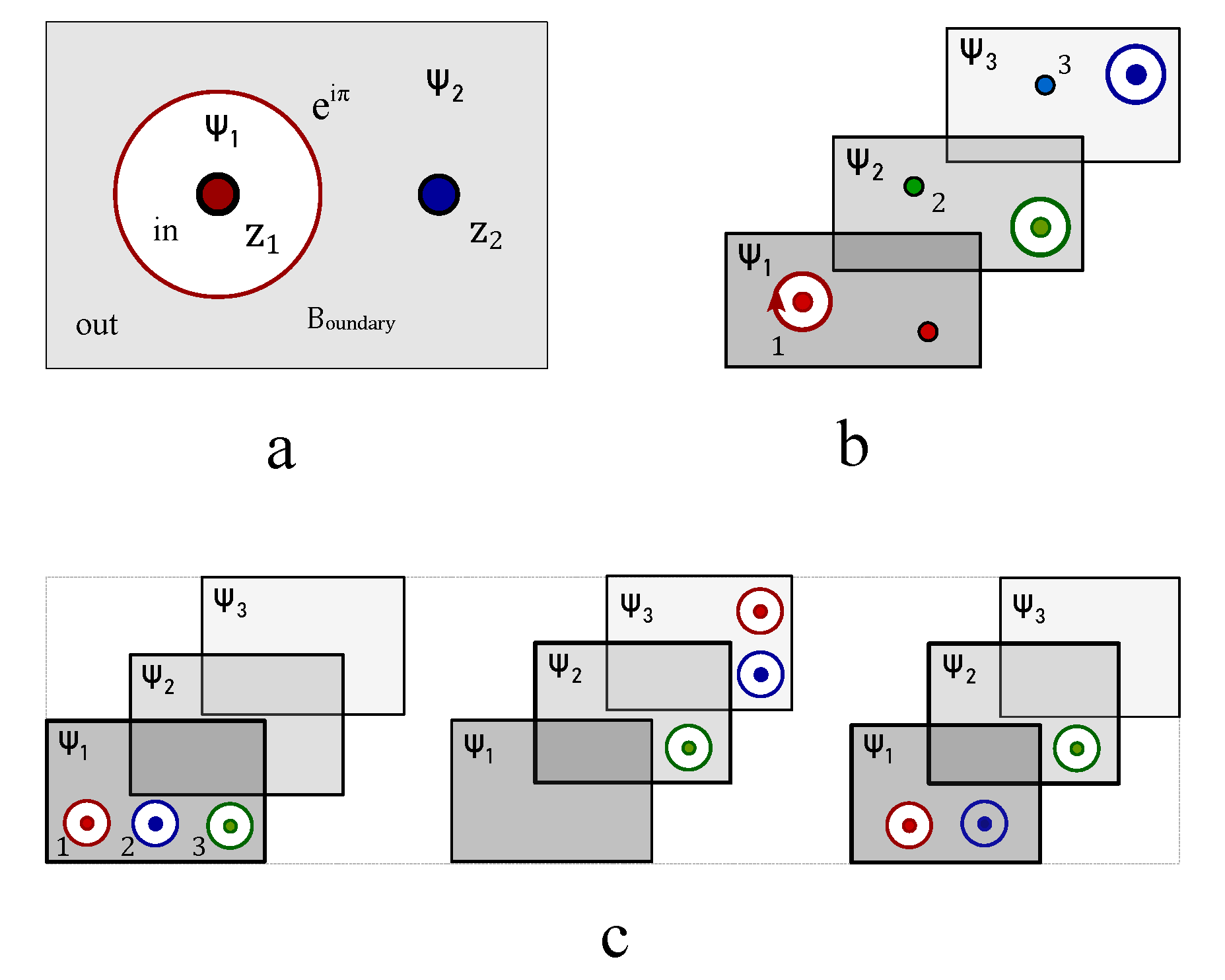
Two coupled crossings with independent topological spin numbers generate four possible crossing states,
,
,
and
as shown in
Figure 3. Unlike the four independent basis of two coupled spins in quantum mechanics, the two crossings with opposite topological spin are transformed into the same product state of two vacuum states under Reidemeister moves,
where
is the operator of the Reidemeister move. As showed in
Figure 3b-c and
Figure 3e-f. Applying the Kauffman decomposition rules for the four crossing basis transforms them into four vacuum basis of two coupled spins,
In mind of the orthogonal relations between different basis, i.e.,
,
,
, the transformation matrix of knot polynomial is mapped into the transformation matrix between the two four dimensional basis vectors,
The polynomial vector of
N coupled crossings
transforms into
N coupled uncrossings
following the same decomposition rules as above,
. The transformation matrix
U is a matrix of Kauffman polynomial, which is equivalent to Jones polynomial.
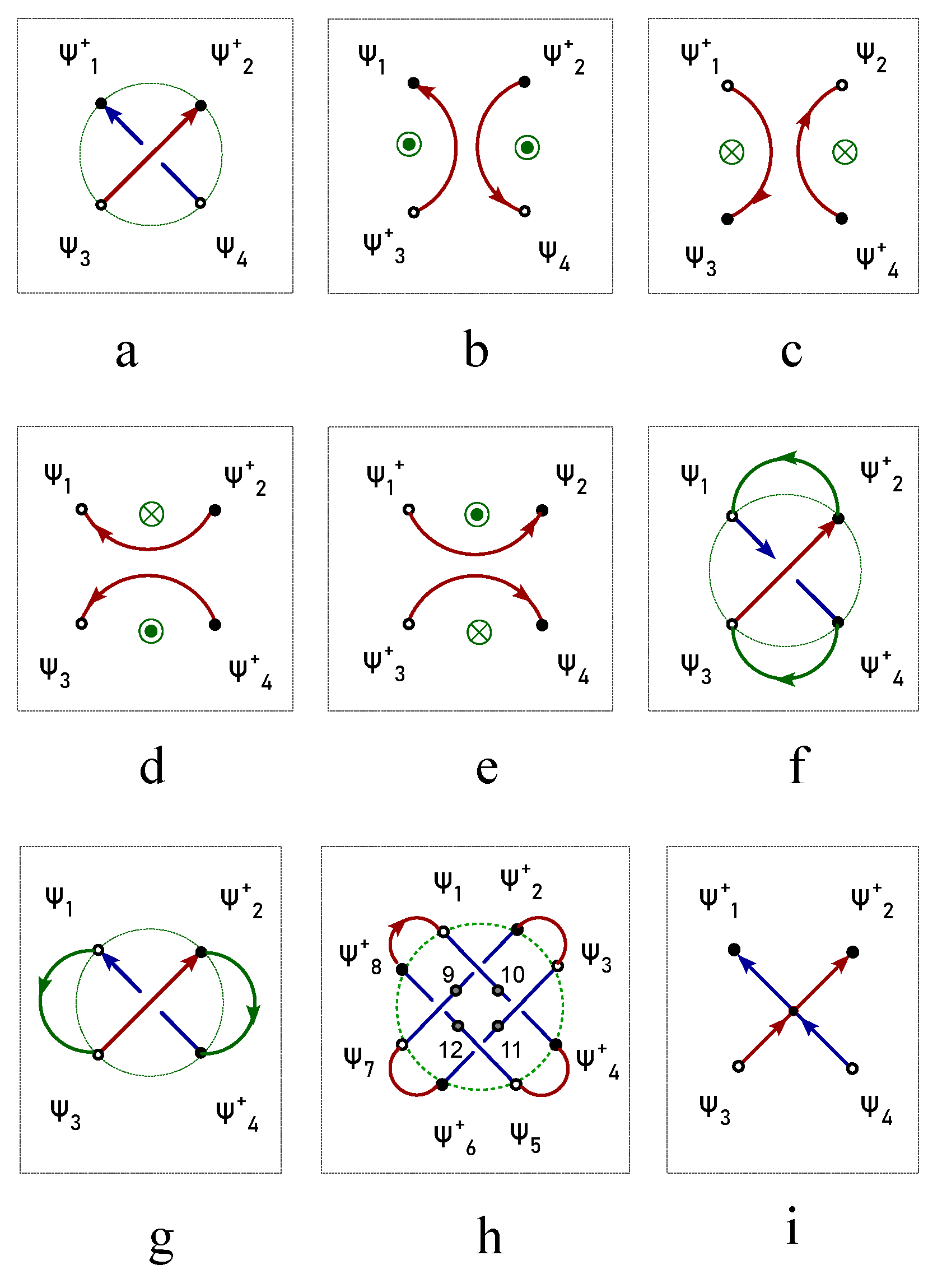
Beside the quantum wavefunction representation of knot, the knot lattice has a straight forward representation by matrix of quantum creation and annihilation operators. Cutting one cross out of its surrounding network generates four open endings in
Figure 4a. The directed flow along the current line is represented by the product of a creation operator and an annihilation operator, i.e.,
and
. The crossing in
Figure 4a is represented by a matrix equation,
where
h is the hopping rate.
is fermion operator and obeys anticommutative relations,
The hopping rate in Eq. (
22) is multiplied by a topological phase term
, where the topological spin is quantified by
where
is the gauge field potential along the current lines. The two crossing current lines that avoid touching each other always bend into opposite directions, since the four ending points are projected into the same plane. When the topological spin
flips to
by exchange the top and bottom lines, the divergence field
or
flips its orientation respectively. The topological spin Eq. (
24) is essentially the abelian Chern-Simons action,
defined on a local crossing. The quadratic fermion operator Eq. (
22) is equivalent to Hamiltonian equation with
t measures the kinetic energy of a hopping particle. Therefore the representation matrix
is termed as topological Hamiltonian matrix here. The topological vacuum state for two uncrossing current lines in
Figure 4b is also represented by four fermion operators which interact with one another following the Hamiltonian equation
,
Since the two current lines in vacuum state avoid crossing each other, the topological spin is defined by the product of the divergence field of the two arc lines,
The divergence of the two arcs in
Figure 4b are oriented in the same direction, denoted by the black dot surrounded by a circle, therefore the eigenvalue of topological spin is
. The topological spin Eq. (
27) for vacuum states shares similar definition with the second Chern number in four dimensional manifold,
The conjugate of
is represented by the same two arcs in
Figure 4c, in which both the flow field and divergence field of the two arcs are reversed simultaneously to preserve the value of topological spin
. When the two arcs in vacuum state generate opposite divergence fields, the topological spin of vacuum state is
. For example, the
Figure 4d is composed of two arcs with opposite divergence, the topological spin in the Hamiltonian matrix,
is
, which is invariant in the conjugate vacuum state
, because both the two opposite divergence fields reversed their orientations (
Figure 4e).
The open endings are connected by edge currents to form a closed loop. In the quantum operator representation of knot, the edge current are also the product of a creation and an annihilation operator. The Hamiltonian matrix of the "8"-shaped knot in
Figure 4f reads
where
is the hopping rate of edge current. A
∞-shaped knot is generated by adding the other two edge states,
and
, on the cross in
Figure 4a. The corresponding Hamiltonian matrix is
The
∞-shaped knot and "8"-shaped knot share the same topology but are distinguishable by the Hamiltonian matrix. This Hamiltonian matrix representation of knot lattice has a straight forward extension to more complex knot lattice. For example, the chiral flow in the knot lattice of
Figure 4h is described by the chiral Hamiltonian matrix
where
is the complex hopping rate. This topological Hamiltonian representation spontaneously eliminated the intersecting current lines out of knot lattice (
Figure 4i), where the product terms of four fermion operators emerges. The dimension of the Hamiltonian matrix of a knot lattice is determined by the total number of nontrivial endings. Each ending represents one fermion particle. This quantum representation provides a natural explanation on the assumption in knot theory, i.e,
. The collective quantum state of a trivial circle composed of
N endings is denoted as
where
is the occupation number on the
ith ending. The Hamiltonian matrix representation of the circle is
dimensional diagonal matrix. The knot polynomial is derived from determinant of the Hamiltonian matrix,
If the occupation number at any one ending points is zero, the track chain remains open, the polynomial equation of circle is spontaneously zero.
The topological Hamiltonian
for a knot lattice is independent of dynamics of interacting crossings. Interacting crossings in knot lattice is described by dynamic Hamiltonian. When the crossing states transform into another crossing states under thermal fluctuation or external field stimuli, the knot lattice is in superposition state of different crossing patterns. For the simplest superposition state of single crossing with opposite topological spin
, the wavefunction is denoted as
, the density matrix is defined as
counts the probability of the cross in the state with topological spin
.
counts the probability of the cross state with
.
or
counts transition rate between the two opposite crossing states. The density matrix obeys the Heisenberg equation of motion,
A general Hamiltonian for the crossing transition dynamics is
measures the reversing frequency of the chiral current in knot.
measures the hopping strength between opposite crossing states. Notice here the Hamiltonian and density operator are expressed by the same basis. If the density operator is expressed by superposition state of topological vacuum basis
The density matrix in the vacuum space is an unitary transformation of the density matrix in the crossing space,
The vacuum state
is transformed into topological crossing state according to the inverse of Eq. (
14),
. The dynamic Hamiltonian Eq. (
37) in the crossing basis also has an equivalent expression in the vacuum basis,
The dynamic Hamiltonian Eq. (
40) is self-consistently applicable on a density matrix originally expressed by topological vacuum states. If the quantum system is a hybrid four level system of two crossing states and two vacuum states, the corresponding dynamic Hamiltonian is expressed by both the crossing basis and the vacuum basis,
The topological invariant polynomial maps the vacuum basis to the crossing basis, providing a topological constraint equation on the hopping process between vacuum state and crossing state. The dynamic hopping in non-topological electron fluid is governed by quantum electrodynamics. The hopping process between different energy levels of topological fluid must take the knot invariant into account.
The Kauffman polynomial of knot lattice
is equivalently mapped into Jones polynomial
by multiplying
with
the writhing number, i.e.,
. The Jones polynomial is equivalent to an evolution operator that maps the initial crossing states of linked knot lattice into all possible full loop states with inequivalent topology,
where
denotes the
ith full loop state. For the initial knot crossing state of the right handed trefoil knot in
Figure 5,
, decomposing the three crossings of
leads to eight possible full loop states,
The four vacuum states with two loops,
,
,
and
, are topologically equivalent. The three vacuum states with one loop,
and
, share the same topology. There is only one vacuum state with three loops,
. The power indices in Jones polynomial with respect to the right handed trefoil knot in
Figure 5 encoded the total number of topologically inequivalent loops state,
where
. The Jones polynomial of the left handed trefoil knot reads
. The Jones polynomial is independent of the sequential order of decompositions of the three crossings. Permutating the spatial locations of the three crossings in decomposition always leads to the same eight vacuum states and the same Jones polynomial. The Jones polynomial of the left handed trefoil knot is expressed by the same counting sequence
, except that the variable
t is replaced by
in Eq. (
44). In the Ising model of knot lattice, the polynomial variable
t is a Boltzmann factor with respect to different energy,
. The value of local spin
with respect to crossing state is
(
) in the right (left) handed trefoil knot. This physical interpretation coincides exactly with the rigorous proof in knot theory. On the other hand, different vacuum states also evolve into different excited states under thermal fluctuation, i.e., different loop configurations evolves into different knot lattices, therefore the Jones polynomial builds a robust bridge between zero energy states and excited states with non-zero spins, as long as thermal fluctuation does not destroy the topology of knot lattice.
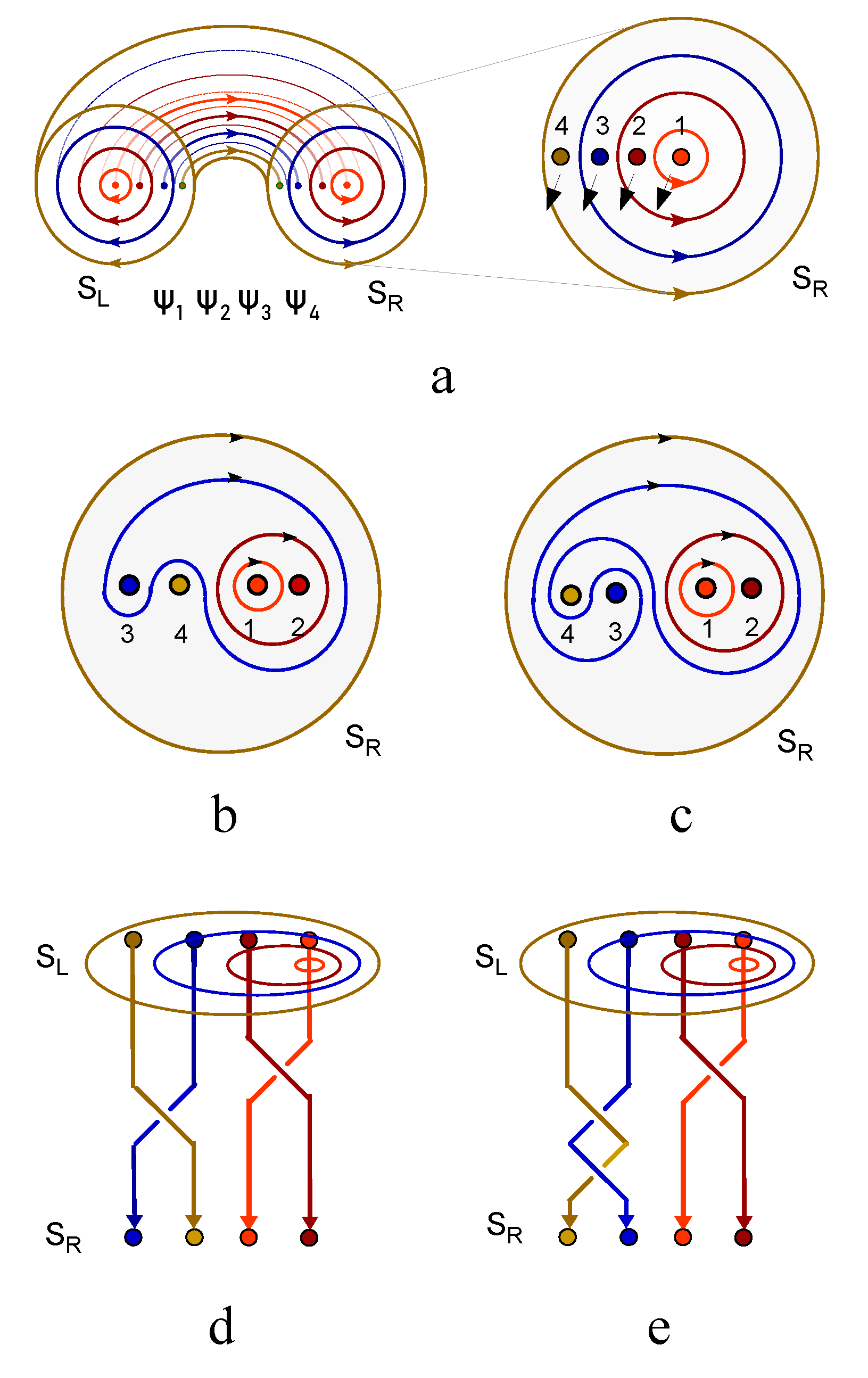
The right handed trefoil knot in
Figure 5,
, is one of the eight crossing basis,
with
. The vacuum basis also has eight components,
with
. The
matrix of Jones polynomials is a transformation matrix from the vacuum space to the crossing space,
This transformation equation holds for the most general case of a knot lattice with
N crossings. The Jones polynomial matrix encodes all possible series decay from a knot lattice of crossings to a lattice of full loops, because the knot lattice with crossings is in excited state and unstable, the fluctuating current lines inevitably touch each other at some time point and fuse into vacuum states. The full loop state is the most stable state against thermal fluctuations.
The Jones polynomial determines the partition distribution of loop states with different number of loops in zero energy state. In the highly degenerated Hilbert space of zero energy state with respect to the right handed trefoil knot (
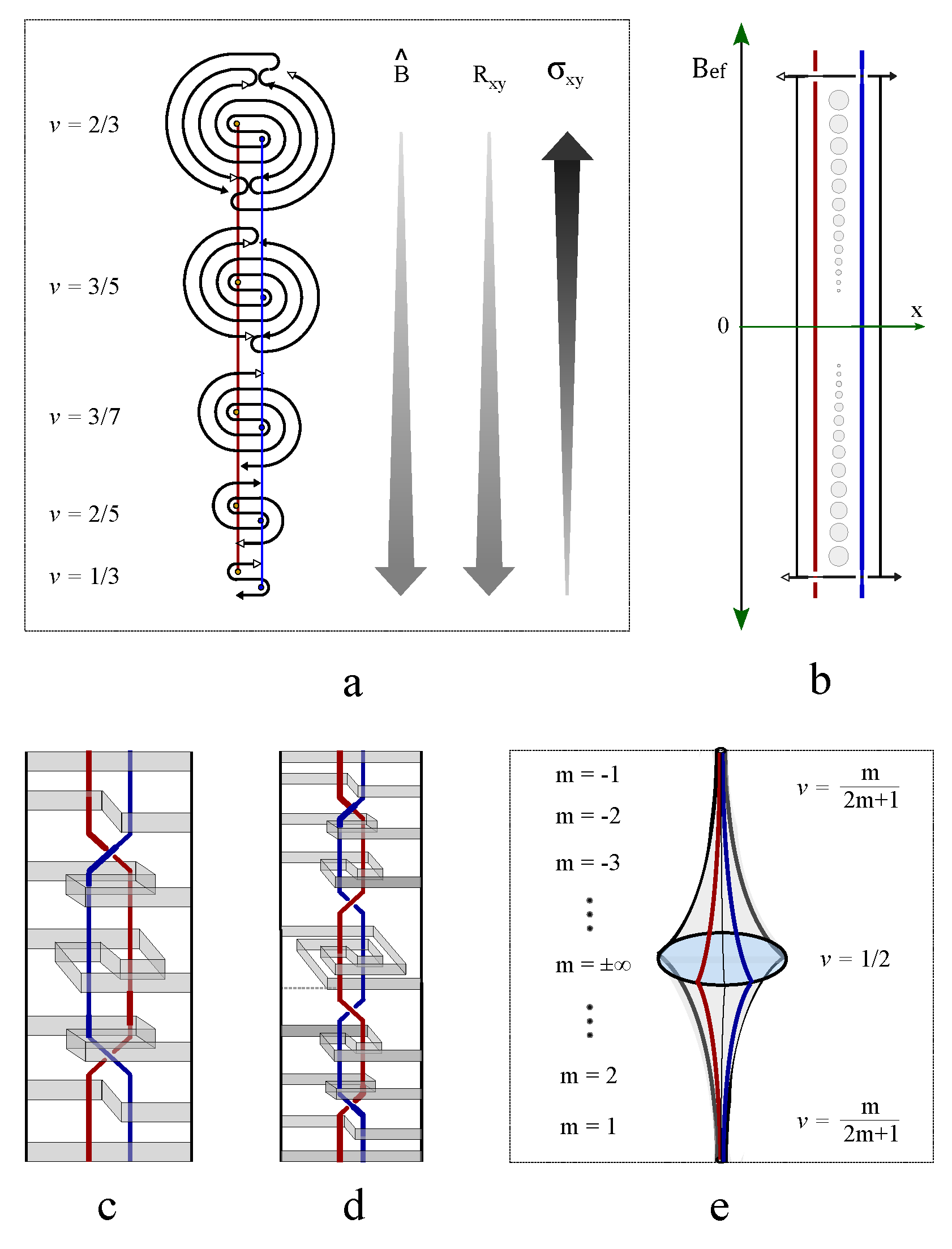
Figure 5), the loop states with three loops contributes the major part to the Jones polynomial. On the contrary, the three loop states contributes the minimal part to the Jones polynomial. This conclusion holds for link on a general knot lattice with many crossings. Only chiral flow in knot lattice survives during thermodynamic evolutions, the flow in knot lattice with opposite chirality exponentially decays to zero (as shown in
Figure 6). Therefore the series decay of knot lattice prefer choosing a chiral path.
The energy of the three crossings of trefoil knot
Figure 7a is quantified by an effective Hamiltonian,
. The high energy state
is defined by three crossing states with the same positive topological spins across the cutting surface in
Figure 7b. The low energy state
is a crossing state formed by two fluxes without penetrating through the boarder. Every topological vortex costs at least two continuous braiding operations as well as two identical crossing states. The total energy of many topological vortices on boarder surface is counted by the linking number of the knot lattice of magnetic fluxes,
The eigenenergy of Hamiltonian Eq. (
46) counts the total energy of the 12 topological vortices in
Figure 7b. When the docking points of the four fluxes in cross section
or
are connected to fuse the four separated flux loops into one flux loop, the knot pattern in Figure 55e realizes a chiral trefoil knot in
Figure 7a. The flux segment that connects the edge points of flux No. 2 and flux No. 3 cross the boarder surface once, while the edge flux segment has to cross three boarder surface to connect flux No. 1 and No. 4. There are four topological vortices created in the left-hand cross section
. On the right-hand cross section
, the edge flux connecting flux No. 1 and No. 3 intersect with four boarder surfaces and created four topological vortices swirling around the intersecting point. Four topological vortices are also created along the edge flux segment connecting flux No. 2 and No. 4. There are eight topological vortices in total in the right-hand cross section
(
Figure 7b). The total number of topological vortices in
grows with respect to an increasing number of periods of braiding.
The Hilbert space of three spin 1 particles is expanded by
basic knot patterns, 15 exemplar knots are listed in
Figure 8. Every knot pattern is labeled by a general quantum state
The left-handed trefoil knot is denoted as
The ferromagnetic state
represents the right-hand trefoil. The Kauffman bracket polynomial of the left-hand trefoil reads
The Kauffman bracket polynomial of the right-hand trefoil is
, in which the parameter
A is
The chirality of the trefoil knot is distinguished by the Kauffman bracket polynomial. Since the trefoil knot in
Figure 7c is created by
braiding operations, the highest power of
A in bracket polynomial Eq. (
47) is
. The fractional quantum Hall state in the cross section
of
Figure 7c carries fractional charge
. Therefore the chiral edge modes in FQHE is distinguishable by Kauffman bracket polynomial. When the ferromagnetic state
flips to
, the total spin
flips to
, driving the Kauffman polynomial of the left-hand trefoil into that of the right-hand trefoil. The chirality of trefoil knot is spontaneously mapped into chiral Jones polynomial as well as Kauffman polynomial,
The Jones polynomial is equivalent to Kauffman polynomial under the exact map of variables
. The trefoil knot in
Figure 7a is mapped to crossing state of three mutually perpendicular fluxes in three dimensions with a special boundary condition (
Figure 7c). Both Jones polynomial and Kauffman polynomial can be interpreted as the Boltzman weight of collective spin state
with respect to eigenenergy
.
At high temperature, a magnetic flux within low magnetic field could cut another flux and reconnect to each other, this dynamic process drives an overcrossing flipping to undercrossing (or vice versa). In the plasma analogy theory of FQHE, the inverse of total number of braiding operations is proportional to effective temperature. At finite temperature, the partition function of three topological spin1 is the sum of Boltzmann weights of all possible collective states of the three crossings,
where
indicates all possible collective spin configurations of three crossings. The simplest formulation of the total energy of three crossings is
. The coupling interaction between crossings leads to more complex energy formulations. The partition function with
is not a topological invariant due to the absence of boundary condition with respect to each knot state. The Kauffman bracket polynomial is the eigenfunction
with respect to eigenenergy
. The Hamiltonian of three crossings
is equivalent to a renormalized writhing number of single loop,
. Therefore topologically nonequivalent knots are classified by writhing number, i.e., the total spin,
The partition function of three crossings is the sum of the Boltzmann weights with respect to different knots states,
where
is the writhing number of the
nth knot states. The Boltzmann weight measures the occupation probability of a knot state at finite temperature.
The knot polynomial of all possible knots that are generated out of three crossings is derived by Kauffman decomposition rules in knot theory,
where
and
. The polynomial of knot including closed loops are decomposed following the conventions,
and
. In
Figure 8, the knot state of
represents two linked loops,
(
) represents two loops circling in the same (opposite) direction. The writhing number equation for
is equivalent to the linking number of two interlocking loops,
. The Kauffman bracket polynomial of nontrivial knot states in
Figure 8 are derived from Kauffman decomposition rules,
An implementation of the knot variable
A by periodical wave
transforms the bracket polynomials into the superposition wavefunction. The simple bracket polynomials
are eigenfunctions of angular momentum operator
. The eigenvalue of
equals to the number of braiding operations as well as the writhing number of single loop, i.e.,
or
. The knot states with the same topology in
Figure 8 are represented by the same Kauffman polynomials,
However the knot states with the same topology do not share the same energy due to the geometric bending or twisting of the loop. Three coupled spins generate 64 possible collective states in total. The total number of knot states with respect to the writhing number
is denoted as
and counted as following,
The energy of knot is assumed to be proportional to the writhing number
,
. The thermodynamic partition function of three coupled topological spins is
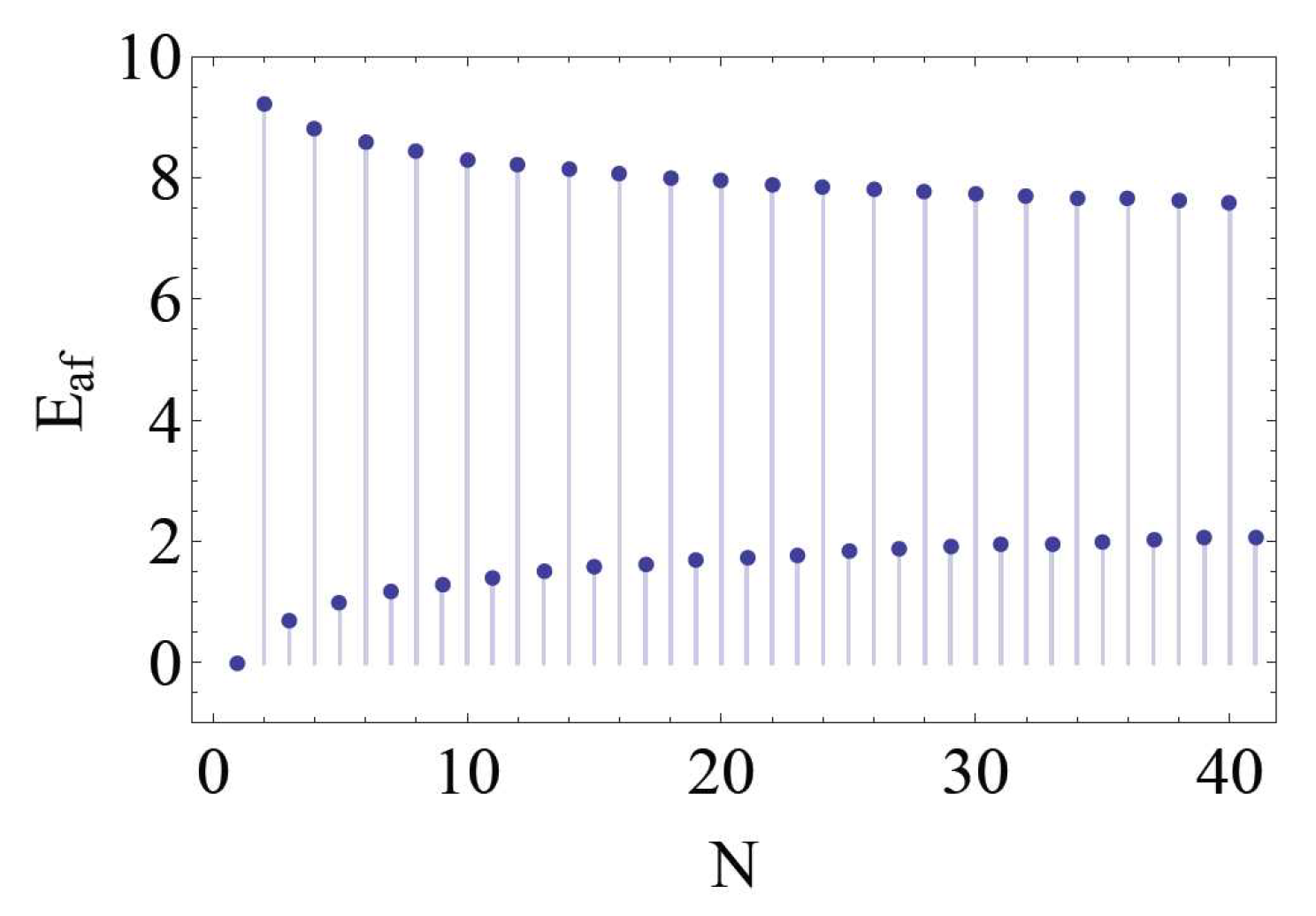
The free energy
and thermodynamics entropy
are spontaneous output of this partition function,
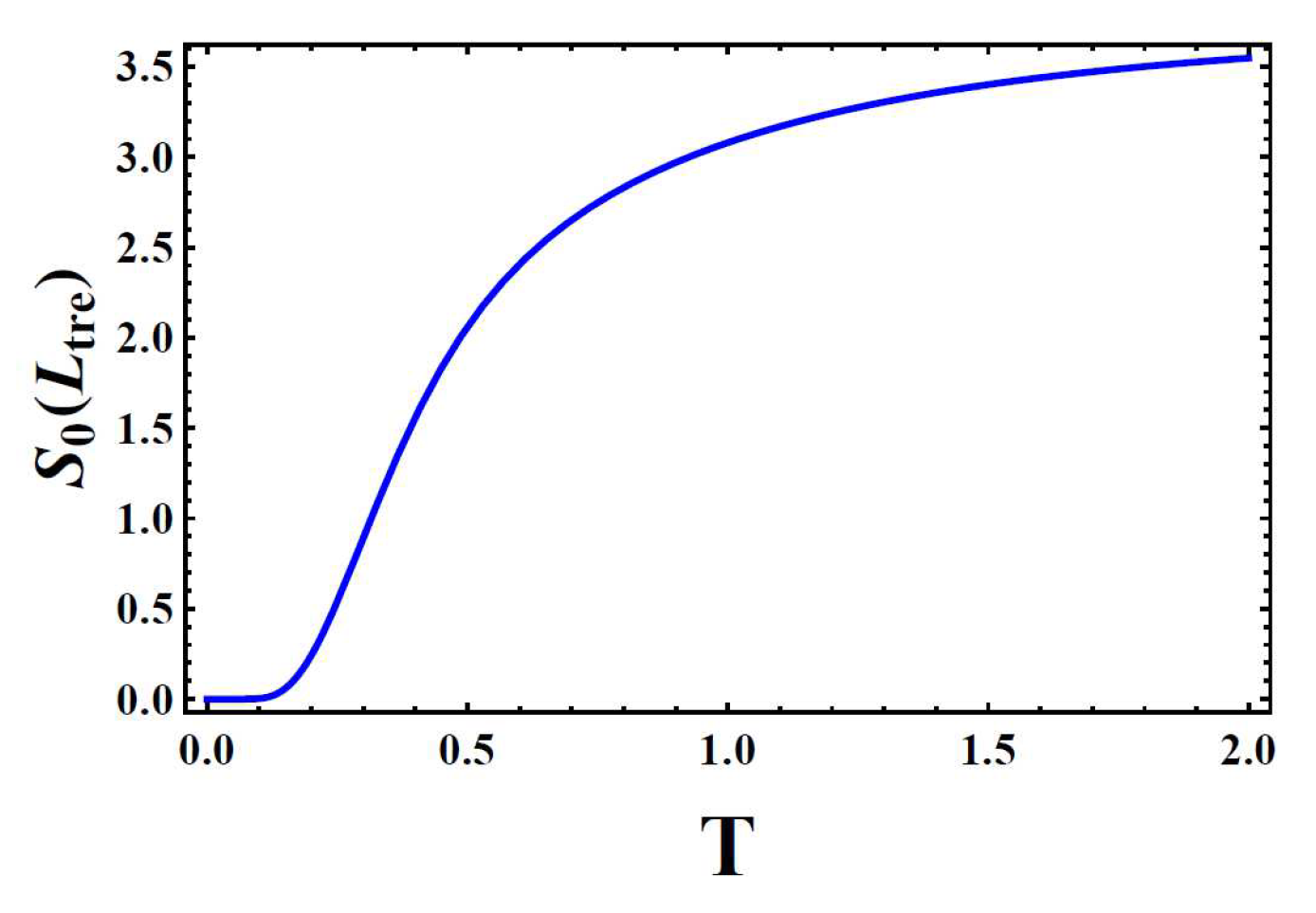
The entropy
approaches to zero when temperature decreases to zero (
Figure 9). The three knot crossings tend to orient their spins in the opposite direction of external field
h. There is no coupling between different crossings. Therefore the entropy of three free crossings (as showed in
Figure 9) is similar to that of three free Ising spins. The crossings in knot lattice are always strongly correlated with one another. It is a reasonable assumption that the left handed trefoil knot shares the same energy as the right handed trefoil knot in absence of external field. Therefore the total Hamiltonian of knot lattice in external field is the sum of the coupling interaction and the interaction with external fields,
where
is the total number of crossings. The output energy of
acting on the knot configurations in
Figure 8 are listed as following,
The eigenenergy of states with writhing number
includes the coupling interaction between a positive crossing and a negative crossing, which is spontaneously eliminated by Hamiltonian
. The corresponding thermodynamic partition function of a knot with three crossings reads
The coupling interaction between crossings introduced non-topological factors into partition function. The thermodynamic entropy
with respect to
is similar to entropy
Eq. (
56) on the cross sectional surface of
, but expands into the extra dimension defined by coupling strength
J.
The knot configurations with different eigenenergy (i.e. writhing number) may share the same topology. The knot with only one crossing keeps its topology invariant when it hops from excited state
to ground state
under thermal fluctuations. The topology experiences a sudden change when the knot hops from the left-hand or the right-hand trefoil knot to ground state with
. The dynamics hopping between the two chiral trefoil knot states,
and
, is governed by the effective Hamiltonian,
Notice here
, the Jones polynomial wavefunction is expressed by orthogonal basis,
The density operator of a mixed state
with the probability
being
and probability
being
is defined as
where
and
. The uncertainty of the mixed state
is measured by the von Neumman entropy,
Because the right hand trefoil knot state is not a pure state in the orthogonal basis space, itself is a mixed state in the orthogonal basis space. Substituting the Kauffman polynomial Eq. (
54) into the von Neumman entropy of the pure state
yields
Substituting the Boltzmann factor
into Eq. (
65) yields the von Neumman entropy that evolves with temperature,
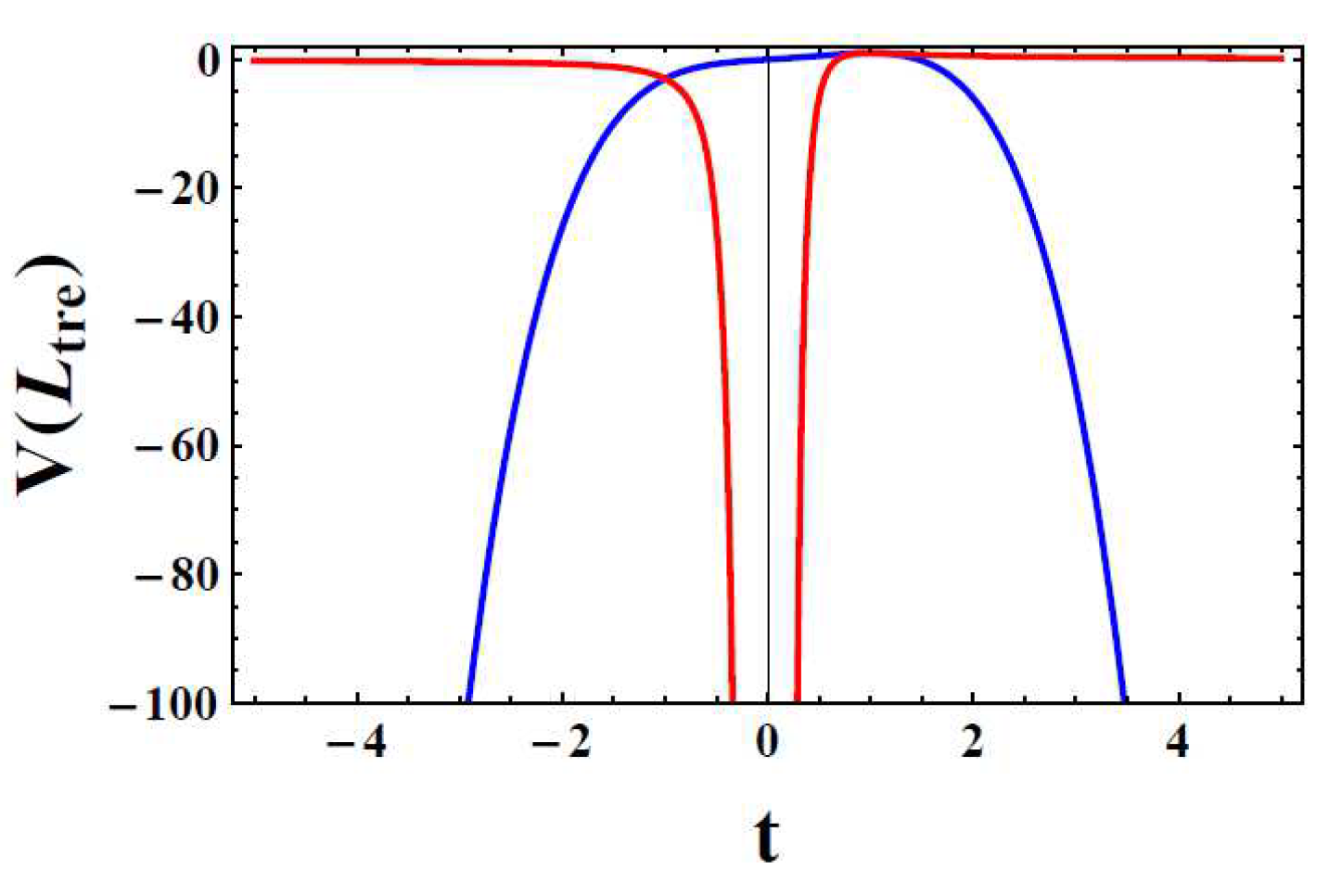
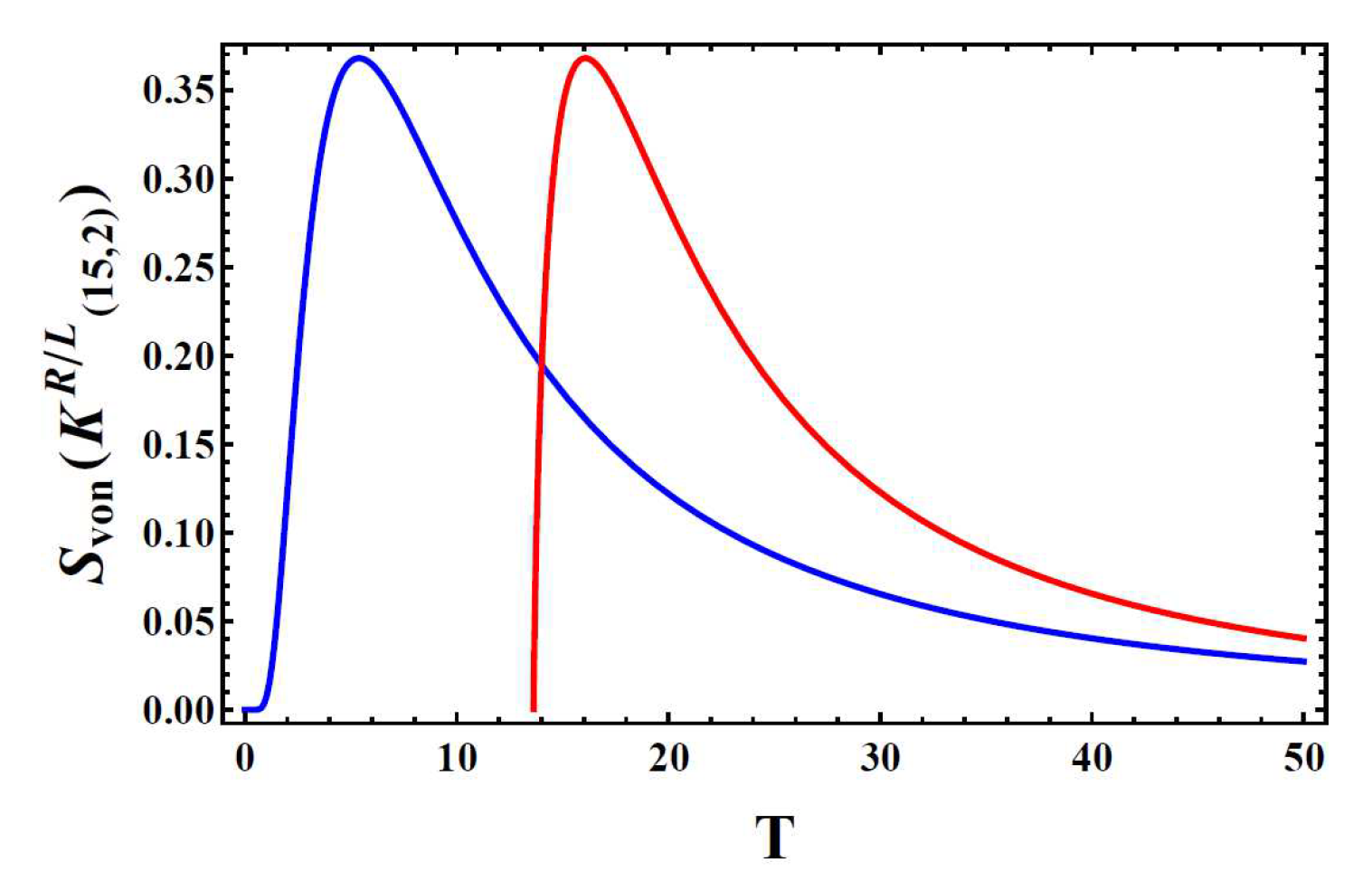
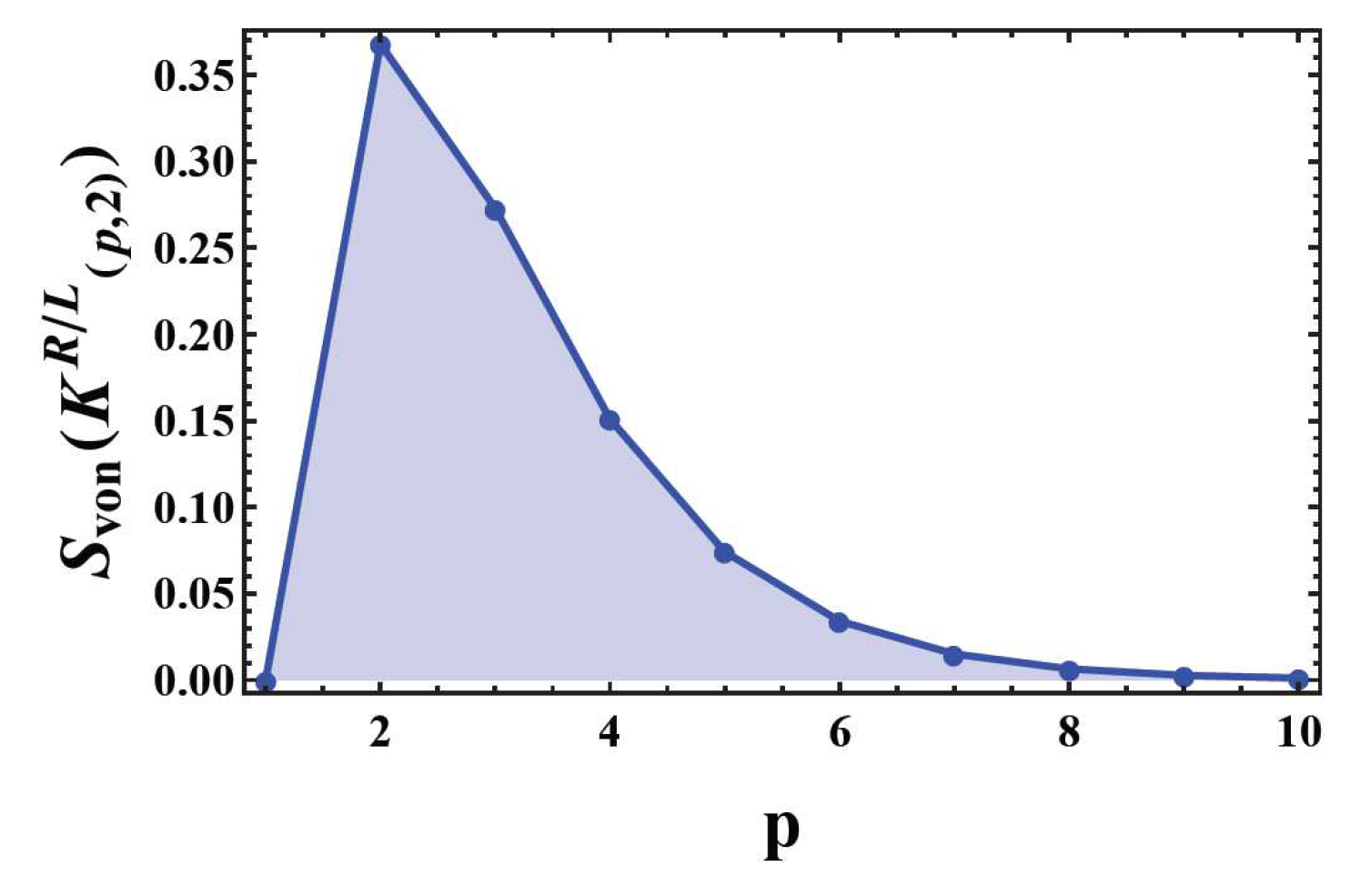
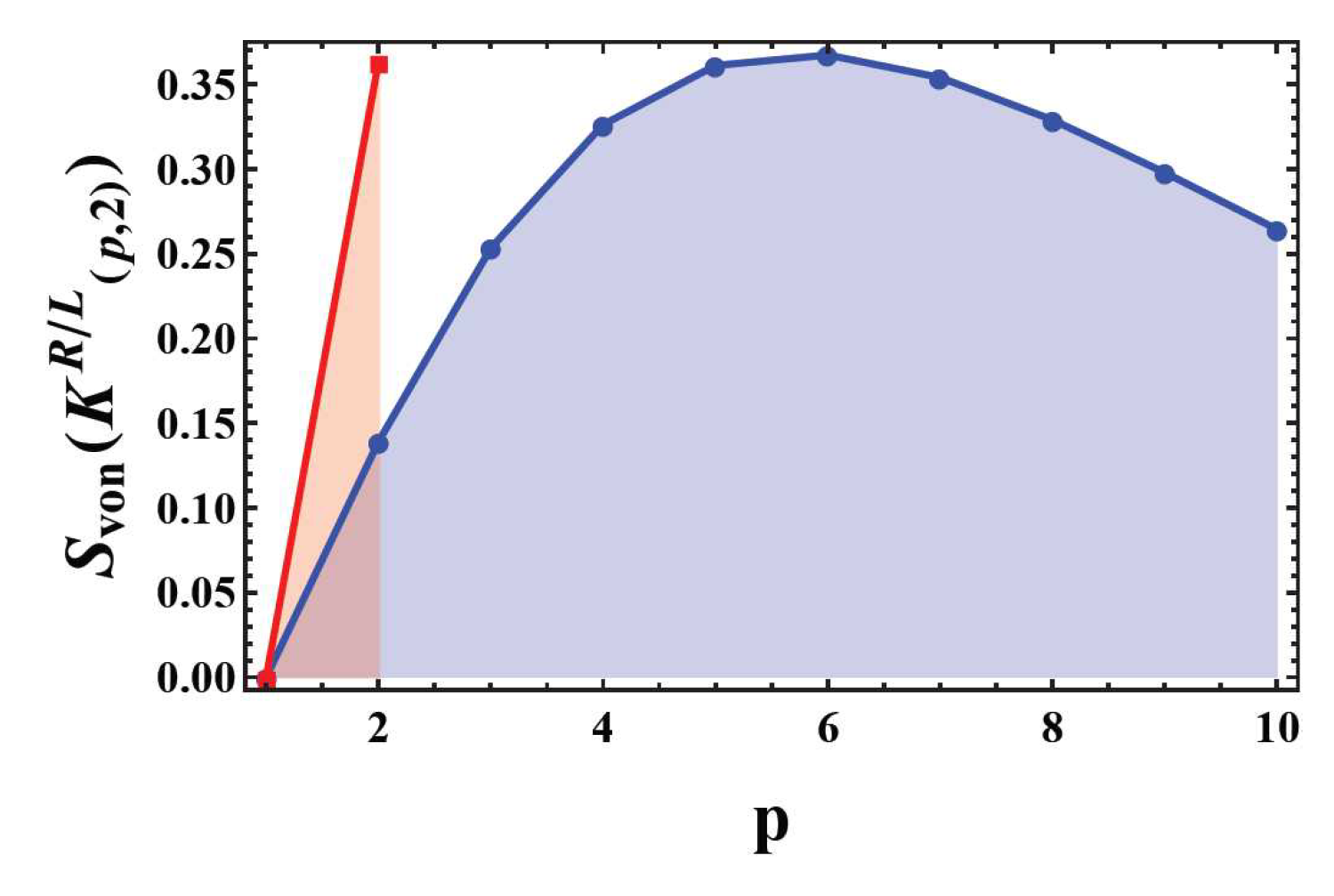
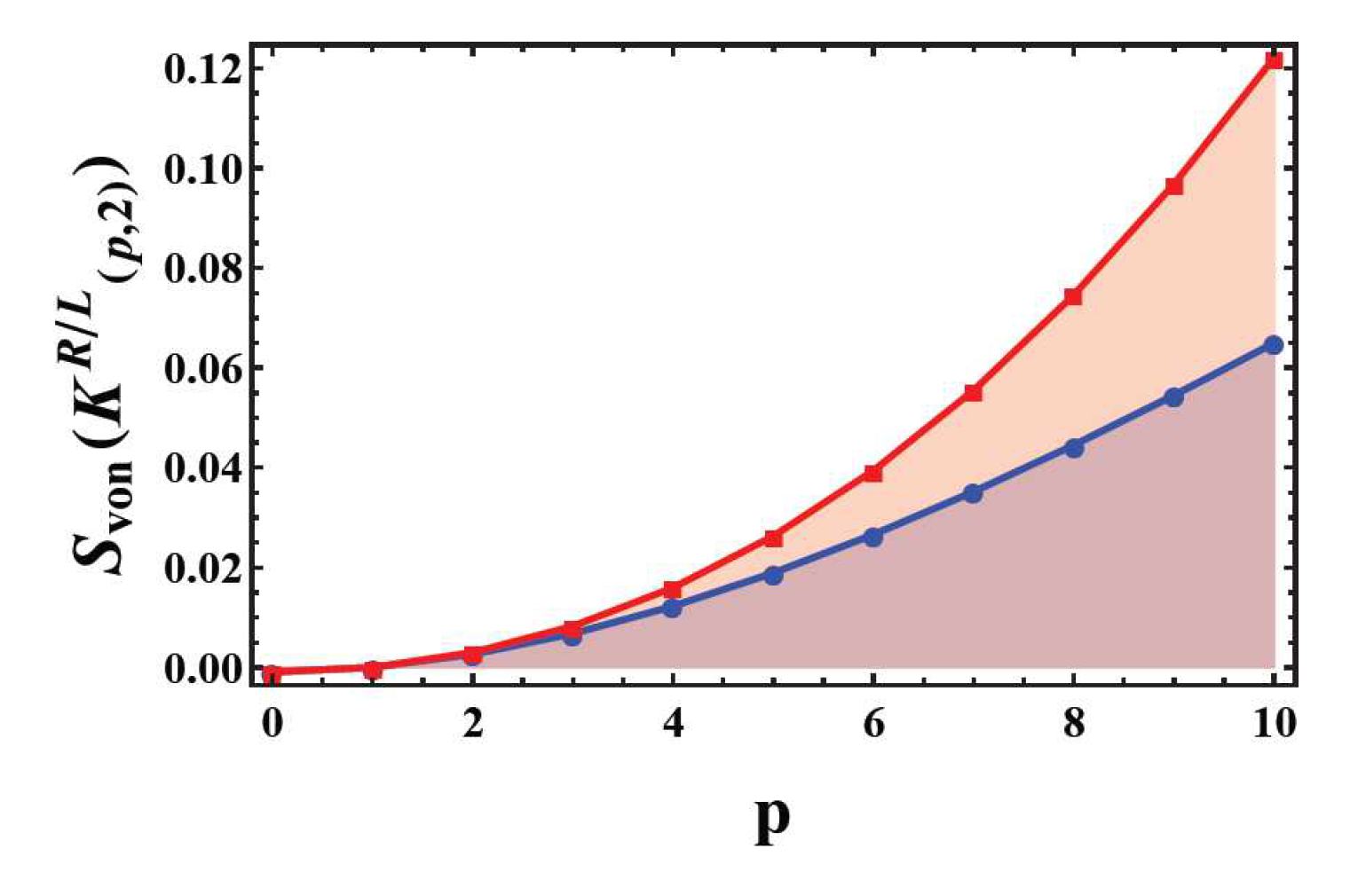
Figure 10 shows that the von Neumman entropy of the right hand trefoil knot reaches the maximal value before it decays to zero near zero temperature. The entropy of the left hand trefoil knot vanishes at finite temperature (
Figure 10). The entropy of other pure states is derived in a similar way of combining Kauffman polynomial Eq. (
54) and the von Neumman entropy Eq. (
64). The entropy of the single loop state
(as shown in
Figure 8) is constantly zero, so does its topological equivalent configuration
in
Figure 8.
A complex topological fluid is composed of many different knots. These knots entangle with one another to form a knot lattice when temperature drops. As temperature gradually increases, the viscous topological fluid gains more kinetic energy to breaks into discrete flowing zones, decomposing a knot lattice into many isolated small loops. The Jones polynomial governs the topological decomposition process, offering an effective density operator to measure the number of all possible states with respect to certain number of loops. For a general knot lattice with
n crossings, the knot polynomial wavefunction is not the direct product of the polynomial of single crossing, instead it is a nonlinear function,
where
denotes topological index of local crossing state. The two crossing states
and topological vacuum state
at the
ith lattice sites are denoted as a vector of two components,
The crossing wavefunction transform into the uncrossing wavefunction under the decomposition operator
, which is derived from the Kauffman decomposition rule in knot theory,
The modular square of the crossing wavefunction is defined as the conventional Jones polynomial or Kauffman polynomial,
. As a result, the transformation operator
between Jones polynomials is the product of the decomposition operator
and its conjugate operator
,
acts on the polynomial with
crossings
. The polynomial with
crossings is further decomposed into the sum of polynomial with
crossings,
The iterative decomposition operation generates a series of Jones polynomials that maps the knot lattice with
i crossings into free loops configuration. The Jones polynomial of knot lattice with
n crossings reads,
The von Neumman entropy of the knot lattice with
n crossings is
The Jones polynomial is a topological invariant, as a result, the entropy Eq. (
73) is the topological entropy of knot lattice.
2.2. The knot invariant of chiral spin liquid of one dimensional spin chain
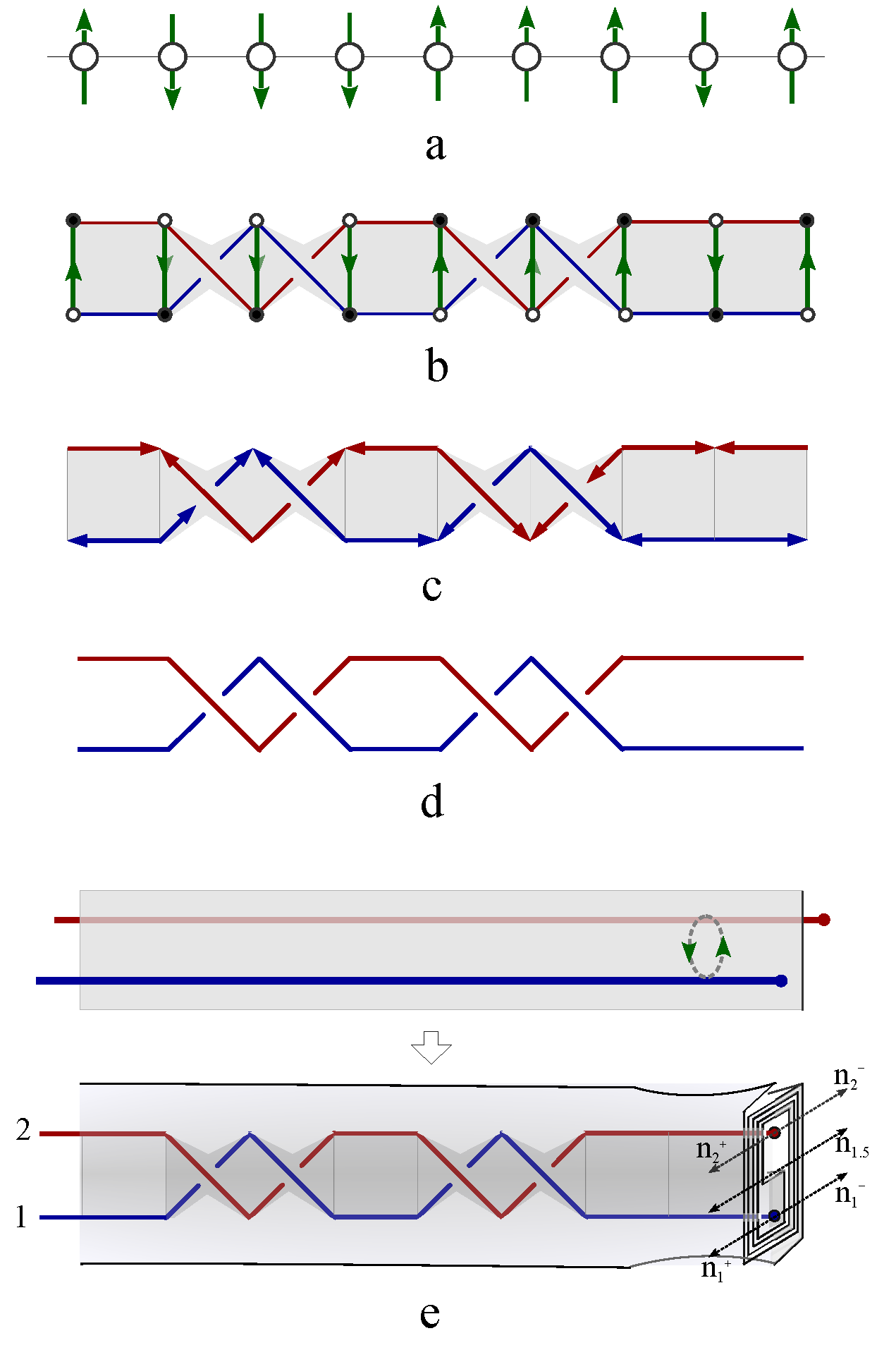
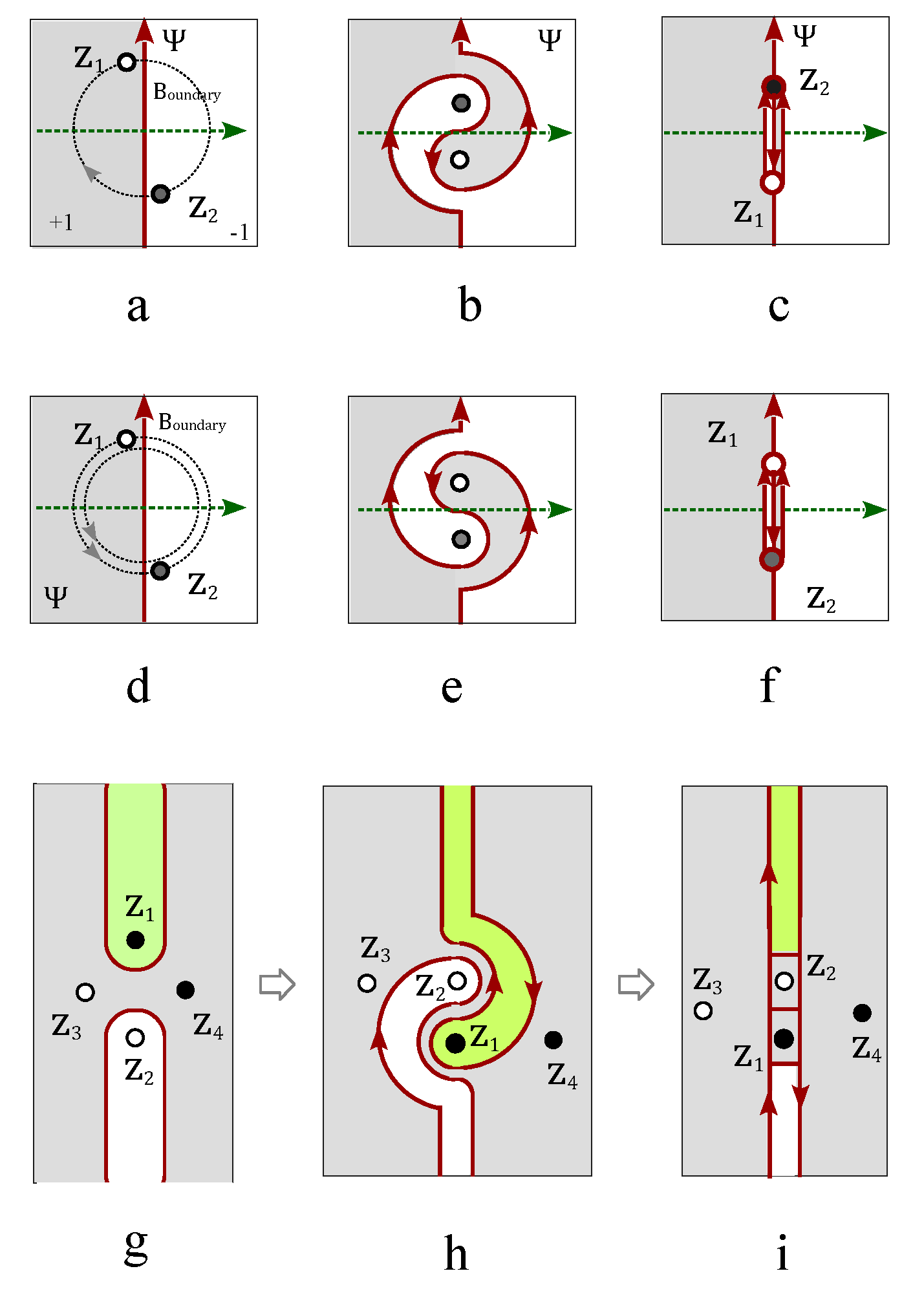
Every electric knot interlocks with an induced magnetic knot current. The electric knot with only one self-crossing interlocks with a simple magnetic loop (
Figure 11a) without self-crossing following electromagnetic induction effect. The link of this electric loop and magnetic loop is characterized by a topological invariant number—Linking number,
where
is the total number of positive (negative) crossings. The link in
Figure 11a has a linking number
. Flipping one of the two spins in
Figure 11a either unties the self-crossing into parallel lines (
Figure 11b) or generates one more crossing both on the electric loop and magnetic loop (
Figure 11c). This linking number is invariant during the flipping process. For a more general case of many coupled spins along one dimensional chain, the antiferromagnetically coupled spins is either represented by a knot lattice of electric loops or a topologically equivalent magnetic knot lattice (
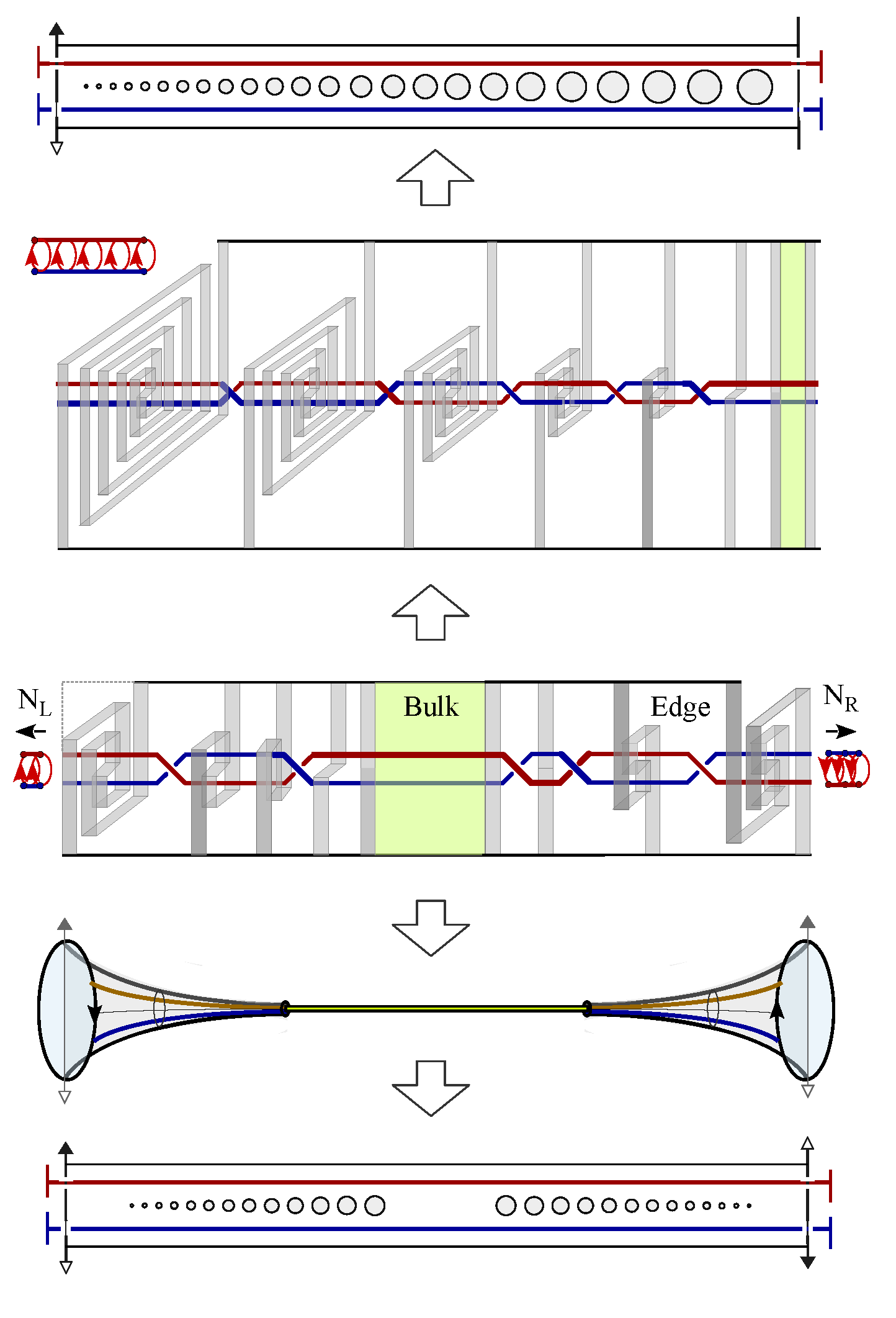
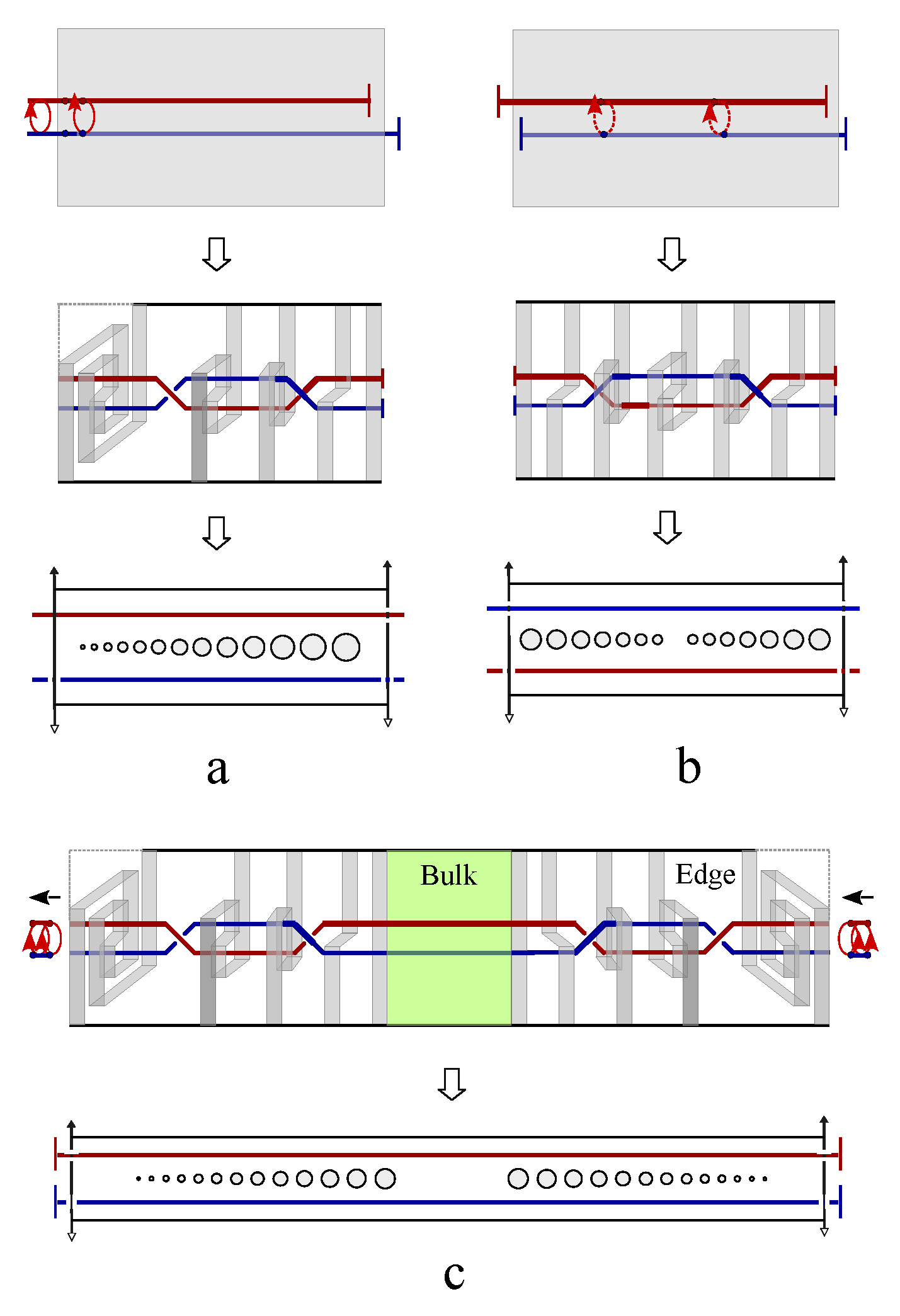
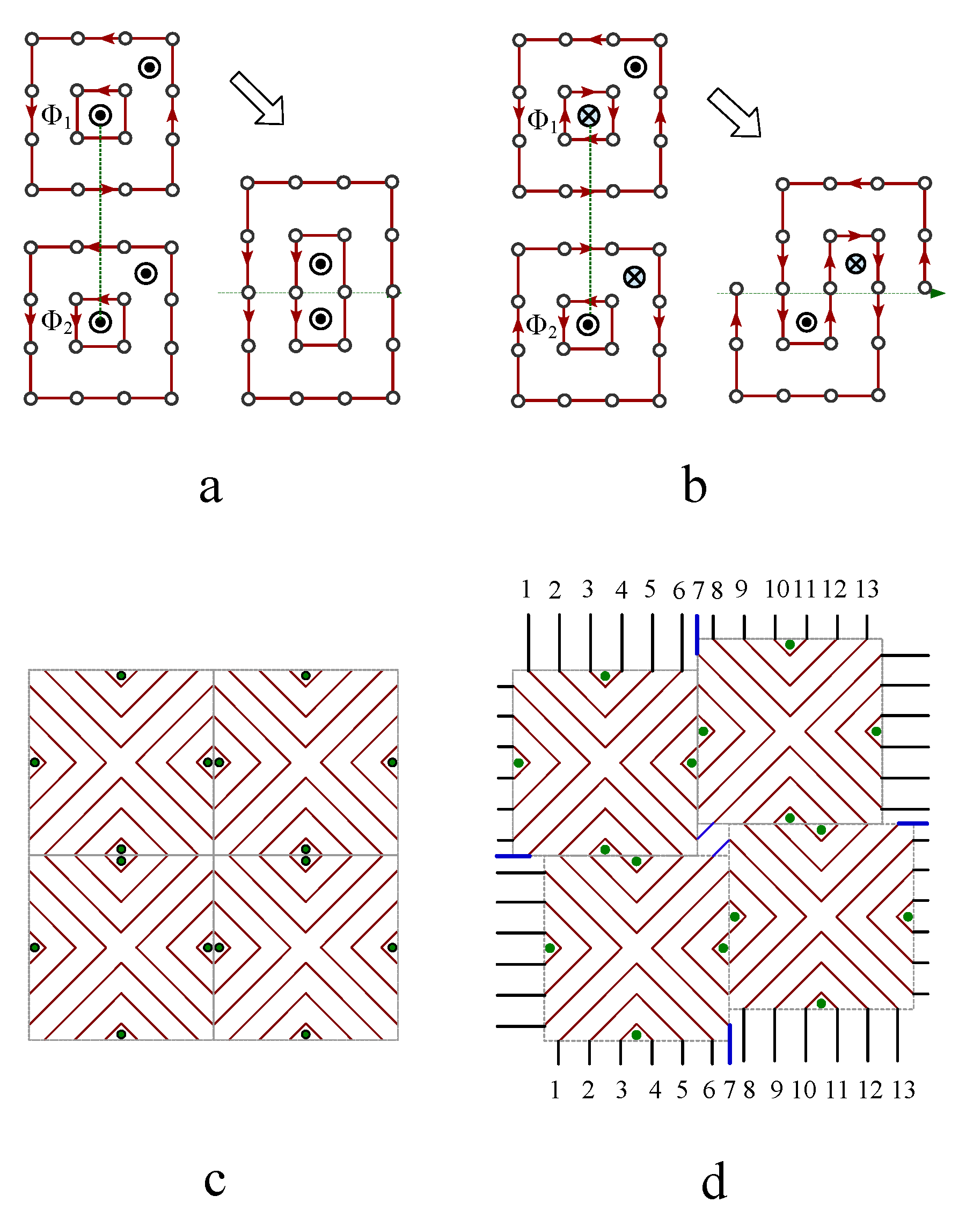
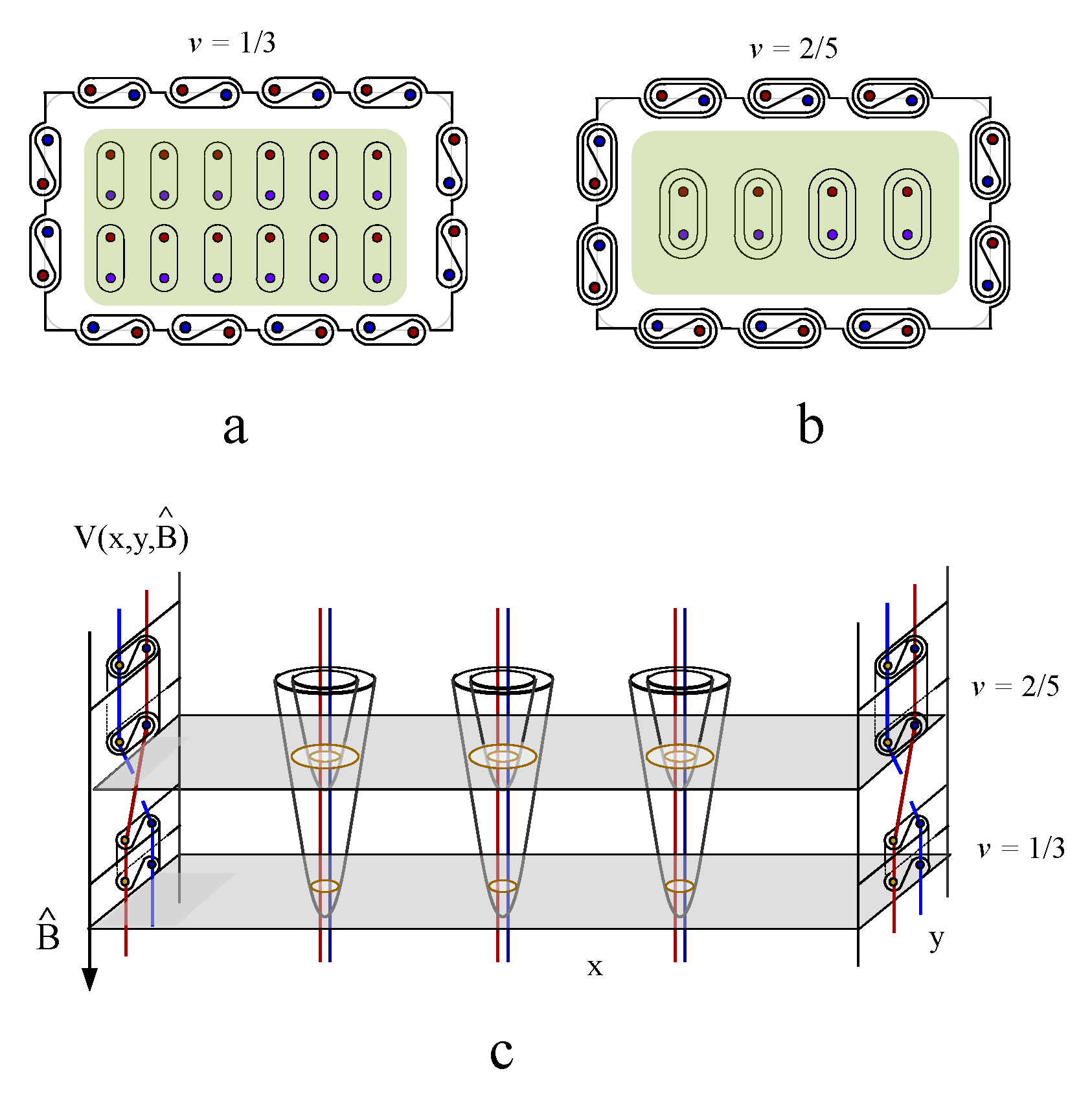
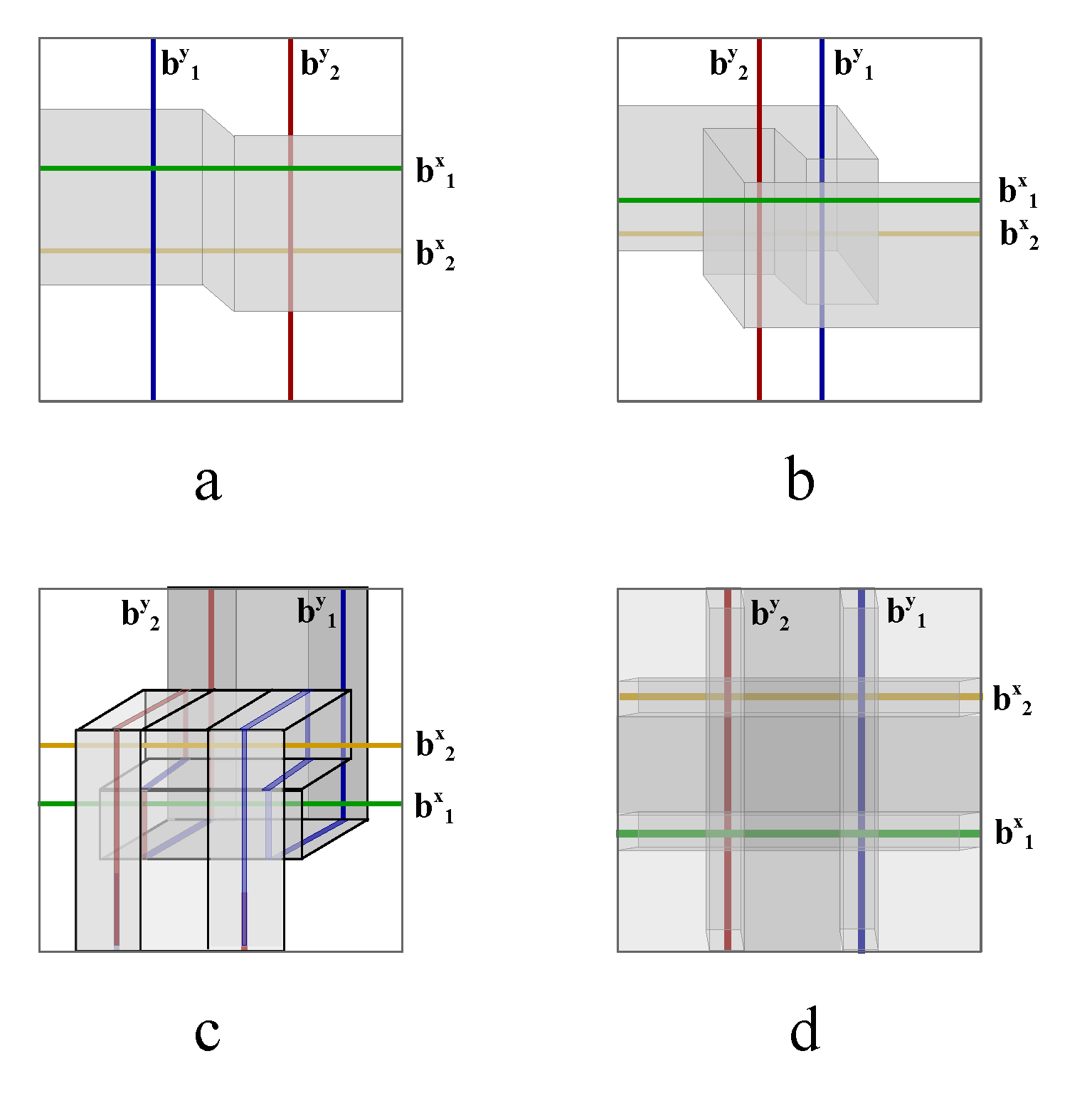
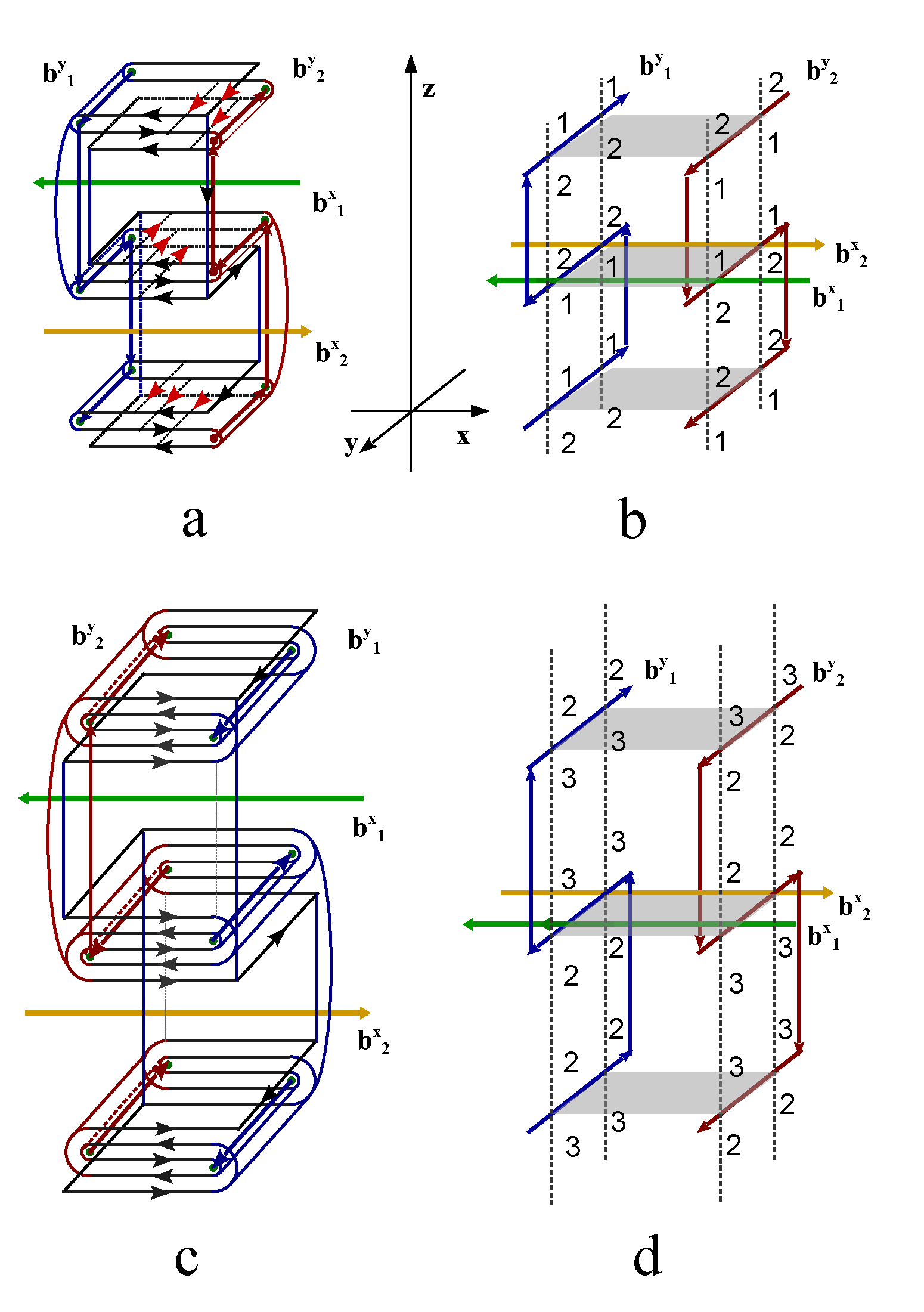
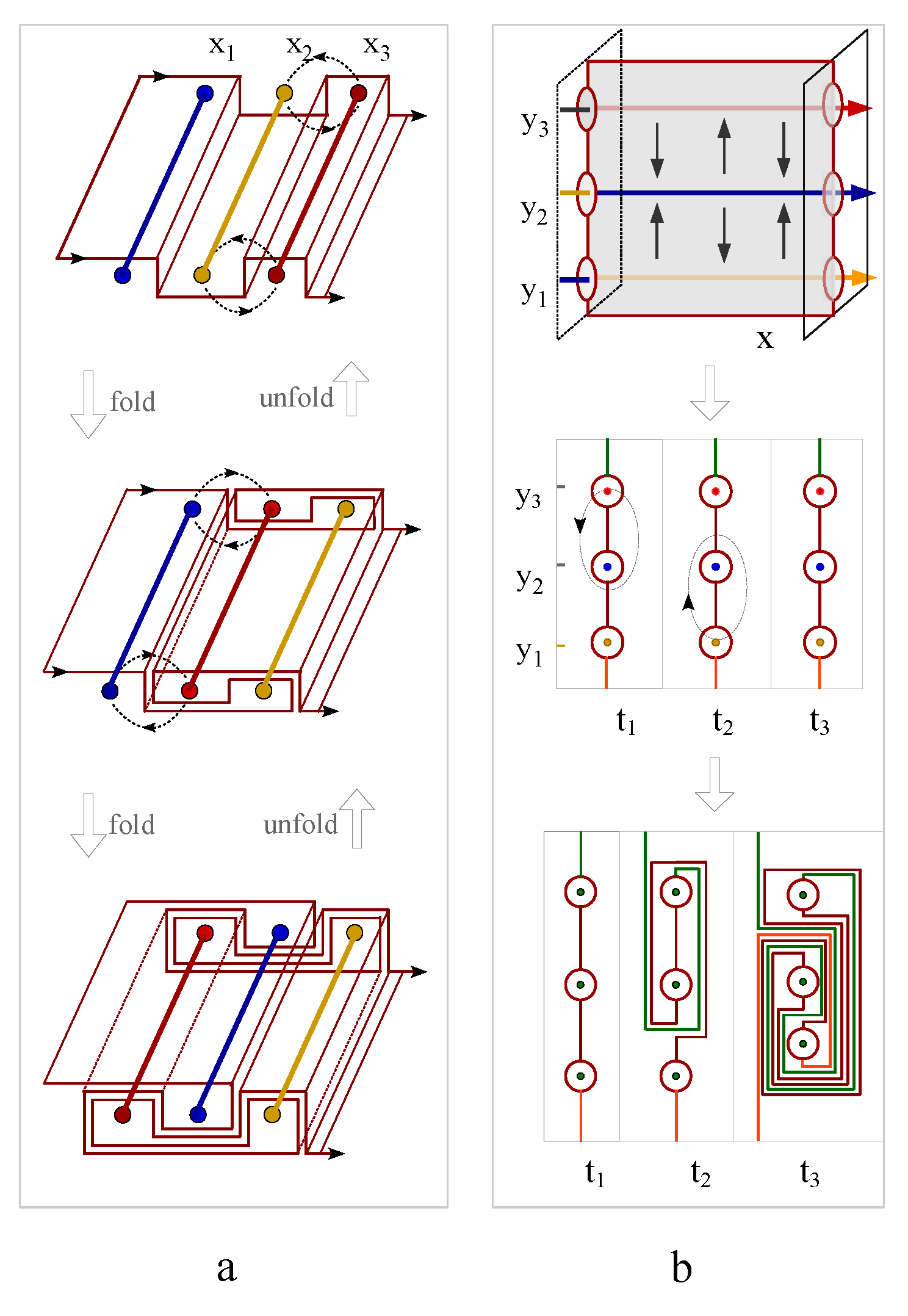
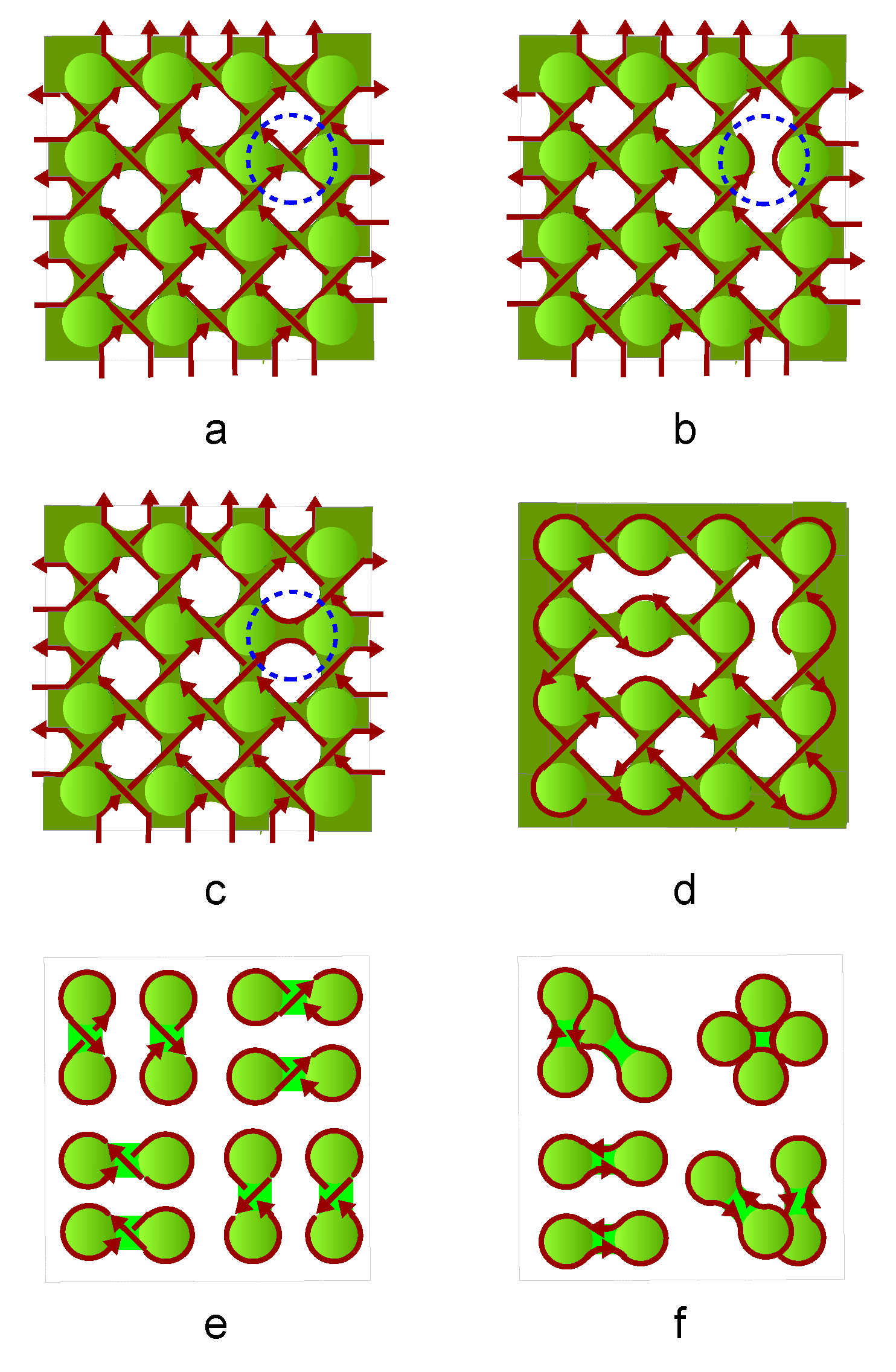
Figure 11 d), there exist an exact one-to-one correspondence between the electric knot lattice and magnetic knot lattice. This exact correspondence also holds for a ferromagnetically coupled spin chain as well as an arbitrary spin liquid state.
The combination of a knot lattice of magnetic fluxes and Thurston’s train track pattern constructs an unique topological representation of a spin liquid state.
Figure 12a shows an exemplar spin liquid state, where Ising spins are represented by arrows pointing up or down. Based on the convention of constructing magnetic knot lattice in
Figure 11 a-b, two antiferromagnetically coupled spins are represented by two parallel magnetic lines, while ferromagnetically coupled spins are represented by crossing magnetic lines. A magnetic line segment always connects two poles of the spin arrows with opposite magnetic charges (
Figure 12c). The linking number of the knot lattice formed by connected magnetic lines is independent of local direction of the line segments, therefore the knot lattice is further mapped into the same knot lattice generated by two magnetic fluxes that are oriented in opposite direction, as represented by the blue and red lines in
Figure 12d. When the two magnetic fluxes are immersed in an electronic fluid, the flowing electron fluid form laminar layers winding around the two magnetic fluxes under the propulsion of Lorentz force,
. To reconstruct exactly the same knot lattice as
Figure 12d, the left endings of the two magnetic fluxes are first fixed, and their corresponding right endings are braid in a designed protocol so that the cross section of the right ending of the electric laminar layer generates a winding path that is described by a topology theory called Thurston’s train track (
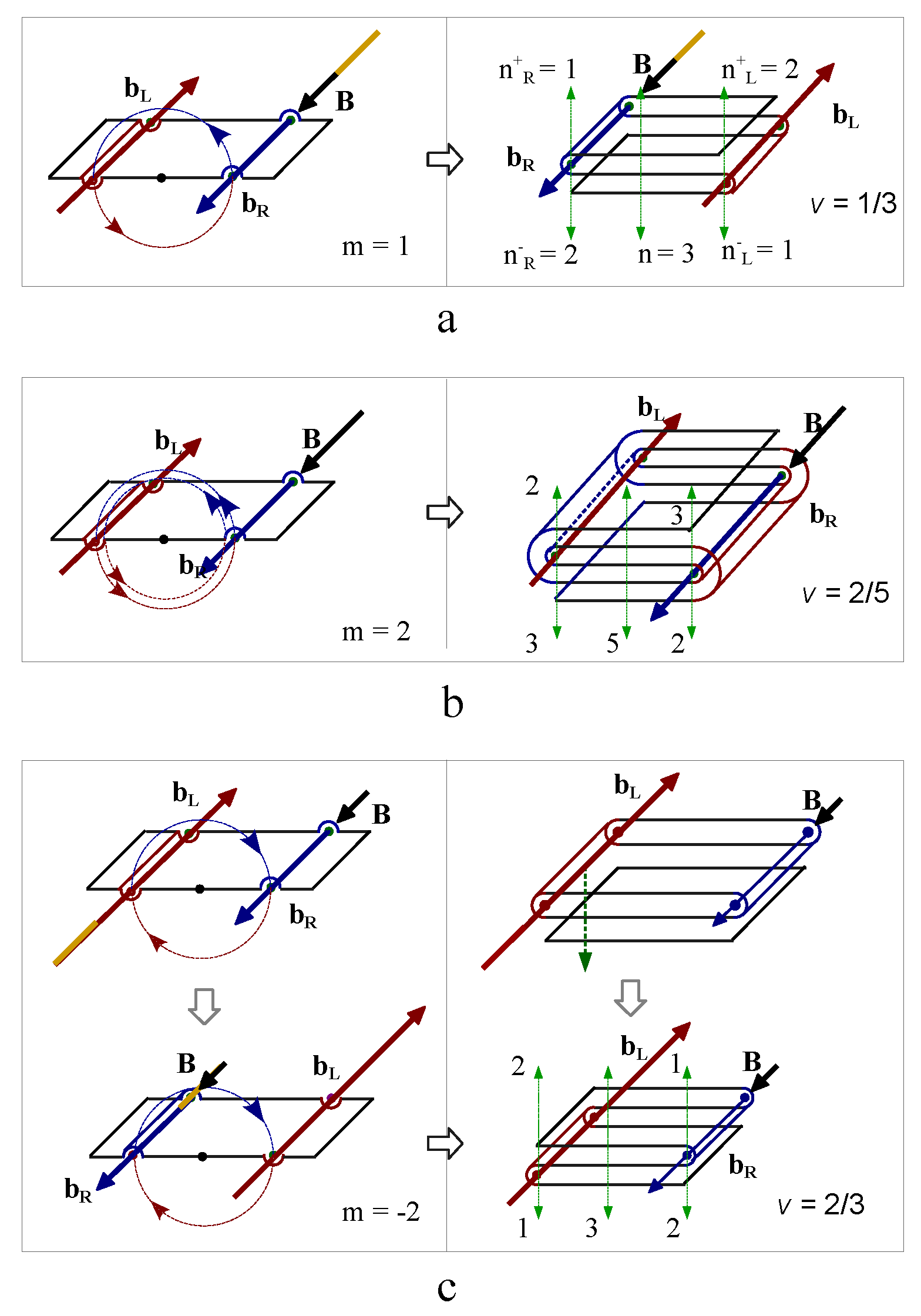
Figure 12e). As an application of Thurston’s train track theory, the number of layers of electric line segments on the two opposite sides of the magnetic fluxes are counted and labeled by
and
correspondingly. An integral electric charge splits into fractional charges passing thorough the train tracks,
leading to fractional Hall resistivity in fractional quantum Hall effect [
12]. The train track pattern in
Figure 12e generates two fractional charges,
and
.
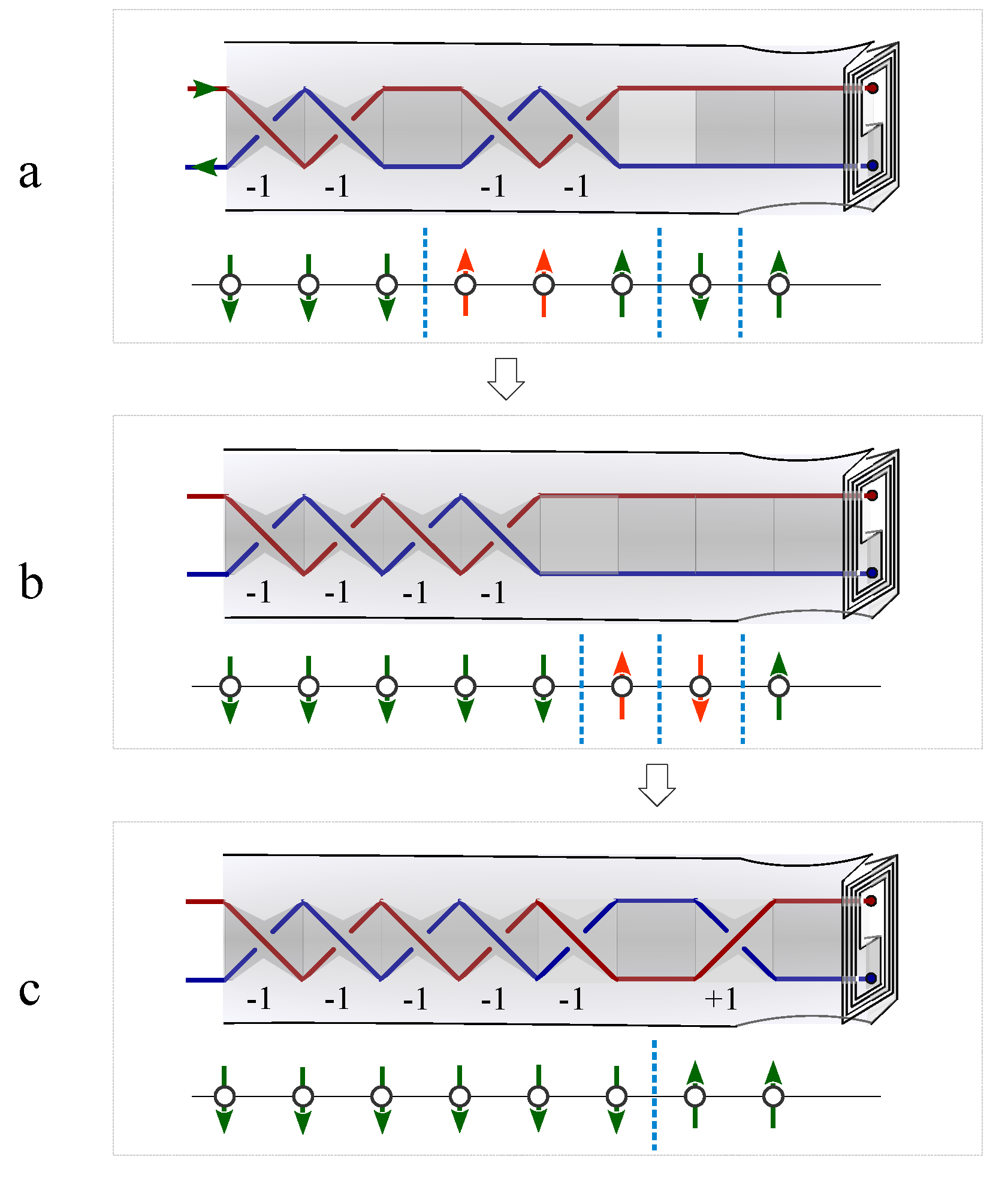
The train track of electric current on the boundary is a stable topological pattern against local perturbations on spins in the bulk chain. In the exemplar spin configuration of spin liquid state in
Figure 13a,
two ferromagnetic domains are separated by a topological kink soliton, (indicated by the orange dash line on the left hand side of the spin pair of red arrows. Flipping the local spin pairs labeled by red arrows does not annihilate the kink,
but transferred it to the right hand side. Therefore,
and
share the same eigenenergy,
. Flipping the local spin pair labeled by red arrows in
Figure 13b annihilates two kinks simultaneously and leaves only one kink behind.
The eigenenergy of this spin liquid state is the energy gap of one kink,
. Topological kink solitons always generate or annihilate by pairs to keep the total topological charge invariant. The linking number of the knot lattice is invariant during these local flipping operations in the bulk,
so does the train tracks on the boundary. The fractional charges on the boundary is quantized by the topological linking number,
where
is the total number of effective braiding operations. As proved by the topological path fusion theory of fractional quantum Hall effect [
12], this fractional charge straightforwardly determines the fractional Hall resistivity,
Therefore, the fractional Hall resistivity is quantized by topological linking number, this quantization rule is different from that of integral quantum Hall effect that is quantized by Chern number [
22].
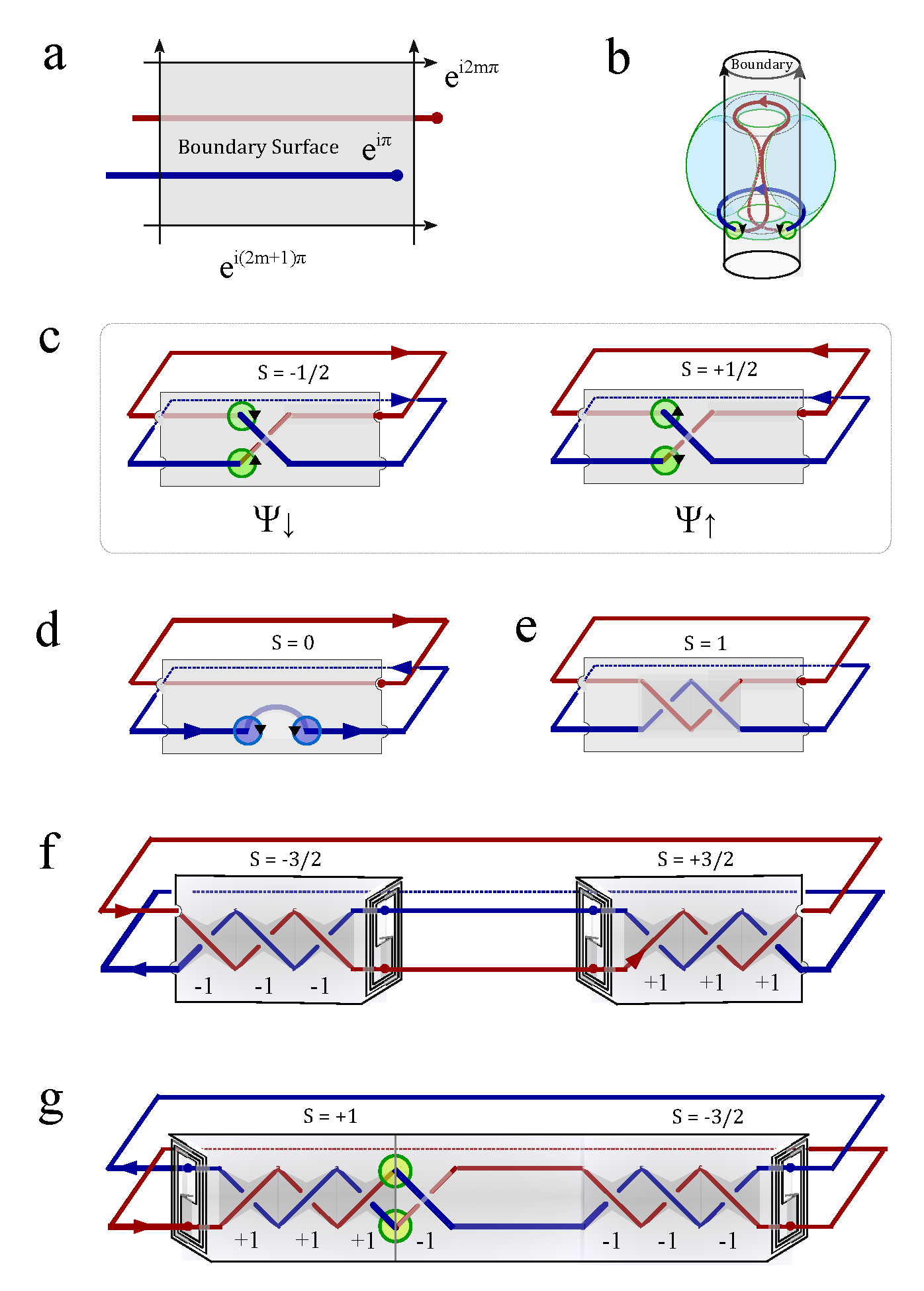
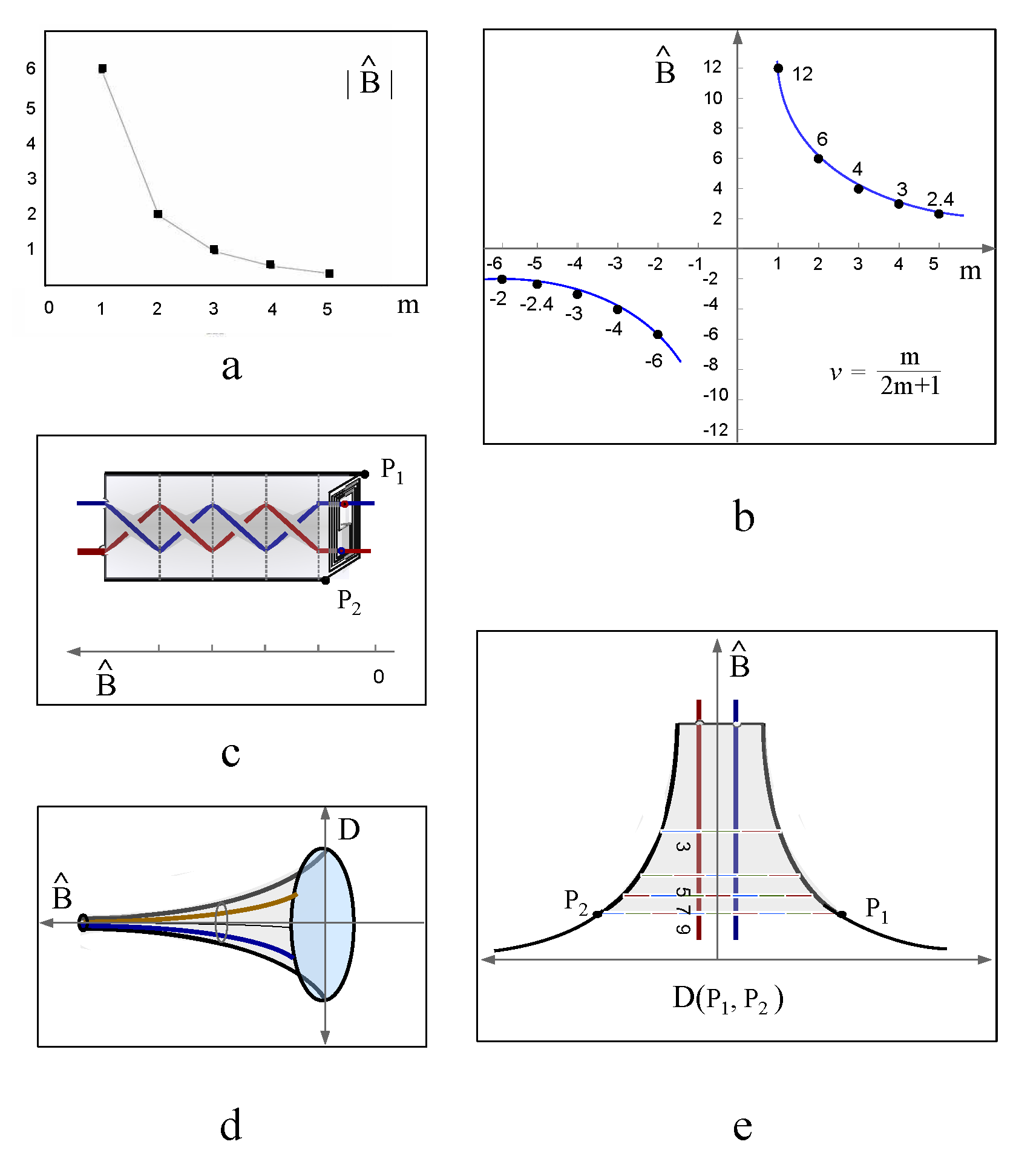
The linking number of the knot lattice determines the energy gap of the spin liquid state, which is similar to the Haldane gap in one-dimensional Heisenberg chain with spin S antiferromagnetic coupling, i.e., an unique gapped ground state exists for an integral Spin [
23]. Here an integral linking number indicates two fully separated magnetic fluxes without any touching point (
Figure 14a). For half-integral linking number, there always exist two vortices penetrating through the electric laminar layer that acts as a boundary layer separating the two magnetic fluxes (
Figure 14b). The two vortices glue the two magnetic rings into one big ring with a self-crossing point, which is exactly the boundary of m
bius strip. The magnetic current along the boundary of m
bius strip represents a topological spin
state,
and
, where
represents the two topological vortices that cannot be eliminated by local operations. The local fluctuation of magnetic fluxes can also generate a pair of vortices crossing the electric laminar layer (
Figure 14c) with topological spin 0, however this vortex pair is unstable and tend to annihilate each other under thermal fluctuations (
Figure 14d). There is no topological vortices on the electric boundary layer for a magnetic knot lattice with an integral linking number, for the exemplar
Figure 14e, the knot lattice of two linking magnetic rings generates electric wrinkles with a topological spin
. Braiding the magnetic flux segments of spin 0 states three times generates two half integer spin states with opposite spin S =
and S =
. The fractional charges
and
on the boundary cross section between the two states S =
and S =
(
Figure 14f) are unstable against local thermal fluctuations, reducing to spin 0 state without topological crossing. The unstable fractional charges can also be generated out of spin
state by local braiding (
Figure 14f), the sum of a S = 1 state and S =
state, however the topological vortex pair is always robust against any local braiding or thermal fluctuations.
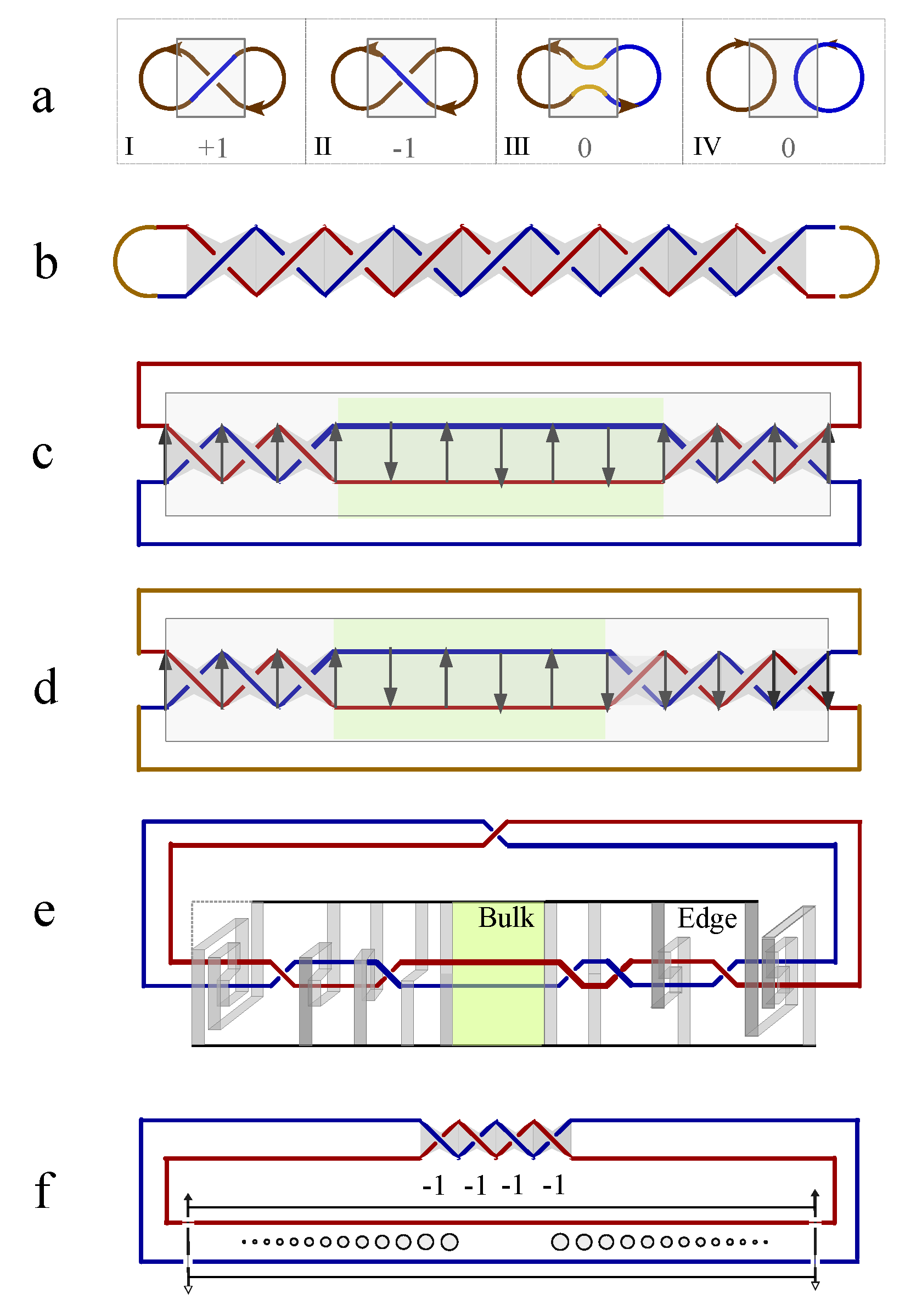
The real spin vectors sandwiched in between two magnetic flux lines represent the spins of real particles. The collective order of real spins fluctuate in thermal environment and transform from one collective phase to another. The two magnetic flux lines form a one dimensional knot chain of crossings, the collective order of many crossings in knot lattice is invariant during thermal fluctuation. A local crossing state in knot lattice is equivalent to topological spin 1,
.
and
represents the overcrossing state, undercrossing state and cross avoiding state respectively in
Figure 15a. The key difference of topological spin 1 from the spin 1 of real particle in nature is that the zero spin state
has two topologically different states, the vertical vacuum and horizontal vacuum states in
Figure 15a III-IV, denoted as
and
respectively. In knot theory, the crossing states in
Figure 15a are represented by Kauffman brackets,
In the knot lattice theory of anyons [
11], the partition function of a spin 1 state is mapped into a Boltzmann weight factor within external magnetic field
h,
which counts the occupation probability of a topological spin 1 on state
with eigenenergy
. The Boltzmann factors are exactly the corresponding Jones polynomials with respect to different crossing states, satisfying the Skein relationship
where the coefficients in Eq. (
83) are
The Jones polynomial is mapped exactly to Kauffman polynomial by redefining the variable
A in Kauffman bracket as
The Kauffman brackets Eq. (
Figure 8) transforms into brief formulations of Boltzmann distribution,
The Kauffman polynomial of spin zero state
measures the probability of finding spin up or spin down,
In statistical physics, the conventional partition function is the sum of Boltzmann weights of all possible states
The magnetization of the knot lattice is topological linking number
[
11], which is an integer at zero temperature but deviates from integer at finite temperature,
The linking number
equivalently counts the total number of braiding,
, where
counts the total number of clockwise (counterclockwise) braiding. In the train track representation of abelian FQHE, the one dimensional knot lattice of magnetic fluxes is generated by
periods of identical braiding, leading to average fractional quantum Hall resistivity
,
Substituting linking number Eq. (
89) into Eq. (
90) yields average fractional Hall resistivity at finite temperature,
where
t is the same parameter in Jones polynomial. At hight temperature, thermal fluctuation drives a local crossing to fluctuate among many different crossing states, different fractional Hall resistivity may appear simultaneously, Eq. (
91) measures the average fractional filling factors at certain temperature.
The single crossing
of
Figure 15 a-II braids the electron fluid surface into a folded lamination with an edge cross section state of
. More braiding operations in the same direction twists the single crossing
into an alternating knot chain in
Figure 15 b, which is represented by Kauffman bracket polynomial,
where
represents the overcrossings with
. If the left-hand endings of the two fluxes in
Figure 15 b are fixed, the right-hand cross section of the alternating knot generates the train track pattern with fractional filling factor,
The Kauffman bracket polynomial is mapped to the eigenfunction of angular momentum operator
,
The eigenvalue of angular momentum
records the total number of continuous braiding in the same direction,
Negative
indicates braiding operations in opposite direction. The fractional Hall conductivity only exist for the alternating knot chain of
Figure 15 b that is confined rigorously in two dimensions, the knot chain is prevented from flipping back to a trivial circle due to dimension reduction. The renormalized Kauffman polynomial of the alternative knot is
where
is the writhing number of a twisted circle. Here
equals to the sum of the signs of all crossings in the knot chain formed by a circle. The constant value of Kauffman polynomial suggests that the twisted circle shares the same topology with the initial unit circle. The fractional Hall conductivity encoded by alternating knot in
Figure 15 b is unstable at finite temperature due to the simple topology.
The collective configurations of many real spins in one dimensional chain can map into the same knot lattice of intertwined magnetic fluxes (
Figure 12). In
Figure 15 c, the leftmost and the rightmost edge zone of the double hyperbolic surface are covered by ferromagnetic phase of classical Ising spins, while antiferromagnetic phase covers the bulk zone in the middle. If the bulk lattice is composed of an even (odd) number of unit cells, the ferromagnetic phase of the leftmost edge zone orients in the same (opposite) direction to that of the rightmost edge zone (
Figure 15 c-d). The collective phases of far separated edge zones in opposite boundaries are strongly correlated, due to the robust topology of two intertwined magnetic fluxes. This topological correlation is stable against local thermal fluctuations unless the magnetic flux line is cut into discrete segments. The two intertwined magnetic flux loops in
Figure 15 c transform into two far separated loops under Reidemeister moves, which are represented by Kauffman bracket polynomial
. While two interlocking loops in
Figure 15 d is equivalent to two magnetic loops linked in a nontrivial way, described by Kauffman bracket polynomial
. If the left-hand and the right-hand edges of
Figure 15 c-d are fixed, a pair of hyperbolic surfaces of electron fluid lamination with opposite normal directions is generated in the middle zone. Each cross section of the hyperbolic lamination represents a qusiparticle with fractional charge
. These quasiparticles are always generated or annihilated by pairs under local fluctuations of real spins in one dimensional chain.
If the collective configuration of real spins in the bulk zone of
Figure 15 e are frozen, finite hyperbolic surfaces of electron fluid lamination are generated on the left-hand and the right-hand edge. Topological quasiparticles carrying opposite topological spin and fractional electric charge as are pushed to the edge zone. The linking number of the two interlocking loops in
Figure 15 e counts the total number of robust crossings which can not be generated or annihilated by local spin fluctuations, unless the loops are cut to reconnect. The two hyperbolic edges are flattened by opposite braiding operations to the initial braiding orientation in
Figure 15 e, the four crossings in bulk zone are transferred to the intertwined magnetic loops in infinity by keeping the topological linking number conserved.
The topological linking number of magnetic flux knot lattice is inadequate to distinguish different boundary states. In
Figure 16, braiding the leftmost edge three times in counterclockwise direction around the left normal direction and braising the rightmost edge three times in clockwise direction around the right normal direction maps into monotonic hyperbolic surface generated by five counterclockwise braiding around the left normal direction. The monotonic hyperbolic surface and double hyperbolic surface in
Figure 16 share the same topological linking number, but their geometric characters and dynamics of electron on the surface are completely different. Therefore quantum states characterized by topological number are usually highly degenerated.
Inhomogeneous magnetic field folds the electron fluid lamination into non-Euclidean geometry, bending the flat lamination into hyperbolic surface with negative curvature. In
Figure 17a, the endings of the flux pairs on the right hand side are fixed. Braiding the endings on the left hand side in counterclockwise direction folds the flat lamination into a hyperbolic surface, which is implementable in experiment by designing a decreasing magnetic field strength from the right hand side to the left hand side. The train track on the left boundary cross section represents fractional filling state
. In
Figure 17b, both the two endings of the flux pair on the left and right hand side are fixed, braiding the middle points of the two fluxes expands the middle zone of the initial flat surface, generating a double hyperbolic surface on which the filling factors decrease from
on the edges to
in the middle.
Figure 17c shows a more complicate magnetic field configuration, a constant magnetic field strength is homogeneously distributed in bulk, but decreases in edge zones on both the left and right hand side. The initial flat lamination in edge zones are folded into hyperbolic surface by braiding operations on the left and right endings of the flux pair in counterclockwise direction. The filling factor decreases from the bulk to the edge, i.e., from
to
, until it reaches
on the outermost boundary. The conducting channel in the edge zone is not pure fractional quantum Hall states, instead is the superposition state of
and
, which forms resistivity in parallel. The resultant edge resistivity in edge zone obeys
Substituting the fractional Hall resistivity Eq. (
179) into edge resistivity Eq. (
97) yields
For a general edge zone covers fractional filling serial
, the resultant edge resistivity obeys the parallel resistivity equation,
Since the electric lamination in the edge zone is continuous during topological braiding, the fractional filling factor equation
for edge lamination in
Figure 17c is generalized to a continuous filling function,
, the resultant edge resistivity obeys
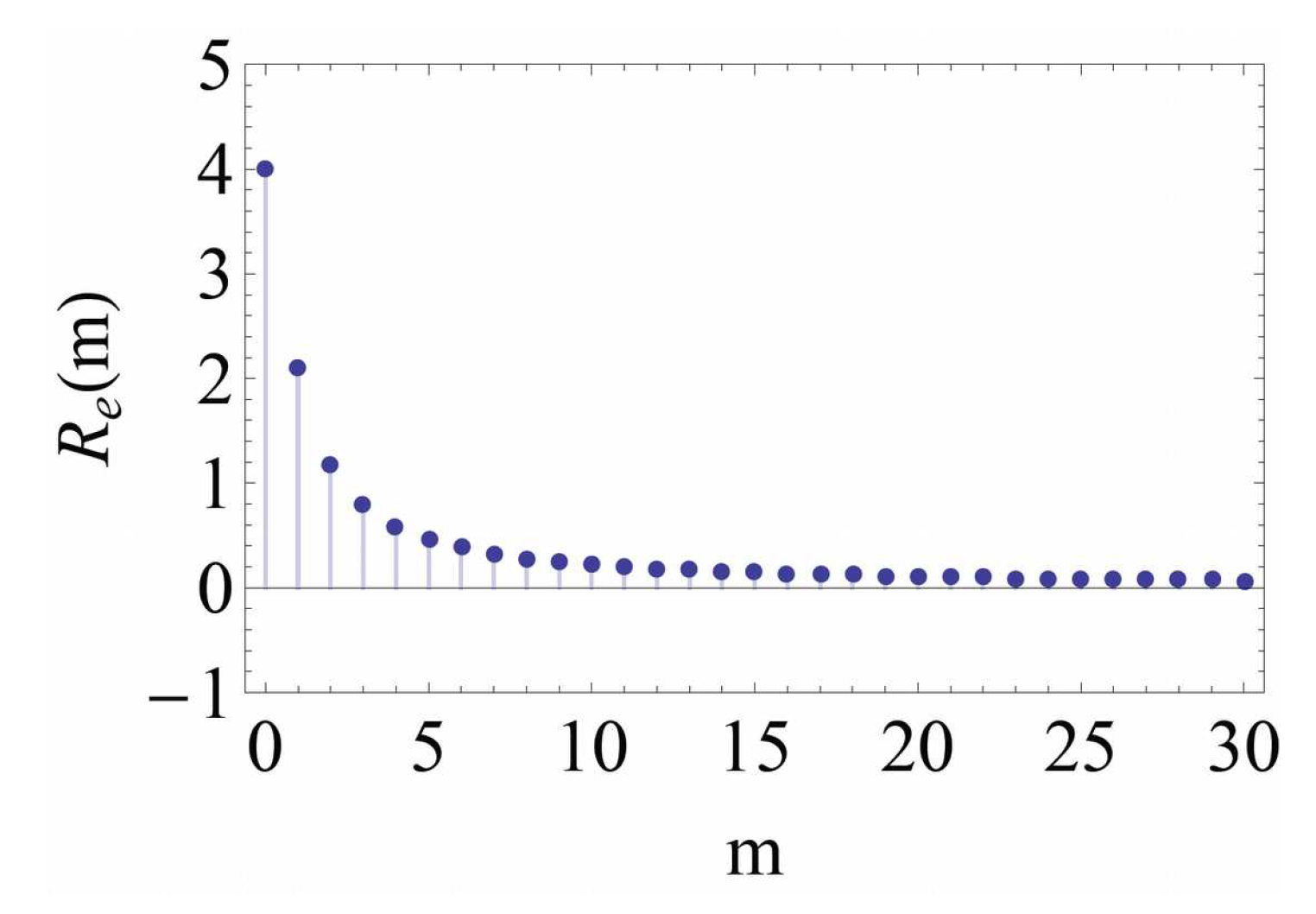
where
and
are the initial and final braiding numbers respectively. The resultant edge resistivity decreases approximately to zero when the topological braiding number
m approaches to 30 as showed in
Figure 18. Every braiding generates a new conducting channel for the electrons in edge zone, the resultant edge resistivity keep decreasing as the number of conducting channels increases. From the point view of hyperbolic geometry, the spatial area of electron fluid lamination expands to infinity as the electrons approach to the horizon boundary of edge zone (
Figure 17c), which corresponds exactly to the outermost boundary line of the edge. The edge space is large enough for electrons to avoid colliding with one another, resulting in zero resistivity.
Opposite boundaries of the folded electron fluid lamination can carry different fractional charges, which is determined by the chirality of braiding operations on boundary. In
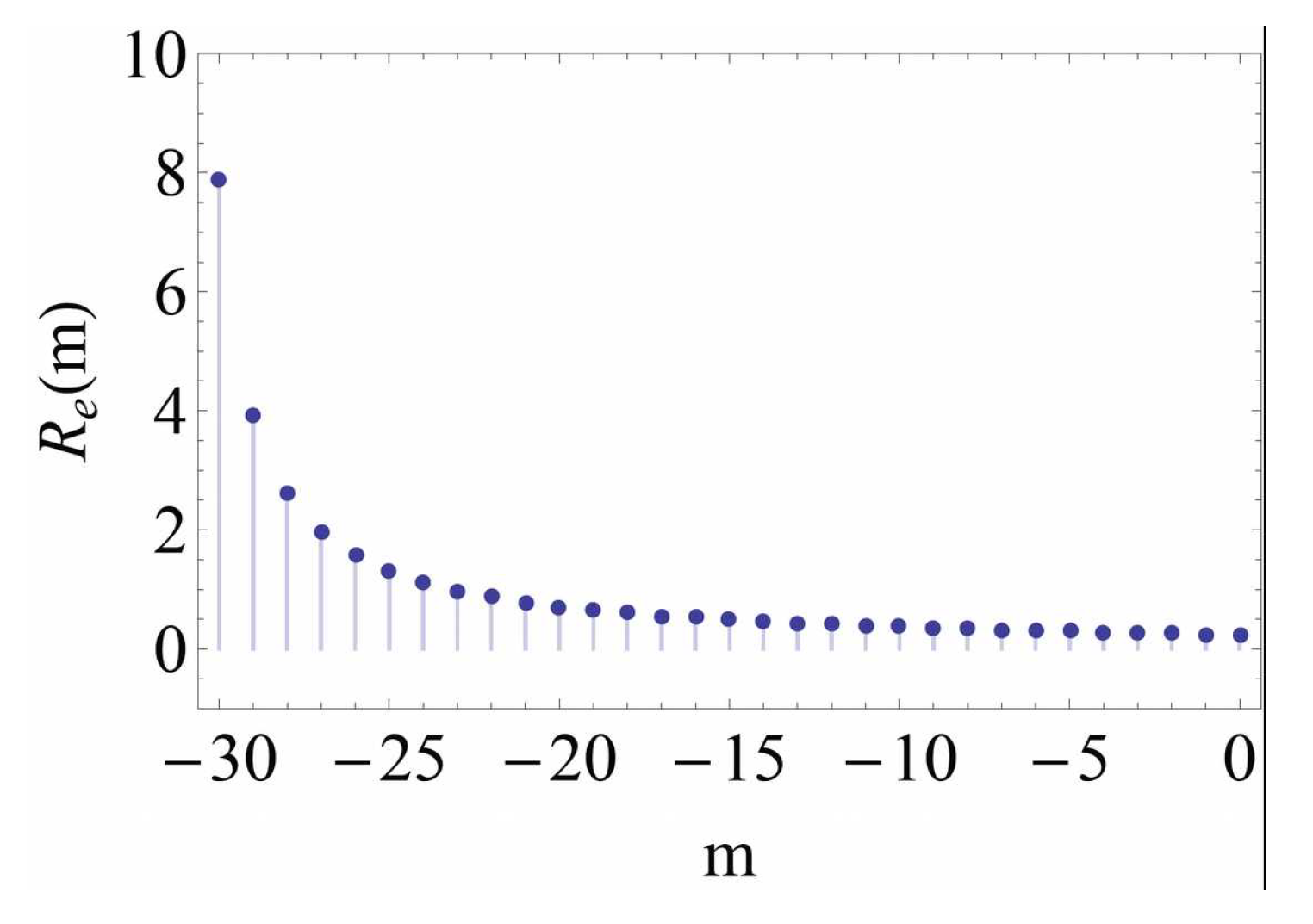
Figure 16, the middle points of the flux pair is fixed, the left endings of the flux pair is braided in opposite direction to its right endings. The fractional filling factors of train track at the left and the right boundaries are respectively,
In
Figure 16, the filling factor on the rightmost edge zone grows from
to
in the normal direction of the outermost boundary. But the filling factors on the leftmost edge zone decreases from
to
along the normal direction of the leftmost boundary (
Figure 19). The resultant edge resistivity on the left boundary grows to the maximal value as the electrons approaches to the leftmost boundary (
Figure 19). This is because the edge lamination twists in the opposite direction to the motion of electrons. The more closer an electron moves to the leftmost boundary channel, the longer distance it covers a geodesic channel against its forward motion.
2.4. Topological phase transition of folded spin chains
The edge cross section of electric lamination is a train track of electric current, which is equivalently modeled as a compact chain of polarized electrons in high magnetic field. The electric laminar surface propagates as running wave, correspondingly induced a electric current wave sandwiched in between two antiparallel fluxes (as showed in
Figure 22a). The wavy current is straightened to form a one dimensional chain of coupled Ising spins,
where
J is the coupling strength,
B is the external magnetic field strength. There is no electromagnetic interaction between the current bonds connected head to tail in a straight line. When the spin chain folds into a spiral vortex pattern in
Figure 22b, the electromagnetic interacting force between stacked electric current bonds obeys the Bio-Savart law,
Parallel (anti-parallel) current bonds attract (repel) one another. Integrating the force vectors along two independent current bonds yields an effective interacting potential,
This long range interaction results in a one dimensional chain of strongly correlated many current bonds
where
is an effective bond operator with respect to ferromagnetic coupling (
) or anti-ferromagnetic coupling (
) between two nearest neighboring Ising spins (as showed in
Figure 22c).
is dielectric coefficient.
is the length of the current bond.
is the perpendicular distance between the nearest neighboring electric bonds, i.e., the unit lattice space of the one dimensional chain of bonds represented by the diamonds in
Figure 22b.
In one dimensional straight chain of Ising spins (
Figure 22a), all spins gradually align to giving rise to a non-zero macroscopic magnetic moment when temperature keeps dropping to zero. At finite temperature, the fluctuating collective spin configurations equivalently correspond to fluctuating orientation configuration of many current bonds. At low temperature, the nearest neighboring current bonds align to form local ferromagnetic clusters. The collective ordered phase of many current bonds with identical orientation is formed at zero temperature. The ferromagnetic phase of the straight chain of many Ising spins corresponds exactly to a dual antiferromagnetic phase of many electric current bonds in the spiral vortex pattern in
Figure 22b. The spiral vortex of current bonds is incompressible due to the repulsive interaction between nearest neighboring anti-parallel bonds. The total electromagnetic energy of
N antiparallel current bonds reads [
12]
A chain with odd number of current bonds always has lower energy that with even number of bonds (
Figure 23). The collective energy
grows to converge to a limit value when the length of current bond chain increase up to infinity.
An one dimensional chain with
antiparallel current bonds generates the fractional quantum Hall state with filling factor
.
Figure 22b and
Figure 22d represents the fractional filling states
and
respectively. When the two fluxes in the innermost gaps of
Figure 22c hop outward into the two second innermost gaps, there is no obstacle to prevent the three current bonds sandwiched in between two fluxes from contracting to single bond topologically (
Figure 22d). The train track in
Figure 22d is a topological representation of
state, since there are only two unshrinkable current bonds on the outer side of the two fluxes. The
state is characterized by single unshrinkable current bond on the outer side of the two fluxes (i.e., the leftmost and rightmost side of
Figure 22e). The five current bonds sandwiched in between the two fluxes in
Figure 22e is topologically equivalent to one current bond. Topological contraction of the five antiparallel currents lowers the electromagnetic interaction energy from
to
following Eq. (
108).
The fractional filling factor is characterized by the ratio of winding number of current bonds on the left hand side of
in
Figure 22c-d-e to the winding number of all unshrinkable bonds bridging
and
. In
Figure 22f, when the input point at
winds around
in counterclockwise direction to fuse with the point
right above
, the winding number of the closed loop around
is exactly
. The current bond
bridging
and
winds exactly half of the total phase of the closed loop,
i.e., twice of the topological number of bond
is exactly the winding number,
. Correspondingly, the topological number of the current bond on the right hand side of
is also
. The middle current bond
sweeps over phase
,
The fractional filling factor is a function of topological winding numbers,
The fraction filling factor with respect to
Figure 22f is
. Even though the middle current bond in
Figure 22e is consists of five layers of currents, the phase accumulation along antiparallel path segments canceled each other, the resultant phase accumulation is still
.
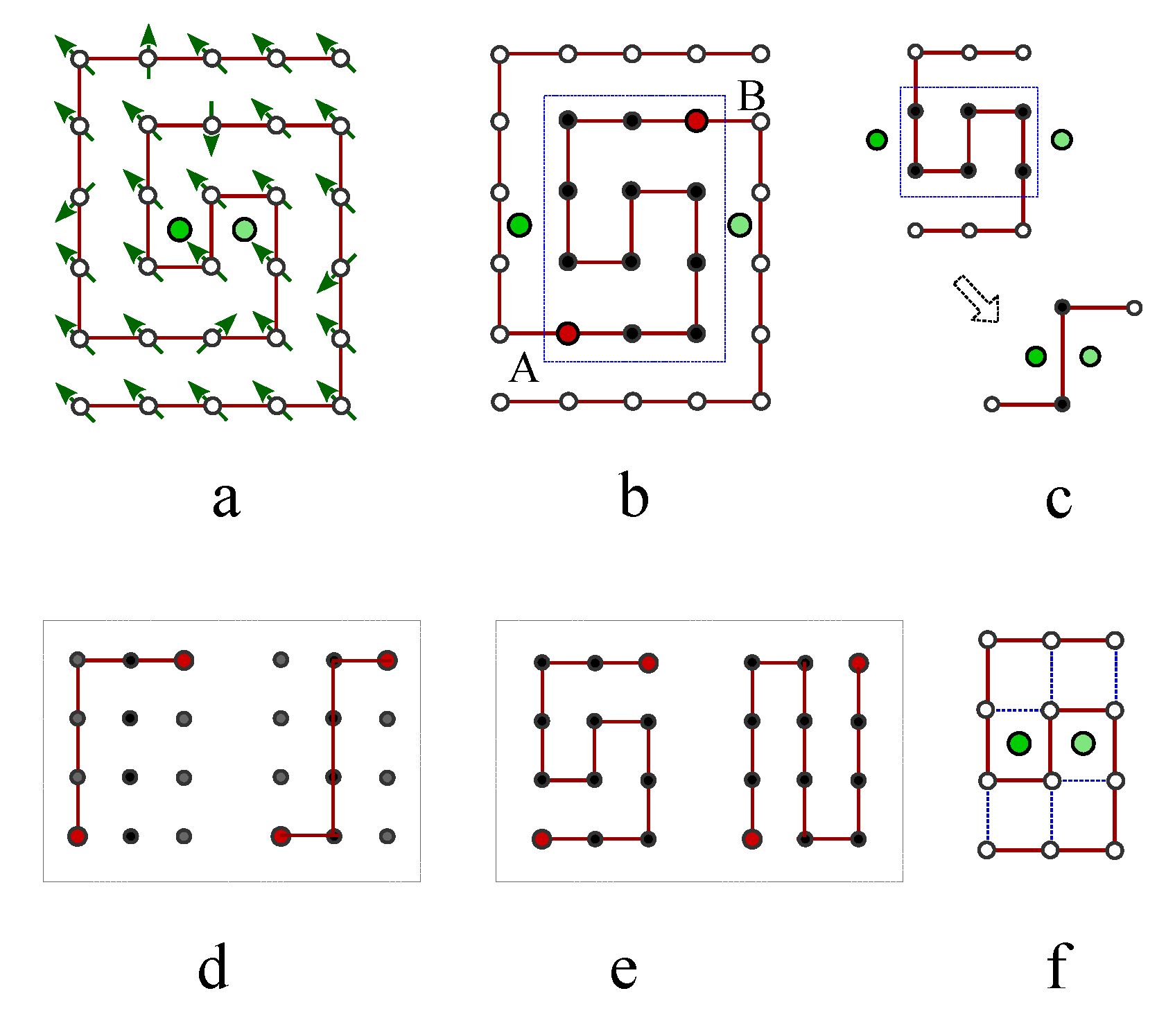
The continuity of the winding path around the magnetic fluxes (or singular points) is the top priority for the existence of fractional filling factors as topological invariant. The conservation law of energy or total particle number along the winding path usually changes under topological transformation, thus it is not a sufficient and necessary condition to extract topological character of spin chain. In
Figure 24a, the double core vortex track is pinned down to a square lattice in the presence of two fluxes in the central zone. When the two fluxes move outward away from the central zone and relocate at the outermost gap zone, separated by single track from the free zone, the spiral track on this finite square lattice is a topological representation of
state (In
Figure 24b). A further hopping of the two fluxes to the open free zone results in an integral filling state in
Figure 24c. The winding track in the bulk zone of
Figure 24b (confined by the blue rectangle) can freely winds or shrinks into all possible configurations as long as it keeps its continuity. The shortest path is consists of six spins, isolated the rest six spins out of the spin chain (
Figure 24d). The longest path covers all lattice sites between
A and
B (
Figure 24e). For a spin chain with only the nearest neighboring interactions, all possible paths connecting the lattice site
A in
Figure 24b to the site
B is denoted as
, which leads to
fold degeneracy of the topological state
. A topological transformation is independent of the distance between two points, a physical implementation of topological transformation for spin chain is to established long range coupling between any two lattice sites. In that case, the total number of possible connected paths from
A to
B is
where
counts the possible states of
i Ising spins in the connected path,
and
counts the number of lattice site in
x- and
y-axis.
For the finite middle zone in
Figure 24b, the entropy with respect to
reads
Notice here this entropy
is not topological invariant. The high entropy results in an insulating state of the bulk zone. On the contrary, the entropy of edge tracks is highly suppressed by the two fluxes, leading to superfluid state. The total energy of a path contains
p spins is countable by a long range coupling Ising model
The probability to find
p-path obeys the Boltzman distribution,
The long range coupling interaction is usually smaller than the nearest neighboring coupling interactions, therefore the minimal energy state of the
p-path is the ground state of spin chain with only nearest neighboring coupling. Spontaneous magnetization does not occur in one dimensional chain of many Ising spins. When the one dimensional chain folds to form a spiral vortex pattern covering a two dimensional square lattice, some far separated spins are relocated to become the nearest neighbors, introducing new coupling bonds in extra dimension perpendicular to its original chain. The newly added coupling bonds strengthened the stability of ferromagnetic phase of the original one dimensional chain against thermal fluctuations (
Figure 24f), results in a critical temperature
of spontaneous magnetization, which is predicted by Onsager’s exact solution of two dimensional Ising model,
The critical temperature of spontaneous magnetization in absence of magnetic field is
where
is the average entropy per bond. The critical temperature is proportional to the coupling energy strength
J. The ground state of the folded Ising spin chain is ferromagnetic phase composed of all polarized spins in the bulk zone. In thermal dynamic limit, both the size of bulk zone and the distance between two fluxes grows to infinity, there are large number of inequivalent path configurations even if the path covers the same number lattice sites.
Figure 24e showed exemplar inequivalent paths with the same number of spins. The two inequivalent paths in
Figure 24e becomes indistinguishable in a two dimensional Ising model.
The free energy of the folded spin chain is determined by the energy of the spin chain
and entropy of the folded paths between fluxes
,
The nearest neighboring approximation of the total energy of spin chain in ground state is
. The critical temperature for the phase transition of spin liquid into a ferromagnetic phase obeys
,
Therefore the critical temperature is proportional inversely to the entropy. The fractional quantum Hall state
has the maximal entropy, and the minimal critical temperature of phase transition from normal metal phase to Hall fluid phase.
2.5. Fractional quantum Hall effect of topological fluid in vortex lattice
The coupling interaction between two nearest neighboring Ising spins can be effectively represented by a rotating current bond in plane, which corresponds to spin in XY model, i.e.,
. The total energy of this current lattice is a dual model of 2D Ising model with long range interaction,
If only the nearest neighboring coupling interactions between current bonds are taken into account, the long range coupling model maps to the XY model of many current bonds on square lattice,
A continuous current flowing along the spiral train track requires a small variation of the orientation of current bonds from site to site, i.e.,
. The spiral current track is described by the effective XY-Hamiltonian,
which predicts Berezinskii-Kosterlitz-Thouless (BKT) phase transition of vortex. The free energy of a free vortex reduces above a critical temperature
,
where
is winding number of the vortex. Below the critical temperature
, single vortex gains higher free energy and becomes unstable, two vortices prefer binding together to form a pair with lower energy.
When a square lattice of current bonds is immersed in strong magnetic field, the center of square plaquette surrounded by four current bonds is penetrated through by a number of magnetic fluxes
(
Figure 25 ab). The velocity of electrons in the current bonds is generated by the gradient of phase field,
, where
is the phase field without magnetic field,
is phase field generated by gauge potential vector due to the presence of magnetic field. The same (or opposite) gradient of phase field
generates current loops circulating around the two fluxes
and
respectively with the same (or opposite) chirality in
Figure 25a (or
Figure 25b). In a weak magnetic field, the vortices are separated far away from one another. The energy of a vortex around one flux is
, with
L the size of the system and
the unit lattice space. All possible locations of the vortex core in a square lattice with periodic boundary condition is
. Two vortices prefer combining to form a pair below critical temperature
. In a finite system with open boundary condition, the vortex core cannot reach the lattice sites in edge zone unless it splits into two half vortices. The entropy of finite system is smaller than that with periodical boundary condition, leading to higher critical temperature.
Because the distance between two vortices
is smaller than the size of finite system
L, the energy of the vortex pair (
Figure 25ab) is smaller than that of single vortex,
The entropy of unfused vortex pair in
Figure 25ab is approximated by
. The free energy of unfused vortex pair is
The critical temperature
is derived from
,
The distance
between two vortices is larger than the unit lattice space of magnetic fluxes, i.e.,
. When the distance
, the critical temperature of vortex pair
is smaller than that of single vortex. Stable vortex pair exist in the temperature zone
. Below the critical temperature
, the vortex pair prefer binding together to form vortex quaternion.
For vortices with
m layers of concentric current loops around the flux core, the distance between the flux cores of two nearest neighboring unfused vortices in
Figure 25ab is
, the critical temperature of vortex pair reads
The energy of vortex pair grows with respect to a growing number of layers
m, while the corresponding entropy decreases, leading to higher value of critical temperature
. The chirality of circling flow within current loop has strong influence on
. A bosonic vortex is surrounded by
m layers of concentric loop current circling with the same chirality. The vorticity of bosonic vortex is the total winding number of
m layers of concentric loops
A fermionic vortex is surrounded by
m layers of antiparallel loop currents, in which the nearest neighboring loop currents circling with opposite chirality. A fermionic vortex is represented by antiferromagnetic state of many concentric current loops (
Figure 25b). The total vorticity of fermionic vortex is defined by the total topological charge
The
m layers of antiparallel loops generates the winding number
for odd
m, and
for even
m. The vorticity of fermionic vortex is a classical spin that only takes two discrete values
for odd
m. For two vortices with the same vorticity in
Figure 25ab, the antiparallel current segments in the contacting zone repel each other, resulting in positive energy increment in free energy Eq. (
126). While for two vortices with opposite vorticity in
Figure 25ab, the parallel currents in the contacting zone attract each other, generating a negative energy increment in free energy Eq. (
126). Therefore a pair of vortices with opposite winding number has lower energy than that with the same winding number, so does the critical temperature
.
Vortex fusion accompanied by topological change occurs in high magnetic field. The magnetic field can be tuned strong enough to squeeze the two vortex cores (which exactly locate at the center of magnetic flux tube) into one unit plaquette. In that case, unit lattice space between fluxes
is smaller than the unit lattice space
between heavy nucleuses within the crystal lattice. The energy of a vortex is determined by unit lattice space of flux lattice. The current segments in the contacting zone of two vortices with the same vorticity is antiparallel. The high magnetic field reforms the local potential landscape to help the current overcome the potential barrier generated by the repulsive interaction between antiparallel currents in the contacting zone. These antiparallel current segments annihilate one another, and unit the rest segments to generate larger concentric loops flowing only in the outer zone of the flux pair (
Figure 25a). The large vortex with double flux core has lower energy than the two initial separated vortices. The swirling electron fluid during vortex fusion is compressible quantum fluid under strong magnetic field, however the effective repulsion between fermions due to Pauli exclusion principal provides a counterbalance interaction to prevent the concentric current loops from overlapping one another. The flow field around each flux of the double core vortex in
Figure 25a carries fractional winding number
. The energy of the double core vortex is
which is smaller than the energy of binding pair of two separated vortices with integral winding number. The energy of single core vortex
diverges when the system size reaches thermal dynamic limit. However the vortex pair has finite energy
limited by the distance between the cores of two vortices, carrying smaller energy than that of single core vortex. For the case of two vortices with opposite vorticity, the current segments in the contacting zone is parallel, the neighboring parallel currents attract one another and finally fuse into one to reduce the total energy of vortex pair. Since the energy barrier between the two opposite vortices is rather small, it takes a weaker magnetic field to push them into smaller unit cell and fuse into one. The effective energy increment of two opposite vortices above single vortex is smaller than that of two identical vortices. The effective magnetic field strength
is proportional inversely to the distance between the cores of two nearest neighboring vortices,
A weaker magnetic field generates vortex with larger radius as well as higher number of layers
m. In the opposite case, a stronger magnetic field reduces the energy of a double core vortex, resulting in lower critical temperature.
A square lattice of many vortices with identical vorticity is unstable (Fig
Figure 25a). The antiferromagnetic vorticity state of many vortices is a stable phase due to the attractive interaction between parallel current segments between neighboring vortices. For a square lattice composed of many fermionic vortices in antiferromagnetic order (Fig
Figure 25b), a dislocation of flux lattice is favored by energy reduction. To keep the continuity of the fused current within every current loop, the magnetic flux
together with the semicircular currents in
Figure 25b translate to the right hand side by one step and reconnect to the currents around
, generating a continuous spiral current pattern without flow orientation frustrations. The total energy of the spiral current track
is lower than that of two fermionic vortices according to the long range-coupling energy Eq. (
121), because the distance between anti-parallel current segments grows larger during the dislocation of magnetic fluxes. The spiral current in
Figure 25b generates a stable collective phase of incompressible fluid due to the diverging repulsive interaction between antiparallel currents. The spiral currents generated by dislocation has lower energy than vortex lattice. This dislocation mechanism is equivalent to the hopping of one flux to the other side of current and braiding with with its original nearest neighboring flux. Two opposite fermionic vortices contributes opposite winding numbers, hence the total winding number of the vortex pair is zero. After the dislocation of magnetic flux lattice, the winding number around flux
(and
) is
(and
), the total winding number of the spiral current is still zero,
. Therefore winding number is not sufficient enough to distinguish the two topologically different states in
Figure 25b.
The double core bosonic vortex generated by fusing two bosonic vortices in
Figure 25a is equivalent to single core bosonic vortex with renormalized magnetic flux,
The unit lattice space is also renormalized as
. In thermodynamic limit, the spatial size of lattice grows to infinity, the same BKT phase transition also occurs for double core bosonic vortices at the same critical temperature Eq. (
124) (
Figure 25a). Two double-core bosonic vortices prefer binding together to form a tetra-core vortex below the critical temperature
. The vortices keep fusing until all bare fluxes gathered together and are enveloped by
n layers of parallel current loops flowing along the edge, resulting in gapless states with respect to integral quantum Hall effect with filling factor
n. The bulk zone is filled by a forest of bare magnetic fluxes without any currents. Conducting electrons are fully confined in the edge zone. The collective condensation of many bosonic vortices phase fulfills integral quantum Hall state and topological insulator state. The vortex fusion of two double core fermionic vortices occurs by connecting two neighboring spiral tracks head to tail, one of flux pair in the center of a spiral track falls in the same domain as another flux of the other flux pair, the two fluxes can be renormalized as new flux
The length of the spiral track also renormalized as
. The fusion of fermionic vortex leads to continuous open current tracks crossing the whole lattice, which represents fractional quantum Hall states.
The collective phase transition from localized vortex pair state to an extended state represented by an open spiral track in
Figure 25b is obviously a topological phase transition, which can be characterized by Euler number of graph of current tracks. Dislocation of magnetic flux lattice creates many open docking points on edge. Different boundary conditions are defined by different docking patterns. For example, the spiral vortex lattice in
Figure 25d has 13 docking points on its four edges. The periodical boundary condition is defined by connecting the
ith docking point on the upper boundary to the
ith docking point of the bottom boundary. The same periodical boundary condition is defined to connect the docking points on the left and right hand side in
Figure 25d. The whole vortex lattice is composed of four localized vortices surrounded by three layers of current loops, and a loop of spiral vortices connected head to tail at the 7th docking point in
Figure 25d. The spiral loop on torus is equivalent to a boundary enveloping four bosonic vortices in the bulk, generating fractional charges
for fractional quantum Hall state. The bulk filled by localized vortices is in insulating state.
Landau’s symmetry breaking theory of phase transition provides a basic understanding for the phase transition from disordered vortex phase to ordered vortex phase. The square vortex lattice in
Figure 25c can be constructed by either bosonic vortex or fermionic vortex. Every vortex generates a local magnetic momentum, which is equivalent to a macroscopic spin. In an extremely high magnetic field, the local magnetic momentum of all electric current loops are polarized in the same direction, generating ferromagnetic phase of bosonic vortices. In weak magnetic field and low temperature environment, the orientation of electron flow within local current loop fluctuates to align with external magnetic field and reduce its local potential energy, driving the collective phase of vortex lattice into ground state. A vortex at the
ith lattice site is represented by an effective vorticity
which is measured by winding number
. The total energy of all vortices on the vortex lattice is summarized as
where
is the distance between vortices (or anti-vortices).
is external magnetic field in
z-axis. For a lattice of many separated vortices, the strongest coupling interaction is assumed to occur between the nearest neighbors. The long range coupling potential
is approximated by constant term
with
the unit lattice space of vortex lattice. Each of the
m layers of concentric orbital around the double core of vortex contributes a vorticity
. If the phase field of the loop orbital fluctuates in thermal environment, the vorticity of certain loop orbital also fluctuates between
. The possible values of vorticity for
m layers of loop orbital are
.
represents bosonic vortex, while
corresponds to fermionic vortex.
The Hamiltonian Eq. (
133) of vortex lattice is equivalent to Heisenberg model for large spins, which is not exactly solvable. In a mean field approximation, the local vorticity is assumed to has a small deviation away from average vorticity
, i.e.,
. The vorticity of vortex lattice is defined in a similar way of magnetic momentum of spins,
where
N is the total number of vortices. The mean field approximation of Hamiltonian Eq. (
133) reads
where
is the absolute value of vorticity.
p is the total number of the nearest neighbors. The effective magnetic field is denoted as
The eigenenergy of the effective Hamiltonian
take a serial of discrete values,
. The partition function sums over all possible vorticity values,
The vorticity is derived from the partition function in a straightforward way,
A self-consistent solution of the transcendental Eq. (
138) is derived under the first order approximation, which outputs a critical temperature in absence of external magnetic field
,
Below the critical temperature
, the vorticity obeys a power-law growth with respect to a decreasing temperature,
Most vortices are aligned to the same direction due to spontaneous breaking of time reversal symmetry. The maximal vorticity is proportional to
at zero temperature. For large vorticity
, the total number of the nearest neighboring parallel current loops is larger than that of antiparallel loops. All vortices are bosonic vortices at zero temperature.
For
, all vortices are spontaneously polarized into fermonic vortices below the critical temperature Eq. (
139), which is consistent with Onsager’s exact solution for two dimensional ising model,
The distance between two vortex cores is
. Notice the spontaneously ordered vortices above are still individual vortices, they are not paired up to form highly ordered state. In the antiferromagnetic phase of many fermionic vortices with double cores, a collective dislocation of magnetic flux lattice occurs to drive the vortex lattice into lower energy state. The
m current loops around double flux core are cut into halves and reconnected to generate spiral current tracks, generating the spiral vortex chain with fractional charge
. These spiral chain is formed by spiral vortex fusion in the edge zone. The spiral vortices connected to one another head to tail to form a closed loop along the edge. All possible locations of the spiral vortex on edge is
. In mind of the internal degree of freedom of spiral vortex, the total number of possible internal state is proportional to
m. As a result, the entropy of the spiral vortex loop in edge zone is
. The effective critical temperature with respect to fractional quantum Hall state with filling factor
reads
increases with respect to an increasing
m as well as
below half-filling state c (
Figure 26), and decays with respect to growing
.
diverges at half-filling state
, where the energy gap between landau levels approaches to zero, and effective magnetic field is also zero. The electron fluid is in a normal metal state in thermal environment at
. The fractional Hall state
has the lowest critical temperature. A growing system size
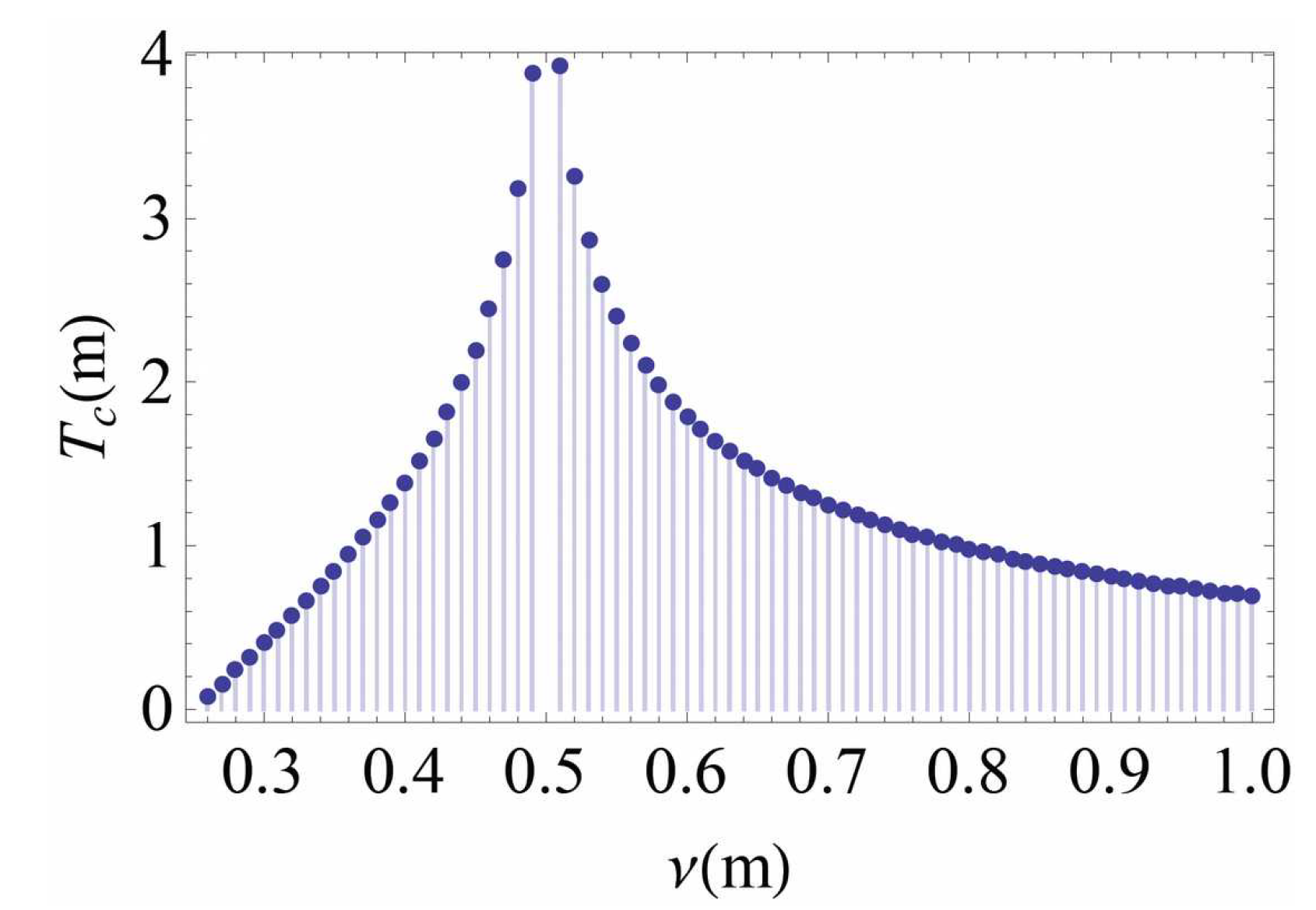
L further reduces the effective critical temperature.
The half-filling factor
is a critical point of the effective magnetic field, at which its orientation reverses from
to
(or vice versa). The correlation length between vortices approaches to infinity at
. Reversing the orientation of an infinite weak magnetic field
results in a global reversal of all vortices. As a result, the electron fluid within the spiral track in edge zone reversed its flowing direction, indicated by reversing the sign of
to
(or vice versa), driving the fractional filling serial with
into the opposite side of
with
. The effective magnetic field for fermionic vortex lattice is the sum of two oppositely oriented magnetic fields,
. In
Figure 25, the alternative distribution
and
in square lattice form antiferromagnetic phase of magnetic fluxes. The fermionic vortex surrounded by
layers of antiparallel current loops carries zero vorticity,
. The total energy of vortex lattice composed of vortices with zero vorticity is zero. The collective zero energy state has
fold degeneracy. Dislocation of flux lattice keeps the zero vorticity of the vortex lattice, but drives the isolated vortices on edge into spiral vortex loops, which has lower energy with respect to fractional filling factors
.
The topological fluid in the vortices lattice generates a serial of fractional Hall resistivity in FQHE. We first focus on topological representation theory of the 0th Landau level. In a homogeneous magnetic field, all vortices have the same flow pattern, we first focus on one vortex at the
jth lattice sites. The
ith current loop around the
ith flux core represents the eigenstate
with eigenenergy
, where
. All current loops around the
ith vortex core has the same degree of degeneracy, which is proportional to the number of fluxes
enveloped by these loops. The locations and total number of fluxes
is not conserved, instead it varies with respect to the external magnetic field strength. The density of electrons in vortex lattice is defined by the ratio of the total number of electrons
to the area of lattice
, i.e.,
. The density of electron defines an effective internal magnetic field strength
, which counts how many layers of loops fully occupied by electrons.
can be viewed as effective magnetic field with respect to Fermi level. The initial current loop has
fold degeneracy and fully occupied by
electrons. The thought experiment to reach such a state is first immersing
electrons in an extremely low magnetic field
, then every vortex is surrounded by almost infinite number of loops, each of which is occupied by one electron. As
grows higher, all loops together with an electron shrink to overlap with one another, finally converging to the single loop in ground state. When the external field strength is higher than
, there are more empty external loops shrink by the external magnetic field to overlap with the initial current loops. These newly overlapped loops are unoccupied since there is no more electrons. The degeneracy of the initial loop in external magnetic field is
. In this case, all electrons are squeezed into ground state loop to form a stacked viscous fluid. The bulk vortex in
Figure 25b is surrounded by only one layer of loop. There is no intersecting between neighboring loops, resulted in fully insulating state. While in the edge zone, dislocation of flux pair connects the initially isolated loop to form a continuous spiral track, forming a conducting edge state. The viscous interaction between the nearest neighboring antiparallel flow currents contributes to Hall resistivity. Since
fold degenerated electron flow contributes simultaneously to Hall resistivity, the Hall resistivity grows linearly with the degree of degeneracy, which is quantified by the external field strength
.
When external magnetic field strength reduces below
, the degeneracy of the initial loop becomes smaller than the number of electrons, the additional electrons are expelled out of the first innermost loop to occupy the second innermost loop with larger radius. As a result, the viscous interaction between the flowing electron lamination is reduced due to the growing distance between current loops, leading to a reduction of Hall resistivity. The Hall resistivity in the edge zone of this vortex lattice obeys the familiar form in FQHE,
The edge current with
in
Figure 25d flows in a crossing avoiding path in the middle zone. A further reduction of external field strength
adds more concentric loop states around the same vortex core, more electrons are expelled out of the inner loops to occupy the outer loops, until there is only one electron occupying one loop state. The spiral vortex pattern on the edge reaches the half-filling state
with respect to zero effective magnetic field
. Then the magnetic field reversed its orientation, leading to a further reduction of
and larger separation distance between neighboring current loops. The flow current in the loop also reversed its circling chirality, topological contraction of two connected nearest neighboring antiparallel current segments generated by folding one longer segment further reduces the Hall resistivity to
. The growing
in negative
z- axis leads to a reducing magnetic field
, until the Fermi level of electron sea is raised up to reach the 1st Laudau level.
In de-Haas-Van Alphen effect, the magnetic moment of electron oscillates with respect to magnetic field strength. The vorticity of fermionic vortex here is equivalent to magnetic momentum of electron, showing similar quantum oscillation effect. In high magnetic field
, all electrons occupy the ground state, i.e., the innermost loop around the vortex core. The ground state energy of the vortex reads
In a low magnetic field initially oriented in
z-axis,
, the degree of degeneracy of ground state loop is smaller than the total number of electrons. Electron are pushed out of ground state loop to occupy higher energy levels. When the magnetic field strength takes the value
all energy loops below the
mth loop with energy
are occupied, but the
th loop are partly occupied, the total energy of the fermion vortex reads
The vorticity of the fermion vortex reads
The unpaired current loop is polarized to the negative direction of
z-axis. A positive increment of magnetic field strength increased the degeneracy of its inner nearest neighboring loop, the electrons of the initial outer loop join in the inner loop. As a result, the magnitude of the negative vorticity decreases linearly with respect to magnetic field. When all electrons of the initial loop flows into its inner nearest neighboring loop, the total number of loops around vortex core becomes even. The vorticity of the fermionic vortex reduces to zero. Further increment of magnetic field increases both the cyclotron frequency and the degeneracy loop current. The vorticity switches to positive
axis when
. Therefore the vorticity oscillates to show the same de-Haas-Van Alphen effect as electron.
2.6. The train track representation of fractional quantum Hall fluid
A high magnetic field at low temperature is the most crucial factor to find fractional quantum Hall resistivity of two dimensional electron gas [
2]. The knot lattice of magnetic fluxes and train tracks around dense magnetic flux lattice is an exact topological representation of strongly correlated electron fluid in high magnetic fluid, leading to a self-consistent explanation to the hierarchy structure of fractional quantum Hall resistivity [
12]. Here we introduce an electric laminar flow around a pair of antiparallel magnetic fluxes to model quantum Hall fluid in high uniform magnetic field (
Figure 27a). The two magnetic fluxes—an external magnetic field
and gauge field strength
—are located in opposite space domains separated by the electric laminar boundary. Rotating the two antiparallel vectors (
and
) counterclockwisely generates folded electric laminations
Figure 27a. The cross sections of the folded lamination in the plane perpendicular to magnetic fluxes is exactly a train track pattern. Therefore, counting the number of intersecting points between a vertical line and laminar layers around the magnetic flux pair can generate the same fractional charges passing through magnetic flux lattice (
Figure 27a). The number of laminar layers is labeled by
and
in
Figure 27a, showing fractional charges
Continuously braiding the two antiparallel vectors (
and
) in counterclockwise direction twice generates fractional charge,
. In the most general case,
m times of braiding over the two antiparallel magnetic vectors generates fractional charges,
The total number of directed braiding
m is determined by the resultant magnetic field strength,
,
Counterclockwise braiding is governed by (
,
). While clockwise braiding are determined by (
,
). The highest magnetic field strength is given by
with respect to fractional charge
. When the resultant magnetic field strength reduced to
,
, the fractional charge reaches
. Further reduction of resultant magnetic field strength drives the train tracks to rotate in clockwise directions. A clockwise braiding on the two vectors (
and
) in
Figure 27c only drives them to touch the electric laminar boundary but without folding effect. One more clockwise braiding of the two magnetic vectors fold the electric laminar boundary into train tracks of fractional charge
, which is derived by substituting
into Eq. (
149). For the special case of only one clockwise braiding
, the fractional charge equation outputs an integral charge
.
The cross section pattern of the electric lamination folding is train track that can be exactly described by Wen-Zee matrix formulation of topological fluid. The Wen-Zee matrix formulation is constructed from abelian Chern-Simons field theory, providing an effective description for fractional quantum Hall resistivity with odd denominator [
9][
17]. When electrons flow around the flux pair, they feel the gauge potential vector
generated by Maxwell magnetic field
as well as U(1) gauge potential
and its corresponding gauge field strength
(
Figure 28a). Cutting the first track loop into two half semicircles creates four open endings, which are equivalent to the Feynman diagram representation of annihilation or generation of particles,
(
) and
(
). The effective Hamiltonian for this topological surgery reads,
The first gauge field strength
is oriented into the opposite direction of Maxwell magnetic field
, because the electric current along the reconnected train track must be continuous and flow in the same direction, the first gauge potential vector
reversed its orientation (
Figure 28c). Therefore the coupling between Maxwell gauge potential
and
shows opposite sign to that between
and
. The corresponding Lagrangian of abelian Chern-Simons action with respect to the first loop is
where
is gauge field strength and
is the charge. Another equivalent way of generating the train track of
Figure 28c is to braid the two fluxes counterclockwisely once (
Figure 28d-e), which is the mother train track pattern of
state. The topological surgery of cutting two electric loops around the magnetic flux pair and reconnect the cutting poins leads to the continuous train track of fractional charge state
(
Figure 28f - e). The second electric loop introduce the second gauge potential vector
and gauge field tensor
. The orientation of
and
is independent of that of
and
before the topological surgery. Since these gauge potential vectorial segments reconnect to form one continuous train track, conflicting orientations are forbidden to fulfil the continuity of field distribution so that the electric lamination flow in a minimum energy state. The effective Hamiltonian with respect to the reconnection process of two cut loops reads,
The effective Lagrangian of Abelian Chern-Simons action with respect to the train track of
in
Figure 28g is
The same train track of
Figure 28g can also be generated by one counterclockwise braiding of two fluxes out of the mother state of
(
Figure 28h-i). For the most general case, the train track generated by
m rounds of braiding on the flux pair is exactly described by Wen-Zee matrix formulation of hierarchy abelian Chern-Simons field action[
9][
17],
Where
is a matrix with its diagonal terms assigned with the integer of filling factors, i.e., (
;
is electromagnetic potential and
is the gauge potential induced by the U(1) gauge symmetry of the
Ith electric loop. Wen-Zee matrix formulation provides an effective description for fractional quantum Hall resistivity with odd denominator [
17],
where the charge vector is
. In this train track model, the Wen-Zee formulation of fractional filling factor is exactly
The train track generated by
m rounds of braiding represents the collective dancing pattern of quantum Hall fluid, which matches the effective wavefunction constructed by Wen-Zee matrix formulation [
17],
This wave function reduces to the celebrated Laughlin wave function with
.
The fractional serial
only characterize the collective dancing pattern of electron fluid around one pair of magnetic fluxes. The celebrated Laughlin wave function
is almost an exact trial wavefunction of fractional charge
state. However, an intuitive physical understanding of Laughlin wave function is still not achieved so far due to the blur physical picture of collective dancing pattern of electron fluid. Here we proposed a physical mechanism based on trains tracks generated by squeezing magnetic fluxes to give an exact characterization of the collective dancing pattern of fractional charge state
. Electrons move around a bundle of magnetic fluxes along concentric circles with different radius
The magnetic field strength of the flux bundle is quantified by the number of fluxes in unit area,
, where
d is the distance between fluxes. As the strength of magnetic flux bundle increases, the electrons along the loop tracks far away from the bundle center are squeezed into inner loops. The condensation of electrons and gauge potentials keep pushing inward until there is only one loop left, circling around a pair of fluxes. However the flux pair here is different from that of Jain’s composite fermion, one flux is determined by Maxwell magnetic field, while the other flux is quantified by U(1) gauge field tensor oriented in opposite direction. The resultant magnetic field strength is determined by the sum of two opposite fluxes. In bulk region, the loop tracks around flux pair are separated from each other (
Figure 29a), constructing an one dimensional lattice of flux pairs. When the flux pairs are squeezed into boundary, every loop track breaks apart into a top half loop and a bottom half loop (
Figure 29a), wrapping around the top flux and bottom flux respectively. The one dimensional lattice of bottom half loop around the bottom flux collectively translocate one step to the right hand side, creating a dislocation of flux lattice. The open endings of the top half loop are reconnected to the open endings of the bottom half loop to construct a continuous winding path (
Figure 29a). When the vertical flux pairs are squeezed into an one dimensional chain with only horizontal flux pairs on the edge, the distance between nearest neighboring fluxes is further reduced to a smaller value, as a result, the higher magnetic field strength on the edge leads to a collective dancing pattern of electron fluid carrying a fractional charge
, which is exactly an one dimensional chain of weakly interacted composite fermions (i.e., one electron combined with two fluxes). This collective dancing pattern matches the Laughlin wave function Eq. (
158) with
.
The Laughlin wave function Eq. (
158) with
describes the fractional charge
state. The corresponding train track of
state can be generated by squeezing two pairs of fluxes of
into one unit space (
Figure 29b), i.e., the
state is the collective state of two composite fermions.
Figure 29b-I shows three pairs of fluxes of
state, braiding the leftmost and rightmost flux in clockwise direction until they squeeze into the gap zone between the two fluxes of the middle flux pair, the train track must be kept continuous without any breaking points during this braiding process. The distance between the nearest neighboring fluxes is further reduced, resulting in higher magnetic strength (
Figure 29b(I-IV)). In fractional quantum Hall theory, the effective magnetic field strength
B is proportional to the inverse of filling factor
. Therefore the magnetic field strength of
state increased by two units comparing with that of
state. Drawing vertical line passing through the center of the middle flux pair in
Figure 29b-III and counting the number of parallel track segments on the two opposite sides of the flux, outputs a pair of fractional charges
(above the flux) and
(below the flux) in
Figure 29b. The same train track of
state can also be generated by the dislocation and compression process of magnetic flux lattice showed in
Figure 29c. The isolated two loops fused into a winding track around four fluxes after the topological surgery on two flux pairs (
Figure 29c). Moving the middle flux No. 2 to the top location and the other middle flux No. 3 to the bottom and squeezing the leftmost flux No. 1 and the rightmost flux No. 4 into the space between flux No. 2 and No. 3, leads to the same train track of
state in
Figure 29b.
The collective dancing train track of electron fluid carrying fractional charge
is generated following similar protocol as
and
state. Three pairs of composite fermions are squeezed and compressed into one unit, matching the Laughlin wave function Eq. (
158) with
. However, there are many different ways to rearrange the spatial ordering of the six fluxes, the degeneracy degree of train track pattern of
is higher than that of
and
state. The leftmost flux No. 1 and the rightmost flux No. 6 in
Figure 29c are fixed to their initial locations, the middle flux pair of No. 3 and No. 4 are relocated to the top and the bottom sites respectively. While the two fluxes No. 2 and No. 5 are translated to the second top and bottom sites respectively. When the six fluxes are translated to squeeze into one column and form a one dimensional chain, the train tracks around the middle flux pair No. 1 and No. 6 outputs fractional charges
. The two fluxes No. 2 and No. 5 carry fractional charge
, while the fluxes No. 3 and No. 4 carry fractional charge 1/3. In another spatial ordering, the two fluxes No. 2 and No. 5 are translated to the top and the bottom respectively, while the fluxes No. 3 and No. 4 are translated to the second top and bottom sites, it also leads to the same fractional charges
around the flux pair of No. 1 and No. 6. But the two fluxes No. 2 and No. 5 carry fractional charge
in this case. The collective train track pattern of
is the mother state of
. Based on the train track pattern of
in
Figure 29b, braiding the leftmost flux and the rightmost flux in counterclockwise direction and squeeze them into the middle flux pairs (
Figure 29e) generates the same train track pattern as
Figure 29d. The distance between magnetic flux is further reduced and magnetic field strength grows higher. This physical picture is consistent with experimental observations in fractional quantum Hall effect.
As a conclusion, the Laughlin wave function Eq. (
158) of fractional charge
can be explained as the condensation of
m composite fermions. The corresponding train track pattern generated by squeezing
m pairs of magnetic fluxes into one unit by keeping the path continuous guides the collective dancing paths of electron fluid in high magnetic field. However,the fractional charge state
is not homogeneous around all fluxes, instead other fractional states alternatively distributed along the flux lattice (as showed in
Figure 29d). The Laughlin wave function Eq. (
158) captured the strongest fractional state
by dropping the other inhomogeneous fractional charge states. While this train track representation reveals the complete distribution of fractional charges around magnetic fluxes.
2.8. The fractional quantum Hall effect in three dimensional magnetic field
For three dimensional homogeneous magnetic field oriented in z-axis, the double Beltrami-Poincare half-plane in
Figure 35b shows straightforwardly that the Fermi wavelength is twice of the wavelength of the charge density wave. There is a discrete energy level in the bulk corresponding to every fractional filling state with
(as showed in
Figure 30). A polarized electron first occupies the ground state with
, when the resultant magnetic field strength decreased to the critical value for
, another electron piles up to fill the second energy level with
, and so on. Since the topological number
m can grow to infinity, the number of quantum energy levels with
m also grows until all electrons are accommodated. The fermi level here is characterized by a critical number
, the quantum states with
are entirely filled, while those states with
are empty. In mind of the enormous number of electrons in a real material, the critical number
is almost infinity. Therefore the Fermi surface is exactly the horizon surface in the double hyperbolic surface in
Figure 35c, which projects the horizon line that produces the mirror images of Beltrami-Poincare half-plane in
Figure 35b. The eigenenergy of Fermi level is straightforwardly derived from the eigenenery Eq. (
215)
The magnetic field strength of Fermi level is
, which is also the critical magnetic field strength for the half-filled state
. The Fermi level locates exactly at the middle point of the energy gap between the 0th and the 1st Landau level (
Figure 33),
The wavelength corresponding to the cyclotron frequency
is inversely proportional to wavelength
. The Fermi wavelength
is twice of the wavelength that bridges the energy gap
, since
. The number of energy levels grows by power law
as
approaches to
, therefore the density of electrons also grows to the maximal value at
and then decays following
as
moving away from
. During this process, the topological linking number first grows to the maximal value and then decays to zero in the end. The charge density wave periodically distributes along z-axis in a homogeneous magnetic field. This topological train track representation agrees with Halperin’s theory of three-dimensional electron gas in a high magnetic field [
30], that is verified by experimental observation in three dimensional quantum Hall effect [
31]. Notice here the topological braiding number is a half-integer,
, which means the two open endings of the track only wind around the flux pair over an angle of
, then they flow along the straight geodesic path in z-axis to complete one period of braiding operations on the top surface. This topological train track configuration agrees with the tunneling theory in three dimensional quantum Hall effect in Weyl semimetals [
32], which was verified by experimental observation of Weyl orbits in
[
33].
The pseudosphere of energy gap against spatial distance
x is experimentally implementable by an inhomogeneous magnetic field distribution in the direction perpendicular to the plane of two dimensional electron fluid. We define the relative value between an arbitrary magnetic field strength and the magnetic field strength at half-filling state
as effective magnetic field strength
,
For the fractional filling with odd denominator
, the effective magnetic field strength reads
. In
Figure 35c, the inhomogeneous effective magnetic field strength
is schematically depicted by a pair of blue and red hyperbolic curves, where the z-axis is defined by defined by
, reformulating
into
. The edge zone is labeled by a white loop corridor surrounding a rectangular bulk zone(indicated by the rectangular yellow green zone). The magnetic field strength is inversely proportional to the separation of the two hyperbolic curves, which also represent the magnetic flux pair. The two magnetic flux lines are pushed away from each other to infinity on the horizon surface in
Figure 35c, which corresponds to zero magnetic field strength. The cross-sectional surface of electron fluid lamination expanded in
plane on the edge (
Figure 35c) can rigorously map to the Beltrami-Poincare half-plane extended by energy gap
and
x in
Figure 35b by applying the initial convention equation
. This inhomogeneous effective magnetic field is generated by an effective gauge potential,
The effective Hamiltonian with respect to this gauge potential vector Eq. (
213) reads
where the resultant magnetic field
. The cyclotron frequency determined by the effective Hamiltonian Eq. (
214) is exactly derived following the same analytical method for the two dimensional gauge potential Eq. (
166),
The eigenenergy levels
determined by this cyclotron frequency distributes symmetrically around
, with
z running from
to
.
Unlike the two dimensional electron fluid in homogeneous magnetic field, the electrons in this inhomogeneous magnetic field tends to move along the semicircular track in
plane or
plane, initially running out of the two dimensional
plane (illustrated by its projected horizon line in
Figure 35b) into the third dimension and finally returning to the
plane. This is because the geodesic curves of the Beltrami-Poincare half-plane are semicircles with different curvatures, or a straight line perpendicular to
plane which is in fact a special semicircle with zero curvature. From physics point of view, the electron fluid must travel through many different fractional filling states in the third dimension in order to move from one location to another within the same plane. The longer distance it covers, the more new Hall states must be excited up along its travel path. For the special case of electrons moving along straight geodesic line in
z axis, the electrons at bottom plane must travel through all fractional quantum Hall states in sequence in order to reach the top plane. There is a high probability to observe many closed circular tracks in
plane or
plane which are exactly divided into two identical semicircles by the horizon line in
Figure 35b. Notice here the circular track in
plane is not the same circular trajectory of an electron under the propulsion of Lorentz force, because there is no magnetic field applied perpendicularly to
plane, they are geodesics of the curved space expanded by energy gap and spatial dimension.
An inhomogeneous charge density wave also exist in three dimensional inhomogeneous magnetic field with its strength determined by the space dependent equation
where
y represents the continuous extension of the quantum number
n of Landau level, and
z is the inverse of topological braiding number
. The double hyperbolic scheme in
Figure 35c visualize spatial distribution of energy magnetic field strength on the cross-sectional plane at
(the 0th Landau level). The wavelength of charge density wave grows up to
for
. While the Fermi wavelength
locates at
. The eigenenergy levels distribute around the Fermi level on the
yth Landau level with a double hyperbolic surface as its boundary outline (
Figure 33). The Fermi wavelength on the 1st Landau level is
Half of Fermi wavelength yields that of charge density wave
, leading to the equation of fractional filling factor
. The topological braiding number must be
to fulfill the fractional filling factor
. Each of the two open endings of the track path sweeps over
in the bottom surface and then tunnels to the top surface to sweeps over
, finally fulfilling the topological constraint of a closed path (
Figure 38). On the
nth Landau level, the general sweeping angle of track arc around flux pair in the bottom plane obeys equation,
decays with an increasing quantum number
n (
Figure 39a). The dual sweeping angle in the top plane is
(
Figure 39b). As the quantum number
of Landau level grows, the charge density wavelength converges to Fermi wavelength and approaches to infinity together, the sweeping angles of electron in bottom plane restores
.
The knot lattice and train track representation theory provides an effective topological characterization for chiral spin liquid in homogeneous magnetic field oriented in the same direction. In a general three dimensional magnetic field distribution, the laminar layer of electron fluid can fold into three independent directions, with interlocking trains tracks as its cross sectional pattern in different cutting plane. We extend the train track theory in two dimensions into laminar folding in three dimensions and combine the Schrdinger equation of electrons in three dimensional magnetic field to give a complete description for 3D fractional quantum Hall effect.
In analogy with the symmetric gauge potential for a constant magnetic field perpendicular to the two dimensional plane, we choose symmetric gauge potentials that generate constant magnetic field in three perpendicular directions,
The magnetic field vector
projects three constant components,
. Spin is assumed to be fully polarized in high magnetic field, so that the spinless Hamiltonian for Schr
dinger equation reads
The eigenstates of Hamiltonian Eq. (
221) are inadequate to deduce fractional Hall resistivity, due to the absence of strong correlations among electrons in quantum Hall fluid. The Coulomb repulsive interaction between electrons is also remodeled to fit in collective potential configuration of viscous electron fluid. In mind of the high similarity of equal energy distribution of harmonic oscillator in parabolic potential well and Landau levels in magnetic field, each magnetic flux
can effectively map into a parabolic potential well with frequency
by following correspondence equation
The Hamiltonian Eq. (
221) effectively describes the electron motion in a parabolic potential determined by
. The strong interaction between electrons in Hall fluid splits this parabolic potential surface into many layers of stacked parabolic surface with respect to different fractional Hall states as showed in
Figure 30, breaking a highly degenerated state into many distinguishable quantum states labeled by topological number
m. This multilayered potential surface is encoded into the effective magnetic field
where
is the fractional filling factor determined by magnetic field strength
. Substituting the multi-valued
Eq. (
223) for the original magnetic field
in Hamiltonian Eq. (
221) yields the effective Hamiltonian
This effective Hamiltonian Eq. (224) for electrons in multilayered three dimensional magnetic field can be reformulated into a three dimensional harmonic oscillator with an angular momentum vector,
,
where
in
are angular momentum operators
The three components of cyclotron frequency vector in
is characterized by the effective magnetic field strength that is renormalized by fractional filling factors
The resultant cyclotron frequency vector
that quantifies the strength of parabolic potential in
obeys the following equations
Without losing generality by firstly dropping
terms in Hamiltonian Eq. (
224), the exact eigenenergy of Hamiltonian
is solved by the same analytical method of Harmonic oscillator,
The resultant cyclotron frequency
in one dimension is utterly determined by the original cyclotron frequencies
oriented into the rest two dimensions,
In mind of the correspondence relation between cyclotron frequency and magnetic field,
the effective resultant magnetic field
is expressed into similar formulation by the initial magnetic field strength,
,
The fractional quantum Hall resistivity in three dimensions is governed by equations
which agrees with the Hall resistivity tensor derived from an extension of classical Drude model into three dimensional magnetic field (Appendix),
The multi-valued magnetic field Eq. (
223) is incorporated into fractional Hall resistivity equation Eq. (
231), which is explicitly expanded by the initial magnetic field strength in three dimensions,
Notice here the initial magnetic field strength
are usually different from
or
, leading to fractional filling factors that depend on initial field strength. In order to eliminate this artificial effect and only keep the topological invariant factor in Hall resistivity, we assume
and finally derived the topological quantum Hall resistivity,
The fractional Hall resistivity in
plane
depends on the braiding operations around x-axis and y-axis (
Figure 40), i.e., the magnetic flux pairs oriented in
x-axis and
y-axis, so does the fractional Hall resistivity
and
. This is a key difference of 3D FQHE from that in two dimensions, where the Hall resistivity
is generated by a magnetic field perpendicular to
plane. At a fixed Hall plateau of
, the topological numbers (
and
) in Eq. (
233) must varies in a see-saw way to output a fixed value, i.e., the increasing of
is always accompanied by an decreasing
, or vice versa. The fractional Hall resistivity
shows competing signals from
and
, which are controlled by magnetic field projected in
x- and
y-axis. When
is smaller than the minimal value,
,
competes with
. When
is larger than the minimal value,
,
grows linearly with
(
Figure 41).The 3D fractional Hall resistivity Eq. (
233) provides a theoretical explanation on the competing fractional Hall states observed in a tilted magnetic field [
27].
The complete Hamiltonian
with
is exactly solvable by Green function method. The angular momentum operator in the interaction term
V is expressed by the same creation and annihilation operators in
,
The creation operator
and annihilation operator
obey the following commutator relations
. The angular momentum operators include the creation or annihilation terms of boson pair,
where the coefficients depends on the ratio of resultant cyclotron frequencies in one direction to another,
For the special case of equal magnetic field strength in three directions,
the resultant cyclotron frequencies are equal,
. Then the coefficients
reduces to (
,
,
). The angular momentum operator reduces to a brief form,
Substituting the second quantization of angular momentum operator Eq. (
234) for
in
, and combining
V with the diagonal Hamiltonian
,
finally yields the complete Hamiltonian
H that is expressed by creation or annihilation operators. The eigenenergy of quasi-excitations locates at the Green’s function poles. The interaction term
V rotates the eigen states around the original frequency vector
by operator,
leading to complex resultant cyclotron frequency that mixed the three original cyclotron frequencies. It is hard to tell the specific spatial directions for measuring Hall resistivity
in an inhomogeneous spatial distribution of magnetic field, because the resultant frequency is the output of mixing all of its three spatial components. However the Hall resistivity for a homogeneous distribution of initial magnetic field strengths and fractional filling factors in three dimensions should has definite values, since the physical effect of the three spatial dimensions are identical. Therefore we choose identical initial magnetic field strength
and fractional filling factors
, the resultant cyclotron frequency
generates two golden ratio solutions
where
. Besides a simple fractional Hall resistivity serial,
which agrees with the Hall resistivity Eq. (
233) derived from
, the Hall resitivity
also takes two golden ratio values
All of the three solutions of Hall resistivity in three dimensions is smaller than that in two dimensions, this is because the total number of transportation paths in three dimensions is much larger than that in two dimensions.
is always larger than
, while
is always smaller than
. The angular momentum
breaks the degeneracy of Hall resistivity at the symmetric point. The most familiar fractional serial
is
, which produces fractional resistivity with odd denominator. Unlike the single serial of fractional resistivity of two dimensional electron fluid, here the fractional resistivity serial splits into three similar branches.
2.9. Fractional filling factors determined by folding electron fluid lamination in three dimensions
The Schrdinger equation is inadequate to determine the fractional filling factors . In two dimensional electron gas, the fractional filling factors with odd denominator can be constructed by Wen-Zee matrix formulation of topological fluid, which is not directly applicable for electron fluid in three dimensional magnetic field due to the non-abelian character of angular momentum operators. In order to construct general fractional filling factors in three dimensional magnetic field, we have to generalize Thurston’s train track that is confined in two dimensions into folded lamination in three dimensions.
The moving electrons are slowed down by low temperature to form viscous fluid, wrapping the magnetic flux lines in three dimensions as folded laminations. The continuous electron lamination has lower energy than the laminations with genus, which pins down the singular point as the core of topological vortex. In order to reduce the energy cost for vortex penetrating through the lamination, the two fluxes in the same direction are placed at the opposite sides of the lamination. In
Figure 42a, one
x-flux (
) and one
y-flux (
) perpendicular to
are located in front of the lamination, while the other two fluxes
and
are placed at the back of the lamination. The four fluxes avoid crossing one another, constructing a knot lattice with four crossing points (
Figure 42a). The single layer lamination folds into a three layer lamination after the two parallel
y-flux lines (
and
) are braided clockwisely (
Figure 42b), and one more clockwise braiding on the two
x-flux lines (
and
) fold the three layer lamination into a nine layer lamination (
Figure 42c). In the end, every flux is fully wrapped by electron fluid lamination and pushed back to its original plane (
Figure 42d). The cross section of the folded lamination in the perpendicular plane to
x- and
axis are both the train track pattern for fractional quantum Hall states with
in high magnetic field strength.
Another way of producing folded electron fluid lamination without intersections is to replace the intersecting lines between two surfaces by vacuum state that is consists of two curved surfaces avoiding touching each other (
Figure 43). In
Figure 43a-I, the two flat electron laminations intersect at a straight line in
y-axis, the strong Coulomb repulsive interaction between electrons drives the quantum state with this electron density distribution to high energy level. The two intersecting lamination reorganize the local electron distribution along the intersecting line into two curved surfaces avoiding touching each other, and stay away from each other as far as possible to reduce the Columb repulsive potential, as showed in
Figure 43a-II and
Figure 43a-III. The two degenerated vacuum states in
Figure 43a reduced the same amount of energy, but can result in different topological configurations.
Figure 43b apply the topological surgery procedure of
Figure 43a to a surface intersection configuration between a flat surface which separates two flux lines in
axis and a tubular surface that fully envelop the
flux pair, folding a flat lamination into a three layer lamination that is identical to
Figure 42b. Similarly, when the magnetic field strength is reduced to a weaker value so that the electrons confined in the innermost tubular surface are release to form a second tubular surface that envelops the innermost surface, the intersecting lamination between two tubular surfaces and one flat surface in
Figure 43c transforms into a folded lamination with five layers. The cross section curve in its horizontal plane perpendicular to
axis is the train track for fractional filling factor
.
For a general folded lamination generated by braiding
y-flux pairs (
Figure 43d-I), a horizontal tubular surface enveloping the
x-flux pairs intersects with all monolayers within the laminations. Mapping the intersecting lines into identical vacuum states leads to the folded lamination of fractional quantum Hall states. The resultant cyclotron frequencies
in
and
fluxes are governed by the cyclotron frequency Eq. (
229) with
,
The fractional filling factor in
z-axis is
The corresponding Hall resistivity with respect to this folded lamination configuration is
. Even though the two perpendicular magnetic fields are confined in
plane, a cyclotron motion around
z-axis is still induced by the non-commutative character of angular momentum operators in three dimensions. As showed by the unfolded electron fluid lamination in Figure 47a, the two topological braiding operations labeled by
result in a loop flow along the four boundaries circling around
z-axis. The resultant energy levels are quantized by three primary quantum numbers
and two topological numbers,
.
The semiclassical representation of these quantum energy levels are many stacked concentric spheres with different constant energy in three dimensional momentum space,
The discrete distribution of spherical contours with constant energy in three dimensional momentum space represents Landau levels characterized by quantum numbers
. There are
hyperorbitals sandwiched in between the nearest neighboring Landau levels in
x-axis (
y-axis). While the total number of hyperorbitals that are sandwiched in between the nearest neighboring Landau levels in
z-axis is
. The energy gap between nearest neighboring hyperorbitals in
z-axis is larger than that in
axis or
axis. The correspondence between energy gap in
z-axis and the energy of classical wave in
z-axis,
suggests that the wavelength
is shorter than that in
x-axis (
y-axis). This physical result is consistent with the topological representation of a highly folded quantum fluid lamination in
z-axis.
The folded lamination is not a simple linear stack of many identical monolayers because the electron fluid must flow continuously passing through each layer of the folded lamination, the orientation of electron flow in each layer determines the collective potential energy of folded lamination. In the train track representation of two dimensional fractional quantum Hall states, the nearest neighboring tracks are always antiparallel. The repulsive interaction between antiparallel electric currents results in incompressible train track pattern, which represents incompressible electron fluid. However in three dimensional lamination representation of 3D fractional Hall states, the electric currents in certain nearest neighboring monolayers are parallel to one another. The attractive interaction between parallel electric currents reduces the collective potential energy, implying a compressible electron lamination in three dimensions. In the nine layer lamination generated by braiding the
y-flux pair and
x-flux pair in sequence (
Figure 44a), each three layer lamination separated by
and
is composed of three antiparallel currents flowing in monolayer. However, the bottom current in the three layer lamination above
is parallel to the top current of the three layer lamination below
, the two nearest neighboring parallel currents attract each other, reducing the total potential energy. For another electron flow pattern that all currents flow along y-axis, the two nearest neighboring currents (labeled by red arrows in
Figure 44a) separated by
is antiparallel to each other, repelling the nearest neighboring three-layer laminations from each other. Unlike the incompressible Hall fluid in two dimensions, the total potential energy of electron fluid lamination in three dimensions is partially compressible according to the current orientation configurations layer by layer. For the first case that the orientation of electric currents are fixed to x-axis (
Figure 44a), the electromagnetic potential of the nine layer lamination is the sum of the potential between the
th and
th layer,
where
and
are the width of the rectangular monolayer projected in
x- and
y-axis.
is the distance between the
th and
th layer.
is the electric current strength of the
th layer. For example,
is bottom layer of the lamination at the crossing point between magnetic fluxes
and
. The interaction strength coefficient
(
) for two antiparallel (parallel) currents. In
Figure 44a, the 3rd and the 4th layer attract each other, so does the 6th and 7th layer. Folding one initial layer around the same flux pair
and
four times generates nine layers of antiparallel currents, which has a total electromagnetic potential energy,
where
(Tm/A) is dielectric coefficient. The area of monolayer in the lamination
is set to
for simplicity. the distance between monolayers is
. For the stacked current configuration with the nine directed monolayer oriented in
axis (as indicated by the black arrows in
Figure 44a), the total electromagnetic potential energy is
In this case, the potential energy is highly reduced comparing with the nine layers of antiparallel monolayers due to the parallel monolayers sandwiched in between laminations. Therefore hybrid folding operations by braiding flux pairs in different directions drives the folded lamination into low energy state. When the currents are all oriented in
y-axis within monolayers of the fold lamination in
Figure 44a, the total electromagnetic potential energy is further lowered to
The No. 1, No. 2 and No. 3 monolayer attract one another and tend to get close to one another to reduce enrgy, constricting a locally compressible lamination cluster. The three monolayers (No. 3, No. 4 and No. 5) are oriented into opposite direction to the lamination cluster of (No. 1, No. 2 and No. 3), therefore the two lamination clusters repel each other, demonstrating incompressible character. The fractional quantum Hall states in three dimension is not only determined by folded lamination pattern, but also depends on the orientation configuration of currents flowing in each monolayer.
The fraction filling factor of the lamination in
Figure 44a can be exactly derived by the spatial distribution of monolayers around the four fluxes.
Figure 44b showed the numbers of layers above or below every flux. The fractional filling factor determined by
y-flux pair and
flux pair are both
,
The resultant filling factor
is not a fractional number and is larger than
. The resultant Hall resistivity is also an irrational number, reducing to a smaller value that that of the
state. Notice here the
flux lines also wind around the
flux lines, constructing a train track of folded fluxes (
Figure 44b). Because these fluxes are fully enveloped by electron fluid lamination, which prevent them from touching each other, as a result, the magnetic fluxes can not fuse to generate fractional fluxes.
An anisotropic magnetic field induces inhomogeneous lamination folding in different directions, than can be decomposed of a number of inhomogeneous lamination clusters. In
Figure 44c, the magnetic field strength in
y-axis is weaker than that in
x-axis, folding the initial monolayer into a five layer lamination. The cross section pattern of this lamination matches the train track of
state. The
flux pair generates the lamination of
state. The three dimensional filling factors is derived from Eq. (
243),
which is close to half-filling factor
. The number of local monolayer distribution is labeled in
Figure 44d. In the ground state of this lamination configuration, all electric currents are oriented in
y-axis,
To generate the magnetic fluxes oriented in
y-axis as showed in
Figure 45a, the simplest gauge potential vector field has a similar form as Landau gauge
. The electron fluid lamination immersed in an one dimensional magnetic flux lattice with lattice spacing
is modulated into collective waves that obeys discrete Schr
dinger equation,
The wave function along
z-axis is assumed as plane wave
, since the gauge potential vector does not explicitly dependent on
z or
y. Substituting the plane wave function into the difference equation (
252) leads to the discrete Harper equation [
34],
In this topological representation theory, the effective magnetic field strength
B is quantified by the inverse of fractional filling factor
, i.e.,
. Then the discrete Harper equation with respect to fractional quantum Hall states with
reads
where
is the flux quanta. The fractional filling factor
is determined by the train track in the cross section plane
at
x,
The train track generated by a pair of antiparallel fluxes always leads to a rational filling factor,
. The wavelength of the oscillating lamination can exactly overlap an integral number of the lattice space between the two fluxes within one pair, generating a stable standing wave pattern crossing the unfolded lamination plane. In this case, the fractal energy spectrum of Hofstadter butterfly[
35] reduced to a collection of many pure fractional quantum Hall states, which matches knotted orbital in phase space [
12].
The fractional filling factor
is not always a rational number, irrational filling factors inevitably emerge when many fluxes (more than two) are braided in a hybrid combination sequence of clockwise or counterclockwise braidings. Irrational filling factors generates open train tracks in phase space, which has exact one-to-one correspondence with the fractal energy spectrum of Hofstadter butterfly [
35]. In real space, the open tracks match running plane waves that never coverage to standing wave. Three fluxes would be squeezed into one local bundle when magnetic field strength grows high enough. The electric lamination around the flux trimer generated superposition state of a number of different fractional Hall states.
Figure 45a shows the simplest initial lamination that single electron fluid layer passes the opposite one side of three nearest neighboring fluxes, No. 1, No. 2 and No. 3 alternatively. The combinatoric braiding operations,
(exchanging the location of fluxes No. 2 and No. 3 counterclockwisely) and
(exchanging the location of fluxes No. 1 and No. 2 clockwisely), is denoted by a product operator, i.e.,
, which maps the initial integral charge into a new distribution of fractional charges around the three fluxes,
The fractional charge passing underneath the
ithe flux is determined by
. The fraction Hall state around the flux trimer is not a pure fractional charged state, it is the superposition of three fractional states,
,
and
. For the most general case of
m-periods of operations of the braiding string operator
, the number of layers around the fluxes obey the following difference equation,
The difference Eq. (
257) is equivalently summarized into matrix formulation,
with the lamination distribution vector
and string operator
matrix defined as
where
is the constant initial lamination distribution. The fractional filling factors after
m times of actions of string operator
reads,
The total number of bonding layers bridging two nearest neighboring fluxes obeys the conservation law,
,
, which is governed by difference equation,
where
and
are constant initial number of layers at the input and output endings. The number of bonding layers obeys the matrix equation,
,
The eigenvalues of the bonding layer matrix
is
, with respect to golden ratio eigenvectors,
The total number of bonding layers grows asymptotically by
under each braiding operation of string operator
, which maps the initial single lamination into a heavily stacked mixed lamination, increasing the topological entropy of the electron fluid lamination. According to the topological chaos theory [
36], the entropy generated by each braiding operation of
is
The fractional charges determined by the filling factor Eq. (
260) finally converge to irrational charges dominated by the golden ratio.
A electron fluid lamination that is confined in two dimensional knot lattice of magnetic fluxes can fold in two independent directions around fluxes in
x- or
y-axis. The flux lines are kept straight without any bending operations during its parallel exchanging motion with another flux for simplicity.
Figure 45b shows the stacked lamination generated by braiding three fluxes in
x-axis under the string operator
, which first counterclockwisely exchanges the location of fluxes No.
and No.
) twice and then clockwisely exchanges the location of fluxes No.
and No.
twice. This braiding operation is implementable by designing a local distribution of magnetic field strength, such as two local magnetic dipoles oriented in antiparallel direction. The number of lamination layers around three fluxes in
x-axis is countable by the same analytical method in topological path fusion theory [
12]. In the limit of infinite number of braiding actions, the ratio of number of laminations above one flux to that below the flux finally converges to a stable value. The largest eigenvalue of the bonding layer between fluxes No.
and No.
is silver ratio
, correspondingly the number of lamination above and below the flux No.
reaches a maximal eigenvalue
and
[
12]. The fractional filling filling factor around the flux No.
is governed by Eq. (
260), in the limit of infinite number of braiding operations, Eq. (
260) yields
The local Hall resistivity around flux No.
is also irrational
The filling factors around fluxes No.
and No.
reaches the half-filling factor,
and
Therefore the local Hall resistivity varies from one flux to another when many fluxes are wrapped into one bundle by electron fluid lamination. If the initial single lamination is braided by hybrid string operator that involves both two directions simultaneously (
Figure 46), i.e.,
the area of the unit square confined by the four bonds:
,
,
and
, converges to
The topological entropy of folding lamination by parallel braiding operations is defined as
Substituting the limit area Eq. (
268) into the entropy Eq. (
269) yields
.
Figure 46.
The number of laminar layers around three magnetic fluxes in axis that over-crossing( or under-crossing) three magnetic fluxes in axis are labelled at the crossing points. The number of bonding laminations are labelled one the bonds of the square knot lattice.
Figure 46.
The number of laminar layers around three magnetic fluxes in axis that over-crossing( or under-crossing) three magnetic fluxes in axis are labelled at the crossing points. The number of bonding laminations are labelled one the bonds of the square knot lattice.
Figure 47.
(a) The unfolded lamination generated by braiding two perpendicular flux pairs in opposite chirality to that for generating the folded lamination in (b). (c) The folded lamination is summarized into two perpendicular bond carrying fractional fluxes. (d) The square lattice of fractional fluxes is generated by translating the unit cell in (c).
Figure 47.
(a) The unfolded lamination generated by braiding two perpendicular flux pairs in opposite chirality to that for generating the folded lamination in (b). (c) The folded lamination is summarized into two perpendicular bond carrying fractional fluxes. (d) The square lattice of fractional fluxes is generated by translating the unit cell in (c).
2.10. Fractional Hall conductance quantized by Chern number of folded lamination in three dimensions
The electron fluid lamination in homogeneous magnetic field is quantum fluid that obeys Schr
dinger equation. The magnetic fluxes in certain direction are all parallel to one another, folding the electron fluid monolayer into stacked flat laminations without buckling or concave (as showed in
Figure 47b). When the unit cell in
Figure 47b translates to fully cover a homogeneous square lattice of magnetic fluxes oriented in two perpendicular directions, the periodic electron fluid confined in x-y plane is described by a magnetic Bloch wave function
,
where the potential
is a periodic function in Schr
dinger equation above,
is the unit lattice space between two nearest neighboring fluxes. The Bloch wave functions
satisfy
. The four magnetic field lines around an unit square cell of unfolded lamination in
Figure 47b confines one
x-flux and one
y-flux, since each flux line segment is shared by two nearest neighboring unit cells. The Hamiltonian
is invariant under magnetic translations [
37],
Here the magnetic translation operator
(
) characterize the periodic distribution of magnetic flux lines oriented in
x-axis (
y-axis).The magnetic translation operators commute with Hamiltonian
.
Without losing generality, we first fold one unit cell in real space (the whole grey rectangular zone in
Figure 47a) by
times of parallel braidings on
x-flux pair (
y-flux pair), to generate a highly folded unit cell of lamination in
Figure 47b. The unit cell lamination in
Figure 47b is overlapped by
layers of stacked monolayers. Every monolayer within the unit cell lamination confines a pair of fractional flux quanta,
The square grid of perpendicular magnetic fluxes in
plane can be generated by choosing generalized Landau gauge
. Unfolding this heavily stacked unit cell lamination into a square array of many unit square monolayers in
Figure 47a extends the original unit lattice space to
The oscillating pattern of electron fluid lamination in the square grid is collective wave formed by intersecting plane wave two dimensions with lattice spacing
and
. Because every unit square monolayer in
Figure 47a carries a fractional flux quanta defined by Eq. (
272), the two magnetic translation operators along
are not commutable,
where the fractional flux within unit square monolayer of
Figure 47a is quantified by the product of two independent filling factors,
The magnetic translation operators over an enlarged unit square consists of
unit square monolayers are commutable,
because the extended unit cell confined by
and
contains two integral flux quanta
, guaranteeing the commutation relation
. The corresponding Bloch wave function on the periodic lattice of extended unit cells reads
The folding (or unfolding) operation in momentum space is exactly the inverse operation of that in real space. Folding the unit cell in real space leads to the unfolding of Brillouin zone in momentum space, because the absolute magnitude of reciprocal unit lattice vector is proportional to the inverse of unit lattice vector in real space. The reciprocal lattice space with respect to the unit cell in real space of
Figure 47a reads
which fulfills the reciprocal relation,
. When the large unit cell in
Figure 47a folds into a small unit cell with stacked lamination in
Figure 47b, the reciprocal unit cell lamination defined by
in momentum space is unfolded and expanded into a large reciprocal unit cell defined by
, covering
small reciprocal unit cells of the original size
. The inverse operation of unfolding the unit cell of stacked lamination in
Figure 47b into
Figure 47a compresses the Brillouin zone with momentum vectors
) into a smaller Brillouin zone with
.
The folding (or unfolding) operation of electron fluid surface is controlled by the effective magnetic field strength. A reduction of magnetic field strength results in corresponding increment on stack number of monolayers around the flux pair. On the contrary case, the stack number of monolayers is reduced with respect to an increasing magnetic field strength. Since folding (or unfolding) operation in real space results in exactly opposite topological effect to that in momentum space, the effective magnetic field strength in real space is the inverse of that in momentum space, i.e.,
In real space, the two fluxes in the same direction are placed in opposite domains of three dimensional space divided by the two dimensional electron fluid surface. Each of the
unit squares covering the unit cell in real space carries a fractional flux
, indicating a decreasing magnetic field strength as
and
grows. In the meantime, the unit square monolayer of Brillouin zone in momentum space folds into stacked unit lamination with
monolayers, resulting in an increasing magnetic field strength in momentum space as
and
grows. The Bloch band denoted by energy curves in unit cells of momentum space correspondingly splits into
stacked sub-bands in unit lamination of stacked Brillouin zones. The two perpendicular flux pairs divide the unit cell in real space into four sub-unit cells carrying four pairs of fractional fluxes respectively (
Figure 47a),
The sum of fractional fluxes in the same side of the electron fluid surface equals to two integral flux quanta,
. The
(
) layers of monolayers above the magnetic fluxes
and
(denoted by the yellow and red bold lines in
Figure 47a) generates fractional fluxes,
which locate at the horizontal and vertical bonds respectively in the folded unit cell (
Figure 47b-c). The two perpendicular flux pairs approaches to the middle lines of the rectangle when
, dividing the unit cell into four equal sub-unit cells filled by half flux quanta
.
When the square lattice composed of many uniform fractional flux pairs
is folded back to the unit cell with two integral fluxes in
Figure 47b, the collective state of electron fluid on the lattice of integral fluxes is described by magnetic Bloch state, which is a complex fibre bundle on base manifold of magnetic Brillouin zone,
The Hall current driven by external electric field
is derived by linear response theory [
22],
where the current operator is defined by the quantum momentum operator,
. The Hall current Eq.(
283) is reformulated into a brief commutator form
by renormalizing the two currents
with energy gaps
The Hall conductance tensor is the coefficient of electric current in response of external electric field,
,
which is exactly the familiar Berry curvature of magnetic Bloch states
which characterize the topology of the magnetic Brillouin zone, leading to a topologically quantized Hall conductivity by the first Chern number
n of the magnetic Brillouin zone [
22],
The Chern number
n is an integer in the magnetic Brillouin zone confined by
.
When the stacked unit cell in
Figure 47b is unfolded and expanded to a square lattice composed of many uniform fractional flux pairs
, the electrons hopping from one site to another in the unfolded square lattice gain fractional phases. Both the magnetic Bloch waves and magnetic Brillouin zone are squeezed into small Brillouin zone, however the Chern number is independent of this scale transformation,
whose value is exactly equal to the topological number in Eq. (
288). The area of Brillouin zone of the unfolded square lattice is
times of the stacked unit cell, i.e.,
Eventhough chiral braiding operation does not change the topology of Brillouin zone, but can split the magnetic Bloch waves into different propagation modes with opposite chirality. The unfolded square lattice are covered by chiral fractional fluxes
, which are defined by its location to the left (or right) hand side of the fluxes in
Figure 47. There are
Brillouin zones to the left hand side of flux
and
to the right hand side of
. The chiral edge states running along the edges of the two dimensional space only occupy the unit cells with the same chirality in the unfolded square lattice. As a result, the Chern number of whole Brillouin zone is decomposed into different fractions with respect to different chiral subzones,
The quantum Hall conductance is quantized by fractional topological numbers,
The fractional filling factors is determined by braiding string operator. For the square lattice of chiral fractional fluxes in
Figure 47, the fractional Hall conductance explicitly reads
where
is the braiding period number in
-axis.
The eigenenergy with respect to certain fractional Hall conductance can be derived from Harper equation [
34]. The collective wave function of the folded electron fluid lamination obeys two dimensional discrete Schr
dinger equation,
which is a generalization of the discrete Harper equation for electrons immersed in homogeneous magnetic field in
z-axis [
34]. Here the effective magnetic field strength
B is quantified by the inverse of fractional filling factor
, i.e.,
. Then the discrete Harper equation with respect to fractional quantum Hall states with
reads
The train track generated by a pair of antiparallel fluxes always leads to a rational filling factor,
. The wavelength of the oscillating lamination can exactly overlap an integral number of the lattice space between the two fluxes within one pair, generating a stable standing wave pattern crossing the unfolded lamination plane. The fractal energy spectrum of Hofstadter butterfly[
35] reduced to a collection of pure fractional Hall fluid states, which matches knotted orbital in phase space [
12].
The Berry curvature acts as an effective magnetic field, attracting an electron to circle around a local extremal point of curvature in momentum space [
37],
where
is an uniform electric field. The tensor equation of motion for electron in three dimensional electric field is
A closed orbit of a moving electron in real space corresponds to a rescaled closed orbit in momentum space that is rotated by
. The physical effect of curvature tensor
is equivalent to an effective magnetic field in momentum space, generated by symmetric gauge potential vectors in three perpendicular directions,
The effective Hamiltonian for Schr
dinger equation in three dimensional magnetic field
is
where
is effective mass of electron in lattice. The covariant derivative operators are
The Berry curvature in three dimensional momentum space is quantized by the Chern number of curvature tensor
in an unfolded three dimensional reciprocal lattice with respect to the folded unit cell in real space,
When the two dimensional unit cell confined by
are folded into stacked unit lamination defined by
, the three dimensional Brillouin zone expands to a large Brillouin zone with reciprocal unit lattice spaces
A train track in real space is also mapped into a rescaled train track in momentum space. The train track pattern in the cross sectional plane perpendicular to fluxes in
x-axis (and
y-axis) defines a chiral fractional flux
(and
) and fractional unit lattice space,
The fractional quantum Hall conductivity with respect to train tracks in
(and
) plane is
(and
),
The fractional Hall conductance tensor above coincides with the Hall conductance coefficient derived from the classical Drude model in three magnetic field (See Appendix A), which also predicts the diagonal resistivity
.
2.11. The collective wave function of 3D fractional quantum Hall states represented by quaternions
If the magnetic fluxes are all located on the same side of the laminar surface, no matter how many times the fluxes lines exchange, the laminar surface is not really folded and can always restore its original unfolded configuration. Therefore the magnetic fluxes split into two separated sets in the simply connected space that is divided by the laminar surface. The plane of two dimensional knot lattice could be oriented to be parallel to the laminar surface. Once a flux that is perpendicular to the laminar surface is introduce to the two dimensional knot lattice, it inevitably penetrates through the laminar surface, driving the electron fluid to flow around itself in a helical path, until a worm hole is finally formed to connect two separated laminar surfaces (the blue surface and red surface in
Figure 48a). Many fluxes are topologically equivalent to many genus of a continuous manyfold (
Figure 48a). In fact, electron fluid lamination can also construct multiply connected surfaces that envelopes the two dimensional lattice completely (
Figure 48b). In that case, even if all magnetic fluxes are locked inside the multiply connected surface, braiding magnetic fluxes in parallel still generates non-trivial folding, which demonstrates the same train track pattern as bare flux knot lattice. The multiply connected surface that envelopes three dimensional knot lattice is generated by cutting two holes at the north pole and south pole of the sphere centered at a crossing point (
Figure 48c), with the equatorial plane overlaping with the plane of two dimensional knot lattice. Three mutually perpendicular fluxes overcross (or undercross) at this crossing point, constructing different local knot configurations. All possible crossing states can be characterized by the relative location vector of projecting the other two fluxes along two different axis to certain flux along the third axis [
12],
The normalized vector
is Ising spin in three dimensions. Besides the eight different crossing states, there are still many vacuum states composed of self-avoiding flux arcs connecting the face centers at different axis and many hybrid states with two vacuum arcs and one crossing flux [
12].
Here we introduce Hamilton quaternion to characterize a general crossing state of three magnetic fluxes in knot lattice. As showed in
Figure 48c, a general magnetic flux vector is expanded by quaternion basis
,
where
, and
,
,
.
is an unit number. The Pauli matrices for spin
is a natural matrix representation of quaternion,
,
,
. This quaternion flux vector exactly characterizes the spin Eq. (
304) due to the anti-commute relations,
The quaternion representation of the vacuum state composed of vortex arc pair and a straight flux line has a similar formulation as following
The full vacuum state composed of three vortex arcs has the following form,
Exchanging the locations of two fluxes maps an over-crossing state to an under-crossing state (or vice versa), flipping a local spin from
S to
. In
Figure 48c, all magnetic fluxes are fully enveloped within the multiply connected electron fluid surface, braiding fluxes does not change the topology of the laminar surface. Therefore the fractional quantum Hall states in the cross section of the multiply connected laminar surface still matches the abelian Chern-Simons field theory, which is described by the effective wavefunction of Wen-Zee matrix formulation [
17].
When the electric tubular surfaces that envelope magnetic fluxes in different axis avoid intersecting with one another, as showed in
Figure 48d, the highly degenerated collective Hall states in three dimensions split into many sub-states which is characterized by crossing states of flux knot lattice. The surface state on the boundary surfaces of finite three dimensional knot lattice is fractional quantum Hall state. When the flux tubes are braided in parallel, the boundary state is identical to any cross-sectional state in the bulk.
Figure 48e showed the stacked lamination after braiding two fluxes in parallel that belong to two separated enveloping tubular surfaces once, the train track pattern on the top and bottom plane corresponds to fractional charge states
.
m times of braiding operations leads to the fractional filling states (
) on the top and bottom boundaries. Parallel braiding is physically implementable by homogeneous magnetic field strength in three perpendicular directions. The fractional states around the eight corners of the cubic knot lattice obey non-abelian statistics [
12]. The abelian Chern-Simons field theory is inadequate to describe the electron fluid flowing along the tubular surfaces in knot lattice, the non-abelian Chern-Simons field theory has to be introduced to establish an effective topological field theory [
15] for the 3D knot lattice of quantum Hall fluid,
where
is the gauge field potential in the tubular surface, and is expanded by the generators of
group (i.e.,
).The hierarchy construction of abelian Chern-Simons Lagrangian for fractional quantum Hall state is extended to non-abelian Chern-Simons theory in a straightforward way,
The Wen-Zee wavefunction for abelian quantum Hall states is constructed in complex plane with locations of electron denoted by complex number
[
17]. In mind of the exact correspondence between quaternion and Pauli matrices, the spatial locations of electrons in three dimensional knot lattice of electric tubular surface can be denoted by quaternions,
In order to construct the wavefunction in three dimensions, the complex variable of locations is extended to quaternions. The effective collective wavefunction with respect to non-abelian Chern-Simons theory is generalized as
In abelian Chern-Simons theory for fractional quantum Hall states, the filling factor Eq. (
79) equivalently maps the fractional filling factor constructed by Wen-Zee formulation into a fraction of linking number of magnetic flux knot lattice. The topological quantum field theory suggested that non-abelian Chern-Simons action is also a topological invariant of link [
15]. The topological linking number of a three dimensional knot lattice is directly countable by projecting every crossing point of three mutually perpendicular tubes into the same two dimensional plane, the projected locations of crossing points must be carefully arranged to avoid overlapping.
Figure 48f showed an exemplar projection of crossing point in three dimensions into a knot configuration in two dimensional plane, which has a linking number
Every local crossing point is characterized by an unique spin state,
, which has one-to-one correspondence with linking number
. Thus the total linking number of the knot lattice is the sum of all local crossing states,
. The total linking number is invariant with respect to an eigenstate. The knot lattice configuration of electron fluid tubes can be reconstructed under thermal fluctuations. The partition function of all possible knot lattice configurations is a topological invariant.
The effective collective wavefunction Eq. (
312) determines the spatial probability distribution of an electron within certain branch of train tracks
where
and
. This probability distribution is reformulated into a Boltzman distribution form by introducing an analogue potential
. Similar to the partition function in statistical physics, the analogue partition function for many electrons is effectively defined by the product of probability distribution of all electrons confined in the train track pattern
The analogue potential of Hall fluid has a similar form of harmonic oscillator potential
, the first two terms at the right hand side of Eq. (
315) summarizes the interaction between parallel electric current segments within a stacked train track pattern, while the third term is a parabola potential well that generates quantized energy levels with equal energy gap, which reflected the physical effect of a homogeneous magnetic field. The effective potential surface deformed into a hyperbolic surface when the electron approaches to the edge.
The locations of electron flowing in the tubular knot lattice is expressed by Pauli matrices to encode the non-abelian nature of three dimensional knot lattice,
The interaction potential between two parallel electric currents and parabola potential well are spontaneously constructed within this non-commutative space,
The coefficients in front of
are collected and summarized into a function
to derive a compact formulation of analogue potential for Hall fluid in three dimensions,
This potential is consistent with the non-abelian Chern-Simon action Eq. (
309), which transforms into similar form as Eq. (
318). The analogue potential
regrouped the energy levels into two energy bands,
The energy gap between two bands
is finite in the bulk, but drops to zero on the edge,
The landscape of effective potential for fractional quantum Hall effect in
Figure 30 is a qualitative visualization of the analogue potential
. In real space, the energy gap closes when the incompressible lamination is penetrated through by magnetic flux lines perpendicular to the folding plane of lamination. Every gap closing point, locating at the solution of
, is characterized by a topological winding number, that counts how many times the unit vectors
winds around the origin point,
Duan’s topological current theorem [
21] suggests that the sum of these local winding numbers equals to the first Chern number of base manifold,
where
is Dirac function,
is the winding number around the
ith energy gap closing point of
.
is the Jacobian of vectorial energy space in real space. The topological vortices locate at the solution of
. There are
m energy gaps closed on the edge with respect to fractional filling factor
, with the energy gap
ruled by the energy Eq. (
198).
The Chern number is an integer as the sum of winding numbers of all singular points, either circling around by clockwise flows or counterclockwise flows, it is independent of the chirality of circling motion around singular points. However, the action of magnetic field breaks time reversal symmetry, only the circling flows with the same fixed chirality are allowed to transport along the edge, the edge flow with opposite chirality are eliminated out of conductivity measurement. The gapless points on the left (right) edge are denoted as
(
), the complete Chern number is the sum of the chiral winding numbers,
The viscous electron flow can only passes one of the two edges in FQHE due to the far distance between them, the measurable chiral Chern number on edge is a fraction of the whole Chern number,
where
is a polynomial of the chiral filling factors. When the transformation operation between different knot states in three dimensional knot lattice are taken into account [
11], the fractional Hall conductivity are quantized by the second Chern number as well as higher order Chern numbers.
The knot lattice of magnetic fluxes generates non-abelian magnetic field in three dimensions. We choose a special symmetric gauge potentials along the knot of magnetic flux tubes and expanded it by quaternions,
The effective magnetic field
with respect to the gauge potential vector above reads
, which is replaced by non-abelian gauge field tensor
in knot lattice,
The abelian magnetic field
corresponds to the gauge field tensor
,
The first term on the right hand side of Eq. (
327) represents the abelian magnetic field, which reduces to
in the absence of quaternion representation of knot. The rest three terms represents the non-commutative character magnetic fluxes in knot lattice. The magnetic field in
z-axis is influenced by the product of
. The magnetic fields in the other two directions both join in the gauge field tensor. The highly entangled magnetic field components results in complex relation between Hall resistivity and magnetic field. The current tracks form closed loops under periodical boundary condition. The gauge field tensor alone these loop tracks is periodical function, which transform into brief formulation under Fourier transformation,
The Hall conductance tensor in the chiral Brillouin zone is fractional number determined by laminar folding of momentum space,
The fractional Hall conductance tensor in three dimensional knot lattice of magnetic fluxes includes nonlinear terms denoted by the product of four fractions. These higher order contribution is much smaller than the dominant fractional terms denoted by the product of two fractions in Eq. (
329), which is also much smaller than the Hall conductance in two dimensions, because the contacting area between viscous laminations is much larger than that between viscous paths in two dimensions. Therefore the fractional Hall conductance in three dimensions hard to detect. More over, the non-abelian fractional Hall conductance tensor can be extended to four dimensional space time, where the Hall conductance is quantized by the second Chern number. The fractional Hall conductance in four dimensions is composed of product terms of eight fractions. Viscous electron flow swirls around a singular time line in curved space time. The three dimensional fractional filling factors predicted here is testable by quantum Hall system in a tilted magnetic field, which is well developed both in theory [
38] and experiment.