Stochastic Extensions of the Elo Rating System

1. Introduction

Rating systems track and predict the performance of competitors in pairwise zero-sum games. They were initially developed to objectively measure the strength of chess players, with the first successful system proposed by Arpad Elo in 1960, and adopted by the United States Chess Federation (USCF) adopted it to replace the more problematic Harkness rating system. The International Chess Federation (FIDE) also started publishing ratings of its players in 1970, and continues to publish them today. The Elo rating system, or variants of it, are also used by most chess websites, where users are automatically matched against other players of similar strength, as well as by federations of go and scrabble players, and several videogames.

The motivation, mathematical basis and problems of the elo rating system are explained in detail in Elo’s book [2], and the academic literature is summarized in [1]. The system gives each player a real parameter called their rating, and defines an algorithm to update it with the result of each new game. Winning a game increases the player’s rating, and losing decreases it, but the increase depends on the rating of the rival. This allows for the ratings to change as the strength of the players also does. More sophisticated systems like glicko, proposed by Mark Glickman [3], include two parameters for each player, representing the strength and its variability, to allow for players gaining strength more quickly than others.

In his thesis, Glickman also extends Elo ratings to sports like American Football to make predictions about the score (not just the result), and more recently, the idea of applying elo ratings to team sports has gained popularity. For instance, fivethirtyeight.com has been keeping computing the ratings of NBA teams since 2014, and other websites like eloratings.net do the same for national soccer teams.

Our contributions are a more formal study of the model underlying the Elo system, with a few results regarding unbiased estimators for the ratings that are used in our computational analysis of league games. We derive how the natural extension of the Elo model for games involving a scoreboard can be used to predict the result during the game, and develop a systematic system for evaluating different systems.

Finally, we show how a discrete stochastic process can be used to model the score, and integrated into a novel type of Elo rating system. For comparison, we implement the rating system behind Nate Silver’s soccer-specific SPI ratings, and show that our system has similar predicting power for the result of the games, despite only tracking one parameter for each team.

The remainder of this paper is organized as follows: Section 2 recalls the main aspects of the (static) Elo rating system. The proposed stochastic extensions of the Elo system are then introduced in Section 3. Their performance at predicting the results of team sports, namely basketball and soccer, is analyzed through the computational study presented in Section 4. Finally, Section 5 is devoted to shed conclusions and expose possible lines of future work.

2. Preliminaries

Although the Elo system has been extensively studied, it’s worth going through its mathematical and statistical basis in order to see how its assumptions can be extended to stochastic processes later. We also go through some basic accuracy metrics that can be used to asses its performance, and a statistical estimator to obtain ratings for players without a preexisting rating.

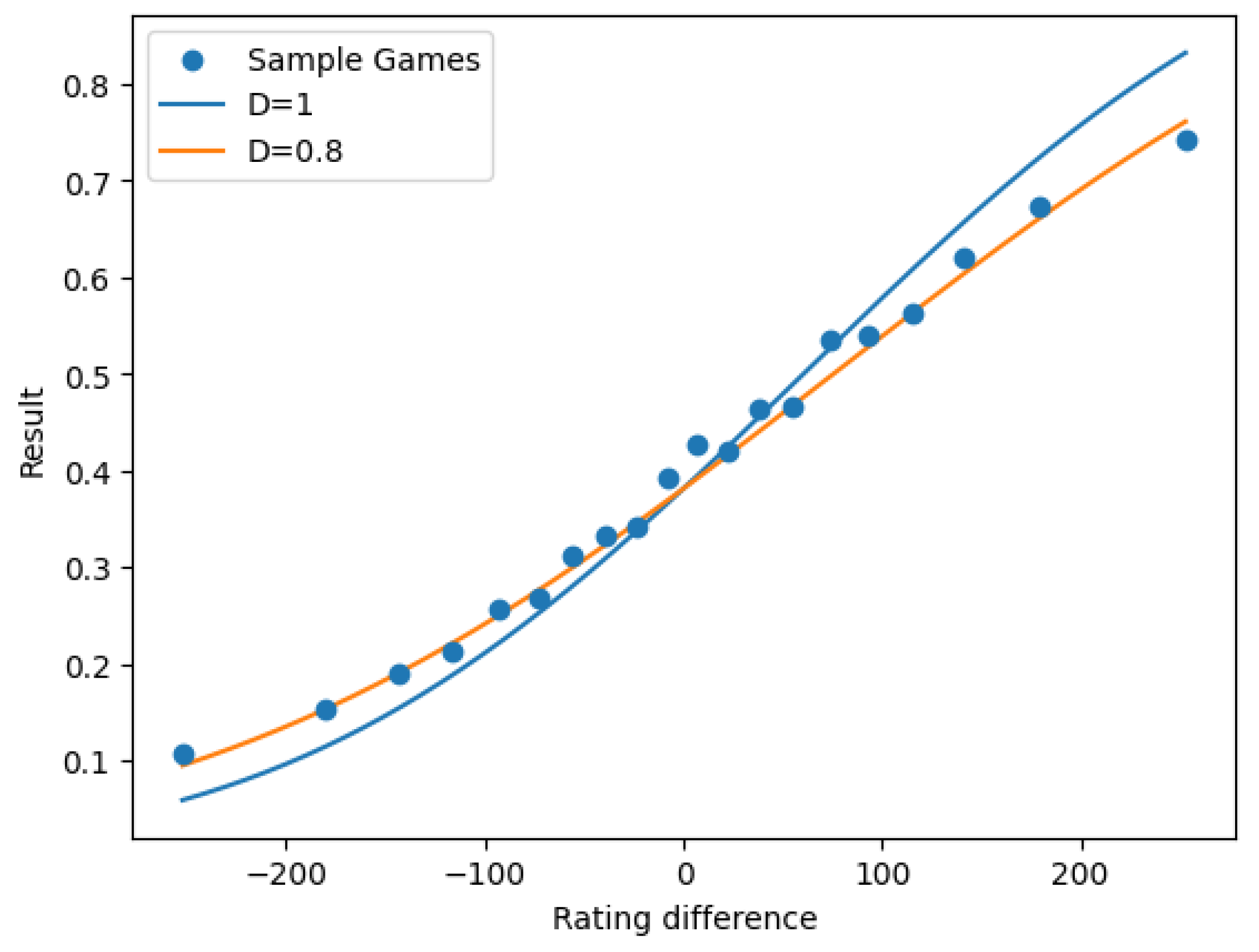
2.1. The Elo Rating System

Elo’s rating system assumes that in a game between two players A and B, the result can be expressed giving points $p_A,p_B\in [0,1]$ to A and B respectively so that $p_B+p_A=0$. The most simple case is a game with two results, in which $p_A$ is 1 if A wins and 0 if B wins, but in chess, a draw is represented by $p_A=p_B={\displaystyle \frac{1}{2}}$, since, in traditional chess tournaments, the player with the higher number of wins plus half the number of draws wins. Then, if A and B respectively have Elo ratings $r_A$ and $r_B$, the updated ratings after the game are given by

$$r_A^{\prime }:=r_A+K(p_A-\mathbb{E}\left[p_A\right|r_A,r_B])\mathrm{and}{r}_B^{\prime }:=r_B+K(p_B-\mathbb{E}\left[p_B\right|r_B,r_A])$$

(1)

where $\mathbb{E}\left[p_A\right|r_A,r_B]$ is the expected score of player A in a game against B, given by

$$E\left[p_A\right|r_A,r_B]:={\mathbf{F}}_X(r_A-r_B)$$

(2)

Here, K is a positive constant, and ${\mathbf{F}}_X$ is the distribution function of some random variable X with mean zero. The distribution function of X must also be symmetrical around zero so that $\mathbb{E}\left[p_A\right|r_A,r_B]+\mathbb{E}\left[p_B\right|r_A,r_B]=1$. X was originally a normal variable, but it was later changed to follow a logistic distribution in the FIDE’s ratings. This has been argued to produce better predictions [2], and it also leads to an explicit and more meaningful expression for $\mathbb{E}\left[p_A\right]$. In fact, sometimes the update rule is given simply as

$$r_A^{\prime }:=r_A+K\left(p_A-{\displaystyle \frac{1}{1+e^{c(r_A-r_B)}}}\right)=r_A+K\left(p_A-{\displaystyle \frac{a^{r_B}}{a^{r_B}+a^{r_A}}}\right)$$

(3)

for some $c=log\left(a\right)\in {\mathbb{R}}^{+}$.

Figure 1. Expected score versus rating difference.

Figure 1. Expected score versus rating difference.

It’s also possible to update the ratings with the results of a set of matches (for instance the results of a tournament). Given a sample $M=\{m_k=(a_k,b_k,p_k^a,p_k^b)\}$ of matches with n intervening players $i=1,\dots ,n$, where the k-th match is between players $a_k$ and $b_k$ and ends with scores $p_k^a$ for $a_k$ and $p_k^b=1-p_k^a$ for $b_k$, and given initial ratings $R:=(r_1,r_2,\cdots ,r_n)$, we similarly compute:

$$r_i^{\prime }:=r_i+K·\sum _{k|a_k=i}\left(p_k^a-\mathbb{E}\left[p_k^a\right|R]\right)+K·\sum _{k|b_k=i}\left(p_k^b-\mathbb{E}\left[p_k^b\right|R]\right)$$

(4)

Obviously, if a player outperforms their expected score, his rating increases, and otherwise it decreases, but the total sum of ratings doesn’t change, as we will see later. However, before discussing the update rule, we need to review the model where the expected score originally comes from, which we will refer to as the static Elo model.

2.2. Basis of the Static Elo Model

The difficulty in rating chess players versus, for instance, olympic runners, is that in the latter sport there is a magnitude, the finish time, which doesn’t depend on the rivals. For instance, taking a weighted mean of the latest times of each athlete would be enough to compare them, and objectively establish which are better and by how much.

However, Elo considers [2](ch. 8.23) what happens if we don’t know the finish times, and can only compare athletes by looking at who finishes first in head to head races. If the finish times of runners A and B follow distributions $T_A\sim N({\mu }_A,{\sigma }^2)$ and $T_B\sim N({\mu }_B,{\sigma }^2)$, and are independent, then:

$$\mathbb{P}\left[A\mathrm{wins}\right]=\mathbb{P}[T_A<T_B]=\mathbb{P}[T_A-T_B<0]=\Phi \left({\displaystyle \frac{{\mu }_B-{\mu }_A}{\sqrt{2{\sigma }^2}}}\right)$$

(5)

In general, if the times follow the same continuous distribution Y with different means, i.e. $T_A\sim Y+{\mu }_A$ and $T_B\sim Y+{\mu }_B$, we can define $X=T_A-T_B+{\mu }_B-{\mu }_A$ and

$$\mathbb{P}\left[A\mathrm{wins}\right]=\mathbb{P}[T_A-T_B<0]={\mathbf{F}}_{T_A-T_B}\left(0\right)={\mathbf{F}}_X({\mu }_B-{\mu }_A)$$

(6)

which is exactly Eq. (2) for $r_i=-{\mu }_i$ (note that the lower the time, the better the athlete, and the higher the rating should be). Also, by definition X has mean zero and follows a symmetrical distribution. Therefore, Elo’s system simply tries to estimate those underlying means ${\mu }_A,{\mu }_B$ from several match results and a given ${\mathbf{F}}_X$.

It also follows that ${\mathbf{F}}_X({\mu }_A-{\mu }_B)={\mathbf{F}}_X(({\mu }_A+h)-({\mu }_B+h))$, so the ${\mu }_i$ can only be determined up to addition of a constant (we can only estimate their pairwise differences). Finally, ${\mathbf{F}}_{\lambda X}\left(\lambda {\mu }_A-\lambda {\mu }_B\right)={\mathbf{F}}_X\left({\mu }_A-{\mu }_B\right)$, so scaling X doesn’t affect the model either (only scales the ratings). This means that both the average of the ratings and the variance of X are an arbitrary choice, and only the shape of ${\mathbf{F}}_X$ affects the behavior of the model.

Traditionally, 1500 is chosen as the average rating [1](p. 621) although Elo’s initial choice was 2000 as the midpoint and ${\sigma }_X=200\sqrt{2}\approx 282.84$[2](ch. 8.21). This was replaced by the logistic distribution ${\mathbf{F}}_X\left(x\right)={\left(1+{10}^{x/400}\right)}^{-1}$, which has a similar standard deviation of ${\displaystyle \frac{400\pi }{log\left(10\right)\sqrt{3}}}\approx 315.09$.

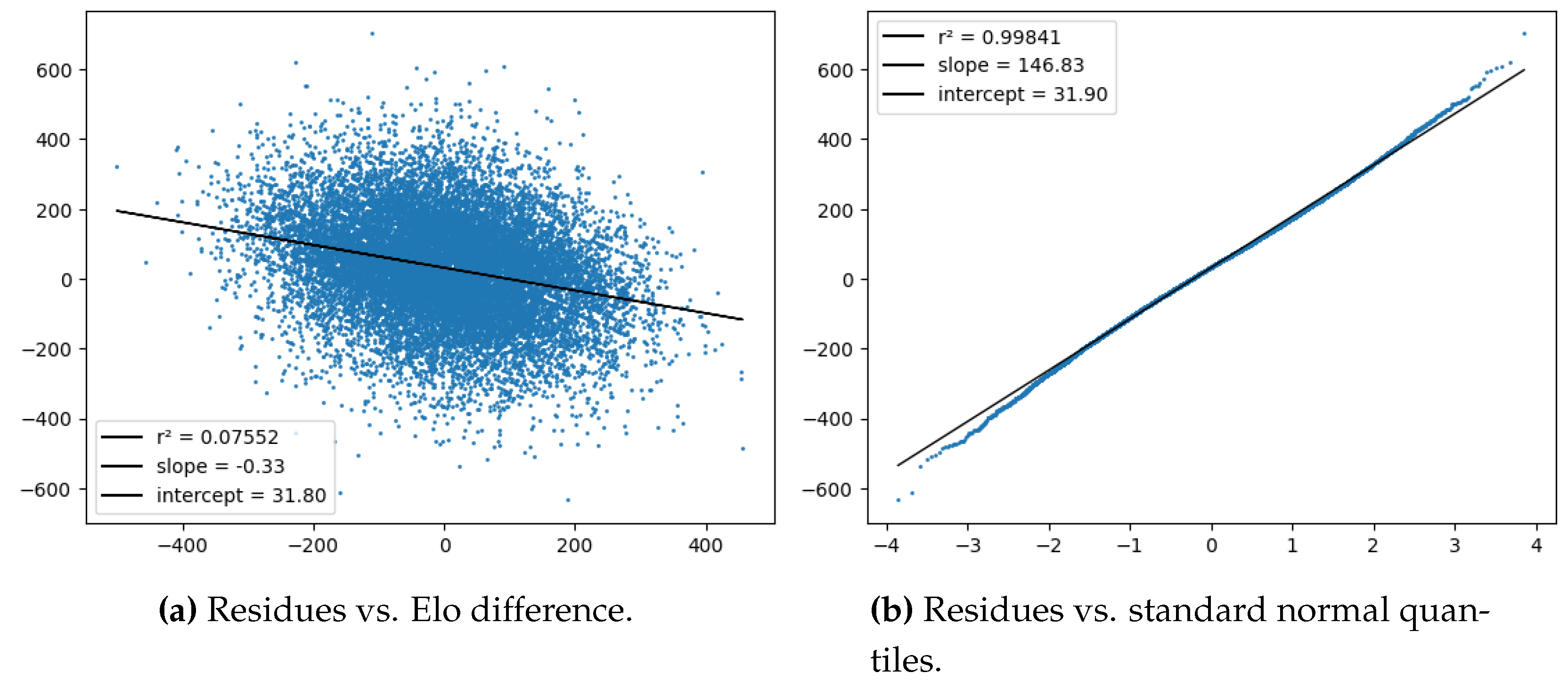
2.3. Statistical Inference in the Static Model

For the model presented above, the next logical step is to estimate the ratings of the players given a sample of matches (for instance a tournament). Again, we denote the sample by $M=\{m_1,\cdots ,m_{\left|M\right|}\}$ with $m_k=(a_k,b_k,p_k^a,p_k^b)$, and if player i played match k, we will use as shorthand $p_{i,k}=p_i^a$ if $i=a_k$ and $p_{i,k}=p_i^b$ if $i=b_k$. We also denote the indices of games played by j with $M^j:=\{1\le k\le |M|:j=a_k\mathrm{or}j=b_k\}$. Then, an interesting estimator $\widehat{R}=({\widehat{r}}_1,\cdots {\widehat{r}}_n)$ is the one that reduces to zero the errors ${\epsilon }_j$ defined by

$${\epsilon }_j(M,\widehat{R}):=\sum _{k|a_k=j}(p_k^a-\mathbb{E}\left[p_k^a\right|\widehat{R}])+\sum _{k|b_k=j}(p_k^b-\mathbb{E}\left[p_k^b\right|\widehat{R}])=:\sum _{k\in M^j}(p_{j,k}-\mathbb{E}\left[p_{j,k}\right|\widehat{R}])$$

As we will see later, this estimator is related with the adjustment formula in Eq.(4), and in particular, if it exists, it’s a fixed point when adjusting with that same sample M:

$${\widehat{r}}_j={\widehat{r}}_j^{\prime }={\widehat{r}}_j+K\sum _{k\in M^j}(p_{j,k}-E\left[p_{j,k}\right|\widehat{R}])⟺0=\sum _{k\in M^j}(p_{j,k}-E\left[p_{j,k}\right|\widehat{R}])={\epsilon }_j$$

In fact, given a sample with n players, there are $n-1$ errors to minimize (since they add up to zero) and $n-1$ ratings to adjust (since the sum doesn’t matter), so we should expect the estimator with zero error to be unique, and thus the only fixed point of the adjustment formula. In Appendix A, we characterize it’s existence and prove uniqueness in the case that it exists. Convergence is easy to see for the case of two players i and j, because if the results of a game follow Elo’s model, i.e. Eq.2, and ${\widehat{r}}_j^m,{\widehat{r}}_i^m$ are the estimators produced by the sample of the first m games, then by the law of large numbers

$${\epsilon }_j=0\Rightarrow {\mathbf{F}}_X({\widehat{r}}_j^m-{\widehat{r}}_i^m)={\displaystyle \frac{1}{m}}\sum _{k=1}^m{\mathbf{F}}_X({\widehat{r}}_j^m-{\widehat{r}}_i^m)={\displaystyle \frac{1}{m}}\sum _{k=1}^m{p}_{j,k}\underset{m\to \infty }{\overset{a.s.}{\to }}E\left[p_{j,k}\right]={\mathbf{F}}_X(r_j-r_i)$$

and since ${\mathbf{F}}_X$ is continuous and has an inverse, ${\widehat{r}}_j^m-{\widehat{r}}_i^m$ converges to $r_j-r_i$. Note that if the average estimated rating is the same at every step m, then ${\widehat{r}}_j^m\underset{m\to \infty }{\overset{a.s.}{\to }}{r}_j+C$ for every j. Therefore, when we look for numerical methods to compute it, it makes sense to keep the average ${\displaystyle \frac{1}{m}}{\sum }_{j=1}^n{\widehat{r}}_j$ constant, and only worry about convergence of the pairwise differences.

Finally, there’s another natural way to estimate the ratings for a sample, if X is a logistic variable and there are only two results in the game ($p_A\in \{0,1\}$). In that case, the sample can be encoded as a set of independent variables $X^1,...,X^n$ where $X_k^j=1$ if $j=a_k$, $X_k^j=-1$ if $j=b_k$, and otherwise (if $k\notin M^j$) $X_k^j=0$. The static model then gives

$$\mathbb{P}(p_k^a=1)=\mathbb{E}\left[p_k^a\right]={\mathbf{F}}_X(r_{a_k}-r_{b_k})={\mathbf{F}}_X\left(\sum _{j=1}^n{X}_k^j{r}_j\right)={\displaystyle \frac{1}{1+e^{\lambda {\sum }_{j=1}^n{r}_j{X}_k^j}}}$$

(7)

which is precisely the formula of the logistic regression of $Y:=(p_k^a:1\le k\le m)$ against X. Since $\lambda$ only depends on the variance of the distribution, and the choice of variance doesn’t affect the model, we can just estimate $r_1,\cdots r_n$ by doing a logistic regression in the $X^j$.

2.4. Basis of the Elo Adjustment Formula

So far we have worked assuming Eq.(2) holds and each player has a constant "true" rating $r_j$. However, in practice the strength of chess players or soccer teams changes over time, and hence the need for a system that updates the ratings with each new game and not with the whole history.

This is the reasoning behind the update formula in Eq.(1): if we consider only one match between A and B, with estimated ratings ${\widehat{r}}_A,{\widehat{r}}_B$ and real ratings $r_A,r_B$ (and for simplicity we pick ${\widehat{r}}_A+{\widehat{r}}_B=r_A+r_B=0$), then using Taylor’s expansion, $\exists \xi \in \mathbb{R}$ such that

$$\mathbb{E}[{\widehat{r}}_A^{\prime }-{\widehat{r}}_A]=K·\mathbb{E}[p_A-{\mathbf{F}}_X({\widehat{r}}_A-{\widehat{r}}_B)]=K·{\mathbf{F}}_X\left(2r_A\right)-K·{\mathbf{F}}_X\left(2{\widehat{r}}_A\right)=2K(r_A-{\widehat{r}}_A)f_X\left(\xi \right)$$

Therefore, for small enough K, in particular for $K<{\left(2{max}_{x\in \mathbb{R}}{f}_X\left(x\right)\right)}^{-1}$, this gives

$$|\mathbb{E}[{\widehat{r}}_A^{\prime }-r_A]|=|\mathbb{E}[{\widehat{r}}_A^{\prime }-{\widehat{r}}_A]+{\widehat{r}}_A-r_A|=|1-2Kf\left(\xi \right)\left|\right|{\widehat{r}}_A-r_A|<|{\widehat{r}}_A-r_A|$$

and thus if $r_A$ is fixed, $E\left[{\widehat{r}}_A\right]$ converges to $r_A$ as ${\widehat{r}}_A$ is updated over an increasing number of games. In practice, K is chosen much smaller than ${\displaystyle \frac{1}{2maxf\left(\mathbb{R}\right)}}$ - for instance, FIDE uses $K=10$ for players with ratings above 2400, and in this case ${\mathbf{F}}_X\left(x\right)={\displaystyle \frac{1}{1+{10}^{-x/400}}}$ so a better K for accelerating the convergence of the expectancy would be ${\displaystyle \frac{1}{2f_X\left(0\right)}}={\displaystyle \frac{4·400}{2log\left(10\right)}}\approx 347$.

The reason for the difference is that faster convergence is at the expense of a much higher variance of ${\widehat{r}}_A^{\prime }$ (the variance is proportional to $K^2$). If we apply the update formula over an infinite number of games, even if the true ratings of the model stay constant, the computed ratings don’t converge, and they approach a limiting distribution [5], the variance of which we would like to minimize.

Therefore, the choice of K depends on the dynamic properties of the strength of the players. If we expect this strength to change significantly from one game to the next, K should be bigger, and if we expect the skill of the players to be relatively stable (for instance, if many games are played in a small lapse of time), we choose a lower K. The FIDE uses $K=40$ for younger players, who may improve quickly, and $K=10$ as said above for players with rating above 2400, which are usually grandmasters and don’t improve their play that fast.

2.5. Asymmetric Games

Until now we have assumed that for two players of equal strength each has expected score $1/2$, but in practice this is not true: in chess, for instance, the player with white pieces makes the first move, and has a slight advantage. In the team sports we will consider later, it is well known that if a team plays in the home field, it also has an advantage over its rival. To incorporate this in the Elo rating system, when A has a systemic advantage against B, we can use the following expectancy formula [3][p. 36]:

$$\mathbb{E}\left[p_A\right]={\mathbf{F}}_X(r_A-r_B+L)=1-{\mathbf{F}}_X(r_B-r_A-L)=1-\mathbb{E}\left[p_B\right]$$

(8)

Here, L is a positive constant, which should obviously be bigger for a bigger advantage of A, since $\mathbb{E}\left[p_A\right]$ is increasing in L, and $L=0$ reduces to our symmetric model. We can estimate it given a sample of matches, provided of course that we know which player has the systematic advantage in each match. From now on, we suppose that in the k-th match $m_k=(a_k,b_k,p_k^a,p_k^b)$ of a sample M, $a_k$ has the advantage. In particular, if X is logistic, L can be estimated as the independent term in the regression formula in Eq.(7).

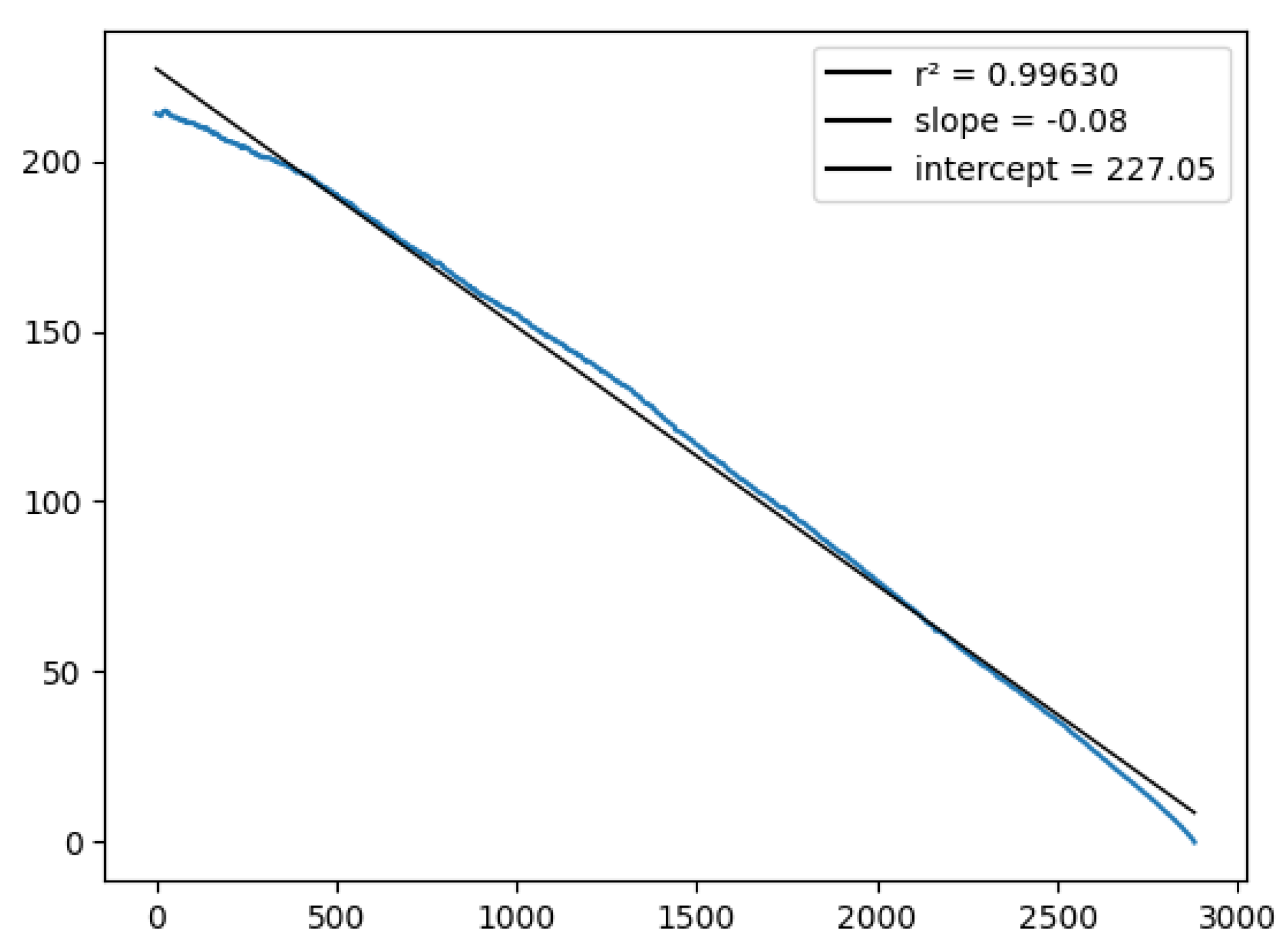
2.6. Accuracy Metrics for Elo Rating Systems

In order to determine the predictive accuracy of a rating system, we will use several tools. The first one, provided by Arpad Elo [2], is a statistical test of normality for a sample in which the players have preexisting ratings R and each player plays m games. Originally the sample was a chess tournament, or a set of tournaments with the same m [2].

Elo proposes to represent the values of the residues ${\epsilon }_j\left(R\right)$ in a histogram and to compare them with the frequencies of a normal variable with mean 0 and the sample variance. Since ${\epsilon }_j\left(R\right)={\sum }_{k\in M^j}\mathbb{E}\left[p_{j,k}\right|R]$ is the sum of m variables, if m is high enough and the rating differences aren’t too high, by the CLT, each ${\epsilon }_j$ should approximately follow a normal distribution, with variance ${\sum }_{k\in M^j}\left(p_{j,k}\right|R)\le {\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\sqrt{m}$. More sophisticated normality tests, like the normal probability plot, can be carried out for the same variables.

In order to compare the accuracy of different systems in the same sample, we propose looking at the average of the squared residues across all matches, i.e. the mean squared error of p:

$$MSE:={\displaystyle \frac{1}{\left|M\right|}}\sum _{k=1}^{\left|M\right|}{\left(p_{a_k,k}-E\left[p_{a_k,k}\right|R]\right)}^2$$

(9)

We can decompose this sum using the known expression of the mean square error, which is the square of the bias plus the mean variance:

$$E\left[{(X-a)}^2\right]={(E\left[X\right]-a)}^2+Var\left(X\right)$$

(10)

In particular, when applied to the results of the games, we obtain:

$$MSE={\displaystyle \frac{1}{\left|M\right|}}\sum _{k=1}^{\left|M\right|}{\left(E\left[p_{a_k,k}\right]-E\left[p_{a_k,k}\right|R]\right)}^2+{\displaystyle \frac{1}{\left|M\right|}}\sum _{k=1}^{\left|M\right|}Var\left(p_{a_k,k}\right)$$

(11)

The advantage of this measure is that we don’t require any of the assumptions of a normality test. The sample can be extended in time (we can update the ratings between games using Eq.(1)) and we don’t need every player to play the same number of games. Also, if we apply two different rating systems to the same number of games, we can look at the variance reduction and extrapolate p-values to determine if one system is better than other.

However, unlike in a linear regression model, the results $p_k^a$ don’t have a constant variance, so the expression $MRV:={\displaystyle \frac{1}{\left|M\right|}}{\sum }_{k=1}^{\left|M\right|}Var\left(p_{a_k,k}\right)$ (mean result variance) can only be understood as the expected variance of a game, i.e. $\mathbb{E}\left[Var\left(p_k^a\right|r_{a_k}-r_{b_k})\right]$, dependent on some distribution of the rating differences $r_{a_k}-r_{b_k}$. We can only compare results from different samples if we assume this average variance to be similar, but this isn’t the case in general (for instance, $MRV$ decreases as the dispersion of the ratings increases).

If we assume the results are binary ($p_k^a\in \{0,1\}$) we can use other approaches. For instance, if ${\mathbf{F}}_X$ is logistic, as we saw in Eq.(7), the model is equivalent to that of a logistic regression, so we can derive the statistics of this type of regression. For instance, the deviance D, which is distributed as a chi-squared variable,

$$D=-2·\ln \left({\displaystyle \frac{{\mathrm{likelyhood}}_{Elo}}{{\mathrm{likelyhood}}_{saturated}}}\right)$$

Finally, the effectiveness of the model can be gauged more visually by plotting the receiver operating characteristic (ROC) curve. Again, this doesn’t work with other possible results besides win or loss, such as a draw ($p_k^a={\displaystyle \frac{1}{2}}$), unless the non-decisive results are removed or imputed (for instance, to 0 and 1 with probabilities $1-p_k^a$ and $p_k^a$).

3. Stochastic Elo Models

In many competitive team sports, we don’t just observe the result of the game, but also a stochastic process $S_t$, which determines the result at time T (we will assume T is positive constant, although it could be any stopping time of $S_t$). In practice, $S_t$ will represent the score difference at time t, positive when the home team is winning, so the home team wins when $S_T>0$, while the visiting team wins when $S_T<0$.

Our goal is to extend the Elo model to incorporate $S_t$, so that the expected result of the game at time $t=0$ matches the static model. In other words, we want to obtain an expression for $\mathbb{E}\left[p_A\right|r_A,r_B,S_t]=g(r_A,r_B,S_t,t)$ such that $g(r_A,r_B,0,0)=F_X(r_A-r_B+L)=\mathbb{E}\left[p_A\right|r_A,r_B]$, i.e. our initial guess matches that of the original Elo model.

We will study several possible models, but there are some properties they should all verify. First, since (in the sports we will see) the past states of the scoreboard aren’t relevant to the game, and only the final score determines the result, $S_t$ should have the Markov property. As a consequence, both $X_t:=\mathbb{E}\left[p_A\right|S_t]=g(r_A,r_B,S_t,t)$ and $Y_t:=\mathbb{E}\left[S_T\right|S_t]$ should be martingales, by the Tower Property of Conditional Expectation [4](p. 46).

Furthermore, for $s>t$, since $S_s$ gives us as much information as $S_s$ and $S_t$ together, our estimation at time s should be better than the one at time t, and therefore

$$\mathbb{E}\left[Var\left(p_A\right|S_s)\right]<\mathbb{E}\left[Var\left(p_A\right|S_t)\right]\mathrm{and}\mathbb{E}\left[Var\left(S_T\right|S_s)\right]<\mathbb{E}\left[Var\left(S_T\right|S_t)\right]$$

3.1. Continuous Models

Recall that in the original Elo model, team A wins if $X+r_A-r_B+L>0$, and that should match the odds of $S_T$ being positive, so we can assume $S_T$ is $X+r_A-r_B+L$ times some constant. Since the incentives of the teams are the same at every point of the game (score the most points and have the opponent score the least), we can also assume the increments $S_{t+h}-S_t$ are independent (for disjoint intervals) and identically distributed.

For this to make sense, $S_T=S_{T/n}+(S_{2T/n}-S_{T/n})+\cdots +(S_T-S_{T-T/n})$ must be infinitely divisible. Although the logistic distribution is infinitely divisible [6], the increments aren’t logistic, so we will suppose that X and $S_T$ are normal, and in that case the increments must also follow the normal distribution by Cramér’s decomposition theorem [7], so $S_t$ has i.i.d. Gaussian increments and it’s a Brownian motion with drift:

$$S_t=\mu t+\sigma B_t\Rightarrow \mathbb{E}\left[p_A\right]=\mathbb{P}[N(\mu T,{\sigma }^{2}T)>0]=\Phi \left({\displaystyle \frac{\mu T}{\sigma \sqrt{T}}}\right)=\Phi \left({\displaystyle \frac{\mu }{\sigma }}\sqrt{T}\right)$$

where $B_t$ is the standard Brownian motion, i.e. $B_0=0$, and B has independent and normal increments $B_t-B_s\sim N(0,|t-s\left|\right)$. If we want this expectation to match the one given by the static model, we must have

$$\Phi \left({\displaystyle \frac{\mu }{\sigma }}\sqrt{T}\right)={\mathbf{F}}_X\left(r_A-r_B+L\right)=\Phi \left({\displaystyle \frac{r_A-r_B+L}{T}}\right)\Rightarrow {\displaystyle \frac{\mu }{\sigma }}\sqrt{T}={\displaystyle \frac{r_A-r_B+L}{{\sigma }_X}}$$

(12)

And from this we immediately obtain the expected score conditioned on $S_t=0$:

$$\mathbb{E}\left[p_A\right|S_t=0]=\mathbb{P}\left[N(\mu (T-t),{\sigma }^2(T-t))>0\right]=\Phi \left({\displaystyle \frac{\mu }{\sigma }}\sqrt{T-t}\right)=$$

$$=\Phi \left({\displaystyle \frac{r_A-r_B+L}{{\sigma }_X}}{\displaystyle \frac{\sqrt{T-t}}{\sqrt{T}}}\right)={\mathbf{F}}_X\left((r_A-r_B+L){\displaystyle \frac{\sqrt{T-t}}{\sqrt{T}}}\right)$$

(13)

Similarly, if we condition on an arbitrary score difference at time $t<T$, we obtain

$$\mathbb{E}\left[p_A\right|S_t=S]=\mathbb{P}\left[S+N(\mu (T-t),{\sigma }^2(T-t))>0\right]=\mathbb{P}\left[N(\mu (T-t)+S,{\sigma }^2(T-t))>0\right]$$

$$=\Phi \left({\displaystyle \frac{\mu }{\sigma }}\sqrt{T-t}+{\displaystyle \frac{S}{\sigma }}{\sqrt{T-t}}^{-1}\right)={\mathbf{F}}_X\left((r_A-r_B+L){\displaystyle \frac{\sqrt{T-t}}{\sqrt{T}}}+{\displaystyle \frac{{\sigma }_X}{\sigma }}{\displaystyle \frac{S}{\sqrt{T-t}}}\right)$$

Denoting by $u_t:=(T-t)/T$ the fraction of the time that remains, and by C the constant coefficient ${\displaystyle \frac{{\sigma }_X}{\sigma \sqrt{T}}}$ we have:

$$\mathbb{E}\left[p_A\right|S_t=S]={\mathbf{F}}_X\left((r_A-r_B+L)\sqrt{u_t}+C{\displaystyle \frac{S}{\sqrt{u_t}}}\right)$$

(14)

In the end, we obtain an expression where the term $(r_A-r_B+L)\sqrt{u_t}$ depends on the ratings, and decreases to zero as the time t approaches T, while the term $C{\sqrt{u_t}}^{-1}S$ depends on the score and becomes larger as the game nears its end, as we would want (unless $S=0$). In other words, the behavior or $\mathbb{E}\left[p_A\right|S_t]$ as $t\to T$ is exactly what we would expect.

Note that setting $t=0\Rightarrow \sqrt{u_t}=1$, and assuming a game starts with a score difference of S points, the expected score is ${\mathbf{F}}_X(r_A-r_B+L+CS)$. This allows us to interpret the constant C as the handicap (measured in rating points) that each goal or point entails at the start of the game. We could in fact use this to estimate C from game data, although we don’t need to pick $t\approx 0$. For any $t\in (0,t)$, C should minimize the mean square error

$$MSE\left(t\right):={\displaystyle \frac{{\sum }_{k\in M}{(p_{a_k,k}-\mathbb{E}\left[p_{a_k,k}\right|S_{t,k}])}^2}{\left|M\right|}}={\displaystyle \frac{1}{\left|M\right|}}\sum _{k\in M}{\left(p_{a_k,k}-{\mathbf{F}}_X\left(\sqrt{u_t}(r_{a_k}-r_{b_k}+L)+C{\displaystyle \frac{S_{t,k}}{\sqrt{u_t}}}\right)\right)}^2$$

as long as the model is correct, and the minimum should be the same for every t. Conversely, if the function above is minimized for $C=C^{*}$ for every t, our model is optimal among a certain class, as the following result showcases.

Lemma 1. 

If there are functions $f:\mathbb{R}\to \mathbb{R}\setminus \left\{0\right\}$ and $V:{\mathbb{R}}^2\to \mathbb{R}$ and there exists a $C^{*}\in \mathbb{R}$ such that $V(x,C^{*}f\left(x\right))\le V(x,Cf\left(x\right))$ for every $x,C\in \mathbb{R}$, then every $g:\mathbb{R}\to \mathbb{R}$ verifies

$$V(x,C^{*}f\left(x\right))\le V(x,g\left(x\right))\forall x\in \mathbb{R}$$

Proof. 

$V(x,g\left(x\right))=V\left(x,{\displaystyle \frac{g\left(x\right)}{f\left(x\right)}}f\left(x\right)\right)\ge V(x,C^{*}f\left(x\right))$□

In particular, for $V(t,g)={\displaystyle \frac{1}{\left|M\right|}}{\sum }_{k\in M}{\left(p_{a_k,k}-{\mathbf{F}}_X(\sqrt{u_t}(r_A-r_B+L)+g{S}_{t,k}\right)}^2$ and the function $f:t\mapsto 1/\sqrt{u_t}$, this means that our model is optimal among the ones with a prediction of the form $\mathbb{E}\left[p_A\right]={\mathbf{F}}_X(\sqrt{u_t}(r_A-r_B+L)+Sg\left(t\right))$. If we further suppose that the true expectancy has the form ${\mathbf{F}}_X(f\left(t\right)(r_A-r_B+L)+Sg\left(t\right))$, we can estimate f by looking at the times in the sample where $S_{t,k}=0$, and if $f:t\mapsto \sqrt{u_t}$ minimizes the mean square error over that restricted sample, our model is optimal among this wider class.

Finally, assuming we already know or have estimated $C={\displaystyle \frac{{\sigma }_X}{\sigma \sqrt{T}}}\Rightarrow \sigma ={\displaystyle \frac{{\sigma }_X}{C\sqrt{T}}}$, we can obtain the drift $\mu ={\displaystyle \frac{\sigma }{\sqrt{T}}}{\displaystyle \frac{r_A-r_B+L}{{\sigma }_X}}$ and express $S_t$ in terms of known quantities as

$$S_t=\mu t+\sigma B_t={\displaystyle \frac{r_A-r_B+L}{C·T}}t+{\displaystyle \frac{{\sigma }_X}{C\sqrt{T}}}{B}_t$$

(15)

Finally, notice also that $\mathbb{E}\left[S_T\right]={\displaystyle \frac{r_A-r_B+L}{C}}$, which gives another way to estimate C.

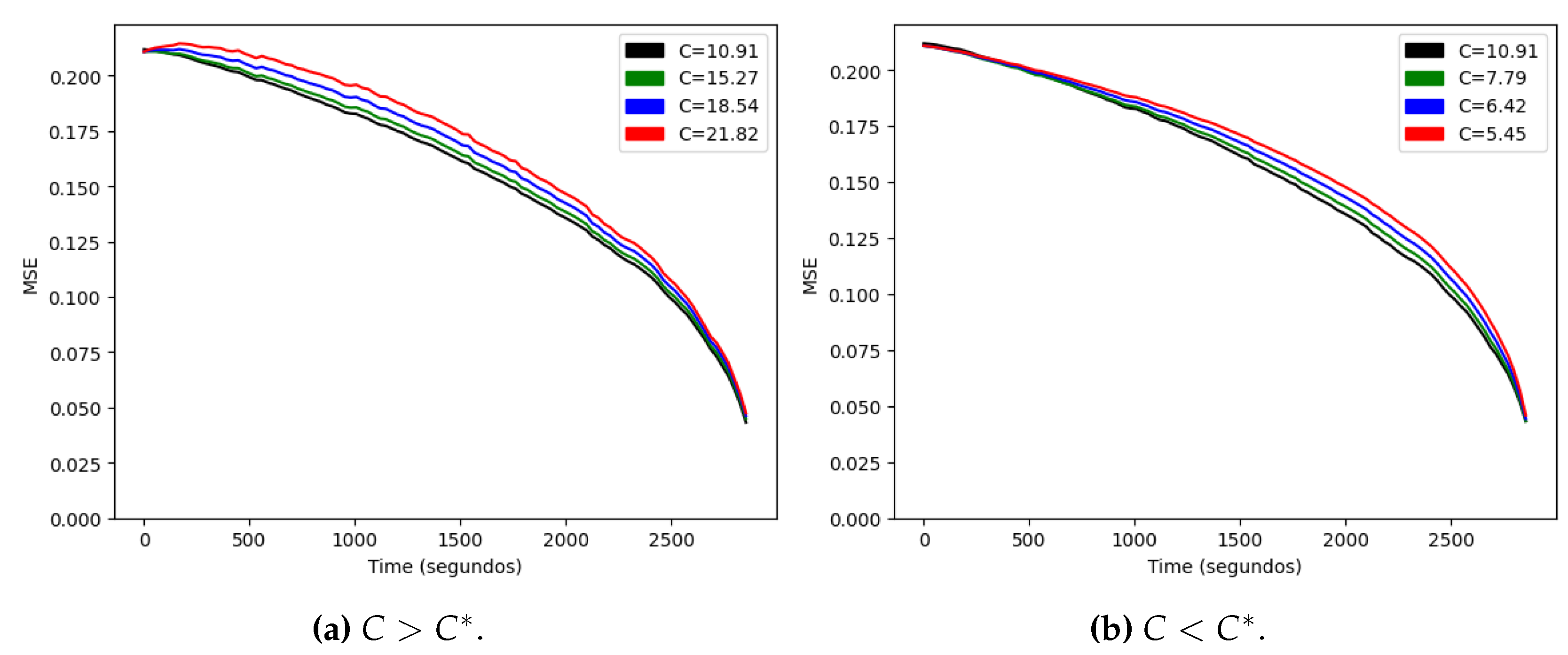
3.2. Accuracy Metrics for the Stochastic Model

If we take $t=T$ in Eq. (15) we obtain

$$C·S_T\sim r_A-r_B+L+{\displaystyle \frac{{\sigma }_X}{\sqrt{T}}}N(0,T)\iff C·S_T-(r_A-r_B+L)\sim N(0,{\sigma }_X^2)\sim X$$

(16)

Therefore, the residuals $C·S_T-(r_A-r_B+L)$ follow the same law as X (the variable used for the static model), and we can do a normality test on them, for instance through a QQ plot or comparing a histogram with the predicted frequencies for X. We could in principle use Eq.(14) with any distribution of X, and in that case $C·S_T$ minus the rating difference follows the law of X and the same test works.

From Eq.(15) we can also reconstruct the standard Brownian motion $S_t$ in the model:

$${\displaystyle \frac{1}{\sqrt{T}}}{B}_t={\displaystyle \frac{1}{{\sigma }_X}}\left(C·S_t-{\displaystyle \frac{t}{T}}·(r_A-r_B+L)\right)$$

(17)

and since ${\displaystyle \frac{1}{\sqrt{a}}}{B}_{at}$ is a standard Brownian motion if and only if $B_t$ is, taking $s_t=1-u_t=t/T$ we get that ${\displaystyle \frac{1}{\sqrt{R}}}{B}_t={\displaystyle \frac{1}{\sqrt{T}}}{B}_{T{s}_t}=C·S_{T{s}_t}-s_t(r_A-r_B+L)$ is a standard Brownian motion in $[0,1]$ as a function of $s_t$, which is just the fraction of the game time elapsed at t.

From Eq.(15) we can also deduce

$$Var\left(S_T\right|S_t)=Var(S_T-S_t)=Var(\mu (T-t)+\sigma B_T-B_t)={\sigma }^2(T-t)=C^{-2}{\sigma }_X^2·u_t$$

(18)

That is, if we compute the mean squared error of $S_T$ instead of $p_A$ at each time t, we should obtain a linear function in t, and we can test this hypothesis via linear regression.

Recall that we are assuming the increments of $S_t$ are independent and identically distributed, and in particular the variance of $S_{t+h}-S_t$ only depends on t. We can test this directly by looking at the points scored by either team at each interval between 0 and T, or, if $S_t$ can increase or decrease by amounts other than one, we can see if the sample variance ${\displaystyle \frac{1}{\left|M\right|-1}}{\sum }_{k\in M}{(S_{t+1,k}-S_{t,k})}^2\underset{\left|M\right|\to \infty }{\overset{a.s.}{\to }}\mathbb{E}\left[{(S_{t+1}-S_t)}^2\right]$ depends on t.

Finally, this continuous model implies expressions for $\mathbb{E}\left[p_A\right|S_t]$ and $\mathbb{E}\left[S_T\right|S_t]$ for each t, and we can check if they behave like martingales in a sample of games.

3.3. Non-Homogeneous Process

In practice , $S_t$ doesn’t always behave like an homogeneous process in time, that is, more points may be scored in some sub-intervals of $[0,T]$ than others. In that case, if $Var\left(S_t\right)=m\left(t\right)$ for some increasing function m, we can model the process as

$$S_t={\int }_0^t\mu dm\left(t\right)+{\int }_0^T{m}^{\prime }\left(s\right)d{B}_s=\mu ·m\left(t\right)+\sigma B_{m\left(t\right)}=S_{m\left(t\right)}^{\prime }$$

where $S^{\prime }$ behaves like the score in the first model. Since this is a map of the process that we were using before, we can use the homogeneous model to compute

$$\mathbb{E}\left[p_A\right|S_t=0]=\mathbb{E}\left[p_A\right|S_{m\left(t\right)}^{\prime }=S]=\mathbb{P}[S_{m\left(T\right)}^{\prime }>0|S_{m\left(t\right)}^{\prime }=S]=$$

$$={\mathbf{F}}_X\left(\sqrt{{\displaystyle \frac{m\left(T\right)-m\left(t\right)}{m\left(T\right)}}}(r_A-r_B+L)+C\sqrt{{\displaystyle \frac{m\left(T\right)}{m\left(T\right)-m\left(t\right)}}}S\right)$$

which is exactly the same as before, for $u_t={\displaystyle \frac{m\left(T\right)-m\left(t\right)}{m\left(T\right)}}$.

3.4. A Discrete Model

The main difference between this model and the actual score difference is that the former is a continuous process, but the latter is discrete in value ($S_t\in \mathbb{Z}$) and continuous in time. The process that fulfills this conditions best is a Skellam process, as described in [11], i.e. the difference of two Poisson processes with different rates, which model the score of each team or player during the game.

If $P_1$ and $P_2$ are two independent Poisson distributions with mean ${\mu }_1$ and ${\mu }_2$, then their difference is said to follow a Skellam distribution, $P_1-P_2\sim Sk({\mu }_1-{\mu }_2)$. If $N_1\left(t\right)$ and $N_2\left(t\right)$ are independent Poisson processes with rates ${\lambda }_1$ and ${\lambda }_2$, the process

$$Z_t:=N_1\left(t\right)-N_2\left(t\right)\sim P\left(t{\lambda }_1\right)-P\left(t{\lambda }_2\right)=Sk(t{\lambda }_1,t{\lambda }_2)$$

has i.d.d. increments as well.

However, in this case, modeling the score with $Z_t$ is not so straightforward. For starters, if we multiply $Z_t$ by a constant, we don’t get another Skellam process. Adding a real-valued function of t also changes the domain of the process from $\mathbb{Z}$ to $\mathbb{R}$. Therefore, the only option is to assume that

$$S_t\sim Z_t({\mu }_1(r_A,r_B),{\mu }_1(r_A,r_B))\Rightarrow S_T\sim Sk(T{\mu }_1(r_A,r_B),T{\mu }_2(r_A,r_B))$$

This in turn means that we can’t assume homocedasticity of the process, because a Skellam distribution with parameters ${\mu }_1$ and ${\mu }_2$ has mean ${\mu }_1-{\mu }_2$ and variance ${\mu }_1+{\mu }_2$. Since ${\mu }_1$ and ${\mu }_2$ are non-negative, the mean is less or equal to the variance, and if we fix ${\mu }_1+{\mu }_2=\sigma$, we would put a bound on the expected final score $\mathbb{E}\left[S_T\right]={\mu }_1-{\mu }_2\le \sigma$, which is not realistic.

However, the distribution of $S_T$, which should have the same shape as X, now depends on two parameters, and not just on the rating difference $r_A-r_B$. We can remove this degree of freedom fixing a relation between ${\mu }_1$ and ${\mu }_2$, and for simplicity’s sake, since the probability that $Sk({\mu }_1,{\mu }_2)$ takes the value k is

$$\mathbb{P}[Sk({\mu }_1,{\mu }_2)=k]=e^{-({\mu }_1+{\mu }_2)}{\left({\displaystyle \frac{{\mu }_1}{{\mu }_2}}\right)}^{k/2}{I}_k\left(2\sqrt{{\mu }_1{\mu }_2}\right)$$

we can fix $2\sqrt{{\mu }_1{\mu }_2}=H$ to compute $I_k$ only once for each $k\in \mathbb{Z}$. Here $I_k(·)$ is the modified Bessel function of the first kind [9], which doesn’t have a closed form expression.

To determine how ${\mu }_1$ and ${\mu }_2$ depend on the ratings, we can take $\mathbb{E}\left[S_T\right]={\mu }_1-{\mu }_2$ to be linear in the rating gap ${\Delta }_r=r_A-r_B+L$ as in Eq.(15), and then if we pick ${\sigma }_X$ so that $C=1$, from the product and difference of ${\mu }_1$ and ${\mu }_2$ we obtain a second degree equation

$$(x+{\mu }_1)(x-{\mu }_2)=x^2+{\Delta }_{r}x-{\displaystyle \frac{H^2}{4}}$$

$$\Rightarrow {\mu }_1={\displaystyle \frac{1}{2}}\left({\Delta }_r+\sqrt{{\Delta }_r^2+H^2}\right)\mathrm{and}{\mu }_2={\displaystyle \frac{1}{2}}\left(-{\Delta }_r+\sqrt{{\Delta }_r^2+H^2}\right)$$

from which we finally obtain not just a prediction for $p_A$, but also a probability for each possible final score, and in this case the probability that $S_T=0$ is positive, so we can include draws in our model. In particular, if we assign a result of $p_A=p_B=1/2$ for draws,

$$E\left[p_A\right]=\mathbb{P}[S_T<0]+{\displaystyle \frac{1}{2}}\mathbb{P}[S_T=0]=\mathbb{P}[Sk({\mu }_1,{\mu }_2)<0]+{\displaystyle \frac{1}{2}}\mathbb{P}[Sk({\mu }_1,{\mu }_2)=0]$$

(19)

Similarly, if we consider that expression as a function of ${\Delta }_r$, it can be shown that it’s increasing (see Appendix B), and with limits 0 and 1 at $-\infty$ and ∞. Therefore, $\mathbb{E}\left[p_A\right]={\mathbf{F}}_X(r_A-r_B+L)$ for some random variable X, and then this model is also an extension of a static Elo model.

4. Computational Study

Next, we evaluate the performance of the proposed stochastic extensions of the Elo system in a computational study implemented in Python. All the results discussed can be replicated with the code available at github using real data from reference databases for each sport, which are also included for download through the previous link. In the case of soccer, a comparison with the more complex methodology of the Soccer Power Index (SPI) developed by Nate Silver [13] is also carried out.

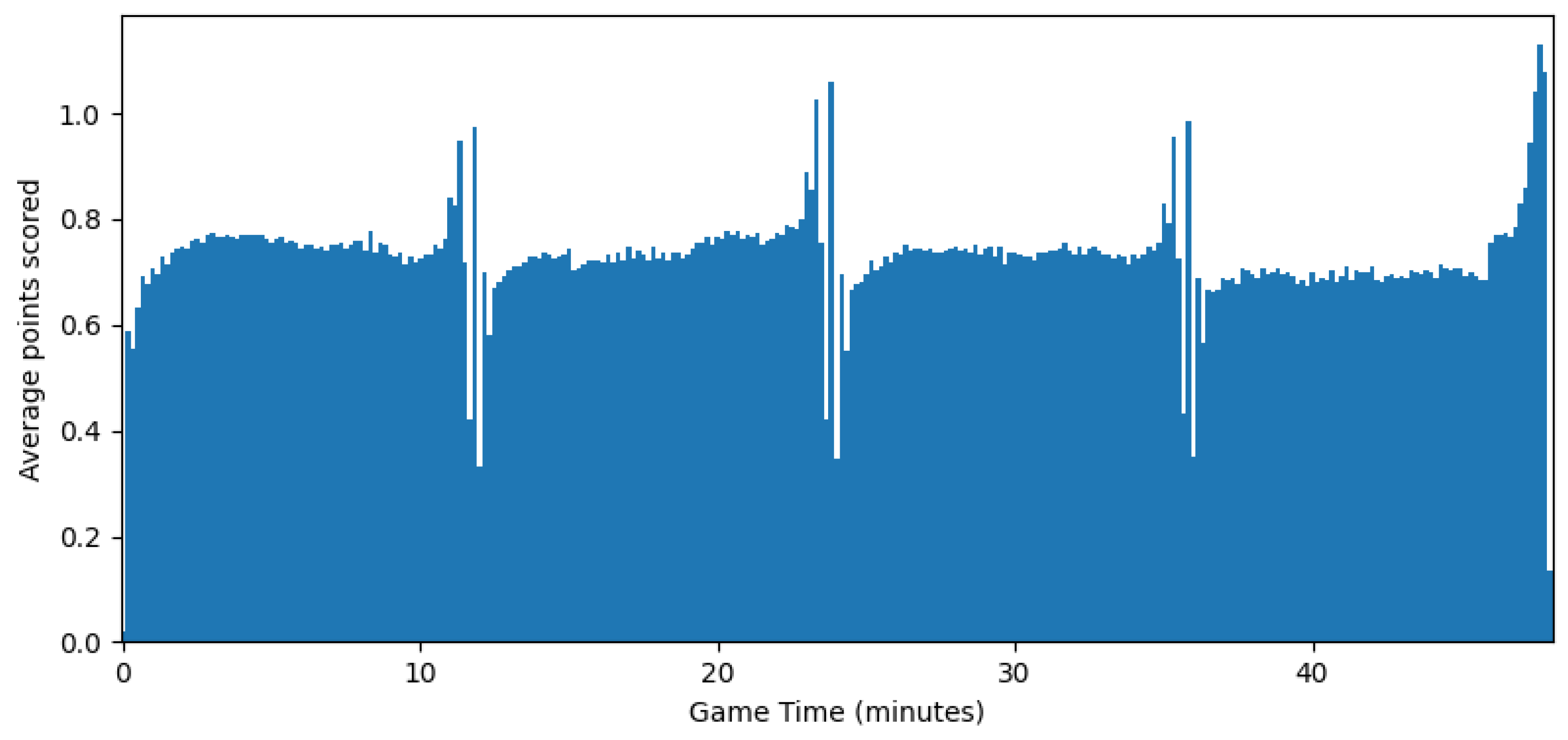
4.1. Experimental Setup

In order to evaluate a rating model with any of the accuracy metrics exposed in Section 2.6, a sample of matches M for which both players have a rating is needed. Furthermore, the update formula in Eq. (1) needs preexisting ratings, so we will have to use some of the games in our dataset to estimate the starting ratings of each team, using the estimator $\widehat{R}$ defined in Section 2.3.

On the other hand, the proposed stochastic models are designed for sports or games where the result depends on a numerical score (S) and the match has a fixed duration (T), such as soccer, basketball or ice hockey, although we will omit the latter in the experimental results for brevity. Moreover, we will focus on league competitions, where each team plays more games and we can use a bigger sample to obtain $\widehat{R}$. For instance, in the Premier League, 20 teams play 380 matches, while in the World Cup, 32 teams play 64 matches.

Most national leagues have a similar format, consisting in yearly seasons in which most of the participating teams remain the same from one year to the next, and all teams play the same number of games each week. We can design an algorithm to extract rated games from any of these sports as follows:

• The expected result is determined by Eq. (8) with constant L.
• During each season, we denote by "entering teams" to the teams that didn’t play the previous season (during the first season, they are all entering teams).
• We divide each season in two parts (I and II), the former comprised of the games that start before every entering team has played at least m games.
• During part I, in each match between two non-entering teams, we update their ratings (from the previous season) according to Eq. (1) using a fixed factor K.
• When part I ends, we compute the rating estimator $\widehat{R}$ for each entering team using the games in part I and the current ratings of non-entering teams.
• During part II, since we have ratings for all teams, we can just update them every match using Eq. (1) with the same K-factor.

In this way, we have a rating before the start of the game for the matches between non-entering teams in part I of each season, and all matches in part II, and we can use them to evaluate the rating system.

This algorithm has (hyper-) parameters m, K and L, that is, respectively the length of part I of each season, the sensitivity of the Elo system to new results, and the home field advantage. We will fix m and estimate K and L by minimizing the mean square error defined in Eq. (9).

4.2. Basketball Results

Basketball has several advantages regarding the Elo system. First, it only admits two results (win or loss), so the result follows a Bernoulli distribution and the logistical model in Eq. (7) can be used. In addition, the score variable $S_t$ has a relatively large range (each team scores around 100 points) and changes quickly (by 1, 2 or 3 points each time), so we don’t lose too much by approximating it by a continuous variable.

On the other hand, an NBA basketball match lasts 48 minutes divided in 4 12-minute quarters, but if the scoreboard is even at the end of that time, additional 5-minute quarters are played until one team is ahead. We will ignore these extra quarters for the sake of simplicity, since we assume T is fixed, but our prediction at the end of the game will be slightly wrong when $S_t=0$.

Our dataset for basketball will consist of the NBA league games between the seasons 2000-01 and 2023-24, obtained from www.basketball-reference.com, which registers every change in the score and its time (in seconds).

4.2.1. Static Elo

We implement the algorithm described above for $m=20$ and $F_X$ corresponding to a normal variable $X\sim N(0,200)$, in a training set of seasons 2000-01 to 2009-10, and in four different ways to test the effectiveness of the Elo model and the significance of its parameters:

• Without Elo, simply assuming $E\left[p_{k,a_k}\right]=\overline{p_{home}}:={\left|M\right|}^{-1}{\sum }_{k=1}^{\left|M\right|}{p}_{k,a_k}=:F_X\left(L\right)$.
• Fixing $K=0$ and minimizing $MSE$ as a function of L (no change in strength).
• Fixing $L=0$ and minimizing $MSE$ as a function of K (no home advantage).
• Minimizing $MSE$ as a function of K and L (standard Elo system).

To avoid overfitting in K and L, we also implement the algorithm for the optimal values $K^{*}$ and $L^{*}$ in a validation set consisting of seasons 2010-11 to 2023-24. The mean squared errors in the training and testing sets are summarized in Table 1:

We can see straight away that the Elo explains a significant part of the variance (around 11%), and both parameters are useful, since setting them to zero increases the mean squared error. The reduction is similar in the training and testing sets, so cross-validation shows the robustness of the algorithm in Section 4.1.

Notice also that the K-factor and home field advantage are similar to those of chess, where $|L^{*}|\approx 50$[2]( ch. 8.93). The sign of $L^{*}$ only reflects that in basketball (and American sports in general) the visiting team is listed first.

We note that setting $K=0$ (which amounts to leaving the rating of a team unchanged until it’s relegated) increases the variance, but still has predictive power, as evidenced by the ROC curves shown in Figure 2.

And finally, setting $L=0$ barely changes the curve, because the map from $F_X\left(z\right)$ to $F_X(z+L)$ is a monotone increasing bijection, and the order of the expected result under the two models are the same for equal $K^{*}$ (and indeed the K-factors are very similar).

After fitting our model and obtaining the sample, we could expect that for a subsample of matches with rating difference $r_A-r_B\approx r$, the average result would be close to $F_X(r+L)$, but this isn’t the case as evidenced by Figure 3.

We observe that the normal distribution function $F_X$ overestimates the effect of the rating difference in the expected result of a match. We can obtain a better predictor if we multiply $r_A-r_B$ by a "dampening" constant $D\le 1$, just like in Fig. 3 of [8].

If we minimize the $MSE$ on $K,L$ and D (only using D for the calculation of the mean squared error, since otherwise it’s equivalent to scaling X), we obtain optimal parameters $K^{*}\approx 19.61$, $L^{*}\approx -58.9$ and $D^{*}\approx 0.786$, reducing the $MSE$ to 0.21064 in the test set.

This seems a small improvement in $MSE$, but it’s straightforward to test the significance of the reduction in variance by looking at the variables $X:={(p_A-{\mathbf{F}}_X(L+r_A-r_B))}^2$ and $Y:={(p_A-{\mathbf{F}}_X(L+D{r}_A-D{r}_B))}^2$ for a random game.

In order to check if $Z:=X-Y$ has a positive mean from our sample of games, we sample the difference $z_k={(p_k^a-{\mathbf{F}}_X(L+r_{a_k}-r_{b_k}))}^2-{(p_k^a-{\mathbf{F}}_X(L+D{r}_{a_k}-D{r}_{b_k}))}^2$ and argue that by the central limit theorem, the sample mean of Z approximately follows a normal distribution with n times the sample variance of Z. In our testing data, Z has negative mean with $p\approx 1.2·{10}^{-6}$, so D significantly improves our predictions.

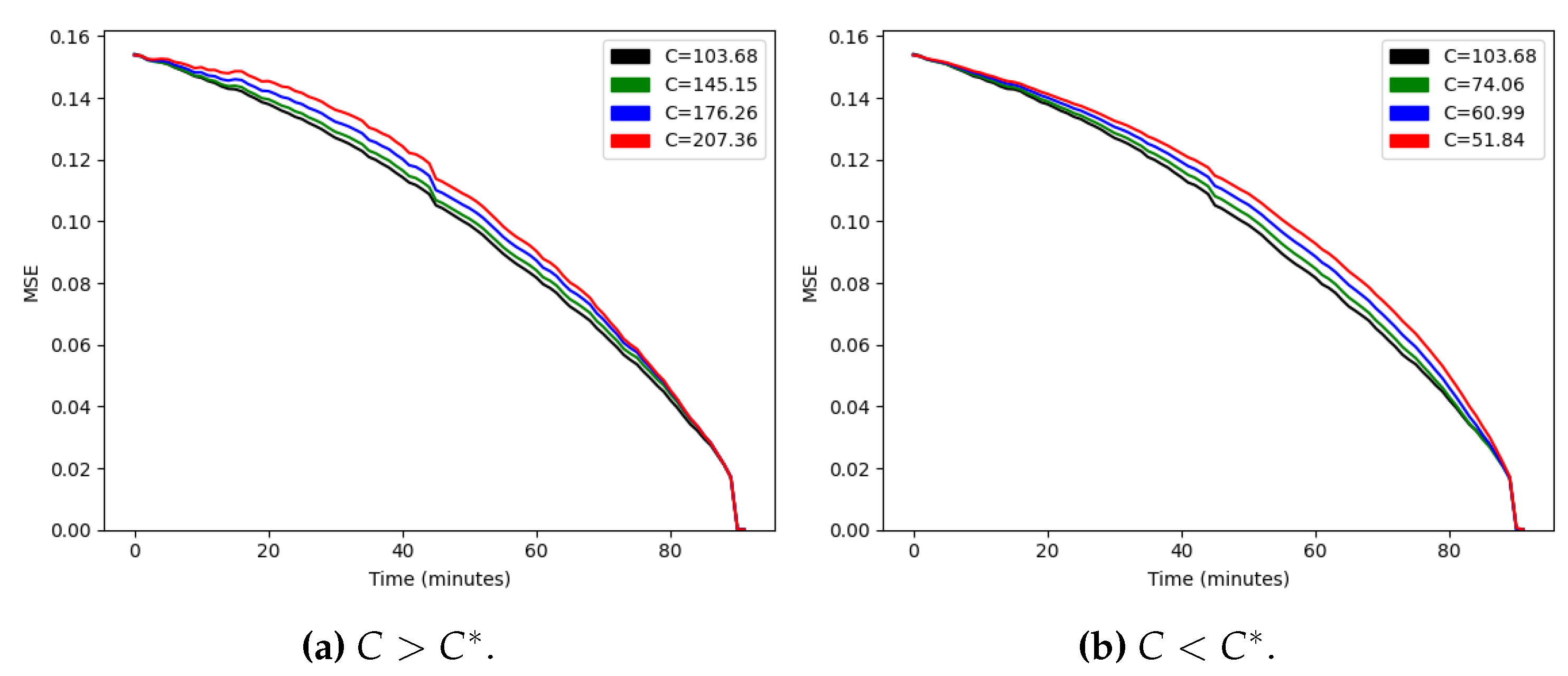
4.2.2. Stochastic Elo

Our algorithm leaves us with 12500 rated games out of the 12933 games in the training set, and 17437 out of the 17820 originally in the testing set. These 17437 matches are the ones used for the analysis of our stochastic model.

We start by estimating the only parameter of the stochastic model, C. As we showed in Lemma 1, if the model is correct, the optimal value $C^{*}$ should minimize the error $MSE\left(t\right)$ at every time t, so we minimize the average of that function at different times for a more robust estimation of $C^{*}$. In the training set, we obtain $C^{*}\approx 10.91$, and we can compare the function $MSE\left(t\right)$ for higher and lower values, as shown in Figure 4. Since every curve lies above the curve for $C=10.91$, Lemma 1 suggests that our formula for the expected result is optimal among the family $E\left[p_A\right]={\mathbf{F}}_X(\Delta r\sqrt{u_t}+g\left(t\right)S_t)$. We also note that the error doesn’t reach zero at the final time $t=T$ of 2880 seconds, since a tied score at that time results in an extra time being played. Our model assumes a fixed duration, so in order to predict the result beyond minute 48 we would need to model another (shorter) match.

Next, Figure 5 shows the result of checking the normality of the score process by computing the normal residues $C·S_T-L-D(r_A-r_B)$ and comparing them with the quantiles of a normal distribution. Here, again, $S_T$ is the score after the first 48 minutes, not the final score of the game. As expected from Eq. (16), the residuals more or less follow a normal distribution, but the mean is not zero, meaning the home team scores better (in terms of $S_T$) than the Elo model predicts. The standard deviation is also smaller than the expected value of the model, namely ${\sigma }_X=200$. From the first plot we can also tell that the residuals are somewhat correlated to the Elo difference, but not to an extent that would invalidate the model.

Finally, Figure 6 checks the lineal relationship between the score variance and time, as described in 18, computing the quantities

$$MS{E}_S\left(t\right):={\displaystyle \frac{1}{\left|M\right|}}\sum _{i=1}^{\left|M\right|}{(S_T-\mathbb{E}\left[S_T\right|S_t])}^2\underset{\left|M\right|\to \infty }{\overset{a.s.}{\to }}\mathbb{E}\left[{(S_T-\mathbb{E}\left[S_T\right|S_t])}^2\right]=Va{r}_t\left(S_T\right)={\displaystyle \frac{{\sigma }_X^2}{C^2}}{u}_t$$

The resulting function is close to a line, but the variance still drops more quickly at the end of the match than at the beginning, suggesting $S_T$ is not completely homogeneous in time. Figure 7 plots the average number of points scored at each 10-second interval of the game by either team, in order to approximate the variance of that interval (they are in fact equal if we assume the score is the difference of two independent Poisson processes as in the discrete model). However, Figure 7 shows that the process is very homogeneous in time, except for brief periods before the end of each quarter.

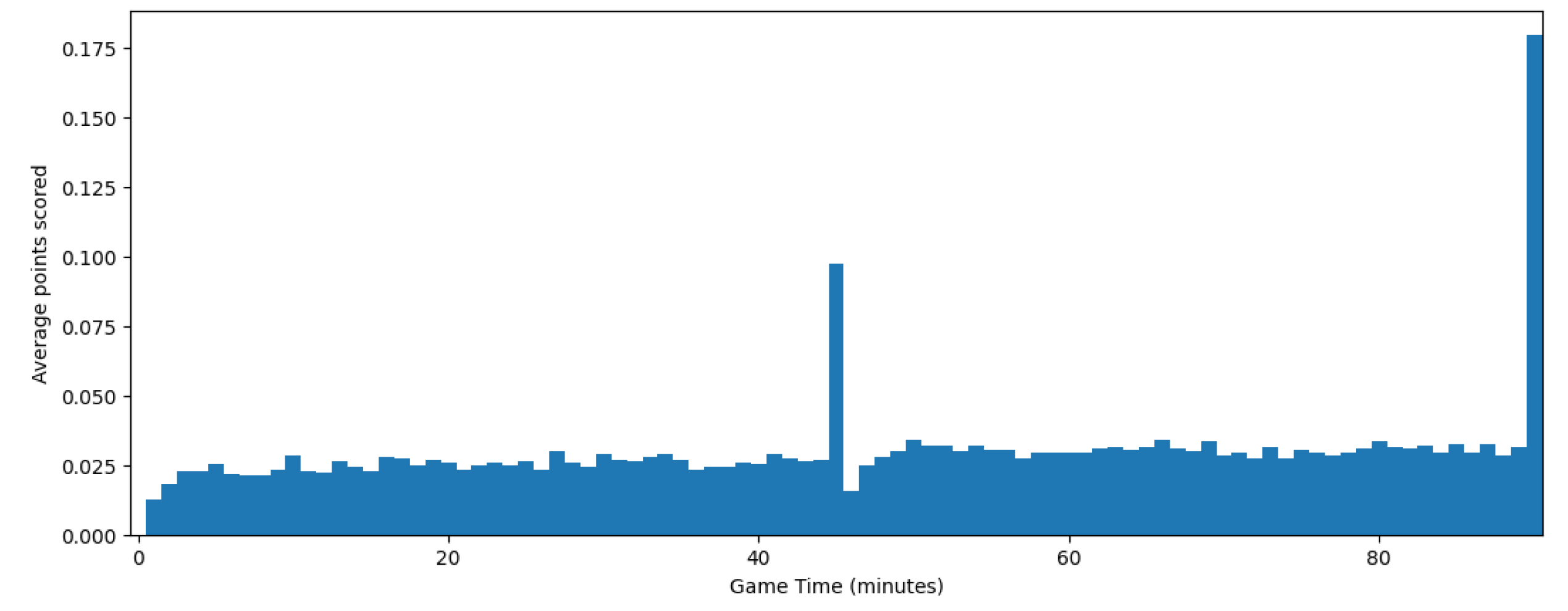
4.3. Soccer Results

Soccer is somewhat more challenging than basketball when it comes to applying Elo models. First, since our database consists of league games, we don’t have extra times, at the expense of allowing for draws ($p_A=p_B={\displaystyle \frac{1}{2}}$) if the score is tied at the end of the match. We should note that in both the Premier League and the Spanish First Division, teams are awarded 3 points for a victory, 1 for a tie and 0 for each loss, so this isn’t entirely a zero-sum game, whereas in the Elo model $p_A+p_B=1$.

Although there are no extra times, there is time added at the end of each half-time, but our database only keeps track of the minute in which each goal is scored, and every goal scored in the added time will appear in the minute 90 or 45. Finally, $S_t$ is relatively small (usually $S_T<5$), so approximating it by a continuous variable is problematic.

Our dataset for soccer consists of the seasons 2003-04 to 2023-24 of the Spanish and English first division leagues, both counting 5320 games. We use the former for training and the latter for testing. The data was obtained from fbref.com.

4.3.1. Static Elo

Since the league structure is similar to the NBA, we will use the same algorithm in Section 4.1 to obtain rated games, this time with a sample of $m=12$ for part I and the same $X\sim N(0,200)$, now adding also the dampened model to the table along with the optimal D. The corresponding results are presented in Table 2.

Just like we saw for basketball, both K and L are clearly significant, but the reduction in variance for adding D is much smaller. The statistical test described for basketball this time gives us that D is significant with $p\approx 0.0013$, and the optimum $D^{*}$ is closer to 1.

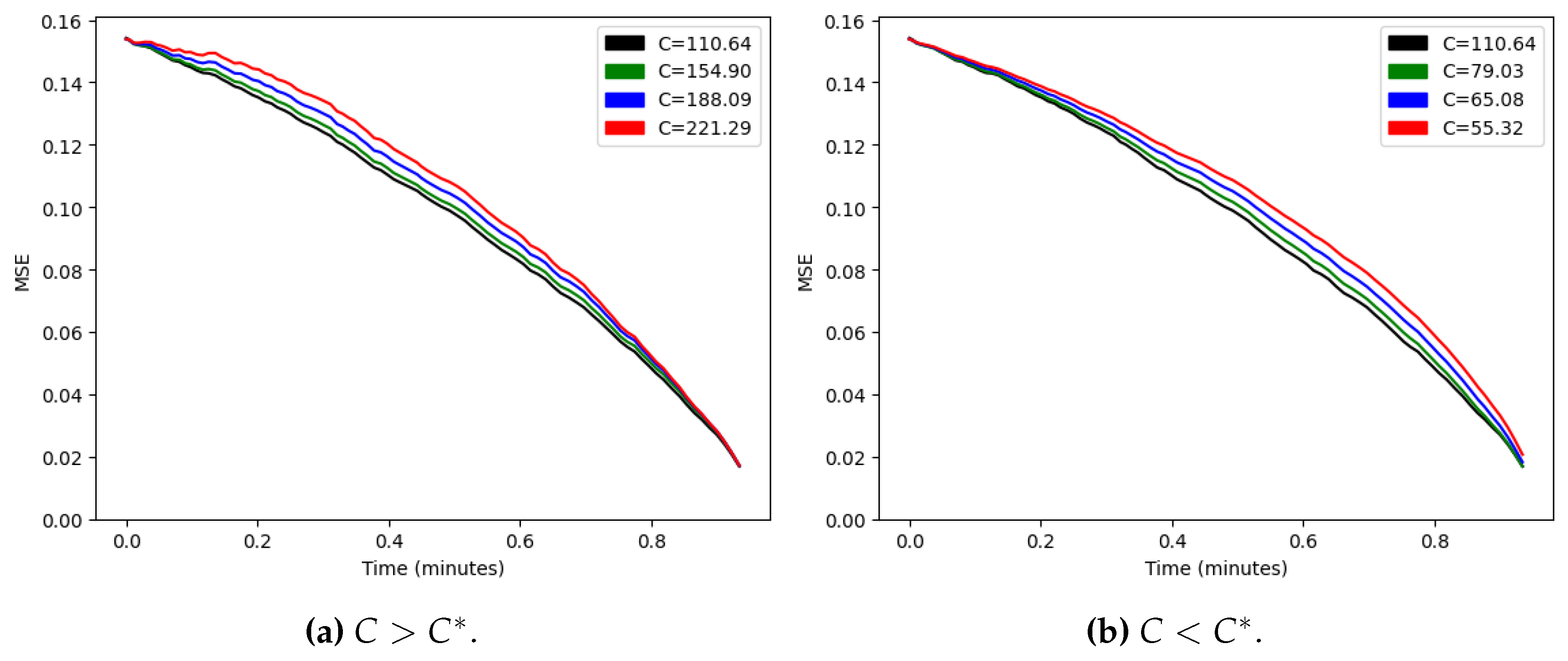
4.3.2. Stochastic Elo

After implementing the static Elo system, we are left with 7176 matches out of the 7980 in our testing set, and we will use these for the analysis of the stochastic model.

However, in this case the irregularity of the process versus the recorded time is stronger. As shown in Figure 8, the number of goals scored by every team each minute increases as the game nears its end, and has two spikes in the added time of each half. This makes the simple model we used for basketball less effective. If we estimate C by minimizing the average of $MS{E}_S\left(t\right)$ at evenly spaced points t, with linear $u_t={\displaystyle \frac{T-t}{T}}$, the resulting functions $MSE\left(t\right)$ and $MS{E}_S\left(t\right)\approx Var\left(S_T\right|S_t)$ are depicted in Figure 9 and Figure 10, respectively.

To tackle this problem, we model the process as a non-homogeneous process, with $u_t$ equal to the fraction of goals in our sample scored after time t. To show the results with this modification, Figure 11 and Figure 12 replaces the match time in the x axis with the modified time $1-u_t$. The last plot showcases that the score variance (conditioned on $S_t$) is almost exactly proportional to $u_t$, and that our assumptions on the process $S_t$ are reasonable.

Finally, Figure 13 plots the residues $C·S_T-L-D(r_A-r_B)$ and compare them to the standard normal quantiles and their respective rating differences $L+D(r_A-r_B)$. The distribution of the residues is close to normal, except for slightly thicker tails. The correlation between the residues and the rating differences is virtually zero compared with the one we saw for basketball.

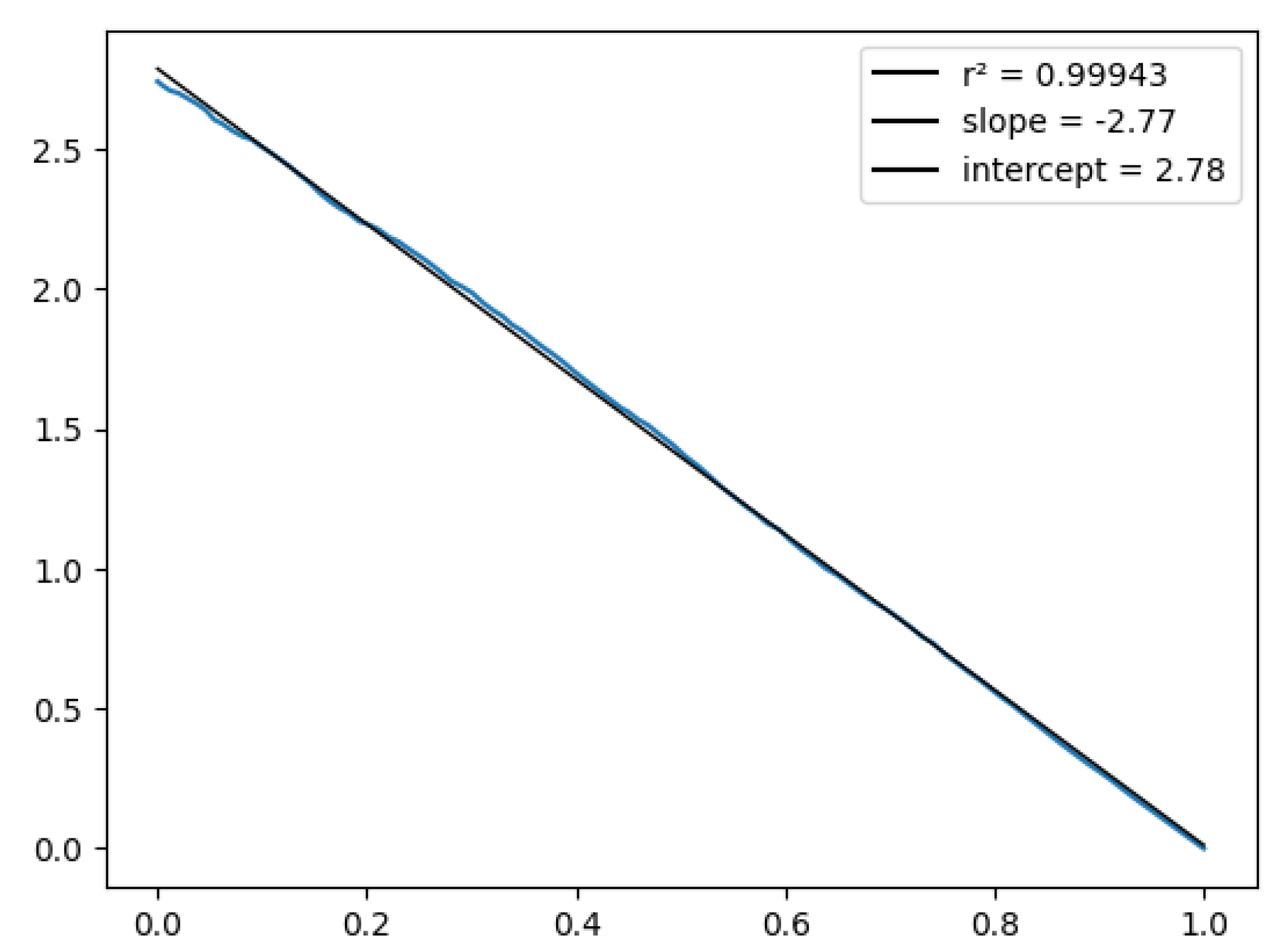
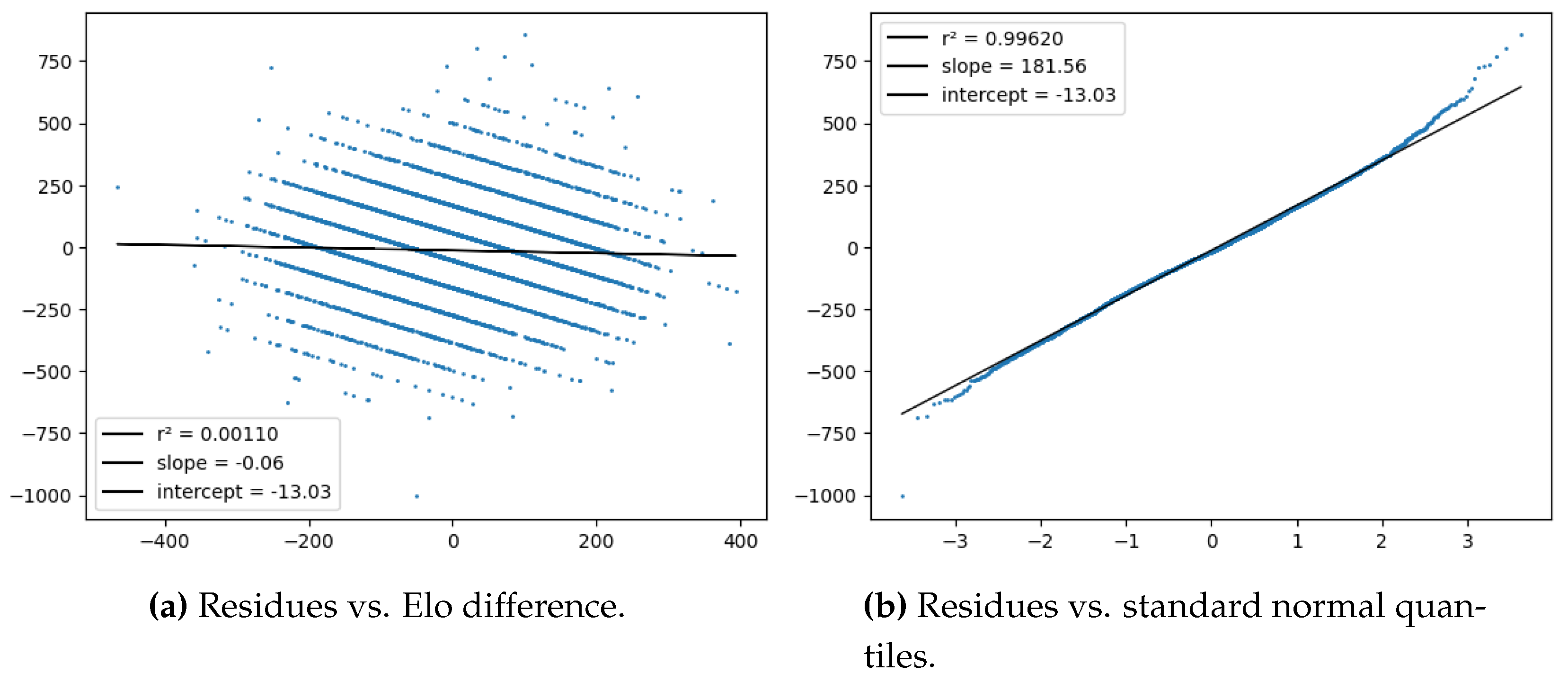
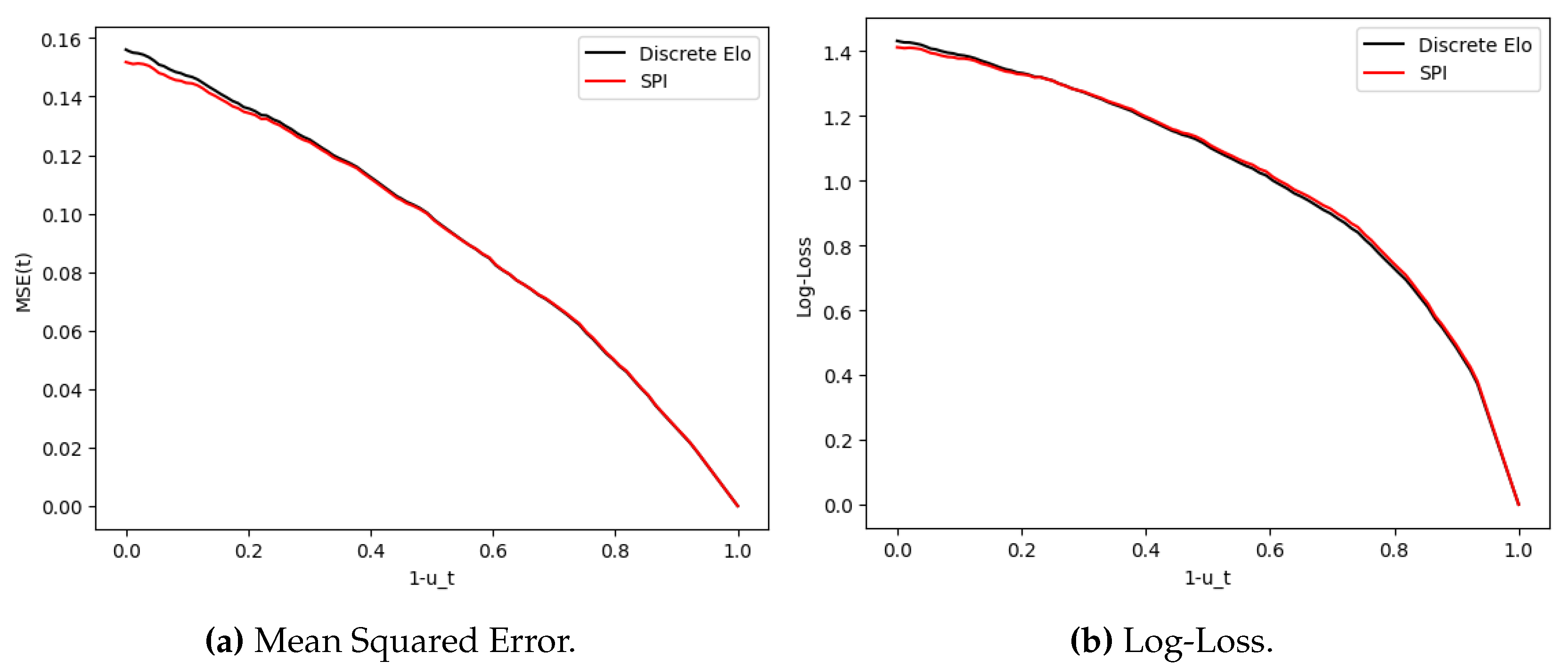
4.3.3. Discrete Elo model

Lastly, we implement the discrete score model based on the Skellam process. As we showed, this is a particular case of an Elo model, and thus the same algorithm can be used to estimate the parameters $K,L$ and D. In this case we use $m=12$ and the function $F_X$ defined in Eq.(19). To estimate the only non-Elo parameter of the model,

$$H=2\sqrt{{\mu }_1{\mu }_2}=2\sqrt{\mathbb{E}\left[goal{s}_{home}\right]+\mathbb{E}\left[goal{s}_{away}\right]}=2\sqrt{\mathbb{E}[goal{s}_{home}·goal{s}_{away}]}$$

we use the sample mean of the product of the goals in our training sample, obtaining $H\approx 2.578$. The corresponding results are presented in Table 3.

Despite the distribution function being different, the mean squared error is very close to that of the standard Elo model with normal $F_X$. However, this model also predicts probabilities for the three possible results, and thus it allows computing metrics like log-loss [10].

For comparison, we implement the rating system used by the Soccer Power Index (SPI) developed by Nate Silver [13], which uses 2 rating parameters for each team: one for their offense (their capacity to score goals) and another for their defense. A concise but complete explanation of the SPI system is given in Appendix C.

The SPI system achieves a $MSE$ of 0.1518 versus the 0.1533 of the discrete Elo system, and the squared errors are significantly lower, with a p-value of $5·{10}^{-5}$. The average log-loss at time zero is also better, with 1.411 beating the 1.432 for the discrete Elo and a p-value of $8·{10}^{-6}$. However, both systems also give probabilities for the result being a victory, loss or draw at any time t during the game, namely

$$\begin{array}{c}\mathbb{P}[p_A=1]=\mathbb{P}[Sk({\mu }_1·u_t,{\mu }_2·u_t)+S_t>0]\\ \mathbb{P}[p_A=1/2]=\mathbb{P}[Sk({\mu }_1·u_t,{\mu }_2·u_t)+S_t=0]\\ \mathbb{P}[p_A=0]=\mathbb{P}[Sk({\mu }_1·u_t,{\mu }_2·u_t)+S_t<0]\end{array}$$

where ${\mu }_1$ and ${\mu }_2$ are the expected goals by the home team (A) and the visiting team, respectively. Computing these for every time t, we obtain the results shown in Figure 14. Note that in the log-loss curve, the Elo system beats SPI in the second half - for instance, at $t=72$ minutes, the log-losses are $0.857$ vs. $0.841$ with a p-value of $2·{10}^{-7}$ showing that the Elo loss achieves a lower loss. This suggests that despite being a 1-parameter model and its relative simplicity, the discrete Elo system is on par with SPI in terms of predictive power when it comes to mid-game predictions (conditioned on $S_t$).

5. Conclusions

In this work, it has been shown how the model underlying the Elo system has a natural extension for fixed-duration sports with which it possible to model the score of each team. The proposed stochastic Elo system can be easily implemented for league competitions using the algorithm in Section 4.1, which in turn uses the estimator defined in Section 2.3, and supported by the results proved in Appendix A.

A discrete model for soccer has been also proposed, which is also an Elo system at time $t=0$, but models the goal difference as a discrete process, thus providing probabilities for each possible outcome of a match. Moreover, we saw that this system has accuracy comparable with that of a biparametric rating system like SPI across the duration of a soccer game. This suggests that the simplicity of the Elo system may favor it as an alternative to sport-specific models, and its use will continue to increase.

5.1. Future Work

These results certainly apply to games or sports with a score board and fixed duration in time, but they could be replicated for other sports with different scoring systems, like table tennis, where the game ends when the first player gets a score of 21, regardless of how long it takes. It’s possible that an Elo system can be derived from these type of "race" processes as we did for our Skellam process.

The concept of predicting the result of a match mid-game could also be applied to chess, where there is no objective score $S_t$ but it’s common to obtain an "evaluation" from the state of the board, using chess engines. Some chess websites store extremely large databases of computer evaluated games in which a study of this kind could be performed.

Another question we didn’t consider when optimizing the parameters of the Elo system, such as K or L, is whether the distribution function $F_X$ can also be inferred from a large enough sample of games. Obviously, the space of distribution functions isn’t finite-dimensional, but a method for choosing $F_X$ hasn’t been proposed, even among a finite-dimensional family of distributions.

Finally, there are games (such as checkers) for which there is a concept of perfect play, i.e. a strategy that guarantees a victory or a draw. It’s easy to see that an expected result above $1/2$ implies an upper bound in ratings from the original model, but the Elo system doesn’t have an upper bound built in. However, some models derived from race processes not only produce odds for a win, draw or loss, but also have a maximum or minimum rating associated with perfect play.

For instance, given ratings $r_1,r_2\in {\mathbb{R}}_{\ge 0}$, we consider Poisson processes $P_1\left(t\right)$ and $P_2\left(t\right)$ with rates $r_1$ and $r_2$, and arrival times $T_1\left(n\right)$ and $T_2\left(n\right)$. Suppose player 1 wins when $T>T_2\left(k\right)<T_1\left(k\right)$, player 2 wins when $T>T_1\left(k\right)<T_2\left(k\right)$ and they tie when $T_1\left(k\right)>T<T_2\left(k\right)$, for fixed $k\in \mathbb{Z}$, $T\in \mathbb{R}$. Then the strength of a player decreases with r, but if $r_1=0$ player 1 will never lose, and 0 is a lower bound for ratings. To the best of our knowledge, this type of systems haven’t been studied computationally at all.