Mathematical Symphonies in Copper Oxide: A Graph Entropy Approach to Topological Analysis and Applications

Nasir Ali; Muhammad Saqlain Zakir; Misbah Arshad; Muhammad Kamran Naseer

doi:10.20944/preprints202407.1499.v1

Submitted:

17 July 2024

Posted:

18 July 2024

You are already at the latest version

Abstract

In the realm of molecular science, intricate relationships between molecular structures and their biomedical and pharmacological characteristics have been revealed through empirical experiments. This exploration hinges on the application of numerical descriptors, known as Topological Indices, which illuminate the inherent properties of diverse molecular structures. With particular significance in the medical and pharmaceutical domains, these indices facilitate the prediction of biological features for new chemical compounds and drugs by quantifying weighted entropies. In the context of this paper, we delve into the concept of graph entropy, weaving it intricately with the topological properties of the crystalline framework of the copper oxide molecule, denoted as Cu\textsubscript{2}O$[i,j,t]$. Our primary objective is to unravel the mathematical symphony underlying the structural intricacies of Cu\textsubscript{2}O$[i,j,t]$ and to imbue it with the conceptual essence of entropy. We accomplish this through the computation of entropy, leveraging various topological indices, including weight. In addition to our analytical journey, we present a graphical comparison that juxtaposes the computed indices and entropies, shedding light on the interplay between mathematical analysis and the structural elegance of Cu\textsubscript{2}O$[i,j,t]$. This endeavor contributes to a deeper understanding of the material's multifaceted applications, spanning domains from chemical sensors to solar cells, photocatalysis, and batteries, where Cu\textsubscript{2}O's crystallographic structure plays a pivotal role.

Keywords:

entropy

;

topological indices

;

entropy measure

;

weighted entropies of Cu₂O[i

;

j

;

t]

;

crystallographic structure

;

entropy of Cu₂O[i

;

graph theory

Subject:

Computer Science and Mathematics - Discrete Mathematics and Combinatorics

Introduction

Graph theory, the foundation of which can be traced back to Leonhard Euler’s ingenious solution to the Seven Bridges Problem in 1735, stands as a crucial branch of applied mathematics that revolves around the study of graphs and their structural intricacies. In mathematical terms, graph theory delves into the realm of graphs, which are fundamental objects of investigation in discrete mathematics. A graph is essentially a collection of vertices (also known as nodes) interconnected by edges (the connecting lines). These graphs serve as versatile mathematical structures, enabling us to explore the relationships between pairs of objects. When all connections within a graph are one-way, it is referred to as a directed graph or a digraph.

The significance of graph theory extends to a multitude of fields. In the realm of computer science, graphs play a pivotal role in constructing and illustrating communication networks, computational devices, data organization, and the flow of computations, among other applications. Moreover, this mathematical framework finds its utility in studying the properties of molecules in fields such as chemistry, physics, and biology. Readers may see the applications of graph theory in [24,25,26,27]. The quantification of weighted entropies through these indices offers a robust framework for anticipating relevant characteristics, thereby contributing to the advancement of medical and pharmaceutical applications see [24].

One intriguing aspect of graph theory is the concept of topological indices, which are real numbers associated with compounds and graph networks. These indices are instrumental in predicting the properties of various compounds and remain constant, making them valuable tools in chemoinformatics. To delve into the properties and chemical bioactivity of compounds, scientists rely on quantitative structure-property relationships and structure-activity relationships, often in conjunction with topological indices.

In the realm of network theory, various polynomials, such as the Wiener polynomial and the Hosoya polynomial [1], come into play, enabling the creation of distance-dependent topological indices. For degree-dependent topological indices, the M-polynomial has been introduced, closely intertwined with the concept of valence in chemistry [2]. This amalgamation of graph theory and chemistry has been instrumental in assigning each molecular structure a real number, paving the way for the study of compounds’ properties.

Since the 1970s, degree-based, invariant graphs, known as the First and Second Zagreb indices, have garnered extensive attention and study. Moreover, We demonstrate the relevance of topological indices-based entropy calculations in facilitating accurate QSAR estimations, particularly in the domain of antiparasitic drug development. Our findings underscore the utility of these methods for enhancing predictive modeling and contributing to advancements in drug discovery.

The investigation conducted by the researchers involves the computation of entropy-based graphical indices for the crystallographic structure of molecular copper oxide. The methods employed and the results obtained exhibit a sound analytical foundation. Some Graphical indices and thermodynamic properties can be seen in [19,20,21]

Moreover, the crystallographic structure of copper oxide holds significant chemical importance. The arrangement of atoms in a crystal lattice provides crucial insights into the material’s properties and behavior. In the case of copper oxide, understanding its crystallographic structure is fundamental for unraveling its electronic, magnetic, and catalytic properties. Readers may see [30,31,32] for Graphical indices and physicochemical properties. Furthermore, some quantum-theoretic applications of graphical indices can be seen in [36,37,38].

These indices, along with various other graph indices, are discussed in more detail below, unveiling the rich tapestry of applications and discoveries within the realm of graph theory.

Definition 1.1. [3] For a graph

G

, First Zagreb index is denoted and defined as:

M_{1} (G) = \sum_{x y \in E (G)} (d_{x} + d_{y})

Definition 1.2. [3] For a graph, The Second Zagreb index is denoted and defined as:

M_{2} (G) = \sum_{x y \in E (G)} (d_{x} d_{y})

Definition 1.3. [4] For a graph, The modified second Zagreb index is denoted and defined as:

{M o d i f i e d M}_{2} (G) = \sum_{x y \in E (G)} \frac{1}{d_{x} d_{y}}

Definition 1.4. [5] For a graph

G

, The augmented Zagreb Index is denoted and defined as:

A Z I (G) = \sum_{x y \in E (G)} {(\frac{d_{x} d_{y}}{d_{x} {+ d}_{y} - 2})}^{3}

Definition 1.5. [6] For a graph

G

, Hyper Zagreb 2nd Index is denoted and defined as:

H_{2} (G) = \sum_{x y \in E (G)} {(d_{x} d_{y})}^{2}

Definition 1.6. [7] For a graph

G

, Redefined 1st Zagreb Index is denoted and defined as:

{R e Z G}_{1} (G) = \sum_{x y \in E (G)} \frac{d_{x} + d_{y}}{d_{x} d_{y}}

Definition 1.7. [8] For a graph

G

, Redefined 2nd Zagreb Index is denoted and defined as:

{R e Z G}_{2} (G) = \sum_{x y \in E (G)} \frac{d_{x} d_{y}}{d_{x} + d_{y}}

Definition 1.8. [8] For a graph

G

, Redefined 3rd Zagreb Index is denoted and defined as:as

{R e Z G}_{3} (G) = \sum_{x y \in E (G)} ((d_{x} d_{y}) (d_{x} + d_{y}))

Definition 1.9. [9] Suppose that we have a probability density function

P_{i j} = \frac{w (x y)}{\sum W (x y)}

The Entropy for any graph G it’s defined as

I (G, w) = - \sum P_{i j} l o g (P_{i j})

One fascinating branch of graph theory that has been gaining significant attention is Chemical Graph Theory, which delves into the intriguing relationship between graphs and chemistry. In recent years, the field of Chemical Graph Theory has sparked my growing interest in research. Back in 1988, numerous researchers were generating around 500 articles annually, each centered on the intersections of chemistry and graph theory.

Among the myriad topics covered in these articles, chemical indices in graph theory have emerged as a particularly vital subject. These indices find their roots in the field of chemistry and yield valuable insights that chemists actively utilize in their work. Notable examples of these chemical indices include the First and Second Zagreb indices, multiplicative Zagreb indices, the Wiener index, the general hyper-Wiener index, the Randic index, the harmonic index, the sum-connectivity index, the general Randic index, and the general sum-connectivity index, among others [10,11,12,13].

Theoretical chemists, as far back as the mid-20th century, recognized the potential of these graph-based invariants to reveal essential insights about the molecular structures of organic materials. By observing appropriately designed invariants of the fundamental molecular graph, they could unveil critical information. These invariants, often referred to as topological indices, serve as graph invariants that offer valuable insights for making chemical determinations.

These topological indices play a pivotal role in various aspects of chemistry, including Numerical Structure-Property Relations (QSPR) and Quantitative Structure-Activity Relations (QSAR). The detailed applicability can be seen in [12,13,14,15,16,17]. They enable chemists to make data-driven decisions and predictions based on the structural characteristics of chemical compounds, underscoring the profound impact of Chemical Graph Theory on the field of chemistry [14, 15, 16, 17, and 18]. The Pauli rejection postulate proposes that two or more electrons do not have the same quantum numbers in a molecule. Thus, if two particular atoms associate to arrange diatomic molecules and every orbit of the atom divert into two molecular orbitals which have distinct energy, it allows electrons in an earlier atomic orbital that possess a new framework of orbits, and each has not have the same energy. Commonly, if any huge number M of atoms are identical to overlap to make a solid substance, like a crystal lattice, the atomic orbital of atoms overlies each other [19].

Here we will discuss topological indices and how to use them

{c u}_{2} o [i, j, t]

Figure 1. Crystallographic molecule.

Figure 2. (a)

{C u}_{2} O [1,1, 1

] unit cell, (b)

{C u}_{2} O

[3,2,3] crystallographic structure.

Figure 2. (a)

{C u}_{2} O [1,1, 1

] unit cell, (b)

{C u}_{2} O

[3,2,3] crystallographic structure.

Table 1. Edge partition of

{c u}_{2} o [i, j, t] \geq 1

based on the degrees of end vertices of each edge.

Table 1. Edge partition of

{c u}_{2} o [i, j, t] \geq 1

based on the degrees of end vertices of each edge.

Table 2. Edge partition of

{c u}_{2} o [i, j, t] \geq 2

based on the degrees of end vertices of each edge.

Table 2. Edge partition of

{c u}_{2} o [i, j, t] \geq 2

based on the degrees of end vertices of each edge.

Here we will discuss topological indices as we wait and Compute the Weighted Entropy for

{c u}_{2} o [i, j, t]

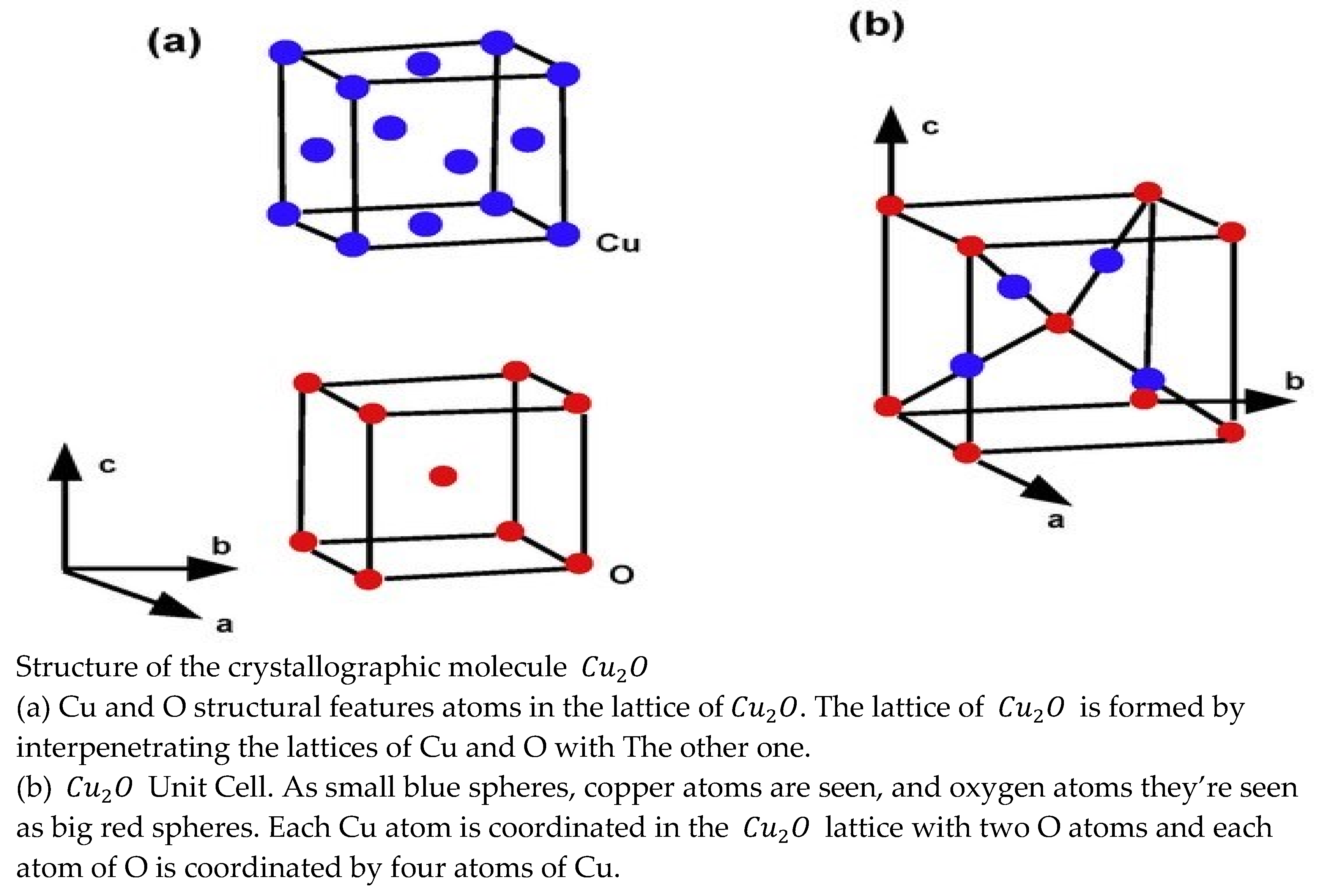
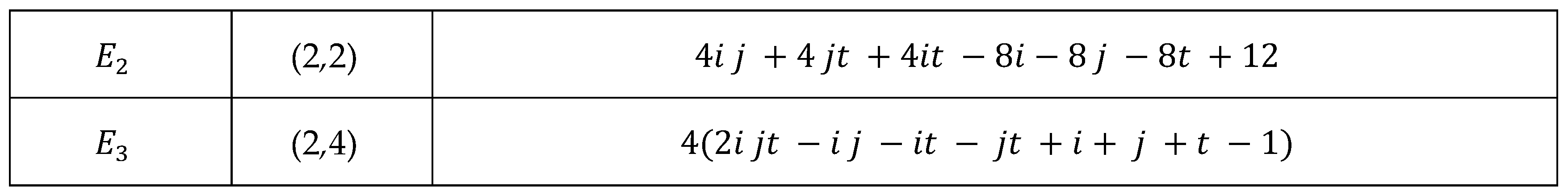
Main Results

Corollary 1: The Modified second Zagreb index ^m

M_{2} (G)

of

{c u}_{2} o

{M o d i f i e d M}_{2} (G) = \sum_{x y \in E (G)} \frac{1}{d_{x} d_{y}}

^{m} M_{2} ({c u}_{2} o) = \frac{1}{2.4} |E_{1}| + \frac{1}{4.6} |E_{2}| + \frac{1}{5.8} |E_{3}| + \frac{1}{6.8} |E_{4}| + \frac{1}{8.8} | E_{5} |

^{m} M_{2} ({c u}_{2} o) = [\begin{matrix} \frac{1}{2} (i + j + t) - 1 + \frac{1}{6} (i j + i t + j t) - \frac{1}{3} (i + j + t) + \frac{1}{2} + \frac{1}{10} (i + j + t) - \frac{1}{5} \\ + \frac{1}{12} (i j + i t + j t) - \frac{1}{6} (i + j + t) + \frac{1}{4} + \frac{1}{8} (i j t) - \frac{1}{8} (i j + i t + j t) \\ + \frac{1}{8} (i + j + t) - \frac{1}{8} \end{matrix}]^{m} M_{2} ({c u}_{2} o) = \frac{1}{8} (i j t) + \frac{1}{8} (i j + i t + j t) + \frac{9}{40} (i + j + t) - \frac{23}{40}

Corollary 2: The Redefined 1st Zagreb Index is

{R e Z G}_{1} ({c u}_{2} o

)

{R e Z G}_{1} (G) = \sum_{x y \in E (G)} \frac{d_{x} + d_{y}}{d_{x} d_{y}}

R e Z G_{1} ({c u}_{2} o) = \frac{3}{4} |E_{1}| + \frac{5}{12} |E_{2}| + \frac{13}{40} |E_{3}| + \frac{7}{24} |E_{4}| + \frac{1}{4} | E_{5} |

R e Z G_{1} ({c u}_{2} o) = [\begin{matrix} 3 (i + j + t) - 6 + \frac{5}{3} (i j + i t + j t) - \frac{10}{3} (i + j + t) + 5 + \frac{13}{10} (i + j + t) - \frac{13}{5} \\ + \frac{7}{6} (i j + i t + j t) - \frac{7}{3} (i + j + t) + \frac{7}{2} + 2 (i j t) - 2 (i j + i t + j t) \\ + 2 (i + j + t) - 2 \end{matrix}]

R e Z G_{1} ({c u}_{2} o) = 2 (i j t) + \frac{5}{6} (i j + i t + j t) + \frac{19}{30} (i + j + t) - \frac{21}{10}

Corollary 3: The Redefined Second Zagreb Index is

R e Z G_{2} ({c u}_{2} o)

)

{R e Z G}_{1} (G) = \sum_{x y \in E (G)} \frac{d_{x} . d_{y}}{d_{x} + d_{y}}

R e Z G_{1} ({c u}_{2} o) = \frac{4}{3} |E_{1}| + \frac{12}{5} |E_{2}| + \frac{40}{13} |E_{3}| + \frac{24}{7} |E_{4}| + 4 | E_{5} |

R e Z G_{1} ({c u}_{2} o) = [\begin{matrix} \frac{16}{3} (i + j + t) - \frac{32}{3} + \frac{48}{5} (i j + i t + j t) - \frac{96}{5} (i + j + t) + \frac{144}{5} + \\ \frac{160}{13} (i + j + t) - \frac{320}{13} + \frac{96}{7} (i j + i t + j t) - \frac{192}{7} (i + j + t) + \frac{288}{7} + \\ 32 (i j t) - 32 (i j + i t + j t) + 32 (i + j + t) - 32 \end{matrix}] R e Z G_{1} ({c u}_{2} o) = 32 (i j t) - \frac{304}{35} (i j + i t + j t) + \frac{4112}{1365} (i + j + t) + \frac{3632}{1365}

Corollary 3: The Redefined Third Zagreb Index is

R e Z G_{3} ({c u}_{2} o)

{R e Z G}_{3} ({c u}_{2} o) = \sum_{x y \in E (G)} (d_{x} + d_{y}) (d_{x} . d_{y})

R e Z G_{3} ({c u}_{2} o) = 48 |E_{1}| + 240 |E_{2}| + 520 |E_{3}| + 672 |E_{4}| + 1024 | E_{5} |

R e Z G_{3} ({c u}_{2} o) = [\begin{matrix} 192 (i + j + t) - 384 + 960 (i j + i t + j t) - 1920 (i + j + t) + 2880 + \\ 2080 (i + j + t) - 4160 + 2688 (i j + i t + j t) - 5376 (i + j + t) + 8064 + \\ 8192 (i j t) - 8192 (i j + i t + j t) + 8192 (i + j + t) - 8192 \end{matrix}]

R e Z G_{3} ({c u}_{2} o) = 8192 (i j t) - 4544 (i j + i t + j t) + 3176 (i + j + t) + 1792

Theorem 1: Weighted Entropy of

{c u}_{2} o [i, j, t] \geq 1

with the first Zagreb Index is

I ({c u}_{2} o [i, j, t], M_{1}) = \log [\begin{matrix} 4 (12 i j t - \\ 2 (i j + i t + j t) \\ + i + j + t) \end{matrix}] - \frac{1}{4 [\begin{matrix} (12 i j t - \\ 2 (i j + i t + j t) + \\ i + j + t) \end{matrix}]} [\begin{matrix} 37.3512600 (i j t) - \\ 9.04267014796 (i j + i t + j t) + \\ 5.13516534335 (i + j + t) - \\ 1.22766053874 \end{matrix}]

Proof. By definition (1.1). We have,

M_{1} ({c u}_{2} o) = 4 (12 i j t - 2 (i j + i t + j t) + i + j + t)

By definition (1.9). We have,

I ({c u}_{2} o, M_{1}) = \log [\begin{matrix} 4 (12 i j t - \\ 2 (i j + i t + j t) \\ + i + j + t) \end{matrix}] - \frac{1}{4 [\begin{matrix} (12 i j t - \\ 2 (i j + i t + j t) + \\ i + j + t) \end{matrix}]} [\begin{matrix} (1 + 2) |E_{1}| \log (1 + 2) + \\ (2 + 2) |E_{2}| \log (2 + 2) + \\ (2 + 4) |E_{3}| \log (2 + 4) \end{matrix}]

I ({c u}_{2} o, M_{1}) = \log [\begin{matrix} 4 (12 i j t - \\ 2 (i j + i t + j t) \\ + i + j + t) \end{matrix}] - \frac{1}{4 [\begin{matrix} (12 i j t - \\ 2 (i j + i t + j t) + \\ i + j + t) \end{matrix}]} [\begin{matrix} 3 |E_{1}| \log (3) + 4 |E_{2}| \log 4 \\ + 6 |E_{3}| \log 6 \end{matrix}]

I ({c u}_{2} o, M_{1}) = \log [\begin{matrix} 4 (12 i j t - \\ 2 (i j + i t + j t) \\ + i + j + t) \end{matrix}] - \frac{1}{4 [\begin{matrix} (12 i j t - \\ 2 (i j + i t + j t) + \\ i + j + t) \end{matrix}]} [\begin{matrix} l o g 2 (48 i j t + 8 i j + 8 i t + 8 j t \\ - 40 i - 40 j - 40 t + 72) + \\ l o g 3 (48 i j t - 24 i j - 24 i t - 24 j t + \\ 36 i + 36 j + 36 t - 48) \end{matrix}]

I ({c u}_{2} o [i, j, t], M_{1}) = \log [\begin{matrix} 4 (12 i j t - \\ 2 (i j + i t + j t) \\ + i + j + t) \end{matrix}] - \frac{1}{4 [\begin{matrix} (12 i j t - \\ 2 (i j + i t + j t) + \\ i + j + t) \end{matrix}]} [\begin{matrix} 37.3512600 (i j t) - \\ 9.04267014796 (i j + i t + j t) + \\ 5.13516534335 (i + j + t) - \\ 1.22766053874 \end{matrix}]

□

Theorem 2: Weighted Entropy of

{c u}_{2} o [i, j, t] \geq 1

with the second Zagreb Index is

I ({c u}_{2} o, M_{2}) = \log [\begin{matrix} 8 (8 i j t - \\ 2 (i j + i t + j t) \\ + i + j + t) \end{matrix}] - \frac{1}{[\begin{matrix} 8 (8 i j t - \\ 2 (i j + i t + j t) \\ + i + j + t) \end{matrix}]} [\begin{matrix} 57.79775916748 (i j t) - \\ 19.26591972249 (i j + i t + j t) + \\ 9.63295986125 (i + j + t) - \\ 4.81647993062 \end{matrix}]

Proof. By definition (1.2). We have,

M_{2} ({c u}_{2} o) = 8 (8 i j t - 2 (i j + i t + j t) + i + j + t)

By definition (1.9). We have,

I ({c u}_{2} o, M_{2}) = \log [\begin{matrix} 8 (8 i j t - \\ 2 (i j + i t + j t) \\ + i + j + t) \end{matrix}] - \frac{1}{[\begin{matrix} 8 (8 i j t - \\ 2 (i j + i t + j t) \\ + i + j + t) \end{matrix}]} [\begin{matrix} (1.2) |E_{1}| \log (1.2) + \\ (2.2) |E_{2}| \log (2.2) + \\ (2.4) |E_{3}| \log (2.4) \end{matrix}]

I ({c u}_{2} o, M_{2}) = \log [\begin{matrix} 8 (8 i j t - \\ 2 (i j + i t + j t) \\ + i + j + t) \end{matrix}] - \frac{1}{[\begin{matrix} 8 (8 i j t - \\ 2 (i j + i t + j t) \\ + i + j + t) \end{matrix}]} [\begin{matrix} 2 |E_{1}| \log (2) + \\ 4 |E_{2}| \log 4 + \\ 8 |E_{3}| \log 8 \end{matrix}]

I ({c u}_{2} o, M_{2}) = \log [\begin{matrix} 8 (8 i j t - \\ 2 (i j + i t + j t) \\ + i + j + t) \end{matrix}] - \frac{1}{[\begin{matrix} 8 (8 i j t - \\ 2 (i j + i t + j t) \\ + i + j + t) \end{matrix}]} [\begin{matrix} l o g 2 (192 i j t - 64 i j - 64 i t - 64 j t \\ + 32 i + 32 j + 32 t - 16) \end{matrix}]

I ({c u}_{2} o [i, j, t], M_{2}) = \log [\begin{matrix} 8 (8 i j t - \\ 2 (i j + i t + j t) \\ + i + j + t) \end{matrix}] - \frac{1}{[\begin{matrix} 8 (8 i j t - \\ 2 (i j + i t + j t) \\ + i + j + t) \end{matrix}]} [\begin{matrix} 57.79775916748 (i j t) - \\ 19.26591972249 (i j + i t + j t) + \\ 9.63295986125 (i + j + t) - \\ 4.81647993062 \end{matrix}]

□

Theorem 3: The Entropy of

{c u}_{2} o [i, j, t] \geq 1

with modified 2nd Zagreb weight is

I ({c u}_{2} o, {^{m}}_{2}) = \log [\begin{matrix} \frac{1}{2} (2 i j t \\ + i j + i t + j t \\ + i + j + t) \end{matrix}] - \frac{1}{[\begin{matrix} \frac{1}{2} (2 i j t \\ + i j + i t + j t \\ + i + j + t) \end{matrix}]} [\begin{matrix} - 0.90308998699 (i j t) - \\ 0.15051499783 (i j + i t + j t) + \\ 0.15051499783 (i + j + t) - \\ 0.15051499783 \end{matrix}]

Proof. By definition (1.3). We have,

^{m} M_{2} ({c u}_{2} o) = \frac{1}{2} (2 i j t + i j + i t + j t + i + j + t)

By definition (1.9). We have,

I ({c u}_{2} o,^{m} M_{2}) = \log [\begin{matrix} \frac{1}{2} (2 i j t \\ + i j + i t + j t \\ + i + j + t) \end{matrix}] - \frac{1}{[\begin{matrix} \frac{1}{2} (2 i j t \\ + i j + i t + j t \\ + i + j + t) \end{matrix}]} [\begin{matrix} \frac{1}{1.2} |E_{1}| l o g \frac{1}{1.2} + \\ \frac{1}{2.2} |E_{2}| l o g \frac{1}{2.2} + \\ \frac{1}{2.4} |E_{3}| l o g \frac{1}{2.4} \end{matrix}]

I ({c u}_{2} o,^{m} M_{2}) = \log [\begin{matrix} \frac{1}{2} (2 i j t \\ + i j + i t + j t \\ + i + j + t) \end{matrix}] - \frac{1}{[\begin{matrix} \frac{1}{2} (2 i j t \\ + i j + i t + j t \\ + i + j + t) \end{matrix}]} [\begin{matrix} \frac{1}{2} |E_{1}| l o g \frac{1}{2} + \\ \frac{1}{4} |E_{2}| l o g \frac{1}{4} + \\ \frac{1}{8} |E_{3}| l o g \frac{1}{8} \end{matrix}]

I ({c u}_{2} o,^{m} M_{2}) = \log [\begin{matrix} \frac{1}{2} (2 i j t \\ + i j + i t + j t \\ + i + j + t) \end{matrix}] - \frac{1}{[\begin{matrix} \frac{1}{2} (2 i j t \\ + i j + i t + j t \\ + i + j + t) \end{matrix}]} [\frac{1}{2} l o g 2 (\begin{matrix} - 6 i j t - (i j + i t + j t) + \\ (i + j + t) - 1 \end{matrix})]

I ({c u}_{2} o, {^{m}}_{2}) = \log [\begin{matrix} \frac{1}{2} (2 i j t \\ + i j + i t + j t \\ + i + j + t) \end{matrix}] - \frac{1}{[\begin{matrix} \frac{1}{2} (2 i j t \\ + i j + i t + j t \\ + i + j + t) \end{matrix}]} [\begin{matrix} - 0.90308998699 (i j t) - \\ 0.15051499783 (i j + i t + j t) + \\ 0.15051499783 (i + j + t) - \\ 0.15051499783 \end{matrix}]

□

Theorem 4: The Entropy of

{c u}_{2} o [i, j, t] \geq 1

with Augmented Zagreb weight is

I ({c u}_{2} o, A Z I) = \log (64 i j t) - \frac{1}{64 i j t} [57.797759 i j t]

Proof. By definition (1.4). We have,

A Z I ({c u}_{2} o) = 64 i j t

By definition (1.9). We have,

I ({c u}_{2} o, A Z I) = \log (64 i j t) - \frac{1}{64 i j t} [\begin{matrix} {(\frac{1.2}{1 + 2 - 2})}^{3} |E_{1}| l o g {(\frac{1.2}{1 + 2 - 2})}^{3} + \\ {(\frac{2.2}{2 + 2 - 2})}^{3} |E_{2}| l o g {(\frac{2.2}{2 + 2 - 2})}^{3} \\ + {(\frac{2.4}{2 + 4 - 2})}^{3} |E_{3}| l o g {(\frac{2.4}{2 + 4 - 2})}^{3} + \end{matrix}]

I ({c u}_{2} o, A Z I) = \log (64 i j t) - \frac{1}{64 i j t} [\begin{matrix} 24 |E_{1}| l o g 2 + \\ 24 |E_{2}| l o g 2 + \\ 24 |E_{3}| l o g 2 \end{matrix}]

I ({c u}_{2} o, A Z I) = \log (64 i j t) - \frac{1}{64 i j t} [24 l o g 2 (8 i j t)]

({c u}_{2} o, A Z I) = \log (64 i j t) - \frac{1}{64 i j t} [57.797759 i j t]

□

Theorem 5: The Entropy of

{c u}_{2} o [i, j, t] \geq 1

with hyper Zagreb second weight is

I ({c u}_{2} o, H_{2}) = l o g [\begin{matrix} 512 (i j t) - \\ 192 (i j + j t + i t) + \\ 144 (i + j + t) - 106 \end{matrix}] - \frac{1}{[\begin{matrix} 512 (i j t) - \\ 192 (i j + j t + i t) + \\ 144 (i + j + t) - 106 \end{matrix}]} [\begin{matrix} 924.7641466798 (i j t) - \\ 376.28749458 (i j + j t + i t) + \\ 317.8876754212 (i + j + t) - \\ 250.4569563924 \end{matrix}]

Proof. By definition (1.5). We have,

H_{2} ({c u}_{2} o) = [\begin{matrix} 512 (i j t) - 192 (i j + j t + i t) + 144 (i + j + t) - 106 \end{matrix}]

By definition (1.9). We have,

I ({c u}_{2} o, H_{2}) = \log [\begin{matrix} 512 (i j t) - \\ 192 (i j + j t + i t) + \\ 144 (i + j + t) - 106 \end{matrix}] - \frac{1}{[\begin{matrix} 512 (i j t) - \\ 192 (i j + j t + i t) + \\ 144 (i + j + t) - 106 \end{matrix}]} [\begin{matrix} {(1.2)}^{2} |E_{1}| l o g {(1.2)}^{2} + \\ {(2.2)}^{2} |E_{2}| l o g {(2.2)}^{2} + \\ {(2.4)}^{2} |E_{3}| l o g {(2.4)}^{2} \end{matrix}]

I ({c u}_{2} o, H_{2}) = \log [\begin{matrix} 512 (i j t) - \\ 192 (i j + j t + i t) + \\ 144 (i + j + t) - 106 \end{matrix}] - \frac{1}{[\begin{matrix} 512 (i j t) - \\ 192 (i j + j t + i t) + \\ 144 (i + j + t) - 106 \end{matrix}]} [\begin{matrix} 8 |E_{1}| l o g 2 + \\ 64 |E_{2}| l o g 2 + \\ 384 |E_{3}| l o g 2 \end{matrix}]

I ({c u}_{2} o, H_{2}) = \log [\begin{matrix} 512 (i j t) - \\ 192 (i j + j t + i t) + \\ 144 (i + j + t) - 106 \end{matrix}] - \frac{1}{[\begin{matrix} 512 (i j t) - \\ 192 (i j + j t + i t) + \\ 144 (i + j + t) - 106 \end{matrix}]} [\begin{matrix} l o g 2 (8 |E_{1}| + 64 |E_{2}| + 384 |E_{3}|) \end{matrix}]

I ({c u}_{2} o, H_{2}) = \log [\begin{matrix} 512 (i j t) - \\ 192 (i j + j t + i t) + \\ 144 (i + j + t) - 106 \end{matrix}] - \frac{1}{[\begin{matrix} 512 (i j t) - \\ 192 (i j + j t + i t) + \\ 144 (i + j + t) - 106 \end{matrix}]} [\begin{matrix} l o g 2 (\begin{matrix} 3072 (i j t) - 1250 (i j + j t + i t) + \\ 1056 (i + j + t) - 832 \end{matrix}) \end{matrix}]

I ({c u}_{2} o, H_{2}) = \log [\begin{matrix} 512 (i j t) - \\ 192 (i j + j t + i t) + \\ 144 (i + j + t) - 106 \end{matrix}] - \frac{1}{[\begin{matrix} 512 (i j t) - \\ 192 (i j + j t + i t) + \\ 144 (i + j + t) - 106 \end{matrix}]} [\begin{matrix} 924.7641466798 (i j t) - \\ 376.28749458 (i j + j t + i t) + \\ 317.8876754212 (i + j + t) - \\ 250.4569563924 \end{matrix}]

□

Theorem 6: The Entropy of

{c u}_{2} o [i, j, t] \geq 1

with redefined first Zagreb weight is

I ({c u}_{2} o, R e Z (G_{1})) = \log [\begin{matrix} 6 (i j t) + \\ (i j + j t + i t) + \\ i + j + t - 3 \end{matrix}] - \frac{1}{[\begin{matrix} 6 (i j t) + \\ (i j + j t + i t) + \\ i + j + t - 3 \end{matrix}]} [\begin{matrix} - 0.749632 (i j t) + \\ 0.374816 (i j + j t + i t) + \\ 0.681731 (i + j + t) - \\ 1.738279 \end{matrix}]

Proof. By definition (1.6). We have,

R e Z G_{1} ({c u}_{2} o) = [\begin{matrix} 6 (i j t) + i j + j t + i t + i + j + t - 3 \end{matrix}]

By definition (1.9). We have,

I ({c u}_{2} o, R e Z (G_{1})) = \log [\begin{matrix} 6 (i j t) + \\ (i j + j t + i t) + \\ i + j + t - 3 \end{matrix}] - \frac{1}{[\begin{matrix} 6 (i j t) + \\ (i j + j t + i t) + \\ i + j + t - 3 \end{matrix}]} [\begin{matrix} \frac{1 + 2}{1.2} |E_{1}| l o g \frac{1 + 2}{1.2} + \frac{2 + 2}{2.2} |E_{2}| l o g \frac{2 + 2}{2.2} + \\ \frac{2 + 4}{2.4} |E_{3}| l o g \frac{2 + 4}{2.4} \end{matrix}]

I ({c u}_{2} o, R e Z (G_{1})) = \log [\begin{matrix} 6 (i j t) + \\ (i j + j t + i t) + \\ i + j + t - 3 \end{matrix}] - \frac{1}{[\begin{matrix} 6 (i j t) + \\ (i j + j t + i t) + \\ i + j + t - 3 \end{matrix}]} [\begin{matrix} \frac{3}{2} |E_{1}| l o g 3 - \frac{3}{2} |E_{1}| l o g 2 + \\ \frac{3}{4} |E_{3}| l o g 3 - \frac{3}{2} |E_{3}| l o g 2 \end{matrix}]

I ({c u}_{2} o, R e Z (G_{1})) = \log [\begin{matrix} 6 (i j t) + \\ (i j + j t + i t) + \\ i + j + t - 3 \end{matrix}] - \frac{1}{[\begin{matrix} 6 (i j t) + \\ (i j + j t + i t) + \\ i + j + t - 3 \end{matrix}]} [\begin{matrix} - \frac{3}{2} l o g 2 (|E_{1}| + |E_{3}|) + \\ l o g 3 (\frac{3}{2} |E_{1}| + \frac{3}{4} |E_{3}|) \end{matrix}]

I ({c u}_{2} o, R e Z (G_{1})) = \log [\begin{matrix} 6 (i j t) + \\ (i j + j t + i t) + \\ i + j + t - 3 \end{matrix}] - \frac{1}{[\begin{matrix} 6 (i j t) + \\ (i j + j t + i t) + \\ i + j + t - 3 \end{matrix}]} [\begin{matrix} - \frac{3}{2} l o g 2 (\begin{matrix} 8 (i j t) - 4 (i j + i t + j t) + \\ 8 (i + j + t) - 12 \end{matrix}) + \\ l o g 3 (\begin{matrix} 6 (i j t) - 3 (i j + i t + j t) + \\ 9 (i + j + t) - 15 \end{matrix}) \end{matrix}]

I ({c u}_{2} o, R e Z (G_{1})) = \log [\begin{matrix} 6 (i j t) + \\ (i j + j t + i t) + \\ i + j + t - 3 \end{matrix}] - \frac{1}{[\begin{matrix} 6 (i j t) + \\ (i j + j t + i t) + \\ i + j + t - 3 \end{matrix}]} [\begin{matrix} - 0.749632 (i j t) + \\ 0.374816 (i j + j t + i t) + \\ 0.681731 (i + j + t) - \\ 1.738279 \end{matrix}]

□

Theorem 7: The Entropy of

{c u}_{2} o [i, j, t] \geq 1

with redefined second Zagreb weight is

I ({c u}_{2} o, R e Z (G_{2})) = \log [\frac{1}{3} [\begin{matrix} 32 (i j t) - \\ 4 (i j + j t + i t - 1) \end{matrix}]] - \frac{1}{[\frac{1}{3} [\begin{matrix} 32 (i j t) - \\ 4 (i j + j t + i t - 1) \end{matrix}]]} [\begin{matrix} 1.33267985716 (i j t) - \\ 0.66633992858 (i j + i t + j t) + \\ 0.19676323776 (i + j + t) + \\ 0.27281345305 \end{matrix}]

Proof. By definition (1.7). We have,

R e Z G_{2} ({c u}_{2} o,) = \frac{1}{3} [32 (i j t) - 4 (i j + j t + i t - 1)]

By definition (1.9). We have,

I ({c u}_{2} o, R e Z (G_{2})) = \log [\frac{1}{3} [\begin{matrix} 32 (i j t) - \\ 4 (i j + j t + i t - 1) \end{matrix}]] - \frac{1}{[\frac{1}{3} [\begin{matrix} 32 (i j t) - \\ 4 (i j + j t + i t - 1) \end{matrix}]]} [\begin{matrix} \frac{1.2}{1 + 2} |E_{1}| l o g \frac{1.2}{1 + 2} + \frac{2.2}{2 + 2} |E_{2}| l o g \frac{2.2}{2 + 2} + \\ \frac{2.4}{2 + 4} |E_{3}| l o g \frac{2.4}{2 + 4} \end{matrix}]

I ({c u}_{2} o, R e Z (G_{2})) = \log [\frac{1}{3} [\begin{matrix} 32 (i j t) - \\ 4 (i j + j t + i t - 1) \end{matrix}]] - \frac{1}{[\frac{1}{3} [\begin{matrix} 32 (i j t) - \\ 4 (i j + j t + i t - 1) \end{matrix}]]} [\begin{matrix} \frac{2}{3} |E_{1}| l o g 2 - \frac{2}{3} |E_{1}| l o g 3 + \\ \frac{8}{3} |E_{3}| l o g 2 - \frac{4}{3} |E_{3}| l o g 3 \end{matrix}]

I ({c u}_{2} o, R e Z (G_{2})) = \log [\frac{1}{3} [\begin{matrix} 32 (i j t) - \\ 4 (i j + j t + i t - 1) \end{matrix}]] - \frac{1}{[\frac{1}{3} [\begin{matrix} 32 (i j t) - \\ 4 (i j + j t + i t - 1) \end{matrix}]]} [\begin{matrix} \frac{2}{3} l o g 2 (|E_{1}| + 4 |E_{3}|) - \\ \frac{2}{3} l o g 3 (|E_{1}| + 2 |E_{3}|)) \end{matrix}]

I ({c u}_{2} o, R e Z (G_{2})) = \log [\frac{1}{3} [\begin{matrix} 32 (i j t) - \\ 4 (i j + j t + i t - 1) \end{matrix}]] - \frac{1}{[\frac{1}{3} [\begin{matrix} 32 (i j t) - \\ 4 (i j + j t + i t - 1) \end{matrix}]]} [\begin{matrix} \frac{2}{3} l o g 2 (\begin{matrix} 32 (i j t) - 16 (i j + i t + j t) + \\ 20 (i + j + t) - 24 \end{matrix}) - \\ \frac{2}{3} l o g 3 (\begin{matrix} 16 (i j t) - 8 (i j + i t + j t) + \\ 12 (i + j + t) - 16 \end{matrix}) \end{matrix}]

I ({c u}_{2} o, R e Z (G_{2})) = \log [\frac{1}{3} [\begin{matrix} 32 (i j t) - \\ 4 (i j + j t + i t - 1) \end{matrix}]] - \frac{1}{[\frac{1}{3} [\begin{matrix} 32 (i j t) - \\ 4 (i j + j t + i t - 1) \end{matrix}]]} [\begin{matrix} 1.33267985716 (i j t) - \\ 0.66633992858 (i j + i t + j t) + \\ 0.19676323776 (i + j + t) + \\ 0.27281345305 \end{matrix}]

□

Theorem 8: The Entropy of

{c u}_{2} o [i, j, t] \geq 1

with redefined third Zagreb weight is

I ({c u}_{2} o, R e Z (G_{3})) = \log [\begin{matrix} 384 (i j t) - \\ 128 (i j + j t + i t) + \\ 88 (i + j + t) - 48 \end{matrix}] - \frac{1}{[\begin{matrix} 384 (i j t) - \\ 128 (i j + j t + i t) + \\ 88 (i + j + t) - 48 \end{matrix}]} [\begin{matrix} 645.59663515 (i j t) - \\ 245.734639 (i j + j t + i t) - \\ 458.25004534686 (i + j + t) - \\ 128.95854092 \end{matrix}]

Proof. By definition (1.8). We have, Entropy with

R e Z G_{3} ({c u}_{2} o) = [384 (i j t) - 128 (i j + j t + i t) + 88 (i + j + t) - 48]

By definition (1.9). We have,

I ({c u}_{2} o, {R e Z (G}_{3})) = \log [\begin{matrix} 384 (i j t) - \\ 128 (i j + j t + i t) + \\ 88 (i + j + t) - 48 \end{matrix}] - \frac{1}{[\begin{matrix} 384 (i j t) - \\ 128 (i j + j t + i t) + \\ 88 (i + j + t) - 48 \end{matrix}]} [\begin{matrix} (1.2) (1 + 2) |E_{1}| \log (1.2) (1 + 2) + \\ (2.2) (2 + 2) |E_{2}| \log (2.2) (2 + 2) + \\ (2.4) (2 + 4) |E_{3}| \log (2.3) (2 + 3) + \end{matrix}]

I ({c u}_{2} o, {R e Z (G}_{3})) = \log [\begin{matrix} 384 (i j t) - \\ 128 (i j + j t + i t) + \\ 88 (i + j + t) - 48 \end{matrix}] - \frac{1}{[\begin{matrix} 384 (i j t) - \\ 128 (i j + j t + i t) + \\ 88 (i + j + t) - 48 \end{matrix}]} [\begin{matrix} 6 |E_{1}| \log 6 + 16 |E_{2}| \log 16 + \\ 48 |E_{3}| l o g 48 \end{matrix}]

I ({c u}_{2} o, {R e Z (G}_{3})) = \log [\begin{matrix} 384 (i j t) - \\ 128 (i j + j t + i t) + \\ 88 (i + j + t) - 48 \end{matrix}] - \frac{1}{[\begin{matrix} 384 (i j t) - \\ 128 (i j + j t + i t) + \\ 88 (i + j + t) - 48 \end{matrix}]} [\begin{matrix} [24 (i + j + t) - 48] l o g 6 + \\ (64 (i j + j t + i t) - 128 (i + j + t) + 192) l o g 16 + \\ (\begin{matrix} 384 (i j t) - 192 (i j + i t + j t) - \\ 192 (i + j + t) - 192 \end{matrix}) l o g 48 \end{matrix}]

I ({c u}_{2} o, R e Z (G_{3})) = \log [\begin{matrix} 384 (i j t) - \\ 128 (i j + j t + i t) + \\ 88 (i + j + t) - 48 \end{matrix}] - \frac{1}{[\begin{matrix} 384 (i j t) - \\ 128 (i j + j t + i t) + \\ 88 (i + j + t) - 48 \end{matrix}]} [\begin{matrix} 645.59663515 (i j t) - \\ 245.734639 (i j + j t + i t) - \\ 458.25004534686 (i + j + t) - \\ 128.95854092 \end{matrix}]

□

Theorem 9: Weighted Entropy of

{c u}_{2} o [i, j, t] \geq 2

with the first Zagreb Index is

I ({c u}_{2} o [i, j, t], M_{1}) = \log [\begin{matrix} (128 i j t - \\ 32 (i j + i t + j t) \\ + 12 (i + j + t) + 8 \end{matrix}] - \frac{1}{[\begin{matrix} (128 i j t - \\ 32 (i j + i t + j t) \\ + 12 (i + j + t) + 8 \end{matrix}]} [\begin{matrix} 154.1273578 (i j t) - \\ 49.9441878 (i j + i t + j t) + \\ 22.3617021 (i + j + t) + \\ 5.2207836 \end{matrix}]

Proof. By definition (1.1). We have,

M_{1} ({c u}_{2} o) = (128 i j t - 32 (i j + i t + j t) + 12 (i + j + t) + 8

By definition (1.9). We have,

I ({c u}_{2} o, M_{1}) = \log [\begin{matrix} (128 i j t - \\ 32 (i j + i t + j t) \\ + 12 (i + j + t) + 8 \end{matrix}] - \frac{1}{[\begin{matrix} (128 i j t - \\ 32 (i j + i t + j t) \\ + 12 (i + j + t) + 8 \end{matrix}]} [\begin{matrix} (2 + 4) |E_{1}| \log (2 + 4) + \\ (4 + 6) |E_{2}| \log (4 + 6) + \\ (5 + 8) |E_{3}| \log (5 + 8) + \\ (6 + 8) |E_{4}| \log (6 + 8) + \\ (8 + 8) |E_{5}| \log (8 + 8) \end{matrix}]

I ({c u}_{2} o, M_{1}) = \log [\begin{matrix} (128 i j t - \\ 32 (i j + i t + j t) \\ + 12 (i + j + t) + 8 \end{matrix}] - \frac{1}{[\begin{matrix} (128 i j t - \\ 32 (i j + i t + j t) \\ + 12 (i + j + t) + 8 \end{matrix}]} [\begin{matrix} 6 |E_{1}| \log (6) + \\ 10 |E_{2}| \log 10 + \\ 13 |E_{3}| \log 13 + \\ 14 |E_{4}| \log 14 + \\ 16 |E_{5}| \log 16 \end{matrix}]

I ({c u}_{2} o, M_{1}) = \log [\begin{matrix} (128 i j t - \\ 32 (i j + i t + j t) \\ + 12 (i + j + t) + 8 \end{matrix}] - \frac{1}{[\begin{matrix} (128 i j t - \\ 32 (i j + i t + j t) \\ + 12 (i + j + t) + 8 \end{matrix}]} [\begin{matrix} l o g 6 (24 (i + j + t) - 48) + \\ l o g 10 [\begin{matrix} 40 (i j + i t + j t) - \\ 80 (i + j + t) + 120 \end{matrix}] + \\ l o g 13 (52 (i + j + t) - 104) + \\ l o g 14 [\begin{matrix} 56 (i j + i t + j t) - \\ 112 (i + j + t) + 168 \end{matrix}] + \\ 128 l o g 16 [\begin{matrix} i j t - (i j + i t + j t) + \\ (i + j + t) - 1 \end{matrix}] \end{matrix}]

I ({c u}_{2} o [i, j, t], M_{1}) = \log [\begin{matrix} (128 i j t - \\ 32 (i j + i t + j t) \\ + 12 (i + j + t) + 8 \end{matrix}] - \frac{1}{[\begin{matrix} (128 i j t - \\ 32 (i j + i t + j t) \\ + 12 (i + j + t) + 8 \end{matrix}]} [\begin{matrix} 154.1273578 (i j t) - \\ 49.9441878 (i j + i t + j t) + \\ 22.3617021 (i + j + t) + \\ 5.2207836 \end{matrix}]

□

Theorem 10: Weighted Entropy of

{c u}_{2} o [i, j, t] \geq 2

with the second Zagreb Index is

I ({c u}_{2} o [i, j, t], M_{2}) = \log [\begin{matrix} (512 i j t - \\ 244 (i j + i t + j t) \\ + 128 (i + j + t) \\ - 32 \end{matrix}] - \frac{1}{[\begin{matrix} (512 i j t - \\ 244 (i j + i t + j t) \\ + 128 (i + j + t) \\ - 32 \end{matrix}]} [\begin{matrix} 924.7641467 (i j t) - \\ 469.465549899 (i j + i t + j t) + \\ 299.3954313 (i + j + t) - \\ 129.3253127309 \end{matrix}]

Proof. By definition (1.2). We have,

M_{2} ({c u}_{2} o) = 512 i j t - 244 (i j + i t + j t) + 128 (i + j + t) - 32

By definition (1.9). We have,

I ({c u}_{2} o, M_{2}) = \log [\begin{matrix} (512 i j t - \\ 244 (i j + i t + j t) \\ + 128 (i + j + t) - 32 \end{matrix}] - \frac{1}{[\begin{matrix} (512 i j t - \\ 244 (i j + i t + j t) \\ + 128 (i + j + t) - 32 \end{matrix}]} [\begin{matrix} (2.4) |E_{1}| \log (2.4) + \\ (4.6) |E_{2}| \log (4.6) + \\ (5.8) |E_{3}| \log (5.8) + \\ (6.8) |E_{4}| \log (6.8) + \\ (8.8) |E_{5}| \log (8.8) \end{matrix}]

I ({c u}_{2} o, M_{2}) = \log [\begin{matrix} (512 i j t - \\ 244 (i j + i t + j t) \\ + 128 (i + j + t) - 32 \end{matrix}] - \frac{1}{[\begin{matrix} (512 i j t - \\ 244 (i j + i t + j t) \\ + 128 (i + j + t) - 32 \end{matrix}]} [\begin{matrix} 8 |E_{1}| \log (8) + \\ 24 |E_{2}| \log (24) + \\ 40 |E_{3}| \log (40) + \\ 48 |E_{4}| \log (48) + \\ 64 |E_{5}| \log (64) \end{matrix}]

I ({c u}_{2} o, M_{2}) = \log [\begin{matrix} (512 i j t - \\ 244 (i j + i t + j t) \\ + 128 (i + j + t) \\ - 32 \end{matrix}] - \frac{1}{[\begin{matrix} (512 i j t - \\ 244 (i j + i t + j t) \\ + 128 (i + j + t) \\ - 32 \end{matrix}]} [\begin{matrix} 8 l o g 8 (4 (i + j + t) - 8) + \\ 24 l o g 24 [\begin{matrix} 4 (i j + i t + j t) - \\ 8 (i + j + t) + 12 \end{matrix}] + \\ 40 l o g 40 (4 (i + j + t) - 8) + \\ 48 l o g 48 [\begin{matrix} 4 (i j + i t + j t) - \\ 8 (i + j + t) + 12 \end{matrix}] + \\ 64 l o g 64 [\begin{matrix} 8 i j t - 8 (i j + i t + j t) + \\ 8 (i + j + t) - 8 \end{matrix}] \end{matrix}]

I ({c u}_{2} o [i, j, t], M_{2}) = \log [\begin{matrix} 512 i j t - \\ 244 (i j + i t + j t) \\ + 128 (i + j + t) \\ - 32 \end{matrix}] - \frac{1}{[\begin{matrix} (512 i j t - \\ 244 (i j + i t + j t) \\ + 128 (i + j + t) \\ - 32 \end{matrix}]} [\begin{matrix} 924.7641467 (i j t) - \\ 469.465549899 (i j + i t + j t) + \\ 299.3954313 (i + j + t) - \\ 129.3253127309 \end{matrix}]

□

Theorem 11: The Entropy of

{c u}_{2} o [i, j, t] \geq 2

with Augmented Zagreb weight is

({c u}_{2} o, A Z I) = \log [\begin{matrix} \frac{262144}{343} (i j t) - \\ \frac{137292}{343} (i j + i t + j t) \\ + \frac{95558696}{113533} (i + j + t) \\ - \frac{55213740}{456533} \end{matrix}] - \frac{1}{[\begin{matrix} \frac{262144}{343} (i j t) - \\ \frac{137292}{343} (i j + i t + j t) \\ + \frac{95558696}{113533} (i + j + t) \\ - \frac{55213740}{456533} \end{matrix}]} [\begin{matrix} 1513.37016310667 (i j t) - \\ 896.40080323762 (i j + i t + j t) + \\ 631.84083470165 (i + j + t) - \\ 367.28086616568 \end{matrix}]

Proof. By definition (1.4). We have,

A Z I ({c u}_{2} o) = [\begin{matrix} \frac{262144}{343} (i j t) - \frac{137292}{343} (i j + j t + i t) + \frac{95558696}{113533} (i + j + t) - \frac{55213740}{456533} \end{matrix}]

By definition (1.9). We have,

I ({c u}_{2} o, A Z I) = \log [\begin{matrix} \frac{262144}{343} (i j t) - \\ \frac{137292}{343} (i j + i t + j t) \\ + \frac{95558696}{113533} (i + j + t) \\ - \frac{55213740}{456533} \end{matrix}] - \frac{1}{[\begin{matrix} \frac{262144}{343} (i j t) - \\ \frac{137292}{343} (i j + i t + j t) \\ + \frac{95558696}{113533} (i + j + t) \\ - \frac{55213740}{456533} \end{matrix}]} [\begin{matrix} {(\frac{2.4}{2 + 4 - 2})}^{3} |E_{1}| l o g {(\frac{2.4}{2 + 4 - 2})}^{3} + \\ {(\frac{4.6}{4 + 6 - 2})}^{3} |E_{2}| l o g {(\frac{4.6}{4 + 6 - 2})}^{3} + \\ {(\frac{5.8}{5 + 8 - 2})}^{3} |E_{3}| l o g {(\frac{5.8}{5 + 8 - 2})}^{3} + \\ {(\frac{6.8}{6 + 8 - 2})}^{3} |E_{3}| l o g {(\frac{6.8}{6 + 8 - 2})}^{3} + \\ {(\frac{8.8}{8 + 8 - 2})}^{3} |E_{3}| l o g {(\frac{8.8}{8 + 8 - 2})}^{3} \end{matrix}]

I ({c u}_{2} o, A Z I) = \log [\begin{matrix} \frac{262144}{343} (i j t) - \\ \frac{137292}{343} (i j + i t + j t) \\ + \frac{95558696}{113533} (i + j + t) \\ - \frac{55213740}{456533} \end{matrix}] - \frac{1}{[\begin{matrix} \frac{262144}{343} (i j t) - \\ \frac{137292}{343} (i j + i t + j t) \\ + \frac{95558696}{113533} (i + j + t) \\ - \frac{55213740}{456533} \end{matrix}]} [\begin{matrix} 24 |E_{1}| l o g 2 + 81 |E_{2}| l o g 3 + \\ \frac{576000}{1331} |E_{3}| l o g 2 + \frac{192000}{1331} |E_{3}| l o g 5 \\ - \frac{192000}{1331} |E_{3}| l o g 11 + 384 |E_{4}| l o g 2 + \\ \frac{491520}{343} |E_{5}| l o g 2 - \frac{98304}{343} |E_{5}| l o g 7 \end{matrix}]

I ({c u}_{2} o, A Z I) = \log [\begin{matrix} \frac{262144}{343} (i j t) - \\ \frac{137292}{343} (i j + i t + j t) \\ + \frac{95558696}{113533} (i + j + t) \\ - \frac{55213740}{456533} \end{matrix}] - \frac{1}{[\begin{matrix} \frac{262144}{343} (i j t) - \\ \frac{137292}{343} (i j + i t + j t) \\ + \frac{95558696}{113533} (i + j + t) \\ - \frac{55213740}{456533} \end{matrix}]} [\begin{matrix} l o g 2 (\begin{matrix} \frac{3932160}{343} (i j t) - \\ \frac{3405312}{343} (i j + i t + j t) + \\ \frac{4665334752}{456533} (i + j + t) - \\ \frac{4798199232}{466533} \end{matrix}) + \\ l o g 3 (\begin{matrix} 324 (i j + i t + j t) - \\ 648 (i + j + t) + 972 \end{matrix}) + \\ l o g 5 (\frac{768000}{1331} (i + j + t) - \frac{1536000}{1331}) \\ - l o g 7 (\begin{matrix} \frac{786432}{343} (i j t) - \\ \frac{786432}{343} (i j + i t + j t) + \\ \frac{786432}{343} (i + j + t) - \\ \frac{786432}{343} \end{matrix}) - \\ l o g 11 (\frac{768000}{1331} (i + j + t) - \frac{1536000}{1331}) \end{matrix}]

({c u}_{2} o, A Z I) = \log [\begin{matrix} \frac{262144}{343} (i j t) - \\ \frac{137292}{343} (i j + i t + j t) \\ + \frac{95558696}{113533} (i + j + t) \\ - \frac{55213740}{456533} \end{matrix}] - \frac{1}{[\begin{matrix} \frac{262144}{343} (i j t) - \\ \frac{137292}{343} (i j + i t + j t) \\ + \frac{95558696}{113533} (i + j + t) \\ - \frac{55213740}{456533} \end{matrix}]} [\begin{matrix} 1513.37016310667 (i j t) - \\ 896.40080323762 (i j + i t + j t) + \\ 631.84083470165 (i + j + t) - \\ 367.28086616568 \end{matrix}]

□

Theorem 12: The Entropy of

{c u}_{2} o [i, j, t] \geq 2

with hyper Zagreb second weight is

I ({c u}_{2} o, H_{2}) = \log [\begin{matrix} 32768 (i j t) - \\ 21248 (i j + j t + i t) + \\ 16384 (i + j + t) \\ - 11520 \end{matrix}] - \frac{1}{[\begin{matrix} 32768 (i j t) - \\ 21248 (i j + j t + i t) + \\ 16384 (i + j + t) \\ - 11520 \end{matrix}]} [\begin{matrix} 118369.81077500801 (i j t) - \\ 81021.1588858941 (i j + j t + i t) + \\ 64641.25695911797 (i + j + t) - \\ 48261.35503234189 \end{matrix}]

Proof. By definition (1.5). We have,

H_{2} ({c u}_{2} o) = [\begin{matrix} 32768 (i j t) - 21248 (i j + j t + i t) + 16384 (i + j + t) - 11520 \end{matrix}]

By definition (1.9). We have,

I ({c u}_{2} o, H_{2}) = \log [\begin{matrix} 32768 (i j t) - \\ 21248 (i j + j t + i t) + \\ 16384 (i + j + t) \\ - 11520 \end{matrix}] - \frac{1}{[\begin{matrix} 32768 (i j t) - \\ 21248 (i j + j t + i t) + \\ 16384 (i + j + t) \\ - 11520 \end{matrix}]} [\begin{matrix} {(2.4)}^{2} |E_{1}| l o g {(2.4)}^{2} + \\ {(4.6)}^{2} |E_{2}| l o g {(4.6)}^{2} + \\ {(5.8)}^{2} |E_{3}| l o g {(5.8)}^{2} + \\ {(6.8)}^{2} |E_{4}| l o g {(6.8)}^{2} + \\ {(8.8)}^{2} |E_{5}| l o g {(8.8)}^{2} \end{matrix}]

I ({c u}_{2} o, H_{2}) = \log [\begin{matrix} 32768 (i j t) - \\ 21248 (i j + j t + i t) + \\ 16384 (i + j + t) \\ - 11520 \end{matrix}] - \frac{1}{[\begin{matrix} 32768 (i j t) - \\ 21248 (i j + j t + i t) + \\ 16384 (i + j + t) \\ - 11520 \end{matrix}]} [\begin{matrix} 128 |E_{1}| \log (8) + \\ 1152 |E_{2}| \log (24) + \\ 3200 |E_{3}| \log (40) + \\ 4608 |E_{4}| \log (48) + \\ 8192 |E_{5}| \log (64) \end{matrix}]

I ({c u}_{2} o, H_{2}) = \log [\begin{matrix} 32768 (i j t) - \\ 21248 (i j + j t + i t) + \\ 16384 (i + j + t) \\ - 11520 \end{matrix}] - \frac{1}{[\begin{matrix} 32768 (i j t) - \\ 21248 (i j + j t + i t) + \\ 16384 (i + j + t) \\ - 11520 \end{matrix}]} [\begin{matrix} 128 l o g 8 (4 (i + j + t) - 8) + \\ 1152 l o g 24 [\begin{matrix} 4 (i j + i t + j t) - \\ 8 (i + j + t) + 12 \end{matrix}] + \\ 3200 l o g 40 (4 (i + j + t) - 8) + \\ 4608 l o g 48 [\begin{matrix} 4 (i j + i t + j t) - \\ 8 (i + j + t) + 12 \end{matrix}] + \\ 8192 l o g 64 [\begin{matrix} 8 i j t - 8 (i j + i t + j t) + \\ 8 (i + j + t) - 8 \end{matrix}] \end{matrix}]

I ({c u}_{2} o, H_{2}) = \log [\begin{matrix} 32768 (i j t) - \\ 21248 (i j + j t + i t) + \\ 16384 (i + j + t) \\ - 11520 \end{matrix}] - \frac{1}{[\begin{matrix} 32768 (i j t) - \\ 21248 (i j + j t + i t) + \\ 16384 (i + j + t) \\ - 11520 \end{matrix}]} [\begin{matrix} 118369.81077500801 (i j t) - \\ 81021.1588858941 (i j + j t + i t) + \\ 64641.25695911797 (i + j + t) - \\ 48261.35503234189 \end{matrix}]

□

Graphical Comparison of the Results:

Figure 3. Comparison of Topological Indices for

{c u}_{2} o [i, j, t] \geq 1

.

Figure 3. Comparison of Topological Indices for

{c u}_{2} o [i, j, t] \geq 1

.

Figure 4. Comparison of Topological Indices for

{c u}_{2} o [i, j, t] \geq 2

.

Figure 4. Comparison of Topological Indices for

{c u}_{2} o [i, j, t] \geq 2

.

Figure 5. Comparison of Entropies for

{c u}_{2} o [i, j, t] \geq 1

.

Figure 5. Comparison of Entropies for

{c u}_{2} o [i, j, t] \geq 1

.

Figure 6. Comparison of Entropies for

{c u}_{2} o [i, j, t] \geq 2

.

Figure 6. Comparison of Entropies for

{c u}_{2} o [i, j, t] \geq 2

.

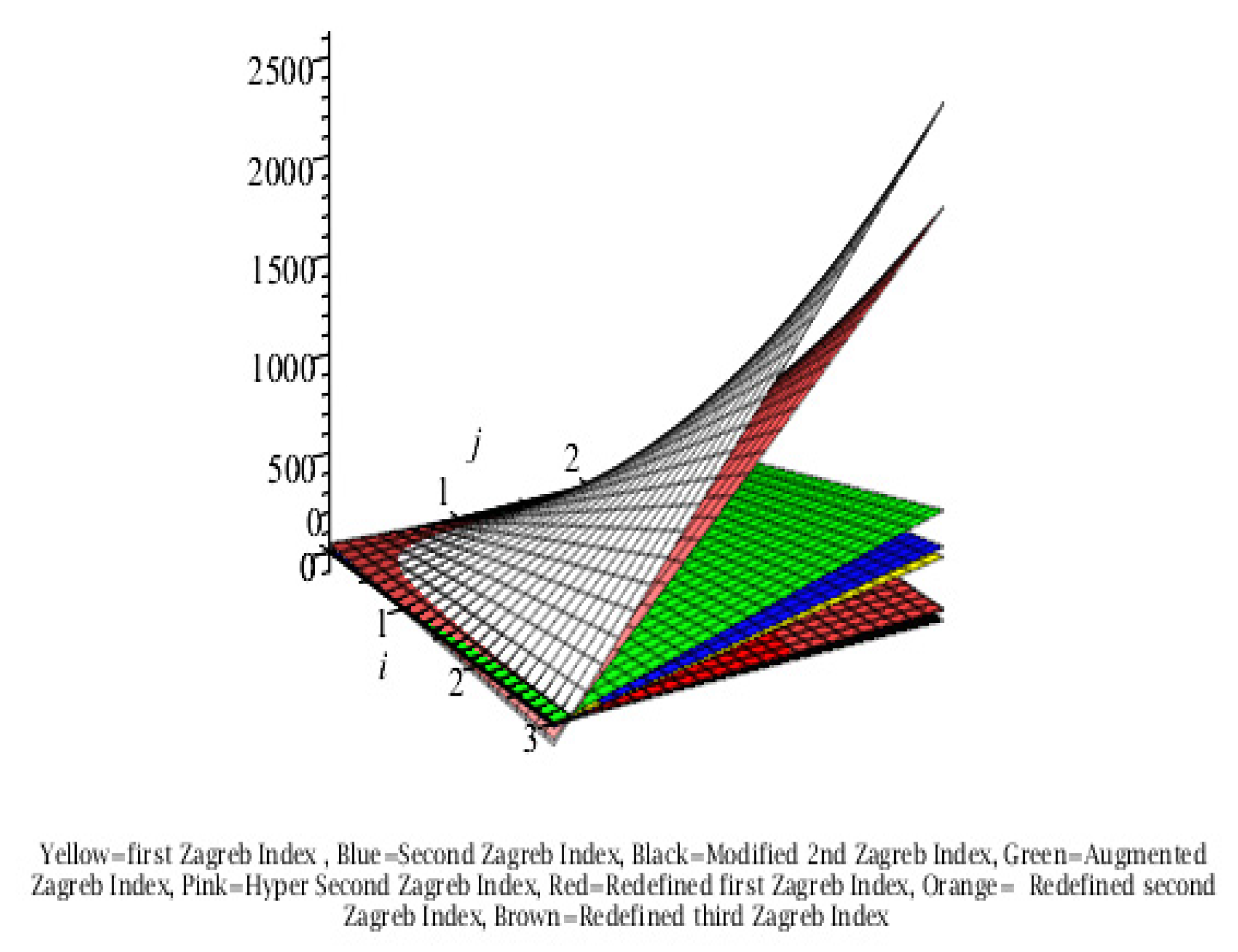
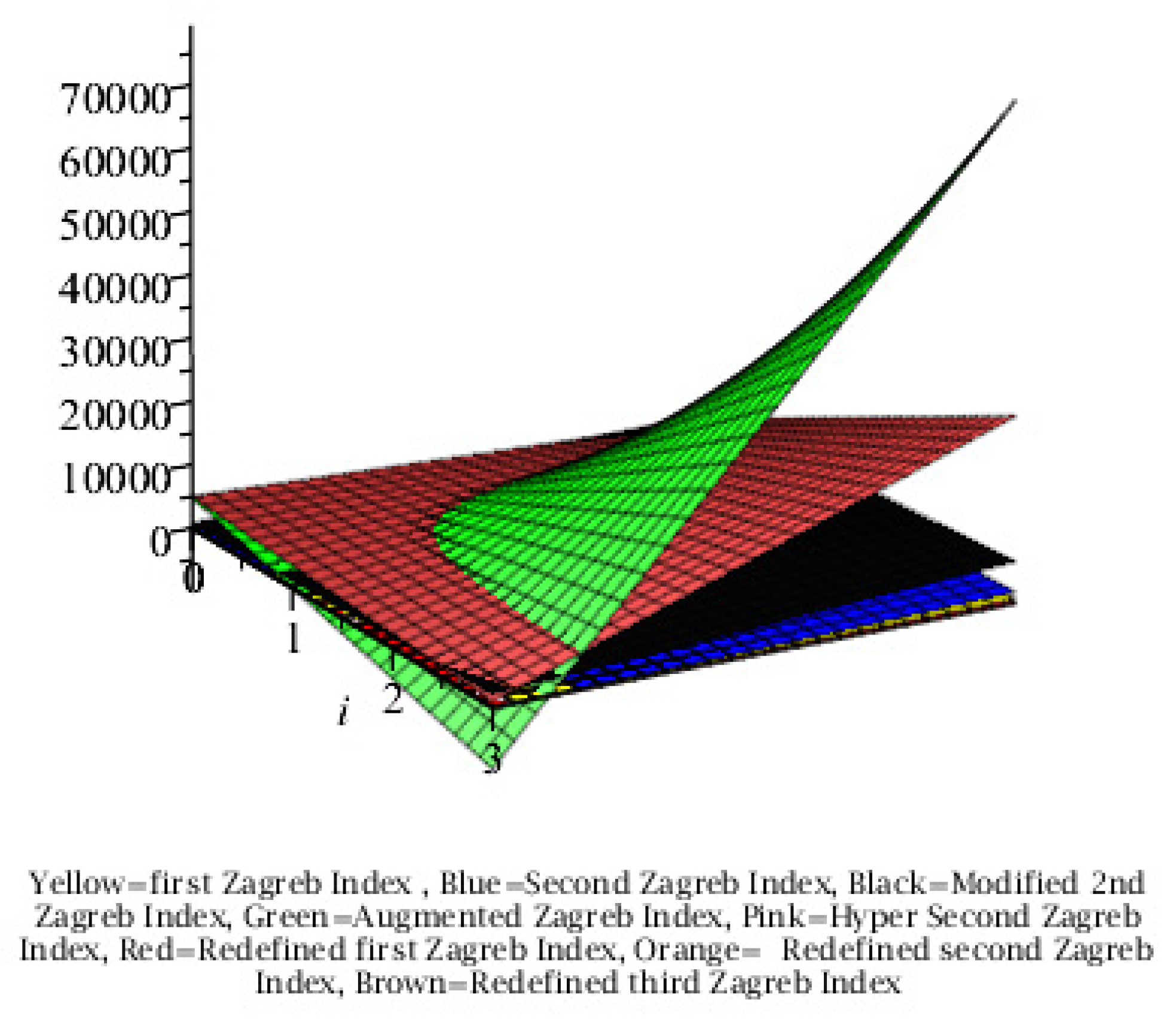
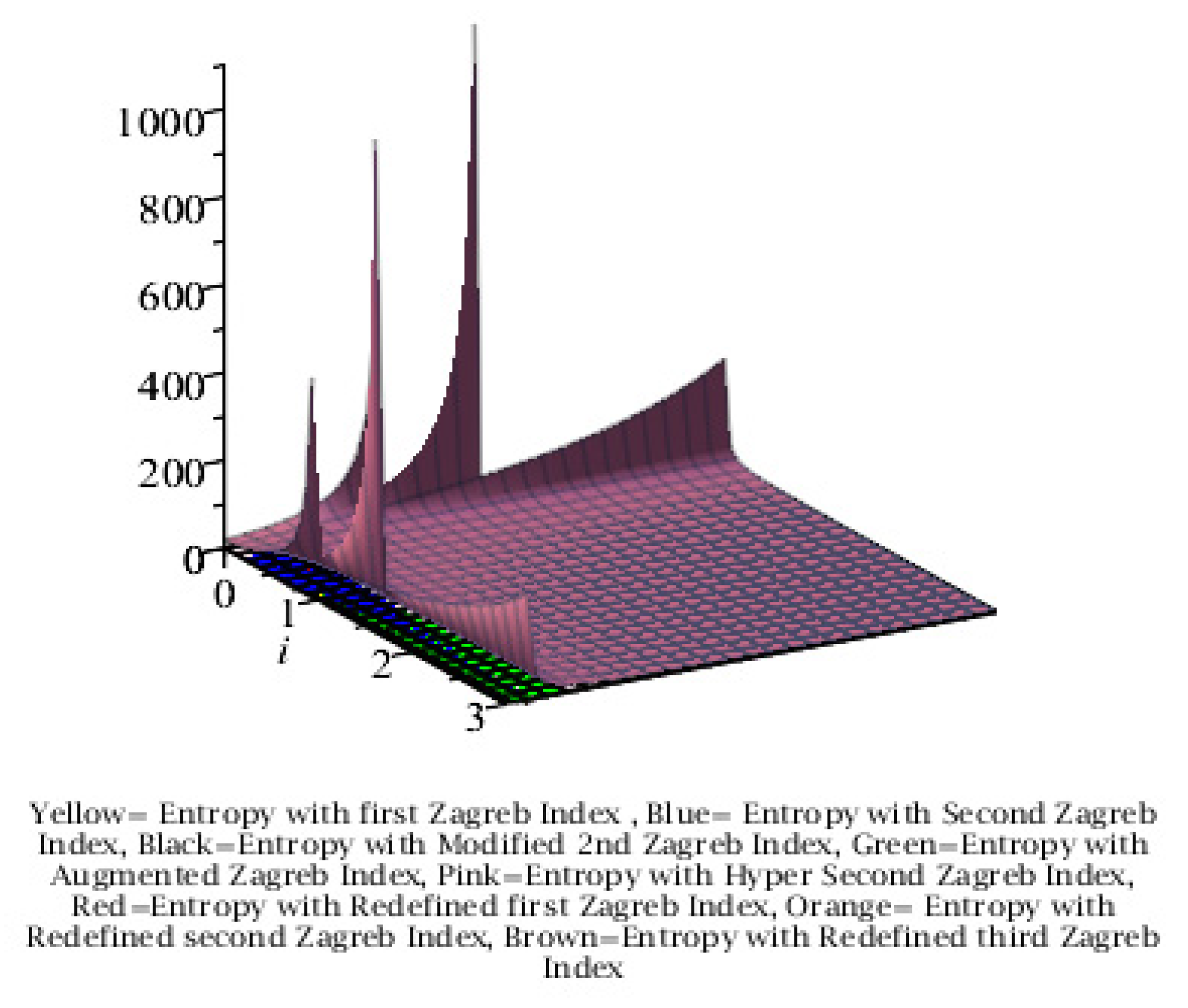
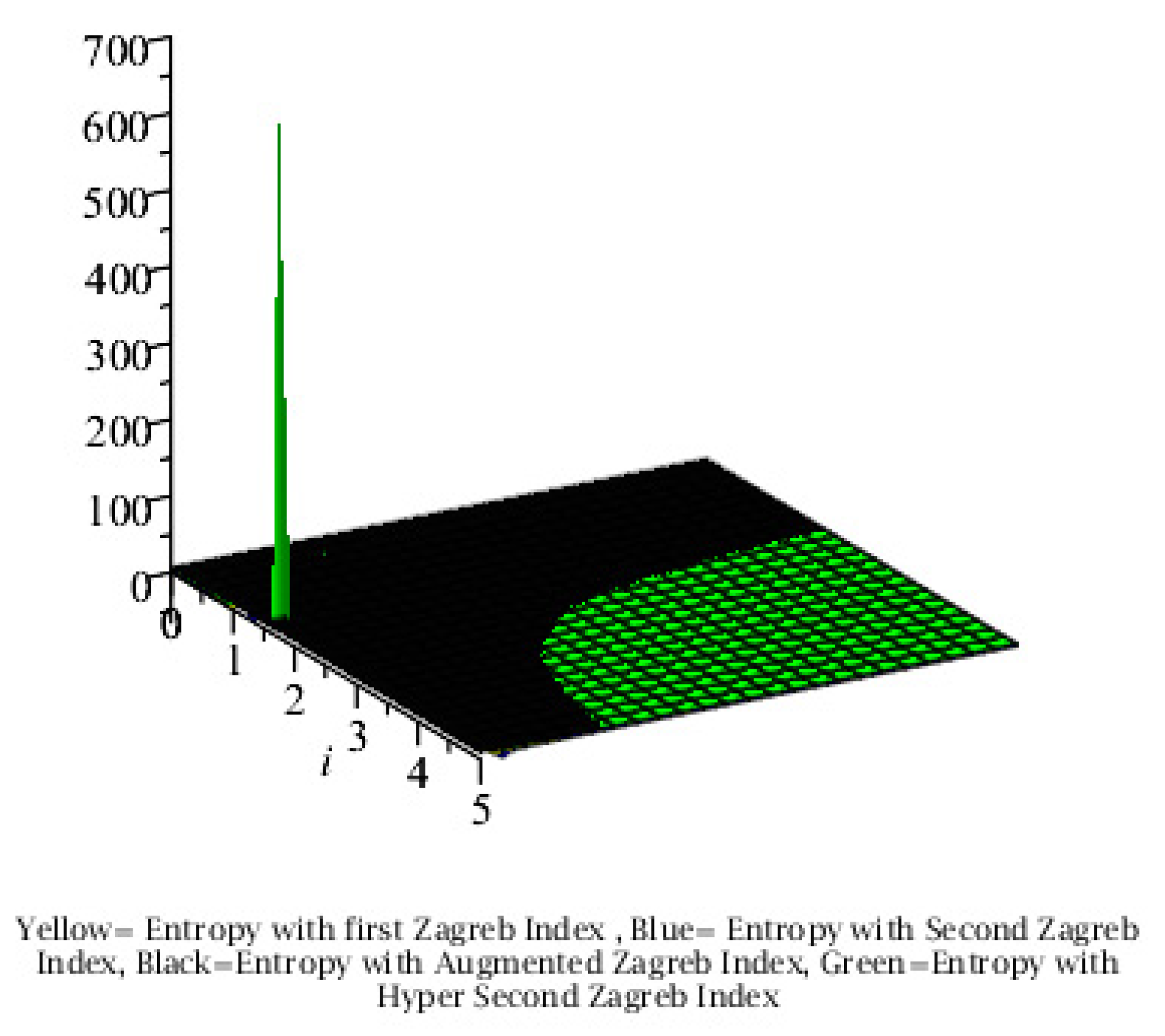
Conclusion

In this paper, we studied the crystallographic structure

{c u}_{2} o

. We work on the structure of Crystallographic Structure of the molecule

{c u}_{2} o [i, j, t]

and apply the definition of entropies based on topological indices to it. Methods to calculate entropies based on topological indices have opened the door to many diverse applications, such as antiparasitic drug QSAR estimations. Topological descriptors help us understand the graphs and networks that underlie topologies. Various chemical graph entropies calculated on topological-based assessments can tackle many complicated schemes in biomedicine, bioinformatics, and chem-informatics, among other fields. This topological study may help in the electronic and atomic structure of oxygen-dosed and clean of for

{c u}_{2} o

single-crystal surfaces and all new experimental information may concern the defect structure in non-stoichiometric for

{c u}_{2} o

. The results are comprehensively calculated and can bring future outcomes. In the future, we are interested in calculating the entropies based on different distance-based topological indices for the chemical structure of for

{c u}_{2} o

.

Data Availability Statement

The data is provided on request to the authors.

Conflicts of Interest

The authors declare that they have no conflicts of interest and all the agree to publish this paper under academic ethics.

References

Gutman I., Some properties of the Wiener polynomials, Graph Theory, Notes New York, 1993, 125, 1318.
Munir M., Nazeer W., Shahzadi S., Kang S.M., Some invariants of circulant graphs, Symmetry, 2016, 8(11), 134, 10.3390/ sym8110134.
Gutman, I., and Trinajstic, N. (1972). Graph theory and molecular orbitals. Total f- electron energy of alternant hydrocarbons. Chemical physics letters, 17(4), 535-538.
Milicevic, A., Nikolic, S., and Trinajstic, N. (2004). On reformulated Zagreb indices. Molecular diversity, 8(4), 393-399. [CrossRef]
Furtula, B., Graovac, A., and Vukicevic, D. (2010). Augmented Zagreb index. Journal of mathematical chemistry, 48(2), 370-380.
Shirdel, G. H., Rezapour, H., and Sayadi, A. M. (2013). The hyper-Zagreb index of graph operations.
Ranjini, P. S., Lokesha, V., and Usha, A. (2013). Relation between phenylene and hexagonal squeeze using harmonic an index. Int. J. Graph Theory, 1(4), 116-121.
Vukicevic, D., and Gaperov, M. (2010). Bond additive modeling 1. Adriatic indices. Croatica chemical Acta, 83(3), 243-260.
Di Crescenzo, A., and Longobardi, M. (2007). On weighted residual and past entropies. ArXiv preprint math/0703489.
Araujo, O., and De La Pena, J. A. (1998). The connectivity index of a weighted graph. Linear algebra and its applications, 283(1-3), 171-177.
Gutman, I., and Trinajstic, N. (1972). Graph theory and molecular orbitals. Total f- electron energy of alternant hydrocarbons. Chemical physics letters, 17(4), 535-538.
Ullah, A., Zaman, S., Hamraz, A., & Saeedi, G. (2022). Network-based modeling of the molecular topology of fuchsine acid dye with respect to some irregular molecular descriptors. Journal of Chemistry, 2022. [CrossRef]
Ullah, A., Qasim, M., Zaman, S., & Khan, A. (2022). Computational and comparative aspects of two carbon nanosheets with respect to some novel topological indices. Ain Shams Engineering Journal, 13(4), 101672. [CrossRef]
Zaman, S., Yaqoob, H. S. A., Ullah, A., & Sheikh, M. (2023). QSPR Analysis of Some Novel Drugs Used in Blood Cancer Treatment Via Degree Based Topological Indices and Regression Models. Polycyclic Aromatic Compounds, 1-17. [CrossRef]
Zaman, S., Ullah, A., & Shafaqat, A. (2023). Structural modeling and topological characterization of three kinds of dendrimer networks. The European Physical Journal E, 46(5), 36.
Ali, N., Kousar, Z., Safdar, M., Tolasa, F. T., & Suleiman, E. (2023). Mapping Connectivity Patterns: Degree-Based Topological Indices of Corona Product Graphs. Journal of Applied Mathematics, 2023.
Zaman, S., & Ullah, A. (2023). Kemeny’s constant and global mean first passage time of random walks on octagonal cell network. Mathematical Methods in the Applied Sciences, 46(8), 9177-9186.
Randic, M. (1975). Characterization of molecular branching. Journal of the American Chemical Society, 97(23), 6609-6615.
Hayat, S., Khan, S., Khan, A., & Liu, J. B. (2022). Valency-based molecular descriptors for measuring the π-electronic energy of lower polycyclic aromatic hydrocarbons. Polycyclic Aromatic Compounds, 42(4), 1113-1129. [CrossRef]
Hayat, S., Khan, S., Khan, A., & Imran, M. (2020). Distance-based topological descriptors for measuring the π-electronic energy of benzenoid hydrocarbons with applications to carbon nanotubes. Mathematical Methods in the Applied Sciences. [CrossRef]
Malik, M. Y. H., Hayat, S., Khan, S., & Binyamin, M. A. (2021). Predictive potential of spectrum-based topological descriptors for measuring the π-electronic energy of benzenoid hydrocarbons with applications to boron triangular and boron α-nanotubes. Mathematical Methods in the Applied Sciences.
Tomescu, I., Arshad, M., and Jamil, M. K. (2015). Extremal topological indices for graphs of given connectivity. Filomat, 29(7), 1639-1643.
Garca, Domenech, R., Glvez, J., de Julin-Ortiz, J. V., and Pogliani, L. (2008). Some new trends in chemical graph theory. Chemical Reviews, 108(3), 1127-1169.
Ali, N., Siddiqui, H. M. A., & Qureshi, M. I. (2023). A Graph-Theoretic Approach to Ring Analysis: Dominant Metric Dimensions in Zero-Divisor Graphs. arXiv preprint arXiv:2312.16005. [CrossRef]
Ullah, A., Zaman, S., Hamraz, A., & Muzammal, M. (2023). On the construction of some bioconjugate networks and their structural modeling via irregularity topological indices. The European Physical Journal E, 46(8), 72. [CrossRef]
Zaman, S., Jalani, M., Ullah, A., & Saeedi, G. (2022). Structural analysis and topological characterization of sudoku nanosheet. Journal of Mathematics, 2022. [CrossRef]
Ullah, A., Zeb, A., & Zaman, S. (2022). A new perspective on the modeling and topological characterization of H-Naphtalenic nanosheets with applications. Journal of Molecular Modeling, 28(8), 211.
Bozkurt, S. B., Gngr, A. D., Gutman, I., and Cevik, A. S. (2010). Randic matrix and Randic energy. MATCH Commun. Math. Compute. Chem, 64(1), 239-250.
Kier, L. B., and Hall, L. H. (1986). Molecular connectivity in structure-activity analysis. Research studies.
Hayat, S., Suhaili, N., & Jamil, H. (2023). Statistical significance of valency-based topological descriptors for correlating thermodynamic properties of benzenoid hydrocarbons with applications. Computational and Theoretical Chemistry, 1227, 114259. [CrossRef]
Hayat, Sakander. “Distance-based graphical indices for predicting thermodynamic properties of benzenoid hydrocarbons with applications.” Computational Materials Science 230 (2023): 112492. [CrossRef]
Hayat, S., Khan, A., Ali, K., & Liu, J. B. (2024). Structure-property modeling for thermodynamic properties of benzenoid hydrocarbons by temperature-based topological indices. Ain Shams Engineering Journal, 15(3), 102586. [CrossRef]
Pogliani, L. (2000). From molecular connectivity indices to semi-empirical connectivity terms: Recent trends in graph-theoretical descriptors. Chemical Reviews, 100(10), 3827-3858.
Todeschini, R., and Consonni, V. (2008). Handbook of molecular descriptors (Vol. 11). John Wiley and Sons.
Van, Z.B. (2017) Section 2.3: Energy Bands. Principles of Semiconductor Devices. Ph.D. Thesis, Electrical, Computer, Energy Engineering Department, University of Colorado, Boulder, CO, USA.
Malik, M. Y. H., Binyamin, M. A., & Hayat, S. (2022). Correlation ability of degree-based topological indices for physicochemical properties of polycyclic aromatic hydrocarbons with applications. Polycyclic Aromatic Compounds, 42(9), 6267-6281. [CrossRef]
Hayat, S., Khan, S., Imran, M., & Liu, J. B. (2020). Quality testing of distance-based molecular descriptors for benzenoid hydrocarbons. Journal of Molecular Structure, 1222, 128927. [CrossRef]
Hayat, S., Khan, S., & Imran, M. (2021). Quality testing of spectrum-based distance descriptors for polycyclic aromatic hydrocarbons with applications to carbon nanotubes and nanocones. Arabian Journal of Chemistry, 14(3), 102994. [CrossRef]
Safdar, M., Mushtaq, T., Ali, N., & Akgül, A. (2023). On study of flow features of hybrid nanofluid subjected to oscillatory disk. International Journal of Modern Physics B, 2450356. [CrossRef]
Zakir, M. S., Arshad, M., Naseer, M. K., Cancan, M. One Study of Weighted Entropy Based on Topological Indices for Triazine-Based Dendrimer: A Mathematical Chemistry Approach. Eur. Chem. Bull. 2023, 12(Special Issue 1, Part-B), 2770-2788.
MAHBOOB, A., HUSSAIN, T., AKRAM, M., MAHBOOB, S., ALI, N., & RAZA, A. (2020). CHARACTERIZATIONS OF CHEVALLEY GROUPS USING ORDER OF THE FINITE GROUPS. Journal of Prime Research in Mathematics, 16(1), 46-51.
Zakir, M. S., Arshad, M., Naseer, M. K., Kanwal, Z., Ahmad, I., & Cancan, M. EVALUATION OF WEIGHTED ENTROPIES BASED ON TOPOLOGICAL INDICES FOR POLY PROPYL ETHER IMINE DENDRIMERS. Eur. Chem. Bull. 2023, 12(Issue 8), 7120-7130.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Mathematical Symphonies in Copper Oxide: A Graph Entropy Approach to Topological Analysis and Applications

Abstract

Keywords:

Subject:

Introduction

Main Results

Graphical Comparison of the Results:

Conclusion

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe