Weak Frequency Band Signal Spectral Detection Based on Pre-Whitening Scale-Transformation Symmetric Bistable Parallel Stochastic Resonance

1. Introduction

Weak target signal detection is a common problem in different applications, such as the radar target detection [1], image object discovery [2], optical damage detection [3], etc.. Lots of research works have been carried out in solving the weak target signal detection problem, especially when the corresponding signal-to-noise ratio (SNR) is relatively very low, for example below 0dB, and the target signal possesses some certain band width.

In the literatures, many researchers investigated the weak target detection problem by using different kinds of methods and techniques. A space-time-waveform joint adaptive detection (STWJAD) method by combining spatial, temporal, and waveform dimensions is proposed, which is based on the linearly constrained minimum variance (LCMV) criterion to achieve effective adaptive processing and detection [4]. The theoretical performance is outstanding, but the complexity for realization remains high. In [5], a new weak maneuvering target detection method is studied in a sea environment with a Radon-fractional Fourier transform (RFrFT) canceller, which can efficiently suppress the sea clutter and detect targets with low computations, but it needs to utilize different representations of the maneuvering target and the sea clutter and hard to apply in other areas applications. To overcome the shortcomings of fractal analysis in the time domain and Fourier transform domain, [6] mainly studies the joint fractal property of sea clutter of autoregressive (AR) spectrum and its application on weak target detection. It combined the box-counting dimension with AR spectrum estimate theory, which considers the correlation property of sea clutter series. Moreover, the intercept is regarded as an auxiliary feature for target detection. While can only solve the binary-classification or binary-detection problem and cannot fit for the weak frequency band signal spectral detection very well. Besides, there also exists traditional energy detection method and spectrum analysis method, which also perform bad under low SNR.

In previous studies, it has been found that the nonlinear stochastic resonance (SR) system possesses the good performance to improve the weak signal detection [7,8]. But to reach an ideal weak signal detection performance, some optimization process should be introduced with some prior knowledge of the SR system [9], which may produce new problems in applications. Although there also exists some other kind of weak signal frequency detection methods such by using nonlinear chaos theory [10], it may only fit for some narrow band signal detection other than wide band signal.

In this research, a novel weak frequency band signal spectral detection approach is proposed, which combines the pre-whitening processing, scale-transformation operation, symmetric bistable parallel SR, and linear response property in SR system. Based on the introduced techniques, the weak frequency band of the target could be enhanced and remained in the middle part of the scale-transformed frequency band of the symmetric bistable parallel SR system output. Finally, computer simulations based on real radar data verify the effectiveness and superiority over traditional weak signal detection method.

2. Proposed Weak Signal Detection Based on Pre-Whitening Scale-Transformation Symmetric Bistable Parallel Stochastic Resonance

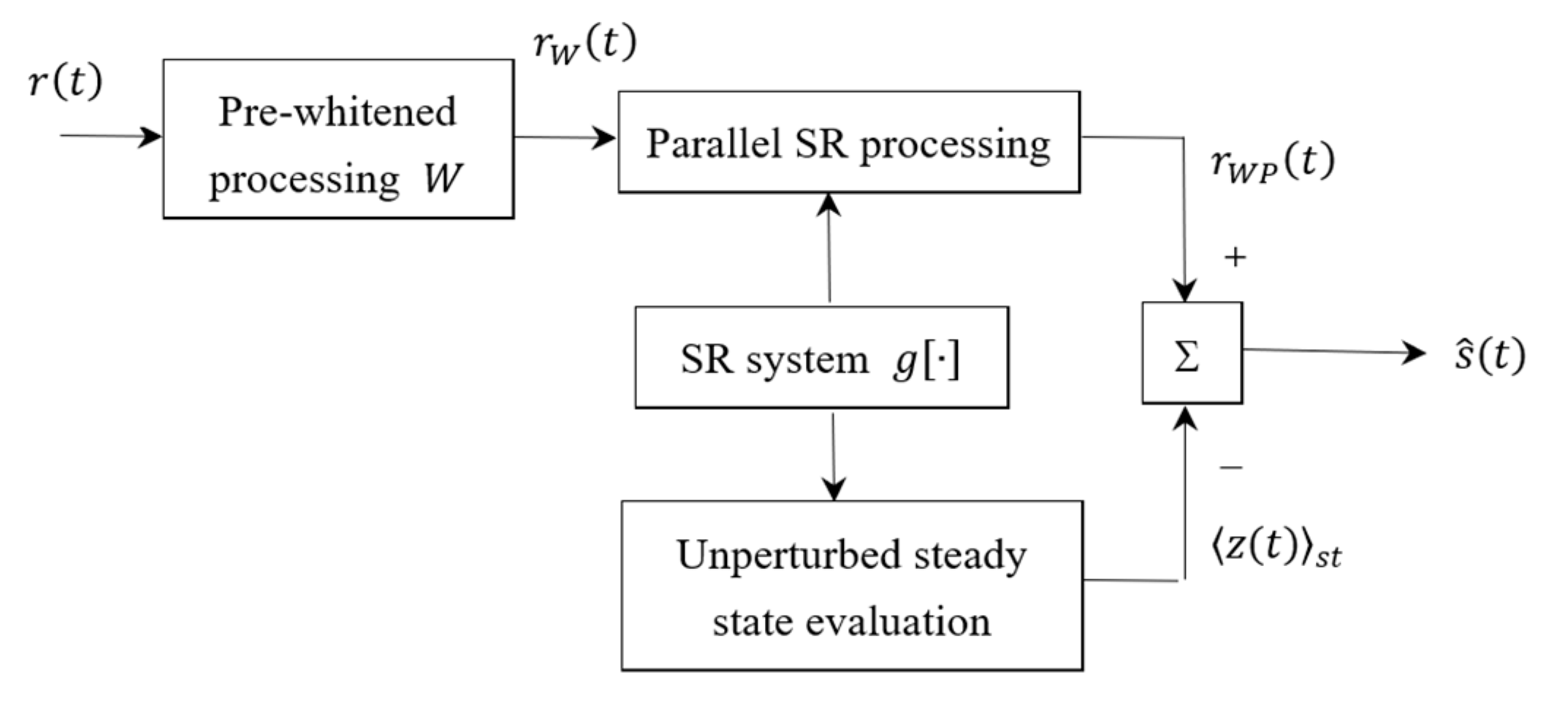
To show a clear structure of the proposed approach, firstly, Figure 1 presents the block diagram of the weak frequency band signal spectral detection based on pre-whitening scale-transformation symmetric bistable parallel stochastic resonance system, and details of each block will be explained in details in the following.

Generally, for the weak target signal detection problem, the signal model can be expressed by

$$\left\{\begin{array}{cc}{H}_0:& r\left(t\right)=c\left(t\right)+n\left(t\right)\\ H_1:& r\left(t\right)=s\left(t\right)+c\left(t\right)+n\left(t\right)\end{array}\right.$$

(1)

where $r\left(t\right)$ is the receiving signal, $c\left(t\right)$ is the clutter signal, $n\left(t\right)$ is the additive noise including measurement noise, $s\left(t\right)$ is the weak frequency band signal. The signal $s\left(t\right)$, $c\left(t\right)$ and $n\left(t\right)$ are independent to each other. So (1) can be regarded as a two-hypotheses detection problem mathematically.

In different applications, the clutter signal $c\left(t\right)$ may have different time-frequency domain characteristics, and the additive noise $n\left(t\right)$ may also possess various distributions. Without full prior knowledge, it will be difficult to carry out corresponding analysis and detection. Here we first consider to let the receiving signal $r\left(t\right)$ pass through a pre-whitening processor or a pre-whitening filter, so that

$$\left\{\begin{array}{cc}{H}_0:& r_W\left(t\right)=\mathrm{W}\left[r\left(t\right)\right]=\mathrm{W}\left[c\left(t\right)\right]+\mathrm{W}\left[n\left(t\right)\right]\\ H_1:& r_W\left(t\right)=\mathrm{W}\left[r\left(t\right)\right]=\mathrm{W}\left[s\left(t\right)\right]+\mathrm{W}\left[c\left(t\right)\right]+\mathrm{W}\left[n\left(t\right)\right]\end{array}\right.$$

(2)

where $r_W\left(t\right)$ is the receiving signal passing through the pre-whitening processor, $\mathrm{W}\left[·\right]$ is the corresponding pre-whitening processing.

Considering the weak target detection condition that the power of $s\left(t\right)$ is much lower than those of $c\left(t\right)$ and $n\left(t\right)$, the pre-whitening processing may result in uniform distribution in the frequency-domain of $r_W\left(t\right)$ under both hypotheses. Without loss of generality, $\mathrm{W}\left[c\left(t\right)\right]+\mathrm{W}\left[n\left(t\right)\right]$ can be regarded as a united random process denoted by $c_W\left(t\right)$, and by denoting $\mathrm{W}\left[s\left(t\right)\right]$ as $s_W\left(t\right)$, we have

$$\left\{\begin{array}{cc}{H}_0:& r_W\left(t\right)=c_W\left(t\right)\\ H_1:& r_W\left(t\right)={s_W\left(t\right)+c}_W\left(t\right)\end{array}\right.$$

(3)

In the weak signal detection problem, among different techniques, it is found that the nonlinear symmetric bistable stochastic resonance (SR) is a kind of good technique which could help improving the weak signal power especially under low SNR, which has been applied in many applications [11,12,13]. To reach an optimal SNR improvement performance, some prior knowledge regarding the distribution and corresponding parameters of strong clutter, additive noise and weak signal are required, which may be difficult in applications. While by using the pre-whitening processing introduced above, it is easy to normalize $r_W\left(t\right)$ to a zero-mean unit-variance symmetric Gaussian white noise process.

When the frequency band of the weak signal can be estimated approximately as $\left[{\widehat{f}}_{min},{\widehat{f}}_{max}\right]$, where ${\widehat{f}}_{min}$ and ${\widehat{f}}_{max}$ represent the estimated minimal and maximal frequencies of the weak signal band, the following scale-transformation-based symmetric bistable SR processing [14] is introduced to enhance the weak signal power as

$${\displaystyle \frac{dz\left(t\right)}{dt}}=z\left(t\right)-z^3\left(t\right)+\sqrt{{\displaystyle \frac{b}{a^3}}}·r_W\left(t\right)+\sqrt{{\displaystyle \frac{b}{a^3}}}·\sqrt{2Da}·\xi \left(t\right)$$

(4)

where $z\left(t\right)$ is the state variable of the symmetric bistable SR system, a and b are bistable potential well parameters of the SR system, $\xi \left(t\right)$ is the SR noise with zero-mean and unit-variance obeying symmetric white Gaussian distribution, and D is the noise power. Here the parameters a and b are chosen to fit the better symmetric bistable SR performance [15] in the scale-transformation bandwidth of the symmetric bistable bistable SR system within $\left(0Hz,10Hz\right)$ as

$$a=0.2\left({\widehat{f}}_{max}-{\widehat{f}}_{min}\right)$$

(5)

$$b=0.7\left({\widehat{f}}_{max}-{\widehat{f}}_{min}\right)$$

(6)

The above settings could ensure that the weak frequency band signal spectrum lies in the middle part of the scale-transformation bandwidth of the symmetric bistable SR system.

Next, although the symmetric bistable SR system in (4) is selected and the scale-transformation in (5) and (6) is introduced, the weak signal enhancement performance of the symmetric bistable SR system is still related to time and frequency properties of $s\left(t\right)$ seriously, or it remains unknown without prior information. To solve this problem, a kind of symmetric parallel SR processing technique is proposed after the previous pre-whitening and scale-transformation processing.

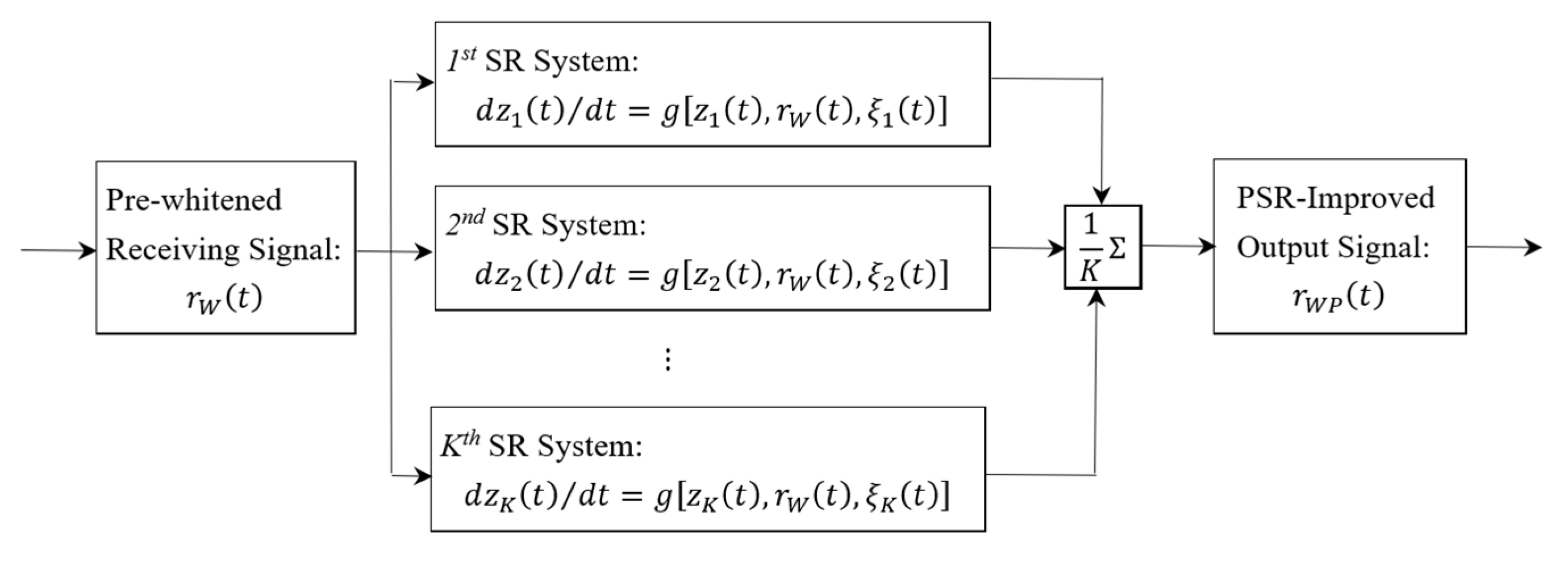
Figure 2 shows the symmetric bistable parallel SR processing structure. The receiving signal $r_W\left(t\right)$ is used as a common driving signal to all K symmetric bistable parallel SR systems. While in these symmetric bistable SR systems, $g\left[·\right]$ represents the scale-transformation-based symmetric bistable SR processing in (4), $z_k\left(t\right)$ is the state variable of the k-th $\left(k=\mathrm{1,2},\cdots ,K\right)$ symmetric bistable SR system, ${\xi }_k\left(t\right)$ is the k-th $\left(k=\mathrm{1,2},\cdots ,K\right)$ SR noise process with the same zero-mean and unit-variance and symmetric white Gaussian distribution, and $r_{WP}\left(t\right)$ is the symmetric bistable parallel SR-improved output signal.

According to the Linear Response Theory of SR [15], it can be found that, under $H_1$ the stable state variable $z\left(t\right)$ can be written as

$${〈z\left(t\right)〉}_{asy}={〈z\left(t\right)〉}_{st}+{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\kappa \left(t-\tau ,a,b\right)\left[\sqrt{{\displaystyle \frac{b}{a^3}}}·r_W\left(\tau \right)+\sqrt{{\displaystyle \frac{b}{a^3}}}·\sqrt{2Da}·{\xi }_k\left(\tau \right)\right]d\tau$$

(7)

where ${〈z\left(t\right)〉}_{asy}$ is the asymptotic response of $z\left(t\right)$, ${〈z\left(t\right)〉}_{st}$ is the mean value of the unperturbed state variable under $r_W\left(t\right)=0$, $\kappa \left(t-\tau ,a,b\right)$ is the response function.

When the receiving signal $r_W\left(t\right)$ is introduced into all K symmetric bistable parallel SR systems, the corresponding response related to $r_W\left(t\right)$ in each symmetric bistable parallel branch will remain the same. And when ${\xi }_k\left(t\right)$ $\left(k=\mathrm{1,2},\cdots ,K\right)$ are independent and identically distributed (i.i.d.), the variance of PSR-improved output signal $r_{WP}\left(t\right)$ in Figure 2 presents

$$var\left[r_{WP}\left(t\right)\right]=var\left[{〈z\left(t\right)〉}_{st}\right]+var\left[{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\kappa \left(t-\tau ,a,b\right)\sqrt{{\displaystyle \frac{b}{a^3}}}·s_W\left(\tau \right)d\tau \right]+{\displaystyle \frac{1}{K}}var\left[{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\kappa \left(t-\tau ,a,b\right)\left(\sqrt{{\displaystyle \frac{b}{a^3}}}·c_W\left(\tau \right)+\sqrt{{\displaystyle \frac{b}{a^3}}}·\sqrt{2Da}·{\xi }_k\left(\tau \right)\right)d\tau \right]$$

(8)

When the initial values of the state variable in each symmetric bistable parallel SR system are chosen randomly, the response of $c_W\left(\tau \right)$ could be also regarded as a random process. And under the assumptions that K is big enough, it can be found that the last term in (8) will approach zero, which may reduce the impacts of $c_W\left(\tau \right)$ and ${\xi }_k\left(\tau \right)$ significantly.

Finally, when the symmetric bistable SR system is chosen and fixed, the first item on the right side of (8), say $var\left[{〈z\left(t\right)〉}_{st}\right]$, can also be got if there is no driving signal introduced into the symmetric bistable SR system. So based on the above analyses, we have the weak frequency band signal estimation $\widehat{s}\left(t\right)$ as

$$\widehat{s}\left(t\right)=r_{WP}\left(t\right)-{〈z\left(t\right)〉}_{st}={\displaystyle \frac{1}{K}}{\sum }_{k=1}^K{z}_k\left(t\right)-{〈z\left(t\right)〉}_{st}$$

(9)

Then the weak frequency band signal spectral detection can be carried out just based on the estimate $\widehat{s}\left(t\right)$. According to the nonlinear SR weak signal enhancement to the weak driving signal, the corresponding frequency band property of $s\left(t\right)$ can be exhibited, which may also remain the same frequency band of the original weak signal.

3. Computer Simulations and Real Experiments

To evaluate the performance of the proposed weak frequency band signal spectral detection approach, some computer simulations using real data are carried out and compared with some conventional method.

In the simulations, a kind of real radar data containing some weak target is used as the objective to be detected, where the frequency band is within [800Hz,1200Hz]. The SNR of the receiving signal is within 0dB to −15dB, which is a relative low SNR for weak signal detection.

In the proposed approach, the following conventional symmetric bistable nonlinear SR system is used for the weak signal enhancement and improvement

$${\displaystyle \frac{dz\left(t\right)}{dt}}=z\left(t\right)-z^3\left(t\right)+r_W\left(t\right)+\sqrt{2D}·\xi \left(t\right)$$

(10)

while the inner SR noise $\xi \left(t\right)$ is chosen as a white Gaussian noise process, and the initial value of the state variable could be selected within [−1,+1] randomly. And the unperturbed steady state ${〈z\left(t\right)〉}_{st}$ could be obtained by setting $r_W\left(t\right)=0$ in (10).

In the proposed symmetric bistable parallel SR processing, totally K=1000 symmetric bistable parallel SR processing units are used and taken for average to get the PSR-improved output signal $r_{WP}\left(t\right)$ in Figure 2. And in the performance comparison, the traditional energy detection method is used as the comparison object, which is widely used in different applications.

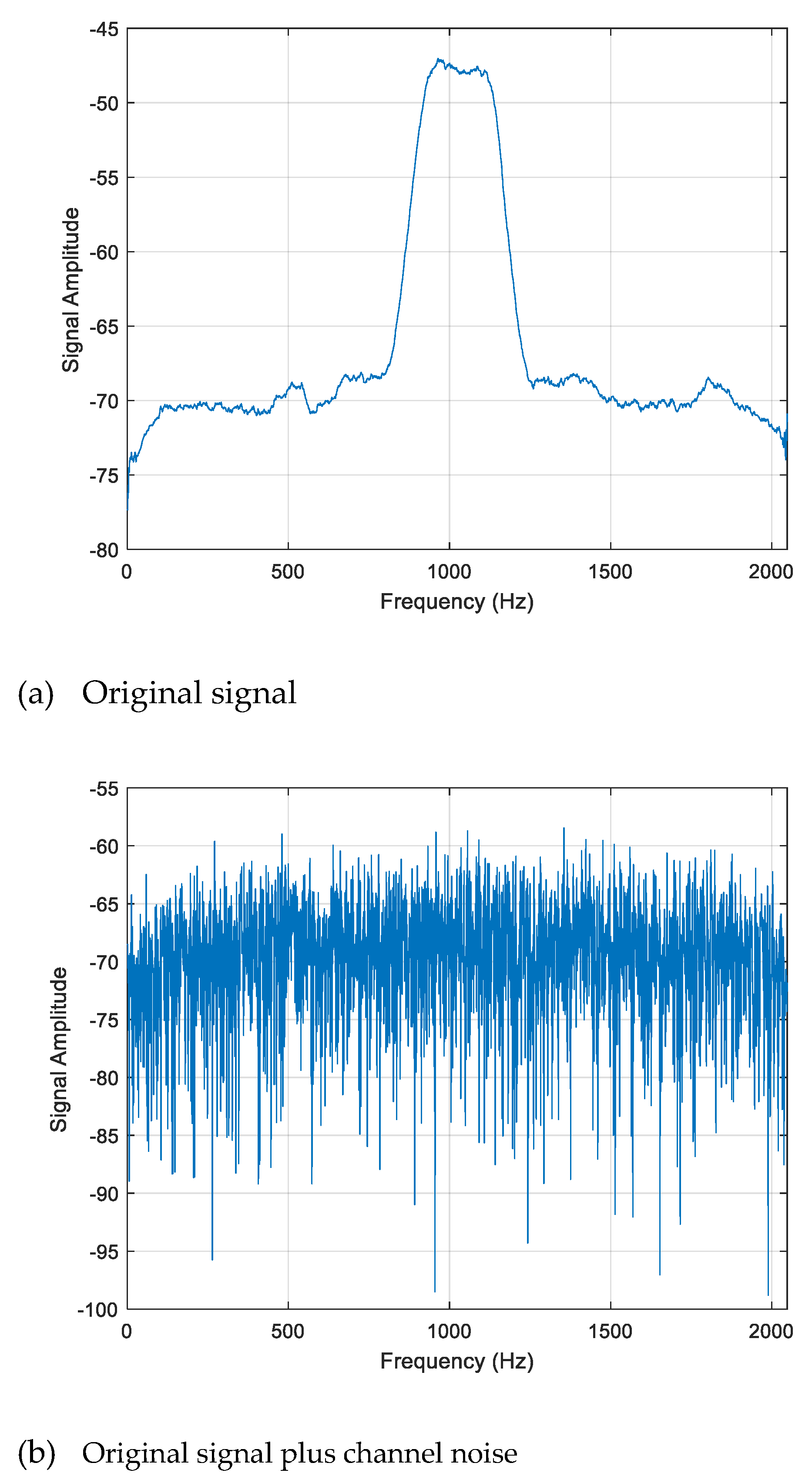
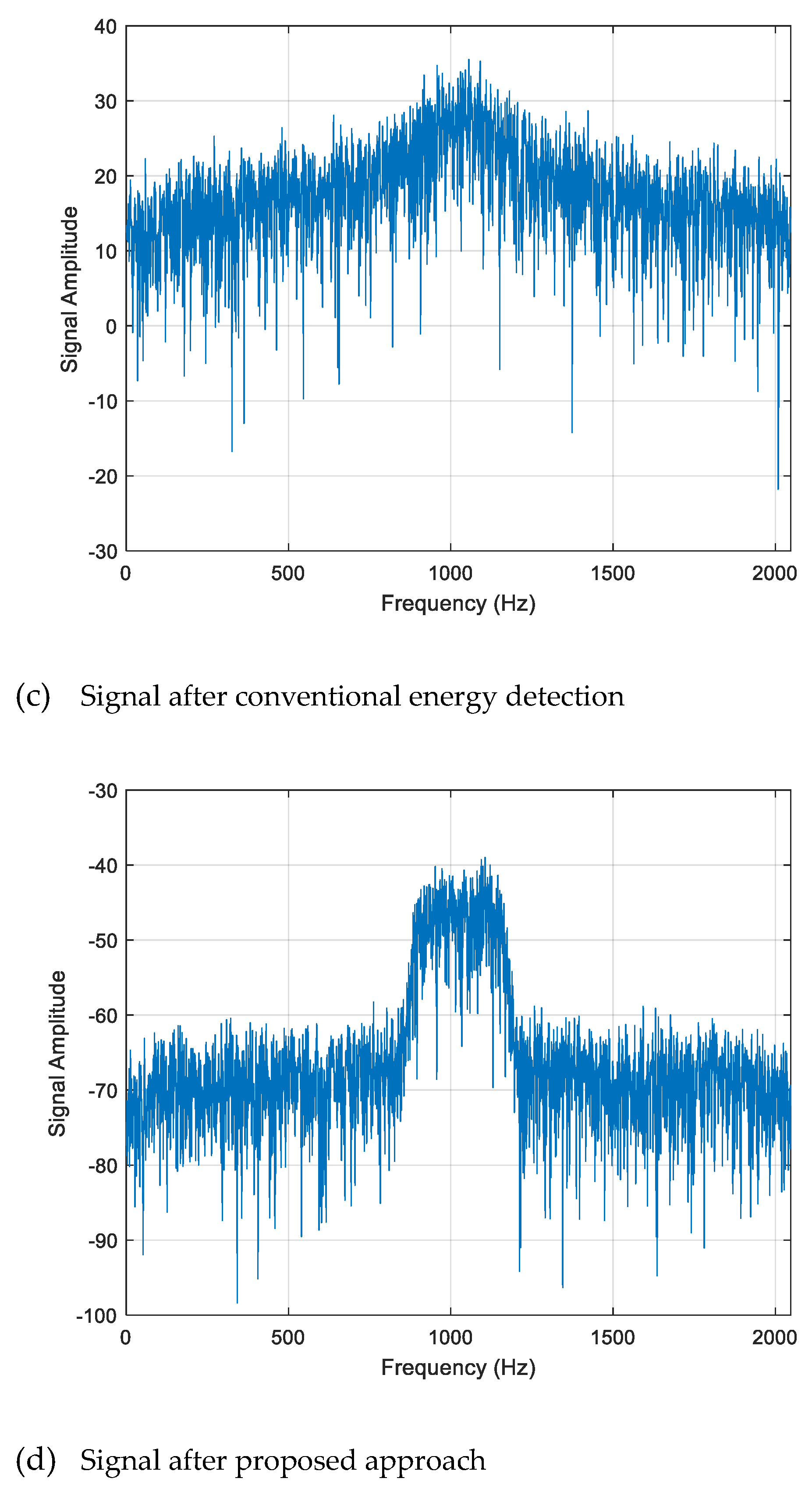
To show the intuitive differentiation between the proposed approach and the traditional method, Figure 3 gives the spectra of the weak frequency band signal under SNR=−15dB. Firstly, Figure 3(a) shows the original signal with certain frequency band. Secondly, Figure 3(b) plots the original signal plus channel noise, where the signal has been merged in the noise spectrum and hard to be detected. Figure 3(c) shows the spectrum after traditional energy detection, where the signal spectrum is still unclear. At last, Figure 3(d) presents the spectrum after the proposed approach, it can be found that the original weak signal band is obvious and can be detected easily compared with Figure 3(c).

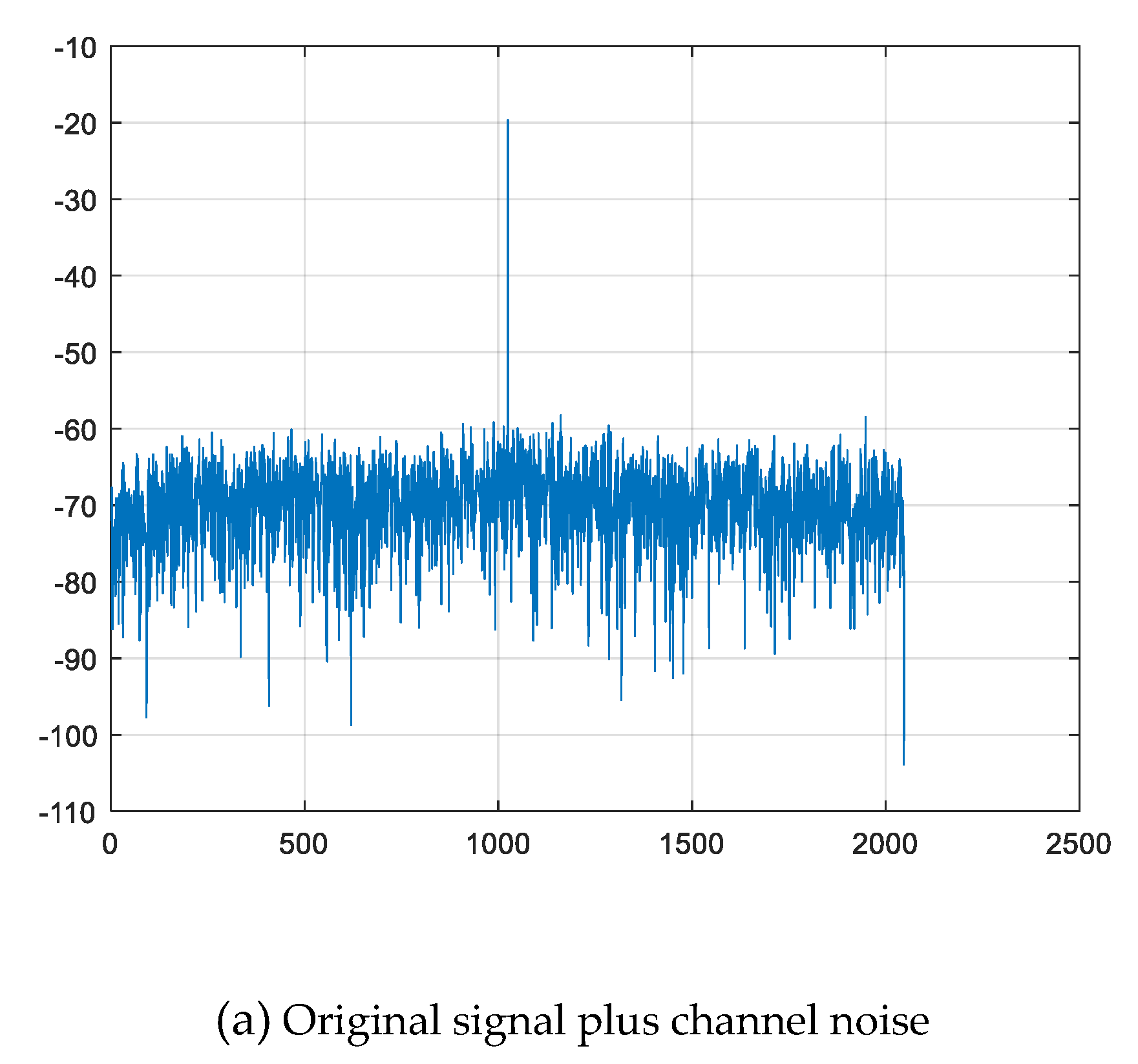
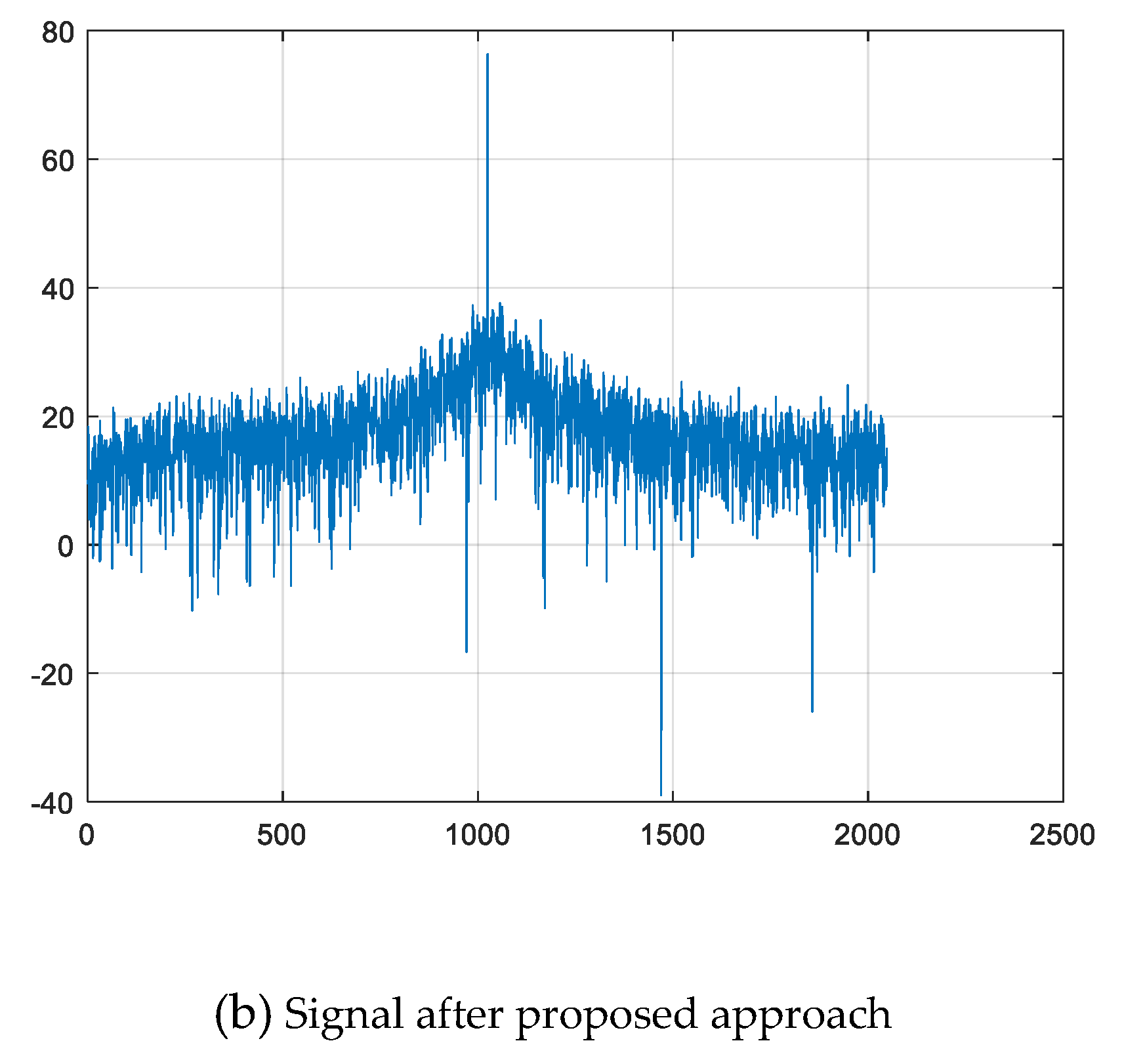
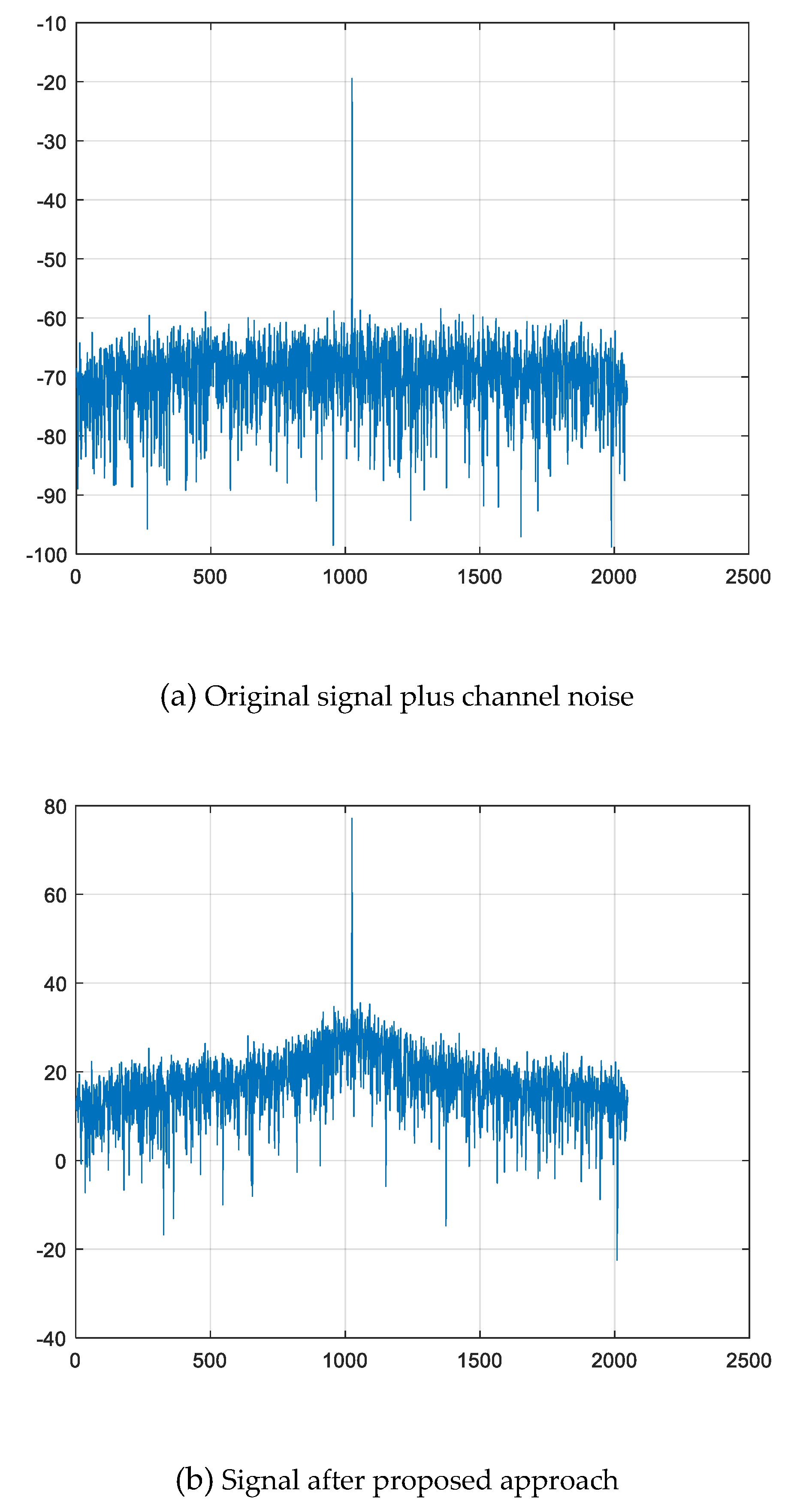
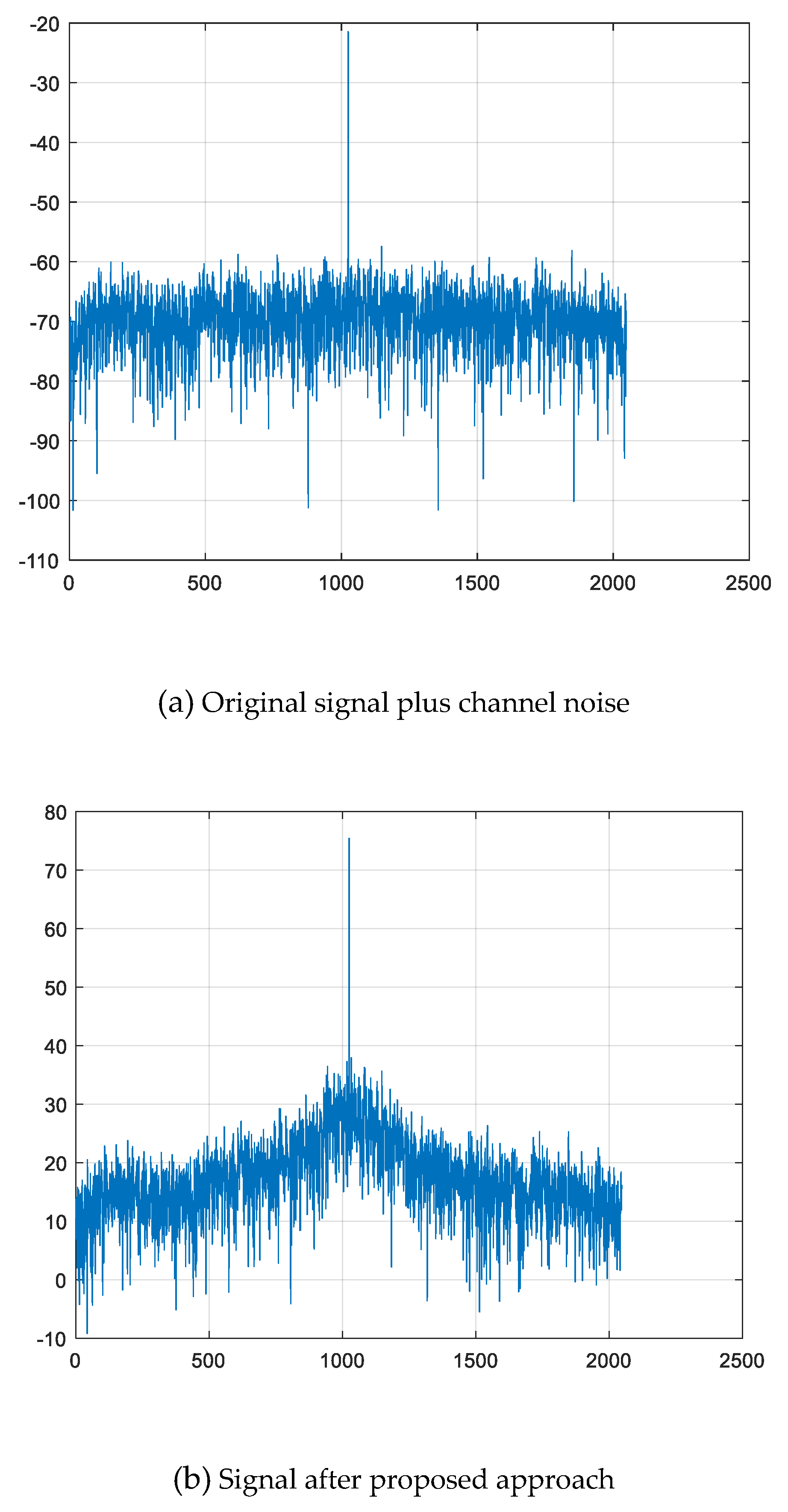
Figure 4, Figure 5 and Figure 6 also present the spectra of the weak frequency band signal before and after the proposed processing for comparison based on real radar data, while the SNR is changed from 0dB, −5dB to −10dB, respectively. The original signal is the summarization of the original signal in Figure 3(a) and a high-peak single-frequency signal at 1020Hz. From these three figures, it can also be discovered that the weak signal under the channel noise can be enhanced effectively with the introduced symmetric bistable PSR processing, which shows good advantage in the weak frequency band signal spectral detection performances over conventional method.

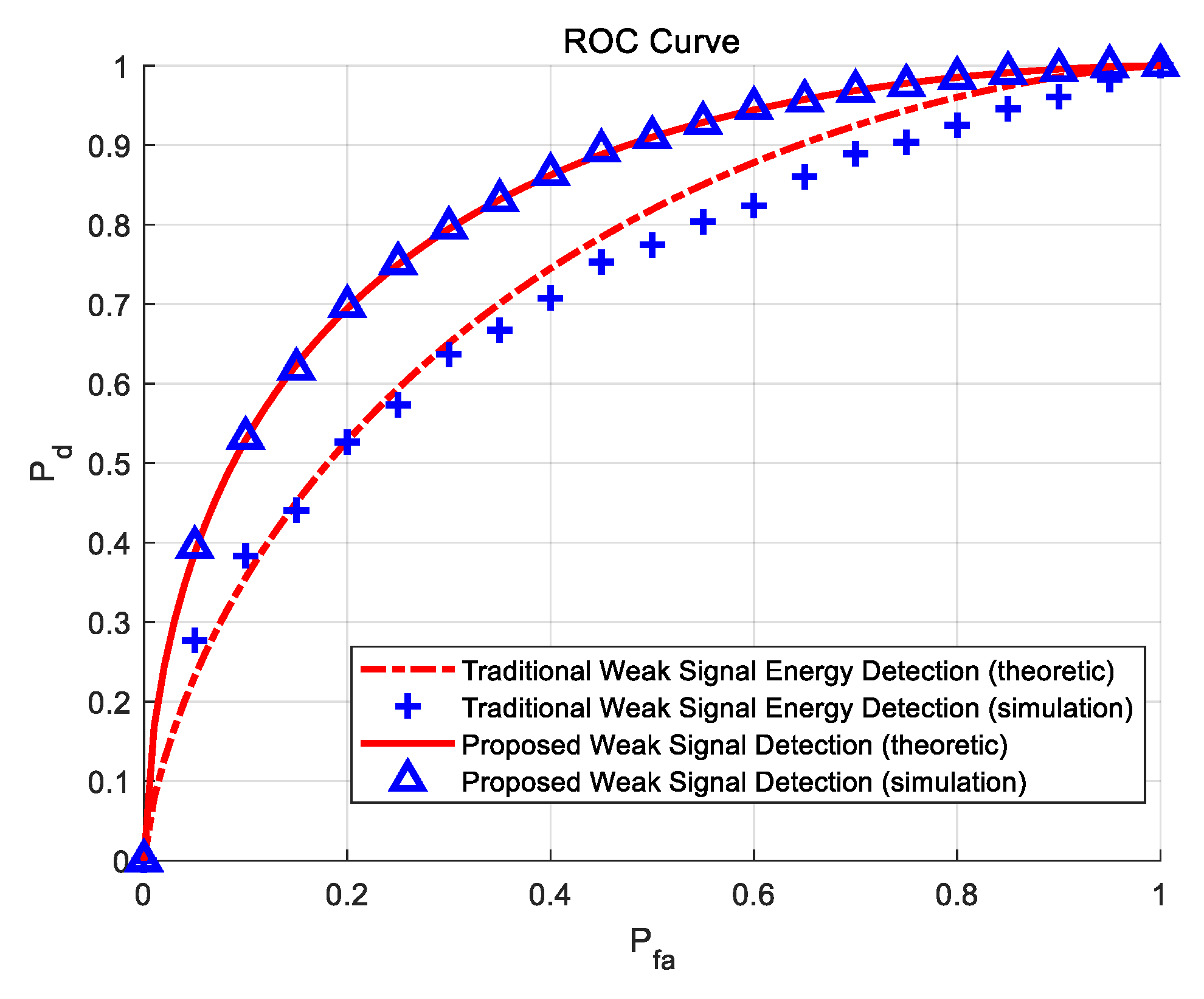
Finally, to compare the weak signal detection performance reasonably, the Receiver Operating Characteristic (ROC) curves are plotted under SNR=−15dB using real sea clutter data with weak target in Figure 7. The performance is also compared with the traditional energy detection method, while both theoretical and simulation results of both methods are given. It can be observed that the performance of the proposed symmetric bistable PSR processing approach overwhelms the traditional energy detection method, and the simulation curve meets the theoretical curve well. The results above guarantee the applicability of the proposed symmetric bistable PSR processing approach commendably.

4. Conclusions

In this study, a novel weak frequency band signal spectral detection approach is proposed, which is based on the pre-whitening scale-transformation symmetric parallel SR technique. The pre-whitening operation helps to regulate the receiving signal; the scale-transformation can ensure the weak frequency band signal spectrum lies in the middle part of the frequency band in the bistable SR system; and the introduction of symmetric parallel SR processing may reduce the influence of clutter and additive noise in the detection. Computer simulations based on real sea clutter radar data evaluate the applicability of this proposed approach.