Submitted:
08 February 2025
Posted:
10 February 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
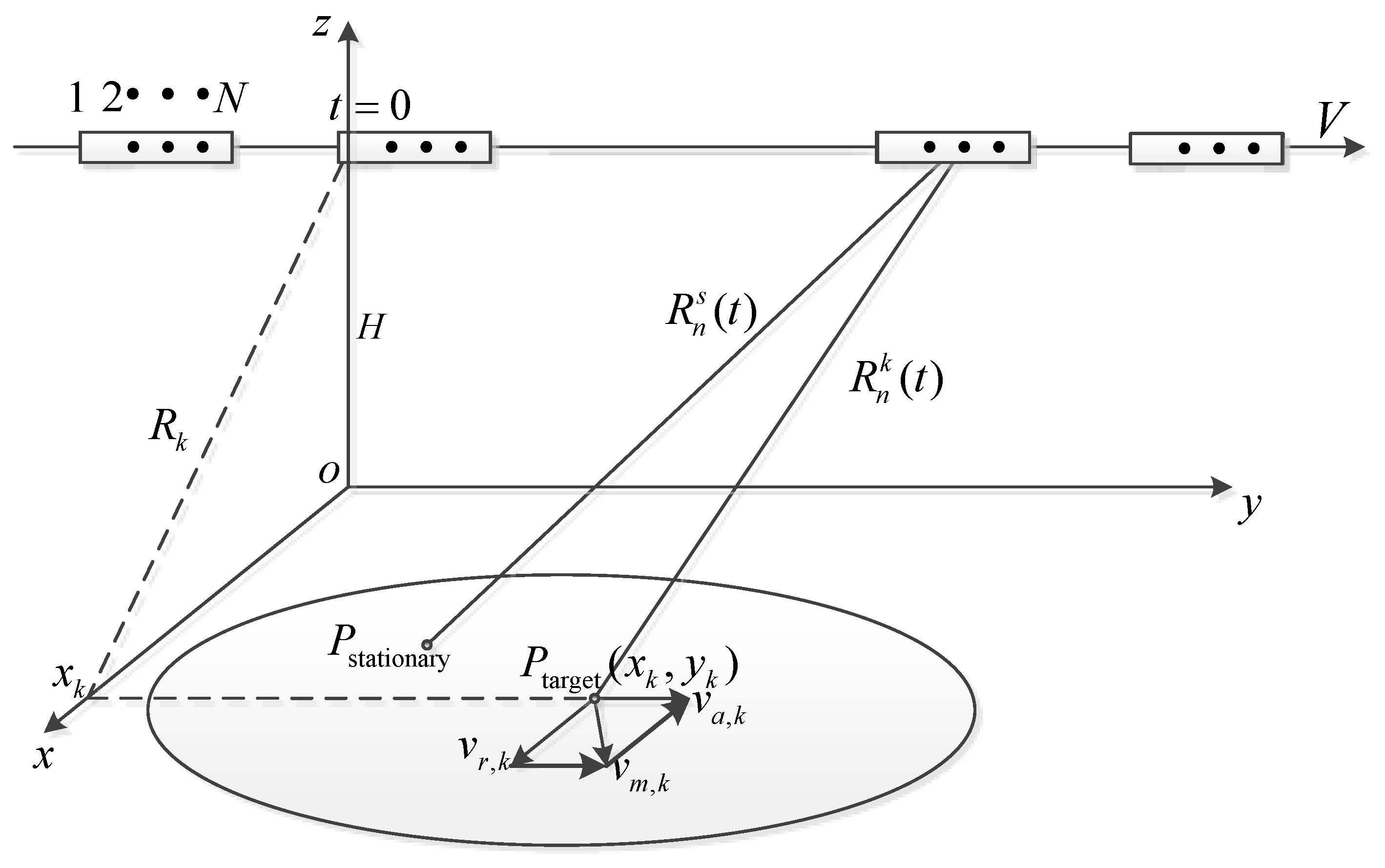
2. Signal Model and Problem Description
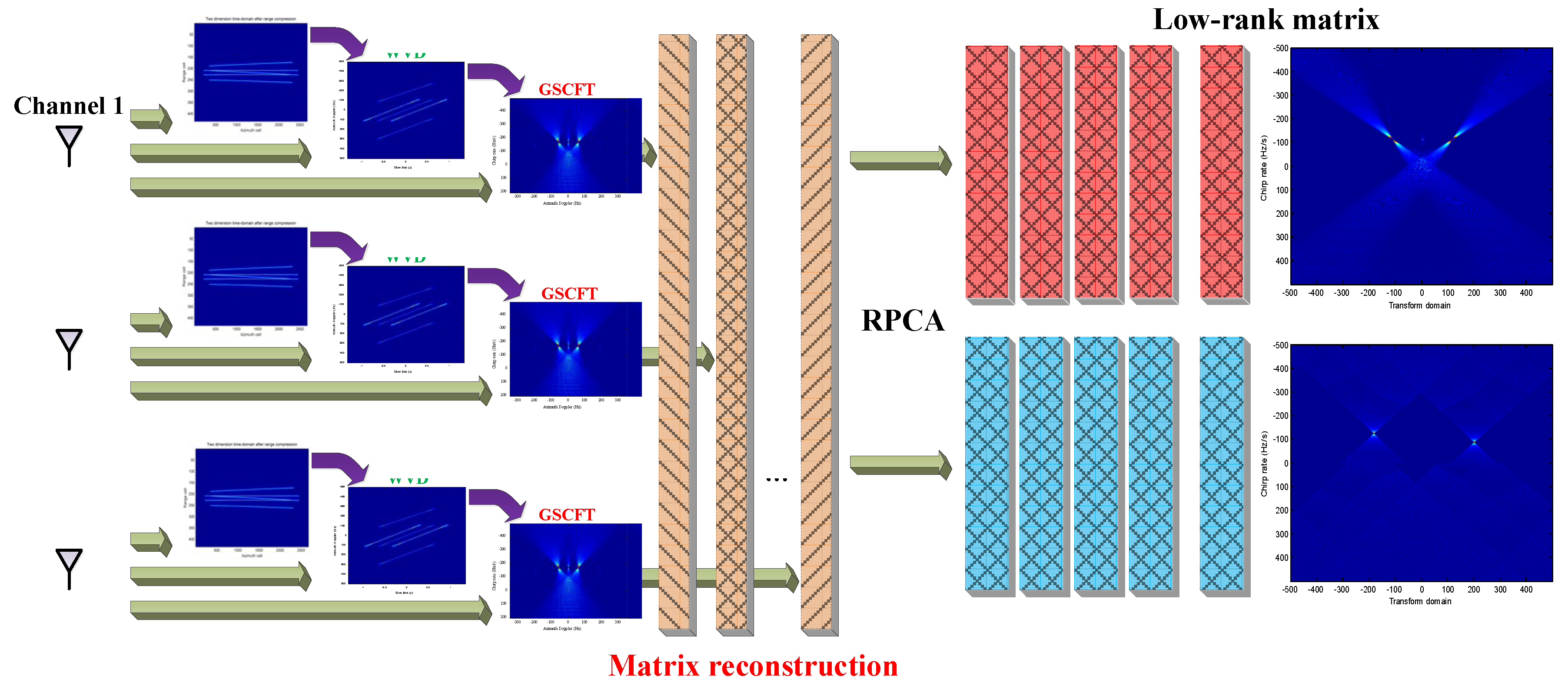
3. The Proposed Moving Target Detection Method Based on GSCFT-RPCA
3.1. Generalized Scale Fourier Transform for Decreasing Correlation Coefficient
3.2. Simultaneously Detect Moving Target and Estimate Azimuth Velocity Based on Improved RPCA
4. Simulations and Results
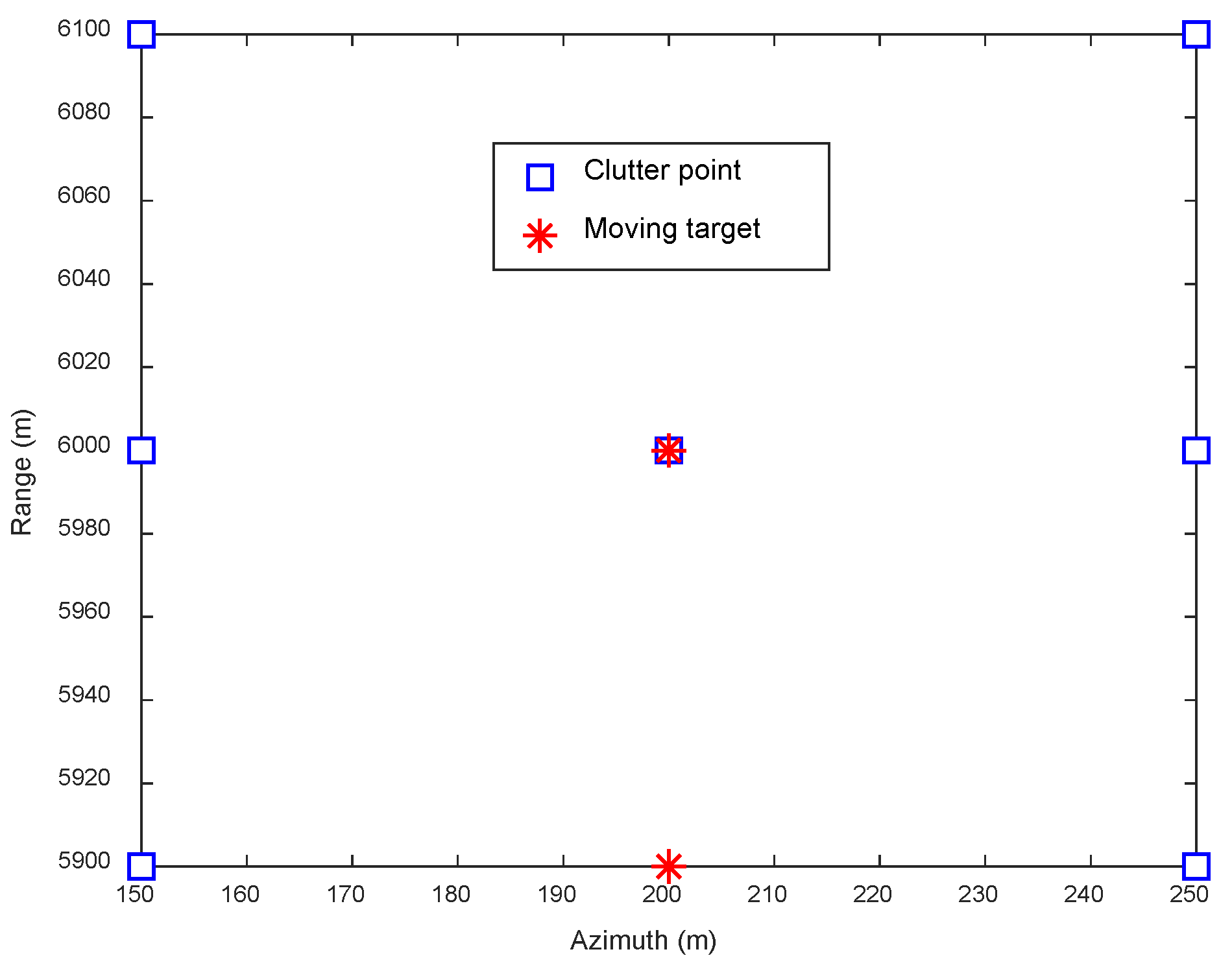
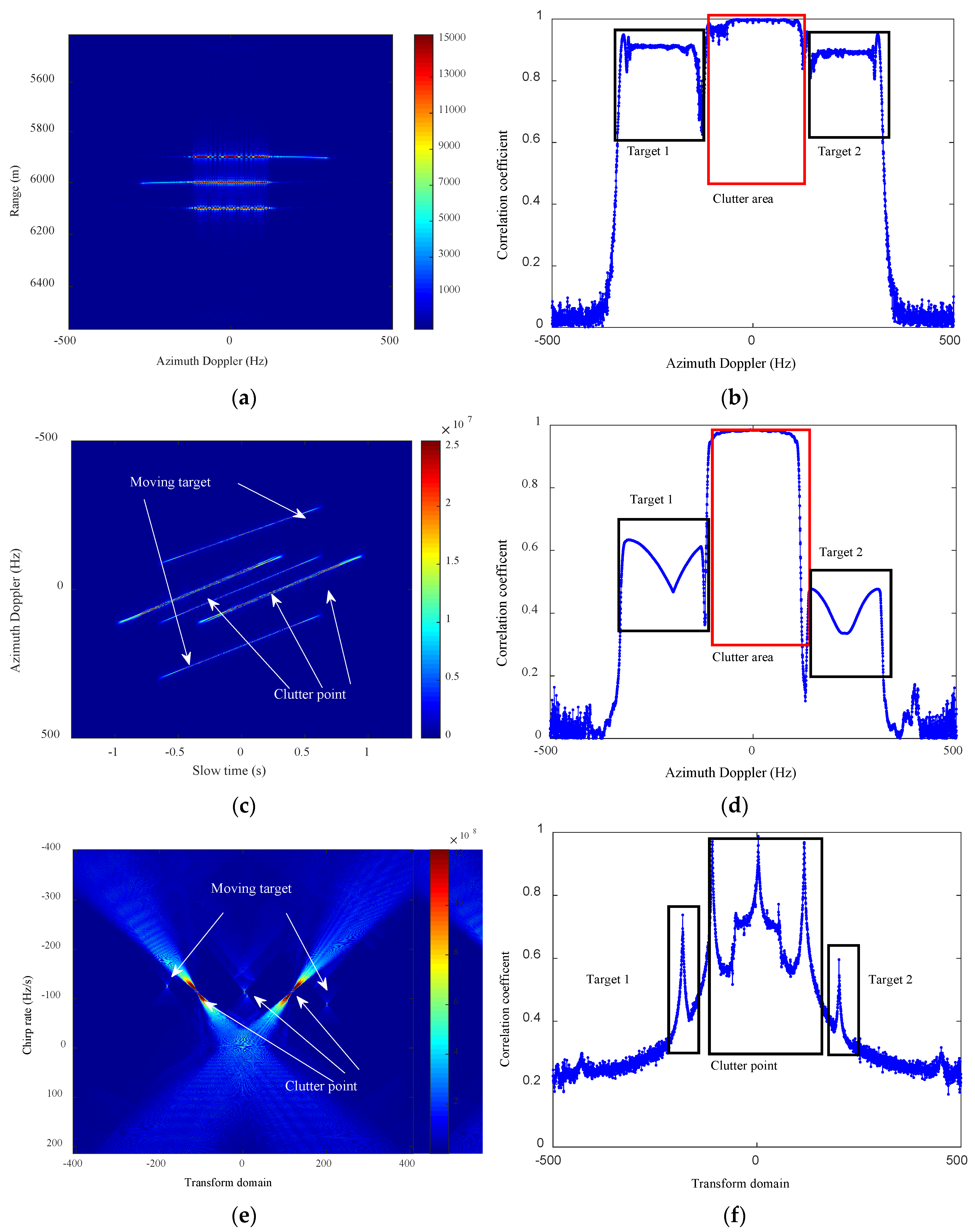
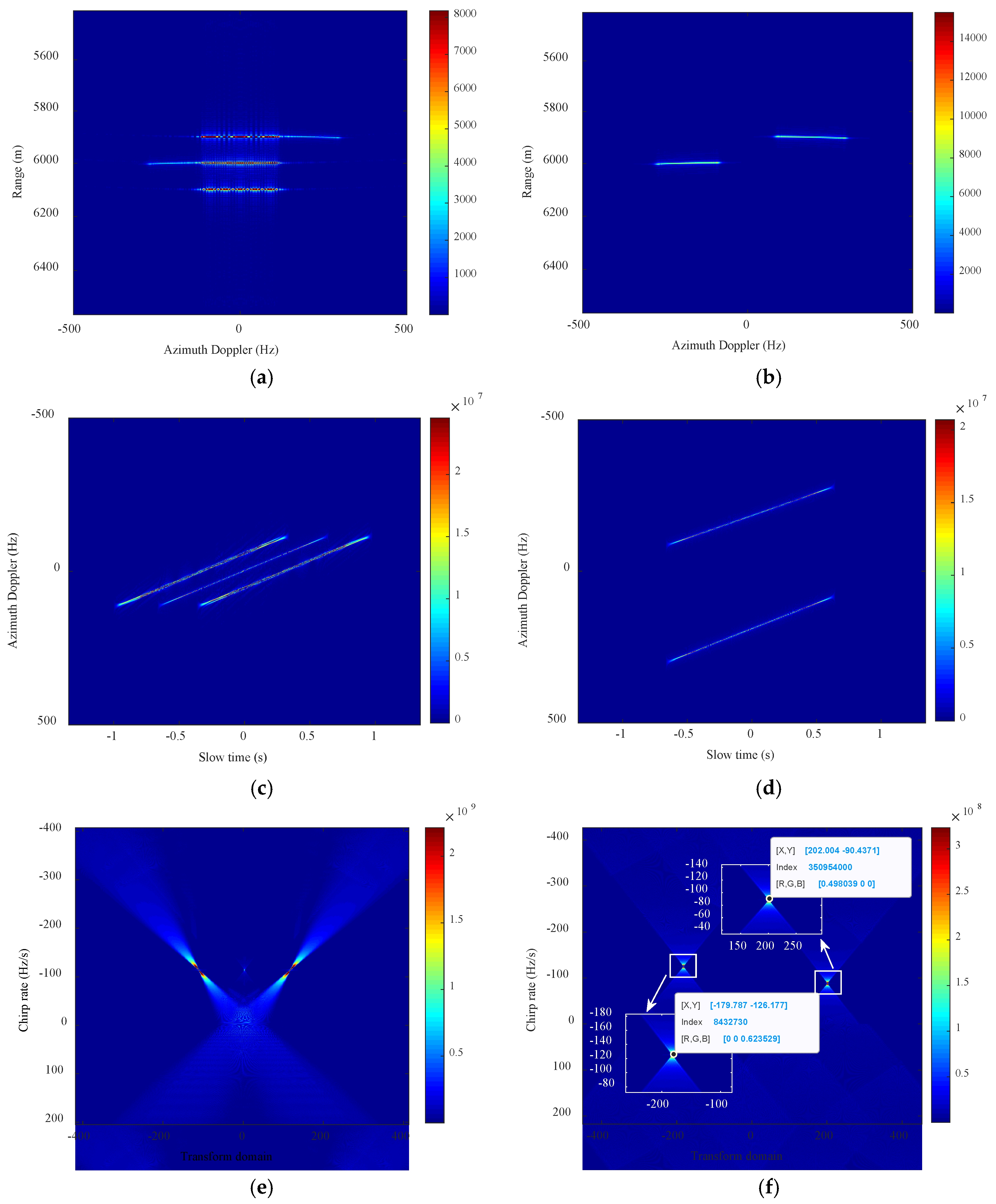
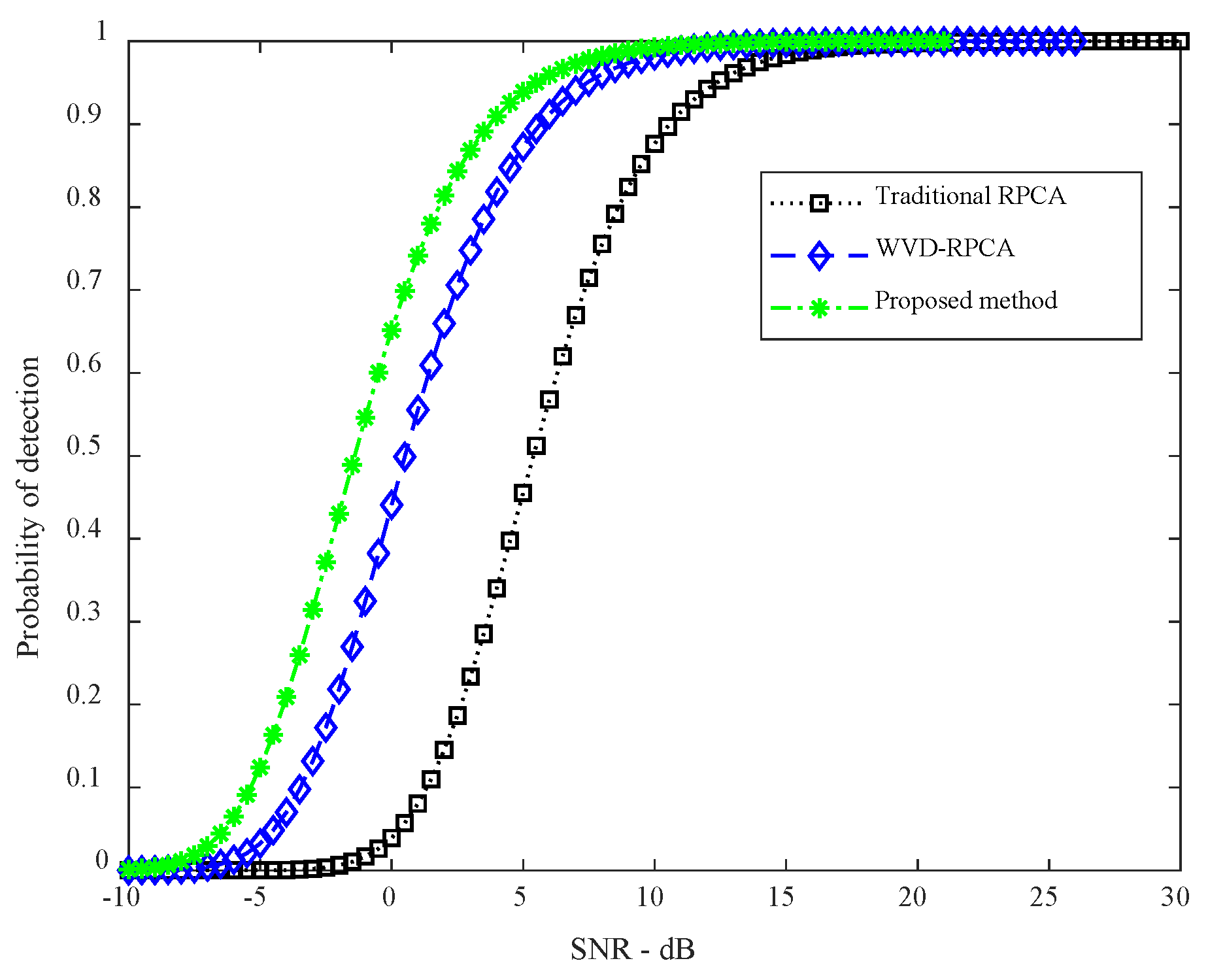
4.1. Simulation Experiments
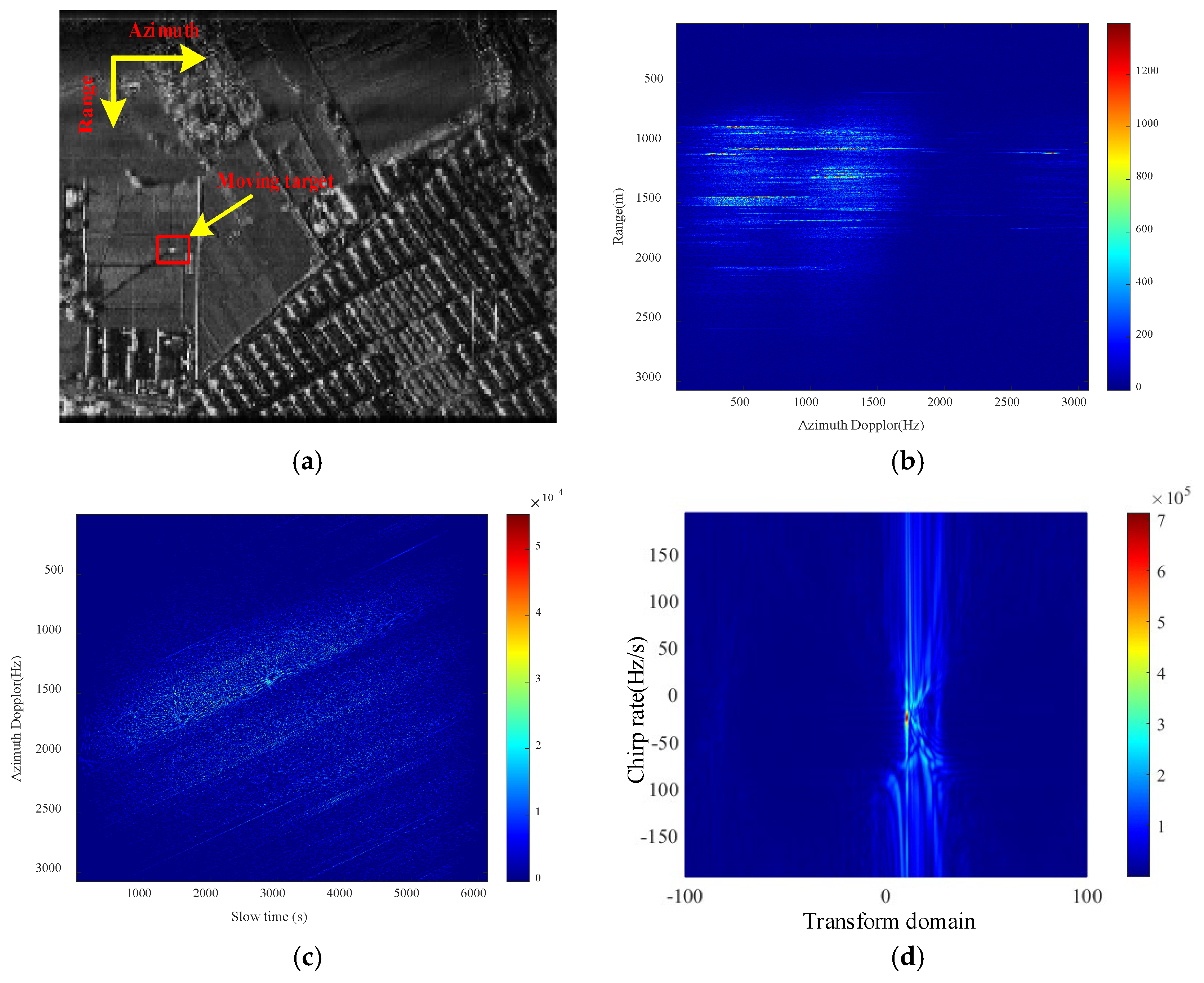
4.2. Measured Data Verification
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- H. Fan, L. Zhang, Z. Zhang, W. Yu, and Y. Deng. On the Processing of Gaofen-3 Spaceborne Dual-Channel Sliding Spot-light SAR Data. IEEE Transactions on Geoscience and Remote Sensing, vol. 60, pp. 5202912, 2022.
- Y. Wang, Q. Song, J. Wang, B. Du, and P. Wang, A Correction Method to Systematic Phase Drift of a High Resolution Radar for Foreign Object Debris Detection. Remote Sensing, vol. 14, no. 8, pp. 1787, 2022. [CrossRef]
- B. Djath, J. Schulz-Stellenfleth, and B. Cañadillas, Study of Coastal Effects Relevant for Offshore Wind Energy Using Spaceborne Synthetic Aperture Radar (SAR). Remote Sensing, vol. 14, no. 7, pp. 1688, 2022. [CrossRef]
- S. Zhang, Z. Jiang, J. Chen, S. Li, Y. Liu, R. Guo, M. Xing, An Effective Clutter Suppression Approach Based on Null-Space Technique for the Space-Borne Multichannel in Azimuth High-Resolution and Wide-Swath SAR System, IEEE Transactions on Geoscience and Remote Sensing, vol. 60, 2022. [CrossRef]
- Y. Guo, G. Liao, J. Li, T. Gu, A Clutter Suppression Method Based on NSS-RPCA in Heterogeneous Environments for SAR-GMTI, IEEE Transactions on Geoscience and Remote Sensing, vol. 58, no. 8, pp. 5880–6891, 2020. [CrossRef]
- D. Cerutti-Maori and I. Sikaneta, A generalization of DPCA processing for multichannel SAR/GMTI radars, IEEE Transactions on Geoscience and Remote Sensing, vol. 51, no. 1, pp. 560–572, Jan. 2013. [CrossRef]
- Budillon, V. Pascazio, and G. Schirinzi, Multichannel along-track interferometric SAR systems: Moving targets detection and velocity estimation, International Journal of Navigation Observation, vol. 2008, no. pp. 1–16, Feb. 2008.
- J. H. G. Ender, “Space-time processing for multichannel synthetic aperture radar,” Electronics and Communication Engineering Journal, vol. 11, no. 1, p. 29, 1999. [CrossRef]
- H. Jeon, Y. Chung, W. Chung, J. Kim, and H. Yang, Clutter covariance matrix estimation using weight vectors in knowledge-aided STAP, Electronics Letters, vol. 53, no. 8, pp. 560–562, April, 2017. [CrossRef]
- R. Klemm, Adaptive airborne MTI: an auxiliary channel approach. Communications Radar and Signal Processing, vol. 134, no. 3, pp. 269-276, 1987. [CrossRef]
- Xiang, D. Feng, H. Lv, J. He, H. Liu, Three-dimensional reduced-dimension transformation for MIMO radar space–time adaptive processing. Signal Processing, vol. 91, no. 8, pp. 2121-2126, 2011. [CrossRef]
- Y. Wang, J. Chen, Z. Bao, and Y. Peng, Robust space-time adaptive processing for airborne radar in nonhomogeneous clutter environments. IEEE Transactions on Aerospace and Electronic Systems , vol. 39, no. 1, pp. 70-81, Jan., 2003.
- T. K. Sarkar, H. Wang, S. Park, and J. Koh, A deterministic least-squares approach to space time adaptive processing (STAP). IEEE Transactions on Antennas and Propagation, vol. 49, no. 1, pp. 91-103, Jan. , 2001. [CrossRef]
- K. Sun, H. Meng, F. D. Lapierre, X. Wang, Direct data domain STAP using sparse representation of clutter spectrum. Signal Processing, vol. 91, no. 10, pp. 2268-2276, 2011. [CrossRef]
- J. Li, Y. Guo, G. Liao, Q. Guo, and J. Xi. Dimension Reduced Sparse Recovery Method for Clutter Suppression in Bistatic MIMO Radar. Radar conference, USA, pp. 1452-1455, 2015.
- J. Chen, J. Yang, “Robust subspace segmentation via low-rank representation,” IEEE Transactions on Cybernetics, vol. 44, no. 8, pp. 1432-1445, August, 2014. [CrossRef]
- M. Davenport, J.Romberg. An Overview of Low-Rank Matrix Recovery From Incomplete Observations, IEEE Journal of Selected Topics in Signal Processing, vol. 10, no. 4, pp. 608–622, 2016. [CrossRef]
- E. J. Candès, X. Li, Y. Ma, and J. Wright, Robust principal component analysis?, J. ACM, vol. 58, no. 3, pp. 1–37, May. 2011.
- Y. Gao, T. Lin, J. Pan, F. Nie, Youwei Xie Fuzzy Sparse Deviation Regularized Robust Principal Component Analysis, IEEE Transactions on Image Processing, vol. 31, pp. 5645–5660, 2022.
- Y. Huang, G. Liao, J. Li, J. Xu, Narrowband RFI Suppression for SAR System via Fast Implementation of Joint Sparsity and Low-Rank Property, IEEE Transactions on Geoscience and Remote Sensing , vol. 56, no. 5, pp. 2748-2761, 2018. [CrossRef]
- E. Mason, I. Son, and B. Yazıcı. Passive Synthetic Aperture Radar Imaging Using Low-Rank Matrix Recovery Methods, IEEE Journal of selected topics in signal processing, vol. 9, no 8, pp.1570-1582, Dec. 2015. [CrossRef]
- Y. Wang, T. Li, L. Chen, Y. Yu, Y. Zhao, J. Zhou, Tensor-Based Robust Principal Component Analysis With Locality Preserving Graph and Frontal Slice Sparsity for Hyperspectral Image Classification, IEEE Transactions on Geoscience and Remote Sensing, vol. 60, no. 5508319, 2022. [CrossRef]
- Yang, X. Yang, G. Liao, S. Zhu, Strong Clutter Suppression via RPCA in Multichannel SAR/GMTI System, IEEE Geoscience and Remote Sensing Letters, vol. 12, pp. 2257-2241, 2015. [CrossRef]
- J. Cai, E. J. Candès, and Z. Shen, A singular value thresholding algorithm for matrix completion, SIAM Journal on Optimization, vol. 20, no. 4, pp. 1956–1982, 2010. [CrossRef]
- Y. Guo, G. Liao, J. Li, and X. Chen. A Novel Moving Target Detection Method Based on RPCA for SAR Systems. IEEE Transactions on Geoscience and Remote Sensing, vol. 58, no. 9, pp. 6677-6690, 2020. [CrossRef]
- L. Donoho, M. Elad, and V. N. Temlyakov, Stable recovery of sparse overcomplete representations in the presence of noise, IEEE Transactions on Information Theory, vol. 52, no. 1, pp. 6-8, 2006.
- L. Zhouchen, C. Minming, and M. Yi, The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices, Eprint Arxiv, 2010.
- J.-F. Cai, E. J. Candès, and Z. Shen, A singular value thresholding algorithm for matrix completion, SIAM Journal on Optimization, vol. 20, no. 4, pp. 1956–1982, Jan. 2010.
- P. Giampouras, K. Themelis, A. Rontogiannis, et al. Simultaneously Sparse and Low-Rank Abundance Matrix Estimation for Hyperspectral Image Unmixing, IEEE Transactions on Geoence and Remote Sensing, vol. 54, no. 8, pp. 4775-4789, 2016.
- C. Kuptametee: N. Aunsri. An EMD with Masked WVDs for Cross-terms Reduction in Non-stationary Signals. 2022 Joint International Conference on Digital Arts, Media and Technology with ECTI Northern Section Conference on Electrical, Electronics, Computer and Telecommunications Engineering (ECTI DAMT & NCON). Chiang Rai, Thailand, January, 2022.
| Parameter | Symbol | Value |
|---|---|---|
| Number of elemnts | N | 10 |
| Radar platform velocity | V | 100 m/s |
| Height of the radar platform | H | 2 km |
| Wavelength | 0.03 m | |
| Inter-element spacing | d | 0.6 m |
| Bandwidth | B | 100 MHz |
| Sampling frequency | 150 MHz | |
| Pulse repetition frequency | PRF | 1000 Hz |
| Signal to clutter ratio | SCR | -30dB |
| Signal to noise ratio | SNR | 10dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




