Submitted:
06 July 2024
Posted:
08 July 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Setups and the Misidentification in the FE and RE Models
2.1. Setups
2.2. The Misidentification in the FE and RE Models
3. The Differential Error Component Model
3.1. The First Differential Random Effects (FDRE) Models
3.2. The Second Differential Random Effects (SDRE) Models
3.3. Comparisons of the Above Identifications
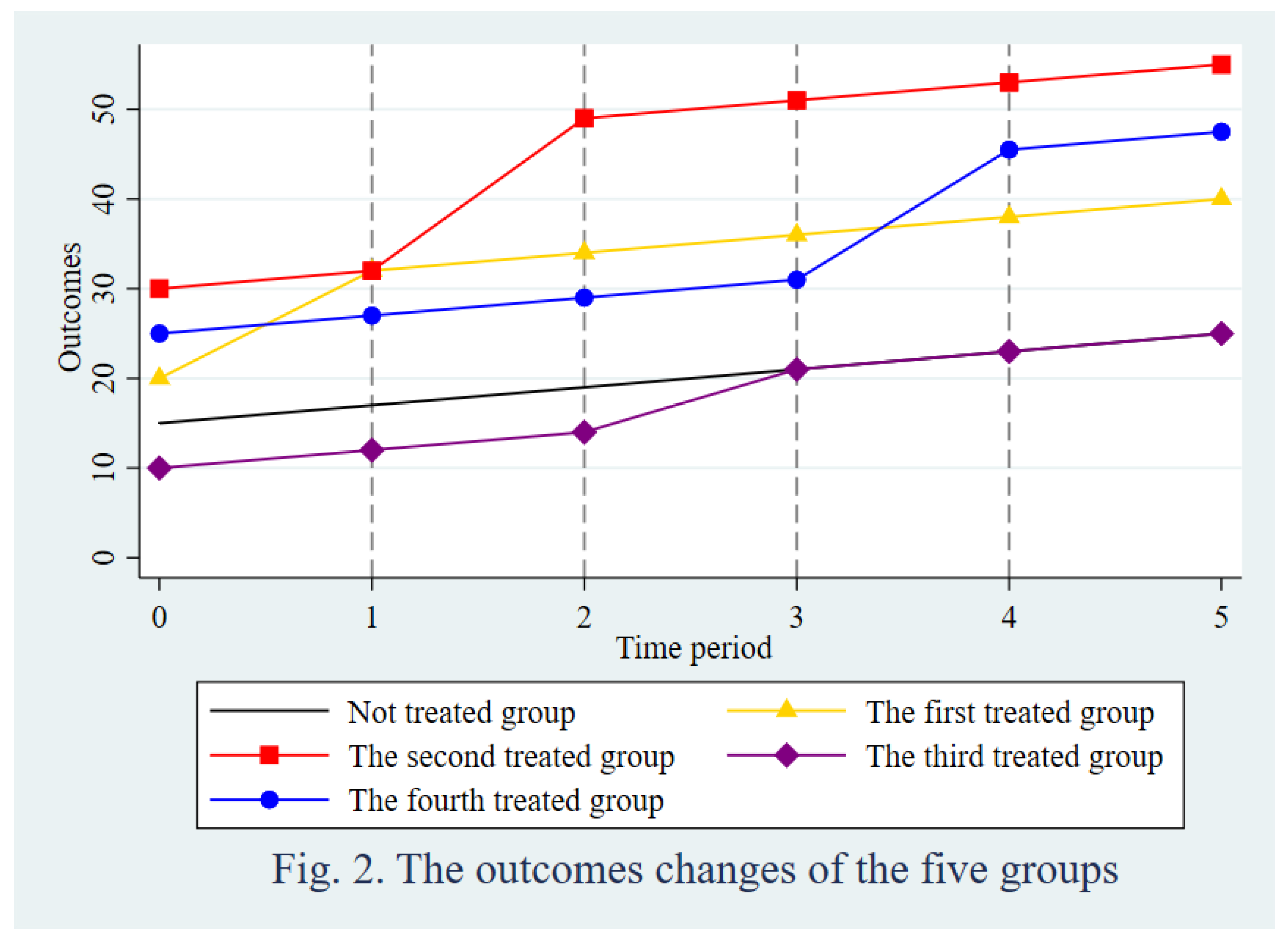
4. Simulation and Application
5. Conclusion
Appendix A. Proofs
A.1 Proof of Theorem 1
A.2 Proof of Corollary 1
A.3 Proof of Corollary 3
A.4 Proof of Corollary 4
A.5 Proof of Theorem 2
A.6 Proof of Corollary 5
Appendix B. Supplementary data
References
- Abadie, A. Semiparametric difference-in-differences estimators. The review of economic studies 2005, 72, 1–19. [Google Scholar] [CrossRef]
- Angrist, J. D.; Imbens, G. W. Two-stage least squares estimation of average causal effects in models with variable treatment intensity. Journal of the American statistical Association 1995, 90, 431–442. [Google Scholar] [CrossRef]
- Arkhangelsky, D.; Imbens, G. W. Doubly robust identification for causal panel data models. The Econometrics Journal 2022, 25, 649–674. [Google Scholar] [CrossRef]
- Baltagi, B. H. Pooling: An experimental study of alternative testing and estimation procedures in a two-way error component model. Journal of Econometrics 1981, 17, 21–49. [Google Scholar] [CrossRef]
- Baltagi, B. H., and Baltagi, B. H. (2008), Econometric analysis of panel data (Vol. 4): Springer.
- Baltagi, B. H.; Song, S. H.; Jung, B. C. The unbalanced nested error component regression model. Journal of Econometrics 2001, 101, 357–381. [Google Scholar] [CrossRef]
- Baltagi, B. H., Song, S. H., and Jung, B. C. A comparative study of alternative estimators for the unbalanced two-way error component regression model. The Econometrics Journal 2002, 5, 480–493. [Google Scholar] [CrossRef]
- Casella, G., and Berger, R. L. (2002), Statistical Inference: Thomson Learning.
- Chamberlain, G. Panel data. Handbook of econometrics 1984, 2, 1247–1318. [Google Scholar]
- de Chaisemartin, C., and d'Haultfoeuille, X. (2020), "Two-way fixed effects regressions with several treatments," arXiv preprint arXiv:2012.10077.
- De Chaisemartin, C., and d’Haultfoeuille, X. Two-way fixed effects estimators with heterogeneous treatment effects. American Economic Review 110, 2964–2996. [CrossRef]
- ---. Two-way fixed effects and differences-in-differences with heterogeneous treatment effects: A survey. The Econometrics Journal 26, C1–C30. [CrossRef]
- Gentzkow, M., Shapiro, J. M., and Sinkinson, M. The effect of newspaper entry and exit on electoral politics. American Economic Review 101, 2980–3018. [CrossRef]
- Goodman-Bacon, A. Difference-in-differences with variation in treatment timing. Journal of Econometrics 2021, 225, 254–277. [Google Scholar] [CrossRef]
- Hausman, J. A. Specification tests in econometrics. Econometrica: Journal of the econometric society 1978, 1251–1271. [Google Scholar] [CrossRef]
- Hausman, J. A., and Taylor, W. E. Panel data and unobservable individual effects. Econometrica: Journal of the econometric society 1981, 1377–1398. [Google Scholar]
- Imai, K., and Kim, I. S. On the use of two-way fixed effects regression models for causal inference with panel data. Political Analysis 2021, 29, 405–415. [Google Scholar] [CrossRef]
- Liu, C., and Sun, Y. A simple and trustworthy asymptotic t test in difference-in-differences regressions. Journal of Econometrics 210, 327–362. [CrossRef]
- Maddala, G. S. The use of variance components models in pooling cross section and time series data, Econometrica: Journal of the econometric society 1971, 341–358. [Google Scholar] [CrossRef]
- Metcalf, G. E. Specification testing in panel data with instrumental variables. Journal of Econometrics 1996, 71, 291–307. [Google Scholar] [CrossRef]
- Mundlak, Y. On the pooling of time series and cross section data. Econometrica: Journal of the econometric society 1978, 69–85. [Google Scholar] [CrossRef]
- Pereda-Fernández, S. Copula-Based Random Effects Models for Clustered Data. Journal of Business & Economic Statistics 2021, 39, 575–588. [Google Scholar] [CrossRef]
- Swamy, P., and Arora, S. S. The exact finite sample properties of the estimators of coefficients in the error components regression models. Econometrica: Journal of the econometric society 1972, 261–275. [Google Scholar]
- Van der Vaart, A. W. (2000), Asymptotic statistics (Vol. 3): Cambridge university press.
- Wallace, T. D., and Hussain, A. The use of error components models in combining cross section with time series data. Econometrica: Journal of the econometric society 1969, 55–72. [Google Scholar]
- Wooldridge, J. M. (2021), "Two-way fixed effects, the two-way mundlak regression, and difference-in-differences estimators," Available at SSRN 3906345.
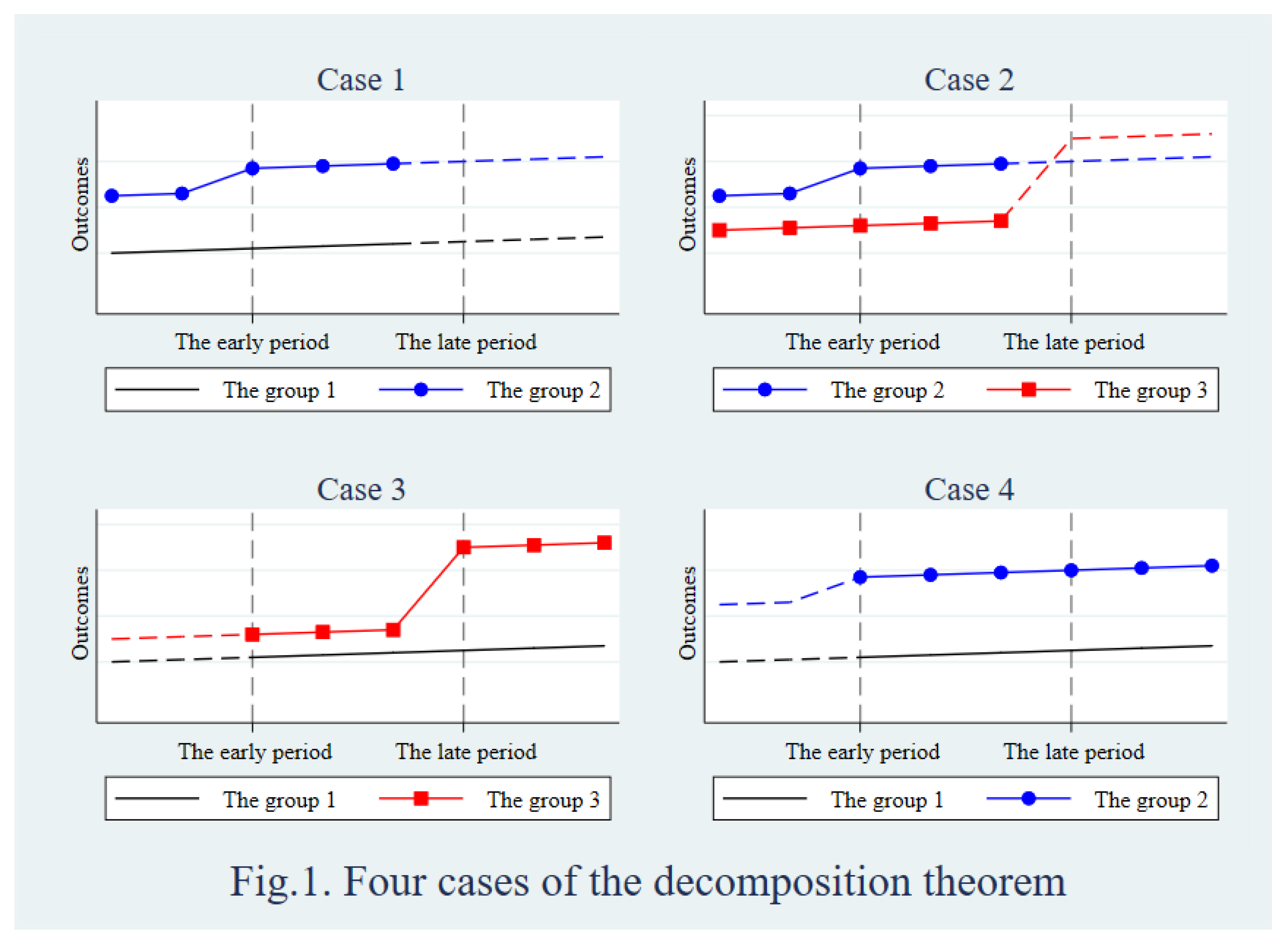
| Small sample | Large sample | |
| Short time periods | TWFE/DM | TWFE/DRE |
| Long time periods | TWFE/DRE | TWRE/DRE |
| Staggered design | Newspapers for all changes | Newspapers for positive changes | |
| TWFE | 10.50 | 0.0032 | 0.0132 |
| (0.1095) | (0.0613) | (0.2130) | |
| FD | 12.63 | 0.0019 | -0.0065 |
| (0.0000) | (0.0785) | (0.9644) | |
| SD | 10.42 | 0.0025 | 0.0036 |
| (0.0000) | (0.0346) | (0.4448) |
| Staggered design | ||||
| OWRE | 15.50 | 16.35 | 15.52 | 16.34 |
| (0.0000) | (0.0000) | (0.0000) | (0.0000) | |
| FDOW | 10.63 | 12.04 | 10.63 | 12.09 |
| (0.0000) | (0.0000) | (0.0000) | (0.0000) | |
| SDOW | 10.31 | 11.13 | 11.13 | 10.31 |
| (0.0000) | (0.0000) | (0.0000) | (0.0000) | |
| Newspapers for all changes | ||||
| OWRE | -0.0241 | 0.0018 | 0.0018 | 0.0032 |
| (1.0000) | (0.0399) | (0.0475) | (0.0021) | |
| FDOW | 0.0026 | 0.0005 | 0.0039 | -0.0010 |
| (0.0292) | (0.3425) | (0.0018) | (0.7595) | |
| SDOW | 0.0024 | 0.0027 | 0.0024 | 0.0028 |
| (0.0414) | (0.0226) | (0.0420) | (0.0217) | |
| Newspapers for positive changes | ||||
| OWRE | -0.0936 | 0.0126 | 0.0126 | 0.0115 |
| (1.0000) | (0.0021) | (0.0026) | (0.0049) | |
| FDOW | -0.0088 | -0.023 | -0.0031 | -0.0285 |
| (0.8542) | (0.9996) | (0.6504) | (1.0000) | |
| SDOW | 0.0011 | 0.0031 | 0.0055 | -0.0014 |
| (0.4523) | (0.3606) | (0.2673) | (0.5601) | |
| Staggered design | ||||||||
| TWRE | 10.50 | 18.26 | 18.26 | 10.56 | 10.56 | 18.26 | 18.26 | 10.50 |
| (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | |
| FDTW | 10.63 | 11.50 | 10.63 | 11.50 | 10.63 | 10.63 | 10.63 | 11.53 |
| (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | |
| Newspapers for all changes | ||||||||
| TWRE | 0.0032 | 0.0022 | 0.0022 | 0.0023 | 0.0032 | 0.0023 | 0.0032 | 0.0032 |
| (0.0014) | (0.0137) | (0.0137) | (0.0113) | (0.0018) | (0.0113) | (0.0018) | (0.0014) | |
| FDTW | 0.0026 | 0.0037 | 0.0037 | 0.0037 | 0.0026 | 0.0037 | 0.0026 | 0.0026 |
| (0.0179) | (0.0012) | (0.0012) | (0.0012) | (0.0181) | (0.0012) | (0.0179) | (0.0181) | |
| SDTW | 0.0031 | 0.0030 | 0.0030 | 0.0031 | 0.0031 | 0.0030 | 0.0031 | 0.0031 |
| (0.0079) | (0.0084) | (0.0084) | (0.0084) | (0.0080) | (0.0084) | (0.0080) | (0.0078) | |
| Newspapers for positive changes | ||||||||
| TWRE | 0.0115 | 0.0043 | 0.0043 | 0.0123 | 0.0033 | 0.0123 | 0.0033 | 0.0115 |
| (0.0215) | (0.2128) | (0.2128) | (0.0140) | (0.2739) | (0.0140) | (0.2739) | (0.0215) | |
| FDTW | 0.0075 | 0.0102 | 0.0105 | 0.0107 | 0.0066 | 0.0110 | 0.0069 | 0.0071 |
| (0.1606) | (0.0786) | (0.0732) | (0.0691) | (0.1885) | (0.0642) | (0.1783) | (0.1701) | |
| SDTW | 0.0050 | 0.0084 | 0.0084 | 0.0085 | 0.0050 | 0.0085 | 0.0050 | 0.0051 |
| (0.2694) | (0.1475) | (0.1475) | (0.1446) | (0.2739) | (0.1445) | (0.2737) | (0.2695) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





