Submitted:
05 July 2024
Posted:
08 July 2024
Read the latest preprint version here
Abstract
Keywords:
1. Introduction
2. Manipulability Measures
2.1. Jacobian Matrix
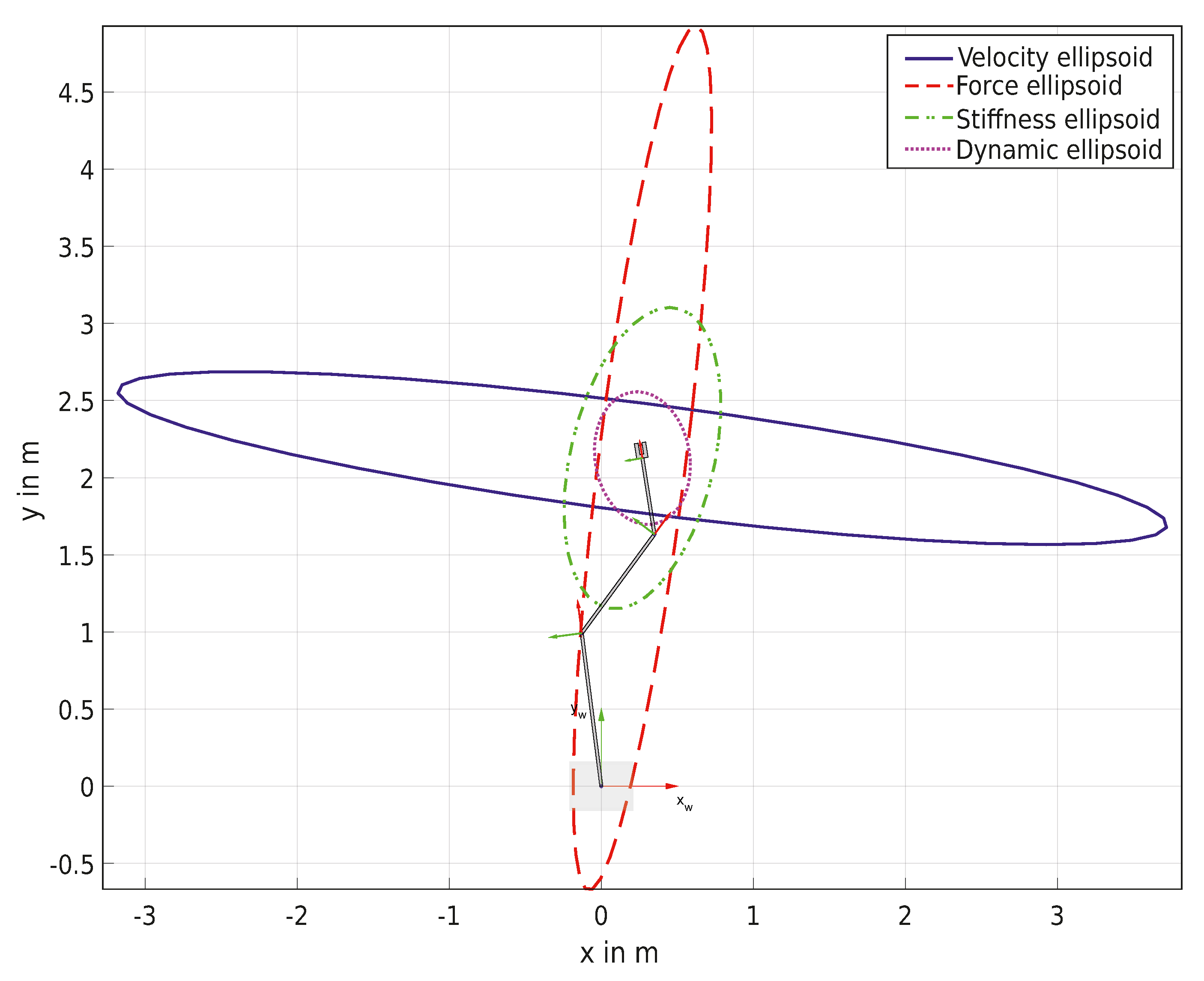
2.2. Velocity Manipulability Measure
2.3. Force Manipulability Measure
2.4. Stiffness Manipulability Measure
2.5. Dynamic Manipulability Measure
3. Task Dependent Comfort Zone
3.1. Task Classification
3.2. Motivation
3.3. Recommended Workspace
3.4. Manipulability Measure Norm, Combination, and Constrains
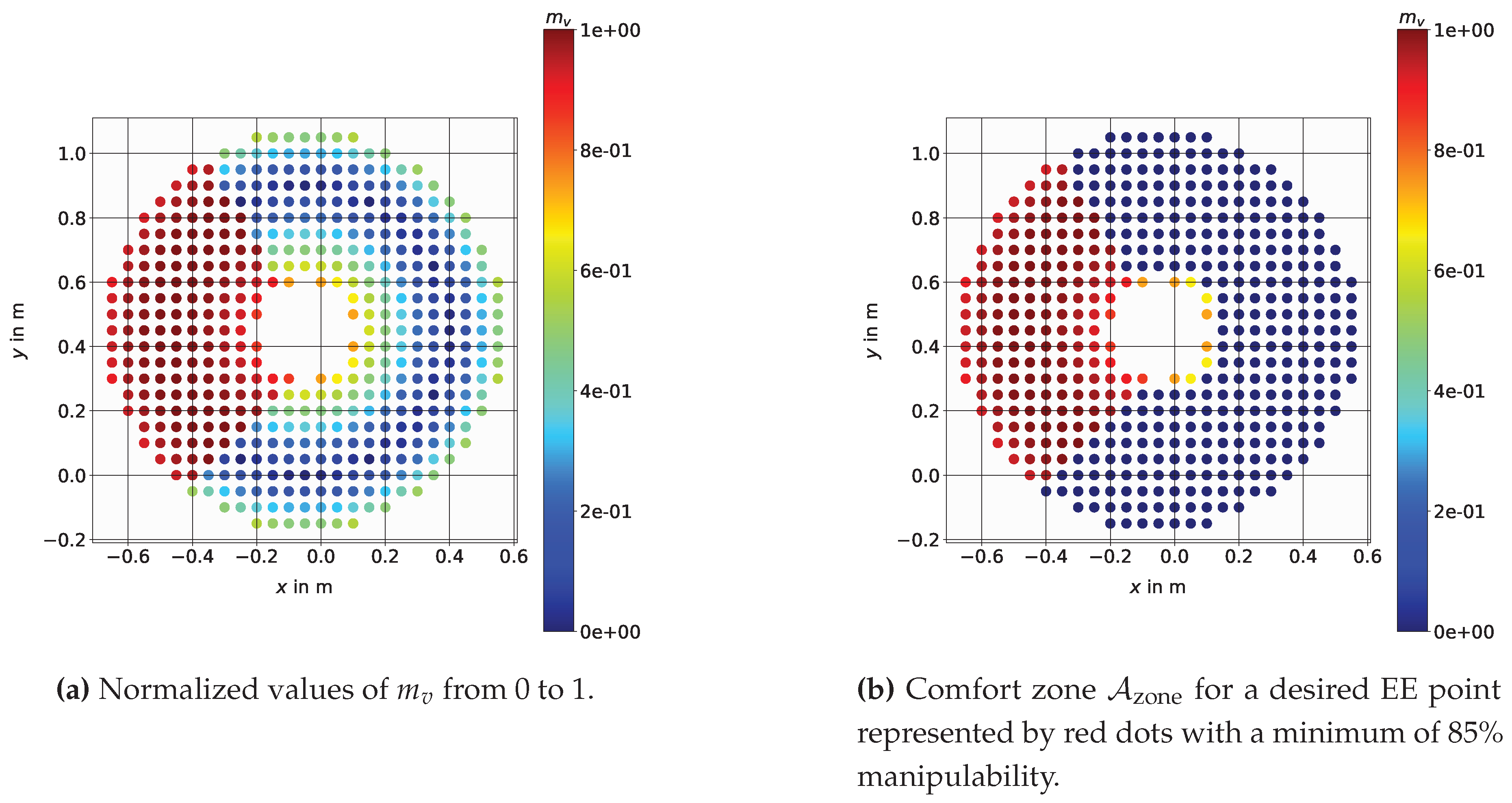
3.5. Comfort Zone Definition
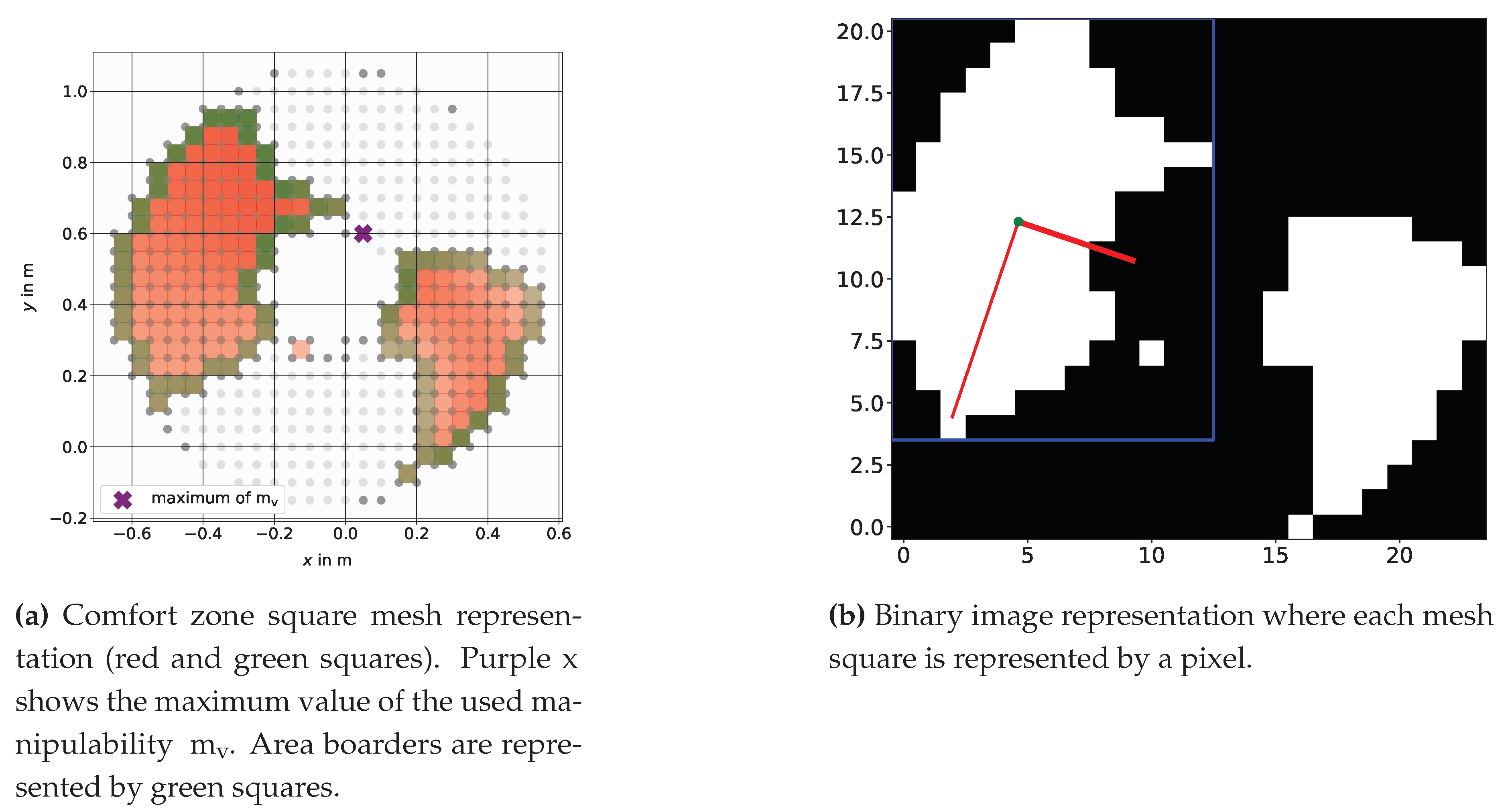
3.6. Comfort Zone Mesh Representation and Target Points
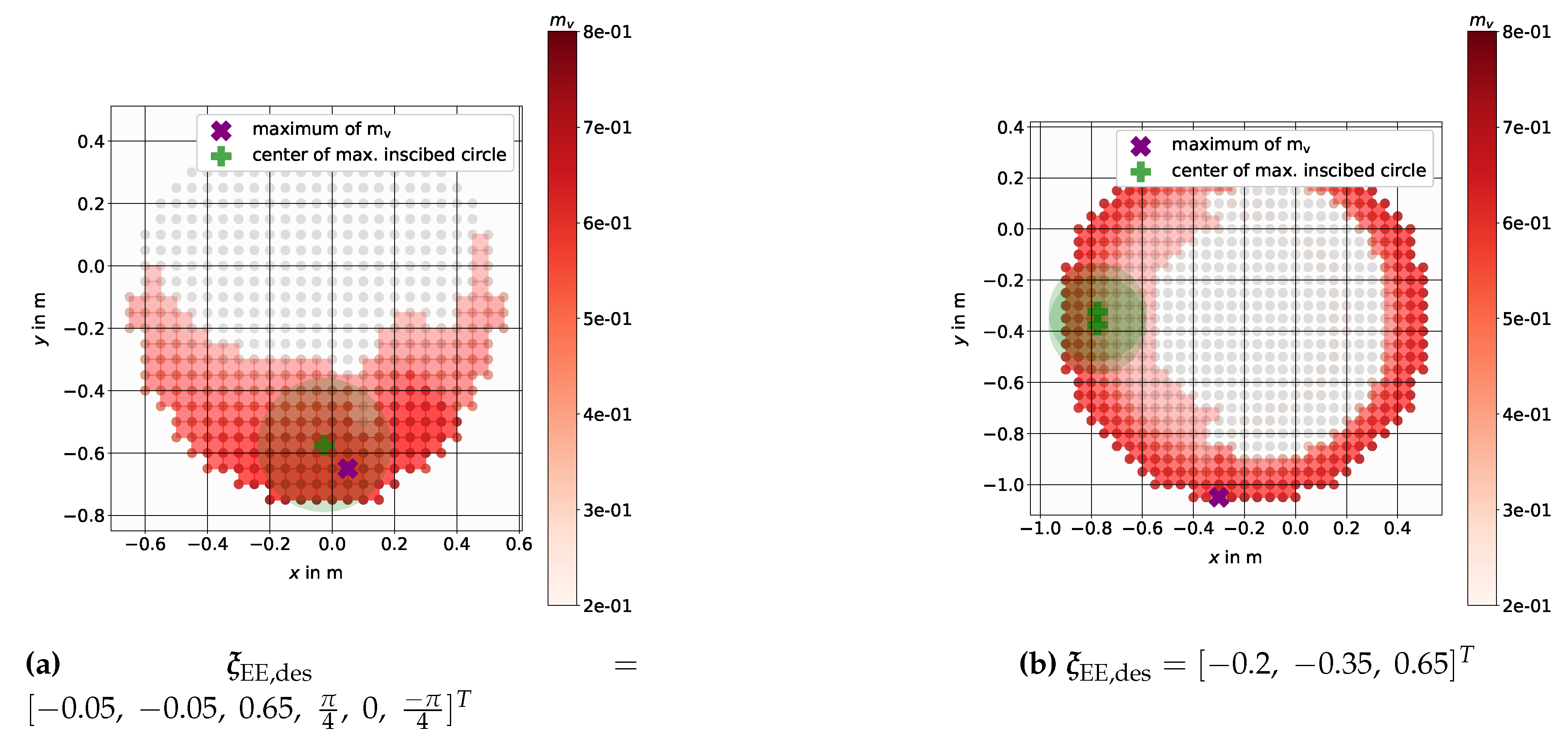
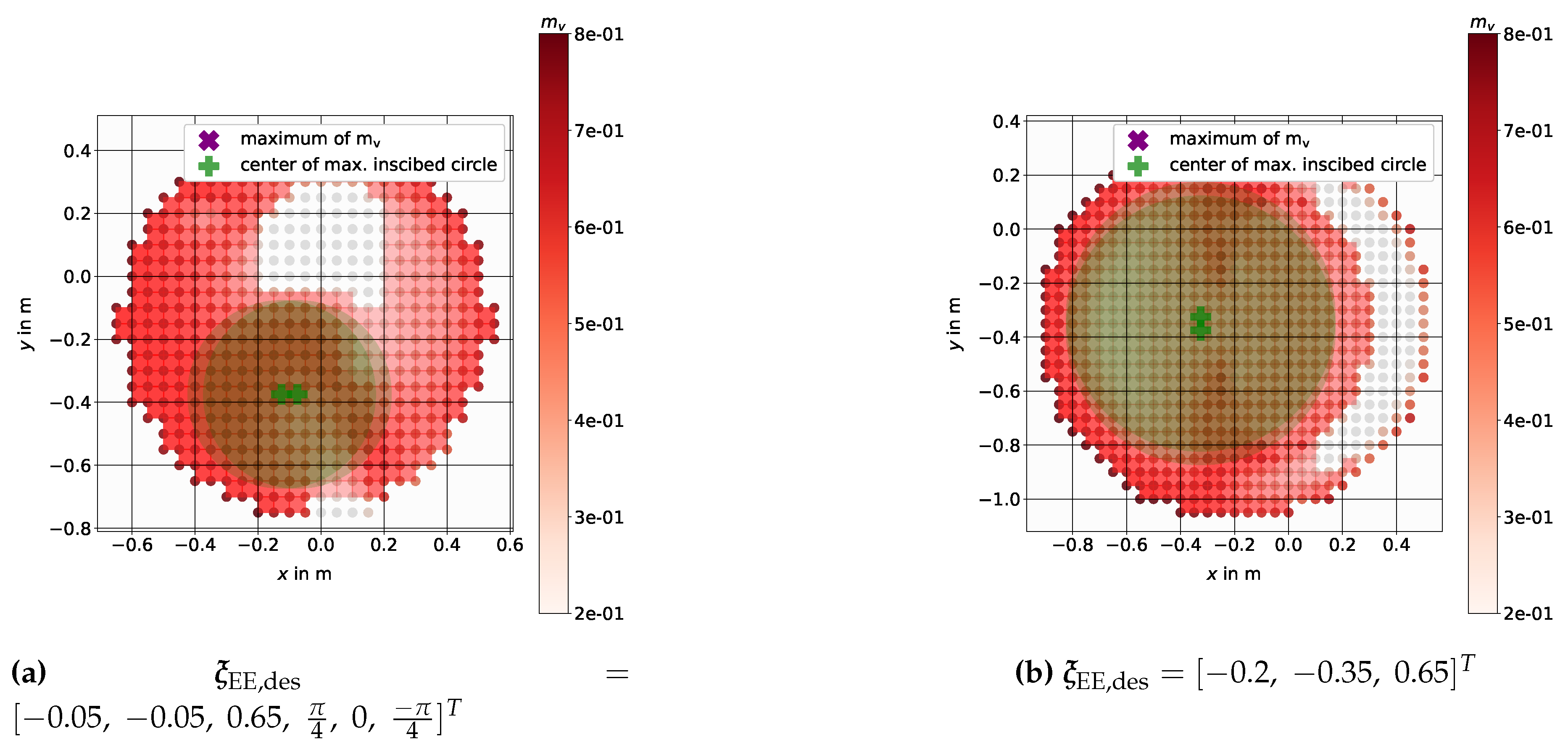
4. Comfort Zone Simulation Examples
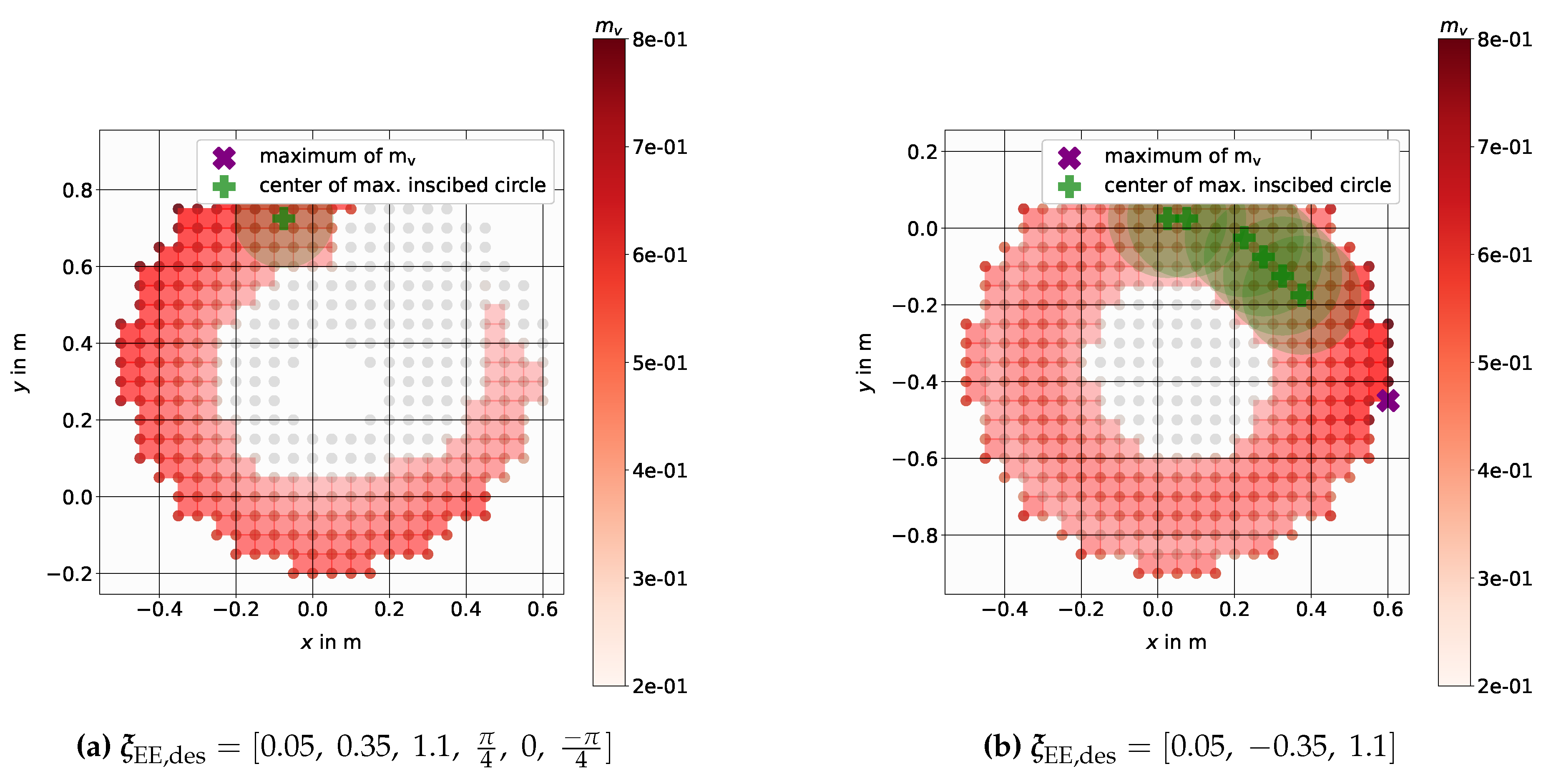
4.1.
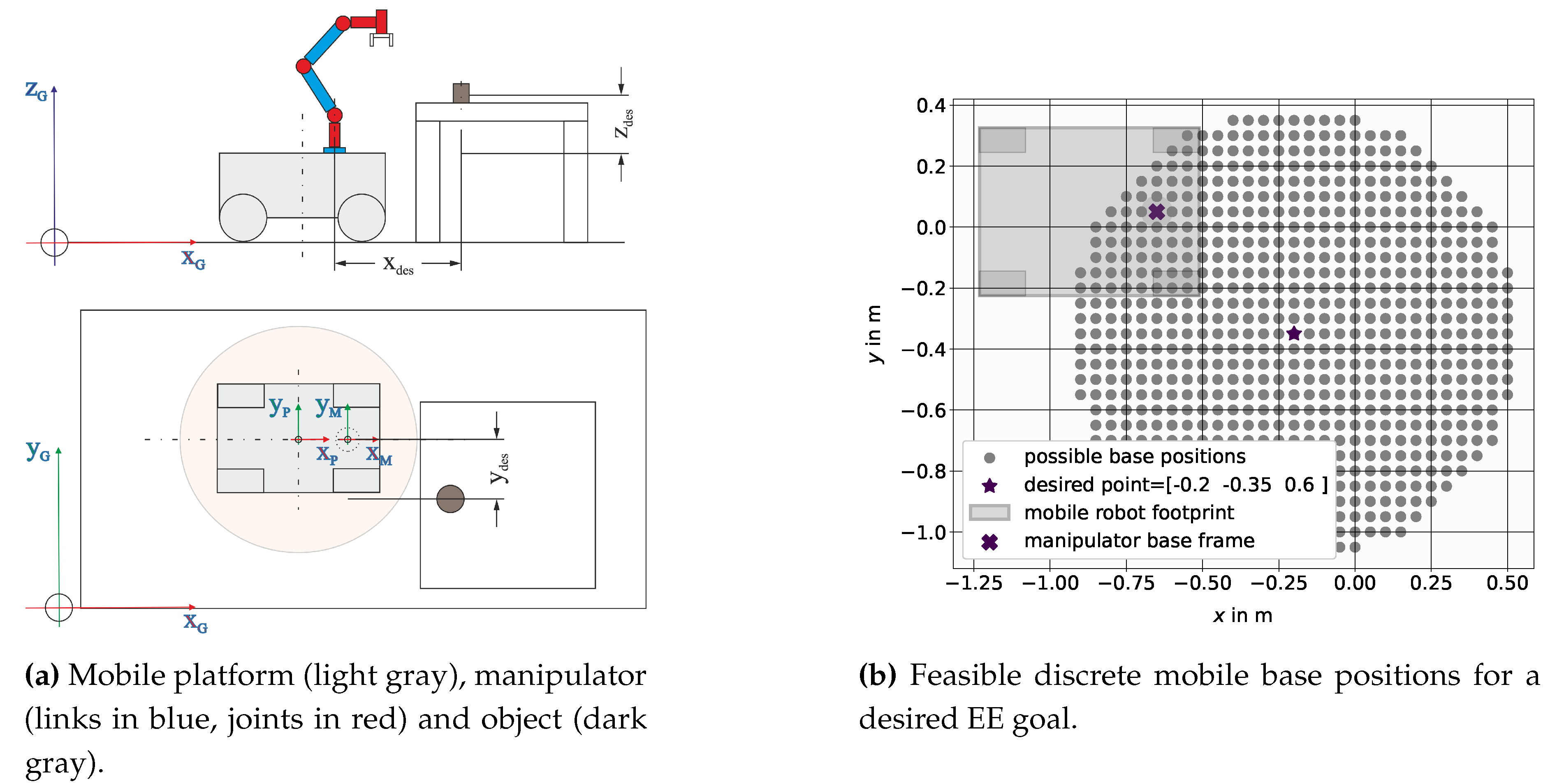
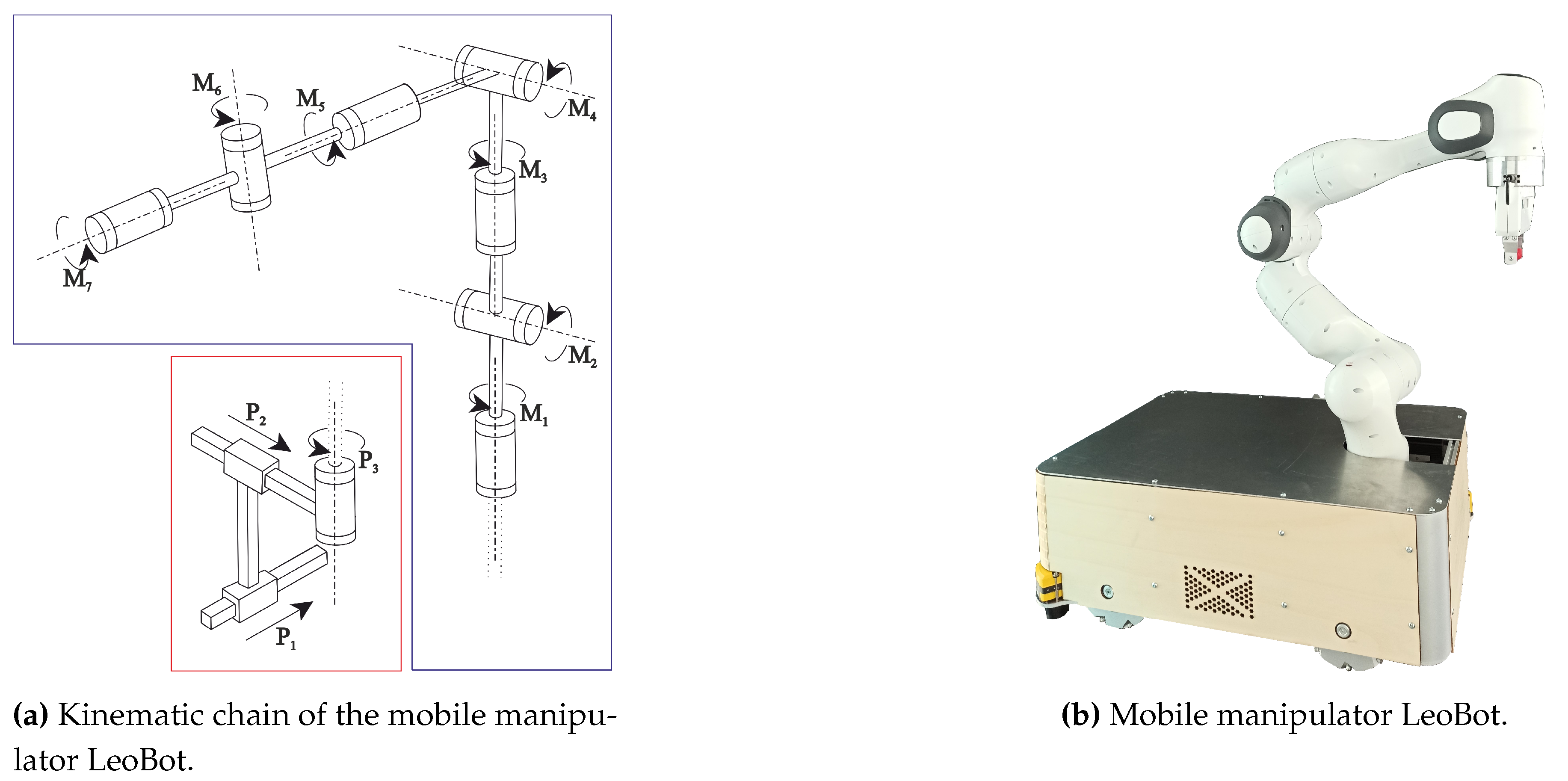
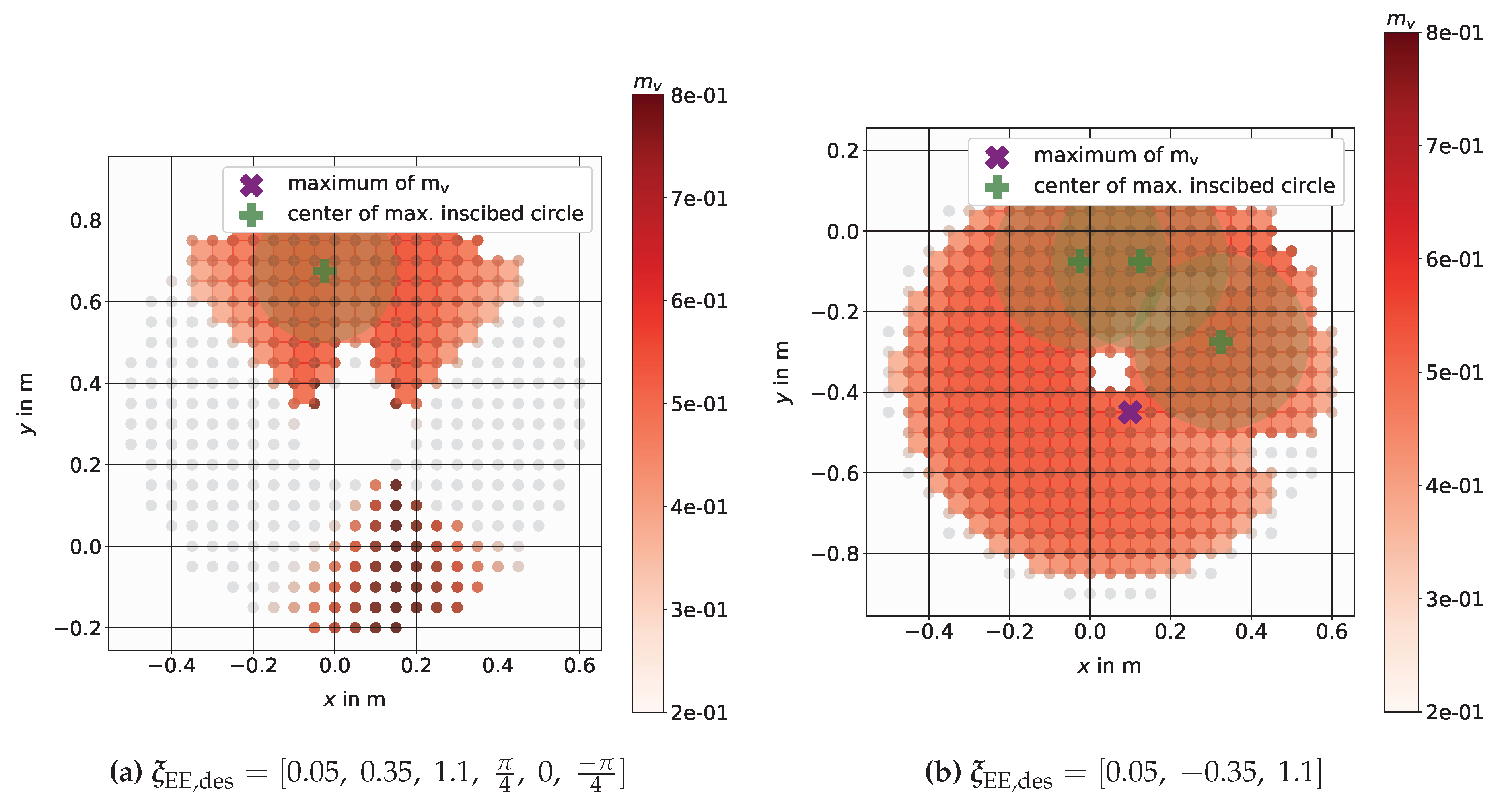
4.2. Mobile Manipulator
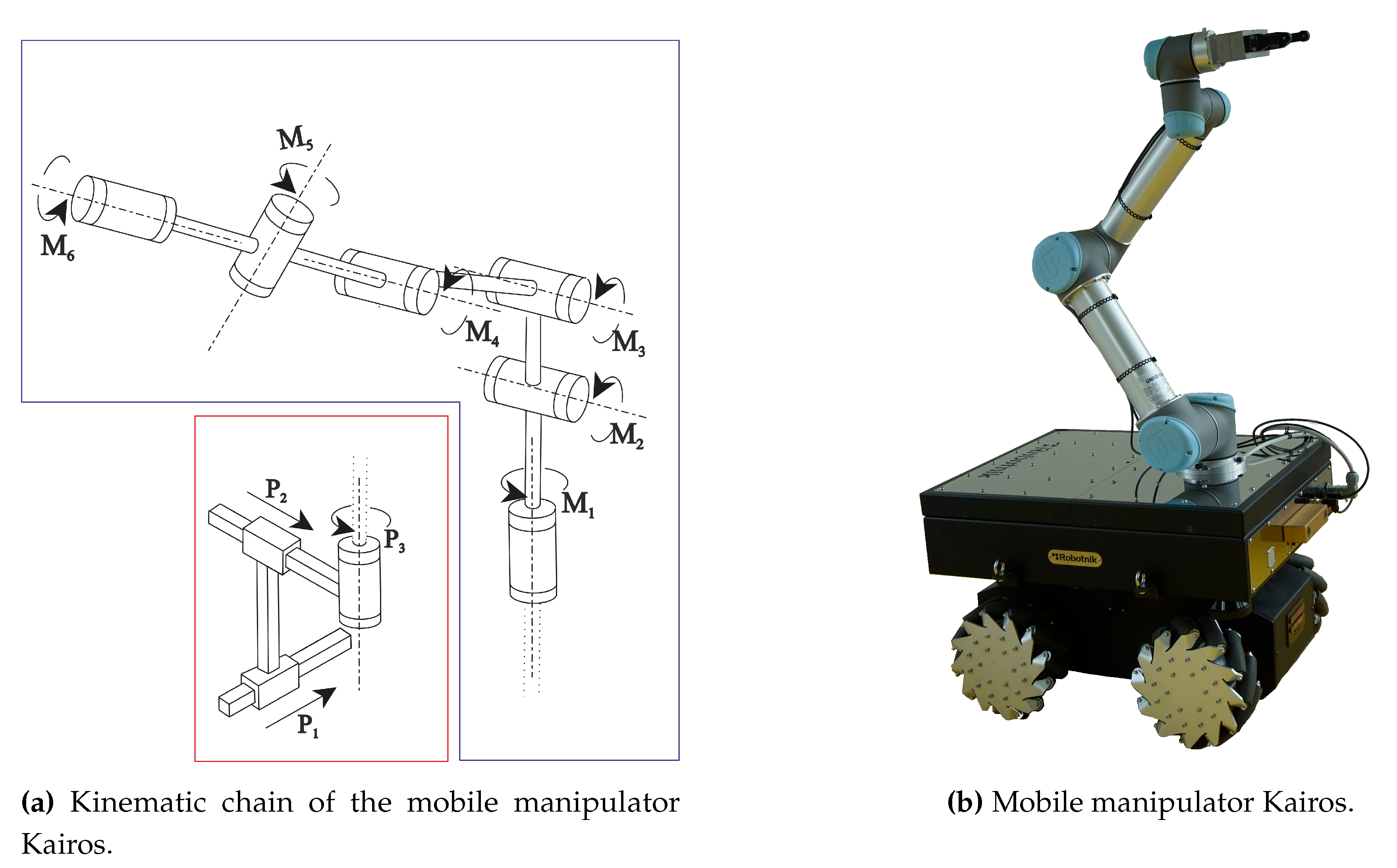
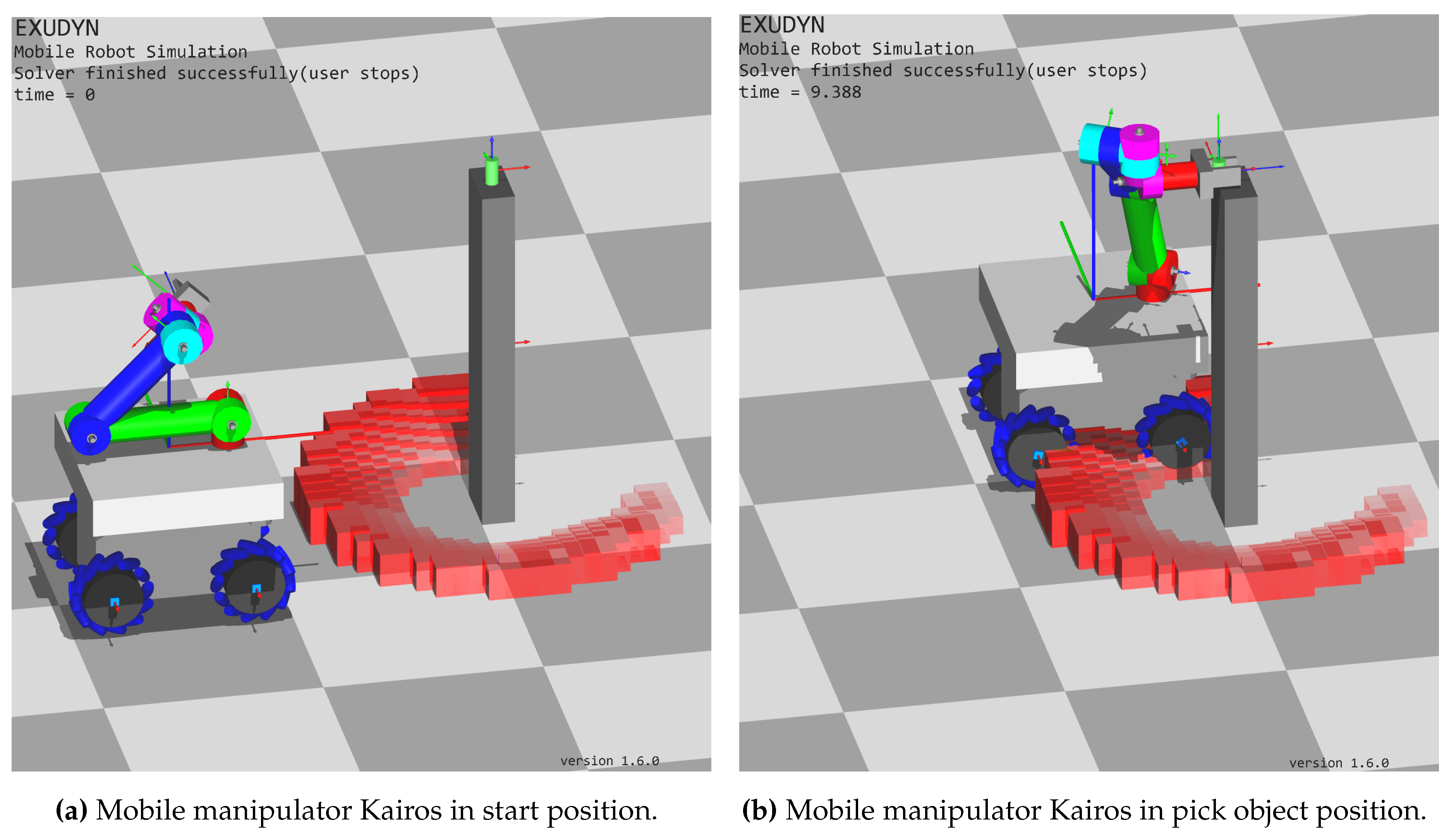
4.3. Mobile Manipulator Kairos
5. Conclusion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brandstötter, M.; Mirkovic, D.; Hofbaur, M. Mobile Manipulation – Eine altbekannte Technologie findet durch sensitive Robotertechnologie Einzug in die Industrie. C-AR2017 – Conference on Automation and Robotics, 2017, pp. 1–6.
- Sereinig, M.; Werth, W.; Faller, L.M. A review of the challenges in mobile manipulation: systems design and RoboCup challenges. e & i Elektrotechnik und Informationstechnik, 2020. [Google Scholar] [CrossRef]
- Haviland, J.; Sünderhauf, N.; Corke, P. A Holistic Approach to Reactive Mobile Manipulation. IEEE Robotics and Automation Letters 2022, 7, 3122–3129. [Google Scholar] [CrossRef]
- Manzl, P.; Gerstmayr, J. An Improved Dynamic Model of the Mecanum Wheel for Multibody Simulations. Volume 9: 17th International Conference on Multibody Systems, Nonlinear Dynamics, and Control (MSNDC), 2021, International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. [CrossRef]
- Luca, A.D.; Oriolo, G.; Giordano, P.R. Kinematic modeling and redundancy resolution for nonholonomic mobile manipulators. Proceedings 2006 IEEE International Conference on Robotics and Automation, 2006. ICRA 2006., 2006, pp. 1867–1873. [CrossRef]
- Chiaverini, S. Singularity-robust task-priority redundancy resolution for real-time kinematic control of robot manipulators. IEEE Transactions on Robotics and Automation 1997, 13, 398–410. [Google Scholar] [CrossRef]
- Siciliano, B.; Khatib, O. Springer Handbook of Robotics; Springer Handbooks, Springer International Publishing, 2016.
- Zanchettin, A.M.; Rocco, P.; Bascetta, L.; Symeonidis, I.; Peldschus, S. Kinematic motion analysis of the human arm during a manipulation task. 2010, Vol. 2, pp. 1–6.
- Rastegarpanah, A.; Gonzalez, H.C.; Stolkin, R. Semi-Autonomous Behaviour Tree-Based Framework for Sorting Electric Vehicle Batteries Components. Robotics 2021, 10. [Google Scholar] [CrossRef]
- Saoji, S.; Rosell, J. Flexibly configuring task and motion planning problems for mobile manipulators. 2020 25th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), 2020, Vol. 1, pp. 1285–1288. [CrossRef]
- Castaman, N.; Pagello, E.; Menegatti, E.; Pretto, A. Receding Horizon Task and Motion Planning in Changing Environments. Robotics and Autonomous Systems 2021, 145, 103863. [Google Scholar] [CrossRef]
- Brock, O.; Kavraki, L. Decomposition-based motion planning: a framework for real-time motion planning in high-dimensional configuration spaces. Proceedings 2001 ICRA. IEEE International Conference on Robotics and Automation (Cat. No.01CH37164), 2001, Vol. 2, pp. 1469–1474 vol.2. 10.1109/ROBOT.2001. 932817.
- Su, J.; Xie, W. Motion Planning and Coordination for Robot Systems Based on Representation Space. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics) 2011, 41, 248–259. [Google Scholar] [CrossRef]
- LaValle, S.M. Rapidly-exploring random trees : a new tool for path planning. The annual research report 1998. [Google Scholar]
- Kavraki, L.; Svestka, P.; Latombe, J.C.; Overmars, M. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Transactions on Robotics and Automation 1996, 12, 566–580. [Google Scholar] [CrossRef]
- Hsu, D.; Latombe, J.C.; Motwani, R. Path planning in expansive configuration spaces. Proceedings of International Conference on Robotics and Automation, 1997, Vol. 3, pp. 2719–2726 vol.3.
- Ratliff, N.; Zucker, M.; Bagnell, J.A.; Srinivasa, S. CHOMP: Gradient optimization techniques for efficient motion planning. 2009 IEEE International Conference on Robotics and Automation, 2009, pp. 489–494. [CrossRef]
- Kalakrishnan, M.; Chitta, S.; Theodorou, E.; Pastor, P.; Schaal, S. STOMP: Stochastic trajectory optimization for motion planning. 2011 IEEE International Conference on Robotics and Automation, 2011, pp. 4569–4574. [CrossRef]
- Coleman, D.; Sucan, I.; Chitta, S.; Correll, N. Reducing the Barrier to Entry of Complex Robotic Software: a MoveIt! Case Study, 2014. [CrossRef]
- Sandakalum, T.; Ang, M.H. Motion Planning for Mobile ManipulatorsA Systematic Review. Machines 2022, 10. [Google Scholar] [CrossRef]
- Makhal, A.; Goins, A.K. Reuleaux: Robot Base Placement by Reachability Analysis. CoRR, 2017; abs/1710.01328. [Google Scholar]
- Zhang, H.; Sheng, Q.; Sun, Y.; Sheng, X.; Xiong, Z.; Zhu, X. A novel coordinated motion planner based on capability map for autonomous mobile manipulator. Robotics and Autonomous Systems 2020, 129, 103554. [Google Scholar] [CrossRef]
- Zhang, H.; Sheng, Q.; Hu, J.; Sheng, X.; Xiong, Z.; Zhu, X. Cooperative Transportation With Mobile Manipulator: A Capability Map-Based Framework for Physical Human–Robot Collaboration. IEEE/ASME Transactions on Mechatronics 2022, 27, 4396–4405. [Google Scholar] [CrossRef]
- Yoshikawa, T. Manipulability of Robotic Mechanisms. The International Journal of Robotics Research 1985, 4, 3–9. [Google Scholar] [CrossRef]
- Zacharias, F.; Borst, C.; Hirzinger, G. Capturing robot workspace structure: representing robot capabilities. 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2007, pp. 3229–3236. [CrossRef]
- Sereinig, M.; Manzl, P.; Gerstmayr, J. Komfortzone mobiler Manipulatoren. Sechste IFToMM D-A-CH Konferenz 2020: 27./28. Februar 2020, Campus Technik Lienz; IFToMM D-A-CH., Ed., 2020, Vol. 2020. [CrossRef]
- Spong, M.; Hutchinson, S.; Vidyasagar, M. Robot Modeling and Control; Wiley, 2005.
- Lynch, K.M.; Park, F.C. Modern Robotics: Mechanics, Planning, and Control, 1st ed.; Cambridge University Press: USA, 2017. [Google Scholar]
- Corke, P. Robotics, Vision and Control: Fundamental Algorithms in MATLAB, 1st ed.; Springer Publishing Company, Incorporated, 2013.
- Jin-Oh, Kim.; Khosla, K. Jin-Oh Kim.; Khosla, K. Dexterity measures for design and control of manipulators. Proceedings IROS ’91:IEEE/RSJ International Workshop on Intelligent Robots and Systems, 1991, pp. 758–763 vol.2.
- Melchiorri, C. Force manipulability ellipsoids for general manipulation systems. IFAC Proceedings Volumes 1994, 27, 235–240. [Google Scholar] [CrossRef]
- Ajoudani, A.; Tsagarakis, N.G.; Bicchi, A. Choosing Poses for Force and Stiffness Control. IEEE Transactions on Robotics 2017, 33, 1483–1490. [Google Scholar] [CrossRef]
- Chen, C.; Peng, F.; Yan, R.; Li, Y.; Wei, D.; Fan, Z.; Tang, X.; Zhu, Z. Stiffness performance index based posture and feed orientation optimization in robotic milling process. Robotics and Computer-Integrated Manufacturing 2019, 55, 29–40. [Google Scholar] [CrossRef]
- Kövecses, J.; Angeles, J. The stiffness matrix in elastically articulated rigid-body systems. Multibody System Dynamics 2007, 18, 169–184. [Google Scholar] [CrossRef]
- Dumas, C.; Caro, S.; Cherif, M.; Garnier, S.; Furet, B. Joint stiffness identification of industrial serial robots. Robotica 2012, 30, 649–659. [Google Scholar] [CrossRef]
- Busson, D.; Bearee, R.; Olabi, A. Task-oriented rigidity optimization for 7 DOF redundant manipulators. IFAC-PapersOnLine 2017, 50, 14588–14593. [Google Scholar] [CrossRef]
- Salisbury, J.K. Active stiffness control of a manipulator in cartesian coordinates. 19th IEEE Conference on Decision and Control including the Symposium on Adaptive Processes, 1980, pp. 95–100.
- Guo, Y.; Dong, H.; Ke, Y. Stiffness-oriented posture optimization in robotic machining applications. Robotics and Computer-Integrated Manufacturing 2015, 35, 69–76. [Google Scholar] [CrossRef]
- YOSHIKAWA, T. Dynamic Manipulability of Robot Manipulators. Transactions of the Society of Instrument and Control Engineers 1985, 21, 970–975. [Google Scholar] [CrossRef]
- Chiacchio, P.; Concilio, M. The dynamic manipulability ellipsoid for redundant manipulators. Proceedings. 1998 IEEE International Conference on Robotics and Automation (Cat. No.98CH36146) 1998, 1, 95–100. [Google Scholar] [CrossRef]
- El Makrini, I.; Merckaert, K.; De Winter, J.; Lefeber, D.; Vanderborght, B. Task allocation for improved ergonomics in Human-Robot Collaborative Assembly. Interaction Studies 2019, 20, 103–134. [Google Scholar] [CrossRef]
- Burdet, E.; Osu, R.; Franklin, D.W.; Milner, T.E.; Kawato, M. The central nervous system stabilizes unstable dynamics by learning optimal impedance. Nature 2001. [Google Scholar] [CrossRef]
- Khatib, O. A unified approach for motion and force control of robot manipulators: The operational space formulation. IEEE Journal on Robotics and Automation 1987, 3, 43–53. [Google Scholar] [CrossRef]
- Chen, H.; Lee, S.I.; Do, J.H.; Lee, J.M. , held June 26-29, 2012, Jeju Island, Korea; Lee, S.; Cho, H.; Yoon, K.J.; Lee, J., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2013; pp. 595–602. doi:10.1007/978-3-642-33926-4_56.Grasping. In Intelligent Autonomous Systems 12: Volume 1 Proceedings of the 12th International Conference IAS-12, held June 26-29, 2012, Jeju Island, Korea; Lee, S., Cho, H., Yoon, K.J., Lee, J., Eds.; Lee, S.; Cho, H.; Yoon, K.J.; Lee, J., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2013; Springer Berlin Heidelberg: Berlin, Heidelberg, 2013; pp. 595–602. [Google Scholar] [CrossRef]
- Kraetzschmar, G.K. ; others. RoboCup@Work: Competing for the Factory of the Future. In RoboCup 2014: Robot World Cup XVIII; Springer International Publishing, 2015; pp. 171–182. [CrossRef]
- Abdel-Malek, K.; Yang, J. Workspace boundaries of serial manipulators using manifold stratification. The International Journal of Advanced Manufacturing Technology 2006, 28, 1211–1229. [Google Scholar] [CrossRef]
- Cao, Y.; Lu, K.; Li, X.; Zang, Y. Accurate Numerical Methods for Computing 2D and 3D Robot Workspace. International Journal of Advanced Robotic Systems 2011, 8, 76. [Google Scholar] [CrossRef]
- Patel, S.; Sobh, T. Task based synthesis of serial manipulators. Journal of Advanced Research 2015, 6, 479–492. [Google Scholar] [CrossRef] [PubMed]
- van der Walt, S.; Schönberger, J.L.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.D.; Yager, N.; Gouillart, E.; Yu, T.; the scikit-image contributors. scikit-image: image processing in Python. PeerJ 2014, 2, e453. [Google Scholar] [CrossRef]
- Fiorio, C.; Gustedt, J. Two linear time Union-Find strategies for image processing. Theoretical Computer Science 1996, 154, 165–181. [Google Scholar] [CrossRef]
- Jähne, B. Digital Image Processing 6th Edition; Springer Berlin, Heidelberg, 2005. [CrossRef]
- Felzenszwalb, P.; Huttenlocher, D. Distance Transforms of Sampled Functions. Theory of Computing 2004, 8. [Google Scholar] [CrossRef]
- Doty, K.L.; Melchiorri, C.; Schwartz, E.M.; Bonivento, C. Robot manipulability. IEEE Transactions on Robotics and Automation 1995, 11, 462–468. [Google Scholar] [CrossRef]
- Gerstmayr, J. Exudyn – A C++ based Python package for flexible multibody systems. Multibody System Dynamics 2023. [Google Scholar] [CrossRef]
- Sugihara, T. Solvability-Unconcerned Inverse Kinematics by the Levenberg–Marquardt Method. IEEE Transactions on Robotics 2011, 27, 984–991. [Google Scholar] [CrossRef]
- Corke, P.; Haviland, J. Not your grandmother’s toolbox–the Robotics Toolbox reinvented for Python. 2021 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2021, pp. 11357–11363.
- Holmberg, R.; Khatib, O. Development and Control of a Holonomic Mobile Robot for Mobile Manipulation Tasks. The International Journal of Robotics Research 2000, 19, 1066–1074. [Google Scholar] [CrossRef]
- Corke, P.I. Visual Control of Robots: High-Performance Visual Serving; John Wiley amp Sons Inc.: USA, 1997. [Google Scholar]
- Kim, H.; Streit, D. Configuration dependent stiffness of the PUMA 560 manipulator: Analytical and experimental results. Mechanism and Machine Theory 1995, 30, 1269–1277. [Google Scholar] [CrossRef]
- Chang, K.S.; Holmberg, R.; Khatib, O. The augmented object model: cooperative manipulation and parallel mechanism dynamics. Proceedings ICRA. IEEE International Conference on Robotics and Automation., 2000, Vol. 1, pp. 470 – 475 vol.1. [CrossRef]
- Sereinig, M.; Manzl, P.; Hofmann, P.; Neurauter, R.; Pieber, M.; Gerstmayr, J. Omnidirectional Mobile Manipulator LeoBot for Industrial Environments, Developed for Research and Teaching. RoboCup 2022:; Eguchi, A.; Lau, N.; Paetzel-Prüsmann, M.; Wanichanon, T., Eds. Springer International Publishing, 2023, pp. 127–139. [CrossRef]
- Gaz, C.; Cognetti, M.; Oliva, A.; Robuffo Giordano, P.; De Luca, A. Dynamic Identification of the Franka Emika Panda Robot With Retrieval of Feasible Parameters Using Penalty-Based Optimization. IEEE Robotics and Automation Letters 2019, 4, 4147–4154. [Google Scholar] [CrossRef]
- Kebria, P.M.; Al-wais, S.; Abdi, H.; Nahavandi, S. Kinematic and dynamic modelling of UR5 manipulator. 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), 2016, pp. 004229–004234.
- Kovincic, N.; Müller, A.; Gattringer, H.; Weyrer, M.; Schlotzhauer, A.; Brandstötter, M. Dynamic parameter identification of the Universal Robots UR5. Proceedings of ARW & OAGM Workshop 2019. Verlag der Technischen Universität Graz, 2019, pp. 44–53. [CrossRef]
- Lu, D.V.; Hershberger, D.; Smart, W.D. Layered costmaps for context-sensitive navigation. 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2014, pp. 709–715.
- Marder-Eppstein, E.; Berger, E.; Foote, T.; Gerkey, B.; Konolige, K. The Office Marathon: Robust navigation in an indoor office environment. 2010 IEEE International Conference on Robotics and Automation, 2010, pp. 300–307. [CrossRef]
| 1 |
https://scikit-image.org/ (accessed 19.04.2023) |
| 2 |
https://docs.opencv.org/4.x/d6/d00/tutorial_py_root.html (accessed 19.04.2023) |
| 3 |
https://github.com/jgerstmayr/exudyn (accessed 19.04.2023) |
| 4 |
https://github.com/petercorke/robotics-toolbox-python (accessed 19.04.2023) |
| 5 |
https://robotnik.eu/(accessed 19.04.2023) |

| Symbol | Formula | Description |
|---|---|---|
| Eq. (13) | Proportional to the volume of the EE velocity ellipsoid, which represents the ability to move the EE with a certain velocity in all directions. | |
| Eq. (17) | Proportional to the volume of the EE force ellipsoid, which represents the ability to act with a certain force in all directions. | |
| Eq. (26) | Represents the minimum eigenvalue of the Cartesian stiffness matrix, which characterizes the smallest stiffness in a certain configuration. | |
| Eq. (34) | Represents the minimum eigenvalue of the weighted dynamic manipulability matrix, which characterizes the smallest acceleration in a certain direction. |
| Task Type | Velocity | Force | Stiffness | Acceleration |
|---|---|---|---|---|
| Pick and Place | High | Moderate | Low | High |
| Assembly | Moderate | High | High | Moderate |
| Painting | Moderate | Low | Low | Low |
| Milling | Low | High | High | Low |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





