The Muon g-2 in a Regularized Electrodynamics

1. Introduction

The study of the electron’s anomalous magnetic moment have played an essential role in the development of quantum theory [1,2,3,4]. Its successful theoretical description led to the expectation that the followed calculation of the anomalous component in the muon’s intrinsic magnetic moment will strengthen and crystallize the established knowledge [5,6,7,8,9,10]. Over the decades, however, with the improvement of the experimental setup and the consequent collection of more data from highly precise measurements the gap between the measured and calculated values not only remained but thickened [11,12,13,14,15,16]. The difference between the most recent experimental average [17,18] and the most recent consensus on the average theoretical value [19] is about $2.49$ ppb, which is significantly larger than the relevant uncertainty. It is expected that the analysis of more experimental data will only result in a negligible variation in the measured average value reaffirming the obtained gap. As a result, a variety of theoretical approaches to the calculation of the corresponding anomalous component were proposed, see Ref. [20] and the references therein.

In the light of the apparent discrepancy many efforts to revise and improve the hadronic vacuum polarization corrections [21,22,23,24,25] and the hadronic light-by-light scattering one [24,25,26,27,28] have been considered, see also the revision of Dyson-Schwinger approach [29]. Despite the increasing number of fitting parameters and relevant ambiguity in the choice of observables needed to calculate these contributions, it is believed that the used quantum field theory approaches have the prospect to reduce the obtained tension.

On the other hand, the utility of refining the regularization technique is also considered. Any progress in the regularization of electromagnetic self-interaction is expected to have a significant contribution to the resolution of named tension. Over the years the application of regularization method in electrodynamics and field theory in general has demonstrated great effectiveness [30,31,32,33,34,35,36,37,38,39,40]. The regularization of self-interaction implies minimal number of effective parameters and leads to high precision results, with Yukawa cut-offs [41,42] being the most prominent tools for removing radial singularities at a microscopic scale in both classical and quantum field approaches. Recently a direct regularization scheme with Yukawa terms describing a massive off shell photons and no free parameters was successfully applied to quantify the electron $g-2$ value and the associated self-interaction [40]. To the best of our knowledge calculations of the muon $g-2$ value based on the direct regularization of its electromagnetic self-interaction via Yukawa coupling have not been undertaken yet.

The present paper introduce a study that implements the regularization technique proposed in Ref. [40] with the aim to quantify the self-energy and anomalous component in the muon’s magnetic moment. The applied approach represents a regularized electrodynamics of non-composite particles and conjugate to the quantum theory beyond the corresponding principle. Accordingly, exact results for the muon’s self-energy, anomalous g-factor and all intrinsic characteristics underlying the dynamics of its self-interaction are reported. Improved accuracy in the calculation of the muon anomalous g-factor is obtained ($0.46$ ppb), overcoming the existing gap between the average value predicted by the quantum theory [19] and the measured one [17,18]. An essential outcome of the obtained accuracy is an exact bound on the sum of the muon and electron neutrinos rest masses.

The rest of the report is structured as follows. Section 2 briefly introduce the used method starting with the notation and definition of all relevant physical quantities. Section 3 presents the obtained results with all derived equations and their solutions. Section 4 discusses and summarizes the obtained results.

2. Theoretical Framework

In this section we set-out the mathematical notation of all needful physical quantities and ab-initio relations. We find it convenient to restrict all representations within the mathematical framework of three-dimensional vector formalism.

2.1. Generalities

Consider a free muon with rest mass and electric charge denoted by $m_{\mu }$ and $\overline{e}=-e$, respectively, where e is the elementary charge. Let $\mathbf{R}$ be the muon’s rest frame of reference and $r_{c\mu }=\alpha {\overline{\lambda }}_{c\mu }$ be its electromagnetic radius in $\mathbf{R}$, where $\alpha$ and ${\overline{\lambda }}_{c\mu }$ are the fine structure constant and associated reduced Compton wavelength, respectively. Let ${\mathbf{r}}_{\mu }$ be the intrinsic field vector associated to the muon, with magnitude $r_{\mu }$, and ${\tilde{u}}_{\mu }$ be the magnitude of the tangential velocity ${\tilde{\mathbf{u}}}_{\mu }$ related to its rotation about the origin of $\mathbf{R}$ in the plane perpendicular to the muon’s relative velocity ${\mathbf{u}}_{\mu }=u_{\mu }\kappa$ defined with respect to an observer with frame of reference $\mathbf{O}$, where $\kappa$ is the respective unit vector (see Figure 1). Since the system is closed, we have the constraint ${\mathbf{u}}_{\mu }={\tilde{\mathbf{u}}}_{\mu }$. Furthermore, the oscillation of ${\mathbf{r}}_{\mu }$ is characterized by an angular velocity ${\omega }_{\mu }$, with magnitude ${\omega }_{\mu }={\tilde{u}}_{\mu }{r}_{\mu }^{-1}$ representing the angular frequency of the corresponding circularly polarized field. For comparison with the classical representation of the electron’s intrinsic dynamics the reader may consult Ref. [40]. Within the applied approach the quantities $r_{\mu }$ and ${\tilde{u}}_{\mu }$ are conjugate and satisfy

$$r_{\mu }{\tilde{u}}_{\mu }={\overline{\lambda }}_{c\mu }c,$$

(1)

where c is the light speed in vacuum.

The charge ${\rho }_e$ and mass ${\rho }_{m_{\mu }}$ densities satisfying ${\rho }_e{\rho }_{m_{\mu }}^{-1}=e{m}_{\mu }^{-1}$ are defined within the spherically symmetric spatial domain ${\Omega }_{c\mu }\in {\mathbb{R}}^3$, with radius $r_{c\mu }$, boundary $\partial {\Omega }_{c\mu }$ and volume $V_{c\mu }$. Moreover, ${\rho }_{M_{\mu }}$ is the muon’s effective mass density and $M_{\mu }=m_{\mu }(1+a_{\mu })$ is the corresponding effective rest mass defined in ${\Omega }_{c\mu }$, where $a_{\mu }$ is the muon’s anomalous g-factor. Here, ${\rho }_{M_{\mu }}={\rho }_{M_{\mu }}\left(r\right)$ is a smooth function of the radial parameter r, with $r\in (0,+\infty )$ and ${\rho }_{M_{\mu }}>{\rho }_{m_{\mu }}$ for all r. Note that if $\nexists e$, then ${\rho }_{M_{\mu }}={\rho }_{m_{\mu }}$.

The inherent dynamics of ${\mathbf{r}}_{\mu }$ underpin the occurrence of intrinsic magnetic moment ${\mu }_{\mu }=-\frac{1}{2}{g}_{\mu }{\mu }_{\mu }\kappa$, where $g_{\mu }=2(1+a_{\mu })$ is the g-factor of the muon and ${\mu }_{\mu }=e\hslash {\left(2m_{\mu }\right)}^{-1}$ is the corresponding magneton. We further have

$$g_{\mu }={\displaystyle \frac{2}{V_{c\mu }}}{\int }_{{\Omega }_{c\mu }}{G}_{\mu }\mathrm{d}\mathrm{v},G_{\mu }={\displaystyle \frac{e{\rho }_{M_{\mu }}}{m_{\mu }{\rho }_e}}.$$

(2)

In the case shown in Figure 1 the field associated to the muon reads ${\Phi }_{\mu }\left(\mathrm{x}\right)=A_{\mu }{\Phi }_{\mu }\left(\mathrm{x}\right){\mathbf{n}}_{\mu }$, where the amplitude $A_{\mu }\equiv r_{\mu }$, ${\mathbf{n}}_{\mu }\in {\mathbb{C}}^3$ is the field’s unit vector and the phase factor ${\Phi }_{\mu }\left(\mathrm{x}\right)$ satisfies the Klein-Gordon equation, with $\mathrm{x}\in {\mathbb{R}}^{1,3}$ denoting the four-vector of the origin of $\mathbf{R}$. In particular, we have ${\mathbf{r}}_{\mu }=\sqrt{2}\mathrm{Re}\left\{{\Phi }_{\mu }(\mathrm{x}=ct)\right\}$, where ${\mathbf{n}}_{\mu }=(\frac{1}{\sqrt{2}},\pm \frac{i}{\sqrt{2}},0)$.

2.2. Electromagnetic Field Regularization

Within the considered approach the classical representation of the electromagnetic field coupled to the muon is time independent. Accordingly, for an observer in $\mathbf{O}$ the electromagnetic field potentials are not retarded and the Lorenz gauge is trivially satisfied. Moreover, the radial singularity in the electromagnetic field is removed via a regularization defined by two cut-off Yukawa terms, with screening constants defined in accordance to the most probable decay of the free muon.

In particular, with respect to an observer in $\mathbf{O}$ the electromagnetic field potentials inherent to the muon read

$${\phi }_{\mu }\left(r\right)={\gamma }_{\mu }{\eta }_{\mu }{\psi }_{\mu }\left(r\right),{\mathbf{A}}_{\mu }\left(r\right)=2{\gamma }_{\mu }{\displaystyle \frac{{\mathbf{u}}_{\mu }}{c^2}}{\psi }_{\mu }\left(r\right),$$

(3)

where ${\gamma }_{\mu }$ is the Lorentz factor, ${\eta }_{\mu }=1+u_{\mu }^2{c}^{-2}$ and

$${\psi }_{\mu }\left(r\right)={\displaystyle \frac{\overline{e}}{4\pi {\epsilon }_{o}r}}\left(2-e^{-{\chi }_{\mu }r}-e^{-{\tilde{\chi }}_{\mu }r}\right),$$

(4)

${\epsilon }_o$ is the electric constant. The screening constant ${\tilde{\chi }}_{\mu }$ is defined in accordance to the most probable decay of a self-interacting muon ${\mu }^{-}\to e^{-}+{\overline{\nu }}_e+{\nu }_{\mu }$. We have

$${\chi }_{\mu }={\displaystyle \frac{{\gamma }_{\mu }{m}_{\mu }c}{(1+a_e)h}},{\tilde{\chi }}_{\mu }={\displaystyle \frac{{\gamma }_{\mu }(m_e+m_{\nu })c}{(1+a_{\mu })h}},$$

(5)

where $m_e$ and $a_e$ denote the electron’s rest mass and anomalous g-factor, respectively. Here, h is Planck’s constant, $m_{\nu }=m_{{\nu }_{\mu }}+m_{{\overline{\nu }}_e}$, where $m_{{\nu }_{\mu }}$ is the muon neutrino rest mass and $m_{{\overline{\nu }}_e}$ is the electron anti-neutrino rest mass. Therefore, we have $m_{\nu }>0$ for all $r\in (0,+\infty )$. The exact value of respective neutrinos’ rest masses is unknown leaving the mass term $m_{\nu }$ as a model parameter. Nevertheless, the value of $m_{\nu }$ is bound by the value of $a_{\mu }$ and therefore it is unique within the used approach.

The classical field equation satisfied by the function in Equation (4) reads

$${\Delta }_r{\psi }_{\mu }\left(r\right)-{\chi }_{\mu }^2{\varphi }_{\mu }\left(r\right)-{\tilde{\chi }}_{\mu }^2{\tilde{\varphi }}_{\mu }\left(r\right)=0,$$

(6)

where ${\Delta }_r$ represents the radial Laplace operator in spherical symmetry, ${\varphi }_{\mu }$ and ${\tilde{\varphi }}_{\mu }$ are the cut-off terms implying the following boundary conditions

$${\psi }_{\mu }\left(r\right)=\left\{\begin{array}{ccc}0,& r\to \infty ,& u_{\mu }<c,\\ ({\chi }_{\mu }+{\tilde{\chi }}_{\mu }){\displaystyle \frac{\overline{e}}{4\pi {\epsilon }_o}},& r\to 0,& u_{\mu }<c.\end{array}\right.$$

We would like to point out, furthermore, that the two Yukawa terms in Equation (4) do not represent an on shell massive photons [43]. For all $r\in (0,+\infty )$, both ${\chi }_{\mu }$ and ${\tilde{\chi }}_{\mu }$ represent the wave numbers of effectively massive off shell photons coupled to the muon, with total effective mass $m_{\mu }{(1+a_e)}^{-1}$ and $(m_e+m_{\nu }){(1+a_{\mu })}^{-1}$, respectively. Both massless photon terms with Yukawa potentials reduced to Coulomb ones (see eq. (4)) are implicitly accounted for in Equation (6).

2.3. Electromagnetic Field Energy Regularization

The energy of the electromagnetic field in the considered system, $W_{\mu }\left(r\right)$, is also regularized. In general, integrating the corresponding energy density ${\epsilon }_o{|\nabla {\phi }_{\mu }\left(r\right)|}^2$ over ${\mathbb{R}}^3$, we obtain

$$\begin{array}{cc}\hfill W_{\mu }\left(r\right)& =C_{\mu }{\displaystyle \frac{r_{c\mu }}{2r}}(8\left(e^{2({\chi }_{\mu }+{\tilde{\chi }}_{\mu })r}-e^{(2{\chi }_{\mu }+{\tilde{\chi }}_{\mu })r}-e^{({\chi }_{\mu }+2{\tilde{\chi }}_{\mu })r}\right)\hfill \\ \hfill & +(2+{\chi }_{\mu }r)e^{2{\tilde{\chi }}_{\mu }r}+(2+{\tilde{\chi }}_{\mu }r)e^{2{\chi }_{\mu }r}\hfill \\ \hfill & +4{\displaystyle \frac{({\chi }_{\mu }+{\tilde{\chi }}_{\mu }+{\chi }_{\mu }{\tilde{\chi }}_{\mu }r)}{{\chi }_{\mu }+{\tilde{\chi }}_{\mu }}})e^{-2({\chi }_{\mu }+{\tilde{\chi }}_{\mu })r},\hfill \end{array}$$

where $C_{\mu }={\gamma }_{\mu }^2{\eta }_{\mu }^2{m}_{\mu }{c}^2$. At the origin of $\mathbf{R}$ and for $u_{\mu }<c$ the electromagnetic field energy in the considered system is finite. Thus, we have

$$\underset{r\to 0}{lim}{W}_{\mu }\left(r\right)=C_{\mu }{r}_{c\mu }{\displaystyle \frac{{\chi }_{\mu }^2+6{\chi }_{\mu }{\tilde{\chi }}_{\mu }+{\tilde{\chi }}_{\mu }^2}{2({\chi }_{\mu }+{\tilde{\chi }}_{\mu })}}.$$

(7)

In contrast to the non-regularized electrodynamics, here for $r\to 0$ the discussed electromagnetic field energy vanish when the particle’s rest mass is negligible. In other words, the charge screening (Yukawa cloud) is nearly complete making the electrically charged particle to appear as electrically neutral.

3. Results

3.1. Self-Energy

By analogy to the case of self-interacting electron (see Ref. [40]), the classical Hamiltonian describing a self-interacting muon do not depend explicitly on time. We have

$$H_{\mu }={\gamma }_{\mu }{m}_{\mu }{c}^2+{\Sigma }_{\mu },$$

(8)

where ${\Sigma }_{\mu }$ is the self-energy term. The latter is not a potential energy of a gradient field and equals the spatial average over the domain ${\Omega }_{c\mu }$ of the interaction energy $\overline{e}{\phi }_{\mu }$. In particular, with respect to Equation (3), we have the representation

$${\Sigma }_{\mu }={\gamma }_{\mu }{c}^2{\int }_{{\Omega }_{c\mu }}({\rho }_{M_{\mu }}-{\rho }_{m_{\mu }})\mathrm{d}\mathrm{v},$$

(9)

where the effective mass density reads

$$\begin{array}{cc}\hfill {\rho }_{M_{\mu }}& ={\rho }_{m_{\mu }}\left(1+{\eta }_{\mu }{\displaystyle \frac{r_{c\mu }}{r}}\left(2-e^{-{\chi }_{\mu }r}-e^{-{\tilde{\chi }}_{\mu }r}\right)\right)\hfill \\ \hfill & ={\rho }_{m_{\mu }}\left(1+{\displaystyle \frac{{\eta }_{\mu }\overline{e}}{m_{\mu }{c}^2}}{\psi }_{\mu }\right).\hfill \end{array}$$

(10)

3.2. The Hamiltonian Density

The information about the muon’s intrinsic dynamics is embedded in the Hamiltonian density ${\mathcal{H}}_{\mu }$ associated to Equation (8). Taking into account Equation (1) for $r\equiv r_{\mu }$ we get

$${\mathcal{H}}_{\mu }=c^2{\rho }_{m_{\mu }}\left({\gamma }_{\mu }+{\displaystyle \frac{\alpha }{m_{\mu }c}}{\mathcal{P}}_{\mu }\right),$$

where

$${\mathcal{P}}_{\mu }={\gamma }_{\mu }{\eta }_{\mu }{m}_{\mu }{\tilde{u}}_{\mu }\left(2-e^{-{\chi }_{\mu }{r}_{\mu }}-e^{-{\tilde{\chi }}_{\mu }{r}_{\mu }}\right)$$

is the corresponding generalized momentum. Accordingly, we have the equations of motion

$${\tilde{u}}_{\mu }={\int }_{{\Omega }_{c\mu }}{\displaystyle \frac{\partial {\mathcal{H}}_{\mu }}{\partial {\mathcal{P}}_{\mu }}}\mathrm{d}\mathrm{v},{\dot{\mathcal{P}}}_{\mu }=0$$

and subsequently the exact values

$${\tilde{u}}_{\mu }=\alpha c,{\eta }_{\mu }=1+{\alpha }^2,{\gamma }_{\mu }^{-1}=\sqrt{1-{\alpha }^2}.$$

(11)

In contrast to the relative velocity, from Equation (11) there follows that the magnitude of the tangential velocity is scale invariant.

3.3. Effective Mass-Energy Equivalence

Taking into account Equation (2), from Equations (9) and (10) we obtain ${\Sigma }_{\mu }=a_{\mu }{\gamma }_{\mu }{m}_{\mu }{c}^2$. As a result, from Equation (8) we get the effective relativistic energy

$${\mathcal{E}}_{\mu }={\gamma }_{\mu }{M}_{\mu }{c}^2,\mathrm{with}{M}_{\mu }={\displaystyle \frac{1}{2}}{g}_{\mu }{m}_{\mu }.$$

(12)

Therefore, as a result of the self-interaction the total energy of a free muon is ${\gamma }_{\mu }(1+a_{\mu })$ times higher than its rest energy and the system’s total mass will be $(1+a_{\mu })$ times higher than the muon’s rest mass.

3.4. The Anomalous g-Factor

In addition to the Standard Model calculations [14,19], the implemented regularized electrodynamics yields a single-parametric transcendental equation for the calculation of the muon’s anomalous g-factor. Accounting for Equations (2), (10) and (11), we obtain

$$a_{\mu }=a_e+3{\eta }_{\mu }\left({\displaystyle \frac{1}{2}}-\left({\displaystyle \frac{1-e^{-\frac{\alpha {\gamma }_{\mu }{\xi }_{\mu }}{2\pi (1+a_{\mu })}}\left(1+\frac{\alpha {\gamma }_{\mu }{\xi }_{\mu }}{2\pi (1+a_{\mu })}\right)}{{\left(\frac{\alpha {\gamma }_{\mu }{\xi }_{\mu }}{2\pi (1+a_{\mu })}\right)}^2}}\right)\right),$$

(13)

where

$${\xi }_{\mu }={\displaystyle \frac{m_e+m_{\nu }}{m_{\mu }}}.$$

(14)

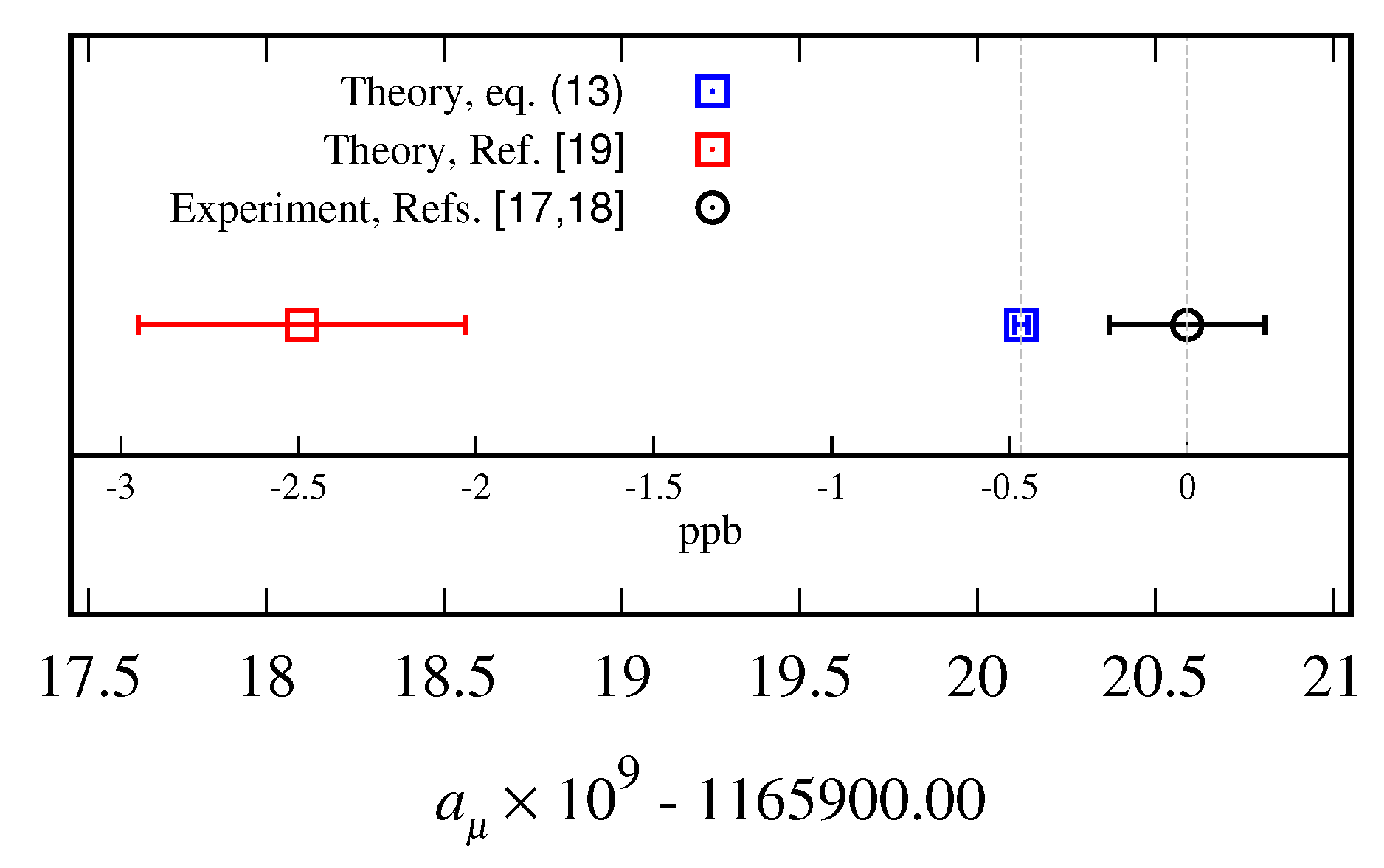
The value of $a_{\mu }$ calculated from Equation (13) is given in the second row of Table 1, where the values of $a_e$ and $\alpha$ are taken from Ref. [40]. The obtained accuracy with respect to the most recent experimental measurements [17] is about $0.46$ ppb, see Figure 2. On the same figure, a comparison with the most recent agreement on the value of $a_{\mu }$ predicted by the Standard Model is also depicted. The value of mass ratio in Equation (14) is given in the third column in Table 1. We have $m_{\nu }=3.58686\times {10}^{-38}$ kg, where the values of electron’s and muon’s rest masses are taken from NIST [44]. This result suggest that the sum of the muon neutrino and electron anti-neutrino rest energies is approximately $0.02012$ eV, which is consistent with the reported upper bound on the sum of the three flavor neutrino rest energies of about $0.120$ eV (see Ref. [45]). Moreover, it suggests that the electron anti-neutrino mass satisfies the inequality $m_{{\overline{\nu }}_e}<3.58686\times {10}^{-38}$ kg. This bound is approximately 40 times lower than the one set by KATRIN collaboration [46], see also Ref. [47].

3.5. Electromagnetic Field Energy

The total energy of the muon given in Equation (12) is only a fraction of the considered system’s energy that accounts for the electromagnetic field energy associated to the muon.

In the non-regularized electrodynamics the electromagnetic field energy associated to the three flavors of charged leptons does not depend on their rest mass and is not defined at the origin of $\mathbf{R}$. Consequently the corresponding energy density is quantitatively indistinguishable with respect to the flavor state of these particles.

Here, as a result of the applied regularization the electromagnetic field energy and its density are flavor dependent. The larger the lepton’s rest mass the higher corresponding electromagnetic field energy. In the considered case, substituting the obtained from Equation (13) values of $m_{\nu }$ and $a_{\mu }$ in Equation (7), we obtain $W_{\mu }(r\to 0)=4.673\times {10}^{21}$ eV, which is $43.783\times {10}^3$ times the value of electromagnetic field energy associated to the electron at the same limit (see Ref. [40]) and about $4.42274\times {10}^{13}$ times the muon’s rest energy.

4. Summary and Conclusions

The present paper reports on the most recent progress in the application of the regularization technique in electrodynamics of electrically charged non-composite particles thus uncovering key aspects from the elusive interrelationship between the classical and quantum theory on a microscopic level. The effectiveness of regularization method is demonstrated by calculating exactly the self-energy and anomalous g-factor of the muon. The used regularization implies two Yukawa cut-off terms with unique to the muon decay screening constants (see Equation (5)) that remove the radial singularity in the classical representation of the off shell electromagnetic field governing the muon’s self-interaction. Accordingly, exact solutions to the system’s equations of motion are derived.

In particular, the muon’s self-energy is calculated exactly showing the genuine contribution of the corresponding electromagnetic self-interaction into the muon’s total mass and energy, see Equation (12). In addition, the muon’s anomalous g-factor is calculated with high accuracy, improving the one obtained from the latest quantum theory calculations, see Figure 2 and Table 1. The obtained accuracy implies that the electromagnetic field contribution into the muon anomalous magnetic moment is significantly larger than previously evaluated. The main contribution results from massive off shell photons with wave vectors given in Equation (5), propagators corresponding to both Yukawa terms given in Equation (4) and interacting with the muon as given in Equation (9). The effective mass of these photons further implies that the muon and electron neutrinos have a rest mass, with upper bound on their sum equal to $3.58686\times {10}^{-38}$ kg, see Equations (13) and (14). Moreover, it points out that the contribution of both neutrinos’ rest masses into the electron-muon mass ratio should be taken by the quantum theory approach in order to improve the relevant result.

The used regularization technique can be applied to quantify the intrinsic dynamics of the tau lepton and to fix the range of values of the corresponding anomalous g-factor determined by the multiplicity of branching fractions. It is, furthermore, applicable to non-composite particles with constant electric charge. Equation (12) points out that the effective rest energy of a self-interacting proton should be at least $2.79$ times its rest energy. Essentially, it shows that the total rest energy of a multi-particle system is always greater than the anticipated value obtained by accounting for only the rest masses of constituent particles.