A Conjecture on the Possible Another Supermassive Black Hole in the Bar of Our Milky Way

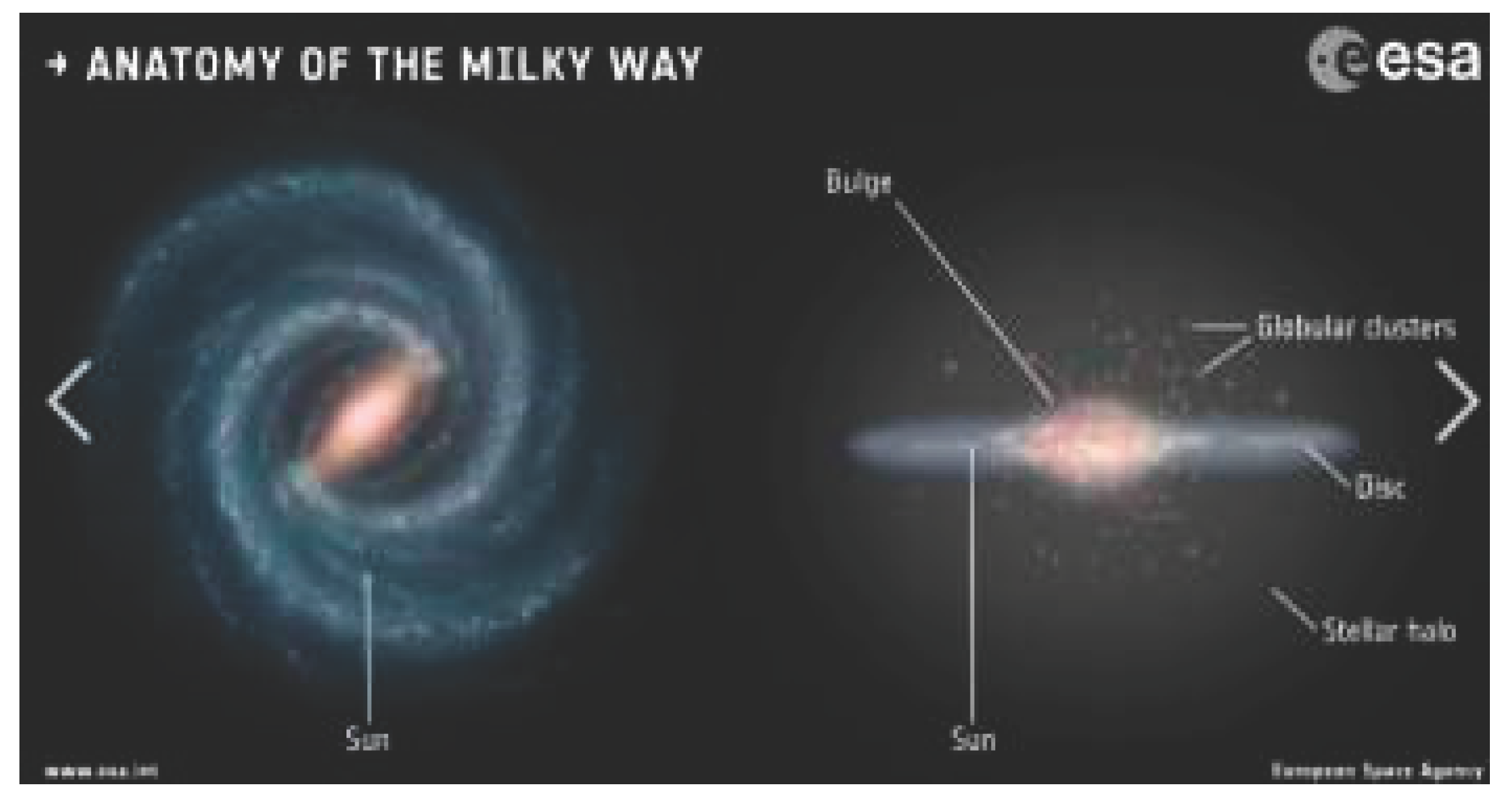
1. Introduction

The Milky Way is with a super gigantic scale. It only can be observed with modern technology. Therefore, the outline of the galaxy only can have been known in recent time and a long time was spent in knowing the whole image of it. First, in 1958, it was observed by Oort et al[1] that the hydrogen clouds are in pure circular rotation about the galactic center. Second, in 1976, it was observed by Georgelin & Georgelin[2] that the galaxy is with four spiral arms. Third, it was known a line about the galactic bar by Oort & Rougoor[3,4] in 1959 and in 1960; and the bar was further confirmed by de Vaucouleurs[5] in 1964; and, it was observed that the bar is with the “x-shaped structure” and with the shape of peanut.[6,7] Fourth, it was observed[8] that a supermassive black hole, Sgr A*, is at the center of the galaxy. Firth, it is currently thought that the radius of the Milky Way is 105 lightyears, the thickness at the center of the galaxy is 104 lightyears; the mass of the Milky Way is almost 5.8×1011 Msun. The observed image of the Milky Way is shown as that in the Figure 1. The structure and shape of the Milky Way was generally known while the reason for the bar and arms are unknown.[9]

On another line, for detecting gravitational waves, the supermassive black hole binaries was generally observed and studied. [10,11,12,13,14,15,16,17,18,19,20] It was presented that there is a pair of black holes with a separation less than 1 pc at the active galactic nuclei in a single galaxy or less than 30 kpc in an interacting system. Therefore, it is not impossible that there are two supermassive black holes in one single galaxy. (It need be noted that only a little fraction of the supermassive black hole binaries can merge.) And, abundance of “x-shaped radio” galaxies was observed.[11,12] It was pointed out that the “x-shaped radio” may be a signposts of supermassive black hole binaries.[10]

In this work, from the studying about the supermassive black hole binaries[10,11,12,13,14,15,16,17,18,19,20] and the “x-shaped structure and the peanut shape of the bar, we present that there should be another supermassive black hole in the bar of our milky way.

2. The “x-Shaped Structure” and Peanut Shape of the Bar: The Possible Another Supermassive Black Hole in the Bar of the Milky Way

2.1. The Bar

As shown in Figure 2, if there should be two supermassive black holes Sgr A* and B, there should be a lots of stars orbit around Sgr A* while another lots of stars around the B. And, other a lots of stars orbit around both A* and B. It is noted that, the black hole B is orbiting around A*. And, the shape and structure of the bar cannot be changed by the orbit of B. The orbits around the pair of supermassive black holes in the bar is analogous to the orbits of the planets around the triple stars in [21].

Bar pattern speed. Figure 2 shows that, the speed of the stars orbiting the two black holes is different and complicated. It was known that the circular velocity curve in the bar of the Milky Way is very complicated.[22,23,24] Maybe, there is not a single bar pattern speed or circular velocity curve. From that the bar is with a thickness of 10,000 ly, it could be concluded that the orbits around A* and B are in a sphere and around both A* and B are in an ellipsoid, rather than in a disk. It is analogous to the orbits of the moons around the Jupiter. And, it is analogous to the orbits of the S-stars around the Sgr A*.[25,26,27,28,29,30] It results in that it is very difficult to observe the speed of the orbit around one of or both of the two black holes. But, the speed of the orbit of the black hole B around the Sgr A* could be observed. And, the mass of Sgr A* can be accurately and precisely known from this speed.

Strong and weak bar. It is observed that 44% of the spiral galaxies are with a bar with different strength. [31] Here, we present, the strength of a bar is determined with these factors: 1) the ratio of ${\displaystyle \frac{M_B}{M_{A*}}}$ . There is $0<{\displaystyle \frac{M_B}{M_{A*}}}<1$. As ${\displaystyle \frac{M_B}{M_{A*}}}$ larger, the bar is stronger; as ${\displaystyle \frac{M_B}{M_{A*}}}$ is less, the bar is weaker; as ${\displaystyle \frac{M_B}{M_{A*}}}$ is very little, B shall become a satellite of A*, the bar is vanished. 2) The distance d between B and A*. As d is very large, no star can orbit both A* and B. Therefore, the necessary condition to form a bar is that the orbit of the stars is affected by both of the two black holes in the same way. 3) As d is very little, no star can orbit around B while many stars orbit around both A* and B. It is a strong bar.

Multi black holes of a bar. There should be more than two supermassive black holes in a bar and all of the black holes have a same effect on the orbit around these black holes.

There were many observations and different discussions about the galactic bar.[9,31,32,33,34,35] However, we think, as 44% of the observed 4378 disc galaxies are with a bar,[31] these bars should be formed by dynamics and kinematics, rather than by accidental event, such as a collision of two galaxies.

2.2. The Galactic Spiral Arms and Hill Sphere

The galactic spiral arms could be understood with the Hill sphere. For two celestial bodies, as the body with less mass is in the Hill radius of the larger one, it can have a stable orbit around the larger one. Or, the less one can move away from the larger one. Therefore, as two stars are orbiting around the Sgr A* with orbit ab and a’b’ as shown in Figure 3, if the distance between ab and a’b’ is less than the Hill radius of the two stars, the two orbits shall merge into one single orbit. Therefore, the condition for the two orbits ab and a’b’ is that the distance between two orbits is larger than the Hill radius of the two stars.

From $r=d\sqrt{m/3M}$ we know, for one same stars, the Hill radius of a star is determined with the distance d between the star and the center mass which the star is orbiting around. In the Figure 3, because the distance d for the star at point a is different from that at b, the Hill radius of the same star at point b is larger than that at point a. As the Hill radius of the star at point b is $r=d\sqrt{m/3M}=bb\text{'}$, then, only the orbit with the distance L ≥ bb′ can be remained. It makes the spiral arm produced.

, we know, for a same star, the Hill radius of this star at point b’ is larger than that at a’ for that db′ = b′A∗ > a′A∗ = da′, where point a’ and b’ are at the orbit around both the two black holes. It results in that the distance bb′ > a′a.

There were different understandings about the reason for the arms.[9,31,32,33,34,35,36] Here, we presented that the reason need be accordant with celestial dynamics and kinematics. As the reason is not accordant with dynamics and kinematics, the orbit should be broken off.

It is noted that, in the solar system, although the distance between the orbits of two neighboring planets is affected by the Hill sphere, the factual distance is much larger than the Hill radius of the planets. And, the factual distance of the neighboring orbits can be described with the Titius-Bode law. So, it could be concluded that the distance between two neighboring arms in a galaxy is much larger than that obtained from the Hill sphere.

2.3. The Mass and Position of the Black Hole B

Assuming that the black hole B is orbiting around Sgr A*, The Hill radius of B is $r=d\sqrt{m_B/3M_{SgrA*}}$. It is known that the length of the bar of our Milky Way is almost 20,000 lightyears, the largest thickness is 10,000 lightyears. Under the condition that the thickness is determined with the radius of the stars orbiting around the Sgr A*, in the Figure 3, it could be concluded that the distance between Sgr A* and a’ is less than 5,000 lightyears. For the same reason, the distance between B and b’ can be observed. Here, for convenience, we assume that Bb’=1,500 lightyears. From the Hill radius, it could be concluded that $m_B~{\displaystyle \frac{1}{30}}{M}_{SgrA*}$. And, the distance between B and Sgr A* should be d~20,000 − 5,000 − 1,500 =13,500 ly. If Bb’=250ly, it could be concluded that $m_B~{\displaystyle \frac{1}{\mathrm{72,000}}}{M}_{SgrA*}$. From Figure 1, it could be guessed that the radius of the orbit of the stars around B is almost 250~2,500 ly. Therefore, the mass of B should be in the range of 10−2~10−5MSgrA∗. This is only a conclusion based on the assuming condition. To accurately know the mass and position of B, the radius of the orbits around B and Sgr A* need be accurately measured.

3. Discussion

Currently, only the supermassive black hole binaries with a separation less than 10 pc in a single galaxy was focused on.[10,11,12,13,14,15,16,17,18,19,20] While, in our work, it is predicted that the distance between two black holes should be larger than 3.5 kpc (10,000—14,500 ly). Therefore, the orbits around the possible pair of black holes in the Milky Way is much more complicated.

It is emphasized that, in the Newtonian theory of orbit, only the black hole with the larger mass is the center of the galaxy. The black hole with the less mass is orbiting around the larger one while the larger one can be treated as that it is at rest. If the two black holes were orbiting around the center of mass of them as usually thought, it should result in that, relative to the stars orbiting around them, the distribution and the center of the mass of the two black holes are varying. It should further result in that the orbits of the stars around the two black holes is unstable. This case can be known as soon as a real orbit is considered. Therefore, only the larger one is at the center. It can be called the center black hole. Any other celestial bodies, including other supermassive black holes, are orbiting around the center black hole. And, the Circular Velocity Curve of the Milky Way is only determined with the mass of the center black hole.[22,23,24]

If the mass of Sgr A* is with the mass of ~4.3 × 106 MSun as current thought,[8] from the Hill sphere, it could be concluded that B is the center black hole with the mass of ~1 × 1011 MSun. And, the distance between the two black holes is ~10,000 ly.

In the stellar system, the stability of the orbit can be described with the Hill sphere, such as the orbits in the triple system in[21]. The orbit in the Hill radius is stable. It is clear, the orbit in a galaxy is stable. Therefore, a theory is needed to describe the stability of the orbit in a galaxy. Factually, no evidence shows that the Hill sphere is invalid to the orbit in a galaxy. But, the Hill sphere is little used to study the orbit in a galaxy. In this work, the Hill sphere is directly used to understand the orbits of stars around the supermassive black hole and to predict the possible supermassive black hole. It should be a necessary way to make galactic dynamics more completed.

From Figure 2 and Figure 3 we know, if there should be a pair of supermassive black holes in the bar, the origin and orbital motion of the bar and the arms can be well understood. Therefore, to confirm the possible another supermassive black hole is significant to well understand our Milky Way.

4. Conclusion

The “x-shaped structure” and peanut shape of the bar very strongly implies that there should be two supermassive black holes in the bar of our Milky Way. The “x-shaped structure” is an important line to detect the possible black hole, i.e. the possible black hole is at another side of the “x”. In addition, the possible black hole could be more easily detected in the weak bar with a large distance between them.