A Regularized Physics-Informed Neural Network to support Data-Driven Nonlinear Constrained Optimization

1. Introduction

Optimization approaches have emerged as tools for solving complex problems across various disciplines. Unlike traditional linear models, nonlinear optimization (NOPT) methods are capable of incorporating the intricate and interdependent relationships inherent in real-world scenarios [1]. These techniques are particularly valuable in fields such as engineering, economics, and operations research, where they enable the formulation and solution of models that more accurately reflect the underlying dynamics [2]. By leveraging advanced algorithms and computational solutions, NOPT facilitates improved decision-making and implementation, thereby enhancing efficiency and effectiveness in tackling multifaceted challenges. As research and technology continue to evolve, their significance in achieving optimal outcomes in diverse applications is becoming increasingly evident [3,4]. Nonetheless, NOPT comprises salient issues: First, data variability and noisy input measurements yield erroneous and fluctuating solutions. Second, nonlinear constraints greatly complicate the task of achieving optimal outputs [5]. Moreover, system scalability should be considered.

Data variability and noisy samples, in particular, are known to be a problem that makes stochastic measurements less accurate and increases the number of errors in NOPT [6]. The presence of unwanted effects in the data not only reduces the solution quality but also adds complications to the computation, making it more difficult to choose suitable optimization parameters [7]. The instability greatly impedes the optimization process, rendering the algorithm vulnerable to external effects and significantly reducing its overall efficiency [8]. Besides, the intricacies of nonlinear constraints might result in outcomes that are either infeasible or suboptimal [9]. Then, the NOPT may have a slow rate of convergence, with a tendency to become trapped at a local minimum. This might present a challenge when both speed and accuracy are crucial [10]. Hence, optimization techniques become impractical for large-scale applications [11], and as the number of variables increases, scalability becomes a significant hindrance, underscoring the pressing need for specialist software and more processing time [12]. Consequently, it is important to deal with large optimization problems, reduce runtime, and simplify the inherent complexity of noisy inputs and nonlinear constraints [11]. Indeed, many NOPT tasks are nondeterministic polynomial-time (NP-hard), making it difficult to find an exact solution for large instances because there is not a polynomial-time algorithm that works well or that does not introduce errors into the final output [13]. Additionally, some NOPT tasks have non-convex nonlinear programming (NLP) issues. The latter are especially challenging because they involve a lot of non-convex and integer functions [14].

Typically, mathematical programming or other classical techniques solve NOPT. These methods are capable of effectively handling non-linearities and discontinuities [9]. Customized strategies are also implemented to refine the iterative search [15]. Gradient-based techniques, mostly based on descent methods, have also shown they can deal with problems like non-linear and convex constraints [16]. Similarly, decomposition methods simplify complexity by segmenting the optimization into more manageable subproblems [17]. Additionally, search approaches and metaheuristics are crucial for maintaining a proper balance between exploration and exploitation [18], which enhances efficiency in finding optimal outputs. However, conventional methods often converge on solutions that may not be useful, especially in stochastic and noisy environments with high uncertainty and intrinsic data variability, which can reduce their accuracy [19].

Nowadays, artificial neural networks (ANNs) employ supervised learning to tackle nonlinear and stochastic problems through regression tasks. These networks are trained to find complex patterns and make accurate predictions even when there is a lot of uncertainty using data-driven strategies [20]. Commonly, ANN-based approaches employ automatic differentiation (AD), a computational technique used to evaluate the derivatives of functions efficiently and accurately. Unlike numerical alternatives, which can suffer from precision issues, or symbolic differentiation, which can be computationally expensive, AD works by breaking down functions into elementary operations for which derivatives are known and applying the chain rule systematically [21]. This process ensures that the derivative calculations are exact to machine precision and enables the calculation of loss function gradients with respect to network parameters, which is essential for gradient-based optimization algorithms like back-propagation.

Recently, physics-informed neural networks (PINNs) have emerged as an effective ANN-based optimization technique. Designed to align training with relevant physical principles, they have proven successful in various NOPT applications [22]. Commonly, the Karush-Kuhn-Tucker (KKT) criteria are used to represent constraints and integrate them into the network’s cost function during supervised training [23]. Additionally, a novel approach for integrating constraints using Runge-Kutta (RK) in unsupervised training has been proposed in [24]. Nevertheless, putting these networks into action is hard, especially when it comes to defining the right loss functions, choosing the best hyperparameters, and making sure that computations run quickly while complex systems are being trained [25]. Also, although PINNs have remarkable capabilities, their ability to generalize to nonlinear optimization problems is limited [26].

In this paper, we present a novel regularized PINN framework, termed RPINN, as a NOPT optimization tool for both supervised and unsupervised data-driven scenarios. As a result, we deal with three key NOPT issues. We first address data variability and noisy input measurements by appropriately adapting custom activation and regularization penalties within an ANN scheme. Second, we effectively integrate nonlinear constraints into the network architecture, adhering to the principles of model physics. Specifically, we utilize the network weights and/or learned features within a functional composition framework to determine the NOPT variables. Third, our ANN-based strategy employs AD training, which favors system scalability and computational time through batch-based back-propagation. Experimental results from both supervised and unsupervised data-driven NOPT tasks confirm that our proposal is robust and competitive against state-of-the-art optimization approaches. The primary advantage of our proposal lies in its stability against noisy input measurements, making it a particularly valuable solution in contexts with fluctuating information. Furthermore, because RPINN is based on ANN, it offers flexibility in terms of network architecture.

The agenda for this paper is as follows: Section 2 summarizes the related work. Section 3 describes the materials and methods. Section 5 and Section 6 depict the experiments and discuss the results. Lastly, Section 7 outlines the conclusions and future work.

2. Related Work

Some studies have shown that mathematical programming has become a crucial tool in numerical optimization. A notable example is the analysis by [9], which employs a sequential linear programming algorithm to address nonlinearities and discontinuities. In this context, the simplex method proves essential, being a classic technique effective for solving linear programming problems through iterative adjustments of solutions within a feasible set [27]. Similarly, the study by [15] explores a solution via quadratic programming (QP). Mixed-integer programming (MIP), on the other hand, is an optimization strategy that uses both integer and continuous variables. It is widely used to solve difficult problems [28], focusing on how the branch-and-cut (BC) algorithm can be employed to find the best solution [29]. Furthermore, second-order cone programming (SOCP) facilitates effective solutions for problems involving linear and quadratic constraints [30]. New studies, like [31], look into semidefinite programming (SDP), and the work in [32] uses convexification techniques. Likewise, exponential programming (EXP), which models NOPT objectives and constraints through exponential functions [33]. Additionally, power cone programming (PCP) is considered for modeling product and square relationships [34]. Yet, these classical methods face challenges such as scalability, computation time, convergence, and practical precision, underscoring their inherent complexity and limitations. Furthermore, the use of relaxations or approximations affects the optimization accuracy [35].

On the other hand, gradient methods’ efficiency and precision in identifying optimal solutions highlight their relevance for practical optimization tasks. The work in [36] uses the Dai-Liao conjugate gradient method and hyperplane projections for global convergence to solve nonlinear equations. In addition, [37] faces the non-convex issue based on a set of starting points. Moreover, nonlinear decomposition using linear programming (LP) and gradient descent was also proposed [38]. Further, the work in [39] examined the Newton-based search to deal with convergence issues in poorly conditioned systems. Also, the semi-sweeping Newton technique was applied for optimization in Hilbert spaces [40]. For noisy problems, the authors in [41] use piecewise polynomial interpolation and box reformulations, along with an interior-point (IP) method. Authors in [42] tackle similar problems with integrated penalty techniques. Overall, gradient methods are effective at solving NOPT tasks, but they have a challenging time convergent and are expensive to run in noisy and nonlinear situations [43]. Besides, it can be challenging to choose the best learning rate, and they run the risk of finding local minima [44]. As seen in [45], it is also important to make sure that at least first-degree differentiation continuity is maintained when using techniques like the conjugate gradient, the IP, and the Newton-based approach.

Of note, most of the available optimization solvers are based on the classical approaches mentioned above. Among them, Clarabel stands out for its versatility in optimizing a wide variety of problems. However, it still faces significant challenges in areas such as MIP [46]. Gurobi is renowned for its proficiency in MIP due to its extensive range of techniques, including simplex and IP methods. However, because it is proprietary software, it might not be able to be used in situations that require license flexibility [47]. Mosek is efficient concerning the IP approach, but its support for MIP is relatively limited, and its aptitude for NLP remains under debate, which could be a hindrance for developers who prefer open-source solutions [48]. Xpress specializes in solving MIP, offers conditional support for NLP, but is a closed-license alternative [49]. In turn, SCS, leveraging its open-source status, promotes adaptability and collaborative development, although its limitations in NLP reduce its effectiveness in certain optimization areas [50]. IPOPT excels at solving NLP problems, and its open access allows for flexibility [51].

Now, in this multifaceted optimization environment, the integration of tools such as MATPOWER, GEKKO, and CVXPY significantly expands the available options. MATPOWER is essential for solving energy system issues and supports solvers like Gurobi, Xpress, and IPOPT for linear, mixed-integer, and nonlinear programming [52,53,54]. GEKKO specializes in dynamic systems and nonlinear models, offering a holistic and open-source Python platform [55,56]. CVXPY is an open-source modeling language for convex optimization problems embedded in Python. It allows you to express your problems naturally, mirroring the mathematical formulation rather than conforming to the restrictive standard form required by solvers [57,58]. Table 1 summarizes the mentioned solvers.

Recently, ANNs have positioned themselves as fundamental tools in optimization by incorporating deep learning techniques, effectively addressing the complexity and non-linearities of various problems. Conventional ANNs employ supervised learning to tackle nonlinear and stochastic problems through regression tasks. To this end, historical data or solutions precomputed by specialized NOPT tools are used to train these networks [60]. This approach enables ANNs to learn complex patterns and make accurate predictions even under significant uncertainty [20]. Typically, ANN-based approaches utilize AD, a computational method for efficiently and accurately evaluating function derivatives. Instead of numerical or symbolic differentiation, which can have issues with accuracy and require a lot of computing power, AD breaks functions down into simple operations whose derivatives are known and uses the chain rule consistently [21]. Thereby, AD ensures machine-level accuracy in derivative calculations and simplifies the determination of loss function gradients in relation to network parameters, enabling the use of gradient-based search with back-propagation. The work in [61] combines quasi-Newton methods and ANNs for NOPT. Furthermore, the authors in [60] utilize deep learning to solve optimal flow problems. Similarly, the work in [62] introduces an integrated training technique that, while effective, requires larger neural networks and presents challenges in generalization. Concurrently, [63] uses elastic layers and incremental training as optimization-based solvers. Furthermore, the method by [64] combines convex relaxation with graph neural networks.

Besides, PINN has recently emerged as a powerful optimization tool. These training approaches have proven effective in various NOPT applications, integrating relevant physical principles within ANNs [22]. The KKT criteria are applied to formulate constraints that are incorporated into an ANN’s cost function during supervised training [23]. In [65], a PINN framework is detailed that imposes penalties for constraint violations in the loss function. The study in [66] proposes a loss function that combines errors from differential and algebraic states with normative equation violations. Additionally, a novel strategy has been proposed to include constraints in unsupervised training using an RK-based technique [24]. Nevertheless, complete approaches based on ANNs and PINNs face challenges such as optimality degradation. In response, advanced alternatives like [67] have emerged, integrating system constraints into the cost function and applying penalties for violations. Furthermore, [68] introduces an algorithm to address nonlinear problems modeled by partial differential equations with noisy data through Bayesian physics-informed neural networks (B-PINNs). Additionally, [69] proposes a parametric differential equation-based approach holding functional connections to enhance the robustness and accuracy of PINNs. In turn, [70] presents a truncated Fourier decomposition, termed Modal-PINNs, to optimize the reconstruction of periodic signals. However, these alternatives often lack adequate precision, generalization capability, and scalability [71]. Finally, supervised data is usually required, complicating their application in various NOPT scenarios.

3. Materials and Methods

3.1. Nonlinear Optimization Fundamentals (NOPT)

Let $\mathbf{x}\in {\mathbb{R}}^P$ be a vector in P variables. The conventional NOPT problem can be summarized as follows:

$$\begin{array}{cc}\hfill & \underset{\mathbf{x}}{min}\varrho \left(\mathbf{x}\right)\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.{\xi }_{\min }\le \mathbf{x}\le {\xi }_{\max }\hfill \\ \hfill & h_L\left(\mathbf{x}\right)\le \mathbf{0}\hfill \\ \hfill & h_N\left(\mathbf{x}\right)\le \mathbf{0},\hfill \end{array}$$

(1)

where the objective function $\varrho :{\mathbb{R}}^P\to \mathbb{R}$ is real-valued. Also, the bound constraints are shown by ${\xi }_{\min },{\xi }_{\max }\in {\mathbb{R}}^P$. The linear and nonlinear constraints are described by $h_L:{\mathbb{R}}^P\to {\mathbb{R}}^{C_L}$ and $h_N:{\mathbb{R}}^P\to {\mathbb{R}}^{C_N}$, where $C_L\in \mathbb{N}$ and $C_N\in \mathbb{N}$.

Figure 1 depicts the main pipeline of the classical approaches for NOPT. First, it includes the physical system’s parameters, constraints, limits, and the objective function to be optimized. Second, starting from an initial point, the optimization algorithm iterates until convergence. Of note, the number of iterations, the level of improvement, and the objective function thresholding are the relevant stopping criteria to return the final output.

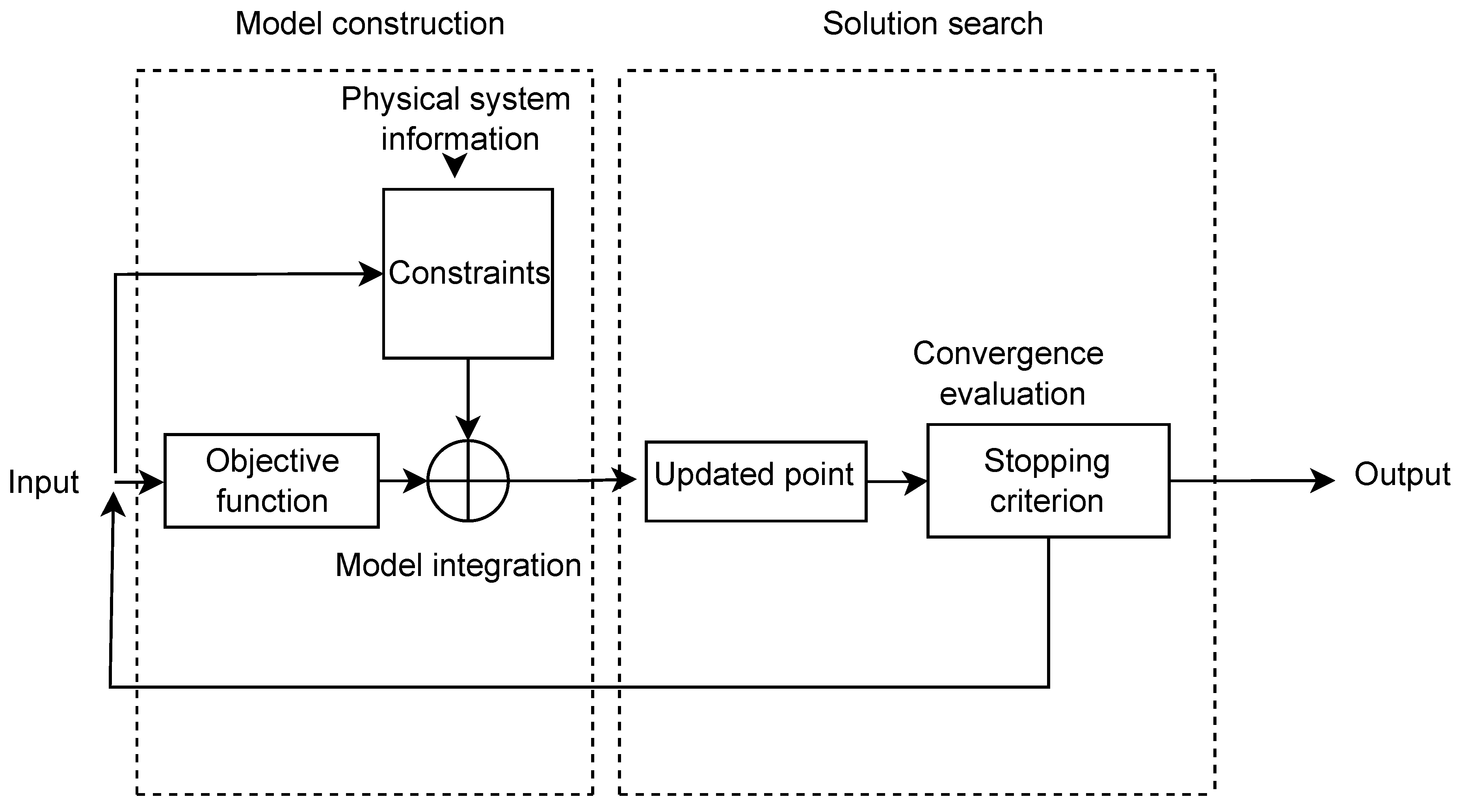
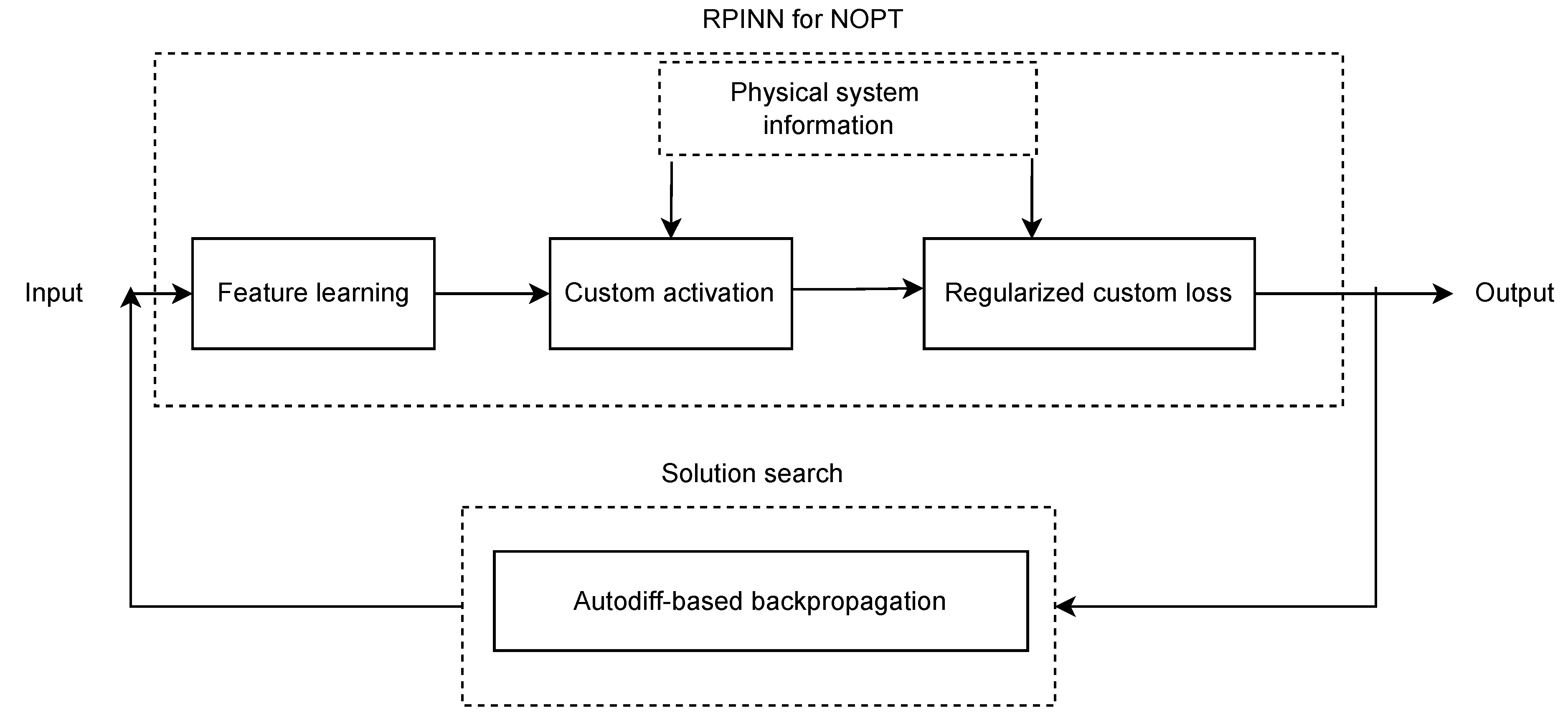
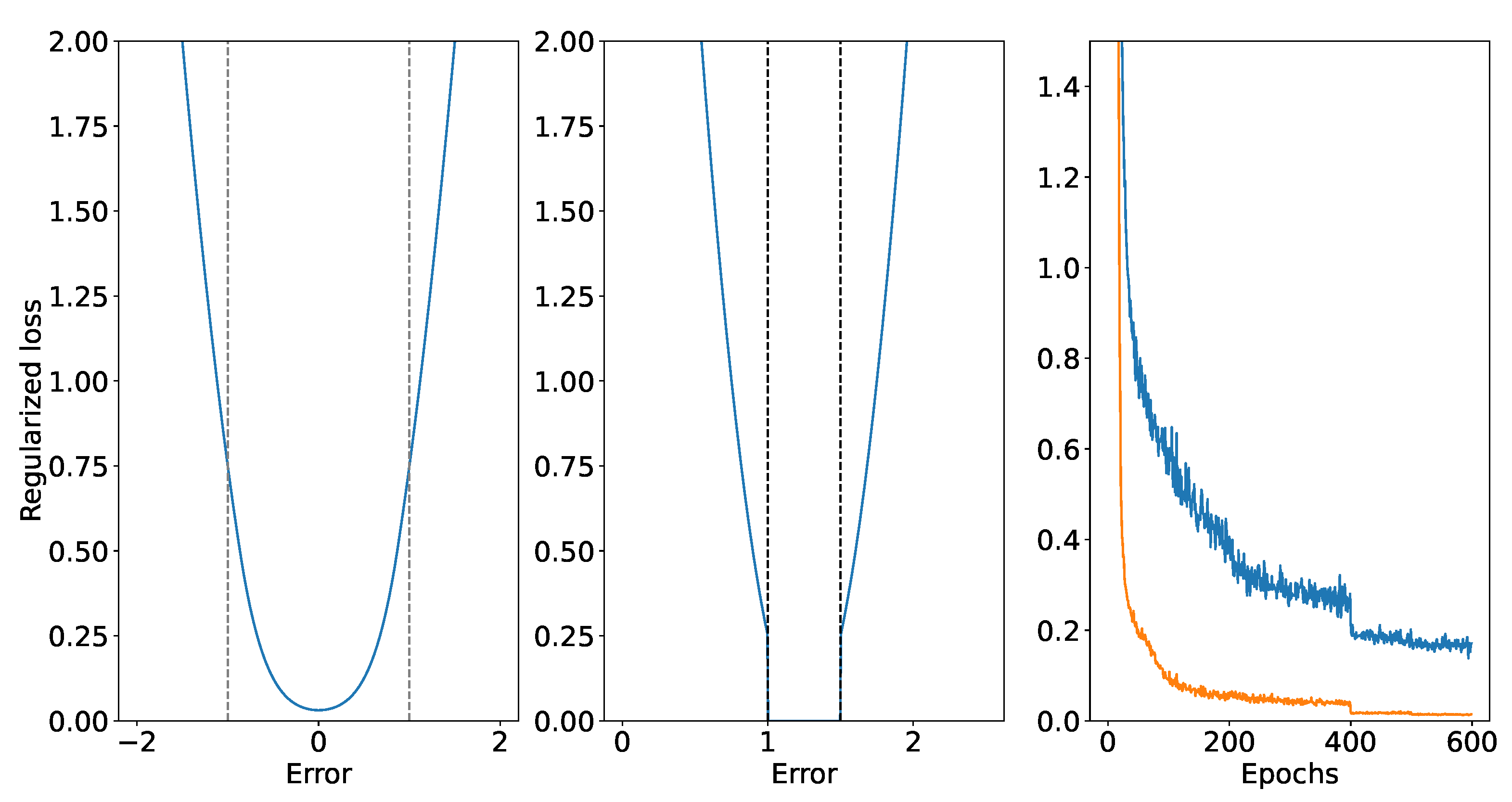
3.2. Regularized Physics-Informed Neural Network (RPINN)

Let ${\{y_r\in \mathcal{Y},z_r\in \mathcal{Z}\}}_{r=1}^R$ be an input-output set holding R samples. Our data-driven RPINN approach aims to couple the optimization problem in Eq. 1 as a penalty-based loss with bounded constraints from both network weights and learned features, as follows:

$$\begin{array}{cc}\hfill & \underset{\tilde{\mathbf{X}},\tilde{\mathbf{Z}}}{min}\frac{{\lambda }_{\mathcal{L}}}{R}\sum _{r=1}^R\mathcal{L}\left(y_r,\tilde{f}\left(z_r\right|\tilde{\mathbf{X}},\tilde{\mathbf{Z}})\right)+\sum _{i=1}^{C_L}\frac{{\lambda }_{Li}}{R}\sum _{r=1}^R{\tilde{h}}_{Li}(y_r,\tilde{f}\left(z_r\right|\tilde{\mathbf{X}},\tilde{\mathbf{Z}}))+\sum _{j=1}^{C_N}\frac{{\lambda }_{Nj}}{R}\sum _{r=1}^R{\tilde{h}}_{Nj}(y_r,\tilde{f}\left(z_r\right|\tilde{\mathbf{X}},\tilde{\mathbf{Z}}))\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.{\lambda }_{\mathcal{L}}+\sum _{i=1}^{C_L}{\lambda }_{Li}+\sum _{j=1}^{C_N}{\lambda }_{Nj}=1\hfill \\ \hfill & {\zeta }_{\min }\le \tilde{\mathbf{X}}\le {\zeta }_{\max }\hfill \\ \hfill & {\psi }_{\min }\le \tilde{f}\left(z_r\right|\tilde{\mathbf{X}},\tilde{\mathbf{Z}})\le {\psi }_{\max },\forall r\in R;\hfill \end{array}$$

(2)

where $\tilde{f}:\mathcal{Z}\to \mathcal{Y}$ is an ANN-based mapping function, $\mathcal{L}:\mathcal{Y}\times \mathcal{Y}\to \mathbb{R}$ is a given loss, $\tilde{\mathbf{X}}$ holds the network parameters, and $\tilde{\mathbf{Z}}$ gathers the learned features along layers. Also, ${\tilde{h}}_{Li}(·,·)$ and ${\tilde{h}}_{Ni}(·,·)$ are the i-th linear and j-th nonlinear penalty functions to follow the NOPT constraints set by the regularization terms ${\lambda }_{\mathcal{L}},{\lambda }_{Li},{\lambda }_{Nj}\in [0,1],$ where $i\in \{1,2,\cdots ,C_L\}$ and $j\in \{1,2,\cdots ,C_N\}$. Furthermore, ${\zeta }_{\min }$ and ${\zeta }_{\max }$ collect the network parameter limit values, and ${\psi }_{\min }$ and ${\psi }_{\max }$ capture the network output and feature bounds.

For a given input $z\in \mathcal{Z}$, our deep learning-based function with $\widehat{L}$ layers yields:

$$\begin{array}{cc}\hfill & \tilde{f}\left(z\right|\tilde{\mathbf{X}},\tilde{\mathbf{Z}})=(f_{\widehat{L}}\circ \cdots \circ f_1|\tilde{\mathbf{X}},\tilde{\mathbf{Z}})\left(z\right),\hfill \\ \hfill & {\tilde{\mathbf{z}}}_l=f_l\left({\tilde{z}}_{l-1}\right|{\tilde{\mathbf{x}}}_l,b_l)={\nu }_l({\tilde{\mathbf{x}}}_l^{\top }{\tilde{\mathbf{z}}}_{l-1}+b_l).\hfill \end{array}$$

(3)

In the l-th layer of Eq. 3, where $l\in \{1,2,\cdots ,\widehat{L}\}$, the weights and bias are ${\tilde{\mathbf{x}}}_l,b_l\in \tilde{\mathbf{X}}$, the learned feature vector is ${\tilde{\mathbf{z}}}_l\in \tilde{\mathbf{Z}}$, and ${\nu }_l(·)$ is a nonlinear activation function to deal with both network representation and customized bounds to fulfill the Eq. 2 limit constraints. Furthermore, the RINN optimization problem can be solved via gradient descent with AD and back-propagation [72].

It is worth noting that our baseline RINN studies a supervised scenario for simplicity, but by addressing its regularized loss, we can easily achieve an unsupervised extension. Figure 2 depicts the RINN main sketch.

4. Tested Scenarios for NOPT Using RPINN

We study two main datasets to test our RPINN as a data-driven NOPT approach: i) a constrained uniform mixture model with nonlinear loss and supervised target; and ii) a constrained flow and pressure gas-powered system optimization with unsupervised loss. Below, we provide a detailed description of each experiment.

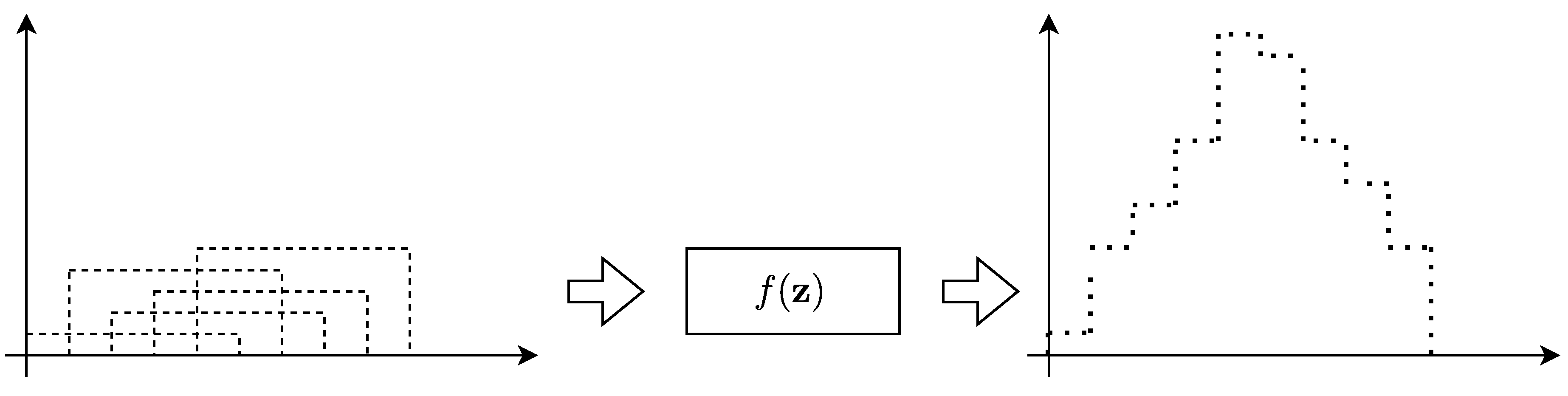
4.1. Supervised Constrained Optimization: Uniform Mixture Model

This task comprises a linear and bound-constrained optimization of a nonlinear cost [73]:

$$\begin{array}{cc}\hfill & \underset{\mathbf{x}}{min}\sum _{r=1}^R{|y_r-{\mathbf{x}}^{\top }{\mathbf{z}}_r|}_2^2\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\mathbf{0}\le \mathbf{x}\le \mathbf{1},\hfill \\ \hfill & {\mathbf{x}}^{\top }\mathbf{1}=1;\hfill \end{array}$$

(4)

where $y_r\in {\mathbb{R}}^{+}$ is the r-th target output, $\mathbf{x}\in {\mathbb{R}}^P$ denotes the mixing coefficients, and ${\mathbf{z}}_r\in {\mathbb{R}}^P$ holds random samples drawn from a uniform distribution as: $z_{rp}\sim \mathcal{U}\left(z\right|p-1,p)$. $\mathbf{0}$ and $\mathbf{1}$ are all-zeros and all-ones vectors of proper size.

Figure 3. Uniform mixture model optimization. Left: weighted uniform probabilities. Right: visual representation of the mixing results.

Figure 3. Uniform mixture model optimization. Left: weighted uniform probabilities. Right: visual representation of the mixing results.

The optimization problem in Eq. 4 can be solved through our RPINN as follows:

$$\begin{array}{cc}\hfill & \underset{\tilde{\mathbf{X}}}{min}\frac{{\lambda }_{\mathcal{L}}}{R}\sum _{r=1}^R{\mathcal{L}}_H\left(y_r,\tilde{f}\left({\mathbf{z}}_r\right|\tilde{\mathbf{X}});ϵ\right)+\frac{{\lambda }_L}{R}{\tilde{\mathbf{x}}}_{\widehat{L}}^{\top }\mathbf{1}\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.{\lambda }_{\mathcal{L}}+{\lambda }_L=1,\forall {\lambda }_{\mathcal{L}},{\lambda }_L\in [0,1]\hfill \\ \hfill & \mathbf{0}\le {\tilde{\mathbf{x}}}_{\widehat{L}}\le \mathbf{1}.\hfill \end{array}$$

(5)

For concrete testing and to mitigate noisy samples, a Huber-based loss is used in Eq. 5:

$$\begin{array}{c}\hfill {\mathcal{L}}_H\left(y,\tilde{f}\left(\mathbf{z}\right|\tilde{\mathbf{X}});ϵ\right)=\left\{\begin{array}{cc}\frac{1}{2}{\parallel y-\tilde{f}\left(\mathbf{z}\right|\tilde{\mathbf{X}})\parallel }^2\hfill & \parallel y-\tilde{f}\left(\mathbf{z}\right|\tilde{\mathbf{X}})\parallel \le ϵ\hfill \\ ϵ·(\parallel y-\tilde{f}\left(\mathbf{z}\right|\tilde{\mathbf{X}})\parallel -\frac{1}{2}ϵ)\hfill & \parallel y-\tilde{f}\left(\mathbf{z}\right|\tilde{\mathbf{X}})\parallel >ϵ,\hfill \end{array}\right.\end{array}$$

(6)

where $ϵ\in {\mathbb{R}}^{+}.$ Next, we fix a scaled exponential linear (SELU) activation for the network function composition, as follows:

$$\begin{array}{c}\hfill \mathrm{SELU}\left(x\right)=\left\{\begin{array}{cc}\theta x\hfill & x>0\hfill \\ \theta \vartheta ·(e^x-1)\hfill & x\le 0,\hfill \end{array}\right.\end{array}$$

(7)

where $\theta ,\vartheta \in \mathbb{R}$. Then, ${\tilde{\mathbf{x}}}_{\widehat{L}}$. To fulfill the former NOPT limit restriction, RPINN’s weights at the output layer $\widehat{L}$ hold a l1-based max-constraint.

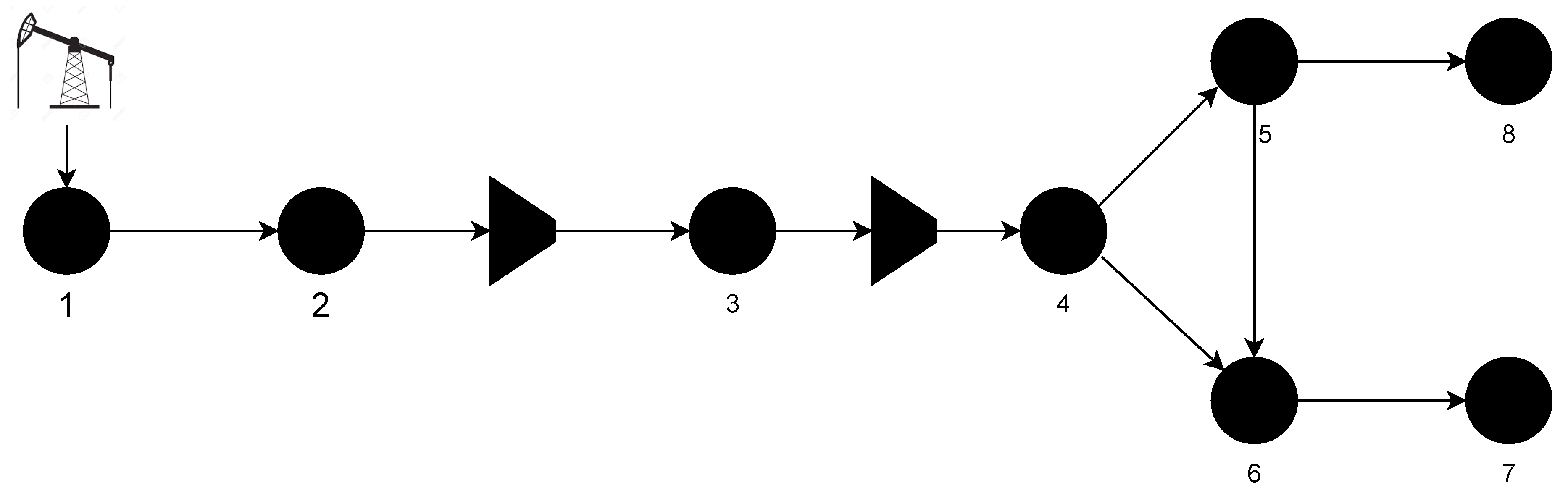
4.2. Unsupervised Constrained Optimization: Gas-Powered System

We study a gas-powered system as a function of flow and pressure. For this purpose, a synthetic network of eight nodes is used, as detailed in [74] and illustrated in Figure 4.

In particular, the NOPT problem is written as:

$$\begin{array}{cc}\hfill & \underset{\mathbf{x},\pi }{min}{\mathbf{x}}^{\top }\mathbf{a}\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\mathbf{B}\mathbf{x}=\mathbf{z}\hfill \\ \hfill & x_q=\mathrm{sgn}\left({\pi }_{w\left(q\right)}^2-{\pi }_{w^{\prime }\left(q\right)}^2\right)\sqrt{k_q|{\pi }_{w\left(q\right)}^2-{\pi }_{w^{\prime }\left(q\right)}^2|},\hfill \\ \hfill & \forall q\in Q;w\left(q\right),w^{\prime }\left(q\right)\in W\hfill \\ \hfill & {\beta }_{\min }(n,n^{\prime })\le \frac{{\pi }_n}{{\pi }_{n^{\prime }}}\le {\beta }_{\max }(n,n^{\prime }),\forall n,n^{\prime }\in V\hfill \\ \hfill & {\gamma }_{\min }\le \mathsf{\pi }\le {\gamma }_{\max }\hfill \\ \hfill & {\delta }_{\min }\le \mathbf{x}\le {\delta }_{\max },\hfill \end{array}$$

(8)

where $\mathbf{a}\in {\mathbb{R}}^P$ represents the gas transport costs for the P flows in $\mathbf{x}\in {\mathbb{R}}^P$. The incidence matrix $\mathbf{B}\in {\mathbb{R}}^{W\times P}$ encodes the gas network structure, with W nodes and $\mathbf{z}\in {\mathbb{R}}^W$ the input gas demand. The first equality constraint is what encodes the linear-based flow and gas demand equilibrium along the network nodes. Next, the node pressure is stored in $\mathsf{\pi }\in {\mathbb{R}}^W$. In turn, the q-th flow $x_q\in \mathbf{x}$ is selected according to the network structure from $\mathbf{B}$ to fulfill the Weymouth equality with $k_q\in \mathbb{R}$ and $Q\le P$ [54]. Then, the function $w\left(q\right)$ extracts the related pressure ${\pi }_{w\left(q\right)}\in \mathsf{\pi }$ regarding such a Weymouth-based physic constraint. Furthermore, ${\pi }_n,{\pi }_{n^{\prime }}\in \pi$ chose the inlet and outlet pressures to fulfill the system compression ratio, with V components ($n,n^{\prime }\in \{1,2,\cdots ,V\}$, $V\le W$) and compression factor limits ${\beta }_{\min }(n,n^{\prime }),{\beta }_{\max }(n,n^{\prime })\in {\mathbb{R}}^{+}$. Also, ${\gamma }_{\min },{\gamma }_{\max }\in {\mathbb{R}}^W$ and ${\delta }_{\min },{\delta }_{\max }\in {\mathbb{R}}^P$ are the minimum and maximum pressure and flow limits, respectively.

Now, let ${\{{\mathbf{z}}_r\in {\mathbb{R}}^W\}}_{r=1}^R,$ be an unsupervised input set concerning the required gas demand for R observations. Our RPINN solution of Eq. 8 is as follows:

$$\begin{array}{cc}\hfill \underset{{\{{\tilde{\mathbf{z}}}_r,{\tilde{\mathsf{\pi }}}_r\}}_{r=1}^R}{min}& \frac{{\lambda }_{\mathcal{L}}}{R}\sum _{r=1}^R{\tilde{\mathbf{z}}}_r^{\top }\mathbf{a}+\frac{{\lambda }_{L1}}{R}\sum _{r=1}^R{\tilde{h}}_{L1}(\mathbf{B}{\tilde{\mathbf{z}}}_r,{\mathbf{z}}_r;{ϵ}_{L1})+\hfill \\ \hfill & \frac{{\lambda }_{N1}}{R}\sum _{r=1}^R{\tilde{h}}_{N1}({\tilde{\mathbf{z}}}_r,{\tilde{\mathsf{\pi }}}_r;\mathbf{B},{ϵ}_{N1})+\frac{{\lambda }_{N2}}{R}\sum _{r=1}^R{\tilde{h}}_{N2}({\tilde{\mathsf{\pi }}}_r;\mathbf{B},\beta ,{ϵ}_{N2})\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.{\lambda }_{\mathcal{L}}+{\lambda }_{L1}+{\lambda }_{N1}+{\lambda }_{N2}=1\hfill \\ \hfill & \tilde{f}={\tilde{f}}^{†}\cup {\tilde{f}}^{‡}\hfill \\ \hfill & {\tilde{\mathbf{z}}}_r={\tilde{f}}^{†}\left({\mathbf{z}}_r\right|{\tilde{\mathbf{X}}}^{†},{\tilde{\mathbf{Z}}}^{†}),{\tilde{\mathsf{\pi }}}_r={\tilde{f}}^{‡}\left({\mathbf{z}}_r\right|{\tilde{\mathbf{X}}}^{‡},{\tilde{\mathbf{Z}}}^{‡})\hfill \\ \hfill & {\gamma }_{\min }\le {\tilde{\mathsf{\pi }}}_r\le {\gamma }_{\max }\hfill \\ \hfill & {\delta }_{\min }\le {\tilde{\mathbf{z}}}_r\le {\delta }_{\max },\forall r\in R.\hfill \end{array}$$

(9)

Given the r-th gas demand vector ${\mathbf{z}}_r\in {\mathbb{R}}^W$, ${\tilde{\mathbf{z}}}_r\in {\mathbb{R}}^P$ predicts the flow vector based on $f^{†}$, and ${\tilde{\mathsf{\pi }}}_r\in {\mathbb{R}}^W$ the corresponding pressure vector using $f^{‡}$. Moreover:

$$\begin{array}{cc}\hfill {\tilde{h}}_{L1}(\mathbf{B}{\tilde{\mathbf{z}}}_r,{\mathbf{z}}_r;{ϵ}_{L1})=& {\mathcal{L}}_H(\mathbf{B}{\tilde{\mathbf{z}}}_r,{\mathbf{z}}_r;{ϵ}_{L1})\hfill \\ \hfill {\tilde{h}}_{N1}({\tilde{\mathbf{z}}}_r,{\tilde{\mathsf{\pi }}}_r;\mathbf{B},{ϵ}_{N1})=& \frac{1}{Q}\sum _{q=1}^Q{\mathcal{L}}_H({\tilde{z}}_{rq},{\phi }_q({\tilde{\mathsf{\pi }}}_r;\mathbf{B});{ϵ}_{N1})\hfill \\ \hfill {\tilde{h}}_{N2}({\tilde{\mathsf{\pi }}}_r;\mathbf{B},\beta )=& \frac{1}{V^2}\sum _{n,n^{\prime }\in V}{\mathcal{L}}_{\tilde{H}}({\tilde{\mathsf{\pi }}}_{rn},{\tilde{\mathsf{\pi }}}_{r{n}^{\prime }};\mathbf{B},\beta ,{ϵ}_{N2}),\hfill \end{array}$$

(10)

where notation ${\mathcal{L}}_H(·,·;{ϵ}_{·})$ stands for a Huber-based penalty (see Eq. 6), $\phi ({\tilde{\mathsf{\pi }}}_r;\mathbf{B})\in {\mathbb{R}}^Q$ holds elements:

$${\phi }_q({\tilde{\mathsf{\pi }}}_r;\mathbf{B})=\mathrm{sgn}\left({\tilde{\mathsf{\pi }}}_{rw\left(q\right)}^2-{\tilde{\mathsf{\pi }}}_{r{w}^{\prime }\left(q\right)}^2\right)\sqrt{k_q|{\tilde{\mathsf{\pi }}}_{rw\left(q\right)}^2-{\tilde{\mathsf{\pi }}}_{r{w}^{\prime }\left(q\right)}^2|},\forall q\in Q,$$

(11)

and:

$${\mathcal{L}}_{\tilde{H}}({\tilde{\pi }}_{rn},{\tilde{\pi }}_{r{n}^{\prime }};\mathbf{B},\beta ,{ϵ}_{N2})=\left\{\begin{array}{cc}0\hfill & {\beta }_{\min }(n,n^{\prime })\le \frac{{\tilde{\pi }}_{rn}}{{\tilde{\pi }}_{r{n}^{\prime }}}\le {\beta }_{\max }(n,n^{\prime })\hfill \\ {\left(\frac{\frac{{\tilde{\mathsf{\pi }}}_{rn}}{{\tilde{\mathsf{\pi }}}_{r{n}^{\prime }}}-0.5{\beta }_{\min }(n,n^{\prime })}{{\beta }_{\max }(n,n^{\prime })}\right)}^2\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(12)

It is worth mentioning that the custom penalty in Eq. 10 aims to deal with noisy inputs while preserving the NOPT limits and constraints. In particular, ${\mathcal{L}}_{\tilde{H}}(·,·;\mathbf{B},\beta ,{ϵ}_{N2})$ penalizes pressures that are far from the middle of the compression factor range, according to ${\beta }_{\min }(n,n^{\prime }),{\beta }_{\max }(n,n^{\prime })\in \beta$. Finally, a scaled sigmoid function $\tilde{\sigma }(·)\in [u_{\min },u_{\max }]$ addresses the predicted flow and pressure limits in Eq. 9, as:

$$\tilde{\sigma }\left(x\right)=\alpha \frac{1}{1+e^{-x}}+\iota ,$$

(13)

where $\alpha ,\iota \in \mathbb{R}.$

5. Experimental Set-Up

The scenarios in Section 4 will be used to test our RPINN in both supervised and unsupervised settings. They will be utilized to look at sample variability, noisy input measurements, and nonlinear constraints.

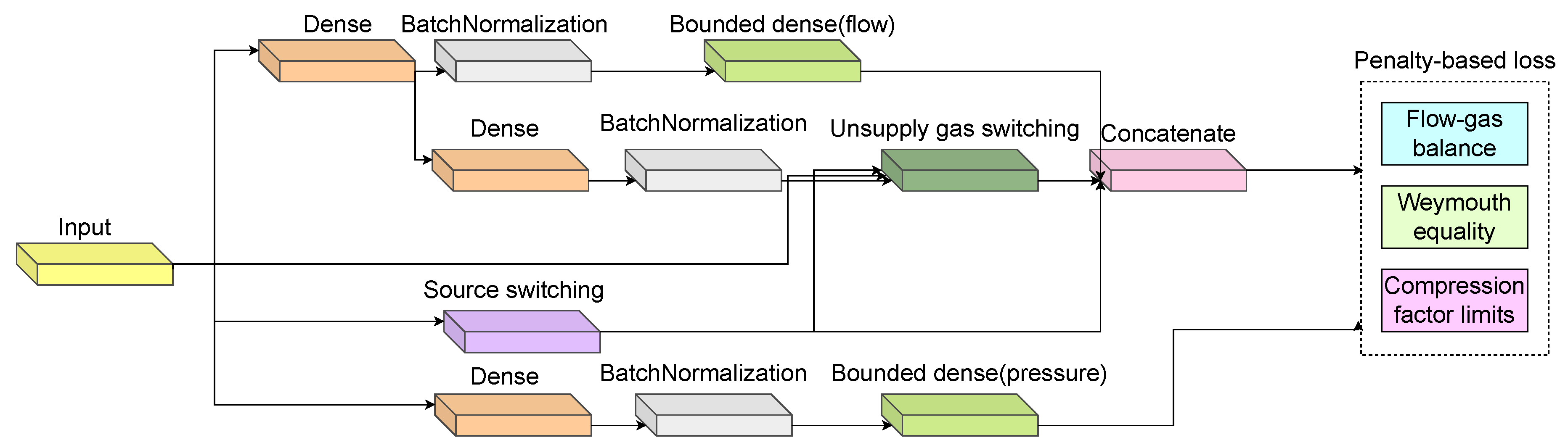
5.1. Deep Learning Architectures

To address the uniform mixture model NOPT (supervised constrained optimization), our RPINN consists of two dense layers, as shown in Figure 5 and Table 2.

Next, as seen in Figure 6 and Table 3, a wide ANN architecture is proposed for our RPINN-based gas-powered system scenario. We can specifically focus on essential variables—flows and pressures—in our sketch, adapting it to the unique characteristics of the gas network. To achieve this, our model incorporates blocks of dense layers designed to map input data, as well as batch normalization layers that help stabilize and normalize the features and gradient along the back-propagation. Additionally, it includes custom layers named: custom dense, bounded dense, source switching, and unsupply gas switching. We design these to encode the source behavior of the system, manage unmet demand, and delineate system boundaries.

5.2. Training Details and Method Comparison

To evaluate the effectiveness of our methodology in addressing optimization problems, we utilized the mean absolute percentage error (MAPE) as the primary performance measure across all conducted experiments, defined as:

$$\begin{array}{c}\hfill \mathrm{MAPE}({\tilde{y}}_r,{\widehat{y}}_r)=\frac{100}{R}\sum _{r=1}^R\left|\frac{{\tilde{y}}_r-{\widehat{y}}_r}{{\tilde{y}}_r}\right|[\%],\end{array}$$

(14)

where ${\tilde{y}}_r,{\widehat{y}}_r\in \mathbb{R}$ stands for r-th target and predicted value, $\mathrm{MAPE}(·,·)\in [0,100][\%]$, and $|·|$ is the absolute value operator.

Now, for the uniform mixture model, we generate 500 samples, each composed of five variables. We trained our RPINN architectures on a total of 400 samples, allocating 30% for the validation phase. We used the remaining 100 samples to evaluate the model’s performance. To see how well NOPT works with noisy inputs, we add white Gaussian noise to the model output while keeping the signal-to-noise ratio (SNR) value within the set $\left\{-1,3,5\right\}$. Further, for the gas-powered system, we defined three distinct scenarios to evaluate the network’s capacity under varying demand conditions. This process yielded a total of 20.000 samples, of which 30% were designated for testing. We produced 320 samples using GEKKO v1.0.6 to compare the model’s performance with IPOPT v3.12 [75].

We implemented RPINN using Python 3.10.12 and the TensorFlow API 2.15.0 on Google Colaboratory. For training, we fixed 500 epochs, a batch size of 64 samples, an Adam optimizer, and a learning rate value of $1e-3$. The regularization hyperparameters, namely ${\lambda }_{·}$ in Eq. 2, are experimentally set using a gridsearch strategy within the set $\{0,0.25,0.5,0.75,1\}.$ Since IPOPT excels at solving NOPT, not to mention its open access, we fix it as a method comparison [51]. Our codes and studied datasets are publicly available at https://github.com/UN-GCPDS/python-gcpds.optimization (accessed on 1 March 2024).

6. Results and Discussion

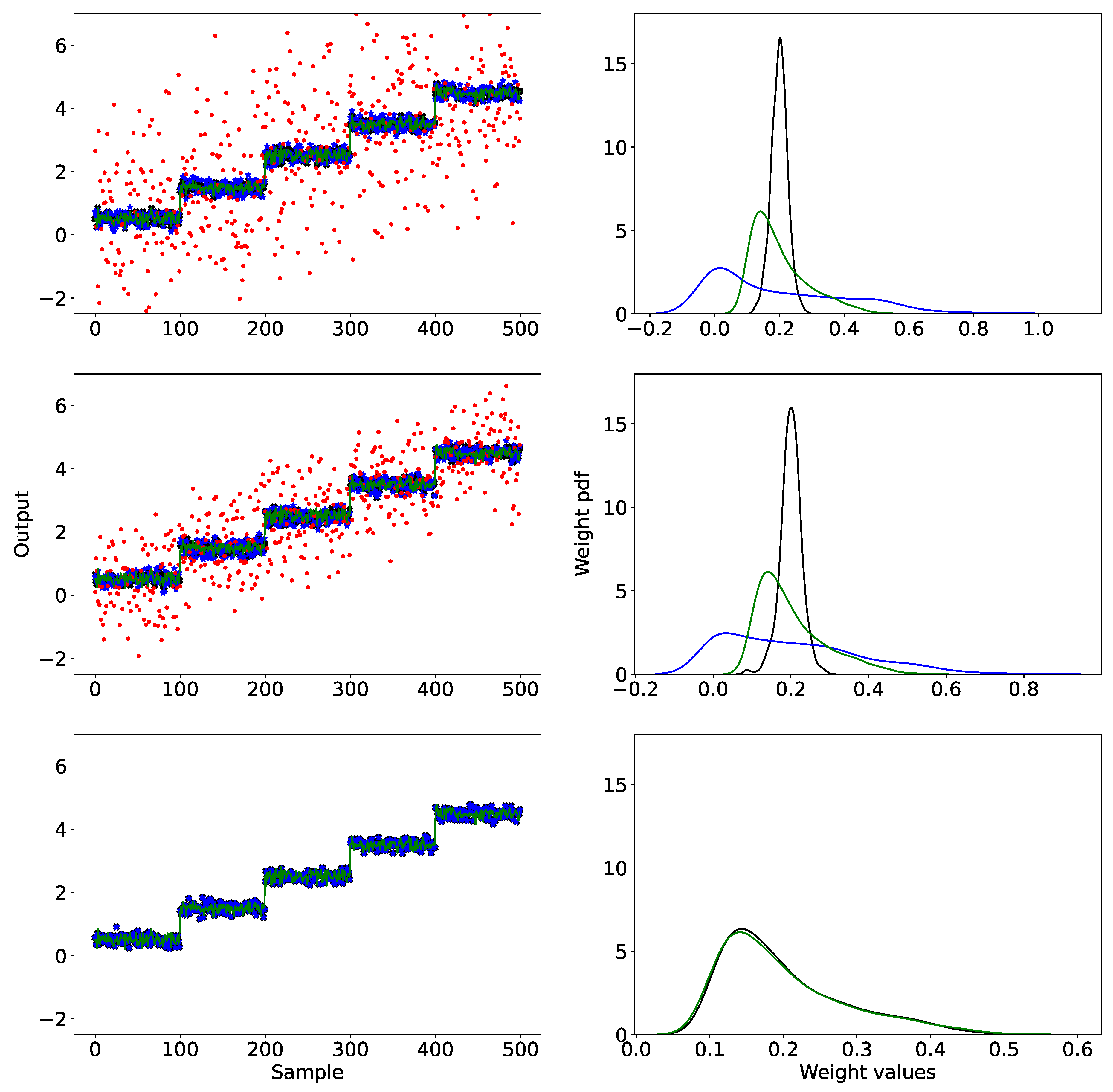
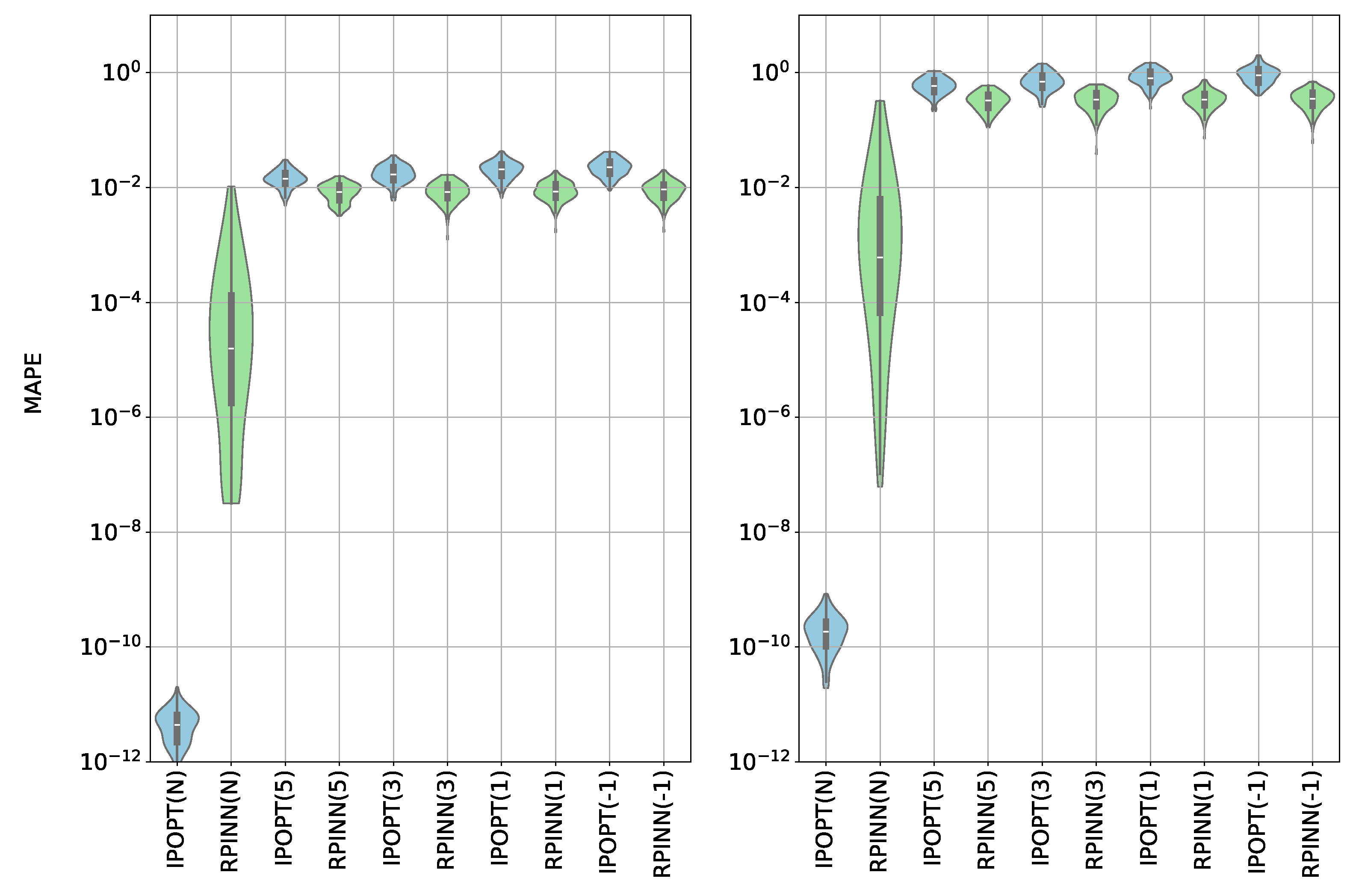
6.1. Supervised Constrained Optimization Results

As shown in Figure 7 (left) and Figure 8, for noisy-free data on the uniform mixture model scenario, both our proposal and the IPOPT solution exhibit similar results. The similarity of the results stems from the fact that the problem defined in Eq. 4 is convex. Next, for noisy inputs, our RPINN, based on the Huber loss function, shows greater robustness against data variability and noise issues. In fact, the Huber function applies the l1-norm for errors exceeding a defined threshold, reducing sensitivity to extreme values, while for smaller errors it uses the l2-norm, ensuring accuracy by penalizing smaller errors. In contrast, the classical IPOPT technique uses an objective function based on the l2-norm, which is sensitive to outliers because it significantly penalizes large deviations. The weight distributions provide support for the latter hypothesis. Noise-free data leads to similar strength predictions for both RPINN and IPOPT. Conversely, for noisy inputs, our proposal regularizes the network weights, yielding concentrated values to find the main output dynamics, and outperforms the IPOPT regarding the MAPE for all considered SNR values.

6.2. Unsupervised Constrained Optimization Results

Figure 9 depicts our RPINN regularized penalty illustration for the gas-powered system NOPT. We adopted a standard variant of the Huber loss for the node balance and Weymouth constraints. As shown, the threshold ${ϵ}_{·}$ transitions between the $l1$ and $l2$ norms. Regarding the constraint on the compression ratio limit, it was essential to alter the structure due to its inequality behavior. This enhancement stabilizes the transition between the l2 and l1 norms at zero, based on the distance to the central value of the required range. Furthermore, it is crucial to correctly integrate these cost functions into our RPINN. Then, the right plot in Figure 9 shows the Weymouth (blue) and compression ratio (orange) penalty evolution. As seen, the obtained loss shows a decreasing trend, indicating that the Huber-based approach can handle the physical limitations of the gas-powered NOPT.

In turn, we designed three evaluation scenarios in comparison with the IPOPT framework to validate the performance of regularization functions in data generation. In the first scenario, data remain below the source’s maximum capacity. In the second scenario, 50 percent of the samples exceed this capacity, while in the third, about 100 percent of the data surpasses it. Figure 10 shows that even though IPOPT has a lower MAPE, its precision (variance) changes a lot over the iterations. This means that conventional methods for NOPT are not strong against data variability and nonlinear constraints. In contrast, our RPINN achieves acceptable MAPE with low variability across experiments due to its regularized strategy based on ANNs. In fact, both approaches share similar costs and adhere to compression ratio constraints. In the first two cases, traditional solutions to the Weymouth equation work better than ours. But in the third case, our proposal is better because it is more stable and less affected by outliers, thanks to the Huber-based penalty.

Finally, to see if our RPINN model can handle the limits in Eq. 9 well, we looked at the results of the flow and pressure prediction layers and how they behaved, as shown in Figure 11. The parameters analyzed, including injection and pipe flows as well as pipeline pressures, remain within acceptable limits. This behavior is attributed to custom activation in Eq. 13, which ensures a smooth and steady transition between the established ranges.

6.3. Computational Cost Results

Figure 12 shows the training and prediction times needed by the RPINN compared to IPOPT. Our model needs more time to process during the training phase because it has to do both forward and backward passes in each iteration within an ANN-based framework. However, in the prediction phases, our RPINN outperforms IPOPT, resulting in significantly shorter prediction times. This is due to the fact that the model only requires forward passes after training the weights. These tools demonstrate the RPINN’s capability to generate fast and accurate predictions for NOPT solutions, not only by reducing processing times but also by narrowing interquartile ranges.

6.4. Limitations

The RPINN framework, while innovative and effective in addressing many challenges of NOPT, has several limitations that need to be considered. One significant limitation is the complexity involved in defining appropriate loss functions and selecting optimal hyperparameters, which can make the implementation process cumbersome. Additionally, extremely high levels of noise or complex nonlinear constraints can hinder the performance of RPINN, despite its robustness against data variability and noisy inputs. Although AD has improved the model’s scalability, it may still face challenges when applied to very large-scale problems due to computational resource limitations.

Furthermore, integrating precise physical principles into the network architecture can be intricate and may not always generalize well across different types of NOPT problems. Current trends in PINNs emphasize improving these models’ generalization capabilities and computational efficiency [76]. To better solve the problems of scalability and accuracy, researchers are focusing on hybrid approaches that mix PINNs with other advanced optimization methods, like metaheuristics and gradient-based methods. The latter indicates a growing recognition of the need for more flexible and adaptive frameworks that can handle a broader range of NOPT scenarios.

7. Conclusions

We introduce a novel Regularized Physics-Informed Neural Network (RPINN) framework, named RPINN, presenting a significant advancement in addressing the challenges associated with nonlinear constrained optimization. By integrating custom activation functions and regularization penalties within an ANN architecture, RPINN effectively handles data variability and noisy inputs. Besides, the incorporation of physics principles into the network architecture allows for the computation of optimization variables based on network weights and learned features, leading to competitive performance compared to state-of-the-art solvers. Furthermore, the use of automatic differentiation for training enhances scalability and reduces computation time, making RPINN a robust solution for various NOPT tasks. Experimental results included two scenarios regarding supervised and unsupervised datasets.

The uniform mixture model experiments (supervised constrained NOPT) show that the RPINN is good at dealing with data variability and noisy samples. For noise-free data, both RPINN and the IPOPT solver achieved similar results due to the convex nature of the problem. Still, in scenarios with noisy inputs, RPINN significantly outperformed IPOPT. The RPINN framework, leveraging the Huber loss function, showed greater robustness against noise by effectively regularizing the network weights. This resulted in more accurate and stable output predictions compared to IPOPT, which relied on an objective function based on the l2-norm and was more sensitive to outliers. The RPINN weight distributions were concentrated, which showed that the model could find the main output dynamics even when noise was present, as shown by the lower mean absolute percentage error across all signal-to-noise ratio values.

Then, the results of the gas-powered system (unsupervised constrained optimization) highlight the capability of the RPINN framework to effectively manage complex, nonlinear constraints under varying conditions of gas demand. Compared to the IPOPT framework, the RPINN showed consistent performance with low changes in the mean absolute percentage error. This was especially true when the gas demand was higher than the source’s maximum capacity. While IPOPT showed lower MAPE in terms of node balance and Weymouth constraints, its precision fluctuated significantly with data variability. In contrast, RPINN maintained stable performance, ensuring compliance with physical constraints such as the Weymouth equation and compression ratio limits. The custom penalty functions within RPINN facilitated this stability, proving particularly valuable when traditional methods struggled with outliers and extreme values. Overall, RPINN offered a robust, scalable solution with reduced prediction times.

As future work, authors plan to include Bayesian hyperparameter optimization for RPINN fine tuning [77]. We will also look at normalized and information theoretic learning-based loss as ways to deal with noisy inputs and complicated constraints [78,79]. Finally, Bayesian PINN and graph neural networks will be coupled with our RPINN for representation learning enhancement [68,80].