Hybrid Euclidean-Lorentzian Universe

1. Introduction

I a recent paper [1] an extensive introduction to the subject of Euclidean and Lorentzian space-times was given, it will not be repeated here, the interested reader is referred to the original paper. We shall only mention that great luminaries of the physical sciences such as Sakharov [2,3], Hawking [4] and Ellis [5] have considered the possibility that near it inception the metric of the universe had an Euclidean signature. It was shown [6] that such a metric cannot be sustained for a long time for an expanding universe since the density of the universe diminishes. The reason is that for a (nearly) empty universes only a Lorentzian metric is stable. So naturally all other metric signature must be confined to a limited portion of space time. This of course also true for the Euclidean signature which is confined as suggested here to a tiny duration after the universe was created. This coupled with the radical dynamics of particles in this primordial Euclidean universe with no upper velocity limit and bizarre physical statistics that favours high velocities [1], suggest an alternative for scalar-field driven cosmic inflation.

The structure of the current paper is as follows: we start with a general geometry and apply the standard restrictions that are implied by homogeneity and isotropy, however, we do not restrict our metric to be either Lorentzian or Euclidean. This will result in a metric with reduced degrees of freedom. Next we use Einstein equations and obtain the generalized Freedman Lemaître Robertson Walker (FLRW) equations which are valid for both Lorentzian and Euclidean signatures. Finally we discuss the solutions of those equations for some simple equations of state, in which we shall attempt to describe a continuous solution describing the evolution of the universe during its entire history from the Euclidean epoch till the current Lorentzian epoch.

2. The Metric

The metric $g_{\mu \nu }$ of a four dimensional space is connected to the infinitesimal square interval $d{s}^2$ by the well known equation:

$$d{s}^2=\left|g_{\mu \nu }d{x}^{\mu }d{x}^{\nu }\right|,\mu ,\nu \in [0,1,2,3]$$

(1)

in which $x^{\mu }$ are the coordinates describing the location of some point P in this space and we use the Einstein summation convention. We shall single out one coordinate $x^0$ and refer to it as "temporal". This can be easily understood in a Lorentzian space-time in which the diagonalize form of $g_{\mu \nu }$ will have a different sign for this coordinate with respect to the other coordinates. For the Euclidean case the choice seems arbitrary, however, if one bears in mind that any Euclidean portion of space-time will turn into a Lorentzian then the direction of "symmetry breaking" allows us to define a temporal direction. Thus we may write:

$$d{s}^2=\left|g_{00}{\left(d{x}^0\right)}^2+2g_{0k}d{x}^{0}d{x}^k+g_{jk}d{x}^{j}d{x}^k\right|.j,k\in [1,2,3]$$

(2)

Next we invoke isotropy in the usual spatial sense, which is assumed in standard cosmological models to claim that there cannot be a preferred direction in our space at any given time. As the vector $\overrightarrow{v}$ whose components are $v_k\equiv g_{0k}$ is such a vector, it follows that we must have: $g_{0k}=0$ and thus:

$$d{s}^2=\left|g_{00}{\left(d{x}^0\right)}^2+g_{jk}d{x}^{j}d{x}^k\right|.j,k\in [1,2,3]$$

(3)

The next step [7] is to look at a "comoving observer", that is an observer that does not feel himself moving in the coordinate system. Such an observer will report that $d{x}^k=0$ and thus will be displaced by an interval:

$$d{s}_0^2=\left|g_{00}{\left(d{x}^0\right)}^2\right|.$$

(4)

As the observer is not displaced in space he will interpret the change he is feeling as a change of time, this is denoted "proper time" ${\tau }_0$. Till now we have measure all dimensions in the same units (say meters), however, it is customary to measure time using a different set of units (seconds). To convert between the units we introduce the conversion factor $c\simeq 3{10}^8$ m/s (which appears later in the theory as the velocity of gravitational and electromagnetic waves in vacuum). Thus:

$$d{\tau }_0^2=\frac{d{s}_0^2}{c^2}=\left|\frac{g_{00}}{c^2}{\left(d{x}^0\right)}^2\right|.$$

(5)

There are two alternatives:

$$d{\tau }_0^2=\left\{\begin{array}{cc}+\frac{g_{00}}{c^2}{\left(d{x}^0\right)}^2& g_{00}>0\\ -\frac{g_{00}}{c^2}{\left(d{x}^0\right)}^2& g_{00}<0\end{array}\right.$$

(6)

So we obtain:

$$d{s}^2=\left|\pm c^{2}d{\tau }_0^2+g_{jk}d{x}^{j}d{x}^k\right|.$$

(7)

Now consider an observer who inspects his surroundings in a given instant of time, since space is assumed to be isotropic he may choose spherical coordinates $r,\theta ,\varphi$ in which case [7]:

$$g_{jk}d{x}^{j}d{x}^k=A\left({\tau }_0\right)\left[{\lambda }^2\left(r\right)d{r}^2+r^2(d{\theta }^2+{sin}^2\theta d{\varphi }^2)\right]$$

(8)

As we do not specify in advance the signature of the metric it follows that:

$$A\left({\tau }_0\right)=\pm a^2\left({\tau }_0\right)$$

(9)

Thus we may write the line interval square as:

$$d{s}^2=\left|\pm c^{2}d{\tau }_0^2\pm a^2\left[{\lambda }^2\left(r\right)d{r}^2+r^2(d{\theta }^2+{sin}^2\theta d{\varphi }^2)\right]\right|.$$

(10)

It follows that there are two equivalent Euclidean choices ($++$ and $--$) and two equivalent Lorentzian choices ($+-$ and $-+$). Hence without loss of generality we choose a positive sign for the spatial component, leaving the metric type to be determined by the temporal part.

$$d{s}^2=\left|\pm c^{2}d{\tau }_0^2+a^2\left[{\lambda }^2\left(r\right)d{r}^2+r^2(d{\theta }^2+{sin}^2\theta d{\varphi }^2)\right]\right|.$$

(11)

Following [7] we shall choose from now on units in which $c=1$ and use the notation:

$$d{t}^2\equiv \pm c^{2}d{\tau }_0^2.$$

(12)

Such that:

$$d{s}^2=\left|-d{t}^2+a^2\left[{\lambda }^2\left(r\right)d{r}^2+r^2(d{\theta }^2+{sin}^2\theta d{\varphi }^2)\right]\right|.$$

(13)

This means that for the Euclidean regions of space-time we use an imaginary time coordinate while for the Lorentzian regions the time coordinate is real:

$$t_E=i{\tau }_0,i=\sqrt{-1},t_L={\tau }_0.$$

(14)

As the spatial scalar curvature is:

$${ }^{3}R=\frac{3}{2a^2{r}^3}\frac{d}{dr}\left[r^2\left(1-\frac{1}{{\lambda }^2}\right)\right].$$

(15)

If we assume that space must be homogeneous it follows that the spatial scalar curvature of space cannot depend on r but of course it can depend on t. It follows that:

$$r^2\left(1-\frac{1}{{\lambda }^2}\right)=c_1{r}^4+c_2$$

(16)

since $\lambda$ is by assumption independent of t. To avoid a singular expression we may choose $c_2=0$ and thus obtain:

$${\lambda }^2=\frac{1}{1-c_1{r}^2}$$

(17)

It is now customary to redefine r such that $\overline{r}\equiv r\sqrt{|c_1|}$ for the cases that $|c_1|\ne 0$, which will lead to the customary form:

$$d{s}^2=\left|-d{t}^2+{\overline{a}}^2\left[\frac{d{\overline{r}}^2}{1-k{\overline{r}}^2}+{\overline{r}}^2(d{\theta }^2+{sin}^2\theta d{\varphi }^2)\right]\right|.{\overline{a}}^2\equiv \frac{a^2}{|c_1|},k\in [-1,0,+1]$$

(18)

For the case $|c_1|=0$ we take $\overline{r}\equiv r,\overline{a}\equiv a$. Finally we drop the bars for convenience and write:

$$d{s}^2=\left|-d{t}^2+a^2\left[\frac{d{r}^2}{1-k{r}^2}+r^2(d{\theta }^2+{sin}^2\theta d{\varphi }^2)\right]\right|.$$

(19)

3. The FLRW Equations

In the previous section we have went as far as is possible to determine the metric from symmetry considerations (isotropy & homogeneity). However, in order to gain more information one must solve Einstein’s equations which are [7]:

$$G_{\mu }^{\nu }=R_{\mu }^{\nu }-\frac{1}{2}{\delta }_{\mu }^{\nu }R=4\pi G{T}_{\mu }^{\nu },$$

(20)

in the above $G_{\mu }^{\nu }$ is the Einstein’s tensor, $R_{\mu }^{\nu }$ is the Ricci tensor, R is the four dimensional curvature scalar, G is Newton’s universal gravitational constant, and $T_{\mu }^{\nu }$ is the energy momentum tensor. Isotropy means that $T_0^k$ must be zero, and $T_j^k$ must be diagonal and the diagonal components must be equal. Homogeneity implies that the components of $T_{\mu }^{\nu }$ must not depend on spatial coordinate but may depend on time. Thus:

$$T_{\mu }^{\nu }=\mathrm{diag}(-\rho \left(t\right),p\left(t\right),p\left(t\right),p\left(t\right))$$

(21)

which means that the source can be thought as an ideal fluid with energy density $\rho$ and pressure p. Using the metric components of equation (19) on can easily calculate the Einstein tensor components:

$$G_0^0=-\frac{3}{a^2}({\dot{a}}^2+k),$$

(22)

$$G_i^j=-\frac{1}{a^2}(2a\ddot{a}+{\dot{a}}^2+k){\delta }_i^j$$

(23)

in the above $\dot{a}\equiv \frac{da}{dt},\ddot{a}\equiv \frac{d^{2}a}{d{t}^2}$. This will lead using equation (20) and equation (21) to the FLRW model equations:

$$\frac{{\dot{a}}^2+k}{a^2}=\frac{8\pi G}{3}\rho ,$$

(24)

$$\frac{2\ddot{a}}{a}+\frac{{\dot{a}}^2+k}{a^2}=-8\pi Gp$$

(25)

It is assumed that p and $\rho$ are connected through an equation of state and thus given appropriate initial conditions those equations can be integrated.

4. Implications of the FLRW Equations

Let us combine equation (24) and equation (25), this will lead to:

$$\frac{\ddot{a}}{a}=-\frac{4\pi G}{3}(\rho +3p),$$

(26)

implying $\ddot{a}<0$ for normal matter for which:

$$\rho +3p>0$$

(27)

now since $\dot{a}>0$ the plot of $a\left(t\right)$ must be convex. This means the a was smaller in previous times. Thus if we look far enough in the past $a\left(t_{sing}\right)=0$ and in this case the Riemann tensor diverges and thus we obtain an essential singularity that cannot be removed by coordinate transformation. This of course means the the Lorentzian FLRW model is not a valid physical model for the entire history of the universe and can only describe in the best case part of it. However, this is only true for normal matter, for exotic types of matter, "dark energy" or "cosmological constant" being the most popular examples, the above inequality does not hold and we have:

$$\rho +3p<0\Rightarrow p<-\frac{1}{3}\rho .$$

(28)

Indeed in the dark energy case $p=-\rho$ the above inequality is satisfied and the universe is accelerating. If this is taken as the correct equation of state near the inception of the universe this means that [8] we have $\ddot{a}>0$ at those early time, meaning that if we go back enough to some $t_c$ then $\dot{a}\left(t_c\right)=0$, and the scale factor reaches a minimal finite size $a_c=a\left(t_c\right)$ and thus the singularity is avoided. However, this scenario is not plausible because ordinary matter density is expected to be much higher than dark energy density at those early times making the above accelerating scenario invalid.

Of course in the above paragraph we assumed that the Universe is Lorentzian throughout its history. However, suppose now that at a time $t_E$ it becomes Euclidean (see Figure 1) then equation (26) will be still correct but now only for imaginary time according to equation (14). In terms of proper time ${\tau }_0$ it will take the form:

$$\frac{1}{a}\frac{d^{2}a}{d{\tau }_0^2}=\frac{4\pi G}{3}(\rho +3p),$$

(29)

Assuming that the normal matter rule $\rho +3p>0$ apply in the Euclidean domain as well, we see that now a is accelerating, meaning that $\frac{da}{d{\tau }_0}$ was smaller at earlier times, as a consequence if we go back far enough $\frac{da}{d{\tau }_0}=0$. Thus at that particular time $t_c$, a reached a minimal value $a_c$ and was not expanding, hence no unphysical singularity should be expected. Moreover, if the duration $t_E-t_c$ is sufficiently long, thermal equilibrium of all components of the universe should be achieved explaining the outstanding smoothness of CMB background. This is augmented by the fact that there is no velocity upper limit in an Euclidean space-time [1]. At times $t<t_c$$\frac{da}{d{\tau }_0}<0$ meaning that the universe is contracting rather than expanding and thus $a\left(t\right)>a_c$.

Let us now write equation (24) as:

$$\rho a^3=\frac{3}{8\pi G}a({\dot{a}}^2+k)$$

(30)

It thus follows that:

$$\frac{d}{dt}\left(\rho a^3\right)=\frac{d}{da}\left(\rho a^3\right)\dot{a}=\frac{3}{8\pi G}\frac{d}{dt}\left(a({\dot{a}}^2+k)\right)$$

(31)

Or:

$$\frac{d}{da}\left(\rho a^3\right)=\frac{3}{8\pi G\dot{a}}\frac{d}{dt}\left(a({\dot{a}}^2+k)\right)=-3a^{2}p.$$

(32)

In which we used equation (25). Now, it is customary to assume a simple equation of state.

$$p=w\rho$$

(33)

In which $w=0$ for non-relativistic matter, $w=\frac{1}{3}$ for relativistic matter and radiation, $w=-1$ for dark energy or cosmological constant, and $w=1$ for "stiff" matter in which the speed of sound is the same as speed of light in vacuum. Inserting equation (33) into equation (32) leads to:

$$\frac{d}{da}\left(\rho a^3\right)=-3a^{2}p=-3w{a}^2\rho \Rightarrow \rho =\Gamma a^{-3(1+w)}.$$

(34)

Thus a completely Lorentzian space-time is not physical as in this case in the instant of creation $a=0$ and thus $\rho =\infty$ for all $w>-1$. On the other hand equation (34) holds also for the Euclidean part of space-time and in the scenario in which space-time is partly Euclidean and partly Lorentzian we simply write:

$$\rho ={\rho }_c{\left(\frac{a}{a_c}\right)}^{-3(1+w)}.$$

(35)

in which ${\rho }_c$ is the finite value of the energy density obtained when the scale factor takes its minimum value of $a_c$ (and is not connected to the critical density that determines the value of k in ordinary Lorentzian space time [7]). The important examples of equation (35) are non relativistic matter with $w=0$:

$$\rho ={\rho }_c{\left(\frac{a}{a_c}\right)}^{-3}.$$

(36)

The case of relativistic matter and radiation with $w=\frac{1}{3}$:

$$\rho ={\rho }_c{\left(\frac{a}{a_c}\right)}^{-4}.$$

(37)

And the dark energy case with $w=-1$:

$$\rho ={\rho }_c.$$

(38)

5. Time Dependence of the Scale Factor

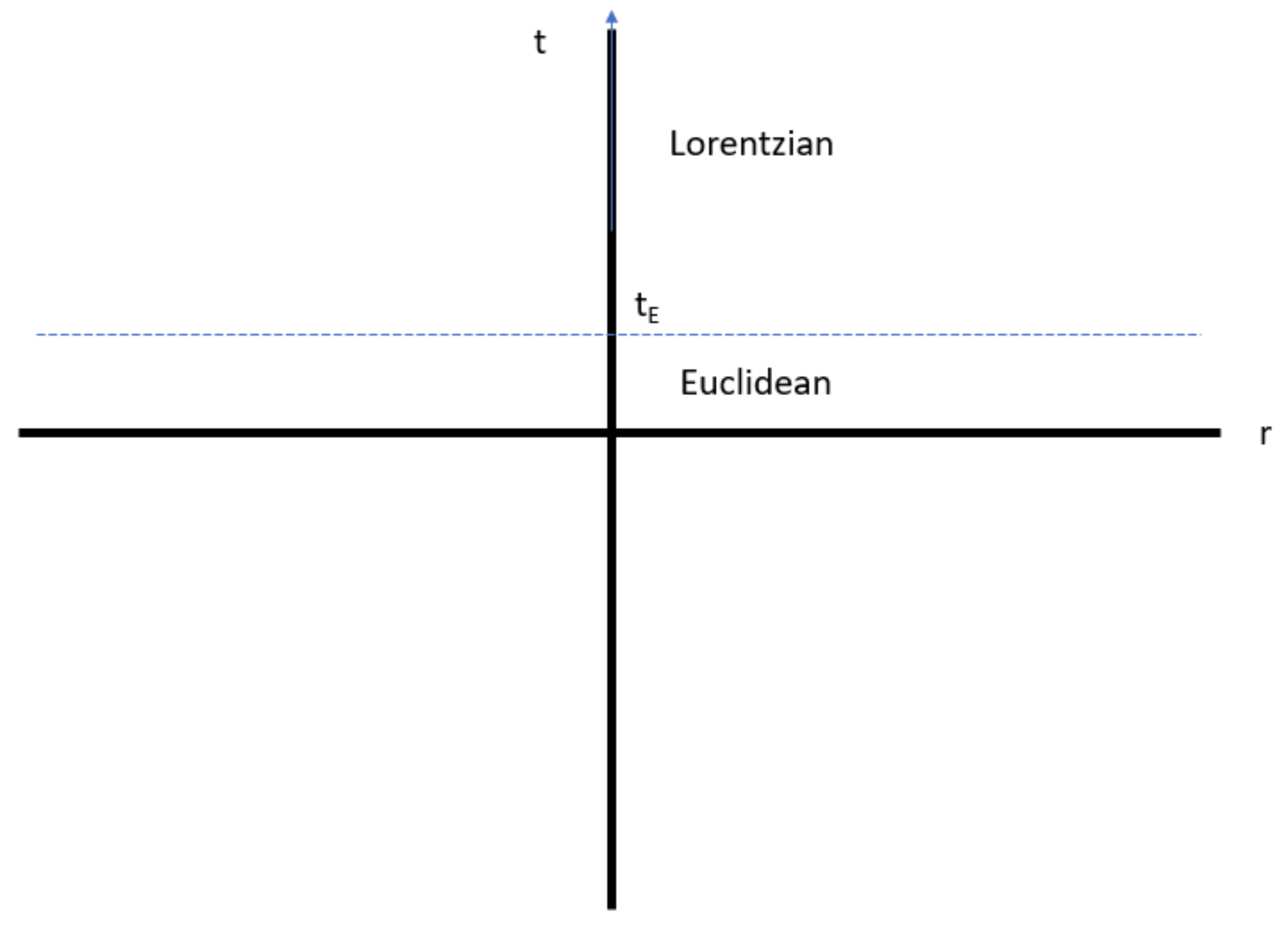
5.1. The Lorentzian Sector

As we know the dependence of the energy density $\rho$ on the scale factor a, we are in a position to integrate equation (24) which is an ordinary first order differential equation and thus has a solution provided an initial condition is specified at some time $t_0$. We rewrite equation (24) in the form:

$${\dot{a}}^2=\frac{8\pi G}{3}\rho a^2-k,$$

(39)

For a Lorentzian space-time (or the Lorentzian sector of a hybrid Lorentzian-Euclidean space-time) the left hand side is positive and thus can always be satisfied for $k=0,-1$. However, for $k=1$ it cannot be satisfied unless:

$$\frac{8\pi G}{3}\rho a^2>1.$$

(40)

Or taking into account equation (34):

$$\frac{8\pi G}{3}\Gamma a^{-(1+3w)}>1,\Rightarrow a<a_L,a_L\equiv {\left(\frac{8\pi G\Gamma }{3}\right)}^{\frac{1}{1+3w}}.$$

(41)

Thus a closed universe with $k=1$ must have an upper limit $a_L$ for its scale factor. Equation (39) being non-linear admits two solutions:

$$\dot{a}=\pm \sqrt{\frac{8\pi G}{3}\rho a^2-k}.$$

(42)

However, since we know from observations that currently the universe is expanding $\dot{a}>0$ we choose the positive sign. This defines the direction of time to be the direction in which the universe is expanding:

$$\dot{a}=+\sqrt{\frac{8\pi G}{3}\rho a^2-k}=+\sqrt{{\left(\frac{a_L}{a}\right)}^{1+3w}-k}.$$

(43)

For the case $k=0$ equation (43) can be written as:

$$\dot{a}={\left(\frac{a_L}{a}\right)}^{\frac{1}{2}(1+3w)},$$

(44)

this is also approximately true for the $k=\pm 1$ cases provided that $a\ll a_L$, that is in the early universe. Let us set $\gamma =\frac{1}{2}(1+3w)$, we shall also assume that $a\left(t_0\right)=a_0$. For the case $\gamma \ne -1$ only one solution is possible:

$$a\left(t\right)={\left[(\gamma +1)a_L^{\gamma }(t-t_0)+a_0^{\gamma +1}\right]}^{\frac{1}{\gamma +1}},$$

(45)

and this solution only exist for part of the universe history, that is for:

$$t>t_{min}\equiv t_0-\frac{a_0^{\gamma +1}}{(\gamma +1)a_L^{\gamma }}.$$

(46)

Moreover, at $a\left(t_{min}\right)=0$ the Riemann tensor diverges, and the solution (if stretched to those early times) becomes unphysical. Hence for ordinary matter one cannot assume that the universe is Lorentzian for its entire history. Some authors [7] choose because of this $t_0=0$ and $a_0=a\left(t_0\right)=0$ this will lead to $t_{min}=0$. And equation (45) can be written in a simple form:

$$a\left(t\right)={\left[(\gamma +1)a_L^{\gamma }\right]}^{\frac{1}{\gamma +1}}{t}^{\frac{1}{\gamma +1}},$$

(47)

The two most popular examples are non relativistic matter with $w=0,\gamma =\frac{1}{2}$ such that:

$$a\left(t\right)={\left(\frac{3}{2}\right)}^{\frac{2}{3}}{a}_L^{\frac{1}{3}}{t}^{\frac{2}{3}},$$

(48)

And relativistic matter (including radiation) with $w=\frac{1}{3},\gamma =1$ such that:

$$a\left(t\right)={\left(2\right)}^{\frac{1}{2}}{a}_L^{\frac{1}{2}}{t}^{\frac{1}{2}}.$$

(49)

Another somewhat farfetched example is the "stiff" material with velocity of sound which is equal to the velocity of light. In this case $w=1,\gamma =2$ and we have:

$$a\left(t\right)={\left(3\right)}^{\frac{1}{3}}{a}_L^{\frac{2}{3}}{t}^{\frac{1}{3}}.$$

(50)

Of course when t is large enough and $k=\pm 1$ one needs to solve the exact equation (43) to obtain an accurate solution for $a\left(t\right)$.

It remains to look at the $\gamma =-1$ or $w=-1$ which is the dark energy or cosmological constant case. For this case integration of equation (44) leads to:

$$a\left(t\right)=a_0{e}^{\frac{t-t_0}{a_L}}.$$

(51)

Such a solution will never vanish for a finite t if $a_0\ne 0$, but will vanish identically if $a_0=0$. It will vanish of course for $t=-\infty$ for any $a_0$. If $k=0$, $a\left(t\right)$ will diverge at infinity, but if $k=\pm 1$ the solution in equation (51) becomes inaccurate for $t\gg t_0$.

5.2. The Euclidean Sector

Let us now consider equation (39) for the Euclidean sector, in this case according to equation (14) t is imaginary, and thus it should be expressed in terms of the proper time in the form:

$$-{\left(\frac{da}{d{\tau }_0}\right)}^2=\frac{8\pi G}{3}\rho a^2-k,$$

(52)

this cannot be solved for either $k=0$ nor $k=-1$, solutions are limited to the case $k=1$. Such that:

$$\frac{8\pi G}{3}\rho a^2<1.$$

(53)

Taking into account equation (35) it follows that in the Euclidean sector the scale factor a must be always larger than a minimal value $a_{min}$:

$$a\ge a_{min}={\left[\frac{8\pi G}{3}{\rho }_c{a}_c^{3(1+w)}\right]}^{\frac{1}{1+3w}}.$$

(54)

In terms of equation (54) we may rewrite equation (52) in the form:

$$\frac{da}{d{\tau }_0}=\pm \sqrt{1-{\left(\frac{a_{min}}{a}\right)}^{1+3w}}.$$

(55)

As in the Lorentzian sector the sign determines the direction of time according to the direction in which the scale factor is growing, thus we choose:

$$\frac{da}{d{\tau }_0}=+\sqrt{1-{\left(\frac{a_{min}}{a}\right)}^{1+3w}}.$$

(56)

Now, according to equation (35) and the discussion that follows $a\left(t_c\right)=a_c$ is the minimal value of a for which $\frac{da}{d{\tau }_0}{|}_{t_c}=0$. Thus $a_c=a_{min}$, and a must be slightly larger than $a_c$ in order for the scale factor to grow. It follows from equation (54) that:

$$a_c=a_{min}\Rightarrow a_c=\sqrt{\frac{3}{8\pi G{\rho }_c}}.$$

(57)

Remarkably, the minimal scale factor does not depend on the equation of state, but depends on the inverse square of the maximal density. Written in MKS units the minimal scale is:

$$a_c=c\sqrt{\frac{3}{8\pi G{\rho }_c}}.$$

(58)

The maximal density that is considered by some authors is Planck’s density:

$${\rho }_{Planck}\equiv \frac{c^5}{\hslash G^2}\simeq 5.2·{10}^{96}\mathrm{kg}/{\mathrm{m}}^3.$$

(59)

ℏ is Planck’s constant over $2\pi$. This will lead to a minimal scale factor of:

$$a_{Planck}\simeq 5.6·{10}^{-36}\mathrm{m}<l_p=\sqrt{\frac{\hslash G}{c^3}}\simeq 16·{10}^{-36}\mathrm{m}$$

(60)

that is for the extreme case of the planck density the scale factor will have a minimal value about third of the planck length $l_p$. This is rather small but not zero, thus no unphysical or diverging behaviour is to be expected.

Equation (56) can be integrated analytically for various values of w, for this we normalize the scale factor and proper time by $a_c$ such that $\overline{a}\equiv \frac{a}{a_c}$ and $\overline{\tau }\equiv \frac{{\tau }_0}{a_c}$, thus we may write equation (56) in a dimensionless form:

$$\frac{d\overline{a}}{d\overline{\tau }}=\sqrt{1-{\overline{a}}^{-(1+3w)}}.$$

(61)

Thus:

$$\overline{\tau }-{\overline{\tau }}_c={\int }_1^{\overline{a}}\frac{1}{\sqrt{1-{\overline{a}}^{-(1+3w)}}}=F\left(\overline{a}\right)-F\left(1\right).$$

(62)

The integral function $F\left(\overline{a}\right)$ which depends on w can be chosen such that $F\left(1\right)=0$, and thus:

$$a=a_c\overline{a}=a_c{F}^{-1}(\overline{\tau }-{\overline{\tau }}_c)=a_c{F}^{-1}\left(\frac{{\tau }_0-t_c}{a_c}\right),$$

(63)

in which $F^{-1}$ is the inverse function of F. For relativistic matter or radiation $w=\frac{1}{3}$ and thus:

$$F\left(\overline{a}\right)=\sqrt{{\overline{a}}^2-1}$$

(64)

Thus:

$$a\left({\tau }_0\right)=\sqrt{a_c^2+{({\tau }_0-t_c)}^2}.$$

(65)

And in particular at the Euclidean transition time $t_E$ we have:

$$a\left(t_E\right)=\sqrt{a_c^2+{(t_E-t_c)}^2},$$

(66)

which is depicted in Figure 2. This value serves as an initial condition for integration of the scale factor in the Lorentzian sector that is for equation (43). To conclude this subsection we mention that for non-relativistic matter $w=0$ and we have:

$$F\left(\overline{a}\right)=\sqrt{{\overline{a}}^2-\overline{a}}+ln[\sqrt{\overline{a}-1}+\sqrt{\overline{a}}]$$

(67)

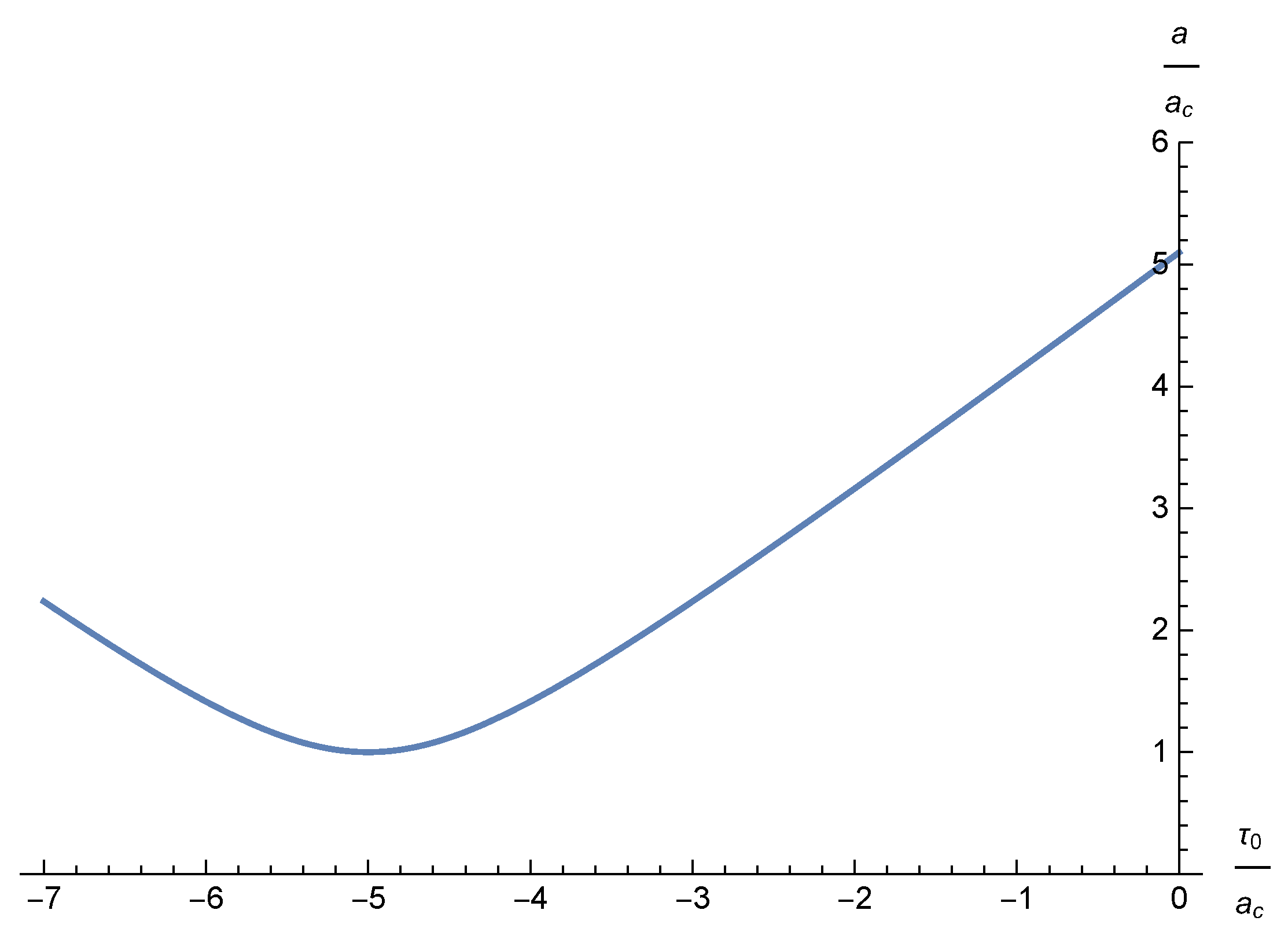
5.3. The Transition between Euclidean and Lorentzian Sectors

The transition between the Euclidean and Lorentzian sectors of space time occurs at a three dimensional hyper surface designated by $x_E^0$. Although the definition of proper time is different in both sides of this hyper surface, still there may be a coordinate system (an "atlas") that is valid for both sectors. In such a coordinate system $g_{00}<0$ in the Lorentzian sector while $g_{00}>0$ in the Euclidean sector. In the interface which is of zero measure we have $g_{00}\left(x_E^0\right)=0$. Hence although the transition described in terms of proper times seems discontinuous, this description is chosen for convenience and does not reflect an essential discontinuity but rather a smooth transition. All other metric components may be continuous over the boundary hyper surface provided that $k=1$ if we choose the scale factor such that:

$$a\left(t_{E-}\right)=a\left(t_{E+}\right)$$

(68)

For $k=0,-1$ the $g_{rr}$ component cannot be continuous across the interface at every point because the Euclidean sector does not admit such solutions.

6. Conclusions

We have shown that completely Lorentzian Cosmology described in many textbooks [7,9,10,11] cannot describe the entire history of the universe, as it must breakdown at some time and lead to unphysical divergences. While a Cosmology of a Euclidean and Lorentzian sectors does not contain unphysical singularities and provides sufficient time [1] to the CMB to achieve thermal equilibrium. Indeed black hole singularities can also be avoided in a similar fashion [12,13,14]. Thus the need to introduce cosmological inflation using ad-hoc (and redundant anywhere else in physics) scalar fields[16] is avoided. We mention that the scale factor at the end of the Euclidean epoch serves as an initial condition for the scale factor in the Lorentzian epoch and this may have some bearing on the apparent scale factor acceleration as evident in the red shift of distant super novae[17]. However, some authors suggest to keep the cosmological constant and show how a signature change may affect its value[15].

The current work of course does not deal with all issues related to the Euclidean Lorentzian transition. A major concern is related to the exact time of this transition which is conjectured to be related to an instability in the metric which develops as the density drops according to (35) [6,17]. Other concerns are related to the dynamics of particles moving from the Euclidean to the Lorentzian sectors, and the thermodynamics of matter in the Euclidean sector which may be different [1] from the thermodynamics in the Lorentzian sector used in the current paper for both sectors. Those subjects will be dealt with, hopefully, in future works.