Parameter Identification of Flexible Link Manipulators Using Evolutionary Algorithms

1. Introduction

Flexible manipulators equipped with compliant structures have garnered significant interest due to their adaptability, dexterity, and safety features. Flexible manipulators have been applied to diverse application domains, ranging from manufacturing and healthcare to space exploration and beyond, highlighting the versatility and potential impact of flexible manipulator technology. In manufacturing, flexible manipulators improve efficiency and accuracy in tasks such as assembly, pick-and-place operations, and quality inspection [1]. In healthcare, they enhance patient outcomes and reduce procedural risks in minimally invasive surgeries, rehabilitation therapies, and medical diagnostics [2]. Flexible manipulators also play integral roles in space exploration missions, enabling tasks such as satellite servicing, planetary exploration, and maintenance of space infrastructure [3]. In addition, several research studies about flexible manipulator have been conducted to enhance their performance: modeling [4], optimization [5,6,7], and control [8].

In this context, several approaches have been proposed to identify the dynamic parameters for implementing control schemes that enhance the dynamic performance in the execution of the afore-mentioned applications [9]. Considering, robotic manipulators with rigid link and transmissions different parameter identification methods have been applied, such as least squares, extended Kalman filter, Adaptive Linear Neuron (Adaline) neural networks, Hopfield recurrent neural networks, and genetic algorithms [10].

In this context, several approaches have been proposed to identify the dynamic parameters for implementing control schemes that enhance the dynamic performance in executing the applications mentioned above [9]. Considering robotic manipulators with rigid links and transmissions, different parameter identification methods have been applied, such as least squares, extended Kalman filter, Adaptive Linear Neuron (Adaline) neural networks, Hopfield recurrent neural networks, and genetic algorithms [10].

Gray-box model identification methods have widely been applied to flexible-link manipulators. The identification of a two-link flexible manipulator belonging to a class of multi-input, multi-output (MIMO) nonlinear systems was carried out by using adaptive time-delay neural networks (ATDNNs) [11]. The identified model based on modal responses of individual modes was evaluated; this approach allowed obtaining the parameters of the modal model of a flexible-link manipulator [12]. The generalized orthonormal basis functions (GOBF) were used for model identification of flexible-link manipulators [13]. Moreover, The stiffness and damping ratio of a 3-TPT parallel manipulator with flexible links were identified using simulation and experiment in [14]. An array of fundamental system identification procedures, which includes the ARX (AutoRegressive eXogenous method), SSEST (State-Space Estimation method), N4SID (Numerical Algorithm for Subspace State-Space System Identification), ERA/OKID (Eigensystem Realization Algorithm combined with the Observer/Kalman Filter Identification method), and TFEST (Transfer Function Estimation method) methods were applied to flexible-link manipulators [15]. In this direction, the model identification of single-link flexible manipulator was performed in [12,13,15], and the two-link flexible manipulator model identification was also considered in [11].

However, the approaches mentioned above do not permit obtaining the dynamic parameters based on the complete model of the manipulation, i.e., these approaches updated the parameters of a simplified model that represents the flexible-link manipulator dynamics.

Several approaches to identifying the parameters of flexible structures based on their input/output analysis and evolutionary algorithms have been successfully implemented. A modified genetic algorithm (GA) strategy was proposed to improve the accuracy and computational time for parameter identification of multiple degree-of-freedom structural systems in [16]. A GA-based substructural identification strategy for large structural systems was conducted in [17] using an improved identification method based on multi-feature GA. The inverse identification of elastic properties of composite materials was carried out using a hybrid GA-ACO-PSO algorithm in [18]. The structural parameter identification with evolutionary algorithms and correlation functions was carried out in [19]. A hybrid identification method in [20] is applied to structural health monitoring to detect the reduction of stiffness with limited sensors and contaminated measurements by applying evolutionary algorithms. The parameter identification of the sound absorption model of porous materials based on a modified particle swarm optimization algorithm was performed in [21]. Nevertheless, the approach mentioned above has not been applied to flexible manipulators. In this context, it is necessary to develop parameter identification methods that permit the identification of the physical parameters of flexible manipulators. Consequently, the present contribution proposed a parameter identification method to estimate the dynamic parameters of a flexible-link manipulator based on the complete model. Thus, the dynamic model is initially obtained using the finite element method and the Lagrange principle. Then, an optimization problem minimizes the difference between numerical and experimental outputs to determine the set of parameters using evolutionary algorithms. A comparative analysis to obtain the identified parameters is established using genetic algorithms, particle swarm optimization, and differential evolution. The proposed identification approach permitted the determination of the dynamic parameters based on the complete dynamic model of the flexible-link manipulator, which is different from the approaches reported in the literature that identify a simplified model.

The paper is organized into five sections. Section 2 presents the flexible-link manipulator modeling and the parameter identification approach. Section 3.2 shows the case study wherein the proposed parameter identification approach is applied. Then, Section 4 presents the experimental results. Finally, Section 5 presents the conclusions and future work.

2. Materials and Methods

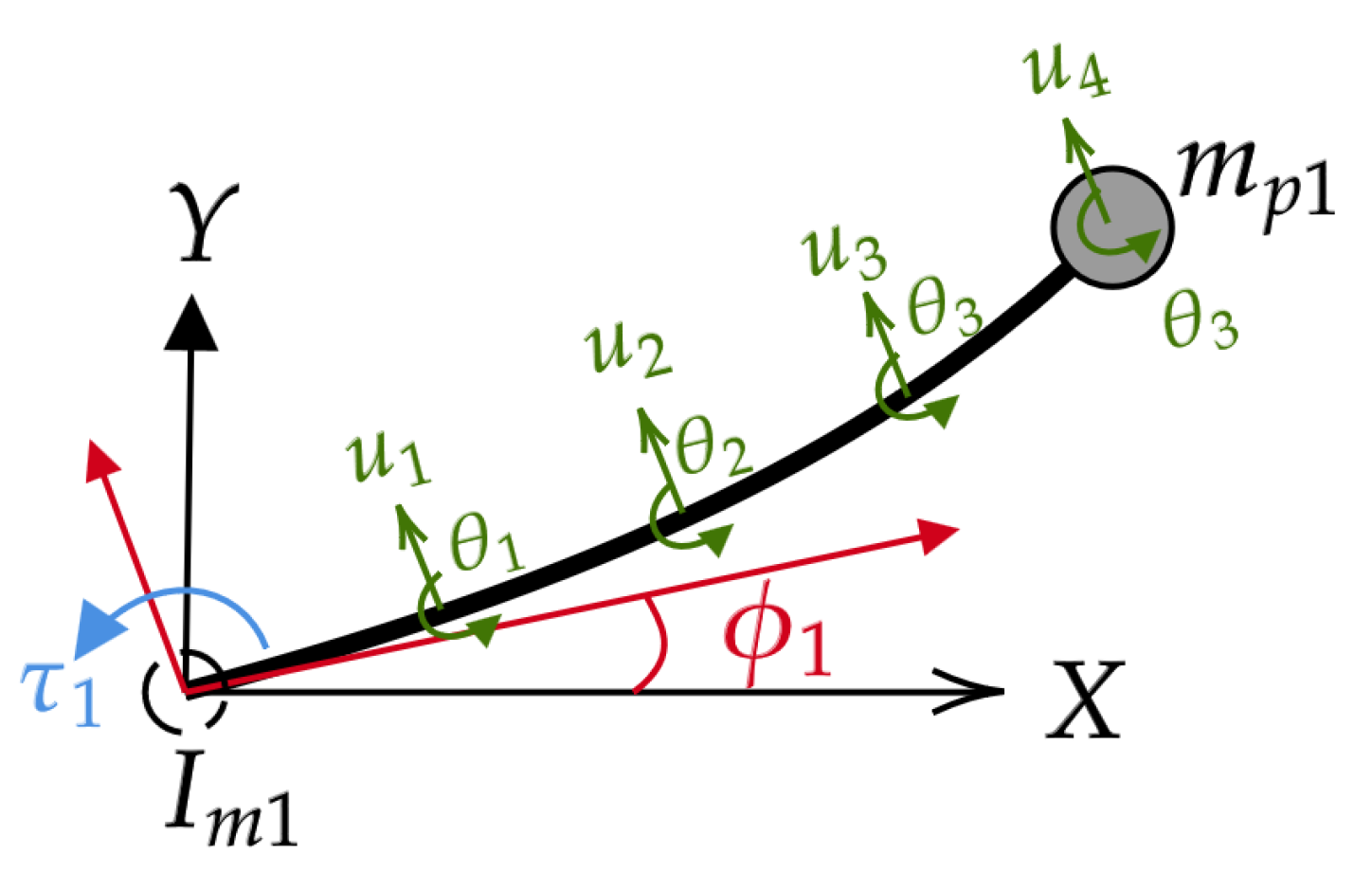
2.1. Flexible-Link Manipulator Dynamics

Several methods have been used to obtain the dynamic equation of flexible-link manipulators. These methods can be summarized into four main approaches: lumped-parameter system [22], Assumed Modes Method (AMM) [23,24], perturbation method [24] and Finite Element (FE) method [25,26]. The methods above lead to the dynamic equation of the flexible-link manipulator in the following form:

$$\mathbf{M}\left(\mathbf{q}\right)\ddot{\mathbf{q}}+\mathbf{h}\left(\mathbf{q},\dot{\mathbf{q}}\right)+\mathbf{C}\dot{\mathbf{q}}+\mathbf{K}\mathbf{q}=\mathbf{f}$$

(1)

where $\mathbf{q}$ is the vector of generalized coordinates, $\mathbf{M}\left(\mathbf{q}\right)$ is the total inertia matrix, $\mathbf{h}(\mathbf{q},\dot{\mathbf{q}})$ is the the Coriolis/centripetal vector, $\mathbf{C}$ is the total damping matrix, $\mathbf{K}$ is the total stiffness matrix, and $\mathbf{f}$ is the vector of generalized force/torque inputs. The control inputs correspond to the generalized force/torque $\tau$ applied by motors or actuators in the vector generalized force/torque $\mathbf{f}$.

Differently from the rigid body manipulator models, the flexibility of the links introduces additional generalized coordination to the model. Thus, the control inputs are less than the number of generalized coordinates.

The least-squares methods have been widely applied to identify the parameters of the rigid body manipulators [9,10]. However, the traditional method for parameter identification based on the least-squares method widely applied to rigid body manipulators can not be applied to flexible-links manipulators since the identified parameters can not express the control inputs as a linear combination of the parameters. Therefore, an alternative approach should be proposed to identify the parameters of the flexible-link manipulators.

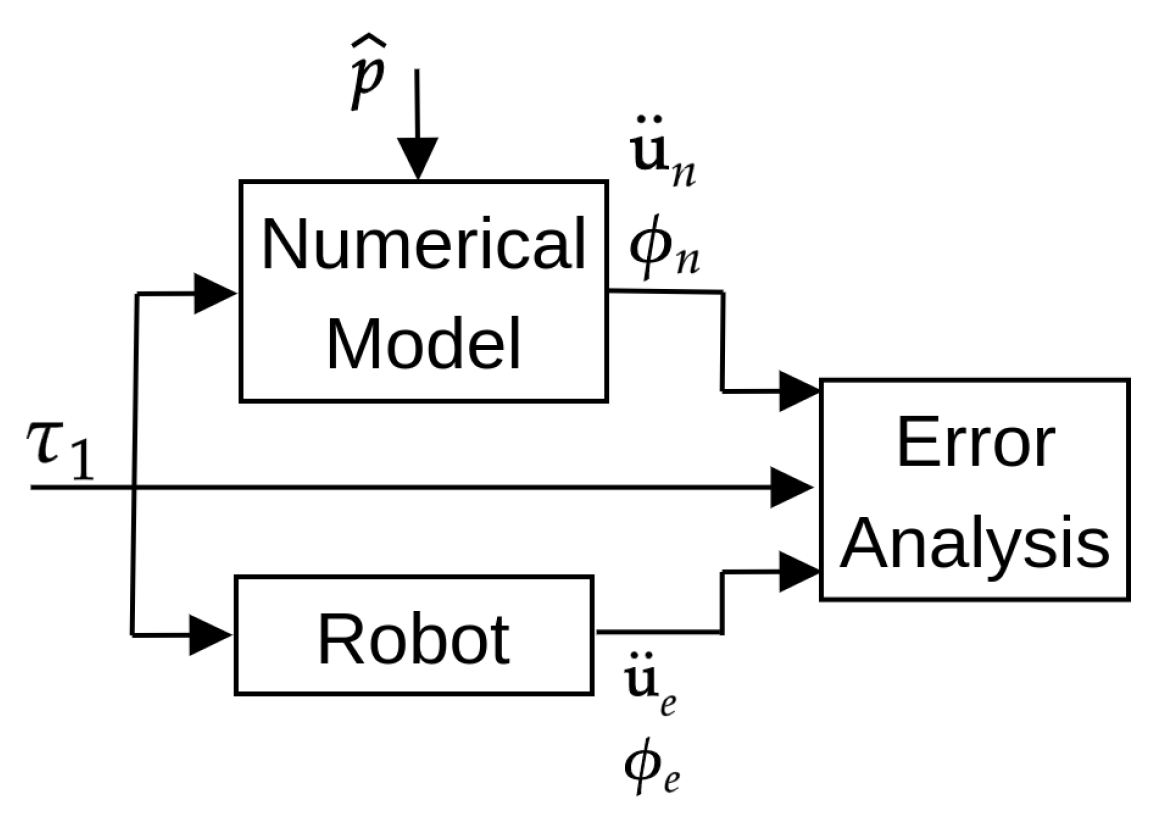
2.2. Parameter Identification Approach

Inverse problems are employed to estimate system parameters by examining experimental inputs/outputs to infer the characteristics or properties of a given system. This process involves working backward from the effects or outputs of a system to determine the underlying causes or parameters that govern its behavior. Mathematical models that describe the relationship between inputs and outputs are often formulated to estimate system parameters. These models are then inverted to obtain the best-fit parameters that align with the experimental outputs to the numerical model outputs [18,20].

The present approach aims at identifying the parameters of the flexible-link manipulator based on an inverse problem approach that adjusts the parameters of the model to minimize the differences between the experimental inputs/outputs of the manipulator and the numerical model of Section 2.1.

The proposed approach is presented in the diagram of Figure 1. This approach is composed of two main steps: experimental measurements of the flexible link-manipulator inputs/outputs and numerical procedure.

Initially, the actuator’s inputs and the generalized coordinate’s outputs are measured. For this approach, the inputs correspond to the actuator torques (${\tau }_1$), and the outputs correspond to joint angles (${\varphi }_e$) and the acceleration at the tip of the link. The dynamic behavior of the flexible-link manipulator encompasses the joint motion and the vibration of the flexible link. For this purpose, two different inputs should be considered for the actuator torque: $a)$ a pulse input to mainly excite the flexible link dynamics and $b)$ a step input to excite the joint dynamics. Moreover, the measurement outputs of the generalized coordinates are the joint actuator of the actuator ($\varphi$) and the link’s tip acceleration (${\ddot{u}}_e$).

Then, the numerical procedure to minimize the difference between the numerical model outputs (${\ddot{u}}_e$ and ${\varphi }_e$) and the measurement outputs of the prototype by fitting the parameters to be identified within the numerical model. The numerical model outputs ${\ddot{u}}_e$ and ${\varphi }_e$ correspond to the link’s tip acceleration and joint angle, respectively. Moreover, the Frequency Response Function (FRF) is obtained to evaluate the vibratory dynamics of the flexible link by applying the pulse torque and measuring the link’s tip acceleration. The minimization of the output difference between the experimental measurements and numerical model outputs derives from an optimization problem that aims at minimizing the objective function $J\left(\widehat{\mathbf{p}}\right)$.

$$\underset{\widehat{\mathbf{p}}\in ({\widehat{\mathbf{p}}}_l,{\widehat{\mathbf{p}}}_r)}{min}J\left(\widehat{\mathbf{p}}\right)$$

(2)

where $\mathbf{p}$ is the identified parameters vector, and the objective function is defined as $J\left(\widehat{\mathbf{p}}\right)=\left|\right|FR{F}_e-FR{F}_n\left(\mathbf{p}\right)\left|\right|+\left|\right|{\varphi }_e-{\varphi }_n\left(\mathbf{p}\right)\left|\right|$.

The optimization problem of Eq. (2) can be solved by using evolutionary algorithms such as Genetic Algorithms (GA), Differential Evolution (DE), and Particle Swarm Optimization (PSO).

3. Case Study: One-Link Flexible Manipulator

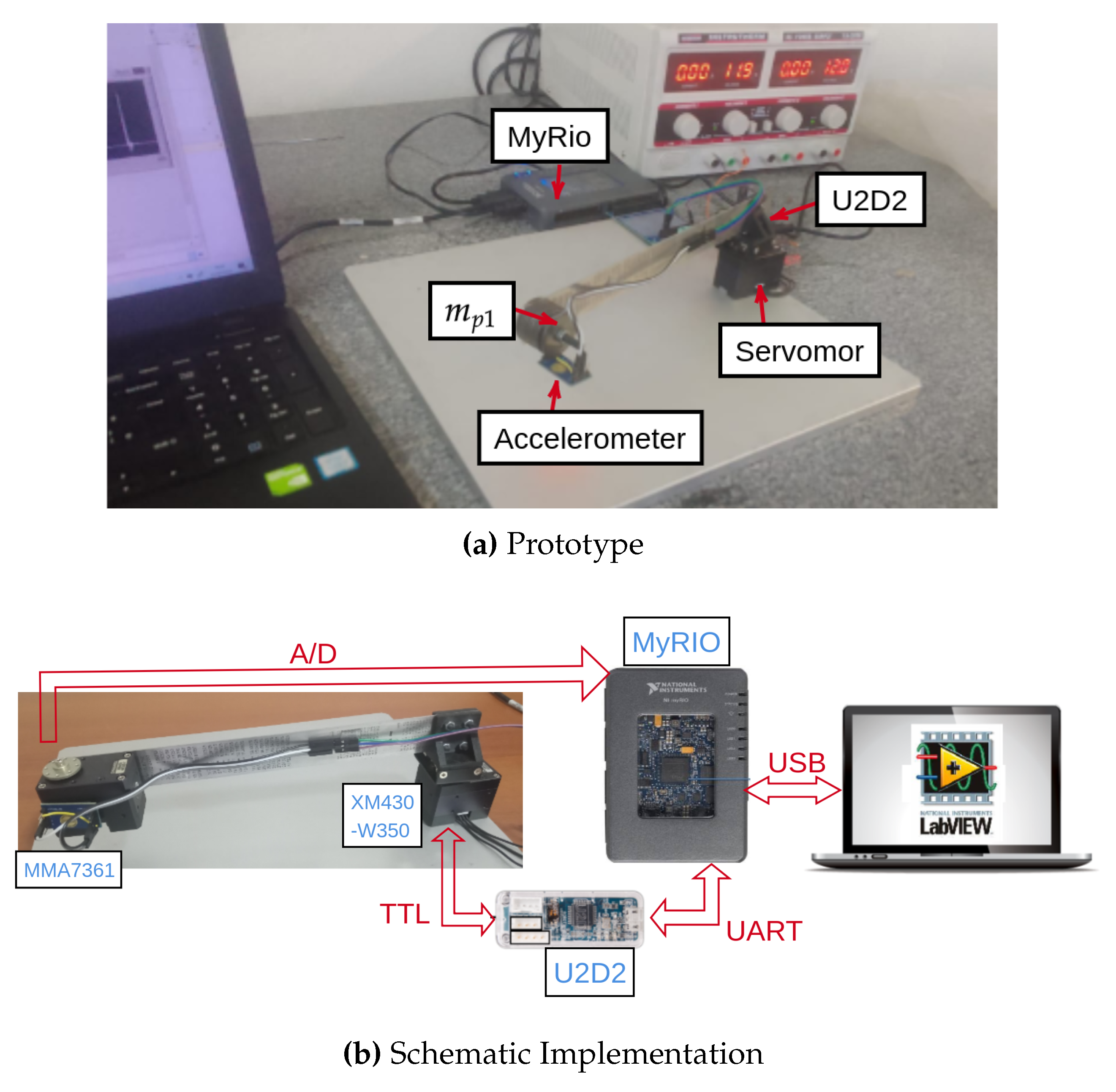
3.1. Testbed

Figure 2a shows the prototype of the one-link flexible manipulator used in the experimental application. The servomotor applies the input torque (${\tau }_1$). The outputs are the joint angle ($\varphi$) and the link’s tip acceleration (${\ddot{u}}_4$), which are measured by the servomotor encoder and the tip’s link accelerometer, respectively.

Figure 2b shows the schematic diagram of the flexible manipulator’s instrumentation, data acquisition, and actuation. The NI myRIO board controls the XM430-W350 Dynamixel servomotor, and the U2D2 interface couples the servomotor and the NI myRIO board. The accelerometer MMA7361 is connected to the input of the A/D (Analog to Digital Converter). The programs of NI myRIO were coded using LabVIEW ®.

3.2. Numerical Model

The schematic model of the one-link flexible manipulator is presented in Figure 3. The manipulator has one revolute joint defined by the angle ${\varphi }_1$. The inertia of the actuator hub is defined as $I_{m1}$, the flexible link with length $l_1$ and Young modulus E is attached to the actuator hub. Moreover, a payload mass $m_{p1}$ is attached at the link’s tip. Initially, the flexible link is split into four Euler-Bernoulli beam elements, as presented in Figure 3. The link length is defined as $l_i=$0.197m. The link cross-section area A is defined as a rectangle with dimensions $h=0.001$m by $b=0.0266$m; thus, $A=bh$, and the moment of inertia of the cross-section area is $I=b{h}^3/12$. Moreover, the mass density is $\rho =$6404.3 kg/m³ and the payload mass is $m_{p1}$=0.09466 kg.

The finite element model was applied to obtain the dynamic equation of the manipulator according to the procedure presented in [25,26]. Thus, the dynamic equation is presented in Eq. (3).

$${\mathbf{M}}_1\left({\mathbf{q}}_1\right){\ddot{\mathbf{q}}}_1+{\mathbf{h}}_1({\mathbf{q}}_1,{\dot{\mathbf{q}}}_1)+{\mathbf{C}}_1{\dot{\mathbf{q}}}_1+{\mathbf{K}}_1{\mathbf{q}}_1+{\mathbf{f}}_b={\mathbf{f}}_1$$

(3)

where ${\mathbf{f}}_1={\left[\begin{array}{cccccccc}{\tau }_1& 0& 0& 0& 0& 0& 0& 0\end{array}\right]}^T$ means that the input torque ${\tau }_1$ of the motor is applied only on the joint ${\varphi }_1$. The generalized coordinates are defined as ${\mathbf{q}}_1={\left[\begin{array}{cc}{\varphi }_1& {\psi }_1\end{array}\right]}^T$ with ${\psi }_1$ being generalizes coordinates of the link ${\psi }_1={\left[\begin{array}{cccccccc}{u}_1& {\theta }_1& u_2& {\theta }_2& u_3& {\theta }_3& u_4& {\theta }_4\end{array}\right]}^T$. Moreover, ${\mathbf{M}}_1\left(\mathbf{q}\right)$ is the total inertia matrix, ${\mathbf{h}}_1({\mathbf{q}}_1,{\dot{\mathbf{q}}}_1)$ is the Coriolis/centripetal vector, and ${\mathbf{K}}_1$ is the total stiffness matrix. The motor applies the input torque ${\tau }_1$; the outputs considered in the model are the joint angle of the motor $\varphi$ and the link’s tip acceleration defined as ${\ddot{u}}_n=l_1{\ddot{\varphi }}_1+{\ddot{u}}_4$.

The mass matrix and the total stiffness matrix of Eq. (3) can be written in the following form:

$$\left\{\begin{array}{cc}\hfill {\mathbf{M}}_1\left({\mathbf{q}}_1\right)& =\left[\begin{array}{cc}{m}^{{\varphi }_1{\varphi }_1}& {\mathbf{m}}^{{\varphi }_1{\psi }_1}\\ {\mathbf{m}}^{{\psi }_1{\varphi }_1}& {\mathbf{M}}^{{\psi }_1{\psi }_1}\end{array}\right]\hfill \\ \\ \hfill {\mathbf{K}}_1& =\left[\begin{array}{cc}0& \mathbf{0}\\ \mathbf{0}& {\mathbf{K}}^{{\psi }_1{\psi }_1}\end{array}\right]\hfill \end{array}\right.$$

(4)

where ${\mathbf{M}}^{{\psi }_1{\psi }_1}$ is related to the transverse displacements or the elastic degrees of freedom of the links that correspond to ${\psi }_1$; ${\mathbf{m}}^{{\varphi }_1{\psi }_1}$ indicates the coupling between the joint ${\varphi }_1$ and these elastic degrees of freedom ${\psi }_1$, and ${\mathbf{m}}^{{\psi }_1{\varphi }_1}={\mathbf{m}}^{{\varphi }_1{\psi }_{1}T}$; $m^{{\varphi }_1{\varphi }_1}$ takes into account the dynamics of the joint. Moreover, ${\mathbf{K}}_{{\psi }_1{\psi }_1}$ of the total stiffness matrix is the elementary stiffness matrix of the link; the total stiffness matrix does not have a coupling between the joint motion and the elastic degrees of freedom.

${\mathbf{C}}_1$ of Eq. (3) is the damping matrix which is based on the Rayleigh damping formulation with ${\mathbf{C}}_1=\alpha {\mathbf{M}}^{{\psi }_1{\psi }_1}+\beta {\mathbf{K}}^{{\psi }_1{\psi }_1}$ where $\alpha$ and $\beta$ are constants of proportionality.

Moreover, ${\mathbf{f}}_b$ considers the viscous friction and Coulomb friction of the motor; thus:

$${\mathbf{f}}_b={\left[\begin{array}{cccccccc}v\dot{\varphi }+{\tau }_{c}sgn\left(\dot{\varphi }\right)& 0& 0& 0& 0& 0& 0& 0\end{array}\right]}^T$$

(5)

where v is the viscous friction coefficient, ${\tau }_c$ is the Coulomb torque, and $sgn(.)$ refers to the sign function.

The inertia, joint friction, stiffness, and damping parameters significantly influence the manipulator dynamics. Nevertheless, these parameters cannot be measured experimentally. Therefore, the parameters to be identified in the flexible-link manipulator model are set in the vector $\widehat{\mathbf{p}}=\left[\begin{array}{cccccc}\widehat{E}& \widehat{I_m}& \widehat{v}& \widehat{{\tau }_c}& \widehat{\alpha }& \widehat{\beta }\end{array}\right]$

4. Results and Discussion

The parameter identification process based on the finite-element model was carried out according to the method of Section 2.2. The parameters to be identified are set in vector $\widehat{\mathbf{p}}=\left[\begin{array}{cccccc}\widehat{E}& \widehat{I_m}& \widehat{v}& \widehat{{\tau }_c}& \widehat{\alpha }& \widehat{\beta }\end{array}\right]$. The objective function $J\left(\widehat{\mathbf{p}}\right)$ to be minimized is defined as the difference between the outputs of the numerical model and those measured experimentally in the flexible-link manipulator prototype. Thus, the objective function $J\left(\widehat{\mathbf{p}}\right)$ considers the frequency domain response that takes into account the vibrational dynamics of the flexible link and the time domain response of the motor angle $\varphi$ as presented in Eq. (6).

$$J\left(\widehat{\mathbf{p}}\right)=\frac{\parallel FR{F}_e-FR{F}_n\left(\widehat{\mathbf{p}}\right)\parallel }{\parallel FR{F}_e\parallel }+\frac{\parallel {\varphi }_e-{\varphi }_n\left(\widehat{\mathbf{p}}\right)\parallel }{\parallel {\varphi }_e\parallel }$$

(6)

The experimental frequency response functions $FR{F}_e$ (toque input/link’s tip acceleration) were measured on the flexible manipulator by applying a pulse torque input ${\tau }_1$ at the motor and the link’s tip acceleration; the response output of the acceleration at the tip ${\ddot{u}}_e$ in a range of 0-50 Hz and steps of 0.2Hz.

The identified parameters are obtained by solving the optimization problem of Eq. (2). Table 1 shows the set of lower (${\widehat{\mathbf{p}}}_l$) and upper bounds (${\widehat{\mathbf{p}}}_r$) on the design variables that correspond to the identified parameters, thus $\widehat{\mathbf{p}}\in ({\widehat{\mathbf{p}}}_l,{\widehat{\mathbf{p}}}_r)$.

This optimization problem is solved by using Differential Evolution (DE), Genetic Algorithm (GA), and Particle Swarm Optimization (PSO). Some assumptions are defined regarding the numerical application of the evolutionary algorithms:

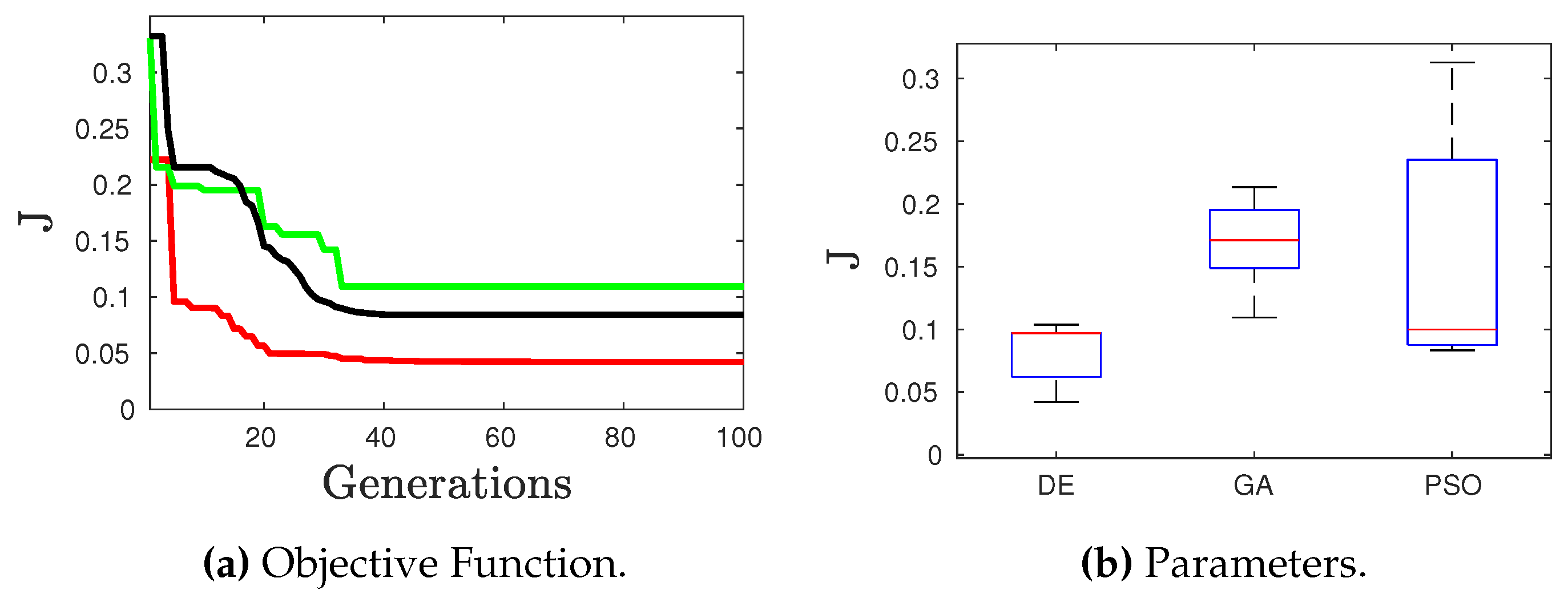
• The parameters used by the DE algorithm [27] are: population size $NP$=100, weighting factor F=0.5, crossover probability $CR=0.8$, 100 generations and $DE/rand/1/exp$ strategy for the generation of candidates.
• The parameters used by the GA algorithm [28] are: $NP$=100, selection rate $SR$=0.5, crossover rate $CR=0.8$, mutation rate $MR=$0.2 and 100 generations.
• The parameters used by the PSO algorithm [29] are: number of particles $NP$=100, inertia weigth w=1.4, $c_1=1.5$, $c_2=$2.5 and 100 iterations.
• Stopping criteria considered was the maximum number of generations/iterations.
• The study cases were run 10 times, and the average values were obtained.
• To establish a fair comparison among the evolutionary algorithms. The seeds $0,1,2,\cdots ,9$ were used to initialize the random generator for each simulation.
• The aforementioned case studies, using DE, GA, and PSO, were run 10 times to obtain the upcoming average values.

Figure 4 shows the convergence of the objective function $J\left(\widehat{\mathbf{p}}\right)$ of Eq. (6) during the optimization process solution considering the best solution for DE, GA and PSO. Figure 4a exhibits the best individual of the population along the generations. One can observe that the DE algorithm exhibited the best performance because it obtained the minimum value of $J\left(\widehat{\mathbf{p}}\right)$ at the twelfth generation. The GA algorithm presented the worst behavior for solving the optimization problem.

For comparison purposes, the dispersion range obtained by minimizing the objective function $J\left(\widehat{\mathbf{p}}\right)$ of Eq. (6) 10 times considering the evolutionary algorithms is presented in Figure 4b. The PSO presented the highest dispersion of the results; nevertheless, GA obtained the highest mean, indicating that the solution of the optimization problem using GA is inaccurate in the present application. On the other hand, DE presented the lowest mean and dispersion.

Table 2 shows the best result of Figure 4a obtained using evolutionary algorithms. One can observe that the results found using the considered evolutionary algorithms are similar. It is worth pointing out that the joint friction and damping coefficients identified showed an expressive difference. These results are expected because the model has three types of energy dissipation: joint friction (viscous and Coulomb friction) and the proportional damping of the flexible link.

Figure 5 shows the dynamic response obtained from the DE, GA, and PSO algorithms. These results considered the joint angle $\varphi$ and the FRF that were used in the objective function $J\left(\widehat{\mathbf{p}}\right)$. These results consider the FRF (see Figure 5b, obtained by applying a pulse torque input in the motor) and the joint angle $\varphi \left(t\right)$ (see Figure 5a). As expected, the solution of the numerical model using the identified parameters obtained with DE is close to the experimental results (see Figure 5a). In addition, the FRF obtained with the numerical model considering the identified parameters are satisfactory (see Figure 5b) close to the peak; nevertheless, expressive differences are observed for high frequencies.

Model Validation

The model validation aims at evaluating confidence in the estimated robot model by comparing the numerical model outputs to the experimental outputs. The model validation approach is presented in Figure 6. A test input ${\tau }_1$ is applied to the flexible robot prototype (of Fig. ) to obtain the experimental outputs ${\ddot{u}}_e$ and ${\varphi }_e$. In this procedure, the same test input ${\tau }_1$ is applied to the numerical model considering the identified parameters $\widehat{\mathbf{p}}$ to obtain the numerical outputs ${\ddot{u}}_n$ and ${\varphi }_n$. Finally, an error analysis assesses the differences between numerical and experimental outputs.

The model validation of the proposed identification approach was carried out, and the following results were obtained:

• Three different test inputs were considered: triangular (see Figure 7b), pulse (see Figure 8b), and sinusoidal that considers the positive part (see Figure 9b).
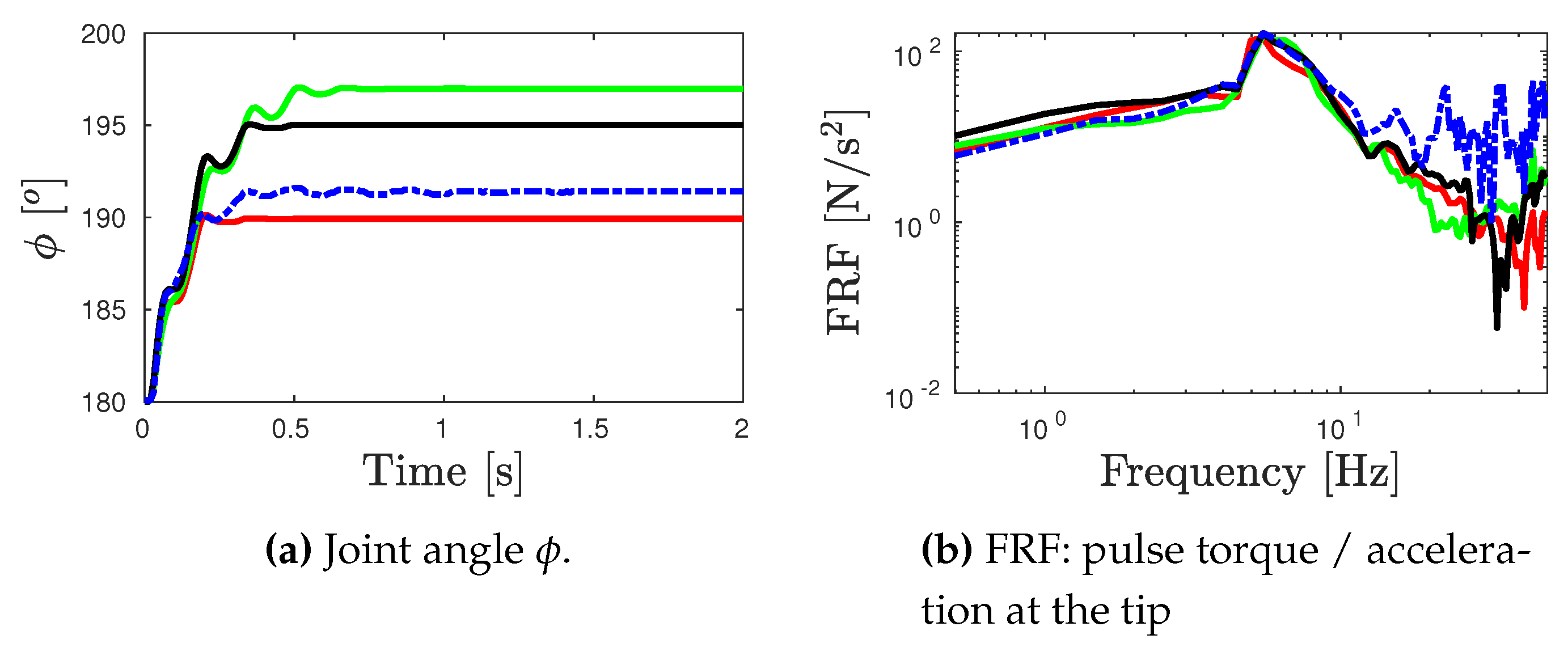
• The identified parameters $\widehat{\mathbf{p}}$ considered in the numerical model were obtained for the best case of DE, and these parameters are presented in Table 2.
• The numerical and experimental outputs of the joint angle $\varphi$ for the corresponding test inputs are presented in Figure 7b, Figure 8b and Figure 9b.
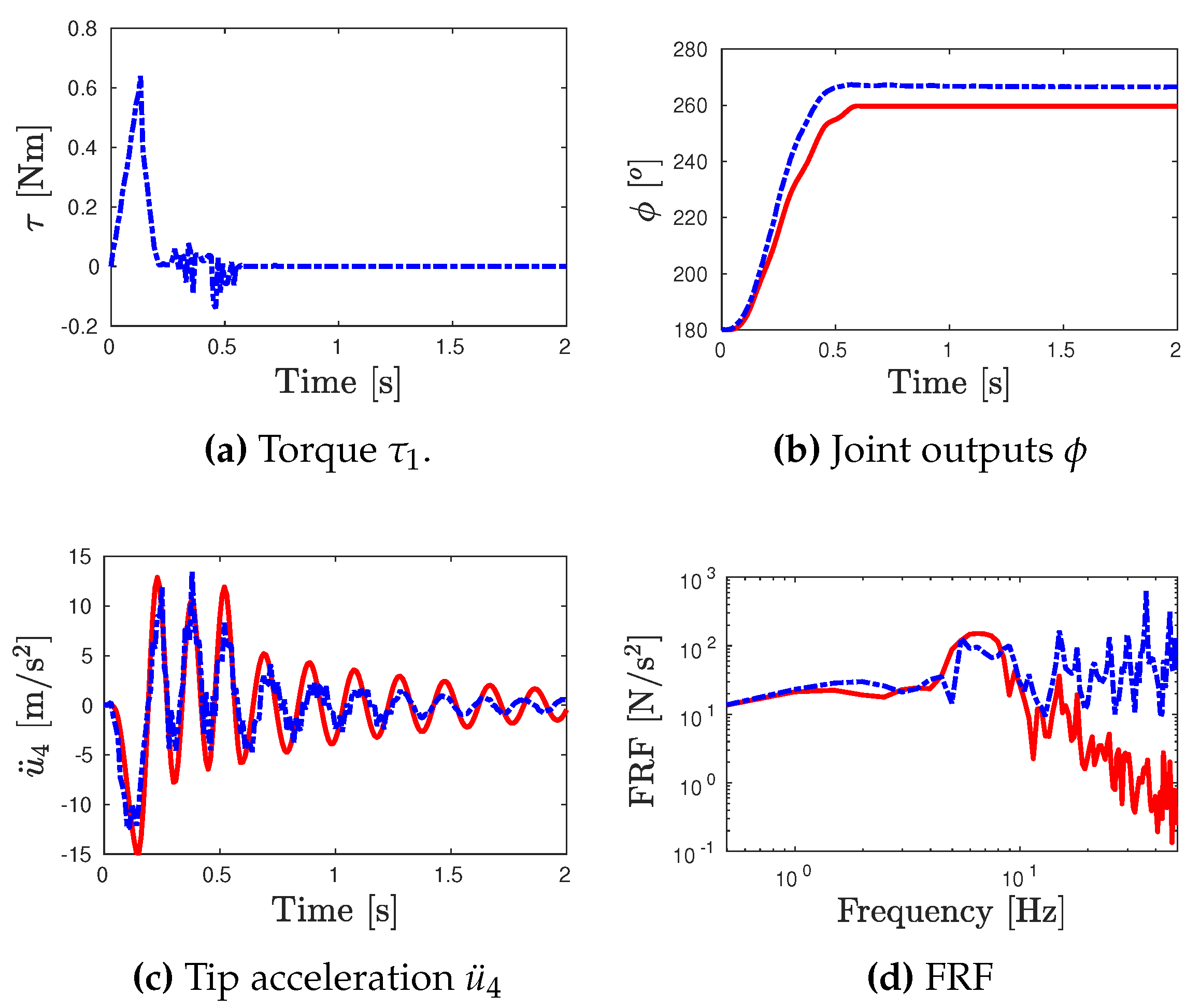
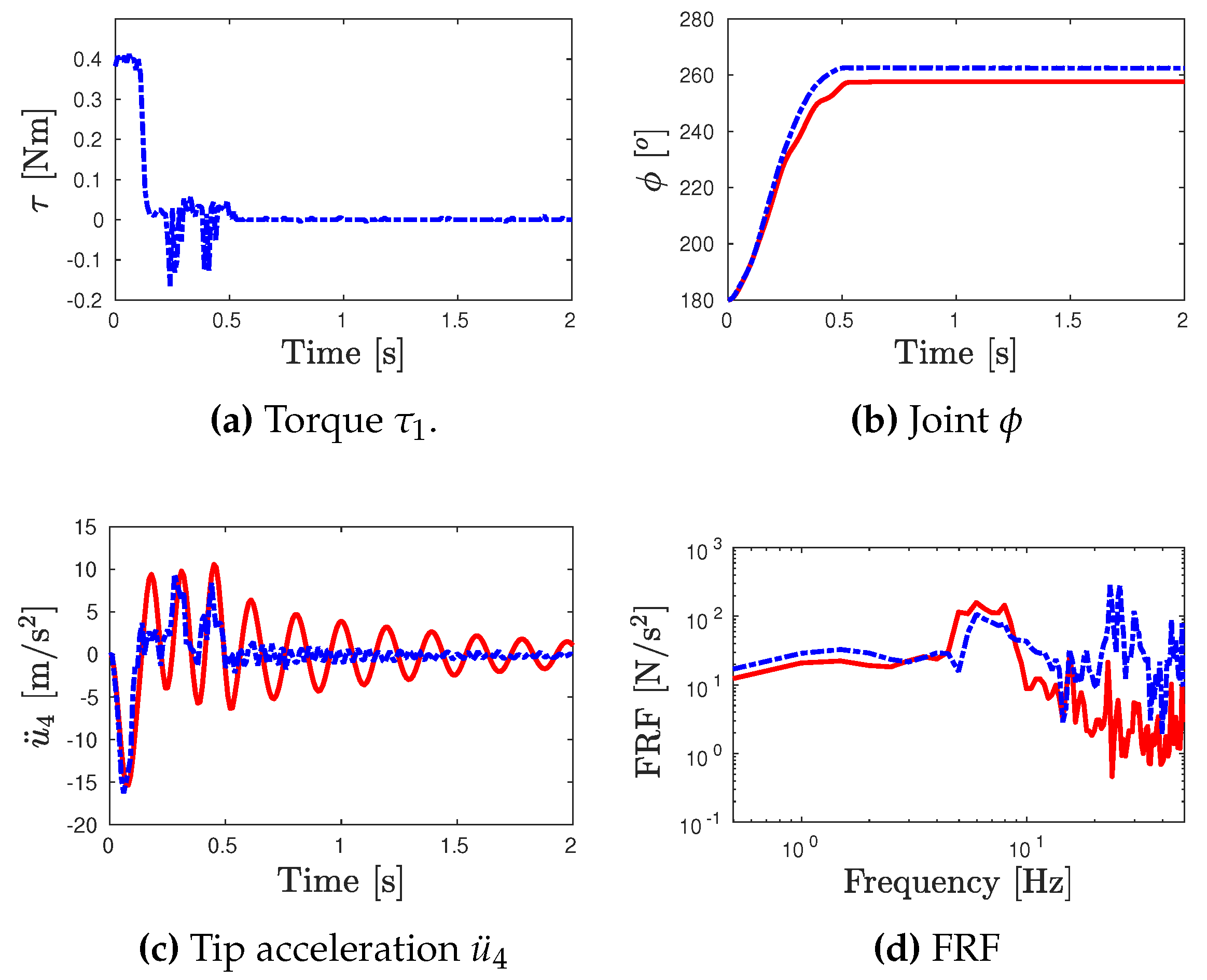
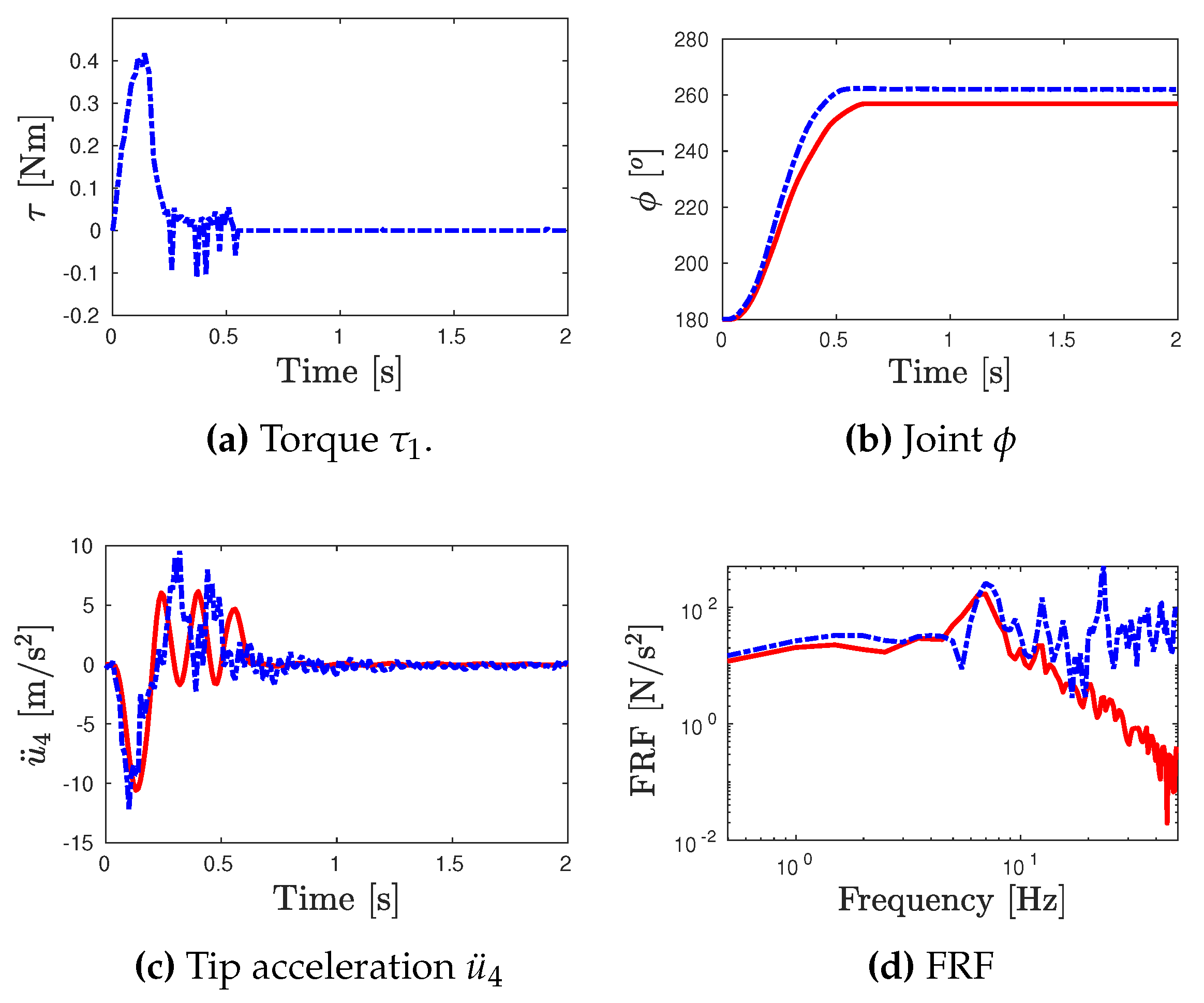
• The numerical and experimental outputs of link’s tip acceleration $\ddot{u}$ for the corresponding test inputs are presented in Figure 7c, Figure 8c and Figure 9c. Moreover, the frequency response functions (toque input/link’s tip acceleration) for the numerical and experimental outputs are also computed in Figure 7d, Figure 8d and Figure 9d.
• For the error analysis, the error between the numerical model and experimental outputs in terms of the joint angle $\varphi$ and the FRFs are estimated based on the Normalized Root Mean Square Error (RMSE) according to the expressions of Eq. (7).

  $$NRMS{E}_{\varphi }=\frac{\sqrt{{\displaystyle \sum _{t=0}^T}{({\varphi }_e\left(t\right)-{\varphi }_n\left(t\right))}^2}}{\overline{{\varphi }_e\left(t\right)}}NRMS{E}_{FRF}=\frac{\sqrt{{\displaystyle \sum _{f=0}^F}{(FR{F}_e\left(f\right)-FR{F}_n\left(f\right))}^2}}{\overline{FR{F}_e\left(f\right)}}$$

  (7)

  where $T=$2s and $F=$15Hz. The Root Mean Square (RMS) outputs are presented in Table 3.

The results of the model validation show that the numerical model adequately represents the dynamic behavior of the flexible-link manipulator according to the results of Figure 7, Figure 8 and Figure 9 . Moreover, the normalized RMSEs of Table 3 show that the percentage error between the numerical and experimental output is less acceptable for the present application. However, the numerical FRF does not have an acceptable representation for high frequencies due to the noise introduced by the accelerometer during the experiment.

5. Conclusions

The present contribution presented a novel approach to identifying the dynamic parameters of flexible-link manipulators, such as inertia, stiffness, and damping parameters, based on the inverse problem associated with the parameter identification problem. The proposed approach minimizes the difference between the numerical model’s outputs and the experimental measurements of the prototype. Then, an optimization problem that minimizes the difference between numerical and experimental outputs was used to determine the dynamic parameters. This optimization was solved using genetic algorithms, particle swarm optimization, and differential evolution. The proposed identification approach permitted the determination of the dynamic parameters based on the complete dynamic model of a one-link flexible manipulator.

The DE was demonstrated to be the most appropriate algorithm to solve the optimization associated with the identification approach compared to the PSO and GA. The proposed methodology permitted the estimation of the joint friction, stiffness, and damping coefficients of the flexible link that experimental measurements can not determine. Additionally, the numerical model with the identified parameters adequately simulates the dynamics regarding the joint response and the vibrational flexible-link dynamics of the manipulator, as demonstrated in the model validation approach.

Finally, the results showed that the approach represents an alternative method to identify the dynamic parameters of flexible-link manipulators. Further research will aim to develop control schemes of flexible-link manipulators based on the identified model.