Fixed-time Consensus-based Attitude Control of Large Telescope On-orbit Construction

This study investigates the fixed-time consensus-based attitude control problem for large telescope on-orbit construction subject to discrete-time communication, unknown tiny disturbance torque, model uncertainty, and actuator saturation under an undirected communication graph. Motivated by the need to save wireless communication resources, the communication scheme was designed to exploit interference, which can save communication resources in proportion to the number of modular unit mirrors. Then, a fixed-time observer with discrete-time communication was proposed, which also handles the unknown channel attenuation problem when exploiting information interference. Moreover, based on the backstepping procedure and the suitably defined adaptive compensation law, the fixed-time attitude consensus control law was proposed to handle unknown tiny disturbance torque, model uncertainty, and actuator saturation. Finally, comparative simulation results were provided to verify the effectiveness of the fixed-time observer and proposed fixed-time control law.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

High-precision, large-diameter space telescopes, unaffected by Earth’s atmosphere and offering high image clarity, are progressively becoming the primary focus for future remote sensing. According to the Rayleigh criterion, the resolution of a telescope is positively correlated with its aperture. However, due to the limited volume and payload of existing launch vehicles, both integral and deployable space telescope structures can easily reach the upper aperture limit. Consequently, the most feasible solution proposed at present is to construct a large aperture space telescope through modular launch and in-orbit assembly [1,2]. For instance, the primary mirror of the James Webb Space Telescope consists of 18 separate hexagonal mirrors.

As shown in Figure 1, with standardized interfaces, modular unit mirror can reconfigure into a large-aperture space telescope in space. If unit mirrors

1 \dots n

are sequentially docked with the main structure 0, the assembly time of the large aperture telescope in orbit will be long, furthermore, the asymmetric moment of inertia will increase the cost of attitude control. Therefore, a new approach is proposed here, firstly, performing consensus-based attitude maneuver of unit mirrors

1 \dots n

, achieving coordinated posture adjustments for modules 0…n, and then docking units

1 \dots n

with the main structure 0 simultaneously. The above consensus-based attitude maneuver of unit mirrors can be regarded as a branch of spacecraft swarm, which requires real-time and high-precision attitude maneuvers applicable to complex constraints such as unknown tiny disturbance torque, model uncertainty, actuator saturation, discrete-time communication, and limited communication.

Numerous studies referring to real-time and high-precision control for spacecraft have proposed various control strategies [3,4]. Asymptotically stable control laws were developed in [5] and [6], where the convergence rate was at best exponential with an infinite settling time. Moreover, finite-time control laws have been developed. Many efforts have been devoted to the finite-time consensus problem of systems with general linear [7], high-order integrator [8,9], other nonlinear dynamics such as typical Euler-Lagrange dynamics [10] and attitude consensus of spacecraft [11,12,13]. Compared with asymptotic control, which requires the system to converge to a given bound exponentially, a finite-time control law can lead to a faster convergence rate (near the equilibrium point) [14,15]. However, the convergent time resulting from finite-time control schemes heavily depends on the initial conditions. Therefore, efforts are now being made toward developing a fixed-time control scheme, which removes the dependence of convergence time on initial conditions [4,16]. Fixed-time output consensus problem of heterogeneous linear multi-agent systems was researched in [17]. Fixed-time consensus for integrator-type multi-agent systems was investigated in [18]. Fixed-time consensus control scheme for high-order multi-agent systems in the presence of external disturbances was proposed in [19]. Fixed-time distributed coordination control for multiple Euler-Lagrange systems was investigated in [20]. Fixed-time formation tracking control of multiple hypersonic flight vehicles with uncertain dynamics and external disturbances was presented in [21]. Fixed-time control law for a group of spacecraft, of which the attitude is represented by modified Rodrigues parameters (MRPs), has been designed in [22,23,24,25,26,27]. Note that because the MRPs are not globally nonsingular, the controller applies only to nonsingular initial attitudes. The distributed fixed-time attitude consensus controller for multiple spacecraft of which the attitude description is based on a unit quaternion, has been proposed in [28,29]; however, the controllers cannot be used where unknown tiny disturbance torque, model uncertainty and actuator saturation exist simultaneously. Further, as the overview of fixed-time cooperative control of multiagent systems in [30] illustrates, the discrete-time communication problem in fixed-time cooperative control is a challenging issue.

Another coordination problem that constrains large telescope on-orbit construction is the design of the communication scheme when a large number of modular unit mirrors are involved in the system or the inter-modules communication channel is limited [31]. Owing to the constraints of modular unit mirror quality, the capability of onboard computers and communication systems is significantly limited. Physically, modular unit mirrors use a low bandwidth to communicate within the system and a high bandwidth for data transfer back to Earth. The low bandwidth of communications limits the availability and timeliness of information transfer among modular unit mirrors. Consequently, if the onboard computer requires more information than the modular unit mirrors can transmit over the communication channel, the system would not be sustained in a complex space environment [32]. Traditionally, orthogonal channel access methods avoid interference by employing time division multiplex access (TDMA) or orthogonal frequency division multiplexing (OFDM) [31]. Consequently, the amount of communication resources (e.g., energy and time consumption) required increases logarithmically with the number of modular unit mirrors. However, the wireless interference property of the channel allows distributed transmitters to broadcast electromagnetic waves in the same frequency band simultaneously and superimpose them at some receivers, which can be advantageous in saving communication resources. Motivated by this observation, the wireless multiple-access channel (WMAC) was proposed in [31] to model the value at the receiver in a wireless communication scheme that exploits interference. Based on this model, a formation consensus control strategy using interference for autonomous agents moving in a plane with continuous-time single integrator dynamics was presented in [33]. The design in [34] exploited interference to achieve finite-time max-consensus in a single integrator multi-agent system. And the event-triggered attitude tracking control exploiting interference for multiple spacecraft systems with tiny disturbance torque is proposed in [35]. It can be concluded from the aforementioned discussion that, considering complex constraints such as unknown tiny disturbance torque, model uncertainty, actuator saturation and discrete-time communication, exploiting interference for large telescope on-orbit construction is nontrivial but effective in saving communication resources. The main contributions of this work are summarized as follows.

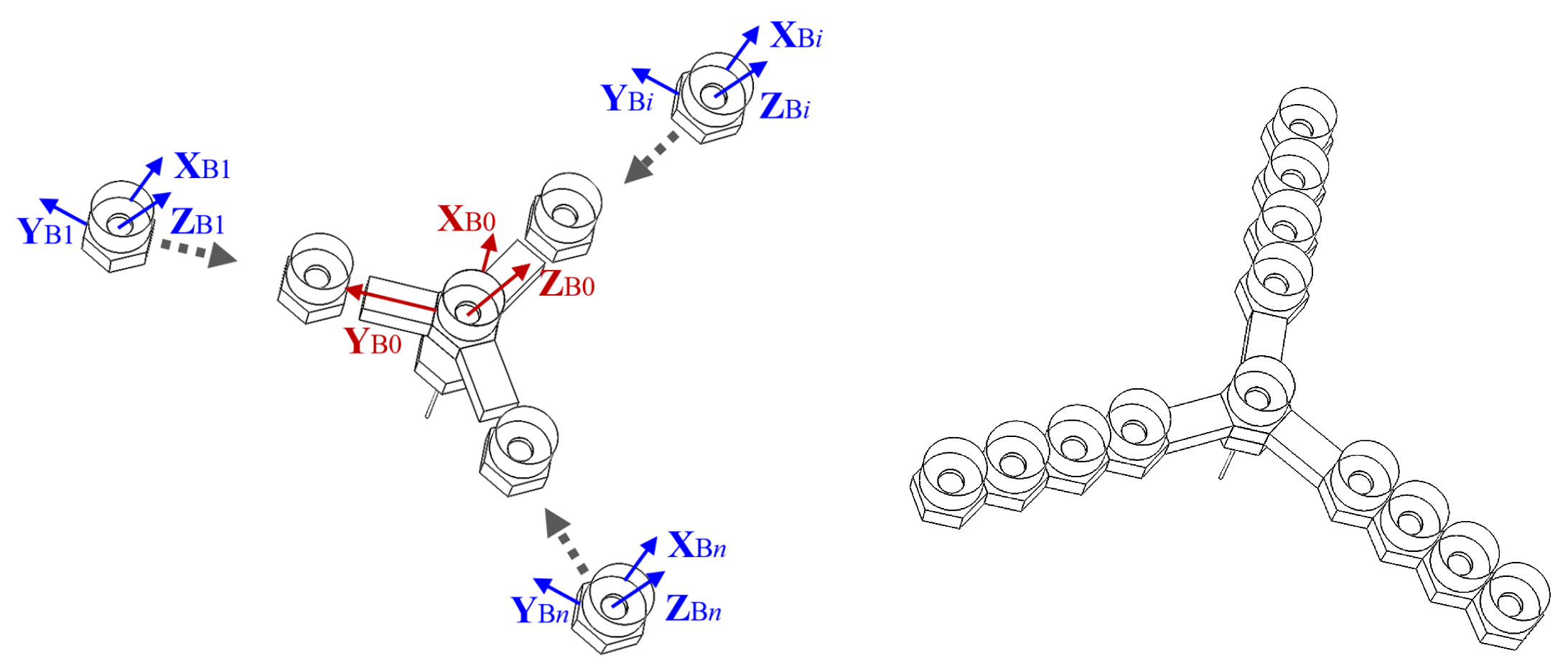
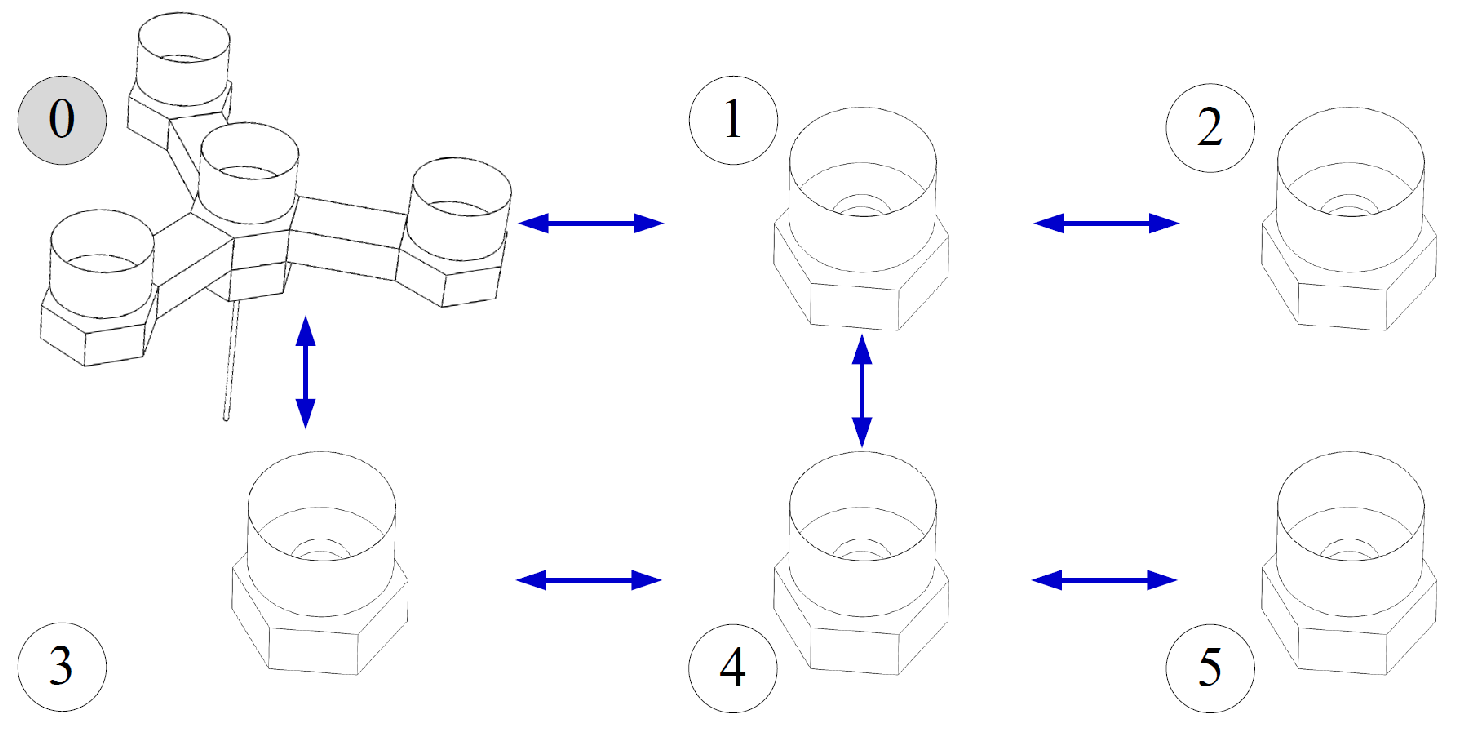
Different from the traditional sequential docking of multiple modules, a new procedure of large telescope on-orbit construction is proposed. Firstly, perform consensus-based attitude maneuver of modular units and main structure, then docking modular units with the main structure simultaneously. In addition, the communication scheme in this study is based on wireless communication interference. As a consequence, the assembly time, cost of attitude control and communication resources are saved proportional to the number of modular unit mirrors.
To provide a singularity-free solution for consensus-based attitude-tracking control, the attitude description is based on a unit quaternion throughout the study. Then, a fixed-time observer was presented for each unit mirrors to cooperatively estimate the attitude quaternion of the main structure. The observer in this study also handles the discrete-time communication in engineering and unknown channel attenuation when exploiting communication interference.
Finally, an observer-based fixed-time control scheme was designed to ensure that the attitude of each unit mirror accurately forms a predetermined attitude angle relative to the main structure. Compared with the existing fixed-time consensus-based attitude controls for multiple satellites [22,23,24,25,26,28,29,36], the controller proposed in this study can simultaneously handle nontrivial issues such as unknown tiny disturbance torque, model uncertainty, and actuator saturation. This implies that the control algorithm introduced in this paper is more applicable in engineering.

Notations: Throughout this study,

R

is introduced as a set of real numbers.

R_{> 0}

represents a set of positive real numbers. The set of non-negative real numbers is defined by

R_{\geq 0}

. The set of non-negative integers is defined as

N_{\geq 0}

. The entry into positions

(i, j)

of matrix

A \in R^{n \times m}

is denoted by

{[A]}_{i, j}

I_{n}

denotes the n-dimensional identity matrix, and

0_{n \times m}

denotes the matrix of zeros with n rows and m columns. ⊗ refers to the Kronecker product. The skew-symmetric matrix

x^{\times} \in R^{3 \times 3}

of a vector

x = {[x_{1}, x_{2}, x_{3}]}^{T} \in R^{3}

is defined by

x^{\times} = [\begin{matrix} 0 & - x_{3} & x_{2} \\ x_{3} & 0 & - x_{1} \\ - x_{2} & x_{1} & 0 \end{matrix}]

. Considering a discrete-time system, the value of state

X \in R^{n}

at instant

t_{k}, k \in N_{\geq 0}

is abbreviated as

X (k)

. A continuous function

α (\cdot) : [0, a) \to R_{\geq 0}

is said to belong to class

K

α (\cdot)

is strictly increasing and subjects to

α (0) = 0

. A continuous function

β (\cdot) : [0, b) \to R_{\geq 0}

is said to belong to class

K_{\infty}

if it belongs to class

K

b = \infty

and

lim_{r \to \infty} β (\infty) = \infty

. Function

γ : R_{\geq 0} \times R_{\geq 0} \to R_{\geq 0}

is of class

K ϖ

\forall t \in R_{\geq 0}, γ (\cdot, t) \in K

, and

γ (s, \cdot)

is decreasing to zero for each

s \in R_{> 0}

. For a vector

X = {[x_{1} \dots x_{n}]}^{T} \in R^{n}

, and a constant

v \in R

{| X |}^{v} = {[| x_{1} |^{v} \dots {| x_{n} |}^{v}]}^{T}

, we define

{sig}^{v} (X) = {[sign (x_{1}) | x_{1} |^{v} \dots sign (x_{n}) {| x_{n} |}^{v}]}^{T}

, where

sign (\cdot)

is the sign function.

Table 1 summarizes all symbols employed in the current work.

2. Preliminary Knowledge

2.1. Kinematics and Dynamics

2.1.1. Quaternion Kinematics

Throughout this study, the attitude of modular unit mirror labeled

i \in {1 \dots n}

regarding an inertial frame is described by unit quaternion

Q_{i} = {[q_{0, i}, q_{i}^{T}]}^{T}

, where

q_{0, i} \in R

and

q_{i} = {[q_{1, i}, q_{2, i}, q_{3, i}]}^{T} \in R^{3}

denote the scalar and vector parts of that quaternion, respectively. For any initial quaternion

Q_{i}

and maneuver quaternion

Q_{j} = {[q_{0, j}, q_{1, j}, q_{2, j}, q_{3, j}]}^{T}

, the final quaternion

Q_{k} = {[q_{0, k}, q_{1, k}, q_{2, k}, q_{3, k}]}^{T}

can be expressed as [37]:

\begin{matrix} \begin{matrix} Q_{k} & = [\begin{matrix} q_{0, j} & - q_{1, j} & - q_{2, j} & - q_{3, j} \\ q_{1, j} & q_{0, j} & - q_{3, j} & q_{2, j} \\ q_{2, j} & q_{3, j} & q_{0, j} & - q_{1, j} \\ q_{3, j} & - q_{2, j} & q_{1, j} & q_{0, j} \end{matrix}] [\begin{matrix} q_{0, i} \\ q_{1, i} \\ q_{2, i} \\ q_{3, i} \end{matrix}] = [\overset{︷}{Q_{j}^{\times}}] Q_{i} . \end{matrix} \end{matrix}

(1)

Furthermore, we state two important properties of unit quaternion here [35]:

Property 1.

Quaternions

{[1, 0, 0, 0]}^{T}

and

{[- 1, 0, 0, 0]}^{T}

correspond to the same attitude.

Property 2.

Every unit quaternion

Q_{i}

satisfies

\begin{matrix} q_{0, i}^{2} + q_{i}^{T} q_{i} = 1 . \end{matrix}

(2)

The vectors

ω_{i} = {[ω_{1, i}, ω_{2, i}, ω_{3, i}]}^{T} \in R^{3}, i \in \{1 \dots n\}

represent the attitude angular velocity of modular unit mirror labeled i in the body-fixed frame. Based on [38], the attitude kinematics for the modular unit mirror labelled i is described by:

\begin{matrix} \begin{matrix} {\dot{Q}}_{i} = \frac{1}{2} [\begin{matrix} 0 & - ω_{1, i} & - ω_{2, i} & - ω_{3, i} \\ ω_{1, i} & 0 & ω_{3, i} & - ω_{2, i} \\ ω_{2, i} & - ω_{3, i} & 0 & ω_{1, i} \\ ω_{3, i} & ω_{2, i} & - ω_{1, i} & 0 \end{matrix}] Q_{i} . \end{matrix} \end{matrix}

(3)

The kinematics in (3) can be transformed into

\begin{matrix} \begin{matrix} {\dot{Q}}_{i} = \frac{1}{2} P_{i} ω_{i}, \end{matrix} \end{matrix}

(4)

where

P_{i} : = [\begin{matrix} - q_{1, i} & - q_{2, i} & - q_{3, i} \\ q_{0, i} & - q_{3, i} & q_{2, i} \\ q_{3, i} & q_{0, i} & - q_{1, i} \\ - q_{2, i} & q_{1, i} & q_{0, i} \end{matrix}] .

It is worth noting that by some calculations, the following property of matrix

P_{i}

is derived

\begin{matrix} \begin{matrix} P_{i}^{T} P_{i} = I_{3} . \end{matrix} \end{matrix}

(5)

2.1.2. Attitude Dynamics

According to [39], the dynamics of modular unit mirror

i \in {1 \dots n}

is described as follows

\begin{matrix} \begin{matrix} J_{i} {\dot{ω}}_{i} + ω_{i} \times J_{i} ω_{i} = T_{i} + δ_{T i}, \end{matrix} \end{matrix}

(6)

where

J_{i} \in R^{3 \times 3}

is the inertia matrix,

T_{i} \in R^{3}

is the control torque, and

δ_{T i}

is the unknown tiny disturbance torque.

Defining

v_{i} = P_{i} ω_{i} \in R^{4}

, using appropriate procedures and definitions, (4)and (6) can be transformed into

\begin{matrix} \begin{matrix} {\dot{Q}}_{i} & = \frac{1}{2} v_{i} \\ {\dot{v}}_{i} & = h_{i} (Q_{i}, v_{i}) + g_{i} (Q_{i}) (T_{i} + δ_{T i}), \end{matrix} \end{matrix}

(7)

where

h_{i} (Q_{i}, v_{i}) = {\dot{P}}_{i} P_{i}^{T} v_{i} - P_{i} J_{i}^{- 1} ((P_{i}^{T} v_{i}) \times J_{i} (P_{i}^{T} v_{i})),

g_{i} (Q_{i}) = P_{i} J_{i}^{- 1} .

2.2. Graph

The information flow among the modular unit mirrors is modeled by an undirected connected graph

G = (V, ε, C)

, where

V = \{1 \dots n\}

represents the node set and

ε \subseteq V \times V

denotes the edge set. Directed arc

(i, j) \in ε

if and only if node i transmit information to node j. The (unknown) channel fading coefficient matrix

C

with

{[C]}_{i, j} = c_{i, j}

is also called the adjacency matrix of graph

G

\forall i, j \in V

c_{i, i} = 0

c_{i, j} > 0

if and only if

(i, j) \in ε

, and

c_{i, j} = 0

otherwise. Notably, as

G

is undirected, one has

c_{i, j} = c_{j, i}, \forall i, j \in V

Considering the attitude consensus tracking control, an augmented undirected graph

\bar{G} = (\bar{V}, \bar{ε}, \bar{C})

is defined to describe the network topology associated with the system consisting of n follower modular unit mirrors and one virtual leader, where the attitude of the main structure acts as the virtual leader, labeled 0.

\bar{V} = \{0 \dots n\}

is the augmented node-set, and

\bar{ε} \subseteq \bar{V} \times \bar{V}

is the augmented edge set. The (unknown) channel fading coefficient matrix

\bar{C}

with

{[\bar{C}]}_{i, j} = c_{i, j}

is the adjacency matrix of graph

\bar{G}

\forall i, j \in \bar{V}

c_{i, i} = 0

, and

c_{i, j} > 0

if and only if

(i, j) \in \bar{ε}

, and

c_{i, j} = 0

otherwise. Referring to the definition of the connected graph in reference [40], for any pair of nodes

i, j \in \bar{V}

, if there exists a path joining i and j, the augmented undirected graph

\bar{G}

is connected. Hence, the augmented undirected graph

\bar{G}

is connected if there exists at least one path from the leader node to every follower node. We define a matrix associated with

\bar{G}

H \in R^{n \times n}

, where

{[H]}_{i, i} = \sum_{j = 0}^{n} c_{i, j}

and

{[H]}_{i, j} = - c_{i, j}

for

i \neq j, i, j \in \{1 \dots n\}

. The following lemma about the

\bar{G}

is presented:

Lemma 1

([41]). If the graph

\bar{G}

is connected, then

H

is symmetric and positive definite.

2.3. WMAC Model for Wireless Interference

In the wireless communication scheme of large telescope on-orbit construction, interference results from the simultaneous access of modular unit mirrors to the available frequency spectrum. Physically, a set of distributed unit mirrors broadcast electromagnetic waves in the same frequency band and then superimposes them at some receiver. To describe a wireless (radio-based) communication scheme that exploits interference, the wireless multiple-access channel (WMAC) model has been widely used. For more information, refer to [31]. The ideal model of the WMAC considering a set of transmitting unit mirrors, say

j, j \in \{0 \dots n\}

, broadcasts real-valued vector signals

Γ_{j} \in R^{p}

, then the value at the receivers

i, i \in \{1 \dots n\}

after interference should be modeled as in [33]:

Υ_{i} = \sum_{j = 0 \dots n} c_{j, i} Γ_{j} .

How interference can be exploited for large telescope on-orbit construction at hand is clarified in Section IV.

3. Problem Description

As a typical multi-spacecraft system, large telescope on-orbit construction require real-time and high-precision attitude maneuvers in the presence of unknown tiny disturbance torque, model uncertainty, actuator saturation, limited communication and discrete-time communication. Motivated by the above requirements, this study considers large telescope on-orbit construction described by (7), and the communication among modular unit mirrors is over the wireless channel that exploits interference. Owing to the discrete communication requirement of engineering, all modular unit mirrors exchange information through wireless channels at discrete broadcasting instants

\forall t_{k} \in R_{\geq 0}, k \in N_{\geq 0}

, and the interval between any two broadcasting instants is

Δ t \in R_{> 0}

This study aims to develop a control strategy to ensure all the attitudes of the modular unit mirrors converge to the desired relative configuration, as shown in Figure 1 (a), within a fixed time, recalling (1), that is,

\begin{matrix} \begin{matrix} \begin{matrix} \forall i \in \{1 \dots n\}, lim_{t \to \infty} Q_{i} & = [\overset{︷}{D_{i}^{\times}}] Q^{*}, \end{matrix} \end{matrix} \end{matrix}

(8)

where

Q^{*} = {[q_{0}^{*}, q^{* T}]}^{T}

is the reference attitude quaternion, which acting as a virtual leader,

q_{0}^{*} \in R

and

q^{*} : = {[q_{1}^{*}, q_{2}^{*}, q_{3}^{*}]}^{T} \in R^{3}

D_{i} = {[d_{0, i}, d_{i}^{T}]}^{T}

is the pre-designed constant desired attitude difference between the attitude of modular unit mirror i (orientation of frame

O_{B i} X_{B i} Y_{B i} Z_{B i}

) and the virtual leader (orientation of frame

O_{B 0} X_{B 0} Y_{B 0} Z_{B 0}

) ,

d_{0, i} \in R

d_{i} : = {[d_{1, i}, d_{2, i}, d_{3, i}]}^{T} \in R^{3}

Equation (8) can be rewritten as:

\begin{matrix} \begin{matrix} \begin{matrix} lim_{t \to \infty} {[\overset{︷}{D_{i}^{\times}}]}^{- 1} Q_{i} = Q^{*}, \end{matrix} \end{matrix} \end{matrix}

(9)

which means that the aim of the study can be regarded as developing a control strategy to achieve consensus for

{[\overset{︷}{D_{i}^{\times}}]}^{- 1} Q_{i}, \forall i \in \{1 \dots n\}

and

Q^{*}

In the following, we present some assumptions for the large telescope on-orbit construction system:

Assumption 1.

The undirected graph

\bar{G}

is connected.

Assumption 2.

The reference attitude quaternion is a constant vector, that is,

{\dot{Q}}^{*} = 0

Assumption 3.

The unknown tiny disturbance torque

δ_{T i}

of modular unit mirror

i, \forall i \in V

satisfies the following inequality:

| | δ_{T i} | | \leq ϖ_{i} < \infty,

where

ϖ_{i} \in R_{> 0}

Assumption 4.

Considering the possible change in the inertia matrix

J_{i}, i \in \{1 \dots n\}

caused by fuel consumption, the model of the modular unit mirrors should satisfy

\forall i \in V

k_{\underset{̲}{J}} I_{3} \leq J_{i} \leq k_{\bar{J}} I_{3}

k_{\underset{̲}{g}} \leq | | g_{i} (Q_{i}) | | \leq k_{\bar{g}}

| | h_{i} (Q_{i}, v_{i}) | | \leq k_{h} | | v_{i} {| |}^{2}

, where

k_{\underset{̲}{J}}

k_{\bar{J}}

k_{\underset{̲}{g}}

k_{\bar{g}}

, and

k_{h}

are positive constants.

4. Design of Communication System Exploiting Interference

Based on the ideal model of the WMAC in section II, at the broadcasting instants

t_{k}

, for each modular unit mirror i in the swarm, the two broadcasting states from the neighbor

j, (j, i) \in \bar{ε}

are designed as:

\begin{matrix} \begin{matrix} \begin{matrix} μ_{j}^{(1)} (t_{k}) & = {\hat{Q}}_{j}^{*} (t_{k}) \in R^{4}, \\ μ_{j}^{'} & = 1, \end{matrix} \end{matrix} \end{matrix}

(10)

where

{\hat{Q}}_{j}^{*}

is the estimation of

Q^{*}

from modular unit mirror j, which will be is introduced in Section

V

. It follows that after wireless interference, the modular unit mirror

i, i \in \{1 \dots n\}

receives two signals:

\begin{matrix} \begin{matrix} \begin{matrix} ζ_{i}^{(1)} (t_{k}) & = \sum_{j = 0 \dots n} (c_{j, i} (t_{k}) {\hat{Q}}_{j}^{*} (t_{k})) \in R^{4}, \\ ζ_{i}^{'} (t_{k}) & = \sum_{j = 0 \dots n} c_{j, i} (t_{k}) \in R_{> 0} . \end{matrix} \end{matrix} \end{matrix}

(11)

To address the (unknown) channel fading coefficient

c_{j, i}

of edge

(j, i) \in \bar{ε}

, signals

ζ_{i}^{(1)}

in (11) should be normalized. Then, signal

ζ_{i}^{(1)}

is converted to

η_{i}^{(1)} (t_{k}) \in R^{4}

as follows:

\begin{matrix} \begin{matrix} \begin{matrix} η_{i}^{(1)} (t_{k}) = \frac{ζ_{i}^{(1)} (t_{k})}{ζ_{i}^{'} (t_{k})} = {[\sum_{j = 0 \dots n} c_{j, i} (t_{k}) I_{4}]}^{- 1} \sum_{j = 0 \dots n} (c_{j, i} (t_{k}) {\hat{Q}}_{j}^{*} (t_{k})) . \end{matrix} \end{matrix} \end{matrix}

(12)

Remark 1.

The communication scheme designed in this section uses interference to allow n follower unit mirrors and 1 virtual leader to broadcast electromagnetic waves in the same frequency band simultaneously. Therefore, for each modular unit mirror in the group, the communication scheme can save communication time (compared with TDMA) or the number of wireless bands (compared with OFDM) proportionally to the number of neighbors.

5. Proposed Solution

In this section, a discrete-time fixed-time observer was presented. It also exploits the channel-superposition property. Then, the backstepping control scheme was proposed for aligning the modular unit mirrors to achieve consensus in a fixed time based on (9). The control strategy was proven to overcome the limited model uncertainty, unknown tiny disturbance torque, and actuator saturation using the backstepping procedure, adaptive compensation, and Lyapunov stability theory.

Before the presentation of the control scheme, the following lemmas are stated.

Lemma 2.

For

A, B \in R^{n}

, the following inequality holds:

- (B^{T} B - 2 B^{T} A) \leq A^{T} A

Proof.

From the fact

{(B - A)}^{T} (B - A) = B^{T} B - 2 B^{T} A + A^{T} A \geq 0

, Lemma 2 is concluded. □

Lemma 3

([42]). For any

X, Y \in R^{n}

, the following inequality holds

\forall a, b, r \in R_{> 0}

{| X |}^{a} {| Y |}^{b} \leq \frac{a}{a + b} {r | X |}^{a + b} + \frac{b}{a + b} r^{- \frac{a}{b}} {| Y |}^{a + b} .

Lemma 4

([43]).

\forall x_{i} \in R, i \in \{1 \dots n\}

, and for any real number

c \in (0, 1]

{(\sum_{i = 1}^{n} | x_{i} |)}^{c} \leq \sum_{i = 1}^{n} {| x_{i} |}^{c} \leq n^{1 - c} {(\sum_{i = 1}^{n} | x_{i} |)}^{c} .

Lemma 5

([43]).

\forall x_{i} \in R, i \in \{1 \dots n\}

, and for any real number

d > 1

\sum_{i = 1}^{n} | x_{i} |^{d} \leq {(\sum_{i = 1}^{n} | x_{i} |)}^{d} \leq n^{d - 1} \sum_{i = 1}^{n} {| x_{i} |}^{d} .

Lemma 6

([43]).

\forall x_{i}, x_{j} \in R, i, j \in \{1 \dots n\}

, and

0 < e \leq 1 \in R

being a ratio of two odd integers, it follows

| x_{i}^{e} - x_{j}^{e} | \leq 2^{1 - e} {| x_{i} - x_{j} |}^{e} .

Lemma 7

([44]). Consider the discrete-time system

\begin{matrix} \begin{matrix} X (k + 1) & = f (X (k), k), k \geq 0 \\ X (0) & = X_{0}, \end{matrix} \end{matrix}

(13)

where

X \in R^{n}

, and

X (0) \in R^{n}

is the initial value of

X

. Furthermore,

f (X (k), k)

satisfies

f (0, k) = 0, k \geq 0

. If there exists a function

ρ (\cdot) \in K_{\infty}

, two constants

c, q \in R_{> 0}

and Lyapunov function

V (X, k)

satisfying

(1): $ρ (| | X (k) | |) \leq V (X, k),$
(2): $V^{c} (X (k + 1), k + 1) - V^{c} (X (k), k) \leq - q {(V (X (k), k) \cdot V (X (k + 1), k + 1))}^{c},$

Then, the system is practically fixed-time stable, that is, for all

X (0) \in R^{n}

, there exist

ξ > 0

and

T (ξ) \leq T_{m a x} = \frac{1}{q ρ^{c} (ξ)}

, such that

V (X, k) \leq ρ (ξ)

for all

t_{k} > T

Lemma 8

([45]). Consider the system

\begin{matrix} \begin{matrix} \dot{X} = f (X, t), \\ f (0, t) = 0, \end{matrix} \end{matrix}

(14)

where

X \in R^{n}

, if there exists a Lyapunov function

V (X (t))

satisfying

\dot{V} (X (t)) \leq - {(k_{1} V^{a} (X (t)) + k_{2} V^{b} (X (t)))}^{k} + v,

where

k_{1}, k_{2}, a, b, k \in R_{\geq 0}

with

a k < 1

b k > 1

and

v \in R_{> 0}

, then the origin of system (14) is practical fixed-time stable. Furthermore, the residual set of system (14) is represented by

\begin{matrix} \begin{matrix} lim_{t \to T} X | V (X) \leq \min \{k_{1}^{\frac{- 1}{a}} {(\frac{v}{1 - ς^{k}})}^{\frac{1}{k a}}, k_{2}^{\frac{- 1}{a}} {(\frac{v}{1 - ς^{k}})}^{\frac{1}{k b}}\}, \end{matrix} \end{matrix}

(15)

where

0 < ς \leq 1

. The settling time satisfies

T \leq \frac{1}{k_{1}^{k} ς^{k} (1 - a k)} + \frac{1}{k_{2}^{k} ς^{k} (b k - 1)}

5.1. Discrete-Time Fixed-Time Observer

As some modular unit mirrors in the system have no access to the information of virtual leader 0, a properly designed observer should be proposed. First, we define

C_{i} = \sum_{j = 0 \dots n} c_{j, i} I_{4} = ζ_{i}^{'} I_{4}, i \in \{1 \dots n\}

C = diag \{C_{1} \dots C_{n}\}

. Then, represent the estimation of

Q^{*}

from modular unit mirror

i, i \in \{1 \dots n\}

{\hat{Q}}_{i}^{*}

. As illustrated in Section II, the target state

Q^{*}

acts as the virtual leader labeled 0, hence the estimation of

Q^{*}

from modular unit mirror

i = 0

itself is given as

{\hat{Q}}_{0}^{*} = Q^{*}

. During all periods

[t_{k}, t_{k + 1})

, we design a fixed-time observer of the following form:

\begin{matrix} \begin{matrix} {\dot{\hat{Q}}}^{*} & = - \frac{1.92}{Δ t} {M_{0}^{- 1}}^{T} (k) y (k), \\ y (k) & = {\hat{Q}}^{*} (k) - η^{(1)} (k), \end{matrix} \end{matrix}

(16)

where

M_{0} = (H^{T} \otimes I_{4}) C^{- 1}

η^{(1)} \in R^{4 n}

and

{\hat{Q}}^{*} \in R^{4 n}

are the column stacks of

η_{i}^{(1)}

and

{\hat{Q}}_{i}^{*}

, respectively.

According to Property 2 and (12), the following inequality can be obtained:

\begin{matrix} \begin{matrix} {[y (k)]}_{m, 1} & \leq 2, m \in \{1 \dots 4 n\} . \end{matrix} \end{matrix}

(17)

Then we construct a theorem based on the fixed-time observer (16).

Theorem 1.

Consider a random constant virtual leader quaternion

Q^{*}

, the estimation of

Q^{*}

from modular unit mirror

i = 0

itself is given as

{\hat{Q}}_{0}^{*} = Q^{*}

, using the discrete-time observer (16) under Assumptions

1 - 4

, there exists a fixed time

T_{0} \geq 0

such that

\forall {\hat{Q}}^{*} (0) \in R^{4 n}

, the estimation error

{\tilde{Q}}_{i}^{*} = {\hat{Q}}_{i}^{*} - {\hat{Q}}_{0}^{*}, i \in \{1 \dots n\}

converges to any small neighborhood of zero within fixed time

T_{0}

. Further, we define the column stacks of

{\tilde{Q}}_{i}^{*}, i \in \{1 \dots n\}

{\tilde{Q}}^{*} \in R^{4 n}

, for any estimation error range:

| | {\tilde{Q}}^{*} | | \leq \frac{\sqrt{2}}{2} ξ, ξ \in R_{> 0}

the settling time

T_{0}

is bounded by

T_{0} \leq \frac{16 n}{0.09 ξ^{2}} λ_{m a x}^{2} (M_{0}^{- 1}) .

The proof of Theorem 1 is provided in Appendix A.

5.2. Fixed-Time Controller

Denote

E_{i} = {[\overset{︷}{D_{i}^{\times}}]}^{- 1} Q_{i}, i \in \{1 \dots n\}

, and

E = {[\begin{matrix} E_{1}^{T} & \dots & E_{n}^{T} \end{matrix}]}^{T}

, then substituting to (7) we have

\begin{matrix} \begin{matrix} {\dot{E}}_{i} & = D_{i} {\dot{Q}}_{i} = \frac{1}{2} D_{i} v_{i}, \end{matrix} \end{matrix}

(18)

where

D_{i} = {[\overset{︷}{D_{i}^{\times}}]}^{- 1}, i \in \{1 \dots n\}

. Note that by some calculations, the following property of matrix

D_{i}

is derived:

\begin{matrix} \begin{matrix} D_{i}^{T} D_{i} = I_{4} . \end{matrix} \end{matrix}

(19)

We define the first backstepping state as

\begin{matrix} \begin{matrix} X_{1, i} = & E_{i} - {\hat{Q}}_{i}^{*} \in R^{4}, i \in \{1 \dots n\}, \end{matrix} \end{matrix}

(20)

which represents the attitude tracking error of an individual unit mirror i in the sense of (9). Note that the tracking target

{\hat{Q}}_{i}^{*}

is the estimation of the virtual leader state

Q^{*}

from modular unit mirror i. Then, the time derivative of

X_{1, i}

is calculated as

\begin{matrix} \begin{matrix} {\dot{X}}_{1, i} = \frac{1}{2} D_{i} v_{i} - {\dot{\hat{Q}}}_{i}^{*}, \end{matrix} \end{matrix}

(21)

According to Theorem 1 and Assumption 2, after settling time

T_{0}

{\dot{\hat{Q}}}_{i}^{*}

can be approximated to zero. Consequently, the above equation can be rewritten as

\begin{matrix} \begin{matrix} {\dot{X}}_{1, i} = \frac{1}{2} D_{i} v_{i} . \end{matrix} \end{matrix}

(22)

When consensus in the sense of formula (9) is realized, we should have

X_{1, i} = 0_{4}

. A virtual control input is defined as

\begin{matrix} \begin{matrix} {\dot{X}}_{1, i} = f (X_{1, i}) + X_{2, i}, \end{matrix} \end{matrix}

(23)

where

f (X_{1, i}) \in R^{4}

is the virtual controller and

X_{2, i} \in R^{4}

is the second backstepping state. Then, a backstepping procedure is performed to develop the fixed-time controller for each modular unit mirror i as follows

Step 1 .

Construct the first candidate Lyapunov function for

X_{1, i}

as:

\begin{matrix} V_{1, i} = \frac{1}{2} | | X_{1, i} {| |}^{2} + \frac{1}{\frac{k_{2}}{k_{1}} + 1} | | X_{1, i} {| |}^{\frac{k_{2}}{k_{1}} + 1}, \end{matrix}

(24)

where

\frac{1}{2} < k_{1} < 1

and

k_{2} > 1

be two specified rational numbers of the ratio of two odd integers, then the derivative of

V_{1}

\begin{matrix} \begin{matrix} {\dot{V}}_{1, i} & = {(X_{1, i} + X_{1, i}^{\frac{k_{2}}{k_{1}}})}^{T} (f (X_{1, i}) + X_{2, i}), \end{matrix} \end{matrix}

(25)

according to (23) and Lemma 6, one can get

\begin{matrix} \begin{matrix} | X_{2, i} | = & | {({\dot{X}}_{1, i}^{\frac{1}{k_{1}}})}^{k_{1}} - {(f^{\frac{1}{k_{1}}} (X_{1, i}))}^{k_{1}} | \\ \leq & 2^{1 - k_{1}} {| {\dot{X}}_{1, i}^{\frac{1}{k_{1}}} - f^{\frac{1}{k_{1}}} (X_{1, i}) |}^{k_{1}} \\ = & 2^{1 - k_{1}} {| ϵ_{i} |}^{k_{1}}, \end{matrix} \end{matrix}

(26)

where

ϵ_{i} = {\dot{X}}_{1, i}^{\frac{1}{k_{1}}} - f^{\frac{1}{k_{1}}} (X_{1, i})

. By Lemma 3, we obtain

\begin{matrix} \begin{matrix} {(X_{1, i} + X_{1, i}^{\frac{k_{2}}{k_{1}}})}^{T} X_{2, i} \\ \leq & 2^{1 - k_{1}} | X_{1, i} |^{T} | ϵ_{i} |^{k_{1}} + 2^{1 - k_{1}} | X_{1, i}^{\frac{k_{2}}{k_{1}}} |^{T} {| ϵ_{i} |}^{k_{1}} \\ \leq & 2^{1 - k_{1}} (\frac{1}{1 + k_{1}} | | X_{1, i}^{1 + k_{1}} {| |}_{1} + \frac{k_{1}}{1 + k_{1}} | | ϵ_{i}^{1 + k_{1}} {| |}_{1}) + 2^{1 - k_{1}} (\frac{\frac{k_{2}}{k_{1}}}{\frac{k_{2}}{k_{1}} + k_{1}} | | X_{1, i}^{\frac{k_{2}}{k_{1}} + k_{1}} {| |}_{1} + \frac{k_{1}}{\frac{k_{2}}{k_{1}} + k_{1}} | | ϵ_{i}^{\frac{k_{2}}{k_{1}} + k_{1}} {| |}_{1}) . \end{matrix} \end{matrix}

(27)

Substituting (27) into (25) yields

\begin{matrix} \begin{matrix} {\dot{V}}_{1, i} & \leq {(X_{1, i} + X_{1, i}^{\frac{k_{2}}{k_{1}}})}^{T} f (X_{1}) + \frac{2^{1 - k_{1}}}{1 + k_{1}} | | X_{1, i}^{1 + k_{1}} {| |}_{1} + \frac{2^{1 - k_{1}} k_{1}}{1 + k_{1}} | | ϵ_{i}^{1 + k_{1}} {| |}_{1} + \frac{2^{1 - k_{1}} \frac{k_{2}}{k_{1}}}{\frac{k_{2}}{k_{1}} + k_{1}} | | X_{1, i}^{\frac{k_{2}}{k_{1}} + k_{1}} {| |}_{1} + \frac{2^{1 - k_{1}} k_{1}}{\frac{k_{2}}{k_{1}} + k_{1}} | | ϵ_{i}^{\frac{k_{2}}{k_{1}} + k_{1}} {| |}_{1} . \end{matrix} \end{matrix}

(28)

Design the virtual controller as

\begin{matrix} \begin{matrix} f (X_{1}) = - γ_{1} X_{1, i}^{k_{1}} - γ_{2} X_{1, i}^{k_{2}}, \end{matrix} \end{matrix}

(29)

then (28) can be transformed as

\begin{matrix} \begin{matrix} {\dot{V}}_{1, i} \leq & - (γ_{1} - \frac{2^{1 - k_{1}}}{1 + k_{1}}) | | X_{1, i}^{1 + k_{1}} {| |}_{1} - γ_{2} | | X_{1, i}^{1 + k_{2}} {| |}_{1} - (γ_{1} - \frac{2^{1 - k_{1}} \frac{k_{2}}{k_{1}}}{\frac{k_{2}}{k_{1}} + k_{1}}) | | X_{1, i}^{\frac{k_{2}}{k_{1}} + k_{1}} {| |}_{1} - γ_{2} | | X_{1, i}^{\frac{k_{2}}{k_{1}} + k_{2}} {| |}_{1} \\ + \frac{2^{1 - k_{1}} k_{1}}{1 + k_{1}} | | ϵ_{i}^{1 + k_{1}} {| |}_{1} + \frac{2^{1 - k_{1}} k_{1}}{\frac{k_{2}}{k_{1}} + k_{1}} | | ϵ_{i}^{\frac{k_{2}}{k_{1}} + k_{1}} {| |}_{1} . \end{matrix} \end{matrix}

(30)

Step 2 .

Construct the second candidate Lyapunov function for

X_{2, i}

\begin{matrix} V_{2, i} = | | d (f (X_{1, i}), {\dot{X}}_{1, i}) {| |}_{1}, \end{matrix}

(31)

where

d (f (X_{1, i}), {\dot{X}}_{1, i}) = \int_{f (X_{1, i})}^{{\dot{X}}_{1, i}} {(s^{\frac{1}{k_{1}}} - f {(X_{1, i})}^{\frac{1}{k_{1}}})}^{2 - k_{1}} d s,

we have

\begin{matrix} \begin{matrix} {\dot{V}}_{2, i} = & (2 - k_{1}) \frac{\partial X_{1, i}^{T}}{\partial t} \frac{- \partial f^{\frac{1}{k_{1}}} (X_{1, i})}{\partial X_{1, i}} \int_{f (X_{1, i})}^{{\dot{X}}_{1, i}} {(s^{\frac{1}{k_{1}}} - f^{\frac{1}{k_{1}}} (X_{1, i}))}^{1 - k_{1}} d s + \frac{\partial {\dot{X}}_{1, i}^{T}}{\partial t} {({\dot{X}}_{1, i}^{\frac{1}{k_{1}}} - f^{\frac{1}{k_{1}}} (X_{1, i}))}^{2 - k_{1}}, \end{matrix} \end{matrix}

(32)

by (26), it is deduced that

\begin{matrix} \begin{matrix} \int_{f (X_{1, i})}^{{\dot{X}}_{1, i}} {(s^{\frac{1}{k_{1}}} - f^{\frac{1}{k_{1}}} (X_{1, i}))}^{1 - k_{1}} d s \leq diag (| {\dot{X}}_{1, i} - f (X_{1, i}) |) | ϵ_{i} |^{1 - k_{1}} \leq 2^{1 - k_{1}} | ϵ_{i} | . \end{matrix} \end{matrix}

(33)

Using (32) and (33), we have

\begin{matrix} \begin{matrix} {\dot{V}}_{2, i} & \leq A_{1} + A_{2}, \end{matrix} \end{matrix}

(34)

where

\begin{matrix} \begin{matrix} A_{1} & = (2 - k_{1}) 2^{1 - k_{1}} | {\dot{X}}_{1, i} |^{T} | \frac{\partial f^{\frac{1}{k_{1}}} (X_{1, i})}{\partial X_{1, i}} | | ϵ_{i} |, \\ A_{2} & = {(ϵ_{i}^{2 - k_{1}})}^{T} \frac{\partial {\dot{X}}_{1, i}}{\partial t} . \end{matrix} \end{matrix}

(35)

\frac{1}{2} < k_{1} < 1

and

k_{2} > 1

are two specified rational numbers of the ratio of two odd integers, by Lemma 4, we can obtain

\begin{matrix} \begin{matrix} | \frac{\partial f^{\frac{1}{k_{1}}} (X_{1, i})}{\partial X_{1, i}} | \\ = & | diag ({(γ_{1} X_{1, i}^{k_{1}} + γ_{2} X_{1, i}^{k_{2}})}^{\frac{1}{k_{1}} - 1}) diag ((γ_{1} X_{1, i}^{k_{1} - 1} + \frac{γ_{2} k_{2}}{k_{1}} X_{1, i}^{k_{2} - 1})) | \\ \leq & | diag ((γ_{1}^{\frac{1}{k_{1}} - 1} X_{1, i}^{1 - k_{1}} + γ_{2}^{\frac{1}{k_{1}} - 1} X_{1, i}^{\frac{k_{2}}{k_{1}} - k_{2}})) diag ((γ_{1} X_{1, i}^{k_{1} - 1} + \frac{γ_{2} k_{2}}{k_{1}} X_{1, i}^{k_{2} - 1})) | \\ \leq & γ_{1}^{\frac{1}{k_{1}}} I_{4} + γ_{1}^{\frac{1}{k_{1}} - 1} \frac{γ_{2} k_{2}}{k_{1}} diag (X_{1, i}^{k_{2} - k_{1}}) + γ_{1} γ_{2}^{\frac{1}{k_{1}} - 1} diag (X_{1, i}^{\frac{k_{2}}{k_{1}} - k_{2} + k_{1} - 1}) + γ_{2}^{\frac{1}{k_{1}}} \frac{k_{2}}{k_{1}} diag (X_{1, i}^{\frac{k_{2}}{k_{1}} - 1}) \end{matrix} \end{matrix} .

that implies

A_{1} \leq (2 - k_{1}) 2^{1 - k_{1}} \sum_{j = 1}^{4} ι_{j} | {\dot{X}}_{1, i} |^{T} diag (X_{1, i}^{ν_{j}}) | ϵ_{i} |,

where

ν_{1} = 0, ν_{2} = k_{2} - k_{1}, ν_{3} = \frac{k_{2}}{k_{1}} - k_{2} + k_{1} - 1, ν_{4} = \frac{k_{2}}{k_{1}} - 1

ι_{1} = γ_{1}^{\frac{1}{k_{1}}}, ι_{2} = γ_{1}^{\frac{1}{k_{1}} - 1} \frac{γ_{2} k_{2}}{k_{1}}, ι_{3} = γ_{1} γ_{2}^{\frac{1}{k_{1}} - 1}, ι_{4} = γ_{2}^{\frac{1}{k_{1}}} \frac{k_{2}}{k_{1}} .

Then, using (26), we have

\begin{matrix} \begin{matrix} ι_{j} | {\dot{X}}_{1, i} |^{T} diag (X_{1, i}^{ν_{j}}) | ϵ_{i} | \\ \leq & ι_{j} | {\dot{X}}_{1, i} - f (X_{1, i}) |^{T} diag (X_{1, i}^{ν_{j}}) | ϵ_{i} | + ι_{j} | f (X_{1, i}) |^{T} diag (X_{1, i}^{ν_{j}}) | ϵ_{i} | \\ \leq & ι_{j} 2^{1 - k_{1}} | ϵ_{i}^{k_{1} + 1} |^{T} | X_{1, i}^{ν_{j}} | + ι_{j} | γ_{1} X_{1, i}^{k_{1}} + γ_{2} X_{1, i}^{k_{2}} |^{T} diag (X_{1, i}^{ν_{j}}) | ϵ_{i} | \\ \leq & ι_{j} 2^{1 - k_{1}} | ϵ_{i}^{k_{1} + 1} |^{T} | X_{1, i}^{ν_{j}} | + ι_{j} γ_{1} | ϵ_{i} |^{T} X_{1, i}^{k_{1} + ν_{j}} + ι_{j} γ_{2} {| ϵ_{i} |}^{T} X_{1, i}^{k_{2} + ν_{j}}, \end{matrix} \end{matrix}

(36)

by Lemma 3, it is deduced that

\forall r \in R_{> 0}

\begin{matrix} \begin{matrix} ι_{j} 2^{1 - k_{1}} | ϵ_{i}^{k_{1} + 1} |^{T} | X_{1, i}^{ν_{j}} | \leq & 2^{1 - k_{1}} \frac{ι_{j} ν_{j}}{k_{1} + 1 + ν_{j}} r | X_{1, i} |^{k_{1} + 1 + ν_{j}} + 2^{1 - k_{1}} \frac{ι_{j} (k_{1} + 1)}{k_{1} + 1 + ν_{j}} r^{- \frac{ν_{j}}{k_{1} + 1}} {| ϵ_{i} |}^{k_{1} + 1 + ν_{j}}, \end{matrix} \end{matrix}

(37)

let

r = ι_{j}^{- 1}

, then

\begin{matrix} \begin{matrix} ι_{j} 2^{1 - k_{1}} | ϵ_{i}^{k_{1} + 1} |^{T} | X_{1, i}^{ν_{j}} | \leq & 2^{1 - k_{1}} \frac{ν_{j}}{k_{1} + 1 + ν_{j}} | X_{1, i} |^{k_{1} + 1 + ν_{j}} + 2^{1 - k_{1}} \frac{(k_{1} + 1)}{k_{1} + 1 + ν_{j}} ι_{j}^{1 + \frac{ν_{j}}{k_{1} + 1}} {| ϵ_{i} |}^{k_{1} + 1 + ν_{j}}, \end{matrix} \end{matrix}

(38)

similarly, the following inequalities hold

\begin{matrix} \begin{matrix} ι_{j} γ_{1} | ϵ_{i} |^{T} X_{1, i}^{k_{1} + ν_{j}} \leq \frac{k_{1} + ν_{j}}{k_{1} + 1 + ν_{j}} | X_{1, i} |^{k_{1} + 1 + ν_{j}} + \frac{1}{k_{1} + 1 + ν_{j}} {(ι_{j} γ_{1})}^{k_{1} + ν_{j} + 1} {| ϵ_{i} |}^{k_{1} + 1 + ν_{j}}, \end{matrix} \end{matrix}

(39)

\begin{matrix} \begin{matrix} ι_{j} γ_{2} {| ϵ_{i} |}^{T} X_{1, i}^{k_{2} + ν_{j}} \leq & \frac{k_{2} + ν_{j}}{k_{2} + 1 + ν_{j}} | X_{1, i} |^{k_{2} + 1 + ν_{j}} + \frac{1}{k_{2} + 1 + ν_{j}} {(ι_{j} γ_{2})}^{k_{2} + ν_{j} + 1} {| ϵ_{i} |}^{k_{2} + 1 + ν_{j}} . \end{matrix} \end{matrix}

(40)

Consequently, equation (36) yields

\begin{matrix} \begin{matrix} ι_{j} | {\dot{X}}_{1, i} |^{T} diag (X_{1, i}^{ν_{j}}) | ϵ_{i} | \leq ℓ_{1, j} | X_{1, i} |^{k_{1} + ν_{j} + 1} + ℓ_{2, j} X_{1, i}^{k_{2} + ν_{j} + 1} + ℓ_{3, j} | ϵ_{i} |^{k_{1} + ν_{j} + 1} + ℓ_{4, j} {| ϵ_{i} |}^{k_{2} + ν_{j} + 1}, \end{matrix} \end{matrix}

(41)

where

ℓ_{1, j} = 2^{1 - k_{1}} \frac{ν_{j}}{k_{1} + 1 + ν_{j}} + \frac{k_{1} + ν_{j}}{k_{1} + 1 + ν_{j}},

ℓ_{2, j} = \frac{k_{2} + ν_{j}}{k_{2} + 1 + ν_{j}},

ℓ_{3, j} = 2^{1 - k_{1}} \frac{(k_{1} + 1)}{k_{1} + 1 + ν_{j}} ι_{j}^{1 + \frac{ν_{j}}{k_{1} + 1}} + \frac{1}{k_{1} + 1 + ν_{j}} {(ι_{j} γ_{1})}^{k_{1} + ν_{j} + 1},

ℓ_{4, j} = \frac{1}{k_{2} + 1 + ν_{j}} {(ι_{j} γ_{2})}^{k_{2} + ν_{j} + 1} .

Consequently,

A_{1}

is bounded by

\begin{matrix} \begin{matrix} A_{1} \leq & (2 - k_{1}) 2^{1 - k_{1}} \sum_{j = 1}^{4} ι_{j} | {\dot{X}}_{1, i} |^{T} diag (X_{1, i}^{ν_{j}}) | ϵ_{i} | \\ \leq & (2 - k_{1}) 2^{1 - k_{1}} \sum_{j = 1}^{4} (ℓ_{1, j} | X_{1, i} |^{k_{1} + ν_{j} + 1} + ℓ_{2, j} X_{1, i}^{k_{2} + ν_{j} + 1} + ℓ_{3, j} | ϵ_{i} |^{k_{1} + ν_{j} + 1} + ℓ_{4, j} {| ϵ_{i} |}^{k_{2} + ν_{j} + 1}) . \end{matrix} \end{matrix}

(42)

From (7) and (22) we can arrive at

\begin{matrix} \begin{matrix} \frac{\partial {\dot{X}}_{1, i}}{\partial t} = \frac{1}{2} D_{i} (h_{i} (Q_{i}, v_{i}) + g_{i} (Q_{i}) (T_{i} + δ_{T i})), \end{matrix} \end{matrix}

(43)

which leads to

\begin{matrix} \begin{matrix} A_{2} = {(ϵ_{i}^{2 - k_{1}})}^{T} (\frac{1}{2} D_{i} (h_{i} (Q_{i}, v_{i}) + g_{i} (Q_{i}) (T_{i} + δ_{T i}))) . \end{matrix} \end{matrix}

(44)

Next, the fixed-time attitude controller

T_{i}

can be designed as:

\begin{matrix} \begin{matrix} u_{i} & = {\hat{J}}_{i} (u_{a, 1 i} + u_{a, 2 i}), \\ T_{i} & = s a t (u_{i}), \\ Δ u_{i} & = T_{i} - u_{i} . \end{matrix} \end{matrix}

(45)

where

\begin{matrix} \begin{matrix} u_{a, 1 i} = - & κ {\hat{J}}_{i}^{- 1} J_{i} P_{i}^{T} \frac{D_{i}^{T} (ϵ_{i}^{2 - k_{1}})}{| | D_{i} | | | | {(ϵ_{i}^{2 - k_{1}})}^{T} | |} (k_{h} | | v_{i} {| |}^{2} + | | P_{i} | | ρ | | u_{a, 2 i} | |) - {\hat{J}}_{i}^{- 1} J_{i} P_{i}^{T} \frac{D_{i}^{T} (ϵ_{i}^{2 - k_{1}})}{| | D_{i} | | | | {(ϵ_{i}^{2 - k_{1}})}^{T} | |} k_{\bar{g}} ϖ_{i}, \end{matrix} \end{matrix}

(46)

\begin{matrix} \begin{matrix} u_{a, 2 i} = 2 P_{i}^{T} D_{i}^{- 1} (- m_{1} ϵ_{i}^{2 k_{1} - 1} - m_{2} ϵ_{i}^{\frac{k_{2}}{k_{1}} + k_{1} + k_{2} - 2} + k_{3} x_{a, i} - ϵ_{i}^{2 - k_{1}}), \end{matrix} \end{matrix}

(47)

\begin{matrix} s a t (u_{i}) = \{\begin{matrix} \frac{u_{i \max}}{| | u_{i} | |} u_{i} & | | u_{i} | | > u_{i \max}, \\ u_{i} & | | u_{i} | | \leq u_{i \max}, \end{matrix} \end{matrix}

(48)

and

ρ = \frac{k_{\underset{̲}{J}}^{- 1} - k_{\bar{J}}^{- 1}}{k_{\underset{̲}{J}}^{- 1} + k_{\bar{J}}^{- 1}}

{\hat{J}}_{i} = \frac{2 I_{3}}{k_{\underset{̲}{J}}^{- 1} + k_{\bar{J}}^{- 1}}

κ > 1

m_{1} > 0

m_{2} > 0

k_{3} > 0

. The constant

u_{i \max} \in R_{> 0}

is the magnitude constraint of the actuator. Moreover, the adaptive compensation law

x_{a, i}

satisfies the following equation:

\begin{matrix} \begin{matrix} {\dot{x}}_{a, i} = & - h_{1} {sig}^{k_{1}} (x_{a, i}) - h_{2} {sig}^{\frac{k_{2}}{k_{1}} + k_{2} - 1} (x_{a, i}) - h_{3} x_{a, i} + \frac{1}{2} D_{i} g_{i} (Q_{i}) J_{i} Δ u_{i}, \end{matrix} \end{matrix}

(49)

where

h_{1}

h_{2}

h_{3}

, and

k_{3}

are constrained by the following inequalities:

\begin{matrix} \begin{matrix} h_{1} > \frac{1}{2} k_{3}^{2}, h_{2} > \frac{1}{2} k_{3}^{2}, h_{3} > 1 . \end{matrix} \end{matrix}

(50)

Inspired by Assumption 3 and Remark 2 in [25], the following similar assumption and remark are added:

Assumption A5.

For the practical modular unit mirror attitude system described by (7), (22), (23), and (45), a feasible commanded input

u_{i}

that the specified consensus control objective can be achieved should exist.

Remark 2.

Assumption A5 implies that the modular unit mirror attitude system described by (7), (22), (23), and (45) is controllable and the input difference

Δ u_{i}

between the saturation input

T_{i}

and commanded control input

u_{i}

is bounded, namely

Δ u_{i} \leq \bar{u}

with

\bar{u}

being an unknown positive constant. The upper bound of

Δ u_{i}

does not need to be known, which will only be used to analyze the stability of the closed-loop system later.

According to (47), we have

\begin{matrix} \begin{matrix} \frac{1}{2} D_{i} (h_{i} (Q_{i}, v_{i}) + g_{i} (Q_{i}) (T_{i} + δ_{T i})) = - m_{1} ϵ_{i}^{2 k_{1} - 1} - m_{2} ϵ_{i}^{\frac{k_{2}}{k_{1}} + k_{1} + k_{2} - 2} + Z_{i}, \end{matrix} \end{matrix}

(51)

where

\begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} Z_{i} & = \frac{1}{2} D_{i} (h_{i} (Q_{i}, v_{i}) + g_{i} (Q_{i}) (T_{i} + δ_{T i})) - \frac{1}{2} D_{i} g_{i} (Q_{i}) J_{i} u_{a, 2 i} + k_{3} x_{a, i} - ϵ_{i}^{2 - k_{1}} \\ = \frac{1}{2} D_{i} g_{i} (Q_{i}) (T_{i} + δ_{T i}) + \frac{1}{2} D_{i} h_{i} (Q_{i}, v_{i}) - \frac{1}{2} D_{i} g_{i} (Q_{i}) J_{i} u_{a, 2 i} + k_{3} x_{a, i} - ϵ_{i}^{2 - k_{1}}, \end{matrix} \end{matrix} \end{matrix} \end{matrix}

(52)

then substituting (45) yields

\begin{matrix} \begin{matrix} \begin{matrix} {(ϵ_{i}^{2 - k_{1}})}^{T} Z_{i} \\ = & {(ϵ_{i}^{2 - k_{1}})}^{T} (\frac{1}{2} D_{i} h_{i} (Q_{i}, v_{i})) + {(ϵ_{i}^{2 - k_{1}})}^{T} (\frac{1}{2} D_{i} g_{i} (Q_{i}) ({\hat{J}}_{i} u_{a, 1 i} + {\hat{J}}_{i} u_{a, 2 i} + Δ u_{i} + δ_{T i})) \\ + {(ϵ_{i}^{2 - k_{1}})}^{T} (- \frac{1}{2} D_{i} g_{i} (Q_{i}) J_{i} u_{a, 2 i}) + {(ϵ_{i}^{2 - k_{1}})}^{T} k_{3} x_{a, i} - {(ϵ_{i}^{2 - k_{1}})}^{T} ϵ_{i}^{2 - k_{1}} \\ \leq & \frac{1}{2} | | {(ϵ_{i}^{2 - k_{1}})}^{T} | | | | D_{i} | | k_{h} | | v_{i} {| |}^{2} + \frac{1}{2} {(ϵ_{i}^{2 - k_{1}})}^{T} D_{i} g_{i} (Q_{i}) {\hat{J}}_{i} u_{a, 1 i} + \frac{1}{2} {(ϵ_{i}^{2 - k_{1}})}^{T} D_{i} g_{i} (Q_{i}) ({\hat{J}}_{i} u_{a, 2 i} + Δ u_{i} - J_{i} u_{a, 2 i}) \\ + \frac{1}{2} {(ϵ_{i}^{2 - k_{1}})}^{T} D_{i} g_{i} (Q_{i}) δ_{T i} + {(ϵ_{i}^{2 - k_{1}})}^{T} k_{3} x_{a, i} - {(ϵ_{i}^{2 - k_{1}})}^{T} ϵ_{i}^{2 - k_{1}}, \end{matrix} \end{matrix} \end{matrix}

(53)

According to Assumption 3, we have

\begin{matrix} \begin{matrix} | | g_{i} (Q_{i}) {\hat{J}}_{i} - P_{i} I_{3} | | & = | | P_{i} J_{i}^{- 1} {\hat{J}}_{i} - P_{i} I_{3} | | \leq | | P_{i} | | ρ, \end{matrix} \end{matrix}

(54)

where

ρ = \frac{k_{\underset{̲}{J}}^{- 1} - k_{\bar{J}}^{- 1}}{k_{\underset{̲}{J}}^{- 1} + k_{\bar{J}}^{- 1}}

, then (53) can be converted to

\begin{matrix} \begin{matrix} \begin{matrix} {(ϵ_{i}^{2 - k_{1}})}^{T} Z_{i} \leq & \frac{1}{2} | | {(ϵ_{i}^{2 - k_{1}})}^{T} | | | | D_{i} | | (k_{h} | | v_{i} {| |}^{2} + | | P_{i} | | ρ | | u_{a, 2 i} | |) + \frac{1}{2} {(ϵ_{i}^{2 - k_{1}})}^{T} D_{i} g_{i} (Q_{i}) {\hat{J}}_{i} u_{a, 1 i} \\ + \frac{1}{2} {(ϵ_{i}^{2 - k_{1}})}^{T} D_{i} g_{i} (Q_{i}) δ_{T i} + \frac{1}{2} {(ϵ_{i}^{2 - k_{1}})}^{T} D_{i} g_{i} (Q_{i}) Δ u_{i} + {(ϵ_{i}^{2 - k_{1}})}^{T} k_{3} x_{a, i} - {(ϵ_{i}^{2 - k_{1}})}^{T} ϵ_{i}^{2 - k_{1}} . \end{matrix} \end{matrix} \end{matrix}

(55)

Then according to (46), as

κ > 1

, one has

\begin{matrix} \begin{matrix} \begin{matrix} {(ϵ_{i}^{2 - k_{1}})}^{T} Z_{i} \leq & \frac{1}{2} {(ϵ_{i}^{2 - k_{1}})}^{T} D_{i} g_{i} (Q_{i}) Δ u_{i} + {(ϵ_{i}^{2 - k_{1}})}^{T} k_{3} x_{a, i} - {(ϵ_{i}^{2 - k_{1}})}^{T} (ϵ_{i}^{2 - k_{1}}) . \end{matrix} \end{matrix} \end{matrix}

(56)

Then, substituting (51) and (56) into (44) yields the following inequality:

\begin{matrix} \begin{matrix} A_{2} \leq & - m_{1} | | ϵ_{i}^{k_{1} + 1} {| |}_{1} - m_{2} | | ϵ_{i}^{\frac{k_{2}}{k_{1}} + k_{2}} {| |}_{1} + \frac{1}{2} {(ϵ_{i}^{2 - k_{1}})}^{T} D_{i} g_{i} (Q_{i}) Δ u_{i} + {(ϵ_{i}^{2 - k_{1}})}^{T} k_{3} x_{a, i} - {(ϵ_{i}^{2 - k_{1}})}^{T} (ϵ_{i}^{2 - k_{1}}), \end{matrix} \end{matrix}

(57)

and combining Lemma 2, equation (57) can be transformed to

\begin{matrix} \begin{matrix} A_{2} \leq & - m_{1} | | ϵ_{i}^{k_{1} + 1} {| |}_{1} - m_{2} | | ϵ_{i}^{\frac{k_{2}}{k_{1}} + k_{2}} {| |}_{1} + \frac{1}{8} | | D_{i} g_{i} (Q_{i}) Δ u_{i} {| |}^{2} + \frac{1}{2} k_{3}^{2} x_{a, i}^{T} x_{a, i} . \end{matrix} \end{matrix}

(58)

Then, the following theorem can be obtained.

Theorem 2.

Consider a system composed of (7), (22), and (23) under Assumptions

1 - 5

, using virtual controller (29), the fixed-time attitude controller given by (45)-(48), and the adaptive compensation law in (49)-(50), if the control parameters

γ_{1}

γ_{2}

m_{1}

, and

m_{2}

satisfy

\begin{matrix} \begin{matrix} γ_{1} & > max \{\begin{matrix} \frac{2^{1 - k_{1}}}{1 + k_{1}} + (2 - k_{1}) 2^{1 - k_{1}} ℓ_{1, 1} + 2 {\hat{ℓ}}_{1}, \\ \frac{2^{1 - k_{1}} \frac{k_{2}}{k_{1}}}{\frac{k_{2}}{k_{1}} + k_{1}} + (2 - k_{1}) 2^{1 - k_{1}} ℓ_{2, 3} + (2 - k_{1}) 2^{1 - k_{1}} ℓ_{1, 4} \end{matrix}\} \\ γ_{2} & > max \{\begin{matrix} (2 - k_{1}) 2^{1 - k_{1}} ℓ_{2, 1} + (2 - k_{1}) 2^{1 - k_{1}} ℓ_{1, 2}, \\ (2 - k_{1}) 2^{1 - k_{1}} ℓ_{2, 4} + 2 {\hat{ℓ}}_{1} \end{matrix}\} \\ m_{1} & > \frac{2^{1 - k_{1}} k_{1}}{1 + k_{1}} + (2 - k_{1}) 2^{1 - k_{1}} ℓ_{3, 1} + 4 {\hat{ℓ}}_{2}, \\ m_{2} & > (2 - k_{1}) 2^{1 - k_{1}} ℓ_{4, 4} + 4 {\hat{ℓ}}_{2}, \end{matrix} \end{matrix}

(59)

where

\begin{matrix} \begin{matrix} {\hat{ℓ}}_{1} & = max \{(2 - k_{1}) 2^{1 - k_{1}} ℓ_{2, 2}, (2 - k_{1}) 2^{1 - k_{1}} ℓ_{1, 3}\}, \\ {\hat{ℓ}}_{2} & = max \{\begin{matrix} (2 - k_{1}) 2^{1 - k_{1}} ℓ_{4, 1} + (2 - k_{1}) 2^{1 - k_{1}} ℓ_{3, 2}, \\ \frac{2^{1 - k_{1}} k_{1}}{\frac{k_{2}}{k_{1}} + k_{1}} + (2 - k_{1}) 2^{1 - k_{1}} ℓ_{4, 3} + (2 - k_{1}) 2^{1 - k_{1}} ℓ_{3, 4}, \\ (2 - k_{1}) 2^{1 - k_{1}} ℓ_{4, 2}, \\ (2 - k_{1}) 2^{1 - k_{1}} ℓ_{3, 3} \end{matrix}\}, \end{matrix} \end{matrix}

(60)

there exists a fixed time

T_{1} \geq 0

such that

X_{1, i}

and

X_{2, i}

converges to the neighborhood of the origin.

The proof of Theorem 2 is provided in Appendix B.

Finally, we can obtain that considering the system composed of a random virtual leader quaternion

Q^{*}

and follower unit mirror

i \in \{1 \dots n\}

described by (7), using the discrete-time observer given in Theorem 1 and the controller given in Theorem 2, the consensus in the sense of formula (9) under Assumptions

1 - 5

can be realized within fixed-time bounded by

T = T_{0} + T_{1}

6. Simulation Results

In this section, we illustrate the performance of the control scheme proposed in this study, which considers discrete-time communication, unknown tiny disturbance torque, model uncertainty, and actuator saturation in case I. To evaluate the effectiveness of the control scheme, in comparison to case II, the continuous control law in [28] is used for the same large telescope on-orbit construction system without unknown tiny disturbance torque, model uncertainty, and actuator saturation.

First, consider the case subject to Assumptions

1 - 5

where five unit mirrors labeled

i, i \in \{1 \dots 5\}

track a constant reference attitude. The reference attitude

Q^{*}

is a randomly chosen constant, and the corresponding Euler angle is

{[\begin{matrix} 0 & 26.5 & 0 \end{matrix}]}^{\circ} .

Further, the initial attitude and angular velocity of the five follower unit mirrors

i, i \in \{1 \dots 5\}

are chosen randomly, as summarized in Table 2. For more information about the relationship between the quaternion and Euler angle, please refer to [39]. The augmented communication graph

\bar{G}

is presented in Figure 2, which satisfies Assumption 1.

6.1. Case I: Simulation with the Discrete-Time Control Scheme Proposed in this Study

The desired attitude difference

D_{i}

between the attitude of modular unit mirror i, namely

Q_{i}

and reference attitude, namely

Q^{*}

correspond to Euler angles

{[\begin{matrix} 0 & 0 & 0 \end{matrix}]}^{\circ}

{[\begin{matrix} 0.2 & 0 & 0 \end{matrix}]}^{\circ}

{[\begin{matrix} 0 & 0.2 & 0 \end{matrix}]}^{\circ}

{[\begin{matrix} 0 & 0 & 0.2 \end{matrix}]}^{\circ}

, and

{[\begin{matrix} 0 & - 0.2 & 0 \end{matrix}]}^{\circ}

. The channel fading coefficients

c_{i, j} = c_{j, i}, \forall (i, j) \in \bar{ε}

are generated randomly, which implies that the coefficients are independent and identically distributed in

(0, 1]

. Considering unknown inertia attenuation, the unit mirrors have moments of inertia

\begin{matrix} \begin{matrix} J_{i} = [\begin{matrix} 10 & 0 & 0 \\ 0 & 15 & 0 \\ 0 & 0 & 20 \end{matrix}] - 0.01 \sin (0.1 t) I_{3}, i \in \{1 \dots 5\} . \end{matrix} \end{matrix}

(61)

The tiny disturbance torque

δ_{T i}, i \in \{1 \dots 5\}

is selected as

\begin{matrix} \begin{matrix} δ_{T i} = [\begin{matrix} 3 c o s (10 ω_{1, i} t) + 4 s i n (3 ω_{1, i} t) - 10 \\ 1.5 s i n (3 ω_{2, i} t) + c o s (10 ω_{2, i} t) + 15 \\ 3 s i n (10 ω_{3, i} t) + 8 s i n (4 ω_{3, i} t) + 10 \end{matrix}] \times 10^{- 3} N \cdot m . \end{matrix} \end{matrix}

(62)

The following parameters were used in the simulation:

k_{1} = \frac{9}{11}

k_{2} = \frac{11}{9}

k_{3} = 0.5

κ = 1.01

γ_{1} = 0.05

γ_{2} = 0.025

m_{1} = 5.1

m_{2} = 4.6

h_{1} = 1

h_{2} = 1

, and

h_{3} = 5

The constant communication interval

Δ t \in R_{> 0}

between any two broadcasting instants

t_{k} \in R_{\geq 0}, k \in N_{\geq 0}

and

t_{k + 1} \in R_{\geq 0}, k \in N_{\geq 0}

was set as

0.1 s

. Notably, each unit mirror receives two signals, as presented in (11). Traditionally, a decimal requires eight bytes, namely, 64 bits. Therefore, using the methodology in this study, the channel required by each unit mirror for attitude control is

\begin{matrix} \begin{matrix} 64 \times (4 + 1) \times (1 / 0.1) = 3200 (b / s), \end{matrix} \end{matrix}

(63)

which can be satisfied by the inter-module communication capability [46]. Contrarily, when using the traditional OCAM, every unit mirror should receive at least one signal

{\hat{Q}}_{j}^{*}

from each neighbor j. Basically, if a unit mirror has n neighbors, the required bit rate is

(4 n) / (4 + 1) = 4 n / 5

times the size of that in this study.

Figure 3 shows the performance of the discrete-time fixed-time observer constructed in Theorem 1. It is observed that the estimation errors

{\tilde{Q}}_{i}^{*}, i \in \{1 \dots 5\}

, represented by Euler angle

{\tilde{E}}_{i} = [{\tilde{ϕ}}_{i}^{★}, {\tilde{θ}}_{i}^{★}, {\tilde{ψ}}_{i}^{★}]

converges to

{[- 0.001, 0.001]}^{\circ}

within

0.8 s

. Figure 4 reflects the containment errors

{[\overset{︷}{D_{i}^{\times}}]}^{- 1} Q_{i} - Q^{*}, \forall i \in \{1 \dots 5\}

represented by Euler angle

E_{i} = [ϕ_{e i}, θ_{e i}, ψ_{e i}]

. It can be observed that the attitude consensus errors based on (9) converge to

{[- 0.01, 0.01]}^{\circ}

within

130 s

. As shown in Figure 5, the control torque is bounded by

0.02 N \cdot m

throughout the process.

6.2. Comparison Case II: with Continuous Control Scheme

Without regard to unknown tiny disturbance torque, model uncertainty, and actuator saturation, using the continuous solution in [28], with parameters

α_{1} = 2

β_{1} = 2

v_{1} = 2

v_{2} = \frac{5}{3}

λ_{1} = 0.001

k_{1} = 1

k_{2} = 1

g_{1} = 0.95

g_{2} = 1.5

ϵ = 0.005

κ_{1} = 1

κ_{2} = 1

p_{1} = 0.6

p_{2} = 1.5

\bar{ϵ} = 0.005

, and

c_{i} = 0.3

, the estimation errors represented by Euler angle are depicted in Figure 6. It is observed that the estimation errors converge to

{[- 0.001, 0.001]}^{\circ}

within

4 s

. Figure 7 reflects the containment errors represented by Euler angle, it can be observed that the attitude consensus errors converge to

{[- 0.01, 0.01]}^{\circ}

within

50 s

. As shown in Figure 8 , the maximum control torque was

5 N \cdot m

The simulation performances of cases I and II are listed in Table 3. This clearly shows that the controller proposed in this study can obtain similar convergence accuracy with the controller in [28], even when unknown tiny disturbance torque, model uncertainty, and actuator saturation are considered.

7. Conclusion

This study proposes a consensus-based attitude control solution for large telescope on-orbit construction. By incorporating discrete-time communication scheme exploiting interference, a fixed-time consensus-based attitude-tracking control scheme was designed for multiple modular unit mirrors. The undirected communication graph was assumed to be connected, and the reference attitude was available only to a subset of the unit mirrors. The control law in this study handles the unknown channel attenuation, limited model uncertainty, unknown tiny disturbance torque, and actuator saturation. The numerical simulation demonstrated that the proposed control scheme can guarantee the attitude of unit mirrors simultaneously tracking a common constant attitude within a fixed time, thus maintaining the predetermined relative configuration. Moreover, the convergence time is guaranteed within a fixed time, independent of the initial conditions, and the convergence accuracy is within

0 . 01^{\circ}

. A comparative simulation was performed to demonstrate the superiority of the proposed solution. It is worth mentioning that the communication scheme in this study can save resources proportionally to the number of unit mirrors, as stated in Remark 1.

Author Contributions

P.L. is responsible for original draft preparation and mathematical derivation, C.G. is responsible for funding acquisition and guidance, Z.Y. is responsible for project administration and supervision, C.C. is responsible for simulation verification, and R.Z. is responsible for review and editing. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by Hong Kong-Macao-Taiwan Science and Technology Cooperation Project of Science and Technology Innovation Action Plan in Shanghai [grant number 23510760200], Oriental Talent Youth Program of Shanghai [grant number Y3DFRCZL01], Outstanding Program of the Youth Innovation Promotion Association of the Chinese Academy of Sciences [grant number Y4ZKRCZL01], Strategic Priority Research Program of the Chinese Academy of Sciences (Category A) [grant number Y3ZKXDZL04], Shanghai Rising-Star Program [grant number 19QA1408400] and Chinese Scholarship Council [grant number201906830037].

Appendix A. Proof of Theorem 1

According to observer (16), during period

[t_{k}, t_{k + 1})

, the derivative of

{\tilde{Q}}^{*}

is:

\begin{matrix} \begin{matrix} {\dot{\tilde{Q}}}^{*} & = {\dot{\hat{Q}}}^{*} - 1_{n} \otimes {\dot{\hat{Q}}}_{0}^{*} = - \frac{1.92}{Δ t} {M_{0}^{- 1}}^{T} (k) y (k), \\ y (k) & = {\hat{Q}}^{*} (k) - η^{(1)} (k), \end{matrix} \end{matrix}

(A1)

By solving the differential equation, the exact discrete model of system (A1) is obtained as follows:

\begin{matrix} \begin{matrix} {\tilde{Q}}^{*} (k + 1) & = {\tilde{Q}}^{*} (k) - 1.92 {M_{0}^{- 1}}^{T} (k) y (k) . \end{matrix} \end{matrix}

(A2)

Consider the following Lyapunov function:

\begin{matrix} \begin{matrix} V (y) & = {\tilde{Q}}^{* T} {\tilde{Q}}^{*}, \end{matrix} \end{matrix}

(A3)

noting that

\begin{matrix} \begin{matrix} \begin{matrix} C_{i} y_{i} = & \sum_{j = 1}^{n} c_{j, i} ({\hat{Q}}_{i}^{*} - {\hat{Q}}_{j}^{*}) + c_{0, i} ({\hat{Q}}_{i}^{*} - {\hat{Q}}_{0}^{*}) = \sum_{j = 1}^{n} c_{j, i} ({\tilde{Q}}_{i}^{*} - {\tilde{Q}}_{j}^{*}) + c_{0, i} {\tilde{Q}}_{i}^{*}, \end{matrix} \end{matrix} \end{matrix}

(A4)

it leads to

\begin{matrix} C y = (H^{T} \otimes I_{4}) {\tilde{Q}}^{*}, \end{matrix}

(A5)

which is equal to

\begin{matrix} {\tilde{Q}}^{* T} (k) = y^{T} (k) M_{0}^{- 1} (k) . \end{matrix}

(A6)

Then, based on (A2) and (A6), the following equation is obtained:

\begin{matrix} \begin{matrix} V^{c} ({\tilde{Q}}^{*} (k + 1), k + 1) = {({\tilde{Q}}^{* T} (k + 1) \tilde{Q} (k + 1))}^{c} = {(0.8464 y^{T} (k) M_{0}^{- 1} (k) {M_{0}^{- 1}}^{T} (k) y (k))}^{c} . \end{matrix} \end{matrix}

(A7)

Combining (A3) and (A6), as

\begin{matrix} \begin{matrix} V^{c} ({\tilde{Q}}^{*} (k), k) = {(y^{T} (k) M_{0}^{- 1} (k) {M_{0}^{- 1}}^{T} (k) y (k))}^{c}, \end{matrix} \end{matrix}

(A8)

the following equation is calculated:

\begin{matrix} \begin{matrix} V^{c} ({\tilde{Q}}^{*} (k + 1), k + 1) - V^{c} ({\tilde{Q}}^{*} (k), k) = (0 . 8464^{c} - 1) {(y^{T} (k) M_{0}^{- 1} (k) {M_{0}^{- 1}}^{T} (k) y (k))}^{c}, \\ - q V^{c} ({\tilde{Q}}^{*} (k), k) V^{c} ({\tilde{Q}}^{*} (k + 1), k + 1) = - 0 . 8464^{c} q {(y^{T} (k) M_{0}^{- 1} (k) {M_{0}^{- 1}}^{T} (k) y (k))}^{2 c} . \end{matrix} \end{matrix}

(A9)

Define an intermediate variable

X \in R_{\geq 0}

\begin{matrix} \begin{matrix} X = y^{T} (k) M_{0}^{- 1} (k) {M_{0}^{- 1}}^{T} (k) y (k), \end{matrix} \end{matrix}

(A10)

the intermediate variable X satisfies the following inequality:

\begin{matrix} \begin{matrix} X \leq λ_{m a x}^{2} (M_{0}^{- 1} (k)) y^{T} (k) y (k) . \end{matrix} \end{matrix}

(A11)

From (17), we can derive:

\begin{matrix} \begin{matrix} y^{T} (k) y (k) \leq 4 n (2^{2}), \end{matrix} \end{matrix}

(A12)

therefore, the inequality about X is obtained as follows:

\begin{matrix} \begin{matrix} X \leq 16 n \cdot λ_{m a x}^{2} (M_{0}^{- 1} (k)) . \end{matrix} \end{matrix}

(A13)

Equations (A9), (A10), and (A13) indicate that there exists two constants

c, q \in R_{> 0}

as follows:

\begin{matrix} \begin{matrix} c & = 1, \\ q & = 0.18 \times {(16 n \cdot λ_{m a x}^{2} (M_{0}^{- 1} (k)))}^{- 1}, \end{matrix} \end{matrix}

(A14)

which reduces to

\begin{matrix} \begin{matrix} V^{c} ({\tilde{Q}}^{*} (k + 1), k + 1) - V^{c} ({\tilde{Q}}^{*} (k), k) \leq - q {(V ({\tilde{Q}}^{*} (k), k) V ({\tilde{Q}}^{*} (k + 1), k + 1))}^{c} . \end{matrix} \end{matrix}

(A15)

Consequently, according to Lemma 7, by selecting

ρ (| | {\tilde{Q}}^{*} | |) = 0.5 | | {\tilde{Q}}^{*} {| |}^{2}

, the estimation error

{\tilde{Q}}^{*}

reaches to

| | {\tilde{Q}}^{*} | | \leq \frac{\sqrt{2}}{2} ξ

within fixed time

\begin{matrix} \begin{matrix} T_{0} \leq T_{m a x} = \frac{16 n}{0.09 ξ^{2}} λ_{m a x}^{2} (M_{0}^{- 1} (k)) . \end{matrix} \end{matrix}

(A16)

The proof is completed.

Appendix B. Proof of Theorem 2

We define the third candidate Lyapunov function as

\begin{matrix} V_{3, i} = \frac{1}{2} x_{a, i}^{T} x_{a, i}, \end{matrix}

(A17)

then the derivative of

V_{3}

\begin{matrix} \begin{matrix} {\dot{V}}_{3, i} = x_{a, i}^{T} {\dot{x}}_{a, i}, \end{matrix} \end{matrix}

(A18)

According to (49) :

\begin{matrix} \begin{matrix} {\dot{V}}_{3, i} = & - h_{1} | | x_{a, i} {| |}^{k_{1} + 1} - h_{2} | | x_{a, i} {| |}^{\frac{k_{2}}{k_{1}} + k_{2}} - h_{3} x_{a, i}^{T} x_{a, i} + \frac{1}{2} x_{a, i}^{T} D_{i} g_{i} (Q_{i}) J_{i} Δ u_{i}, \end{matrix} \end{matrix}

(A19)

then invoking Lemma 2, and considering the fact

h_{3} > 1

, we have

\begin{matrix} \begin{matrix} {\dot{V}}_{3, i} \leq & - h_{1} | | x_{a, i} {| |}^{k_{1} + 1} - h_{2} | | x_{a, i} {| |}^{\frac{k_{2}}{k_{1}} + k_{2}} + \frac{1}{16} | | D_{i} g_{i} (Q_{i}) J_{i} Δ u_{i} {| |}^{2} . \end{matrix} \end{matrix}

(A20)

By selecting

V_{i} = V_{1, i} + V_{2, i},

and combining (30), (34), (42), and (58), for

T \geq T_{0}

, yields

\begin{matrix} \begin{matrix} {\dot{V}}_{i} & \leq - (γ_{1} - \frac{2^{1 - k_{1}}}{1 + k_{1}}) | | X_{1, i}^{1 + k_{1}} {| |}_{1} - γ_{2} | | X_{1, i}^{1 + k_{2}} {| |}_{1} - (γ_{1} - \frac{2^{1 - k_{1}} \frac{k_{2}}{k_{1}}}{\frac{k_{2}}{k_{1}} + k_{1}}) | | X_{1, i}^{\frac{k_{2}}{k_{1}} + k_{1}} {| |}_{1} - γ_{2} | | X_{1, i}^{\frac{k_{2}}{k_{1}} + k_{2}} {| |}_{1} \\ + \frac{2^{1 - k_{1}} k_{1}}{1 + k_{1}} | | ϵ_{i}^{1 + k_{1}} {| |}_{1} \\ + \frac{2^{1 - k_{1}} k_{1}}{\frac{k_{2}}{k_{1}} + k_{1}} | | ϵ_{i}^{\frac{k_{2}}{k_{1}} + k_{1}} {| |}_{1} + (2 - k_{1}) 2^{1 - k_{1}} \sum_{j = 1}^{4} (ℓ_{1, j} | X_{1, i} |^{k_{1} + ν_{j} + 1} + ℓ_{2, j} X_{1, i}^{k_{2} + ν_{j} + 1} + ℓ_{3, j} | ϵ_{i} |^{k_{1} + ν_{j} + 1} + ℓ_{4, j} {| ϵ_{i} |}^{k_{2} + ν_{j} + 1}) \\ - m_{1} | | ϵ_{i}^{k_{1} + 1} {| |}_{1} - m_{2} | | ϵ_{i}^{\frac{k_{2}}{k_{1}} + k_{2}} {| |}_{1} + \frac{1}{8} | | D_{i} g_{i} (Q_{i}) Δ u_{i} {| |}^{2} + \frac{1}{2} k_{3}^{2} x_{a, i}^{T} x_{a, i} \\ = - (γ_{1} - \frac{2^{1 - k_{1}}}{1 + k_{1}} - (2 - k_{1}) 2^{1 - k_{1}} ℓ_{1, 1}) | | X_{1, i}^{1 + k_{1}} {| |}_{1} - (γ_{2} - (2 - k_{1}) 2^{1 - k_{1}} ℓ_{2, 1} - (2 - k_{1}) 2^{1 - k_{1}} ℓ_{1, 2}) | | X_{1, i}^{1 + k_{2}} {| |}_{1} \\ - (γ_{1} - \frac{2^{1 - k_{1}} \frac{k_{2}}{k_{1}}}{\frac{k_{2}}{k_{1}} + k_{1}} - (2 - k_{1}) 2^{1 - k_{1}} ℓ_{2, 3} - (2 - k_{1}) 2^{1 - k_{1}} ℓ_{1, 4}) | | X_{1, i}^{\frac{k_{2}}{k_{1}} + k_{1}} {| |}_{1} - (γ_{2} - (2 - k_{1}) 2^{1 - k_{1}} ℓ_{2, 4}) | | X_{1, i}^{\frac{k_{2}}{k_{1}} + k_{2}} {| |}_{1} \\ + (2 - k_{1}) 2^{1 - k_{1}} ℓ_{2, 2} X_{1, i}^{2 k_{2} - k_{1} + 1} + (2 - k_{1}) 2^{1 - k_{1}} ℓ_{1, 3} | X_{1, i} |^{\frac{k_{2}}{k_{1}} - k_{2} + 2 k_{1}} - (m_{1} - \frac{2^{1 - k_{1}} k_{1}}{1 + k_{1}} - (2 - k_{1}) 2^{1 - k_{1}} ℓ_{3, 1}) | | ϵ_{i}^{k_{1} + 1} {| |}_{1} \\ + ((2 - k_{1}) 2^{1 - k_{1}} ℓ_{4, 1} + (2 - k_{1}) 2^{1 - k_{1}} ℓ_{3, 2}) | ϵ_{i} |^{k_{2} + 1} + (\frac{2^{1 - k_{1}} k_{1}}{\frac{k_{2}}{k_{1}} + k_{1}} + (2 - k_{1}) 2^{1 - k_{1}} ℓ_{4, 3} + (2 - k_{1}) 2^{1 - k_{1}} ℓ_{3, 4}) | | ϵ_{i}^{\frac{k_{2}}{k_{1}} + k_{1}} {| |}_{1} \\ - (m_{2} - (2 - k_{1}) 2^{1 - k_{1}} ℓ_{4, 4}) | | ϵ_{i}^{\frac{k_{2}}{k_{1}} + k_{2}} {| |}_{1} + (2 - k_{1}) 2^{1 - k_{1}} ℓ_{4, 2} | ϵ_{i} |^{2 k_{2} - k_{1} + 1} + (2 - k_{1}) 2^{1 - k_{1}} ℓ_{3, 3} {| ϵ_{i} |}^{\frac{k_{2}}{k_{1}} - k_{2} + 2 k_{1}} \\ + \frac{1}{8} | | D_{i} g_{i} (Q_{i}) Δ u_{i} {| |}^{2} + \frac{1}{2} k_{3}^{2} x_{a, i}^{T} x_{a, i} . \end{matrix} \end{matrix}

(A21)

Note that

γ_{1}

γ_{2}

m_{1}

, and

m_{2}

satisfy (59); hence, there exists

K_{1} > 0

and

K_{2} > 0

satisfying

\begin{matrix} \begin{matrix} γ_{1} - \frac{2^{1 - k_{1}}}{1 + k_{1}} - (2 - k_{1}) 2^{1 - k_{1}} ℓ_{1, 1} & \geq 2 {\hat{ℓ}}_{1} + K_{1}, \\ γ_{2} - (2 - k_{1}) 2^{1 - k_{1}} ℓ_{2, 4} & \geq 2 {\hat{ℓ}}_{1} + K_{1}, \\ m_{1} - \frac{2^{1 - k_{1}} k_{1}}{1 + k_{1}} - (2 - k_{1}) 2^{1 - k_{1}} ℓ_{3, 1} & \geq 4 {\hat{ℓ}}_{2} + K_{2}, \\ m_{2} - (2 - k_{1}) 2^{1 - k_{1}} ℓ_{4, 4} & \geq 4 {\hat{ℓ}}_{2} + K_{2} . \end{matrix} \end{matrix}

(A22)

It is easy to verify the following inequalities

\begin{matrix} \begin{matrix} \frac{k_{2}}{k_{1}} + k_{2} > 2 k_{2} - k_{1} + 1 > k_{1} + 1, \\ \frac{k_{2}}{k_{1}} + k_{2} > \frac{k_{2}}{k_{1}} - k_{2} + 2 k_{1} > k_{1} + 1, \\ \frac{k_{2}}{k_{1}} + k_{2} > \frac{k_{2}}{k_{1}} + k_{1} > k_{1} + 1, \\ \frac{k_{2}}{k_{1}} + k_{2} > k_{2} + 1 > k_{1} + 1, \end{matrix} \end{matrix}

(A23)

and

\forall A \in R^{4 n}

a < b < c \in R

, we can obtain the following inequality

\begin{matrix} \begin{matrix} | | A^{b} {| |}_{1} < | | A^{a} {| |}_{1} + | | A^{c} {| |}_{1} . \end{matrix} \end{matrix}

(A24)

Based on (60) and (A21)-(A24), it can be obtained that

\begin{matrix} \begin{matrix} {\dot{V}}_{i} \leq & - (γ_{1} - \frac{2^{1 - k_{1}}}{1 + k_{1}} - (2 - k_{1}) 2^{1 - k_{1}} ℓ_{1, 1}) | | X_{1, i}^{1 + k_{1}} {| |}_{1} - (γ_{2} - (2 - k_{1}) 2^{1 - k_{1}} ℓ_{2, 4}) | | X_{1, i}^{\frac{k_{2}}{k_{1}} + k_{2}} {| |}_{1} \\ + 2 {\hat{ℓ}}_{1} (| | X_{1, i}^{1 + k_{1}} {| |}_{1} + | | X_{1, i}^{\frac{k_{2}}{k_{1}} + k_{2}} {| |}_{1}) - (m_{1} - \frac{2^{1 - k_{1}} k_{1}}{1 + k_{1}} - (2 - k_{1}) 2^{1 - k_{1}} ℓ_{3, 1}) | | ϵ_{i}^{k_{1} + 1} {| |}_{1} \\ - (m_{2} - (2 - k_{1}) 2^{1 - k_{1}} ℓ_{4, 4}) | | ϵ_{i}^{\frac{k_{2}}{k_{1}} + k_{2}} {| |}_{1} + 4 {\hat{ℓ}}_{2} (| | ϵ_{i}^{k_{1} + 1} {| |}_{1} + | | ϵ_{i}^{\frac{k_{2}}{k_{1}} + k_{2}} {| |}_{1}) \\ + \frac{1}{8} | | D_{i} g_{i} (Q_{i}) Δ u_{i} {| |}^{2} + \frac{1}{2} k_{3}^{2} x_{a, i}^{T} x_{a, i} \\ \leq & - K_{1} | | X_{1, i}^{1 + k_{1}} {| |}_{1} - K_{1} | | X_{1, i}^{\frac{k_{2}}{k_{1}} + k_{2}} {| |}_{1} - K_{2} | | ϵ_{i}^{k_{1} + 1} {| |}_{1} - K_{2} | | ϵ_{i}^{\frac{k_{2}}{k_{1}} + k_{2}} {| |}_{1} \\ + \frac{1}{8} | | D_{i} g_{i} (Q_{i}) Δ u_{i} {| |}^{2} + \frac{1}{2} k_{3}^{2} x_{a, i}^{T} x_{a, i} . \end{matrix} \end{matrix}

(A25)

Consider the Lyapunov function candidate

V_{a, i} = V_{i} + V_{3, i}

, then according to (A20) and (A25), we obtain

\begin{matrix} \begin{matrix} {\dot{V}}_{a, i} \leq & - K_{1} | | X_{1, i}^{1 + k_{1}} {| |}_{1} - K_{1} | | X_{1, i}^{\frac{k_{2}}{k_{1}} + k_{2}} {| |}_{1} - K_{2} | | ϵ_{i}^{k_{1} + 1} {| |}_{1} - K_{2} | | ϵ_{i}^{\frac{k_{2}}{k_{1}} + k_{2}} {| |}_{1} \\ + \frac{1}{8} | | D_{i} g_{i} (Q_{i}) Δ u_{i} {| |}^{2} + \frac{1}{2} k_{3}^{2} x_{a, i}^{T} x_{a, i} - h_{1} | | x_{a, i} {| |}^{k_{1} + 1} - h_{2} | | x_{a, i} {| |}^{\frac{k_{2}}{k_{1}} + k_{2}} + \frac{1}{16} | | D_{i} g_{i} (Q_{i}) J_{i} Δ u_{i} {| |}^{2} \end{matrix} \end{matrix}

(A26)

From the fact

\begin{matrix} \begin{matrix} | | d (f (X_{1, i}), {\dot{X}}_{1, i}) {| |}_{1} = & | | \int_{f (X_{1, i})}^{{\dot{X}}_{1, i}} {(s^{\frac{1}{k_{1}}} - f {(X_{1, i})}^{\frac{1}{k_{1}}})}^{2 - k_{1}} d s {| |}_{1} \\ \leq & | {\dot{X}}_{1, i} - f (X_{1, i}) |^{T} {| ϵ_{i} |}^{2 - k_{1}} \\ \leq & 2^{1 - k_{1}} | | ϵ_{i} {| |}_{1}^{2}, \end{matrix} \end{matrix}

(A27)

we can arrive at

\begin{matrix} \begin{matrix} V_{a, i} & = \frac{1}{2} | | X_{1, i} {| |}^{2} + \frac{1}{\frac{k_{2}}{k_{1}} + 1} | | X_{1, i} {| |}^{\frac{k_{2}}{k_{1}} + 1} + | | d (f (X_{1, i}), {\dot{X}}_{1, i}) {| |}_{1} + \frac{1}{2} x_{a, i}^{T} x_{a, i} \\ \leq \frac{1}{2} | | X_{1, i} {| |}^{2} + \frac{1}{\frac{k_{2}}{k_{1}} + 1} | | X_{1, i} {| |}^{\frac{k_{2}}{k_{1}} + 1} + 2^{1 - k_{1}} | | ϵ_{i} {| |}_{1}^{2} + \frac{1}{2} x_{a, i}^{T} x_{a, i} . \end{matrix} \end{matrix}

(A28)

Direct calculation, using Lemma 4 and Lemma 5, yields

\begin{matrix} \begin{matrix} V_{a, i}^{\frac{k_{1} + 1}{2}} & \leq {\frac{1}{2}}^{\frac{k_{1} + 1}{2}} | | X_{1, i} {| |}^{k_{1} + 1} + {\frac{1}{\frac{k_{2}}{k_{1}} + 1}}^{\frac{k_{1} + 1}{2}} | | X_{1, i} {| |}^{(\frac{k_{2}}{k_{1}} + 1) \frac{k_{1} + 1}{2}} \\ + 2^{(1 - k_{1}) \frac{k_{1} + 1}{2}} | | ϵ_{i} {| |}_{1}^{k_{1} + 1} + {\frac{1}{2}}^{\frac{k_{1} + 1}{2}} | | x_{a, i} {| |}^{k_{1} + 1}, \\ V_{a, i}^{\frac{\frac{k_{2}}{k_{1}} + k_{2}}{\frac{k_{2}}{k_{1}} + 1}} \leq & 4^{\frac{k_{2} - 1}{\frac{k_{2}}{k_{1}} + 1}} {\frac{1}{2}}^{\frac{\frac{k_{2}}{k_{1}} + k_{2}}{\frac{k_{2}}{k_{1}} + 1}} | | X_{1, i} {| |}^{\frac{2 \frac{k_{2}}{k_{1}} + 2 k_{2}}{\frac{k_{2}}{k_{1}} + 1}} + 4^{\frac{k_{2} - 1}{\frac{k_{2}}{k_{1}} + 1}} {\frac{1}{\frac{k_{2}}{k_{1}} + 1}}^{\frac{\frac{k_{2}}{k_{1}} + k_{2}}{\frac{k_{2}}{k_{1}} + 1}} | | X_{1, i} {| |}^{\frac{k_{2}}{k_{1}} + k_{2}} \\ + & 4^{\frac{k_{2} - 1}{\frac{k_{2}}{k_{1}} + 1}} 2^{\frac{(1 - k_{1}) (\frac{k_{2}}{k_{1}} + k_{2})}{\frac{k_{2}}{k_{1}} + 1}} | | ϵ_{i} {| |}_{1}^{\frac{2 \frac{k_{2}}{k_{1}} + 2 k_{2}}{\frac{k_{2}}{k_{1}} + 1}} + 4^{\frac{k_{2} - 1}{\frac{k_{2}}{k_{1}} + 1}} {\frac{1}{2}}^{\frac{\frac{k_{2}}{k_{1}} + k_{2}}{\frac{k_{2}}{k_{1}} + 1}} | | x_{a, i} {| |}^{\frac{2 \frac{k_{2}}{k_{1}} + 2 k_{2}}{\frac{k_{2}}{k_{1}} + 1}} . \end{matrix} \end{matrix}

(A29)

It follows that

\begin{matrix} \begin{matrix} V_{a, i}^{\frac{k_{1} + 1}{2}} & \leq M_{1} | | X_{1, i} {| |}^{k_{1} + 1} + M_{1} | | X_{1, i} {| |}^{(\frac{k_{2}}{k_{1}} + 1) \frac{k_{1} + 1}{2}} + M_{1} | | ϵ_{i} {| |}_{1}^{k_{1} + 1} + M_{1} | | x_{a, i} {| |}_{1}^{k_{1} + 1}, \\ V_{a, i}^{\frac{\frac{k_{2}}{k_{1}} + k_{2}}{\frac{k_{2}}{k_{1}} + 1}} & \leq M_{2} | | X_{1, i} {| |}^{\frac{2 \frac{k_{2}}{k_{1}} + 2 k_{2}}{\frac{k_{2}}{k_{1}} + 1}} + M_{2} | | X_{1, i} {| |}^{\frac{k_{2}}{k_{1}} + k_{2}} + M_{2} | | ϵ_{i} {| |}_{1}^{\frac{2 \frac{k_{2}}{k_{1}} + 2 k_{2}}{\frac{k_{2}}{k_{1}} + 1}} + M_{2} | | x_{a, i} {| |}_{1}^{\frac{2 \frac{k_{2}}{k_{1}} + 2 k_{2}}{\frac{k_{2}}{k_{1}} + 1}}, \end{matrix} \end{matrix}

(A30)

where

\begin{matrix} M_{1} & = max \{{\frac{1}{2}}^{\frac{k_{1} + 1}{2}}, {\frac{1}{\frac{k_{2}}{k_{1}} + 1}}^{\frac{k_{1} + 1}{2}}, 2^{(1 - k_{1}) \frac{k_{1} + 1}{2}}, {\frac{1}{2}}^{\frac{k_{1} + 1}{2}}\}, \\ M_{2} & = max \{\begin{matrix} 4^{\frac{k_{2} - 1}{\frac{k_{2}}{k_{1}} + 1}} {\frac{1}{2}}^{\frac{\frac{k_{2}}{k_{1}} + k_{2}}{\frac{k_{2}}{k_{1}} + 1}}, \\ 4^{\frac{k_{2} - 1}{\frac{k_{2}}{k_{1}} + 1}} {\frac{1}{\frac{k_{2}}{k_{1}} + 1}}^{\frac{\frac{k_{2}}{k_{1}} + k_{2}}{\frac{k_{2}}{k_{1}} + 1}}, \\ 4^{\frac{k_{2} - 1}{\frac{k_{2}}{k_{1}} + 1}} 2^{\frac{(1 - k_{1}) (\frac{k_{2}}{k_{1}} + k_{2})}{\frac{k_{2}}{k_{1}} + 1}}, \\ 4^{\frac{k_{2} - 1}{\frac{k_{2}}{k_{1}} + 1}} {\frac{1}{2}}^{\frac{\frac{k_{2}}{k_{1}} + k_{2}}{\frac{k_{2}}{k_{1}} + 1}} \end{matrix}\} \end{matrix}

Again, It is easy to verify the following inequalities

\begin{matrix} \begin{matrix} \frac{k_{2}}{k_{1}} + k_{2} & > (\frac{k_{2}}{k_{1}} + 1) \frac{k_{1} + 1}{2} > k_{1} + 1, \\ \frac{k_{2}}{k_{1}} + k_{2} & > \frac{2 (\frac{k_{2}}{k_{1}} + k_{2})}{\frac{k_{2}}{k_{1}} + 1} > k_{1} + 1 . \end{matrix} \end{matrix}

(A31)

combining (A30) and (A31) results in

\begin{matrix} \begin{matrix} V_{a, i}^{\frac{k_{1} + 1}{2}} & \leq 2 M_{1} | | X_{1, i} {| |}^{k_{1} + 1} + M_{1} | | X_{1, i} {| |}^{\frac{k_{2}}{k_{1}} + k_{2}} + M_{1} | | ϵ_{i} {| |}_{1}^{k_{1} + 1} + M_{1} | | x_{a, i} {| |}_{1}^{k_{1} + 1}, \\ V_{a, i}^{\frac{\frac{k_{2}}{k_{1}} + k_{2}}{\frac{k_{2}}{k_{1}} + 1}} & \leq M_{2} | | X_{1, i} {| |}^{k_{1} + 1} + 2 M_{2} | | X_{1, i} {| |}^{\frac{k_{2}}{k_{1}} + k_{2}} + M_{2} | | ϵ_{i} {| |}_{1}^{k_{1} + 1} + M_{2} | | ϵ_{i} {| |}_{1}^{\frac{k_{2}}{k_{1}} + k_{2}} \\ + M_{2} | | x_{a, i} {| |}_{1}^{k_{1} + 1} + M_{2} | | x_{a, i} {| |}_{1}^{\frac{k_{2}}{k_{1}} + k_{2}} . \end{matrix} \end{matrix}

(A32)

Note that

k_{3}

h_{1}

and

h_{2}

satisfy (50); hence, there exists

K_{3} > 0

satisfying

\begin{matrix} \begin{matrix} h_{1} - \frac{1}{2} k_{3}^{2} & \geq K_{3}, \\ h_{2} - \frac{1}{2} k_{3}^{2} & \geq K_{3} . \end{matrix} \end{matrix}

(A33)

Comparing (A24) with (A26) and (A33), we can conclude that

\begin{matrix} \begin{matrix} {\dot{V}}_{a, i} \leq & - K_{1} | | X_{1, i}^{1 + k_{1}} {| |}_{1} - K_{1} | | X_{1, i}^{\frac{k_{2}}{k_{1}} + k_{2}} {| |}_{1} - K_{2} | | ϵ_{i}^{k_{1} + 1} {| |}_{1} - K_{2} | | ϵ_{i}^{\frac{k_{2}}{k_{1}} + k_{2}} {| |}_{1} + \frac{1}{8} | | D_{i} g_{i} (Q_{i}) Δ u_{i} {| |}^{2} \\ + \frac{1}{2} k_{3}^{2} x_{a, i}^{T} x_{a, i} - h_{1} | | x_{a, i} {| |}^{k_{1} + 1} - h_{2} | | x_{a, i} {| |}^{\frac{k_{2}}{k_{1}} + k_{2}} + \frac{1}{16} | | D_{i} g_{i} (Q_{i}) J_{i} Δ u_{i} {| |}^{2} \\ \leq & - K_{1} | | X_{1, i}^{1 + k_{1}} {| |}_{1} - K_{1} | | X_{1, i}^{\frac{k_{2}}{k_{1}} + k_{2}} {| |}_{1} - K_{2} | | ϵ_{i}^{k_{1} + 1} {| |}_{1} - K_{2} | | ϵ_{i}^{\frac{k_{2}}{k_{1}} + k_{2}} {| |}_{1} \\ + \frac{1}{2} k_{3}^{2} | | x_{a, i} {| |}^{k_{1} + 1} + \frac{1}{2} k_{3}^{2} | | x_{a, i} {| |}^{\frac{k_{2}}{k_{1}} + k_{2}} + \frac{1}{8} | | D_{i} g_{i} (Q_{i}) Δ u_{i} {| |}^{2} \\ - h_{1} | | x_{a, i} {| |}^{k_{1} + 1} - h_{2} | | x_{a, i} {| |}^{\frac{k_{2}}{k_{1}} + k_{2}} + \frac{1}{16} | | D_{i} g_{i} (Q_{i}) J_{i} Δ u_{i} {| |}^{2} \\ \leq & - K_{1} | | X_{1, i}^{1 + k_{1}} {| |}_{1} - K_{1} | | X_{1, i}^{\frac{k_{2}}{k_{1}} + k_{2}} {| |}_{1} - K_{2} | | ϵ_{i}^{k_{1} + 1} {| |}_{1} - K_{2} | | ϵ_{i}^{\frac{k_{2}}{k_{1}} + k_{2}} {| |}_{1} \\ - K_{3} | | x_{a, i} {| |}^{k_{1} + 1} - K_{3} | | x_{a, i} {| |}^{\frac{k_{2}}{k_{1}} + k_{2}} + \frac{1}{16} | | D_{i} g_{i} (Q_{i}) J_{i} Δ u_{i} {| |}^{2} + \frac{1}{8} | | D_{i} g_{i} (Q_{i}) Δ u_{i} {| |}^{2} . \end{matrix} \end{matrix}

(A34)

Comparing (A32) with (A34), we can conclude that

\begin{matrix} \begin{matrix} {\dot{V}}_{a, i} \leq - P_{1} V_{a, i}^{\frac{k_{1} + 1}{2}} - P_{2} V_{a, i}^{\frac{\frac{k_{2}}{k_{1}} + k_{2}}{\frac{k_{2}}{k_{1}} + 1}} + Δ M, \end{matrix} \end{matrix}

(A35)

where

P_{1} = min \{\frac{K_{1}}{4 M_{1}}, \frac{K_{2}}{2 M_{1}}, \frac{K_{3}}{2 M_{1}}\},

P_{2} = min \{\frac{K_{1}}{4 M_{2}}, \frac{K_{2}}{2 M_{2}}, \frac{K_{3}}{2 M_{2}}\},

\begin{matrix} \begin{matrix} Δ M & = \frac{1}{16} | | D_{i} g_{i} (Q_{i}) J_{i} Δ u_{i} {| |}^{2} + \frac{1}{8} | | D_{i} g_{i} (Q_{i}) Δ u_{i} {| |}^{2} \\ \leq \frac{1}{16} | | Δ u_{i} {| |}^{2} | | D_{i} {| |}^{2} | | P_{i} {| |}^{2} + \frac{1}{8} | | Δ u_{i} {| |}^{2} | | D_{i} {| |}^{2} | | P_{i} {| |}^{2} | | J_{i}^{- 1} {| |}^{2}, \end{matrix} \end{matrix}

(A36)

Recalling the properties of

D_{i}

and

P_{i}

in Eq. (19) and (5), the upper bound of

Δ M

becomes

Δ M \leq \frac{1}{16} | | Δ u_{i} {| |}^{2} + \frac{1}{8} \frac{| | Δ u_{i} {| |}^{2}}{λ_{m i n} {(J_{i})}^{2}} .

By Lemma 8, inequality (A35) implies that

X = {[X_{1, i}^{T}, X_{2, i}^{T}, x_{a, i}^{T}]}^{T}

reach region

\begin{matrix} \begin{matrix} lim_{t \to T_{1}} X | V_{a, i} (X) \leq \min \{\begin{matrix} P_{1}^{- 2 / (k_{1} + 1)} {(\frac{Δ M}{1 - ς})}^{\frac{2}{k_{1} + 1}}, \\ P_{2}^{- 2 / (k_{1} + 1)} {(\frac{Δ M}{1 - ς})}^{\frac{\frac{k_{2}}{k_{1}} + 1}{\frac{k_{2}}{k_{1}} + k_{2}}} \end{matrix}\} \end{matrix} \end{matrix}

(A37)

within fixed time

T_{1}

given by

\begin{matrix} \begin{matrix} T_{1} \leq \frac{2}{P_{1} ς (1 - k_{1})} + \frac{k_{1} + k_{2}}{P_{2} ς k_{1} (k_{2} - 1)}, 0 < ς \leq 1 . \end{matrix} \end{matrix}

(A38)

The proof is completed.

References

Li, W.J.; Cheng, D.Y.; Liu, X.G.; Wang, Y.B.; Shi, W.H.; Tang, Z.X.; Gao, F.; Zeng, F.M.; Chai, H.Y.; Luo, W.B.; et al. On-orbit service (OOS) of spacecraft: A review of engineering developments. Progress in Aerospace Sciences 2019, 108, 32–120. [Google Scholar] [CrossRef]
Sanfedino, F.; Thiébaud, G.; Alazard, D.; Guercio, N.; Deslaef, N. Advances in fine line-of-sight control for large space flexible structures. Aerospace Science and Technology 2022, 130, 107961. [Google Scholar] [CrossRef]
LI, P.; WEN, X.; LIU, H.; LU, Y. Event-triggered and consensus-based attitude tracking alignment for discrete-time multiple spacecraft system exploiting interference. Chinese Journal of Aeronautics 2023, 36, 241–255. [Google Scholar] [CrossRef]
Zhang, T.; Mu, R. Attitude Tracking Adaptive Control of a Geocentric Polar Displaced Solar Sail. Aerospace 2023, 10. [Google Scholar] [CrossRef]
Fan, S.; Cui, Z.; Chen, X.; Liu, X.; Xing, F.; You, Z. Magnetic Fault-Tolerant Attitude Control with Dynamic Sensing for Remote Sensing CubeSats. Remote Sensing 2023, 15. [Google Scholar] [CrossRef]
Song, C.; Fan, C.; Wang, M. Image-Based Adaptive Staring Attitude Control for Multiple Ground Targets Using a Miniaturized Video Satellite. Remote Sensing 2022, 14. [Google Scholar] [CrossRef]
Amato, F.; Ambrosino, R.; Cosentino, C.; Tommasi, G.D. Input-output finite time stabilization of linear systems. Automatica 2010, 46, 1558–1562. [Google Scholar] [CrossRef]
Sun, Z.Y.; Yun, M.M.; Li, T. A new approach to fast global finite-time stabilization of high-order nonlinear system. Automatica 2017, 81, 455–463. [Google Scholar] [CrossRef]
Sun, Z.Y.; Shao, Y.; Chen, C. Fast finite-time stability and its application in adaptive control of high-order nonlinear system. Automatica 2019, 106, 339–348. [Google Scholar] [CrossRef]
Hu, H.X.; Wen, G.; Yu, W.; Cao, J.; Huang, T. Finite-Time Coordination Behavior of Multiple Euler-Lagrange Systems in Cooperation-Competition Networks. IEEE Transactions on Cybernetics 2019, 1–13. [Google Scholar] [CrossRef] [PubMed]
Gui, H.; de Ruiter, A.H. Global finite-time attitude consensus of leader-following spacecraft systems based on distributed observers. Automatica 2018, 91, 225–232. [Google Scholar] [CrossRef]
Yu, L.; Ye, D.; Sun, Z. Finite-time resilient attitude coordination control for multiple rigid spacecraft with communication link faults. Aerospace Science and Technology 2021, 111, 106560. [Google Scholar] [CrossRef]
Gui, H.; Ruiter, A.H.J.D. Global finite-time attitude consensus of leader-following spacecraft systems based on distributed observers. Automatica 2018. [Google Scholar] [CrossRef]
Zhang, Y.; Li, S.; Wang, S.; Wang, X.; Duan, H. Distributed bearing-based formation maneuver control of fixed-wing UAVs by finite-time orientation estimation. Aerospace Science and Technology 2023, 136, 108241. [Google Scholar] [CrossRef]
Doostmohammadian, M. Single-Bit Consensus With Finite-Time Convergence: Theory and Applications. IEEE Transactions on Aerospace and Electronic Systems 2020, 56, 3332–3338. [Google Scholar] [CrossRef]
Xu, C.; Wang, Y.; Niu, Z.; Luo, S.; Du, F. Fixed-Time Convergent Guidance Law with Angle Constraint and Autopilot Lag Compensation Using Partial-State Feedback. Aerospace 2023, 10. [Google Scholar] [CrossRef]
Zhan, X.; Hao, L.; Han, T.; Yan, H. Adaptive bipartite output consensus for heterogeneous multi-agent systems with quantized information: A fixed-time approach. Journal of the Franklin Institute 2021, 358, 7221–7236. [Google Scholar] [CrossRef]
Wang, J.; Fang, Y.M.; Li, J.X.; Li, K.D. Fixed-Time Sliding Mode Fault-Tolerant Consensus Control for Second-Order Multi-Agent System with Actuator Fault. 2022 41st Chinese Control Conference (CCC), 2022, pp. 4153–4158. [CrossRef]
Ni, J.; Shi, P.; Zhao, Y.; Wu, Z. Fixed-Time Output Consensus Tracking for High-Order Multi-Agent Systems With Directed Network Topology and Packet Dropout. IEEE/CAA Journal of Automatica Sinica 2021, 8, 817–836. [Google Scholar] [CrossRef]
Xu, T.; Duan, Z.; Sun, Z.; Chen, G. Distributed Fixed-Time Coordination Control for Networked Multiple Euler-Lagrange Systems. IEEE Transactions on Cybernetics 2020, 1–12. [Google Scholar] [CrossRef]
Wu, X.; Wei, C.; Chen, T.; Dai, M.Z. On novel distributed fixed-time formation tracking of multiple hypersonic flight vehicles with collision avoidance. Aerospace Science and Technology 2023, 141, 108517. [Google Scholar] [CrossRef]
Zhou, Z.; Wang, Y. Coordinated Attitude Control of Spacecraft Formation Flying via Fixed-Time Estimators under a Directed Graph. Remote Sensing 2022, 14. [Google Scholar] [CrossRef]
Zou, A.M.; Fan, Z. Distributed fixed-time attitude coordination control for multiple rigid spacecraft. International Journal of Robust and Nonlinear Control 2020, 30, 266–281. [Google Scholar] [CrossRef]
Sui, W.; Duan, G.; Hou, M.; Zhang, M. Distributed fixed-time attitude coordinated tracking for multiple rigid spacecraft via a novel integral sliding mode approach. Journal of the Franklin Institute 2020, 357, 9399–9422. [Google Scholar] [CrossRef]
Han, G.; Yuanqing, X.; Zhang, X.; Zhang, G. Distributed fixed-time attitude coordinated control for multiple spacecraft with actuator saturation. Chinese Journal of Aeronautics 2022, 35, 292–302. [Google Scholar]
Hong, H.; Yu, C.; Yu, W. Adaptive fixed-time control for attitude consensus of disturbed multi-spacecraft systems with directed topologies. IEEE Transactions on Network Science and Engineering 2022, 9, 1451–1461. [Google Scholar] [CrossRef]
Yin, T.; Zhang, K.; Jiang, B.; Liu, Q. Fixed-time attitude cooperative fault-tolerant control with prescribed performance for heterogeneous multiple satellite. Aerospace Science and Technology 2022, 128, 107752. [Google Scholar] [CrossRef]
Xu, C.; Wu, B.; Wang, D.; Zhang, Y. Distributed fixed-time output-feedback attitude consensus control for multiple spacecraft. IEEE Transactions on Aerospace and Electronic Systems 2020, 56, 4779–4795. [Google Scholar] [CrossRef]
Chen, R.Z.; Li, Y.X.; Ahn, C.K. Reinforcement-learning-based fixed-time attitude consensus control for multiple spacecraft systems with model uncertainties. Aerospace Science and Technology 2023, 132, 108060. [Google Scholar] [CrossRef]
Zuo, Z.; Han, Q.L.; Ning, B.; Ge, X.; Zhang, X.M. An overview of recent advances in fixed-time cooperative control of multiagent systems. IEEE Transactions on Industrial Informatics 2018, 14, 2322–2334. [Google Scholar] [CrossRef]
Utschick, W. Communications in Interference Limited Networks 2016.
Truszkowski, W.; Hinchey, M.; Rash, J.; Rouff, C. NASA’s swarm missions: The challenge of building autonomous software. IT professional 2004, 6, 47–52. [Google Scholar] [CrossRef]
Molinari, F.; Raisch, J. Efficient consensus-based formation control with discrete-time broadcast updates. 2019 IEEE 58th Conference on Decision and Control (CDC). IEEE, 2019, pp. 4172–4177.
Molinari, F.; Agrawal, N.; Stanczak, S.; Raisch, J. Max-Consensus Over Fading Wireless Channels 2020.
Peiran, L.; Xin, W.; Haiying, L.; Yuping, L. Event-triggered and consensus-based attitude tracking alignment for discrete-time multiple spacecraft system exploiting interference. Chinese Journal of Aeronautics 2023, 36, 241–255. [Google Scholar]
Hu, D.; Zhang, S.; Zou, A.M. Velocity-free fixed-time attitude cooperative control for spacecraft formations under directed graphs. International Journal of Robust and Nonlinear Control 2021, 31, 2905–2927. [Google Scholar] [CrossRef]
Yatzunsky, I.M.; Gurko, O.V.; Kwon, O.C.; Hassan, M.I.; Faeth, G.M.; Ickes, B.P. A new method for performing digital control system attitude computations using quaternions. AIAA Journal 1970. [Google Scholar]
Sidi, M.J. Spacecraft dynamics and control: a practical engineering approach; Vol. 7, Cambridge university press, 1997.
Wie, B. Space Vehicle Dynamics and Control, 2008.
Li, P.; Wen, X.; Zheng, M.; Liu, H.; Long, D.; Lu, Y. Discrete-Time Attitude Tracking Synchronization for Swarms of Spacecraft Exploiting Interference. Aerospace 2022, 9, 134. [Google Scholar] [CrossRef]
Hong, Y.; Hu, J.; Gao, L. Tracking control for multi-agent consensus with an active leader and variable topology. Automatica 2006, 42, 1177–1182. [Google Scholar] [CrossRef]
Qian, C.; Lin, W. Non-Lipschitz continuous stabilizers for nonlinear systems with uncontrollable unstable linearization. Systems & Control Letters 2001, 42, 185–200. [Google Scholar] [CrossRef]
Zou, A.M.; de Ruiter, A.H.; Kumar, K.D. Distributed finite-time velocity-free attitude coordination control for spacecraft formations. Automatica 2016, 67, 46–53. [Google Scholar] [CrossRef]
Chen, G.; Yang, Y.; Deng, F. On practical fixed-time stability of discrete-time impulsive switched nonlinear systems. International Journal of Robust and Nonlinear Control 2020, 30, 7822–7834. [Google Scholar] [CrossRef]
Jiang, B.; Hu, Q.; Friswell, M.I. Fixed-time rendezvous control of spacecraft with a tumbling target under loss of actuator effectiveness. IEEE Transactions on Aerospace and Electronic Systems 2016, 52, 1576–1586. [Google Scholar] [CrossRef]
Farrag, A.; Othman, S.; Mahmoud, T.; ELRaffiei, A.Y. Satellite swarm survey and new conceptual design for Earth observation applications. The Egyptian Journal of Remote Sensing and Space Science 2021, 24, 47–54. [Google Scholar] [CrossRef]

Figure 1. Large telescope on-orbit construction: (a) Consensus-based attitude maneuver of unit mirrors

1 \dots n

. (b) Docking and assembly of unit mirrors

1 \dots n

and main structure 0.

Figure 1. Large telescope on-orbit construction: (a) Consensus-based attitude maneuver of unit mirrors

1 \dots n

. (b) Docking and assembly of unit mirrors

1 \dots n

and main structure 0.

Figure 2. The augmented communication graph.

Figure 3. The estimation errors of case I.

Figure 4. The control errors of case I.

Figure 5. The control torque of case I.

Figure 6. The estimation errors of case II.

Figure 7. The control errors of case II.

Figure 8. The control torque of case II.

Table 1. Notation.

Notation	Meaning
$Q^{*}$	the reference attitude quaternion
$Q_{i}$	attitude quaternion of modular unit mirror i
$ω_{i}$	attitude angular velocity of modular unit mirror i
$D_{i}$	pre-designed constant desired attitude difference
$t_{k} \in R_{\geq 0}, k \in N_{\geq 0}$	update instants
$G$	communication graph
$\bar{G}$	augmented communication graph
$H \in R^{n \times n}$	a matrix associated with $\bar{G}$
$c_{i, j}$	(unknown) channel fading coefficient of the edge $(i, j)$
$η_{i}^{(1)} (t_{k})$	the normalized signal modular unit mirror i received at update instants $t_{k}$
$η^{(1)} = {[η_{1}^{(1) T} \dots η_{n}^{(1) T}]}^{T}$	a column stack vector of all $η_{i}^{(1)}, i = 1 \dots n$
$J_{i} \in R^{3 \times 3}$	the initial momentum of inertia of modular unit mirror i
$X_{1, i} \in R^{4}, X_{2, i} \in R^{4}$	backstepping states of modular unit mirror i
$x_{a, i} \in R^{4}$	the adaptive compensation law
${\hat{Q}}_{i}^{*}$	the estimation of $Q^{*}$ from modular unit mirror i
${\hat{Q}}^{} = {[{\hat{Q}}_{1}^{ T} \dots {\hat{Q}}_{n}^{* T}]}^{T}$	a column stack vector of all ${\hat{Q}}_{i}^{*}, i = 1 \dots n$
${\tilde{Q}}_{i}^{*}$	the estimation error of modular unit mirror i
${\tilde{Q}}^{} = {[{\tilde{Q}}_{1}^{ T} \dots {\tilde{Q}}_{n}^{* T}]}^{T}$	a column stack vector of all ${\tilde{Q}}_{i}^{*}, i = 1 \dots n$
$T_{i} \in R^{3}$	control torque for modular unit mirror i
$δ_{T i}$	unknown tiny disturbance torque of modular unit mirror i

Table 2. Initial state of the large telescope on-orbit construction system.

Unit mirror	Initial attitude $(^{\circ})$	Initial angular velocity $(^{\circ} / s)$
1	[13; 11; 11]	[-0.001; 0.001; -0.002]
2	[20; 16; 17]	[-0.001; -0.002; 0.001]
3	[12; 21; 18]	[0.001; -0.001; -0.002]
4	[13; 14; 16]	[-0.001; 0.001; -0.002]
5	[15; -2; 19]	[-0.002; -0.001; 0.002]

Table 3. Simulation performance of case I and case II.

Case	Observer convergence time $(s)$	Observer error $(^{\circ})$	Controller convergence time $(s)$	Controller error $(^{\circ})$	Maximum torque $(N \cdot m)$
I	0.8	0.001	130	0.01	0.02
II	4	0.001	50	0.01	5

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Fixed-time Consensus-based Attitude Control of Large Telescope On-orbit Construction

Abstract

1. Introduction

2. Preliminary Knowledge

2.1. Kinematics and Dynamics

2.1.1. Quaternion Kinematics

2.1.2. Attitude Dynamics

2.2. Graph

2.3. WMAC Model for Wireless Interference

3. Problem Description

4. Design of Communication System Exploiting Interference

5. Proposed Solution

5.1. Discrete-Time Fixed-Time Observer

5.2. Fixed-Time Controller

6. Simulation Results

6.1. Case I: Simulation with the Discrete-Time Control Scheme Proposed in this Study

6.2. Comparison Case II: with Continuous Control Scheme

7. Conclusion

Author Contributions

Funding

Appendix A. Proof of Theorem 1

Appendix B. Proof of Theorem 2

References

MDPI Initiatives

Important Links

Subscribe