Spin Phase Space Entropy

1. Introduction

This paper addresses the problem of quantifying the randomness associated with a spin state. Our broader motivation is to study the role of randomness in quantum physics. We follow the Geometric Quantization method (GQ) [1,2,3,4,5] a formulation of quantum physics derived from classical physics in phase space. One can then view quantum physics as embedding randomness into phase space classical physics and so seeing it as an information theory. Previous work addressed information theory aspects of quantum physics, see [6,7,8,9,10,11,12,13,14,15,16] and their references. We point out the GK-Law[15], a hypothesis that in a closed physical system information cannot be gained. Thus, the entropy of a quantum state could and should play a role in helping us make predictions about particle physics.

The degrees of freedom (DOFs) of a quantum state are associated with the position and spin values of a particle, i.e., all randomness of a quantum state is captured by Born’s rule once the DOFs are specified as well as its phase space. Thus, our attempt to capture the information content of a quantum state, must address these degrees of freedom as well as their phase space. We point out that in quantum physics, von Neumann entropy [6] quantifies only the lack of knowledge an observer has about a quantum state, i.e., it quantifies only the randomness in specifying its DOFs. Thus, for all pure states, von Neumann entropy is zero, while our entropy formulation is focused on pure states.

With respect to the position DOF Geiger and Kedem [15] formulated the x-p phase space quantum entropy. Let us then focus on the spin DOF.

Note that quantifying the randomness of the spin state along the z-direction alone is not sufficient, since a measurement of an eigenstate of $S_z$ is certain to yield the eigenvalue of this eigenstate, and yet there is the randomness associated with any spin measurement in the x-y plane as demonstrated by the Stern-Gerlach experiments[17]. It is in the spin phase space where all the randomness of a spin state is captured.

Historically, spin was first conceived as a quantum concept, but GQ derives it as the quantization of the classical two-sphere ${\mathbb{S}}^2$. In this Hilbert space two independent variables, such as the zenith and azimuth angles, $\theta$ and $\varphi$ respectively, are required to specify a spin wave function $\psi (\theta ,\varphi )$. These classical variables are associated with the polarization of spin particles. Not only does GQ produces a description for the spin, originated from classical ideas, but also provides the spin phase space where the wave function and all its randomness is defined.

The information content, or lack thereof, associated with the phase space wave function $\psi (\theta ,\varphi )$ is captured by the differential entropy [18], i.e.,

$$\begin{array}{c}\hfill \mathrm{S}\left(\psi \right)=-{\int }_0^{2\pi }{\int }_0^{\pi }{\left|\psi (\theta ,\varphi )\right|}^{2}ln{\left|\psi (\theta ,\varphi )\right|}^{2}sin\theta d\theta d\varphi .\end{array}$$

We will refer to (1) as spin-entropy. While many of the properties exhibited by the spin-entropy also hold for the more general Rényi entropy of order $\alpha$ given by

$$\begin{array}{c}\hfill {\mathrm{S}}_{\alpha }\left(\psi \right)=\frac{1}{1-\alpha }log\left({\int \left|\psi (\theta ,\varphi )\right|}^{2\alpha }sin\theta d\theta d\varphi \right),\end{array}$$

we focus on the spin-entropy in this paper.

1.1. Previous Work

Wehrl entropy [19] was introduced to approximate a classical entropy for a quantum state, and Lieb studied spin-coherent states to evaluate Wehrl spin entropy [20,21,22] As in the case of spatial coherent states, spin coherent states constitute an overcomplete set of states. Since Werhl entropy is based on an overcomplete basis representation, projections onto this basis lead to quasi-probabilities violating the Kolmogorov third axiom. The overcomplete basis decomposition and the arbitrariness of the choice of spin-coherent states basis to define the probability distribution prevent Wehrl entropy from accurately quantifying the randomness associated with the spin observables.

This work does start from a similar view as [23] and here we steer it differently, correcting their attempt to decompose the wave function in phase space.

1.2. Paper Organization

The paper is organized as follows: Section 2 provides a summary of GQ concepts, based on [5], applied to the sphere and focus on a derivation of the wave function in spin phase space. Extensions to these GQ concepts are also in the Appendix A and references. Section 3 derives the main spin-entropy properties, including a formula for all the eigenstates of the z-direction for any spin s. Section 4 analyzes the connection between phase space entanglement and spin-entropy. We show that the more the entanglement between two particles the larger is the spin-entropy. Section 5 concludes the paper with speculations about the role of spin-entropy in particle physics.

2. Some Geometric Quantization Concepts

We first provide a summary of concepts used in this paper developed by the GQ of the two-sphere ${\mathbb{S}}^2$ to describe spin operators and eigenfunctions in phase space. Some extra material to complete the descriptions presented in this summary is presented in the Appendix A.

2.1. Complex Plane and the Sphere

Consider the local variable $z=x+\mathrm{i}y$ to describe the complex plane ${\mathbb{CP}}^1$. The stereographic projection of the 3D embedding of the sphere ${\mathbb{S}}^2$ of radius s via the south pole $Z=-1$, to the plane $Z=0$ is given as

$$\begin{array}{c}\hfill X=ssin\theta cos\varphi =s\frac{z+z^{*}}{1+z{z}^{*}},Y=ssin\theta sin\varphi =-\mathrm{i}s\frac{z-z^{*}}{1+z{z}^{*}},Z=scos\theta =s\frac{1-z{z}^{*}}{1+z{z}^{*}}\end{array}$$

where $(\theta ,\varphi )\in [0,\pi )\times [0,2\pi )$ are the zenith and azimuth spherical angles, respectively. The inverse mapping is then given by

$$\begin{array}{c}\hfill z=\frac{X+\mathrm{i}Y}{1+Z}=tan\frac{\theta }{2}{\mathrm{e}}^{\mathrm{i}\varphi }\to z^{*}=\frac{X-\mathrm{i}Y}{1+Z}=tan\frac{\theta }{2}{\mathrm{e}}^{-\mathrm{i}\varphi }.\end{array}$$

and the mapping of the south pole $Z=-1$ to z requires the stereographic projection via the north pole, i.e., $z=\frac{X+\mathrm{i}Y}{1-Z}$.

2.2. Symplectic Structure for the Sphere and Canonical Transformations

A symplectic structure for the sphere manifold is given by

$$\begin{array}{c}\hfill \Omega =2\mathrm{i}s\frac{dz\wedge d{z}^{*}}{{(1+z{z}^{*})}^2}=ssin\theta d\theta \wedge d\varphi \end{array}$$

where $2s$ is an integer. Canonical transformations preserve $\Omega$. Consequently for vector fields $\xi =({\xi }^z,{\xi }^{z^{*}})$ to be generators of canonical transformations in the sphere, the transformation $\overrightarrow{z}=(z,z^{*})\to \overrightarrow{z}+\xi \left(\overrightarrow{z}\right))$ must satisfy

$$\begin{array}{cc}\hfill 0={\delta }_{\xi }\Omega & =\frac{1}{2}{\Omega }_{\mu ,\nu }(\overrightarrow{z}+\xi )d(z^{\mu }+{\xi }^{\mu }\left(\overrightarrow{z}\right))\wedge d(z^{\nu }+{\xi }^{\nu }\left(\overrightarrow{z}\right))-\frac{1}{2}{\Omega }_{\mu ,\nu }d{z}^{\mu }\wedge d{z}^{\nu }\hfill \\ \hfill & =\frac{1}{2}\left[{\partial }_{z^{\mu }}\left({\xi }^{\alpha }{\Omega }_{\alpha ,\nu }\right)-{\partial }_{z^{\nu }}\left({\xi }^{\alpha }{\Omega }_{\alpha ,\mu }\right)\right]d{z}^{\mu }\wedge d{z}^{\nu }\hfill \\ \hfill & =\left({\xi }^{\alpha }{\Omega }_{\alpha ,\nu }d{z}^{\nu }\right).\hfill \end{array}$$

Thus, for every infinitesimal canonical transformation we can associate a function J on ${\mathbb{S}}^2$ such that $-dJ={\xi }^{\alpha }{\Omega }_{\alpha ,\nu }d{z}^{\nu }$ is a closed one form. Also, by inverting $\Omega$ we get

$$\begin{array}{c}\hfill {\xi }^{\mu }{\Omega }_{\mu ,\nu }={-}_{z^{\nu }}J\to {\xi }^{\mu }={\Omega }_{z^{\nu }}^{\mu ,\nu }J.\end{array}$$

Thus, conversely, given a classical observable J the generators $\xi$ of the infinitesimal canonical transformation can be readily obtained.

2.3. Spin Operator and Eigenfunctions

In order to derive the spin operators $S_x,S_y,S_z$ one consider the classical functions $J_X=X(z,z^{*})$, $J_Y=Y(z,z^{*})$, $J_Z=Z(z,z^{*})$ in the sphere, as described by (2.1). The generators of the canonical transformations associated with these functions, derived from (2.2), are isometries of the sphere. In Appendix A we give a summary of the GQ steps to obtain the quantum operator operators (A.3) acting on the two-sphere ${\mathbb{S}}^2$ associated to these functions $J_X,J_Y,J_Z$. These are the spin operators and can then be written as

$$\begin{array}{cc}\hfill {\mathcal{S}}_X& ={\frac{(1-z^2)}{2}}_z+s\frac{1}{(1+z{z}^{*})}\left(z+\frac{(z^{*}+z^2{z}^{*})}{2}\right)\hfill \\ \hfill {\mathcal{S}}_Y& =\mathrm{i}{\frac{(1+z^2)}{2}}_z-\mathrm{i}s\frac{1}{(1+z{z}^{*})}\left(z-\frac{(z^{*}-z^2{z}^{*})}{2}\right)\hfill \\ \hfill {\mathcal{S}}_Z& =-z_z+s\frac{1}{(1+z{z}^{*})}\hfill \end{array}$$

The eigenfunctions of the operator ${\mathcal{S}}_Z$ (due to the polarization condition, see appendix (A.3), (A.3)) are of the form

$$\begin{array}{c}\hfill {\Psi }_{s,m}(z,z^{*})=\frac{1}{{(1+z{z}^{*})}^s}{f}_{s,m}\left(z\right)\end{array}$$

which leads to

$$\begin{array}{cc}\hfill {\mathcal{S}}_Z{\Psi }_{s,m}(z,z^{*})& =sz\frac{z^{*}}{{(1+z{z}^{*})}^{1+s}}{f}_{s,m}\left(z\right)-{\frac{z}{{(1+z{z}^{*})}^s}}_z{f}_{s,m}\left(z\right)+s\frac{1}{{(1+z{z}^{*})}^{1+s}}{f}_{s,m}\left(z\right)\hfill \\ \hfill & =\frac{1}{{(1+z{z}^{*})}^s}\left(-z{\partial }_z+s\right)f_{s,m}\left(z\right)\hfill \\ \hfill & =m{\Psi }_{s,m}(z,z^{*})\hfill \\ \hfill & \Downarrow \hfill \\ \hfill \left(-z_z+s\right)f_{s,m}\left(z\right)& =m{f}_{s,m}\left(z\right)\hfill \end{array}$$

with solutions of the form

$$\begin{array}{cc}\hfill f_{s,m}\left(z\right)& =\frac{1}{\sqrt{4\pi }}\sqrt{(2s+1)C_{s+m}^{2s}}{z}^{s-m},\hfill \end{array}$$

where $C_p^n=\frac{n!}{p!(n-p)!}$ and we note that compare to the presentation of Nair[5] the functions $f_{s,m}\left(z\right)$ do have an extra factor $\frac{1}{\sqrt{4\pi }}$ for normalization purposes. In the representation (2.1) the wave function (2.3) is written as

$$\begin{array}{cc}\hfill {\Psi }_{s,m}(\theta ,\varphi )& =\frac{\sqrt{(2s+1)}}{2^s\sqrt{4\pi }}{\left[C_{s+m}^{2s}\right]}^{\frac{1}{2}}{\left(1+cos\theta \right)}^{\frac{s+m}{2}}{\left(1-cos\theta \right)}^{\frac{s-m}{2}}{\mathrm{e}}^{\mathrm{i}(s-m)\varphi }.\hfill \end{array}$$

These wave functions form an orthonormal basis, i.e.,

$$\begin{array}{cc}\hfill {\int }_{{\mathbb{S}}^2}\frac{\Omega }{s}{\Psi }_{s,m}{\Psi }_{s,m^{\prime }}^{*}& =\mathrm{i}{\int }_{{\mathbb{S}}^2}\frac{dz\wedge d{z}^{*}}{2\pi {(1+z{z}^{*})}^{2s+2}}{f}_{s,m}^{*}\left(z\right)f_{s,m^{\prime }}\left(z\right)\hfill \\ \hfill & =\frac{1}{2^{2s+1}}{\int }_0^{2\pi }\frac{d\varphi }{2\pi }{\int }_0^{\pi }sin\theta d\theta {(1+cos\theta )}^{2s}{f}_{s,m}^{*}\left(z(\theta ,\varphi )\right)f_{s,m^{\prime }}\left(z(\theta ,\varphi )\right)\hfill \\ \hfill & ={\delta }_{m,m^{\prime }}\frac{(2s+1)C_{s+m}^{2s}}{2^{2s+1}}{\int }_0^{\pi }{(1+cos\theta )}^{s+m}{(1-cos\theta )}^{s-m}sin\theta d\theta \hfill \\ \hfill & ={\delta }_{m,m^{\prime }}.\hfill \end{array}$$

Then, through linear superposition of these eigenstates, all spin-wave functions in phase space for spin s are constructed.

Note that a wave function in the x-p phase space is decomposed as a product of a wave function on x and a wave function on p, related to each other by the Fourier transform. In contrast, a wave function in the spin phase space cannot be “reduced”, i.e., cannot be decomposed as a product of wave functions where each contains just one variable of phase space. Instead, a wave function over the entire spin phase space, the entire sphere, is required.

3. Spin-Entropy in Phase Space

Lemma 1 

(Space Homogeneity). The spin-entropy, given by (1), is invariant under rotations and reflections of the coordinate system.

Proof. 

Given a function $g:{\mathbb{S}}^2\to \mathbb{R}$, define a functional on the sphere

$$F\left(g\right)={\int }_{{\mathbb{S}}^2}g(z,z^{*})d\sigma (z,z^{*}),$$

where $d\sigma (z,z^{*})=\frac{1}{s}\Omega =2\mathrm{i}\frac{dz\wedge d{z}^{*}}{{(1+z{z}^{*})}^2}$.

The spin-entropy is one such functional $F\left(g\right)$ for the function

$$\begin{array}{c}\hfill g(z,z^{*})=-|\psi (z,z^{*}){|}^{2}log{\left|\psi (z,z^{*})\right|}^2.\end{array}$$

Consider an isometry transformation $\xi :{\mathbb{S}}^2\to {\mathbb{S}}^2$, so $\xi (z,z^{*})=\left({\xi }^z(z,z^{*}),{\xi }^{z^{*}}(z,z^{*})\right)$. Applying an isometry to the wave function $\psi (z,z^{*})$, i.e., applying it to g leads to

$$\begin{array}{cc}\hfill F(g\circ \xi )& ={\int }_{{\mathbb{S}}^2}g\left(\xi (z,z^{*})\right)d\sigma (z,z^{*})\hfill \\ \hfill & \mathrm{changing}\mathrm{coordinates}d\sigma (z,z^{*})=detJ\left(\xi \right)d\sigma \left(\xi (z,z^{*})\right)\hfill \\ \hfill & ={\int }_{{\mathbb{S}}^2}g\left({\xi }^z(z,z^{*}),{\xi }^{z^{*}}(z,z^{*})\right)detJ\left(\xi \right)d\sigma \left({\xi }^z(z,z^{*}),{\xi }^{z^{*}}(z,z^{*})\right)\hfill \\ \hfill & \xi \mathrm{is}\mathrm{a}\mathrm{canonical}\mathrm{transformation}\hfill \\ \hfill & ={\int }_{{\mathbb{S}}^2}g\left({\xi }^z,{\xi }^{z^{*}}\right)d\sigma \left({\xi }^z,{\xi }^{z^{*}}\right)=F\left(g\right)\hfill \end{array}$$

where we used the fact that isometries of the sphere are canonical transformations that preserve the symplectic form, i.e., the determinant of a Jacobian of a canonical transformations is 1, i.e., $detJ\left(\xi \right)=1$.

Thus the spin-entropy is invariant under isometries. The isometries of the sphere are the three reflections, and combinations of two reflections gives the rotations. □

One immediate conclusion is that the homogeneity of the space is reflected by the invariance of the spin-entropy to rotations and reflections of the coordinate system. So given a spin-state associated with $s=1$ and such that for some choice of z-coordinate it has $m=1$, this state will have a spin-entropy value regardless if one chooses or not this z-coordinate to describe it.

Let us consider the eigentstates along the z-direction, described by (2.3). The spin-entropy (1) associated with these eigenfunctions is

$$\begin{array}{cc}\hfill S\left({\psi }_{s,m}\right)& =-{\int }_0^{2\pi }{\int }_0^{\pi }\left(\frac{{\left(1+cos\theta \right)}^{s+m}{\left(1-cos\theta \right)}^{s-m}}{2\pi Z(s,m)}\right)ln\left(\frac{{\left(1+cos\theta \right)}^{s+m}{\left(1-cos\theta \right)}^{s-m}}{2\pi Z(s,m)}\right)sin\theta d\theta d\varphi \hfill \\ \hfill & =ln\left(2\pi Z(s,m)\right)-\frac{1}{Z(s,m)}{\int }_{-1}^1{\left(1+u\right)}^{s+m}{\left(1-u\right)}^{s-m}ln\left[{\left(1+u\right)}^{s+m}{\left(1-u\right)}^{s-m}\right]du,\hfill \end{array}$$

where the probability normalization constant is given by $2\pi Z(s,m)=2\pi \frac{2^{2s+1}}{(2s+1)C_{s+m}^{2s}}$ and $u=cos\theta$.

For the rest of this section, and for manipulation purposes, let us define the integer variables $p=s+m$ and $q=s-m$, and since $-s\le m\le s$, we have $p,q\in [0,1,\cdots ,2s-1,2s]$. We may refer to $p,q,s,m$ as it is more convenient during manipulations.

Lemma 2 

(Spin-Entropy Formula for z-Eigenstates). The spin-entropy in phase space for the z-eigenstates ${\psi }_{s,m}$ is invariant under the reflection $m\to -m$ and can be written as

$$\begin{array}{c}\hfill S\left({\psi }_{s,m}\right)=ln\left(4\pi \right)-ln{C}_{s+m}^{2s}+\sum _{j=1}^{s-m+1}\frac{s+m}{(s+m+j)}+\sum _{j=1}^{s+m+1}\frac{s-m}{(s-m+j)}\end{array}$$

where $\theta (.)$ is the heaviside function, i.e. for $x\ge 0,\theta \left(x\right)=1$ and for $x<0,\theta \left(x\right)=0$.

Proof. 

Following on (3), let us first proceed to evaluate the spin-entropy. We will refer to $S_{p,q}$ as the spin-entropy of the eigenstate $S\left({\psi }_{s,m}\right)$ and $Z_{p,q}=\left[\frac{2^{s+1}}{2s+1}\frac{p!q!}{2s!}\right]$ refers to the normalization $Z(s,m)$. We then write (3) as

$$\begin{array}{cc}\hfill S_{p,q}& =ln\left(2\pi Z_{p,q}\right)-\frac{1}{Z_{p,q}}{\int }_{-1}^1{(1+u)}^p{(1-u)}^{q}ln\left({(1+u)}^p{(1-u)}^q\right)du\hfill \\ \hfill & =ln\left(2\pi Z_{p,q}\right)-\frac{1}{Z_{p,q}}[p{I}_{p,q}+q{I}_{q,p}]\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill I_{p,q}& ={\int }_{-1}^1{(1+u)}^p{(1-u)}^{q}ln(1+u)du\hfill \\ \hfill & \Downarrow \hfill \\ \hfill I_{q,p}& ={\int }_{-1}^1{(1+u)}^q{(1-u)}^{p}ln(1+u)du={\int }_{-1}^1{(1-u^{\prime })}^q{(1+u^{\prime })}^{p}ln(1-u^{\prime })d{u}^{\prime }.\hfill \end{array}$$

and in the last step we applied the transformation $u\to u^{\prime }=-u$.

Noting that $Z_{p,q}=\left[\frac{2^{s+1}}{2s+1}\frac{p!q!}{2s!}\right]=Z_{q,p}$, it is then clear that the spin-entropy (3) have the property $S_{p,q}=S_{q,p}$. And since the transformation $m\to -m$ is equivalent to $p\leftrightarrow q$, we obtain that $S\left({\psi }_{s,-m}\right)=S\left({\psi }_{s,m}\right)$ to conclude the first statement of the lemma.

In order to evaluate $I_{p,q}$ define

$$\begin{array}{c}\hfill \left\{\begin{array}{c}U={(1-u)}^q\\ V=\frac{{(1+u)}^{p+1}}{(p+1)}[ln(1+u)-\frac{1}{(p+1)}]\end{array}\right.\Rightarrow \left\{\begin{array}{c}dU=q{(1-u)}^{q-1}du\\ dV={(1+u)}^{p}ln(1+u)du\end{array}\right.\end{array}$$

Thus,

$$\begin{array}{cc}\hfill I_{p,q}& ={\int }_{-1}^1{(1+u)}^p{(1-u)}^{q}ln(1+u)du\hfill \\ \hfill & =\frac{{(1-u)}^q{(1+u)}^{p+1}}{p+1}\left[ln(1+u)-\frac{1}{p+1}\right]{|}_{-1}^1-\frac{q}{p+1}{\int }_{-1}^1{(1-u)}^{q-1}{(1+u)}^{p+1}\left[ln(1+u)-\frac{1}{p+1}\right]du\hfill \\ \hfill & =\left\{\begin{array}{cc}\frac{{(1+u)}^{2s+1}}{(2s+1)}\left[ln(1+u)-\frac{1}{(2s+1)}\right]{|}_{-1}^1=Z_{2s,0}\left[ln2-\frac{1}{(2s+1)}\right]& p=2s,q=0\\ -\frac{q}{p+1}\left(I_{p+1,q-1}-\frac{1}{p+1}{Z}_{p+1,q-1}\right)& 0\le p<2s,0<q\le 2s\end{array}\right.\hfill \end{array}$$

Considering the Ansatz that $I_{p,q}=Z_{p,q}{F}_{p,q}$. Then, the case $p=2s,q=0$ is already solved in (3), i.e., $I_{2s,0}=Z_{2s,0}{F}_{2s,0}=Z_{2s,0}\left[ln2-\frac{1}{(2s+1)}\right]$. We can then advance (3) for $0\le p<2s,0<q\le 2s$ by a recursive method

$$\begin{array}{cc}\hfill I_{p,q}& =Z_{p,q}{F}_{p,q}=-\frac{q}{(p+1)}{Z}_{p+1,q-1}\left(F_{p+1,q-1}-\frac{1}{(p+1)}\right)\hfill \\ \hfill & \Downarrow \mathrm{solving}\mathrm{for}{F}_{p,q}\hfill \\ \hfill F_{p,q}& =-\frac{q}{p+1}\frac{Z_{p+1,q-1}}{Z_{p,q}}\left(F_{p+1,q-1}-\frac{1}{p+1}\right)\hfill \\ \hfill & =F_{p+1,q-1}-\frac{1}{(p+1)}=F_{p+2,q-2}-\frac{1}{p+2}-\frac{1}{p+1}=\cdots \hfill \\ \hfill & =F_{p+q,0}-\sum _{j=1}^n\frac{1}{(p+j)},0\le p<2s,0<q\le 2s\hfill \\ \hfill & \mathrm{inserting}\mathrm{the}\mathrm{case}{F}_{p+q,0}=F_{2s,0}=\left[ln2-\frac{1}{(2s+1)}\right]\hfill \\ \hfill & =\left[ln2-\frac{1}{(2s+1)}\right]-\sum _{j=1}^n\frac{1}{(p+j)},0\le p,q\le 2s\hfill \\ \hfill & =ln2-\sum _{j=1}^{n+1}\frac{1}{(p+j)},0\le p,q\le 2s\hfill \end{array}$$

We can then apply (3) to (3), while using $Z_{p,q}=Z_{q,p}$, to get

$$\begin{array}{cc}\hfill S_{p,q}& =ln\left(2\pi \frac{q!p!}{\left(2s\right)!}\frac{2^{s+1}}{2s+1}\right)-[p{F}_{p,q}+q{F}_{q,p}]\hfill \\ \hfill & =ln\left(4\pi \right)-ln\left(\frac{(2s+1)!}{q!p!}\right)+\sum _{j=1}^{q+1}\frac{p}{(p+j)}+\sum _{j=1}^{p+1}\frac{q}{(q+j)}.\hfill \end{array}$$

Replacing $p=s+m$ and $q=s-m$ into (3) concludes the lemma. □

The entropies for the special cases $s=0,\frac{1}{2},1$ and $m=-s,-s+1,\cdots ,s$ are readily derived

$$\begin{array}{cc}\hfill S_{s=0,m=0}& =ln\left(4\pi \right)\approx 2.5310.\hfill \\ \hfill S_{s=\frac{1}{2},m=\pm \frac{1}{2}}& =\frac{1}{2}+ln\left(2\pi \right)\approx 2.3379.\hfill \\ \hfill S_{s=1,m=\pm 1}& =\frac{2}{3}+ln\left(\frac{4}{3}\pi \right)\approx 2.0991.\hfill \\ \hfill S_{s=1,m=0}& =\frac{5}{3}+ln\left(\frac{2}{3}\pi \right)\approx 2.4059.\hfill \end{array}$$

Lemma 3 

(Spin-Entropy Variation Across z-Eigenstates). Let ${\psi }_{s,m}$ be the z-eigenstates of spin s. Let $m^{+}$ represent m restricted to the range $2m+1\in {\mathbb{Z}}^{+}$, i.e., $mod(s,1)\le m^{+}\le s$. The spin-entropy $S\left({\psi }_{s,m^{+}}\right)$ decreases as $m^{+}$ increases. Moreover, the decrease in $S\left({\psi }_{s,m^{+}}\right)$ as one vary from $m^{+}$ to $1+m^{+}$ is given by

$$\begin{array}{cc}\hfill S\left({\psi }_{s,1+m^{+}}\right)-S\left({\psi }_{s,m^{+}}\right)& =ln\left(\frac{s+1+m^{+}}{s-m^{+}}\right)-\sum _{j=s-m^{+}}^{s+m^{+}}\frac{1}{j},m^{+}<s\hfill \\ \hfill & ={\int }_{s-m^{+}}^{s+1+m^{+}}\frac{1}{x}dx-\sum _{j=s-m^{+}}^{s+m^{+}}\frac{1}{j}\hfill \\ \hfill & <0\hfill \end{array}$$

Proof. 

Adopting the notation $p=s+m,q=s-m$ we can rewrite the last two terms in (2) as

$$\begin{array}{c}\hfill \sum _{j=1}^{q+1}\frac{p}{(p+j)}+\sum _{j=1}^{p+1}\frac{q}{(q+j)}=\sum _{j=p+1}^{2s+1}\frac{2s}{j}+\theta \left(p-q-1\right)\sum _{j=q+1}^p\frac{q}{j}\end{array}$$

where $\theta \left(x\right)$ is the heaviside function, i.e., $\theta \left(x\right)=1$ for $x\ge 0$ and $\theta \left(x\right)=0$ otherwise. Consider the difference of consecutive values of the spin-entropy described by (2) for $m\in m^{+}$, i.e.,

$$\begin{array}{cc}\hfill S\left({\psi }_{s,m+1}\right)-S\left({\psi }_{s,m}\right)& =ln\left(\frac{(p+1)!(q-1)!}{p!q!}\right)+\sum _{j=p+2}^{2s+1}\frac{2s}{j}-\sum _{j=p+1}^{2s+1}\frac{2s}{j}+\sum _{j=q}^{p+1}\frac{q-1}{j}-\sum _{j=q+1}^p\frac{q}{j}\hfill \\ \hfill & =ln\left(\frac{p+1}{q}\right)-\frac{2s}{p+1}+1+\frac{q}{p+1}-\sum _{j=q}^{p+1}\frac{1}{j}\hfill \\ \hfill & =ln\left(\frac{p+1}{q}\right)+\frac{1}{p+1}-\sum _{j=q}^{p+1}\frac{1}{j}\hfill \\ \hfill & =ln\left(\frac{p+1}{q}\right)-\sum _{j=q}^p\frac{1}{j}\hfill \\ \hfill & ={\int }_q^{p+1}\frac{1}{x}dx-\sum _{j=q}^p\frac{1}{j}\hfill \\ \hfill & <0\mathrm{for}p\ge q\iff m^{+}\mathrm{set}\hfill \end{array}$$

For the last step we used Lemma 8. □

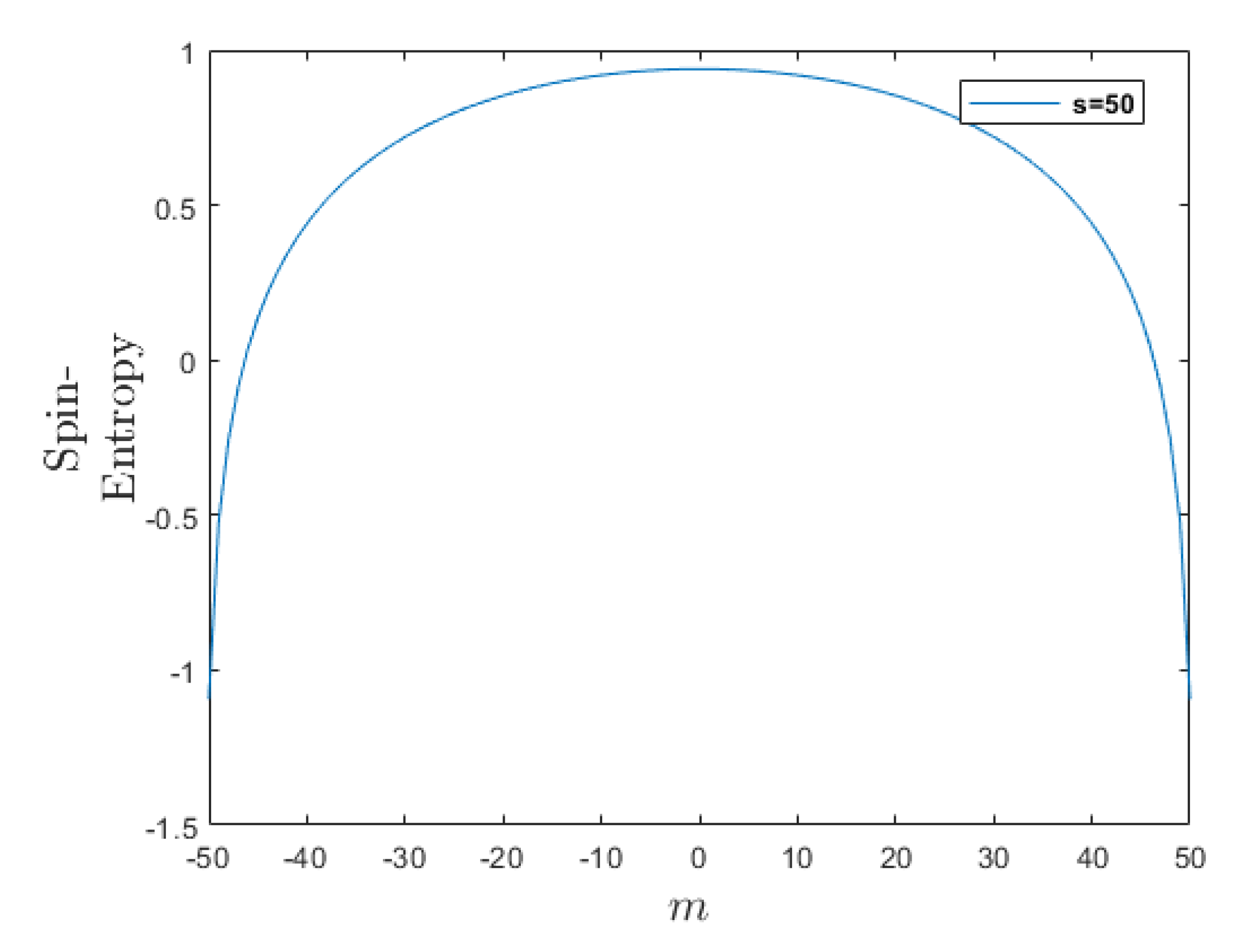
Figure 1. Spin-Entropy for $s=50$ eigenstates along z-direction. It is invariant by transforming $m\to -m$ and it is decreasing as m increases in the range $m\in [0,50)$ (see Lemma 3).

Figure 1. Spin-Entropy for $s=50$ eigenstates along z-direction. It is invariant by transforming $m\to -m$ and it is decreasing as m increases in the range $m\in [0,50)$ (see Lemma 3).

Lemma 4 

(Negative Spin-Entropy across z-Eigenstates). Let ${\psi }_{s,m}$ be the z-eigenstates of spin s. For the spin-entropy of ${\psi }_{s,m}$ to have a negative value it is required that $s\ge 16\frac{1}{2}$.

Proof. 

From Lemma 3 the lowest entropy of a spin s particle is attained for $m=\pm s$. Examining the the spin-entropy formula (2) for such cases and requiring it to be negative we get

$$\begin{array}{c}\hfill S\left({\psi }_{s,m=\pm s}\right)=ln\left(4\pi \right)-ln(2s+1)+\frac{2s}{2s+1}<0\iff ln\frac{2s+1}{4\pi }>\frac{2s}{2s+1}\end{array}$$

and since s must be a multiple of $\frac{1}{2}$, the minimum value of s for which this is possible is $s_{min}=16\frac{1}{2}$. □

Since the visible universe does not seem to contain particles with spin $s>1$, such mathematical property may not be relevant to physical systems. Let us examine some properties of spin $s=\frac{1}{2}$ and $s=1$ for all spin states.

3.1. Spin One-Half

Lemma 5 

(Spin $\frac{1}{2}$ Entropy). All $s=\frac{1}{2}$ spin states have the same spin-entropy

Proof. 

Let us refer to $|\psi \rangle$ as an arbitrary $s=\frac{1}{2}$ spin-state. All $s=\frac{1}{2}$ spin states are reached by the application of an element of the $SU\left(2\right)$ to $|\psi \rangle$.

There exists a two-to-one homomorphic mapping of the group $SU\left(2\right)$ onto the group $SO\left(3\right)$. If $A\in SU\left(2\right)$ maps onto $R\left(A\right)\in SO\left(3\right)$, then $R\left(A\right)=R(-A)$. This implies that the representations of $SO\left(3\right)$ are also representations of $SU\left(2\right)$.

By Lemma 1 we conclude that all $s=\frac{1}{2}$ spin-states will be reached by a canonical transformations of any given $|\psi \rangle$$s=\frac{1}{2}$ spin-state and therefore have the same spin-entropy. □

3.2. Spin One

The most general normalized $s=1$ spin state can be written as

$$\begin{array}{c}\hfill {\Psi }^{s=1}(\theta ,\varphi )={\mathrm{e}}^{\mathrm{i}{\varphi }_1}\left(cos{\theta }_0{\mathrm{e}}^{\mathrm{i}{\varphi }_0}{\psi }_{1,0}+sin{\theta }_{0}cos{\theta }_1{\psi }_{1,1}+sin{\theta }_{0}sin{\theta }_1{\mathrm{e}}^{\mathrm{i}{\varphi }_{-1}}{\psi }_{1,-1}\right)\end{array}$$

where ${\psi }_{1,-1},{\psi }_{1,0},{\psi }_{1,1}$ are derived from (12) as

$$\begin{array}{c}\hfill {\psi }_{1,1}(\theta ,\varphi )=\frac{\sqrt{3}}{2}(1+cos\theta )\mathrm{and}{\psi }_{1,0}(\theta ,\varphi )=\sqrt{3}sin\theta {\mathrm{e}}^{\mathrm{i}\varphi }\mathrm{and}{\psi }_{1,-1}(\theta ,\varphi )=\frac{\sqrt{3}}{2}(1-cos\theta ){\mathrm{e}}^{\mathrm{i}2\varphi }\end{array}$$

Lemma 6. 

The maximum value of the spin-entropy for $s=1$ is $S_{max}^1=ln\frac{2\pi }{3}+\frac{5}{3}\approx 2.4059$ and it is reached by the state ${\psi }_{1,0}(\theta ,\varphi )$ and all its canonical transformations (rotations and reflections). The minimum value of the spin-entropy for $s=1$ is $S_{min}^1=ln\frac{4\pi }{3}+\frac{2}{3}\approx 2.0991$ and it is reached by the states ${\psi }_{1,-1}(\theta ,\varphi )$ and ${\psi }_{1,1}(\theta ,\varphi )$ and all their canonical transformations (rotations and reflections).

Proof. 

The probability density does not depend to the global phase term ${\mathrm{e}}^{\mathrm{i}{\varphi }_1}$ and thus, the spin-entropy vary according to the four parameters ${\varphi }_{-1},{\varphi }_0,{\theta }_0,{\theta }_1$. Note that for a given a set of these parameters all canonical transformations (rotations and reflections) of this wave function will correspond to transformations in parameter space.

For example for the canonical transformation of a rotation around the z-axis we have $\varphi \to \varphi +\delta$ and the wave function (3.2) is then written as

$$\begin{array}{cc}\hfill {\Psi }^{s=1}(\theta ,\varphi +\delta ;{\varphi }_1,{\varphi }_{-1},{\varphi }_0,{\theta }_0,{\theta }_1)& =\frac{\sqrt{3}}{2}{\mathrm{e}}^{\mathrm{i}{\varphi }_1}\left(2cos{\theta }_0{\mathrm{e}}^{\mathrm{i}{\varphi }_0}sin\theta {\mathrm{e}}^{\mathrm{i}\delta }{\mathrm{e}}^{\mathrm{i}\varphi }+sin{\theta }_{0}cos{\theta }_1(1+cos\theta )\right.\hfill \\ \hfill & \left.+sin{\theta }_{0}sin{\theta }_1{\mathrm{e}}^{\mathrm{i}{\varphi }_{-1}}(1-cos\theta ){\mathrm{e}}^{\mathrm{i}2\delta }{\mathrm{e}}^{\mathrm{i}2\varphi }\right)\hfill \\ \hfill & =\frac{\sqrt{3}}{2}{\mathrm{e}}^{\mathrm{i}{\varphi }_1}\left(2cos{\theta }_0{\mathrm{e}}^{\mathrm{i}({\varphi }_0+\delta )}sin\theta {\mathrm{e}}^{\mathrm{i}\varphi }+sin{\theta }_{0}cos{\theta }_1(1+cos\theta )\right.\hfill \\ \hfill & \left.+sin{\theta }_{0}sin{\theta }_1{\mathrm{e}}^{\mathrm{i}({\varphi }_{-1}+2\delta )}(1-cos\theta ){\mathrm{e}}^{\mathrm{i}2\varphi }\right)\hfill \\ \hfill & ={\Psi }^{s=1}(\theta ,\varphi ;{\varphi }_1,{\varphi }_{-1}+2\delta ,{\varphi }_0+\delta ,{\theta }_0,{\theta }_1)\hfill \end{array}$$

corresponding to a translation in the parameters $({\varphi }_0,{\varphi }_{-1})\to ({\varphi }_0+\delta ,{\varphi }_{-1}+2\delta )$.

The rotations have three degrees of freedom and thus, the space of parameters that cause the spin-entropy to vary is reduced to one. This degree of freedom still have a reflection to reduce it further by one half the possible variations of the spin-entropy values. Thus, we examine the wave function restricted to varying one parameter.

Consider the spin-1 state (3.2) for the case of ${\varphi }_{-1}={\varphi }_0=0$ and ${\theta }_0=\frac{\pi }{2}$, i.e.,

$$\begin{array}{c}\hfill {\Psi }_{{\theta }_1}^{s=1}(\theta ,\varphi )=\frac{\sqrt{3}}{2}{\mathrm{e}}^{\mathrm{i}{\varphi }_1}\left(cos{\theta }_1(1+cos\theta )+sin{\theta }_1(1-cos\theta ){\mathrm{e}}^{\mathrm{i}2\varphi }\right),\end{array}$$

where ${\theta }_1$ is the free parameter. All canonical transformations of such state lead to the same spin-entropy distribution. The probability is then

$$\begin{array}{cc}\hfill P_{{\theta }_1}^{s=1}(u,\varphi )& =\frac{3}{4}\left({cos}^2{\theta }_1{(1+u)}^2+{sin}^2{\theta }_1{(1-u)}^2+sin2{\theta }_1(1-u^2)cos\left(2\varphi \right)\right)\hfill \\ \hfill & =\frac{3}{4}\left((1+u^2)+2ucos\left(2{\theta }_1\right)+sin2{\theta }_1(1-u^2)cos\left(2\varphi \right)\right)\hfill \end{array}$$

where $u=cos\theta$. The spin-entropy of this state is

$$\begin{array}{cc}\hfill S_{{\theta }_1}& =ln4\pi -{\int }_{-1}^1{\int }_0^{2\pi }\frac{1}{4\pi }{P}_{{\theta }_1}^{s=1}(u,\varphi )ln{P}_{{\theta }_0}^{s=1}(u,\varphi )dud\varphi .\hfill \end{array}$$

The extremes of the entropy occur when $\frac{\partial S_{{\theta }_1}}{\partial {\theta }_1}=0$, i.e., when

$$\begin{array}{cc}\hfill 0& =\frac{\partial S_{{\theta }_1}}{\partial {\theta }_1}=-\frac{1}{4\pi }{\int }_{-1}^1{\int }_0^{2\pi }\frac{\partial P_{{\theta }_1}^{s=1}}{{\theta }_1}ln{P}_{{\theta }_0}^{s=1}(u,\varphi )dud\varphi \hfill \\ \hfill & =-\frac{3}{8\pi }{\int }_{-1}^1{\int }_0^{2\pi }\left(-2usin2{\theta }_1+cos2{\theta }_1(1-u^2)cos\left(2\varphi \right)\right)\hfill \\ \hfill & \times ln\left((1+u^2)+2ucos\left(2{\theta }_1\right)+sin2{\theta }_1(1-u^2)cos\left(2\varphi \right)\right).\hfill \end{array}$$

They occur for ${\theta }_1=0,\frac{\pi }{4},\frac{\pi }{2},\frac{3\pi }{4}$. By investigation, the cases ${\theta }_1=0,\frac{\pi }{2}$ are the z-eigenstates $s=1,m=\pm 1$ and yield the minimum spin-entropy. The cases ${\theta }_1=\frac{\pi }{4},\frac{3\pi }{4}$ are associated with the x-eigenstates and y-eigenstates, $s=1,m_x,m_y=0$, respectively, i.e., they are canonical transformations of the z-eigenstates, $s=1,m=0$ and yield the maximum spin-entropy. □

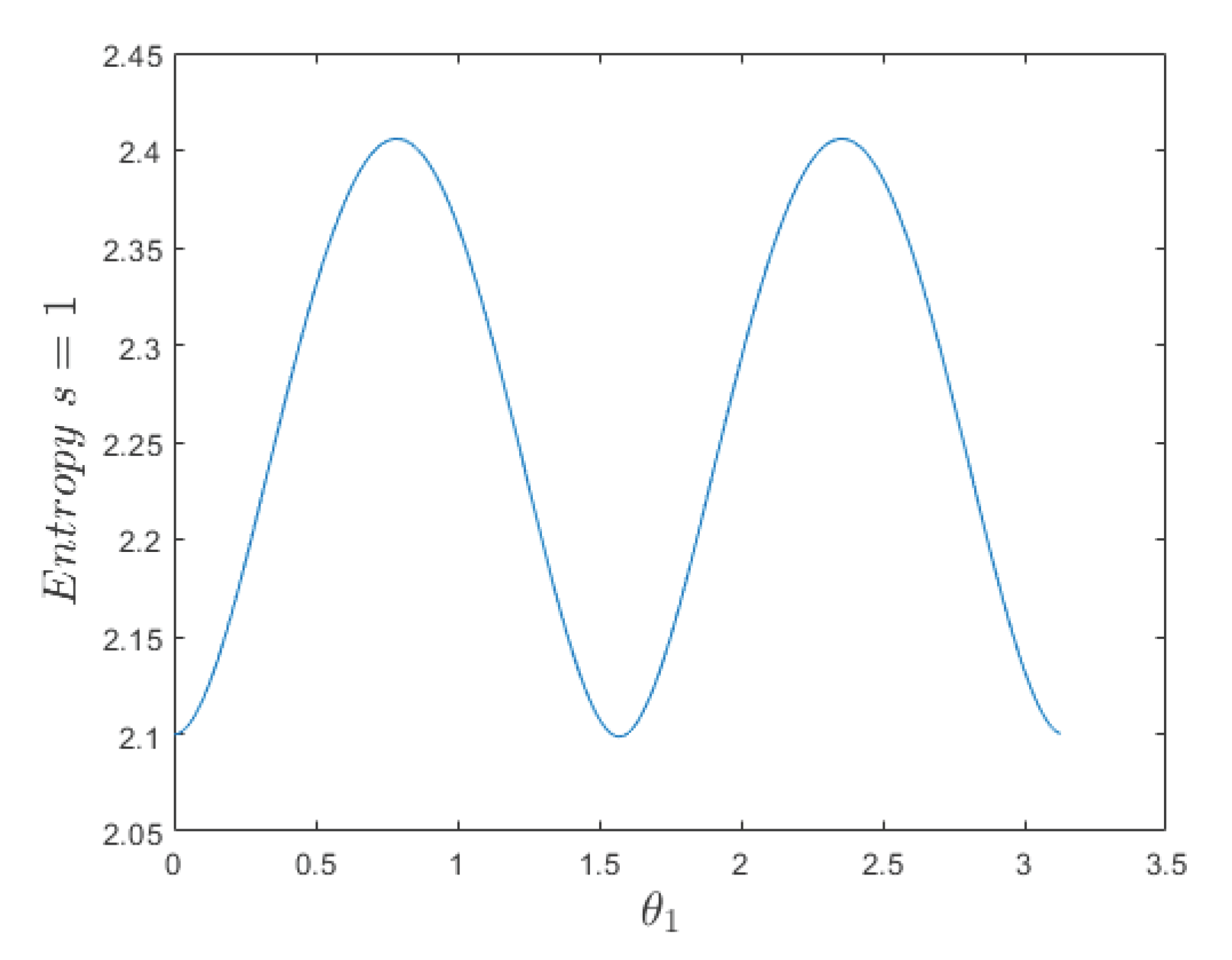
We show in Figure 2 a simulation for this spin-entropy as ${\theta }_1$ vary.

Note that the state ${\psi }_{s=1,m=0}(\theta ,\varphi )$ have a higher spin-entropy than the states ${\psi }_{s=1,m=\pm 1}(\theta ,\varphi )$, i.e., there is more randomness and less information at the $m=0$ state. The GK-law [15] says that the arrow of time in quantum physics, for a closed system, is given by an increase in quantum entropy. If GK-law holds and if the laws of conservation allow, then transition from a spin-state ${\psi }_{s=1,m=\pm 1}(\theta ,\varphi )$ to the spin-state ${\psi }_{s=1,m=0}(\theta ,\varphi )$ can occur. However, a transition from a spin-state ${\psi }_{s=1,m=0}(\theta ,\varphi )$ to either of the spin-states ${\psi }_{s=1,m=\pm 1}(\theta ,\varphi )$ cannot occur.

In order to test such hypothesis, one may investigate $W^{\pm },Z^0$, bosons of $s=1$, where such phenomena or lack thereof would be observed. These particles decay quickly (usually attributed to their large masses) and we speculate the trigger may be due to these forbidden transitions. More precisely, the state (3.2) is a superposition of z-eigenstates ${\psi }_{s=1,m=1}(\theta ,\varphi )$ and ${\psi }_{s=1,m=-1}(\theta ,\varphi )$ and oscillates as ${\theta }_1$ vary. At its maximum spin-entropy the state is either the x-eigenstate $s=1,m_x=0$ (${\theta }_1=\frac{\pi }{4}$) or the y-eigenstate $s=1,m_y=0$ (${\theta }_1=\frac{3\pi }{4}$). The spin-entropy (3.2) will also oscillate as ${\theta }_1$ vary following the same cycle as the state probability (3.2). For ${\theta }_1$ varying over time (due to the quantum Hamiltonian) the spin-entropy would oscillate and if the GK-law holds, these particles decay would be a mechanism to bar the spin-entropy from decreasing.

Conjecture 1. 

The spin-entropy associated with any spin state of magnitude s has its maximum value for the states $m=\pm mi{n}_m=\pm mod(s,1)$ and all its canonical transformations. The spin-entropy associated with any spin state of magnitude s has its minimum value for the pair of states $m=\pm s$ and all its canonical transformations.

We have shown to be true for the cases of $s=1$ and $s=\frac{1}{2}$ and $s=0$. Also, by Lemma 3 the z-direction eigenstates, for any s value, will have lower spin-entropy the larger $m^{+}$ is. All canonical transformations of a state will have the same spin-entropy. It remains to be proven that any spin state will have the spin-entropy between these values or that the extremes of the spin-entropy occur for the spin-eigenstates.

4. Phase Space Entanglement Increases Entropy

Consider two orthonormal spin eigenstates along the z-direction, ${\psi }_{s,m_1}\left(\theta \right){\mathrm{e}}^{\mathrm{i}(s-m_1)\varphi }$ and ${\psi }_{s,m_2}\left(\theta \right){\mathrm{e}}^{\mathrm{i}(s-m_2)\varphi }$ where from (12) we have

$$\begin{array}{cc}\hfill {\psi }_{s,m_{1,2}}\left(\theta \right)& ={(2s+1)}^{\frac{1}{2}}{\left[C_{s+m_{1,2}}^{2s}\right]}^{\frac{1}{2}}{\left(cos\frac{\theta }{2}\right)}^{s+m_{1,2}}{\left(sin\frac{\theta }{2}\right)}^{s-m_{1,2}}\hfill \end{array}$$

Following [7,8,24,25,26] and their references, let us define the entanglement of these two orthonormal spin eigenstates as

$$\begin{array}{cc}\hfill {\Psi }_{s,m_1,m_2}(\theta ,\varphi ,{\theta }^{\prime },{\varphi }^{\prime };{\theta }^{\mathrm{e}})& =cos{\theta }^{\mathrm{e}}{\psi }_{s,m_1}\left(\theta \right){\psi }_{s,m_2}\left({\theta }^{\prime }\right){\mathrm{e}}^{\mathrm{i}[(s-m_1)\varphi +(s-m_2){\varphi }^{\prime }]}\hfill \\ \hfill & +sin{\theta }^{\mathrm{e}}{\psi }_{s,m_2}\left(\theta \right){\psi }_{s,m_1}\left({\theta }^{\prime }\right){\mathrm{e}}^{\mathrm{i}[(s-m_2)\varphi +(s-m_1){\varphi }^{\prime }]},\hfill \end{array}$$

where ${\theta }^{\mathrm{e}}\in [0,\pi )$ controls periodically the amount of entanglement. With minimum (no) entanglement occurring at ${\theta }^{\mathrm{e}}=0,\frac{\pi }{2}$ and maximum entanglement occurring at ${\theta }^{\mathrm{e}}=\frac{\pi }{4},\frac{3\pi }{4}$.

By Born’s rule this spin-state has a probability density

$$\begin{array}{cc}\hfill {\mathrm{P}}_{s,m_1,m_2}(\theta ,\varphi ,{\theta }^{\prime },{\varphi }^{\prime };{\theta }^{\mathrm{e}})& =|{\Psi }_{s,m_1,m_2}(\theta ,\varphi ,{\theta }^{\prime },{\varphi }^{\prime };{\theta }^{\mathrm{e}}){|}^2,\hfill \end{array}$$

The spin-entropy of state (4) is

$$\begin{array}{cc}\hfill S_{s,m_1,m_2}\left({\theta }^{\mathrm{e}}\right)& =2ln\left(4\pi \right)\hfill \\ \hfill & -\frac{1}{{\left(4\pi \right)}^2}{\int }_{-1}^1{\int }_0^{2\pi }{\int }_{-1}^1{\int }_0^{2\pi }{\mathrm{P}}_{s,m_1,m_2}(u,\varphi ,u^{\prime },{\varphi }^{\prime };{\theta }^{\mathrm{e}})ln{\mathrm{P}}_{s,m_1,m_2}(u,\varphi ,u^{\prime },{\varphi }^{\prime };{\theta }^{\mathrm{e}})dud\varphi d{u}^{\prime }d{\varphi }^{\prime }.\hfill \end{array}$$

The extremes of the entropy occur when $\frac{\partial S_{s,m_1,m_2}\left({\theta }^{\mathrm{e}}\right)}{\partial {\theta }^{\mathrm{e}}}=0$, i.e., when

$$\begin{array}{cc}\hfill 0& =\frac{\partial S_{s,m_1,m_2}\left({\theta }^{\mathrm{e}}\right)}{\partial {\theta }^{\mathrm{e}}}\hfill \\ \hfill & =-\frac{1}{{\left(4\pi \right)}^2}{\int }_{-1}^1{\int }_0^{2\pi }{\int }_{-1}^1{\int }_0^{2\pi }\frac{\partial {\mathrm{P}}_{s,m_1,m_2}(u,\varphi ,u^{\prime },{\varphi }^{\prime };{\theta }^{\mathrm{e}})}{\partial {\theta }^{\mathrm{e}}}ln{\mathrm{P}}_{s,m_1,m_2}(u,\varphi ,u^{\prime },{\varphi }^{\prime };{\theta }^{\mathrm{e}})dud\varphi d{u}^{\prime }d{\varphi }^{\prime }.\hfill \end{array}$$

We conjecture that they occur for ${\theta }^{\mathrm{e}}=0,\frac{\pi }{4},\frac{\pi }{2},\frac{3\pi }{4}$. By investigation of these four cases, the cases ${\theta }^{\mathrm{e}}=0,\frac{\pi }{2}$, associated with no entanglement, yield the minimum spin-entropy which is the sum of the spin-entropy of each state. We have already calculated each state spin-entropy in (2). The cases ${\theta }^{\mathrm{e}}=\frac{\pi }{4},\frac{3\pi }{4}$ yield the maximum spin-entropy and are associated with maximum entanglement.

We present "a sketch of a proof" by reasoning about randomness. Let us examine the role of each of the wave functions, ${\psi }_{s,m_1}\left(\theta \right){\mathrm{e}}^{\mathrm{i}(s-m_1)\varphi }$ and ${\psi }_{s,m_2}\left({\theta }^{\prime }\right){\mathrm{e}}^{\mathrm{i}(s-m_2){\varphi }^{\prime }}$, that are being entangled (4). Each represent a distribution in a two-sphere ${\mathbb{S}}^2$, or let us call it a “container”. The phase space of the entanglement is the product of these two “container”. For ${\theta }^{\mathrm{e}}=0,\frac{\pi }{2}$, when there is no entanglement, despite the phase space being the product of two “container”, each of the distributions occupies only one of the containers. Thus, the entanglement spin-entropy is the sum of the spin-entropy of each container. For ${\theta }^{\mathrm{e}}=\frac{\pi }{4},\frac{3\pi }{4}$, when there is maximum entanglement, the wave functions occupy equally both containers, i.e., they are mixed in the containers. The more spread is a distribution the larger is the entropy. The parameter ${\theta }^{\mathrm{e}}$ controls the mixture, and so the more is the mixture the larger is the spin-entropy. This reasoning is not specific about spin entanglement, it also applies to position entanglement.

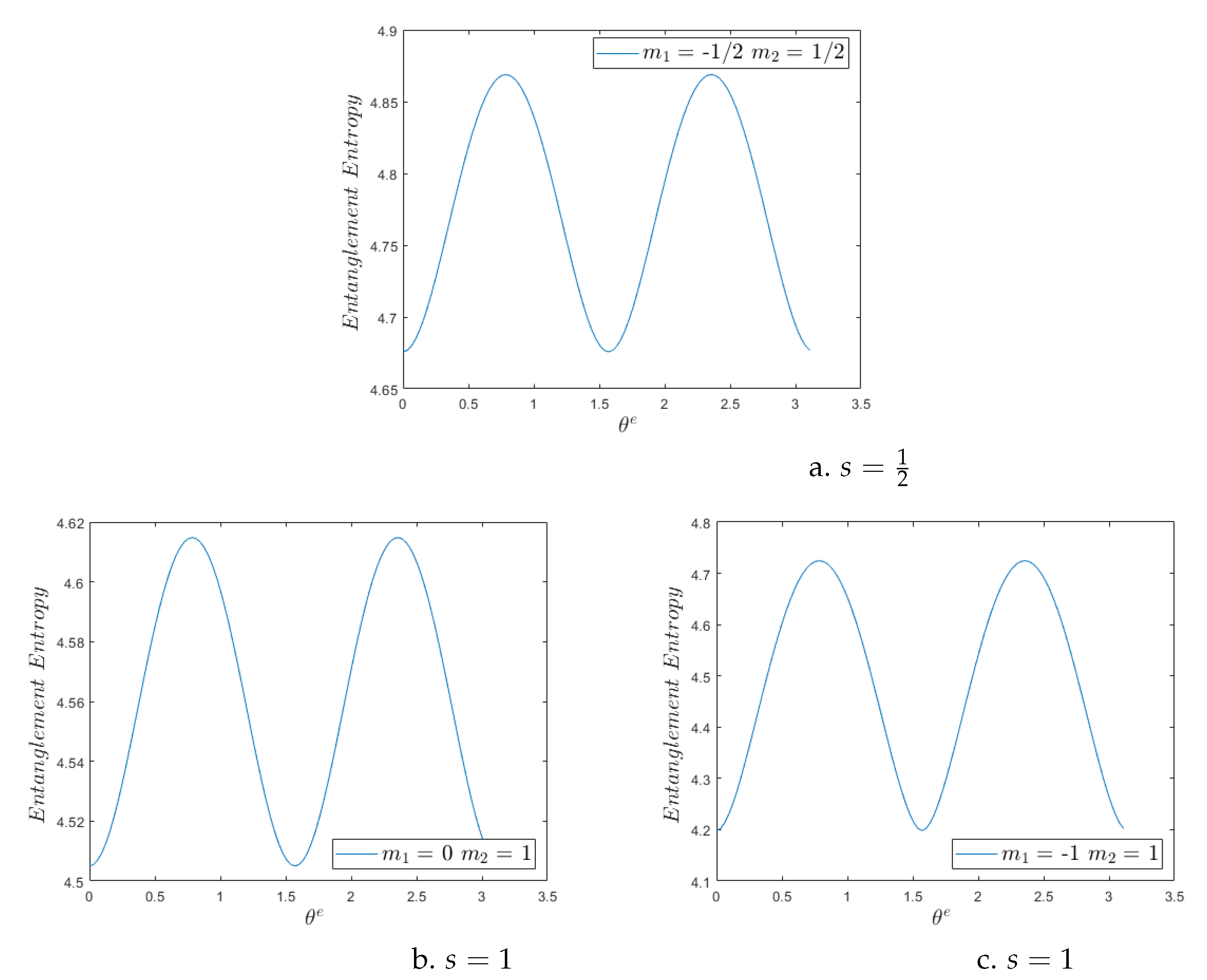
In Figure 3 we plot the spin-entropy (4) vs ${\theta }^{\mathrm{e}}$ for z eigenstates of $s=\frac{1}{2}$ and for z eigenstates of $s=1$. Clearly, spin-entropy increases as the entanglement increases. It is noticeable that the spin-entropy of the entanglement $s=\frac{1}{2}$, for any given ${\theta }^{\mathrm{e}}$, is larger than the spin-entropy for the same ${\theta }^{\mathrm{e}}$ of any of the possible entanglements for $s=1$. For the case $s=1$, the cases b. $m_1=0,m_2=1$ has the same entanglement entropy as the case $m_1=-1,m_2=0$. This can be inferred from the mapping $m_1=-1,m_2=0\to m_1=-1,m_2=0$, i.e., the mapping $(\theta ,{\theta }^{\prime })\to (\pi -\theta ,\pi -{\theta }^{\prime })$ lead to the same probabilities (4) and thus, to the same spin-entropy (4). Comparing the cases b. $m_1=0,m_2=1$ with c. $m_1=-1,m_2=1$, it is noticeable that it is for c. that the minimum entanglement value as well as the maximum entanglement value occurs. The minimum entanglement is the product states and so the spin-entropy is simply the sum of the spin-entropy of both states, thus c. is smaller. The maximum value of the spin-entropy being awarded to c. is of interest. We wonder if it maybe related to the fact that the superposition of these two states is a canonical transformation of the higher entropy state ${\psi }_{s=1,m=0}$, see Figure 2.

5. Conclusion

This paper quantified the randomness associated with a spin state by defining the spin-entropy in phase space.

At the formal level we used differential entropy from information theory and the Geometric Quantization method (GQ) applied to the two-sphere. The GQ produces a description for the spin, originated from classical ideas, and also provides the spin phase space where the spin-wave function and all its randomness is defined. Local canonical transformation in phase space preserve the area element of the sphere and guarantees the spin-entropy satisfies the homogeneity hypothesis, and so Lemma 1 showed the spin-entropy of a spin state is invariant under 3D rotations and reflections of the coordinate system.

Lemma 2 provides a spin-entropy formula for the z-direction spin-eigenstates. Lemma 3 and a plot of the spin-entropy of a given spin s versus different values of $m=-s,-s+1,\cdots ,s-1,s$, see Figure 1, showed that the spin entropy is symmetric with respect to $m\leftrightarrow -m$, and decreases as m increases for $m\ge 0$. Thus, in particular, the state ${\psi }_{s=1,m=0}(\theta ,\varphi )$ has a higher spin-entropy than the spin states ${\psi }_{s=1,m=\pm 1}(\theta ,\varphi )$, i.e., there is more randomness and less information at the $m=0$ state.

If the GK-Law [15] holds, i.e., the arrow of time in quantum physics is given by an increase in quantum entropy for closed systems, and if the laws of conservation allow, then a transition from a spin-state ${\psi }_{s=1,m=\pm 1}(\theta ,\varphi )$ to a spin-state ${\psi }_{s=1,m=0}(\theta ,\varphi )$ can occur. However, a transition from a spin-state ${\psi }_{s=1,m=0}(\theta ,\varphi )$ to either of the spin-states ${\psi }_{s=1,m=\pm 1}(\theta ,\varphi )$cannot occur. In order to test the GK-Law, one may investigate $W^{\pm },Z^0$, bosons of $s=1$, where such phenomena or lack thereof would be observed. We speculate that their fast decays, with a half-life of about $3\times {10}^{-25}$s, are triggered by oscillatory behavior of a superposition of their eigenstates (see Figure 2 with the interpretation that the parameter ${\theta }_1$ is varying with time, thus the oscillations) coupled with the GK-Law of an impossibility of transitions from $m=0\to m=\pm 1$. After all, if a transition is forbidden and in order to bar the spin-entropy to decrease, then a mechanism to avoid this event, and satisfying the conservation laws, is to annihilate such particles and create new particles.

The phase space of the entanglement of two states is the product of two phase spaces. We reasoned that the entanglement correspond to a distribution that mixes the two phase spaces while the product of states does not mix. The larger is the entanglement, the more is the mixture, the more randomness, and so the larger is the entropy. We speculate that the phenomena of decoherence [7,8,24,26,27] of a subsystem immersed in an environment occurs so that parts of such subsystem will entangle with the environment and the total entanglement increases. An interesting future direction could exploit a connection of this work to the work on quantum thermalization [10,28,29,30] and their references, where they suggest a procedure that by tracing out the environment and evaluating the reduced density matrix of a system of interest may lead to the entropy of classical physics.

Appendix A.1. Symplectic Structure

Considering the symplectic structure to be the oriented surface area element of a sphere scaled down by the radius s, it is written as

$$\begin{array}{c}\hfill \Omega =ssin\theta d\varphi \wedge d\theta =2\mathrm{i}s\frac{dz\wedge d{z}^{*}}{{(1+z{z}^{*})}^2}\end{array}$$

This symplectic structure can be derived from a Kähler potential $\Omega =\mathrm{i}\partial \partial K$ where

$$\begin{array}{c}\hfill K=2sln(1+z{z}^{*}),\end{array}$$

and $2s$ is an integer associated with a spin magnitude s. The symplectic potential $\mathcal{A}=-\frac{\mathrm{i}}{2}\partial K=\mathrm{i}s\left[\frac{zd{z}^{*}-z^{*}dz}{(1+z{z}^{*})}\right]$ has the components given by

$$\begin{array}{c}\hfill {\mathcal{A}}_z=-\frac{\mathrm{i}}{2}{\partial }_{z}K=-\mathrm{i}s\frac{z^{*}}{(1+z{z}^{*})}\mathrm{and}{\mathcal{A}}_{z^{*}}=\frac{\mathrm{i}}{2}{\partial }_{z^{*}}K=\mathrm{i}s\frac{z}{(1+z{z}^{*})},\end{array}$$

Here we abused the notation that $z,z^{*}$, when used as superscript or subscripts, do represent the index of the component of a vector. A special case occurs for $\partial ={\partial }_z\wedge {\partial }_{z^{*}}$ which represents both, the index of as well as the variable for which the partial derivative is differentiating. We may also switch to the component notation $z^{\mu },\mu =1,2$ to indicate $z=z^1$ and $z^{*}=z^2$, which will help with manipulations. In this case we may represent the vector potential by ${\mathcal{A}}^{\mu },\mu =1,2$. We will use both notations.

The corresponding covariant derivatives are

$$\begin{array}{c}\hfill D_z={\partial }_z-\mathrm{i}{A}_z=\left({\partial }_z-s\frac{z^{*}}{(1+z{z}^{*})}\right),\mathrm{and}{D}_{z^{*}}={\partial }_{z^{*}}-\mathrm{i}{A}_{z^{*}}=\left({\partial }_{z^{*}}+s\frac{z}{(1+z{z}^{*})}\right).\end{array}$$

Appendix A.2. From Canonical Transformations to PreQuantum Operators

Canonical transformations preserve $\Omega$. Consequently for the vector fields $\xi =({\xi }^z,{\xi }^{z^{*}})$ to be generators of canonical transformations in the sphere, written as $\overrightarrow{z}=(z,z^{*})\to \overrightarrow{z}+\xi \left(\overrightarrow{z}\right))$, must satisfy ${\delta }_{\xi }\Omega =\left({\xi }^{\alpha }{\Omega }_{\alpha ,\nu }d{z}^{\nu }\right)=({\xi }^z{\Omega }_{z,z^{*}}d{z}^{*}+{\xi }^{z^{*}}{\Omega }_{z^{*},z}dz)$ (derived in (2.2)). Thus, for every infinitesimal canonical transformation we can associate a function J on ${\mathbb{S}}^2$ such that $-dJ={\xi }^z{\Omega }_{z,z^{*}}d{z}^{*}+{\xi }^{z^{*}}{\Omega }_{z^{*},z}dz=0$ is a closed one form.

The symplectic potential $\mathcal{A}$ change under a canonical transformation is given by

$$\begin{array}{cc}\hfill {\delta }_{\xi }\mathcal{A}& ={\mathcal{A}}_{\mu }(\overrightarrow{z}+\xi )d(z^{\mu }+{\xi }^{\mu }\left(\overrightarrow{z}\right))-{\mathcal{A}}_{\mu }\left(\overrightarrow{z}\right)d{z}^{\mu }\hfill \\ \hfill & =\left[{\xi }_{{\partial }_{z^{\alpha }}}^{\alpha }{\mathcal{A}}_{\mu }+{\mathcal{A}}_{\alpha }\frac{{\xi }^{\alpha }}{z^{\mu }}\right]d{z}^{\mu }\hfill \\ \hfill & =\left[{\xi }^{\alpha }\left({\partial }_{z^{\alpha }}{\mathcal{A}}_{\mu }{-}_{z^{\mu }}{\mathcal{A}}_{\alpha }\right){+}_{z^{\mu }}\left({\xi }^{\alpha }{\mathcal{A}}_{\alpha }\right)\right]d{z}^{\mu }\hfill \\ \hfill & =\left[{\xi }^{\alpha }{\Omega }_{\alpha ,\mu }{+}_{z^{\mu }}\left({\xi }^{\alpha }{\mathcal{A}}_{\alpha }\right)\right]d{z}^{\mu }\hfill \\ \hfill & {=}_{z^{\mu }}\left({\xi }^{\alpha }{\mathcal{A}}_{\alpha }-J\right)d{z}^{\mu }\hfill \end{array}$$

Thus, under a canonical transformation $\mathcal{A}\to \mathcal{A}+d\Lambda$, where $\Lambda ={\xi }^{\alpha }{\mathcal{A}}_{\alpha }-J$. The symplectic potential may be thought of as a $\mathit{U}$(1) gauge field, with the transformations $\mathcal{A}\to \mathcal{A}+d\Lambda$. In order for $\mathcal{D}\psi \left(\overrightarrow{z}\right)$ to be a covariant derivative under canonical transformation the wave function must transform as $\psi \left(\overrightarrow{z}\right)\to {\psi }^{\prime }\left({\overrightarrow{z}}^{\prime }\right)={\mathrm{e}}^{\mathrm{i}\Lambda }\psi \left(\overrightarrow{z}\right)$. This form of the canonical transformation of $\psi$ will lead to the unitary operators associated with observable J.

Consider a function $J\left(\overrightarrow{z}\right)$ in phase space generating a canonical transformation $\overrightarrow{z}\to \overrightarrow{z}+\xi$ and described by the change of the symplectic potential $\Lambda ={\xi }^{\alpha }{\mathcal{A}}_{\alpha }-J$. The corresponding change in $\psi$ is thus

$$\begin{array}{cc}\hfill \delta \psi \left(\overrightarrow{z}\right)& ={\xi }_{z^{\mu }}^{\mu }\psi \left(\overrightarrow{z}\right)-\mathrm{i}({\xi }^{\alpha }{\mathcal{A}}_{\alpha }-J)\psi \left(\overrightarrow{z}\right)\hfill \\ \hfill & ={\xi }^{\mu }\left({\partial }_{z^{\mu }}-\mathrm{i}{\mathcal{A}}_{\mu }\right)\psi \left(\overrightarrow{z}\right)+\mathrm{i}J\psi \left(\overrightarrow{z}\right)\hfill \\ \hfill & =\left({\xi }^{\mu }{\mathcal{D}}_{\mu }+\mathrm{i}J\right)\psi \left(\overrightarrow{z}\right)\hfill \end{array}$$

Thus, associated to the classical function $J\left(\overrightarrow{z}\right)$ the GQ method creates the prequantum operator for the classical observable J

$$\begin{array}{c}\hfill \mathcal{P}\left(J\right)=-\mathrm{i}(\xi ·\mathcal{D}+\mathrm{i}J),\end{array}$$

and so canonical transformations are implemented as quantum unitary transformations of the wave function, $\psi ={\mathrm{e}}^{\mathrm{i}\mathcal{P}\left(J\right)}\psi$.

Appendix A.3. From 3D Embedding Functions to Quantum Spin Operators

Let us refer to the 3D embedding in the sphere (2.1) as the “classical spin variables” for which the quantum spin operators will be derived as follows. From these variables we can evaluate the canonical transformations (2.2) for the symplectic (2.2) or its inverse, i.e., we can obtain the Hamiltonian vector field coefficients

$$\begin{array}{cc}\hfill {\xi }^z& =({\xi }_X^z,{\xi }_Y^z,{\xi }_Z^z)={\Omega }_{z^{*}}^{z,z^{*}}(X(z,z^{*}),Y(z,z^{*}),Z(z,z^{*}))=\frac{\mathrm{i}}{2}\left((1-z^2),\mathrm{i}(1+z^2),-2z\right)\hfill \\ \hfill {\xi }^{z^{*}}& =({\xi }_X^{z^{*}},{\xi }_Y^{z^{*}},{\xi }_Z^{z^{*}})={\Omega }_z^{z,z^{*}}(X(z,z^{*}),Y(z,z^{*}),Z(z,z^{*}))=-\frac{\mathrm{i}}{2}\left((1-{\left(z^{*}\right)}^2,-\mathrm{i}(1+{\left(z^{*}\right)}^2,2z^{*}\right)\hfill \end{array}$$

Similarly to the abuse of notation of $z,z^{*}$, the abuse of notation to the 3D variables $X,Y,Z$ occurs when using them as superscripts or subscripts, then they represent an index to a component of a vector. The vector field coefficients form the following Hamiltonian vector fields

$$\begin{array}{cc}\hfill {\xi }_X·\nabla & =\frac{\mathrm{i}}{2}\left({\partial }_z{-}_{z^{*}}+{\left(z^{*}\right)}_{z^{*}}^2-z_z^2\right),{\xi }_Y·\nabla =-\frac{1}{2}\left({\partial }_z{+}_{z^{*}}+{\left(z^{*}\right)}_{z^{*}}^2+z_z^2\right),\hfill \\ \hfill {\xi }_Z·\nabla & =-\mathrm{i}\left(z_z-z_{z^{*}}^{*}\right)\hfill \end{array}$$

where $\nabla ={(}_z{,}_{z^{*}})$, which are the standard isometries of the sphere. The Lie commutator of these vector fields give the $\mathit{SU}$(2) algebra. The prequantum spin operators (A.2) for these “classical spin variables” are then

$$\begin{array}{cc}\hfill \mathcal{P}\left(J\right)& =-\mathrm{i}({\xi }_J·\mathcal{D}+\mathrm{i}J)\mathrm{for}J(z,z^{*})=X(z,z^{*}),Y(z,z^{*}),Z(z,z^{*}).\hfill \\ \hfill & =-\mathrm{i}\left({\xi }_J^z\left({\partial }_z-s\frac{z^{*}}{(1+z{z}^{*})}\right)+{\xi }_J^{z^{*}}\left({\partial }_{z^{*}}+s\frac{z}{(1+z{z}^{*})}\right)\right)+\mathrm{i}J(z,z^{*})\hfill \end{array}$$

where the covariant derivatives in the sphere are given by (A.1). The polarization condition

$$\begin{array}{c}\hfill {\mathcal{D}}_{z^{*}}\Psi (z,z^{*})=\left({\partial }_{z^{*}}+{\frac{1}{2}}_{z^{*}}K\right)\Psi (z,z^{*})=\left({\partial }_{z^{*}}+s\frac{z}{(1+z{z}^{*})}\right)\Psi (z,z^{*})=0\end{array}$$

leads to an irreducible representation of the spin operators solved by

$$\begin{array}{c}\hfill \Psi (z,z^{*})={\mathrm{e}}^{-\frac{1}{2}K}f\left(z\right)=\frac{1}{{(1+z{z}^{*})}^s}f\left(z\right)\end{array}$$

where $\Psi (z,z^{*})$ is the spin wave function and $f\left(z\right)$ is a holomorphic function. Applying the polarization condition (A.3) to the prequantum operators (A.3) we obtain the spin quantum operators

$$\begin{array}{c}\hfill {\mathcal{S}}_{J_k}=-\mathrm{i}{\xi }_J^z\left({\partial }_z-s\frac{z^{*}}{(1+z{z}^{*})}\right)+\mathrm{i}{J}_k(z,z^{*})\mathrm{for}k=X,Y,Z.\end{array}$$