1. Introduction
1.1. The Future of Wind Turbines and the Novelty of the Paper
Wind energy has seen remarkable growth over the past decade and continues to be on an upward trend in the power generation industry. In the current context of the reduction and even abandonment of conventional energy sources, wind energy becomes a basic source, along with nuclear and hydro. In these conditions, the reliability and stability of the operation are necessary to maintain the production capacity for the longest possible periods and with the best possible predictability [
1]. With the rapid development of the wind turbine technology and according with a higher demand of renewable energy the number of wind turbine (WT) units had a major increase, but under these conditions the failure rate also increased [
2]. Power transmission is influenced by all components in the kinematic chain, rotor, gearbox, and generator. After an experience of over 20 years, both in operation and research, it can be concluded that the component with the highest level of vulnerability is the gearbox, with a very high failure and downtime [
1,
2,
3]. To make wind power more competitive, it is necessary to reduce turbine downtime and increase reliability. Condition monitoring can help reduce the chances of catastrophic failures, enabling cost-effective operation and maintenance practices. Compared to other applications, the representatives of the wind industry recognized quite late, the benefits and importance of monitoring the operating status through the use of artificial intelligence (AI) and vibration analysis [
4]. Substantial research has been conducted to establish algorithms based on a large volume of data that train on specific moments of failure, through machine learning to obtain specific failure models [
4,
5].
This paper presents a method that leverages Fourier spectrum analysis and machine learning-based data extraction techniques for predicting wear in wind turbine operation. The novelty of the applied method lies in its utilization of unlabeled and uncategorized data to infer meaningful results for the predictive maintenance of wind turbines. In this study functions representing the vibration trends of turbines across certain speed parameters, power levels, and wind flow conditions have been constructed. Furthermore, a density-based data filtering technique drawn from a machine learning-based method; Based Density Support Vector Machines (BDSVM) has been employed at the data acquisition stages of the experiments.
The research was carried out over a period of about two months. The Fourier spectrum was analyzed at different points in time while maintaining regulated and controlled parameters. With the help of at least 5 points from the Fourier spectrum, the objective functions were defined. The evolution over time of these Fourier spectra's maximum points (amplitude-frequency) offers an effective approach to ensure predictive maintenance. The established objective functions can be utilized to determine the wear evolution in both the low-frequency and high-frequency areas of a wind turbine. As a result of the experiments the envelope of normal operation and the envelope of maximum limit of operation are obtained for the gearbox, which is the most vulnerable part of the wind turbine. The envelope of a maximum limit of operation refers to wind turbine operation until the appearance of a defect. These experiments define the frequency-amplitude limits, which allow predictive maintenance of turbine components by setting the intervention thresholds without the need for extensive data collection.
The organization of the paper is as follows.
Section 1 includes the details of the current scenario of predictive maintenance of wind turbines and the state-of-the-art methods used for the condition monitoring of wind turbines. The research methods and experiments conducted in this study are discussed in
Section 2. The results of the experiments and their interpretations are presented in
Section 3 and the conclusion and future work is briefed in
Section 4.
1.2. Overview of Wind Turbine Condition Monitoring and Its Need
Wind energy has seen remarkable growth over the past decade and continues to be on an upward trend in the power generation industry [
3]. In the current context of the reduction and even abandonment of conventional energy sources, wind energy emerges as a primary source, along with nuclear energy and hydropower [
5]. In these conditions, the reliability and stability of the wind turbine operations are crucial to maintaining the production capacity for prolonged periods and with optimal predictability [
1].
The monitoring of wind turbine (WT) condition is defined as a complex process of monitoring the parameters of the state of the machine so that a significant change is detected, which indicates a possible developing fault [
6]. This can potentially help in different stage of wear: early detection of incipient failures, thus reducing the chances of catastrophic failures, accurately assessing the proper functioning of the components and reducing maintenance costs, the analysis of the fundamental causes of the occurrence of defects and can ensure the optimal determination of the input parameters for an improved operation of the turbine, the establishment of the control strategy as well as the optimal design of the components [
7,
8,
9,
10]. In a broad sense, the CMS of a wind turbine can target almost all of its major subsystems, including blades, nacelle, power transmission, tower, and foundation [
9]. This paper presents a method that focuses on the monitoring of wind turbine, and can be applied to the different components of the wind turbine: rotor shaft with main bearings, gearbox, and generator. From a CMS perspective, the three major monitored transmission components are the rotor shaft, the gearbox, and the generator. Of these three components the gearbox causes the longest downtime [
11,
12,
13]. For this reason, the gearbox was chosen as the main subsystem targeted in this study. In detail, this paper will cover the typical practices, challenges, and future research opportunities related to CM wind turbine drivetrains [
14].
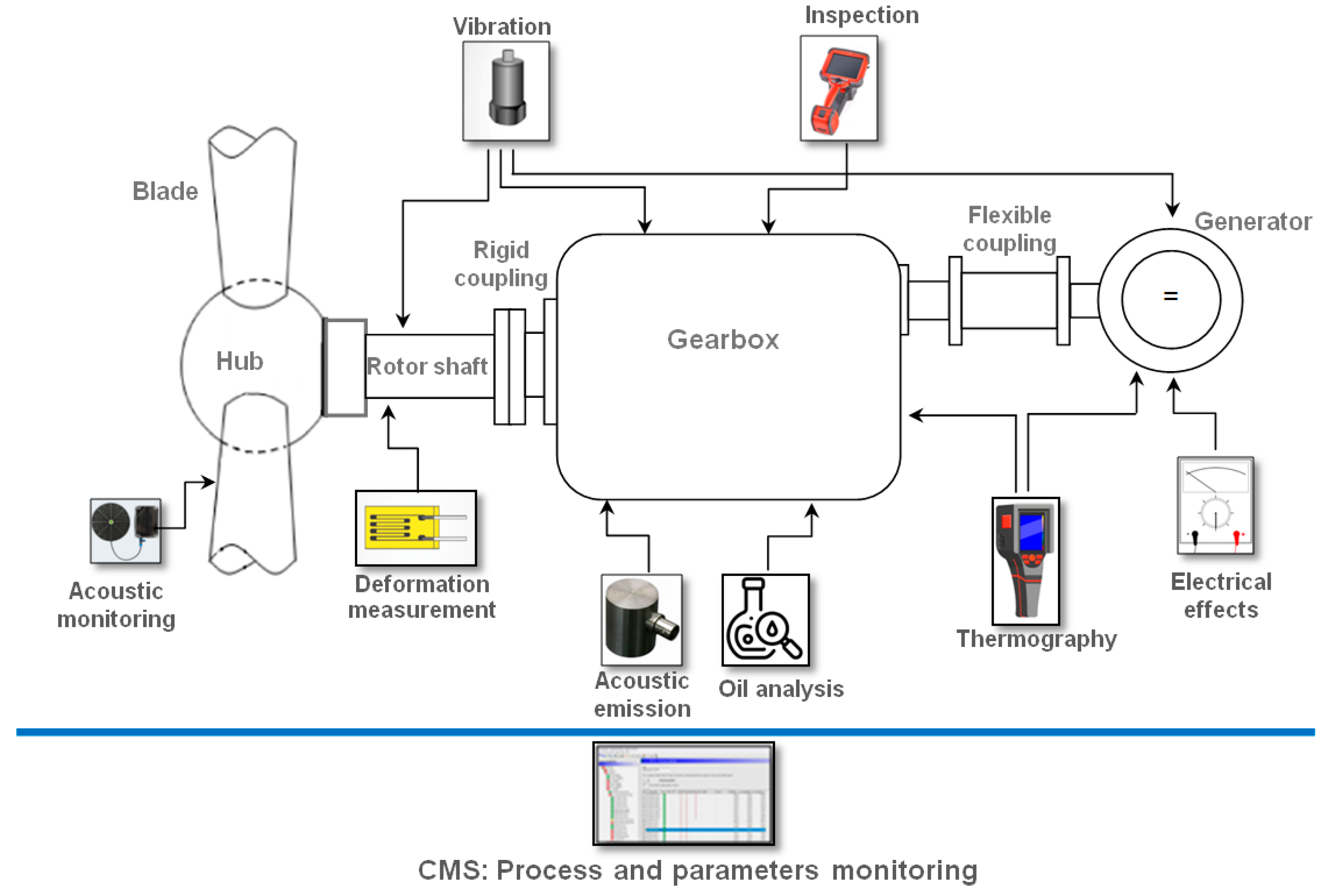
To understand the dynamic beahviour of a WT and especially of a planetary gearbox, a number of techniques have been used in reserch and in intustrial field: vibration analysis, oil condition analysis, thermography, aqustique measurmenet, acoustic, boroscopic inspection, electrical parameters effects, self-diagnostic of sensors, etc [
15]. In order to ensure optimal conditions for predictive maintenance, a combination of different techniques is needed. Even if the vibration technique has a dominant proportion, it is supported in the decision by the other specific technologies.
However, vibration analysis on component fault diagnosis in wind turbines is a hard challenge due to the complex mechanical conditions of the power transmission kinematic chain, the variable operating conditions with transient phenomena, and the speed differences between the different elements of the gearbox [
15,
16,
17]. The use of vibration transducers, respectively piezoelectric accelerometers, is the most used method, with different sensitivities depending on the speed and with rigid fixation on the structure of the components [
7,
8,
9]. The repartition of the sensors in the monitoring process of the wind turbine from the actual stage of the research is shown in
Figure 1 and
Table 1.
In this paper, the focus is on the monitoring of wind turbine drivetrains. The drive trains consist of the main bearing, main shaft, gearbox, brake, generator shaft, and generator. From a CM perspective, the three major monitored transmission components are the main bearing, the gearbox, and the generator. Of these three components [
6] the gearbox causes the longest downtime. Other research has also shown that the gearbox is the most expensive subsystem to maintain during the 20-year operating life of a turbine [
1,
2,
3,
4,
5,
6,
7]. For this reason, the gearbox was chosen as the main subsystem targeted in this study.
1.3. State of the Art in Turbine Wear Monitoring and Trend Analysis
Current research has led to the identification of the following monitoring techniques and directions, which can be applied to wind turbines [
14,
15]: Vibration analysis; Oil condition analysis; Thermography of important elements in the turbine structure (gearbox); Analysis of the physical condition of the materials; Measurement of elastic yielding and deformation of various components; Acoustic measurements in various sensitive areas of the turbine; Measurement of various electrical effects; Process parameter measurement; Visual inspection; Performance monitoring by comparing output sizes for the same input data; Use of self-diagnostic sensors (
Figure 1).
a)
Vibration analysis- Vibration analysis is the most well-known technology for monitoring the working conditions, especially for rotating equipment [
15]. The type of sensors used depends: on the frequency range used for monitoring, position of transducers on the transmision chain for the low-frequency range, velocity sensor in the 5- 1000 Hz frequency domain, accelerometers for the high-frequency range; acoustic sensor for gearbox monitoring or blades.
b)
Oil analysis - Oil analysis is another evaluation criterion, which, coupled with vibration analusis, contributes to decision-making in predictive maintenance. Oil analysis is mostly done offline, by sampling but also ensuring the quality of the oil, contamination with dirt from the parts in contact, moisture, degradation of additives and maintaining the oil filter. However, to protect oil quality, the application of online sensors is used more and more often, especially for particle counter. In addition, protecting the condition of the oil filter is currently mainly applied to both hydraulic oil and lubricating oil. In case of excessive pollution of the filter, or change in the characteristics of the oil, this leads to excessive wear [
15].
c)
Thermography- Thermography is often applied for monitoring and fault identification of electrical and elecronic components [
15]. Hot spots due to component degeneration or poor contacts can be identified in a simple and fast way by using cameras and diagnostic software. Mainly they are used in generator and power converter monitoring but also for the thermal gear contact.
d)
Inspection of compoenets condition- This type of monitoring mainly focuses on detecting and tracking the evolution of wear, using borosocpe device. The methods are normally offline and are a very important decision criterion for stopping, limiting or planning the repair [
15,
16].
e)
Deformation measurement- Deformation measurement using manometers is a common technique but not often applied in a case of wind turbine monitoring. Strain gauges are not robust in the long term [
15,
16,
17]. For wind turbines, deformation measurement can be very useful for life prediction and stress level protection, especially for blades [
18] and also for the main shaft.
f)
Acoustic monitoring - Acoustic monitoring is related to vibration monitoring using the noise measurement. Acoustic monitoring technology can be used for blades condition monitoring using acoustic mircophone or for bearings and gearboxes monitoring using acoustic emission sensor fixed directly to the housing [
15].
g)
Electrical effects – Electrical parameters monitoring of generator represent a mandatory conditin in based condition maintenance (CBM). The analysis of electrical parameters, such as: electrical current,voltage, insultation, power, etc., they allow both the evaluation of the quality of the generated power and the analysis of the potential faults [
17].
h)
Process parameters- Control systems monitoring (CMS) are becoming more sophisticated and their diagnostic capabilities are improving. However, protection is mostly based on level detection or signal comparison, which directly leads to an alarm when the signals exceed predefined threshold values. The integration of machine learing is still at the beginning, but in the future, solutions using AI will be sought for the large-scal development [
15].
i)
Performance monitoring- Wind turbine performance is often gauged through the relationship between power, wind speed, rotor speed, and blade angle, and in case of large deviations, an alarm or even stopping is generated [
15]. Detection of margins are large to prevent false alarms [
19]. Similar to process parameter estimation, more sophisticated methods like performance evolution monitoring are still not a common practice.
Thus, to obtain reliable predictive maintenance results, a combination of different techniques is needed. While vibration analysis may hold a predominant role, it is complemented by other specific technologies to perform decision-making accurately (
Figure 1).
2. Applied Research Methods
2.1. Condition Monitoring System
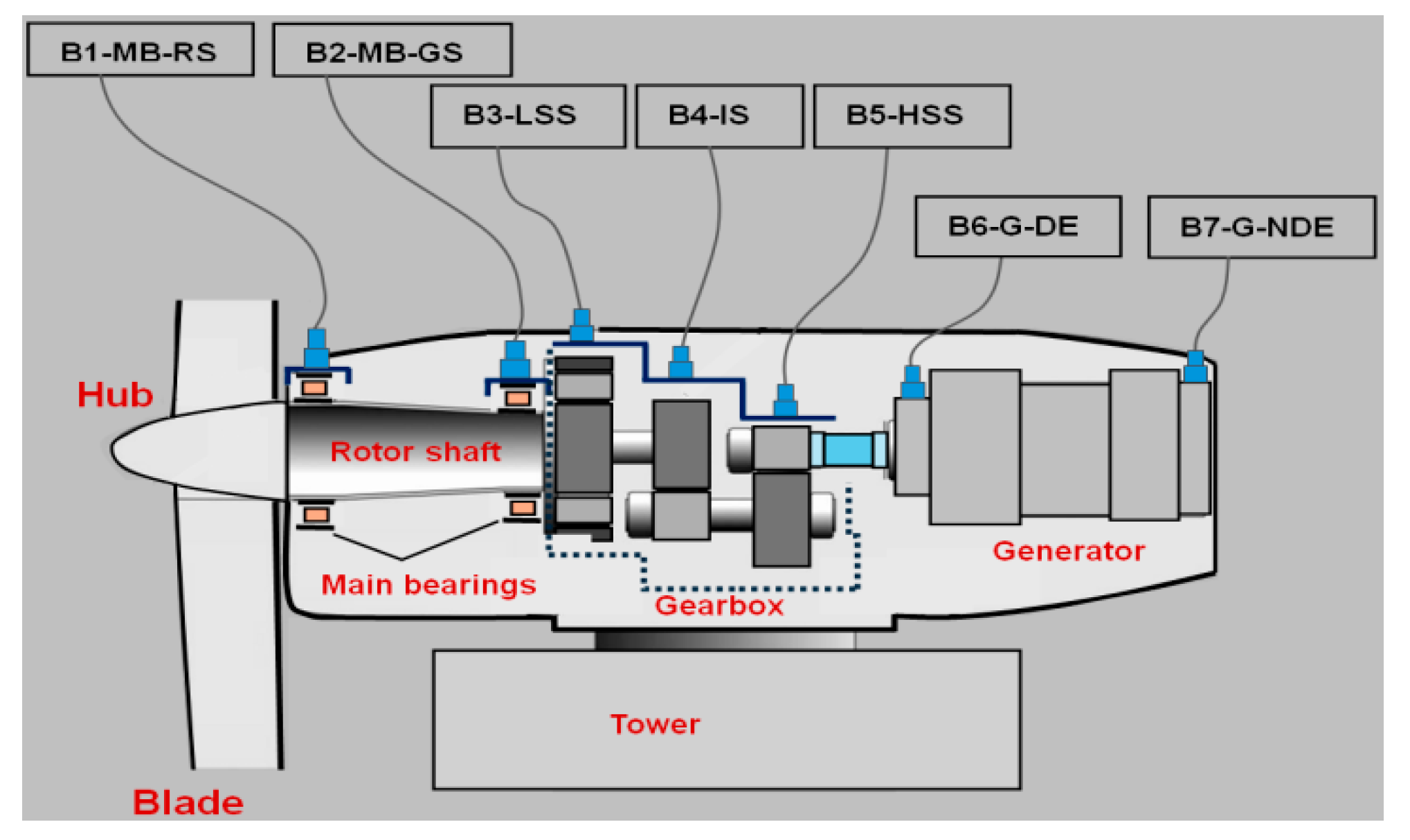
In this research, the experimental protocol is based on the Condition Monitoring System (CMS) The data used is part of the online data protocol regarding the wind turbines' state of operation. The recorded data is analyzed using signal evaluation both in the time domain and in the frequency domain. The CMS provides all data sets as originally optimized for all turbines. The data is collected from a wind turbine gearbox. The repartition of the sensors in the monitoring process of the wind turbine from the actual stage of the research is shown in
Figure 2.
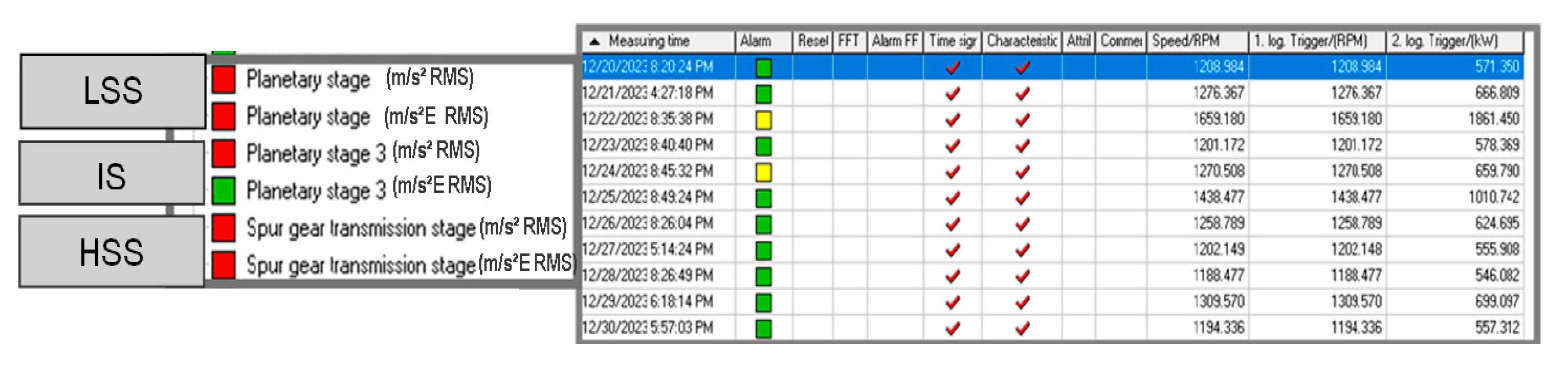
The analysis is centered on the gearbox, examining the vibrations at three specific points of the gearbox: Low-speed Shaft (LSS), Intermediary Shaft (IS), and High-Speed Shaft (HSS). The data acquisition is conducted using vibration sensors fixed on the bearings of the kinematic chain, starting from the input, which is the rotor side, and extending to the output, which is the generator side.
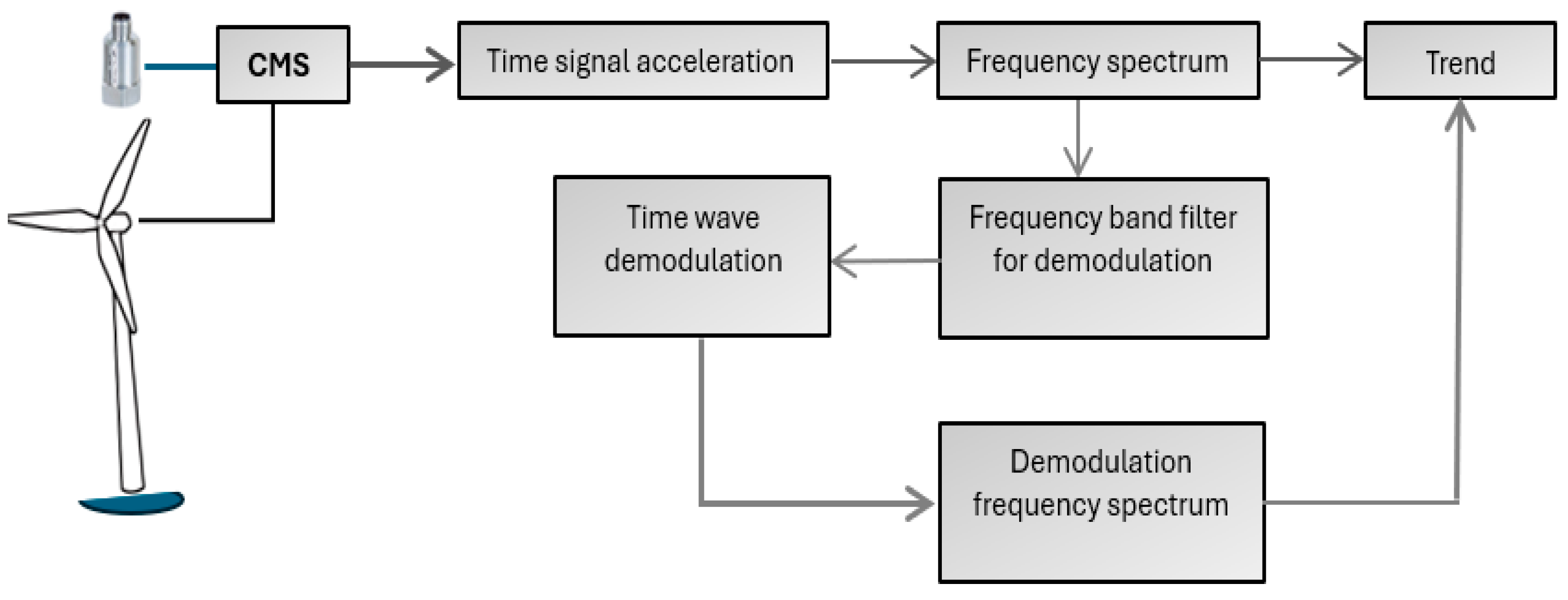
The data transmission and processing chain is described in
Figure 3. The online acquisition system allows the data to be recorded according to the original settings thus capturing signals along with their speed and power readings. In this way, the evolution of vibrations can be determined specific to certain values of speed and power [
20]. The system allowed the definition of parameters in the frequency domain both in the acquisition and analysis phases. The selected frequency range is according to ISO10816-21 standards, including the rotor, gearbox, generator, and tower/nacelle.
Figure 3 shows the data sets according to CMS, for the gearbox in the 3 entry points, LSS, intermediate IS, and HSS.
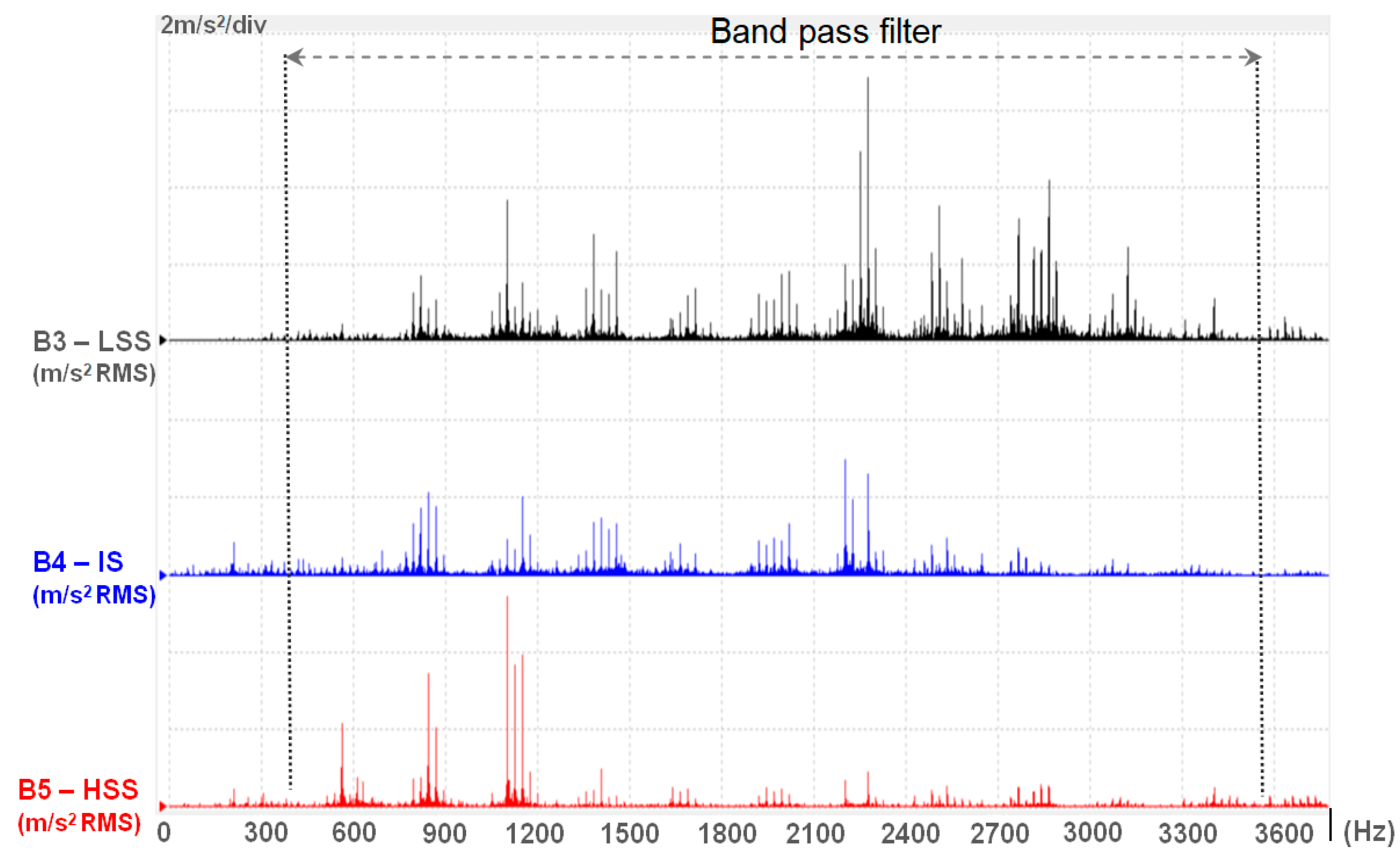
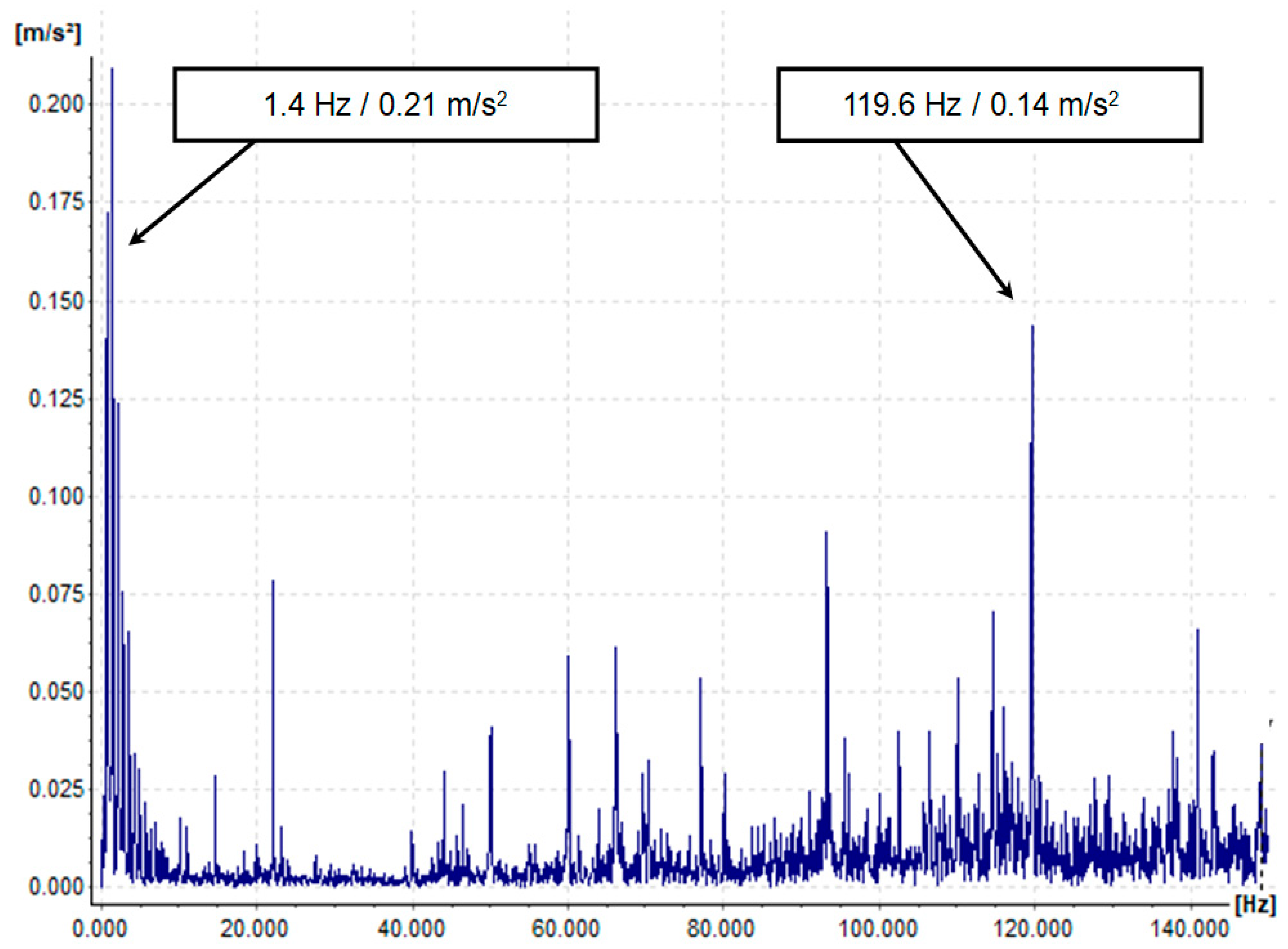
In these experiments the data from the input of the gearbox, the acceleration in the frequency domain at LSS, and the data of the gearbox output, in the frequency domain at HSS is taken into account,
Figure 4.
2.2. Signal Processing and Defect Detection
The experimental is based on real-time vibration monitoring, using National Instrument equipment cRIO-9076, with 12 input chanels, 24 bits resolution and a 50kSamples/s/ch. max. speed,
Figure 5. The real time monitoring data is set on 25kSamples/s, a buffer size with 32768Samples and a block size with 10kSamples. The vibration monitoring provide the signal data from the 3 acceleormteres fixed on the 3 gearbox points: the LSS with the 1-2 stages, the IS- the 3 stage and the HSS with the spur gear stage. The accelerometers used are with the 100mV/g sensitivity for the IS and HSS point and with 500mV/g sensistivity for the LSS point. For a precise synchronization between vibration singnals and speed signal, a laser speed sensor fixed at the generator side was used.
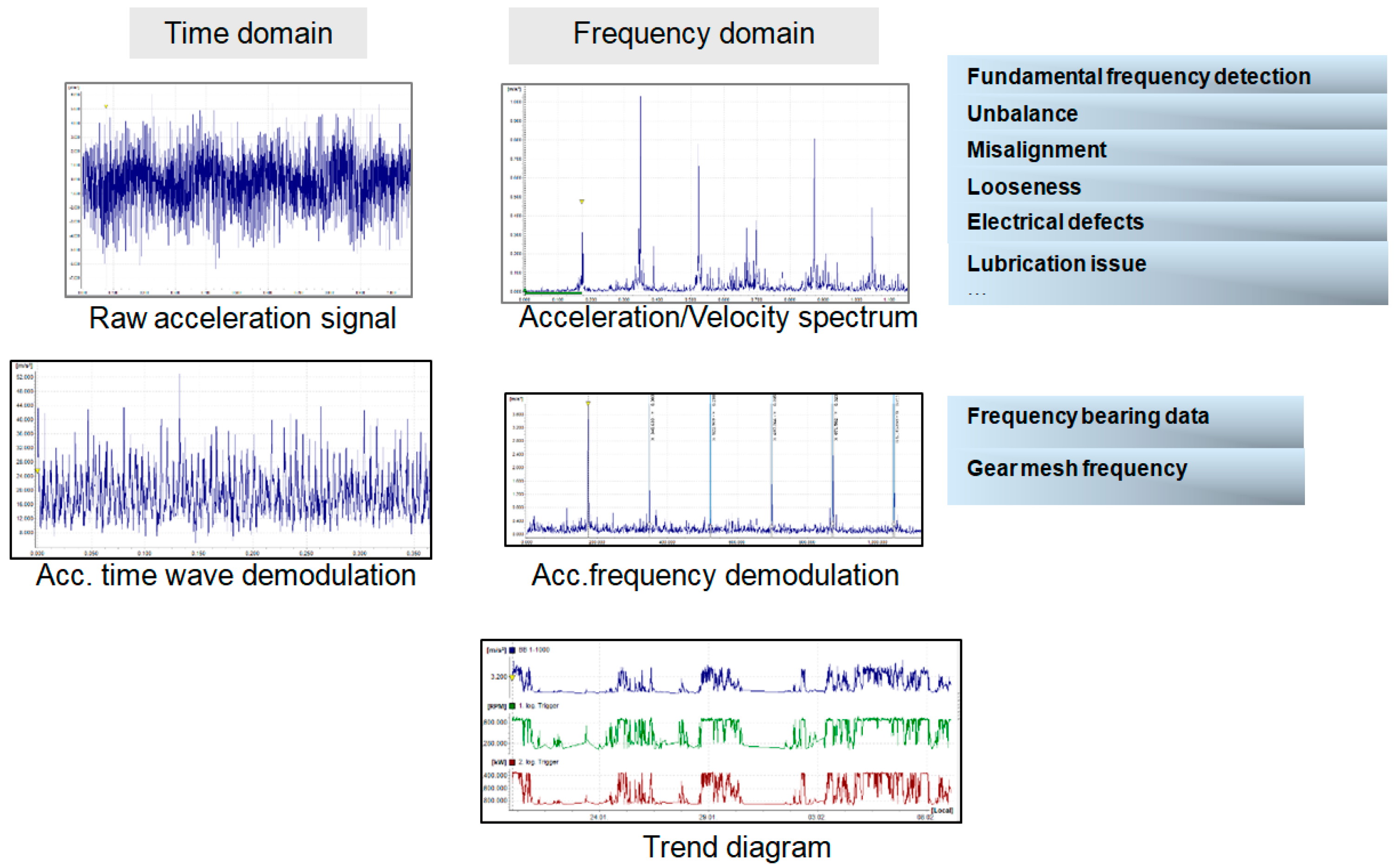
Signal analysis was done by numerical processing taking into account the parameters (frequency and amplitude) being monitored. Thus,
Figure 6 shows the waveforms obtained with the help of the monitoring software both in the time domain and in the frequency domain and in
Figure 7 and
Figure 8 are shown acceleration signal in the case of the gearbox wear. The vibration parameters are set according to the ISO10816-21 standard, specifying acceleration in m/s² RMS, vibration velocity in mm/s RMS, and demodulated acceleration in m/s ²E. With the bearing frequency data, the characteristic frequency of the bearing defect can be identified. The structure of the vibration parameters is complex and based on the vibration defect theory [
21,
22]. The vibration limits for wind turbines, provided by the ISO standard 10816-21, present an integrated base defining the recommended state of operation [
23,
24,
25]. Even in this situation, many specific cases of vibration of the wind turbine components are difficult to classify according to this standard [
26]. For this purpose, it is proposed to develop a model that can interpret the state of operation in real operating conditions using data provided by CMS
The processing datat and anlalysis aproch for bearing detection is applied alos for gear characterization by using the gear mesh frequency data according to the kinematic chain of the gearbox [
9,
10,
11,
12]. The signal processing and analysis is perform with Fastview software, which allows the use of both vibration monitoring and analysis in real time. The software allows the identification of the specific failure frequencies of the gear and bearings by the method of vibration demodulanting using envelope function [
27] with a dynamic filtering of the specific domain frequencies (
Figure 7).
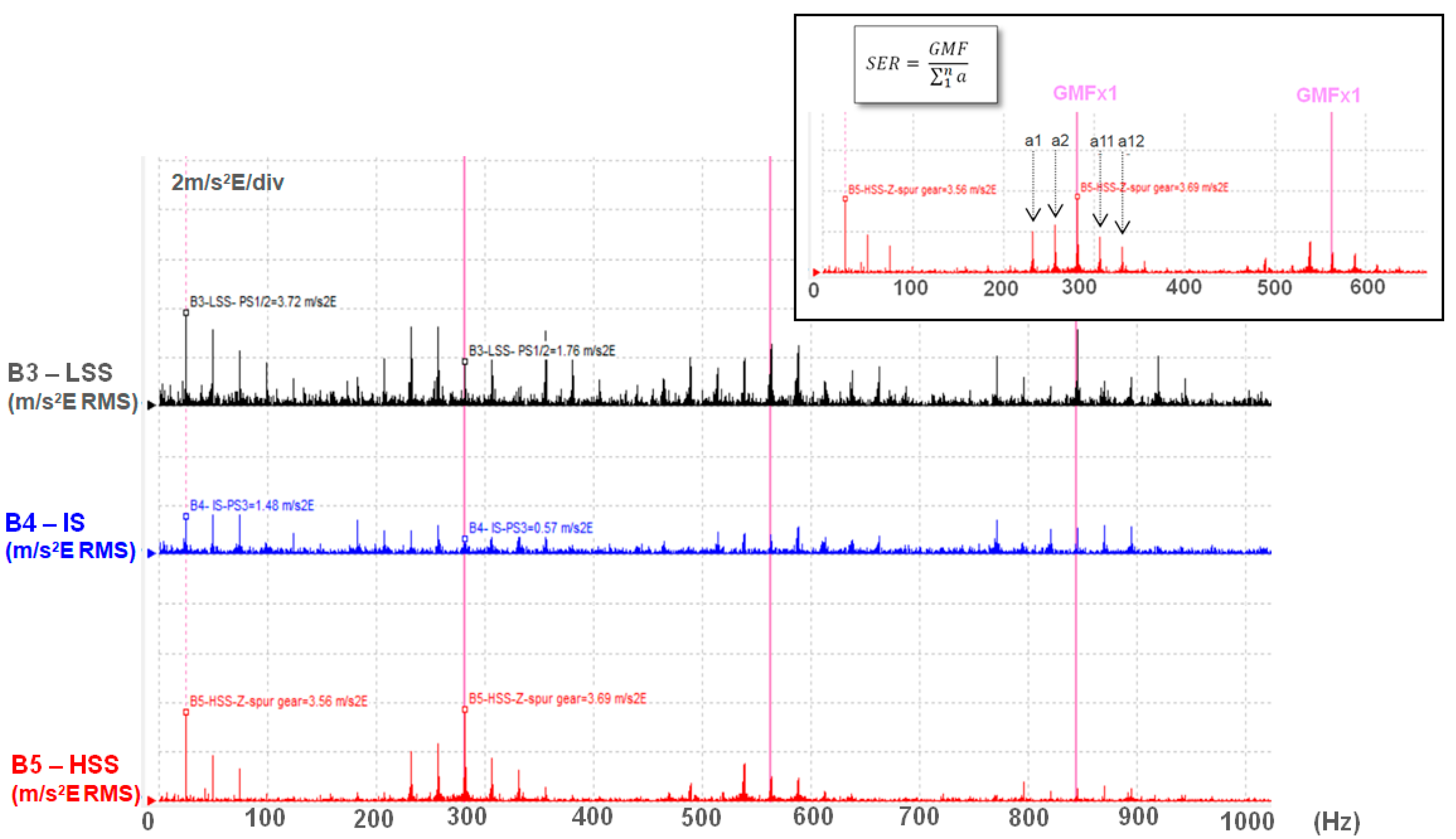
A novelty in the evaluation analysis of the gearboxes wear condition is the envelope method using the Hilbert transform [
27] with side bands energy coefficient integration, called SER coefficenent (Sideband Energy Ratio™, a patent pending algorithm utilized in the General Electric) [
28,
29,
30] so that the impact energy generated by the defect can be quantified (
Figure 8).
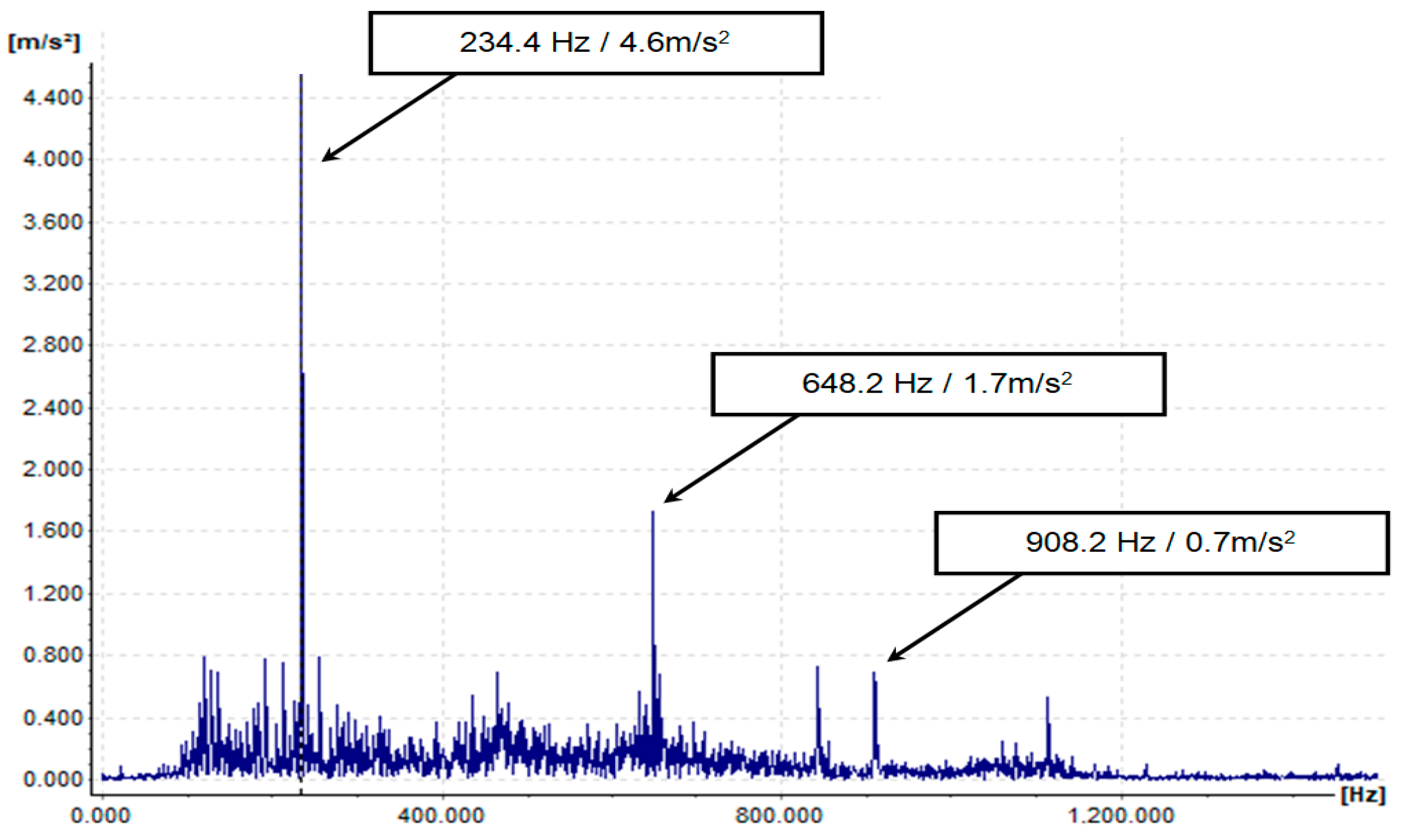
Figure 8 shows the spectrum of the acceleration envelope in the case of the gearbox defect. The quantification of the defective condition is evaluated by means of the gear mesh frequency presence (GMF) in relation to the side bands, as well as its harmonics. According to the quantification of the level of sidebands in relation to the amplitude of the GMF frequency, it can be found that the ratio is less than one, which means that the defect on the HSS stage is present, and is in an advanced state.
2.3. Using BDSVM-Based Data Extraction Technique
The Base density of the Support Vector for Machine Learning (
BDSVM) [
30] has been beneficial in establishing the basic data for neural network learning. In any monitoring activity, it is more efficient to train the neural network using BDSVM as it reduces the learning input data (decreasing computational complexity) and determines the resulting weights matrices to identify a mechanical failure without being impacted by the outliers. This study exploits this method to find the most relevant data points and establish the objective function (
FO).
This data extraction method is based on the filtering of data points based on their population density. Population density of data points refers to the correlation between the population size and the space they occupy. The rationale behind this data filtering is to deal with the data points that are influenced by random noises or gross errors. These data points do not accurately represent the general trend. These points are considered outliers and can affect the accuracy of the established objective functions and subsequently the analysis. The densely populated areas in the input space are determined by calculating the Mahalanobis distance (9). The points lying in this region are considered meaningful points while the points lying outside of this region are considered outliers.
The Mahalanobis distance is calculated from the quantity
μ which represents the average of the points' distances, to each point. The
cov-1 represents the inverse covariance matrix. This distance is [
33,
34]. The Mahalanobis distance takes into account the correlation of the data set and does not depend on the measurement scale [
34,
35,
36]. The population variance is calculated with a variance-convariance matrix [
35]. The Mahalanobis distance from the point to the mean of the distribution
μ can be calculated by (9), and the Mahalanobis distance from one point to another can be calculated by (10):
Where the population variance is calculated with [
12]:
and population covariance with:
If cov(xi) & cov(yi)>0
both of them increase or decrease;
If cov(xi) & cov(yi)<0
when xi increases yi decreases or vice-versa;
If cov(xi) & cov(yi)=0
not exist any relation between xi & yi;
If var(xi)> var(yi)
xi increase or decrease faster than yi;
End.
The average of
d is:
where
di is the distance between the points and
d is the average of these distances
If di >d,
the point i is in the outlier group;
Else
the point i will be considered important (meaningful) points in BDSVM;
End.
2.4. Objective Functions
The optimization function (
FO) was proposed as a polynomial function of the fifth order with real coefficients that will be constructed by using the data from the acquisition of Fourier spectrum of the vibrations:
where
ai will be determined by using the matrix equation:
with the following constraints:
- xi>0;
- xi must be meaningful points, xi group 1;
- xi BDSVM,
where FOi is the amplitude of the vibration evolution in time where the defect will appear and xi is the frequency in time. To define the FO, 5 boundary points (xi, FOi)BDSVM will be used for each moment of time vs. frequency points but under the same conditions of forced vibration and for the same wind turbine. The BDSVM points must strictly adhere to the condition of belonging to BDSVM which is that:
The boundary of FO will be the limit of the optimal functioning of the wind turbine. In this way, the moment of time for intervention on the gearbox will be determined, to eliminate the danger of an imminent defect.
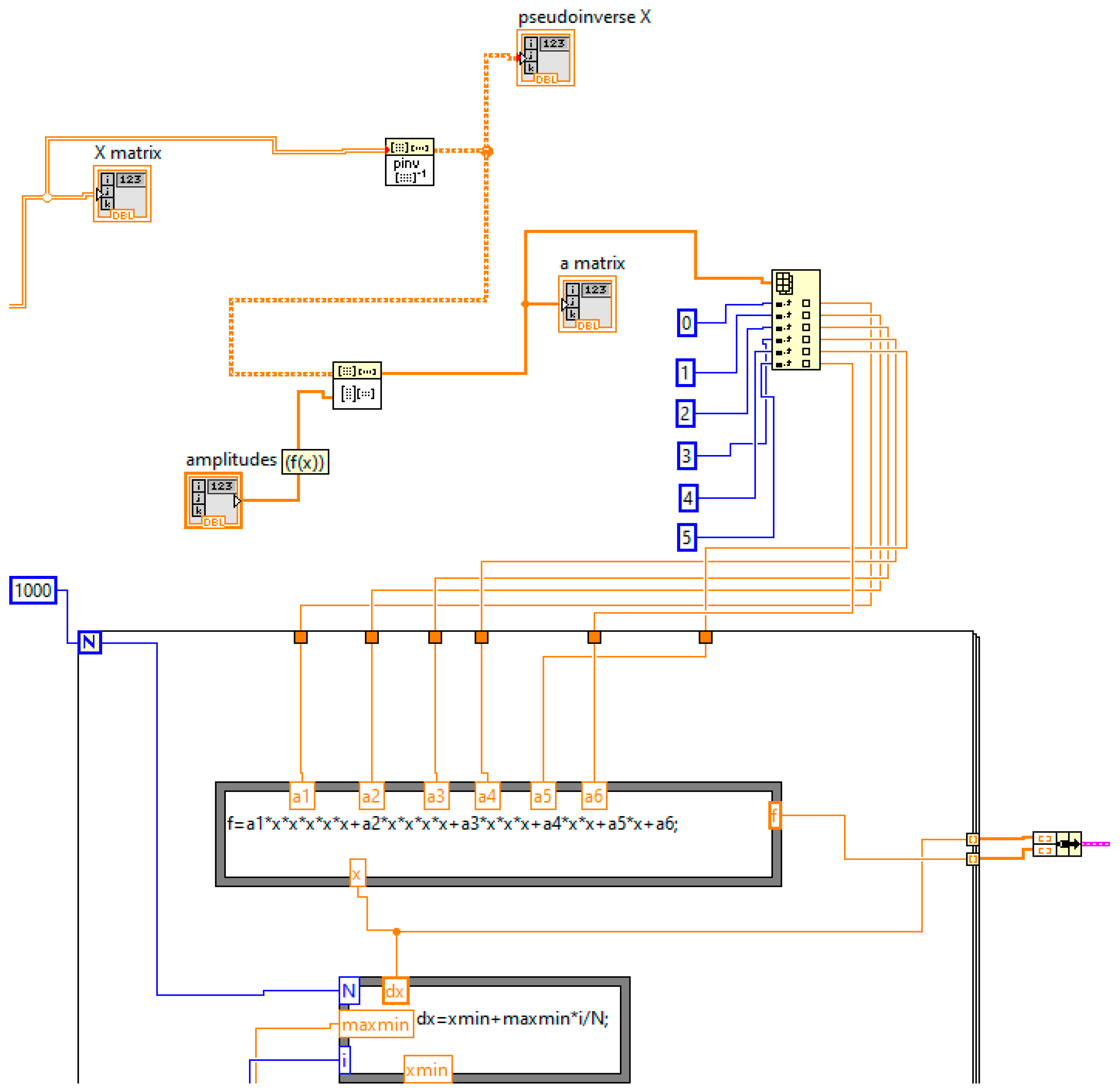
2.5. The Used Proper LabView Virtual Instrument for FO
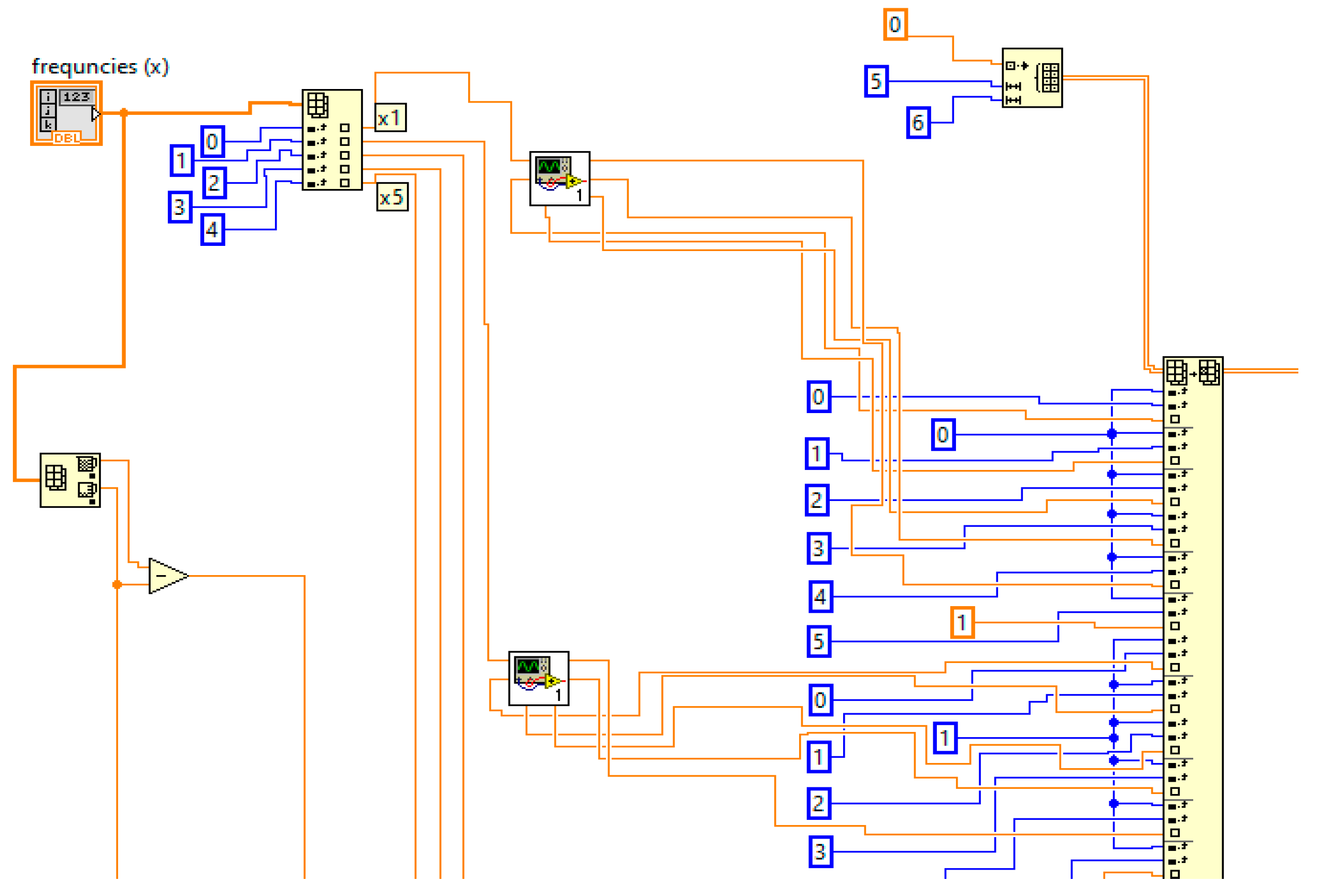
To solve the objective function
FO, proper LabView virtual instrumentation was used and the block schemas are shown in
Figure 9,
Figure 10 and
Figure 11.
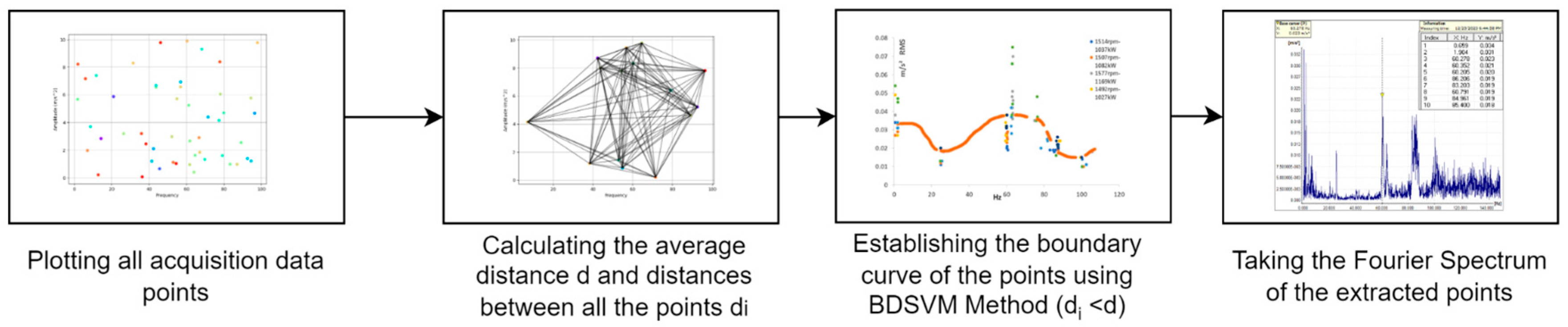
2.6. Description of the Used Algorithm
The used algorithm includes the following stages, as depicted in
Figure 12 and
Figure 13: (i) acquisition of data at different moments of time, for the same parameters of wind, power, speed; (ii) application of relation (12) for calculating the distances between points
di (max. amplitude, frequency of the fourier spectra acquired); (iii) applying relation (13) to determine the average distance,
d; (iv) defining group 1 of the BDSVM after checking the condition
di<
d; (v) establishing the boundary curve of BDSVM; (vi) analysis of Fourier spectra from group 1; (vii) defining the 5 maximum points from the Fourier spectra both for the upwind position and for the downwing position of the sensors; (viii) the use of LabView virtual instrumentation to determine the 5th order objective functions; (ix) plotting multiple objective functions for Fourier spectra acquired during three months of operation, under the same conditions of wind, power, speed; (x) defining the maximum points of the objectively drawn functions, in order to determine the trend; (xi) determining the coefficients of the 5th order objective functions of the trend for both low and high frequencies, as well as for upwind and downwind of the gear box sensors positions.
3. Results and Analysis
3.1. Establishing FO Boundary of Fourier Spectrum
If the operational limit of the turbine is set at a specific FO, a defect can be easily detected through control at each frequency. This can be done by checking if the operational point (frequency, magnitude) is in the normal functioning area or outside of this. In this way, it is possible to determine the maximum permissible magnitude of vibration.
In this case, the equation of the
FO will be:
For predictive maintenance, the following relation would be applied:
where
xi is the frequency for the imposed five points
BDSVM, the points from boundary limits, and
fi is the all current frequencies that must be checked. If this condition is false, the respective points could be the potential mechanical wear.
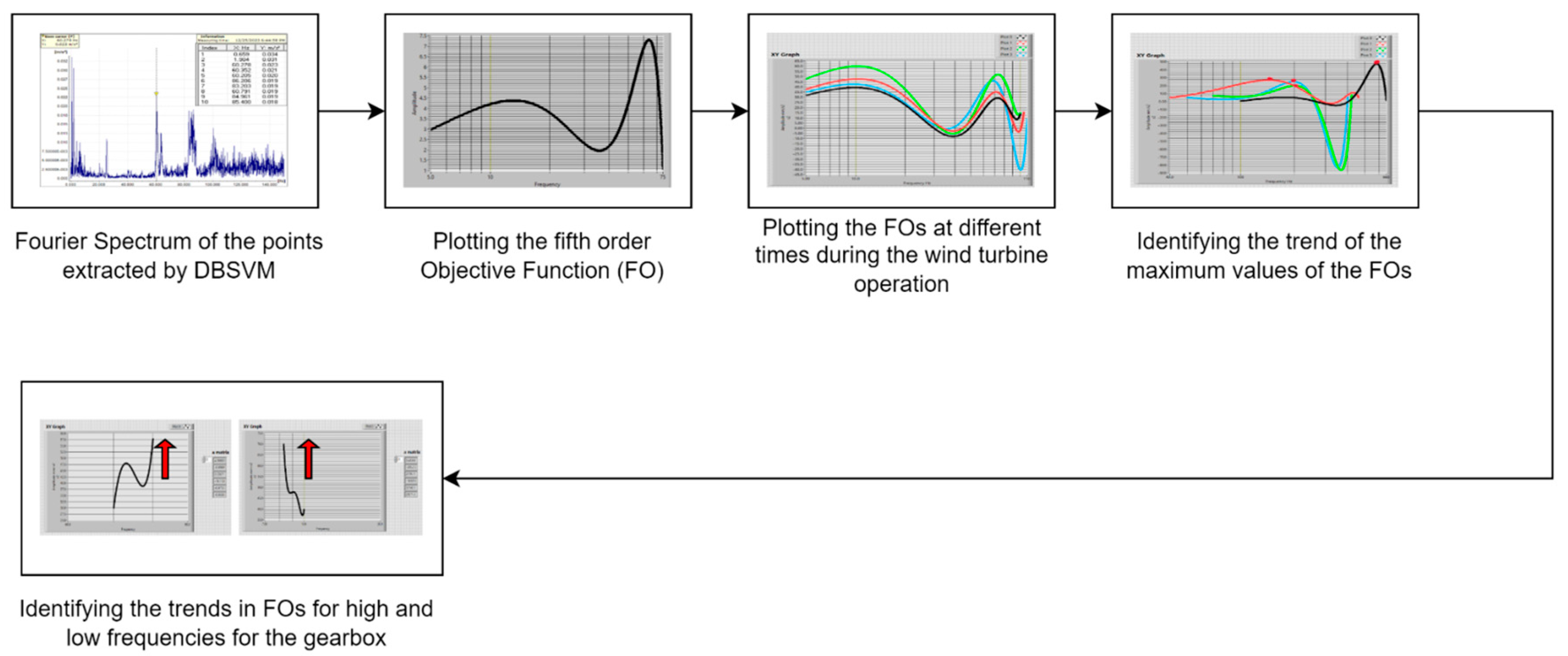
Using the Fourier spectra, the objective functions (
FOi) were constructed the objective functions (
FOi) for each of these data sets. All these
FOs were shown in
Figure 12,
Figure 13,
Figure 14 and
Figure 15, for upwind and downwind sensors from the wind turbine gearbox. All objective functions
FO, were determined by using the maximal values of magnitude from each of the used Fourier spectra, see the table of each acquisition Fourier spectrum.
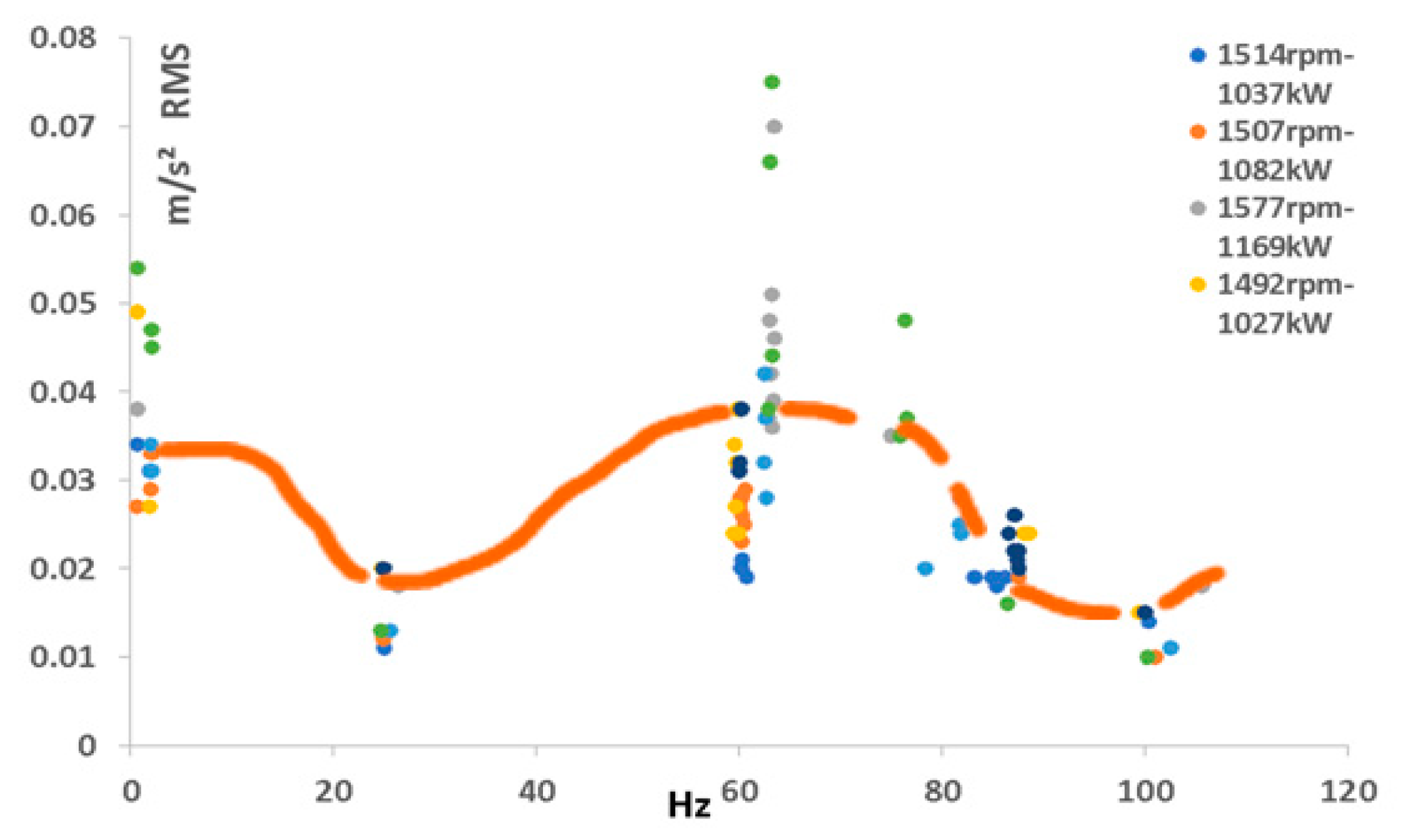
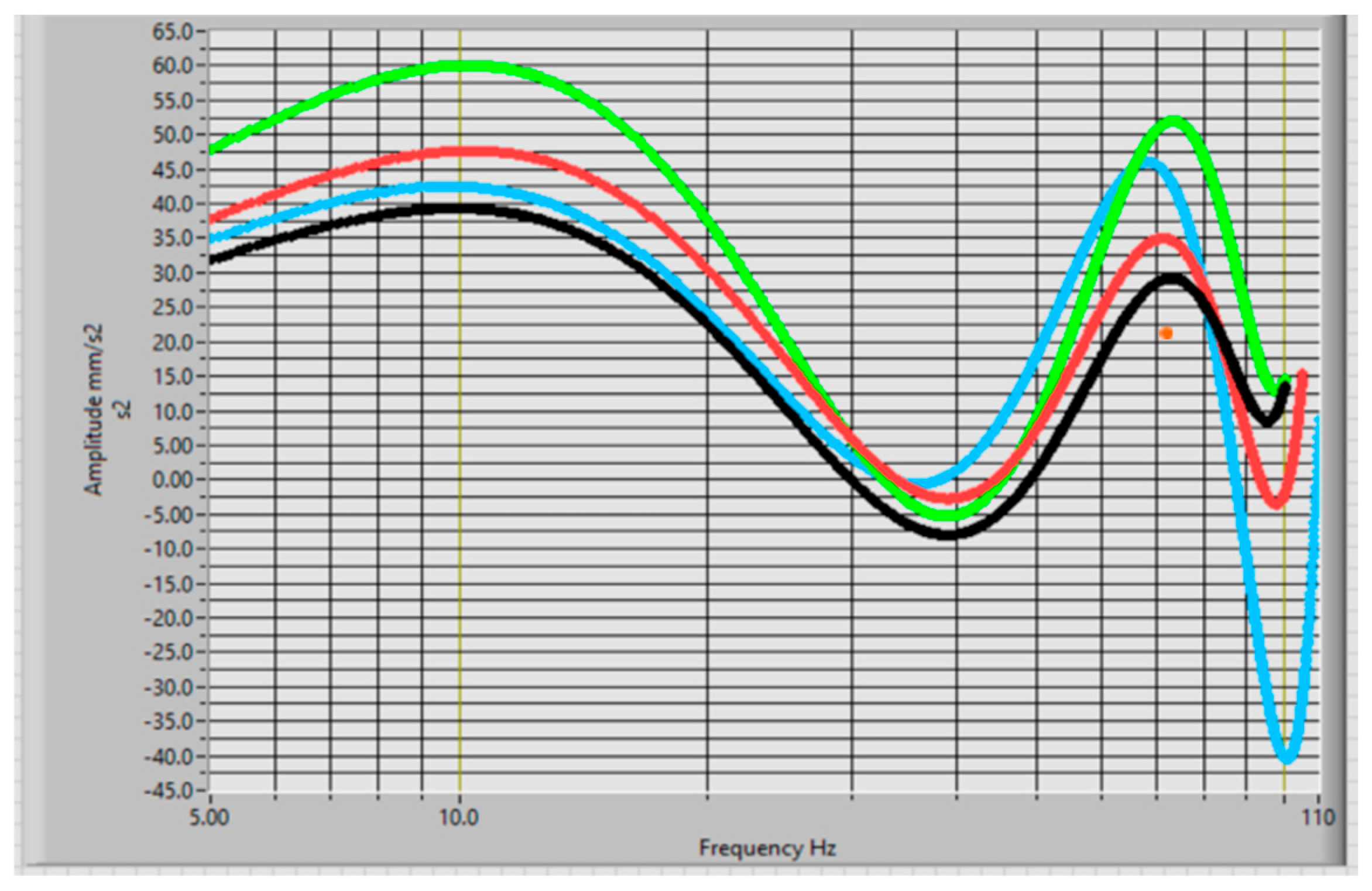
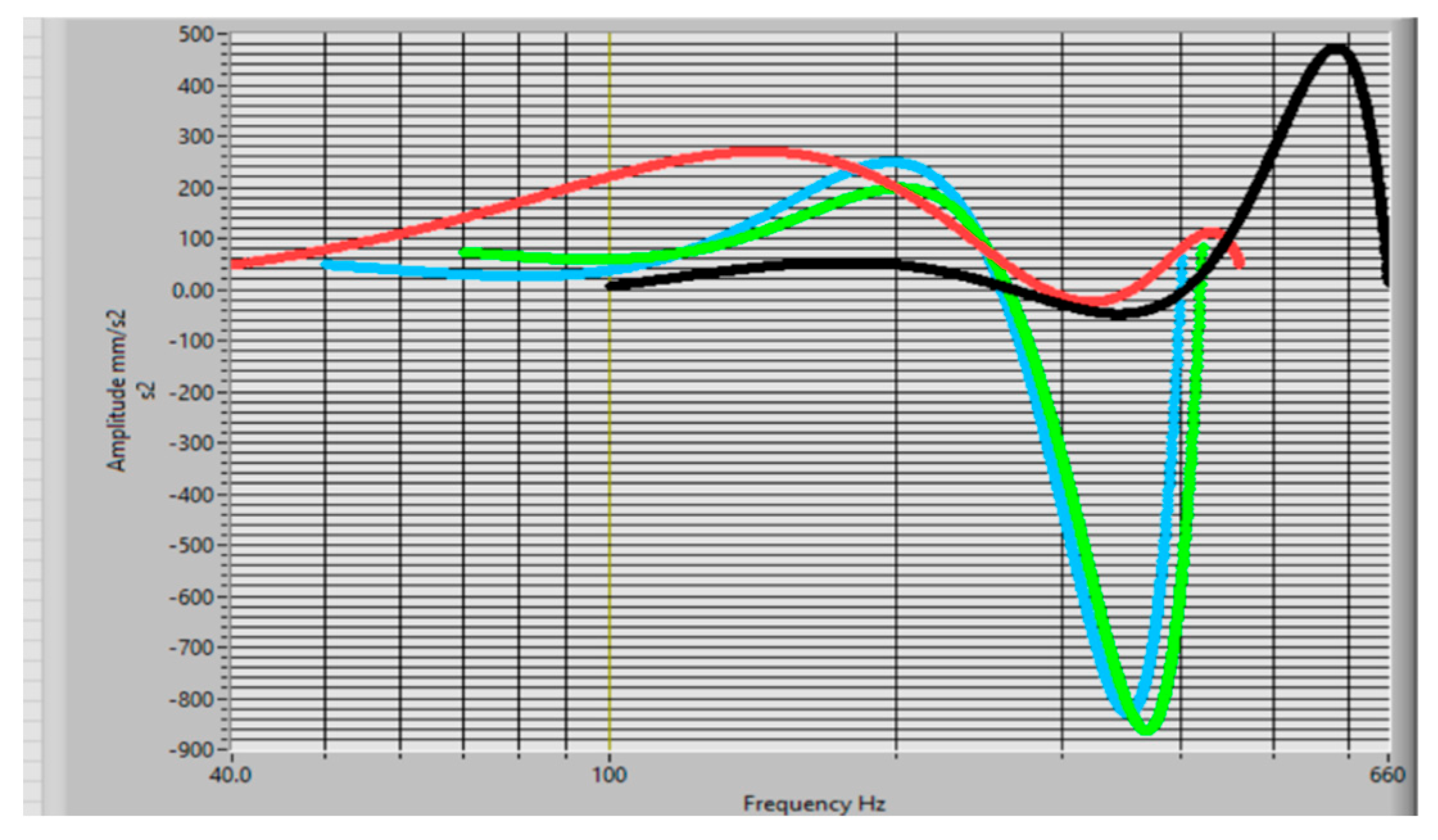
3.2. Construct the Objective Functions FO for All Selected Fourier Spectra
To construct the
FO for the data acquisition and establish the trend of the maximum values of the vibration magnitude vs. frequency were used four Fourier spectra for the upwind and downwind bearings, see
Figure 15. The results of
FOi are shown in
Figure 16 and
Figure 18.
To validate the mathematical vibration model proposed (
Figure 13), the vibration data is obtained from the CMS of 2.0 MW industrial WT gearbox, based on the acceleration position and data acquisition shown in
Figure 2 and
Figure 5. The gearbox is planetary type with a transmissions ratio 116. This model was applied to synthesize the data acquisition of the wind turbine in the period between December 2023 to February 2024. The conditions that were imposed are the following: (i) the data acquisition was for the same, or very similar wind turbines; (ii) the data acquisition was carried out from the sensors from the gearbox, B3-LSS, and B5-HSS, HSS upwind bearing radial and similarly HSS downwind bearing radial; (iii) the data acquisition was performed in the similar dynamic conditions of wind intensity, speed, and power; (iv) the acquisition data that was synthesized is the data that falls under the condition to be classified as a meaningful point,
xi group
1,
xi BDSVM, see
Figure 14.
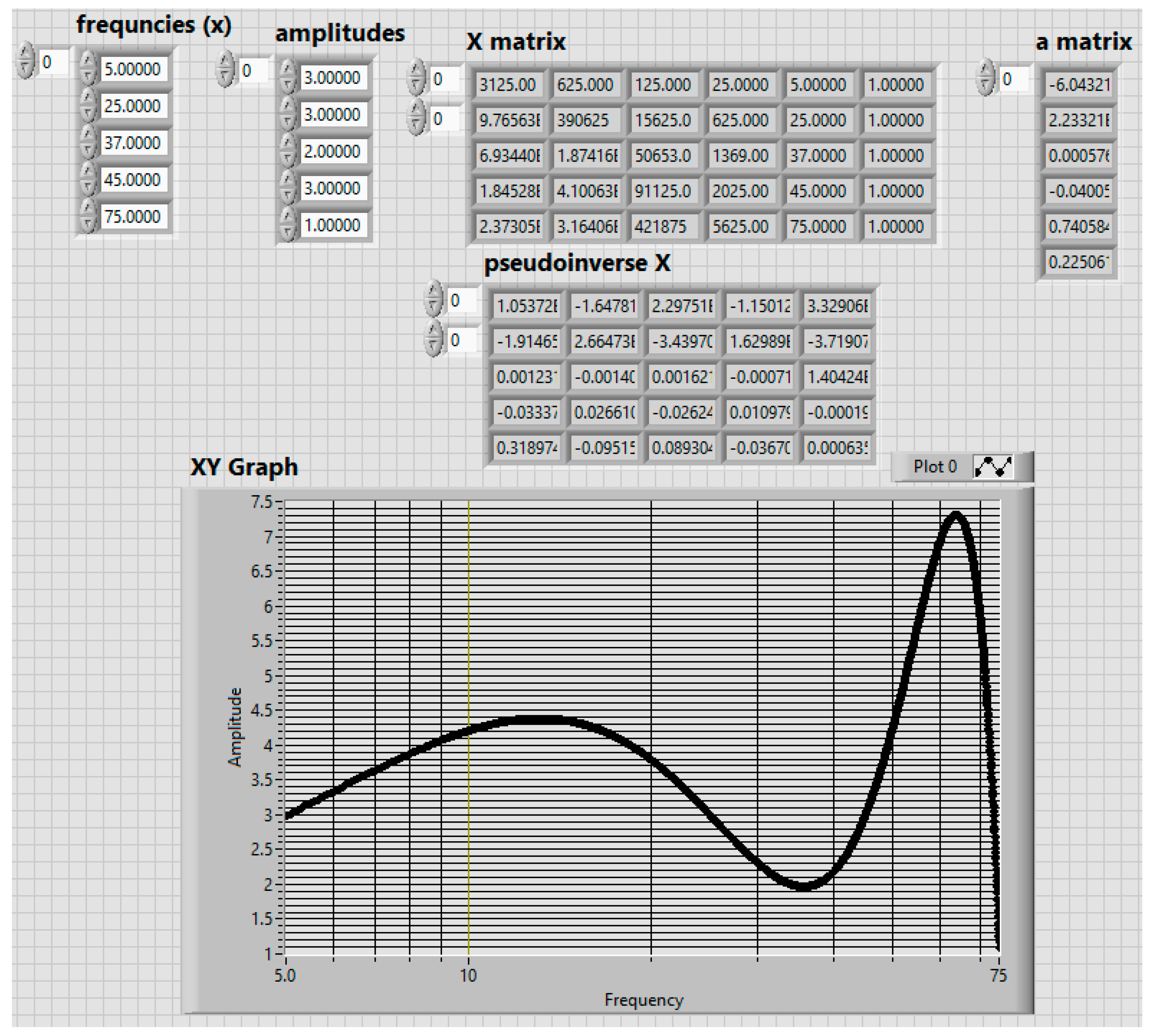
Using the data from the column matrices
ai, the fifth-order equation for
FOi will be determined. The
FOi for the upwind position of the sensor is shown in relation (19) and for the downwind position in relation (20).
All determined FOs represent different stages of the mechanical condition of the turbine gearbox assembly.
3.3. Determine the FO for the Trend
With the help of these functions, the trend of potential defects in the turbine gearbox area can be assessed. The characteristic frequencies of the WT gearbox in the damage case are presented in the
Figure 20 and
Figure 21, corresponding to LSS-upwind and HSS-downwind. The frequency spetrum of acceleration for LSS – upwind position shows the fundamental frequency of planet pin (
Figure 20) and the frequency spectrum of HSS – downwind position, shows the existence gear meash frequency (GMF) generated by the HSS pin gear and planet pin gear. In the case of a fault gear the amplitude is much higher, reaching up to 10 times higher than in the normal condition case.
At any given moment, it is possible to check if the function is approaching the period close to the appearance of a defect or not [
37,
38]. Throughout this timeframe, it will be possible to examine whether the points (Frequency, Magnitude) fall within the first or last
FO or between them, providing information on the proximity of a potential defect, as per relations (19) and (20). The trends of these functions are depicted in
Figure 22, represented by the maximum of the
FO for each of the cases.
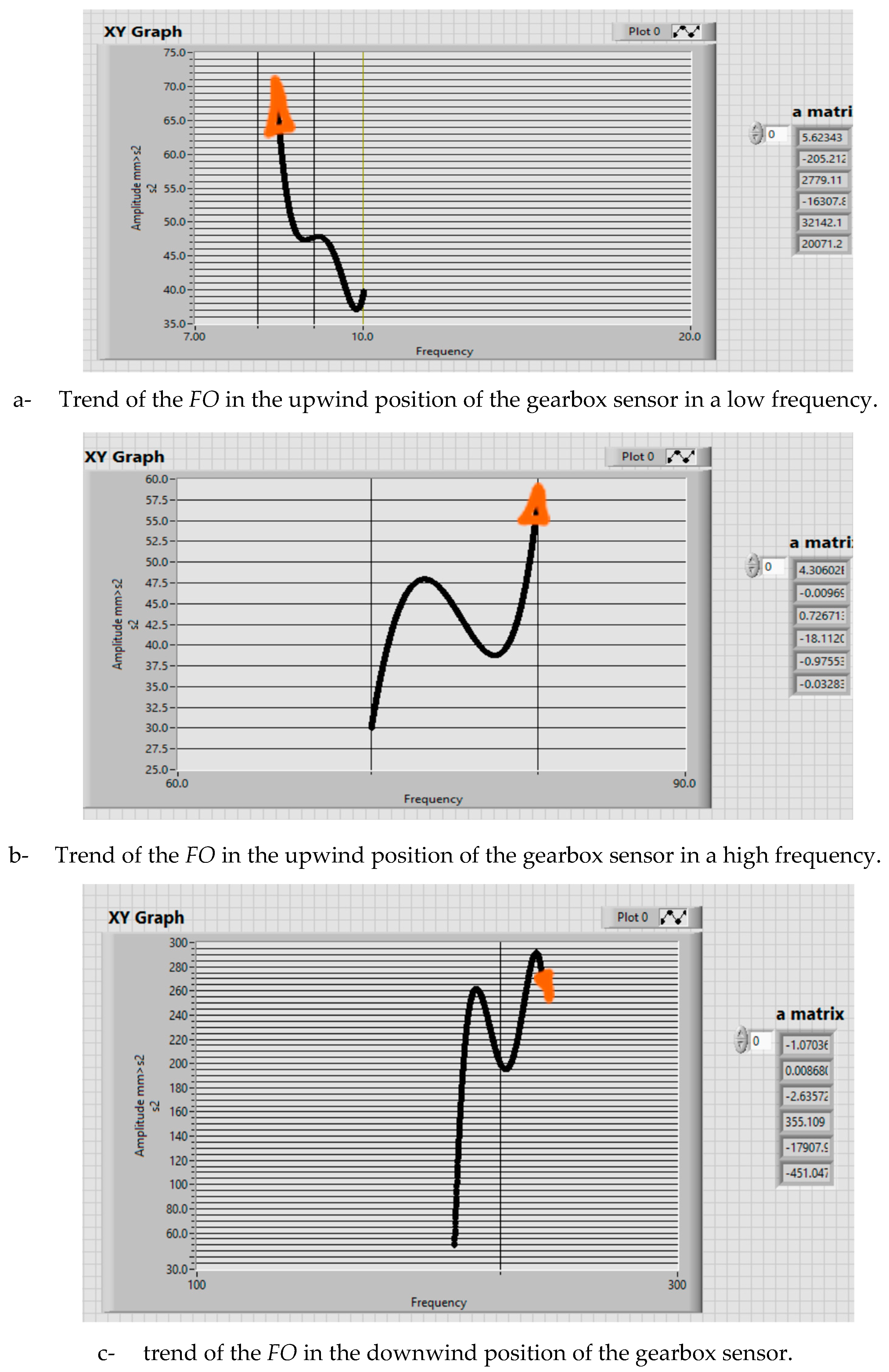
The trend functions are the following: (21)
for the low frequency in the upwind position
for high frequency in the upwind position
for high frequency in the downwind position
If the first FO objective function is defined after an intervention when the gearbox is working correctly, and the last function is determined close to the appearance of a defect, the position of any point (frequency, amplitude) can be determined between these limits. Intermediate FOs define the intermediate limits. By using this method, it will be possible to implement preventive maintenance and also monitor the normal operation of the gearbox of the wind turbine. The validation of this developed method can be carried out by checking whether the maximum points (frequency, magnitude) from the Fourier spectrum belonging to a certain trend as identified by the objective functions, correspond to any known instances of gearbox malfunction or failure in wind turbines. This would be done through collaboration with a wind turbine expert.
4. Conclusions and Future Work
This paper presents a novel approach to address the complexities of vibration monitoring and analysis in wind turbine gearboxes. By leveraging mathematical modeling and AI techniques, we have developed a method for evaluating gearbox conditions during operation that can help make meaningful interpretations from uncategorized vibration data from wind turbines. After analyzing the obtained results, the objective functions, and the trend of the monitoring results, we can make the following remarks: (i) The applied method is general and can be applied to many other dynamic monitoring processes; (ii) The designed LabView instrumentation for the synthetic analysis of the obtained acquisition data opens the way to applying more virtual instrumentation in monitoring the dynamic behavior across various mechanical fields; (iii) Using BDSVM to filter out the meaningful data adds a new front to applying machine learning in monitoring processes; (v) Establishing the trend of the FO for each position of the gearbox sensors ensures the design of an intelligent monitoring system for predictive maintenance; (vi) The trend for the low frequency in the upwind sensor position is a decrease in frequency and an increase in magnitude; (vii) conversely, the trend involves an increase in both frequency and magnitude for the high frequency; (viii) in the downwind sensor position, the trend is characterized by an increase in frequency and a decrease in magnitude.
In future work, we propose to generalize this method and leverage neural networks for the rapid establishment of weight matrices, objective functions, and wear trends in wind turbines across all sensors. This will be integrated into a comprehensive matrix comprising objective functions, alongside a monitoring and trend matrix.
In the next stage of this research SVM Regression analysis will be implemented to predict the magnitude of vibrations based on various input features (e.g., frequency, time). This information will help obtain a quantitative measure of potential defects. Upon further assessment of the FFT spectrum of vibrations leading up to failures or defects, we also aim to study and explore other features (fluctuations in phase, etc.) that could indicate upcoming defects. This condition-based maintenance strategy can also be further enhanced by incorporating supervised classification. We plan to label the datasets indicating different points (labeled points) in time leading up to the developing fault. This would be done through collaboration with the industry specialists. The classification algorithm can be employed to identify the definite states of the system (normal operation, potential fault, critical fault). The combination of regression and classification would allow for a more comprehensive predictive maintenance approach.
The proposed method is intended to be applied in other industrial applications in the case of condition monitoring of machine-tool spindles.
Author Contributions
Conceptualization, B.C. and O.A.; methodology, B.C and O.A.; software, B.C. and O.A; validation, B.C., O.A., O.S. and A.A.; formal analysis O.A., O.S., and A.A.; investigation, B.C., O.A., O.S., A.A., M.N. and U.H.; resources, B.C.; writing—original draft preparation, O.A. and B.C.; writing—review and editing, B.C. and O.A., O.S., A.A., M.N. and U.H.; supervision, O.A.; funding acquisition, B.C. and O.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The requested data is currently unavailable as the owner has deemed it confidential for economic reasons.
Acknowledgments
This work was supported by a grant from the National Program for Research of the National Association of Technical Universities - GNAC ARUT 2023.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nie, Y.; Li, F.; Wang, L.; Li, J.; Sun, M.; Wang, M.; Li, J. A mathematical model of vibration signal for multistage wind turbine gearboxes with transmission path effect analysis. Mechanism and Machine Theory 2022, 167. [Google Scholar] [CrossRef]
- Spinato, F.; Tavner, P.J.; Bussel, G.J.W.; Koutoulakos, E. Reliability of wind turbine subassemblies. IET Renew. Power Gener. 2009, 3, 387–401. [Google Scholar] [CrossRef]
- Dao, C.; Kazemtabrizi, B.; Crabtree, C. Wind turbine reliability data review and impacts on levelised cost of energy. Wind Energy 2019, 22, 1848–1871. [Google Scholar] [CrossRef]
- Ren, B.; Chi, Y.; Zhou, N.; Wang, Q.; Wang, T.; Luo, Y.; Ye, J.; Zhu, X. Machine learning applications in health monitoring of renewable energy systems. Renewable and Sustainable Energy Reviews 2024, 189. [Google Scholar] [CrossRef]
- Sheng, S.; Veers, P. Wind Turbine Drivetrain Condition Monitoring – An Overview, Mechanical Failures Prevention Group: Applied Systems Health Management Conference 2011 Virginia Beach, Virginia May 10 – 12, 2011.
- Zhu, Y.; Xie, B.; Wang, A.; Qian, Z. Fault diagnosis of wind turbine gearbox under limited labeled data through temporal predictive and similarity contrast learning embedded with self-attention mechanism. Expert Systems with Applications 2024, 245. [Google Scholar] [CrossRef]
- Teng, W.; Ding, X.; Zhang, X.; Liu, Y.; Ma, Z. Multi-fault detection and failure analysis of wind turbine gearbox using complex wavelet transform. Renew. Energy 2016, 93, 591–598. [Google Scholar] [CrossRef]
- Vamsi, I.; Sabareesh, G.R.; Penumakala, P.K. , Comparison of condition monitoring techniques in assessing fault severity for a wind turbine gearbox under nonstationary loading. Mech. Syst. Signal Process. 2019, 124, 1–20. [Google Scholar] [CrossRef]
- Teng, W.; Ding, X.; Tang, S.; Xu, J.; Shi, B.; Liu, Y. Vibration Analysis for Fault Detection of Wind Turbine Drivetrains—A Comprehensive Investigation. Sensors 2021, 21, 1686. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Liang, X.; Zuo, M.J. Vibration signal modeling of a planetary gear set with transmission path effect analysis. Measurement 2016, 20–31. [Google Scholar] [CrossRef]
- Liang, X.; Zuo, M.J.; Liu, L. A windowing and mapping strategy for gear tooth fault detection of a planetary gearbox. Mechanical Systems and Signal Processing 2016, 80, 445–459. [Google Scholar] [CrossRef]
- Feng, Z.; Ma, H.; Zuo, M.J. Vibration signal models for fault diagnosis of planet bearings. Journal of Sound and Vibration 2016, 370, 372–393. [Google Scholar] [CrossRef]
- Wang, T.; Han, Q.; Chu, F.; Feng, Z. Vibration based condition monitoring and fault diagnosis of wind turbine planetary gearbox: A review. Mechanical Systems and Signal Processing 2019, 126, 662–685. [Google Scholar] [CrossRef]
- Salameh, J.P.; Cauet, S.; Etien, E.; Sakout, A.; Rambault, L. Gearbox condition monitoring in wind turbines: A review. Mechanical Systems and Signal Processing 2018, 111, 251–264. [Google Scholar] [CrossRef]
- Hameeda, Z.; Honga, Y.S.; Choa, Y.M.; Ahnb, S.H. Condition monitoring and fault detection of wind turbines and related algorithms: A review. Renewable and Sustainable Energy Reviews 2009, 13, 1–39. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, K.; Wei, D.; Zuo, M.J. Amplitudes of characteristic frequencies for fault diagnosis of planetary gearbox. Journal of Sound and Vibration 2018, 432, 119–132. [Google Scholar] [CrossRef]
- McNiff, B.; Keller, J.; Fernandez-Sison, A.; Demtröder, J. A Revised International Standard for Gearboxes in Wind Turbine Systems. Presented at the Conference for Wind Power Drives Aachen, Germany March 21-22, 2023.
- Cao, L.; Liu, S. Vibration Suppression of an Input-Constrained Wind Turbine Blade System. Mathematics 2023, 11, 3946. [Google Scholar] [CrossRef]
- Peng, J.; Bian, Y.; Tian, D.; Liu, P.; Gao, Z. Vibration alleviation for wind turbine gearbox with flexible suspensions based on modal interaction. Journal of Low Frequency Noise, Vibration and Active Control 2023, 42, 1390–1418. [Google Scholar] [CrossRef]
- Global Energy Research Council, Global Wind Report, 2009. [Online] http://www.gwec.net/fileadmin /documents/Publications/Global_Wind_2007_report/GWEC_Global_Wind_2009_Report_Lowres_15th.520Apr./pdf.
- Verbruggen, T.W. Condition Monitoring: Theory and Practice, 2009, Wind Turbine Condition Monitoring Workshop, October 8-9, 2009, Broomfield, CO.
- Sheng, S.; Veers, P. Wind Turbine Drivetrain Condition Monitoring – An Overview, Mechanical Failures Prevention Group: Applied Systems Health Management Conference, 2011, Virginia Beach, Virginia, May 10 – 12, 2011.
- Lloyd, G. , Guideline for the Certification of Condition Monitoring Systems for Wind Turbines, 2007, Hamburg, Germany.
- Gellermann, T.; Walter, G. , Requirements for Condition Monitoring Systems for Wind Turbines, 2003, AZT Report no.03.01.068.
- Wind Stats Newsletter, 2003-2009, vol.16, no.1 to vol.22, no.4, Haymarket Business, Media, London, UK.
- Veers, P. Databases for Use in Wind Plant Reliability Improvement, 2009, Wind Turbine Condition Monitoring Workshop, October 8-9, 2009, Broomfield, CO.
- Bisu, C.F.; Zapciu, M.; Cahuc, O.; Gérard, A.; Anica, M. Envelope Dynamic Analysis: A New Approach For Milling Process Monitoring. The International Journal of Advanced Manufacturing Technology 2012, 62, 471–486. [Google Scholar] [CrossRef]
- Zhang, M.; Cui, H.; Li, Q.; Liu, J.; Wang, K.; Wang, Y. An improved sideband energy ratio for fault diagnosis of planetary gearboxes. Journal of Sound and Vibration 2021, 491. [Google Scholar] [CrossRef]
- A Pattabiraman, T.R. a, *, Srinivasan K.b, Malarmohan K.b, Assessment of sideband energy ratio technique in detection of wind turbine gear defects. Case Studies in Mechanical Systems and Signal Processing 2015, 2, 1–11. [Google Scholar]
- Hanna, J.; Hatch, C.; Kalb, M. Detection of Wind Turbine Gear Tooth Defects Using Sideband Energy Ratio, GE Enregy, Nevada USA, 2012.
- Verbruggen, T.W. Wind Turbine Operation and Maintenance Based on Condition Monitoring, 2003, Energy Research Center of the Netherlands, Petten, The Netherlands. [Online] www.ecn.nl/publicaties/PdfFetch.aspx?nr=ECN-C-- 03-047.
- Dodge, Y. The Concise Encyclopedia of Statistics, Springer 2008.
- Nazari, Z.; Kang, D.; Endo, H. Density Based Support Vector Machines, The 29th International Technical Conference on Circuits/Systems, Computers and Communications (ITC-CSCC), pp.1-3, 2014.
- El Moutaouakil, K.; El Ouissari, A.; Olaru, A.; Palade, V.; Ciorei, M. OPT-RNN-DBSVM: OPTimal Recurrent Neural Network and Density-Based Support Vector Machine. Mathematics 2023, 11, 3555. [Google Scholar] [CrossRef]
- Variance-covariance matrix- GeeksforGeeks.html.
- Nazari, Z.; Kang, D. Density Based Support Vector Machines for Classification. International Journal of Advanced Research in Artificial Intelligence (IJARAI) 2015, 4. [Google Scholar] [CrossRef]
- Bo Ren; Chi, Y. ; Zhou, N.; Wang, Q.; Wang, T.; Luo, Y.; Ye, J.; Zhu, X. Machine learning applications in health monitoring of renewable energy systems. Renewable and Sustainable Energy Reviews 2024, 189. [Google Scholar]
- Valikhani, M.; Jahangiri, V.; Ebrahimian, H.; Moaveni, B.; Liberatore, S.; Hines, E. Inverse modeling of wind turbine drivetrain from numerical data using Bayesian inference. Renewable and Sustainable Energy Reviews 2023, 171. [Google Scholar] [CrossRef]
Figure 1.
The position of the sensors for the monitoring process.
Figure 1.
The position of the sensors for the monitoring process.
Figure 2.
Schema of the experimental stand with the position of the used sensors.
Figure 2.
Schema of the experimental stand with the position of the used sensors.
Figure 3.
Synopsis of data acquisition and signal processing.
Figure 3.
Synopsis of data acquisition and signal processing.
Figure 4.
Example of CMS data presentation.
Figure 4.
Example of CMS data presentation.
Figure 5.
Vibration monitoring devices.
Figure 5.
Vibration monitoring devices.
Figure 6.
Signal processing and defect detection from CMS.
Figure 6.
Signal processing and defect detection from CMS.
Figure 7.
Acceleration signal in the case of the gearbox wear.
Figure 7.
Acceleration signal in the case of the gearbox wear.
Figure 8.
Envelope acceleration in the case of a gearbox wear.
Figure 8.
Envelope acceleration in the case of a gearbox wear.
Figure 9.
Part of the block schema of the LabView virtual instrument to determine the FO5 order.
Figure 9.
Part of the block schema of the LabView virtual instrument to determine the FO5 order.
Figure 10.
Part of the block diagram represents the FO (polynomial function of the 5-degree order) characteristic.
Figure 10.
Part of the block diagram represents the FO (polynomial function of the 5-degree order) characteristic.
Figure 11.
Front panel with the results of the optimization function FO for known points from the BDSVM (the maximal values from the Fourier spectrum).
Figure 11.
Front panel with the results of the optimization function FO for known points from the BDSVM (the maximal values from the Fourier spectrum).
Figure 12.
Block schema of the part of the used algorithm to establish the BDSVM of the collected data.
Figure 12.
Block schema of the part of the used algorithm to establish the BDSVM of the collected data.
Figure 13.
Block schema of the part of the used algorithm to establish the objective functions (FO) by using the Fourier spectrum collected from the boundary of the BDSVM. .
Figure 13.
Block schema of the part of the used algorithm to establish the objective functions (FO) by using the Fourier spectrum collected from the boundary of the BDSVM. .
Figure 14.
The acquisition data distribution and the establishment of boundary values for group 1, representing meaningful points of BDSVM, occur under similar dynamic conditions of speed and power. This characteristic is constructed by applying the BDSVM algorithm.
Figure 14.
The acquisition data distribution and the establishment of boundary values for group 1, representing meaningful points of BDSVM, occur under similar dynamic conditions of speed and power. This characteristic is constructed by applying the BDSVM algorithm.
Figure 15.
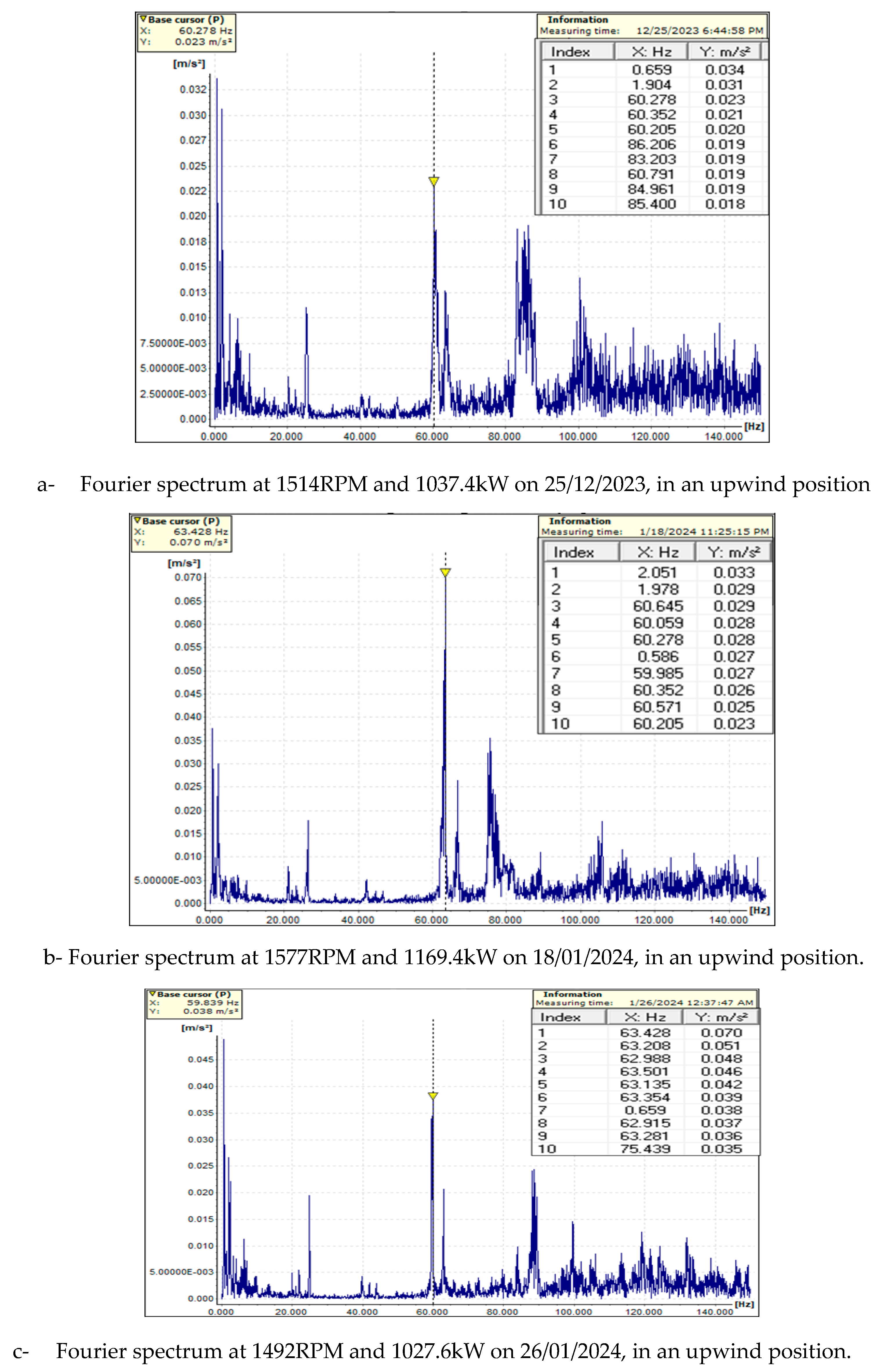
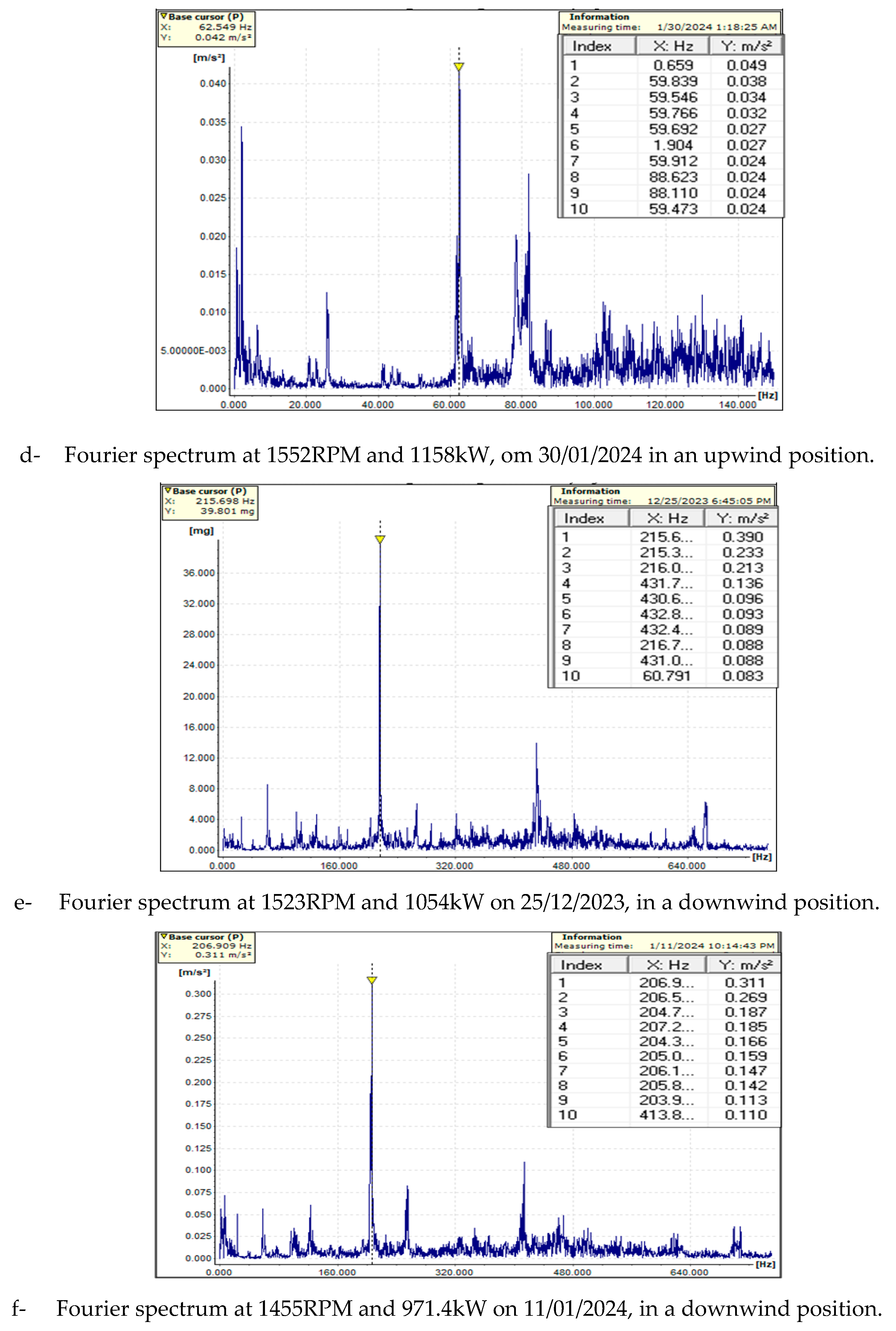
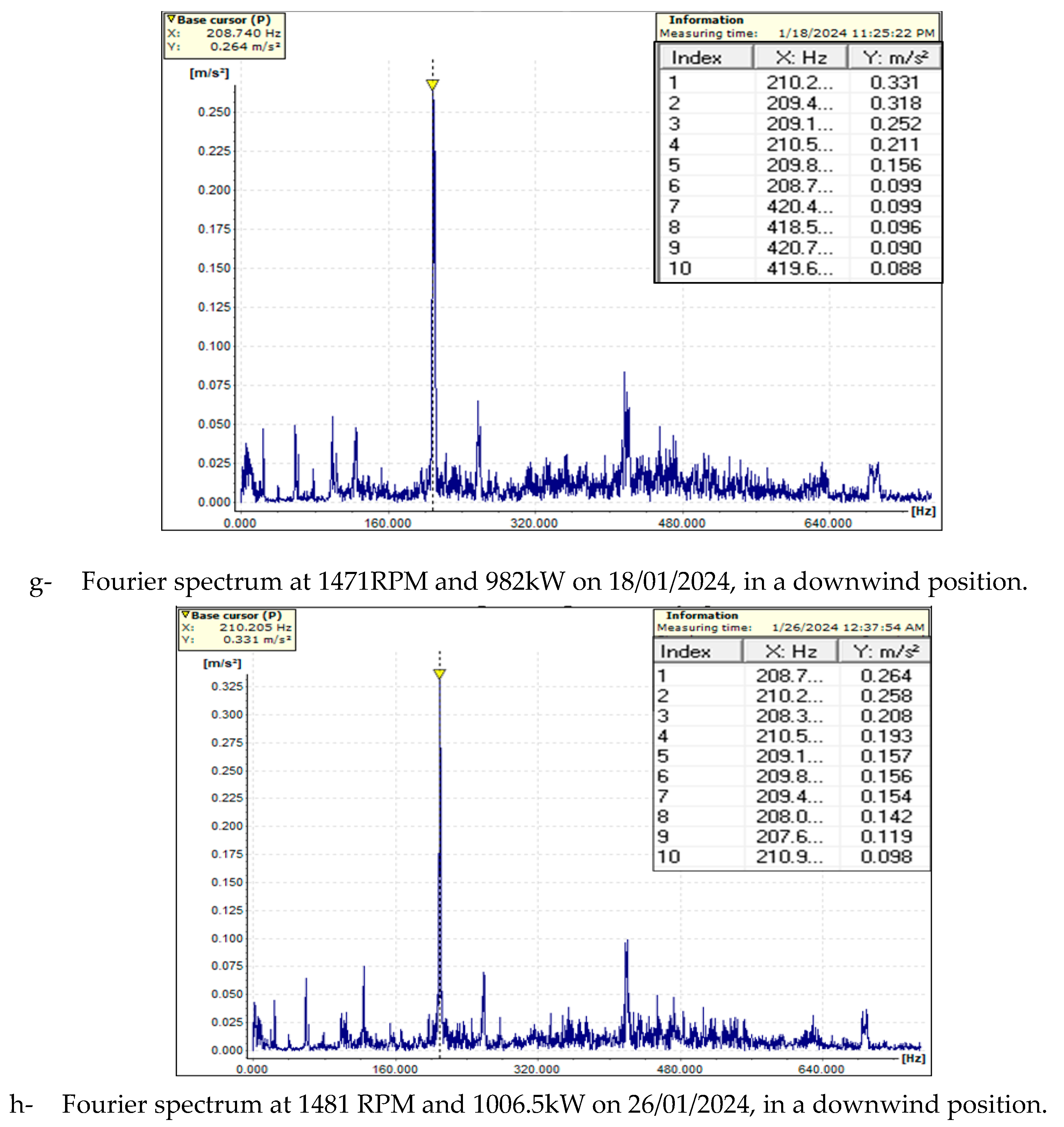
Fourier spectrum from data acquisition between December 2023 to February 2024, in an upwind and downwind position of the sensors in the gearbox of WT.
Figure 15.
Fourier spectrum from data acquisition between December 2023 to February 2024, in an upwind and downwind position of the sensors in the gearbox of WT.
Figure 16.
Objective functions (FOi) for all four selected acquisition data in the upwind sensor position.
Figure 16.
Objective functions (FOi) for all four selected acquisition data in the upwind sensor position.
Figure 17.
The front panel of the used LabView VI-s with input and output data for the upwind position sensor.
Figure 17.
The front panel of the used LabView VI-s with input and output data for the upwind position sensor.
Figure 18.
Objective functions (FOi) for all four selected acquisition data in a downwind sensor position.
Figure 18.
Objective functions (FOi) for all four selected acquisition data in a downwind sensor position.
Figure 19.
The front panel of the used LabView VI-s with input and output data for the downwind position sensor.
Figure 19.
The front panel of the used LabView VI-s with input and output data for the downwind position sensor.
Figure 20.
The frequency spectrum at LSS poistion in the case of gearbox defect.
Figure 20.
The frequency spectrum at LSS poistion in the case of gearbox defect.
Figure 21.
The frequency spectrum at HSS poistion in the case of gearbox defect.
Figure 21.
The frequency spectrum at HSS poistion in the case of gearbox defect.
Figure 22.
The trend of the magnitude- -frequency points from the FO.
Figure 22.
The trend of the magnitude- -frequency points from the FO.
Table 1.
Sensors notation and position on the wind turbine.
Table 1.
Sensors notation and position on the wind turbine.
| Sensor label |
Description |
| B1-MB-RS |
Main bearing accelerometer- rotor side |
| B2-MB-GS |
Main bearing accelerometer- generator side |
| B3-LSS |
Gearbox accelerometer- low-speed shaft |
| B4-IS |
Gearbox accelerometer- intermediary shaft |
| B5-HSS |
Gearbox accelerometer- high-speed shaft |
| B6-G-DE |
Generator accelerometer drive end-side |
| B7-G-NDE |
Generator accelerometer non-drive end-side |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).