Physical Modeling of a Water Hydraulic Proportional Cartridge Valve for a Digital Twin in a Hydraulic Press Machine

1. Introduction

A digital twin is a virtual representation of a physical entity. It aims to be the digital mirror of a system’s behavior by accounting for condition monitoring, its control, and for creating predictions of its behavior. It is also one of the enablers of Industry 4.0. We can find different definitions in the literature, but this concept was introduced in 2003 [1]. According to a narrower definition [2], a digital twin has the following characteristics: it is a model of a physical object that exists; it is associated with a data set that evolves and grows with time; the parameters of the model are updated continuously from the data; and it can render predictions with a high enough level of accuracy and confidence for application. Furthermore, according to this definition, the model should be a physics-based type of model. Therefore, digital twins of mechatronic devices-where sensors collect data that are sent to their virtual mirror and actuators allow one to control the system’s behavior-play an essential role in the digitalization of the industry [3,4]. In this study, we will formulate a digital twin of a valve that fits the definition in [2]. Such digital twins have the advantage of being interpretable for engineers who work with certain specific applications [5].

Digital twins can be used for modeling various technical systems in the steel industry. Feng Xiang described how to apply digital twins when considering data over the entire life-cycle of a product [6]. Karandaev et al. (2021) developed a digital twin for the purpose of mirroring and controlling metal behavior in wire-rolling processes [7]. Gasiyarova et al. (2021) developed an observer of angular gaps in a rolling stand’s mechanical transmission, and this observer contained information about the transmission’s failure, which was achieved by considering the algorithm’s computational cost for real-time monitoring [8]. A comparison of some types of behavioral models used for digital twins of a ring rolling machine was investigated in Bautista and Rönnow (2023); specifically, autoregressive with exogenous variables (ARX), autoregressive moving averge with exogenous variables (ARMAX), and orthonormal basis functions (OBF) models were investigated [9]. OBF-ARX and OBF-ARMAX were used for digital twins of the various subsystems of a ring rolling machine in [10].

Hydraulic valves are used in hydraulic control systems for the modulation and control of the position, speed, or force of actuators. They provide the interface between the power elements, which generally are pumps, and the actuators, which are usually hydraulic cylinders. A more detailed description of hydraulic valves and its classification can be found in [11]. Electro-hydraulic proportional/servo valves have certain disadvantages compared to high-speed on/off valves, such as complex structure and high power losses. Research on high-speed valves is currently being carried out because of their fast response. However, the flow capabilities of high-speed on/off valves are insufficient for applications with large flow requirements. Two-stages proportional cartridge valves are used in such applications. Two-stages proportional cartridge valves with a poppet type construction, which gives better sealing compared to the traditional large flow proportional cartridge valve, have been used succesfully in large flow, fast response, and high-pressure applications [12,13].

Research on cartridge valves has been ongoing for the last two decades [14,15]. The energy required by a system to control the hydraulic cylinder position was reduced in Song Liu and Bin Yao (2002) through a particular combination of five proportional cartridge valves [16]. The same authors developed an adaptive robust control of the same hydraulic system by considering the valve manufacturer’s information about flow characteristics instead of identifying the flow model parameters with experimental data [17]. Then, they identified the flow mapping of the cartridge valve in different ways[18,19]. A reduction of the energy consumption was achieved by introducing an accumulator and designing a new controller [20]. A directional control valve with a three-stage structure based on two high-speed on/off solenoid valves as the pilot stage and two poppet-type cartridge valves as the secondary stage was proposed in [21] to get fast response and to maximize flow and pressure. Daling Yue et al. (2021) proposed a control strategy based on optimizing the duty ratios of positive and negative pulse voltages so as to decrease the opening and closing times of a screw-in cartridge valve [22]. The same research group further developed optimizations in the opening and closing times of a valve by proposing a hybrid voltage control strategy, in which a preload voltage and hold voltage stage were added to the positive pulse and negative pulse voltages [13]. A cartridge proportional valve, similar to the one under study in this work, was investigated in prior studies. In these studies, the medium used to transfer energy between the power element and the actuator was water, and the valves were used for large flows under high-pressure conditions, as is the case in our study. The analytical expressions for non-linear flow forces under different poppet geometries of a cartridge valve were studied and validated by physical simulations using AMESim of the behavior of an injection machine, thereby demonstrating that using the most optimal choice of parameters results in improved process performance [12]. An optimal design of a two-stage proportional cartridge valve with two 2/2-way water hydraulic proportional valves as the pilot stage and a poppet-type cartridge valve as the main valve was proposed in [23]. An extensive physical model of the valve was also developed and implemented in Matlab/Simulink to simulate the dynamic behaviour of the valve. A multi-objective optimization was carried out to obtained a desired step respone of the valve. The flow force was obtained from CFD simulations after optimizing the dimensional parameters of the valve orifice to minimize the flow force. A prototype was developed and tested experimentally to validate the simulated dynamic simulations [23].

Hydraulic valves are dynamic systems; as such, they can be modeled by physics-based or behavioral models, in which the former are derived from laws of physics, and the latter describe the relation between input and output signals via, for example, artificial neural networks[24]. Junhui et al. proposed a proportional directional valve, and they described its dynamical behavior by a physics-based model [25]. A physics-based model for describing the non-linear valve flow of a proportional valve was developed for the robust control of its position [26]. Physics-based models have been used to model and control the position of proportional directional valves [27]. A physics-based model was proposed for a proportional pressure-reducing valve, and was formulated by considering the dead zone and hysteresis effects for pressure tracking with a robust control method [28]. Regarding poppet-type cartridge valves and physics-based model, parameter identification has been used to identify the valve flow mapping as well as the valve flow rate [18,19,21]. Michele proposed a novel Hammerstein dynamical model for modeling a hydraulic actuation system; this model was constructed for the purpose of control, and the model was constructed using a neural network in the non-linear static part and an ARX model for the linear dynamical part [29]. Black-box models have been used for system identification in hydraulic directional control valves [30]. A large servo-valve-controlled hydraulic system’s pressure dynamics was modeled using neural network model structures [31].

In this study, we derive for the first time-to our knowledge-a model and identify the parameters of a water two-stage proportional cartridge valve for high-pressure hydraulics. The pilot stage has two 2/2-way water proportional valves, and the main valve is a marginally stable poppet-type cartridge valve. In contrast, previous studies of poppet-type cartridge valves used a stable configuration. Additionally, this work is based on identifying the model parameters rather than optimizing the design parameters [23]. We also approximate the orifice equation via a polynomial so as to make the parameter estimation easier, as well as to make modeling possible without a pressure sensor in the control volume (which is situated in the pilot stage, c.f. [23]). The parameters related to the flow mappings and flow rate have been estimated for several poppet-type cartridge valves [18,19,21] with data collected in the laboratory. This is the first identification of a system of two valves, i.e., the control valve and the main valve, where the main valve is a poppet-type cartridge valve. Moreover, the data used to estimate the model parameters were collected when the valve was part of a hydraulic press. It was operated as the plant in a closed-loop system. The hydraulic press machine, which is composed of more than 50 valves and 5 hydraulic cylinders, was situated in a steel manufacturing plant. Each hydraulic cylinders reaches pressures up to $2.5\times {10}^7$ Pa during a production cycle. The proposed model is derived from physical modeling based on fluid mechanics, dynamics, and electrical principles. The model parameters are related to the design parameters of the valve, and the parameter estimation is sufficiently fast to update the model parameters between production cycles. The estimated parameters could be used for real-time monitoring of the valve’s status as well as diagnosis. The interpretation of the model parameters is relatively easy since we use a physical model. The model can be used as a digital twin, where the parameters are monitored to show the aging of the valve; this was seen in data from industrial production.

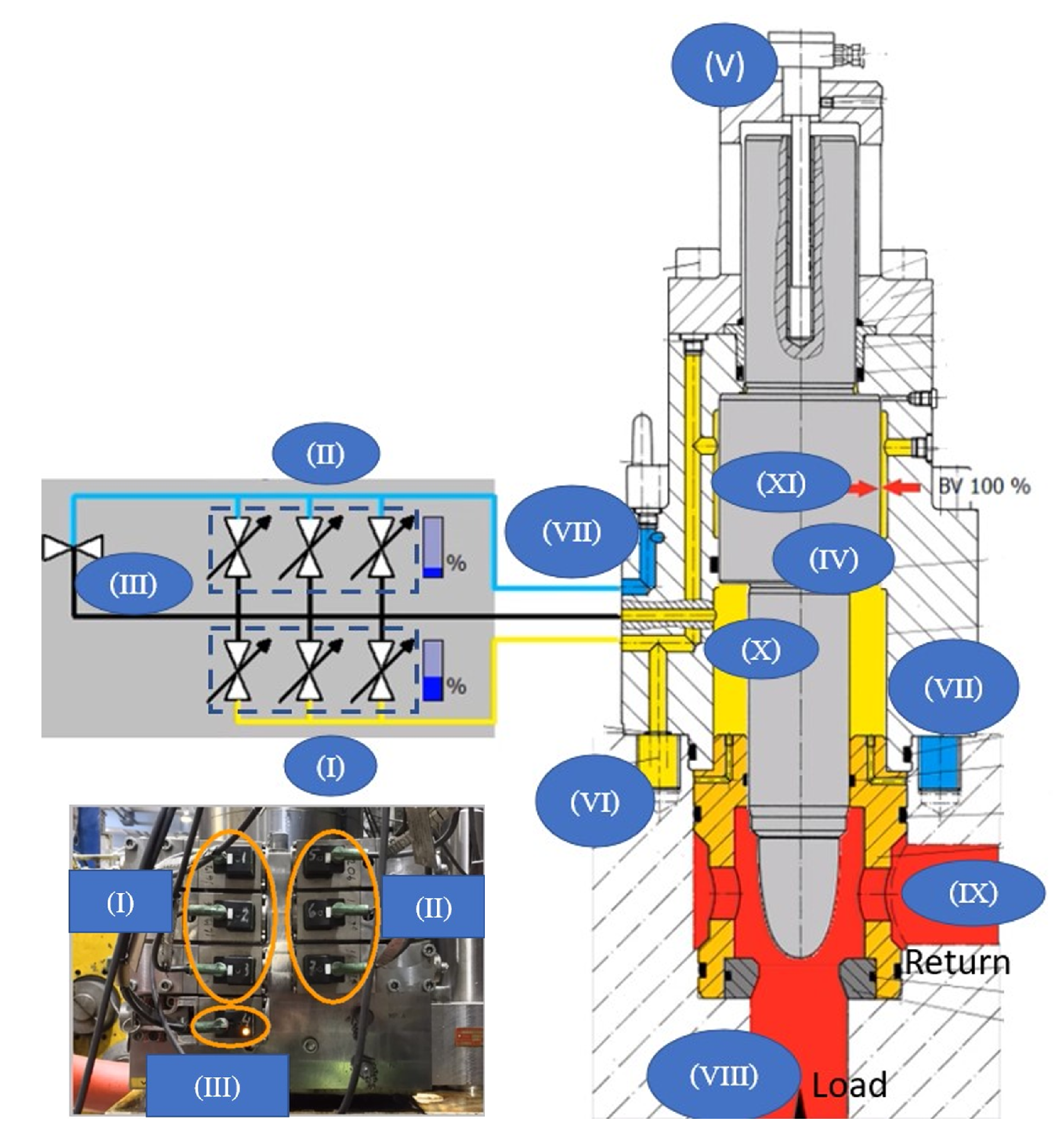
2. Device and Operating

Figure 1 shows, in detail, the two-stage 2/2 proportional cartridge valves under study. The pilot stage involves two groups of proportional spool valves: Group (I) with three valves, and Group (II) with another three. Each pilot valve is controlled by a solenoid, and they contain a pre-loaded spring attached. An emergency shut-down valve (III), a pilot-operated spindle (IV), an LDTV sensor (V), and two hydraulic circuits (one from (VI) to (VII), and another one from (VIII) to (IV), of which represents the lower chamber (X) and the upper chamber (XI)) are included. Notice that there is no spring attached to the spindle (IV).

Figure 2 illustrates how the valve operates. There are certain differences, as can be seen from Figure 1. The three valves of Group (I) in Figure 1 are represented by an equivalent single valve (I) in Figure 2. The valves (II) in Figure 1 are also represented by one equivalent valve (II) in Figure 2. There is a difference between the area of the upper part of the spindle, $A_T$, and the area of the lower part, $A_B$ (see Figure 2). Thus, the cross-sectional areas in contact with the fluid were different. $P_L{A}_L$ is the force exerted by the liquid going from (VIII) to (IX) to the spindle (IV); M is the mass of the spindle (IV); $P_z\left(t\right)$ is the pressure of the fluid in the upper chamber (XI); $P_c\left(t\right)$ in the lower chamber (X); $Q_{in}\left(t\right)$ is the volumetric flow rate that goes from (VI) to the lower chamber through the group of valves (I); and $Q_{out}\left(t\right)$ the volumetric flow rate from the lower chamber (X) to (VII). In addition, $v_{in}\left(t\right)$ is the voltage applied to Group (I), and $v_{out}\left(t\right)$ the one applied to Group (II). The liquid that enters through (VI) is pressurized at a pressure of $P_Z$, and the liquid that leaves through exit (VII) is pressurized at a pressure of $P_R$ in the reservoir.

To illustrate the valve’s behavior, we assumed the initial position of the spindle to be at its lowest position. That is to say that when the lower part of the spindle touches the bottom part of the container ($x=0$), the pilot valves are closed, i.e., $v_{in}\left(t\right)=v_{out}\left(t\right)=0$, $P_R=0$, $P_Z>0$, and $P_L{A}_L<P_Z{A}_T+Mg$. If $v_{in}>0$ and $v_{out}=0$, $Q_{in}>0$, then $Q_{out}=0$ , x increases and fluid goes from (XI) to (VI). On the contrary, if $v_{in}=0$ and $v_{out}>0$ when there is fluid in (X) and $P_L{A}_L<P_Z{A}_T$, then $Q_{in}=0$ and $Q_{out}>0$, which makes x decrease when the fluid goes from (X) to (VII). In this study, the liquid that goes from (VI) to (VII) as well as the one that goes from (VIII) to (IX) was 94% drinking water and 6% Hysol SL 36 XBB, respectively. Other additives that are used to harden the water and reduce the foam were Castrol Antifoam 101 and Castrol Antifoam S 105.

The operating conditions of the valve are determined by the fact that this is used for production of steel tubes and as a plant in a closed-loop system. The operating conditions can be split in (i), (ii), and (iii), see Figure 3: (i) The initial conditions of the valve occurs when $x=0$ for the spindle (IV) of the main valve, when $v_{in}=v_{out}=0$ for the pilot valves (I) and (II), when the upper chamber of the main valve (XI) is full of water with $P_z\left(t\right)=3\times {10}^7$ Pa, and when $P_L\left(t\right)=0.6\times {10}^7$ Pa (see Figure 2 and Figure 3(i)). (ii) Once $v_{in}\left(t\right)>0$, then Group (I) of the pilot valves let $Q_{in}>0$, and the spindle (IV) of the main valve starts to move to being $x\left(t\right)>0$; furthermore, $P_L\left(t\right)$ drops to $0.3\times {10}^7$ Pa in a few seconds (see Figure 3d)). (iii) If $v_{in}\left(t\right)=0$ and $v_{out}\left(t\right)>0$, then the water from the lower chamber of the main valve (X) leaves the valve to the reservoir of Group (II); hence, $x\left(t\right)$ decreases. This last step takes place when $P_L$ is approximately $0.1\times {10}^7$ Pa (see Figure 3d)). It is noted that the value of $P_Z=2.9\times {10}^7$ Pa holds for most of the time but drops to $P_Z=2.7\times {10}^7$ Pa in the last third of the valve operation time; however, the spindle’s position x is not affected by it due to the ratio between $P_Z$ and $P_L$ (see Figure 3a,c). As a consequence of how the valve operates, x remains constant as far as $v_{in}\left(t\right)=v_{out}\left(t\right)=0$. However, this is not the case between $t=10$ s and $t=20$ s in (ii) due to the valve’s leakage (see Figure 3a,b). This last observation was discussed with maintenance engineers.

The experimental data collected for this study were of the valve operating as the interface between a hydraulic pump and a single-rod linear actuator of one of the hydraulic control systems of a hydraulic press machine from a steel manufacturing plant. The signals from position x of the spindle (IV) and the voltages applied to the coils of the pilot valves (I) and (II) are $v_{in}\left(t\right)$ and $v_{out}\left(t\right)$, respectively. These signals are recorded by the data acquisition system IBA-DAQ with a sampling time of 0.03 s and an amplitude range of 0–1, where 0 corresponds to the minimum value and 1 to the maximum one, respectively. $v_{in}\left(t\right)$ and $v_{out}\left(t\right)$ are generated by a programmable logic computer with pulse width modulated signals of 24 V. The position of spindle $x\left(t\right)$ is controlled by a feedback control structure with a proportional–integral–derivative digital controller.

3. Modeling

This section is divided into three sub-sections: The first one describes the physical model of the valve; in the second, we describe the parameter estimation of the models; and in the last, the model validation is explained.

3.1. Physical Model

We present a physical model of the valve shown in Figure 1 and Figure 2. It is based on the formulation detailed in Chapter 4 of [11]. In this work, the pressure in the upper chamber of the spindle (XI) $P_c\left(t\right)$ and the armature’s position of the pilot valves (I) and (II) are not measured; hence, we derive a model that connects the position x and the control signals $v_{in}\left(t\right)$ and $v_{out}\left(t\right)$ (see Figure 3 (a) and (b), respectively). These signals are given in normalized scale. This section is divided based on the analysis of the valve as a system composed of different sub-systems, as well as a system that is subject to different principles: The first part is the proportional pilot valves of both Groups, (I) and (II); for the second, we have the the volumetric flow rate of the pilot valves; next, a description of the the main valve’s control volume (X) is written; in the the fourth part, the equation of motion for the spindle (IV) of the main valve is shown; then, an approximation of the $P_c$ in the main valve’s (X) is described in detail; and then lastly, in the sixth part, the input–output system model is shown. This input–output model implicitly describes all sub-systems of the valve.

1

Pilot valve model (I and II): These pilot valves consist of a solenoid, its armature, and a pre-loaded spring. Equations (3.6) and (3.7) in [11] describe a third-order coupled system, which, in this case, is the dynamics of the armature and the electrical circuit of the coil. We assumed that the time-constants of the armature’s motion are much smaller than those of the spindle’s motion. Therefore, we neglect the inductance of the coil’s circuit, the linear momentum, the viscous force, the flow forces acting on the armature, and the induced electromagnetic force from the armature’s motion. The last is allowed because the electromagnetic force to the armature is greater; as such, we obtain

$$k_i{y}_i=\frac{{\alpha }_i{v}_{max}}{R_i}{v}_i-F_{0,i}$$

(1)

for valve i, where $i=\left\{1,...,m\right\}$ corresponds to the m pilot valves of Group (I), and $i=\left\{m+1,...,m+n\right\}$ to the n of Group (II). In this case, $m=n=3$ (see Figure 1); $k_i$ is the spring rate of the spring; $y_i$ is the armature position; ${\alpha }_i$ is the magnetic coupling coefficient, which provides the constant of proportionality for the electromagnetic force; $v_{max}$ is the maximum supplied voltage applied to the coil; $R_i$ is the resistance of the electrical circuit of the coil; $v_i$ is the supplied voltage with respect to its maximum value applied to the coil; and $F_{0,i}$ is the pre-load force acting on the armature by the spring when $y_i=0$. By setting $v_i=v_0$ for $y_i=0$, we obtain

$$y_i\left({\overline{v}}_i\right)=\frac{{\alpha }_i{v}_{max}}{R_i{k}_i}{\overline{v}}_i$$

(2)

where ${\overline{v}}_i=v_i-v_0$. ${\overline{v}}_i$ assumes $v_0$ as the offset of $v_i$, which is assumed to be the same for all i (see Figure 3b).

2

Volumetric flow rate of the pilot valves (I and II): we use the standard equation (4.1) in [11] for describing the flow (which assumes the fluid to be incompressible with a high Reynold number (i.e. laminar flow)). As such, we obtain

$$Q_i=c_{d}A\left({\overline{v}}_j\right)\sqrt{\frac{2}{\rho }\left(P_i\right)},$$

(3)

where $c_d$ is the discharge coefficient; $A_i\left({\overline{v}}_j\right)=w{y}_i\left({\overline{v}}_j\right)$ is the discharge flow area when assuming a rectangular section, which depends on the voltage applied to the coil of the pilot valve i; and $\rho$ is the fluid density and $P_i$ is the pressure drop across the valve, which is $P_i=(P_z-P_c)$ for $i=\left\{,2,...,m\right\}$, and $P_i=(P_c-P_r)$ for $i=\left\{m+1,...,m+n\right\}$. We substitute j by subindexing $in$ for $i=\left\{1,2,...,m\right\}$, as well as by subindexing $out$ for $i=\left\{m+1,...,m+n\right\}$.

3

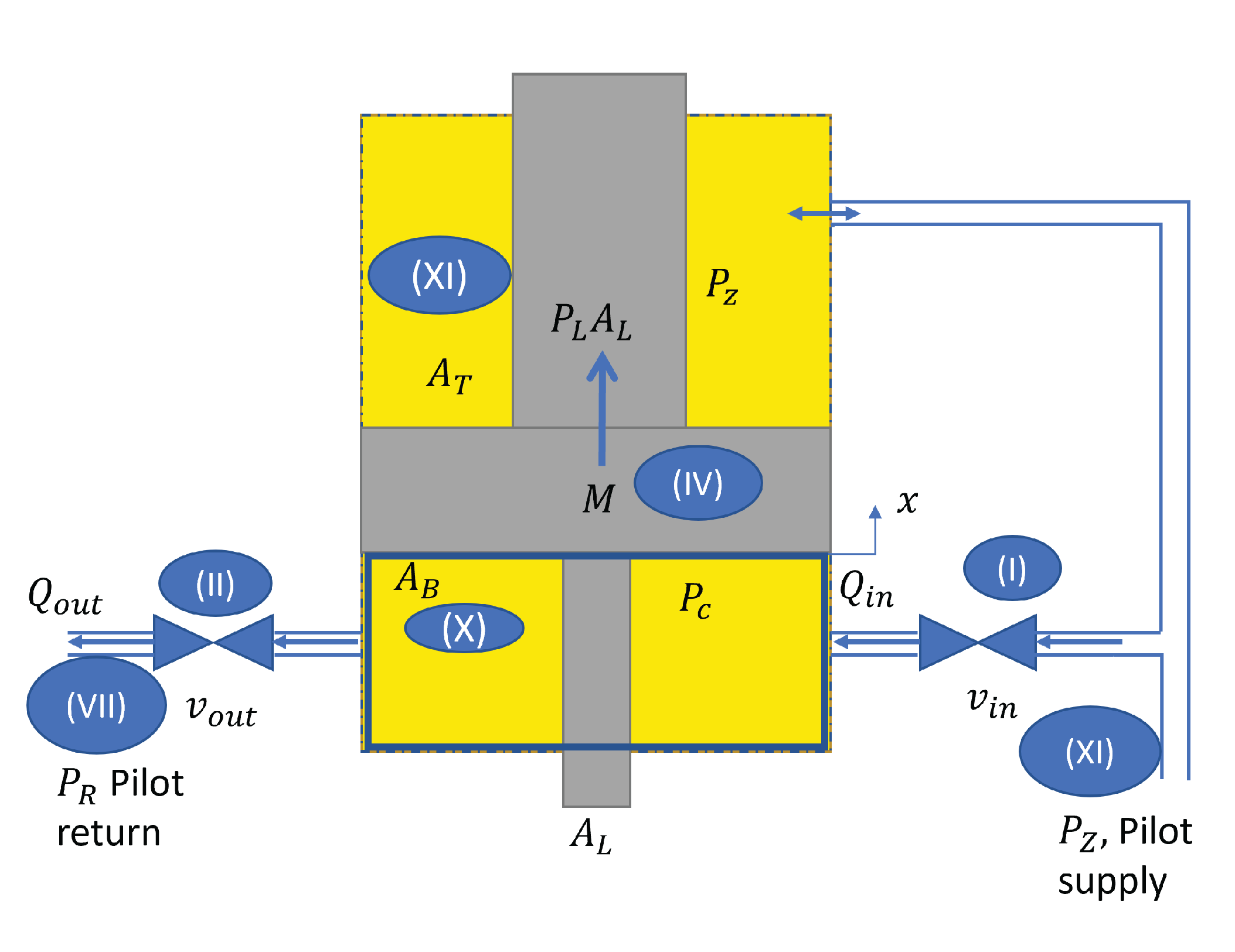
The deformable volume (X) of the main valve is chosen as the control volume, as indicated by the solid blue line in Figure 2. The change in the control volume is understood as a function of the spindle’s position. For an incompressible fluid, the continuity Equation (5.5) in [32] becomes

$$A_B\dot{x}=Q_1+...+Q_i+...+Q_m-Q_{m+1}-...-Q_{m+n},$$

(4)

where $A_B$ is the cross-sectional area of the lower chamber subtracting $A_L$, which is assumed to be constant along x; $\dot{x}$ is the derivative of the spindle’s position; and $Q_i$ is the volumetric flow rate of valve i (see Figure 1 and Figure 2).

4

The spindle (IV) equation of motion of the main valve determines the motion of the main valve’s spindle, which is

$$M\ddot{x}+B\dot{x}=A_B{P}_c\left(t\right)-A_T{P}_z-F_{fm}sgn\left({\dot{x}}_m\right)-F_{flow}+A_L{P}_L-Mg,$$

(5)

when ${\overline{v}}_{in}>0$ or ${\overline{v}}_{in}>0$, and where M is the main valve’s spindle mass, and B is the viscous drag coefficient. For a marginally stable valve, as the one under study, there is no spring; hence, no term is proportional to x. $F_{fm}$ is the coefficient of the Coulomb friction, and $F_{flow}$ is the force exerted by the flow going from (VIII) to (IX) in Figure 1. An analysis of the flow forces allows for the term $A_L{P}_L$ to appear in the equation. $Mg$ is the force given by the main valve’s spindle mass. We assumed that the Coulomb friction term can be neglected in contrast to $A_B{P}_c\left(t\right)$ and $A_T{P}_z$ due to a difference of 3–5 orders of magnitude when assuming friction between steel and rubber, i.e., the seal’s material. Furthermore, as we had values of $P_L\ll P_z$ (c.f. scale of Figure 3 (c) and (d)) and $A_L\ll A_T$ (c.f. Figure 2), we thus obtained $A_L{P}_L\ll A_T{P}_z$, as well as $Mg\ll A_T{P}_z$. The flow forces can be described by

$$F_{flow}=\rho L{K}_q\dot{x}+\rho L{K}_c{P}_L+K_{fq}(x-x_0)+K_{fc}(P_L-P_{L_0})$$

(6)

which can be obtained after deriving and linearizing with respect to x and $P_L$ (see (4.20) in [11]), where $K_q$ is the flow gain coefficient, $K_c$ is the pressure-flow coefficient, $K_{fq}$ is the flow force gain, and $K_{fc}$ is the pressure flow force. Considering the control volume, as illustrated in Figure 4–21 by dashed lines and the dimension given in (4.122) in [11], as well as the operating conditions of the hydraulic valve under study, we consider $F_{flow}$ to be negligible in contrast to $A_B{P}_c\left(t\right)$ and $A_T{P}_z$. This was performed because there was a difference of two orders of magnitude. More information about how to derive the expression of the coefficients in (6) can be found in Chapter 4, more specifically in Section 4.3 and Section 4.6, in [11]. Finally, we obtained the main valve’s spindle equation of motion, which is

$$\left\{\begin{array}{cc}M\ddot{x}+B\dot{x}=A_B{P}_c\left(t\right)-A_T{P}_z\hfill & \mathrm{if}{\overline{v}}_{in}\mathrm{or}{\overline{v}}_{out}>0\hfill \\ \dot{x}=0,\hfill & \mathrm{if}{\overline{v}}_{in}={\overline{v}}_{out}=0\hfill \end{array}\right..$$

(7)

These equations are valid for $x\in [0,x_{max}]$, where $x_{max}$ is the maximum position of the spindle. The case of ${\overline{v}}_{in}\left(t\right)={\overline{v}}_{out}\left(t\right)=0$ describes the system when $P_c\left(t\right)$ cannot be derived from (3) and (4).

5

Approximation of $P_c$ in the main valve (X): Since $P_c$ is not measured, it is derived from (3) and (4). Furthermore, assuming that the pilot parallel valves are identical, and knowing that ${\overline{v}}_{in}\left(t\right)$ is applied to all of the coils of pilot valves (I) and ${\overline{v}}_{out}\left(t\right)$ to (II) (see Figure 1 and (4)), we obtain

$$A_B\dot{x}=m{Q}_{in}-n{Q}_{out},$$

(8)

where $Q_{in}=Q_1=...=Q_m$ and $Q_{out}=Q_{m+1}=...Q_{m+n}$. For $Q_{in}$, we use the auxiliary function

$$f_{in}\left(P_c\right)=\sqrt{(2/\rho )(P_Z-P_c)}$$

(9)

and, for $Q_{out}$, we use

$$f_{out}\left(P_c\right)=\sqrt{(2/\rho )\left(P_c\right)},$$

(10)

which are derived from (3). We approximate $f_{in}$ and $f_{out}$ by a Taylor series in $P_c$ around the operating point $P_c=P_{c,0}=\frac{A_T}{A_B}{P}_z$, which is the equilibrium point of (7). By performing this, keeping the linear terms, and substituting these in (8), we obtain

$$\begin{array}{cc}\hfill P_c\left(t\right)& =P_{c,0}+g({\overline{v}}_{in},{\overline{v}}_{out})\times \hfill \\ \hfill & (f_{in}(P_{c,0}{\overline{R}}_1{\overline{v}}_{in}\left(t\right)-f_{out}\left(P_{c,0}\right){\overline{R}}_2{\overline{v}}_{out}\left(t\right)-A_B\dot{x}),\hfill \end{array}$$

(11)

where

$$g({\overline{v}}_{in},{\overline{v}}_{out})=\frac{1}{f_{out}^{\prime }\left(P_{c,0}\right){\overline{R}}_2{\overline{v}}_{out}\left(t\right)-f_{in}^{\prime }\left(P_{c,0}\right){\overline{R}}_1{\overline{v}}_{in}\left(t\right)},$$

(12)

In the above, $f_{in}^{\prime }\left(P_{c,0}\right)$ is the first derivative of $f_{in}\left(P_c\right)$, which is evaluated at $P_{c,0}$, $f_{out}^{\prime }\left(P_{c,0}\right)$ is the one of $f_{out}$, ${\overline{R}}_1=m{c}_d{w}_{in}\frac{{\alpha }_{in}{v}_{max}}{k_{in}{R}_{in}}$, and ${\overline{R}}_2=n{c}_d{w}_{out}\frac{{\alpha }_{out}{v}_{max}}{k_{out}{R}_{out}}$.

6

The input–output system model is obtained by substituting (11) in (7), where

$$\begin{array}{cc}\hfill M\ddot{x}& +B\dot{x}=A_{B}g({\overline{v}}_{in},{\overline{v}}_{out})\times \hfill \\ \hfill & (f_{in}\left(P_{c,0}\right){\overline{R}}_1{\overline{v}}_{in}\left(t\right)-f_{out}\left(P_{c,0}\right){\overline{R}}_2{\overline{v}}_{out}\left(t\right)-A_B\dot{x}).\hfill \end{array}$$

(13)

We approximate the auxiliary function $g(\overline{v_{in}},\overline{v_{out}})$ by a Taylor series in ${\overline{v}}_{in}\left(t\right)$ and ${\overline{v}}_{out}\left(t\right)$ around ${\overline{v}}_{in,0}$ and ${\overline{v}}_{out,0}$, respectively, where ${\overline{v}}_{in,0}={\overline{v}}_{out,0}={\overline{v}}_0\ne 0$. We keep the linear terms and (13) is approximated by

$$\begin{array}{c}\hfill {\gamma }_1\ddot{x}+{\gamma }_2\dot{x}={\varphi }_1{\overline{v}}_{in}\left(t\right)+{\varphi }_2{\overline{v}}_{out}\left(t\right)+{\varphi }_3{\overline{v}}_{in}^2\left(t\right)+{\varphi }_4{\overline{v}}_{out}^2\left(t\right)+...\\ \hfill ...+{\varphi }_5{\overline{v}}_{in}\left(t\right){\overline{v}}_{out}\left(t\right)+{\varphi }_6{\overline{v}}_{in}\left(t\right)\dot{x}+{\varphi }_7{\overline{v}}_{out}\left(t\right)\dot{x},\end{array}$$

(14)

where

$$\left\{\begin{array}{c}{\gamma }_1=\frac{M}{A_B}\ge 0\hfill \\ {\gamma }_2=\frac{B}{A_B}+\overline{g}{A}_B\ge 0\hfill \\ {\varphi }_1=\overline{g}{f}_{in}\left(P_{c,0}\right){\overline{R}}_1\ge 0\hfill \\ {\varphi }_2=-\overline{g}{f}_{out}\left(P_{c,0}\right){\overline{R}}_2\le 0\hfill \\ {\varphi }_3=g_{{\overline{v}}_{in}}^{\prime }({\overline{v}}_0,{\overline{v}}_0)f_{in}\left(P_{c,0}\right){\overline{R}}_1\le 0\hfill \\ {\varphi }_4=-g_{{\overline{v}}_{out}}^{\prime }({\overline{v}}_0,{\overline{v}}_0)f_{out}\left(P_{c,0}\right){\overline{R}}_2\ge 0\hfill \\ {\varphi }_5=g_{{\overline{v}}_{out}}^{\prime }({\overline{v}}_0,{\overline{v}}_0)f_{in}\left(P_{c,0}\right){\overline{R}}_1-g_{{\overline{v}}_{in}}^{\prime }({\overline{v}}_0,{\overline{v}}_0)f_{out}\left(P_{c,0}\right){\overline{R}}_2\in \mathcal{R}\hfill \\ {\varphi }_6=-g_{{\overline{v}}_{in}}^{\prime }({\overline{v}}_0,{\overline{v}}_0)A_B\ge 0\hfill \\ {\varphi }_7=-g_{{\overline{v}}_{out}}^{\prime }({\overline{v}}_0,{\overline{v}}_0)A_B\ge 0\hfill \end{array}\right.,$$

(15)

where $\overline{g}=g({\overline{v}}_0,{\overline{v}}_0)-g_{{\overline{v}}_{in}}^{\prime }({\overline{v}}_0,{\overline{v}}_0){\overline{v}}_0-g_{{\overline{v}}_{out}}^{\prime }({\overline{v}}_0,{\overline{v}}_0){\overline{v}}_0$, $g_{{\overline{v}}_{in}}^{\prime }({\overline{v}}_0,{\overline{v}}_0)$ is the derivative of $g({\overline{v}}_{in},{\overline{v}}_{out})$ with respect to ${\overline{v}}_{in}$, and $g_{{\overline{v}}_{out}}^{\prime }({\overline{v}}_0,{\overline{v}}_0)$ is the derivative of $g({\overline{v}}_{in},{\overline{v}}_{out})$ with respect to ${\overline{v}}_{out}$. Indeed, both are evaluated at ${\overline{v}}_{in}={\overline{v}}_{out}={\overline{v}}_0$. The sign of each of the parameters is specified explicitly in (15), and this is performed in accordance with the physics of the device described in (1-13). ${\varphi }_5$ is positive or negative depending on $A_T/A_B$. Notice that (14) is a non-linear input–output model and linear in the parameters. The non-linearities are related to ${\overline{v}}_{in}^2$, ${\overline{v}}_{out}^2$, ${\overline{v}}_{in}\dot{x}$, and ${\overline{v}}_{out}\dot{x}$. These terms are obtained from the square root in $\sqrt{\frac{2}{\rho }\left(P_i\right)}$ and the product $A\left({\overline{v}}_j\right)\times \sqrt{\frac{2}{\rho }\left(P_i\right)}$ in (3).

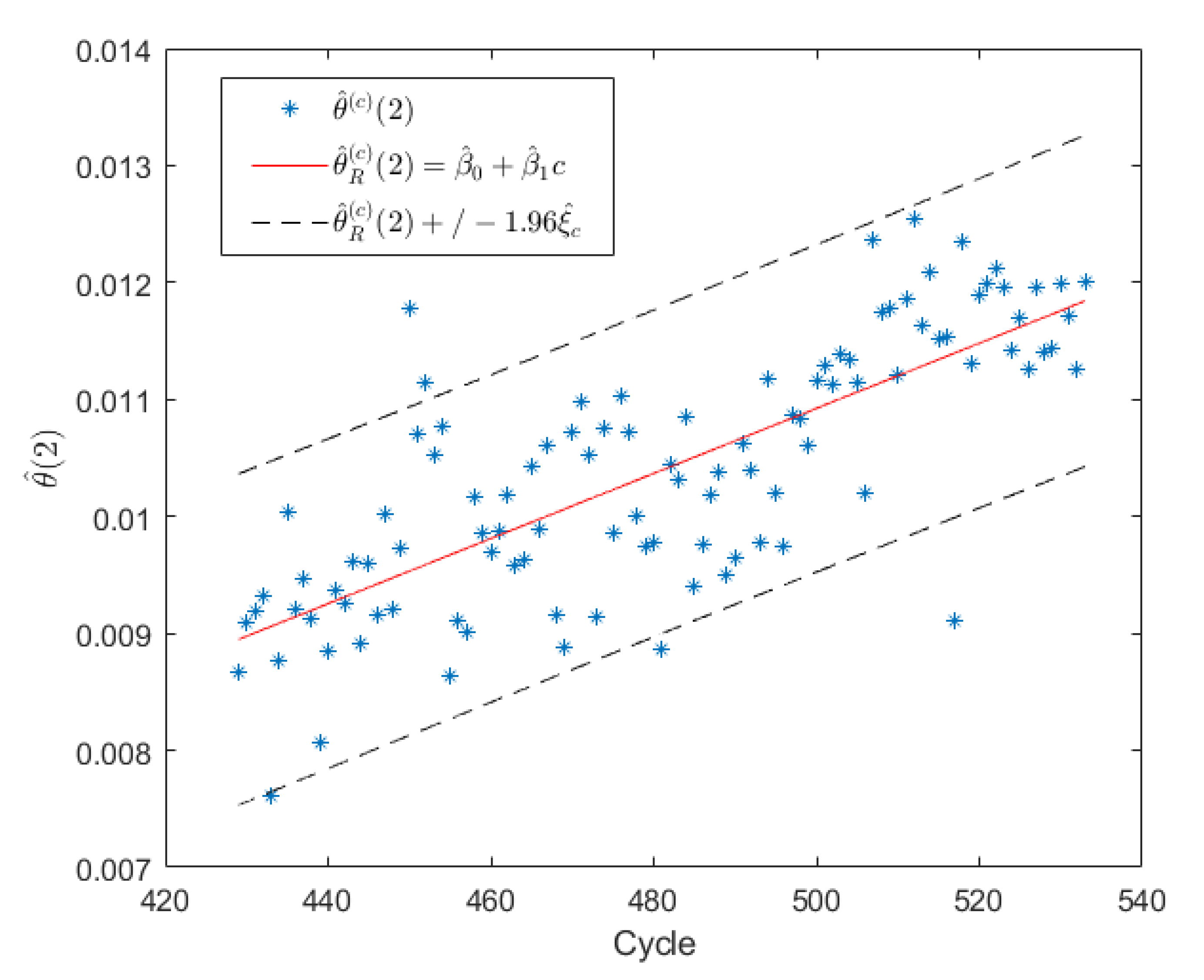
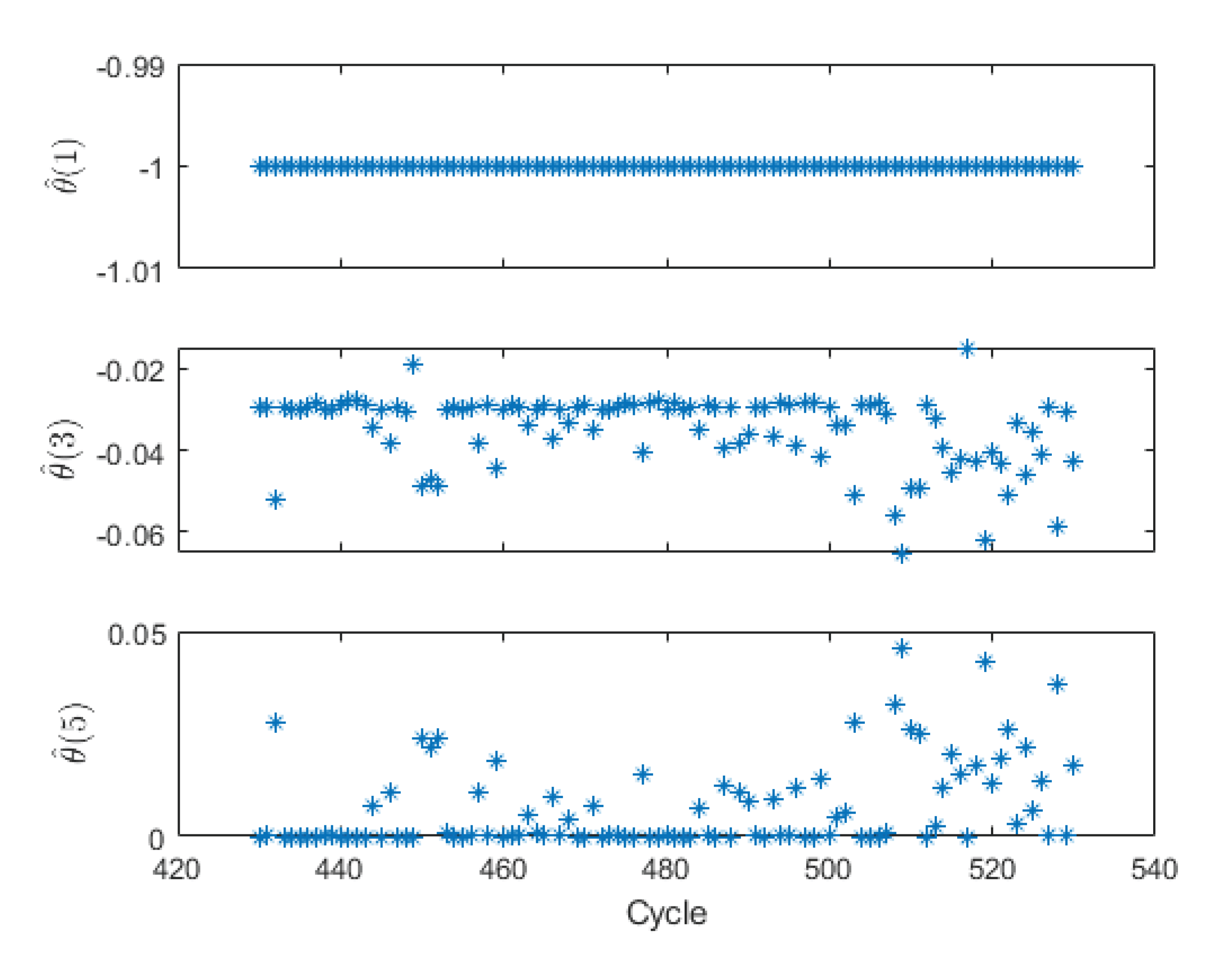
3.2. Parameter Estimation

The parameters are estimated based on (14). (14) represents a non-linear system that relates the inputs ${\overline{v}}_{in}$ and ${\overline{v}}_{out}$ to the output x, and it is also linear in the parameters. The data acquired by DAQ was saved in time discrete form. Therefore, we need to transform (14) to an equivalent time discrete version. By following Eq. (6.2.3) in [33], i.e., when using the forward Euler method in (14), we obtain

$$\begin{array}{c}\hfill \widehat{x}\left[n\right]=2x[n-1]-x[n-2]+{\mathit{\theta }}^{\mathbf{⊺}}\mathit{u}\left[n\right]\end{array}$$

(16)

where n is the sample number, and x and $\widehat{x}$ are the experimental and model position of the main valve’s spindle (IV), respectively.

$$\mathit{\theta }={\left[\begin{array}{cccccccc}-\frac{{\gamma }_2{T}_s}{{\gamma }_1}& \frac{{\varphi }_1{T}^2}{{\gamma }_1{x}_{max}}& \frac{{\varphi }_2{T}^2}{{\gamma }_1{x}_{max}}& \frac{{\varphi }_3{T}^2}{{\gamma }_1{x}_{max}}& \frac{{\varphi }_4{T}^2}{{\gamma }_1{x}_{max}}& \frac{{\varphi }_5{T}^2}{{\gamma }_1{x}_{max}}& \frac{{\varphi }_6{T}_s}{{\gamma }_1}& \frac{{\varphi }_7{T}_s}{{\gamma }_1}\end{array}\right]}^{\mathbf{⊺}},$$

(17)

where $x_{max}$ is a scale factor, $T_s$ is the sampling time, and

$$\mathit{u}\left[n\right]=\left[\begin{array}{cc}& x[n-1]-x[n-2]\\ & {\overline{v}}_{in}[n-2]\\ & {\overline{v}}_{out}[n-2]\\ & {\overline{v}}_{in}^2[n-2]\\ & {\overline{v}}_{out}^2[n-2]\\ & {\overline{v}}_{in}[n-2]{\overline{v}}_{out}[n-2]\\ & {\overline{v}}_{in}[n-2](x[n-1]-x[n-2])\\ & {\overline{v}}_{out}[n-2](x[n-1]-x[n-2])\end{array}\right].$$

(18)

We formulate the parameter estimation problem as

$${\widehat{\mathit{\theta }}}_{LS}=argmi{n}_{\theta }\frac{1}{N}\sum _{n=1}^N\epsilon {[n;\mathit{\theta }]}^2,$$

(19)

where $\epsilon [n;\mathit{\theta }]=x\left[n\right]-\widehat{x}[n;\mathit{\theta }]$, which gives an estimation of $\theta$ in (16) by solving

$$\left(\sum _{n=1}^{N}u\left[n\right]u{\left[n\right]}^{⊺}\right){\widehat{\mathit{\theta }}}_{LS}=\sum \mathit{u}\left[n\right]\overline{x}\left[n\right]$$

(20)

as a system of linear equations, where $\overline{x}\left[n\right]=x\left[n\right]-2x[n-1]+x[n-2]$.

Alternatively, we formulate the problem of estimating the parameters in (16) by accordingly referring to (4.1) in [34] as

$$\begin{array}{cc}\hfill & \underset{\theta \in {\mathcal{R}}^7}{min}\frac{1}{N}\sum _{n=1}^N\epsilon {[n;\mathit{\theta }]}^2\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill \\ \hfill & \overline{\mathit{\theta }}\le 0\hfill \end{array}$$

(21)

where

$$\overline{\mathit{\theta }}={\left[\begin{array}{cccccccc}\theta \left(1\right)& -\theta \left(1\right)-1& -\theta \left(2\right)& \theta \left(3\right)& \theta \left(4\right)& -\theta \left(5\right)& -\theta \left(7\right)& -\theta \left(8\right)\end{array}\right]}^{⊺},$$

(22)

cf. (19).

(22) is built from (17) and use in (21) to satisfy the standard form specified by (4.1) in [34] and the physical constraints of the valve in (15). $\overline{\theta }\left(1\right)=\theta \left(1\right)\le 0$ and $\overline{\theta }\left(2\right)=-\theta \left(1\right)-1\le 0$ are defined so as to obtain two poles in the discrete pole-zero map related to (16), which is equivalent to a pole in the origin and a pole in the real left axis of the pole-zero map related to (14). This is because ${\gamma }_1\ge 0$ and ${\gamma }_2\ge 0$ are such in 15), and because there is no x term in (14). (21) is a quadratic program (QP) and can be efficiently solved by iterative methods like the interior-point method [34]. To solve (21), we use CVX, a package for specifying and solving convex programs [35,36].

We used convex optimization to overcome problems caused by the closed-loop operation and the signals used in one production cycle. Thus, the excitation signals are narrow band at low frequencies and have a limited number of amplitudes. A system operating under feedback control is identifiable under specific conditions. For linear systems, if the feedback transfer function is persistently excited, then the system is identifiable (see ch 10 in [37]). The order of the controller and reference signal should be larger than that of the system, which is easily met in our case; furthermore, if the PID controller is of order two, then the system of order five and the discrete time signal are of order ≥ 30.

3.3. Model Validation

The cross-validation was carried out with the data corresponding to a one-hour production after the production from which the data were used to estimate $\theta$ in (16). We checked that the estimated values were in agreement with the physics of the valve described in (15); in addition, we analyzed the residuals, i.e., $\epsilon [n;\widehat{\mathit{\theta }}]=x\left[n\right]-\widehat{x}[n;\widehat{\mathit{\theta }}]$. The mean squared error (MSE) indicator

$$MSE=\frac{1}{N}\sum _{n=1}^N{(x\left[n\right]-\widehat{x}\left[n\right])}^2$$

(23)

was computed, where N is the number of samples for the training or validation data sets. A dimensional analysis of the parameters of (14), as described in (15), was carried out, and the size of the estimated parameter values were checked as to whether they were reasonable with the physical parameters described in (15). We ended the model validation by computing the relative errors of the estimated parameters for different error sources [24].

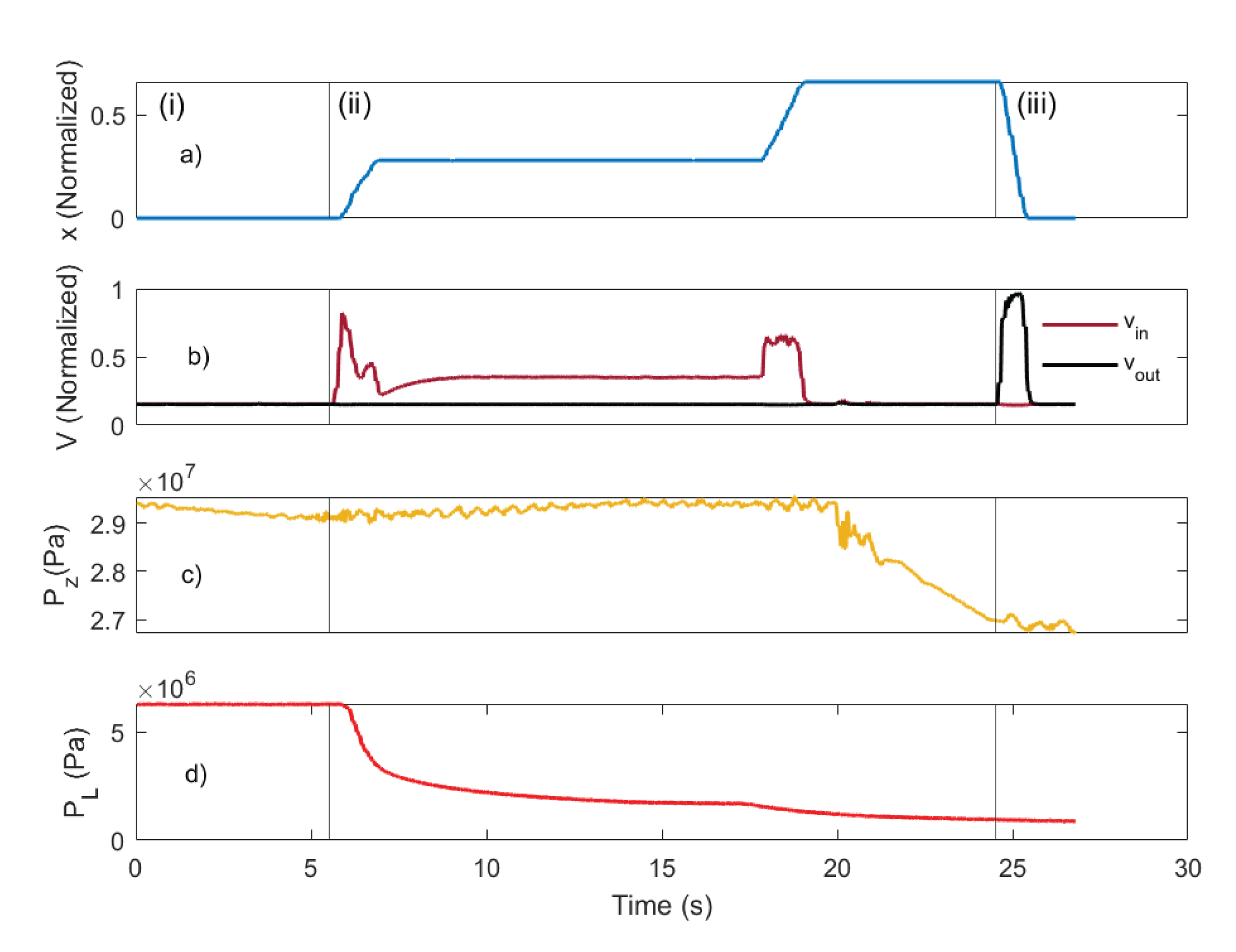
4. Results and Discussion

This section is divided into three subsections: the first reports and analyzes the estimated parameters of the physical model; in the second, the relative errors of the estimated parameters for different error sources are computed and analyzed; and in the last section, the aging of the valve is analyzed over different production cycles.

4.1. Physical Model

Table 1 presents the results of the parameter estimation problem that were defined in (19) and (21) in order to obtain the input–output system model described in (16). We carried out three different parameter estimations. The first one was given by solving the standard least squares problem defined in (19) with (20). This provided

$$\begin{array}{c}{\widehat{\mathit{\theta }}}_1={\left(\begin{array}{ccc}\widehat{\theta }\left(1\right)& \widehat{\theta }\left(2\right)& \widehat{\theta }\left(3\right)\end{array}\right)}^{⊺},\end{array}$$

(24)

which is an estimation of $\theta \left(1\right)$, $\theta \left(2\right)$ and $\theta \left(3\right)$ in (17). Then, (16) becomes

$${\widehat{x}}_1[n;{\widehat{\mathit{\theta }}}_1]=2x[n-1]-x[n-2]+{\mathit{\theta }}_1^{⊺}{u}_1\left[n\right]$$

(25)

with

$$\begin{array}{c}{u}_1\left[n\right]={\left(\begin{array}{ccc}u\left(1\right)& u\left(2\right)& u\left(3\right)\end{array}\right)}^{⊺},\end{array}$$

(26)

where $u\left(1\right)$, $u\left(2\right)$ and $u\left(3\right)$ are found in (18). In the second case, we obtained ${\widehat{\theta }}_2$ by solving (19) with (20) as in the first case. The difference between the first and second case is that, for the second case, we considered certain non-linear terms as having

$${\widehat{x}}_2[n;{\widehat{\mathit{\theta }}}_2]=2x[n-1]-x[n-2]+{\mathit{\theta }}_2^{⊺}{\mathit{u}}_2\left[n\right],$$

(27)

where

$$\begin{array}{c}{\widehat{\mathit{\theta }}}_2={\left(\begin{array}{ccccc}\widehat{\theta }\left(1\right)& \widehat{\theta }\left(2\right)& \widehat{\theta }\left(3\right)& \widehat{\theta }\left(4\right)& \widehat{\theta }\left(5\right)\end{array}\right)}^{⊺},\end{array}$$

(28)

and

$$\begin{array}{c}{u}_2\left[n\right]={\left(\begin{array}{ccccc}u\left(1\right)& u\left(2\right)& u\left(3\right)& u\left(4\right)& u\left(5\right)\end{array}\right)}^{⊺}.\end{array}$$

(29)

The third and last case correspond to solving (21), which gave ${\widehat{\mathit{\theta }}}_3$. Then, (16) becomes

$${\widehat{x}}_3[n;{\widehat{\mathit{\theta }}}_3]=2x[n-1]-x[n-2]+{\mathit{\theta }}_3^{⊺}{\mathit{u}}_3\left[n\right],$$

(30)

where

$$\begin{array}{c}{\widehat{\mathit{\theta }}}_3={\left(\begin{array}{cccc}\widehat{\theta }\left(1\right)& \widehat{\theta }\left(2\right)& \widehat{\theta }\left(3\right)& \widehat{\theta }\left(5\right)\end{array}\right)}^{⊺},\end{array}$$

(31)

and

$$\begin{array}{c}{\mathit{u}}_3\left[n\right]={\left(\begin{array}{cccc}u\left(1\right)& u\left(2\right)& u\left(3\right)& u\left(5\right)\end{array}\right)}^{⊺}.\end{array}$$

(32)

$\widehat{\theta }\left(4\right)$ and $\widehat{\theta }\left(8\right)$ are not considered in (31) since their absolute value $\le 1\times {10}^{-6}$ when solving (21) and (22). $\widehat{\theta \left(6\right)}$, which is the parameter for the cross term in ${\overline{v}}_{in}$ and ${\overline{v}}_{out}$, is ignored because during operation ${\overline{v}}_{in}=0$ when ${\overline{v}}_{out}>0$ and ${\overline{v}}_{out}=0$ when ${\overline{v}}_{in}>0$. We ignore $\widehat{\theta }\left(7\right)$ because $u\left(7\right)$ is highly correlated with $u\left(1\right)$ and $u\left(2\right)$, and the MSE for training and test data shown in Table 1 do not change if it is considered. We did not consider higher order terms in (14) and (15) because their absolute values were found to be $\le 1\times {10}^{-6}$ when solving (21) and (22).

Table 1. Estimated parameter values for the input–output system model in (16) and (17). ${\widehat{\theta }}_1$ and ${\widehat{\theta }}_2$ are least squares estimates, and ${\widehat{\theta }}_3$ was obtained by solving (21). $-1\le \theta \left(1\right)\le 0$, $\theta \left(2\right)\ge 0$, $\theta \left(3\right)\le 0$, $\theta \left(4\right)\le 0$, and $\theta \left(5\right)\ge 0$ are based on the physical constraints of the device.

$\mathit{\theta }$	Description	${\widehat{\mathit{\theta }}}_1$	${\widehat{\mathit{\theta }}}_2$	${\widehat{\mathit{\theta }}}_3$
$\theta \left(1\right)$	$-\frac{{\gamma }_2{T}_s}{{\gamma }_1}$	-1.16	-1.24	-0.99
$\theta \left(2\right)$	$\frac{{\varphi }_1{T}^2}{{\gamma }_1{x}_{max}}$	$1.01\times {10}^{-2}$	$7.04\times {10}^{-3}$	$1.01\times {10}^{-2}$
$\theta \left(3\right)$	$\frac{{\varphi }_2{T}^2}{{\gamma }_1{x}_{max}}$	$-4.34\times {10}^{-2}$	$-6.03\times {10}^{-2}$	$-5.61\times {10}^{-2}$
$\theta \left(4\right)$	$\frac{{\varphi }_3{T}^2}{{\gamma }_1{x}_{max}}$	-	$6.33\times {10}^{-2}$	-
$\theta \left(5\right)$	$\frac{{\varphi }_4{T}^2}{{\gamma }_1{x}_{max}}$	-	$3.37\times {10}^{-2}$	$2.78\times {10}^{-2}$
MSE training		$3.5\times {10}^{-5}$	$3.2\times {10}^{-5}$	$3.6\times {10}^{-5}$
MSE test		$3.8\times {10}^{-5}$	$3.8\times {10}^{-5}$	$4.5\times {10}^{-5}$

Table 1. Estimated parameter values for the input–output system model in (16) and (17). ${\widehat{\theta }}_1$ and ${\widehat{\theta }}_2$ are least squares estimates, and ${\widehat{\theta }}_3$ was obtained by solving (21). $-1\le \theta \left(1\right)\le 0$, $\theta \left(2\right)\ge 0$, $\theta \left(3\right)\le 0$, $\theta \left(4\right)\le 0$, and $\theta \left(5\right)\ge 0$ are based on the physical constraints of the device.

$\mathit{\theta }$	Description	${\widehat{\mathit{\theta }}}_1$	${\widehat{\mathit{\theta }}}_2$	${\widehat{\mathit{\theta }}}_3$
$\theta \left(1\right)$	$-\frac{{\gamma }_2{T}_s}{{\gamma }_1}$	-1.16	-1.24	-0.99
$\theta \left(2\right)$	$\frac{{\varphi }_1{T}^2}{{\gamma }_1{x}_{max}}$	$1.01\times {10}^{-2}$	$7.04\times {10}^{-3}$	$1.01\times {10}^{-2}$
$\theta \left(3\right)$	$\frac{{\varphi }_2{T}^2}{{\gamma }_1{x}_{max}}$	$-4.34\times {10}^{-2}$	$-6.03\times {10}^{-2}$	$-5.61\times {10}^{-2}$
$\theta \left(4\right)$	$\frac{{\varphi }_3{T}^2}{{\gamma }_1{x}_{max}}$	-	$6.33\times {10}^{-2}$	-
$\theta \left(5\right)$	$\frac{{\varphi }_4{T}^2}{{\gamma }_1{x}_{max}}$	-	$3.37\times {10}^{-2}$	$2.78\times {10}^{-2}$
MSE training		$3.5\times {10}^{-5}$	$3.2\times {10}^{-5}$	$3.6\times {10}^{-5}$
MSE test		$3.8\times {10}^{-5}$	$3.8\times {10}^{-5}$	$4.5\times {10}^{-5}$

In Table 1, we find the estimated parameter values obtained for the parameters defined in (25), (27), and (30). For ${\widehat{\theta }}_1$, we have no agreement between $\widehat{\theta }\left(1\right)$ and the physics of the system defined in (15). From a system theory perspective, this parameter value implies that the poles of (16) were $z=1$ and $z=-0.16$, where the last one relates to a pole in $f=16.67$ Hz, which is not possible when looking at Figure 3(a) and (b). The $\widehat{\theta }\left(2\right)$ and $\widehat{\theta }\left(3\right)$ signs are in agreement with the physics; however, when assuming that both pilot valves (I) and (II) are equal to each other, there seems to be an anomaly in the valve. After discussion with maintenance engineers on the manufacturing plant, a manual calibration of the springs in the pilot valves was performed after the maintenance of the valve. In ${\widehat{\theta }}_2$, the values of $\widehat{\theta }\left(1\right)$ and $\widehat{\theta }\left(4\right)$ are different in sign than (15). Considering the non-linear terms in (27) increases the conditioning number of $\left({\sum }_{n=1}^N{\mathit{u}}_1\left[n\right]{\mathit{u}}_1{\left[n\right]}^{⊺}\right)$ by two orders of magnitude, and this could be the reason to obtain these parameter values because of the poor excitation of the signals (see Figure 3(a) and (b)). ${\widehat{\theta }}_3$ gives values in agreement with the signs defined in (15) regarding the physics of the valve. As for ${\widehat{\theta }}_2$, there are differences between the second and third element of the estimated parameter vector.

Figure 4(a) shows a comparison between $x\left[n\right]$ and ${\widehat{x}}_3\left[n\right]$, and this is achieved using validation data, i.e., signals from a different production time than the ones used for estimating ${\widehat{\theta }}_3$. The signals ${\overline{v}}_{in}$, ${\overline{v}}_{out}$, and x in Figure 4 show that the valve operates under the same conditions as for the signals that are used for estimating the parameters (see. Figure 3(a) and (b)). We can see that $x\left[n\right]$ and ${\widehat{x}}_3\left[n\right]$ are overlapped, and that these results are seen in the error signal (see Figure 4(c)). There was a small offset between both signals when the main valve’s spindle was at rest, i.e., between $n=250$ and $n=60$, and $n=650$ and $n=850$ ($T_s=0.03$ s). In addition, the error signal shows a process that is close to white noise with a small offset when $\dot{x}\ne 0$. The error signal seems to have a component with a 0.09 s period, i.e., three samples. The error signal agrees with the MSE values shown in Table 1. The difference between the error signal when $\dot{x}>0$ and $\dot{x}<0$ agrees with the difference in the parameter values $\widehat{\theta }\left(2\right)$ and $\widehat{\theta }\left(3\right)$ , as for the difference between $\widehat{\theta }\left(4\right)$, which is negligible, and $\widehat{\theta }\left(5\right)$.

Figure 4. Modeling results with the validation data: a) the measured output $x_{exp}$ (position of IV) and the modeled output ${\widehat{x}}_3$; b) the normalized input signals ${\overline{v}}_{in}$ and ${\overline{v}}_{out}$; and c) the error signal obtained by subtracting ${\widehat{x}}_3$ from $x_{exp}$.

Figure 4. Modeling results with the validation data: a) the measured output $x_{exp}$ (position of IV) and the modeled output ${\widehat{x}}_3$; b) the normalized input signals ${\overline{v}}_{in}$ and ${\overline{v}}_{out}$; and c) the error signal obtained by subtracting ${\widehat{x}}_3$ from $x_{exp}$.

In addition to analyzing the modeling results with cross-validation and inspecting the poles, we performed a dimensional analysis and checked the size of the parameter values. Table 2 shows the units of some of the parameters in (14). These parameter units can be derived by using (15), and by knowing that $f_{in}\left(P_c\right)$ and $f_{out}\left(P_c\right)$ have the units $[\mathrm{m}·{\mathrm{s}}^{-1}]$, $f_{in}^{\prime }\left(P_c\right)$ and $f_{out}^{\prime }\left(P_c\right)$, which have $[{\mathrm{m}}^2·\mathrm{s}·{\mathrm{kg}}^{-1}]$; $g({\overline{v}}_{in},{\overline{v}}_{out})$, $g_{{\overline{v}}_{in}}^{\prime }({\overline{v}}_{in},{\overline{v}}_{out})$, $g_{{\overline{v}}_{out}}^{\prime }({\overline{v}}_{in},{\overline{v}}_{out})$ have $[{\mathrm{m}}^{-4}·{\mathrm{s}}^{-1}·\mathrm{kg}]$; and ${\overline{R}}_1$ and ${\overline{R}}_2$ have $\left[{\mathrm{m}}^2\right]$. The parameter elements of $\theta$ in (17) are dimensionless as ${\widehat{\theta }}_1$, ${\widehat{\theta }}_2$, and ${\widehat{\theta }}_3$ in (25), (27), and (30), respectively. This finding agrees with the normalized units of the output x, as well as the inputs ${\overline{v}}_{in}$ and ${\overline{v}}_{out}$. Table 3 shows the values of the valve as related to its mechanical, hydraulic, electronic, and physical dimension characteristics. These values have been used to compute intervals for the estimated parameter vector ${\theta }_{\mathbf{3}}$ in (30). The interval for the mass of the spindle M was given by maintenance engineers. The damping coefficient B was obtained from the knowledge of the poles of the system, as discussed in Section 4.1. The physical $A_B$ and $A_T$ dimensions were obtained from the manufacturer drawings of similar valves. $c_d\frac{\alpha v_{max}}{KR}w$ is related to the flow through the pilot valves, and it was obtained from the manufacturer’s flow graphs. ${\overline{v}}_0$ and $P_z$ were selected based on the measured signals (see Figure 3). Table 4 shows the computed intervals from the values and intervals in Table 3, as well as in (4) to (17). We can see that the obtained parameter values for ${\widehat{\theta }}_3$ are within the intervals. In Table 3, the intervals correspond up to an order of magnitude; furthermore, the interval in Table 3 is up to three orders of magnitude, which is due the products used to compute the elements of ${\theta }_3$ (see (9), (10), (12), and (15)).

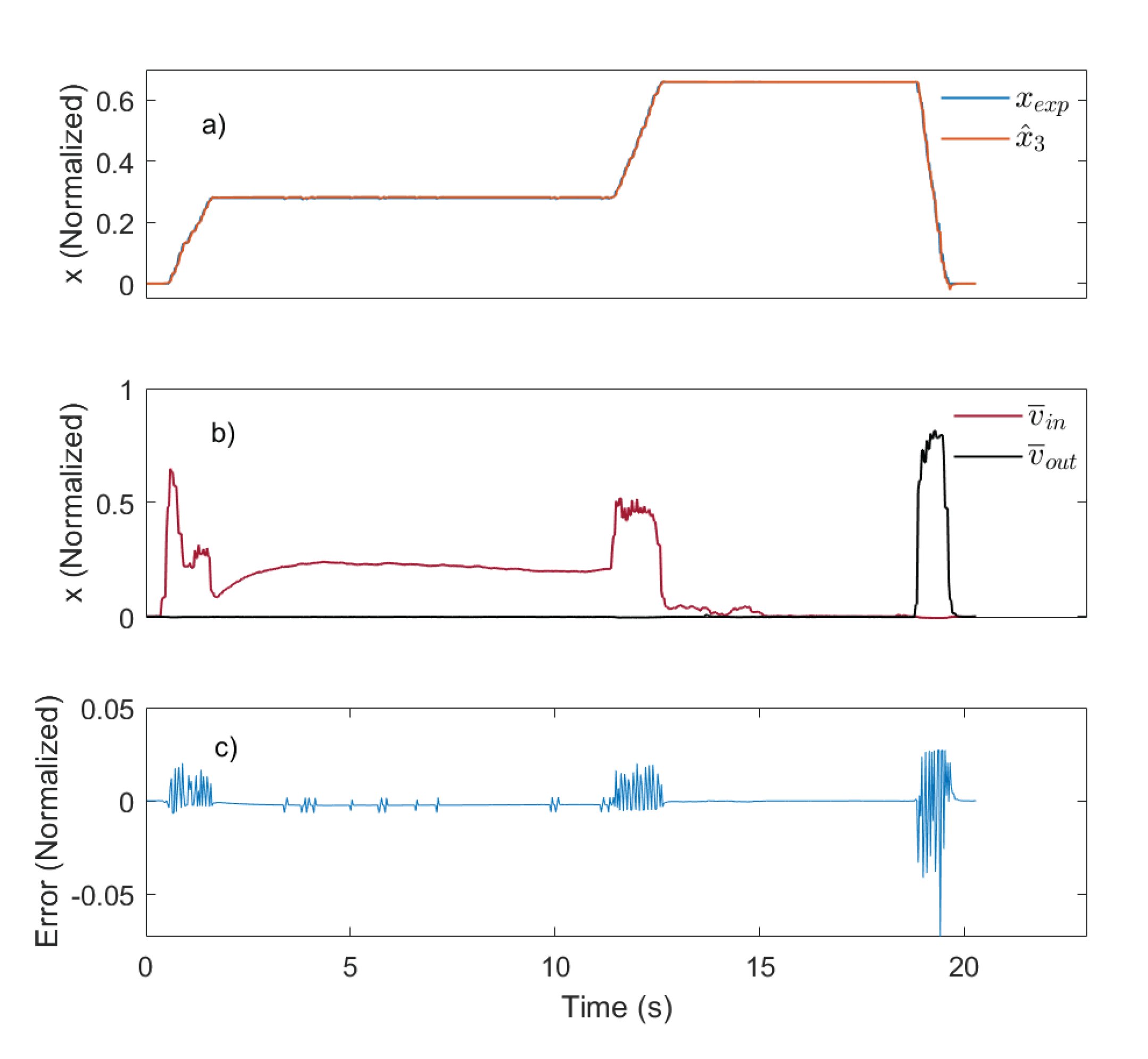
4.2. Modeling Errors

The relative errors in the elements of ${\widehat{\theta }}_3$ were estimated from the known error sources. The different sources are listed in the second column of Table 5. First, we explain how the relative errors were estimated for each error source. Then, we describe the relative errors obtained from each error source.

The rows (a), (b), and (c) give the relative errors from the offset in the measured data in ${\overline{v}}_{in}$, ${\overline{v}}_{out}$, and x. The offset changes between the cycles. The errors in ${\overline{v}}_{in}$ were calculated for a cycle with a negligible offset. We added positive and negative offset values, $\Delta {\overline{v}}_{in}\in [-0.001,0.001]$ to ${\overline{v}}_{in}$, and determined the parameter values $\widehat{\theta }\left(i\right)$ for $i=\left\{1,2,3,5\right\}$. A straight line was fitted for each $\widehat{\theta }\left(i\right)$ versus $\Delta {\overline{v}}_{in}$. The estimated errors $\Delta \theta \left(i\right)$ were calculated with $\Delta {\overline{v}}_{in}=0.001$, which is the highest offset in the measured signal ${\overline{v}}_{in}$. The errors due to the offset $\Delta {\overline{v}}_{out}$ and $\Delta x$ were calculated in the same way.

The relative errors from the noise in the measured data in ${\overline{v}}_{in}$, ${\overline{v}}_{out}$, and x are given in rows (d), (e), and (f). We added a noise signal with a variance of ${\sigma }^2\in (0,1\times {10}^{-7}]$ to ${\overline{v}}_{in}$, as well as estimated the parameter values $\widehat{\theta }\left(i\right)$ for $i=\left\{1,2,3,5\right\}$. A straight line was fitted for each $\widehat{\theta }\left(i\right)$ versus ${\sigma }^2$. A ${\sigma }^2=1\times {10}^{-10}$ was used to calculate $\Delta \widehat{\theta }\left(i\right)$, which was also the highest observed ${\sigma }^2$ in the measured signals. The errors due to noise in ${\overline{v}}_{out}$ and x were calculated in the same way.

In order to estimate the relative errors from the Euler Forward method, as shown in row (g) in Table 5, we compared a continuous and discrete time model of the system. The continuous time model uses (14) and (15) with input signals ${\overline{u}}_{in}$ and ${\overline{u}}_{out}$ as being combinations of ramp and step functions similar to the measured of ${\overline{v}}_{in}$ and ${\overline{v}}_{out}$, respectively (see Figure 4(b)). An analytical output signal was derived by solving the differential Equation (14) with the conventional Laplace transform method. A discrete-time output signal was calculated after discretization of the differential equation by the Euler Forward method (see (14) to (16)). When comparing the discrete- time to the analytical output, an error signal was obtained. The variance of that signal was determined and used to generate different realizations of the error signal. These realizations were added to the measured output signal x, and the parameters $\theta \left(i\right)$ for $i=\left\{1,2,3,5\right\}$ were identified. $\Delta \widehat{\theta }\left(i\right)$ was determined as the difference to the case with no added error signals.

The rows (h), (i), and (j) provide the relative errors caused by the approximations in (9), (10), and (12). The remainder term of a Taylor polynomial of order 2 was estimated for each approximation and included in (14). We used $P_c\in [2.8\times {10}^7,2.9\times {10}^7]$ Pa based on the ratio of the areas $A_B$ and $A_T$, as shown in Figure 2, to estimate the remainder term of (9) and (10), as well as to calculate $\Delta \widehat{\theta }\left(i\right)$ for $i=\left\{1,2,3,5\right\}$ (which is given in row (h)). ${\overline{v}}_{in},{\overline{v}}_{out}\in [0.01,0.8]$ were used to estimate the remainder term of (12), and this was based on the signals in Figure 4(b) and the obtained relative errors that are given in row (i). The relative errors from the product of the remainder term of each approximation included in (14) are given in row (j).

Row (k) gives the relative errors from the approximation that the fluid is incompressible, (4). We compared the model output obtained from (1) to (18) with that of a Matlab/Simulink model, which models water as compressible (details are given in section 7). An error signal was calculated as the difference of the model outputs. The mean and variance of that signal were estimated and used to generate different realizations, that were added to the measured output signal x. The parameters $\theta \left(i\right)$ for $i=\left\{1,2,3,5\right\}$ were estimated. $\Delta \widehat{\theta }\left(i\right)$ were determined as the difference to the case with no added error signal.

Table 5 provides the relative errors. The relative errors in $\widehat{\theta }\left(2\right)$, $\widehat{\theta }\left(3\right)$, and $\widehat{\theta }\left(5\right)$ are bigger than that of $\widehat{\theta }\left(1\right)$ from offsets in ${\overline{v}}_{in}$, ${\overline{v}}_{out}$, and x (see rows (a), (b), and (c) in Table 5). These relative errors could be reduced by decreasing the offset levels in the calibration process. In rows (d), (e), and (f), the relative errors of $\widehat{\theta }\left(3\right)$ and $\widehat{\theta }\left(5\right)$ are bigger than those of $\widehat{\theta }\left(1\right)$ and $\widehat{\theta }\left(2\right)$. The sensitivity of the non-linear term and the poor data of ${\overline{v}}_{out}$ cause these relative errors. Sensors with lower additive noise could be used to reduce these relative errors. Regarding the discretization of (14) (see row (g)), large relative errors for $\widehat{\theta }\left(2\right)$, $\widehat{\theta }\left(3\right)$, and $\widehat{\theta }\left(5\right)$ are obtained when compared to $\widehat{\theta }\left(1\right)$. These relative errors come from the fast changes in x relative to the sampling time (0.03 s) at the initial and final time of the steps in the input signals. One could reduce the sampling time or use more advanced discretization methods to minimize these relative errors. The relative errors of $\widehat{\theta }\left(1\right)$ and $\widehat{\theta }\left(2\right)$ are found to be bigger than those of the other elements in ${\widehat{\theta }}_3$ for the approximations of (9), (10), and (12) (see rows (h), (i), and (j)). The approximations of (9) and (10) could be avoided by having a sensor for $P_c\left(t\right)$, as well as by estimating $\dot{x}$ (see (8), (9), and (10)). One cannot avoid the approximation (12) by using more sensors, but one could collect further informative data to estimate more of the parameters of the Taylor polynomial that was used in the approximation (see ${\overline{v}}_{in}$ and ${\overline{v}}_{out}$ in Figure 4(b)). The largest relative errors of the elements in $\widehat{\theta }$ are due to the incompressibility approximation. The assumption of water being incompressible could be avoided by having a sensor for $P_c\left(t\right)$ and estimating ${\dot{P}}_c$ and $\dot{x}$. The final row provides the total relative error of the parameters $\widehat{\theta }\left(i\right)$ for $i=\left\{1,2,3,5\right\}$. They were calculated as the sum of the relative errors of $\widehat{\theta }\left(i\right)$ from rows (a) to (k). The largest relative error is $\widehat{\theta }\left(5\right)$, which is the parameter that describes the nonlinear effect of ${\overline{v}}_{out}^2$.

4.3. Aging

This section evaluates a potential use of the system model described in (30). The elements of ${\theta }_3$ in (30) were estimated for different production cycles (see (21)). The elements of the estimated parameter vectors are denoted as ${\widehat{\theta }}^{\left(c\right)}\left(i\right)$, where $c=\left\{,2,...,l\right\}$ and l is the total number of cycles.

We observe a linear trend in ${\widehat{\theta }}^{\left(c\right)}\left(2\right)$ for the cycles $c\in [429,533]$ (see Figure 5). We fitted the linear regression model

$${\widehat{\theta }}_R^{\left(c\right)}\left(2\right)={\widehat{\beta }}_0+{\widehat{\beta }}_{1}c,$$

(33)

where ${\widehat{\beta }}_0$ and ${\widehat{\beta }}_1$ are the least square estimators, and ${\widehat{\theta }}_R^{\left(c\right)}\left(2\right)$ is the estimated ${\widehat{\theta }}^{\left(c\right)}\left(2\right)$ at cycle c. The confidence intervals of ${\widehat{\theta }}_R^{\left(c\right)}\left(2\right)$ were calculated as (13.17) in [38], and this was achieved by assuming the residuals of (33) to be white Gaussian noise. In addition, we considered a confidence level of 95% by estimating ${\widehat{\xi }}_c$ as (13.16), as shown in [38]. The estimated relative error of 6.5% in $\widehat{\theta }\left(2\right)$ is similar to but slightly smaller than 95% intervals shown in Figure 5. Thus, the scattering around the trend line is explained by the different error sources summarized in Table 5. The trend line reveals the aging of the valve.

Figure 6 shows the values of the other elements of ${\widehat{\theta }}^{\left(c\right)}$ for $c\in [429,533]$. We can see that ${\widehat{\theta }}^{\left(c\right)}\left(1\right)$ is constant over the cycles, and that it stays at the limits of the constraints defined in Section 4.1. The scattering in ${\widehat{\theta }}^{\left(c\right)}\left(3\right)$ and ${\widehat{\theta }}_3^{\left(c\right)}\left(5\right)$ show an increasing trend with the number of cycles. The estimated parameter values of ${\widehat{\theta }}^{\left(c\right)}\left(3\right)$ are bigger in magnitude than ${\widehat{\theta }}^{\left(c\right)}\left(5\right)$ for $c\in [430,500]$. The total estimated error of $\widehat{\theta }\left(3\right)$ and $\widehat{\theta }\left(5\right)$, as given in Table 5, describe most of the scattering of the estimated parameters ${\widehat{\theta }}^{\left(c\right)}\left(3\right)$ and ${\widehat{\theta }}^{\left(c\right)}\left(5\right)$, respectively.

5. Conclusions

An input–output model of a novel two-stage 2/2 proportional cartridge valve was derived from a physical modeling that was based on fluid mechanics, dynamics, and electrical principles. This is possible because of the relative simplicity of the device when compared to more complex systems, such as machines with multiple components [9]. Therefore, each of the model parameters can be related to the design parameters of the valve. The main difference from other two-stages cartridge valves is that the valve under study is marginally stable (c.f. [23]). Moreover, parameter estimation was performed with data that were collected in industrial conditions, with the valve operating as a subsystem of a press mill, and with the valve being the plant of a closed-loop system.

In this work, we did not use a sensor for $P_c\left(t\right)$, which is usually the case in other studies of similar valves. This limitation was addressed successfully in the derivation of the input-output model, which was achieved by using Taylor polynomials. The closed loop operation results in poor system excitation, which delivered numerical problems when applying the least-squares method. This problem was solved by estimating the parameters by a convex optimization problem. The constraints of the convex optimization problem were defined based on the physics of the valve and system knowledge regarding the poles of the device. An in-depth study of the contributions to the errors of the estimated parameters from different error sources were carried out.

The identified model of the valve showed that the non-linear terms were not negligible compared to the linear ones. Thus, a non-linear controller of the valve position could improve the performance of the closed-loop system compared to a linear controller. The estimated parameters of the model showed several trends vs. the production cycles. Analyses of more data should be carried out to check if a prognosis of the valve’s health status could be conducted. In future studies, the developed method could be used to investigate and identify different failure models of the valve, such as for leakages.