Submitted:
02 March 2024
Posted:
04 March 2024
You are already at the latest version
Abstract
Keywords:
I. Introduction
II. Noncommutative Geometry and Minimal Uncertainty in Momentum
- 1.
- The ★-product under the integral sign
- 2.
- The Complex conjugation
III. Schrödinger and Continuity Equations in Commutative Case
A. Schrödinger Equation with NLP in the Context of MUM
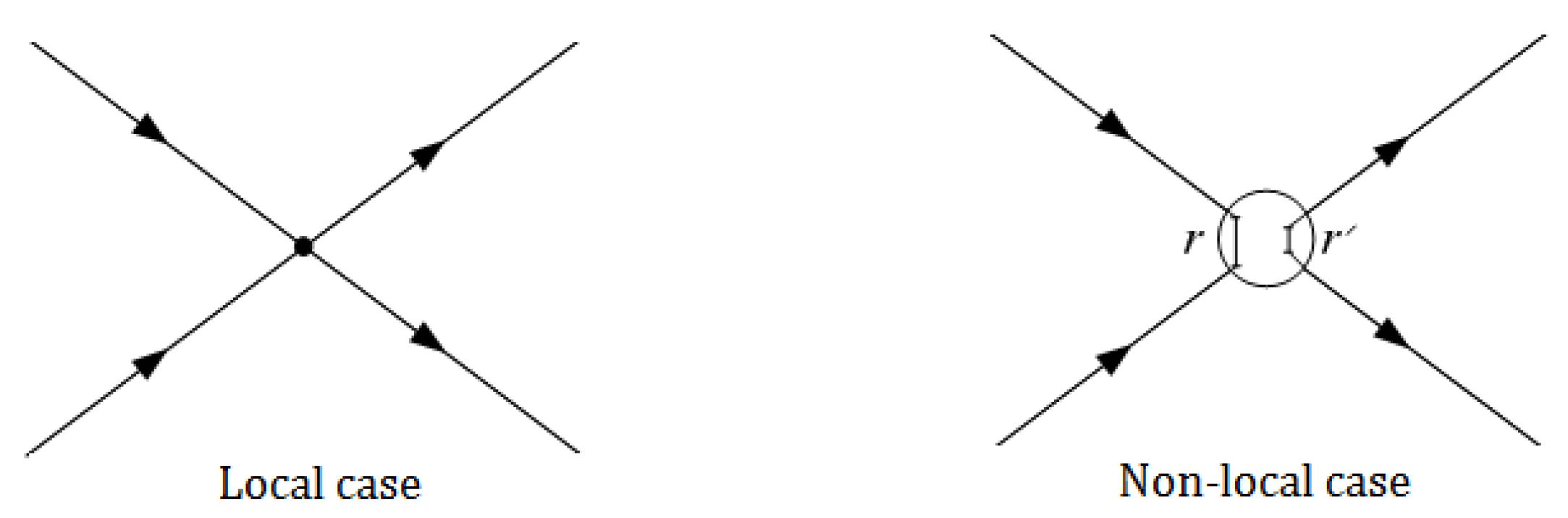
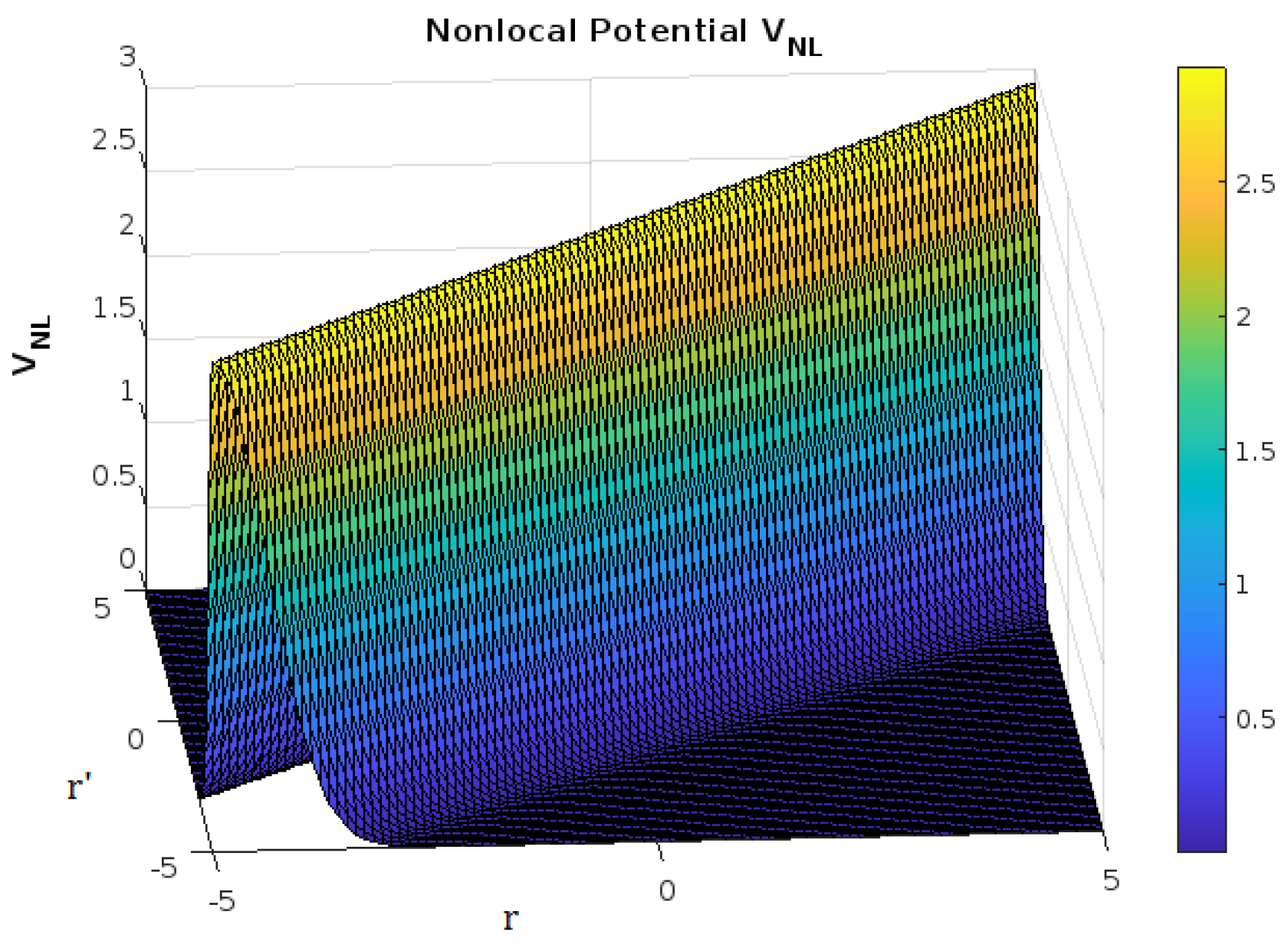
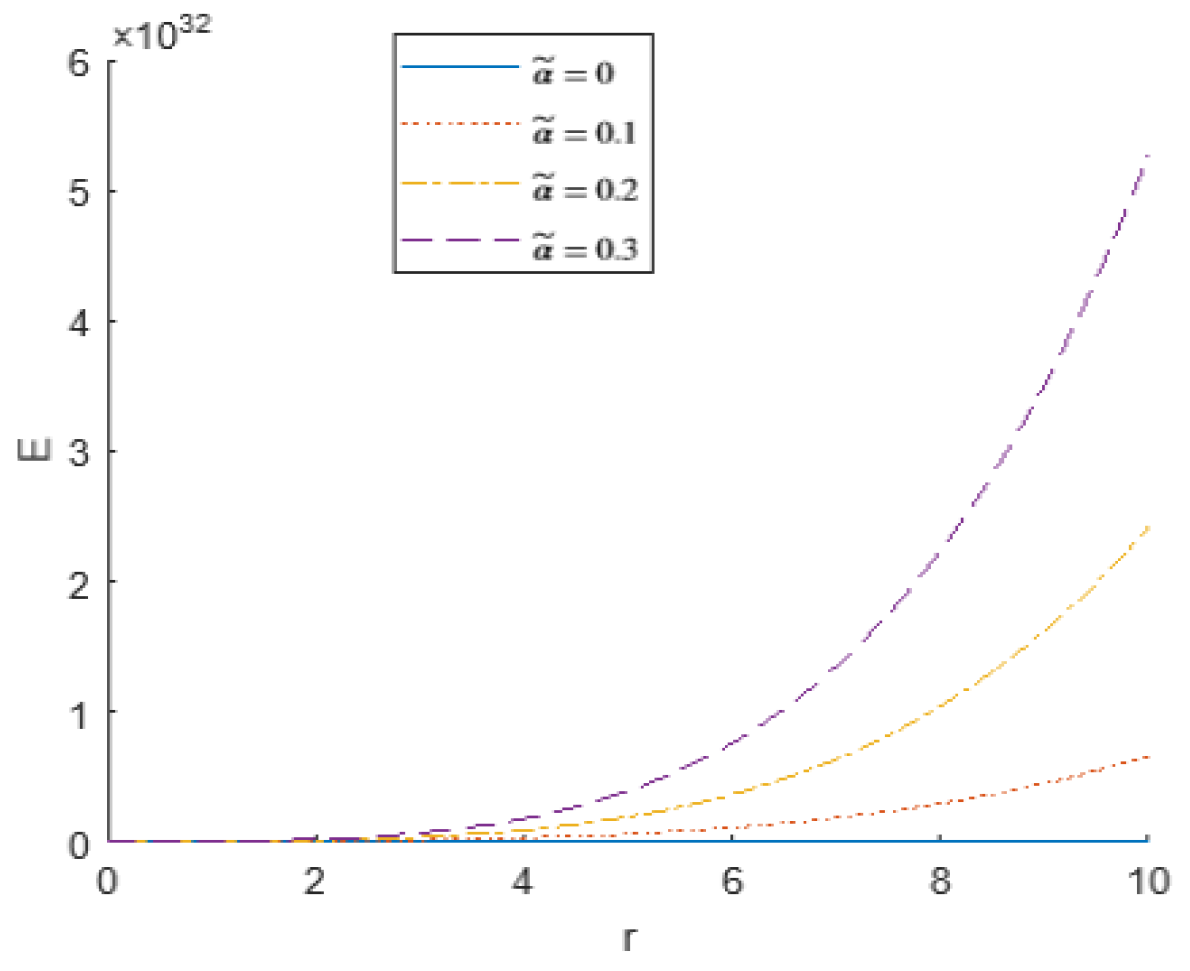
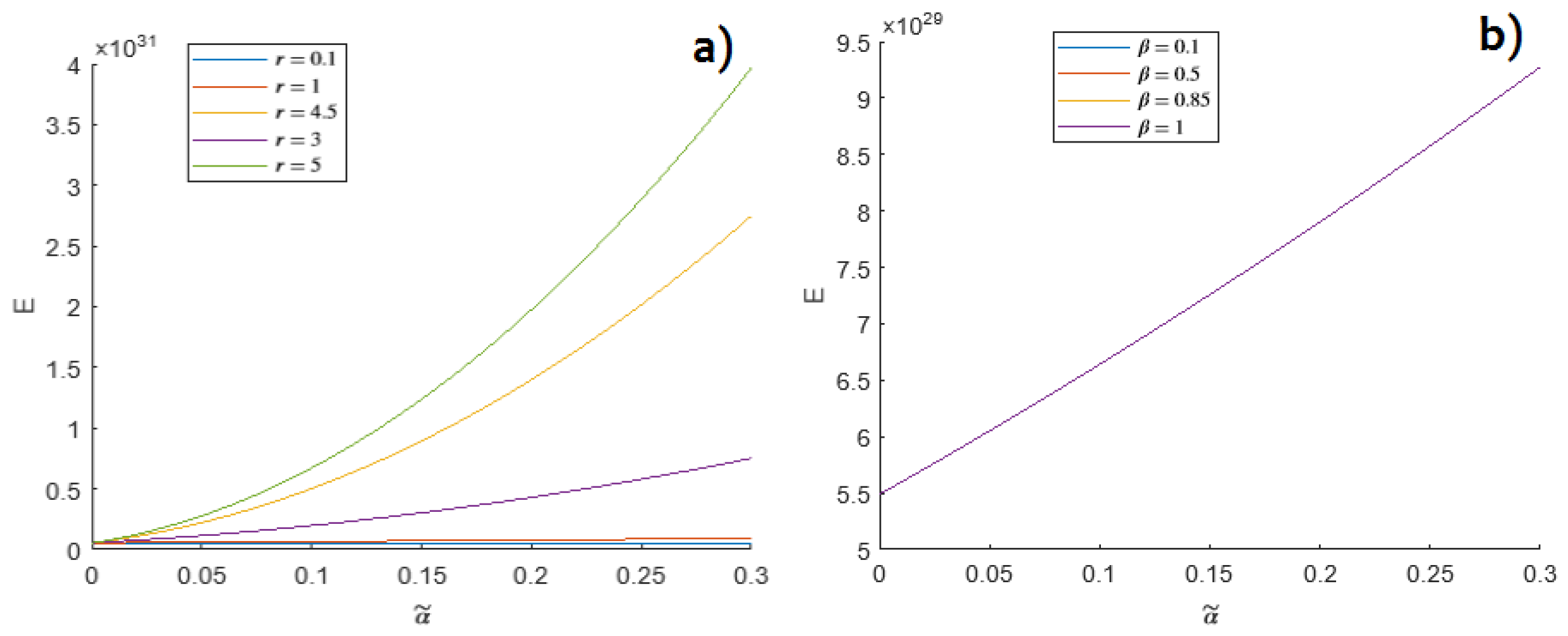
B. Continuity Equation with NLP in the Context of MUM
IV. Schrödinger and Continuity Equations in Noncommutative Case
A. Noncommutative Schrödinger Equation with NLP in the Context of MUM
B. Noncommutative Continuity Equation with NLP in the Context of MUM
V. Conclusions
Funding
Conflicts of Interest
References
- Michael, G, et al. Heat conduction in molecular transport junctions. Phys. Rev. B 75, 155312. [CrossRef]
- Nayak, G.C. General form of the color potential produced by color charges of the quark. J. High Energ. Phys. 2013, 1 (2013). [CrossRef]
- Nayak, G.C. General form of color charge of the quark. Eur. Phys. J. C, 73, 2442 (2013). [CrossRef]
- Mott, N. F., Massey, H. S. The Theory of Atomic Collisions, (Oxford Univ. Press, London). (1965).
- Baseia, B., Nussenzveig, H. M. Semiclassical theory of laser transmission loss. Optica Acta: International Journal of Optics, 31(1), 39(1984). [CrossRef]
- Balantekin, A.B, et al. Green’s function for nonlocal potentials. J. Phys. G: Nucl. Part. Phys. 24(11), 2087 (1998). [CrossRef]
- Li, C, et al. Definition of current density in the presence of a non-local potential. Nanotechnology. 19, 15, 155401 (2008). [CrossRef]
- Reeves, M., Owen, L. W. Solution of a Schroedinger equation with a nonlocal potential. J. Comput. Phys. 4(4), 572 (1969). [CrossRef]
- Pattanayak, D. N. Wolf, E.Scattering states and bound states as solutions of the schrödinger equation with nonlocal boundary conditions. Phys. Rev. D, 13(4), 913 (1976). [CrossRef]
- Kidun, O., et al. Scattering and bound-state problems with non-local potentials: application of the variable-phase approach. J. Phys. A: Math. Gen. 35, 9413 (2002). [CrossRef]
- Perey, F., Buck, B. A Non-Local Potential Model for the Scattering of Neutrons by Nuclei. Nucl. Phys, 32, 353 (1962). [CrossRef]
- Fetter, A.L., Walecka, J.D. Quantum Theory of Many-Particle Systems. McGraw-Hill, New York. (1971).
- Balantekin, A.B., et al. Green’s Function for Nonlocal Potentials. J. Phys. G: Nucl. Part. Phys, 24, 2087 (1998). [CrossRef]
- Taylor, J., et al. Initio Modeling of Quantum Transport Properties of Molecular Electronic Devices. Phys. Rev. B, 63, 245407 (2001). [CrossRef]
- Deltuva, A. Three-body direct nuclear reactions: Nonlocal optical potential. Phys. Rev. C, 79(2), 021602 (2009). [CrossRef]
- Jaghoub, M. I., et al. Exploration of the energy dependence of proton nonlocal optical potentials. Physical Review C, 98(2), 024609 (2018). [CrossRef]
- Deltuva, A., Jurčiukonis, D. Nonlocal optical potential with core excitation in Be10(d,p)11 Be and Be11(p,d)10 Be reactions. Phys. Lett. B, 840, 137867 (2023). [CrossRef]
- Coz, M., Arnold, L. G., & MacKellar, A. D. Nonlocal potentials and their local equivalents. Ann. Phys. 59(1), 219 (1970). [CrossRef]
- De Forest. Jr, T. Equivalence of local and non-local potentials and the perey effect. Nucl. Phys. A, 163(1), 237 (1971). [CrossRef]
- Lassaut, M., Mau, N. V. l-Dependent local potentials equivalent to a non-local potential. Nucl. Phys. A, 518(3), 441(1990). https://doi.org/10.1016/0375-9474(90)90139-D. [CrossRef]
- Madore, J.: An introduction to noncommutative geometry. In: H. Gausterer, L. Pittner, H. Grosse, (eds) Geometry and Quantum Physics. Lecture Notes in Physics, vol 543. (Springer, Berlin, Heidelberg, 2000). [CrossRef]
- Haouam, I. Two-dimensional Pauli equation in noncommutative phase-space. Ukr. J. Phys.66(9), 771 (2021). [CrossRef]
- Seiberg. N., Witten. E, String theory and noncommutative geometry. J. High Energy Phys. 1999(09), 032 (1999). [CrossRef]
- Calmet, X., Jurčo, B., Schupp, P. et al. The standard model on non-commutative space-time. Eur. Phys. J. C 23, 363 (2002). [CrossRef]
- Haouam, I. On the Fisk-Tait equation for spin-3/2 fermions interacting with an external magnetic field in noncommutative space-time. J. Phys. Stud. 24, 1801 (2020). [CrossRef]
- Grosse, H., Klim£ík, C. & Prešnajder, P. On finite 4D quantum field theory in non-commutative geometry. Commun.Math. Phys. 180, 429 (1996). [CrossRef]
- Moffat, J. W. Noncommutative quantum gravity. Phys. Lett. B, 491(3-4), 345 (2000). [CrossRef]
- Spallucci, E., Smailagic, A., & Nicolini, P. Non-commutative geometry inspired higher-dimensional charged black holes. Phys. Lett. B, 670(4-5), 449 (2009). [CrossRef]
- Haouam, I. Dirac oscillator in dynamical noncommutative space. Acta. Polytech.61(6), 689 (2021). [CrossRef]
- Haouam, I. Analytical solution of (2+1) dimensional Dirac equation in time-dependent noncommutative phase-space. Acta. Polytech. 60(2), 111 (2020). [CrossRef]
- Haouam, I., Hassanabadi, H. Exact solution of (2+1)-dimensional noncommutative Pauli equation in a time-dependent background. Int. J. Theor. Phys. 61, 215 (2022). [CrossRef]
- Haouam, I., Alavi, S.A. Dynamical noncommutative graphene. Int. J. Mod. Phys. A. 37(10), 2250054 (2022). [CrossRef]
- Haouam, I. Solutions of Noncommutative Two-Dimensional Position–Dependent Mass Dirac Equation in the Presence of Rashba Spin-Orbit Interaction by Using the Nikiforov–Uvarov Method. Int. J. Theor. Phys. 62, 111 (2023). [CrossRef]
- Chaichian., M., et al. Hydrogen Atom Spectrum and the Lamb Shift in Noncommutative QED. Phys. Rev. Lett. 86, 2716 (2001). [CrossRef]
- Haouam, I. On the noncommutative geometry in quantum mechanics. J. Phys. Stud. 24(2), 2002 (2020). [CrossRef]
- Gouba, L. A comparative review of four formulations of noncommutative quantum mechanics. Int. J. Mod. Phys. A, 31, 1630025 (2016). [CrossRef]
- Haouam, I. On the three-dimensional Pauli equation in noncommutative phase-space. Acta Polytech. 61(1), 230 (2021). [CrossRef]
- Hassanabadi, H. et al. Noncommutative phase space Schrödinger equation with minimal length. Adv. High Energy Phys. 2014, article ID 459345, 6 (2014). [CrossRef]
- Dossa, F.A et al. Non-commutative phase space Landau problem in the presence of a minimal length. Vestnik KRAUNC. Fiz.-mat. nauki. 33(4), 188 (2020). [CrossRef]
- Haouam, I. Foldy–Wouthuysen Transformation of Noncommutative Dirac Equation in the Presence of Minimal Uncertainty in Momentum. Few-Body. Syst. 64, 9 (2023). [CrossRef]
- Haouam, I. The non-relativistic limit of the DKP equation in non-commutative phase-space. Symmetry. 11, 223 (2019). [CrossRef]
- Zarei, M., Mirza, B. Minimal uncertainty in momentum: the effects of IR gravity on quantum mechanics. Phys. Rev. D, 79, 125007 (2009). [CrossRef]
- Chang, L. N., et al. Exact solution of the harmonic oscillator in arbitrary dimensions with minimal length uncertainty relations. Physical Review D, 65(12), 125027 (2002). [CrossRef]
- Brau, F., Buisseret, F. Minimal length uncertainty relation and gravitational quantum well. Physical Review D, 74 (3), article ID 036002, 5 (2006). [CrossRef]
- Nairz. O., et al. Experimental verification of the Heisenberg uncertainty principle for fullerene molecules. Phys. Rev. A. 65, 032109 (2002). [CrossRef]
- Stetsko, M. M. Corrections to the ns levels of the hydrogen atom in deformed space with minimal length. Phys.Rev. A. 74(6), 062105 (2006). [CrossRef]
- Das, S., Vagenas, E. C. Universality of quantum gravity corrections. Phys. Rev. Lett. 101(22), 221301 (2008). [CrossRef]
- Kempf, A. On quantum field theory with nonzero minimal uncertainties in positions and momenta, J. Math. Phys. 38, 1347 (1997). [CrossRef]
- Feshbach. H, et al. Model for Nuclear Reactions with Neutrons. Phys. Rev. 96, 448 (1954). [CrossRef]
- Schiff, L. I. Quantum Mechanics (New York: McGraw-Hill), 1968.
- Horiuchi, H. A Semi-Classical Treatment of Non-Local Potentials. Progress of Theoretical Physics, 64, 184 (1980). [CrossRef]
- Peierls, R., Mau, N. V. Local approximation to a non-local potential. Nuclear Physics A, 343, 1 (1980). [CrossRef]
- Frahn, W.E,. Lemmer, R.H. Velocity-Dependent Nuclear Interaction. Il Nuovo Cimento, 6, 1221 (1957). [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




