Elementary Particles and Their Interaction with Space-Time Curvature

Eran Magshim Lavi

doi:10.20944/preprints202402.0809.v3

Preprint

Article

Elementary Particles and Their Interaction with Space-Time Curvature

This version is not peer-reviewed.

Eran Magshim Lavi^*

This version is not peer-reviewed.

Downloads

306

Views

Comments

Submitted:

08 April 2024

Posted:

09 April 2024

Read the latest preprint version here

Abstract

This article begins with exploring fundamental limits in the universe. It examines key principles, such as the uniformity of physical laws and Energy conservation, that lead to maximum speed, locality, and maximum density. These universal limits govern physical phenomena, leading to very interesting results.I demonstrate that quarks and leptons comprise smaller entities named "Quantum Black Holes." These Quantum black holes are relativistically rotating miniature charged black holes consisting of a single core at the highest possible density. Quantum black holes are the only structures small enough in space-time capable of keeping all charges quantized (including gravitational charges.)By the end of the article, I prove that Quantum black holes explain the deficiencies of SM. They facilitate explanations of quantized gravity, the nature of Luminous and dark Matter, establishing the Mass, size, and (quantized) charges quantities of elementary particles, the nature of neutrino oscillations, and more. Elementary particles release their Energy outward, altering the curvature of nearby space-time and providing new insights into the nature of space-time curvature change. With this understanding, we can characterize movements and processes in local space-time using five sets of equations simultaneously: four representing the four charge types and one representing Dark Matter.

Keywords:

elementary particles

;

space-time

;

spacetime curvature

;

relativity

;

charges

Subject:

Physical Sciences - Particle and Field Physics

1. Preliminaries

Throughout this article, when referring to Matter, Energy also applies.

For clarity and conciseness, I will employ the term "particles" to denote housing for charges.

I will not distinguish between left-handed and right-handed particles; when I must choose a process, I will choose the one that happens.

The Universe often follows an unwritten rule: "Occam Razor Rule," which shows a preference for the simpler route. The "Occam Razor Rule" solution must conform to actual observations. (It does not always work – in which case I use a more elaborate solution.)

2. Limits

Space-time has built-in limits.

To understand the source of the limits, I examined the following two physical laws (stated as principles):

Uniformity of Physical Laws in the Universe Principle:

Each physical law is the same throughout the Cosmos.

The “Uniformity of Physical Laws in the Universe Principle” is a fundamental tenet in physics and forms the foundation of our understanding of the Cosmos.

All experiments and observations conducted on Earth thus far have consistently upheld this principle. Moreover, additional evidence gathered from distant galaxies further supports the validity of this principle across the vast reaches of the Universe, leading us to accept its validity throughout the Cosmos. (1)

Based on many observations, we conclude that Energy is conserved in closed systems.

Energy Conservation Principle:

Energy is conserved in a closed system.

No known physical phenomenon or process has ever contradicted the "Energy Conservation Principle."

Applying the "Uniformity of Physical Laws in the Universe Principle" to the "Energy Conservation Principle" leads us to deduce that Energy conservation is a universal characteristic of closed systems, including the Universe as a whole.

Consequently, we can infer that the total amount of Energy in the Cosmos is constant.

Since our Universe has a fixed amount of Energy, it cannot contain infinite Energy in any given region. This conclusion is a very fundamental quality of our Cosmos and leads to limits in our Universe.

Remark: The only way to guarantee that no region in the Cosmos has infinite Energy under any circumstances is to ensure that even a point in space-time cannot have infinite Energy density.

If there is no infinite Energy anywhere in the Universe, then no Universe part can travel at infinite speeds because infinite speeds require infinite Energy.

Thus, all Universe parts must have a speed limit of influence propagation, movement, or change.

We never observed any Universe part that moves at speeds higher than the speed of light. Therefore, we deduce that the highest possible influence propagation speed, a Universe part's speed, or a Universe part's speed of change, is the speed of light, marked as "c" [m].

Maximal Speed Principle:

Nothing in our Cosmos propagates, changes, or moves faster than the speed of light.

Note: If there were an infinite speed of influence propagation or movement in our Universe, we would get instant reactions to all processes all over the Universe. We would get a completely Uniform Universe. Our Universe is not completely uniform, corroborating the "Maximal Speed Principle."

This result leads to another important principle:A Universe part cannot influence "almost instantly" any part of the Universe that is not its immediate neighbor. Otherwise, there was a possibility of influencing a very far Universe part in a way that violates the "Maximal Speed Principle."

Therefore, a Universe part can only "almost instantly" influence the Universe parts in its immediate neighborhood.

Note: combining physics and mathematics converts "almost instantly" into infinitesimally close.

The Locality Principle:

Universe parts can only influence Universe parts that are immediately in their neighborhood.

There is a third consequence - a new and fundamental limit:

The Universe cannot compress Energy indefinitely because I have shown that there is no infinite Energy anywhere in the Universe (not even the possibility of infinite Energy density at a point). This restriction leads us to conclude that a state of Matter with a maximum density MUST exist.

I name this state of maximum Matter density "Dachus" (derived from the Hebrew word for compressed.) I use the term "Dachus density" to denote this maximal density.

Maximal Density Principle:

Nothing in our Cosmos has a density greater than Dachus’ density.

I denote Dachus density by

ρ_{D} [K g m^{- 3}]

. (I will calculate its value later.)

Question: Where can we find Dachus density in the Universe?

We should look at extreme places where attraction forces are mighty.

In this context, I investigated what happens Inside a black hole.

Continual compression of Matter within a black hole ultimately compresses its Matter until it reaches Dachus density within a non-zero volume in the center of the black hole. As the Matter inside the black hole compresses to its maximum degree, any further compression only contributes to the expansion of the black hole's core size, which maintains its Dachus state.

Remark: The concept of a black hole without a singularity challenges some calculations by esteemed physicists who predict singularities at the core of black holes. However, it is important to note that these calculations, which suggest the existence of singularities within black holes as a mathematical necessity, did not consider the presence of an upper limit for Matter density. Consequently, the conclusion that geodesics inside a black hole converge in a singularity is invalid.

3. Quantum Black Holes

Dachus state occurs in the core of any black hole composed of one body.

I will continue by examining the smallest black holes that have a profound physical meaning:

Quantum Black Hole Definition:

A "Quantum black hole" is a relativistically fast rotating, charged, miniature black hole whose core composes the entire black hole.

Going forward, I will use "QBH" as an abbreviation for a Quantum black hole.

By miniature, I refer to sizes in the order of

1 \cdot 10^{- 59} [m]

and less.

QBH (quantum black hole) is slightly oblated as it rotates relativistically fast, but this minor deformity does not affect my calculations in this article.

I will use "Naked core" to refer to a black hole composed of a single core (without two horizons.) QBH is a naked core, as I will prove through calculations.

Question: Is there a single value to Dachus density?

In the Dachus state, there is absolutely no room for additional contraction. Thus, in this state, all Energy squeezes to the same limit as Dachus density.

Energy represents both the substance of the Cosmos and embodies the ability to cause changes in the Cosmos.

Energy composes everything in our Universe.

The Completeness Principle:

Energy and nothing but Energy composes the Cosmos.

Therefore, in Dachus state, QBHs compress charges (composed of Energy according to the “Completeness Principe”) to the highest possible degree.

The Kerr-Newman solution describes a rotating, electrically charged black hole. (2)

Following the Kerr-Newman metric, I present an adaptation to include all charges:

Equation 1 Quadratic QBH radius

{(r_{Q B H})}^{2} - \frac{2 \cdot M_{Q B H} \cdot G}{c^{2}} r_{Q B H} + a^{2} + \sum \frac{C_{i} \cdot e^{2} \cdot G \cdot {(# u n i t s o f c h a r g e q_{i})}^{2}}{c^{4}}

Where

r_{Q B H}

is the

Q B H

radius,

C_{i}

is the force coefficient of the non-gravitational charge

q_{i}

, “i” = E – electric, W – weak, Q -quarkic (also known as color or strong.)

For a solid sphere rotating relativistically

J = \frac{3}{4} M c r_{Q B H}

(3) under the limit

ω r < c

a = \frac{J}{M C}

Equation 2 QBH Dachus core radius (first version)

r_{Q B H \pm} = \frac{\frac{2 \cdot M_{Q B H} \cdot G}{c^{2}} \pm \sqrt{{(\frac{2 \cdot M_{Q B H} \cdot G}{c^{2}})}^{2} - 4 \cdot \frac{25}{16} \cdot (\frac{e^{2} \cdot G}{c^{4}}) \cdot \sum C_{i} \cdot {(# u n i t s o f c h a r g e q_{i})}^{2}}}{\frac{50}{16}}

When using the “real charges” numbers, the root for the QBH radius equation is always imaginary (as I will show through calculations later,) and we get a naked core as in the QBH definition. Solving yields:

r_{Q B H} = \frac{16 \cdot M_{Q B H} \cdot G}{25 c^{2}}

Equation 3 QBH Mass, density, and radius

M_{Q B H} = \frac{4 π ρ_{D} \cdot {(r_{Q B H})}^{3}}{3}, ρ_{D} = \frac{3 M_{Q B H}}{4 π {\cdot (r_{Q B H})}^{3}}, {r_{Q B H} = (\frac{3 M_{Q B H}}{4 π ρ_{D}})}^{\frac{1}{3}}

Interestingly, since there is only one Dachus density, when comparing the radius in these two different equations, we get a restriction on the QBH Mass:

M_{Q B H} = \sqrt{\frac{46,875 c^{6}}{16,384 π ρ_{D} G^{3}}}

, which is the quantization of the gravitational charge!

4. Elementary Particles Must Be QBHs

We know that elementary particles have quantized charges, and very small dimensions. (4)

Therefore, we must look for physical structures that keep the quantization of charges and are small enough to house elementary particles.

Let us look at what happens to Energy added to a QBH:

Suppose an uncertainty-related Energy emerges within the QBH, including its border - which are always at Dachus state.

We must remember that the Universal physical limits we listed, the speed of light, and the maximal Matter density cannot be circumnavigated – they hold at every possible physical phenomenon.

Therefore, no amount of Energy will make Matter move at the speed of light or higher, and no amount of Energy will squeeze Matter and Energy further than the Dachus state.

Thus, when uncertainty-related Energy emerges within a QBH up to and including its border, the Matter density there cannot increase. Therefore, the uncertainty-related Energy exits the QBH swiftly.

Outside the QBH, when Energy contacts the QBH, the QBH’s strong and very relativistic centrifugal force deflects any such Energy.

If no additional (to existing) Energy can become a permanent part of the QBH and being a black hole at Dachus state, it cannot lose charges. I found what I sought: a tiny structure that always keeps its existing quantized angular momentum and charges.

As there are no other candidates besides QBHs for elementary particles, I conclude that QBHs are the only structures in space-time that are elementary particles.

5. Quarks and Leptons as QBH?

It is common practice that quarks and leptons are elementary particles.

Therefore, as elementary particles, quarks and leptons should be QBHs.

Using the QBH radius equation, I calculated the radii of all quarks and leptons: (5)

Table 1. Calculated radii of quarks and leptons as QBHs.

Particle	$M [K g]$	$r [m]$
Up	$3.8505 \cdot 10^{- 30}$	$1.8230 \cdot 10^{- 57}$
Down	$8.3250 \cdot 10^{- 30}$	$2.3664 \cdot 10^{- 57}$
Charm	$2.2640 \cdot 10^{- 27}$	$1.5332 \cdot 10^{- 56}$
Strange	$1.6650 \cdot 10^{- 28}$	$6.4235 \cdot 10^{- 57}$
Top	$3.0785 \cdot 10^{- 25}$	7.8840 $\cdot 10^{- 56}$
Bottom	$7.4515 \cdot 10^{- 27}$	$2.2806 \cdot 10^{- 56}$
Electron	$9.1094 \cdot 10^{- 31}$	$1.1319 \cdot 10^{- 57}$
Muon	$1.8835 \cdot 10^{- 28}$	$6.6931 \cdot 10^{- 57}$
Tau	$3.1675 \cdot 10^{- 27}$	$1.7148 \cdot 10^{- 56}$
Electron neutrino (6)	$2.3769 \cdot 10^{- 38} *$	$3.3572 \cdot 10^{- 60}$
Muon neutrino	$7.1306 \cdot 10^{- 38} *$	$4.8419 \cdot 10^{- 60}$
Tau neutrino	$1.1844 \cdot 10^{- 37} *$	$5.7407 \cdot 10^{- 60}$

*Neutrinos masses values are not certain (I used

\sum m_{ν} = 0.12 [e V]

and results I discovered later in the chapter “RishonisL” about neutrinos composition, which yields the appropriate NH.).

We know that the maximal radius of an up quark is

4.3 \cdot 10^{- 19} [m]

We also know the upper limit for the electron radius is

10^{- 22} [m]

(7)

Discussion: Empirical observations of quarks and leptons’ radii vastly exceed the magnitude observed if they were indeed elementary particles.

Their Dachus density varies with their type.

The apparent discrepancy in size is too significant to ignore, and they have different values for Dachus density in contrast to the equations for QBHs.

Therefore, because the only miniature structure that keeps quantization of Energy and charges for elementary particles is a QBH, I MUST conclude that quarks and leptons are NOT elementary particles.

Note: Quarks and leptons still exist and compose particles like protons and neutrons. (But they are not elementary particles.) The SM that describes them is very successful but imperfect: It has infinities corrected by mathematical procedures; it does not include gravity. It cannot explain dark Matter, Mass of elementary particles, quantization of elementary particles, size of elementary particles, neutrino oscillations, and more. This article explains and solves many of these problems (see summary in “Validity check” chapter.)

6. Rishonis

I name the real (new) elementary particles (QBHs) that compose quarks and leptons: “Rishonis.” The singular is “Rishoni” (from the Hebrew word “Rishoni,” which means first one.)

Naming:

Rishonis who build quarks: “RishonisQ.”

RishoniQ with a negative electric charge “NegativiumQ.” Plural form: “NegativiumsQ.”

RishoniQ with a positive electric charge: “PositiviumQ.” Plural form: “PositiviumsQ.”

Rishonis who build leptons: “RishonisL.”

RishoniL with a negative electric charge: “NegativiumL.” Plural form: “NegativiumsL.”

RishoniL with a positive electric charge: “PositiviumL.” Plural form: “PositiviumsL.”

All RishonisQ and RishonisL share the same Dachus density but have different compositions of charges.

To determine Rishonis’ charges, I must explore Energy types, charges, and forces.

7. Luminous and Hidden Energy

From observations: everything we directly observe has a QBH source.

Therefore, the only structures we can observe in space-time are the QBHs and their products, like photons, expanding Energy from QBHs charges, and the particles they build.

Luminous Energy Definition:

Luminous Energy aggregates all the QBHs and QBHs’ products Energy.

Our current observational devices cannot directly observe Energy that does not emanate from a QBH source.

Hidden Energy Definition:

Hidden Energy aggregates all charges and their Energies that are not part of Luminous Energy.

Hidden Energy is also known as “Dark Matter” (but as Energy composes everything in our Universe, and the term “Dark Energy’ is taken, I prefer the term hidden Energy.)

We can deduce hidden Energy existence by its influence on substantial structures in our Universe. (For example, the rotation speed of galaxies.) (8)

Scientists estimate the volume of the known Universe

U_{V} = 3.559 \cdot 10^{80} [m^{3}]

We estimate the Mass of the hidden Energy in the Universe

M (E_{H})

7.42857 \cdot 10^{53} [K g]

. (Energy in space-time (without Dark Energy) comprises close to 16.8% of Luminous Energy and 83.2% of Hidden Energy.) (9)

Therefore, the average density of hidden Energy in the observable Universe:

ρ_{H E} = \frac{M (E_{H})}{U_{V}} = 2.087269 \cdot 10^{- 27} [K g m^{- 3}]

Remark: the data above assume an inflationary Universe expansion, which may be wrong. Without an inflationary era

ρ_{H E} = \frac{M (E_{H})}{U_{V}} = 7.98541 \cdot 10^{- 26} [K g m^{- 3}]

Hidden Energy contains an extremely thin soup-like aggregate of gravitational, electric, and weak charges. In many cases, it also contains quarkic (color) charges.

The low density of hidden Energy charges (many orders of magnitude less than QBHs' Dachus density) emits very faint Energy and is, therefore, too faint to observe with current instruments.

Luminous Energy aggregates through quarks and leptons, atoms, molecules, gas clouds, stars, galaxies, and galaxy groups, clusters, and superclusters.

Hidden Energy surrounds Luminous Energy; in the case of attraction, it is denser near concentrations of corresponding Luminous Energy (for example, the center of the Milky Way galaxy). As gravitational charges have the most extensive range, they influence hidden Energy throughout space-time at varying degrees of density, creating the “Cosmic web.” Scientists still need more observation to detect the exact distribution of hidden Energy. (10)

Remark: Dark Energy influences the Universe's expansion. It is probably pure kinetic Energy without charges. (It is not part of this article.)

8. Charges and Their Influence on Space-Time Curvature

Charge Definition:

A charge is a Universe part that constantly emits Energy that changes the space-time curvature it encounters in a specific way attributed to the charge type.

Note: Charges continuously affect their neighborhoods by changing space-time curvature. Charges do that by their Energy and its momentum. (For brevity, from now on, whenever I refer to charge Energy that changes space-time curvature, it will always also include the momentum associated with this space-time curvature change.)

Every charge changes space-time curvature in an amount specific to the charge type.

Charges invest Energy in any change they affect.

The influence of charges propagates from the charge outward.

Therefore, charge Energy continues to propagate away from the charge, modifying the space-time curvature it encounters, as long as some charge's Energy (and momentum) remains.

Question: Can a Universe part possess several charge types on any scale (no matter how small)?

According to the “Completeness Principle,” Energy composes charges. Therefore, the question is: Can a Universe part possess several Energy (charges) types on any scale (no matter how small)?

As long as the combination of Energies does not exceed the Dachus density, several types of charges can coexist in the same volume (no matter how small)

In legacy terms, we use forces:

Force Definition:

A force is the influence of a Universe part’s charge on its surroundings with the same charge type. A force always causes a change in the influenced Universe part.

I name the point where the charge's Energy is completely spent: "Charge diminishing point." (Equivalently, where a force stops its effect: "Force diminishing point.")

Gravitational charges:

The gravitational charge diminishing point is the largest, maybe even up to the size of the Universe. Its value: ~ substantial part of the Universe’s size?

Electric charges: Magnetars can affect space-time up to several astronomical units away. (Other sources provide a much shorter range.) Therefore, the electric charge diminishing point is ~

{1 \cdot 10}^{12} [m]

. (We require additional data.)

Quarkic charges: The charge diminishing point of the quarkic charge is about the radius of the last stable nucleus – the 208 lead nucleus. Its value: ~

{7.61 \cdot 10}^{- 15} [m]

(11)

Weak charges: The weak charge diminishing point is the smallest. Its value:

{~ 1 \cdot 10}^{- 17}

. (12)

According to the "Locality Principle" and "Charge Definition," a charge Energy continuously propagates from the charge outward, changing the space-time curvature it encounters. Now imagine a particle that moves to a new neighborhood and has to change the new neighborhood and exert new Energy to do it. This perpetual state seems to contradict the "Energy Conservation Principle" since it implies a ceaseless Energy production at the charge location, which then ceaselessly expands from the charge outwards.

Surprisingly, from observations, this continuous influence does occur up to the charges' diminishing points.

Recalling the explanation of how the QBH guards' quantization, we know of just such a renewable Energy source: "Thus, when uncertainty-related Energy emerges within a QBH up to and including its border, the Matter density there cannot increase. Therefore, the uncertainty-related Energy exits the QBH swiftly."

This conclusion reveals exciting knowledge of space-time curvature behavior.

Every QBH repeatedly emits Energy, altering space-time curvature around it. A state of equilibrium forms: the ongoing charge's Energy from the QBH continuously tries to change space-time curvature. Space-time curvature resists and counters by trying to return to its initial flat state (The source of Newton's third law?). Thus, this space-time curvature remains "constant" - fluctuating around an equilibrium value.

Remark: Inside and at the border of the QBH, some uncertainty-related Energy keeps the substantial space-time curvature in check, and some propagates outside the QBH.

When a new QBH comes into play, it modifies the existing space-time curvature, creating a new, altered space-time curvature by simultaneously superpositioning its charges' Energy influences.

All charges have the same form of behavior. They emit Energy that propagates and changes space-time curvature. They emit radiation when accelerated. (2) (13)

This behavior embodies the "Uniformity of Physical Laws in the Universe Principle" applied to charges' Energy.

Constructing the equations for QBH influence on space-time curvature:

“Uniformity of Physical Laws in the Universe Principle” requires a tensorial form.

Premise: Space-time curvature exists at every point of space-time. According to the “Completeness Principle,” Energy also exists at every point in space-time. Whenever space-time curvature encounters charges’ Energy (and momentum) or kinetic Energy without charges, it changes. This same changed space-time curvature strives to be zero (“flat space-time curvature”): when Energy changes it, it will respond in an opposing manner, trying to return to its zeroth value - a state of equilibrium forms.

So, I can write an equation at a point in space-time that never encountered charge’s Energy or kinetic Energy (a hypothetical case):

R_{μ ν} - \frac{1}{2} R g_{μ ν} = 0

The equations that describe changes in space-time curvature need tensors of the curvature from one side and tensors of the Energy and its momentum on the other side. These equations cover the entire space-time because charges’ Energy and momentum (and in some cases kinetic Energy) and space-time curvature exist throughout all of space-time.

Specifically, the resulting equations describe the equilibrium point between the space-time curvature resisting change and the Energy enforcing change on the space-time curvature.

We can form an Energy-momentum tensor

(T_{μ ν - i})

in space-time as a (0,2) tensor. We know that the Energy-momentum tensor must follow the “Energy conservation Principle”; consequently, the Curvature tensors on the opposite side of the equation must do the same and be (0,2) tensors.

Therefore,

\nabla^{μ} {k_{i} T}_{μ ν - i} = 0

, and correspondingly

\nabla^{μ} ({(R i)}_{μ ν} - \frac{1}{2} (R i) g_{μ ν}) = 0

, where

k_{i}

is a conversion factor between the Energy and the curvature (I will discuss later), and “i” associates with charge

q_{i}

The result is four sets of equations, one for each charge (The first is EFE.)

Equation 4 Rishonis charges influence on space-time curvature

{(R G)}_{μ ν} - \frac{1}{2} (R G) g_{μ ν} = {k_{G} T}_{μ ν - G}, \forall r | r_{Q B H < r < r_{G}}

{(R E)}_{μ ν} - \frac{1}{2} (R E) g_{μ ν} = {k_{E} T}_{μ ν - E}, \forall r | r_{Q B H < r < r_{E}}

{(R W)}_{μ ν} - \frac{1}{2} (R W) g_{μ ν} = {k_{W} T}_{μ ν - W}, \forall r | r_{Q B H < r < r_{W}}

{(R Q)}_{μ ν} - \frac{1}{2} (R Q) g_{μ ν} = {k_{Q} T}_{μ ν - Q}, \forall r | r_{Q B H < r < r_{Q}}

{(R i)}_{μ ν}

is the Ricci curvature tensor of the charge

q_{i}

(R i)

is Ricci scalar of the charge

q_{i}

g_{μ ν}

is the metric.

T_{μ ν - i}

is the Energy-momentum (stress-Energy) tensor of the charge

q_{i}

k_{i}

is a conversion constant corresponding to the Energy expenditure of the charge

q_{i}

while changing space-time curvature. [Einstein calculated

k_{G} = \frac{8 π G}{c^{4}}

] (14) [I calculated

k_{E} = - \frac{2 q ρ_{E}}{m {c^{2} ϵ}_{0}^{2} E^{2}}

] (15)

r_{i}

is the charge

q_{i}

diminishing point.

These equations describe Luminous Energy sources. Each Rishoni type will have specific stress-Energy tensors according to its specific charges’ quantities.

What about hidden Energy?

Outside the QBH, other charges exist in small densities as hidden Energy. There, the uncertainty-related Energy that acts on them induces changes in space-time curvature:

Equation 5 Hidden Energy charges influence on space-time curvature

{(R i)}_{μ ν} - \frac{1}{2} (R i) g_{μ ν} = {k_{i} Λ}_{i}, \forall r | r_{Q B H < r < r_{i}}

Λ_{i}

is a tensor similar to

T_{μ ν - i}

for the charge

q_{i}

of hidden Energy and the uncertainty-related Energy acting on it. Only the hidden Energy of gravitational charges influences space-time curvature on cosmic scales. The electric charges spread evenly so their influence cancels on large scales. The other charges have tiny diminishing points, and their influence does not carry far.

Remark: I separated hidden Energy from Luminous Energy for clarity, as their charges' Energy sources exist in separate locations. I did not write equations for Dark Energy; they will appear in an article about the Cosmos expansion.

Note: When solving the equations of Rishonis' influence on space-time curvature, it is best to do so simultaneously, considering the sequence, the influences of charges' Energy and momentum reach the space-time curvature under consideration (taking into account the maximal speed of influence propagation.) This way, we will incorporate the non-linear terms that may appear in some equations in the correct sequence and ultimately produce the correct space-time curvature change value.

Note: A known path to produce equations of motion: Form an action as an integral of Lagrange density up to the charge diminishing point. Then, perform an extremization procedure on the action. (16)

Examining photons and space-time curvature produces very important results.

"Photons" are particles without rest Energy (known as rest Mass.) They only have kinetic Energy. They are chargeless.

I can express photons as stress-Energy tensors containing pure kinetic Energy and momentum (without rest Energy.)

From current observations, although chargeless, photons respond to gravitation and electric charges!

Using the “Uniformity of Physical Laws in the Universe Principle,” I deduced that the only way space-time curvature influences a chargeless particle can happen is if and only if all charges’ Energy or chargeless kinetic Energy change the same space-time curvature and all particles (with or without charges) follow space-time curvature. Thus, when a photon moves along space-time curvature, it follows it even though it is chargeless.

The photon cannot use its charge’s Energy influence on the space-time curvature because it has no charges. However, it has kinetic Energy and momentum, and with them, it can influence the space-time curvature, which is usually negligible.

Discussion: All charges change the same space-time curvature. However, electric and weak charges have two types of charges, marked “+” and “-“. The effect of the signs is mirrored in the space-time curvature. The same sign-charged particles always change space-time curvature in the same manner. So, a particle with a “+” sign electric charge will change the curvature of space-time around it in a way that when another particle with a “-“ electric charge that follows the space-time curvature appears, it will move towards the “+” electrically charged particle.

The gravitational and quarkic charges have only a single sign charge. They always change space-time curvature similarly – always causing attraction.

When we do the calculations of Rishonis charges, we notice that in very close range, all charges, have significant non-linear components in their stress-Energy tensors. These components change the space-time curvature most when they act on corresponding non-linear components of existing space-time curvature (a “compound accumulated effect”).

The weak and quarkic charges have short charge diminishing points and stop affecting the space-time curvature beyond these distances.

The electric charge has a significant diminishing point, but beyond atom nuclei sizes, it has an even electric charge distribution (in hidden Energy), and therefore, its space-time curvature effects over large distances cancel out.

Ony the gravitational charges affect space-time curvature on large scales.

9. RishonisQ

Discussion:

There are equal amounts of opposing electric charges in the Universe.

Both electric charges have the same intensity.

Only QBHs possesses net quantized electric charges (as Rishonis.)

Electric charges of hidden Energy (outside the QBHs) have an equal amount of opposing charges, even on a very small scale. Therefore, the net electric charge of hidden Energy is zero. So, when determining the quarks and leptons’ electric charge, I do not need to consider the “space” between the Rishonis that construct the quarks and leptons.

Therefore, the electric charge of any Rishoni will directly correspond to the charge of the quarks and leptons they construct. In the case of RishonisQ:

Table 2. Electric charge for RishonisQ.

Elementary particles	Electric charge $q_{E}$
PositiviumQ	+2e/3
NegativiumQ	-1e/3

Before continuing, I want to check the possible influence of hidden Energy on the structure of quarks and leptons :

If we take an Up quark, for example, its volume is

3.3304 \cdot 10^{- 55} [m^{3}]

, and the hidden Energy (presented as Matter) within this volume is

6.9541 \cdot 10^{- 82} [K g]

, which is

1.81 \cdot 10^{- 52}

of the total Mass of the Up quark – quite insignificant.

To identify the other charges of Rishonis, I plan to propose a structure that consists of Rishonis forming quarks and leptons. At the end of the article, in a "Sensitivity analysis," I will investigate the influence of other options for Rishonis' composition on the conclusions.

Using the "Occam Razor Rule," I will look for the least number of RishonisQ constituting the different quarks and the least number of RishonisL composing the different leptons.

Composite QBH definition:

Composite QBH is a compound particle composed of several QBHs.

To avoid a state of a quark composed of one elementary particle (that would return us to the original state of a quark as an elementary particle,) I need an electric neutral Composite QBH in addition to the charged RishoniQ. The simplest additional particle would be a composite particle with 2 NegativiumsQ and 1 PositiviumQ – which do not change the electric charge of the entire ensemble.

I name this neutral compound particle: "ImpartialQ."

When discussing QBHs, I have shown that all Rishonis have a single quantized Mass.

To get the values of PositiviumQ and NegativiumQ charges, I use the data known for quarks:

F o r u p, c h a r m a n d t o p q u a r k s : q_{E} = + \frac{2 e}{3}, q_{W} = + \frac{1 e}{3} . q_{Q} = + 1

F o r d o w n, s t r a n g e a n d b o t t o m q u a r k s : q_{E} = - \frac{1 e}{3}, q_{W} = - \frac{2 e}{3} . q_{Q} = + 1

Therefore:

An Up quark has 1 PositiviumQ and 1 ImpartialQ = 2 PositiviumQ + 2 NegativiumQ.

A Down quark has 1 NegativiumQ + 1 ImpartialQ = 1 PositiviumQ + 3 NegativiumQ.

Example for calculating charges: Equation for

q_{E}

(2 q_{E - N e g a t i v i u m Q} + 2 q_{E - P o s i t i v i u m Q} = \frac{2}{3}) \land (3 q_{E - N e g a t i v i u m Q} + 1 q_{E - P o s i t i v i u m Q} = - \frac{1}{3})

, yields:

q_{E - N e g a t i v i u m Q} = - \frac{1}{3}, q_{E - P o s i t i v i u m Q} = \frac{2}{3}

RishoniQ contains gravitational, electric, weak, and quarkic charges. To maintain its existence, the QBH attraction forces must overcome the repulsion forces, so the QBH does not disintegrate.

I use

q_{G} = X_{R} \cdot 1 e

(X_{R} \in R)

with a corresponding

C_{G}

to place all charges on the same footing. As there is only one

M_{Q B H}

(because there is only one

ρ_{D}

,) then, then there is only one

X_{R}

for all Rishonis.

Table 3. RishonisQ charges.

	Gravitational charge $q_{G}$	Electric charge $q_{E}$	Weak charge $q_{W}$	Quarkic charge $q_{Q}$
PositiviumQ	$1 X_{R} e$	+2e/3	7e/12	1e/4
NegativiumQ	$1 X_{R} e$	-1e/3	-5e/12	1e/4
ImpartialQ: 1 PositiviumQ + 2 NegativiumsQ	3 $X_{R}$ e	0e	-1e/4	3e/4
Up: 1 PositiviumQ + 1 ImpartialQ = 2 PositiviumQ + 2 NegativiumsQ	4 $X_{R}$ e	+2e/3	1e/3	1e
Down: 1 NegativiumQ + 1 ImpartialQ = 1 PositiviumQ + 3 NegativiumsQ	4 $X_{R}$ e	-1e/3	-2e/3	1e
Charm: 1 PositiviumQ + 2 ImpartialsQ + 1 antiImpartialQ = 3 PositiviumsQ + 4 NegativiumsQ + 1 anti PositiviumsQ + 2 antiNegativiumsQ	10 $X_{R}$ e	+2e/3	1e/3	1e
Strange: 1 NegativiumQ + 2 ImpartialsQ + 1 antiImpartialQ = 2 PositiviumsQ + 5 NegativiumsQ + 1 anti PositiviumsQ + 2 antiNegativiumsQ	10 $X_{R}$ e	-1e/3	-2e/3	1e
Top: 1 PositiviumQ + 3 ImpartialsQ + 2 antiImpartialsQ = 4 PositiviumsQ + 6 NegativiumsQ + 2 anti PositiviumsQ + 4 antiNegativiumsQ	16 $X_{R}$ e	+2e/3	1e/3	1e
Bottom: 1 NegativiumQ + 3 ImpartialsQ + 2 antiImpartialsQ = 3 PositiviumsQ + 7 NegativiumsQ + 2 anti PositiviumsQ + 4 antiNegativiumsQ	16 $X_{R}$ e	-1e/3	-2e/3	1e

10. RishonisL

Following the “Occam Razoe Principle,” I chose an electric neutral composite QBH particle for RishonisL with 1 NegativiumL and 1 PositiviumL. I call this neutral compound particle: “ImpartialL.”

RishoniL contains gravitational, electric, and weak charges. To maintain its existence, the QBH attraction forces must overcome the repulsion forces, so the QBH does not disintegrate.

11. Rishonis Mass Radius and Density

The complete, accurate solution of Rishonis Mass, radii, and Dachus density must incorporate the Rishonis influence over space-time curvature, but we do not yet possess the entire data. Instead, I used existing data about protons and quarks to calculate

M_{Q B H}

. The binding Energy inside a proton is ~99% of its Mass.

I chose the electron neutrino as the test case because it has the smallest Mass of quarks and leptons. A word of caution: the exact value of its Mass is not yet certain. However, the possible variance in its value does not change the article’s conclusions about QBHs as elementary particles, their charges (besides the gravitational charge), their charges quantization, and their impact on space-time curvature.

One PositiviumL and one NegativiumL compose an electron neutrino.

q_{P o s i t i v i u m L} = (q_{G}, q_{E}, q_{W}) = (1 X_{R} e, + 1 e, 2 e) .

q_{N e g a t i v i u m L} = (q_{G}, q_{E}, q_{W}) = (1 X_{R} e, - 1 e, - 1 e) .

As there is only one value for

M_{Q B H}

r_{Q B H}

, and

ρ_{D}

M_{P o s i t i v i u m L} = {M_{N e g a t i v i u m L} = M}_{P o s i t i v i u m Q} = {M_{N e g a t i v i u m Q} = M}_{Q B H} = \frac{M_{e l e c t r o n n e u t r i n o} \cdot (1 - (99 % b i n d i n g E n e r g y))}{2} \cdot 1 = 1.1884415 \cdot 10^{- 40} [K g]

Now I will solve the equation of the radius:

r_{P o s i t i v i u m L} = r_{N e g a t i v i u m L} = r_{P o s i t i v i u m Q} = r_{N e g a t i v i u m Q} = r_{Q B H} = \frac{\frac{2 \cdot M_{P o s i t i v i u m L} \cdot G}{c^{2}} + \sqrt{{(\frac{2 \cdot M_{P o s i t i v i u m L} \cdot G}{c^{2}})}^{2} - 4 \cdot \frac{25}{16} \cdot (\frac{e^{2} \cdot G}{c^{4}}) \cdot (C_{E} \cdot {(1)}^{2} + C_{W \cdot} {(1)}^{2})}}{\frac{50}{16}} = 5.648357 \cdot 10^{- 68} [m]

The radius calculation result yields only one value (the root is imaginary), as appropriate for a naked core.

ρ_{D} = \frac{3 M_{Q B H}}{4 π {\cdot (r_{Q B H})}^{3}} = 1.574428 \cdot 10^{161} [K g m^{- 3}]

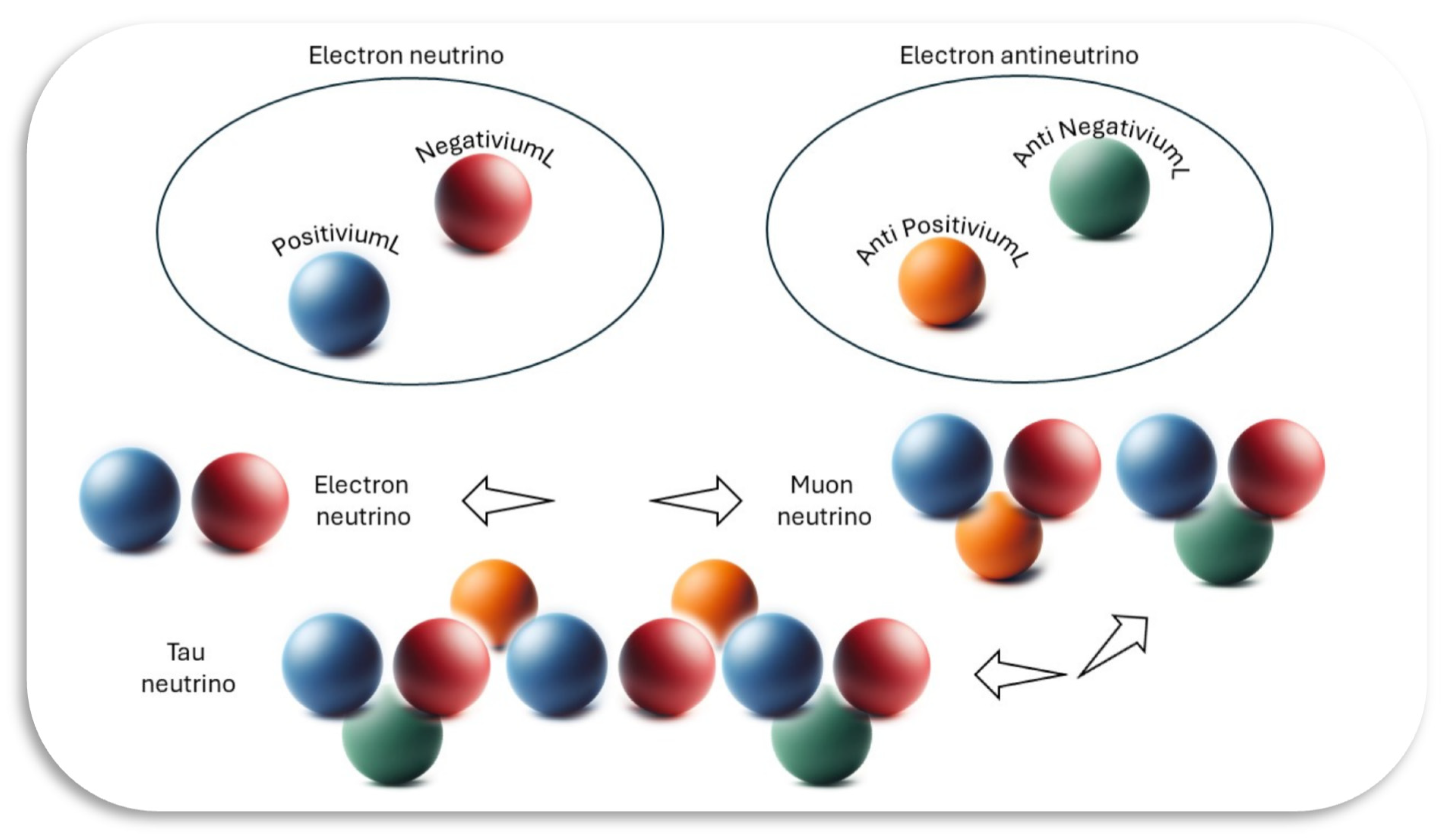
12. Neutrinos oscillations

Neutrino oscillations are easy to explain by adding or removing electron neutrinos and electron antineutrinos as required – see Table 4 RishonisL charges.

Table 4. RishonisL charges.

	Gravitational charge $q_{G}$	Electric charge $q_{E}$	Weak charge $q_{W}$
PositiviumL	$1 X_{R} e$	1e	2e
NegativiumL	$1 X_{R}$ e	-1e	-1e

Electron neutrino = 1 PositiviumL + 1 NegativiumL	$2 X_{R} e$	0	1e
Electron lepton = 1 NegativiumL + 1 Electron neutrino	3 $X_{R}$ e	-1e	0

Muon neutrino = 2 electron neutrinos + 1 electron antineutrino	$6 X_{R} e$	0	1e
Muon lepton = 1 NegativiumL + 1 Muon neutrino	$7 X_{R} e$	-1e	0

Tau neutrino = 3 electron neutrinos + 2 electron antineutrinos	$10 X_{R} e$	0	1e
Tau lepton= 1 NegativiumL + 1 Tau neutrino	$11 X_{L} e$	-1e	0

Figure 1. Neutrinos oscillations.

13. QBH Spin-Like Quality Origin

New possibility: Now that I have shown that Rishonis gravitational charges are quantized, have a non-zero volume, and revolve relativistically fast, it is plausible to talk about the origin of Rishonis quantized spin-like quality as an intrinsic angular momentum of non-zero-volume QBHs with the same Mass, radius, and angular velocity.

14. Compound Particles Half Lives

Protons, neutrons, electrons, and electron neutrinos are composed exclusively of Rishonis, without their corresponding antiRishonis. This unique composition is a crucial factor contributing to their exceptionally long half-lives, leading to the widespread assumption that they are stable. In contrast, other particles, characterized by a composition that includes both Rishonis and antiRishonis, exhibit significantly shorter half-lives. This is primarily due to the potential for annihilation events between Rishonis and antiRishonis within these particles, resulting in their more transient nature.

15. Discovering Hidden Energy

As hidden Energy (dark Matter) is a very thin soup-like mixture of all charges, we can discover it by looking for very lethargic photons.

For example, a quark size hidden Energy Universe part, moving at

2,000 [K m s^{- 1}]

, has a de Broglie wavelength of

3.8 \cdot 10^{43} [m]

16. Validity Check

Direct observations of Rishonis are beyond the ability of current particle accelerators.

However, the resultant neutrino oscillations are not!

As opposed to the standard model, I have successfully explained the following:

The nature of elementary particles (QBH.)
Quantization of gravitational charges.
Neutrinos oscillations source.
The nature of Dark Matter.
The nature of Luminous Matter.
Sizes of quantization of all charges of all elementary particles.
Sizes ([m]) of elementary particles.
The Dachus density existence and value.
The origin of a quantized spin-like quality in QBHs.
The source of protons, neutrons, and electrons stability versus other particles.
The influence of charges on space-time curvature.
The equations that govern all Luminous and hidden Energy local movements in space-time.

Therefore, as the only theory that (easily) explains the source of observed neutrinos' oscillations, some compound particle longevity, the source of spin-like quality of elementary particles, and solves many deficiencies of the SM, I have established this article's validity.

17. Sensitivity Analysis

Binding energies

The exact value of

M_{P o s i t i v i u m L}

is not certain. What will happen if it changes?

In this article, I assumed 99% as the guide for the value of binding Energy, yielding

M_{Q B H} = \frac{M_{e l e c t r o n n e u t r i n o} \cdot (1 - (99 % b i n d i n g E n e r g y))}{2} \cdot 1 = 1.1884415 \cdot 10^{- 40} [K g]

Let me test what occurs when the binding Energy is 1% instead of 99%.

M_{Q B H} = \frac{M_{e l e c t r o n n e u t r i n o} \cdot (1 - (1 % b i n d i n g E n e r g y))}{2} \cdot 1 = 1.176557 \cdot 10^{- 38} [K g]

. The result is roughly two magnitude orders larger than the article's value. Changing the value of the binding Energy percent, only affects the radius

(5.591873 \cdot 10^{- 66} [m])

, Mass, and Dachus density

(1.606396 \cdot 10^{+ 157} [K g m^{- 3}])

of Rishonis. The new binding Energy does not change the non-gravitational charges values of any Rishoni. All Rishonis are still QBHs that affect space-time curvature. Therefore, the characteristics and essential conclusions of the article will not change.

Number of constituents Rishonis

What will happen if the number of Rishonis composing quarks and leptons is much higher than the proposed model?

The Mass, radii, and charge values will change in this case. However, the conclusions will not change; elementary particles are still QBHS that change space-time curvature.

Additional options for Rishonis charges

There is another alternative to RishonisQ compositions, one that does not require quarks to possess antiRishonisQ at the cost of many more RishonisQ (12 types instead of 2):

Table 5. Alternative RishonisQ charges.

	Gravitational charge $q_{G}$	Electric charge $q_{E}$	Weak charge $q_{W}$	Quarkic charge $q_{Q}$
PositiviumQ-up	$1 X_{R} e$	+2e/3	1e/3	1e/4
NegativiumQ-up	$1 X_{R} e$	-1e/3	-1e/6	1e/4
Up quark = 1 PositiviumQ-up + 1 ImpartialQ-up	4 $X_{R}$ e	+2e/3	+1e/3	1e

PositiviumQ-charm	$1 X_{R} e$	+2e/3	1e/3	1e/7
NegativiumQ-charm	$1 X_{R} e$	-1e/3	-1e/6	1e/7
Charm quark = 1 PositiviumQ- charm + 2 ImpartialsQ- charm	7 $X_{R}$ e	+2e/3	+1e/3	1e

PositiviumQ-top	$1 X_{R} e$	+2e/3	1e/3	1e/10
NegativiumQ-top	$1 X_{R} e$	-1e/3	-1e/6	1e/10
Top quark = 1 PositiviumQ-top + 3 ImpartialsQ-top	10 $X_{R}$ e	+2e/3	+1e/3	1e

PositiviumQ-down	1 $X_{R}$ e	+2e/3	-2e/3	1e/4
NegativiumQ-down	1 $X_{R}$ e	-1e/3	1e/3	1e/4
Down quark = 1 NegativiumQ-down + 1 ImpartialQ-down	4 $X_{R}$ e	-1e/3	-2e/3	1e

PositiviumQ-strange	1 $X_{R}$ e	+2e/3	-2e/3	1e/7
NegativiumQ-strange	1 $X_{R}$ e	-1e/3	1e/3	1e/7
Strange quark = 1 NegativiumQ- strange + 2 ImpartialsQ- strange	7 $X_{R}$ e	-1e/3	-2e/3	1e

PositiviumQ-bottom	1 $X_{R}$ e	+2e/3	-2e/3	1e/10
NegativiumQ-bottom	1 $X_{R}$ e	-1e/3	1e/3	1e/10
Bottom quark = 1 NegativiumQ- bottom + 3 ImpartialsQ- bottom	10 $X_{R}$ e	-1e/3	-2e/3	1e

The same for Leptons without antiRishonisL (at the cost of 6 types instead of 2):

Table 6. Alternative RishonisL charges.

	Gravitational charge $q_{G}$	Electric charge $q_{E}$	Weak charge $q_{W}$
PositiviumL-electron	$1 X_{R} e$	1e/2	1e
NegativiumL-electron	$1 X_{R}$ e	-1e	-1e

Electron neutrino = 1 NegativiumL-electron + 2 PosiviumsL-electron	$3 X_{R} e$	0	1e

Electron lepton = 1 NegativiumL-electron + 1 electron neutrino	$4 X_{R} e$	-1e	0

PositiviumL-muon	$1 X_{R}$ e	1e/2	3e/4
NegativiumL-muon	$1 X_{R}$ e	-1e	-1e
Muon neutrino	$6 X_{R} e$	0	1e
Muon lepton	$7 X_{R} e$	-1e	0

PositiviumL-tau	$1 X_{R}$ e	1e/2	2e/3
NegativiumL-tau	$1 X_{R}$ e	-1e	-1e
Tau neutrino	$9 X_{R} e$	0	1e
Tau lepton	$10 X_{R} e$	-1e	0

This alternate version is more complicated and does not explain neutrino oscillations or the shorter half-life of some particles. Only experimental data will decide which occurs.

Both choices of the Rishonis types provide a Cosmos where QBHs are the elementary particles that influence space-time curvature.

18. Conclusions

Rishonis – the elementary particles in space-time are Quantum black holes: miniature, relativistically fast rotating spheres at Dachus state (slightly oblated) that are naked cores. They keep quantization of all charges (including the gravitational charge) and spin.

Rishonis, in different combinations, compose all quarks and leptons.

The Dachus density (according to available data) is

ρ_{D} \approx 1.574428 \cdot 10^{161} [K g m^{- 3}]

Rishonis Energy is replenished by the uncertainty-related Energy that appears in them.

All Rishonis release Energy that changes the space-time curvature it encounters.

The uncertainty-related Energy within Rishonis (including their border) maintains the highly curved space-time curvature inside the QBH. Some of this Energy exits the QBH, expands outward, and changes space-time curvature as far as the QBH's charges diminishing points.

Space-time curvature strives to return to its flat state.

The space-time curvature value is an oscillation of values around an equilibrium value between the QBH charge’s Energy, which changes the space-time curvature at a point and the reaction of the space-time curvature trying to revert to its flat state.

References

Evidence for large-scale uniformity of physical laws.Tubbs, A. D. s.l. : The Astrophysical Journal, Vol. 236. [CrossRef]
C.W. Misner, K. S. Thorne, J. A. Wheeler. Gravitation. s.l. : W. H. Freeman.
On the Dependence of the Relativistic Angular Momentum of a Uniform Ball on the Radius and Angular Velocity of Rotation.F., Sergey G. s.l. : International Frontier Science Letters, Vol. 15. [CrossRef]
Goldberg, Dave. The Standard Model in a Nutshell. s.l. : Princeton University Press, 2017.
Group, Particle Data. https://pdg.lbl.gov/2022/booklet/2022dev/2022/summary-tables.html. [Online] 2022.
Updated results on neutrino mass and mass hierarchy from cosmology with Planck 2018 likelihoods.Choudhury, Shouvik Roy. s.l. : https://arxiv.org/pdf/1907.12598.pdf. [CrossRef]
Direct neutrino-mass measurement with sub-electronvolt sensitivity.Collaboration, The KATRIN. 18, s.l. : nature physics, 2022. [CrossRef]
Limits on the effective quark radius from inclusive ep scattering at HERA.Collaboration, ZEUS. s.l. : Physics Letters B, 2016. [CrossRef]
Dehmelt, Hans. A Single Atomic Particle Forever Floating at Rest in Free Space: New Value for Electron Radius. Physica Scripta. 1988, Vol. 102. [CrossRef]
Corbelli, Edvige. The extended rotation curve and the dark matter halo of M33. Astronomical society. 2000. [CrossRef]
https://www.wolframalpha.com/input/?i=size+of+universe. Size of the Universe.
Weakly Interacting Stable Pions.Bai, Yang. 2010. [CrossRef]
On the dark matter distribution in the Milky Way.Iocco, Fabio. 718, s.l. : J. Phys.: Conf. Ser. [CrossRef]
Constraints on neutron skin thickness in 208Pb and density-dependent symmetry energy.Dong, Jianmin. s.l. : Phys. Rev. C, 2015, Vol. 91. [CrossRef]
ON The Bosons’ Range of The Weak Interaction.PUCCINI, Antonio. 3, s.l. : Journal of Advances in Physics, Vol. 14. [CrossRef]
Griffiths, David 1. Introduction to Electrodynamics. s.l. : Prentice Hall, 1999.
Janssen, Michel and Renn, Jürgen. How Einstein Found His Field Equations: Sources and Interpretation. s.l. : Springer Nature, 2022.
Electric charge influence on space-time curvature.Lavi, E. M. s.l. : Zenodo, 2023. [CrossRef]
Sean, Carroll. Spacetime and geometry an introduction to general relativity. s.l. : Pearson, 2014.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

306

Views

Comments

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Elementary Particles and Their Interaction with Space-Time Curvature

Abstract

Keywords:

Subject:

1. Preliminaries

2. Limits

3. Quantum Black Holes

4. Elementary Particles Must Be QBHs

5. Quarks and Leptons as QBH?

6. Rishonis

7. Luminous and Hidden Energy

8. Charges and Their Influence on Space-Time Curvature

9. RishonisQ

10. RishonisL

11. Rishonis Mass Radius and Density

12. Neutrinos oscillations

13. QBH Spin-Like Quality Origin

14. Compound Particles Half Lives

15. Discovering Hidden Energy

16. Validity Check

17. Sensitivity Analysis

18. Conclusions

References

MDPI Initiatives

Important Links

Subscribe