Submitted:
19 January 2024
Posted:
22 January 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Data and Methods
2.1. Data
2.2. Methods
3. Results
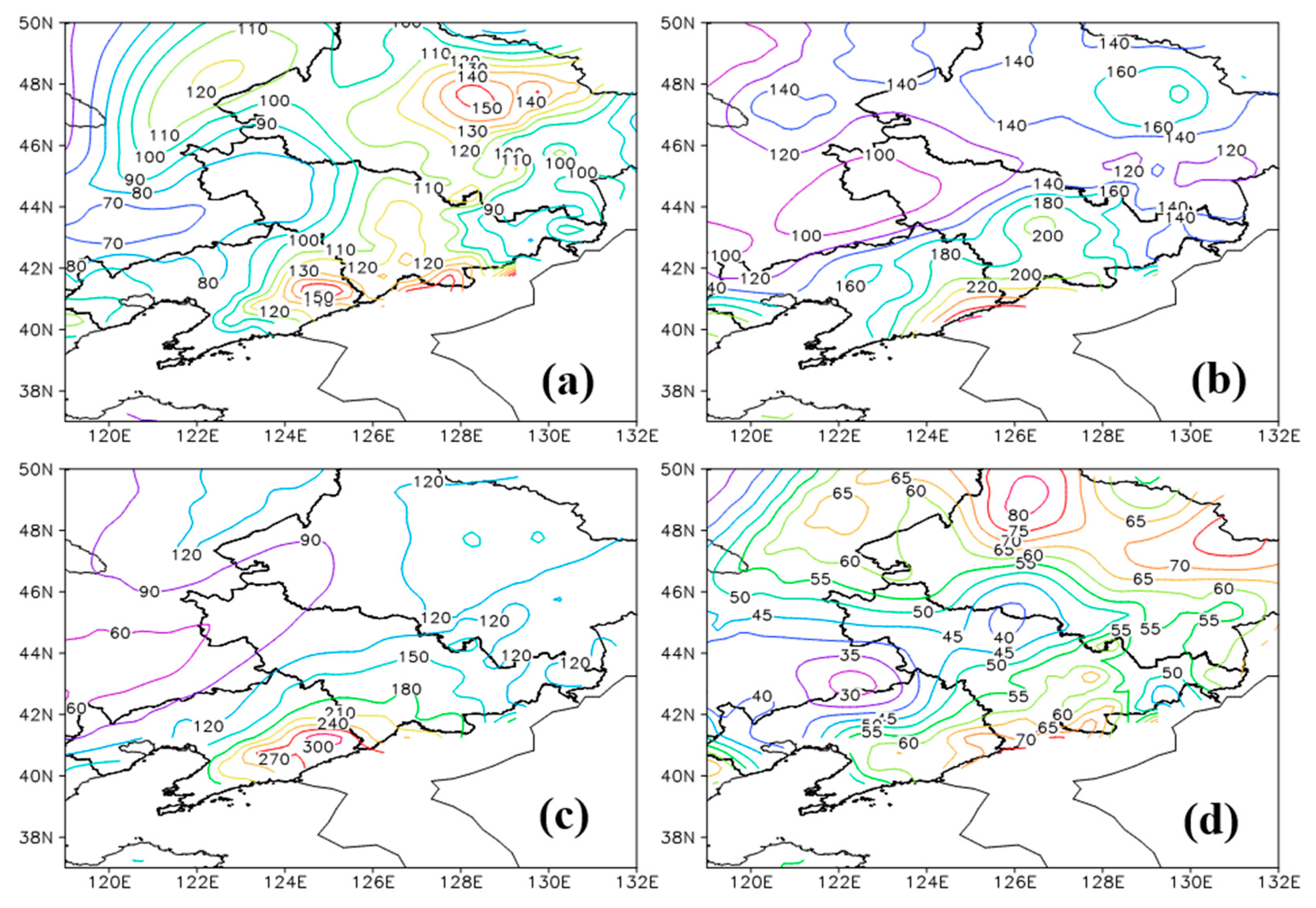
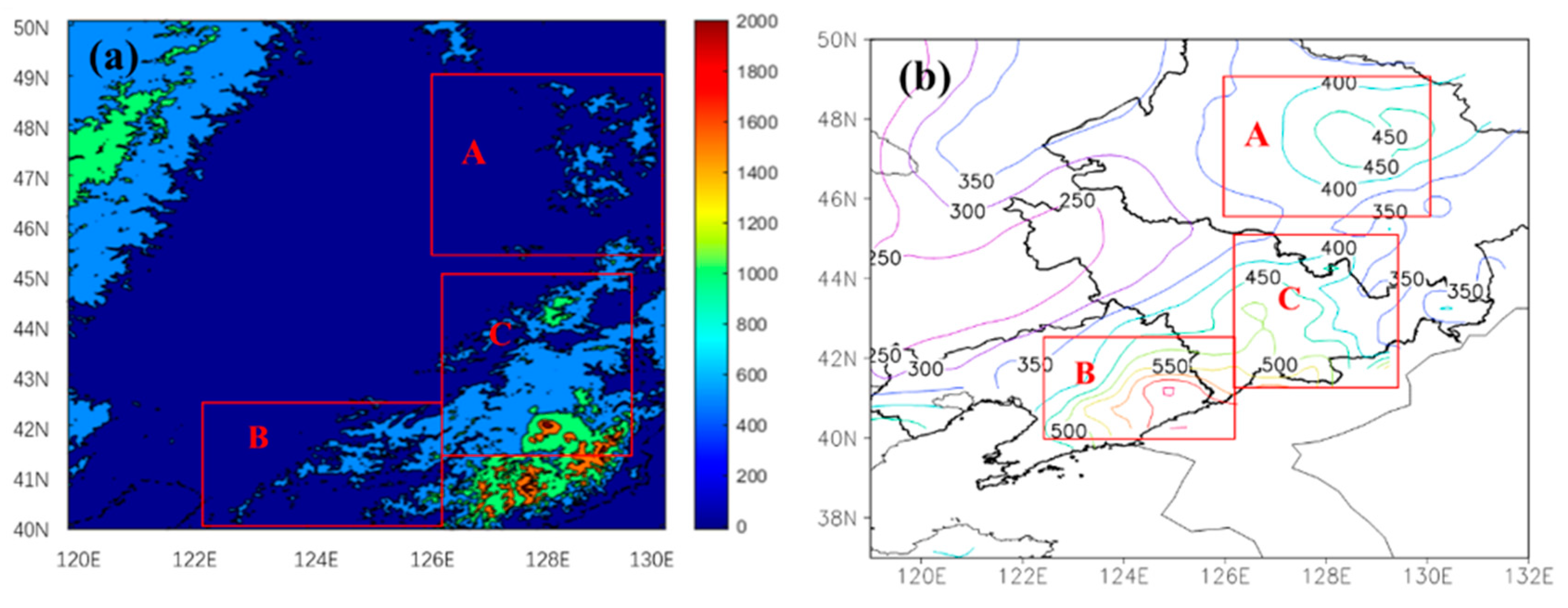
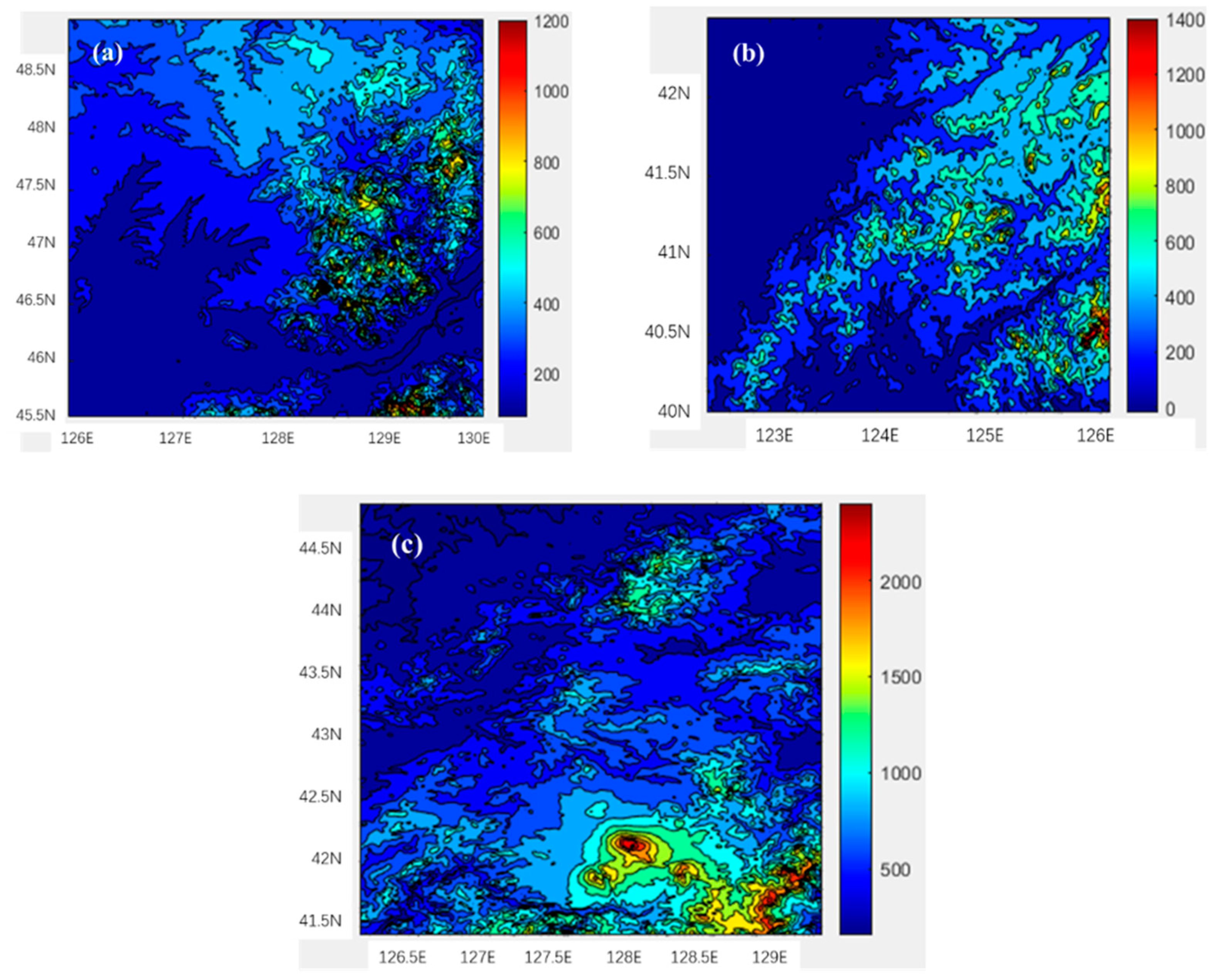
3.1. Precipitation Distribution in Changbai Mountain Region and Selection of Study Region
3.2. The Terrain Spectra of Changbai Mountain Region
3.3. The Spectral Analysis of Terrain, Precipitation and Wind Field
4. Discussion and Conclusions
References
- Sun, W.Y.; Mu, X.M.; Song, X.Y.; Wu, D.; Cheng, A.F.; Qiu, B. Changes in extreme temperature and precipitation events in the Loess Plateau (China) during 1960–2013 under global warming. Atmosphere 2016, 168, 33–48. [Google Scholar] [CrossRef]
- Zhao, Y.F.; Zou, X.Q.; Cao, L.G.; Xu, X. Changes in precipitation extremes over the Pearl River Basin, southern China, during 1960–2012. Quat. Int. 2014, 333, 26–39. [Google Scholar] [CrossRef]
- Domroes, M.; Schaefer, D. Recent climate change affecting rainstorm occurrences: a case study in East China. Clim. Past, 2008, 4, 303–309. [Google Scholar] [CrossRef]
- Chen, S.J.; Wang, W.; Lau, K.H.; Zhang, Q.H.; Chung, Y.S. Mesoscale convective systems along the Meiyu front in a numerical model. Meteorol. Atmos. Phys. 2000, 75, 149–160. [Google Scholar] [CrossRef]
- Hu, B.W.; Cui, C.G.; Fang, C.H. Causes of a two-day successively heavy rain along the Changjiang Valley in the eastern Hubei Province during 21–22 July 1998. Chinese J. Atmos. Sci. 2001, 25, 479–491. (In Chinese) [Google Scholar]
- Ding, Z.Y.; Zhang, X.Q.; Shou, S.W. Analysis of relation of South Asia High and rainstorm caused by northwesterly upper-level jet. J. Appl. Meteor. Sci. 2002, 13, 671–679. (In Chinese) [Google Scholar]
- Chen, J.; Liu, L. Characteristics of urban rainstorm and its disaster cause over Beijing in flood season of 2011. Torrential Rain Disasters 2011, 30, 282–287. (in Chinese). [Google Scholar]
- Wang, C.X.; Gao, S.T.; Liang, L.; Ding, D.F.; Gong, H.N. Multi-scale characteristics of moisture transport during a rainstorm process in North China. Atmos. Res. 2014, 145–146, 189–204. [Google Scholar] [CrossRef]
- Scorer, R.S. Theory of waves in the lee of mountains. Q. J. R. Meteorol. Soc. 1949, 75, 41–56. [Google Scholar] [CrossRef]
- Mclntyre, M.E. On Long’s hypothesis of no upstream influence in uniformly stratified or rotating flow. J. Fluid Mech. 1972, 52, 209–243. [Google Scholar] [CrossRef]
- Klemp, J.B.; Lilly, D.K. Numerical simulation of hydrostatic mountain waves. J. Atmos. Sci. 1978, 35, 78–107. [Google Scholar] [CrossRef]
- Tucker, D.F.; Reiter, E.R. Modeling heavy precipitation in complex terrain. Meteorol. Atmos. Phys. 1988, 39, 119–131. [Google Scholar] [CrossRef]
- Johnson, G.L.; Hanson, C.L. Topographic and atmospheric influences on precipitation variability over a mountainous watershed. J. Appl. Meteor. 1995, 34, 68–87. [Google Scholar] [CrossRef]
- Aebischer, U.; Schar, C. Low-level potential vorticity and cyclogenesis to the lee of the Alps. J. Atmos. Sci. 1998, 55, 186–207. [Google Scholar] [CrossRef]
- Jiang, Q.F. Precipitation over concave terrain. J. Atmos. Sci. 2006, 63, 2269–2288. [Google Scholar] [CrossRef]
- Jiang, Q.F. Precipitation over multiscale terrain. Tellus. 2007, 59, 321–335. [Google Scholar] [CrossRef]
- Steeneveld, G.J.; Holtslag, A.A.M.; Nappo, C.J.; van de Wiel, B.J.H.; Mahrt, L. Exploring the possible role of small-scale terrain drag on stable boundary layers over land. J. Appl. Meteor. Climatol. 2008, 47, 2518–2530. [Google Scholar] [CrossRef]
- Jia, B.S.; Jia, F.N.; Zhang, W.T.; Liu, G.Y.; Cui, Z.Q. Analysis of heavy rainstorm weather process in Jilin province from July 13 to 14, 2017. Modern Agricultural Science and Technology 2021, 4, 176–180. (In Chinese) [Google Scholar]
- Yu, J.H.; Gong, Y.F.; Mao, W.S. Comparative analysis on two extreme severe precipitation events in Yongji county, Jinlin province in July 2017. J. Chengdu University of information technology 2019, 3, 287–296. (In Chinese) [Google Scholar]
- Zhang, L.; Li, Z.C. The reason of a heavy rain event in Nenjiang valley in August, 1998. Meteor. Mon. 2003, 8, 7–12. (In Chinese) [Google Scholar]
- Zheng, X.Y.; Zhang, Y.Z.; Bai, R.H. Rainstorm in Northeast China; Meteorology Press: Beijing, China, 1992; pp. 142–145. [Google Scholar]
- He, B.H.; Sun, J.Q.; Yu, E.T.; Wang, H.J.; Zhang, M.Q.; Hua, W. Simulation study on the Influence of the great Khingan Strip and Changbai Mountain on summer rainfall in Northeast China. Climatic and Environmental Research 2020, 3, 268–280. (in Chinese). [Google Scholar]
- Liu, C.H.; Wang, Y.; Yan, Q.; Tan, Z.H.; Liu, S.; Jiao, H.R.; Jin, Y. Impact of flow over and flow around caused by super low-level jet on a sudden rainstorm over the Changbai Mountains. Torrential Rain Disaster. 2023, 3, 273–282. (in Chinese). [Google Scholar]
- Pielke, R.A.; Kennedy, E. Mesoscale Terrain Features. Report UVA-ENV SCI-MESO-1980-1; University of Virginia: Charlottesville, VA, USA, 1980; p. 19. [Google Scholar]
- Young, G.S.; Pielke, R.A. Application of terrain height variance spectra to mesoscale modeling. J. Atmos. Sci. 1983, 40, 2555–2560. [Google Scholar] [CrossRef]
- Young, G.S.; Pielke, R.A.; Kessler, R.C. A comparison of the terrain height variance spectra of the Front Range with that of a hypothetical mountain. J. Atmos. Sci. 1984, 41, 1249–1252. [Google Scholar] [CrossRef]
- Srinivasan, K.; Ramanathan, N. Terrain variance spectra for Indian Western Ghats. Proc. Indian natn Sci. Acad. 1994, 60A, 133–138. [Google Scholar]
- Ramanathan, N.; Srinivasan, K. An estimation of optimum grid size for Kashmir Valley by spectral method. J. Appl. Meteor. 1995, 34, 2783–2786. [Google Scholar] [CrossRef]
- Steyn, D.G.; Ayotte, K.W. Application of two-dimensional terrain height spectra to mesoscale modeling. J. Atmos. Sci. 1985, 42, 2884–2887. [Google Scholar] [CrossRef]
- Salvador, R.; Calbo, J.; Millan, M.M. Horizontal grid size selection and its influence on mesoscale model simulations. J. Appl. Meteor. 1999, 38, 1311–1329. [Google Scholar] [CrossRef]
- Wang, C.X.; Liang, L.; Zhang, W.C.; Gao, S.T.; Yang, S. The Impact of Improved Topographic Resolution on the Distribution of Terrain Spectra and Grid-Size Selection for Mesoscale Models. Atmosphere 2022, 13, 708. [Google Scholar] [CrossRef]
- Wang, W.T.; Wang, Y. A spectral analysis of satellite topographic profile: A coincident pattern between latitudinal topographic and westerly perturbation on the lee side of Qinghai-Tibet Plateau. J. Nanjing Univ. 2004, 40, 304–317. (In Chinese) [Google Scholar]
- Shu, S.J.; Wang, Y.; Li, Y. Effect of topographic perturbation on the precipitation distribution in Tibetan Plateau. Adv. Water Sci. 2006, 17, 585–591. (In Chinese) [Google Scholar]
- Denis, B.; Cote, J.; Laprise, R. Spectral decomposition of two-dimensional atmospheric fields on limited-area domains using the discrete cosine transform (DCT). Mon. Wea. Rev. 2002, 130, 1812–1829. [Google Scholar] [CrossRef]
- Zheng, Y.J.; Jin, Z.Y.; Chen, D.H. Kinetic energy spectrum analysis in a semi-implicit semi-Lagrangian dynamical frame work. Acta Meteor. Sinica 2008, 70, 371–386. (In Chinese) [Google Scholar]
- Jiang, C.; Shen, X.S. Assessment of the simulative performance of the GRAPES model on the convective boundary layer based on the large eddy simulations. Acta Meteor. Sinica 2013, 71, 879–890. (In Chinese) [Google Scholar]
- Prein, A.F.; Holland, G.J.; Rasmussen, R.M. Importance of regional climate model grid spacing for the simulation of heavy precipitation in the Colorado Headwaters. J. Climate 2013, 26, 4848–4857. [Google Scholar] [CrossRef]
- Ricard, D.; Lac, C.; Riette, S.; Legrand, R.; Mary, A. Kinetic energy spectra characteristics of two convection-permitting limited-area models AROME and Meso-NH. Q. J. R. Meteorol. Soc. 2013, 139, 1327–1341. [Google Scholar] [CrossRef]
- Huang, Y.J.; Cui, X.P. Spectral characteristics of terrain in the Sichuan basin and the horizontal grid size selection for a mesoscale model. Acta Meteor. Sinica 2016, 1, 114–126. (In Chinese) [Google Scholar]
- Pan, Y.; Shen, Y.; Yu, J.J.; Zhao, P. Analysis of the combined gauge-satellite hourly precipitation over China based on the OI technique. Acta Meteor. Sinica 2012, 6, 1381–1389. (In Chinese) [Google Scholar]
- Pielke, R.A. Mesoscale Meteorological Modeling; Academic Press: SanDiego, CA, USA, 1984; p. 599. [Google Scholar]
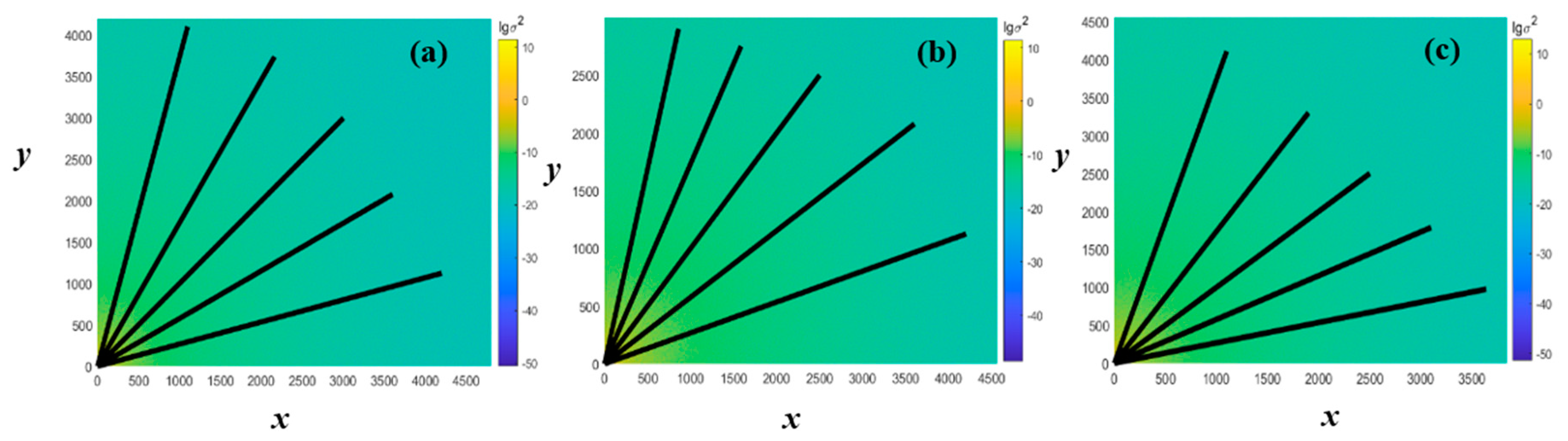
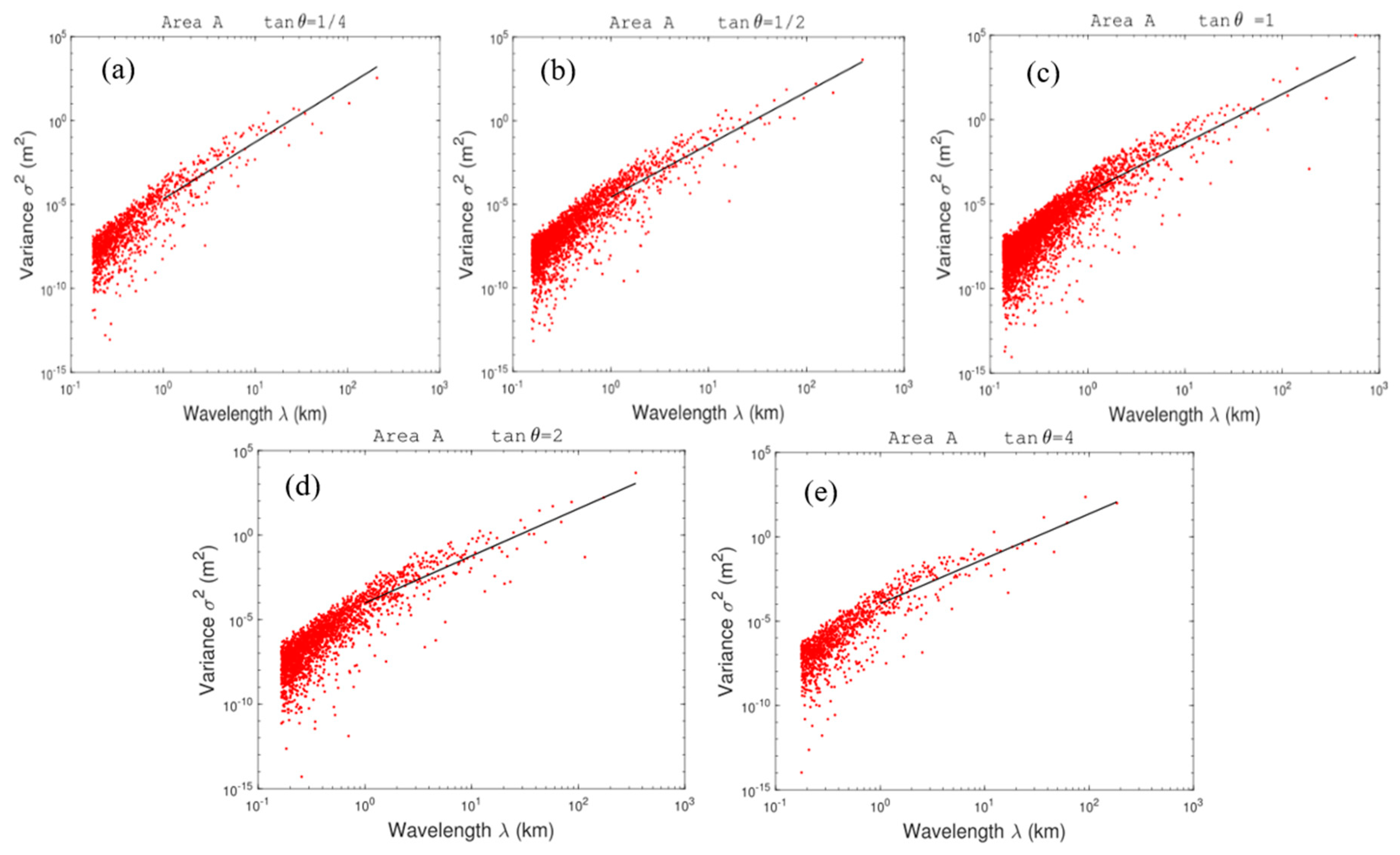
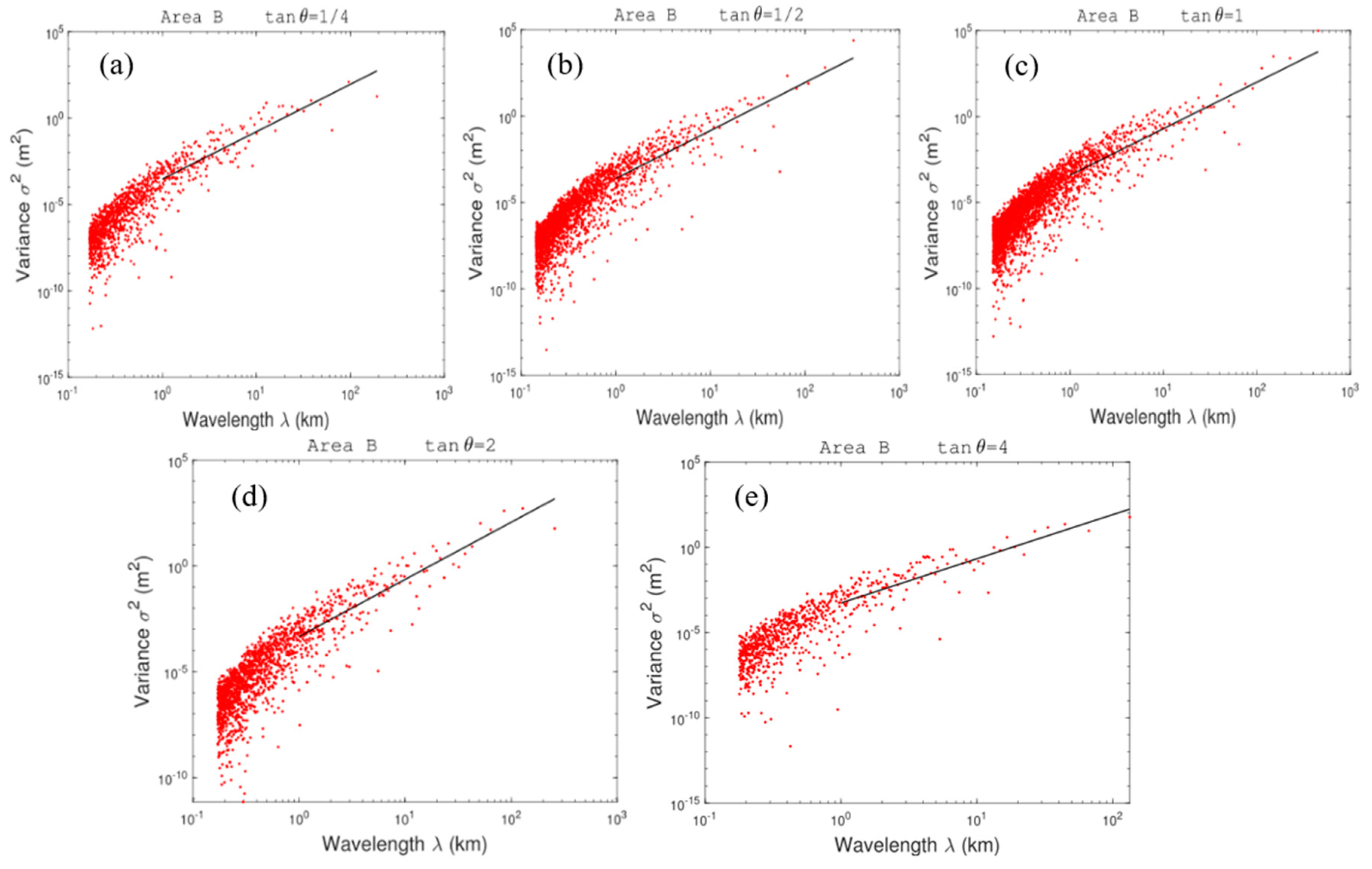
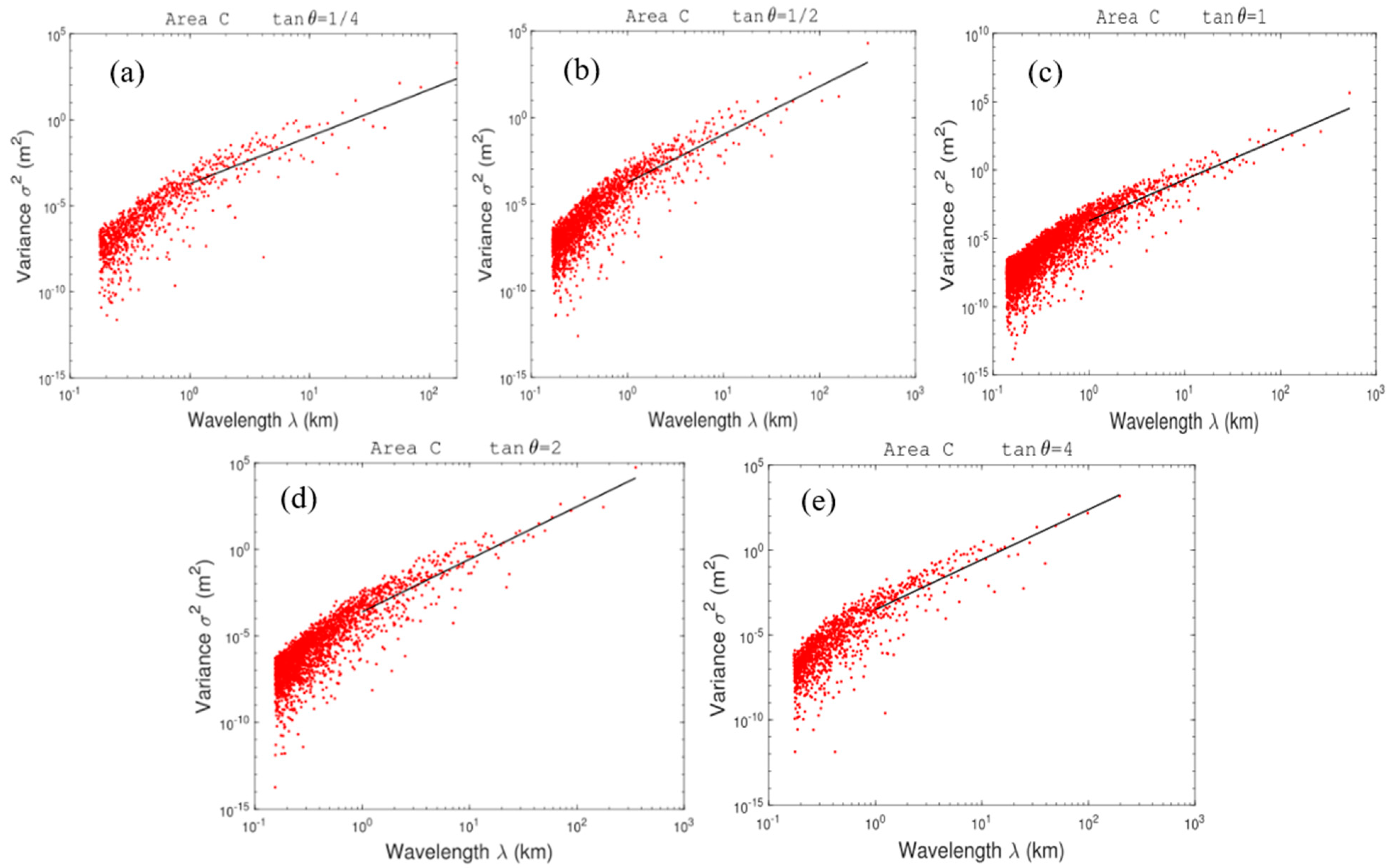
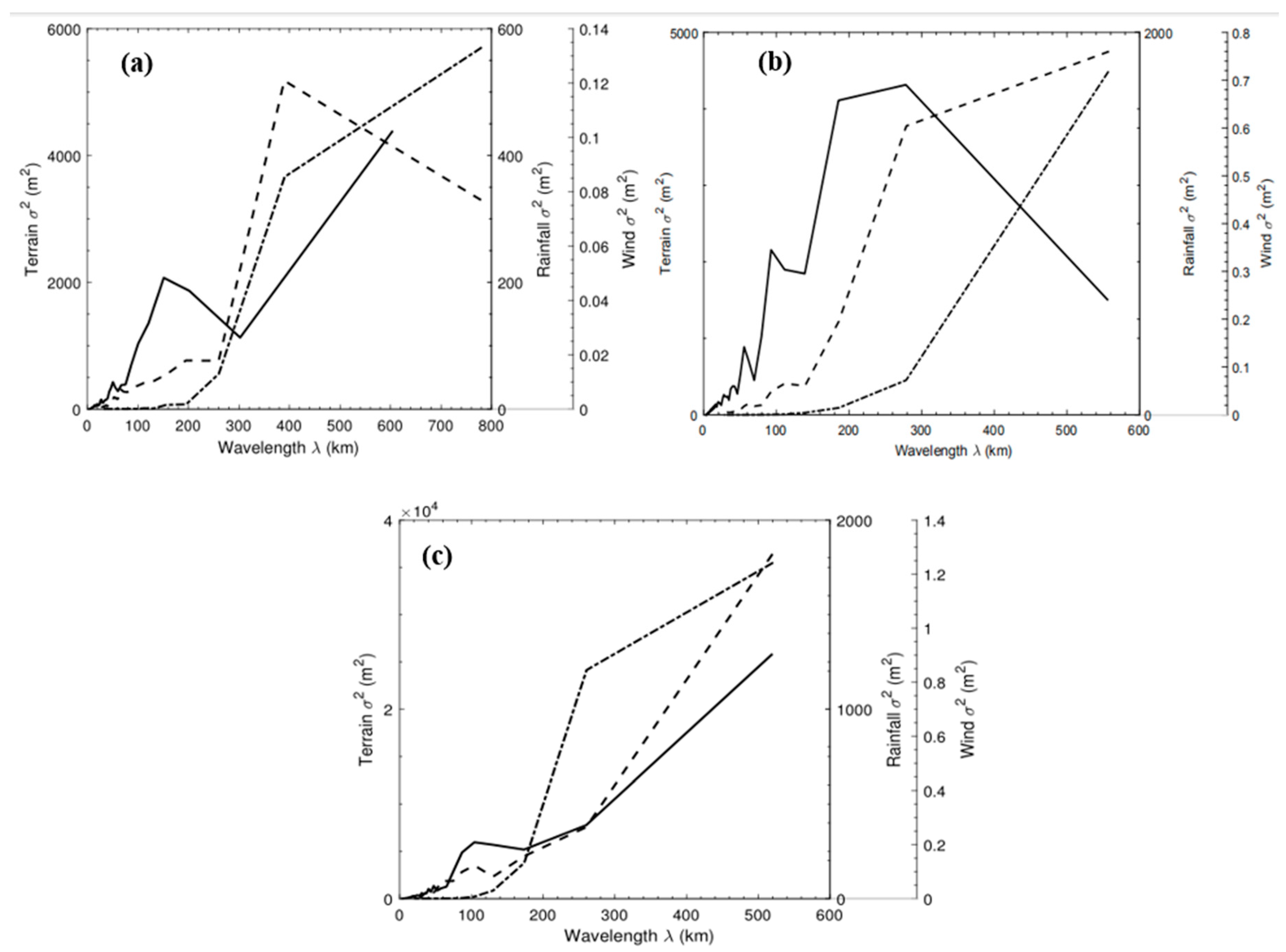
| Domain | tan θ | 1/4 | 1/2 | 1 | 2 | 4 | Average |
| A |
a(10-4) b r |
0.21 3.40 0.94 |
0.27 3.14 0.93 |
0.50 2.90 0.93 |
0.94 2.79 0.93 |
1.07 2.66 0.92 |
0.60 2.98 |
| B |
a(10-4) b r |
2.90 2.75 0.93 |
2.37 2.78 0.94 |
3.80 2.70 0.91 |
4.50 2.70 0.92 |
5.41 2.59 0.91 |
3.80 2.70 |
| C |
a(10-4) b r |
1.90 2.74 0.90 |
1.70 2.77 0.90 |
1.87 3.03 0.91 |
2.38 3.04 0.92 |
3.03 2.95 0.91 |
2.18 2.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




