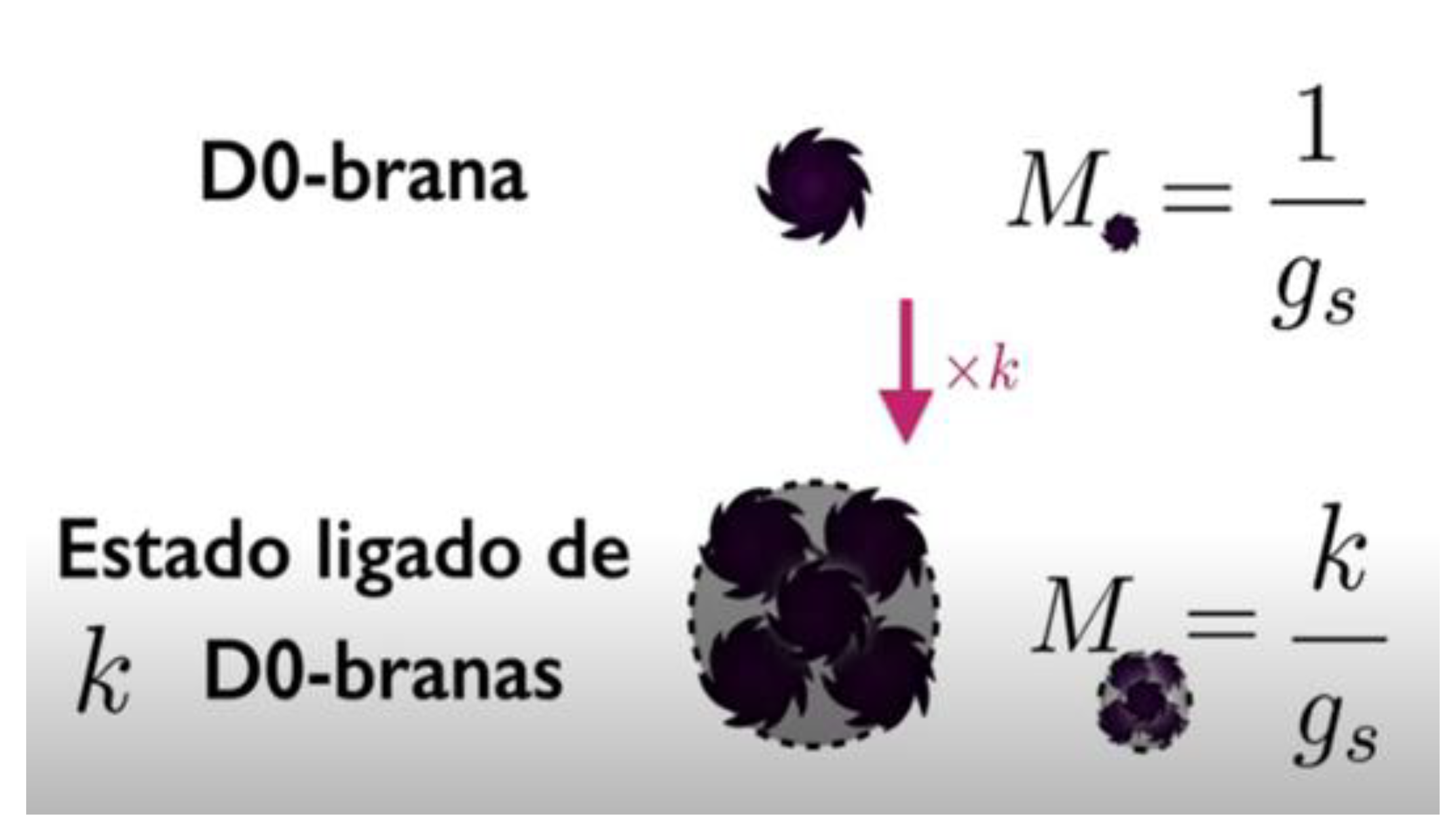
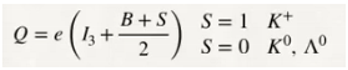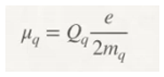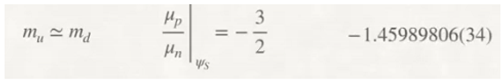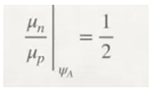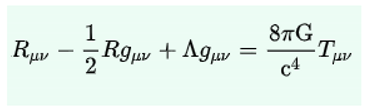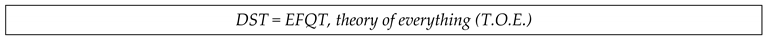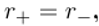1. INTRODUCTION
In the introduction topic, we are going to make a general summary of all the theory that we will need to be able to develop our main objective, determining how the elementary particles that make up the table of the standard model are formed, emphasizing the relationship between gravity, space-time and temperature. Finally, we are going to present a theory of everything (TOE), which includes dark matter, dark energy and matter-antimatter asymmetry.
Let's start from Einstein's most famous equation, E = mc²; this will allow us to make a series of assumptions, which will be our basis in the development of this paper, both for the particles that belong to the standard model and the particles of gravity.
We are going to skip all of Dirac's mathematical development and analyse the following equation:
The correct interpretation of this equation will provide us with very valuable information, which we will use to develop our theory.
Next, we are going to start our interpretation:
a) We are going to analyse equation (1), from the point of view of the electric charge.
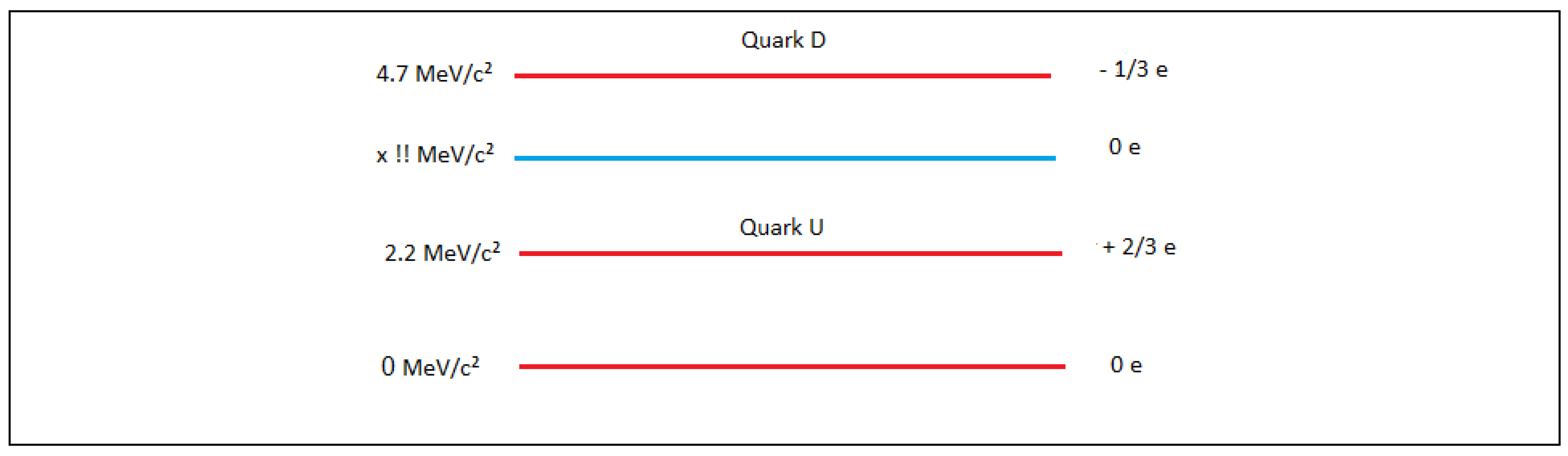
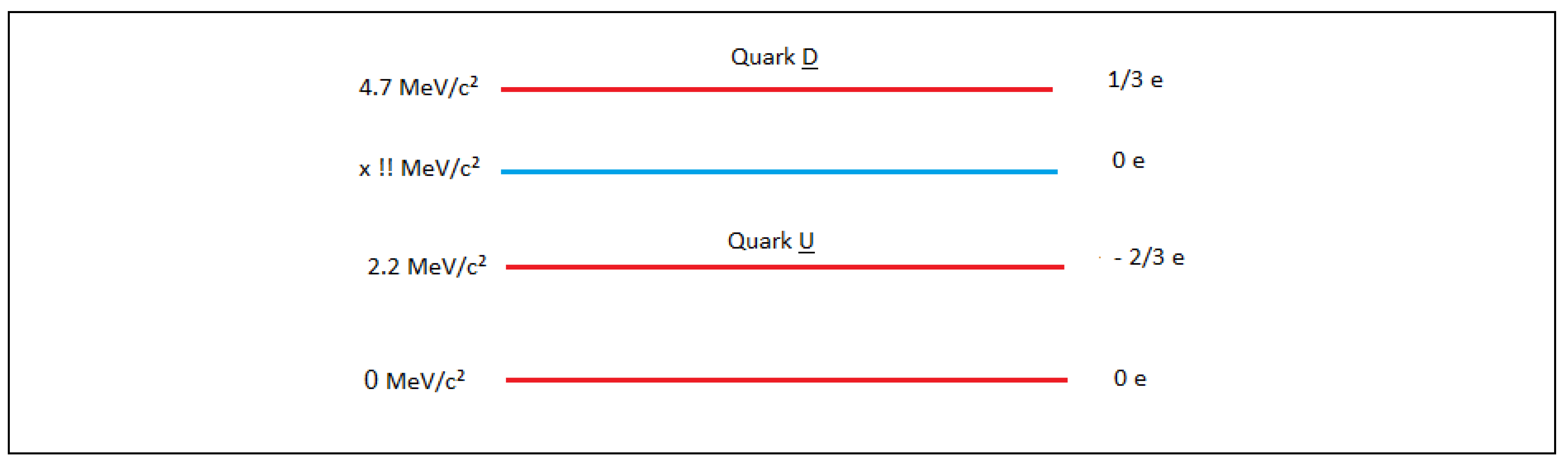
a.1) The sign (+) in equation (1) tells us that there is a positive charge, which can be matter or antimatter. Example, U quark.
a.2) The sign (-) of equation (1) tells us that there is a negative charge, which can be matter or antimatter. Example, U antiquark.
a.3) There is a third possibility, neutral charge or no charge, in other words matter and antimatter without charge. Examples neutrinos and antineutrinos.
b) We are going to analyse equation (1), from the point of view of the mass.
b.1) The sign (+) of the equation tells us that there is a force of attraction for matter and antimatter.
Example: anti de Sitter space-time, ADS.
b.2) The sign (-) of the equation tells us that there is a repulsive force for matter and antimatter.
Example: De Sitter space-time DS, expansion of the universe.
Now that we have concluded our preliminary analysis, we are going to propose the following hypotheses:
- 1)
Here, we hypothesize the existence of elementary particles that have mass and also have a positive charge. These particles are included in the standard model and are characterized by having spin ½. Example, Up quark.
- 2)
Here, we hypothesize the existence of elementary particles that have mass and also have a negative charge. These particles are included in the standard model and are characterized by having spin ½. Example: Down quark.
- 3)
Here, we hypothesize the existence of elementary particles that have mass and have a neutral charge. These particles are included in the standard model and are characterized by having spin ½. Example: electron neutrino.
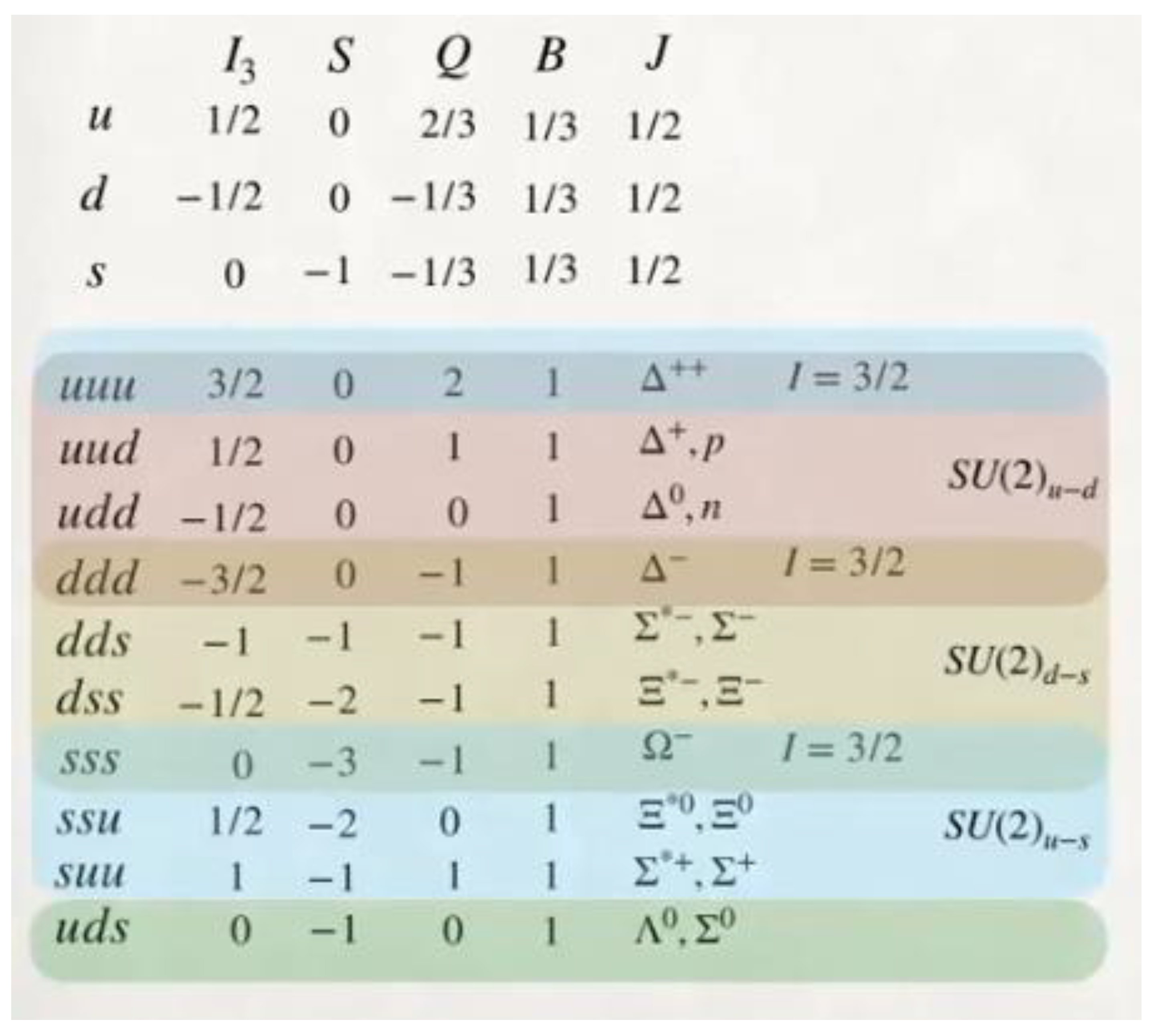
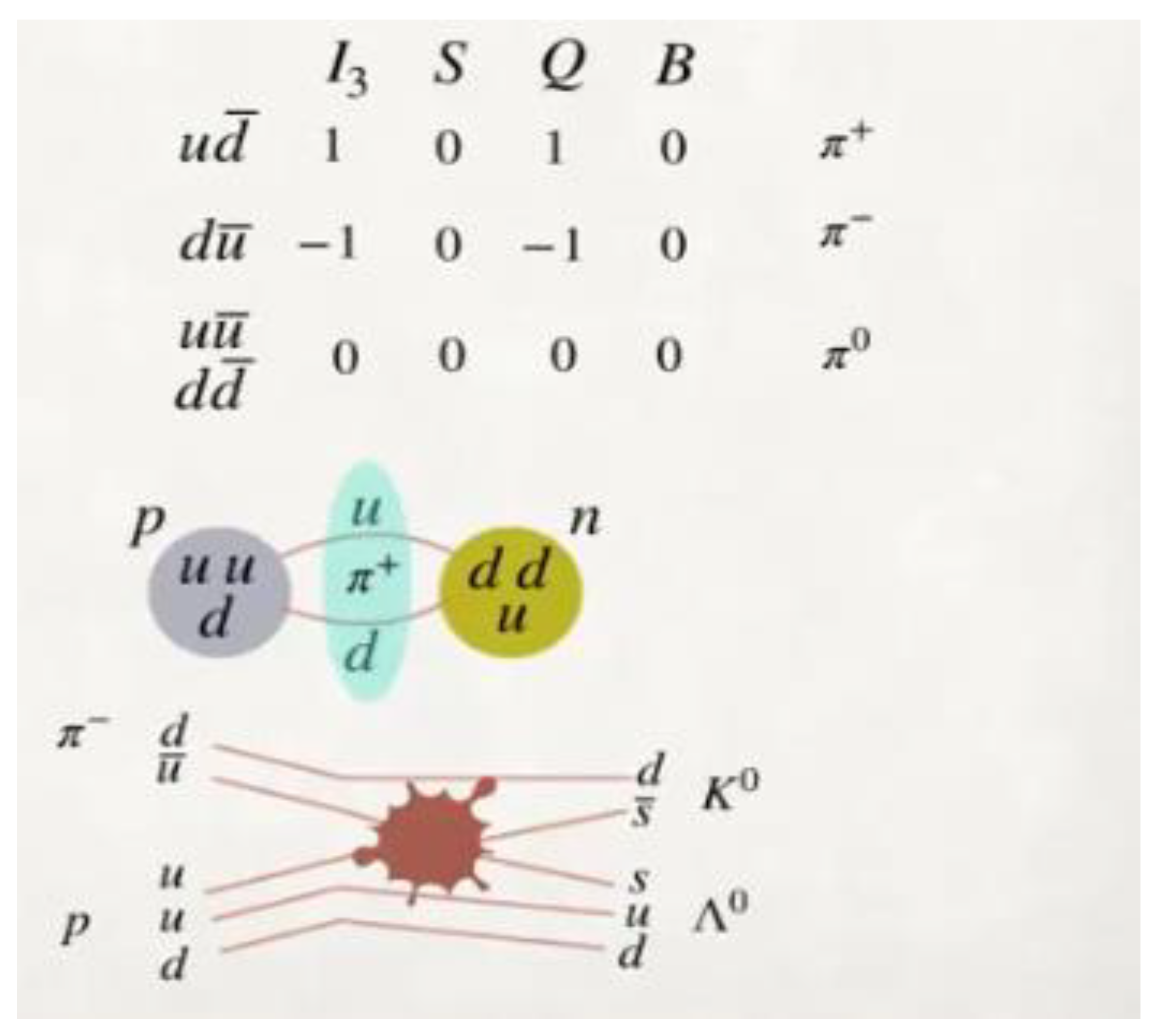
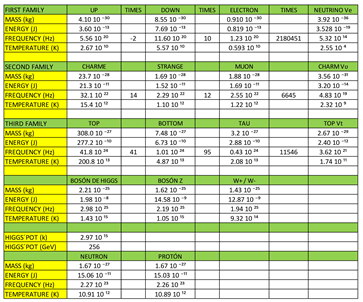
These particles are part of our standard model, when we talk about particles implicitly, we also refer to the existence of their antiparticles. With the exception of leptons that can be found in isolation in nature, quarks or fermions cannot be found in isolation in nature due to their quantum property of colour, they form more complex structures such as bosons, neutrons, protons, etc.
- 4)
Here we hypothesize the existence of sub-particles or elemental quanta that have mass and can also have a positive, negative or neutral charge. These sub-particles are not included in the standard model. Generally, elemental quanta never remain individually with a positive, neutral or negative charge, they form elemental particles such as the Up quark and Down quark.
- 5)
Here, we hypothesize the very existence of the structure of space-time which is quantized and acts as a support for all particles and sub-particles described in hypotheses 1), 2), 3) and 4). A turning point in the structure of space-time is the Planck longitude. Above the Planck length we are in the domain of the 4 fundamental interactions, electromagnetic force, weak force, strong force and gravitational force. Below the Planck length, we are inside a black hole, in the domain of gravitational force.
These 5 hypotheses will support all our theoretical development in this paper.
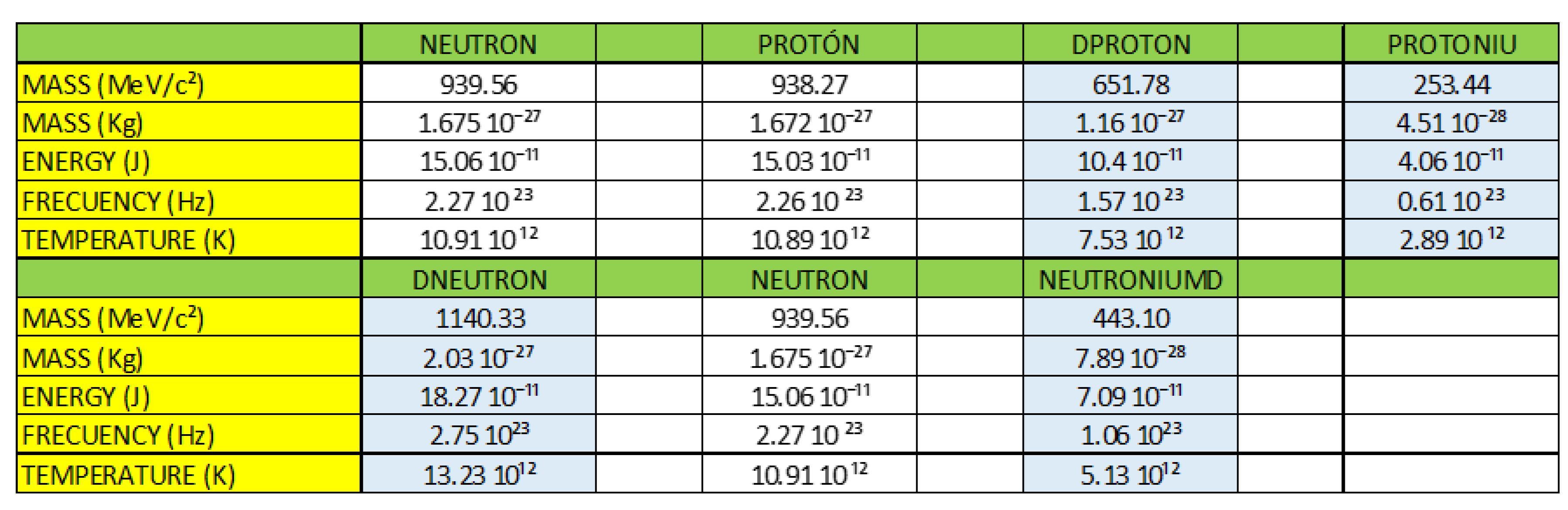
Later we will demonstrate that the elementary particles that form the table of the standard model described by items 1), 2) and 3); they are formed by the combination of factors such as temperature, the effective Boltzmann´s constant, etc.; which are associated with items 4) and 5).
If we analyse the left side of the equation (1), E(energy), we can say that E represents energy in its pure state, quanta of elemental energy.
If we analyse the right side of equation (1), mc², we will say that m represents energy in its concentrated state, where c² represents a proportionality factor.
m, is not energy in a pure state and for this purpose we designate it as a capacitive property of matter to store energy in a state such that it is not pure energy as represented by E.
When we talk about the capacitive property that matter has, we are referring to the property that elementary quanta have to interact with space-time and form elementals particles which give rise to bosons and more complex structures such as protons and neutrons; these in turn give rise to the periodic table of elements.
The difference between m and E is the following, m is the result of the interaction of the elemental quanta of energy and space-time that occurs at a certain temperature, this capacitive property of matter allows the formation of neutrons, protons and all the complex matter that makes up the periodic table of chemical elements. In E, the energy is pure, elemental energy quanta, space-time encapsulates the energy E. This property allows us to form the table we call the standard model of elementary particles.
In both cases where matter is found, E or m, it is important to highlight that a curvature and contraction of space-time occurs. This curvature and contraction of space-time structure is a function of temperature, it is a direct function of temperature, the higher the temperature, the greater the curvature and contraction of space-time.
Example:
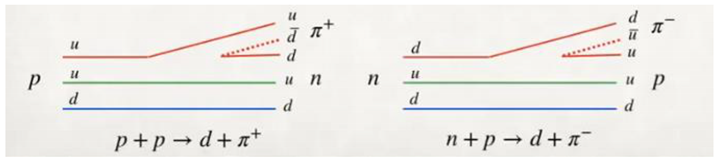
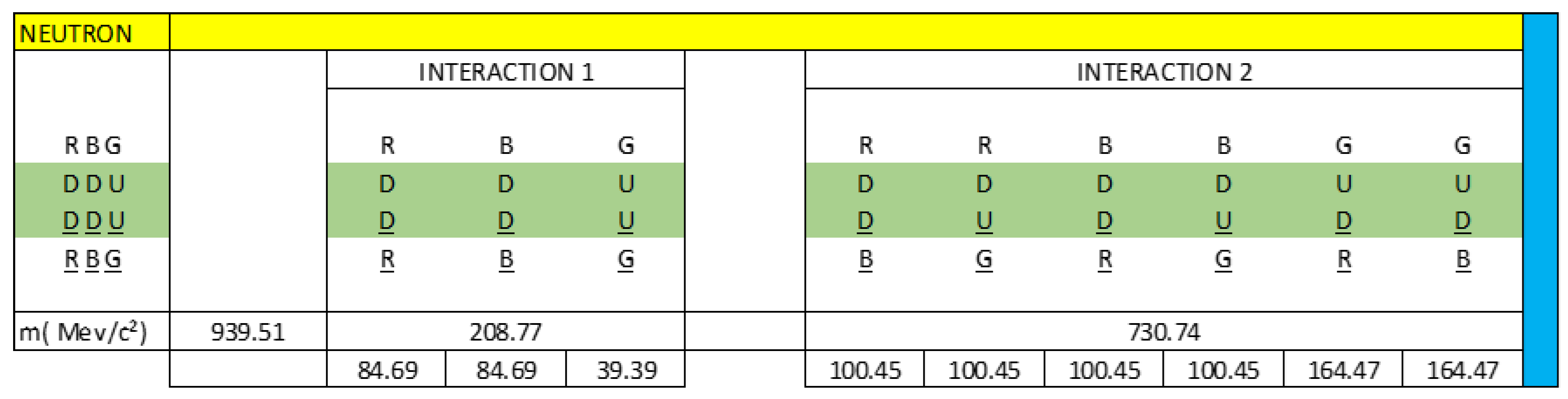
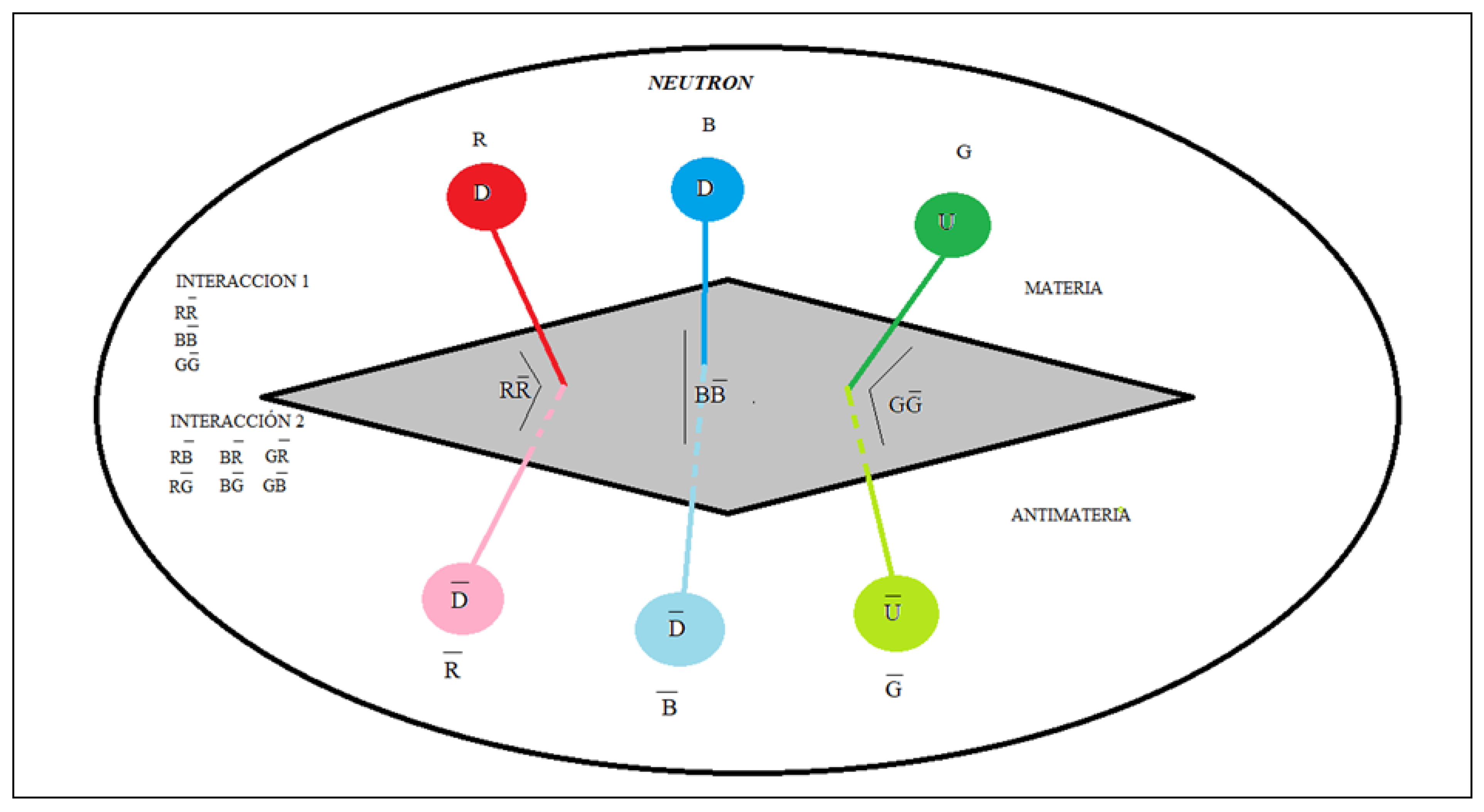
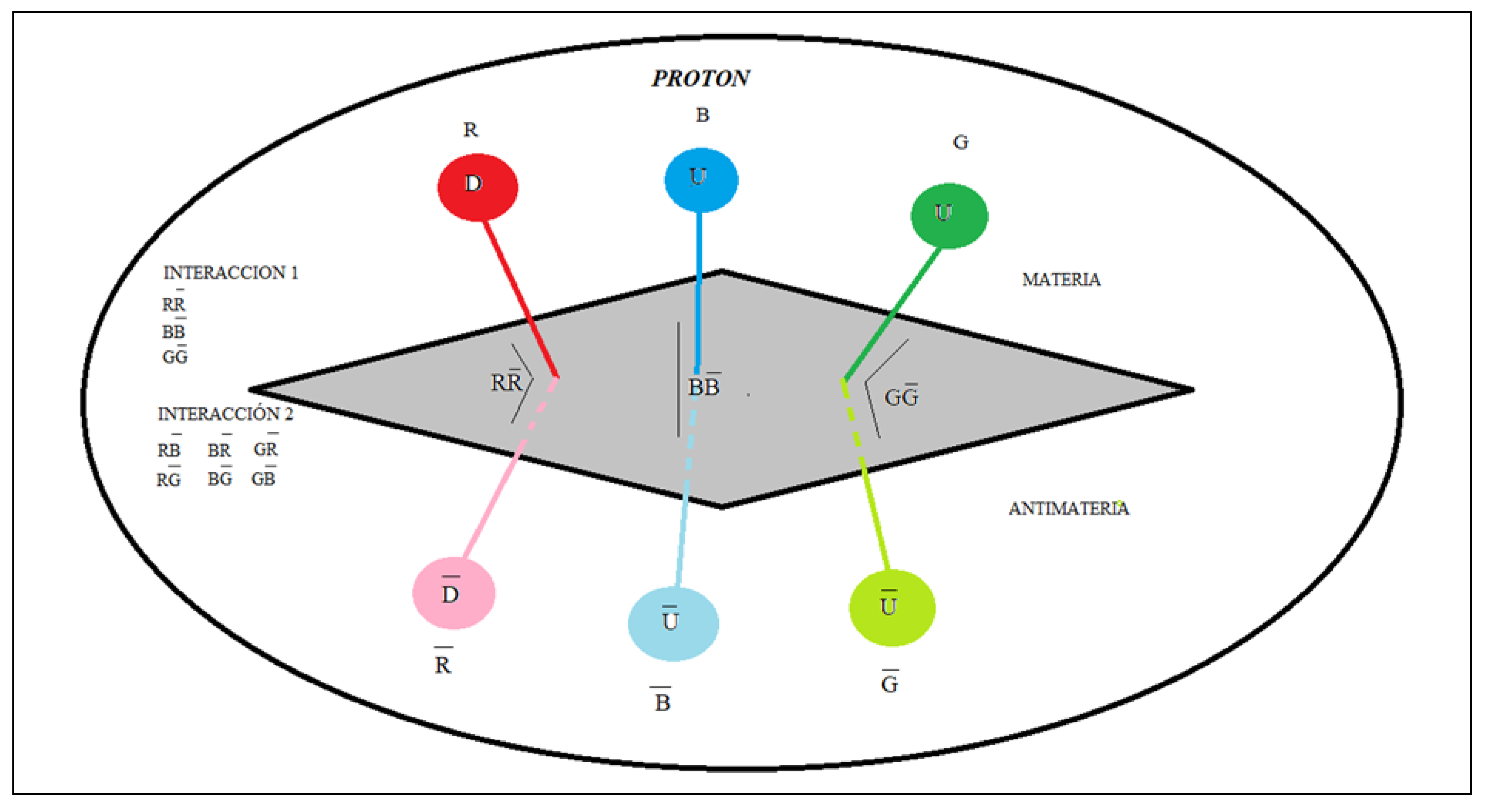
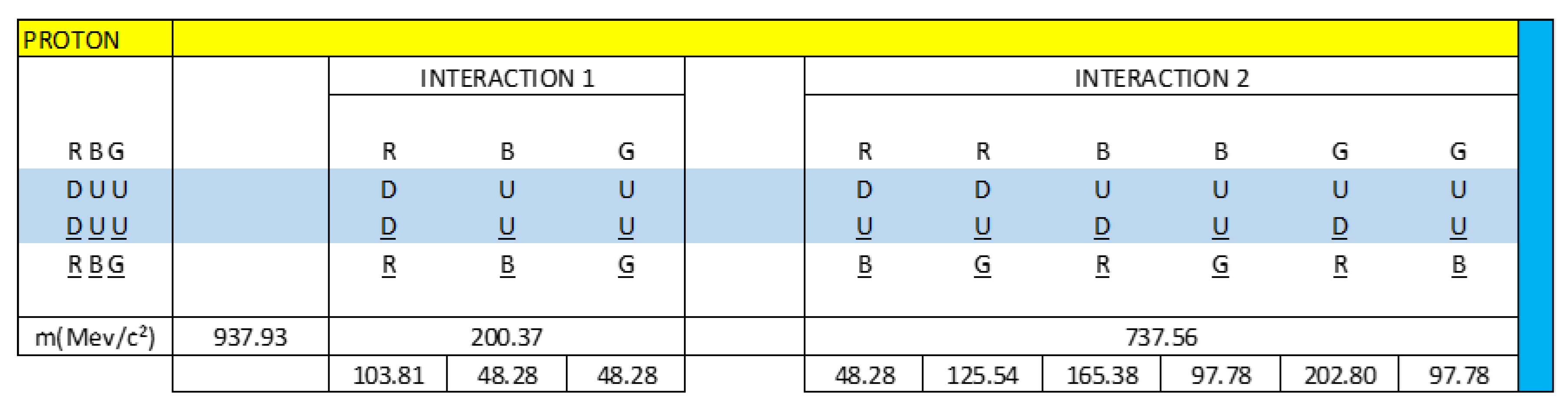
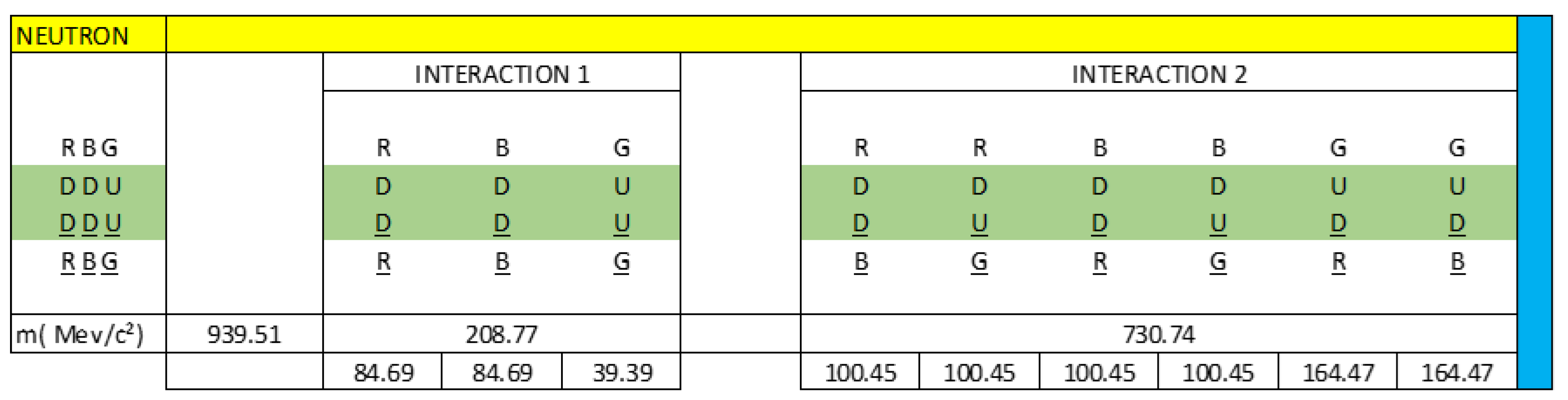
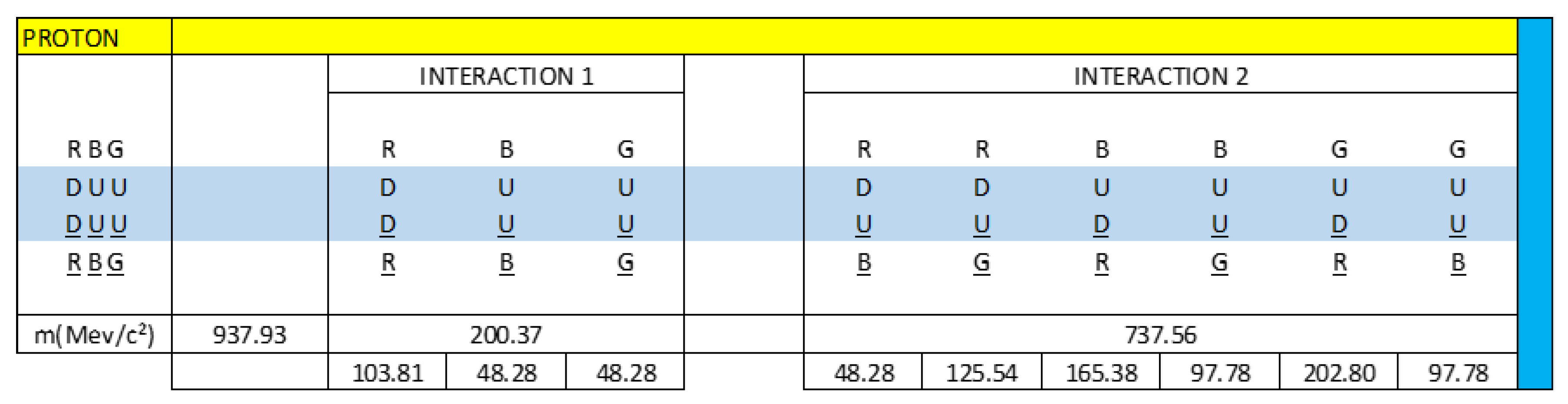
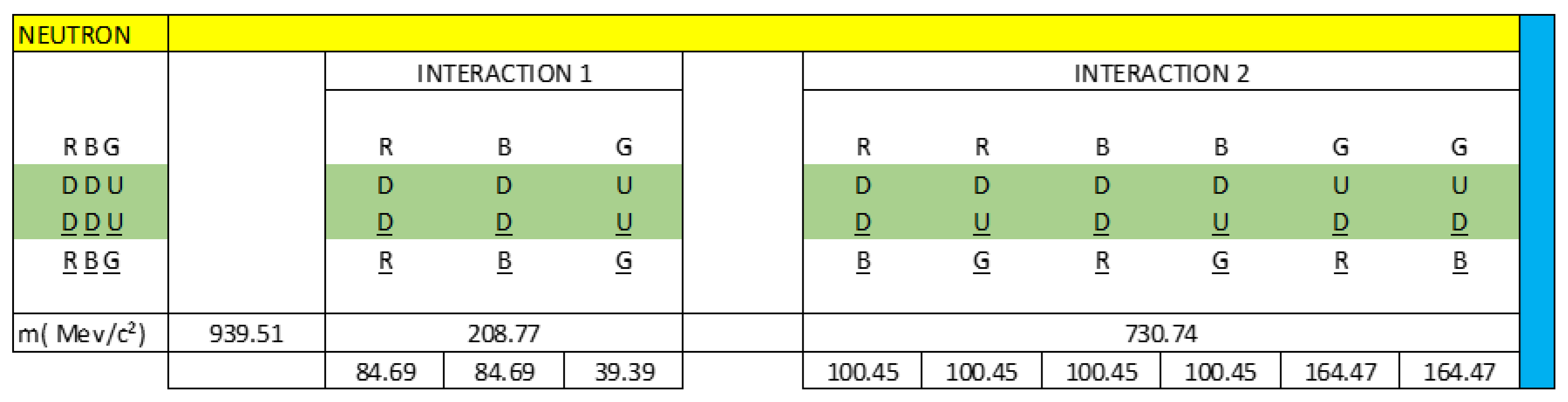
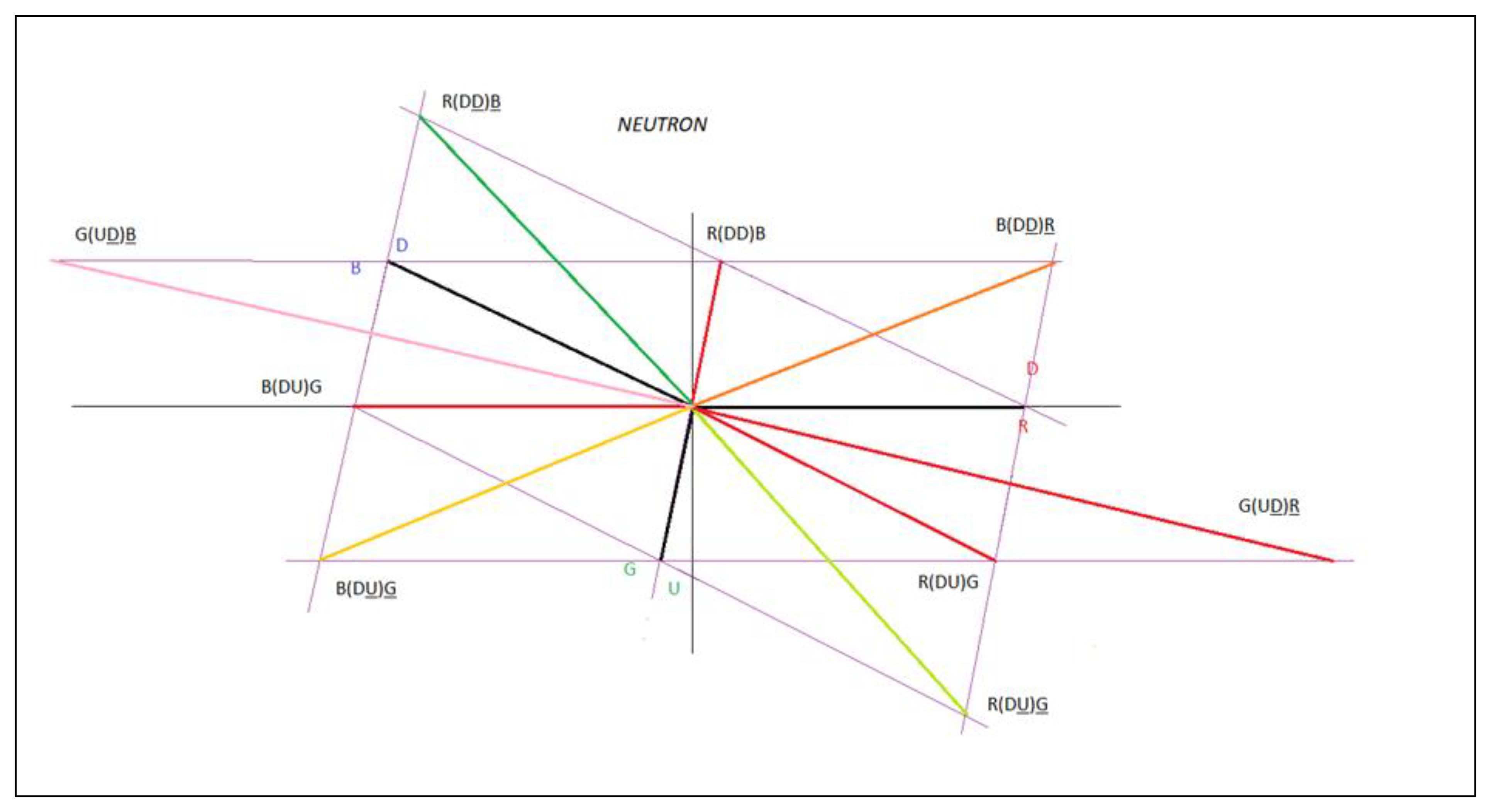
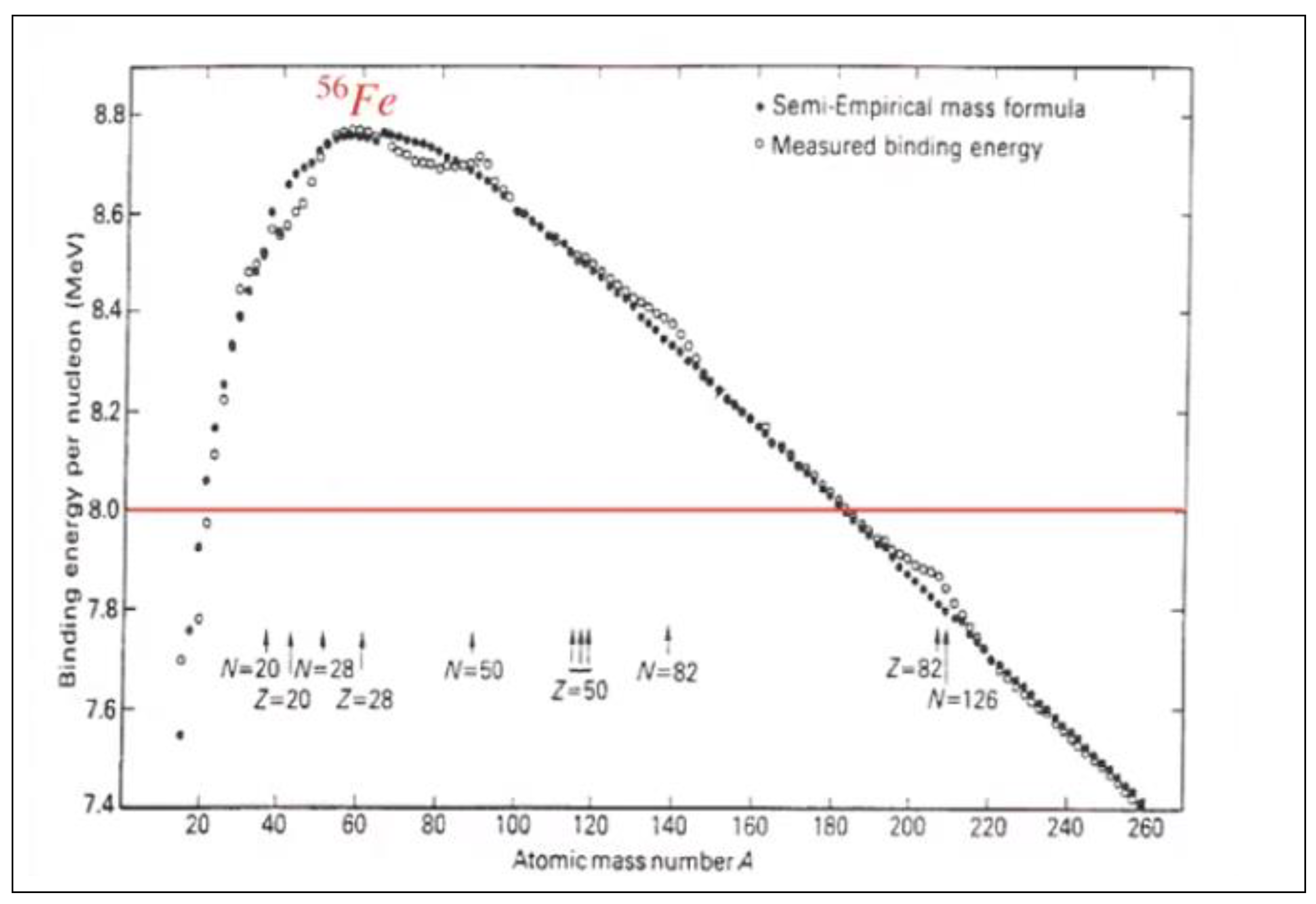
In
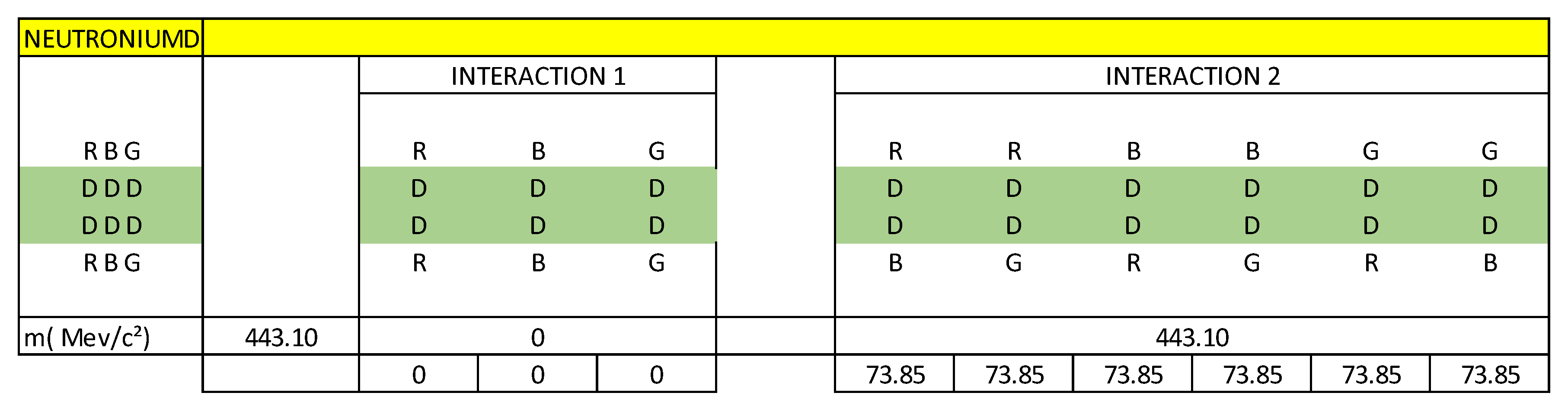
Figure 1, we observe that the neutron is a clear example that represents the capacitive property of matter, we see through the interactions of quarks, antiquarks and gluons how the neutron is formed.
Now that we understand the difference between E and m, from the point of view of the theory of the generalization of the Boltzmann´s constant in curved space-time, we continue with our development.
Let's analyse the correspondence of Maldacena, ADS/CFT.
In my opinion, this equation, ADS = CFT, is the most important equation in all of physics, it is the equation that shows us the path we must follow to reach the theory of everything (T.O.E.), so sought after by scientists.
The Maldacena ADS/CFT correspondence, considering the theory of the generalization of the Boltzmann´s constant, can be generalized to the equation DST = EQFT, where DST represents dynamic space-time with a negative curve, plane or positive curve. EFQT, stands for electromagnetic field quantum theory and includes electromagnetic field theory linked to weak field theory (QED) and strong field theory (QCD).
Here, let it be very clear, the EFQT theory is a reductionist theory; later we will demonstrate through the theory of the neutron and the proton as a three-phase alternating current electric generator, that the interactions of the strong force and weak force can be reduced to simple electromagnetic interactions.
The equation DST = EFQT is reductionist. We are going to explain the meaning of a reductionist theory. For example, in the standard model, we explain the electromagnetic interactions by U(1), the weak force interactions by SU(2) and the strong force interactions by SU(3); a reductionist theory means that we can explain the interactions of electromagnetic forces, weak and strong, only through U(1), a simplification.
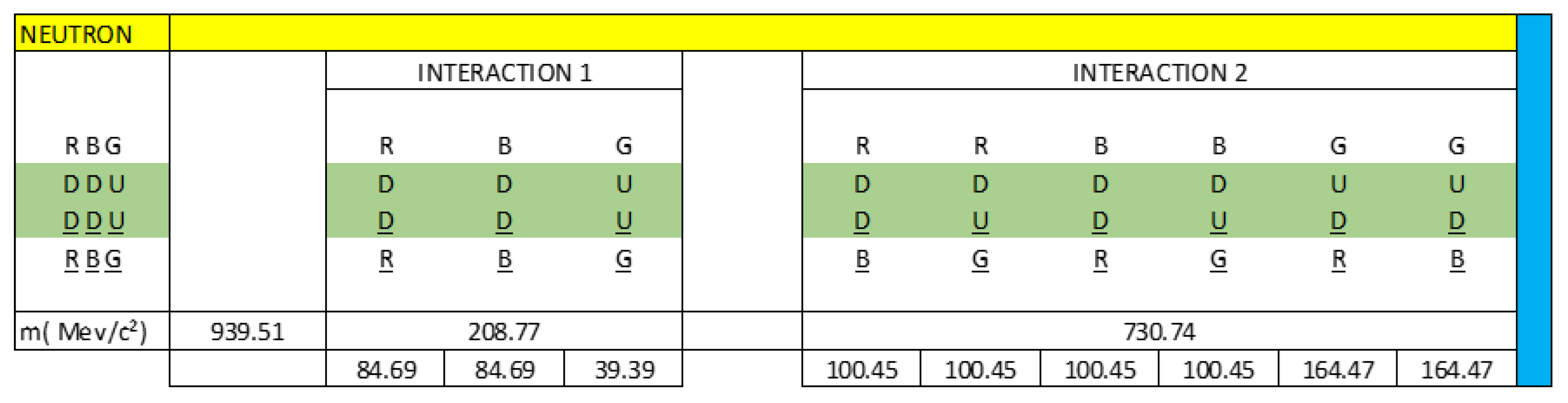
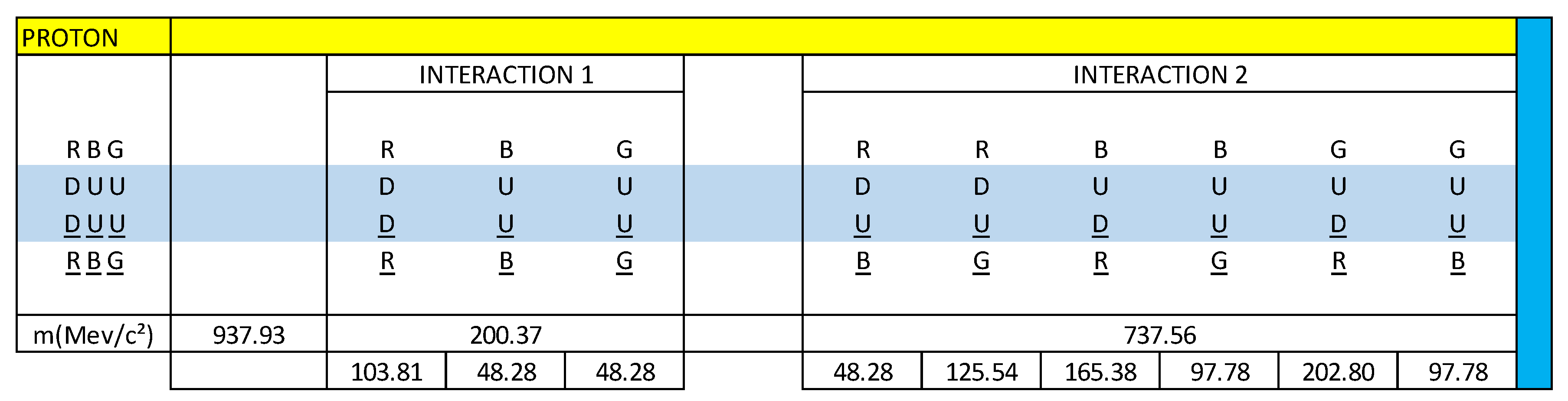
In the paper: Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electric Generator. Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons, inside a Neutron; we analyse how gravity is quantified and exemplify it for the neutron.
Therefore, we will show that the gravity in DST space-time is quantized and is on equal footing with the quantization of EFQT field theory.
DST, represents a theory of quantum gravity associated with the theory of the generalization of the Boltzmann´s constant in curved space-time.
EFQT represents a electromagnetic field quantum theory, which unites the electromagnetic field theory, the weak field theory and the strong field theory and is associated with the theory: Electrical-Quantum Modelling of the Neutron and Proton as a Three- Phase Alternating Current Electric Generator. Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons, inside a Neutron.
The equation DST = EFQT is telling us that there is an intrinsic relationship, a direct relationship, a duality, between matter and space-time. We are going to show that the space-time represented by DST is quantized and in addition the curvature of the space-time DST is also quantized. It is important to note that we do not use conformal field theory. The DST = EFQT equation is even more general than the ADS/CFT correspondence.
Based on this equation DST = EFQT, here in this work we are going to propose that fundamental particles are formed due to a relationship that exists between the curvature of space-time, matter in its elemental or pure state and the temperature or state of the matter; in other words, it is the curvature of space-time or the gravity associated with a temperature, which is responsible for the origin of elementary particles.
To conclude, here we are going to try to solve how to unite Albert Einstein's general relativity theory of gravity and quantum mechanics. We are talking about uniting a classical theory with a quantum theory; with this we are saying that we must quantify gravity and then unite this theory with the theory of quantum mechanics.
It is here where black holes appear and acquire fundamental importance, it is the link that allows this union.
We should not confuse the quantization of gravity with the quantization of space-time, let it be very clear.
When we talk about quantifying gravity, we are referring to determining the existence of the graviton, a boson.
Just as photons have an electromagnetic wave spectrum; similarly, gravitons have a gravitational wave spectrum.
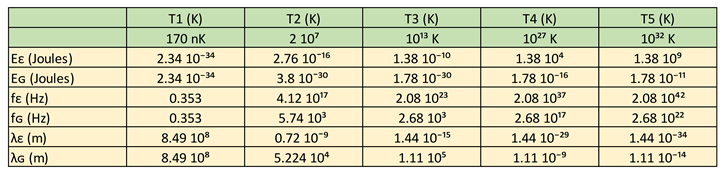
Next, we are going to represent the equations that define the electromagnetic wave spectrum and the gravitational wave spectrum.
Electromagnetic wave spectrum:
Eε = h x fε
Cε = λε x fε
Eε = h x Cε / λε
Eε = Kʙε x Tε
Kʙε = 1.38 10⁻²³ J/K
Gravitational wave spectrum:
Eɢ = h x fɢ
Cɢ = λɢ x fɢ
Eɢ = h x Cɢ / λɢ
Eɢ = Kʙɢ x Tɢ
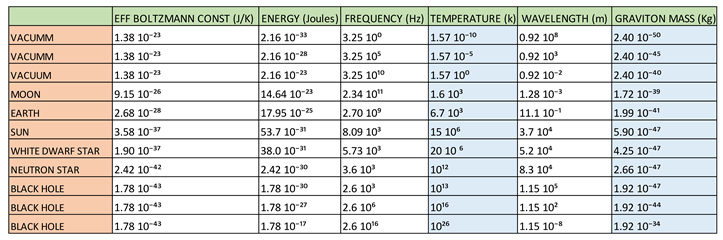
Kʙɢ = 1.38 10⁻²³ J/K > Kв-eff > 1.78 10⁻⁴³ J/K
When we analyze the equations of the electromagnetic wave spectrum, the Boltzmann´s constant is unique for the entire spectrum and is equal to Kʙε = 1.38 10⁻²³ J/K.
However, when we analyze the equations of the gravitational wave spectrum, we observe that the Boltzmann´s constant is not unique and varies according to, Kʙɢ = 1.38 10⁻²³ J/K > Kв-eff > 1.78 10⁻⁴³ J/K.
When we talk about quantifying space-time, we are referring to Planck's constant h, in other words, we are going to determine how h varies in the presence of a mass M. This is precisely when black holes become important, allowing us to quantify the space-time.
We can affirm that space-time represents a sea of gravitons (bosons).
If we analyze the equation DST = EFQT; both members of the equation must be quantized; from the point of view of matter, the quantization of the left side of matter is carried out through gravitons, and the quantization of the right side of matter through the particles defined in the standard model; if we consider the space-time point of view, both sides of the equation will be quantized by the Planck length. Let us remember that outside a black hole Lp dominates the dynamics of space-time and inside a black hole Lpԍ < Lp dominates the dynamics of space-time.
To finish with our introduction, we are going to unravel the origin of dark matter, dark energy and explain the discrepancy that exists in the universe between matter and antimatter. These topics have already been developed in other of my papers, but given the importance of the title of this paper, I consider it appropriate to include these topics since they allow us to have a much broader, much more complete idea of the scope of the theory developed in this paper; really understand the true meaning and scope of the theory of generalization of the standard model. Theory of everything (TOE).
2. RLC ELECTRICAL MODELLING OF BLACK HOLE AND EARLY UNIVERSE
Here, it is important to make the following comment, the theory developed in this item, together with the theory of the neutron and proton model as an alternating current electric generator, served as a base theory to be able to constitute the theory of everything (TOE). The importance of this base theory is such that once again I consider that it should be included in this paper as an integral part.
2.1. RC Electrical Model for a Black Hole
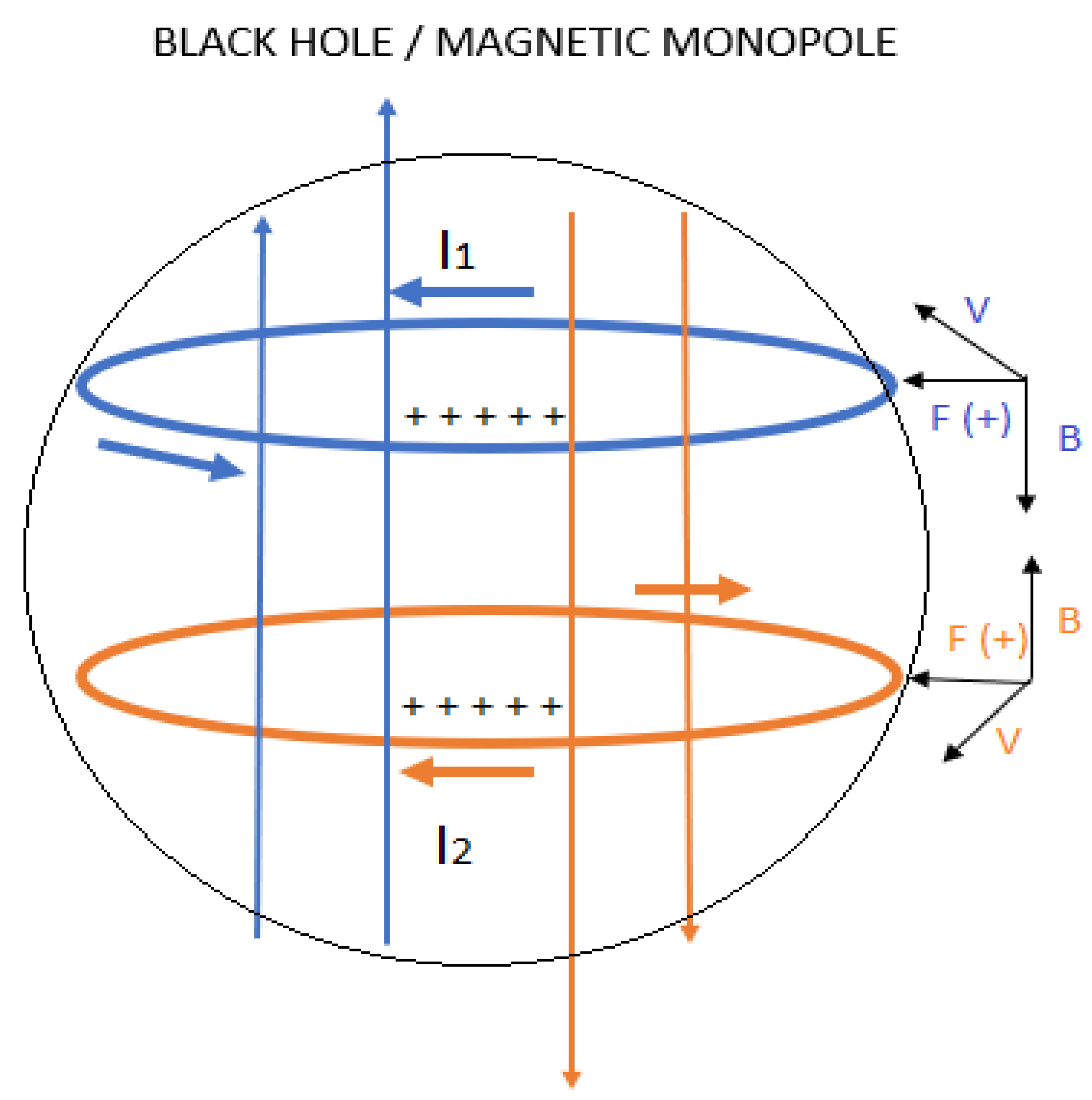
If considering mass and electric charge as fundamental properties of matter.
If we consider the electric charge, we know that a capacitor stores electrical energy and we can represent it as an RC circuit.
Analogously, if we consider the mass, we can consider a black hole as a capacitor that stores gravitational potential energy.
Continuing with the analogy, the space-time that surrounds a black hole can be represented as the inductance L.
from this simple conceptual idea was born RLC electrical modelling of black hole and early universe.
RC electrical model for a Black Hole:
Here we put forward the hypothesis of a black hole growth in analogy to an RC electrical circuit that grows according to a constant Tau being defined as:
We will consider the total mass of a black hole to consist of the sum of baryonic mass and dark matter mass (equation 3), considering dark matter as an imaginary number.
Where M is the total mass of a black hole, m is the baryonic mass;
corresponds to dark matter and i is the irrational number
. This equation is in analogy to impedance of an RC circuit.
Where Z represents impedance; R represents resistance and Xc represents capacitive reactance.
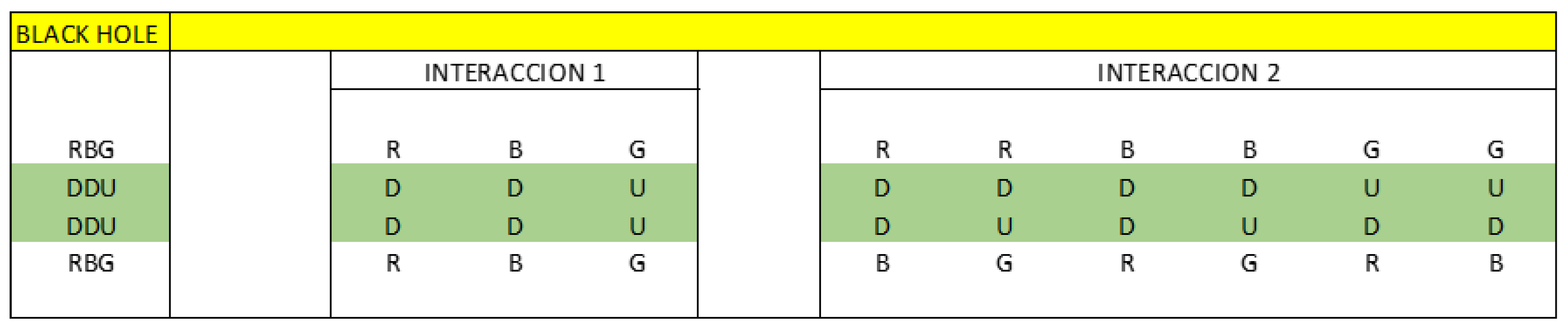
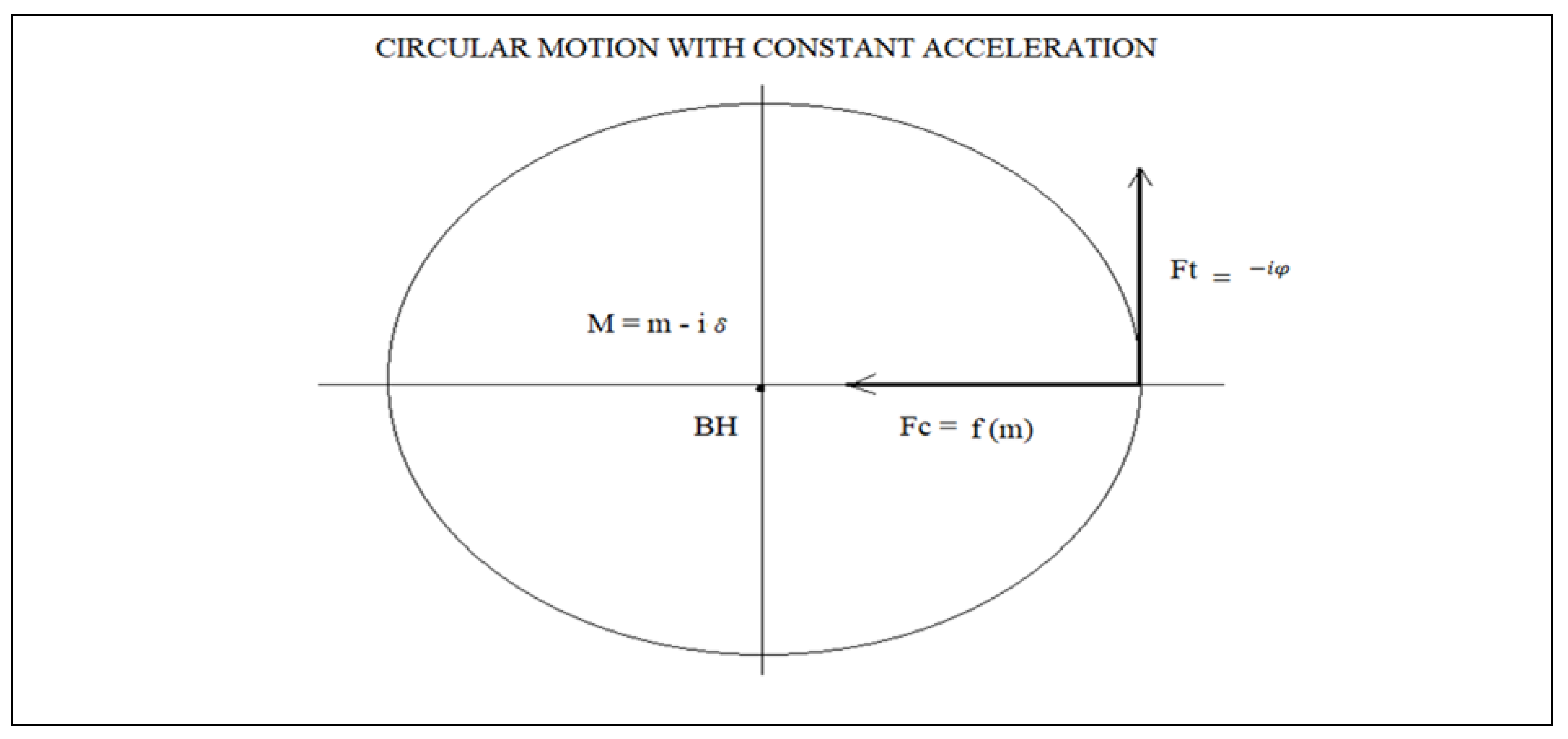
If proper accelerations for the masses are introduced in equation (3) we obtain the following:
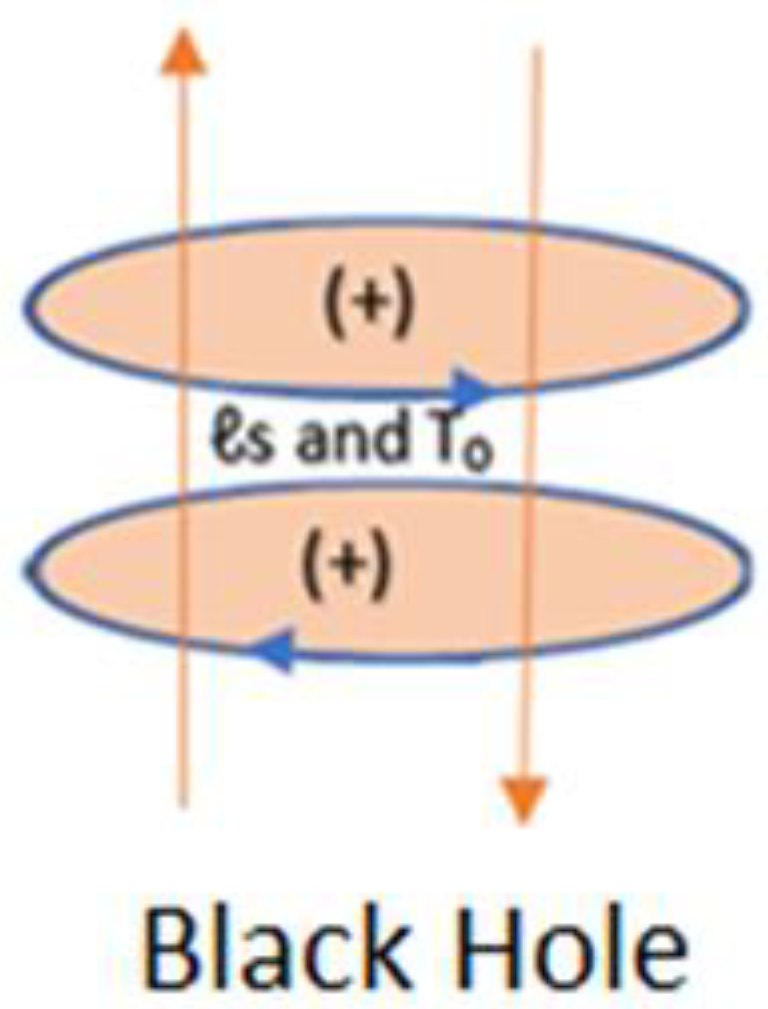
Where F is the total force, f is the force associated to baryonic mass, and i
is the force associated to dark matter mass. In analogy to a phasor diagram for an RC circuit, in which the reactance phasor Xc lags the resistance phasor R by
, we can represent the two forces associated to barionic matter and dark matter as two orthogonal vectors (
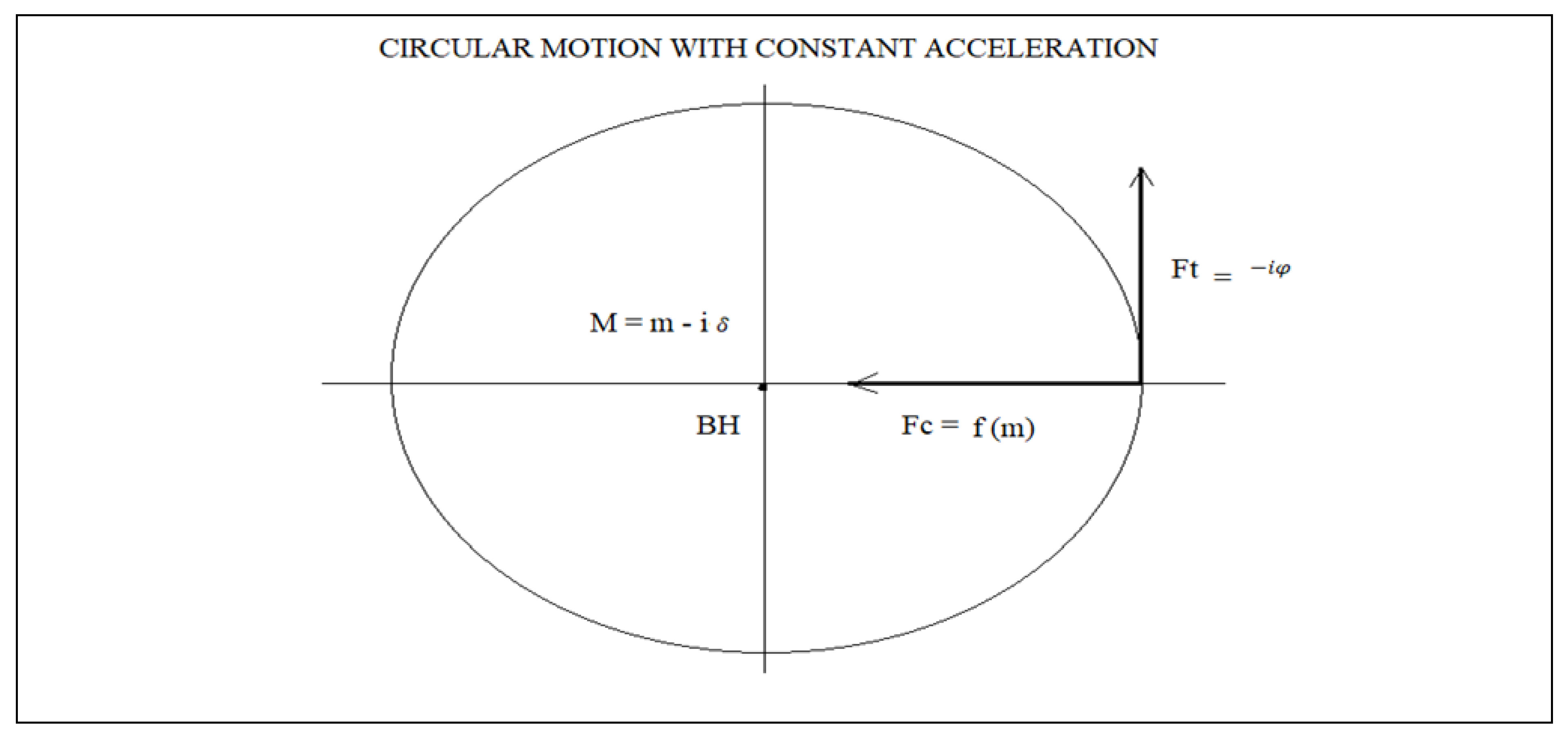
Figure 1).
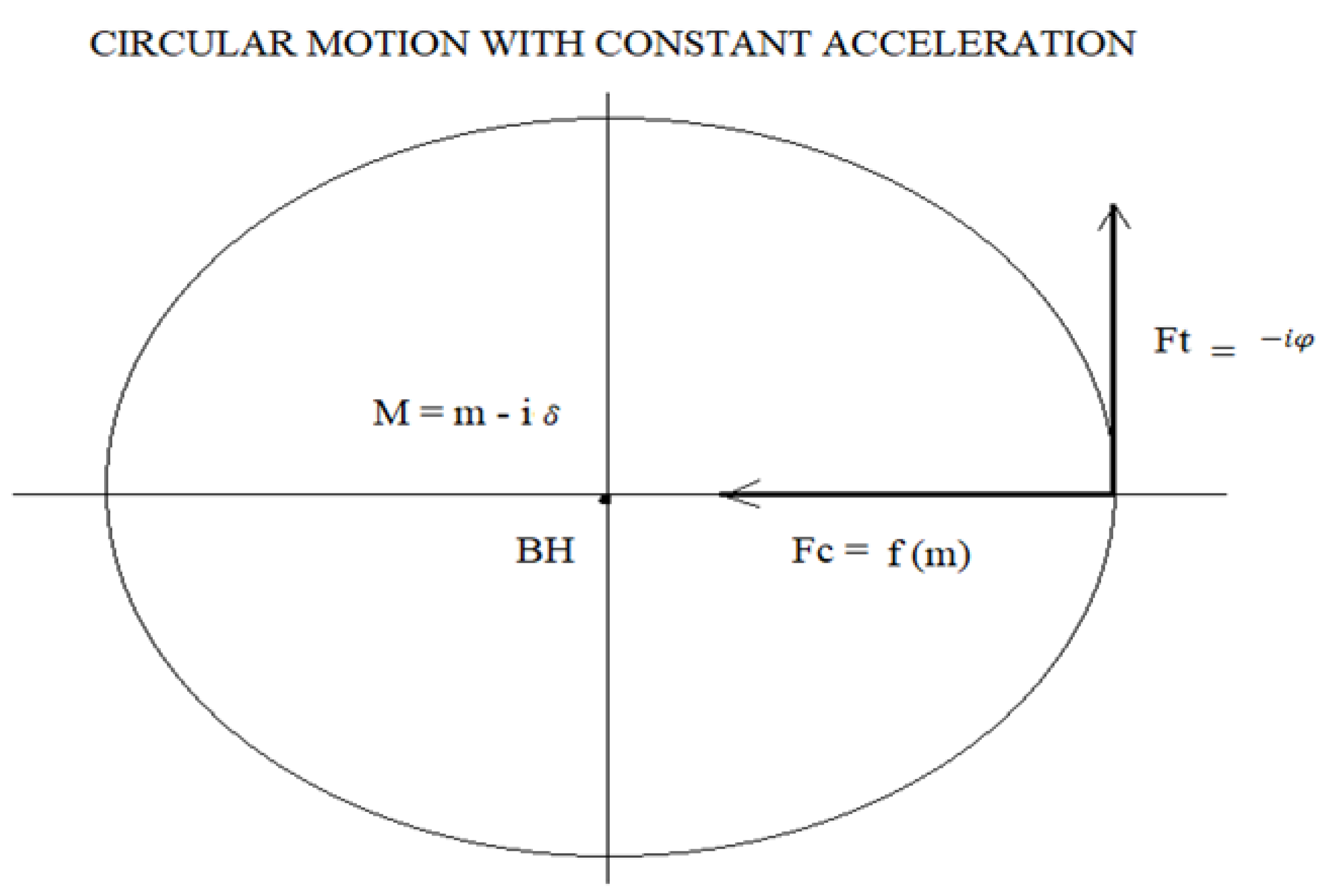
Vector diagram of forces in a black hole for circular motion with constant acceleration:
taking into account Newton's equation of universal gravitation:
The sign (-) of the equation means that the force Fc is at 180 degrees with respect to the resistance R and the force Ft is also at 180 degrees from the capacitive reactance Xc.
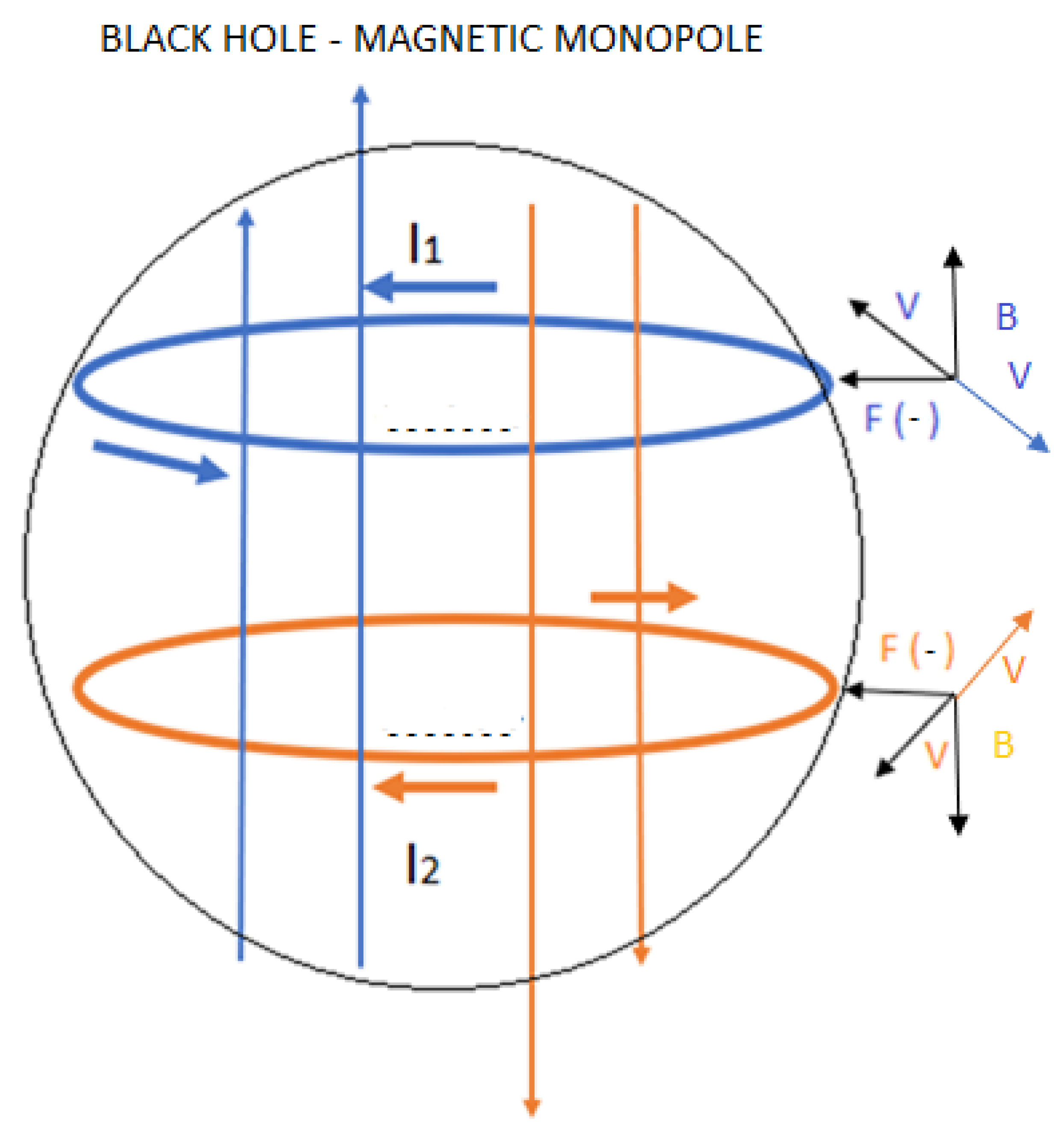
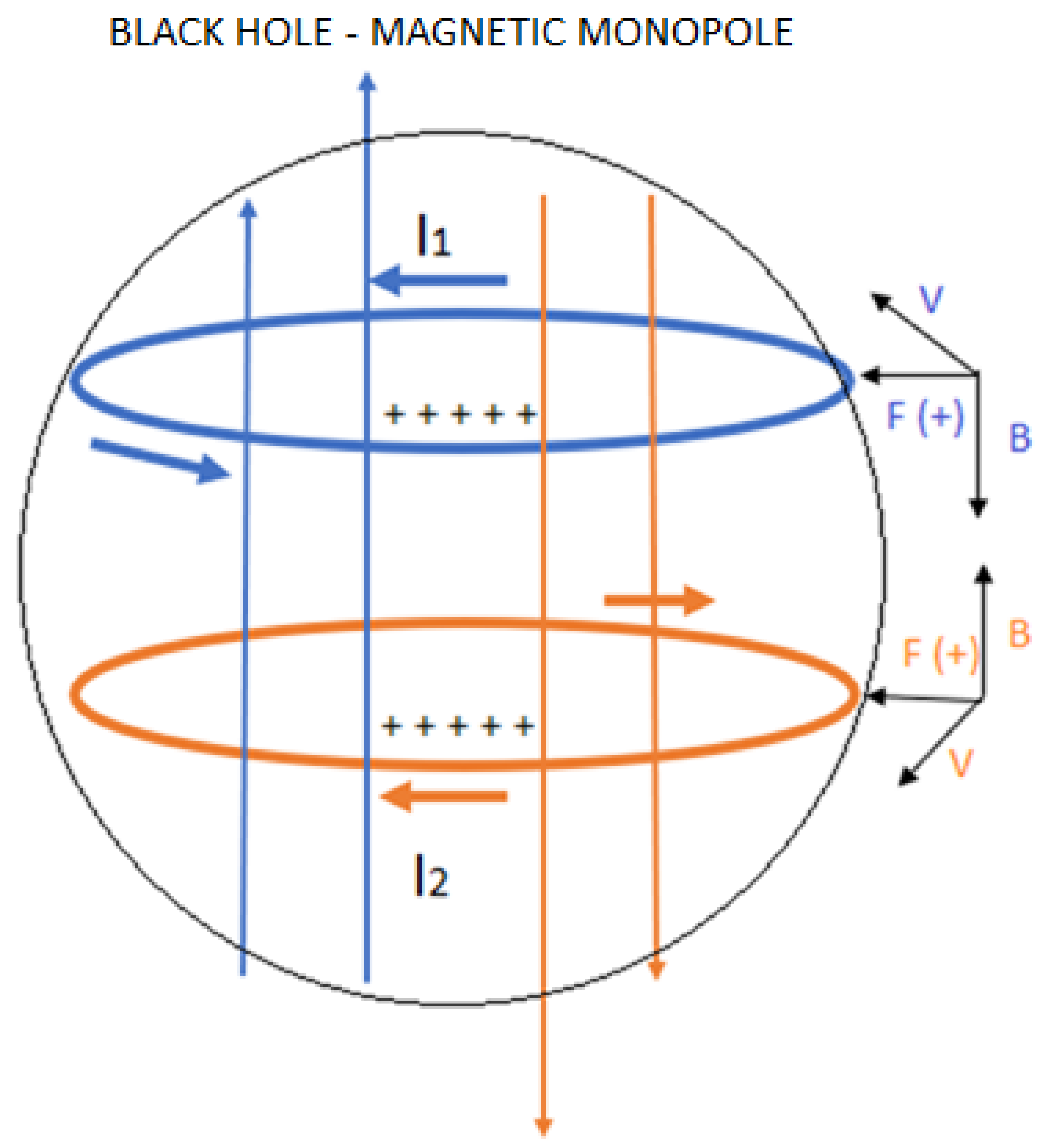
It is important to make clear the physical interpretation of the dark matter mass δ, it is simply telling us that the force Ft due to the mass δ lag the force fc by 90 degrees, that lag is represented by the imaginary number i. Later we will determine that the mass δ, is the result of v > c inside a black hole.
Where v is the speed of a massless particle and c is the speed of light in a vacuum.
Figure 2 is represented for a circular motion with constant acceleration simply because the tangential velocity of a particle is proportional to the radius from the centre of the black hole multiplied by the average angular frequency.
The contribution of (Ft, Vt) is what makes the speed of the galaxy remain constant as the radius of the galaxy grows.
Where Vt represents the tangential rotation velocity of a galaxy, r is the radius from the galaxy, and ω is the average angular rotation velocity of the galaxy.
Circular motion with constant acceleration tells us that the mass input into a black hole is negligible with respect to the black hole's own mass.
The growth of a black hole according to the tau constant is an intrinsic property of a black hole and is independent of the amount of matter that enters a black hole.
To calculate the total energy associated to the black hole, we can introduce its total mass (equation 3) into:
Where E is energy; c represents the speed of light and m represents the mass. This lead to:
We can assume that during the big bang inflation phase baryonic matter was overrepresented compared to dark matter together with an infinitesimal momentum, which would give us from equation (7) the following:
As expected, this result corresponds to the total energy of the universe at the big bang if we consider it to be made of dark matter represented as a reactance in an RC circuit.
The positive value of E is determined by matter, there is no antimatter inside a black hole.
If we consider charge as a fundamental property of matter, , represents the amount of relativistic dark matter mass inside the black hole at the time of disintegration.
If we consider mass as a fundamental property of matter, , represents the amount of relativistic dark matter mass inside a black hole, which exerts a repulsive gravitational force at the moment of disintegration. This repulsive gravitational force is what generates the dark energy after the Big Bang.
At time T0⁺, when the black hole disintegrates and the Big Bang occurs, roughly all matter was dark matter.
We could also consider a universe at infinity proper time in which baryonic matter is dominant over dark matter mass, which would transform equation (7) back into equation (6) but with baryonic matter.
2.2. RLC Electrical Model of the Universe
We will analyse the Dirac delta function &(t).
If we perform the Fourier transform of the function Dirac delta &(t) and analyse the amplitude spectrum, we observe that the frequency content is infinite.
If we perform the Fourier transform of the function Dirac delta &(t) and analyse the phase spectrum, we observe that the phase spectrum is zero for all frequencies.
We say that it is a non-causal zero phase system.
The most important thing to emphasize in this system is that an infinite impulse has an infinite frequency content.
When we work in seismic prospecting looking for gas or oil, using explosives, the detonations produce an energy peak that generates a frequency spectrum that propagates in the layers of the earth. The energy produced in the detonation explosion is not instantly transferred to the ground, a time delay occurs, it is said to be causal system of minimum phase.
In analogy, we are going to suppose that the Big Bang also behaves like a causal system of minimum phase.
Here we put forward the hypothesis that the big bang is the convolution of the energy released by disintegration of the black hole with the space-time surrounding the black hole, being defined as:
Where is the total mass M of a black hole, Ɛ is the space-time surrounding the black hole and ``*´´ is the convolution symbol.
Equation (10) can be simplified and considered analogous to an RLC circuit.
Where RC represents a black hole and L represents the space-time around a black hole
the resolution of the quadratic differential equation of the RLC circuit, will determine how space-time will expand after the Big Bang and the bandwidth of the equation will give us the spectrum of gravitational waves that originated during the Big Bang.
2.3. Generalization of Boltzmann's Constant in Curved Space-Time
Equation of state of an ideal gas as a function of the Boltzmann´s constant.
Where, P is the absolute pressure, V is the volume, N is the number of particles, Kв is Boltzmann's constant, and T is the absolute temperature.
Boltzmann's constant is defined for 1 mole of carbon 12 and corresponds to 6.0221 10²³ atoms.
Equation (13) applies for atoms, molecules and for normal conditions of pressure, volume and temperature.
We will analyse what happens with equation (13) when we work in a degenerate state of matter.
We will consider an ideal neutron star, made only for neutrons.
We will analyse the condition:
This condition tells us that the number of particles remains constant, under normal conditions of volume, pressure and temperature
However, in an ideal neutron star, the smallest units of particles are neutrons and not atoms.
This leads us to suppose that number of neutrons would fit in the volume of a carbon 12 atom, this amount can be represented by the symbol Dn.
In an ideal neutron star,
Where Dn represents the number of neutrons in a C12 atom.
However, equation (15) is not constant, with respect to equation (14), the number of particles increased by a factor Dn, to make it constant again, I must divide it by the factor Dn.
Where N' = (Dn N), is the new number of particles if we take neutrons into account and not atoms as the fundamental unit.
Where Kв' = (Kв / Dn), is the new Boltzmann´s constant if we take neutrons into account and not atoms as the fundamental unit.
We can say that equation (14) is equal to equation (17), equal to a constant
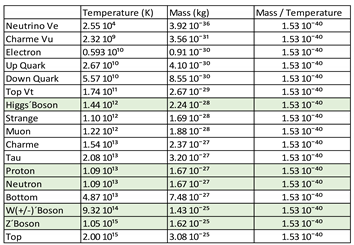
Generalizing, it is the state in which matter is found that will determine Boltzmann's constant.
A white dwarf star will have a Boltzmann´s constant Kвe, a neutron star will have a Boltzmann´s constant Kвn, and a black hole will have a Boltzmann´s constant Kвq.
There is a Boltzmann´s constant Kв that we all know for normal conditions of volume, pressure and temperature, for a flat space-time.
There is an effective Boltzmann´s constant, which will depend on the state of matter for curved space-time.
The theory of general relativity tells us that in the presence of mass (energy), space-time curves but it does not tell us how to quantify the curvature of space-time.
Here we put forward the hypothesis that there is an effective Boltzmann´ constant that depends on the state of matter and through the value that the Boltzmann´ constant takes we can measure or quantify the curvature of space-time.
Quantifying space-time considering the variable Boltzmann´s constant is also quantizing gravitational waves and as with the electromagnetic spectrum, we will determine that there is a spectrum of gravitational waves.
2.4. Black Hole´s Radiation
Equation (3) defines the mass of a black hole, as shown below:
Where M is the total mass of a black hole, m is the baryonic mass; corresponds to dark matter and i is the irrational number .
Also, here we put forward the hypothesis of a black hole growth in analogy to an RC electrical circuit that grows according to a constant Tau being defined as:
If we consider the black hole´s radiation that produces pairs of particles and antiparticles at the event horizon.
Here we put forward the hypothesis:
the HR (matter & antimatter) particle, with frequency ω and energy hω, falls into the black hole and adds to m and δ increasing the mass of the black hole, that is, it adds mass.
This is defined with the assumption that a black hole grows according to the tau constant just like an RC circuit.
The P particle (matter & antimatter), with frequency ω and energy -hω, moves away from the black hole in the form of a gravitational wave.
According to the proposed hypothesis, a black hole always grows, following the curve of the tau constant in analogy to an RC electrical circuit.
2.5. Cosmic Inflation
From the following equation:
We will analyse the Schwarzschild solution for a punctual object in which mass and gravity are introduced.
Where M is the mass of a black hole, c is the speed of light, and G is the gravitational constant.
if we consider dθ = 0; and dφ = 0; that is, we move in the direction of dR. (22)
R = Rs, ds = 0, let's analyse this specific situation. (23)
Replacing the conditions given in (21), (22) and (23) in equation (20), we have:
(dR / dt) ² = v² = c² (1 - (2MG/Rc²) ²
R = Rs, v = 0; ds² = 0; Rs is Schwarzschild´s radius. (24)
R > Rs, v < c; ds < 0, time type trajectory. (25)
R < Rs, v > c; ds > 0, space type trajectory. (26)
Condition (26) is very important because to the extent that R < Rs, v > c is fulfilled, it is precisely this speed difference that generates the dark matter mass in a black hole given by
Planck length equation:
where h is Planck's constant, G is the gravitational´s constant, and c is the speed of light.
If we consider condition (26) and equation (27), to the extent that R < Rs and v > c, are fulfilled, we deduce that the Planck length decreases in value.
We define the following:
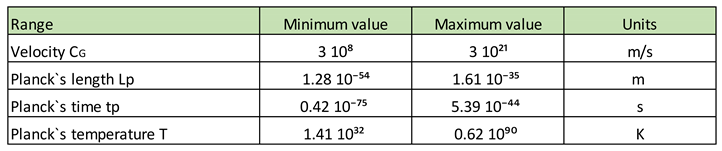
Lpɛ = Lp = 1.616199 10⁻³⁵ m; electromagnetic Planck length.
Lpɢ = gravitational Planck length.
Always holds:
Lpɢ < Lpɛ
Here we put forward the hypothesis that cosmic inflation is the expansion of space-time that is given by Lpɢ that tends to reach its normal value Lpɛ after a black hole disintegrates.
If we consider the Planck length Lpɛ, the minimum length of space-time, like a spring and due to the action of v > c (300,000 km/s), this length decreases in values of Lpɢ, that is, Lpɢ < Lpɛ, allowing us to imagine the immense forces involved in compressing space-time of length Lpɛ into smaller values of space-time Lpɢ. The immense energy stored and released in the spring of length Lpɢ, to recover its initial length Lpɛ, is the cause of the exponential expansion of space-time in the first moments of the Big Bang.
At time T0⁺, when the black hole disintegrates and the Big Bang occurs, roughly all matter was dark matter, relativistic dark matter.
2.6. Additional Calculations. Growth of a Black Hole in Analogy to the Tau Growth Curve of an RC Circuit
In the ADS/CFT correspondence to calculate the viscosity of quark-gluon plasma, the following assumption is used: a black hole is equivalent to quark-gluon plasma.
We consider the temperature of a black hole equal to the temperature of the quark-gluon plasma, equal to T = 10¹³ K.
Another way of interpreting it is as follows:
When a star collapses; a white dwarf star, a neutron star or a black hole is formed.
A white dwarf star has a temperature of about 10⁶ K, a neutron star has a temperature of about 10¹¹ K. If we consider that a black hole is a plasma of quarks and gluons, its temperature is expected to be higher than 10¹¹ K.
Hypothesis: the temperature of a black hole is 10¹³ K.
We will make the following approximation:
T = 0.0000000000001τ, T = 10⁻¹³τ
τ = 10²⁶ K
Cɢ(T) = Cɢmax (1 - e⁻(ᵀ/τ))
Cɢ(T) = Cɢmax (1 - e ⁻ ⁰·⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰¹(τ/τ))
Cɢ(T) = Cɢmax (1 - e ⁻ ⁰·⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰¹)
Cɢ(T) = Cɢmax (1 - e ⁻ (¹ / 10¹³)
Cɢ(T) = Cɢmax (1 - 1 / e (¹/ 10¹³))
Cɢ(T) = Cɢmax (1 – 0.9999999999999)
Cɢ(T) = Cɢmax x 10⁻¹³
Cɢmax = Cɢ(T) / 10⁻¹³ = 3 10⁸ m/s x 10¹³
Cɢmax ≡ 3 10²¹ m/s.
Where T is the absolute temperature, τ represents the growth constant tau, Cɢ = v, represents the speed of a massless particle greater than the speed of light and Cɢmax represents the maximum speed that Cɢ can take.
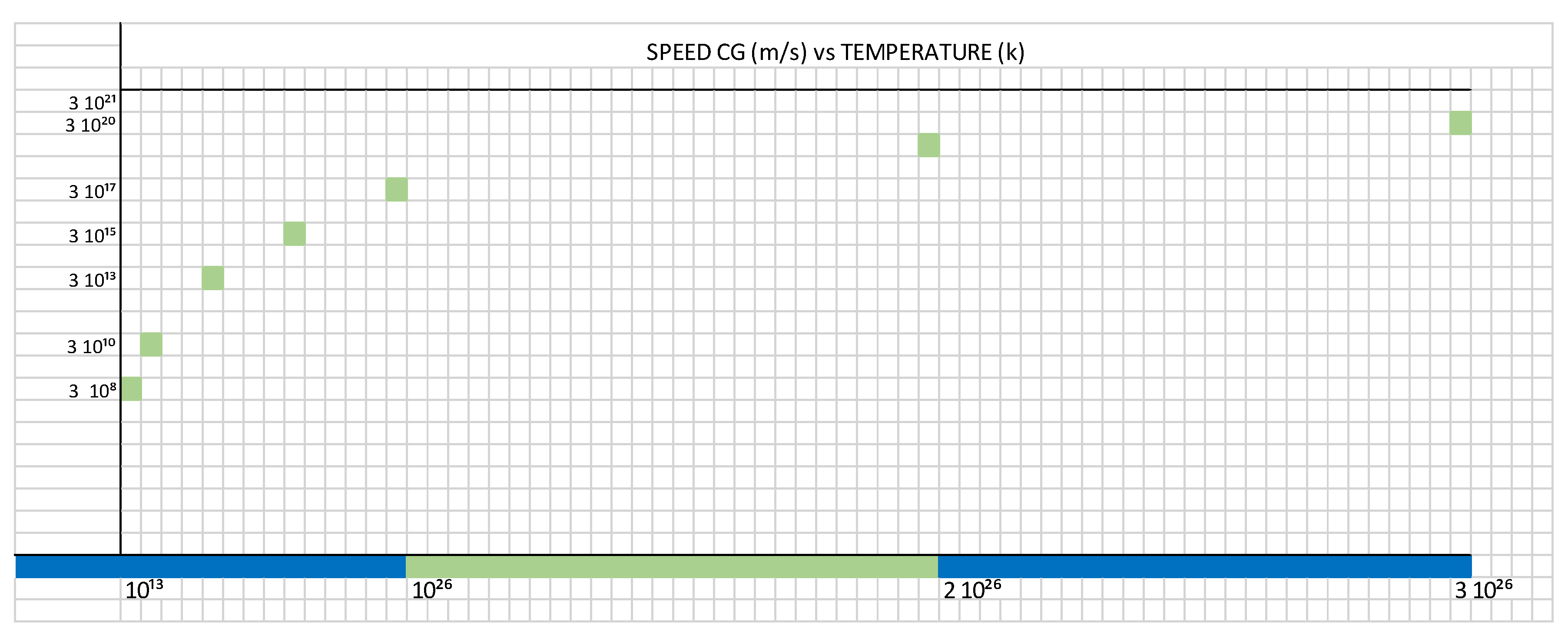
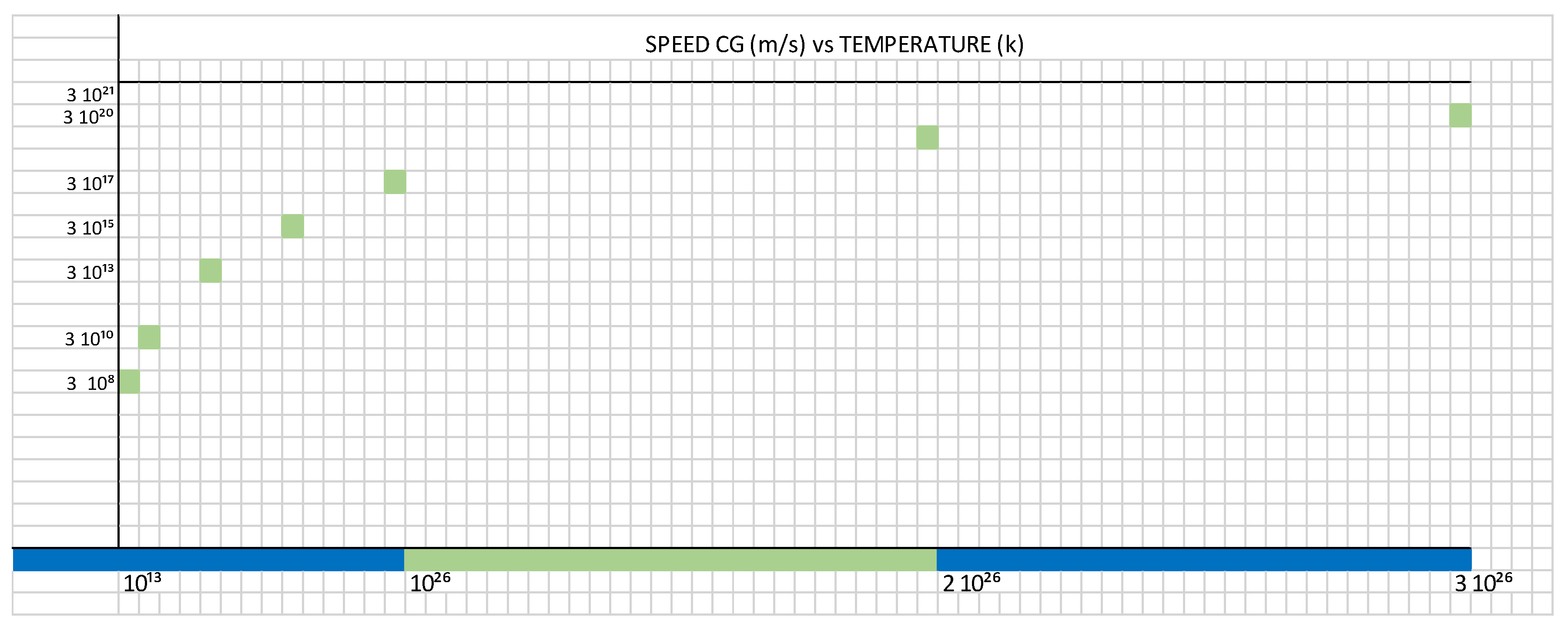
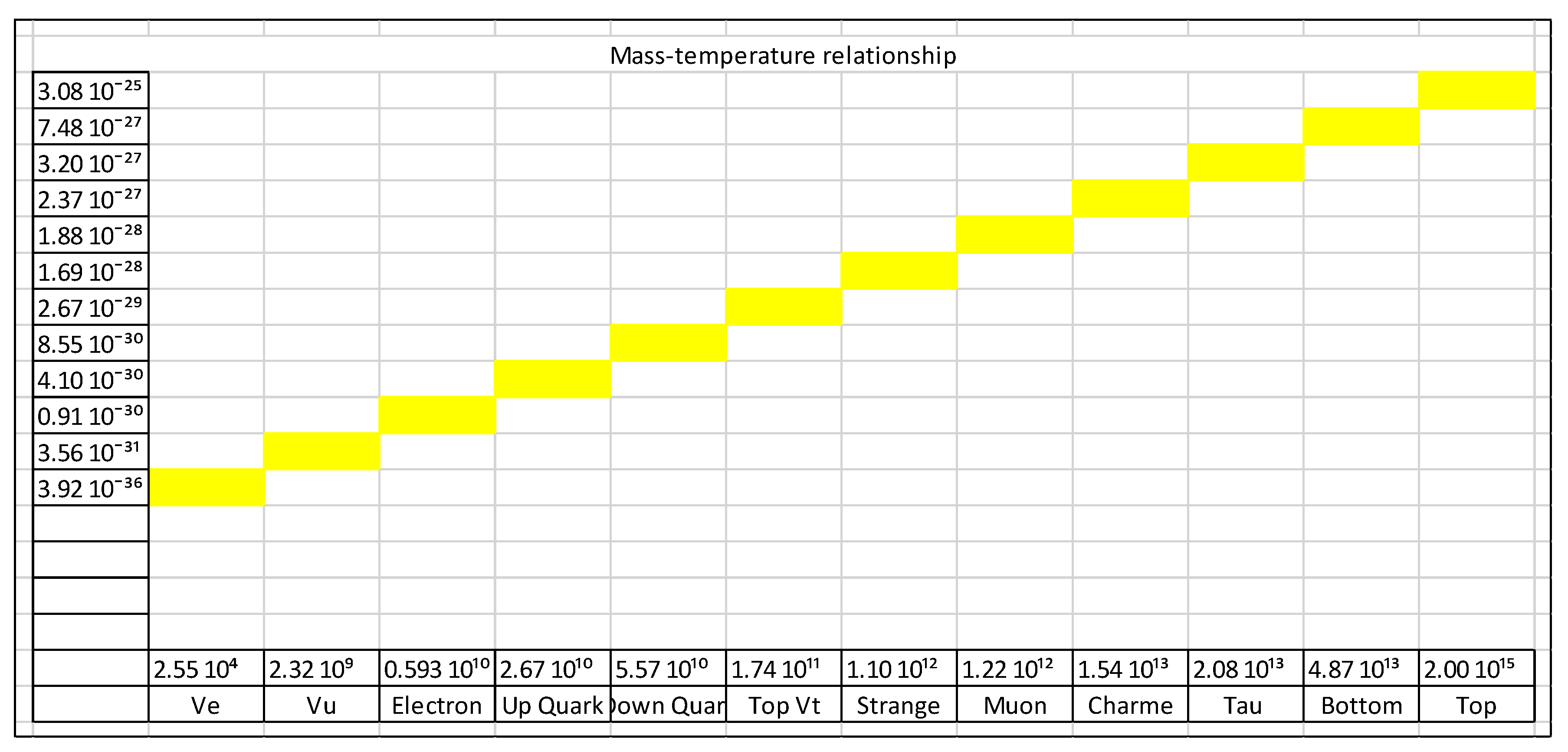
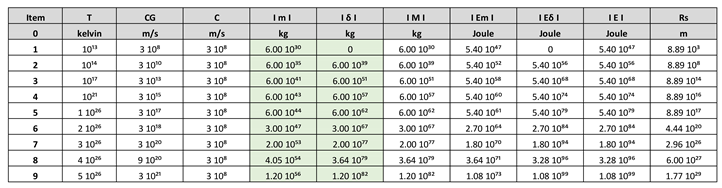
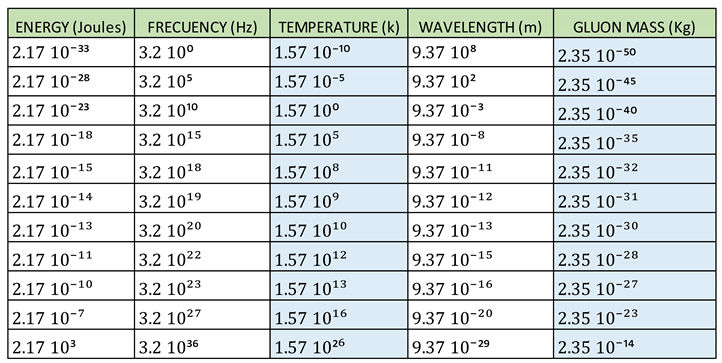
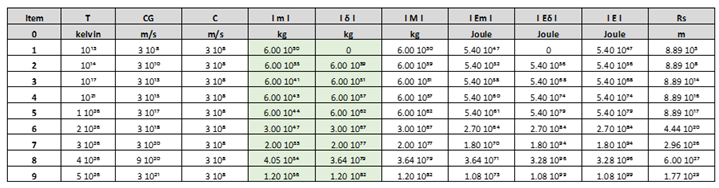
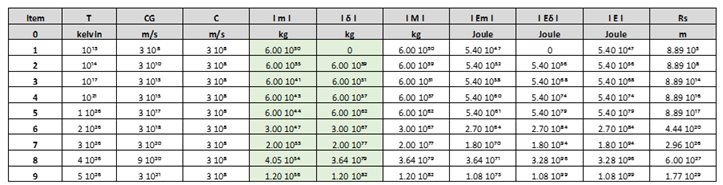
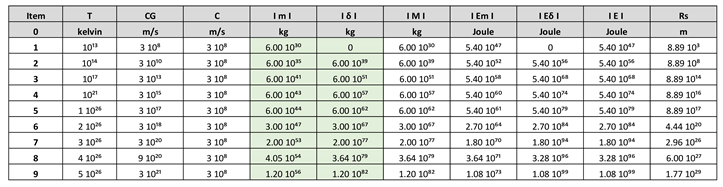
With the following equations, we obtain the following graphs, represented by
Table 1 and
Figure 2:

- a)
-
In item 1 of the
Table 1, for the following parameters: T = 10¹³ K, Cɢ = C = 310⁸ m/s, calculating we get the following values:
m = 6 10³⁰ kg, baryonic mass.
δ = 0, dark matter mass.
M = m = 6 10³⁰ kg
Rs = 8,89 10³ m, Schwarzschild´s radius.
- b)
-
In Item 9 of the
Table 1, for the following parameters: T = 5 10²⁶ K, Cɢ = 3 10²¹ m/s, C = 310⁸ m/s, calculating we get the following values:
m = 1.20 10⁵⁶ kg, baryonic mass.
δ = 1.20 10⁸² kg, dark matter mass.
M = δ = 1.20 10⁸² kg
Rs = 1.77 10²⁹ m, Schwarzschild´s radius.
- c)
It is Important to emphasize, for the time t equal to 5τ, at the moment the disintegration of the black hole occurs, the big bang originates; the total baryonic mass of the universe corresponds to m = 10⁵⁶ kg. Let us remember that the baryon mass calculated by scientists is approximately m = 10⁵⁴ kg.
- d)
Figure 3 shows the growth of the tau (τ) constant, as a function of speed vs. temperature.
2.7. Dark Matter: Calculation of the Amount of Dark Matter That Exists in the Milky Way
Mass and Schwarzschild´s radius of the black hole Sagittarius A*:
m = 4.5 10⁶ Ms = 4.5 x 10⁶ x 1.98 10³⁰ kg
Where Ms is the mass of the sun.
m = 8.1 x 10³⁶ kg
Rs = 6 million kilometres
Where Rs is the Schwarzschild´s radius of the Sagittarius A*.
Rs = 6 x 10⁹ m
If we look at
Figure 3; for m = 8.1 x 10³⁶ kg and Rs = 6 x 10⁹ m, extrapolating we have approximately that T = 3 10¹⁴ K.
To calculate the speed Cɢ we are going to use the Hawking temperature equation:
T = hc³ / (8ᴨ x KB x G x M)
Where h is Boltzmann's constant, c is the speed inside a black hole, Kв is Boltzmann's constant, G is the universal constant of gravity, and M is the mass of the black hole.
Substituting the values and calculating the value of C we have:
Cɢ = c = 10.30 10¹⁰ m/s
If we look at
Figure 3, we see that this value corresponds approximately to the calculated value.
With the value of Cɢ we calculate δ and M:
E = m C²
Where E is energy, m is mass, and C is the speed of light.
Eɢ = m Cɢ ²
Eɢ = K m C²
Eɢ = M C²
Cɢ ² = K C²
M = K m
Where K is a constant.
Calculation of the constant K:
C = 3 10⁸ m/s,
Cɢ = 10.30 10¹⁰ m/s,
m = 8.1 10³⁶ kg
E = 8.1 10³⁶ kg x 9 10¹⁶ m²/s²
Eɢ = 8.1 10³⁶ x (10.30 10¹⁰) ² = 8.1 10³⁶ x 106 10²⁰
Eɢ = (106 / 9) 10⁴ x 8.1 10³⁶ x 9 10¹⁶
Eɢ = K E
K = 11.77 10⁴
Calculation of the total mass M:
M = K m
M = (11.77 10⁴) x (8.1 10³⁶ kg)
M = 9.54 10⁴¹ kg, Total mass of black hole Sagittarius A*
m = 8.1 x 10³⁶ kg, total baryonic mass inside the black hole Sagittarius A*
Calculation of the mass of dark matter δ:
M = δ
δ = 9.54 10⁴¹ kg, total dark matter inside the black hole Sagittarius A*
Calculation of the ratio of the mass of dark matter δ and the mass of the Milky Way Mvl.
Mvl = 1.7 10⁴¹ kg, mass of the milky way
δ = 9.54 10⁴¹ kg, total dark matter inside the black hole Sagittarius A*
δ / Mvl = (9.54 10⁴¹ kg / 1.7 10⁴¹ kg)
δ / Mvl = 5.61, ratio of the mass of dark matter and the mass of the Milky Way
δ = 5.61 Mvl
The total dark matter δ is 5.61 times greater than the measured amount of baryonic mass of the Milky Way Mvl.
Let's consider circular motion with constant acceleration. See
Figure 2.
Let's remember that in a circular motion with constant acceleration, the tangential rotation velocity can be written with the following equation:
Equation (28) is very important, based on this equation we are going to work.
Let's consider the
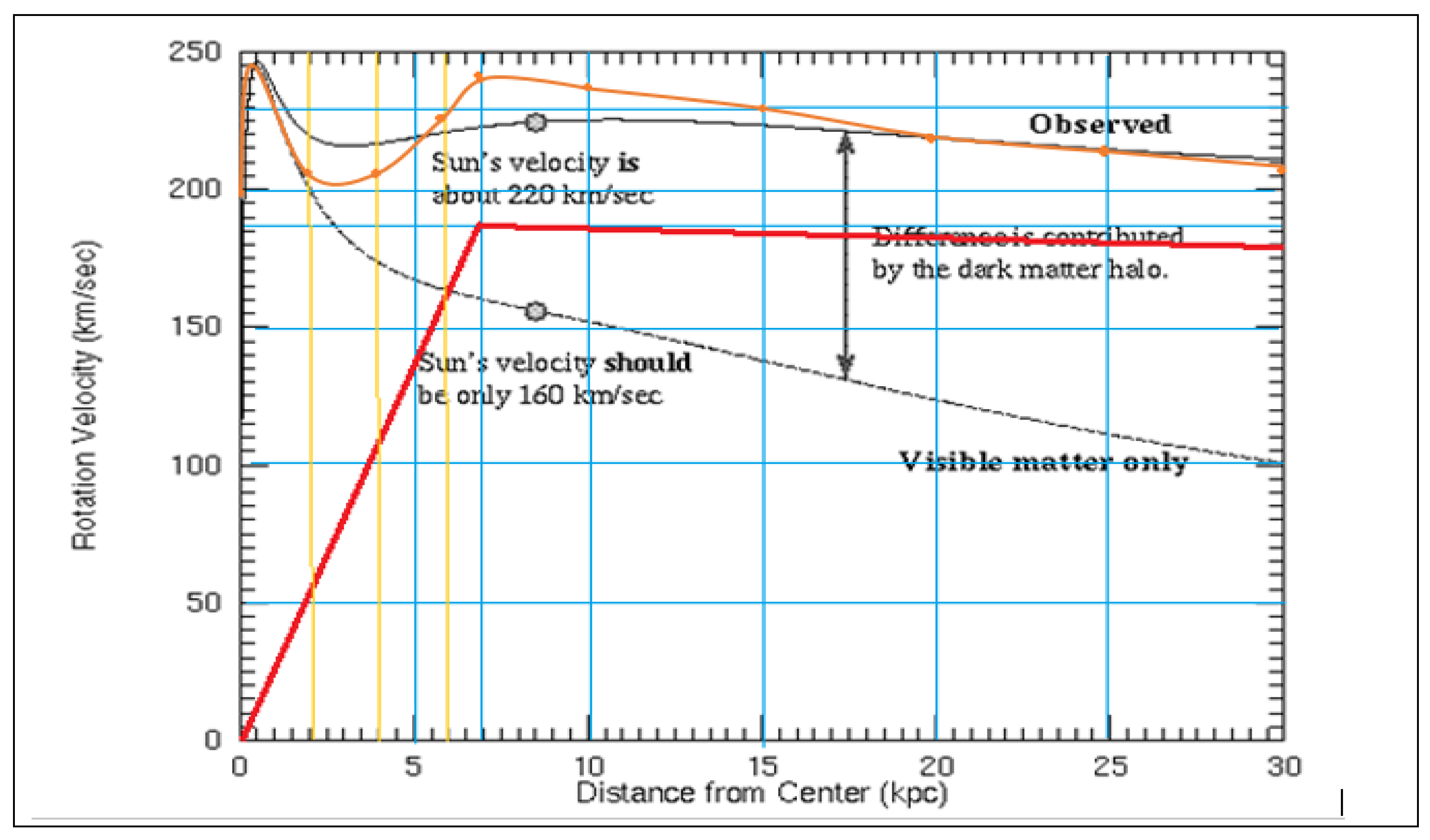
Figure 4, provided by the Federal University of Rio Grande do Sul UFRS:
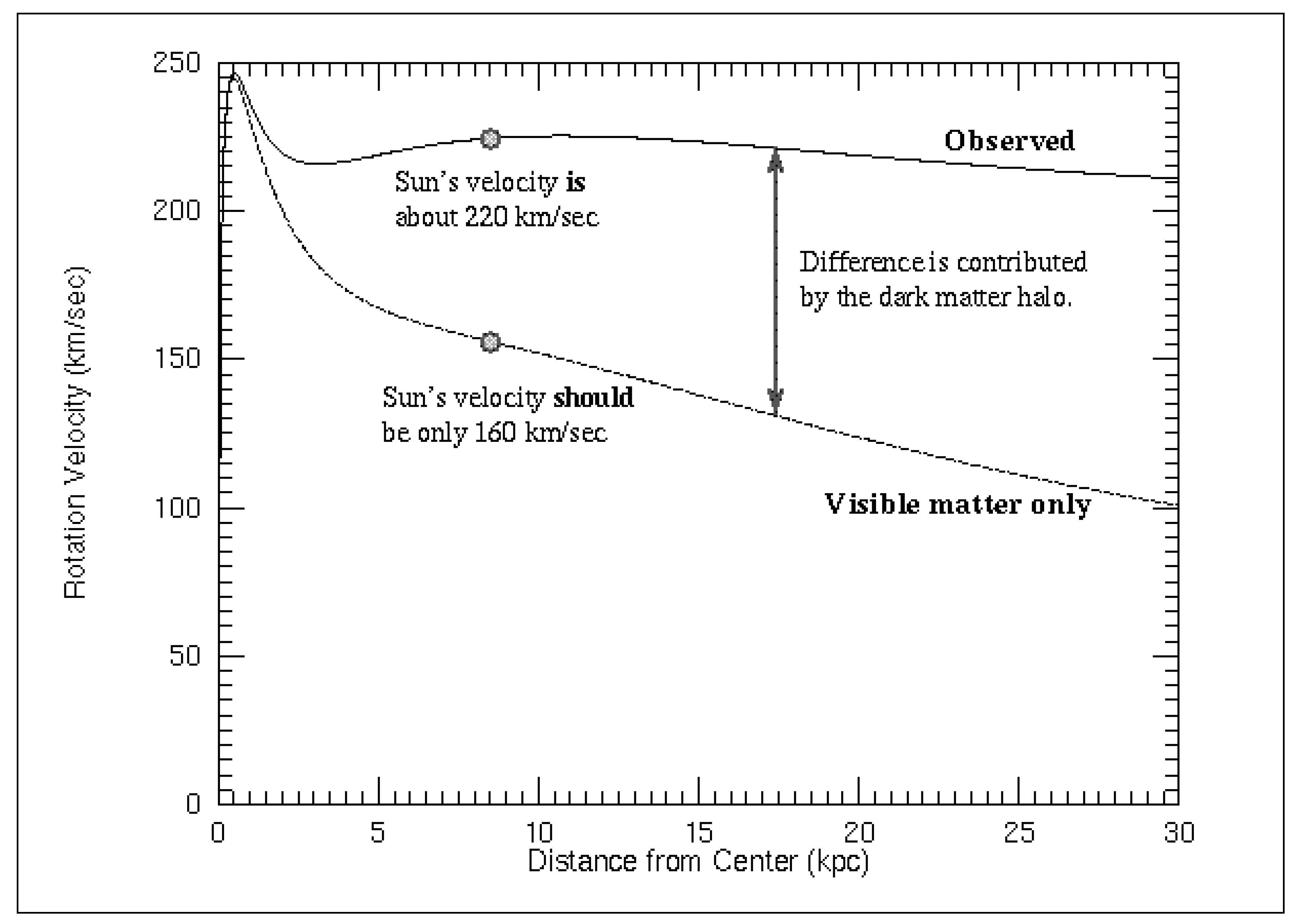
In
Figure 4, we observe that there is a difference between the observed or measured rotation speed of the Milky Way and the rotation speed considering only visible matter.
This difference is attributed to the existence of an invisible matter that we call dark matter mass, because we do not know its origin.
However, if we look at
Figure 3, as the black hole grows, a tangent force Ft appears, as a consequence of v > c inside a black hole, which generates additional mass. This tangential rotation force Ft delays the force Fc by 90 degrees. Both forces are gravitational forces.
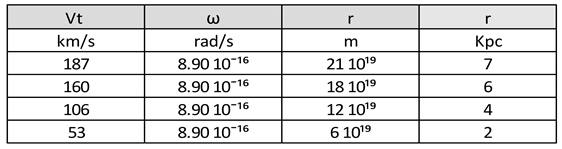
Taking as reference (28) and the distance r in Kpc to the centre of the Milky Way; We are going to generate the
Table 2:
Let's calculate ω:
To calculate ω, we are going to consider
Figure 5.
ω = (187 km/s) / (7 Kpc)
ω = 187 / 10 x 21 10¹⁶ = 8.9 10ˉ¹⁶
ωt = 8.9 10ˉ¹⁶ rad/s (29)
ωt, constant angular rotation velocity of the Milky Way.
ωt is theoretical omega ou proposed omega.
We are going to carry out the calculations of the angular rotation speed considering the data provided by the University of São Paulo, USP.
For the position of the sun, we have:
r = 8.5 Kpc
Vt = 224.4 km/s
Vt = ω x r
ω = Vt / r
ω = 224.4 km/s / 8.5 Kpc = 224.4 /8.5 x 3 10¹⁶
ωc = 8.8 10ˉ¹⁶ rad/s (30)
ωc, calculated value given by USP university.
We observe that the angular rotation velocity ωt given by (30), is approximately equal to the value calculated ωc, in (29)
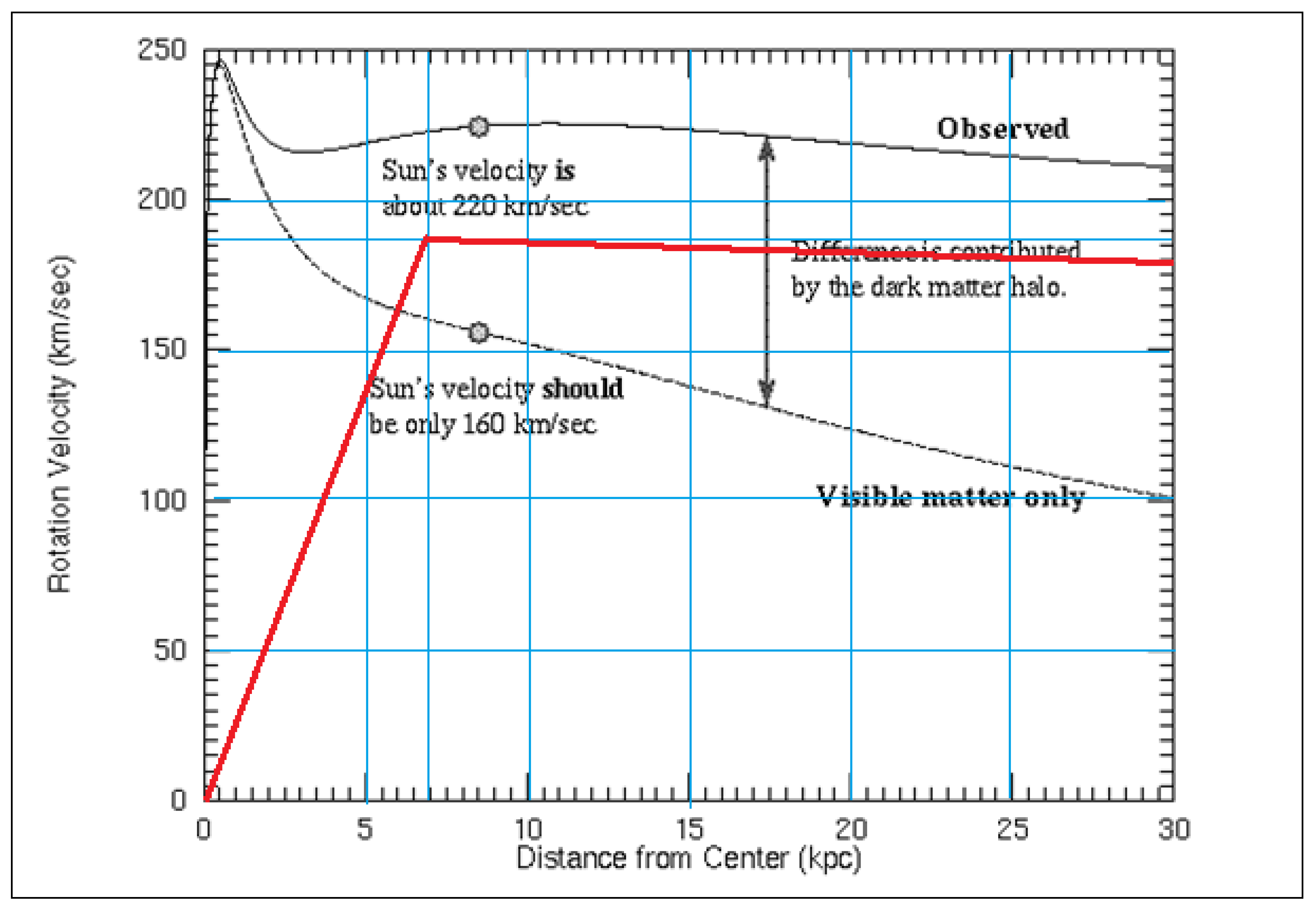
If we look at
Figure 5, starting at 7 Kpc, we see that the speed begins to decrease gently, therefore, we are going to consider r = 7 Kpc
Taking all this data into consideration, we are going to make the following table:
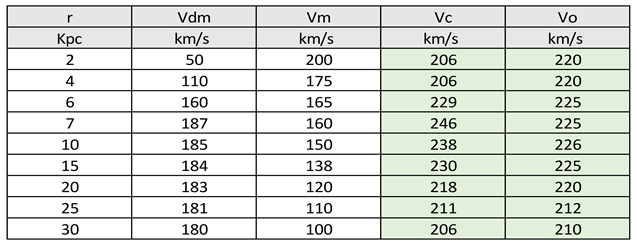
If we analyse
Figure 5, we observe that the relationship Vt = ω r, is fulfilled up to 7 Kpc, from 7 Kpc onwards, we observe that the rotation speed does not comply with the relationship Vt = ω r. From 7 Kpc onwards, the rotation velocity due to the contribution of dark matter mass decreases parallel to the rotation velocity curve of the Milky Way, measured or observed.
Considering the graph of the rotation speed of only the visible matter and the graph in red, of the rotation speed of the dark matter mass, we are going to calculate the vector sum of both rotation speeds to obtain a total rotation speed and compare it with the graph of the observed or measured rotation speed.
In the following table we represent the calculations:
2.7.1. Calculation of the Amount of Dark Matter Existing in the Andromeda Galaxy M31
We will consider the mass of the black hole at the centre of the Andromeda galaxy equal to:
Let's assume m the following value:
m = 1.5 10⁷ Ms = 1.5 x 10⁷ x 2 10³⁰ kg
Where Ms is the mass of the sun.
m = 3 x 10³⁷ kg
m, mass of the black hole at the centre of the Andromeda galaxy
Let's assume ML the following value:
ML = 3 10⁴² kg
Where ML is the luminous mass of the Andromeda galaxy
If we look at
Figure 3, for m = 4 x 10³⁷ kg, extrapolating we have approximately that:
T = 4 10¹⁵ K and c = 5 10¹¹ m/s.
T = 4 10¹⁵ K (31)
Cɢ = 3 10¹¹ m/s (32)
We are going to verify if these extrapolated values are correct or within the order of error.
Mвн = hc³ / (8ᴨ x Kв x G x T) (33)
Where h is Boltzmann's constant, c is the speed inside a black hole, Kв is Boltzmann's constant, G is the universal constant of gravity, and M is the mass of the black hole.
Substituting (31) and (32) into (33), we have:
Mвн = 1.5 10³⁷ kg
We see that m = 3 10³⁷ kg, is approximately equal to Mвн = 1.5 10³⁷ kg
If we look at
Figure 3, we see that this value corresponds approximately to the calculated value.
We will take m = 1.5 10³⁷ kg, as true.
With the value of Cɢ we calculate δ and M:
E = m C²
Where E is energy, M is mass, and C is the speed of light.
Eɢ = m Cɢ²
Eɢ = K m C²
M = K m
Where K is a constant.
Calculation of the constant K:
C = 3 10⁸ m/s
Cɢ = 3 10¹¹ m/s
m = 1.5 10³⁷ kg
E = 1.5 10³⁷ kg x 9 10¹⁶ m²/s² = 13.5 10⁵³
E = 13.5 10⁵³ J
Eɢ = 1.5 10³⁷ x (3 10¹¹) ² = 1.5 10³⁷ x 9 10²²
Eɢ = 13.5 10⁵⁹ J
Eɢ = K E
K = Eɢ / E = 13.5 10⁵⁹ / 13.5 10⁵³ = 10⁶
K = 10⁶
Calculation of the total mass M of the black hole of the Andromeda galaxy M31:
M = K m
M = (10⁶) x (1.5 10³⁷ kg)
M = 1.5 10⁴³ kg
Where M is the total mass of the central black hole of the Andromeda Galaxy.
m = 1.5 x 10³⁷ kg, total baryonic mass inside the black hole of the Andromeda Galaxy.
Calculation of the mass of dark matter δ:
M = δ
δ = 1.5 10⁴³ kg,
Where δ, is total dark matter inside the black hole.
Calculation of the ratio of the mass of dark matter δ and the mass of the andromeda galaxy ML.
ML= 3 10⁴² kg (34)
Where ML is the luminous mass of the Andromeda galaxy M31.
δ = 1.5 10⁴³ kg (35)
δ / ML= (1.5 10⁴³ kg / 3 10⁴² kg)
δ / ML = 5
δ = 5 ML
The total dark matter δ is 5 times greater than the measured amount of baryonic mass of the andromeda galaxy ML.
Let's consider circular motion with constant acceleration.
Let's remember that in a circular motion with constant acceleration, the tangential rotation velocity can be written with the following equation:
Vt = ω r (36)
Equation (36) is very important, based on this equation we are going to work.
From now on, I inform you that the data and graphs with which we are going to work were provided in the Cosmology 1 course, taught by Dr Alexander Sabot, from the federal university of Santa Catarina, UFSC. The graphs were made in Python with real astronomical data.
We are going to carry out the calculations of the angular rotation speed ω:
- a)
-
r = 33,000 Ly; Vt = 250 km km/s
1 Ly = 9.46 10¹⁵ m
ω = Vt / r
ω = 250 10³ / 308 10³ 10¹⁵
ωa = 8.11 10ˉ¹⁶ rad/s (37)
- b)
-
r = 80,000 Ly; Vt = 200 km/s
ω = Vt / r
ω = 200 10³ / 752 10³ 10¹⁵
ωb = 2.6 10ˉ¹⁶ rad/s (38)
We observe that the angular rotation velocity ωa, given by (37), is approximately equal to the value calculated ωb, in (38)
THEORETICAL ANALYSIS - CALCULATION OF DARK MATTER IN THE COSMOLOGY 1 COURSE, UFSC:
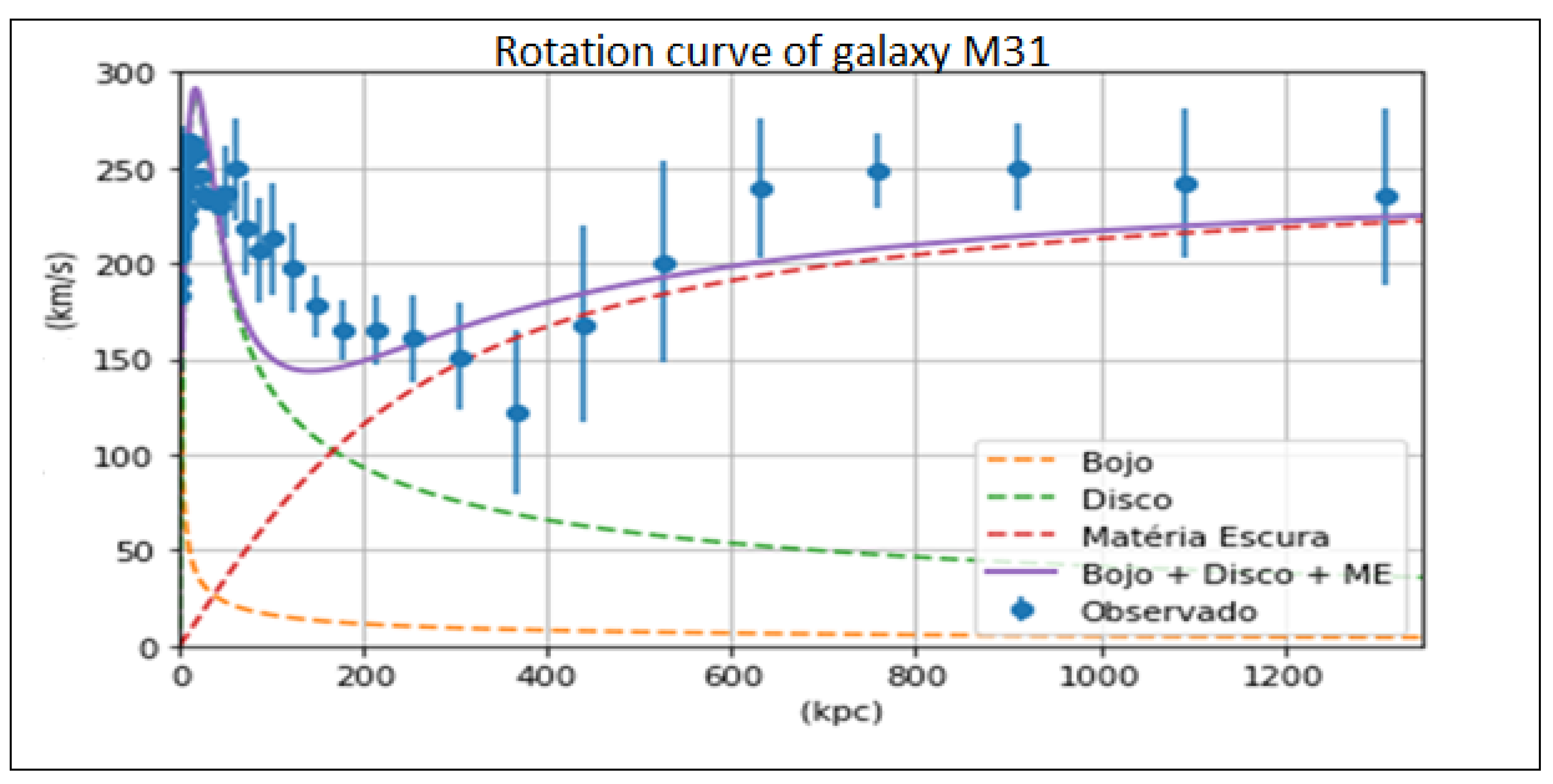
The Python program, developed by Dr Alexander Zabot, from the Cosmology I course, is used to calculate the rotation curves of the Andromeda galaxy due to dark matter mass, the galactic nucleus and the galactic disk.
Value of parameters used in Python.
Figure 7.
Parameter values used in the Python program to generate the graph in
Figure 8.
Figure 7.
Parameter values used in the Python program to generate the graph in
Figure 8.
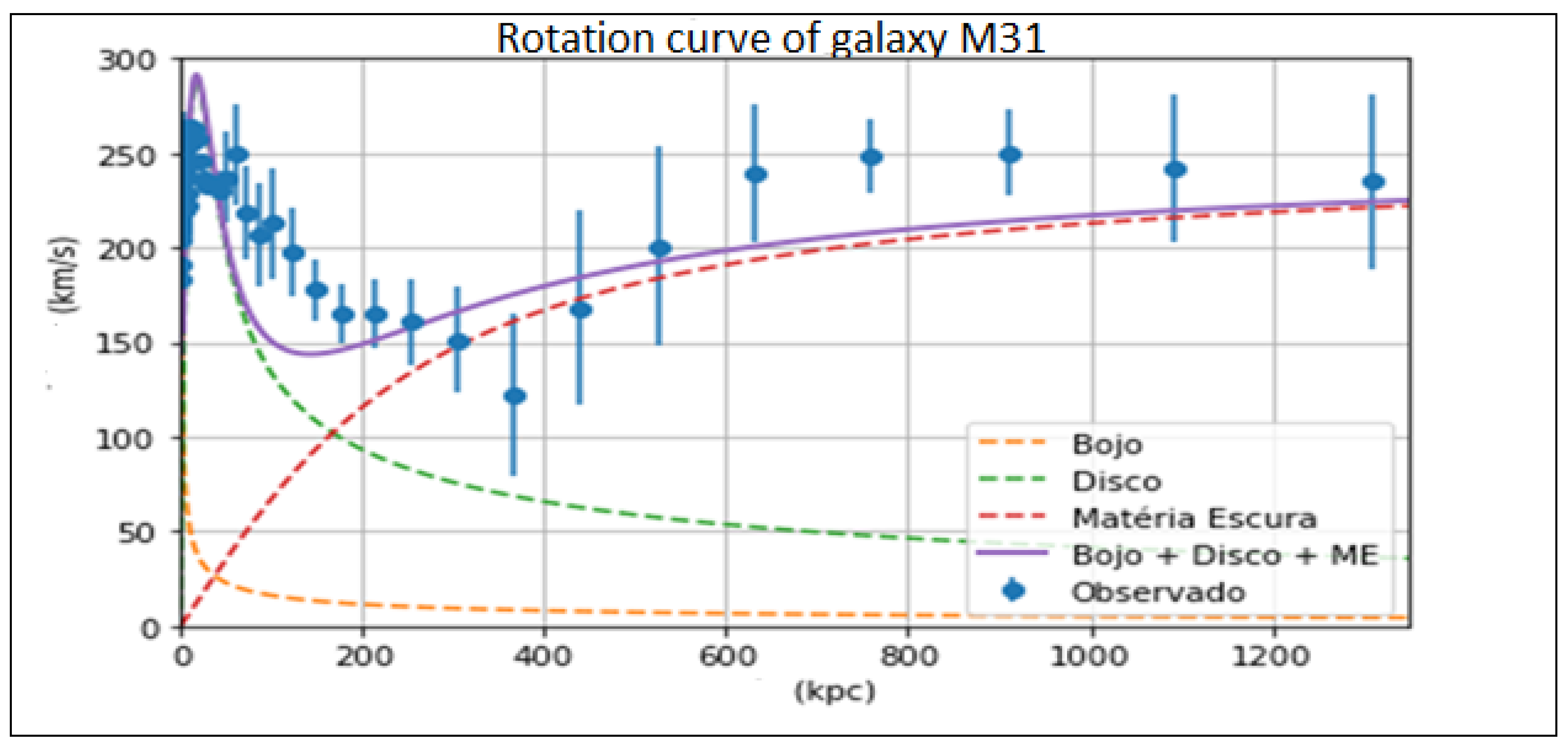
We observe in
Figure 8, how the calculated rotation curve values, in purple, are close to the measured or observed values, in blue.
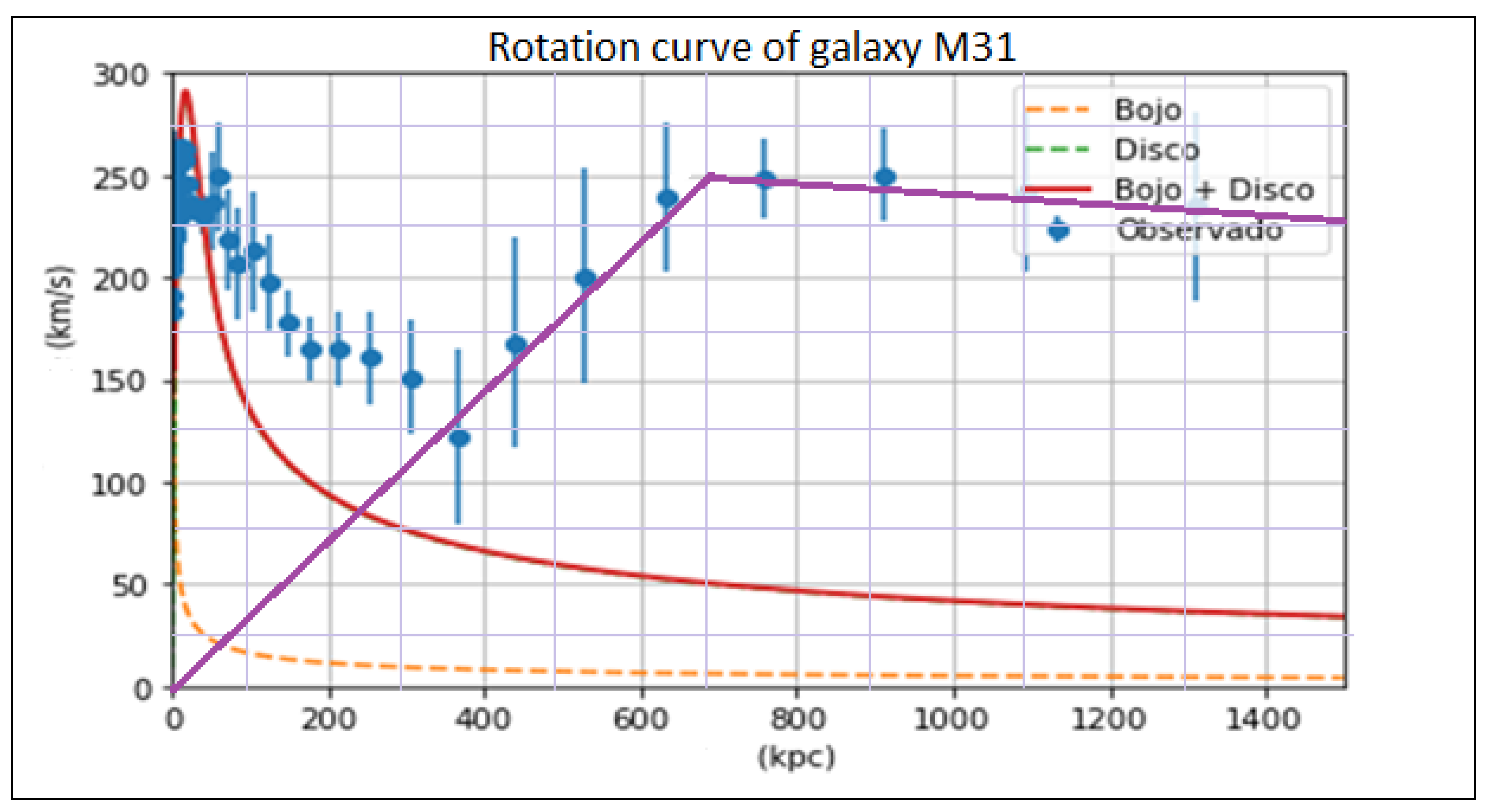
THEORETICAL ANALYSIS - WE CONSIDER THAT THE BLACK HOLE IS COMPOSED OF THE MASS M = m - i δ, THAT IS, THAT THERE IS A TANGENTIAL FORCE Ft. WE ASSUME THAT THE RELATIONSHIP, Vt = ω r, IS FULFILLED.
The Python program, developed by Dr Alexander Zabot, from the Cosmology I course, is used to calculate the rotation curves of the Andromeda galaxy M31 due to dark matter mass, the galactic nucleus and the galactic disk.
Value of parameters used in Python.
Figure 9.
Parameter values used in the Python program to generate the graph in
Figure 10.
Figure 9.
Parameter values used in the Python program to generate the graph in
Figure 10.
Figure 10.
M31 rotation curve; blue, represents the measured or observed values of the rotation speed of M31; red, represents the values of the rotation speed due to the galactic disk; orange, represents the values of the rotation speed due to the galactic centre.
Figure 10.
M31 rotation curve; blue, represents the measured or observed values of the rotation speed of M31; red, represents the values of the rotation speed due to the galactic disk; orange, represents the values of the rotation speed due to the galactic centre.
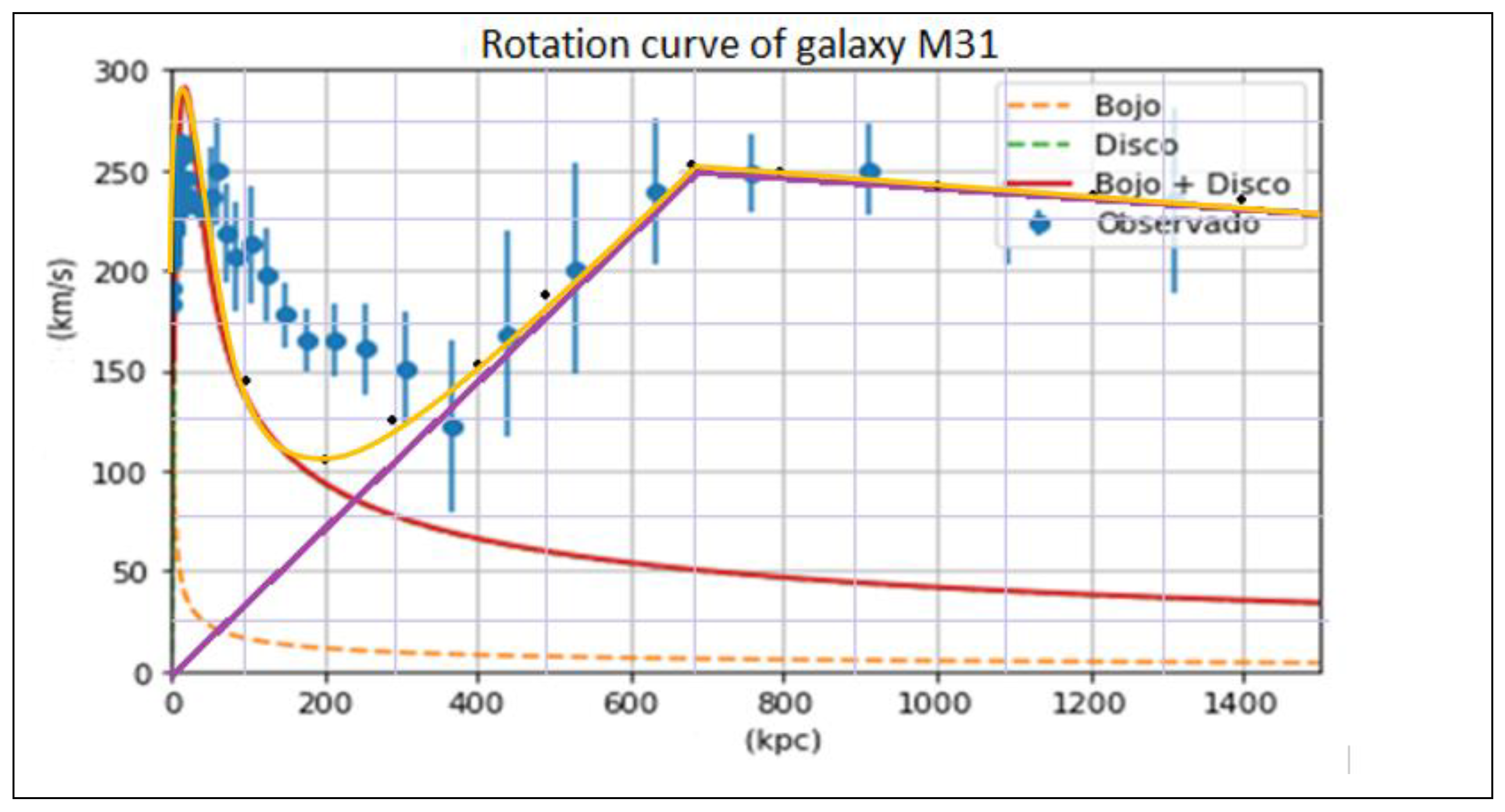
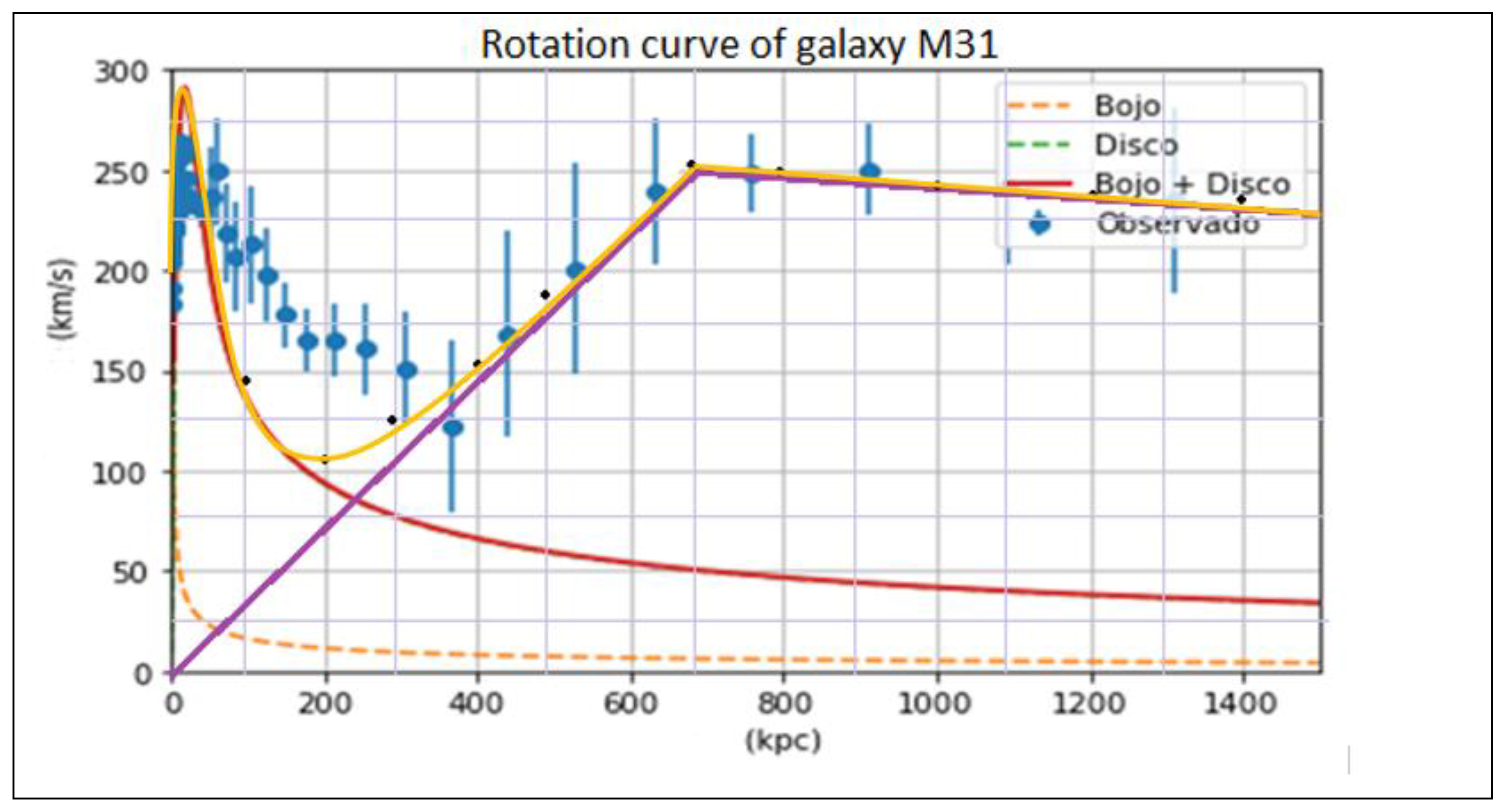
Taking into account
Figure 11, we are going to perform the following calculations:
Vt = ω r
ω = Vt / r
ω = 250 km/s / 700 Kpc = (250 10³ m/s) / 700 10³ 3 10¹⁶
ω = 250 / 2100 10¹⁶ = 0.119 10ˉ¹⁶ = 1.19 10ˉ¹⁷ rad/s
ω = 1.19 10ˉ¹⁷ rad/s
With the value of ω, we do the following and fill out the following table:
Table 4.
Represents the values of the rotation velocity Vt, angular rotation velocity ω, as a function of the radius r.
Table 4.
Represents the values of the rotation velocity Vt, angular rotation velocity ω, as a function of the radius r.
If we analyse
Figure 11, we observe that the relationship Vt = ω r, is fulfilled up to 700 Kpc; from 700 Kpc onwards, we observe that the rotation speed does not comply with the relationship Vt = ω r; from 700 Kpc onwards, the rotation velocity due to the contribution of dark matter mass decreases parallel to the rotation velocity curve of the Galaxy M31 measured or observed.
Considering the graph of the rotation speed of only the visible matter and the graph in red, of the rotation speed of the dark matter mass, we are going to calculate the vector sum of both speeds to obtain a total rotation speed and compare it with the graph of the observed or measured rotation speed.
In the following table we represent the calculations:
Table 5.
We represent Vdm, rotation speed due to dark matter mass; Vm, rotation speed due only to visible matter; Vc, calculated rotation speed that results from the vector sum of Vdm + Vm and Vo, is the observed or measured rotation speed.
Table 5.
We represent Vdm, rotation speed due to dark matter mass; Vm, rotation speed due only to visible matter; Vc, calculated rotation speed that results from the vector sum of Vdm + Vm and Vo, is the observed or measured rotation speed.
As seen in
Figure 11, from 400 Kpc onwards, the influence of dark matter is predominant.
It is important to remember that the rotation speeds are vectors, therefore, the sum of rotation speeds is vector and for this we use Pythagoras.
If we look at
Figure 12, we see that the observed rotation speed Vo is approximately coincident with the calculated rotation speed Vc, in yellow.
Vc is the vector sum of the velocity Vdm plus the velocity Vm, Vdm + Vm.
Let's compare the following figures:
If we look at
Figure 13, it corresponds to the theoretical model that we used in the cosmology course 1 and compare with
Figure 14, it corresponds to the RC model of a black hole that has mass M = m - i δ and that satisfies the equation Vt = ω r; We conclude that the rotation curve calculated in
Figure 14 fits the observed or measured data of the Andromeda galaxy.
To improve, you could combine both methods; below 400 Kpc, we use the theoretical analysis applied in Cosmology 1; above 400 Kpc, we apply the RC model of a black hole, in which the mass is M = m - i δ and it holds that Vt = ω r.
Finally, we have shown that using the theory of RLC electrical modelling of a black hole and the primitive universe and the theory of the generalization of the Boltzmann constant in curved space-time, we can determine the rotation curve of the galaxy M31, in coincidence with the observed or calculated values. This is another method that we can use to calculate the rotation speeds of galaxies.
2.7.2. We Will Describe the Contribution of All the Forces Involved in Determining the Rotation Speed of a Galaxy Using the RC Electrical Model of a Black Hole.
Let us remember that all forces and velocity are vector magnitudes. We are also going to remember that in the RC electrical model of a black hole it is true that M = m - i δ and Vt = ω r.
Ḟв + Ḟᴅ + Ḟdm = [(m / r) (Vв² + Vᴅ²)] + [(δ / r) Vdm ²] (39)
Ḟв + Ḟᴅ + Ḟdm = [(m / r) x (Vв² + Vᴅ²)] + [(δ/ r) x (ω r) ²] (40)
Ḟв + Ḟᴅ + Ḟdm = [(m / r)(Vв² + Vᴅ²)] + [δ ω² r] (41)
Equation (39), (40) y (41); represents the contribution of all the forces that intervene in the rotation curve of a galaxy.
Where m is baryonic matter; δ is dark matter mass.
Where Ḟв, force of the bojo or galactic nucleus; Ḟᴅ, force of the galactic disk; Ḟdm, force of the dark matter mass inside a black hole and r, radius of the galaxy.
Where Vв, is the rotation speed due to the bojo or galactic nucleus; Vᴅ, is the rotation speed due to the galactic disk; Vdm, is the rotation speed due to dark matter.
m >> δ, r near the black hole, we have:
V, the rotation speed of the galaxy will be the vector sum of the rotation speed of the galactic disk Vᴅ plus the rotation speed of the galactic nucleus Vв, that is:
V = Vв + Vᴅ (42)
V, is vector sum of rotation velocity.
Ḟв + Ḟᴅ + Ḟdm ≈ (m / r) x (Vв² + Vᴅ²)
δ >> m, r far from the galactic centre, we have:
The speed of the rotation curve of the galaxy will be approximately Vdm, due to the contribution of dark matter mass.
V = Vdm (43)
Ḟв + Ḟᴅ + Ḟdm ≈ (δ / r) Vdm ²
m ≈ δ, baryon mass of the order of the mass of dark matter.
V = Vв + Vᴅ + Vdm (44)
V, is vector sum of velocity.
Ḟв + Ḟᴅ + Ḟdm = [(m / r) (Vв² + Vᴅ²)] + [(δ / r) Vdm ²]
Ḟв + Ḟᴅ + Ḟdm ≈ (m / r) (Vв² + Vᴅ² + Vdm²)
The speed of the rotation curve of the galaxy will be the vector sum of the rotation speed of the galactic nucleus plus the rotation speed of the galactic disk and plus the rotation speed due to dark matter mass.
Vm = Vв + Vᴅ (45)
Where Vm represents the rotation curve of visible matter and is the vector sum of the rotation velocity due to the galactic nucleus plus the velocity due to the galactic disk.
Using the criteria described here in a), b) y c), the mentioned approaches; we perform calculations to determine the speed of the rotation curve of a galaxy Vc, calculated rotation speed represented in the tables; which we compare with Vo, which is the observed or measured rotation speed.
2.8. Dark Energy and Gravitational Waves: Origin of the Accelerated Expansion of the Universe and the Hubble Tension
All the mathematical and conceptual development that we are going to describe is based on the mathematical model described in the paper: RLC Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time; which we will use as a basis to develop our idea.
The mathematical approach to the origin of dark energy, which we describe in the paper: RLC Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time; It is framed in totally theoretical ideas, in this paper, we are going to support all those theoretical ideas through a demonstration of a practical example of the origin of dark energy that causes an accelerated expansion of the universe and creates the Hubble tension.
As a practical example to demonstrate the existence of dark energy we are going to use a test that is used in terrestrial seismic with vibroseis, Hardwire Similarity, in gas and oil exploration.
2.8.1. Theoretical Analysis of the Dirac Delta Function (Impulse) and Its Analogy with the Big Bang
The collision of two stellar black holes with an average mass of 40 solar masses, detected by the LIGO and Virgo observatory, confirmed the existence of gravitational waves.
If we take this to the Big Bang, to the inflationary period, the immense energy released would be expected to generate a spectrum of gravitational waves; this affirmation is very important and based on this we are going to work.
Let us define the impulse function &(t) or also called the Dirac delta function.
Graphical representation of the impulse function:
Figure 15.
impulse function.
Figure 15.
impulse function.
We see that for t = 0 the value of the impulse function &(t) tends to infinity (In some literature for t = 0, the Dirac delta function has a generic unitary amplitude) and that for t ≠ 0 the value is 0. Based on what has been said, we can make an analogy with the expansion of the Big Bang and say that at time t = 0, its expansion would behave like a pulse of infinite energy.
If we analyse the amplitude and phase spectrum of the Fourier transform of the impulse function &(t), we see that the amplitude spectrum is equal to a constant K for all frequencies and the phase spectrum is equal to 0 for all frequencies.
Making an analogy between the impulse and the burst of energy of the Big Bang released at time t = 0, we can say that for all frequencies the amplitude spectrum is constant and the phase spectrum is zero.
Figure 16.
Amplitude spectrum of the function &(t) in the frequency domain.
Figure 16.
Amplitude spectrum of the function &(t) in the frequency domain.
Figure 17.
Phase spectrum of the function &(t) in the frequency domain.
Figure 17.
Phase spectrum of the function &(t) in the frequency domain.
Let's try to clarify what has been explained and let's say that at t = 0 at the moment of the Big Bang explosion, the enormous amount of energy released generates infinite waves of energy (infinite frequency spectrum) that will propagate through space in all directions, each wave with the same amplitude and the same phase.
For the amplitude spectrum to be constant and the phase spectrum to be zero, we will infer that it is a zero-phase system.
We will introduce the concept of convolution and for this we will make the following analogy. When we do seismic exploration studies to look for gas or oil and use explosive as a source of energy, the signal that we pick up on our seismic sensors is the result of the energy released by exploding the dynamite that mixes or convolves with the physical characteristics of the earth. If we analyse the signals captured by geophones sensors in the frequency domain, we see that the amplitude and phase spectra depend on the physical characteristics of the earth. We are dealing with a causal type minimal phase system.
We will consider the explosion of the dynamite as the explosion of a black hole and the physical characteristics of the Earth analogous to the physical characteristics of the space-time of our universe that surrounds the black hole. According to the above, we can say that the energy released and produced by the Big Bang mixes or convolves with the physical characteristics of the existing universe to produce infinite waves spectrum of energy that propagate through space-time (gravitational wave spectrum), whose spectrum of amplitude and phase in the frequency domain, will depend on the physical characteristics of space-time at the moment of the explosion in analogy with the physical characteristics of the Earth. In other words, we can consider the Big Bang as a minimum phase causal system.
In the following example, we will show the difference that exists between a zero-phase non-causal system and a minimal-phase causal system.
Figure 18.
wavelet with minimum phase in the upper graph and a wavelet with zero phase in the lower graph.
Figure 18.
wavelet with minimum phase in the upper graph and a wavelet with zero phase in the lower graph.
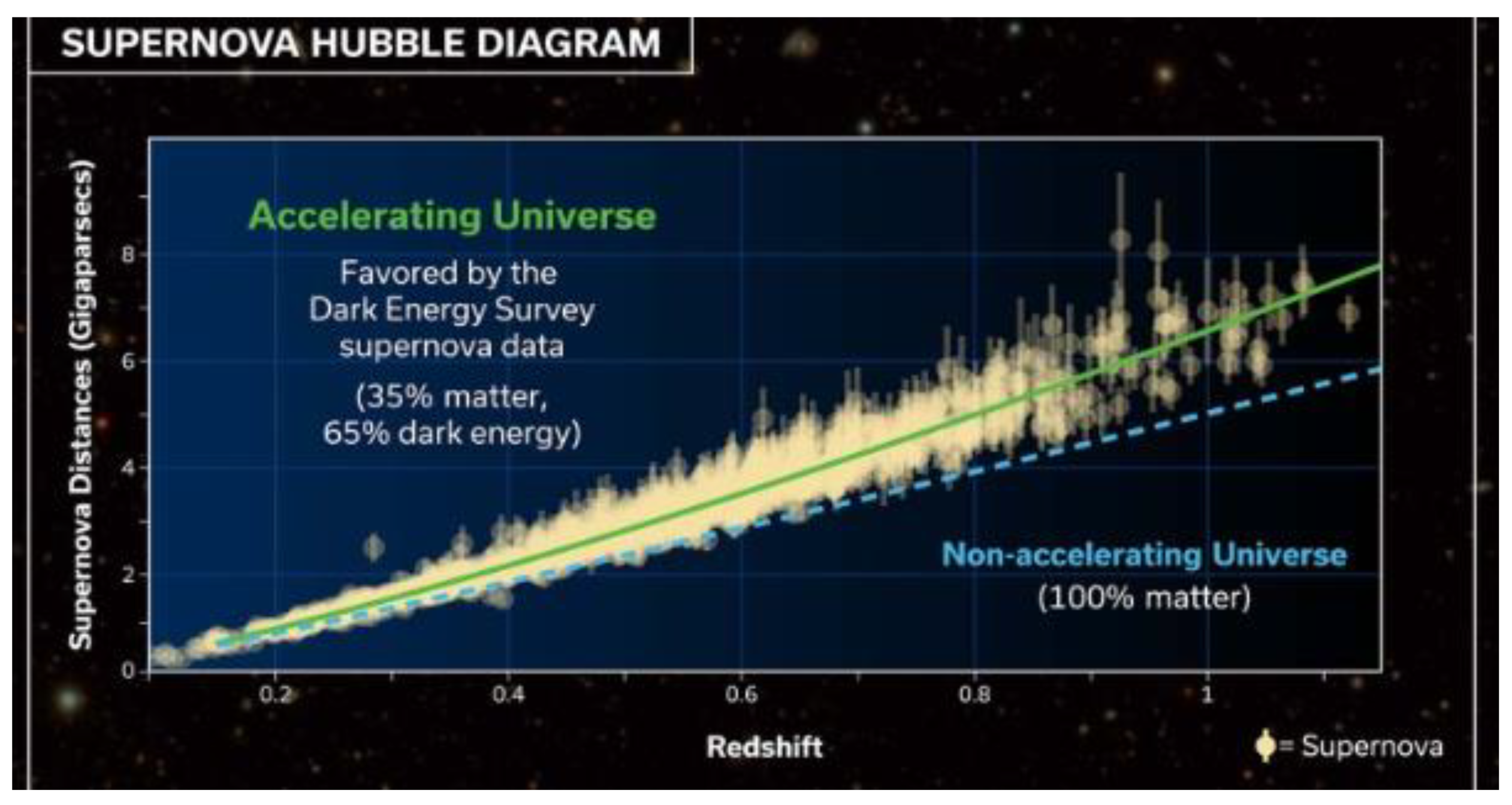
The Lambda-CDM model and the FLRW metric are indicating that the expansion period of the universe, called inflation, behaves as an approximation of the Dirac function for t = 0, the energy released is infinite, spectrum of constant amplitude and spectrum of phase 0.
What would happen if we consider the big bang as a minimal phase causal system? that is, that the energy released during inflation is not transmitted instantaneously to space-time and that the expansion of gravitational waves during inflation is a function of time. Possibly these considerations could end or solve the problem of dark energy generated by an incorrect conjecture when considering the isotropic universe, that is, we would be affirming that Einstein's field equations would not be adequate to analyse the evolution of the universe or would eventually be needing of a fine adjustment.
I propose that the space-time expansion of the inflationary era of the Big Bang behaves as a minimal phase causal system, in which the released energy is transmitted to space-time with a minimum delay and the propagation of the generated gravitational waves depend of the physical characteristics of the space-time. An example of this behaviour is analogous to the seismic exploration method with explosives, in which the entire system is of minimum phase (causal) and the waves generated by the explosion are transmitted to an anisotropic medium, that is, with different refractive and reflection coefficients.
We are going to highlight the following in this analysis:
1) If we analyse the Dirac delta impulse function &(t), in the frequency domain, the amplitude spectrum tells us that we have infinite frequencies and the zero-phase spectrum tells us that all the energy is transmitted to the medium instantaneously. We are facing a zero-phase non-causal system.
2) If we analyse the Big Bang as a real system analogous to the explosion of dynamite in seismic prospecting; In the frequency domain, the amplitude spectrum tells us that we have infinite gravitational waves spectrum and the phase spectrum tells us that energy is not transmitted instantaneously to space-time, the transmission of energy to space-time is a function of time; we are faced the presence of a minimal phase causal system. It is precisely this characteristic that a minimal phase causal system has, which takes on significant importance in order to explain the origin of dark energy.
2.8.2. Analysis of the Propagation of Seismic Waves Using the Vibroseis Method and Its Analogy with the Big Bang.
Real example:
In our analysis, we are going to use a Hardwire Similarity, Start up.
The Hardwire Similarity is a test carried out in Seismic that uses Vibroseis, to measure the polarity of the Recording system and the polarity of the Vibroseis system as a whole; which must comply with the SEG (Geophysical Exploration Society) standards.
The Hardwire Similarity also serves to measure the start time or zero adjustment, that is, the synchronization of the system.
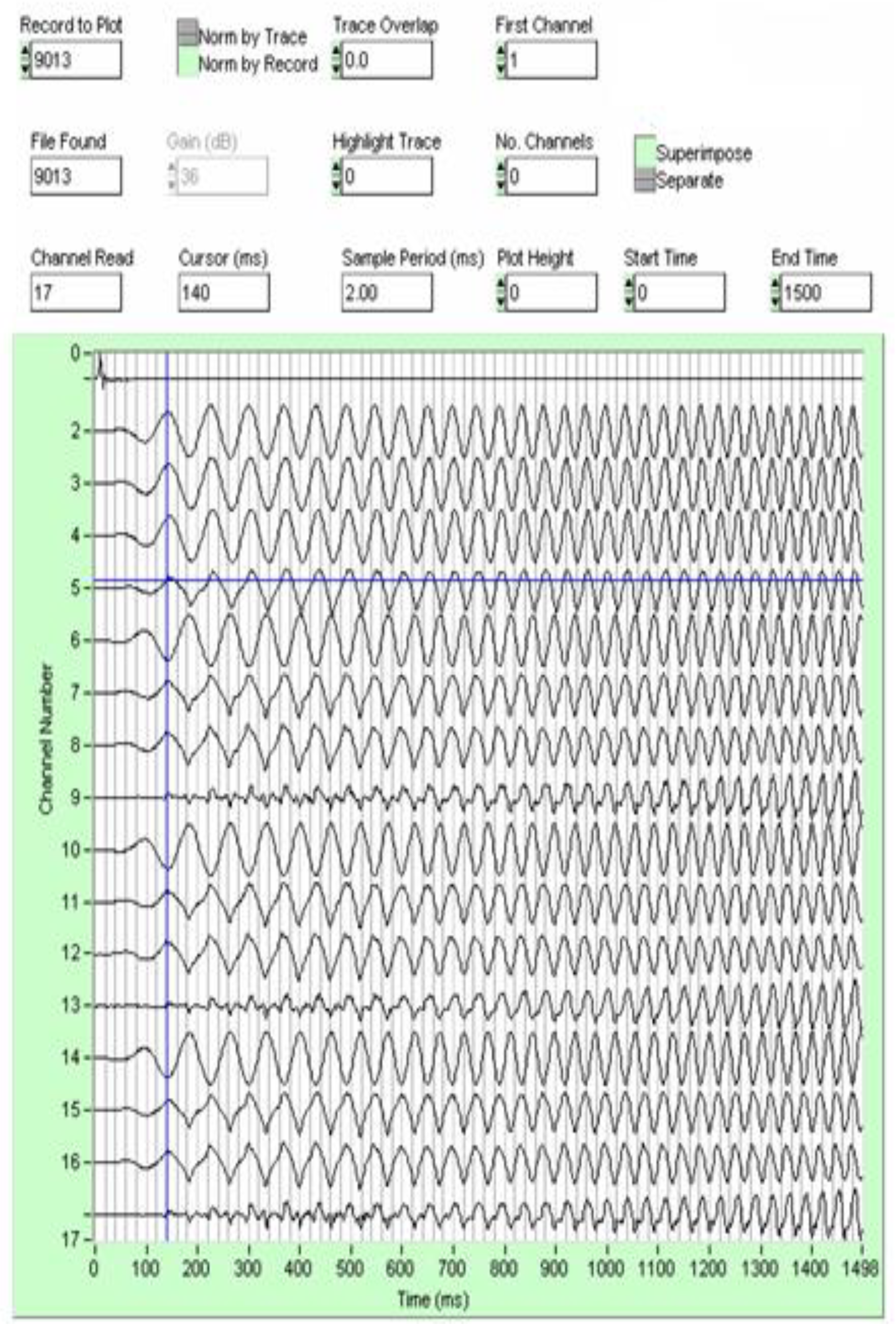
Figure 19, shows the graph of the signals recorded on tape, which we used to process the tests.
In
Figure 20, the signals are described per channel; the graph on the right describes what each signal is in the first 5 channels, from the graph in
Figure 19.
On the left, it is described what each signal is, from channel 6 to channel 17, from the graph in
Figure 19.
Figure 21, describes the sweep used in the test vs File. It tells us that its frequency ranges from 8 Hz to 96 Hz, that the sweep time is 8 s and that the sweep type used is 0.2 Db/Hz.
As a general comment, to process the signals we have used a Testif-i key.
Now, using graphs we are going to try to understand the mathematical process of correlation.
Figure 22.
Graphic explanation of the convolution, cross-correlation and autocorrelation process.
Figure 22.
Graphic explanation of the convolution, cross-correlation and autocorrelation process.
To begin our signal analysis, it is necessary to explain the following:
Vibroseis: It is a truck that consists of a servomechanism system that is divided into two parts; an electrical part, which generates the pure electronic sweep called True Reference. A mechanical part, which is responsible for transforming the pure electrical sweep into a mechanical sweep, which is applied to the ground. In our work we use 60,000 Lb Vibroseis.
Casa Blanca: It is the Recording truck where is the heart of recording electronics. When the vibroseis executes the seismic sweep, this signal is transmitted to the different layers of the earth, is reflected in the different interfaces and returns to the surface, where it is captured by the geophones. This signal is transported from the geophones to recording truck, where it is processed (correlated) and recorded on tape.
Spread: It is the set of geophones, cables and boxes that are connected to the recording truck, which are distributed on the ground, used to capture the seismic signals emitted by the vibroseis.
Now we are going to analyze the following signals:
Figure 23.
Analysis of channel (2, 2), True Reference signal (see
Figure 19).
Figure 23.
Analysis of channel (2, 2), True Reference signal (see
Figure 19).
From the processing of this signal we are going to rescue the following image:
Figure 24.
Envelope of autocorrelation canal (2,2).
Figure 24.
Envelope of autocorrelation canal (2,2).
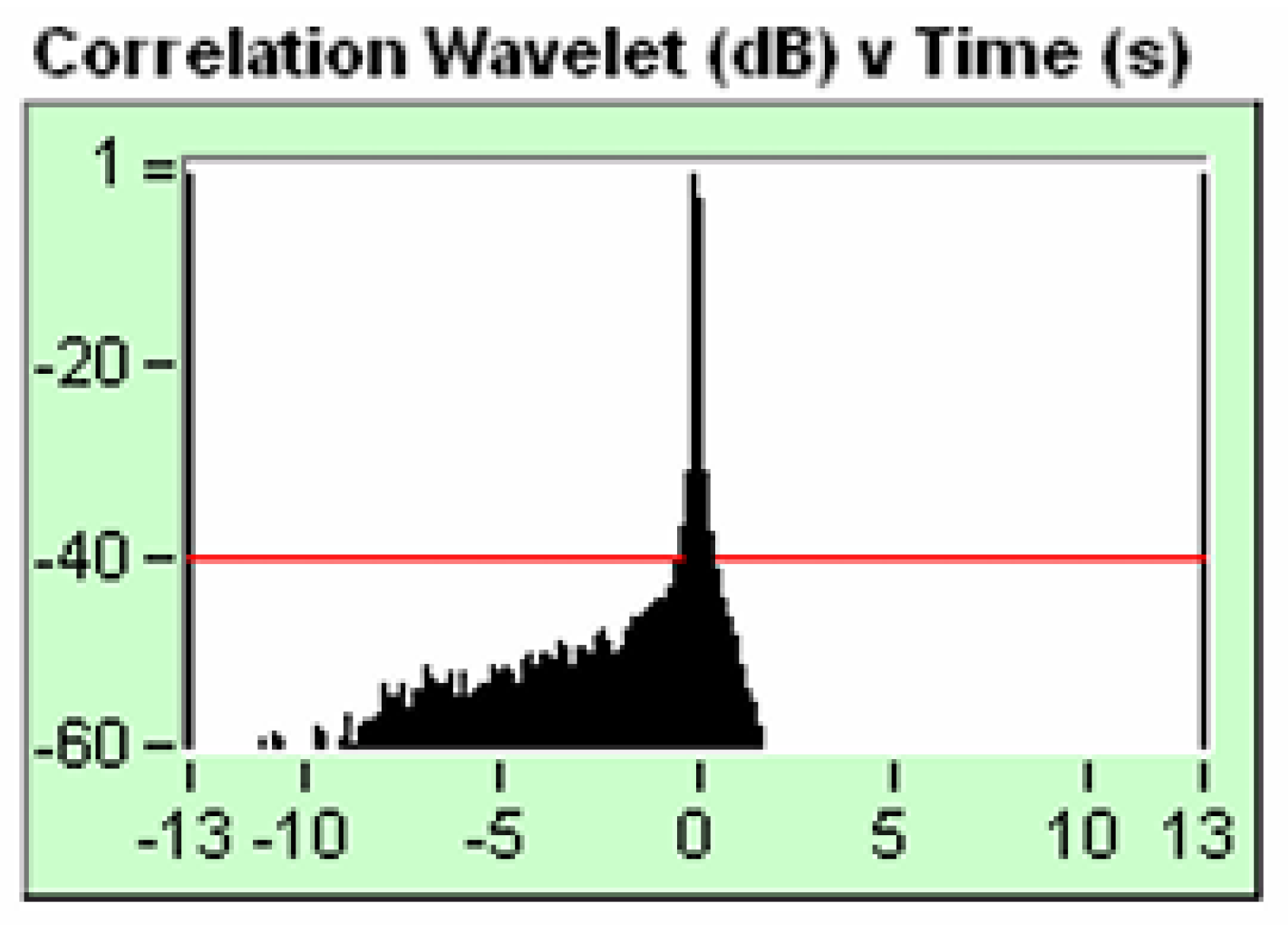
It is important to highlight that this signal is symmetrical on both sides, has no noise and reaches up to -120 dB common mode rejection of the signal/noise , It is a pure electronic signal.
Now we are going to analyze the following signal:
Figure 25.
Analysis of channel (2, 15), True Reference signal vs - Ground Force (see
Figure 19).
Figure 25.
Analysis of channel (2, 15), True Reference signal vs - Ground Force (see
Figure 19).
It is important to note that we are analyzing the signal from channel 2, true reference (it is a pure electronic signal) and the signal from channel 15, - ground force (It is the signal that the accelerometers of the Vibrosis truck capture, they are processed and sent to the recording truck, which are recorded on tape and displayed on the monitor, see
Figure 19).
From the processing of this signal we are going to rescue the following image:
Let's first analyze image 26 and 27.
If we analyze
Figure 22, the envelope of cross correlation; we see that it is not the same to cross correlate the channels (2, 15) or cross-correlate the channels (15, 2); from now on
, we are going to use Figure 27, the envelope of cross correlation of the channels (15, 2) for the simple reason that in this picture the noise corresponds to the right of zero, that is, for positive time, this is the main reason why we use this envelope of cross-correlation configuration. In Figure 26, the signal/noise is to the left of zero, for negative times and that confuses our interpretation.
The correct thing would be to use the Testif-i key to process the signal again, perform the envelope of cross-correlation of the signals (15, 2) and obtain the correct image, unfortunately I do not have that Testif-i key; for which I am forced to use the mirror image and give a good explanation.
Now we are going to analyze how everything explained is related to the Big Bang.
If we analyze
Figure 24, it shows the autocorrelation envelope of the signal that corresponds to channel 2 (True Reference, pure electronic signal), it is a symmetrical signal and reaches up to -120 db common mode rejection of the Signal/noise, It has no noise and we can see this in the FK filter that we show below.
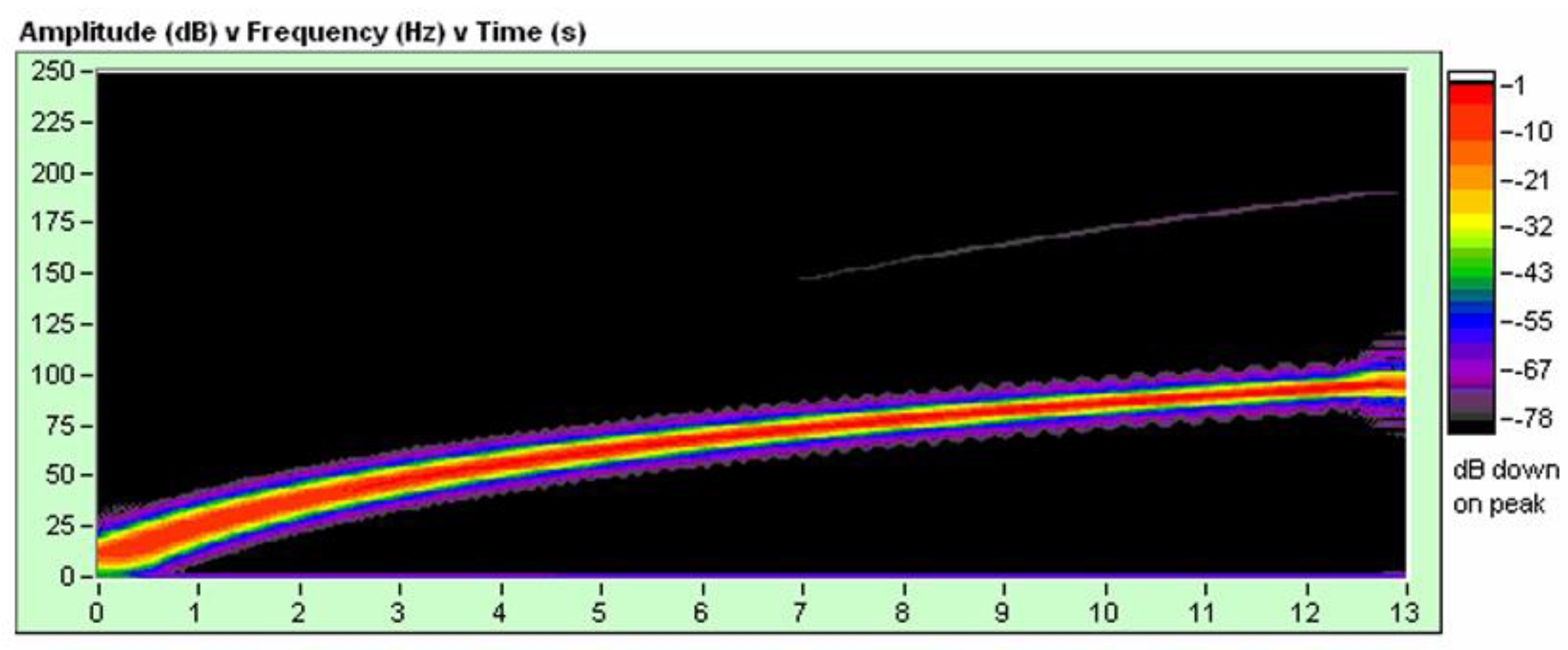
Figure 28, shows the frequency content of the pure electronic sweep of channel 2 (True Reference), we see that it does not have even or odd harmonics and we do not see noise in the signal; in other words it is a pure electronic sweep.
This pure electronic sweep that corresponds to channel 2 (True Reference) is the perfect analogy with the Big Bang. The theory developed to explain the Big Bang, the Lambda-CDM model (metrica FLRW), analyzes the Big Bang as if the expansion were of a single fundamental frequency, this makes us think that the expansion should have a single Hubble constant. This expansion does not consider even and odd harmonic frequencies or noise in the signal, which is very important because these additional energy contributions make the Hubble´s constant variable and most importantly, the additional energy makes the expansion of the universe accelerate.
If we analyze
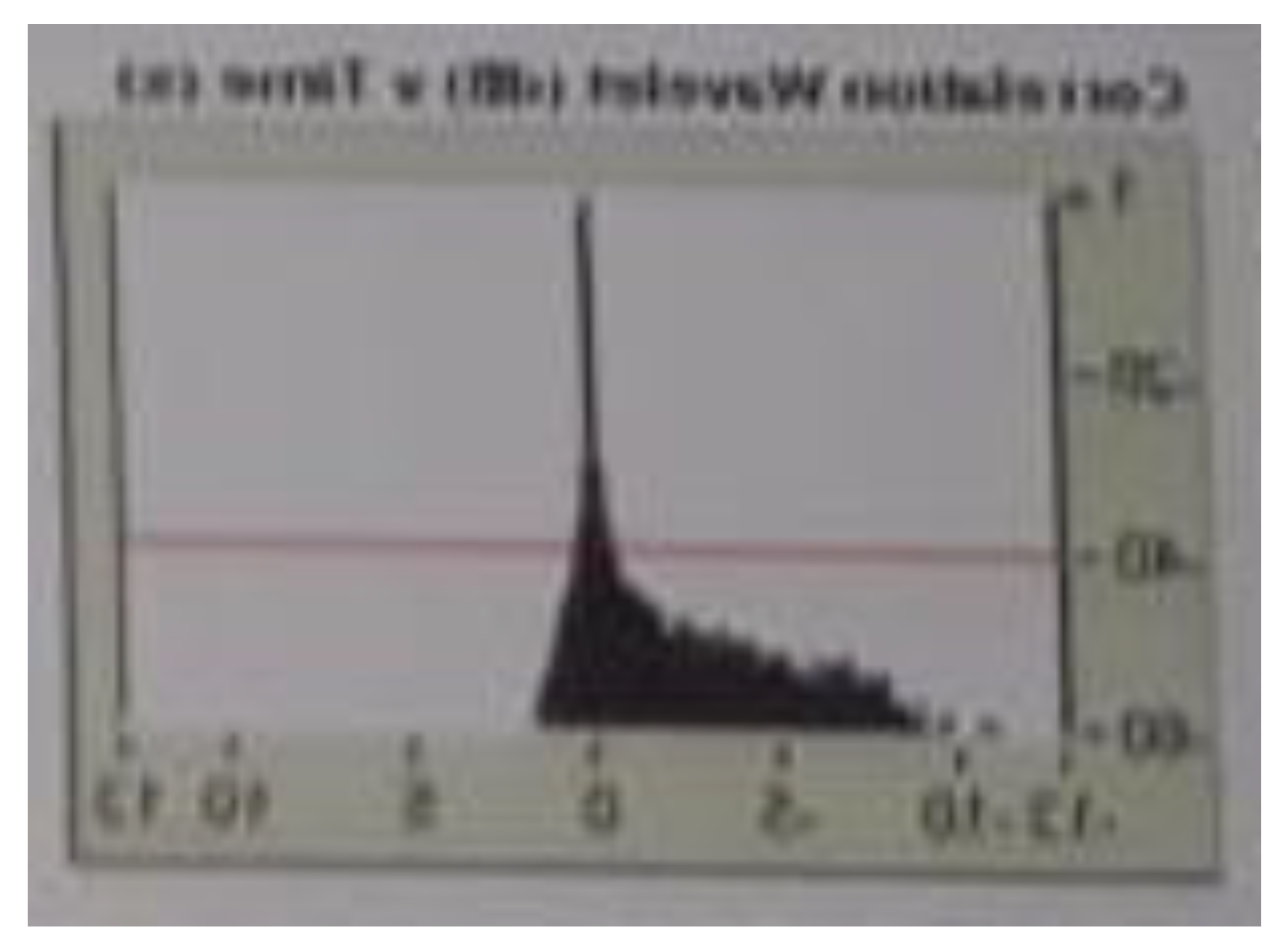
Figure 27, it shows the envelope of the autocorrelation of the signal that corresponds to the channel (15, 2) that corresponds to the signal [-Ground Force vs True Reference], it is an antisymmetric signal and we observe that from - 40 db common mode rejection of the signal/noise, there is a noise content and we can see this in the FK filter shown below.
Figure 29.
Shows the frequency content, FK filter of the channel 15, signal (-Ground Force).
Figure 29.
Shows the frequency content, FK filter of the channel 15, signal (-Ground Force).
The signal from channel 15, see
Figure 19, which corresponds to the mechanical signal emitted by the Vibroseis Truck, which is captured by the Vibroseis accelerometers, processed and recorded; It is a real signal that contains the fundamental frequencies, odd and even harmonic frequencies, and additional noise.
If we make an analogy with the Big Bang, in addition to the fundamental frequency, we must consider the harmonics and inherent noise to be able to correctly interpret the expansion of the universe.
Now we are going to analyze it from another point of view, to understand the origin of dark energy.
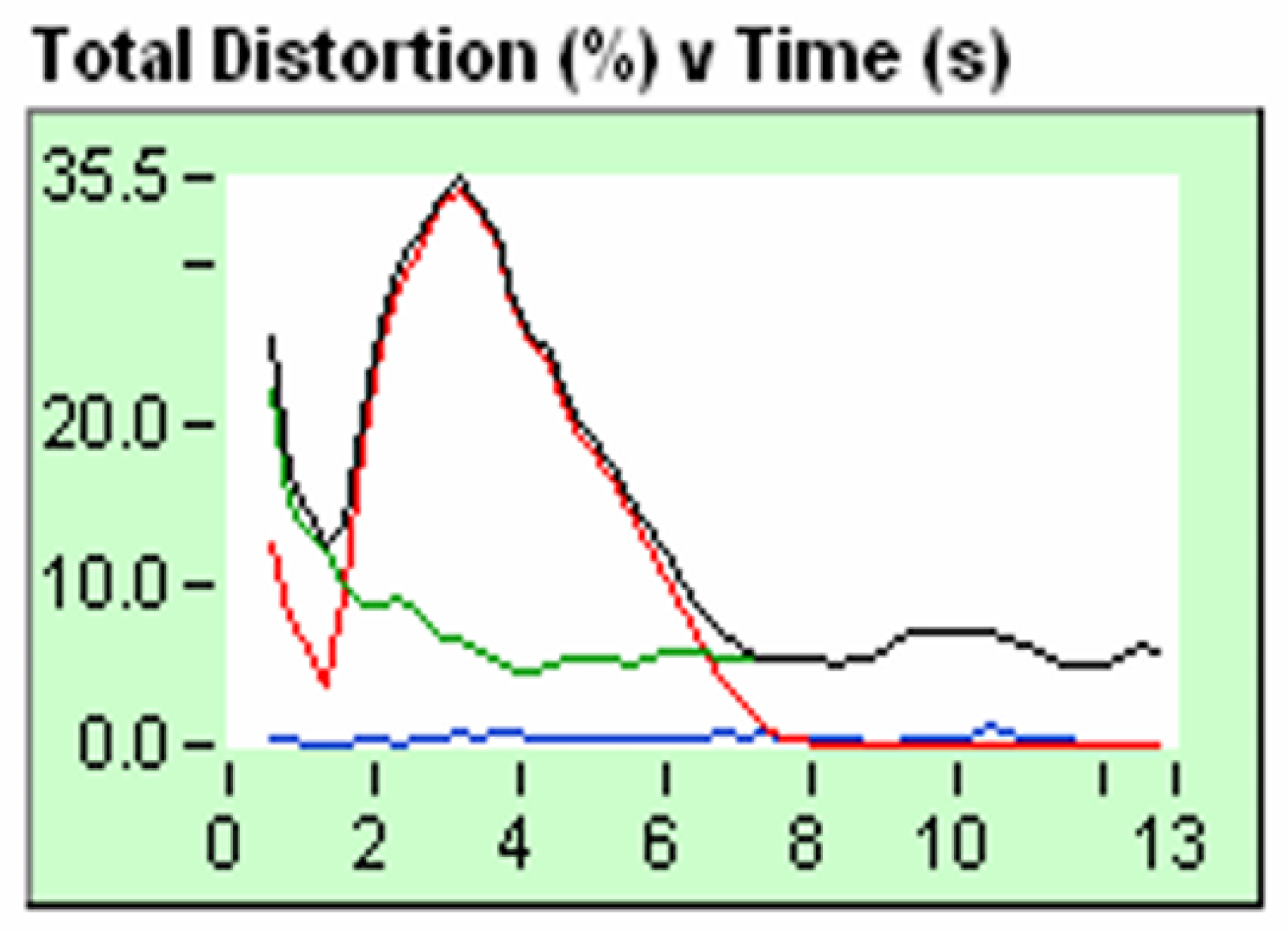
Let's analyze the distortion graph, from
Figure 23, we rescue the following graph :
Remember that
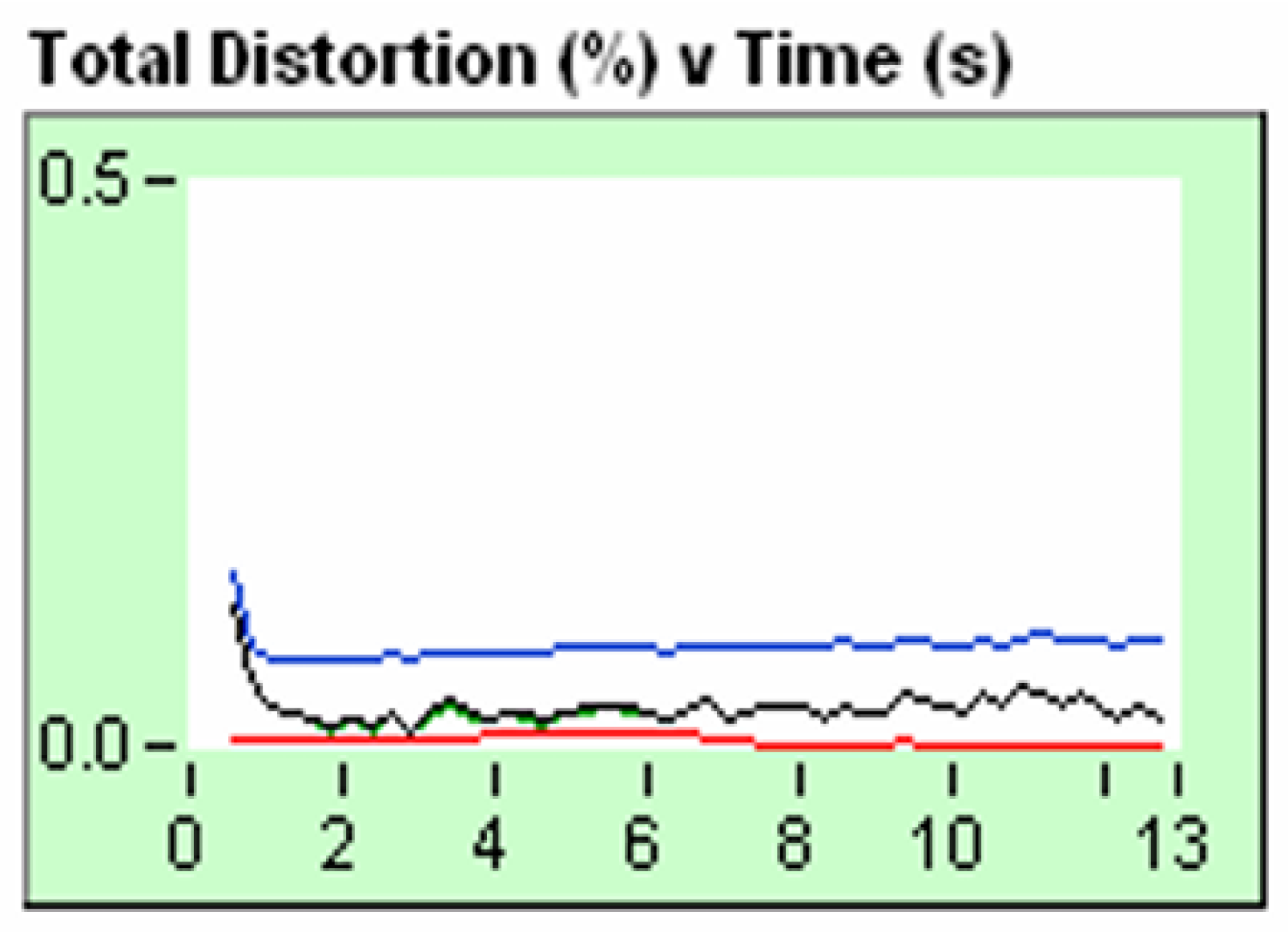
Figure 23, represents a pure electronic sweep signal without distortion. If we look at
Figure 30, we see that the distortion is approximately of the order of 0.1%. We can also see this in
Figure 28, FK filter, in which it is observed that there is no dostortion.
If we make an analogy with the Big Bang, the expansion of space-time, we can consider the example of the balloon that inflates, it does so with a fundamental frequency, there is no distortion, noise; it is an ideal expansion that follows the FRWL metric, the equations of general relativity and all the theoretical development framed in the theory of modern Cosmology.
Let's analyze the distortion graph, from
Figure 25, we rescue the following graph :
In
Figure 31, we are analyzing the distortion graph of a real signal, it is a signal emitted by the vibroseis truck that interacts with the terrain. We see that the distortion peak is approximately 35%. That distortion is produced by even harmonics, odd harmonics and additional noise. We can see this in
Figure 29, FK filter, in which the frequencies of even, odd harmonics and additional noise are observed.
Again, if we make an analogy with the Big Bang, it is important to understand the following concept. The expansion of space-time produced by the Big Bang, in addition to producing a spectrum of fundamental frequencies of gravitational waves, produces an additional spectrum of even and odd harmonics, additional noise that is a result of the energy released by the Big Bang which convolves with space-time. Space-time being the medium through which gravitational waves propagate.
The sum of additional energy due to the frequency of even and odd harmonics and additional noise is what causes dark energy. Since this energy distribution is not constant as a function of time, it generates what we call Hubble´s tension, which is nothing more than considering variable the Hubble´s constant.
In general, when the vibroseis truck carries out the sweep, depending on the type of terrain, a distortion of the order of 20% to 50% is produced; when the terrain is volcanic rock the distortion goes up to 80%; also on occasions the distortion exceeds 100% producing a decoupling of the vibroseis truck from the ground, in this situation the force exerted by the earth on the vibroseis truck is greater than the weight of the vibroseis, causing it to make sudden jumps.
Recall that we have hypothesized that the Big Bang behaves as a minimal phase causal system, in other words, the energy contribution is a function of time.
This is how we can correctly understand the following graph:
The difference that exists between the dotted light blue line, which corresponds to the non-accelerated universe, and the green line, which corresponds to the accelerated universe, is simply that we are not considering the energy contributions that correspond to the harmonics of the fundamental frequency and the noise inherent, as was analyzed for the example of Hardwire Similarity that is carried out in seismic prospecting. If we consider the contributions of additional energies to the fundamental frequency (harmonics of the fundamental frequency and the noise inherent) as a function of time, we will understand why the expansion of the universe is accelerated and deduce that the Hubble´s constant must be variable.
In
Figure 27, we can see that additional energy contribution corresponding to the harmonics and noise in the signal, we can see how from time t = 1 to t = 13 sec; the additional energy decreases from -40 dB to -60 dB common mode rejection of the signal/noise. In
Figure 24, which corresponds to a pure electronic sweep, we can see that this additional energy does not exist precisely because the signal does not have harmonics and noise. In this case, if we observe for t = 13 s, we see that the signal takes the value of - 120 Db common mode rejection of the signal/noise
Continuing with the analogies of our example, just as we consider that the area in which the seismic survey is carried out exists, it is the physical space which we are going to study to find out if there is gas or oil, this leads us to an important conclusion; when the Big Bang occurred, space-time already existed, in this case we could consider a local big bang in an infinite space-time full of big bang or multiverses.
2.8.3. Accelerated Expansion of the Universe and the Variation of the Hubble´s Constant
We will carry out the following analysis:
Figure 33.
Hubble's constant and the isotropic principle.
Figure 33.
Hubble's constant and the isotropic principle.
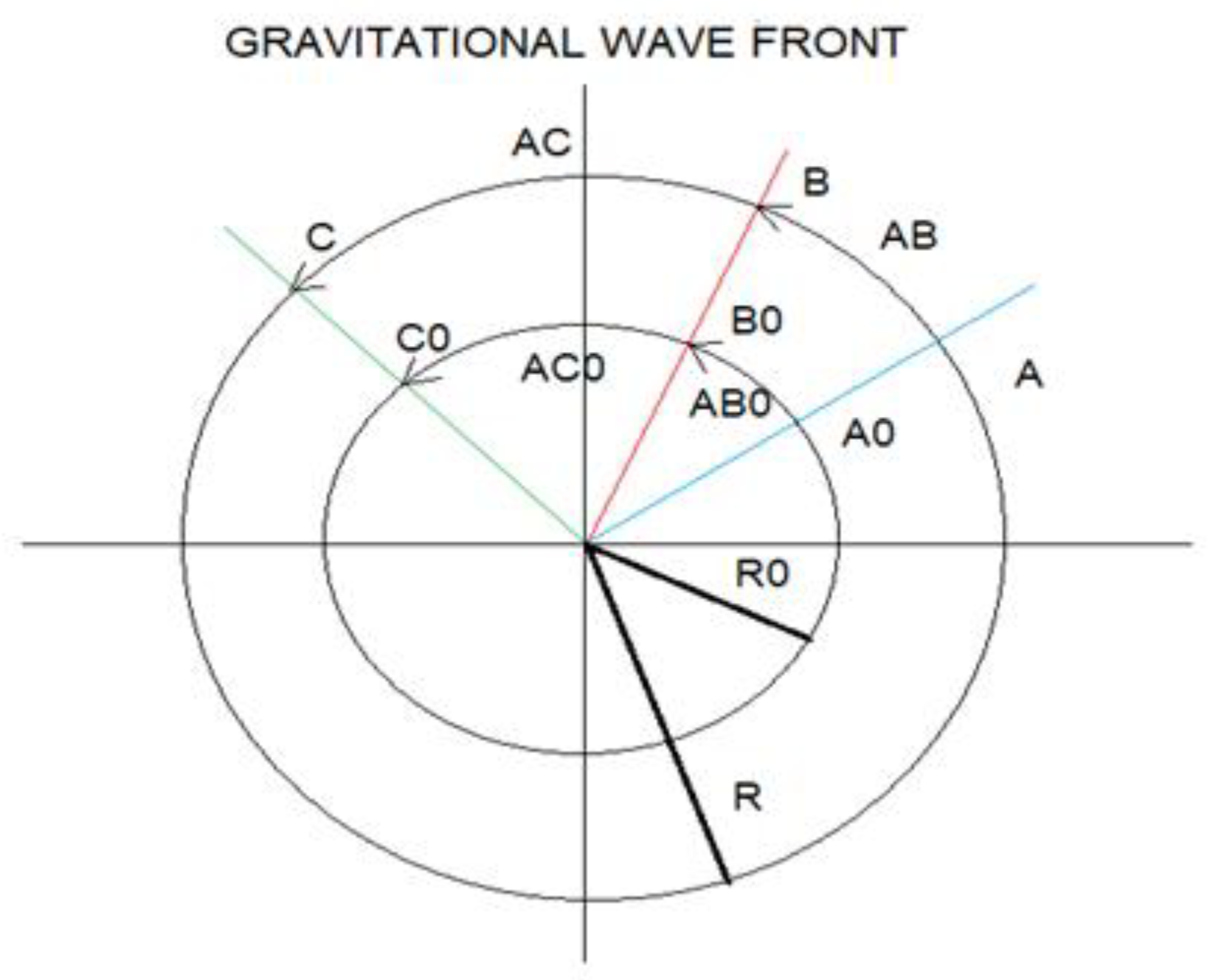
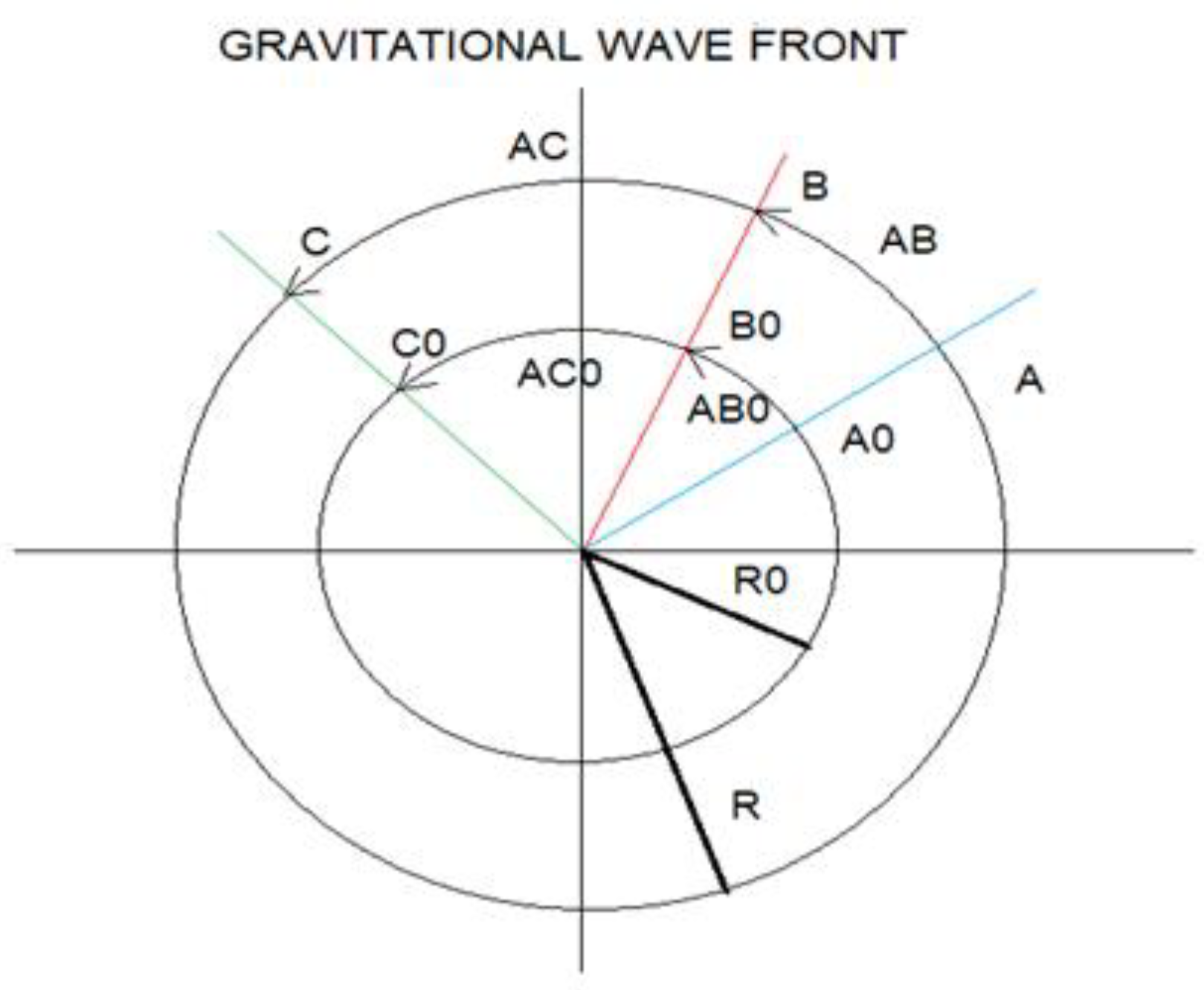
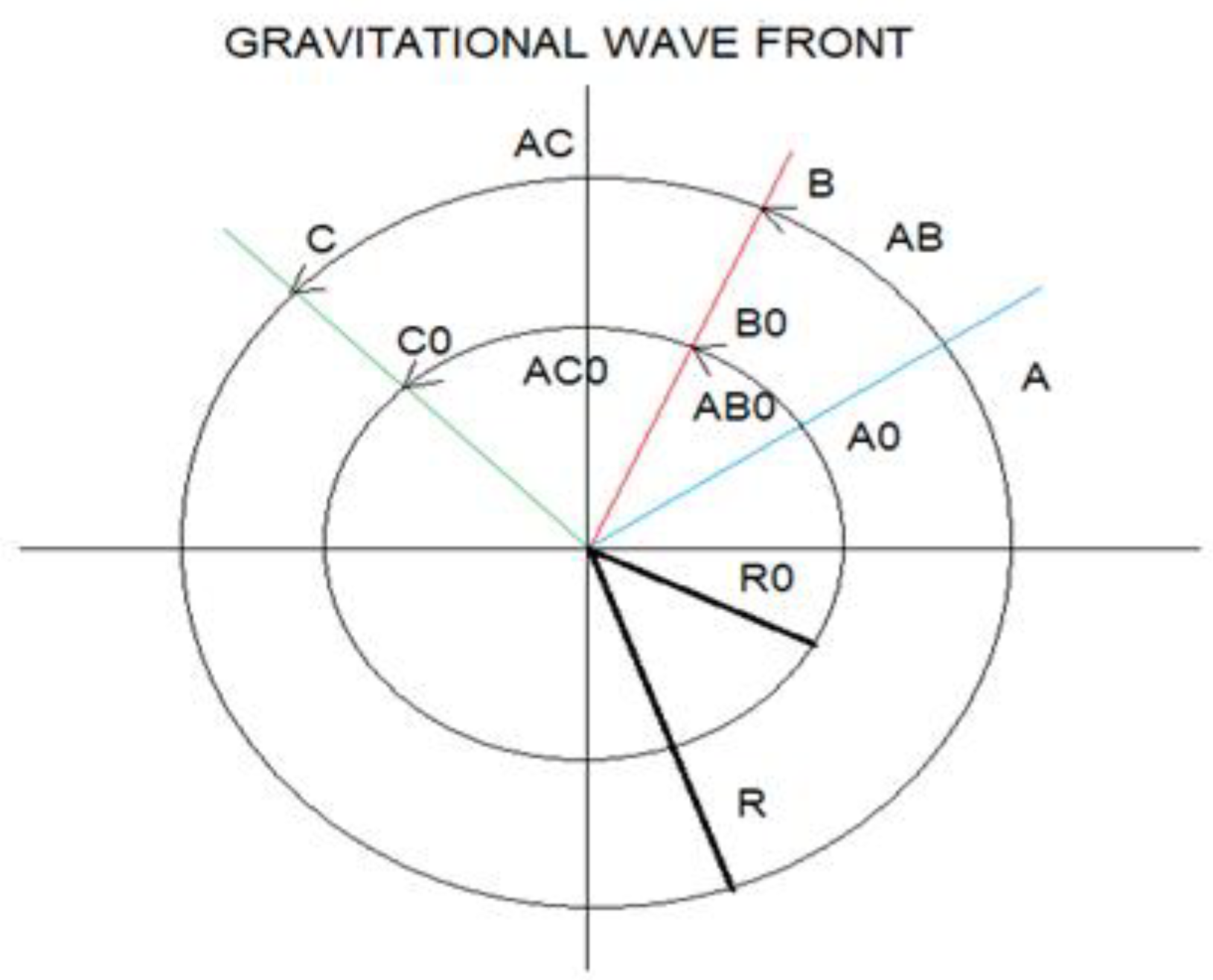
We are going to give a mathematical interpretation to the gravitational wave front:
D(ABo) = Ro α(ABo)
D(ACo) = Ro α(ACo)
D(AB) = R α(AB)
D(AC) = R α(AC)
Deriving with respect to time we have:
V(AB) = (d/dt) D(AB) = (d/dt) R α(AB)
V(AB) = R´α(AB)
in the same way it is fulfilled:
V(AC) = R`α(AC)
Working mathematically, we have:
D(AB) = R α(AB)
V(AB) = R´α(AB)
V(AB) = (R´/R) D(AB)
H(t) = R`/R
V(AB) = H(t) D(AB)
V = H D, Hubble’s law
H = R´/ R, Hubble's constant
Mathematically we can deduce that the propagation of a single gravitational wave front, in an isotropic medium, produces a single Hubble´s constant.
Now we return to our hypothesis that in the inflationary era a gravitational waves spectrum is produced.
Let us remember that in a minimal phase causal system in which the frequency spectrum produced is a function of time, we have: the fundamental frequency occurs at a time t, the first harmonic at a time t1, the second harmonic at a time t2, the third harmonic at a time t3 and so on for the rest of the frequencies of the spectrum, with t > t1 > t2 > t3 > ...........> tn.
Suppose that in this wave spectrum, the main wave has the highest energy are the fundamental frequency and the first and second harmonics wave frequency.
If we consider the first wave front, that is, the fundamental frequency, it is to be expected that for this wave front there is a Hubble´s constant.
Now let's consider the second wave front or first harmonic, it is expected that with the arrival of the energy pulse of the first harmonic that is added to the energy pulse of the fundamental frequency, the Hubble´s constant will vary.
Now let's consider the third wave front or second harmonic, again with the arrival of this pulse of energy that is added to the energy of the fundamental frequency and the frequency of the first harmonic, it is expected that the Hubble´s constant will vary again.
In short, for a spectrum of gravitational waves produced in the inflationary era, it is expected that with the arrival of the energy impulse of each of the gravitational waves, a variation in the Hubble´s constant will occur.
Now, we will consider the geometric interpretation, as shown below, and relate each graph as a propagation of a gravitational wave front with energy E, wavelength λ, time t, velocity C, and temperature T.
E1, λ1, t1, C, T1
E2, λ2, t2, C, T2
E3, λ3, t3, C, T3
Where t1 > t2 > t3 > ..........tn
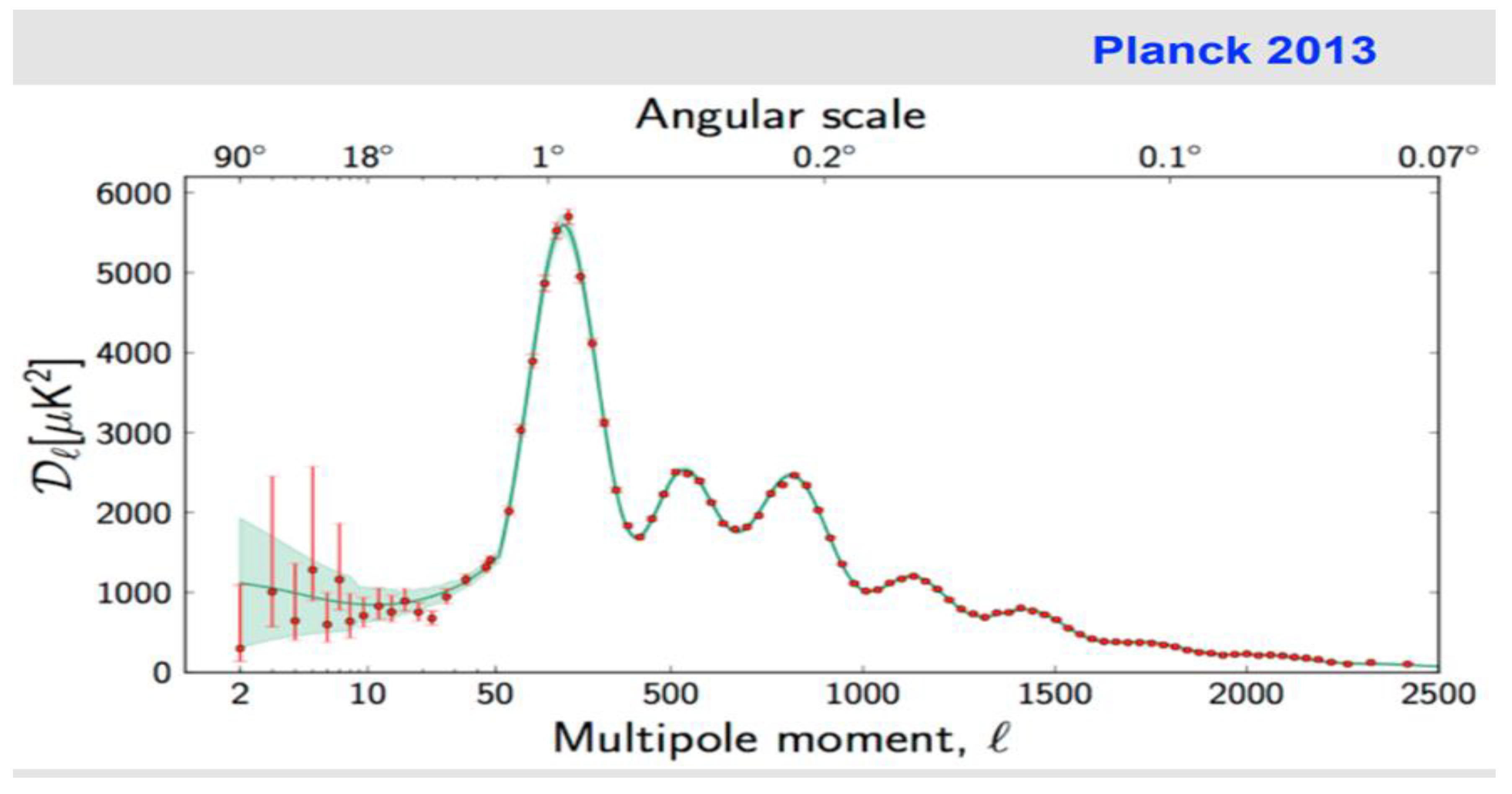
Let's consider the power spectrum of the CMB acoustic waves, and relate it to the 3 graphs, shown above.
We can see in the graph of
Figure 37, which corresponds to the power spectrum of acoustic waves. They have 3 well-defined peaks that are related to the graphs of
Figure 34,
Figure 35 and
Figure 36; this would correspond to three wave fronts, that are They propagate through space-time with different energies E, wavelength λ, out of phase at time t, with the speed C and different temperatures T.
This can be interpreted as follows:
E1, λ1, t1, C, T1: characteristics of the gravitational wave front for the fundamental frequency.
E2, λ2, t2, C, T2: characteristics of the gravitational wave front for the first harmonic frequency.
E3, λ3, t3, C, T3: characteristics of the gravitational wave front for the second harmonic frequency.
En, λn, tn, C, Tn: characteristics of the gravitational wave front for the harmonic of the nth frequency
In conclusion, the expansion of the universe and the Hubble´s constant, will depend on the characteristics of the spectrum of the gravitational wave front H (En, λn, tn, C, Tn).
For example, for the first peak of the power spectrum that corresponds to the fundamental frequency, this gravitational energy E1 will define the wave front λ1 +Δλ, and this will occur at time t1; this wave front will define the Hubble´s constant H1 (E1, λ1, t1, C, T1). Finally, we must consider the contributions of all wave fronts; with this criterion we must update our Lambda-CDM model. It is also expected that whenever a gravitational wave front with an energy E exists, will result in a variation in the Hubble´s constant.
Let us remember, in our RLC electrical model of black hole and the early universe, the expansion of the universe is divided into two phases:
Phase 1, Cosmic inflation: If we consider the Planck length Lpɛ, the minimum length of space-time, like a spring and due to the action of v > c (300,000 km/s); inside a black hole, this length decreases in values of Lpɢ, that is, Lpɢ < Lpɛ, allowing us to imagine the immense forces involved in compressing space-time of length Lpɛ into smaller values of space-time Lpɢ. The immense energy stored and released in the spring of length Lpɢ, to recover its initial length Lpɛ, is the cause of the exponential expansion of space-time in the first moments of the Big Bang.
Let us remember that inside a black hole, as it grows, the speed v > C, therefore it is true that the Planck length Lpɢ < Lpɛ.
Here we put forward the hypothesis that cosmic inflation is the expansion of space-time that is given by Planck Length Lpɢthat tends to reach its normal value Lpɛ, after a black hole disintegrates.
Lpɛ, electromagnetic Planck length.
Lpɢ, gravitational Planck length.
Where, Lpɢ< Lpɛ
- 2.
Phase 2, occurs when the propagation speed of gravitational waves spectrum is equal to c = 300,000 km/s, as in the events detected by LIGO and Virgo. In this phase the universe stabilizes. In this phase, the Boltzmann constant Kʙ = 1.78 10⁻⁴³ J/K (curved space time) tends to reach the value of Kʙ = 1.38 10⁻²³ J/K (flat space time).
Now, we are going to explain the two phases of the universe stated, to do so we are going to begin by analysing the following equation:
Where E0 corresponds to the temperature of 2.7 K
The mathematical development of this equation is in the paper: Rlc Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time.
The equation (46) represents the gravitational wave spectrum equation of the early universe.
λ = 1.000.000 Light years = 10⁶ x 9.46 10¹⁵ m
where λ is the fundamental wavelength
λ is a data provided by the IFT UAM.
λ = 9.46 10²¹ m
c = λ x f, f = c/λ, f = 3 10²¹ / 9.46 10²¹ = 0.317 Hz
f = 0.317 Hz
Where f is the fundamental frequency
Where c is the value of the expansion of the universe in the period of cosmic inflation; see the paper: Rlc Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time
ω = 2.ᴨ.f = 2 x 3.14 x 0.317 = 2
ω = 2.00 rad/s
Where ω is the fundamental angular frequency
We will perform the calculations of ω0, B, ω1 and ω2 for our RLC circuit.
R = 3.60 10⁵¹ Ohms
L = 1.98 10⁶² Hy
C = 1.26 10⁻⁶³ F
ω0 = 1 / √ LC rad/s
ω0 = 1 / √ LC = 1 / √ (1.98 10⁶² Hy x 1.26 10⁻⁶³ F) = 1 / √2.49 x 10⁻¹
ω0 = 2.00 rad/s
Where ω0, is the resonance frequency or fundamental angular frequency.
Calculation of the high cut-off frequency
ω2 = + 1 / 2RC + √ (1 / 2RC) ² - (1 / LC)
S2 = - α - √ (α) ² - (ω0) ²
ω2 = 11.00 10¹⁰ + √ (121.00 10²⁰ - 4)
ω2 = 2.19 10¹¹ rad/s
ω2 is the high cut-off frequency
ω2 = 2.19 10¹¹ rad/s
f2 = ω2 / 2π = 2.19 10¹¹ / 2 x 3.14 = 0.348 10¹¹
f2 = 0.348 10¹¹ Hz
λ2 = C / f2 = 3 10²¹ / 0.348 10¹¹ = 8.60 10¹⁰
λ2 = 8.60 10¹⁰ m
Calculation of the low cut-off frequency
ω1 = -1 / 2RC + √ (1 / 2RC) ² + (1 / LC)
S1 = - α + √ ((α)² - (ω0) ²)
ω1 = -11.00 10¹⁰ + √ (121.00 10²⁰ - 4)
ω1 = 1.81 10⁻¹¹ rad/s
Where ω1 is the low cut-off frequency
ω1 = 1.81 10⁻¹¹ rad/s
f1 = ω1 / 2π = 1,81 10⁻¹¹ rad/s / 2 x 3.14 = 2.88 10⁻¹²
f1 = 2.88 10⁻¹² Hz
λ1 = C / f1 = 3 10²¹ / 2.88 10⁻¹² = 1.08 10³³
λ1 = 1.08 10³³ m
Bandwidth Calculation
B = ω2 - ω1
B = 2.2 10¹¹ rad/s
B is the bandwidth
Remember that the energy stabilizes when the space reaches 2.7 K, which corresponds to 3.72 10⁻²³ J.
3.72 10⁻²³ = 1.08 10⁷³ e⁻ (1.81 10⁻¹¹ t)
e⁻ (1.81 10⁻¹¹ t) = 0.290 10⁹⁶
1.81 10⁻¹¹ t = ln (0.290 10⁹⁶)
t = ln (0.290 10⁹⁶) / 1.81 10⁻¹¹ = 219.84 / 1.81 10⁻¹¹ = 121.46 10¹¹
t = 1.22 10¹³ s
Where t is the time in which the equation (46) reaches 2.7 K
At, t = 1.22 10¹³ s, space-time has expanded by a factor of:
e = v x t
e = 1.22 10¹³ s x 3 10²¹ m/s = 3.66 10³⁴ m.
e = 3.66 10³⁴ m
Calculation of the number of seconds in 380,000 years:
t = 11.81 10¹² s
low cut-off frequency: ω1 = 1.81 10⁻¹¹ rad/s
High cut-off frequency: ω2 = 2.19 10¹¹ rad/s
Fundamental or resonant frequency: ω0 = 2.00 rad/s
Bandwidth: B =2.2 10¹¹ rad/s
Space travelled that corresponds to the total bandwidth: e = 3.66 10³⁴ m
Minimum time: approximately t = 10ˉ¹³ s
Maximum time: t = 1.22 10¹³ s
Now we are going to analyse something very important that will help us understand the origin of dark energy.
We said, to form a black hole, the Boltzmann´s constant changes from Kв = 1.38 10ˉ²³ J/K (flat space-time) to Kв = 1.78 10ˉ⁴³ J/K (curved space-time). Once the black hole forms, the Boltzmann´s constant remains constant at Kв = 1.78 10ˉ⁴³ J/K. As the black hole grows, the Planck´s length varies from Lp = 1.61 10⁻³⁵ m to 1.28 10⁻⁵⁴ m. When it reaches the Planck´s length Lp = 1.28 10⁻⁵⁴ m, the speed of massless particles inside a black hole is c = 10²¹ m/s.
How can we relate the above statement to the Big Bang? Let's try to interpret this as follows:
If we consider Planck's constant as a spring, as a black hole grows, Planck's constant decreases; that is, the spring decreases in size, increasing its potential energy.
Here, it is important to mention that the spring decreases and twists, like a corkscrew, storing gravitational potential energy and generating a rotation movement in the black hole.
When the disintegration of the ultra-massive black hole occurs and causes the Big Bang, Planck's constant that was at the value of Lp = 1.28 10⁻⁵⁴ m tries to reach its normal or stable value of Lp = 1.61 10⁻³⁵ m, expanding to a speed of c = 10²¹ m/s, generating the period of cosmic inflation.
This implies, in the first instance, each generated frequency, shown in the bandpass circuit in
Figure 38, must travel a distance e = 3.66 10³⁴ m, which brings the total time to 10²⁶ s. Example, the fundamental frequency that originates in 1 sec goes up to 1.22 10¹³ s, the last frequency that originates in 1.22 10¹³ s goes up to 10²⁶ s, where each of the frequencies of the wave spectrum travels a distance e = 3.66 10³⁴ m.
This is the first phase that contributes to the origin of dark energy, where each gravitational wave generated in the big bang, travels at a speed c = 10²¹ m/s and travels through a space of e = 3.66 · 10³⁴ m.
This is precisely what we meant when we hypothesized that the Big Bang behaves as a minimal phase causal system; that is, the energy contribution of the gravitational wave spectrum produced in cosmic inflation is a function of time, in other words it varies with time.
Now we are going to analyse the second phase, it will help us understand dark energy even more.
The second phase is related to the Boltzmann´s constant; in this process the Boltzmann´s constant Kв = 1.78 10ˉ⁴³ J/K (curved space-time) must reach the value of Kв = 1.38 10ˉ²³ J/K (flat space-time), in this process each gravitational wave travels at the speed of light c = 3 10⁸ m/s.
In the second phase, we will propose as a hypothesis that the shape of the CMB power spectrum will determine the shape of the contribution of gravitational wave energies.
The energy contribution of both phases is what will determine the expansion of the universe and will allow us to understand why the expansion of the universe is accelerated and why we must consider variable the Hubble´s constant.
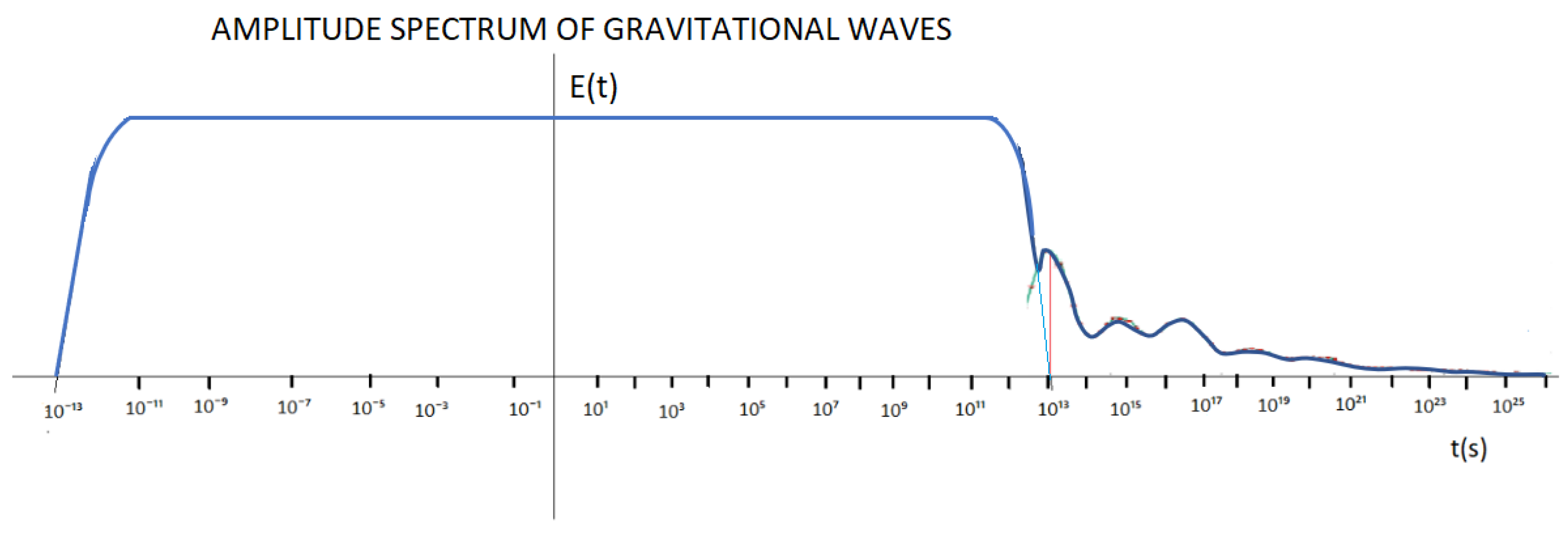
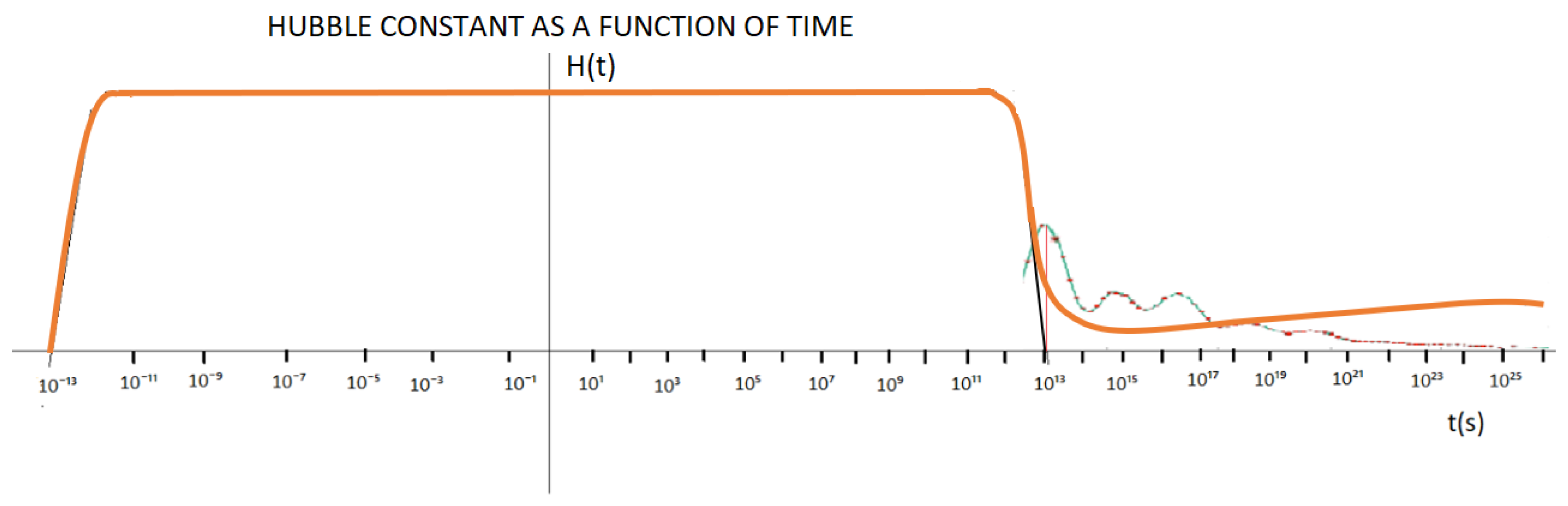
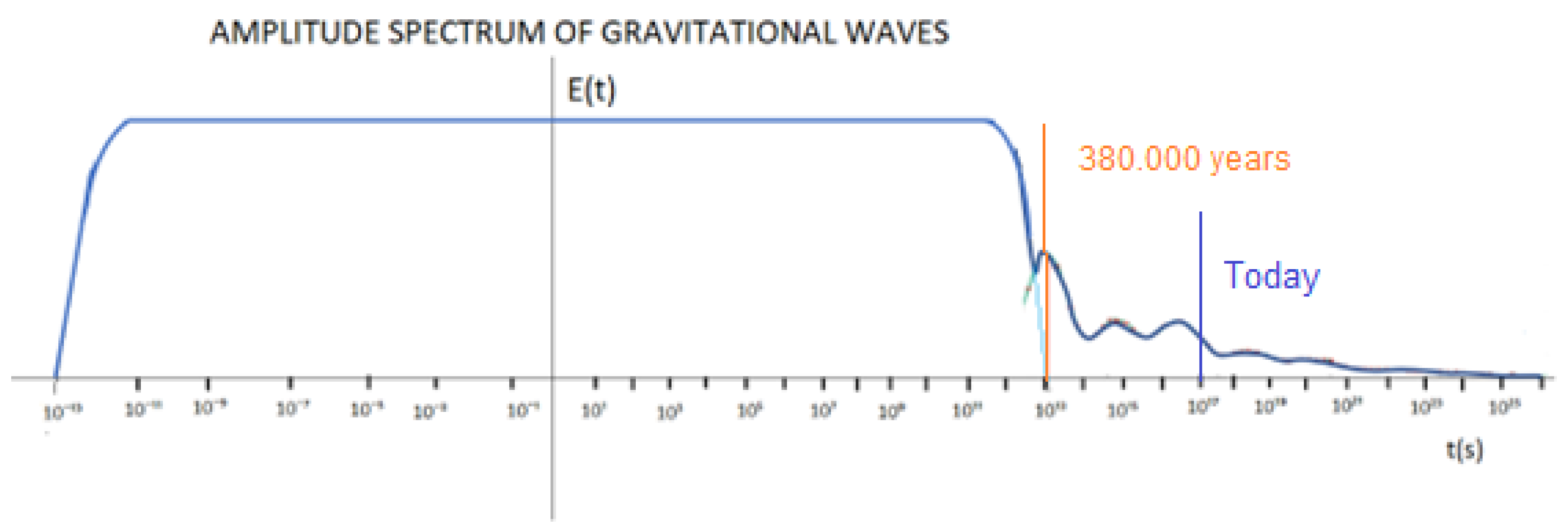
Finally, considering the statement above, in the following graph we will try to represent the energy [E(t) vs t(s)] and [H(t) vs t(s)].
In
Figure 39 and
Figure 40, we can see that phase 1, cosmic inflation, corresponds to the period determined between 10⁻¹³ s < t < 10¹³ s; phase 2 corresponds to the period of time between 10¹³ s < t < 10²⁶ s.
In figures 39 and 40, the X axis is represented to scale, the y axis is not represented to scale.
In
Figure 39, I try to represent the contribution of the energy of gravitational waves up to a time t = 10²⁶ s.
In
Figure 40, I try to represent the variation of the Hubble´s constant up to a time t = 10²⁶ s, considering the energy contribution of gravitational waves.
Observing
Figure 40, we see that from t = 10¹² s, there is an inflection point in which the Hubble´s constant goes from negative to positive slope, this is due to the energy gravitational wave front, which has the shape of the CMB acoustic wave spectrum distributed in time, which adds energy, causing the universe to go from decelerated expansion to accelerated expansion. This is manifested by a variable Hubble´s constant as shown in
Figure 40. This is analogous to what happens in
Figure 27, where on the right side you can see the energy added by the harmonic frequencies and noise.
We also observe for t = 10²⁶ s,
Figure 40, another inflection point occurs due to the absence of gravitational waves, as shown in
Figure 40, in which the slope is horizontal.
It is very important to make clear that the accelerated expansion of the universe has a limit and it is given for t = 10²⁶ s, after that time, space-time stabilizes.
When we measure the Hubble´s constant using the IA supernova method, it gives us H = 74 km/s/Mpc.
When we measure the Hubble´s constant, using the CMB microwave radiation background, it gives us H = 67 km/s/Mpc.
When we measure the Hubble´s constant using merged neutron stars, using the electromagnetic spectrum and gravitational waves, it gives us H = 66.2 km/s/Mpc.
When we measure the Hubble´s constant using an IA supernova and gravitational lensing, it gives us H = 64 km/s/Mpc.
Which of all these values is correct? Or are they all correct values?
Possibly the values of the Hubble´s constants determined by the four different methods are correct and the difference between the calculated values for the Hubble´s constants is due to the fact that the expansion of space-time is different in each place where the measurements are carried out, because the measurements were made in different time periods of the expansion of the space-time of the universe, as shown in
Figure 40, which represents the variation of the Hubble´s constant (H vs t).
Example 1:
According to
Figure 39 and 40, if we divide by power of 10, logarithmic scale, we have approximately 26 steps, neglecting negative exponent stages.
Let's calculate the time t today.
t = 4.35 10¹⁷ s, correspond to 17 steps.
(17,5 / 26) x 100 = 67.3%
This is similar to the dark energy content of the universe.
100% - 67.3 % = 32.7 %
This is similar to the dark matter content of the universe.
Calculation of the number of seconds in 380,000 years:
t = 11.81 10¹² s
Calculation of the number of seconds for when the universe stabilizes and reaches the temperature of 2.7 K
t = 1.22 10¹³ s
We divide the time t, we get:
(11.81 10¹² s / 1.22 10¹³ s) x 100 = 96.72 %
100% - 96,72% = 3.28%
This is similar to the baryonic matter content in the universe.
The true interpretation of this result is the following, the fundamental wavelength that corresponds to λ = 1,000,000 light years, represents the highest amplitude peak of the CMB power spectrum, has convolved 96% with the space-time of the universe; still needs to be convolved 4%.
The following values:
Dark energy = 67.3%
Dark matter = 29.42 %
Baryonic matter = 3.28 %
They represent the proportions of dark energy, dark matter and baryonic matter in the universe in relation to the energy of the fundamental wavelength.
If we consider the total energy contribution of all frequencies of the gravitational wave spectrum produced during cosmic inflation, the percentage values of dark energy, dark matter and baryonic matter should change.
Example 2:
Comment:
At present, the new discoveries of the James Webb telescope have raised a controversy in the astronomical scientific community. The new galaxies discovered 500 million years after the Big Bang appear smooth (well defined), big, old and numerous; have cast doubt on the Big Bang theory of evolution.
Well defined galaxies similar to the Milky Way, whose size exceeds our galaxy as well as discovered black holes with sizes up to 10 Millon solar masses, break the Big Bang theory of evolution.
If we consider the theory of the RLC electrical model of a black hole and early universe, in which RC represents a black hole that grows in a universe represented by L; in this approach, it is to be expected until the moment T0 in which the black hole disintegrates, that around the black hole, we can find perfectly developed galaxies similar to the Milky Way; it is also to be expected to find large numbers of galaxies as well as supermassive black holes; which would imply that the theory of the RLC electrical model of a black hole and early universe does not contradict the recent discoveries of the James Webb telescope and would be in line.
Therefore, the theory of the RLC electrical model of a black hole and early universe does not contradict the new discoveries of the James Webb telescope and is in complete harmony. It considers our universe as a local universe and also predicts the existence of multiverses.
2.8.4. Calculation of the Existing Relationship of Baryonic Matter, Dark Matter and Dark Energy at Time T0⁻, at the Moment When the Big Bang Occurs
We are going to need the information contained in the following figure:
Figure 41.
It represents the growth of a black hole from its birth to its disintegration.
Figure 41.
It represents the growth of a black hole from its birth to its disintegration.
This graph is obtained from the paper: RLC Electrical Modelling of a Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time.
At time T0⁻, just before the disintegration of the ultra-massive black hole, dark energy does not exist, it is zero (0); Inside the black hole there are only baryon matter and dark matter.
For T0⁻, we have:
Baryonic matter = 1.20 10⁵⁶ kg
Dark matter = 1.20 10⁸² kg
Dark energy = 0 kg
If we express it in terms of energy, we have:
Baryonic matter = 1.08 10⁷³ Joules
Dark matter = 1.08 10⁹⁹ Joules
Dark energy = 0 Joules
We see that the dark matter mass content is of the order of 10²⁶ times the baryon matter mass content.
In other words, the energy content of baryon matter mass is negligible compared to the energy content of dark matter mass.
It is important to note that the calculation estimate made by scientists of the total mass of the universe corresponds to 10⁵⁴ kg. If we compare it with the calculation in our RLC electrical model of a black hole and early universe, 10⁵⁶ kg, we see that the difference is in the order 10², there is practically no difference, they are in the approximate order.
2.8.5. Calculation of the Relationship Between Baryon Matter, Dark Matter and Dark Energy at Time t = 5 10¹⁷ s, Which Corresponds to the Current Moment, Today.
Current time = 5 10¹⁷ s (Today)
If we look at
Figure 40, on the horizontal axis we express time in powers of base 10, we will consider from 10⁻¹³ s to 10²⁶ s, 39 steps.
It is important to express that the content of baryon matter in our universe does not change, it is always the same.
After time T0⁺, after big bang, the dark matter content decreases and the dark energy content increases.
We are going to hypothesize that during the period of cosmic inflation, much of the energy of dark matter has been transformed into dark energy.
It is also important to note that both dark matter and dark energy originate from a gravitational interaction force.
Dark matter produces a gravitational attractive force and dark energy produces a gravitational repulsive force.
Taking into account the energy values that exist between baryon matter, dark matter and dark energy, any relationship that existed at a later time T0⁺, will always be true that the amount of energy of baryon matter is negligible.
If we look at
Figure 42, the amplitude spectrum of gravitational wave of the universe tells us that the maximum value of energy during the inflation period corresponds to Emax = 1.08 10⁷³ Joules; above the time t = 10¹³ s, we see that there is an energy contribution similar to the CMB power spectrum, but in reality, the energy contribution is not to scale, it is simply to tell us that there is an additional energy contribution.
If we look at
Figure 42; we see that until time t = 10¹³ s, practically all the energy corresponding to dark matter has been converted into dark energy.
We remember again, the energy contribution corresponding to baryonic matter is negligible.
If we look at
Figure 42, we see that the contribution of dark energy as a function of time is constant.
Taking this relationship into account we are going to carry out the following calculation:
For time T0⁻, the instant before the Big Bang, we have:
The total energy of dark matter (universe) will be:
Dark matter energy = 1.08 10⁹⁹ Joules
Now we are going to calculate the dark energy that corresponds to the epoch of cosmic inflation.
We are going to calculate the total area that corresponds to the era of cosmic inflation, knowing that we know the energy and time, as an integration.
From the gravitational wave equation of the universe, we have that the universe expands with a constant energy of E = 1.08 10⁷³ Joules.
Gravitational wave equation of the universe:
E (t) = 1.08 10⁷³ {e ⁻ (1.81 10⁻¹¹ t)} – 1.08 10⁷³ {e ⁻ (2.19 10¹¹ t)} + E0
A = ∫ E(t) dt, between time limits [10⁻¹³ s, 10¹³ s]
A = 1.08 10⁷³ x 10²⁶
A = 1.08 10⁹⁹ Joules
Dark Energy = A = 1.08 10⁹⁹ Joules
This calculation is telling us that during the time that cosmic inflation lasted, all the energy that corresponded to dark matter was transformed into dark energy.
In conclusion, according to our calculations, for t = 5 10¹⁷ s, today, the proportion of baryon matter, dark matter and dark energy is as follows:
Dark Energy ≈ 100%
Dark Matter = negligible
Baryonic matter = negligible
These proportions calculated for baryon matter, dark matter and dark energy are fulfilled as long as we consider the energy of the entire spectrum of gravitational waves that originate during cosmic inflation.
If we consider only the energy content of the fundamental frequency and not the entire energy content of the frequency spectrum of gravitational waves produced during the era of cosmic inflation, the relationship of baryon matter, dark matter and dark energy is as follows, according to what was calculated above:
Dark energy = 67.3%
Dark matter = 29.42 %
Baryonic matter = 3.28 %
2.9. Space-Time Contraction Factor and the Effective Boltzmann Constant.
In the paper, Theory of the Generalization of the Boltzmann’s Constant in Curved Space-Time. Shannon-Boltzmann Gibbs Entropy Relation and the Effective Boltzmann’s Constant; we analyse the theory that gives rise to the space-time contraction factor, that is, to the origin of the effective Boltzmann´s constant. We also calculate the space-time contraction factor of the Earth, the Sun, the white dwarf star, the neutron star and a black hole.
Briefly, let's remember how the space-time contraction factor is calculated for a black hole.
Taking into account the Maldacena correspondence ADS = CFT, we are going to assume that a black hole is formed by a plasma of quarks-gluons, with this premise we calculate the space-time contraction factor for a black hole and its effective Boltzmann´s constant.
The mass of the black hole is 3.0 Mϴ
Where Mϴ is solar mass
The temperature of a black hole at its formation is 10¹³ K, it is the temperature that corresponds to the quark-gluon plasma.
Here it is important to clarify that the temperature of a black hole is chosen when it is formed, T = 10¹³ K; equal to the temperature at which, in particle collisions, matter forms the soup of quarks-gluons.
M = 3Mϴ = 3 x 2 10³⁰ = 6.0 10³⁰ kg
T = 10¹³ K
Kʙ = hc³ / (8ᴨTGM)
Kʙq = 6.63 10⁻³⁴ x 27 10²⁴ / (8 x 3.14 x 10¹³ x 6.67 10⁻¹¹ x 6.0 10³⁰)
Kʙq = 179.01 10⁻¹⁰ / 1005.30 10³² = 0.1780 10⁻⁴² = 1.78 10⁻⁴³ J/k
Kʙq = 1.78 10⁻⁴³ J/K
Kʙq, effective Boltzmann´s constant of a black hole
D = Kʙ / Kʙq, D = 1.38 10⁻²³ / 1.780 10⁻⁴³ = 0.7752 10²⁰ = 7.752 10¹⁹
D = 7.752 10¹⁹
Where D, Scale contraction factor for a black hole of three solar masses
D = Vc12 / Vq, Vq = (Vc12 / D) = 1.33 x 3.13 x 0.4218 10⁻³⁰ / 7.752 10¹⁹
Vq = 1.76 10⁻³⁰ / 7.752 10¹⁹ = 0.2270 10⁻⁴⁹ = 2.270 10⁻⁵⁰ mᶾ
Vq = 2,270 10⁻⁵⁰ mᶾ, volume of the quark.
Where Mϴ is solar mass, T is temperature, Kʙq is Boltzmann´s constant for black hole, D is scale factor of Boltzmann´s constant and Vq is quark volume.
V = (4/3) x π x R³, R = ᶾ √ (V / 1.33 x π) = ᶾ √ (2.270 10⁻⁵⁰ / 4.17)
R = ᶾ √ 0.5435 10⁻⁵⁰
R = ᶾ √ 5.435 10⁻⁵¹ = 1.758 10⁻¹⁷ m
R = 1.758 10⁻¹⁷ m
Where R, corresponds to the radius of the quark when a black hole is formed.
We are going to interpret the meaning of the space-time contraction factor and the effective Boltzmann´s constant.
Rc12 = 0.75 10ˉ¹⁰ m
Where Rc12 is radius of the C12 atom
The contraction factor D of space-time tells us that the volume of the carbon 12 atom with a radius of Rc12 = 0.75 10ˉ¹⁰ m is reduced by a factor D = 7.752 10¹⁹, to the volume of the quark of radius R = 1.758 10⁻¹⁷ m.
For a black hole, the effective Boltzmann´s constant corresponds to Kʙq = 1.78 10⁻⁴³ J/K.
The most important thing we have to rescue is that to form a black hole, space-time contracts by a factor D = 7.752 10¹⁹ times, in three dimensions and approximately 10⁶ in one dimension.
Unlike the theory of general relativity which tells us that in the presence of mass space-time is curved; in the theory of the generalization of the Boltzmann´s constant in curved space-time, in the presence of mass or energy, space-time is curved and contracts.
2.10. Space-Time Torsion Mechanism
In the paper: Theory of the Generalization of the Boltzmann’s Constant in Curved Space-Time. Shannon-Boltzmann Gibbs Entropy Relation and the Effective Boltzmann’s Constant, we have determined that we can quantify the curvature of space-time through the effective Boltzmann´s constant which varies from:
Now we are going to determine that there is a mechanism that generates a torsional force in the Space-time structure that adds to the contraction force. The contraction force is inward, towards the centre of mass of the body in question. The torsion force is a tangent force that lags the contraction force by 90 degrees. It is similar to the phasor diagrams that occur in an RC electrical circuit.
We can represent it in the following diagram:
From the following equation:
We will analyse the Schwarzschild solution for a punctual object in which mass and gravity are introduced.
Where M is the mass of a black hole, c is the speed of light, and G is the gravitational constant.
if we consider dθ = 0; and dφ = 0; that is, we move in the direction of dR. (50)
R = Rs, ds = 0, let's analyse this specific situation. (51)
Replacing the conditions given in (49), (50) and (51) in equation (48), we have:
(dR / dt) ² = v² = c² (1 - (2MG/Rc²) ²
R = Rs, v = 0; ds² = 0; Rs is the Schwarzschild´s radius. (52)
R > Rs, v < c; ds < 0, time type trajectory. (53)
R < Rs, v > c; ds > 0, space type trajectory. (54)
Condition (54) is very important because to the extent that R < Rs, v > c is fulfilled; it is precisely this speed difference that generates the dark matter mass in a black hole given by
Planck length equation:
Where h is Planck's constant, G is the gravitational constant, and c is the speed of light.
If we consider condition (54) and equation (55), to the extent that R < Rs and v > c, are fulfilled; we deduce that the Planck length decreases in value.
We define the following:
Lpɛ = Lp = 1.616199 10⁻³⁵ m; electromagnetic Planck length.
Lpɢ = gravitational Planck length. (56)
Always holds:
Lpɢ < Lpɛ (57)
This is telling us that as the black hole grows, the Planck length inside a black hole decrease; this mechanism generates a torsional force or rotation force, which delays the force of gravitational attraction by 90 degrees, this mechanism is what generates dark matter mass.
A more rigorous explanation is given in the paper: Rlc Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time.
Up to this point we have explained that there are two forces that act in the structure of space-time. As we place mass in a given space-time structure, a gravitational force of attraction acts, which curves and contracts space-time structure until a black hole is formed. As the black hole grows, in addition to the force of gravitational attraction or contraction of space-time, a rotation or torsion force of space-time begins to act, which delays the force of gravitational attraction by 90 degrees.
The behaviour of the system is analogous to an RC circuit. We can say that an RC Circuit stores electrical energy and a black hole stores gravitational potential energy.
In the following diagram we are going to represent the force of attraction (compression) and the force of torsion or rotation, inside a black hole.
In
Figure 43 and
Figure 44, we can see the compression (attraction) and torsion (rotation) force that act on the Planck length, inside a black hole.
2.11. Generalization of the Boltzmann’s Constant in Curved Space-Time. Quantization of the Curvature of Space-Time
This theory proposes the quantification of the curvature of space-time considering the Boltzmann´s constant variable; thus, the concept of effective Boltzmann´s constant was born. This allows us to measure the curvature of space-time.
The Boltzmann´s constant varies between the following limits:
1.38 10⁻²³ J/K > Kв-eff > 1.78 10⁻⁴³ J/K
The curvature of space-time is a direct function of temperature, the higher the temperature, the greater the curvature of space-time.
1.38 10⁻²³ J/K => flat space-time structure
0⁻²³ J/K > Kв-eff > 1.78 10⁻⁴³ J/K => curved space-time structure
2.12. Calculation of the Curvature of Space-Time for Different States of Matter
In the paper: Theory of the Generalization of the Boltzmann’s Constant in Curved Space-Time. Shannon-Boltzmann Gibbs Entropy Relation and the Effective Boltzmann’s Constant; we have calculated the curvature of space-time for different states of matter.
In the following table, we show these calculations:
In
Table 6, for different states of matter, we have calculated the curvature of space-time with respect to flat space-time, for a Boltzmann´s constant corresponding to Kʙ = 1.38 10ˉ²³ J/K.
For a black hole, whose space-time curvature, Cv = 7.72 10¹⁹ times with respect to flat space-time, corresponds to a gravitational force of F = 5 10¹² N.
2.13. Calculation of the Critical Mass to Produce a Black Hole in the LHC Applying the Theory of the Generalization of Boltzmann´s Constant in Curved Space-Time
In the paper: RLC Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann's Constant in Curved Space-Time; we have calculated the critical mass to produce a black hole at the LHC and we have also shown that according to the proton packets that are used in particle collisions LHC, we are at the limit or threshold to produce a black hole.
Next, we are going to put the equations that define the critical mass to produce a black hole in the LHC:
mc = 13.33 10¹⁰ GeV/C² = 2.37 10⁻¹⁶ kg
mc = h x c / (2π x G x M1) (59)
mc = 13.33 10¹⁰ GeV/C² = 2.37 10⁻¹⁶ kg
This equality is given for Kʙ = 1.78 10⁻⁴³ J/K
In two different ways, we have calculated the critical mass to produce a black hole at the LHC.
mc = 13.33 10¹⁰ GeV/C² = 2.37 10⁻¹⁶ kg
Example:
Currently, the CERN particle accelerator LHC, is working with energies of the order of 14 TeV.
If we consider that the LHC works with proton packages of 100,000 10⁶ protons, we have:
Mp = 100,000 10⁶ x mp
Where Mp, total mass of the collision and mp, proton mass.
Mp = 10¹¹ x 1.672 10⁻²⁷ kg = 1.672 10⁻¹⁶ kg
Mp = 1.672 10⁻¹⁶ kg
Mc = 2.37 10⁻¹⁶ kg
Mp ≈ mc, we are working on the order of the critical mass to produce a black hole at the LHC.
Note that in the RLC electrical theory of the universe, black holes always grow until they disintegrate.
3. STANDARD MODEL OF ELEMENTARY PARTICLES
We are going to work with the table that represents the standard model of fundamental particles. Let's transform the characteristics of fundamental particles into parameters that are easy to work with as shown in
Table 7.
Figure 45.
Standard Model.
Figure 45.
Standard Model.
4. NEUTRON AND PROTON ANALYSIS
4.1. Summary of the Theory of Three-Phase Alternating Current Electric Generators
We are going to make a brief introduction to understand the theory of three-phase alternating current electric generators, this theory is very important to understand the context and be able to relate the concepts of matter, antimatter, left-handed particles and right-handed particles.
Here we put forward the hypothesis for a neutron, as a quark-antiquark-gluon interaction, and not as represented in the formal theory of QCD, as a quark-gluon interaction. See
Figure 46.
Where D corresponds to the D quark and D corresponds to the D antiquark.
Where U corresponds to the U quark and U corresponds to the U antiquark.
The gluon interaction is given by (R, B, G) and (R, B, G).
Here we put forward the hypothesis for a proton, as a quark-antiquark-gluon interaction, and not as represented in the formal theory of QCD, as a quarks-gluons interaction. See
Figure 47.
If we look at figures 48 and 49, which correspond to the electrical circuit of a three-phase alternating current electric generator, we see that the electrical circuit of a neutron represented in
Figure 46 and the electrical circuit of a proton represented in
Figure 47, have an identical diagram. Basically, the difference is the following, in a three-phase generator, the pairs, XX', YY' and ZZ' have the same frequency and in the case of a proton and neutron the D
D pairs have twice the frequency of the U
U pairs.
Figure 48.
Three-phase alternating current electric generator.
Figure 48.
Three-phase alternating current electric generator.
Figure 49.
Three phase alternating current electric generator.
Figure 49.
Three phase alternating current electric generator.
Figure 50.
Three-phase voltage generated with a phase shift of 120 degrees.
Figure 50.
Three-phase voltage generated with a phase shift of 120 degrees.
In analogy to what happens in an electric generator; in the proton and the neutron, the DD dipoles vibrate at approximately twice the frequency of the UU dipoles. Continuing with the analogy, the dipoles, XX', YY' and ZZ' in a generator would be analogous to the dipoles DD, DD and UU in a neutron and the dipoles DD, UU and UU in a proton.
If we consider that the voltages, VL1, VL2 and VL3 are the result of rotating the rotor, which produces a variation of the magnetic field and ends up inducing and generating the three-phase voltages in the stator; continuing with the analogy, we can say that the dipoles DD, DD and UU in a neutron and the dipoles DD, UU and UU in a proton, is the result of a variable magnetic field that is generated from the interaction of quarks-antiquarks-gluons; precisely this mechanism makes protons and neutrons generate their mass and are self-sustaining, this is the mechanism that allows the existence of hadrons.
The dipoles DD, DD and UU in a neutron and the dipoles DD, UU and UU in a proton, are also out of phase with a phase angle that we are going to determine; the nomenclature of the gluons (R, B, G) and (R, B, G) serves to remind us that the Interactions between quarks-antiquarks-gluons are vectors.
If we look at
Figure 50, we see that in red, green and blue the sinusoidal lines of tension generated in the stator of the three-phase alternating current electric generator are drawn.
By construction of the generator stator, the sine waves marked in red, green and blue are out of phase by 120 degrees.
We are going to analyse the sinusoidal voltage marked in red VL2.
If we look at
Figure 50, the voltage value that VL2 takes between 0 degrees and 180 degrees is positive, positive half-cycle. However, between 180 degrees and 360 degrees, the voltage value of VL2 is negative, negative half-cycle.
If we return to our analogy between the neutron and the proton with three-phase alternating current electric generator; we can consider that the upper or positive semi-cycle corresponds to matter and the lower or negative semi-cycle corresponds to antimatter. It is a very nice analogy.
This analogy is very important, it is telling us that matter and antimatter are always linked, twinned. However, the theory of quantum chromodynamics QCD does not treat matter and antimatter in a twinned manner and discriminates matter over antimatter.
In my personal opinion, the theory of quantum chromodynamics QCD describes half of the story, it excludes antimatter from history. Precisely this perception is what led me to develop the theory of the neutron and the proton as a three-phase alternating current generator, in which matter and antimatter are included in the theory.
Next, we are going to describe a new analogy.
To do this we are going to run the generator like an engine.
A generator works in the following way: a generator is made up of a rotor and a stator. The stator is fixed. The magnetic field is located in the rotor. When the rotor rotates, it produces a variation in the magnetic field that induces a current and a voltage in the stator. The voltage and current in the stator are what we use. If the generator is three-phase, then the generated voltages can be represented by (X, Y, Z).
A motor works in the following way: the motor is made up of a stator and a rotor. If it is a three-phase motor then the voltage (X, Y, Z) is applied to the stator. This voltage (X, Y, Z) that is applied to the stator is analogous to that in
Figure 50. This voltage generates a current and therefore generates an induced field in the rotor that causes the rotor to rotate. This is the operating principle of an engine described in a simplified way.
The importance in this analogy is the following, if we apply a voltage (X, Y, Z) to the stator, we will assume that the rotor rotates to the left, this corresponds to the left-handed particles; however, if we make a phase change and apply the voltage (X, Z, Y) to the motor stator, then the rotor rotates to the right, this corresponds to right-handed particles.
In these two simple analogies we have compared matter, antimatter, left-handed particles and right-handed particles with the operation of three-phase alternating current electric generator.
These analogies that we have described here will represent the base guide for the development of this paper.
4.2. Nuclear Phenomenology - Sum of Spins ½ of Subatomic Particles
We are not going to carry out the mathematical development, we are going to put the final results and we are going to focus on the application.
Spin 1/2 particles, Definition of Isospin:
Isospin is a symmetry associated with interchangeability or coupling between spin 1/2 particles.
Later we are going to describe the concept of symmetry, in particular we are going to analyse the SU(2) and SU(3) symmetries in order to compare them with our model that we are going to develop below.
We are going to represent the quantum states of spin 1/2 particles in the following way:
│↑ >, │↓ > (60)
Let's represent the superposition states:
│↑ > (+⁄-) │↓ > (61)
These operators have a certain algebra or commutation relationship.
Isospin:
│↑ > ≡ │1⁄2, 1⁄2 ˃ (62)
We consider this subatomic particle that has spin 1/2 and angular projection 1/2.
│↓ > ≡ │ 1⁄2, - 1⁄2 ˃ (63)
We consider this subatomic particle that has spin 1/2 and angular projection – 1/2.
Now we are going to apply the following algebraic operation and we are going to calculate the results:
│↑ ↑ > ≡ │1, 1 ˃ (64)
│↓ ↓ > ≡ │ 1, - 1 ˃ (65)
(1 ⁄ √2) x │↑↓ + ↓↑ > ≡ │1,0 > (66)
(1 ⁄ √2) x │↑↓ - ↓↑ > ≡ │0,0 > (67)
Example of a phenomenon where the proton and the neutron behave like two states of the same particle:
│p >, │n >
Where p corresponds to the proton and n corresponds to the neutron.
The superposition states correspond to:
│p > (+/-) │n >
│p > ≡ │1/2, 1/2 >
│n > ≡ │1/2, -1/2 >
│pp > ≡ │1, 1 >
│nn > ≡ │1, -1 >
(1/√2) │pn + np > ≡ │1, 0 >
(1/√2) │pn - np > ≡ │0, 0 >
Using this same procedure, we are going to apply the spin ½ addition mechanism to the quarks (U, U, D, D).
We are going to extend or generalize the symmetry of the neutron and the proton to the other particles, especially to the particles (U, U, D, D).
- 1)
Sum of quark U and antiquark U
│U >, │U >
Where U corresponds to the quark U; U corresponds to the antiquark U.
The superposition states correspond to:
│U > (+/-) │U >
│U > ≡ │1/2, 1/2 > (68)
│U > ≡ │1/2, -1/2 > (69)
│UU > ≡ │1, 1 > (70)
│UU > ≡ │1, -1 > (71)
(1/√2) │UU + UU > ≡ │1, 0 > (72)
(1/√2) │UU - UU > ≡ │0, 0 > (73)
We can write equation 14 as follows:
(1/√2) │UU + UU > ≡ │1, 0 >
│UU + UU > ≡ │2, 0 >
│UU > + | UU > ≡ │1, 0 > + │1, 0 >
│UU > ≡ │1, 0 > (72a)
│UU > ≡ │1, 0 > (72b)
- 1)
-
Sum of quark D and antiquark D
│D >, │D >
where D corresponds to the quark D and D corresponds to the antiquark D.
The superposition states correspond to:
│D > (+/-) │D >
│D > ≡ │1/2, 1/2 > (74)
│D > ≡ │1/2, -1/2 > (75)
│DD > ≡ │1, 1 > (76)
│DD > ≡ │1, -1 > (77)
(1/√2) │DD + DD > ≡ │1, 0 > (78)
(1/√2) │DD - DD > ≡ │0, 0 > (79)
We can write equation 78 as follows:
(1/√2) │DD + DD > ≡ │1, 0 >
│DD + DD > ≡ │2, 0 >
│DD > + | DD > ≡ │1, 0 > + │1, 0 >
│DD > ≡ │1, 0 > (78a)
│DD > ≡ │1, 0 > (78b)
- 2)
Sum of quark U and antiquark D
│U >, │D >
where U corresponds to the quark U and D corresponds to the antiquark D.
The superposition states correspond to:
│U > (+/-) │D >
│U > ≡ │1/2, 1/2 > (80)
│D > ≡ │1/2, -1/2 > (81)
│UU > ≡ │1, 1 > (82)
│DD > ≡ │1, -1 > (83)
(1/√2) │UD + DU > ≡ │1, 0 > (84)
(1/√2) │UD - DU > ≡ │0, 0 > (85)
- 1)
Sum of quark D and antiquark U
│D >, │U >
where D corresponds to the quark D and U corresponds to the antiquark U.
The superposition states correspond to:
│D > (+/-) │U >
│D > ≡ │1/2, 1/2 > (86)
│U > ≡ │1/2, -1/2 > (87)
│DD > ≡ │1, 1 > (88)
│UU > ≡ │1, -1 > (89)
(1/√2) │DU + UD > ≡ │1, 0 > (90)
(1/√2) │DU - UD > ≡ │0, 0 > (91)
We are going to follow the following rule for spins:
Left-handed particles
Rule 1, for matter:
| MATTER |
| CHARGE |
SPIN |
SPIN |
CHARGE |
| |
← |
← |
|
| - 1/3 e |
D |
U |
2/3 e |
| 1/3 e |
D |
U |
- 2/3 e |
| |
→ |
→ |
|
Rule 2, for antimatter:
| ANTIMATTER |
| CHARGE |
SPIN |
SPIN |
CHARGE |
| |
← |
← |
|
| 1/3 e |
D |
U |
- 2/3 e |
| - 1/3 e |
D |
U |
2/3 e |
| |
→ |
→ |
|
Right-handed particles
Rule 3, for matter:
| MATTER |
| CHARGE |
SPIN |
SPIN |
CHARGE |
| |
→ |
→ |
|
| - 1/3 e |
D |
U |
2/3 e |
| 1/3 e |
D |
U |
- 2/3 e |
| |
← |
← |
|
Rule 4, for antimatter:
| ANTIMATTER |
| CHARGE |
SPIN |
SPIN |
CHARGE |
| |
→ |
→ |
|
| 1/3 e |
D |
U |
- 2/3 e |
| - 1/3 e |
D |
U |
2/3 e |
| |
← |
← |
|
Example:
│U > ≡ │1/2, 1/2 >
│U > ≡ │1/2, -1/2 >
Using rule 1 for matter we have: for the quark U, we see that the spin is 1/2 and its angular projection that results from applying the left-hand rule is also 1/2, it is telling us that the magnetic field in the inside of the coil is upward. For the antiquark U, we see that the spin is 1/2 and its angular projection that results from applying the left-hand rule is also -1/2, this is telling us that the magnetic field inside the loop is downwards.
Now that we have established a spin rule, we are going to perform the following interactions between quarks.
- 2)
Sum of quark D and anti-quark U
│D >, │U >
Where D corresponds to the quark D and U corresponds to the antiquark U.
The superposition states correspond to:
│D > (+/-) │U >
│D > ≡ │1/2, 1/2 > (92)
│U > ≡ │1/2, -1/2 > (93)
│DU > ≡ │1, -1 > (94)
If we add the spin of the D quark (equation 92) and the spin of the U antiquark (equation 93), the sum of the spins would have to give us:
│DU > ≡ │1,0 >
However, the correct sum of the spins is represented by equation 94.
Equation 94 can be interpreted as follows:
If we consider the D quark, the spin rule tells us that the D quark generates an upward magnetic flux; If we consider the U antiquark, the U antiquark generates a downward magnetic flux; If we consider that the magnetic flux of the U antiquark is greater than the flux generated by the D quark, the resulting magnetic field flux is directed downwards.
This can also be interpreted in the following way:
(1/√2) │DU + UD > ≡ │1, 0 >
│DU + UD > ≡ │2, 0 >
│DU > + │UD > ≡ │1, -1 > + │1, 1 >
│DU > ≡ │1, -1 >
│UD > ≡ │1, 1 >
- 2)
Sum of quark U and anti-quark D
│U >, │D >
Where U corresponds to the quark U and D corresponds to the antiquark D.
The superposition states correspond to:
│U > (+/-) │D >
│U > ≡ │1/2, 1/2 > (95)
│D > ≡ │1/2, -1/2 > (96)
│UD > ≡ │1, 1 > (97)
If we add the spin of the U quark (equation 95) and the spin of the D antiquark (equation 96), the sum of the spins would have to give us:
│UD > ≡ │1,0 >
However, the correct sum of the spins is represented by equation 97.
Equation 97 can be interpreted as follows:
If we consider the U quark, the spin rule tells us that the U quark generates an upward magnetic flux; If we consider the D antiquark, the D antiquark generates a downward magnetic flux; If we consider that the magnetic flux of the U quark is greater than the flux generated by the D antiquark, the resulting magnetic field flux is directed upwards.
This can also be interpreted in the following way:
(1/√2) │UD + DU > ≡ │1, 0 >
│UD + DU > ≡ │2, 0 >
│UD > +│ DU > ≡ │1, 1 > + │1, -1 >
│UD > ≡ │1, 1 >
│DU > ≡ │1, -1 >
Taking into account what has been developed, we are going to define the following particles:
│p > ≡ │1/2, 1/2 >
│n > ≡ │1/2, -1/2 >
│ν > ≡ │1/2, 0 >
│ν > ≡ │1/2, 0 >
│νν > ≡ │1, 0 >
│e⁻ > ≡ │1/2, 1/2 >
│e⁺ > ≡ │1/2, -1/2 >
│ e⁻e⁺ > ≡ │1, 0 >
│U > ≡ │1/2, 1/2 >
│U > ≡ │1/2, -1/2 >
│D > ≡ │1/2, 1/2 >
│D > ≡ │1/2, -1/2 >
│UU > ≡ │1, 0 >
│UU > ≡ │1, 1 >
│UU > ≡ │1, -1 >
│DD > ≡ │1, 0 >
│DD > ≡ │1, 1 >
│DD > ≡ │1, -1 >
│UD > ≡ │1, 1 >
│DU > ≡ │1, -1 >
│DU > ≡ │1, -1 >
│UD > ≡ │1, 1 >
(1/√2) │UD + DU > ≡ │2, 0 >
(1/√2) │UD - DU > ≡ │0, 0 >
(1/√2) │DU + UD > ≡ │1, 0 >
(1/√2) │DU - UD > ≡ │0, 0 >
These are the base particles, with which we are going to work.
Example:
- a)
We make two protons collide and we obtain deuterium plus the particle π⁺. Exceeding a certain energy threshold, one of the protons transforms into a neutron plus the pion (+), the neutron unites with the proton and transforms into deuterium.
p + p → d + π⁺ < Ɣʹ, 1, 1| Uᵗ | Ɣ, 1, 1>
d ₁ H², (1, 1) → (1/ √2) |pn – np > ≡ |0, 0 >
We observe that deuterium couples to isospin (0) and its angular projection is also zero (0).
If we analyse the initial state, we see that the sum of the two protons couple with isospin 1 and their angular projection also 1; if we analyse the final state, we see that the deuterium does not contribute to the sum, therefore for symmetry to be preserved, the π⁺particle has to have isospin 1 and angular projection 1.
π⁺, │UD > ≡ │1, 1 >
- b)
We collide two neutrons and obtain deuterium plus the particle π⁻. Once a certain energy threshold is exceeded, one of the neutrons transforms into a proton plus the pion (-), the proton joins the neutron and becomes deuterium.
n + n → d + π⁻ < Ɣʹ, 1, -1| Uᵗ | Ɣ, 1, -1>
d → ₁ H ², (1, 1) → (1/ √2) |pn – np > ≡ |0, 0 >
We observe that deuterium couples to isospin (0) and its angular projection is also zero (0).
If we analyse the initial state, we see that the sum of the two neutrons couples with isospin (1) and its angular projection (-1); if we analyse the final state, we see that deuterium does not contribute to the sum, therefore for symmetry to be preserved, the π⁻ particle has to have isospin (1) and angular projection (-1).
π⁻, │DU > ≡ │1, -1 >
- c)
We collide neutrons against protons and obtain deuterium plus the particle π⁰.
n + p → d + π⁰ < Ɣʹ, 1, 0| Uᵗ | Ɣ, 1, 0>
d → ₁ H ², (1, 1) → (1/ √2) |pn – np > ≡ |0, 0 >
We observe that deuterium couples to isospin (0) and its angular projection is also zero (0).
If we analyse the initial state, we see that the sum of the neutron plus the proton couples with the isospin (1) and its angular projection (0); if we analyse the final state, we see that deuterium does not contribute to the sum, therefore for symmetry to be preserved, the π⁰ particle has to have isospin (1) and angular projection (0).
π⁰, │UU > ≡ │1, 0 >
π⁰, │DD > ≡ │1, 0 >
4.3. Electrical-Quantum Modelling of the Neutron as a Three-Phase Alternating Current Electric Generator
In analogy to a three-phase alternating current electric generator, we are going to represent interaction 1 and interaction 2, using vectors whose resulting vector is null. In this way, we are going to simulate a neutron as a three-phase alternating current electric generator.
Taking these values as reference we are going to make our vector diagram of the neutron.
Quark Down = 4.7 MeV/c²
Quark up = 2.2 MeV/c²
It is important to make it clear that all interactions are vector, although we do not represent them as such in the figures.
Figure 52.
interaction 1 of the neutron.
Figure 52.
interaction 1 of the neutron.
Figure 53.
Interaction 1 & 2 of the neutron.
Figure 53.
Interaction 1 & 2 of the neutron.
Knowing that the total mass of the neutron is 939.56 MeV/c², we are going to calculate the mass content in each interaction:
R(DD)R = 8.6 x 9.8486 = 84.69 MeV/c²
B(DD)B = 8.6 x 9.8486 = 84.60 MeV/c²
G(UU)G = 4.0 x 9.8486 = 39.39 MeV/c²
R(DD)B = 10.2 x 9.8486 = 100.45 MeV/c²
R(DU)G = 10.2 x 9.8486 = 100.45 MeV/c²
B(DD)R = 10.2 x 9.8486 = 100.45 MeV/c²
B(DU)G = 10.2 x 9.8486 = 100.45 MeV/c²
G(UD)R = 16.7 x 9.8486 = 164.47 MeV/c²
G(UD)B = 16.7 x 9.8486 = 164.47 MeV/c²
(2 x (8.6) + 4.0 + 4(10.2) + 2 x (16.7) = 95.4
NECF = Mn / 95.4 = (939.56 MeV/c²) / 95.4 = 9.8486 MeV/c², neutron electromagnetic coupling factor. The value: 95.4, could have any type of units, for practical purposes we are going to leave it without units.
If we divide the electromagnetic coupling factor of the neutron NECF, by the energy 0.388 MeV/c², corresponding to unit binding energy per nucleon, we will have the approximate number of protons to which the neutron can be stably couple.
Qtyp = NECF / ∆Eα = (9.8486 MeV/c²) / (0.388 MeV/c²) = 25.38
Where ∆Eα could be considered unit binding energy per nucleon.
Qtyp = 25 proton.
Where Qtyp represents the number of protons that the neutron-proton binding energy stably supports, considering the electromagnetic coupling factor of the Neutron NECF.
Let us remember that the maximum binding energy is obtained for iron, Fe (26,30); which has 26 protons and 30 neutrons and this coincides with being the most abundant element on Earth.
According to our calculation, starting at proton number 26, the neutron-proton binding energy begins to weaken.
We are going to represent these values in
Figure 54:
The electric model of a neutral as a three-phase alternating current electric generator allows us to assign a mass value in MeV/c² to interactions 1 & 2, which we represent using a phasor diagram, as shown in
Figure 54. It also allows us to verify that the resulting vector sum in interactions 1 & 2 is zero, and the scalar sum is equal to 939.56 MeV/c², as appropriate.
Analysing the vector diagrams in
Figure 52 and 53, we see that the degrees of freedom of the vectors are practically zero, there is no possibility of deviations, the hypothesis that the charge has to be zero restricts any possibility of changes in the position of the vectors; that is, the vectors have a unique configuration, given in
Figure 52 and 53.
It is important to keep in mind that the relationship between the interactions of quarks-antiquarks-gluons is vector-type, that is, each interaction will be represented by a module and an angle.
In the neutron, if we add the phasors of interaction 1 and interaction 2 vector-wise, we see that the resulting vector is zero, in other words, the net charge is zero; but if we add the module of each vector in MeV/c² scalarly, the sum gives us 939.56 MeV/c²; we represent this in
Figure 53 and 54, which corresponds to the neutron.
Definitely, we can assure that neutrons are true generators of energy, mass and gravity; we have verified how with three quarks that add up to approximately 10 MeV/c², we can generate a mass of 939.56 MeV/c² through the interactions of quarks-antiquarks-gluons.
4.3. Neutron Analysis
For our analysis we will need the following figure:
In
Figure 55, we observe that there are 9 dipoles, 3 dipoles belong to interaction 1 or direct interaction and 6 dipoles belong to interaction 2 or crossed interaction.
Interaction 1
Dipole 1, is represented by R(DD)R, which generates a neutral quark electric current (DD) in the RR direction, in phase.
R(DD)R →│DD > ≡ │1, 0 >
Dipole 2, is represented by B(DD)B, which generates a neutral quark electric current (DD) in the BB direction, in phase.
B(DD)B →│DD > ≡ │1, 0 >
Dipole 3, is represented by G(UU)G, which generates a neutral quark electric current (UU) in the GG direction, in phase.
G(UU)G →│UU > ≡ │1, 0 >
The quark current (DD) in the RR and BB directions can escape confinement by generating photons.
The quark current (UU) in the GG direction can escape confinement by generating photons.
This can be seen when we analyse the B⁻ decay.
Interaction 2
Dipole 4, is represented by R(DD)B; generates two quarks electric currents (DD), one electric current in the R direction, D quarks; the other electric current in the B direction, D antiquarks. Both currents are out of phase.
R(DD)B →│DD >
Dipole 5, is represented by R(DU)G; generates two quarks electric currents (DU), one electric current in the R direction, D quarks; the other electric current in the G direction, U antiquarks. Both currents are out of phase.
R(DU)G →│DU >
Dipole 6, is represented by B(DD)R; generates two quarks electric currents (DD), one electric current in the B direction, D quarks; the other electric current in the R direction, D antiquarks. Both currents are out of phase.
B(DD)R →│DD >
Dipole 7, is represented by B(DU)G; generates two quarks electric currents (DU), one electric current in the B direction, D quarks; the other electric current in the G direction, U antiquarks. Both currents are out of phase.
B(DU)G →│DU >
Dipole 8, is represented by G(UD)R; generates two quarks electric currents (UD), one electric current in the G direction, U quarks; the other electric current in the R direction, D antiquarks. Both currents are out of phase.
G(UD)R →│UD >
Dipole 9, is represented by G(UD)B; generates two quarks electric currents (UD), one electric current in the G direction, U quarks; the other electric current in the B direction, D antiquarks. Both currents are out of phase.
G(UD)B →│UD >
If we analyse the dipoles of interaction 2, we see that they are crossed interactions; generate two quarks currents that are characterized by being out of phase, they are not in phase. These currents are confined to the neutron.
In this simple analysis we have replaced the quantum model of quantum chromodynamics QCD with the electric model of the neutron as a three-phase alternating current electrical generator. In the QCD model, quarks and gluons are used to represent the interactions in the neutron; in the electric model of the neutron as a three-phase alternating current electrical generator, the interactions in the neutron are carried out through quarks-antiquarks, the gluons are just indicative notations to remind us that we are working with vectors with module and phase, as happens in an electric generator.
Here, it is important to highlight that we have simplified the quarks-antiquarks-gluons interactions by quarks-antiquarks interactions (U, U, D, D).
4.4. Electrical-Quantum Modelling of the Proton as a Three-Phase Alternating Current Electric Generator.
We are going to work with
Figure 56 to create our electric model of the proton as a three-phase alternating current electric generator.
In analogy to a three-phase alternating current electric generator, we are going to represent interaction 1 and interaction 2, using vectors whose resulting vector is not zero. In this way we are going to simulate a proton as a three-phase alternating current electric generator.
Taking these values as reference we are going to make our vector diagram of the proton.
D Quark = 4.7 MeV/c²
U Quark = 2.2 MeV/c²
It is important to make it clear that all interactions are vector, although we do not represent them as such in the figures.
Figure 57.
Proton interaction 1.
Figure 57.
Proton interaction 1.
Figure 58.
Interaction 1 & 2 of the proton.
Figure 58.
Interaction 1 & 2 of the proton.
Knowing that the total mass of the proton is 938.27 MeV/c², we are going to calculate the mass content in each interaction:
R(DD)R = 8.6 x 12.0720 = 103.81 MeV/c²
B(UU)B = 4.0 x 12.0720 = 48.28 MeV/c²
G(UU)G = 4.0 x 12.0720 = 48.28 MeV/c²
R(DU)B = 4.0 x 12.0720 = 48.28 MeV/c²
R(DU)G = 10.4 x 12.0720 = 125.54 MeV/c²
B(UD)R = 13.7 x 12.0720 = 165.38 MeV/c²
B(UU)G = 8.1 x 12.0720 = 97.78 MeV/c²
G(UD)R = 16.8 x 12.0720 = 202.80 MeV/c²
G(UU)B = 8.1 x 12.0720 = 97.78 MeV/c²
8.6 + 4 x (3) + 10.4 + 13.7 + 2 x (8.1) + 16.8 = 77.7
PECF = Mp ̸ 77.7 = (938.27 MeV/c²) ̸ 77.7 = 12.0720 MeV/c², proton electromagnetic coupling factor. The value: 77.7, could have any type of units, for practical purposes we are going to leave it without units.
If we divide the proton electromagnetic coupling factor PECF, by the energy 0.388 MeV/c², corresponding to unit binding energy per nucleon, we will have the approximate number of neutrons to which the proton can be stably associated.
Qtyn = PECF / ∆Eα = (12.0720 MeV/c²) / (0.388 MeV/c²) = 31.11
Where ∆Eα could be considered unit binding energy per nucleon.
Qtyn = 31 neutron.
Where Qtyn represents the number of neutrons that the proton-neutron binding energy stably supports, considering the proton electromagnetic coupling factor PECF.
According to our calculation, starting at neutrons number 31, the proton-neutron binding energy begins to weaken.
If we consider the electromagnetic coupling factor NECF and PECF, the maximum stability of an atomic nucleus would be achieved with a maximum number of 25 protons and a maximum number of 31 neutrons, these quantities roughly coincide with that of the iron atom Fe (26,30), a excellent approximation.
We are going to represent these values in
Figure 59:
The electric model of a proton as a three-phase alternating current electric generator allows us to assign a mass value to interactions 1 and 2, which we represent using a vector diagram, as shown in
Figure 58 & 59.
It is important to keep in mind that the relationship between the interactions of quarks-antiquarks-gluons is vector-type, that is, each interaction will be represented by a module and an angle.
We can assure that protons are true generators of energy, mass and gravity; we have verified how with three quarks that add up to approximately 10 MeV/c², we can generate a mass of 938.27 MeV/c² through the interactions of quarks-anti-quarks-gluons.
4.5. Proton Analysis
For our analysis we will need the following figure:
In
Figure 60, we observe that there are 9 dipoles, 3 dipoles belong to interaction 1 or direct interaction and 6 dipoles belong to interaction 2 or crossed interaction.
Dipole 1, is represented by R(DD)R; generates a quarks electric current (DD) in the RR direction, in phase.
R(DD)R →│DD > ≡ │1, 0 >
Dipole 2, is represented by B(UU)B; generates a quarks electric current (UU) in the BB direction, in phase.
B(UU)B →│UU > ≡ │1, 0 >
Dipole 3, is represented by G(UU)G; generates a quarks electric current (UU) in the GG direction, in phase.
G(UU)G →│UU > ≡ │1, 0 >
The quark current (DD) in the RR directions can escape confinement by generating photons.
The quark current (UU) in the BB and GG direction can escape confinement by generating photons.
This can be seen when we analyse the B⁻ decay.
Interaction 2
Dipole 4, is represented by R(DU)B; generates two quarks electric currents (DU), one electric current in the R direction, D quarks; the other electric current in the B direction, U antiquarks. Both currents are out of phase.
R(DU)B →│DU >
Dipole 5, is represented by R(DU)G; generates two quarks electric currents (DU), one electric current in the R direction, D quarks; the other electric current in the G direction, U antiquarks. Both currents are out of phase.
R(DU)G →│DU >
Dipole 6, is represented by B(UD)R; generates two quarks electric currents (UD), one electric current in the B direction, U quarks; the other electric current in the R direction, D antiquarks. Both currents are out of phase.
B(UD)R →│UD >
Dipole 7, is represented by B(UU)G; generates two quarks electric currents (UU), one electric current in the B direction, U quarks; the other electric current in the G direction, U antiquarks. Both currents are out of phase.
B(UU)G →│UU >
Dipole 8, is represented by G(UD)R; generates two quarks electric currents (UD), one electric current in the G direction, U quarks; the other electric current in the R direction, D antiquarks. Both currents are out of phase.
G(UD)R →│UD >
Dipole 9, is represented by G(UU)B; generates two quarks electric currents (UU), one electric current in the G direction, U quarks; the other electric current in the B direction, U antiquarks. Both currents are out of phase.
G(UU)B →│UU >
If we analyse the dipoles of interaction 2, we see that they are crossed interactions; generate two quarks currents that are characterized by being out of phase, they are not in phase. These currents are confined to the proton.
In this simple analysis we have replaced the quantum model of quantum chromodynamics QCD with the electrical model of the proton as a three-phase alternating current electric generator. In the QCD model, quarks and gluons are used to represent the interactions in the proton; in the electric model of the proton as a three-phase alternating current electric generator, the interactions in the proton are carried out through quarks-antiquarks, the gluons are just indicative notations to remind us that we are working with vectors with module and phase, as happens in an electric generator.
Here, it is important to highlight that we have simplified the quarks-antiquarks-gluons interactions by quarks-antiquarks interactions (U, U, D, D).
5. NEW PHYSICAL MODEL PROPOSED FOR PHOTONS, GLUONS, W⁺ BOSON, W⁻ BOSON, Z⁰ BOSON, GRAVITONS AND HIGGS BOSON.
In version 1 of the paper: Generalization of the standard model. Theory of Everything (T.O.E.); we have proposed a generalized model for the photons, gluons and gravitons. Here, in this paper, we are going to delve into our model and propose specific models with their respective examples.
The proposed models are developed in the paper: Theory of Unification of the Interactions of Fundamental Forces: SU(3) x SU(2) --> U(1)
5.1. Analysis of the Proposed Models for the Photons
Main characteristics of photons:
Mass = 0
Electric charge = 0
Spin = 1
Next, we will hypothesize and propose the following model for photons:
(DD) → │DD > ≡ │1, 0 >, in phase (98)
(UU) → │UU > ≡ │1, 0 >, in phase (99)
We are going to highlight that photons are part of the group of gluons. It is important to note that the photons (DD) are in phase. The photons (UU) are also in phase.
Photon modelled as quarks (DD)
- I)
First analysis:
Figure 61.
Feynmann diagram, (a) emission of a photon by an electron (b) absorption of a photon by an electron.
Figure 61.
Feynmann diagram, (a) emission of a photon by an electron (b) absorption of a photon by an electron.
This can be exemplified with the electrons that orbit around an atom, as they gain or lose energy, the electrons jump from their orbits and can even escape from the atom.
If we analyse β⁻ Decay, specifically the interaction [B(DD)B]n → [B(UU)B]p; We conclude that the energy involved in the emission or absorption of a photon by an electron is distributed partly in the electron and partly in the nucleus of the atom. Let us remember that electrons are attached to the nucleus through the exchange of photons.
- II)
Second analysis:
Figure 62.
(c) emission of a photon by a positron (d) absorption of a photon by a positron.
Figure 62.
(c) emission of a photon by a positron (d) absorption of a photon by a positron.
Considering antimatter, this can be exemplified by positrons orbiting an antiatom, as they gain or lose energy, the positrons jump out of their orbits and can even escape the antiatom.
If we analyse β⁺ Decay, specifically the interaction [B(DD)B]n → [B(UU)B]p, We conclude that the energy involved in the emission or absorption of a photon by an positron is distributed partly in the positron and partly in the nucleus of the antiatom. Let us remember that the positrons are linked to the antiatom through the exchange of photons.
- III)
Third analysis:
Figure 63.
Feynmann diagram, (e) a photon creates an electron and positron, (f) an electron and a positron create a photon.
Figure 63.
Feynmann diagram, (e) a photon creates an electron and positron, (f) an electron and a positron create a photon.
This interaction can be observed in particle collider LHC, it is more intuitive to understand. In particle collisions in LHC, a photon (DD) can decay into an electron and a positron. The same thing happens if we make electrons and positrons collide in LHC, these collisions can create photons (DD).
To finish this item, these three interactions can be understood by considering the photon as the combination of quarks (DD).
To begin our analysis, let's consider the following figure:
Let's analyse
Figure 64, in which protons are made to collide at high speeds, this causes the fusion of a quark top with a antiquark top to generate a Higgs boson; this Higgs boson decays in a couple of bottom and antibottom bosons, which decay into a pair of photons. The photons are what we really measure in the detection of the Higgs Boson.
We are going to hypothesize the following; when the interaction of the D quark with the
D antiquark occurs, the resulting interaction is analogous to the interaction in
Figure 64. The resulting interaction is shown in
Figure 65, where the fusion of the D quark and the
D antiquark produces a Higgs boson, which in turn decays into a pair of U quark and
U antiquark and this in turn produces a pair of photons.
If the diagram in
Figure 65 is true, we wonder, could there be three families of Higgs bosons? In my opinion, there are three Higgs Bosson families.
Figure 65 represents an example of how we can produce photons formed by quark (U
U).
5.2 Analysis of the proposed models for the gluons
If we analyse
Figure 66, corresponding to the neutron and
Figure 67 corresponding to the proton, we observe that we can represent the gluons by combining the following markers (R, B, G), which represents matter and (
R,
B,
G) which represents antimatter.
The combination of these markers tells us the number of gluons that exist, 9 in total.
Next, we are going to describe the existing gluon combinations:
(RR), (BB), (GG), (RB), (RG), (BR), (BG), (GR) and (GB)
These gluons had the following characteristics:
Mass = 0
Electric charge = 0
Colour charge = yes
Spin = 1
However, in this paper we make the following hypothesis:
Here, working with the theory of the neutron and proton as a three-phase alternating current electric generator, we hypothesize that (R, B, G) and (R, B, G) are simply markers that tell us that the interactions between quark-antiquark-gluon have magnitude and angles that must be met, as happens in an electric generator.
In other words, quarks-antiquarks-gluons interactions reduce to interactions between quarks-antiquarks.
This implies that in the strong interaction the colour charge disappears and is transformed into simple electromagnetic interactions.
Strong interaction → Electromagnetic interaction
The strong interaction reduces to 6 combinations of quarks-antiquarks interactions. Below we are going to list these 6 combinations.
Direct interactions
(DD) → │DD > ≡ │1, 0 >, in phase (100)
(UU) → │UU > ≡ │1, 0 >, in phase (101)
These interactions that correspond to the strong force are analogous to the electromagnetic interaction that gives rise to photons.
We can explain this in the following way. When a neutron decays into a proton and this in turn traps the electron and forms the hydrogen atom; It is the electron that is linked to the nucleus of the atom through the exchange of photons.
Initially, the gluon (DD) was part of the neutron; after the decay of the neutron into a proton occurs, that gluon (DD) is transformed into a photon and becomes part of the binding energy between the electron and the nucleus of the atom.
The interactions of the quarks (DD) and (UU) called gluons or photons, are the only ones that can escape the confinement of an atom.
Cross interactions
(DU) → │DU >, out of phase (102)
(UD) → │UD >, out of phase (103)
(DD) → │DD >, out of phase (104)
(UU) → │UU >, out of phase (105)
These interactions that correspond to the strong force are analogous to the electromagnetic.
The interactions of the quarks (DU), (UD), (DD) and (UU) cannot escape confinement.
The property that the electric charge is different from zero allows W⁻ bosons to be produced during β⁻ decay and W⁺ bosons to be produced during β⁺ decay.
It is important to see how the strong and weak-electromagnetic force interactions can be reduced to six quarks-antiquarks interactions given by equations 100, 101, 102, 103, 104 and 105.
It is important to highlight the following; when we work with the theory of electric model of the proton and neutron as a three-phase alternating current electric generator, our model includes matter and antimatter together. However, in the standard model, there is one equation that determines matter and another for antimatter; for example, when we model a neutron or proton in QCD, we consider only matter and not antimatter.
I think that the theory corresponding to the electric model of a neutron and proton as a three-phase alternating current electric generator would be a very important complement to the standard model, it would help us develop particle physics in leaps and bounds and discover the great mysteries that we have today, thanks to his visionary ideas.
The theory corresponding to the electric model of the neutron and proton as a three-phase alternating current electric generator, in addition to being a complement to the theory of the standard model of particle physics, is a generalization of the same, simply because it includes matter and antimatter, directly in their interactions.
It is important to highlight our reductionist model, in which we have reduced the quarks-gluons interactions of the proton and neutron in the QCD model to quarks-antiquarks-gluons interactions in the theory of the proton and neutron model as an three-phase alternating current electric generator. Finally, we have reduced the quarks-antiquarks-gluons interactions to simple quarks-antiquarks interactions (U, U, D, D).
5.3. Analysis of the Proposed Models for the Gravitons
When we analyse the standard model, we see that it does not include gravity.
We are going to develop a model of the graviton using vector thinking; that is, we are going to use the theory of electric model a neutron and proton as a three-phase alternating current electric generator, which will allow us to develop a model for the graviton.
Vector thinking is a very powerful tool. Vector thinking allows us to imagine a black hole formed by positively charged particles (quark up) or negatively charged particles (quark down) but whose resulting net charge is zero, in perfect balance.
What is a black hole? A black hole is a stellar body in which the electromagnetic force interactions, weak force interactions and strong force interactions have been disconnected; there is only the gravitational force.
Saying that only the gravitational force exists inside a black hole is the way to follow to discover the graviton particle.
We are going to mention the paper: Analysis of the Kerr-Newman Diagram. Unravelling the interior of a black Hole; in which we define two types of black holes.
First black hole model formed by D quark
If we analyse
Figure 72, we observe that the black hole is formed by
neutroniumd particles, which contain D quark in a special configuration that is characterized because the resulting net charge is zero. The interior of the black hole is made up only of matter, it does not contain antimatter.
Second black hole model formed by U quark
If we analyze
Figure 73, we observe that the black hole is formed by
protoniu particles, which contain U quark in a special configuration that is characterized because the resulting net charge is zero. The interior of the black hole is made up only of matter, it does not contain antimatter.
Continuing along our path, we observe that the minimum fundamental particles inside black holes correspond to the D quark (
Figure 72) and the U quark (
Figure 73).
However, we also said, when a black hole forms, antimatter is ejected out of the black hole into space-time; therefore, we must consider and include the D antiquark and the U antiquark in our theory of the graviton.
Here, we are going to hypothesize that the quarks (U, U, D, D) are the fundamental particles that contribute to the existence of the graviton.
We are going to represent the quantum states in the following way:
│U > ≡ │1/2, 1/2 > (106)
│U > ≡ │1/2, -1/2 > (107)
│D > ≡ │1/2, 1/2 > (108)
│D > ≡ │1/2, -1/2 > (109)
Using the quantum states described in equations 106, 107, 108 and 109; we are going to use the following mathematical expressions to calculate the different graviton models.
│↑ ↑ > ≡ │1, 1 ˃
│↓ ↓ > ≡ │ 1, - 1 ˃
(1⁄√2) │↑↓ + ↓↑ > ≡ │1,0 >
(1⁄√2) │↑↓ - ↓↑ > ≡ │0,0 >
Model 1 for gravitons:
(1⁄√2) │↑↓ + ↓↑ > ≡ │1,0 >
│↑↓ + ↓↑ > ≡ │2,0 >
│U > ≡ │1/2, 1/2 >
│U > ≡ │1/2, -1/2 >
│UU + UU > ≡ |UU > + |UU > = │1, 0 > + │1, 0 > =│2, 0 >
│UU + UU > ≡ │2, 0 > (110)
Model 2 for gravitons:
(1⁄√2) │↑↓ + ↓↑ > ≡ │1,0 >
│↑↓ + ↓↑ > ≡ │2,0 >
│D > ≡ │1/2, 1/2 >
│D > ≡ │1/2, -1/2 >
│DD + DD > ≡ |DD > + |DD > = │1, 0 > + │1, 0 > =│2, 0 >
│DD + DD > ≡ │2, 0 > (111)
Here, we have hypothesized the existence of two gravitons particles given by equation 110 and 111; we observe that in all of them, their spin corresponds to 2 and their angular projection is zero.
If we add the spins of the graviton particle formed by two U quark and two U antiquark or of the graviton particle formed by two D quark and two D antiquark; the spin of the resulting particle is 2, as can be seen in equations 110 and 111.
What is more difficult to imagine or visualize is the sum of the angular projection of the four particles equal or zero (0). If the angular projection of the 4 particles is in phase, aligned on the Z axis, the angular momentum of the two U quarks is up and the angular momentum of the two U antiquarks are down, the resulting angular momentum is zero.
However, after carrying out a rigorous analysis, we came to the conclusion that graviton models 1 and 2 are not viable.
In the upper loop there are a U quark and a U antiquark which annihilate each other; In the lower loop there are a U antiquark and a U quark, which also annihilate.
In the upper loop there are a D quark and a D antiquark which annihilate each other; In the lower loop there are a D antiquark and a D quark, which also annihilate.
Model 3 for gravitons:
(1⁄√2) │↑↓ + ↓↑ > ≡ │1,0 >
│↑↓ + ↓↑ > ≡ │2,0 >
│UD + DU > ≡ |UD > + |DU > = │1, 1 > + │1, -1 > =│2, 0 >
│UD + DU > ≡ │2, 0 > (112)
Model 4 for gravitons:
(1⁄√2) │↑↓ + ↓↑ > ≡ │1,0 >
│↑↓ + ↓↑ > ≡ │2,0 >
│DU + UD > ≡ |DU > + |UD > = │1, -1 > + │1, 1 > =│2, 0 >
│DU + UD > ≡ │2, 0 > (113)
After carrying out a rigorous analysis, we came to the conclusion that graviton models 3 and 4 are viable.
From now on we are going to use model 3 and 4 to represent gravitons.
If we analyze our model, we observe that photons are made up of quarks (U, U, D, D); the same happens with the W⁺ boson, W⁻ boson, Z⁰boson, gluons and gravitons. Absolutely all bosons are made up of quarks (U, U, D, D).
Taking into account what was stated above, that all bosons of gauge corresponding to the forces of strong, weak and electromagnetic interactions are formed by quarks (U, U, D, D); it is assumed that the graviton is also made up of quarks (U, U, D, D), this is the reason why we define gravitons according to equations 112 and 113.
Another reason is the quantum fluctuation that exists in the fabric of space-time; virtual particles that are born and disappear; let's assume that these virtual particles are the result of the creation and decay of gravitons.
A third reason is related to the behavior of the graviton with respect to the photon, we can see this in
Table 8 and
Table 9; at low temperatures the mass of the graviton is approximately equal to the mass of the photon; as the temperature increases, the mass of the graviton is less than 10²⁰ times the mass of the photon; this is due to the differences that exist between the magnetic field and the electric field of the photon and graviton, as a function of temperature.
Until now, detecting gravitons with the intention of discovering a new exotic particle has been very difficult in the particle collider at the LHC at CERN. With the definition of the graviton given by equations 112 and 113; I think that it may be much easier to design an experiment at the LHC at CERN that allows us to detect quarks (U, U, D, D) or some of their associated disintegrations, in such a way that allows us to identify gravitons in particle collisions.
When we analyze bodies like the moon, earth, sun, white dwarf stars, neutron stars and black holes; absolutely all the bodies we know; all the mentioned bodies have a mass and therefore an associated gravity. They are the quarks (U, U, D, D), the reason for the link between the mass of the body and its associated gravity.
Knowing that gravitons are made up of quarks (U, U, D, D), it is easier to imagine the relationship between the mass of the bodies their associated gravity and the curvature of space-time.
Knowing that gravitons are made up of quarks (U, U, D, D), it is now easy for us to imagine and understand the sea of virtual particles that exist in the fabric of space-time, which is the result of decays and formation of gravitons.
Now that we know that gravitons are made up of quarks (U, U, D, D), we can conclude that gravity is a force and affirm that gravitons are the gauge bosons of the gravitational force.
Figure 74.
-│UD + DU > ≡ │2, 0 >.
Figure 74.
-│UD + DU > ≡ │2, 0 >.
In equation 112, we observe the graviton model given by │UD + DU > ≡ │2, 0 >; we observe that the graviton has a positive charge, however its net charge is zero; it has spin 2 and zero angular projection. If we analyze from the point of view of the electric field, the upper and lower coils exert a repulsive force; if we analyze from the point of view of the magnetic field, the upper and lower coil exert an attractive force. It is important to note that UD corresponds to the internal coils and DU corresponds to the external coils. The direction of rotation of the arrows is obtained by applying rules 1 and 2 for matter and antimatter (left-handed particles).
Figure 75.
-│DU + UD > ≡ │2, 0 >.
Figure 75.
-│DU + UD > ≡ │2, 0 >.
In
Figure 30, we observe the graviton model given by │D
U +
UD > ≡ │2, 0 >; we observe that the graviton has a negative charge, however its net charge is zero; it has spin 2 and zero angular projection. If we analyze from the point of view of the electric field, the upper and lower coils exert a repulsive force; if we analyze from the point of view of the magnetic field, the upper and lower coil exert an attractive force. It is important to highlight that D
U corresponds to the internal coils and
UD corresponds to the external coils. The direction of rotation of the arrows is obtained by applying rule 1 and 2 for matter and antimatter (left-handed particles).
If we compare the interactions of the quarks that we denote as gluons with the interactions of the quarks which we denote as gravitons, we can see that gluons are made up of two elementary particles, a quark and an antiquark; however, gravitons are made up of four elementary particles, 2 quarks and 2 antiquarks.
This difference is very important, it is telling us the reason for the stability of gravitons, because the electromagnetic force is 10⁴⁰ times greater than the gravitational force.
We are going to comment on why we defined the graviton according to equation 112 and 113; its definition is related to the virtual particles that exist in space-time. When we excite space-time, generally by the Heisenberg principle, a set of pairs of virtual particles are produced, particles and their antiparticles, that is the main reason for the definition given for the graviton.
Vacuum fluctuations should not be interpreted as small quantum violations of the principle of conservation of energy.
We could have defined the graviton as the sum of the following quarks (UUUU) or (DDDD), but this last definition does not coincide with the sea of virtual particles that exist in space-time. By this we mean that gravitons are responsible for the existence of virtual particles.
It is also worth mentioning the definition of graviton that we have adopted, represented in equations 112 and 113; is telling us that space-time is made up of matter and antimatter, it is telling us that there is no imbalance between matter and antimatter, that all matter and antimatter are in perfect balance in the universe.
We can also observe this difference if we compare the mass of gluons as a function of temperature,
Table 8, with the mass of gravitons as a function of temperature,
Table 9.
Up to this point, using the electric model of the neutron and the proton as an three-phase alternating current electric generator, we have proposed a model that corresponds to graviton particles. We have also shown that the bosons corresponding to the electromagnetic, weak, strong and gravitational forces can be described by quarks-antiquarks interactions (U, U, D, D).
It is important to make it clear that the bosons that represent the standard model corresponding to the interactions of the electromagnetic, weak and strong forces are born from the equations denoted as 100, 101, 102, 103, 104 and 105, including the Higgs boson.
It is also necessary to highlight that the model proposed for gravitons is also born from equation 116.
For this we use as a premise that bosons are the result of the combination of fermions. Taking into account the above, from the point of view of color, nature requires that the wave function of hadrons be anti-symmetrical, that is, singlet, without color. It is also important to highlight that nature demands of us, from the point of view of spin and flavor, that the wave function of hadrons be symmetrical, behaving like bosons.
Next, we are going to represent the base equations with which we work to define the bosons.
│↑ ↑ > ≡ │1, 1 ˃ (114)
│↓ ↓ > ≡ │ 1, - 1 ˃ (115)
(1⁄√2) │↑↓ + ↓↑ > ≡ │1,0 > (116)
(1⁄√2) │↑↓ - ↓↑ > ≡ │0,0 > (117)
5.4. Analysis of the Proposed Models for the Higgs Boson.
To hypothesize the model corresponding to the Higgs boson, we are going to work with equation 117.
Model 1 for the Higgs boson
(1⁄√2) │↑↓ - ↓↑ > ≡ │0,0 >
│↑↓ - ↓↑ > ≡ │0,0 >
│UD - DU > ≡ |UD > - |DU > = |UD > + |DU > =│1, 1 > - │1, -1 > =│0, 0 >
│UD - DU > ≡ |UD > + |DU > │0, 0 > (118)
Model 2 for the Higgs boson
(1⁄√2) │↑↓ - ↓↑ > ≡ │0,0 >
│↑↓ - ↓↑ > ≡ │0,0 >
│DU - UD > ≡ |DU > - |UD > = |DU > + |UD > =│1, -1 > - │1, 1 > =│0, 0 >
│DU - UD > ≡ |DU > + |UD > │0, 0 > (119)
In equation 118 and 119, we observe model 1 and 2 of the Higgs bosons as a combination of quarks (U, U, D, D).
Note that in both models represented in equation 118 and 119; the Higgs boson is not stable, its decay immediate.
If we analyze equation 118, we observe that the upper loop is formed by the quark up, with charge (+) and the quark down, with charge (-); both are annihilated instantly.
If we analyze equation 118, we observe that the lower loop is formed by the D antiquark, with charge (+) and the U antiquark, with charge (-); both are also instantly annihilated.
In other words, the Higgs boson formed by equation 118 is not stable, it decays instantly. This condition in which we affirm that the Higgs bosons decays instantly is very important, too important.
We are going to explain the importance of the meaning of the decay of the Higgs Boson. When the Higgs Boson decays, the important thing is not the Higgs boson, it is the Higgs field, it is the Higgs potential, it is the temperature it generates; there is the importance of the decay of the Higgs Boson, in temperature. Let us remember that there is a relationship between temperature, energy, frequency and Boltzmann's constant; given by the following equations.
E = h x ν (120)
E = Kв-eff x T (121)
Equation 120 and 121 tell us that for a given energy or temperature, space-time has a certain frequency or wavelength and a certain effective Boltzmann´s constant.
Here is the importance of the Higgs Boson, the combination of frequency (wavelength), temperature (energy) and the effective Boltzmann´s constant which is related to temperature; they are the fundamental pillars to form the elementary particles that form the standard model, which constitute the three families of quarks and leptons.
The combination of quarks (U, U, D, D) that give rise to the Higgs boson, which decays instantly; they create the conditions for the elementary particles that form the standard model to originate.
The analysis we carried out for model 1 of the Higgs boson is also valid for model 2 of the Higgs boson.
Up to this point, we have analyzed the existence of the Higgs boson for the first family of quarks, we could generalize and hypothesize the existence of Higgs bosons for the three families of quarks, that is, each family of quarks has its Higgs boson.
First family of Higgs boson formed by quarks (U, U, D, D). Second family of Higgs boson formed by quarks (c, c, s, s). Third family of Higgs boson formed by quarks (t, t, b, b).
6. QUANTIZATION OF SPACE-TIME AND THE GRAVITY
Here it is important to make it clear that when we talk about quantizing gravity, we are talking about gravitons. We know that there is a spectrum of electromagnetic waves related to photons. When we talk about quantizing gravity, we are talking about finding a spectrum of gravitational waves for gravitons in analogy to photons. However, when we talk about quantizing the structure of space-time, we are referring to Planck's constant; outside a black hole, in the domain of the four fundamental interactions, the dynamics are dominated by the Planck´s constant Lp = Lpɛ; inside a black hole, the dynamics is dominated by a Planck´s constant Lpɢ < Lpɛ.
Where Lpɛ is the electromagnetic Planck´s constant and Lpɢ is the gravitational Planck´s constant, it is true whenever Lpɢ < Lpɛ.
Electromagnetic wave spectrum:
Eε = h x fε
Cε = λε x fε
Eε = h x Cε / λε
Eε = Kʙε x Tε
Kʙε = 1.38 10⁻²³ J/K
Gravitational wave spectrum:
Eɢ = h x fɢ
Cɢ = λɢ x fɢ
Eɢ = h x Cɢ / λɢ
Eɢ = Kʙɢ x Tɢ
Kʙɢ = 1.38 10⁻²³ J/K > Kв-eff > 1.78 10⁻⁴³ J/K
When we analyze the equations of the electromagnetic wave spectrum, the Boltzmann´s constant is unique for the entire spectrum and is equal to Kʙε = 1.38 10⁻²³ J/K.
However, when we analyze the equations of the gravitational wave spectrum, we observe that the Boltzmann´s constant is not unique and varies according to: Kʙɢ = 1.38 10⁻²³ J/K > Kв-eff > 1.78 10⁻⁴³ J/K.
If we consider the equation ADS = CFT, Maldacena correspondence; from the point of view of matter, both sides of the equation have to be quantized. From the space-time point of view, both sides of the equation also have to be quantized. Precisely what we are stating is what we want to demonstrate.
6.1 Quantization of the gravity. ``Gravity is a force´´
Next, we are going to show that gravity is a force.
To do this, we are going to resort to the theory developed in the paper: Theory of the Generalization of the Boltzmann’s Constant in Curved Space-Time. Shannon-Boltzmann Gibbs Entropy Relation and the Effective Boltzmann’s Constant.
In the analysis of this theory, we show that the Boltzmann´s constant is variable. There is a Boltzmann´s constant that we all know and that I call the electromagnetic Boltzmann´s constant and a variable or effective Boltzmann´s constant that I call the gravitational Boltzmann´s constant. We also show that Boltzmann's constant is related to the curvature of space-time.
Kв = 1.38 10⁻²³ J/K, for flat space-time
Where Kв is called the electromagnetic Boltzmann´s constant.
1.38 10⁻²³ J/K > Kв-eff > 1.78 10⁻⁴³ J/K, for curved space-time
Where Kв-eff is called the gravitational Boltzmann´s constant.
We can observe in
Table 6, according to the state of matter, how the Kв, frequency, wavelength, etc, vary; according to whether we are in a flat space-time or in a curved space-time.
In
Table 6, it can be seen that there is a relationship between the Boltzmann´s constant Kв-eff, the curvature of space-time and gravity.
In the following graph, we are going to demonstrate why gravity is a force!!!!
If we look at
Figure 76, in the upper part we represent the flat space-time by a straight line and we mark that space-time by a point which we designate as A.
Now, we imagine that we can bring the sun and we place it in the center of flat space-time, curving it. We can see this in the drawing represented at the bottom. Now we see that the sun curves space-time and also contracts it, we can see this because point A moves to the right and the location of point A at the beginning corresponds to point B. In other words, the presence of curved mass and contracts space-time.
The stretching of space-time between point A and B produces a force F; from this simple example we can show that Newton was right, gravity is a force and the bosons that transport gravity exist and are the gravitons defined in equation 112 and 113.
The force F, which stretches space-time from Point B to Point A, is responsible for keeping our feet on the ground, for the fall of bodies, for the rotation of bodies, etc.
From another point of view, we can also see gravity as the curvature of space-time; the greater the curvature, the greater gravity and the greater the stretching of space-time.
Next, through images we will try to interpret what happens to space-time as the force of gravity increases.
If we look at
Figure 76, we see that for the sun,
Table 6 shows us that gravity is of the order of g = 2.73 10² m/s²; if we now consider a neutron star, the gravity is of the order of g = 2.0 10¹² m/s². When a black hole of three solar masses forms, the value of gravity corresponds to g = 5.0 10¹² m/s²; in this last condition, space-time reaches the Planck length.
In all these situations, we observe that as the mass increases, gravity increases, therefore the force of gravity and the curvature of space-time; this is indicating to us that there is a compression of space-time, we can see this in
Figure 76.
A special condition occurs when a black hole of three solar masses is formed, in this condition the length of space-time reaches the Planck length.
As the black hole grows, that is, its mass increases, space-time experiences two forces, a compression force and a torsion force, we can see this in
Figure 44.
As the black hole grows, the Planck length, which initially has the shape of a rod, as shown in
Figure 44, transforms into a spring similar to a corkscrew; the compression force produces a force of gravity towards the interior of the black hole, towards the center. The torsion force produces a tangential force that generates rotation in black holes. This tangential or torsion force is responsible for the origin of dark matter mass.
Lp = Lpɛ = 1.61 10⁻³⁵ m;
Where Lpɛ is Electromagnetic Planck length
1.61 10⁻³⁵ m > Lpɢ > 1.28 10⁻⁵⁴ m
Where Lpɢ is Gravitational Planck length
When the black hole reaches its critical mass, it disintegrates and transforms into a white hole (Big Bang). The Planck length Lpɢ that was compressed, after disintegration tends to reach its normal value Lpɛ and the immense energy released gives rise to cosmic inflation.
In the following table, we are going to analyze how gluon varies with temperature. Gluon is understood as the quarks-antiquarks interactions given by equations 100, 101, 102, 103, 104 and 105.
All the calculations presented in
Table 8 are developed in the paper:
Electrical-quantum modeling of the neutron and proton as a three-phase alternating current electric generator. Determination of the number of quarks-antiquarks-gluons and gravitons, inside a neutron.
In the following table, we are going to analyze how graviton varies with temperature. Graviton is understood as the quark-antiquarks interactions given by equations 112 and 113.
All the calculations presented in
Table 9 are developed in the paper:
Electrical-quantum modeling of the neutron and proton as a three-phase alternating current electric generator. Determination of the number of quarks-antiquarks-gluons and gravitons, inside a neutron.
We are going to analyse the behaviour of the mass of the gluon and the graviton as a function of temperature, we are going to make a comparison to obtain important conclusions.
If we analyze tables 8 and 9, for a temperature less than 2 K, we see that the mass of the gluon coincides with the mass of the graviton.
T = 1.57 10⁻¹⁰ K, gluon mass = 2.35 10⁻⁵⁰ kg; graviton mass = 2.40 10⁻⁵⁰ kg
T = 1.57 10⁻⁵ K, gluon mass = 2.35 10⁻⁴⁵ kg; graviton mas = 2.40 10⁻⁴⁵ kg
T = 1.57 10⁰ K, gluon mass = 2.35 10⁻⁴⁰ kg; graviton mass = 2.40 10⁻⁴⁰ kg
We observe that as the temperature increases, the mass of the gluon and graviton also increases.
We observe that for a temperature below 2⁰K, the mass of the gluon is approximately equal to the mass of the graviton.
We observe that as the temperature increases, the mass of the gluon also increases.
T = 1.57 10⁰ K, gluon mass = 2.35 10⁻⁴⁰ kg
T = 1.57 10¹³ K, gluon mass = 2.35 10⁻²⁷ kg
However, the same does not happen with the mass of the graviton; in the interval we are analyzing, we observe that the mass of the graviton decreases.
T = 1.57 10⁰ K, graviton mass = 2.40 10⁻⁴⁰ kg
T = 10¹³ K, graviton mass = 1.92 10⁻⁴⁷ kg
We observe for a temperature of T = 10¹³ K, the difference between the mass of the gluon and the graviton is of the order Δ = 10²⁰ kg.
If we look at tables 8 and 9, we see that this difference 10²⁰ kg, is maintained in the temperature range between T = 10⁶ K and T = 10¹³ K.
Above T > 10¹³ K, we observe that as the temperature increases, the mass of the gluon also increases.
T = 1.57 10¹³ K, gluon mass = 2.35 10⁻²⁷ kg
T = 1.57 10²⁶ K, gluon mass = 2.35 10⁻¹⁴ kg
Above T > 10¹³ K, we observe that as the temperature increases, the mass of the graviton also increases.
T = 10¹³ K, graviton mass = 1.92 10⁻⁴⁷ kg
T = 10²⁶ K, gluon mass = 1.92 10⁻³⁴ kg
If we look at tables 8 and 9, we see that this difference Δ = 10²⁰ kg, is maintained in the temperature range between T = 10¹³ K and T = 10²⁶ K.
In conclusion, for a temperature higher than T > 10⁶ K, the mass difference between the gluon and the graviton is of the order of Δ = 10²⁰ kg. For a temperature lower than T < 10⁰ K, the mass of the gluon and that of the graviton are approximately equal or coincident. There is a temperature interval between T = 10⁰ K and T = 10⁶ K, in which the difference between the mass of the gluon and that of the graviton widens between 10⁰ kg and 10²⁰ kg.
Here, using the theory from the paper: Theory of the Generalization of the Boltzmann’s Constant in Curved Space-Time. Shannon-Boltzmann Gibbs Entropy Relation and the Effective Boltzmann’s Constant and the theory of the paper: Electrical-Quantum Modeling of the Neutron and Proton as a Three-Phase Alternating Current Electric Generator. Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons, inside a Neutron; we have shown that gravity is a force and furthermore, gravity is quantized. Later we will demonstrate that space-time is also quantized.
6.2. Quantization of Space-Time (DST)
DST, Dynamic space-time with quantum gravity, with negative, positive and flat curvature.
EFQT, Electromagnetic field Quantum theory is a generalization of conformal quantum field theories; this theory is the result of uniting the field theory of electromagnetic interactions, the field theory of weak interactions and the field theory of strong interactions in a single field theory of electrical interactions.
In order to carry out the quantification of space-time we will need the following table:
If we look at
Table 10, we see that Cɢ varies between the following limits:
10⁸ m/s < Cɢ < 3 10²¹ m/s (123)
Replacing (123) into (122), we have:
Cɢ = 3 x 10⁸ m/s to 3 x 10²¹ m/s
Lp = 1.61 10⁻³⁵ m to 1.28 10⁻⁵⁴ m
To quantify gravity, we will use the principle of minimal action:
The action we call S has the following dimensions:
S = {M} C² x {T} , C = L/T
S = Energy involved in a process x Time the process lasts
S = {M} C x {L}, C speed of light.
S = momentum x spatial size
Now we ask ourselves, what is the minimum value of the action?
Quantum mechanics postulates that there is a minimum value for the action and it is defined by h, where h is Planck's constant and is non-zero. If we consider S = h, we have:
Lg = h / (M x C)
Where Lg we call this length quantum size, minimum gravitational length.
This tells us that a mass M cannot be located in a region smaller than Lg.
Let's calculate the quantum size Lg:
For a black hole of 3 solar masses, 6 10³⁰ kg, we have:
Lg = 6.63 10⁻³⁴ / 6 10³⁰ x 3 10⁸ = 6.63 10⁻³⁴ / 18 10³⁸
Lg = 0.368 10⁻⁷²
Lg = 3.68 10⁻⁷³ m
For a black hole of 1.20 10⁸² kg, we have:
Lg = h / M x C
Lg = 6.63 10⁻³⁴ / 1.20 10⁸² x 3 10⁸
Lg = 6.63 10⁻³⁴ / 3.6 10⁹⁰ = 1.84 10⁻¹²⁴
Lg = 1.84 10⁻¹²⁴ m
Taking into account the calculations just carried out and the values in
Table 10, we generate the following table:
Table 11.
represents the quantization of matter Lp and the quantization of space-time Lg.
Table 11.
represents the quantization of matter Lp and the quantization of space-time Lg.
According to calculations, in a black hole we see that the quantization of space-time is different from the quantization of matter and varies as the black hole grows.
We can also infer that column 1 would correspond to the quantization of matter and space-time outside a black hole, in the domain of the 4 elemental forces.
Inside a black hole the following is true:
The quantization values of the matter would vary in the following range:
1.61 10⁻³⁵ m to 1.27 10⁻⁵⁴ m (124)
The space-time quantization values would vary in the following range:
3.68 10⁻⁷³m to 1.84 10⁻¹²⁴ m (125)
Comments:
When we talk about quantizing matter, we mean that ordinary matter as we know it needs a minimum space-time that is given by the Planck length Lp, which is different from Lg, which represents the quantization value of the space-time. The Planck length Lp, determines the limiting space in which matter below this value becomes a black hole, that is, it loses the properties of the electromagnetic force field, the weak and strong force field.
Lp = Lpɛ = 1.61 10⁻³⁵ m, electromagnetic Planck longitude.
Lɢ < Lpɛ
Lɢ = gravitational Planck length.
Lɢ varies from 1.61 10⁻³⁵ m > Lɢ > 1.27 10⁻⁵⁴ m
Lp >> Lg
Lg varies from 3.68 10ˉ⁷³ m > Lg > 1.84 10ˉ¹²⁴ m
Up to this point we have shown that the DST space-time is quantized in values of Lg between:
3.68 10ˉ⁷³ m > Lg > 1.84 10ˉ¹²⁴ m
We have also shown that the matter/energy, represented by the EQFT quantum fields, are also quantized in values of Lp between:
1.61 10⁻³⁵ m > Lɢ > 1.27 10⁻⁵⁴ m
We have demonstrated that space-time and matter are quantized.
7. ANALYSIS OF THE ORIGIN OF ELEMENTARY PARTICLES USING THE THEORY OF THE GENERALIZATION OF THE BOLTZMANN´S CONSTANT IN CURVED SPACE-TIME
Now that we have described the bases on which we are going to stand, we are going to begin to analyse the origin of elementary particles.
We will also remember that the theory electrical-quantum modelling of the neutron and proton as a three-phase alternating current electric generator, tells us:
E = mc², the difference between m and E is the following; in m, energy and gravity are mixed, this capacitive property of matter allows the formation of neutrons, protons and all the complex matter that make up the periodic table of chemical elements. In E, the energy is pure, quanta of elemental energy, gravity encapsulates the E energy, gravity and E energy are not mixed. This property allows us to form the table that we call the standard model of elementary particles.
In both cases where matter is found, E or m, it is important to highlight that a curvature and contraction of space-time occurs. This curvature and contraction of space-time is a function of temperature, it is a direct function of temperature; the higher the temperature, the greater the curvature and contraction of space-time.
This can be seen in
Table 6, for different states of matter, different temperatures and different curvature and contraction of space-time correspond. We are going to use this concept to determine the origin of elementary particles.
In the calculations that we are going to carry out below, we are going to consider the models proposed in item 5), for photons, gluons and quarks.
Equations that we are going to use in our calculations:
Coulomb's law:
Fq = K (q1 x q2) / r² (126)
Where, k is a constant, q1 and q2 are the quantities of each charge, and the scalar r is the distance between the charges.
K = 8.98 10⁹ N⋅m²⋅Cˉ²
Newton's law of universal gravitation:
Fg = - G (m1 x m2) / r² (127)
where F is the gravitational force acting between two objects, m1 and m2 are the masses of the objects, r is the distance between the centres of their masses, and G is the gravitational constant.
G = 6.674 10ˉ¹¹ m³⋅kgˉ¹⋅sˉ²
Before starting the analysis of the first family, we are going to analyse a black hole.
Black Hole:
If we analyse
Table 6, we observe that the gravitational force of attraction of a black hole is Fg = 5 10¹² N.
In item 2.13), we determine the value of the critical mass to produce a black hole in the LHC, mc = 2.37 10ˉ¹⁶ kg. This occurs at a temperature of 10¹³ K.
With these data we are going to calculate the minimum distance r, this corresponds to a temperature of 10¹³ K
Fg = G (m1 x m2) / r²
r = √ [G (m1 x m2)/Fg]
r = √ (6.67 10ˉ¹¹ x 25 x 2.37 10ˉ¹⁶ x 25 2.37 10ˉ¹⁶) / 5 10¹²)
= √ (23515.45 10ˉ⁴³ / 5 10¹²)
rg = √ (4.70 10ˉ⁵²) = 2.16 10ˉ²⁶ m
We have calculated the distance r, moments before a black hole occurs in the LHC, that is, T0ˉ.
rg = 2.16 10ˉ²⁶ m (128)
We are going to perform the same calculations using equation (126):
Fq = K (q1 x q2) / r²
r = √ [k (q1 x q2)/Fg]
r = √ [(8.98 10⁹ x 0.8 10ˉ¹⁹ x 0.8 10ˉ¹⁹) / 10¹⁰]
r = √ (5.74 10ˉ³⁹)
rq = 7.57 10ˉ²⁰ m (129)
The calculated values given by (128) and (129) tell us that ℓs has to take a value between:
7.57 10ˉ²⁰ m > ℓs > 2.16 10ˉ²⁶ m
The value calculated for ℓsq for Up and Down quarks is above the value of 5 10ˉ²² m.
Taking into account the models proposed for photons, quarks and gluons, we are going to propose the following value of ℓs = 10ˉ²⁴ m
rq > ℓsq > ℓs
ℓsq >> ℓs
ℓs = 10ˉ²⁴ m,
ℓs = 10ˉ²⁴ m, proposed value to perform our calculations below.
It is very important to make clear, in the following calculations in which we are going to apply the formula to each elementary particle, Fg = (G (m1 x m2)) / r², the value of (m1 x m2) will be replaced by the value of the mass of the elementary particle to be analysed, this results from applying the new model of photons and gluons.
For example, we divide the up quark into two, separated by the distance ℓs, the product of those two masses m1 x m2 will be equal to the total mass of the up quark. With this same scheme we are going to calculate Fg, for all the elementary particles.
Figure 77.
Model of an up quark analogous to the model of a black hole.
Figure 77.
Model of an up quark analogous to the model of a black hole.
We are going to begin by analysing the first family or generation of elementary particles.
I) First family of elementary particles
In
Figure 78, we see that the down quark is 2 times larger than the up quark and approximately 10 times larger than the electron.
Quark Up:
C = λ x f
λ = C / f
λ = 3 10⁸ / 5.56 10²⁰ = 0.54 10⁻¹² m = 5.4 10⁻¹³
λ / 2 = 2.7 10⁻¹³ m
If we consider for T = 2.67 10¹⁰ K and a contraction in a dimension of 10⁵ times, with respect to flat space-time.
Dqu = (λ/2) / 10⁵ = 2.7 10⁻¹³ / 10⁵ = 2.7 10⁻¹⁸ m
Dqu = 2.7 10⁻¹⁸ m; up quark diameter
Rqu = 1.35 10⁻¹⁸ m, radius of the up quark.
Let's calculate Fg:
Fg = G (m1 x m2) / r²
We know that ℓs is of the order of 10ˉ²² m, between quarks and antiquarks. The value of ℓs was calculated in the paper: Electrical-quantum modelling of the neutron and proton as a three-phase alternating current electric generator. Determination of the number of quarks-antiquarks-gluons and gravitons, inside a neutron.
Let's consider the radius Rs = r = 10ˉ²⁴ m
Fg = (6.67 10ˉ¹¹ x (4 10ˉ³⁰)) / (10ˉ²⁴) ² = 26.68 10ˉ⁴¹ / 10ˉ⁴⁸ = 26.68 10⁷ = 2.66 10⁸
Fg = 2.66 10⁸ N
Note that the product of the mass (m1 x m2) is replaced by the mass of the up-quark, this results from applying the up-quark model in
Figure 77. We generalize this for all elementary particles.
If we compare with
Table 6, we see that the gravitational force that compresses an up quark, Fg = 2.66 10⁸ N, is of the order of the gravitational force of a white dwarf star.
It is true that Fg > Fq, the up quark is stable and does not decay, it can form hadrons. The force of gravitational attraction or compression Fg is greater than the force of repulsion or disintegration Fq.
Quark Down:
C = λ x f
λ = C / f
λ = 3 10⁸ / 11.60 10²⁰ = 0.258 10⁻¹² m = 2.58 10⁻¹³
λ / 2 = 1.29 10⁻¹³ m
We consider T = 10¹⁰ K and a contraction of space-time in a dimension of 10⁵ times with respect to flat space-time.
Dqd = (λ/2) / 10⁵ = 1.29 10⁻¹³ / 10⁵ = 1.29 10⁻¹⁸ m
Dqd = 1.29 10⁻¹⁸ m; Down quark diameter
Rqd = 6.45 10⁻¹⁹ m, radius of the Down quark.
Let's calculate Fg:
Fg = G (m1 x m2) / r²
We know that ℓs is of the order of 10ˉ²² m, between quarks and antiquarks.
Let's consider the radius Rs = r = 10ˉ²⁴ m
Fg = (6.67 10ˉ¹¹ x (8.55 10ˉ³⁰)) / (10ˉ²⁴) ² = 57.02 10ˉ⁴¹ / 10ˉ⁴⁸ = 57.02 10⁷
Fg = 5.70 10⁸ N
If we compare with
Table 6, we see that the gravitational force that compresses a down quark, Fg = 5.70 10⁸ N, is of the order of the gravitational force of a white dwarf star.
It is true that Fg > Fq, the quark down is stable and does not decay, it can form hadrons. The force of gravitational attraction or compression Fg is greater than the force of repulsion or disintegration Fq.
Electron:
C = λ x f
λ = C / f
λ = 3 10⁸ / 1.23 10²⁰ = 2.44 10⁻¹² m
λ / 2 = 1.22 10⁻¹² m
We consider T = 10¹⁰ K and a contraction of space-time in a dimension of 10⁵ times, with respect to flat space-time.
De = (λ/2) / 10⁵ = 1.22 10⁻¹² / 10⁵ = 1.22 10⁻¹⁷ m
De = 1.22 10⁻¹⁷ m; diameter of the electron.
Re = 6.1 10⁻¹⁸ m, radius of the electron.
We know that ℓs is of the order of 10ˉ²² m, between quarks and antiquarks.
Let's consider the radius Rs = r = 10ˉ²⁴ m
Fg = (6.67 10ˉ¹¹ x (0.91 10ˉ³⁰)) / (10ˉ²⁴) ² = 6.06 10ˉ⁴¹ / 10ˉ⁴⁸ = 6.06 10⁷
Fg = 6.06 10⁷ N
If we compare with
Table 6, we see that the gravitational force that compresses an electron, Fg = 6.06 10⁷ N, is of the order of the gravitational force of a white dwarf star. The force of gravitational attraction or compression Fg is greater than the force of repulsion or disintegration Fq, Fg > Fq.
Neutrino Ve:
C = λ x f
λ = C/f
λ = 3 10⁸ / 5.32 10¹⁴ = 0.563 10⁻⁶ m = 5.63 10⁻⁷ m
λ / 2 = 2.81 10⁻⁷ m
Fg >> Fq, Stable half-life.
Here, it is important to highlight that neutrinos have no charge, or eventually if they do, it is negligible.
The neutrino has no charge, Fq = 0; the neutrino is bound by the gravitational force of attraction Fg.
If we analyse
Figure 78 and compare it with table 6, we observe that the frequency of the neutrino corresponds to the characteristics of the earth, that is, a curvature of space-time of the order of Cv = 10², in one dimension. The gravitational force of attraction on the neutrino is very small, similar to the gravitational force of attraction of the earth.
In the case of the neutrino, since the temperature is of the order of T = 2.55 10⁴ K, we can say that the contraction of space-time is very small, of the order of 10² times, with respect to flat space-time for Kв = 1.38 10⁻²³ J/K; this is why neutrinos move almost at the speed of light, as fast as photons because the space-time envelope is practically negligible.
Now we can glimpse and understand when we talk that particles that have mass travel at a speed less than light and particles without mass travel at the speed of light; in reality all particles have mass, what really happens is that the particles with mass travel at a speed lower than that of light because they have an associated space-time curvature (gravitons) that surrounds the particle, decreasing their speed with respect to that of light and massless particles do not have an associated space-time envelope, by which they can move freely at the speed of light.
We are going to explain why we use λ/2, in the calculation of the diameter and radius of the fundamental particles.
In
Figure 79, the ball represented moves with respect to the vertical axis. If this displacement is small with respect to λ/2, we can consider that the movement is that of a harmonic oscillator and if we have several balls, they will all move with the same frequency or period; this is an important characteristic of the motion of a harmonic oscillator, as shown in
Figure 79. According to what has been stated, we can say that the movement of the energy quanta inside an elementary particle is similar to the movement of a harmonic oscillator. We can also say that the temperature of space-time has an associated wavelength λ, which determines the diameter of an elementary particle given by λ/2.
II) Second family of elementary particles
In
Figure 80, we see that the quark charme is 14 times larger than the quark strange and approximately 12 times larger than the muon.
Quark Charme:
C = λ x f
λ = C/f
λ = 3 10⁸ / 32.1 10²² = 0.0934 10⁻¹⁴ m = 9.34 10⁻¹⁶ m
λ / 2 = 4.67 10⁻¹⁶ m
We consider T = 10¹³ K and a contraction of space-time in a dimension of 10⁶ times, with respect to flat space-time.
Dqc = (λ/2) / 10⁶ = 4.67 10⁻¹⁶ / 10⁶ = 4.67 10⁻²² m
Dqc = 4.67 10⁻²² m; diameter of the charme quark.
Rqc = 2.33 10⁻²² m, radius of the charme quark.
We know that ℓs is of the order of 10ˉ²² m, between quarks and antiquarks.
Let's consider the radius Rs = r = 10ˉ²⁴ m
Fg = (6.67 10ˉ¹¹ x (23.7 10ˉ²⁸)) / (10ˉ²⁴) ² = 158.07 10ˉ³⁹ / 10ˉ⁴⁸ = 158.07 10⁹
Fg = 1.58 10¹¹ N
Fq > Fg, the disintegration of the particle occurs.
If we look at
Table 6, we see that the contraction force of space-time is approximately that of a neutron star.
Quark Strange:
C = λ x f
λ = C/f
λ = 3 10⁸ / 2.29 10²² = 1.31 10⁻¹⁴ m = 1.31 10⁻¹⁴ m
λ / 2 = 0.655 10⁻¹⁴ m = 6.55 10⁻¹⁵ m
We consider T = 10¹² K and a contraction of space-time in a dimension of 10⁶ times, with respect to flat space-time.
Dqs = (λ/2) / 10⁶ = 6.55 10⁻¹⁵ / 10⁶ = 6.55 10⁻²¹ m
Dqs = 6.55 10⁻²¹ m; diameter of the strange quark
Rqs = 3.27 10⁻²¹ m; radius of the strange quark
We know that ℓs is of the order of 10ˉ²² m, between quarks and antiquarks.
Let's consider the radius Rs = r = 10ˉ²⁴ m
Fg = (6.67 10ˉ¹¹ x (1.69 10ˉ²⁸)) / (10ˉ²⁴) ² = 11.27 10ˉ³⁹ / 10ˉ⁴⁸ = 11.2710⁹
Fg = 1.12 10¹⁰ N
Fq > Fg, the disintegration of the particle occurs.
If we look at
Table 6, we see that the contraction force of space-time is approximately that of a neutron star.
Muon:
C = λ x f
λ = C/f
λ = 3 10⁸ / 2.55 10²² = 1.17 10⁻¹⁴ m
λ / 2 = 0.588 10⁻¹⁴ m = 5.88 10⁻¹⁵ m
We consider T = 10¹² K and a contraction of space-time in a dimension of 10⁶ times, with respect to flat space-time.
Dm = (λ/2) / 10⁶ = 5.88 10⁻¹⁵ / 10⁶ = 5.88 10⁻²¹ m
Dm = 5.88 10⁻²¹ m; diameter of the muon
Rm = 2.94 10⁻²¹ m; radius of the Muon
We know that ℓs is of the order of 10ˉ²² m, between quarks and antiquarks.
Let's consider the radius Rs = r = 10ˉ²⁴ m
Fg = (6.67 10ˉ¹¹ x (1.88 10ˉ²⁸)) / (10ˉ²⁴) ² = 12.53 10ˉ³⁹ / 10ˉ⁴⁸ = 12.53 10⁹
Fg = 1.25 10¹⁰ N
Fq > Fg, the disintegration of the particle occurs.
If we look at
Table 6, we see that the contraction force of space-time is approximately that of a neutron star.
Muon neutrino Vט:
C = λ x f
λ = C/f
λ = 3 10⁸ / 4.83 10¹⁹ = 0.621 10⁻¹¹ m = 6.21 10⁻¹² m
λ / 2 = 3.10 10⁻¹² m
We consider T = 10¹⁰ K and a contraction of space-time in a dimension of 10⁵ times, with respect to flat space-time.
Dmn = (λ/2) / 10⁵ = 3.10 10⁻¹² / 10⁵ = 3.10 10⁻¹⁷ m
Dmn = 3.10 10⁻¹⁷ m; diameter of the muon neutrino
Rmn = 3.10 10⁻¹⁷ m; radius of the Muon neutrino
We know that ℓs is of the order of 10ˉ²² m, between quarks and antiquarks.
Let's consider the radius Rs = r = 10ˉ²⁴ m
Fg = (6.67 10ˉ¹¹ x (3.56 10ˉ³¹)) / (10ˉ²⁴) ² = 23.74 10ˉ⁴² / 10ˉ⁴⁸ = 23.74 10⁶
Fg = 2.37 10⁷ N
Fg > Fq, stable half-life.
If we look at
Table 6, we see that the contraction force of space-time is approximately that of a white dwarf star.
III) Third family of elementary particles
In
Figure 81, we see that the quark top is 41 times larger than the quark bottom and approximately 95 times larger than the particle tau.
Quark top:
C = λ x f
λ = C / f
λ = 3 10⁸ / 4.18 10²⁵ = 0.71 10⁻¹⁷ m = 7.1 10⁻¹⁸ m
λ / 2 = 3.55 10⁻¹⁸ m
We consider T = 10¹⁵ K and a contraction of space-time in a dimension of 10⁶ times, with respect to flat space-time.
Dqt = (λ/2) / 10⁶ = 3.55 10⁻¹⁸ / 10⁶ = 3.55 10⁻²⁴ m
Dqt = 3.55 10⁻²⁴ m; diameter of the Top quark
Rqt = 2.33 10⁻²⁴ m, radius of the Top quark.
We know that ℓs is of the order of 10ˉ²² m, between quarks and antiquarks.
Let's consider the radius Rs = r = 10ˉ²⁴ m
Fg = (6.67 10ˉ¹¹ x (308 10ˉ²⁷)) / (10ˉ²⁴) ² = 2054.36 10ˉ³⁸ / 10ˉ⁴⁸ = 2054.36 10¹⁰
Fg = 2.05 10¹³ N
Fq > Fg, the disintegration of the particle occurs.
If we look at
Table 6, we see that the contraction force of space-time is approximately that of a black hole.
Quark Bottom:
C = λ x f
λ = C/f
λ = 3 10⁸ / 1.01 10²⁴ = 2.97 10⁻¹⁶ m
λ / 2 = 1.48 10⁻¹⁶ m
We consider T = 10¹³ K and a contraction of space-time in a dimension of 10⁶ times, with respect to flat space-time.
Dqb = (λ/2) / 10⁶ = 1.48 10⁻¹⁶ / 10⁶ = 1.48 10⁻²² m
Dqb = 1.48 10⁻²² m; diameter of the Bottom quark
Rqb = 0.74 10⁻²² m, radius of the Bottom quark.
We know that ℓs is of the order of 10ˉ²² m, between quarks and antiquarks.
Let's consider the radius Rs = r = 10ˉ²⁴ m
Fg = (6.67 10ˉ¹¹ x (7.48 10ˉ²⁷)) / (10ˉ²⁴) ² = 49.89 10ˉ³⁸ / 10ˉ⁴⁸ = 49.89 10¹⁰
Fg = 4.98 10¹¹ N
Fq > Fg, the disintegration of the particle occurs.
If we look at
Table 6, we see that the contraction force of space-time is approximately that of a neutron star.
Tau:
C = λ x f
λ = C/f
λ = 3 10⁸ / 0.43 10²⁴ = 6.97 10⁻¹⁶ m
λ / 2 = 3.48 10⁻¹⁶ m
We consider T = 10¹³ K and a contraction of space-time in a dimension of 10⁶ times, with respect to flat space-time.
Dqtau = (λ/2) / 10⁶ = 3.48 10⁻¹⁶ / 10⁶ = 3.48 10⁻²² m
Dqtau = 3.48 10⁻²² m; diameter of the Lepton Tau
Rqtau = 1.74 10⁻²² m, radius of the Lepton Tau.
We know that ℓs is of the order of 10ˉ²² m, between quarks and antiquarks.
Let's consider the radius Rs = r = 10ˉ²⁴ m
Fg = (6.67 10ˉ¹¹ x (3.2 10ˉ²⁷)) / (10ˉ²⁴) ² = 21.34 10ˉ³⁸ / 10ˉ⁴⁸ = 21.34 10¹⁰
Fg = 2.13 10¹¹ N
Fq > Fg, the disintegration of the particle occurs.
If we look at
Table 6, we see that the contraction force of space-time is approximately that of a neutron star.
Tau Neutrino:
C = λ x f
λ = C/f
λ = 3 10⁸ / 3.62 10²¹ = 0.628 10⁻¹³ m = 6.28 10⁻¹⁴ m
λ / 2 = 3.14 10⁻¹⁴ m
We consider T = 10¹¹ K and a contraction of space-time in a dimension of 10⁵ times with respect to flat space-time.
Dtau = (λ/2) / 10⁵ = 3.14 10⁻¹⁴ / 10⁵ = 3.14 10⁻¹⁹ m
Dtau = 3.14 10⁻¹⁹ m; diameter of the tau neutrino
Rtau = 3.10 10⁻¹⁹ m, radius of the Tau neutrino
We observe that ℓs is of the order of 10ˉ²² m, between quarks and antiquarks.
Let's consider the radius Rs = r = 10ˉ²⁴ m
Fg = (6.67 10ˉ¹¹ x (2.67 10ˉ²⁹)) / (10ˉ²⁴) ² = 17.80 10ˉ⁴⁰ / 10ˉ⁴⁸ = 17.80 10⁸
Fg = 1.78 10⁹ N
Fg > Fq, stable half-life.
If we look at
Table 6, we see that the contraction force of space-time is approximately that of a white dwarf star.
8. APPLICATION OF THE MODEL AND RESULTS
We are going to remember again the capacitive property of matter, according to the equation E = mc²; matter is in two states, pure energy as is the case of elementary particles in which gravity encapsulates the energy in state pure; and mixed, that is, the energy is mixed with gravity, as happens with protons, neutrons and stellar bodies.
8.1. Comparison Between Stellar Bodies and Elementary Particles Considering the Theory of the Generalization of the Boltzmann´s Constant in Curved Space-Time.
In
Table 12, for a gravitational force Fg = 10¹⁰ N, we can divide the elementary particles into two groups; in blue, the stable elementary particles correspond to a gravitational force less than 10¹⁰ N, ( Fg > Fq); in orange, unstable elementary particles, correspond to a gravitational force greater than 10¹⁰ N, (Fq > Fg).
Fg = 10¹⁰ N, it is an inflection point, between the gravitational forces Fg and the coulomb force Fq; below 10¹⁰ N, Fg > Fq, the elementary particles are stable; above 10¹⁰ N, Fq > Fg, the elementary particles are unstable.
However, this inflection point only exists for elementary particles, for pure energy type E, according to the Einstein equation E = mc².
For stellar bodies, in which the energy is given by the mass m, from the equation E = mc², there is no inflection point.
If we analyse
Table 7, we see that the temperature corresponding to the quark top is slightly lower than the temperature of the Higgs potential.
Temperature Quark top = 2.00 10¹⁵ K
Temperature Higgs boson = 2.97 10¹⁵ K
Taking into account that the decay time of the quark top is of the order of 10ˉ²⁵ s.
We are going to propose the following, for a temperature higher than the temperature of the Higgs potential, T Higgs = 2.97 10¹⁵ K, the coulomb force is much greater than the gravitational force, Fq >> Fg; under these conditions, the coulomb force is so great that it does not allow the gravitational force field to encapsulate matter in the pure energy state E, consequently breaking the inverse symmetry of the electroweak force.
Above the Higgs potential temperature, the gravitational force field cannot encapsulate matter in the form of pure energy, the energy of the electromagnetic field moves freely independent of the force of gravity; below the Higgs temperature, the gravitational force field interacts with the electromagnetic force field, this interaction allows the formation of elementary particles.
If we look at
Table 6, the gravitational force of a black hole is 5 10¹² N and the force of the Top quark is 2 10¹³ N; we see that the gravitational force of the top quark is greater than the force of a black hole, this is because a top quark does not have the critical mass to form a black hole, even though its temperature reaches 10¹⁵ K. In this example it is true that the force Fq >> Fg and the top quark ends up decaying.
Another very important deduction that we can make is the following, it is the gravitational field together with the Higgs field that give rise to elementary particles. It is the Higgs potential that determines the temperature that causes the gravitational field to encapsulate elemental energy to form elemental particles.
In conclusion, to form elementary particles we need:
Let us remember that the Higgs field H has a value of 246 GeV (2.85 10¹⁵ K) in a vacuum.
The Higgs potential is the value of energy that the Higgs field stores at a given moment, it is a scalar field, it is a temperature field.
The Higgs boson is the excitation of the Higgs field and is produced in particle accelerator LHC.
The potential of the Higgs field has a maximum at the origin and falls to its minimum, which is the current vacuum that corresponds to 246 GeV, the value of the Higgs field.
8.2. Mass-Temperature Relationship in Elemental and Non-Elemental Particles.
It is observed for all situations that the mass-temperature relationship is 1.53 10ˉ⁴⁰ kg / k.
In
Table 13, it is observed that the mass-temperature relationship is constant for all the particles of the standard model, including the W (+/-) bosons, z⁰ Boson, Higgs boson, protons and neutrons.
In
Figure 82, we represent the mass-temperature relationship, which gives us a straight line whose slope is 1.53 10ˉ⁴⁰ kg/k.
In red, the elementary particles are represented; in blue, the stellar bodies are represented.
In
Figure 83, we can see that elementary particles have a gravitational attraction force of the order of stellar bodies; for example, electrons have a gravitational force on the order of white dwarf stars and the quark bottom has a gravitational force on the order of neutron stars.
Let us remember that 2.97 10¹⁵ K is the temperature at which the symmetry break occurs. Above that temperature, the electroweak repulsion force Fq is much greater than the gravitational attraction force Fg, Fq >> Fg; therefore, which makes the formation of elementary particles impossible.
In
Figure 83, the yellow line marks the boundary between stable and unstable elementary particles, below the yellow line, the elementary particles are stable; above the yellow line, the elementary particles are unstable.
According to the models proposed for the quarks, the instability of the particles occurs because for Fg = 10¹⁰ N, the force Fq of repulsion or electrostatic disintegration exceeds the force Fg of gravitational attraction.
Up to this point we have carried out an intuitive analysis of why some elementary particles are stable and why other elementary particles are unstable.
Now we are going to analyse intuitively, why the first family of quarks can form hadrons and why the second and third families of quarks cannot form hadrons.
In the paper: Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electric Generator. Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons, inside a Neutron; we have modelled a neutron and a proton as a three-phase alternating current electric generator.
In the following graph, we are going to bring the figures that represent the neutron as a reminder example:
If we analyse
Table 7, we observe that there is a relationship of 2 between the parameters of the up and down quark.
It is also important to consider that the up and down quarks are in the stable zone of
Figure 26; these two combinations are very important and are what gives the first family of quarks the ability to form hadrons.
For the second family of charme and strange quarks, the relationship between the parameters of the quarks is 14 and in addition both quarks are in the unstable zone of
Figure 83, these two combinations mean that the second family of quarks does not have the ability to form hadrons. It would be very difficult to form a vector diagram analogous to that of the neutron,
Figure 84, with the charme and strange quarks.
For the third family of top and bottom quarks, the relationship between the parameters of the quarks is 41 and in addition both quarks are in the unstable zone of
Figure 26, these two combinations mean that the third family of quarks does not have the ability to form hadrons. It would be very difficult to form a vector diagram analogous to that of the neutron,
Figure 28, with the bottom and top quarks.
At this point we wonder, if the gravitational force of the stellar bodies is of the order of the gravitational force of the elementary particles, why the stellar bodies move at a speed v << c and the elementary particles move at a speed approximate to the speed of the light?
The answer to this question can be related to the capacitive property of matter, to the extent that matter forms complex bodies, gravity mixes with energy and this manifests itself in our daily life, in which we perceive that the bodies are they move slowly v << c, that is, our classical world, deterministic. For elementary particles, in which the gravity-energy relationship is minimal, we see that the speed v of the elementary particles is approximately the speed of light c, v approximately c, quantum world, probabilistic.
We are going to try to find a relationship between the sun-earth and proton-electron model.
First relationship
Ms / Mp = 1.98 10³⁰ / 1.67 10ˉ²⁷ = 1.18 10⁵⁷
Mt / Me = 5.97 10²⁴ / 9.1 10ˉ³¹ = 0.656 10⁵⁵
(Ms / Mp) / (Mt / Me) = 1.18 10⁵⁷ / 0.656 10⁵⁵ = 1.79 10²
Where Ms is the mass of the sun, Mt is the mass of the earth, Mp is the mass of the proton and Me is the mass of the electron.
Second relationship
Ms / Mt = 1.98 10³⁰ / 5.97 10²⁴ = 3.31 10⁵
Mp / Me = 1.673 10ˉ²⁷ / 9.1 10ˉ³¹ = 1.83 10³
(Ms / Mt) / (Mp / Me) = 3.31 10⁵ / 1.83 10³ = 1.80 10²
Where Ms is the mass of the sun, Mt is the mass of the earth, Mp is the mass of the proton and Me is the mass of the electron.
Third relationship
Dts = 1.5 10¹¹ m, earth-sun distance
Dpe = 5.3 10ˉ¹¹ m, proton-electron distance
If we consider zero (0) as a reference and measure to the left the distance Dpe = 5.3 10ˉ¹¹ m, now if we change the reference to the left then the distance Dpe = 5.3 10¹¹ m.
With this we want to demonstrate that the distance Dpe and Dts are equivalent in relation to the size of the bodies Ms/Mt vs Mp/Me.
We apply the Bohr model to calculate the speed of the electron around the nucleus of the atom, proton:
Ve = n h / (r me 2 π)
Ve = 1 x 6.62 10ˉ³⁴ / 5.3 10ˉ¹¹ x 9.1 10ˉ³¹ x 2 x 3,14
Ve = 2.18 10⁶ m/s, velocity of the electron
We are going to calculate the speed of the earth around the sun:
Vt = ꙍ x Rt
Vt = (2π /T) x Rt
Vt = (2 x 3,14 x 1.5 10¹¹ m) / 3.15 10⁷ s
Vt = 2.99 10⁴ m/s
Ve / Vt = 2.18 10⁶ / 2.99 10⁴ = 0.72 10²
Where Ve is electron velocity and Vt is earth velocity.
We have shown that the difference between the speed of the electron Ve and the speed of the earth with respect to the sun Vt is two order of magnitude; this is due to the difference between the mass ratio Ms/Mt vs Mp/Me, 1.8 10², if an equal mass ratio existed, surely Vt would be the same as the speed of the electron Ve. Therefore, the sun-earth model is equivalent to the proton-electron model.
To conclude, we have demonstrated that gravity is fundamental in determining the parameters that elementary particles acquire when they are formed. Furthermore, we have shown that the attractive force of elementary particles is similar to that of stellar bodies.
In the next section, we will analyse β ˉ decay, to emphasize how electrons, antineutrinos and photons are produced.
8.3. Origin of the Electron and Antineutrino - β ˉ Decay
In the paper: Theory of Unification of the Interactions of Fundamental Forces: SU(3) x SU(2) → U(1); we have analysed β ˉ decay, considering the electric model of the proton and the neutron as a three-phase alternating current electric generator.
We are going to develop the vector diagrams of the neutron and the proton, considering the
Figure 87 and
Figure 88.
From the vector diagram the following table is obtained:
Table 14 shows that the total energy involved in β⁻ decay corresponds to IEtI = 385.37 MeV/c².
In order to find a relationship between fermions and bosons, we are going to analyse the 9 interactions in
Table 14 one by one.
Direct interactions:
- i)
[R(DD)R]n → [R(DD)R]p
There is a neutral current in (RR), which adds mass; causes the mass of [R(DD)R]n to reach the value of (R(DD)R)p.
Let's remember that gluons (RR) do not exist, it simply tells us that the exchange of quarks (DD) is vector and has a magnitude and angle that must be respected.
Figure 87, we see that (R(D
D)
R)n has a mass of: 84.69 MeV/c²
Figure 88, we see that (R(D
D)
R)p has a mass of: 103.81 MeV/c²
Figure 89, we see that there is a potential difference that gives rise to E1, therefore what is really produced is a neutral electric current that makes (R(D
D)
R)n → (R(D
D)
R)p , as shown in
Table 15 in green.
- ii)
[B(DD)B]n → [B(UU)B]p
There is a non-neutral current in (BB), that removes mass; causes the mass of [B(DD)B]n to reach the value of [B(UU)B]p.
Let's remember that gluons (BB) do not exist, it simply tells us that the exchange of quarks (DD) is vector and has a magnitude and angle that must be respected.
Figure 87, we see that (B(D
D)
B)n has a mass of: 84.69 MeV/c²
Figure 88, we see that (B(U
U)
B)p has a mass of: 48.28 MeV/c²
Figure 89, we see that there is a potential difference that gives rise to E2, therefore what really occurs is the decay of the quarks (D
D) into quarks (U
U) which makes B(D
D)
B]n → [B(U
U)
B]p as shown in
Table 16 in green.
Here we are going to carry out the following reasoning, for this we are going to use the following graph:
If we look at the graph in
Figure 90, there is a mass value between 2.2 Mev/c² and 4.7 Mev/c² marked with x, in blue, which corresponds to zero charge (0 e).
Let's give an interpretation to this graph that relates the D quark to the U quark.
We see that for 0 Mev/c² it corresponds to a charge of zero, 0 e. As the mass increases, the charge also increases, reaching 2.2 Mev/c², with a charge of +2/3 e, which corresponds to the U quark. We continue adding mass, but now we add negative charge until we reach a value of null charge or zero charge, we do not know this mass value and we denote it with an X. We continue adding mass and negative charge until we reach a mass of 4.7 Mev/c² and a charge of - 1/3 e, which corresponds to the D quark.
We are going to hypothesize that quarks (D, D) are composite particles within which the elementary particles (U, U) are contained.
- iii)
[G(UU)G]n → [G(UU)G]p
There is a neutral electric current in (GG), that adds up to mass; causes the mass of [G(UU)G]n to reach the value of [G(UU)G]p
Let's remember that gluons (GG) do not exist, it simply tells us that the exchange of quarks (UU) is vector and has a magnitude and angle that must be respected.
Figure 87, we see that (G(U
U)
G)n has a mass of: 39.39 MeV/c²
Figure 88, we see that (G(U
U)
G)p has a mass of: 48.28 MeV/c²
Figure 89, we see that there is a potential difference E3, therefore what is really produced is a neutral electric current that makes [G(U
U)
G]n → [G(U
U)
G]p as shown in
Table 17 in green.
Cross interactions:
- iv)
[R(DD)B]n → [R(DU)B]p
there are two electric currents that removes mass; causes the mass of [R(DD)B]n to reach the value of [R(DU)B]p.
There is a neutral electric current of D quarks in the direction of R.
There is an electric current of D antiquarks in the direction of B.
Let's remember that gluons (RB) do not exist, it simply tells us that the exchange of quarks (DD) is vector and has a magnitude and angle that must be respected.
Figure 87, we see that [R(D
D)
B]n has a mass of: 100.45 MeV/c²
Figure 88, we see that [R(D
U)
B]p has a mass of: 48.28 MeV/c²
Figure 89, we see that there is a potential difference E4, we observe that there is a neutral electric current in the direction of R that goes from the quark Dn → Dp and we also observe in the direction of
B the decay of the quark
Dn →
Up; therefore, what really occurs is that [R(D
D)
B]n → [R(D
U)
B]p as shown in
Table 18 in green.
We can represent this transformation in the following way:
D → U + e⁺ + ʋ
In this interaction: [R(DD)B]n → [R(DU)B]p; we observe that U antiquark, positrons and neutrinos are produced.
- v)
[R(DU)G]n → [R(DU)G]p
there are two neutral electric currents that adds up to mass; causes the mass of [R(DU)G]n to reach the value of [R(DU)G]p
There is a neutral electric current of D quarks in the direction of R.
There is a neutral electric current of U antiquarks in the direction of G.
Let's remember that gluons (RG) do not exist, it simply tells us that the exchange of quarks (DU) is vector and has a magnitude and angle that must be respected.
Figure 87, we see that [R(D
U)
G]n has a mass of: 100.45 MeV/c²
Figure 88, we see that [R(D
U)
B]p has a mass of: 125.54 MeV/c²
Figure 89, we see that there is a potential difference E5; if we observe in the direction of R, we see that there is a neutral electric current that goes from Dn → Dp and if we observe in the direction of
G, we also observe that there is a neutral electric current that goes from
Un →
Up; therefore, what really occurs is that [R(D
U)
G]n →[R(D
U)
G]p as shown in
Table 19, in green.
- vi)
[B(DD)R]n → [B(UD)R]p
there are two electric currents that adds up to mass; causes the mass of [B(DD)R]n to reach the value of [B(UD)R]p.
There is an electric current of D quarks in the direction of B.
There is a neutral electric current of D antiquark in the direction of R.
Let's remember that gluons (BR) do not exist, it simply tells us that the exchange of quarks (DD) is vector and has a magnitude and angle that must be respected.
Figure 87, we see that [B(D
D)
R]n has a mass of: 100.45 MeV/c²
Figure 88, we see that [B(U
D)
R]p has a mass of: 165.38 MeV/c²
Figure 89, we see that there is a potential difference E6, note that in the direction of B the D quark decays into the U quark, D → U; also note that in the direction of
R there is a neutral electric current between the
U quarks,
U -- >
U; therefore what really occurs is that [B(D
D)
R]n --> [B(U
D)
R]p as shown in
Table 20 in green.
We can represent this transformation in the following way:
D → U + e⁻ + ʋ
In this interaction: [B(DD)R]n → [B(UD)R]p; we observe that U quark, electron and antineutrinos and are produced.
- vii)
[B(DU)G]n → [B(UU)G]p
there are two electric currents that removes mass; causes the mass of [B(DU)G]n to reach the value of [B(UU)G]p.
There is an electric current of D quarks in the direction of B.
There is a neutral electric current of U antiquark in the direction of G.
Let's remember that gluons (BG) do not exist, it simply tells us that the exchange of quarks (DU) is vector and has a magnitude and angle that must be respected.
Figure 87, we see that [B(D
U)
G]n has a mass of: 100.45 MeV/c²
Figure 88, we see that [B(U
U)
G]p has a mass of: 97.78 MeV/c²
In
Figure 89, we see that there is a potential difference E7. If we look in the direction of B, the D quark decays into the U quark, D --> U; if we look in the direction of
G, there is a neutral electric current between the
U antiquarks,
U -->
U; therefore, what is actually produced is [B(D
U)
G]n →[B(U
U)
G]p as show in
Table 21 in green.
We can represent this transformation in the following way:
D → U + e⁻ + ʋ
In this interaction: [B(DU)G]n → [B(UU)G]p; We observe that U quark, electron and antineutrinos are produced.
- viii)
G(UD)R → G(UD)R
There are two neutral electric currents that adds up to mass; causes the mass of [G(UD)R]n to reach the value of [G(UD)R]p.
There is a neutral electric current of U quarks in the direction of G.
There is a neutral electric current of D antiquark in the direction of R.
Let's remember that gluons (GR) do not exist, it simply tells us that the exchange of quarks (UD) is vector and has a magnitude and angle that must be respected.
Figure 87, we see that [G(U
D)
R]n has a mass of: 164.47 MeV/c²
Figure 88, we see that [G(U
D)
R]p has a mass of: 202.80 MeV/c²
Figure 89, we see that there is a potential difference E8. If we observe in the direction of G, there is a neutral current that goes from the Un quark to the Up quark, Un --> Up; if we observe in the direction of
R, there is a neutral electric current that goes from the
Dn antiquark to the
Dp antiquark,
Dn -->
Dp; therefore, what really occurs is that [G(U
D)
R]n → [G(U
D)
R]p as shown in
Table 22 in green.
- ix)
G(UD)B → G(UU)B
There are two electric currents that removes mass; causes the mass of [G(UD)B]n to reach the value of [G(UU)B]p.
There is a neutral electric current of U quarks in the direction of G.
There is an electric current of D antiquarks in the direction of B.
Let's remember that gluons (GB) do not exist, it simply tells us that the exchange of quarks (UD) is vector and has a magnitude and angle that must be respected.
Figure 87, we see that [G(U
D)
B]n has a mass of: 164.47 MeV/c²
Figure 88, we see that [G(U
U)
B]p has a mass of: 97.78 MeV/c²
Figure 89, we see that there is a potential difference E9, if we look in the direction of G we see that there is a neutral electric current that goes from the Un quark to the Up quark, Un → Up; if we look in the direction of
B, we see that the
Dn antiquark decays into the
Up antiquark,
Dn →
Up; therefore, what really occurs is that [G(U
D)
B]n → [G(U
U)
B]p as shown in
Table 23 in green.
We can represent this transformation in the following way:
D → U + e⁺ + ʋ
In this interaction: G(UD)B → G(UU)B; We observe that U antiquark, positrons and neutrinos are produced.
We observe that in
Table 16 (E2), an electron and a positron are emitted; in
Table 18 (E4), a positron is emitted; in
Table 20 (E6), an electron is emitted; in
Table 21 ((E7), an electron is emitted and finally in
Table 23 (E9), a positron is emitted. The important thing in our analysis is the net emission, which we will demonstrate below that it consists of the emission of an electron and an electron antineutrino.
Origin of the electron
In
Figure 87 and 88, we see that the neutron and proton interactions are divided into direct interactions and cross interactions.
If we analyze the direct interaction in the decay of the neutron → proton, we observe that the dipole [B(DD)B]n --> [B(UU)B]p undergoes transformations.
E2 = [B(DD)B]n → [B(UU)B]p = 36.41 MeV/c²
When analyzing the cross interaction, we observe that the following dipoles undergo transformations,
E4 = [R(DD)B]n → [R(DU)B]p = 80.75 MeV/c²
E6 = [B(DD)R]n → [B(UD)R]p = 72.87 MeV/c²
E7 = [B(DU)G]n → [B(UU)G]p = 41.35 MeV/c²
E9 = [G(UD)B]n → [G(UU)B]p = 68.93 MeV/c²
We observe that in the dipoles E2, E4, E6, E7 and E9; transformations occur in the (BB) interaction.
Using
Table 14, we are going to make the following graphs:
The interactions that occur in RR and GG are neutral currents that do not produce transformations in the quarks.
The interactions in (BB) produce transformations in the quarks.
Now we are going to try to interpret the values given in
Table 24, in (B
B) interactions.
In
Table 14, we observe that the interaction at
B = 36.41 MeV/c². If we compare with the interaction
B in
Table 24, we observe that there is a difference of 0.95 MeV/c².
In
Table 14, we observe that the interaction at B = 36.41 MeV/c². If we compare with the interaction
B in
Table 24, we observe that there is a difference of 36.41 MeV/c²
The difference between the (BB) interactions is given by:
Δ(BB) = 36.41 MeV/c² - 35.46 MeV/c² = 0.95 MeV/c²
This difference in mass or energy given by Δ(BB) = 0.95 MeV/c², it is what gives rise to the electron.
Origin of the electron antineutrino
We are going to represent the neutrino and antineutrino in the following way:
│ν > ≡ │1/2, 0 >
│ν > ≡ │1/2, 0 >
Let us observe that the neutrino and antineutrino have spin 1/2 and zero angular projection (0).
We know that electron neutrino has very small mass, therefore they can transport energy and transfer it through their linear momentum. Let's remember that neutrinos are particles that have no electrical charge.
An example occurs when an electron antineutrino interacts with an electron and changes the speed of the electron and its angle. The change in speed of the electron produces a change in energy and therefore a change in its mass.
The interaction of the antineutrino with the electron acts as a neutral current, which causes the electron to change its speed, its energy and therefore its mass.
We are going to perform the following analysis on βˉ decay.
Initially, the decay of potassium into calcium was analysed and it was observed that a neutron transformed into a proton and emitted an electron. The decay of copper into Zinc was also analysed and again it was observed that a neutron transformed into a proton and emitted an electron, that is:
n →p + e⁻
A → B + e⁻
Where A is the parent nucleus, B is the daughter nucleus and e⁻, is the electron.
Let's represent this in the following way,
Where A is a quadruple-vector and represents the parent nucleus, Eᴀ is the energy and Pᴀ represents the ordinary impulse in (X, Y, Z).
Where B is a quadruple-vector and represents the daughter nucleus, Eв is the energy and Pв represents the ordinary impulse in (X, Y, Z).
Where e⁻ is a quadruple-vector and represents the electron, Ee is the energy and Pe represents the ordinary momentum in (X, Y, Z).
Now if I stand at the centre of mass, that is, at the parent nucleus, we have:
Pᴀ= 0 ; Eᴀ= mᴀ
Pв = - Pe
The process is defined by these equations.
We now consider the following equations:
We can determine the value of Ee.
However, what was observed is that Ee is not fixed, it is variable and represents a continuous energy spectrum, which at that time violated the law of conservation of energy and momentum. This led to the postulation of a new particle that they called electron antineutrino.
This particle, the electron antineutrino, allowed the conservation of energy, impulse and lepton number.
To determine the origin of the electron antineutrino on βˉ decay, we are going to analyse
Figure 87, 88 and 89.
Let's remember that we are using the theory: modelling a neutron and proton as a three-phase alternating current electric generator.
In the previous item we analysed the origin of the electron, we observed that it is related to (BB) interactions.
We observe that the dipoles E2, E4, E6, E7 and E9; they are involved in the (BB) interactions that give rise to the electron.
However, if we analyze
Table 8 to
Table 16, we observe that there are neutral electric currents.
Figure 87, we see that [R(D
D)
R]n has a mass of: 84.69 MeV/c²
Figure 88, we see that [R(D
D)
R]p has a mass of: 103.81 MeV/c²
Figure 89, we see that there is a potential difference E1, therefore what is really produced is a neutral electric current (D
D) that goes from (R(D
D)
R)n
→ (R(D
D)
R)p, as show in
Table 25 in green.
If we analyse in the RR direction, we observe that there are no changes in flavour in the DD quark, there is only a change in mass that goes from 84.69 MeV/c² in the neutron to 103.81 MeV/c² in the proton. We could attribute this mass variation to the interaction of neutrinos and antineutrinos that act as neutral currents.
If we observe in the direction of R, the change in mass D quarks, is attributed to the neutrinos, if we observe in the direction of R, the change in mass D antiquarks, is attributed to the antineutrinos.
Figure 87, we see that [B(D
U)
G]n has a mass of: 100.45 MeV/c²
Figure 88, we see that [B(U
U)
G]p has a mass of: 97.78 MeV/c²
Figure 89, we see that there is a potential difference E7, therefore what is really produced is a electric current (D
U) that goes from [B(D
U)
G]n → [B(U
U)
G]p as show in
Table 26 in green.
If we analyse in the direction of B, we observe that there is a change in flavour in the D quarks, which transforms into the U quarks; if we analyse in the direction of G, we observe that there is no change in flavour in the U antiquarks.
The cross interaction is related to the direct interaction, therefore the change of flavour in the direction of B, in which the D quarks transforms into the U quarks inTable 13, is related to the origin of the electron. However, in the G direction, there is no change in flavour in the U antiquarks, this is related to a current of antineutrinos.
Here, it is necessary to make the following comment.
We are going to use the following equation:
n → p + e⁻ + ν
If we bombard neutrons with electron neutrinos in a nuclear reactor, we obtain protons and electrons. We can represent this in the following equation:
ν +n → p + e⁻
However, if we bombard neutrons with electron antineutrinos in a nuclear reactor, we do not obtain protons and electrons. We can represent this in the following equation:
Figure 87, we see that [G(U
D)
B]n has a mass of: 164.47 MeV/c²
Figure 88, we see that [G(U
U)
B]p has a mass of: 97.78 MeV/c²
Figure 89, we see that there is a potential difference E9, therefore what is really produced is a electric current (U
D) that goes from [G(U
D)
B]n → [G(U
U)
B]p as show in
Table 27, in green.
In
Table 27, if we analyse in the direction of G, we observe that there is no change in flavour in the U quarks. If we analyse in the direction of
B, we observe that there is a change in flavour in the
D antiquarks, which becomes U antiquarks.
The cross interaction is related to the direct interaction, therefore the flavour change in the direction of B, in which the D antiquarks transforms into the U antiquarks in Table 27, is related to the origin of the positron. However, in the G direction, there is no flavour change in the U quarks, this is related to a current of neutrinos.
In
Table 19, we clearly see that when the D quarks transforms into U quarks, there is an associated neutral antineutrino current.
In
Table 20, we clearly see that when the
D antiquarks transforms into
U antiquarks, there is an associated neutral neutrino current.
When we analyse the origin of the electron, we determine that in the (BB) interaction, there is a net mass value corresponding to 0.95 MeV/c², which gives rise to the electron and therefore has associated a neutral current corresponding to the electron antineutrino; as can be seen in Table 27. Therefore, the emission of the electron is associated with the emission of an antineutrino, in the process in which a neutron decays into a proton.
By analysing the decay of a neutron into a proton in β⁻ decay, we determine the importance of the neutral currents of neutrinos and antineutrinos; they help us conFigure the direct and cross interactions inside the proton.
We are going to propose a model that explains the process by which neutrinos and antineutrinos are created.
In the following figure, we will recall the proposed model for the D quark and D antiquark.
In
Figure 92, we are proposing that the D quark is a composite particle, in which the U quark and electron neutrinos are included.
In
Figure 93, we are proposing that the
D antiquark is a composite particle, in which the
U antiquark and the electron antineutrinos are included.
We are going to write the βˉ decay as a function of the D quark and the U quark.
D → U + e⁻ + ν
We are going to perform the following calculation:
We are going to calculate the mass of the electron neutrino for the temperature of the electron.
T = 5.93 10 ⁹ K
E = K x T
E = 1.38 10⁻²³ x 5.93 10 ⁹ K = 8.18 10 ⁻¹⁴
E = 8.18 10 ⁻¹⁴ J
E = h x f; f = E / h
f = 8.18 10 ⁻¹⁴ / 6.63 10⁻³⁴
f = 1.23 10²⁰ Hz
c = λ x f; λ = c/f = 3 10⁸ / 1.23 10²⁰
λ = 2.43 10 ⁻¹² m
M(neutrino) = h / (λ x C) = 6.63 10⁻³⁴ / (2.43 10 ⁻¹² x 3 10⁸)
M(neutrino) = 0.909 10 ⁻³⁰ = 9.09 10⁻³¹ kg
These calculations also hold true for electron antineutrinos.
We have shown that if we consider the temperature of the electron T = 5.93 10 ⁹ K, the mass of the electron antineutrino is exactly equal to the mass of the electron. It is important to remember that the linear momentum of the electron is different from the linear momentum of the electron antineutrino.
|Pe| ≠ |Pν| → Me.Ve ≠ Mν.Vν
The calculations that we are going to carry out below are approximate calculations, we want to determine the number of electron antineutrinos that are emitted when a D quark decays into a U quark, considering the temperature.
Md = 8.55 10⁻³⁰ kg
Mu = 4.10 10 ⁻³⁰ kg
Me = 9.10 10 ⁻³¹ kg, T = 5.93 10 ⁹ K
Mν = Me = 9.10 10 ⁻³¹ kg, T = 5.93 10 ⁹ K
Δ = Md – Mu = 4.45 10 ⁻³⁰ kg
Qν = Δ / Mν = 4.45 10 ⁻³⁰ kg / 9.10 10 ⁻³¹ kg = 0.489 10 = 5
These calculations are telling me that at the temperature at which βˉ decay of the neutron into a proton occurs, the mass of the electron antineutrino is approximately the mass of the electron.
If we consider an intermediate temperature between the U quark and the electron, possibly the mass corresponding to Δ = 4.45 10 ⁻³⁰ kg is divided into two, one for the electron and another for the electron antineutrino and not in 5 as the calculation carried out.
Now when the electron antineutrino reaches the temperature of empty space, that is, 2.7 K, it is evident that its mass takes on the value we know, M
ν = 1.6 10 ⁻³⁶ kg, or perhaps even lower. See
Figure 82 and 83.
These calculations show us the importance of considering the temperature at which particle interactions occur.
Mν = Mν = 1.6 10 ⁻³⁶ kg, T = 2.55 10⁴ K
Mν = Mν = 9.10 10 ⁻³¹ kg, T = 5.93 10 ⁹ K
Generalizing, just as the βˉ decay, represented by
Figure 89 is the result of interactions between quarks and antiquarks; in other words, the Wˉ boson is an ideal boson, it would represent a black box given the impossibility of a physical-mathematical definition that would describe such an interaction. We could extrapolate this for the W⁺ bosons and Z bosons, they are ideal bosons, they are the result of quark, antiquark interactions and neutral current.
In this simple analysis we have replaced the quantum model of QCD with the electric model of a proton and neutron as a three-phase alternating current electric generator. Quarks and gluons are used in the QCD model; in the electric model as a three-phase alternating current electrical generator, the interactions are carried out through quarks and antiquarks, the gluons are only indicative notations to remind us that we are working with vectors with module and phase, as happens in an electric generator. In this model, the W⁻, W⁺ and Z⁰ bosons are replaced by quark-antiquark interactions (U, U, D, D).
8.4. Fine Structure Constant
In this item, we will determine the origin of the fine structure constant α.
To do this, let's remember the definition of NECF and PECF.
NECF = Mn / 95.4 = (939.56 MeV/c²) / 95.4 = 9.8486 MeV/c²
Where NECF is Neutron electromagnetic coupling factor.
95.4 = 8.6 + 8.6 + 4 + 10.2 + 10.2 + 10.2 + 10.2+ 16.7 + 16.7
Where 95.4 is the sum of segments measured in units of centimeter, in the neutron phasor diagram.
NECF = 9.8486 MeV/c²
If we divide the electromagnetic coupling factor of the neutron NECF, by the energy 0.388 MeV/c², corresponding to unit binding energy per nucleon, we will have the approximate number of protons to which the neutron can be stably associated.
Qtyp = NECF / ∆Eα = (9.8486 MeV/c²) / (0.388 MeV/c²) = 25.38
Qtyp = 25 proton.
Where Qtyp represents the number of protons that the neutron-proton binding energy stably supports, considering the electromagnetic coupling factor of the Neutron NECF.
According to our calculation, starting at proton number 26, the neutron-proton binding energy begins to weaken.
PECF = Mp ̸ 77.7 = (938.27 MeV/c²) ̸ 77.7 = 12.0720 MeV/c²
Where PECF is Neutron electromagnetic coupling factor.
77.7 = 8.6 + 4 + 4 + 4 + 10.4 + 13.7 + 8.1 + 16.8 + 8.1
Where 77.7 is the sum of segments measured in units of centimeter, in the proton phasor diagram.
PECF = 12.0720 MeV/c²
If we divide the electromagnetic coupling factor of the proton PECF, by the energy 0.388 MeV/c², corresponding to unit binding energy per nucleon, we will have the approximate number of neutrons to which the proton can be stably associated.
Qtyn = PECF / ∆Eα = (12.0720 MeV/c²) / 0.388 MeV/c² = 31.11
Qtyn = 31 neutron.
Where Qtyn represents the number of neutrons that the proton-neutron binding energy stably supports, considering the electromagnetic coupling factor of the proton PECF.
According to our calculation, starting at neutrons number 31, the proton-neutron binding energy begins to weaken.
If we consider the electromagnetic coupling factor, NECF and PECF; the maximum binding energy is obtained for Iron (26,30), which has 26 protons and 30 neutrons; Above the number of protons and neutrons that Iron has, the binding energy begins to decrease, we can see this in
Figure 94.
we are going to calculate the value of the fine structure constant α, considering NECF and PECF and then we are going to make a description of the parameters that influence NECF and PECF.
Calculation of the fine structure constant α:
∆Eα / NECF = (0.388 MeV/c²) / (9.8486 MeV/c²) = 0.0393964
∆Eα / PECF = (0.388 MeV/c²) / (12.0720 MeV/c²) = 0.0321404
α´ = (∆Eα / NECF) – (∆Eα / PECF)
α´ = 0.0393964 - 0.0321404 = 0.007256
α´ = 0.007256
1/α´ = 137.81
Where, α´ is calculated theoretical value.
α = 0.00729
Where α is calculated experimental value.
1/α = 137.17
% = {(137.81 – 137.17) / 137.17} x 100 = 0.46 %
The difference is very small considering that the calculated theoretical value α´ is obtained from vector diagrams.
We can define the fine structure constant α, as an interaction between the electromagnetic coupling factor of the neutron NECF and the proton PECF. The electromagnetic coupling factor in the neutron and proton is determined by the quarks-antiquarks interaction.
It is the quarks-antiquarks interactions in the protons and neutron that determine the fine structure constant α, we can see this by analysing βˉ decay.
The electromagnetic coupling factor of the neutron and the proton is very important, it determines the configuration of baryonic matter as we know it.
∆Eα = (1 / α) x [(1 / NECF) – (1 / PECF)]
∆Eα = (1 / α) x [(PECF - NECF) / (NECF x PECF)]
Where ∆Eα is the unit binding energy per nucleon.
∆Eα = 0.388 MeV
Up to this point, we have seen how the fine structure constant is a consequence of the parameters given by the unit binding energy per nucleon ∆Eα, the electromagnetic coupling factor of the neutron NECF and the electromagnetic coupling factor of the proton PECF.
where α is fine structure constant.
M = Z mp + (A-Z)mn – B, B >0
Where, B is binding energy.
The binding energy B is what makes the nucleus stable and is preferable to its parts being free.
The average binding energy, B = 8 MeV, is of the order of 1% of the energy of the mass of the proton or neutron.
The maximum binding energy is found in iron Fe (26,30), and this is consistent with it being the most stable nucleus.
For stable atomic nuclei, the strong nuclear force is greater than the electromagnetic repulsion force; for unstable atomic nuclei, the electromagnetic force begins to be relevant.
Now, we are going to give a brief description of the relationship that exists between the fine structure constant α and the atomic orbitals.
As spectroscopy developed, it was observed that the fundamental orbital levels were divided into two, this led us to a much more complex atomic model, which introduced relativistic corrections, spin corrections, etc.; which allowed us to describe the atomic orbitals more precisely.
In our approximate model as a three-dimensional harmonic oscillator, the electromagnetic coupling factor of the proton PECF and the neutron NECF, given by the interactions of the quarks-antiquarks, is related to the following parameters:
N, No. of nodes
n, principal quantum number
L, quantum number of angular momentum.
m, quantum number of the magnetic moment.
The most rigorous way to take into account relativistic corrections is to pose the Dirac equation. But we won't do that now.
It is also important to mention that NECP and PECP electromagnetic coupling is also related to corrections due to relativistic and spin effects.
The most important corrections that contribute to the fine structure constant α are three, induce order corrections mc²α⁴:
Relativistic correction in kinetic energy
The first term that we will consider in the fine structure has to do with the fact that the kinetic energy of the electron has a correction due to relativistic effects.
where we use that the speed v in the first orbit of the Bohr atom is v/c ≈ e² / hc. Consequently, as we already mentioned, the correction is very small compared to the 13.6 eV scale (i.e., it is about 10⁻⁴ eV, which corresponds to a typical frequency of tens of GHz, microwave).
Finite size of the electron: Darwin's term
Taking into account relativistic effects, the electron cannot be considered a point particle. Indeed, it is impossible to locate a particle of mass m below a length of the order of the Compton wavelength. The heuristic argument on which this statement is based is that to locate a particle below a length λc it is necessary to use photons that have a energy hω which is greater than that necessary to create a pair of particles (consequently, in that limit the theory for a single particle does not make sense). This length is λc = h /mc. Taking into account the above, to understand this correction, we can assume that the electron is a cloud of charge located around a certain point r of radius λc, which interacts with the electrostatic potential produced for the atom.
Consequently, this term also has a magnitude α² times smaller than the typical energies of E0
Spin-orbit coupling
There is a third relativistic effect that appears naturally in the Hydrogen atom. As we said, the electron has spin, and therefore has a momentum associated magnetic.
Consequently, this term also has a magnitude α² times smaller than the typical energies of E0.
We observe that the corrections given by H(TE), H(Darwin) and H(SO) are α² smaller than their original energy.
We can see through these two descriptions how the fine structure constant α relates the stability of the atomic nuclei to the shell model that describes the atomic orbitals.
Summing up to conclude, it is the quarks-antiquarks interactions that determine the electromagnetic coupling factor of the neutron and the proton and this, in turn, determines the fine structure constant α; we can see this by applying the concepts in βˉ decay.
8.5. We Will Demonstrate the Existence of a Force Tangential to the Repulsive Force in Subatomic Disintegrations, This Force Advances to Repulsive Force by 90 Degrees.
We will analyse the following equation:
E² = m²c⁴ + P²c²
where E is energy, m is mass, and c is the speed of light in a vacuum.
If we consider 0 the moment P of a particle, P = 0, we have:
E² = m²c⁴
E = (+/-) mc²
If we consider mass as a fundamental property of matter we have:
E = + mc², positive energy, (+ m), gravitational attraction
E = - mc², negative energy, (- m), gravitational repulsion
According to the equation E = (+/-) mc², we have that gravity acts in two ways, (+m) as an attractive force or (-m) as a repulsive force.
METRIC FOR TIME TYPE TRAJECTORIES
Figure 96.
Time-like trajectory, light cone, ds < 0.
Figure 96.
Time-like trajectory, light cone, ds < 0.
This metric is defined for speeds less than light, v < c.
We skip the mathematical steps and with this metric we calculate the moment P and the energy E.
Where P is lineal moment of a particle.
Where E is energy of a particle
If we analyse the energy, we see that when the particle is at rest the energy corresponds to E = mc²; when the speed tends to c, the energy tends to infinity.
v = 0, E = mc²
v → c, E → ∞
Now we are going to perform the following mathematical operation; although the metric does not allow us to do this because it is not defined for speeds greater than light, v > c, we are going to see the consequences of the following mathematical operation.
E = mc² / √-1 √(v²/c²) – 1
multiplying the numerator and denominator by the imaginary number i:
we see that the terms – i appear.
If we compare with the mass of a black hole:
m, baryonic mass.
= , for v > c; mass of dark matter.
How can we interpret this, what meaning does it have?
Although the metric we use is not defined for particles that move at a speed greater than that of light, there are massless tachyonic particles that can cross this barrier and travel at a speed greater than that of light.
These tachyonic particles produce a tangential force Ft to the attractive force Fc of gravity and as the speed increases with respect to the speed of light, they generate dark matter mass. It must be made clear that these particles are inside the black hole, only inside the black hole.
METRIC FOR SPACE TYPE TRAJECTORIES
Figure 97.
Space-like trajectory, light cone, ds > 0.
Figure 97.
Space-like trajectory, light cone, ds > 0.
We skip the mathematical steps and with this metric we calculate the moment P and the energy E.
These equations for momentum P and energy E are valid for speeds greater than light and can never reach speeds of light.
v → ∞, E = 0
v → c, E = -∞
How can we interpret this, what does it mean?
We are going to relate the equations of P and E with the RLC electrical modelling of black hole an early universe; at the moment that the black hole explodes, let us remember that the space-time that was compressed begins to expand and generates a well of gravitational potential of negative energy analogous to the equation E = - mc² / √(v²/c²) – 1; in other words, a gravitational wave spectrum is produced that produce a repulsive force that gives rise to the expansion of space-time. In this case, tachyons are related to gravitons and particles of elemental energy, in which, during the period of cosmic inflation, they travel at a speed greater than that of light.
Now we are going to perform the following mathematical operation, although the metric does not allow us to do this because it is not defined for speeds less than light, v < c, we are going to see what happens if a particle exceeds the limit for speeds less than c.
E = - mc² / √(v²/c²) – 1
E = - mc² / √-1 √ (1 - v²/c²)
Multiplying and dividing by the imaginary number i.
If we compare with the mass of a black hole:
m, baryonic mass.
Where M represents the total mass, the minus sign indicates that the mass M generates a repulsive force; - m represents the baryonic mass, the minus sign indicates that the mass m generates a repulsive force and iδ is a mass that generates a tangential rotation force the force generated by the mass - m and advance 90 degrees to the force generated by the mass - m.
The subatomic disintegrations that occur in particle accelerator LHC represent a clear example.
Here we put forward the hypothesis that, for v < c, there is an additional force that corresponds to the mass iδ that leads 90 degrees to the force given by the mass – m; in other words, when the subatomic disintegration of particles occurs, two forces act, a repulsive force given by the mass - m and a tangential rotation force that leads 90 degrees to the force given by - m, resulting from the mass iδ.
In the following tables we will define the statement.
Table 28.
From left to right represented by the numbers 1,2 and 3; we describe the forces that act on matter. In phase 1, for v < c, only an attractive force acts; in phase 2, for v = c, only an attractive force acts; in phase 3, for v > c, inside a black hole, we can see that two forces act, an attractive force and a tangential force that delays the attractive force by 90 degrees.
Table 28.
From left to right represented by the numbers 1,2 and 3; we describe the forces that act on matter. In phase 1, for v < c, only an attractive force acts; in phase 2, for v = c, only an attractive force acts; in phase 3, for v > c, inside a black hole, we can see that two forces act, an attractive force and a tangential force that delays the attractive force by 90 degrees.
| TIME TYPE PATH |
LIGHT TYPE PATH |
SPACE TYPE PATH |
| 1 |
2 |
3 |
| ds < 0 |
ds = 0 |
ds > 0 |
| v < c |
v = c |
v > c |
|
|
|
| attraction |
attraction |
attraction and torsion |
| Lp = Lpɛ |
Lpɢ = Lpɛ = Lp |
Lpɢ < Lpɛ |
| E = c² / √[1 - (v²/c²)] |
Phase change |
E = - i c² / √[(v²/c²) – 1] |
Table 29.
From right to left, represented by the numbers 1,2 and 3, we will describe the forces that act on matter. In phase 1, for v > c, we see that a repulsive force acts; in phase 2, for v = c, we see that a repulsive force acts; in phase 3, for v < c, we see that two forces act, a repulsive force and a tangential force that leads the repulsive force by 90 degrees.
Table 29.
From right to left, represented by the numbers 1,2 and 3, we will describe the forces that act on matter. In phase 1, for v > c, we see that a repulsive force acts; in phase 2, for v = c, we see that a repulsive force acts; in phase 3, for v < c, we see that two forces act, a repulsive force and a tangential force that leads the repulsive force by 90 degrees.
| TIME TYPE PATH |
LIGHT TYPE PATH |
SPACE TYPE PATH |
| 3 |
2 |
1 |
| ds < 0 |
ds = 0 |
ds > 0 |
| v < c |
v = c |
v > c |
|
|
|
| Repulsion |
Repulsion |
Repulsion |
| Lp = Lpɛ |
Lpɢ = Lpɛ = Lp |
Lpɢ < Lpɛ |
| E = c² / √[1 - (v²/c²)] |
Phase change |
E = - m c² / √[(v²/c²) – 1] |
Figure 98.
Diagram of forces that act in the disintegration of subatomic particles.
Figure 98.
Diagram of forces that act in the disintegration of subatomic particles.
In conclusion, two forces act inside a black hole; a force of attraction towards the interior of the black hole and a rotation (torsion) force that delays the force of attraction by 90 degrees.
Two forces also act in the disintegration of elementary particles, a repulsion force and a rotation (torsion) force that advances the repulsion force by 90 degrees.
8.6. Symmetries in Particles
In the paper: Theory of Unification of the Interactions of Fundamental Forces: SU(3) x SU(2) → U(1), we developed this topic.
In physics, symmetry is defined as an operation to which it is applied to a state or system and leaves it invariant.
U, Symmetry operation
If we apply the symmetry operator U to the Ψ function, it transforms it into the Ψʹ function, simply by applying the operator.
| Ψ > → | Ψʹ > = U | Ψ >
Now if I transform my state and also transform the rest of the universe, with the same transformation operator; It is to be expected that the expectation values are the same.
< Φ | Ψ >
We can interpret this from the point of view of probabilities.
| < Φ | Ψ > |² = | < Φʹ | Ψʹ > |² = | < Φ | Uᵗ U | Ψ > |²
The probability of the untransformed states is the same as the probability of the transformed states. I can express the transformed states in terms of the symmetry operators, which leads me to the following condition.
Uᵗ U = I → The operator U has to be unitary.
A characteristic that we are going to ask of all symmetry operators is that they be unitary transformations.
Noether's theorem
It tells me that for every symmetry my system had there would have to be a conserved quantity. In quantum mechanics, Noether's theorem relates symmetries to conservation laws.
Symmetry of spatial translations, P → Conservation of linear momentum
symmetry of spatial rotations, L → Conservation of angular momentum
Symmetry of temporal translations, H → Conservation of energy
Symmetry of phase transformations, e → Conservation of charge
Isospin symmetry, I → Conservation of isospin
In general, symmetry transformations generate mathematical groups, which satisfy the following conditions:
The identity function, must be an element of the group
The inverse function, must be an element of the group
Let there be associativity
If the group of transformations is commutative it is said to be an abelian group, if the group of transformations is non-commutative it is said to be non-abelian.
Symmetry groups
U(n), unitary group nxn; example, group U(1), complex phase transformations.
SU(n), unitary group nxn + determinant = 1; example, SU(2), Isospin / weak interactions; SU(3), strong interactions.
Representation of the group SU(2) of dimension 2
For SU(2), the fundamental representation is given by two base 2 elements, as shown below:
, fundamental, representation.
Considering these elements of base 2, of dimension 2, I am going to define the following generators.
Where σ₁, σ₂ and σ₃, are the Pauli matrices, which satisfy a certain commutation relation.
The elements of the group (transformations) would be given by the following equation:
The elements of the group, which would be the unitary matrices with a determinant equal to 1 and order 2x2, would be given by the exponential of the generator; the transformations are the matrices U that materialize the rotations which are applied to the two spin (1/2) projections.
Representation of the group SU(2) of dimension 3
For SU(2) of dimension 3, the representation is given by three base 3 elements, as shown below:
Now, I have 3 generators ĵ of dimension 3 x 3, which satisfy the following commutation relation.
And the elements of the group are the transformations or matrices U that I build with the generators.
Combination of two spins ½ in SU(2), dimension 2; I get:
2⊗ 2 = 3ѕ + 1ᴀ
Combination of three spins ½ in SU(2), dimension 3; I get:
2⊗ 2⊗ 2 = 4ѕ + 2мѕ + 2мᴀ
Representation of the group SU(3) of dimension 3
For SU(3) of dimension 3, the representation is given by two base 3 elements, as shown below:

, fundamental,
representation.
The group SU(3) are 3x3 unitary matrices with determinate equal to 1.
The SU(2) generators of dimension 3x3 are different from the generators of SU(3) dimension 3x3.
The SU(3) generators of dimension 3x3, which I need to describe a transformation, are going to be different from the SU(2) generators of dimension 3x3 and we are also going to need more generators, a total of 8.
The elements of the group, which would be the unitary matrices with a determinant equal to 1 and order 3x3, would be given by the exponential of the generator; the transformations are the matrices U that materialize the rotations which are applied to the three spin (1/2) accoupling.
The generators of SU(3) are called Gell-Mann matrices.
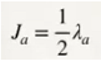
Where λ
a are Gell-Mann, matrices.
Combination of two spins ½ in SU(3); I get:
3⊗ 3 = 6ѕ + 3ᴀ
Combination of three spins ½ in SU(3); I get:
3⊗ 3⊗ 3 = 10ѕ + 8мѕ + 8мᴀ + 1ᴀ
Isospin, electric charge and strangeness
Correlation between electric charge and isospin:
- i)
- ii)
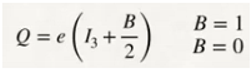
B = 1, baryons; B = 0,
mesons.
ii) includes baryons and mesons and does not include strange particles.
- iii)
iii) includes baryons, mesons and particles with strangeness.
Quark model (1964)
Use SU(3) symmetry where the elements are the quarks (u, d, s).
3⊗ 3⊗ 3 = 10ѕ + 8мѕ + 8мᴀ + 1ᴀ
3⊗ 3 = 8ѕ + 1ᴀ
To accept this quark model, the following premises had to be met:
Quarks have to have a fractional electric charge.
Individual quarks never occur in isolation.
Quarks only combine in three or as quarks and antiquarks.
Example 1:
Figure 99.
Particle classification.
Figure 99.
Particle classification.
Example 2:
In
Figure 99 and 100, we have generalized the isospin theory of the proton and neutron to the particles (u, d, s).
Figure 101.
Functions SU(2) and SU(3) that have symmetry defined under permutations.
Figure 101.
Functions SU(2) and SU(3) that have symmetry defined under permutations.
8.6.1. Fermions, Bosons, Spin and Color Symmetry
Bosons: Particles that are described by symmetric wave functions due to the exchange of positions of the particles. They obey the Bose-Einstein statistics.
Example: Bose-Einstein condensate.
Fermions: Particles that are described by antisymmetric wave functions due to the exchange of position of the particles. They obey the Fermi-Dirac statistics.
Example: The filling of the layers around the nucleus to form atoms, obeying the Pauli principle.
Now we are going to carry out a brief analysis of the magnetic moment of the particles.
Magnetic moment
Let us remember that the Dirac equation predicts the magnetic moment of elementary particles, it predicts what the spin of elementary fermionic particles would be.
For example, it predicts the magnetic moment of the electron or muon to nine significant digits.
The equation for the magnetic moment tells us that it is proportional to the electric charge and inversely proportional to the mass. We use natural units.
However, the prediction fails for the neutron and the proton. We know that this is because the neutron and proton are not elementary particles.
We can approximately calculate the relationship of the magnetic moment of the quarks.
Where μq is the magnetic moment of a quark.
With this we can create operators that allow us to calculate the ratio of the magnetic moment of the proton and the neutron.
Where μp is the magnetic moment of the proton and μn is the magnetic moment of the neutron.
Let us observe that the quotient of the magnetic moments of the proton and the neutron gives me as a result of the calculation an error of the order of 3%, without knowing the mass of the U quark and the D quark, as long as I use a flavor and spin wave function totally symmetrical.
If I use a completely asymmetric flavor and spin wave function, the result is not correct and not even the sign agrees.
This tells us that the way in which the flavor and spin of the quarks combine inside the protons and neutrals is symmetrical in the face of perturbations.
Color symmetry
Now we are going to analyze the color symmetry, we are going to analyze what ant-symmetrizes the wave function; in other words, how can I put together a totally antisymmetric wave function.
For this we are going to draw the following equations:
3⊗ 3⊗ 3 = 10ѕ + 8мѕ + 8мᴀ + 1ᴀ
Let us observe that in the combination of three particles with spins ½, SU(3), already exists a singlet state defined as 1ᴀ, whose wave function is totally antisymmetric.
3⊗ 3 = 8ѕ + 1ᴀ
Let us also observe that in the combination of 2 particles with spins ½, SU(3), there already exists a singlet state defined as 1ᴀ, whose wave function is totally antisymmetric.
Now, I postulate that quarks have a quantum number that has SU(3) symmetry, different from the flavor and spin that makes the combinations of quarks in hadrons and mesons anti-symmetrize the wave function.
I am expressing the following:
This tells us that the way the color of the quarks combine within the protons and the neutrals is anti-symmetric to perturbations.
Let us observe that the fundamental representation of the quarks is given by (R, B, G) and that the combination of the quarks that gives me a completely anti-symmetric wave function is represented in the equation above.
A spin singlet is a state that has no spin or projection.
A color singlet is an essentially colorless state.
This is telling me that the wave function of hadrons has no color, that is, mesons and baryons are colorless combinations.
This is telling me that nature demands that the hadron wave function be antisymmetric, singlet, colorless.
This is one of the reasons why quarks cannot exist in isolation.
This is also telling us that the lowest energy state corresponds to the singlet state.
In conclusion, the interactions of quarks inside protons and neutrons abhor explicit color, they always combine in singlets, whose wave function is antisymmetric, which correspond to the minimum energy state.
Example:
Here, color symmetry is represented in that both processes represent colorless singlets.
Now we can understand the SU(3) symmetry which predicts what the interactions between quarks would be like.
Here, we reach a point where it becomes inevitable to compare the bases on which the entire theory of quantum chromodynamics QCD of SU(3) symmetry is based and the theory that corresponds to the model of the neutron and proton as an three-phase alternating current electric generator.
Nature requires that the wave function of hadrons be asymmetrical, that they behave as colorless singlets, that is, that baryons and mesons reach their minimum energy state.
We have verified that this premise is fulfilled in the SU(3) theory of quantum chromodynamics QCD, but with a very important reservation, it is developed only for matter and does not contemplate antimatter.
However, if we analyze the theory of the electric model of the proton and neutron as a three-phase alternating current electric generator; it also meets the premise, but there is a very important difference with respect to the QCD theory, it includes matter and antimatter.
In my humble personal opinion, I believe that we must consider both complementary theories, taking advantage of everything they can provide us to enrich science.
With this I am meaning the following; when we analyze β ˉ decay, in the conventional theory everything is represented as a black box. The neutron represents the input and the output represents the proton, electron and antineutrino. However, in the black box there is no theory that explains what really happens in the decay of the neutron into a proton. This is where the theory of electric model the neutron and proton as a three-phase alternating current electric generator comes into play, providing a logical explanation of what could really happen with the interactions of quarks in the decay of the neutron into a proton; in other words, this theory explains to us what really happens inside the black box.
I think that the theory of electric model of the proton and neutron as a three-phase alternating current electric generator should be considered very seriously and used as a complement to the theory of quantum chromodynamic QCD.
Taking into account everything we have developed in this paper, we could generalize the theory of electric model of the neutron and proton as a three-phase alternating current electric generator and consider including SU(2) in the generalization.
Let us remember that quantum electrodynamics QED unites SU(2) with U(1)
QED → SU(2) x U(1)
I think we have started a path in which SU(3) symmetries and SU(2) symmetries can be represented by a single U(1) symmetry, where all interactions included in the standard model can be represented by a single electromagnetic interaction; we can also include gravity.
We are saying that the symmetries of the standard model can be replaced by a unique symmetry U(1) that corresponds to electromagnetic interactions of quarks-antiquarks (U, U, D, D).
SU(3) x SU(2) → U(1)
We can express this as follows:
Quark interactions, gluons:
(DD) → │DD > ≡ │1, 0 >, in phase.
(UU) → │UU > ≡ │1, 0 >, in phase.
(DU) → │DU >, out of phase.
(UD) → │UD >, out of phase.
(DD) → │DD >, out of phase.
(UU) → │UU >, out of phase.
Quark interactions, gravitons:
│UD + DU > ≡ │2, 0 >, in phase.
│DU + UD > ≡ │2, 0 >, in phase.
Let's note that all the interactions that are included in the standard model can be represented by 6 bosons that we define as gluons.
Also note that the interaction that corresponds to the gravitational force is represented by two bosons that we define as gravitons.
Note that both gluons and gravitons are made up of quarks (U, U, D, D).
Now we are going to give a 3.0 explanation of the subtle difference that exists between the electromagnetic force and the gravitational force.
For this, we are going to need Einstein's field equation of general relativity and eventually, the Maldacena correspondence.
ADS = CFT
The right side of both equations corresponds to matter or energy and is under the domain of the strong, weak and electromagnetic interaction forces.
Let us remember again that the theory of electric model of a proton and neutron as a three-phase alternating current electric generator reduces strong and weak interactions to simple electromagnetic interactions, we can express this as follows:
SU(3) x SU(2) → U(1)
Therefore, in both equations we have; on the left side the interactions of the gravitational force, which represents the curvature of space-time; on the right side the interactions of the electromagnetic force, which represents matter or energy. This equality is fulfilled as long as the gravitons and the carriers of the electromagnetic force, the gluons, are made up of the fundamental bricks of the universe, the quarks (U, U, D, D).
This is very important; we are saying that space-time and matter (energy) are made up of the same fundamental bricks.
We are saying that gravity is matter (energy), as long as they are made up of quarks (U, U, D, D); only under this condition are the Einstein´s field equation of General Relativity and the Maldacena correspondence true.
Now we are going to carry out a new analysis adopting another point of view.
To do this we are going to adopt the following premises:
- i)
Nature requires that the wave function of spin 1/2 baryons with respect to flavor and spin, combine symmetrically in the face of permutations.
- ii)
Nature requires that the wave function of the Hadrons, with respect to color, combine in an antisymmetric way in the face of permutations.
If we observe any corner of the universe, we see that practically all matter is made up of baryons, therefore the wave function that characterizes the baryons with respect to color is antisymmetric when faced with permutations. If we look under the magnifying glass of the quantum number that represents color, the wave function that represents the baryons is singlet, it has no color; in other words, the baryons are in a state of minimum energy, with this we are wanting to affirm that the energy of their individual constituents is greater than the energy of the whole. Premise ii) is met.
When we say that the baryons are in a state of minimum energy, it leads us to premise i), that is, we are referring to the wave function, with respect to flavor and spin, which is symmetric in the face of permutations.
Saying that its state is of minimum energy and that its wave function is symmetry in the face of permutations, with respect to flavor and spin, means that its behavior is analogous to that of bosons, this is very important and we are going to explain it in the following example.
Example:
D Quarks are fermions, they have color, which is why they cannot exist in a free state in nature. D quarks join with a D antiquark to form a photon (DD), that is, a Boson. The boson has a wave function that is symmetric under permutations and has no color, a singlet state.
If we analyze gravitons, they are also bosons, that is, their wave function is symmetrical in the face of permutations (flavor and spin) and they have no color, they are singlets.
To conclude, gravitational interactions and electromagnetic interactions are totally equivalent, both interactions are the result of interactions between quarks (U, U, D, D).
When we say that space-time is flat, we are saying that space-time has an effective Boltzmann´s constant Kʙɛ = 1.38 10⁻²³ J/K.
Under these conditions the matter content is reduced to the graviton content.
As the temperature increases, the quantities of virtual particles that make up space-time increase, the decay of gravitons gives rise to matter; as the temperature continues to increase, material structures such as the Earth, stars, white dwarfs, neutron stars and black holes begin to form, all types of celestial material bodies that we know; this causes the Boltzmann´s constant to reach its minimum value Kʙԍ = 1.78 10⁻⁴³ J/K.
Let us remember that the maximum curvature of space-time is reached for a Boltzmann´s constant equal to Kʙԍ = 1.78 10⁻⁴³ J/K, this occurs when a black hole forms.
Now we are going to analyze a celestial body, an ideal neutron star, we are going to assume that this neutron star is made up only of neutrons.
We know that neutrons are made up of quarks (U, U, D, D); therefore, we can say that the neutron star forms a pocket of quarks (U, U, D, D).
Now we are going to analyze from the point of view of the curvature of space-time, we know that the curvature of the space-time of a neutron star is approximately the curvature of the space-time of a black hole and corresponds to a Boltzmann´s constant in the order of Kʙn = 1.78 10⁻⁴¹ J/K.
In
Table 6, we see that the curvature of space-time for a neutron star is in the order of 10¹⁹ times the curvature corresponding to flat space-time, it is very large, therefore its gravity is also very large.
In
Figure 76, we observe that a body that has mass and curves space-time produces a stretching of space-time due to its contraction, this generates a force and is what we call gravitational force.
In summary, we could represent the neutron star as a bag of compacted quarks (U, U, D, D) that has a very large gravity, that is, it produces a fairly large stretching of space time; in other words, the number of gravitons that surround the neutron star is also large, therefore the number of quarks (U, U, D, D).
Another way of looking at it is the following, we said that we can represent the neutron star as a compact bag of quarks (U, U, D, D), surrounded by a space-time whose gravity is very great. Let us remember that space-time is made up of gravitons, that is, quarks (U, U, D, D); by saying that the curvature of space-time is great, we are saying that its gravity is great and therefore the number of gravitons is also great.
This is telling us that there is a continuity in the quantity of quarks (U, U, D, D); if we consider the interior of the neutron star as we move away, this quantity decreases and consequently the gravitational force decreases. This continuity is given by the existence of gravitons and is represented by the curvature of space-time that we call gravity.
Therefore, we can affirm that space-time represents a sea of gravitons (bosons) formed by quarks (U, U, D, D).
To conclude, the quarks (U, U, D, D) are those that dominate the dynamics that determine the origin of matter and antimatter and the interactions of the strong force, weak force, electromagnetic force and gravitational force. They are the fundamental bricks on which the entire universe we know is based. In this dynamic, we can also include dark matter and dark energy, which we can also say is dominated by quark interactions (U, U, D, D).
Additional comment:
In a talk at a conference dedicated to the 100th birthday of Erwin Schrödinger, Chen Ning Yang quoted from a lecture on quantum mechanics given by Paul Dirac. The topic here is the non-commutability of operators, often presented as the essential feature of quantum theory in the literature. Dirac said:
“The question arises whether the noncommutation is really the main new idea of quantum mechanics. Previously I always thought it was but recently I have begun to doubt it and to think that maybe from the physical point of view, the noncommutation is not the only important idea and there is perhaps some deeper idea, some deeper change in our ordinary concepts which is brought about by quantum mechanics.”
Dirac then continued, according to Yang, as follows:
“So, if one asks what is the main feature of quantum mechanics, I feel inclined now to say that it is not noncommutative algebra. It is the existence of probability amplitudes which underlie all atomic processes. Now a probability amplitude is related to experiment but only partially. The square of its modulus is something that we can observe. That is the probability which the experimental people get. But besides that, there is a phase, a number of modulus unity which can modify without affecting the square of the modulus. And this phase is all important because it is the source of all interference phenomena but its physical significance is obscure. “
8.6.2. Generalization of Gauge Symmetries
The idea of Gauge theory is the following, we take a field that has a symmetry s, from that we extract the fundamental characteristics of the field, which in the case of gauge theory are the interactions, that is, a force field.
Adding a field to restore the invariance of physics is the basis of all fundamental interactions in particle physics.
This is the basic idea, of which the interactions of electromagnetic force fields interactions , weak force field interactions and strong force field interactions are born.
The study of the symmetries of the universe allows us to understand in a deeper way the origin of the laws that govern it.
Standard Model
The standard model is the unification of three different symmetry, the symmetry of electromagnetism, the symmetry of isospin and the symmetry of colours.
We can represent this in the following way:
SU(3) x SU(2) x U(1)
-
i)
U(1) Symmetry and electromagnetic interaction field
The quantum field of the electrons has a global symmetry when we shift all the complex numbers in the same way, but if we locally shift the different parts of the field in a different way, the laws that describe the electrons seem to change, this change of reference does not obey to symmetry; if we want to re-establish the absolute nature of the laws of physics, whatever the reference level we choose, we must introduce a force field with which it interacts with the field of electrons, called the electromagnetic field, which has particles that interact with electrons called photons.
-
ii)
SU(2) symmetry and the weak force interaction field
interaction between protons and neutrons.
SU(2)
W(+/-) bosons and Z boson are excitations of the SU(2) field
-
iii)
SU(3) ) symmetry and the strong force interaction field
Interactions between quarks.
SU(3)
Gauge field: gluons
We will analyse and compare the theory of the standard model vs theory: electric model of the proton and neutron as a three-phase alternating current electric generator.
When we analyse the standard model, to describe the electromagnetic interactions we use U(1), to describe the weak force interactions we use SU(2) and to describe the strong force interactions we use SU(3) which is associated with the theory of quantum chromodynamics QCD. We see that it is a vertical system. Doing a deeper analysis, it has been shown that the union of U(1) x SU(2) is possible and gives rise to the theory of quantum electrodynamics QED. However, when we want to unite QED and QCD the task becomes quite complicated to find a single theoretical framework that explains this union.
In my personal opinion, I believe that the complication lies in postulating protons and neutrons made up only of three quarks, not considering antiquarks; that is, it considers quarks made up of matter and does not consider antimatter; however, in experimental calculations antimatter is considered.
All this becomes even more complicated if in addition to the interactions that form the standard model, we add the gravitational interaction; uniting the four interactions becomes a titanic task, an almost impossible challenge.
For now our best description of the world around us is represented by the standard model, it is a vertical and segmented description represented by U(1) x SU(2) x SU(3). The unification of U(1) x SU(2) gives rise to quantum electrodynamics QED and SU(3) gives rise to quantum chromodynamics QCD.
In the paper: Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electric Generator. Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons, inside a Neutron; we develop a model for the neutron and proton, equivalent to a three-phase electric generator.
This model uses quarks-antiquarks interactions (U, U, D, D)
We define two types of interactions, interaction 1 or direct interaction and interaction 2 or cross interaction.
The markers, R B G and R B G, are used to remind us that interactions 1 and 2 are vectors that have magnitude and angle.
When we analyse β ˉ decay, we discover that photons are a particular case of gluons that can escape confinement.
When we analyse β ˉ decay, we show that the Wˉ boson is the result of quarks-antiquarks interactions; they are ideal bosons, which originate when a neutron transforms into a proton. This allowed us to generalize for the W+ and Z⁰ bosons, which are also ideal bosons, the result of quarks-antiquarks interactions (U, U, D, D).
When we analyse the models proposed for photons and gluons, we observe that they are composed of elementary particle (U, U, D, D).
Photons, W⁺ bosons, W⁻ bosons, Z⁰ bosons, gluons, gravitons and the Higgs boson are reduced to quarks-antiquarks interactions (U, U, D, D).
In our model, the weak interaction is reduced to an electromagnetic interaction given by the quarks-antiquarks interactions (U, U, D, D).
In our model, the strong interaction is reduced to an electromagnetic interaction given by the quarks-antiquarks interactions (U, U, D, D).
In our model, the gravitational interaction is reduced to an electromagnetic interaction given by the quarks-antiquarks interactions (U, U, D, D).
To conclude, I want to say that in our model, all force interactions are reduced to a single electromagnetic interaction (U, U, D, D).
It is a reductionist, simplifying model. It is a model that allows the four existing fundamental interactions to be represented through a single electromagnetic interaction, given by the quarks-antiquarks interactions (U, U, D, D).
In other words:
SU(3) x SU(2) x U(1), standard model
is reduced to:
U(1), proposed model
Finally, our proposed model simplifies the three interactions that exist in the standard model and the gravitational interaction into a single electromagnetic interaction. Importantly, our model includes gravitational interaction.
In order to explain what we are saying, once again we are going to need the Maldacena correspondence equation and our proposed equation for the theory of everything (TOE).
In equation (130), CFT is associated with the interactions of the weak force, strong force and electromagnetic forces. ADS is associated with the hyperbolic curvature of space-time. However, we say that gravity represents the curvature of space-time. Here, it is important to highlight that the quantization of gravity is different from the quantization of space-time, but it is also important to highlight that gravity is related to the curvature of space-time; the greater the gravity, the greater the curvature of space-time and we can represent this by the effective Boltzmann´s constant of a system. see
Table 6.
Now we are going to analyse equation (131), remember that this equation is much more general than equation (130) and is the equation proposed by us as the equation that represents the theory of everything (T.O.E.).
It is also important to remember that matter is quantized, gravity is quantized and space-time is also quantized.
When we refer to the right side of the equation (EFQT), we are talking about matter; let us remember that in our model, the interactions of the weak force, strong force and electromagnetic forces are replaced by interactions of quarks-antiquarks (U, U, D, D).
When we refer to the left side of the equation (DST), we are also talking about matter; let us remember that in our model, the interaction of gravitational forces is replaced by quark-antiquark interactions (U, U, D, D).
If we express this according to equation (130), it is as if we are saying that the interactions of the electromagnetic force, weak force and strong force, are equal or equivalent to the gravitational force interaction. Now, if we express this according to equation (131), we are saying that the quark-antiquark interaction on the right side of the equation is equal or equivalent to the quark-antiquark interaction on the left side of the equation. This is true if we look at it from the point of view of mass or matter.
Now we are going to analyse equation (131). from the point of view of space-time.
Let us remember that EFQT is associated with quarks-antiquarks interactions (U, U, D, D) which in turn are associated with interactions electromagnetic force, weak force and strong force. The right side of equation (131), EFQT, is telling me that the distortion of space-time given by the interactions of the quarks-antiquarks (U, U, D, D) has to be equivalent to the distortion of space- time on the left side of equation (131), DST.
Let us remember that DST is associated with quarks-antiquarks interactions (U, U, D, D) which in turn are associated with gravitational interaction. The left side of equation (131), DST, is telling me that the distortion of space-time given by the interactions of the quarks-antiquarks (U, U, D, D) has to be equivalent to the distortion of space -time on the right side of equation (131), EFQT.
When we analysed a neutron star in the previous example, we said that we could consider it as a bag of quarks (U, U, D, D). As we move away from the neutron star, gravity decreases as does the curvature of space-time, according to the inverse of the distance squared (1/r²), until we reach flat space-time. This transition that occurs, from the neutron star to reaching flat space-time, does so continuously through gravitons; It is the gravitons formed by quarks (U, U, D, D) that allow this transition.
A neutron star is a bag of quarks (U, U, D, D), which has a maximum density. As we move away from the neutron star, gravity and the curvature of space-time decrease until we reach flat space-time, minimum density. That continuity that occurs in density is given by the gravitons (U, U, D, D).
After having concluded our analysis, we see that equation (131) is a generalization of equation (130); furthermore, equation (131) includes the gravitational interaction as a quark-antiquark interaction (U, U, D, D), on equal footing to the rest of the interactions.
8.6.3. Phase Transitions in the Early Universe – Symmetries
According to the Big Bang theory, the universe emerged 13.8 billion years ago.
First Phase Transition:
The first phase transition occurs at t = 10ˉ³⁸ s.
The temperature was of the order of T = 10³⁰ K, which corresponds to an energy of the order of E = 10¹⁶ GeV.
It goes from a large-unified phase to a phase with less symmetry, the standard model.
GUTs SU(5) → Standard Model SUc(3) x SUʟ(2) x Uʀ(1)
The SU(5) symmetry is broken for the symmetry of the standard model
A sector of the Higgs is the one that makes the first symmetry break.
The SU(5) symmetry has 24 generators, the standard model symmetry has 12 generators.
In this phase transition, 12 generators are broken, thereby generating very massive vector bosons. Also, in this phase, very massive magnetic monopoles are generated. Energy scale of the order of E = 10¹⁶ GeV.
This first Higgs sector is what gives mass to vector bosons and magnetic monopoles.
Second Phase Transition:
The second phase transition occurs at a time of t = 10ˉ¹⁰ s, also called the electro-weak transition.
This phase transition is guided by the Higgs field.
The estimated temperature in this transition was of the order of T = 10¹⁵ K, corresponding to an energy of the order of 250 GeV.
Estimated magnetic fields in the order of 10¹⁹ Tesla.
SUc(3) x SUʟ(2) x Uʀ(1) → SUc(3) x Uem(1)
A second Higgs sector is the one that performs the second symmetry break, different from the Higgs sector of the first phase transition.
The Higgs in this second transition is what gives mass to the quarks and particles of the standard model.
Third Phase Transition:
The third and final phase transition occurs at t = 10ˉ⁵ s, after the Big Bang.
The estimated temperature was of the order T = 10¹² K, with energies corresponding to E = 200 GeV.
Estimated magnetic fields of the order of 10¹⁶ Tesla.
In this phase transition the quarks become confined.
It is important to highlight that magnetic monopoles occur between the first and second phase transition:
Estimated temperature range, T = 10¹⁵ K to 10³⁰ K
Estimated Energy Range, E = 250 GeV to 10¹⁶ GeV
Estimated magnetic field, B > 10¹⁹ Tesla
8.7. Generalization of the ADS/CFT Correspondence
In theoretical physics, the ADS/CFT correspondence is a conjectured relationship between two kinds of physical theories. On one side are anti-de Sitter spaces (ADS) which are used in theories of quantum gravity, formulated in terms of string theory or M-theory. On the other side of the correspondence are conformal field theories (CFT) which are quantum field theories, including theories similar to the Yang–Mills theories that describe elementary particles.
It also provides a powerful toolkit for studying strongly coupled quantum field theories. Much of the usefulness of the duality results from the fact that it is a strong–weak duality: when the fields of the quantum field theory are strongly interacting, the ones in the gravitational theory are weakly interacting and thus more mathematically tractable. This fact has been used to study many aspects of nuclear and condensed matter physics by translating problems in those subjects into more mathematically tractable problems in string theory.
Quantum gravity is the branch of physics that seeks to describe gravity using the principles of quantum mechanics. Currently, a popular approach to quantum gravity is string theory, which models elementary particles not as zero-dimensional points but as one-dimensional objects called strings. In the ADS/CFT correspondence, one typically considers theories of quantum gravity derived from string theory or its modern extension, M-theory.
The application of quantum mechanics to physical objects such as the electromagnetic field, which are extended in space and time, is known as quantum field theory. In particle physics, quantum field theories form the basis for our understanding of elementary particles, which are modelled as excitations in the fundamental fields. Quantum field theories are also used throughout condensed matter physics to model particle-like objects called quasiparticles.
In the ADS/CFT correspondence, one considers, in addition to a theory of quantum gravity, a certain kind of quantum field theory called a conformal field theory. This is a particularly symmetric and mathematically well-behaved type of quantum field theory. Such theories are often studied in the context of string theory, where they are associated with the surface swept out by a string propagating through spacetime, and in statistical mechanics, where they model systems at a thermodynamic critical point.
8.7.1. M-Theory, Extra Dimensions and the Theory of the Generalization of Boltzmann's Constant in Curved Spacetime
In the paper: RLC Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time, we developed this topic.
In this section, we will use the information from the IFT UAM, as a guide and technical-scientific support.
In string theory, the fundamental degrees of freedom are extended one-dimensional objects, strings that live in 10-dimensional space-time; 9 for space and 1 for time. These strings can interact by division-recombination, and the strength of this interaction is measured by a parameter gs; gs is the string coupling constant, which can range from 0 to infinity. When the coupling constant gs is small, it is called a perturbative regime; when the coupling constant gs is large, it is called a non-perturbative regime.
In the non-perturbative regime, gs is large, new components appear, the P-Branes, which are extensive and have P extended spatial dimensions; the strings no longer play an essential role, they are on an equal footing with all those branes and all these objects of different extensive dimensions coexist.
When gs is small, the regime is perturbative. This regime is dominated by a single object, the strings, and in this regime the energy required to create a brane is greatly increased. In this perturbative regime, string theory is well explained, well formulated, and well defined.
Figure 102.
Perturbative regime, dominated by strings, small gs.
Figure 102.
Perturbative regime, dominated by strings, small gs.
There are 5 different types of super-symmetric string theory in 10 dimensions namely: TYPE IIA, TYPE IIB, TYPE I, HETEROTIC E8 X E8 AND HETEROTIC SO (32). These theories are very different from each other, they have different particle contents, different interactions, different supersymmetries, different symmetry groups, and they also have different P-Brane contents.
Figure 103.
TYPE IIA, TYPE IIB, TYPE I, HETEROTIC E8 X E8 AND HETEROTIC SO (32).
Figure 103.
TYPE IIA, TYPE IIB, TYPE I, HETEROTIC E8 X E8 AND HETEROTIC SO (32).
To study how branes behave as gs approaches infinity, gs → ∞, it is important to specify which particular string theory we are going to study. For our case we are going to study the TYPE IIA theory, a theory that lives in 10 dimensions and has a perturbative content corresponding to the graviton and its companions, as well as a non-perturbative content of P-Branes. D0 branes are objects without extended dimension, they are like point particles.
Figure 104.
Non-perturbative regime, dominated by D0 branes, gs infinite.
Figure 104.
Non-perturbative regime, dominated by D0 branes, gs infinite.
It is observed that the limit when the coupling tends to infinity , gs → ∞, is dominated by the D0-branes. This is very interesting, it is a single object that dominates all dynamics and they are not strings, they are point particles and it is a theory that has quantum gravity.
In the case of D0-Branes, the binding energy is zero (0), basically because these branes are BPS supersymmetry (state with certain properties protected by supersymmetry). Supersymmetry causes the cancellation of many quantities, specifically the binding energy between D0-Brans.
Figure 105.
mass of a set of particles in a bound state is M* = k / gs.
Figure 105.
mass of a set of particles in a bound state is M* = k / gs.
Therefore, the mass of a particle is equal to M = 1/gs and the mass of a set of particles in a bound state is M* = k / gs. With that we have that the different states for the different values of k; the different sets of non-perturbative particles would form a tower whose masses would be x-spaced by the value 1/gs.
Now, if we make gs → ∞, that is, an infinitely strong coupling, all the particles in that tower will have mass equal to zero (0); there would be an infinite number of particles with mass zero (0).
How do you discover an extra dimension? We have seen that if you have a theory in which there is an extra dimension packed into a circle of radius R, the way this extra dimension manifests are that a tower of state appears with masses spaced 1/R and that is exactly what we are seeing in our TYPE IIA theory in strong coupling, gs → ∞. That is, the theory has a hidden extra dimension with a radius R controlled by the coupling constant gs. The D0-Branas are the Kaluza-Klain replicas of the states of the theory in 10 dimensions, that is, of the graviton.
So, we have an 11-dimensional theory, where one of the dimensions is packed into a radius of size R that is related to the coupling constant gs. When R is small, gs is also small, gs → 0; that is, we recover a loosely coupled 10-dimensional theory that exactly matches the TYPE IIA, perturbative theory we started with.
When we go to the strong coupling, gs → ∞, in the limit where R and gs tend to infinity, the circle of dimension 11 is decompressed, that is, we recover a theory in 11 dimensions.
M-theory is the 11-dimensional theory that is recovered when the circle that is hidden in the extra dimension of TYPO IIA theory is decompressed.
Let's give an example explaining what it means when we talk about a perturbative regime and a non-perturbative regime.
We can explain the meaning of a perturbative regime, gs → 0, through a hydrodynamic analogy, saying: if we consider a lake with calm waters and we throw a small stone, small waves are produced that propagate in the water; we say that we are in a perturbative regime and it would be analogous to space-time in which small significant disturbances occur.
When we talk about a non-perturbative regime, gs → ∞; hydrodynamically we refer as an example to very rough seas, giant waves; in the space-time regime it would be analogous, for example, to black holes, neutron stars; large disturbances in space-time, very large space-time curvature.
After having explained the perturbative and non-perturbative regime, let's try to explain M-theory with its 11 dimensions by comparing it with the theory of the generalization of Boltzmann's constant in curved space-time.
Three spatial dimensions plus one temporal (3 + 1), these are the dimensions in which we live every day, the ones that our senses perceive. Next, we have the theory of superstrings consisting of 10 dimensions, in addition to the 4 dimensions, 6 more dimensions are added. Finally, we have an additional dimension that when decompressed creates the 11 dimensions of M-theory.
the theory of the generalization of Boltzmann's constant in curved space-time, has 3 stages. The first stage corresponds to the regime in which the Boltzmann´s constant is equal to Kʙ = 1.38 10⁻²³ J/K, for a flat space-time; the second stage corresponds to the regime in which the Boltzmann´s constant varies from 1.38 10⁻²³J/K > Kʙ >1.78 10⁻⁴³ J/K, for a curved space-time; the third stage corresponds to the regime where the Boltzmann´s constant is maximum, equal to Kʙ = 1.78 10⁻⁴³ J/K, maximum curvature of space-time.
Considering these two theories: the M-theory and the theory of the generalization of Boltzmann's constant in curved space-time, we will make the following comparison, in 3 stages.
Here we put forward the following hypothesis:
First stage: Corresponds to the (3 + 1) dimensions in which we live, the three spatial dimensions plus time. In the theory of the generalization of the Boltzmann´s constant in curved space-time, it corresponds to the regime in which the Boltzmann´s constant is equal to Kʙ = 1.38 10⁻²³ J/K. We are in a perturbative regime, that is, gs → 0, dominated by the strings. This regime is characterized by the fact that the space-time structure does not undergo modifications, flat space-time.
Second stage: matter undergoes the first compaction process. This would be represented by the 10-dimensional superstring theory, that is, by the dimensions (3 + 1) plus 6 additional dimensions that arise from the first compaction process. In the theory of the generalization of the Boltzmann´s constant in curved space-time, this regime would be characterized because the Boltzmann constant varies between 1.38 10⁻²³ J/K > Kʙ > 1.78 10⁻⁴³ J/K. We are in a perturbative to non-perturbative transition regime, that is, gs tends to a large value. This regime is characterized by the fact that the space-time structure undergoes modifications. An example of this regime would be white dwarf stars and neutron stars. This is a regime in which space-time is curved.
Third stage: In this stage of M-Theory, the second compaction process occurs, that is, the decompression of dimension 11 occurs, the radius R becomes infinitely large and gs = ∞. In the theory of the generalization of the Boltzmann´s constant in curved space-time, in this regime, the Boltzmann´s constant assumes the value of Kʙ = 1.78 10⁻⁴³ J/k. We are in the non-perturbative regime, that is, gs is infinite. In this regime, the space-time structure undergoes great changes, a concrete example would be the creation of black holes. The decompression of dimension 11 in M-theory is equivalent to creating a black hole. In this stage the maximum curvature of space-time occurs. At this stage, as the black hole grows, inside a black hole, it is true that the gravitational Planck length Lpɢ is less than the electromagnetic Planck length Lpɛ.
Decompactification of dimension 11
It is important to understand that the concept of dimension depends on the scale of energies or distances. We are used to the four dimensions of everyday life (x, y, z, t), now when we work at high energies in the LHC, at small distances we introduce 6 more dimensions, that is, we would be working in 10 dimensions, which is the case of the plasma of quarks and gluons. In the theory of the generalization of the Boltzmann´s constant in curved spacetime, we can represent this by varying the Boltzmann´s constant in the range of 1.38 10⁻²³ J/K > Kʙ > 1.78 10⁻⁴³ J/ K.
If we imagine dimension 11 as a circle, unroll the circle to represent it as an interval, then all particles have a wave function in on that interval, which must be periodic. This type of wave is characterized by a number K and we can represent it as follows: k = 0, (+/-) 1, (+/-) 2, (+/-) 3,.…etc.
The momentum or energy that the particles possess does not reside in the 10 dimensions, it is hidden in the dimension 11. This internal energy manifests as additional mass in the dimension 11.
Using equations, we can represent it as follows:
λ = (2 π R) / K
λ = h / p
p = m v
p = (h k) / 2 π R = m c
p² = (h k / 2 π R) ² = m² c²
The energy can be written as:
E = √ {(m² c⁴) + (Px² + Py² +Pz²) c² + (h k / 2 π R) ² c²}
Where the rest mass seen by an observer is equal to:
M² = m² + (h k / 2 π R c) ²
This is the general formula that tells us how to detect an extra dimension.
We define that the mass of a black hole is equal to:
Where represents the dark matter mass of a black hole that results from decompactification of dimension 11 of the M theory and m represents the baryonic mass.
We can complement all the development presented with the analysis carried out in section 3. COSMIC INFLATION, of the paper: RLC Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time.
Specifically, in (26):
R < Rs, v > c; ds > 0, space type trajectory.
Condition (26) is very important because to the extent that R < Rs, v > c is fulfilled, it is precisely this speed difference that generates the dark matter mass in a black hole given by -iδ.
8.7.2 ADS/CFT correspondence and the theory of the generalization of Boltzmann's constant in curved spacetime
When analysing M-theory and the theory of the generalization of the Boltzmann´s constant in curved space-time, it is inevitable to make a comparison with the ADS/CFT correspondence.
According to the analysis carried out in M-theory and the theory of the generalization of Boltzmann's constant in curved space-time, in a non-perturbative regime, when gs is infinitely large (gs → ∞), we can equate a theory of gravity in anti-de Sitter space ADS n+1-dimensional, with a field theory according to CFT n-dimensional.
We wonder why we can do this? And the answer lies in the value that the Boltzmann´s constant takes.
We will give the answer with an example where the plasma viscosity of quarks-gluons is calculated. For the non-perturbative regime, gs → ∞, for very large gs tending to infinity, we are comparing two theories in which the Boltzmann´s constants are approximately equal.
For the case of the 11-dimensional ADS theory, where we introduce a black hole, Boltzmann's constant is equal to Kʙ = 1.38 10⁻⁴³ J/K. For the 10-dimensional CFT theory, in which we want to calculate the plasma viscosity of quarks-gluons, the Boltzmann´s constant is of the order of 0.76 10⁻⁴¹ J/K > Kʙ-eff > 1.78 10⁻⁴³ J/ K.
This tells us that we can use the ADS and CFT theories to calculate the plasma viscosity of quarks-gluons because both theories work in an almost identical non-perturbative regime, which is why whichever of the theories we use to calculate, the answer will be practically the same.
In strong coupling, in the limit where gs tends to infinity, that is, in the non-perturbative regime; we can reduce superstring theory to general relativity and with that we can simply use a theory of gravity in anti-de Sitter space ADS, to describe the strong coupling regime of a particle theory, we call dual QCD. This becomes a very useful duality.
In other words, whenever we use a CFT theory that works with a Boltzmann´s constant close to Kʙ = 1.78 10⁻⁴³ J/K, we can say that the duality ADS/CFT is fulfilled.
Up to this point, we have analysed superstring theory and M theory. I consider it very important to make a small summary of the first bosonic string theory.
Bosonic string theory
Describes the behaviour of both open strings and closed strings; however, the theory has several problems, three being the main ones: absence of fermions, existence of tachyons and the number of dimensions.
The name bosonic string theory is a consequence of the fact that theory is only capable of describing bosons and therefore does not include to ordinary matter that is composed of fermions.
When developing the theory, a particle emerges that has a speed greater than that of light and therefore, according to relativity, an imaginary mass. This particle is known as Tachyon and has been tried to eliminate it from the theory, although without result.
Finally, for this theory to have quantum consistency, it is necessary to consider that the background space-time has 26 dimensions: 1 temporal and 25 spatial.
If we analyse the interior of a black hole or the beginning of the Big Bang, we can hypothesize that space-time structure is dominated by bosonic strings; that is, space-time is in the domain of the inverse symmetry break of the electro-weak theory, dominated only by elementary bosons, T > 10¹⁶ K.
Let us remember that the dimensions are a function of the energy, therefore at high temperatures, high energies correspond and this implies that the dimensions are high.
Finally, there is the tachyon, a bosonic particle whose speed v >> c; let us remember that in the inside a black hole or at the beginning of the big bang with the expansion of the universe, it is true that gravitons as well as elementary bosons move at a speed v greater than c, in accordance with space-time.
Here we are postulating the following hypothesis in which we say that the bosonic string theory applies only to the interior of a black hole and to the beginning of the big bang.
When we say that the speed of tachyons is greater than the speed of light inside black holes, this does not contradict Einstein's theories. This is the result of analysing the interior of black holes using Albert Einstein's theory of general relativity.
Let's explain it, according to the theory of the RLC electrical modelling of black hole and early universe, it happens that inside a black hole as it grows following the law of the constant Tau of the RC circuit, the Planck length Lp decreases.
If we consider that the speed is equal to V = e/t, as the Planck length decreases, time also decreases, now if we consider that the Planck length is constant, as time decreases the speed increases.
This is what makes us think that the speed increases inside a black hole, but in reality, if we combine the correct variation of the gravitational Planck length Lpɢ with the correct time variations, the speed really remains c, the speed of light.
That is why we say that inside a black hole the trajectories are of the time type, while on the outside of a black hole the trajectories are of the space type.
Inside a black hole, the gravitational Planck length Lpɢ is smaller than the electromagnetic Planck length Lpɛ.
Generalizing, inside black holes and at the beginning of the Big Bang, they are under the domain of bosonic string theory. Outside of black holes, it is under the domain of superstring theory and M-theory.
Both theories are complementary to the theory proposed in this paper, DST = EFQT duality.
8.7.3 DST = EFQT, theory of everything (T.O.E.)
Based on the development of the following items:
2. RLC ELECTRICAL MODELLING OF BLACK HOLE AND EARLY UNIVERSE
2.1 RC electric model for a black hole
2.2 RLC electric model of the universe
2.3 Generalization of Boltzmann's constant in curved space-time.
2.4 Black Hole´s radiation
2.5 Cosmic inflation
2.6 Additional calculations. Growth of a black hole in analogy to the tau growth curve of an RC circuit
2.7 Dark Matter: Calculation of the amount of dark matter that exists in the Milky Way
2.7.1 Calculation of the amount of dark matter existing in the Andromeda galaxy M31
2.7.2 We will describe the contribution of all the forces involved in determining the rotation speed of a galaxy using the RC electric model of a black hole.
2.8 Dark energy and gravitational waves: Origin of the Accelerated Expansion of the Universe and the Hubble´s Tension
2.8.1 Theoretical analysis of the Dirac delta function (Impulse) and its analogy with the Big Bang
2.8.2 Analysis of the propagation of seismic waves using the Vibroseis method and its analogy with the Big Bang.
2.8.3 Accelerated expansion of the universe and the variation of the Hubble´s constant
2.8.4 Calculation of the existing relationship of baryonic matter, dark matter and dark energy at time T0⁻, at the moment when the Big Bang occurs.
2.8.5 Calculation of the relationship between baryon matter, dark matter and dark energy at time t = 5 10¹⁷ s, which corresponds to the current moment, today.
2.9 Space-time contraction factor and the effective Boltzmann´s constant.
2.10 Space-time Torsion Mechanism
2.11 Generalization of the Boltzmann’s Constant in Curved Space-Time. Quantization of the curvature of space-time
2.12 Calculation of the curvature of space-time for different states of matter
2.13 Calculation of the critical mass to produce a black hole in the LHC applying the theory of the generalization of Boltzmann´s constant in curved spacetime
3. STANDARD MODEL OF ELEMENTARY PARTICLES
4. NEUTRON AND PROTON ANALYSIS
4.1 Summary of the theory of three-phase alternating current electric generators.
4.2 Nuclear phenomenology - sum of spins ½ of subatomic particles
4.3 Electrical-quantum modelling of the neutron as a three-phase alternating current electricl generator.
4.4 Neutron analysis
4.5 Electrical-quantum modelling of the proton as a three-phase alternating current electric generator.
4.6 Proton analysis
5. NEW PHYSICAL MODEL PROPOSED FOR PHOTONS, GLUONS, GRAVITONS AND HIGGS BOSON.
5.1 Analysis of the proposed models for the photon
5.2 Analysis of the proposed models for the gluons
5.3 Analysis of the proposed models for the gravitons
5.4 Analysis of the proposed models for the Higgs boson.
6. QUANTIZATION OF SPACE-TIME AND THE GRAVITY
6.1 Quantization of the gravity.``Gravity is a force´´
6.2 Quantization of space-time
7. ANALYSIS OF THE ORIGIN OF ELEMENTARY PARTICLES USING THE THEORY OF THE GENERALIZATION OF THE BOLTZMANN´S CONSTANT IN CURVED SPACE-TIME
8. APPLICATION OF THE MODEL AND RESULTS
8.1 Comparison between stellar bodies and elementary particles considering the theory of the generalization of the Boltzmann´s constant in curved space-time.
8.2 Mass-temperature relationship in elemental and non-elemental particles.
8.3 Origin of the electron and antineutrino - β ˉ decay
8.4 Fine structure constant
8.5 We will demonstrate the existence of a force tangential to the repulsive force in subatomic disintegrations, this force advances to repulsive force by 90 degrees.
8.6 Symmetries in particles
8.6.1 Fermions, bosons, spin and color symmetry
8.6.2 Generalization of gauge symmetries
8.6.3 Phase transitions in the early universe – symmetries
8.7 Generalization of the ADS/CFT correspondence
8.7.1 M-theory, extra dimensions and the theory of the generalization of Boltzmann's constant in curved spacetime
8.7.2 ADS/CFT correspondence and the theory of the generalization of Boltzmann's constant in curved spacetime
8.7.3 DST = EFQT, theory of everything (T.O.E.)
9. BLACK HOLE AND BIG BANG
9.1 The Penrose Property with a Cosmological Constant
9.2 Modelling of a black hole
9.3 Correlation between Kerr-Newman Black hole vs RLC electrical modelling of a black hole and early universe
9.4 Inside a black hole
9.5 Black holes are true generators of matter in the universe
We will propose a generalization of the ADS/CFT correspondence. Here we hypothesize that we replace the ADS/CFT correspondence with a general equation given by DST = EFQT duality.
ADS is replaced by DST; DST represents a theory of quantum gravity associated with the theory of the generalization of the Boltzmann´s constant in curved space-time.
CFT is replaced by EFQT. EFQT represents unique electromagnetic field quantum theory, which unites the electromagnetic field theory, the weak field theory and the strong field theory and is associated with the theory: Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electric Generator.
Here we put forward the hypothesis that the equation DST = EFQT, represents the theory of everything, is the equation that unites gravity and quantum mechanics, this fact is achieved through the theory of the generalization of the Boltzmann´s constant in a curved space-time and the theory electrical-quantum modelling of the neutron and proton as a three-phase alternating current electric generator
We can represent it using the following general equations:
We will describe simple equations that represent the electromagnetic wave spectrum.
Eε = h x fε
Cε = λε x fε
Eε = h x Cε / λε
Eε = Kʙε x Tε
Kʙε = 1.38 10⁻²³ J/K
We will describe simple equations that represent the gravitational wave spectrum.
Eɢ = h x fɢ
Cɢ = λɢ x fɢ
Eɢ = h x Cɢ / λɢ
Eɢ = Kʙɢ x Tɢ
Kʙɢ = 1.38 10⁻²³ J/K > Kв ef > 1.78 10⁻⁴³ J/K
In the paper: RLC Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time, we explain the origin of the universe, the origin of cosmic inflation, the origin of dark matter and the origin of dark energy.
In the paper: Theory of the Generalization of the Boltzmann’s Constant in Curved Space-Time. Shannon-Boltzmann Gibbs Entropy Relation and the Effective Boltzmann’s Constant, we explain how we can quantify the curvature of space-time and show using the Shannon-Boltzmann-Gibbs entropy relation that information is conserved.
In the paper: RC Electrical Modelling of Black Hole. New Method to Calculate the Amount of Dark Matter and the Rotation Speed Curves in Galaxies, we explain how we can calculate the amount of dark matter in a galaxy and how we can model the rotation curves of a galaxy using a new method.
In the paper: Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electric Generator. Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons, inside a Neutron; we explain how the mass is generated (we calculate the number of quarks-antiquarks-gluons) and the gravity (we calculate the number of gravitons) in a neutron.
In the paper: Theory of Unification of the Interactions of Fundamental Forces: SU(3) x SU(2) --> U(1); we explain that electromagnetic, weak, strong and gravitational interactions; they can be replaced by a single electromagnetic force interaction.
In this paper: Generalization of the Standard Model. Theory of Everything (T.O.E.) version 1; we proposed a method to determine the origin of elementary particles and how matter/energy is related to gravity, this allowed us to generalize the correspondence ADS/CFT, for a general theory or theory of everything.
The theory of the generalization of the Boltzmann´s constant and the quantum-electrical modelling of the neutron and the proton as a three-phase alternating current electric generator, are the fundamental basis or pillar that allows us to unite the theory of general relativity and quantum mechanics.
This theory allows us to quantify space-time, it allows us to quantify the curvature of space-time, it does not allow us to unite the field theory of electromagnetic interactions, weak interaction, strong interaction and gravitational interaction in a single quantum field theory of electromagnetic interactions EFQT.
Finally, it allows us to generalize the ADS/CFT correspondence. It allows us to propose a universal theory or theory of everything, represented by the equation:
From the point of view of mass, the dynamics of both sides of the equation are dominated by quarks-antiquarks interactions (U, U, D, D).
From the space-time point of view, the dynamics of both sides of the equation are dominated by the Planck constant. Outside a black hole, in the domain of the four existing force interactions, space-time is dominated by Planck length Lp; inside a black hole, in the domain of gravitational force, space-time is dominated by Lpԍ, where Lpԍ < Lp.
Higgs mechanism versus conformal mechanism
Gauge symmetry demands massless particles. The Higgs mechanism, on the other hand, is a technique for determining particle mass. In this case, the symmetry is broken at the price of providing particles with mass. This interaction occurs in a flat space. However, in curved space, particle mass may violate a symmetry known as conformal symmetry.
Breaking this symmetry is proven to give gravitons, photons, scalar fields (bosons), and Dirac particles mass in flat space. This mass is directly proportional to the conformal factor's (field) temporal derivative. The equation of motion of a particle in conformal space in curved space looks to be moving in a fluid (viscous), which may be the cause of inertia. There appears to be a background (conformal) field present with which particles and fields interact.
This text was posted by Arbab Ibrahim (Abdus Salam Intentional Centre for Theoretical Physics (ICTP)- Trieste-Italy), in QUANTUM PHYSICS.
This text, highlights the essence of this paper, shows us how the breakdown of symmetry in curved space-time provides mass to fermionic and bosonic particles as a function of temperature, as the temperature increases, the curvature of space-time increases; the fermionic and bosonic particles of the standard model acquire mass, it includes photons and gravitons to be clear.
It is precisely this reasoning that led us to generalize the ADS/CFT correspondence, where conformal quantum fields CFT, a particular case of quantum field theory, are generalized to the electromagnetic field quantum theory EFQT.
DST represents dynamic space-time, which we have shown is quantized; is on a plane of equality with EFQT, represented by electromagnetic field quantum theory; this duality, DST = EFQT, represents the equation of the theory of everything.
We are going to perform the following examples:
Example 1:
Quantification of space-time curvature
In the paper: RLC Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time; we perform this example.
The observation of the 1919 solar eclipse in Brazil and Africa provided the first experimental proof of the validity of Albert Einstein's theory of general relativity. We will calculate the Boltzmann´s constant for the sun and show how it adjusts to the deviation found.
No solar eclipse has had as much impact in the history of science as that of May 29, 1919, photographed and analysed at the same time by two teams of British astronomers. One of them was sent to the city of Sobral, Brazil, in the interior of Ceara state; the other group go to the island of Principe, then a Portuguese territory off the coast of West Africa. The goal was to see if the path of starlight would deviate when passing through a region with a strong gravitational field, in this case the surroundings of the Sun, and by how much this change would be if the phenomenon was measured.
Einstein introduced the idea that gravity was not a gravitational force exchanged between matter, as Newton said, but a kind of secondary effect of a property of energy: that of deforming space-time and everything that propagates over it, including waves like light. “For Newton, space was flat. For Einstein, with general relativity, it curves near bodies with great energy or mass”, comments physicist George Matsas, from the Institute of Theoretical Physics of the São Paulo State University (IFT- Unesp). With curved space-time, Einstein's calculated value of light deflection nearly doubled, reaching 1.75 arc-seconds.
The greatest weight should be given to those obtained with the 4-inch lens in Sobral. The result was a deflection of 1.61 arc-seconds, with a margin of error of 0.30 arc seconds, slightly less than Einstein's prediction.
Demonstration:
Let us calculate the Boltzmann´s constant for the Sun, Kʙs, curved space-time.
Hawking's temperature equation:
Kʙs = (h x c³) / (8 x π x Ts x G x Ms)
Where Kʙs is the Boltzmann´s constant for the sun, Ts is the temperature of the sun's core, G is the universal constant of gravity, and Ms is the mass of the sun.
Kʙs = (6.62 10⁻³⁴ x 27 10²⁴) / (8 x 3.14 x 1.5 10⁷ x 6.67 10⁻¹¹ x 1.98 10³⁰)
Kʙs = 3.59 10⁻³⁷ J/K, Boltzmann's constant of the sun.
We use the following equation:
Es = Kʙs x Ts
Es = 3.59 10⁻³⁷ x 1.5 10⁷
Es = 5.38 10⁻³⁰ J/K
We use the following equation:
Es = h x fs
fs = Es / h
fs = 5.38 10⁻³⁰ / 6.62 10⁻³⁴ = 0.81 10⁴ = 8.1 10³ Hz
fs = 8.1 10³ Hz
We use the following equation:
c = λs x fs
λs = c / fs
λs = 3 10⁸ / 8.1 10³
λs = 3.7 10⁴ m
We use the following equation:
Degree = λs / 360
Degree =102.77 m
We use the following equation:
Arc-second = degree / 3600
Arc-second = 102.77 m / 3600 = 0.0285 m
1.61 arc-second = 0.0458 m
1 inch = 0.0254 m
4 inch = 0.1016 m
With a 4-inch lens, we can measure the deflection produced by the 1.61 arc-second curvature of space-time, which was predicted by Albert Einstein's theory of general relativity, and corresponds to a wavelength λs = 3.7 10⁴ m, a frequency fs = 8.1 10³ Hz, for an effective Boltzmann´s constant of the sun Kʙs = 3.59 10⁻³⁷ J/K.
We will carry out the same calculations for Kʙ = 1.38 10⁻²³ J/K, flat space-time.
Kʙ = 1.38 10⁻²³ J/K
We use the following equation:
E = Kʙ x Ts
E = 1.38 10⁻²³ x 1.5 10⁷
E = 2.07 10⁻¹⁶ J/K
We use the following equation:
E = h x f
f = E / h = 2.07 10⁻¹⁶ / 6.62 10⁻³⁴
f = 3.12 10¹⁷ Hz
We use the following equation:
c = λ x f
λ = c / f
λ = 3 10⁸ / 0.312 10¹⁸
λ = 9.61 10⁻¹⁰ m
We use the following equation:
Degree = λ / 360
Degree = 0.02669 10⁻¹⁰ m
We use the following equation:
Arc-second = degree / 3600
Arc-second = 7.41 10⁻¹⁶ m
Using the Boltzmann´s constant Kʙ = 1.38 10⁻²³ J/K, we cannot correctly predict by mathematical calculations the deflection of light given by Albert Einstein's general theory of relativity, to be measured in the telescope at Sobral.
Through the example given, we can conclude that the Boltzmann´s constant Kʙs = 3.59 10⁻³⁷ J/K fits the calculations of the deflection of light in curved space-time.
Example 2:
Quark-gluon viscosity
We ask ourselves, why do we use the Boltzmann´s constant of a black hole to calculate the viscosity of a quark-gluon plasma?
We will give the answer with an example where the plasma viscosity of quarks-gluons is calculated. For the non-perturbative regime, for very large gs tending to infinity, we are comparing two theories in which the Boltzmann´s constants are approximately equal.
For the case of the 11-dimensional ADS theory, where we introduce a black hole, Boltzmann's constant is equal to Kʙ = 1.38 10⁻⁴³ J/K. For the 10-dimensional CFT theory, in which we want to calculate the plasma viscosity of quarks-gluons, the Boltzmann´s constant is of the order of 0.76 10⁻⁴¹ J/K > Kʙ > 1.78 10⁻⁴³ J/ K.
This tells us that we can use the ADS(DST) and CFT(EQFT) theories to calculate the plasma viscosity of quarks-gluons because both theories work in an almost identical non-perturbative regime, which is why whichever of the theories we use to calculate, the answer will be practically the same.
In strong coupling, in the limit where gs tends to infinity, that is, in the non-perturbative regime, we can reduce superstring theory to general relativity and with that we can simply use a theory of gravity in anti-de Sitter space ADS, to describe the strong coupling regime of a particle theory, we call dual QCD. This becomes a very useful duality.
In other words, whenever we use a CFT theory that works with a Boltzmann´s constant close to Kʙ = 1.78 10⁻⁴³ J/K, we can say that the duality ADS/CFT is fulfilled.
Using the following formula, we have:
VQGP = 3 h c² / (4 π Kʙ T)
ɲ/S = VQGP T
Where ɲ is shear viscosity, VQGP is Kinematic viscosity and ɲ/S is viscosity entropy ratio
Calculation of the viscosity of quark-gluon plasma:
Considering that a quark-gluon plasma has a Boltzmann´s constant given by:
Kʙ-eff = 1.78 10⁻⁴³ J/K
VQGP = 3 h c² / (4 π Kʙ-eff T), ħ = h / (2π)
c = 3 10⁸ m/s
T = 10¹³ K
h = 6,62 10⁻³⁴ (m² x kg)/s
VQGP = (3 x 6.62 10⁻³⁴ x 9 10¹⁶) / (4 x 3.14 x 1.78 10⁻⁴³ x 10¹³ x (2 x 3.14))
VQGP = (178.74 10⁻¹⁸) / (140.40 10⁻³⁰)
VQGP = 1.27 10¹²
ɲ/s = VQGP T; Applying the following formula we have:
ɲ/s = 1.27 10¹² 10¹³ = 1.27 10²⁵
ɲ/s = 1.27 10²⁵; viscosity-entropy relationship.
Figure 106.
QGP plasma viscosity applying the Maldacena correspondence.
Figure 106.
QGP plasma viscosity applying the Maldacena correspondence.
Considering that a quark-gluon plasma has a Boltzmann´s constant given by:
Kʙ = 1.78 10⁻²³ J/K
VQGP = 3 h c² / (4 π Kʙ-eff T), ħ = h / (2π)
c = 3 10⁸ m/s
T = 10⁻⁹ K
h = 6,62 10⁻³⁴ (m² x kg)/s
VQGP = (3 x 6.62 10⁻³⁴ x 9 10¹⁶) / (4 x 3.14 x 1.78 10⁻²³ x 10⁻⁹ x (2 x 3.14))
VQGP = (178.74 10⁻¹⁸) / (140.40 10⁻³²)
VQGP = 1.27 10¹⁴
ɲ/s = VQGP T; Applying the following formula we have:
ɲ/s = 1.27 10¹⁴ x 10⁻⁹ = 1.27 10⁵
ɲ/s = 1.27 10⁵; viscosity-entropy relationship.
If we look at
Figure 51, we will see that the viscosity of the QGP plasma by the holographic method is ɲ/s = 0.1, less than liquid helium (superfluid) and less than water. We ask ourselves, is this value correct? Could it be that a black hole with a density of approximately 10²¹ kg/m³, a density similar to that of QGP plasma, behaves like a superfluid whose viscosity is lower than that of liquid helium?
In the paper: RLC Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann's Constant in Curved Space-Time; the critical temperature for the Bose-Einstein condensate of rubidium atoms was calculated for the following values of the Boltzmann´s constants, Kʙ = 1.38 10⁻²³ J/K and Kʙ = 1.78 10⁻⁴³ J/K; both values of the Boltzmann´s constant indicate that there are two types of temperatures that allow the creation of a Bose-Einstein condensate:
• Tc, min = 170 10⁻⁹ K, minimum critical temperature of the Bose-Einstein condensate for low temperatures, with rubidium atoms.
• Tc, max = 1.01 10¹³ K, maximum critical temperature of the Bose-Einstein condensate for high temperatures with rubidium atoms.
At this point, we have to clarify that a black hole is a QGP plasma, a high-temperature Bose-Einstein condensate in which the quarks behave as if they were free, generating a cascade of gluons of infinite energy, forming the state most energetic that exists in the universe.
If we look again atFigure 51, we see that the viscosityɲ/s = 10¹¹ for brea. In our calculation, for a black hole of 3 solar masses, a density of approximately 10²¹ kg/mᶾ, the value of the viscosity is of the order ofɲ/s = 10²⁵; I interpret that this value is more in line with reality, it is the correct value, taking into account the density.
Let's try to understand why the behaviour of the quark-gluon plasma resembles that of a superfluid. If we remember how we generate the scale factor of the Boltzmann´s constant, as matter gains energy and goes through the states of a white dwarf star, neutron star, until forming a QGP plasma; we see that the Boltzmann´s constant changes from 1.38 10⁻ ²³ J/K > Kʙ > 1.78 10⁻⁴³ J/K; this gives us an idea of how compacted or concentrated the mass is (gains energy) and how curved space-time is. This curvature of space-time is proportional to the amount of energy that the mass gains and we can compare it to a spring that compresses.
When we produce the QGP in a particle accelerator LHC, the quark-gluon plasma has stored energy but this state is not stable and at this point the QGP has an approximate Boltzmann´s constant Kʙ-eff = 1.78 10⁻⁴³ J/K. For curved space-time and matter to return to their stable state, the Boltzmann´s constant must go from Kʙ = 1.78 10⁻⁴³ J/K to 1.38 10⁻²³ J/K, that is, in this point all the energy stored in the compressed spring, is released until it reaches its natural state, that is, until the Boltzmann´s constant reaches the value of Kʙ = 1.38 10⁻²³ J/K. It is this energy that makes QGP look like a superfluid, but in reality, if we consider the scale factor of the Boltzmann´s constant, we will see that ɲ/s = 1.27 10²⁵ (viscosity-entropy relationship). The energies involved in this process are very great.
I can't imagine how something that has a density on the order of 10²¹ kg/mᶾ behaves like a superfluid with a lower viscosity than liquid helium.
Possibly, the Boltzmann´s constant Kʙ-eff is the response to the discrepancy that exists with the holographic method to calculate the viscosity of the QGP, ɲ/s = 0.1; I let the reader draw their own conclusions.
Example 3:
The two states of the Higgs field
By studying the Higgs field, theoretical physicists have discovered that the Higgs field, which permeates all of spacetime, exists in two states, in addition to the state known today; there is a second state thousands of times denser called the ultra-dense state of the Higgs field. This creates a potential problem, which is the possibility of a transition between the two states. We will analyse that this transition is almost impossible to happen.
First state of the Higgs field:
The Higgs field that we know today fills the entire space-time of our universe and together with the gravitational field, gives mass to the particles, for example, when the elemental energy corresponding to the electron moves in the Higgs field and the field gravitational, its interaction with the two fields gives the mass to the electron as we know it in the standard model table.
The Higgs boson is the excitation of the Higgs field; the Higgs field should not be confused with the Higgs boson.
The Higgs field has a value in vacuum and corresponds to:
H = 246 GeV (2.85 10¹⁵ K), this corresponds to a minimum potential energy V that gives stability to our current universe.
Second state of the Higgs field - Ultra dense state
Hypothesis: I propose that the ultra-dense state of the Higgs field occurs inside black holes.
In the paper: Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electric Generator. Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons, inside a Neutron; we proposed a model for black holes which we are going to represent in the following figure:
The explosion of a supernova goes beyond chemical energy or nuclear energy; that is why we propose that a supernova when it explodes separates matter and antimatter m (hw) from matter and antimatter m (-hw), in other words, the black hole that remains would be made up of matter and antimatter m (hw), m (-hw) expands in the space-time that surrounds the black hole.
With this we are proposing that inside a black hole there is no m (-hw), that is, the interior of a black hole is made up only of matter m (hw). This is represented in
Figure 107 and 108.
To conclude, let's consider the following table:
Conclusion:
The ultra-dense Higgs field inside a black hole is not constant and varies between the following extremes:
H1 = 8.6 GeV (10¹³ K), minimum value of the ultra-dense Higgs field, occurs when a stellar black hole of three solar masses forms. See
Table 30.
H2 = 4.4 10¹⁵ GeV (5 10²⁶ K), maximum value of the ultra-dense Higgs field, is the value that the Higgs field takes inside a black hole at the moment T⁰, it explodes and produces a white hole or Big Bang. See
Table 30.
The ultra-dense state of the Higgs field varies between the values of H1 = 8.6 GeV (10¹³ K) < ultra-dense Higgs field < H2 = 4.4 10¹⁵ GeV (5 10²⁶ K); and only occurs inside black holes.
The first state of the Higgs field is associated with the false vacuum, domain of the four fundamental forces; the ultra-dense state of the Higgs field is associated with the true vacuum inside black hole, domain of the gravitational force field.
Figure 109.
The two states of the Higgs field.
Figure 109.
The two states of the Higgs field.
Example 4:
Calculation of the entropy of a black hole, neutron star and white dwarf star
To perform entropy calculations for stellar bodies such as white dwarf stars and neutron stars or possibly any stellar body, we will first calculate the equivalent black hole of the body of interest and then using the entropy formula of a black hole, we will calculate the entropy value for that body in question; as a final result, the entropy of the body of interest will be less than or equal to the entropy of its counterpart black hole. Using this mechanism, we can estimate the approximate entropy value of any stellar body knowing that it cannot be greater than the entropy of its equivalent black hole.
We will calculate the entropy value for the following situations:
A) Calculation of the entropy of a black hole of three solar masses.
B) Calculation of the entropy of a black hole at the moment of the Big Bang.
C) Calculation of entropy for a neutron star.
D) Calculation of entropy for a white dwarf star.
We are going to use the following entropy equations:
S = (4 π Kʙ-eff G² M²) / Lp²C⁴ (132)
S = (π Kʙ-eff Rs²) / Lp² (133)
Kʙ-eff = effective Boltzmann´s constant, G = Universal gravitational constant, M = mass of a body to calculate entropy, Lp = Planck length, C = Speed of light and Rs = Schwarzschild radius.
Comments:
When applying the formula to calculate the entropy of a black hole, it is important to clarify that the Boltzmann´s constant used corresponds to the Boltzmann´s constant of a black hole and assumes the following value, Kʙ = 1.78 10⁻⁴³ J/K.
A) Calculation of the entropy of a black hole of three solar masses
M = 3ϴ = 6 10³⁰ kg
Kʙ-eff = 1.78 10⁻⁴³ J/K
C = 3 10⁸ m/s
Lp = 1.61 10⁻³⁵ m
S = (4 π Kʙ-eff G² M²) / Lp² C⁴
Replacing the values,
S = 4 x 3.14 x 1.78 10⁻⁴³ x 36 10⁶⁰ x 44.48 10⁻²² / (2.59 10⁻⁷⁰ x 81 10³²)
S = 35799.49 10⁻⁵ / 209.79 10⁻³⁸
S = 1.70 10³⁵ J/K
B) Calculation of the entropy of a black hole at the moment of the Big Bang
M = 1.20 10⁸² kg
Kʙ-eff = 1.78 10⁻⁴³ j/k
C = 3 10²¹ m/s
Lp = 1.27 10⁻⁵⁴ m
Rs = 1.59 10³⁰ m
S = 4 π Kʙ G² M² / (Lp² C⁴)
Replacing the values,
S = 4 x 3.14 x 1.78 10⁻⁴³ x 1.44 10¹⁶⁴ x 44.48 10⁻²² / (1.61 10⁻¹⁰⁸ x 81 10⁸⁴)
S = 1431.97 10⁹⁹ / 130.41 10⁻²⁴
S = 1.098 10¹²⁴ J/K
S = π Kʙ x Rs² / Lp²
S = 3.14 x 1.78 10⁻⁴³ x 2.52 10⁶⁰ / 1.61 10⁻¹⁰⁸
S = 14.08 10¹⁷ / 1.61 10⁻¹⁰⁸
S = 8.74 10¹²⁵ J/K
C) Calculation of entropy for a neutron star
M = 2.2Mϴ = 4.4 10³⁰ kg
Calculation of the Schwarzschild´s radius.
Rs = 2 G M/C²
Rs = 2 x 6.67 10⁻¹¹ x 4.4 10³⁰ / 9 10¹⁶ = 58.69 10³⁰ / 9 10¹⁶ = 6.52 10³ m
Rs = 6.52 10³ m
Entropy calculation:
S = π Kʙ-eff Rs² / Lp²
S = 3.14 x 1.78 10⁻⁴³ x 42.51 10⁶ / 2.59 10⁻⁷⁰
S = 237.59 10⁻³⁷ / 2.59 10⁻⁷⁰
S = 9.173 10³⁴ J/K
D) Calculation of entropy for a white dwarf star
M = 1.2 Mϴ = 2.4 10³⁰ kg
Calculation of the Schwarzschild´s radius:
Rs = (2 G M) / C²
Rs = 2 x 6.67 10⁻¹¹ x 2.4 10³⁰ / 9 10¹⁶ = 32.016 10³⁰ / 9 10¹⁶ = 3.55 10³ m
Rs = 3.55 10³ m
Entropy calculation:
S = π Kʙ-eff Rs² / Lp²
S = 3.14 x 1.78 10⁻⁴³ x 12.60 10⁶ / 2.59 10⁻⁷⁰
S = 70.43 10⁻³⁷ / 2.59 10⁻⁷⁰
S = 2.719 10³⁴ J/K
Finally, in
Table 31, we will represent a summary of the entropy calculations for different stellar bodies.
Example 5:
Analysis of the equations of the electromagnetic and gravitational wave spectrum
We will describe simple equations that represent the electromagnetic wave spectrum.
Eε = h x fε
Cε = λε x fε
Eε = h x Cε / λε
Eε = Kʙε x Tε
Kʙε = 1.38 10⁻²³ J/K
We will describe simple equations that represent the gravitational wave spectrum.
Eɢ = h x fɢ
Cɢ = λɢ x fɢ
Eɢ = h x Cɢ / λɢ
Eɢ = Kʙɢ x Tɢ
Kʙɢ = 1.38 10⁻²³ J/K > Kв-eff > 1.78 10⁻⁴³ J/K
We are going to carry out our analysis from the point of view of temperature, we are going to consider the following equations:
Eε = Kʙε x Tε (134)
Eɢ = Kʙɢ x Tɢ (135)
- i)
T = 170 nK, temperature of the Bose-Einstein condensate for Rubidium atoms.
Eε = Kʙε x Tε
Eε = Kʙε x Tε = 1.38 10⁻²³ J/K x 170 10⁻⁹ K = 234.6 10⁻³² = 2.34 10⁻³⁴ J
Eε = 2.34 10⁻³⁴ J
Eε = h x fε
fε = Eε / h = 2.34 10⁻³⁴ J / 6.62 10⁻³⁴ = 0.353
fε = 0.353 Hz
C = λε x fε
λε = C / fε = 3 10⁸ / 0.353 = 8.49 10⁸ m
Eɢ = Kʙɢ x Tɢ
Eɢ = Kʙɢ x Tɢ = 1.38 10⁻²³ J/K x 170 10⁻⁹ K = 234.6 10⁻³² = 2.34 10⁻³⁴ J
Eɢ = 2.34 10⁻³⁴ J
Eɢ = h x fɢ
fɢ = Eɢ / h = 2.34 10⁻³⁴ J / 6.62 10⁻³⁴ = 0.353
fɢ = 0.353 Hz
C = λɢ x fɢ
λɢ = C / fɢ = 3 10⁸ / 0.353 = 8.49 10⁸ m
λɢ = 8.49 10⁸ m
- ii)
T = 2 10⁷ K, temperature of a white dwarf star
Eε = Kʙε x Tε
Eε = 1.38 10ˉ²³ x 2 10⁷
Eε = 2.76 10ˉ¹⁶ J
Eε = h x fε
fε = Eε / h = 2.76 10ˉ¹⁶ / 6.62 10ˉ³⁴ = 0.4123 10¹⁸
fε = 4.12 10¹⁷ Hz
C = λε x fε
λε = C / fε = 3 10⁸ / 4.12 10¹⁷ = 0.72 10ˉ⁹ m
Eɢ = Kʙɢ x Tɢ
Eɢ = 1.9 10ˉ³⁷ x 2 10⁷
Eɢ = 3.8 10ˉ³⁰ J
Eɢ = h x fɢ
fɢ = Eɢ / h = 3.8 10ˉ³⁰ / 6.62 10ˉ³⁴ = 0.5740 10⁴ = 5.74 10³
fɢ = 5740 Hz = 5.74 10³ Hz
C = λɢ x fɢ
λɢ = C / fɢ = 3 10⁸ / 5.740 10³
λɢ = 0.5226 10⁵ m = 52264 m = 5.224 10⁴ m
- iii)
T = 10¹³ K, temperature of a black hole of three solar masses
Eε = Kʙε x Tε
Eε = 1.38 10⁻²³ J/K x 10¹³ K = 1.38 10⁻¹⁰
Eε = 1.38 10⁻¹⁰ J
Eε = h x fε
fε = Eε / h = 1.38 10⁻¹⁰ / 6.62 10⁻³⁴ = 0.208 10²⁴ = 2.08 10²³
fε = 2.08 10²³ Hz
C = λε x fε
λε = C / fε = 3 10⁸ / 2.08 10²³ = 1.44 10⁻¹⁵ m
Eɢ = Kʙɢ x Tɢ
Eɢ = 1.78 10⁻⁴³ J/K x 10¹³ K = 1.78 10⁻³⁰ J
Eɢ = 1.78 10⁻³⁰ J
Eɢ = h x fɢ
fɢ = Eɢ / h = 1.78 10⁻³⁰ J / 6.62 10⁻³⁴ = 0.268 10⁴
fɢ = 2.68 10³ Hz
C = λɢ x fɢ
λɢ = C / fɢ = 3 10⁸ / 2.68 10³ = 1.11 10⁵ m
λɢ = 1.11 10⁵ m
T = 10²⁷ K, black hole decay temperature
- iv)
Eε = Kʙε x Tε
Eε = 1.38 10⁻²³ J/K x 10²⁷ K = 1.38 10⁴
Eε = 1.38 10⁴ J
Eε = h x fε
fε = Eε / h = 1.38 10⁴ / 6.62 10⁻³⁴ = 0.208 10³⁸ = 2.08 10³⁷
fε = 2.08 10³⁷ Hz
C = λε x fε
λε = C / fε = 3 10⁸ / 2.08 10³⁷ = 1.44 10⁻²⁹ m
λε = 1.44 10⁻²⁹ m
Eɢ = Kʙɢ x Tɢ
Eɢ = 1.78 10⁻⁴³ J/K x 10²⁷ K = 1.78 10⁻¹⁶
Eɢ = 1.78 10⁻¹⁶ J
Eɢ = h x fɢ
fɢ = Eɢ / h = 1.78 10⁻¹⁶ J / 6.62 10⁻³⁴ = 0.268 10¹⁸
fɢ = 2.68 10¹⁷ Hz
C = λɢ x fɢ
λɢ = C / fɢ = 3 10⁸ / 2.68 10¹⁷ = 1.11 10⁻⁹ m
λɢ = 1.11 10⁻⁹ m
- v)
T = 10³² K, Planck´s temperature
Eε = Kʙε x Tε
Eε = 1.38 10⁻²³ J/K x 10³² K = 1.38 10⁹
Eε = 1.38 10⁹ J
Eε = h x fε
fε = Eε / h = 1.38 10⁹ / 6.62 10⁻³⁴ = 0.208 10⁴³ = 2.08 10⁴²
fε = 2.08 10⁴² Hz
C = λε x fε
λε = C / fε = 3 10⁸ / 2.08 10⁴² = 1.44 10⁻³⁴ m
λε = 1.44 10⁻³⁴ m
Eɢ = Kʙɢ x Tɢ
Eɢ = 1.78 10⁻⁴³ J/K x 10³² K = 1.78 10⁻¹¹
Eɢ = 1.78 10⁻¹¹ J
Eɢ = h x fɢ
fɢ = Eɢ / h = 1.78 10⁻¹¹ J / 6.62 10⁻³⁴ = 0.268 10²³
fɢ = 2.68 10²² Hz
C = λɢ x fɢ
λɢ = C / fɢ = 3 10⁸ / 2.68 10²² = 1.11 10⁻¹⁴ m
λɢ = 1.11 10⁻¹⁴ m
If we analyse the lower temperature limit, it corresponds to the Bose-Einstein condensate for rubidium atoms.
Table 32.
Energy, frequency and wavelength as a function of temperature.
Table 32.
Energy, frequency and wavelength as a function of temperature.
In my opinion, if we continue to lower the temperature, we will reach a critical point, an inflection point, in which a transition or phase change of matter will occur.
In item 7. ANALYSIS OF THE ORIGIN OF ELEMENTARY PARTICLES USING THE THEORY OF THE GENERALIZATION OF THE BOLTZMANN CONSTANT IN CURVED SPACE-TIME, we analyse how important temperature is in the formation of elemental particles.
For low temperatures, the reverse process occurs, we will reach a critical inflection point Tc, in which the disintegration of the elementary particles occurs, separating the gravitons from the elemental electrical content.
The critical temperature, or inflection point, is the temperature at which the matter reaches (0) Kelvin.
This separation produces a repulsive force, which causes the temperature to reach values close to zero (0) kelvin.
In a simple analysis we are going to justify why the temperature reaches absolute zero, in an environment of repulsive gravity.
i) Let's consider the ideal gas equation:
PV = n Kв T
V = constant, repulsive forces act
ΔP V = n Kв ΔT
(Pf – Pi) V = n Kв (Tf – Ti)
In an environment in which repulsive gravity act, the final pressure will be lower than the initial pressure, therefore the value of (Pf - Pi) will be negative; this implies that the final temperature will be lower than the initial temperature.
In conclusion, in an environment in which repulsive gravity act, disintegration of matter, the temperature is zero (0) Kelvin.
The lower temperature limit corresponds to when the particles and bosons disappear. Only the elemental energy quanta remain in minimum energy values.
Example 6:
Quantum entanglement and the Bose-Einstein condensate
In the paper: RLC Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time; we write the equation that defines the temperature of the Bose Einstein condensate:
According to the information of Cauê Muraro - Agência USP - 10/30/2007, the temperature of a Bose-Einstein condensate for 100,000 rubidium atoms corresponds to Tcmin = 180 nK.
Where Tcmin, low temperature Bose-Einstein condensate.
For Kв = 1.38 10⁻²³ J/K and rubidium atoms corresponds:
Tcmin = 180 nk
Approximate critical temperature of the Bose-Einstein condensate for low temperatures, with rubidium atoms.
Let's calculate Tcmax, for Kʙ-eff = 1.78 10⁻⁴³ J/K
Where Tcmax, High temperature Bose-Einstein condensate.
Tcmax, we are going to calculate considering the relationship between the Boltzmann´s constant Kʙ = 1.38 10⁻²³ J/K, for flat space-time and Kв-eff = 1.78 10⁻⁴³ J/K for curved space-time.
For Kʙ-eff = 1.78 10⁻⁴³ J/K and rubidium atoms corresponds:
Tcmax = 180 nk / 1.78 10⁻²⁰ = 1.01 10¹³ K
Tcmax = 1.01 10¹³ K
Critical temperature of the Bose-Einstein condensate for high temperatures with rubidium atoms.
Here we put forward the hypothesis that for an effective Boltzmann´s constant Kʙ-eff = 1.78 10⁻⁴³ J/K, there is a temperature Tcmax, that corresponds to a high temperature Bose Einstein condensate.
For a temperature of approximately 1.01 10¹³ K, in a plasma of quarks-gluons, a phase transition occurs that gives rise to a Bosonic condensate at high temperatures, which is characterized by being very energetic.
We can interpret it as follows, when a star collapses and a black hole is formed, we can affirm that a high-temperature Bose-Einstein condensate exists inside a black hole.
In analogy with the properties of materials at very low temperatures, super fluids and superconductivity; quark-gluon plasma achieves similar exotic properties, but not with atoms and molecules as we normally know.
these properties are achieved for the quark-gluon plasma, a superfluid or super solid, the main property of which makes this liquid or solid behave like isolated quarks, allowing the gluons to stack up neatly in an infinite cascade of energy; making it the most energetic matter in the universe.
We also said that quarks are fermions and gluons are bosons, but in black holes, by analogy with what happens with superconducting materials and super fluids and super solids; the plasma of quarks and gluons as a whole act as a Bose-Einstein condensate, as a single atom whose macroscopic properties are unique.
Here we hypothesize that quantum entanglement is related to the Bose-Einstein condensate, that is, there is quantum entanglement for a Bose-Einstein condensate of low temperature Tcmin and there is also quantum entanglement for a Bose-Einstein condensate of high temperature Tcmax.
We are familiar with low temperature quantum entanglement, Tcmin, in quantum computers, for Kʙ = 1.38 10⁻²³ J/K.
At high temperatures, Tcmax, for Kʙ = 1.78 10⁻⁴³ J/K, quantum entanglement is given to calculate the viscosity of the quark-gluon plasma.
Using duality DST (ADS) = EFQT (CFT)
We can use the Boltzmann´s constant of the quark-gluon plasma or eventually the Boltzmann´s constant for a black hole, interchangeably, to calculate the viscosity of the quark-gluon plasma, which will give us the same result.
Boltzmann´s constant for quark-gluon plasma: Kʙ-eff = 0.76 10⁻⁴¹ J/K.
Boltzmann´s constant for black hole: Kʙ-eff = 1.78 10⁻⁴³ J/K.
9. BLACK HOLE AND BIG BANG
To conclude and demonstrate the scope of the theory of everything (T.O.E.) that we have developed; in this section, we are going to propose a physical-mathematical model for black holes and we are also going to demonstrate using the Newman-Kerr diagrams that the Big Bang originates through the disintegration of a black hole.
9.1. The Penrose Property with a Cosmological Constant
Before beginning our analysis, we are going to make a reference to the paper entitled: The Penrose Property with a Cosmological Constant; which provides us with a description of the characteristics of space-time, according to the cosmological constant being ꓥ > 0, ꓥ = 0, ꓥ < 0, with respect to its mass, m > 0, m = 0 and m < 0.
We can represent this in the following table:
where a dash indicates that this spacetime has not been considered here.
A detailed analysis of the equations that demonstrate the results of
Table 33 can be seen in the paper:
The Penrose Property with a Cosmological Constant
In
Table 33, it is observed for a space-time anti de Sitter ADS (ꓥ < 0), of dimension n > 3, the Penrose property is satisfied for: m < 0.
Next, we are going to analyse a very important segment of the conclusion of the paper:
The Penrose Property with a Cosmological Constant, which is related to what is shown in
Table 33:
In order to rule out a formulation of quantum gravity based on a fixed background Minkowski spacetime, Penrose showed that it was sufficient to find one physically relevant spacetime which satisfies the non-timelike boundary version of the Penrose property. For asymptotically de Sitter spacetimes, the Schwarzschild-de Sitter black hole satisfies this property and hence rules out a SO(d+11) covariant construction of quantum gravity based on a background de Sitter spacetime. Note that unlike in the asymptotically at case, such a construction is ruled out in d+1 dimensions for any d > 3. For asymptotically anti-de Sitter spacetimes we can rule out a quantum gravity construction if we are able to find a physically relevant spacetime satisfying the timelike boundary version of the Penrose property (Definition 2.9). However, the spacetime we have found which satisfies this is the negative mass Schwarzschild-AdS spacetime which we may regard as not being physically relevant. Furthermore, the Theorem of Gao and Wald (Theorem 2.10) shows that this property fails for spacetimes which focus null geodesics. These are spacetimes we would like to regard as physical since they are associated with spacetimes containing positive energy densities. As a result, we are unable to rule out a quantum gravity construction based on a fixed background anti-de Sitter spacetime.
In this segment of the conclusion, we are going to highlight the following:
However, the spacetime we have found which satisfies this is the negative mass Schwarzschild-AdS spacetime which we may regard as not being physically relevant.
I want to get to this point precisely; if we look at
Table 33 and consider the negative mass as not relevant in an ADS space-time, I think it is a very serious error.
It is here, where the theory: RLC electrical modelling of a black hole and the universe, appears and becomes relevant.
Which proposes the following:
We will consider the total mass of a black hole to consist of the sum of baryonic mass m and dark matter mass
, considering dark matter as an imaginary number.
Which we can write in the following way:
Where M is the total mass of a black hole, m is the baryonic mass;
corresponds to dark matter mass and i is the irrational number
. This equation is in analogy to impedance of an RC circuit.
Where Z represents impedance; R represents resistance and Xc represents capacitive reactance.
Here we put forward the hypothesis that the big bang is the convolution of the energy released by disintegration of the black hole with the space-time surrounding the black hole, being defined as:
Where is the total mass M of a black hole, Ɛ is the space-time surrounding the black hole and ``*´´ is the convolution symbol.
We can simplify it and consider it analogous to an RLC circuit.
Where RC represents a black hole and L represents the space-time around a black hole.
the resolution of the quadratic differential equation of the RLC circuit will determine how space-time will expand after the Big Bang and the bandwidth of the equation will give us the spectrum of gravitational waves that originated during the Big Bang.
Briefly, we have described the theory: RLC electrical modelling of a black hole and the early universe.
We can see that the definition of a black hole contains negative mass, which is very relevant; It determines the relativistic mass of the dark matter contained inside a black hole.
Just as a capacitor stores electrical energy, in analogy, we can consider a black hole as a capacitor that stores gravitational potential energy.
Just as a capacitor is made up of a real part and a negative imaginary part, analogously, the physical idea of considering a black hole formed by a baryon mass and a negative mass or negative imaginary mass, depending on how we consider it, is physically possible.
The introduction of the imaginary number i = , associated with the mass δ, adds a new dimension to the interpretation given to the mass δ; however, in analogy to the RC circuit; despite talking about negative mass or negative imaginary mass, mass δ has a real existence. The interpretation given for the mass δ is the following: mass δ generates a rotation force Ft that makes the black hole rotate; Ft lag by 90 degrees the force Fg that is generated by the mass m, which directed into the interior of the hole black. Let us remember that the total mass of a black hole is M = m - i δ.
The analysis carried out by Dr Peter Cameron, which is represented in
Table 33, is of utmost importance, will allow us to carry out a new interpretation of the extended Kerr-Newman diagram using the theory of the paper:
Rlc Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time; for a space-time anti de Sitter ADS (ꓥ < 0) of dimension n > 3, for m < 0.
It is also important to highlight the conditions:
These conditions are very relevant in flat space-time (ꓥ = 0) and de Sitter space-time (ꓥ > 0).
In analogy to what happens in a curved space-time (ꓥ < 0); in a flat space-time (ꓥ = 0) and in a de Sitter space-time (ꓥ > 0), there is a rotation(torsion) force to the force of gravitational attraction, which makes a body rotate clockwise.
In the case of a black hole, the rotation force generated by dark matter mass causes the black hole to rotate counter-clockwise. In the case of particle disintegrations, the particles experience a repulsion force and a rotation(torsion) force that causes them to rotate clockwise.
This is demonstrated in the paper: Rlc Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time.
9.2. Modelling of a Black Hole
We are going to use the theory developed in the paper: Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electric Generator. Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons, Inside a Neutron.
Let us remember the following, in the particle accelerator LHC, it has been successfully isolated antimatter, that is, matter with energy (-ℏω).
We will also remember, when a black hole forms, a star of more than 25 solar masses explodes in a supernova and collapses due to gravity, giving rise to a black hole of approximately 3 solar masses. It is important to note that the star loses 22 solar masses to produce a black hole of 3 solar masses.
Let's also remember the following definition of a black hole:
A black hole is a plasma of quarks and gluons, a superfluid or a super-solid, which forms a high-temperature bosonic-fermionic condensate, characterized because the matter is in its state of maximum energy, that is, as a whole it behaves like an isolated quark.
This definition is in the paper: Rlc Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time.
In the definition of a black hole, we are going to highlight the word isolated quark, we could interpret this as meaning that inside a black hole there is no quarks - antiquarks - gluons interaction, only the quarks interaction exists.
With this we are proposing that inside a black hole there is no antimatter (-ℏω), that is, the interior of a black hole is made up only of matter (ℏω).
Recalling again that at the LHC it was possible to isolate antimatter, that is, matter (-ℏω) and also remembering that to form a black hole a star of 25 solar masses explodes in a supernova and by gravitational collapse forms a black hole of 3 solar masses, we are wondering!!!!!!
Could it happen that the gravitational collapse process separates matter from anti-matter in analogy to what happens at the LHC?
The explosion of a supernova goes beyond chemical energy or nuclear energy; that is why we propose that a supernova when it explodes separates matter from antimatter, in other words, the black hole that remains would be made up of matter and the antimatter expands in the space-time that surrounds the black hole.
Let us remember that for temperatures greater than 10¹⁵ kelvin, the symmetry breaking of the electro-weak force occurs and consequently the separation of the electromagnetic force field and the weak force field; for higher temperatures, the interactions of the electromagnetic force field and those of weak force do not exist.
According to what is stated in the theory RLC Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann's Constant in Curved Space-Time; a black hole has a temperature of 10¹³ K, that is, the supernova explosion to form a black hole produces a temperature higher than 10¹³ K; in this way, it is possible to reach at the temperature of symmetry breaking, which would mean that a black hole would form a high-temperature Bose-Einstein condensate, a single primordial atom.
Hypothesis: the disappearance of the interactions of the electromagnetic force field and the weak force field together with the gravitational collapse of a star of more than 25 solar masses due to the explosion of a supernova generates a black hole of mass (ℏω), matter and antimatter; that is, a black hole without mass (-ℏω), matter and antimatter.
Taking the above into account, we are going to propose the following vector model of a black hole and we are going to compare it with the vector model of a neutron.
We compare it with a neutron because we assume that the net charge of a black hole is also zero.
Figure 111.
Equivalent Neutron / Black Hole.
Figure 111.
Equivalent Neutron / Black Hole.
We are going to carry out mathematical calculations to see if we can obtain important conclusions:
We will calculate the Schwarzschild´s radius for a black hole of 3 solar masses.
M = 6 10³⁰ kg
mn = 939.56 MeV/c²
mn = 1.675 10ˉ²⁷ kg
Where mn is mass of the neutron.
Rs = 2GM / c²
Rs = (2 x 6.67 10¯¹¹ x 6 10³⁰) / 9 10¹⁶ = 80.04 10¹⁹ / 9 10¹⁶
Rs = 8.89 10³ m
Where Rs is Schwarzschild´s radius.
We will calculate the volume of a black hole of three solar masses:
V = 4/3 ᴨ R³
V = 1.33 x 3.14 x (8.89 10³) ³
V = 1.33 x 3.14 x 702.59 10⁹
V = 2934.15 10⁹
Where V is volume of the black hole.
We will calculate the volume of a neutron.
Rn = 0.4 10⁻¹⁵ m
Where Rn is radius of the neutron.
Vn = 4/3 ᴨ R³
Vn = 4/3 ᴨ R³ = 4/3 x 3.14 x (0.4 10⁻¹⁵) ³ = 0.267 10⁻⁴⁵ mᶾ, volume of the neutron.
Vn = 0.267 10⁻⁴⁵ mᶾ,
Where Vn is volume of the neutron.
We will define D, a scale factor that represents the ratio of the volume of a black hole of 3 solar masses to the volume of the neutron.
D = V / Vn
Where D is scale factor.
D = V / Vn
D = V / Vn = 2934.15 10⁹ / 0.267 10⁻⁴⁵ = 10989.34 10⁵⁴
D = 10.98 10⁵⁷
We divide the mass of the black hole by the factor D.
Mn = M/D
Mn = 6 10³⁰ kg / 10.98 10 ⁵⁷ kg
Mn = 0.54 10 ⁻²⁷ kg
If we divide Mn by mn, we obtain:
K = Mn / mn = 0.54 10⁻²⁷ / 1.67 10⁻²⁷ = 0.32
K = 0.32
Mn = 939.56 x 0.32 = 300.65 MeV/c
Mn = 300.65 MeV/c
Where Mn is the mass contained in a black hole, in a volume equivalent to that of the neutron.
This result that we obtained for Mn is very interesting, it is telling us that the mass content in a volume equivalent to that of a neutron inside a black hole is less than the mass of the neutron; precisely this coincides with our assumption that inside a black hole we do not have antimatter, a black hole is formed only by matter.
If the statement is true: a black hole is formed only by matter, the antimatter is expelled when the collapse of a star occurs and a supernova explosion occurs; this would explain the enigma of antimatter during the Big Bang, it would explain why the Big Bang produces a universe of matter and not antimatter.
Figure 112.
Vector Diagram of a Black Hole.
Figure 112.
Vector Diagram of a Black Hole.
Considering the conversion factor, we calculate the value of interaction 2, for the six corresponding dipoles, which we will represent below:
R(DD)B = 28.54 MeV/c²
R(DU)G = 60.88 MeV/c²
B(DD)R = 28.54 MeV/c²
B(DU)G = 60.88 MeV/c²
G(UD)R = 60.88 MeV/c²
G(UD)B = 60.88 MeV/c²
We are going to represent these values in
Figure 113:
In
Figure 113, we see that the equivalent mass of the neutron inside a black hole is approximately one-third of the mass of the neutron.
We observe that the direct interaction, interaction 1, is null (0).
We observe that the cross interaction, interaction 2, the scalar sum is equal to 300.60 MeV/c² and the vector sum is zero (0).
Now we are going to present the graphic representation of the electric model of the black hole in
Figure 113:
Next, using
Figure 114 and 115, we are going to make a brief description of the internal behaviour of a black hole.
Before starting our description, let us remember that in our RLC electric model, a black hole is represented by:
Here we put forward the hypothesis of a black hole growth in analogy to an RC electric circuit that grows according to a constant Tau being defined as:
First, we will consider the total mass of a black hole to consist of the sum of baryonic mass and dark matter mass (equation 137), considering dark matter as an imaginary number.
Where M is the total mass of a black hole, m is the baryonic mass;
corresponds to dark matter mass and i is the irrational number
. This equation is in analogy to impedance of an RC circuit.
Where Z represents impedance; R represents resistance and Xc represents capacitive reactance.
If proper accelerations for the masses are introduced in equation (137) we obtain the following:
Where F is the total force, f is the force associated to baryonic mass m, and i
is the force associated to dark matter mass δ. In analogy to a phasor diagram for an RC circuit, in which the reactance phasor lags the resistance phasor R by
, we can represent the two forces associated to barionic matter and dark matter as two orthogonal vectors (
Figure 12).
Vector diagram of forces in a black hole for circular motion with constant acceleration:
taking into account Newton's equation of universal gravitation:
The sign (-) of the equation means that the force Fc is at 180 degrees with respect to the resistance R and the force Ft is also at 180 degrees from the reactance Xc.
It is important to make clear the physical interpretation of the dark matter mass δ, it is simply telling us that the force Ft due to the mass δ lag the force fc by 90 degrees, that lag is represented by the imaginary number i. Later we will determine that the mass δ, is the result of v > c inside a black hole.
Where v is the speed of a massless particle and c is the speed of light in a vacuum.
Figure 115 is represented for a circular motion with constant acceleration simply because the tangential rotation velocity of a particle is proportional to the radius from the centre of the black hole multiplied by the average angular frequency.
The contribution of (Ft, Vt) is what makes the speed of the galaxy remain constant as the radius of the galaxy grows.
Where Vt represents the rotation velocity of a galaxy, r is the radius from the galaxy, and ω is the average angular velocity of the rotation of the galaxy.
Circular motion with constant acceleration tells us that the mass input into a black hole is negligible with respect to the black hole's own mass.
The growth of a black hole according to the tau constant is an intrinsic property of a black hole and is independent of the amount of matter that enters a black hole.
To calculate the total energy associated to the black hole, we can introduce its total mass (equation 137) into:
Where E is energy; c represents the speed of light and m represents the mass. This lead to:
We can assume that during the big bang inflation phase baryonic matter mass was overrepresented compared to dark matter mass together with an infinitesimal momentum, which would give us from equation (141) the following:
As expected, this result corresponds to the total energy of the universe at the big bang if we consider it to be made of dark matter represented as a reactance in an RC circuit.
The positive value of E is determined by matter, there is no antimatter inside a black hole.
If we consider charge as a fundamental property of matter, , represents the amount of relativistic dark matter inside the black hole at the time of disintegration.
If we consider mass as a fundamental property of matter, , represents the amount of relativistic dark matter inside a black hole, which exerts a repulsive gravitational force at the moment of disintegration. This repulsive gravitational force is what generates the dark energy after the Big Bang.
At time T0⁺, when the black hole disintegrates and the Big Bang occurs, roughly all matter was dark matter, relativistic dark matter.
We could also consider a universe at infinity proper time in which baryonic matter mass is dominant over dark matter mass, which would transform equation (141) back into equation (140) but with baryonic matter.
We are also going to remember, the collapse of a star to form a black hole, separates the matter from the antimatter, the matter remains inside the black hole and the antimatter is expelled to the outside of the black hole, that is, into space-time.
This is telling us that the vacuum inside a black hole is less dense than the vacuum outside. We call the vacuum inside a black hole true vacuum and the vacuum outside a black hole (space-time) we call it meta-stable vacuum.
If we look at it from the point of view of the density of virtual particles, the density of virtual particles inside a black hole is lower than the density of virtual particles outside a black hole. Therefore, inside black hole, a particle like the photon could travel at a speed v > c, this allows us to state again, as the difference of v with respect to c increases, the Planck length decreases. Inside a black hole, the gravitational Planck length Lpԍ decreases with respect to the electromagnetic Planck length Lpԑ.
The decrease in Lpԍ with respect to Lpԑ is not linear like that of a shock absorber, it is similar to the movement of a corkscrew, precisely that is what generates the torsion or rotation force. This torsion force is what makes the black hole rotate counter clockwise.
This model resembles a Kerr black hole, dynamic and rotating, with a singularity inside in the form of a spiral/coil or ring, ring singularity. See
Figure 116.
Everything we have stated was analysed in the paper: RLC Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time.
Figure 116, we see that the black hole is divided into two parts, an upper hemisphere and a lower hemisphere.
The dynamics of the upper hemisphere is dominated by bosonic particles that rotate counter clockwise, these particles resemble a ring or coil, which we represent by the current I₁.
If we consider the right-hand rule, the current I₁ generates a magnetic field B that goes up inside the coil (upper hemisphere) and goes down outside the coil, as shown in
Figure 116.
The dynamics of the lower hemisphere is dominated by bosonic particles that rotate in a clockwise direction, these particles resemble a ring or coil, which we represent by the current I₂.
If we consider the right-hand rule, the current I₂ generates a magnetic field B that flows downwards inside the coil (lower hemisphere) and rises outside the coil, as shown in
Figure 116.
If we take an infinitesimal part of the upper and lower coil, we can assume that they behave like two parallel wires in which the current is in the opposite direction, in this case the magnetic force generated between the two wires whose current is in the opposite direction is a force of repulsion. Both coils generate repulsive forces between each other.
If we look at
Figure 116; the electric current I₁ with a positive charge moves counter clockwise, now if we look at the electric current I₂ with positive charges it moves clockwise; in other words, the electric field between the upper and lower coils generates a repulsion magnetic force between the upper coil and the lower coil.
In other words, there is a magnetic field B, which generates a force that causes the upper coils and the lower coil to repel each other, and there is an electric field E, which generates a force between the upper coil and the lower coil that causes both coils also repel each other.
The repulsion forces between the upper hemisphere coil and the lower hemisphere coil, generated by the magnetic and electric fields, are counteracted by the gravitational force towards the interior of the black hole.
Again, if we look at
Figure 116, there is an equatorial zone of the black hole between the upper and lower coil in which the magnetic field and the electric field are not defined. It is an indeterminate region, a turning point.
If we analyse the magnetic fields outside the black hole, at the height of the upper coil, we observe that the magnetic field has a downward direction, if we consider a particle with a positive charge, we see that the magnetic field B generates a force towards the interior of the black hole. see
Figure 116.
If we analyse the magnetic fields outside the black hole, at the height of the lower coil, we observe that the magnetic field has an upward direction, if we consider a particle with a positive charge, we see that the magnetic field B generates a force inward of the black hole. see
Figure 116.
This mechanism, recently described, tells us that the magnetic field that surrounds the black hole at the equator generates a force that causes positively charged particles to move towards the interior of the black hole and negatively charged particles are repelled, moving away from the black hole.
If we consider Hawking radiation, which tells us that a pair of particles of matter (ℏω) and antimatter (-ℏω) are produced in the event horizon of a black hole; it is assumed that the matter particles (ℏω) fall into a black hole and antimatter (-ℏω) are repelled out of a black hole. However, the magnetic field B outside a black hole at the height of the equator tells us that the particles with a positive charge of matter (ℏω) and antimatter (-ℏω), are those that fall into the interior of a black hole; and the particles with a negative charge of matter (ℏω) and antimatter (-ℏω), are repelled and move away from the black hole.
Here, let's go one step further; when we refer to (ℏω), it means positively charged particle and can be made of matter and antimatter, (-ℏω), it means negatively charged particle and can be made of matter and antimatter.
The statement is very important, it is telling us, the interior of a black hole is made up only of positive charges particles.
Inside a black hole, in the domain of gravitational force, there are only positively charged particles which behave like a Bose-Einstein condensate. The black hole becomes a giant atom with a positive charge and its event horizon indicates the limit of the gravitational envelope that encloses the positively charged particles.
Let us remember that from the scalar point of view, the black hole is made up of positively charged particles, but if we consider it from the vector point of view, the net charge resulting from a black hole is zero.
If we consider the magnetic field outside the black hole between the two coils, strong enough to generate pairs of particles with positive charge (ℏω) and negative charged (-ℏω) in a vacuum, we can affirm that this mechanism would be powerful enough to produce an accretion disk around the equator of the black hole, which the black hole would use to feed on particles and grow. The black hole is self-sustaining, it feeds itself and is not dependent on devouring stars and other bodies to grow.
If we look at the upper hemisphere, above the upper coil there is an area in which the dynamics become dominated by the magnetic field B in an upward direction. The same thing happens with the lower hemisphere, from a certain distance, the dynamics become dominated by the magnetic field B in the lower direction. An example of what is stated is a quasar.
9.3. Correlation Between Kerr-Newman Black Hole vs RLC Electrical Modelling of a Black Hole.
1) We are going to perform an analysis for the condition: M² > Q² + a²
If we observe and compare
Figure 117 and 118, we see the following:
In both models the black holes rotate around their axial axis.
In
Figure 117, we can see an ergosphere, an outer horizon and an inner horizon. We also observe that the outer and inner horizons are co-focal oblate spheroids whose focus is the ring singularity.
In
Figure 118, we can also observe an event horizon and a ring singularity, we can assume that the event horizon is co-focal oblate spheroids and whose focus is the ring singularity.
Under this condition, M² > Q² + a²; the black hole is born and grows, we can say that it represents the first moments of the life time of a black hole.
As the black hole grows, the distance between the outer horizon and the inner horizon decreases.
The particles that enter the black hole pass through the ergosphere, cross the outer horizon and the inner horizon and finally fall into the ring singularity. Inside the ring singularity (r ≤ 0) the bosonic particles move at a speed greater than the speed of light , v > c, which generates an additional mass which we represent in our model as – iδ (see equation 137). This additional mass generates a gravitational force that is not attractive and is the gravitational force that gives rise to dark matter δ.
Let us remember that a black hole grows in the same way as the Tau constant of an RC circuit (equation 136).
We are going to represent the graphs and calculations that describe the growth of a black hole, the complete mathematical development can be found in the paper: RLC Electrical Modelling of Black Hole and Early Universe. Generalization of the Boltzmann´s constant in curved spacetime.
Figure 119.
Represents the variation of speed Cɢ, as a function of temperature T, inside a black hole.
Figure 119.
Represents the variation of speed Cɢ, as a function of temperature T, inside a black hole.
Now we are going to present the Penrose Diagram:
Figure 118, we see that the spheroid that represents a black hole can be divided into two parts, an upper part and a lower part.
Figure 120, if we consider the yellow vertical line, we can also divide the graph into two parts, a spatial part representing the right side and a spatial part representing the left side.
If we consider a test particle, we see in
Figure 118 that it can enter the upper part, at the equator of the spheroid, cross the event horizon and head to the upper singularity. There is also another option in which the test particle could enter the lower part of the equator, in the spheroid, cross the event horizon and head to the lower singularity.
If we consider a test particle, we see in
Figure 120, in analogy with
Figure 118, that it can enter the left side of the black hole, in the ergosphere, cross the event horizon, pass through the wormhole region and end up in the antiverse region. There is also another option in which the test particle could enter on the right side of the black hole, in the ergosphere, cross the event horizon, cross the parallel wormhole region and end up in the parallel antiverse region.
If we look at
Figure 118, both currents I₁ and I₂ have a positive charge and move in the opposite direction. We observe that current I₁ moves counter clockwise and generates an upward magnetic field (blue); Current I₂ moves clockwise and generates a downward magnetic field (orange).
Both the electric and magnetic force generated by currents I₁ and I₂ produce a repulsion force between the coils, this is counteracted only by the gravitational force.
Figure 120, if we consider a test particle, we see that there is a repulsion force between the left side of the graph and the right side, for example, if a test particle (1) that enters the black hole, enters the ergosphere, enter the wormhole and antiverse; if we consider
Figure 118, by analogy the particle heads upward until it reaches the ring singularity.
Now we consider the test particle (2) that enters the black hole, ergosphere, parallel wormhole, parallel antiverse, by analogy to
Figure 118, the test particle heads downward until it reaches the ring singularity. The test particle (1) is directed upward, while the test particle (2) is directed downward, as if both positive particles were under opposite forces.
There is an analogy between graph 118 and graph 120; the upper part of graph 118, from the equator up, corresponds to the left symmetrical region of the vertical yellow line of graph 120; the lower part of graph 118, from the equator downwards, corresponds to the right symmetrical part of the vertical yellow line of graph 120.
Another important analogy that we must highlight is the ring singularity, above the equator in
Figure 118, which corresponds to the antiverse in the left symmetry of graph 120; We must also highlight the ring singularity below the equator in
Figure 118, which corresponds to the parallel antiverse in the right symmetry of graph 120.
Finally, it is important to note that the black hole grows and as it increases in size, the regions of the black hole that we call ergosphere, wormhole (parallel wormole) and antiverse (parallel antiverse) also grow.
Here, it is important to note that although the black hole grows, nothing material comes out of the black hole, therefore we can represent this in Figure 120 only with the yellow triangle. What is stated here is very important.
2) We are going to perform an analysis for the condition: M² = Q² + a²
The Kerr-Newman geometry is called extremal when the outer and inner horizons coincide:
We see that in this condition there is a single event horizon, which we are going to represent in the following figure:
We could express the relationship M² = Q² + a² in another way:
M² / (Q² + a²) = 1
This is telling us that the growth of a black hole has a limit, that the amount of matter it devours is limited and if it exceeds that limit it has to be expelled in some way; therefore, the amount of matter that enters the interior of the ring singularity (antiverse) is limited by the mass M of the black hole.
For example, we could assume that this limit is generally exceeded when a stellar black hole devours a star, a quasar forms.
Here, it is important to note that although the black hole grows, nothing material comes out of the black hole, therefore we can represent this inFigure 120only with the yellow triangle.
3) We are going to perform an analysis for the condition: M² < Q² + a²
We could express the relationship M² < Q² + a² in another way:
M² / (Q² + a²) < 1
In this condition, the event horizon disappears and we say that we have a naked singularity.
In this condition, we can observe that the amount of matter (charge) that the black hole devours exceeds its mass.
We said that the growth of a black hole is limited by its mass M, that is, if the black hole devours a greater amount of matter that its mass M, then somehow the black hole has to eliminate the excess matter it is ingesting.
We are going to represent the statement in the following figure:
Figure 122.
Spatial geometry of a super-extremal Kerr black hole with spin parameter a = 104M. A super-extremal black hole has no horizons.
Figure 122.
Spatial geometry of a super-extremal Kerr black hole with spin parameter a = 104M. A super-extremal black hole has no horizons.
Let's interpret what we said in a Penrose diagram.
Figure 123, Let's consider two sets of test particles, the two sets of test particles enter the black hole (ergosphere), one set through the horizon and the other set through the parallel horizon; now let's look at
Figure 118, one set of test particles enters above the equator of the spheroid and the other set of particles enters below the equator of the spheroid.
Let us remember that we are under the condition: M² < Q² + a²
Figure 123, the first set that was in the parallel universe, enters the black hole (ergosphere) through the parallel horizon, part of that set of particles is devoured by the black hole and ends up in the antiverse; the rest of the particles leave the black hole, crosses the inner antihorizon and ends in the new parallel universe. The second set of particles follows a similar path, it enters the black hole (ergosphere) through the horizon, part of that set of particles is devoured by the black hole and ends up in the parallel antiverse; the rest of the particles leave the black hole, crosses the parallel inner antihorizon and ends in the new universe.
If we look at
Figure 118, the first set of particles enters the black hole above the equator of the spheroid, part of the set of particles is devoured by the black hole and goes to the ring singularity and the rest of the particles are expelled out of the black hole, upwards. Similarly, the second set of particles enters the black hole through the lower part of the equator of the spheroid, part of the set of particles is devoured by the black hole and goes to the ring singularity and the rest of the particles are expelled from the hole black, downwards.
Figure 120 represents a black hole that grows, under the condition M² ≥ Q² + a², which is telling us that no matter comes out of the black hole. This is represented by the inverted yellow triangle.
Figure 123 represents a black hole that grows and has an associated relativistic jet, under the condition M² < Q² + a², which is telling us that part of the matter that the black hole devours is expelled. This is represented by the two highlighted triangles; the yellow triangle representing the black hole devouring matter and the orange triangle (white hole) representing the amount of matter ejected from the black hole.
An example of the true meaning of what
Figure 123 represents would be a quasar.
Reissner-Nordström Black Hole, the inflationary instability, under the condition Q > M, at point X, an inflationary instability occurs that produces feedback which generates the relativistic jets. The interior mass is not the only thing that increases exponentially during mass inflation. The proper density and pressure, and the Weyl scalar (all gauge-invariant scalars) exponentiate together.
This is analogous to what happens in a black hole with the Kerr-Newman geometry, part of the mass that enters the black hole ends up in the antiverse (ring singularity) and the rest of the mass is ejected in the form of a relativistic jet, is given for the condition M² < Q² + a².
Under this interpretation, the universe, the parallel universe, the new universe and the new parallel universe actually represent our only universe. See
Figure 123.
Under this interpretation, the antiverse and the parallel antiverse in
Figure 120 and 123, represent in
Figure 118, the ring singularity that is at the top of the equator of the spheroid and the ring singularity that is at the bottom of the equator of the spheroid.
According to our description, the black hole model in
Figure 118 perfectly emulates the black hole model represented in
Figure 123, corresponding Penrose diagram of the Newman-Kerr geometry.
4) We are going to perform an analysis for the condition: M = Mc
This condition arises from the theory of the RLC electric model of a black hole and the early universe. However, the Newman Kerr diagram is used to give it a double interpretation.
Here, we are going to analyse the condition in which the black hole reaches its critical mass Mc.
In the theory of the paper
: RLC Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time; we put forward the hypothesis of a black hole growth in analogy to an RC electric circuit that grows according to a constant Tau being defined as:
In a capacitor when its charge reaches the value of 5, we say that the capacitor reached its maximum charge, in analogy to the capacitor; when the black hole reaches the value of 5 it reaches its maximum mass value; Let us remember that a capacitor stores electric energy and a black hole stores gravitational potential energy.
Let us remember that the mass of a black hole in the theory of the paper:
Rlc Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time; it is represented by the following equation:
Where M is the total mass of a black hole, m is the baryonic mass m; corresponds to dark matter and (i) is the irrational number . This equation is in analogy to impedance of an RC circuit.
To calculate the total energy associated to the black hole, we can introduce its total mass (equation 145) into:
Where E is energy; c represents the speed of light and m represents the mass. This lead to:
We can assume that during the big bang inflation phase baryonic matter was overrepresented compared to dark matter together with an infinitesimal momentum, which would give us from equation (51) the following:
As expected, this result corresponds to the total energy of the universe at the big bang if we consider it to be made of dark matter represented as a reactance in an RC circuit.
The positive value of E is determined by matter, there is no antimatter inside a black hole.
If we consider charge as a fundamental property of matter, , represents the amount of relativistic dark matter inside the black hole at the time of disintegration.
If we consider mass as a fundamental property of matter, , represents the amount of relativistic dark matter inside a black hole, which exerts a repulsive gravitational force at the moment of disintegration. This repulsive gravitational force is what generates the cosmic inflation and dark energy after the Big Bang.
At time T0, when the black hole disintegrates and the Big Bang occurs, roughly all matter was dark matter . Relativistic dark matter.
We could also consider a universe at infinity proper time in which baryonic matter is dominant over dark matter, which would transform equation (147) back into equation (146) but with baryonic matter.
Here we put forward the hypothesis that the big bang is the convolution of the energy released by disintegration of the black hole with the space-time surrounding the black hole, being defined as:
Where is the total mass M of a black hole, Ɛ is the space-time surrounding the black hole and ``*´´ is the convolution symbol.
Equation (150) can be simplified and considered analogous to an RLC circuit.
Where RC represents a black hole and L represents the space-time around a black hole.
the resolution of the quadratic differential equation of the RLC circuit will determine how space-time will expand after the Big Bang and the bandwidth of the equation will give us the gravitational waves spectrum that originated during the Big Bang.
The growth of the black hole from its birth until it reaches the value of 5
is represented in
Table 34 and
Figure 119.
e) In item 1 of the
Table 34, for the following parameters, T = 10¹³ K, Cɢ = C = 310⁸ m/s, calculating we get the following values:
m = 6 10³⁰ kg, baryonic mass.
δ = 0, dark matter mass.
M = m = 6 10³⁰ kg
Rs = 8.89 10³ m, Schwarzschild´s radius.
f) In item 9 of the
Table 34, for the following parameters, T = 5 10²⁶ K, Cɢ = 3 10²¹ m/s, C = 310⁸ m/s, calculating we get the following values:
m = 1.20 10⁵⁶ kg, baryonic mass.
δ = 1.20 10⁸² kg, dark matter mass.
M = δ = 1.20 10⁸² kg
Rs = 1.77 10²⁹ m, Schwarzschild´s radius.
It is important to emphasize, for the time t equal to 5τ, at the moment the disintegration of the black hole occurs, the big bang originates, the total baryonic mass of the universe corresponds to: m = 10⁵⁶ kg.
g) It is important to highlight, for time t equal to 5τ, at the moment in which the disintegration of the black hole occurs, the big bang originates, the total mass of the dark matter of the universe corresponds to: δ = 10⁸² kg.
h) It is important to highlight the following, when scientists calculated the total baryon mass of the universe, they gave them the following value m = 10⁵⁴ kg, in our calculation, the total baryon mass of the universe gave the following value, m = 10⁵⁶ kg; 100 times greater, I think the difference between the calculations is in the order taking into account the complexity of the calculation.
Figure 119, shows the growth of the tau (τ) constant, as a function of speed vs. temperature.
Figure 118, we see that the upper and lower ring singularity are formed by positively charged particles.
If we consider the electric field E, both (ring singularity) exert a repulsive force. If we consider the magnetic field B, both (ring singularity) exert a repulsive force. Therefore, the only force holding the black hole together is the gravitational force. Above the critical mass of the black hole, the force of repulsion of the electric field and the magnetic field Fr is greater than the force of gravitational attraction Fg, the disintegration of the black hole occurs, that is, a white hole is produced, what we call the Big Bang, this process gives rise to cosmic inflation.
Next, we are going to explain the process that gives rise to cosmic inflation.
Cosmic Inflation
Let's look at
Figure 120 and 123; consider that we move only in the vertical Y time axis, the X axis of space is null. If we consider the instant of time To⁻, we observe that we are in a black hole; if we consider the instant of time To⁺, we observe that we are in a white hole. The instant of time To is an inflection point at which the transition from a black hole to a white hole occurs.
Now let's consider a test particle (1) that moves in the X axis, the Y time axis is null. We begin our movement on the right side through the parallel antiverse, we continue to the left and cross the region of the parallel wormhole, until we reach the inflection point.
Now let's consider a test particle (2) that moves in the X axis, the Y time axis is null. We begin our movement on the left side along the antiverse, we continue to the right, we cross the wormhole region, until we reach the inflection point X.
Let us observe that the test particles (1) and the test particle (2) are at the inflection point, but cannot exceed it.
Now, if we analyse the inflection point, we see that it is a space-type point, its trajectory is space-type, this implies that in order to cross it we need to move at a speed greater than the speed of light, v > c.
If we analyse section 2.9, Antiverse; we see that there is a region for negative radii, r < 0 which corresponds to a negative mass, M < 0.
Later we will analyse the importance of negative mass.
Now we will analyse
Figure 118, we will use two test particles for our analysis, the test particle (1) and the test particle (2). We will consider that the test particle (1) is directed towards the upper singularity ring and the test particle (2) is directed towards the lower singularity ring.
The test particle (1) that is in the upper singularity ring cannot go to the lower singularity ring.
The test particle (2) that is in the lower singularity ring cannot go to the upper singularity ring.
Therefore, in the black hole model represented in
Figure 118, there is also an inflection point.
Here, we are going to hypothesize that the black hole reaches its critical mass Mc, collapses, disintegrates and transforms into a white hole, this process generates cosmic inflation.
This is the only condition in which a test particle can cross the inflection point whose velocity v > c.
If we look at
Figure 123, at time To, the amount of matter in the black hole is the same as that of the white hole. We can deduce this by comparing the orange triangle with the yellow triangle.
There is a second condition in which a test particle can cross the inflection point, it is when a black hole behaves like a quasar, generating relativistic jets. In this condition that we have already analysed, the inflection point exhibits a feedback inflationary instability, which is what generates the relativistic jets and occurs for the condition M² < Q² + a²
Now we are going to analyse the importance of negative mass, M < 0 (Antiverse), in the origin of cosmic inflation.
We said that the mass of a black hole can be represented in analogy to that of an RC circuit as follows:
Where M is the total mass of a black hole, m is the baryonic mass; δ corresponds to dark matter and (i) is the irrational number √(-1).
We can represent this equation in the following way:
In equation 154, we see that the mass of dark matter δ can be represented as a negative mass.
We said that a black hole grows like a capacitor, following the Tau constant.
In item 9 of the
Table 33, for the following parameters, T = 5 10²⁶ K, Cɢ = 3 10²¹ m/s, C = 310⁸ m/s, calculating we get the following values:
m = 1.20 10⁵⁶ kg, baryonic mass.
δ = 1.20 10⁸² kg, dark matter mass.
M = δ = 1.20 10⁸² kg
Rs = 1.77 10²⁹ m, Schwarzschild radius.
These values correspond to the moment of time To, in which the black hole reaches its critical mass Mc, collapses, disintegrates, transforming into a white hole.
We will use these values to calculate your Plank Length.
At instant To, the Planck length inside a black hole (white hole) corresponds to Lpԍ = 1.28 10⁻⁵⁴ m.
If we consider the Planck length Lpɛ, the minimum length of space-time, like a spring and due to the action of v > c (c = 300,000 km/s), this length decreases in values of Lpɢ, that is, Lpɢ < Lpɛ, allowing us to imagine the immense forces involved in compressing space-time of length Lpɛ into smaller values of space-time Lpɢ. The immense energy stored and released in the spring of length Lpɢ, to recover its initial length Lpɛ, is the cause of the exponential expansion of space-time (cosmic inflation) in the first moments of the Big Bang.
At time T0, when the black hole disintegrates and the Big Bang occurs, roughly all matter was dark matter, relativistic dark matter. This is represented in equation (148).
9.3. Inside a Black Hole
We are going to use the paper: Proton decay and inverse neutron decay, we will use the new particles proposed in this article to determine what really exists inside black holes.
The new proposed particles are the following:
• Dproton
• Protoniu
• Dneutron
• Neutroniumd
In the following Figure we are going to present the main characteristics of these particles along with those of the proton and the neutron for comparison.
We said that the collapse of a star of more than 25 solar masses produces a black hole of 3 solar masses.
In section 9.2 Modelling of a black hole; we calculated the equivalent neutron/black hole model, which gave us an equivalent neutron mass of 300 MeV/c².
Figure 125.
Equivalent Neutron/ Black Hole.
Figure 125.
Equivalent Neutron/ Black Hole.
Taking into account the above and considering the equivalent neutron/black hole model, we are going to hypothesize that the collapse of a star larger than 25 suns produces a black hole of 3 solar masses, which contains the neutroniumd particle inside.
We are going to show the graph of the neutroniumd particle:
If we look at
Figure 126, the
neutroniumd particle is made up of three D quarks, matter (-ℏ
ω), it does not contain matter (ℏ
ω); the configuration of these three D quarks is analogous to that of an electric generator, that is to say that each quark can be represented by three vectors out of phase by 120 degrees whose vector sum is zero and whose scalar sum is (-1).
As seen in
Figure 126, the
neutroniumd particle has a mass m = 443.10 MeV/c².
The scalar charge of the neutroniumd particle is (-1) but the vectorial charge is zero (0). In other words, the black hole would be formed by negatively charged particles (-ℏω) but whose vector sum is zero (0). The distribution of the D-quark vectors inside the black hole is such that the resulting charge on the black hole is zero (0).
In the following graph, we are going to represent the black hole model formed by neutromiumd particles.
It can be seen in
Figure 127 that negatively charged particles (-ℏ
ω) enter the black hole and positively charged particles (ℏ
ω) are repelled from the black hole.
At this stage, the black hole grows by devouring negatively charged particles (-ℏω).
As the black hole grows, the mass, pressure, density, etc. increases and another transformation occurs inside the black holes.
We are going to analyse the following transformation that happens inside black holes.
Let's hypothesize the following, as a black hole grows and reaches a critical point of pressure, volume, temperature, density, etc., the neutroniumd particle decays into the protoniu particle.
This decay of the neutroniumd particle in the protoniu particle is very important and explains the jets that quasars produce.
If we compare
Figure 126 and 128, we observe that the mass of the Neutroniumd particle is 443 MeV/c² and the mass of the protoniu particle is 253 MeV/c².
We observe that the D quarks have to decay into U quarks, this is analogous to βˉ decay, therefore electrons, antineutrinos and electromagnetic energy will be produced.
Neutroniumd → protoniu + e⁻ + ṽ + ∆E
D → U + e⁻ + ṽ + ∆E
Inside a black hole the neutroniumd particle (-ℏω) decays into the protoniu particle (ℏω).
Electrons, antineutrinos and electromagnetic radiation are sent in the jet, this would explain why the jet particles are so collimated.
The relativistic jet could be explained for the condition M² < Q² + a², in which there is a naked singularity.
Along with the jet, we must include the particles that are expelled by the action of the magnetic field of the accretion disk.
When the black hole is formed by the neutroniumd particle, the magnetic field B, forces negative particles (-ℏω) into the interior of the black hole.
When the black hole is formed by the protoniu particle, the magnetic field B, forces positive particles (ℏω) to enter the interior of the black hole.
In other words, we have black holes formed by negative charges neutroniumd and black holes formed by positive charges protoniu.
According to this theory, the relativistic jet of quasars is produced when the neutroniumd particles, formed by the D quark, decay into the protoniu particle, formed by the U quark, inside the black hole; this is another condition in which quasers occur.
If we compare
Figure 125 - Equivalent Neutron/ Black Hole with
Figure 128 - protoniu; We observe that the masses are approximately equal (300 ≈ 253) Mev/c².
In the following graph, we are going to represent the black hole model formed by protoniu particles.
Black holes can be formed by negatively charged particles (neutroniumd) or positively charged particles (protoniu), however, it is important to know that the net charge of black holes is zero, due to their vector configuration, whether they are formed by positively or negatively charged particles.
Another important characteristic of black holes is that they are formed by positively charged matter (ℏω), and negatively charged matter (-ℏω); the process of formation of a black hole separates (ℏω) of the (-ℏω).
If we look atFigure 116, 118, 127 and 129; We see that we write 'Black Hole / Magnetic Monopole', this is due to the following: if we carefully analyse our black hole model, they behave the same as magnetic monopoles.
9.5. Black Holes Are True Generators of Matter in the Universe
We will determine the temperature of a stellar black hole of three solar masses, using the Boltzmann constants given by Kʙε and Kʙɢ.
Where Kʙε is the electromagnetic Boltzmann´s constant and Kʙɢ is the gravitational Boltzmann´s constant.
Kʙε = 1.38 10ˉ²³ J/K
Kʙɢ = 1.78 10ˉ⁴³ J/K
Tʙʜ = Tε + Tɢ, temperature of a BH.
Tε = hc³ / (8 x ᴨ x Kʙε x G x M) = 9.9 10⁻¹⁶ K
Tɢ = hc³ / (8 x ᴨ x Kʙɢ x G x M) = 10¹³ K
Tʙʜ = Tε + Tɢ = 0 K + 10¹³ K
Tʙʜ = Tɢ = 10¹³ K
We show that the temperature of a black hole is 10¹³ K, it is a gravitational temperature, not an electromagnetic temperature.
According to our calculation, Tʙʜ = Tɢ = 10¹³ K
If we look at
Table 7, we see that the temperature of the elementary particles of the first family, second family and third family in the standard model, vary between 10¹⁰ K to 10¹⁵ K. Taking into account the above, we are going to propose that black holes can be true generators of elementary particles, generators of matter; quasars would be responsible for distributing this matter throughout the universe.
Here we put forward the hypothesis of that the accretion disk that surrounds a black hole or quasar is partly formed by interstellar matter and partly by matter created by the black hole itself. With this we are saying that we can find in the universe, quasars practically alone, without matter that is feeding them; this could be explained if we consider that the accretion disk is created by the black hole itself.
10. Harshit Jain – Comment on
It seems like your text touches on several complex concepts related to the Boltzmann constant, string theory, particle formation, and their relationship with temperature. Here's a restructured version to make it more coherent:
"Within our paper, a key focus was leveraging the Boltzmann constant as a foundational element for constructing a more accurate model of the universe. Utilizing temperature as a distinguishing factor between flat and curved space-time structures was pivotal in this pursuit.
In our exploration, we delved into the Vlasov Equations, particularly emphasizing the role of the Boltzmann constant in interactions, such as the Debye electron interaction. This interaction aids in delineating temperature variations, contributing to our understanding of the overall wave function of the universe.
Another significant aspect of our paper revolved around string theory. We addressed the deep damping of interaction Maxwell state equations, specifically examining the formation of strings with varying constants (Homotropy). This exploration led us to consider the application of the Boltzmann Hagedorn conjecture, particularly in understanding how different temperatures contribute to the formation of various particles, such as mesons and bosons.
Our investigation into the interaction between temperature, matter, and space-time fabrics was fundamental in establishing a coherent understanding, aligning with your previously considered stability of different particle generations through the Boltzmann-derived energy capacity.
Furthermore, in the realm of string theory, where entities are viewed as strings at the Planck scale, the relationship between these strings and temperature (represented by the Boltzmann constant) becomes crucial. Here, we delve into the implications of Boltzmann interaction fields and other relevant factors.
Specifically discussing gluons and leptons, your classification based on stability is noteworthy. However, our paper strives to connect this stability classification with temperature within the quantum scenario. For instance, considering the RLC modelling you've previously provided, we explore the nexus between stability and temperature, especially when two entities are mixed our work aims to bridge the gap between fundamental constants like the Boltzmann constant, string theory, particle stability, and their interrelation with temperature in the complex fabric of the universe." Energy, as understood through the lens of stability classes determined by the hyperfine structure constant (group theory), Quantum Field Theory (QFT), and conformal field theory, plays a pivotal role in quantum-level interactions with help of Boltzmann constant. These interactions manifest in stable clusters and the Zeno interaction during quark formation in the event horizon of a black hole (phasor interaction) in one form of formation.
By introducing new models for photons, quarks, and gluons and extending the Boltzmann constant theory to curved space-time, our work demonstrates the generalization of the standard model. This extension incorporates gravity as a fundamental component, influencing the properties governing elementary particles through Einsteinian Hamiltonian interactions within their fields. Our aim in generalizing the standard model is to unify quantum field theory (as represented by the standard model) and gravity. Our calculations indicate that the gravitational forces acting on elementary particles approximate those acting on stellar bodies like white dwarf stars, neutron stars, and black holes.
The Higgs potential, a mass internal interaction, and its associated temperature are directly related to the curvature of space-time. Observing the temperatures of quarks reveals their proximity to those of these stellar bodies, hence the similarity in gravitational effects on elementary particles and stellar bodies. Our model describing quarks posits two opposing forces within them: a repulsive/disintegrative force (Fq) and a gravitational attractive force (Fg), offering insight into different modes of bubble formation in their interactions.
Our calculations elucidate the stability of the first quark family and the instability of the second and third quark families. The critical point occurs at the gravitational force Fg = 10¹⁰ N; below this value, elementary particles remain stable (Fg > Fq), whereas above this threshold, they become unstable (Fg < Fq).
In section 5.5, we have demonstrated the existence of a force tangential to the repulsive force in the disintegration of subatomic particles interaction. This tangential or torsion force precedes the repulsive force by 90 degrees. Analogously, within a black hole, two forces operate: a gravitational force drawing inward and a tangential or torsional gravitational force delaying the gravitational force by 90 degrees.
Finally, we propose the equation DST = EFQT as representative of the Theory of Everything (TOE), serving as a generalization of the Maldacena ADS/CFT correspondence, in our research, we have showcased the quantization of both space-time and matter. 'DST' signifies dynamic space-time and is associated with the theory that expands the Boltzmann constant concept into curved space-time.
On the other hand, 'EFQT' represents electromagnetic quantum field theory. Our focus lies in understanding quantum complexity in electrodynamics and its influence on the formation of various elementary particles.
The theory extending the Boltzmann constant into curved space-time unifies general relativity and quantum mechanics. Evidence of this convergence is visible in CP interactions within string theory, entanglement, and other disintegration functions or may be integration function inherent to these interactions. Utilizing vector interactions becomes crucial across various scenarios. However, detailing its importance everywhere would require extensive additional formulations, as these interactions permeate numerous scenarios.
For instance, in calculating the entropy of celestial bodies like white dwarf stars and neutron stars, we calculate their equivalent black hole entropy. This method allows us to estimate the approximate entropy of any stellar body, understanding that it cannot surpass the entropy of its equivalent black hole. When we generate Quark-Gluon Plasma (QGP) in particle accelerators, it initially stores energy but remains an unstable state. At this stage, the QGP exhibits an approximate Boltzmann constant Kʙ = 1.78 10⁻⁴³ J/K. To revert space-time and matter to their stable state, the Boltzmann constant needs to transition from Kʙ = 1.78 10⁻⁴³ J/K to 1.38 10⁻²³ J/K. This release of energy causes the QGP to resemble a superfluid, despite the substantial energy involved (ɲ/s = 1.27 10²⁵, depicting the viscosity-entropy relationship).
The viscosity of a quark-gluon plasma utilizes the Boltzmann constant of a black hole for calculation. For instance, comparing theories like 11-dimensional ADS theory (Kʙ = 1.38 10⁻⁴³ J/K) and 10-dimensional CFT theory (with a collision Boltzmann constant around 0.76 10⁻⁴¹ J/K > Kʙ > 1.78 10⁻⁴³ J/K) allows for nearly identical calculations, reflecting the non-perturbative regime's similarity in both theories.
In the strong coupling regime, utilizing superstring theory in the limit where gs tends to infinity approximates general relativity, facilitating the use of anti-de Sitter space ADS as a tool to describe the strong coupling regime of a particle theory (dual QCD). Our research emphasizes the breakdown of symmetry in curved space-time, attributing mass to fermionic and bosonic particles concerning temperature. As temperature rises, space-time curvature increases, affecting particles in the standard model, including photons and gravitons. This reasoning led us to generalize the Maldacena ADS/CFT correspondence, extending conformal quantum fields CFT to the entire quantum field theory EFQT.
The equation DST = EFQT symbolizes the duality between dynamic space-time and quantum field theory, representing the theory of everything. In conclusion, our work elucidates complex interactions between space-time, matter, and various fields, showcasing how their interplay leads to the emergence of mass and fundamental forces in the universe, quantifying space-time curvature was a pivotal aspect explored in the paper 'RC Electrical Modelling of Black Hole: New Method to Calculate the Amount of Dark Matter and the Rotation Speed Curves in Galaxies.' The 1919 solar eclipse observed in Brazil and Africa provided crucial experimental validation for Albert Einstein's theory of relativity. In this context, we aim to calculate the Boltzmann constant for the Sun and demonstrate how it aligns with the observed deviation. No solar eclipse in history impacted science as profoundly as the one on May 29, 1919. Photographed and analysed simultaneously by two British astronomer teams—one in Sobral, Brazil, and the other on Principe, a Portuguese territory—the goal was to measure the deviation of starlight passing through the Sun's gravitational field. Einstein's theory of general relativity proposed that space-time curved around bodies with high energy or mass, altering the trajectory of light.
Einstein's predicted light deflection nearly doubled, reaching 1.75 arcseconds due to curved space-time. The most significant results emerged from observations made in Sobral, using a 4-inch lens, indicating a deflection of 1.61 arcseconds with a 0.30 arcsecond margin of error—slightly less than Einstein's forecast. Our calculations for the number of gravitons within a neutron equate to a temperature of T = 10¹² K. As per
Table 12, the graviton's mass decreases with rising temperature for particular interaction.
The culmination of various aspects in our research leads to the proposition of a theory of everything (TOE), symbolized by the equation DST = EFQT:
Quantization of space-time (DST) and matter and its interaction (EFQT)
Quantization of space-time curvature
Electrical modelling of a neutron as a three-phase alternating current generator, revealing the origin of mass and gravity in particles as double Boltzmann understanding
Mechanisms generating mass and gravity within neutrons, calculating the constituent particles and gravitons
Proposed generalization of the ADS/CFT correspondence with the equation DST = EFQT, unifying gravity and quantum mechanics across space-time scenarios—negative, positive, or flat curvature
This equation, DST = EFQT, symbolizes the theory of everything, representing an interaction field unifying gravity and quantum mechanics. It extends from the generalization of the Boltzmann constant in curved space-time
In the paper 'RLC Electrical Modelling of Black Hole and Early Universe: Generalization of Boltzmann’s Constant in Curved Space-Time,' we delve into the origins of the universe, cosmic inflation, dark matter, and dark energy. And this paper also ‘Theory of the Generalization of the Boltzmann’s Constant in Curved Space-Time: Shannon-Boltzmann Gibbs Entropy Relation and the Effective Interacted Boltzmann’s Constant,’ having to we quantify space-time curvature and demonstrate, using the Shannon-Boltzmann-Gibbs entropy relation, the conservation of information.
The paper 'RC Electrical Modelling of Black Hole: New Method to Calculate the Amount of Dark Matter and the Rotation Speed Curves in Galaxies' details how we quantify dark matter in a galaxy and model its rotation curves using an innovative approach and a newly introduced constant in interactive work.
In the paper 'Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electrical Generator: Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons inside a Neutron,' we elucidate the generation of mass (calculating the number of quarks-antiquarks-gluons) and gravity (calculating the number of gravitons) within a neutron, treating it as a three-phase alternating current energy generator.
Utilizing the theory of the generalization of the Boltzmann constant in curved space-time, this paper proposes a methodology to elucidate the origin of elementary particles and their relation to gravity. This allowed us to generalize the ADS/CFT correspondence, extending it into a general theory or theory of everything.
The theory of the generalization of the Boltzmann constant serves as the fundamental pillar uniting general relativity and quantum mechanics, enabling the quantification of space-time and its curvature. Ultimately, it facilitates the generalization of the Maldacena ADS/CFT correspondence, leading to the proposal of a universal theory represented by the equation 'entangled DST = EFQT.'
Reflections: Comparing the Higgs mechanism with the conformal mechanism reveals their distinctions. Gauge symmetry necessitates massless particles, but the Higgs mechanism confers mass by breaking symmetry. While this interaction occurs in flat space, in curved space, it might disrupt conformal symmetry.
In curved space, breaking this symmetry could endow particles like gravitons, photons, scalar fields (bosons), and Dirac particles with mass through interaction. This mass appears proportional to the conformal factor's temporal derivative. In a conformal space within curved space, a particle's motion resembles movement through a fluid (viscous), potentially accounting for inertia.
Regarding mass, envisioning quark and anti-quark dipoles as vibrating point masses linked by a spring (Gravitons with spin 2), these vibrating masses interact together, causing disturbances in space-time propagating as gravitational waves.
This could elucidate the generation of gravitational waves through gravitons' propagation within space-time interaction in my view, the equation ADS = CFT holds paramount significance in physics, paving the way toward the sought-after Theory of Everything (TOE) in science. Extending the Maldacena ADS/CFT correspondence, considering the generalization of the Boltzmann constant, leads us to the equation DST = EFQT, where DST symbolizes space-time with negative, positive, or plane curvature, while EFQT encompasses Electromagnetic Quantum Field Theory, comprising electromagnetic field theory linked to weak field theory (QED) and strong field theory (QCD) for formulating various functions.
In your paper 'Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electrical Generator: Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons inside a Neutron,' we explore gravity quantification, specifically exemplifying it for the neutron. We've demonstrated that DST space-time quantization aligns with the quantization of EFQT field theory, representing a theory of quantum gravity associated with the generalization of the Boltzmann constant in curved space-time. This understanding assists in comprehending interactions within both curved and flat space-time.
The equation DST = EFQT elucidates an intrinsic, direct relationship between matter and space-time, revealing quantized space-time and its curvature. It's important to note that conformal field theory is not utilized in this context. This equation holds broader implications than the ADS/CFT correspondence, especially within different regions of self and inner interactions forming ADS/CFT. Building upon DST = EFQT, we propose that fundamental particles originate due to the relationship between space-time curvature, elemental matter, and temperature.
Essentially, it's the curvature of space-time and gravity associated with temperature that accounts for elementary particle genesis, a topic we will delve into extensively later.
In our paper 'Theory of the Generalization of the Boltzmann’s Constant in Curved Space-Time: Shannon-Boltzmann Gibbs Entropy Relation and the Effective Boltzmann’s Constant,' we analyse the space-time contraction factor for various celestial bodies, incorporating Shannon-Gibbs energy within its interaction. Let's briefly recap the calculation of the space-time contraction factor for a black hole: Assuming a black hole comprises a plasma of quarks and gluons based on the Maldacena correspondence ADS = CFT, we calculate the space-time contraction factor and its effective Boltzmann constant. For instance, considering a black hole's mass at 3.0 solar masses (Mϴ), and its formation temperature at 10¹³ K, aligning with the temperature at which matter forms a soup of quarks and gluons in particle collisions Boltzmann understanding.
This paper concludes by emphasizing the significance of these analyses in our research, contributing comprehensively to various analytical aspects by which we take whole interaction to formation of particle by generalization.
11. Conclusions:
By studying β ˉ decay and introducing new models of photons, gluons, gravitons and Higgs bosons; applying the theory of the generalization of the Boltzmann´s constant in curved space-time and the theory of modelling the neutron and proton as a three-phase alternating current electric generator; we have shown how the standard model of particle physics can be generalized.
In principle, we have shown that the origin of elementary particles depends on a combination of factors such as the geometry of space-time associated with gravity, temperature and the effective Boltzmann´s constant. The combination of such factors makes possible the origin of the elementary particles that make up the standard model. It is a mechanism analogous to the Higgs mechanism and much more realistic, it even manages to explain the origin of the neutrino. To support this mechanism, it is compared to the forces involved in stellar bodies such as white dwarf stars, neutron stars and black holes. The analogies that result from comparing stellar bodies with elementary particles are of utmost importance to have a clear idea of the forces involved inside the elementary particles, repulsive force Fq vs gravitational attractive force Fg.
We must remember that the Higgs potential, its associated temperature, is a direct function of the curvature of space-time. If we observe the temperatures of the quarks, we see that they are close to the temperatures of the stated stellar bodies, which is why the gravitational forces on elementary particles are similar to the gravitational forces on stellar bodies.
Our proposed model for quarks tells us that inside them there are two forces that act in opposite directions, a repulsion or disintegration force Fq and a gravitational attraction force Fg; our calculation allows us to demonstrate why the first quark family is stable and why the second and third quark families are unstable.
The inflection point is given by the gravitational force Fg = 10¹⁰ N, below that value the elementary particles are stable Fg > Fq, above that value, the elementary particles are unstable Fg < Fq.
In item 8.5), we have demonstrated the existence of a tangential rotation force to the repulsive force in the disintegrations of subatomic particles, this rotation or torsion force advances by 90 degrees to the repulsive force. Very possibly, this rotation force is the cause of the existing discrepancies in lepton universality, discrepancy between the percentage of electronic decay vs. muonic decay.
In analogy to the forces that act in the disintegration of sub-atomic particles, we have also demonstrated that two forces act inside a black hole; a gravitational force of attraction towards the interior of the black hole and a second rotation or torsional gravitational force that delays the gravitational force by 90 degrees.
In our analysis of the symmetry of the particles, applying the theory of the neutron and proton model as an electric generator of three-phase alternating current; we have shown that weak, strong, gravitational and electromagnetic interactions can be reduced to a single electromagnetic interaction. In other words, we can represent this by the following equation:
This allows us to affirm that photons, gluons, W⁺ bosons, W⁻ bosons, Z bosons, gravitons and the Higgs boson can be replaced by quark-antiquark interactions (U, U, D, D).
Applying the theory of the generalization of the Boltzmann constant and curved space-time; we have demonstrated the quantization of gravity and space-time. The quantization of gravity is associated with gravitons and is analogous to the quantization of photons. The quantization of space-time is associated with Planck's constant. This allowed us to unite Albert Einstein's theory of general relativity with the theory of quantum mechanics.
Finally, we have proposed the equation DST = EFQT, as the equation that represents the theory of everything (T.O.E.), it is a generalization of the ADS/CFT Maldacena correspondence.
DST, stands for dynamic space-time and is related to the theory of the generalization of the Boltzmann´s constant in curved space-time. It is a theory of quantum gravity.
EFQT, stands for electromagnetic field quantum theory; it is related to the quantum-electrical modelling of neutrons and protons as a three-phase alternating current electrical generator. This EFQT theory is equivalent to the quantum theory of strong interactions, weak interactions and electromagnetic interactions.
The theory of the generalization of the Boltzmann´s constant in curved space-time and the theory of the electrical-quantum modelling of the neutron and the proton as an three-phase alternating current electric generator, are the theories that allow us to unite general relativity and quantum mechanics, allowing the duality DST = EQFT to be defined as a theory of everything.
It is important to highlight that the theory of everything (TOE); it also explains the origin of the universe, the origin of dark matter, the origin of dark energy, cosmic inflation and matter-antimatter asymmetry.
About the Authors
HECTOR GERARDO FLORES (ARGENTINA, 1971). I studied Electrical Engineering with an electronic orientation at UNT (Argentina); I worked and continue to work in oil companies looking for gas and oil for more than 25 years, as a maintenance engineer for seismic equipment in companies such as Western Atlas, Baker Hughes, Schlumberger, Geokinetics, etc.
Since 2010, I study theoretical physics in a self-taught way.
In the years 2020 and 2021, during the pandemic, I participated in the course and watched all the online videos of Cosmology I and Cosmology II taught by the Federal University of Santa Catarina UFSC (graduate level).
MARIA ISABEL GONÇALVEZ DE SOUZA (Brazil, 1983). I studied professor of Portuguese language at the Federal University of Campina Grande and professor of pedagogy at UNOPAR University, later I did postgraduate, specialization. I am currently a qualified teacher and I work for the São Joao do Rio do Peixe Prefecture, Paraiba. I am Hector's wife and my studies served to collaborate in the formatting of his articles, corrections, etc.; basically, help in the administrative part with a small emphasis in the technical part analysing and sharing ideas.
HARSHIT JAIN (India ,2008) I was born on July 14, 2008, into a loving family. My father, Ajitendra Kumar Jain, and my mother, Preeti Jain, have been incredibly supportive throughout my life and education. I grew up in Lalitpur, where I attended Jawahar Navodaya Vidyalaya (JNV) for my high school education.
My passion for learning has always driven me toward subjects that explore the mysteries of the universe. I have a particular interest in physics, biology, cosmology, and mathematics. This interest led me to the Pacific Institute of Cosmology, where I am currently pursuing advanced studies in these fields.
One of the most significant influences on my academic journey has been Professor Padhi, a renowned scholar who works with several professors who hold the prestigious title of Fellow of the Royal Society (FRS). His mentorship has been invaluable, guiding me through complex concepts and encouraging me to delve deeper into research.
Throughout my studies, I've engaged in various research projects, some of which have challenged conventional thinking and opened new avenues for exploration. These experiences have not only honed my analytical skills but also strengthened my resolve to contribute meaningfully to the scientific community.
In summary, I am Harshit Jain, a young scientist with a passion for discovery. My journey is just beginning, but I'm excited about the endless possibilities that lie ahead. I owe much of my success to my supportive family, dedicated mentors, and the enriching educational environments I've been fortunate to be a part of. I look forward to continuing my research and making meaningful contributions to the fields I hold dear.
Acknowledgments
I sincerely appreciate the comments and suggestions provided by Mr. Harshit Jain and Premachand Mahapatra
Conflicts of Interests
The authors declares that there are no conflicts of interest.
References
- Flores, H.G.; Gonçalves de Souza, M.I. Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electrical Generator. Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons, Inside a Neutron. Preprints 2023, 2023102076. [CrossRef]
- Flores, H.G.; Gonçalvez de Souza, M.I. Theory of the Generalization of the Boltzmann’s Constant in Curved Space-Time. Shannon-Boltzmann Gibbs Entropy Relation and the Effective Boltzmann’s Constant. Preprints 2023, 2023090301. [CrossRef]
- Flores, H.G. Rlc Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time. Preprints 2023, 2023052246. [CrossRef]
- Flores, H.G.; Gonçalves de Souza, M.I. RC Electrical Modelling of Black Hole. New Method to Calculate the Amount of Dark Matter and the Rotation Speed Curves in Galaxies. Preprints 2023, 2023092017. [CrossRef]
- Gerardo Flores, H.; Jain, H.; Gonçalves de Souza, M. I. Proton Decay and Inverse Neutron Decay. Preprints 2024, 2024050023. [CrossRef]
- Flores, H. G.; Jain, H.; Gonçalves de Souza, M. I. Origin of the Dark Energy. Preprints 2024, 2024051639. [CrossRef]
- Gerardo Flores, H.; Jain, H.; Mahapatra, P.; Gonçalves de Souza, M. I. Theory of Unification of the Interactions of Fundamental Forces: SU(3) x SU(2) --> U(1). Preprints 2024, 2024100660. [CrossRef]
- Flores, H. G.; Jain, H.; Mahapatra, P.; Gonçalves de Souza, M. I. Analysis of the Kerr-Newman Diagram. Unravelling the Interior of a Black Hole. Preprints 2024, 2024080101. [CrossRef]
- Arbab Ibrahim, (Abdus Salam Intentional Centre for Theoretical Physics (ICTP)- Trieste-Italy), in QUANTUM PHYSICS. https://www.linkedin.com/groups/1892648/?highlightedUpdateUrn=urn%3Ali%3AgroupPost%3A1892648-7142083157524205568&q=highlightedFeedForGroups.
- Kostya Trachenko, Vadim Brazhkin, Matteo Baggioli. Similarity between the kinematic viscosity of quark-gluon plasma and liquids at the viscosity minimum. https://arxiv.org/pdf/2003.13506.pdf.
- Cauê Muraro - Agência USP - 30/10/2007 Cientistas brasileiros criam átomo artificial https://www.inovacaotecnologica.com.br/noticias/noticia.php?artigo=010160071030&id=010160071030.
- Diego Marinho Rodrigues. A Correspondencia AdS/CFT: Um Estudo Introdutorio UNIVERSIDADE FEDERAL DO RIO DE JANEIRO, INSTITUTO DE FISICA. https://pos.if.ufrj.br/wp-content/uploads/2021/06/Diego-Marinho_prelim.pdf.
- Horatiu Nastase. Introduction to AdS-CFT Global Edge Institute, Tokyo Institute of Technology https://professores.ift.unesp.br/horatiu.nastase/AdS-CFTnotes.pdf.
- Alberto Zaffaroni. Introduction to the AdS/CFT correspondence Universita di Milano-Bicocca and INFN, sezione di Milano-Bicocca, Piazza della Scienza, 3; I-20126 Milano, Italy. https://laces.web.cern.ch/laces09/notes/dbranes/lezionilosanna.pdf.
- Gaston Luciano Giordano. Aplicaciones de la Correspondencia AdS/CFT en el ambito de la Fısica de la Materia Condensada. UNIVERSIDAD NACIONAL DE LA PLATA, TRABAJO DE TESIS DOCTORAL. http://sedici.unlp.edu.ar/bitstream/handle/10915/68984/Documento_completo.pdf-PDFA.pdf?sequence=1&isAllowed=y.
- P.H.E. Meijer, E. Bauer (2004) Group Theory: The Application To Quantum Mechanics (Dover).
- M. Hamermesh (1962) Group theory and its application to physical problems (Dover).
- Aula 02: circuitos Trifásicos Universidad Federal de Parana, UFPR https://www.eletrica.ufpr.br/sebastiao/wa_files/te344%20aula%2002%20-%20circuitos%20trifasicos_(2).pdf.
- Circuitos Trifasicos Universidad de São Paulo, USP. https://edisciplinas.usp.br/pluginfile.php/5335698/mod_resource/content/1/Slides%231.pdf.
- Gabriel Vinicius Vian. Introdução à Eletrodinâmica e Cromodinâmica Quântica. UNIVERSIDADE FEDERAL DA FRONTEIRA SUL, CAMPUS REALEZA. CURSO DE FÍSICA – LICENCIATURA – 2022 https://rd.uffs.edu.br/bitstream/prefix/5440/1/VIAN.pdf.
- Jefferson Taneo Shida Gonçalves. Introdução à QCD, Fundamentos e aplicações na física do LHC. Universidade Federal do Rio Grande - Instituto de Matemática, Estatística e Física. Rio Grande, 2017 https://imef.furg.br/images/stories/Monografias/Fisica_bacharelado/2017/2017-2_Jefferson_Shida.pdf.
- Michelangelo L. Mangano. INTRODUCTION TO QCD CERN, TH Division, Geneva, Switzerland https://cds.cern.ch/record/454171/files/p41.pdf.
- P. Z. Skands. Introduction to QCD. Theoretical Physics, CERN, 1211 Geneva 23, Switzerland School of Physics & Astronomy, Monash University, Clayton VIC 3800, Australia Updated: July, 2017 https://arxiv.org/pdf/1207.2389.pdf.
- Thomas Gehrmann and Bogdan Malaescu. Precision QCD Physics at the LHC Annual Review of Nuclear and Particle Science https://www.annualreviews.org/docserver/fulltext/nucl/72/1/annurev-nucl-101920-014923.pdf?expires=1711222185&id=id&accname=guest&checksum=718297BFB633C2F332DE04F95BB9CFE2.
- François Gieres. ABOUT SYMMETRIES IN PHYSICS Institut de Physique Nucleaire de Lyon, IN2P3/CNRS, Universit´e Claude Bernard 43, boulevard du 11 novembre 1918, F - 69622 - Villeurbanne CEDEX https://arxiv.org/pdf/hep-th/9712154.
- Stefano Disca, Roberto Demaria, Lorenzo Formaggio INTRODUCTIVE EXERCISES TO QUANTUM FIELD THEORY https://arxiv.org/pdf/2406.01393.
- Valentin Benedetti, Horacio Casini, Javier M. Magán ABJ anomaly as a U(1) symmetry and Noether’s theorem Instituto Balseiro, Centro Atómico Bariloche 8400-S.C. de Bariloche, Río Negro, Argentina https://arxiv.org/pdf/2309.03264.
- John L. Friedman Notes on Gravitational Physics Department of Physics, University of Wisconsin-Milwaukee; May 17, 2024. https://arxiv.org/pdf/2308.09826.
- James T. Wheeler SU(3) × SU(2) × U(1) : The residual symmetry of extended conformal gravity. Utah State University, Logan, UT 84322; November 13, 2018 https://arxiv.org/pdf/hep-th/9109033.
- Logan Nye Entangled Origins of SU(3) × SU(2) × U(1): Emergence of Gauge Symmetries in the Standard Model Carnegie Mellon University file:///C:/Users/55839/Downloads/Entangled_Origins_of_SU_3__x_SU_2__x_U_1___Emergence_of_Gauge_Symmetries_the_Standard_Model_Nye.pdf.
- Thomas Görnitz, Goethe-Universität Frankfurt am Main · Institut für Didaktik der Physik. Uwe Schomäcker, Technische Universität Braunschweig · Institut für Mathematische Physik. The Structures of Interactions: How to Explain the Gauge Groups U(1), SU(2) and SU(3) file:///C:/Users/55839/Downloads/2016_Structures_of_interactions_GrnitzSchomcker_Res_gate.pdf.
- Lucas Carvalho Simões Quebra Espontânea da Simetria Quiral em Modelos de Yukawa-Higgs Universidade Federal do Espírito Santo – UFES, Programa de Pós-Graduação em Física. 5 de abril de 2019, Vitória - ES, Brasil. https://sappg.ufes.br/tese_drupal//tese_13252_Disserta%E7%E3o%20Lucas%20Sim%F5es%20-%20PPGFis.pdf.
- Jean-Bernard Zuber Invariances in Physics and Group Theory M2/International Centre for Fundamental Physics. https://www.lpthe.jussieu.fr/~zuber/Cours/InvariancesGroupTheory-2014.pdf.
- Matthew Robinson Book: Symmetry and the Standard Model Mathematics and Particle Physics https://www.docdroid.net/QGtZ58X/matthew-robinson-auth-symmetry-and-the-standard-model-mathematics-and-particle-physics-2011-springer-verlag-new-york-libgenlc-pdf#page=4.
- Scott Willenbrock Symmetries of the Standard Model Department of Physics, University of Illinois at Urbana-Champaign, February 2, 2008. https://arxiv.org/pdf/hep-ph/0410370.
- J. Zupan Introduction to flavor physics Department of Physics, University of Cincinnati, Cincinnati, Ohio, USA https://cds.cern.ch/record/2702255/files/939-4115-1-PB.pdf.
- Álvaro Pastor-Gutiérrez(1,2), Jan M. Pawlowski(2,3) and Manuel Reichert(4) The Asymptotically Safe Standard Model: From quantum gravity to dynamical chiral symmetry breaking 1 Max-Planck-Institut für Kernphysik P.O. Box 103980, D 69029, Heidelberg, Germany 2 Institut für Theoretische Physik, Universität Heidelberg, Philosophenweg 16, 69120 Heidelberg, Germany 3 ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung mbH, Planckstr. 1, 64291 Darmstadt, Germany 4 Department of Physics and Astronomy, University of Sussex, Brighton, BN1 9QH, U.K. https://scipost.org/SciPostPhys.15.3.105/pdf.
- Gustavo Garcia de Melo Simetria conforme e covariância galileana Universidade de Brasília, 2015. http://icts.unb.br/jspui/bitstream/10482/19882/1/2015_GustavoGarciaMelo.pdf.
- FILIPE JOAQUIM Introduction to particle Physics https://indico.cern.ch/event/1328014/contributions/6081852/attachments/2922272/5129762/Joaquim%20Aula%204.pdf.
- Noether’s Theorem CERN https://indico.cern.ch/event/106673/contributions/1306809/attachments/20980/30332/Natal_Lectures_Part_III.pdf.
- Igor R. Klebanov Joseph Henry Laboratories, Princeton University, Princeton, New Jersey 08544 Edward Witten Institute for Advanced Study, Olden Lane, Princeton, New Jersey 08540 AdS/CFT Correspondence and Symmetry Breaking https://arxiv.org/pdf/hep-th/9905104.
- Erin Blauvelt,a; Laura Engelbrecht,b; and Kurt Hinterbichler,c a: Department of Physics, Lehigh University, Bethlehem, PA, 18018. U.S.A. b: Institute for Theoretical Physics, ETH Zürich, Wolfgang-Pauli-Strasse 27, 8093, Zürich, Switzerland. c: CERCA, Department of Physics, Case Western Reserve University, 10900 Euclid Ave, Cleveland, OH 44106, U.S.A. Shift Symmetries and AdS/CFT file:///C:/Users/55839/Downloads/Shift_Symmetries_and_AdSCFT.pdf.
- Michaelmas 2014, Prof. N. Manton Symmetries, Fields and Particles University of Cambridge https://www.damtp.cam.ac.uk/user/examples/3P2.pdf.
- Howard Georgi Book: Lie Algebras in Particle Physics Cambridge, MA; May, 1999. https://library.oapen.org/bitstream/handle/20.500.12657/50876/9780429967764.pdf.
- CHONG LEONG ONG SUPERSYMMETRIC MODELS FOR QUARKS AND LEPTONS WITH NONLINEARLY REALIZED E8 SYMMETRY * Submitted to Physical Review D Stanford Linear Accelerator Center https://www.slac.stanford.edu/pubs/slacpubs/3250/slac-pub-3459.pdf.
- Thomas T. Dumitrescu Lectures on Generalized Symmetries and Phases of Gauge Theory Lectures at IHES Summer School (June/July 2024) on Symmetries and Anomalies, June 26, 2024. https://indico.math.cnrs.fr/event/11080/attachments/4585/8220/Lecture%20Notes_DumitrescuT.pdf.
- Elina Rischke Symmetries in Quantum Mechanics and Particle Physics Frankfurt Digital Summer School 2021 https://itp.uni-frankfurt.de/~drischke/Script_Symmetries_GU2021.pdf.
- Goran Senjanović; Alejandra Melfo Introductory Course Standard Model of particle physics https://www2.physik.uni-muenchen.de/lehre/vorlesungen/sose_22/Introduction-to-Physics-of-Neutrinos/Materials/SMcourse.pdf.
- IAN LIM SYMMETRIES, FIELDS, AND PARTICLES https://lim.physics.ucdavis.edu/teaching/files/sfp-notes-partiii.pdf.
- GABRIEL J. H. KHAN WHAT IS NOETHER’S THEOREM? https://math.osu.edu/sites/math.osu.edu/files/Noether_Theorem.pdf.
- Juan Maldacena The symmetry and simplicity of the laws of physics and the Higgs boson Institute for Advanced Study, Princeton, NJ 08540, USA https://arxiv.org/pdf/1410.6753.
- Juan Maldacena The Illusion of Gravity https://www.ias.edu/sites/default/files/sns/sciam-maldacena-3a.pdf.
- Roger Penrose THE ROAD TO REALITY. A Complete Guide to the Laws of the Universe First published in Great Britain in 2004 by Jonathan Cape https://chaosbook.org/library/Penr04.pdf.
- Edmund Bertschinger & Edwin F. Taylor Inside the Spinning Black Hole, CHAPTER 21 https://www.eftaylor.com/exploringblackholes/Ch21TravelThroughTheSpinningBH170831v1.pdf.
- H. Nagakura and S. Yamada, The standing accretion shock instability in the disk around the Kerr black hole, The Astrophysical Journal 696, 2026 (2009).
- P. Tarafdar, S. Maity, and T. K. Das, Influence of flow thickness on general relativistic low angular momentum accretion around spinning black holes, Phys. Rev. D 103, 023023 (2021).
- V. Moncrief, Stability of stationary, spherical accretion onto a Schwarzschild black hole, Astrophysical Journal 235, 1038 (1980).
- P. Tarafdar and T. K. Das, Influence of the geometric configuration of accretion flow on the black hole spin dependence of relativistic acoustic geometry, International Journal of Modern Physics D 27, 1850023 (2018).
- M. A. Shaikh and T. K. Das, Linear perturbations of low angular momentum accretion flow in the Kerr metric and the corresponding emergent gravity phenomena, Phys. Rev. D 98, 123022 (2018).
- B. Carter, Complete analytic extension of the symmetry axis of Kerr’s solution of Einstein’s equations, Phys. Rev. 141, 1242 (1966).
- B. Carter, Global structure of the Kerr family of gravitational fields, Phys. Rev. 174, 1559 (1968).
- P. Tarafdar, D. A. Bollimpalli, S. Nag, and T. K. Das, Influence of geometrical configuration on low angular momentum relativistic accretion around rotating black holes, Phys. Rev. D 100, 043024 (2019).
- M. A. Abramowicz, A. Lanza, and M. J. Percival, Accretion disks around Kerr black holes: Vertical equilibrium revisited, The Astrophysical Journal 479, 179 (1997).
- S. W. Hawking, “Breakdown of predictability in gravitational collapse,” Phys. Rev. D 14, 2460 (1976).
- L. Susskind, L. Thorlacius and J. Uglum, “The Stretched horizon and black hole complementarity,” Phys. Rev. D 48, 3743 (1993) [hep-th/9306069].
- D. Marolf and J. Polchinski, “Gauge/Gravity Duality and the Black Hole Interior,” Phys. Rev. Lett. 111, 171301 (2013) [arXiv:1307.4706 [hep-th]].
- J. Maldacena and L. Susskind, “Cool horizons for entangled black holes,” Fortsch. Phys. 61, 781 (2013) [arXiv:1306.0533 [hep-th]].
- M. R. Mbonye and D. Kazanas, “Non-singular black hole model as a possible end product of gravitational collapse,” Phys. Rev. D 72, 024016 (2005); “Can Gravitational Collapse Sustain Singularity-Free Trapped Surfaces?” Int. J. Mod. Phys. D 17, 165 (2008).
- V. P. Frolov, “Notes on non-singular models of black holes,” Phys. Rev. D 94, no. 10, 104056 (2016) [arXiv:1609.01758 [gr-qc]].
- V. P. Frolov and A. Zelnikov, “Quantum radiation from an evaporating non-singular black hole,” Phys. Rev. D 95, no. 12, 124028 (2017) [arXiv:1704.03043 [hep-th]].
- J. B. Hartle, “Tidal Friction in Slowly Rotating Black Holes,” Phys. Rev. D 8, 1010 (1973).
- R. Brustein, A. J. M. Medved and K. Yagi, “When black holes collide: Probing the interior composition by the spectrum of ringdown modes and emitted gravitational waves,” Phys. Rev. D 96, no. 6, 064033 (2017) [arXiv:1704.05789 [gr-qc]].
- R. Carballo-Rubio, F. Di Filippo, S. Liberati and M. Visser, “Phenomenological aspects of black holes beyond general relativity,” Phys. Rev. D 98, no. 12, 124009 (2018). [CrossRef]
- Richard A. Matzner, Texas Cosmology Centre, University of Texas at Austin The Kerr-de Sitter Universe https://arxiv.org/pdf/1011.0479.
- Middleton, M.: Black hole spin: theory and observation, Chapter 3. In: Bambi, C. (ed.) Astrophysics of Black Holes: From Fundamental Aspects to Latest Developments, pp. 99–151. Springer, Berlin (2016).
- Gou, L., McClintock, J.E., Reid, M.J., Orosz, J.A., Steiner, J.F., Narayan, R., Xiang, J., Remillard, R.A., Arnaud, K.A., Davis, S.W.: The extreme spin of the black hole in Cygnus X-1. Astrophys. J. 742, 85 (2011). [CrossRef]
- Stuchlík, Z., Slaný, P.: Equatorial circular orbits in the Kerr–de Sitter spacetimes. Phys. Rev. D 69, 064001 (2004). [CrossRef]
- de Felice, F., Calvani, M.: Causality violation in the Kerr metric. Gen. Relativ. Gravit. 10, 335–342 (1979). [CrossRef]
- Hackmann, E., Lämmerzahl, C., Kagramanova, V., Kunz, J.: Analytical solution of the geodesic equation in Kerr–(anti) de Sitter space-times. Phys. Rev. D 81, 044020 (2010). [CrossRef]
- Stuchlík, Z., Hledík, S.: Some properties of the Schwarzschild-de Sitter and Schwarzschild-anti-de Sitter spacetimes. Phys. Rev. D 60, 044006 (1999). [CrossRef]
- GERADORES DE CORRENTE ALTERNADA Universidad Federal Rio Grande do Norte UFRN – Apostille. https://docente.ifrn.edu.br/heliopinheiro/Disciplinas/maquinas-acionamentos-eletricos/apostila-de-maquinas-de-cc.
- Eisberg Resnick, Física Cuántica.
- Eyvind H. Wichmann. Física cuántica.
- Sears – Zemansky. Física Universitaria con Física Moderna Vol II.
- M. Tinkham, Group Theory and Quantum Mechanics, McGraw-Hill, New York, 1964.
- Bernard Carr, and Florian Kühnel - Annual Review of Nuclear and Particle Science. Primordial Black Holes as Dark Matter: Recent Developments https://www.annualreviews.org/doi/10.1146/annurev-nucl-050520-125911.
- D. T. Son - University of Washington. AdS/CFT correspondence and the Quark-Gluon Plasma https://www.phenix.bnl.gov/WWW/publish/jfrantz/ou_nucl_lunch/DamTSon_lectures.pdf.
- Marc Kamionkowski and Adam G. Riess. The Hubble tension and Early Dark Energy https://arxiv.org/pdf/2211.04492.pdf.
- Luis Anchordoqui, Carlos Nuñez and Kasper Olsen Quantum cosmology and AdS/CFT.
- https://arxiv.org/abs/hep-th/0007064.
- Jefferson Londoño and Eduardo Velasquez. Agujeros Negros de Kerr Escuela de Fsica, Universidad Nacional de Colombia https://www.researchgate.net/publication/328380970_Agujeros_Negros_de_Kerr.
- Kostas kokkotas, Field Theory.
- James B. Hartle, Gravity and introduction to Einstein´s General Relativity.
- Charles W. Misner, Kip S. Thorne and Jhon Archibald Wheelher, Gravitation.
- Benito Marcote, Cosmologia Cuantica y creacion del universe.
- Carlos Rovelli, Quantum Gravity. Vinicius Miranda Bragança, Singularidades em teorias f(r) da gravitação. http://arcos.if.ufrj.br/teses/mestrado_vinicius_miranda.pdf.
- Laurent Pitre ∗, Mark D. Plimmer, Fernando Sparasci, Marc E. Himbert; 2019. Determinations of the Boltzmann constant. https://hal.science/hal-02166573/file/1-s2.0-S1631070518301348-main.pdf.
- ZEUS Collaboration, 2016. Limits on the effective quark radius from inclusive ep scattering at HERA. Accepted for publication in Physics Letters B.
- Dissertação de Mestrado, Wallas Santos Nascimento, Universidade Federal da Bahia, Instituto de Física, Programa de Pós-Graduação em Física, Junho de 2013. Dissertação intitulada: Sobre algumas características da entropia de Shannon para sistemas atômicos confinados. https://repositorio.ufba.br/bitstream/ri/28664/1/disserta%C3%A7%C3%A3o_wallas_final.pdf.
Figure 1.
Capacitive property of matter, mass distribution in interactions 1 & 2.
Figure 1.
Capacitive property of matter, mass distribution in interactions 1 & 2.
Figure 2.
Vector representation of the forces in a black hole. Fc = f, represents the force towards the interior of the black hole generated by the mass m and Ft = -iφ, is a tangential rotation force that retards Fc by 90 degrees, generated by the dark matter mass δ.
Figure 2.
Vector representation of the forces in a black hole. Fc = f, represents the force towards the interior of the black hole generated by the mass m and Ft = -iφ, is a tangential rotation force that retards Fc by 90 degrees, generated by the dark matter mass δ.
Figure 3.
Represents the variation of speed Cɢ, as a function of temperature T, inside a black hole.
Figure 3.
Represents the variation of speed Cɢ, as a function of temperature T, inside a black hole.
Figure 4.
It represents the observed rotation speed of the Milky Way versus the rotation speed of visible matter.
Figure 4.
It represents the observed rotation speed of the Milky Way versus the rotation speed of visible matter.
Figure 5.
In red you can see the rotation velocity Vt that results from the contribution of dark matter mass.
Figure 5.
In red you can see the rotation velocity Vt that results from the contribution of dark matter mass.
Figure 6.
In red is represented the rotation speed Vdm, due to the contribution of dark matter mass; in orange, is represented the sum of the rotation speed due to dark matter plus the rotation speed due only to visible matter, Vdm + Vm.
Figure 6.
In red is represented the rotation speed Vdm, due to the contribution of dark matter mass; in orange, is represented the sum of the rotation speed due to dark matter plus the rotation speed due only to visible matter, Vdm + Vm.
Figure 8.
M31 rotation curve; blue, represents the measured or observed values of the rotation speed of M31; green, represents the values of the rotation speed due to the galactic disk; orange, represents the values of the rotation speed due to the galactic centre; red, represents the rotation speed due to dark matter mass; purple, represents the vector sum of the rotation speed that corresponds to the galactic centre, galactic disk and dark matter mass.
Figure 8.
M31 rotation curve; blue, represents the measured or observed values of the rotation speed of M31; green, represents the values of the rotation speed due to the galactic disk; orange, represents the values of the rotation speed due to the galactic centre; red, represents the rotation speed due to dark matter mass; purple, represents the vector sum of the rotation speed that corresponds to the galactic centre, galactic disk and dark matter mass.
Figure 11.
The rotation speed due to dark matter mass is represented in purple.
Figure 11.
The rotation speed due to dark matter mass is represented in purple.
Figure 12.
M31 rotation curve; blue, represents the measured or observed values of the rotation speed of M31; red, represents the values of the rotation speed due to the galactic disk; orange, represents the values of the rotation speed due to the galactic centre; purple, represents the rotation speed due to dark matter mass; yellow, represents the vector sum of the rotation speed that corresponds to the galactic centre, galactic disk and dark matter.
Figure 12.
M31 rotation curve; blue, represents the measured or observed values of the rotation speed of M31; red, represents the values of the rotation speed due to the galactic disk; orange, represents the values of the rotation speed due to the galactic centre; purple, represents the rotation speed due to dark matter mass; yellow, represents the vector sum of the rotation speed that corresponds to the galactic centre, galactic disk and dark matter.
Figure 13.
M31 rotation curve; blue, represents the measured or observed values of the rotation speed of M31; green, represents the values of the rotation speed due to the galactic disk; orange, represents the values of the rotation speed due to the galactic centre; red, represents the rotation speed due to dark matter mass; purple, represents the vector sum of the rotation speed that corresponds to the galactic centre, galactic disk and dark matter.
Figure 13.
M31 rotation curve; blue, represents the measured or observed values of the rotation speed of M31; green, represents the values of the rotation speed due to the galactic disk; orange, represents the values of the rotation speed due to the galactic centre; red, represents the rotation speed due to dark matter mass; purple, represents the vector sum of the rotation speed that corresponds to the galactic centre, galactic disk and dark matter.
Figure 14.
M31 rotation curve; blue, represents the measured or observed values of the rotation speed of M31; red, represents the values of the rotation speed due to the galactic disk; orange, represents the values of the rotation speed due to the galactic centre; purple, represents the rotation speed due to dark matter mass; yellow, represents the vector sum of the rotation speed that corresponds to the galactic centre, galactic disk and dark matter.
Figure 14.
M31 rotation curve; blue, represents the measured or observed values of the rotation speed of M31; red, represents the values of the rotation speed due to the galactic disk; orange, represents the values of the rotation speed due to the galactic centre; purple, represents the rotation speed due to dark matter mass; yellow, represents the vector sum of the rotation speed that corresponds to the galactic centre, galactic disk and dark matter.
Figure 19.
Plot of seismic channels for file 9013.
Figure 19.
Plot of seismic channels for file 9013.
Figure 20.
Description of acquisition channels vs File.
Figure 20.
Description of acquisition channels vs File.
Figure 21.
Description of the seismic sweep vs File.
Figure 21.
Description of the seismic sweep vs File.
Figure 26.
Envelope of cross-correlation canal (2,15).
Figure 26.
Envelope of cross-correlation canal (2,15).
Figure 27.
Envelope of cross-correlation canal (15,2), mirror image.
Figure 27.
Envelope of cross-correlation canal (15,2), mirror image.
Figure 28.
Shows the frequency content, FK filter of the channel 2 signal (True Reference).
Figure 28.
Shows the frequency content, FK filter of the channel 2 signal (True Reference).
Figure 30.
Total distortion % vs Time (s).
Figure 30.
Total distortion % vs Time (s).
Figure 31.
Total distortion % vs Time (s).
Figure 31.
Total distortion % vs Time (s).
Figure 32.
Supernova Hubble Diagram.
Figure 32.
Supernova Hubble Diagram.
Figure 34.
fundamental wave front.
Figure 34.
fundamental wave front.
Figure 35.
first harmonic wave front.
Figure 35.
first harmonic wave front.
Figure 36.
second harmonic wave front.
Figure 36.
second harmonic wave front.
Figure 37.
The power spectrum of the CMB acoustic waves.
Figure 37.
The power spectrum of the CMB acoustic waves.
Figure 38.
Spectrum of gravitational waves produced in the era of cosmic inflation, ω0 is the resonant or fundamental frequency, ω1 is the low cut-off frequency and ω2 is the high cut-off frequency. The time t corresponds to the moment when the amplitude spectrum reaches 2.7 K.
Figure 38.
Spectrum of gravitational waves produced in the era of cosmic inflation, ω0 is the resonant or fundamental frequency, ω1 is the low cut-off frequency and ω2 is the high cut-off frequency. The time t corresponds to the moment when the amplitude spectrum reaches 2.7 K.
Figure 39.
In blue, it represents the energy contribution of gravitational waves as a function of time, it is observed for t = 10²⁶ s, the energy contribution of gravitational waves becomes zero (0).
Figure 39.
In blue, it represents the energy contribution of gravitational waves as a function of time, it is observed for t = 10²⁶ s, the energy contribution of gravitational waves becomes zero (0).
Figure 40.
In orange, it represents the variation of the Hubble´s constant as a function of time, for t = 10²⁶ s, the slope of the Huble constant becomes horizontal.
Figure 40.
In orange, it represents the variation of the Hubble´s constant as a function of time, for t = 10²⁶ s, the slope of the Huble constant becomes horizontal.
Figure 42.
Distribution of energy as a function of time.
Figure 42.
Distribution of energy as a function of time.
Figure 43.
Vector representation of the forces in a black hole. Fc = f, represents the force towards the interior of the black hole generated by the mass m and Ft = -iφ, is a rotation force that retards Fc by 90 degrees, generated by the mass δ.
Figure 43.
Vector representation of the forces in a black hole. Fc = f, represents the force towards the interior of the black hole generated by the mass m and Ft = -iφ, is a rotation force that retards Fc by 90 degrees, generated by the mass δ.
Figure 44.
compression and torsion forces that act in space-time corresponding to a Planck length inside a black hole.
Figure 44.
compression and torsion forces that act in space-time corresponding to a Planck length inside a black hole.
Figure 46.
Electric model of the neutron considering matter and antimatter.
Figure 46.
Electric model of the neutron considering matter and antimatter.
Figure 47.
Electric model of the proton considering matter and antimatter.
Figure 47.
Electric model of the proton considering matter and antimatter.
Figure 54.
Mass distribution in interactions 1 & 2.
Figure 54.
Mass distribution in interactions 1 & 2.
Figure 59.
Mass distribution in interactions 1 & 2.
Figure 59.
Mass distribution in interactions 1 & 2.
Figure 64.
Collision of protons produces the Higgs boson which is detected by the detector of photons.
Figure 64.
Collision of protons produces the Higgs boson which is detected by the detector of photons.
Figure 65.
Collision of D & D Quarks produces the Higgs boson which is detected by the detector of photons.
Figure 65.
Collision of D & D Quarks produces the Higgs boson which is detected by the detector of photons.
Figure 72.
black hole formed by Neutroniumd particles.
Figure 72.
black hole formed by Neutroniumd particles.
Figure 73.
- black hole model formed by protoniu particles.
Figure 73.
- black hole model formed by protoniu particles.
Figure 76.
Gravity is a force.
Figure 76.
Gravity is a force.
Figure 78.
first family of elementary particles.
Figure 78.
first family of elementary particles.
Figure 79.
harmonic oscillator.
Figure 79.
harmonic oscillator.
Figure 80.
second family of elementary particles.
Figure 80.
second family of elementary particles.
Figure 81.
Third family of elementary particles.
Figure 81.
Third family of elementary particles.
Figure 82.
The mass-temperature relationship is a straight line whose slope takes the value of 1.53 10ˉ⁴⁰ kg/k.
Figure 82.
The mass-temperature relationship is a straight line whose slope takes the value of 1.53 10ˉ⁴⁰ kg/k.
Figure 83.
Gravitational force vs temperature for elementary particles and stellar bodies.
Figure 83.
Gravitational force vs temperature for elementary particles and stellar bodies.
Figure 85.
Neutron vector diagram.
Figure 85.
Neutron vector diagram.
Figure 89.
Vector diagram of β⁻ Decay.
Figure 89.
Vector diagram of β⁻ Decay.
Figure 90.
Mass distribution vs charge distribution.
Figure 90.
Mass distribution vs charge distribution.
Figure 91.
Mass distribution vs charge distribution.
Figure 91.
Mass distribution vs charge distribution.
Figure 92.
Proposed model for the D quark.
Figure 92.
Proposed model for the D quark.
Figure 93.
Proposed model for the D antiquark.
Figure 93.
Proposed model for the D antiquark.
Figure 94.
Atomic mass number A vs binding energy per nucleon (MeV).
Figure 94.
Atomic mass number A vs binding energy per nucleon (MeV).
Figure 95.
Shell model, first orbitals.
Figure 95.
Shell model, first orbitals.
Figure 107.
Equivalent Neutron / Black Hole.
Figure 107.
Equivalent Neutron / Black Hole.
Figure 108.
Black Hole, the orange arrows represent magnetic fields, the blue arrows represent electric fields.
Figure 108.
Black Hole, the orange arrows represent magnetic fields, the blue arrows represent electric fields.
Figure 113.
Equivalent Neutron/ Black Hole.
Figure 113.
Equivalent Neutron/ Black Hole.
Figure 114.
Electric model of a black hole.
Figure 114.
Electric model of a black hole.
Figure 115.
Vector representation of the forces in a black hole. Fc = f, represents the force towards the interior of the black hole generated by the mass m and Ft = -iφ, is a tangential rotation force that retards Fc by 90 degrees, generated by the mass δ.
Figure 115.
Vector representation of the forces in a black hole. Fc = f, represents the force towards the interior of the black hole generated by the mass m and Ft = -iφ, is a tangential rotation force that retards Fc by 90 degrees, generated by the mass δ.
Figure 116.
Diagram of the black hole model.
Figure 116.
Diagram of the black hole model.
Figure 117.
Spatial geometry of a Kerr-Newman black hole with charge Q = 08M and spin parameter a = 056M. The lower half shows r ≤ 0, the Antiverse. The outer and inner horizons are confocal oblate spheroids whose focus is the ring singularity. The Sisytube is a torus enclosing the ring singularity, that contains closed time like curves.
Figure 117.
Spatial geometry of a Kerr-Newman black hole with charge Q = 08M and spin parameter a = 056M. The lower half shows r ≤ 0, the Antiverse. The outer and inner horizons are confocal oblate spheroids whose focus is the ring singularity. The Sisytube is a torus enclosing the ring singularity, that contains closed time like curves.
Figure 118.
Diagram of the black hole model.
Figure 118.
Diagram of the black hole model.
Figure 120.
Penrose diagram of the Kerr-Newman geometry, M² > Q² + a².
Figure 120.
Penrose diagram of the Kerr-Newman geometry, M² > Q² + a².
Figure 121.
Spatial geometry of an extremal Kerr-Newman black hole with charge Q = 08M and spin parameter a = 06M.
Figure 121.
Spatial geometry of an extremal Kerr-Newman black hole with charge Q = 08M and spin parameter a = 06M.
Figure 123.
Penrose diagram of the Kerr-Newman geometry, M² < Q² + a².
Figure 123.
Penrose diagram of the Kerr-Newman geometry, M² < Q² + a².
Figure 124.
Characteristic parameters of the following particles: Neutron, Proton, Dproton, Protoniu, Dneutron and Neutroniumd.
Figure 124.
Characteristic parameters of the following particles: Neutron, Proton, Dproton, Protoniu, Dneutron and Neutroniumd.
Figure 127.
black hole formed by Neutroniumd particles.
Figure 127.
black hole formed by Neutroniumd particles.
Figure 129.
black hole model formed by protoniu particles.
Figure 129.
black hole model formed by protoniu particles.
Table 1.
Represents values of ImI, baryonic mass; IδI, dark matter mass; IMI, mass of baryonic matter plus the mass of dark matter; IEmI, energy of baryonic matter; IEδI, dark matter energy; IEI, Sum of the energy of baryonic matter plus the energy of dark matter and Rs, Schwarzschild´s radius, as a function of, c, speed of light; Cɢ, speed greater than the speed of light; T, temperature in Kelvin.
Table 1.
Represents values of ImI, baryonic mass; IδI, dark matter mass; IMI, mass of baryonic matter plus the mass of dark matter; IEmI, energy of baryonic matter; IEδI, dark matter energy; IEI, Sum of the energy of baryonic matter plus the energy of dark matter and Rs, Schwarzschild´s radius, as a function of, c, speed of light; Cɢ, speed greater than the speed of light; T, temperature in Kelvin.
Table 2.
Represents the values of the tangential rotation velocity Vt, angular rotation velocity ω, as a function of the radius r.
Table 2.
Represents the values of the tangential rotation velocity Vt, angular rotation velocity ω, as a function of the radius r.
Table 3.
We represent Vdm, rotation speed due to dark matter mass in red; Vm, rotation speed due only to visible matter; Vc, calculated rotation speed that results from the sum of Vdm + Vm and Vo, is the observed or measured rotation speed.
Table 3.
We represent Vdm, rotation speed due to dark matter mass in red; Vm, rotation speed due only to visible matter; Vc, calculated rotation speed that results from the sum of Vdm + Vm and Vo, is the observed or measured rotation speed.
Table 6.
We can observe in
Table 6, according to the state of matter, how the KB, frequency, wavelength, etc, vary; according to whether we are in a flat space-time or in a curved space-time.
Table 6.
We can observe in
Table 6, according to the state of matter, how the KB, frequency, wavelength, etc, vary; according to whether we are in a flat space-time or in a curved space-time.
| Earth |
Flat space-time |
Curved space-time |
units |
| Kʙ (Boltzmann´s constant) |
1.38 10ˉ²³ |
2.97 10ˉ²⁸ |
(J/K) |
| f (frequency) |
1.25 10¹⁴ |
2.69 10⁹ |
Hz |
| λ (wavelength) |
2.4 10ˉ⁶ |
0.11 |
m |
| second of arc |
1.85 10ˉ¹² |
8.49 10ˉ⁸ |
m |
| Cv (curvature) |
1 |
4.58 10⁴ |
times |
| F (gravity) |
|
9.81 |
N |
| Sun |
Flat space-time |
Curved space-time |
units |
| Kʙ (Boltzmann´s constant) |
1.38 10ˉ²³ |
3.59 10ˉ³⁷ |
(J/K) |
| f (frequency) |
3.12 10¹⁷ |
8.1 10³ |
Hz |
| λ (wavelength) |
9.61 10ˉ¹⁰ |
3.7 10⁴ |
m |
| second of arc |
7.41 10ˉ¹⁶ |
0.0285 |
m |
| Cv (curvature) |
1 |
3.84 10¹³ |
times |
| F (gravity) |
|
2.73 10² |
N |
| White dwarf star |
Flat space-time |
Curved space-time |
units |
| Kʙ (Boltzmann´s constant) |
1.38 10ˉ²³ |
1.97 10ˉ³⁷ |
(J/K) |
| f (frequency) |
4.12 10¹⁷ |
5.74 10³ |
Hz |
| λ (wavelength) |
0.72 10ˉ⁹ |
5.224 10³ |
m |
| second of arc |
5.55 10ˉ¹⁶ |
0.0403 |
m |
| Cv (curvature) |
1 |
7.2 10¹³ |
times |
| F (gravity) |
|
4.7 10⁶ |
N |
| Neutron star |
Flat space-time |
Curved space-time |
units |
| Kʙ (Boltzmann´s constant) |
1.38 10ˉ²³ |
2.42 10ˉ⁴² |
(J/K) |
| f (frequency) |
2.084 10²² |
3.655 10³ |
Hz |
| λ (wavelength) |
1.43 10ˉ¹⁴ |
8.207 10⁴ |
m |
| second of arc |
1.1 10ˉ²⁰ |
0.0633 |
m |
| Cv (curvature) |
1 |
5.75 10¹⁸ |
times |
| F (gravity) |
|
2.0 10¹² |
N |
| Black hole |
Flat space-time |
Curved space-time |
units |
| Kʙ (Boltzmann´s constant) |
1.38 10ˉ²³ |
1.78 10ˉ⁴³ |
(J/K) |
| f (frequency) |
2.084 10²³ |
2.688 10³ |
Hz |
| λ (wavelength) |
1.439 10ˉ¹⁵ |
1,11 10⁵ |
m |
| second of arc |
1.108 10ˉ²¹ |
0.0856 |
m |
| Cv (curvature) |
1 |
7.72 10¹⁹ |
times |
| F (gravity) |
|
5.0 10¹² |
N |
Table 7.
particles of the standard model as a function of mass in kg, energy in Joules, frequency in Hz and temperature in K.
Table 7.
particles of the standard model as a function of mass in kg, energy in Joules, frequency in Hz and temperature in K.
Table 8.
Variation of the mass of gluons with temperature.
Table 8.
Variation of the mass of gluons with temperature.
Table 9.
Calculation of the mass of the graviton as a function of temperature.
Table 9.
Calculation of the mass of the graviton as a function of temperature.
Table 10.
Represents values of ImI, baryonic mass; IδI, dark matter mass; IMI, mass of baryonic matter plus the mass of dark matter; IEmI, energy of baryonic matter; IEδI, dark matter energy; IEI, Sum of the energy of baryonic matter plus the energy of dark matter and Rs, Schwarzschild´s radius, as a function of, c, speed of light; Cɢ, speed greater than the speed of light; T, temperature in Kelvin.
Table 10.
Represents values of ImI, baryonic mass; IδI, dark matter mass; IMI, mass of baryonic matter plus the mass of dark matter; IEmI, energy of baryonic matter; IEδI, dark matter energy; IEI, Sum of the energy of baryonic matter plus the energy of dark matter and Rs, Schwarzschild´s radius, as a function of, c, speed of light; Cɢ, speed greater than the speed of light; T, temperature in Kelvin.
Table 12.
Compare the gravitational force between stellar bodies and elementary particles.
Table 12.
Compare the gravitational force between stellar bodies and elementary particles.
Table 13.
Mass-temperature relationship for elemental and non-elemental particles.
Table 13.
Mass-temperature relationship for elemental and non-elemental particles.
Table 14.
β⁻ Decay.
| βˉ DECAY |
| NEUTRON |
PROTON |
INTERACTION |
INTERACTION (MeV/c²) |
| R(DD)R |
R(DD)R |
E1 = 1.94 |
IE1I = 19.12 |
| B(DD)B |
B(UU)B |
E2 = 3.69 |
IE2I = 36.41 |
| G(UU)G |
G(UU)G |
E3 = 0.9 |
IE3I = 08.89 |
| R(DD)B |
R(DU)B
|
E4 = 8.2 |
IE4I = 80.75 |
| R(DU)G |
R(DU)G |
E5 = 2 |
IE5I = 19.69 |
| B(DD)R |
B(UD)R |
E6 = 7.4 |
IE6I = 72.87 |
| B(DU)G |
B(UU)G
|
E7 = 4.2 |
IE7I = 41.35 |
| G(UD)R
|
G(UD)R
|
E8 = 3.8 |
IE8I = 37.42 |
| G(UD)B
|
G(UU)B
|
E9 = 7 |
IE9I = 68.93 |
| TOTAL INTERACTION |
IEtI = 385.37 MeV/c² |
Table 15.
Electric current (DD) in green, between (R(DD)R)n and (R(DD)R)p.
Table 15.
Electric current (DD) in green, between (R(DD)R)n and (R(DD)R)p.
| 84.69 MeV/c² |
E1 = 19.12 MeV/c² |
103.81 MeV/c² |
| N |
--> |
P |
| R |
|
R |
| D |
D |
D |
| D |
D |
D |
| R |
|
R |
Table 16.
Electric current (DD) in green, between (R(DD)B)n and (B(UU)B)p.
Table 16.
Electric current (DD) in green, between (R(DD)B)n and (B(UU)B)p.
| 84.69 MeV/c² |
E2 = 36.41 MeV/c² |
48.28 MeV/c² |
| N |
--> |
P |
| B |
|
B |
| D |
D |
U |
| D |
D |
U |
| B |
|
B |
Table 17.
- Electric current (UU) in green, between (G(UU)G)n and (G(UU)G)p.
Table 17.
- Electric current (UU) in green, between (G(UU)G)n and (G(UU)G)p.
| 39.39 MeV/c² |
E3 = 8.89 MeV/c² |
48.28 MeV/c² |
| N |
--> |
P |
| G |
|
G |
| U |
U |
U |
| U |
U |
U |
| G |
|
G |
Table 18.
Electric current (DD) in green, between (R(DD)B)n and (R(DU)B)p.
Table 18.
Electric current (DD) in green, between (R(DD)B)n and (R(DU)B)p.
| 100.45 MeV/c² |
E4 = 80.75 MeV/c² |
48.28 MeV/c² |
| N |
--> |
P |
| R |
|
R |
| D |
D |
D |
| D |
D |
U |
| B |
|
B |
Table 19.
Electric current (DU) in green, between (R(DU)G)n and (R(DU)G)p.
Table 19.
Electric current (DU) in green, between (R(DU)G)n and (R(DU)G)p.
| 100.45 MeV/c² |
E5 = 19.69 MeV/c² |
125.54 MeV/c² |
| N |
--> |
P |
| R |
|
R |
| D |
D |
D |
| U |
U |
U |
| G |
|
G |
Table 20.
Electric current (DD) in green, between [B(DD)R]n and [B(UD)R]p.
Table 20.
Electric current (DD) in green, between [B(DD)R]n and [B(UD)R]p.
| 100.45 MeV/c² |
E6 = 72.84 MeV/c² |
165.38 MeV/c² |
| N |
--> |
P |
| B |
|
B |
| D |
D |
U |
| D |
D |
D |
| R |
|
R |
Table 21.
Electric current (UD) in green, between [G(DU)G]n and [G(UU)G]p.
Table 21.
Electric current (UD) in green, between [G(DU)G]n and [G(UU)G]p.
| 100.45 MeV/c² |
E7 = 41.35 MeV/c² |
97.78 MeV/c² |
| N |
--> |
P |
| B |
|
B |
| D |
D |
U |
| U |
U |
U |
| G |
|
G |
Table 22.
Electric current (UD) in green, between [G(UD)R]n and [G(UD)R]p.
Table 22.
Electric current (UD) in green, between [G(UD)R]n and [G(UD)R]p.
| 164.47 MeV/c² |
E8 = 37.42 MeV/c² |
202.80 MeV/c² |
| N |
--> |
P |
| G |
|
G |
| U |
U |
U |
| D |
D |
D |
| R |
|
R |
Table 23.
Electric current (UD) in green, between [G(UD)R]n and [G(UD)R]p.
Table 23.
Electric current (UD) in green, between [G(UD)R]n and [G(UD)R]p.
| 164.47 MeV/c² |
E9 = 68.93 MeV/c² |
97.78 MeV/c² |
| N |
--> |
P |
| G |
|
G |
| U |
U |
U |
| D |
D |
U |
| B |
|
B |
Table 24.
Analysis of (BB) interactions.
Table 24.
Analysis of (BB) interactions.
| R |
R |
B |
B |
G |
G |
| MeV/c² |
MeV/c² |
MeV/c² |
MeV/c² |
MeV/c² |
MeV/c² |
| 80.75 |
72.87 |
72.87 |
80.75 |
68.93 |
41.35 |
| |
|
41.35 |
68.93 |
|
|
| |
|
114.22 |
149.68 |
|
|
| |
|
149.68 - 114.22 = 35.46 |
|
|
Table 25.
Electric current (DD) in green, between (R(DD)R)n and (R(DD)R)p.
Table 25.
Electric current (DD) in green, between (R(DD)R)n and (R(DD)R)p.
| 84.69 MeV/c² |
E1 = 19.12 MeV/c² |
103.81 MeV/c² |
| N |
--> |
P |
| R |
|
R |
| D |
D |
D |
| D |
D |
D |
| R |
|
R |
Table 26.
Electric current (DU) in green, between [B(DU)G]n and [B(UU)G]p.
Table 26.
Electric current (DU) in green, between [B(DU)G]n and [B(UU)G]p.
| 100.45 MeV/c² |
E7 = 41.35 MeV/c² |
97.78 MeV/c² |
| N |
--> |
P |
| B |
|
B |
| D |
D |
U |
| U |
U |
U |
| G |
|
G |
Table 27.
Electric current (UD) in green, between [G(UD)R]n and [G(UD)R]p.
Table 27.
Electric current (UD) in green, between [G(UD)R]n and [G(UD)R]p.
| 164.47 MeV/c² |
E9 = 68.93 MeV/c² |
97.78 MeV/c² |
| N |
--> |
P |
| G |
|
G |
| U |
U |
U |
| D |
D |
U |
| B |
|
B |
Table 30.
Represents values of ImI, baryonic mass; IδI, dark matter mass; IMI, mass of baryonic matter plus the mass of dark matter; IEmI, energy of baryonic matter; IEδI, dark matter energy; IEI, Sum of the energy of baryonic matter plus the energy of dark matter and Rs, Schwarzschild´s radius, as a function of, c, speed of light; Cɢ, speed greater than the speed of light; T, temperature in Kelvin.
Table 30.
Represents values of ImI, baryonic mass; IδI, dark matter mass; IMI, mass of baryonic matter plus the mass of dark matter; IEmI, energy of baryonic matter; IEδI, dark matter energy; IEI, Sum of the energy of baryonic matter plus the energy of dark matter and Rs, Schwarzschild´s radius, as a function of, c, speed of light; Cɢ, speed greater than the speed of light; T, temperature in Kelvin.
Table 31.
Entropy values for white dwarf stars, neutron stars, and black holes.
Table 31.
Entropy values for white dwarf stars, neutron stars, and black holes.
Table 33.
Space-time dimension vs cosmological constant for: m > 0, m = 0 and m < 0.
Table 33.
Space-time dimension vs cosmological constant for: m > 0, m = 0 and m < 0.
Table 34.
Represents values of ImI, baryonic mass; IδI, dark matter mass; IMI, mass of baryonic matter plus the mass of dark matter; IEmI, energy of baryonic matter; IEδI, dark matter energy; IEI, Sum of the energy of baryonic matter plus the energy of dark matter and Rs, Schwarzschild´s radius, as a function of, c, speed of light; Cɢ, speed greater than the speed of light; T, temperature in Kelvin.
Table 34.
Represents values of ImI, baryonic mass; IδI, dark matter mass; IMI, mass of baryonic matter plus the mass of dark matter; IEmI, energy of baryonic matter; IEδI, dark matter energy; IEI, Sum of the energy of baryonic matter plus the energy of dark matter and Rs, Schwarzschild´s radius, as a function of, c, speed of light; Cɢ, speed greater than the speed of light; T, temperature in Kelvin.
Table 35.
Calculations of Planck parameters as a function of Cɢ.
Table 35.
Calculations of Planck parameters as a function of Cɢ.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

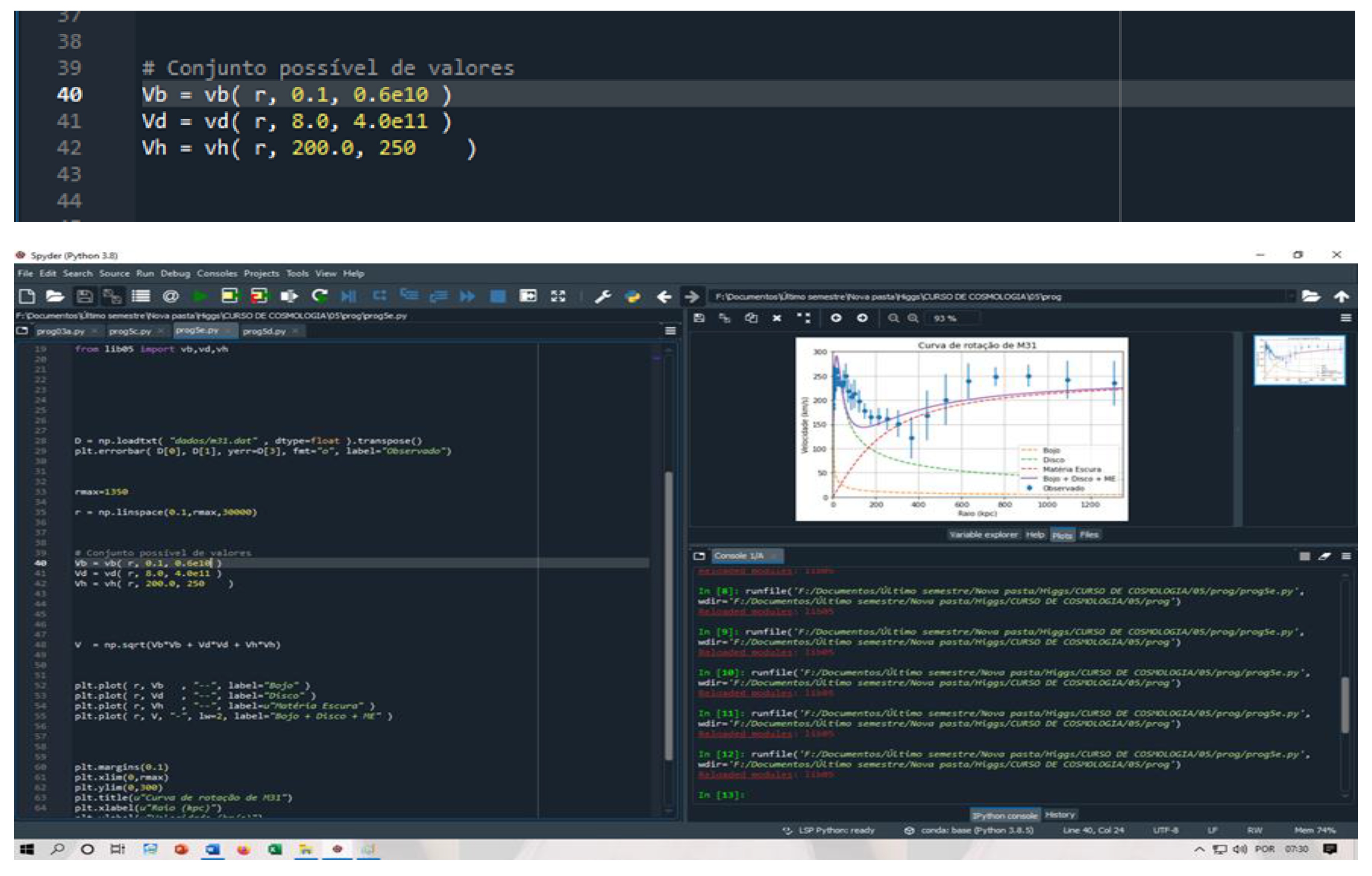

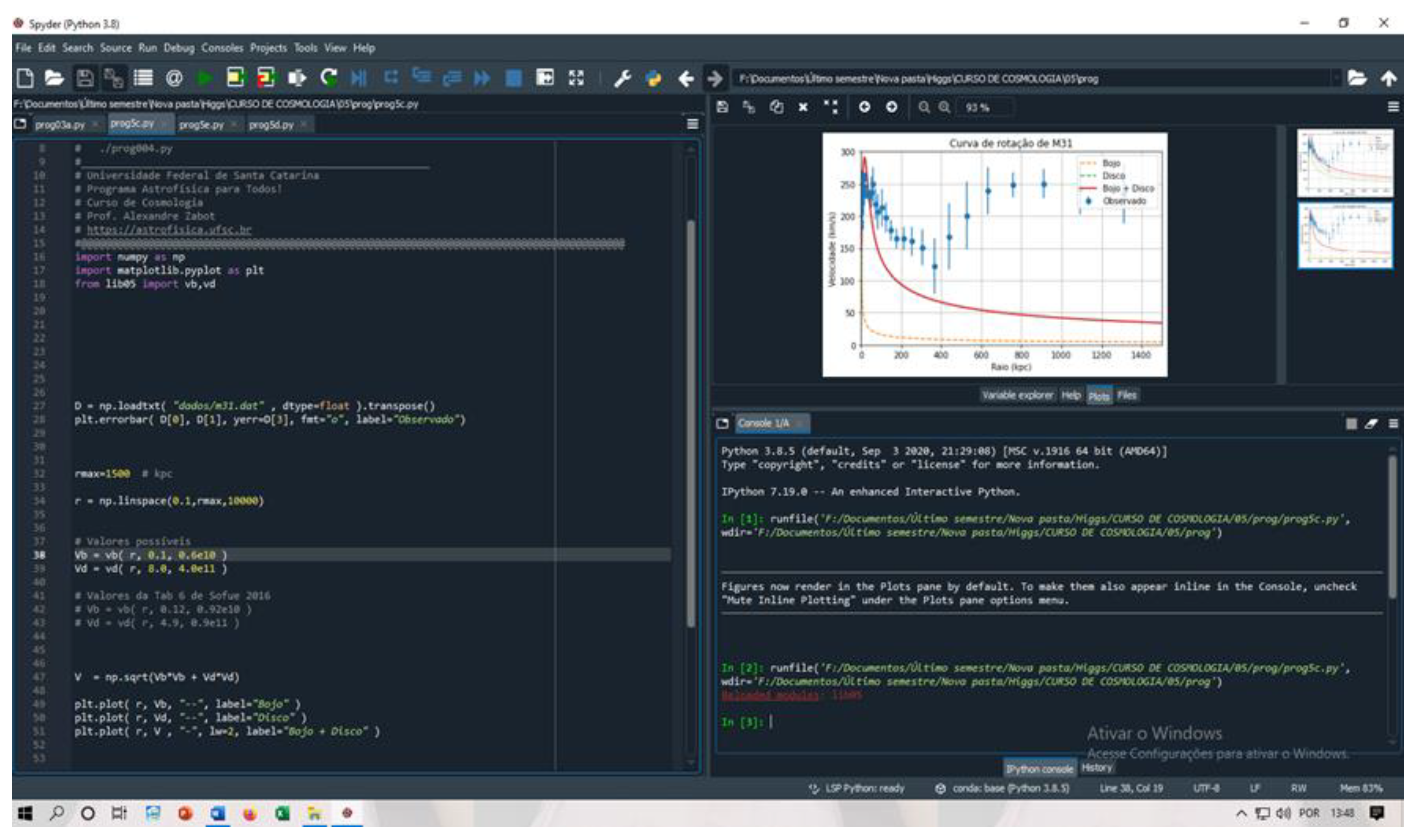
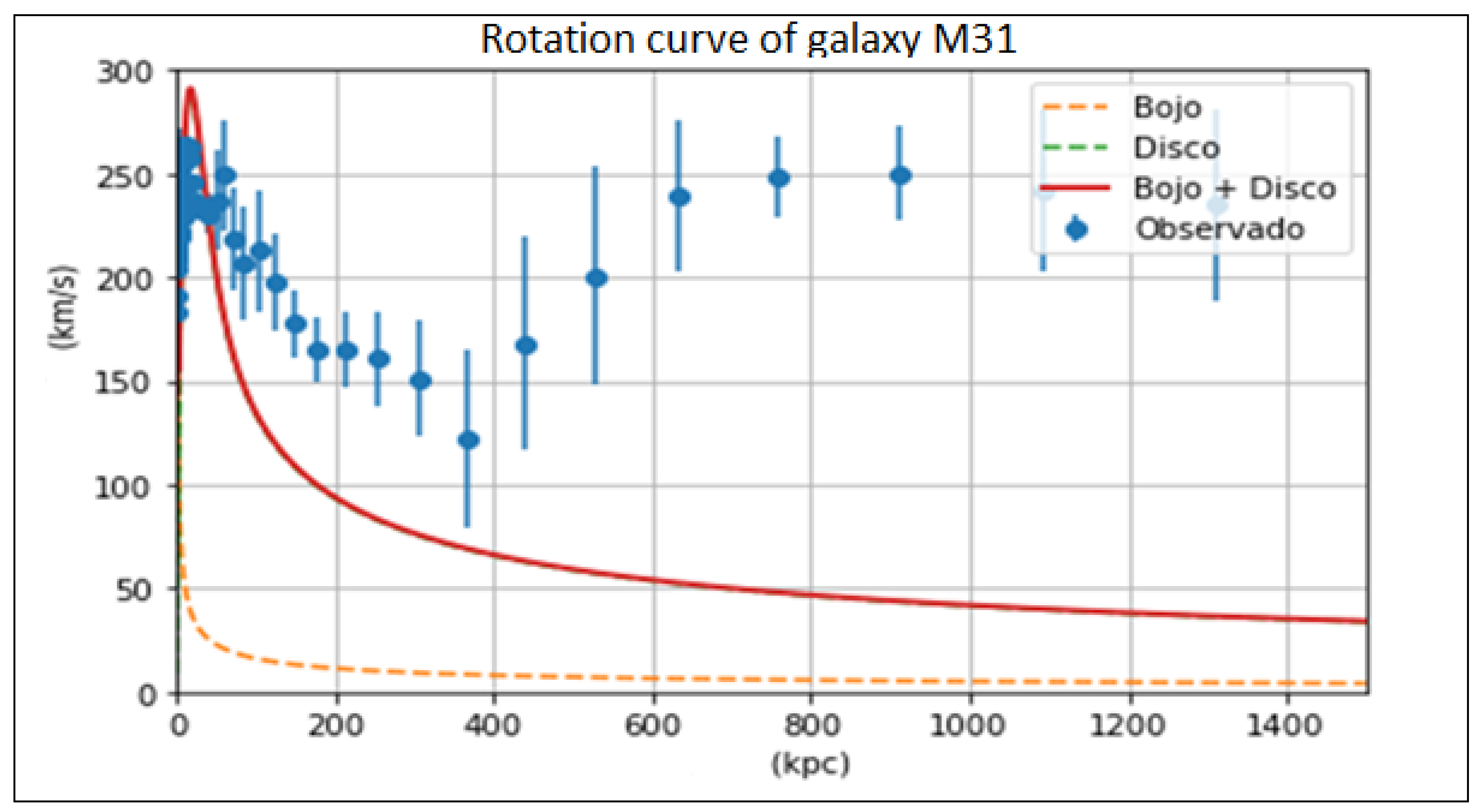
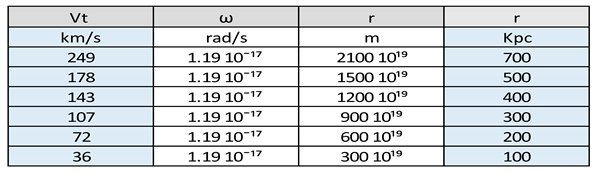
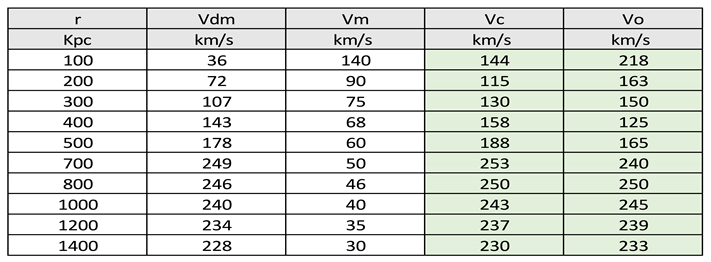
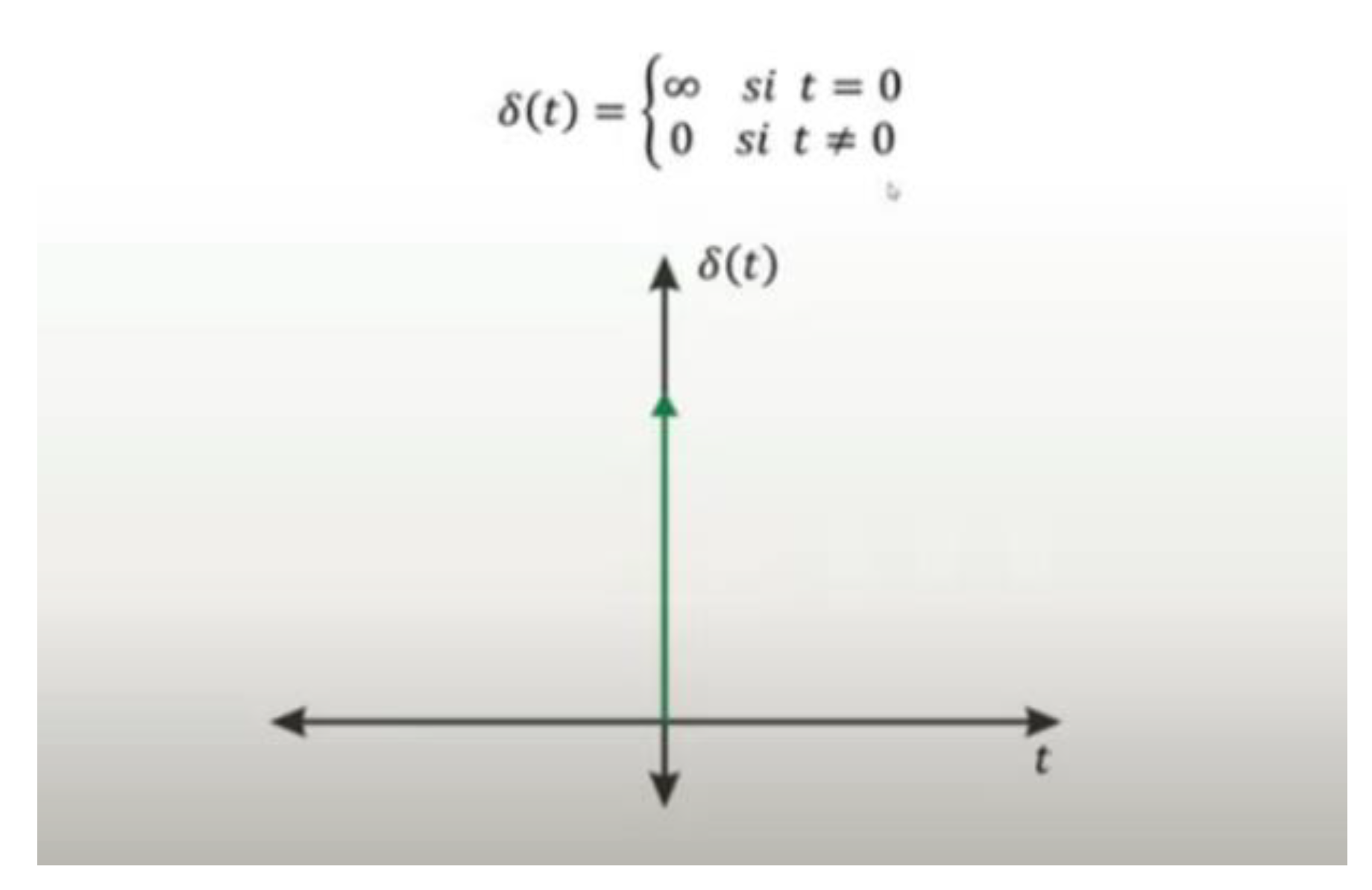
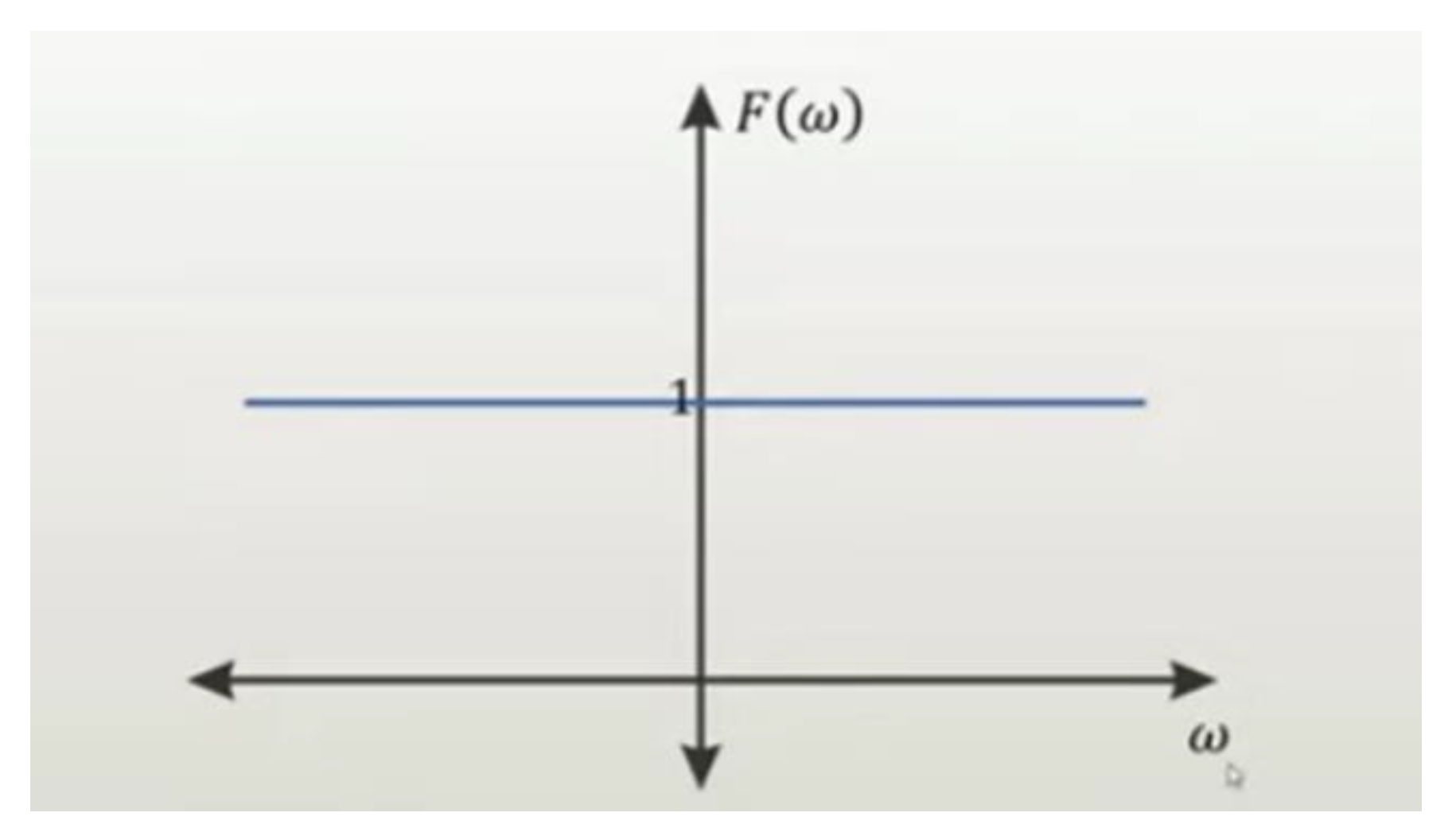
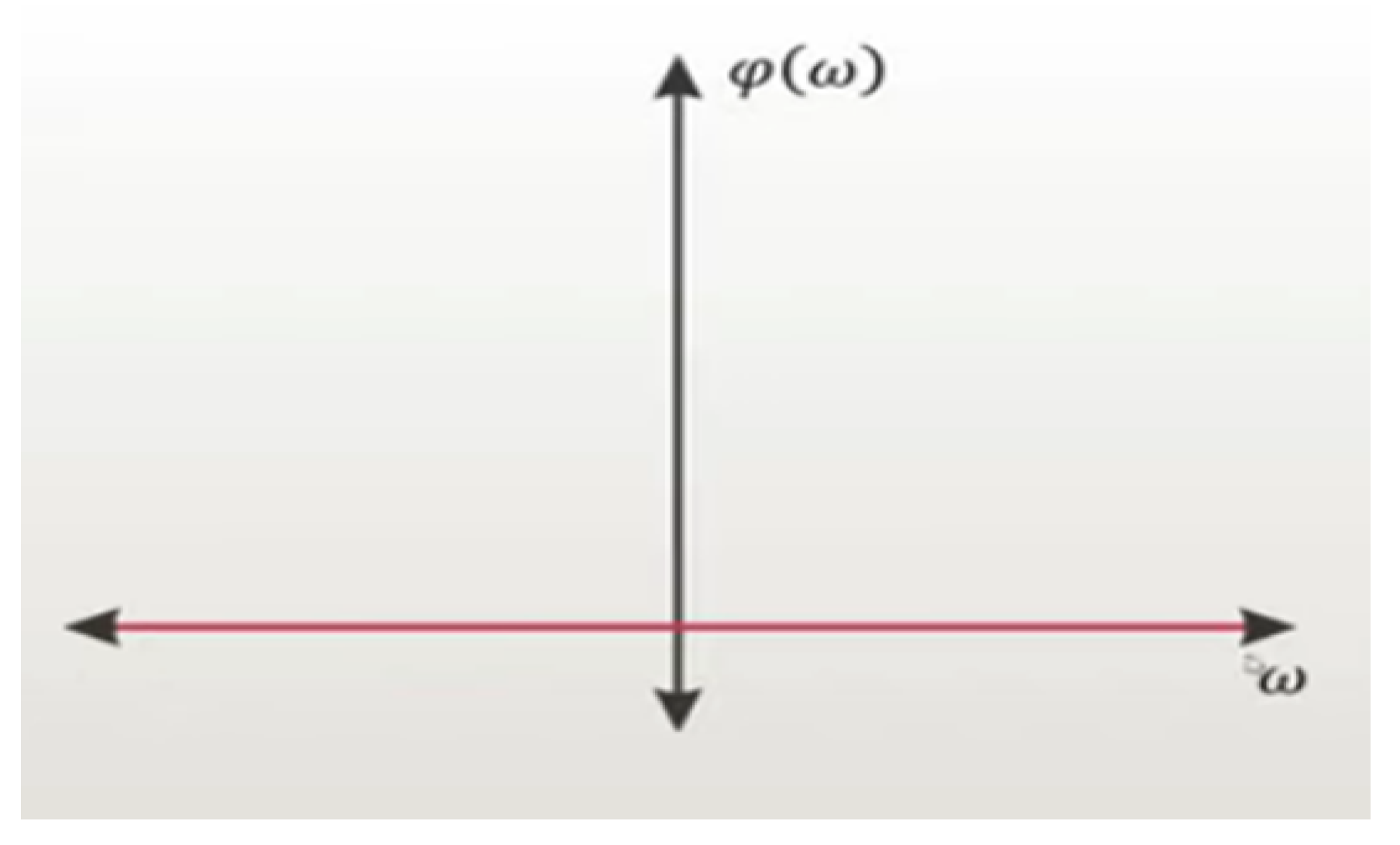
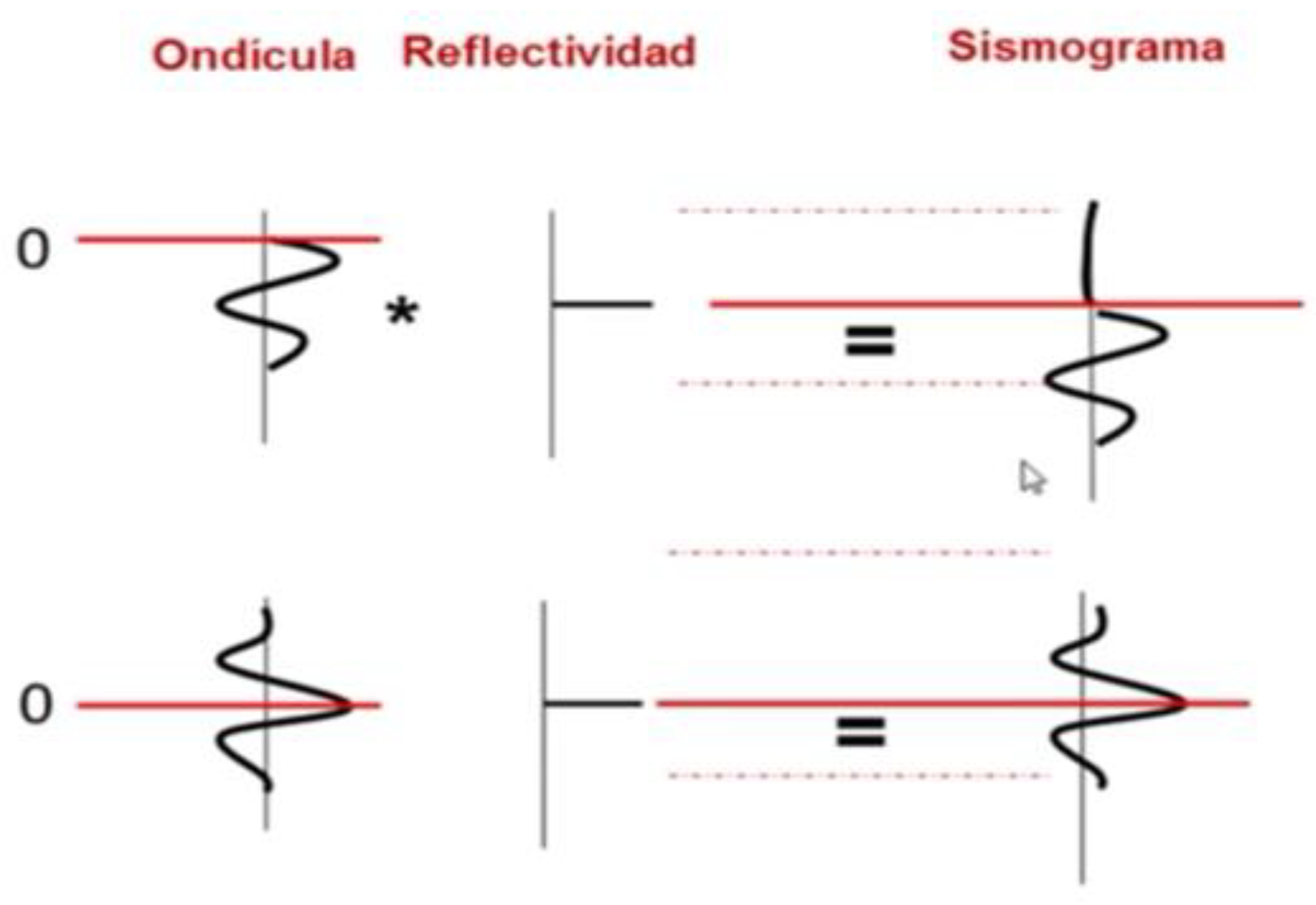
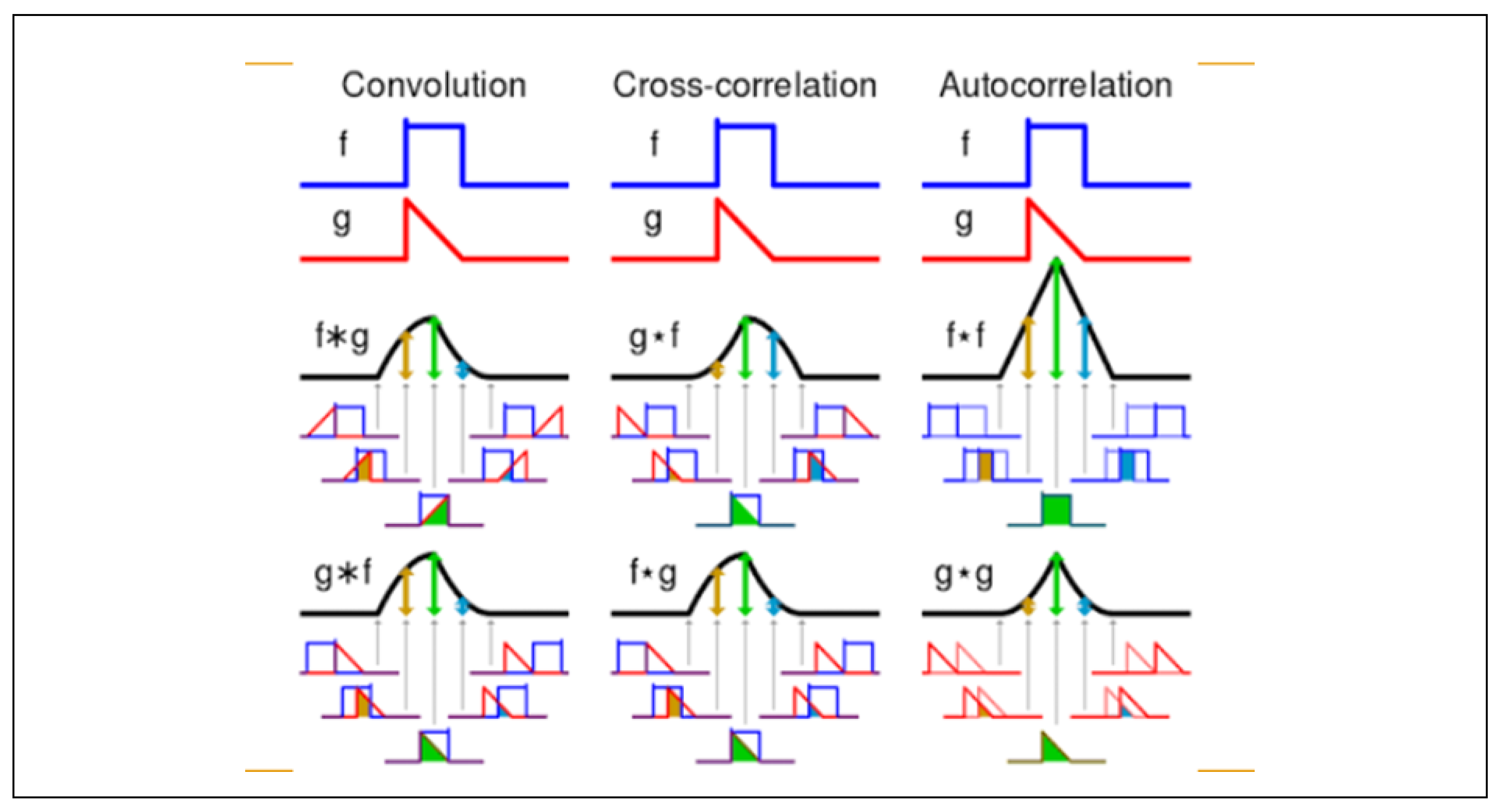

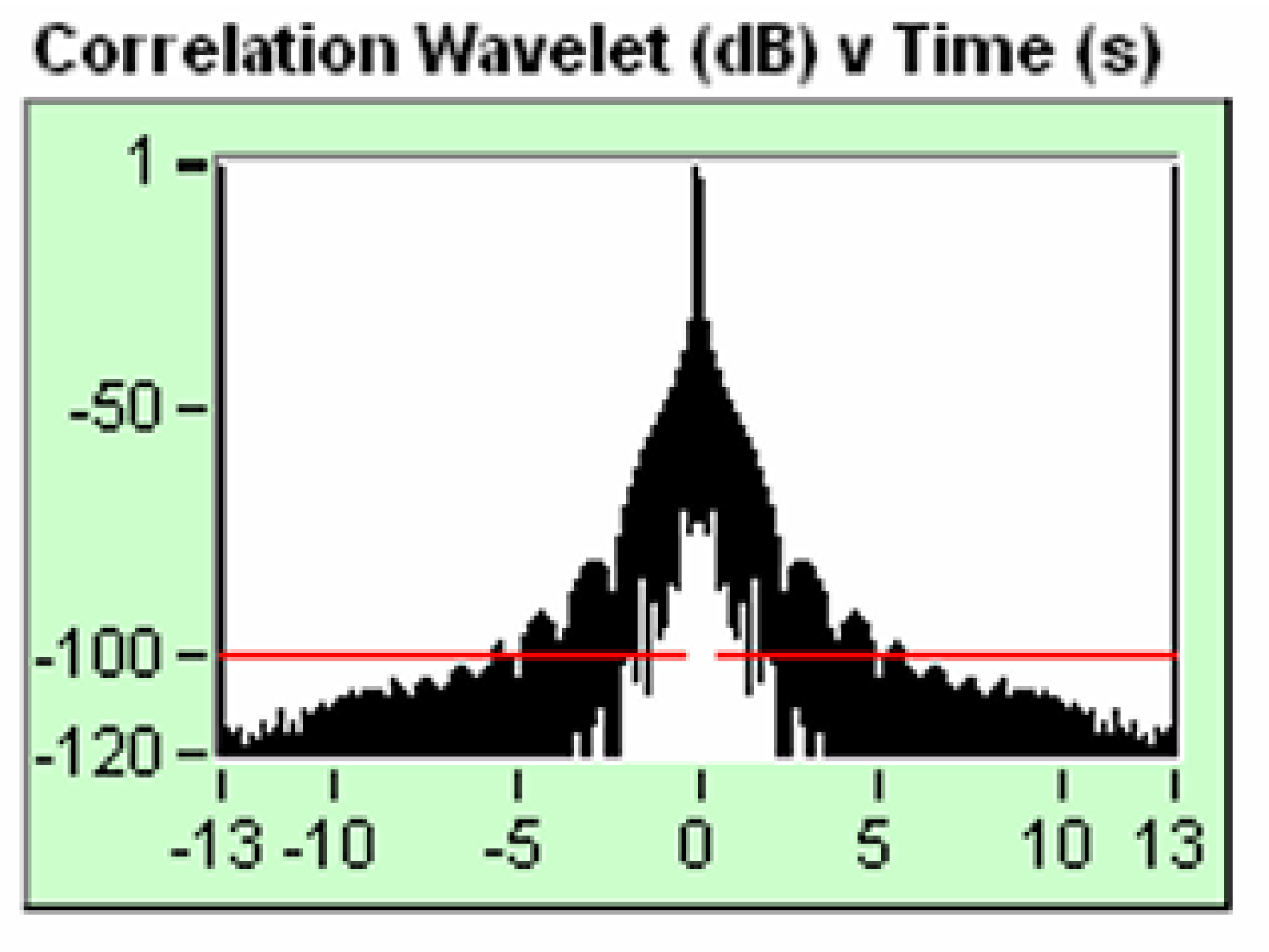
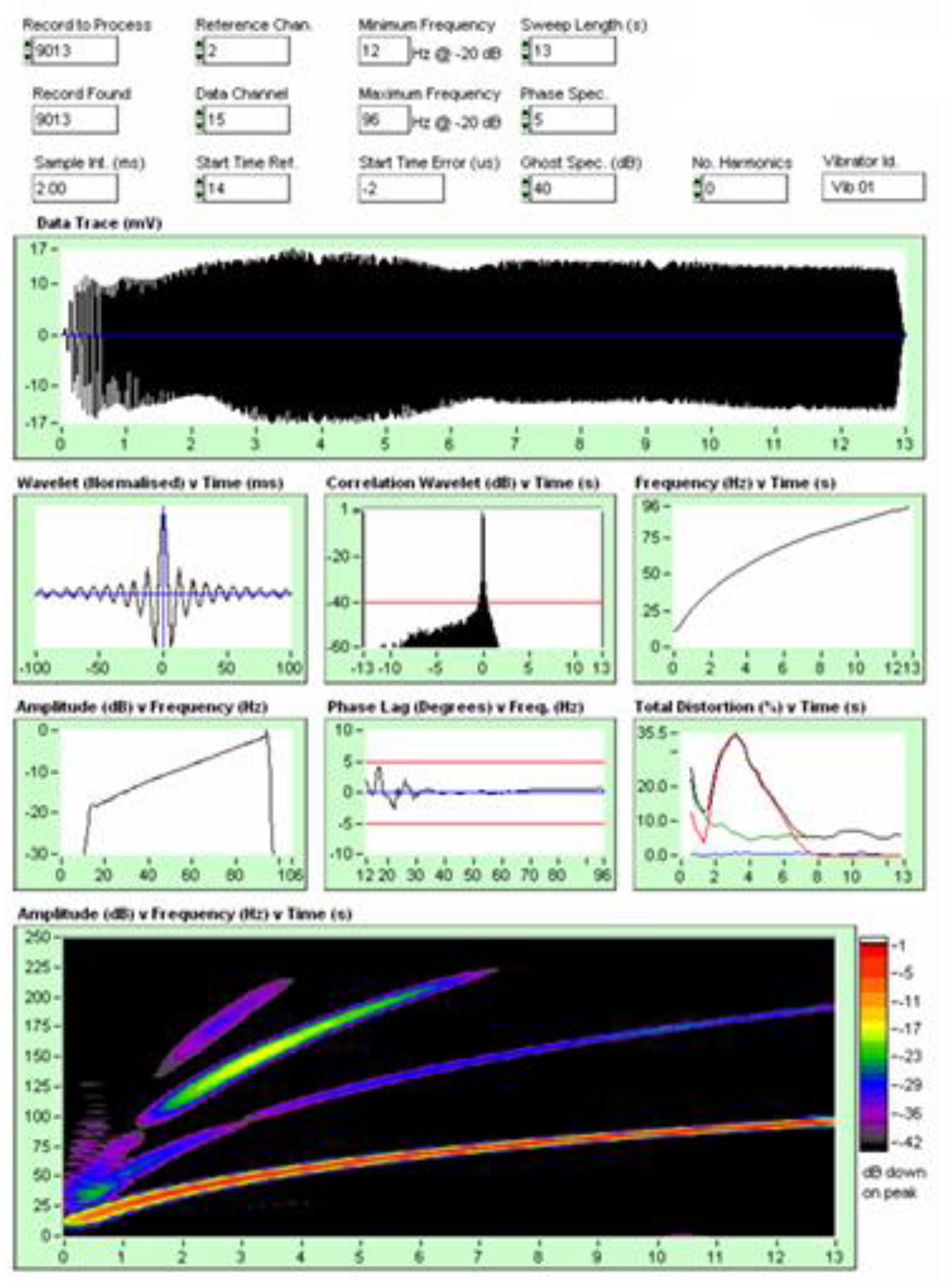
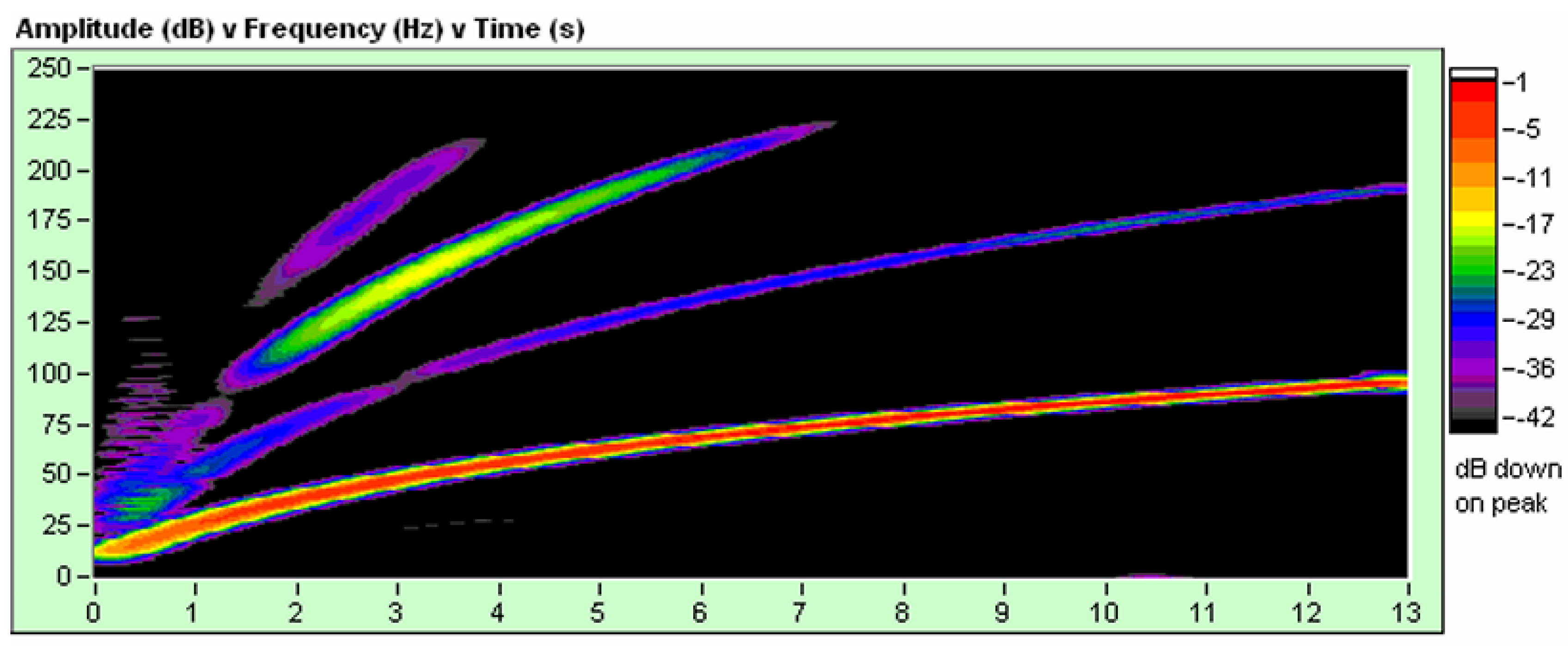
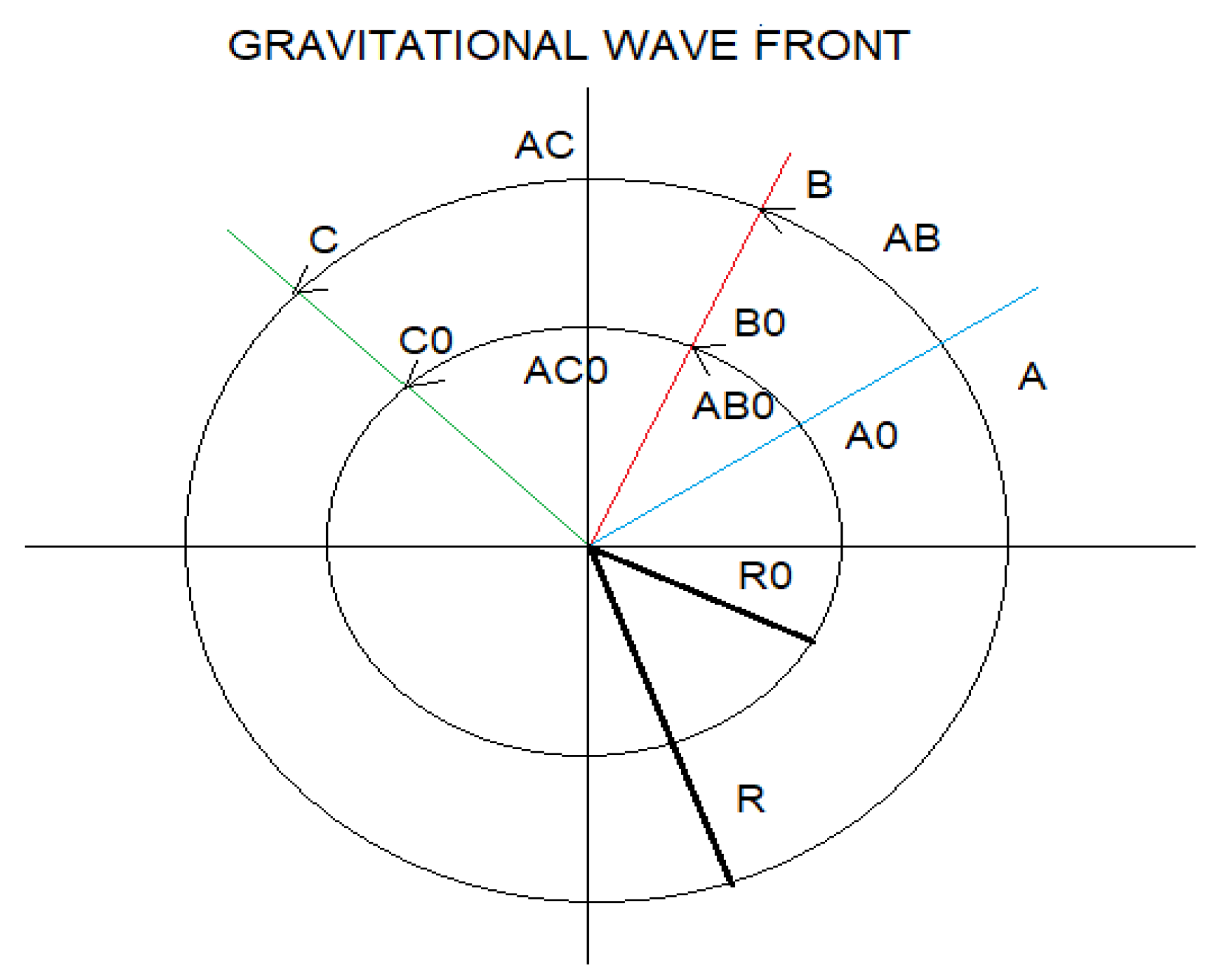
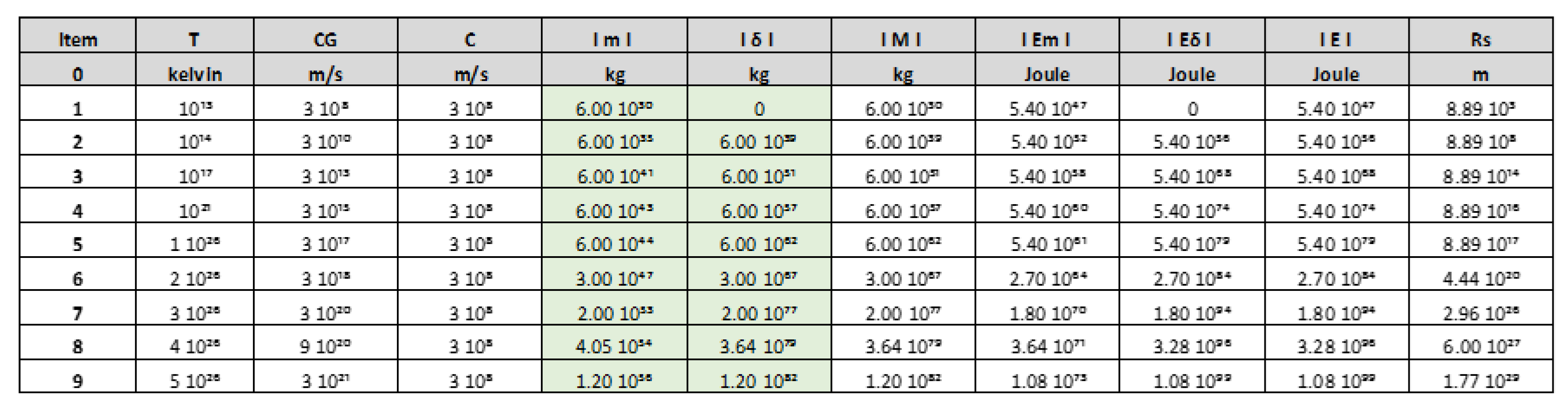
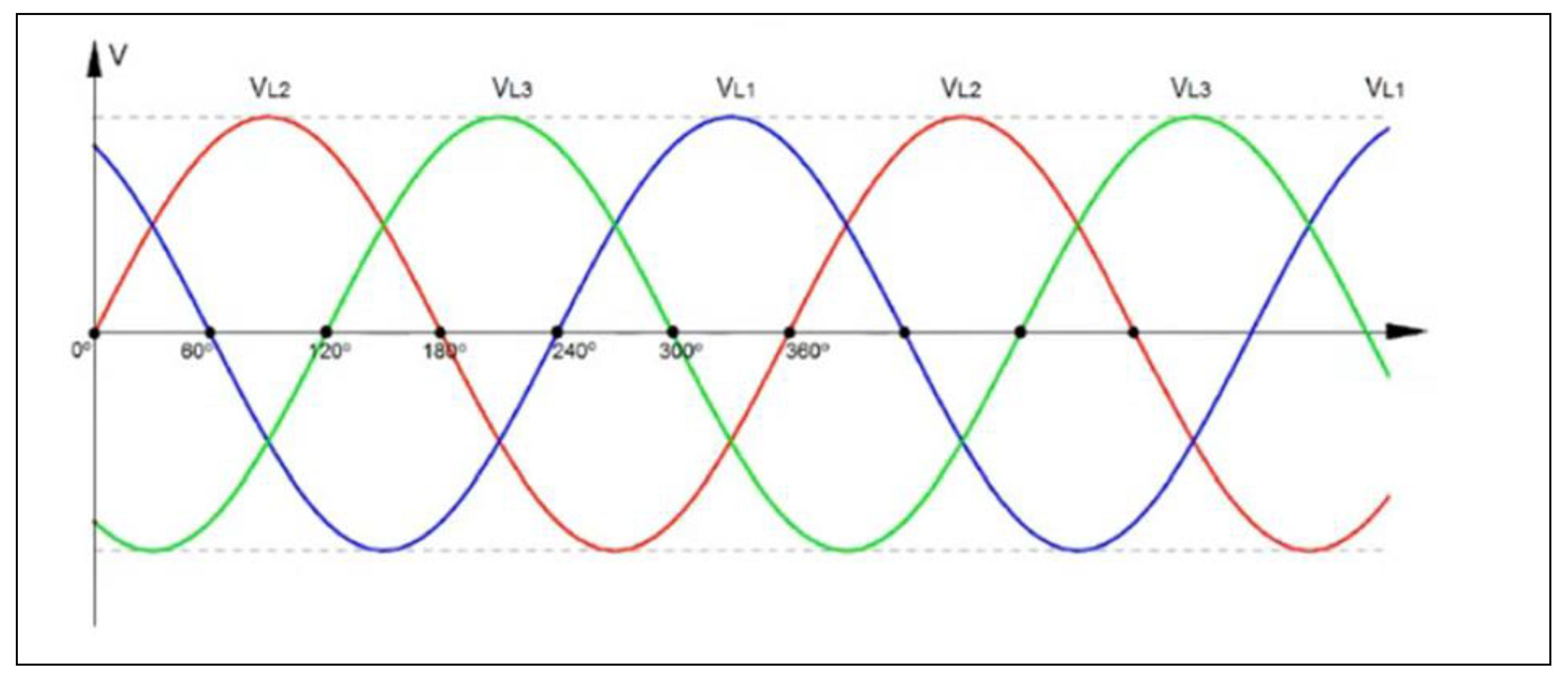
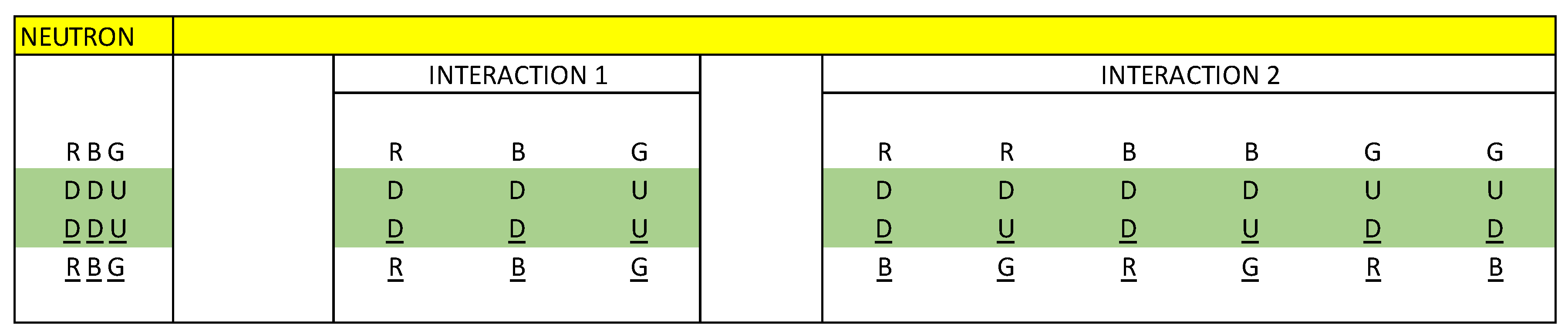
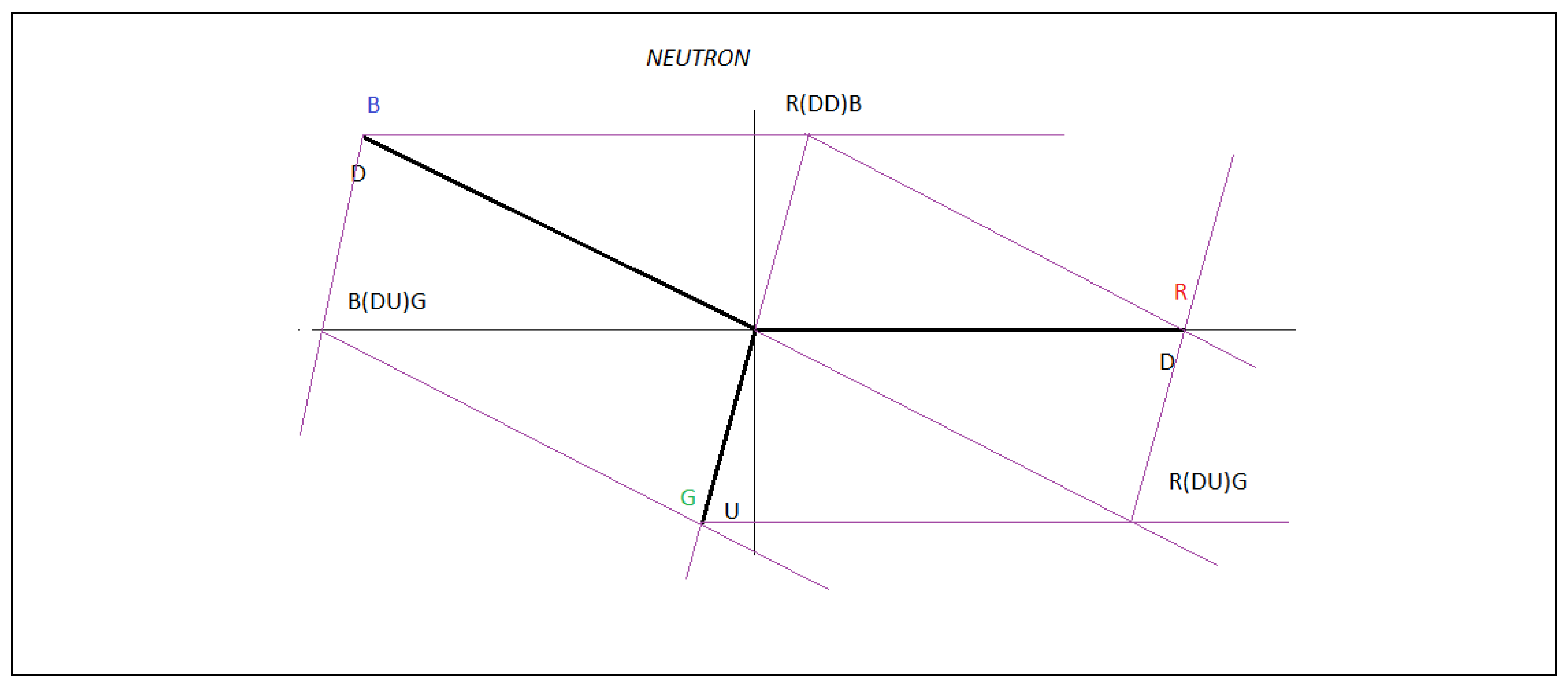

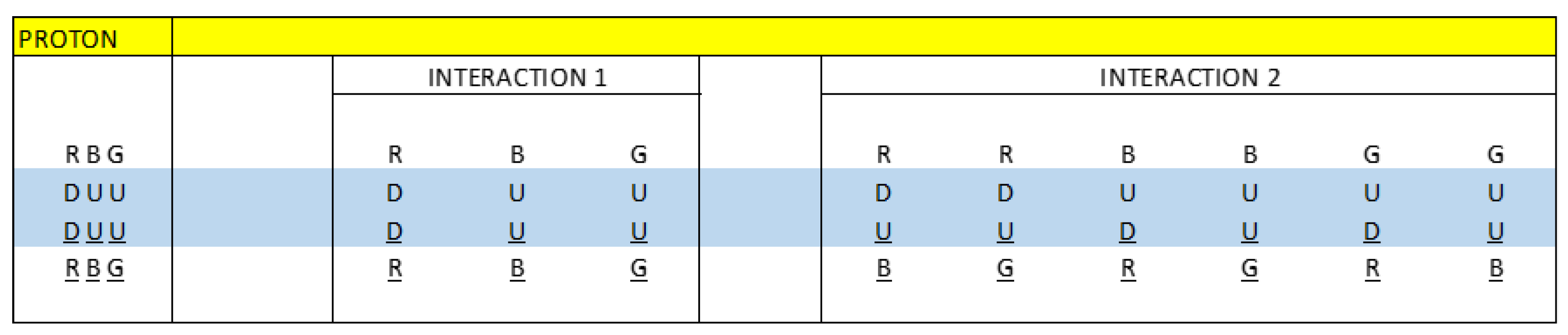
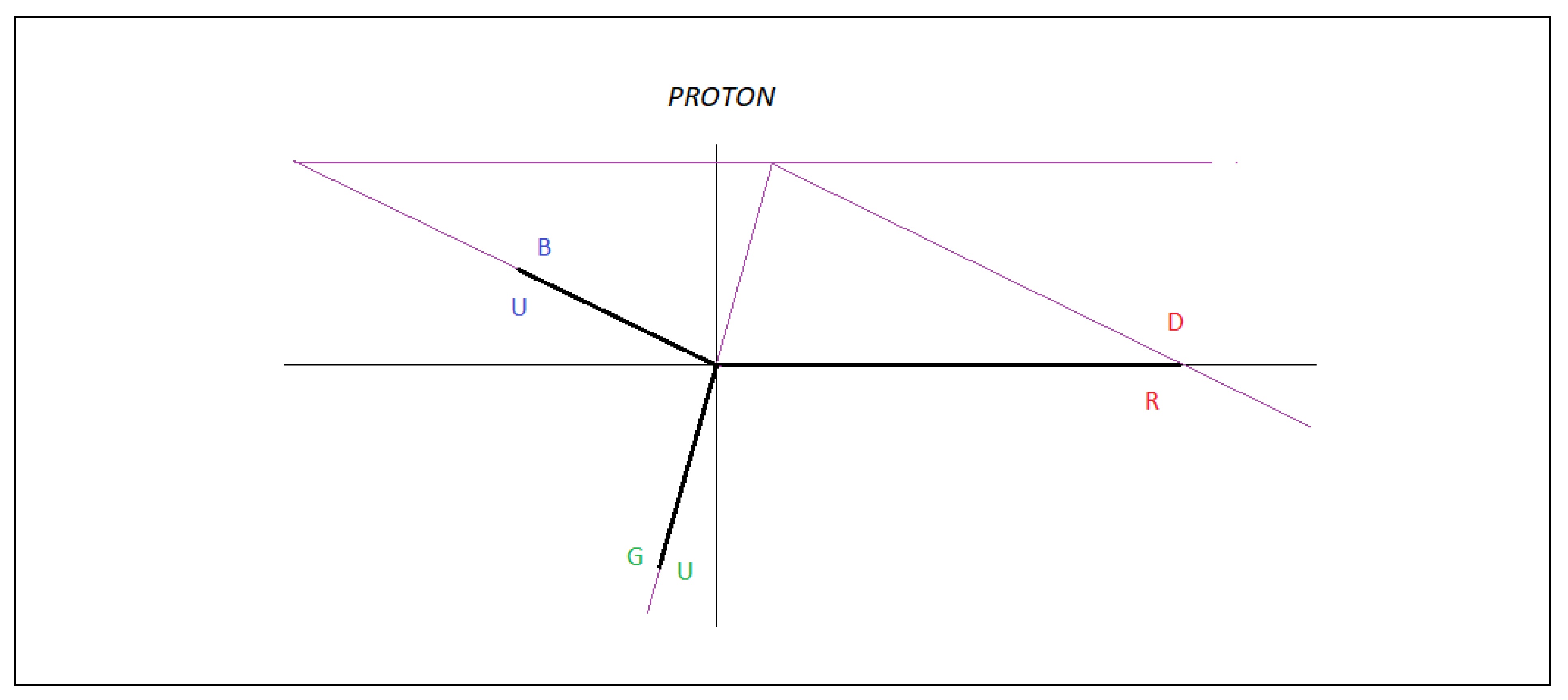
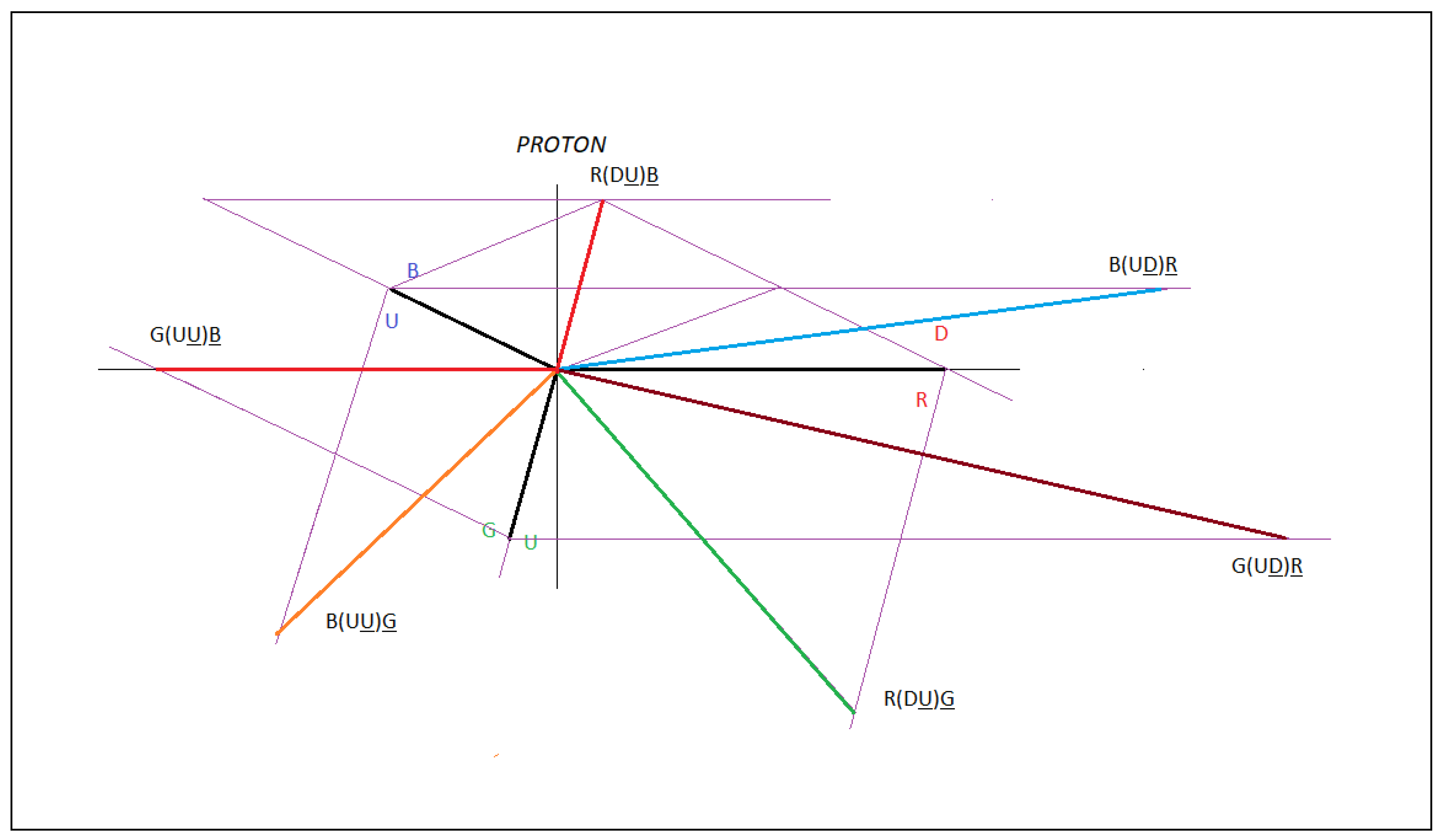
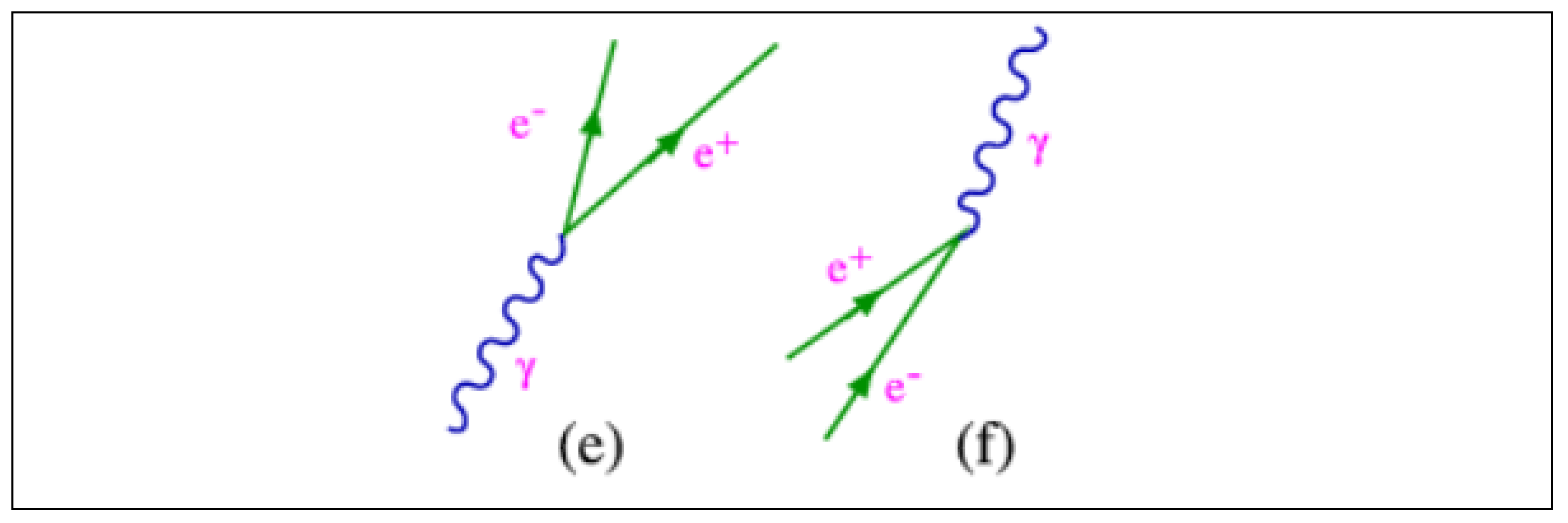
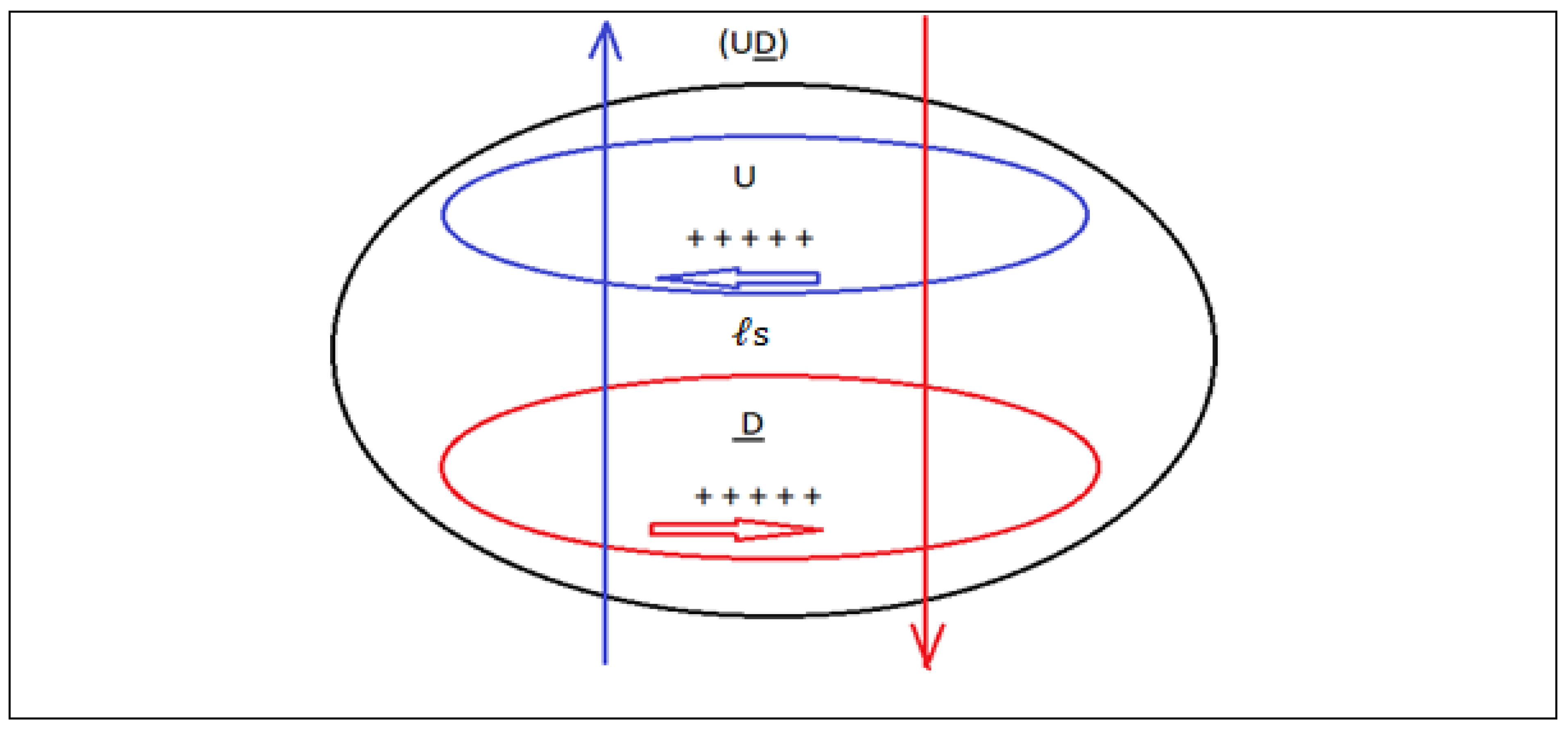


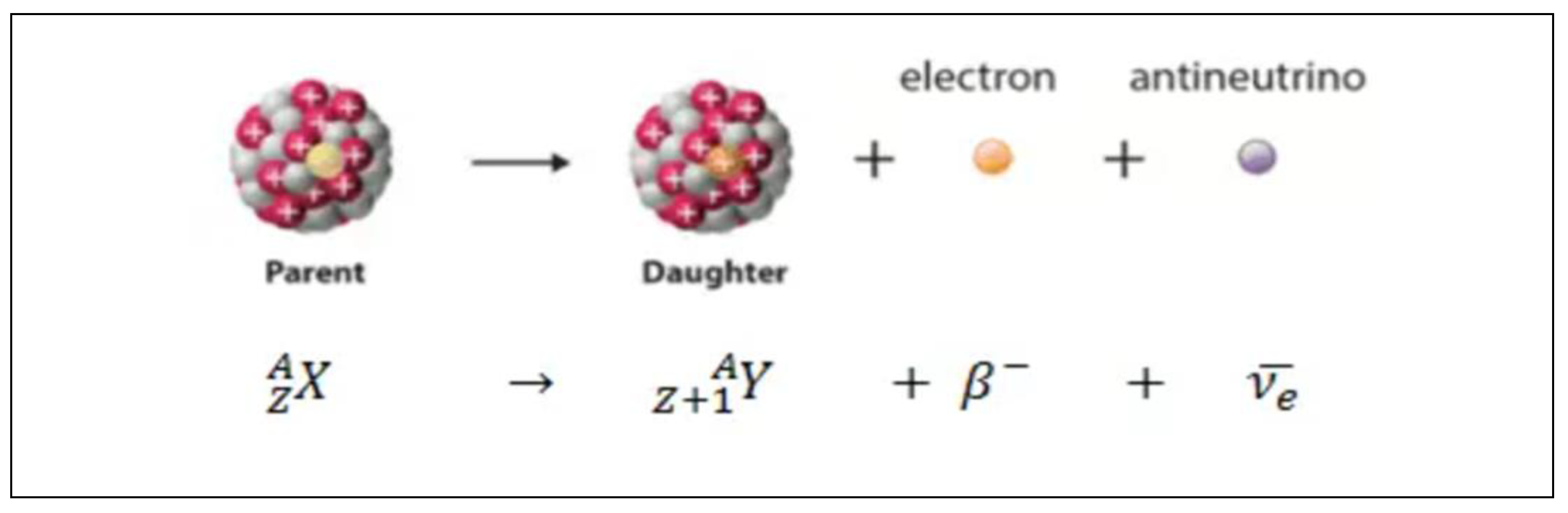
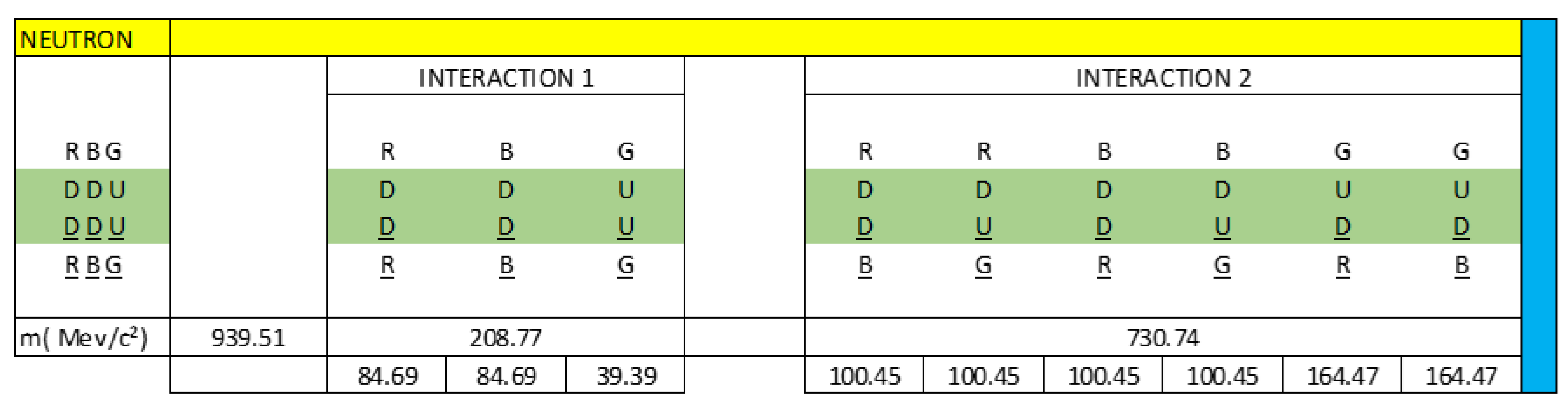
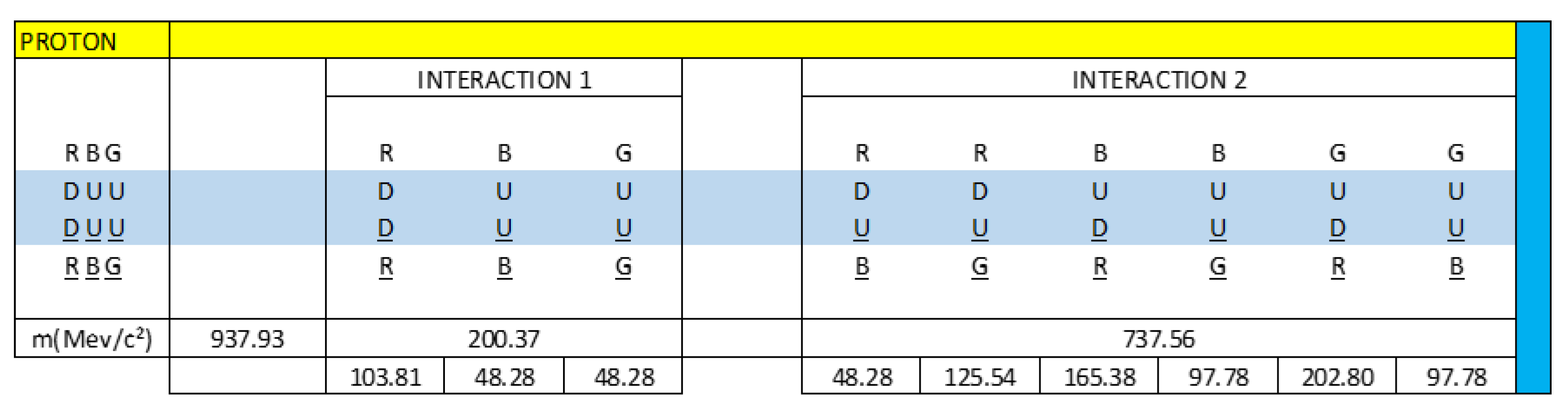
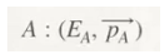
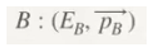
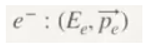
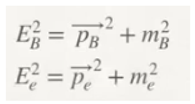
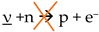
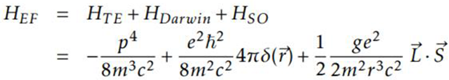
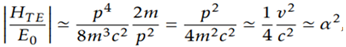
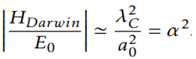
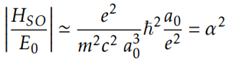
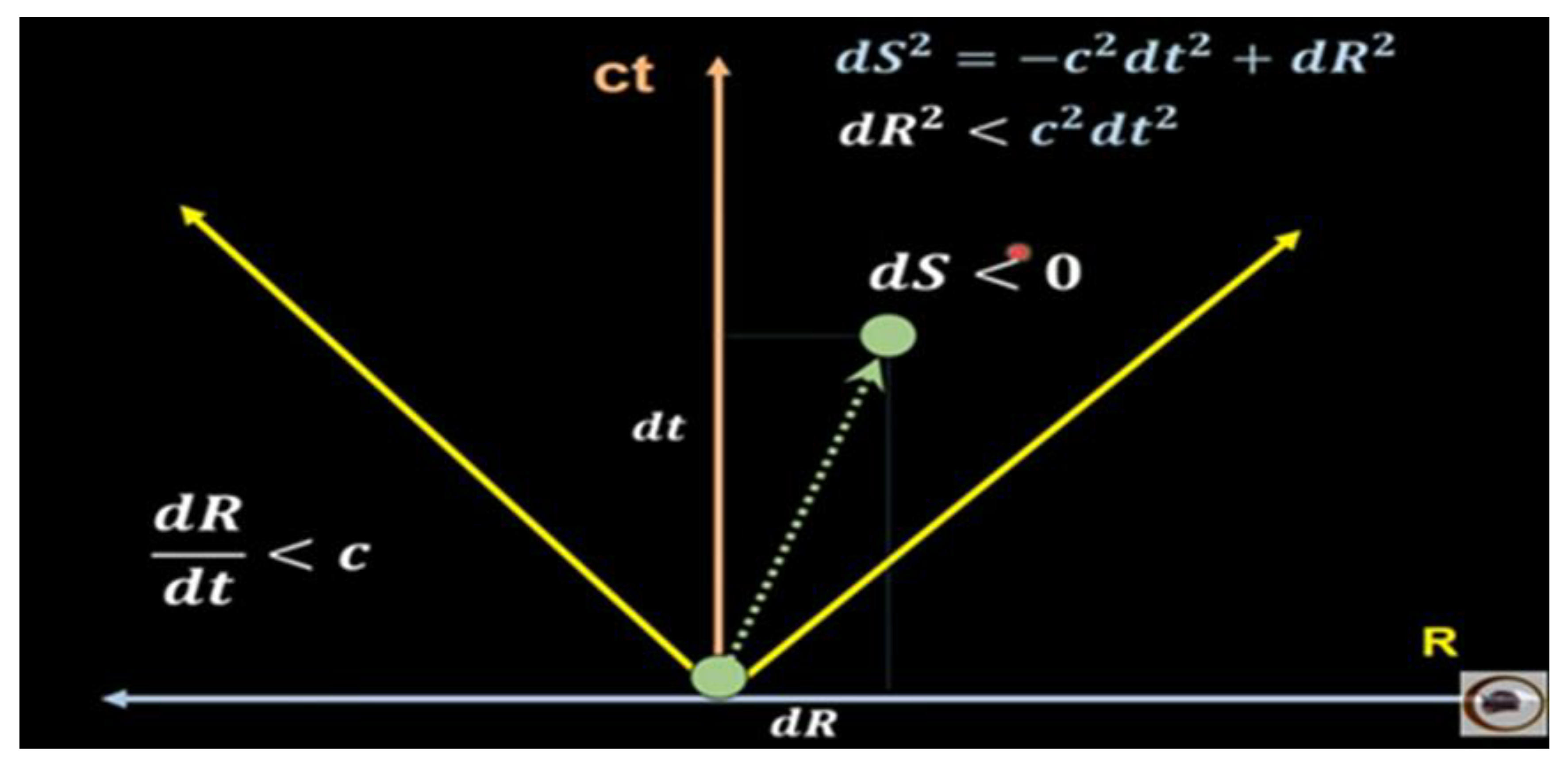
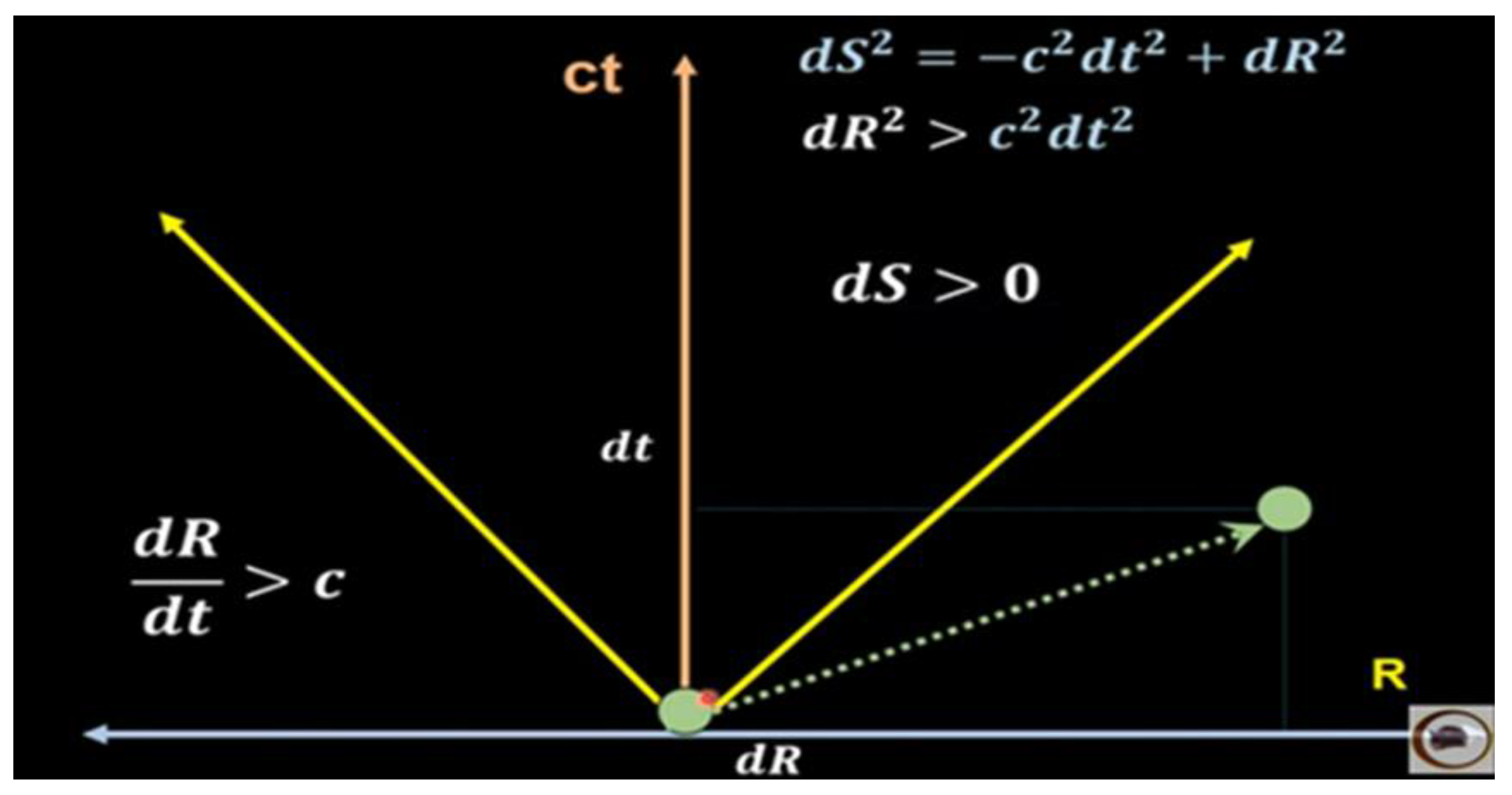
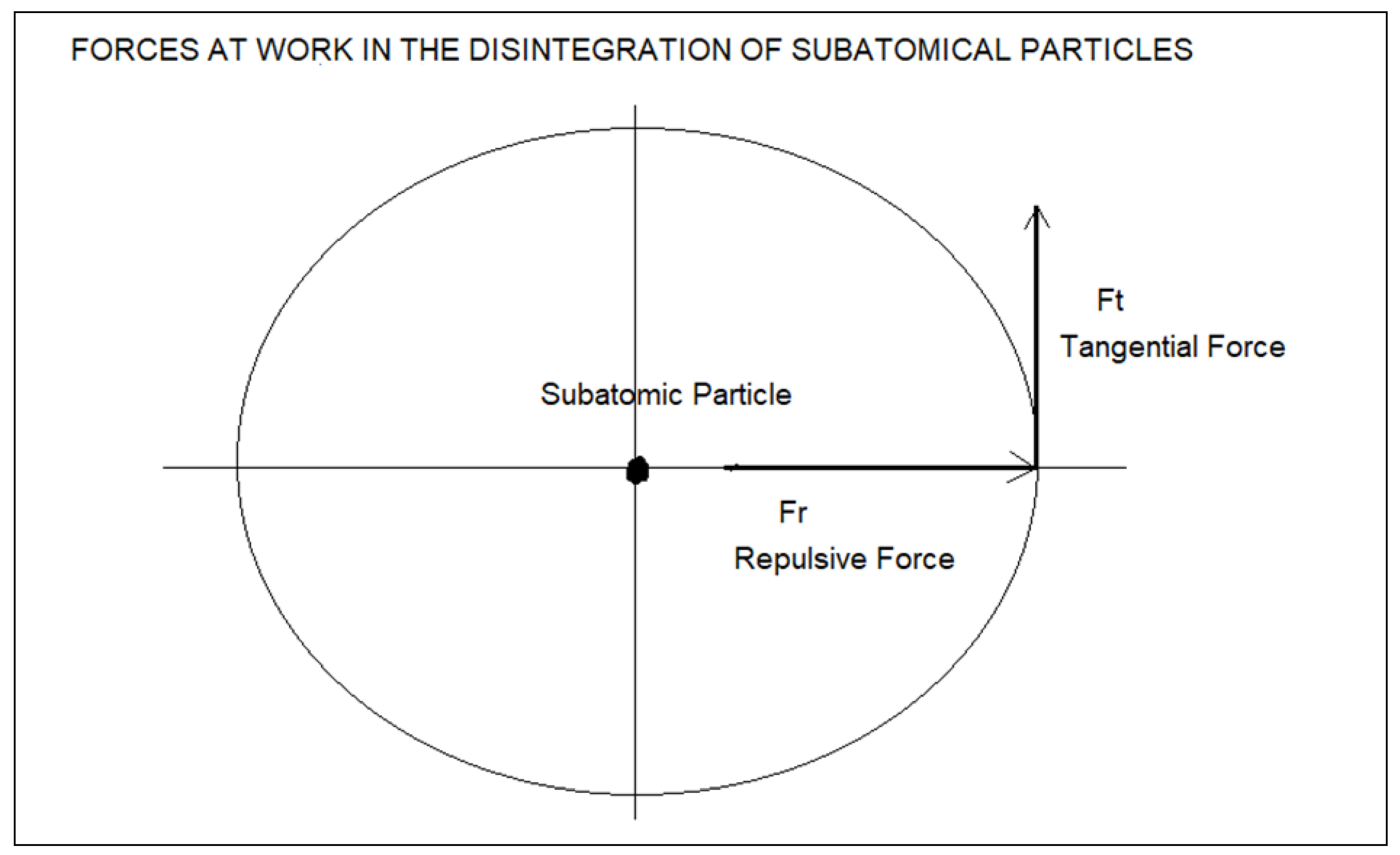
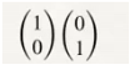 , fundamental, representation.
, fundamental, representation.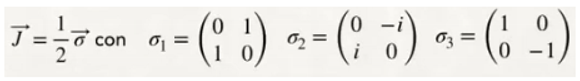
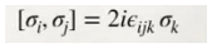
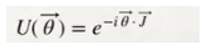
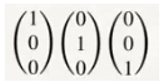
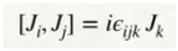
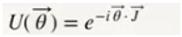
 , fundamental,
representation.
, fundamental,
representation.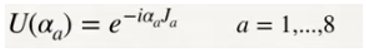
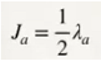 Where λa are Gell-Mann, matrices.
Where λa are Gell-Mann, matrices.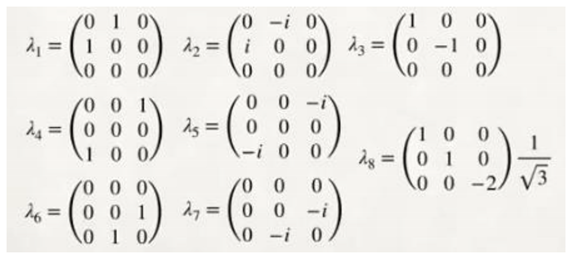
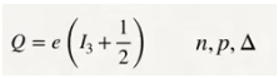
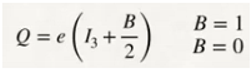 B = 1, baryons; B = 0,
mesons.
B = 1, baryons; B = 0,
mesons.