Submitted:
07 January 2024
Posted:
08 January 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
- Development of a novel statistical model: We introduce a new statistical model specifically designed for optimizing PV-battery system sizes with a primary focus on peak demand reduction. This model addresses a critical gap in the current literature by considering both energy consumption and peak demand costs, which are essential factors for utility companies.
- Incorporation of modified Monte Carlo Simulation: The study utilizes a modified Monte Carlo simulation approach to generate realistic and varied operational scenarios. This methodological innovation allows for a more understanding of PV-battery system performance under diverse conditions, enhancing the robustness of our optimization model.
- Operational and financial analysis for utilities: By providing a method to effectively flatten up to 95% of daily load demand profiles, the model offers a practical tool for utility companies. It enables them to make informed decisions regarding the optimal sizing of PV-battery systems, balancing technical feasibility with financial viability.
2. Materials and Methods
2.1. Data Collection Analyzing
2.2. PV-Battery System Component Model
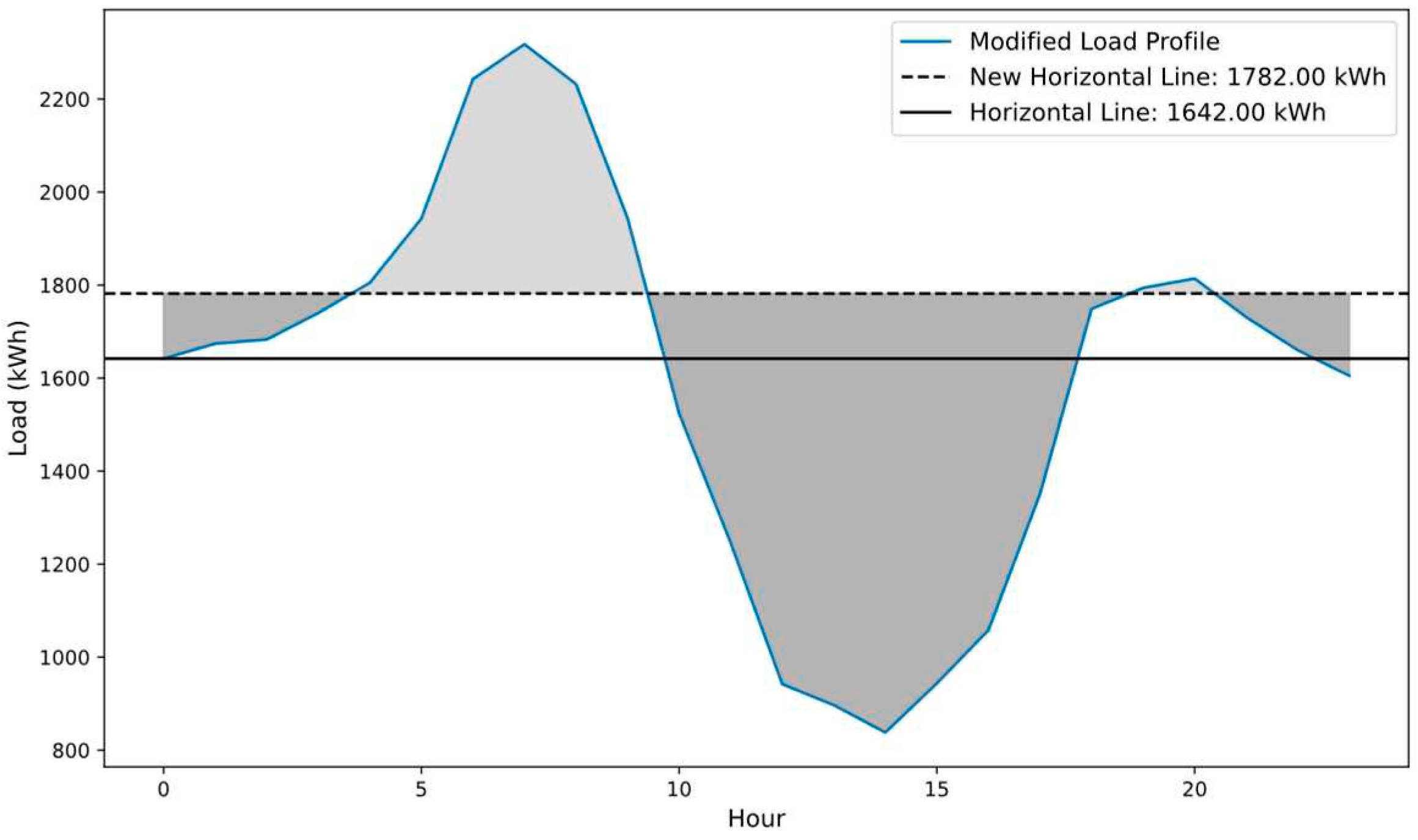
2.3. Updated Peaks
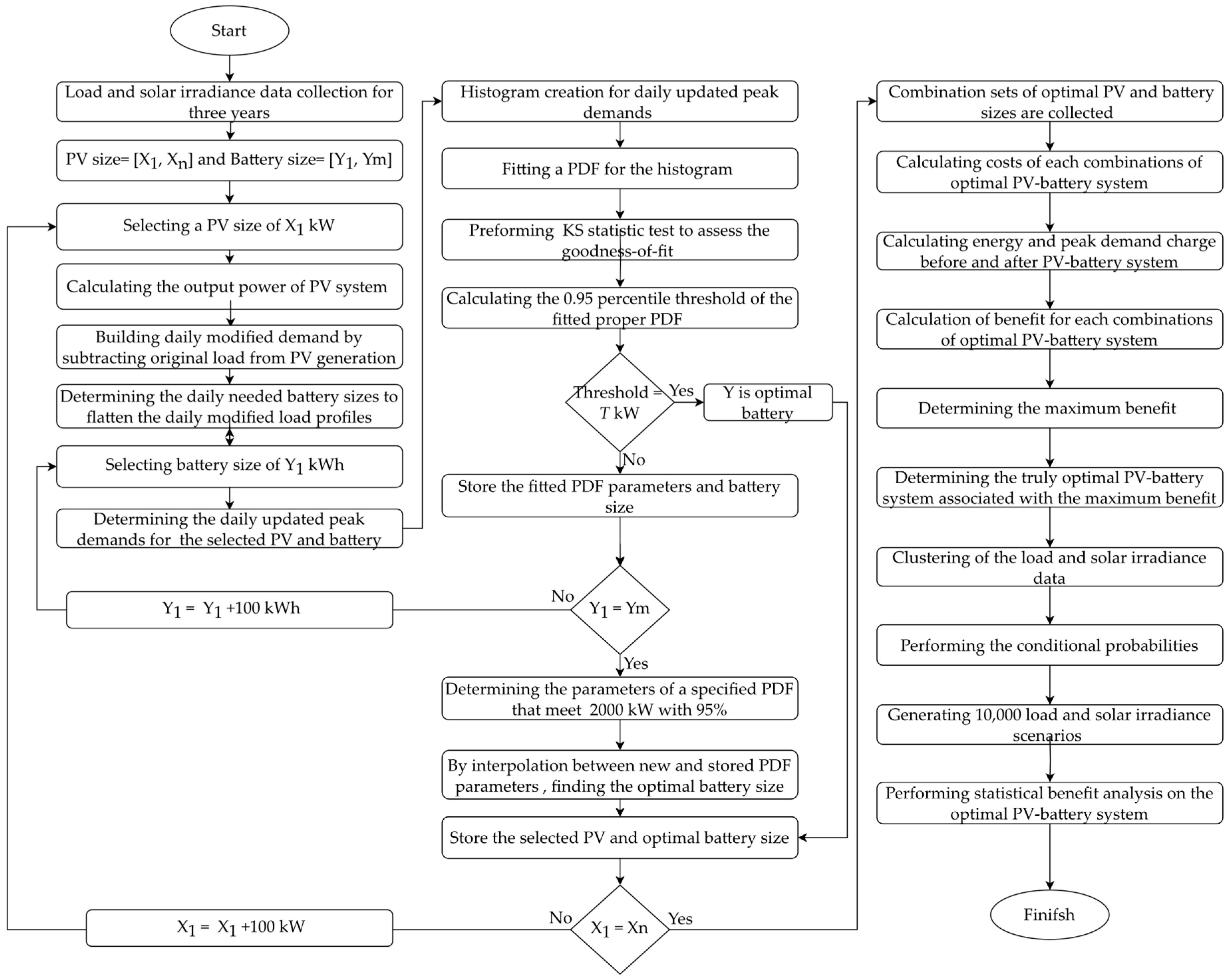
2.4. Optimal Battery Sizes
2.5. Statistical Analysis
- 1.
- Selection of PV and battery sizes: We started by selecting a single PV size and evaluating it across a range of various battery sizes.
- 2.
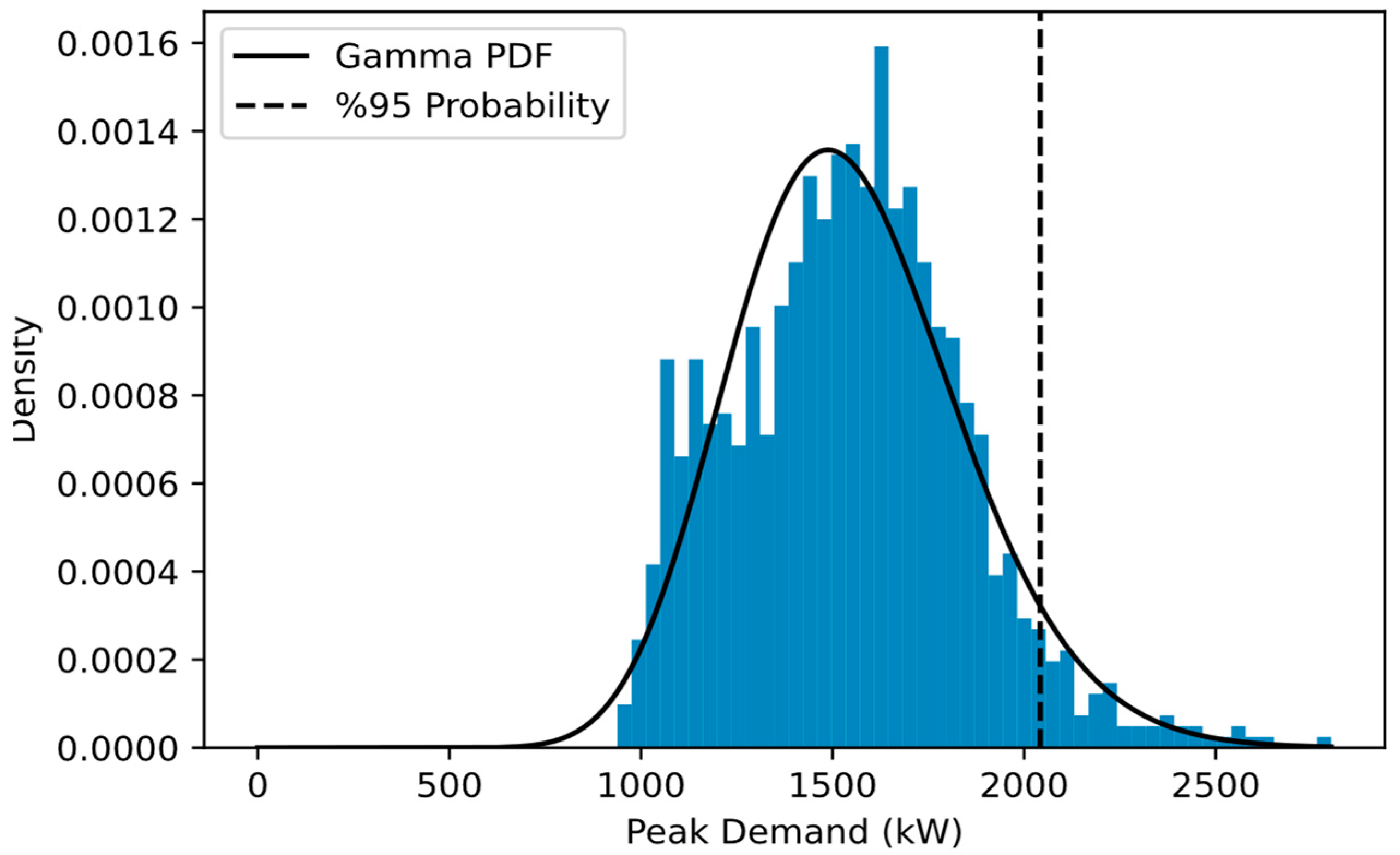
- Histogram creation and PDF fitting: For each PV-battery size, we generated scaled histograms of daily peak demands following PV-battery installation. These histograms were then fitted with a PDF, specifically chosen for its relevance, characterized by PDF parameters
- 3.
- Determining the 0.95 threshold: For each PDF, we calculated the threshold value that corresponds to the 95th percentile. Mathematically, this is represented as:where is the inverse of the cumulative distribution function for the fitted PDF. This calculation yields multiple threshold values for each PV-battery combination.
- 4.
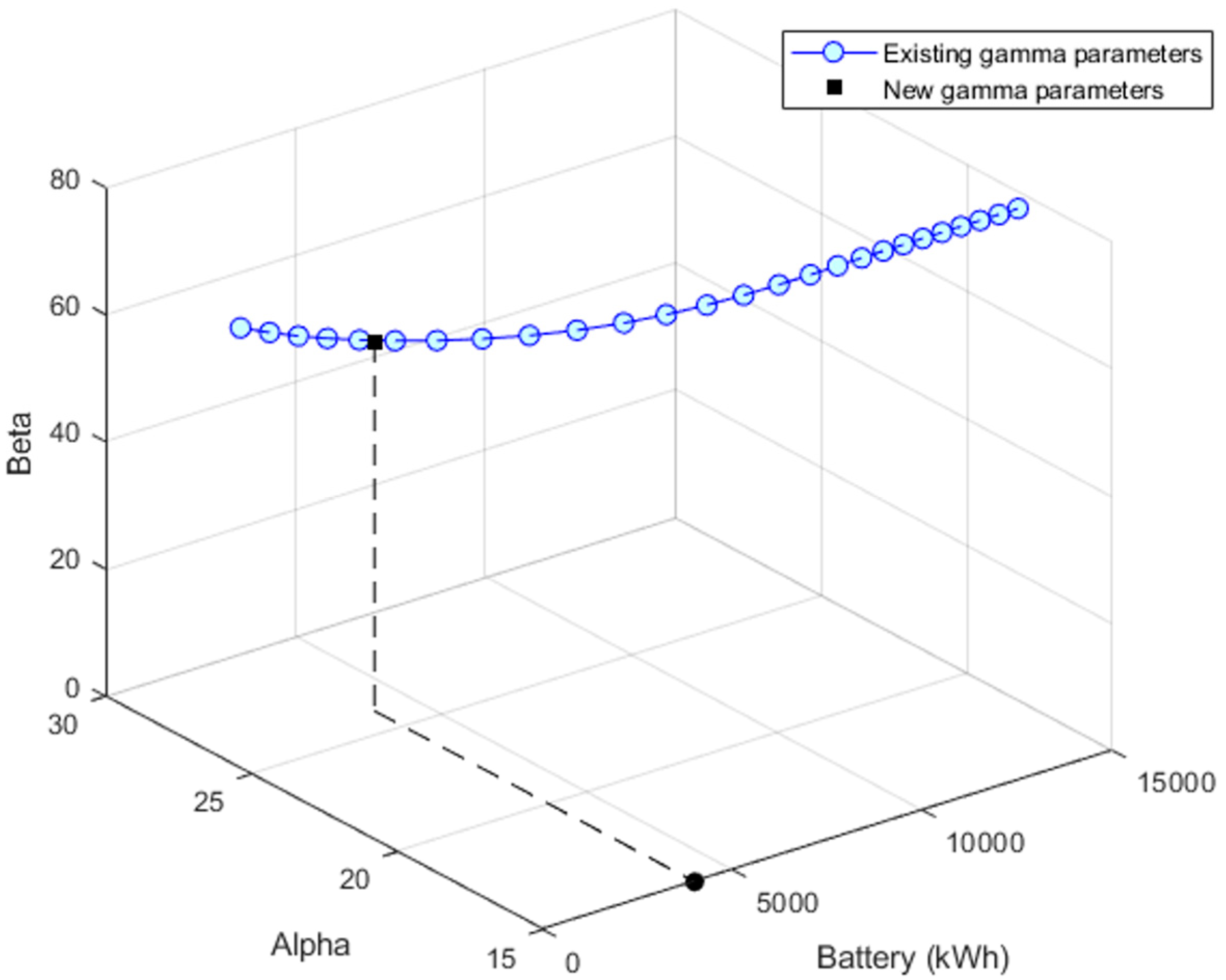
- Optimal sizing criteria: The objective is to find the PV-battery size combination that meets a predetermined threshold of T kW with a 95% probability. If the desired threshold T aligns with the thresholds found in equation (9), the corresponding battery size is considered optimal for the chosen PV size. In cases where the desired threshold T does not align with the previously determined thresholds, we adjust our approach and recalculate the parameters of a new PDF to match the T kW threshold with a 95% probability. This is achieved through the formula:After recalibrating the new parameters of a new PDF to align with the T kW threshold at a 95% probability level, we use interpolation between the newly found parameters and those determined in step 3. This interpolation helps us identify the corresponding battery size for these updated parameters.
- 5.
- Optimal PV-battery system: By repeating all the aforementioned steps for a wide range of PV sizes, we eventually compile an extensive set of optimal PV-battery combinations. Each of these combinations is capable of flattening 95% of the daily peaks up to a fixed threshold of T kW, which meets the technical requirement.
2.6. Economic Analysis
2.6.1. Initial Investment Cost
- PV Installation [38]:
- Inverter Cost [39]:
- Labor cost [40]:
- Equipment costs [41]:
- Overhead costs:
- Battery cost:
2.6.2. Operation, Maintenance, and Insurance Costs
2.6.3. Peak Demand and Energy Costs
2.6.4. Economic Benefit
2.7. Modified Monte Carlo Simulation
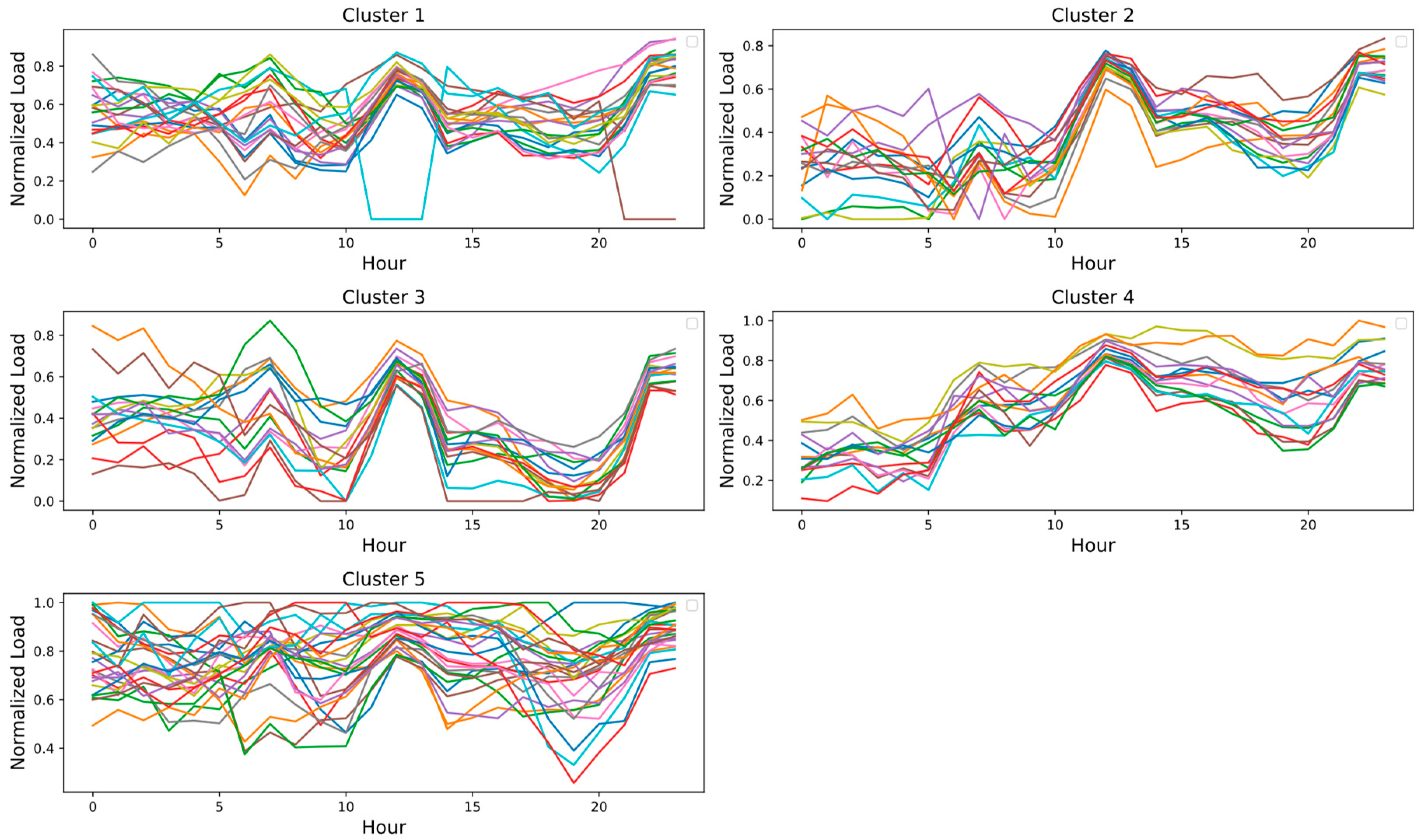
2.7.1. Time Series Clustering
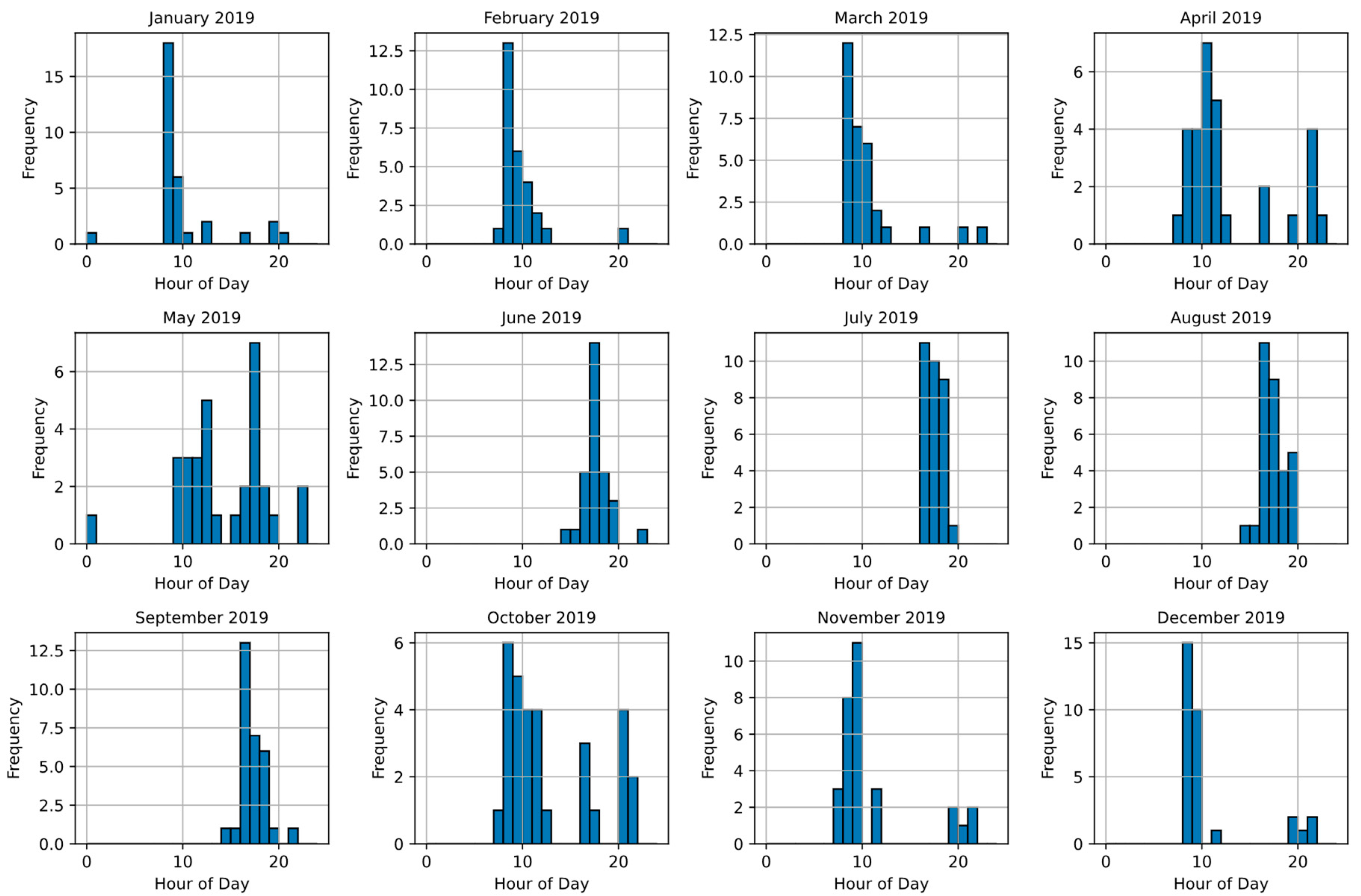
- Data preprocessing: The first step involves comprehensive data preparation. This includes cleaning the data to remove any inconsistencies or errors, addressing outliers, and ensuring that all data is correctly formatted. Subsequently, we normalized the data values to fall between 0 and 1. This standardization is crucial for comparability analysis. Then, we grouped the data monthly, aggregating three years of data for further analysis.
- Similarity measures: The objective of time series clustering is to categorize time series datasets into clusters where datasets within each cluster exhibit maximum similarity among themselves and minimal similarity with datasets in other clusters. A similarity measure is crucial in quantifying the degree of resemblance between two time series datasets. In this study, we have employed Dynamic Time Warping (DTW), a technique that has demonstrated significant efficacy in assessing similarity, particularly in the energy management sector [47,48]. DTW compares each point of one time series with multiple points of another, finding the best alignment by minimizing the cumulative distance between these matched points. By allowing such flexibility in the alignment, DTW effectively captures the inherent patterns and shapes within the time series data, even when these occur at different rates or phases.
- Clustering algorithms: The next step is to employ an appropriate time series clustering algorithm.
- Initialization: The process began by randomly selecting k data points as the initial centroids of the clusters.
- Assignment step: In this phase, each data in the dataset was assigned to the nearest centroid. The closeness was determined based on the DTW distance.
- Update step: The centroids of the clusters were then recalculated as the mean of all points assigned to each cluster.
- Convergence: These steps were repeated until the positions of the centroids stabilized, indicating that the clusters had converged and were no longer changing significantly.
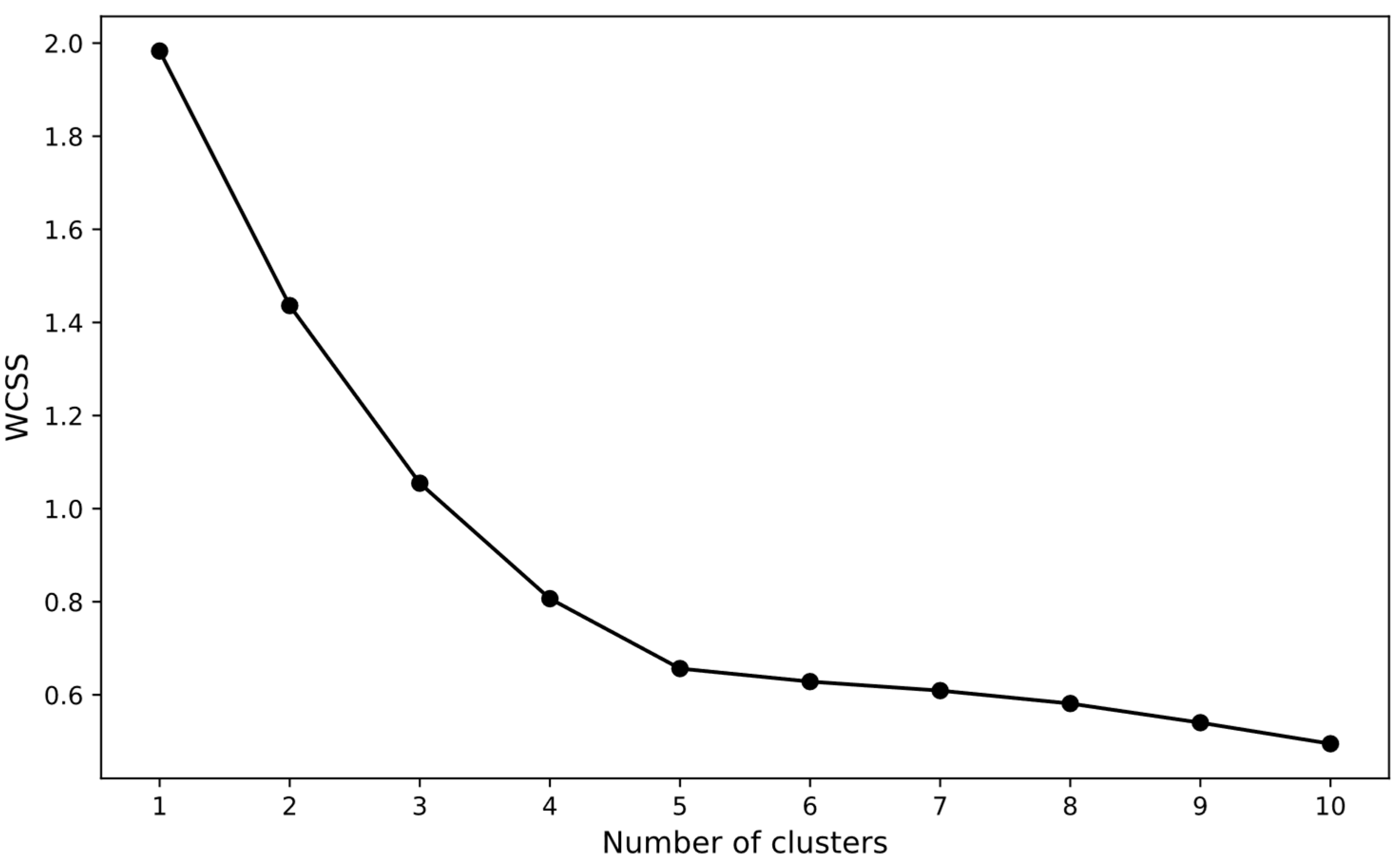
- Optimal number of clusters: Determining the optimal number of clusters is a critical aspect of the K-means algorithm. We employed the Elbow method to identify this number. To apply the Elbow method, we first executed the K-means algorithm over a range of K values from 1 to a predefined maximum, then computed the Within-Cluster Sum of Squares (WCSS) for each K, and finally plotted these WCSS values against their cluster number. By observing the WCSS curve, we looked for a point where the rate of decrease in WCSS significantly slows down, creating an elbow in the plot. The K value at this elbow point is considered the optimal number of clusters as it indicates a trade-off between maximizing the number of clusters and minimizing WCSS [49].
- Initialization: We start by initializing the SOM neural network with weight vectors, through random selection.
- Competitive learning: For each data point in our dataset, SOM identifies the Best Matching Unit (BMU) by finding the neuron with the closest weight vector to the data point.
- Weight adjustment: The weights of the BMU and its neighbors within the network are adjusted to become more similar to the input data point, with the adjustment magnitude decreasing over time and distance from the BMU.
- Iterative process: This cycle of competitive learning and weight adjustment was repeated across numerous iterations, allowing the SOM to evolve and form a map that reflects the intrinsic structure of the data.
- Cluster visualization: The final output is a map where similar data points are clustered together.
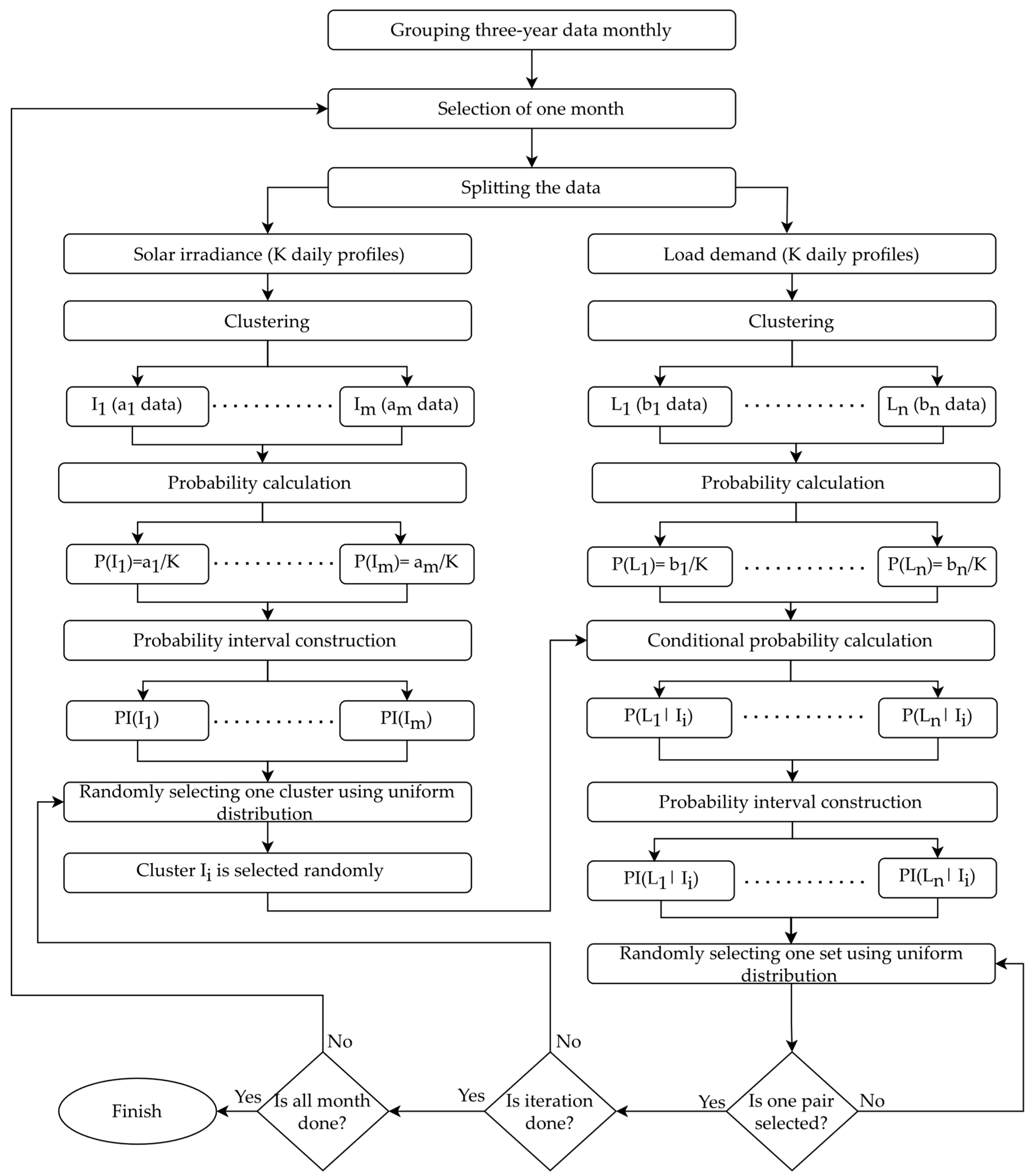
2.7.2. Modified Monte Carlo Simulation
- Assign probabilities to solar irradiance clusters: For each solar irradiance cluster (i = 1 to m), calculate its probability:
- Establish probability intervals: This is done by sequentially adding the probabilities of the clusters. For the first cluster , its probability interval is:For the second cluster , the interval is defined as:This continues for each cluster , where:
- Random cluster selection for solar irradiance: A random number R within the range [0, 1] is selected uniformly. Selecting the solar irradiance cluster for which the random number R falls within its probability interval.
- Determine the specific days that are included in the selected solar irradiance cluster.
- Match days with load clusters: For each identified day in the solar irradiance cluster , finding the corresponding days within the load demand clusters from to .
- Calculate conditional probability for load clusters: After selecting the solar irradiance cluster , the probability of each load demand cluster conditioned on the selection of is calculated. The conditional probability is calculated as:
- Establish probability intervals for each conditional probability like step 2.
- Random selection of load cluster based on conditional probability intervals.
- Final scenario selection: From the selected solar irradiance cluster and the randomly chosen load cluster , a specific pair of solar irradiance and load demand profile is identified. If multiple profile pairs are available within the selected clusters, one pair is selected randomly. This random selection can be done using a uniform distribution, ensuring each pair has an equal chance of being chosen.
3. Results
3.1. Data Analysis
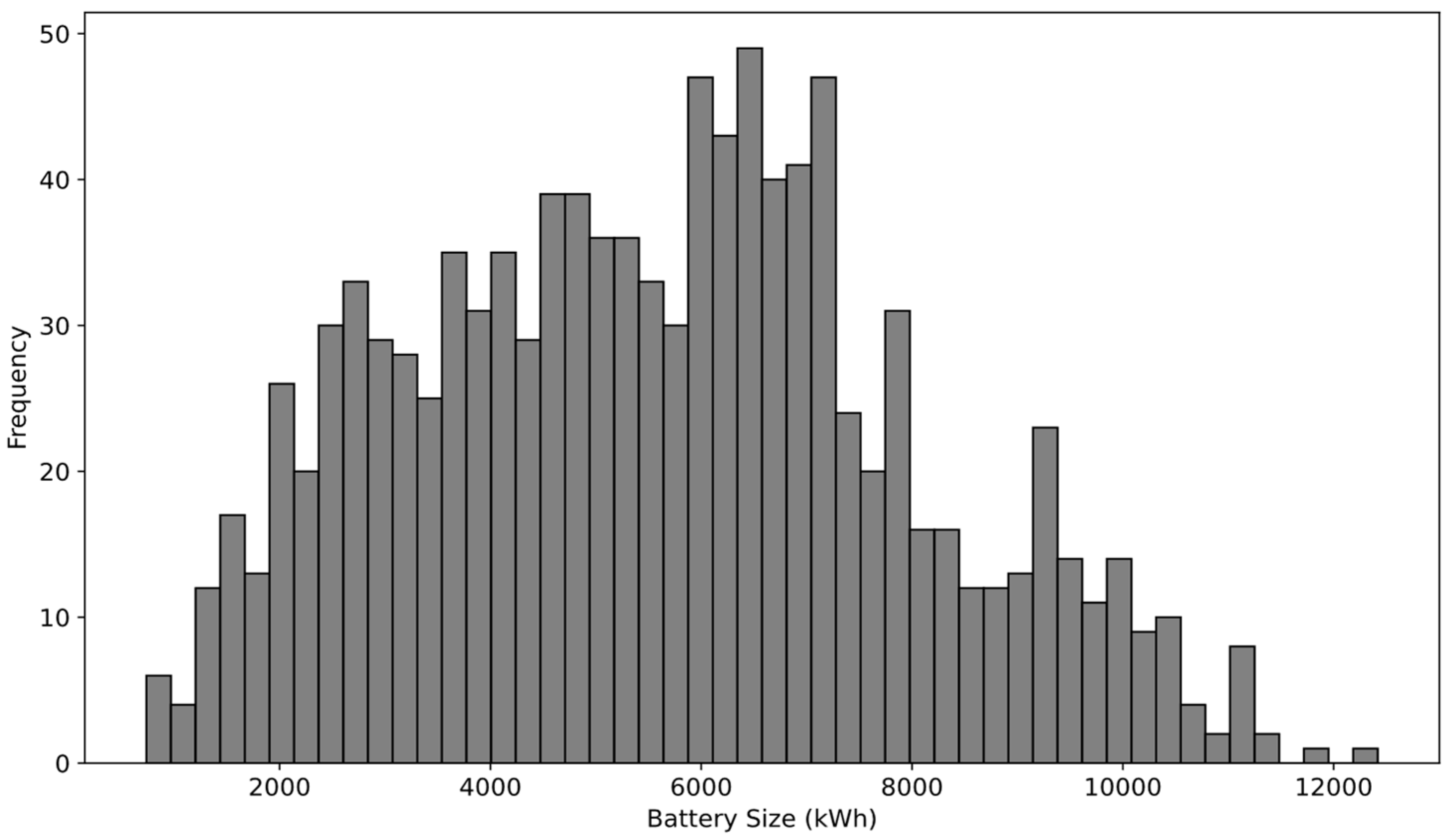
3.2. Battery Operation Daily Needed Battery Sizes
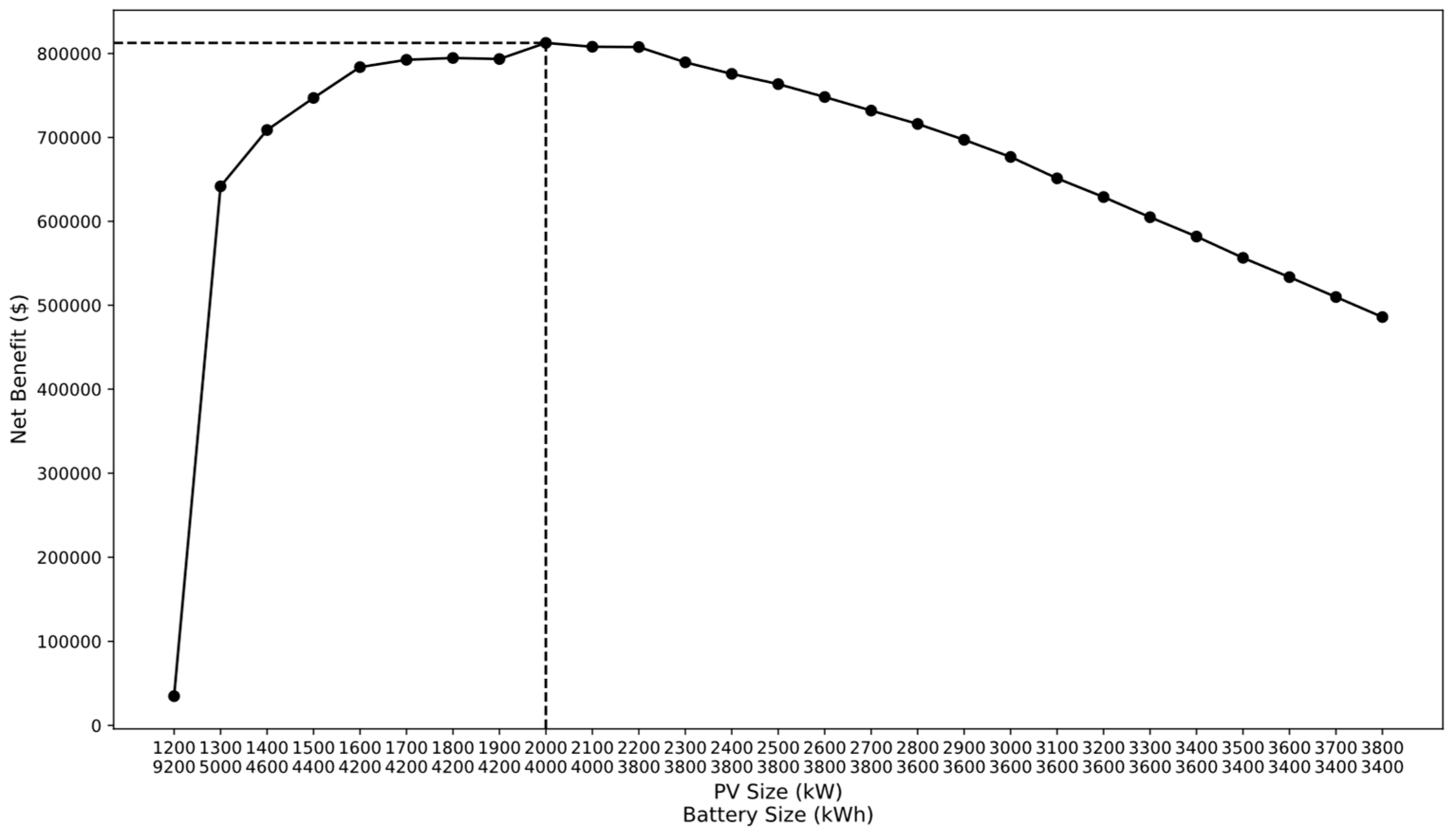
3.3. Optimal PV-Battery System
3.4. Benefit Analysis
3.5. Modified Monte Carlo simulation
4. Conclusions
- Integrating various energy technologies and evolving market dynamics into the model to enhance its scalability and adaptability.
- Examining the influence of grid topology and related constraints on the effectiveness of the proposed methodology.
- Extending the methodology to integrate other renewable energy sources, such as wind turbines, in a hybrid system.
- Refining the methodology to determine the desired demand threshold in alignment with specific utility company requirements and operational capacities.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Betancourt Schwarz, M.; Veyron, M.; Clausse, M. Impact of Flexibility Implementation on the Control of a Solar District Heating System. Solar 2023, 4, 1–14. [Google Scholar] [CrossRef]
- Nematirad, reza; Ardehali, M.M.; Khorsandi, A. Optimization of Residential Demand Response Program Cost with Consideration for Occupants Thermal Comfort and Privacy. arXiv preprint arXiv:2305.08077. 2023. [CrossRef]
- Banibaqash, A.; Hunaiti, Z.; Abbod, M. Assessing the Potential of Qatari House Roofs for Solar Panel Installations: A Feasibility Survey. Solar 2023, 3, 650–662. [Google Scholar] [CrossRef]
- Ali, A.; Volatier, M.; Darnon, M. Optimal Sizing and Assessment of Standalone Photovoltaic Systems for Community Health Centers in Mali. Solar 2023, 3, 522–543. [Google Scholar] [CrossRef]
- Nematirad, R.; Pahwa, A.; Natarajan, B.; Wu, H. Optimal Sizing of Photovoltaic-Battery System for Peak Demand Reduction Using Statistical Models. Front Energy Res 2023, 11. [Google Scholar] [CrossRef]
- Jayathunga, D.; Weliwita, J.A.; Karunathilake, H.; Witharana, S. Economic Feasibility of Thermal Energy Storage-Integrated Concentrating Solar Power Plants. Solar 2023, 3, 132–160. [Google Scholar] [CrossRef]
- Shavolkin, O.; Shvedchykova, I.; Gerlici, J.; Kravchenko, K.; Pribilinec, F. Use of Hybrid Photovoltaic Systems with a Storage Battery for the Remote Objects of Railway Transport Infrastructure. Energies (Basel) 2022, 15, 4883. [Google Scholar] [CrossRef]
- Agajie, T.F.; Ali, A.; Fopah-Lele, A.; Amoussou, I.; Khan, B.; Velasco, C.L.R.; Tanyi, E. A Comprehensive Review on Techno-Economic Analysis and Optimal Sizing of Hybrid Renewable Energy Sources with Energy Storage Systems. Energies (Basel) 2023, 16, 642. [Google Scholar] [CrossRef]
- Owosuhi, A.; Hamam, Y.; Munda, J. Maximizing the Integration of a Battery Energy Storage System–Photovoltaic Distributed Generation for Power System Harmonic Reduction: An Overview. Energies (Basel) 2023, 16, 2549. [Google Scholar] [CrossRef]
- Vossos, V.; Garbesi, K.; Shen, H. Energy Savings from Direct-DC in U.S. Residential Buildings. Energy Build 2014, 68, 223–231. [Google Scholar] [CrossRef]
- Beck, T.; Kondziella, H.; Huard, G.; Bruckner, T. Assessing the Influence of the Temporal Resolution of Electrical Load and PV Generation Profiles on Self-Consumption and Sizing of PV-Battery Systems. Appl Energy 2016, 173, 331–342. [Google Scholar] [CrossRef]
- Tervo, E.; Agbim, K.; DeAngelis, F.; Hernandez, J.; Kim, H.K.; Odukomaiya, A. An Economic Analysis of Residential Photovoltaic Systems with Lithium Ion Battery Storage in the United States. Renewable and Sustainable Energy Reviews 2018, 94, 1057–1066. [Google Scholar] [CrossRef]
- Bendato, I.; Bonfiglio, A.; Brignone, M.; Delfino, F.; Pampararo, F.; Procopio, R.; Rossi, M. Design Criteria for the Optimal Sizing of Integrated Photovoltaic-Storage Systems. Energy 2018, 149, 505–515. [Google Scholar] [CrossRef]
- Belboul, Z.; Toual, B.; Kouzou, A.; Mokrani, L.; Bensalem, A.; Kennel, R.; Abdelrahem, M. Multiobjective Optimization of a Hybrid PV/Wind/Battery/Diesel Generator System Integrated in Microgrid: A Case Study in Djelfa, Algeria. Energies (Basel) 2022, 15, 3579. [Google Scholar] [CrossRef]
- Mukhopadhyay, B.; Das, D. Multi-Objective Dynamic and Static Reconfiguration with Optimized Allocation of PV-DG and Battery Energy Storage System. Renewable and Sustainable Energy Reviews 2020, 124, 109777. [Google Scholar] [CrossRef]
- Shivam, K.; Tzou, J.-C.; Wu, S.-C. A Multi-Objective Predictive Energy Management Strategy for Residential Grid-Connected PV-Battery Hybrid Systems Based on Machine Learning Technique. Energy Convers Manag 2021, 237, 114103. [Google Scholar] [CrossRef]
- Zhi, Y.; Yang, X. Scenario-Based Multi-Objective Optimization Strategy for Rural PV-Battery Systems. Appl Energy 2023, 345, 121314. [Google Scholar] [CrossRef]
- Song, Z.; Guan, X.; Cheng, M. Multi-Objective Optimization Strategy for Home Energy Management System Including PV and Battery Energy Storage. Energy Reports 2022, 8, 5396–5411. [Google Scholar] [CrossRef]
- Park, H. A Stochastic Planning Model for Battery Energy Storage Systems Coupled with Utility-Scale Solar Photovoltaics. Energies (Basel) 2021, 14, 1244. [Google Scholar] [CrossRef]
- Javidsharifi, M.; Pourroshanfekr Arabani, H.; Kerekes, T.; Sera, D.; Guerrero, J.M. Stochastic Optimal Strategy for Power Management in Interconnected Multi-Microgrid Systems. Electronics (Basel) 2022, 11, 1424. [Google Scholar] [CrossRef]
- Guo, E.; He, B.; Zhang, J. Effects of Photovoltaic Panel Type on Optimum Sizing of an Electrical Energy Storage System Using a Stochastic Optimization Approach. J Energy Storage 2023, 72, 108581. [Google Scholar] [CrossRef]
- Ntube, N.; Li, H. Stochastic Multi-Objective Optimal Sizing of Battery Energy Storage System for a Residential Home. J Energy Storage 2023, 59, 106403. [Google Scholar] [CrossRef]
- Zheng, Z.; Li, X.; Pan, J.; Luo, X. A Multi-Year Two-Stage Stochastic Programming Model for Optimal Design and Operation of Residential Photovoltaic-Battery Systems. Energy Build 2021, 239, 110835. [Google Scholar] [CrossRef]
- Rong, S.; Zhao, Y.; Wang, Y.; Chen, J.; Guan, W.; Cui, J.; Liu, Y. Information Gap Decision Theory-Based Stochastic Optimization for Smart Microgrids with Multiple Transformers. Applied Sciences 2023, 13, 9305. [Google Scholar] [CrossRef]
- Chaerani, D.; Shuib, A.; Perdana, T.; Irmansyah, A.Z. Systematic Literature Review on Robust Optimization in Solving Sustainable Development Goals (SDGs) Problems during the COVID-19 Pandemic. Sustainability 2023, 15, 5654. [Google Scholar] [CrossRef]
- Bakhtvar, M.; Al-Hinai, A. Robust Operation of Hybrid Solar–Wind Power Plant with Battery Energy Storage System. Energies (Basel) 2021, 14, 3781. [Google Scholar] [CrossRef]
- Aghamohamadi, M.; Mahmoudi, A.; Haque, M.H. Two-Stage Robust Sizing and Operation Co-Optimization for Residential PV–Battery Systems Considering the Uncertainty of PV Generation and Load. IEEE Trans Industr Inform 2021, 17, 1005–1017. [Google Scholar] [CrossRef]
- Coppitters, D.; De Paepe, W.; Contino, F. Robust Design Optimization and Stochastic Performance Analysis of a Grid-Connected Photovoltaic System with Battery Storage and Hydrogen Storage. Energy 2020, 213, 118798. [Google Scholar] [CrossRef]
- Nematirad, R.; Pahwa, A. Solar Radiation Forecasting Using Artificial Neural Networks Considering Feature Selection. In Proceedings of the 2022 IEEE Kansas Power and Energy Conference (KPEC); IEEE, April 25 2022; pp. 1–4. [CrossRef]
- Mellit, A.; Massi Pavan, A.; Ogliari, E.; Leva, S.; Lughi, V. Advanced Methods for Photovoltaic Output Power Forecasting: A Review. Applied Sciences 2020, 10, 487. [Google Scholar] [CrossRef]
- Kaufhold, E.; Meyer, J.; Myrzik, J.; Schegner, P. Harmonic Stability Assessment of Commercially Available Single-Phase Photovoltaic Inverters Considering Operating-Point Dependencies. Solar 2023, 3, 473–486. [Google Scholar] [CrossRef]
- Li, R.; Huang, S.; Dou, H. Dynamic Risk Assessment of Landslide Hazard for Large-Scale Photovoltaic Power Plants under Extreme Rainfall Conditions. Water (Basel) 2023, 15, 2832. [Google Scholar] [CrossRef]
- de Figueiredo, F.A.P.; Dias, C.F.; de Lima, E.R.; Fraidenraich, G. Capacity Bounds for Dense Massive MIMO in a Line-of-Sight Propagation Environment. Sensors 2020, 20, 520. [Google Scholar] [CrossRef]
- Althubyani, F.A.; Abd El-Bar, A.M.T.; Fawzy, M.A.; Gemeay, A.M. A New 3-Parameter Bounded Beta Distribution: Properties, Estimation, and Applications. Axioms 2022, 11, 504. [Google Scholar] [CrossRef]
- Valvo, P.S. A Bimodal Lognormal Distribution Model for the Prediction of COVID-19 Deaths. Applied Sciences 2020, 10, 8500. [Google Scholar] [CrossRef]
- Upreti, D.; Pignatti, S.; Pascucci, S.; Tolomio, M.; Li, Z.; Huang, W.; Casa, R. A Comparison of Moment-Independent and Variance-Based Global Sensitivity Analysis Approaches for Wheat Yield Estimation with the Aquacrop-OS Model. Agronomy 2020, 10, 607. [Google Scholar] [CrossRef]
- Kyeong, S.; Kim, D.; Shin, J. Can System Log Data Enhance the Performance of Credit Scoring?—Evidence from an Internet Bank in Korea. Sustainability 2021, 14, 130. [Google Scholar] [CrossRef]
- Dehwah, A.H.A.; Asif, M.; Budaiwi, I.M.; Alshibani, A. Techno-Economic Assessment of Rooftop PV Systems in Residential Buildings in Hot–Humid Climates. Sustainability 2020, 12, 10060. [Google Scholar] [CrossRef]
- Hazim, H.I.; Baharin, K.A.; Gan, C.K.; Sabry, A.H.; Humaidi, A.J. Review on Optimization Techniques of PV/Inverter Ratio for Grid-Tie PV Systems. Applied Sciences 2023, 13, 3155. [Google Scholar] [CrossRef]
- Raza, F.; Tamoor, M.; Miran, S.; Arif, W.; Kiren, T.; Amjad, W.; Hussain, M.I.; Lee, G.-H. The Socio-Economic Impact of Using Photovoltaic (PV) Energy for High-Efficiency Irrigation Systems: A Case Study. Energies (Basel) 2022, 15, 1198. [Google Scholar] [CrossRef]
- Shepovalova, O.; Izmailov, A.; Lobachevsky, Y.; Dorokhov, A. High-Efficiency Photovoltaic Equipment for Agriculture Power Supply. Agriculture 2023, 13, 1234. [Google Scholar] [CrossRef]
- Ershad, A.M.; Ueckerdt, F.; Pietzcker, R.C.; Giannousakis, A.; Luderer, G. A Further Decline in Battery Storage Costs Can Pave the Way for a Solar PV-Dominated Indian Power System. Renewable and Sustainable Energy Transition 2021, 1, 100006. [Google Scholar] [CrossRef]
- Asad, M.; Mahmood, F.I.; Baffo, I.; Mauro, A.; Petrillo, A. The Cost Benefit Analysis of Commercial 100 MW Solar PV: The Plant Quaid-e-Azam Solar Power Pvt Ltd. Sustainability 2022, 14, 2895. [Google Scholar] [CrossRef]
- Boonluk, P.; Khunkitti, S.; Fuangfoo, P.; Siritaratiwat, A. Optimal Siting and Sizing of Battery Energy Storage: Case Study Seventh Feeder at Nakhon Phanom Substation in Thailand. Energies (Basel) 2021, 14, 1458. [Google Scholar] [CrossRef]
- Quiles-Cucarella, E.; Marquina-Tajuelo, A.; Roldán-Blay, C.; Roldán-Porta, C. Particle Swarm Optimization Method for Stand-Alone Photovoltaic System Reliability and Cost Evaluation Based on Monte Carlo Simulation. Applied Sciences 2023, 13, 11623. [Google Scholar] [CrossRef]
- Hoffmann, M.; Kotzur, L.; Stolten, D.; Robinius, M. A Review on Time Series Aggregation Methods for Energy System Models. Energies (Basel) 2020, 13, 641. [Google Scholar] [CrossRef]
- Yang, M.; Zhao, M.; Huang, D.; Su, X. A Composite Framework for Photovoltaic Day-Ahead Power Prediction Based on Dual Clustering of Dynamic Time Warping Distance and Deep Autoencoder. Renew Energy 2022, 194, 659–673. [Google Scholar] [CrossRef]
- Li, F.; Su, J.; Sun, B. An Optimal Scheduling Method for an Integrated Energy System Based on an Improved K-Means Clustering Algorithm. Energies (Basel) 2023, 16, 3713. [Google Scholar] [CrossRef]
- Onumanyi, A.J.; Molokomme, D.N.; Isaac, S.J.; Abu-Mahfouz, A.M. AutoElbow: An Automatic Elbow Detection Method for Estimating the Number of Clusters in a Dataset. Applied Sciences 2022, 12, 7515. [Google Scholar] [CrossRef]
- Criado-Ramón, D.; Ruiz, L.G.B.; Pegalajar, M.C. An Improved Pattern Sequence-Based Energy Load Forecast Algorithm Based on Self-Organizing Maps and Artificial Neural Networks. Big Data and Cognitive Computing 2023, 7, 92. [Google Scholar] [CrossRef]
|
PV module ($/W) 0.035 |
Inverter ($/W) 0.04 |
Equipment ($/W) 0.18 |
| Overhead ($/W) | O&M ($/kW) | Transformer ($) |
| 0.1 | 15 | 150,000 |
| Energy cost ($/kWh) | Power cost ($/kW) | Tax credit (%) |
| 0.025 | 22 | 30 |
| Initial battery ($/kWh) | Replacement battery ($/kWh) | Project lifetime |
| 150 | 100 | 20 years |
| Labor ($/W) | Discount rate | Battery roundtrip efficiency |
| 0.1 | 0.08 | 0.9025 |
| Inverter coefficient | Battery efficiency | Battery utilization |
| 1.2 | 0.95 | 0.7 |
| Lognormal | Gamma | Beta | ||||
| Battery | KS_statistic | P-value | KS_statistic | P-value | KS_statistic | P-value |
| 2000 | 0.041089 | 0.0480 | 0.031794 | 0.65124 | 0.08 | 0.005355 |
| 2500 | 0.03537 | 0.12579 | 0.029497 | 0.55618 | 0.11 | 0.027578 |
| 3000 | 0.040364 | 0.15470 | 0.026193 | 0.56416 | 0.09 | 0.005044 |
| 3500 | 0.026193 | 0.43233 | 0.053331 | 0.42345 | 0.12 | 0.04289 |
| 4000 | 0.062428 | 0.037 | 0.027589 | 0.65164 | 0.16 | 0.01455 |
| 4500 | 0.039343 | 0.06544 | 0.03461 | 0.32136 | 0.13 | 0.004353 |
| 5000 | 0.046593 | 0.01660 | 0.030778 | 0.32103 | 0.14 | 0.000539 |
| 5500 | 0.051666 | 0.00554 | 0.062428 | 0.27564 | 0.15 | 0.000127 |
| 6000 | 0.054413 | 0.00292 | 0.034076 | 0.24565 | 0.25 | 5.58E-05 |
| PV (kW) | 500 | 1000 | 1200 | 1500 | 2000 | 2500 | 3000 | 3500 | 4000 |
| Battery (kW) | NAN | NAN | 9200 | 4400 | 4000 | 3800 | 3600 | 3400 | 3300 |
| Before PV-battery | PV-only | After PV-battery | |
| Equipment cost ($) | 0 | 1,638,688 | 2,015,246 |
| Energy Cost ($) | 3,788,907 | 3,036,927 | 3,023,569 |
| Peak demand charge ($) | 6,913,926 | 6,472,805 | 4,901,679 |
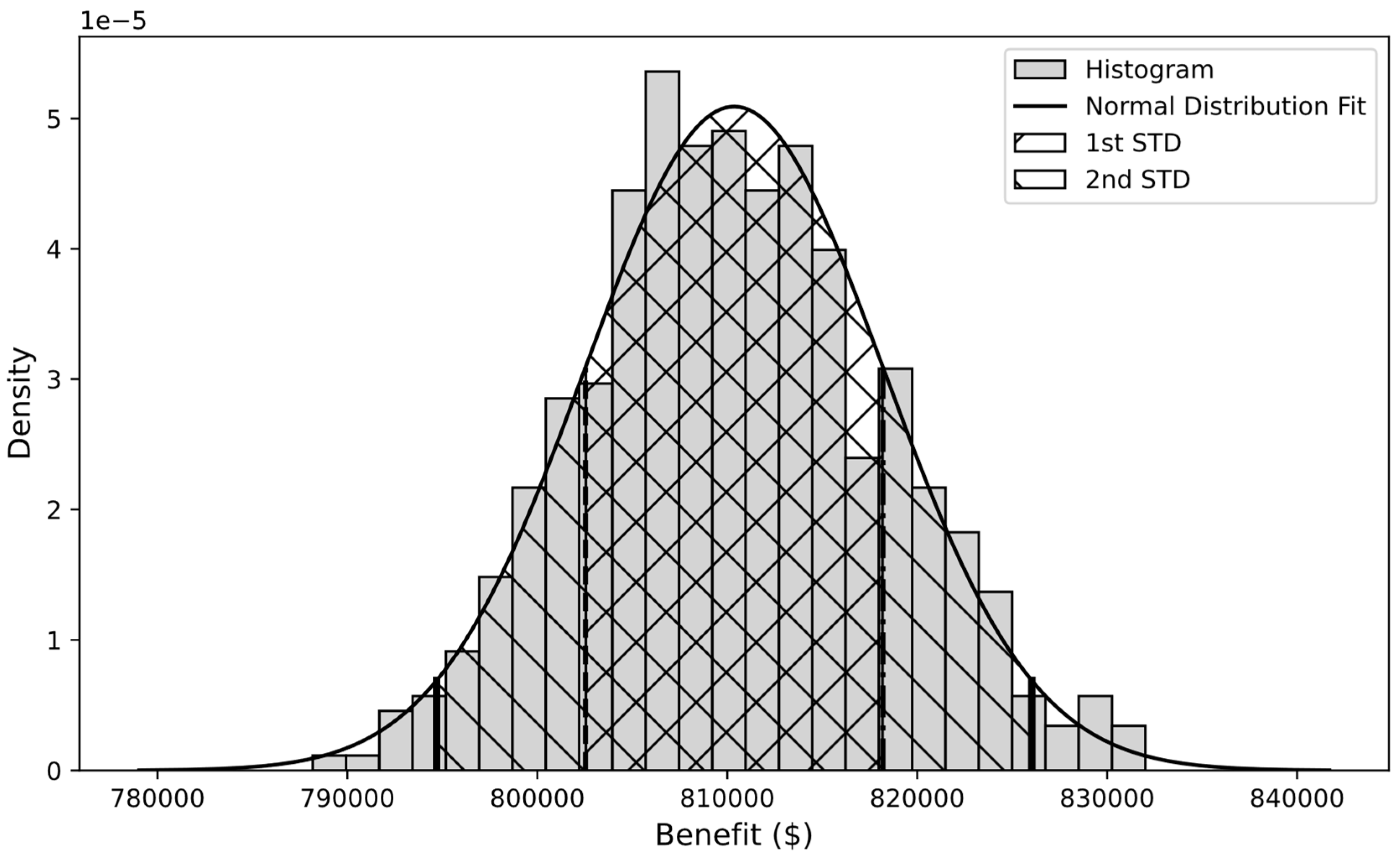
| Benefit ($) | 0 | -445,587 | 812,648 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





